Лекция
№2. Основные типовые звенья систем автоматического управления
Содержание
лекции:
- понятие и
определение динамического
звена, основные типы динамических звеньев;
- уравнения взаимосвязи между входной и выходной
величинами; основных динамических звеньев и их передаточные функции.
Цели лекции:
- изучить принципы построения
основных типовых звеньев САУ;
- изучить математическое описание основных
типовых звеньев.
Как указывалось выше, для
изучения динамических свойств системы целесообразно рассматривать отдельные ее
элементы только с точки зрения их динамических свойств независимо от их
конкретного исполнения.
Для того чтобы можно было
рассматривать общие свойства элементов системы и знать различие между ними,
очевидно, необходимо воздействовать на них однотипными возмущениями.
Одним из таких типовых
возмущений принято считать единичную ступенчатую (толчкообразную) функцию.
Тогда в зависимости от вида возникающего в элементе переходного процесса можно
относить этот элемент к тому или иному типу. Такое различение элементов по
динамическим характеристикам приводит к понятию динамического звена или просто
звена. Динамическим звеном называют
часть системы, описываемую тем или иным уравнением, вид которого в общем случае
может быть любым. Однако уравнение сложного звена представляется возможным
изобразить в виде той или иной совокупности более простых уравнений; число
видов таких элементарных уравнений невелико. Следовательно, сложное звено
можно разложить на несколько наиболее простые элементарные типовые звенья.
При таком рассмотрении все
разнообразие существующих линейных элементов удается характеризовать небольшим
числом типовых звеньев или их комбинаций. Обычно различают следующие типы
звеньев: а) безынерционное; б) инерционное; в) колебательное; г)
интегрирующее; д) дифференцирующее; е)
интегро-дифференцирующее; ж)
запаздывающее.
Иногда в литературе встречаются
и несколько отличные от указанных типы и наименования звеньев.
Безынерционное звено. Звено принято называть
безынерционным, если связь между входом и выходом звена определяется алгебраическим
уравнением
 , (2.1)
, (2.1)
где k - коэффициент усиления
звена;
xВХ, хВЫХ-
соответственно входная и выходная его величины.
Это звено иногда называют также усилительным или
безъемкостным.
Очевидно, что характер изменения
во времени выходной величины при подаче на вход возмущения, равного хВХ = const = A[1],
будет определяться уравнением (2.1), т. е. хВЫХ = kxВЫХ. Примером конструктивного
выполнения такого звена могут служить:
электронная усилительная лампа; рычажное сочленение;
механический редуктор, и др.
Передаточная функция
безынерционного звена может быть из (2.1) записана как отношение выходной величины
к входной в следующем виде
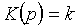 .
.
Инерционное звено. Звено называется инерционным,
если связь между входом и выходом звена определяется дифференциальным
уравнением вида
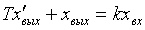 , (2.2)
, (2.2)
где Т- постоянная времени звена;
k - коэффициент усиления звена;
xВЫХ, хВХ - соответственно выходная и входная величины
звена.
Такое звено также называют
апериодическим, статическим, одноемкостным, релаксационным.
В качестве примеров конструктивного выполнения подобного звена можно назвать ряд устройств. Так,
сюда можно отнести пассивный четырехполюсник, состоящий из емкости и омического
сопротивления или из индуктивности и омического сопротивления, термопару,
магнитный усилитель, электрический двигатель (если вход - напряжение, а выход
- угловая скорость) и т. д.
Передаточная функция
инерционного звена может быть записана в следующем виде
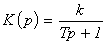 . (2.3)
. (2.3)
Колебательное звено. Звено называют колебательным, если связь между входной и выходной
величинами звена определяется уравнением вида
или 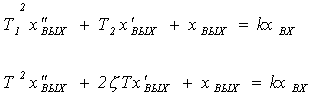
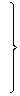 (2.4)
(2.4)
и при этом соблюдается условие
 .
.
Иногда встречается
другая форма уравнений
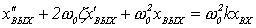 . (2.5)
. (2.5)
В этих уравнениях Т1 - постоянная времени
звена, равная 1/ω0;
Т2 -
постоянная времени звена, равная 2ζ/ω0; k -
коэффициент усиления звена, равный отношению установившихся значений выходной и входной величин; ζ=T2/2T1 --
постоянная затухания звена (степень успокоения); ω0-собственная
частота незатухающих колебаний
звена.
Если ζ = 0, то колебания
звена будут незатухающими - звено будет колебаться с частотой ω0,
чем и объясняется термин «собственная частота». Такое звено иногда называют
консервативным. Колебательное звено получается при наличии в звене двух
емкостей, способных запасать энергию двух видов и взаимно обмениваться этими
запасами. При этом обычно одна емкость запасает кинетическую энергию, а другая
потенциальную и процесс обмена запасами энергии сопровождается переходом
одного вида энергии в другой и наоборот. Если в процессе колебаний запас
энергии в звене, полученный в начале возмущения, уменьшается, то колебания
затухают и звено является устойчивым колебательным звеном.
Примером конструктивного
выполнения устойчивого колебательного звена могут служить: конический центробежный
тахометр; электрический контур, содержащий емкость, индуктивность и омическое
сопротивление; масса, подвешенная на пружине и имеющая успокоительное
устройство.
Передаточная функция
колебательного звена, может быть
записана так
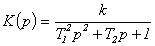 . (2.6)
. (2.6)
Интегрирующее звено. Звено называют интегрирующим, если его выходная величина пропорциональна
интегралу по времени от величины, подаваемой на вход, и определяется
уравнением вида
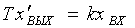 (2.7)
(2.7)
или в другой часто встречающейся
форме
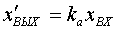 , (2.8)
, (2.8)
где  является отношением скорости изменения выходной величины к
входной величине.
является отношением скорости изменения выходной величины к
входной величине.
Обозначения в (2.7) аналогичны
приведенным для других звеньев.
Проинтегрировав почленно (2.7) и
(2.8), получим
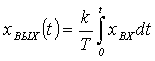
или 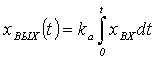 ,
,
что и дает основание называть такое звено интегрирующим.
Кроме того, такое звено называют астатическим или нейтральным.
Примерами конструктивного
выполнения интегрирующего звена могут служить: поршневой гидравлический
исполнительный двигатель, у которого массой и силами трения можно пренебречь и
у которого входом является количество жидкости подаваемой в цилиндр, а выходом
- перемещение поршня; электрический двигатель, у которого можно пренебречь
электромеханической постоянной времени и механической постоянной времени
ротора и у которого входом считается напряжение питания, а выходом - угол
поворота вала ротора; идеализированный интегрирующий контур с емкостью и тому
подобные устройства.
Передаточная функция
интегрирующего звена, получаемая из уравнения
(2.7), может быть записана так
 . (2.8)
. (2.8)
Дифференцирующие звенья. Различают идеальное и реальное дифференцирующие
звенья. Идеальное дифференцирующее звено характеризуется уравнением
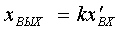 . (2.9)
. (2.9)
Следовательно, в таком звене выходная величина пропорциональна
скорости изменения входной величины, такое звено называется идеальным.
Однако практически осуществить
идеальное звено, строго удовлетворяющее уравнению (2.9), не представляется
возможным. Поэтому применяются звенья, выполняющие дифференцирующее действие
более или менее приближенно. Такие звенья называют реальными дифференцирующими
звеньями.
Их уравнения
могут быть записаны в
следующей форме
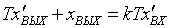 . (2.10)
. (2.10)
Из уравнения (2.10) видно, что
при Т→0, но при конечном kТ оно переходит в уравнение,
аналогичное уравнению идеального дифференцирующего звена, и подходит к нему
тем больше, чем меньше Т. Но тогда
при малом значении постоянной времени звена необходимо увеличивать значение k.
Это обычно приводит к необходимости ставить дополнительный безынерционный
усилитель, особенно если требуется производить дифференцирование достаточно
точно.
Примеры конструктивного
выполнения реальных дифференцирующих звеньев это обычно пассивные
четырехполюсники, содержащие RС (реже RL и RLM) в электрических цепях, успокоитель
с пружиной в механических цепях и другие устройства.
Сообразно с уравнением (2.10)
передаточная функция реального дифференцирующего звена может быть записана так
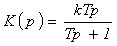 .
.
Интегро-дифференцирующее звено. Звено называют
интегро-дифференцирующим (или упругим), если его уравнение имеет вид
 , (2.11)
, (2.11)
где Т1 и Т2
- постоянные времени;
k -
коэффициент усиления звена.
В зависимости от соотношения
постоянных времени T1 и Т2, т. е. от схемы
исполнения, звено будет обладать различными свойствами: будет работать либо в
режиме дифференцирования, либо в режиме интегрирования.
Передаточная функция
звена, согласно уравнению (2.11) будет
 . (2.12)
. (2.12)
Запаздывающее звено. Звено определяется как запаздывающее, если оно
описывается уравнением следующего вида
 , (2.13)
, (2.13)
где τ - время запаздывания.
В качестве примера
запаздывающего звена можно назвать длинный трубопровод, в первом приближении
некоторые тепловые объекты (печи, нагреватели), длинную электрическую линию
без потерь и некоторые другие.
Передаточная функция звена
запаздывания легко выводится из уравнения (2.14) и имеет вид
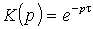 . (2.14)
. (2.14)
Лекция №3. Структурные схемы систем автоматического управления
Содержание лекции:
- назначение
структурных схем САУ и основные правила их составления;
- операторный метод исследования и расчета САУ, принцип наложения.
Цели лекции:
- усвоить основные правила составления структурных схем САУ;
-
изучить операторный метод изображения зависимости между входной и
выходной величинами САУ.
При исследовании и расчете систем
автоматического управления исходят из математического описания происходящих в
них физических процессов. Обычно это описание бывает представлено в виде
системы дифференциальных уравнений, выражающих связи между переменными
величинами и их производными. Такой подход, когда уравнения описывают
поведение исследуемой системы в целом, является наиболее общим в математическом
плане и применимым во всех случаях.
Вместе с тем для большого класса САУ (линейных
систем) широко применяется и другой способ, связанный с использованием
операторного метода. При этом способе исследуемая система разделяется на части
- звенья направленного действия, обладающие свойством передачи сигнала только
в одном направлении: от входа к выходу. Совокупность этих звеньев совместно с
линиями связи между ними, характеризующими их взаимодействие, образует
структурную схему системы управления.
Между функциональными и структурными
схемами есть определенная общность - те и другие отражают процесс передачи и
переработки информации в замкнутом контуре системы управления. Однако между
ними существует и четкое различие: функциональные схемы характеризуют систему
по составу входящих в нее элементов, рассматриваемых с точки зрения их назначения,
т. е. выполняемых ими функций; структурные схемы, состоящие из звеньев направленного
действия, описывают математически динамические свойства системы. Исходя из
структуры системы и вида входящих в нее функциональных элементов, можно
произвести разделение систем на звенья направленного действия в общем виде
так, чтобы для каждого из них можно было наиболее просто определить
передаточную функцию звена как отношение операторных изображений выходной
величины звена к входной и соединить отдельные звенья между собой линиями
связи.
Хвх (р) Хвых(р)
Рисунок 3.1 - Система направленного действия
Передаточная функция каждого звена направленного
действия представляет собой записанное в операторной форме и разрешенное
относительно изображения выходной величины дифференциальное уравнение данного
звена. Таким образом, задача составления дифференциальных уравнений САУ в целом
сводится к составлению уравнений отдельных звеньев. Получаемый при этом выигрыш
в части трудоемкости становится более очевидным, так как на практике в подавляющем большинстве случаев структурные
схемы САУ представляют собой различные комбинации небольшого числа так
называемых типовых звеньев направленного действия, передаточные функции и
динамические свойства которых могут быть определены раз и навсегда.
Рассмотрим разомкнутую систему, обладающую
свойством направленного действия (рисунок 3.1). Это может быть как одно звено,
так и любая их комбинация.
По определению передаточной функции
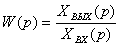 , (3.1)
, (3.1)
откуда следует основное свойство
направленной системы
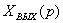 =
= 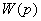
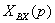 (3.2)
(3.2)
т. е. операторное изображение выходной
величины равняется передаточной функции системы, умноженной на изображение
входной величины.
В действительности, кроме управляющего
входного воздействия, всякая реальная система подвержена различным возмущающим
воздействиям (колебания нагрузки, нестабильность характеристик элементов,
помехи и т. д.), которые могут поступать в систему в любом месте. Для учета
их влияния нужно уметь при помощи структурной схемы устанавливать
зависимости между этими
возмущениями и изменениями управляемой (выходной)
величины системы. Рассмотрим структурную схему САУ, (рисунок 3.2).
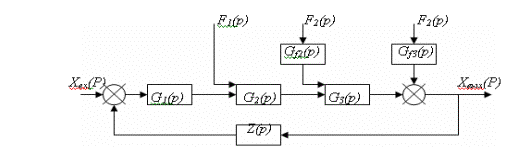
Рисунок 3.2 - Структурная схема системы автоматического управления
Прямая цепь системы состоит из
последовательно включенных звеньев направленного действия с передаточными
функциями G1(р),
G2(р), G3(р). На входы двух последних звеньев поступают возмущающие
воздействия F1(р)
и F2(р), суммирующиеся с соответствующими выходными величинами
предыдущих звеньев. Кроме того, возмущение F3(р) действует непосредственно на выходную величину системы,
что обозначено на схеме специальным элементом суммирования. При этом
принципиально важно, что место приложения возмущения F3(р) охвачено обратной связью, т. е. на звено с передаточной
функцией Z(р) поступает выходная величина системы уже с учетом действия F3(р). В противном случае никакого эффекта регулирования не было
бы, так как управляемая величина системы, искаженная влиянием возмущающего
воздействия, не корректировалась бы обратной связью.
Из структурной схемы (рисунок 3.2) видно,
что возмущающие воздействия F2(р),
F3(р)
поступают на входы
звеньев прямой цепи системы не непосредственно, а через дополнительные звенья
с передаточными функциями G j1(р),
G j3(р), которые отражают характер зависимости данной величины
системы от конкретного возмущающего воздействия.
В силу линейности рассматриваемой системы
управления, к ней применим принцип наложения, дающий возможность определить
общую реакцию системы (изменение выходной величины как сумму частных реакций от
каждого из внешних воздействий в отдельности).
Положим 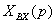 =0, F2(р)=0, Fз(р)=0 и определим зависимость
=0, F2(р)=0, Fз(р)=0 и определим зависимость 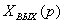 от
F1(р).При этом на входе звена G2(р) действует сумма сигналов F1(р)+G1(р)[0 –-Z(p)
от
F1(р).При этом на входе звена G2(р) действует сумма сигналов F1(р)+G1(р)[0 –-Z(p)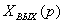 ], которые, пройдя
через звенья G2(р), G3(р), дадут на выходе
], которые, пройдя
через звенья G2(р), G3(р), дадут на выходе
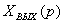 = G2(р) G3(р)[
F1(р)-G1(р) Z(p)
= G2(р) G3(р)[
F1(р)-G1(р) Z(p) 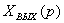 ].
].
Разрешив
последнее равенство
относительно  , будем
иметь
, будем
иметь
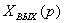
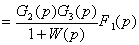 , (3.3)
, (3.3)
где 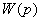 = G1(р)
= G1(р)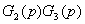 Z(p) -
передаточная функция разомкнутой системы.
Z(p) -
передаточная функция разомкнутой системы.
Полученный результат можно обобщить в виде
следующего правила: операторное изображение выходной величины системы равняется
дроби, числитель которой есть произведение изображения внешнего воздействия на
передаточные функции звеньев, включенных последовательно между точкой приложения
воздействия и выходом системы, а знаменатель - увеличенная на единицу
передаточная функция разомкнутой системы.
Аналогичным путем получим выражения и для
остальных внешних воздействий
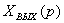
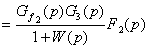 , (3.4)
, (3.4)
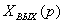
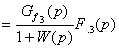 , (3.5)
, (3.5)
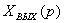
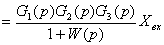 . (3.6)
. (3.6)
При одновременном воздействии всех
возмущений результирующее значение ХВЬ1Х
(р) определится как сумма полученных частных значений, что может быть
записано следующим образом
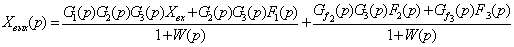 . (3.7)
. (3.7)
Из выражения (3.7) можно получить (как
частный случай) формулы, характерные для следящих систем. Особенностью последних,
как отмечалось ранее, является передача выходной величины θвых к элементу сравнения, т. е. на вход системы, с коэффициентом
передачи, равным единице. Кроме того, основным видом внешних воздействий в
следящих системах обычно считают входное (управляющее) воздействие θвх
, отрабатываемое системой с некоторой ошибкой (рассогласованием) θ = θвх - θвых//.
С учетом сказанного, положив в формулу (3.6)
Z(р) = 1, будем иметь
W(p) = G(p)
после чего, заменив в (3.5) обозначения
входной и выходной величин, получим
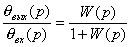 . (3.8)
. (3.8)
Соответствующая структурная схема следящей
системы приведена на рисунке 3.3.
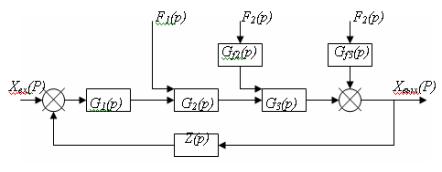
Рисунок 3.3 -
Структурная схема следящей системы
В силу линейности преобразований Лапласа,
операторные изображения ошибки, входной и выходной величин связаны между собой
так же, как и их оригиналы, т. е.
 =
= -
-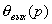 . (3.9)
. (3.9)
Определив  из (3.9) и подставив в (3.8), получим после
несложных преобразований
из (3.9) и подставив в (3.8), получим после
несложных преобразований
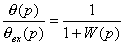 . (3.10)
. (3.10)
Выражения (3.8) и (3.10) называются
соответственно передаточными функциями следящей системы по выходной величине и
по ошибке.
Во всех рассмотренных случаях передаточные
функции замкнутых систем управления определялись через передаточную функцию
разомкнутой системы 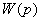 . Последняя обычно
может быть представлена в виде
. Последняя обычно
может быть представлена в виде
 =
= ,
(3.11)
,
(3.11)
где А(р), В(р) - полиномы от р.
Подставив (3.11) в выражения (3.8) и (3.10),
можно получить полезные для расчетов следящих систем формулы
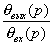 =
= , (3.12)
, (3.12)
 =
=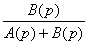 . (3.13)
. (3.13)
Рассматривалась отрицательная обратная
связь.
Весьма
важным преимуществом
структурных схем является их физическая наглядность, дающая более ясное представление
о процессах, происходящих в исследуемой системе, по сравнению с общей формой
записи дифференциальных уравнений.
После того как составлена структурная
схема и получены передаточные функции входящих в нее звеньев, необходимо определить
передаточную функцию всей системы. При
этом для определения передаточной функции системы по ее структурной схеме
можно, воспользоваться специальными правилами преобразования структурных схем,
основные из которых приводятся ниже.
Рекомендуется внимательно разобрать сам
процесс их вывода, являющийся примером преобразования структурных схем в
наиболее общем виде. Кроме того, в сложных случаях может оказаться выгоднее не
пытаться применить окончательные формулы преобразования, а идти путем,
намеченным при их выводе.
Лекция №4. Преобразования структурных
схем САУ
Содержание
лекции:
- основные способы
включения звеньев САУ;
- методы
преобразования структурных схем САУ.
Цели лекции:
- изучить основные
способы включения звеньев САУ;
- изучить методы
преобразования структурных схем САУ.
Рассмотрим основные случаи включения
звеньев направленного действия.
Последовательное
включение (одноконтурная
разомкнутая система). Структурная схема приведена на рисунке 4.1.

Рисунок 4.1 - Последовательное
включение звеньев
направленного действия
Для каждого из п звеньев можно
записать
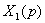 =
= 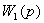
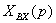 ,
,
 =
= 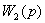
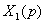 ,
,
…………………………….
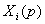 =
= 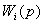
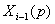 ,
,
…………………………… (4.1)
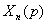 =
= 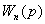
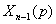 .
.
Исключая все промежуточные величины, т. е.
подставляя предыдущие в последующие, получим выражение для последнего члена
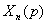 =
=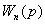
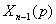 =
=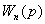

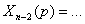
Учитывая, что выход последнего n-го звена является одновременно выходной величиной системы, т. е.
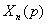 =
=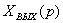
получим  =
=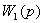
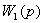 …
…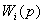 …
…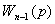
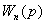
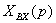 . (4.2)
. (4.2)
Так как отношение
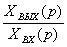
по определению есть передаточная функция
всей системы то окончательно будем иметь
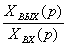 =
= =
=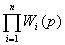 . (4.3)
. (4.3)
Итак, передаточная функция последовательно включенных звеньев равняется произведению передаточных функций
отдельных звеньев.
Параллельное, согласное включение. Параллельным согласным
включением звеньев направленного действия считается такое, при котором
входная величина системы подается параллельно на входы всех звеньев, а их
выходные величины алгебраически суммируются на выходе системы. На рисунке 4.2
изображен частный случай параллельного согласного включения трех звеньев направленного
действия.
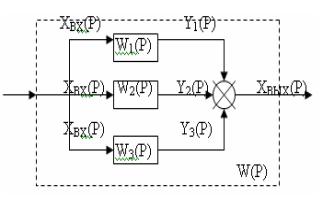
Рисунок 4.2 -
Параллельное согласное включение
звеньев
направленного действия
На основании формулы (4.2) для каждого из п
параллельно, включенных звеньев можно записать
 =
= 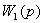
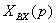 ,
,
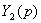 =
= 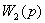
 ,
,
…………………………….
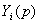 =
= 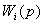
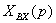 ,
,
……………………………
 =
= 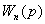
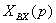 .
.
Суммируя написанные равенства и принимая
во внимание, что по определению параллельного согласного включения, звеньев
направленного действия сумма левых частей является выходной величиной системы,
получим
 =
= +
+ +…+
+…+ +…+
+…+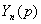 = (
= ( +
+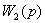 +…+
+…+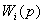 +…+
+…+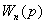 )
)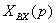 .
.
Согласно определению передаточной функции
(4.1), из последнего выражения будем иметь
 =
=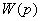 =
=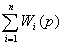 . (4.4)
. (4.4)
Таким образом, передаточная функция
параллельных согласно включенных звеньев направленного действия равняется алгебраической
сумме передаточных функций отдельных звеньев.
Параллельное
встречное включение
(обратная связь). Рассмотрим сначала основной случай - отрицательную обратную
связь.
На рисунке 4.3. изображена структурная
схема замкнутой системы автоматического управления в наиболее общем виде, где G(р) и
Z(р) -
передаточные функции соответственно прямой цепи системы и цепи обратной связи.
Сигнал обратной связи Хo.с(р) вычитается из входного сигнала Хвх(р) (в
случае положительной обратной связи они не вычитаются, а складываются). Передаточные
функции G(р) и Z(р) могут соответствовать как простым звеньям направленного
действия, так и их любым комбинациям.
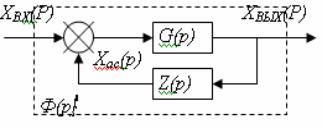
Рисунок 4.3 - Параллельное встречное включение звеньев,
направленного
действия (обратная связь)
Для схемы,
изображенной на рисунке 4.3,
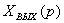 = G(р)(
= G(р)(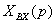 - Хo.с(р)),
- Хo.с(р)),
Хo.с(р)= Z(р)  .
.
Исключив из них промежуточную величину Хо.с,
получим передаточную функцию замкнутой системы
 =Ф(р)=
=Ф(р)=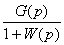 , (4.5)
, (4.5)
где 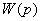 = G(р)Z(р) (4.6)
= G(р)Z(р) (4.6)
есть передаточная функция разомкнутой
системы. Смысл последнего названия становится понятным, если мысленно
разомкнуть контур управления в любом месте и, «выпрямив» его, рассматривать
прохождение сигнала, поданного в месте размыкания, по цепочке последовательно
включенных звеньев направленного действия.
Итак, передаточная функция замкнутой
системы автоматического управления равняется отношению передаточной функции прямой цепи к увеличенной
на единицу передаточной функции разомкнутой системы.
Следует отметить, что этот вывод, равно
как и формула (4.5), справедливы только для изображенного на рисунке 4.3
случая, когда внешнее воздействие поступает на вход системы управления.
Поэтому Ф(р) иногда называют передаточной
функцией замкнутой системы по входному воздействию.
а)

б)
Рисунок 4.4 - Структурные
схемы САР напряжения генератора постоянного тока, а – первоначальная, б –
преобразованная.
Преобразование многоконтурных структурных
схем с перекрещивающимися связями производят по способу переключения
(перенесения) связей, сущность которого поясняется на примере, рисунок 4.4.
Лекция №5. Преобразование
Лапласа в применении к теории автоматического регулирования
Содержание лекции:
-
математический метод -
преобразование Лапласа для САУ (прямое и обратное преобразование);
-
определение лапласового
изображения для дифференциальных уравнений САУ, рассмотрение конкретных
примеров.
Цели лекции:
-
изучить математический метод - преобразование
Лапласа для систем САУ (прямое и
обратное преобразование);
-
научиться, на конкретных
примерах, преобразовывать дифференциальные уравнения САУ рассмотренным методом.
При исследовании и расчетах
систем автоматики широко используется математический метод - преобразование
Лапласа.
Основанием для этого служит то
обстоятельство, что такое преобразование существенно облегчает исследование
сложных систем, заменяя дифференциальные уравнения алгебраическими. В
частности, при решении дифференциальных уравнений систем преобразование Лапласа
позволяет легко учитывать начальные условия и избежать сложных выкладок,
связанных с вычислением постоянных интегрирования. Достаточно просто решаются
также неоднородные уравнения, позволяющие учитывать влияние возмущений (записанных
в правой части уравнения) на динамику процессов. Некоторые понятия,
касающиеся обычного преобразования Лапласа и используемые при исследовании
систем автоматики, приводятся ниже, а также в последующих главах.
Преобразование Лапласа
преобразует функцию вещественного переменного (в том числе времени) в функцию
комплексного переменного. Такое преобразование превращает дифференциальные
уравнения в алгебраические, что дает определенные преимущества при решении
ряда задач.
Распространенное в теории САР
понятие так называемой передаточной функции также использует понятие лапласова
изображения.
Общее представление о прямом и обратном преобразованиях Лапласа. Если имеется некоторая функция
ƒ(t) независимой вещественной
переменной t (обычно времени), то преобразование
Лапласа, производимое над функцией ƒ(t) и обращающее ее в функцию F(р), определяется соотношением
 (5.1)
(5.1)
здесь р - произвольная
комплексная величина, обозначаемая  , где σ и ω - вещественные переменные.
, где σ и ω - вещественные переменные.
Функциональное преобразование
вида (5.1), осуществляемое над функцией ƒ(t), часто
сокращенно обозначается так
 или
или 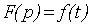 .
(5.2)
.
(5.2)
Функция ƒ(t) называется оригиналом, а функция
F(р) - изображением функции ƒ(t).
Следует заметить, что при
применении преобразования Лапласа к функции ƒ(t) рассматриваются
значения этой функции лишь при t>0, т. е. в технических задачах после
приложения к системе внешних возмущающих воздействий, а именно это и
представляет практический интерес при решении задач автоматического регулирования.
Для того чтобы преобразованная
функция была определена, достаточно потребовать, чтобы интеграл (5.1)
существовал для некоторой области р, за пределами которой этот интеграл может
и не иметь смысла. Так, например, изображение оригинала, равного единице, т.
е. если ƒ(t) = [1], будет равно
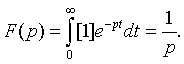
Здесь при вычислении интеграла
предполагается, что вещественная часть р
положительна (σ>0). При
σ≤0 интеграл не существует, но преобразованная функция от
единицы всегда равняется 1/р.
Может случиться, что интеграл (5.1) не существует ни при каких значениях р.
В этом случае преобразование (5.2) невозможно. Однако в физических задачах,
описываемых дифференциальными уравнениями в полных производных с постоянными
коэффициентами, и при обычном типе возмущающих воздействий это преобразование
всегда осуществимо.
Наряду с прямым преобразованием
(5.1) функции времени ƒ(t) в F(р), т. е. наряду с операцией перехода от функции вещественного
переменного t к функции комплексного
переменного р, пользуются обратным
преобразованием, т. е. преобразованием изображения в оригинал. При этом
производится обратная операция определения оригинала ƒ(t) по заданному изображению F(р). Эта операция обозначается символом
L-1 или 1/L. Таким образом, в этом случае имеем
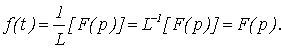 (5.3)
(5.3)
При этом преобразовании теорема
о начальном значении функции ƒ(t) записывается так
 ,
,
 а теорема о
конечном значении
а теорема о
конечном значении
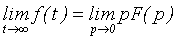 .
.
Преобразования Лапласа, часто
используемые при расчетах систем автоматики, приведены в учебниках.
Нахождение лапласова изображения для линейного дифференциального уравнения. Положим, что линейная система автоматического регулирования описывается
дифференциальным уравнением n-го порядка с постоянными коэффициентами следующего
вида
 . (5.4)
. (5.4)
Умножая левую и правую части
уравнения (5.4) на е-pt и интегрируя в пределах от 0 до
∞, получим
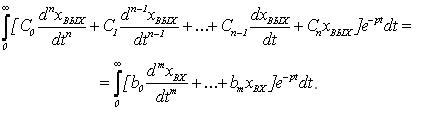
Воспользовавшись вышеприведенными обозначениями,
правилами о преобразованиях Лапласа, можно написать
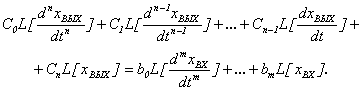
Полагая, что система находится при нулевых начальных
условиях и зная лапласово изображение для производных, для данного случая
получим
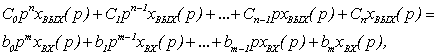 (5.5)
(5.5)
или
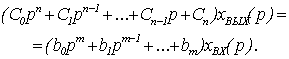 (5.6)
(5.6)
Выражение (5.6) является
лапласовым изображением дифференциального уравнения (5.4) при нулевых начальных
условиях.
Лекция
№6. Статическое и астатическое регулирование
Содержание лекции:
- статическое регулирование, рассмотрение
примеров, основные характеристики;
- астатическое регулирование, рассмотрение
примеров, основные характеристики.
Цели лекции:
-
изучить
принцип построения статического регулятора, основные определения и
характеристики;
-
изучить
принцип построения астатического регулятора, основные определения и характеристики.
Одной из существенных
характеристик систем автоматического регулирования является зависимость между
значением регулируемого параметра и величиной внешнего воздействия (нагрузкой)
на объект регулирования. По виду таких рабочих характеристик различают
статическое и астатическое регулирование.
Статическое регулирование. Регулированием со
статической характеристикой называется такое, при котором в установившемся состоянии имеется определенная зависимость между
величиной отклонения регулируемого параметра от заданного значения и
величиной внешнего возмущения, например нагрузкой объекта регулирования. При
статическом регулировании величина регулирующего воздействия однозначно
связана с отклонением регулируемого параметра от заданного значения. Отсюда
следует, что для создания требуемого регулирующего воздействия, устраняющего
соответствующее влияние внешнего возмущения, обязательно должно иметь место
отклонение регулируемого параметра. Поэтому при статическом регулировании
всегда имеется остаточное отклонение
регулируемого параметра от номинального значения. Равновесие системы при
статическом регулировании для разных нагрузок имеет место при различных
значениях регулируемого параметра, лежащих в заданных заранее пределах.
Пример статического
регулятора приведен на рисунке 6.1,а.
Принцип действия этого регулятора достаточно ясно виден из рассмотрения схемы
и особых пояснений не требует. Заметим лишь, что требуемое возбуждение
генератора 1 осуществляется путем
изменения входного сигнала электронного усилителя 2. В свою очередь, этот сигнал пропорционален отклонению регулируемого
параметра uГ от заданного значения uЗАД. Поэтому такое отклонение, т. е. наличие Δu, является неизбежным и должно быть тем больше, чем
больше изменяется величина внешнего возмущения. Очевидно, что это отклонение
регулируемого параметра от заданного значения сохраняется также и в
установившемся положении. Рабочая характеристика (зависимость напряжения от
нагрузки) статического регулятора, называемого иногда пропорциональным
регулятором, приведена на рисунке 6.1,6.
На рисунке 6.1, в показан переходный процесс в системе
при уменьшении нагрузки генератора. Выходное напряжение uГ при этом увеличивается с uГ1 до uГ2.
При решении
однотипных задач статические регуляторы обычно имеют сравнительно менее сложное
конструктивное исполнение, чем астатические регуляторы. Вместе с тем такие
регуляторы органически обладают погрешностью в поддержании постоянства величины
регулируемого параметра при разных внешних нагрузках.
Рисунок 6.1 -
Пример статического регулятора и его характеристика
Астатическое регулирование. Регулированием с астатической характеристикой называется
такое регулирование, при котором в установившемся состоянии системы отклонение регулируемого параметра от
заданного значения равно нулю при любой величине внешнего возмущения.
Равновесие системы имеет место всегда при заданном значении регулируемого
параметра. В установившемся состоянии при неизменном возмущении неизменным
должно быть также и регулирующее воздействие, т. е. скорость его изменения
должна быть равна нулю, а это возможно, если отклонение параметра
регулирования от номинального значения равно нулю.
Характеристика астатического
регулятора приведена на рисунке 6.2,б,
а кривая переходного процесса - на рисунке 6.2,в.
Астатические
регуляторы, следовательно, более точно поддерживают заданное значение
регулируемого параметра, но имеют, как правило, по сравнению со статическими
регуляторами более сложное конструктивное исполнение.
К числу регуляторов, имеющих
астатическую характеристику, следует отнести так называемые изодромные
регуляторы, действие которых слагается из элементов статического и астатического
регулирования.
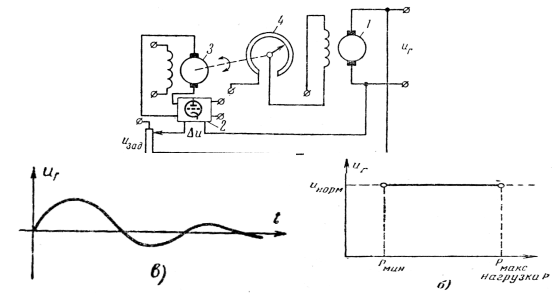
Рисунок 6.2 - Пример астатического регулятора и его
характеристика.
Статизм регулирования (точность
в установившемся режиме). Если при
изменении нагрузки от нуля до номинального значения в статической системе
значение регулируемого параметра изменилось от хМИН до хНОМ,
то статизмом системы s называют следующее соотношение
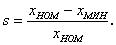 (6.1)
(6.1)
Предварительно отметим, что при
установившемся состоянии в статической замкнутой системе имеет место следующее
соотношение
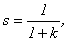 (6.2)
(6.2)
где k – коэффициент усиления разомкнутой системы.
Как видно из (6.2), статизм
системы регулирования обратно пропорционален коэффициенту усиления разомкнутой
системы, сложенному с единицей.
При достаточно больших
коэффициентах усиления эти величины можно считать обратно пропорциональными,
т.е.
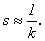 (6.3)
(6.3)
Составление уравнений и определение
передаточных функций объектов управления.
Лекция №7. Уравнения и частотные
характеристики систем автоматического управления
Содержание лекции:
-
методика
составления операторных уравнений САУ;
-
определение передаточных функции звеньев САУ.
Цели лекции:
-
изучить
методику составления операторных уравнений систем САУ:
-
научиться
определять передаточные функции звеньев
САУ.
Достоверность динамических расчетов САУ,
прежде всего, определяется тем, насколько близко к действительности принятое
математическое описание происходящих в системе физических процессов.
Математическое описание динамики САУ обычно
производится путем составления системы дифференциальных (иногда
интегро-дифференциальных) уравнений. Строго говоря, любая реальная
динамическая система является нелинейной. Однако большинство непрерывных
систем управления могут быть линеаризованы, т. е. заменены приближенно
эквивалентными системами, переходные процессы в которых описываются
обыкновенными линейными дифференциальными уравнениями с постоянными
коэффициентами. Такие системы управления принято называть линейными.
Линеаризация исходных систем основывается
на методе малых отклонений. Сущность этого метода заключается в том, что
динамические свойства системы управления исследуются не во всем возможном
диапазоне изменения переменных систем, а вблизи их некоторых значений,
соответствующих характерным режимам работы (например, установившимся режимам).
Составление и линеаризация уравнений
обычно производится по отдельным звеньям. Разлагая в ряд Тейлора непрерывную
аналитическую функцию, связывающую переменные звеньев и их производные, и
отбрасывая члены второго и высших порядков малости, получим линейное уравнение
звена. Однако в расчетной практике, как правило, не прибегают к разложению
функций в ряд, а пользуются заранее линеаризованными характеристиками звеньев,
которые чаще всего задаются не в аналитической форме, а в виде графиков,
таблиц, паспортных данных и т. д.
Полученные дифференциальные уравнения
линейных звеньев направленного действия обычно выражают в операторной форме и
представляют в виде передаточных функций. Структурная схема, для всех звеньев
которой передаточные функции определены, представляет собой наглядную форму
записи дифференциальных уравнений исследуемой системы управления в операторной
форме.
Составление уравнений и определение передаточных
функций объектов управления, вообще говоря, выходит за рамки теории
автоматического управления и должно производиться на основе физических законов,
характеризующих эксплуатационные режимы этих объектов (например, законы
аэродинамики для “летательных”
аппаратов). Однако нужно уметь правильно представлять и преобразовывать
уравнения объектов управления к наиболее удобному для расчетов виду.
Специалисту по автоматическому управлению
необходимо также уметь определять и преобразовывать передаточные функции тех
звеньев, которые входят в управляющую часть системы (чувствительные элементы,
усилители, исполнительные двигатели, корректирующие звенья и т. д.).
Частотные характеристики получили
исключительно широкое использование при анализе и синтезе систем автоматического
управления.
Выражения для частотных характеристик
отдельных звеньев и системы легко могут быть получены из соответствующих передаточных
функций, написанных в операторной форме, путем замены оператора р на d/dt).
Физически частотная характеристика
замкнутой или разомкнутой системы имеет место при подаче на вход системы гармонического
воздействия при изменении его частоты от нуля до бесконечности и сохранении
постоянной амплитуды входного сигнала на всем диапазоне изменения частот. Подобного
же рода частотная характеристика свойственна и отдельным звеньям системы.
Очевидно, что при экспериментальном получении подобной характеристики диапазон
изменения частоты входного гармонического воздействия ограничен определенными
техническими возможностями того или иного устройства для подачи гармонических
воздействий.
При подаче на вход линейной системы
автоматического управления гармонического воздействия
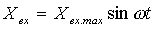 ,
,
характеристика отработки системы по
окончании переходного процесса будет также представлять собой периодическую
функцию вида
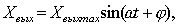
отличающуюся от входной функции по
амплитуде и по фазе, но имеющую ту же частоту, что и входная функция. При этом
система будет находиться в режиме вынужденных колебаний. Отношение
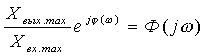 , (7.1)
, (7.1)
представляет собой комплексную
частотную функцию, которая называется комплексным коэффициентом усиления
системы.
Таким образом, при подаче на вход системы
гармонического сигнала, установившаяся гармоническая величина на выходе
определяется произведением входной функции на комплексную частотную функцию,
которая может быть непосредственно получена из передаточной функции, т.е.
 .
.
Выражение для Ф(jω) может быть разделено на вещественную и
мнимую части
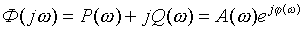 ,
(7.2)
,
(7.2)
где Р(ω), Q (ω), А (ω),
φ(ω) - полиномы от ω.
При определенном значении ω комплексная частотная функция Ф(ω) представляет собой вектор на плоскости комплексного
переменного и характеризуется амплитудой А и фазой φ.
При изменении частоты ω
амплитуда и фаза векторов Ф(ω)
будут изменяться, а их конец будет описывать на плоскости комплексного
переменного кривую (геометрическое место концов векторов частотной функции),
представляющую собой амплитудно-фазовую характеристику замкнутой системы.
Очевидно, что при изменении частоты будут
изменяться также и величины Р, Л и ф, что позволяет построить частотные характеристики и для этих величин.
Соответственно имеются:
-
Р(ω)
- вещественная
частотная характеристика замкнутой системы;
- Q (ω) - мнимая частотная характеристика замкнутой системы;
- А3(ω) - амплитудная частотная характеристика
замкнутой системы;
- Φ3(ω) - фазовая частотная характеристика
замкнутой системы.
Соотношения между характеристиками
определяются выражениями
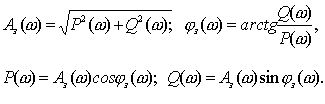 (7.3)
(7.3)
Для получения частотных характеристик экспериментальным путем для каждого
значения частоты определяют амплитуду гармонического воздействия, амплитуду
выходной величины, а также фазовый сдвиг между обеими амплитудами.
Кривые зависимости отношения амплитуд и
фазового сдвига от частоты воздействующей величины и являются амплитудной и
фазовой частотными характеристиками. По этим характеристикам могут быть
построены и другие характеристики: амплитудно-фазовая, вещественная и др.
Подобные характеристики могут быть получены как для замкнутой системы, так и
для разомкнутой, а также для отдельных звеньев системы.
Частотные характеристики
разомкнутой системы обычно обозначают:
-
W(jω) - амплитудно-фазовая характеристика разомкнутой системы (А.Ф.Х.);
- U (ω) - вещественная частотная характеристика
разомкнутой системы;
- V(ω) - мнимая
частотная характеристика разомкнутой
системы;
- А(ω)- амплитудная частотная характеристика разомкнутой системы;
-
φ(ω) -
фазовая частотная характеристика разомкнутой системы.
Соотношения между этими характеристиками
определяются выражениями, аналогичными выражениям для замкнутых систем.
Кроме амплитудно-фазовой характеристики,
на плоскости комплексного переменного может быть построена также и так
называемая характеристическая кривая, или кривая Михайлова, получаемая
в результате формальной замены в характеристическом уравнении замкнутой
системы оператора р на jω.
Выражение для этой характеристики может быть написано как
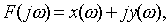 (7.4)
(7.4)
где x(ω) и
y(ω) - соответственно ее вещественная и мнимая
составляющие.
Ценность использования частотных
характеристик заключается в том, что они позволяют косвенно, т. е. без решения
дифференциального уравнения системы, судить о поведении последней в отношении
устойчивости и ряда показателей качества, а также определять и рассчитывать
средства коррекции системы для получений заданных динамических показателей.
Наибольшее использование получили
характеристики разомкнутой системы благодаря их наглядности и простоте построения.
В особенности это следует отметить относительно логарифмических частотных
характеристик (амплитудной и фазовой), позволяющих производить синтез системы
наиболее простым образом.
Для расчета кривой переходного процесса
удобно использование вещественной частотной характеристики замкнутой системы.
Лекция №8. Устойчивость
систем автоматического управления
Содержание лекции:
- общие понятия об
устойчивости систем автоматического управления;
- критерии устойчивости линейных
систем.
Цели лекции:
- изучить общие понятия об
устойчивости систем автоматического управления;
- изучить критерии
устойчивости линейных систем.
Для того чтобы система автоматического управления
могла нормально функционировать, она должна, прежде всего, удовлетворять
требованию устойчивости.
Система является устойчивой, если она возвращается к установившемуся состоянию
после прекращения действия возмущения, которое вывело ее из этого состояния.
Общее решение х(t) дифференциального
уравнения линейной системы управления может быть представлено в виде суммы
двух функций времени
х(t) = хs (t)+ хd (t) ,
из которых хs(t) характеризует так называемое вынужденное движение системы
и зависит от внешнего воздействия, а хd (t) определяет
свободное движение или переходный процесс в системе.
Математическая форма записи условия устойчивости представляет
собой требование обращения в нуль хd (t)
при неограниченном возрастании
времени с момента начала переходного процесса, т. е.
 .
.
Функция хd (t),
являющаяся общим решением
соответствующего однородного дифференциального уравнения (т. е. уравнения
системы управления с нулевой правой частью) для линейной системы n-го порядка имеет вид
хd (t)= ,
,
где с1, с2, ..., сn - —
постоянные интегрирования, а λ1, λ2, ...,
λn - неравные корни характеристического уравнения системы
управления.
Из последнего выражения видно, что при 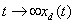 будет стремиться к нулю
только в том случае, если все п корней характеристического уравнения
имеют отрицательные вещественные части.
будет стремиться к нулю
только в том случае, если все п корней характеристического уравнения
имеют отрицательные вещественные части.
Следовательно, для суждения об устойчивости системы управления
нет необходимости определять значения корней характеристического уравнения,
что связано обычно с трудоемкими вычислениями. Достаточно располагать
косвенными признаками, которые позволяли бы судить об отсутствии в характеристическом
уравнении системы управления корней с неотрицательной вещественной частью
(действительные корни могут рассматриваться как частный случай комплексных с нулевой
мнимой частью). Такие признаки получили название критериев устойчивости.
Известно несколько критериев устойчивости. Наиболее
употребительными из них являются алгебраические
критерии Рауса и Гурвица, основанные на рассмотрении системы неравенств,
образуемых из коэффициентов характеристического уравнения, а также связанные с
частотными представлениями критерии Найквиста и Михайлова.
Ниже приводятся без доказательства формулировки этих
критериев устойчивости.
При использовании операторного исчисления характеристическое
уравнение системы управления легко находится приравниванием нулю знаменателя
передаточной функции замкнутой системы
1+W(p) . (8.1)
Учитывая выражение (8.1), получим характеристическое
уравнение в виде
H(p)=A(p)+B(p)=0. (8.2)
Для системы n-го
порядка функция H(p), представляющая собой левую часть
характеристического уравнения, имеет вид многочлена n-й степени
Н(р) = а0 рп +
а, рn-1 +... + ап-1р
+ ап.
(8.3)
Критерий Гурвица. Проверка устойчивости по Гурвицу сводится к вычислению по
коэффициентам характеристического уравнения так называемых определителей
Гурвица, которые для устойчивой системы управления должны быть положительными.
Для получения определителей Гурвица составляется таблица
из коэффициентов характеристического уравнения n-й степени
 .
.
Правила составления таблицы просты: по главной диагонали
выписываются по порядку п коэффициентов характеристического уравнения
от а1 до аn; каждая
строка содержит п элементов; строки с нечетными и четными индексами
чередуются; недостающие элементы строк заполняются нулями. Отчеркивая соответствующие
строки и столбцы таблицы, получим п определителей Гурвица
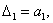
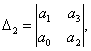
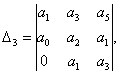
………………………..
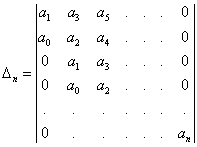 .
.
Критерий устойчивости Гурвица заключается в требовании
положительности всех п определителей (при а0>0), т. е.
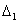 >0,
>0, 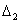 >0,...,
>0,..., 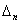 >0.
>0.
Необходимым (но недостаточным) условием устойчивости
системы n-го порядка при а0>0 является требование
положительности всех коэффициентов характеристического уравнения
 >0,
>0,  >0,
>0, 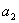 >0,...,
>0,..., 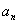 >0.
>0.
Поскольку последнее условие легко проверяется по виду
уравнения, записанного с конкретными числовыми коэффициентами, то
целесообразно проанализировать критерии Гурвица с учетом этого необходимого
условия. В результате такого анализа, излагаемого в большинстве руководств по
теории автоматического управления и регулирования, можно получить систему неравенств,
соблюдение которых эквивалентно выполнению условий устойчивости.
Для систем первого и второго порядка необходимое условие
устойчивости
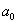 >0,
>0, 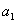 >0,
>0, 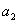 >0
>0
одновременно является и достаточным.
Для систем более высокого порядка, кроме выполнения
требования положительности всех коэффициентов характеристического уравнения,
необходимо и достаточно соблюдение следующих неравенств
для системы третьего порядка

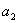 -
-
 >0;
>0;
для системы четвертого порядка
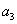 (
(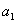
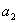 -
-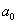
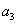 )
)
 >0;
>0;
для системы пятого порядка

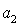 -
-
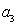 >0,
>0,
(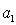
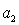 -
-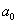
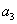 )(
)(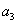
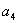 -
-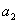
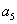 )-(
)-(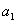
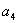 -
-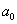
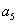 )2>0;
)2>0;
для системы шестого порядка
(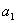
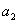 -
-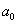
 ) -
) -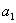 (
(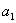
 -
-
 )>0,
)>0,
(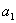
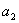 -
-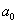
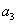 )[
)[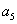 (
(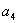
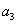 -
-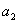
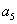 )+
)+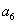 (2
(2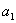
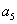 -
-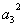 )]+
)]+
+(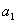
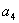 -
-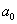
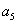 )[
)[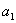

 -
-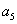 (
(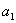
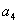 -
-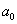
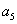 )]-
)]-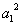
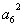 >0.
>0.
Критерий Рауса. Практически критерием Гурвица выгодно пользоваться при исследовании
устойчивости систем автоматического управления не выше пятого порядка. Для
систем более высоких порядков удобнее применять критерий Рауса.
Составим таблицу-схему из коэффициентов, характеристического
уравнения (таблица 6.1). В первую строку таблицы вписываются коэффициенты с четными
индексами, а во вторую — с нечетными. Все последующие строки получаются в
результате делений разности перекрестных произведений коэффициентов двух
предыдущих строк на коэффициент первого столбца предыдущей строки. Всего
таблица содержит n+1 строку.
Согласно критерию Рауса, для устойчивости системы необходимо
и достаточно, чтобы при a0>0 все коэффициенты первого столбца таблицы 8.1
были положительны, т. е. чтобы
 >0,
>0,  >0,
>0,  >0,
>0, 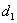 >0,...
>0,...
Таблица 8.1 - Коэффициенты
характеристического уравнения
Лекция№9. Частотные
критерии устойчивости САУ
Содержание лекции:
- основные частотные критерии
устойчивости САУ;
- методика исследования
устойчивости критериями Найквиста и Михайлова.
Цели лекции:
- изучить основные частотные
критерии устойчивости САУ;
- изучить методику исследования
устойчивости критериями Найквиста и Михайлова.
Частотные критерии устойчивости в
настоящее время получили широкое признание. Одним из таких критериев является критерий Найквиста, или, как его также
называют, частотный
амплитудно-фазовый критерий, являющийся
следствием известной теоремы Коши, другим является критерий Михайлова.
Амплитудно-фазовый
критерий дает возможность судить об устойчивости замкнутой системы посредством исследования разомкнутой системы. Исследование
же разомкнутой системы проще, чем замкнутой
и, кроме того, его можно производить также экспериментально.
Руководствуясь формой
и расположением на комплексной плоскости амплитудно-фазовой характеристики разомкнутой системы, можно судить о динамических
свойствах замкнутой системы.
Частотные критерии
обладают большой наглядностью в силу их простой геометрической интерпретации.
Критерий Найквиста. Критерий Найквиста основан на рассмотрении амплитудно-фазовой
характеристики W(jω) разомкнутой
системы, по виду которой можно судить об устойчивости замкнутой системы, что
обусловлено наличием однозначной зависимости между передаточной функцией W(р) разомкнутой системы и характеристическим уравнением
замкнутой [1,2,3].
Амплитудно-фазовая характеристика W(jω) может быть построена расчетным путем на основании
аналитического выражения функции W(р) при
замене в последней р на jω и изменении ω от 0 до ∞ (практически расчет заканчивается,
когда значения модуля |W(jω)|
становятся достаточно малыми).
Эта характеристика может быть также получена экспериментально,
в частности, по снятым опытным путем частотным характеристикам отдельных
звеньев системы. Это обстоятельство является важным практическим преимуществом
частотного критерия Найквиста.
Формулировка критерия устойчивости замкнутой системы управления
зависит от свойств разомкнутой системы.
Согласно критерию Найквиста, если разомкнутая система
устойчива, т.е. ее характеристическое
уравнение не имеет корней с положительной вещественной частью (но может иметь
нулевые корни), то для устойчивости замкнутой системы автоматического
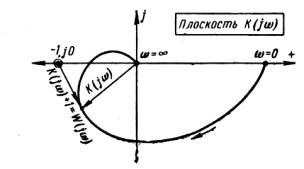
управления необходимо и достаточно, чтобы амплитудно-фазовая характеристика W(jω) не охватывала точку с координатами (-1, j0).
На рисунке 9.1, приведена амплитудно-фазовая характеристика (годограф), частотной функции разомкнутой системы 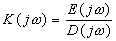 если задана частотная функция
разомкнутой системы K(jω).
если задана частотная функция
разомкнутой системы K(jω).
Если же разомкнутая система имеет т корней с
положительной вещественной частью, то для устойчивости замкнутой системы
требуется, чтобы характеристика W(jω) охватывала
точку (-1, j0) в
положительном направлении  раз.
раз.
|
|
|
Рисунок 9.1 - Взаиморасположение
векторов K(jω)
и W(jω)
|
Критерий Михайлова. Критерий устойчивости Михайлова основан на построении так называемой
кривой Михайлова, представляющей собой годограф вектора H(jω), вычерчиваемый при изменении ω от 0
до ∞ (практически ограничиваются достаточно большими значениями ω, при
которых - угол поворота вектора перестает изменяться с увеличением ω).
Комплексная функция Н(jω) получается подстановкой р=jω в
характеристический полином Н(р), стоящий в левой части
характеристического уравнения.
Согласно критерию Михайлова, для устойчивости системы
автоматического управления n-го порядка
необходимо и достаточно, чтобы характеристическая кривая Михайлова при изменении
ω
от 0 до ∞ , начиная с положительной вещественной оси, обошла
последовательно в положительном направлении (т. е. против часовой стрелки) п
квадрантов.
Если представить комплексную функцию Н(jω) в виде
Н(jω)=x(ω)+jy(ω)
и построить графики вещественных функций x(ω) и y(ω), откладывая
ω
по оси абсцисс в положительном направлении, то можно указать другую формулировку
критерия Михайлова. Согласно этой формулировке, графики функций х(ω) и y(ω) для
устойчивой системы должны пересекать ось ω, последовательно чередуясь друг с другом.
Рисунок 9.2,а показывает годографы устойчивой системы, где для уравнений
п-го порядка кривая, вычерченная вектором F(jω), проходит без пропусков последовательно
п квадрантов справа налево; на рисунке. 9.2,б приведена кривая,
вычерченная вектором F(jω) для неустойчивой системы регулирования; на рисунке 9.2,в приведена проходящая через начало
координат кривая F(jω) для системы, находящейся на границе устойчивости.
Алгебраические критерии Гурвица и Рауса удобны при проверке
устойчивости систем до пятого-шестого порядка. Для систем высших порядков выгоднее
применять частотные критерии Найквиста и Михайлова.
|

|
|
Рисунок 9.2 - Вид годографов F(jω) замкнутой системы для устойчивой, неустойчивой и
нейтральной систем
|
При исследовании устойчивости систем автоматического
управления может ставиться задача не только проверки устойчивости системы при
заданных значениях ее параметров, но также и определения некоторой области
изменения отдельных параметров, внутри которой система остается устойчивой.
Построение областей устойчивости в функции одного и
двух параметров системы управления может быть выполнено при помощи любого
критерия устойчивости. Существуют различные формальные способы выделения
областей устойчивости. Однако эффективность применения того или иного способа
в сильной степени зависит от конкретного содержания решаемой задачи. Поэтому
целесообразно не приводить общее описание этих способов, а предоставить
читателю, освоить сущность некоторых из них на конкретных примерах, рассматриваемых
в пособии, с указанием, по мере необходимости, на соответствующие руководства
по теории.
Лекция № 10. Переходные
процессы в системах автоматического управления
Содержание лекции:
-
основные способы определения переходных процессов в САУ;
- методы построения кривых переходных процессов в САУ.
Цели лекции:
- освоить основные
способы определения переходных процессов;
- изучить и освоить методы
построения кривых переходного процесса.
По окончании расчета системы автоматического управления,
в процессе которого из условия обеспечения устойчивости и заданных косвенных
показателей качества (времени переходного процесса, величины перерегулирования
и т. д.) оказываются выбранными структура и значения параметров системы,
обычно производится приближенное построение кривой переходного процесса в
системе при каком-либо типовом воздействии.
Различные методы определения переходных процессов (в
биде графиков изменения во времени выходной величины или ошибки) для наиболее
характерных режимов работы системы можно разбить на две основные группы.
В первую группу входят различные (аналитические,
графические, графоаналитические) способы приближенного решения
дифференциальных уравнений системы управления, из которых наибольшее
распространение получил операторный метод, основанный на использовании
преобразований Лапласа.
Вторую группу составляют методы, основанные на
использовании частотных характеристик систем автоматического управления.
Здесь наиболее известным является метод построения кривой переходного процесса
при помощи так называемых трапецеидальных вещественных частотных
характеристик.
При использовании операторного метода, благодаря
алгебраизации дифференциальных уравнений (при переходе к операторным изображениям
величин), существенно упрощается процесс составления уравнений систем автоматического
управления, который сводится к определению передаточных функций отдельных
звеньев и преобразованию структурных схем систем управления.
После определения передаточной функции замкнутой системы
Ф(р) операторное изображение выходной величины может быть получено как
XВЫХ(р) = Ф(р)XВХ(р).
В качестве типового входного воздействия хвх(t), являющегося
оригиналом по отношению к изображению Хвх(р), чаще всего
применяется воздействие в виде единичной (скачкообразной) функции времени
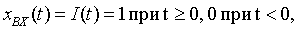
операторное изображение которой по Лапласу
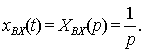
Кроме единичной функции в качестве типовых воздействий
при исследовании систем автоматического управления (главным образом, следящих
систем), принимаются также следующие входные воздействия:
в виде линейной функции времени
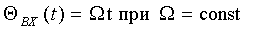 ,
,
для которой операторное изображение
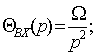
в виде квадратичной функции времени
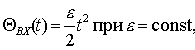
для которой операторное изображение
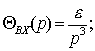
в виде синусной функции времени

для которой
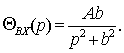
Следует иметь в виду, что в ряде руководств по
операционному исчислению операторные изображения функций определяются не
преобразованием Лапласа (принятым в данной книге), а так называемым
преобразованием Карсона - Хевисайда, отличающимся наличием множителя р перед
интегралом Лапласа. Поэтому, пользуясь таблицами из этих руководств, нужно все
операторные изображения разделить на р.
Если известна передаточная функция системы Ф(р) и
задано входное воздействие, то определение переходного процесса сводится к
нахождению оригинала хВЫХ(t) по его
операторному изображению XВЫХ(р). При этом должны быть заданы начальные условия,
которые большей частью принимаются нулевыми.
Для нахождения оригиналов в системах невысокого
порядка могут быть использованы таблицы операторных изображений.
В системах выше третьего порядка обычно пользуются второй
теоремой разложения Хевисайда, сущность которой заключается в следующем. Пусть
операторное изображение F(р) некоторой
функции f(t)
представлено в виде дроби
F(p)=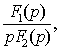
где  ,
, 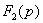 - полиномы от р.
- полиномы от р.
Тогда оригинал может быть определен как
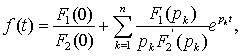 (10.1)
(10.1)
где
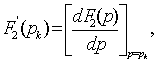
а р1,
р2,..., рк — суть корни алгебраического
уравнения, среди которых нет кратных и
нулевых, корней.
Применение теоремы разложения позволяет избежать трудоемкой
процедуры определения постоянных интегрирования, необходимой при использовании
классических методов решения дифференциальных уравнений, но не избавляет от
нахождения корней уравнения Р2(р)=0, являющегося характеристическим
уравнением исследуемой системы управления.
Из многочисленных способов определения приближенных
значений корней характеристического уравнения наиболее эффективными, по мнению
авторов, являются метод деления многочленов
и итерационный метод, применение - которых показано на примерах.
Построение кривой переходного процесса при помощи
трапецеидальных вещественных - частотных характеристик основано на наличии
однозначной связи между функцией хвых(t), определяющей
переходный процесс в системе управления, и частотной функцией Р(ω), представляющей
собой вещественную часть комплексного выражения
Ф(jω)=Р(ω)+jQ(ω),
получаемого
подстановкой р=jω в
передаточную функцию замкнутой
системы управления Ф(р).
Метод трапецеидальных вещественных частотных характеристик
подробно изложен в учебниках по теории автоматического управления.
В следящих системах переходный процесс часто
определяется в виде графика изменения не выходной величины системы  , а ошибки
, а ошибки 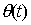 . В этом случае передаточная функция замкнутой системы
определяется иной формулой, а начальные условия пересчитываются с учетом соотношения
. В этом случае передаточная функция замкнутой системы
определяется иной формулой, а начальные условия пересчитываются с учетом соотношения
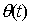 =
=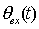 -
-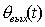 .
.
Лекция №11. Расчет систем
автоматического управления по методу логарифмических частотных характеристик
Содержание лекции:
-
основные положения метода логарифмических
частотных характеристик;
- логарифмические характеристики основных звеньев САУ.
Цели лекции:
-
изучить основные положения метода логарифмических
частотных характеристик;
-
изучить логарифмические характеристики основных звеньев
САУ.
Находят широкое практическое
применение частотные характеристики, построенные в логарифмическом масштабе,
называемые логарифмическими частотными характеристиками. Если частотную
характеристику  прологарифмировать,
то можно записать
прологарифмировать,
то можно записать
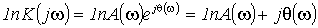 . (11.1)
. (11.1)
Характеристика lnA(ω), построенная в
логарифмическом масштабе частот по
оси абсцисс и
в обычном натуральном масштабе по оси ординат,
называется логарифмической амплитудной частотной характеристикой (ЛАЧХ). Характеристика, построенная в
логарифмическом масштабе частот
(ось абсцисс) и в обычном
масштабе для фазы (ось ординат), называется логарифмической фазовой частотной характеристикой (ЛФЧХ).
При построении логарифмических
характеристик частоты по оси абсцисс откладываются в логарифмическом масштабе
в октавах и декадах.
Октавой называется частотный
интервал, соответствующий удвоению частот, т. е. изменению частоты в 2 раза.
Декадой называется частотный
интервал, соответствующий изменению частоты в 10 раз.
В одной декаде содержится 3,32
октавы. Декадный интервал применяется чаще. Обычно по оси ординат фаза
откладывается в угловых градусах или в радианах, а ординатой амплитудной
частотной характеристики принимается не величина lnA(ω),
а пропорциональная ей величина L(ω) в децибелах, где
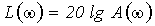 , дб.
(11.2)
, дб.
(11.2)
Связь между натуральным числом
А(ω) и значением L(ω) в
децибелах, определяемая выражением (11.2), дает для некоторых часто
встречающихся значений А (ω)
таблица 11.1.
Таблица 11.1- Связь между натуральным числом А(ω) и значением
L(ω)
|
А(ω)
|
1
|
2
|
10
|
100
|
0,2
|
0,1
|
0,01
|
|
L(ω)
|
0
|
6
|
20
|
40
|
-14
|
-20
|
-40
|
Координатные системы для
логарифмических характеристик приведены на рисунке 11.1.
Рисунок 11.1- Координатные
системы для логарифмических характеристик
В соответствии с
видом передаточных функций типовых звеньев легко найти их логарифмические
характеристики.
Рассмотрим
логарифмические характеристики некоторых часто встречающихся типовых звеньев
САУ.
Логарифмические
характеристики безынерционного звена. Передаточная функция безынерционного звена
K(p) = k.
Следовательно,
 и
и  ,
(11.3)
,
(11.3)
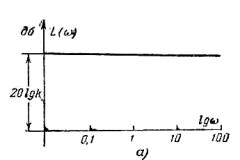
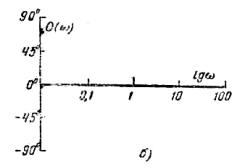
Рисунок 11.2 - Логарифмические характеристики безынерционного звена
т.е. амплитудная
характеристика
представляет собой прямую,
параллельную оси абсцисс и проходящую на
расстоянии 20lgk от нее, а фазовая характеристика показывает
отсутствие
фазового сдвига (рисунок 11.2, а и б).
Логарифмические
характеристики инерционного звена. Зная, что частотная
характеристика
инерционного звена имеет вид
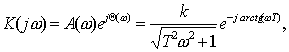 (11.4)
(11.4)
и логарифмируя выражение (9.4), получим
 .
.
Обозначая
соответственно амплитудную и фазовую характеристики через 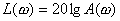 в децибелах и
в децибелах и 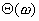 в градусах, можем
записать
в градусах, можем
записать
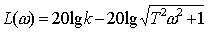 (11.5)
(11.5)
и
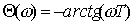 . (11.6)
. (11.6)
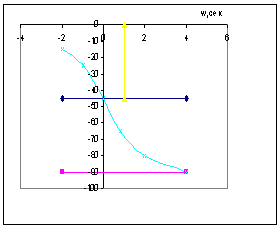
Как видно из
равенства (11.5), искомая логарифмическая амплитудная характеристика равна
сумме двух слагаемых, из которых первое представляет собой постоянную величину. Таким образом, форма
логарифмической амплитудной характеристики
не зависит от коэффициента усиления
звена k. Изменение величины k приводит лишь к перемещению характеристики по оси ординат, поэтому для
определения вида амплитудной характеристики можно положить k=1
и в соответствующих случаях переместить ее на требуемую величину.
Следовательно, при k=1
имеем 20lgk=0 и соответственно
 . (11.7)
. (11.7)
Из рассмотренного
выражения (11.7) видно, что можно приближенно записать:
а) при ω «1/T, т. е. при низких частотах
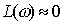 ;
;
б) при ω »1/T, т. е. при высоких частотах
 ;
;
с) при ω = 1/T (эту частоту принято называть сопрягающей)
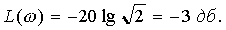
Из рассмотренных
соотношений следует, что искомая логарифмическая амплитудная характеристика
может быть приближенно
представлена двумя прямыми (асимптотами),
сопрягающимися друг с другом при ω = 1/T.
Максимальная ошибка, отличающая истинную характеристику от приближенной, при этом
получается равной 3 дб, и возникает она также при ω = 1/T.
Первая прямая 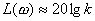 , очевидно, представляет прямую, параллельную оси
абсцисс, вторая прямая
, очевидно, представляет прямую, параллельную оси
абсцисс, вторая прямая  имеет наклон к оси абсцисс, определяемый из следующего соотношения: если при любом значении ω=ω1 имеем
имеет наклон к оси абсцисс, определяемый из следующего соотношения: если при любом значении ω=ω1 имеем  , то при ω=10ω1 имеем
, то при ω=10ω1 имеем  следовательно,
следовательно, 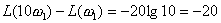 дб. Замечая, что изменение частоты в 10 раз принято называть изменением
частоты на декаду, можно сказать, что
наклон второго отрезка прямой
равен -20 дб/дек (или -6 дб/окт). Таким образом, для построения логарифмической амплитудной частотной характеристики инерционного
звена с параметрами k и Т следует
провести прямую, параллельную оси частот и отстоящую от нее на величину 20lgk
до частоты ω = 1/T,
а из точки этой прямой, соответствующей
частоте ω = 1/T, провести прямую с наклоном, равным —20дб/дек (или —6 дб/окт). Логарифмическая фазовая характеристика легко строится по
формуле (11.6).
дб. Замечая, что изменение частоты в 10 раз принято называть изменением
частоты на декаду, можно сказать, что
наклон второго отрезка прямой
равен -20 дб/дек (или -6 дб/окт). Таким образом, для построения логарифмической амплитудной частотной характеристики инерционного
звена с параметрами k и Т следует
провести прямую, параллельную оси частот и отстоящую от нее на величину 20lgk
до частоты ω = 1/T,
а из точки этой прямой, соответствующей
частоте ω = 1/T, провести прямую с наклоном, равным —20дб/дек (или —6 дб/окт). Логарифмическая фазовая характеристика легко строится по
формуле (11.6).
Рисунок 11.3 - Логарифмические характеристики
инерционного звена
На рисунке 11.3,а и б
приведены логарифмические асимптотическая амплитудная L(ω)
и фазовая Θ(ω) частотные характеристики инерционного звена. Фазовая характеристика
представляет собой кососимметричную кривую.
Можно также строить
приближенно фазовую характеристику по точкам, в которых имеются следующие постоянные
соответствия:
0 декад.............................. —45°
0,25 декады....................... —29°
0,6 декады........................ —14°
1,0 декада......................... —6°
2,0 декады........................ —0,5°
Логарифмические характеристики
колебательного звена. Для колебательного звена частотная функция может быть записана в виде
 . (11.8)
. (11.8)
Логарифмируя выражение
(11.8), найдем
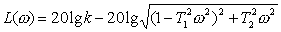 (11.9)
(11.9)
и
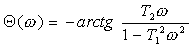 . (11.10)
. (11.10)
Используя формулы
(11.9) и (11.10), можно найти вид логарифмических характеристик колебательного звена. Делая
допущения, аналогичные тем, которые имели место при нахождении приближенной
характеристики инерционного звена, и приняв 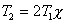 , можно построить приближенные логарифмические амплитудные и
фазовые характеристики
колебательного звена. Для построения приближенной амплитудной характеристики нужно
найти значение
, можно построить приближенные логарифмические амплитудные и
фазовые характеристики
колебательного звена. Для построения приближенной амплитудной характеристики нужно
найти значение 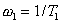 , затем провести прямую, параллельную оси частот и
отстоящую от нее на величину 20lgk, до точки с частотой
, затем провести прямую, параллельную оси частот и
отстоящую от нее на величину 20lgk, до точки с частотой 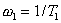 и, наконец, из
этой точки
провести прямую с наклоном —40 дб/дек (или —12 дб/окт). Такое
построение приведено на рисунке 11.4,а.
и, наконец, из
этой точки
провести прямую с наклоном —40 дб/дек (или —12 дб/окт). Такое
построение приведено на рисунке 11.4,а.
Приближенная фазовая
характеристика может быть построена по следующим формулам (дающим ошибку не более
2°)
для T1ω<0,4

(11.11)
Однако следует
учитывать, что построение приближенной логарифмической амплитудной
характеристики колебательного звена связано с наличием существенной погрешности,
зависящей от коэффициента затухания 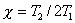 . При χ= 0,5 ошибка минимальна. При условии 0,4≤х≤0,7
ошибка не превышает 3 дб.
. При χ= 0,5 ошибка минимальна. При условии 0,4≤х≤0,7
ошибка не превышает 3 дб.
Вид реальных
логарифмических амплитудных L(ω) и фазовых  характеристик для
колебательного звена приведен на рисунке
11.4,б и в.
характеристик для
колебательного звена приведен на рисунке
11.4,б и в.
Рисунок 11.4 - Приближенные (а)
и реальные (б и в) логарифмические
характеристики колебательного звена.
Лекция №12. Построение амплитудных и фазовых логарифмических характеристик системы, логарифмический критерий
устойчивости
Содержание лекции:
- основы методики построения логарифмических
характеристик САУ;
- логарифмический критерий
устойчивости САУ.
Цели лекции:
- изучить основы методики построения
логарифмических характеристик САУ;
- изучить логарифмический критерий
устойчивости САУ.
Пользуясь
рассмотренным выше в применении к отдельным звеньям методом построения
логарифмических характеристик, можно
сравнительно просто построить логарифмические
характеристики и для сложных систем автоматического регулирования по
логарифмическим характеристикам
отдельных звеньев.
При построении логарифмических амплитудных
и фазовых характеристик системы можно руководствоваться
следующими соображениями.
Обычно передаточная
функция системы в общем виде (без запаздывающих звеньев) имеет следующий вид
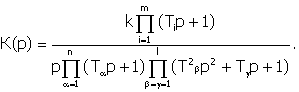 (12.1)
(12.1)
Делая в этом
выражении подстановку 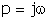 и находя модуль |К(jw)|, можно записать
и находя модуль |К(jw)|, можно записать
 (12.2)
(12.2)
Для построения
суммарной логарифмической амплитудной частотной характеристики можно построить ЛАЧХ типовых звеньев и затем в соответствии с общим
выражением для L(w) просуммировать их с соответствующими знаками. Однако проще
поступить несколько иначе, порядок такого построения рассмотрим на следующем частном примере.
Пусть система имеет в
разомкнутом состоянии частотную функцию следующего вида
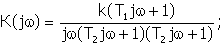 (12.3)
(12.3)
согласно сказанному
можем записать
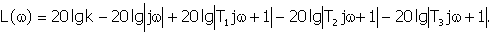 (12.4)
(12.4)
Предположив для
определенности T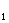 >T2>T3 и
обозначив сопрягающие
частоты
>T2>T3 и
обозначив сопрягающие
частоты 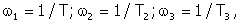 нанесем на оси абсцисс их, а также частоту w=1 (рисунок 12.1) и отложим в
выбранном масштабе величину 20lgk. При частоте (w<w
нанесем на оси абсцисс их, а также частоту w=1 (рисунок 12.1) и отложим в
выбранном масштабе величину 20lgk. При частоте (w<w ) все слагаемые, кроме
) все слагаемые, кроме  , могут не учитываться ввиду их малой величины. Поэтому в интервале 0<w<w
, могут не учитываться ввиду их малой величины. Поэтому в интервале 0<w<w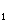 вычерчивается прямая АБ с наклоном 20 дб/дек.
При частотах, лежащих в интервале w
вычерчивается прямая АБ с наклоном 20 дб/дек.
При частотах, лежащих в интервале w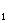 <w<w
<w<w , должен учитываться член +20lg|T
, должен учитываться член +20lg|T jw+1|, в результате чего получается прямая БВ, параллельная оси абсцисс. При w
jw+1|, в результате чего получается прямая БВ, параллельная оси абсцисс. При w <w<w3 должен быть учтен
член —20lg|T2jw+1|, поэтому логарифмическая характеристика в
этом интервале частот будет изображаться прямой ВГ с наклоном - 20 дб/дек.При
частотах w больших, чем w3, необходимо в частотной функции системы учитывать все слагаемые, т. е. и
<w<w3 должен быть учтен
член —20lg|T2jw+1|, поэтому логарифмическая характеристика в
этом интервале частот будет изображаться прямой ВГ с наклоном - 20 дб/дек.При
частотах w больших, чем w3, необходимо в частотной функции системы учитывать все слагаемые, т. е. и
Рисунок 12.1 - Пример построения амплитудной логарифмической
характеристики системы
член —20lg|T3jw+1|,; и суммарная кривая в этом случае может быть изображена отрезком ГД
с наклоном - 40 дб/дек. Таким
образом, общий вид приближенной амплитудной логарифмической характеристики рассматриваемой системы с достаточной степенью
точности может быть изображен
ломаной линией АБВГД. Построение
фазовой логарифмической характеристики
системы, соответствующей записанному выше выражению для передаточной функции этой системы, можно произвести согласно следующему выражению
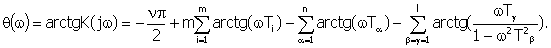 (12.5)
(12.5)
Из приведенного
выражения следует, что для построения ЛФЧХ системы нужно сложить с
соответствующими знаками ЛФЧХ отдельные звенья системы.
Такое построение для
системы с передаточной функцией, аналогичной функции предыдущего примера, но
при T1<T2<Tз
приведено на рисунке 12.2. Частоты сопряжения w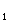 ,w
,w ,w3 получены в соответствии со значениями постоянных времени.
Для интегрирующего звена фазовая характеристика изображена прямой 1, для двух
инерционных звеньев - кососимметричными кривыми 2 и 3, а для дифференцирующего звена -
кососимметричной кривой 4. Суммарная фазовая характеристика изображена кривой 5.
,w3 получены в соответствии со значениями постоянных времени.
Для интегрирующего звена фазовая характеристика изображена прямой 1, для двух
инерционных звеньев - кососимметричными кривыми 2 и 3, а для дифференцирующего звена -
кососимметричной кривой 4. Суммарная фазовая характеристика изображена кривой 5.
Рисунок
12.2 - Пример построения фазовой частотной характеристики системы
Логарифмический критерий устойчивости. Амплитудно-фазовый частотный критерий
устойчивости Найквиста легко может быть интерпретирован в логарифмической
форме. Соответствующим точкам и значениям
амплитудно-фазовой частотной характеристики, очевидно, будут соответствовать вполне определенные точки и значения
логарифмических амплитудной и фазовой
частотных характеристик. Так, точкам пересечения кривой K(jω) с отрезком -1 -∞ отрицательной вещественной полуоси будут соответствовать
фазы θ(ω)=-π,-Зπ, -5π и т. д. и значения
амплитуды в
логарифмическом масштабе L(ω) >0. Принимается, что когда
логарифмическая фазовая характеристика при положительных значениях L(ω) пересекает при возрастании частоты фазовое значение, равное - 180° (иначе - π), снизу вверх, то это является положительным переходом, а сверху вниз -
отрицательным переходом.
-∞ отрицательной вещественной полуоси будут соответствовать
фазы θ(ω)=-π,-Зπ, -5π и т. д. и значения
амплитуды в
логарифмическом масштабе L(ω) >0. Принимается, что когда
логарифмическая фазовая характеристика при положительных значениях L(ω) пересекает при возрастании частоты фазовое значение, равное - 180° (иначе - π), снизу вверх, то это является положительным переходом, а сверху вниз -
отрицательным переходом.
Амплитудно-фазовые
характеристики трех систем (устойчивых в разомкнутом состоянии) показаны на рисунке 12.3,а и в.
Одна из этих систем, неустойчивая в замкнутом состоянии, имеет характеристику 2, показанную на рисунке 12.3,а.
Для всех трех систем построены
соответствующие логарифмические амплитудные
и фазовые частотные характеристики
(рисунок 12.3 ,6 и г).
Для наглядности предполагается,
что фазовая характеристика в θ(ω), приведенная на
рисунке 12.3, 6, общая для обеих амплитудных характеристик L1(ω) и L2(ω). Для систем обычного (не клювообразного)
вида амплитудно-фазовая характеристика,
приведенная на рисунке 12.3, а, при изменении ω от 0 до
+∞
пересекает отрицательную вещественную полуось
Рисунок
12.3 - Обычные и логарифмические
частотные характеристики системы
только 1 раз при
частоте ω1, где θ(ω)=-π.
Этим
точкам соответствует на ЛФЧХ (рисунке12.3,6)
точка М пересечения фазовой кривой θ(ω)с линией θ°= - π = - 180°. Из рисунка 12.3,а видно, что амплитуда вектора K(jω) становится равной единице при
пересечении амплитудно-фазовой характеристики с окружностью единичного радиуса,
проходящей через точку (- 1, j0) и имеющей центр в точке 0; этой точке пересечения соответствует частота, обозначенная на рисунке 12.3,а и б
через ωс.
Обозначения ωс1 и ωс2 относятся соответственно
к характеристикам 1 и 2. На ЛАЧХ (рисунок 12.3,6) этим частотам соответствуют частоты ωс1 и ωс2. Частоты, при которых
происходит пересечение характеристик, L1(ω) и L2(ω) с осью абсцисс называются частотой среза и обозначаются ωс.
Согласно критерию
устойчивости Найквиста замкнутая система будет устойчива при рассматриваемых
формах
амплитудно-фазовых характеристик, если точка с частотой ω1 (рисунок 12.3,а) будет лежать правее точки (-1, j0). Расстояние между
этими точками характеризует запас устойчивости по амплитуде.
Из рисунке 12.3,а видно, что если замкнутая система устойчива, то ωс1< ω1,
а
если она неустойчива, то ωс2< ω1. Это означает, что для системы (устойчивой в замкнутом состоянии) точка ЛФЧХ, определяемая фазой - 180°, должна соответствовать области
отрицательных значений L(ω). Величина отрицательной ординаты L(ω) б1 (рисунок 10.4,6) представляет собой запас устойчивости
по
амплитуде. Величина а1 (рисунок
12.3,6) ординаты ЛФЧХ, соответствующая
точке ωс1 на ЛАЧХ, характеризует запас устойчивости по фазе (угол а на рисунке 12.3,а).
Положительная ордината 62
на рисунке 12.3,6 свидетельствует о неустойчивости замкнутой
системы.
Для клювообразной АФХ (рисунок 12.3,в) число точек пересечения отрицательной вещественной полуоси при изменении ω от 0 до
+∞
больше одной (при частотах ω1, ω2, ω3). В этом случае для системы, устойчивой в замкнутом состоянии, число таких точек, лежащих
левее точки (-1, j0) должно быть четным. Поскольку каждая такая точка
соответствует θ=- 180°, условием устойчивости замкнутой
системы при клювообразных АФХ будет наличие четного числа пересечений логарифмической фазовой
частотной характеристики θ(ω) с прямой, соответствующей θ= - 180° в области
положительных ординат L(ω), т.е. лежащих левее частоты среза ωс (точки пересечения L(ω) с осью абсцисс, рисунок 10.4,г). Запас устойчивости замкнутой системы по амплитуде и по фазе применительно к рисунку 12.3,г представляет более сложную картину,
он может характеризоваться несколькими величинами.
В частности он может быть представлен соответственно в виде отрезков - для амплитуды отрезок б, а для фазы отрезок а (однако здесь можно отметить также запас по амплитуде при частотах ω1 и ω2,).
Равным образом
сообразно со сформулированными ранее при рассмотрении критерия Найквиста условиями о числе и виде пересечений отрезка -∞  - 1 вещественной
оси годографом АФХ можно найти логарифмический критерий устойчивости
для замкнутых САР, неустойчивых в
разомкнутом состоянии: подобные системы устойчивы, если разность чисел
положительных и отрицательных
переходов логарифмической фазовой частотной и отрицательных переходов
логарифмической фазовой частотной
характеристики θ(ω)через значение θ=-
180°, лежащих в области
положительных L(ω), равна k/2 при изменении ω от 0 до
+∞. Здесь k - число положительных корней характеристического уравнения разомкнутой системы.
- 1 вещественной
оси годографом АФХ можно найти логарифмический критерий устойчивости
для замкнутых САР, неустойчивых в
разомкнутом состоянии: подобные системы устойчивы, если разность чисел
положительных и отрицательных
переходов логарифмической фазовой частотной и отрицательных переходов
логарифмической фазовой частотной
характеристики θ(ω)через значение θ=-
180°, лежащих в области
положительных L(ω), равна k/2 при изменении ω от 0 до
+∞. Здесь k - число положительных корней характеристического уравнения разомкнутой системы.
При подсчете числа
пересечений следует считать 1/2 пересечения, если АФХ имеет при ω = 0 точку, лежащую на отрезке (-∞, - 1, j0) вещественной оси. В этом случае при ω = 0 ЛФЧХ пересекает прямую, соответствующую θ= - 180°, а значение L(0) -положительно.
Лекция №13. Нелинейные системы
автоматического управления
Содержание лекции:
- основные определения о нелинейных САУ;
- обзор методов расчета нелинейных систем.
Цели лекции:
- изучить основные определения о нелинейных
САУ;
- иметь представление о методах расчета
нелинейных систем.
Анализ и синтез нелинейных систем автоматического
управления значительно сложнее, чем линейных систем, что объясняется
необходимостью решения нелинейных дифференциальных уравнений. В большинстве
случаев подобное решение не может быть дано в общем виде, в связи с чем приходится
прибегать к частным решениям, выполняемым с той или иной степенью приближения.
Поэтому большую роль приобретают различные упрощенные и приближенные методы,
при помощи которых можно получить ответы на отдельные вопросы (устойчивость в
определенных условиях; наличие автоколебаний; поведение системы в каком-либо
частном режиме, например при установившейся скорости, при воздействии и
возмущении определенного вида и т. п.).
Следует подчеркнуть, что принцип суперпозиции, широко
применяемый в линейной теории, при анализе и синтезе нелинейных систем не
применим. Таким образом, в последнем случае выходной сигнал в статике не
пропорционален входному, форма выходной величины при ступенчатом воздействии
оказывается зависимой от величины этого воздействия, а реакция на произвольное
входное воздействие не может быть найдена как сумма реакций на отдельные
составляющие входного воздействия.
Невозможность применения принципа суперпозиции связана
с невозможностью использования экстраполяции. Определенные сведения о
переходном процессе в нелинейной системе при ступенчатом воздействии на входе
не позволяют сделать заключения о характере реакции системы на подобное воздействие
большей или меньшей величины. Таким же образом оказывается невозможным
использовать известную реакцию системы на сигнал одного вида для суждения о
реакции на сигнал другого типа (нарушается формальное соотношение между
временной и частотной областями, которое существует для линейных систем).
В настоящее время разработано весьма большое число
методов исследования нелинейных систем. Некоторые из этих методов годятся
только для анализа отдельных элементов, другие применимы для систем в целом.
Полного решения поставленной задачи редко удается достичь при помощи
какого-либо одного метода. Чаще приходится использовать несколько методов, каждый
из которых обеспечивает некоторую часть необходимой информации при анализе и
расчете.
Приведем краткую характеристику основных групп методов
и остановимся в дальнейшем на применении в расчетах лишь некоторых из них, как
получивших наибольшее использование для, решения практических задач.
Методы,
интегрируемой аппроксимации: а)
линейная, б) кусочно-линейная, в) нелинейная интегрируемая.
Принцип первого вида аппроксимации основывается на допущении,
что основные параметры системы имеют постоянное значение, соответствующее
выбранной точке, что позволяет применить, методику .линейного анализа. Последний
имеет силу лишь для ограниченной зоны вблизи рабочей точки (малые сигналы или
малые отклонения, или же малая степень нелинейности).
Второй вид аппроксимации предназначен для случая
сравнительно больших сигналов и заключается в составлении линейных
дифференциальных уравнений для каждого прямолинейного участка, на которые
разбита нелинейная характеристика. Общее решение сводится в этом случае к
решению ряда неоднородных линейных уравнений. Требуемый объем вычислений
обычно велик, особенно если система высокого порядка или нелинейность такова,
что для точной аппроксимации требуется разбивка характеристики на большое число
линейных отрезков.
В случае применения третьего вида аппроксимации
решение уравнения находят путем замены характеристики нелинейного элемента
некоторой близкой к ней кривой, которая может быть написана аналитически. Таким
образом, производится замена «точного» уравнения приближенным, которое может
быть точно проинтегрировано, что практически является не менее точным, чем приближенное
решение «точного» уравнения.
В ряде случаев значительной точности аппроксимации не
требуется, причем часто соображения физического характера указывают на
требуемую точность аппроксимации.
Из видов аппроксимации нелинейных характеристик можно
отметить:
а) аппроксимацию целой рациональной функцией
Н = αВ +βВn
(α>0; β>0);
б) аппроксимацию дробной рациональной функцией
В-Н=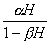 (при Н > 0);
(при Н > 0);
в) аппроксимацию при помощи степенной функции
В=α Нβ;
г) аппроксимацию при помощи логарифмической функции
В =
α1n(1 + ) (при Н>0).
) (при Н>0).
Выбор того или иного вида аппроксимации зависит от
вида нелинейной характеристики и от желательной степени упрощения решения
задачи.
Численно-графические
методы. Исследование и расчет
нелинейных систем может производиться путем численных и графических методов
интегрирования нелинейных дифференциальных уравнений.
Целесообразно проводить расчет нелинейной системы
комбинированным путем, т. е. предварительно использовать какой-либо
приближенный метод, а затем для уточнения и проверки правильности выбранных
параметров провести расчет численным или графическим путем или же при помощи
моделирования.
В настоящее время известен целый ряд численных и графических
способов, из которых следует отметить: способ численного интегрирования по разностному
методу Адамса [Л. 17], способ приближенного интегрирования акад. Чаплыгина,
метод Эйлера (один из наиболее простых методов), численное интегрирование
методом разложения в ряд Тейлора, численное интегрирование методом разложения
во временный ряд (использование импульсной функции}, метод Боксера и Тэйлора с
использованием преобразования и др. [Л.
29].
За последнее время появились достаточно простые
графические методы, из которых следует отметить метод секущих, метод
касательных [Л. 19] и метод с
использованием решения уравнения в конечных разностях [Л. 9]. В ряде случаев
вместо применения трудоемких численно-графических методов может быть применено
моделирование, позволяющее получить большое число вариантов решения нелинейных
задач.
Методы
фазовых траекторий. Эти методы основаны на введении некоторых наглядных
понятий и представлений геометрического характера. Основным из них является
понятие фазового пространства, которое дает полное представление о характере
возможных движений в системе.
Пусть система описывается дифференциальным уравнением n-го порядка. Ее состояние может быть охарактеризовано n числами, которые можно рассматривать как задание
некоторой точки в n-мерном пространстве, причем каждой
точке этого пространства будет соответствовать одно определенное состояние
(определенная фаза) системы. Поэтому такое пространство называется фазовым
пространством.
В основном область применения этого метода ограничена
системами не выше третьего порядка, однако он может оказаться полезным и для
проверки различных приближенных методов, применяемых к системам более высокого
порядка.
Для систем, описываемых дифференциальным уравнением
второго порядка, фазовое пространство (в этом частном случае) превращается в
фазовую плоскость.
Практически наибольшее распространение для
исследования нелинейных систем получил метод фазовой плоскости. Результаты
исследования этим методом дают полную картину поведения систем в том смысле,
что могут быть получены все решения данного дифференциального уравнения для
широкой совокупности начальных условий и возмущающих функций в виде скачка или
линейно возрастающего сигнала. Метод фазовой плоскости применим для любого
типа нелинейности, а также для сочетания нелинейностей. Путем графического
интегрирования на его основе можно получить кривую переходного процесса.
Недостатком метода является его ограничение системами
второго порядка и возмущающими функциями вида ступенчатого воздействия или
линейно нарастающего сигнала.
В некоторых случаях можно аппроксимировать системы высших
порядков системой второго порядка с запаздыванием, что расширяет область
применения метода фазовой плоскости. Однако подобный прием не гарантирует, в
отдельных случаях, от существенных неточностей. Этот метод дает возможность установить
физическую картину влияния на систему того или иного типа нелинейности в
большей степени, чем какой-либо другой.
Методы малого
параметра. Основные исследования по
методу малого параметра были проведены французским математиком Пуанкаре и
русским ученым Ляпуновым. В дальнейшем были разработаны различные варианты
метода малого параметра, успешно применяемые в радиотехнике и теории
автоматического управления, составившие целую группу методов малого параметра.
Последняя может быть разделена на две подгруппы методов: аналитические и
графоаналитические.
Наиболее ранними являются методы Ляпунова, Рэлея и Ван
дер Поля. Метод последнего был строго обоснован Мандельштамом, Папалекси и
Андроновым, которые также развили метод Пуанкаре.
Булгаков развил свой оригинальный метод малого
параметра применительно к системам высокого порядка. Крылов и Боголюбов
разработали на этой же научной базе принцип так называемого гармонического
баланса, а Теодорчик - принцип энергетического баланса. Графоаналитические
варианты, базирующиеся на указанных принципах, разрабатывались Гольдфарбом,
Теодорчиком, Поповым и др.
Наибольшее распространение в инженерной практике получили
графоаналитические методы Гольдфарба и Попова, базирующиеся на принципе гармонического
баланса.
Ниже приводятся примеры расчета по этим методам. Общая
идея метода малого параметра основана на том, что ряд членов, входящих в левую
часть дифференциальных уравнений нелинейных систем, можно считать малыми по
сравнению с остальными членами, в основном определяющими характер движения
системы. Поэтому рассматриваются упрощенные уравнения без малых членов как
уравнения, близкие к линейным (в определенных условиях). Следовательно, можно
говорить о так называемых квазилинейных, системах.
В связи с этим методы малого параметра, направленные к
исследованию периодических режимов нелинейных систем, являются приближенными,
так как они позволяют определить лишь приближенные значения амплитуды и частоты
основной гармоники периодических колебаний, предполагаемых близкими к
гармоническим.
Графоаналитический метод гармонического баланса (метод
гармонической линеаризации) представляет собой результат распространения
частотной линейной методики на исследование нелинейных систем. Как известно,
при гармонических сигналах на входе нелинейного звена на выходе последнего
будут иметь место периодические несинусоидальные величины, которые можно разложить
на основную и высшие гармоники. Если последними пренебречь, а рассматривать
только основную гармонику, то можно вычислить комплексный коэффициент усиления
нелинейного звена по первой гармонике, который является своеобразным аналогом
передаточной функции. Таким образом, этот метод позволяет использовать обычный
линейный частотный аппарат с некоторыми видоизменениями.
Методы моделирования. Исключительно
важное значение для анализа и синтеза нелинейных систем автоматического управления
за последнее время приобретают методы математического моделирования в связи с
широким распространением электронных вычислительных машин, как
специализированных, так и общего назначения.
Поскольку сложная нелинейная задача не может быть,
решена в общем виде, то для нахождения оптимального, или просто приемлемого
варианта, нужно решить значительное число частных задач. Подобная работа проще
всего может быть выполнена на моделирующей установке. С её помощью можно промоделировать
весьма сложные системы со многими нелинейностями и обследовать широкую область
начальных условий и внешних возмущений, причем коррекцию целесообразно
выполнять при помощи последовательных приближений.
Однако и в этом случае аналитические и графические
методы анализа могут оказаться весьма полезными, так как они позволят
предварительно нащупать оптимальную структуру системы и зону варьирования
параметрами.
В некоторых случаях существенные черты влияния
отдельных нелинейностей проще раскрываются при помощи фазовой характеристики
(фазового портрета системы), а не переходной. Поэтому предварительное изучение
задачи тем или иным методом может дать значительную экономию времени, уменьшить объем полученного
материала и сократить время для его анализа.
Список литературы
1.
Егоров
К.В. «Основы теории автоматического регулирования»: Учебное пособие для ВУЗов.
– М.: Энергия, 1967.
2.
Бесекерский В.А., Попов Е.П. « Теория систем
автоматического регулирования». - М: Наука, 1975.
3.
Лукас В.А. «Теория автоматического управления»:
Учебник для ВУЗов: Недра, 1990.
4.
Теория автоматического управления. - ч.1. –
Под ред. А.А. Воронова. – М.: Высш. шк., 1986.
5.
Цыба Ю.А., Сагитов П.И. «Элементы теории
автоматического управления»: Учебное пособие для ВУЗов. – Алматы: КАУ, 2006.
Приложение
А
Примеры решения задач по разделам курса САУ
А1 Составление
функциональных схем по принципиальным схемам
Пример А1.1 Составление функциональной схемы системы автоматического
регулирования напряжения генератора постоянного тока.
Принципиальная схема системы регулирования
изображена на рисунке А 1.1. Система работает следующим образом. Напряжение обратной связи Uo.c, пропорциональное регулируемой величине – напряжению генератора UГ, сопоставляется с напряжением сравнения Uср.. Разность Uср - Uo.c поступает на
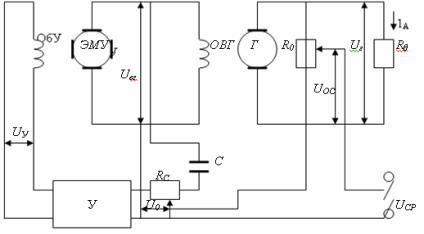
Рисунок А1.1 - Упрощенная
принципиальная схема системы автоматического регулирования напряжения
генератора постоянного тока
вход электронного усилителя У, питающего
обмотку управления ОбУ электромашинного усилителя с поперечным полем ЭМУ,
являющегося возбудителем генератора Г. Для повышения динамической устойчивости
системы в ней предусмотрена стабилизирующая местная обратная связь по напряжению
ЭМУ, осуществляемая при помощи конденсатора С и делителя напряжения
Rс. Величина главной обратной связи
устанавливается делителем R0.
При разделении системы автоматического
регулирования на функциональные элементы выделим, прежде всего, генератор,
который будем рассматривать как объект регулирования ОР. На него
действует напряжение возбуждения UВГ, являющееся регулирующим воздействием, и возмущающее воздействие
- ток нагрузки Iн.
Регулируемая величина UГ преобразуется в напряжение Uo.c элементом главной обратной связи ОСГЛ и сравнивается с напряжением
Uср при помощи элемента сравнения ЭС, который в данном случае
является электрическим соединением,
поскольку в рассматриваемой системе
регулирования сравниваются электрические величины Uср и Uo.c.
В качестве усилительного элемента принят
электронный усилитель У, а ЭМУ в данном случае является исполнительным элементом ИЭ.
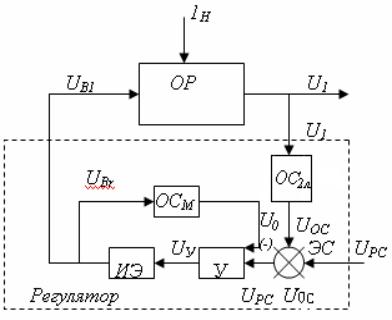
Рисунок А1.2 -
Функциональная схема системы автоматического регулирования напряжения
генератора постоянного тока
Стабилизирующий контур СRс представим как элемент местной обратной связи ОСМ, входной величиной
которого является напряжение ЭМУ (напряжение на обмотке возбуждения
генератора ОВГ), а выходной - напряжение U0, представляющее собой сигнал местной обратной связи, подаваемый на
вход усилителя и вычитаемый из основного сигнала Uср - Uo.c.
При указанном разделении системы
регулирования напряжения генератора на элементы функциональная схема будет
иметь вид, изображенный на рисунке 1. 2.
Пример А1.2 Составление функциональной схемы простейшей следящей
системы с асинхронным двухфазным двигателем АД.
Принципиальная схема простейшей следящей
системы приведена в [1]. Система работает следующим образом. Положение входной
и выходной осей системы сравнивается при помощи механического дифференциала Др,
с которым связан движок потенциометра П.
Напряжение Uc снимаемое с потенциометра, усиливается однокаскадным ламповым
усилителем У, собранным на двойном триоде Л. Выходное напряжение
усилителя Uу
подается на управляющую
обмотку ОбУ асинхронного двухфазного двигателя с полым ротором, обмотка
возбуждения 0В которого
питается переменным напряжением от той же сети, к которой подключен
потенциометр. Конденсатор С,
включенный параллельно вторичной обмотке выходного трансформатора, служит для
фазирования напряжения Uу с напряжением на обмотке возбуждения
двигателя.
Приняв механический дифференциал за
элемент сравнения ЭС, а потенциометр— за преобразующий элемент, ПЭ, получим
функциональную схему следящей системы, изображенную на рисунке А 4. На схеме
асинхронный двигатель объединен вместе с редуктором в один элемент —
исполнительный двигатель ИД.
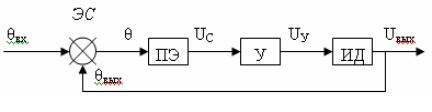
Рисонок А1.4 - Функциональная схема следящей системы
А 2 Примеры
составления структурных схем и определения передаточных функций систем в общем
виде
Пример А2.1 Составление структурной схемы
и определение передаточных функций системы автоматического регулирования
напряжения генератора постоянного тока.
Принципиальная схема системы регулирования
приведена на рисунке А 1.1.
Будем обходить основной контур системы
регулирования, начиная с электронного усилителя, в направлении передачи воздействия.
В качестве первого звена направленного
действия примем участок контура от входа электронного усилителя до поперечной
цепи якоря ЭМУ. Запаздывание передачи воздействий в этом звене будет
определяться отставанием изменения тока в обмотке управления ЭМУ от
изменения напряжения на обмотке. За выходную величину этого звена можно принять
э. д. с. eq в поперечной цепи якоря ЭМУ, пропорциональную току в
обмотке управления. Тогда передаточная функция первого звена
где  и
и  - соответственно
операторные изображения э.д.с, поперечной цепи якоря ЭМУ и напряжения на
входе электронного усилителя.
- соответственно
операторные изображения э.д.с, поперечной цепи якоря ЭМУ и напряжения на
входе электронного усилителя.
Вторым звеном направленного действия будем
считать часть контура системы регулирования, динамические процессы в котором
характеризуются изменением тока в поперечной цепи якоря ЭМУ под
действием э. д. с. eq, являющейся для данного звена входной
величиной. В качестве выходной величины звена примем э. д. с. ed продольной
цепи якоря ЭМУ. Передаточная функция второго звена
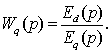
В качестве последнего звена направленного
действия в прямой цепи системы регулирования примем звено с передаточной функцией
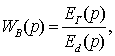
где Ег(р) - операторное
изображение э. д. с. якоря генератора. В цепи главной обратной связи,
замыкающей основной контур системы автоматического регулирования, будем иметь
одно безынерционное звено — делитель напряжения R0. В общем случае передаточная функция звена главной обратной
связи

где
 - изображение напряжения обратной связи;
- изображение напряжения обратной связи;
 - изображение регулируемой величины (напряжения генератора).
- изображение регулируемой величины (напряжения генератора).
Основной контур системы регулирования
оказался разделенным на четыре звена направленного действия, из которых три
входят в прямую цепь системы и одно - в цепь обратной связи. Остается выделить
звено направленного действия в
цепи местной обратной связи, образуемой стабилизирующим RС-контуром.
Входной величиной этого звена является
напряжение  на обмотке возбуждения генератора,
несколько отличающееся от еd за счет падения напряжения в якоре ЭМУ,
однако это отличие может быть учтено введением соответствующего коэффициента
в передаточную функцию звена местной обратной связи
на обмотке возбуждения генератора,
несколько отличающееся от еd за счет падения напряжения в якоре ЭМУ,
однако это отличие может быть учтено введением соответствующего коэффициента
в передаточную функцию звена местной обратной связи
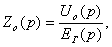
где Uо(р) - изображение напряжения местной обратной связи, подаваемого на
вход электронного усилителя.
Структурная схема системы регулирования,
составленная из рассмотренных звеньев направленного действия, приведена на
рисунке А2.1, а, где Uср(р) - напряжение сравнения, с помощью которого производится
настройка системы на требуемое значение регулируемого напряжения; F(р) - возмущающее воздействие (например, изменение нагрузки
генератора); Gf (р)
- передаточная функция
возмущающего воздействия, определяющая характер зависимости регулируемой
величины от данного возмущения (если, в частном случае, возмущающим
воздействием служит ток нагрузки, то Gf (р)
является постоянной величиной,
равной сопротивлению якоря генератора).
Для определения передаточной функции
разомкнутой системы необходимо преобразовать полученную, структурную
многоконтурную схему с помощью основных правил, приведенных в лекции 3. С этой
целью выделим пунктиром на схеме участок прямой цепи системы, охваченный
местной обратной связью, и, используя свойство параллельного встречного
включения звеньев направленного действия, заменим его эквивалентным звеном с
передаточной функцией
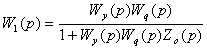 ,
,
после чего структурная схема примет более
простой вид (рисунок А2.1,6).
Передаточная функция разомкнутой системы,
составленная из последовательно включенных звеньев направленного действия,
примет вид
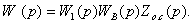
Имея  , можно получить передаточную функцию
замкнутой системы для возмущающего воздействия
, можно получить передаточную функцию
замкнутой системы для возмущающего воздействия
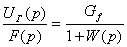
и передаточную функцию замкнутой системы
для управляющего воздействия
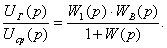
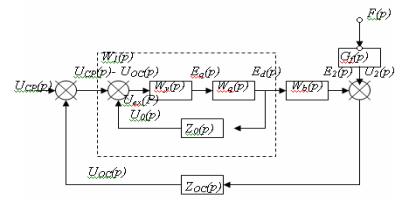

а) б)
Рисунок А2.1 - Структурные схемы системы автоматического
регулирования напряжения генератора постоянного тока: а – первоначальная; б – преобразованная
А3 Примеры расчета статических параметров
отдельных элементов
Пример А3.1 Определение передаточных
коэффициентов двигателя постоянного тока с независимым возбуждением.
Двигатель имеет следующие номинальные
данные: Рн = 9 кет; UН=220 в; Iя.н = 46 а;
пн = 780 об/мин; Rя.в=0,218
ом.
Необходимо определить передаточные
коэффициенты двигателя: по скорости - kдв и по моменту - си.
Передаточный коэффициент двигателя по
скорости kдв =
представляет собой коэффициент пропорциональности
между э. д. с. двигателя и угловой скоростью вращения якоря, номинальное
значение которой

Скоростной коэффициент
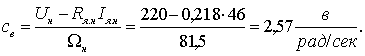
Передаточный коэффициент двигателя по
скорости
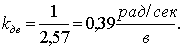
Передаточный коэффициент двигателя по
моменту
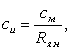
где см - коэффициент
пропорциональности между током якоря и
вращающим моментом MВР
двигателя.
Так как
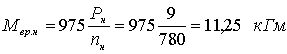 ,
,
то 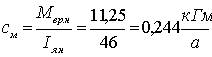 ,
,
 .
.
Произведение сеси
представляет собой коэффициент внутреннего скоростного трения в двигателе,
определяющий наклон его механической характеристики
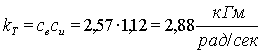 .
.
Определение одного из передаточных
коэффициентов двигателя через другой в
некоторых пособиях рекомендуется производить с помощью зависимости св
= 9,81 <7М. В этом случае используется в расчете не момент на
валу, а электромагнитный момент двигателя.
А4 Примеры определения передаточных
функций отдельных элементов
Пример А4.1 Определение передаточной
функции генератора постоянного тока с независимым возбуждением.
Сопротивление и индуктивность обмотки
возбуждения генератора соответственно равны: Rв = 65,5 ом и LB - 27,5 гн; угловой коэффициент характеристики холостого хода
генератора в ее линейной части
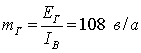 ,
,
где ЕГ - э. д. с,
генератора.
Подставив в операторное уравнение цепи
возбуждения генератора
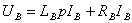
значение тока возбуждения Iв,
получим после преобразований
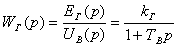 .
.
Полученное выражение представляет собой
передаточную функцию апериодического звена направленного действия с передаточным
коэффициентом kг и
постоянной времени ТВ. Подставляя численные значения,
получим
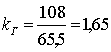 ,
,
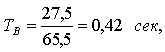
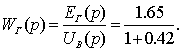
Пример А4.2 Определение передаточной
функции электромашинного усилителя с поперечным полем.
Параметры ЭМУ имеют следующие
значения: сопротивление, индуктивность и число витков обмотки управления
соответственно Rу =
2000 ом, Lу = 80 гн, ωу = 3200; сопротивление и индуктивность поперечной цепи якоря ЭМУ
-Rq -1,23 ом,
Lq =
0.16гн; угловой
коэффициент характеристики холостого хода ЭМУ, определяемый как
отношение э. д. с. якоря по продольной оси к м. д. с., создаваемой обмоткой
управления, mэ =
4,2 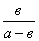 - ЭМУ считается скомпенсированным.
- ЭМУ считается скомпенсированным.
Передаточная функция ЭМУ
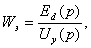
где Ed(p) и Uy(p)— соответственно операторные изображения э. д. с. якоря по
продольной оси и напряжения па управляющей обмотке.
Операторные уравнения для цепи обмотки
управления и поперечной цепи якоря ЭМУ
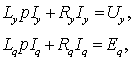
где
Iу и Iq — соответственно токи в обмотке управления
и в поперечной цепи якоря.
Электродвижущая сила, действующая по
поперечной оси якоря, в пределах линейного участка кривой намагничивания машины
пропорциональна м, д. с. Р7, развиваемой обмоткой управления
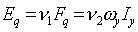 .
.
Электродвижущая сила якоря по продольной
оси пропорциональна поперечной м. д. с. якоря Fq создаваемой
током Iq

А5 Примеры
построения амплитудных и фазовых частотных характеристик в вещественной и
комплексной плоскостях
Пример А5.1 Построение амплитудно-частотной, фазо-частотной и амплитудно-фазовой
характеристик апериодического звена.
Примем передаточный коэффициент k = 1 и постоянную времени T= 2,5 и 0,5 сек.
Передаточная функция апериодического звена
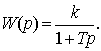
Заменяя р на jω, получим соответственно выражения для
амплитудно-частотной и фазо-частотной характеристик
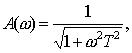

Подставив числовые значения Т, вычислим
A(ω) и
φ(ω). Результаты вычислений представлены в таблице А5.1, по которой
построены кривые A(ω)
и φ(ω) (рисунок 5.1, а и б).
Амплитудно-фазовая характеристика
апериодического звена (рисунок А5.1,в)
представляет собой расположенную в четвертом квадранте полуокружность с
диаметром, равным отрезку k и координатами центра на вещественной
оси 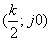 .
.
Таблица А5.1- Результаты
вычислений представлены A(ω) и φ(ω)
|
T=2,5 ceк
|
T=0,5 ceк
|
|
ω
|
А(ω)
|
φ(ω)
|
ω
|
А(ω)
|
φ(ω)
|
|
0,5
1
1,5
2
2,5
3
20
|
0,622
0,372
0,258
0,195
0,158
0,127
0,02
|
–51º6’
–68º24’
–75º6’
–78º48’
–81º
–82º6’
–86º30’
|
1
2
3
5
7
10
50
|
0,895
0,708
0,554
0,372
0,279
0,196
0,04
|
–26º36’
–46º
–56º18’
–68º12’
–74º
–78º42’
–87º48’
|
а)
б)

в)
Рисунок А5.1 - Частотные характеристики апериодного звена: а)амплитудные;
б)фазовые; в)амплитудно-фазовые
А6 Примеры исследования
устойчивости по критериям Рауса и Гурвица
Пример А6.1 Проверка
устойчивости системы автоматического, регулирования по критерию Гурвица.
Характеристическое уравнение системы имеет вид
Р3+ 1,48р3 + 4,6р
+ 4 = 0.
Для уравнения третьей степени условием устойчивости по
Гурвицу, помимо положительности коэффициентов уравнения, является выполнение
неравенства
 = а1 а2 — а0 а3 >
0,
= а1 а2 — а0 а3 >
0,
где 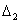 - определитель второго
порядка.
- определитель второго
порядка.
В данном случае а0 = 1; а1 =
1,48; а2 = 4,6; а3 = 4. Следовательно, система
устойчива.
Пример А6.2 Проверка устойчивости системы
автоматического регулирования.
Характеристическое уравнение имеет вид
р6 + 0,212р5
+ 2,42р4 + 36,2 р3 + 228р2 + 1408 = 0.
Система неустойчива, так как не выполняется
необходимое условие положительности всех коэффициентов уравнения (отсутствует
член с первой производной).
Пример А 6.3 Проверка по критерию Рауса устойчивости
следящей системы.
Система задана характеристическим уравнением
0,0008 р5 +
0,03р4 + 1,36р3 + 4р2 + 52,5 р + 50 = 0.
Составим таблицу Рауса в соответствии с таблицей 8.1.
Система устойчива,
так как из таблицы следует, что
а0 > 0, а1
> 0, 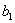 >0,
>0, 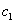 >0,
>0, 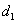 >0, е1 > 0.
>0, е1 > 0.
А7 Примеры решения уравнений
операторным методом
Пример А7.1 Определение переходного процесса в
апериодическом звене при единичном входном воздействии. Передаточная функция
звена
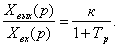
Входная величина представляет собой единичную функцию
времени хвх(t) = I(t); к=1; постоянная времени звена Т = 0,05; 0,5 и 2,5 сек.
При хвх(t) = I(t)

и
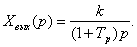
Получено простое операторное изображение, для которого
оригинал

На рисунке А7.1 построен график функции хвых(t) при
заданных значениях Т.
Рисунок А7.1 – Кривые хвых(t) для апериодического звена при единичной входной
функции при заданных значениях Т
Пример А7.2 Построение графика изменения выходной величины
апериодического звена при линейном входном воздействии хвх(t)=at.
Параметры звена: k = 10; а = 40 ; Т = 0,05; 0,5 и 2,5 сек.
; Т = 0,05; 0,5 и 2,5 сек.
При хвх(t) = at
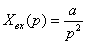 .
.
Тогда 
Функцию хвых(t) можно
найти по таблицам или интегрированием в пределах от 0 до t оригинала, соответствующего изображению

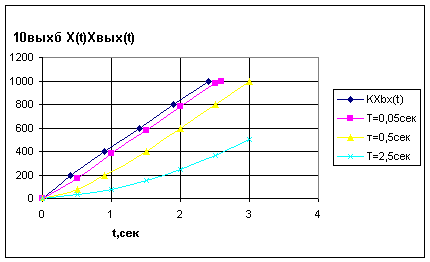
Рисунок А7.2 - Кривые хвых(t) для апериодического звена при линейной входной
функции
В обоих случаях
хвых(t) = akt - akT(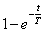 ).
).
После подстановки численных величин
хвых(t) = 400 t - 400T(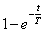 ).
).
График хвых(t) для указанных значений Т построен на рисунке А7.2.
А8 Примеры определения
передаточных функций построения частотных характеристик корректирующих звеньев
Пример А8.1 Определение
передаточной функции и построение частотных характеристик простейшего
инерционного (апериодического) звена
(рисунок А8.1, а).
1. Составляем уравнение э. д. с. звена при единичном
возмущении, т.е. при подаче на вход звена напряжения постоянного тока
U1=IR+ U2.
Выражение для тока имеет вид
I=CpU2,
откуда
U1=(CRp+1)+ U2.
Полагая CR = T, получим
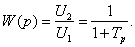
2. Для построения амплитудно-фазовой частотной характеристики
заменим р на jω, тогда
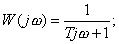
освобождаемся от мнимой величины в знаменателе
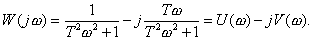

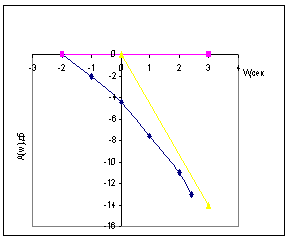 а) б)
а) б)
в) г)
Рисунок А8.1 - Апериодическое
звено и его характеристики
Амплитудно-фазовая характеристика звена может быть также
изображена в виде
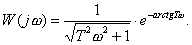
Амплитудно-фазовая
характеристика
представляет собой (при изменении
частоты в пределах  ) полуокружность (рисунок А8.1,6).
) полуокружность (рисунок А8.1,6).
3. Для построения логарифмической амплитудной характеристики (л. а. х.) звена запишем
20lgA(ω) = - 10lg(T2ω2+1) db
На рисунке А8.1, в
представлена л. а. х., построенная по точкам (кривая 1), причем масштаб частоты
взят относительный (частота ωГ =  принята за единицу).
На этом же рисунке построена приближенная, асимптотическая л. а. х. (характеристика 2), состоящая
из двух участков - горизонтального, полученного в предположении, что T2ω2 <<1 и, следовательно, при малых частотах A(ω)
принята за единицу).
На этом же рисунке построена приближенная, асимптотическая л. а. х. (характеристика 2), состоящая
из двух участков - горизонтального, полученного в предположении, что T2ω2 <<1 и, следовательно, при малых частотах A(ω) 1, и наклонного
участка (с наклоном - 6 дб/окт), соответствующего предположению, что 20lgA(ω)
1, и наклонного
участка (с наклоном - 6 дб/окт), соответствующего предположению, что 20lgA(ω)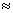 -20lgTω(T2ω2>>1) (единицей на этом участке пренебрегаем). Указанные
участки соединяются при сопрягающей частоте ωT =
-20lgTω(T2ω2>>1) (единицей на этом участке пренебрегаем). Указанные
участки соединяются при сопрягающей частоте ωT =
 . Как видно из рисунка А8.1,в, наибольшая ошибка при построении приближенной л. а. х.
апериодического звена имеет место при частоте ω= ωT и составляет - 3 дб.
. Как видно из рисунка А8.1,в, наибольшая ошибка при построении приближенной л. а. х.
апериодического звена имеет место при частоте ω= ωT и составляет - 3 дб.
а)
б)
Рисунок А8.2 - Апериодическое
звено при учете входного сопротивления следующего звена
а- схема звена; б- логарифмическая амплитудная
характеристика
4. Фазовая характеристика строится по точкам по
формуле φ(ω) = - агсtgTω. На
рисунке А8,1, г приведена
фазовая характеристика, построенная в функции частоты в логарифмическом масштабе
(частота взята в относительных единицах 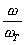 ). Очевидно, что при ω
= ωT значение агсtgTω = 450.
). Очевидно, что при ω
= ωT значение агсtgTω = 450.
Св. пл. 2006
поз. 141
Пулат Исмаилович Сагитов
Юрий Александрович Цыба
СИСТЕМЫ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Конспект лекций
(для студентов
всех форм обучения специальности 050718 – Электроэнергетика)
Редактор Т.С. Курманбаева
Подписано
в печать ______ Формат 60x84 1/16
Тираж 50 экз.
Бумага типографская № 1
Объем
4,5 уч. – изд. л. Заказ____ Цена_____
Копировально – множительное бюро
Алматинского института энергетики и связи
050013, Алматы, ул. Байтурсынова, 126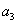
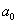

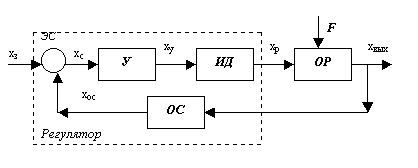
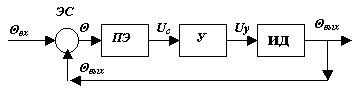
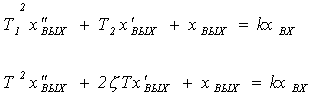
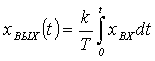
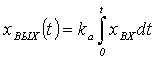 ,
, .
. .
. 







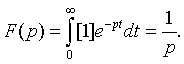
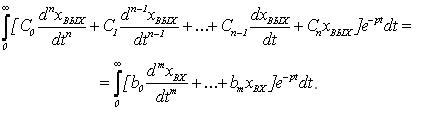
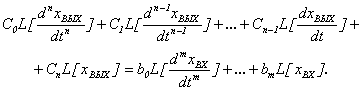
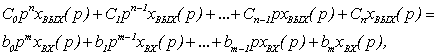
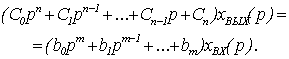
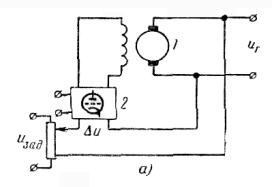
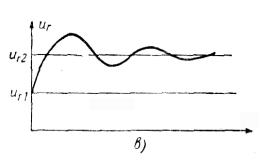
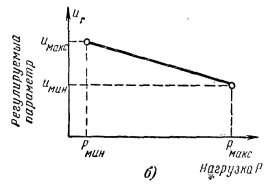

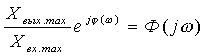
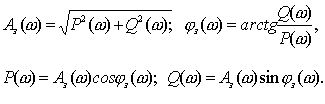

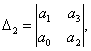
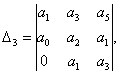



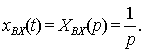
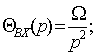
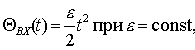
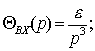
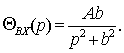
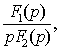
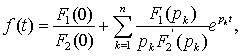
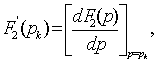



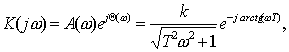
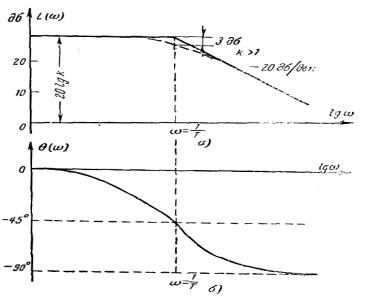
 .
.


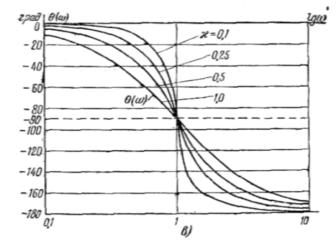
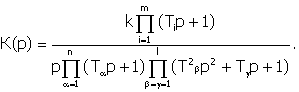

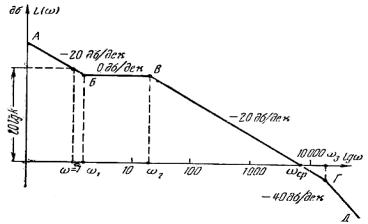



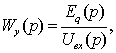
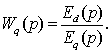
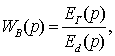



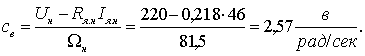
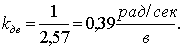
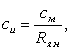
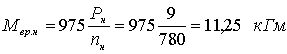 ,
,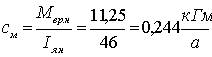 ,
, .
.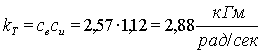 .
. ,
,