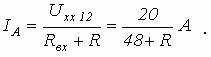Алматинский институт энергетики и связи
Теория электрических цепей 1
Конспект лекций
(для специальност 050719 – Радиотехника, электроника и телекоммуникации, 050704 - Вычислительная техника и программное обеспечение )
Алматы 2007
СОСТАВИТЕЛИ: З.И. Жолдыбаева, Е.Х.Зуслина, Т.И. Коровченко. Теория электрических цепей 1. Конспект лекций для студентов всех форм обучения специальностей 050704 - Вычислительная техника и программное обеспечение и 050719 – Радиотехника, электроника и телекоммуникации.– Алматы: АИЭС, 2006.- 80с.
Конспект лекций содержит 17 лекций по разделам: линейные электрические цепи постоянного тока, электрические цепи однофазного синусоидального тока, резонансные явления в электрических цепях, четырехполюсники и фильтры. Конспект лекций предназначен для студентов специальности 050704 - Вычислительная техника и программное обеспечение и о50719- Радиотехника, электроника и телекоммуникации.
Содержание
Введение
1Лекция 1
2Лекция 2
3Лекция 3
4Лекция 4
5Лекция 5
6Лекция 6
7Лекция 7
8Лекция 8
9Лекция 9
10Лекция 10
11Лекция 11
12Лекция 12
13Лекция 13
14Лекция 14
15Лекция 15
16Лекция 16
17Лекция 17
Список литературы
Введение
Дисциплина «Теория электрических цепей 1» является основным базовым обязательным курсом для подготовки бакалавров в области радиотехники, вычислительной техники и связи. Назначение дисциплины заключается в изучении и описании как с качественной, так и с количественной стороны электромагнитных процессов и явлений, происходящих в различного рода радиотехнических установках, устройствах вычислительной техники и связи.
Предлагаемый конспект лекций включает следующие разделы: линейные электрические цепи постоянного тока, электрические цепи однофазного синусоидального тока, резонансные явления в электрических цепях, четырехполюсники и фильтры. В первом разделе рассмотрены основные свойства линейных электрических цепей постоянного тока, такие как метод по законам Кирхгофа, метод контурных токов, метод узловых потенциалов, метод эквивалентного генератора.
Во втором разделе рассмотрены особенности описания цепей при синусоидальных токах и напряжениях, показано применение метода комплексных амплитуд с использованием векторных и топографических диаграмм для анализа цепей синусоидального тока, рассмотрено явление фазового резонанса в последовательном и параллельном контурах, показан расчет цепей при наличии взаимной индукции.
В третьем разделе рассмотрены четырехполюсники и электрические фильтры.
Конспект лекций предназначен для студентов, обучающихся по специальностям 050719 – Радиотехника, электроника и телекоммуникации, 050704 - Вычислительная техника и программное обеспечение.
1Лекция 1.Элементы электрических цепей и электрических схем
Цель лекции: ознакомить с основными понятиями электрических цепей.
1.1 Основные понятия
Электромагнитные процессы, протекающие в электрических цепях можно описать с помощью таких интегральных понятий, как: напряжение, ток, электродвижущая сила (ЭДС). Электротехнические устройства, производящие электрическую энергию, называются генераторами или источниками электрической энергии, а устройства, потребляющие ее – приемниками электрической энергии. Все элементы электрической цепи условно можно разделить на активные и пассивные. Активным называется элемент, содержащий в своей структуре источник электрической энергии. К пассивным относятся элементы, в которых рассеивается (резисторы) или накапливается (катушка индуктивности и конденсаторы) энергия. Если элементы описываются линейными дифференциальными или алгебраическими уравнениями, то они называются линейными, в противном случае они относятся к классу нелинейных. Если параметры элемента не являются функциями пространственных координат, определяющих его геометрические размеры, то он называется элементом с сосредоточенными параметрами. Цепи, содержащие только линейные элементы, называются линейными. Наличие в схеме хотя бы одного нелинейного элемента относит ее к классу нелинейных.
1.2 Резистивный элемент (резистор)
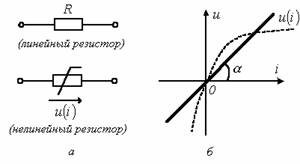
Рисунок 1.1
Резистор – это пассивный элемент, характеризующийся резистивным
сопротивлением (рисунок 1.1,а). Основной характеристикой
резистивного элемента является зависимость ![]() , называемая вольтамперной характеристикой
(ВАХ). Если зависимость
, называемая вольтамперной характеристикой
(ВАХ). Если зависимость ![]() представляет
собой прямую линию, проходящую через начало координат (см.рисунок 1.1,б), то
резистор называется линейным и описывается соотношением
представляет
собой прямую линию, проходящую через начало координат (см.рисунок 1.1,б), то
резистор называется линейным и описывается соотношением
![]()
Нелинейным резистивным элементом называется элемент, ВАХ которого нелинейна (рисунок 1.1,б).
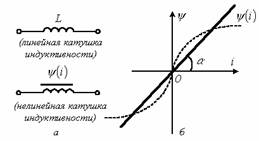 1.3 Индуктивный элемент
1.3 Индуктивный элемент
Рисунок 1.2
Индуктивность определяется отношением потокосцепления к току, протекающему по виткам катушки (рисунок 1.2,а),
![]()
Основной характеристикой катушки индуктивности является
зависимость ![]() , называемая
вебер-амперной характеристикой. Для линейных катушек индуктивности зависимость
, называемая
вебер-амперной характеристикой. Для линейных катушек индуктивности зависимость ![]() представляет собой прямую
линию ( рисунок 1.2,б); при этом
представляет собой прямую
линию ( рисунок 1.2,б); при этом![]() . Для нелинейных - зависимость
. Для нелинейных - зависимость ![]() нелинейная ( рисунок 1.2,б).
нелинейная ( рисунок 1.2,б).
1.4 Емкостный элемент
Конденсатор ( рисунок 1.3,а) – это пассивный элемент,
характеризующийся емкостью. Емкость определяется отношением ![]() .
.

Рисунок 1.3
Большинство
диэлектриков, используемых на практике, линейны, т.е. у них относительная
диэлектрическая проницаемость
![]() =const. В этом случае зависимость
=const. В этом случае зависимость ![]() представляет собой прямую
линию, проходящую через начало координат, (см. рисунок 1.3,б) и
представляет собой прямую
линию, проходящую через начало координат, (см. рисунок 1.3,б) и
![]() .
.
У нелинейных диэлектриков
(сегнетоэлектриков) диэлектрическая проницаемость является функцией
напряженности поля, что обусловливает нелинейность зависимости ![]() (рисунок 1.3,б ).
(рисунок 1.3,б ).
1.5 Источники электрической энергии
Источники электрической энергии, питающие электрические цепи могут быть независимыми и зависимыми.
Источники напряжения или источники тока, в которых напряжение или ток в одной из ветвей зависит от напряжения или тока в другой, называются зависимыми. Различают четыре типа зависимых источников: источник напряжения, управляемый напряжением (ИНУН) (рисунок 1.4, а ) источник напряжения, управляемым током (ИНУТ) (рисунок 1.4, б) источник тока, управляемый напряжением (ИТУН) (рисунок 1.4,в) источник тока, управляемый током (ИТУТ) (рисунок 1.4,г). На рисунках приведены соотношения, описывающие связи зависимых значений, выраженные через коэффициенты k, r, g, β, которые, как правило, являются положительными или отрицательными числами и однозначно полно характеризуют зависимый источник.

Рисунок 1.4
Источники напряжения или источники тока, в которых напряжение или ток в одной из ветвей не зависит от напряжения или тока в другой, называются независимыми.
Свойства источника электрической энергии описываются ВАХ ![]() , называемой внешней
характеристикой источника. ВАХ источника может быть определена экспериментально
( рисунок 1.5,а).
, называемой внешней
характеристикой источника. ВАХ источника может быть определена экспериментально
( рисунок 1.5,а).

Рисунок 1.5
В общем случае ВАХ источника является нелинейной (кривая 1 на
рисунке 1.5,б). Она имеет две характерные точки, которые соответствуют: а – режиму холостого хода![]() ;в – режиму короткого замыкания
;в – режиму короткого замыкания ![]() .
.
Прямая 2 на рисунке 1.5,б описывается линейным уравнением
![]() (1.1)
(1.1)
где ![]() -
напряжение на зажимах источника при отключенной нагрузке;
-
напряжение на зажимах источника при отключенной нагрузке; ![]() - внутреннее сопротивление источника.
- внутреннее сопротивление источника.
Уравнение (1.1) позволяет составить последовательную схему
замещения источника энергии источником Э.Д.С. (см. рисунок 1.6,а). На этой
схеме символом Е обозначен элемент, называемый идеальным источником ЭДС, ему
соответствует ВАХ на рисунке 1.6,б, у такого источника ![]() .
.
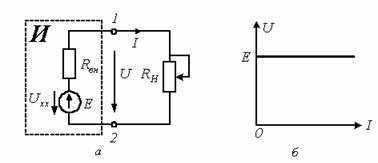
Рисунок 1.6
Существует также параллельная схема замещения источника . Для ее
описания разделим левую и правую части соотношения (1.1) на ![]() . В результате получим
. В результате получим
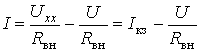 или
или
![]()
где ![]() ;
; ![]() - внутренняя проводимость
источника.
- внутренняя проводимость
источника.
Уравнению (1.2) соответствует схема замещения источника на рисунке 1.7,а.
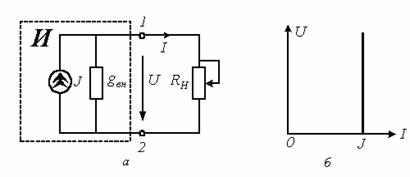
Рисунок 1.7
На этой схеме символом J обозначен элемент, называемый идеальным
источником тока. Ток в ветви с этим элементом равен ![]() и не зависит от напряжения на зажимах источника,
следовательно, ему соответствует ВАХ на рисунке 1.7,б. На этом основании с
учетом (1.2) у такого источника
и не зависит от напряжения на зажимах источника,
следовательно, ему соответствует ВАХ на рисунке 1.7,б. На этом основании с
учетом (1.2) у такого источника ![]() , т.е. его внутреннее сопротивление
, т.е. его внутреннее сопротивление ![]() .В расчетном плане при
выполнении условия
.В расчетном плане при
выполнении условия ![]() последовательная
и параллельная схемы замещения источника являются эквивалентными. На практике
важное значение имеет согласованный режим работы? когда
последовательная
и параллельная схемы замещения источника являются эквивалентными. На практике
важное значение имеет согласованный режим работы? когда ![]() ,
при котором нагрузкой от источника потребляется максимальная мощность
,
при котором нагрузкой от источника потребляется максимальная мощность
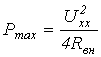 . (1.3)
. (1.3)
2 Лекция 2. Методы преобразования электрических цепей. Закон Ома. Потенциальная диаграмма
Цель лекции: ознакомить с простейшими методами преобразования цепей и законом Ома.
2.1 Методы преобразования
Во всех cлучаях преобразования замена одних схем другими, им эквивалентными, не должна привести к изменению токов или напряжений участках цепи, не подвергшихся преобразованию.
Замена последовательно соединенных сопротивлений одним эквивалентным.Сопротивления соединены последовательно, если они обтекаются одним и тем же током.
Эквивалентное сопротивление цепи, состоящей из последовательно соединенных сопротивлений, равно сумме этих сопротивлений
RЭК =![]() .
(2.1)
.
(2.1)
При последовательном соединении n сопротивлений напряжения на них распределяются прямо пропорционально этим сопротивлениям
U1: U2: …: Un = R1: R2: …: Rn.
В частном случае двух последовательно соединённых сопротивлений
U1 / U2 = R1 / R2; U1= U R1 / (R1+ R2); U2=U R2 / ( R1+ R2)
где U — общее напряжение, действующее на участке цепи, содержащем два сопротивления R1 и R2.
Замена параллельно соединенных сопротивлений одним эквивалентным. Сопротивления соединены параллельно, если все они присоединевны к одной паре узлов.
Эквивалентное сопротивление цепи, состоящей из n параллельно соединенных сопротивлений, определяется из формулы
![]() , или
, или ![]() . (2.2)
. (2.2)
В частном случае параллельного соединения двух сопротивлений R1 и R2 эквивалентное сопротивление
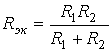 .
.

Рисунок 2.1
При параллельном соединении n сопротивлений (рисунок 2.1, а) токи в них распределяются обратно пропорционально их сопротивлениям или прямо пропорционально их проводимостям
I1 : I2 : … : In = ![]() :
:![]() : … :
: … : ![]() = G1:
G2
: … : Gn.
= G1:
G2
: … : Gn.
Ток IS в каждой из них вычисляется через ток I в неразветвленной части цепи
Is = I ![]() .
.
В частном случае двух параллельных ветвей (рисунок 2.1, б)
I2 = I1 ![]() , I3 = I1
, I3 = I1![]()
или
I2 = I1![]() , I3 =
I1
, I3 =
I1![]() .
.
Замена смешанного соединения сопротивлений одним эквивалентным. Смешенное соединение это сочетание последовательного и параллельного соединений сопротивлений. Например, сопротивления R1 , R2 и R3 (рисунок 2.1,б) соединены смешанно.
Их эквивалентное сопротивление
Rэк = R1 + ![]() =
= ![]() .
.
Формулы преобразования треугольника сопротивлений (рисунок 2.2, а) в эквивалентную звезду сопротивлений (рисунок 2.2, б) и наоборот имеют вид
R1 = 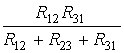 , R2 =
, R2 = ![]() ,
, ![]() R3 =
R3 = ![]() , (2.3)
, (2.3)
G12 =![]() , G23 =
, G23 = ![]() , G31 =
, G31 =
![]() (2.4)
(2.4)
где G – проводимость соответствующей ветви.
Формулы (2.4) можно записать через сопротивления
R12=R1+R2+![]() ,
R23= R2+R3+
,
R23= R2+R3+![]() , R31=R3+R1+
, R31=R3+R1+![]() .
(2.5)
.
(2.5)
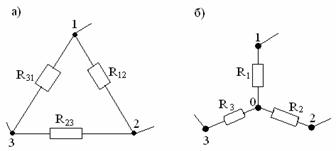 |
Рисунок 2.2
2.2 Закон Ома
Этот закон применяется для ветви или для одноконтурной замкнутой цепи (не имеющей разветвлений).
При написании закона Ома следует, прежде всего, выбрать произвольно некоторое положительное направление тока.
Для ветви, состоящей только из резисторов и не содержащей э. д. с. (например, для ветви вка), при положительном направлении тока от точки в к точке а (рисунок 2.3)
Ι
= ![]() =
= ![]()
 |
где
Uва - разность потенциалов или напряжение между точками в и а;
Rва = R4 + R5 – полное сопротивление ветви между точками в и а.
Рисунок 2.3
Для ветви цепи, содержащей э. д. с. и резисторы (например, для ветви асb, рисунок 2.3)
I1
= 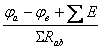 =
=
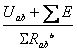 (2.6)
(2.6)
где
Uab =
![]() - напряжение
на концах ветви аb, отсчитываемое по выбранному положительному
направлению тока;
- напряжение
на концах ветви аb, отсчитываемое по выбранному положительному
направлению тока;
![]() — алгебраическая сумма
э. д. с., находящихся в этой ветви;
— алгебраическая сумма
э. д. с., находящихся в этой ветви; ![]() Rab - арифметическая
сумма ее сопротивлений.
Rab - арифметическая
сумма ее сопротивлений.
В ветви асb ![]() = Е1 - Е2,
= Е1 - Е2,
![]() Rab =R1+R2+R3.
Rab =R1+R2+R3.
Формулу (2.6) называют обобщенным законом Ома.
Для замкнутой одноконтурной цепи
I = ![]() (2.7)
(2.7)
где ∑R — арифметическая сумма всех внешних и внутренних сопротивлений цепи;
∑Е — алгебраическая сумма электродвижущих сил.
Со знаком плюс берут те эдс., направления которых совпадают с выбранным положительным направлением тока, а со знаком минус - э. д. с. с противоположными направлениями.
2.3 Потенциальная диаграмма
Потенциальная диаграмма применяется при анализе цепей постоянного тока. Она представляет собой график распределения потенциала вдоль участка цепи или контура, при этом по оси абсцисс откладываются сопротивления резистивных элементов, встречающихся на пути обхода ветви или контура, а по оси ординат – потенциалы соответствующих точек. Таким образом, каждой точке рассматриваемого участка или контура соответствует точка на потенциальной диаграмме. Рассмотрим построение потенциальной диаграммы на примере схемы на рисунке 2.4.
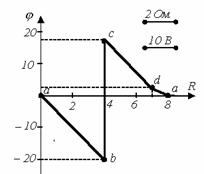 Рисунок 2.4 |
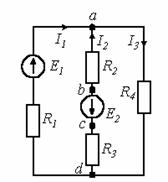
Рисунок 2.5
При параметрах схемы ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() и
и ![]() токи в ветвях схемы равны:
токи в ветвях схемы равны: ![]() ;
; ![]() ;
; ![]() .
.
Построим потенциальную диаграмму для контура abcda.Для
выбора масштаба по оси абсцисс просуммируем сопротивления резисторов вдоль
рассматриваемого контура: ![]()
![]() после чего определим потенциалы точек контура
относительно потенциала произвольно выбранной точки a, потенциал которой
принят за нуль
после чего определим потенциалы точек контура
относительно потенциала произвольно выбранной точки a, потенциал которой
принят за нуль
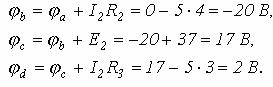
Таким образом, координаты точек потенциальной диаграммы: а(0;0);b(4;-20); c(4;17); d(7;2). С учетом выбранных масштабов на рисунке 2.5 построена потенциальная диаграмма для выбранного контура.
2.4 Метод наложения
Если в электрической цепи заданными величинами являются э.д.с. источников и токи источников тока, то расчет токов по методу наложения состоит в следующем. Ток в любой ветви можно рассчитать как алгебраическую сумму токов, вызываемых в ней э.д.с. каждого источника
э. д. с. в отдельности и током, проходящим по этой же ветви от действия каждого источника тока. При этом надо иметь в виду, что когда ведется расчет токов, вызванных каким-либо одним источником э. д. с. или тока, то остальные источники э. д. с. в схеме заменяются короткозамкнутыми участками, а ветви с источниками тока размыкаются .
3 Лекция 3. Основные законы и методы расчета линейных электрических цепей постоянного тока
Цель лекции: ознакомить с основными методами расчета линейных электрических цепей постоянного тока.
3.1 Законы Кирхгофа
Для написания законов Кирхгофа необходимо задаться положительными направлениями токов каждой ветви.
Первый закон Кирхгофа - алгебраическая сумма всех токов, сходящихся в любом узле, равна нулю
 .
( 3.1)
.
( 3.1)
Токи, направленные от узла, условно принимаются положительными, а направленные к нему – отрицательными (или наоборот).
Второй закон Кирхгофа - алгебраическая сумма э. д. с. замкнутого контура равна алгебраической сумме падений напряжений в нём
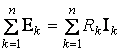 .
(3.2)
.
(3.2)
Направление обхода контура выбирается произвольно. При записи левой части равенства э. д. с., направления которых совпадают с выбранным направлением обхода, принимаются положительными, а э. д. с., направленные против - отрицательными. При записи правой части равенства со знаком плюс берутся падения напряжения в тех ветвях, в которых выбранное положительное направление тока совпадает с направлением обхода, а со знаком минус падения напряжения в тех ветвях, в которых положительное направление тока противоположно.
Пусть цепь состоит из Nв ветвей, имеет Nу узлов и Nт источников тока.
П р и м е н е н и е з а к о н о в К и р х г о ф а. Устанавливаем число неизвестных токов, равное Nв — Nт. Для каждой ветви задаются положительным направлением тока.
Общее число уравнений, составляемых по первому и второму законам Кирхгофа, равно числу (Nв — Nт) неизвестных токов. Число уравнений, составляемых по первому закону Кирхгофа, равно (Nу - 1). Число взаимонезависимых уравнений, составляемых по второму закону Кирхгофа
К =( Nв —Nт ) — (Nу - 1). (3.3)
При составлении уравнений по второму закону Кирхгофа следует выбирать независимые контуры, не содержащие источников тока.
3.2 Метод контурных токов
Метод основан на том, что ток в любой ветви цепи можно представить в виде алгебраической суммы контурных токов, протекающих по этой ветви. При пользовании этим методом выбирают и обозначают контурные токи (по любой ветви цепи должен проходить хотя бы один выбранный контурный ток). Общее число контурных токов равно К =( Nв —Nт ) — (Nу - 1). Рекомендуется выбирать Nт, контурных токов так, чтобы каждый из них - проходил через один источник тока. Эти контурные токи можно считать совпадающими с соответствующими токами источников тока J1, J2, . . ., JNT, и они обычно являются заданными условиями задачи. Для них уравнения не составляют, но учитывают при составлении уравнений для других контуров.
Оставшиеся К =( Nв —Nт ) — (Nу - 1) контурные токи выбирают проходящими по ветвям, не содержащим источников тока. Для определения последних контурных токов по второму закону Кирхгофа для этих контуров составляют К уравнений в виде
R11I11 + R12Ι22 + … +R1kIkk+ … +![]() JnRn = Е11,
JnRn = Е11,
R21I11 + R22Ι22
+ … +R2kIkk+ … +![]() JnRn = Е22,
(3.4)
JnRn = Е22,
(3.4)
Rk1I11
+ Rk2Ι22 + … +RkkIkk+ … +![]() JnRn
= Еkk
JnRn
= Еkk![]()
где Rnn — собственное сопротивление контура n (сумма сопротивлений всех ветвей, входящих в контур n);
Rnl — общее сопротивление
контуров n и L, причем Rnl = Rln.. Если направления контурных токов в общей ветви для n и L, совпадают, то Rnl положительно, в противном случае Rnl отрицательно;
Еnn- алгебраическая сумма э. д. с., включенных в ветви, образующие контур n;
Rn — общее сопротивление ветви контура n с контуром, содержащим источник тока Jn.
3.3 Метод узловых потенциалов.
Он позволяет уменьшить количество уравнений системы до числа
m = Nу - 1. (3.5)
Сущность метода заключается в том, что вначале путем решения системы уравнений определяют потенциалы всех узлов схемы, а токи ветвей, соединяющих узлы, находят с помощью закона Ома.
При составлении уравнений по методу узловых потенциалов вначале полагают равным нулю потенциал какого-либо узла (его называют базисным).
Для определения потенциалов оставшихся (m = Nу —1) узлов составляется следующая система уравнений
 (3.6)
(3.6)
Здесь Gss – сумма проводимостей ветвей, присоединённых к узлу S;
Gsq – сумма проводимостей ветвей, непосредственно соединяющих узел S с узлом q ;
![]() - алгебраическая сумма
произведений э.д.с. ветвей, примыкающих к узлу S , на их
проводимости; при этом со знаком плюс берутся те э.д.с., которые действуют в
направлении узла S, и со знаком минус –в направлении от узла S;
- алгебраическая сумма
произведений э.д.с. ветвей, примыкающих к узлу S , на их
проводимости; при этом со знаком плюс берутся те э.д.с., которые действуют в
направлении узла S, и со знаком минус –в направлении от узла S;
![]() - алгебраическая сумма
источников тока, присоединённых к узлу S; при этом со
знаком плюс берутся те токи, которые направлены к узлу S , а
со знаком минус – в направлении от узла S.
- алгебраическая сумма
источников тока, присоединённых к узлу S; при этом со
знаком плюс берутся те токи, которые направлены к узлу S , а
со знаком минус – в направлении от узла S.
Методом узловых потенциалов рекомендуется пользоваться в тех случаях, когда число уравнений будет меньше числа уравнений, составленных по методу контурных токов.
Если в схеме некоторые узлы соединяются идеальными источниками э.д.с., то число m уравнений, составляемых по методу узловых потенциалов, уменьшается
m = Nу – Nи – 1 (3.7)
где Nи – число ветвей, содержащих только идеальные источники э.д.с. В этом случае за нуль принимается один из узлов, принадлежащих ветви с идеальным источником э.д.с., тогда потенциал другого равен _± Е. Плюс, если двигаться по э.д.с., минус –если против.
3.5 Метод двух узлов
Для схем, имеющих два узла (например,узлы a и b), узловое напряжение Uab определяется формулой
Uab =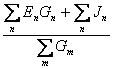 (3.8)
(3.8)
где ∑Εn Gn - алгебраическая сумма произведений э.д.с. ветвей (э.д.с. считаются положительными, если они направлены к узлу а, и отрицательными, если направлены от узла а, к узлу b) на проводимости этих ветвей;
Jn – токи источников тока (положительны, если они направлены к узлу а, и отрицательны, если направлены от узла а, к узлу b);
![]() - сумма проводимости всех
ветвей, соединяющих узлы а и b.
- сумма проводимости всех
ветвей, соединяющих узлы а и b.
3.6 Метод замены нескольких соединенных параллельно источников э.д.с. одним эквивалентным
Если имеется несколько источников с э.д.с. Е1, Е2 … , Е п и внутренним сопротивлениями R1, R2, … , Rn, работающих параллельно на общее сопротивление нагрузки R (рисунок 3.1, а), то они могут быть заменены одним эквивалентным источником, э.д.с. которого Еэк, а внутреннее сопротивление Rэк (рисунок 3.1, б). При этом
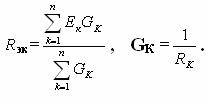 (3.9)
(3.9)
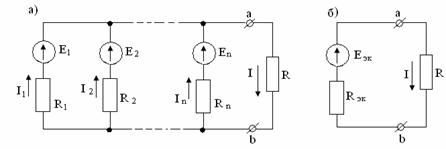 |
Рисунок 3.1
3.7 Метод замены параллельно соединенных источников тока одним эквивалентным
Если несколько источников тока с токами J1 , J2, … , Jn и внутренними проводимостями G1, G2, …, Gn соединены параллельно (рисунок 3.2,а), то их можно заменить одним эквивалентным источником тока (рисунок 3.2, б), ток которого Jэк равен алгебраической сумме токов, а его внутренняя проводимость Gэк равна сумме внутренних проводимостей отдельных источников
J = ![]()
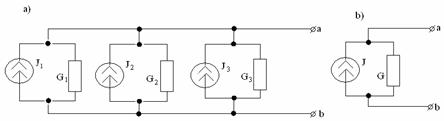 Gэк=
Gэк=![]() .
(3.10)
.
(3.10)
Рисунок 3.2
Лекция 4. Метод эквивалентного генератора. Баланс мощностей
Цель лекции: научить пользоваться методом эквивалентного источника и составлять баланс мощностей.
4.1 Метод эквивалентного генератора
Применение метода эквивалентного генератора (метода активного двухполюсника или метода холостого хода и короткого замыкания) целесообразно для определения тока в какой-либо одной ветви сложной электрической цепи. Имеется два варианта метода: 1) метод эквивалентного источника э.д.с. и 2) метод эквивалентного источника тока.
Метод эквивалентного источника э.д.с. Для нахождения тока I в произвольной ветви ab, сопротивление которой R (рисунок 4.1, а; буква А означает активный двухполюсник), надо эту ветвь разомкнуть (рисунок 4.1, б), а часть цепи, подключенную к этой ветви, заменить эквивалентным источником с э.д.с. Еэк и внутренним сопротивлением Rэк (рисунок 4.1, в).
Э.д.с. Еэк этого источника равняется напряжению на зажимах разомкнутой ветви (напряжение холостого хода)
Еэк = Uabx =(φa - φb). (4.1)
Расчет схем в режиме холостого хода (рисунок 4.1,б) для определения Еэк проводится любым известным способом.
Внутреннее сопротивление Rэк эквивалентного источника э.д.с. равняется входному сопротивлению пассивной цепи относительно зажимов a и b исходной схемы, из которой исключены все источники (источники э.д.с. заменены короткозамкнутыми участками, а ветви с источниками тока отключены, рисунок 4.1, г; буква П указывает на пассивный характер цепи), при разомкнутой ветви ab. Сопротивление Rэк можно вычислить непосредственно по схеме рисунка 4.1, г.
Ток в искомой ветви схемы (рисунок 4.1, д), имеющей сопротивление R, определяется по закону Ома
I
=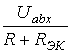 =
=![]() (4.2)
(4.2)
Метод эквивалентного источника тока. Для расчета тока в ветви ab, сопротивление которой R, надо заменить часть схемы относительно зажимов a и b (при замкнутой ab) эквивалентным источником тока, ток которого Jэк а проводимость Gэк (рисунок 4.1, е).
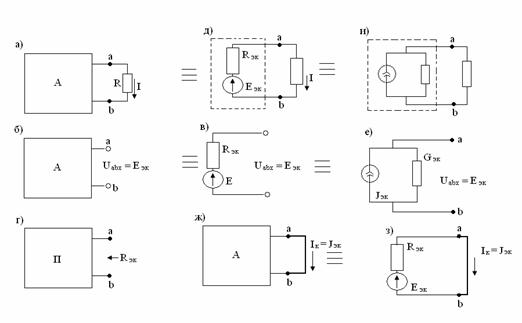
Рисунок 4.1
Для нахождения тока Jэк надо зажимы a и b закоротить и любым способом рассчитать ток которого замыкания Ik , протекающий по закороченному участку (рисунок 4.1, ж). При этом Jэк = Ik . Сопротивление Rэк можно найти, как и при расчете по методу эквивалентного источника э.д.с. (см. рисунок 4.1,г). Это же сопротивление может быть рассчитано, как это видно из схемы замещения заданной схемы в режиме короткого замыкания (рисунок 4.1,з) по формуле
Rэк=Еэк/Ik=Еэк/Jэк=1/Gэк. (4.3)
Ток в ветви R (рисунок 4.1,и)
I=Jэк![]() .
(4.4)
.
(4.4)
В качестве примера использования метода
эквивалентного генератора для анализа определим зависимость показаний
амперметра в схеме на рисунке 4.2 при изменении сопротивления R переменного
резистора в диагонали моста в пределах ![]() . Параметры цепи Е=100 В; R1=R4=40 Ом; R2=R3=60
Ом.
. Параметры цепи Е=100 В; R1=R4=40 Ом; R2=R3=60
Ом.
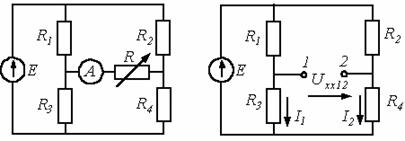
Рисунок 4.2 Рисунок 4.3
Для нахождения значения ![]() перейдем к схеме на рис. 4.3, где напряжение
перейдем к схеме на рис. 4.3, где напряжение ![]() на разомкнутых зажимах 1 и 2
определяет искомую ЭДС
на разомкнутых зажимах 1 и 2
определяет искомую ЭДС ![]() .
В данной цепи
.
В данной цепи
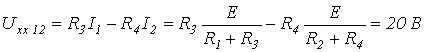 .
.
Для определения входного сопротивления активного двухполюсника трансформируем его в схему на рисунке 4.4.
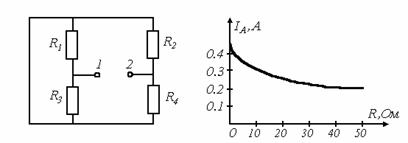
Рисунок 4.4 Рисунок 4.5
Со стороны зажимов 1-2 данного пассивного двухполюсника его сопротивление равно
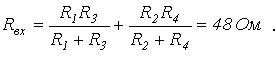
Таким образом, для показания амперметра в схеме на рисунке 4.2 в соответствии с (4.2) можно записать
|
|
Задаваясь значениями R в пределах его изменения, на основании (4.2) получаем кривую на рисунке 4.5.
4.2 Баланс мощностей
Баланс мощностей является следствием закона сохранения энергии и может служить критерием правильности расчета электрической цепи. Для любой замкнутой электрической цепи сумма мощностей РИ, развиваемых источниками электрической энергии, равна сумме мощностей Рп, расходуемых в приемниках энергии
![]() =
=![]() , или
, или
![]() .
(4.6)
.
(4.6)
Это уравнение представляет собой математическую форму записи баланса мощностей: суммарная мощность, генерируемая источниками электрической энергии, равна суммарной мощности, потребляемой в цепи.
Следует указать, что в левой части (4.6) слагаемые имеют знак “+”, поскольку активная мощность рассеивается на резисторах. В правой части (4.6) сумма слагаемых больше нуля, но отдельные члены здесь могут иметь знак “-”, что говорит о том, что соответствующие источники работают в режиме потребителей энергии (например, заряд аккумулятора).
Где Σ Εk Ik – алгебраическая сумма; здесь положительны те из слагаемых, для которых направления действия э.д.с. Εk и соответствующего тока Ik совпадают, в противном случае слагаемое отрицательно;
Σ Εk Jk - алгебраическая сумма; здесь положительны те из слагаемых, для которых напряжение на источнике тока (оно определяется расчетом цепи внешней по отношению к зажимам источника тока) и его ток Jk совпадают по направлению, в противном случае слагаемое отрицательно .
4.3 Расчет цепей с зависимыми источниками
Для расчета цепей, содержащих зависимые источники, применимы все методы, известные для расчета цепей с независимыми источниками.
Наиболее часто используются методы узловых напряжений и контурных токов.
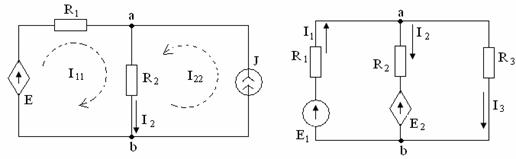 |
Пример 1. В цепи (рисунок 4.6) действуют независимый источник тока J и ИНУТ с ЭДС Е =rI2. Дано: R1, R2, r, J. Найти напряжение Uab.
Решение. Выберем для решения метод контурных токов. Контурное уравнение: I11 (R1+R2)+J R2=E.Учитывая, что I2=I11+J, I11 (R1+R2)+J R2=r(I11+J) или I11(R1+R2 - r)= J (r - R2). Из этого уравнения определим ток I11. Напряжение Uab = I2 R2.
Пример 2. В цепи (рис.4.7) действуют независимые источник напряжения с ЭДС E1 и ИНУН с ЭДС E2=k Uab. Найти токи в ветвях, если даны R1,R2,R3, k. Решение. Для решения выберем метод узловых потенциалов. Приняв φb = 0, запишем уравнение для узла α
φα (1 / R1+1 / R2+1 / R3) = E1 / R1+E2 / R2.
Учитывая, что Uab = φa-φb, E2=kφа имеем
φα (1 / R1+1 / R2+1 / R3) = E1 / R1+ kφа / R2.
Решая уравнение, получим φa= Uab. Токи в ветвях I1= (Uab+E1)/ R1;
I2=( Uab- E2) / R2,
I3= Uab / R3.![]()
Лекция 5.Синусоидальный ток и основные характеризующие его величины
Цель лекции: усвоить основные понятия о синусоидальных токах и напряжениях и особенности их протекания в основных элементах.
5.1 Синусоидальные электрические величины
Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.
В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися (переменными ) токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.
Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи.
Переменным током (напряжением, ЭДС и т.д.) называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, - периодом Т. Для периодического тока имеем
![]()
Величина, обратная периоду, есть частота, измеряемая в герцах (Гц)
![]()
Диапазон частот, применяемых в технике: от сверхнизких частот (0.01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: (радиолокация, радиоастрономия). Промышленная частота f = 50Гц.
Мгновенное значение переменной величины есть функция
времени. Ее принято обозначать строчной буквой: i -
мгновенное значение тока![]() ; u–
мгновенное значение напряжения
; u–
мгновенное значение напряжения![]() ; е - мгновенное значение ЭДС
; е - мгновенное значение ЭДС ![]() ; р -
мгновенное значение мощности
; р -
мгновенное значение мощности ![]() . Наибольшее мгновенное значение
переменной величины за период называется амплитудой (ее обозначают заглавной
буквой с индексом m):
. Наибольшее мгновенное значение
переменной величины за период называется амплитудой (ее обозначают заглавной
буквой с индексом m): ![]() - амплитуда тока;
- амплитуда тока;![]() -
амплитуда напряжения;
-
амплитуда напряжения;![]() - амплитуда ЭДС.
- амплитуда ЭДС.
5.2 Действующее значение переменного тока
Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока
 (5.3)
(5.3)
Аналогично определяются действующие значения ЭДС и напряжения. В соответствии с выражением (5.3) для действующего значения синусоидального тока запишем:
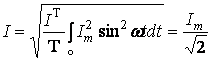 . (5.4)
. (5.4)
Аналогичный результат можно получить для
синусоидальных ЭДС и напряжений. Таким образом, действующие значения
синусоидальных токов, ЭДС и напряжения меньше своих амплитудных значений в ![]() раз.
раз.
5.3 Изображение синусоидальных ЭДС, напряжений и токов на плоскости декартовых координат
Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.
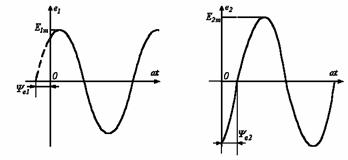 |
Рисунок 5.1 Рисунок 5.2
Приведенным на рисунке 5.1, 5.2 графикам двух синусоидальных ЭДС е1 и е2 соответствуют уравнения
![]()
![]() .
.
Значения аргументов синусоидальных функций ![]() и
и ![]() называются фазами синусоид, а
значение фазы в начальный момент времени (t=0):
называются фазами синусоид, а
значение фазы в начальный момент времени (t=0):![]() и
и ![]() - начальной фазой (
- начальной фазой (![]()
![]() ).
).
Величину ![]() , характеризующую скорость изменения
фазового угла, называют угловой частотой. Так как фазовый угол синусоиды
за время одного периода Т изменяется на
, характеризующую скорость изменения
фазового угла, называют угловой частотой. Так как фазовый угол синусоиды
за время одного периода Т изменяется на ![]() рад., то угловая частота есть
рад., то угловая частота есть![]() где f– частота.
где f– частота.
При совместном рассмотрении двух синусоидальных величин одной частоты разность их начальных фаз, называют углом сдвига фаз.
![]() (5.5).
(5.5).
5.4 Синусоидальный ток в сопротивлении
Если синусоидальное напряжение ![]() приложено к сопротивлению r
(рисунок 5.3а), то через сопротивление пройдет синусоидальный ток
приложено к сопротивлению r
(рисунок 5.3а), то через сопротивление пройдет синусоидальный ток ![]() .
.

Риунок 5.3
Напряжение на зажимах сопротивления и ток, проходящий через это сопротивление, имеют одинаковую начальную фазу или, как говорят, совпадают по фазе. (рисунок 5.3 ,б).
В данном случае сдвиг по фазе равен нулю
![]() (5.6)
(5.6)
При прохождении синусоидального тока через сопротивление r не только мгновенные значения напряжения на сопротивлении и тока в нем, но и амплитуды и соответственно действующие значения напряжения и тока связаны законом Ома
![]()
![]()
5.5 Синусоидальный ток в индуктивности
Пусть через индуктивность L (рисунок 5.4,
а ) проходит ток ![]()

Рисунок 5.4
Электродвижущая сила самоиндукции определяется по формуле
![]() (5.7)
(5.7)
Значит напряжение на индуктивности
![]() (5.8)
(5.8)
Полученное выражение показывает, что напряжение на индуктивности
опережает
ток на угол ![]() (рисунок
5.4,б).
(рисунок
5.4,б).
Фазовый сдвиг равен
![]() (5.9)
(5.9)
Амплитуда так же, как и действующие значения напряжения и тока, связаны соотношением, подобным закону Ома
![]() (5.10)
(5.10)
Величина
![]() , имеющая
размерность сопротивления, называется индуктивным сопротивлением; обратная ей
величина
, имеющая
размерность сопротивления, называется индуктивным сопротивлением; обратная ей
величина ![]() называется
индуктивной проводимостью.
называется
индуктивной проводимостью.
![]() (5.11)
(5.11)
5.6 Синусоидальный ток в емкости
Пусть напряжение на емкости С (рисунок 5.5,а)
синусоидально: ![]()

Рисунок 5.5
Ток в емкости
![]() (5.12)
(5.12)
Выражение (5.12) показывает, что ток i опережает
приложенное напряжение и на угол ![]() (рисунок 5.5,б).
(рисунок 5.5,б).
Сдвиг по фазе ![]() .
.
Амплитуды и соответственно действующие значения напряжения и тока связаны соотношением, подобным закону Ома
![]() (5.13)
(5.13)
Величина ![]() , имеющая размерность сопротивления,
называется емкостным сопротивлением. Обратная ей величина
, имеющая размерность сопротивления,
называется емкостным сопротивлением. Обратная ей величина ![]() называется
емкостной проводимостью. Следовательно,
называется
емкостной проводимостью. Следовательно,
![]() (5.14)
(5.14)
6 Лекция 6. Основы символического метода расчета цепей синусоидального тока
Цель лекции: ознакомить с применением метода комплексных амплитуд.
6.1 Представление синусоидальных функций в виде векторов и комплексных чисел.
Известно, что каждая точка на комплексной плоскости определяется радиус-вектором этой точки (рисунок 6.1).
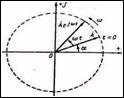
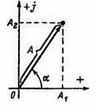
Рисунок 6.1 Рисунок 6.2
Комплексное число может быть представлено в показательной тригонометрической и алгебраической формах
![]()
здесь А - модуль;
![]() - аргумент или фаза;
- аргумент или фаза;
![]() .
.
Вектор, вращающийся в положительном направлении, т.
е. против хода часовой стрелки, с угловой скоростью ![]() может быть выражен следующим образом
может быть выражен следующим образом
![]() (6.1)
(6.1)
где ![]() - комплексная амплитуда, представляющая данный
вектор
- комплексная амплитуда, представляющая данный
вектор
в момент t = 0 (рисунок 6.2).
Синусоидальная функция ![]() может
рассматриваться как мнимая часть комплексной функции (6.1) или как проекция
вращающегося вектора на мнимую ось.
может
рассматриваться как мнимая часть комплексной функции (6.1) или как проекция
вращающегося вектора на мнимую ось.
Условно это
записывается так ![]() (6.2)
(6.2)
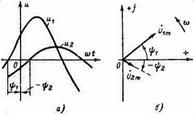
Рисунок 6.3
На рисунке 6.3, а показаны две синусоидальные функции:
![]() и
и ![]() имеющие одинаковую угловую частоту
имеющие одинаковую угловую частоту ![]() . Функция
. Функция ![]() опережает по фазе функцию
опережает по фазе функцию ![]() , причем фазовый сдвиг равен
разности начальных фаз
, причем фазовый сдвиг равен
разности начальных фаз![]() Этот угол образует векторы, показанные
на рисунке 6.3,б. При равенстве начальных фаз, т. е. при фазовом сдвиге,
равном нулю, векторы совпадают по фазе. При фазовом сдвиге 1800
векторы находятся в противофазе. Диаграмма, изображающая совокупность векторов,
построенных с соблюдением их взаимной ориентации по фазе, называется векторной
диаграммой.
Этот угол образует векторы, показанные
на рисунке 6.3,б. При равенстве начальных фаз, т. е. при фазовом сдвиге,
равном нулю, векторы совпадают по фазе. При фазовом сдвиге 1800
векторы находятся в противофазе. Диаграмма, изображающая совокупность векторов,
построенных с соблюдением их взаимной ориентации по фазе, называется векторной
диаграммой.
6.2 Основы символического метода расчета цепей синусоидального тока
Расчет цепей переменного синусоидального тока может производиться не только путем построения векторных диаграмм, но и аналитически – путем операций с комплексами, символически изображающими синусоидальные ЭДС, напряжения и токи. Достоинством векторных диаграмм является их наглядность, недостатком – малая точность графических построений. Применение символического метода позволяет производить расчеты цепей с большой степенью точности. Символический метод расчета цепей синусоидального тока основан на законах Кирхгофа и законе Ома в комплексной форме. Уравнения, выражающие законы Кирхгофа в комплексной форме, имеют совершенно такой же вид, как и соответствующие уравнения для цепей постоянного тока. Только токи, ЭДС, напряжения и сопротивления входят в уравнение в виде комплексных величин.
6.3 Последовательное соединение сопротивления, индуктивности и емкости. Рассмотрим применение метода комплексных амплитуд в случае последовательного соединения элементов r, L и С (рисунок 6.4).
Рисунок 6.4
Положим, что в уравнении Кирхгофа
заданными
являются параметры r, L, С и
напряжение ![]() ,
а искомой величиной является ток i. Решение этого дифференциального уравнения должно
дать синусоидальную функцию вида
,
а искомой величиной является ток i. Решение этого дифференциального уравнения должно
дать синусоидальную функцию вида ![]() .
.
Комплексные амплитуды напряжения и тока равны соответственно
![]()
Комплексное уравнение, соответствующее уравнению (6.3)
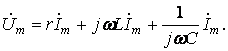 (6.4)
(6.4)
Комплексное сопротивление рассматриваемой электрической цепи
![]() (6.5)
(6.5)
Таким образом, получается уравнение, выражающее закон Ома для комплексных амплитуд и действующих значений.
![]()
![]() и
и ![]() . (6.6)
. (6.6)
Комплексное сопротивление ![]() в тригонометрической и показательной
формах имеет вид
в тригонометрической и показательной
формах имеет вид
 (6.8)
(6.8)
Здесь ![]() - модуль комплексного числа
- модуль комплексного числа![]() , представляет собой
полное сопротивление цепи; а
, представляет собой
полное сопротивление цепи; а ![]() — аргумент комплексного числа
— аргумент комплексного числа ![]()
![]() (6.9)
(6.9)
На основании (6.6) комплексная амплитуда тока
где ![]() - начальная фаза тока. Следовательно,
искомый ток в тригонометрической форме
- начальная фаза тока. Следовательно,
искомый ток в тригонометрической форме
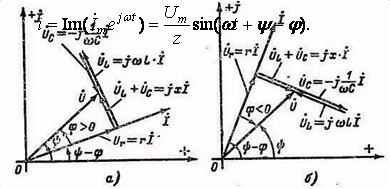 |
Рисунок 6.5
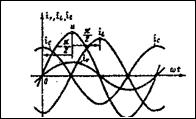
На рисунке 6.5 дана геометрическая интерпретация на
комплексной плоскости уравнения (6.4). Рисунок 6.5,а относится к случаю, когда
реактивное сопротивление цепи имеет индуктивный характер (х>0) и ![]() >0. Рисунок 6.5,б
относится к случаю, когда реактивное сопротивление цепи имеет емкостный
характер (х<0), и
>0. Рисунок 6.5,б
относится к случаю, когда реактивное сопротивление цепи имеет емкостный
характер (х<0), и ![]() <0.
<0.
Как видно из векторных диаграмм, приведенных на
рисунке 6.5, ![]() —
напряжение на сопротивлении r (совпадает по фазе с током
—
напряжение на сопротивлении r (совпадает по фазе с током ![]() ),
), ![]() —напряжение на индуктивности L
(опережает ток
—напряжение на индуктивности L
(опережает ток ![]() на
угол
на
угол ![]() ) и
) и ![]() — напряжение на емкости С (отстает от тока I
на угол
— напряжение на емкости С (отстает от тока I
на угол ![]() ).
).
Геометрическая сумма векторов ![]() дает
вектор приложенного к цепи напряжения U.
дает
вектор приложенного к цепи напряжения U.
6.4 Параллельное соединение сопротивления, индуктивности и емкости
 |
Рисунок 6.6 Рисунок 6.7
Если к зажимам электрической цепи, состоящей из
параллельно соединенных элементов r, L
и С (рисунок 6.6), приложено синусоидальное напряжение ![]() , то
синусоидальный ток, проходящий через эту цепь, равен .
, то
синусоидальный ток, проходящий через эту цепь, равен .![]()
Ток ![]() в сопротивлении r совпадает
по фазе с напряжением и, ток
в сопротивлении r совпадает
по фазе с напряжением и, ток ![]() в индуктивности L отстает, а
ток
в индуктивности L отстает, а
ток ![]() в емкости С
опережает напряжение на
в емкости С
опережает напряжение на ![]() (рисунок 6.7).
(рисунок 6.7).
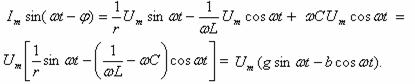 |
Следовательно, суммарный ток i в цепи равен
![]()
![]()
Величина называется реактивной проводимостью цепи, которая в зависимости от знака может иметь индуктивный (b>0) или емкостный (b<0) характер. Величина g = 1/r называется активной проводимостью.
В соответствии с первым законом Кирхгофа
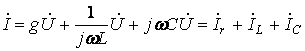 (6.11)
(6.11)
где ![]() - ток в сопротивлении (совпадает по фазе
с напряжением
- ток в сопротивлении (совпадает по фазе
с напряжением ![]() );
);
![]() - ток в индуктивности (отстает от напряжения на -
- ток в индуктивности (отстает от напряжения на -![]() );
);
![]() - ток в емкости
(опережает напряжение на
- ток в емкости
(опережает напряжение на ![]() ).
).
Выражение комплексной проводимости
![]() .
(6.12)
.
(6.12)
Уравнение закона Ома в комплексной форме
![]() .
(6.13)
.
(6.13)
Тригонометрическая и показательная формы комплексной проводимости имеют следующий вид
![]()
здесь ![]() - модуль комплексного числа;
- модуль комплексного числа;
![]() - представляет собой полную
проводимость цепи;
- представляет собой полную
проводимость цепи;
а ![]() — аргумент комплексного числа
— аргумент комплексного числа ![]() .
.
![]() .
(6.14)
.
(6.14)
Комплексный ток равен
что соответствует синусоидальному току
На рисунке 6.8 дана геометрическая интерпретация на
комплексной плоскости уравнения (6.11). Рисунок 6.8, а относится
к случаю, когда реактивная проводимость цепи имеет индуктивный характер (b>0) и соответственно ток отстает по фазе от напряжения ![]() . Рисунок 6.8, б
относится к случаю, когда реактивная проводимость цепи имеет емкостный характер
(b<0) и соответственно ток опережает по фазе
напряжение (
. Рисунок 6.8, б
относится к случаю, когда реактивная проводимость цепи имеет емкостный характер
(b<0) и соответственно ток опережает по фазе
напряжение (![]() ).
).
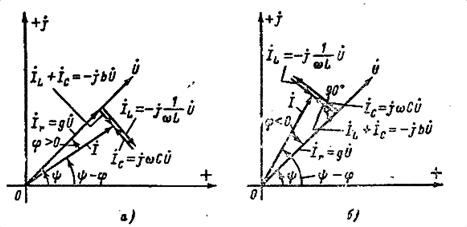 |
Рисунок 6.8
7 Лекция 7. Применение законов Кирхгофа, метода контурных токов и узловых потенциалов для расчета цепей синусоидального тока символическим методом. Векторные и топографические диаграммы
Цель лекции: познакомить с основными методами расчета цепей синусоидального тока, научиться строить векторные и топографические диаграммы.
7.1 Применение законов Кирхгофа, метода контурных токов и узловых потенциалов для расчета цепей синусоидального тока символическим метом.
7.1.1 Законы Кирхгофа.
Первый закон Кирхгофа в комплексной форме
![]() (7.1)
(7.1)
Второй закон Кирхгофа в комплексной форме
![]() (7.2)
(7.2)
Пример. Составим уравнения по законам Кирхгофа
(рисунок 7.1)
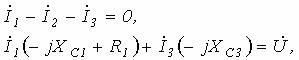
![]()

Рисунок. 7.1
7.1.2 Метод контурных токов
Пример. Составим уравнения методом контурных токов(рисунок 7.2)
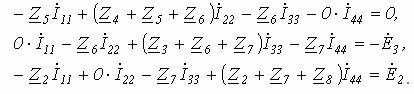
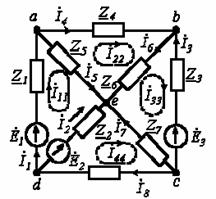
Рисунок 7.2
Решим их относительно контурных токов и затем по уравнениям,
связывающим контурные токи и токи ветвей, найдем последние. ![]()
![]()
![]()
![]() ,
, ![]() .
.
7.1.3 Метод узловых потенциалов
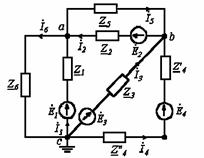
Рисунок 7.3
Пример. Составим уравнения методом узловых потенциалов (рисунок 7.3).
Составим уравнения по методу узловых потенциалов для узлов а и в.
Потенциал узла ![]() =0.
=0.
![]()
![]() .
.
Токи ветвей выразим по закону Ома
 .
.
7.2 Векторные и топографические диаграммы
Совокупность радиус-векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называется векторной диаграммой. Векторные диаграммы наглядно иллюстрируют ход решения задачи. При точном построении векторов можно непосредственно из диаграммы определить амплитуды и фазы искомых величин. Приближенное (качественное) построение диаграмм при аналитическом решении служит надежным контролем корректности хода решения. При построении векторных диаграмм для цепей с последовательным соединением элементов за базовый вектор следует принимать вектор тока. Для цепей с параллельным соединением элементов за базовый вектор следует принять вектор напряжения, ориентируя относительно него векторы токов в параллельных ветвях. Для наглядного определения величины и фазы напряжения между различными точками электрической цепи удобно использовать топографические диаграммы. Они представляют собой соединенные соответственно схеме электрической цепи точки на комплексной плоскости, отображающие их потенциалы. На топографической диаграмме, представляющей собой в принципе векторную диаграмму, порядок расположения векторов напряжений строго соответствует порядку расположения элементов в схеме, а вектор падения напряжения на каждом последующем элементе примыкает к концу вектора напряжения на каждом предыдущем элементе.
В качестве примера построим векторную диаграмму токов, а также топографическую диаграмму потенциалов для схемы (см. рисунок 7.4).
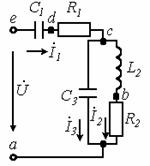 |
Рисунок 7.4
Параметры схемы ![]()
![]()
![]()
![]()
При данных параметрах и заданном напряжении на входе схемы ![]() предварительно найденные
значения токов равны
предварительно найденные
значения токов равны ![]() ,
, ![]() ,
,![]() .
.
При построении векторной диаграммы зададимся масштабами токов и напряжений (см. рисунок 7.5). Векторную диаграмму можно строить, имея запись комплекса в показательной форме, т.е. по значениям модуля и фазы. Однако на практике удобнее проводить построения, используя алгебраическую форму записи, поскольку при этом вещественная и мнимая составляющие комплексной величины непосредственно откладываются на соответствующих осях комплексной плоскости, определяя положение точки на ней. Построение векторной диаграммы токов осуществляется непосредственно на основании известных значений их комплексов. Для построения топографической диаграммы предварительно осуществим расчет комплексных потенциалов.
Обозначив на схеме ( рисунку 7.4) разнопотенциальные точки и
приняв потенциал точки а за нуль( ![]() ), определим потенциалы остальных точек
), определим потенциалы остальных точек
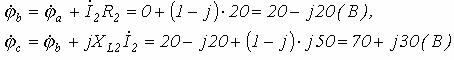
или ![]()
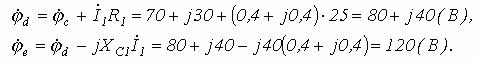
Таким образом, в результате проведенных вычислений получено, что ![]() , т.е равно напряжению U,
приложенному к цепи. В соответствии с полученными результатами строится топографическая
диаграмма ( рисунок 7.5). В заключение заметим, что векторы напряжений
ориентированы относительно точек топографической диаграммы противоположно
положительным направлениям напряжений относительно соответствующих точек
электрической цепи.
, т.е равно напряжению U,
приложенному к цепи. В соответствии с полученными результатами строится топографическая
диаграмма ( рисунок 7.5). В заключение заметим, что векторы напряжений
ориентированы относительно точек топографической диаграммы противоположно
положительным направлениям напряжений относительно соответствующих точек
электрической цепи.
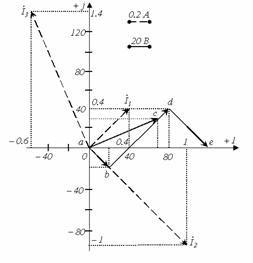
Рисунок 7.5
8.Лекция 8. Мощность в цепях синусоидального тока. Входные и передаточные характеристики
Цель лекции: рассмотреть вопросы преобразования энергии в электрической цепи, в мгновенную, активную, реактивную и полную мощности синусоидального тока.
8.1 Мгновенная, активная, реактивная и полная мощности в цепях синусоидального тока
Передача энергии w по электрической цепи , рассеяние энергии, то есть переход электромагнитной энергии в тепловую, а также и другие виды преобразования энергии характеризуются интенсивностью, с которой протекает процесс. Интенсивность передачи или преобразования энергии называется мощностью р
![]() (8.1)
(8.1)
Выражение для мгновенного значения мощности в электрических цепях имеет вид
![]() (8.2)
(8.2)
Приняв начальную фазу напряжения за нуль, а сдвиг фаз между
напряжением и током за ![]() ,
получим
,
получим
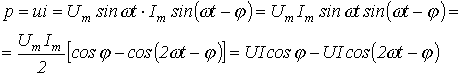 (8.3)
(8.3)

Рисунок 8.1
Когда мгновенная мощность отрицательна ( рисунок 8.1), , т.е. когда направления напряжения и тока в двухполюснике противоположны, энергия возвращается из двухполюсника к источнику питания. Среднее за период значение мгновенной мощности называется активной мощностью .
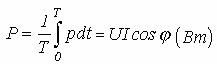 (8.4)
(8.4)
Активная мощность, потребляемая пассивным двухполюсником, не
может быть отрицательной (иначе двухполюсник будет генерировать энергию),
поэтому ![]() , т.е. на входе
пассивного двухполюсника
, т.е. на входе
пассивного двухполюсника ![]() .
Случай Р=0,
.
Случай Р=0, 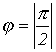 теоретически
возможен для двухполюсника, не имеющего активных сопротивлений, а содержащего
только идеальные индуктивные и емкостные элементы.
теоретически
возможен для двухполюсника, не имеющего активных сопротивлений, а содержащего
только идеальные индуктивные и емкостные элементы.
Резистор (идеальное активное сопротивление).
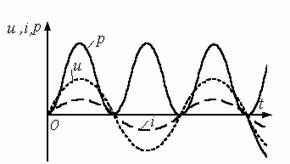
Рисунок 8.2
Здесь напряжение и ток (см. рисунок 8.2) совпадают по фазе ![]() , поэтому мощность
, поэтому мощность ![]() всегда положительна, т.е.
резистор потребляет активную мощность
всегда положительна, т.е.
резистор потребляет активную мощность
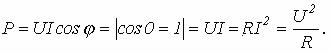 (8.5)
(8.5)
Катушка индуктивности (идеальная индуктивность)
При идеальной индуктивности ток отстает от напряжения по фазе на ![]() . Поэтому в соответствии с (8.3)
можно записать
. Поэтому в соответствии с (8.3)
можно записать
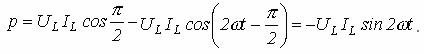 (8.6)
(8.6)
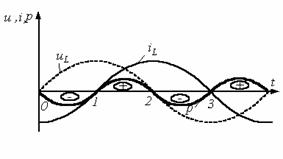
Рисунок 8.3
Участок 1-2: энергия ![]() , запасаемая в магнитном поле катушки,
нарастает.
, запасаемая в магнитном поле катушки,
нарастает.
Участок 2-3: энергия магнитного поля убывает, возвращаясь в источник.
Конденсатор (идеальная емкость).
Аналогичный характер имеют процессы и для
идеальной емкости. Здесь ![]() .
Поэтому из (8.3) вытекает, что
.
Поэтому из (8.3) вытекает, что ![]() . Таким образом, в катушке индуктивности и
конденсаторе активная мощность не потребляется (Р=0). Происходит только
циркуляция энергии: электрическая энергия запасается в электрическом поле
конденсатора на протяжении четверти периода, а на протяжении следующей четверти
периода вновь возвращается в сеть. В силу этого катушку индуктивности и
конденсатор называют реактивными элементами, а их сопротивления ХL и
ХС, в отличие от активного сопротивления R резистора, – реактивными.
Интенсивность обмена энергии принято характеризовать реактивной мощностью.
. Таким образом, в катушке индуктивности и
конденсаторе активная мощность не потребляется (Р=0). Происходит только
циркуляция энергии: электрическая энергия запасается в электрическом поле
конденсатора на протяжении четверти периода, а на протяжении следующей четверти
периода вновь возвращается в сеть. В силу этого катушку индуктивности и
конденсатор называют реактивными элементами, а их сопротивления ХL и
ХС, в отличие от активного сопротивления R резистора, – реактивными.
Интенсивность обмена энергии принято характеризовать реактивной мощностью.
![]() (8.7)
(8.7)
Она положительна при отстающем токе
(индуктивная нагрузка- ![]() )
и отрицательна при опережающем токе (емкостная нагрузка-
)
и отрицательна при опережающем токе (емкостная нагрузка- ![]() ). Единицу измерения реактивной
мощности называют вольт-ампер реактивный (ВАр).
). Единицу измерения реактивной
мощности называют вольт-ампер реактивный (ВАр).
8.2 Полная мощность
Помимо понятий активной и реактивной мощностей в электротехнике широко используется понятие полной мощности
![]() (8.8)
(8.8)
Активная, реактивная и полная мощности связаны следующим соотношением
![]() (8.9)
(8.9)
Отношение активной мощности к полной называют коэффициентом
мощности. Из приведенных выше соотношений видно, что коэффициент мощности ![]() равен косинусу угла сдвига между
током и напряжением. Итак
равен косинусу угла сдвига между
током и напряжением. Итак
![]() (8.10)
(8.10)
8.3 Комплексная мощность
Активную, реактивную и полную мощности можно определить, пользуясь
комплексными изображениями напряжения и тока. Пусть ![]() , а
, а ![]() .
.
Тогда комплекс полной мощности
![]() (8.11)
(8.11)
где ![]() - комплекс, сопряженный с комплексом
- комплекс, сопряженный с комплексом ![]() .
.
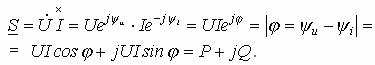 (8.12)
(8.12)
Комплексной мощности можно поставить в
соответствие треугольник мощностей (см. рисунок 8.4). Рисунок 8.4
соответствует ![]() (активно-индуктивная нагрузка).
(активно-индуктивная нагрузка).

Рисунок 8.5
8.4 Баланс мощностей
Из закона сохранения энергии следует, что сумма всех отдаваемых активных мощностей равна сумме всех потребляемых активных мощностей, т.е.
 (8.13)
(8.13)
Баланс соблюдается и для реактивных мощностей
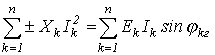 (8.14)
(8.14)
“-” где знак “+” относится к индуктивным
элементам ![]() ; – к
емкостным
; – к
емкостным ![]() .
.
Умножив (8.14) на “j” и сложив полученный результат с (8.13), придем к аналитическому выражению баланса мощностей в цепях синусоидального тока (без учета взаимной индуктивности)
 или
или
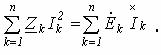 (8.16)
(8.16)
9 лекция 9. Входные и передаточные характеристики
Цель лекции: исследовать входные и передаточные характеристики простейших цепей.
9.1 Входные характеристики
Под входной характеристикой понимают зависимость
![]() , которая в свою очередь состоит из двух
характеристик
, которая в свою очередь состоит из двух
характеристик
АЧХ -![]() и ФЧХ -
и ФЧХ - ![]() .
.
Рассмотрим входные характеристики
простейших цепей ![]() (рисунок
9.1) и
(рисунок
9.1) и ![]() (рисунок
9.4). Граничная частота- это частота, при которой модуль реактивного
сопротивления равен активному.
(рисунок
9.4). Граничная частота- это частота, при которой модуль реактивного
сопротивления равен активному.
Для цепи ![]() тогда
тогда
![]() или
или ![]() .
.
Для цепи 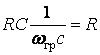 ,тогда
,тогда
![]() или
или ![]() .
.

Рисунок 9.1
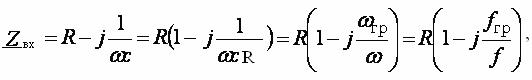

(9.1)
(9.2)
На основании (9.1 и 9.2) построим соответственно ![]() (рисунок 9.2) и
(рисунок 9.2) и ![]() (рисунок 9.3) для цепи
(рисунок 9.3) для цепи ![]() .
.
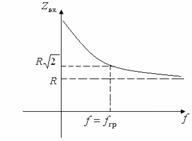
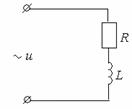

Рисунок 9.2 Рисунок 9.3 Рисунок 9.4

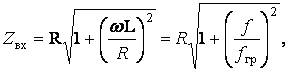 (9.3)
(9.3)
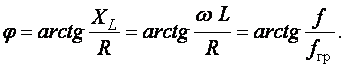
(9.4)
На основании (9.3 и 9.4) построим соответственно ![]() (рисунок 9.5) и
(рисунок 9.5) и ![]() (рисунок 9.6) для цепи
(рисунок 9.6) для цепи ![]() .
.
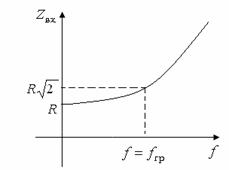
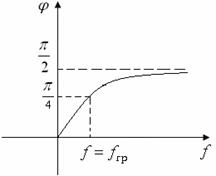
Рисунок 9.5 Рисунок 9.6
9.2 Передаточная функция по напряжению
Комплексным
коэффициентом передачи по напряжению называется отношение 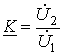
где ![]() -
выходное;
-
выходное;
![]() - входное напряжение.
- входное напряжение.
Совокупность коэффициентов передачи на различных частотах называется комплексной передаточной функцией и обозначается
![]() или
или ![]()
где H- АЧХ передаточной функции;
![]() - ФЧХ передаточной
функции.
- ФЧХ передаточной
функции.
Рассмотрим
передаточные функции по напряжению на примере простейших цепей ![]() (рисунок 9.7) и
(рисунок 9.7) и ![]() (рисунок 9.10).
(рисунок 9.10).
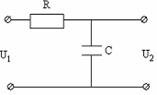
Рисунок 9.7
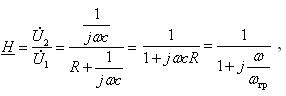
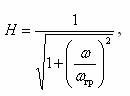 (9.5)
(9.5)
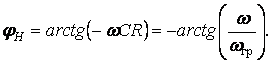 (9.6)
(9.6)
По выражениям (9.5) и (9.6) построим соответственно АЧХ передаточной функции ( рисунок 9.8) и ФЧХ передаточной функции (рисунок 9.9).

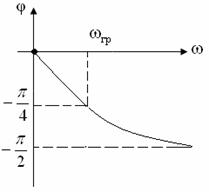
Рисунок 9.8 Рисунок 9.9
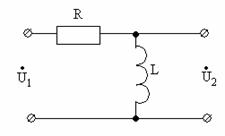 |
Рисунок 9.10

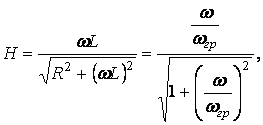 (9.7)
(9.7)
 (9.8)
(9.8)
![]() По выражениям (9.7) и (9.8) построим соответственно АЧХ (рисунок 9.11)
и ФЧХ передаточной функции (рисунок 9.12) для цепи
По выражениям (9.7) и (9.8) построим соответственно АЧХ (рисунок 9.11)
и ФЧХ передаточной функции (рисунок 9.12) для цепи ![]() .
.

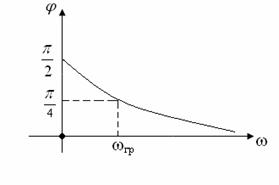
Рисунок 9.11 Рисунок 9.12
![]()
10 Лекция 10. Индуктивно связанные цепи
Цель лекции: изучение методов расчета электрических цепей с взаимной индуктивностью.
10.1 Индуктивно связанные элементы цепи
Два элемента индуктивно связаны, если изменение тока в одном элементе приводит к появлению э.д.с. в другом элементе. Возникающая э.д.с. называется э.д.с. взаимной индукции (рисунок 10.1,а,б).
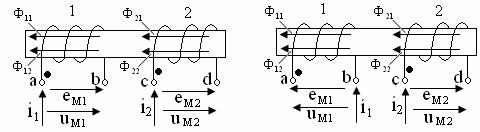
а) б)
Рисунок 10.1
При наличии тока i1 в первой катушке, витки первой катушки сцеплены с магнитным потоком самоиндукции Ф11, а витки второй катушки сцеплены с
магнитным потоком взаимной индукции Ф21. (рисунок 10.1).
Потокосцепления самоиндукции и взаимной индукции
первой и второй катушек ![]() ,
,
![]()
где w1,w2- число витков первой и второй катушек. При наличии
тока i2 во второй катушке, витки второй катушки сцеплены с магнитным
потоком самоиндукции Ф22, а витки первой катушки сцеплены с
магнитным потоком взаимной индукции Ф12. Потокосцепления
самоиндукции и взаимной индукции второй и первой катушек: ![]() ;
; ![]() , где w1,w2- число
витков первой и второй катушек. Индуктивность первой и второй катушек и их
взаимная индуктивность определяются по формулам
, где w1,w2- число
витков первой и второй катушек. Индуктивность первой и второй катушек и их
взаимная индуктивность определяются по формулам
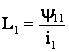 ,
, 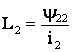 ,
,  ,
, 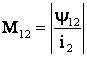 ,
, ![]() . (10.1)
. (10.1)
Степень индуктивной связи двух индуктивно связанных элементов цепи характеризуется коэффициентом связи
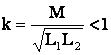 .
(10.2)
.
(10.2)
10.2 Электродвижущая сила (э.д.с.) и напряжение взаимной индукции
При изменении тока в одном из индуктивно связанных элементов в другом элементе возникает э.д.с. взаимной индукции ем и на его разомкнутых выводах появляется напряжение uм:
![]() ;
; ![]() . (10.3)
. (10.3)
Для определения знака ем и uм делают специальную разметку выводов индуктивно связанных элементов.
Два вывода принадлежащие двум разным индуктивно
связанным элементам называются одноимёнными и обозначаются одинаковыми
значками: **,![]() ,∆∆, если при одинаковом направлении токов в обоих
элементах относительно этих выводов магнитные потоки самоиндукции и взаимной
индукции в каждом элементе складываются.
,∆∆, если при одинаковом направлении токов в обоих
элементах относительно этих выводов магнитные потоки самоиндукции и взаимной
индукции в каждом элементе складываются.
При одинаковом
направлении тока ![]() в
элементе 2,
в
элементе 2, ![]() ,
,![]() в элементе 1 и тока
в элементе 1 и тока ![]() в элементе 1,
в элементе 1, ![]() ,
,![]() в элементе 2 (рисунок 10.1,а)
в элементе 2 (рисунок 10.1,а) ![]() ,
, ![]() , (10.4)
, (10.4)
![]() ,
, ![]() . (10.5)
. (10.5)
Напряжение взаимной индукции ![]() опережает ток
опережает ток ![]() на
на ![]() , напряжение взаимной индукции
, напряжение взаимной индукции ![]() опережает ток
опережает ток ![]() на
на ![]() .
.
При различном направлении
тока ![]() в
элементе 2,
в
элементе 2, ![]() ,
,![]() в элементе 1 и тока
в элементе 1 и тока ![]() в элементе 1,
в элементе 1, ![]() ,
,![]() в элементе 2 (рисунок 10.1,б)
в элементе 2 (рисунок 10.1,б) ![]() ,
, ![]() . (10.6)
. (10.6)
![]() ,
, ![]() . (10.7)
. (10.7)
Напряжение взаимной индукции ![]() отстаёт от тока
отстаёт от тока ![]() на
на ![]() , напряжение взаимной индукции
, напряжение взаимной индукции ![]() отстаёт от тока
отстаёт от тока ![]() на
на ![]() .
.
Величина ![]() называется сопротивлением взаимной
индукции,
называется сопротивлением взаимной
индукции,
величина![]() называется комплексным
сопротивлением взаимной индукции.
называется комплексным
сопротивлением взаимной индукции.
10.3 Последовательное соединение индуктивно связанных элементов цепи
Две индуктивно связанные катушки с сопротивлениями ![]() ,
, ![]() и индуктивностями
и индуктивностями ![]() соединены
последовательно. Возможны два вида включения: согласное и встречное.
соединены
последовательно. Возможны два вида включения: согласное и встречное.

а) б)
Рисунок 10.2
Согласное включение. При согласном включении токи в обоих элементах в любой момент времени направлены одинаково относительно одноименных выводов (рисунок 10.2,а). Поэтому потокосцепления самоиндукции и взаимной индукции в каждом элементе складываются
![]() ,
,![]() .
.
Индуктивность двух последовательно соединенных индуктивно связанных элементов при согласном включении равна
![]() (10.8)
(10.8)
Напряжение на зажимах первой и второй катушках в комплексной форме
![]() ,
(10.9)
,
(10.9)
![]() .
(10.10)
.
(10.10)
Напряжение на зажимах цепи (рисунок 10.2,а)
![]() (10.11)
(10.11)
где ![]() - входное сопротивление цепи при согласном
включении;
- входное сопротивление цепи при согласном
включении;
![]() ;
;
![]() ;
;
![]() .
.
Векторная диаграмма для согласного включения показана на рисунке 10.3,а.
Встречное включение. При встречном включении токи в
обоих элементах в любой момент времени направлены различно относительно
одноименных выводов (рисунок 10.2,б). Поэтому потокосцепления самоиндукции и
взаимной индукции в каждом элементе вычитаются ![]() ,
, ![]() . Индуктивность двух последовательно
соединенных индуктивно связанных элементов при встречном включении равна
. Индуктивность двух последовательно
соединенных индуктивно связанных элементов при встречном включении равна
![]() (10.12)
(10.12)
Напряжение на зажимах первой и второй катушках в комплексной форме
![]() , (10.13)
, (10.13)
![]() . (10.14)
. (10.14)
Напряжение на зажимах цепи (рисунок 10.2,б)
![]() (10.15)
(10.15)
где ![]() - входное сопротивление цепи при встречном
включении;
- входное сопротивление цепи при встречном
включении;
![]() ;
;
![]() .
.
Векторная диаграмма для встречного включения (при ![]() и
и ![]() ) показана на рисунке 10.3,б.
) показана на рисунке 10.3,б.
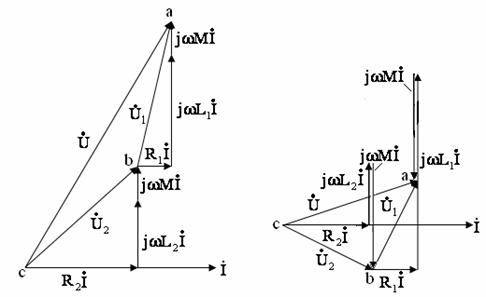
а) б)
Рисунок 10.3
10.4 Параллельное соединение индуктивно связанных элементов цепи
Две индуктивно
связанные катушки с сопротивлениями ![]() ,
, ![]() и индуктивностями
и индуктивностями ![]() соединены параллельно, причем
одноименные выводы присоединены к одному и тому же узлу (рисунок 10.4).
соединены параллельно, причем
одноименные выводы присоединены к одному и тому же узлу (рисунок 10.4).
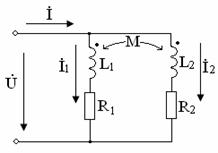
Рисунок 10.4
Запишем законы Кирхгофа для цепи (рисунок 10.4)
 } (10.16 )
} (10.16 )
где ![]() ,
, ![]() ,
,![]() .
.
Решая систему уравнений ( 10.16), получим

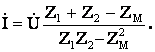 (10.17)
(10.17)
Входное сопротивление цепи
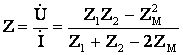 . (10.18)
. (10.18)
Если индуктивно связанные элементы присоединены к узлу разноименными выводами
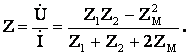 (10.19)
(10.19)
10.5 Расчёт разветвлённых цепей при наличии взаимной индуктивности
Для
разветвлённых цепей с индуктивными связями применяются законы Кирхгофа и метод
контурных токов. При составлении уравнений по второму закону Кирхгофа э.д.с.
взаимной индукции учитывается как соответствующее напряжение ![]() на элементе К,
обусловленное током в элементе S. Напряжение записывается с положительным знаком, если
направление обхода элемента К и положительное направление тока в элементе S одинаковы относительно
одноимённых выводов.
на элементе К,
обусловленное током в элементе S. Напряжение записывается с положительным знаком, если
направление обхода элемента К и положительное направление тока в элементе S одинаковы относительно
одноимённых выводов.
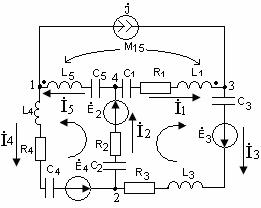
Рисунок 10.5
Запишем уравнения по второму закону Кирхгофа для схемы (рисунок 10.5).
 }(10.20)
}(10.20)
11 Лекция 11.Резонанс напряжений
Цель лекции: изучить резонансные явления в последовательном колебательном контуре.
11.1 Резонанс напряжений
Резонансом называется такой режим работы цепи, включающей в себя индуктивные и емкостные элементы, при котором ее входное сопротивление вещественно. Следствием этого является совпадение по фазе тока на входе цепи с входным напряжением.
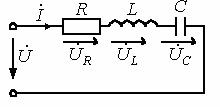
Рисунок 11.1
Для цепи на рисунке 11.1 имеет место
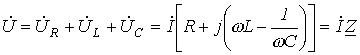
где
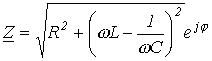 (11.1)
(11.1)
![]() (11.2)
(11.2)
В зависимости от соотношения величин ![]() и
и ![]() возможны три различных случая.
возможны три различных случая.
1. В цепи преобладает индуктивность, т.е. ![]() , а, следовательно,
, а, следовательно,
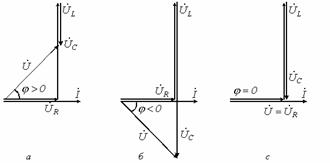 |
Рисунок 11.2
2. В цепи преобладает емкость, т.е. ![]() , а значит,
, а значит, ![]() . Этот случай отражает векторная
диаграмма на рисунке 11.2,б.
. Этот случай отражает векторная
диаграмма на рисунке 11.2,б.
3. ![]() - случай резонанса напряжений (рисунок 11.2,с).
- случай резонанса напряжений (рисунок 11.2,с).
Условие резонанса напряжений
![]() (11.3)
(11.3)
При этом, как следует из (11.1) и (11.2), ![]() .
.
При резонансе напряжений ток в цепи наибольший ![]() . Соответственно возрастанию тока
увеличиваются напряжения на индуктивном и емкостном элементах, которые могут во
много раз превысить величину напряжения источника питания. Физическая сущность
резонанса заключается в периодическом обмене энергией между магнитным полем
катушки индуктивности и электрическим полем конденсатора, причем сумма энергий
полей остается постоянной.
. Соответственно возрастанию тока
увеличиваются напряжения на индуктивном и емкостном элементах, которые могут во
много раз превысить величину напряжения источника питания. Физическая сущность
резонанса заключается в периодическом обмене энергией между магнитным полем
катушки индуктивности и электрическим полем конденсатора, причем сумма энергий
полей остается постоянной.
Как показывает анализ уравнения (11.3), режима резонанса можно добиться путем изменения параметров L и C, а также частоты. На основании (11.3) для резонансной частоты можно записать
 (11.4)
(11.4)
11.2 Добротность и затухание последовательного колебательного контура
Добротность Q определяется отношением напряжения на индуктивном (емкостном) элементе в режиме резонанса к входному напряжению
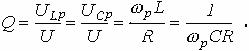 (11.5)
(11.5)
Добротность характеризует
“избирательные” свойства резонансного контура, в частности его полосу
пропускания ![]() .
.
Другим параметром резонансного контура является характеристическое сопротивление, связанное с добротностью соотношением
![]() (11.6)
(11.6)
или с учетом
(11.4) и (11.5) для ![]() можно
записать
можно
записать
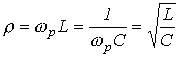 (11.7)
(11.7)
Тогда добротность
![]() .
(11.8)
.
(11.8)
Затухание величина обратная добротности
 .
(11.9)
.
(11.9)![]()
11.3 Частотные характеристики последовательного колебательного контура
Зависимость реактивного сопротивления
контура от частоты ![]() (рисунок
11.3), где
(рисунок
11.3), где ![]() ,
,
![]() .
.
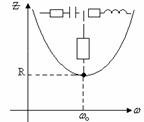

Рисунок 11.3 Рисунок 11.4
Зависимость
полного сопротивления контура от частоты ![]() ,
, ![]() (рисунок 11.4).До резонанса характер сопротивления контура
активно- емкостной, при резонансе активный, после резонанса активно-
индуктивный.
(рисунок 11.4).До резонанса характер сопротивления контура
активно- емкостной, при резонансе активный, после резонанса активно-
индуктивный.
Зависимость
![]() - амплитудно -
частотная характеристика (АЧХ),
- амплитудно -
частотная характеристика (АЧХ), ![]() (рисунок 11.5).
(рисунок 11.5).
Зависимости ![]()
![]()
![]() ,
,![]() ,
, ![]() (рисунок 11.6).
(рисунок 11.6).
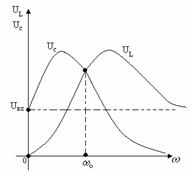
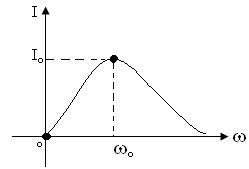
Рисунок 11.5 Рисунок 11.6
Зависимость ![]() - фазо- частотная характеристика (ФЧХ),
- фазо- частотная характеристика (ФЧХ), ![]() (рисунок 11.7).
(рисунок 11.7).
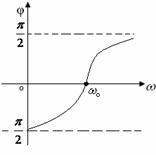
Рисунок 11.7
11.4 Последовательный колебательный контур при узкой полосе частот
В технике связи часто имеют дело с контурами высокой добротности, работающими в диапозоне частот, мало отличающихся от резонансной. В этом случае расчетным формулам можно придать более общий вид, если ввести в них новые независимые переменные.
Обобщенная расстройка ![]() , при резонансе (
, при резонансе (![]() )
)![]() , при
, при ![]()
![]() (11.10)
(11.10)
где ![]() (11.11)
(11.11)
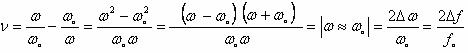 (11.13)
(11.13)
Абсолютная расстрой-ка: ![]()
Относительная расстройка .
.
Удобно для сравнения резонансных кривых пользоваться относительными единицами.
АЧХ в относительных единицах 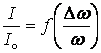 - (рисунок 11.8)
- (рисунок 11.8)
 (11.14)
(11.14)
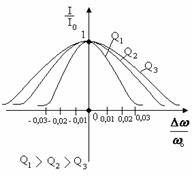 |
 |
||
где ![]()
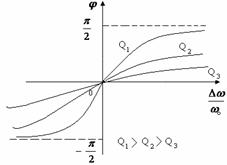
ФЧХ в относительных единицах (рисунок 11.9)
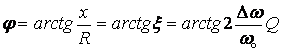 . (11.5)
. (11.5)
12. Лекция 12. Резонанс токов
Цель лекции: исследование резонансных явлений в параллельном колебательном контуре.
12.3 Резонанс токов
Резонанс токов возникает в параллельном колебательном контуре при условии, что входная реактивная проводимость
![]()
![]() ,
,![]() .
(12.1)
.
(12.1)
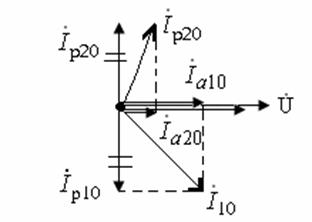

Рисунок 12.1 Рисунок 12.2
Учитывая (12.1), видно, что полная проводимость чисто активная
![]() (12.2)
(12.2)
При резонансе токов общий ток наименьший и совпадает с напряжением на входе (рисунок 12.2)
![]() , (12.3)
, (12.3)
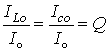 . (11.4)
. (11.4)
Добротность контура
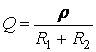 (12.5)
(12.5)
где ![]() -активное сопротивление контура;
-активное сопротивление контура;
![]() - полоса пропускания.
- полоса пропускания.
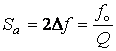 . (12.6)
. (12.6)
12.2 Резонансная частота параллельного колебательного контура
По условию резонанса токов ![]()
где 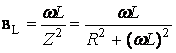 ,
,  (12.7)
(12.7)
Решая совместно (12.7), получим
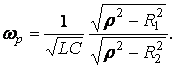 (12.8)
(12.8)
Резонанс токов возможен при ![]() , если:
, если:
а) R1>r; R2>r R1<r; R2<r;
б) R1=R2¹r или R1<< r и R2<< r.
В случае, когда R1=R2=r получаем неопределенность, т.е. может быть любое значение резонансной частоты.
Резонанс, не при какой частоте не возникает, если R1>r, а R2![]() r или наоборот.
r или наоборот.
12.3 Сопротивление параллельного колебательного контура
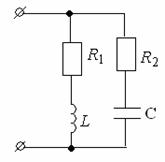
Рисунок 12.3
Эквивалентное сопротивление параллельного колебательного контура
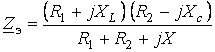 ;
;
где X=XL-XC ; R1<< XLR2 << Xc.
После преобразований, получим
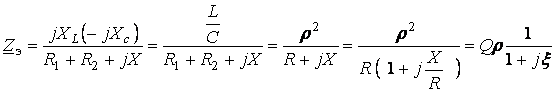 (12.9)
(12.9)
где R=R1+R2 активное сопротивление.
При резонансе ![]()
![]() (12.10)
(12.10)
Тогда в режиме, отличном от резонансного
 =
= (12.11)
(12.11)
Из выражения (12.11) видно, что
 ;
;  (12.12)
(12.12)
Модуль эквивалентного сопротивления
![]() (12.13)
(12.13)
Найдем ![]() для эквивалентной схемы
для эквивалентной схемы
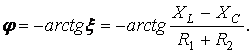
12.4 Влияние шунта на свойства параллельного колебательного контура
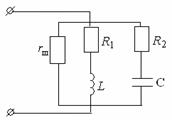
Рисунок 12.4
При резонансе активное сопротивление шунтированного контура
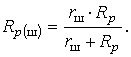
Учитывая (12.10), получим
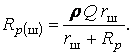
С другой стороны ![]() , т.е
, т.е 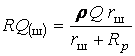 .
.
Таким образом добротность шунтированного контура
 (12.14)
(12.14)
12.5 Частотные характеристики идеального параллельного контура

Рисунок 12.5
Так как ![]() то в этом случае резонансная частота
то в этом случае резонансная частота ![]() .
.
Проводимость катушки ![]() , проводимость конденсатора
, проводимость конденсатора ![]()
![]() в=вL- вс
(рисунок 12.6).
в=вL- вс
(рисунок 12.6).


Рисунок 12.6 Рисунок 12.7
Так как ток I=/в/ U,
значит в соответствующем масштабе резонансная кривая тока это график ![]() .
.
Угол 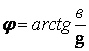 , график
, график ![]() приведен на рисунке 12.7
приведен на рисунке 12.7
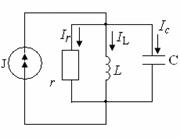 |
12.5 Идеальный колебательный контур,
шунтированный активным сопротивлением
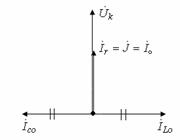
Рисунок 12.9
Для
рассматриваемого контура резонансная частота ![]()
Для резонансного режима векторная диаграмма привидена на рисунке 12.9
где ![]() .
.
Напряжение на контуре  .
.
В режиме резонанса ![]()
![]()
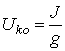 .
.
Частотные зависимости приведены на рисунках 12.10, 12.11
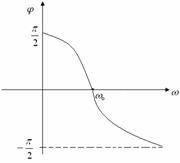 |
Рисунок 12.10

Рисунок 12.11
Полосой пропускания параллельного
колебательного контура называется полоса частот, в пределах которой напряжение
на контуре не падает ниже ![]() (рисунок 12.12).
(рисунок 12.12).
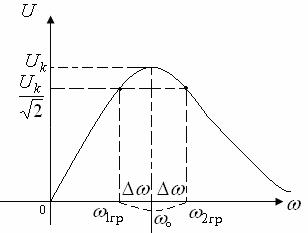
Рисунок 12.12
Полоса пропускания
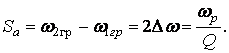 (12.15)
(12.15)
Добротность
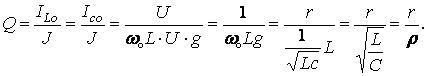 (12.16)
(12.16)
13 Лекция 13. Линейные электрические цепи при несинусоидальных периодических токах
Цель лекции: изучение методов расчета линейных электрических цепей при несинусоидальных периодических токах.
13.1 Несинусоидальные ЭДС, напряжения и токи
На практике э.д.с., напряжения и токи в большей или меньшей степени являются несинусоидальными. Это связано с тем, что реальные генераторы не обеспечивают, строго говоря, синусоидальной формы кривых напряжения, а с другой стороны, наличие нелинейных элементов в цепи обусловливает искажение формы токов даже при синусоидальных ЭДС источников. В радиотехнике, вычислительной технике и т.п. применяются генераторы периодических несинусоидальных импульсов.
В общем случае характер изменения несинусоидальных величин может быть периодическим, почти периодическим и непериодическим. В данной лекции будут рассматриваться цепи только с несинусоидальными периодическими э.д.с., напряжениями и токами.
В качестве примера (рисунок 13.1,а) представлена цепь с нелинейным резистором (НР), нелинейная вольт-амперная характеристика (ВАХ) которого обусловливает несинусоидальную форму тока i в цепи при синусоидальном напряжении u на ее входе (рисунок 13.1,б).
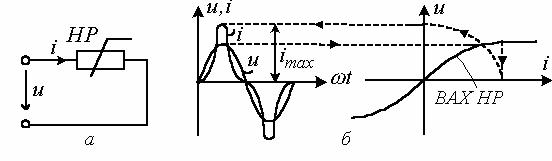
Рисунок 13.1
13.2 Разложение периодических несинусоидальных кривых в ряд Фурье
Периодическая
функция ![]()
где Т – период, удовлетворяющая условиям Дирихле, может быть разложена в тригонометрический ряд Фурье
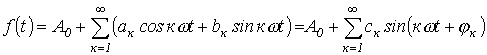 (13.1)
(13.1)
Здесь ![]() - постоянная составляющая или нулевая
гармоника;
- постоянная составляющая или нулевая
гармоника;
![]() - первая (основная) гармоника,
изменяющаяся с угловой частотой
- первая (основная) гармоника,
изменяющаяся с угловой частотой ![]()
где Т – период несинусоидальной периодической функции.
В выражении (13.1) ![]() . Коэффициенты А0, аК
и bK определяются
по формулам
. Коэффициенты А0, аК
и bK определяются
по формулам
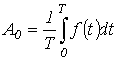 ,
, 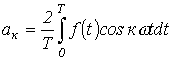 ,
, 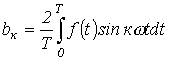 .
.
Свойства периодических кривых, обладающих симметрией:
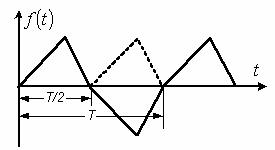
Рисунок 13.2
а) кривые, симметричные относительно оси абсцисс.
К данному типу относятся
кривые, удовлетворяющие равенству ![]() ( рисунок 13. 2). В их разложении отсутствуют
постоянная составляющая и четные гармоники, т.е.
( рисунок 13. 2). В их разложении отсутствуют
постоянная составляющая и четные гармоники, т.е. ![]() ;
;

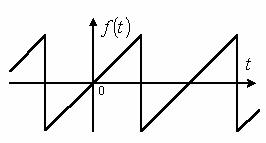
Рисунок 13.3 Рисунок 13.4
б) кривые, симметричные относительно оси ординат.
К
данному типу относятся кривые, для которых выполняется равенство ![]() ( рисунок 13.3). В их разложении
отсутствуют синусные составляющие, т.е.
( рисунок 13.3). В их разложении
отсутствуют синусные составляющие, т.е. ![]() ;
;
в) кривые, симметричные относительно начала координат.
К этому типу относятся кривые, удовлетворяющие
равенству![]() (рисунок
13.4). При разложении таких кривых отсутствуют постоянная и косинусные
составляющие, т.е.
(рисунок
13.4). При разложении таких кривых отсутствуют постоянная и косинусные
составляющие, т.е. ![]() .
.
13.3 Действующее значение периодической несинусоидальной переменной. Действующее значение периодического тока
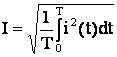 .
(13.2)
.
(13.2)
Разложим периодический несинусоидальный ток в тригонометрический ряд
![]() и подставим в формулу (13.2),
после преобразования получим
и подставим в формулу (13.2),
после преобразования получим 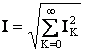 . (13.3)
. (13.3)
Аналогичные выражения имеют место для э.д.с. напряжения
 ,
, 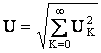 .
.
13.4 Мощность в цепях периодического несинусоидального тока
Выразим мгновенные значения напряжения и тока в виде тригонометрических рядов
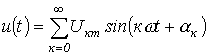
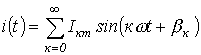 .
.
Тогда для активной мощности можно записать
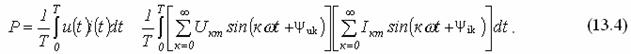
После интегрирования, получим:
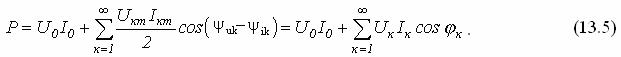
Таким образом, активная мощность несинусоидального тока равна сумме активных мощностей отдельных гармонических
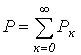 .
.
Аналогично для реактивной мощности можно записать
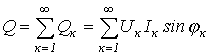 .
.
Полная мощность
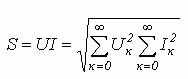 .
.
Для несинусоидального тока ![]() .
.
13.5 Расчёт цепей с несинусоидальными периодическими э.д.с., напряжениями, токами
Расчёт линейных электрических цепей несинусоидального тока распадается на три этапа:
а) разложение несинусоидальных э.д.с. и токов источников на постоянную и синусоидальные составляющие (т.е. в тригонометрический ряд Фурье);
б) применение принципа наложения и расчет токов и
напряжений в цепи для каждой из составляющих в отдельности. При расчете цепи с
постоянными составляющими э.д.с. и тока источника следует учитывать, что
индуктивное сопротивление равно 0 и индуктивность в эквивалентной схеме
заменяется короткозамкнутым участком, а ёмкостное равно![]() и ветвь с ёмкостью размыкается.
При расчете цепи для каждой синусоидальной составляющей э.д.с. и тока источника
можно пользоваться комплексным методом, но недопустимо сложение комплексных
токов и напряжений различных синусоидальных составляющих. Необходимо учитывать,
что индуктивное и емкостное сопротивления для различных частот неодинаковы,
индуктивное сопротивление для k-й гармоники равно:
и ветвь с ёмкостью размыкается.
При расчете цепи для каждой синусоидальной составляющей э.д.с. и тока источника
можно пользоваться комплексным методом, но недопустимо сложение комплексных
токов и напряжений различных синусоидальных составляющих. Необходимо учитывать,
что индуктивное и емкостное сопротивления для различных частот неодинаковы,
индуктивное сопротивление для k-й гармоники равно:![]() , а емкостное сопротивление для k-й гармоники
равно:
, а емкостное сопротивление для k-й гармоники
равно: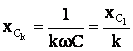 ;
;
в) совместное рассмотрение решений, полученных для каждой из составляющих. Причём суммируются только мгновенные значения составляющих токов и напряжений.
14 Лекция 14. Четырёхполюсники. Уравнения передачи четырёхполюсников
Цель лекции: изучение основ теории четырёхполюсников и получение навыков расчета линейных пассивных четырёхполюсников.
14.1 Основные определения и классификация четырёхполюсников
Четырёхполюсником называется электрическая цепь или её часть, имеющая две пары зажимов (полюсов), для подключения к источнику и приемнику электрической энергии. К четырёхполюсникам относятся трансформаторы, усилители, электрические фильтры, линии передачи электрической энергии и т.д. Таким образом, теория четырёхполюсников позволяет едиными методами анализировать системы различные по структуре и принципу действия.
Условное изображения четырёхполюсников показано на рисунке 14.1.
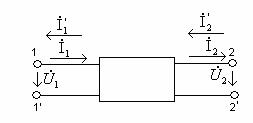
Рисунок 14.1
Пара зажимов ![]() называются первичными,
называются первичными, ![]() называются вторичными,
зажимы, к которым подключается источник называются входными, зажимы, к которым
подключается приёмник называются выходными. Положительные направления напряжений
и токов показано на рисунке 14.1.
называются вторичными,
зажимы, к которым подключается источник называются входными, зажимы, к которым
подключается приёмник называются выходными. Положительные направления напряжений
и токов показано на рисунке 14.1.
Активные и пассивные четырехполюсники.
Активные четырехполюсники содержат независимые и зависимые источники, пассивные четырехполюсники не содержат источников электрической энергии.
Линейные и нелинейные четырёхполюсники.
Линейные четырёхполюсники не содержат нелинейные элементы, нелинейные четырёхполюсники содержат нелинейные элементы.
Обратимые и необратимые четырёхполюсники.
Для обратимых четырёхполюсников выполняется теорема обратимости или взаимности: отношение напряжения на входе к току на выходе не меняется при перемене местами зажимов. Пассивные четырёхполюсники всегда обратимы.
Симметричные и несимметричные четырёхполюсники.
В симметричном четырёхполюснике перемена местами входных и выходных зажимов не изменяет напряжений и токов в цепи.
Схемы типовых пассивных четырёхполюсников показаны на рисунках 14.2 а), 14.2 б), 14.2 в),14.2 г).
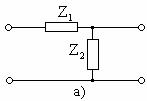
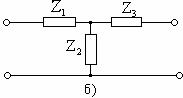
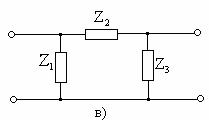
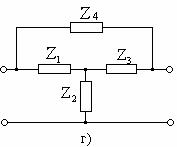
Рисунок 14.2
14.2 Уравнения передачи четырёхполюсника
Уравнения определяющие зависимость между ![]() называются уравнениями
передачи четырёхполюсника. Величины, связывающие в уравнениях передачи
напряжения и токи, называются параметрами четырёхполюсника.
называются уравнениями
передачи четырёхполюсника. Величины, связывающие в уравнениях передачи
напряжения и токи, называются параметрами четырёхполюсника.
Уравнения передачи в Y-параметрах
 }. (14.1)
}. (14.1)
Коэффициенты ![]() называются Y-параметрами
и имеют размерность проводимостей.
называются Y-параметрами
и имеют размерность проводимостей.
Уравнения передачи в Z-параметрах
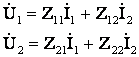 }. (14.2)
}. (14.2)
Коэффициенты ![]() называются Z-параметрами и
имеют размерность сопротивлений.
называются Z-параметрами и
имеют размерность сопротивлений.
Уравнения передачи в А- параметрах
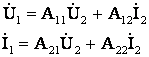 }. (14.3)
}. (14.3)
Коэффициенты ![]() называются А- параметрами или
обобщенными параметрами. А11,А22-безразмерные, А12
имеет размерность сопротивления, А21 имеет размерность проводимости.
называются А- параметрами или
обобщенными параметрами. А11,А22-безразмерные, А12
имеет размерность сопротивления, А21 имеет размерность проводимости.
Уравнения передачи в А - параметрах
применяют при передаче энергии через четырёхполюсник от зажимов ![]() к зажимам
к зажимам![]() .
.
При передаче энергии от зажимов ![]() к зажимам
к зажимам ![]() уравнения передачи для обратимых
четырёхполюсников могут быть записаны через А – параметры, при этом
коэффициенты А11 и А22 меняются местами
уравнения передачи для обратимых
четырёхполюсников могут быть записаны через А – параметры, при этом
коэффициенты А11 и А22 меняются местами
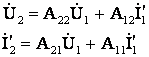 }. (14.4)
}. (14.4)
Уравнение передачи в Н – параметрах
 }. (14.5)
}. (14.5)
Системы Y-,Z-,A-,H-параметров
называются параметрами коэффициентами. Параметры – коэффициенты являются
комплексными величинами, определяются только схемой четырёхполюсника и её
элементами, между различными системами параметров – коэффициентов существует
однозначная связь. Для пассивного четырёхполюсника ![]() ,
, ![]() ,для А- параметров справедливо
соотношение
,для А- параметров справедливо
соотношение
∆А=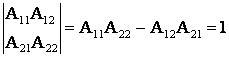 .
.
Для симметричного четырёхполюсника: А11=А22, Y11=-Y22, Z11=-Z22.
14.3 Входные сопротивления четырёхполюсника, параметры холостого
хода и короткого замыкания.
Если к зажимам![]() подключить произвольное
сопротивление нагрузки ZH2 (рисунок
14.3, а), то входное сопротивление четырёхполюсника со стороны зажимов
подключить произвольное
сопротивление нагрузки ZH2 (рисунок
14.3, а), то входное сопротивление четырёхполюсника со стороны зажимов ![]() будет равно
будет равно 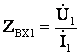 . Входное
сопротивление
. Входное
сопротивление ![]() можно
выразить через А-параметры
можно
выразить через А-параметры
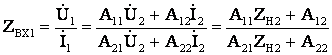 .
(14.6)
.
(14.6)
Аналогично определяется входное
сопротивление четырёхполюсника со стороны зажимов![]() , если к к зажимам
, если к к зажимам ![]() подключить произвольное
сопротивление нагрузки ZH1 (рисунок
14.3,б)
подключить произвольное
сопротивление нагрузки ZH1 (рисунок
14.3,б)
 . (14.7)
. (14.7)
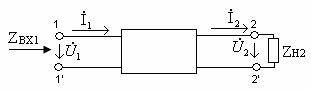
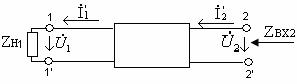
а) б)
Рисунок 14.3
Параметрами холостого хода (ХХ) и
короткого замыкания (КЗ) называются ![]() и
и ![]() при разомкнутых и замкнутых накоротко
зажимах четырёхполюсника.
при разомкнутых и замкнутых накоротко
зажимах четырёхполюсника.
Входные
сопротивления четырёхполюсника в режиме холостого хода на зажимах ![]() ( ZH2=
( ZH2=![]() , I2=0) и
, I2=0) и ![]() ( ZH1=
( ZH1=![]() , I1=0) соответственно равны
, I1=0) соответственно равны
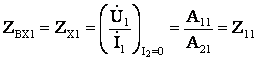 ,
,  .
.
При коротком замыкании зажимов ![]() (ZH2=0, U2=0) и
(ZH2=0, U2=0) и ![]() (ZH1=0, U1=0)
входные сопротивления четырёхполюсника, соответственно, равны
(ZH1=0, U1=0)
входные сопротивления четырёхполюсника, соответственно, равны
 ,
,  .
.
Параметры ХХ и КЗ удовлетворяют
соотношению: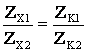 ,
т.е.только три параметра из четырёх независимы и их достаточно для составления
уравнений передачи пассивных четырёхполюсников, из параметров ХХ и КЗ может
быть получена любая система параметров-коэффициентов пассивных
четырёхполюсников. Для симметричных четырёхполюсников А11=А22,
ZX1=ZX2, ZK1=ZK2.
,
т.е.только три параметра из четырёх независимы и их достаточно для составления
уравнений передачи пассивных четырёхполюсников, из параметров ХХ и КЗ может
быть получена любая система параметров-коэффициентов пассивных
четырёхполюсников. Для симметричных четырёхполюсников А11=А22,
ZX1=ZX2, ZK1=ZK2.
15 Лекция 15. Характеристические параметры четырёхполюсника. Уравнения четырёхполюсника с гиперболическими функциями
Цель лекции: изучение характеристических параметров четырехполюсника, получение навыков расчета режимов работы линейных пассивных четырёхполюсников с использованием характеристических параметров.
Характеристические параметры четырёхполюсника
К характеристическим параметрам четырёхполюсника относятся характеристические сопротивления и характеристическая постоянная передачи.
15.1 Характеристические сопротивления четырёхполюсника
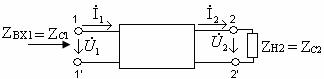
а)
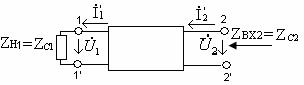
б)
Рисунок 15.1
Характеристическими сопротивлениями
четырёхполюсника называется такая пара сопротивлений ![]() и
и ![]() , которая удовлетворяет условию:
, которая удовлетворяет условию:
при
![]() имеем
имеем ![]() и при
и при ![]() имеем
имеем ![]() (рисунки 15.1а,15.1б).
(рисунки 15.1а,15.1б).
![]() можно
выразить через А- параметры и параметры ХХ и КЗ
можно
выразить через А- параметры и параметры ХХ и КЗ
 ,
, 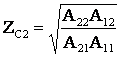 , (15.1)
, (15.1)
![]() ,
, ![]() (152)
(152)
Для симметричного четырёхполюсника: 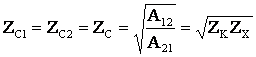 .
.
Согласованное включение четырёхполюсника
Режим, при котором внутреннее
сопротивление генератора выбрано равным ![]() , а сопротивление нагрузки
, а сопротивление нагрузки ![]() (рисунок15.2)
называется режимом согласованного включения. Режим согласованного включения
наиболее благоприятен при передаче сигнала.
(рисунок15.2)
называется режимом согласованного включения. Режим согласованного включения
наиболее благоприятен при передаче сигнала.
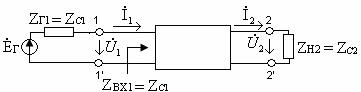
Рисунок 15.2
Режим согласованного включения
симметричного четырёхполюсника (рисунок 15.3) ![]() ;
; ![]() .
.
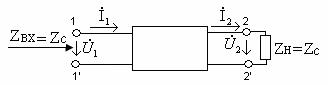
Рисунок 15.3
Характеристическая постоянная передачи четырёхполюсника
Характеристическая постоянная передачи четырёхполюсника определяется в режиме согласованного включения и равна
 , (15.3)
, (15.3)
так как ![]() и
и ![]() получим
получим
 .
(15.4) Характеристическую постоянную передачи
можно выразить через
.
(15.4) Характеристическую постоянную передачи
можно выразить через
А-параметры и параметры ХХ и КЗ
![]() ,
, ![]() . (15.5)
. (15.5)
Подставим в уравнение (15.3)![]() ,
,
получим
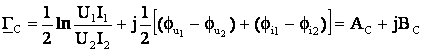 (15.6)
(15.6)
где АС –характеристическое (собственное) ослабление четырёхполюсника
 (15.7)
(15.7)
единица измерения АС в масштабе натуральных логарифмов называется непером (Нп). На практике принято измерять АС в децибелах (дБ).
ВС – фазовая постоянная четырёхполюсника,
измеряется в радианах или градусах ![]() (15.8)
(15.8)
![]() симметричного четырёхполюсника
симметричного четырёхполюсника 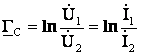 ,
,
 ,
, ![]() .
.
15.2 Уравнения передачи четырёхполюсника с гиперболическими функциями
А- параметры могут быть выражены через характеристические параметры
![]()
![]() (15.9)
(15.9)
Подставим (15.9) в уравнение передачи в А-параметрах (14.3) и получим уравнение передачи с гиперболическими функциями
![]() ,
,
![]() . (15.10)
. (15.10)
Для симметричного четырёхполюсника (![]() ) уравнение передачи с
гиперболическими функциями имеет вид
) уравнение передачи с
гиперболическими функциями имеет вид
![]() ,
, ![]() .
(15.11)
.
(15.11)
15.3 Характеристические параметры Т- и П- образных симметричных четырёхполюсников (рисунки 15.4 а, 15.4 б).
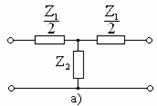
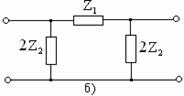
Рисунок 15.4
Для Т- и П-образных симметричных
четырёхполюсников ![]()
Характеристические сопротивления для Т-и П- образных схем
![]() ,
, ![]() . (15.12)
. (15.12)
16 Лекция 16. Электрические частотные фильтры и их классификация
Цель лекции: изучение частотных электрических фильтров и их принципа действия.
16.1 Электрическим фильтром называется четырехполюсник, устанавливаемый между источником питания и нагрузкой и служащий для беспрепятственного (с малым ослаблением) пропускания токов одних частот и задержки (или пропускания с большим ослаблением) токов других частот.
Диапазон частот, пропускаемых фильтром без ослабления (или с малым ослаблением), называется полосой пропускания или полосой прозрачности; диапазон частот, пропускаемых с большим ослаблением, называется полосой затухания или полосой задерживания. Качество фильтра считается тем выше, чем ярче выражены его фильтрующие свойства.
Таблица 16.1- Классификация фильтров
|
Название фильтров |
Диапазон пропускаемых частот |
|||
|
Низкочастотные фильтры (НЧФ) |
|
|||
|
Высокочастотные фильтры (ВЧФ) |
|
|||
|
Полосовые фильтры (ПФ) |
|
|||
|
Заграждающие или режекторные фильтры (ЗФ или РФ) |
где |
Частота ![]() называется частотой среза или граничной
частотой.
называется частотой среза или граничной
частотой.
Фильтры используются как в радиотехнике и технике связи, где имеют место токи достаточно высоких частот, так и в силовой электронике и электротехнике.
Применяются: пассивные LC-фильтры и RC-фильтры ; активные RC-фильтры (АRC-фильтры); цифровые фильтры.
16.2 RC- фильтры
В
устройствах техники связи широко применяются активные RC- фильтры (ARC-фильтры).
Элементной базой ARC-фильтров являются: пассивные (резисторы и
конденсаторы) и активные элементы. В качестве активного элемента обычно служит
операционный усилитель (ОУ). Рассмотрим пассивные RC- фильтры. Для
всех RC- фильтров в рабочей зоне коэффициент ослабления ![]() .
.
Для
НЧФ (рисунок 16.1) рабочая зона находится в диапазоне частот от ![]() до
до![]() , при
, при ![]() , а =3дБ (рисунок 16.2).
Коэффициент ослабления определяется по формуле
, а =3дБ (рисунок 16.2).
Коэффициент ослабления определяется по формуле
![]() . (16.1)
. (16.1)
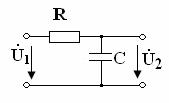
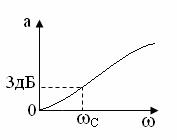
Рисунок 16.1 Рисунок 16.2
Для
ВЧФ (рисунок 16.3) рабочая зона находится в диапазоне частот от ![]() , при которой, а =3дБ,
до
, при которой, а =3дБ,
до ![]() , когда
, когда ![]() (рисунок 16.4).
(рисунок 16.4).
Коэффициент ослабления определяется по формуле
![]() . (16.2)
. (16.2)

Рисунок 16.3 Рисунок 16.4
Для ПФ (рисунок 16.5) минимальное значение
коэффициента ослабления имеет место при ![]() (рисунок 16.6) , коэффициент ослабления
определяется по формуле
(рисунок 16.6) , коэффициент ослабления
определяется по формуле
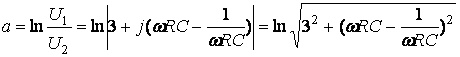 . (16.3)
. (16.3)
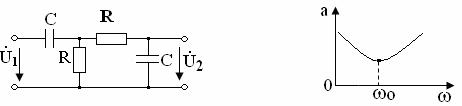
Рисунок 16.5 Рисунок 16.6
16.3 Пассивные реактивные LC-фильтры. Фильтры типа К.
Фильтры, у которых произведение их комплексных сопротивлений во всём диапазоне частот не зависит от частоты, называются фильтрами типа К.
К фильтрам типа К относятся низкочастотные, высокочастотные, полосовые и заграждающие реактивные LC-фильтры. Рассмотрим пассивные реактивные LC-фильтры, составленные из идеальных катушек индуктивности и конденсаторов, т.е. элементов соответственно с нулевыми активными сопротивлением и проводимостью.
Фильтрующие свойства четырехполюсников обусловлены возникающими в них резонансными режимами – резонансами токов и напряжений. Фильтры обычно собираются по симметричной Т - или П-образной схеме.

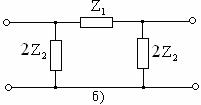
Рисунок 16.7
Симметричный фильтр определяется двумя
параметрами характеристическим сопротивлением![]() и постоянной передачи
и постоянной передачи ![]() , где
, где ![]() -коэффициент
ослабления,
-коэффициент
ослабления, ![]() -
коэффициент фазы. Для фильтров с согласованной нагрузкой (
-
коэффициент фазы. Для фильтров с согласованной нагрузкой (![]() при всех частотах)
при всех частотах)
![]()
 . (16.4)
. (16.4)
Так как ![]() - реактивные сопротивления, то
- реактивные сопротивления, то![]() действительная величина,
отсюда получим
действительная величина,
отсюда получим 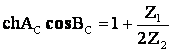 ,
(16.5)
,
(16.5)
![]() . (16.6)
. (16.6)
16.4 Полоса пропускания и полоса задерживания реактивного LC- фильтра
При
согласованной нагрузки фильтра (![]() )
)
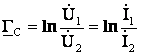 и
и  . (16.6)
. (16.6)
В идеальном случае в полосе
пропускания (прозрачности) фильтра ![]() ,
, ![]() отсюда следует, что в полосе пропускания
отсюда следует, что в полосе пропускания ![]() (формула 16.6).
(формула 16.6).
Выражение
(16.5) запишется в виде ![]() и
и 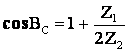 . (16.7)
. (16.7)
Так как ![]() , то
, то 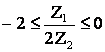 . (16.8)
. (16.8)
Из условия (16.7) следует, что сопротивления ![]() должны
иметь различный характер: а)
должны
иметь различный характер: а) ![]() или б)
или б) ![]() .
.
Выражение (16.8) можно записать в виде 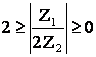 , отсюда получим условие для граничных
частот
, отсюда получим условие для граничных
частот 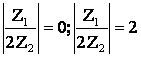 .
(16.9)
.
(16.9)
Условия для полосы пропускания и полосы задерживания.
Полоса
пропускания ![]()
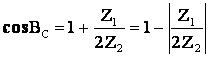 . (16.10)
. (16.10)
Полоса
задерживания ![]()
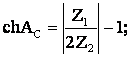
![]() . (16.11)
. (16.11)
17 Лекция 17. Пассивные реактивные LC-фильтры
Цель лекции: изучение принципа действия низкочастотных, высокочастотных, полосовых и задерживающих пассивных реактивных LC-фильтров.
17.1 Низкочастотные фильтры
Т-и П- образные схемы низкочастотного фильтра приведены на рисунке17.1.


Рисунок 17.1
Найдём произведение сопротивлений ![]() и
и ![]() :
: ![]() (17.1)
(17.1)
где 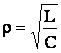 - номинальное характеристическое
сопротивление.
- номинальное характеристическое
сопротивление.
Как видно из выражения (17.1), НЧФ являются фильтрами типа К.
Определим 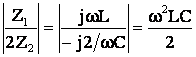 . (17.
2)
. (17.
2)
Условия для полосы пропускания и полосы задерживания НЧФ получим из (16.10) и (16.11) с учетом выражения (17.2).
Полоса пропускания ![]()
 . (17. 3)
. (17. 3)
Полоса задерживани ![]()
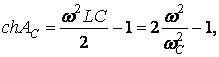
![]() . (17. 4)
. (17. 4)
Из условий (16.9) 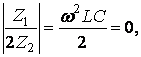 и
и 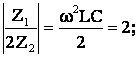 получим граничные
частоты
получим граничные
частоты ![]() и
и 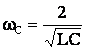 .
.
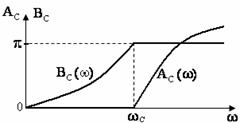 |
АЧХ
Рисунок 17.2
Условия для полосы пропускания и полосы
задерживания и частотные характеристики ![]() и
и ![]() получены при согласовании фильтра с
нагрузкой (
получены при согласовании фильтра с
нагрузкой (![]() )
во всем диапазоне частот.
)
во всем диапазоне частот.
17.2 Характеристические сопротивления НЧФ
В лекции 15 были получены характеристические сопротивления для Т-и П- образных симметричных схем
![]() ,
, ![]() .
.
Отсюда получим характеристические сопротивления для НЧФ
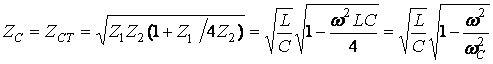 , (17.5)
, (17.5)
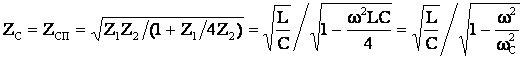 . (17.6)
. (17.6)
Как видно из (17.5) и (17.6), характеристические
сопротивления зависят от частоты, при ![]() :
: ![]() , при
, при ![]() :
:![]() ,
, ![]() .
.
В полосе пропускания характеристические сопротивления ![]() активные.
При согласовании фильтра с нагрузкой(
активные.
При согласовании фильтра с нагрузкой(![]() ) входное сопротивление
фильтра
) входное сопротивление
фильтра ![]() ,
отсюда следует, что напряжение и ток на входе фильтра совпадают по фазе
и в полосе пропускания фильтр работает в режиме резонанса.
,
отсюда следует, что напряжение и ток на входе фильтра совпадают по фазе
и в полосе пропускания фильтр работает в режиме резонанса.
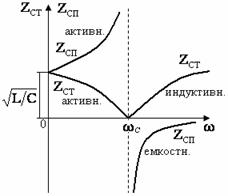 |
Зависимость
Рисунок 17.3
17.3 Высокочастотные фильтры
Т-и П- образные схемы высокочастотного фильтра приведены
на рисунке 17.4.
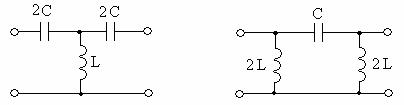
Рисунок 17.4
Найдём произведение сопротивлений ![]() и
и ![]() :
: ![]() (17.7)
(17.7)
где 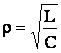 - номинальное характеристическое
сопротивление.
- номинальное характеристическое
сопротивление.
Как видно из выражения (17.7), ВЧФ являются фильтрами типа К.
Определим 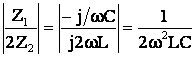 . (17.8)
. (17.8)
Условия для полосы пропускания и полосы задерживания ВЧФ получим из (16.10) и (16.11) с учетом выражения (17. 8).
Полоса пропускания ![]()
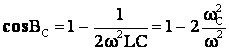 . (17. 9)
. (17. 9)
Полоса задерживания ![]()
 ,
,
![]() . (17.10)
. (17.10)
Из условий (16.9) 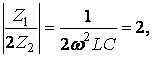
 и получим граничные частоты
и получим граничные частоты 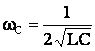 и
и ![]() .
.
 |
 |
||
АЧХ
Рисунок 17.5 Рисунок 17.6
Условия для полосы пропускания и полосы задерживания и
частотные характеристики ![]() и
и ![]() получены при согласовании фильтра с
нагрузкой (
получены при согласовании фильтра с
нагрузкой (![]() )
во всем диапазоне частот.
)
во всем диапазоне частот.
17.4 Характеристические сопротивления ВЧФ
В лекции 15 были получены характеристические сопротивления для Т-и П- образных симметричных схем
![]() .
.
Отсюда получим характеристические сопротивления для ВЧФ
![]() , (17.11)
, (17.11)
![]() . (17.12)
. (17.12)
Как видно из (17.11) и (17.12), характеристические
сопротивления зависят от частоты, при ![]() :
: ![]() , при
, при ![]() :
:![]() ,
, ![]() .
.
В полосе пропускания характеристические сопротивления ![]() активные. При
согласовании фильтра с нагрузкой(
активные. При
согласовании фильтра с нагрузкой(![]() ) входное сопротивление фильтра
) входное сопротивление фильтра ![]() , отсюда следует, что
напряжение и ток на входе фильтра совпадают по фазе и в полосе пропускания
фильтр работает в режиме резонанса.
, отсюда следует, что
напряжение и ток на входе фильтра совпадают по фазе и в полосе пропускания
фильтр работает в режиме резонанса.
Зависимость ![]() ,
, ![]() представлена на рисунке 17.6.
представлена на рисунке 17.6.
17.5 Полосовые фильтры
 |
Полоса пропускания полосового фильтра лежит в
диапазоне частот от ![]() до
до
![]() . Полосовой
фильтр может быть образован путём соединения низкочастотного фильтра с полосой
пропускания от 0 до
. Полосовой
фильтр может быть образован путём соединения низкочастотного фильтра с полосой
пропускания от 0 до ![]() и
высокочастотного фильтра с полосой пропускания от
и
высокочастотного фильтра с полосой пропускания от ![]() до
до ![]() , причем
, причем ![]() >
>![]() .
.
Т-и П- образные схемы полосового фильтра приведены на рисунке 17.7.
Выберем ![]() , тогда при частоте
, тогда при частоте ![]() в продольной
ветви наступает резонанс напряжений, в поперечной резонанс токов. Поэтому
частота
в продольной
ветви наступает резонанс напряжений, в поперечной резонанс токов. Поэтому
частота ![]() принадлежит
полосе пропускания. Частотные характеристики полосового фильтра представлены на
рисунке 17.8.
принадлежит
полосе пропускания. Частотные характеристики полосового фильтра представлены на
рисунке 17.8.
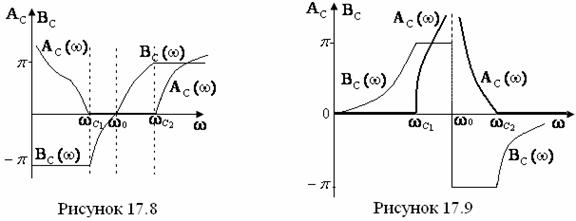 |
17.6 Заграждающие или режекторные фильтры
Полоса пропускания заграждающего фильтра лежит в
диапазоне частот от 0 до![]() и от
и от![]() до
до![]() . Заграждающие фильтры могут быть получены
путём совмещения свойств НЧФ и ВЧФ. Т-и П- образные схемы заграждающего фильтра
приведены на рисунке 17.10.
. Заграждающие фильтры могут быть получены
путём совмещения свойств НЧФ и ВЧФ. Т-и П- образные схемы заграждающего фильтра
приведены на рисунке 17.10.
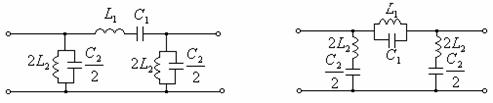 |
Рисунок 17.10
Частотные характеристики ЗФ представлены на рисунке 17.9.
В заключение необходимо отметить, что для улучшения характеристик фильтров всех типов их целесообразно выполнять в виде цепной схемы, представляющей собой каскадное включенные четырехполюсники. При обеспечении согласованного режима работы всех n звеньев схемы.
Список литературы
1.Бакалов В. П., Дмитриков В.Ф., Крук Б.Е. Основы теории цепей: Учебник для вузов. – М.: Радио и связь, 2000.-592с.
2.Демирчян К.С., Нейман Л.Р., Коровкин Н.В., Чечурин В.Л. Теоретические основы электротехники. - т.1. – Санкт-Петербург, Питер, 2003.-463с.
3. Демирчян К.С., Нейман Л.Р., Коровкин Н.В., Чечурин В.Л. Теоретические основы электротехники. - т.2. – Санкт-Петербург, Питер, 2003.-576с.
4.Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. – М.: Энергоатомиздат, 1989.-528с.
5.Шебес М. Р., Каблукова М. В. Задачник по теории линейных электрических цепей. – М.: Высшая школа, 1990.-544с.