АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра теоретических основ электротехники
Теория
электрических цепей 2
Конспект лекций
(для специальност ей 050719 –
Радиотехника, электроника и телекоммуникации, 050704 - Вычислительная техника и
программное обеспечение)
Алматы 2006
СОСТАВИТЕЛИ: З.И. Жолдыбаева, Е.Х.Зуслина, Т.И.
Коровченко. Теория электрических цепей 2. Конспект лекций (для студентов всех форм обучения специальностей 050719 – Радиотехника, электроника и
телекоммуникации, 050704 - Вычислительная техника и программное обеспечение ). – Алматы: АИЭС, 2006.- 52с.
Конспект лекции содержит 9
лекций по 3 разделам: переходные процессы, нелинейные электрические цепи и цепи
с распределенными параметрами.
Конспект лекций
предназначен для студентов специальности 050704 - Вычислительная техника и
программное обеспечение
Ил.32 ,
табл.1 , библиогр.- 5 назв.
Рецензент: канд. техн. наук, доцент каф. ТКС Г.С. Казиева.
Печатается по плану издания Алматинского института
энергетики и связи на 2006 г.
Ó Алматинский институт энергетики и связи, 2006г.
Содержание
Введение………………………………………………...………………………………4
1 Лекция 1………….………………………………...………………………………….5
2 Лекция 2…………………………….…………………………………………………8
3 Лекция………………………………………………………………………………..11
4 Лекция………………………………………………………………………………..14
5 Лекция 5….…………………………………………………………………………..15
6 Лекция 6….…………………………………………………………………………..20
7 Лекция 7….…………………………………………………………………………..23
8 Лекция 8………………………………………………………………………….…..27
9 Лекция 9………...……………………………………………………………………34
Список литературы……………………...…………...………………………..............41
Введение
Дисциплина «Теория электрических
цепей 2» является основным базовым
обязательным курсом для подготовки бакалавров в области радиотехники,
вычислительной техники и связи. Назначение дисциплины заключается в изучении и
описании как с качественной, так и с количественной стороны электромагнитных
процессов и явлений, происходящих в различного рода радиотехнических
установках, устройствах вычислительной техники и связи.
Предлагаемый конспект лекций включает
три основных раздела: переходные процессы, нелинейные электрические цепи и
цепи с распределенными параметрами.
В первом разделе рассмотрены
следующие методы расчета переходных процессов: классический, операторный,
спектральный и интеграл Дюамеля.
Во втором разделе рассмотрены
нелинейные электрические цепи постоянного тока.
В третьем разделе рассмотрены
цепи с распределенными параметрами.
Конспект лекций предназначен для студентов,
обучающихся по специальностям 050719 – Радиотехника, электроника и
телекоммуникации, 050704 - Вычислительная техника и программное обеспечение.
1 Лекция 1. Переходные процессы в линейных
электрических цепях с сосредоточенными
параметрами
Цель лекции: изучение классического метода
расчета переходных процессов в линейных электрических цепях.
Содержание:
- переходный, принужденный и свободный
режимы;
- законы коммутации;
- выражение свободных составляющих общего
решения однородных дифференциальных уравнений;
- постоянная времени цепи.
При всех изменениях в электрической цепи: включении, выключении,
коротком замыкании, колебаниях величины какого-либо параметра и т.п. – в ней
возникают переходные процессы, которые не могут протекать мгновенно, так как
невозможно мгновенное изменение энергии, запасенной в электромагнитном поле
цепи. Таким образом, переходный процесс обусловлен несоответствием величины
запасенной энергии в магнитном поле катушки и электрическом поле конденсатора
ее значению для нового состояния цепи.
При переходных процессах могут возникать большие перенапряжения,
сверхтоки, электромагнитные колебания, которые могут нарушить работу устройства
вплоть до выхода его из строя. С другой стороны, переходные процессы находят
полезное практическое применение, например, в различного рода электронных
генераторах. Все это обусловливает необходимость изучения методов анализа
нестационарных режимов работы цепи.
Классический
метод расчета
Классический метод расчета переходных
процессов заключается в непосредственном интегрировании дифференциальных уравнений,
описывающих изменения токов и напряжений на участках цепи в переходном
процессе.
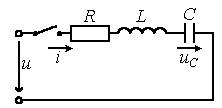
Рисунок 1.1
Для последовательной цепи, содержащей
линейные резистор R, катушку индуктивности L и конденсатор С, при ее
подключении к источнику с напряжением u (рисунок 1.1) можно записать
|
|
(1.1) |
Подставив в (1.1) значение тока через
конденсатор
![]()
получим линейное дифференциальное уравнение второго порядка
относительно ![]()
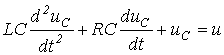
В общем случае уравнение, описывающее переходный процесс в цепи с
n независимыми накопителями энергии,
имеет вид
|
|
(1.2) |
где х – искомая функция времени (напряжение, ток, потокосцепление
и т.п.);
![]() - известное возмущающее воздействие (напряжение и (или)
ток источника электрической
энергии);
- известное возмущающее воздействие (напряжение и (или)
ток источника электрической
энергии);
![]() - к-й постоянный коэффициент, определяемый параметрами цепи.
- к-й постоянный коэффициент, определяемый параметрами цепи.
Как известно из математики, общее решение уравнения (1.2)
представляет собой сумму частного решения исходного неоднородного уравнения и
общего решения однородного уравнения, получаемого из исходного путем
приравнивания его левой части к нулю. Частное решение ![]() уравнения (1.2) определяется видом функции
уравнения (1.2) определяется видом функции![]() , стоящей в его правой части, и поэтому называется принужденной составляющей. Для цепей с
заданными постоянными или периодическими напряжениями (токами) источников
принужденная составляющая определяется путем расчета установившегося режима
работы схемы после коммутации любым из рассмотренных ранее методов расчета
линейных электрических цепей.
, стоящей в его правой части, и поэтому называется принужденной составляющей. Для цепей с
заданными постоянными или периодическими напряжениями (токами) источников
принужденная составляющая определяется путем расчета установившегося режима
работы схемы после коммутации любым из рассмотренных ранее методов расчета
линейных электрических цепей.
Вторая составляющая ![]() общего решения х уравнения (1.2) – решение (1.2) с нулевой
правой частью – соответствует режиму, когда внешние (принуждающие) силы
(источники энергии) на цепь непосредственно не воздействуют. Влияние источников
проявляется здесь апосредованно через энергию, запасенную в полях катушек
индуктивности и конденсаторов. Данный режим работы схемы называется свободным,
а переменная
общего решения х уравнения (1.2) – решение (1.2) с нулевой
правой частью – соответствует режиму, когда внешние (принуждающие) силы
(источники энергии) на цепь непосредственно не воздействуют. Влияние источников
проявляется здесь апосредованно через энергию, запасенную в полях катушек
индуктивности и конденсаторов. Данный режим работы схемы называется свободным,
а переменная ![]() - свободной
составляющей.
- свободной
составляющей.
В соответствии с вышесказанным общее решение уравнения (1.2) имеет
вид
|
|
(1.3) |
Начальные условия. Законы коммутации
В соответствии с определением свободной составляющей ![]() в ее выражении имеют
место постоянные интегрирования
в ее выражении имеют
место постоянные интегрирования![]() , число которых равно порядку дифференциального уравнения.
Постоянные интегрирования находятся из начальных условий, которые принято
делить на независимые и зависимые.
, число которых равно порядку дифференциального уравнения.
Постоянные интегрирования находятся из начальных условий, которые принято
делить на независимые и зависимые.
К независимым начальным
условиям относятся потокосцепление (ток) для катушки индуктивности и заряд
(напряжение) на конденсаторе в момент времени ![]() (момент
коммутации). Независимые начальные условия определяются на основании законов
коммутации.
(момент
коммутации). Независимые начальные условия определяются на основании законов
коммутации.
Первый закон коммутации
– в ветви
с катушкой индуктивности ток в момент коммутации сохраняет
свое докоммутационное значение и в дальнейшем начинает изменяться с него ![]() .
.
Второй закон
коммутации – напряжение на конденсаторе в момент
коммутации сохраняет свое докоммутационное значение и в дальнейшем начинает
изменяться с него ![]() .
.
Зависимыми начальными условиями называются
значения остальных токов и напряжений, а также производных от искомой функции в
момент коммутации, определяемые по независимым начальным условиям при помощи
уравнений, составляемых по законам Кирхгофа для ![]() . Необходимое число начальных условий равно числу постоянных
интегрирования.
. Необходимое число начальных условий равно числу постоянных
интегрирования.
Корни
характеристического уравнения. Постоянная времени
Выражение свободной составляющей ![]() общего решения х
дифференциального уравнения определяется видом корней характеристического
уравнения
общего решения х
дифференциального уравнения определяется видом корней характеристического
уравнения ![]()
Таблица 1.1 -
Выражения свободных составляющих общего решения
|
Вид корней характеристического
уравнения |
Выражение свободной составляющей |
|
Корни |
|
|
Корни |
|
|
Пары
комплексно-сопряженных корней |
|
Необходимо помнить, что, поскольку в линейной цепи с течением
времени свободная составляющая затухает, вещественные части корней
характеристического уравнения не могут быть положительными.
При вещественных корнях ![]() монотонно затухает, и
имеет место апериодический переходный
процесс. Наличие пары комплексно - сопряженных корней
обусловливает появление затухающих синусоидальных колебаний (колебательный переходный процесс).
монотонно затухает, и
имеет место апериодический переходный
процесс. Наличие пары комплексно - сопряженных корней
обусловливает появление затухающих синусоидальных колебаний (колебательный переходный процесс).
Поскольку физически колебательный процесс связан с периодическим
обменом энергией между магнитным полем катушки индуктивности и электрическим
полем конденсатора, комплексно-сопряженные корни могут иметь место только для
цепей, содержащих оба типа накопителей. Быстроту затухания колебаний принято
характеризовать отношением
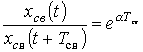 ,
,
которое называется декрементом
колебания, или натуральным логарифмом этого отношения
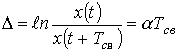 ,
,
называемым логарифмическим
декрементом колебания, где ![]() ,
, ![]() - угловая частота собственных или свободных колебаний.
- угловая частота собственных или свободных колебаний.
Важной характеристикой при исследовании переходных процессов
является постоянная времени ![]() , определяемая для цепей первого порядка, как
, определяемая для цепей первого порядка, как
 ,
,
где р – корень характеристического уравнения.
Постоянную времени можно интерпретировать как временной интервал,
в течение которого свободная составляющая уменьшится в е раз по сравнению со
своим начальным значением. Теоретически переходный процесс длится бесконечно
долго. Однако на практике считается, что он заканчивается при ![]() .
.
2 Лекция 2. Способы
составления характеристического уравнения
Цель лекции:
получение навыков составления характеристических уравнений и расчета переходных
процессов в RL цепи.
Содержание:
- способы
составления характеристических уравнений;
- подключение RL цепи к источнику постоянного
напряжения;
- подключение RL цепи к источнику синусоидального
напряжения;
- короткое замыкание
в RL
цепи.
Рисунок
2.1
Характеристическое уравнение составляется для цепи
после коммутации. Оно может быть получено следующими способами.
Непосредственно на
основе дифференциального уравнения (1.2).
Согласно
первому способу, в предыдущей лекции было получено дифференциальное уравнение
относительно напряжения ![]() на конденсаторе для
последовательной R-L-C-цепи, на базе которого записывается характеристическое
уравнение.
на конденсаторе для
последовательной R-L-C-цепи, на базе которого записывается характеристическое
уравнение.
Следует
отметить, что, поскольку линейная цепь охвачена единым переходным процессом,
корни характеристического уравнения являются общими для всех свободных
составляющих напряжений и токов ветвей схемы, параметры которых входят в
характеристическое уравнение. Поэтому по первому способу составления
характеристического уравнения в качестве переменной, относительно которой оно
записывается, может быть выбрана любая.
Применение второго
способа составления характеристического уравнения рассмотрим на примере
цепи (рисунок 2.1).
Составление характеристического уравнения по методу входного
сопротивления заключается в следующем:
- записывается входное сопротивление цепи на
переменном токе;
- jw заменяется на оператор р;
- полученное выражение ![]() приравнивается к нулю.
приравнивается к нулю.
Уравнение совпадает с характеристическим.
![]()
Для
цепи на рисунке 2.1 относительно зажимов источника
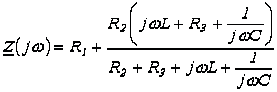
Заменив
jw на р и приравняв полученное выражение к нулю, запишем
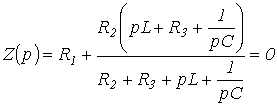
или
|
|
(2.1) |
Общая методика расчета переходных процессов
классическим методом
В
общем случае методика расчета переходных процессов классическим методом
включает следующие этапы:
а)
определение независимых начальных условий -![]() ;
;
б) запись
выражения для искомой переменной в виде
|
|
(2.2) |
в)
нахождение принужденной составляющей общего решения на основании расчета
установившегося режима послекоммутационной цепи;
г)
составление характеристического уравнения и определение его корней. Запись
выражения свободной составляющей в форме, определяемой типом найденных корней;
д)
подстановка полученных выражений принужденной и свободной составляющих в
соотношение (2.2);
е)
определение начальных условий и на их основе – постоянных интегрирования.
Примеры расчета переходных процессов классическим
методом
Переходные процессы в R-L цепи при ее подключении
к источнику напряжения
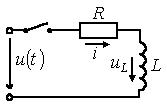
Рисунок 2.2
Такие процессы имеют место, например, при подключении
к источнику питания электромагнитов, трансформаторов, электрических двигателей
и т.п.
Рассмотрим два случая:
а) ![]()
б) ![]() .
.
Согласно рассмотренной методике, определим независимое
начальное условие ![]() , для тока в цепи на рисунке 2.2 можно записать
, для тока в цепи на рисунке 2.2 можно записать
|
|
(2.3) |
Тогда
для первого случая принужденная составляющая тока
|
|
(2.4) |
Характеристическое уравнение
![]() ,
,
откуда ![]() и постоянная времени
и постоянная времени![]() .
.
Таким образом,
|
|
(2.5) |
Подставляя (2.4) и (2.5) в соотношение (2.3), запишем
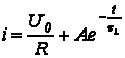 .
.
Так как ![]() , получим
, получим
![]()
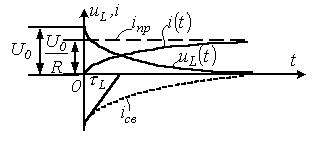
Рисунок 2.3
откуда ![]() .
.
Таким образом, ток в цепи в переходном процессе
описывается уравнением
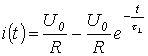 ,
,
а напряжение на катушке индуктивности – выражением
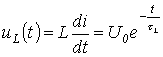 .
.
Качественный вид кривых ![]() и
и ![]() , соответствующих
полученным решениям, представлен на рисунке 2.3.
, соответствующих
полученным решениям, представлен на рисунке 2.3.
При втором типе источника принужденная составляющая
рассчитывается с использованием символического метода
 ,
,
где ![]() .
.
Отсюда
![]() .
.
Выражение свободной составляющей не зависит от типа
источника напряжения. Следовательно,
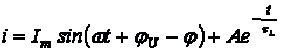 .
.
Поскольку ![]() , то
, то
![]() .
.
Таким образом, окончательно получаем
|
|
(2.6) |
Анализ
полученного выражения (2.6) показывает:
а) при
начальной фазе напряжения ![]() постоянная
интегрирования А=0. Таким образом, в этом случае коммутация не повлечет за
собой переходного процесса, и в цепи сразу возникнет установившийся режим;
постоянная
интегрирования А=0. Таким образом, в этом случае коммутация не повлечет за
собой переходного процесса, и в цепи сразу возникнет установившийся режим;
б) при ![]() свободная
составляющая максимальна по модулю. В этом случае ток переходного процесса
достигает своей наибольшей величины.
свободная
составляющая максимальна по модулю. В этом случае ток переходного процесса
достигает своей наибольшей величины.

Рисунок 2.4
Если ![]() значительна
по величине, то за полпериода свободная составляющая существенно не
уменьшается. В этом случае максимальная величина тока переходного процесса
значительна
по величине, то за полпериода свободная составляющая существенно не
уменьшается. В этом случае максимальная величина тока переходного процесса ![]() может
существенно превышать
амплитуду тока установившегося режима. Как
видно из рисунке 2.4, где
может
существенно превышать
амплитуду тока установившегося режима. Как
видно из рисунке 2.4, где
![]() , максимум тока имеет место примерно через
, максимум тока имеет место примерно через![]() . В пределе при
. В пределе при ![]()
![]() .
.
Таким образом, для линейной цепи максимальное значение
тока переходного режима не может превышать удвоенной амплитуды принужденного
тока ![]() .
.
Аналогично для линейной цепи с конденсатором: если в
момент коммутации принужденное напряжение равно своему амплитудному значению и
постоянная времени ![]() цепи
достаточно велика, то примерно через половину периода напряжение на
конденсаторе достигает своего максимального значения
цепи
достаточно велика, то примерно через половину периода напряжение на
конденсаторе достигает своего максимального значения ![]() , которое
не может превышать удвоенной амплитуды принужденного напряжения
, которое
не может превышать удвоенной амплитуды принужденного напряжения ![]() .
.
Переходные процессы при отключении катушки
индуктивности
от источника питания
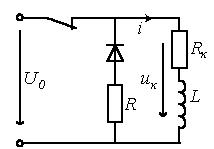 При размыкании ключа в цепи на рисунке 2.5
принужденная составляющая тока через катушку индуктивности
При размыкании ключа в цепи на рисунке 2.5
принужденная составляющая тока через катушку индуктивности ![]() .
.
Рисунок 2.5
Характеристическое
уравнение
![]() ,
,
откуда ![]() и
и ![]() .
.
В
соответствии с первым законом коммутации
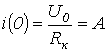 .
.
Таким
образом, выражение для тока в переходном режиме

и
напряжение на катушке индуктивности
|
|
(2.7) |
3
Лекция 3. Заряд и разряд конденсатора
Цель лекции: получение
навыков анализа и классического метода расчета переходных процессов в RC – цепи и RLC – цепи.
Содержание:
- переходные процессы в RC –цепи;
- подключение RLC –
цепи к источнику постоянного напряжения.
При переводе ключа в положение 1 (рисунок 3.1)
начинается процесс заряда конденсатора
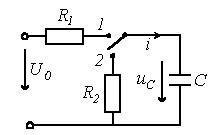
Рисунок 3.1
![]() .
.
Принужденная составляющая напряжения на конденсаторе ![]() .
.
Из характеристического уравнения
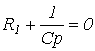
определяется корень ![]() . Отсюда
постоянная времени
. Отсюда
постоянная времени ![]() .
.
Таким образом,
![]() . (3.1)
. (3.1)
При t=0 напряжение на конденсаторе равно ![]() (в общем
случае к моменту коммутации конденсатор может быть заряженным, т.е.
(в общем
случае к моменту коммутации конденсатор может быть заряженным, т.е. ![]() ). Тогда
). Тогда ![]() и
и
![]() . (3.2)
. (3.2)
Соответственно для зарядного тока можно записать
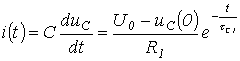 . (3.3)
. (3.3)
В
зависимости от величины![]() : 1 -
: 1 -![]() ; 2 -
; 2 -![]() ; 3 -
; 3 -![]() ; 4 -
; 4 - ![]() - возможны четыре вида кривых переходного процесса, которые
иллюстрирует рисунок 3.2.
- возможны четыре вида кривых переходного процесса, которые
иллюстрирует рисунок 3.2.

Рисунок 3.2
При
разряде конденсатора на резистор ![]() (ключ на рисунке 3.1 переводится в положение 2)
(ключ на рисунке 3.1 переводится в положение 2) ![]() . Постоянная времени
. Постоянная времени ![]() .
.
Тогда,
принимая, что к моменту коммутации конденсатор был заряжен до напряжения ![]() (в частном случае
(в частном случае ![]() ), для напряжения на нем в переходном режиме можно записать
), для напряжения на нем в переходном режиме можно записать
![]() .
(3.4)
.
(3.4)
Соответственно
разрядный ток
|
|
(3.5) |
Переходные процессы при
подключении последовательной
R-L-C-цепи к источнику напряжения
Рассмотрим случай
![]()
Согласно изложенной в предыдущей лекции
методике расчета переходных процессов классическим методом для напряжения на
конденсаторе в цепи на рисунке 3.3, можно записать
|
|
(3.7) |
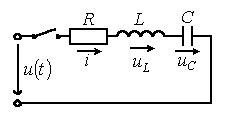
Рисунок 3.3
Тогда для первого случая принужденная составляющая
этого напряжения
|
|
(3.8) |
Характеристическое уравнение цепи
![]() ,
,
решая
которое, получаем
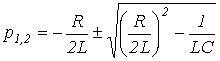 .
.
В
зависимости от соотношения параметров цепи возможны три типа корней и
соответственно три варианта выражения для свободной составляющей:
1.
![]() или
или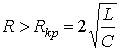 , где
, где ![]() - критическое
сопротивление контура, меньше которого свободный процесс носит
колебательный характер.
- критическое
сопротивление контура, меньше которого свободный процесс носит
колебательный характер.
В
этом случае
|
|
(3.9) |
2.
![]() - предельный случай апериодического режима.
- предельный случай апериодического режима.
В
этом случае ![]() и
и
|
|
(3.10) |
3.
![]() - периодический
(колебательный) характер переходного процесса.
- периодический
(колебательный) характер переходного процесса.
В
этом случае ![]() и
и
|
|
(3.11) |
где
![]() - коэффициент затухания;
- коэффициент затухания;
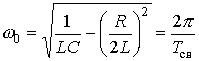 - угловая частота
собственных или свободных колебаний;
- угловая частота
собственных или свободных колебаний;
![]() - период собственных колебаний.
- период собственных колебаний.
Для
апериодического характера переходного процесса можно записать
![]() .
.
Для
нахождения постоянных интегрирования, учитывая, что в общем случае ![]() и в соответствии с первым законом коммутации
и в соответствии с первым законом коммутации 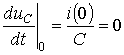 , запишем для t=0 два уравнения
, запишем для t=0 два уравнения

решая
которые, получим
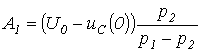 ;
; 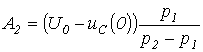 .
.
Таким
образом,
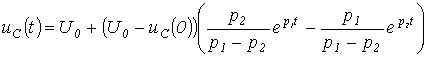 .
.
Тогда
ток в цепи
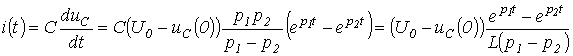
и
напряжение на катушке индуктивности
 .
.
На
рисунке 3.4 представлены качественные кривые ![]() ,
, ![]() и
и ![]() ,
соответствующие апериодическому переходному процессу при
,
соответствующие апериодическому переходному процессу при ![]() .
.
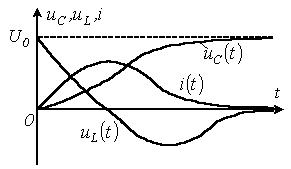
Рисунок 3.4
Для критического режима можно записать
![]() .
.
При ![]()
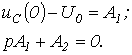
Таким образом,
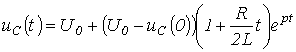
и
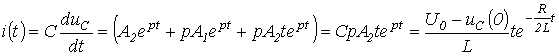 .
.
Для колебательного переходного режима имеем
![]() .
.
Для
нахождения постоянных интегрирования запишем ![]()
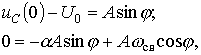
откуда
![]() и
и ![]() .
.
тогда
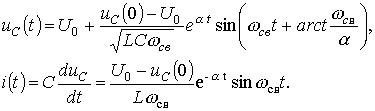
На
рисунке 3.5 представлены качественные кривые ![]() и
и![]() , соответствующие колебательному переходному процессу при
, соответствующие колебательному переходному процессу при ![]() .
.
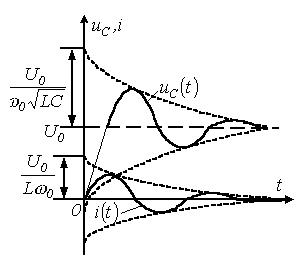
Рисунок 3.5
4
Лекция 4. Операторный
метод расчета переходных процессов
Цель лекции:
получение навыков расчета переходных процессов операторным методом.
Содержание:
- прямое
преобразование Лапласа;
- изображение
напряжений на индуктивном и емкостном элементах;
- закон Ома в
операторных методах;
- операторная схема
замещения;
- законы Кирхгофа в
операторной форме;
- переход от
изображений к оригиналам.
Сущность операторного метода заключается в том, что
функции ![]() вещественной
переменной t, которую называют оригиналом,
ставится в соответствие функция
вещественной
переменной t, которую называют оригиналом,
ставится в соответствие функция ![]() комплексной переменной
комплексной переменной![]() , которую называют изображением.
В результате этого производные и интегралы от оригиналов заменяются
алгебраическими функциями от соответствующих изображений (дифференцирование
заменяется умножением на оператор р, а интегрирование – делением на него), что
в свою очередь определяет переход от системы интегродифференциальных уравнений
к системе алгебраических уравнений относительно изображений искомых переменных.
При решении этих уравнений находятся изображения и далее путем обратного
перехода – оригиналы. Важнейшим моментом при этом в практическом плане является
необходимость определения только независимых начальных условий, что существенно
облегчает расчет переходных процессов в цепях высокого порядка по сравнению с
классическим методом.
, которую называют изображением.
В результате этого производные и интегралы от оригиналов заменяются
алгебраическими функциями от соответствующих изображений (дифференцирование
заменяется умножением на оператор р, а интегрирование – делением на него), что
в свою очередь определяет переход от системы интегродифференциальных уравнений
к системе алгебраических уравнений относительно изображений искомых переменных.
При решении этих уравнений находятся изображения и далее путем обратного
перехода – оригиналы. Важнейшим моментом при этом в практическом плане является
необходимость определения только независимых начальных условий, что существенно
облегчает расчет переходных процессов в цепях высокого порядка по сравнению с
классическим методом.
Изображение
![]() заданной функции
заданной функции ![]() определяется в соответствии с прямым преобразованием Лапласа
определяется в соответствии с прямым преобразованием Лапласа
|
|
(4.1) |
В
сокращенной записи соответствие между изображением и оригиналом обозначается,
как
|
|
или |
|
Изображения производной и интеграла
В
курсе математики доказывается, что если ![]() , то
, то![]() , где
, где ![]() - начальное значение функции
- начальное значение функции ![]() .
.
Таким
образом, для напряжения на индуктивном элементе можно записать
![]()
или
при нулевых начальных условиях
![]()
Отсюда операторное
сопротивление катушки индуктивности
![]() .
.
Аналогично для интеграла: если ![]() , то
, то .
.
С учетом ненулевых начальных условий для напряжения на
конденсаторе можно записать
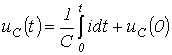
Тогда
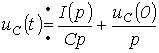
или при нулевых начальных условиях
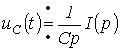
откуда операторное
сопротивление конденсатора
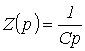
Закон Ома в операторной форме
Пусть имеем некоторую ветвь ![]() (рисунок4.1), выделенную из некоторой
(рисунок4.1), выделенную из некоторой
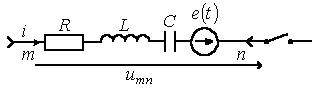
Рисунок 4.1
сложной
цепи. Замыкание ключа во внешней цепи приводит к переходному процессу, при этом
начальные условия для тока в ветви и напряжения на конденсаторе в общем случае
ненулевые.
Для
мгновенных значений переменных можно записать

Тогда
на основании приведенных выше соотношений получим:
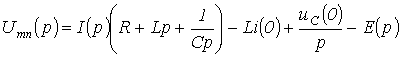
Отсюда
|
|
(4.2) |
где
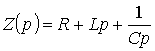 - операторное сопротивление рассматриваемого участка цепи.
- операторное сопротивление рассматриваемого участка цепи.
Следует
обратить внимание, что операторное сопротивление ![]() соответствует
комплексному сопротивлению
соответствует
комплексному сопротивлению ![]() ветви в
цепи синусоидального тока при замене оператора р на
ветви в
цепи синусоидального тока при замене оператора р на ![]() .
.
Уравнение
(4.2) есть математическая запись закона Ома для участка цепи с источником ЭДС в
операторной форме. В соответствии с ним для ветви на рисунке 4.1 можно
нарисовать операторную схему замещения, представленную на рисунке 4.2.

Рисунок 4.2
Законы Кирхгофа в операторной форме
Первый закон Кирхгофа: алгебраическая
сумма изображений токов, сходящихся в узле, равна нулю
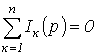
Второй
закон Кирхгофа: алгебраическая сумма изображения ЭДС, действующих в контуре,
равна алгебраической сумме изображения на пассивных элементах этого контура
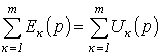
При
записи уравнений по второму закону Кирхгофа следует помнить о необходимости
учета ненулевых начальных условий (если они имеют место). С их учетом последнее
соотношение может быть переписано в развернутом виде
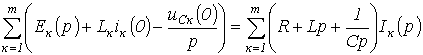 (4.3)
(4.3)
Переход от изображений к оригиналам
Переход
от изображения искомой величины к оригиналу может быть осуществлен следующими способами:
а)
посредством обратного преобразования
Лапласа
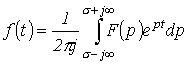
которое
представляет собой решение интегрального уравнения (4.1) и сокращенно
записывается, как
![]() .
.
На
практике этот способ применяется редко;
б) по
таблицам соответствия между оригиналами и изображениями
В
специальной литературе имеется достаточно большое число формул соответствия,
охватывающих практически все задачи электротехники. Согласно данному способу,
необходимо получить изображение искомой величины в виде, соответствующем
табличному, после чего выписать из таблицы выражение оригинала;
в) с
использованием формулы разложения
Пусть
изображение ![]() искомой переменной определяется отношением двух полиномов
искомой переменной определяется отношением двух полиномов
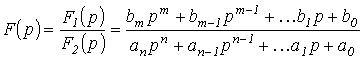 ,
,
где
![]() .
.
Тогда
|
|
(4.4) |
Соотношение
(4.4) представляет собой формулу разложения.
Если
один из корней уравнения ![]() равен нулю, т.е.
равен нулю, т.е.![]() , то уравнение (4.4) сводится к виду
, то уравнение (4.4) сводится к виду
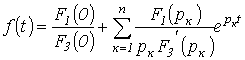 (4.5)
(4.5)
Комплексно-сопряженным корням уравнения ![]() в формуле
разложения соответствуют комплексно-сопряженные слагаемые, которые в сумме дают
удвоенный вещественный член, т.е. для к-й пары комплексно-сопряженных корней
имеет место
в формуле
разложения соответствуют комплексно-сопряженные слагаемые, которые в сумме дают
удвоенный вещественный член, т.е. для к-й пары комплексно-сопряженных корней
имеет место
 (4.6)
(4.6)
Последовательность расчета переходных
процессов
операторным методом:
а) определение независимых начальных условий путем расчета
докоммутационного режима работы цепи;
б) составление операторной схемы замещения цепи;
в) запись уравнений по законам Кирхгофа или другим методам расчета
линейных цепей в операторной форме с учетом начальных условий;
г) решение полученных уравнений относительно изображений искомых
величин;
д) определение оригиналов (с помощью формулы разложения или таблиц
соответствия оригиналов и изображений) по найденным изображениям.
5 Лекция 5.Переходная проводимость
Цель лекции:
получение навыков расчета переходных процессов с использованием интеграла
Дюамеля и методом переменных состояния.
Содержание:
- переходная
функция цепи;
- расчет
переходных процессов с использованием интеграла Дюамеля;
- метод
переменных состояния.
При рассмотрении метода наложения было
показано, что ток в любой ветви схемы может быть представлен в виде
![]() ,
,
где ![]() -
собственная (к=m) или взаимная
-
собственная (к=m) или взаимная ![]() проводимость.
проводимость.
Это соотношение, трансформированное в уравнение
|
|
(5.1) |
будет иметь силу и в переходном режиме, т.е. когда замыкание ключа
в m-й ветви подключает к цепи находящийся в этой ветви источник постоянного
напряжения ![]() . При этом
. При этом ![]() является
функцией времени и называется переходной проводимостью.
является
функцией времени и называется переходной проводимостью.
В соответствии с (5.1) переходная проводимость численно равна току
в ветви при подключении цепи к постоянному напряжению ![]() .
.
Переходная функция по напряжению
Переходная функция по напряжению наиболее часто используется при
анализе четырехполюсников.
Если линейную электрическую цепь с нулевыми начальными условиями
подключить к источнику постоянного напряжения ![]() , то между
произвольными точками m и n цепи возникнет напряжение
, то между
произвольными точками m и n цепи возникнет напряжение
![]() ,
,
где ![]() - переходная функция по напряжению,
численно равная напряжению между точками m и n схемы при подаче на ее вход
постоянного напряжения
- переходная функция по напряжению,
численно равная напряжению между точками m и n схемы при подаче на ее вход
постоянного напряжения ![]() .
.
Расчет
переходных процессов с использованием интеграла Дюамеля
Зная реакцию цепи на единичное возмущающее воздействие, т.е.
функцию переходной проводимости ![]() или (и)
переходную функцию по напряжению
или (и)
переходную функцию по напряжению ![]() , можно
найти реакцию цепи на воздействие произвольной формы. В основе метода – метода
расчета с помощью интеграла Дюамеля – лежит принцип наложения.
, можно
найти реакцию цепи на воздействие произвольной формы. В основе метода – метода
расчета с помощью интеграла Дюамеля – лежит принцип наложения.
При использовании интеграла Дюамеля для разделения переменной, по
которой производится интегрирование, и переменной, определяющей момент времени,
в который определяется ток в цепи, первую принято обозначать как ![]() , а вторую
- как t.
, а вторую
- как t.
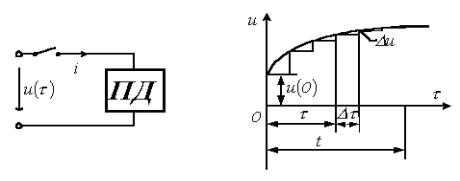
Рисунок
5.1
Рисунок 5.2
Пусть в момент времени ![]() к цепи с
нулевыми начальными условиями (пассивному двухполюснику ПД на рисунке
5.1) подключается источник с напряжением
к цепи с
нулевыми начальными условиями (пассивному двухполюснику ПД на рисунке
5.1) подключается источник с напряжением ![]() произвольной
формы. Для нахождения тока
произвольной
формы. Для нахождения тока ![]() в цепи
заменим исходную кривую ступенчатой (рисунок 5.2), после чего с учетом, что
цепь линейна, просуммируем токи от начального скачка напряжения
в цепи
заменим исходную кривую ступенчатой (рисунок 5.2), после чего с учетом, что
цепь линейна, просуммируем токи от начального скачка напряжения ![]() и всех
ступенек напряжения до момента t, вступающих в действие с запаздыванием по
времени.
и всех
ступенек напряжения до момента t, вступающих в действие с запаздыванием по
времени.
В момент времени t составляющая общего тока, определяемая
начальным скачком напряжения ![]() , равна
, равна ![]() .
.
В момент времени ![]() имеет место
скачок напряжения
имеет место
скачок напряжения ![]() , который с
учетом временного интервала от начала скачка до интересующего момента времени t
обусловит составляющую тока
, который с
учетом временного интервала от начала скачка до интересующего момента времени t
обусловит составляющую тока ![]() .
.
Полный ток ![]() в момент
времени t равен, очевидно, сумме всех составляющих тока от отдельных скачков
напряжения с учетом
в момент
времени t равен, очевидно, сумме всех составляющих тока от отдельных скачков
напряжения с учетом ![]() , т.е.
, т.е.
![]() .
.
Заменяя конечный интервал приращения времени ![]() на
бесконечно малый, т.е. переходя от суммы к интегралу, запишем
на
бесконечно малый, т.е. переходя от суммы к интегралу, запишем
|
|
(5.1) |
Соотношение (5.1) называется интегралом Дюамеля.
Следует отметить, что с использованием интеграла Дюамеля можно
определять также напряжение. При этом в (5.1) вместо переходной проводимости ![]() будет
входить переходная функция по напряжению.
будет
входить переходная функция по напряжению.
Последовательность
расчета с использованием
интеграла Дюамеля:
а) определение функции ![]() (или
(или ![]() ) для
исследуемой цепи;
) для
исследуемой цепи;
б) запись выражения ![]() (или
(или ![]() ) путем
формальной замены t на
) путем
формальной замены t на ![]() ;
;
в) определение производной ![]() ;
;
г) подстановка найденных функций в (5.1) и
интегрирование определенного интеграла.
6 Лекция 6. Спектральный метод анализа переходных
процессов в линейных электрических цепях.
Цель лекции: получение навыков анализа и расчета
переходных процессов в линейных электрических цепях спектральным методом.
Содержание:
-интеграл Фурье;
- спектры непериодических функций;
- спектральный метод анализа линейных электрических
цепей при непериодических воздействиях;
- основные этапы расчета переходных процессов
спектральным методом.
Интеграл Фурье
При воздействии на цепь сигналов произвольной формы
широко используется спектральный (частотный) метод анализа, основанный на
спектральных представлениях сигнала. Для непериодических сигналов используются
спектральные представления, базирующиеся на преобразованиях Фурье.
Непериодическая функция ![]() , удовлетворяющая условию абсолютной интегрируемости в
бесконечных пределах
, удовлетворяющая условию абсолютной интегрируемости в
бесконечных пределах
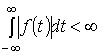 ,
,
может быть представлена интегралом Фурье
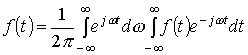 .
(6.1)
.
(6.1)
Внутренний интеграл в уравнении (6.1) называется
спектром заданной функции или спектральной плотностью ![]()
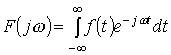 . (6.2)
. (6.2)
С учетом выражения (6.2) формула (6.1) примет вид
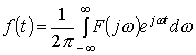 . (6.3)
. (6.3)
Уравнение (6.2) называют прямым преобразованием Фурье,
уравнение 6.3 – обратным преобразованием Фурье.
Спектральная плотность ![]() является комплексной
функцией частоты и может быть записана в показательной форме
является комплексной
функцией частоты и может быть записана в показательной форме
![]() , (6.4)
, (6.4)
где ![]() - амплитудно –
частотная характеристика АЧХ (четная функция частоты);
- амплитудно –
частотная характеристика АЧХ (четная функция частоты);
![]() - фазочастотная
характеристика ФЧХ (нечетная функция частоты).
- фазочастотная
характеристика ФЧХ (нечетная функция частоты).
Если функция ![]() задана на
положительной полуоси времени
задана на
положительной полуоси времени ![]() , т.е.
, т.е. ![]() при
при ![]() , то прямое преобразование Фурье имеет вид
, то прямое преобразование Фурье имеет вид
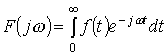 (6.5)
(6.5)
и называется односторонним преобразованием Фурье.
Сравнивая прямое и обратное преобразования Лапласа с
прямым (6.5) и обратным (6.3) преобразованием Фурье, можно сделать вывод, что
преобразования Фурье являются частным случаем преобразований Лапласа и
получаются из него при ![]() . Следовательно, спектральный метод, основанный на
преобразованиях Фурье, может быть применен для расчета переходных процессов.
. Следовательно, спектральный метод, основанный на
преобразованиях Фурье, может быть применен для расчета переходных процессов.
Спектры
непериодических функций
Применение прямого преобразования Фурье позволяет
определить спектры входных воздействий. Определим спектральную плотность
прямоугольного видеоимпульса с амплитудной ![]() и длительностью
и длительностью ![]() (рисунок 6.1).
(рисунок 6.1).
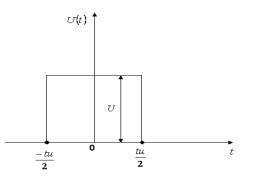
Рисунок 6.1
Спектральную плотность определим по формуле (6.2)
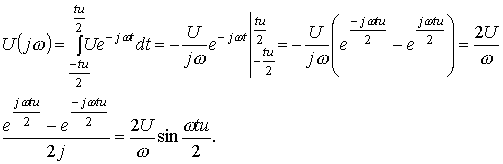 (6.8)
(6.8)
Амплитудно-частотная характеристика
 .
.
Фазо-частотная характеристика ![]() при положительных
значениях синуса и
при положительных
значениях синуса и ![]() при отрицательных.
при отрицательных.
АЧХ ![]() и ФЧХ
и ФЧХ ![]() показаны на
рисунках 6.2 и 6.3.
показаны на
рисунках 6.2 и 6.3.
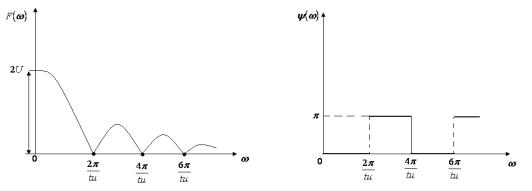
Рисунок
6.2
Рисунок 6.3
Спектральный метод анализа линейных
электрических цепей при непериодических воздействиях.
Спектральный метод применяется для
определения спектральной плотности входного сигнала (воздействия) и вычисления
спектральной плотности реакции цепи по спектральной плотности воздействия.
Для RLC - цепи закон
Ома для частотных спектров при ненулевых начальных условиях можно получить из
закона Ома в операторной форме при ![]()
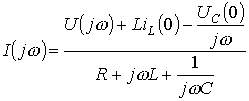 , (6.9)
, (6.9)
где ![]() - спектральная
плотность воздействия.
- спектральная
плотность воздействия.
Знаменатель этого выражения
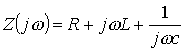 (6.10)
(6.10)
представляет собой комплексное
сопротивление RLC цепи, которое применялось
ранее для расчета установившихся гармонических процессов.
Если цепь находится при нулевых
начальных условиях, закон Ома для частотных спектров имеет вид
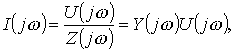 (6.11)
(6.11)
где
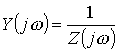 - комплексная
проводимость.
- комплексная
проводимость.
При помощи ![]() по формулам (6.9) и
(6.11) можно найти спектральную плотность тока
по формулам (6.9) и
(6.11) можно найти спектральную плотность тока ![]()
Законы Кирхгофа для частотных спектров
при нулевых начальных условиях
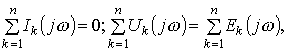 (6.12)
(6.12)
где ![]() - спектры токов, напряжений и ЭДС.
- спектры токов, напряжений и ЭДС.
В общем случае спектральную плотность ![]() реакции цепи
(спектральную плотность напряжения
реакции цепи
(спектральную плотность напряжения ![]() или тока
или тока ![]() произвольного
элемента цепи) вычисляют по спектральной плотности воздействия
произвольного
элемента цепи) вычисляют по спектральной плотности воздействия ![]() источника и
соответствующей комплексной функции передачи цепи
источника и
соответствующей комплексной функции передачи цепи ![]()
![]() (6.13)
(6.13)
Частные случаи комплексной функции
передачи – комплексное сопротивление передачи ![]() и комплексная проводимость
передачи
и комплексная проводимость
передачи ![]() .
.
Для определения выходного сигнала цепи
в виде четырехполюсника при воздействии на входе непериодического сигнала
используют комплексную передаточную функцию четырехполюсника. Например,
спектральная плотность выходного напряжения
![]() определяется по
формуле
определяется по
формуле
![]() (6.14)
(6.14)
где
![]() - спектральная
плотность входного сигнала;
- спектральная
плотность входного сигнала;
![]() - комплексная
передаточная функция цепи по напряжению.
- комплексная
передаточная функция цепи по напряжению.
Основные этапы расчета переходных
процессов спектральным методом:
а) определение спектральной плотности
входного воздействия ![]() ;
;
б) определение комплексной функции передачи цепи;
в) определение спектральной плотности
реакции цепи ![]() ;
;
г) определение реакции цепи ![]() , которая может быть найдена с помощью обратного
преобразования Фурье, теоремы разложения или по таблицам.
, которая может быть найдена с помощью обратного
преобразования Фурье, теоремы разложения или по таблицам.
7 Лекция 7.Нелинейные электрические цепи постоянного
тока
Цель лекции: изучение характеристик нелинейных
резистивных элементов и получение навыков графического метода расчета
нелинейных электрических цепей постоянного метода.
Содержание:
- нелинейные резистивные элементы и их характеристики;
- статическое и дифференциальное сопротивление;
- вольт – амперные
характеристики активного нелинейного двухполюсника;
- графический метод расчета нелинейных резистивных
цепей.
Нелинейные резистивные элементы и их характеристики
При постоянных токах и напряжениях в качестве
нелинейных могут рассматриваться только резистивные электрические цепи.
Резистивными нелинейными цепями называются цепи,
содержащие хотя бы один нелинейный резистивный элемент (НЭ), хотя бы один
источник напряжения или тока и линейные сопротивления. Нелинейным резистивным
элементом называется резистивный элемент с нелинейной вольт-амперной
характеристикой ВАХ.
По виду ВАХ нелинейные резистивные элементы можно
разбить на две основные группы: симметричные и несимметричные. Симметричными
называются нелинейные резистивные элементы, у которых ВАХ не зависит от
направления тока в них и напряжения на их зажимах: ![]() (рисунок 7.1,а).
(рисунок 7.1,а).
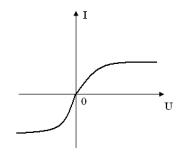
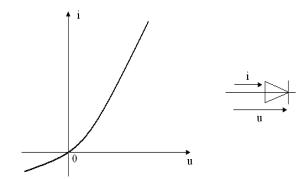
а) б)
Рисунок 7.1
Несимметричными называются нелинейные резистивные
элементы, у которых ВАХ неодинаковы при
различных направлениях тока и напряжения на зажимах (рисунок 7.1,б).
Статическое и
дифференциальное сопротивления
Различают два вида сопротивлений: статическое и
дифференциальное (динамическое).
Статическое сопротивление
Статическое сопротивление определяется по формуле
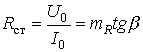 . (7.1)
. (7.1)
Статическое сопротивление всегда положительное ![]() .
.
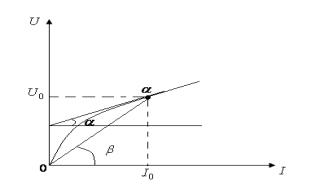
Рисунок 7.2
Дифференциальное сопротивление
Дифференциальное сопротивление определяется по формуле
![]() (7.2)
(7.2)
Дифференциальное сопротивление
может быть как положительным ![]() (на восходящем
участке ВАХ), так и отрицательным
(на восходящем
участке ВАХ), так и отрицательным ![]() (на падающем участке
ВАХ).
(на падающем участке
ВАХ).
Вольт – амперные характеристики
активного нелинейного двухполюсника
Нелинейный активный двухполюсник
(рисунок 7.3) содержит один нелинейный резистор с ВАХ, изображенной на рисунке
7.4, и один идеальный источник ЭДС.
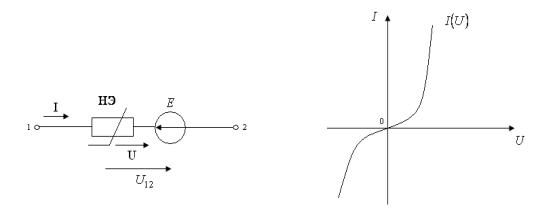
Рисунок
7.3 Рисунок 7.4
Для построения ВАХ активного
нелинейного двухполюсника ![]() определяется
напряжение
определяется
напряжение ![]() .
.
Пользуясь вольт – амперной
характеристикой нелинейного резистора ![]() , построим вольт – амперную характеристику
, построим вольт – амперную характеристику ![]() , абсциссы которой получены сложением абсцисс ВАХ
, абсциссы которой получены сложением абсцисс ВАХ ![]() и ЭДС Е для различных
значений тока (рисунок 7.5).
и ЭДС Е для различных
значений тока (рисунок 7.5).
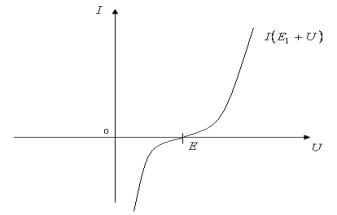
Рисунок 7.5
При изменении положительного
направления ЭДС Е кривая ![]() получается путем
сдвига ВАХ нелинейного резистора
получается путем
сдвига ВАХ нелинейного резистора ![]() влево на величину,
равную Е. При изменении положительного направления тока на противоположное в
активном нелинейном двухполюснике (рисунок 7.3) кривая
влево на величину,
равную Е. При изменении положительного направления тока на противоположное в
активном нелинейном двухполюснике (рисунок 7.3) кривая ![]() получается путем
зеркального отображения ВАХ
получается путем
зеркального отображения ВАХ ![]() с последующим сдвигом
вправо на величину Е, т.к. в этом случае
с последующим сдвигом
вправо на величину Е, т.к. в этом случае ![]() .
.
Графические методы расчета
нелинейных резистивных цепей
Графический метод расчета
неразветвленных цепей с нелинейными резистивными элементами.
К цепи (рисунок 7.6) с
последовательным соединением двух нелинейных резисторов НЭ1 и НЭ2, ВАХ которых ![]() , приложено постоянное напряжение
, приложено постоянное напряжение ![]() . Требуется определить ток
. Требуется определить ток ![]() и напряжения
и напряжения ![]() на элементах НЭ1 и
НЭ2.
на элементах НЭ1 и
НЭ2.

Рисунок 7.6 Рисунок 7.7
Запишем второй закон Кирхгофа для нелинейной цепи
(рисунок 7.6)
![]() . (7.3)
. (7.3)
Ток в обоих элементах один и тот же ![]() .
.
Построим ВАХ ![]() , для построения которой просуммируем напряжения
, для построения которой просуммируем напряжения ![]() при одинаковых
значениях тока (рисунок 7.7), отложим на оси абсцисс напряжение
при одинаковых
значениях тока (рисунок 7.7), отложим на оси абсцисс напряжение ![]() , из точки а проведем прямую параллельно оси ординат до
пересечения с кривой
, из точки а проведем прямую параллельно оси ординат до
пересечения с кривой ![]() . Отрезок ав равен в масштабе
. Отрезок ав равен в масштабе ![]() току
току ![]() . Из точки в проводим прямую вс, параллельную оси абсцисс, в
результате получим отрезки
. Из точки в проводим прямую вс, параллельную оси абсцисс, в
результате получим отрезки ![]() , равные в масштабе
, равные в масштабе ![]() напряжениям
напряжениям ![]() :
: ![]() .
.
Графический метод
расчета цепей с параллельным соединением нелинейных элементов.
К цепи (рисунок 7.8) с
параллельным соединением нелинейных
резистивных элементов НЭ1 и НЭ2 с вольт – амперными характеристиками ![]() и
и ![]() (рисунок 7.9)
приложено постоянное напряжение
(рисунок 7.9)
приложено постоянное напряжение ![]() .
.

Рисунок
7.8 Рисунок 7.9
При параллельном
соединении ![]() и согласно первому закону Кирхгофа
и согласно первому закону Кирхгофа
![]() . (7.4)
. (7.4)
Если задано
напряжение ![]() , то токи
, то токи ![]() в нелинейных
элементах определяются по ВАХ
в нелинейных
элементах определяются по ВАХ ![]() ,
, ![]() , а ток в неразветвленной части цепи на основании уравнения
(7.4).
, а ток в неразветвленной части цепи на основании уравнения
(7.4).
Если задан ток ![]() , то для определения напряжения
, то для определения напряжения ![]() и токов
и токов ![]() строят
вспомогательную характеристику
строят
вспомогательную характеристику ![]() путем суммирования
ординат кривых
путем суммирования
ординат кривых ![]() и
и ![]() для одних и тех же
значений напряжения
для одних и тех же
значений напряжения ![]() Далее откладывается
га оси ординат отрезок
Далее откладывается
га оси ординат отрезок ![]() , равный в масштабе
, равный в масштабе ![]() току
току ![]() , из точки
, из точки ![]() проводим прямую до
пересечения с характеристикой
проводим прямую до
пересечения с характеристикой ![]() , полученный отрезок
, полученный отрезок ![]() равен в масштабе
равен в масштабе ![]() напряжению
напряжению ![]() . Из точки в проведем прямую ва до пересечения с осью абсцисс, получим отрезки
. Из точки в проведем прямую ва до пересечения с осью абсцисс, получим отрезки ![]() , которые в масштабе
, которые в масштабе ![]() равны токам
равны токам ![]() :
: ![]() .
.
8 Лекция 8.
Цепи с распределенными параметрами
Цель лекции: получение навыков анализа и расчета
различных режимов в цепях с распределенными параметрами.
Содержание:
- цепи
с распределенными параметрами, однородная линия;
-
дифференциальные уравнения однородной линии;
-
уравнения однородной линии в стационарном режиме;
-
прямая и обратная бегущая волны;
-
согласованный режим работы линии;
- линия
без искажений;
В предыдущих лекциях
рассматривались электрические цепи, геометрические размеры которых, а также
входящих в них элементов не играли роли, т.е. электрические и магнитные поля
были локализованы соответственно в пределах конденсатора и катушки
индуктивности, а потери мощности – в резисторе. Однако на практике часто
приходится иметь дело с цепями (линии электропередачи, передачи информации,
обмотки электрических машин и аппаратов и т.д.), где электромагнитное поле и потери
равномерно или неравномерно распределены вдоль всей цепи. В результате
напряжения и токи на различных участках даже неразветвленной цепи отличаются
друг от друга, т.е. являются функциями двух независимых переменных: времени t и
пространственной координаты x. Такие цепи называются цепями с распределенными
параметрами. Смысл данного названия заключается в том, что у цепей данного
класса каждый бесконечно малый элемент их длины характеризуется сопротивлением,
индуктивностью, а между проводами – соответственно емкостью и проводимостью.
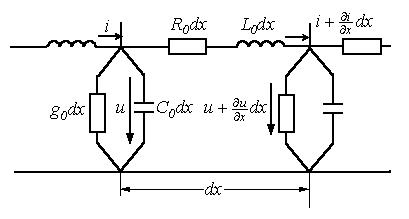 Для исследования процессов в цепи с
распределенными параметрами (другое название – длинная линия) введем дополнительное условие о равномерности
распределения вдоль линии ее параметров: индуктивности, сопротивления, емкости
и проводимости. Такую линию называют однородной.
Линию с неравномерным распределением параметров часто можно разбить на однородные участки.
Для исследования процессов в цепи с
распределенными параметрами (другое название – длинная линия) введем дополнительное условие о равномерности
распределения вдоль линии ее параметров: индуктивности, сопротивления, емкости
и проводимости. Такую линию называют однородной.
Линию с неравномерным распределением параметров часто можно разбить на однородные участки.
Рисунок 8.1
Уравнения однородной линии в
стационарном режиме
Под первичными параметрами линии будем понимать сопротивление ![]() ,
индуктивность
,
индуктивность ![]() ,
проводимость
,
проводимость ![]() и емкость
и емкость ![]() ,
отнесенные к единице ее длины. Для получения уравнений однородной линии
разобьем ее на отдельные участки бесконечно малой длины
,
отнесенные к единице ее длины. Для получения уравнений однородной линии
разобьем ее на отдельные участки бесконечно малой длины ![]() со
структурой, показанной на рисунок 8.1.
со
структурой, показанной на рисунок 8.1.
Пусть напряжение и ток в начале такого элементарного
четырехполюсника равны u и i, а в конце соответственно - ![]() и
и ![]() .
.
Разность напряжений в начале и конце участка определяется падением
напряжения на резистивном и индуктивном элементах, а изменение тока на участке
равно сумме токов утечки и смещения через проводимость и емкость. Таким
образом, по законам Кирхгофа
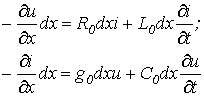
или после сокращения на ![]()
|
|
(8.1) |
|
|
(8.2) |
Теорию цепей с распределенными параметрами в установившихся
режимах будем рассматривать для случая синусоидального тока. Тогда полученные
соотношения при ![]() можно
распространить и на цепи постоянного тока, а воспользовавшись разложением
в ряд Фурье – на линии периодического несинусоидального тока.
можно
распространить и на цепи постоянного тока, а воспользовавшись разложением
в ряд Фурье – на линии периодического несинусоидального тока.
Вводя комплексные величины и заменяя ![]() на
на ![]() , на
основании (8.1) и (8.2) получаем
, на
основании (8.1) и (8.2) получаем
|
|
(8.3) |
|
|
(8.4) |
где ![]() и
и ![]() -
соответственно комплексные сопротивление и проводимость на единицу длины линии.
-
соответственно комплексные сопротивление и проводимость на единицу длины линии.
Продифференцировав (3) по х и подставив выражение ![]() из (8.4),
запишем
из (8.4),
запишем
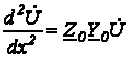 .
.
Характеристическое уравнение
![]() ,
,
откуда
![]() .
.
Таким образом,
|
|
(8.5) |
где ![]() -
постоянная распространения;
-
постоянная распространения; ![]() -
коэффициент затухания;
-
коэффициент затухания; ![]() - коэффициент фазы.
- коэффициент фазы.
Для тока согласно уравнению (8.3) можно записать
|
|
(8.6) |
где ![]() - волновое
сопротивление.
- волновое
сопротивление.
Волновое сопротивление ![]() и
постоянную распространения
и
постоянную распространения ![]() называют
вторичными параметрами
линии, которые характеризуют ее свойства как устройства для передачи энергии
или информации.
называют
вторичными параметрами
линии, которые характеризуют ее свойства как устройства для передачи энергии
или информации.
Определяя ![]() и
и ![]() , на
основании (8.5) запишем
, на
основании (8.5) запишем
|
|
(8.7) |
Аналогичное уравнение согласно (8.6) можно записать для тока.
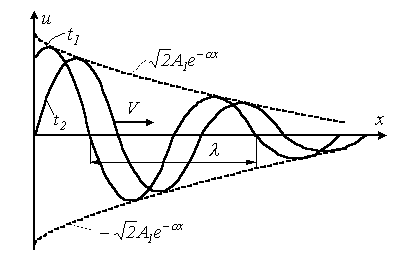
Рисунок 8.2
Слагаемые в правой части соотношения (8.7) можно трактовать как
бегущие волны: первая движется и затухает в направлении возрастания х, вторая –
убывания. Действительно, в фиксированный момент времени каждое из слагаемых
представляет собой затухающую (вследствие потерь энергии) гармоническую функцию
координаты х, а в фиксированной точке – синусоидальную функцию времени.
Волну, движущую от начала линии в сторону возрастания х, называют прямой, а движущуюся от конца линии в
направлении убывания х – обратной.
На рисунке 8.2 представлена затухающая синусоида прямой волны для
моментов времени ![]() и
и ![]()
![]() .
Перемещение волны характеризуется фазовой
скоростью. Это скорость перемещения по линии неизменного фазового
состояния, т.е. скорость, с которой нужно перемещаться вдоль линии, чтобы
наблюдать одну и ту же фазу волны
.
Перемещение волны характеризуется фазовой
скоростью. Это скорость перемещения по линии неизменного фазового
состояния, т.е. скорость, с которой нужно перемещаться вдоль линии, чтобы
наблюдать одну и ту же фазу волны
|
|
(8.8) |
Продифференцировав (8) по времени, получим
|
|
(8.9) |
Длиной волны ![]() называется
расстояние между двумя ее ближайшими точками, различающимися по фазе на
называется
расстояние между двумя ее ближайшими точками, различающимися по фазе на ![]() рад. В
соответствии с данным определением
рад. В
соответствии с данным определением
![]() ,
,
откуда
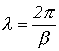
и с учетом (8.9)
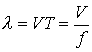
В соответствии с введенными понятиями прямой и обратной волн
распределение напряжения вдоль линии в любой момент времени можно трактовать
как результат наложения двух волн: прямой и обратной, - перемещающихся вдоль
линии с одинаковой фазовой скоростью, но в противоположных направлениях:
|
|
(8.10) |
где в соответствии с (8.5) ![]() и
и ![]() .
.
Аналогично для тока на основании (8.6) можно записать
|
|
(8.11) |
где
![]() и
и ![]() .
.
На основании (10) и (11) для прямых и обратных волн напряжения и
тока выполняется закон Ома
|
|
|
|
Бесконечно длинная однородная линия. Согласованный режим работы
В случае бесконечно длинной линии в выражениях (8.5) и (8.6) для
напряжения и тока слагаемые, содержащие ![]() , должны
отсутствовать, т.к. стремление
, должны
отсутствовать, т.к. стремление ![]() лишает эти
составляющие физического смысла. Следовательно, в рассматриваемом случае
лишает эти
составляющие физического смысла. Следовательно, в рассматриваемом случае ![]() . Таким
образом, в решении уравнений линии бесконечной длины отсутствуют обратные волны
тока и напряжения. В соответствии с вышесказанным
. Таким
образом, в решении уравнений линии бесконечной длины отсутствуют обратные волны
тока и напряжения. В соответствии с вышесказанным
|
|
; |
|
. |
(8.12) |
На основании соотношений (8.12) можно сделать важный вывод, что
для бесконечно длинной линии в любой ее точке, в том числе и на входе,
отношение комплексов напряжения и тока есть постоянная величина, равная
волновому сопротивлению
![]()
Таким образом, если такую линию мысленно рассечь в любом месте и
вместо откинутой бесконечно длинной части подключить сопротивление, численно
равное волновому, то режим работы оставшегося участка конечной длины не
изменится. Отсюда можно сделать два вывода:
Уравнения бесконечно длинной линии распространяются на линию
конечной длины, нагруженную на сопротивление, равное волновому. В этом случае
также имеют место только прямые волны напряжения и тока.
У линии, нагруженной на волновое сопротивление, входное
сопротивление также равно волновому.
Режим работы длинной линии, нагруженной на сопротивление, равное
волновому, называется согласованным,
а сама линия называется линией с согласованной нагрузкой.
Отметим, что данный режим практически важен для передачи
информации, поскольку характеризуется отсутствием отраженных (обратных) волн,
обусловливающих помехи.
Согласованная нагрузка полностью поглощает мощность волны,
достигшей конца линии. Эта мощность называется натуральной. Поскольку в любом
сечении согласованной линии сопротивление равно волновому, угол сдвига ![]() между
напряжением и током неизменен. Таким образом, если мощность, получаемая линией
от генератора, равна
между
напряжением и током неизменен. Таким образом, если мощность, получаемая линией
от генератора, равна ![]() , то
мощность в конце линий длиной
, то
мощность в конце линий длиной ![]() в данном
случае
в данном
случае
![]() ,
,
откуда КПД линии
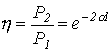
и затухание
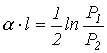 .
.
Как указывалось
при рассмотрении четырехполюсников, единицей затухания является непер,
соответствующий затуханию по мощности в ![]() раз, а по напряжению
или току – в
раз, а по напряжению
или току – в ![]() раз.
раз.
Линия без искажений
Пусть
сигнал, который требуется передать без искажений по линии, является
периодическим, т.е. его можно разложить в ряд Фурье. Сигнал будет искажаться,
если для составляющих его гармонических затухание и фазовая скорость различны,
т.е. если последние являются функциями частоты. Таким образом, для отсутствия
искажений, что очень важно, например, в линиях передачи информации, необходимо,
чтобы все гармоники распространялись с одинаковой скоростью и одинаковым
затуханием, поскольку только в этом случае, сложившись, они образуют в конце
линии сигнал, подобный входному.
Идеальным
в этом случае является так называемая линия без потерь, у которой сопротивление ![]() и
проводимость
и
проводимость ![]() равны нулю.
равны нулю.
Действительно,
в этом случае
![]() ,
,
т.е.
независимо от частоты коэффициент затухания ![]() и фазовая
скорость
и фазовая
скорость
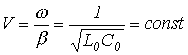 .
.
Однако
искажения могут отсутствовать и в линии с потерями. Условие передачи сигналов
без искажения вытекает из совместного рассмотрения выражений для постоянной
распространения
|
|
(8.13) |
и
фазовой скорости
|
|
(8.14) |
Из
(8.13) и (8.14) вытекает, что для получения ![]() и
и ![]() , что
обеспечивает отсутствие искажений, необходимо, чтобы
, что
обеспечивает отсутствие искажений, необходимо, чтобы ![]() , т.е.
чтобы волновое сопротивление не зависело от частоты.
, т.е.
чтобы волновое сопротивление не зависело от частоты.
|
|
(8.15) |
Как
показывает анализ (8.15), при
|
|
(8.16) |
![]() есть
вещественная константа.
есть
вещественная константа.
Линия,
параметры которой удовлетворяют условию (8.16), называется линией без
искажений.
Фазовая
скорость для такой линии
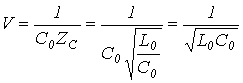
и
затухание
![]() .
.
Следует
отметить, что у реальных линий (и воздушных, и кабельных) ![]() . Поэтому
для придания реальным линиям свойств линий без искажения искусственно
увеличивают их индуктивность путем включения через одинаковые интервалы
специальных катушек индуктивности, а в случае кабельных линий – также за счет
обвивания их жил ферромагнитной лентой.
. Поэтому
для придания реальным линиям свойств линий без искажения искусственно
увеличивают их индуктивность путем включения через одинаковые интервалы
специальных катушек индуктивности, а в случае кабельных линий – также за счет
обвивания их жил ферромагнитной лентой.
9 Лекция 9.
Уравнения линии конечной длины
Цель лекции: изучение различных режимов в однородной
линии без потерь.
Содержание:
-
уравнения линии с гиперболическими функциями;
- линия
без потерь;
- входное сопротивление линии.
 Постоянные
Постоянные ![]() и
и ![]() в
полученных в предыдущей лекции формулах
определяются на основании граничных условий.
в
полученных в предыдущей лекции формулах
определяются на основании граничных условий.
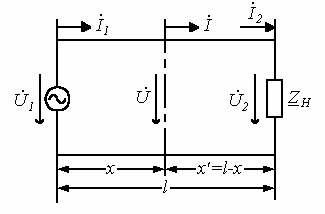
Рисунок 9.1
|
|
(9.1) |
|
|
(9.2) |
Пусть для линии длиной l ( рисунок (9.1) заданы
напряжение ![]() и ток
и ток ![]() в начале
линии, т.е. при
в начале
линии, т.е. при ![]() .
.
Тогда из (9.1) и (9.2) получаем
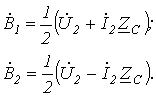
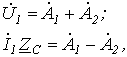
откуда

Подставив найденные выражения ![]() и
и ![]() в (9.1) и
(9.2), получим
в (9.1) и
(9.2), получим
|
|
(9.3) |
|
|
(9.4) |
Уравнения (9.3) и (9.4) позволяют определить ток и
напряжение в любой точке линии по их известным значениям в начале линии. Обычно
в практических задачах бывают заданы напряжение ![]() и ток
и ток ![]() в конце
линии. Для выражения напряжения и тока в линии через эти величины перепишем
уравнения (9.1) и (9.2) в виде
в конце
линии. Для выражения напряжения и тока в линии через эти величины перепишем
уравнения (9.1) и (9.2) в виде
|
|
(9.5) |
|
|
(9.6) |
Обозначив ![]() и
и ![]() , из
уравнений (9.5) и (9.6) при
, из
уравнений (9.5) и (9.6) при ![]() получим
получим

откуда
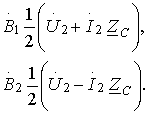
После
подстановки найденных выражений ![]() и
и ![]() в (9.5) и
(9.6) получаем уравнения, позволяющие определить ток и напряжение по их
значениям в конце линии
в (9.5) и
(9.6) получаем уравнения, позволяющие определить ток и напряжение по их
значениям в конце линии
|
|
(9.7) |
|
|
(9.8) |
Линия без потерь
Линией без потерь называется линия, у которой
первичные параметры ![]() и
и ![]() равны нулю.
В этом случае, как было показано ранее,
равны нулю.
В этом случае, как было показано ранее, ![]() и
и ![]() . Таким
образом,
. Таким
образом,
![]() ,
,
откуда
![]() .
.
Раскроем
гиперболические функции от комплексного аргумента ![]()

Тогда
для линии без потерь, т.е. при ![]() , имеют
место соотношения:
, имеют
место соотношения:
![]() и
и ![]()
Таким
образом, уравнения длинной линии в гиперболических функциях от комплексного
аргумента для линии без потерь трансформируются в уравнения, записанные с
использованием круговых тригонометрических функций от вещественного аргумента
|
|
(9.9) |
|
|
(9.10) |
Строго
говоря, линия без потерь (цепь с распределенными параметрами без потерь)
представляет собой идеализированный случай. Однако при выполнении ![]() и
и ![]() , что имеет
место, например, для высокочастотных цепей, линию можно считать линией без
потерь и, следовательно, описывать ее уравнениями (9.9) и (9.10).
, что имеет
место, например, для высокочастотных цепей, линию можно считать линией без
потерь и, следовательно, описывать ее уравнениями (9.9) и (9.10).
Стоячие волны в длинных линиях
Как
было показано выше, решение уравнений длинной линии можно представить в виде
суммы прямой и обратной волн. В результате их наложения в цепях с
распределенными параметрами возникают стоячие волны.
Рассмотрим
два предельных случая: ХХ и КЗ в линии без потерь, когда поглощаемая приемником
активная мощность равна нулю.
При
ХХ на основании уравнений (9.9) и (9.10) имеем
![]() и
и 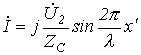
откуда для
мгновенных значений напряжения и тока можно записать
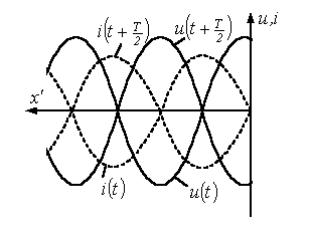
Рисунок 9.2
|
|
(9.11) |
|
|
(9.12) |
Последние
уравнения представляют собой уравнения стоячих волн, являющихся результатом
наложения прямой и обратной волн с одинаковыми амплитудами.
При ХХ в соответствии с (9.11) и (9.12) в
точках с координатами ![]() , где
, где ![]() - целое
число, имеют место максимумы напряжения, называемые пучностями, и нули тока, называемые узлами. В точках с координатами
- целое
число, имеют место максимумы напряжения, называемые пучностями, и нули тока, называемые узлами. В точках с координатами ![]() пучности и
узлы напряжения и тока меняются местами (рисунок 9.2). Таким образом, узлы и
пучности неподвижны, и пучности одной переменной совпадают с узлами другой и
наоборот.
пучности и
узлы напряжения и тока меняются местами (рисунок 9.2). Таким образом, узлы и
пучности неподвижны, и пучности одной переменной совпадают с узлами другой и
наоборот.
При
КЗ на основании уравнений (9.9) и (9.10)
![]() и
и ![]() ,
,
откуда для мгновенных значений можно записать
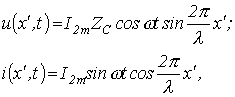
т.е. и в этом случае напряжение и ток представляют собой стоячие волны, причем
по сравнению с режимом ХХ пучности и узлы напряжения и тока соответственно
меняются местами.
Поскольку
в узлах мощность тождественно равна нулю, стоячие волны в передаче энергии
вдоль линии не участвуют. Ее передают только бегущие волны. Чем сильнее
нагрузка отличается от согласованной, тем сильнее выражены обратные и,
следовательно, стоячие волны. В рассмотренных предельных случаях ХХ и КЗ имеют
место только стоячие волны, и мощность на нагрузке равна нулю.
Входное сопротивление длинной линии
Входным
сопротивлением длинной линии (цепи с распределенными параметрами) называется
такое сосредоточенное сопротивление, подключение которого вместо линии к
зажимам источника не изменит режим работы последнего.
В
общем случае для линии с произвольной нагрузкой ![]() для
входного сопротивления можно записать
для
входного сопротивления можно записать
|
|
(9.13) |
Полученное
выражение показывает, что входное сопротивление является функцией параметров
линии ![]() и
и ![]() , ее длины
, ее длины ![]() и нагрузки
и нагрузки ![]() . При этом
зависимость входного сопротивления от длины линии, т.е. функция
. При этом
зависимость входного сопротивления от длины линии, т.е. функция ![]() , не является
монотонной, а носит колебательный характер, обусловленный влиянием обратной
(отраженной) волны. С ростом длины линии как прямая, так соответственно и
отраженная волны затухают все сильнее. В результате влияние последней
ослабевает и амплитуда колебаний функции
, не является
монотонной, а носит колебательный характер, обусловленный влиянием обратной
(отраженной) волны. С ростом длины линии как прямая, так соответственно и
отраженная волны затухают все сильнее. В результате влияние последней
ослабевает и амплитуда колебаний функции ![]() уменьшается.
При согласованной нагрузке, т.е. при
уменьшается.
При согласованной нагрузке, т.е. при ![]() , как было
показано ранее, обратная волна отсутствует, что полностью соответствует
выражению (9.13), которое при
, как было
показано ранее, обратная волна отсутствует, что полностью соответствует
выражению (9.13), которое при ![]() трансформируется
в соотношение
трансформируется
в соотношение
![]() .
.
Такой
же величиной определяется входное сопротивление при ![]() .
.
При
некоторых значениях длины линии ее входное сопротивление может оказаться чисто
активным. Длину линии, при которой ![]() вещественное,
называют резонансной. Как и в цепи с сосредоточенными параметрами,
резонанс наиболее ярко наблюдается при отсутствии потерь. Для линии без потерь
на основании (9.13) можно записать
вещественное,
называют резонансной. Как и в цепи с сосредоточенными параметрами,
резонанс наиболее ярко наблюдается при отсутствии потерь. Для линии без потерь
на основании (9.13) можно записать
|
|
(9.14) |
Из
(9.14) для режимов холостого хода (ХХ) и короткого замыкания (КЗ), т.е.
случаев, когда потребляемая нагрузкой активная мощность равна нулю,
соответственно получаем:
|
|
(9.15) |
|
|
(9.16) |
Исследование
характера изменения ![]() в
зависимости от длины
в
зависимости от длины ![]() линии на
основании (9.15) показывает, что при
линии на
основании (9.15) показывает, что при ![]()
![]() по модулю
изменяется в пределах
по модулю
изменяется в пределах ![]() и имеет
емкостный характер, а при
и имеет
емкостный характер, а при ![]() - в
пределах
- в
пределах ![]() и имеет
индуктивный характер. Такое чередование продолжается и далее через отрезки
длины линии, равные четверти длины волны (рисунок 3,а).
и имеет
индуктивный характер. Такое чередование продолжается и далее через отрезки
длины линии, равные четверти длины волны (рисунок 3,а).
В
соответствии с (1.16) аналогичный характер, но со сдвигом на четверть волны
будет иметь зависимость ![]() при КЗ
(рисунок 3б).
при КЗ
(рисунок 3б).
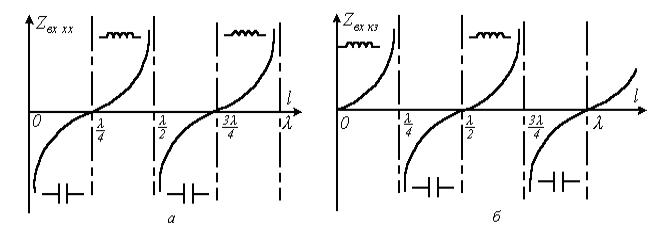
Рисунок
9.3
Точки,
где ![]() ,
соответствуют резонансу напряжений, а точки, где
,
соответствуют резонансу напряжений, а точки, где ![]() , -
резонансу токов.
, -
резонансу токов.
Таким
образом, изменяя длину линии без потерь, можно имитировать емкостное и
индуктивное сопротивления любой величины. Поскольку длина волны ![]() есть
функция частоты, то аналогичное изменение
есть
функция частоты, то аналогичное изменение ![]() можно
обеспечить не изменением длины линии, а частоты генератора. При некоторых
частотах входное сопротивление цепи с распределенными параметрами также
становится вещественным. Такие частоты называются резонансными.
можно
обеспечить не изменением длины линии, а частоты генератора. При некоторых
частотах входное сопротивление цепи с распределенными параметрами также
становится вещественным. Такие частоты называются резонансными.
Список литературы
1.Бакалов В. П.,
Дмитриков В.Ф., Крук Б.Е. Основы теории цепей: Учебник для вузов. – М.: Радио и
связь, 2000.-592с.
2.Демирчян К.С.,
Нейман Л.Р., Коровкин Н.В., Чечурин В.Л. Теоретические основы электротехники. -
т.1. – Санкт-Петербург: Питер, 2003.-463с.
3. Демирчян К.С.,
Нейман Л.Р., Коровкин Н.В., Чечурин В.Л. Теоретические основы электротехники. -
т.2. – Санкт-Петербург: Питер, 2003.-576с.
4.Зевеке Г.В., Ионкин
П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. – М.: Энергоатомиздат,
1989.-528с.
5.Шебес М. Р.,
Каблукова М. В. Задачник по теории линейных электрических цепей. – М.: Высшая
школа, 1990.-544с.
Сводный план 2006 г., поз. 144
Зухра Исламовна Жолдыбаева
Екатерина Хаскелевна Зуслина
Татьяна Ивановна
Коровченко
ТЕОРИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ 2
Конспект лекций
(для студентов всех форм обучения
специальностей 050719 –
Радиотехника, электроника и телекоммуникации, 050704 - Вычислительная техника и
программное обеспечение)
Редактор
Ж.М. Сыздыкова
Подписано в печать
_________ Формат 60х84 1/16
Тираж 110 экз. Бумага
типографская №1
Объем уч. - изд. л. Заказ
____. Цена ____тенге.
Копировально-множительное бюро
Алматинского института энергетики и связи
050013, Алматы, Байтурсынова 126.

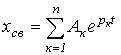
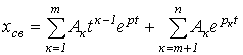
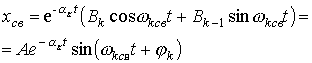
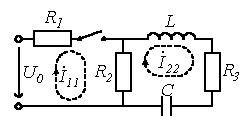
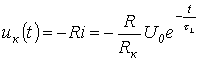 .
.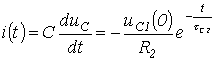 .
.
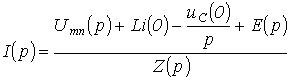
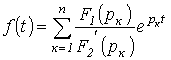
 .
.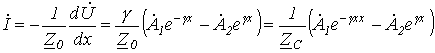 ,
,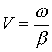
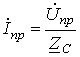
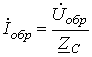
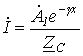
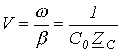

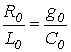
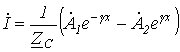


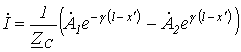
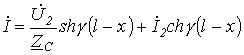
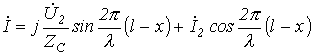
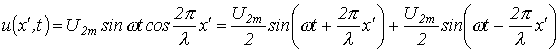
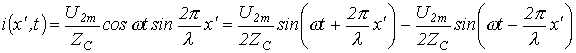 .
. 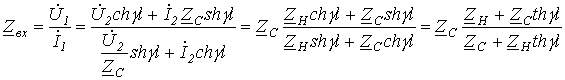 .
.