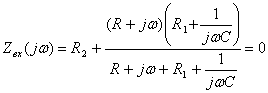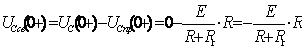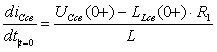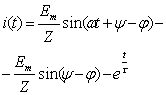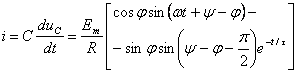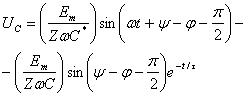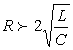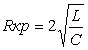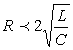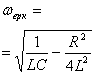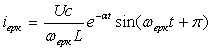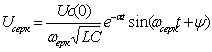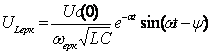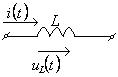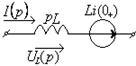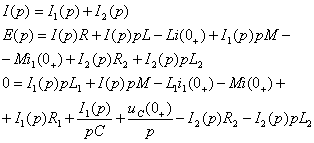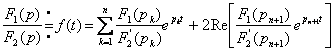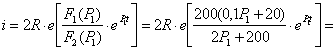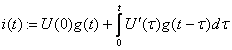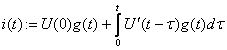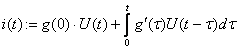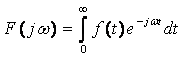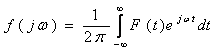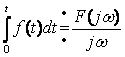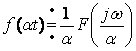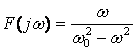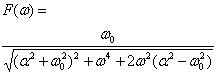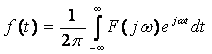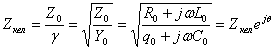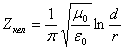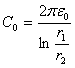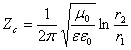НЕКОММЕРЧЕСКОЕ НЕКОММЕРЧЕСКОЕ АКЦИОНЕРНОЕ ОБЩЕСТВО

Алматинский институт энергетики и связи 

Кафедра теоретических основ электротехники

 

 

 

Теория электрических цепей 2

 

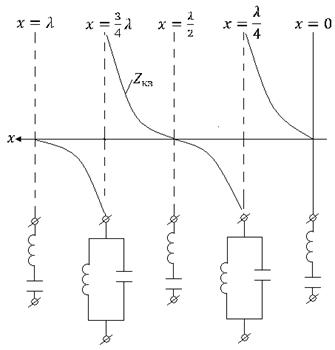
Методические указания к расчету установившихся и переходных процессов в электрических цепях

 для специальностей 5В0719 – Радиотехника, электроника и телекоммуникации, 5В0704 - Вычислительная техника и программное обеспечение,  5В0703 – Информационная система 

 

 

Алматы 2010

СОСТАВИТЕЛЬ: Х.А. Иманбаев. Теория электрических цепей 2. Методические указания к расчету установившихся и переходных процессов в электрических цепях  (для специальностей 5В0719 – Радиотехника, электроника и телекоммуникации, 5В0704 – Вычислительная техника и программное обеспечение,  5В0703 – Информационная система). – Алматы: АИЭС, 2010.- 42с.

 

Методические указания к  расчету переходных процессов в электрических цепях «Теория электрических цепей 2» содержат четыре работы по темам: «Переходные процессы в линейных электрических цепях», «Расчет переходных процессов методом интеграла Дюамеля», «Спектральный (Частотный) метод», «Цепи с распределенными параметрами (однородная линия)». Методические указания к расчету соответствует типовой программе по дисциплине ТЭЦ 2 для специальностеи 5В0719, 5В0704, 5В0703.

 

1 Переходные процессы в линейных электрических цепях

 

1.1 Возникновение переходных процессов

 

Под переходным процессом понимают процесс перехода от одного режима работы электрической цепи к другому, чем-либо отличающемуся от предыдущего.

Под коммутацией понимают различные включения, выключения пассивных и активных   ветвей и элементов электрической цепи, приводящие к изменению схемы и ее параметров. Обычно считают, что коммутация совершается мгновенно.

При наличии в цепи накопителей энергии (индуктивности и емкости) переходный процесс имеет конечную длительность. Практически длительность переходного процесса составляет доли секунды (например, сотые); теоретически время протекания переходного процесса t=∞.

Методами расчета переходных процессов являются:

1. Классический метод

2. Операторный метод

3. Метод расчета путем применения интеграла Дюамеля

4. Частотный метод.

Расчет переходных процессов состоит из следующих основных операции:

а) Выбор положительных направлений токов в ветвях цепи.

б) Определение значений токов и напряжений непосредственно до  коммутации.

в) Составление характеристического уравнения и определение корней.

г) Получение выражений для искомых токов и напряжений, как функции времени.

 

1.2 Классический метод

 

Классическим методом расчета переходных процессов называется метод расчета, в котором решение дифференциального уравнения берется в виде суммы принужденного и свободного решений и в котором определение постоянных интегрирования, входящих в выражение для свободного тока (напряжения), производится путем совместного решения системы алгебраических уравнений по известным значениям корней характеристического уравнения и известным значениям свободной составляющей тока и ее производных, взятых при   

 

Законы коммутации

Т а б л и ц а 1.1

Законы коммутации	Пример
Ток и магнитный поток в ветви с индуктивностью не могут изменятся скачком и в момент коммутации равны тем значения, которые они имели непосредственно передней (условие непрерывности тока и магнитного потокосцепления)
Напряжение и заряд на емкости не могут изменяться скачком и в момент коммутации равны тем значениям, которые они имели непосредственно передней (условие непрерыв- ности напряжения и заряда):

 

1.3 Расчет классическим методом

 

Решение дифференциального для схемы, образованный после коммутации, записывают без его составления в виде принужденной и свободной составляющих.

Например, для переходных токов  и напряжения:

  

Такие составляющие являются вспомогательными (расчетными) величинами.

 

Т а б л и ц а 1.2

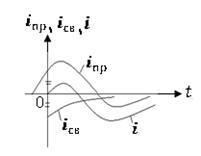
Переходный ток (напряжение), т.е. реакция цепи на производимую в ней  коммутацию

 

 

 

Продолжение таблицы 1.2

Принужденная составляющая пере- ходного тока (напряжения), т.е. частное решение неоднородного дифферен- циального уравнения, определяемое по схеме, образованное  после коммутации. В схеме с периодическими (постоян- ными) источниками принужденная составляющая является установившей величиной и также будет периодической (постоянной во времени)

Свободная составляющая пере- ходного тока (напряжения) представляет со- бой решение однородного дифференциаль- ного уравнения для коммутационной схемы.    При расчете сводной составляющей в схеме, образованной после коммутации, ЭДС и токи источников тока принимают равным нулю (источники ЭДС закорачивают, а источники тока разрывают)    Значение  свободной составляющей зависит от вида электрической схемы, ее параметров и перераспределения запасов в накопителях энергии. Свободная составляющая затухает с течением времени (теоретически ).

 

 

 Характер свободного процесса в зависимости от корней характеристического уравнения

Т а б л и ц а 1.3

Характер корней	Уравнение свободного процесса
Корни действительные неравные (всегда отрицательные): (апериодическим процесс). Корни действительные равные (всегда отрицательные):(критический процесс). Один корень действительный (всегда отрицательный) а два корня комплексные сопряженные (действительные части всегда отрицательные):

Составление  характеристического уравнения и определение степени

Т а б л и ц а 1.4

Способы составления

Пример

Первый способ: Входные  комплексные сопротивления (проводимость) после коммутационной схемы приравнивают нулю и заменяют на или Полученное алгебраическое  уравнение решают относительно корней В общем случае входное сопротивление(проводимость) находят по отношению к зажимам, к которым подключена ветвь с искомой переходной функции  Решая уравнение относительно  получаем два корня Степень характеристического уравнения равна сумме порядков дифференциальных уравнений для независимых контуров, выбранных так, чтобы порядок дифференциальных уравнений для них был наименьшим. Характеристическое уравнение нечетной степени имеет хотя бы один действительный корень(отрицательный). Характеристическое уравнение четной степени имеет четное число действительных или комплекно-сопряженных корней. Коэффициенты характеристического уравнения должны быть действительными и положительными. Наличие в схеме ветвей с взаимной индуктивностью не повышает степень характеристи- ческого уравнения.

 

 

Начальные условия (начальные значения токов и напряжений при )

    

Независимые начальные условия – значения токов (потоков) в индуктивном и напряжения (заряда) на емкостном элементах в момент коммутации определяемые по законам коммутации.

 Зависимые начальные условия-значения токов и напряжений в момент коммутации определяемые по схеме, образованной после коммутации по законам Кирхгофа с учетом законов коммутации.

Схема имеет нулевые начальные условия, если в момент коммутации токи и напряжения на всех ее пассивных элементах равны нулю При нулевых начальных условиях наличии индуктивности  равносильно разрыву ветви а емкости – короткому замыканию Постоянные интегрирования, число которых рано порядку уравнения, определяют по зависимым и независимым начальным условиям.

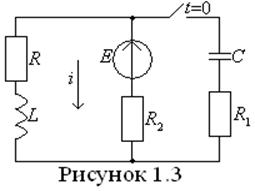
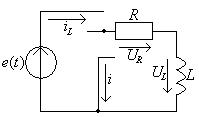
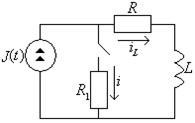
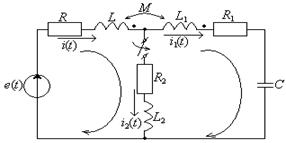
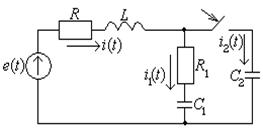
Найдем независимые и зависимые начальные условия для схемы рис.1.3

Т а б л и ц а 1.5

Начальные условия	Схема	Математическая запись
Независимые
Зависимые	В момент коммутации   (Законы Кирхгофа) Откуда   производную   находим из уравнения

Определение зависимых начальных условии по законам Кирхгофа.

1. По законам коммутации определяется 

2. Для цепи, образованной после коммутации, составляют уравнения Кирхгофа и записывают их для момента коммутации  с учетом

3. Полученную систему алгебраических уравнений решают относительно искомых величин при  В случае необходимости, например для определения первой и второй производных при  уравнения Кирхгофа дифференцируют и решают совместно для

 

Определение начальных условии для свободных составляющих токов и напряжений

 

Начальные значения свободных составляющих токов на индуктивности и напряжениях на емкостных элементах, а также их производные определяются с учетом законов коммутации по следующим соотношениям:

В других элементах схемы начальные значения свободных составляющих токов и напряжении рассчитывают на основании уравнении, составленных по законам Кирхгофа для после коммутационной схемы без источников энергии.

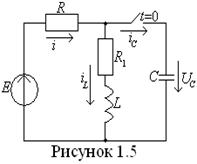
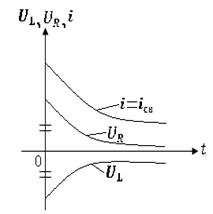
Пример: определить начальные значения свободных составляющих токов и напряжении при  (рис.1.5,  1.6)

Т а б л и ц а 1.6

Начальные условия	Схема
Для свободных составляю-щих		Схема для расчета свободных составляющих дана на рис 1.6 по законам Кирхгофа   откуда

 Алгоритм расчета переходных процессов классическим методом

1. В после коммутационной схеме известными методами находят принужденные составляющие искомых токов и напряжении.

2. Составляют характеристическое уравнение и определяют его корни. Исходя из характера корней, записывают выражения для искомых свободных составляющих токов и напряжений через постоянные интегрирования. Переходные значения искомых функций рассматривают как сумму найденных значений принужденной и свободной составляющих данной функции, например .

3. До коммутации рассчитывают токи в индуктивных   и напряжениях на емкостных элементах, в соответствии с которыми по законам коммутации определяют независимые начальные условия:

4. Зависимые начальные условия находят по законам Кирхгофа в после коммутационной схеме с учетом независимых начальных условий. Постоянные интегрирования вычисляют с помощью начальных условий для искомых функции и их производных. Найденные начальные условия подставляют в уравнение искомых переходной функции для  и в уравнениях их производных, записанных для  Полученную систему алгебраических уравнений решают относительно постоянных интегрирования. 

 

1.4 Переходные процессы  в простейших схемах

Т а б л и ц а 1. 7

Напряжение(ток)	Схема Переходные величины	Графики переходных величин
а) начальные условия нулевые

 

Продолжение таблицы 1.7

Не нулевые начальные условия	;  ; ;
	где ;

  

Т а б л и ц а 1.8

Напряжение (ток)	Схема Переходные величины	Графики переходных величин
а) Нулевые начальные условия
Не нулевые начальные условия

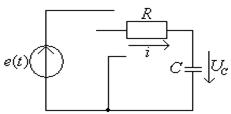
1.5 Переходные процессы в -цепи

 

Свободные состовляющие при переходном процессе  описываются дифференциальными уравнениями второго порядка:

 

 

 

 

 

Характер свободного процнсса зависит от начальных условии и корней харатеристического уравнения откуда  Рассмотрим разряд конденсатора  при подключения схемы к постоянному напряжению.

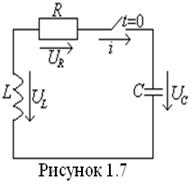
При разряде конденсатор  на  (рис 1.7)в момент коммутации напряжение на нем равно а ток в контуре При этом в контуре наблюдается только свободный процесс, характер которого определяется корнями характеристического уравнения.

    

 

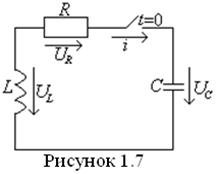
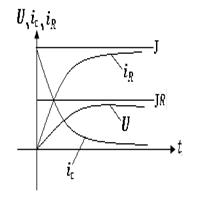
         Т а б л и ц а 1.9

Вид разряда	Корни характерис-тического уравнения	Свободные составляющие тока и напряжения	Графики свободных составляющих тока и напряжения
Апериодический	Два действительных отрицательных неравных корня
Предельный (критический) процесс	Два действительных отрицательных неравных корня
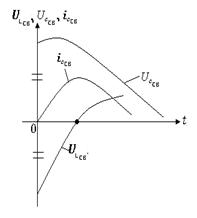
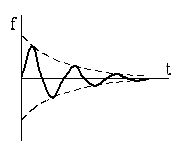
Колебательный	Два комплексно сопряжен ных корня  где  коэффициент затухания  частота  собственных колебаний

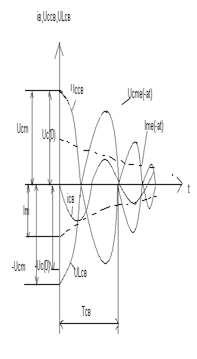
Быстроту затухания собственных колебании характеризуют отношением напряжений в момент времени и

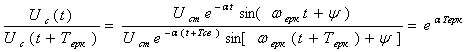
Это отношение называемое декрементом колебания- постоянная величина, не зависящая от времени а зависящая от параметров -контура

логарифмический декремент колебании

 

1.6 Операторный метод расчета переходных процессов

 

Суть операторного метода заключается в том, что функции действительной переменной  сопоставляется функция комплексной переменной  Это сопоставление осуществляется с помощью прямого преобразования

Лапласа: 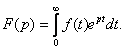  Функция называемся оригиналом, функция называется изображением.

Обозначение:  

Изображение постоянной :

Изображения производных:  

где  начальные значения функции и её производной. При нулевых начальных значениях 

Изображение интеграла:

 

Таблица оригиналов и изображений по Лаплас

Т а б л и ц а 1.10

Оригинал	Изображение	Обозначение

Продолжение таблицы 1.10

 

 

Изображения напряжений на пассивных элементах

Т а б л и ц а 1.11

Изображения напряжений на	Оригинал	Изображение
Сопротивление
Индуктивность.  В момент ток в индуктивности:
Ёмкость.  В момент напряжение на ёмкости:

 

Система интегро-дифференциальных уравнений Кирхгофа относительно оригиналов: , заменяется системой алгебраических уравнений относительно их изображений:

 

Эквивалентные операторные схемы

Т а б л и ц а 1.12

Исходная схема	Операторная схема

Продолжение таблицы 1.12

	или
	или

 

 

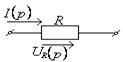
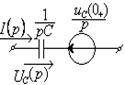
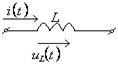
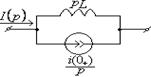
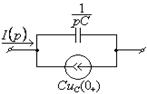
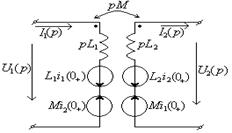
1.7 Законы Ома и Кирхгофа в операторной форме. Эквивалентные схемы

Т а б л и ц а 1.13

Исходная схема	Операторная схема
	Если  операторная схема не содержит

         Продолжение таблицы 1.13

 

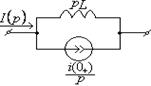
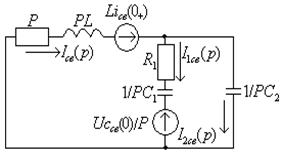
Расчет свободных составляющих операторным методом. Операторная схема

Т а б л и ц а 1.14

Исходная схема	Операторная схема

 

1.8 Теорема разложения

Т а б л и ц а 1.15

 

 

 

Продолжение таблицы 1.15

Знаменатель имеет один  нулевой корень:
1. Характеристическое уравнение  имеет простые корни  и комплексные сопряженные корни 2.- ком-плексные сопряженные корни уравнения	1.       2.

 

1.9 Алгоритм расчета переходных процессов операторным методом

 

1. По законам коммутации определяют независимые начальные условия: 

2. Составляют эквивалентную операторную схему. Ненулевые начальные условия     учитываются введением внутренних (расчетных) эдс (или источников тока): в ветвях с индуктивностью вводится эдс  (направление эдс совпадает с положительным направлением тока в данной ветви); в ветвях с емкостью вводится эдс  (направление  эдс противоположно положительному направлению тока) Сопротивления ветвей вычисляются в операторной форме

где -операторные сопротивления, соответ- ственно, на индуктивности и  емкости.

3. Изображения токов и напряжений рассчитывают по операторной схеме известными методами (законы Ома и Кирхгофа, МКТ, МУП, МЭГ и т.п.).

4.Оригинал определяют по теореме разложения, по таблице оригиналов и   изображений или с помощью обратного преобразования Лапласа.

 

Эквивалентные операторные схемы

         Т а б л и ц а 1.16

Исходная схема	Операторная схема
	или

Продолжение таблицы 1.16

	или

 

1.10 Приведение схемы к нулевым начальным условиям

 

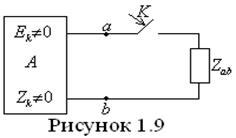
Переходный процесс в схеме с ненулевыми начальными условиями при подключении (выключении) к ней какой-либо ветви может быть рассчитан методом наложения.

В рассматриваемой ветви переходный ток получают суммированием установившего, протекающего до коммутации, и переходного тока, возникающего в этой ветви при подключении схемы с нулевыми начальными условиями к источнику ЭДС (ток) которого равен напряжению (току) на переключателе до коммутации Переходный процесс  в схеме с нулевыми начальными условиями рассчитывают классическим или операторным методом.

         Т а б л и ц а 1.17

Исходная схема	Схема для расчета режима до коммутации	Схема с нулевыми начальными условиями

         Продолжение таблицы 1.17

К выводам 1-2 активного двухполюсника ключом  «» подключается ветвь с операторным сопротив- лением

Для расчета тока в подключаемой ветви опре- делим В ветвь включим два источника с противо- положно направленным ЭДС  При этом режим не изменится в цепи.

Рассмотрим расчет при включении «». Система линейна, применяем метод наложения. а) Находим токи по схеме   «», т.е. при действии всех источников  актив- ного двухполюсника и ЭДС которая дейс- твует противоположно напряжению  В схеме «» после замыкания ключа, ток  так как  Следовательно для всей схемы будет режим до коммутации. б) В схеме «» ЭДС действует в ветви в том же направлении, что и напряжение  т.е. рассчитывается переход -ный процесс при замы -кании ключа «» ветви с источником ЭДС  к пассивному двухполюс- нику. Процесс рассма- тривается для нулевых начальных условии.

Изображение свободной составляющей тока (напряжения) может быть найдено по операторной схеме, построенной для этой составляющей. При этом схема содержит только дополнительные источники ЭДС и тока, ЭДС которых определяются ненулевыми начальными условиями для свободных составляющих токов в ветвях с индуктивными элементами  и напряжений на емкостных элементах  а так же операторными сопротивлениями  В операторной схеме для свободных составляющих заданные источники тока не учитывают (источники ЭДС закорачивают, а источники тока размыкают).

Т а б л и ц а 1.18

Исходная схема	Операторная схема

 

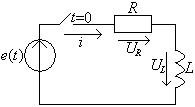
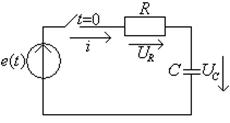
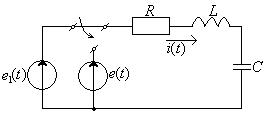
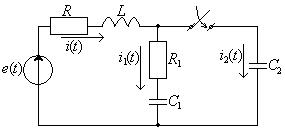
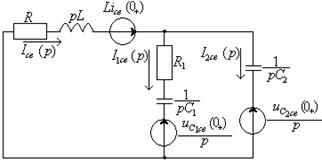
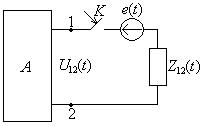
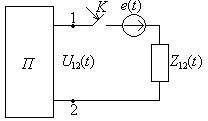
Пример: Сведение расчета переходного к нулевым начальным условиям. Найти ток в конденсаторе (рис.1.8) после включения ключа.

Дано:

 

_{Т а б л и ц а 1.19}

Схема	Переходные величины
Представим всю схему в виде активного двухполюсника, кроме ключа.	Выбрав положительное направление напряжение на ключе, как показано на рис.1.8, найдем  Входное сопротивление активного и соответствующего пассивного  двух- полюсника (рис.1.10)

 

_{Продолжение таблицы 1.19}

Изображение искомого тока найдем по закону Ома в операторной форме: Приравниваем находим корни характеристического уравнения: Оригинал найдем по теореме разло- жения при комплексных корнях:

 

 

2 Расчет переходных процессов методом интеграла Дюамеля 

 

 Интеграл Дюамеля (интеграл наложения) применяют для расчета переходного тока (напряжения) в ветвях с нулевым начальными условии при подключении ее к источнику эдс произвольной формы. Использования интеграла Дюамеля требует знания переходной функции (характеристики) схемы  Если определяют переходный ток, то переходная функция является переходной проводимостью  если рассчитывают переходное напряжение, то переходная функция является переходной функцией напряжения

Существует несколько форм записи интеграла Дюамеля. Для каждой конкретной задачи выбирают ту форму, которая имеет более простое подынтегральное выражение и приводит к меньшему числу слагаемых. Для всех форм записи переменной интегрирования является, например,

 Тогда производные в подынтегральном выражении  определяются по времени после чего в полученном выражении заменяют на и производят вычисление интеграла в пределах фиксированных

 

Т а б л и ц а 2.1

 

 2.1 Единичные и переходные функции

         Т а б л и ц а 2.2

Функция и ее обозначения	Определения	Свойства функции
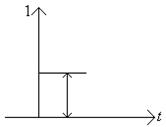
Единичная функция  (имеет нулевую размерность)	Соответствует подклю- чению постоянного на- пряжения (тока) на вход электрической цепи в момент времени	Если  произвольная функция, то при
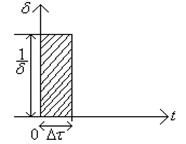
Единичный импульс (дельта функция, имея размерность с)	Бесконечно большой импульс в момент времени  площадь которого равна единице:    при
Переходная проводимость (имеет размерность )	Функция времени рав- ная отношению электри- ческого тока в цепи при подключении этой цепи к постоянному напря- жению	при

         Продолжение таблицы 2.2

Переходная функция напряжения	Переходное напряжение на участке схемы, возникающее при под- ключении ее к единич- ному постоянному напря- жению	при
Импульсная характеристика	Реакция цепи при нуле- вых начальных условиях на единичный импульс напряжения (тока)	Где,  переменная интегри- рования

 

2.2 Действие единичных ступенчатых и единичных импульсов источников на индуктивный и емкостной элементы

         Т а б л и ц а 2.3

Элемент	Воздействующий источник	Напряжение (ток) на элементе
	ступенчатая функция величиной когда  -им- пульсное напряжение. При воздействии им- пульсного источника напряжения в момент времени  ток на индуктивности изменяется скачком.	- импульсная функция, определяемая площадью           при            при  сту- пенчатая функция, определяемая величиной
	- импульсный ток  ступенчатая функция, определяемая величии- ной   При действии импульс- ного источника тока в момент времени  на- пряжение на емкостном элементе изменяется скачкообразно.	Ступенчатая функция, определяемая величиной    импульсная функция, определяемая площадью

2.3 Алгоритм расчета переходных процессов методом интеграла Дюамеля

1. Классическим (операторным) методом находят переходную проводимость (переходную функцию напряжения ), если искомым является ток (напряжение)

2. Вычисляют производную подынтегральной функции интеграла Дюамеля. Для этого сначала определяют производную по времени а затем заменяют переменной интегрирования

3. Записывают интеграл Дюамеля (в форме наиболее рациональной для решаемой задачи) с момента времени до фиксированного момента времени. При этом учитывают возможные скачи тока (напряжения) в начале и конце каждого интервала до фиксированного момента вызываемые наличием скачков приложенного напряжения

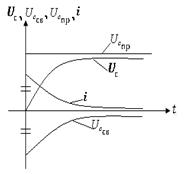
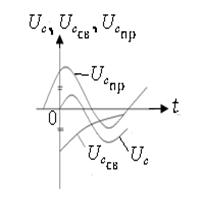
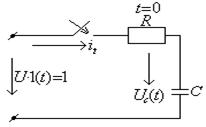
 Пример: Найти выражения для напряжения в схеме рис 2.1 а, при подключении ее к напряжению рис 2.2 б.

                                

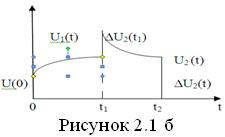
Решение: Воспользуемся третьей (наиболее рациональной в данном случае) формой записи интеграла Дюамеля:

Определим переходную функцию напряжения (напряжение на емкостном элементе при включении схемы к постоянному напряжению, равному )

         _где      

Найдем производную переходной функции на интервале времени

        где  – переменная интегрирования.

Запишем интеграл Дюамеля для трех интервалов времени

Т а б л и ц а 2.4

Интервал	Интеграл Дюамеля

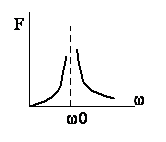
 3 Спектральный (Частотный) метод

 

Частотный метод основан на преобразованиях Фурье и является частным случаем преобразования Лапласа. Оно может быть осуществлено на основе преобразования Лапласа путем замены на

В схеме с нулевыми начальными условиями на спектральной характеристике входного напряжения частотной характеристике цепи определяют спектральную характеристику искомого тока . Функцию времени находят с помощью обратного преобразования Фурье (интеграл Фурье) по таблицам изображений или формулой разложения. Переходный процесс при ненулевых начальных условиях схема сводится к схеме с нулевыми начальными условиями.

 

3.1 Преобразование Фурье

Т а б л и ц а 3.1

Апериодическая функция времени, удовлетворяющая условие абсолют- ной интегрируемости:
Спектральная функция (спектральная характеристика)
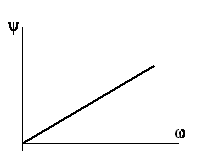
Модуль спектральной функции (амплитудная характеристика)
Аргумент спектральной функции (фазовая характеристика)
Соответствие спектральной функции и апериодической функции времени
Одностороннее прямое преобра- зование Фурье, применяемое, если  при
Двухсторонне прямое преобра- зование Фурье, применяемое, если при
Обратное преобразование Фурье (интеграл Фурье)
Переход от спектральной функции к функции времени путем замены  на  в ее изображение по Лапласу

 

3.2 Основные свойства преобразования Фурье

Т а б л и ц а 3.2

Свойство линейности
Дифференцирование функции времени
Интегрирование функции времени
Дифференцирование спектральной характеристики
Изменение масштаба независимого переменного
Смещение функции времени
Смещение спектральной характеристики
Умножение спектральных характеристик
Умножение функции времени на косинус
Умножение функции времени на синус

 

3.3 Спектральные характеристики некоторых функции

 

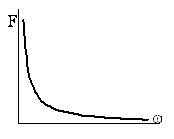
Функции времени, неудовлетворяющих условию абсолютной интегрируемости.

Абсолютная характеристика функции в этом случае, должна, хотя бы в одной точке равна бесконечности.

Т а б л и ц а 3.3

Функция времени	Амплитудная характеристика	Фазовая характеристика
при (единичная функция)

Продолжение таблицы 3.3

при  (косинусоидальная функция)
при   (синусоидальная функция)

 

 

3.4 Функции времени, удовлетворяющие условию абсолютной интегрируемости

Т а б л и ц а 3.4

Функция времени	Абсолютная характеристика	Фазовая характеристика
(убывающая показательная функция)

  

Продолжение таблицы 3.4

(затухающая синусоида)
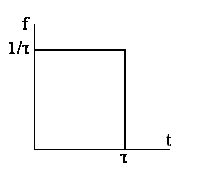
при (прямоугольный импульс)
единичный импульс или - функция

 

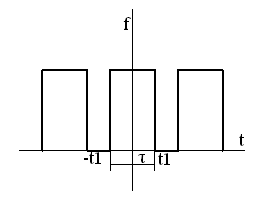
3.5 Спектральная характеристика периодических прямоугольных импульсов

Т а б л и ц а 3.5

Вид импульса	Спектральная характеристика
при

 

 

3.6 Ряд и интеграл Фурье

Т а б л и ц а 3.6

Ряд Фурье для периодической функции	Интеграл Фурье для непериодической функции
или   (дискретный спектр периодической функции)	или (сплошной спектр периодической функции)

 

 

3.7 Алгоритм расчета переходных процессов частотным методом

 

1. Схему с ненулевыми начальными условиями, применяя принцип наложения, сводят к схеме с нулевыми начальными условиями.

2. Частотную характеристику определяют с помощью прямого преобразования Фурье или по аналогии с изображением Лапласа.

3. По заданной схеме находят частотную характеристику, которая представляет собой комплексное сопротивление, аналогичное сопротивление цепи синусоидальному току

4. По частотной характеристике тока  определяют функцию времени В зависимости от вида выражения функция времени может быть найдена по таблицам изображении, теореме разложения.

 Пример: Расчет переходных процессов частотным методом

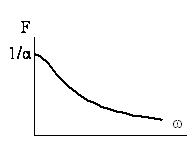
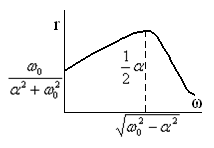
Рассмотрим -цепь, которая была подключена к источнику ЭДС и в момент переключается на источник ЭДС

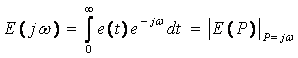                                                    (1)

Запишем закон Ома для частотных спектров при ненулевых начальных условиях, с учетом изображении производных и интегралов при Р= jω:

                                                      (2)

При помощи найдем частотный спектр затем находим ток переходного процесса                                                  (3)

Из формулы (3) заключаем, что ток так же может быть представлен в виде суммы элементарных гармонии тока с частотами, непрерывно изменяющимися от  до  а величина  представляют собой гармонику с частотной  функции

 

4 Цепи с распределенными параметрами (однородная линия)

 

4.1 Уравнение однородной линии

 

Длинной линией (линия с распределенными параметрами) называется линия, в которых в любой момент времени ток и напряжение в различных точах имеют различные значения. Электрическая и магнитная энергиинепрерывно распределены по длине линии, поэтому линию рассматривают как цепь с распределенными вдоль проводов индуктивностьюи соптотивлением емкостью и проводимостью между проводами. Токи и напряжения в длинных линиях зависят от времени и расстояния точки на линии от начала (конца) и описывается дифференциальными уравненями в часных прозводных. Однородные длинные линии имеют равномерное распределение параметров по всей длине линии.

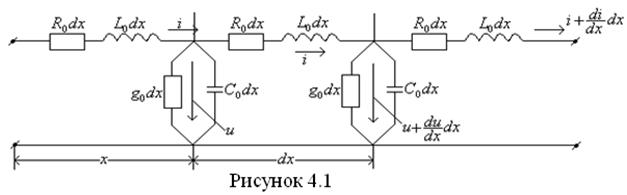
На рис 4.1 дана эквивалентная схема элемента по отношению к входным, выходным токами и напряжениям линии.

Т а б л и ц а 4.1

Первичные параметры	Уравнение длинной линии
	Дифференциальные	В комплексной форме
	При отчете от начала линии
	При отчете от конца линии

  

4.2 Параметры длинной линии

 

Т а б л и ц а 4.2

Определение	Обозначение и размерность
Продольное активное сопротив- ление прямого и обратного проводов на единицу длины линий
Индуктивность петли
Проводимость утечки между про- водами
Емкость двух проводов линий на единицу длины
Комплексное продольное сопро- тивление
Компленксная поперечная прово- димость
Комплескный коэффициент рас- пространения -коэффициент затухания -коэффициент фазы
Длина волны, определяюще рас- стояния, на которые распрос- траняется волна за один период
Фазовая скорость-скорость пере мещения постоянной фазы волны
Коэффициент затухания, характериует уменьшение амплитуды волны на единицу длины линии
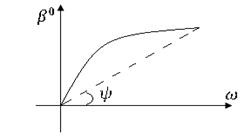
Коэффициент фазы, характеризующий изменение фазы волны на единицу длины линии

  

Продолжение таблицы 4.2

Волновое (характеристическое) сопротивление линии падающей и отраженной волны

 

 

4.3 Зависимость , ,   от геометрических размеров линий

 

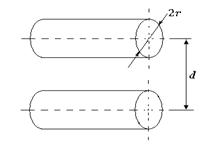
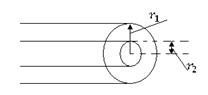
Т а б л и ц а 4.3

Линия	Емкость на единицу длины линии	Индуктивность единицу длины линии	Волновое сопротивление
Коаксиальная

 

 

4.4 Линия без искажений

 

Линия, в начале и конце которой передаваемый сигнал имеет одинаковую фазу, называют линией без искажений, в такой линии коэффициент затуханияи фазовая скорость не зависят от частоты   а коэффициент фазы пропорционален

 

Т а б л и ц а 4.4

Необходимое соотношение между параметрами линии без искажений	условие для линии без искажений
Коэффициент распространения
Коэффициент затухания
Коэффициент фазы
Фазовая скорость
Волновое сопротивление

 

4.5 Линия с согласованной нагрузкой

Т а б л и ц а 4.5

( коэф. отражения)	В согласованной линии  отраженная волна не возникает
	В любой точке линии входное сопротивление равно волновому.

 

4.6 Линия без потерь

Т а б л и ц а 4.6

Коэффициент расространения
Коэффициент затухания
Коэффициент фазы
Волновое сопротивление
Уравнение линии без потерь при отсчете длины  от начале линии
Уравнение линии без потерь при отсчете длины  от конца линии
Уравнение линии для мгновенных значений при отсчете длины  от конца линии

4.7 Входное сопротивление линии без потерь

 

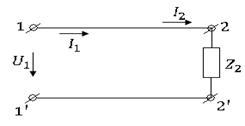
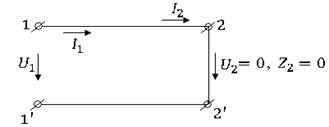
Т а б л и ц а 4.7

Схема	Входное сопротивление
Комплексная нагрузка	или
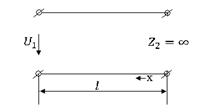
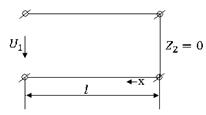
Линия, разомнутная на конце (хх)
Линия, закороченная на конце (кз)
Согласованная нагрузка

 

 

4.8 Стоячая волна

 

 Стоячие волны образуеются в линии без потерь, разомкнутой на конце, короткозамкнутой и нагруженной на чисто реактивное сопративление

Т а б л и ц а 4.8

Уравнения	Распределение действующих значении напряжении и ток	Изменение	Пояснения
Для стоячей волны в разомкутой линии (хх)			Пучности напряже- нии и узлы токов находятся в точках при а узлы напряжений и пучности токов в точках

 

Продолжение таблицы 4.8

Для стоячей волны в короткозамкнутой линии (кз) или

Пучность тока и узлы напряжений находятся в точках   при  а узлы тока и пуч- ности напряжения в точках

Содержание

 

1	Переходные процессы в линейных электрических цепях	3
1.1	Возникновение переходных процессов	3
1.2	Классический метод	3
1.3	Расчет классическим методом	4
1.4	Переходные процессы  в простейших схемах	9
1.5	Переходные процессы в -цепи	12
1.6	Операторный метод расчета переходных процессов	14
1.7	Законы Ома и Кирхгофа в операторной форме. Эквивалентные схемы	16
1.8	Теорема разложения	17
1.9	Алгоритм расчета переходных процессов операторным методом	18
1.10	Приведение схемы к нулевым начальным условиям	19
2	Расчет переходных процессов методом интеграла Дюамеля	23
2.1	Единичные и переходные функции	24
2.2	Действие единичных ступенчатых и единичных импульсов источников на индуктивный и емкостной элементы	25
2.3	Алгоритм расчета переходных процессов методом интеграла Дюамеля	26
3	Спектральный (Частотный) метод	27
3.1	Преобразование Фурье	27
3.2	Основные свойства преобразования Фурье	28
3.3	Спектральные характеристики некоторых функции	28
3.4	Функции времени, удовлетворяющие условию абсолютной интегрируемости	29
3.5	Спектральная характеристика периодических прямоугольных импульсов	31
3.6	Ряд и интеграл Фурье	31
3.7	Алгоритм расчета переходных процессов частотным методом	31
4	Цепи с распределенными параметрами (однородная линия)	33
4.1	Уравнение однородной линии	33
4.2	Параметры длинной линии	34
4.3	Зависимость , ,   от геометрических размеров линий	35
4.4	Линия без искажений	35
4.5	Линия с согласованной нагрузкой	36
4.6	Линия без потерь	36
4.7	Входное сопротивление линии без потерь	37
4.8	Стоячая волна	37
Содержание		40
Список литературы		41

 

 

 

Список литературы

 

1. Бакалов В.П., Дмитриков В.Ф., Крук Б.И. Основы теории цепей.- М.: Радио и связь, 2000.-592с.

2. Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей.-  М.: Энергоатомиздат, 1989.–528с.

3. Демирчян  К.С.,   Нейман  Л.Р.,   Коровкин  Н.В.,   Чечурин В.Л. Тео- ретические основы электротехники.- т.1. Санкт-Петербург: Питер, 2003. 463с.

4. Демирчян  К.С.,  Нейман Л.Р.,  Коровкин  Н.В., Чечурин В.Л. Теоре- тические основы электротехники. – т.2. Санкт- Петербург: Питер, 2003.-576с.

5. Бессонов Л.А. Теоретические основы электротехники. – М.: Гардарики, 1999. – 638с.

6. Шебес М.Р., Каблукова М.В. Задачник по теории линейных электри- ческих цепей. - М.: Высш. шк., 1990.- 544с.

7. Карлащук В.И. Электронная лаборатория на IВМ РС. Программа Electronics Workbench и её применение.-М.: Солон-Р, 1999.-506с.

          8. Жолдыбаева З.И., Зуслина Е.Х., Коровченко Т.И. Теория электричес- ких цепей 1. Конспект лекций. – Алматы: АИЭС, 2007.- 80с.