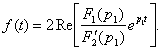З.И. Жолдыбаева
Е.Х. Зуслина
ТЕОРИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ 2
Примеры расчета установившихся и переходных режимов
в электрических цепях с сосредоточенными и распределенными параметрами
Учебное пособие
Алматы 2011
УДК 621.3 (01)
ББК 31. 221 Я73
Ж 79. Учебное пособие. З.И. Жолдыбаева., Е.Х. Зуслина
Примеры расчета установившихся и переходных режимов в электрических цепях с сосредоточенными и распределенными параметрами
АУЭС. Алматы, 2010. - 78 с.
I SBN 9965-850-35-6
В пособии представлены типовые задачи с подробными решениями и пояснениями, примеры применения основных методов расчета электрических цепей в установившемся и переходных режимах.
Предназначается для студентов специальностей 5В070400 – «Вычислительная техника и программное обеспечение».
Табл.1, ил.114, библиогр. - 8 назв.
ББК 31. 221 Я73
РЕЦЕНЗЕНТЫ: КазНТУ канд. техн. наук. доц. Иманбекова Т.Ж.,
АУЭС канд. тех. наук, проф. Г.С.Казиева
Печатается по плану издания Министерства образования и науки Республики Казахстан на 2010 г.
ISBN 9965-850-35-6
©НАО «Алматинский университет энергетики и связи», 2010г.
Введение
Теории электрических цепей являются базовым курсом, на который опираются профилирующие дисциплины радиотехнических специальностей, специальностей по вычислительной технике и информационным системам. В соответствии с новыми учебными планами курс ТЭЦ изучается в течение двух семестров. При этом существенно увеличен объем самостоятельной работы студентов (до 60% от общего числа часов).
Цель настоящего учебного пособия состоит в оказании помощи студентам в их самостоятельной работе. Поэтому все задачи даны с подробными решениями, пояснениями, методическими указаниями, приведены основные положения теории и необходимые расчетные формулы.
В пособии рассмотрены различные методы расчёта переходных процессов в линейных электрических цепях с сосредоточенными параметрами: классический, операторный, спектральный методы, интеграл Дюамеля. Показаны методы расчёта различных режимов в цепях с распределёнными параметрами и в нелинейных цепях постоянного тока.
1 Классический метод расчета переходных процессов
1.1 Основные теоретические сведения
В работе электрических цепей различают два режима процессов: установившийся и переходный.
Установившимся режим – это режим, при котором токи и напряжения либо не зависят от времени, либо являются периодическими функциями времени в зависимости от вида приложенного воздействия.
Переходным
процессом называют электромагнитный
процесс, возникающий в цепи, содержащей накопители энергии (индуктивности и
ёмкости) при переходе от одного установившегося режима к другому. Возникновение
переходных процессов в цепях с энергоемкими элементами обусловлено тем, что
энергии электрических полей конденсаторов ![]() и магнитных полей индуктивных
катушек
и магнитных полей индуктивных
катушек ![]() вследствие
закона непрерывности изменения энергии не могут изменяться скачком.
вследствие
закона непрерывности изменения энергии не могут изменяться скачком.
Переходный процесс возникает в электрических цепях, при различного рода
воздействиях (подключении к цепи или отключении от цепи источников
электрической энергии, а также при скачкообразном изменении схемы цепи или
параметров входящих в нее элементов), которые называются коммутациями.
Коммутация осуществляется с помощью идеального ключа: сопротивление ключа в
разомкнутом положении равно ![]() , в замкнутом – 0.
, в замкнутом – 0.
![]()
Будем считать, что
коммутация происходит мгновенно ![]() . Начало отсчёта времени
. Начало отсчёта времени ![]() совмещается с моментом
коммутации.
совмещается с моментом
коммутации.
Законы коммутации:
1) Ток в индуктивности непосредственно после
коммутации ![]()
сохраняет значение, которое он имел
непосредственно до коммутации ![]() :
:
![]() (1.1)
(1.1)
2) Напряжение на ёмкости непосредственно после
коммутации ![]()
сохраняет значение, которое
оно имело непосредственно до коммутации ![]() :
: ![]() (1.2)
(1.2)
Начальные условия − значения токов и напряжений при t = 0.
Независимые начальные условия − это значения тока в индуктивности ![]() и напряжения на ёмкости
и напряжения на ёмкости ![]() в момент коммутации
в момент коммутации ![]() , которые определяются
на основании законов коммутации путем расчета установившегося режима в цепи до
коммутации. Зависимые начальные условия − это значения токов и
напряжений и их производных в момент коммутации
, которые определяются
на основании законов коммутации путем расчета установившегося режима в цепи до
коммутации. Зависимые начальные условия − это значения токов и
напряжений и их производных в момент коммутации ![]() , которые в момент коммутации могут
изменяться скачком, например:
, которые в момент коммутации могут
изменяться скачком, например: ![]() и т.п. Они определяются по схеме,
образованной после коммутации, по законам Кирхгофа с учетом законов коммутации.
Пример дан в задаче 1.1.
и т.п. Они определяются по схеме,
образованной после коммутации, по законам Кирхгофа с учетом законов коммутации.
Пример дан в задаче 1.1.
При анализе переходных процессов в электрических цепях классическим методом составляется система уравнений для мгновенных значений токов и напряжений по законам Кирхгофа или с помощью других методов расчета цепей, например метода контурных токов или метода узловых потенциалов. При этом используются соотношения между токами и напряжениями:
![]()
![]()
![]()
![]()
![]()
![]() (1.3)
(1.3)
В полученной таким образом системе уравнений выбирается основная переменная (ток или напряжение), и исключением других переменных из системы уравнений получают одно дифференциальное уравнение с постоянными коэффициентами, содержащее только основную переменную. Полученное, в общем случае, линейное неоднородное дифференциальное уравнение с постоянными коэффициентами, имеет вид:
![]() (1.4)
(1.4)
где ![]() − постоянные коэффициенты,
зависящие от схемы цепи и её параметров;
− постоянные коэффициенты,
зависящие от схемы цепи и её параметров; ![]() − выходная величина, основная переменная (ток
− выходная величина, основная переменная (ток ![]() или напряжение
или напряжение ![]() );
); ![]() − функция, описывающая
характер воздействия на цепь.
− функция, описывающая
характер воздействия на цепь.
Порядок высшей производной дифференциального уравнения определяет порядок цепи. Если этот порядок будет первым, то и цепь называют цепью первого порядка, эти цепи содержат только однотипные реактивные элементы (ёмкости или индуктивности. Цепь, содержащая два независимых накопителя энергии (и ёмкость и индуктивность), описывается уравнением второго порядка и называется цепью второго порядка.
Решение уравнения
(1.4) ищется в виде: ![]() (1.5)
(1.5)
где ![]() − принуждённая составляющая,
являющаяся частным решением уравнения (1.4), и определяется путём расчёта установившегося
режима в цепи после коммутации;
− принуждённая составляющая,
являющаяся частным решением уравнения (1.4), и определяется путём расчёта установившегося
режима в цепи после коммутации; ![]() − свободная составляющая,
являющаяся общим решением однородного дифференциального уравнения:
− свободная составляющая,
являющаяся общим решением однородного дифференциального уравнения:
![]() . (1.6)
. (1.6)
Общая формула свободной составляющей ![]() имеет вид:
имеет вид:
![]() (1.7)
(1.7)
где ![]() - постоянная интегрирования;
- постоянная интегрирования; ![]() - корни
характеристического уравнения
- корни
характеристического уравнения ![]() .
.
Выражение свободной составляющей ![]() зависит от вида корней
характеристического уравнения. Для
цепи второго порядка выражение свободной
составляющей
зависит от вида корней
характеристического уравнения. Для
цепи второго порядка выражение свободной
составляющей ![]() имеет
вид:
имеет
вид:
при действительных и различных корнях ![]() < 0 и
< 0 и ![]() < 0
< 0
![]() ,
,
при действительных и равных корнях ![]() =
=![]() =р < 0
=р < 0
![]() ,
,
при комплексно-сопряжённых корнях ![]() (α – коэффициент
затухания, ωСВ –
частота свободных колебаний)
(α – коэффициент
затухания, ωСВ –
частота свободных колебаний)
![]()
где А и ψ постоянные интегрирования;
или ![]()
Характеристическое
уравнение. Методы составления
характеристического уравнения: 1) по однородному дифференциальному уравнению,
например, для уравнения (1.6), характеристическое уравнение имеет вид: ![]() ; 2) методом главного
определителя суть которого состоит в следующем: записывают определитель
матрицы комплексных контурных сопротивлений (узловых проводимостей) и, заменив
; 2) методом главного
определителя суть которого состоит в следующем: записывают определитель
матрицы комплексных контурных сопротивлений (узловых проводимостей) и, заменив ![]() на р, приравнивают его
к нулю; 3) методом входного сопротивления: а) записывают входное комплексное
сопротивление
на р, приравнивают его
к нулю; 3) методом входного сопротивления: а) записывают входное комплексное
сопротивление![]() цепи после коммутации относительно любой ветви, кроме ветви с идеальным
источником тока; б) в формуле
цепи после коммутации относительно любой ветви, кроме ветви с идеальным
источником тока; б) в формуле![]() заменяют
заменяют ![]() на р; в) полученное выражение
на р; в) полученное выражение ![]() приравнивают к нулю:
приравнивают к нулю: ![]() .Пример дан в задаче
1.2.
.Пример дан в задаче
1.2.
Постоянные интегрирования.
Особенностью классического метода является необходимость определения постоянных
интегрирования, число которых зависит от порядка цепи. Постоянные
интегрирования определяются по значениям искомой выходная величины ![]() и её производных, рассматриваемых в момент
и её производных, рассматриваемых в момент ![]() :
:
а) для цепи первого порядка
постоянная интегрирования определяется из уравнения: ![]() ;
;
б) для цепи второго порядка
постоянные интегрирования определяются по начальным значениям ![]() .
.
Корни действительные и различные:
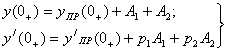
Корни комплексно-сопряжённые: 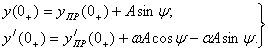
Порядок расчета переходных процессов классическим методом:
а) определяют независимые
начальные условия ![]() и
и
![]() ;
;
б) записывают дифференциальные
уравнения по законам Кирхгофа, решение которых представляют в виде: ![]() ;
;
в) определяют принуждённую
составляющую ![]() ;
;
г) определяют ![]() : составляют характеристическое
уравнение, вычисляют его корни и находят постоянные интегрирования,
: составляют характеристическое
уравнение, вычисляют его корни и находят постоянные интегрирования,
д) построение графика ![]()
1.2 Примеры расчёта типовых задач
1.2.1 Определение начальных значений и составление характеристических уравнений.
Задача 1.1 Решение: Определить независимые и зависимые начальных условий для электрической цепи (см. рисунок 1.1). Независимые начальные условия определяют по второму закону коммутации по схеме до коммутации (см. рисунок 1.2).
![]() (1.8)
(1.8)
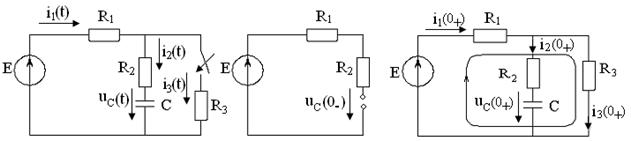
Рисунок 1.1 Рисунок 1.2 Рисунок 1.3
Зависимые начальные условия находят для цепи после коммутации (см. рисунок 1.3), записав уравнения в соответствии с законами Кирхгофа:
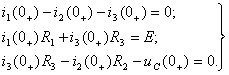 (1.9)
(1.9)
Выразим из первого уравнения
системы уравнений (1.9) ![]() и подставим во второе уравнение. С учетом
того, что
и подставим во второе уравнение. С учетом
того, что ![]() ,
получим:
,
получим:
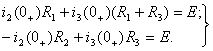 (1.10)
(1.10)
Решая систему уравнений (1.10), определим
зависимые начальные условия ![]() .
.
Задача 1.2 Для схемы (см. рисунок 1.4) составить характеристическое уравнение и определить его корень: а) по однородному дифференциальному уравнению;
б) по методу входного сопротивления; в)
определить корень по постоянной времени цепи ![]() .
.

Рисунок 1.4 Рисунок 1.5 Рисунок 1.6
Решение: а) Составим характеристическое уравнение по
однородному дифференциальному уравнению. Запишем неоднородное дифференциальное уравнение относительно тока ![]() :
: ![]() ,
,
приравняем к нулю правую часть
неоднородного уравнения, получим однородное дифференциальное уравнение: ![]() .
.
Заменим ![]() на р,
на р, ![]() на 1, получим
характеристическое уравнение:
на 1, получим
характеристическое уравнение:
![]() ,
(1.11)
,
(1.11)
отсюда корень характеристического уравнения
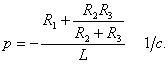 (1.12)
(1.12)
б) Составление характеристического уравнения по методу входного сопротивления. Перейдём от заданной схемы цепи после коммутации к комплексной схеме (рис. 1.5) и запишем комплексное входное сопротивление
![]() , заменим
, заменим ![]() на р , выражение
на р , выражение ![]() приравняем к нулю и получим
характеристическое уравнение:
приравняем к нулю и получим
характеристическое уравнение:
![]() ,
(1.13)
,
(1.13)
корень которого вычисляется по формуле (1.12).
в) Определить корни по постоянной времени цепи ![]() .
.
Известно, что ![]() . Для цепи с одним индуктивным
элементом постоянная времени
. Для цепи с одним индуктивным
элементом постоянная времени ![]() . Эквивалентное сопротивление цепи
. Эквивалентное сопротивление цепи ![]() определяется
относительно зажимов реактивного элемента (индуктивности), при этом
определяется
относительно зажимов реактивного элемента (индуктивности), при этом
необходимо закоротить входной источник ЭДС
(см. рисунок 1.6):![]() .
.
1.2.2 Расчёт переходных процессов в цепях первого порядка.
Задача 1.3 Накопительная емкость импульсного модулятора передающего устройства РЛС (см. рисунок 1.7, а) после включения разряжается через разрядное сопротивление. Определить время, через которое напряжение на емкости уменьшится до уровня U=20 В, если U0 = 20 кВ, С= 5 мкФ, разрядное сопротивление Rp=10 кОм.
Решение: Конденсатор заряжен до напряжения ![]() =U0=20 кВ. Составим дифференциальное уравнение по второму
закону Кирхгофа для цепи после коммутации (см. рисунок 1.7,б):
=U0=20 кВ. Составим дифференциальное уравнение по второму
закону Кирхгофа для цепи после коммутации (см. рисунок 1.7,б):
![]() (1.14)
(1.14)
где ![]()
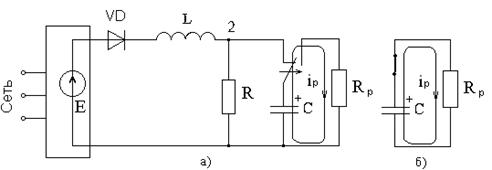
Рисунок 1.7
Решением дифференциального уравнения (1.14) является переходное напряжение на емкости, которое имеет вид
![]()
Принуждённая составляющая
напряжения ![]() (для
схемы после коммутации (см. рисунок 1.7,б) при
(для
схемы после коммутации (см. рисунок 1.7,б) при ![]() ) равна нулю:
) равна нулю:
![]()
Свободная составляющая напряжения:
![]() B.
B.
И переходное напряжение будет равно: ![]()
Определим постоянную времени цепи
![]() , используя
соотношение
, используя
соотношение
![]()
Определим постоянную
интегрирования А из начальных условий (при ![]() ).
).
![]()
Напряжение на ёмкости в переходном режиме будет равно:
![]() (1.15)
(1.15)
Вычислим время разряда накопительной емкости до U=20 В из уравнений:
![]() или
или ![]() отсюда
отсюда ![]()
После логарифмирования получаем:
![]()
![]()
таким образом, время разряда накопительной емкости до U=20 В составляет примерно 7τ.
График напряжения на емкости ![]() построен в среде Mathcad (см. рисунок 1.8).
построен в среде Mathcad (см. рисунок 1.8).
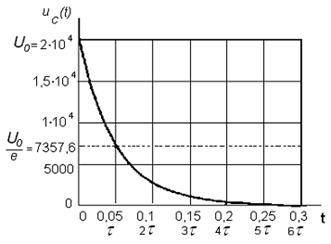
Рисунок 1.8
Вывод. Для
регулирования длительности переходного процесса необходимо изменять в цепи
постоянную времени ![]() .
Это достигается путем выбора параметров R
и С. За время
.
Это достигается путем выбора параметров R
и С. За время ![]() свободная составляющая
уменьшается в е = 2,718 раз.
свободная составляющая
уменьшается в е = 2,718 раз.
Задача 1.4 Интегрирующая цепь (см. рисунок 1.9) с параметрами R1 = 30 Ом, R2 = 20 Ом, С= 50 мкФ, Е= 100 В подключается к сопротивлению R2.
Определить закон изменения напряжения на конденсаторе и токов в ветвях в переходном режиме.
Решение: Определяют независимые начальные условия ![]() . Из эквивалентной
схемы для
. Из эквивалентной
схемы для ![]() (см.
рисунок 1.10) находят
(см.
рисунок 1.10) находят ![]()
Составляют систему дифференциальных уравнений по законам Кирхгофа для цепи после коммутации:
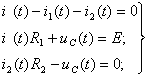 (1.16)
(1.16)
Переходное напряжение ![]() является решением ддифференциальных
уравнений и представляется в виде:
является решением ддифференциальных
уравнений и представляется в виде: ![]()

Рисунок 1.9 Рисунок 1.10 Рисунок 1.11
Определяют
принуждённую составляющую напряжения ![]() в установившемся режиме цепи после
коммутации
в установившемся режиме цепи после
коммутации ![]() из
схемы (см. рисунок 1.11):
из
схемы (см. рисунок 1.11):
![]()
![]()
![]()
Определяют
свободную составляющую напряжения ![]() .
.
Постоянная
времени цепи ![]() находится
по формуле:
находится
по формуле:
![]() (1.17)
(1.17)
Постоянную
интегрирования определяют по начальному значению напряжения ![]() :
: ![]() , отсюда
, отсюда
![]() .
.
Записывают аналитические выражения для переходного напряжения
![]() . (1.18)
. (1.18)
Токи найдём по формулам:
![]()
![]() (1.19)
(1.19)
![]()
Построение графиков напряжения и токов среде Mathcad (см. рисунок 1.12, 1.13).
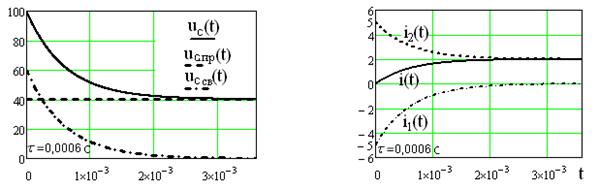
Рисунок 1.12 Рисунок 1.13
Цепи в виде резисторно-конденсаторного делителя нашли широкое применение в импульсных устройствах РЭТ.
1.2.3 Расчёт переходных процессов в цепях второго порядка.
Задача 1.5 Параллельный колебательный контур (см. рисунок 1.14)
подключается к источнику ЭДС Е= 125В. Определить закон изменения
напряжения ![]() для
трех случаев: 1.R =
250 Ом, L =
667 мГн, С = 2 мкФ;
для
трех случаев: 1.R =
250 Ом, L =
667 мГн, С = 2 мкФ;
2. R = 100 Ом, L = 40мГн, С= 1 мкФ; 3. R = 100 Ом, L = 40мГн, С = 5мкФ.
 Рисунок 1.14
Рисунок 1.15
Рисунок 1.14
Рисунок 1.15
Решение: Записывают независимые начальные условия ![]()
![]() . Составляют систему дифференциальных
уравнений по законам Кирхгофа для
цепи после коммутации:
. Составляют систему дифференциальных
уравнений по законам Кирхгофа для
цепи после коммутации:
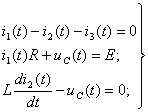 (1.20)
(1.20)
Переходное
напряжение ![]() представляют в виде суммы принуждённой и свободной
составляющих:
представляют в виде суммы принуждённой и свободной
составляющих: ![]()
Определяют принуждённую составляющую напряжения на
ёмкости. Так как в установившемся режиме цепи после коммутации (при ![]() ) конденсатор
шунтирован катушкой индуктивности накоротко (см. рисунок 1.15), принуждённая
составляющую равна нулю:
) конденсатор
шунтирован катушкой индуктивности накоротко (см. рисунок 1.15), принуждённая
составляющую равна нулю: ![]()
Вычисляют свободную составляющую напряжения на ёмкости. Для этого составляют характеристическое уравнение, например, методом входного сопротивления и определяют его корни:
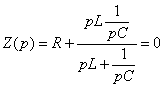 или (после преобразований)
или (после преобразований) ![]()
откуда ![]() (1.21.)
(1.21.)
Вид свободной составляющей напряжения зависит от типа корней характеристического уравнения. Для трех заданных значений параметров рассчитывают корни р1,2.
1) R = 250 Ом, L = 667 мГн, С = 2 мкФ.
![]()
![]()
![]()
Корни действительные и различные.
Свободная составляющая напряжения на конденсаторе имеет вид: ![]()
2) R =
100 Ом, L = 40мГн, С= 1
мкФ ![]()
![]()
Корни действительные и равные ![]() , следовательно,
, следовательно,
![]()
3) R = 100 Ом, L = 40мГн, С = 5мкФ
![]()
![]()
Корни комплексные сопряженные.
Свободная составляющая напряжения на конденсаторе имеет вид: ![]()
Постоянные интегрирования
![]() и
и ![]() определяют из
начальных условий
определяют из
начальных условий
![]() . Из выражения
. Из выражения ![]() следует, что
следует, что ![]() , и задача сводится к
определению
, и задача сводится к
определению ![]() .Зависимое
начальное условие
.Зависимое
начальное условие ![]() определяют
из уравнений составленных по законам Кирхгофа (1.20), записанных для момента
времени
определяют
из уравнений составленных по законам Кирхгофа (1.20), записанных для момента
времени ![]() :
:

и с учётом независимых начальных условий ![]()
![]() , получим:
, получим:
![]() (1.22)
(1.22)
Найдём uc(t) для трех случаев корней:
1) R = 250 Ом, L = 667 мГн, С = 2 мкФ. Корни действительные и
различные: ![]() тогда:
тогда:
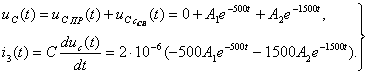
При ![]() :
:![]() ,
, ![]() , получим
, получим
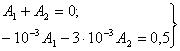
отсюда А1=250, А2=-250, и напряжение на ёмкости равно:
![]()
Графики напряжения uc(t) и его составляющих выполнены в среде Mathcad (см. рисунок 1.16, а).
2) R = 100 Ом, L =
40мГн, С= 1 мкФ. Корни действительные и равные: ![]() , тогда
, тогда
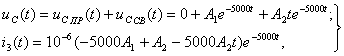
при ![]() :
:![]() ,
, ![]() , получим
, получим ![]()
![]() , и напряжение на ёмкости равно:
, и напряжение на ёмкости равно: ![]()
Графики напряжения uc(t) и его составляющих выполнены в среде Mathcad (см. рисунок 1.16,б).
3) R = 100 Ом, L = 40мГн, С = 5мкФ. Корни комплексные сопряженные
![]() тогда
тогда
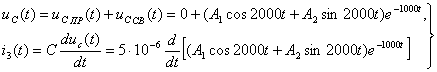
при ![]() :
:![]() ,
, ![]() , получим
, получим ![]()
![]() , отсюда
, отсюда ![]() и напряжение на ёмкости будет равно:
и напряжение на ёмкости будет равно: ![]()
Графики напряжения uc(t) и его составляющих выполнены в среде Mathcad (см. рисунок 1.16,в).
Выводы
1 Напряжение uc(t) при колебательном режиме представляет собой затухающее колебание.
2 Переходной процесс в параллельном колебательном контуре при при колебательном режиме используют в автоколебательных системах, где контур является нагрузочной цепью.
а) б) в)
Рисунок 1.16
Задача
1.6 Электрическая цепь (см. рисунок
1.17), в которой действует источник постоянной ЭДС ![]() =
=![]() , находится в установившимся режиме.
Параметры цепи:
, находится в установившимся режиме.
Параметры цепи:![]() Ом,
Ом,
![]() Ом,
Ом, ![]() Ом,
Ом, ![]() мГн, С=0,7 мкФ. В момент времени
t=0 путем замыкания ключа К в цепи осуществляется коммутация.
Определить ток
мГн, С=0,7 мкФ. В момент времени
t=0 путем замыкания ключа К в цепи осуществляется коммутация.
Определить ток ![]() после
замыкания ключа.
после
замыкания ключа.
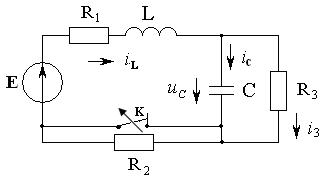
Рисунок 1.17
Решение: 1) Определение независимые начальные условия (ННУ). ННУ ![]() и
и ![]() определяются путём расчета
установившегося режима в цепи до коммутации. Установившийся режим до коммутации
создается постоянной ЭДС, поэтому на схеме индуктивность заменяется коротко
замкнутым участком, а ёмкость размыкается (см. рисунок 1.18).
определяются путём расчета
установившегося режима в цепи до коммутации. Установившийся режим до коммутации
создается постоянной ЭДС, поэтому на схеме индуктивность заменяется коротко
замкнутым участком, а ёмкость размыкается (см. рисунок 1.18).
Ток в индуктивности и напряжение на ёмкости до коммутации найдём по формулам:
![]() А;
А; ![]() В.
В.
Независимые начальные условия определим по законам коммутации:
![]() А,
А, ![]() В.
В.
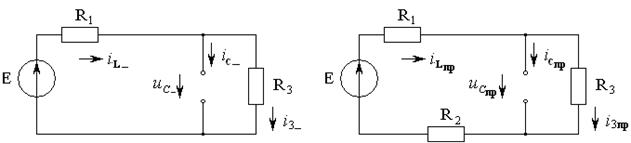
Рисунок 1.18 Рисунок 1.19
2) Составляется систему дифференциальных уравнений по законам Кирхгофа для цепи после коммутации, при t ≥0:
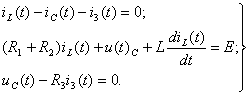 (1.23)
(1.23)
Переходный
ток ![]() удовлетворяет
системе уравнений (1.23) и может быть представлен в виде суммы токов
принужденного и свободного режимов цепи:
удовлетворяет
системе уравнений (1.23) и может быть представлен в виде суммы токов
принужденного и свободного режимов цепи:
![]() (1.24)
(1.24)
3) Определение тока в принужденном режиме. Принужденный ток ![]() определяется путем
расчета установившегося режима в цепи после коммутации. Установившийся режим
после коммутации создается постоянной ЭДС, поэтому на схеме индуктивность
заменяется короткозамкнутым участком, а ёмкость размыкается (см. рисунок 1.19).
Принужденный ток
определяется путем
расчета установившегося режима в цепи после коммутации. Установившийся режим
после коммутации создается постоянной ЭДС, поэтому на схеме индуктивность
заменяется короткозамкнутым участком, а ёмкость размыкается (см. рисунок 1.19).
Принужденный ток ![]() определяется
по закону Ома:
определяется
по закону Ома:
![]() А; (1.25)
А; (1.25)
4)
Определение свободного тока ![]() . Для определения свободного тока
. Для определения свободного тока ![]() необходимо составить
характеристическое уравнение цепи после коммутации. Наиболее простой способ
составления характеристического уравнения – это метод входного сопротивления.
Комплексное входное сопротивление для цепи после коммутации относительно ветви
с источником ЭДС имеет вид:
необходимо составить
характеристическое уравнение цепи после коммутации. Наиболее простой способ
составления характеристического уравнения – это метод входного сопротивления.
Комплексное входное сопротивление для цепи после коммутации относительно ветви
с источником ЭДС имеет вид:
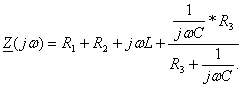 , (1.26)
, (1.26)
В
формуле ![]()
![]() заменяется на р и
полученное сопротивление
заменяется на р и
полученное сопротивление ![]() приравнивается к нулю:
приравнивается к нулю: ![]() :
:
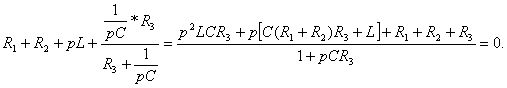
Приравняем к нулю числитель выражения ![]() и получим
характеристическое уравнение:
и получим
характеристическое уравнение:
![]() (1.27)
(1.27)
Подставим числовые значения:
![]()
отсюда
![]() (1.28)
(1.28)
Корни характеристического уравнения (1.28):
![]() .
.
Так
как корни характеристического уравнения комплексно-сопряженные, свободный ток ![]() записывается в виде:
записывается в виде:
![]() (1.29)
(1.29)
5)
Определение постоянных интегрирования ![]() . Постоянные интегрирования определяются
по начальным значениям тока
. Постоянные интегрирования определяются
по начальным значениям тока ![]() и его первой производной
и его первой производной ![]() Записывается
переходный ток:
Записывается
переходный ток:
![]()
находится
производная тока ![]()
![]()
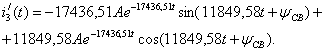
Записывается переходный ток ![]() и производная тока
и производная тока ![]() для момента времени
для момента времени ![]() . Система уравнений для
определения постоянных интегрирования имеет вид:
. Система уравнений для
определения постоянных интегрирования имеет вид:
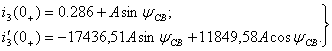 ; (1.30)
; (1.30)
Чтобы решить систему уравнений
(1.30) и определить постоянные интегрирования ![]() , нужно найти начальные значения
(зависимые начальные условия)
, нужно найти начальные значения
(зависимые начальные условия) ![]() и
и ![]() Зависимые начальные условия
Зависимые начальные условия ![]() и
и ![]() определяются по независимым
начальным условиям
определяются по независимым
начальным условиям ![]() путем
решения системы дифференциальных уравнений (1.23), составленных по законам
Кирхгофа для цепи после коммутации и рассматриваемых для момента времени t=0+.
Выразим ток
путем
решения системы дифференциальных уравнений (1.23), составленных по законам
Кирхгофа для цепи после коммутации и рассматриваемых для момента времени t=0+.
Выразим ток ![]() через
независимые переменные
через
независимые переменные ![]() . Из третьего уравнения системы (1.23)
определим ток
. Из третьего уравнения системы (1.23)
определим ток ![]() и
найдём производную
и
найдём производную ![]() :
:![]() ;
; ![]() .
.
Так
как ток в ёмкости равен ![]() , производную
, производную![]() определим по формуле:
определим по формуле: ![]() . Ток
. Ток ![]() найдём из первого закона
Кирхгофа:
найдём из первого закона
Кирхгофа: ![]() .
Вычислим
.
Вычислим ![]() и
и ![]() для момента времени
для момента времени ![]() :
:
![]()
![]() ;
;
![]() , отсюда
, отсюда ![]() =0.
=0.
Подставим
![]() и
и ![]() в систему (1.30) и определим
постоянные интегрирования А и
в систему (1.30) и определим
постоянные интегрирования А и ![]() :
:
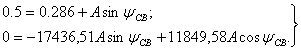 (1.31)
(1.31)
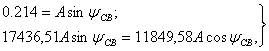 (1.32)
(1.32)
отсюда
![]()
![]()
![]()
Подставим найденные значения А и ![]() в выражения для тока
в выражения для тока ![]()
![]() и окончательно получим:
и окончательно получим:
![]() .
.
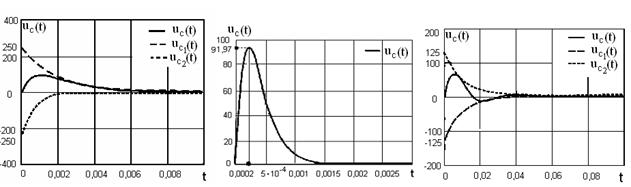
График тока ![]() (см.рисунок 1.20) построен в среде Mathcad, в
интервале времени
(см.рисунок 1.20) построен в среде Mathcad, в
интервале времени
от 0 до 5τ, где ![]() .
.
Чтобы наглядно показать, как ![]() →
→ ![]() , и
, и ![]() → 0, построены отдельно
графики
→ 0, построены отдельно
графики ![]() и
и ![]() (рис.1 21) и
(рис.1 21) и ![]() (рис.1.22) в интервале
от 3τ до 8τ.
(рис.1.22) в интервале
от 3τ до 8τ.
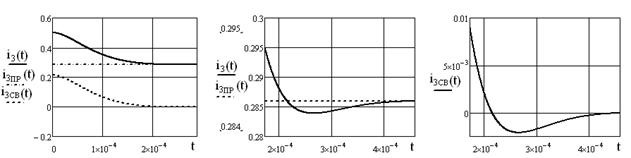
Рисунок 1.20 Рисунок 1.21 Рисунок 1.22
Задача
1.7 Электрическая цепь (см. рисунок 1.23), в которой действует
источник синусоидальной ЭДС ![]() =
=![]() , находится в установившимся режиме.
Параметры цепи:
, находится в установившимся режиме.
Параметры цепи:![]() Ом,
Ом,
![]() Ом,
Ом, ![]() Ом,
Ом, ![]() мГн, С=0,5мкФ. В момент времени t=0
путем замыкания ключа К в цепи осуществляется коммутация. Определить ток
мГн, С=0,5мкФ. В момент времени t=0
путем замыкания ключа К в цепи осуществляется коммутация. Определить ток ![]() после замыкания ключа.
после замыкания ключа.
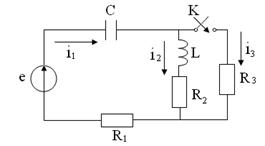
Рисунок 1.23
Решение: 1)
Определение независимых начальных условий (ННУ): ![]() . ННУ определим путём расчета
установившегося режима в цепи до коммутации. Установившийся режим до коммутации
создается синусоидальной ЭДС. Для расчета установившегося режима применим
комплексный метод. Эквивалентная схема цепи до коммутации для расчета
комплексным методом показана на рисунке 1.24.
. ННУ определим путём расчета
установившегося режима в цепи до коммутации. Установившийся режим до коммутации
создается синусоидальной ЭДС. Для расчета установившегося режима применим
комплексный метод. Эквивалентная схема цепи до коммутации для расчета
комплексным методом показана на рисунке 1.24.
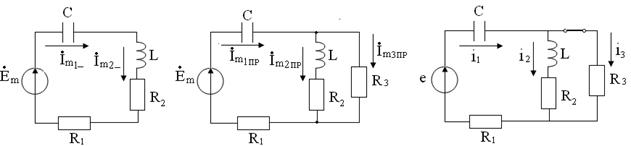
Рисунок 1.24 Рисунок 1.25 Рисунок 1.26
Комплексная
амплитуда ЭДС: ![]() Индуктивное
и емкостное сопротивления:
Индуктивное
и емкостное сопротивления: ![]() Ом,
Ом, ![]() Ом. Комплексное сопротивление цепи,
комплексная амплитуда тока и комплексная амплитуда напряжения на ёмкости равны:
Ом. Комплексное сопротивление цепи,
комплексная амплитуда тока и комплексная амплитуда напряжения на ёмкости равны:
![]() Ом,
Ом,
![]() А,
А,
![]() В.
В.
Запишем
мгновенные значения тока в индуктивности ![]() и напряжения на емкости
и напряжения на емкости ![]() :
:
![]() А,
А, ![]() В. (1.33)
В. (1.33)
Определим
мгновенные значения тока в индуктивности ![]() и напряжения на емкости
и напряжения на емкости ![]() в момент времени t=0−:
в момент времени t=0−:
![]() А,
А, ![]() В.
В.
Независимые начальные условия найдем по законам коммутации:
![]() А,
А, ![]() В. (1.34)
В. (1.34)
2) Составление системы дифференциальных уравнений. Дифференциальные уравнения составляются по законам Кирхгофа для цепи после коммутации (см. рисунок 1.26) для t ≥0 и имеют вид:
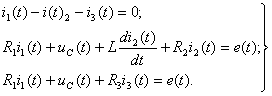 (1.35)
(1.35)
Переходный
ток ![]() удовлетворяет
системе уравнений (1.35) и может быть представлен в виде суммы токов
принужденного и свободного режимов цепи:
удовлетворяет
системе уравнений (1.35) и может быть представлен в виде суммы токов
принужденного и свободного режимов цепи:
![]() (1.36)
(1.36)
3)
Определение тока ![]() в
принужденном режиме.
в
принужденном режиме.
Принужденный
ток ![]() определяется
путем расчета установившегося режима в цепи после коммутации. Установившийся
режим после коммутации создается синусоидальной ЭДС. Для расчета установившегося
режима применим комплексный метод (см. рисунок 1.25). Комплексная амплитуда
ЭДС:
определяется
путем расчета установившегося режима в цепи после коммутации. Установившийся
режим после коммутации создается синусоидальной ЭДС. Для расчета установившегося
режима применим комплексный метод (см. рисунок 1.25). Комплексная амплитуда
ЭДС: ![]() Комплексное
сопротивление цепи:
Комплексное
сопротивление цепи:
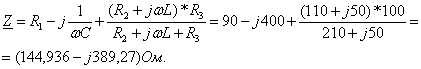
Найдём
комплексные амплитуды принужденных токов ![]() , используя закон Ома и формулу разброса:
, используя закон Ома и формулу разброса:
![]()
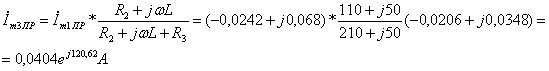
Мгновенное
значение принужденного тока ![]() равно:
равно:
![]() (1.37)
(1.37)
4)
Определение свободного тока ![]() .
.
Для
определения свободного тока ![]() составляют характеристическое уравнение
цепи после коммутации. Наиболее простой способ составления характеристического
уравнения – это метод входного сопротивления.
составляют характеристическое уравнение
цепи после коммутации. Наиболее простой способ составления характеристического
уравнения – это метод входного сопротивления.
Запишем комплексное входное сопротивление для цепи после коммутации относительно ветви с источником ЭДС:
![]() .
.
В
формуле ![]() заменяют
заменяют
![]() на р и
полученное сопротивление
на р и
полученное сопротивление ![]() приравнивают к нулю:
приравнивают к нулю: ![]()
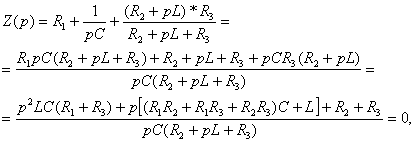 (1.38)
(1.38)
Приравнивают к нулю
числитель ![]() и
получают характеристическое уравнение:
и
получают характеристическое уравнение:
![]() .
(1.39)
.
(1.39)
После подстановки числовых значений:
![]()
получают:
![]() (1.40)
(1.40)
Определяют корни характеристического уравнения (1.40):

Корни
характеристического уравнения комплексно-сопряженные, свободный ток ![]() представляют в виде:
представляют в виде:
![]() (1.41)
(1.41)
Переходный ток равен:
![]() (1.42)
(1.42)
5) Определение
постоянных интегрирования ![]() .
.
Постоянные
интегрирования определяются по начальным значениям тока ![]() и его первой производной
и его первой производной ![]() Запишем переходный ток
Запишем переходный ток
![]() и найдем
производную тока
и найдем
производную тока ![]()
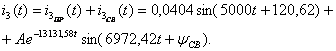
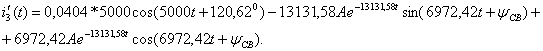
Записываются
начальные значения тока ![]() и его первой производной
и его первой производной ![]() , в момент времени t=0+
и получают систему уравнений для определения постоянных интегрирования
, в момент времени t=0+
и получают систему уравнений для определения постоянных интегрирования![]() :
:
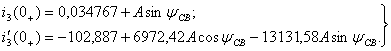 (1.43)
(1.43)
Чтобы
решить систему уравнений (1.43) и определить постоянные интегрирования ![]() , нужно найти
, нужно найти ![]() и
и ![]() ,которые определяются по
независимым начальным условиям
,которые определяются по
независимым начальным условиям ![]() путем решения системы дифференциальных
уравнений (1.35), рассматриваемых для момента времени t=0+.
Выражают ток
путем решения системы дифференциальных
уравнений (1.35), рассматриваемых для момента времени t=0+.
Выражают ток ![]() через
независимые переменные
через
независимые переменные ![]() , из первого закона Кирхгофа имеем:
, из первого закона Кирхгофа имеем: ![]() , подставляют
полученное выражение для тока
, подставляют
полученное выражение для тока ![]() в третье уравнение системы (1.35):
в третье уравнение системы (1.35):
![]() , и найдем
, и найдем ![]() и
и ![]()
![]() ;
; ![]()
где
![]() .
.
Для
момента времени t=0+ рассчитывают ![]() :
:
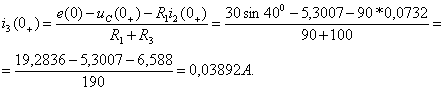
Чтобы
определить ![]() вычисляют
вычисляют
![]() ;
; ![]() и
и ![]()
находят из системы дифференциальных уравнений (1.35), рассматриваемых для момента времени t=0+:
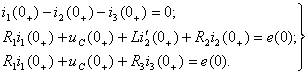 (1.44)
(1.44)
Ток
![]() определяют из
первого уравнения системы (1.44):
определяют из
первого уравнения системы (1.44):
![]()
По
найденному значению тока ![]() , вычисляют:
, вычисляют:
![]()
Производную
тока ![]() определяют
из второго уравнения системы (1.44):
определяют
из второго уравнения системы (1.44):
![]()
![]()
По
найденным значениям ![]() определяют
определяют
![]()
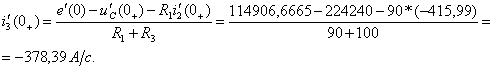
Подставляют
найденные значения ![]() в
систему уравнений (1.43) и определяют постоянные интегрирования
в
систему уравнений (1.43) и определяют постоянные интегрирования ![]() .
.
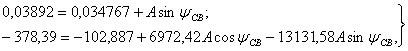 (1.45)
(1.45)
отсюда:
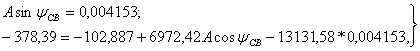 (1.46)
(1.46)
или
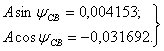 (1.47)
(1.47)
Делят первое уравнение системы (1.47) на второе определяют постоянные интегрирования:
![]() ,
, ![]() и
и
![]()
Подставляют найденные значения ![]() в выражение (1.42) и получают
переходный ток
в выражение (1.42) и получают
переходный ток ![]() :
:
![]()
где
![]() -
принуждённый ток,
-
принуждённый ток,
![]() - свободный
ток.
- свободный
ток.
График тока ![]() (см. рисунок 1.27) построен в среде Mathcad, в интервале
времени
(см. рисунок 1.27) построен в среде Mathcad, в интервале
времени
от 0 до 6τ, где ![]() .
.
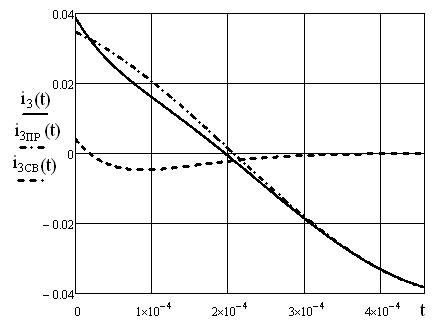
Рисунок 1.27
2 Операторный метод расчета переходных процессов
2.1 Основные теоретические сведения
Преобразования Лапласа. Операторный метод расчёта переходных процессов широко применяется в теории электрических цепей для решения линейных дифференциальных и интегро-дифференциальных уравнений
Суть операторного метода заключается в том, что
функции f(t) действительной переменной t сопоставляется
функция ![]() комплексной
переменной
комплексной
переменной ![]() . Это сопоставление осуществляется
с помощью прямого преобразования Лапласа:
. Это сопоставление осуществляется
с помощью прямого преобразования Лапласа:
 .
(2.1)
.
(2.1)
Функция f(t) называется оригиналом, функция ![]() называется изображение.
Это сопоставление обозначается:
называется изображение.
Это сопоставление обозначается: ![]()
![]()
![]() и
и ![]()
Из
выражения (2.1) следует, что изображение постоянной равно: ![]()
![]()
![]() . Изображения производных:
. Изображения производных: ![]()
![]()
![]()
![]()
![]()
![]() где
где ![]() − начальные значения функции и её
производной. При нулевых начальных значениях
− начальные значения функции и её
производной. При нулевых начальных значениях ![]() :
: ![]()
![]()
![]()
![]()
![]()
![]()
Изображение
интеграла: ![]()
![]()
![]() .
.
Таким образом изображения производных и интегралов от оригинала выражаются алгебраическими функциями от изображения и от начальных значений самой функции и её производных. Отсюда следует, что система интегро-дифференциальных уравнений относительно оригиналов заменяется системой алгебраических уравнений относительно их изображений. При этом нет необходимости вычислять постоянные интегрирования.
Изображения напряжений на пассивных элементах и их эквивалентные операторные схемы замещения.
а) Резистивное сопротивление.
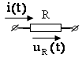
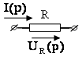
![]()
![]()
б) Индуктивность

![]()
![]()
в) Ёмкость.

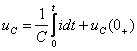 ;
; ![]() ;
;
Законы Ома и Кирхгофа в операторной форме. Эквивалентные операторные схемы.
Для исходной схемы после коммутации (см. рисунок 2.1) запишем второй уравнение по второму закону Кирхгофа в дифференциальной форме:
![]() . (2.2)
. (2.2)
Перейдём от оригинала к изображению, получим второй закон Кирхгофа в операторной форме:
![]() (2.3)
(2.3)
где I(p) - изображение тока; Е(р) - изображение источника ЭДС е(t);
![]() ,
, ![]() - внутренние (расчетные) ЭДС,
показывающие, что в магнитном поле катушки и в электрическом поле конденсатора
в момент коммутации была запасена энергия. ЭДС
- внутренние (расчетные) ЭДС,
показывающие, что в магнитном поле катушки и в электрическом поле конденсатора
в момент коммутации была запасена энергия. ЭДС ![]() совпадает с положительным направлением
тока в ветви, ЭДС
совпадает с положительным направлением
тока в ветви, ЭДС ![]() противоположно
положительному направлению тока в ветви (здесь
противоположно
положительному направлению тока в ветви (здесь ![]() - ток в индуктивности).
- ток в индуктивности).
![]() - операторное сопротивление,
- операторное сопротивление, ![]() -
операторная проводимость.
-
операторная проводимость.
Из уравнения (2.3) получим закон Ома в операторной форме:
![]() .
(2.4)
.
(2.4)
Законы Кирхгофа в операторной форме.
Система интегро-дифференциальных уравнений Кирхгофа относительно
оригиналов:![]()
![]() заменяется системой
заменяется системой
алгебраических уравнений относительно их изображений:
![]()
![]() (2.5)
(2.5)
Чтобы сразу записывать уравнения по законам Кирхгофа, а также уравнения расчета по МКТ, МУП, МЭГ и т.п, составляют эквивалентную операторную схему. (см. рисунок 2.2).

Рисунок 2.1 Рисунок 2.2
Определение оригинала по изображению.
Оригинал ![]() можно
определить по его изображению
можно
определить по его изображению ![]() , используя таблицы, обратное
преобразование Лапласа, теорему разложения.
, используя таблицы, обратное
преобразование Лапласа, теорему разложения.
Таблица 2.1-Теорема разложения
|
Изображение имеет вид рациональной дроби: где
m<n, |
|
|
по вид корней характеристического
уравнения |
Теорема разложения |
|
|
где |
|
знаменатель имеет один нулевой
корень: |
|
|
1. характеристическое уравнение |
1.
|
Продолжение таблицы 2.1
|
2. |
2. |
Порядок расчета переходных процессов операторным методом
1) По законам коммутации определяют независимые начальные условия:
![]()
2)
Составляют эквивалентную операторную схему. Ненулевые начальные условия ![]() учитываются введением
внутренних (расчетных) эдс (или источников тока): в ветвях с индуктивностью
вводится ЭДС
учитываются введением
внутренних (расчетных) эдс (или источников тока): в ветвях с индуктивностью
вводится ЭДС ![]() ,
в ветвях с емкостью вводится ЭДС
,
в ветвях с емкостью вводится ЭДС ![]()
3) Изображения токов и напряжений рассчитывают по операторной схеме известными методами (законы Ома и Кирхгофа, МКТ, МУП, МЭГ и т.п.).
4) Оригинал определяют по теореме разложения, по таблице оригиналов и изображений или с помощью обратного преобразования Лапласа.
2.2 Примеры решения типовых задач
Задача 2.1 В интегродифференцирующем контуре постоянного тока (см.
рисунок 2.3), применяемом для коррекции ЭЦ и САУ, определить напряжение ![]() ,
построить его график, если:
,
построить его график, если: ![]() ,
, ![]() ,
, ![]() мкФ,
мкФ, ![]() мкФ.
мкФ.
Решение: Определяют независимые начальные условия — напряжения
на емкостях. До коммутации ключ был разомкнут, напряжение на емкостях отсутствовало: ![]() .
.
Эквивалентная операторная схема после коммутации имеет вид (см. рисунок 2.4).
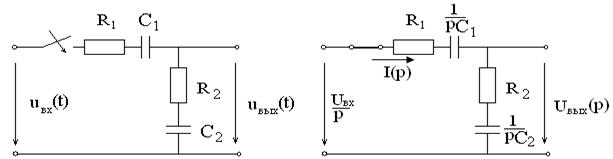
Рисунок 2.3 Рисунок 2.4
Находят изображение выходного напряжения ![]() :
:
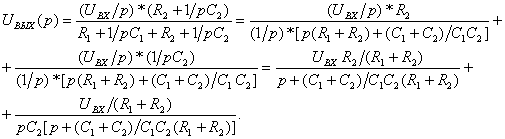 (2.6)
(2.6)
После подстановки числовых значений, получают:
![]() (2.7)
(2.7)
Оригинал определяют по теореме разложения:
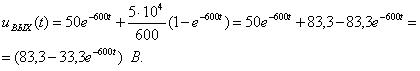
График напряжения ![]() построен в среде Mathcad (см. рисунок 2.5).
построен в среде Mathcad (см. рисунок 2.5).
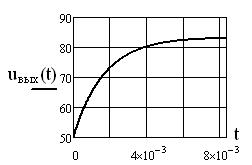
Рисунок 2.5
Задача
2.2 Электрическая цепь (см. рисунок
2.6), в которой действует источник постоянной ЭДС ![]() =
=![]() , находится в установившимся режиме. Параметры
цепи:
, находится в установившимся режиме. Параметры
цепи:![]() Ом,
Ом, ![]() Ом,
Ом, ![]() Ом,
Ом, ![]() мГн, С=0,7 мкФ. В момент времени
t=0 путем замыкания ключа К в цепи осуществляется
коммутация. Определить ток
мГн, С=0,7 мкФ. В момент времени
t=0 путем замыкания ключа К в цепи осуществляется
коммутация. Определить ток ![]() после замыкания ключа.
после замыкания ключа.

Рисунок 2.6
Решение:
1) Определение
независимых начальных условия (ННУ): ![]() и
и ![]() .ННУ определяют путём расчета
установившегося режима в цепи до коммутации. Установившийся режим до коммутации
создается постоянной ЭДС, поэтому на схеме индуктивность заменяется коротко
замкнутым участком, а ёмкость размыкается (см. рисунок 2.7).
.ННУ определяют путём расчета
установившегося режима в цепи до коммутации. Установившийся режим до коммутации
создается постоянной ЭДС, поэтому на схеме индуктивность заменяется коротко
замкнутым участком, а ёмкость размыкается (см. рисунок 2.7).
Ток в индуктивности и напряжение на ёмкости до коммутации найдём по формулам:
![]() А;
А; ![]() В.
В.
Рисунок 2.7 Рисунок 2.8
Независимые начальные условия определим по законам коммутации:
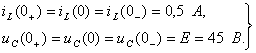 (2.8)
(2.8)
2) Составление эквивалентной операторной схемы.
Эквивалентная
операторная схема (см. рисунок 2.8) составляется для цепи после коммутации. При
составлении операторной схемы i(t), u(t), e(t) заменяют их операторными
изображениями: ![]() Индуктивность
и ёмкость заменяют эквивалентными операторными схемами:
Индуктивность
и ёмкость заменяют эквивалентными операторными схемами:
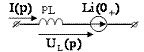 ,
,
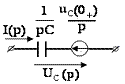
3) Определение изображения искомой величины ![]()
Изображение ![]() можно определить, используя законы Ома и
Кирхгофа в операторной форме, МКТ, МУП, МЭГ и т.п.
можно определить, используя законы Ома и
Кирхгофа в операторной форме, МКТ, МУП, МЭГ и т.п.
Изображение тока ![]() проще всего определить
методом контурных токов:
проще всего определить
методом контурных токов:
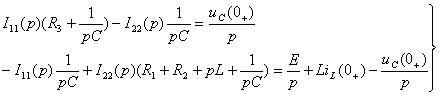 (2.9)
(2.9)
Из системы (2.9) находят:
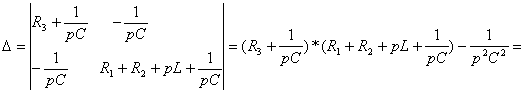
=![]() ;
;

![]() .
.
Изображение тока ![]() вычисляют по формуле:
вычисляют по формуле:
![]()
![]() (2.10)
(2.10)
где
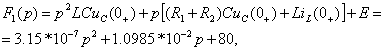
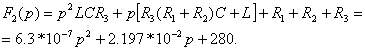
![]()
Определяют
корни характеристического уравнения ![]()
![]()
![]()
Корни
характеристического уравнения комплексно-сопряженные, ток ![]() находят по теореме разложения:
находят по теореме разложения:
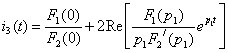 . (2.11)
. (2.11)
Рассчитывают:
![]()
![]()
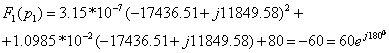
![]()
![]()
![]()
Подставляют значения ![]() в формулу (2.11):
в формулу (2.11): 
Переходный
ток ![]() равен:
равен:
![]() .
.
Примечание.
Если в рассматриваемой схеме требуется найти напряжение на ёмкости ![]() , то для определения
изображения
, то для определения
изображения ![]() более
рационально применить метод двух узлов.
более
рационально применить метод двух узлов.
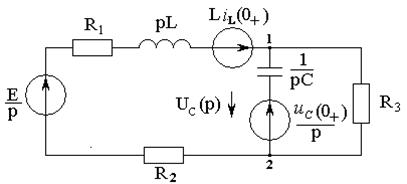
Рисунок 2.9
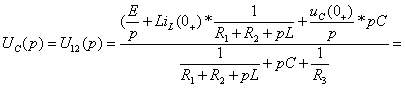
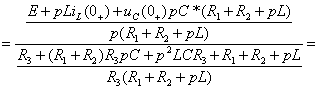 (2.12)
(2.12)
![]()
Задача 2.3
Электрическая цепь (см. рисунок 2.10) содержит источник синусоидальный ЭДС ![]() , резистивные
сопротивления, индуктивность, емкость и находится в установившимся режиме. В
момент времени
, резистивные
сопротивления, индуктивность, емкость и находится в установившимся режиме. В
момент времени ![]() в
цепи происходит коммутация (ключ замыкается). Определить ток
в
цепи происходит коммутация (ключ замыкается). Определить ток ![]() после коммутации.
после коммутации.
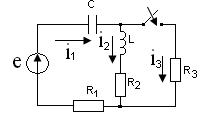
Рисунок 2.10
Значения
ЭДС и параметров цепи: ![]() В,
В, ![]() ,
, ![]()
![]() ,
, ![]() Ом,
Ом, ![]() Ом,
Ом, ![]() Ом.
Ом.
Решение: При расчёте переходных процессов в электрической цепи с синусоидальным источником ЭДС операторным методом целесообразно применить метод наложения: принужденные токи и напряжения определяются путем расчёта установившихся режимов в цепи после коммутации комплексным методом (как в классическом методе), а свободные токи и напряжения определяются операторным методом.
1)
Определяют независимые начальные условий (ННУ): ![]() ,
, ![]() .
.
Независимые начальные условия определяются путём расчёта установившегося режима в цепи до коммутации. Установившийся режим до коммутации создаётся источником синусоидальной ЭДС и при расчёте применяется комплексный метод (см. рисунок 2.11).
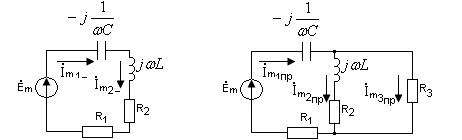
Рисунок 2.11 Рисунок 2.12
Комплексная
амплитуда ЭДС: ![]() ;
;
Индуктивное
и ёмкостное сопротивления:![]()
![]() Ом;
Ом;
![]() Ом;
Ом;
Комплексное
сопротивление всей цепи до коммутации равно: ![]() Ом .
Ом .
Комплексную
амплитуду тока ![]() и
напряжение
и
напряжение ![]() определяют
по закону Ома.
определяют
по закону Ома.
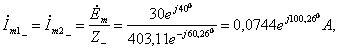 (2.13)
(2.13)
![]() (2.14)
(2.14)
Записывают мгновенные значения тока на индуктивности и напряжения на ёмкости до коммутации:
![]() ;
; ![]() .
.
Определяют
значения тока на индуктивности и напряжение на ёмкости в момент ![]()
![]()
![]() (4)
(4)
Независимые
начальные условия ![]() ,
,
![]() определим по
законам коммутации:
определим по
законам коммутации:
 (2.15)
(2.15)
2) Рассчитывают установившийся режим в цепи после
коммутации, создаваемый источником синусоидальной ЭДС ![]() В, комплексным методом (см. рисунок
2.12).Определяют принужденный ток
В, комплексным методом (см. рисунок
2.12).Определяют принужденный ток ![]() , а также принужденного тока в индуктивности
, а также принужденного тока в индуктивности
![]() и
принуждённого напряжения на ёмкости
и
принуждённого напряжения на ёмкости ![]() .
.
Комплексная
амплитуда ЭДС: ![]() =22,98+19,84
В.
=22,98+19,84
В.
Комплексное
входное сопротивление цепи после коммутации, токи ![]() и напряжение
и напряжение ![]() равны:
равны:
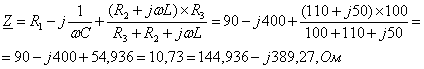 (2.16)
(2.16)
![]() (2.17)
(2.17)
 (2.18)
(2.18)
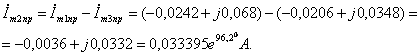 (2.19)
(2.19)
 (2.20)
(2.20)
Мгновенные
принуждённые токи ![]() ,
,![]() и мгновенное
напряжение
и мгновенное
напряжение ![]() соответственно
равны:
соответственно
равны:
![]() (2.21)
(2.21)
![]() (2.22)
(2.22)
![]() (2.23)
(2.23)
3) Определение свободного тока ![]() .
.
Свободный
ток ![]() определяют
операторным методом.
определяют
операторным методом.
а)
Составляют эквивалентную операторную схему для определения ![]() , которая содержит только
внутренние (расчётные ) ЭДС:
, которая содержит только
внутренние (расчётные ) ЭДС: ![]()
![]() и не содержит изображение внешнего
источника ЭДС
и не содержит изображение внешнего
источника ЭДС ![]() .
Направление ЭДС
.
Направление ЭДС ![]() совпадает
с направлением тока в ветви, направление ЭДС
совпадает
с направлением тока в ветви, направление ЭДС ![]() противоположно направлению тока в ветви. Эквивалентная
операторная схема представлена на рисунке 2.13.
противоположно направлению тока в ветви. Эквивалентная
операторная схема представлена на рисунке 2.13.
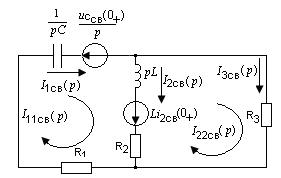
Рисунок 2.13
Находят
![]() и
и ![]() :
:
![]() ,
,
![]()
где ![]()
![]()
б)
Определение изображения. ![]() .
.
По
эквивалентной операторной схеме (см. рисунок 2.13) определяют изображение тока ![]() , используя метод
контурных токов:
, используя метод
контурных токов:

Из
системы контурных уравнений находят изображение ![]() :
:
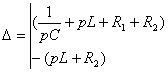
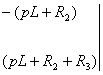 =
=
![]()
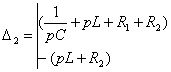
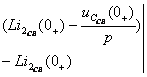 =
=

 (2.24)
(2.24)
где

в)
Определение свободного тока ![]() по его изображению
по его изображению ![]() . Вычисляют корни
характеристического уравнения
. Вычисляют корни
характеристического уравнения ![]() :
:
![]()
![]() (2.25)
(2.25)
Корни характеристического уравнения комплексно сопряжённые:
![]()
Свободный
ток ![]() находят
по теореме разложения:
находят
по теореме разложения:
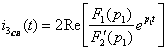 . (2.26)
. (2.26)
Вычисляют:
![]() ,
,![]() ,
,![]() :
:


![]()
![]()
Подставляют
![]() ,
, ![]() в формулу (2.26) и
вычисляют
в формулу (2.26) и
вычисляют ![]() :
:

Переходный
ток записывают в виде ![]()
![]()
3 Интервал Дюамеля
3.1 Основные теоретические сведения
Этот метод применяется для расчета переходных процессов в пассивной линейной электрической цепи при подключении ее к источнику напряжения или тока произвольной формы.
Порядок расчёта с помощью интеграла Дюамеля:
1) Определение переходной характеристики цепи.
2) Определение искомого напряжения или тока с помощью одной из форм записи интеграла Дюамеля.
Существует 4 формулы записи интеграла Дюамеля (есть еще производные от них формы):
1 форма 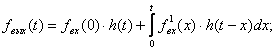 (3.1)
(3.1)
2 форма
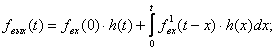 (3.2)
(3.2)
3 форма
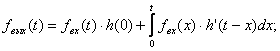 (3.3)
(3.3)
4 форма
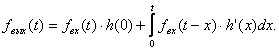 (3.4)
(3.4)
где ![]() (t)
-входное воздействие [
(t)
-входное воздействие [![]() или
или ![]() ];
];
![]() - начальное
значение входного воздействия;
- начальное
значение входного воздействия;
![]() - производная
входного воздействия;
- производная
входного воздействия;
![]() - переходная
характеристика
- переходная
характеристика ![]()
где t –заменено, соответствие на х или t-х;
![]()
![]()
![]() -реакция цепи.
-реакция цепи.
Выбирают ту форму записи интеграла Дюамеля, для которой будет проще под интегральное выражение, что зависит от конкретной задачи.
Реакция цепи на единичное воздействие ![]() называется переходной
характеристикой цепи
называется переходной
характеристикой цепи ![]() .
Переходная характеристика цепи численно равна искомому напряжению или
току при подключении цепи в момент времени
.
Переходная характеристика цепи численно равна искомому напряжению или
току при подключении цепи в момент времени ![]() при нулевых начальных условиях к
источнику единичного постоянного напряжения.
при нулевых начальных условиях к
источнику единичного постоянного напряжения.
1 Переходная
характеристика по напряжению ![]() .
.
2 Переходная
проводимость ![]() .
.
Переходную характеристику цепи находят путем расчета
переходных процессов классическим или операторным методом при подключении
пассивной линейной электрической цепи в момент ![]() при нулевых начальных условиях к
источнику постоянного единичного напряжения.
при нулевых начальных условиях к
источнику постоянного единичного напряжения.
Например,
при подключении к источнику напряжения производной формы ![]() первая форма записи интеграла
Дюамеля для тока в любой ветви или напряжения на любом участке цепи имеет вид:
первая форма записи интеграла
Дюамеля для тока в любой ветви или напряжения на любом участке цепи имеет вид:
 (3.5)
(3.5)
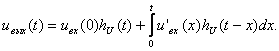 (3.6)
(3.6)
Интеграл
Дюамеля применяют и в тех случаях, когда входное воздействие ![]() , представляет собой
кусочно-непрерывную функцию, содержащую скачки напряжения конечной величины (
см.рисунок 3.1.)
, представляет собой
кусочно-непрерывную функцию, содержащую скачки напряжения конечной величины (
см.рисунок 3.1.)
В интервале времени 0 ≤ t ≤ t1:
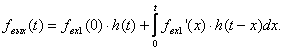 (3.7)
(3.7)
В интервале времени t1 ≤ t ≤ t2:
 (3.8)
(3.8)
В интервале времени t ≥ t2
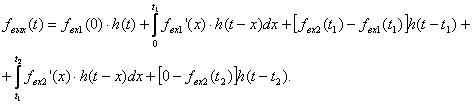 (3.9)
(3.9)
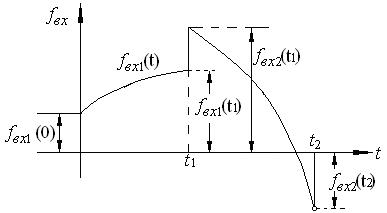
Рисунок 3.1
3.2 Примеры решения типовых задач
Задача 3.2.1 Определить
напряжение на сопротивлении R интегрирующей
RL-цепи (см.рисунок
3.2), если напряжение на входе ![]() В(см. рисунок 3.3), параметры:U=50В,
α=50с-1, R=47Oм, L=0,25Гн
В(см. рисунок 3.3), параметры:U=50В,
α=50с-1, R=47Oм, L=0,25Гн
Рисунок 3.2 Рисунок 3.3
Решение: Выбираем аналитическое выражение интеграла Дюамеля (3.3)
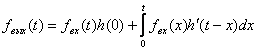 (3.10)
(3.10)
Конкретизируя величины, входящие в интеграл Дюамеля, получаем
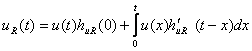 (3.11)
(3.11)
Определяем переходную характеристику по напряжению на сопротивлении R
![]() (3.12)
(3.12)
Используем известное выражение переходного тока для цепи RL, при подключении ее к источнику постоянного напряжения
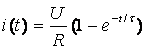 (3.13)
(3.13)
Тогда напряжение на сопротивлении в переходном режиме
![]() (3.14)
(3.14)
где ![]()
Следовательно,
![]() (3.15)
(3.15)
Вычисляем компоненты, входящие в интеграл Дюамеля:
![]()
![]()
Производя интегрирование в соответствии с выражением (3.11), находят искомое напряжение

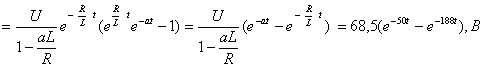 (3.16)
(3.16)
Графическое изображение выходного напряжения, построенное в среде Mathcad, показано на рисунке. 3.4.
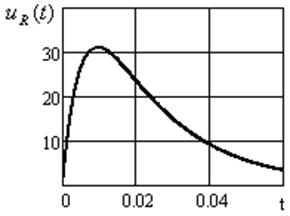
Рисунок 3.4
 Задача 3.2.2 На вход цепи
Задача 3.2.2 На вход цепи ![]() (см.рисунок
3.5) подается прямоугольный видеоимпульс
(см.рисунок
3.5) подается прямоугольный видеоимпульс ![]() (см. рисунок 3.6) с параметрами U=
10В,
(см. рисунок 3.6) с параметрами U=
10В, ![]() =2мс.
Параметры RC -цепи: R= 100 Ом; С= 25мкФ. Найти уравнения напряжения на
конденсаторе и тока в цепи, построить графики.
=2мс.
Параметры RC -цепи: R= 100 Ом; С= 25мкФ. Найти уравнения напряжения на
конденсаторе и тока в цепи, построить графики.

![]()
![]()
![]()
![]()
Рисунок 3.5 Рисунок 3.6
Решение: Используем известное выражение переходного напряжения для цепи RС, при подключении ее к источнику постоянного напряжения
![]() , (3.17)
, (3.17)
Определяем переходную характеристику по напряжению на емкости
![]() (3.18)
(3.18)
Запишем выражения для ![]() с помощью интеграла Дюамеля в интервале
времени
с помощью интеграла Дюамеля в интервале
времени ![]()
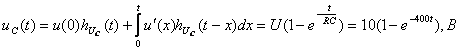 (3.19)
(3.19)
так как ![]()
![]()
![]() (3.20)
(3.20)
В интервале времени ![]()
 (3.21)
(3.21)
![]() (3.22)
(3.22)
Графики для интервала времени ![]() строим по формулам
(3.19), (3.20). Для интервала времени
строим по формулам
(3.19), (3.20). Для интервала времени ![]() графики строят по формулам (3.21) и
(3.22).
графики строят по формулам (3.21) и
(3.22).
Графическое изображение выходного напряжения и тока, построенное в среде Mathcad, показано на рисунках. 3.7, 3.8.
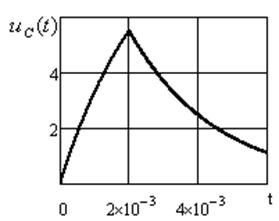
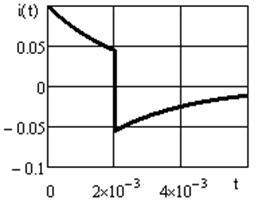
Рисунок 3.7 Рисунок 3.8
Задача 3.2.3 На
вход цепи ![]() (см.
рисунок 3.9) с параметрами
(см.
рисунок 3.9) с параметрами ![]()
![]() подается напряжение, изменяющееся по
закону
подается напряжение, изменяющееся по
закону ![]() (см.
рисунок 3.10), где
(см.
рисунок 3.10), где ![]() ,
,
![]() Найти
уравнения напряжения на конденсаторе и тока в цепи, построить графики.
Найти
уравнения напряжения на конденсаторе и тока в цепи, построить графики.
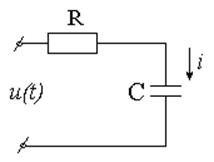
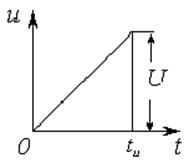
Рисунок 3.9 Рисунок 3.10
Решение: В расчетах используем, найденную в предыдущей задаче, переходную характеристику по напряжению на емкости
![]() (3.23)
(3.23)
Рассмотрим интервал времени ![]() :
:
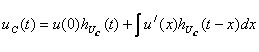 (3.24)
(3.24)
где ![]()
![]() ;
; ![]() .
.
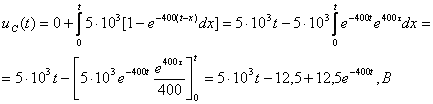 (3.25)
(3.25)
![]() , А (3.26)
, А (3.26)
Рассмотрим
интервал времени ![]()
![]()
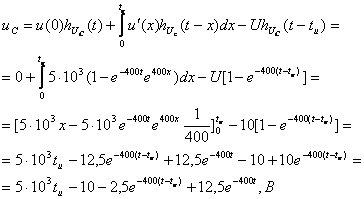 (3.27)
(3.27)
Подставив в последнее выражение ![]() получим
получим
![]() (3.28)
(3.28)
![]() (3.29)
(3.29)
Графики для интервала времени ![]() строим по формулам
(3.25), (3.26); для интервала времени
строим по формулам
(3.25), (3.26); для интервала времени ![]() по формулам (3.28), (3.29). Построение
произведено в среде Mathcad (см.
рисунки 3.11, 3.12).
по формулам (3.28), (3.29). Построение
произведено в среде Mathcad (см.
рисунки 3.11, 3.12).
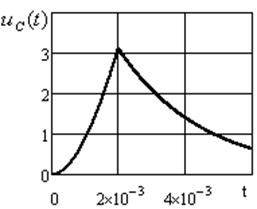
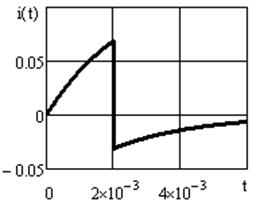
Рисунок 3.11 Рисунок 3.12
Задача 3.2.4 Электрическая цепь
(см.рисунок 3.13), параметры которой равны: ![]() подключается на импульс
напряжения с
подключается на импульс
напряжения с ![]() (см.
рисунок 3.14). Найти выражение тока
(см.
рисунок 3.14). Найти выражение тока ![]() на индуктивности.
на индуктивности.
Решение: 1. Определение переходной характеристики для тока в ветви с индуктивностью.
Для определения переходной проводимости цепи ![]() рассчитаем переходной
процесс при подключении цепи при нулевых начальных условиях
рассчитаем переходной
процесс при подключении цепи при нулевых начальных условиях ![]() к источнику единичного
постоянного напряжения (см. рисунок 3.15) и определим ток
к источнику единичного
постоянного напряжения (см. рисунок 3.15) и определим ток ![]() .
.
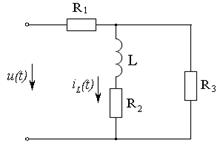

Рисунок 3.13 Рисунок 3.14
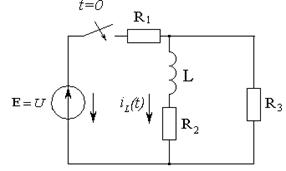
Рисунок 3.15
Независимое
начальное условие ![]() Ток в переходном режиме в индуктивности
можно записать в виде
Ток в переходном режиме в индуктивности
можно записать в виде
![]() (3.30)
(3.30)
Принужденная составляющая тока
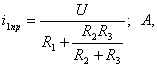
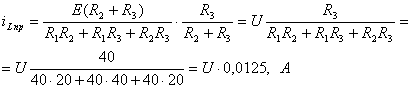 (3.31)
(3.31)
Для
определения свободной составляющей тока ![]() составим характеристическое уравнение
цепи после коммутации методом входного сопротивления относительно ветви с
индуктивностью (см. рисунок 3.16).
составим характеристическое уравнение
цепи после коммутации методом входного сопротивления относительно ветви с
индуктивностью (см. рисунок 3.16).
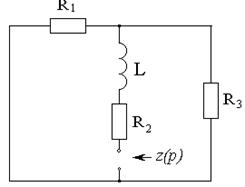
Рисунок 3.16
![]() (3.32)
(3.32)
тогда, ![]() (t)
:
(t)
:
![]() (3.33)
(3.33)
Для определения постоянной интегрирования, перепишем
выражение (3.33) для момента времени t=0, откуда ![]()
![]() , значит
, значит
![]() (3.34)
(3.34)
Определяем переходную характеристику для тока в ветви с индуктивностью
![]()
![]() (3.35)
(3.35)
2. Определение тока ![]() при включения цепи на импульс напряжения
при включения цепи на импульс напряжения ![]() с помощью интеграла
Дюамеля.
с помощью интеграла
Дюамеля.
Напряжения ![]() имеет разные аналитические выражения в
разных интервалах времени
имеет разные аналитические выражения в
разных интервалах времени

Рассмотрим
интервал времени ![]() (не
включая скачок напряжения):
(не
включая скачок напряжения): 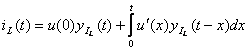 (3.36)
(3.36)
где ![]()
![]()
![]() ;
; ![]()
 (3.37)
(3.37)
Рассмотрим интервал времени ![]()
 (3.38)
(3.38)
 (3.39)
(3.39)
График для интервала времени ![]() строим по формуле
(3.37); для интервала времени
строим по формуле
(3.37); для интервала времени ![]() по формуле (3.39). Построение
произведено в среде Mathcad (см.
рисунок 3.17).
по формуле (3.39). Построение
произведено в среде Mathcad (см.
рисунок 3.17).
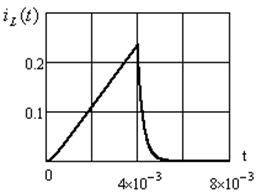
Рисунок 3.17
4 Спектральный метод анализа электрических цепей
4.1 Основные теоретические сведения
4.1.1 Преобразования Фурье. При воздействии на
цепь сигналов произвольной формы широко используется спектральный (частотный)
метод анализа электрических цепей. Спектральный метод позволяет определять
спектр входного воздействия и вычислять спектральную плотность реакции цепи по
спектру входного воздействия и соответствующей комплексной функции передачи
цепи ![]() , а
также находить реакцию цепи в переходном и установившемся режимах.
, а
также находить реакцию цепи в переходном и установившемся режимах.
Математической основой спектрального метода анализа
электрических цепей являются преобразования Фурье. Непериодическая функция,
удовлетворяющая условию абсолютной интегрируемости в бесконечных пределах ![]() , может быть
представлена интегралом Фурье:
, может быть
представлена интегралом Фурье:
![]() (4.1)
(4.1)
Внутренний
интеграл в выражении (4.1) является спектром или спектральной плотностью ![]() заданной функции
заданной функции ![]() и называется прямым
преобразованием Фурье:
и называется прямым
преобразованием Фурье:
![]() (4.2)
(4.2)
Заданную
функцию ![]() можно
определить по спектру
можно
определить по спектру ![]() с помощью обратного преобразования Фурье:
с помощью обратного преобразования Фурье:
![]() (4.3)
(4.3)
Одностороннее
обратное преобразование Фурье (если ![]() при
при![]() ):
):
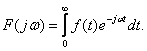 (4.4)
(4.4)
Спектральная
плотность ![]() является
комплексной функцией частоты и может быть записана в показательной форме:
является
комплексной функцией частоты и может быть записана в показательной форме: ![]() , где
, где ![]() −
амплитудно-частотная характеристика АЧХ (чётная функция частоты),
−
амплитудно-частотная характеристика АЧХ (чётная функция частоты),
![]() − фазочастотная
характеристика ФЧХ (нечётная функция частоты).
− фазочастотная
характеристика ФЧХ (нечётная функция частоты).
Обратное преобразование Фурье в тригонометрической форме:
![]()
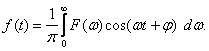 (4.5)
(4.5)
Сравнивая
прямое и обратное преобразование Лапласа с прямым (4.3) и обратным
преобразованием Фурье (4.4), можно сделать вывод, что преобразования Фурье
являются частным случаем преобразований Лапласа и получаются из него при ![]() .
.
4.1.2 Некоторые свойства преобразований.
Фурье
теорема линейности: ![]()
![]()
![]() ;
;
спектры
производной и интеграла: если ![]()
![]()
![]() , то
, то ![]()
![]()
![]() и
и
![]()
![]()
![]() ;
;
теорема
запаздывания: если ![]()
![]()
![]() , то
, то ![]()
![]()
![]() .
.
4.1.3
Определение спектра непериодических функций. Спектры непериодических
входных воздействий определяют по формуле прямого преобразования Фурье или
используя таблицы операторных изображений по Лапласу, в которых ![]() заменяют на
заменяют на ![]() . Пример в задаче 4.1.
. Пример в задаче 4.1.
4.1.4 Определение спектральной плотности реакции цепи. Спектральную плотность реакции цепи вычисляют по спектральной плотности входного воздействия и соответствующей комплексной функции передачи цепи.
Расчет спектра тока в ![]() , закон Ома для частотных спектров при
нулевых начальных значениях):
, закон Ома для частотных спектров при
нулевых начальных значениях):
![]() (4.6)
(4.6)
где ![]() - спектр
непериодического входного воздействия;
- спектр
непериодического входного воздействия;
![]() - комплексное
сопротивление
- комплексное
сопротивление ![]() ,
которое применялось ранее для расчёта установившихся гармонических процессов.
,
которое применялось ранее для расчёта установившихся гармонических процессов.
Расчет спектра тока двухполюсника:
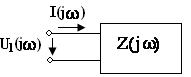
![]() (4.7)
(4.7)
где
![]() -
комплексные входные сопротивление и проводимость.
-
комплексные входные сопротивление и проводимость.
В
общем случае спектральную плотность реакции цепи (напряжение ![]() или ток
или ток ![]() произвольного элемента
цепи) вычисляют по спектральной плотности входного воздействия по формулам
(4.8):
произвольного элемента
цепи) вычисляют по спектральной плотности входного воздействия по формулам
(4.8):

 (4.8)
(4.8)
где
![]() ,
, ![]() - спектры
непериодических входных воздействий (напряжения и тока);
- спектры
непериодических входных воздействий (напряжения и тока);
![]() - комплексные
передаточные функции цепи.
- комплексные
передаточные функции цепи.
Для расчёта комплексных передаточных функций цепи применяется комплексный метод, который применялся ранее для расчёта установившихся гармонических процессов Примеры в задачах 4.2; 4 .
4.1.5 Определение реакции цепи в переходном и
установившемся режимах. Спектральный метод может быть применён для расчета
переходных процессов в линейных электрических цепях, так как преобразования
Фурье являются частным случаем преобразований Лапласа и получаются из него при ![]() .
.
Порядок расчета переходных процессов спектральным методом:
а) определение спектра входного воздействия;
б) определение соответствующей передаточной функции цепи;
в) определение спектра реакции цепи;
г) определение реакции цепи по её спектру с помощью обратного преобразования Фурье, по таблице, по теореме разложения.
Примеры в задачах 4.2; 4.
4.2 Примеры решения типовых задач
Задача 4.1 Определить спектральную
плотность ![]() ,
АЧХ
,
АЧХ ![]() , ФЧХ
, ФЧХ ![]() прямоугольного
видеоимпульса с амплитудой U и длительностью tu (см.
рисунок 4.1, а, б, в).
прямоугольного
видеоимпульса с амплитудой U и длительностью tu (см.
рисунок 4.1, а, б, в).

а) б) в)
Рисунок 4.1
Решение: Спектр ![]() определяют, используя
прямое преобразование Фурье
определяют, используя
прямое преобразование Фурье
а) для видеоимпульса (см. рисунок 4.1,а):
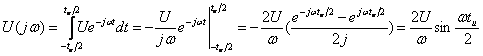 , (4.9)
, (4.9)
АЧХ:
![]() ; ФЧХ:
; ФЧХ: ![]() 0 ,если
0 ,если ![]() и
и ![]() , если
, если ![]() .
.
б) для видеоимпульса (см. рисунок 4.1,б), применяя теорему запаздывания, получают:
![]() АЧХ:
АЧХ: ![]() , ФЧХ
, ФЧХ![]() , если
, если ![]() и
и![]() , если
, если ![]() .
.
в) для видеоимпульса (см. рисунок 4.1,в), применяя теорему запаздывания, получают:
![]() АЧХ:
АЧХ: ![]() ; ФЧХ:
; ФЧХ: ![]() если
если ![]() и
и ![]()
![]() , если
, если ![]() .
.
Графики АЧХ (см. рисунок 4.2) для видеоимпульсов (см. рисунок 4.1, а, б, в), ФЧХ (см. рисунки 4.3; 4.4) для видеоимпульсов (см. рисунок 4.1, а, б) с амплитудой U=20B и длительностью импульса tu=0,004c построены в среде Mathcad.

Рисунок 4.2 Рисунок 4.3
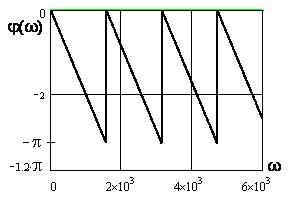
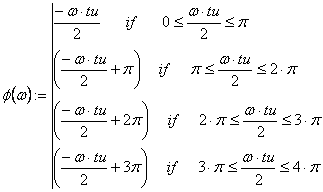
Рисунок 4.4
Задача 4.2 На входе электрической цепи
(см. рисунок 4.5), параметры которой ![]()
![]()
![]()
![]() , действует прямоугольный импульс
, действует прямоугольный импульс ![]() амплитудой
амплитудой ![]() и длительностью
и длительностью ![]() (см. рисунок 4.6).
(см. рисунок 4.6).
Определить
комплексную передаточную функцию по напряжению ![]() и спектральную плотность напряжения
и спектральную плотность напряжения ![]() .
.
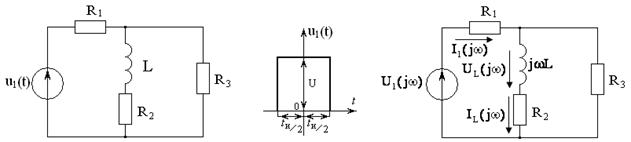
Рисунок 4.5 Рисунок 4.6 Рисунок 4.7
Решение: 1) Определение спектральной плотности входного напряжения.
Спектр
входного напряжения найден в задаче 4.1: ![]() ,
,
АЧХ: ![]() ; ФЧХ:
; ФЧХ: ![]() 0 ,если
0 ,если ![]() и
и ![]() , если
, если ![]() .
.
2)
Определение комплексной передаточной функции по напряжению ![]() Комплексную передаточную
функцию находят по формуле:
Комплексную передаточную
функцию находят по формуле: ![]() . Будем считать, что на вход цепи подано
синусоидальное напряжение, комплексное действующее значение которого
. Будем считать, что на вход цепи подано
синусоидальное напряжение, комплексное действующее значение которого ![]() . Применяя комплексный
метод расчёта, определяют комплексное действующее значение напряжение
. Применяя комплексный
метод расчёта, определяют комплексное действующее значение напряжение ![]() (см. рисунок 4.7) и
(см. рисунок 4.7) и ![]() :
:
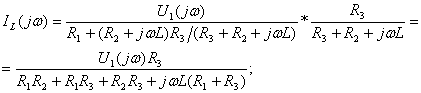
![]() (4.10)
(4.10)
![]() (4.11)
(4.11)
АЧХ: ![]()
ФЧХ: ![]()
3)
Определение спектральной плотности ![]() по спектру входного напряжения
по спектру входного напряжения ![]() и соответствующей
комплексной функции передачи
и соответствующей
комплексной функции передачи ![]() . Спектральную плотность
. Спектральную плотность ![]() находят по формуле:
находят по формуле:
![]() (4.12)
(4.12)
АЧХ: 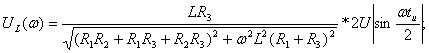
ФЧХ: ![]() , если
, если ![]() и
и
![]() , если
, если ![]() .
.
Подставляют числовые
значения: ![]() ,
,  ,
, ![]() если
если ![]() и
и ![]() если
если ![]() .
.
4) Графики АЧХ: ![]()
![]() ,
, ![]() (см. рисунки 4.8, 4.10, 4.12) и ФЧХ
(см. рисунки 4.8, 4.10, 4.12) и ФЧХ ![]() ,
, ![]() (см. рисунки 4.9, 4.11, 4.13)
построены в среде Mathcad.
(см. рисунки 4.9, 4.11, 4.13)
построены в среде Mathcad.

Рисунок 4.8 Рисунок 4.9
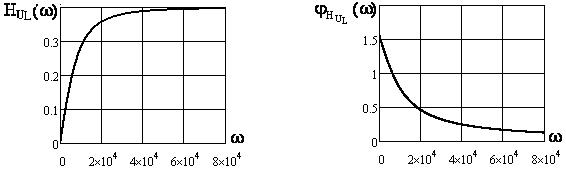
Рисунок 4.10 Рисунок 4.11
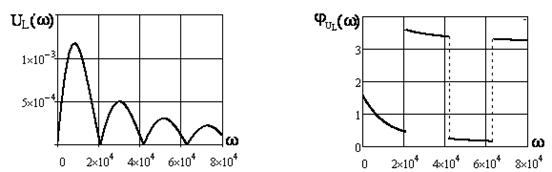
Рисунок 4.12 Рисунок 4.13
Задача 4.3 На входе
электрической цепи (см. рисунок 4.15), параметры которой ![]()
![]()
![]()
![]() , действует импульс напряжения
, действует импульс напряжения ![]() (см. рисунок 4.14) c
(см. рисунок 4.14) c ![]() и α=900 c-1.
и α=900 c-1.
Определить:
1) спектральную плотность импульса напряжения
![]() , АЧХ,ФЧХ;
, АЧХ,ФЧХ;
2) комплексную передаточную функцию по
напряжению ![]() ,
АЧХ,ФЧХ;
,
АЧХ,ФЧХ;
3) спектральную плотность реакции цепи ![]() ,АЧХ,ФЧХ;
,АЧХ,ФЧХ;
4)
реакцию цепи ![]() .
.
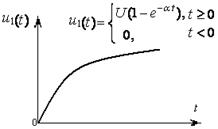
Рисунок 4.14
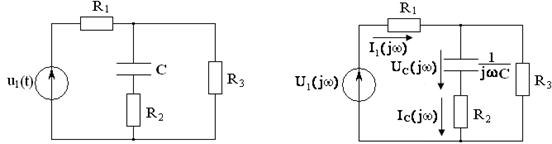
Рисунок 4.15 Рисунок 4.16
Решение: а)
Определение спектральной плотности входного импульса напряжения ![]() .
.
Спектральную
плотность импульса напряжения ![]() определяют с помощью прямого
преобразования Фурье:
определяют с помощью прямого
преобразования Фурье:
 (4.13)
(4.13)
АЧХ: ![]()
ФЧХ: ![]() (4.14)
(4.14)
2)
Определение комплексной передаточной функции по напряжению ![]()
![]() находят по формуле:
находят по формуле: ![]() . Будем считать, что на вход
цепи подано синусоидальное напряжение, комплексное действующее значение
которого
. Будем считать, что на вход
цепи подано синусоидальное напряжение, комплексное действующее значение
которого ![]() .
Применяя комплексный метод расчёта (см. рисунок 4.16), определяют
.
Применяя комплексный метод расчёта (см. рисунок 4.16), определяют ![]() , АЧХ
, АЧХ ![]() , ФЧХ
, ФЧХ ![]() :
:
![]()
![]()
![]()
![]()
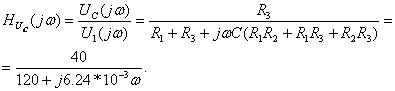 (4.15)
(4.15)
 ,
,
![]()
3)
Определение спектральной плотности ![]() по спектру входного напряжения
по спектру входного напряжения ![]() и соответствующей
комплексной функции передачи
и соответствующей
комплексной функции передачи ![]() . Спектральную плотность реакции цепи
. Спектральную плотность реакции цепи ![]() вычисляют по формуле
вычисляют по формуле![]() :
:
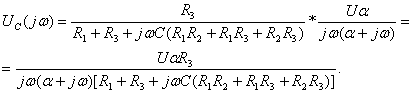 (4.16)
(4.16)
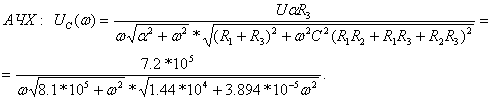
![]()
Графики
АЧХ: ![]()
![]() ,
, ![]() (см. рисунки 4.17, 4.19 4.21) и
ФЧХ
(см. рисунки 4.17, 4.19 4.21) и
ФЧХ ![]() ,
, ![]() (см. рисунки 4.18,
4.20, 4.22) построены в среде Mathcad.
(см. рисунки 4.18,
4.20, 4.22) построены в среде Mathcad.

Рисунок 4.17 Рисунок 4.18
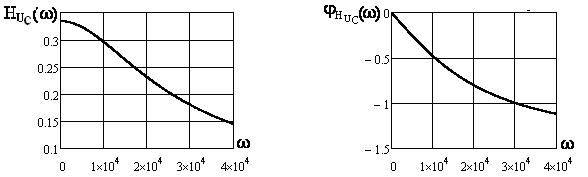
Рисунок 4.19 Рисунок 4.20
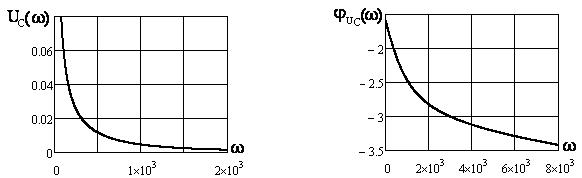
Рисунок 4.21 Рисунок 4.22
4)
Определение реакции цепи ![]() .
.
Реакцию
цепи ![]() определяют
по соответствующей спектральной плотности
определяют
по соответствующей спектральной плотности ![]() по теореме разложения. В выражении (4.15)
заменяют
по теореме разложения. В выражении (4.15)
заменяют ![]() на
р:
на
р:
![]() (4.17)
(4.17)
где
![]() ,
,
![]() Находят
корни характеристического уравнения
Находят
корни характеристического уравнения ![]() :
:
![]()
Реакцию
цепи ![]() определяют
по теореме разложения:
определяют
по теореме разложения:
![]() (4.18)
(4.18)
где ![]()
Рассчитывают:
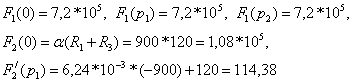
![]()
Подставляют
полученные значения ![]()
![]() в выражение (4.18) и
вычисляют реакцию цепи
в выражение (4.18) и
вычисляют реакцию цепи ![]() :
:
![]() .
.
Ток
![]() в ветви с
ёмкостью находят по формуле:
в ветви с
ёмкостью находят по формуле:
![]()
Графики ![]() ,
, ![]() (см. рисунки 4.23, 4.24)
построены в среде Mathcad .
(см. рисунки 4.23, 4.24)
построены в среде Mathcad .
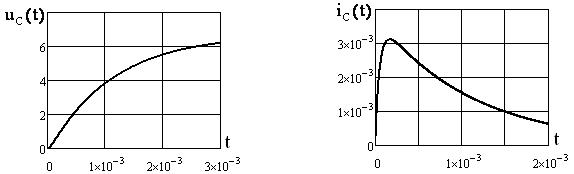
Рисунок 4.23 Рисунок 4.24
5 Расчет цепей с распределенными параметрами
5.1 Основные теоретические сведения
5.1.1 Параметры однородной линии. Первичными параметрами однородной линии на единицу ее длины являются: R0 - сопротивление, Ом; L0 - индуктивность, Гн; C0 - емкость, Ф; G0 - проводимость изоляции между проводами (утечка), См.
Вторичные
параметры однородной линии: ![]() -волновое (характеристическое)
сопротивление и
-волновое (характеристическое)
сопротивление и ![]() -
коэффициент распространения
-
коэффициент распространения
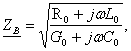 (5.1)
(5.1)
![]() (5.2)
(5.2)
где γ -модуль коэффициента
распространения, ![]() -коэффициент
ослабления,
-коэффициент
ослабления, ![]() -
коэффициент фазы.
-
коэффициент фазы.
Длина волны λ и фазовая скорость υф
![]()
![]() (5.3)
(5.3)
5.1.2 Решение уравнений однорядной линии в гиперболических функциях. Запишем выражения для определения комплексов напряжения и тока в любой точке М линии (см. рисунок 5.1):
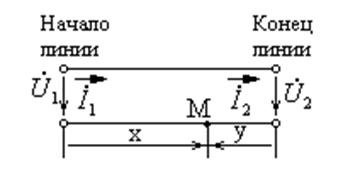
Рисунок 5.1
При отсчете х от начала линии
![]() (5.4)
(5.4)
![]() (5.5)
(5.5)
При отсчете у от ее конца
![]() (5.6)
(5.6)
![]() (5.7)
(5.7)
Входное сопротивление линии представляет отношение комплексного напряжения к току в точках подключения источника
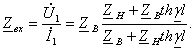 (5.8)
(5.8)
5.1.3
Линия без потерь - это линия, у которой![]() . Для линии без потерь
. Для линии без потерь 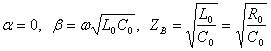 .
.
В
линии без потерь гиперболические функции заменяются круговыми ![]() ;
; ![]() .
.
Тогда решение уравнений длиной линии без потерь в комплексной форме:
При отсчете х от начала линии
![]() (5.9)
(5.9)
![]() (5.10)
(5.10)
При отсчете расстояний у от ее конца
![]() (5.11)
(5.11)
![]() (5.12)
(5.12)
Входное сопротивление линии без потерь
![]() (5.13)
(5.13)
В режимах холостого хода и короткого замыкания входное сопротивление линии без потерь
![]() ,
, ![]() . (5.14)
. (5.14)
5.1.4 Линия, согласовонная с нагрузкой.
Режим работы длинной линии, при ![]() называется согласованным. При этом в любой точке линии
называется согласованным. При этом в любой точке линии ![]() .
.
В решении уравнений линий с согласованной нагрузкой отраженная волна соответствует:
При отсчете х от начала линии
![]() (5.15)
(5.15)
![]() (5.16)
(5.16)
При отсчете у от конце линии
![]() (5.17)
(5.17)
![]() (5.18)
(5.18)
5.2 Примеры решения типовых задач
Задача 5.2.1
Линия передачи электроэнергии длиной ![]() км имеет первичные параметры:
км имеет первичные параметры: ![]() Ом,
Ом, ![]() См/км,
См/км, ![]() Гн/км,
Гн/км, ![]() Ф/км. ЭДС генератора
Ф/км. ЭДС генератора ![]() кВ, внутренние
сопротивление генератора
кВ, внутренние
сопротивление генератора ![]() Ом,
Ом, ![]() Гц. Сопротивление нагрузки
Гц. Сопротивление нагрузки ![]() Ом.
Ом.
1) Определить напряжение в конце линии, ток в начале и в конце линии.
2) Рассчитать мощность в начале и в конце линии, к.п.д.
Расчеты
произвести для двух режимов ![]() и
и ![]()
Решение: 1) Определим вторичные параметры линии:
Продольное сопротивление единицы длины линии
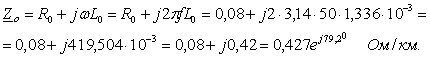 (5.19)
(5.19)
Поперечная проводимость единицы длины линии
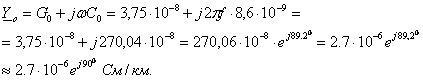 (5.20)
(5.20)
Волновое сопротивление
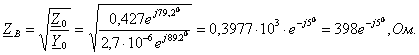 (5.21)
(5.21)
Коэффициент распростронения
![]() (5.22)
(5.22)
Коэффициент затухания и коэффициент фазы
![]()
![]()
2) Произведем расчет линии, нагруженной на
сопротивление Z2. Определим
входное сопротивление линий, для этого рассчитаем ![]() ,
, ![]() ,
, ![]()
![]()
![]()


![]()
Учитывая, найденные значения, определим входное сопротивление линии:
 (5.23)
(5.23)
По схеме замещения линии (см. рисунок 5.2) определим ток и напряжение в начале линии
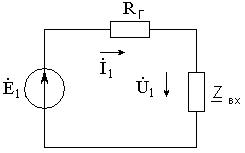
Рисунок 5.2
 (5.24)
(5.24)
![]() (5.25)
(5.25)
Используя выражение (5.8), определим напряжение в конце линии
 (5.26)
(5.26)
Ток в конце линии найдем по закону Ома
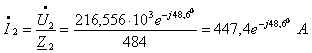 (5.27)
(5.27)
Рассчитаем мощность в начале и в конце линии. к.п.д.
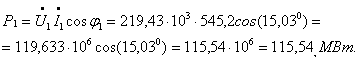 (5.28)
(5.28)
![]() (5.29)
(5.29)
![]() (5.30)
(5.30)
3) Произведем расчет линии с согласованной нагрузкой, то есть когда
![]()
Определим ток и напряжение в начале линии
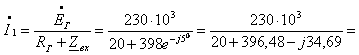
![]() (5.31)
(5.31)
![]() (5.32)
(5.32)
Из уравнений линии в согласованном режиме при х =l, определим напряжение конце линии
 (5.33)
(5.33)
И ток в конце линии
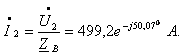 (5.34)
(5.34)
Рассчитаем мощность в начале и в конце линии. к.п.д
![]() (5.35)
(5.35)
![]() (5.36)
(5.36)
![]() (5.37)
(5.37)
Задача 5.2.2
Линия передачи электроэнергии без потерь длиной ![]() км имеет следующие параметры:
км имеет следующие параметры: ![]() Гн/км,
Гн/км, ![]() Ф/км,
Ф/км, ![]() кВ,
кВ, ![]() Гц. Сопротивления
Гц. Сопротивления ![]() Ом,
Ом, ![]() . Для каждого из четырех режим
(х.х; к.з; согласованный режим и линия нагружена на активное сопротивление),
определить:
. Для каждого из четырех режим
(х.х; к.з; согласованный режим и линия нагружена на активное сопротивление),
определить:
1) Входное сопротивление линии ![]() .
.
2) Напряжение и ток в начале и в конце линии.
3) Активную мощность в нагрузке, к.п.д. линии.
4) Построить графики распределения мгновенного
значения напряжения вдоль линии для двух моментов времени: когда напряжение в
конце линии максимально и спустя ![]() период.
период.
5) Построить графики распределения действующих напряжений и токов вдоль линий.
Решение: 1)
Определим вторичные параметры линии ![]() и
и ![]()
Волновое сопротивление линии
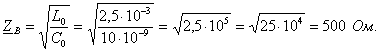 (5.38)
(5.38)
Коэффициент распростронения линии
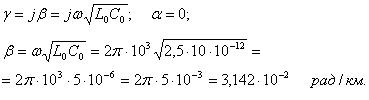 (5.39)
(5.39)
Длина волны:
![]() (5.40)
(5.40)
![]()
![]()
1) Линия работает в режиме ХХ ![]()
Входное сопротивление линии
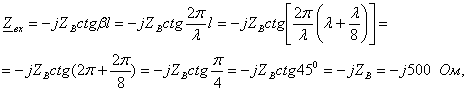 (5.41)
(5.41)
или
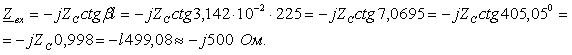
Ток в начале линии
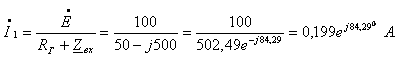 (5.42)
(5.42)
Напряжение в начале линии
![]() (5.43)
(5.43)
Из выражения (5.11), учитывая что ![]() и
и ![]() найдем напряжение в конце линии
найдем напряжение в конце линии
![]() ;
; ![]()
Значит
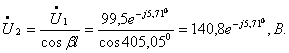 (5.44)
(5.44)
Активная мощность в нагрузке и к.п.д. линии
![]()
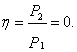
Из выражения (5.11), учитывая, что ![]() , получим
, получим
![]() (5.45)
(5.45)
Запишем мгновенное значение напряжения
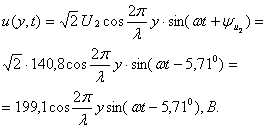 (5.46)
(5.46)
Запишем мгновенное значение напряжения для момента
времени, когда напряжение в конце линии максимально при ![]()
![]()
![]() . (5.47)
. (5.47)
Мгновенное значение напряжение через 1/6 периода при ![]()
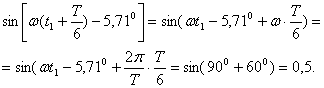
![]() (5.48)
(5.48)
Учитывая, что в режиме х.х. из(5.11) и (5.12):
![]()
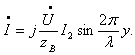
Запишем действующие значения напряжения и тока
![]() (5.49)
(5.49)
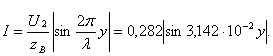 (5.50)
(5.50)
Графики распределения мгновенного значения напряжения вдоль линии для двух моментов времени построены по выражениям (5.47) и (5.48) в среде Mathcad (см. рисунок 5.3)
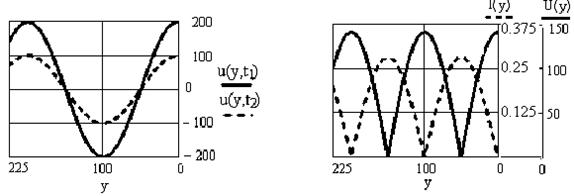
Рисунок 5.3 Рисунок 5.4
Графики распределения действующих значений, напряжения и тока вдоль линии построены по выражениям (5.49) и (5.50) с помощью программы (см. рисунок 5.4).
2) Линия работает в режиме КЗ ![]()
Входные сопротивление линии
![]() (5.51)
(5.51)
Ток в начале линии
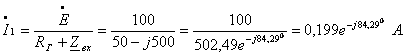 (5.52)
(5.52)
Напряжение в начале линии
![]() (5.53)
(5.53)
Из выражения (5.12), учитывая, что ![]() ,
, ![]() найдем ток в конце линии
найдем ток в конце линии
![]() (5.54)
(5.54)
Значит
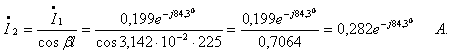
Активная мощность в нагрузке и к.п.д. линии
![]()
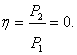
Из
выражения (5.11), учитывая, что ![]() получим
получим
![]() (5.55)
(5.55)
Мгновенное значение напряжение
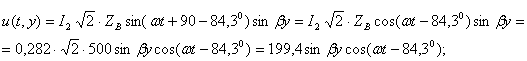 (5.56)
(5.56)
Запишем мгновенное значение напряжение для момента
времени, когда напряжение в конце линии максимально при ![]()
![]()
![]()
![]()
![]() (5.57)
(5.57)
Мгновенное
значение напряжения для момента времени спустя ![]() периода, при
периода, при ![]()
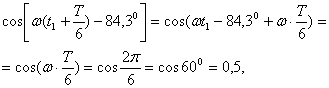
![]()
![]() (5.58)
(5.58)
Учитывая, что в режиме к.з. из (5.11) и (5.12)
![]()
![]()
![]()
Запишем действующие значения напряжения и тока
![]() (5.59)
(5.59)
![]() (5.60)
(5.60)
Графики распределения мгновенного значения напряжения вдоль линии для двух моментов времени построена по выражениям (5.57) и (5.58) в среде Mathcad (см. рисунок 5.5)
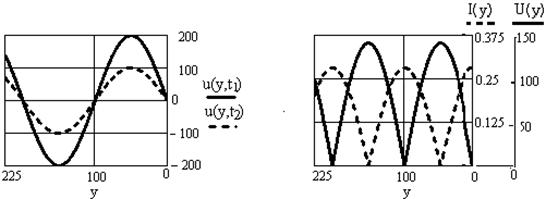
Рисунок 5.5 Рисунок 5.6
Графики распределения действующих значений напряжения и тока вдоль линии построены по выражениям (5.59) и (5.60) с помощью программы Mathcad (см. рисунок 5.6).
3) Линия работает в режиме согласованной нагрузки
При согласованной нагрузке
![]()
Ток в начале линии
 (5.61)
(5.61)
Напряжение в начале линии
![]() (5.62)
(5.62)
Из выражения (5.16), учитывая, что ![]() и
и ![]() , найдем напряжение в конце линии
, найдем напряжение в конце линии
![]() (5.63)
(5.63)
Ток в конце линии найдем по закону Ома
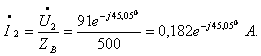 (5.64)
(5.64)
Активная мощность в нагрузке и к.п.д. линии
![]()
![]()
![]()
Из выражения (5.18), учитывая, что ![]() получим
получим
![]() (5.65)
(5.65)
Запишем мгновенное значение напряжения:
![]() (5.66)
(5.66)
Запишем мгновенное значение напряжения для момента
времени, при котором напряжение в конце линии (при ![]() ) максимально. При
) максимально. При ![]() ,
, ![]() , значит
, значит ![]()
будет максимально при ![]() (5.67)
(5.67)
Тогда,
![]() (5.68)
(5.68)
Мгновенное
значение напряжение для момента времени, спустя ![]() т.е. при
т.е. при ![]()
 (5.69)
(5.69)
![]() (5.70)
(5.70)
Перепишем
выражения (5.18) и (5.19) для линии без потерь ![]()
![]()
![]()
Тогда действующие значения напряжения и тока
![]() ;
; ![]() (5.71)
(5.71)
Графики распределение мгновенного значения напряжения вдоль линии для двух моментов времени построены по выражениям (5.68) и (5.70) с помощью программы Mathcad (см. рисунок 5.7)
Графики распределения действующих значений напряжения и тока построены по выражениям (5.71) с помощью программы Mathcad.

Рисунок 5.7 Рисунок 5.8
4) Линия работает в смешанном режиме ![]()
Входное сопротивление линии
![]() (5.72)
(5.72)
Ток в начале линии
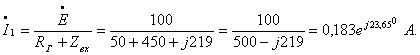 (5.73)
(5.73)
Напряжение в начале линии
![]() (5.74)
(5.74)
Из выражения (5.9) найдем напряжение в конце линии
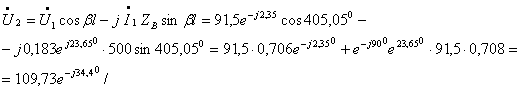 (5.75)
(5.75)
Определим ток в конце линии
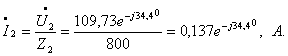 (5.76)
(5.76)
Активная мощность в нагрузке и к.п.д. линии
![]()
![]()
![]()
Из выражение (5.11), получим
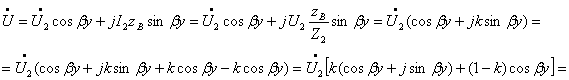
![]() (5.77)
(5.77)
Учитывая, что ![]() , получил
, получил
![]() (5.78)
(5.78)
Перейдем к мгновенному значению напряжения:
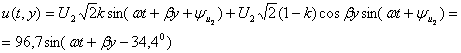 (5.79)
(5.79)
где
![]() - прямая
бегущая волна,
- прямая
бегущая волна,
![]() - стоячая волна.
- стоячая волна.
Запишем мгновенное значение напряжения для момента
времени, при котором напряжение в конце линии (при ![]() ) максимально. При
) максимально. При ![]()
![]() если,
если, ![]() тогда
тогда
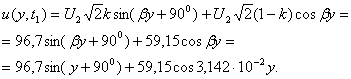 (5.80)
(5.80)
Мгновенное значение напряжения для момента времени
спустя ![]() т.е.
при
т.е.
при ![]()
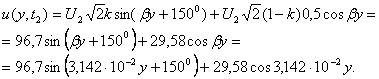 (5.81)
(5.81)
Найдем действующие значение напряжения
![]()
![]() (5.82)
(5.82)
Найдем действующие значение тока
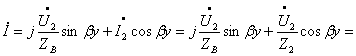
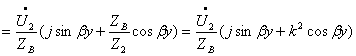
![]() (5.83)
(5.83)
Графики распределения мгновенного значения напряжения вдоль линии для двух моментов времени построены по выражениям (5.80) и (5.81) с помощью программы Mathcad.
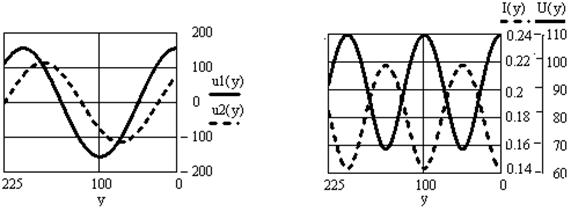
Рисунок 5.9 Рисунок 5.10
Графики распределения действующих значений напряжения и тока построены по выражениям (5.82) и (5.83) с помощью программы Mathcad. (см. рисунок 5.10).
6 Нелинейные электрические цепи постоянного тока
6.1 Основные теоретические сведения
Нелинейные резистивные электрические цепи – это цепи содержащие хотя бы один резистивный элемент, т.е. с нелинейной вольт-амперной характеристикой.
6.1.1 Статическое и дифференциальное сопротивления нелинейного элемента. Статическое сопротивление определяется по формуле (см.рисунок 6.1):
![]() (6.1)
(6.1)
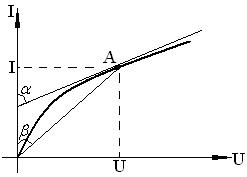
Рисунок 6.1
Дифференциальное сопротивление определяется по формуле (см. рисунок 6.1)
![]() (6.2)
(6.2)
1. Расчет нелинейных цепей постоянного тока. Простые нелинейные схемы постоянного тока рассчитывают графическим способом. При последовательном соединении нелинейных элементов (см.рисунок 6.2) существует два способа расчета.
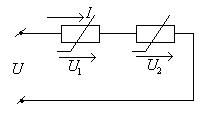
Рисунок 6.2
Первый
способ – метод сложения: напряжение на нелинейных элементах складываются ![]() при одном и том же
токе
при одном и том же
токе ![]() (см.
рисунок 6.3).
(см.
рисунок 6.3).
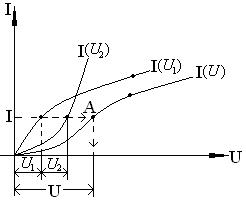
Рисунок 6.3
Второй способ – метод пересечения (см. рисунок 6.4):
- начало в.а.х. ![]() зеркально отражено и сдвинуто по оси
ординат на величину входного напряжения
зеркально отражено и сдвинуто по оси
ординат на величину входного напряжения ![]()
- точка пересечения кривой ![]() и в.а.х. первого элемента
является рабочей точкой А.
и в.а.х. первого элемента
является рабочей точкой А.
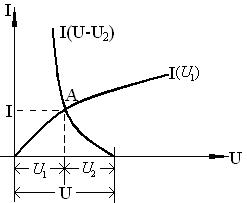
Рисунок 6.4
При параллельном соединении нелинейных элементов (см.
рисунок 6.5) токи через элементы складывают ![]() при одинаковом напряжение на них, А -
рабочая точка (см. рисунок 6.6).
при одинаковом напряжение на них, А -
рабочая точка (см. рисунок 6.6).
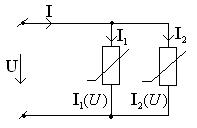
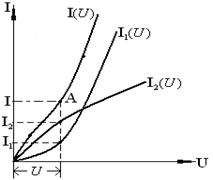
Рисунок 6.5 Рисунок 6.6
6.2 Примеры решение типовых задач
Задача 6.2.1 Цепь
(см. рисунок 6.1) состоит из последовательно включенных ЭДС ![]() линейного сопротивления
линейного сопротивления ![]() и участка АК (анод
– катод) электронного триода. Ток цепи (он же анодный ток триода)
и участка АК (анод
– катод) электронного триода. Ток цепи (он же анодный ток триода) ![]() образует между анодом и
катодом напряжение
образует между анодом и
катодом напряжение ![]() (анодное
напряжение). Между сеткой C и катодом K триода
включена ЭДС
(анодное
напряжение). Между сеткой C и катодом K триода
включена ЭДС ![]() при
которой вольт-амперная характеристика (зависимость анодного тока
при
которой вольт-амперная характеристика (зависимость анодного тока ![]() от анодного напряжения
от анодного напряжения ![]() ) определяется графиком
НЭ (см. рисунок 6.3). Требуется:
) определяется графиком
НЭ (см. рисунок 6.3). Требуется:
1) Определить ток ![]() напряжения
напряжения ![]() и
и ![]()
2) Заменить нелинейный элемент (триод) эквивалентным
линейным участком и определить ток цепи ![]() обеспечивающий напряжение
обеспечивающий напряжение ![]() в пределах 140-170В.
в пределах 140-170В.
Решение: Представим
схему замещения заданной цепи (см. рисунок 6.2), состоящую из последовательного
соединения линейного ![]() и
нелинейного НЭ сопротивлений. Вольт-амперная характеристика НЭ известна (см.
рисунок 6.3), а для линейного сопротивления
и
нелинейного НЭ сопротивлений. Вольт-амперная характеристика НЭ известна (см.
рисунок 6.3), а для линейного сопротивления ![]() ее легко построить (дальше будет
показано).
ее легко построить (дальше будет
показано).
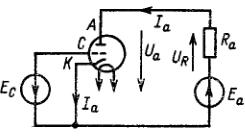
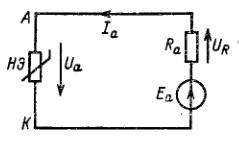
Рисунок 6.1 Рисунок 6.2
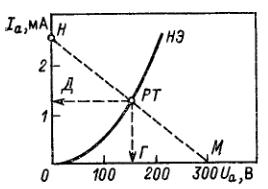
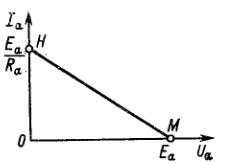
Рисунок 6.3 Рисунок 6.4
В данной цепи один из элементов является линейным сопротивлением. Такме цепи весьма распространены на практике, и их расчет представляет особый интерес. Кроме того существует простой метод расчета последовательного соединения линейного и нелинейного элементов. Он основан на построении так называемой нагрузочной характеристики.
Покажем этот метод на примере заданной цепи (см. рисунок 6.2), для которой
![]() (6.3)
(6.3)
откуда
![]() (6.4)
(6.4)
Обозначив
постоянные величины ![]() и
и ![]() получим уравнение прямой
получим уравнение прямой
![]() (6.5)
(6.5)
Оказывается,
имеем две зависимости для тока ![]() от напряжения
от напряжения ![]() одна задана графиком
НЭ (см. рисунок 6.3) и определяется только свойствами нелинейного элемента
(триода), другая – уравнением прямой (6.5) и выражает свойства цепи из
последовательно соединенных
одна задана графиком
НЭ (см. рисунок 6.3) и определяется только свойствами нелинейного элемента
(триода), другая – уравнением прямой (6.5) и выражает свойства цепи из
последовательно соединенных ![]() и НЭ. Поэтому совместное решение двух
указанных зависимостей позволит найти значения тока
и НЭ. Поэтому совместное решение двух
указанных зависимостей позволит найти значения тока ![]() и напряжения
и напряжения ![]() удовлетворяющие как
свойствам НЭ (триода), так и свойствам цепи (см. рисунок 6.2).
удовлетворяющие как
свойствам НЭ (триода), так и свойствам цепи (см. рисунок 6.2).
Требуемое решение обычно выполняется графически, так как одна из зависимостей уже задана графиком НЭ (см. рисунок 6.3). Чтобы построить другой график (прямую), выбираем две характерные точки:
а)
![]() или
или ![]() откуда
откуда
![]() т.е. имеем
точку М (см. рисунок 6.4) с координатами
т.е. имеем
точку М (см. рисунок 6.4) с координатами ![]()
![]()
б)
![]() или
или ![]() т.е. точку H
(см. рисунок 6.4) с координатами
т.е. точку H
(см. рисунок 6.4) с координатами ![]()
![]()
Искомую прямую, называемую нагрузочной характеристикой, можно построить по точкам ее пересечения с осями напряжения и тока точки М и H (см. рисунок 6.4).
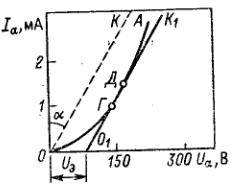
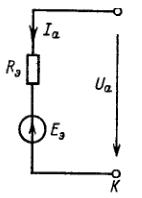
Рисунок 6.5 Рисунок 6.6
На
рисунке 6.3 в дополнение к графику НЭ построим другую зависимость ![]() от
от ![]() т.е. нагрузочную характеристику МH.
Ее точка М определяется напряжением
т.е. нагрузочную характеристику МH.
Ее точка М определяется напряжением ![]() а точка H –
значением
а точка H –
значением ![]()
![]()
Прямая МH пересекает характеристику нелинейного элемента в точке РТ (рабочая точка), которая и является графическим решением двух рассмотренных зависимостей. Иначе говоря, точка РТ определяет единственно возможный режим цепи (см. рисунок 6.2).
Этот режим определяется током ![]() - ордината ОД точки РТ
и напряжением
- ордината ОД точки РТ
и напряжением ![]() абсцисса
ОГ точки РТ (см. рисунок 6.2).
абсцисса
ОГ точки РТ (см. рисунок 6.2).
Напряжение на линейном сопротивлении
![]()
определяется отрезком МГ (см. рисунок 6.3).
Так как решение задачи найдено на основе пересечения вольт-амперной и нагрузочной характеристик, то использованный метод часто называют “методом пересечений”.
Затем заменим участок кривой ГД отрезком прямой ГД и найдем параметры последнего. В этих целях через точки Г и Д проведем прямую О1К1 и сместим ее в начало координат (прямая ОК).
Все точки прямой ОК (см. рисунок 6.5) имеют
одинаковое отношение ![]() поэтому
его можно найти для одной любой точки. Так, при
поэтому
его можно найти для одной любой точки. Так, при ![]() имеем
имеем ![]() и
и
![]() (6.6)
(6.6)
Следовательно, прямая ОК является
вольт-амперной характеристикой линейного сопротивления ![]()
Абсциссы соответствующих точек прямых ОК и О1К1
смещены на постоянное напряжение ![]() определяемое отрезком ОО1. Поэтому
если прямая ОК определяется уравнением
определяемое отрезком ОО1. Поэтому
если прямая ОК определяется уравнением ![]() то пряма О1К1
- уравнением
то пряма О1К1
- уравнением
![]()
или
![]() (6.7)
(6.7)
Последнему уравнению соответствует участок цепи АК (см. рисунок 6.6), который эквивалентен (в заданных условиях) участку АК (см. рисунок 6.2).
Определим ток ![]() в цепи для рисунка
6.2, если вместо НЭ включен участок АК по рисунку 6.6. При этом
в цепи для рисунка
6.2, если вместо НЭ включен участок АК по рисунку 6.6. При этом
![]() (6.8)
(6.8)
т.е.
результат очень близок к ранее найденному ![]() Погрешность менее 2% является весьма малой
при графических расчетах.
Погрешность менее 2% является весьма малой
при графических расчетах.
Итак, если нелинейный элемент работает на небольшом участке своей вольт-амперной характеристики и этот участок с известным приближением может быть заменен прямой линией, то НЭ может быть представлен на схеме замещения эквивалентными сопротивлением и ЭДС.
Эту
задачу можно решить методом сложения характеристик триода и сопротивления ![]() На рисунке 6.7
построены вольт-амперная характеристика триода1 (перенесена с рисунка 6.3
кривая НЭ) и прямая 2, являющаяся характеристикой линейного
сопротивления
На рисунке 6.7
построены вольт-амперная характеристика триода1 (перенесена с рисунка 6.3
кривая НЭ) и прямая 2, являющаяся характеристикой линейного
сопротивления ![]() Эта
прямая построены по уравнению
Эта
прямая построены по уравнению ![]() метод показанном выше при анализе прямой ОК
(см. рисунок 6.5).
метод показанном выше при анализе прямой ОК
(см. рисунок 6.5).
Сложением
абсцисс соответствующих точек кривой 1 и прямой 2 получена кривая 3 (см.
рисунок 6.7), являющаяся результирующей вольт-амперной характеристикой
соединения НЭ и ![]() (см. рисунок 6.2).
(см. рисунок 6.2).
Воспользуемся
кривой 3 (см. рисунок 6.7) и определим при ![]() ток
ток ![]() который был уже ранее найден для
рассматриваемой цепи (см. рисунок 6.2).
который был уже ранее найден для
рассматриваемой цепи (см. рисунок 6.2).
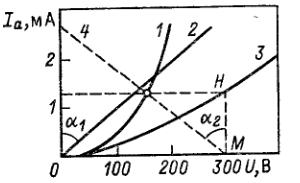
Рисунок 6.7
Задача
6.2.2 В цепь (см. рисунок 6.8) с номинальным током ![]() включены соединенные
параллельно нелинейный элемент (бареттер) с вольт-амперной характеристикой
включены соединенные
параллельно нелинейный элемент (бареттер) с вольт-амперной характеристикой ![]() (см. рисунок 6.9) и
линейное сопротивление
(см. рисунок 6.9) и
линейное сопротивление ![]() Определить прнеделы изменения напряжения на бареттере при колебаниях
общего тока цепи
Определить прнеделы изменения напряжения на бареттере при колебаниях
общего тока цепи ![]() на
на
![]() % номинального значения.
% номинального значения.

Рисунок 6.8
Решение: 1) Построение суммарной вольт-амперной характеристики.
При параллельном соединении, очевидно, можно получить
общую вольт-амперную характеристику по условию равенства общего тока и суммы
токов ветвей, т.е. в нашем случае ![]() (см. рисунок 6.9).
(см. рисунок 6.9).
Построим сначала вольт-амперную характеристику
сопротивления ![]() проведя
прямую
проведя
прямую ![]() из
начала координат (см. рисунок 6.9), например через точку
из
начала координат (см. рисунок 6.9), например через точку ![]() с координатами
с координатами ![]() и
и ![]()
Общая вольт-амперная характеристика ![]() на рисунке 6.9
получена сложением ординат (токов) кривых
на рисунке 6.9
получена сложением ординат (токов) кривых ![]() и
и ![]() при одинаковых абсциссах (напряжениях).
при одинаковых абсциссах (напряжениях).
Например, при напряжении ![]() точка
точка ![]() (см. рисунок 6.9) получена сложением
ординат точки
(см. рисунок 6.9) получена сложением
ординат точки ![]() и
точка
и
точка ![]()
![]() Аналогичным образом
построены точки
Аналогичным образом
построены точки ![]() и
и
![]()
2) Определение пределов изменения напряжения на
бареттере. Ток цепи изменяется (по условию задачи) от значения ![]() до
до ![]() или на
или на ![]() Обозначив на рисунке
6.9
Обозначив на рисунке
6.9 ![]() и
и ![]() найдем, используя
характеристику
найдем, используя
характеристику ![]() пределы
изменения напряжения
пределы
изменения напряжения ![]()
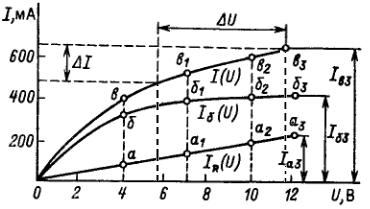
Рисунок 6.9
Список литературы
1. Белецкий А.Ф. Теория линейных электрических цепей. - М.: Радио и связь, 1986. – 544 с.
2. Матханов П.Н. Основы анализа электрических цепей. Линейные цепи.-М.: Высшая школа,1981. – 333 с.
3. Основы теории цепей. Учебник для вузов /Г.В.Зевеке и др.- М.: Энергоиздат, 1989. – 528 с.
4. Теория линейных электрических цепей. /Под редакцией И.Г.Кляцкина.-М.: Высшая школа, 1975.
5. Зернов И.В., Карпов В.Г. Теория радиотехнических цепей.-Л.: Энергия, 1972.
6. Шебес М.Р., Каблукова М.В. Задачник теории линейных электрических цепей: Учебное пособие для вузов.-М.: ВШ, 1990.-544 с.
7. Основы теории цепей: Учебник для вузов / В.П.Бакалов и др. -М.: 2000. - 592с.
8. Попов В.П. Основы теории цепей: Учебник для вузов. - М.: 2000. -576 с.
Содержание
|
|
Введение |
3 |
|
1 |
Классический метод расчета переходных процессов |
4 |
|
2 |
Операторный метод расчета переходных процессов |
24 |
|
3 |
Интеграл Дюамеля |
36 |
|
4 |
Спектральный метод анализа электрических цепей |
46 |
|
5 |
Расчет цепей с распределенными параметрами |
56 |
|
6 |
Нелинейные электрические цепи постоянного тока |
69 |
Список литературы 76