АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра теоретических основ электротехники

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ 1

Конспект лекций

(для бакалавриата специальности 050718 – Электроэнергетика)

Алматы 2006

СОСТАВИТЕЛИ: В.И. Денисенко, С.Ю. Креслина. Теоретические основы электротехники 1. Конспект лекций (для студентов всех форм обучения специальности 050718 – Электроэнергетика). – Алматы: АИЭС, 2006.- 63 с.

Конспект лекции содержит 13 лекций по 2 разделам: линейные электрические цепи постоянного тока и электрические цепи однофазного синусоидального тока.

Конспект лекций предназначен для студентов специальности 050718-Электроэнергетика.

Ил.48, библиограф.-5 назв.

Рецензент: канд. техн. наук, профессор кафедры ЭАПУ М.А.Мустафин

Печатается по плану издания Алматинского института энергетики и связи на 2006г.

Ó Алматинский институт энергетики и связи, 2006г.

Содержание

Введение…………………………………………...…………………………..….4

1 Лекция 1………………….………………………...…………………………....5

2 Лекция 2……………………………………………………………………....…9

3 Лекция 3………………………………………………………………………...12

4 Лекция 4……………………………………………………………………...…20

5Лекция 5………………………………………………………………………....22

6 Лекция 6………………………………………………………………………...27

7 Лекция 7…………………………………………………………………….......32

8 Лекция 8……………………………………………………………………...…37

9 Лекция 9…………………………………………………………………….......42

10 Лекция 10………………………………………………………………….......47

11 Лекция 11…………………………………………………………………..….51

12 Лекция 12……………………………………………………………………...54

13 Лекция 13………………………………………………………………….......58

Список литературы……………………………………………………………...63

Введение

Дисциплина «Теоретические основы электротехники1» является основным базовым обязательным курсом для подготовки бакалавров в области электроэнергетики. Назначение дисциплины заключается в изучении и описании как с качественной, так и с количественной стороны электромагнитных процессов и явлений, происходящих в различного рода электротехнических установках, представленных эквивалентными схемами замещения с помощью основных элементов электрических цепей.

Предлагаемый конспект лекций включает два основных раздела: линейные электрические цепи постоянного тока и электрические цепи однофазного синусоидального тока. В первом разделе рассмотрены основные свойства линейных электрических цепей постоянного тока, и на их примере произведено теоретическое обоснование и показано применение основных методов анализа и расчета электрических цепей, таких, как метод преобразований, метод законов Кирхгофа, метод контурных токов, метод узловых потенциалов, метод суперпозиции, метод активного двухполюсника.

Во втором разделе рассмотрены особенности описания цепей при синусоидальных токах и напряжениях, показано применение метода комплексных амплитуд с использованием векторных и топографических диаграмм для анализа цепей синусоидального тока, представлены энергетические соотношения в цепи синусоидального тока, рассмотрено явление фазового резонанса в последовательной и параллельной цепях, показан расчет цепей при наличии взаимной индуктивности.

Конспект лекций предназначен для студентов, обучающихся в бакалавриате по специальности 050718 – Электроэнергетика.

Линейные электрические цепи постоянного тока

1Лекция 1. Элементы электрических цепей и электрических схем, эквивалентные схемы для источников энергии, закон Ома для участка цепи с э.д.с.

Цель лекции: познакомить с основными понятиями электрических цепей при постоянных токах и напряжениях.

1.1 Элементы электрических цепей и электрических схем

Электрической цепью называется совокупность устройств, предназначенных для передачи, распределения и взаимного преобразования электрической и других видов энергии, если процессы, протекающие в устройствах, могут быть описаны при помощи понятий об электродвижущей силе (эдс), токе и напряжении. Основными элементами электрической цепи являются источники и приемники электрической энергии, которые соединяются между собой проводами.

В источниках электрической энергии (гальванические элементы, аккумуляторы, электромашинные генераторы и т.п.) химическая, механическая, тепловая энергия или энергия других видов превращается в электрическую, а в приемниках электрической энергии (электрические лампы, резисторы, электрические двигатели и т.п.), наоборот, электрическая энергия преобразуется в тепловую, световую, механическую и др. Электрические цепи, в которых получение электрической энергии в источниках, ее передача и преобразование в приемниках происходят при неизменных во времени токах и напряжениях, называют цепями постоянного тока.

Чтобы облегчить изучение процессов в электрической цепи, ее заменяют расчетной схемой замещения, т.е. идеализированной цепью, которая служит расчетной моделью реальной цепи. При этом пользуются понятиями двух основных элементов схемы: источника энергии с э.д.с. и внутренним сопротивлением и сопротивления приемников и проводов (рисунок1.1).

Электродвижущая сила Е (рисунок1.1) численно равна разности потенциалов или напряжению между положительным и отрицательным зажимами 1 и 2 источника энергии при отсутствии в нем тока.

Рисунок 1.1

(1.1)

Направление действия эдс (от отрицательного зажима к положительному) указывается на схеме стрелкой.

Если к зажимам источника энергии присоединить приемник (нагрузить), то в замкнутом контуре этой простейшей цепи возникает ток . При этом напряжение или разность потенциалов на зажимах 1 и 2 уже не будет равна эдс вследствие падения напряжения

внутри источника энергии, т.е. на его внутреннем сопротивлении.

На рисунке 1.2 представлена внешняя характеристика, т.е. зависимость напряжения на зажимах нагруженного источника энергии от тока. Развиваемая источником энергии мощность определяется равенством

(1.2)

Сопротивление приемника (рисунок 1.2) идеализированной цепи характеризует потребление электрической энергии, т.е. превращение электрической энергии в другие виды при мощности

(1.3)

По закону Ома напряжение на сопротивлении

. (1.4)

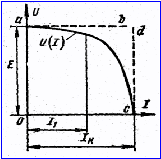
Рисунок 1.2

Наряду с сопротивлением для расчета цепей вводят понятие проводимости .

Если принять э.д.с. источников энергии, их внутренние сопротивления и сопротивления приемников не зависящими от токов и напряжений, то внешние характеристики источников энергии и вольт – амперные характеристики источников будут линейными (рисунок 1.2). Электрические цепи, состоящие только из элементов с линейными характеристиками, называют линейными.

1.2 Эквивалентные схемы для источников энергии

Простейшая электрическая цепь и ее схема замещения состоят из одного источника энергии с э.д.с. и внутренним сопротивлением и одного приемника с сопротивлением (рисунок 1.3), где сопротивление соединяющих проводов не показано, если для этой цепи им можно пренебречь. Ток во внешней по отношению к источнику энергии части цепи, т.е. в приемнике или сопротивлении , принимается направленным от точки с большим потенциалом к точке с меньшим потенциалом .Покажем, что источник энергии с известными э.д.с. и внутренним сопротивлением может быть представлен двумя основными эквивалентными схемами.

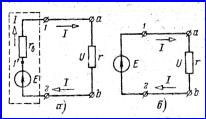
Рисунок 1.3

Как уже указывалось, напряжение на зажимах источника энергии меньше э.д.с, на падение напряжения внутри источника

. (1.5)

С другой стороны, напряжение на сопротивлении

. (1.6)

Ввиду равенства и , из (1.5) и (1.6) следует, что или

(1.7)

(1.7а)

На эквивалентной схеме можно показать внутреннее сопротивление соединенным последовательно с сопротивлением приемника .в зависимости от соотношения между напряжениями на этих сопротивлениях получим две разновидности первой эквивалентной схемы для источника энергии (рисунок 1.3).

На эквивалентной схеме рисунка 1.4, с источником э.д.с, напряжение зависит от тока приемника и равно разности между э.д.с. источника энергии и падением напряжения . Источник энергии может быть представлен и одной из двух эквивалентных схем по рисунку 1.4. Чтобы обосновать эту возможность, разделим правую и левую части уравнения (1.7) на .

В результате получим

, (1.8)

где - ток при коротком замыкании источника энергии

(т.е. ток при сопротивлении );

- некоторый ток, равный отношению напряжения на зажимах источника энергии к его внутреннему сопротивлению;

- ток приемника;

- проводимость приемника.

Полученному уравнению (1.8) удовлетворяет эквивалентная схема с источником тока (рисунок 1.4,а), при этом внутреннее сопротивление включено параллельно сопротивлению приемника .

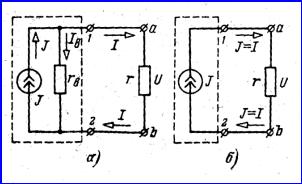
Рисунок 1.4

Такой источник с внутренней проводимостью , обозначенный кружком с двойной стрелкой с разрывом внутри и буквой , называют идеальным источником тока (источником с заданным током). Ток источника тока не зависит от сопротивления приемника .

Источники э.д.с и источники тока называют активными элементами электрических схем, а сопротивления и проводимости - пассивными.

1.3 Закон Ома для участка цепи с э.д.с.

Для однозначного определения потенциала любой точки электрической цепи необходимо произвольно выбрать потенциал какой – нибудь одной точки.

Ток во внешней части простейшей электрической цепи, а в общем случае в любом пассивном элементе цепи направлен от точки с более высоким потенциалом () к точке с более низким ().

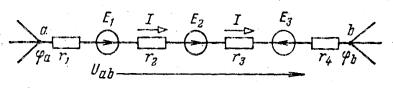
Рисунок 1.5

Если принять за положительное направление тока на участке направление от точки к точке , то потенциал определяется через потенциал выражением

. (1.9)

Из этого равенства следует

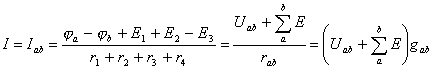, (1.10)

где - суммарное сопротивление участка схемы;

- разность потенциалов или напряжение между зажимами рассматриваемого участка, взятые по выбранному направлению тока;

- алгебраическая сумма э.д.с., действующих на том же участке, причем каждая э.д.с., совпадающая по направлению с положительным направлением тока, записывается с положительным знаком, а не совпадающая - с отрицательным.

Формула (1.10) представляет собой закон Ома для участка цепи с э.д.с.

2Лекция 2. Распределение потенциала вдоль неразветвленной электрической цепи, применение законов Кирхгофа для расчета разветвленных цепей.

Цель лекции: познакомить с основными понятиями электрических цепей при постоянных токах и напряжениях.

2.1 Распределение потенциала вдоль неразветвленной электрической цепи

Распределение потенциала вдоль неразветвленной электрической цепи можно наглядно представить при помощи графика, который называют потенциальной диаграммой.

На рисунке 2.1 изображена схема простейшей неразветвленной цепи с двумя э.д.с. и и внутренними сопротивлениями и и двумя сопротивлениями и .Пусть э.д.с. больше э.д.с. .

Действительный ток и совпадает по направлению с э.д.с. . Для однозначного определения потенциала каждой точки рассматриваемой цепи можно положить, например, потенциал точки , равный нулю (заземление на рисунке 2.1). Теперь легко найти потенциалы остальных точек.

. (2.1)

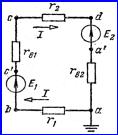
Рисунок 2.1

Потенциал точки меньше потенциала точки

При переходе через первый источник энергии потенциал повышается на значение э.д.с. и понижается на внутреннее падение напряжения, так что потенциал точки

Для определения потенциала точки надо из потенциала вычесть падение напряжения , т.е.

Наконец, при переходе через второй источник энергии потенциал понижается не только на значение э.д.с. (по определению понятия э.д.с. ), но и на внутреннее падение напряжения, причем потенциал точки должен быть равен нулю

Если по оси абсцисс отложить в выбранном масштабе сопротивления участков в той последовательности, в которой они включены в цепь, а по оси ординат - потенциалы соответствующих точек (рисунок 2.2), то получится график распределения потенциала вдоль неразветвленной цепи. Пользуясь этим графиком, можно определить напряжение между любыми точками цепи.

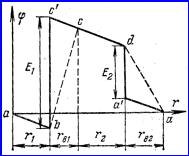
Рисунок 2.2

Отношение напряжения к сопротивлению любого пассивного участка цепи равно току участка и на графике потенциала определяется в некотором масштабе тангенсом угла наклона соответствующей прямой к оси абсцисс. Поэтому одинаков наклон прямых (например, и на рисунке 2.2), определяющих изменение потенциала вдоль всех пассивных участков неразветвленной цепи с одним и тем же током.

2.2 Применение законов Кирхгофа для расчета разветвленных цепей

Ветвью электрической цепи называется такой ее участок, который состоит только из последовательно включенных источников э.д.с. и сопротивлений и вдоль которого протекает один и тот же ток. Узлом электрической цепи называется место (точка) соединения трех и более ветвей.

При обходе по соединенным в узлах ветвям можно получить замкнутый контур электрической цепи; каждый контур представляет собой замкнутый путь, проходящий по нескольким ветвям; при этом каждый узел в рассматриваемом контуре встречается не более одного раза.

На рисунке 2.3 в качестве примера показана электрическая цепь с пятью узлами и девятью ветвями. В частных случаях встречаются ветви только с сопротивлениями без э.д.с. (ветвь ) и с сопротивлениями, практически равными нулю (ветвь ). Так как напряжение на зажимах ветви равно нулю (сопротивление равно нулю), то потенциалы точек и одинаковы и оба узла можно объединить в один.

Режим электрической цепи произвольной конфигурации полностью определяется первым и вторым законами Кирхгофа.

Первый закон Кирхгофа применяется к узлам и формулируется следующим образом: алгебраическая сумма токов в узле равна нулю, т.е.

. (2.2)

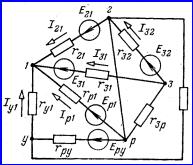
Рисунок 2.3

в этом уравнении одинаковые знаки должны быть взяты для токов, имеющих одинаковые положительные направления относительно узловой точки.

Если к данному узлу присоединен источник тока, то ток этого источника также должен быть учтен. В ряде случаев целесообразно писать одной части равенства (2.2) алгебраическую сумму токов в ветвях, а в другой части – алгебраическую сумму токов, обусловленных источниками токов

, (2.3)

где I – ток одной из ветвей, присоединенной к рассматриваемому узлу, а J – ток одного из источников тока, присоединенного к тому же самому узлу; этот ток входит в уравнение (2.3) с положительным знаком, если направлен к узлу, с отрицательным, если направлен от узла.

Второй закон Кирхгофа применяется к контурам электрической цепи и формулируется следующим образом: в любом замкнутом контуре алгебраическая сумма напряжений на сопротивлениях, входящих в этот контур, равна алгебраической сумме э.д.с., т. е.

. (2.4)

В этом уравнении положительные знаки принимаются для токов и э.д.с., положительные направления которых совпадают с произвольно выбранным направлением обхода рассматриваемого контура.

Часто применяется другая формулировка второго закона Кирхгофа: в любом контуре алгебраическая сумма напряжений на зажимах ветвей, входящих в этот контур, равна нулю

. (2.5)

При этом положительные направления для напряжений на зажимах ветвей выбираются произвольно; в уравнении (2.5) положительные знаки принимаются для тех напряжений, положительные направления которых совпадают с произвольно выбранным направлением обхода контура.

3 Лекция 3. Метод контурных токов, метод узловых потенциалов.

Цель лекции: познакомить с основными методами расчета электрических цепей при постоянных токах и напряжениях.

3.1 Метод контурных токов

Для расчета режима сложной электрической цепи можно ограничиться совместным решением лишь независимых уравнений, составленных на основании второго закона Кирхгофа, воспользовавшись методом контурных токов; здесь - число ветвей и - число узлов. При этом первый закон Кирхгофа, конечно, всегда удовлетворяется.

Для иллюстрации применения метода контурных токов рассмотрим схему на рисунке 3.1,а. Прежде чем составлять уравнения по второму закону Кирхгофа (рисунок 3.1), надо выбрать взаимно независимые контуры так, чтобы одна из ветвей каждого контура входила только в этот контур. Например, в схеме рисунка 3.1,а первая, вторая и третья ветви входят соответственно только в контуры 1-2-4-1, 2-3-4-2 и 1-4-3-1.

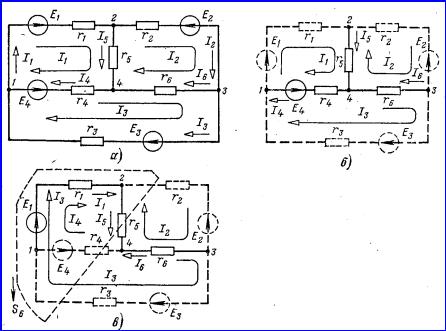
Рисунок 3.1

Для схемы рисунка 3.1,а по первому закону Кирхгофа

(3.1)

На основании второго закона Кирхгофа

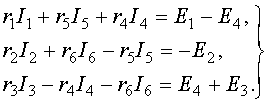(3.2)

Пользуясь уравнениями (3.1), исключим из уравнений (3.2) токи и всех ветвей дерева, общих для нескольких контуров;

в результате получим: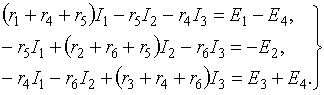 (3.3)

В соответствии с уравнениями (3.3) можно принять, что каждый из токов и замыкается через соответствующую ветвь связи в одном из контуров (рисунок 3.1 а и б) и назвать такие токи контурными. Напряжения на сопротивлениях любого контура равны алгебраической сумме напряжений, обусловленных токами своего и смежных контуров. Например, в контуре из сопротивлений и разность э.д.с. равняется сумме трех напряжений: от собственного контурного тока на всех сопротивлениях этого контура и от токов и соответственно на сопротивлениях и . Действительные токи в ветвях, общих для нескольких контуров, равны алгебраическим суммам контурных токов

, , . (3.4)

В этих уравнениях сопротивление вида (с двумя одинаковыми индексами) называется собственным сопротивлением контура , а сопротивление вида (с двумя различными индексами) называется общим сопротивлением контуров и . Правые части уравнений (3.5) называются контурными э.д.с. Каждая из контурных э.д.с. вида равна алгебраической сумме э.д.с, всех источников в ветвях контура . Положительные знаки в каждом уравнении (3.5) должны быть взяты для токов и э.д.с., положительные направления которых совпадают с произвольно выбранным направлением обхода соответствующего контура.

В более общем случае, когда электрическая цепь содержит как источники э.д.с., так и источники тока, контурное уравнение для его контура записывается в виде

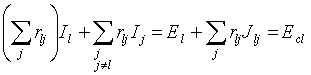, (3.5)

где 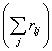обозначает собственное сопротивление контура ;

- общее сопротивление двух контуров и ;

- ток источника тока, замыкающийся по сопротивлению .

3.2 Метод узловых потенциалов

Режим любой цепи полностью характеризуется уравнениями, составленными на основании первого и второго законов Кирхгофа, причем для определения токов во всех ветвях необходимо составить и решить систему уравнений .

Число уравнений, подлежащих решению, можно сократить, если пользоваться методом узловых потенциалов, основанным на применении первого закона Кирхгофа и закона Ома.

Для выяснения сущности этого метода рассмотрим, например, электрическую схему, показанную на рисунке 3.2.

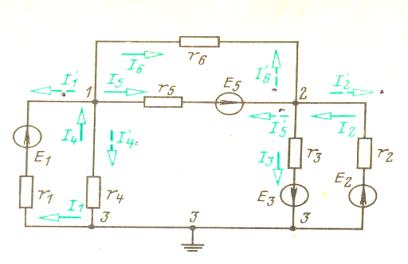
Рисунок 3.2

Пусть потенциал одного из узлов, например узла 3, принят равным нулю, т.е.. Такое допущение не изменяет условий задачи, так как ток в каждой ветви зависит не от абсолютных значений потенциалов узлов, к которым присоединена ветвь, а от разности потенциалов между концами ветви.

Запишем уравнения на основании первого закона Кирхгофа для узлов 1 и 2 этой схемы при выбранных положительных направлениях токов

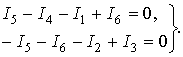(3.6)

Токи в ветвях согласно закону Ома

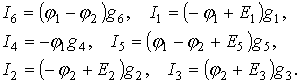(3.7)

где - потенциалы узлов 1 и 2.

После подстановки (3.7) в (3.6) и группировки членов получим

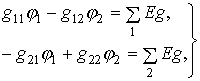. (3.8)

В этих уравнениях - суммы проводимостей ветвей, присоединенных соответственно к узлам 1 и 2; - сумма проводимостей ветвей, соединяющих эти узлы.

Правая часть каждого из уравнений (3.8) равна алгебраической сумме произведений ЭДС в каждой ветви на проводимость ветви, присоединенной к рассматриваемому узлу. Произведение вида Eg записывается с положительным знаком в том случае, если ЭДС направлена к узлу, для которого записывается уравнение, и с отрицательным, если ЭДС направлена от узла.

Уравнения (3.8) не зависят от выбранных положительных направлений токов в ветвях.

Таким образом, можно написать уравнения для определения потенциалов узлов произвольной электрической цепи, не задаваясь положительными направлениями токов в ветвях, при этом потенциал одного из узлов надо принять равным нулю.

Если электрическая схема содержит не только источники ЭДС, но и источники тока, то в уравнения, составленные по первому закону Кирхгофа, войдут и токи источников тока. При составлении уравнений токи заданных источников тока учитываются для каждого узла в виде слагаемых в правой части, причем, как было отмечено выше, с положительными знаками должны быть взяты токи источников тока, направленные к узлу, с отрицательными – от узла.

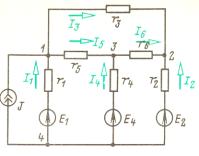
Рисунок 3.3

Например, для узлов 1, 2 и 3, показанной на рисунке 3.3, при получим соответственно следующие уравнения

где

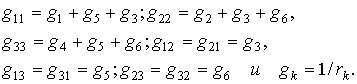
источников тока. При составЛI уравнений вида (1.30) токи зада~ источников тока учитываются для

дого узла в виде слагаемых в пр; части, причем, как было отмечено ВI с положительными знаками должны ( взяты токи источников тока, нап ленные к узлу, с отрицательными

узла.

Например, для узлов 1, 2 и 3 СХI показанной на рис. 1.17, при <Р4 = О лучим соответственно следующие )' нения:

Если электрическая схема имеет в своем составе У узлов (У - любое целое число), а потенциал, например, У-го узла принят равным нулю, то для определения У - 1 потенциалов У остальных у получается - 1 уравнений

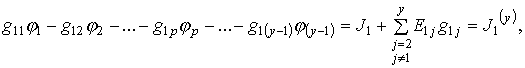
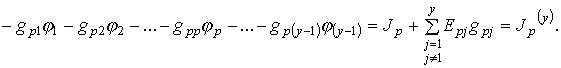(3.9)

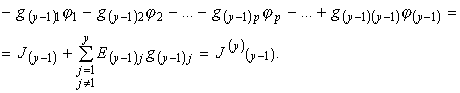
Или более в общей форме для любого узла р при

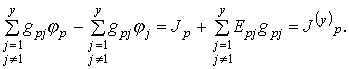(3.10)

В этих уравнениях так же, как и в уравнениях (3.8), проводимость

(с двумя одинаковыми индексами) представляет собой суммарную проводимость ветвей, присоединенных к узлу р, и называется собственной узловой проводимостью этого узла; проводимость с двумя различными индексами равна сумме проводимостей ветвей, соединяющих между собой рассматриваемые узлы j и р, и называется общей узловой проводимостью этих узлов. Правая часть каждого из уравнений содержит алгебраические суммы произведений эдс на соответствующие проводимости для всех ветвей, присоединенных к узлу р, ток J р равен алгебраической сумме токов всех источников тока, присоединенных к тому же узлу. В свою очередь ток - узловой ток - равен алгебраической сумме и токов, определяемых источниками эдс, которые присоединены к узлу р, при этом следует иметь в виду, что для замкнутых поверхностей сумма всех узловых токов, как это

вытекает из первого закона Кирхгофа, равна нулю. К узловым токам можно отнести и уже известные в каких-либо ветвях токи. Проводимости таких ветвей в выражения вида и не входят.

Решив уравнения (3.10), можно определить потенциалы узлов, а зная потенциалы, найти токи во всех ветвях по закону Ома.

Если в цепи имеются ветви с идеальными источниками эдс и сопротивлениями этих ветвей можно пренебречь, то при составлении уравнений (3.10) получается неопределенность, поскольку проводимости таких ветвей бесконечно большие. Такое затруднение преодолевается путем переноса заданной эдс из ветви с нулевым сопротивлением через соответствующий узел в другие ветви, присоединенные к тому же узлу и имеющие конечные значения сопротивлений. В результате такого преобразования токи во всех ветвях заданной схемы не изменяются.

Для иллюстрации рассмотрим схему (рисунок 3.4), у которой сопротивление ветви 2-4 равно нулю, а эдс равна Е. Если в каждую ветвь, присоединенную, например, к узлу 2, включить источник напряжения с эдс, равной Е и направленной от узла 2 (на рисунке 3.4, а эти эдс изображены штриховой линией), то токи во всех ветвях останутся без изменения, поскольку разности потенциалов между точками 1', 3', 4' будут так же, как и в заданной схеме, равны нулю. Теперь потенциалы узлов 2 и 4, очевидно, одинаковы и их можно объединить в одну точку (рисунок 3.4,б). Для полученной схемы с тремя узлами (вместо четырех) можно составить два независимых уравнения вида (3.10), из которых определяются искомые потенциалы двух узлов, а затем по закону Ома токи во всех ветвях схемы, после чего легко найти ток в ветви с сопротивлением r = О (рисунок 3.4,а) по первому закону Кирхгофа.

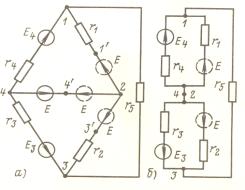
Рисунок 3.4

Рассмотренную и аналогичные ей задачи можно решить и без предварительного переноса эдс через узел в другие ветви. Действительно, если принять в заданной схеме (рисунок 3.4, а) , то потенциал узла 2, очевидно, будет равен Е. Для определения двух неизвестных потенциалов нужно составить уравнения (3.10), которые полностью совпадут с уравнениями, составленными для тех же узлов эквивалентной схемы (рисунок 3.4,б).

Рассмотрим применение уравнений (3.9) для частного случая схемы с двумя узлами и произвольным числом ветвей, все или часть которых содержат источники эдс. Требуется определить напряжение между этими узлами.

Пусть между узлами 1 и 2 включено m ветвей (рисунок 3.5). Найдем напряжение , записав уравнение (3.9) для первого узла

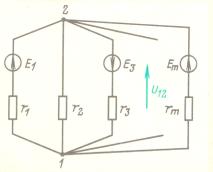
Рисунок 3.5

откуда

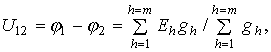(3.11)

где числитель представляет собой алгебраическую сумму произведений эдс на проводимость для всех ветвей, содержащих эдс (с положительным знаком записываются эдс, направленные к узлу 1), а знаменатель - арифметическую сумму проводимостей всех ветвей, включенных между узлами.

Если между узлами 1 и 2 включены еще источники тока, то их значения следует добавить в числитель (3.11), причем со знаком плюс записываются токи, направленные к узлу 1.

Если преобразуется часть электрической схемы, не содержащая источников энергии, то, как будет видно из дальнейшего, неизменность токов и напряжений в остальной части схемы обеспечивает и неизменность мощностей, потребляемых ветвями. В случае преобразования электрических схем, содержащих источники энергии, суммарные мощности источников и приемников в исходной схеме не равны в общем случае соответствующим мощностям в эквивалентной схеме.

4 Лекция 4. Преобразование линейных электрических схем

Цель лекции: познакомить с основными преобразованиями линейных электрических цепей.

4.1 Преобразование линейных электрических схем

Расчет и исследование сложных электрических цепей во многих случаях можно значительно облегчить и сделать более наглядными путем преобразования электрических схем одного вида в схемы другого вида. Целесообразное преобразование электрической схемы приводит к уменьшению числа ее ветвей или узлов, а следовательно, и числа уравнений, определяющих ее электрическое состояние.

Во всех случаях замены заданных электрических схем эквивалентными схемами другого вида необходимо выполнять условия неизменности токов и напряжений в тех частях схемы, которые не затронуты преобразованиями.

Для того чтобы схема, показанная на рисунке 4.1 ,б, была эквивалентна схеме рисунке 4.1,а, необходимо равенство токов (, , и т.д.) в обеих схемах при одинаковых напряжениях (, , и т.д.), что выполняется при

(4.1)

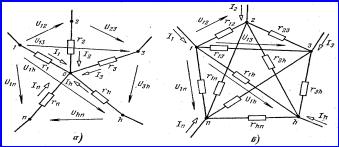
Рисунок 4.1

Из формул (4.1) при n = 3 сразу получаются формулы для преобразования трехлучевой звезды в эквивалентный треугольник в следующем виде:

для эквивалентных проводимостей

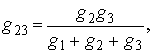
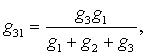(4.2)

или для эквивалентных сопротивлений

(4.3)

формулы (4.2) позволяют определить эквивалентные сопротивления звезды по заданным сопротивлениям треугольника.

, (4.4)

где

Если сложная электрическая схема имеет одну или несколько групп, параллельно соединенных ветвей с источниками э.д.с, то расчет и исследование такой схемы можно значительно облегчить, заменив каждую группу параллельных ветвей одним источником с эквивалентной э.д.с, и эквивалентным внутренним сопротивлением. На рисунке 4.2,а показана группа из m параллельно

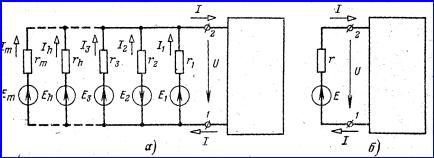
соединенных ветвей, выделенная в электрической схеме. Остальная часть схемы условно обозначена прямоугольником. Требуется заменить m параллельных ветвей (рисунке 4.2,а) одной эквивалентной ветвью (рисунок 4.2,б) так, чтобы ток и напряжение в эквивалентной схеме и все токи и напряжения в остальной части схемы были такими же, как в заданной.

Рисунок 4.2

Для токов ветвей и суммарного тока схемы (рисунок 4.2,а) справедливо следующее выражение

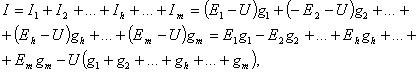(4.5)

где .

В схеме рисунка 4.2,б ток

(4.6)

где

Так как условия эквивалентности должны быть выполнены при любых токе и напряжении , то, приравнивая правые части выражений (4.5) и (4.6), нужно положить

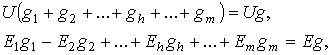
откуда

(4.7)

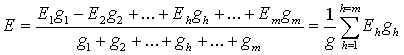. (4.8)

При вычислении эквивалентной э.д.с. с положительным знаком записываются те э.д.с. , которые направлены к тому же узлу, что и эквивалентная э.д.с. , и с отрицательным знаком - направленные к другому узлу. Если какая-либо из параллельных ветвей, например третья, не содержит источника э.д.с. , то в выражении (4.8) слагаемого не будет, но в состав проводимости входит проводимость этой ветви .

Из выражения (4.7) следует, что эквивалентная проводимость не зависит от э.д.с., в то время как эквивалентная э.д.с. (4.8) зависит не только от э.д.с, ветвей, но и от их проводимостей.

Если к узлам 1 и 2 (рисунок 4.2,а) присоединены, кроме m ветвей с источниками э.д.с, еще n ветвей с источниками тока, то при вычислении эквивалентной э.д.с. (4.8) нужно учесть токи заданных источников тока

(4.9)

причем с положительным знаком берутся токи, направленные к тому же узлу, что и эквивалентная э.д.с. , а с отрицательным знаком - направленные к другому узлу.

5 Лекция 5. Принцип наложения, свойство взаимности, входные и взаимные проводимости и сопротивления ветвей; коэффициенты передачи напряжений и токов, теорема о компенсации

Цель лекции: познакомить с основными свойствами электрических цепей при постоянных токах и напряжениях.

5.1 Принцип наложения

Каждая э.д.с. в уравнении (3.5) представляет собой алгебраическую сумму э.д.с. во всех ветвях контура . Если в уравнении (3.5) заменить все контурные э.д.с. алгебраическими суммами э.д.с. ветвей, то получится выражение для контурного тока в виде алгебраической суммы составляющих токов, вызванных каждой из э.д.с ветвей в отдельности.

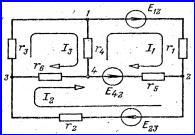
Рисунок 5.1

Это чрезвычайно важное свойство носит название принципа наложения и непосредственно следует из линейности уравнений для цепей с линейными элементами.

В качестве примера, иллюстрирующего принцип наложения, рассмотрим электрическую схему, показанную на рисунке 5.1, для которой, пользуясь методом контурных токов, запишем следующие уравнения

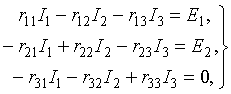(5.1)

где

Из уравнений (5.1) вытекает

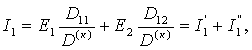(5.2)

где

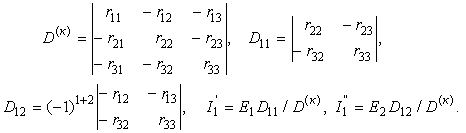
Аналогично определяются токи и .

Если в выражении (5.2) контурные э.д.с. заменить через э.д.с. ветвей, то получим

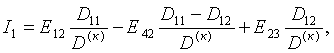(5.3)

откуда и следует, что ток равен алгебраической сумме составляющих токов, вызываемых каждой из э.д.с. в отдельности. Таким образом, при определении токов ветвей при помощи принципа наложения можно поочередно оставлять в схеме по одной э.д.с., считая все остальные э.д.с. источников равными нулю, но сохраняя в схеме их внутренние сопротивления. Действительные токи ветвей определятся как алгебраические суммы токов, вызываемых каждой э.д.с. Если схема содержит не только источники э.д.с., но и источники тока, то следует найти составляющие токов, вызываемые каждой э.д.с. и каждым источником тока, после чего определить действительные токи ветвей путем алгебраического суммирования этих составляющих.

5.2 Свойство взаимности

Пользуясь методом контурных токов, установим еще одно важное свойство линейных электрических цепей - свойство взаимности или как его иногда называют, принцип взаимности.

Сущность этого свойства заключается в следующем. Пусть в схеме произвольной конфигурации единственный источник э.д.с. действует в ветви с сопротивлением в направлении от точки

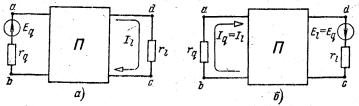
Рисунок 5.2

к точке (рисунок 5.2,а) и создает в ветви с сопротивлением ток , направленный от точки к точке . Тогда такой же единственный источник э.д.с. , включенный в ветвь с сопротивлением и действующий в направлении от к (рисунок 5.2,б), создаст в ветви с сопротивлением ток , направленный от к и равный току .

На рисунке 5.2,а изображены ветви и с сопротивлениями и , а остальная часть схемы, не содержащая источников энергии, условно показана в виде прямоугольника с буквой (пассивная).

Пусть ветвь является частью контура , а ветвь входит в состав другого контура (рисунок 5.2,а) и, как указано, других источников э.д.с., кроме , эта цепь не содержит. Контуры выберем так, чтобы ветви и вошли каждая в один контур соответственно и . Тогда ток в контуре , равный току ветви , определится

. (5.4)

Если источник э.д.с. переставить в ветвь контура (рисунок1-18,б), то после этого ток в контуре , т.е. ток в ветви , определится выражением

(5.5)

Алгебраическое дополнение вида получается из определителя путем вычеркивания в нем столбца н строки и умножения получаемого определителя на , а алгебраическое дополнение вида - вычеркиванием столбца и строки и умножением получаемого определителя на . Так как в контурных уравнениях общие сопротивления и равны друг другу, т.е. и т.д., то и (отличаются только тем, что строки являются столбцами или наоборот). Следовательно, при равенстве э.д.с. токи в ветвях (рисунок 5.2,а) и (рисунок 5.2,б) равны друг другу.

5.3 Входные и взаимные проводимости и сопротивления ветвей

Пользуясь принципом наложения, напишем уравнение для тока в любой ветви, например , линейной электрической цепи в виде

(5.6)

В этом уравнении ток обозначает ток ветви , а , и т. д. -э.д.с. соответственно в первой, второй и так далее ветвях. При этом если положительное направление для тока выбрано совпадающим с направлением э.д.с. , то составляющие токов в той же ветви вида , создаваемые э.д.с. других ветвей, могут иметь отрицательные знаки.

В уравнении (5.6) множители при э.д.с. имеют размерность проводимости. Поэтому каждый из множителей с двумя одинаковыми индексами вида называется входной проводимостью ветви , а величина, обратная входной проводимости, - входным сопротивлением той же ветви. Любой из множителей с двумя различными индексами называется взаимной проводимостью ветвей и , а величина, обратная взаимной проводимости, - взаимным сопротивлением тех же ветвей.

Численные значения входных и взаимных проводимостей и сопротивлений ветвей могут быть определены следующим путем. Приравняем в рассматриваемой схеме все э.д.с., кроме , нулю. Тогда ток , откуда

(5.7)

Следовательно, входная проводимость любой ветви определяется отношением тока к э.д.с. в этой ветви при равных нулю э.д.с. в остальных ветвях, а входное сопротивление ветви обратно входной проводимости.

Электродвижущая сила , включенная в ветвь , вызывает в общем случае токи во всех ветвях и, в частности, в ветви . Ток в ветви определяется по уравнению, аналогичному (5.6), при равных нулю всех э.д.с., кроме , т.е. откуда

(5.8)

Отметим, что , как это непосредственно следует из свойства взаимности.

Таким образом, взаимная проводимость двух любых ветвей определяется отношением тока в одной ветви к э.д.с. в другой при равных нулю э.д.с. в остальных ветвях, а взаимное сопротивление двух ветвей обратно взаимной проводимости тех же ветвей.

В общем случае входная проводимость некоторой ветви равна сумме взаимных проводимостей данной ветви и каждой из остальных ветвей, присоединенных к одному из двух узлов, к которым присоединена эта ветвь.

Например, входная проводимость первой ветви (рисунок 1-19) равняется сумме проводимостей и или , и , т.е.

Эти соотношения непосредственно следуют из первого закона Кирхгофа и свойства взаимности и могут быть применены для расчета электрических цепей.

5.4 Теорема о компенсации

В электрической схеме, показанной на рисунок 5.3,а, выделена ветвь с сопротивлением и током .

Включим в эту ветвь два источника с э.д.с. и (рисунок 5.3,б), численно равными напряжению и направленными навстречу друг другу; токи во всех ветвях схемы, очевидно, останутся без изменения. При переходе из точки (рисунок 5.3,б) в точку потенциал повышается на величину э.д.с. , а при переходе из точки в точку понижается на ту же величину, вследствие чего потенциалы точек и равны. Эти точки можно соединить проводником (закоротить), как показано на рисунке 5.3,б пунктиром, т.е. источник э.д.с. , и сопротивление удалить из схемы, не изменив токов во всех ветвях (рисунок 5.3, в).

Из сравнения схем рисунок 5.3, а и в непосредственно следует, что любое сопротивление можно заменить источником с э.д.с., направленной навстречу току и равной напряжению на этом сопротивлении. Это положение называют теоремой о компенсации.

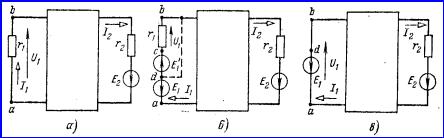
Рисунок 5.3

6 Лекция 6. Линейные соотношения между напряжениями и токами, теорема об активном двухполюснике и ее применение для расчета разветвленных цепей. Передача энергии от активного двухполюсника пассивному.

6.1 Линейные соотношения между напряжениями и токами

В эквивалентных схемах (рисунок 5.3,a), кроме ветви с сопротивлением , выделена еще ветвь с источником э.д.с. и сопротивлением . Пользуясь принципом наложения, напишем выражения для токов и в ветвях схемы (рисунок 5.3,в)

(6.1)

Пусть в схеме (рисунок 5.3,в) ЭДС первого источника может изменяться, а эдс остальных источников , и т.д. неизменны. Так как входные и взаимные проводимости не зависят от э.д.с. , то, обозначив

получим (6.2)

заменив в (6.2) эдс через ,

(6.3)

Для определения постоянных и расчетом или опытным путем необходимо, как следует из (6.3), рассчитать или измерить токи , и

напряжение при двух режимах первой ветви (двух значениях сопротивления ). Наиболее наглядно и просто эти постоянные определяются из режимов короткого замыкания и режима холостого хода .

При коротком замыкании , токи и . При размыкании первой ветви ток . Обозначив разность потенциалов между точками разрыва через , а ток , получим согласно (6.3)

откуда входная проводимость

и взаимная проводимость

После замены постоянных в первом из уравнений (6.3) получается

(6.4)

Отметим, что изменение напряжения в пределах от до соответствует изменению сопротивления от нуля до бесконечности.

Токи и рассматриваемых ветвей также связаны линейными соотношениями. Действительно, исключив из уравнений (6.3) напряжение , получим

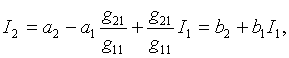(6.5)

где

и - постоянные, которые определяются из двух любых режимов первой ветви или вычисляются при известных значениях входных и взаимных проводимостей.

6.2 Теорема об активном двухполюснике и ее применение для расчета разветвленных цепей

Выделим в электрической цепи одну ветвь с сопротивлением , присоединенную в точках к активному двухполюснику (рисунок 6.1).

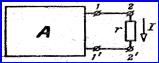
Рисунок 6.1

Покажем, что для расчета тока в ветви активный двухполюсник можно заменить источником э.д.с. и пассивным двухполюсником. Чтобы найти э.д.с. источника, разомкнем цепь между точками и (рисунок 6.2,а) и определим разность потенциалов опытным или расчетным путем. Затем подключим к точкам и источник с э.д.с. , направленной навстречу U_x (рисунок 6.2,б); ток в ветви останется равным нулю, так как при этом разность потенциалов любых двух точек не изменилась. Схема, показанная на рисунке 1-22,б, отличается от заданной (рисунок 6.1) тем, что в ней между точками и включен источник э.д.с. и ток в ветви равен нулю.

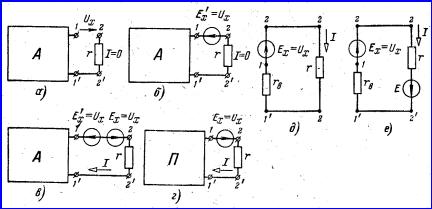
Рисунок 6.2

Эта схема будет эквивалентна заданной, если между точками и ввести еще одну э.д.с. , противоположно направленную э.д.с. (рисунок 6.2, в). По принципу наложения ток в ветви эквивалентной схемы (рисунок 6.2,е), а значит и заданной (рисунок 6.1), найдем как алгебраическую сумму токов, создаваемых каждым из источников. Но все источники, находящиеся внутри активного двухполюсника, совместно с источником э.д.с. не вызывают тока в ветви (рисунок 6.2,б). Поэтому ток в ветви , создаваемый одним источником э.д.с. (рисунок 6.2,г), равен действительному току в этой ветви (рисунок 6.1)

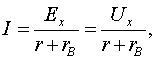(6.6)

где - входное сопротивление пассивного двухполюсника, получающегося из заданного активного после того, как все э.д.с. источников напряжения и все токи источников тока приняты равными нулю. В частности, при , т. е. при коротком замыкании ветви , , т. е. входное сопротивление активного двухполюсника можно определить как отношение напряжения холостого хода к току короткого замыкания

Формулу (6.6) можно еще записать так

(6.7)

Сопротивление в общем случае может быть входным сопротивлением пассивного двухполюсника, присоединенного к зажимам заданного активного двухполюсника.

Уравнение (6.6) представляет собой математическое выражение теоремы об активном двухполюснике, называемой также теоремой об эквивалентном генераторе или теоремой Гельмгольца и Тевенена. Эту теорему можно формулировать следующим образом: если активную цепь, к которой присоединена некоторая ветвь, заменить источником с э.д.с, равной напряжению на зажимах разомкнутой ветви, и сопротивлением, равным входному сопротивлению активной цепи, то ток в этой ветви не изменится.

Активный двухполюсник можно также представить в виде источника тока и параллельно ему присоединенного сопротивления . Если рассматриваемая ветвь содержит не только сопротивление , но и э.д.с. , то ток в этой ветви

(6.8)

где э.д.с. берется с положительным знаком, когда обе э.д.с. и действуют в одном и том же направлении (рисунок 6.2,е), и с отрицательным, когда направлена навстречу .

Остановимся теперь на применении теоремы об активном двухполюснике и принципа наложения для расчета разветвленных электрических цепей.

Рассмотрим, например, схему на рисунке 6.3, в которой требуется определить токи во всех ветвях при заданных э.д.с. источников, напряжении и сопротивлениях ветвей.

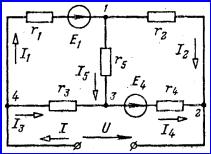
Рисунок 6.3

Разомкнем ветвь с сопротивлением (рисунок 6.4,а) и определим ток из уравнения и ток из уравнения

Зная токи и , вычислим напряжение по формуле

Затем положим э.д.с. и и напряжение равными нулю и включим в ветвь с сопротивлением источник с э.д.с. (рисунок 6.4,б), а затем найдем токи во всех ветвях. Входное сопротивление двухполюсника на зажимах и (ветви с сопротивлением ) .

Ток

Токи в остальных ветвях

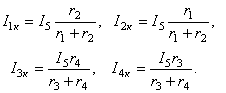
Токи в ветвях заданной схемы (рисунок 6.3) определяются при помощи принципа наложения:

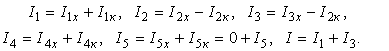
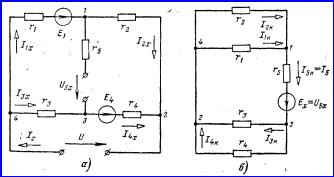
Рисунок 6.4

6.3 Передача энергии от активного двухполюсника пассивному

Для исследования передачи энергии от активного двухполюсника к пассивному вернемся к эквивалентной схеме, показанной на рисунке 6.2,д, и будем считать, что - входное сопротивление активного двухполюсника (источника энергии) и - эквивалентная э.д.с. - остаются постоянными, а -входное сопротивление пассивного двухполюсника - может принимать любое значение.

Прежде всего установим соотношение между сопротивлениями и , при выполнении которого мощность пассивного двухполюсника максимальна.

Мощность пассивного двухполюсника определяется выражениями

, (6.9)

(6.10)

где - мощность, развиваемая эквивалентным активным двухполюсником;

- мощность потерь в сопротивлении .

Для определения тока , при котором мощность максимальна, найдем производную от по из уравнения (6.9) и приравняем ее нулю

откуда искомый ток

[уравнением (6.9) пользоваться нельзя, так как его правая часть содержит две переменные: и ]. Но в общем случае (рисунок 6.9,д) ток . Значит, мощность максимальна при

(6.11)

т.е. при равенстве входных сопротивлений пассивного и активного двухполюсников.

По формуле (6.10) при мощность

(6.12)

Отношение мощности пассивного двухполюсника к мощности , развиваемой эквивалентным активным двухполюсником, называется к. п. д. эквивалентного активного двухполюсника

(6.13)

Из выражения (6.13) следует, что при максимальной мощности пассивного двухполюсника к.п. д. равен 0,5. Более высокие значения к.п.д. будут при .

Электрические цепи однофазного синусоидального тока.

7Лекция 7. Синусоидальные электрические величины, генерирование синусоидальной э.д.с., среднее и действующее значение функции.

Цель лекции: усвоить основные понятия о синусоидальных токах и напряжениях.

7.1 Синусоидальные электрические величины

Электромагнитный процесс в электрической цепи, при котором мгновенные значения напряжений и токов повторяются через равные промежутки времени, называется периодическим. Наименьшее время, по истечении которого мгновенные значения периодической величины повторяются, называется периодом Т.

Величина, обратная периоду, т. е. число периодов в единицу времени, называется частотой

Частота имеет размерность 1/сек, а единицей измерения частоты служит герц ( гц ); частота равна 1 гц, если период равен 1 сек.

Преобладающим видом периодического процесса в электрических цепях является синусоидальный режим, характеризующийся тем, что все напряжения и токи являются синусоидальными функциями одинаковой частоты. На рисунке 7.1 изображена синусоидальная функция

, (7.1)

здесь - максимальное значение, или амплитуда;

- скорость изменения аргумента ( угла ), называемая угловой частотой; она равна произведению частоты на 2

, рад/сек ; (7.2)

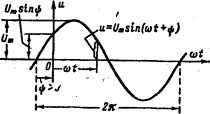
Рисунок 7.1

- начальная фаза, определяемая величиной смещения синусоиды относительно начала координат; она измеряется абсциссой точки перехода отрицательной полуволны в положительную.

Начальная фаза представляет собой алгебраическую величину. Угол положителен и отсчитывается вправо к точке t = 0, когда синусоидальная функция смещена влево относительно начала координат ( рисунок 7.1).

За аргумент функции (7.1) может быть принято время t или соответственно угол . Аргументу t соответствует период Т, а аргументу - период = 2л. Следует иметь в виду, что аргумент измеряется в радианах, причем в тех же единицах измеряется и начальная фаза.

Если угол вычисляется в градусах, то аргумент также переводится в градусы; в этом случае период составляет 360°.

Величина , определяющая стадию изменения синусоидальной величины (7.1), называется фазовым углом или фазой. С течением времени фаза возрастает, причем после увеличения фазы на 2л цикл изменения синусоидальной величины повторяется.

7.2 Генерирование синусоидальной э.д.с.

Наиболее распространенным в промышленности способом получения синусоидального тока является применение синхронных генераторов, приводимых во вращение тепловыми, газовыми, гидравлическими или другими турбинами.

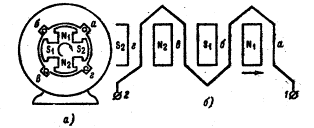
Рисунок 7.2

Генератор переменного тока состоит из двух частей: неподвижного статора и вращающегося ротора. На одном из них (чаще на роторе) располагаются полюсы, т. е. электромагниты, обмотка которых питается от источника постоянного тока, или постоянные магниты. На другом (обычно на статоре) располагается главная обмотка, в которой наводится переменная э. д. с. На рисунке 7.2,а упрощенно показан явнополюсный генератор с двумя парами полюсов, размещенных на роторе. Указанному на рисунке 7.2, а положению ротора относительно статора соответствует на рисунке 7.2, б развернутая на плоскость схема расположения обмотки и полюсов.

В каждом проводе обмотки, находящемся в пазу статора, при вращении ротора наводится по закону Фарадея э. д. с. е = Blv, где В — магнитная индукция поля под проводом; —длина провода; v—линейная скорость перемещения магнитного поля. В международной системе В измеряется в теслах (тл), т. е. вб/м².

При постоянных значениях и v закон изменения э. д. с. e(t) определяется законом распределения магнитной индукции в воздушном зазоре машины. Благодаря специальной форме полюсных наконечников закон изменения магнитной индукции делается приблизительно синусоидальным вдоль всей окружности зазора между ротором и статором; магнитная индукция максимальна против середин и постепенно убывает к краям полюсных наконечников.

В момент времени, которому соответствует указанное на рисунке 7.2 положение ротора, магнитная индукция под проводом равна нулю, и поэтому э. д. с. е также равна нулю.

После поворота ротора на одну восьмую часть полного оборота (половина полюсного шага) э. д. с. достигнет максимума и будет направлена от зажима 1 к зажиму 2 (по правилу правой руки). Когда ротор повернется еще на половину полюсного шага, э. д. с. вновь обратится в нуль. При последующем вращении ротора еще на одну восьмую часть оборота э. д. с. достигнет максимума, но будет противоположно направлена от зажима 2 к зажиму 1 и так далее. Таким образом, на зажимах генератора возникнет практически синусоидальная э. д. с.

При числе пар полюсов р и числе оборотов ротора в минуту частота наводимой переменной э. д. с. равна

. (7.3)

В энергосистемах СНГ и большинства других стран частота промышленного тока равна 50 гц. В США принята частота 60 гц.

7.3 Среднее и действующее значения синусоидальных величин

Среднее значение периодической функции за период Т определяется по формуле

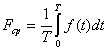. (7.4)

В случае синусоидальной функции среднее значение за период равно нулю, так как площадь положительной полуволны компенсируется площадью отрицательной полуволны синусоиды. Поэтому здесь пользуются понятием среднего значения функции, взятой по абсолютной величине, или, что то же, среднего полупериодного значения, соответствующего положительной полуволне синусоиды (рисунок 7.4).

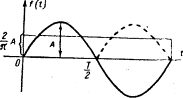
Рисунок 7.4

В соответствии с этим среднее значение синусоидального тока с амплитудой А = 1т будет

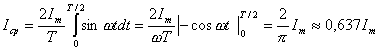. (7.5)

Аналогично среднее значение синусоидального напряжения

. (7.6)

Тепловое действие тока, а также механическая сила взаимодействия двух проводников, по которым проходит один и тот же ток, пропорциональны квадрату тока. Поэтому о величине тока судят обычно по так называемому действующему

( среднеквадратическому) значению за период.

Действующее значение периодической функции вычисляется по формуле

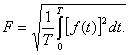(7.7)

В соответствии с (7.7) действующее значение периодического тока

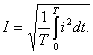(7.8)

Возведя (7.8) в квадрат и умножив обе части полученного выражения на rT, найдем

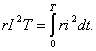
Это равенство показывает, что действующее значение периодического тока равно по величине такому постоянному току, который, проходя через неизменное сопротивление r, за период времени Т выделяет то же количество тепла, что и данный ток i.

Аналогично действующее значение периодического напряжения

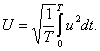(7.9)

При синусоидальном токе

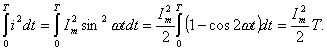
Следовательно, согласно (7.8)

(7.10)

аналогично действующее значение синусоидального напряжения

(7.11)

Номинальные токи и напряжения электротехнических устройств определяются, как правило, действующими значениями; поэтому действующие значения представляют наиболее распространенный электрический параметр.

8 Лекция 8. Синусоидальный ток в сопротивлении, индуктивности и емкости.

Цель лекции: усвоить особенности протекания тока в основных элементах

8.1 Синусоидальный ток в сопротивлении

Если синусоидальное напряжение подвести к сопротивлению r (рисунок 8.1, а), то через сопротивление пройдет синусоидальный ток .

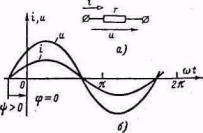
Рисунок 8.1

Следовательно, напряжение на зажимах сопротивления и ток, проходящий через это сопротивление, имеют одинаковую начальную фазу или, как говорят, совпадают по фазе: они одновременно достигают своих амплитудных значений ии соответственно одновременно проходят через нуль (рисунок 8.1,б).

Разность начальных фаз двух синусоид, имеющих одинаковую частоту, называется фазовым сдвигом. В данном случае фазовый сдвиг между напряжением и и током i равен нулю

При прохождении синусоидального тока через сопротивление r не только мгновенные значения напряжения на сопротивлении и тока в нем, но и амплитуды и соответственно действующие значения напряжения и тока связаны законом Ома

Пользуясь величиной проводимости g =1/r, получаем

Мгновенная мощность, поступающая в сопротивление

(8.1)

изменяется с угловой частотой, удвоенной по сравнению с частотой напряжения и тока, и колеблется в пределах от 0 до 2UI (рисунок 8.2).

Как видно из (8.1), кривая состоит из двух слагающих: постоянной слагающей UI и косинусоидальной функцией, имеющей амплитуду UI и угловую частоту 2 .

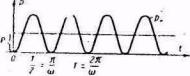
Рисунок 8.2

Ввиду того, что в рассматриваемом случае напряжение и ток совпадают по фазе, т. е. всегда имеют одинаковый знак (плюс или минус), их произведение всегда положительно.

Среднее значение мощности за период Р = 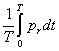называется активной мощностью и измеряется в ваттах. В рассматриваемом случае, как это видно из выражения (8.1) и рисунка 8.2, активная мощность Р = UI =r1².

8.2 Синусоидальный ток в индуктивности

Пусть через индуктивность L (рисунок 8.3, а ) проходит ток

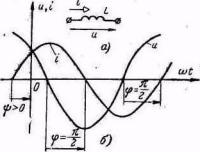
Рисунок 8.3.

Электродвижущая сила самоиндукции определяется по формуле

(8.2)

Значит напряжение на индуктивности

(8.3)

Полученное выражение показывает, что напряжение на индуктивности

опережает ток на угол максимум напряжения смещен влево относительно максимума тока на (рисунок 8.3,б), когда ток проходит через нуль, напряжение достигает положительного или отрицательного максимума, так как оно пропорционально скорости изменения тока (di/dt), которая в момент прохождения тока через нуль максимальна (синусоида тока в этот момент имеет наибольшую крутизну). Когда ток достигает максимума, скорость его изменения, а следовательно, и напряжение на индуктивности обращаются в нуль.

Фазовый сдвиг равен

Амплитуда так же, как и действующие значения напряжения и тока, связаны соотношением, подобным закону Ома

(8.4)

Величина , имеющая размерность сопротивления, называется индуктивным сопротивлением; обратная ей величина называется индуктивной проводимостью.

(8.5)

Индуктивное сопротивление представляет собой расчетную величину, с помощью которой учитывается явление самоиндукции.

Мгновенная мощность, поступающая в индуктивность, будет

.(8.6)

Она колеблется по синусоидальному закону с угловой частотой , имея амплитуду UI. Мгновенная мощность в данном случае равна скорости изменения энергии магнитного поля индуктивности.

Энергия магнитного поля индуктивности

(8.7)

изменяется периодически с угловой частотой в пределах от 0 до (рисунок 8.4).

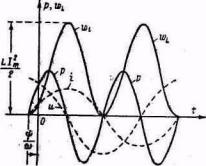
Рисунок 8.4

Поступая от источника, энергия временно запасается в магнитном поле индуктивности, затем возвращается в источник при исчезновении магнитного поля. Энергия магнитного поля достигает максимума в момент перехода тока в индуктивности через амплитудное значение, затем она убывает и обращается в нуль при токе, равном нулю.

Таким образом, происходит колебание энергии между источником и индуктивностью, причем активная мощность, поступающая в индуктивность, равна нулю.

8.3 Синусоидальный ток в емкости

Пусть напряжение на емкости С (рисунок 8.5, а) синусоидально:

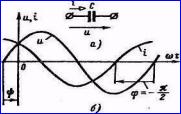
Рисунок 8.5

Ток в емкости

(8.8)

Изменение электрического заряда происходит по синусоидальному закону в соответствии с приложенным напряжением и. Величина тока определяется скоростью изменения заряда на емкости (dq/dt).

Выражение (8.8) показывает, что ток i опережает приложенное напряжение и на угол (рисунок 8.5,б). Нулевым значениям тока соответствуют максимальные (положительные или отрицательные) значения напряжения и. Физически это объясняется тем, что когда электрический заряд q и соответственно напряжение и = q/C достигают максимального значения (положительного или отрицательного), ток i равен нулю.

Разность начальных фаз напряжения и тока, т. е. . Таким образом, в отличие от цепи с индуктивностью, где , фазовый сдвиг тока относительно напряжения в случае емкости отрицателен ().

Амплитуды и соответственно действующие значения напряжения и тока связаны соотношением, подобным закону Ома

(8.9)

Величина , имеющая размерность сопротивления, называется емкостным сопротивлением. Обратная ей величина называется емкостной проводимостью. Следовательно,

(8.10)

Мгновенная мощность, поступающая в емкость,

(8.11)

колеблется синусоидально с угловой частотой , имея амплитуду, равную UI; выражение в рассматриваемом случае аналогично выражению для .

Мгновенная мощность, поступающая в емкость, равна скорости изменения энергии электрического поля емкости, которая равна

(8.12)

и изменяется периодически с угловой частотой в пределах от 0 до (рисунок 8.6).

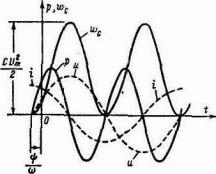
Рисунок 8.6

Поступая от источника, энергия временно запасается в электрическом поле емкости, а затем возвращается в источник при исчезновении электрического поля.

Энергия электрического поля достигает максимума при амплитудном значении напряжения на емкости. Затем она убывает и обращается в нуль при напряжении, равном нулю.

Таким образом, так же как в случае индуктивности, происходит колебание энергии между источником и емкостью, причем активная мощность Р = 0.

9 Лекция 9. Основы комплексного метода расчета цепей синусоидального тока.

Цель лекции: познакомиться с применением метода комплексных амплитуд.

9.1 Представление синусоидальных функций в виде векторов

Известно, что каждая точка на комплексной плоскости определяется радиус-вектором этой точки, т. е. вектором, начало которого совпадает с началом координат, а конец находится в точке, соответствующей заданному комплексному числу (рисунок 9.1).

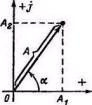
Рисунок 9.1

Пользуясь показательной или полярной формой записи комплексного числа, имеем

здесь А - модуль; - аргумент или фаза;

. Применив формулу Эйлера, можно получить тригонометрическую форму записи комплексного числа

или соответственно алгебраическую форму

где

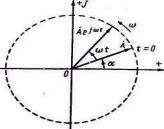
Рисунок 9.2

Очевидно,

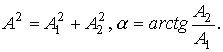
Вектор, вращающийся в положительном направлении, т. е. против хода часовой стрелки, с угловой скоростью может быть выражен следующим образом

(9.1)

где - комплексная амплитуда, представляющая данный вектор в момент t = О (рисунок 9.2). Иначе говоря, это комплексная величина, не зависящая от времени, модуль и аргумент которой равны соответственно амплитуде и начальной фазе заданной синусоидальной функции.

Записывая комплексную функцию (9.1) в тригонометрической форме

заключаем, что синусоидальная функция может рассматриваться как мнимая часть комплексной функции (9.1), взятая без множителя j, или, что то же, как проекция вращающегося вектора на мнимую ось.

Условно это записывается так

Символ Im обозначает, что берется мнимая часть комплексной функции.

Если синусоидальные функции имеют одну и ту же частоту, то соответствующие этим функциям векторы вращаются с одинаковой угловой скоростью и поэтому углы между ними сохраняются неизменными.

На рисунке 9.3, а показаны две синусоидальные функции: и имеющие одинаковую угловую частоту . Функция опережает по фазе функцию , причем фазовый сдвиг равен разности начальных фаз

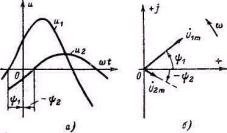
Рисунок 9.3

Этот угол и образуют между собой векторы, показанные на рисунке 9.3, б.

При равенстве начальных фаз, т. е. при фазовом сдвиге, равном нулю, векторы направлены в одну и ту же сторону (совпадают по фазе). При фазовом сдвиге 180⁰ векторы направлены в диаметрально противоположные стороны (находятся в противофазе).

Диаграмма, изображающая совокупность векторов, построенных с соблюдением их взаимной ориентации по фазе, называется векторной диаграммой.

9.2 Последовательное соединение сопротивления, индуктивности и емкости

Рассмотрим применение метода комплексных амплитуд в случае последовательного соединения элементов r, L и С (рисунок 9.4).

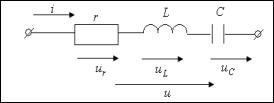
Рисунок 9.4

Положим, что в уравнении Кирхгофа

(9.2)

заданными являются параметры r, L, С и синусоидальное напряжение на зажимах цепи, а искомой величиной является ток i. Ввиду того что здесь рассматривается установившийся режим цепи синусоидального тока, решение этого дифференциального уравнения должно дать синусоидальную функцию вида

где - пока неизвестные амплитуда и начальная фаза тока.

Пусть заданное синусоидальное напряжение символизируется комплексной

функцией ,а искомый синусоидальный ток—комплексной функцией комплексные амплитуды напряжения и тока равны соответственно

Сложение, дифференцирование и интегрирование синусоидальных функций в уравнении (9.2) заменяются теми же математическими операциями над комплексными функциями

(9.3)

В результате сокращения всех частей уравнения (9.3) на множитель получается алгебраическое комплексное уравнение

(9.4)

Ток может быть вынесен за скобки. При этом вводится условное обозначение для комплексного сопротивления рассматриваемой электрической цепи

(9.5)

Таким образом, получается уравнение

(9.6)

выражающее закон Ома для комплексных амплитуд.

Разделив обе части уравнения (9.6) на , получим закон Ома для комплексных действующих значений

(9.7)

Следовательно, комплексное сопротивление электрической цепи равно отношению комплексного напряжения на зажимах данной цепи к комплексному току в этой цепи.

Комплексное сопротивление Z представлено в выражении (9.5) в алгебраической форме. Та же величина в тригонометрической и показательной (полярной) формах имеет вид

(9.8)

Здесь - модуль комплексного числа Z— представляет собой полное сопротивление цепи, а — аргумент комплексного числа Z

(9.9)

На основании (9.6) комплексная амплитуда тока

где - начальная фаза тока. Следовательно, искомый ток в тригонометрической форме

На рисунке 9.5 дана геометрическая интерпретация на комплексной плоскости уравнения (9.4). Рисунок 9.5, а относится к случаю, когда реактивное сопротивление цепи имеет индуктивный характер (х>0) и соответственно ток отстает по фазе от напряжения (>0). Рисунок 9.5,б относится к случаю, когда реактивное сопротивление цепи имеет емкостный характер (х<0), и поэтому ток опережает по фазе напряжение (<0).

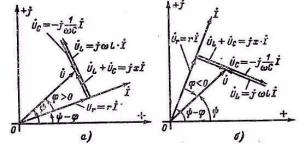
Рисунок 9.5

В случае чисто реактивной цепи (r = 0) ток отстает от напряжения по фазе на , если сопротивление цепи индуктивно, и опережает напряжение на при емкостном сопротивлении цепи.

Как видно из векторных диаграмм, приведенных на рисунке 9.5, — напряжение на сопротивлении r (совпадает по фазе с током ), —напряжение на индуктивности L (опережает ток на угол ) и — напряжение на емкости С (отстает от тока I на угол ).

Геометрическая сумма векторов дает вектор приложенного к цепи напряжения

10 Лекция 10. Параллельное соединение сопротивления, индуктивности и емкости, топографические диаграммы

Цель лекции: Усвоить расчет цепей комплексным методом и построение топографической диаграммы.

10.1 Параллельное соединение сопротивления, индуктивности и емкости

Если к зажимам электрической цепи, состоящей из параллельно соединенных элементов r, L и С (рисунок 10.1), приложено синусоидальное напряжение , то синусоидальный ток, проходящий через эту цепь, равен алгебраической сумме синусоидальных токов в параллельных ветвях (первый закон Кирхгофа)

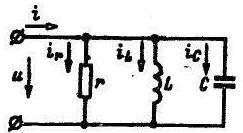
Рисунок 10.1

Рисунок 10.2

Ток в сопротивлении r совпадает по фазе с напряжением и, ток в индуктивности L отстает, а ток в емкости С опережает напряжение на (рисунок 10.2).

Следовательно, суммарный ток i в цепи равен

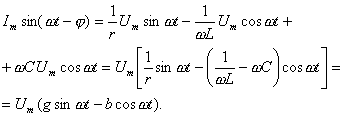(10.1)

Уравнение (10.1) представляет собой тригонометрическую форму записи первого закона Кирхгофа для мгновенных значений токов. Входящая в него величина называется реактивной проводимостью цепи, которая в зависимости от знака может иметь индуктивный (b>0) или емкостный (b<0) характер. В отличие от реактивной проводимости Ь величина g = 1/r, которая в данном случае называется активной проводимостью, всегда положительна.

Перейдем к комплексной форме законов Ома и Кирхгофа для электрической цепи, состоящей из элементов r, L и С, соединенных параллельно.

Ограничиваясь записью для комплексных действующих значений, пропорциональных комплексным амплитудам, имеем в соответствии с первым законом Кирхгофа

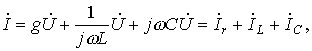(10.2)

здесь - ток в сопротивлении г (совпадает по фазе с напряжением );

- ток в индуктивности (отстает от напряжения на );

- ток в емкости (опережает напряжение на ).

Выражение

(10.3)

представляет собой комплексную проводимость рассматриваемой цепи; g и b—активная и реактивная проводимости цепи.

Уравнение

(10.4)

выражает закон Ома в комплексной форме. Следовательно, комплексная проводимость электрической цепи равна отношению комплексного тока в данной цепи к комплексному напряжению на ее зажимах.

Тригонометрическая и показательная (полярная) формы комплексной проводимости имеют следующий вид

здесь - модуль комплексного числа;

Y представляет собой полную проводимость цепи;

а — аргумент комплексного числа Y

На основании (10.4) комплексный ток равен

что соответствует синусоидальному току

На рисунке 10.3 дана геометрическая интерпретация на комплексной плоскости уравнения (10.2). Рисунок 10.3, а относится к случаю, когда реактивная проводимость цепи имеет индуктивный характер (b>0) и соответственно ток отстает по фазе от напряжения . Рисунок 10.3, б относится к случаю, когда реактивная проводимость цепи имеет емкостный характер (b<0) и соответственно ток опережает по фазе напряжение ().

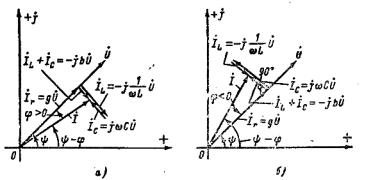
Рисунок 10.3

Прямоугольный треугольник с катетами и и гипотенузой называется треугольником токов; и представляют собой соответственно активную и реактивную слагающие тока и .

10.2 Топографические диаграммы

Топографическая диаграмма представляет собой векторную диаграмму, на которой отложены комплексные потенциалы отдельных точек заданной цепи по отношению к одной точке, потенциал которой принят за нуль. Таким образом, порядок расположения векторов падения напряжения на диаграмме строго соответствует порядку расположения элементов цепи на схеме. Конец вектора напряжения на каждом последующем элементе примыкает к началу вектора напряжения предыдущего элемента. При таком построении векторной диаграммы напряжений каждой точке электрической цепи соответствует определенная точка на топографической диаграмме. Топографическая диаграмма позволяет весьма просто находить напряжения между любыми точками цепи: действующее значение и фаза искомого напряжения определяются прямой, соединяющей соответствующие точки потенциальной диаграммы.

На рисунке 10.4 изображена схема неразветвленной электрической цепи и для нее построена топографическая диаграмма напряжений. Направления векторов напряжений на топографической диаграмме увязаны с произвольно выбранным направлением вектора тока .

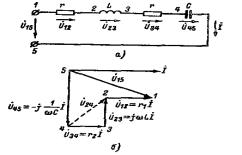
Рисунок 10.4

Обход схемы ведется навстречу положительному направлению тока . В соответствии с порядком расположения в схеме элементов на диаграмме изображены векторы напряжений

Начала и концы векторов (рисунок 10.4,б) пронумерованы в соответствии с нумерацией точек, принятой на схеме (рисунок 10.4, а).

Напряжение между какими-либо двумя точками схемы, например, на участке 2—4 схемы, взятое в положительном направлении тока , определяется по топографической диаграмме вектором , соединяющим точки 2 и 4 диаграммы и направленным на диаграмме от точки 4 к точке 2. Это соответствует известному правилу вычитания векторов, согласно которому какой-либо вектор , представляющий собой разность напряжений (или потенциалов) , направлен от конца вектора к концу вектора . Итак, вектор напряжения на диаграмме направлен к точке высшего (уменьшаемого) потенциала, а то же напряжение на схеме указывается стрелкой, направленной от высшего потенциала к низшему. Если при построении топографической диаграммы обход схемы совершался бы в положительном направлении тока , то изменилась бы нумерация начала и конца каждого вектора напряжения на топографической диаграмме, что противоречило бы принятому правилу расстановки индексов при вычитании векторов.

11 Лекция 11. Мощности в цепях синусоидального тока, баланс мощностей

Цель лекции: изучить виды мощностей в цепях синусоидального тока

11.1 Мощности в цепях синусоидального тока

Мгновенная мощность в электрических цепях имеет вид

. (11.1)

Приняв начальную фазу напряжения за нуль, а сдвиг фаз между напряжением и током за , получим

(11.2)

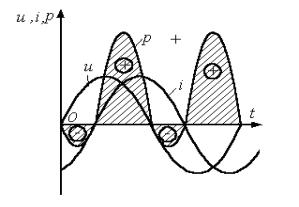
Рисунок 11.1

Итак, мгновенная мощность имеет постоянную составляющую и гармоническую составляющую, угловая частота которой в 2 раза больше угловой частоты напряжения и тока. Когда мгновенная мощность отрицательна, а это имеет место ( рисунок 11.1), когда u и i разных знаков, т.е. когда направления напряжения и тока в двухполюснике противоположны, энергия возвращается из двухполюсник источнику питания.

Среднее за период значение мгновенной мощности называется активной мощностью.

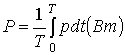. (11.3)

Принимая во внимание, что 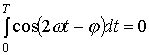, из (11.3) получим

(11.4)

Активная мощность, потребляемая пассивным двухполюсником, не может быть отрицательной (иначе двухполюсник будет генерировать энергию), поэтому, т.е. на входе пассивного двухполюсника .

Интенсивность обмена энергии принято характеризовать наибольшим значением скорости поступления энергии в магнитное поле катушки или электрическое поле конденсатора, которое называется реактивной мощностью.

В общем случае выражение для реактивной мощности имеет вид:

. (11.5)

Она положительна при отстающем токе (индуктивная нагрузка-) и отрицательна при опережающем токе (емкостная нагрузка-). Единицу мощности в применении к измерению реактивной мощности называют вольт-ампер реактивный (ВАр).

В частности, для катушки индуктивности имеем

, (11.6)

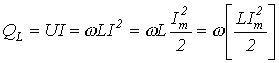. (11.7)

Из последнего видно, что реактивная мощность для идеальной катушки индуктивности пропорциональна частоте и максимальному запасу энергии в катушке. Аналогично можно получить для идеального конденсатора

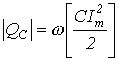. (11.8)

Помимо понятий активной и реактивной мощностей в электротехнике широко используется понятие полной мощности

. (11.9)

Активная, реактивная и полная мощности связаны следующим соотношением

. (11.10)

Отношение активной мощности к полной называют коэффициентом мощности. Из приведенных выше соотношений видно, что коэффициент мощности равен косинусу угла сдвига между током и напряжением. Итак,

. (11.11)

Активную, реактивную и полную мощности можно определить, пользуясь комплексными изображениями напряжения и тока. Пусть , а . Тогда комплекс полной мощности

, (11.12)

где - комплекс, сопряженный с комплексом .

Комплексной мощности можно поставить в соответствие треугольник мощностей (рисунок 11.2). Рисунок 11.2 соответствует (активно-индуктивная нагрузка), для которой имеем:

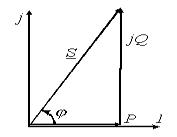
Рисунок 11.2

11.2 Баланс мощностей в цепях синусоидального тока

Баланс мощностей является следствием закона сохранения энергии и может служить критерием правильности расчета электрической цепи.

Из закона сохранения энергии следует, что сумма всех отдаваемых активных мощностей равна сумме всех потребляемых активных мощностей, т.е.

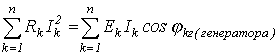. (11.13)

Баланс соблюдается и для реактивных мощностей

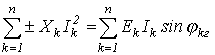, (11.14)

где знак “+” относится к индуктивным элементам ,

“-” – к емкостным .

Умножив (11.14) на “j” и сложив полученный результат с (11.13), придем к аналитическому выражению баланса мощностей в цепях синусоидального тока для комплексных мощностей

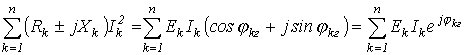(11.15)

или

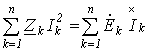(11.16)

12 Лекция 12.Резонанс напряжений, резонанс токов.

Цель лекции: изучить резонансные явления в последовательной и параллельной цепях.

Резонансом называется такой режим работы цепи, включающей в себя индуктивные и емкостные элементы, при котором ее входное сопротивление (входная проводимость) вещественно. Следствием этого является совпадение по фазе тока на входе цепи с входным напряжением.

12.1 Резонанс в цепи с последовательно соединенными элементами
(резонанс напряжений)

Для цепи на рисунке 12.1 имеет место

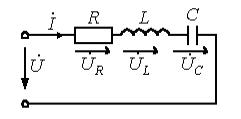
Рисунок 12.1

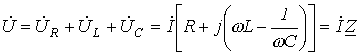, (12.1)

где

, (12.2)

В зависимости от соотношения величин и возможны три различных случая:

а) в цепи преобладает индуктивность, т.е. , а следовательно, . Этому режиму соответствует векторная диаграмма на рисунке 12.2,а;

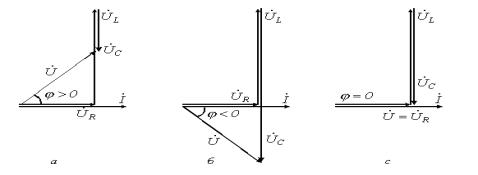
Рисунок 12.2

б) в цепи преобладает емкость, т.е. , а значит, . Этот случай отражает векторная диаграмма на рисунке 12.2,б;

в) - случай резонанса напряжений (рисунок 12.2,в).

Условие резонанса напряжений

. (12.3)

При этом, как следует из (12.1) и (12.2), .

При резонансе напряжений или режимах, близких к нему, ток в цепи резко возрастает. В теоретическом случае при R=0 его величина стремится к бесконечности. Соответственно возрастанию тока увеличиваются напряжения на индуктивном и емкостном элементах, которые могут во много раз превысить величину напряжения источника питания. Пусть, например, в цепи на рисунке 1 . Тогда , и соответственно .

Явление резонанса находит полезное применение на практике, в частности, в радиотехнике. Однако если он возникает стихийно, то может привести к аварийным режимам вследствие появления больших перенапряжений и сверхтоков. Физическая сущность резонанса заключается в периодическом обмене энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, причем сумма энергий полей остается постоянной.

Как показывает анализ уравнения (12.3), режима резонанса можно добиться путем изменения параметров L и C, а также частоты. На основании (12.3) для резонансной частоты можно записать

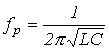. (12.4)

Резонансными кривыми называются зависимости тока и напряжения от частоты. В качестве их примера на рисунке 12.3 приведены кривые I(f); и для цепи на рисунке 12.1 при U=const.

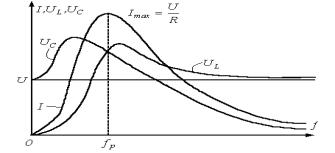
Рисунок 12.3

Важной характеристикой резонансного контура является добротность Q, определяемая отношением напряжения на индуктивном (емкостном) элементе при резонансе к входному напряжению

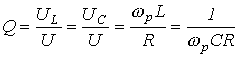, (12.5)

и характеризующая “избирательные” свойства резонансного контура, в частности, его полосу пропускания . Другим параметром резонансного контура является характеристическое сопротивление, связанное с добротностью соотношением

, (12.6)

или с учетом (12.4) и (12.5) для можно записать

. (12.7)

12.2 Резонанс в цепи с параллельно соединенными элементами
(резонанс токов)

Для цепи рисунка 12.4 имеем

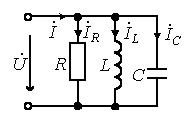
Рисунок 12.4

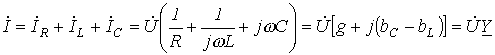, (12.8)

где

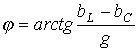; . (12.9)

В зависимости от соотношения величин и , как и в рассмотренном выше случае последовательного соединения элементов, возможны три различных случая.

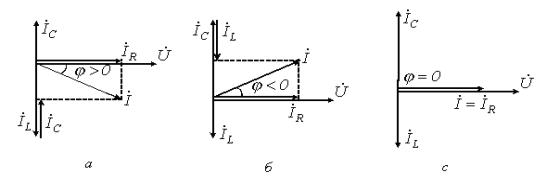
Рисунок 12.5

В цепи преобладает индуктивность, т.е. , а следовательно, . Этому режиму соответствует векторная диаграмма на рисунке 12.5,а. В цепи преобладает емкость, т.е. , а значит, . Этот случай иллюстрирует векторная диаграмма на рисунке 12.5,б. - случай резонанса токов (рисунок 12.5,в).

Условие резонанса токов или

. (12.10)

При этом, как следует из (12.8) и (12.9), . Таким образом, при резонансе токов входная проводимость цепи минимальна, а входное сопротивление, наоборот, максимально. В частности, при отсутствии в цепи на рисунке 12.4 резистора R ее входное сопротивление в режиме резонанса стремится к бесконечности, т.е. при резонансе токов ток на входе цепи минимален.

Идентичность соотношений (12.3) и (12.5) указывает, что в обоих случаях резонансная частота определяется соотношением (12.4). Однако не следует использовать выражение (12.4) для любой резонансной цепи. Оно справедливо только для простейших схем с последовательным или параллельным соединением индуктивного и емкостного элементов.

При определении резонансной частоты в цепи произвольной конфигурации следует исходить из условия вещественности входного сопротивления (входной проводимости) цепи.

Например, для цепи на рисунке 12.6 имеем

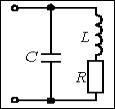
Рисунок 12.6

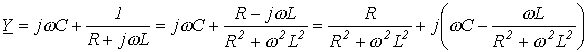
Поскольку в режиме резонанса мнимая часть должна быть равна нулю, то условие резонанса имеет вид

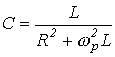
откуда, в частности, находится резонансная частота.

13 Лекция 13. Цепи с индуктивно связанными элементами.

Цель лекции: рассмотреть особенности расчета цепей при наличии взаимной индуктивности.

13.1 Индуктивно связанные элементы цепи

Электрические цепи могут содержать элементы, индуктивно связанные друг с другом. Такие элементы могут связывать цепи, электрически (гальванически) разделенные друг от друга.

В том случае, когда изменение тока в одном из элементов цепи приводит к появлению ЭДС в другом элементе цепи, говорят, что эти два элемента индуктивно связаны, а возникающую э.д.с. называют э.д.с. взаимной индукции. Степень индуктивной связи элементов характеризуется коэффициентом связи

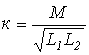, (13.1)

где М – взаимная индуктивность элементов цепи (размерность – Гн);

и -собственные индуктивности этих элементов. Следует отметить, что всегда к<1.

Пусть имеем две соосные катушки с ферромагнитным сердечником (рисунок 13.1). На рисунке 13.1 схематично показана картина магнитного поля при наличии тока в первой катушке (направление силовых линий магнитного потока определяется по правилу правого буравчика). Витки первой катушки сцеплены с магнитным потоком самоиндукции Ф11 , а витки второй катушки – с магнитным потоком взаимной индукции Ф21, который отличается от Ф11 (Ф21< Ф11) за счет потоков рассеяния.

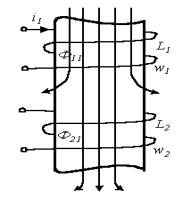
Рисунок 13.1

По определению

(13.2)

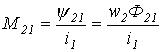(13.3)

Если теперь наоборот пропустить ток i₂ по второй катушке, то соответственно получим

(13.4)

(13.5)

При этом

(13.6)

Следует отметить, что коэффициент связи мог бы быть равным 1, если бы и , то есть когда весь поток, создаваемый одной катушкой, полностью пронизывал бы витки другой катушки. Практически даже различные витки одной и той же катушки пронизываются разными потоками. Поэтому с учетом рассеяния и . В этой связи

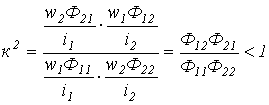
13.2 Последовательное соединение индуктивно связанных элементов

Рассмотрим цепь переменного тока на рисунке 13.2, в которую последовательно включены две катушки индуктивности и , индуктивно связанные друг с другом, и резистор R.

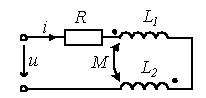
Рисунок 13.2

При изменении тока i в цепи в катушках индуцируются ЭДС само- и взаимоиндукции. При этом э.д.с. взаимной индукции должна по закону Ленца иметь такое направление, чтобы препятствовать изменению потока взаимной индукции.

Тогда если в цепи протекает гармонически изменяющийся ток , то в первой катушке индуцируется э.д.с.

(13.7)

а во второй –

(13.8)

Катушки можно включить так, что э.д.с. самоиндукции будет суммироваться с э.д.с. взаимоиндукции; при переключении одной из катушек ЭДС взаимоиндукции будет вычитаться из э.д.с. самоиндукции. Один из зажимов каждой катушки на схеме помечают, например, точкой или звездочкой. Этот знак означает, что при увеличении, например, тока в первой катушке, протекающего от точки, во второй катушке индуцируется э.д.с. взаимоиндукции, действующая от другого конца к точке. Различают согласное и встречное включения катушек. При согласном включении токи в катушках одинаково ориентированы по отношению к их одноименным зажимам. При этом э.д.с. само- и взаимоиндукции складываются – случай, показанный на рисунке 13.2. При встречном включении катушек токи ориентированы относительно одноименных зажимов различно. В этом случае э.д.с. само- и взаимоиндукции вычитаются. Таким образом, тип включения катушек (согласное или встречное) определяется совместно способом намотки катушек и направления токов в них.

Перейдя к комплексной форме записи (13.7) и (13.8), получим

, (13.9)

, (13.10)

где - сопротивление взаимоиндукции (Ом).

Для определения тока в цепи на рисунке 13.2 запишем

откуда

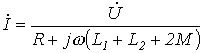
13.3 Расчет разветвленных цепей при наличии взаимной индуктивности

Расчет разветвленных цепей при наличии взаимной индуктивности может быть осуществлен путем составления уравнений по законам Кирхгофа или методом контурных токов. Непосредственное применение метода узловых потенциалов для расчета таких цепей неприемлемо, поскольку в этом случае ток в ветви зависит также от токов других ветвей, которые наводят ЭДС взаимной индукции.

В качестве примера расчета цепей с индуктивно связанными элементами составим контурные уравнения для цепи на рисунке 13.3:

Рисунок 13.3

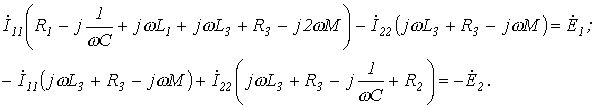
Список литературы

1.К.С.Демирчян, Л.Р.Нейман, Н.В.Коровкин, В.Л. Чечурин. Теоретические основы электротехники. – том 1. – СПб.: Питер, 2003.-463с.

2.Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. Основы теории цепей.- М.: Энергоатомиздат, 1989.-528с.

3.Л.А.Бессонов. Теоретические основы электротехники. – М.: Гардарики, 1999.-638с.

4.Г.В.Бакалов, В.Ф.Дмитриков, Б.Е.Крук. Основы теории цепей.- М.: Радио и связь, 2000.-592с.

5.Сборник задач по теоретическим основам электротехники/Л.Д.Бессонов, И.Г.Демидова, М.Е.Заруди и др.-М.: Высшая школа, 2003.-543с.

Сводный план 2006 г., поз. 142