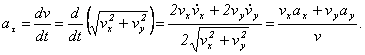МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН
Некоммерческое акционерное общество
«Алматинский университет энергетики и связи»
А.Д.Динасылов, Р.К.Койлыбаева
МЕХАНИКА.
сборник заданий для самостоятельной
работы студентов
Учебное пособие
Алматы 2012
УДК 621.01(075.8)
ББК 22.21я73
Д46. Механика. Сборник заданий для самостоятельной работы студентов:
Учебное пособие /А.Д. Динасылов, Р.К. Койлыбаева;
Алматы: АУЭС, 2011. – 88 с.
Ил. 128, табл. 2, библиогр. - 10 назв.
ISBN 978-601-7098-77-3
В учебном пособии содержатся задания для самостоятельной работы студентов по курсу «Механика». Данный курс состоит из разделов теоретической механики и сопротивления материалов. Для успешного освоения курса важно научиться применять законы и общие теоремы механики к определению движения материальных тел и механических систем, составлять расчетные схемы и проводить расчеты на прочность, жесткость и устойчивость. На практических занятиях и при выполнении расчетно-графических работ студенты получают навыки решения типовых задач. Вместе с тем имеется необходимость в рассмотрении более широкого и разнообразного круга задач, имеющих прикладное значение. Представленные в учебном пособии задачи предназначены для закрепления теоретического материала и получения навыков решения задач при выполнении домашних заданий, подготовке к рубежному контролю и экзамену, они могут использоваться также на аудиторных занятиях. По каждой теме имеются примеры решения задач, некоторые из них решены с использованием компьютерной системы Mathcad.
Учебное пособие предназначено для студентов, обучающихся по специальности 5В071700 – Теплоэнергетика. Оно может быть полезно также студентам других специальностей, изучающим курсы «Механика» или «Прикладная механика».
ББК 22.21я73
РЕЦЕНЗЕНТЫ: АТУ, канд.техн.наук, доц. Н.М.Ержанов,
АЭжБУ, доктор техн.наук, доц. С.Н.Тойбаев.
ISBN 978-601-7098-77-3
Печатается по плану издания Министерства образования и науки Республики Казахстан на 2011 г.
ã НАО «Алматинский университет энергетики и связи», 2012 г.
Содержание
|
1 Равновесие систем сходящихся сил |
4 |
|
2 Равновесие плоских систем сил |
8 |
|
3 Равновесие пространственных систем сил |
14 |
|
4 Кинематика точки |
18 |
|
5 Кинематика простейших движений твердого тела |
23 |
|
6 Плоское движение твердого тела |
27 |
|
7 Сложное движение точки |
33 |
|
8 Динамика точки |
37 |
|
9 Динамика системы |
42 |
|
10 Расчеты на прочность при растяжении – сжатии |
48 |
|
11 Расчеты заклепочных, сварных и других видов соединений |
58 |
|
12 Расчеты на прочность и жесткость при кручении. |
63 |
|
13 Расчеты на прочность при изгибе |
67 |
|
14 Расчет стержней при совместном действии изгиба и кручения |
76 |
|
15 Расчет сжатых стержней на устойчивость |
82 |
|
Список литературы |
88 |
1 Равновесие систем сходящихся сил
Задача 1.1. Определить силу давления на гладкую плоскость однородного шара весом 30кН и натяжение удерживающей его нити (см. рисунок 1,а).
Решение.
Рассмотрим равновесие шара, покажем действующую на него
активную силу – силу тяжести ![]() ,
которая приложена в центре тяжести тела О и направлена вертикально вниз.
Мысленно отбросим наложенные на шар связи (плоскость и нить) и
заменим их действие реакциями. Реакция гладкой плоскости
,
которая приложена в центре тяжести тела О и направлена вертикально вниз.
Мысленно отбросим наложенные на шар связи (плоскость и нить) и
заменим их действие реакциями. Реакция гладкой плоскости ![]() приложена в точке касания А
и направлена по общей нормали плоскости и шара от плоскости к шару; реакция
нити
приложена в точке касания А
и направлена по общей нормали плоскости и шара от плоскости к шару; реакция
нити ![]() направлена вдоль нити от шара (см. рисунок
1,б). При этом искомая сила давления шара на плоскость равна по величине
ее реакции R и направлена в противоположную
сторону. Аналогично сила натяжения нити равна S
и направлена в противоположную сторону. По теореме о равновесии тела под
действием 3-ех непараллельных сил, лежащих в одной плоскости, линии действия трех
показанных сил пересекаются в одной точке О. Перенесем все силы по линиям
их действия в эту точку и изобразим в виде плоской системы сходящихся сил на
отдельном чертеже (см. рисунок 1,в).
направлена вдоль нити от шара (см. рисунок
1,б). При этом искомая сила давления шара на плоскость равна по величине
ее реакции R и направлена в противоположную
сторону. Аналогично сила натяжения нити равна S
и направлена в противоположную сторону. По теореме о равновесии тела под
действием 3-ех непараллельных сил, лежащих в одной плоскости, линии действия трех
показанных сил пересекаются в одной точке О. Перенесем все силы по линиям
их действия в эту точку и изобразим в виде плоской системы сходящихся сил на
отдельном чертеже (см. рисунок 1,в).
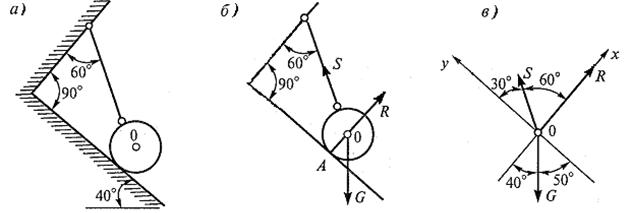
Рисунок 1
Для решения задачи аналитическим способом выберем систему координат хОу, направив для удобства одну из осей вдоль неизвестной силы, а вторую перпендикулярно ей, и составим 2 уравнения равновесия:
![]()
![]()
Из второго уравнения находим
![]()
Из первого уравнения находим
![]()
Ответ: ![]()
![]()
Задача 1.2. Определить силу натяжения нити АВ и реакцию невесомого стержня АС, удерживающих груз весом 30 Н (см. рисунок 2,а).
Решение.
Рассмотрим равновесие точки А, на которую через
нить передается сила тяжести груза ![]() . Мысленно отбросим
наложенные на точку А связи (нить и стержень) и заменим их действие
реакциями. Реакцию нити
. Мысленно отбросим
наложенные на точку А связи (нить и стержень) и заменим их действие
реакциями. Реакцию нити ![]() направим
вдоль нити от точки А, так как нить может испытывать только растяжение.
Реакцию стержня
направим
вдоль нити от точки А, так как нить может испытывать только растяжение.
Реакцию стержня ![]() направим
также от точки А, предполагая, что стержень растянут (см. рисунок 2,б).
При этом, если в результате решения знак реакции
направим
также от точки А, предполагая, что стержень растянут (см. рисунок 2,б).
При этом, если в результате решения знак реакции ![]() получится
отрицательным, то это означает, что действительное направление реакции
противоположно принятому, то есть стержень испытывает сжатие. Можно изобразить
полученную плоскую систему сходящихся сил отдельно, как показано на рисунке 2,в.
Выберем систему координат, направив ось х вдоль линии действия
получится
отрицательным, то это означает, что действительное направление реакции
противоположно принятому, то есть стержень испытывает сжатие. Можно изобразить
полученную плоскую систему сходящихся сил отдельно, как показано на рисунке 2,в.
Выберем систему координат, направив ось х вдоль линии действия![]() , а ось у перпендикулярно ей.
, а ось у перпендикулярно ей.
Рисунок 2
Составим для полученной системы сил 2 уравнения равновесия:

![]()
![]()
Из второго уравнения находим
![]()
Из первого уравнения находим
![]()
Систему координат можно выбрать по-другому, при этом уравнения равновесия зависят от выбора системы координат, но искомые величины получатся такими же. При выборе системы координат, как показано на рисунке 2,д, в каждом уравнении равновесия будет по два неизвестных. На рисунке 3 представлен пример решения системы уравнений в Mathcad с использованием блока Given-Find.
Ответ: N1=23,4 Н, N2=43,9 Н (сжат).
|
|
Ответ: 3,68 кН, 3,39 кН (стержень сжат).
|
|
Задача 1.4 Кронштейн АВСD (см. рисунок 5) изготовлен из четырех шарнирно соединенных между собой стержней. К шарниру А прикреплен груз весом 8 кН. Определить методом вырезания узлов усилия во всех четырех стержнях.
Ответ: N1 = 9,6 кН (сжат), N2 =12,5 кН (растянут), N3 = 12,5 кН (сжат), N4 =19,2 кН (растянут).
|
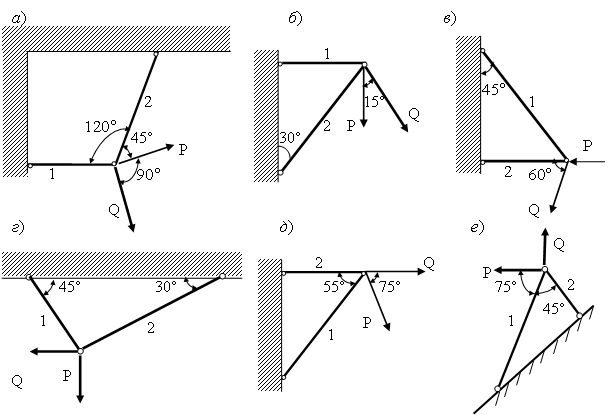
Задача 1.5. Определить усилия в стержнях конструкций, изображенных на рисунке 6, а–е, если Р=5 кН, Q=8 кН.
Ответ: а) N1 = 10,6 кН, N2 =7,43 кН (оба растянуты);
б) N1 = 9,42 кН (растянут), N2 =14,7 кН (сжат);
в) N1 = 9,8 кН (растянут), N2 =15,9 кН (сжат);
г) N1 = 0,35 кН, N2 =9,52 кН (оба растянуты);
д) N1 = 5,7 кН (сжат), N2 =12,7 кН (растянут);
е) N1 = 0,47 кН (сжат), N2 =9,76 кН (растянут).
Задача 1.6. Определить усилия в стержнях пространственной конструкции, изображенной на рисунке 7,a, если F=4 кН.
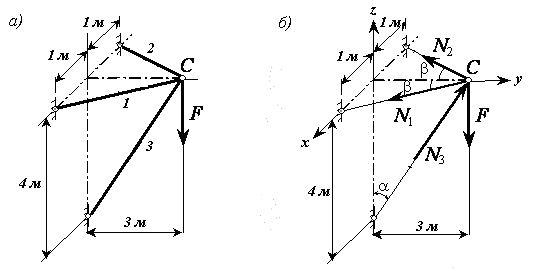
Рисунок 7
Решение.
Рассмотрим равновесие узла С. Реакции невесомых стержней направим вдоль стержней, при этом 1-й и 2-й
стержни испытывают растяжение и их реакции ![]() ,
,
![]() направлены
от узла, 3-й стержень испытывает сжатие, его реакция
направлены
от узла, 3-й стержень испытывает сжатие, его реакция ![]() направлена к узлу (см. рисунок 11,б). Выберем систему координат
Оxyz и составим уравнения равновесия для
полученной пространственной системы сходящихся сил.
направлена к узлу (см. рисунок 11,б). Выберем систему координат
Оxyz и составим уравнения равновесия для
полученной пространственной системы сходящихся сил.
åFkx = 0, N1sinb - N2sinb = 0, N1 = N2;
å Fkz = 0, N3cosa - F = 0,
å Fky = 0, N3sina - 2N1cosb =0, N1 = N3sina/(2cosb)
![]()
Ответ:
![]()
Рисунок 8
Задача 1.7. Определить усилия в стержнях пространственных конструкций, изображенных на рисунке 8,а,б, если Р=4 кН, Q=6 кН, α=60º.
Ответ: а) N1 = 16,5 кН, N2 = 10,5 кН (растянуты), N3 =15,4 кН (сжат) .
б) N1 = N2 = 8,3 кН (сжаты), N3 =12 кН (растянут) .
2 Равновесие плоских систем сил
Задача 2.1. Определить реакции связей балки, показанной на рисунке 9. В точке А балка имеет неподвижную шарнирную опору, в точке В – подвижную шарнирную опору на катках. На балку действует силы Р=5 кН; пара сил с моментом М = 2 кН∙м, равномерно распределенная нагрузка интенсивностью q = 1 кН/м. Заданы размеры: а1=2 м, а2=3 м, l=10 м.

Рисунок 9
Рисунок 10
Задача 2.2. Определить реакции связей балок, показанных на рисунке 11,а-г.
Задача 2.3. Определить реакции связей балок, показанных на рисунке 12, а,б при следующих данных: М=8 кН∙м, F=12 кН, q=4 кН/м.
Ответ: а) 3,1 кН, 21,5 кН, 30,1 кН; б) 4,97 кН, 3,07 кН, 2,85 кН.
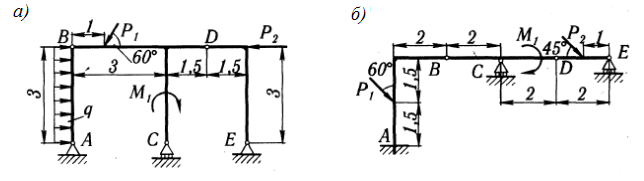
Задача 2.4. Определить реакции связей рамных конструкций, показанных на рисунке 13,а,б при следующих данных:
а) М=15 кН∙м, F=20 кН, q=4 кН/м, АВ=СD=3 м, ВС=4 м, СЕ=2 м;
б) М=9 кН∙м, F=12 кН, q=2 кН/м, АВ=5 м, ВС=3 м, ВЕ=2 м.
Ответ: а) 17,6 кН, 2 кН, 0,25 кН; б) 14,4 кН, 0,4 кН.
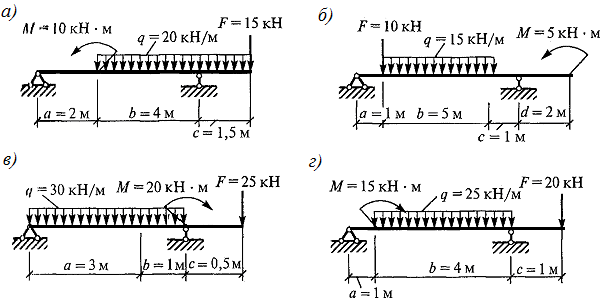
Рисунок 11
 Рисунок 12
Рисунок 12

Рисунок 13
Задача 2.5. Определить реакции жесткой заделки ломаного стержня, изображенного на рисунке 14,а, если F=10 кН, q=5 кН/м, M=15 кН∙м, AB=4 м, BC=2 м, CD=1 м.
Решение. Рассмотрим равновесие ломаного стержня, находящегося под действием сосредоточенной силы F, пары сил с моментом М и равномерно распределенной нагрузки интенсивностью q. Заменим распределенные силы равнодействующей, равной Q=q·АВ=20 кН и приложенной в середине участка АВ. Покажем реакции жесткой заделки А: две составляющие реактивной силы и момент жесткой заделки МА (см. рисунок 14,б).
Для полученной плоской системы сил составим 3 уравнения равновесия.
![]()
![]()
![]()
![]()

Рисунок 14
Выполним проверку правильности решения, составив дополнительное
уравнение равновесия:
![]()
![]()
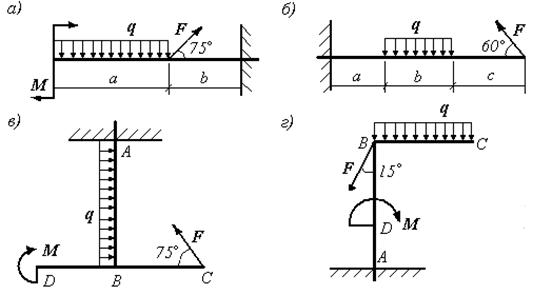
Рисунок 15
Задача 2.6. Определить реакции жестких заделок конструкций, показанных на рисунке 15,а-г при следующих данных:
а) М=12 кН∙м, F=10 кН, q=8 кН/м, а =2 м, b=1,5 м;
б) F=20 кН, q=6 кН/м, а =1 м, b=с=1,5 м;
в) М=15 кН∙м, F=12 кН, q=4 кН/м, АВ=CD=3 м, ВС=2 м;
г) М=6 кН∙м, F=14 кН, q=10 кН/м, АВ=5 м, ВС=BD=3 м.
Ответ: а) 2,6 кН, 6,3 кН, 13,5 кН∙м; б) 10 кН, 8,3 кН, 53,5 кН∙м;
в) 8,9 кН, 11,6 кН, 16,9 кН∙м; г) 3,6 кН, 42,5 кН, 32,9 кН∙м.
Задача 2.7. Мост состоит из двух одинаковых горизонтальных балок, соединенных шарниром А и прикрепленных шарнирно к основанию жесткими стержнями 1, 2, 3 и 4, причем крайние стержни вертикальны, а средние наклонены к горизонту под углом α=60° (см. рисунок 16,а). Даны размеры: АВ=8 м, ВС=6 м. Определить реакции внешних и внутренних связей моста, если мост несет вертикальную нагрузку P=15 кН, приложенную на расстоянии а=4 м от точки В.
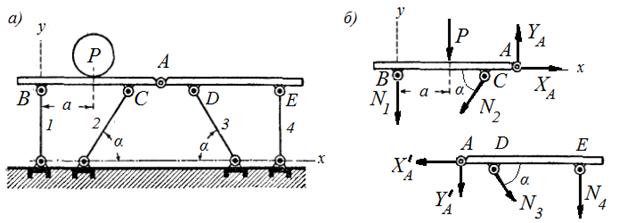
Рисунок 16
Решение. Расчленим конструкцию на 2 части и рассмотрим равновесие каждой балки в отдельности (см. рисунок 16,б). Направим реакции стержней от балок, предполагая, что стержни испытывают растяжение. Реакцию шарнира А разложим на две составляющие, при этом по аксиоме о равенстве действия и противодействия ХА′= ХА, YА ′=YА , а направлены они в противоположные стороны. Составим для каждой балки по 3 уравнения равновесия. В этих уравнениях будет 6 неизвестных, то есть задача является статически определимой.
Уравнения равновесия для балки АВ:
![]()
![]()
![]()
Уравнения равновесия для балки АЕ:
![]()
![]()
![]()
Решение
полученной системы уравнений проведем в системе Mathcad,
как показано на рисунке 17. Для проверки правильности решения составим
уравнение равновесия для всей конструкции, а именно вычислим сумму проекций на
ось у всех сил, приложенных к мосту: ![]()
Как видно на рисунке 17, проверочное условие сходится.
Ответ: N1 =-6,25кН, N2 =- 5,77кН, N3 =-5,77кН, N4 =1,25кН, ХА=-2,89кН, YА=3,77кН.
Задача 2.8. Определить реакции внешних связей составных конструкций, показанных на рисунке 18, а)-б) при следующих данных:
а) М=7 кН∙м, Р1=6 кН, Р2=8 кН, q=3 кН/м;
б) М=4 кН∙м,Р1=10 кН, Р2=12 кН, q=5 кН/м.
Ответ: а) ХА=3 кН, YА=8,49 кН, ХВ=-4,77 кН, YB=3,75 кН;
б) ХА=2,91 кН, YА=12,8 кН, ХВ=-2,52 кН, YB=8,23 кН.

Рисунок 17
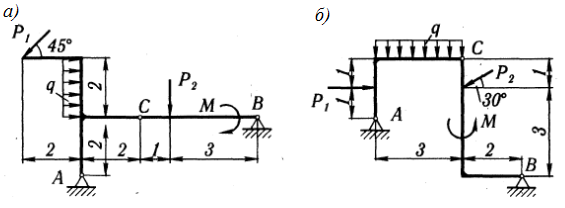
Рисунок 18
Задача 2.9. Определить реакции внешних связей составных конструкций, показанных на рисунке 19,а-б при следующих данных:
а) М1=5 кН∙м, Р1=3 кН, Р2=4 кН, q=2 кН/м;
б) М1=10 кН∙м, Р1=12 кН, Р2=15 кН.
Ответ: а) ХА=-3 кН, YА=-2,4 кН, RC=10 кН, ХE=2,5 кН, YЕ=-5 кН;
б) ХА=-21 кН, YА=-4,3 кН, МА=26,8 кН∙м, RC=15,6 кН, RE=5,3 кН.
 Рисунок
19
Рисунок
19
3 Равновесие пространственных систем сил
Задача 3.1. Определить реакции подшипников вала червячного редуктора, изображенного на рисунке 20, и уравновешивающий его момент М, если червяк находится под действием сил: F=3 кН, N=2 кН, Т1=2T2=6 кН, силы тяжести колес Р1=0,5 кН, Р2=0,4 кН, Р3=0,3 кН, вес груза Q=5 кН, вес вала G =0,2 кН. Заданы размеры: a=d=1,8 м, b=c=1,4 м, R1=0,6 м, R2=0,4 м, R3=0,5 м, угол α=30°.
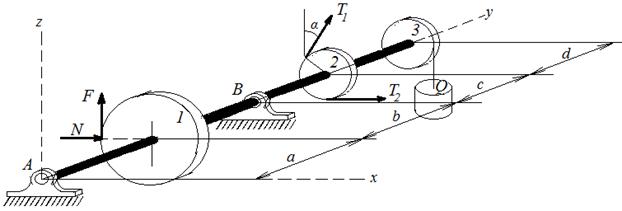
Рисунок 20
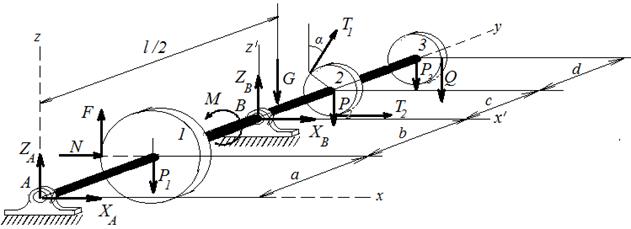
Рисунок 21
Задача 3.2. Определить удерживающую вал в равновесии силу Р и реакции опор вала (см. рисунок 22, а-г) при следующих данных:
а) Q=2 кН, G=3 кН, r=R/2, a=b=1 м, c=0,3 м;
б) Q=8 кН, G=4 кН, r=0,4 м, R=0,5 м, a=2 м, b=1 м, c=3 м;
в) Т=4 кН, G=5 кН, r=0,3 м, R=0,4 м, a=1 м, b=3 м, c=2 м;
г) Q=18 кН, G=10 кН, r=0,1 м, R=0,3 м, a=4 м, b=3 м, c=1 м.
Ответ: а) P=1 кН, XA=-0,68 кН, ZA=2,16 кН, XB =0,27кН, ZВ = 2,16 кН;
б) P=5 кН, XA=-2 кН, ZA=-2,8 кН, XB =-2 кН, ZВ = -0,13 кН;
в) P=5,2 кН, XA=-2 кН, ZA=-6,5 кН, XB =-11,9 кН, ZВ = -5,5 кН;
г) P=4,9 кН, XA=-0,3 кН, ZA=9,35 кН, XB =0,3 кН, ZВ =17,6 кН.
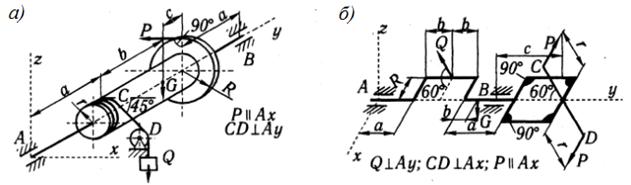
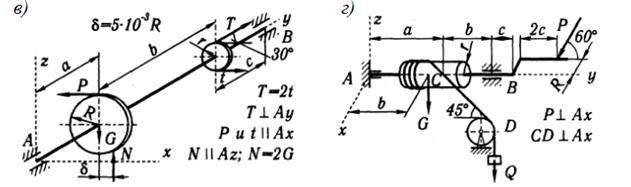
Рисунок 22
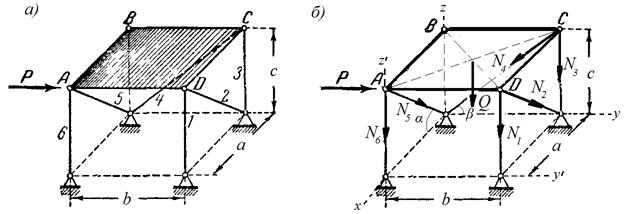
Рисунок 23

Рисунок 24
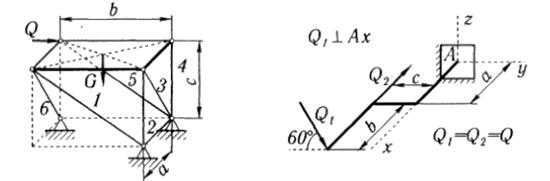
Рисунок 25 Рисунок 26
Задача 3.4. Определить реакции стержней, поддерживающих плиту весом G=6 кН при действии на нее горизонтальной силы Q=3 кН (см. рисунок 25), если а=3 м, b=5 м, c=4 м.
Ответ: N1 =-0,96 кН, N2 =-2,4 кН, N3 =0,75 кН, N4 =-1,2 кН, N5 =-2,88 кН, N6 = =-0,75 кН.
Задача 3.5. Определить реакции жесткой заделки А, если Q1=Q2=10 кН, а=2 м, b=3 м, c=1 м (см. рисунок 26).
Задача 3.6. Определить реакции сферического шарнира А, петли В и стержня СD, удерживающих плиту весом G (см. рисунок 27, а-б), при следующих данных: а) Q=8 кН, G=10 кН, а=5 м, b=1 м, c=3 м;
б) Q=5 кН, G=3 кН, а=4 м, b=3 м.
Ответ: а) XA = -11,85 кН, YA =2,31 кН, ZA =4,67 кН, XB =3,85 кН, ZB=1,33 кН, NCD=4,62 кН; б) XA = 6,13 кН, YA =0, ZA =-2,04 кН, XB =-3,54 кН, ZB=5,04 кН, NCD =-7,08 кН.
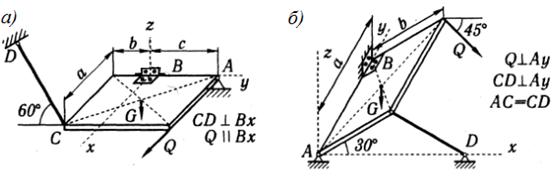
Рисунок 27
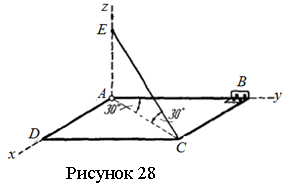 Задача 3.7.
Однородная
прямоугольная рама ABCD весом
20 Н прикреплена к стене при помощи сферического шарнира А и
петли В и удерживается в горизонтальном положении веревкой СЕ,
как показано на рисунке 28. Определить натяжение веревки и опорные реакции.
Задача 3.7.
Однородная
прямоугольная рама ABCD весом
20 Н прикреплена к стене при помощи сферического шарнира А и
петли В и удерживается в горизонтальном положении веревкой СЕ,
как показано на рисунке 28. Определить натяжение веревки и опорные реакции.
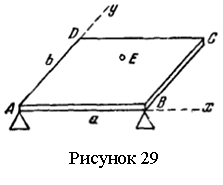 Задача 3.8.
Однородная
прямоугольная пластинка ABCD, опираясь на три точечные опоры, две из которых расположены
в вершинах прямоугольника А и В, а третья в некоторой точке Е,
удерживается в горизонтальном положении (см. рисунок 29). Вес пластинки равен Р,
давления на опоры в точках А и В соответственно равны Р/4
и Р/5 . Найти давление на опору Е и координаты этой точки, если
длины сторон пластины равны a и
b.
Задача 3.8.
Однородная
прямоугольная пластинка ABCD, опираясь на три точечные опоры, две из которых расположены
в вершинах прямоугольника А и В, а третья в некоторой точке Е,
удерживается в горизонтальном положении (см. рисунок 29). Вес пластинки равен Р,
давления на опоры в точках А и В соответственно равны Р/4
и Р/5 . Найти давление на опору Е и координаты этой точки, если
длины сторон пластины равны a и
b.
Ответ:
![]()
4 Кинематика точки
Задача 4.1. Точка движется равноускоренно из состояния покоя по окружности радиуса 100 м, при этом через 4 с от начала движения ее скорость равна 20 м/c. Определить скорость и ускорение точки в момент времени 6 с и пройденный за это время путь.
Задача 4.2. Точка движется по дуге радиуса 50 м с переменным касательным ускорением 6t м/с2, имея в начальный момент скорость 10 м/с. Определить скорость, ускорение и перемещение точки через 5 с от начала движения.
Задача 4.3. При отходе от станции скорость поезда возрастает равномерно и достигает величины 72 км/ч через 3 мин после отхода; путь расположен на закруглении радиуса 800 м. Определить касательное, нормальное и полное ускорения поезда через 2 мин после отхода от станции.
Задача 4.4. Поезд, имея начальную скорость 54 км/ч, прошел 600 м за 30 с. Считая движение поезда равнопеременным, определить скорость и ускорение поезда в этот момент времени, если путь находится на закруглении радиуса 1 км.
Задача 4.5. Считая посадочную скорость самолета равной 400 км/ч, определить его замедление при посадке на пути 1200 м, приняв замедление постоянным.
Задача 4.6. Точка движется по дуге окружности радиуса 2 м со скоростью v=30sin(2t) м/c. Определить ускорение точки в момент времени t=π/3 c.
Задача 4.7. Заданы уравнения движения точки на плоскости: x=2t, y=4t2-3 (координаты заданы в сантиметрах, время в секундах). Найти траекторию точки, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории в момент времени t=1 c.
Ответ: траектория – парабола y=x2-3, v=8,25см/с, a=8см/с2, aτ=7,76 см/с2, an=1,94 см/с2, ρ=35 см.
Задача 4.8. По заданным уравнениям движения точки на плоскости найти траекторию точки, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории в момент времени t1. Координаты заданы в сантиметрах, время в секундах.
Ответ: а) окружность радиуса 10 см с центром в начале координат, v = const = 31,4 см/с, aτ = 0, a = an = const = 98,6 см/с2, ρ = 10 см;
б) эллипс ![]() , v=35,1 см/с,
a=55,1 см/с2,
aτ=44,1 см/с2,
an=33 см/с2,
ρ=37,3 см;
, v=35,1 см/с,
a=55,1 см/с2,
aτ=44,1 см/с2,
an=33 см/с2,
ρ=37,3 см;
в) синусоида x =20 sin(πy/2), v = 62,9 см/с, a=683,1 см/с2, aτ =-682см/с2, an = 38,8 см/с2, ρ = 102 см;
г) парабола y= 10 - 1,25x2, v=0, aτ=0, a = an= 394,6 см/с2, ρ=0.
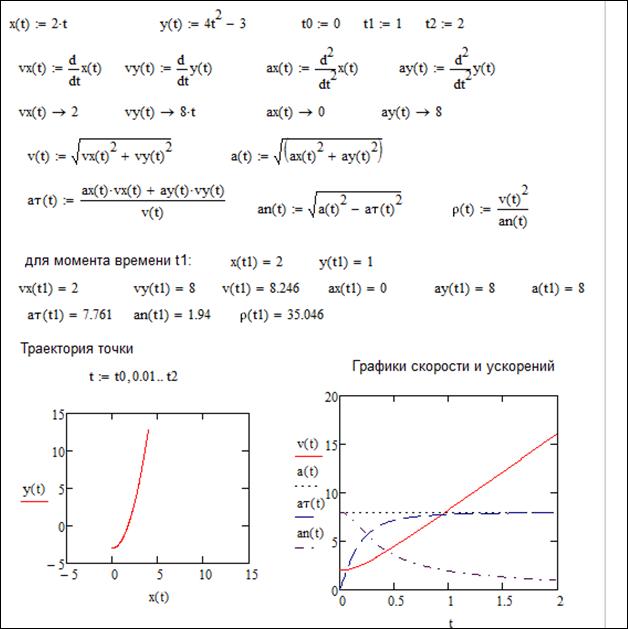
Рисунок 31
![]()
![]()
![]()
![]()
Уравнения
движения точки М имеют вид: ![]() . Найдем уравнение
траектории, исключив время t из уравнений
движения:
. Найдем уравнение
траектории, исключив время t из уравнений
движения: ![]()
Найдем проекции и модуль скорости точки:
![]()
![]()
![]()
Максимальное и
минимальное значения скорости: ![]() .
.
Найдем проекции и модуль ускорения точки:
![]()
![]()
![]() ,
,
где r – расстояние от
точки М до начала координат О, т.е. ускорение точки
пропорционально ее расстоянию до т.О. Найдем направляющие косинусы
вектора ускорения: ![]() . Отсюда следует, что
ускорение направлено к т. О (см. рисунок 32,б).
. Отсюда следует, что
ускорение направлено к т. О (см. рисунок 32,б).
Ответ:
эллипс ![]() ,
, ![]() ,
, ![]() .
.
Задача 4.10. Найти величину и направление ускорения, а также радиус кривизны траектории точки колеса, катящегося без скольжения по горизонтальной оси х (см. рисунок 33), если точка описывает циклоиду согласно уравнениям: x = 20t - sin(20t), y = 1 – cos(20t). Здесь t – в секундах, x,y - в метрах.
Ответ: ускорение a=400 м/с2 и направлено по МС к центру колеса, ρ=2МА.
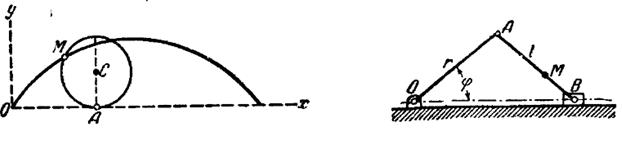
Рисунок 33 Рисунок 34
Задача 4.11. Найти траекторию точки М шатуна кривошипно-ползунного механизма, если r=l=60 см, МВ=l/3, φ=4π∙t (t – в секундах), а также определить скорость, ускорение и радиус кривизны траектории точки в момент времени, когда φ=0 (см. рисунок 34).
Ответ: эллипс ![]() , v = 80π см/с, a = 1600 π2 см/с2, ρ = 4 см.
, v = 80π см/с, a = 1600 π2 см/с2, ρ = 4 см.
Задача 4.12. Снаряд движется в вертикальной плоскости согласно уравнениям: x = 300t, y = 400t - 5t2 (t – в секундах, x,y – в метрах). Найти скорость и ускорение снаряда в начальный момент времени, высоту и дальность обстрела, радиус кривизны траектории в начальной и наивысшей точке.
Ответ: v0=500 м/с, a0=10 м/с2, h=8 км, s=24 км , ρ0=41,67 км , ρ=9 км.
Задача 4.13. Уравнения движения пальца кривошипа в период пуска имеют вид : x = 75cos4t2, y = 75sin4t2 (t – в секундах, x,y – в сантиметрах). Найти скорость, касательное и нормальное ускорения пальца.
Ответ: v=600t cм/с, aτ=600 cм/с2,an=4800t2 cм/c2.
Задача 4.14. Движение
точки задано уравнениями: x=a(ekt+e-kt),
y=a(ekt-
e-kt), где
a и
k
– заданные постоянные величины. Найти
уравнение траектории, скорость и ускорение точки, как функции радиуса-вектора ![]() .
.
Ответ: гипербола x2-y2=4a2, v=kr, a=k2r.
5 Кинематика простейших движений твердого тела
Задача 5.1. Тело, получившее в начальный момент времени угловую скорость 10 рад/с, через 4 секунды имеет угловую скорость 30 рад/с. Считая вращение тела равнопеременным, найти количество оборотов за это время.
Решение. Используем формулы угловой скорости и угла поворота при равнопеременном вращении: w=w0+et, j=j0+w0t+et2/2. Из первой формулы определяем угловое ускорение тела: e=(w-w0)/t =(30-10)/4=5 рад/c2. Считая начальный угол поворота j0 равным нулю, определяем угол поворота за 4 секунды: j=j0+w0t+et2/2=10×4+ +5×42/2=80 рад. Количество оборотов в минуту N=j /2p=12,74 обор.
Ответ: 12,74 оборота.
Задача 5.2. Вал, вращающийся из состояния покоя равноускоренно, за первые 5 секунд делает 12,5 оборота. Найти его угловую скорость в этот момент времени.
Ответ: 10p рад/с.
Задача 5.3. Тело с неподвижной осью вращения получает начальную угловую скорость 2p рад/с. Совершив 10 оборотов, тело вследствие трения в подшипниках остановилось. Считая вращение тела равнопеременным, найти его угловое ускорение.
Ответ: - 0,1p рад/с2.
Задача 5.4. Маховик, вращавшийся с частотой вращения n0=90 об/мин, с некоторого момента начинает вращаться равноускоренно и через 1,5 мин достигает частоты вращения n=150 обор/мин. Определить угловое ускорение маховика и количество совершенных им оборотов за 1,5 мин.
Ответ: p/45 рад/с2, 180 оборотов.
Задача 5.5. Тело
вращается по закону: ![]() Определить, за какое время
от начала движения тело достигнет угловой скорости 70 рад/с и сколько
оборотов оно успеет совершить за это время.
Определить, за какое время
от начала движения тело достигнет угловой скорости 70 рад/с и сколько
оборотов оно успеет совершить за это время.
Ответ: 4,25 с, около 18 оборотов.
Задача 5.6. Заданы
угловая скорость 1-го колеса
![]() и радиусы колес:
R1=0,3 м,
R2=0,2 м,
R3=0,4
м (см. рисунок 35,а). Найти в
момент времени t=3 с скорость
и ускорение груза 4, а также скорость и ускорение точки А,
лежащей на ободе 3-го колеса.
и радиусы колес:
R1=0,3 м,
R2=0,2 м,
R3=0,4
м (см. рисунок 35,а). Найти в
момент времени t=3 с скорость
и ускорение груза 4, а также скорость и ускорение точки А,
лежащей на ободе 3-го колеса.
Решение. Вращение от 1-го колеса передается 2-му, при этом направления вращений противоположны (см. рисунок 35,б), а отношение их угловых скоростей обратно пропорционально отношению радиусов колес:
![]()

Рисунок 35 Рисунок 36
Угловое
ускорение 2-го колеса ![]() Колесо 3
располагается на одной оси с колесом 2, поэтому их угловые скорости и
угловые ускорения одинаковы:
Колесо 3
располагается на одной оси с колесом 2, поэтому их угловые скорости и
угловые ускорения одинаковы: ![]() Найдем скорость и
ускорение груза 4 при t=3 c:
Найдем скорость и
ускорение груза 4 при t=3 c: ![]() Скорость и ускорение
точки А при t=3 c:
Скорость и ускорение
точки А при t=3 c:
![]()
![]()
Направление
полного ускорения точки А определим с помощью угла наклона вектора
полного ускорения к радиусу: ![]() .
.
Ответ: ![]()
![]()
![]()
Задача 5.7. Подвешенный на нити груз, опускаясь с ускорением a=2t м/с2, приводит во вращение вал радиуса R=0,2 м (см. рисунок 36). Считая, что начальная скорость груза равна нулю, определить через 5 секунд от начала движения скорость, касательное и нормальное ускорения точки М, лежащей на поверхности вала.
Ответ:
v=25 м/с, ![]()
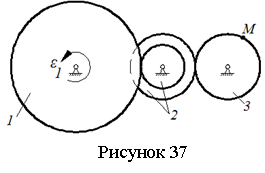 Задача 5.8.
Колесо 1 начинает вращаться из состояния покоя с угловым ускорением
Задача 5.8.
Колесо 1 начинает вращаться из состояния покоя с угловым ускорением ![]() и приводит в движение колеса 2 и
3. Заданы радиусы колес: R1=0,6
м, R2=0,3 м,
r2=0,2 м,
R3=0,15
м (см. рисунок 37). Найти в момент
времени t=4 с скорость,
касательное и нормальное ускорения точки М, лежащей на его ободе.
и приводит в движение колеса 2 и
3. Заданы радиусы колес: R1=0,6
м, R2=0,3 м,
r2=0,2 м,
R3=0,15
м (см. рисунок 37). Найти в момент
времени t=4 с скорость,
касательное и нормальное ускорения точки М, лежащей на его ободе.
Ответ:
![]()
![]()
Задача 5.9. Груз 1 опускается по заданному закону x=x(t) (см. рисунок 38, а-б). Найти в момент времени t1 скорость, касательное и нормальное ускорения точки М при следующих данных:
а) x=5t2-2t cм, t1 =1 с, R2=30 cм, r2=10 cм, R3=15 cм;
б) x=25t2+10t+40 cм, t1 =2 с, R2=40 cм, r2=20 cм, R3=80 cм, r3=18 cм;
в) x=0,4t2-0,5t+0,3 м, t1 =4 с, R2=0,3 м, r2=0,15 м, R3=0,4 м.
Ответ:
а)![]()
б)![]()
в)![]()
Задача 5.10. Редуктор скорости, служащий для замедления вращения и передающий вращение вала I валу II , состоит из четырех шестерен с соответствующим числом зубцов: z1=10, z2=60, z3=12, z4=70. Определить передаточное отношение механизма (см. рисунок 39).
Ответ:
![]()
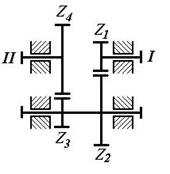
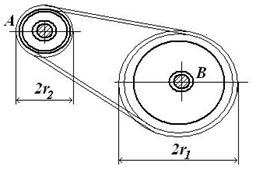
Рисунок 39 Рисунок 40
Задача 5.11. Станок со шкивом А приводится в движение из состояния покоя бесконечным ремнем от шкива В электромотора (см. рисунок 40). Радиусы шкивов: r1=75 см, r2=30 см. После пуска электромотора его угловое ускорение равно 0,4p рад/с2. Пренебрегая скольжением ремня по шкивам, определить через какое время угловая скорость станка будет равна 10p рад/с.
Ответ: 10 с.
Задача 5.12. В механизме стрелочного индикатора движение от рейки мерительного штифта 1 передается шестерне 2, на оси которой укреплено зубчатое колесо 3, сцепляющееся с шестерней 4, несущей стрелку (см. рисунок 41). Определить угловую скорость стрелки, если движение штифта задано уравнением x=asinkt и радиусы зубчатых колес равны r2, r3 и r4.
Ответ: ![]()
Задача 5.13. В механизме домкрата при вращении рукоятки А начинают вращаться шестерни 1,2,3,4 и 5 , которые приводят в движение зубчатую рейку В домкрата (см. рисунок 42). Числа зубцов шестерен: z1=10, z2=60, z3=12, z4=70, радиус пятой шестерни r5=4 см. Определить скорость рейки В, если рукоятка А вращается с угловой скоростью p рад/с .
Ответ: 7,8 мм/с.
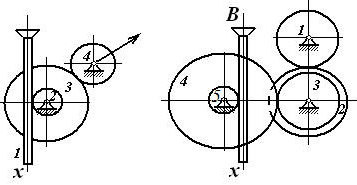
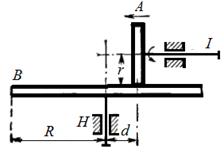
Рисунок 41 Рисунок 42 Рисунок 43
Задача 5.14. Ведущий вал I фрикционной передачи (см. рисунок 43) вращается с угловой скоростью 20p рад/с и на ходу передвигается (направление указано стрелкой) так, что расстояние d меняется по закону d=(10-0,5t) см (t в секундах). Радиусы колес r=5 см, R=15 см. Определить угловое ускорение вала II как функцию расстояния d, а также ускорение точки на ободе колеса В в тот момент, когда d=r .
 Ответ:
Ответ:![]()
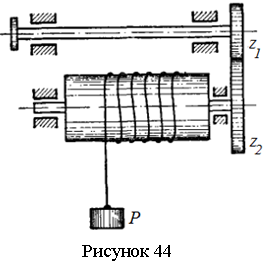
Задача 5.15. Для подъема груза Р служит электрическая лебедка, состоящая из ведущего вала с насаженной на нем шестеренкой с числом зубцов z1 (см. рисунок 44). Груз поднимается при вращении ведомого вала, на который насажена шестеренка с числом зубцов z2. При этом канат, на котором подвешен груз Р, наматывается на барабан радиусом R. Уравнение вращения ведущего вала имеет вид: φ1=2π∙t2 рад. Определить ускорение груза Р.
 Ответ:
Ответ:
![]()
6 Плоское движение твердого тела
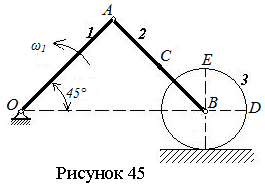
 Задача 6.1.
Механизм
состоит из двух стержней и колеса, соединенных между собой с помощью шарниров
(см. рисунок 45). Заданы размеры: ОА=АВ=40 см,
R=10
см, угловая скорость 1-го
тела ω1=6 рад/с, колесо 3 катится без
скольжения. Найти в показанном на рисунке положении механизма скорости точек
А,
В, С, D, Е и
угловые скорости 2-го и 3-го тел.
Задача 6.1.
Механизм
состоит из двух стержней и колеса, соединенных между собой с помощью шарниров
(см. рисунок 45). Заданы размеры: ОА=АВ=40 см,
R=10
см, угловая скорость 1-го
тела ω1=6 рад/с, колесо 3 катится без
скольжения. Найти в показанном на рисунке положении механизма скорости точек
А,
В, С, D, Е и
угловые скорости 2-го и 3-го тел.
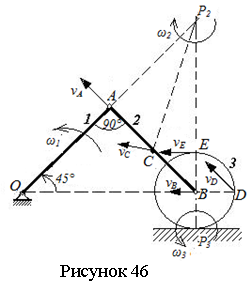
Решение. Стержень ОА вращается вокруг неподвижной оси, проходящей через точку О, стержень АВ и колесо совершают плоское движение. Найдем скорость точки А: vА=w1·OA=240 см/с. Вектор скорости точки А направим перпендикулярно ОА в сторону вращения 1-го тела (см. рисунок 46). Точка В движется по горизонтальной прямой, поэтому можно показать направление ее скорости. Зная направления скоростей двух точек 2-го тела, можно найти его мгновенный центр скоростей Р2, как точку пересечения перпендикуляров к скоростям двух точек А и В. Угловая скорость 2-го тела находится по формуле: w2=vA/AP2. Так как AP2=АВ, получаем w2=vA/AВ=6 рад/с. Скорости точек В и С, принадлежащих 2-му телу, найдем по формулам: vВ=w2·Р2В, vC=w2·Р2C. Из геометрии находим
![]()
Тогда vВ=339,4 см/с, vC=268,3 см/с.
Так как направление скорости точки В известно, ее можно было найти также по теореме о проекциях скоростей двух точек тела на прямую, проходящую через эти точки: vВх= vАх или vB·cos45°=vA . Отсюда vB=vA/cos45°=339,4 см/с.
Так как колесо 3 катится без скольжения, то его мгновенный центр скоростей Р3 находится в точке касания колеса о неподвижную плоскость. Найдем угловую скорость 3-го тела и скорости его точек:
![]()
![]()
Ответ: vА=240 см/с, vВ=339,4 см/с, vC=268,3 см/с, vD=450 см/с, vE=678,8 см/с.
Задача 6.2. В кривошипном механизме длина кривошипа ОА=40 см, длина шатуна АВ=2 м (см. рисунок 47). Кривошип вращается равномерно с угловой скоростью ωOA=6π рад/с. Найти угловую скорость шатуна и скорость его средней точки М при четырех положениях кривошипа, для которых угол АОВ соответственно равен 0, π/2, π, 3π/2.
Ответ: I) ωАВ= -6π/5 рад/с, vM=377 см/; II) ωАВ= 0, vM=754 см/; III) ωАВ= 6π/5 рад/с, vM=377 см/с; IV) ωАВ= 0, vM=754 см/с.
Рисунок 47 Рисунок 48
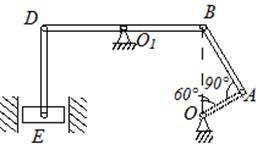
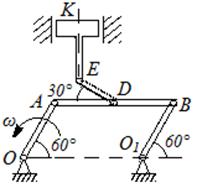
Рисунок 49 Рисунок 50
Задача 6.4. Стержень ОВ вращается вокруг оси О с постоянной угловой скоростью ω=2 рад/с и приводит в движение стержень АD, точки А и С которого движутся по осям (см. рисунок 48). Определить скорость точки D при φ=45°, если ОВ=АВ=ВС=СD=12 см.
Ответ: 53,7 см/с.
Задача 6.5. Определить скорость поршня Е приводного механизма насоса в положении, указанном на рисунке 49, если звено ОА=20 см, О1В=О1D. Кривошип ОА вращается равномерно с угловой скоростью 2 рад/с.
Ответ: 46,2 см/с.
Задача 6.6. К середине D стержня AB шарнирного параллелограмма ОАВО1 присоединен с помощью шарнира D стержень DЕ, приводящий в возвратно-поступательное движение ползун К. Определить скорость ползуна К и угловую скорость стержня DЕ в положении, указанном на рисунке 50, если ОА=О1В=2DЕ=20 см, а угловая скорость звена ОА равна в данный момент 1 рад/с.
Ответ: vK =40 см/с, ωDЕ = 3,46 рад/с.
Задача 6.7. Найти угловую скорость шатуна АВ и скорости точек В, С в показанном на рисунке 51 положении механизма, если ωОА=5 рад/с, ОА=40 см, АВ=70 см, ВС=20 см.
Ответ: ωАВ = 2 рад/с, vВ =141 см/с, vС = 146 см/с.
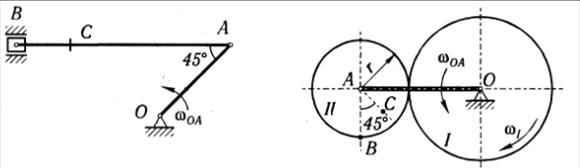
Рисунок 51 Рисунок 52
Задача 6.8. Заданы угловые скорости колеса I и водила ОА: ωI=3 рад/с, ωОА=4 рад/с. Найти угловую скорость колеса II и скорости его точек В, С, если ОА=60 см, r=20 см, АС=15 см (см. рисунок 52).
Ответ: ωII = 18 рад/с, vВ =433 см/с, vС = 197 см/с.
Задача 6.9. Колесо радиуса R=0,4 м катится без скольжения по неподвижной плоскости с замедлением, имея в данный момент времени vС=3м/с, аС=2 м/с2 ( см. рисунок 53,а). Определить в рассматриваемый момент скорости и ускорения точек колеса А, В и D.
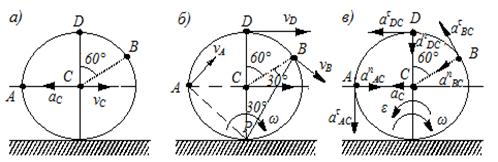
Рисунок 53
Решение.
Так как колесо катится без скольжения, то его мгновенный центр скоростей
Р находится в точке касания колеса о неподвижную плоскость (см. рисунок
53,б). Найдем угловую скорость колеса: ![]() Скорости
точек колеса:
Скорости
точек колеса:
Угловое
ускорение колеса находим как производную по времени от его угловой скорости: ![]() Так как движение колеса замедляется, то
направление углового ускорения противоположно направлению угловой скорости (см.
рисунок 53,в).
Так как движение колеса замедляется, то
направление углового ускорения противоположно направлению угловой скорости (см.
рисунок 53,в).
Ускорения
точек найдем по теореме об ускорениях точек тела при плоском движении: ![]() Здесь
Здесь ![]() Вектор
Вектор
![]() и направлен в соответствии с направлением
ε, вектор
и направлен в соответствии с направлением
ε, вектор ![]() направлен от точки А к
полюсу С. Аналогично находим для других точек колеса:
направлен от точки А к
полюсу С. Аналогично находим для других точек колеса: ![]()
![]()
Для определения ускорений точек, проецируем векторные равенства для их ускорений на оси х и у:
![]()
![]()
Модуль
ускорения точки А:
![]()
Аналогично найдем ускорения точек B и D:
![]()
![]()
Ответ: vА=4,23 м/с, vВ=5,2м/с, vD=6 м/с, aА=20,6м/с2, aВ=24,4м/с2, aD=22,9м/с2.
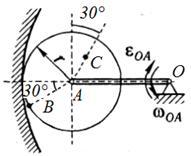

Рисунок 54 Рисунок 55 Рисунок 56
Задача 6.10. Колесо катится без скольжения в вертикальной плоскости по наклонному прямолинейному пути (см. рисунок 54). Найти ускорения двух взаимно перпендикулярных концов диаметров колеса, один из которых параллелен рельсу, если в рассматриваемый момент скорость центра колеса vО=1 м/с, ускорение центра колеса аО=3 м/с2 , радиус колеса R=0,5 м.
Ответ: аМ1=2 м/с2 , аМ2=3,16 м/с2 , аМ3=6,32 м/с2 , аМ4=5,83 м/с2 .
Задача 6.11. Найти угловую скорость и угловое ускорение колеса, катящегося без скольжения по неподвижной поверхности, а также скорости и ускорения его точек В и С, если ωОА=2 рад/с, εОА=6 рад/с2, ОА=0,6 м, r=0,4 м, АC=0,2 м (см. рисунок 55).
Ответ: ω=3 рад/с, ε=9 рад/с2, vВ =0,6 м/с, vС = 1,6 м/с, аB=7,5 м/с2, аC=3,4 м/с2.
Задача 6.12. Найти угловую скорость и угловое ускорение колеса, катящегося без скольжения по неподвижному колесу, а также скорости и ускорения его точек В и С, если ωОА=4 рад/с, εОА=2 рад/с2, ОА=1 м, r=0,4 м, АC=0,3 м (см. рисунок 56).
Ответ: ω=10 рад/с, ε=5 рад/с2, vВ =8 м/с, vС =4 м/с, аB=56,1 м/с2, аC=33,7 м/с2.
Задача 6.13. Кривошип ОА шарнирно-рычажного механизма вращается с постоянной угловой скоростью ωОА=2 рад/с (см. рисунок 57,а). Определить в изображенном положении механизма угловые скорости и угловые ускорения звеньев АВ и ВD, а также скорости и ускорения его точек В и С, если ОА=20 см, АВ=ВD=30 см.
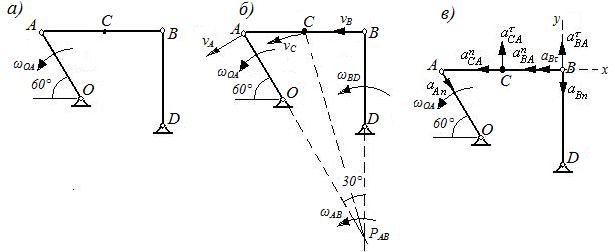
Рисунок 57
Решение.
Найдем скорость точки А: vА=w1·OA=40
см/с. Вектор скорости точки А направим перпендикулярно ОА в
сторону вращения кривошипа (см. рисунок 57,б). Так как точка В
принадлежит вращающемуся звену ВD, направление
ее скорости известно. Зная направления скоростей двух точек звена АВ,
найдем его мгновенный центр скоростей РАВ, как точку
пересечения перпендикуляров к скоростям двух точек А и В.
Угловая скорость звена АВ находится по формуле: wАВ=vA/APАВ. Так как APАВ=2АВ,
получаем wАВ=vA/(2AВ)=2/3 рад/с.
Скорости точек В и С, принадлежащих звену АВ, найдем по формулам:
vВ=wАВ·ВРАВ,
vC=wАВ·СРАВ. Из геометрии ![]()
![]() Тогда
vВ=34,6 см/с,
vC=36,1
см/с.
Тогда
vВ=34,6 см/с,
vC=36,1
см/с.
Найдем угловую скорость звена BD: wВD = vB / BD = 1,15 рад/с.
Ускорение
точки А кривошипа: ![]() где нормальное
ускорение
где нормальное
ускорение ![]() и направлено к оси вращения О,
касательное ускорение
и направлено к оси вращения О,
касательное ускорение ![]() так как ωОА=const. Ускорение точки В, принадлежащей
вращающемуся звену ВD, находится по
формуле:
так как ωОА=const. Ускорение точки В, принадлежащей
вращающемуся звену ВD, находится по
формуле: ![]() где нормальное ускорение
где нормальное ускорение ![]() и направлено к оси вращения D, а касательное ускорение
и направлено к оси вращения D, а касательное ускорение ![]() неизвестно
по величине, но известно, что
неизвестно
по величине, но известно, что ![]() выберем направление
вектора
выберем направление
вектора ![]() , как показано на рисунке 57,в.
, как показано на рисунке 57,в.
Ускорение
точки В можно найти по теореме об ускорениях точек тела при плоском
движении, приняв за полюс точку А: ![]() или
или
![]() . Здесь
. Здесь ![]() вектор
вектор
![]() направлен от точки В к полюсу А.
Вектор
направлен от точки В к полюсу А.
Вектор![]() , а его величина определяется по формуле
, а его величина определяется по формуле![]() , где
, где ![]() пока
неизвестно. Направим ось х по АВ, ось у перпендикулярно АВ
и спроецируем векторное равенство для ускорений на координатные оси (см. рисунок
57,в). Получаем два уравнения:
пока
неизвестно. Направим ось х по АВ, ось у перпендикулярно АВ
и спроецируем векторное равенство для ускорений на координатные оси (см. рисунок
57,в). Получаем два уравнения:
на х: ![]() на у:
на у: ![]()
Из первого
равенства находим: ![]() Тогда модуль ускорения точки В:
Тогда модуль ускорения точки В:
![]() , угловое ускорение звена ВD:
, угловое ускорение звена ВD: ![]() , где отрицательный
знак показывает, что вращение звена BD в данный момент замедляется.
, где отрицательный
знак показывает, что вращение звена BD в данный момент замедляется.
Из второго
равенства найдем: ![]() . Тогда угловое ускорение
звена АВ :
. Тогда угловое ускорение
звена АВ :
![]()
Найдем теперь
ускорение точки С по той же теореме, принимая за полюс точку А: ![]() . Здесь
. Здесь ![]() вектор
вектор![]() и направлен в ту же сторону, что и
и направлен в ту же сторону, что и ![]() , поскольку
, поскольку ![]() положительно,
положительно,
![]() вектор
вектор ![]() направлен
от точки С к полюсу А. Проецируем векторное равенство для
ускорений на координатные оси:
направлен
от точки С к полюсу А. Проецируем векторное равенство для
ускорений на координатные оси:
![]()
Модуль
ускорения точки С:
![]()
Ответ: wАВ=0,67 рад/с, εАВ=0,99 рад/с2, wВD= 1,15 рад/с, εВD=-0,89 рад/с2, vВ=34,6 cм/с, vC=36,1 cм/с, aB=47,8 cм/с2, aC=63,8 cм/с2.
Задача 6.14. Найти скорости и ускорения точек В и С в показанном положении (см. рисунок 58, а-в) при следующих данных:
а) ωОА=1 рад/с, εОА=2 рад/с2, ОА=0,4 м, АВ=0,7 м, АC=0,3 м;
б) vА=10 м/с, аС=30 м/с2 , АВ=1 м, АC=0,6 м;
в) ωОА=2 рад/с, εОА=3 рад/с2, ОА=0,3 м, АВ=1 м, АC=0,5 м.
Ответ: а) vВ =0,35 м/с, vС =0,37 м/с, аB=0,44 м/с2, аC=0,89 м/с2;
б) vВ =5,78 м/с, vС =5,29 м/с, аB=136,7 м/с2, аC=94,3 м/с2;
в) vВ =0,52 м/с, vС =0,54 м/с, аB=0,27 м/с2, аC=0,77 м/с2.
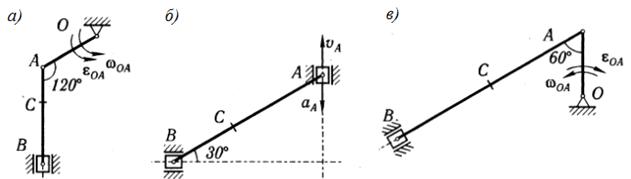
Рисунок 58
7 Сложное движение точки
Задача 7.1. Кривошип ОА=r вращается в плоскости чертежа вокруг неподвижной точки О согласно уравнению φ=kt (см. рисунок 59,а). Ползун А при этом перемещается в наклонной кулисе В, которая может перемещаться поступательно вдоль оси Ох. Угол наклона кулисы к оси Ох равен α. Найти абсолютную, относительную и переносную скорость точки А.
Решение.
Свяжем систему координат О1х1у1
с кулисой В и рассмотрим движение точки А, как сложное, состоящее
из двух движений. Движение точки А вместе с подвижной системой координат
О1х1у1 является переносным, ее
переносная скорость ![]() равна скорости кулисы и
направлена параллельно оси х. Движение точки А относительно
подвижной системы координат О1х1у1, т.е
движение по отношению к кулисе, является относительным, относительная скорость
точки
равна скорости кулисы и
направлена параллельно оси х. Движение точки А относительно
подвижной системы координат О1х1у1, т.е
движение по отношению к кулисе, является относительным, относительная скорость
точки ![]() направлена вдоль кулисы. Движение точки
А относительно неподвижной системы координат Оху является
абсолютным, по данным задачи можно найти ее абсолютную скорость:
направлена вдоль кулисы. Движение точки
А относительно неподвижной системы координат Оху является
абсолютным, по данным задачи можно найти ее абсолютную скорость: ![]() Вектор абсолютной скорости точки А
Вектор абсолютной скорости точки А
![]() направлен перпендикулярно ОА в
сторону вращения кривошипа.
направлен перпендикулярно ОА в
сторону вращения кривошипа.
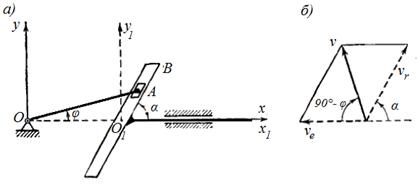

Рисунок 59 Рисунок 60
По теореме о
сложении скоростей ![]() . Начнем построение с вектора
абсолютной скорости
. Начнем построение с вектора
абсолютной скорости ![]() , известной по величине и
направлению, с начала вектора
, известной по величине и
направлению, с начала вектора ![]() проведем линию,
параллельную относительной скорости
проведем линию,
параллельную относительной скорости ![]() , с конца - линию,
параллельную переносной скорости
, с конца - линию,
параллельную переносной скорости ![]() , в результате
получим треугольник, расставим в нем стрелки векторов согласно теореме о
сложении скоростей (см. рисунок 59,б). По теореме синусов имеем
, в результате
получим треугольник, расставим в нем стрелки векторов согласно теореме о
сложении скоростей (см. рисунок 59,б). По теореме синусов имеем
![]() или
или ![]()
Отсюда ![]()
Ответ:
![]()
Задача 7.2. Шары центробежного регулятора Уатта (см. рисунок 60), вращающегося вокруг вертикальной оси с угловой скоростью ω=10 рад/с, благодаря изменению нагрузки машины отходят от этой оси, имея для своих стержней в данном положении угловую скорость ω1=1,2 рад/с. Найти абсолютную скорость шаров регулятора в данный момент, если длина стержней l=50 см, расстояние между осями их привеса 2e=10 см, углы, образованные стержнями с осью регулятора α1=α2=α=30°.
Ответ: 306 см/с.
Задача 7.3. Корабль
плывет на юг со скоростью ![]() км/час. Второй корабль
идет курсом на юго-восток со скоростью 30 км/час. Найти величину и
направление скорости второго корабля, определяемые наблюдателем, находящемся на
палубе первого корабля.
км/час. Второй корабль
идет курсом на юго-восток со скоростью 30 км/час. Найти величину и
направление скорости второго корабля, определяемые наблюдателем, находящемся на
палубе первого корабля.
Ответ: vr =30 км/час, скорость направлена на северо-восток.
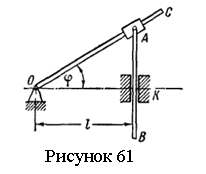 Задача 7.4.
В
кулисном механизме при качании кривошипа ОС вокруг оси О, перпендикулярной
плоскости чертежа, ползун А, перемещаясь вдоль кривошипа ОС,
приводит в движение стержень АВ, движущийся в вертикальных направляющих К
(см. рисунок 61). Расстояние ОК=l
. Определить скорость движения ползуна А относительно
кривошипа ОС в функции от угловой скорости ω и угла поворота
кривошипа φ.
Задача 7.4.
В
кулисном механизме при качании кривошипа ОС вокруг оси О, перпендикулярной
плоскости чертежа, ползун А, перемещаясь вдоль кривошипа ОС,
приводит в движение стержень АВ, движущийся в вертикальных направляющих К
(см. рисунок 61). Расстояние ОК=l
. Определить скорость движения ползуна А относительно
кривошипа ОС в функции от угловой скорости ω и угла поворота
кривошипа φ.
Ответ: ![]()
 Задача 7.5.
В
кривошипно-кулисном механизме с поступательно движущейся кулисой ВС кривошип
ОА, расположенный позади кулисы (см. рисунок 62), длины ОА=0,2 м
вращается с постоянной угловой скоростью 3π рад/с. Концом А,
соединенным шарнирно с камнем, скользящим в прорези кулисы, он сообщает кулисе
возвратно-поступательное движение. Определить скорость кулисы в момент, когда
кривошип образует с осью кулисы угол 30°.
Задача 7.5.
В
кривошипно-кулисном механизме с поступательно движущейся кулисой ВС кривошип
ОА, расположенный позади кулисы (см. рисунок 62), длины ОА=0,2 м
вращается с постоянной угловой скоростью 3π рад/с. Концом А,
соединенным шарнирно с камнем, скользящим в прорези кулисы, он сообщает кулисе
возвратно-поступательное движение. Определить скорость кулисы в момент, когда
кривошип образует с осью кулисы угол 30°.
Ответ: 0,942 м/с.
Задача 7.6. Квадратная плита А движется по вертикали согласно уравнению z1=3t-t2 м (см. рисунок 63,а). Находящаяся на плите точка М движется по дуге радиуса R=0,3 м согласно уравнению s=OM=0,1π∙t2 м (s измеряется по дуге). Определить абсолютную скорость и абсолютное ускорение точки М в момент времени t=1 c.
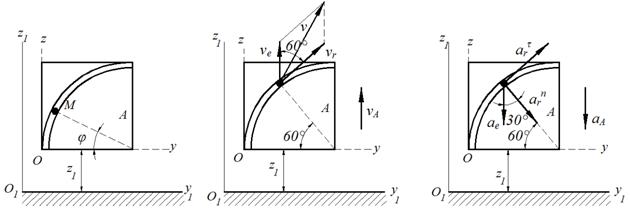 Рисунок 63
Рисунок 63
Решение.
Движение точки М является сложным, ее движение по плите является
относительным, а движение вместе с плитой – переносным. По теореме о сложении
скоростей ![]() , по теореме о сложении ускорений
, по теореме о сложении ускорений ![]() .
.
Рассмотрим
относительное движение точки М. Положение точки на плите можно
определить с помощью центрального угла дуги: φ=s/R. Относительные скорость и ускорение точки М
определяются по формулам: ![]()
При t=1с имеем:
s=0,1π, φ=s/R=π/3=60°, ![]()
Рассмотрим
переносное движение точки М. Так как движение плиты А является поступательным,
переносная скорость и переносное ускорение точки М равны соответственно
скорости и ускорению плиты: ![]() В рассматриваемый
момент
В рассматриваемый
момент ![]() В случае поступательного переносного движения
кориолисово ускорение точки равно нулю: ас=0.
В случае поступательного переносного движения
кориолисово ускорение точки равно нулю: ас=0.
Покажем в рассматриваемый момент времени положение точки М, векторы ее относительной и переносной скорости, относительного касательного, относительного нормального и переносного ускорений, как показано на рисунках 63,а-б.
Проецируем векторные равенства абсолютной скорости и абсолютного ускорения на координатные оси y и z:

Найдем модуль абсолютной скорости и абсолютного ускорения точки М:

![]()
Ответ: v=1,42 м/с, а=3,04 м/с2.
Задача 7.7. На тележке, движущейся по горизонтали вправо с ускорением а=49,2см/с, установлен электрический мотор, ротор которого при пуске в ход вращается согласно уравнению φ=t2 , где угол φ измеряется в радианах (см. рисунок 64). Радиус ротора равен 20 см. Определить абсолютное ускорение точки А, лежащей на ободе ротора, при t=1 c, если в это момент точка А находится в положении, указанном на рисунке.
Ответ: аА =74,6 см/с2, ускорение направлено по вертикали вверх.
Задача 7.8. Точка М движется по телу D согласно уравнению sr=OM=16-8cos(3π∙t) cм, которое, в свою очередь, вращается вокруг вертикальной оси согласно уравнению φе=0,9t2-9t3 рад ( см. рисунок 65,а). Определить при t1=2/9 c абсолютные скорость и ускорение точки М.
Решение.
Будем считать, что в заданный момент времени плоскость рисунка совпадает
с плоскостью треугольника D. Относительные
скорость и ускорение точки М определяются по формулам: ![]() При t1=2/9c имеем: sr=16-8cos(3π·2/9)=20см,
При t1=2/9c имеем: sr=16-8cos(3π·2/9)=20см,
![]() Вектор
Вектор ![]() направлен в сторону
положительных значений sr , а вектор
направлен в сторону
положительных значений sr , а вектор ![]() направлен в
противоположную сторону, так как
направлен в
противоположную сторону, так как ![]() отрицательно (см. рисунки 65,б-в).
отрицательно (см. рисунки 65,б-в).
Рассмотрим переносное
движение точки М, т.е. движение той точки тела D,
с которой в данный момент времени совпадает точка М. Траекторией этого
движения является окружность L радиуса R=sr·sin30°=10 см. Переносные скорость и ускорение точки М
определяются по формулам: ![]() , где
, где ![]()
![]() При
t1=2/9c
имеем:
При
t1=2/9c
имеем: ![]()
![]() Отрицательные значения ωе и
εе означают, что их направления противоположны
направлению отсчета угла φе. Модуль вектора переносной
скорости
Отрицательные значения ωе и
εе означают, что их направления противоположны
направлению отсчета угла φе. Модуль вектора переносной
скорости ![]() вектор
вектор ![]() направлен
по касательной к траектории переносного движения в сторону ωе.
Модули переносных ускорений
направлен
по касательной к траектории переносного движения в сторону ωе.
Модули переносных ускорений ![]() Вектор
Вектор ![]() направлен так же, как
направлен так же, как ![]() , вектор
, вектор ![]() направлен
к центру окружности L.
направлен
к центру окружности L.
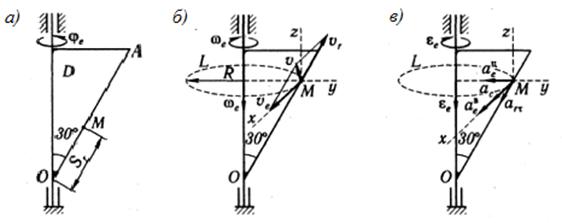
Рисунок 65
Вектор
кориолисова ускорения точки равен ![]() Найдем величину кориолисова
ускорения:
Найдем величину кориолисова
ускорения: ![]() где угол
где угол ![]() С учетом
найденных значений получаем ас=61 см/с2. Направление
кориолисова ускорения можно найти по правилу векторного произведения или по
правилу Жуковского. Для определения направления
С учетом
найденных значений получаем ас=61 см/с2. Направление
кориолисова ускорения можно найти по правилу векторного произведения или по
правилу Жуковского. Для определения направления ![]() по
правилу Жуковского проецируем вектор
по
правилу Жуковского проецируем вектор ![]() на плоскость,
перпендикулярную оси переносного вращения, и затем повернем полученный вектор
на 90° в сторону переносного вращения (см. рисунок 65,в).
на плоскость,
перпендикулярную оси переносного вращения, и затем повернем полученный вектор
на 90° в сторону переносного вращения (см. рисунок 65,в).
По теореме о
сложении скоростей ![]() . Так как
. Так как ![]() , то модуль абсолютной скорости
, то модуль абсолютной скорости ![]()
По теореме о
сложении ускорений ![]() или
или ![]() .
Найдем абсолютное ускорение способом проекций:
.
Найдем абсолютное ускорение способом проекций:
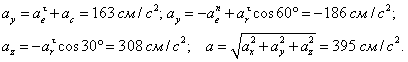
Ответ: v=65,9 см/с, а=395 см/с2.
Задача 7.9. Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t1 (см. рисунок 66,а-в) при следующих данных:
а) φe=π∙t(2-3t) рад, ОM=30t2 cм, t1=1 c;
б) φe=0,5t2 рад, ОM=20sin(π∙t) cм, t1=1/3 c;
в) φe=4t2 рад, ОM=πRt2 cм, R=a=10 см, t1=1/2 c.
Ответ: а) v=134 cм/с, а=782 cм/с2; б) v= 31,9 cм/с, а=177 cм/с2;
в) v=61 cм/с, а=297 cм/с2.
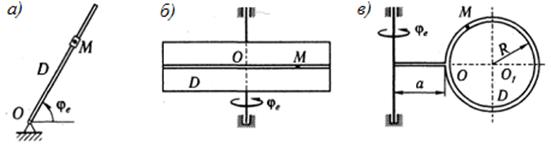
Рисунок 66
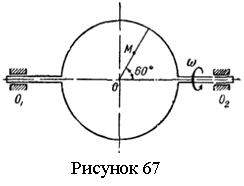 Задача 7.10. По
радиусу диска, вращающегося вокруг оси О1О2 с угловой
скоростью ω=2t рад/с, в
направлении от центра диска к его ободу движется точка М по закону
OM=4t2
см (см. рисунок 67). Радиус ОМ
составляет с осью О1О2 угол 60°. Найти
величину абсолютного ускорения точки М в момент времени
t=1с.
Задача 7.10. По
радиусу диска, вращающегося вокруг оси О1О2 с угловой
скоростью ω=2t рад/с, в
направлении от центра диска к его ободу движется точка М по закону
OM=4t2
см (см. рисунок 67). Радиус ОМ
составляет с осью О1О2 угол 60°. Найти
величину абсолютного ускорения точки М в момент времени
t=1с.
Ответ: а= 35,56 cм/с2.
8 Динамика точки
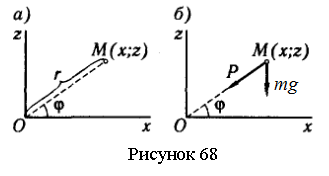 Задача 8.1.
Материальная
точка М массой m=1 кг
движется в вертикальной плоскости xOz
под действием силы притяжения к началу координат
Задача 8.1.
Материальная
точка М массой m=1 кг
движется в вертикальной плоскости xOz
под действием силы притяжения к началу координат ![]() , где
, где ![]() - радиус-вектор
точки, коэффициент пропорциональности
c=4 Н/м (см. рисунок 68,а). Начальные координаты точки
x0=0,
z0=10
м, начальная скорость точки
v0=20 м/с направлена горизонтально. Найти уравнения движения и
траекторию точки М.
- радиус-вектор
точки, коэффициент пропорциональности
c=4 Н/м (см. рисунок 68,а). Начальные координаты точки
x0=0,
z0=10
м, начальная скорость точки
v0=20 м/с направлена горизонтально. Найти уравнения движения и
траекторию точки М.
Решение.
Покажем действующие на материальную точку силы: силу тяжести![]() и силу притяжения
и силу притяжения ![]() (см. рисунок 68,б). Так как
действующие силы и начальная скорость точки расположены в плоскости xOz, движение точки будет происходить в этой плоскости.
Запишем уравнение движения точки в векторном виде:
(см. рисунок 68,б). Так как
действующие силы и начальная скорость точки расположены в плоскости xOz, движение точки будет происходить в этой плоскости.
Запишем уравнение движения точки в векторном виде: ![]() или
или ![]() Проецируем уравнение движения на
координатные оси:
Проецируем уравнение движения на
координатные оси: ![]() Так как
Так как ![]()
![]()
![]()
![]() дифференциальные уравнения движения
точки примут вид:
дифференциальные уравнения движения
точки примут вид:
![]() или
или ![]()
Окончательно запишем дифференциальные уравнения движения в виде:
![]() где
где ![]()
Первое
уравнение является однородным дифференциальным уравнением 2-го порядка с
постоянными коэффициентами. Составим характеристическое уравнение и найдем его
корни: ![]() где
где ![]() Так
как корни мнимые, то общее решение дифференциального уравнения имеет вид: x=C1coskt+C2sinkt. Для определения констант интегрирования надо найти
производную координаты, т.е. проекцию скорости на ось х:
Так
как корни мнимые, то общее решение дифференциального уравнения имеет вид: x=C1coskt+C2sinkt. Для определения констант интегрирования надо найти
производную координаты, т.е. проекцию скорости на ось х: ![]() Подставим начальные условия движения t=0, x0=0, v0x=20 в
полученные выражения для координаты и проекции скорости точки: 0=С1,
20=С2 . Тогда С1= 0, С2=10. Получаем
уравнение движения по оси х: x=10sin2t м.
Подставим начальные условия движения t=0, x0=0, v0x=20 в
полученные выражения для координаты и проекции скорости точки: 0=С1,
20=С2 . Тогда С1= 0, С2=10. Получаем
уравнение движения по оси х: x=10sin2t м.
 Второе
дифференциальное уравнение движения является неоднородным, его общее решение
ищем в виде: z = zо.о.+
zчаст., где общее решение
соответствующего однородного уравнения такое же, как для первого уравнения: zо.о =C3coskt+C4sinkt . Частное решение данного уравнения ищем по виду
правой части в виде: zчаст.=А. После
подстановки частного решения в дифференциальное уравнение получаем
Второе
дифференциальное уравнение движения является неоднородным, его общее решение
ищем в виде: z = zо.о.+
zчаст., где общее решение
соответствующего однородного уравнения такое же, как для первого уравнения: zо.о =C3coskt+C4sinkt . Частное решение данного уравнения ищем по виду
правой части в виде: zчаст.=А. После
подстановки частного решения в дифференциальное уравнение получаем ![]() Общее решение принимает вид:
Общее решение принимает вид: ![]() Найдем проекцию скорости на ось z:
Найдем проекцию скорости на ось z: ![]() Подставим начальные
условия движения t=0, z0=10,
v0z=0
в полученные выражения для координаты и проекции скорости точки: 10=С3
–g/k2,
0=С4k . Тогда С3=
10+ g/k2=12,45,
С4=0. Получаем уравнение движения по оси z:
z = 12,45cos2t -
2,45 м.
Подставим начальные
условия движения t=0, z0=10,
v0z=0
в полученные выражения для координаты и проекции скорости точки: 10=С3
–g/k2,
0=С4k . Тогда С3=
10+ g/k2=12,45,
С4=0. Получаем уравнение движения по оси z:
z = 12,45cos2t -
2,45 м.
Таким образом, точка движется согласно уравнениям: x =10sin2t м , z =12,45cos2t - 2,45 м. Исключив время из уравнений движения, получим уравнение траектории точки:
![]()
Как видно, траекторией точки является эллипс, центр которого А смещен от начала координат по оси z на 2,45 м вниз. Полуоси эллипса: горизонтальная а=10 м, вертикальная b=12,45 м (см. рисунок 69).
Ответ: x=10sin2t м , z=12,45cos2t - 2,45 м,
уравнение траектории
![]()
Задача 8.2. Найти
уравнения движения точки по условию задачи 8.1 с учетом силы сопротивления
среды, пропорциональной скорости точки: ![]() где
μ=2 Нс/м.
где
μ=2 Нс/м.
Ответ:
![]()
![]()
Задача 8.3. Решить
задачу 8.1 с учетом силы сопротивления среды, пропорциональной квадрату скорости
точки: ![]() где μ=0,2
кг/м.
где μ=0,2
кг/м.
Решение.
Проекции
силы сопротивления на координатные оси равны: ![]()
![]() где модуль скорости
где модуль скорости ![]() . С учетом этого дифференциальные уравнения
движения точки примут вид:
. С учетом этого дифференциальные уравнения
движения точки примут вид: ![]() или окончательно:
или окончательно:
![]()
Полученные
дифференциальные уравнения являются нелинейными, получить их аналитическое решение
не представляется возможным. Численное решение можно получить в системе Mathcad. Для этого дифференциальные уравнения движения надо
записать в виде системы дифференциальных уравнений 1-го порядка: ![]() Тогда вектор неизвестных имеет вид
Тогда вектор неизвестных имеет вид ![]() .
.
В Mathcad имеется несколько встроенных функций решения задачи
Коши (решения дифференциальных уравнений с начальными условиями). Решение
проведем с помощью встроенной функции rkfixed(U0,0,t2,200,DU), реализующей метод Рунге-Кутта с фиксированным шагом.
Здесь первый параметр означает начальный вектор, второй и третий параметры –
интервал интегрирования, 200 – число шагов интегрирования, последний
параметр – векторная функция, задающая систему дифференциальных уравнений.
Результатом численного решения будет матрица значений координат точки x, z и проекций скорости vx , vz
на отрезке времени [0,t2]
с шагом ![]()
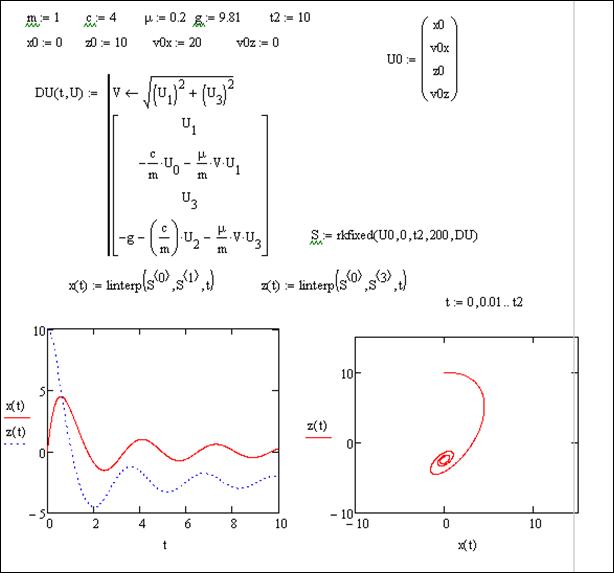
Рисунок 70
Для построения графиков необходимо по найденным дискретным значениям переменных получить их функции от времени путем интерполяции. Используем линейную интерполяцию с помощью встроенной функции вида linterp(x,y,t), которая возвращает значение в точке t линейного интерполяционного многочлена векторов х и у. Решение в Mathcad представлено на рисунке 70. Здесь видно, что точка движется по спирали.
Задача 8.4. Материальная точка массы m совершает прямолинейное движение под действием силы, изменяющейся по закону F=F0cosωt, где F0 и ω –постоянные величины. В начальный момент точка имела скорость v0. Найти уравнение движения точки.
Ответ: ![]()
Задача 8.5. Частица массы m, несущая заряд электричества e, находится в однородном электрическом поле с переменным напряжением E=Asinkt (A и k – заданные постоянные). Определить движение частицы, если известно, что в электрическом поле на заряженную частицу действует сила F=eE, направленная в сторону напряжения Е. Влиянием силы тяжести пренебречь, начальное положение частицы принять за начало координат, начальная скорость равна нулю.
 Ответ:
Ответ:
![]()
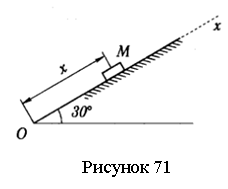
Задача 8.6. Тело массы m=100 кг движется под действием направленной вверх по наклонной плоскости переменной силы F=120(6+t) Н (см. рисунок 71). Коэффициент трения скольжения f=0,1. Определить скорость тела при t=3 c, если его начальная скорость равна нулю.
Ответ: 9,75 м/с.
Задача 8.7. Точка
массы m
движется
в горизонтальной плоскости xOу под
действием силы отталкивания от начала координат ![]() , где
, где
![]() - радиус-вектор точки. В начальный
момент точка находилась в М0(а,0) и имела скорость
v0 , направленную
параллельно оси у. Определить траекторию точки.
- радиус-вектор точки. В начальный
момент точка находилась в М0(а,0) и имела скорость
v0 , направленную
параллельно оси у. Определить траекторию точки.
Ответ:
![]() (гипербола).
(гипербола).
Задача 8.8. Тело массы 2 кг, брошенное вертикально вверх со скоростью 20 м/с, испытывает сопротивление воздуха, которое при скорости v м/с равно 0,4v H. Найти, через сколько секунд тело достигнет наивысшего положения.
Ответ: 1,71с.
Задача 8.9. По шероховатой наклонной плоскости, составляющей с горизонтом угол 30°, спускается тяжелое тело без начальной скорости. Определить за какое время тело пройдет путь 39,2 м, если коэффициент трения скольжения f=0,2.
Ответ: 5 с.
Задача 8.10. Масса поезда без локомотива равна 2·105 кг . Двигаясь по горизонтальному пути равноускоренно, поезд через 60 с от начала движения приобрел скорость 15 м/с. Сила трения равна 0,005 веса поезда. Определить натяжение стяжки между поездом и локомотивом.
Ответ: 59800 Н.
 Задача 8.11.
Груз
массы М=600 кг посредством ворота поднимают по наклонному шурфу,
составляющему угол 60° с горизонтом (см. рисунок 72). Коэффициент трения
груза о поверхность шурфа f=0,2. Ворот
радиуса 0,2 м вращается по закону φ=0,4t3. Найти натяжение
троса как функцию времени.
Задача 8.11.
Груз
массы М=600 кг посредством ворота поднимают по наклонному шурфу,
составляющему угол 60° с горизонтом (см. рисунок 72). Коэффициент трения
груза о поверхность шурфа f=0,2. Ворот
радиуса 0,2 м вращается по закону φ=0,4t3. Найти натяжение
троса как функцию времени.
Ответ: (5,68+0,288t) кН.
Задача 8.12. Тело массы 50 кг подвешено на нити. Точка привеса нити движется равноускоренно сверху вниз и за время t=2 с проходит 5 м. Определить силу натяжения нити.
Ответ: 615 Н.
Задача 8.13. Гиря массы 0,2 кг подвешена к концу нити длины 1 м. Вследствие толчка гиря получила горизонтальную скорость 5 м/с. Определить силу натяжения нити непосредственно после толчка.
Ответ: 6,96 Н.
Задача 8.14. Автомобиль массы 1000 кг движется по выпуклому мосту с постоянной скоростью 10 м/с. Радиус кривизны в середине моста ρ=50 м. Определить силу давления автомобиля на мост в момент прохождения его через середину моста.
Ответ: 7800 Н.
Задача 8.15. Груз массы 1 кг подвешен на нити длины 0,5 м. В начальный момент груз отклонен от вертикали на угол 60° , и ему сообщена скорость в вертикальной плоскости по перпендикуляру к нити вниз, равная 2,1 м/с. Определить натяжение нити в самом нижнем положении груза и высоту, на которую груз поднимется над этим положением.
 Ответ: 28,4 Н, 47,5 см.
Ответ: 28,4 Н, 47,5 см.
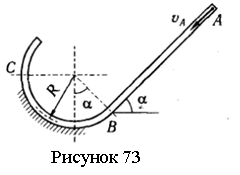
Задача 8.16. Шарик массы 0,2 кг движется в трубке из положения А, имея начальную скорость vA=3 м/с (см. рисунок 73). Определить скорость шарика в положениях В и С, а также давление шарика на трубку в положении С, если R=3 м , α=45°, время движения на участке АВ равно t=4 с. Трением пренебречь.
Ответ: vB=16,9 м/с, vC= 15,6 м/с, N=16,3 Н.
Задача 8.17. Парашютист массы 70 кг выбросился из самолета и, пролетев 100 м, раскрыл парашют. Найти силу натяжения стропов, на которых человек подвешен к парашюту, если в течение первых 5 с с момента раскрытия парашюта скорость парашютиста уменьшилась до 4,3 с. Сопротивлением воздуха движению человека пренебречь.
Ответ: 1246 Н.
9 Динамика системы
Задача 9.1. Механическая система, состоящая из связанных между собой невесомой нерастяжимой нитью трех тел, под действием сил тяжести приходит в движение из состояния покоя, начальное положение системы показано на рисунке 74,а. Заданы массы тел m1=m, m2=m/2, m3=m/3, радиусы внешнего и внутреннего обода 3-го колеса R3=30 см и r3=20 см, коэффициент трения скольжения f=0,2, коэффициент трения качения δ=0,1 см, углы α=30°, β=45°. Масса 2-го тела равномерно распределена по его ободу, радиус инерции 3-го колеса относительно оси, проходящей через его центр масс, равен i3=20 см. Найти скорость тела 1 в тот момент, когда пройденный им путь станет равным s=2 м.
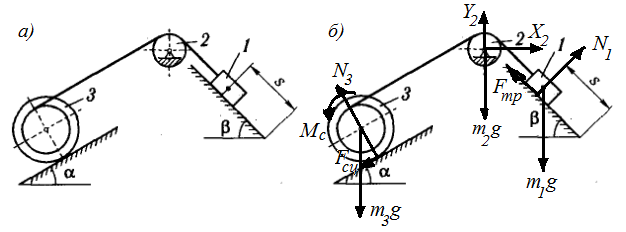
Рисунок 74
Решение.
Применим теорему об изменении кинетической энергии системы в конечной
форме: ![]() , то есть изменение
кинетической энергии системы на каком-то ее перемещении равно сумме работ
действующих на систему внешних и внутренних сил на этом перемещении. В
начальный момент система находилась в покое, поэтому Т0=0.
Все тела системы являются абсолютно жесткими, а нить – нерастяжимой, поэтому внутренние
силы работу не совершают:
, то есть изменение
кинетической энергии системы на каком-то ее перемещении равно сумме работ
действующих на систему внешних и внутренних сил на этом перемещении. В
начальный момент система находилась в покое, поэтому Т0=0.
Все тела системы являются абсолютно жесткими, а нить – нерастяжимой, поэтому внутренние
силы работу не совершают: ![]() Тогда теорема
запишется в виде:
Тогда теорема
запишется в виде:
![]()
Кинетическую
энергию системы в конечном положении найдем как сумму кинетических энергий тел,
входящих в систему: ![]() . Груз 1
движется поступательно, блок 2 вращается вокруг неподвижной оси, колесо 3
совершает плоскопараллельное движение. Тогда
. Груз 1
движется поступательно, блок 2 вращается вокруг неподвижной оси, колесо 3
совершает плоскопараллельное движение. Тогда ![]()
![]()
![]() , где моменты инерции тел
, где моменты инерции тел ![]()
![]()
Выразим все
скорости и угловые скорости через искомую скорость 1-го тела, учитывая,
что колесо 3 катится без скольжения, и точка его касания о плоскость
является мгновенным центром скоростей: ![]()
![]()
![]() С учетом этого
С учетом этого
![]()
Окончательно
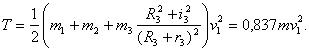
Покажем
действующие на механическую систему внешние силы (см. рисунок 74,б) и найдем
сумму работ внешних сил. Заметим, что ![]() так
как
так
как![]() ; работа сил, приложенных к
блоку 2, также равна нулю, так как они приложены в неподвижной точке; сила
сцепления Fсц и N3
работу не совершают, т.к. приложены в мгновенном центре скоростей колеса 3.
Тогда
; работа сил, приложенных к
блоку 2, также равна нулю, так как они приложены в неподвижной точке; сила
сцепления Fсц и N3
работу не совершают, т.к. приложены в мгновенном центре скоростей колеса 3.
Тогда ![]() Здесь работа сил тяжести
Здесь работа сил тяжести ![]()
![]() работа силы трения скольжения
работа силы трения скольжения ![]() работа момента сопротивления качению
работа момента сопротивления качению ![]() Найдем силу трения
Найдем силу трения ![]() и момент сопротивления качению
и момент сопротивления качению ![]() Соотношения между перемещениями тел
такие же, как между скоростями, поэтому имеем
Соотношения между перемещениями тел
такие же, как между скоростями, поэтому имеем ![]()
![]() С
учетом этого
С
учетом этого ![]() . Окончательно
. Окончательно
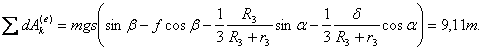
Подставив
полученные выражения в теорему об изменении кинетической энергии, получаем
![]()
Ответ:
![]()
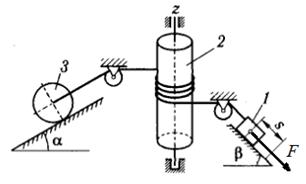
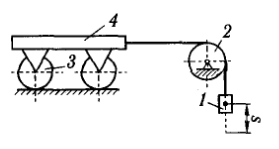
Рисунок 75 Рисунок 76
Задача 9.2. Механическая система движется из состояния покоя под действием постоянной силы F=20 Н, приложенной к грузу 1 массы m1=4 кг (см. рисунок 75). Тело 2 считать однородным сплошным цилиндром массы m2=8 кг, колесо 3 катится без скольжения, его масса m3=5 кг равномерно распределена по ободу, коэффициент трения скольжения f=0,1, углы α=45°, β=60°. Нить считать невесомой и нерастяжимой, сопротивлением качению колеса и трением в подшипниках пренебречь. Найти скорость тела 1 в тот момент, когда пройденный им путь станет равным s=1 м.
Ответ:
![]()
Задача 9.3. Механическая система приходит в движение из состояния покоя под действием сил тяжести (см. рисунок 76). Блок 2 и четыре колеса 3 тележки считать однородными дисками, нить - невесомой и нерастяжимой, сопротивлениями движению пренебречь. Найти скорость тела 1 в зависимости от пройденного им пути s, если массы равны m1=m, m2=m/2, m3=m/8, m4=m/2.
Ответ:
![]()
Задача 9.4. На вал диаметром 60 мм насажен маховик диаметром 50 см, делающий 180 обор/мин. Определить коэффициент трения скольжения f между валом и подшипниками, если после выключения привода маховик сделал 90 оборотов до остановки. Массу маховика считать равномерно распределенной по его ободу. Массой вала пренебречь.
Ответ: f=0,07.
Задача 9.5. Какой путь проедет велосипедист, не вращая педалями, до остановки, если в начальный момент он двигался со скоростью 9 км/час? Общая масса велосипедиста и велосипеда 80 кг, масса каждого из колес 5 кг. Массу каждого колеса считать равномерно распределенной по ободу радиуса 50 см. Коэффициент трения качения колес о землю равен 0,5 см.
Ответ: 35,6 м.
Задача 9.6. Скорость автомашины, движущейся по прямой горизонтальной дороге, возросла от v1 до v2 за счет увеличения мощности мотора. При этом был пройден путь s. Вычислить работу, совершенную мотором на этом перемещении автомашины, если Р1 - вес каждого из четырех колес, Р2 -вес кузова, v1 – радиус колес, fк - коэффициент трения качения колес о шоссе. Колеса, катящиеся без скольжения, считать однородными сплошными дисками. Кинетической энергией всех деталей, кроме колес и кузова, пренебречь.
Ответ:
![]()
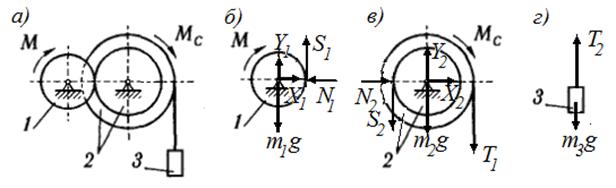
Рисунок 77
Задача 9.7. Механическая система движется под действием вращающего момента М=300+2t Нм, приложенного к колесу 1 (см. рисунок 77,а). К ведомому колесу 2 приложен момент сопротивления Мс=150 Нм. В начальный момент времени угловая скорость 1-го колеса равна ω1,0=4 рад/с, начальный угол поворота φ1,0=0 . Заданы массы тел m1=10 кг, m2=30 кг, m3=50 кг, радиусы колес R1=20 см, R2=60 см, r2=40 см, радиус инерции 2-го колеса относительно его оси вращения i2z=50 см. Колесо 1 считать однородным диском, другими сопротивлениями движению пренебречь . Найти уравнение движения колеса 1, а также натяжение нити, на которой подвешен груз, и окружное усилие в точке касания колес в момент времени t=2 c.
Решение. Рассмотрим движение каждого тела системы в отдельности (см. рисунок 77,б-г). Покажем действующие на них силы и запишем уравнения движения тел.
Дифференциальное
уравнение вращения колеса 1 имеет вид: ![]() , где
, где ![]() Дифференциальное уравнение вращения
колеса 2 имеет вид:
Дифференциальное уравнение вращения
колеса 2 имеет вид: ![]() ,
где
,
где ![]() Дифференциальное уравнение
поступательного движения груза 3 имеет вид:
Дифференциальное уравнение
поступательного движения груза 3 имеет вид: ![]() ,
где
,
где ![]() . Учитывая, что
. Учитывая, что ![]() , получаем систему дифференциальных
уравнений:
, получаем систему дифференциальных
уравнений:
![]()
В этих
уравнениях можно выразить угловое ускорение 2-го колеса и ускорение
груза 3 через угловое ускорение колеса 1, пользуясь такими же
соотношениями, как и для скоростей: ![]() Тогда
будем иметь три уравнения с тремя неизвестными. Сначала можно из третьего
уравнения выразить натяжение нити
Тогда
будем иметь три уравнения с тремя неизвестными. Сначала можно из третьего
уравнения выразить натяжение нити ![]() и
подставить во второе уравнение:
и
подставить во второе уравнение: ![]() Отсюда
можно выразить окружное усилие
Отсюда
можно выразить окружное усилие ![]() и
подставить в первое уравнение:
и
подставить в первое уравнение: ![]() После
подстановки выражений для
После
подстановки выражений для ![]() и
и ![]() , получаем
, получаем ![]() . Отсюда выразим угловое ускорение 1-го
колеса:
. Отсюда выразим угловое ускорение 1-го
колеса:
 или
или 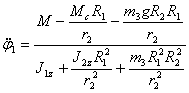 .
.
Подставив выражения моментов инерции и заданные величины, получим:
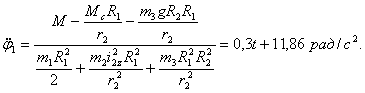
Проинтегрируем
два раза: ![]() Подставив сюда начальные
условия движения t=0, ω1,0=4
рад/с, φ1,0=0, получим С1=4, С2=0.
Окончательно уравнение движения 1-го колеса запишется:
Подставив сюда начальные
условия движения t=0, ω1,0=4
рад/с, φ1,0=0, получим С1=4, С2=0.
Окончательно уравнение движения 1-го колеса запишется: ![]()
Найдем натяжение нити и окружное усилие:
![]()
![]()
При t=2 c получим ![]()
Ответ:
![]()
Задача 9.8. Маховик с моментом инерции относительно неподвижной оси вращения, равным J=15 кгм2, разгоняется из состояния покоя при действии постоянного вращающего момента Мвр=75 Нм. Пренебрегая сопротивлениями установить, через какое время маховик приобретает заданную частоту вращения n=150 обор/мин.
Ответ: π с.
Задача 9.9. Натяжения ведущей и ведомой ветвей ремня, приводящего во вращение шкив радиуса r=20 см и массы m=3 кг, соответственно равны: Т1=10 Н, Т2=5 Н. Чему равен момент сил сопротивления, если угловое ускорение шкива ε=1,5 рад/с? Шкив считать однородным диском.
Ответ: 0,91 Нм.
Задача 9.10. Тормозной шкив, масса которого m=2 кг, диаметр d=0,8 м, имеет форму сплошного диска и вращается по инерции с угловой скоростью ω0=10 рад/с. Для остановки вала к шкиву прижимают тормозную колодку с силой Q=5 Н. Через сколько секунд вал остановится и сколько оборотов он сделает до остановки, если коэффициент трения колодки о шкив f=0,4? Трением в подшипниках вала и массой вала пренебречь.
Ответ: 6,28 с, 15,7 оборота.
Задача 9.11. Зубчатая передача состоит из двух колес, радиусы которых r1 и r2, а соответствующие осевые моменты инерции J1 и J2 (см. рисунок 78). К первому колесу приложен вращающий момент Мвр, на второе действует момент сил сопротивления Мс. С учетом заданных соотношений Мс = Мвр /4, r2=2r1, J1=J2= J определить угловое ускорение ε1 первого колеса передачи, а также окружное усилие S взаимодействия колес в контактной точке.
Ответ:
![]()

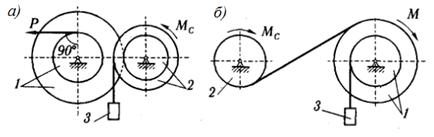
Рисунок 78 Рисунок 79
Задача 9.12. Определить ускорение груза 3 при следующих данных (см. рисунок 79,а,б):
а) движущая сила Р=2500 Н, момент сопротивления Мс=50 Нм, m1=20кг, m2=10 кг, m3=30 кг, радиусы колес R1=50 см, r1=20 см, R2=40 см, r2=25 см, радиусы инерции колес относительно осей вращения i1z=i2z=30 см;
б) движущий момент М=600 Нм, момент сопротивления Мс=100 Нм, m1=30 кг, m2=20 кг, m3=40 кг, радиусы колес R1=60 см, r1=40 см, R2=30 см, радиусы инерции колес относительно их осей вращения i1z=50 см , i2z=30 см.
Ответ: а) 5,36 м/с2 ; б) 2,57 м/с2.
Задача 9.13. При пуске в ход электрической лебедки к барабану А приложен вращающий момент, пропорциональный времени mвр=at, где a – постоянная (см. рисунок 80). Груз В весом Р1 поднимается посредством каната, навитого на барабан А радиуса r и весом Р2. Определить угловую скорость барабана, считая его сплошным однородным цилиндром. В начальный момент лебедка находилась в покое.
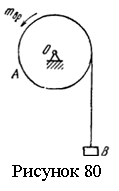 Ответ:
Ответ: ![]()
 Задача 9.14.
По
горизонтальной платформе А, движущейся по инерции со скоростью v0 перемещается тележка
В с постоянной относительной скоростью
u0
(см. рисунок 81). В некоторый момент времени тележка
была заторможена. Определить общую скорость
v
платформы с тележкой после остановки тележки, если
M
- масса платформы, m - масса тележки.
Задача 9.14.
По
горизонтальной платформе А, движущейся по инерции со скоростью v0 перемещается тележка
В с постоянной относительной скоростью
u0
(см. рисунок 81). В некоторый момент времени тележка
была заторможена. Определить общую скорость
v
платформы с тележкой после остановки тележки, если
M
- масса платформы, m - масса тележки.
Ответ:
![]()
Задача 9.15. Граната массы 2 кг, летевшая со скоростью 15 м/с, разорвалась в воздухе на две части. Скорость осколка массы 8 кг возросла в направлении движения до 25 м/с. Определить скорость второго осколка.
Ответ: 5 м/с в направлении, противоположном движению первого осколка.
Задача 9.16. Колесо катится со скольжением по горизонтальной прямой под действием силы F (см. рисунок 82). Найти закон движения центра масс С колеса, если коэффициент трения скольжения равен f , а F=5 f P, где P – вес колеса. В начальный момент колесо находилось в покое.
Ответ:
![]()
 Задача 9.17.
Колесо
катится со скольжением по горизонтальной прямой под действием приложенного к
нему момента (см. рисунок 83). Найти закон движения центра масс С
колеса, если коэффициент трения скольжения равен
f. В
начальный момент колесо находилось в покое.
Задача 9.17.
Колесо
катится со скольжением по горизонтальной прямой под действием приложенного к
нему момента (см. рисунок 83). Найти закон движения центра масс С
колеса, если коэффициент трения скольжения равен
f. В
начальный момент колесо находилось в покое.
Ответ:
![]()
Задача
9.18. При полете снаряда вращение
его вокруг оси симметрии замедляется действием момента сопротивления
воздуха, равного kω , где
ω - угловая скорость вращения снаряда,
k
– постоянный коэффициент пропорциональности.
Определить закон убывания угловой скорости, если начальная угловая скорость
ω0 , а
момент инерции снаряда относительно оси симметрии равен
J.
Ответ: ![]()
10 Расчеты на прочность и жесткость при растяжении-сжатии
Задача 10.1. Для изображенного на рисунке 84,а стержня построить эпюру нормальных сил и перемещений поперечных сечений вдоль оси стержня. Рассмотреть различные виды расчетов на прочность, задавшись необходимыми данными.
|
а)
в)
г) |
|
|
Рисунок 84 |
|
Решение.
1)
Определение
реакции опоры. Из уравнения равновесия ![]() найдем
реакцию в заделке
найдем
реакцию в заделке
![]() .
.
2)
Определение
нормальных сил и построение эпюры N(z).Стержень имеет три участка, границами которых служат
сечения, где приложены внешние силы. Для определения нормальных сил используем
метод сечений. Мысленно рассекаем стержень на каждом из участков на расстояниях
z1, z2,
z3 и рассматриваем равновесие
одной из частей рассеченного стержня, заменяя действие отброшенных частей
внутренними нормальными силами N1, N2, N3.
(см. рисунок 84,б). Для каждого участка записываем выражение для нормальной
силы![]() ,
причем проекция силы берется со
знаком “плюс”, если сила направлена кнаружи от отсеченной части стержня; если сила
направлена вовнутрь отсеченной части, то ее следует брать со знаком “минус”. В
результате получаем
,
причем проекция силы берется со
знаком “плюс”, если сила направлена кнаружи от отсеченной части стержня; если сила
направлена вовнутрь отсеченной части, то ее следует брать со знаком “минус”. В
результате получаем ![]()
![]() .
Строим эпюру (график) нормальных сил, показывающую, как изменяется N при переходе от одного сечения к другому вдоль оси
стержня (см. рисунок 84,в).
.
Строим эпюру (график) нормальных сил, показывающую, как изменяется N при переходе от одного сечения к другому вдоль оси
стержня (см. рисунок 84,в).
3) Расчет на прочность. Т.к. сечение стержня постоянно, то опасными сечениями являются все сечения, принадлежащие второму участку, где нормальная сила максимальна по модулю (принимаем, что материал стержня одинаково сопротивляется растяжению и сжатию), Nmax≠N2̸=2P. Составляем условие прочности
![]() .
.
C помощью условия прочности можно решать три вида задач.
3.1Проверочный
расчет на прочность. Известны все величины в условии прочности, требуется
проверить, выполняется ли оно. Пусть, например ![]()
![]() , тогда
, тогда
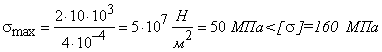 .
.
Т.к. ![]() ,то
приходим к заключению, что условие прочности выполняется.
,то
приходим к заключению, что условие прочности выполняется.
3.2 Проектировочный расчет на
прочность. Требуется найти диаметр d круглого поперечного сечения стержня, для которого площадь сечения
определяется формулой ![]() . Из условия прочности выражаем
площадь
. Из условия прочности выражаем
площадь ![]() , тогда
, тогда 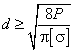 . Сохраняя
значения
. Сохраняя
значения![]() , получаем
, получаем
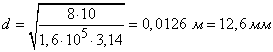 .
.
Округляя, принимаем d=13 мм. Т.к. выполнено округление в большую
сторону, то расчетное напряжение  меньше допускаемого
на
меньше допускаемого
на 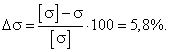
3.3 Определение допускаемой нагрузки. Из условия прочности имеем
![]() .
.
Пусть ![]() , тогда
, тогда
![]() .
.
4 Построение эпюры перемещений. Для определения перемещений на различных участках будем использовать формулу
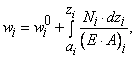
где ![]() –
номер участка;
–
номер участка; ![]() – значение перемещения в
начале i-го участка;
– значение перемещения в
начале i-го участка; ![]() –
текущая координата сечения i-го участка;
–
текущая координата сечения i-го участка; ![]() – жесткость i-го
участка,
– жесткость i-го
участка, ![]() – координаты начального сечения i-го участка.
– координаты начального сечения i-го участка.
На участке 1 ![]() имеем
имеем 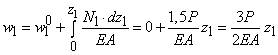 , следовательно,
эпюра − прямая линия. При
, следовательно,
эпюра − прямая линия. При ![]() имеем
имеем ![]() , т. е. в заделке
, т. е. в заделке ![]() . При
. При ![]() получаем
получаем
![]() .
.
На участке 2 ![]() имеем
имеем
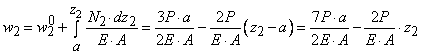 , так
что на втором участке эпюра также представляет собой прямую линию. При
, так
что на втором участке эпюра также представляет собой прямую линию. При ![]() получаем
получаем ![]() .
.
На участке 3 ![]() получаем также линейную зависимость
получаем также линейную зависимость
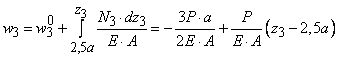 . При
. При
![]() получаем
получаем ![]() .
.
Используя
полученные данные, строим график - эпюру перемещений ![]() поперечных
сечений (см. рисунок 84,г).
поперечных
сечений (см. рисунок 84,г).
5
Расчеты на жесткость. Пусть полное удлинение стержня не должно
превышать допустимого значения ![]() , тогда условие
жесткости имеет вид
, тогда условие
жесткости имеет вид
![]() .
.
Отсюда можно найти другое допускаемое значение силы
![]() .
.
Сравнивая два значения ![]() окончательно выбираем наименьшее.
окончательно выбираем наименьшее.
Задача 10.2.
Построить эпюры ![]() для стержня,
изображенного на рисунке 85,а при его нагружении силой
для стержня,
изображенного на рисунке 85,а при его нагружении силой ![]() и равномерно распределенной нагрузкой
и равномерно распределенной нагрузкой ![]() . Допускаемое напряжение
. Допускаемое напряжение ![]() (дерево),
(дерево), ![]() ,
, ![]() . Определить из условия прочности
размеры поперечного сечения стержня в виде прямоугольника с соотношением сторон
1:2.
. Определить из условия прочности
размеры поперечного сечения стержня в виде прямоугольника с соотношением сторон
1:2.
Решение.
1
Определение опорной реакции. Из уравнения статики ![]() находим
находим ![]() .
.
2
Определение
внутренних усилий N методом
сечений. На первом участке проводим сечение на расстоянии ![]() и из рассмотрения левой отсеченной
части (см. рисунок 84,б) находим
и из рассмотрения левой отсеченной
части (см. рисунок 84,б) находим ![]() . Следовательно,
на этом участке эпюра N -
наклонная прямая. Строим эпюру по двум точкам: при
. Следовательно,
на этом участке эпюра N -
наклонная прямая. Строим эпюру по двум точкам: при ![]() имеем
имеем
![]() , а при
, а при ![]() получаем
получаем
![]() .
.
На участке 2 отсекаем
на расстоянии ![]() правую часть стержня.
Действие левой части на правую определяет усилие
правую часть стержня.
Действие левой части на правую определяет усилие ![]() ,
которое находим как
,
которое находим как![]() , и на этом участке
, и на этом участке ![]() имеет постоянное значение. Эпюра
имеет постоянное значение. Эпюра ![]() показана на рисунке 84,в. На расстоянии
показана на рисунке 84,в. На расстоянии
![]() усилие
усилие ![]() .
Найдем это расстояние
.
Найдем это расстояние
![]() ;
; ![]() .
.
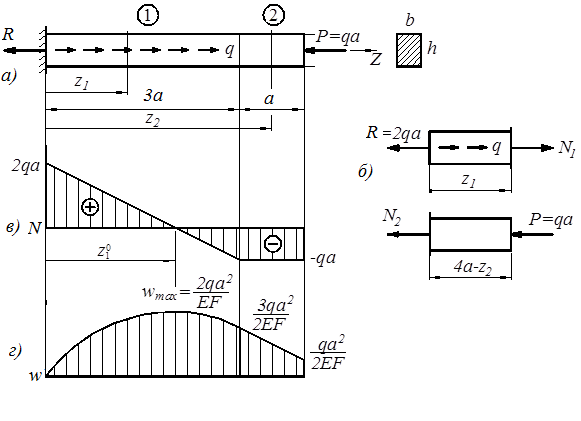 Опасным по
прочности является сечение у заделки, где
Опасным по
прочности является сечение у заделки, где ![]() .
.
3
Расчет на прочность. Условие
прочности стержня ![]() . Для
прямоугольного поперечного сечения с соотношением сторон
. Для
прямоугольного поперечного сечения с соотношением сторон ![]() имеем
имеем ![]() . Тогда
из условия прочности находим
. Тогда
из условия прочности находим
![]() ,
,
откуда ![]() .
Округляем значение
.
Округляем значение ![]() до значения
до значения ![]() , тогда
, тогда ![]()
![]() . Проверяем стержень на прочность с подобранными
размерами поперечного сечения
. Проверяем стержень на прочность с подобранными
размерами поперечного сечения
![]() ,
,
Перегрузка составит 
4 Построение
эпюры перемещений ![]() . На первом участке
. На первом участке 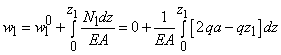 е или
е или 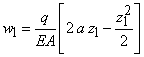 . Эпюра
– парабола. В сечении
. Эпюра
– парабола. В сечении ![]() , где
, где ![]() ,
перемещение достигает максимального значения, при этом
,
перемещение достигает максимального значения, при этом ![]() .
При
.
При ![]() имеем
имеем 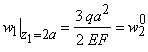 .
.
На участке 2 ![]() имеем
имеем 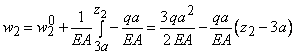 , эпюра
− прямая. При
, эпюра
− прямая. При ![]() имеем
имеем ![]() ,
при
,
при ![]() -
-  .
.
Окончательно, эпюра перемещений принимает вид, как на рисунке 85,г.
Задача 10.3. Для конструкции, показанной на рисунке 86,а, определить из расчетов на прочность и жесткость допускаемое значение силы F, если для материала стержней 1 и 2 допускаемое напряжение [s] = 120 МПа, допускаемое вертикальное перемещение точки С [δС] = 1,7 мм, А1=2А, А2 = А = 5 см2, l1 = l2 = l = 1 м, Е = 2∙105 МПа.
 Решение.
Решение.
1 Определение усилий в стержнях. Из условий равновесия бруса АС имеем
åmA = 0, F×3a - N1×a = 0, N1 = 3F;
åmB = 0, F×2a - N2×a = 0, N2 = 2F.
2 Расчет на прочность. Находим напряжения в стержнях s1 = N1/A1 = 3F/(2A), s2 = N2/A2 = 2F/A. Как видим, наиболее нагруженным является стержень 2, прочность которого определяет прочность всей конструкции в целом. Из условия прочности smax = s2 = 2F/A£[s] находим
[Fпр] = 0,5[s]×A = 30 кН.
3 Расчет на жесткость. Вычисляем деформации стержней Dl1 = N1l/(EA1) = =3Fl/(2EA), Dl2 = N2l/(EA2) = 2Fl/(2EA), а по ним - перемещение точки С. Из подобия треугольников В1А1В2 и С1А1С2 имеем В1В2/А1В2 = С1С2/А1С2 или (Dl1 + Dl2)/a = (dC + +Dl2)/3a, откуда dC = 3Dl1 + 2Dl2 = 9Fl/(2EA) + 4Fl/(EA) = 8,5Fl/(EA). Записываем условие жесткости dC = 8,5Fl/(EA) £ [dC], откуда
[Fж] = EA[dC]/(8,5l) = 2×1011×5×10-4×1,7×10-3/(8,5×1) = 2∙104 Н = 20 кН.
Допускаемая нагрузка из расчета на жесткость получилась меньше, чем из расчета на прочность, поэтому ее и принимаем в качестве окончательной, т.е.
[F] = min{[Fпр], [Fж]} = [Fж] = 20 кН.
Задача 10.4. Для настенного поворотного крана (см. рисунок 87,а) требуется подобрать из расчетов на прочность стальной стержень АВ круглого поперечного сечения и деревянный брус BD квадратного сечения, если F=240 кН; l1=l2=1,2 м; для стали [s]ст = 160 МПа, Еcт=2⋅105 МПа, для дерева [s]д = 10 МПа, 160 МПа, Ед=104 МПа. Определить вертикальное перемещение δB узла В.
Решение. Воспользовавшись методом вырезания узлов, рассмотрим равновесие узла В (см. рисунок 87,б).
åFx = - N1×cos45° + N2×cos45° = 0, N1 = N2,
åFy = F- N1×sin45° - N2× ° = 0, F-2N1×sin45° = 0,
N1 = N2=F/(2∙sin45°)=170,2 кН.
Стержень АВ испытывает растяжение, стержень BD сжатие.
Определяем размеры поперечных сечений стержней. Из условия прочности s= N/A£[s] находим для стержня AB
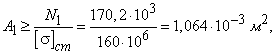
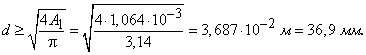
Принимаем d=37 мм. Для стержня BD
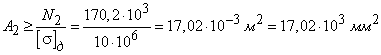
и сторона квадрата ![]() Пересчитаем значения площадей
Пересчитаем значения площадей
![]()
![]()
Для определения перемещения узла В рассмотрим схему деформирования на рисунке 87,в. Найдем удлинение стержня АВ и укорочение стержня BD
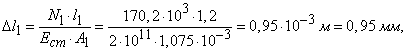
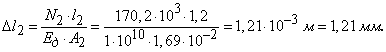
Т.к. абсолютные деформации стрежней малы по сравнению с общими размерами конструкции, то можно считать, что в деформированной конструкции углы остаются такими же, как до деформации. Тогда, учитывая, что вертикальное перемещение узла B складывается их двух составляющих, найдем
![]()
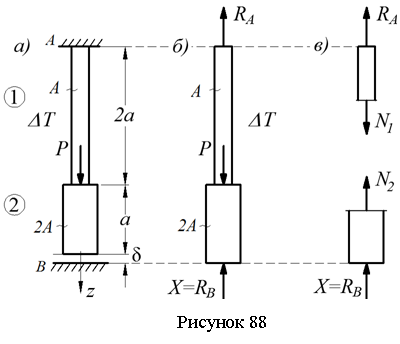 Задача 10.5.
Определить усилия и
нормальные напряжения в стержне с зазором
Задача 10.5.
Определить усилия и
нормальные напряжения в стержне с зазором ![]() ,
изображенном на рисунке 88,а, при действии силы
P
и нагревании на
,
изображенном на рисунке 88,а, при действии силы
P
и нагревании на ![]() . Дано:
. Дано:![]()
![]()
![]()
![]()
![]()
Решение.
В результате сборки конструкции (выборки зазора δ), действия силы P и температуры ΔT в опорах возникнут
реакции RA и
RB=X.
Уравнение равновесия имеет вид ![]() . Задача один раз статически
неопределима. Для эквивалентной системы (см. рисунок 88,б) составляем
дополнительное уравнение совместности деформаций. Перемещение сечения wB ограничено, поэтому
. Задача один раз статически
неопределима. Для эквивалентной системы (см. рисунок 88,б) составляем
дополнительное уравнение совместности деформаций. Перемещение сечения wB ограничено, поэтому
![]() . Используя
принцип независимости действия сил и закон Гука для эквивалентной системы
получаем
. Используя
принцип независимости действия сил и закон Гука для эквивалентной системы
получаем ![]() , или
, или
![]() , откуда
, откуда ![]() .
.
C учетом этого выражения из уравнения равновесия получаем
![]() .
.
Методом сечения находим усилия
на участках стержня
![]()
и напряжения ![]()
![]()
В выражениях для напряжений содержатся по три вида слагаемых. Первые возникают за счет действия силы P, вторые – за счет изменения температуры, третьи − за счет устранения зазора δ.
В случае, когда ![]() , возникают напряжения только от
действия силы P. При этом
, возникают напряжения только от
действия силы P. При этом ![]() ,
, ![]() ,
т.е. первый участок растягивается, а второй сжимается.
,
т.е. первый участок растягивается, а второй сжимается.
В случае,
когда действует только температура (![]() ), во всем стержне
возникают сжимающие температурные напряжения
), во всем стержне
возникают сжимающие температурные напряжения ![]() ,
,
![]() .
.
В случае, когда ![]() и только выбирается зазор
и только выбирается зазор ![]() ,
, ![]() ,
,
в обоих участках возникают растягивающие монтажные напряжения; здесь стержень был растянут для выборки зазора и закреплен.
Задача 10.6.
Сила ![]() передаётся через абсолютно жёсткую плиту
на сплошной стальной цилиндр 1 площадью поперечного сечения 15 см2
и полый медный цилиндр 2 площадью 20 см2 (см. рисунок 89).
Сила действует вдоль оси обоих цилиндров. Требуется: найти усилия в стальном
передаётся через абсолютно жёсткую плиту
на сплошной стальной цилиндр 1 площадью поперечного сечения 15 см2
и полый медный цилиндр 2 площадью 20 см2 (см. рисунок 89).
Сила действует вдоль оси обоих цилиндров. Требуется: найти усилия в стальном![]() и медном
цилиндрах
и медном
цилиндрах ![]() ;
изменить температуру конструкции, чтобы усилия в стальном и медном цилиндрах
были одинаковы
;
изменить температуру конструкции, чтобы усилия в стальном и медном цилиндрах
были одинаковы ![]() ; изменить температуру конструкции,
чтобы напряжения в стальном и медном цилиндрах были одинаковы
; изменить температуру конструкции,
чтобы напряжения в стальном и медном цилиндрах были одинаковы ![]() . Принять: Р = 45 кН;
A1 = 15 см2;
A2 = 20 см2;
E1 =
2∙105 МПа; E2 = 1∙105 МПа;
коэффициент линейного расширения для стали
a1 =
1,2∙10 -5 1/град, для меди
a2 =
1,6∙10 -5 1/град.
. Принять: Р = 45 кН;
A1 = 15 см2;
A2 = 20 см2;
E1 =
2∙105 МПа; E2 = 1∙105 МПа;
коэффициент линейного расширения для стали
a1 =
1,2∙10 -5 1/град, для меди
a2 =
1,6∙10 -5 1/град.
Ответ: N1=-27 кН, N2=-18 кН; 9,4°С; 16°С.
Задача 10.7. Для стержней (см. рисунок 90), нагруженных сосредоточенными силами и распределенной нагрузкой, построить эпюры нормальных сил.
Задача 10.8. Для показанных на рисунке 91 стержней построить эпюры нормальных сил и нормальных напряжений.
Задача 10.9. Тяжелая жесткая плита весом G=1,2 кН нагружена силой F=8 кН (см. рисунок 92). Определить из условия прочности диаметр стержня CD, если α=45°, [σ]=150 Н/мм2.
Ответ: 12 мм.
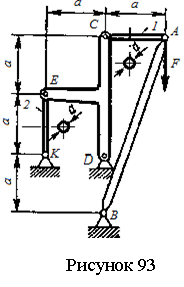
Задача 10.10. Трос составлен из 100 стальных проволок диаметром 2 мм. Вычислить напряжения в поперечном сечении троса, если сила, растягивающая трос, равна 50 кН.
Ответ: 159 МПа.
Задача 10.11. Из условия прочности стержней 1 и 2 рычажного механизма (см. рисунок 93) определить допускаемую нагрузку F, если d=4 мм, [σ]=140 МПа.
Ответ: 2,64 кН.
Задача 10.12. Вычислить напряжения в поперечных сечениях стержней (см. рисунок 94).
Ответ: а) 140 МПа, 97,8 МПа; б) 136 МПа; в) 120 МПа, 83,6 МПа; г) 115 МПа, д)126 МПа; е) 177 МПа; ж) 156МПа, 141 МПа; з) 74,7 МПа.
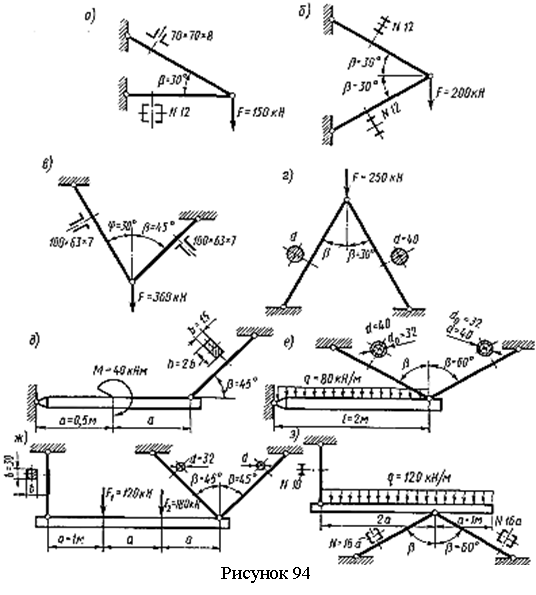
11 Расчеты заклепочных, сварных и других видов соединений
Задача 11.1.
Проверить прочность заклёпочного соединения (см. рисунок 95). Принять: для
полосы допускаемое напряжение на растяжение ![]() = 200
МПа; для заклёпок допускаемое напряжение на срез
= 200
МПа; для заклёпок допускаемое напряжение на срез ![]() ;
допускаемое напряжение на смятие
;
допускаемое напряжение на смятие ![]() = 240 МПа.
= 240 МПа.
Решение.
1. Построим эпюру нормальных сил действующих в сечениях 1-1, 2-2, 3-3 полосы (см. рисунок 93). При этом будем учитывать, что на каждую заклёпку приходиться сила Q, равная в среднем P/5=40 кН, т.к. число заклёпок i = 5.
2. Проверка прочности полосы при растяжении. Выполним расчёт для сечения 3-3. Здесь действует наибольшая нормальная сила N3=P. Площадь поперечного сечения полосы (см. рисунок 96,а) A3=tп∙(b-d)=12∙(180-22) = 1896 мм2 =1,896∙10-3 м2. Найдем напряжения и проверим условие прочности
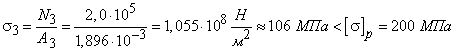 .
.
Условие прочности выполняется.
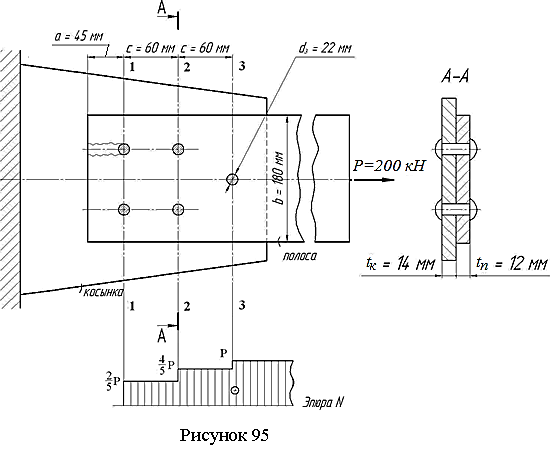
Для сечения 2-2 усилие меньше, но и расчётная площадь поперечного сечения меньше, чем в сечении 3-3 (см. рисунок 96,б): N3=4P/5, A2=tп∙(b-2d)=12∙(180-2∙22)= =1632 мм2 = 1,632∙10-3 м2. Найдем напряжения и проверим условие прочности
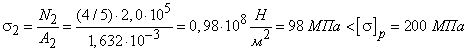 .
.
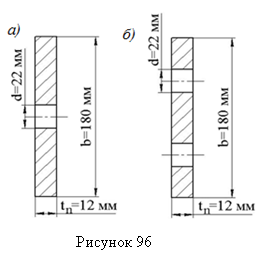 Условие
прочности выполняется.
Условие
прочности выполняется.
3. Проверка прочности заклёпок на срез
Условие прочности
![]()
Здесь Q − перерезывающая сила, приходящаяся на одну заклёпку;
![]() − площадь среза заклёпки.
− площадь среза заклёпки.
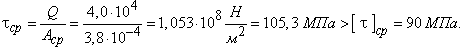
Условие прочности не выполняется.
4. Проверка прочности заклёпок на смятие
Условие прочности
![]()
где ![]() 22·12 = 264 мм2
− условная площадь смятия.
22·12 = 264 мм2
− условная площадь смятия.
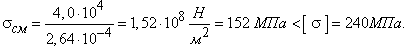
Условие прочности выполняется.
5. Проверка условия прочности на срез по длине а (см. рисунок 95)
Условие прочности
![]()
где ![]() 2·45·12 = 1080 мм2 =
1,08·10-3 м2
− площадь среза;
2·45·12 = 1080 мм2 =
1,08·10-3 м2
− площадь среза;
![]() - допускаемое напряжение на срез для
материала полосы; это напряжение не задано, поэтому согласно рекомендациям оно
может быть принято равным
- допускаемое напряжение на срез для
материала полосы; это напряжение не задано, поэтому согласно рекомендациям оно
может быть принято равным ![]() . Тогда
. Тогда
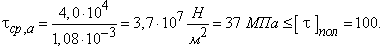
Условие прочности выполняется.
Т.о., прочность соединения по напряжениям среза в заклёпках не обеспечена, по остальным критериям условия прочности выполняются. Чтобы обеспечить прочность по всем критериям, можно увеличить количество заклепок (поставить, например, 6 заклепок, по 2 в каждом ряду) или использовать заклепки большего диаметра.
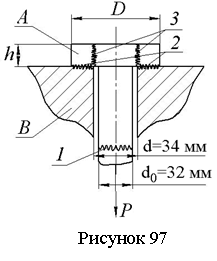 Задача
11.2. Определить размеры
Задача
11.2. Определить размеры ![]() детали А (см. рисунок 97) из условия
равнопрочности на растяжение, срез и смятие, если
детали А (см. рисунок 97) из условия
равнопрочности на растяжение, срез и смятие, если ![]()
![]()
![]()
Решение. Нарушение прочности данного соединения возможно от разрыва по сечению 1, от смятия по поверхности 2 и от среза по поверхности 3.
1. Определение
допускаемой нагрузки Р из условия прочности стрежня диаметром ![]() на растяжение. Условие прочности
на растяжение. Условие прочности ![]() откуда
откуда ![]() Здесь
Здесь
![]() − площадь поперечного сечения
стержня диаметра
− площадь поперечного сечения
стержня диаметра ![]() . Тогда
. Тогда
![]()
2. Определение размера D из условия прочности на смятие
Условие
прочности ![]()
Здесь ![]() −
площадь смятия. Тогда
−
площадь смятия. Тогда 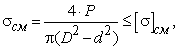 откуда
откуда
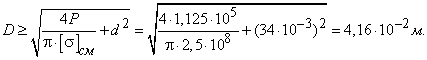
Примем D = 42 мм.
3. Определение размера h из условия прочности на срез
Условие
прочности ![]() Здесь
Здесь ![]() −
площадь среза. Условие прочности примет вид
−
площадь среза. Условие прочности примет вид ![]() откуда
откуда
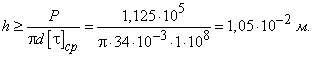 Примем
Примем ![]() мм.
мм.
Задача 11.3.
Определить необходимую длину фланговых швов для прикрепления стержня
фермы, состоящего из двух равнобоких уголков (см. рисунок 96). Принять
N
= 320 кН; ![]() = 160 МПа;
= 160 МПа; ![]() = 110 МПа.
= 110 МПа.
Решение.
1 Расчёт
стержня фермы на прочность. Стержень фермы, состоящий из двух равнобоких
уголков, растягивается силой N, приложенной в
центре тяжести сечения (точка ![]() на рисунке 98). Усилие,
приходящееся на один уголок
на рисунке 98). Усилие,
приходящееся на один уголок ![]() и оно приложено в центре тяжести уголка
и оно приложено в центре тяжести уголка ![]() .
.
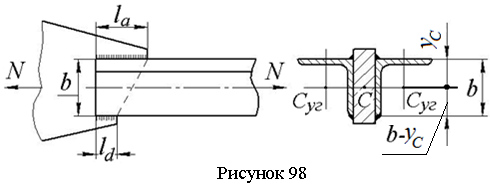
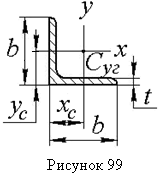 Условие прочности
уголка
Условие прочности
уголка 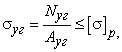 откуда необходимая площадь поперечного сечения
уголка
откуда необходимая площадь поперечного сечения
уголка 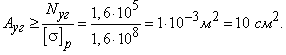
По сортаменту
выбираем уголок с ближайшей большей площадью поперечного сечения. Принимаем
уголок 7,5´7,5´0,8. Из таблицы имеем ![]() = 11,5 см2, b = 7,5 см,
= 11,5 см2, b = 7,5 см, ![]() 2,15 см, t = 0,8 см (см. рисунки 98, 99).
2,15 см, t = 0,8 см (см. рисунки 98, 99).
2
Определение длины сварных швов ![]() и
и ![]() Рассмотрим равновесие уголка под
действием сил
Рассмотрим равновесие уголка под
действием сил ![]() ,
, ![]() и
и ![]() (см. рисунок 100). Составим уравнения
равновесия и определим усилия
(см. рисунок 100). Составим уравнения
равновесия и определим усилия ![]() и
и ![]() , возникающие в сварных швах,
, возникающие в сварных швах,

![]() ,
,
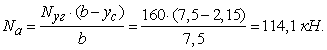
![]() ,
,
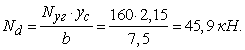
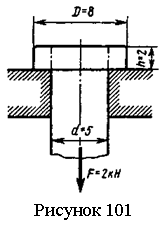 Из условия прочности для сварного
шва
Из условия прочности для сварного
шва 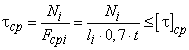 определяем необходимую длину швов
определяем необходимую длину швов
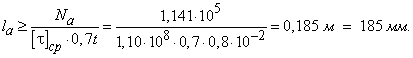
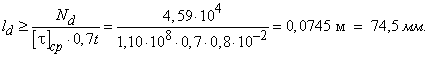
Окончательно
примем ![]() = 190 мм,
= 190 мм,![]() = 80 мм.
= 80 мм.
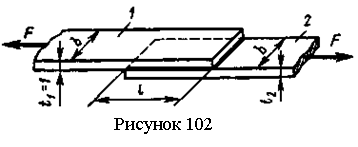 Задача 11.4.
Для стержня, изображенного на рисунке 101, определить напряжения от
растяжения, напряжения среза в его головке и напряжения смятия на опорной поверхности.
Задача 11.4.
Для стержня, изображенного на рисунке 101, определить напряжения от
растяжения, напряжения среза в его головке и напряжения смятия на опорной поверхности.
Ответ: σр=102 МПа, τср=63,7 МПа, : σсм=65 МПа.
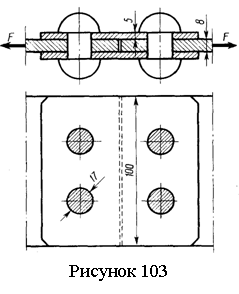 Задача 11.5.
На рисунке 102 показано клеевое соединение дюралюминиевой пластины 1
толщиной t1=1 мм
и стеклопластиковой пластины 2. Определить из расчетов на прочность ширину
обеих пластин b, толщину
t2
пластины 2 и длину
l
клеевого шва, если сила F=500
Н, допускаемое напряжение на растяжение для дюралюминия [σ]д=100
МПа, для стеклопластика [σ]с=75 МПа, допускаемое
напряжение на срез для клея [τ]ср=5 МПа.
Задача 11.5.
На рисунке 102 показано клеевое соединение дюралюминиевой пластины 1
толщиной t1=1 мм
и стеклопластиковой пластины 2. Определить из расчетов на прочность ширину
обеих пластин b, толщину
t2
пластины 2 и длину
l
клеевого шва, если сила F=500
Н, допускаемое напряжение на растяжение для дюралюминия [σ]д=100
МПа, для стеклопластика [σ]с=75 МПа, допускаемое
напряжение на срез для клея [τ]ср=5 МПа.
Ответ:b=5 мм, t2=1,33 мм, l=20 мм.
Задача 11.6. При каком значении силы и в каком элементе разрушится заклепочный шов, показанный на рисунке 103, если для материала полос и накладок σвр=400 МПа, для материала заклепок τвр=270 МПа?
Ответ:Fразр=219,5кН.
Задача 11.7. Вал передает момент M=300 Н∙м (см. рисунок 104). Определить напряжения среза в шпонке и напряжения смятия между шпонкой и ступицей колеса.
Ответ: τср=20,8 МПа, σсм=62,5 МПа.
 |
Задача 11.8. Валы, имеющие по концам фланцы, выкованные с ними заодно, соединены болтами, которые вставлены без зазора в отверстия во фланцах (см. рисунок 105). Определить из расчета на срез требуемый диаметр болтов, если валы передают момент M=6 кН∙м, число болтов 6, [τcр]=270 МПа?
Ответ:dб=15 мм.
12 Расчеты на прочность и жесткость при кручении
Задача 12.1. Для стержня (см. рисунок 106,а) построить эпюру крутящих моментов, определить из условия прочности диаметр стержня и построить и эпюру углов закручивания поперечных сечений стержня.
Решение.
1.
Определение
опорного реактивного момента из уравнения равновесия.
Из уравнения
равновесия для стержня ![]() получаем
получаем
![]() .
.
2. Построение эпюры крутящих моментов. У стержня два участка с различными выражениями для внутреннего крутящего момента. Методом сечений (см. рисунок 106,б) находим
![]() ,
, ![]()
и строим эпюру крутящих моментов ![]() (см. рисунок 106,в).
(см. рисунок 106,в).
3. Расчет на прочность
Из эпюры
крутящих моментов определяем ![]() во всех сечениях
первого участка. Условие прочности
во всех сечениях
первого участка. Условие прочности
 .
.
|
а)
в)
г)
|
б) |
||
|
Рисунок 106 |
|||
Если сечение
круглое, то ![]() , и из условия прочности
получаем
, и из условия прочности
получаем
 .
.
Если,
например, ![]() , то
, то
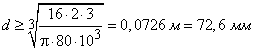 .
.
Округляем
полученные значения до целых значений и принимаем ![]() . Выполним
проверку условия прочности при этом значении диаметра; получаем
. Выполним
проверку условия прочности при этом значении диаметра; получаем
![]() ,
, 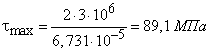 .
.
Перенапряжение
составит ![]() , что нельзя считать приемлемым. Если
принять d=75 мм, то
, что нельзя считать приемлемым. Если
принять d=75 мм, то ![]() и
и ![]() МПа.
МПа.
4. Построение эпюры углов закручивания (см. рисунок 104,г).
На первом
участке в заделке ![]() , поэтому
, поэтому
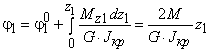 .
.
При ![]() а при
а при 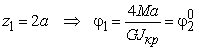 .
.
На втором
участке ![]() имеем
имеем
 .
.
При ![]() получаем
получаем ![]() , а
при
, а
при ![]() .
.
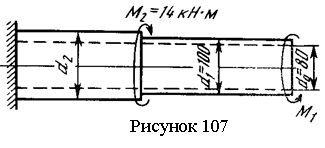 Задача 12.2. Определить
диаметр d2 ступенчатого
стержня кольцевого сечения (см. рисунок 107), если наибольшие касательные напряжения
на обоих участках равны 40 МПа.
Задача 12.2. Определить
диаметр d2 ступенчатого
стержня кольцевого сечения (см. рисунок 107), если наибольшие касательные напряжения
на обоих участках равны 40 МПа.
Указание: уравнение для определения d2 решать подбором.
Ответ: 125 мм.
Задача 12.3 Определить диаметр вала круглого сечения, передающего мощность P=125 кВт и вращающегося со скоростью n=150 об/мин, если допускаемое касательное напряжение [τ]=200 МПа, а допускаемый относительный угол закручивания [θ]=0,6 град/м.
Решение.
Определяем угловую скорость вращения вала и крутящий момент, равный вращающему моменту
![]() с-1,
с-1, ![]() кН∙м.
кН∙м.
Из условия
прочности при кручении ![]() находим полярный
момент сопротивления поперечного сечения вала и его диаметр
находим полярный
момент сопротивления поперечного сечения вала и его диаметр ![]()
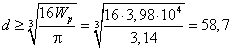 мм.
мм.
Из условия
жесткости при кручении ![]() находим полярный момент инерции
поперечного сечения вала и его диаметр
находим полярный момент инерции
поперечного сечения вала и его диаметр
![]()
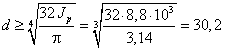 мм. Округляя, принимаем d=60 мм.
мм. Округляя, принимаем d=60 мм.
Задача 12.4. Как изменится максимальное касательное напряжение в скручиваемом стержне круглого поперечного сечения, при увеличении площади в 2 раза?
Ответ: уменьшится в 2,8 раза.
Задача 12.5.
Как изменится
Рисунок 105
максимальное касательное напряжение в стержне круглого
поперечного сечения, если крутящий момент увеличится площади в 2 раза, а
диаметр стержня увеличится в 1,5 раза?
Ответ: уменьшится в 1,69 раза.
Задача 12.6. Найти размеры поперечного сечения стержня кольцевого поперечного сечения, если он должен быть равнопрочным со стержнем круглого поперечного сечения диаметром 300 мм, а по массе в 2 раза легче.
Ответ: 360 и 288 мм.
Задача 12.7. Определить из расчета на прочность диаметр вала круглого сечения, передающего мощность P=48 кВт и вращающегося со скоростью n=970 об/мин, если [τ]=40 МПа.
Ответ: 40 мм.
Задача 12.8. Во сколько раз возрастет жесткость при кручении для стержня круглого поперечного сечения при увеличении площади сечения в 2 раза?
Ответ: в 4 раза.
Задача 12.9. Для стержней на рисунке 108 построить эпюры Mкр, наибольших касательных напряжений и углов закручивания.
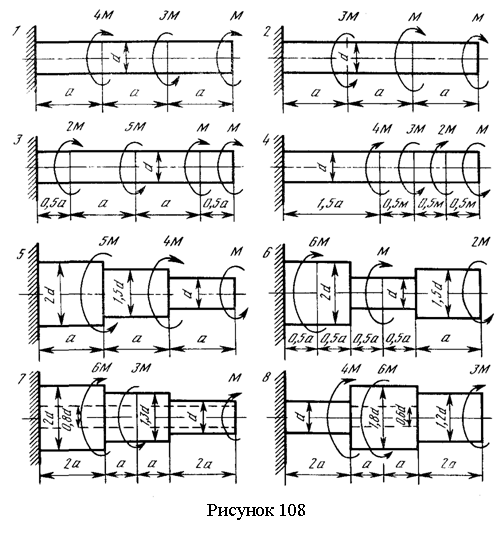
Задача 12.10. Проверить прочность и жесткость стальных стержней, изображённых на рисунке 109, если [τ]=40 МПа, а [θ]=0,6 град/м.
Ответ:
|
Схема |
а) |
б) |
в) |
г) |
д) |
е) |
|
τmax, МПа |
68,4 |
55,7 |
27,6 |
44,6 |
33,4 |
65,6 |
|
θmax, град/м |
1,63 |
1,23 |
0,4 |
0,86 |
0,74 |
1,18 |
|
|
|
|
|
|
|
|
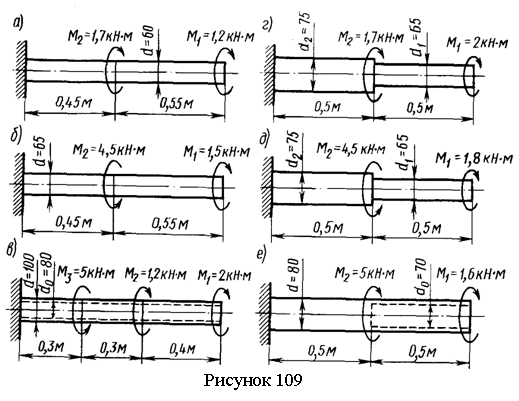
13 Расчеты на прочность при изгибе
Задача 13.1.
Для балки,
изображенной на рисунке 107,а, построить эпюры поперечной силы Q и
изгибающего момента M. Проверить прочность балки по нормальным напряжениям,
если![]() сечение балки – швеллер №36.
сечение балки – швеллер №36.
Решение.
1. Определение опорных реакций. Из уравнений равновесия
![]()
![]()
находим
![]()
![]()
Выполним проверку![]()
2. Построение эпюр. Для нахождения Qy и Mx используем метод сечений.
Поперечная
сила Qy численно равна сумме проекций
на ось y всех внешних сил, приложенных к стержню
по одну сторону от рассматриваемого сечения ![]() ; проекцию
силы, стремящуюся повернуть отсеченную часть стержня по часовой стрелке относительно
центра тяжести рассматриваемого поперечного сечения, следует брать со знаком
«плюс», в противном случае проекцию нужно взять со знаком «минус».
; проекцию
силы, стремящуюся повернуть отсеченную часть стержня по часовой стрелке относительно
центра тяжести рассматриваемого поперечного сечения, следует брать со знаком
«плюс», в противном случае проекцию нужно взять со знаком «минус».
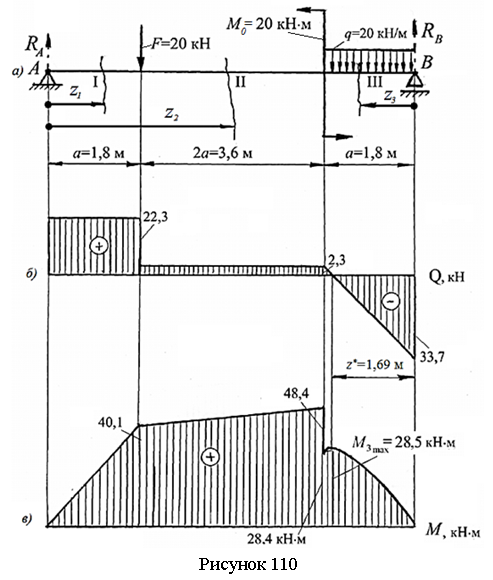
Изгибающий
момент Mx численно равен
алгебраической сумме моментов всех внешних сил, приложенных к стержню по одну
сторону от рассматриваемого сечения, относительно оси x ![]() ; знак момента
внешней силы (или пары сил) следует брать со знаком «плюс», если эта сила
(пара сил) стремится изогнуть рассматриваемую часть балки относительно
рассматриваемого сечения выпуклостью вниз; в противном случае момент следует
взять со знаком «минус».
; знак момента
внешней силы (или пары сил) следует брать со знаком «плюс», если эта сила
(пара сил) стремится изогнуть рассматриваемую часть балки относительно
рассматриваемого сечения выпуклостью вниз; в противном случае момент следует
взять со знаком «минус».
Балка имеет 3 участка. Строим эпюры по участкам (см. рисунок 110,б,в)
Участок I (0≤ x1 ≤ a):
![]() эпюра
Q – прямая, параллельная
оси z.
эпюра
Q – прямая, параллельная
оси z.
![]() -
эпюра M – наклонная прямая;
при z1 =0 M1 =0 , при z1 = a M1 = RА ⋅a = 22,3⋅1,8
= 40,1 кН∙м.
-
эпюра M – наклонная прямая;
при z1 =0 M1 =0 , при z1 = a M1 = RА ⋅a = 22,3⋅1,8
= 40,1 кН∙м.
Участок II (0≤ x2 ≤3a):
![]() эпюра
Q – прямая, параллельная
оси z.
эпюра
Q – прямая, параллельная
оси z.
![]() -
эпюра M – наклонная прямая;
при z2 = a
M2 = RА
⋅a = 22,3⋅1,8 = 40,1 кН∙м, при z2 = 3a M2 = RА ⋅3a-F∙2a =
48,4 кН∙м.
-
эпюра M – наклонная прямая;
при z2 = a
M2 = RА
⋅a = 22,3⋅1,8 = 40,1 кН∙м, при z2 = 3a M2 = RА ⋅3a-F∙2a =
48,4 кН∙м.
Участок III (0≤ z3 ≤a, справа налево):
![]() , эпюра
Q – наклонная прямая; при
z3 =0 Q3
=- RB = -33,7
кН, при z3 = a Q3 = -RB +q∙a =
2,3 кН.
, эпюра
Q – наклонная прямая; при
z3 =0 Q3
=- RB = -33,7
кН, при z3 = a Q3 = -RB +q∙a =
2,3 кН.
![]() - эпюра M
– квадратичная парабола; при z3 =0 M3 =0,
при z3 =3a
M3 = RB ⋅a-q∙a2/2 = 28,4 кН∙м. Т.к. эпюра Q изменяет знак на участке (с
плюса на минус в правосторонней системе координат), то, в соответствии с
дифференциальной зависимостью Журавского между M и Q, в сечении, где Q=0, на эпюре M имеет место максимум для участка. Для того, чтобы определить
это значение, приравняем нулю выражение для Q.
Тогда
- эпюра M
– квадратичная парабола; при z3 =0 M3 =0,
при z3 =3a
M3 = RB ⋅a-q∙a2/2 = 28,4 кН∙м. Т.к. эпюра Q изменяет знак на участке (с
плюса на минус в правосторонней системе координат), то, в соответствии с
дифференциальной зависимостью Журавского между M и Q, в сечении, где Q=0, на эпюре M имеет место максимум для участка. Для того, чтобы определить
это значение, приравняем нулю выражение для Q.
Тогда ![]() , откуда
, откуда![]() и
и
![]()
3. Проверка
прочности. Опасным сечением по нормальным напряжениям σ является
сечение чуть левее границы между участками II и III, где ![]() Для балки постоянного поперечного
сечения условие прочности по нормальным напряжениям имеет вид
Для балки постоянного поперечного
сечения условие прочности по нормальным напряжениям имеет вид ![]() . По таблице сортамента для швеллера №30 находим момент сопротивления
изгибу относительно оси x Wx=387 см3.
. По таблице сортамента для швеллера №30 находим момент сопротивления
изгибу относительно оси x Wx=387 см3.
Проверим выполнение условия прочности. Вычисляем
![]() ,
,
так что условие прочности выполняется.
Задача 13.2.
Построить эпюры поперечной силы![]() и
изгибающего момента
и
изгибающего момента
![]() для балки (см. рисунок 111,а) и подобрать
стандартное двутавровое поперечное сечение, если
для балки (см. рисунок 111,а) и подобрать
стандартное двутавровое поперечное сечение, если ![]()
![]()
![]()
![]() Провести проверку
прочности балки по касательным напряжениям,
Провести проверку
прочности балки по касательным напряжениям, ![]()
Решение
1. Определение опорных реакций. Из уравнений равновесия
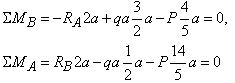
находим

Для проверки правильности найденных реакций составляем уравнение равновесия в виде суммы проекций сил на вертикальную ось
![]() .
.
Подставляя численные значения,
получим![]() . Следовательно, опорные реакции найдены
верно.
. Следовательно, опорные реакции найдены
верно.
2.
Определение ![]() и
и
![]() , построение эпюр.
Балка состоит из трех участков, на которых внутренние усилия имеют
различные аналитические выражения. Методом сечений (см. рисунок 111,б)
находим
, построение эпюр.
Балка состоит из трех участков, на которых внутренние усилия имеют
различные аналитические выражения. Методом сечений (см. рисунок 111,б)
находим
На первом
участке ![]() :
:
![]() эпюра поперечных сил – прямая линия;
при
эпюра поперечных сил – прямая линия;
при ![]() имеем
имеем ![]() а
а ![]() (см. рисунок 111,в).
(см. рисунок 111,в).
![]() эпюра моментов – квадратичная парабола, обращенная
выпуклостью вверх; при
эпюра моментов – квадратичная парабола, обращенная
выпуклостью вверх; при ![]()
![]() , при
, при ![]()
![]() . Экстремум параболы
имеет место в сечении, где
. Экстремум параболы
имеет место в сечении, где ![]() откуда
откуда ![]() Максимальное значение момента
Максимальное значение момента ![]() .
.
На втором
участке ![]() :
:
![]() поперечная сила
постоянная, эпюра – прямая линия, параллельная оси z.
поперечная сила
постоянная, эпюра – прямая линия, параллельная оси z.
![]() , эпюра – наклонная прямая; при
, эпюра – наклонная прямая; при
![]()
![]() , при
, при
![]()
![]()
На третьем
участке ![]() , выбирая начало координаты z там же, но рассматривая силы, приложенные к правой
части, имеем:
, выбирая начало координаты z там же, но рассматривая силы, приложенные к правой
части, имеем:
![]() поперечная сила постоянная, эпюра – прямая линия, параллельная
z.
поперечная сила постоянная, эпюра – прямая линия, параллельная
z.
 эпюра – наклонная прямая; при
эпюра – наклонная прямая; при ![]()
![]() , при
, при ![]()
![]()
3. Расчет
на прочность. Из эпюры ![]() находим в опасном
сечении
находим в опасном
сечении ![]() . Условие прочности записываем в виде
. Условие прочности записываем в виде 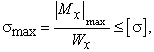 откуда
откуда
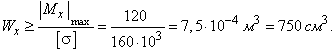
В таблице
ГОСТ 8239-89 находим двутавр № 36, у которого ![]() , и
двутавр № 40, для которого
, и
двутавр № 40, для которого ![]() . Последний дает значительную
недогрузку (свыше 20%), а первый – некоторую перегрузку, при этом
. Последний дает значительную
недогрузку (свыше 20%), а первый – некоторую перегрузку, при этом ![]() так что перегрузка не превышает 1%.
Следовательно, выбираем двутавр № 36.
так что перегрузка не превышает 1%.
Следовательно, выбираем двутавр № 36.
4. Проверка прочности балки по касательным напряжениям. Условие прочности в рассматриваемом случае имеет вид
![]()
Опасным по
касательным напряжениям будет сечение балки чуть правее опоры A, где ![]() В таблице
сортаментов для двутавра № 36 находим осевой момент сопротивления Jx=13380 см4, статический
момент половины площади поперечного сечения относительно нейтральной оси Sx=423 см3 , толщину стенки
двутавра d=7,5 мм. Тогда
В таблице
сортаментов для двутавра № 36 находим осевой момент сопротивления Jx=13380 см4, статический
момент половины площади поперечного сечения относительно нейтральной оси Sx=423 см3 , толщину стенки
двутавра d=7,5 мм. Тогда
![]()
Т.о., касательные напряжения пренебрежимо малы, так что в подавляющем большинстве случаев их можно не принимать во внимание и расчет на прочность проводить только по нормальным напряжениям.
Задача 13.3.
Для
балки, изображенный на рисунке 112,а, построить эпюры ![]() и
и ![]() , если
, если
![]()
![]()
![]()
![]()
![]() . Из расчета на прочность определить
размеры поперечного сечения в виде прямоугольника с соотношением сторон
h/b=2, если
. Из расчета на прочность определить
размеры поперечного сечения в виде прямоугольника с соотношением сторон
h/b=2, если
![]() Сопоставить расход материала для случая, когда балка
ориентирована таким образом, что длинная сторона сечения параллельна плоскости
изгиба, и для случая, когда короткая сторона сечения параллельна плоскости
изгиба.
Сопоставить расход материала для случая, когда балка
ориентирована таким образом, что длинная сторона сечения параллельна плоскости
изгиба, и для случая, когда короткая сторона сечения параллельна плоскости
изгиба.
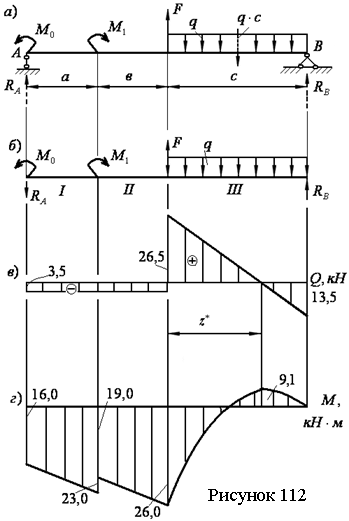
Решение. Начинаем с определения реакций, для чего составляем уравнения равновесия (реакции показаны пунктиром на рисунке 112,а).
![]()
![]()
откуда
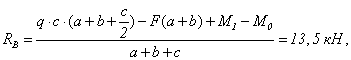
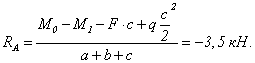
Знак «минус» показывает, что реакция направлена противоположно предварительно принятому направлению; на рисунке 112,б показаны действительные направления.
Проверка показывает, что реакции определены правильно
![]()
Эпюры будем строить по характерным точкам.
На участке І
(см. рисунок 112,б) эпюра
поперечных сил QI постоянна
(распределенная нагрузка отсутствует), равна по модулю RA=3,5
кН, отрицательна (направлена вниз слева от любого сечения на участке І)
– строим эпюру на рисунке 112,в. Эпюра изгибающих моментов здесь
линейная, убывающая (QI отрицательна),
начинается от значения
![]() на
левой границе, а на правой границе участка
на
левой границе, а на правой границе участка
![]() (здесь значение подставляем со знаком
«плюс», так как в выражении для
(здесь значение подставляем со знаком
«плюс», так как в выражении для
![]() мы
учли действительное направление RA
). Эпюра показана на рисунке 112,г.
мы
учли действительное направление RA
). Эпюра показана на рисунке 112,г.
На участке ІІ
эпюра QII имеет
такой же вид, как на участке І:
![]() Изгибающий момент изменяется по
линейному закону и на левой границе имеет значение
Изгибающий момент изменяется по
линейному закону и на левой границе имеет значение
![]() (скачок на
(скачок на ![]() вверх);
на правой границе
вверх);
на правой границе
![]() .
.
На участке ІІІ
поперечная сила меняется по линейному закону (на участке имеется равномерно
распределенная нагрузка). На левой границе участка ІІІ эпюра изменяется
скачком на величину
![]() :
:
![]() . На
правой границе, если рассматривать левую часть балки,
. На
правой границе, если рассматривать левую часть балки, ![]()
![]() . Если же смотреть справа, то в этом
сечении
. Если же смотреть справа, то в этом
сечении ![]() т.е. все сходится. Изгибающий момент на
участке ІІІ изменяется по квадратичному закону. Эпюра на левой границе
начинается со значения
т.е. все сходится. Изгибающий момент на
участке ІІІ изменяется по квадратичному закону. Эпюра на левой границе
начинается со значения ![]() , там, где эпюра
, там, где эпюра ![]() проходит через нулевое значение - достигает
максимального значения и на правой границе должна приходить к нулевому
значению. Проверим:
проходит через нулевое значение - достигает
максимального значения и на правой границе должна приходить к нулевому
значению. Проверим: ![]()
![]()
![]() . Найдем теперь
значения максимального момента на участке . Из подобия треугольников,
составляющих эпюру
. Найдем теперь
значения максимального момента на участке . Из подобия треугольников,
составляющих эпюру ![]() , запишем
, запишем ![]() , откуда
, откуда ![]() .
Поскольку изменение значения изгибающего момента между левой границей участка и
сечением, где момент максимален, положительно и равно площади под эпюрой
поперечной силы между этими двумя сечениями, то
.
Поскольку изменение значения изгибающего момента между левой границей участка и
сечением, где момент максимален, положительно и равно площади под эпюрой
поперечной силы между этими двумя сечениями, то ![]() .
.
Переходим к подбору
сечения. Из условия прочности
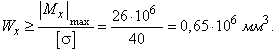
В случае,
когда балка ориентирована таким образом, что длинная сторона сечения
параллельна плоскости изгиба, момент сопротивления![]() Тогда
Тогда![]() Округляя, получаем b=100
мм, h= 200 мм.
Округляя, получаем b=100
мм, h= 200 мм.
В случае же,
когда балка ориентирована так, что короткая сторона сечения параллельна
плоскости изгиба, момент сопротивления![]() Тогда
Тогда![]() и h= 250 мм.
и h= 250 мм.
Сопоставляя значения площадей поперечных сечений в двух случаях, видим, что во втором случае расход материала больше в 100х200/125х250= 1,56 раза.
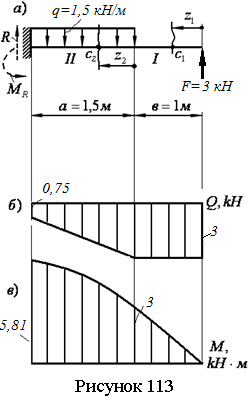 Задача 13.4.
Для
балки, изображенной на рисунке 113,а, построить эпюры
Задача 13.4.
Для
балки, изображенной на рисунке 113,а, построить эпюры ![]() и
и ![]() , а также
подобрать из условия прочности диаметр, если
, а также
подобрать из условия прочности диаметр, если ![]()
Решение. Балка имеет два участка. Для того чтобы не определять реакцию R и реактивный момент MR в заделке, будем рассматривать на обоих участках правую отсеченную часть.
На участке I
![]() :
:
![]() , от
z2 не зависит;
, от
z2 не зависит;
![]() - уравнение прямой; при
- уравнение прямой; при
![]()
![]() , при
, при
![]() ,
, ![]() .
.
На участке II ![]() :
:
![]() -
уравнение прямой; при
-
уравнение прямой; при ![]()
![]()
![]() , при
, при ![]() ,
, ![]() . Изгибающий момент
. Изгибающий момент
![]() -
уравнение параболы; поскольку Q2
не меняет знак на участке, в пределах участка парабола вершины не имеет;
при
-
уравнение параболы; поскольку Q2
не меняет знак на участке, в пределах участка парабола вершины не имеет;
при ![]() ,
,
![]() ; при
; при
![]() ,
,
![]() .
Эпюры
показаны на рисунке 113,б,в.
.
Эпюры
показаны на рисунке 113,б,в.
Переходим к
подбору сечения. Из условия прочности 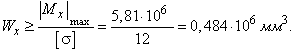
Для круглого
поперечного сечения осевой момент сопротивления ![]() ,
отсюда определяем диаметр
,
отсюда определяем диаметр 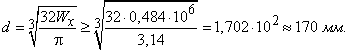
Задача 13.5.
Для
стальных балок, изображенных на рисунке 114, построить эпюры ![]() и
и ![]() , а также
подобрать из условия прочности номера прокатных профилей из условия прочности,
если
, а также
подобрать из условия прочности номера прокатных профилей из условия прочности,
если ![]() Данные принять по таблице 3.
Данные принять по таблице 3.
Указание: в рассматриваемых случаях значение осевого момента сопротивления, найденное в результате расчета, следует разделить на два и по полученному значению подбирать номер профиля.
Т а б л и ц а 1
|
Схема |
Вариант |
q, кН/м |
F, кН |
M, кН∙м |
a, м |
l, м |
|
|
||||||
|
1 |
I II III IV |
- - - - |
40 50 40 40 |
20 30 30 40 |
2 2 3 2 |
|
|
2 |
I II III IV |
- - - - |
80 60 50 70 |
40 30 20 30 |
2 3 3 2 |
4 4 6 5 |
|
3 |
I II III IV |
30 20 20 40 |
50 80 60 40 |
- - - - |
2 3 4 2 |
6 5 6 5 |
|
4 |
I II III IV |
20 30 40 30 |
- - - - |
60 50 40 20 |
3 2 4 3 |
5 6 6 6 |
|
5 |
I II III IV |
20 30 30 30 |
- - - - |
40 50 50 40 |
2 3 2 4 |
6 5 5 7 |
|
6 |
I II III IV |
20 30 40 20 |
60 50 50 60 |
- - - - |
4 2 3 2 |
7 6 7 5 |
|
7 |
I II III IV |
20 20 30 30 |
20 30 20 30 |
- - - - |
2 2 2 3 |
6 5 6 5 |
|
8 |
I II III IV |
20 30 40 30 |
- - - - |
40 40 30 20 |
2 3 2 2 |
4 5 5 6 |
14 Расчет стержней круглого поперечного сечения при совместном действии изгиба и кручения
Задача 14.1. Из расчета на прочность определить диаметр промежуточного вала цилиндрического косозубого редуктора (см. рисунок 115,а). Вал изготовлен из стали с пределом текучести σт=340 МПа, требуемый коэффициент запаса прочности [n]=2,5. При расчете использовать гипотезу прочности наибольших касательных напряжений. Влиянием продольных и поперечных сил пренебречь. Вал передает мощность P=55 кВт и вращается со скоростью n=300 об/мин. Принять Fr=0,36Ft, Fa=0,2Ft.
Решение
Определяем угловую скорость вращения вала и крутящий момент, равный вращающему моменту
![]() с-1,
с-1, ![]() кН∙м.
кН∙м.
Определяем окружные силы на зубчатых колесах
![]()
![]()
Радиальные и осевые силы на колесах
![]()
![]()
На рисунке 115,б показана расчетная схема вала, на основе которой определены опорные реакции и построены эпюры Mкр, Mx, My. Значения реакций приведены на рисунке 115,б, а эпюры – на рисунке 115,в. Очевидно, что опасным является сечение вала чуть левее середины второго колеса, где расчетный момент по гипотезе прочности наибольших касательных напряжений равен
![]()
Условие прочности записывается в виде
![]()
![]()
Отсюда

Округляя,
принимает d=55 мм, при этом максимальное значение эквивалентных напряжений
будет равно ![]() и перегрузку, равную
и перегрузку, равную ![]() ,
можно принять.
,
можно принять.
Если требуется выполнить расчёт по гипотезе прочности удельной потенциальной энергии формоизменения, то получим
![]()

Округляя, принимаем d=55 мм.
 Задача 14.2.
Из расчета на прочность, принимая [σ]=100 МПа,
определить диаметры dA,
dB,
dC,
dE,
вала лебедки (см. рисунок 116). Расчёт выполнить по
гипотезе прочности потенциальной энергии формоизменения.
Задача 14.2.
Из расчета на прочность, принимая [σ]=100 МПа,
определить диаметры dA,
dB,
dC,
dE,
вала лебедки (см. рисунок 116). Расчёт выполнить по
гипотезе прочности потенциальной энергии формоизменения.
Указание: Расчет начать с определения силы F, радиальную силу в зубчатом зацеплении не учитывать.
Ответ: dA=62 мм, dB=62 мм, dC=116 мм, dE=98 м.
Задача 14.3. Из расчета на прочность, принимая [σ]=45 МПа, определить диаметр опасного сечения вала цилиндрического косозубого колеса (см. рисунок 117), передающего мощность P=32 кВт при угловой скорости ω=51 рад/с. Расчёт выполнить по гипотезе прочности потенциальной энергии формоизменения.
Указание: Окружная сила Ft направлена по касательной к окружности колеса. Сжатием вала осевой силой Fa пренебречь.
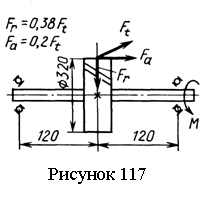 Ответ: 52 мм.
Ответ: 52 мм.
Задача 14.4. Из расчета на прочность, принимая [σ]=45 МПа, определить диаметр опасного сечения вала конической шестерни (см. рисунок 118), передающего мощность P=12,5 кВт при n=970 об/мин. Расчёт выполнить по гипотезе прочности потенциальной энергии формоизменения, учесть указания к предыдущей задаче.
Ответ: 36 мм.
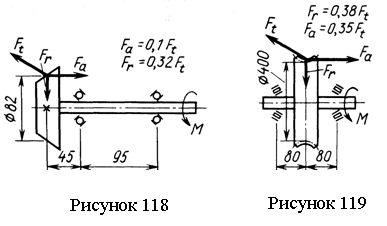
Задача 14.5. Из расчета на прочность, принимая [σ]=50 МПа, определить диаметр опасного сечения вала червячного колеса (см. рисунок 119), передающего мощность P=9 кВт при n=65 об/мин. Расчёт выполнить по гипотезе прочности потенциальной энергии формоизменения, учесть указания к задаче 14.3.
Ответ: 63 мм.
Задача 14.6. К горизонтальному валу (см. рисунок 120,а) с помощью ременной передачи подводится мощность P=31 кВт, угловая скорость вала ω=43 рад/с. От этого вала движение передается через коническую зубчатую передачу на вертикальный вал. По приведенной на рисунке 120,б расчетной схеме построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях.
Определить, используя гипотезу прочности наибольших касательных напряжений, диаметр опасного сечения вала, если [σ]=50 МПа. Сжатие вала осевой силой Fa не учитывать.
Ответ: 66 мм.
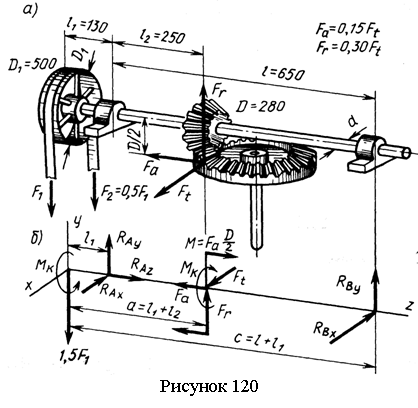
 Задача 14.7.
Вал с насаженным на (см. рисунок 121) коническим прямозубым колесом
вращается со скоростью ω=35 рад/с. Материал вала – сталь, предел
текучести σт=300 МПа.
Задача 14.7.
Вал с насаженным на (см. рисунок 121) коническим прямозубым колесом
вращается со скоростью ω=35 рад/с. Материал вала – сталь, предел
текучести σт=300 МПа.
При каком значении передаваемой мощности вал имеет коэффициент запаса по отношению к σт равный 4,0? Влиянием продольной силы, вызывающей осевую деформацию вала, пренебречь, использовать гипотезу прочности наибольших касательных напряжений.
Ответ: 27,9 кВт.
Задача 14.9. Для стального вала постоянного поперечного сечения, изображенного на рисунке 122, требуется: а) построить эпюры крутящего момента и изгибающих моментов в вертикальной и горизонтальной плоскостях; б) определить диаметр вала, принимая [σ]=60 МПа.
Расчет выполнить, используя гипотезу прочности наибольших касательных напряжений, полученное значение диаметра вала в миллиметрах округлить до ближайшего числа, оканчивающегося на 0, 2, 5 или 8.
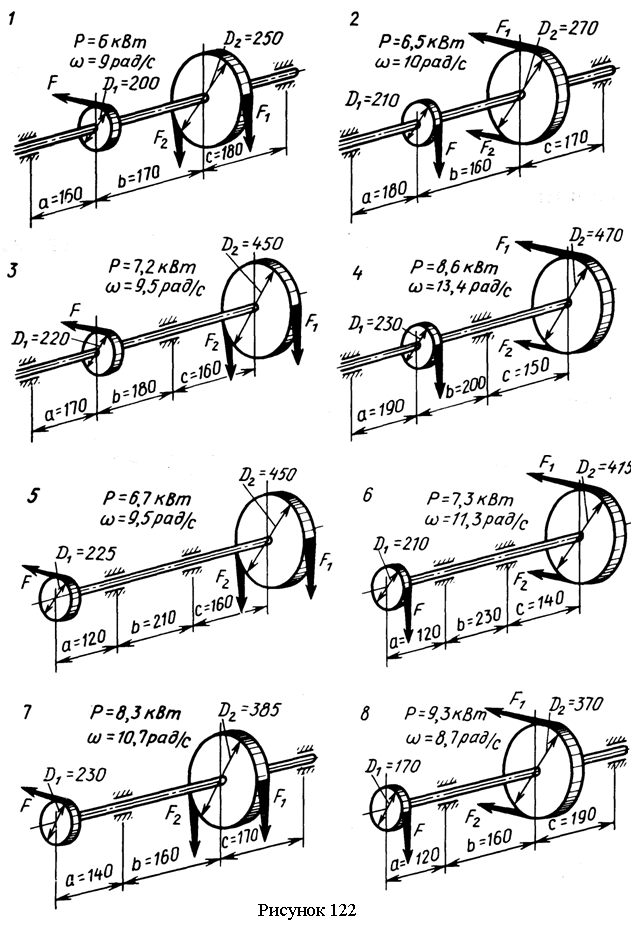
15 Расчет сжатых стержней на устойчивость
Задача 15.1. Стальной стержень двутаврового сечения №18, шарнирно
закреплённый на одном краю и жёстко на другом (см. рисунок 123,в), сжимается
силой F. Длина стержня
l
= 4 м. Требуется определить допускаемое и критическое значения силы
F,
а также коэффициент запаса устойчивости, если ![]()
![]()
![]()
Решение. Из таблицы сортамента стального проката
для двутавра №18 находим параметры поперечного сечения стержня: площадь A = 23,4 см2, минимальные радиус
инерции и момент инерции ![]()
![]() Коэффициент приведения длины для
данного типа закрепления (см. рисунок 123,в)
Коэффициент приведения длины для
данного типа закрепления (см. рисунок 123,в) ![]() Определяем
гибкость стержня
Определяем
гибкость стержня 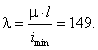 Т.к. в рассматриваемом случае
Т.к. в рассматриваемом случае 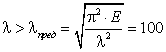 ,
то критическая сила определяется по формуле Эйлера
,
то критическая сила определяется по формуле Эйлера
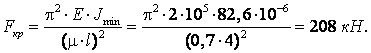
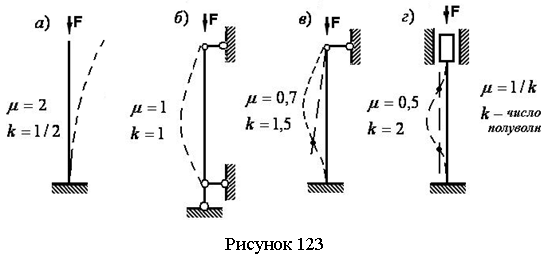
По таблице 4 определяем с помощью интерполяции коэффициент снижения основного допускаемого напряжения φ=0,333. Вычисляем допускаемое значение силы
![]()
Запас устойчивости
![]()
Если принять длину l=2 м, то ![]() В этом случае для определения
критической силы использовать формулу Эйлера нельзя. Воспользуемся формулой Ясинского,
тогда
В этом случае для определения
критической силы использовать формулу Эйлера нельзя. Воспользуемся формулой Ясинского,
тогда
![]()
Коэффициент
запаса: ![]()
Т а б л и ц а 2 - Коэффициент продольного изгиба
|
Гибкость, λ |
Материал |
|||
|
Сталь Ст.2, Ст.3, Ст.4. |
Сталь Ст.5 |
Чугун |
Дерево |
|
|
|
||||
|
0 |
1,00 |
1,00 |
1,00 |
1,00 |
|
10 |
0,99 |
0,98 |
0,97 |
0,99 |
|
20 |
0,96 |
0,95 |
0,91 |
0,97 |
|
30 |
0,94 |
0,92 |
0,81 |
0,93 |
|
40 |
0,92 |
0,89 |
0,89 |
0,87 |
|
50 |
0,89 |
0,86 |
0,57 |
0,80 |
|
60 |
0,86 |
0,82 |
0,44 |
0,71 |
|
70 |
0,81 |
0,76 |
0,34 |
0,60 |
|
80 |
0,75 |
0,70 |
0,26 |
0,48 |
|
90 |
0,69 |
0,62 |
0,20 |
0,38 |
|
100 |
0,60 |
0,51 |
0,16 |
0,31 |
|
110 |
0,52 |
0,43 |
- |
0,15 |
|
120 |
0,45 |
0,37 |
- |
0,22 |
|
130 |
0,40 |
0,36 |
- |
0,18 |
|
140 |
0,36 |
0,29 |
- |
0,16 |
|
150 |
0,32 |
0,26 |
- |
0,14 |
|
160 |
0,29 |
0,24 |
- |
0,12 |
|
170 |
0,26 |
0,21 |
- |
0,11 |
|
180 |
0,23 |
0,19 |
- |
0,10 |
|
190 |
0,21 |
0,17 |
- |
0,09 |
|
200 |
0,19 |
0,16 |
- |
0,08 |
Задача 15.2. Подобрать диаметр круглого поперечного сечения стойки
длиной ![]() из дерева (сосна), нагруженной силой
F=100
кН, если
из дерева (сосна), нагруженной силой
F=100
кН, если ![]() Один конец стержня жёстко
защемлён, а другой свободен от закрепления.
Один конец стержня жёстко
защемлён, а другой свободен от закрепления.
Решение. Условие устойчивости записываем в виде
![]()
Подбор диаметра D сечения производим методом последовательных приближений.
Первое приближение. Принимаем ![]() Тогда:
Тогда:
![]()
Т.к. ![]() то
то ![]()
Для найденного диаметра d=130 мм находим![]()
![]()
![]()
Учитывая, что в рассматриваемом случае (см. рисунок 123,а) коэффициент
приведения длины μ=2, находим гибкость стержня![]() По таблице коэффициентов
По таблице коэффициентов ![]() с учётом интерполирования
находим
с учётом интерполирования
находим ![]() то есть значение коэффициента
продольного изгиба не совпадает с предварительно принятым значением.
то есть значение коэффициента
продольного изгиба не совпадает с предварительно принятым значением.
Второе
приближение. Зададимся значением ![]()
Находим
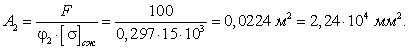
Диаметр ![]() Далее находим
Далее находим
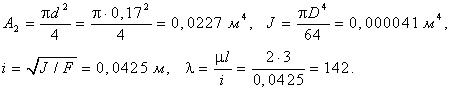
По таблице находим ![]() и видим, что значение
коэффициента продольного изгиба не совпадает с предварительно принятым
значением
и видим, что значение
коэффициента продольного изгиба не совпадает с предварительно принятым
значением![]() .
.
Третье приближение. Принимаем
![]()
Вычисляем
![]()
Находим диаметр
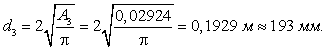
Округляя, получаем D3 = 200 мм. Корректируем новую площадь
![]()
Вычисляем
![]()
![]()
По таблице 1 находим ![]()
Проверим, насколько сошелся полученный результат. Фактическое
напряжение равно ![]() Допускаемое напряжение на
устойчивость
Допускаемое напряжение на
устойчивость ![]() недогрузка составляет
недогрузка составляет ![]()
Выполним проверку для диаметра d4= 195 мм. Вычисляем
![]()
Вычисляем
![]()
![]()
По таблице 1 находим ![]()
Проверим полученный результат. Фактическое напряжение равно ![]() Допускаемое напряжение на устойчивость
Допускаемое напряжение на устойчивость
![]() так что перегрузка составляет
так что перегрузка составляет ![]() , что недопустимо.
, что недопустимо.
Окончательно принимаем значение диаметра d = 200 мм.
Задача 15.3. Как изменится значение критической силы для стержня, показанного на рисунке 123,а и имеющего круглое поперечное сечение, если: а) площадь поперечного сечения увеличить вдвое; б) если диаметр стержня увеличить вдвое? Потеря устойчивости происходит при σ<[σкр].
Ответ: а) увеличится в 4 раза; б) увеличится в 16 раз.
Задача 15.4. Сравнить значения критической силы для стержней, показанных на рисунке 124; поперечное сечение и материал стержней одинаковы. Потеря устойчивости происходит при λ>λпред.
Ответ: Fкр,2=1/4Fкр,1, Fкр,3=4 Fкр,1, Fкр,4=2,04 Fкр,1.
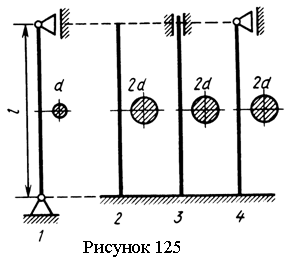 |
Задача 15.5 Сравнить значения критической силы для стержней, показанных на рисунке 125; материал стержней одинаков. Потеря устойчивости происходит при σ<[σкр].
Ответ: Fкр,2=4Fкр,1, Fкр,3=64 Fкр,1, Fкр,4=32,6 Fкр,1.
Задача 15.6. Сравнить значения критической силы для стержней, показанных на рисунке 125; материал стержней одинаков. Потеря устойчивости происходит при λ>λпред.
Ответ: Fкр,2=4Fкр,1, Fкр,3=64 Fкр,1, Fкр,4=32,6 Fкр,1.
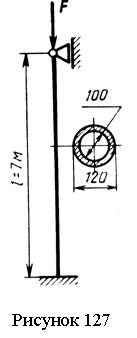
Задача 15.7. Как изменится значение критической силы для сжатого стержня, если его поперечное сечение – круг с диаметром d заменить сечением с равновеликой площадью в виде: а) квадрата; б) кольца, d1:d=0,8; прямоугольника со сторонами bx2b? Потеря устойчивости происходит при σ<[σкр].
Ответ: а) увеличится на 4,9%; б) увеличится в 1,9 раза.
Задача 15.8. Для колонны, показанной на рисунке 127, определить допускаемое значение силы F. Материал колонны сталь Ст.3. Требуемый коэффициент запаса устойчивости [nу]=3.
Решение. Для поперечного сечения колонны
определяем момент инерции ![]() , площадь
, площадь ![]() и радиус инерции
и радиус инерции ![]() и ее гибкость
и ее гибкость![]() Т.к. в
рассматриваемом случае
Т.к. в
рассматриваемом случае ![]() , то критическая сила определяется по
формуле Эйлера
, то критическая сила определяется по
формуле Эйлера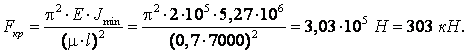 Тогда
Тогда
![]()
Задача 15.9. Определить запас устойчивости для стрежней, показанных на рисунке 128.
Ответ: а) 3,28; б) 3,12; в) 3,3; г) 5,06; д) 5,03; е) ?.
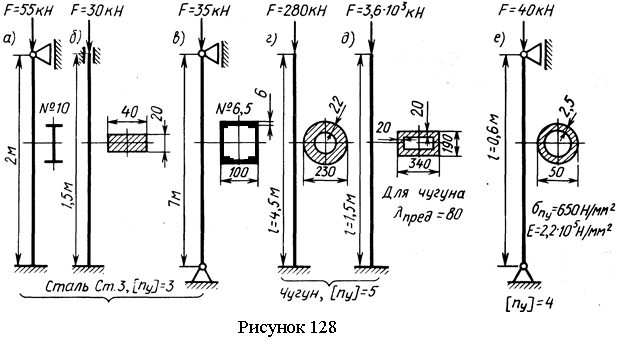
Список литературы
1. Сборник заданий для курсовых работ по теоретической механике: Учебное пособие /А.А.Яблонский, ред. – М.: Интеграл-Пресс, 2007. – 384 с.
2. Мещерский И.В. Сборник задач по теоретической механике: Учебное пособие. - М.: Наука, 1986. – 448 с.
3. Сборник задач по теоретической механике: Учебное пособие. - А.С.Кельзон, ред. – М.: Высш. шк., 1987. – 176 с.
4. Аркуша А.И. Техническая механика. Руководство к решению задач по теоретической механике: – М.: Высш. шк., 2000. – 176 с.
5. Бертяев В.Д. Теоретическая механика на базе Mathcad/ Практикум. – СПб.: БХВ-Петербург, 2005. – 752 с.
6. Буланов Э.А. Рещение задач по сопротивлению материалов. – М.: Бином, 2010. – 215 с.
7. Винокуров А.И. Сборник задач по сопротивлению материалов. – М.: Высш. шк., 1990. – 383 с.
8. Динасылов А.Д. Прикладная механика. Основы расчетов на прочность и жесткость: Учебное пособие. – Алматы: АИЭС, 2009. - 84 c.
9. Механика. Конспект лекций /А.Д.. Р.К.Койлыбаева. – Алматы: АИЭС, 2008. – 76 с.
10. Пособие к решению задач по сопротивлению материалов: Учебное пособие /И.Н.Миролюбов, ред. – М.: Высш. шк., 1985. – 399 с.

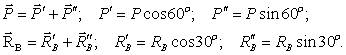
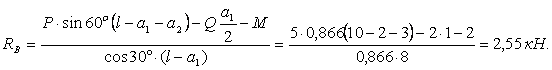
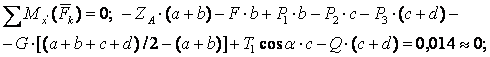
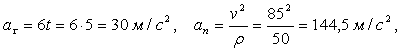
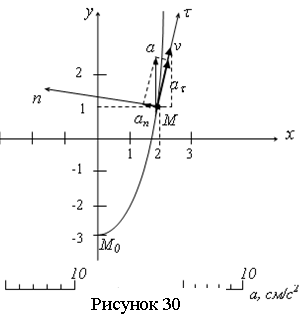 Решение. Для
определения траектории точки исключим из уравнений ее движения время, для этого
выразим из первого уравнения время
Решение. Для
определения траектории точки исключим из уравнений ее движения время, для этого
выразим из первого уравнения время