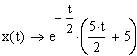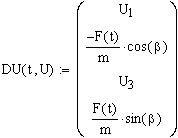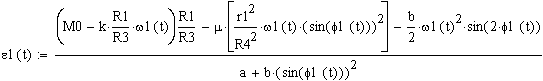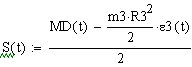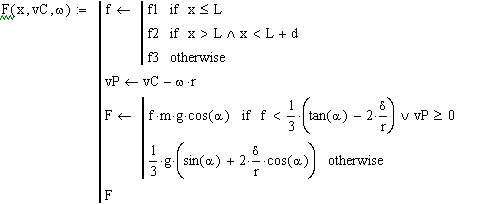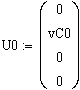Некоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра инженерной графики и прикладной механики
МЕХАНИКА.
Динамика ТОЧКИ И СИСТЕМЫ
Методические указания к выполнению лабораторных работ
для студентов специальностей
5В074600 – Космическая техника и технологии,
5В071700 – Теплоэнергетика
Алматы 2012
СОСТАВИТЕЛЬ: Р.К.Койлыбаева. Механика. Динамика точки и системы. Методические указания к выполнению лабораторных работ для студентов специальностей 5В074600 – Космическая техника и технологии, 5В071700 – Теплоэнергетика. – Алматы: АУЭС, 2012. – 38 с.
В методических указаниях содержатся задания и пошаговые указания к выполнению лабораторных работ по разделу «Динамика». Лабораторные работы выполняются с использованием компьютерной системы Mathcad. В каждой лабораторной работе предусмотрено проведение численного эксперимента, что позволяет выявить влияние начальных условий движения, инерционных характеристик и других параметров на движение точки и системы. Каждая лабораторная работа выполняется за 2 контактных часа.
Методические указания предназначены для студентов специальностей 5В074600 – Космическая техника и технологии, 5В071700 – Теплоэнергетика. Они могут также использоваться на лабораторных занятиях по дисциплинам «Механика» и «Прикладная механика» для студентов других специальностей.
Ил. 32, табл. 1, библиогр. – 5 назв.
Рецензент: канд.техн.наук, проф. А.Д.Динасылов.
Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2012 г.
ã НАО «Алматинский университет энергетики и связи», 2012 г.
Введение
В разделе «Динамика» изучается движение материальных тел и их систем под действием приложенных сил. В динамике решаются две основные задачи – определение сил, обеспечивающих заданное движение, и определение движения при заданных силах и начальных условиях. Задачи динамики материальной точки и твердого тела решаются с помощью дифференциальных уравнений движения и общих теорем динамики. При решении задач динамики механической системы используются общие теоремы динамики системы, метод кинетостатики, принцип виртуальных перемещений, уравнения Лагранжа 2-го рода и другие методы.
1 Интегрирование дифференциальных уравнений движения материальной точки
1.1 Цель лабораторной работы и задание
Цель: закрепление знаний по теме «Динамика точки», получение навыков составления дифференциальных уравнений движения материальной точки и отработка приемов их интегрирования аналитическим и численным способами.
Лабораторная работа выполняется на персональном компьютере с установленной в среде Windows XP системой Mathcad.
В работе предусмотрено выполнение 3-х заданий.
Задание 1: материальная точка массой m (см.рисунок
1) движется в горизонтальной плоскости Оху под действием силы притяжения
к началу координат, пропорциональной расстоянию от точки до начала координат ![]() , где
, где ![]() – радиус-вектор
точки, k – коэффициент пропорциональности. Материальная точка при
движении испытывает линейную силу сопротивления среды
– радиус-вектор
точки, k – коэффициент пропорциональности. Материальная точка при
движении испытывает линейную силу сопротивления среды ![]() , пропорциональную скорости
точки. В начальный момент точка находилась в положении М0(x0,y0)
и имела начальную скорость v0, направленную под углом α0
к оси х.
, пропорциональную скорости
точки. В начальный момент точка находилась в положении М0(x0,y0)
и имела начальную скорость v0, направленную под углом α0
к оси х.
Необходимо составить дифференциальные уравнения движения материальной точки, проинтегрировать их в системе Mathcad аналитическим способом, а также построить графики движения и траекторию точки на отрезке времени [0,t2] при следующих данных: m=1 кг, k=0,5 c-1, μ=0,1 кг/с, х0=5 м, у0=0, v0=2 м/с, α0=π/2, t2=20 c. Провести численный эксперимент, меняя коэффициент сопротивления среды μ.
Задание 2: рассмотреть случай силы сопротивления, пропорциональной квадрату скорости, составить дифференциальные уравнения движения и получить их решение численным способом.
Задание 3: по указанному преподавателем варианту составить дифференциальные уравнения движения материальной точки, проинтегрировать их аналитическим или численным способом и построить траекторию точки.
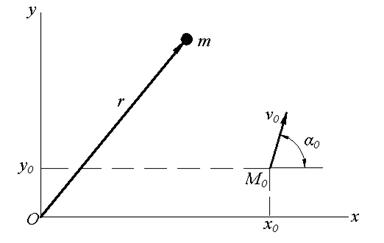
Рисунок 1
1.2 Выполнение лабораторной работы
Задание 1. Запишем уравнение движения материальной точки в векторном виде
![]() ,
,
с учетом выражений для заданных сил
![]() .
(1.1)
.
(1.1)
Спроектируем векторное уравнение (1.1) на оси х
и у, учитывая, что проекции радиуса-вектора точки равны ее координатам:
![]() . Тогда уравнения запишутся в виде:
. Тогда уравнения запишутся в виде:
![]()
Используя известные из кинематики формулы для проекций
скорости и ускорения точки ![]() ,
получаем
,
получаем
![]() .
.
Запишем дифференциальные уравнения в виде
![]() .
.
Обозначив ![]() , получаем
, получаем
![]() . (1.2)
. (1.2)
Необходимо найти решение дифференциальных уравнений (1.2) при следующих начальных условиях:
t=0, x=x0, vx=v0х , у=у0, vу=v0у . (1.3)
Уравнения (1.2) совпадают по виду, каждое из них является однородным линейным дифференциальным уравнением 2-го порядка с постоянными коэффициентами. Для получения общего решения первого уравнения (1.2) запишем соответствующее ему характеристическое уравнение и найдем его корни:
![]() .
.
Здесь возможны случаи: 1) n>k, 2) n=k, 3) n<k. Рассмотрим каждый из них.
1) n>k, тогда корни характеристического уравнения являются вещественными отрицательными числами:
![]()
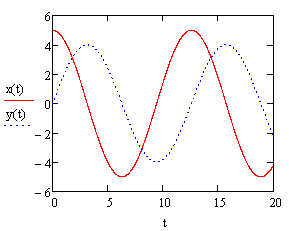
В этом случае общее решение дифференциального уравнения имеет вид:
![]() . (1.4)
. (1.4)
Очевидно, что х(t) является убывающей по экспоненциальному закону функцией.
Для определения констант интегрирования запишем вначале выражение для проекции скорости на ось х:
![]() . (1.5)
. (1.5)
Подставим начальные условия движения t=0, x=x0, vx=v0х в выражения (1.4) и (1.5):
![]() ,
, ![]() .
.
Решая данную систему уравнений, получим
 .
.
2) n=k, тогда корни характеристического
уравнения являются вещественными кратными числами: ![]() В этом случае общее решение
дифференциального уравнения имеет вид:
В этом случае общее решение
дифференциального уравнения имеет вид:
![]() . (1.6)
. (1.6)
Так как скорость убывания функции х(t) по экспоненциальному закону больше скорости ее возрастания по линейному закону, х(t) является в данном случае убывающей функцией. Запишем выражение для проекции скорости:
![]() . (1.7)
. (1.7)
Подставив начальные условия движения t=0, x=x0, vx=v0х в выражения (1.6) и (1.7), получаем
![]() ,
, ![]() .
.
Отсюда ![]() .
.
3) n<k, тогда корни характеристического
уравнения являются комплексно-сопряженными числами: ![]() где
где ![]()
В этом случае общее решение дифференциального уравнения имеет вид:
![]() . (1.8)
. (1.8)
В данном случае изменение х(t) носит характер
затухающих гармонических колебаний с циклической частотой k1
и периодом 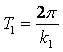 .
Запишем выражение для проекции скорости:
.
Запишем выражение для проекции скорости:
![]() .
(1.9)
.
(1.9)
Подставив начальные условия движения t=0, x=x0,
vx=v0х в выражения (1.8) и (1.9), получаем ![]() ,
, ![]() .
.
Отсюда 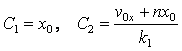 .
.
Поскольку второе дифференциальное уравнение совпадает по виду с первым, его решение находится по таким же формулам, при этом константы интегрирования определяются из начальных условий t=0, у=у0 , vу=v0у .
Для получения решения в системе Mathcad создадим с использованием полученных выше формул пользовательскую подпрограмму-функцию sol(n,k,s0,v0,t), где n и k – коэффициенты дифференциального уравнения, s0 – начальная координата, v0 –начальная скорость (см.рисунок 2).
|
|
Рисунок 2
При вводе подпрограммы-функции необходимо использовать имеющиеся на панели инструментов Программирование кнопку Add Line (добавить линию), стрелку ← и операторы if , otherwise. Здесь if («если») – условный оператор, при этом в случае выполнения условия справа вычисляется выражение слева; если условие не выполняется, управление передается следующей строке, в которой могут располагаться другой оператор if, выражение или условный оператор otherwise («в противном случае»). Данная подпрограмма-функция дает решение дифференциального уравнения вида (1.2) при любых значениях коэффициентов n и k.
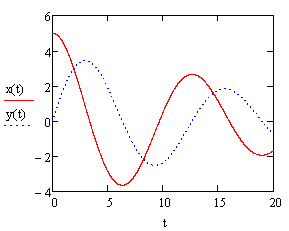
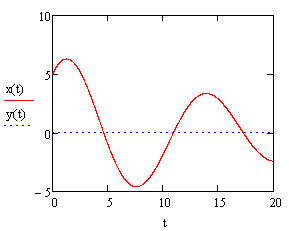
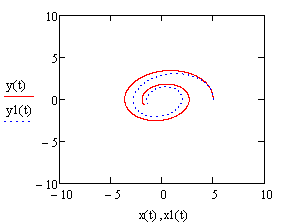
Внесем в документ Mathcad исходные данные, найдем решение дифференциальных уравнений и построим графики изменения координат и траекторию движения точки, как показано на рисунке 3.
Как видно, координаты х, у с течением времени затухают по гармоническому закону с циклической частотой k1=0,497 с-1, траектория точки похожа на спираль, точка стремится к началу координат. Это случай n<k, т.е. случай малого сопротивления движению.
|
|
Рисунок 3
Проведем численный эксперимент, меняя в документе Mathcad коэффициент сопротивления среды μ.
При μ =1 координаты х, у с течением времени убывают, точка стремится к началу координат и попадает в начало координат примерно за 15 с (см.рисунок 4). Это случай n=k, т.е. случай значительного сопротивления движению.
При μ =2 координаты х, у также с течением времени убывают, точка стремится к началу координат (см.рисунок 5). Это случай n>k, т.е. случай большого сопротивления движению.
|
|
Рисунок 4
|
|
Рисунок 5
|
|
Рисунок 6
|
|
Рисунок 7
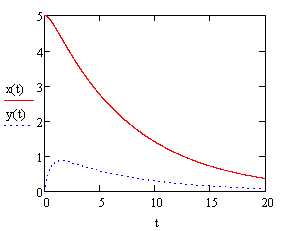
При μ =0 (случай отсутствия сопротивления движению) координаты х, у меняются по гармоническому закону с циклической частотой k=0,5 с-1, точка движется по замкнутой траектории – эллипсу и никогда не попадет в начало координат (см.рисунок 6).
Можно также проверить влияние на движение начальных условий. Если, например, при заданном значении коэффициента сопротивления μ=0,1 принять α0=0, то, как видно из рисунка 7, точка движется по прямой, при этом ее движение носит характер затухающих колебаний.
Задание 2. Рассмотрим
случай силы сопротивления, пропорциональной квадрату скорости. В этом случае
вектор силы сопротивления удобно записать в виде ![]() . Тогда уравнение движения в векторном
виде имеет вид:
. Тогда уравнение движения в векторном
виде имеет вид:
![]() .
(1.10)
.
(1.10)
Спроектируем векторное уравнение (1.10) на оси х и у:
![]()
Используя известные из кинематики формулы
![]()
![]() , получаем
, получаем
![]() . (1.11)
. (1.11)
Разделим обе части уравнений на m, тогда уравнения (1.11) примут вид
![]() .
(1.12)
.
(1.12)
Необходимо решить задачу Коши, т.е. получить решение дифференциальных уравнений (1.12) при заданных начальных условиях (1.3). Дифференциальные уравнения (1.12) являются нелинейными, получить их аналитическое решение невозможно. Для численного решения задачи Коши надо записать дифференциальные уравнения (1.12) в виде системы дифференциальных уравнений 1-го порядка:
 . (1.13)
. (1.13)
Тогда вектор неизвестных имеет вид
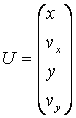 .
(1.14)
.
(1.14)
В начальный момент времени имеем вектор
 .
.
Вектор правых частей дифференциальных уравнений (1.13) имеет вид
 . (1.15)
. (1.15)
Учитывая, что в Mathcad нижний индекс элементов матриц по умолчанию равен 0, получаем с учетом (1.14)
 . (1.16)
. (1.16)
В Mathcad имеется несколько встроенных функций решения
задачи Коши. Решение методом Рунге-Кутта с фиксированным шагом реализуется с
помощью встроенной функции rkfixed(U0,0,t2,200,DU). Здесь первый параметр
означает начальный вектор, второй и третий параметры – интервал интегрирования,
200 – фиксированное число шагов интегрирования, последний параметр –
векторная функция, задающая правую часть системы дифференциальных уравнений.
Результатом численного решения будет матрица значений координат точки x,
y и проекций ее скорости vx , vy на
отрезке времени [0,t2] с шагом ![]() .
.
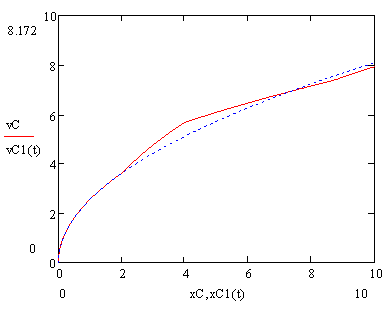
Для построения графиков необходимо по найденным дискретным значениям переменных получить их функции от времени путем интерполяции. Используем линейную интерполяцию с помощью встроенной в Mathcad функции вида linterp(x,y,t), которая возвращает значение в точке t линейного интерполяционного многочлена векторов х и у. Чтобы различать аналитическое и численное решения, будем обозначать полученные интерполяцией функции x1(t) и y1(t) (см.рисунок 9).
Обращаем внимание на то, что при вводе индексов
элементов матрицы необходимо использовать кнопку ![]() на панели инструментов Матрица, а при
вводе номера столбца матрицы - кнопку
на панели инструментов Матрица, а при
вводе номера столбца матрицы - кнопку ![]() на той же панели.
на той же панели.
|
|
Рисунок 9
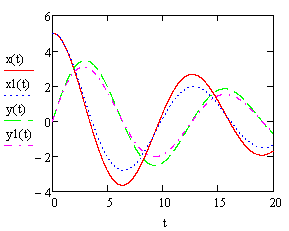
 Численное решение дифференциальных уравнений (1.12),
полученных для силы сопротивления, пропорциональной квадрату скорости, конечно,
отличается от аналитического решения дифференциальных уравнений (1.2), полученных
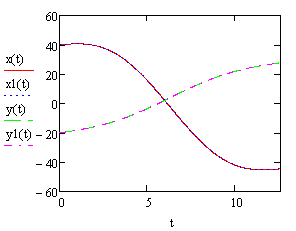
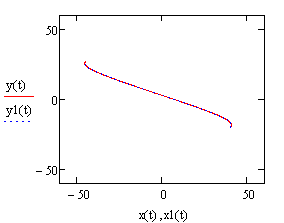
для линейной силы сопротивления. Как видно из рисунка 9, точка в случае силы
сопротивления, пропорциональной квадрату скорости, быстрее приближается к
началу координат.
Численное решение дифференциальных уравнений (1.12),
полученных для силы сопротивления, пропорциональной квадрату скорости, конечно,
отличается от аналитического решения дифференциальных уравнений (1.2), полученных
для линейной силы сопротивления. Как видно из рисунка 9, точка в случае силы
сопротивления, пропорциональной квадрату скорости, быстрее приближается к
началу координат.
Задание 3. Для схемы (см.рисунок 12) и данных из таблицы 1 по указанному преподавателем варианту составьте дифференциальные уравнения движения материальной точки, проинтегрируйте их аналитическим или численным способом, постройте траекторию точки. Пример выполнения задания приводится ниже.
Пример выполнения задания (см.рисунок 10). Дано: m=0,5 кг, х0=40 м, у0=20 м, v0=2 м/с, α0=60°, F=2sin(0,5t) Н, β=15°, t2=2π c.
Составим уравнения движения материальной точки в проекции на оси х и у:
![]()
Подставив выражение силы и значение массы, получаем:
![]()
Два раза проинтегрируем оба уравнения:
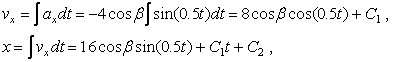
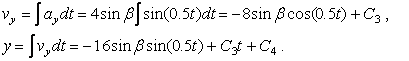
Для определения констант интегрирования используем начальные условия движения: t=0, х = х0, vx =v0x= v0 cosα0 , y =y0, vy =v0y= v0sinα0 .
Подставив начальные условия в выражения для координат и проекций скорости, получаем:
![]()
![]()
Отсюда находим константы интегрирования
![]()
Для численного решения запишем дифференциальные уравнения движения в виде системы дифференциальных уравнений 1-го порядка:
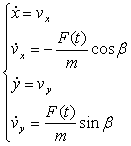 .
.
Тогда вектор неизвестных и вектор правых частей системы дифференциальных уравнений имеют вид
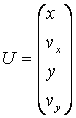 ,
, 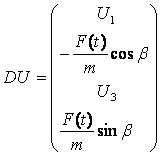 .
.
Результаты решения в Mathcad представлены на рисунке 11. Как видно, аналитическое и численное решения дифференциальных уравнений движения точки совпадают, что свидетельствует о правильности решения и о хорошей сходимости метода Рунге-Кутта.
|
ДАНО:
АНАЛИТИЧЕСКОЕ РЕШЕНИЕ
|
Рисунок 11
1.3 Варианты заданий
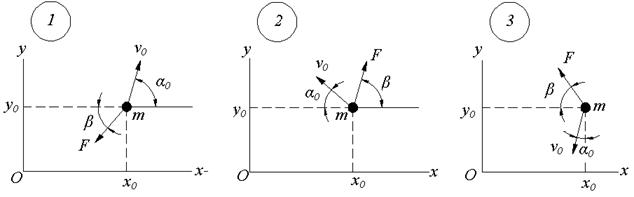
Рисунок 12
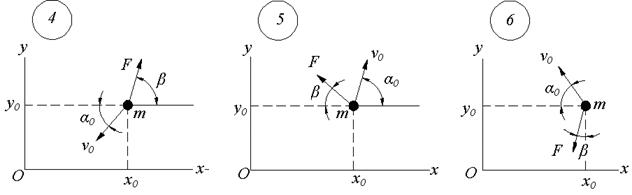
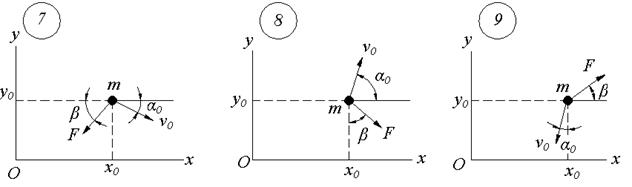
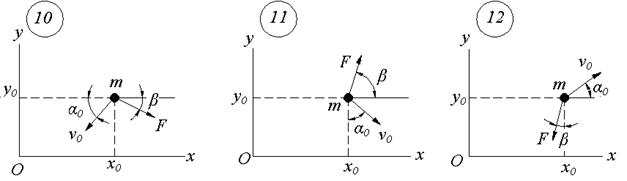
Продолжение рисунка 12
Т а б л и ц а 1
|
Вариант |
m, кг |
x0 , м |
y0 , м |
v0 , м/c |
α0 ,° |
F=F(t), H |
β ,° |
t2 , c |
|
|
||||||||
|
1 |
0,2 |
20 |
10 |
15 |
45 |
10sin(πt) |
15 |
2 |
|
2 |
0,5 |
0 |
10 |
20 |
30 |
8sin(πt/2) |
60 |
4 |
|
3 |
0,1 |
0 |
5 |
15 |
60 |
10cos(πt/2) |
30 |
4 |
|
4 |
0,1 |
-5 |
30 |
10 |
15 |
5cos(πt/2) |
75 |
4 |
|
5 |
0,2 |
-10 |
25 |
20 |
50 |
10cos(πt/3) |
60 |
6 |
|
6 |
0,5 |
0 |
0 |
10 |
20 |
6sin(πt/3) |
50 |
6 |
|
7 |
2 |
0 |
-10 |
15 |
30 |
20sin(πt/4) |
20 |
8 |
|
8 |
2 |
10 |
-5 |
25 |
75 |
40cos(πt/4) |
30 |
8 |
|
9 |
0,2 |
10 |
0 |
20 |
40 |
12cos(πt) |
55 |
3 |
|
10 |
0,5 |
0 |
0 |
10 |
25 |
10sin(2πt) |
45 |
2 |
Ответьте на вопросы:
1) Как записывается основное уравнение динамики материальной точки?
2) Как записываются дифференциальные уравнения движения материальной точки в декартовой системе координат?
3) Что означает знак «-» в формуле силы сопротивления среды?
4) Что задается и что определяется в первой задаче динамики точки?
5) Что задается и что определяется во второй задаче динамики точки?
6) Как определяются константы интегрирования дифференциальных уравнений движения?
7) В каких случаях необходимо использовать численные методы интегрирования дифференциальных уравнений движения?
8) В каком виде необходимо записать дифференциальные уравнения движения для их численного интегрирования?
2 Исследование динамики машины с кулисным приводом
2.1 Цель лабораторной работы и задание
Цель: закрепление знаний по темам «Общие теоремы динамики системы» и «Дифференциальные уравнения движения твердого тела», получение навыков составления дифференциальных уравнений движения механической системы и твердых тел, отработка приемов численного интегрирования дифференциальных уравнений в Mathcad.
Лабораторная работа выполняется на персональном компьютере с установленной в среде Windows XP системой Mathcad.
В работе предусмотрено выполнение 3-х заданий.
Задание 1: машина
с кулисным приводом (см.рисунок 13) приводится в движение моментом ![]() , приложенным к шкиву 3. Шкив связан с
маховиком 1 ременной передачей. Полезная нагрузка моделируется моментом
, приложенным к шкиву 3. Шкив связан с
маховиком 1 ременной передачей. Полезная нагрузка моделируется моментом
![]() ,
приложенным к катку 4. Здесь
,
приложенным к катку 4. Здесь ![]() - постоянные параметры. Элементы конструкции машины
считаются абсолютно жесткими. Предполагается, что ремень невесомый,
нерастяжимый, не проскальзывающий относительно шкива 3 и маховика 1.
Трение между пальцем А маховика и прорезью кулисы 2 отсутствует.
Каток 4 катится без скольжения. Шкив 3 и каток 4 можно
считать однородными сплошными цилиндрами.
- постоянные параметры. Элементы конструкции машины
считаются абсолютно жесткими. Предполагается, что ремень невесомый,
нерастяжимый, не проскальзывающий относительно шкива 3 и маховика 1.
Трение между пальцем А маховика и прорезью кулисы 2 отсутствует.
Каток 4 катится без скольжения. Шкив 3 и каток 4 можно
считать однородными сплошными цилиндрами.
Необходимо составить дифференциальное уравнение движения данной механической системы, используя теорему об изменении кинетической энергии системы в дифференциальной форме, и проинтегрировать его в системе Mathcad на отрезке времени [0,t2] при следующих данных: O1A=r1= 0,1м, R1=0,4 м, R3=0,2м, R4=0,1 м, J1=1,4 кгм2, m2=8 кг, m3=5 кг, m4=10 кг, М0=65 Нм, k=1Нм·c, μ=5 Нм·c, t2=2 c.
Начальные условия движения нулевые: φ1(0)=0, ω1(0)=0.
Построить графики изменения кинематических характеристик всех звеньев системы, вычислить их для момента времени t1=t2/2, а также найти их максимальные и минимальные значения в установившемся режиме.
Задание 2: составить дифференциальные уравнения движения твердых тел, входящих в механическую систему, и получить выражения для динамических реакций связей. В системе Mathcad построить графики зависимости от времени заданных моментов и найденных реакций связей.
Задание 3: провести численный эксперимент, меняя инерционные характеристики механической системы, и выявить их влияние на время установления движения.

Рисунок 13
2.2 Выполнение лабораторной работы
Задание 1. Для составления дифференциальных уравнений движения заданной механической системы применим теорему об изменении кинетической энергии в дифференциальной форме:
![]() ,
(2.1)
,
(2.1)
где dT -
элементарное
изменение кинетической энергии системы; ![]() - сумма элементарных работ действующих на систему внешних
и внутренних сил.
- сумма элементарных работ действующих на систему внешних
и внутренних сил.
Кинетическая энергия системы равна сумме кинетических энергий тел, входящих в систему:
![]() .
.
Маховик 1 и шкив 3 совершают вращательное движение, кулиса 2 движется поступательно, каток 4 совершает плоскопараллельное движение. Тогда кинетические энергии тел, входящих в систему, определяются по формулам:
 ,
,
где моменты инерции 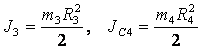 .
.
Запишем кинематические соотношения для тел системы, выражая все скорости и угловые скорости через первую производную по времени угла поворота 1-го тела:
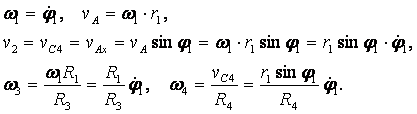 (2.2)
(2.2)
С учетом этого


Тогда кинетическая энергия системы запишется в виде:
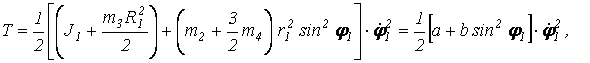
где 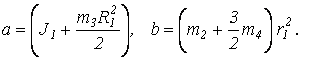
Так как кинетическая энергия системы является функцией
двух переменных ![]() , то ее полный дифференциал находится следующим
образом:
, то ее полный дифференциал находится следующим
образом:
 (2.3)
(2.3)
Найдем частные производные и дифференциалы:
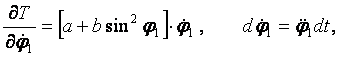
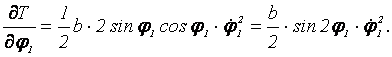
Учитывая, что ![]() получаем
получаем
![]() .
(2.4)
.
(2.4)
Найдем сумму элементарных работ внешних и внутренних сил системы. Сумма элементарных работ внутренних сил равна нулю, поскольку все тела системы являются абсолютно жесткими, а ремень нерастяжимым. Внешними являются заданные моменты МД и МН, силы тяжести, а также реакции внешних связей в точках О1, О2, В и К. В данной системе работа сил тяжести и реакций внешних связей равна нулю, поскольку они либо приложены в неподвижных точках, либо направлены перпендикулярно перемещению. Найдем сумму работ внешних моментов:
![]() ,
(2.5)
,
(2.5)
где ![]() .
.
Используя кинематические соотношения (2.2), получаем:
 ,
,
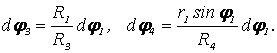
С учетом этого
 (2.6)
(2.6)
Подставляя (2.4) и (2.6) в выражение (2.1) и сокращая
на ![]() , получаем
, получаем
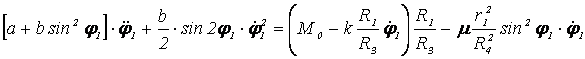 .
(2.7)
.
(2.7)
Это и есть дифференциальное уравнение движения механической системы. Оно является нелинейным, его аналитическое решение найти невозможно, поэтому будем искать численное решение полученного дифференциального уравнения в системе Mathcad. Для этого вначале запишем уравнение (2.7) в виде:
 .
.
Далее запишем данное дифференциальное уравнение 2-го порядка в виде системы двух дифференциальных уравнений 1-го порядка.
 (2.8)
(2.8)
Вектор неизвестных обозначим 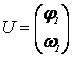 , тогда элементы вектора
, тогда элементы вектора ![]()
![]() .
.
Вектор правых частей дифференциальных уравнений (2.8) запишется в виде:
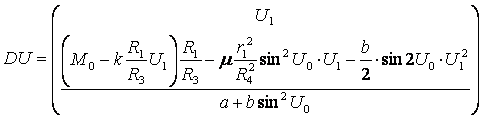 .
.
Систему дифференциальных уравнений с заданными
начальными условиями (задачу Коши) в Mathcad
можно решить с помощью встроенной функции
rkfixed(U0,0,t2,200,DU), реализующей метод
Рунге-Кутта. Здесь первый параметр означает начальный вектор, второй и третий
параметры – интервал интегрирования, 200 – фиксированное число шагов интегрирования,
последний параметр – векторная функция, задающая систему дифференциальных
уравнений. Результатом численного решения будет матрица значений угла поворота
и угловой скорости
маховика 1
на отрезке времени [0,t2] с шагом ![]() . Для построения графиков необходимо по
найденным дискретным значениям переменных получить их функции от времени путем
интерполяции. Используем линейную интерполяцию с помощью встроенной функции
вида linterp(x,y,t).
. Для построения графиков необходимо по
найденным дискретным значениям переменных получить их функции от времени путем
интерполяции. Используем линейную интерполяцию с помощью встроенной функции
вида linterp(x,y,t).
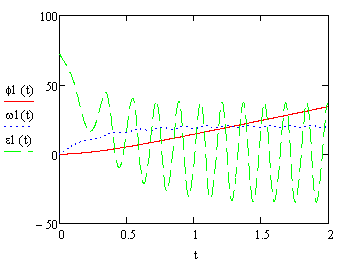
Проведем решение и построим графики зависимости от времени угла поворота, угловой скорости и углового ускорения маховика 1, как показано на рисунке 14. Как видно, вначале движение маховика, а значит и механизма, является неустановившимся. Примерно через 1 с движение устанавливается и становится периодическим.
С помощью режимов ![]() (Лупа) и
(Лупа) и ![]() (Слежение), можно выяснить, что в установившемся
режиме угловая скорость маховика 1 меняется примерно от 19 рад/с
до 21 рад/с, а его угловое ускорение меняется от -34 рад/с2
до 37 рад/с2. Относительная неравномерность вращения
маховика равна
(Слежение), можно выяснить, что в установившемся
режиме угловая скорость маховика 1 меняется примерно от 19 рад/с
до 21 рад/с, а его угловое ускорение меняется от -34 рад/с2
до 37 рад/с2. Относительная неравномерность вращения
маховика равна
 .
.
|
Р Е Ш Е Н И Е
|
Рисунок 14
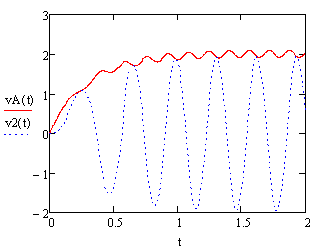
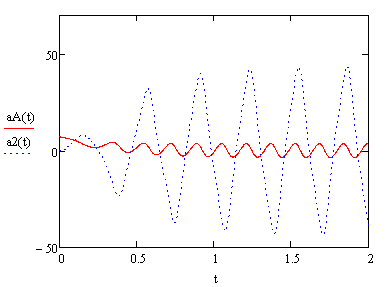
Используя кинематические соотношения, построим графики зависимости от времени линейных и угловых скоростей тел системы (см.рисунок 15). Как видно, скорость кулисы v2 и угловая скорость катка ω4 меняются по знаку, так как они перемещаются влево-вправо.
|
|
Рисунок 15
Дифференцируя по времени кинематические соотношения для линейных и угловых скоростей (2.2), получим выражения для ускорений точки А и кулисы 2, а также для угловых ускорений шкива 3 и катка 4:
![]()
![]()

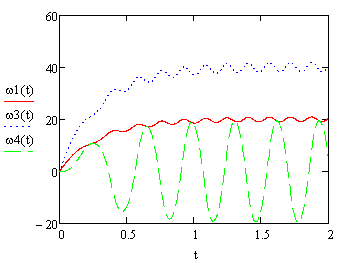
Введем полученные формулы и построим графики зависимости от времени ускорений точки А и кулисы 2, угловых ускорений шкива 3 и катка 4 (см.рисунок 16).
|
|
Рисунок 16
Анализируя полученные графики с помощью режимов ![]() (Лупа) и
(Лупа) и ![]() (Слежение), можно выяснить для
установившегося режима движения минимальные и максимальные значения скоростей и
ускорений точки А и кулисы 2, а также угловых скоростей и ускорений
шкива 3 и катка 4.
(Слежение), можно выяснить для
установившегося режима движения минимальные и максимальные значения скоростей и
ускорений точки А и кулисы 2, а также угловых скоростей и ускорений
шкива 3 и катка 4.
Задание 2. Рассмотрим систему сил, приложенных к шкиву 3 (см.рисунок 17). Составим для шкива дифференциальное уравнение вращательного движения:
![]()
Отсюда можно выразить разность натяжений ведущей и
ведомой ветвей ремня шкива:  .
.
Рассмотрим систему сил, приложенных к маховику 1 (см.рисунок 18), и составим для него дифференциальное уравнение вращательного движения:
![]()
Учитывая, что ![]() ,
получим
,
получим
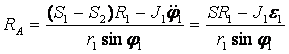 .
.
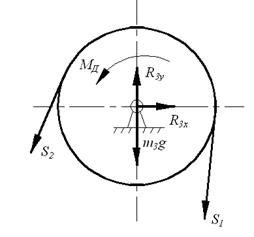
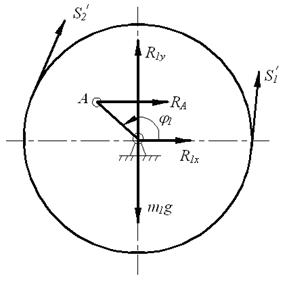
Рисунок 17 Рисунок 18
Рассмотрим систему сил, приложенных к кулисе 2 (см.рисунок 19). Составим для кулисы уравнение поступательного движения в проекции на ось х:
![]()
Так как ![]() , получаем
, получаем
![]()
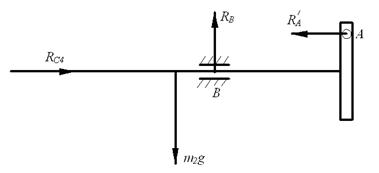
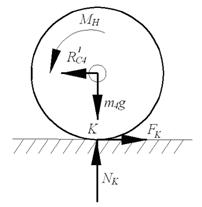
Рисунок 19 Рисунок 20
Рассмотрим систему сил, приложенных к катку 4 (см.рисунок 20). Составим для катка уравнения плоскопараллельного движения:
![]()
![]()
![]()
Выразим
силу сцепления из первого уравнения:
![]() .
.
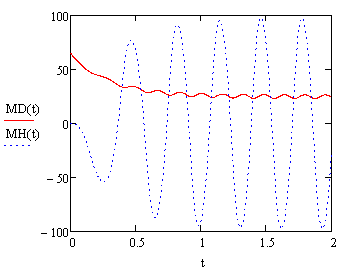
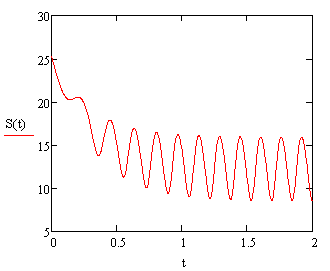
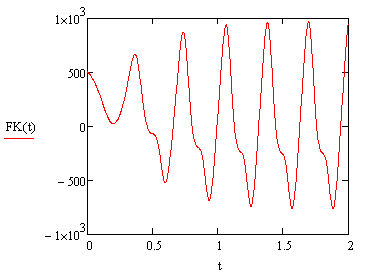
Введем формулы и построим графики зависимости моментов и реакций связей от времени, как показано на рисунках 21, 22, 23 и 24.
|
|
Рисунок 21
|
|
Рисунок 22
|
|
Рисунок 23
|
|
Рисунок 24
Анализируя полученные графики, можно найти для установившегося режима движения минимальные и максимальные значения моментов и реакций связей.
Задание 3. Проведите численный эксперимент, поочередно увеличивая в 2 раза инерционные характеристики тел системы: момент инерции J1 маховика и массы m2 , m3 , m4. При этом выяснится, что наибольшее влияние на время установления движения имеет момент инерции J1. При J1 =2,8 кгм2 движение устанавливается примерно через 1,5 с, а при J1 =5,6 кгм2 движение устанавливается примерно через 2,5 с. Увеличение момента инерции маховика приводит также к снижению относительной неравномерности вращения маховика, т.е. к его более равномерному вращению.
Ответьте на вопросы:
1) Как записывается теорема об изменении кинетической энергии системы в дифференциальной форме?
2) Как вычисляется кинетическая энергия твердого тела в случае его поступательного (вращательного, плоскопараллельного) движения?
3) В каком случае сумма работ внутренних сил системы равна нулю?
4) Как определяется элементарная работа силы в общем случае?
5) Как определяется элементарная работа силы тяжести?
6) Как определяется элементарная работа вращающего момента?
7) Каков характер изменения кинематических и динамических характеристик системы в установившемся режиме движения?
8) Как вычисляется относительная неравномерность вращения тела?
3 Динамика плоского движения твердого тела
3.1 Цель лабораторной работы и задание
Цель: закрепление знаний по теме «Динамика плоского движения тела», получение навыков составления и решения дифференциальных уравнений плоского движения тела.
Лабораторная работа выполняется на персональном компьютере с установленной в среде Windows XP системой Mathcad.
В работе предусмотрено выполнение 3-х заданий.
Задание 1: колесо массой m и радиуса r движется под действием силы тяжести по наклонной плоскости, составляющей угол α с горизонтом (см.рисунок 25). Колесо представляет собой однородный сплошной цилиндр. Начальная скорость центра колеса параллельна наклонной плоскости и равна vС0. Коэффициент трения скольжения колеса о наклонную плоскость на участке ОА длиной L равен f1, на участке АВ длиной d - f2, на оставшейся части наклонной плоскости - f3 . Коэффициент трения качения колеса равен δ.
Необходимо составить дифференциальные уравнения движения колеса, решить их в системе Mathcad численным методом при следующих данных: m=1 кг, r=0.5 м, L=2 м, d=2 м, vC0=0, α=π/6, f1=0.2, f2=0.01, f3=0,3, δ=0.0001м, Т =2.5 с.
Задание 2: построить неподвижную центроиду колеса на отрезке времени [0,Т].
Задание 2: провести численный эксперимент, меняя значения коэффициентов трения скольжения, начальной скорости колеса и угла наклона плоскости. Выяснить влияние этих параметров на характер качения колеса.
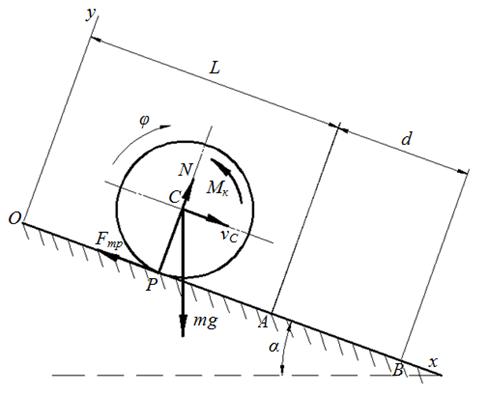
Рисунок 25
3.2 Выполнение лабораторной работы
Задание 1. Выберем
систему координат, направив ось Ох вдоль наклонной плоскости, а ось Оу
перпендикулярно ей. Начало системы координат совместим с начальным положением
колеса так, чтобы ось Оу проходила через его центр масс С. Угол
φ направим по ходу часовой стрелки. На колесо действуют сила тяжести
![]() ,
нормальная реакция опорной плоскости
,
нормальная реакция опорной плоскости
![]() , сила трения скольжения
, сила трения скольжения
![]() и
момент сопротивления качению
и
момент сопротивления качению ![]() .
.
Запишем дифференциальные уравнения плоского движения колеса:
![]()
![]() (3.1)
(3.1)
![]()
Здесь момент инерции колеса относительно оси
Cz,
проходящей через его центр масс, равен ![]() Учитывая, что
Учитывая, что
![]() и
и
![]() ,
получаем из второго уравнения системы (3.1) нормальную реакцию опорной
плоскости
,
получаем из второго уравнения системы (3.1) нормальную реакцию опорной
плоскости ![]() . Момент сопротивления качению равен
. Момент сопротивления качению равен
![]() .
Сила трения скольжения в случае качения со скольжением равна своему предельному
значению
.
Сила трения скольжения в случае качения со скольжением равна своему предельному
значению ![]() , где коэффициент трения скольжения принимает значения
f1, f2 или f3 в зависимости от
участка. В случае качения без скольжения сила трения
, где коэффициент трения скольжения принимает значения
f1, f2 или f3 в зависимости от
участка. В случае качения без скольжения сила трения
![]() и
определяется из дифференциальных уравнений движения. Так как заранее неизвестно,
какой вид качения имеет место, то сила трения также неизвестна.
и
определяется из дифференциальных уравнений движения. Так как заранее неизвестно,
какой вид качения имеет место, то сила трения также неизвестна.
Таким образом, имеем два дифференциальных уравнения движения колеса:
 (3.2) Начальные условия движения имеют вид:
(3.2) Начальные условия движения имеют вид:
![]() (3.3)
(3.3)
Необходимо решить систему дифференциальных уравнений (3.2) с начальными условиями (3.3). В общем случае в двух дифференциальных уравнениях (3.2) содержатся 3 неизвестных: хС, φ и Fтр.
Для решения задачи рассмотрим подробнее оба возможных вида качения: без скольжения и со скольжением.
В случае качения без скольжения сила трения неизвестна, но известно, что мгновенный центр скоростей (МЦС) колеса находится в точке Р касания колеса о наклонную плоскость, поскольку скорость этой точки равна нулю (колесо не проскальзывает). Тогда скорость центра колеса и его угловая скорость связаны соотношением:
![]() или
или
![]() .
.
Отсюда после дифференцирования по времени получаем
![]() . (3.4)
. (3.4)
Решая систему (3.2) с учетом (3.4), можно найти ускорение центра масс колеса и силу трения:
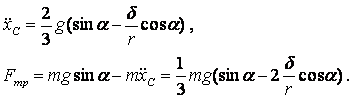 (3.5)
(3.5)
Находим затем угловое ускорение колеса:
![]() (3.6)
(3.6)
В случае качения со скольжением ![]() ,
тогда из (3.2) получаем ускорение центра масс и угловое ускорение колеса:
,
тогда из (3.2) получаем ускорение центра масс и угловое ускорение колеса:
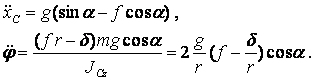 (3.7)
(3.7)
При этом скорость точки Р касания колеса о наклонную плоскость не равна нулю. Она направлена в сторону движения колеса и находится по формуле:
![]() . (3.8)
. (3.8)
МЦС колеса смещается от точки Р вниз перпендикулярно скорости его центра масс. Расстояние от центра масс колеса до его МЦС определяется по формуле:
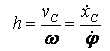 .
(3.9)
.
(3.9)
Можно получить условие качения без скольжения,
используя неравенство ![]() .
.
Подставим сюда выражение силы трения для качения без скольжения:
![]() .
.
Отсюда получим условие качения без скольжения:
![]() .
(3.10)
.
(3.10)
Тогда условие качения со скольжением запишется в виде:
![]() . (3.11)
. (3.11)
Учитывая условие (3.11) и формулы для силы трения в обоих случаях качения, решим поставленную задачу в Mathcad.
Введем данные и подпрограмму-функцию для определения силы трения, как показано на рисунке 26. При этом необходимо использовать панели инструментов Программирование и Логический.
|
|
Рисунок 26
Для численного решения двух дифференциальных уравнений второго порядка (3.2) запишем их в виде системы дифференциальных уравнений 1-го порядка:
 (3.12)
(3.12)
Вектор неизвестных обозначим 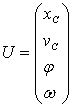 , тогда элементы вектора
, тогда элементы вектора ![]()
С учетом этого вектор правых частей дифференциальных уравнений (3.12) запишется в виде:
 .
.
Систему дифференциальных уравнений (3.12) с заданными
начальными условиями (3.3) можно решить в
Mathcad с помощью встроенной функции
rkfixed(U0,0,T,200,DU), реализующей метод
Рунге-Кутта. Здесь первый параметр означает начальный вектор, второй и третий
параметры – интервал интегрирования, 200 – фиксированное число шагов интегрирования,
последний параметр – векторная функция, задающая систему дифференциальных уравнений.
Результатом численного решения будет матрица значений координаты и скорости
центра масс колеса, угла поворота и угловой скорости
колеса на
отрезке времени [0,T] с шагом ![]() .
.
Проведем решение дифференциальных уравнений движения и
построим график изменения силы трения, как показано на рисунке 27. При вводе
индексов элементов векторов U, хС
, vC, ω и номеров столбцов
матрицы S необходимо
использовать кнопки ![]() и
и
![]() на панели инструментов
Матрица.
на панели инструментов
Матрица.
|
|
Рисунок 27
С помощью режимов ![]() (Лупа) и
(Лупа) и ![]() (Слежение), можно выяснить значения
силы трения на разных участках движения и установить характер качения.
(Слежение), можно выяснить значения
силы трения на разных участках движения и установить характер качения.
При ![]() (на участке ОА) сила трения
Fтр=1,636 Н, что меньше максимального значения силы трения на
этом участке
(на участке ОА) сила трения
Fтр=1,636 Н, что меньше максимального значения силы трения на
этом участке ![]() , следовательно, колесо катится без скольжения.
, следовательно, колесо катится без скольжения.
При ![]() (на участке АВ)
Fтр=0,085 Н, что
равно максимальному значению силы трения на этом участке
(на участке АВ)
Fтр=0,085 Н, что
равно максимальному значению силы трения на этом участке
![]() ,
т.е. колесо катится со скольжением.
,
т.е. колесо катится со скольжением.
При ![]() Fтр=2,55
Н, что также равно максимальному
значению силы трения
Fтр=2,55
Н, что также равно максимальному
значению силы трения ![]() , следовательно, колесо продолжает катиться со скольжением.
, следовательно, колесо продолжает катиться со скольжением.
При ![]() Fтр=1,64 Н
<
Fтр=1,64 Н
<
![]() , т.е.
колесо катится без скольжения.
, т.е.
колесо катится без скольжения.
Для сравнения запишем ускорение центра масс колеса в предположении качения без скольжения на всех участках, используя формулу (3.5), а затем скорость, уравнение движения центра масс и угловую скорость колеса, как показано на рисунке 28. Построим графики изменения скорости центра масс и угловой скорости колеса для данной задачи и в предположении качения без скольжения (см. рисунки 28,29). Как видно, решения совпадают только на участке ОА, когда колесо катится без скольжения.
|
|
Рисунок 28
|
|
Рисунок 29
Задание 2. Как
известно, неподвижной центроидой называется геометрическое место мгновенных
центров скоростей плоской фигуры, отмеченных на неподвижной плоскости. Положение
МЦС в произвольный момент времени определяется по формуле (3.9). Внесем
формулы для отображения на графике колеса и неподвижной центроиды, как показано
на рисунке 30. Меняя переменную i
от 0 до 200 , можно получать положения
колеса в моменты времени ![]() . При вводе вектора
h
по найденным векторам vc
и ω необходимо
использовать кнопку векторизации
. При вводе вектора
h
по найденным векторам vc
и ω необходимо
использовать кнопку векторизации ![]() на панели инструментов Матрица.
на панели инструментов Матрица.
|
|
Рисунок 30
При построении графика во избежание искажения необходимо указать одинаковые границы изменения абсциссы и ординаты от -1 до 8. Вызвав двойным щелчком мыши диалоговое окно форматирования графика, необходимо в поле Стиль осей установить Пересекающиеся и Равные масштабы, как показано на рисунке 31. Кроме того, на закладке Графики диалогового окна форматирования необходимо установить типы и цвета линий (см. рисунок 32). Как видно из рисунка 30, на участке ОА неподвижная центроида совпадает с осью х, то есть колесо катится без скольжения. На участке АВ точка Р касания колеса о наклонную плоскость скользит, достигая максимальной скорости в точке В. На остальной части наклонной плоскости скорость точки Р уменьшается до нуля, после чего колесо вновь катится без скольжения.

Рисунок 31
Рисунок 32
Задание 3. Проведите численный эксперимент, меняя данные задачи в указанном ниже порядке, и выясните характер качения колеса для каждого случая:
1) угол наклона плоскости α=π/4;
2) угол наклона плоскости α=0, начальная скорость vC0=4 м/с;
3) коэффициенты трения скольжения на всех участках одинаковы f1=f2= f3=0.2, а остальные параметры имеют исходные значения.
Ответьте на вопросы:
1) Как записываются уравнения динамики плоского движения тела в общем случае?
2) Каким соотношением связаны скорость центра масс и угловая скорость колеса при его качении без скольжения?
3) Что такое мгновенный центр скоростей (МЦС) плоской фигуры?
4) Где находится МЦС колеса при его качении без скольжения и при качении со скольжением?
5) Что можно сказать о величине силы трения скольжения при качении без скольжения?
6) Чему равна сила трения скольжения при качении со скольжением?
7) Как запишутся дифференциальные уравнения движения колеса при его качении по горизонтальной плоскости под действием приложенной в центре масс горизонтальной силы F(t)?
8) Как запишутся дифференциальные уравнения движения колеса при его качении по горизонтальной плоскости под действием вращающего момента М(t) ?
Список литературы
1. Сборник заданий для курсовых работ по теоретической механике: Учебное пособие для технических вузов / Под ред. проф. А.А.Яблонского. –15-е изд., стереотипное. – М.: Интеграл-Пресс, 2006. – 384.
2. Добронравов В.В., Никитин Н.Н. Курс теоретической механики. - М.: Высш.шк., 1983.
3. Бертяев В.Д. Теоретическая механика на базе Mathcad. Практикум. – СПб.: БХВ-Петербург, 2005. – 752 с.
4. Охорзин В.А. Прикладная математика в системе MATHCAD: Учебное пособие. 2-е изд, испр.и доп. – СПб.: Издательство «Лань», 2008. – 352 с.
5. Динасылов А.Д., Койлыбаева Р.К. Механика. Сборник заданий для самостоятельной работы студентов: Учебное пособие. – Алматы: АУЭС, 2011. – 88 с.
Содержание
|
Введение |
3 |
|
1 Интегрирование дифференциальных уравнений движения материальной точки |
3 |
|
2 Исследование динамики машины с кулисным приводом |
16 |
|
3 Динамика плоского движения твердого тела |
27 |
|
Список литературы |
37 |
Св.план 2012 г., поз. 239