Некоммерческое акционерное общество

АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра инженерной графики и прикладной  механики

 

  

МЕХАНИКА

Конспект лекций

для студентов всех форм обучения специальности

5B074600 – Космическая техника и технологии

  

 

Алматы 2013

СОСТАВИТЕЛЬ: А.Д.Динасылов. Механика. Конспект лекций для студентов специальности 5B074600 – Космическая техника и технологии. – Алматы: АУЭС, 2013. – 64 с.

 

Конспект лекций содержит основной теоретический материал дисцип-лины «Механика», излагаемый в лекционном курсе для студентов 5B074600 – Космическая техника и технологии. В конспекте излагаются основные положения статики, кинематики и динамики механических систем, а также рассматриваются начала аналитической механики и теории космических движений.

Ввиду ограниченности объема ряд положений дан без выводов, количество примеров недостаточно для полного усвоения материала, поэтому предполагается, что при изучении дисциплины студенты будут пользоваться дополнительной литературой, список которой приведен в конце конспекта.

Конспект лекций может использоваться студентами других специальностей,  изучающих дисциплину «Механика» или «Прикладная механика».

Ил.53, библиогр. - 17 назв.  

 

Рецензент: канд. техн. наук, доц. Ни А.Г.      

 

Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2012 г.                       

 

© НАО «Алматинский университет энергетики и связи», 2013 г.

Содержание 

1 Лекция №1. Введение. Основные понятия и аксиомы статики.  Системы сходящихся сил	4
2 Лекция №2. Момент силы относительно точки и оси. Пара сил. Приведение системы сил к заданному центру	8
3 Лекция №3. Равновесие  систем сил. Трение. Центр тяжести	11
4 Лекция №4. Кинематика точки и простейших движений твердого тела	16
5 Лекция №5. Плоскопараллельное движение твердого тела. Сложное движение точки	20
6 Лекция №6. Вращение твердого тела вокруг неподвижной точки. Общий случай движения свободного твердого тела	24
7 Лекция №7. Сложение движений твердого тела	28
8 Лекция №8. Введение в динамику.  Законы и задачи динамики точки.  Общие теоремы динамики точки	34
9 Лекция №9. Прямолинейные колебания материальной точки	40
10 Лекция №10. Основы  динамики  системы и  твердого  тела.   Общие  теоремы динамики системы	46
11 Лекция №11. Элементы аналитической механики	51
12 Лекция №12.  Движение    точки   переменной   массы.      Задачи Циолковского	57
Список литературы	61

 

1 Лекция №1. Введение. Основные понятия и аксиомы статики. Системы сходящихся сил

Содержание лекции: механика, как основа техники; вводные понятия и аксиомы статики, системы сходящихся сил и условия их равновесия.

Цели лекции: определить роль механики в подготовке бакалавров, сформулировать вводные понятия и аксиомы статики, рассмотреть упрощение и условия равновесия системы сходящихся сил.

«Механика» - дисциплина, лежащая в основе общетехнической подготовки бакалавров для отраслей энергетики. Механика является теоретической базой машиностроения и играет большую роль в повышении  надежности, качества проектирования и правильной эксплуатации машин, механизмов, приборов в энергетике. Дисциплина включает в себя  разделы механики твердого тела, которые относятся к теоретической механике.

Теоретическая механика (ТМ) есть наука об общих законах механического движения (МД) и равновесия материальных тел. Под МД понимается изменение относительного положения материальных тел в пространстве с течением времени. Наблюдать и изучать МД материальных тел можно по отношению к другим материальным телам, с которыми связывают систему координатных осей, называемую системой отсчета. Частным случаем МД является равновесие материальных тел, под которым надо понимать не только состояние покоя, но и состояние равномерного прямолинейного движения. В теоретической механике изучаются механические взаимодействия тел, в результате которых происходит изменение движения тел.

ТМ принято делить на статику, кинематику и динамику. Статикой называют раздел ТМ, в котором изучаются методы преобразования системы сил, а также устанавливаются условия их равновесия. В кинематике изучается движение тел без учета действующих на них сил. В динамике изучается движение материальных тел с учетом действующих на них сил. Последние две лекции посвящена рассмотрению некоторых методов аналитической динамики и динамике точки переменной массы.

1.1 Основные понятия и аксиомы статики

Объектами изучения ТМ являются модели материальных тел, а именно, материальная точка (МТ), система МТ и абсолютно твердое тело (АТТ).

МТ называют материальное тело, размеры которого в рассматриваемых условиях можно не учитывать, считая, что масса тела сосредоточена в точке. Системой МТ называются совокупность МТ, положения и движения которых взаимосвязаны между собой (любой механизм). АТТ называют такое тело, в котором расстояния между любыми его точками остаются неизменными. Все реальные тела в результате воздействий в какой-то мере изменяют свою геометрическую форму (деформируются). Эти деформации зачастую малы, и при решении ряда задач ими можно пренебречь, считая тело абсолютно твердым.

Состояние равновесия или движения тела зависит от характера его механических взаимодействий с другими телами, мерой которых является сила. Сила - вектор, характеризующийся численной величиной, направлением и точкой приложения. Графически сила изображается направленным отрезком прямой. Прямая, вдоль которой направлена сила, называется ее линией действия (ЛД). Силу будем обозначать прописной буквой латинского алфавита с надчеркиванием, например , тогда ‌F= -‌‌ модуль силы. Совокупность сил, действующих на какое-либо твердое тело или точку, называют системой сил. Обозначать ее будем .

Если систему сил (СС), действующих на твердое тело, можно заменить другой СС, не изменяя при этом состояния покоя или движения тела, то эти СС называют эквивалентными ~.

Если данной СС эквивалентна одна сила, то эта сила называется равнодействующей для рассматриваемой СС. Если обозначить ее как ^*, то ^*~. Не каждая СС имеет равнодействующую.

СС называют уравновешенной, если она, будучи приложенной к телу, не изменяет его состояния покоя или движения. Действие уравновешенной СС эквивалентно нулю, т.е. ~0. Силой, уравновешивающей СС, называют силу, которая, будучи присоединенной к этой СС, составит вместе с ней новую СС, эквивалентную нулю.

Сила, приложенная к телу в какой-нибудь одной его точке, называется сосредоточенной. Силы, действующие на часть точек данного объема или данной части поверхности тела, называются распределенными.

В основе статики лежит ряд аксиом.

1. Аксиома равновесия системы двух сил. Для равновесия двух сил, приложенных к телу, необходимо и достаточно, чтобы эти силы были равны по величине и направлены вдоль прямой, соединяющей их точки приложения, в противоположные стороны: F₁ = F₂, но .

2. Аксиома добавления и отбрасывания уравновешенной СС. Не изменяя действия системы сил на твердое тело, можно к этой системе прибавить или отнять от нее уравновешенную СС. Следствие: не изменяя действия силы на АТТ, ее можно переносить в любую точку тела вдоль ее ЛД.

3. Аксиома параллелограмма сил. Равнодействующая двух сил, приложенных в одной точке под углом друг к другу, определяется диагональю параллелограмма, построенного на этих силах как на сторонах.

4. Аксиома взаимодействия. Силы, с которыми действуют друг на друга два тела, всегда равны по величине и направлены вдоль одной прямой в противоположные стороны: F₂₁ = F₁₂, .

Прежде чем сформулировать 5-ю аксиому, введем несколько понятий.

Если тело может получать любые перемещения в пространстве, то оно называется свободным. Если же некоторые перемещения для тела невозможны, то тело называется несвободным. Условия, ограничивающие свободу движения тела, называются связями. Связи осуществляются при помощи материальных тел, твердых или гибких. Тело, стремясь под действием приложенных сил осуществить перемещение, которому препятствует связь, действует на нее с некоторой силой. Одновременно связь действует на тело с такой же по модулю, но противоположно направленной силой, называемой реакцией связи. Силы, не являющиеся реакциями, будем называть активными. Реакция связи отличается от активных сил тем, что ее численная величина зависит от активных сил и наперед неизвестна. Направление реакции противоположно направлению, по которому связь препятствует движению тела. Рассмотрим, как направлены реакции некоторых видов связей (опор):

а) гладкая поверхность (можно пренебречь трением) не препятствует скольжению по ней тела, а препятствует только его движению по нормали к поверхности. Поэтому ее реакция направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена в этой точке;

б) гибкая нить или цепь. Здесь реакция направлена вдоль нити или цепи;

в) цилиндрический шарнир (подшипник) или шарнирно-неподвижная опора. Два тела, соединенные валом, проходящим через отверстия в этих телах, образуют шарнирное соединение. Осевая линия вала называется осью шарнира. Тело не может перемещаться по направлению, перпендикулярному к оси шарнира, но может поворачиваться вокруг оси. Поэтому реакция может иметь любое направление в плоскости, перпендикулярной оси шарнира. Обычно ее раскладывают на две составляющие;

г) опора типа катка или шарнирно-подвижная опора. Если пренебречь трением, то реакция направлена по нормали к поверхности качения;

д) сферический шарнир и подпятник. Этот вид связи закрепляет какую-либо точку тела так, что она не может совершать никаких перемещений в пространстве, при этом тело может как угодно поворачиваться вокруг этой точки. Реакция проходит через закрепленную точку, а направление ее заранее неизвестно. Поэтому реакцию разлагают на три составляющие;

е) невесомый стержень, закрепленный с двух сторон шарнирами. На стержень действуют только две силы, приложенные в центрах шарниров. Стержень находится в равновесии, поэтому эти силы (реакции) должны быть направлены вдоль прямой, проходящей через центры шарниров.

Для несвободного тела имеет место следующая аксиома.

5. Аксиома связей. Несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие реакциями.

6. Аксиома затвердевания. Равновесие изменяемого (деформируемого) тела, находящегося под действием данной СС, не нарушится, если наложить на него дополнительные связи  вплоть до того, что рассматривать тело, как затвердевшее (абсолютно твердое).

1.2 Система сходящихся сил

Различают следующие типы систем сил (СС): система сходящихся сил, система параллельных сил, произвольная СС. СС сил называется сходящейся, если линии действия (ЛД) всех сил системы пересекаются в одной точке. СС называется параллельной, если ЛД сил параллельны между собой. Произвольной называется такая СС, ЛД которых не параллельны и не пересекаются в одной точке. Все указанные СС могут быть как плоскими, так и пространственными. СС называется плоской, если ЛД всех сил лежат в одной плоскости; в противном случае СС пространственная.

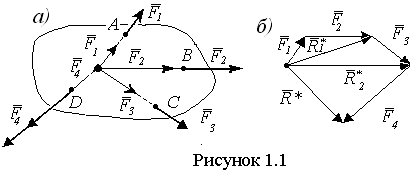Пусть к телу в точках А, В, С, D приложены силы , ЛД которых пересекаются в точке О (см. рисунок 1.1,а). Перенесем силы вдоль их ЛД в точку О и будем последовательно складывать силы по правилу силового треугольника (см. рисунок 1.1,б). Сначала найдем равнодействующую  сил  и , затем  сил  и  и т.д. Получим следующее: ,   ,   =. Если сил n, то

                                                                 (1.1)

 можно определить также, отложив вектор  и приложив к его концу вектор , затем к концу  - вектор , и т.д. Равнодействующая   соединяет начало первого вектора с концом последнего.

Т.о., равнодействующая системы сходящихся сил равна векторной сумме сил, входящих в систему, и ее ЛД проходит через точку пересечения ЛД слагаемых сил. Чтобы найти равнодействующую геометрическим способом, надо построить в точке пересечений их ЛД силовой многоугольник на слагаемых силах; замыкающая силового многоугольника будет равнодействующей.

Рассмотрим аналитический способ определения равнодействующей системы сходящихся сил. Спроецируем векторное равенство (1.1) на оси прямоугольных координат и найдем проекции равнодействующей

,  ,    .                                 (1.2)

Модуль равнодействующей силы определяется, как

                                        (1.3)

а направление - по трем направляющим косинусам

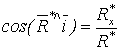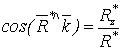,              ,            .      (1.4)

  Для равновесия системы сходящихся сил необходимо и достаточно, чтобы ее равнодействующая была равна нулю, т.е.,  или  (условия равновесия в векторном виде). Условия равновесия в геометрическом смысле выражаются в том, что силовой многоугольник должен быть замкнут, т.е., конец последнего вектора должен совпасть с началом первого вектора. В аналитическом виде они выражаются в том, что должны равняться нулю суммы проекций на три координатные оси всех сил, входящих в систему,

,   ,    .                                    (1.5)

Условия равновесия для плоской системы сходящихся сил

,   .                                                    (1.6)

Теорема о трех силах: если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.

2 Лекция №2.  Момент  силы  относительно точки и оси.   Пара сил. Приведение системы сил к заданному центру

Содержание лекции: момент силы относительно точки и оси; пара сил, свойства пар сил, приведение системы сил к центру.

Цели лекции: изучить свойства момента силы относительно точки и оси, свойства пары сил, упрощение и условия равновесия системы пар сил, упрощение произвольной си стемы сил.

2.1 Момент силы относительно точки и относительно оси

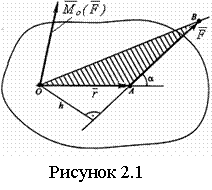Моментом силы относительно точки О (см. рисунок 2.1) называется вектор , прило­женный в точке О перпендикулярно плоскости треугольника ОАВ и равный

                           (2.1)

где  - радиус-вектор, проведенный из точки О в точку А приложения силы .

Модуль вектора равен произведению модуля силы F на расстоя­ние h от точки О до линии действия силы, которое называется плечом силы относительно точки О, т. е.

=F∙h.                                (2.2)

Момент  характеризует вращательное действие силы относительно точки О. Радиус-вектор  может быть проведен из точки О не только в точку А, но и в любую другую точку, лежащую на линии действия силы . Момент силы относительно точки равен нулю, когда линия действия силы проходит через эту точку.

Для системы сил вектор

,                                             (2.3)

равный сумме моментов всех этих сил относительно точки О, называется главным моментом системы сил относительно точки О.

В случае плоской системы сил удобно вместо векторного момента силы относительно точки использовать понятие алгебраического момента силы относительно точки, т.к. в этом случае векторные моменты всех сил параллельны друг другу. Алгебраическим моментом силы относительно точки называют произведение модуля силы на плечо силы

.                                                 (2.4)

Знак «плюс» берется, если сила стремится вращать тело относительно точки против часовой стрелки, «минус» – если по часовой стрелке.

Моментом силы  относительно оси называется проекция векторного момента этой силы, взятого относительно любой точки оси, на эту ось, т. е.

.                          (2.5)

Проекция на ось момента силы , взятого относительно какой-либо точки О этой оси Oz, не зависит от положения точки на оси.

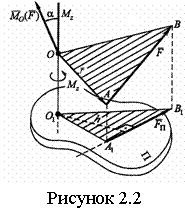
Иначе: момент силы относительно оси - это алгебраический момент проекции этой силы на плоскость, перпендикулярную оси, взятый отно­сительно точки пересечения оси с плоскостью (см. рисунок 2.2)

 .                (2.6)

Момент силы относительно оси равен нулю, если сила и ось находятся в одной плоскости.         Момент силы относительно начала координат  равен по (2.1)

,

откуда получим моменты силы относительно осей координат

,     ,     .    (2.7)

2.2 Сложение параллельных сил

Две  приложенные к АТТ и направленные в одну сторону параллельные силы имеют равнодействующую, параллельную им, равную по модулю сумме их модулей и направленную в ту же сторону. Линия действия (ЛД) равнодействующей расположена между ЛД заданных сил и делит внутренним образом отрезок прямой между ЛД этих сил на части, обратно пропорциональные модулям сил. Обратно, любую силу можно разложить на две параллельные силы, направленные в ту же сторону.

Две неравные параллельные силы, направленные в противоположные стороны имеют равнодействующую, равную по модулю разности модулей сил, параллельную им и направленную в сторону большей силы. ЛД равнодействующей расположена за ЛД большей из них и делит внешним образом отрезок прямой между ЛД заданных сил на части, обратно пропорциональные модулям сил.

2.3 Пара сил. Момент пары сил

Парой сил, приложенной к АТТ, называют систему двух равных по модулю параллельных сил, направленных в противоположные стороны (см. рисунок 2.3). Сумма сил пары равна нулю, но пара сил не уравновешена. Кратчайшее расстояние между ЛД сил пары называют плечом пары, а плоскость, в которой действуют силы пары - плоскостью действия пары. Совокупность нескольких пар сил, действующих на тело, называется системой пар сил. Пара сил не приводится к равнодействующей. Действие пары на тело характеризуется моментом пары, равным по модулю F∙d, а также положением плоскости действия пары в пространстве и направлением, в котором пара стремится вращать тело, т.о., момент пары сил есть вектор.

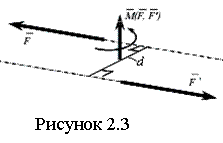Векторный момент пары сил - это вектор , перпендикулярный плоскости действия пары и направленный в ту сторону, откуда видно, что пара стремится повернуть тело против часовой стрелки, и численно равный произведению модуля одной из сил пары на ее плечо. Пару сил можно переносить куда угодно в плоскости и в параллельную плоскость, изменяя модуль силы и плечо пары, но, сохраняя при этом неизменными модуль момента пары и направление, в котором она стремится вращать твердое тело, т.е. пара сил – свободный вектор.

Две пары сил, имеющие одинаковые векторные моменты, эквивалентны независимо от того, где каждая из них расположена (на одной плоскости или в параллельных плоскостях) и чему равны модули сил и плечи пар.

Если пары расположены в одной плоскости, то их векторные моменты направлены перпендикулярно этой плоскости в ту или иную сторону в зависимости от направления, в котором пара стремится вращать тело. Поэтому в данном случае моменты пар можно различать по модулю и знаку, рассматривая как алгебраические величины. Момент пары считают положительным, если пара стремится вращать тело против часовой стрелки, и отрицательным при противоположном направлении. Тогда для плоской системы пар сил

                                                     (2.8)

и                                         .                                                    (2.9)

Теорема о сложении пар сил. Совокупность пар сил, действующих на тело, эквивалентна одной паре сил, векторный момент которой равен сумме векторных моментов всех пар сил, 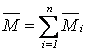. Тогда условия равновесия системы пар сил, действующих на твердое тело, имеют вид

.                                                     (2.10)

2.4 Теорема о параллельном переносе силы

Силу, приложенную к твердому телу, можно, не изменяя ее действия, перенести параллельно самой себе в любую точку тела, прибавляя при этом пару с моментом, равным моменту переносимой силы относительно точки, в которую она переносится (см. рисунок 2.4).

 

 

 

 

 

 

 

 

 

2.5 Приведение системы сил к заданному центру

Произвольную систему сил, действующих на АТТ, можно привести к какому-либо центру, заменив все действующие силы одной силой, равной главному вектору системы сил, приложенному в этом центре, и одной парой сил с моментом, равным главному моменту системы сил относительно того же центра (см. рисунок 2.5)

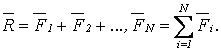                               (2.11)

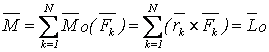.                      (2.12)

При этом  не зависит от выбора центра приведения, а  – зависит.  

Две системы сил, приложенных к АТТ, эквивалентны, если они имеют одинаковые главные векторы и главные моменты относительно одного и того же центра.

В механике широко используется теорема Вариньона: если система сил имеет равнодействующую, то момент равнодействующей относительно любой точки или оси равен сумме моментов сил системы относительно той же точки или оси.

3 Лекция №3. Равновесие  систем сил. Трение. Центр тяжести

Содержание лекции: условия равновесия  систем сил; трение скольжения и качения; центр тяжести твердых тел.

Цели лекции: изучить условия равновесия пространственных и плоских систем сил, рассмотреть особенности решения задач при наличии трения, научиться определять центры тяжести тел.

3.1 Условия равновесия системы сил

Произвольная СС, приложенных к телу, эквивалентна силе, равной главному вектору , и паре сил с моментом, равным главному моменту  относительно какого-либо центра О. Чтобы такая система находилась в равновесии, необходимо и достаточно равенство нулю  и . Поэтому условия равновесия могут быть представлены в векторной форме как

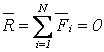          ,                                            (3.1)

.                                     (3.2)

Эти условия эквивалентны аналитическим условиям равновесия в виде      

     ,           ,         ,             

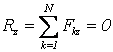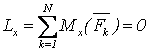   ,   ,    ,                             (3.3)

т.е., для равновесия произвольной СС, приложенных к АТТ, необходимо и достаточно равенства нулю сумм проекций всех сил на оси декартовой системы координат и сумм моментов всех сил относительно этих осей.

Условия равновесия для пространственной системы параллельных сил (ось Oz параллельна направлению действия сил) имеют вид

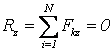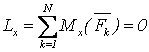       ,       ,       .      (3.4)

  Первая форма условий равновесия произвольной плоской СС: необходимо и достаточно, чтобы суммы проекций всех сил на две координатные оси и сумма алгебраических моментов сил относительно любого центра были равны нулю

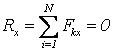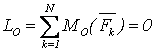       ,       ,      .      (3.5)

Вторая форма

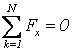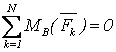,            ,                        (3.6)

при этом   не перпендикулярна .

Третья форма

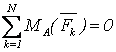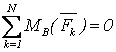,       ,                  (3.7)

при этом А, В, С не лежат на одной прямой.

  Условия равновесия для плоской системы параллельных сил имеют вид

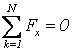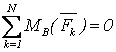,                                (3.8)

(при этом ось Ox не должны быть перпендикулярной направлению сил) или

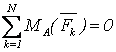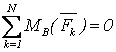,                     (3.9)

причем прямая, проходящая через А и В, не параллельна силам.

3.2 Статически определимые и статически неопределимые системы

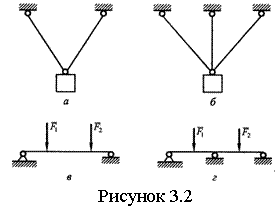Если число неизвестных состав­ляющих реакций связей равно числу неза­висимых уравнений равновесия (см. рисунок 3.2,а,в), то рассматриваемую систему на­зывают статически определимой, если больше - статически неопределимой (см. ри­сунок 3.2,б,г). Определить реакции в ста­тически неопределимых системах мето­дами, изложенными в этом разделе для АТТ, невозможно. Для решения таких за­дач необходимо учитывать деформируемость тел и дополнительно состав­лять уравнения деформаций, рассматриваемые в курсе «Сопротивление ма­териалов».

 

3.3 Равновесие системы тел

Связи, соеди­няющие части системы тел, называют внутрен­ними. Если внешние связи заменить силами, то ус­ловий равновесия недостаточно для их определе­ния. Методы решения таких задач:

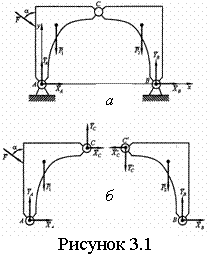
а) пользуясь свойствами внутренних связей, составляют дополнительные условия равновесия. Так, для системы на рисунке 3.1 а, четвертым уравнением будет равенство нулю суммы момен­тов относительно шарнира С всех сил, приложен­ных  к какую-либо одной из ее половин;

б) мысленно расчленяют конструкцию на от­дельные части, заменяя внутренние связи силами (см. рисунок 3.1 б). Для каждой половины имеем по 3 независимых условия равновесия, из которых находим 6 неизвестных.

3.4. Трение скольжения. Законы трения скольжения

Законы трения скольжения (Кулона – Амонтона):

1) При стремлении сдвинуть одно тело относительно другого в плоскости их соприкосновения возникает сила трения , модуль которой может принимать любые значения  в интервале 0≤F≤ F_max. Сила трения приложена к телу и направлена в сторону, противоположную возможному направлению скорости точки приложения силы.

2) Максимальная сила трения равна произведению коэффициента трения f на силу нормального давления N          

F_max=f∙N.                                                  (3.10)

Коэффициент трения - безразмерная величина, зависящая от материалов и состояния поверхностей соприкасающихся тел (шероховатость, температура, влажность и т. п.) и определяемая опытным путем. Значения f: дерево по дереву 0,4-0,7; металл по металлу 0,15-0,25; сталь по льду 0,027.

 Различают коэффициенты трения покоя и трения скольжения. Коэффициент трения покоя определяется по максимальной силе трения F_max, соответствующей предельному состоянию равновесия, когда малейшее увеличение внешних сил вызывает движение. Обычно он больше коэффициента трения скольжения. С увеличением скорости скольжения значение последнего сначала незначительно уменьшается, а затем остается практически неизменным.

3) Максимальная сила трения в довольно широких пределах не зависит от площади соприкасающихся поверхностей.

3.5 Реакция шероховатой поверхности. Угол трения

Реакцию шероховатой поверхности представляют в виде двух составляющих: нормальной реакции  (равна по модулю силе нормального давления) и перпендикулярной ей силы трения  (см. рисунок 3.3). Полная реакция отклонена от нормали на угол α (tg α = F/N).

Если тело лежит на горизонтальной шероховатой поверхности и на него не действуют никакие внешние силы, кроме силы тяжести, то F = 0, а полная реакция R = N и перпендикулярна опорной поверхности. Приложив к телу силу , мы стремимся вызвать его движение, но оно не происходит, так как возникает сила трения , причем F≤ F_max. С увеличением силы  будет возрастать и сила . При F₁ = F_max наступит предельное состояние равновесия, при котором  отклонится от вертикали на угол α_max, называемый углом трения. Обозначив его через φ, находим, что тангенс угла трения равняется коэффициенту трения  

tg φ= F_max/N=f .                                             (3.11)

Полная реакция неидеальной связи при равновесии имеет направление в пределах угла трения. Равновесие тел с учетом сил трения скольжения рассматривают обычно для предельного состояния, когда сила трения достигает максимального значения. Реакция неидеальной связи представляется двумя составляющими: нормальной реакцией N и максимальной силой трения F_max.

3.6 Реакция связи при качении

На рисунке 3.4,а показано, что при качении цилиндр вдавливается в опорную плоскость и контактирует с ней по некоторой поверхности, которая образует дугу СD, сдвинутую в направлении качения.

Полная реакция  опорной поверхности на цилиндр как сумма системы распределенных сил, вы­званных деформацией по­верхности, препятствует ка­чению цилиндра. Это со­противление, возникающее при качении одного тела по поверхности другого, называют трением качения. В инженерных рас­четах нас интересует момент сопротивления качению (см. рисунок 3.4 б). Схема­тизируя явление, рассматривают качение по недеформируемой поверх­ности, а полную реакцию   представляют в виде двух составляющих, прило­женных в точке В, смещенной от точки А в сторону возможного качения на некоторую величину δ (см. рисунок 3.4,в). Сила  - сила трения скольжения, а сила - нормальная реакция. Из условий равновесия имеем

N = P,       F = Q,      Q_max∙r = δ∙N.                                 (3.12)

Произведение δ∙N = (М_тр)_max называется моментом сопротивления качению, или моментом трения качения. Если сила Q мала, то смещение силы N от вертикального диаметра цилиндра также незначительно; с увеличением Q это смещение возрастает. При Q_max цилиндр достигнет предельного состояния равновесия, и нормальная реакция N будет отстоять от вертикального диаметра на предельном расстоянии δ, которое называется коэффициентом трения качения. Коэффициент δ зависит от свойств материалов и состояния поверхностей соприкасающихся тел, определяют его опытным путем. Так, при качении колеса по рельсу δ = 0,005 см, в шариковом подшипнике δ = 0,001 см.

3.7 Центр тяжести твердого тела

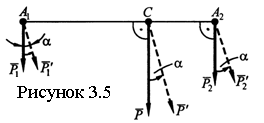Рассмотрим сначала две параллельные силы  и , приложен­ные к телу в точках А₁ и A₂ (см. рисунок 3.5). Равнодействующая, линия действия которой параллельна слагаемым силам и проходит через некоторую точку С, лежащую на прямой A₁ A₂, . Положение точки С найдем с помощью теоремы Вариньона  , откуда

     .                 (3.13)

Повернув силы   и  на один и тот же угол α вокруг точек А₁, А₂, придем к выводу, что и равнодействующая повернется в ту же сторону на угол α и будет приложена в той же точке С, называемой центром параллельных сил. Аналогично -  для любого числа сил.

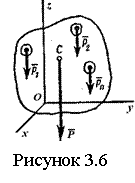
Равнодействующую сил тяжести , ,…, , приложенных к частицам данного тела, обозначим  (см. рисунок 3.6). Модуль этой силы  называется весом тела и определяется  равенством

.                                              (3.14)

Точка С является центром параллельных сил тяжести и  называется центром тяжести тела.. Т.о., центр тяжести АТТ - неизменно связанная с телом точка, через которую проходит ЛД равнодействующей сил тяжести, приложенных к частицам дан­ного тела, при любом положении тела в пространстве. Координаты центра тяжести определяются формулами

,   ,      (3.15)

где  , , – координаты точек приложения сил тяжести  .

4 Лекция №4. Кинематика точки и простейших движений тела

Содержание лекции: вводные понятия кинематики, кинематика точки, траектория, скорость, ускорение точки; поступательное и вращательное движение твердого тела.

Цели лекции: изучить кинематические параметры движения точки и простейших движений твердого тела.

4.1 Введение в кинематику

Кинематика - раздел механики, в котором изуча­ются геометрические свойства движения тел без учета их инертно­сти и действующих на них сил. Под движением понимают изменение с течением времени положения данного тела в пространстве по отношению к другим телам, образующим вместе с системой координат систему отсчета (СО), выбор которой в кинематике произволен.

Движение тел совершается в пространстве с течением времени. Пространство рассматривают как трехмерное евкли­дово пространство. Время считается. протекающим одинаково во всех рассматриваемых СО. В задачах кинематики время t принимают за независимое пере­менное (аргумент). Все другие переменные величины (расстояния, скорости и т. д.) рассматривают как функции от t. Отсчет времени ведется от не­которого начального момента.

Для решения задач кинематики надо, чтобы изучаемое движение тела (точ­ки) было кинематически задано, что означает задать положение этого тела (точки) относительно данной СО в любой момент времени. Изучение движения начинается с  установления способов задания  движения. Основная задача кинематики - зная закон движения точки (тела), установить методы определения всех кинематических величин, характеризующих дан­ное движение.

Непрерывную линию, которую описывает движущаяся точка от­носительно данной СО, называют траекторией точки. Если траекторией является прямая, движение точки называ­ют прямолинейным, а если кривая - криволинейным.

4.2 Способы задания движения точки

Движение точки может быть задано одним из трех способов.

1. Векторный способ. Пусть точка М движется по отношению к некоторой си­стеме отсчета Oxyz. Положение точки в любой момент времени можно опре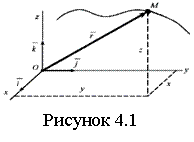делить, задав ее радиус-вектор  (см. рисунок 4.1) как функцию от времени t

.                                          (4.1)

Это и есть закон движения точки в векторной форме.

 

2. Координатный способ. Положение точки можно непосредственно опре­делять ее координатами, изме­няющимися при движении с течением времени

.           (4.2)

Это - закон движения точки в прямоугольных декартовых координатах.

3. Естественный способ. Задать движение точки естественным способом – это задать (см. рисунок 4.2) ее траекторию, начало отсчета на траектории с указанием направлений отсчета и закон движения в виде         

.                                                     (4.3)

4.3 Скорость и ускорение точки при векторном способе задания

движения

Доказывается (см. рисунок 4.4), что скорость точки есть первая производная от вектора  по аргументу t

.                                                        (4.4)

 

 

 

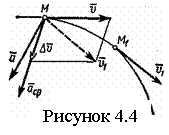
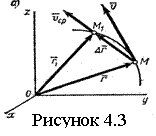
 Доказывается также, что вектор ускорения точки в данный момент време­ни равен первой производной от вектора скорости  или второй произ­водной от радиуса-вектора точки по времени.

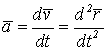.                                                     (4.5)

Т.о., вектор ускорения точки в данный момент време­ни равен первой производной от вектора скорости  или второй произ­водной от радиуса-вектора точки по времени.

Для определения скорости и ускорени точки при координатном способе задания движения используем следующую теорему: про­екция производной от вектора на ось, неподвижную в данной СО, равна производной от проекции дифференцируемого вектора на ту же ось.

Тогда проекции скорости на координатные оси равны первым производным от от координат точки по времени

                                            (4.6)

или                                          .                                          (4.7)

Для проекций ускорения получаем

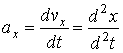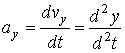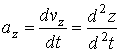,      ,                      (4.8)

или                                                  ,                                           (4.9)

т.е. проекции ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от координат точки по времени.

При естественном способе задания движения скорость и ускорение точки определяют по их проек­циям на оси естественного трехгранника Мtnb, имеющие начало в точке М и движущиеся вместе с нею. Направления осей: Мt - по касательной к траектории в сторону положительного отсчета s; главная нормаль Мn - по нормали к траектории, лежащей в соприкасающейся плоскости, и направленной в сторону вогнутости траектории; бинормаль Mb - перпендикулярно к первым двум так, чтобы она образовывала с ними правую систему осей.

Определим скорость точки

.                                         (4.10)

Проекция скорости точки на касательную к ее траектории

      .                                                          (4.11)

Очевидно, что  и модуль скорости .

Для ускорения  точки имеем

 .                     (4.12)

Т.к. 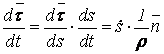  (ρ – радиус кривизны траектории точки в рассматриваемом положении), то

,                                                    (4.13)

т.е., ускорение равно сумме касательной и нормальной составляющих

.                                                             (4.14)

Вектор  лежит в соприка­сающейся плоскости, т. е. в плоскости Mtn. Проецируя обе части равенства (4.13) на оси Мt, Мn  и Mb, получим

 .                                        (4.15)

 4.3 Поступательное движение твердого тела и вращательное движение твердого тела вокруг неподвижной оси

Поступательным называется такое движение АТТ, при котором любая прямая, проведенная в теле, перемещается, оставаясь параллельной себе, при этом траектории его точек могут быть любыми кривыми. Справедлива теорема: при поступательном движении все точки тела описывают одинаковые траектории и имеют в каждый момент времени одинаковые по модулю и направлению ско­рости и ускорения. Кинематика АТТ в этом случае сводится к кинематике точки.

При вращении АТТ вокруг неподвижной оси, его точки, лежащие на оси, остаются неподвижными (АВ на рисунке 4.5). Через ось проведем две плоскости - неподвижную и подвижную, связанную с телом. Двугранный угол j между ними называют углом поворота тела и считают положительным, когда он отсчитывается от неподвижной плоскости к подвижной против часовой стрелки, если смотреть со стороны положительного направления оси вращения. Закон вращения АТТ вокруг неподвижной оси – это зависимость

j = j (t).                                       (4.16)

Угловая скорость характеризует изменение j

w = dj/dt  или  .                                    (4.17)

Угловую скорость тела можно изоб­разить в виде вектора  с модулем, равным |w|, и направленного вдоль оси вращения тела в ту сторону, откуда вращение видно происходящим против хода часовой стрелки.

Угловое ускорение характеризует изменение с те­чением времени

e = dw/dt  = d² j/dt²  или  .                          (4.18)

Если во все время движения w=cons, то вращение называют равномерным. Из формулы (4.17), интегрируя, найдем его закон    .                              (4.19)

При равномерном вращении, если  , то  .                                  (4.20)

Если угловое ускорение тела во все время дви­жения остается постоянным (e=const), то вращение называется равно­переменным, закон которого имеет вид

.                                (4.21)

Если w  и e имеют одинаковые знаки, вращение - равноуско­ренное, если разные — равнозамедленное.

Определим скорости и ускорения точек вращающегося тела (см. рисунок 4.6).

При вращении точка М описывает окружность радиуса h, плоскость которой перпендикулярна оси вращения, а центр P лежит на оси. За время dt тело поворачивается на угол dj, точка М совершает перемещение ds = h∙ dj. Тогда

.                                                 (4.21)

Ускоре­ния точки найдем как

.                    (4.22)

Ускорение  направлено по каса­тельной к траектории (в сторону движения при ускоренном вра­щении и в обратную сторону при замедленном), ускорение  всегда направлено по радиусу МP к оси. Полное ускорение точки равно

,                                          (4.23)

а угол m  (рисунок 4.6) определяется через зависимость

.                                                 (4.24)

Для векторов  и  можно получить формулы

                                ,                                                                     (4.25)

                       .                                                (4.26)

5 Лекция №5. Плоскопараллельное движение твердого тела. Сложное движение точки

Содержание лекции: кинематика плоскопараллельного движения тела; сложное движение точки.

Цели лекции: изучить кинематические параметры плоскопараллельного движения тела и сложного движения точки.

5.1  Уравнения   плоскопараллельного  движения и его  разложение на поступательное и вращательное движения

Плоскопараллельным или плоским движением АТТ называют движение, при котором все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости (см. рисунок 5.1).

 

 

 

 

 

 

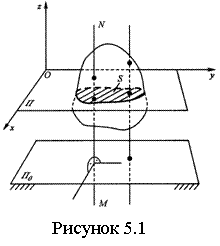
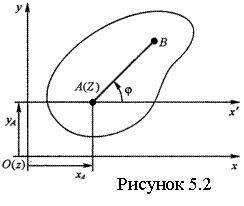
 Для изучения движения тела дос­таточно изучить, как движется в плоскости Оху сечение S  тела. Положение фигуры S в плоскости Оху определяется положением отрезка АВ (см. рисунок 5.2.). Зная коор­динаты х_А, у_А точки А (полюса) и угол j, можно определить положение отрезка АВ. Чтобы знать закон движения, т. е. положение фигуры в плоскости Оху в любой момент времени, надо знать зависимости

.                                               (5.1)

Плоское движение можно рассматривать как слагающееся из поступательного движения вместе с полюсом, и вращательного движения вокруг полюса.

Рассмотрим теперь определение скоростей точек плоской фигуры. Пусть поступательная составляющая движения характеризуется скоростью . Положение любой точки B фигуры определяется по отношению к осям Оху радиусом-вектором  (см. рисунок 5.3). Тогда    

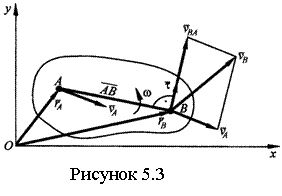
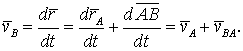    (5.2)

При этом скорость , которую точка B получает при вращении фигуры вокруг полюса А, будет равна

                          (5.3)

где  w  - угловая  скорость  фигуры.                                                                                 

При определении скоростей точек АТТ оказывается полезной следующая теорема (справедлива для произвольного движения): проекции скоростей двух точек тела на соединяющую их прямую равны.

5.2  Определение  скоростей  точек  плоской  фигуры  с  помощью

мгновенного центра скоростей

Другой метод определения скоростей точек плоской фигуры основан на поня­тии о мгновенном центре скоростей (МЦС) - это точка плоской фигу­ры, скорость которой в данный момент времени равна нулю.

Пусть в момент времени t точки А и В плоской фигуры имеют скорости  и , не параллельные друг другу (см. рисунок 5.4). Тогда точка Р, лежащая на пересечении пер­пендикуляров Аа к вектору  и Вb к векто­ру , и будет мгновенным центром скоростей, так как = 0.

Если теперь в момент времени t взять точку Р за полюс, то по формуле (5.2) скорость точки А будет

.

Т.о., скорости точек фигуры определяются в данный момент времени так, как если бы движение фигуры было вращением вокруг МЦС.  При этом

                             ,     .             (5.4)

Из равенства (5.4) следует, что   

 ,                                                              (5.5)

т.е., скорости точек плоской фигуры пропорциональны их расстояниям от МЦС.

Полученные результаты приводят к следующим выводам:

а) для определения МЦС достаточно знать то­лько направления  и  каких-либо двух точек А и В плоской фигуры; МЦС находится в точке пересечения перпендикуляров, вос­ставленных из точек А и В к скоростям этих точек;

б) для определения скорости любой точки плоской фигуры достаточно знать модуль и направление скорости какой-нибудь одной точки А фигуры и направление скорости другой ее точки В. Тогда, вос­становив из точек А и В перпендикуляры к  и , найдем МЦС и по направлению  определим направ­ление поворота фигуры. После этого, зная , найдем по (5.5) скорость  любой точки М плоской фигуры. Направлен век­тор  перпендикулярно РМ в сторону поворота фигуры;

в) угловая скорость w плоской фигуры равна в каждый момент времени отношению скорости какой-нибудь точки фигуры к ее расстоянию от МЦС

 .                                                               (5.6)

5.3 Определение ускорений точек плоской фигуры

Ускорение любой точки М плоской фигуры складывается из ускорений, которые точка получает при поступательном и вращательном движениях этой фи­гуры. Положение точки М по отношению к осям Оху определяется радиусом-вектором  , где = AM. Тогда

.                                      (5.7)

Т.о., ускорение любой точки М плоской фигуры гео­метрически складывается из ускорения какой-нибудь другой точки А, принятой за полюс, и ускорения, которое точка М получает при вращении фигуры вокруг этого полюса. При решении задач удобно вектор  заменять его касательной () и нормальной () составляющими и пред­ставить равенство (5.7) в виде

  .                                                        (5.8)

 5.4 Сложное движение точки. Относительное, переносное и абсолютное движения

При реше­нии задач оказывается целесообразным рассматривать движе­ние точки  по отношению к двум СО, из которых одна считается основной (условно неподвиж­ной), а другая - движущейся по отношению к первой. Движение, совершаемое при этом точкой, называют сложным. Рассмотрим точку М, движущуюся по отношению к подвижной СО Oxyz, которая, в свою очередь, движется отно­сительно неподвижной СО О₁х₁у₁z₁ (см. рисунок 5.5). Введем определения:

а) движение, совершаемое точкой М по отношению к подвижной СО (к осям Oxyz), называется относительным движением;

б) движение, совершаемое подвижной СО Oxyz по отношению к неподвижной системе О₁х₁у₁z₁, является для точки М переносным движением. Скорость неизменно связанной с подвижными осями Охуz точки m, с которой в данный момент времени совпадает движущаяся точка М, называется переносной скоростью точки М в этот момент времени (), а ускорение этой точки m - переносным ускорением точки М. Тогда

,            ;                                          (5.9)

в) движение, совершаемое точкой по отношению к неподвижной системе отсчета О₁х₁у₁z₁, называется абсолютным или сложным.

Рассмотрим сложное движение точки М. Пусть она совершает за промежуток времени  Dt=t₁-t относительное перемещение вдоль траектории АВ, определяемое вектором  (см. рисунок 5.6 а). Сама кривая АВ, двигаясь вместе с подвижными осями Oxyz, перейдет за тот же промежуток времени в какое-то новое положение A₁B₁. Одновременно точка m кривой АВ, с которой в момент времени t совпадает точка М, совершит пере­носное перемещение . В результате точка М придет в положение М₁ и совершит за время Dt абсолютное перемещение . Из векторного треугольника  Мm₁М₁ имеем .

Деля обе части этого равенства на Dt  и переходя к пределу, получим .  В   результате   находим,   что

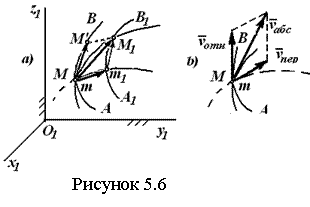
.            (5.10)

Направлены  по касательным к соответствую­щим траекториям  (см. рисунок 5.6 б). Т.о., дока­зана теорема о сложении скоростей: при сложном движении абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей. Если угол между  и  равен a, то по модуль скоро­сти

.                                      (5.11)

Найдем зависимость между относительным, переносным и абсолютным ускорениями точки. Из равенства (5.10) получим

.                            (5.12)

Здесь изменения, которые векторы  и  получают при относительном движении, отмечены индексом 1, а при переносном движении - индексом 2.

Но, по определению, относительное ускорение характеризует изменение относительной скорости только при относительном движении; движение осей Охуz, т. е.  переносное движение при этом во внимание не принимается. Поэтому

 .                                                       (5.13)

В свою очередь, переносное ускорение характеризует изменение переносной скорости только при переносном движении, так как , где m - точка, неизменно связанная с осями Охуz и, следовательно, получающая ускорение только при движении вместе с этими осями, т. е. при переносном движении. Поэтому

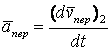.                                                    (5.14)

В результате из равенства (5.12) получим

 .                              (5.15)

Введем обозначение

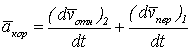.                                               (5.16)

Величина , характеризующая изменение относительной ско­рости точки при переносном движении и переносной скорости точки при ее относительном движении, называется поворотным, или кориолисовым, ускорением точки. В результате равенство (5.15) примет вид

.                                               (5.17)

Формула (5.17) выражает теорему Кориолиса о сложении ускорений: при сложном движении ускорение точки равно геометри­ческой сумме трех ускорений, от­носительного, переносного и пово­ротного (кориолисова).

Доказывается, что вектор ускорения Кориолиса определяется как

.                                                    (5.18)

При нахождении и нужно учитывать, что каждый из них может являться суммой нескольких составляющих, например, касательного и нормального ускорений.

В частном случае, когда переносное движение является поступательным движением, =0, и теорема о сложении ускорений упрощается

.                                               (5.19)       

6 Лекция №6. Вращение твердого тела вокруг неподвижной точки. Общий случай движения свободного твердого тела

Содержание лекции: движение тела с одной неподвижной точкой, общий случай свободного движения тела.

Цели лекции: изучить кинематику сферического движения и общего случая движения твердого тела.

 

6.1 Движение тела с одной неподвижной точкой

Движение твердого тела с одной неподвижной точкой принято называть вращательным или сферическим. Расстояние от неподвижной точки до любой точки тела при его движения остается неизменным, поэтому траектории всех точек располагаются на поверхностях концентрических сфер.

Тело с одной неподвижной точкой имеет три степени свободы. Для описания движения такого тела необходимо задать три независимых параметра, однозначно определяющих в любой момент времени его положение в выбранной СО. Наиболее распространены углы Эйлера (см. рисунок 6.1).

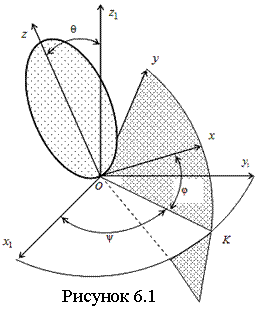  С телом, движение которого изучается в неподвижной системе координат Ox₁y₁z₁, жестко связывают подвижную систему координат Oxyz. Плоскость xOy подвижной системы пересекается с плоскостью x₁Oy₁ по т.н. линии узлов ОК. Положение Oxyz относительно Ox₁y₁z₁ определяют углами Эйлера:

  ψ – угол прецессии, определяющий вращение тела вокруг неподвижной оси;

  φ – угол собственного вращения, определяющий вращение тела вокруг оси собственного вращения;

  θ – угол нутации, определяющий вращение тела вокруг линии узлов.

  Уравнения движения имеют вид

                                 (6.1)

Теорема Эйлера-Даламбера устанавливает, что любое элементарное перемещение тела, имеющего неподвижную точку, представляет собой элементарный поворот вокруг некоторой мгновенной оси вращения, проходящей через эту точку. Мгновенная ось вращения является неподвижной в лишь данный момент времени, и в любой другой момент времени это уже другая ось. Мгновенная ось описывает в процессе движения тела коническую поверхность с образующей, проходящей через неподвижную точку.

  Для описания движения тела вводятся векторы угловой скорости и углового ускорения. Вектор угловой скорости  расположен на мгновенной оси вращения и направлен так, что с его вершины вращение наблюдается против хода стрелки часов. Начало вектора расположено в неподвижной точке. Вектор углового ускорения  определяется формулой

.                                                    (6.2)

Здесь  характеризует изменение  как по величине, так и по направлению, и поэтому  и  неколлинеарны;   направлен по касательной к траектории, описываемой концом вектора , так же как вектор скорости точки.

Скорость и ускорение точки тела определяют по формулам:

,               (6.3)

где  – радиус-вектор точки, проведенный из неподвижной точки. Заметим, что вектор осестремительного ускорения направлен к мгновенной оси вращения тела и перпендикулярен вектору скорости так же, как и при вращении тела вокруг неподвижной оси. Вектор вращательного ускорения не лежит на одной прямой с вектором скорости, т.е. на касательной к траектории точки и не тождествен ее касательному ускорению.

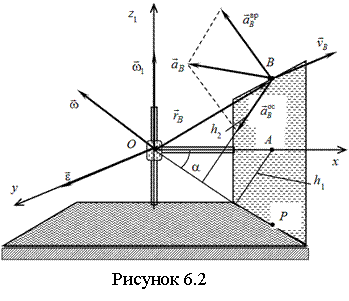Пример 6.1 - Ось подвижного конуса Ox вращается вокруг неподвижной оси Oz₁ с постоянной угловой скоростью  (см. рисунок 6.2). При этом подвижный конус катится без скольжения по боковой поверхности неподвижного конуса. Определить скорости точек  P, A, B и угловую скорость подвижного конуса, а также ускорение точки В, если  = 1 рад/с, OA = 50 см, α= 30°.

Решение. Вначале установим положение мгновенной оси вращения тела. Так как качение подвижного конуса по неподвижному происходит без скольжения, то все точки подвижного конуса, включая точку P, в данный момент времени совпадают с точками неподвижного конуса. Следовательно, скорости этих точек равны нулю. Отсюда следует, во-первых, что мгновенная ось вращения тела в данный момент времени расположена на прямой OP, и, во-вторых, что скорость точки P равна нулю.

Определим скорость точки А, которая лежит на оси Ox, . Обозначив через расстояние от точки А до мгновенной оси вращения, найдем угловую скорость тела: . Далее определим скорость точки B. Она направлена параллельно оси y, перпендикулярной осям z₁ и x.

  Определим ускорение точки В. Вектор  вращается вокруг неподвижной оси Oz₁, а поскольку угловая скорость его вращения  постоянна по модулю, то модуль вектора  также постоянен

.

Следовательно, его производную по времени, т.е. вектор , определим по формуле . Этот вектор направлен по оси y, перпендикулярно плоскости, в которой расположены векторы и . Его модуль .

  Проведем из неподвижной точки радиус-вектор точки В  и определим составляющие вектора ее ускорения

;

;

.

По теореме косинусов, поскольку угол между векторами  и  равен 120°, найдем модуль ускорения точки

                                                            

Вектор вращательного ускорения не лежит на одной прямой с вектором скорости, а перпендикулярен ему.

 

6.1 Движение свободного твердого тела

Свободным называют такое движение тела, при котором на его положение в пространстве не наложено никаких ограничений. В этом случае тело имеет 6 степеней свободы. Для описания движения его введем в рассмотрение три системы координат (см. рисунок 6.3):   – неподвижная, относительно которой изучается движение;  – подвижная, оси которой движутся поступательно вместе с началом координат (т. О);  – подвижная, жестко скрепленная с телом.

 

 

 

 

 

 

 

 

 

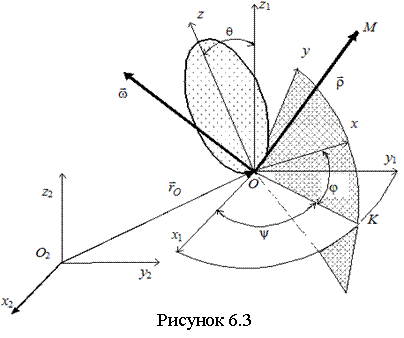
Движение тела слагается из поступательного вместе с точкой О, являющейся полюсом, и движения относительно точки О. Последнее является движением тела с одной неподвижной точкой в системе координат .

Т.о., движение свободного твердого тела в общем случае слагается из поступательного движения, при котором все точки тела движутся как произвольно выбранный полюс О, и из сферического движения, определяемого углами Эйлера. Все перемещения являются независимыми и поэтому уравнениями движения могут быть записаны в виде

      

                               (6.4)

Первые три зависимости соответствуют поступательному движению, а вторые три – сферическому.

Поскольку сферическое движение может быть представлено серией элементарных поворотов вокруг мгновенных осей вращения, проходящих в данном случае через полюс О, то скорость и ускорение любой точки тела будут равны геометрическим суммам скорости и ускорения, соответственно, поступательного движения, т.е. полюса, а также скорости и ускорения точки при движении относительно полюса. Приведем формулы для определения скорости и ускорения свободного твердого тела:

.                 (  6.5)

Здесь  и  – скорость и ускорение точки М тела;  и  – скорость и ускорение полюса О;  – угловая скорость тела;  радиус-вектор точки М в подвижной системе координат .

 

7 Лекция №7. Сложение движений твердого тела

Содержание лекции: сложное движение АТТ; сложение поступательных движений, вращательных движений, вращательного и поступательного движений.

Цели лекции: рассмотреть сложение поступательных движений, вращательных движений, вращательного и поступательного движения.

7.1 Сложение поступательных движений твердого тела

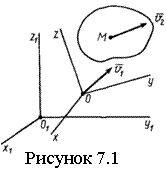
Имеем АТТ, движущееся относительно подвижной системы координат Oxyz поступательно со ско­ростью v₂, а подвижная система координат движется относи­тельно неподвижной O₁x₁y₁z₁ тоже поступательно со скоростью v₁ (см. рисунок 7.1). Движение тела относительно основной системы координат является сложным.

Установим вид сложного движения. Для этого вычислим скорость к.-л. точки М тела относительно O_lx₁y₁z₁ по теореме сложения скоростей для случая, когда оба движения являются поступа­тельными

                                   (7.1)

Это справедливо для лю­бой точки рассматриваемого тела, поэтому сложное движение тела является поступательным со скоро­стью  Т.о., при сложении двух поступательных движений АТТ получается поступатель­ное движение со скоростью, рав­ной векторной сумме скоростей составляющих поступательных дви­жений.

Если имеется последовательность поступательных движений тела, то от сложения этих движений путем последовательного применения (7.1) получим поступательное движение тела со скоростью                (7.2)

7.2 Сложение вращательных движений твердого тела

1. Сложение вращений вокруг пересекающихся осей. Пусть АТТ участвует одновременно в двух вращениях: переносном с угловой скоростью  и относительном с угловой скоростью  Оси вращений пересекаются в точке О (см. рисунок 7.2,а). Вектора угловых скоростей как скользящие вектора можно считать перенесенными в точку пересечения осей вращения О. Пример тела, совершающего такое движение, показан на рисунке 7.2,б).

 

 

 

 

 

 

 

 

 

 

 

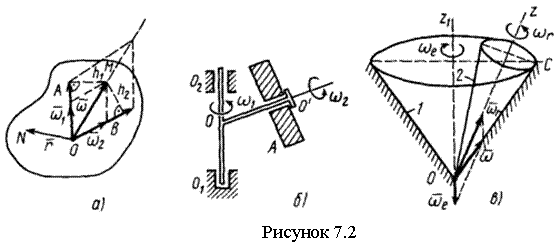
Определим вид движения АТТ, участвующего в двух вращениях вокруг пересекающихся осей. Точка О тела, расположенная на пересечении осей вращения, является непод­вижной, и ее абсолютная скорость v_О = 0. Доказывается, что любая точка М тела, находящаяся на диагонали парал­лелограмма, построенного на векторах угловых скоростей  и , в рассматриваемый момент имеет скорость, равную нулю. Следовательно, ОМ является мгновенной осью вращения, т. е. при сложении двух вращений вокруг пересекающихся осей получается вращение тела вокруг мгновенной оси.

Для определения абсолютной угловой скорости вращения вокруг ОМ выберем на теле точку N и вычислим ее скорость. Доказывается, что

                                               (7.3)

т. е. угловая скорость абсолютного вращения равна векторной сумме угловых скоростей составляющих вращений.

Последовательное применение этого правила сложения вра­щений вокруг пересекающихся осей позволяет заменить любое количество вращений вокруг пересекающихся осей одним вращением, угловая скорость которого  равна векторной сумме угловых скоростей составляющих вращений, т. е.

Тело, участвующее в двух вращениях вокруг пересекающихся осей, имеет неподвижную точку, расположенную на пересечении осей. Оно вращается вокруг неподвижной точки, т. е. совершает сферическое движение. Т.о., сферическое движение АТТ можно считать состоящим из двух вращений вокруг пересекающихся осей, переносного и относительного.

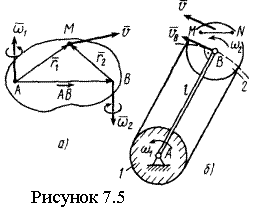
Сферическое движение совершает конус 2 при качении без скольжения по неподвижному конусу 1 (см. рисунок7.2,в).

2. Сложение вращений вокруг параллельных осей. Следует рассмотреть три случая.

А) Вращения имеют одинаковые направления. Тело участвует в двух вращениях: переносном со скоростью и от­носительном со скоростью  (см. рисунок 7.3,а). Примером является диск, представленный на рисунке 7.3,б. Пересечем оси вращения перпендикулярной прямой. Получим точки пересечения А и В, в которые можно перенести векторы угловых скоростей и. На отрезке АВ тела в рассматриваемый момент имеется точка С, скорость которой равна нулю. Доказывается, что

ω₁∙AC= ω₂∙BC   или 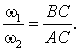                                     _(7.4)

 

 

 

 

 

 

Доказывается также, что при сложении двух вращений тела вокруг параллельных осей в одинаковых направлениях получается враще­ние вокруг параллельной оси в том же направлении с угловой скоростью

                                                (7.5)

Мгновенная ось полученного вращения делит отрезок между осями составляющих вращений на части, обратно пропорциональные угловым скоростям этих вращений, внутрен­ним образом.

                                                 (7.6)

С другой стороны, вращение АТТ вокруг оси можно разложить на два вращения вокруг двух параллельных осей.

Тело, участвующее в двух вращениях вокруг параллельных осей, совершает плоское движение. Плоское движение АТТ можно представить как два вращения, переносное и от­носительное, вокруг параллельных осей. Пример - движение колеса сателлита 2 по неподвижному колесу 1 (см. рисунок 7.2,в).

Б) Вращения имеют противоположные направления. Рассмот­рим случай, когда  >  (см. рисунок 7.4,а). Доказывается, что

                                                    (7.7)

                                                            (7.8)

 

 

 

 

 

 

 

 

Т.е., при сложении двух вращений твердого тела вокруг параллельных осей в противоположных направлениях получается вращение вокруг параллельной оси с угловой скоростью, равной разности угловых скоростей составляющих вращений, в сторону вращения с большей угловой скоростью. Ось абсолютного вращения делит отрезок между осями составляющих вращений на части, обратно пропорциональные угловым скоростям этих вращений внешним образом. Точка С находится на отрезке АВ за точкой А, через которую проходит ось вращения с большей угловой скоростью. Можно также одно вращение разложить на два вокруг параллельных осей с противоположными направлениями враще­ния.

Примером плоского движения твердого тела, которое может быть представлено двумя вращениями вокруг параллель­ных осей в противоположных направлениях, является движение колеса сателлита, катящегося внутри неподвижного колеса без скольжения (см. рисунок 7.4,в).

В)Пара вращений. Парой вращений называется совокуп­ность двух вращений АТТ вокруг параллельных осей с одина­ковыми угловыми скоростями в противоположных направлениях (см. рисунок 7.5,а). В этом случае  По теореме сложения скоростей для точки М имеем

                                (7.9)

Составляющие движения явля­ются вращениями с угловыми скоростями и  По формуле Эйлера для них получим

   

Тогда для абсолютной скорости имеем

так как  Учитывая, что , получаем

.                           (7.9')

Векторное произведение  можно назвать моментом угловой скорости  относительно точки В, поэтому

Заменяя  на  получим

Обобщая, имеем

или                                                           (7.10)

Здесь  является векторным моментом пары вращений

Т.о., если АТТ участвует в паре вращений, то скорости всех точек тела одинако­вы, т. е. тело совершает мгновенное поступательное движение. Скорость поступательного движения тела равна векторному моменту пары вращений. Скорость поступательного дви­жения тела, участвующего в паре вращений, зависит только от характеристик пары вращений. Она перпендику­лярна осям пары вращений и равна

                                 (7.11)

Здесь d - кратчайшее расстояние между осями пары или плечо пары.

Пару вращений и ее эквивалентность поступательному движению наглядно демонстрирует прибор (см. рисунок 7.5,б), состоящий из неподвижной 1 и подвижной 2 ше­стеренок, соединенных цепью.

 

7.3 Сложение поступательного и вращательного движений

Если АТТ участвует в переносном поступа­тельном движении со скоростью и относительном вращатель­ном с угловой скоростью , то в зависимости от взаимного расположения и нужно рассмотреть три случая.

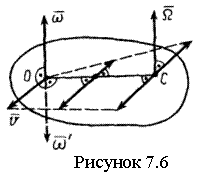А) Скорость поступательного движе­ния перпендикулярна оси относительного вращения. В этом случае векторы  и  перпендикулярны (см. рисунок 7,6). На линии ОС, перпендикулярной плоскости, в которой расположены  и , имеется точка С, скорость которой равна нулю.

Определим ее расстояние от точки О. По теореме сложения скоростей имеем  т.к. при вращении вокруг оси   Учитывая, что скорости  и  противоположны по направле­нию, получим v_С = v - ω∙ОС. Т.к.v_С =0, то v - ω∙ОС =0 и, следовательно,

                                                (7.12)

Другие точки, имеющие скорости, равные нулю, располагаются на линии, проходящей через точку С, параллельно оси вращения тела с угловой скоростью . Т.о, имеется мгновенная ось вращения, параллельная оси от­носительного вращения и проходящая через точку С. Доказывается, что угловая скорость абсолютного вращения  равна  Т.о., в рассматриваемом случае эквивалентное аб­солютное движение является вращением вокруг мгновенной оси, параллельной оси относительного вращения с угловой скоростью, совпадающей с угловой скоростью относительного вращения.

На поступательное переносное и вращательное относитель­ное с осью вращения, перпендикулярной к скорости переносного движения, разлагается плоское движение твердого тела (пример -  плоское движение без скольжения колеса по прямой).

Б) Винтовое движение. Движение, при котором скорость переносного поступательного движения тела параллельна оси относительного вращения, называется винтовым движени­ем (ВД) твердого тела (см. рисунок 7.7). Ось вращения тела в этом случае называется винтовой осью. При ВД тело движется поступательно параллельно оси винтового движения и вращается вокруг этой оси. ВД не приводится к к.-л. другому одному эквивалентному движению.

При ВД векторы  и могут иметь как одинаковые, так и противоположные направления. ВД тела характеризуют параметром р = v/ω. Если v и ω изменяются с течением времени, то и параметры винтового движения являются переменными. В общем случае т.е., р есть перемещение тела вдоль оси винтового движения при повороте на один радиан.

Для скорости точки М тела можно показать, что

                                           (7.13)

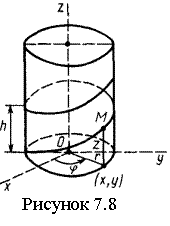Если тело вращается с постоянной угловой скоростью и имеет постоянную скорость поступательного движения, то такое движение тела называется постоянным ВД. В этом случае точка тела при движении все время находится на поверхности кругового цилиндра с радиу­сом r. Траекторией точки является винтовая линия. Кроме параметра в рассматриваемом случае вводят шаг винта, т. е. расстояние, на которое переместится какая-либо точка тела при одном обороте тела вокруг оси винтового движения. Угол поворота тела φ при ω = const вычисляется по формуле φ =ω∙t. Для одного оборота тела φ =2π. Необходимое для этого время  За время Т точка переместится в направлении, параллельном винтовой оси, на шаг винта h = v∙ Т = v∙Отсюда найдем h =

Уравнения движения точки М тела по винтовой линии (см. рисунок 7.8) в декартовых координатах выражаются в следующей форме

   

Здесь ω, r и v являются постоянными.

В) Общий случай. Пусть вектора  и образуют угол α. Разложим скорость  (см. рисунок 7.9) на две перпендикулярные составляющие и , причем  направим параллельно . Тогда

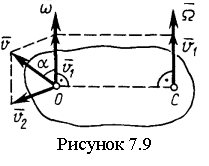Переносное движение со скоростью  и относительное враще­ние с угловой скоростью эквивалентны вращению вокруг оси, проходящей через точку С с угловой скоростью  (согласно случаю А), причем

Скорость поступательного движения имеют все точки тела. Т.о., получено ВД с винтовой осью, отстоящей от первоначальной оси вращения на величину  Параметр ВД  Т.о., общий случай эквивалентен мгновенному ВД.

 

8 Лекция №8 Введение в динамику. Законы и задачи динамики точки. Общие теоремы динамики точки

Содержание лекции: вводные понятия и аксиомы динамики точки; дифференциальные уравнения движения; общие теоремы динамики точки.

Цели лекции: изучить понятия динамики, дифференциальные уравнения движения точки, научиться применять общие теоремы динамики точки для определения характеристик движения точки.

 

8.1 Аксиомы динамики

Динамикой называют раздел механики, в котором рассматривается движение материальных тел под действием приложенных к ним сил с учетом инерции. Инерцией называется свойство материального тела сохранять состояние движения или покоя при отсутствии действующих на тело сил. Физическую величину, зависящую от количества вещества и являющуюся мерой инерции тела в поступательном движении, называется массой тела m.

Основой динамики точки являются 4 аксиомы, изложенные ниже.

1-я аксиома (закон инерции): материальная точка (МТ), к которой не приложены силы, находится в состоянии покоя или равномерного прямолинейного движения, пока приложенные к ней силы не изменяют этого состояния. Движение МТ при отсутствии сил называют инерциальным. Систему отсчета (СО), в которой действует закон инерции, называют инерциальной СО. В большинстве задач СО, связанная с Землей, считается инерциальной.

2-я аксиома (основной закон динамики): ускорение МТ пропорционально приложенной к ней силе и направлено по силе. Основное уравнение

.                                                        (8.1)

3-я аксиома (закон о действии и противодействии): две МТ действуют друг на друга с равными по модулям силами, которые лежат на соединяющей эти точки прямой и направлены в противоположные стороны.

4-я аксиома (закон независимости действия сил): геометрическая сумма ускорений, которые сообщаются МТ отдельно каждой приложенной к ней силой, равна ускорению, которое МТ получит под действием на нее всех сил.

                                               (8.2)

Вместо (8.2) можно использовать уравнение (8.1), понимая под силой  равнодействующую.

Под действием на тело силы тяжести у тела возникает одно и то же ус­корение , которое называют ускорением силы тяжести (ускорением свобод­ного падения). Если к МТ приложена только сила тяжести , то по (8.1)

.                                                       (8.3)

Масса тела не зависит от его местонахождения и от сил, приложенных к телу, а вес тела меняется с изменением ускорения силы тяжести в зависимости от географической широты места и расстояния от центра Земли.

 

8.2 Дифференциальные уравнения движения материальной точки

Рассмотрим движение МТ под действием сил {} относительно инерциальной СО Оxyz. Проецируя уравнение (8.2) на естественные оси, получаем естественные дифференциальные уравнения движения (ДУД)

;                              (8.4)

проецируя на декартовы оси, получаем ДУД точки в декартовых координатах

                             (8.5)

ДУД применяются к решению двух основных задач динамики МТ:

1-я основная задача: по движению точки найти приложенную к ней силу. Здесь нужно продифференцировать уравнения движения МТ и результаты подставить в (8.4) или (8.5), откуда определяется приложенная к точке сила;

2-я основная задача: по силам, приложенным к точке, найти ее движение. Решая эту задачу, нужно в общем случае найти вторые интегралы дифференциальных уравнений (8.4) или (8.5).

8.3 Относительное движение материальной точки

Законы динамики справедливы только в инерциальной СО. Рассмотрим движение МТ относительно СО, которая движется произвольно относительно инерциальной СО. Рассмотрим МТ под действием сил {}. В инерциальной СО справедливо основное уравнение динамики (8.2). Абсолютное ускорение точки можно найти по формуле (5.17)

                                             (8.6)

Подставим (8.6) в равенство (8.2) и преобразуем его

                                  (8.7)

Примем обозначения

                                                (8.8)

                                                                                         (8.9)

Векторы  и  называют соответственно переносной и кориолисовой силами инерции. Равенство (8.7) можно записать в виде

                                        (8.10)

Уравнение (8.10) называют основным уравнением динамики относительного движения МТ. Уравнения относительного движения МТ составляются также, как в случае абсолютного движения, если к числу действующих сил добавить переносную и кориолисову силы инерции. Наблюдатель, который находится в движущейся неинерциальной системе отсчета, воспринимает переносную и кориолисову силы инерции, как реально существующие силы. Но это неверно, т.к. в неинерциальной СО законы механики Ньютона не действуют, и рассматривать явления с точки зрения предыдущих аксиом нельзя.

Частные случаи основного уравнения относительного движения МТ:

а) при поступательном переносном движении

                                             (8.11)

б) при прямолинейном и равномерном переносном движении

                                                (8.12)

Уравнения (8.12) и (8.2) совпадают, так как . Следовательно, данная CO инерциальна. Механическими опытами невозможно установить, неподвижна ли CO, или она движется поступательно, равномерно и прямолинейно (принцип относительности Галилея);

в) в относительном состоянии покоя

                                                   (8.13)

Это уравнение относительного равновесия МТ.

8.4 Движение несвободной материальной точки

Основной закон динамики для несвободной МТ, а следовательно, и ее ДУД имеют такой же вид, как и для свободной точки, только к действующим на точку силам добавляют не известные заранее силы реакций связей.

При решении первой основной задачи динамики по заданному движению точки из ДУД определяется равнодействующая. Затем, раскладывая равнодействующую на составляющие, по заданным связям выделяют силу реакции связей. Полную силу реакции точки при ее движении обычно раскладывают на две составляющие. Составляющая силы реакции связей, уравновешивающая заданные силы, приложенные к точке, называется статической реакцией. Составляющая реакции, зависящая только от движения точки под действием заданных сил, называется динамической реакцией. Она уравновешивает силу инерции движущейся точки.

При решении второй основной задачи динамики, когда по заданным силам и начальным условиям требуется определить движение несвободной точки, все силы реакций связей, заранее не известны, и их необходимо определить по заданным связям в процессе решения. Т.о., вторую основную задачу динамики для несвободной МТ можно сформулировать так: по заданным силам, начальным условиям и связям, наложенным на точку, определить движение этой точки и силы реакции связей.

А) Движение точки по поверхности. Пусть гладкая неподвижная поверхность, по которой движется точка массой m под действием данной силы , задана уравнением f(x, у, z) = 0, где х, у, z - координаты движущейся точки. Сила трения отсутствует. Обозначив через неизвестную нормальную силу реакции поверхности, получим следующие ДУД

                          (8.14)

Из дифференциальной геометрии известно, что косинусы углов внешней нормали к поверхности с осями координат, а следовательно, и силы , параллельной главной нормали, можно вычислить по формулам

 

Здесь  Тогда

       

                                                             (8.15)

                                                      

Обозначив λ = N/Δf и подставив (8.15) в (8.14), получим 

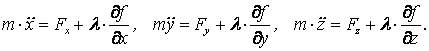
Эти дифференциальные уравнения (ДУ) называют ДУ Лагранжа 1-го рода для движения несвободной МТ. Из этих трех ДУ и уравнения поверхности f(x, у, z) = 0 можно найти 4 неизвестных - координаты точки х, у, z и неопределенный множитель Лагранжа λ как функции времени и произвольных постоянных интегрирования. Произвольные постоянные определяют из начальных условий. По множителю Лагранжа λ определяют реакции поверхности N = λ∙Δf, которая в общем случае зависит от времени.

Если поверхность не гладкая, то кроме нормальной реакции возникает предельная сила трения , проекции которой надо добавить в ДУД точки. Это усложнит решение задачи, но задача разрешима, т.к. наряду с добавлением неизвестной силы добавляется и конечное уравнение, связывающее эту силу с нормальной реакцией , где k - коэффициент трения.

Проекции силы трения на оси координат можно представить в виде

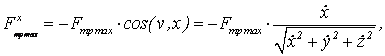
аналогично,  

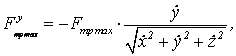
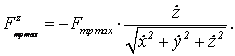
Учет трения усложняет задачу интегрирования ДУД несвободной МТ.

Б) Движение точки по гладкой кривой линии. Кривую неподвижную линию можно рассматривать как линию пересечения двух поверхностей  f₁(х, у, z) = 0 и f₂ (х, у, z) = 0. Эти поверхности создают для движущейся точки нормальные реакции  и , и полная реакция кривой линии

ДУ Лагранжа 1-го рода движения точки по кривой линии имеют вид

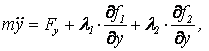                                                          (8.16)

 

Здесь

Присоединяя к ДУ (8.16) два уравнения поверхностей f₁(х, у, z) = 0 и f₂ (х, у, z) = 0, получаем пять уравнений для определения пяти величин х, у, z, λ₁,  λ₂ как функций времени, т.о., поставленная задача может быть решена.

 

8.5 Теорема об изменении количества движения точки

При решении многих задач динамики вместо интегрирования ДУД оказывается более эффективным использо­вание т.н. общих теорем динамики.

Рассмотрим теорему об изменении количества движения точки. Количеством движения МТ называют величину , равную произведению массы точки на ее скорость. Вектор направлен по ка­сательной к траектории точки.

Элементарным импульсом силы называют величину

                                                             (8.17)

равную произведению силы на элементарный промежуток времени. Направлен импульс вдоль линии действия силы. Импульс  силы  за конечное время t₁

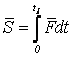               .                                                                (8.18)

Модуль и направление импульса можно вычислить по его проекциям

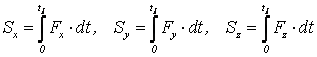.                                  (8.19)

Основной закон динамики можно представить в виде              

                  .                                                         (8.20)

Это теорема об изменении количества движения точки в дифференциальной форме: производная по времени от количества движения точки равна сумме действующих на точку сил. Та же теорема в конечном виде: изменение количества движения точки за некоторый промежуток вре­мени равно сумме импульсов всех действующих на точку сил за этот промежуток времени

.                                                         (8.21)

При решении задач обычно поль­зуются уравнениями в проекциях.

 

8.6 Теорема об изменении момента количества движения точки

Моментом количества движения точки относи­тельно некоторого центра О называется векторная величина , определяемая равенством

 ,                                                      (8.22)

где   — радиус-вектор  движущейся точки, проведенный из центра О.

При этом вектор направлен перпендикулярно плоскости, проходящей через  и центр О, a .

Момент количества движения точки относительно какой-нибудь оси Оz, проходящей через центр О, равен проекции вектора на эту ось

,                         (8.23)

где  g — угол между вектором  и осью Оz.

Теорема: производная по времени от момента количества движения точки, взятого относительно какого-либо неподвижного центра, равна моменту действующей на точку силы относительно того же центра

.                                               (8.24)

Теорема моментов относительно оси

.                                              (8.25)

Из уравнения (8.25) следует, что если , то .

 

8.7 Работа силы. Мощность силы. Теорема об изменении кинетической  энергии точки

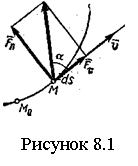Элементарной работой силы , приложенной в точке М (см. рисунок 8.1), называют скалярную величину

dW = F_t ∙ds,                                         (8.26)

где F_t  — проекция силы  на касательную Мt  к траектории точки М, направленную в сторону перемещения точки;

ds — модуль элемен­тарного перемещения точки М.

Т.к. ds = |d| (здесь d - вектор элементарного переме­щения точки), то равенство (8.26) можно представить в виде

dW= .                                                 (8.27)

Т.е., элементарная работа силы равна скалярному произведению силы на вектор элементарного перемещения точки ее приложения.   

Работа силы на конечном перемещении M₀M₁ (см. рисунок 8.1) равна

,                                                   (8.28)

 .                             (8.29)

Мощностью  называют величину, равную работе, совершаемой силой в единицу времени. Если работа совершается равномерно, то мощность P = W/t₁ (здесь t₁ - время, течение которого произведена работа W). В общем случае

,                                   (8.30)

т.е., мощность равна произведению касательной составляющей силы на скорость.

Кинетической энер­гией (КЭ) точки называют скалярную величину . Теорема: изменение КЭ точки при некотором ее перемещении равно алгебраической сумме работ всех действующих на точку  сил на том же перемещении.

.                                          (8.31)

 

8.8 Принцип Даламера для точки

Пусть на МТ с массой m действует система активных  сил, равнодействующую которых обозначим , и реакция связи . Под действием этих сил точка будет двигаться по отношению к инерциальной СО с некоторым ускорением .

Введем в рассмотрение величину

,                                                                (8.32)

имеющую размерность силы. Векторную величину, равную по модулю произведению массы точки на ее ускорение и направленную противоположно этому ускорению, называют силой инерции точки. Тогда оказывается, что если в любой момент времени к действующим на точку активным силам и реакции связи присоединить силу инерции, то полученная система сил будет уравновешенной, т. е.

.                                                   (8.33)

Это положение выражает принцип Даламбера для МТ.

 

9 Лекция №9. Прямолинейные колебания материальной точки

Содержание лекции: прямолинейные колебания материальной точки; свободные колебания, вынужденные колебания, резонанс.

Цели лекции: изучить методику составления дифференциальных уравнений движения и их интегрирования на примере прямолинейных колебаний.

 

9.1 Дифференциальное уравнение прямолинейных колебаний МТ

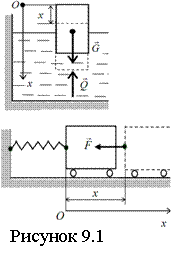Рассмотрим прямолинейные колебания МТ, считая восстанавливающие силы пропорциональными отклонениям точки от положения равновесия (см. рисунок 9.1), а силы сопротивления – пропорциональными скорости МТ.

Пусть т. М массой m притягивается к точке O силой , пропорциональной расстоянию OM, а начальная скорость точки направлена вдоль прямой OM или равна нулю (см. рисунок 9.2). В этом случае т. M движется прямолинейно, а ее положение определяется одной координатой x, отсчитываемой от положения равновесия (т.  O). Проекция  на ось x равна , с > 0. Пусть на т. M действует также сила сопротивления , проекция её на x равна , β > 0. Кроме того, на т. M действует гармоническая возмущающая сила  направленная вдоль x; проекция  на ось x равна , > 0 – амплитуда возмущающей силы, р – ее частота.

Запишем ДУД точки М

  или .

После преобразования, обозначив , получим неоднородное линейное ДУ с постоянными коэффициентами

.                                  (9.1)

9.2 Свободные колебания в среде без сопротивления

Рассмотрим колебания МТ под действием только восстанавливающей силы . Такие колебания называют свободными; они описываются однородным ДУ, которое получается из (9.1) при n = 0 и h = 0,

.                                               (9.2)

Характеристическое уравнение (ХУ) этого ДУ имеет чисто мнимые корни , поэтому общее решение (9.2) запишем в виде

                                    (9.3)

Постоянные интегрирования С₁ и С₂ определяем из начальных условий

.                                     (9.4)

Продифференцируем функцию (9.3)

.                                  (9.5)

Воспользовавшись (9.3) - (9.5), получим

.

Подставив С₁ и С₂ в уравнение (9.3), запишем закон движения точки

                                      (9.6)

и преобразуем его к более удобному виду, ввоедя обозначения

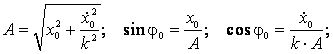                         (9.7)

тогда из (9.6) получим

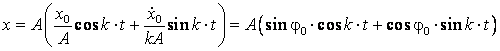
или                                    .                                             (9.8)

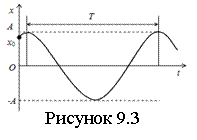  Т.о., свободные колебания МТ в среде без сопротивления являются гармоническими с амплитудой A и фазой , где  – начальная фаза. Здесь  - круговая или циклическая частота колебаний. Период колебаний  является периодом функции . Круговая частота k равна числу полных колебаний точки за 2π секунд, k = 2π/T. Частота и период гармонических колебаний зависят от массы точки и коэффициента пропорциональности восстанавливающей силы, но не зависят от начальных условий (свойство изохронности свободных колебаний). А и зависят как от параметров  m и c, так и от начальных условий. График свободных незатухающих колебаний приведен на рисунке 9.3.

Отметим, что выбор начала отсчета координаты в положении статического равновесия позволяет получить наиболее простую форму ДУД.

9.3 Свободные колебания при наличии вязкого сопротивления

Рассмотрим прямолинейное движение МТ под действием восстанавливающей силы и силы сопротивления. ДУД получим из  (9.1) при h = 0    

.                                         (9.9)

Его ХУ  имеет корни

.                                          (9.10)

Рассмотрим три возможных случая соотношения величин n и k.

1.       Случай малого сопротивления  Корни ХУ (9.10) комплексно сопряженные , . Общее решение (9.9) имеет вид

                             (9.11)

Постоянные интегрирования С₁ и С₂ определяют из начальных условий.

Введем новые постоянные А и φ₀

,

тогда из (9.11) получим

.                                       (9.12)

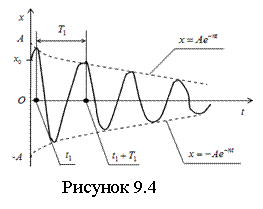Это уравнение описывает затухающие колебания (см. рисунок 9.4). Они не являются периодическими, но промежуток времени между двумя последовательными максимальными отклонениями точки от положения равновесия в одну и ту же сторону остается неизменным. Его условно называют периодом затухающих колебаний,  и k₁ – их частота.

Скорость затухания колебаний характеризуется отношением величин двух последовательных максимальных отклонений точки от положения равновесия в одну и ту же сторону

,

которое называют декрементом колебаний. Используют также величину , называемую логарифмическим декрементом колебаний. Т.к., появление силы сопротивления приводит к увеличению периода колебаний, . Это изменение может быть незначительным.

2.   Случай критического сопротивления          Корни характеристического уравнения (9.10) вещественные, равные и отрицательные , а общее решение дифференциального уравнения (9.9) имеет вид

.                                      (9.13)

3.   Случай большого сопротивления  Корни ХУ (9.10) вещественные, отрицательные и различные, а общее решение (9.9) имеет вид

                     (9.14)

В двух последних случаях движение точки становится апериодическим. В зависимости от величины и направления начальной скорости график движения имеет вид одной из трех кривых, приведенных на рисунке 9.5.

 

9.4 Вынужденные колебания. Общий случай

Колебания, которые совершает МТ под действием восстанавливающей силы, силы сопротивления и возмущающей силы, называют вынужденными. Их описывают неоднородным ДУ (9.1), которое имеет общее решение

_.                                                     (9.15)

Здесь  – общее решение однородного ДУ (9.9);  – частное решение неоднородного ДУ (9.1).

  Решение  является затухающим, и через достаточно большой промежуток времени после начала движения в решении (9.15) остается только слагаемое , которое будем искать в виде

.                                      (9.16)

Определим производные

,            (9.17)

затем преобразуем правую часть уравнения (9.1)

и подставим в него выражения (9.16) и (9.17)

  

                         

Чтобы это равенство выполнялось тождественно, приравняем коэффициенты при  и  в левой и правой его частях  и найдем

.                        (9.18)

Т.к.  и полностью определяется своим тангенсом.

Т.о,, уравнение вынужденных колебаний имеет следующий вид

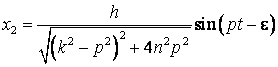.                     (9.19)

Из (9.19) следует, что вынужденные колебания являются незатухающими, а их частота и период равны частоте и периоду возмущающей силы.

Преобразуем выражение для амплитуды вынужденных колебаний

.    (9.20)

Отношение частоты возмущающей силы p к частоте свободных гармонических колебания k называют коэффициентом расстройки. Обозначим

Здесь  – статическое отклонение точки от положения равновесия под действием постоянной силы . Введем в рассмотрение коэффициент динамичности η, равный отношению амплитуды вынужденных колебаний  к величине статического отклонения ,

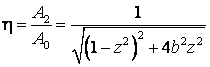.                                    (9.21)

Этот коэффициент зависит от коэффициента расстройки  z и коэффициента вязкости b (см. рисунок 9.6).

Исследуя на экстремум подкоренное выражение в (9.21), найдем, что при  коэффициент динамичности имеет максимум при  и минимум при  

             ,                        (9.22)

На рисунке 9.6 видно, что при малых значениях b, т.е. ,  и происходит резкое увеличение коэффициента динамичности η и, следовательно, амплитуды вынужденных колебаний . С увеличением коэффициента b, т.е. с ростом сопротивления среды, максимумы амплитуды уменьшаются и сдвигаются влево.

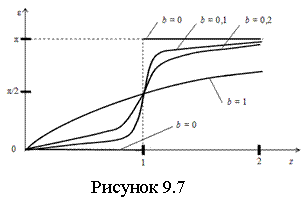  При  коэффициент динамичности η имеет лишь 1 экстремум - максимум при.

  Фаза вынужденных колебаний  отстает от фазы возмущающей силы  на величину ε, называемую сдвигом фаз. Из (9.18) получим

.                   (9.23)

Кривые зависимости ε от z для различных значений b приведены на рисунке 9.7. При z = 1 сдвиг фаз равен π/2 при любых значениях b, при дальнейшем росте z сдвиг фаз стремится к π.

9.5 Вынужденные колебания в среде без сопротивления

При отсутствии сопротивления (n = 0) при  из (9.18) следует, что 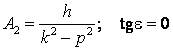, и уравнение вынужденных колебаний принимает вид

,                                (9.24)

а коэффициент динамичности

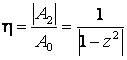                                            (9.25)

имеет разрыв 2-го рода при z = 1 (это кривая на рисунке 9.6 при b = 0). Если , то  и фаза вынужденных колебаний совпадает с фазой возмущающей силы. Если , то  и

,

т.е. сдвиг фаз ε = π (кривая на рисунке 9.7 при b = 0).

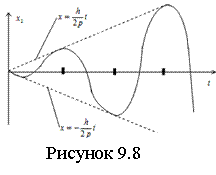  В случае совпадения частоты возмущающей силы p и частоты свободных гармонических колебаний k (собственной частоты) возникает явление резонанса. Тогда частное решение ДУ

,                              (9.26)

которое можно получить из уравнения (9.1) при n = 0, будем искать в виде

.                                           (9.27)

Определим производные

     

   (9.28)

Подставим (9.27) и (9.28) в уравнение (9.26)

.

Учтем, что p = k, тогда , откуда 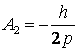 и

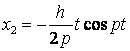.                                      (9.29)

Т.о., при резонансе возникают колебания с частотой p = k, размахи которых неограниченно растут пропорционально времени (см. рисунок 9.8).

 

10 Лекция №10. Основы динамики системы и твердого тела. Общие теоремы динамики системы

Содержание лекции: механическая система, ее масса, центр масс и моменты инерции; дифференциальные уравнения движения системы; общие теоремы динамики и принцип Даламбера для системы.

Цели лекции: изучить динамические характеристики системы, ДУД системы, основные теоремы динамики для МС.

 

10.1 Механическая система. Масса, центр масс и моменты инерции

Механической системой (МС) называют совокупность взаимодействующих МТ или тел. Материальное тело является МС составляющих его частиц. МС, движение точек которой не ограничено связями, называется системой свободных материальных точек. Внешними силами , k= 1,2 …,n называют силы, c которыми на точки системы действуют тела, не принадлежащие к этой системе. Внутренними силами , k= 1,2 …,m называют силы, c которыми взаимодействуют точки системы. Можно показать, главный вектор и главный момент системы внутренних сил равны нулю. Отсюда не вытекает, что внутренние силы уравновешиваются в общем случае, т.к. они могут вызывать перемещения точек системы (уравновешиваются в АТТ).

Массой системы называют сумму масс частиц системы

M=Σm_k.                                                (10.1)

Положение центра масс системы (т. С)  определяется по формулам

,                                                (10.2)

 .                     (10.3)

Для тела имеем 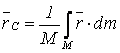              ,                                                (10.4)

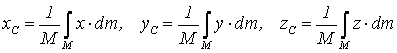 .                     (10.5)

В однородном поле силы тяжести центры масс и тяжести совпадают.

Моментами инерции МС относительно оси и точки называют величины

J_l=Σm_k∙h_k².                                                    (10.6)

                                         J_O=Σm_k∙r_k²                                                     (10.7)

где h_k и r_k – расстояние точки тела с массой m_k от оси l и точки O.

Для твердого тела момент инерции относительно оси и точки

,                                                 (10.8)

.                                                (10.9)

Моменты инерции относительно декартовых осей и начала координат

         J_x=Σm_k∙(y_k²+z_k²),    J_y=Σm_k∙(x_k²+z_k²),   J_z=Σm_k∙( x_k²+y_k²),              (10.10)

J_O=Σm_k∙r_k²=  Σm_k∙∙( x_k²+y_k²+z_k²).                                 (10.11)                                                

Моменты инерции относительно координатных плоскостей равны

          J_xy=Σm_k∙ z_k²,    J_yz=Σm_k∙x_k²,   J_xz=Σm_k∙y_k².                   (10.12)             

Имеются зависимости      2J_O= J_x+ J_y+ J_z,                                             (10.13)

J_O= J_xy+ J_yz+ J_xz.                                            (10.14)

Для тела моменты инерции определяются интегралами по массе

,   ,   .   (10.15)

Теорема Гюйгенса-Штейнера: момент инерции  системы J_z относительно какой-либо оси z равен сумме момента инерции системы J_zC  относительно параллельной ей оси z_C, проходящей через центр масс, и произведения массы системы M  на квадрат расстояния между осями d

.                                       (10.16)

Среди моментов для семейства параллельных осей момент инерции относительно оси, проходящей через центр масс, - наименьший.

10.2 ДУД системы. Теорема о движении центра масс системы

Для точек, входящих в МС,  можно записать ДУД в векторной форме

                                       (10.17)

Проецируя (10.17) на оси, получим ДУД в проек­циях оси. Полное решение основной задачи динамики для системы состоит в том, чтобы проинтегрировать ДУД и определить закон движения каждой точки системы и реакции связей. Выполнить это аналитически удается лишь в частных случаях, когда число точек мало, иначе приходится интегри­ровать уравнения численно. Однако при решении многих задач бывает достаточным найти некоторые характеристики, определяющие движение системы в целом. Сложив почленно уравнения (10.17), получим

.                                      (10.18)

С учетом формулы (10.2) можно получить соотношение

.                                  (10.19)

Это теорема о движении центра масс системы: центр масс системы движется как МТ, масса которой равна массе всей системы и к кото­рой приложены все внешние силы, действующие на систему. Проецируя обе части равенства (10.19) на координатные оси, можно по­лучить ДУД центра масс в проекциях на оси декартовой системы коор­динат.

Из (10.19) следует, что поступательно движущееся тело можно рассматривать как МТ с массой, равной массе тела. В остальных слу­чаях тело можно рассматривать как МТ, когда допустимо не принимать во внимание вращательную часть движения тела. При определении закона движения центра масс МС можно исключать из рассмотрения все неиз­вестные внутренние силы.

Следствие из теоремы (закон сохранения движения центра масс системы): внутренние силы не изменяют движение центра масс системы.

10.3 Теорема об изменении количества движения системы

Количеством движения системы (КДС) называют вели­чину

.                                              (10.20)

Можно показать, что

,                                                   (10.21)

т. е. КДС равно произведению массы всей системы на скорость ее центра масс. Если система движется так, что центр масс остается неподвижным, то КДС равно нулю (например, в случае тела, вращаю­щегося вокруг неподвижной оси, проходящей через его центр масс). Если же движение тела является сложным, то величина  КДС не зависит от его вращательного движения вокруг центра масс (для катящегося колеса  независимо от вращения).

Теорема об изменении КДС в дифферен­циальной форме: производная по времени от количества движения системы равна геометрической сумме всех действующих на систему внешних сил

.                                               (10.22)

В интеграль­ной форме: изменение КДС за некото­рый промежуток времени равно сумме импульсов, действующих на систему внешних сил за тот же промежуток времени

                                                 .                                                         (10.24)

Следствие (закон сохранения КДС): внутренние силы не могут изменить КДС, и при решении задач внутренние силы можно не рассматривать.

10.4 Теорема об изменении главного момента количеств движения

Главным моментом количеств движения системы (ГМКДС) или кинетическим моментом относительно данного цент­ра О называется величина , равная геометрической сумме моментов количеств движения всех точек системы относительно этого центра

.                                         (10.25)

Аналогично  имеем относительно координатных осей

,     ,    .    (10.26)

Теорема об изменении ГМКДС (теорема мо­ментов): производная  по времени от ГМКДС относительно некоторого неподвижного центра равна сумме моментов всех внешних сил системы относитель­но того же центра

.                             (10.27)

Проецируя на неподвижные оси 0хyz, получим теорему в проекциях.

Теорема применяется для изучения враща­тельного движения тела, а также движения системы в общем случае, т.к. последнее слага­ется из поступательного и вращательного движения. Если за полюс выбрать центр масс, то поступательная часть движения тела может быть изучена с помощью теоремы о движении центра масс, а вращательная - с помощью теоремы моментов. При этом из рассмотрения исключаются наперед неизвестные внутренние силы.

Для системы координат, движущейся поступательно вместе с телом, справедлива теорема моментов относительно его центра масс. Она имеет тот же вид, что и относительно неподвижного центра. Для моментов относительно осей такой системы также получаются схожие урав­нения.

Следствие из теоремы (закон сохранения ГМКДС): внутренние силы не изменяют ГМКДС. При этом если система неизменяема, то она  вращается с постоянной угловой скоростью, а если изменяема, то под действием внутренних (или внешних) сил расстояния отдельных ее точек от оси могут изменяться, что вы­зовет изменение угловой скорости.

 

10.5 Теорема об изменении кинетической энергии системы 

Кинетической энергией (КЭ) системы называют скалярную величину

.                                            (10.28)

КЭ является характеристикой и поступатель­ного, и вращательного движений системы. Отличие Т от  и  состоит в том, что КЭ является скалярной су­щественно положительной величиной, не зависящей от направлений движения частей МС, и не характеризует их изменение. Внутренние силы действуют на части системы по взаимно противоположным на­правлениям, поэтому они не изменяют векторные величины  и . Но если под действием внутренних сил будут изменяться модули скоростей точек системы, то при этом будет изменяться и величина Т. Т.о., T отличается от величин  и  еще и тем, что на ее изме­нение влияет действие и внешних, и внутренних сил. КЭ тела в частных случаях движения:

а) при поступательном движении

                                      ,                                                 (10.29)      

б)  при вращательном движении

,                                                 (10.30)      

в) при плоскопараллельном  движении

.                                 (10.31)      

Теорема об изменении КЭ сиcтемы в дифферен­циальной форме

.                                     (10.32)

В интегральной форме: изменение КЭ системы при некотором перемещении равно сумме работ на этом перемещении всех приложенных к системе внешних и внут­ренних сил.

.                                       (10.33)

10.6 Принцип Даламбера для системы

Силы инерции, действующие на точки МС, можно привести к главному вектору и главному моменту (точка O – неподвижный центр приведения). Формулировка принципа Даламбера для МС: систему, находящуюся в движении, можно рассматривать как находящуюся в состоянии равновесия, включая в число и . Можно доказать, что при любом движении системы  равен взятому со знаком «минус» произведению массы системы на ускорение центра масс . Для АТТ, совершающего плоскопараллельное движение в плоскости материальной симметрии тела Oxy, силы инерции могут быть приведены к подвижному центру масс С. Тогда ось Cz - главная центральная ось инерции тела. Обозначая  через  момент инерции относительно этой оси и через ε – угловое ускорение, можно доказать, что .

10.7 Основное уравнение динамики тела, вращающегося вокруг неподвижной оси

Для тела, вращающегося вокруг неподвижной оси, получаем уравнение движения в виде                                

                                                (10.34)

   _{где Iz –момент инерции тела относительно оси варащения;}

          _{ε  – угловое ускорение тела;}

          _{Mz – сумма моментов относительно оси вращения всех внешних сил, приложенных к телу.}

11 Лекция №11. Элементы аналитической механики

Содержание лекции: связи и их классификация, обобщенные перемещения и обобщенные силы, общее уравнение динамики, уравнения Лагранжа 2-го рода, принцип виртуальных перемещений.

Цели лекции: изучить основные понятия и методы  аналитической механики.

Общие теоремы динамики позволяют решать большинство задач динамики МС, однако невозможно знать заранее, в каком случае какая теорема является наиболее эффективной. Аналитическая механика дает наиболее общие методы составления дифференциальных уравнений движения МС.

 

11.1 Связи и их классификация

На координаты и скорости точек несвободной МС наложены ограничения, называемые связями. Уравнения, которым должны удовлетворять координаты и скорости точек несвободной МС, называют уравнениями связей.

Пример 11.1 - Две материальные точки, показанные на рисунке 11.1, соединены нерастяжимым стержнем длиной l. Уравнение связи имеет вид

,      (11.1)

где  – декартовы координаты точек.

Пример 11.2 - Рассмотрим конёк, движущийся по поверхности льда. Пусть лезвие касается льда в одной точке А (см. рисунок 11.2). Зададим положение конька тремя координатами: . Будем считать, что точка А не проскальзывает в направлении, перпендикулярном лезвию, тогда ее скорость  направлена вдоль лезвия и справедливо , откуда получаем уравнение связи

.                          (11.2)

Если время явно входит в уравнение связи, то связь называют нестационарной, в противном случае – стационарной. Геометрическими называют связи, уравнения которых содержат только координаты точек МС и, возможно, время. Если, кроме того, в уравнения входят первые производные от координат по времени, то связи называют дифференциальными. Геометрические связи и те дифференциальные связи, уравнения которых могут быть проинтегрированы, называют голономными. Дифференциальные связи, уравнения которых не могут быть проинтегрированы, называют неголономными. По виду связей МС разделяют на голономные и неголономные. Голономной называют МС, на которую наложены только голономные связи. Если хотя бы одна связь является неголономной, то МС - неголономная.

Связи могут быть удерживающими (если описывают уравнениями) и неудерживающими (если описывают неравенствами).

Пример 11.3 - Две движущиеся по плоскости точки (корабли) связаны нитью, длина которой увеличивается каждую секунду на 0.5 метра (см. рисунок 11.3). Здесь связь - голономная, нестационарная, неудерживающая

.              (11.3)

Далее будем рассматривать только голономные удерживающие связи.

 

11.2 Возможные и виртуальные перемещения

Рассмотрим одну МТ, подчиненную нестационарной голономной связи

f(x, y, z, t) = 0.                                                    (11.4)

Это уравнение изменяющейся с течением времени поверхности. Из (11.4) следует, что МТ должна перемещаться по этой поверхности, поэтому

.                              (11.5)

Вектор , определяемый своими проекциями dx, dy, dz при бесконечно малом времени , называют вектором возможного перемещения точки.

Зафиксируем теперь время t в уравнении (11.4) и рассмотрим допускаемое связью перемещение МТ из положения, занимаемого ею в данный момент времени, в бесконечно близкое положение, которое она может занимать в тот же момент времени. Это перемещение выражают изохронной вариацией радиус-вектора точки  и называют вектором виртуального перемещения. Вариации координат δx, δy, δz связаны соотношением

                                        (11.6) 

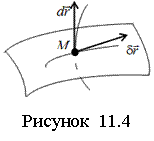которое получается из (11.4) при фиксированном  t. В случае стационарной голономной связи и совпадает с .

  Различие между возможными и виртуальными  перемещениями рассмотрим на примере связи в виде поверхности, которая перемещается относительно неподвижной СО, не деформируясь. Тогда точка участвует в относительном движении (по поверхности) и переносном (вместе с поверхностью). Вектор  направлен по касательной к этой траектории абсолютного движения (см. рисунок 11.4), а вектор  - по касательной к траектории относительного движения.

  11.3 Число степеней свободы системы и обобщенные координаты

  Виртуальным перемещением МС называют любую совокупность виртуальных перемещений ее точек, допускаемую связями. Система имеет множество различных виртуальных перемещений, из которых можно выбрать независимые между собой перемещения, а через них выразить любое виртуальное перемещение. Число независимых между собой виртуальных перемещений МС называют ее числом степеней свободы (ЧСС).

  Рассмотрим систему из N материальных точек, подчиненную d голономным связям. Положение системы определяется 3N декартовыми координатами ее точек, из которых независимыми будут s = 3N – d. Для голономной системы число независимых координат совпадает с ЧСС.

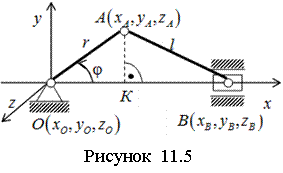  Положение МС можно однозначно определить с помощью любых независимых между собой параметров, - т.н. обобщенных координат.

  Пример 11.4 - Положение кривошипно-шатунного механизма (см. рисунок 11.5) определяется точками O, A, B.

Запишем уравнения связей

 .

Здесь количество связей  d = 8, количество точек  N = 3 и ЧСС системы s = 3N– d = 1. Выберем в качестве обобщенной координаты угол φ , тогда

      .

Т.о., обобщенная координата φ однозначно определяет положение системы.

  11.4 Основная задача динамики несвободной МС. Идеальные связи

  Силы, действующие на точки МС, делятся на активные силы  и реакции связей . В отличие от заранее неизвестных реакций, активные силы являются заданными функциями времени, положений и скоростей точек МС

.

Запишем ДУД системы:

.     (11.7)

  Основная задача динамики несвободной МС: определить движение системы и реакции связей, если известны активные силы и заданы совместимые со связями начальные положения и начальные скорости точек системы. Здесь 6N неизвестных: 3N декартовых координат точек  и 3N проекций реакций связей . Количество скалярных соотношений, связывающих неизвестные величины, равно 3N + d: 3N уравнений (11.7) и d уравнений связей. Необходимо дополнительно иметь 6N – (3N + d) = 3N – d = s соотношений, которые можно получить, считая все связи системы идеальными.

  Связи называют идеальными, если сумма работ реакций связей на любом виртуальном перемещении системы из любого ее положения равна нулю

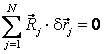 или 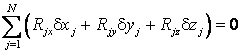   .            (11.8)

Среди 3N вариаций координат  есть 3N – d = s независимых. Выразив 3N – s = d зависимых вариаций в (11.8) через независимые и приравнивая коэффициенты при независимых вариациях нулю, получим необходимые s соотношений.

Примером идеальной связи является гладкая неподвижная поверхность, по которой движется МТ. Т.к. реакция поверхности направлена по нормали, а вектор любого виртуального перемещения лежит в плоскости, касательной к поверхности в точке М, скалярное произведение .       

Гладкая поверхность является идеальной связью и тогда, когда она движется или деформируется. Действительно, определяя виртуальное перемещение, фиксируют время, чем «останавливают» связь, поэтому  остается в касательной плоскости. Реакция гладкой поверхности в любом случае направлена по нормали, поэтому условие (11.8) выполняется.

Идеальными связями являются шарниры без трения, невесомые недеформируемые стержни, внутренние связи АТТ и др. В тех случаях, когда трением пренебречь нельзя, можно учитывать только нормальные составляющие реакций шероховатых поверхностей, относя силы трения к числу неизвестных активных сил. В дальнейшем все связи будем считать идеальными.

  11.5 Обобщенные силы

  Рассмотрим МС, положение которой однозначно определяется заданием .          Выразим радиус-векторы точек через и t

                                 (11.9)

и найдем вариации радиус-векторов

.                              (11.10)

Определим сумму работ всех активных сил на некотором  

.                                              (11.11)

Из формул (11.11) и (11.10), изменяя порядок суммирования, получим

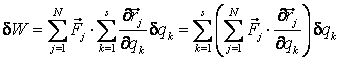.                    (11.12)

Введем обозначения

,                                    (11.13)

тогда равенство (11.12) примет вид

.                                         (11.14)

Величину , равную коэффициенту при  в выражении для виртуальной работы активных сил системы, называют обобщенной силой, соответствующей обобщенной координате . При определении обобщенных сил системе сообщают такое виртуальное перемещение, при котором изменяется только одна обобщенная координата, соответствующая искомой обобщенной силе, и вычисляют сумму работ активных сил. Тогда

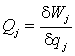.                                                   (11.15)

  11.6 Общее уравнение динамики

  Далее везде будем рассматривать МС, состоящую из N точек, с идеальными и голономными связями, положение которой однозначно через . Для каждой МТ системы можно записать или

.                             (11.16)

  Зафиксируем время и дадим системе виртуальное перемещение, при котором радиус-векторы точек получат приращения . Умножим скалярно каждое уравнение (11.16) на  и сложим полученные произведения

.                          (11.17)

Последняя сумма равна нулю т.к. связи идеальные, и тогда

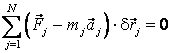.                                  (11.18)

Т.к.  – сила инерции j-й МТ,  – работы активной силы и силы инерции, перепишем (11.18) как

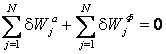.                                  (11.19)

Это общее уравнение динамики (ОУД): при движении системы с идеальными связями в любой момент времени сумма работ активных сил и сил инерции на любом виртуальном перемещении системы равна нулю.

  ОУД позволяет получать ДУД системы, в которые не входят реакции идеальных связей. Оно может быть использовано для систем с любым ЧСС. Однако при большом ЧСС удобнее применять уравнения Лагранжа 2-го рода.

  11.7 Уравнения Лагранжа второго рода

  Приводится вывод уравнений Лагранжа 2-го рода

.                             (11.20)

  После дифференцирования в левые части этих уравнений входят t, ,  и . Обобщенные силы  зависят от параметров t, , . Т.о., уравнения Лагранжа представляют собой систему s ОДУ 2-го порядка, и порядок всей системы равен 2s. Это наименьший возможный порядок системы ДУ.

  Интегрирование (11.20) позволяет получить зависимости  , что полностью определяет движение МС. В случае несвободной МС следует также определить реакции идеальных связей. Подставив зависимости  в (11.9), получим зависимости , дифференцируя которые, определим скорости и ускорения  всех точек. Далее из (11.16) найдем

.                                   (11.21)

  11.8 Принцип виртуальных перемещений

Необходимые и достаточные условия равновесия МС устанавливает принцип виртуальных перемещений: для того чтобы некоторое положение системы, подчиненной идеальным, голономным, стационарным и удерживающим связям, было положением равновесия, необходимо и достаточно, чтобы начальные скорости всех точек системы были равны нулю и сумма работ всех активных сил на любом ее виртуальном перемещении из данного положения была равна нулю, т.е.

.                                (11.22)

12 Лекция №12. Движение МТ переменной массы. Задачи

Циолковского

Содержание лекции: Дифференциальные уравнения движения МТ переменной массы, уравнение Мещерского, 1-я и 2-я задачи Циолковского.

Цели лекции: изучить элементы теории космических движений.

При полете космических ракет вследствие выбрасывания продуктов сгорания и отделения ненужных частей ракет изменяется их масса. В лекции рассматриваются особенности, связанные с изменением массы МТ.

12.1 Дифференциальные уравнения движения МТ переменной массы

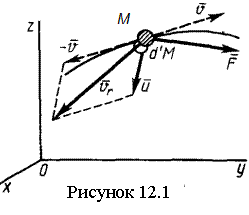ДУД точки переменной массы получим, применяя закон независимости действия сил и теорему об изменении КДС. Здесь кроме приложенной к точке силы , действуют силы, вызванные отделением от точки частицы массой d'M.

Общее изменение скорости за время dt_ складывается из изменения скорости dv_l от действия силы при постоянной массе точки и измене­ния скорости dv₂, вызванного изменением массы точки в от­сутствие силы .

Имеем точку переменной массы М. От действия  скорость точки постоянной массы изменяется за время dt на

                                             (12.1)

Изменение скорости точки за время dt, вызванное изменением ее массы в отсутствие действия силы , определяют по теореме об изменении количества движения системы постоянной массы. Т.к. МС, состоящая из точки переменной массы и отделившихся от нее частиц, свободна от действия внешних сил, то ее количество движения является постоянной величиной. Внутренние силы взаимо­действия точки с отделяющимися частицами не изменяют КДС. Из закона сохранения КДС имеем

                                                (12.2)

Учитываем только взаимодействие точки переменной массы с отделившейся от нее частицей массы d'M за время dt и пренебрегаем действием на точку и эту частицу ранее отделившихся частиц (см. рисунок 12.1). Получаем , т.к. в момент t  имеется одна точка массой M(t), движущаяся со скоростью  относительно системы координат Oxyz.

В момент t + dt имеются точка массой  M - d'M, скорость которой , и отделившаяся частица массой d'M, ско­рость которой  относительно той же системы координат Oxyz. Количество движения их в момент t + dt

Согласно (12.2) после преобразования, считая , получаем

при d'M >0 или, включая знак минус в dМ (тогда dM<0), имеем

                                              (12.3)

Общее изменение скорости  или, учитывая (12.1) и (12.2)

После преобразования получаем ДУД Мещерского (1897 г.)

                                     (12.4)

Если с точкой переменной массы связать подвижную систему координат, поступательно движущуюся относительно системы координат Oxyz, то абсолютную скорость отделив­шейся частицы массой dM по теореме о сложении скоростей можно выразить как

Здесьи относительная скорость отделившейся частицы

Подставляя значение  в (12.4), получаем

                                                  (12.5)

Если ввести обозначение  то (12.5) примет вид

                                            (12.6)

Величину  называют реактивной силой, a dM/dt является скоростью изменения массы. Она характеризует изменение массы точки за единицу времени, например за 1 с. Поэтому реактивная сила равна произведению секундного изменения массы точки на относительную скорость отделения частиц массы от точки переменной массы.

В случае уменьшения массы точки с изменением времени величина dM/dt является отрицательной, а при возрастании - положительной. При уменьшении массы точки вследствие отделения от нее частиц реактивная сила  направлена в сторону, противоположную относительной ско­рости отделяющихся частиц , а при увеличении массы точки величина dM/dt больше нуля и реактивная сила направлена в сторону относительной скорости частиц  Для реактивного двигателя скорость изменения массы dM/dt является от­рицательной, равной секундному расходу массы, a  - скорость вылета газа из сопла двигателя. Реактивная сила является тягой двигателя, обусловленной выбросом газа через сопло и направленной противоположно скорости вылета газа из сопла.

Проецируя (12.6) на прямоугольные декартовы оси координат, получаем

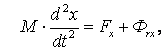
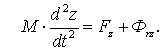             (12.7)

Из (12.6) или (12.7) следует, что ДУД точки переменной массы имеют такой же вид, как и для точки постоянной массы, но здесь дополнительно учитывается реактивная сила, обуслов­ленная изменением массы точки.

Из ДУД точки переменной массы можно вывести общие теоремы для точки и системы переменной массы.

12.1 Дифференциальные уравнения движения МТ переменной массы

Первая задача Циолковского. Пусть точка переменной массы движется прямолинейно в «свободном пространстве» под действием одной только реактивной силы. Считаем, что относительная скорость  отделения частиц постоянна и направлена в сторону, противо­положную скорости  движения точки переменной массы (см. рисунок 12.2). Проецируя (12.5) на ось Ох, направленную по скорости движения точки, получаем

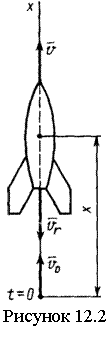
Разделяя переменные и беря интегралы, получаем

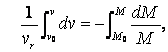
где v₀ и M₀ – начальная скорость (направлена по реактивной силе) и начальная масса соответственно.

Выполняя интегрирование, получаем

                         (12.8)

Подставляя в (12.8) величины, характеризующие конец горения, когда масса точки (ракеты) состоит только из массы несгоревшей части М_р, и обозначая через m массу топлива, для скорости v₁ в конце горения имеем

Вводя число Циолковского Z = m/M_p, получаем формулу Циолковского

                                         (12.9)

Отсюда следует, что скорость v₁ не зависит от закона изменения массы. Скорость в конце горения можно увеличить либо увеличением скорости истечения газа из сопла реактивного двигателя, либо увеличением Z за счет использования многоступенчатой раке­ты, где отбрасываются ступени ракеты.

Для определения уравнения движения точки из (12.8) имеем

или, выполняя интегрирование и считая х = 0 при t = 0, получаем

                            (12.10)

Для случая линейного закона изменения массы можно записать

М = М₀∙(1-α∙t),                                  (12.11)

где α = const - удельный расход,

М₀ - масса точки в начальный момент времени.

При показательном законе изменения массы примем зависимость

  М = М₀∙e ^α∙t.                                        (12.12)

Выполняя интегрирование в (12.10) при линейном законе изменения массы (2.11), получаем следующее уравнение движения

              (12.13)

При показательном законе изменения массы (12.12) соответ­ственно

                             (12.14)

Отметим, что при линейном законе изменения массы (12.11), если v_r = =const, секундный расход массы и реактивная сила

(-dM/dt) = α∙M₀ = const,        Ф_r =(-dM/dt)∙v_r= α∙M₀∙v_r = const.

При показательном законе секундный расход массы и ре­активная сила являются переменными, но ускорение точки переменной массы, вызванное действием на точку реактивной силы Ф_r, является постоянным, т. е.

а_r= Ф_r/M= α∙v_r = const.

Вторая задача Циолковского. Если точка переменной массы (ракета) движется по вертика­ли вверх вблизи Земли (см. рисунок 12.2), то, принимая g=const и пренебрегая сопротивлением воздуха, а также учитывая все допущения первой задачи Циолковского, получаем следующее ДУД точки

    

После интегрирования имеем

Для х, если отсчитывать его от начального положения точки, получаем при линейном законе изменения массы

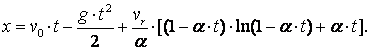            (12.15)

При показательном законе изменения массы соответ­ственно получаем

                                      (12.16)

 

Список литературы 

1. Никитин Н.Н. Курс теоретической механики. – М.: Высшая школа, 1990.

2. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики. Учебник: в 2-х т. - М.: Наука, 2002.

3. Мещерский И.В. Сборник задач по теоретической механике. Учеб. пособие. - СПб.: Изд-во "Лань", 2005.

4. Динасылов А.Д., Койлыбаева Р.К. Механика. Сборник заданий для самостоятельной работы студентов: Учебное пособие. – Алматы: АУЭС, 2012.

5. Тойбаев С.Н., Динасылов А.Д. Механика. Методические указания  и задания к выполнению расчетно-графических работ для студентов специальности 5В074600 - Космическая техника и технологии – Алматы: АУЭС, 2012.  

6. Койлыбаева Р.К. Механика. Статика и кинематика. Методические указания к выполнению лабораторных работ для студентов специальностей 5В074600 - Космическая техника и технологии, 5В071700 - Теплоэнергетика. – Алматы: АУЭС, 2012.

7. Динасылов А.Д.,  Койлыбаева Р.К. Прикладная механика. Кинематический и динамический анализ плоского шарнирно-рычажного механизма в системе АРМ WinMaсhine. Методические указания к выполнению лабораторной работы для студентов специальности 5В071700 - Теплоэнергетика. – Алматы: АУЭС, 2010.  

8. Койлыбаева Р.К. Механика. Динамика. Методические указания к выполнению лабораторных работ для студентов специальностеи 5В074600 - Космическая техника и технологии, 5В071700 - Теплоэнергетика. – Алматы: АУЭС, 2012.

9. Тойбаев С.Н., Динасылов А.Д. Механика. Методические указания  и задания к самостоятельной работе для студентов специальности 5В074600 - Космическая техника и технологии – Алматы: АУЭС, 2012.

10. Тарг С.М. Краткий курс теоретической механики. Учебник. - М.: Наука, 2002.

11. Яблонский А.А. Курс теоретической механики. Учебник: в 2-х т. - М.: Высшая школа, 2002.

12. Сборник заданий для курсовых работ по теоретической механике. Учеб. пособие./Под ред. А.А.Яблонского. - М.: Высшая школа, 1985.

13. Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. Учеб. пособие: в 2-х частях. - М.: Наука, 1984.

14. Лойцянский Л.Г., Лурье А.И. Курс теоретической механики. Учеб. пособие: в 2-х т. - М.: Наука, 1983.

15. Сборник задач по теоретической механике. Учеб. пособие./Под ред. К.С.Колесникова. - М.: Высшая школа, 1983.

16. Сборник коротких задач по теоретической механике: Учеб. пособие./Под ред. О.Э. Кепе. - М.: Высшая школа, 1989.

17. Аркуша А.И. Техническая механика. Руководство к решению задач по теоретической механике. - М.: Высш. шк., 2002.

  Сводный план 2012 г., поз.365