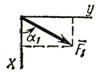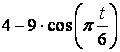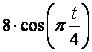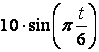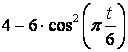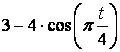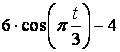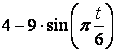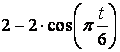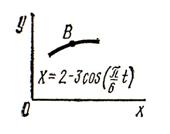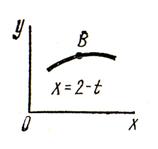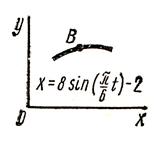Некоммерческое акционерное общество

АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра инженерной  графики и прикладной механики

 

 

МЕХАНИКА

Методические указания и задания к выполнению расчетно-графических работ для студентов специальности

5В074600 – Космическая техника и  технология 

 

 

 

 

Алматы 2012 

СОСТАВИТЕЛИ: Тойбаев С.Н., Динасылов А.Д. Механика. Методические указания и задания к выполнению расчетно-графических работ (для студентов всех форм обучения специальности 5В074600 – Космическая техника и технология). - Алматы: АУЭС, 2012. – 39 с.

 

Дисциплина «Механика» является обязательным предметом для студентов высших учебных заведений, обучающихся по специальности 5В074600 – Космическая техника и технология. В данной методической разработке, предназначенной для студентов, приводятся задания к расчетно-графическим работам, методические указания к их выполнению, примеры выполнения работ. Дан список рекомендуемой литературы.

Ил. 14, табл. 7, библиогр. – 6 назв. 

 

Рецензент: д-р. техн. наук, профессор Иванов К.С.

 

 

Печатается по плану издания некоммерческого акционерного общества «Алматинского университета энергетики и связи» на 2012 г.

© НАО «Алматинский университет энергетики и связи», 2012 г.

 

Содержание

 

1 Общие требования и указания к выполнению расчетно-графических работ	4
2 Задачи, входящие в расчетно-графическую работу №1, указания к их выполнению и примеры решения	5
2.1 Задача 1. Равновесие плоской системы сил	5
2.2 Задача 2. Равновесие пространственной системы сил	8
3 Задачи, входящие в расчетно-графическую работу №2, указания к их выполнению и примеры решения	11
3.1 Задача 3. Кинематика точки	11
3.2 Задача 4. Вращательное движение твёрдого тела	16
3.3  Задача 5. Сложное движение точки	19
4 Задачи, входящие в расчетно-графическую работу №3, указания к их выполнению и примеры решения	24
4.1 Задача 6. Относительное и колебательное движение материальной точки	24
4.2 Задача 7.  Применение  теоремы об   изменении кинетической энергии механической системы	29
Список литературы	38

  

1 Общие требования и указания к выполнению расчетно-графических работ

 

Согласно учебным планам студенты, обучающиеся по специальности 5В074600 – Космическая техника и технология выполняют 3 расчетно-графические работы (РГР) по дисциплине «Механика» в соответствии с числом кредитов, отводимых на изучение дисциплины.

Условия задач приведены в десяти схемах и десяти вариантах, кроме задачи 7. Студент должен взять для выполнения номер схемы, который показан римскими цифрами на соответствующем рисунке, по последней цифре шифра зачетной книжки, а вариант с цифровыми данными из соответствующей таблицы – по предпоследней цифре шифра. Так, студент, зачетная книжка которого имеет шифр 96452, должен для каждой задачи выбрать схему II и цифровые данные, соответствующие варианту 5. Если последняя цифра шифра нуль, то следует взять схему X, а если предпоследняя цифра нуль, то данные из таблицы принимаются по варианту 10. Данные для задачи 7 принимаются согласно номеру студента в списке группы (по журналу).

При окончательной сдаче РГР каждая работа должна быть сброшюрована отдельно. Выполненная работа состоит из текстовой и графической частей. Оформление работы должно выполняться четким почерком на листах белой бумаги формата А4: работа должна содержать титульный лист, содержание, задание, выполненные расчеты, графические построения, выводы и список литературы. Работа должна быть оформлена согласно принятым нормам (СТП 768-01-07-97); на листах текст должен быть только с одной стороны, в конце каждой РГР должен быть приведен список использованной литературы. Как графическая, так и расчетная часть работы, а также текстовый материал могут быть выполнены с помощью компьютерных средств (с разрешения преподавателя).

Прежде чем приступать к решению задачи, студент должен ознакомиться с соответствующим теме задачи теоретическим материалом по лекциям, учебникам и учебным пособиям, с указаниями к решению задачи и примерами, приведенными в настоящих методических указаниях. Выполненные РГР должны быть защищены студентов. Для защиты надо решить подобную задачу или ответить на 5-6 вопросов по теме.

 

2 Задачи, входящие в расчетно-графическую работу №1, указания к их выполнению и примеры решения

 

2.1 Задача 1. Равновесие плоской системы сил

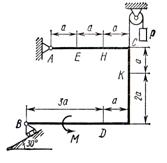
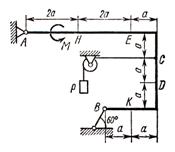
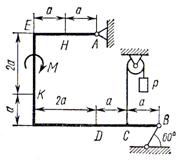
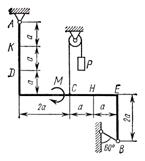
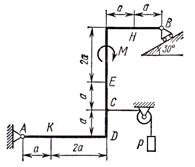
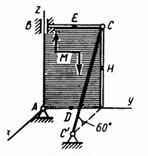
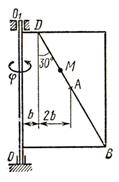
Жесткая рама (см. рисунок 1) закреплена в точке  шарнирно, а в точке  прикреплена или к невесомому стержню , или к шарнирной опоре на катках; стержень прикреплен к раме и к неподвижной опоре шарнирами.

В точке  к раме привязан трос, перекинутый через блок и несущий на конце груз весом . На раму действуют пара сил с моментом  и две силы, значения которых, направления и точки приложения указаны в таблице (например, в условиях №1 на раму действуют сила  под углом 30° к горизонтальной оси, приложенная в точке  и сила  под углом 60° к горизонтальной оси, приложенная в точке ).

Определить реакции связей в точках  и , вызываемые заданными нагрузками. При окончательных подсчетах принять .

 

Т а б л и ц а 1

 

Указания. Задача 1 является задачей на равновесие тела под действием плоской системы сил. Составляя уравнения равновесия, учесть, что уравнение моментов будет более простым (содержать меньше неизвестных), если брать моменты относительно точки, где пересекаются линии действия двух реакций

I	II
III	IV
V	VI
VII	VIII
IX	X
Рисунок 1

связей (в данном случае относительно точки А). При вычислении момента силы  часто бывает удобным разложить ее на составляющие   и , для которых легко вычисляются плечи моментов (в частности, на составляющие, параллельные координатным осям) и как следствие - использование теоремы Вариньона; тогда .

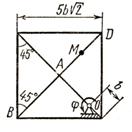
Пример 1. Жесткая пластина ABCD (см. рисунок 2) имеет в точке А неподвижную шарнирную опору, а в точке В – подвижную шарнирную опору на катках. Все действующие нагрузки и размеры показаны на рисунке.

 

 

 

 

 

 

 

 

 

 Рисунок 2 - Схема к примеру 1

 

Дано:  ,  ,  ,  ,   ,  , .

Определить: реакции в точках А и В, вызываемые действующими нагрузками.

Решение: рассмотрим равновесие пластины. Проведем координатные оси  и изобразим действующие на пластину силы: силу  , пару сил с моментом М, натяжение троса  (по модулю Т = Р) и реакции связей  (реакцию неподвижной шарнирной опоры А  изображаем двумя ее составляющими, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости).

Для полученной плоской системы сил составим три уравнения равновесия. При вычислении момента силы  относительно точки А  воспользуемся теоремой Вариньона, т.е. разложим силу   на составляющие   и учтем, что . Получим

Подставив в эти уравнения числовые значения заданных величин, решаем их и определяем искомые реакции.

Ответ: , , . Знаки указывают, что силы  и направлены противоположно направлениям, показанным на рисунке 2. Для проверки правильности решения следует воспользоваться каким-либо другим уравнением равновесия, например, в виде суммы моментов всех сил относительно точки С.

 

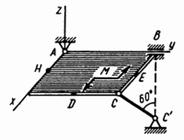
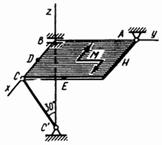
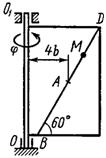
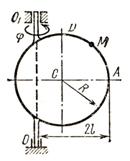
2.2 Задача 2. Равновесие пространственной системы сил

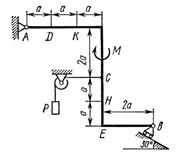
Однородная прямоугольная плита весом  со сторонами  закреплена в точке A сферическим шарниром, а в точке  цилиндрическим шарниром (подшипником) и удерживается в равновесии невесомым стержнем  (см. рисунок 3) и две силы. Значения этих сил, их направления и точки приложения указаны в таблице 2; при этом силы  и  лежат в плоскостях параллельных , сила - в плоскости, параллельной , сила в плоскости параллельной . Точки приложения сил (, , ) находятся в серединах сторон плиты.

Определить реакции связей в точках ,  и . При окончательных подсчетах принять .

Указания. В этой задаче рассматривается равновесие тел под действием пространственной системы сил. При ее решении нужно учесть, что реакция

 

Т а б л и ц а 2

сферического шарнира имеет три составляющие, а реакция цилиндрического шарнира (подшипника) – две составляющие, лежащие в плоскости, перпендикулярной оси шарнира. При вычислении моментов силы  также разложим ее на составляющие  и , параллельные координатным осям; тогда, по теореме Вариньона, и т.д.

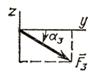
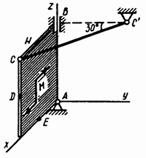
Пример 2. Вертикальная прямоугольная плита весом P (см. рисунок 4) закреплена сферическим шарниром в точке , цилиндрическим (подшипником) в точке  и невесомым стержнем , лежащим в плоскости, параллельной плоскости . На плиту действуют сила  (в плоскости ), сила  (параллельная оси y) и пара сил с моментом  (в плоскости плиты).

Дано: ,

   Определить: реакции опор ,  и стержня .

Решение: 1) Рассмотрим равновесие плиты. На плиту действуют заданные силы , ,  и пара сил с моментом М, а также реакции связей. Реакцию сферического шарнира разложим на три составляющие , , , цилиндрического (подшипника) – на две составляющие ,  (в плоскости, перпендикулярной оси подшипника), реакцию  стержня направим вдоль стержня, предполагая, что он растянут.

2) Для определения шести неизвестных реакций составляем шесть уравнений равновесия для действующей на плиту пространственной системы сил

                                                                      (1)

                                                      (2)

                                     (3)

                                           (4)

          

        (5)

.                                                (6)

Для определения момента силы  относительно оси y разлагаем  на составляющие  и , параллельные осям x и z  и применяем теорему Вариньона. Аналогично можно поступить при определении моментов реакции  относительно оси x.

Подставив в составленные уравнения числовые значения всех заданных величин и решив затем эти уравнения, найдем, чему равны искомые реакции.

Ответ:    

. Знаки (-) указывают, что реакции ,  и  направлены в сторонупротивоположную направлениям, показанным на рисунке 4.

 

3 Задачи, входящие в расчетно-графическую работу № 2, указания к их выполнению и примеры решения

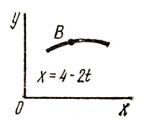
3.1 Задача 3. Кинематика точки

Точка  движется в плоскости  (траектория точки показана на рисунке 5 условно). Закон движения точки задан уравнениями: , где  и  выражены в сантиметрах, а в секундах.

Т а б л и ц а 3

 

I	II
III	IV
V	VI
VII	VIII
IX	X
Рисунок 5

 

Найти уравнение траектории точки; для момента времени  определить скорость и ускорение точки, а также касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории. Вычертить в масштабе траекторию точки, показать ее начальное положение и положение в заданный момент времени, показать на рисунке полные скорость и ускорение точки, их проекции на координатные оси, касательное и нормальное ускорения точки. Зависимость  указана непосредственно на рисунке 5, а зависимость  дана в таблице 3  (для схем I - III во втором столбце, для схем IV - VII в третьем столбце, для схем VIII - X в четвертом столбце).

Указания. Задача 3 относится к теме «Кинематика точки» и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются нормальное и касательное ускорения точки.

В данной задаче все искомые величины нужно определить только для момента времени . В некоторых вариантах задачи при определении траектории или при последующих расчетах (для их упрощения) следует учесть известные из тригонометрии формулы: ; .

Пример 3. Даны уравнения движения точки в плоскости

,

где  ,  даны в сантиметрах, в секундах.

Выполнить решение по условиям задачи 3.

Решение: 1) Для определения траектории точки исключим время  из заданных уравнений движения. Используем формулу .

Из заданных уравнений движения выражаем соответствующие функции

.

Подставляя эти выражения, получаем

.

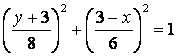Это  уравнение эллипса.

Траектория точки показана на рисунке 6, a;  в  начальный момент времени  точка находится в положении , а когда  – в положении M.

2) Скорость точки найдем по ее проекциям на координатные оси

,

,  .

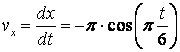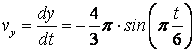При   .

,  ,

.

3) Аналогично найдем ускорение точки

,

,

.

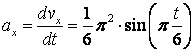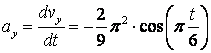При    находим

,

,

.

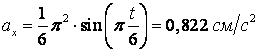4) Касательное ускорение найдем, дифференцируя по времени равенство

.

Получаем

.

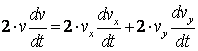Отсюда

.

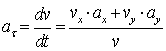Подставив в полученное выражение числовые значения соответствующих величин при ,  найдем

.

5) Нормальное ускорение точки находим, как

.

6) Для определения радиуса кривизны траектории воспользуемся формулой

,

откуда

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

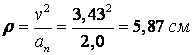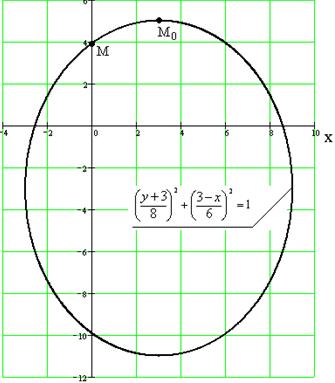
                                  Рисунок 6 – Схема к примеру 3

 

Ответ:  при , , , , , .

На рисунке 6, б показаны скорости и ускорения точки в положении M.

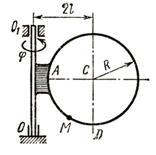
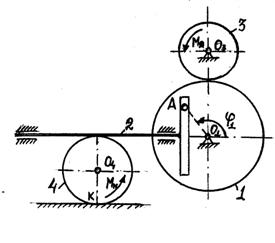
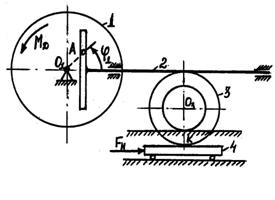
3.2 Задача 4.  Вращательное движение твёрдого тела

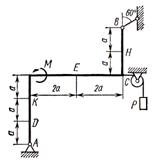
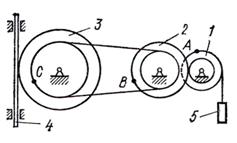
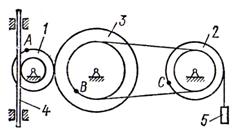
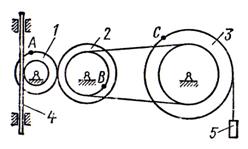
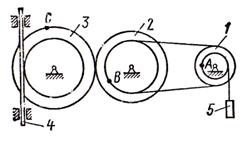
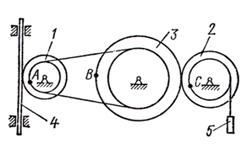
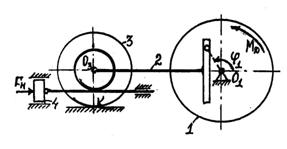
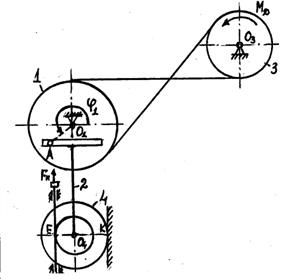
Механизм состоит из ступенчатых колес 1 - 3, находящихся в зацеплении или связанных ременной передачей, зубчатой рейки 4, груза 5, привязанного к концу нити, намотанной на одно из колес (см. рисунок 7). Радиусы ступеней колес равны соответственно: у колеса , , у колеса , , у колеса , . На ободьях колес расположены точки ,  и  (см. рисунок 7).

В столбце «Дано» таблицы указан закон движения или закон изменения скорости ведущего звена механизма, где закон вращения колеса 1, закон движения рейки 4, закон изменения угловой скорости колеса 2, закон изменения скорости груза 5 и т.д. (везде  выражено в радианах, в сантиметрах, в секундах). Положительное направление для  и  против хода часовой стрелки, для ,  и , вниз.

Определить в момент времени  указанные в таблице в столбцах «Найти» скорости (линейные, угловые) и ускорения (линейные, угловые) соответствующих точек или тел (так, скорость груза 5).

Указания. Задача 4 - на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что когда два колеса находятся в зацеплении, скорость точки зацепления каждого колеса одна и та же, а когда два колеса связаны ременном передачей, то скорости всех точек ремня и, следовательно, точек, лежащих на ободе каждого из этих колес, в данный момент времени численно одинаковы; при этом считается, что ремень но ободу колеса не скользит.

Т а б л и ц а 4

Номер условия	Дано	Найти
		скорости	ускорения
1
2
3
4
5
6
7
8
9
10

 

I	II
III	IV
V		VI
VII		VIII
IX		X
Рисунок 7

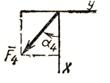
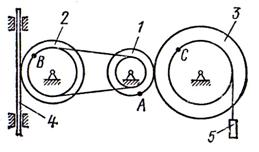
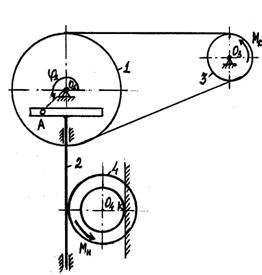
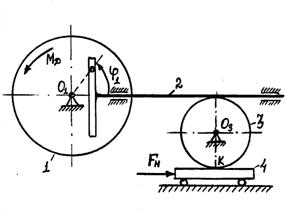
Пример 4. Рейка 1, ступенчатое колесо 2 с радиусами  и  и колесо 3 радиуса , скрепленное с валом радиуса , находятся в зацеплении; на вал намотана нить с грузом 4 на конце (см. рисунок 8). Рейка движется по закону .

Дано: см, , , ,  (в сантиметрах, в секундах),  точка обода колеса 3, .

Определить: , в момент времени .

Решение:  условимся обозначать скорости точек, лежащих на радиусах , через , а точек, лежащих на радиусах , - через .

1) Определяем сначала угловые скорости всех колес как функции времени . Зная закон движения рейки 1, находим ее скорость

.                                                          (1)

Так как рейка и колесо 2 находятся в зацеплении, то  или . Но колеса 2 и 3 тоже находятся в зацеплении, следовательно,  или . Из этих равенств находим

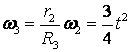,   .                       (2)

Тогда для момента времени  получим .

2) Определяем . Так как , то при  .

3) Определяем . Учитывая второе из равенств (2), получим . Тогда при .

4) Определяем . Для точки , где численно , . Тогда для момента времени  имеем

,

,

.

Все скорости и ускорения точек, а также направления угловых скоростей показаны на рисунке 8.

Ответ: при , , , , .

 

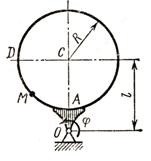
3.3 Задача 5. Сложное движение точки

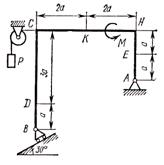
Прямоугольная пластина (схемы I - V) или круглая пластина радиуса  (схемы VI - X) вращается вокруг неподвижной оси по закону , заданному в таблице 5 (см. рисунок 9). Положительное направление отсчета угла  показано на рисунках дуговой стрелкой. На схемы I, II, III, IV, VI, ось вращения перпендикулярно плоскости пластины и проходит через точку  (пластина вращается в своей плоскости); на рис. VI, V, VIII, X ось вращения , лежит в плоскости пластины (пластина вращается в пространстве).

По пластине вдоль прямой  (схемы I - V) или по окружности радиуса  (схемы VI - X) движется точка М; закон ее относительного движения, т. е. зависимость  ( выражено в сантиметрах,  - в секундах), задан в таблице отдельно для схемы I - V и для схемы VI - X; там же даны размеры  и . На рисунках точка  показана в положении, при котором  (при  точка  находится по другую сторону от точки ).

Найти абсолютную скорость и абсолютное ускорение точки  в момент времени .

Т а  б л и ц а 5

Номер условия	Для всех рисунков	Для схемы I - V			Для схемы VI - X
		см
1		12
2		16
3		10
4		16
5		8
6		20
7		12
8		8
9		10
10		20
I				II
III				IV
V				VI
VII				VIII
IX				X
Рисунок 9

Указания. Задача 5 - на сложное движение точки. Для ее решения воспользоваться теоремами о сложении скоростей и о сложении ускорений. Прежде чем производить все расчеты, следует по условиям задачи определить, где находится точка  на пластине в момент времени , и изобразить точку именно в этом положении (а не в произвольном, показанном на рисунках к задаче).

В случаях, относящихся к схемы VI - X, при решении задачи не подставлять числового значения , пока не будут определены положение точки  в момент времени  и угол между радиусами  и  в этот момент.

Пример 5. Шар радиуса  (см. рисунок 10, а) вращается вокруг своего диаметра  по закону  (положительное направление отсчета угла  показано на рис. 10, а в дуговой стрелкой). По дуге большого круга («меридиану»)  движется точка  по закону ; положительное направление отсчета  от  к .

Дано: ,  (в радианах, в метрах, в секундах). Определить:  и  в момент времени .

 

 

 

 

 

 

 

 

 

 

 

 

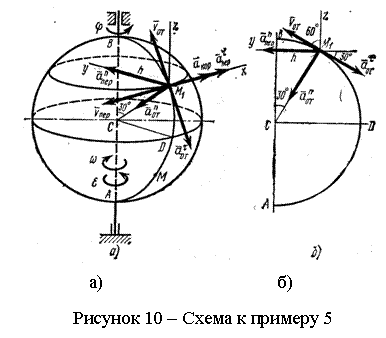Решение: рассмотрим движение точки  как сложное, считая ее движение по дуге  относительным (относительная траектория точки), а вращение шара — переносным движением. Тогда абсолютная скорость  и абсолютное ускорение  точки найдутся по формулам

,                                                      (1)

где, в свою очередь, .

Определим все характеристики относительного и переносного движений.

1) Относительное движение. Это движение происходит по закону

.                                                                   (2)

Сначала установим, где будет находиться точка  на дуге  в момент времени . Полагая в уравнении , получим

.

Тогда ,   или °.

Изображаем на рисунке 10, а точку в положении, определяемом этим углом (точка ).

Теперь находим числовые значения .

,

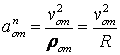где радиус кривизны относительной траектории, т. е. дуги . Для момента времени , учитывая, что , получим

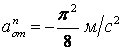,   ,   .                                        (3)

Знаки показывают, что вектор  направлен в сторону положительного отсчета расстояния , а вектор  - в противоположную сторону; вектор  направлен к центру  дуги. Изображаем все эти векторы (рисунок 10, а). Для наглядности приведен рисунок 10, , где дуга  совмещена с плоскостью чертежа.

2) Переносное движение. Это движение (вращение) происходит по закону . Найдем угловую скорость  и угловое ускорение  переносного вращения

,

и при

.                                                                  (4)

Знаки указывают, что при  направление  совпадает с направлением положительного отсчета угла , а направление  ему противоположно; отметим это на рисунке 10,  соответствующими дуговыми стрелками.

Для определения   и  находим сначала расстояние  точки  от оси вращения. Получаем . Тогда в момент времени , учитывая равенства (4), получим

,  ,  .               (5)

Изображаем на рисунке 10, а векторы  и  с учетом направлений  и  и вектор  (направлен к оси вращения).

3) Кориолисово ускорение. Так как угол между вектором и осью вращения (вектором ) равен 60°, то численно в момент времени  [см. равенства (3) и (4)]

.                                                           (6)

Направление  найдем, спроецировав вектор  на плоскость, перпендикулярную оси вращения (проекция направлена так же, как вектор ), и повернув затем эту проекцию в сторону , т. е. по ходу часовой стрелки, на 90°. Иначе направление  можно найти, учтя, что . Изображаем вектор  на рисунке 10, а.

Теперь можно вычислить значения  и .

4) Определение . Так как  а векторы  и  взаимно перпендикулярны (см. рис. 10, а), то в момент времени

.

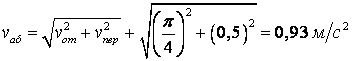5) Определение . По теореме о сложении ускорений

.                                                                            (7)

Для определения  проведем координатные оси  (см. рисунок 10, а) и вычислим проекции вектора  на эти оси. Учтем при этом, что векторы  и  лежат на проведенной оси , а векторы ,  и  расположены в плоскости дуги , т. е. в плоскости  (см. рисунок 10, б). Тогда, проецируя обе части равенства (7) на координатные оси и учтя одновременно равенства (3), (5), (6), получим для момента времени

,

.

Отсюда находим значение  в момент времени

.

Ответ: при , , .

 

4 Задачи, входящие в расчетно-графическую работу № 3, указания к их выполнению и примеры решения

 

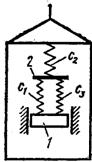
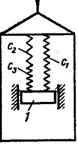
4.1 Задача 6. Относительное и колебательное движение материальной точки

 

Груз 1 массой  укреплен на пружинной подвеске в лифте (см. рисунок 11). Лифт движется вертикально по закону   (ось  направлена по вертикали вверх,  выражено в метрах, в секундах). На груз действует сила сопротивления среды , где скорость груза по отношению к лифту (см. рисунок 11).

Найти закон движения груза по отношению к лифту, т. е, ; начало координат поместить в положении статического равновесия груза при неподвижном лифте (во избежание ошибок в знаках, направить ось  в сторону удлинения пружины, а груз изобразить в положении, при котором  и пружина растянута). При подсчетах можно принять . Массой пружин и соединительной планки 2 пренебречь.

В таблице обозначено:

 коэффициенты жесткости пружин;

удлинение пружины с эквивалентной жесткостью в начальный момент времени ;

начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах  означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна.

Т а б л и ц а 6

Номер условия	кг	H/м	H/м	H/м	м/с2	м/с2	м/с2	1/c	H·c/м	м	м/с
0	1	300	150	-	0	0,1	0	15	0	0	0
1	0,8	-	240	120	-0,5	0	0	-	8	0,1	0
2	0,5	-	100	150	0	0,8	0	5	0	0	4
3	1	240	-	160	0	0	0,5	6	0	0	0
4	0,5	80	120	-		0	0	-	6	0,15	0
5	2	-	400	400	0	0	0,1	16	0	0	0
6	0,4	60	-	120		0	0	-	4	0	2
7	0,5	120	-	180	0	0,1	0	20	0	0	0
8	0,4	50	200	-	0	0	0,2	20	0	0,15	0
9	1	200	-	300	1,5	0	0	-	20	0	3

 

 

I	II
III	IV
V	VI
VII	VIII
IX	X
Рисунок 11

Если при этом конец одной из оставшихся пружин окажется свободным, его следует  прикрепить  в  соответствующем  месте  или  к  грузу  или  к  потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.

Условие  означает, что сила сопротивления  отсутствует.

Указания. Задача 6 охватывает одновременно темы относительное движение и колебания материальной точки. Сначала нужно составить дифференциальное уравнение относительного движения (по отношению к лифту) рассматриваемого в задаче груза, для чего присоединить к действующим силам переносную силу инерции. При этом заменить подвеску одной пружиной с жесткостью, эквивалентной жесткости подвески. Затем проинтегрировать полученное линейное дифференциальное уравнение 2-го порядка, учтя начальные условия.

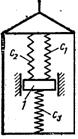
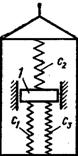
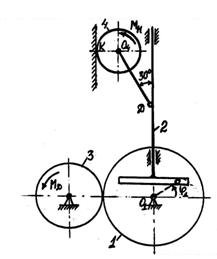
Пример 6. Груз  массой , прикрепленный к двум последовательно соединенным пружинам с коэффициентами жесткости  и , перемещается по пазу  призматической тележки (см. рисунок 12, а). Тележка движется по закону . Начальное удлинение пружины эквивалентной жесткостью , а начальная скорость груза по отношению к тележке  (направлена от  к ).

Дано: , Н/м,  Н/м, м,  м/с, ,  (в метрах, в секундах).

Определить: закон движения груза по отношению к тележке.

Решение: 1) Заменим прикрепленные к грузу пружины одной эквивалентной пружиной с коэффициентом жесткости . Значение с здесь определяется из условия, что при равновесии под действием какой-нибудь приложенной к свободному концу пружин силы  усилия в любом поперечном сечении пружин одинаковы и равны . Тогда если удлинения пружин равны соответственно  и , то удлинение эквивалентной пружины  и должно быть , откуда . Но так как

,                                                                                                     (1)

то

 и 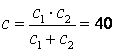 Н/м.                                                              (2)

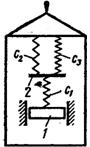
2) Составим теперь дифференциальное уравнение относительного движения груза (по отношению к тележке). Сначала заметим, что при неподвижной тележке в положении статического равновесия груза эквивалентная пружина (длину ее в недеформированном состоянии обозначим ) под действием силы тяжести  будет сжата на величину  (см. рисунок 12, б). Из условия равновесия следует, что

 

 и .                                            (3)

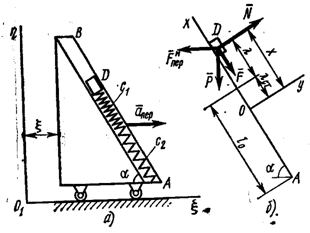Свяжем тогда с тележкой подвижную систему отсчета , начало  которой поместим в положении статического равновесия груза, а ось  направим вдоль паза  в сторону удлинения пружины (см. рисунок 12, б). Рассмотрим груз в положении, при котором  и пружина растянута; изобразим действующие на груз силы: силу тяжести , силу упругости  и реакцию паза . Для составления уравнения относительного движения груза присоединим к этим силам переносную силу инерции ; кориолисова сила инерции здесь равна нулю, так как переносное движение (движение тележки) является поступательным. Тогда уравнение относительного движения в векторной форме будет иметь вид

.

Проецируя обе его части на ось , получим

.                                                                (4)

Найдем значения  и так как при положении груза, определяемом координатой  (см. рисунок 12, б), эквивалентная пружина имеет удлинение , то . Далее , где ускорение тележки. Из равенства (1) находим, что . Кроме того, . Подставляя все эти величины в уравнение (4), получим

.

Согласно равенству (3) члены  и   в правой части сокращаются, и окончательно дифференциальное уравнение относительного движения груза примет вид

,                                                                            (5)

где обозначено

.                                     (6)

3) Для определения закона движения груза надо проинтегрировать уравнение (5). Его общее решение, как известно из теории дифференциальных уравнений

,                                                                                                     (7)

где  общее решение однородного уравнения , т. е.

,                                                                       (8)

а  частное решение уравнения (5). Учитывая, каковы правая и левая части этого уравнения, ищем  в виде

.                                                                                      (9)

Для определения постоянных  и  находим , подставляем значения  и  в уравнение (5) и приравниваем в его обеих частях свободные члены и коэффициенты при . В результате, принимая во внимание обозначения (6), получим

.

Тогда из равенств (7)—(9), учитывая, что , получим следующее общее решение уравнения (5)

.                              (10)

Для определения постоянных интегрирования  и  найдем еще

.                              (11)

По условиям задачи при . Тогда, как видно из рисунок 12, б и равенства (3), . Подставив эти начальные данные в уравнения (10) и (11), найдем из них, что. В результате уравнение (10) примет окончательно вид

.                          (12)

Это уравнение и определяет искомый закон относительного движения груза, т. е. закон совершаемых им колебаний.

Примечания:

1) Если груз был бы прикреплен к двум параллельным пружинам, то при равновесии под действием некоторой силы  каждая из пружин и эквивалентная пружина имели бы одно и то же удлинение . Тогда для двух пружин , а для эквивалентной пружины , отсюда и определяется значение .

2) Если пружины были бы прикреплены к тележке в точке  (см. рисунок 12, а), а груз  находился на другом их конце, то в положении статического равновесия эквивалентная пружина была бы растянута на величину , а не сжата, что следует учесть при изображении схемы, подобной показанной на рисунке 12, б, и при определении зависимости между ,  и  (в этом случае ).

Ответ: .

 

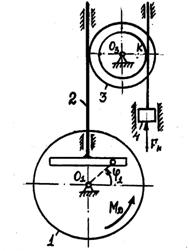
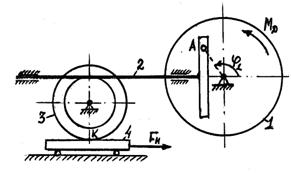
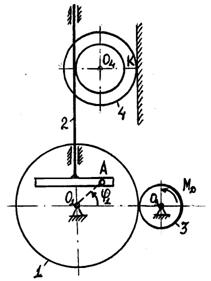
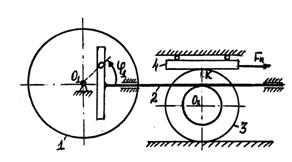
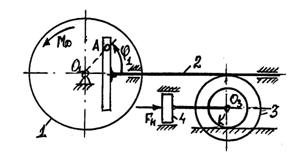
4.2 Задача 7. Теорема об изменении кинетической энергии механической системы

 

Расчет предназначен для обучения методике исследования динамики машин с использованием дифференциальных уравнений движения. Исходные данные подобраны таким образом, что машина работает вблизи установившегося режима. Путем интегрирования на ПК дифференциальных уравнений определяются движения машины.

Варианты схем машин представлены на рисунке 13. Элементы конструкции машин считаются абсолютно жесткими, ремни нерастяжимыми и безинерционными. Проскальзывание колес ремней и т.д. отсутствует. Трением между пальцем  кривошипа и прорезью кулисы пренебрегаем.

Машины приводятся в движение электродвигателем, развивающим момент . Полезная нагрузка моделируется для разных вариантов либо силой , либо моментом .

Исходные данные для расчета задаются формулами (1), параметры по вариантам приведены в таблице 7.

,   ,

,  ,                                           (1)

,   ,

,   .

Здесь и далее для масс, весов, угловых скоростей, радиусов, моментов и радиусов инерции приняты обозначения  , , , , , ,  с индексами, соответствующими номерам звеньев машины, указанным на рисунке 13. Через  обозначены скорости точек, ,   константы, значения которых указаны в таблице 7. интервал времени интегрирования, величина которого близко времени полного оборота маховика в установившемся режиме. номер студенческой группы, номер факультета. Радиус маховика ,  .  Угол  указан на рисунках. Числовые значения величин задаются в системе СИ.

Требуется составить дифференциальное уравнение движения машины.

 

I	II
III	IV
V	VI
Рисунок 13
VII	VIII
IX	X
XI	XII
Продолжение рисунка 13

 

XIII	XIV
XV	XVI
XVII	XVIII
Продолжение рисунка 13
XIX	XX
XXI	XXII
XXIII	XXIV
Окончание рисунка 13

 

 

 

 

Т а б л и ц а 7

 

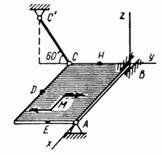
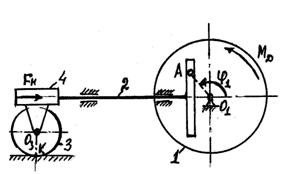
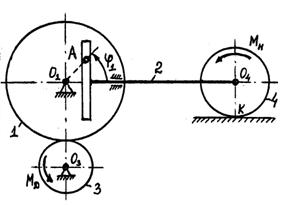
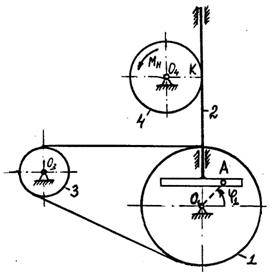
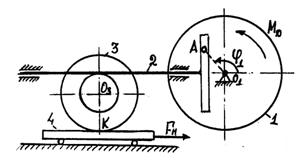
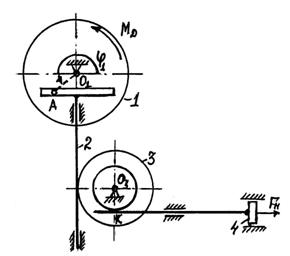
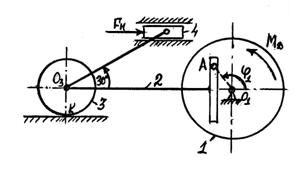
Пример 7. Кинематическая схема машины с кривошипно-кулисным механизмом изображена на рисунке 14. Движущий момент приложен  к шкиву 3. Шкив связан с маховиком ременной передачей. Полезная нагрузка моделируется моментом  Числовые данные: 

,       

.

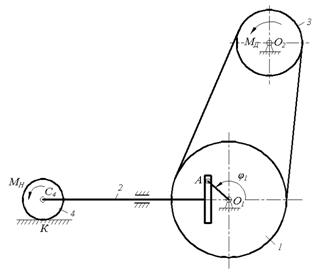
Предполагается, что ремень невесомый, нерастяжимый, проскаль-зывание его относительно шкива и маховика отсутствует. Каток 4 относительно плоскости не проскальзывает.

Составить диффе-ренциальное уравнение движения машины.

Решение. Положение тел данной механической системы определяется следующими геометри-ческими параметрами:

1) маховик 1 - углом поворота ;

2) кулиса 2 - координатами  и  центра масс кулисы;

3) шкив 3 - углом поворота ;

4) каток 4 - координатами  и . центра масс катка и углом поворота . относительно оси, проходящей через точку  перпендикулярно плоскости чертежа.

Перечисленные параметры связаны следующими кинематическими соотношениями:

а) в силу нерастяжимости ремня и непроскальзывания его, относительно маховика 1 и шкива 3, скорости точек В маховика и  шкива равны

  ,  ,  ,                                      (2)

откуда следует

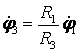;                                                                                                      (3)

б) так как кулиса 2 движется поступательно и прямолинейно, имеем

,                                                                                              (4)

;                                                                                  (5)

в) из условия неразрывности движения абсолютно твердого катка 4 по плоскости получаем

;                                                                                              (6)

г) так как качение катка 4 по плоскости происходит без скольжения (т.е. в точке МЦС катка), запишем

,                                                                                                           (7)

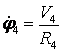 или .                                                                               (8)

Таким образом, семь геометрических параметров    связаны шестью кинематическими соотношениями (3)-(8). Следовательно, независимым является один параметр из семи. Принимаем за основную угол поворота  маховика 1 и выражаем через  остальные

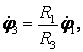                                                                                                  (9)

                                                                                          (10)

                                                                                          (11)

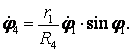                                                                                          (12)

Для определения движения машины применим теорему об изменении кинетической энергии системы в дифференциальной форме

.                                                                                                 (13)

Кинетическая энергия данной механической системы определяется выражением

                                                                                      (14)

где кинетическая энергия маховика 1 во вращательном движении неподвижной оси;

кинетическая энергия кулисы 2 в поступательном движении;

кинетическая энергия шкива во вращательном движении вокруг неподвижной оси

кинетическая энергия 4 в плоском движении.

Заменяя  по формулам (9) - (12) получаем

,    (15)

где .

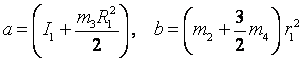Учитывая, что совершают работу движущий момент  и полезная нагрузка , вычисляем сумму элементарных работ

                                                                      (16)

Из уравнений (9) - (12) получаем соотношения для элементарных перемещений

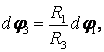                                                                                                (17)

                                                                                     (18)

Учитывая, что  с учетом (17), (18) находим

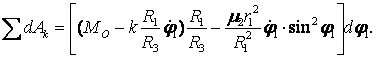                                      (19)

Дифференциал кинетической энергии

.                                    (20)

Подставляя полученные выражения в теорему об изменении кинетической энергии системы и сокращая на , получаем

      . (21)

Это и есть дифференциальное уравнение движения механической системы. Оно является нелинейным, его аналитическое решение найти невозможно, поэтому будем интегрировать его численно, для чего вначале запишем полученное дифференциальное уравнение в виде

.                       (22)

Далее запишем данное дифференциальное уравнение 2-го порядка в виде системы двух дифференциальных уравнений 1-го порядка

           (23)

которая может быть проинтегрирована, например, в системе Mathcad методом Рунге-Кутты.

 

Список литературы

 

1. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики. Учебник: в 2-х т. – М.: Наука, 2002.

2. Мещерский И.В. Сборник задач по теоретической механике. Учеб. пособие. – СПб.: Изд-во «Лань», 2005.

3. Никитин Н.Н. Курс теоретической механики. Учебник. – М.: Высшая школа, 1990.

3. Тарг С.М. Краткий курс теоретической механики. Учебник. – М.: Наука, 2002.

4. Яблонский А.А. Курс теоретической механики. Учебник: в 2-х т. – М.: Высшая школа, 2002.

5. Мещерский И.В. Сборник задач по теоретической механике. Учеб. пособие. – СПб.: Изд-во «Лань», 2005.

6. Сборник заданий для курсовых работ по теоретической механике. Учебное пособие./Под ред. А.А.Яблонского. – М.: Высшая школа, 1985.

7. Динасылов А.Д., Койлыбаева Р.К. Механика. Сборник заданий для самостоятельной работы студентов: Учебное пособие. – Алматы: АУЭС, 2012.

                                                                 Сводный план 2012 г., поз. 243