Некоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра инженерной графики и прикладной механики
МЕХАНИКА
Методические указания и задания к самостоятельной работе для студентов специальности 5В074600–Космическая техника и технология
Алматы 2012
СОСТАВИТЕЛИ: Тойбаев С.Н., Динасылов А.Д., Иванов К.С. Механика. Методические указания и задания к самостоятельной работы студентов для студентов специальности 5В074600–Космическая техника и технология. - Алматы: АУЭС, 2012.–39 с.
Дисциплина «Механика» является дисциплиной обязательной для обучающихся по специальности 5В074600 – Космическая техника и технология. В данной методической разработке, предназначенной для студентов, приводятся задания по темам и методические указания к выполнению самостоятельной работы. Дан список рекомендуемой литературы.
Ил. 27, библиогр. – 6 назв.
Рецензент: канд. техн. наук, профессор Яхъяев Э.А.
Печатается по плану издания некоммерческого акционерного общества «Алматинского университета энергетики и связи» на 2012 г.
© НАО «Алматинский университет энергетики и связи», 2012 г.
Содержание
|
Статика 1 Система сходящихся сил |
4 4 |
|
2 Момент силы относительно центра |
7 |
|
3 Плоская система сил |
7 |
|
4 Равновесие произвольной системы сил |
8 |
|
5 Трения. Центр тяжести |
9 |
|
Кинематика 6 Способы задания движения точки. Траектория и уравнение движение точки |
11 11 |
|
7 Скорость точки при координатном способе задания движения точки. Касательное и нормальное ускорение точки |
12 |
|
8 Поступательное и вращательное движения твердого тела. Плоскопараллельное движение твердого тела |
15 |
|
9 Определение скоростей и ускорений точек плоской фигуры. Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей. Определение ускорений точек плоской фигуры. Сложное движение точки |
17 |
|
10 Сложное движение точки |
20 |
|
Динамика 11 Дифференциальные уравнения движения материальной точки. Решение первой задачи динамики |
24 24 |
|
12 Количество движения точки. Импульс силы. Теорема об изменении количества движения |
25 |
|
13 Работа и мощность. Теорема об изменении кинетической энергии материальной точки. Динамика системы и твердого тела. Механическая система. Масса системы |
26 |
|
14 Теорема о движении центра масс. Теорема об изменении количества движения системы |
31 |
|
15 Теорема об изменении момента количества механической системы. Теорема об изменении кинетической энергии системы |
34 |
|
Список литературы |
38 |
Статика
1 Система сходящихся сил
1.1 Система сходящихся сил на плоскости
Пример 1.1. Однородный
цилиндр, вес которого ![]() , лежит на гладкой горизонтальной
плоскости. Сверху на цилиндр давит вертикальная сила
, лежит на гладкой горизонтальной
плоскости. Сверху на цилиндр давит вертикальная сила ![]() , линия действия которой
проходит через центр тяжести цилиндра (см. рисунок 1.1).
, линия действия которой
проходит через центр тяжести цилиндра (см. рисунок 1.1).
Определить давление цилиндра на горизонтальную плоскость.
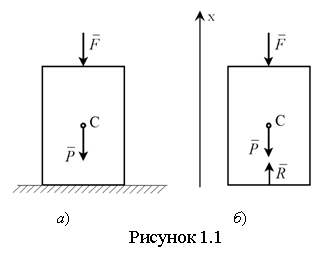
Решение: показываем действующие
на цилиндр заданные силы – силу веса ![]() и вертикальную силу давления
и вертикальную силу давления ![]() , действующие по одной
прямой.
, действующие по одной
прямой.
Мысленно освобождаем тело от
связей, заменяя их действие силами реакций (см. рисунок 1.1,б).
На цилиндр наложена одна связь – гладкая горизонтальная плоскость. Ее реакция ![]() направляется
перпендикулярно плоскости вверх.
направляется
перпендикулярно плоскости вверх.
Теперь данное несвободное тело можно рассматривать как свободное, к которому приложены три силы, лежащие на одной прямой. Запишем условие равновесия этих сил. При равновесии должно быть
![]() .
.
Откуда в проекциях на ось, параллельную силам, получаем
![]() или
или ![]() .
.
Подставив численные значения,
получаем ![]() .
Давление тела на горизонтальную плоскость равно по модулю силе реакции
.
Давление тела на горизонтальную плоскость равно по модулю силе реакции ![]() этой плоскости и
направлено ей противоположно, т.е. по вертикали вниз.
этой плоскости и
направлено ей противоположно, т.е. по вертикали вниз.
Пример 1.2. Стержни АС
и ВС соединены между собой и с вертикальной стеной посредством шарниров.
На шарнирный болт С действует вертикальная сила ![]() (см. рисунок 1.2). Определить
реакции этих стержней на шарнирный болт С, если углы, составляемые
стержнями со стеной, равны:
(см. рисунок 1.2). Определить
реакции этих стержней на шарнирный болт С, если углы, составляемые
стержнями со стеной, равны: ![]() .
.
Решение: для решения задачи рассматриваем равновесие трёх сил, приложенных к узлу C:
- заданной силы ![]() ;
;
- реакций стержней ![]() и
и ![]() , направленных соответственно
по AC и BC.
, направленных соответственно
по AC и BC.
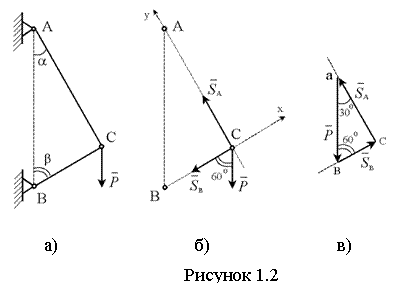 К этой системе применяем
геометрическое условие равновесия плоской системы сходящихся сил, т.е. строим
замкнутый треугольник этих сил. Для этого откладываем заданную силу
К этой системе применяем
геометрическое условие равновесия плоской системы сходящихся сил, т.е. строим
замкнутый треугольник этих сил. Для этого откладываем заданную силу ![]() . Из конца «в»
силы
. Из конца «в»
силы ![]() проведём
прямую, параллельную реакции
проведём
прямую, параллельную реакции ![]() , тогда из начала «a»
силы
, тогда из начала «a»
силы ![]() должна
быть проведена прямая, параллельная другой реакции
должна
быть проведена прямая, параллельная другой реакции ![]() . Точка «c»
пересечения проведённых прямых является третьей вершиной треугольника сил. Стороны
треугольника направляем так, чтобы все силы
. Точка «c»
пересечения проведённых прямых является третьей вершиной треугольника сил. Стороны
треугольника направляем так, чтобы все силы ![]() ,
, ![]() и
и ![]() были направлены в одну сторону по обходу
контура. По треугольнику сил определяем истинное направление реакций
были направлены в одну сторону по обходу
контура. По треугольнику сил определяем истинное направление реакций ![]() и
и ![]() . Устанавливаем, что стержень BC – сжат.
. Устанавливаем, что стержень BC – сжат.
Из треугольника сил (см. рисунок 1.2, в), определив его углы, находим модули искомых реакций
![]() ,
,
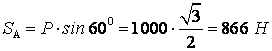 .
.
Пример решения задачи методом проекций.
Решим предыдущий пример методом
проекций, т.е. аналитическим способом. Воспользуемся изображением сил ![]() ,
, ![]() и
и ![]() , данным на рисунок 2,b. Начало системы координат
совместим с шарниром C. Ось x
направим по BC вправо, ось y – по AC вверх.
, данным на рисунок 2,b. Начало системы координат
совместим с шарниром C. Ось x
направим по BC вправо, ось y – по AC вверх.
Составим уравнения равновесия шарнира C в проекциях на оси x и y
![]() ,
, ![]() .
.
Решив эту систему уравнений, находим
![]() ,
, ![]() .
.
Ответ со знаком минус
показывает, что направление силы ![]() , показанное на чертеже, противоположно
действительному, т.е. стержень BC сжат.
, показанное на чертеже, противоположно
действительному, т.е. стержень BC сжат.
Задания для самостоятельного решения
№№ 2.6, 2.7, 2.8, 2.9, 2.15, 2.18, 2.19, 2.21, 2.23, 2.24, [1].
1.2 Система сходящихся сил в пространстве
Пример 1.3. Найти усилия
![]() и
и ![]() в стержнях AB и AC и усилие
в стержнях AB и AC и усилие ![]() в тросе AD, если дано, что Ð
CBA = Ð
BCA = 60°,
Ð EAD
= 30°. Вес груза
в тросе AD, если дано, что Ð
CBA = Ð
BCA = 60°,
Ð EAD
= 30°. Вес груза ![]() равен 3000 Н. Плоскость
ABC горизонтальна. Крепление стержней в точках A, B, C шарнирное (см. рисунок 1.3).
равен 3000 Н. Плоскость
ABC горизонтальна. Крепление стержней в точках A, B, C шарнирное (см. рисунок 1.3).
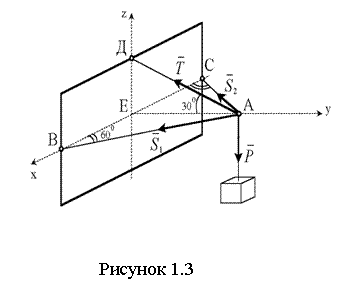 |
Решение: рассмотрим равновесие
сил, приложенных к узлу A: заданной силы – силы
реакции троса ![]() ,
реакций стержней
,
реакций стержней ![]() и
и
![]() и реакции
троса
и реакции
троса ![]() (см. рисунок 1.3).
Все силы реакций направляем от узла A,
предполагая, что стержень и трос растянуты.
(см. рисунок 1.3).
Все силы реакций направляем от узла A,
предполагая, что стержень и трос растянуты.
Оси координат проведем из точки
E по взаимно перпендикулярным направлениям DE, BE и EA. Для определения неизвестных сил ![]() ,
, ![]() и
и ![]() составляем три уравнения равновесия пространственной
системы сходящихся сил
составляем три уравнения равновесия пространственной
системы сходящихся сил
![]() ,
,
![]() ,
,
![]() .
.
Решая эти уравнения, найдем
Т = 6000 Н, S1 = S2 = –3000 Н.
Знак минус в ответе указывает, что стержни AB и AC сжаты.
Задания для самостоятельного решения
№№ 6.1, 6.2, 6.3, 6.4, 6.5, 6.6, 6.7, 6.8, 6.9, 6.10, [1].
2 Момент силы относительно центра
Пример 2.1. Однородная
горизонтальная балка длиной 4 м и весом 0,5 Н заложена в стену, толщина которой
равна 0,5 м, так, что она опирается на неё в точках A и B (см.
рисунок 2.1). Определить реакции в этих точках, если к свободному концу
балки подвешен груз ![]() весом
4 Н.
весом
4 Н.
 |
Решение: показываем
действующие на балку заданные силы: вес груза ![]() в точке C
и вес балки
в точке C
и вес балки ![]() в
середине балки D.
в
середине балки D.
Освобождаем балку от связей,
заменяя их действие реакциями опор ![]() и
и ![]() , направленными перпендикулярно к
поверхности балки.
, направленными перпендикулярно к
поверхности балки.
К полученной системе
вертикальных сил ![]() ,
,
![]() ,
, ![]() ,
, ![]() применяем условия равновесия
параллельных сил на плоскости
применяем условия равновесия
параллельных сил на плоскости
![]() ,
,
![]() .
.
Решая эти уравнения, определяем неизвестные реакции
![]() ,
, ![]() .
.
Значение обеих реакций получено со знаком плюс, значит на расчётной схеме указано действительное направление этих реакций.
Задания для самостоятельного решения
№№ 3.6, 3.7, 3.8, 3.9, 3.12, 3.13, 3.14, 3.15, 3.16, 3.17, [1].
3 Плоская система сил
Пример 3.1. Определить реакции опор A и B балки, находящейся под действием двух сосредоточенных сил и равномерно распределённой нагрузки. Интенсивность распределённой нагрузки, величины сил и размеры указаны на чертеже (см. рисунок 3.1).
Решение: на балку действуют
заданные силы: 6кН, 8кН. Равномерно распределённую нагрузку
заменяем сосредоточенной силой, приложенной в середине загруженного участка.
Модуль этой силы равен: q×l=3(кН/м)×(м)=6кН. Мысленно
отбрасываем связи: неподвижную шарнирную опору A
и шарнирно подвижную опору B. Реакция опоры ![]() направлена перпендикулярно
опорной плоскости. Линия действия реакции опоры A
неизвестна, поэтому заменяем её двумя взаимно перпендикулярными составляющими
направлена перпендикулярно
опорной плоскости. Линия действия реакции опоры A
неизвестна, поэтому заменяем её двумя взаимно перпендикулярными составляющими ![]() ,
, ![]() , направленными вдоль осей
координат.
, направленными вдоль осей
координат.
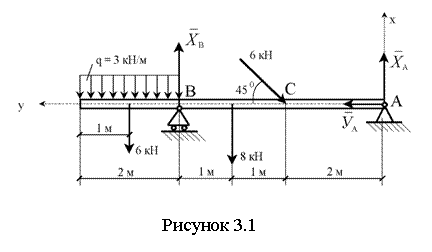 |
Для полученной произвольной плоской системы сил составляем три уравнения равновесия
![]()
![]()
![]()
Решая полученные уравнения, определяем неизвестные
ХА = 2,6 кН, YА = 4,2 кН, ХВ = 15,6 кН.
Знаки ответа показывают, что принятые направления реакций совпадают с действительными.
Задания для самостоятельного решения
№№ 4.19, 4.21, 4.22, 4.25, 4.26, 4.27, 4.28, 4.29, 4.30, 4.31, [1].
4 Равновесие произвольной системы сил
Пример 4.1. Рабочий
удерживает груз ![]() с
помощью ворота, схематически изображенного на чертеже; радиус барабана R = 5 см; длина рукоятки AK
= 40 см, AC = CB
= 50 см (см. рисунок 4.1). Определить давление
с
помощью ворота, схематически изображенного на чертеже; радиус барабана R = 5 см; длина рукоятки AK
= 40 см, AC = CB
= 50 см (см. рисунок 4.1). Определить давление ![]() на рукоятку и давление оси
ворота на опоры A и B
при том положении ворота, когда рукоятка AK
горизонтальна; сила
на рукоятку и давление оси
ворота на опоры A и B
при том положении ворота, когда рукоятка AK
горизонтальна; сила ![]() вертикальна.
вертикальна.
Решение: при равномерном
вращении ворота, действующие на него силы, находятся в равновесии. На ворот
действуют силы: натяжение верёвки ![]() , по модулю равное
, по модулю равное ![]() , искомая сила
, искомая сила ![]() и реакции подшипников
и реакции подшипников
![]() ,
, ![]() ,
, ![]() ,
, ![]() . Реакции
. Реакции ![]() и
и ![]() могут иметь любое направление в
плоскости, перпендикулярной оси, и изображаются двумя составляющими. Для
определения пяти неизвестных составляем пять уравнений равновесия
могут иметь любое направление в
плоскости, перпендикулярной оси, и изображаются двумя составляющими. Для
определения пяти неизвестных составляем пять уравнений равновесия
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
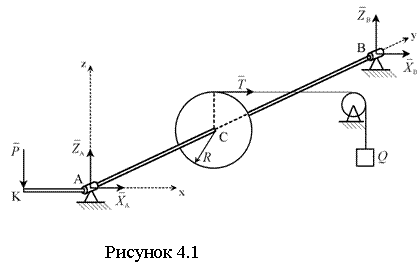 |
Решая полученную систему уравнений, находим
Р = 100 Н, ХА = 400 Н, ZА = – 100 Н, ХВ = – 400 Н, ZВ = 0.
Задания для самостоятельного решения
№№ 8.5, 8.7, 8.8, 8.12, 8.13, 8.14, 8.15, 8.16, 8.17, 8.24, [1].
5 Трения. Центр тяжести
Пример 5.1. К
вертикальной стене приставлена лестница
AB,
опирающаяся своим нижним концом на горизонтальный пол. Коэффициент трения
лестницы о стену f1,
о пол f2.
Вес лестницы вместе с находящимся на ней человеком равен ![]() и приложен в точке
C,
которая делит длину лестницы
и приложен в точке
C,
которая делит длину лестницы
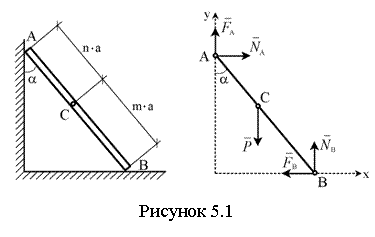 |
в
отношении m : n
(см. рисунок 5.1). Определить
наибольший угол a, составляемый лестницей со стеной в положении
равновесия, а также нормальные составляющие реакций ![]() стены и
стены и ![]() пола для этого значения
a.
пола для этого значения
a.
Решение: на
лестницу действует одна заданная сила ![]() и наложены две связи: пол и стена.
Отбросим мысленно связи и заменим их действие на лестницу силами реакций. Т.к.
пол и стена негладкие, представляем их реакции двумя составляющими:
и наложены две связи: пол и стена.
Отбросим мысленно связи и заменим их действие на лестницу силами реакций. Т.к.
пол и стена негладкие, представляем их реакции двумя составляющими: ![]() и
и ![]() направляем перпендикулярно
шероховатой поверхности, силы трения
направляем перпендикулярно
шероховатой поверхности, силы трения ![]() и
и ![]() – в сторону, противоположную возможному
перемещению соответствующей точки лестницы.
– в сторону, противоположную возможному
перемещению соответствующей точки лестницы.
Т.к. amax имеет место при предельном значении силы трения, то:
![]() ,
, ![]() .
.
Составим уравнения равновесия:
![]() ,
,
![]() ,
,
![]() .
.
Получили пять уравнений с пятью
неизвестными ![]() ,
,
![]() ,
, ![]() ,
, ![]() , a. Задача статически определённая. Решая, находим
, a. Задача статически определённая. Решая, находим
 ,
, 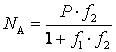 ,
,  .
.
Пример 5.2. Найти центр тяжести C площади кругового сегмента ADB радиуса AO = 30 см, если угол AOB = 60° (см. рисунок 5.2).

Решение: воспользуемся способом отрицательных площадей. Площадь сегмента круга представляет собой разность площадей сектора круга ADBO и треугольника AOB. Примем за ось x биссектрису угла AOB, т.е. ось симметрии сегмента, ось y направим по вертикали вверх. Т.к. центр тяжести кругового сегмента ADB лежит на его оси симметрии, т.е. на оси x, то yC = 0. Остается определить абсциссу хС центра тяжести C. Обозначим: DS1 – площадь кругового сектора ADBO; DS2 – площадь равнобедренного треугольника ABO; х1 и х2 – соответственно абсциссы центров тяжести С1 и С2 кругового сектора ADBO и треугольника AOB. Тогда положение центра тяжести определится формулой
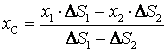 .
.
Находим
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Вывод формул для координат центров тяжести треугольника и кругового сектора даётся в лекционном материале и получим
 .
.
При ![]() и
и ![]() ,
, ![]() .
.
Задания для самостоятельного решения
№№ 9.4, 9.5, 9.6, 9.7, 9.8, 9.9, 9.10, 9.11, 9.12, 9.13, [1].
Кинематика
6 Способы задания движения точки. Траектория и уравнения движения точки
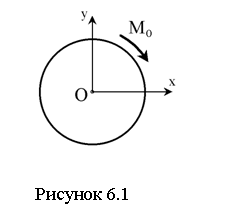
Пример 6.1. По заданным уравнениям движения точки найти уравнение ее траектории, а также указать закон движения точки по траектории, отсчитывая расстояние от начального положения точки.
![]() (см. рисунок 6.1).
(см. рисунок 6.1).
 |
Решение: возводя обе части уравнений движения в квадрат и складывая их почленно, найдем
![]() или
или ![]() .
.
Следовательно, траектория – окружность радиуса 3 ед. длины с центром в начале координат (см. рисунок 6.1).
Определим закон движения вдоль траектории. Вычисляя производные от x и y по t, получим
![]() .
.
Подставляя эти значения в равенство
 ,
(1)
,
(1)
будем иметь 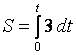 или
или ![]() . (2)
. (2)
Уравнение (2) дает закон
движения точки вдоль траектории. Согласно уравнениям (1), когда ![]() ,
, ![]() , т.е. точка находится в положении
М0 (см. рисунок 6.1), а когда
, т.е. точка находится в положении
М0 (см. рисунок 6.1), а когда ![]() начинает возрастать,
начинает возрастать, ![]() растёт, принимая положительные
значения, а
растёт, принимая положительные
значения, а ![]() убывает.
Следовательно, начало отсчета S лежит в точке
убывает.
Следовательно, начало отсчета S лежит в точке ![]() , а движение по
окружности происходит в направлении, показанном на рисунке 6.1 стрелкой.
, а движение по
окружности происходит в направлении, показанном на рисунке 6.1 стрелкой.
Задания для самостоятельного решения
№№ 10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10 [1].
7 Скорость точки при координатном способе задания движения точки. Касательное и нормальное ускорения точки
7.1 Скорость точки при координатном способе задания движения точки.
Пример 7.1.1. Кривошип
OA вращается с постоянной угловой скоростью w (см. рисунок 7.1). Найти скорость
середины M шатуна кривошипно-шатунного механизма и скорость ползуна B в зависимости от времени, если ![]() .
.
 |
Решение: уравнения движения точек M и B не заданы, следовательно, их необходимо составить. Изобразим механизм в произвольном положении. Оси координат показаны на рисунке 7.1. Из точек M и A опустим на оси перпендикуляры MD, ME и AK. Тогда получим
![]()
![]()
![]()
Подставляя значения ![]() ,
получим уравнения движения точек M и B
,
получим уравнения движения точек M и B
![]()
![]()
![]()
![]() , т.к. ползун B движется по направляющей Ox.
Определяем скорости точек M и B:
, т.к. ползун B движется по направляющей Ox.
Определяем скорости точек M и B:
![]() ,
, ![]() ,
,
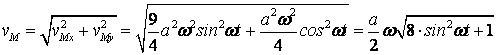 ,
,
![]() .
.
7.2 Определение ускорения точки при координатном способе задания движения
Пример 7.2.1. Уравнения
движения пальца кривошипа дизеля в период пуска имеют вид ![]() (х, у – в
сантиметрах, t – в секундах). Найти скорость,
тангенциальное и нормальное ускорения пальца.
(х, у – в
сантиметрах, t – в секундах). Найти скорость,
тангенциальное и нормальное ускорения пальца.
Решение: для определения скорости вычисляем первые производные от координат по времени, равные проекциям скорости точки на соответствующие оси координат
![]() ,
, ![]() .
.
Величина скорости определяется формулой
![]() (см/с).
(см/с).
Тангенциальное ускорение определится как производная по времени от проекции скорости на касательную ось
![]() (см/с2).
(см/с2).
Находим проекции ускорения на оси координат, вычисляя первые производные по времени от соответствующих проекций скорости
![]() ,
,
![]() .
.
Величина ускорения определится по формуле
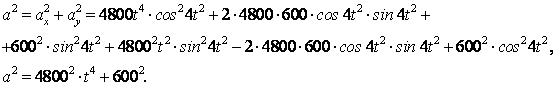
Но величина полного ускорения связана с тангенциальным и нормальным ускорением зависимостью
![]() .
.
Тогда получим
![]() ,
,
откуда
![]() (см/с2).
(см/с2).
7.3 Равномерное и равнопеременное криволинейное движение точки
Пример 7.3.1. Поезд
движется равнозамедленно по дуге окружности радиуса ![]() и проходит путь
и проходит путь ![]() , имея начальную
скорость
, имея начальную
скорость ![]() и
конечную
и
конечную ![]() .
Определить полное ускорение поезда в начале и в конце дуги, а также время
движения по этой дуге.
.
Определить полное ускорение поезда в начале и в конце дуги, а также время
движения по этой дуге.
Решение: рассмотрим
движение одной из точек поезда, например, его центра тяжести. Совместим начало
отсчета O дуговой координаты с начальным
положением точки M, и направление движения
примем за положительное направление. Тогда ![]() (см. рисунок 7.3).
(см. рисунок 7.3).
При равнозамедленном движении точки уравнение движения и формула скорости точки имеют вид
![]() ,
(1)
,
(1)
![]() .
(2)
.
(2)
 |
По условию задачи
известны: дуговая координата движущейся точки M
в конце участка, равная длине участка, т.е. ![]() , скорость точки в начале участка
, скорость точки в начале участка ![]() , скорость точки в
конце участка
, скорость точки в
конце участка ![]() ,
а также радиус окружности во всех её точках
,
а также радиус окружности во всех её точках ![]() .
.
Подставляем в (1), (2) все известные величины
![]() ,
, ![]() .
.
Решая полученные уравнения совместно, находим время движения и тангенциальное ускорение
 ,
,  ,
, ![]() ,
,
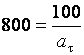 ,
, ![]() .
.
Модуль нормального ускорения точки в начале участка
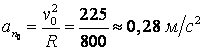 ,
,
в конце участка - 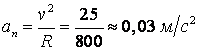 .
.
Модуль полного ускорения в начале и в конце участка
![]() ,
,
![]() .
.
Задания для самостоятельного решения
№№ 10.2, 10.12, 11.3, 11.5, 12.1, 12.2, 12.3, 12.7, 12.8, 12.10, [1].
8 Поступательное и вращательное движения твердого тела. Плоскопараллельное движение твердого тела
8.1 Вращательное движения твердого тела
Пример 8.1.1. Груз A, подвешенный к нити AB, намотанной на барабан, опускается равноускоренно из состояния покоя, приводя во вращение барабан. За первые 3 с барабан совершает 9 оборотов (см. рисунок 8.1).
Решение: барабан вращается равноускоренно, согласно уравнению
![]() . (1)
. (1)
Формула угловой скорости имеет вид
![]() .
(2)
.
(2)
Положим, что ![]() . Барабан вращается из
состояния покоя, следовательно,
. Барабан вращается из
состояния покоя, следовательно, ![]() . При этих условиях формулы (1), (2)
принимают вид
. При этих условиях формулы (1), (2)
принимают вид
![]() ,
(3)
,
(3)
![]() .
(4)
.
(4)
Т.к. ![]() оборотов при
оборотов при ![]() , то из уравнения (3)
определяем одинаковое для всех моментов времени угловое ускорение
, то из уравнения (3)
определяем одинаковое для всех моментов времени угловое ускорение
![]()
![]() .
.
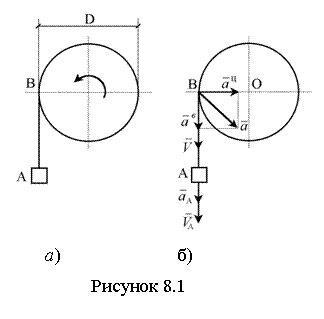 |
Из уравнения (4) найдём угловую скорость барабана в конце 5-й сек
![]() .
.
Определим в точке B обода барабана (см. рисунок 8.1, б) модули линейной скорости, вращательного и центростремительного ускорения в этот же момент времени
![]() м/с,
м/с,
![]() м/с2,
м/с2,
(модуль вращательного ускорения точки тела при равнопеременном вращении одинаков для всех моментов времени)
![]() м/с2.
м/с2.
Модуль полного ускорения точки обода барабана определяется по формуле
![]() м/с2.
м/с2.
Скорость груза равна линейной скорости точки обода барабана
![]() м/с.
м/с.
Ускорение груза равно вращательному ускорению точки обода, т.е.
![]() м/с2.
м/с2.
Задания для самостоятельного решения
№№ 13.2, 13.3, 13.4, 13.5, 13.14, 13.18, 14.1, 14.3, 14.4, 14.5, [1].
9 Определение скоростей и ускорений точек плоской фигуры. Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей. Определение ускорений точек плоской фигуры. Сложное движение точки
9.1 Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей. Определение ускорений точек плоской фигуры
Пример 9.1.1. Колесо
радиуса ![]() катится
без скольжения по прямолинейному участку пути; скорость центра его постоянна и
равна
катится
без скольжения по прямолинейному участку пути; скорость центра его постоянна и
равна ![]() .
Найти скорости концов A, B,
C, D
вертикального и горизонтального диаметров колеса (см. рисунок 9.1). Определить
угловую скорость колеса.
.
Найти скорости концов A, B,
C, D
вертикального и горизонтального диаметров колеса (см. рисунок 9.1). Определить
угловую скорость колеса.
Решение: I способ (применение формулы распределения скоростей).
Примем за полюс центр
колеса O (см. рисунок 9.1). Тогда скорость любой
точки колеса будет равна геометрической сумме скорости полюса и скорости
вращения вокруг полюса, например: ![]() .
.
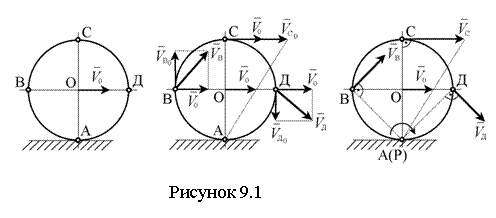 |
Так как колесо катится
без скольжения, то скорость точки A касания
колеса с рельсом равна нулю VА=0.
Точка A является мгновенным центром скоростей. В
этой точке скорость вращения вокруг полюса ![]() и скорость полюса
и скорость полюса ![]() равны по модулю и
противоположны по направлению, т.е.
равны по модулю и
противоположны по направлению, т.е. ![]() . Расстояния от точек A, B, C,
D до полюса O
равны. Следовательно, и вращательные скорости точек вокруг полюса тоже равны,
т.е.
. Расстояния от точек A, B, C,
D до полюса O
равны. Следовательно, и вращательные скорости точек вокруг полюса тоже равны,
т.е.
![]() .
.
Откладывая в каждой точке
скорость полюса ![]() и
вращательную скорость перпендикулярную соответствующему радиусу колеса,
находим:
и
вращательную скорость перпендикулярную соответствующему радиусу колеса,
находим:

Угловая скорость колеса
![]() .
.
II способ (применение мгновенного центра скоростей).
Примем: точка A – мгновенный центр скоростей колеса за полюс. Тогда скорости всех точек колеса определяются как вращательные скорости вокруг мгновенного центра скоростей. Модули скоростей всех точек найдутся по пропорциональности всех скоростей их расстояниям от –мгновенного центра скоростей
![]() ,
,
Так как PB = PД
= ![]() , то
, то
 м/c,
м/c,
![]() м/c.
м/c.
Найденные скорости точек направлены перпендикулярно соответствующим отрезкам в сторону вращения колеса (см. рисунок 17). Угловую скорость колеса можно определить, зная модуль скорости любой его точки, например O, и расстояние этой точки от мгновенного центра скоростей PO
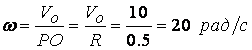 .
.
9.2 Ускорения точек твёрдого тела в плоском движении
Пример 9.2.1. Шестёренка
радиуса ![]() приводится
в движение кривошипом OA, вращающимся вокруг оси
O неподвижной шестёренки с тем же радиусом;
кривошип вращается с угловым ускорением
приводится
в движение кривошипом OA, вращающимся вокруг оси
O неподвижной шестёренки с тем же радиусом;
кривошип вращается с угловым ускорением ![]() 2, имея в данный момент
угловую скорость
2, имея в данный момент
угловую скорость ![]() (см.
рисунок 9.2). Определить ускорение точки N.
(см.
рисунок 9.2). Определить ускорение точки N.
Решение: для решения
задачи надо рассмотреть движение шестерни 2. По данным задачи легко
найти скорость ![]() и
ускорение
и
ускорение ![]() точки
A этой шестерни, которую и выбираем за полюс.
точки
A этой шестерни, которую и выбираем за полюс.
Определим ![]() и
и ![]() . Зная w и e кривошипа, находим
. Зная w и e кривошипа, находим
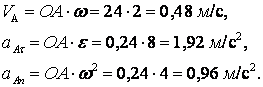
Т.к. знаки ![]() и
и ![]() одинаковые, то движение точки A из данного положения является ускоренным. Направления
векторов
одинаковые, то движение точки A из данного положения является ускоренным. Направления
векторов ![]() ,
, ![]() ,
, ![]() , показаны на рисунке 9.2.
, показаны на рисунке 9.2.
Определим ![]() угловую скорость
шестерни 2. Точка касания P является
мгновенным центром скоростей для шестерни 2, следовательно
угловую скорость
шестерни 2. Точка касания P является
мгновенным центром скоростей для шестерни 2, следовательно
![]() ,
, ![]() .
.
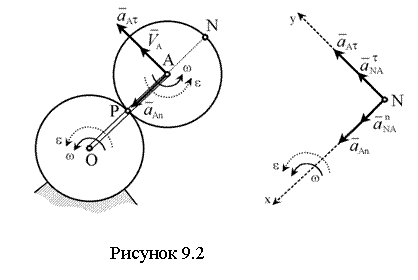 |
Направление ![]() (направление вращения
шестерни) определяется направлением
(направление вращения
шестерни) определяется направлением ![]() .
.
Определим e2 – угловое ускорение шестерни 2. Заметим, что величина AP = R во все время движения постоянна, поэтому
![]() ,
, 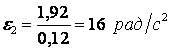 ,
(1)
,
(1)
т.к. знаки и одинаковые, то вращение шестерни 2 является ускоренным.
Ускорение точки N найдем по формуле
![]() .
(2)
.
(2)
Для этого определим ![]() и
и ![]() . В вашем случае
. В вашем случае ![]() и
и
![]() ,
, ![]() .
.
Изображаем на чертеже (см.
рисунок 9.2, b) векторы, из которых слагается
ускорение ![]() ,
а именно:
,
а именно: ![]() ,
, ![]() (переносим из точки A);
(переносим из точки A); ![]() (по ходу вращения, т.к. оно ускоренное);
(по ходу вращения, т.к. оно ускоренное);
![]() (к полюсу A).
(к полюсу A).
Вычисляем ![]() . Проводя оси Nx и Ny, находим, что
. Проводя оси Nx и Ny, находим, что
![]() ,
,
![]() .
.
Откуда ![]() .
.
Задания для самостоятельного решения
№№ 15.2, 16.2, 16.3, 16.4, 16,9, 16.24, 16.29, 18.1, 18.2, 18.15, [1].
10 Сложное движение точки
10.1 Определение траекторий и уравнений движения точки в сложном движении
Пример 10.1.1. Поворотный
кран вращается вокруг оси, перпендикулярной к плоскости рисунка и проходящей
через точку O с постоянной угловой скоростью: ![]() . По стреле крана,
совпадающей с осью
. По стреле крана,
совпадающей с осью ![]() ,
передвигается тележка M с грузом согласно
уравнению
,
передвигается тележка M с грузом согласно
уравнению ![]()
![]() (см. рисунок 10.1, a).
(см. рисунок 10.1, a).
Определить уравнения абсолютного движения тележки M и её траекторию.
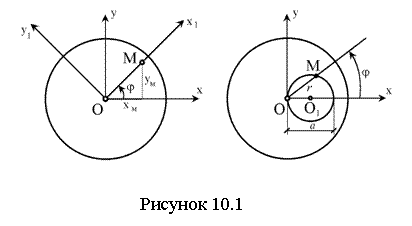 |
Решение: вращение крана
вокруг оси с постоянной угловой скоростью принимаем за переносное движение.
Прямолинейное движение тележки по стреле крана рассматриваем как относительное
движение. Зависимость между координатами точки M
в абсолютной системе координат ![]()
![]() и относительной системе координат
и относительной системе координат ![]() определится формулами
определится формулами
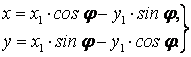
В нашей задаче
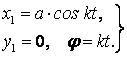
Уравнения абсолютного движения точки M в декартовой системе координат будут иметь вид
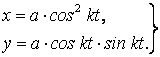
Уравнение траектории абсолютного движения проще получить в полярной системе координат
![]()
Откуда ![]() .
.
Это уравнение окружности диаметром а, проходящей через начало координат (см. рисунок 10.1, b).
10.2 Теорема о сложении скоростей. Определение скоростей при сложном движении точки
Пример 10.2.1. Шары
центробежного регулятора Уатта, вращающегося вокруг вертикальной оси с угловой
скоростью ![]() ,
благодаря изменению нагрузки машины отходят от этой оси, имея для своих
стержней в данном положении угловую скорость
,
благодаря изменению нагрузки машины отходят от этой оси, имея для своих
стержней в данном положении угловую скорость ![]() (см. рисунок 10.2). Найти абсолютную
скорость шаров регулятора в рассматриваемый момент, если дана длина стержней
(см. рисунок 10.2). Найти абсолютную
скорость шаров регулятора в рассматриваемый момент, если дана длина стержней ![]() , расстояние между
осями их привеса
, расстояние между
осями их привеса ![]() ,
углы, образованные стержнями с осью регулятора,
,
углы, образованные стержнями с осью регулятора, ![]() .
.
 |
Решение: подвижную
систему отсчёта связываем с частями регулятора, вращающимися вокруг его оси.
Переносным движением шаров является их вращение вокруг вертикальной оси с
угловой скоростью ![]() ,
а относительным – вращение стержней с шарами вокруг осей их привеса с угловой
скоростью
,
а относительным – вращение стержней с шарами вокруг осей их привеса с угловой
скоростью ![]() .
Траекторией переносного движения центра каждого шара является горизонтальная
окружность с центром на оси регулятора, проходящая через центр шара. Траектория
относительного движения – это дуга окружности радиуса
.
Траекторией переносного движения центра каждого шара является горизонтальная
окружность с центром на оси регулятора, проходящая через центр шара. Траектория
относительного движения – это дуга окружности радиуса ![]() , лежащей в плоскости регулятора,
с центром на оси привеса стержня.
, лежащей в плоскости регулятора,
с центром на оси привеса стержня.
Радиус окружности переносного движения
![]() см.
см.
Абсолютная скорость центра шара определяется как геометрическая сумма его переносной и относительной скоростей (см. рисунок 10.2)
![]() .
.
Скорости ![]() ,
, ![]() направлены по касательным к
соответствующим траекториям, а по модулю равны
направлены по касательным к
соответствующим траекториям, а по модулю равны
![]() .
.
Скорости ![]() и
и ![]() взаимно перпендикулярны,
следовательно, модуль абсолютной скорости будет равен
взаимно перпендикулярны,
следовательно, модуль абсолютной скорости будет равен
![]() .
.
10.3 Теорема о сложении ускорений
Пример 10.3.1. По заданному
уравнению относительного движения точки М ![]() и уравнению вращения тела D
и уравнению вращения тела D
![]() (
(![]() в см,
в см, ![]() в с), найти
абсолютную скорость и абсолютное ускорение точки M в момент
в с), найти
абсолютную скорость и абсолютное ускорение точки M в момент ![]() , если
, если ![]() (см. рисунок 10.3).
(см. рисунок 10.3).

Решение: рассмотрим движение точки М как сложное, считая ее движение в прорези тела D относительным (относительное движение - прямолинейное), а вращение тела D - переносным движением.
Находим положение точки М при
![]()
![]() .
.
Определим все кинематические характеристики относительного и переносного движения.
Относительное движение. Это движение задано
естественным способом. Находим ![]()
![]() .
.
Так как
![]() , то
вектор
, то
вектор ![]() направлен вдоль прямой ОМ в сторону
возрастания S, а
направлен вдоль прямой ОМ в сторону
возрастания S, а ![]() .
.
Находим относительное ускорение точки М: ![]() , так как (движение
прямолинейное)
, так как (движение
прямолинейное)
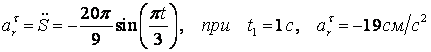 .
.
В связи с тем, что
![]() ,
вектор
,
вектор ![]() направлен вдоль прямой ОМ, в сторону
уменьшения S, а его модуль
направлен вдоль прямой ОМ, в сторону
уменьшения S, а его модуль ![]() .
.
Переносное движение. Это вращение задано уравнением
![]() . Находим угловую скорость и угловое ускорение тела D:
. Находим угловую скорость и угловое ускорение тела D:
![]() , при
, при ![]()
![]() . Так как
. Так как ![]() , то
направление вращения противоположно положительному направлению отсчета угла
, то
направление вращения противоположно положительному направлению отсчета угла ![]() и вращение
ускоренное. Модули
и вращение
ускоренное. Модули ![]() .
Направление вектора
.
Направление вектора ![]() показано
на рисунке 10.3.
показано
на рисунке 10.3.
Для определения переносной скорости и переносного
ускорения точки находим сначала расстояние точки М от оси вращения
![]() . Для
. Для
![]() и
и
![]() в момент времени
в момент времени
![]() получаем
получаем
![]() ,
, ![]() ,
,
![]() .
.
Через точку М проводим пространственные оси
![]() и в соответствии с направлениями угловой скорости и
углового ускорения направляем векторы
и в соответствии с направлениями угловой скорости и
углового ускорения направляем векторы ![]() .
.
Ускорение Кориолиса. Так как угол между вектором
![]() равен (180°-
равен (180°-![]() ), то модуль
), то модуль ![]() в
момент
в
момент ![]() будет
будет
![]() .
.
Воспользовавшись правилом Жуковского, направляем
вектор ![]() вдоль оси
вдоль оси
![]() от нас.
от нас.
Абсолютное движение. В соответствии с теоремами сложения скоростей и ускорений имеем
![]() .
(1)
.
(1)
Так как векторы
![]() взаимно
перпендикулярны, то в момент
взаимно
перпендикулярны, то в момент ![]()
![]() .
.
Для вычисления
![]() спроецируем
(1) на координатные оси
спроецируем
(1) на координатные оси ![]() . Для
момента
. Для
момента ![]() получаем
получаем

Находим значение
![]() в момент
в момент
![]()
![]() .
.
Задания для самостоятельного решения
№№ 21.3, 22.1, 22.3, 22.15, 22.17, 23.14, 23.18, 23.19, 23.27, 23.29, [1].
Динамика
11 Дифференциальные уравнения движения материальной точки. Решение первой задачи динамики
Пример 11.1. Горизонтальная
платформа, на которой лежит груз весом ![]() , опускается вертикально вниз с
ускорением
, опускается вертикально вниз с
ускорением ![]() .
Найти давление, производимое грузом на платформу во время их совместного
спуска.
.
Найти давление, производимое грузом на платформу во время их совместного
спуска.
Решение: к грузу
приложена одна активная сила – его вес ![]() . Применив закон освобождаемости от
связей, мысленно отбросим дно платформы, заменив его действие реакцией
. Применив закон освобождаемости от
связей, мысленно отбросим дно платформы, заменив его действие реакцией ![]() , направленной
вертикально вверх. Направим ось x вертикально
вниз в сторону движения (см. рисунок 11.1). Запишем дифференциальное уравнение
движения груза в проекциях на ось
, направленной
вертикально вверх. Направим ось x вертикально
вниз в сторону движения (см. рисунок 11.1). Запишем дифференциальное уравнение
движения груза в проекциях на ось ![]()
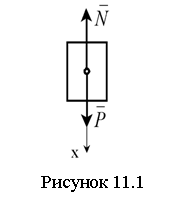
![]() ,
,
отсюда
![]() .
.
Следовательно, ![]() , т.е. давление, оказываемое грузом на платформу также равно
, т.е. давление, оказываемое грузом на платформу также равно ![]() .
.
Пример 11.2. Движение
материальной точки, массой ![]() выражается уравнениями
выражается уравнениями ![]() где
где ![]() выражено в
секундах.
выражено в
секундах.
Определить проекции силы, действующей на точку, в зависимости от её координат.
Решение: движение материальной точки заданно в прямоугольной системе координат. Дифференциальные уравнения движения материальной точки записываются
![]() .
.
Т.к. заданы уравнения движения материальной точки, можно найти её ускорения в проекциях на оси координат
![]() .
.
Подставим эти значения в дифференциальные уравнения движения
![]() .
.
Подставим численные значения, получим
![]() .
.
Задания для самостоятельного решения
№№ 27.1, 27.2, 27.3, 27.4, 27.7, 27.8, 27.30, 27.40, 27.42, 27.43, [1].
12 Количество движения точки. Импульс силы. Теорема об изменении количества движения
Пример 12.1. По шероховатой
наклонной плоскости, составляющей с горизонтом угол ![]() , спускается тяжёлое тело без
начальной скорости (см. рисунок 12.1). Определить, в течение какого времени
, спускается тяжёлое тело без
начальной скорости (см. рисунок 12.1). Определить, в течение какого времени ![]() тело пройдёт путь,
длиной
тело пройдёт путь,
длиной ![]() ,
если коэффициент трения
,
если коэффициент трения ![]() .
.
Решение: изобразим на
чертеже силы, приложенные к грузу: вес груза ![]() нормальную реакцию поверхности
нормальную реакцию поверхности ![]() , сила трения
, сила трения ![]() , причём
, причём
![]() .
.
 |
Направим ось x вдоль наклонной плоскости в сторону движения вниз.
Запишем теорему об
изменении количества движения в проекциях на ось ![]()
 . (*)
. (*)
Согласно условию задачи
![]() ,
,
![]() .
.
Вычислим импульсы каждой силы, учтя, что все действующие на тело силы постоянны
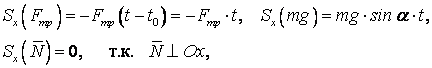
тогда ![]() .
.
Подставим это выражение в (*)
![]() или
или ![]() .
.
Проинтегрируем это уравнение по времени t
![]() ,
,
C![]() определим из начальных
условий при
определим из начальных
условий при ![]() .
.
Итак, закон движения тела имеет вид
![]() .
.
Для того чтобы определить
время ![]() , за
которое время пройдёт путь
, за
которое время пройдёт путь ![]() м, подставим эти значения в
уравнение движения
м, подставим эти значения в
уравнение движения
![]() .
.
Откуда 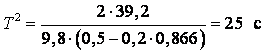 ,
, ![]() .
.
Задания для самостоятельного решения
№№ 28.1, 28.2, 28.3, 28.4, 28.5, 28.6, 28.7, 28.8, 28.9, 28.10, [1].
13 Работа и мощность. Теорема об изменении кинетической энергии материальной точки. Динамика системы и твердого тела. Механическая система. Масса системы
13.1 Работа и мощность. Теорема об изменении кинетической энергии материальной точки
Пример 13.1.1. Определить наименьшую работу, которую нужно затратить для того,
чтобы поднять на ![]() груз
груз
![]() , двигая его
по наклонной плоскости, составляющей с горизонтом угол в 30°; коэффициент трения 0,5 (см. рисунок 13.1).
, двигая его
по наклонной плоскости, составляющей с горизонтом угол в 30°; коэффициент трения 0,5 (см. рисунок 13.1).
Решение: к грузу
приложены следующие силы: ![]() его вес,
его вес, ![]() сила трения,
сила трения, ![]() нормальная реакция наклонной
плоскости.
нормальная реакция наклонной
плоскости.
Направим параллельно
наклонной плоскости вверх ось ![]() , взяв начало координат в начале
движения.
, взяв начало координат в начале
движения.
Работа, которую необходимо затратить, чтобы поднять груз, равна сумме работ всех приложенных сил
![]()
Работа силы тяжести отрицательна, т.к. груз удаляется от земной поверхности
![]() .
.
Работа силы трения определяется по формуле
![]() .
.
![]()
![]()
![]()
 x
x
![]()
![]()
![]()
![]()
![]()
![]()
 s
s
![]()
![]()
![]() h
h
![]()
![]() a
a
O
a
![]()
![]()
![]()
Рисунок 13.1
Из чертежа, когда груз
будет поднят на высоту ![]() ,
, ![]() ,
,
тогда  .
.
Работа нормальной реакции
![]() равна 0,
т.к. эта сила перпендикулярна перемещению
равна 0,
т.к. эта сила перпендикулярна перемещению ![]() .
.
Таким образом, сумма работ равна
![]()
![]() Дж.
Дж.
Берём модуль работы ![]() .
.
Пример 13.1.2. Шахтный
лифт движется вниз со скоростью ![]() . Масса лифта
. Масса лифта ![]() . Какую силу трения между
лифтом и стенками шахты должен развивать предохранительный парашют, чтобы
остановить лифт на протяжении пути
. Какую силу трения между
лифтом и стенками шахты должен развивать предохранительный парашют, чтобы
остановить лифт на протяжении пути ![]() , если канат, удерживающий лифт,
оборвался? Силу трения считать постоянной.
, если канат, удерживающий лифт,
оборвался? Силу трения считать постоянной.
Решение: изобразим на
рисунке силы, приложенные к материальной точке – силу тяжести ![]() и силу трения
и силу трения ![]() (см. рисунок 13.2).
Применим теорему об изменении кинетической энергии материальной точки
(см. рисунок 13.2).
Применим теорему об изменении кинетической энергии материальной точки
 .
.
Вычислим работу сил,
приложенных к лифту, на перемещении ![]()
![]() .
.
Работа сил тяжести положительна, т.к. груз опускается вниз
![]() .
.
Работа силы трения
отрицательна, т.к. угол между направлением ![]() и
и ![]() равен 180°.
равен 180°.
![]()
![]() O
O
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() s
s
![]()
x
Рисунок 13.2
Подставим эти значения в
теорему об изменении кинетической энергии, учтя, что в конечный момент лифт
остановился, т.е. ![]() .
.
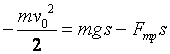 .
.
Отсюда определим
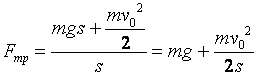 ,
,
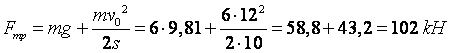 .
.
Задания для самостоятельного решения
№№ 30.1, 30.2, 30.3, 30.4, 30.5, 30.6, 30.7, 30.8, 30.9, 30.10, [1].
13.2 Динамика системы и твердого тела. Механическая система. Масса системы. Геометрия масс: центр масс материальной системы, моменты инерции твёрдого тела
Пример 13.2.1. Определить
траекторию центра масс механизма эллипсографа, состоящего из муфт A и B весом ![]() каждая, кривошипа ОС
весом
каждая, кривошипа ОС
весом ![]() и линейки
AB весом
и линейки
AB весом ![]() .
.
Дано ![]() . Считать, что линейка и
кривошип представляют однородные стержни, а муфты точечные массы.
. Считать, что линейка и
кривошип представляют однородные стержни, а муфты точечные массы.
Решение: выберем оси
декартовых координат (см. рисунок 13.3). Для определения
положения центра масс системы C надо найти его
координаты ![]() по
формулам
по
формулам
 .
.
Т.к. рассматриваемая система состоит из четырёх тел: муфт А и В, кривошипа ОС и линейки АВ, то
 ,
, 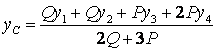 .
.
Как видно из рисунка,
![]() (т. А),
(т. А), ![]() (т. В),
(т. В),
![]() (т. С1),
(т. С1), ![]() (т. С),
(т. С),
![]()
 |
Тогда
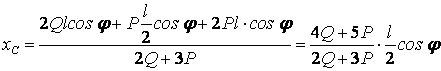 ,
,
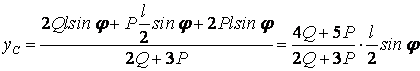 .
.
Для нахождения траектории центра масс надо из этих уравнений исключить время. Для этого возведём обе части каждого уравнения в квадрат и сложим
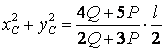 .
.
Итак, траекторией центра
масс является окружность с центром в т. О и радиусом  .
.
Пример
3.2.2.
Вычислить радиус инерции сплошного однородного цилиндра относительно оси z, перпендикулярной к оси цилиндра и отстоящей от его
центра тяжести C на расстоянии ![]() , если радиус цилиндра
равен
, если радиус цилиндра
равен ![]() , а высота
, а высота
![]() .
.
Решение: проведем ось ![]() через центр тяжести
цилиндра параллельно оси
через центр тяжести
цилиндра параллельно оси ![]() . Как известно, момент инерции цилиндра
относительно оси перпендикулярной оси цилиндра и проходящей через центр масс
цилиндра (табличная величина) и равен
. Как известно, момент инерции цилиндра
относительно оси перпендикулярной оси цилиндра и проходящей через центр масс
цилиндра (табличная величина) и равен
 .
.
По теореме Гюйгенса: ![]() , где
, где ![]() .
.
Определим
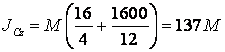 ,
,
![]() .
.
Связь между моментом инерции и радиусом инерции определяется по формуле
![]() .
.
Откуда определим радиус инерции цилиндра относительно оси z
 .
.
Задания для самостоятельного решения
№№ 35.1, 35.2, 35.3, 35.4, 35.5, 35.6, 35.10, 35.17, 35.19, 35.20, [1].
14 Теорема о движении центра масс. Теорема об изменении количества движения системы
14.1 Теорема о движении центра масс
Пример 14.1.1. Грузы Р1 и Р2 соединены нерастяжимой нитью, переброшенной через блок А, скользят по гладким боковым сторонам прямоугольного клина, опирающегося основанием ВС на гладкую горизонтальную плоскость (см. рисунок 14.1). Найти перемещение клина по горизонтальной плоскости при опускании груза Р1 на высоту h = 10 см. Вес клина Р = 4Р1 = 16Р2; массой нити и блока пренебречь.
Решение: изобразим все
внешние силы, приложенные к материальной системе, состоящей из призмы и двух
грузов. Внешними силами являются: ![]() – вес призмы,
– вес призмы, ![]() ,
, ![]() – весы грузов,
– весы грузов, ![]() – суммарная нормальная
реакция горизонтальной плоскости. Т.к. горизонтальная плоскость идеально
гладкая, то сила трения скольжения между клином и горизонтальной плоскостью
отсутствует. Направим ось x по горизонтали
направо и запишем теорему о движении центра масс системы в проекциях на эту ось
– суммарная нормальная
реакция горизонтальной плоскости. Т.к. горизонтальная плоскость идеально
гладкая, то сила трения скольжения между клином и горизонтальной плоскостью
отсутствует. Направим ось x по горизонтали
направо и запишем теорему о движении центра масс системы в проекциях на эту ось
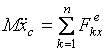 .
.
Т.к. все внешние силы
перпендикулярны к оси x, то ![]() .
.
Следовательно, ![]() ,
,
тогда ![]() .
.
 |
В начальный момент времени система находилась в покое, поэтому
С1 =
0, ![]() .
.
Отсюда следует, что ![]() , т.е. абсцисса центра
масс системы, независимо от перемещений отдельных масс, входящих в систему,
остаётся постоянной. Из определения центра масс системы вытекает, что
, т.е. абсцисса центра
масс системы, независимо от перемещений отдельных масс, входящих в систему,
остаётся постоянной. Из определения центра масс системы вытекает, что
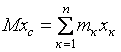 ,
,
т.к. все внешние силы
перпендикулярны к оси x, то ![]() .
.
Следовательно, ![]() ,
,
тогда ![]() .
.
В начальный момент времени система находилась в покое, поэтому
С1 =
0, ![]() ,
,
Отсюда следует, что ![]() , т.е. абсцисса центра
масс системы, независимо от перемещений отдельных масс, входящих в систему,
остаётся постоянной. Из определения центра масс системы вытекает, что
, т.е. абсцисса центра
масс системы, независимо от перемещений отдельных масс, входящих в систему,
остаётся постоянной. Из определения центра масс системы вытекает, что
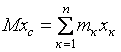 .
.
При t = 0 – начальный момент перемещения точек системы
![]() (см. рисунок 14.1, а).
(см. рисунок 14.1, а).
При t = t` – в конце перемещения
![]() .
.
Вычтем из второго уравнения первое, получим
![]() . или
. или ![]() ,
,
где Dх – искомое перемещение призмы.
При перемещении груза Р1 на высоту h
 .
.
Тогда груз Р2 получит перемещение
![]() .
.
Следовательно,
![]() ,
, ![]() .
.
Получим, выразив массы тел через их веса,
![]() .
.
Учтя, что P = 4Р1 = 16Р2 , получим
 ,
, ![]() .
.
Задания для самостоятельного решения
№№ 35.1, 35.2, 35.3, 35.4, 35.5, 35.6, 35.10, 35.17, 35.19, 35.20, [1].
14.2 Теорема об изменении количества движения материальной системы
Пример 14.2.1. Определить главный вектор количества движения маятника, состоящего из однородного стержня ОА весом Р1, длиной 4r и однородного диска В, весом Р2, радиуса r, если угловая скорость маятника в данный момент равна w (см. рисунок 14.2).
Решение: главный вектор количеств движения системы равен
![]() .
.
Наша система состоит из двух тел: стержня ОА с центром масс в точке С1 и диска В с центром масс в т. С2.
Следовательно,
![]() .
(*)
.
(*)
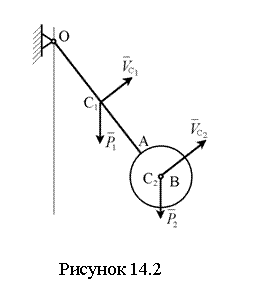 |
Точка С1 движется
по окружности с радиусом 2r, поэтому ![]() .
.
Точка С2
движется вокруг т. О по окружности радиуса 5r,
следовательно: ![]() .
.
Причём ![]() и
и ![]() направлены перпендикулярно
прямой ОВ.
направлены перпендикулярно
прямой ОВ.
Спроецируем векторное
равенство (*) на направление скоростей ![]() и
и ![]() , тогда
, тогда
 .
.
Пример 14.2.2. Ствол
орудия весит ![]() .
Вес снаряда равен
.
Вес снаряда равен ![]() .
Скорость снаряда у дульного среза
.
Скорость снаряда у дульного среза ![]() (см. рисунок 14.3). Определить скорость
свободного отката ствола орудия.
(см. рисунок 14.3). Определить скорость
свободного отката ствола орудия.
Решение: материальная
система состоит из ствола орудия и снаряда. Изобразим все внешние силы системы:
![]() – вес
ствола орудия,
– вес
ствола орудия, ![]() –
вес снаряда. Сила давления пороховых газов для данной системы является
внутренней и поэтому исключается.
–
вес снаряда. Сила давления пороховых газов для данной системы является
внутренней и поэтому исключается.
 |
Направим ось x по горизонтали направо. Запишем теорему об изменении главного вектора количеств движения системы в проекциях на Ox в дифференциальной форме
![]() ,
,
т.к. ![]() , то
, то ![]() .
.
Следовательно, имеет место случай сохранения проекций на ось x главного вектора количеств движения системы.
В начальный момент
система находилась в покое, т.е. ![]() , то и в любой момент
, то и в любой момент ![]() .
.
Обозначим скорость
откатывающихся частей в конечный момент через ![]() , абсолютная скорость снаряда задана
, абсолютная скорость снаряда задана ![]() .
.
Следовательно, 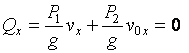 .
.
Отсюда находим:  .
.
Знак минус указывает, что
направление ![]() противоположно
противоположно
![]() .
.
Задания для самостоятельного решения
№№ 36.1, 36.2, 36.3, 36.4, 36.5, 36.7, 36.8, 36.9, 36.10, [1].
15 Теорема об изменении момента количества механической системы. Теорема об изменении кинетической энергии системы
15.1 Теорема об изменении момента количества механической системы. Дифференциальное уравнение вращения твёрдого тела вокруг неподвижной оси
Пример 15.1.1. Упругую проволоку, на которой подвешен однородный шар с радиусом r и массой m, закручивают на угол j0, а затем предоставляют ей свободно раскручиваться. Момент, необходимый для закручивания проволоки на один радиан, равен C.
Определить движение, пренебрегая сопротивлением воздуха и считая момент силы упругости закрученной проволоки пропорциональным углу кручения j.
Решение: направим ось z по оси вращения твёрдого тела. На систему действуют:
сила тяжести шара ![]() и
сила упругости пружины, момент которой равен
и
сила упругости пружины, момент которой равен ![]() . Выберем направление отсчёта угла j по часовой стрелке, если смотреть с
конца оси z, тогда
. Выберем направление отсчёта угла j по часовой стрелке, если смотреть с
конца оси z, тогда ![]() против часовой стрелки (отрицателен),
т.к. противоположен положительному направлению.
против часовой стрелки (отрицателен),
т.к. противоположен положительному направлению.
Запишем дифференциальное уравнение вращения твёрдого тела вокруг неподвижной оси
![]() ,
,
где![]() момент инерции шара, известен и
равен
момент инерции шара, известен и
равен ![]() .
.
Момент силы тяжести относительно оси z равен 0.
Следовательно
![]() или
или ![]() , т.е.
, т.е. ![]() , где
, где 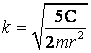 .
.
Это однородное дифференциальное уравнение. Решение его известно
![]() ,
, ![]() .
.
Определим произвольные постоянные:
при ![]() .
.
Таким образом, уравнением вращения является
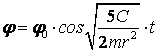 .
.
Задания для самостоятельного решения
№№ 37.1, 37.2, 37.3, 35.4, 37.5, 37.6, 37.7, 37.8, 37.9, 37.10, [1].
15.2 Теорема об изменении кинетической энергии материальной системы
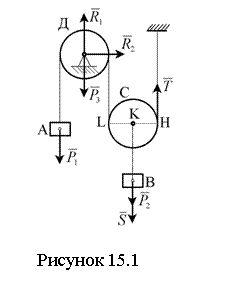
Пример 15.2.1. Груз A весом Р1 опускается вниз при помощи троса, перекинутого через неподвижный блок D, поднимает вверх груз В весом Р2, прикреплённый к оси подвижного блока С. Блоки С и D считать однородными сплошными дисками весом Р3 каждый (см. рисунок 15.1).
Определить скорость груза A в момент, когда он опустится на высоту h. Массой троса, проскальзыванием по ободом блоков и силами сопротивления пренебречь. В начальный момент система находилась в покое.
Решение: направим ось S через центр масс K подвижного блока C по вертикали вниз. Считаем положительным направление угла поворота блока D против часовой стрелки, а блока C – против часовой стрелки. Радиусы блоков обозначим через r. Запишем теорему об изменении кинетической энергии в интегральной форме
 .
.
Т.к. нить, охватывающая
блоки D, C и груз
C, не растягивается, то ![]() , а в начальный момент система
находилась в покое, то Т1 = 0.
, а в начальный момент система
находилась в покое, то Т1 = 0.
Поэтому уравнение (59) примет вид:
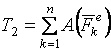 .
.
Изобразим внешние силы
системы: силы тяжести грузов ![]() ,
, ![]() ; блоков –
; блоков – ![]() ;
; ![]() ,
, ![]() – составляющие реакции оси блока;
– составляющие реакции оси блока; ![]() – реакция нити.
– реакция нити.
Дадим элементарное
перемещение ![]() центру
масс K блока C по
вертикали вверх. Блок C совершает
плоскопараллельное движение и имеет мгновенный центр скоростей в т. P. Перемещение точки обода L
диска C равно
центру
масс K блока C по
вертикали вверх. Блок C совершает
плоскопараллельное движение и имеет мгновенный центр скоростей в т. P. Перемещение точки обода L
диска C равно ![]() . Следовательно, перемещение груза A также равно
. Следовательно, перемещение груза A также равно ![]() .
.
 |
Вычислим элементарную работу всех внешних сил системы

Находим:
![]() ;
;
![]() (точка приложения веса тела D неподвижна);
(точка приложения веса тела D неподвижна);
![]() (ось s
направлена вниз, а тело B – движется вверх);
(ось s
направлена вниз, а тело B – движется вверх);
![]() ;
;
![]() (реакция нити в мгновенном
центре скоростей H);
(реакция нити в мгновенном
центре скоростей H);
![]() ;
;
![]() (точка приложения сил
(точка приложения сил ![]() и
и ![]() неподвижна).
неподвижна).
Таким образом
![]() .
.
Для определения полной работы возьмём от (63) определённый интеграл от 0 до S
![]() .
.
Переходим к вычислению кинетической энергии системы, в состав которой входят массы двух грузов и двух блоков. Запишем
![]()
Обозначим через ![]() скорость груза A.
скорость груза A.
Тогда угловая скорость
блока D равна wD = v/r; скорость точки L равна
также ![]() , а
скорость точки K и груза B
равна v/2 (см. рисунок 15.2).
, а
скорость точки K и груза B
равна v/2 (см. рисунок 15.2).
Мгновенная угловая
скорость блока C равна: ![]() .
.
Грузы A и B движутся поступательно, поэтому
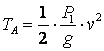 ,
, 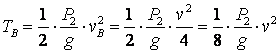 .
.
 |
Блок C совершает плоское движение
 , т.к.
, т.к.  ,
, ![]() ,
,
то
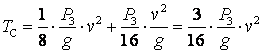 .
.
Блок Д вращается вокруг неподвижной оси
 .
.
Найдём кинетическую энергию системы:
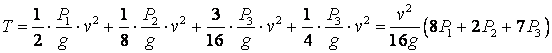 .
.
В конечном положении ![]() , а перемещение груза A равно
, а перемещение груза A равно ![]() .
.
Получим
 .
.
Отсюда определим скорость груза A
 .
.
Задания для самостоятельного решения
№№ 38.1, 38.2, 38.3, 38.4, 38.5, 38.6, 38.7, 38.8, 38.9, 38.10, [1].
Список литературы
1. Мещерский И.В. Сборник задач по теоретической механике: Учеб. пособие. М., 2002.
2. Сборник коротких задач по теоретической механике: Учеб. пособие для втузов / Под ред. О.Э.Кепе. – М.: Высшая школа, 1989.
3. Сборник заданий для курсовых работ по теоретической механике. Учеб. пособие./Под ред. А.А.Яблонского. - М.: Высшая школа, 1985.
4. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики. Учебник: в 2-х т. - М.: Наука, 2002.
5. Никитин Н.Н. Курс теоретической механики. Учебник. - М.: Высшая школа, 1990.
6. Тарг С.М. Краткий курс теоретической механики. Учебник. - М.: Наука, 2002.
Сводный план 2012 г., поз. 244