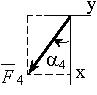Некоммерческое акционерное общество

АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра инженерной графики и прикладной  механики

 

 

   

ПРИКЛАДНАЯ МЕХАНИКА 

Методические указания и задания к выполнению расчетно-графических работ

для студентов всех форм обучения специальностей

5B070200 – Автоматизация и управление,

5B071700 – Теплоэнергетика

 

 

Алматы 2012

     СОСТАВИТЕЛИ: Динасылов А.Д., Тойбаев С.Н., Иванов К.С. Прикладная механика. Методические указания и задания к выполнению расчетно-графических работ для студентов всех форм обучения специальностей 5B070200 – Автоматизация и управление, B071700 – Теплоэнергетика. - Алматы:  АУЭС,  2011. – 48 с.

Дисциплина «Прикладная механика» для студентов высших учебных заведений, обучающихся по специальностям бакалавриата 5B070200 – Автоматизация и управление, и 5B071700  – Теплоэнергетика, является дисциплиной по выбору. В данной методической разработке приводятся  задания к расчетно-графическим работам, методические указания к их выполнению, примеры выполнения работ. Дан список рекомендуемой литературы.

Ил. 30, табл. 16, библиогр. – 10 назв.

 

Рецензент: канд. техн. наук, ст. препод. А.Т.Нурмагамбетова

  

Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2011 г.                        

 

© НАО «Алматинский университет энергетики и связи», 2012 г.

Содержание 

1 Общие   требования   и  указания   к    выполнению расчетно-графических работ

 4

2  Задачи, входящие в расчетно-графические работы, указания к их выполнению и примеры                                                                                            

 5

 

2.1 3адача 1. Равновесие пространственной системы сил

5

 

2.2 3адача 2. Задача на применение теоремы об изменении   кинетической энергии системы   

 8

 

2.3 3адача 3. Кинематический анализ механизма

13

 

2.4 3адача 4. Кинетостатический анализ механизма

25

 

2.5 Задача 5. Расчет на прочность при растяжении-сжатии

30

 

2.6 3адача 6. Расчеты на прочность и жесткость при кручении

33

 

2.7 Проектный расчет на прочность при изгибе

44

Приложение А. Схемы механизмов и исходные данные к задачам 3 и 4

42

Список литературы     

47

 

1 Общие   требования   и  указания   к    выполнению

расчетно-графических работ

 

Согласно учебным планам студенты, обучающиеся по специальности «Автоматизация и управление», выполняют 3 расчетно-графические работы (РГР), а обучающиеся по специальности «Теплоэнергетика» выполняют 4 РГР по дисциплине «Прикладная механика» в соответствии с числом кредитов, отводимых на изучение дисциплины. Тематика РГР относится к разделам «Теоретическая механика», «Теория механизмов» и «Сопротивление материалов» курса.

Условия задач приведены в десяти схемах и десяти вариантах. Студент должен взять для выполнения номер схемы, который показан римскими цифрами на соответствующем рисунке, по последней цифре шифра зачетной книжки, а вариант с цифровыми данными из соответствующей таблицы – по предпоследней цифре шифра. Так, студент, зачетная книжка которого имеет шифр 96472, должен для каждой задачи выбрать схему II и цифровые данные, соответствующие варианту 7. Если последняя цифра шифра нуль, то следует взять схему X, а если предпоследняя цифра нуль, то данные из таблицы принимаются по варианту 10.

При окончательной сдаче РГР каждая работа должна быть сброшюрована отдельно. Выполненная работа состоит из текстовой и графической частей. Оформление работы должно выполняться четким почерком на листах белой бумаги формата А4. Объем графической части в задачах 3 и 4 - два листа формата А3 (по одному на задачу). В этих задачах каждое графическое построение или группа однотипных построений должны иметь поясняющую надпись и масштабный коэффициент (с размерностью), который следует выбирать так, чтобы построения были доста­точно крупными, и листы не имели пустых мест.

 Каждая РГР должна содержать титульный лист, и по каждой задаче, входящей в РГР, должны быть приведены задания, выполненные расчеты, графические построения, выводы. Работа должна быть оформлена согласно принятым нормам (СТП 768-01-07-97); на листах текст должен быть только с одной сто­роны, в конце каждой РГР должен быть приведен список использованной литературы. Как графическая, так и расчетная  часть работы, а также текстовый материал могут быть выполнены с помощью компьютерных средств.

Для студентов специальности «Автоматизация и управление» РГР №1 включает задачи 1, 2, РГР№2 – задачу 3, РГР№3 – задачи 5, 6, 7. Студенты специальности «Теплоэнергетика», кроме перечисленных выше работ, выполняют еще РГР №4, включающую в себя задачу 4.

Прежде чем приступать к решению задачи, студент должен ознакомиться с соответствующим теме задачи теоретическим материалом по лекциям, учебникам и учебным пособиям, а также с указаниями к решению задачи и с примером выполнения работы, приведенными в данной методической разработке.

Выполненные РГР должны быть защищены студентов. Для защиты надо решить подобную задачу или ответить на 4-5 вопросов по теме.

 

2 Задачи, входящие в расчетно-графические работы, указания к их выполнению и примеры

 

2.1 Задача 1. Равновесие пространственной системы сил

 

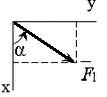
Однородная прямоугольная плита весом P = 6 кН со сторонами AB = 3l, BC = 2l закреплена в точке A сферическим шарниром, а в точке B цилиндрическим шарниром (подшипником) и удерживается в равновесии невесомым стержнем CC' (см. рисунок 1). На плиту действует пара сил с моментом М = 6 кН·м, лежащая в плоскости плиты, и две силы. Значения этих сил, их направления и точки приложения указаны в таблице 1; при этом силы  и  лежат в плоскостях, параллельных плоскости xy, сила  - в плоскости, параллельной плоскости xz, сила - в плоскости, параллельной плоскости yz. Точки приложения сил (D, E, H) находятся в серединах сторон плиты.

Т а б л и ц а 1

Сила

 

F1=14 кH

F2=16 кH

F3=8 кH

F4=10 кH

 

Номер условия

Точка прилож.

a1

Точка прилож.

a2

Точка прилож.

a3

Точка прилож.

a4

1

D

60

–

–

E

0

–

–

2

H

90

D

30

–

–

–

–

3

–

–

E

60

–

–

D

90

4

–

–

–

–

D

60

H

0

5

E

0

–

–

H

60

–

–

6

–

–

D

60

H

0

–

–

7

–

–

H

30

–

–

D

0

8

E

30

H

90

–

–

–

–

9

–

–

–

–

D

0

E

60

10

–

–

E

90

D

30

–

–

 

 

 

Требуется определить реакции связей в точках А, B и C.

При окончательных подсчетах принять l = 1,0 м.

Указания. Эта задача является задачей на равновесие тела под действием пространственной системы сил. При ее решении нужно учесть, что реакция сферического шарнира (или подпятника) имеет три составляющие, а реакция цилиндрического шарнира (подшипника) – две составляющие, лежащие в плоскости, перпендикулярной оси шарнира. При вычислении моментов силы зачастую удобно разложить ее на составляющие и , параллельные координатным осям; тогда, по теореме Вариньона, и т.д.

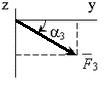
Пример 1 - Вертикальная плита весом P (см. рисунок 2) закреплена сферическим шарниром в точке А, цилиндрическим подшипником в точке В и невесомым стержнем  DD´, лежащим в плоскости, параллельной плоскости yz. На плиту действуют сила  (в плоскости xz), сила  (параллельная оси y) и пара сил с моментом М ( в плоскости плиты).

Дано: P=5 кH, M=3 кH·м, F1=6 кH, F2=7,5 кH, α= 300, AB=1 м, ВС=2 м, СЕ=0,5АВ, ВК=0,5ВС.

Определить: реакции опор А, В и стержня DD´.

Решение:

а) рассмотрим равновесие плиты. На плиту действуют заданные силы ,  и пара сил с моментом М, а также реакции связей. Реакцию сферического шарнира разложим на три составляющие  ,, , цилиндрического подшипника – на две составляющие , (в плоскости, перпендикулярной оси подшипника), реакцию стержня направим вдоль стержня, предполагая, что он растянут;

б) для определения шести неизвестных реакций составляем  шесть уравнений равновесия для действующей на плиту пространственной системы сил:

                                                                                             (1)

                                                                             (2)

                                                              (3)

                                                                    (4)      (5)

                                                                        (6)

Для определения момента силы  относительно оси  разлагаем  на составляющие   и , параллельные осям x и z , и применяем теорему Вариньона. Аналогично можно поступить при определении моментов реакции  .

Подставив в составленные уравнения числовые значения всех заданных величин и решив эти уравнения, найдем, чему равны искомые реакции.

Ответ: XA=-5,2 кН, YA=-3,8 кН, ZA=28,4 кН, YB=-7,5 кН, ZB=-12,4 кН, N=14,5 кН. Отрицательный знак указывает, что силы ,  и  направлены противоположно направлениям, показанным на рисунке 2.

 

2.2 Задача 2. Задача на применение теоремы об изменении кинетической энергии системы       

 

Механическая система (см. рисунок 3) состоит из грузов 1 и 2 (коэффициент трения грузов о плоскость f = 0,1), цилиндрического сплошного однородного катка 3 и ступенчатых шкивов 4 и 5 с радиусами ступеней R4 = 0,3 м, r4 = 0,1 м, R5 = 0,2 м, r5 = 0,1 м (массу каждого шкива считать равномерно распределенной по его внешнему ободу). Тела системы соединены друг с другом гибкими нерастяжимыми нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям. Под действием силы F = F(s), зависящей  от      перемещения    точки   приложения  силы,   система  приходит  в движение из состояния покоя. При движении системы на шкивы 4 и 5 действуют постоянные моменты сил сопротивления M4 и M5.

Значения масс и моментов сопротивлений принять по таблице 2; там же указана величина, которую требуется определить (здесь обозначено: v1 – скорость груза 1, vС3 – скорость центра масс катка, w4 – угловая скорость тела 4 и т.д.). Значение искомой величины нужно найти для момента времени, когда перемещение точки приложения силы F равно s1. В случае, когда какая-либо масса равна нулю, соответствующий груз  на схеме изображать не следует.

 

Т а б л и ц а 2

Вари- aнт

m1,

кг

m2,

кг

m3,

кг

m4,

кг

m5,

кг

M4,

Н м

M5, Н м

F = F(s), Н

s1, м

Найти

 

1

2

0

4

6

0

0

0.8

50 (2+3s)

1.0

v1

2

6

0

2

0

8

0,6

0

20 (5+2s)

1.2

w5

3

0

4

6

8

0

0

0.4

80 (3+4s)

0.8

vC3

4

0

2

4

0

10

0.3

0

40 (4+5s)

0.6

v2

5

8

0

2

6

0

0

0.6

30 (3+2s)

1.4

w4

6

8

0

4

0

6

0.9

0

40 (3+5s)

1.6

v1

7

0

6

2

8

0

0

0.8

60 (2+5s)

1.0

w4

8

0

4

6

0

10

0.6

0

30 (8+3s)

0.8

w5

9

6

0

4

0

8

0.3

0

40 (2+5s)

1.6

vC3

10

0

4

6

10

0

0

0.4

50 (3+2s)

1.4

v2

Указания. Задача 2 является задачей на применение теоремы об изменении кинетической энергии системы (раздел «Основы динамики твердого тела и системы»). При решении задачи следует учитывать, что кинетическая энергия системы равна сумме кинетических энергий всех входящих в систему тел. Эту энергию надлежит выразить через ту  скорость,  которую  требуется  определить в задаче.

При вычислении энергии катка, находящегося в плоскопараллельном движении, для установления зависимости между угловой скоростью и скоростью его центра масс нужно воспользоваться понятием о мгновенном центре скоростей. При определении работы все перемещения следует выразить через заданное перемещение s1, учитывая, что зависимость между перемещениями будет такой же, как между соответствующими скоростями.

Пример 2 - Механическая система (см. рисунок 4) состоит из сплошного цилиндрического катка 1, ступенчатого шкива 2 с радиусами ступеней  r2 и   R2 (массу шкива считать распределенной равномерно по его ободу) и груза 3 (коэффициент трения груза о плоскость равен f). Тела системы соединены между собой гибкими нерастяжимыми нитями, намотанными на шкив 2. Под действием силы  F =F(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя. На шкив при движении действует момент сил сопротивления  M2.

Определить: скорость центра масс катка vС1 в момент времени, когда  s =s1.

Дано:   m1 = 4 кг;  m2 = 10 кг;  m3 = 8 кг; R2 = 0,2 м;  r2 = 0,1 м;  f = 0,2;   M2 =0,6 Н·м;   F = 2(1 +2s) Н;  s1 = 2 м.

Решение.

Рассмотрим движение неизменяемой механической системы, состоящей из тел 1, 2 и 3, соединенных нитями. Изобразим все действующие на систему внешние силы: активные , момент сопротивления M2, реакции  и силы трения  .

Скорость vС1 будем определять, исходя из теоремы об изменении кинетической энергии системы, согласно которой для неизменяемой механической системы изменение кинетической энергии за какое-либо время движения равно сумме работ, которые совершают все внешние силы, действующие на систему, за тот же отрезок времени

T-T0  = .                                                               (1)

Определяем  T0 и T. Т.к. в начальный момент система находится в покое, то T0 = 0. Величина T равна сумме энергий всех тел системы

      T = T1+T2+T3.                                                             (2)

Учитывая, что тело 1 движется плоскопараллельно, тело 3 – поступательно, а тело 2 вращается вокруг неподвижной оси, получаем

T1 = ,      T2 = ,       T3 = .                (3)

Все скорости, входящие в это выражение, нужно выразить через искомую скорость vС1. Учитывая, что точка K1 является мгновенным центром скоростей катка 1, и, обозначив радиус катка через  r1, получаем

      ,        ,       .                    (4)

Моменты инерции определяются как

                          IC1 = 0,5m1·r,              I2 = m2·R,                                      (5)

Подставляя выражения (6) и (5) в формулы (3) и используя равенство (2), получаем

                  T = .                                               (6)

Находим сумму работ всех действующих на систему сил на перемещениях, соответствующих перемещению  точки С1 на величину s1. При этом все перемещения выразим через  s1, для чего учтем, что зависимости между перемещениями имеют такой же вид, как зависимости между соответствующими скоростями в формулах (4), то есть:  φ2 = s1/R2,  s3 = s1∙ (r2/R2). Тогда

                    W() = ,

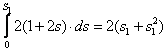                     W() = G1·s1·sin60˚,       

                    W() = - M2·= - M2∙,

                    W() = - G3·s3sin30˚= - G3·s1∙sin30˚,

                    .

Работа остальных сил равна нулю, так как точка  K1, где приложены силы   и – мгновенный центр скоростей, точка O, где приложены   и , неподвижна, а реакция  перпендикулярна перемещению груза 3. Тогда окончательно

             (7)
Подставляя выражения (6) и (7) в уравнение (1) и учитывая, что  T0 = 0, получаем

  

    (8)

Подставляя сюда числовые значения, найдем  vC1= 0,23 м/с.

 

2.3 Задача 3. Кинематический анализ механизма

 

Для заданных схемы механизма (см. рисунки А.1-А.10 в приложении А), варианта числовых данных (см. таблицы А.1-А.10 в приложении А) и расчетного положения требуется выполнить следующее:

а) провести структурный анализ механизма;

б) построить план положений механизма (при общем изображении стойки). Размеры звеньев согласно обозначению их точек на схеме механизма и угловой скорости  входного звена 1 указаны в соответствующем вертикальном столбце таблицы числовых данных;

в) для расчетного положения механизма построить план скоростей. На плане показать векторы скоростей всех точек, обозначенных на схеме механизма буквами, в том числе и точек  S - центров масс звеньев, которые при стержневой форме звена считать находящимися на серединах их полных длин;

г) построить план ускорений механизма для расчетного положения механизма. Найти векторы ускорений всех точек, указанных в пункте в.

Указания. Для успешного выполнения задания рекомендуется:

а) изучить теоретический материал по теме  работы, используя учебную  и методическую литературу, например, [2-4], а также конспект лекций;

б) проработать   материал §6 сборника задач [4]: ознакомиться с методическими указаниями, содержащими подробно разобранные примеры (с.37-39, 43-56);  просмотреть задачи 91-126, ответы к которым приведены в графической форме;

в) для задач 3 и 4, кроме номера схемы и варианта, задается расчетное положение механизма, которое следует принять по третьей от конца цифре шифра зачетной книжки. 

Пример 3 - Для схемы механизма (см. рисунок 5) и числовых данных, приведенных в таблице 3, выполнить решение по приведенным выше условиям. В таблице 3, кроме размеров всех звеньев и скорости  входного звена, приведено значение угла поворота  соответствующее расчетному положению механизма.

Т а б л и ц а 3

w1,

c – 1

j1, град

lOA,

м

lAB,

м

lAC,

м

lCM,

м

lBC = lOU = lBU,

м

lDU,

м

 

15

15

0,05

0,096

0,028

0,18

0,1

0,06

 

1) Структурный анализ механизма

Задачей структурного анализа является определение класса механизма на основе классификации Ассура-Артоболевского, идея которой состоит в том, что любой плоский шарнирно-рычажный механизм может быть образован путём присоединения к ведущему звену (или звеньям) групп нулевой подвижности. Т.о., механизм можно представить состоящим из ведущего звена (или нескольких ведущих звеньев) и указанных групп звеньев, получивших название групп Ассура. Количество ведущих звеньев механизма определяется степенью подвижности  , вычисляемой по формуле Чебышёва

где  n – число подвижных звеньев;

 – число низших кинематических пар.

Шарнирно–рычажные механизмы характеризуются наличием только низших кинематических пар. К этой категории относится и исследуемый механизм. Определяем степень его подвижности .

Полученное значение  показывает, что в рассматриваемом механизме есть одно ведущее звено, которым является кривошип. Остальные звенья составляют группы Ассура. Простейшей группой Ассура является комбинация из двух звеньев (диад Сильвестра) и трёх кинематических пар, получивших название двухповодковых групп.

Расчленение механизма на структурные группы осуществляется методом попыток. Отсоединяя двухповодковую группу, проверяем степень подвижности оставшегося механизма. Если она не изменяется, то отсоединение произведено верно. При неудавшихся попытках следует пытаться расчленить механизм на группы более высокого порядка, например, трёхповодковые, состоящие их четырёх звеньев и шести кинематических пар и т.д.

Рассматриваемый механизм состоит из одного ведущего звена и двух двухповодковых групп (см. рисунок 6) и принадлежит к механизмам второго класса.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

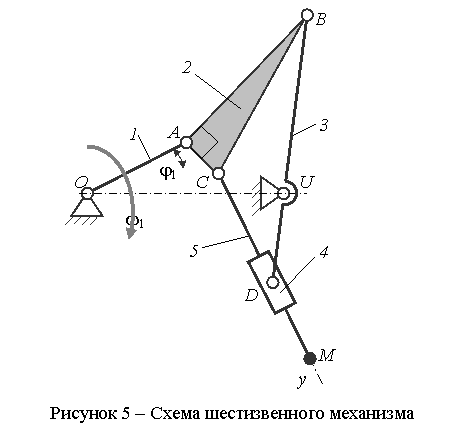
Расчленение механизма на группы Ассура в значительной мере облегчает дальнейшее проведение кинематического исследования механизма. В нашем случае:

общее количество звеньев,

количество подвижных звеньев,

количество кинематических пар 5-го класса,

кинематическая пара 5-го класса (вращательная),

кинематическая пара 5-го класса (вращательная),

кинематическая пара 5-го класса (вращательная),

кинематическая пара 5-го класса (вращательная),

кинематическая пара 5-го класса (вращательная),

кинематическая пара 5-го класса (вращательная),

кинематическая пара 5-го класса (поступательная).

Механизм образован присоединением к начальному механизму двух  групп Ассура 2-го класса: группы 1-го вида, состоящей из звеньев 2 и 3, и группы 3-го вида, состоящей из звеньев 4 и 5. Точку звена 5, совпадающую в рассматриваемом положении с точкой D, обозначим через . Формула строения механизма

1(1) ®2(2,3) ®2(4,5).

 

Из формулы строения механизма видно, что наивысший класс присоединённой группы – второй, поэтому данный механизм при ведущем звене 1 следует отнести ко второму классу (по Джолдасбекову).

 

 

 

 

 

 

 

 

 

 

Подпись: Рисунок 6 - Расчленение механизма на группы Ассура

 

2) Построение плана положений механизма

Обычно при проведении кинематического анализа механизма строят планы положений механизма. Планом положения называется графическое изображение взаимного расположения звеньев, соответствующее выбранному моменту времени. Так как во время движения механизма взаимное расположение звеньев всё время меняется, то для того, чтобы наглядно проследить за его движением, строят целый ряд последовательных планов положения механизма. Такое построение особенно удобно по отношению к механизмам с периодическим движением, у которых период равен времени одного оборота кривошипа. Последовательные планы положения механизма соответствуют в точности стробоскопическому эффекту его движения. Для подобных механизмов строят не менее 12 планов положения механизма.

Построение планов положения механизма имеет своей целью:

- использование его для дальнейших кинематических исследований;

- предохранение от ошибок при выборе размеров звеньев, так как размеры иногда могут быть выбраны такими, что механизм может заклинить;

- получение габаритов машины, так как можно говорить о габаритах машины только имея взаимное расположение звеньев для целого периода её движения.

Для построения планов положения механизма должны быть заданы кинематическая схема механизма, размеры звеньев, закон движения ведущего или начального звена.

В рассматриваемом движении данного механизма ведущее звено движется с постоянной угловой скоростью . Будем строить план положения механизма только для заданного расчетного положения.

Для подсчёта масштабного коэффициента длин    длиной звена  OA  на чертеже задаёмся произвольно. Длину отрезка , изображающего на чертеже размер ведущего звена, принимаем, например, равной 50мм. Тогда масштабный коэффициент длин схемы механизма будет ml = lOA/(OA) = 0,05/50 = 0,001 м/мм, и по нему из таблицы исходных данных длины всех звеньев и расстояния между точками переводим в миллиметры. При построении плана положения механизма пользуемся методом засечек. Вначале отмечаем на чертеже положение неподвижных точек O и U. По заданному начальному углу  строится положение ведущего звена, и определяем положение точки  A. На этом чертеже строится план положения групп Ассура. Положение точки B определяем методом засечек, проводя дуги окружностей с центрами в точках A и U. Пересечение этих дуг даст точку  B. Положение точки  C  находим на пересечении дуг окружностей с центрами в точках A и D и радиусами, равными (AC) и  (BC) соответственно. Так как, судя по заданным сторонам, треугольник ABC прямоугольный, то можно положение точки C найти, другим путём – нужно провести от точки A линию, перпендикулярную построенной стороне  (AB), и на этом направлении отложить отрезок  (AC). При этом обход контура треугольника должен быть таким же, как в заданной исходной схеме. Далее, на продолжении линии BU  по длине отрезка DU  получим точку D. Через точки  C  и  D  проводим направление  Cy и, откладывая на нём отрезок  (CM), получаем точку  M.

 

,  

 мм, 

     

                         

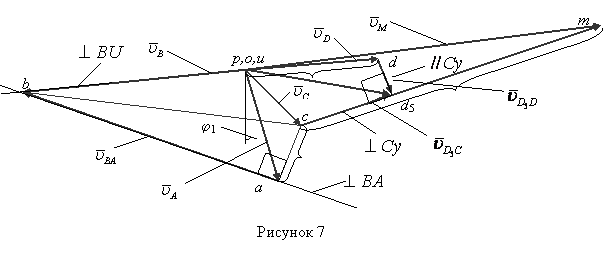
3)  Построение плана скоростей

 

Для данного положения механизма определяются скорости точек графическим методом (см. рисунок 5). Вначале определяем скорость точки  , принадлежащей ведущему звену, которое вращается равномерно с постоянной угловой скоростью . Скорость этой точки по модулю равна  и направлена перпендикулярно оси звена  OA  в сторону вращения. Отложим (см. рисунок 7) от произвольной точки  p, называемой полюсом плана скоростей, отрезок (pa). Длину отрезка (pa) выбираем равной (OA):  (pa) =(OA)= 50 мм. Вычисляем масштабный коэффициент скоростей

.

Строим план скоростей для группы звеньев 2 и 3. Определяем скорость точки  B  по следующим двум векторным уравнениям

где   - скорость точки  ,  нам известная;

 - скорость точки  B  при вращении звена  BA  вокруг оси шарнира A, по модулю равная    (– угловая скорость звена BA, которая пока нам неизвестна) и направленная перпендикулярно линии  BA;

 – скорость точки  U  стойки  6 (она равна нулю, так как звено  6  неподвижно);

 –  скорость точки  B  при вращении звена  BU вокруг оси шарнира  U, по модулю равная   ( - угловая скорость звена  BU, которая пока нам неизвестна) и направленная перпендикулярно линии  BU.

Построение плана скоростей ведём в такой последовательности. Строим решение первого векторного уравнения, указанного выше: из точки   проводим направление скорости  изображающий   - линию, перпендикулярную  BA. Строим решение второго векторного уравнения: из точки  p  надо отложить скорость  , но она равна нулю, поэтому точку  u  совмещаем с полюсом плана скоростей  p;  из точки u  или, что то же, p  проводим направление скорости   - линию, перпендикулярную BU, до пересечения с линией, проведённой перпендикулярно  BA, и получаем точку  b - конец вектора скорости точки  B. Помещаем в полюс плана точку O. Скорость точки  C находим по правилу подобия треугольников: . От точки a проводим линию, перпендикулярную отрезку  (ab). На этой линии лежит точка c.

Составляем пропорцию

Затем откладываем на проведённой линии от точки  a отрезок  (ac). Точку c соединяем с полюсом плана p. Вектор (pc) изображает абсолютную скорость точки  C.

Точку d (конец вектора скорости точки D) находим аналогично

Переходим к построению плана скоростей группы звеньев 4 и 5. Этот план строим по векторным уравнениям

где   – скорость точки    звена  5, которая лежит под точкой  D;

 – скорость точки C, она найдена предыдущим построением (отрезок );

– скорость точки  во вращении звена 5 относительно точки C, по модулю равная    и направленная перпендикулярно  (пока нам неизвестна);

– скорость точки D , она найдена предыдущим построением (отрезок );

– скорость точки  относительно точки D, по модулю неизвестная и направленная параллельно линии . Построение плана сведётся к проведению через точку  линии, перпендикулярной  (направления скорости  ), и через точку    линии, параллельной   (направления скорости , точка ). Точка пересечения этих линий является концом вектора скорости точки    (отрезок ). Точку  m – конец вектора скорости точки M во вращении вокруг полюса  C – находим по правилу подобия из соотношения

Полученную точку  m  соединяем с полюсом плана  p. Вектор   изображает абсолютную скорость точки M. На этом заканчиваем построение плана скоростей механизма.

Определяем скорость точки B73×0,015 » 1,1 м/c.

Определяем скорость точки  C 

34×0,015 = 0,51 м/c.

Определяем скорость точки  B относительно точки  A

 95×0,015 = 1,425 м/c.

Определяем скорость точки  D

 44×0,015 = 0,66 м/c.

Определяем скорость точки 

 м/c.

Определяем скорость точки    относительно точки  C

м/c.

Определяем скорость точки    относительно точки D

 м/c.

Определяем скорость точки  M

 м/c.

Определяем угловую скорость    звена AB

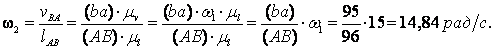Направление угловой скорости  может быть определено следующим образом. Мысленно прикладывая вектор  к точке  B, видим, что вращение звена  2  вокруг оси шарнира  A, принятой за полюс, происходит против вращения часовой стрелки. Отмечаем нужное направление вращения в виде дуговой стрелки на плане положения.

Определяем угловую скорость звена  BD

Направление угловой скорости    звена 3 определяется  таким же образом,  как и . Мысленно прикладывая вектор  к точке  B, видим, что вращение звена 3 вокруг оси шарнира U, принятой за полюс, противоположно направлению вращения часовой стрелки. Отмечаем нужное направление вращения звена в виде дуговой стрелки.

Определяем угловую скорость звена  CM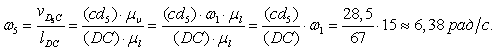

План скоростей механизма

Направление угловой скорости    звена 5  определяем следующим образом. Мысленно прикладывая вектор  к точке D, видим, что вращение звена 5 вокруг оси шарнира C, принятой за полюс, происходит против хода часовой стрелки. Отмечаем нужное направление вращения в виде дуговой стрелки на плане положения. Замечаем, что угловые скорости звеньев 4 и 5 совпадают, т.е. , так как эти звенья входят в поступательную кинематическую пару.

 

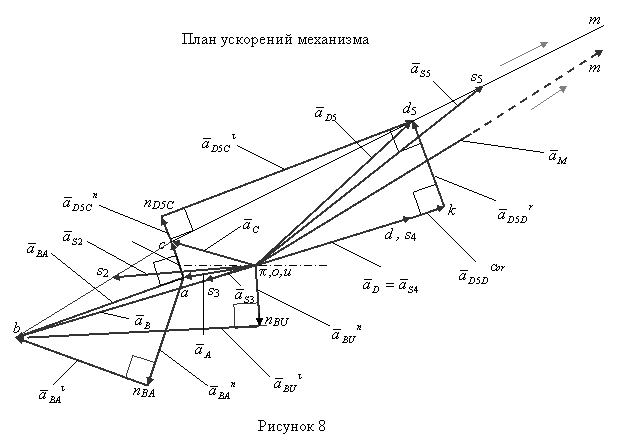
4) Построение плана ускорений

 

Ускорения точек находятся методом плана ускорений (см. рисунок 8). Строим план ускорений для группы звеньев  2  и  3. Этот план строится по двум векторным уравнениям

где   - полное ускорение точки  A, равное нормальному ускорению  , так как звено  1 (кривошип) вращается равномерно и угловое ускорение равно нулю, следовательно, равно нулю и тангенциальное ускорение  . Тогда  и оно направлено параллельно линии   от точки A  к точке  O (к центру кривизны траектории);

- нормальное ускорение точки  B  во вращательном движении звена  AB вокруг точки  A, по модулю равное

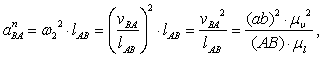
и направленное параллельно линии  AB  от точки  B к точке  A  ();

- тангенциальное ускорение точки  B в том же движении звена  AB, по модулю равное  ( - угловое ускорение звена  AB, пока нам неизвестное) и направленное перпендикулярно линии AB;

- ускорение точки  U, равное нулю, так как звено  6  неподвижно;

- нормальное ускорение точки  B во вращательном движении звена  BU  вокруг точки  U, по модулю равное

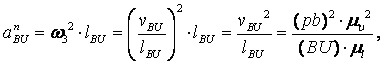
и направленное параллельно линии  BU   от точки  B   к точке  U  ();

- тангенциальное ускорение точки  B в том же движении звена  BU, по модулю равное  ( - угловое ускорение звена  BU, пока нам неизвестное) и направленное перпендикулярно линии  BU.

Построение плана ускорений ведём в следующей последовательности. Строим решение первого векторного уравнения, указанного выше, для чего от полюса плана  π  откладываем отрезок  , изображающий ускорение , параллельно линии  OA. Длину отрезка    принимаем равной  50 мм, тогда масштаб ускорений будет равен

.

От точки  a  откладываем отрезок , изображающий ускорение .  Длина отрезка   вычисляется так

         

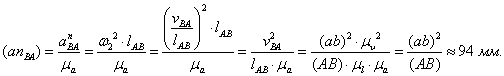
Через точку  проводим направление ускорения - линию, перпендикулярную линии  . Переходим к построению решения второго векторного уравнения, указанного выше. Для этого от полюса плана  π   откладываем вектор ускорения  , но оно равно нулю, поэтому точку u совмещаем с точкой π. От точки π  откладываем отрезок , изображающий ускорение  . Длина отрезка    вычисляется так

        

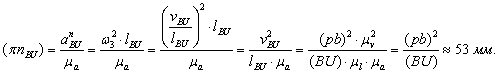
Через точку  проводим направление ускорения   прямую, перпендикулярную отрезку BU. Точка пересечения её с линией, проведённой перпендикулярно  AB, даёт точку b - конец вектора ускорения точки  B. Соединяем точки   и    и  получаем вектор полного ускорения точки  B при вращении звена  AB  относительно точки  A, т.е.   Точку  o  совмещаем с точкой  π (полюсом плана). Ускорение точки  C  находим, как и в плане скоростей, по правилу подобия треугольников: . Составляем пропорцию

Точку  d - конец вектора ускорения точки  D - находим по правилу подобия из соотношения

Переходим к построению плана скоростей группы звеньев 4 и 5. Сначала определим ускорение точки ,  которая принадлежит звену  5. Для этого пользуемся уравнениями

где   - ускорение точки  звена 5, которая в данный момент совпадает с точкой D;

 - ускорение точки  C (отрезок ), его изображающий, найден при построении плана ускорений для группы, состоящей из звеньев  2  и  3);

 - нормальное ускорение точки  во вращении звена 5  относительно точки C, по модулю равное

и направленное параллельно линии  Cy;

 - тангенциальное ускорение точки   в том же движении звена  5, равное по модулю   и направленное перпендикулярно  Cy;

ускорение точки D (отрезок  ), его изображающий, найден ранее);

ускорение Кориолиса в движении точки    относительно звена  4, по модулю равное  . Это ускорение  имеет направление вектора , повёрнутого на угол, равный 90°, в сторону вращения звена  5  или, что то же, звена  4 (звенья  4  и  5  входят в поступательную кинематическую пару, поэтому их угловые скорости одинаковы, т.е.  ). Ускорение  - релятивное ускорение точки    относительно точки D, неизвестное по модулю и направленное параллельно линии  Cy.

Строим решение первого векторного уравнения, указанного выше. От точки  c  откладываем отрезок ускорение  ,  длина которого

 далее через точку    проводим направление ускорения  линию, перпендикулярную  Cy.

Переходим к построению решения второго векторного уравнения, указанного выше. От точки  d  откладываем отрезок ускорении  Кориолиса  , длина которого

.

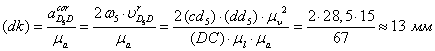Далее через точку  k  проводим направление релятивного ускорения  линию, параллельную Cy, до пересечения с ранее проведённой прямой, перпендикулярной  Cy  (т.е. направлением ускорения ). Точка    пересечения есть конец отрезка  , изображающего абсолютное ускорение  .

Точку m - конец вектора ускорения точки M находим по правилу подобия из соотношения

Соединяем полученную точку  m  с полюсом плана ускорений  π. Отрезок   изображает абсолютное ускорение точки M.

Величины абсолютных ускорений точек определяются так

,

,

.

По правилу подобия найдём ускорения центров масс подвижных звеньев. Точки    и    находятся на серединах соответствующих звеньев, а центр масс звена  4  (камня кулисы) совпадает с точкой D. На плане ускорений это будут векторы:  и . Определяем абсолютные величины ускорений этих центров масс

,

,

,

,

.

Величина углового ускорения звена  AB  равна

.

Направление углового ускорения    звена 2 (звена ) может быть определено следующим образом. Перенося мысленно вектор   в точку  , видим из точки , принятой за полюс, что направление    противоположно  направлению вращения часовой стрелки. Обозначаем направление углового ускорения    на плане положения звена   2  дуговой стрелкой.

Величина углового ускорения звена BD  равна

.

Направление углового ускорения   звена 3 (звена BU) может быть определено таким же образом, как и . Перенося мысленно вектор   в точку , видим из точки , принятой за полюс, что направление   противоположно  направлению вращения часовой стрелки. Обозначаем направление углового ускорения   на плане положения звена  3  дуговой стрелкой.

                 

 

 

 

 

 

 

 

 

 

                          

 

 

 

 

 

 

 

 

 

 

 

 

Величина углового ускорения звена 5 (звена  CM)  равна

.

Направление углового ускорения    звена 5 (звена CM) может быть определено таким же образом, как и  .  Перенося мысленно вектор   в точку D, видим из точки C, принятой за полюс, что направление    противоположно направлению вращения часовой стрелки. Обозначаем направление углового ускорения    на плане положения звена  5  дуговой стрелкой. Звенья  4  и  5  входят в одну поступательную кинематическую пару, поэтому их угловые ускорения совпадают, т.е. .

На этом кинематическое исследование механизма закончено.

 

2.4 Задача 4. Кинетостатический анализ механизма

 

Для схемы механизма, рассмотренной к задаче 3, используя результаты, полученные при решении этой задачи, требуется выполнить следующее:

а) определить инерционные нагрузки механизма в расчетном положении и нанести их на звенья, используя построенный в задаче 3 план ускорений. Массу  звеньев-стержней следует находить по их полной длине  и массе , приходящейся на 1 м длины звена: , приняв кг/м. Массу звеньев-ползунов определять по найденной массе  ведущего звена 1. Масса ползуна 3 в кривошипно-ползунном механизме , в синусном механизме массы ползунов 2 и 3 принять соответственно  и . Моменты инерции звеньев-стержней относительно оси, проходящей через центр масс  перпендикулярно плоскости движения, определять, как ;

б) определить реакции  в кинематических парах группы звеньев 2 и 3 от действия инерционных нагрузок и сил веса, не учитывая трения. Следует вычертить группу звеньев 2 и 3 и нанести на звенья действующие нагрузки. Рядом поместить план сил группы. Если какая-либо сила относительно мала и при достаточно больших векторах других сил должна изображаться вектором меньше миллиметра, то его на плане сил можно не показывать. Однако в общих буквенных выражениях и при подстановках в них значений следует приводить все силы и их плечи, пренебрегать действием силы можно только после того, как будет показана его незначительность по сравнению  с действием других сил;

в) определить уравновешивающий момент на кривошипе 1 и уравновешивающую силу, условно считая ее приложенной в точке  перпендикулярно кривошипу  для данного расчетного положения. Найти реакцию в опоре  учитывая действие уравновешивающей силы. Выяснить роль уравновешивающей силы в данном положении механизма: является она движущей силой или сопротивлением (уравновешивающей в истинном смысле). Следует изобразить отдельно ведущее звено со стойкой, показав действующие на стойку нагрузки, и рядом поместить план сил для ведущего звена.

Указания. Для успешного выполнения задания рекомендуется:

а) изучить теоретический материал по теме  работы, используя учебную  и методическую литературу, например, [2-4], а также конспект лекций;

б) проработать материал методических указаний к §9 сборника задач [4] с примером  (с.78-81) и изучить материал методических указаний к §12 того же сборника с примерами 1, 2 (с.103-109).

Пример 4 - Для механизма, кинематический анализ которого выполнен в примере 3, выполнить кинетостатический анализ по сформулированным выше условиям задачи.

Решение.

1) Определение веса звеньев механизма

Массой кривошипа зададимся, так как кривошип связан с маховиком. Массу звеньев-стержней находим по их полной длине  l  и удельной массе  q, приходящейся на один метр длины звена

= (0,1 + 0,06)×0,5 = 0,08 кг,

= 0,18×0,5 = 0,09 кг.

Массу звена-треугольника находим по его наибольшей стороне  , удельной массе q и коэффициента

кг.

Массу звена  4 (ползуна или камня кулисы) задаём равной  0,01 кг.

Определяем веса звеньев. Ускорение свободного падения  , тогда

                     0,25×9,8 = 2,45 H,           0,06×9,8 = 0,59 H,

0,08×9,8 = 0,784 H,       0,01×9,8 = 0,098 H,

                     0,09×9,8 = 0,088 H.

2)  Определение инерционной нагрузки на звенья механизма

Силы инерции определяем, используя построенный план ускорений. Сила инерции рассматриваемого звена равна

где m – масса звена, кг;

 –  ускорение центра масс звена, . Направление силы инерции   противоположно направлению вектора  . Её размерность - , то есть она измеряется в ньютонах (Н). Считаем, что звено совершает плоскопараллельное движение. При этом в качестве точки приложения сил инерции берём центр масс звена, так как при этом упрощается выражение момента пары сил инерции или инерционного момента. Он равен

Mu = - IS×e,

где  IS  (кг×м2) – момент инерции масс звена относительно оси, проходящей через его центр масс перпендикулярно плоскости его материальной симметрии, или, иначе, центральный момент инерции звена;

 – угловое ускорение звена, .

Инерционный момент  имеет размерность = Н×м. Плоскость, на которой он действует, параллельна плоскости движения звена, она направлена в сторону, противоположную направлению углового ускорения звена.

Сила инерции кривошипа по модулю равна

 » 0,25×5,6 » 1,4 H,

приложена в центре масс кривошипа  и по направлению противоположна вектору ускорения   этого звена.

Сила инерции звена  2 (шатуна) по модулю равна

 » 0,06×25,4 » 1,52 H,

 приложена в центре масс шатуна  и по направлению противоположна вектору ускорения    этого звена.

Сила инерции звена  3 (двуплечего коромысла) по модулю равна

 = 0,08×7,65 = 0,61 H,

приложена в центре масс этого звена   и по направлению противоположна вектору ускорения  .

Сила инерции звена  4 (ползуна или камня кулисы) по модулю равна

» 0,01×22,7 = 0,23 H,

приложена в центре масс  и по направлению противоположна вектору ускорения    этого звена.

Сила инерции звена  5 (кулисы) по модулю равна

» 0,09×40,7 = 3,66 H,

приложена в центре масс  и по направлению противоположна вектору ускорения    этого звена.

Инерционный момент звена 2 (шатуна), имеющего форму треугольника, равен

» 0,2·0,06·0,12·169 » 0,02Н·м

и направлен противоположно угловому ускорению  .

Инерционный момент  звена  3 (двуплечего коромысла), имеющего форму стержня, равен

 »  0,1·0,08·0,162·362 » 0,074 Н·м

и направлен противоположно угловому ускорению  .

Инерционным моментом звена  4 (ползуна или камня кулисы), из-за малых его размеров, пренебрегаем.   » 0.

Инерционный момент звена  5 (кулисы), имеющего форму стержня, равен

 » 0,1·0,09·0,182·547 » 0,16Н·м

и направлен противоположно угловому ускорению  .

3) Силовой расчёт механизма

В задачу силового расчёта входит определение всех сил и моментов пар сил, которые приложены к каждому отдельному звену механизма. Эти силы или моменты надо знать, например, для расчёта на прочность отдельных звеньев механизма или их частей (деталей). Для того чтобы механизм находился в равновесии пол воздействием внешних сил, к одному из звеньев его должна быть приложена уравновешивающая сила    или уравновешивающая пара сил, характеризуемая её моментом уравновешивающим моментом. Эту силу    или момент    обычно считают приложенными к ведущему звену. Так как при силовом расчёте механизма в число известных внешних сил, приложенных к его звеньям, входит инерционная нагрузка на звенья, то силовой расчёт механизма называется кинетостатическим. Трением в кинематических парах механизма пренебрегаем.

Проводится силовой расчёт каждой группы Ассура в отдельности, так как группа Ассура является статически определимой системой. Расчёт следует начинать с группы Ассура, присоединённой к механизму при его образовании в последнюю очередь; затем перейти к следующей группе и так до тех пор, пока не будет произведён силовой расчёт всех групп, образовавших ведомую часть механизма. В заключение производится силовой расчёт ведущего звена. Задачи решают графоаналитическим методом, используя известные из теоретической механики уравнения равновесия всей группы или отдельных её звеньев в форме

В число сил и моментов, входящих в эти уравнения, включаются реакции и моменты реакций в кинематических парах группы.

Для реакций, возникающих между элементами кинематических пар, приняты следующие обозначения: реакция со стороны звена   k  на звено l  обозначается  , реакция же со стороны звена l  на звено k  соответственно обозначается  . Очевидно, что .

a)    Силовой расчёт группы звеньев  4  и  5

Сначала показываем инерционную нагрузку на звенья данной группы Ассура (см. рисунок 9).

К звену  5  приложены следующие силы:  (реакция в шарнире  С  со стороны звена  2 на звено  5),  (реакция в точке  D  со стороны звена  3, направленная перпендикулярно направляющей поступательной пары, т.е. звену  5),  (сила инерции центра масс звена  5, приложенная в середине   звена),  (сила тяжести звена  5, приложенная там же),  (сила инерции центра масс звена  4, приложенная в точке  D),  (сила тяжести звена  4, приложенная там же) и пара сил инерции с моментом  .

             

 

 

 

 

 

 

 

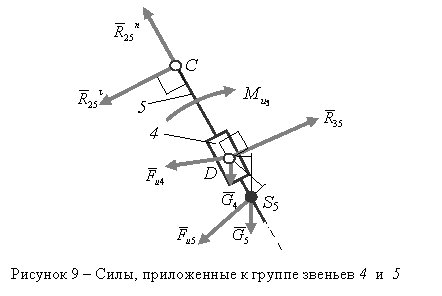
Составляем уравнение равновесия для группы

В этом уравнении содержатся три неизвестных: величина и направление реакции   и величина реакции  . Для того чтобы его решить, т.е. чтобы построить представленную им векторную сумму, разложим реакцию    на две составляющие: , направленную перпендикулярно оси звена CM и , направленную параллельно оси звена CM. Теперь геометрическая сумма сил, приложенных к группе, равна

Величину силы    найдём, рассматривая равновесие звена  5. Напишем равенство нулю суммы моментов относительно точки D всех сил, приложенных к звену  5  (тем самым исключим из него моменты неизвестных реакций   и ). Это уравнение пишется так:  , которое, будучи развёрнутым, примет вид

откуда

Здесь плечи известных сил найдены по чертежу (см. рисунок 9) и выражены в метрах. Остальные две неизвестные силы найдём по первому векторному уравнению равновесия всей группы. Для этого строим план сил в принятом масштабе сил (см. рисунок 10). Здесь масштабный коэффициент сил равен

.

 

 

 

 

 

 

 

 

 

 

 

 

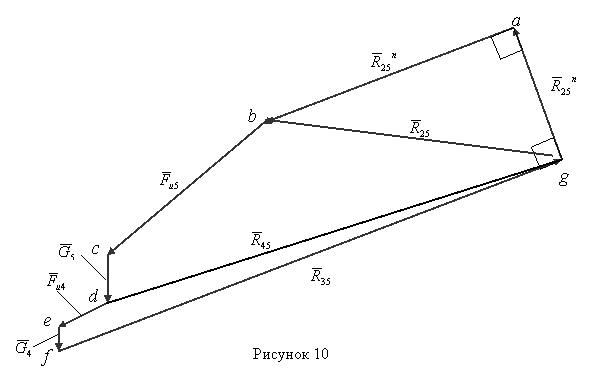Порядок построения векторной суммы безразличен, но применительно к группам Ассура можно рекомендовать следующий: назначаем обход контура группы в каком-либо направлении (например, по ходу часовой стрелки) и силы на плане откладываем в такой последовательности, в какой мы эти силы встречаем на группе при обходе её контура в выбранном направлении. В нашем случае принят обход контура по ходу часовой стрелки. Отложим:

 от точки a силу   в виде отрезка

от точки  b откладываем силу   в виде отрезка

от точки  c откладываем силу   в виде отрезка

от точки  d откладываем силу   в виде отрезка

от точки    откладываем силу    в виде отрезка

Через точку a проводим прямую, параллельную оси звена  CM. Это будет линия действия силы , а через точку f - прямую, перпендикулярную оси звена CM, которое является подвижной направляющей. Последняя  прямая будет линией действия силы   (в поступательной паре направление реакции всегда перпендикулярно оси направляющих пары, т.е. ). Находим точку  g пересечения этих двух прямых.

Отрезок    в масштабе    даёт искомую реакцию  , а отрезок   в том же масштабе – реакцию  , и, наконец, отрезок   даёт искомую реакцию . По полученным  отрезкам  вычисляем  модули  искомых  сил.   Реакция  

H.   Полная   реакция    H.    Реакция

 H.

Для определения реакции   запишем условие равновесия звена  5

На плане сил видно, что отрезок  в масштабе соответствует искомой реакции  . Тогда   H.

б) Силовой расчёт группы звеньев  2  и  3

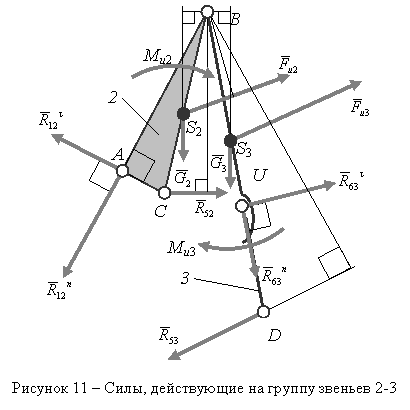
Сначала показываем инерционную нагрузку на звенья данной группы Ассура (см. рисунок 11). К звену  3  приложены следующие силы:  (реакция в шарнире A со стороны звена  1  на звено  2),  (реакция в шарнире  C со стороны звена  5  на звено  2),  (сила инерции центра масс звена  2),   (сила тяжести звена  2),  (сила инерции центра масс звена  3),   (сила тяжести звена  3),  (реакция в шарнире  U со стороны стойки  6  на звено  3),  (реакция в точке D со стороны звена  5  на звено  3), пары сил инерции с моментами    и  .

Составляем уравнение равновесия этой группы

 

 

 

 

 

 

 

 

 

 

 

 

Чтобы найти неизвестную  силу , используем уравнение моментов сил, приложенных к звену  2, относительно точки  B

 

Это уравнение с одним неизвестным. Отсюда находим

Размеры плеч сил = 0,047 м,   = 0,008 м  и  = 0,099 м  найдены по чертежу и выражены  в метрах.

Чтобы найти неизвестную  , используем уравнение моментов сил, приложенных к звену  3, относительно точки  B

  .

 

Из этого уравнения находим

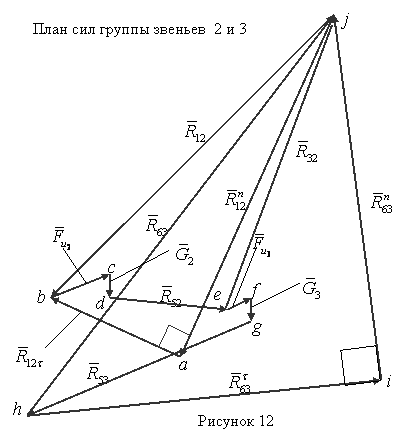
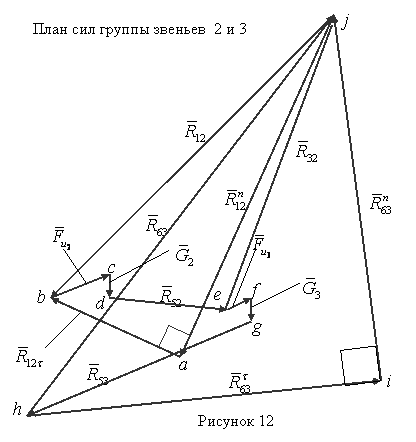
Строим план сил (см. рисунок 12) в масштабе

Отложим:

от точки  a силу   в виде отрезка

от точки  b откладываем силу   в виде отрезка

от точки  c откладываем силу   в виде отрезка

от точки  d откладываем силу   в виде отрезка

от точки  e откладываем силу   в виде отрезка

от точки  f  откладываем силу    в виде отрезка

от точки  g откладываем силу   в виде отрезка

от точки  h  отложим силу   в виде отрезка

 

 

 

 

 

 

 

 

 

 

 

                                                

 

 

 

 

 

 

 

 

 

 

 

 

 

Через точку  a проводим прямую, параллельную отрезку AB. Это будет линия действия силы  , а через точку  i - прямую, параллельную отрезку . Она будет линией действия силы . Находим точку пересечения  j  этих двух прямых. Отрезок  в масштабе    даёт искомую реакцию  , а отрезок   в том же масштабе – реакцию  . Отрезок   даёт полную реакцию  , и, наконец, отрезок   даёт полную искомую реакцию  .

Реакция  H.

Полная реакция  H.

Реакция  H.

Полная реакция  H.

Для нахождения реакции   напишем условие равновесия звена  2

                                      .

На плане сил видно, что отрезок   в масштабе    соответствует искомой реакции   Реакция   H.

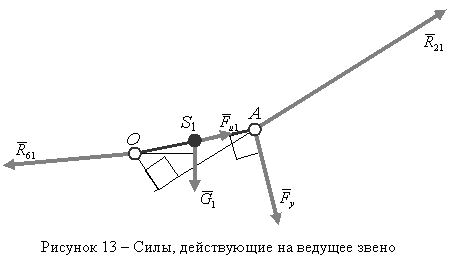
в) Силовой расчёт ведущего звена

К звену  1  приложены (см. рисунок 13) силы:   (реакция в шарнире  A  со стороны звена  2  на звено  1),  (уравновешивающая сила, приложенная в шарнире A перпендикулярно кривошипу OA),  (сила инерции центра масс звена 1, приложенная в середине звена ),  (сила тяжести, приложенная там же) и   (реакция в неподвижном шарнире O). Из этих сил неизвестными являются две силы:   (неизвестен модуль) и   (неизвестны модуль и направление).

Из уравнения моментов сил относительно точки O, приложенных к кривошипу (звено 1), находим величину момента уравновешивающей паря сил

  .

 

                             

 

 

 

 

 

 

Отсюда находим уравновешивающую силу  , считая её приложенной в точке  A  и действующей перпендикулярно к кривошипу

.

Для определения реакции    неподвижного звена  6  (стойки) на звено  1  составим уравнение равновесия сил, приложенных к кривошипу

.

Строим план сил (см. рисунок 14) по уравнению равновесия в том же масштабе сил  .

 

 

 

 

 

 

 

 

Отложим:

реакцию  от произвольной точки a в виде отрезка ;

уравновешивающую силу  – в виде отрезка ,;

силу инерции  – в виде

вес кривошипа  – в виде . 

Отсюда  по  длине  отрезка  (ea)   находим  модуль  реакции    как  

H. На этом кинетостатическое исследование механизма закончено.

 

2.5 Задача 5. Расчет на прочность при растяжении-сжатии

 

Для заданной схемы (см. рисунок 15) требуется проверить прочность стержней, работающих на растяжение и (или) сжатие, приняв допускаемое напряжение на растяжение [sр] = 160 МПа и на сжатие [sс] = 120 МПа. Данные взять  из  таблицы 4.

Указания. Задача 5 является задачей проверочного расчета на прочность при растяжении-сжатии. Для решения задачи следует проверить выполнение условия прочности для элементов конструкции, для чего следует сравнить расчетные напряжения с допускаемыми напряжениями. Расчетные напряжения определяются через значения продольных усилий в стержнях; для нахождения последних используются уравнения равновесия, которые в зависимости от расчетной схемы (произвольная плоская система или плоская система сходящихся сил) имеют тот или иной вид. Для плоской системы сходящихся сил можно составить два независимых уравнения равновесия, а для произвольной плоской системы сил можно составить три уравнения. Для  рассматриваемых в данной задаче схем в последнем случае необходимости в составлении всех трех уравнений равновесия нет, так как нас интересует только продольная сила в растянутом или сжатом стержне, поэтому можно обойтись одним уравнением равновесия.

Т а б л и ц а 4

Вари -ант

F1,

кН

F2,

кН

a,

град

b,

град

a,

м

b,

м

Сечения

стержней

1

2

 

1

40

35

50

45

0,7

0,7

уг 40´3

Æ25

2

45

30

55

40

0,6

0,4

2 уг 20´4

Æ11

3

50

25

60

35

0,5

0,7

2 уг 25´4

Æ12

4

55

20

65

40

0,4

0,8

уг 45´3

Æ14

5

60

15

70

45

0,8

0,5

2 уг 45´4

Æ16

6

40

35

50

45

0,7

0,7

2 уг 20´3

Æ18

7

15

45

25

60

1,2

0,8

уг 50´3

Æ20

8

20

50

30

65

1,0

0,7

уг 50´4

Æ20

9

25

55

35

70

0,8

0,6

2 уг 36´3

Æ12

10

30

60

40

75

0,9

0,5

2 уг 32´3

Æ10

Примечания

1 Обозначение уг 50´4 означает, что стержень изготовлен из равнобокого уголка с шириной полок 50 мм и толщиной полок 4 мм; обозначение 2 уг 403 означает, что стержень составлен из двух равнобоких уголков с шириной полок 40 мм и толщиной полок 3 мм; знак Æ означает, что стержень имеет круглое поперечное сечение с диаметром, указанным после этого знака.

2 На некоторых схемах рисунка 7 отдельные параметры, указанные в таблице 3, отсутствуют; в таких случаях численные значения этих величин не следует принимать во внимание.

            3 Для схем, где имеется два стержня, работающих на растяжение (сжатие), расчет следует выполнить для обоих стержней.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Пример 4 - Для заданной схемы (см. рисунок 16,а) проверить прочность стержня 1, работающего на растяжение или сжатие, приняв допускаемое напряжение на растяжение [sр]=160 МПа и на сжатие [sс]=120 МПа. Дано: F1 = 60 кН, a = 60°, а = 1,2 м,   b = 0,8 м, сечение стержня - 4 уголка 36´3.           

Условие прочности при растяжении-сжатии имеет вид

            где

σ – расчетное напряжение в поперечном сечении стержня;

N – нормальная (продольная) сила;

А – площадь поперечного сечения;

[σ] – допускаемое напряжение (на растяжение или сжатие соответственно тому, что испытывает стержень).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

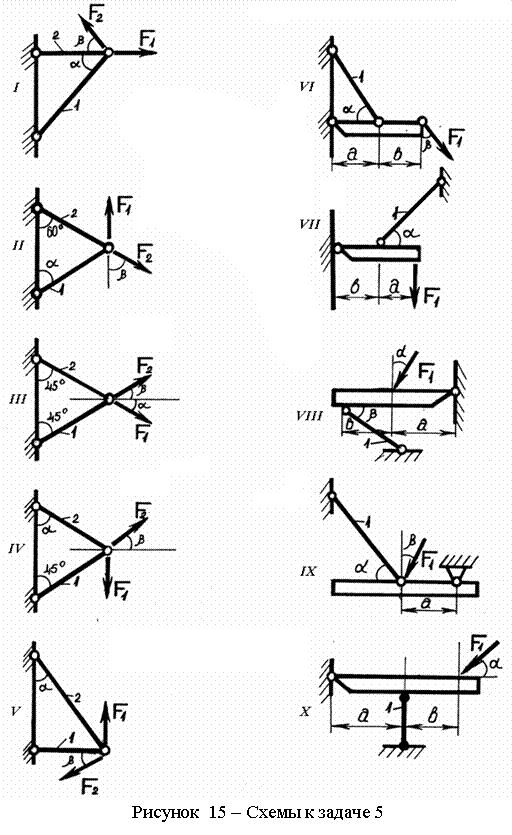Определим продольную силу в стрежне 1. Отбросим мысленно шарнирную опору в точке B, заменив ее действие двумя реакциями HA  и VA, а также разрежем стержень 1, заменив действие отброшенной части силой N (см. рисунок 8,б). Имеем произвольную плоскую систему сил. Три неизвестные силы HA, VA, и N могут быть определены из трех уравнений равновесия. Однако в рассматриваемой задаче реакции HA  и VA  можно не определять, так как нас интересует только нормальная сила N в стержне 1. Уравнение равновесия запишем в виде å МА = 0, тогда реакции HA  и VA  в него не войдут. Имеем

N×a - F1×(a+b)×sin a = 0,

откуда

N = F1×(a+b)×sin a)/а = 60 ×(1,2+0,8)×sin 60°/1,2 =   86,7 кН (стержень 1 сжат).

Определим площадь поперечного сечения стержня 1. Так как стержень представляет собой четыре уголка 36´3, то его поперечное сечение найдем как учетверенное значение площади поперечного сечения уголка, которое найдем в таблицах прокатных профилей. Находим Aуг = 2,1 см2 и площадь поперечного сечения стержня A=4Aуг=840 мм2.

Определим нормальные напряжения в поперечных сечениях стержней и сравним с допускаемым напряжением

Условие прочности выполняется для стержня  и для конструкции в целом.

 

2.6 Задача 6. Расчеты на прочность и жесткость при кручении

 

К стальному валу приложены четыре момента (см. рисунок 17, таблица 5). Требуется: построить эпюру крутящих моментов; при заданном значении допускаемого напряжения при кручении  определить диаметры вала d и d1 из расчета на прочность; построить эпюру максимальных касательных напряжений по длине бруса; вычислить угол закручивания концевого сечения вала при найденных размерах.

Указания. Задача 6 является задачей проектного расчета на прочность при кручении. Для решения задачи следует прежде всего построить эпюру крутящих моментов, а затем из условия прочности при кручении выразить полярный момент сопротивления поперечных сечений. Далее по формуле полярного момента нужно найти необходимые значения диаметров вала.

После того, как диаметры вала на двух участках будут определены, нужно построить эпюру максимальных касательных напряжений по длине бруса, причем на эпюре можно откладывать абсолютные значения максимальных касательных напряжений, так как для изотропного материала знак касательных напряжений не имеет значения. Последний пункт задания – определение угла закручивания концевого сечения вала - относится к расчетам на жесткость; здесь по найденным диаметрам надо подсчитать значения полярных моментов инерции, а затем воспользоваться формулой для определения угла закручивания.

 

Т а б л и ц а 5

Номер условия

 

Размеры, м

Моменты, кН·м

 

,

МПа

a

b

c

M1

M2

M3

M4

 

1

0,8

0,6

1,4

1,1

1,4

1,0

1,0

125

2

0,5

0,7

1,5

0,7

1,5

1,2

0,9

90

3

1,2

1,0

0,6

1,0

1,6

1,4

1,2

100

4

1,0

1,2

0,7

0,9

0,7

1,7

1,0

110

5

1,5

0,8

1,2

0,6

0,7

0,4

1,2

120

6

0,5

1,0

1,3

1,3

1,0

0,6

0,8

140

7

0,8

0,6

1,4

1,0

1,4

1,0

1,1

85

8

0,6

1,1

0,8

0,6

0,8

1,2

1,0

150

9

1,0

1,3

0,9

0,7

0,9

1,2

1,0

75

10

0,8

1,4

1,0

0,9

1,0

1,4

0,6

80

 

Пример 6 - Решить по приведенным выше условиям задачу для схемы, показанной на рисунке 18,а, приняв а = 1,1 м, b = 1,5 м, с = 1,2 м, [t] = 85 МПа, М1 = 0,8 кН×м, М2 = 1,1 кН×м, М3 = 1,7 кН×м, М4 = 0,6 кН×м.

Решение. Сначала построим эпюру крутящих моментов T. Для этого воспользуемся формулой  T=∑M и правилом знаков для крутящих моментов. Начинаем строить эпюру от незакрепленного конца вала (рисунок 18,б). Тогда

T4=M4=0,6 кН×м,

T3=-M3+M4=-1.1 кН×м,

T2=-M2-M3+M4=-2,2 кН×м,

T1=-M1-M2-M3+M4=3 кН×м.

Теперь по заданному значению допускаемого напряжения при кручении [t] определим диаметры вала d и d1 из расчета на прочность.

Найдём диаметр вала d, общий для двух участков слева. Из условия прочности вала при кручении следует, что полярный момент сопротивления поперечного сечения вала должен отвечать условию

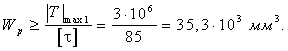
Так как для круглого сечения

, то

Аналогично найдём диаметр d1, общий для двух участков справа

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

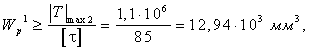
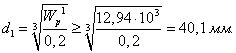
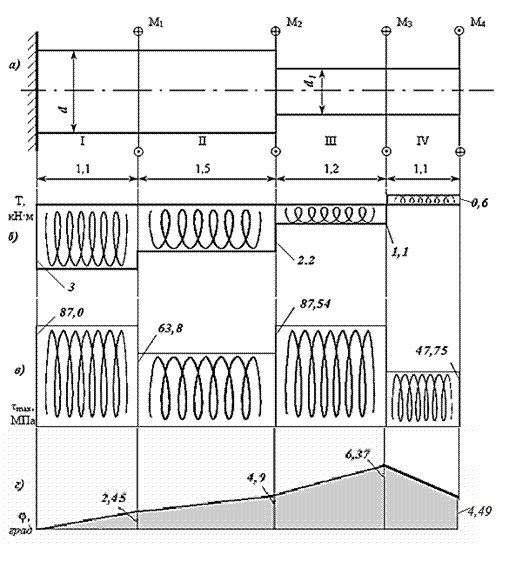Окончательно примем значения диаметров вала из ряда предпочтительных чисел d=56 мм и d1=40 мм. Очевидно, что при этом будет некоторая перегрузка по напряжениям, однако в дальнейшем мы убедимся, что она пренебрежимо мала.

Чтобы построить эпюру максимальных касательных напряжений τmax по длине бруса, сначала пересчитаем значения полярных моментов сопротивления. Найдем

,

.

Тогда τmax определятся, как

I участок:    ,

II участок:    ,

III участок: ,

IV участок: .

Как видим, максимальная перегрузка имеет место на 3-м участке и составляет

, что можно считать приемлемым.

Эпюра τmax приведена на рисунке 18,в.

Вычислим угол закручивания концевого сечения вала при найденных размерах. Для этого предварительно определим значения полярных моментов инерции поперечных сечений вала, входящих в формулы Jp Jp1 для углов закручивания. Получаем

мм4,   мм4.

Теперь, принимая модуль сдвига G= 8·104 МПа для стали, найдем углы закручивания граничных сечений вала, воспользовавшись формулами

, где .

Просчитаем все φ

,

,

,

.

В рассматриваемом случае крутящий момент на трех участках слева имеет одинаковый знак, поэтому значение угла закручивания возрастает – все сечения закручиваются по часовой стрелке, если смотреть со стороны правого торца вала. На четвертом участке знак крутящего момента другой, поэтому знак приращения угла закручивания на этом участке другой, однако концевое сечение все равно повернуто по часовой стрелке, если смотреть со стороны правого торца вала. На рисунке 18,г показана эпюра углов закручивания (по условиям задачи не требуется).

 

2.7 Задача 7. Проектный расчет на прочность при изгибе

 

Для заданной схемы балки (см. рисунок 19) требуется: а) написать выражения для поперечной силы Q и изгибающего момента M для каждого участка в общем виде; б) построить эпюры Q и M; в) из условия прочности выбрать сечение балки в виде стандартного прокатного двутавра или швеллера, приняв для стали Ст.3 допускаемое напряжение [s] = 160 МПа. Данные взять из таблицы 6.

 Указания. Эта задача относится к теме «Изгиб». Так как рассматривается балка на двух опорах, то прежде всего надо определить опорные реакции из уравнений статики и проверить их правильность.

При построении эпюр также следует контролировать их правильность, в том числе и с помощью дифференциальных зависимостей Журавского между изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки. В частности, следует помнить, что изгибающий момент имеет экстремальное значение в сечении, где поперечная сила проходит через нулевое значение.

   Т а б л и ц а 6

 

Вариант

Значения величин

l2,

 м

 

a1/a

 

а2/a

 

а3/a

F,

кН

M,

кН· м

q,

кН/м

Тип

профиля

 

1

10

2,0

0,8

1,6

5

14

20

двутавр

2

9

2,2

1,0

1,8

6

12

18

швеллер

3

8

2,4

1,2

2,0

7

10

16

двутавр

4

7

2,6

1,4

2,2

8

8

14

швеллер

5

6

2,8

1,6

2,4

9

7

12

двутавр

6

5

3,0

1,8

2,6

10

6

10

швеллер

7

4

3,2

2,0

1,4

11

5

8

двутавр

8

3

1,0

2,2

1,2

12

4

      6

швеллер

9

11

1,6

2,4

1,0

14

16

5

двутавр

10

12

1,5

2,6

0,8

16

18

4

швеллер

Примечание -  В расчетах принять  длину балки l2=10a.

 

Опасным с точки зрения прочности сечением для балки постоянного поперечного сечения, изготовленной из материала, одинаково сопротивляющегося растяжению и сжатию, является то сечение, где максимален по абсолютной величине изгибающий момент.

 


 

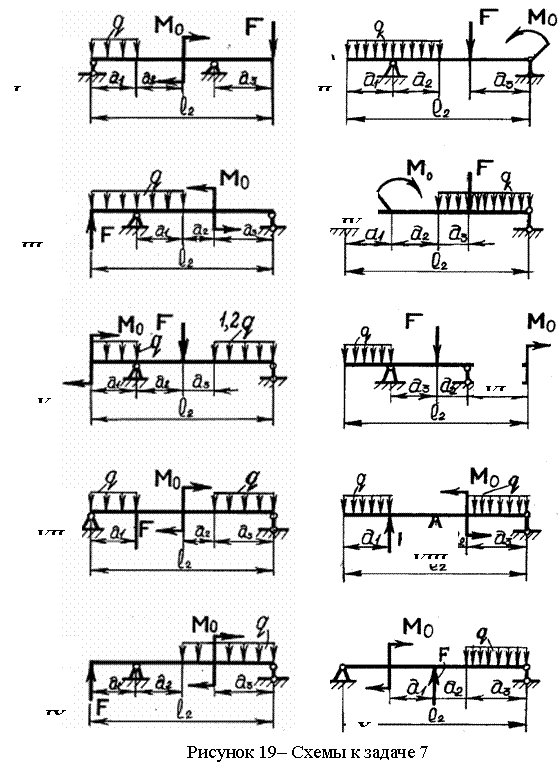Так как задача представляет собой задачу проектного расчета, то далее следует выразить из условия прочности при изгибе необходимую величину осевого момента сопротивления поперечного сечения Wx. По этому значению для стандартных прокатных профилей определяют по таблицам сортамента номер профиля с ближайшим и, как правило, большим значением Wx.  После этого следует определить недогрузку или перегрузку балки в процентах. При решении данной задачи перегрузку более 4% будем считать недопустимой.

Пример 7 - Для схемы, изображенной на рисунке 20,а, выполнить решение по условиям задачи 7. Дано: F=7 кН, M0=10 кН·м, q=9 кН/м, l=14 м, a=3,8 м, b=5 м, c=2,2 м, требуется подобрать сечение балки в виде двутавра..

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

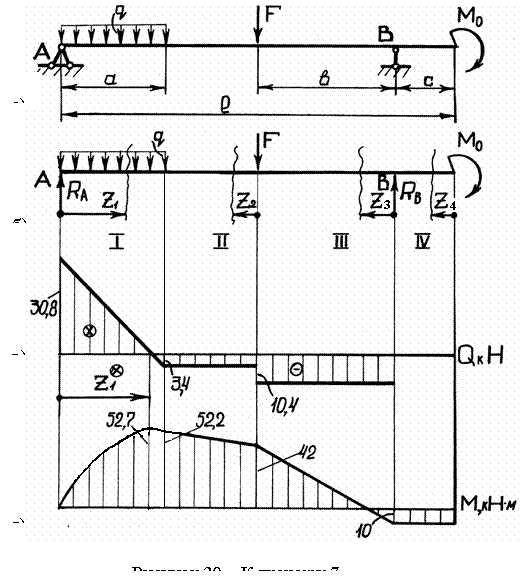Решение. Определяем реакции RA и RB (см. рисунок 20,б) из уравнений равновесия

   

Получаем

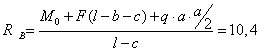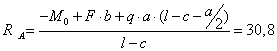 кН,   кН.

Проверяем правильность найденных значений реакций

.

Запишем уравнения для поперечной силы Q и изгибающего момента M на участках I – IV и построим эпюры.

I участок :                                                                                                                 

;                      при z1 = 0                  Q = RA = 30,8 кН;

                                                          при z1 = a = 3,8 м     Q = RA-q·a = -3,4 кН.

;                при z1 = 0                  M = RA = 0;

                                                           при z1 = a = 3,8 м     M = 52 кН∙м.

Так как эпюра Q на участке I проходит через нулевое значение, меняя знак с положительного на отрицательный, то в сечении, где Q равна нулю, на эпюре M имеет место максимальное значение. Чтобы найти его, определим значение координаты , при котором Q = 0:         ;                                 м.

Тогда  кН∙м.

IV участок  :

                  

 кН∙м.

III участок  :

кН;                  

    при z3 = 0              M = -M0 = -10 кН м;

                                               при z3 = b = 5 м     M = -M0 + RB ∙b= 42 кН∙м;

II участок  :

кН;                  

 при z2 = 0              M = -42 кН∙м;

                                                                при z2 = 3 м           M =  52 кН∙м.

Эпюры Q и M приведены на рисунке 20,в г.

Из условия прочности при изгибе для балки постоянного сечения .

определяем необходимую величину осевого момента сопротивления

Из таблицы сортамента выбираем двутавр №24а, для которого Wx=317 см3; при этом

Так что перегрузка составляет  что приемлемо.

Приложение А

Схемы механизмов и исходные данные к задачам 3 и 4


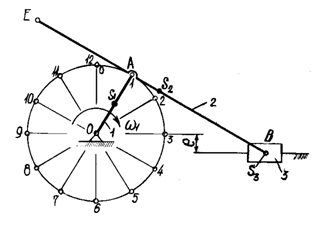Рисунок А.1 - Cхема 1. Кривошипно-ползунный механизм

Т а б л и ц а А.1

Величина

Предпоследняя цифра шифра (вариант числовых данных)

0

1

2

3

4

5

6

7

8

9

 

OA, мм

60

80

100

120

140

160

180

240

20

22

le ,  мм

30

40

30

25

28

0

80

90

14

16

lAB, мм

180

240

300

340

365

400

550

900

68

75

lAE, мм

80

120

80

180

90

200

250

40

26

35

w1, рад/c

32

18

26

15

80

30

60

25

30

35

 

 

 

 

 

 

 

 

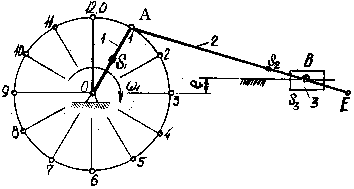
Рисунок А.2 - Схема 2. Кривошипно-ползунный механизм

Т а б л и ц а А.2

Величина

Предпоследняя цифра шифра (вариант числовых данных)

0

1

2

3

4

5

6

7

8

9

 

lOA, мм

65

75

100

120

130

150

170

230

22

24

le,    мм

20

35

60

20

30

0

10-0

80

12

15

lAB, мм

200

250

320

300

330

360

500

650

75

86

lBE, мм

60

100

150

125

150

140

250

200

20

28

w1,  рад/c

20

18

12

15

100

30

28

34

14

25


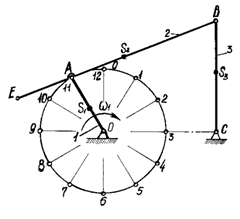Рисунок А.3 - Схема 3. Шарнирный четырехзвенник

Т а б л и ц а А.3

Величина

Предпоследняя цифра шифра (вариант числовых данных)

   0

   1

   2

   3

   4

   5

   6

   7

   8

   9

 

  lOA, мм

  55

  75

  90

 115

130

 150

 170

 200

 22

  24

 lOC, мм

 120

 200

 240

 250

 300

 400

 450

 400

  45

  40

 lBC, мм

 150

 160

 200

 300

 350

 300

 350

 500

  55

  60

 lAB, мм

 180

 240

 280

 350

 400

 500

 540

 600

  60

  64

 lAE, мм

  70

  80

  75

 150

 200

 210

 190

 240

  28

  25

 w1, рад/c

  19

  14

  25

  60

  50

  30

  35

  15

  24

  20


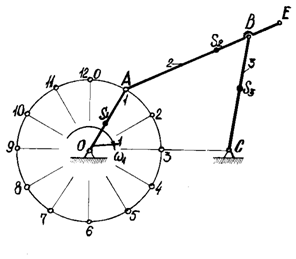Рисунок А.4 - Cхема 4. Шарнирный четырехзвенник

Т а б л и ц а А.4

Величина

Предпоследняя цифра шифра (вариант числовых данных)

   0

1

   2

   3

   4

   5

   6

   7

   8

   9

 

 lOA, мм

  60

  58

  80

  75

 100

 105

 120

  125

  14

 140

 lOC, мм

 120

 140

 160

 200

 200

 240

 245

 250

  30

 300

 lBC, мм

 150

 160

 200

 200

 250

 230

 300

 320

  34

 320

 lAB, мм

 150

 180

 200 

 200

 250

 300

 300

 360

  34

 400

 lBE, мм

 150

 100

 180

 150

 200

 140

 180

 200

  25

 200

 w1, рад/c

  25

  22

  20

  60

  21

  40

  30

  16

  30

  28


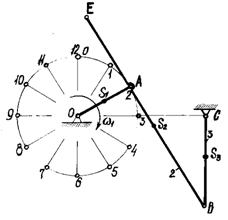Рисунок А.5 - Схема 5. Шарнирный четырехзвенник

Т а б л и ц а А.5

Величина

Предпоследняя цифра шифра (вариант числовых данных)

   0

   1

   2

   3

   4

   5

   6

  7

   8

   9

 

lOA, мм

  60

  80   

  100

 120

 140

 160

 180

 200

  22

 240

lOC, мм

 140

 180

 280

 240

 320

 380

 440

 420

  46

 400

lBC, мм

 160

 200

 180

 300

 300

 320

 300

 500

  50

 600

lAB, мм

 200

 260

 300

 360

 400

 480

 500

 600

  60

 700

lAE, мм

 100

 120

 150

 200

 200

 240

 200

 250

  35

 250

w1, рад/c

  31

  21

  30

  60

  12

  30

  28

  25

  20

  24


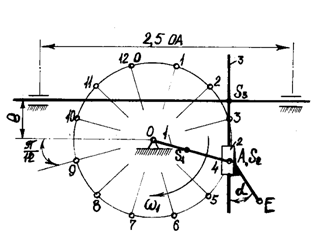Рисунок А.6 - Схема 6. Синусный механизм

Т а б л и ц а А.6

Величина

Предпоследняя цифра шифра (вариант числовых данных)

   0

   1

   2

  3

  4

  5

   6

  7

  8

  9

 

 

 

lOA, мм

  50

 100

 150

 25

  60

  80

 120

 200

 140

 175

 

le,    мм

  10

  30

  60

  10

  30

  40

  60

  80

  70

 100

 

lAE, мм

  20

  40

  30

  10

  25

  30

  50

 100

  56

  80

 

a,   рад

π/6

0

π/2

π/3

π/2

π/4

π/3

π/2

0

π/3

 

w1, рад/c

  40

  25

  15

  28

  18

  20

  15

  30

  50

 35

 


Рисунок А.7 - Схема 7. Двухкривошипный шарнирный четырехзвенник

Т а б л и ц а А.7

Величина

Предпоследняя цифра шифра (вариант числовых данных)

   0

   1

   2

   3

   4

  5

   6

   7

   8

   9

 

lOA, мм

150

 200

  50

 240

  70

  80

  35

  60

  60

  50

lOC, мм

  55

 100

  20

  75

  40

  50

  20

  10

  24

  30

lBC, мм

 170

 240

  60

 200

  80

 100

  40

  80

  64

  60

lAB, мм

 120

 200

  52

 160

  75

  90

  37

  70

  40

  55

lBE, мм

  50

  80

  30

  85

  40

  60

  30

  40

  20

  35

w1, рад/c

  30

  50

  40

  35

  45

  15

  12

  40

  10

  15


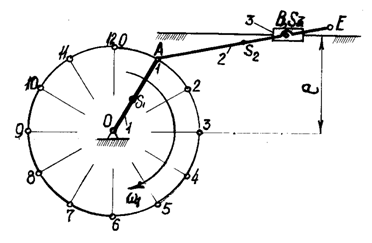Рисунок А.8 - Схема 8. Кривошипно-ползунный механизм с большим дезаксиалом

Т а б л и ц а А.8

Величина

Предпоследняя цифра шифра (вариант числовых данных)

    0 

   1

   2

   3

   4

   5

   6

   7

   8

  9

 

lOA, мм

  40

 100

 200

 150

  80

  60

 120

  70

 110

  30

le,    мм

  60

 120

 220

 210

  90

 120

 150

  80

 130

  40

lAB, мм

 160

 320

 650

 550

 250

 280

 400

 220

 360

 110

lBE, мм

  50

  80

 200

 150

  60

 100

 120

  60

 110

  40

w1, рад/c

  40

  12

  37

  26

  80

  60

  30

  20

  15

  35

 

 

 

 

 

 

 

 

 

Рисунок А.9 - Схема 9. Двухкривошипный шарнирный четырехзвенник

Т а б л и ц а А.9

Величина

Предпоследняя цифра шифра (вариант числовых данных)

   0

   1

   2

   3

   4

   5

   6

   7

   8 

  9

 

lOA, мм

  60

  80

  64

  40

 100

  80

 200

  60

 240

 170

lOC, мм

  25

  10

  20

  20

  50

  40

  75

  20

 100

  60

lBC, мм

  50

  60

  60

  35

  80

  70

 240

  50

 200

 150

lAB, мм

  55

  70

  40

  36

  90

  75

 160

  52

 200

 130

lAE, мм

  30

  35

  25

  26

  40

  40

  70

  25

 120

  60

w1, рад/c

  30

  15

  32

  12

  16

  35

  28

  30

  45

  25

 

 

 

 

 

 

 

 

 

 

Рисунок А.10 -Схема 10. Шарнирный четырехзвенник c большим коромыслом

Т а б л и ц а А10

Величина

Предпоследняя цифра шифра (вариант числовых данных)

  0

   1

  2

  3

  4

   5

  6

  7

  8

  9

 

lOA, мм

  40

  20

 100

  60

  50

  80

  25

 100

 120

  90

lOC, мм

  80

  30

 180

 100

 150

 200

 100

 400

 300

 315

lBC, мм

 160

  60

 350

 200

 250

 400

 150

 550

 420

 315

lAB, мм

 140

  60

 320

 190

 200

 300

  90

 300

 350

 250

lBE, мм

  40

  15

  50

  40

 100

 100

  40

  75

 100

  65

w1, рад/c

  16

  40

  20

  15

  22

  30

  35

  12

  15

  20

Список литературы

 

1. Тарг С.М. Краткий курс теоретической механики. - М.: Высш. шк., 1986.

2. Иосилевич Г.Б., Строганов Г.Б., Маслов Г.М. Прикладная механика. - М.: Высш. шк., 1989.

3. Кореняко А.С. Теория механизмов и машин. – Киев: Вища школа, 1976.

4. Сборник задач по теории механизмов и машин /Артоболевский И.И. и Эдельштейн Б.В. – М.: Наука, 1973.

5. Степин П.А. Сопротивление материалов. - М.: Высш. шк., 1988.

6. Буланов Э.А. Решение задач по сопротивлению материалов. – М.: Высш. шк., 1994.

7. Пособие к решению задач по сопротивлению материалов /Миролюбов  И.Н. и др. – М.: Высш.шк., 1985.

8. Аркуша А.И. Техническая механика. Теоретическая механика и сопротивление материалов. - М.: Высш. шк., 2003.

9. Аркуша А.И. Техническая механика. Руководство к решению задач по теоретической механике. - М.: Высш. шк., 2002.

10. Расчетные и курсовые работы по сопротивлению материалов /Ф.З.Алмаметов, С.И.Арсеньев, С.А.Енгалычев и др. – М.: Высш.шк., 1992.

         11. Динасылов А.Д. Прикладная механика. Основы расчетов на прочность и жесткость. – Алматы, АИЭС, 2009.

 

Сводный план 2011 г., поз.  270