Некоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра «Компьютерные технологии»
МАТЕМАТИЧЕСКОЕ И КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ
Методические укзания по выполнению
лабораторных работ
для магистрантов специальности 6М070400-«Вычислительная техника и программное
обеспечение»
Алматы 2013
Составители: З.К.Куралбаев, А.А.Ержан, А.А.Таурбекова. Методические указания по выполнению лабораторных работ для магистрантов специальности 6М070400 - «Вычислительная техника и программное обеспечение» . – Алматы: АУЭС, 2013. – 32 с.
В методической разработке приведены работы, предназначенные для организации лабораторных занятий по дисциплине «Математическое и компьютерное моделирование» для магистрантов специальности 6М070400-«Вычислительная техника и программное обеспечение»
Здесь предложены двенадцать лабораторных работ, темы которых охватывают различные разделы науки. При выполнении заданий по этим лабораторным работам магистрант знакомится с популярными методами решения математических задач, используемых для решения научных и исследовательских задач, получают навыки решения практических задач.
Знания и навыки, полученные в результате изучения данной дисциплины могут быть использованы в дальнейшем магистрантом при выполнении научно-исследовательской и экспериментальной работы. Поэтому основными постреквизитами данной дисциплины являются научно-исследовательская работа, написание научных статей и диссертации и любые дисциплины, связанные с научной деятельностью магистранта.
Ил. 15, библиогр. – 10 назв.
Рецензент: канд. физ-мат. наук, доцент А.А.Аманбаев
Печатается по плану издания некоммерческого акционерного общества “Алматинский университет энергетики и связи” на 2013 г.
© НАО “Алматинский университет энергетики и связи”, 2013 г.
Св.план 2013г. поз 205
Введение
Изучение дисциплины «Математическое и компьютерное моделирование» базируется на знаний, полученные во время обучения в бакалавриате по дисциплинам, являющимися пререквизитами такие, как «математика», «физика», «теория вероятностей и математическая статистика», «теория электрических цепей», «алгоритмизация и основы программирования», «объектно-ориентированное програмирование», «технологии программирования».
Для закрепления знаний, полученных на лекционных занятиях по данной дисциплине, и получения навыков разработки моделей различных процессов проводятся лабораторные занятия в компьютерных классах. Умение разобраться с поставленной проблемой, разработать математическую или компьютерную модель и сформулировать математическую задачу на основе условий, при которых предполагается решить данную проблему, являются основными требованиями к квалификации современного IT-специалиста. Выполнение заданий по лабораторным работам требует от магистранта умение использовать знания по вышеназванным дисциплинам, полученных во время учебы в бакалавриате.
Здесь предложены двенадцать лабораторных работ, темы которых охватывают различные разделы науки. При выполнении заданий по этим лабораторным работам магистрант знакомится с популярными методами решения математических задач, используемых для решения научных и исследовательских задач, получают навыки решения практических задач.
Знания и навыки, полученные в результате изучения данной дисциплины, могут быть использованы в дальнейшем магистрантом при выполнении научно-исследовательской и экспериментальной работы. Поэтому основными постреквизитами данной дисциплины являются научно-исследовательская работа, написание научных статей и диссертации и любые дисциплины, связанные с научной деятельностью магистранта.
Для каждой лабораторной работы определена цель работы, дано задание, приведены теретические и методические материалы, имеется ссылка к литературным источникам. Каждой лабораторной работе предшествует лекция по теме и предлагается литература для дополнительного изучения. Перед выполнением лабораторной работы магситрант отвечает на контрольные вопросы преподавателя и получает индивидуальное задание. После выполнения лабораторной работы магистрант сдает отчет преподавателю.
Лабораторная работа № 1. Линейная аппроксимация статистических данных
Цель работы: изучение одного из методов обработки статистических или экспериментальных данных с целью получения линейной зависимости между двумя показателями.
Задание и порядок выполнения работы:
1) Изучить теоретические материалы [1-3,12] о линейной аппроксимации данных эксперимента или статистики и ознакомиться с методическими указаниями по выполнению данной работы.
2) Сформулировать постановку задачи.
3) Изучить метод решения задачи и разработать алгоритм ее решения.
4) Решить задачу с помощью MS Excel или программы на алгоритмическом языке.
5) Построить график аппроксимирующей функции.
6) Оформить отчет по данной работе.
Методические указания по выполнению работы
Постановка задачи. Пусть требуется определить функциональную зависимость
между двумя величинами ![]() и
и ![]() . Они
могут быть параметрами некоторого либо физического процесса, либо
экономического показателя, либо других явлений природного характера. Для
определения этой зависимости проводят наблюдения или эксперименты, результаты
которых записывают в виде таблицы значений рассматриваемых величин. Используя
эти данные, требуется определить математическую зависимость между этими
величинами.
. Они
могут быть параметрами некоторого либо физического процесса, либо
экономического показателя, либо других явлений природного характера. Для
определения этой зависимости проводят наблюдения или эксперименты, результаты
которых записывают в виде таблицы значений рассматриваемых величин. Используя
эти данные, требуется определить математическую зависимость между этими
величинами.
Математическая модель задачи. Искомая зависимость записывается в виде
линейной функции ![]() где
где ![]() и
и ![]() неизвестные
пока параметры, значения которых должны быть определены.
неизвестные
пока параметры, значения которых должны быть определены.
Метод решения задачи. Данная задача решается известным методом наименьших квадратов, сущность которого заключается в следующем. График аппроксимирующей функции должен проходить очень близко от статистических точек. Это условие может быть осуществлено, если следующая функция имеет наименьшее значение:
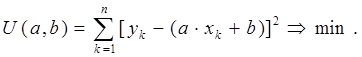
Здесь ![]() количество
статистических точек,
количество
статистических точек, ![]() координаты статистических точек.
Необходимым и достаточным условием минимума данной функции может быть записано:
координаты статистических точек.
Необходимым и достаточным условием минимума данной функции может быть записано:

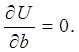
Из этих условий будут определены следующие формулы
для определения значений неизвестных параметров ![]() и
и ![]() :
:
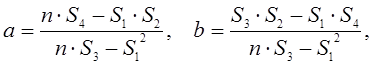
где 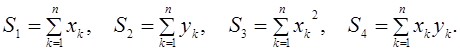
Алгоритм решения задачи:
- ввод массивов ![]() в память компьютера;
в память компьютера;
- определение значений следующих сумм ![]()
- определить
значения искомых параметров ![]() и
и ![]() .
.
Пример. Использовать статистические данные, приведенные в таблице1.
Таблица
1- Статистические данные значений величин ![]() и
и ![]()
|
|
50 |
60 |
70 |
80 |
90 |
100 |
110 |
120 |
130 |
140 |
|
|
65 |
75 |
95 |
100 |
115 |
130 |
155 |
170 |
180 |
190 |
|
|
150 |
160 |
170 |
180 |
190 |
200 |
210 |
220 |
230 |
240 |
|
|
200 |
210 |
235 |
250 |
265 |
290 |
310 |
350 |
370 |
400 |
Результатом решения задачи является линейная
аппроксимирующая функция ![]() и ее график в виде
прямой линии.
и ее график в виде
прямой линии.
Контрольные вопросы:
1) Что такое аппроксимация статистических данных?
2) Какая линия является графиком линейной функции аппроксимации?
3) Почему рассматривается минимум
функции ![]()
4) Почему условие равенства нулю первых
производных функции ![]() является достаточным условием
минимума?
является достаточным условием
минимума?
5) В чем сущность метода наименьших квадратов?
Лабораторная работа № 2. Квадратичная аппроксимация статистических данных
Цель работы: изучение одного из методов обработки статистических или экспериментальных данных с целью получения зависимости между двумя показателями в виде квадратичной функции.
Задание и порядок выполнения работы:
1) Изучить теоретические материалы [2,3,12] о нелинейной аппроксимации данных эксперимента или статистики и ознакомиться с методическими указаниями по выполнению данной работы.
2) Сформулировать постановку задачи.
3) Изучить метод решения задачи и разработать алгоритм ее решения.
4) Решить задачу с помощью MS Excel или программы на алгоритмическом языке.
5) Построить график аппроксимирующей функции.
6) Оформить отчет по данной работе.
Методические указания по выполнению работы
Постановка задачи. Пусть требуется определить функциональную
зависимость между двумя величинами ![]() и
и ![]() в виде квадратичной функции
в виде квадратичной функции ![]() . Для определения этой зависимости используются
данные эксперимента или статистики. Этот процесс называется квадратичной
аппроксимацией.
. Для определения этой зависимости используются
данные эксперимента или статистики. Этот процесс называется квадратичной
аппроксимацией.
Математическая модель задачи. Искомая зависимость записывается в виде
функции ![]() где
где ![]() ,
,![]()
![]() неизвестные пока
параметры, значения которых должны быть определены.
неизвестные пока
параметры, значения которых должны быть определены.
Метод решения задачи. Данная задача решается методом наименьших квадратов. Используется условие минимума следующей функции:
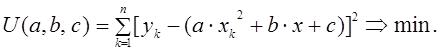
Здесь ![]() количество
статистических точек,
количество
статистических точек, ![]() координаты статистических точек.
Необходимым и достаточным условием минимума данной функции имеет вид:
координаты статистических точек.
Необходимым и достаточным условием минимума данной функции имеет вид:
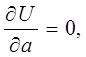
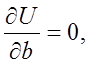
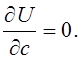
Из этих условий будут получена следующая система алгебраических
уравнений относительно неизвестных параметров ![]() ,
, ![]() и
и ![]() :
:
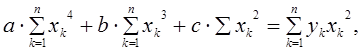

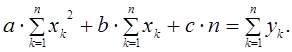
Алгоритм решения. Полученную систему алгебраических уравнений можно решить с помощью MS Excel или с помощью программы на алгоритмическом языке. При этом используется один из существующих методов решения системы алгебраических уравнений. Алгоритм решения этой системы состоит из следующих этапов:
- ввод массивов ![]() в память компьютера;
в память компьютера;
- определение значений следующих сумм ![]()
- решить систему алгебраических уравнений;
- определить
значения искомых параметров ![]() ,
, ![]() ,
, ![]() .
.
Здесь суммы определяются по формулам:

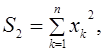
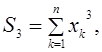
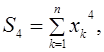
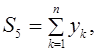
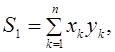

Пример. В качестве статистических данных использовать данные, приведенные в таблице 1.
Результатом решения задачи является квадратичная функция и ее график.
Контрольные вопросы:
1) Почему квадратичная функция является лучшей для аппроксимации статистических данных, чем линейная функция?
2) Что такое репрезентативность статистических данных?
3) Какие методы используются для решения системы алгебраических уравнений, получаемой в результате использования метода наименьших квадратов?
4) Какая линия является графиком аппроксимирующей функции?
5) Почему в третьем уравнении системы коэффициент при ![]() равен
равен ![]() ?
?
6) Можно ли привести систему уравнений из трех уравнений к системе с двумя уравнениями?
Лабораторная работа № 3. Уравнения множественной регрессии
Цель работы: изучение одного из методов определения зависимостей между многими переменными в результате математической обработки статистических (экспериментальных) данных.
Задание и порядок выполнения работы:
1) Изучить теоретические материалы [2,3,12] и методические указания по выполнению данной работы.
2) Сформулировать постановку задачи.
3) Изучить метод решения задачи и разработать алгоритм ее решения.
4) Решить задачу с помощью MS Excel .
5) Получить решение задачи с помощью компьютерной программы, составленной на одном из языков программирования.
6) Оформить отчет по данной работе.
Постановка задачи. В экономических или экспериментальных исследованиях часто встречаются задачи, когда требуется определить зависимость между несколькими переменными. Такие зависимости называются уравнениями множественной регрессии. Здесь для простоты рассматриваются три переменные.
Математическая модель. Если ![]() являются некоторыми показателями, то уравнение,
связывающее их значения, может быть написано в следующем виде
являются некоторыми показателями, то уравнение,
связывающее их значения, может быть написано в следующем виде
![]() (3.1)
(3.1)
где ![]() - неизвестные пока параметры.
- неизвестные пока параметры.
Если будут найдены значения этих параметров, то задача считается решеной. Данное уравнение (3.1) может быть написано в других видах. Например,
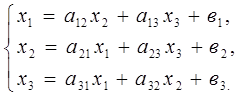 (3.2)
(3.2)
Эти уравнения являются эквивалентными уравнению (3.1).
Метод решения задачи. Для решения поставленной здесь задачи используются статистические (экспериментальные) данные, которые могут быть представлены в виде таблицы 2.
Таблица 2 – Статистические данные для трех переменных
|
|
x11 |
x12 |
x13 |
… |
x1i |
… |
x1m |
|
|
x21 |
x22 |
x23 |
… |
x2i |
… |
x2m |
|
|
x31 |
x32 |
x33 |
… |
x3i |
… |
x3m |
Искомое уравнение может быть написано и в другом виде:
![]() (3.3)
(3.3)
Здесь следующие выражения являются средними статистическими значениями каждой из этих переменных:
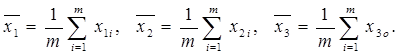 (3.4)
(3.4)
Свободный член в уравнении (3.1) будет иметь вид:
![]() (3.5)
(3.5)
Итак, задача сводится к определению двух
неизвестных параметров ![]() . Для определения их значений используется известный метод наименьших
квадратов. Для этого рассматривается следующая функция от неизвестных
параметров:
. Для определения их значений используется известный метод наименьших
квадратов. Для этого рассматривается следующая функция от неизвестных
параметров:
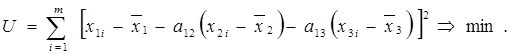
Из условия минимума данной функции получаются следующие алгебраические уравнения:
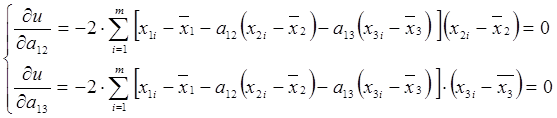 .
.
После ввода обозначений эти уравнения могут быть написаны в следующем виде:
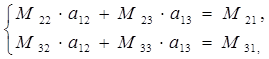 (3.6)
(3.6)
Здесь:
![]()
![]() (3.7)
(3.7)
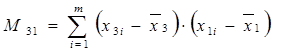
называются моментами второго порядка.
Решение системы уравнений (3.6) будет представлено в виде:
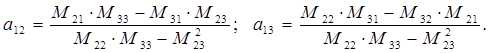 (3.8)
(3.8)
Алгоритм решения задачи состоит из следующих этапов:
-
по формуле (3.4) определяют
средние значения переменных ![]() ;
;
- по формулам (3.7) вычисляют значения моментов второго порядка;
-
по формулам (3.8)
определяют значения параметров ![]() и
и ![]() ;
;
-
по формуле (3.5)
определяют свободный член ![]() уравнения (3.1).
уравнения (3.1).
Пример. Для решения задачи использовать данные, приведенные в таблице 3.
Таблица 3 – Статистические данные для трех переменных
|
|
15,9 |
16,4 |
19,0 |
19,1 |
18,8 |
20,4 |
22,7 |
26,5 |
28,1 |
|
|
149,3 |
161,2 |
171,5 |
175,5 |
180,8 |
190,7 |
202,1 |
212,4 |
226,1 |
|
|
4,2 |
4,1 |
3,1 |
3,1 |
1,1 |
2,2 |
2,1 |
5,6 |
5,0 |
|
|
27,6 |
26,3 |
31,1 |
33,3 |
37,0 |
43,3 |
40,6 |
41,8 |
42,0 |
|
|
231,9 |
239,0 |
258,0 |
269,8 |
288,4 |
304,5 |
305,2 |
308,7 |
310,3 |
|
|
5,1 |
0,7 |
5,6 |
3,1 |
3,1 |
4,6 |
3,4 |
3.7 |
4,0 |
Результатом решения задачи является уравнение (3.1).
Контрольные вопросы:
1) Что такое уравнение регрессии?
2) Можно ли использовать данный метод для четырех и более переменных?
3) Какие величины называются моментами второго порядка?
4) В каких областях знаний могут встречаться задачи множественной регрессии?
5) Каким методом определены формулы (3.8)?
6) Что собой представляет результат решения данной задачи?
Лабораторная работа № 4. Модель нормально распределенных случайных величин
Цель работы: изучение способов компьютерного моделирования случайных величин и определения числовых характеристик по данным наблюдений.
Порядок выполнения работы:
1) Изучить теоретические материалы [5,6] и методические указания к выполнению данной работы.
2) Изучить способы компьютерного моделирования непрерывных случайных величин.
3) Составить алгоритм и программу выполнения расчетов характеристик случайной величины.
4) Выполнить программу решения данной задачи для конкретных данных наблюдений.
5) Оформить отчет по данной работе.
Теоретические материалы и методические указания
Постановка задачи. Случайная величина называется нормально распределенной, если плотность распределения вероятностей имеет следующий вид:
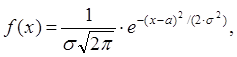 (4.1)
(4.1)
где ![]() математическое
ожидание,
математическое
ожидание, ![]() среднее квадратическое отклонение.
среднее квадратическое отклонение.
Если будут определены характеристики ![]() то считается задача решеной, т.е.
определена функция (4.1). Однако точные значения этих параметров невозможно
определить, поэтому определяются их оценки. Точечной оценкой математического
ожидания является выборочное среднее, а для среднего квадратичного отклонения
корень квадратный из выборочной дисперсии. Для определения их используются
данные наблюдений, приведенные в таблице 4. Эти данные составляют вариационный
ряд.
то считается задача решеной, т.е.
определена функция (4.1). Однако точные значения этих параметров невозможно
определить, поэтому определяются их оценки. Точечной оценкой математического
ожидания является выборочное среднее, а для среднего квадратичного отклонения
корень квадратный из выборочной дисперсии. Для определения их используются
данные наблюдений, приведенные в таблице 4. Эти данные составляют вариационный
ряд.
Таблица 4 – Вариационный ряд
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь ![]() варианты,
варианты, ![]() частота появлений вариант;
частота появлений вариант; ![]() объем выборки.
объем выборки.
Алгоритм решения этой задачи имеет следующие этапы:
- вводятся
значения массивов ![]() и
и ![]()
- вычисление условных вариант ![]() где
где
![]() ложный нуль,
ложный нуль, ![]() шаг
вариационного ряда;
шаг
вариационного ряда;
- вычисление условного момента первого порядка 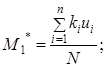
- вычисление условного момента второго порядка 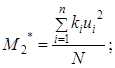
- вычисление выборочного среднего ![]()
- вычисление выборочную дисперсию ![]()
- вычисление выборочного среднего квадратичного
отклонения ![]()
Пример. Пусть дан вариационный ряд.
|
|
0,3 |
0,5 |
0,7 |
0,9 |
1,1 |
1,3 |
1,5 |
1,7 |
1,9 |
2,1 |
2,3 |
|
|
6 |
9 |
19 |
25 |
28 |
30 |
27 |
23 |
20 |
8 |
5 |
Требуется определить точечные оценки математического ожидания и среднего квадратичного отклонения нормального распределения.
Контрольные вопросы:
1) Что такое случайная величина?
2) Какая случайная величина называется нормально распределенной?
3) Что являются основными характеристиками случайной величины?
4) Что такое вариационный ряд?
5) Что такое точечная оценка?
6) Что такое дисперсия случайной величины?
Лабораторная работа № 5. Модель определения цены товара на конкурентном рынке
Цель работы: изучение одного из популярных методов решения задачи об определении цены товара на конкурентном рынке.
Порядок выполнения работы:
1) Изучить теоретические материалы [2,12] и методические указания к выполнению данной работы.
2) Изучить метод решения задачи.
3) Разработать алгоритм решения задачи.
4) Решить задачу с помощью MS EXCEL.
5) Составить программу решения задачи на одном из языков программирования.
6) Отладить программу и выполнить ее для конкретных исходных данных.
7) Получить результат решения задачи в виде таблицы промежуточных значений искомой цены товара.
8) Провести анализ полученного решения.
9) Оформить отчет по данной работе.
Теоретические материалы и методические указания
Постановка задачи. В экономической теории имеется утверждение о том, что цена товара определяется конкурентным рынком. Она зависит от спроса и предложения на этот товар. Требуется показать процесс установления цены товара на модели.
Эконометрическая
модель.
Пусть рассматривается некоторый рынок определенного товара. Обозначения: ![]() –цена товара,
–цена товара, ![]() -функция спроса,
-функция спроса, ![]() – функция
предложения. Для простоты предполагается, что эти функции являются линейными:
– функция
предложения. Для простоты предполагается, что эти функции являются линейными: ![]()
![]() , где
, где ![]() –время
(период),
–время
(период), ![]() – заданные величины, определяющие
функции спроса и предложения. Объемы спроса и предложения должны быть
одинаковыми:
– заданные величины, определяющие
функции спроса и предложения. Объемы спроса и предложения должны быть
одинаковыми: ![]() . Здесь параметр
. Здесь параметр ![]() -текущий момент (период торговли)
времени, а
-текущий момент (период торговли)
времени, а ![]() показывает
предыдущий момент (период торговли) времени. Приведенные выше формулы
определяют эконометрическую модель поставленной задачи.
показывает
предыдущий момент (период торговли) времени. Приведенные выше формулы
определяют эконометрическую модель поставленной задачи.
Метод решения задачи. В данном случае для решения задачи выполняются простые вычисления объема предложения и спроса, в каждом шаге определяется новое значение цены товара.
Алгоритм решения состоит из следующих этапов:
-
рассматривается координатная система, у которой абсцисса ![]() , а ордината
, а ордината ![]() ;
;
-
необходимо строить графики функций ![]() и
и ![]() ;
;
-
задается начальная цена товара ![]() и для нее
определяется объем товара по формуле для
и для нее
определяется объем товара по формуле для ![]() ;
;
- из
равенства ![]() определяется новая цена товара;
определяется новая цена товара;
- цена
товара определяется с определенной точностью; для этого задается либо
количество повторения ![]() , либо условие точности:
, либо условие точности: ![]()
![]()
![]() если выполняется это условие, то
процесс решения задачи завершается; в противном случае вычисляется следующее
значение цены товара.
если выполняется это условие, то
процесс решения задачи завершается; в противном случае вычисляется следующее
значение цены товара.
Пример. Пусть
рассматривается пример, для которого заданы следующие данные: ![]() и начальная цена товара
и начальная цена товара ![]()
В
результате
выполнения программы должно получиться графическое изображение в виде
«паутины», поэтому данную модель называют «паутинообразной» моделью определения
цены товара в конкурентном рынке. Графики функции спроса ![]() и предложения S(p) могут
быть изображены в прямоугольной
системе координат в зависимости от цены товара
и предложения S(p) могут
быть изображены в прямоугольной
системе координат в зависимости от цены товара ![]() :
они стремятся к некоторому окончательному значению цены товара и
соответствующего объема торговли.
:
они стремятся к некоторому окончательному значению цены товара и
соответствующего объема торговли.
Контрольнве вопросы:
1) Что такое функция спроса?
2) Что такое функция предложения?
3) Что такое эконометрическая модель задачи?
4) Что является результатом решения данной задачи?
5) Можно ли определить цену товара, не решая данную задачу?
Лабораторная работа № 6. Численное решение задачи Коши для обыкновенных дифференциальных уравнений
Цель работы: изучение одного из популярных методов решения задачи Коши для обыкновенных дифференциальных уравнений.
Порядок выполнения работы:
1) Изучить теоретические материалы [9,12] и методические указания к выполнению данной работы.
2) Сформулировать постановку задачи.
3) Изучить метод решения задачи и разработать алгоритм ее решения.
4) Решить задачу с помощью Excel .
5) Получить решение задачи с помощью компьютерной программы, составленной на одном из языков программирования.
6) Получить результат решения задачи в виде графика искомой функции.
7) Оформить отчет по данной работе.
Методические указания по выполнению работы
В прикладных задачах часто возникает задача Коши для обыкновенных дифференциальных уравнений. Некоторые из них будут рассмотрены в следующих лабораторных работах.
Постановка задачи. Пусть рассматривается дифференциальное уравнение второго порядка
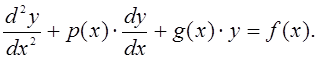 (6.1)
(6.1)
В данном уравнении функции ![]() считаются заданными, а функция
считаются заданными, а функция ![]() является искомой. Требуется найти
решение этого уравнения в промежутке
является искомой. Требуется найти
решение этого уравнения в промежутке ![]() , если заданы следующие начальные условия:
, если заданы следующие начальные условия:
 (6.2)
(6.2)
Метод решения задачи. Для решения этой задачи может быть использован один из методов, в
частности, методы Эйлера, Рунге-Кутта и другие. Эти методы используют замену
дифференциального уравнения алгебраическими уравнениями. Пусть используется
метод Эйлера. Сущность этого метода заключается в следующем. Выбирают маленький
шаг ![]() ; а затем промежуток
; а затем промежуток ![]() делится на
делится на ![]() равных
частей, длина каждой равна
равных
частей, длина каждой равна ![]() . Точки деления данного
промежутка определяются следующей формулой:
. Точки деления данного
промежутка определяются следующей формулой:
![]()
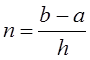 .
.
Значения функции ![]() в этих точках
в этих точках ![]() будут обозначены:
будут обозначены: ![]()
Производные искомой функции 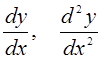 заменяются
конечными разностями:
заменяются
конечными разностями:
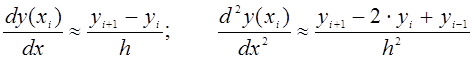 . (6.3)
. (6.3)
Используя замену (3), из уравнения (1) можно получить следующую формулу:
![]() (6.4)
(6.4)
Начальные условия (6.2) могут быть записаны в следующем виде:
![]() или
или ![]() (6.5)
(6.5)
Итак, вместо дифференциального уравнения получены формулы (6.4) и (6.5); они являются простыми алгебраическими соотношениями.
Алгоритм решения задачи может иметь следующие этапы:
1) вычисление по формуле (6.5) значение ![]()
2) начало цикла по параметру ![]()
![]()
3) вычисление по формуле (6.4) значение ![]()
4) переход к следующему номеру ![]()
5) проверка конца цикла ![]() если
это условие выполняется, то осуществляется переход к этапу 3) для вычисления
следующего значения
если
это условие выполняется, то осуществляется переход к этапу 3) для вычисления
следующего значения ![]() в противном случае выполняется
следующий этап;
в противном случае выполняется
следующий этап;
6) вывод значений ![]()
Пример. Пусть рассматривается уравнение:
![]()
Для численного решения использованы следующие значения
параметров: ![]()
Необходимо составить программу решения данной задачи.
Результат решения задачи представить в виде графика функции ![]()
Контрольные вопросы:
1) Какая задача является задачей Коши?
2) Можно ли решать задачу Коши для системы дифференциальных уравнений первого порядка методом Эйлера?
3) Как определяется погрешность метода Эйлера?
4) В чем сущность метода Эйлера?
5) От какого параметра зависит точность метода Эйлера?
6) В каком виде будут представлены результаты решения данной задачи?
Лабораторная работа № 7. Модели процессов в экологических системах
Цель работы: изучение способов моделирования процессов, происходящих в экологических системах, и решение задач, возникающих в результате моделирования.
Порядок выполнения работы:
1) Изучить теоретические материалы [2] и методические указания к выполнению данной работы.
2) Изучить различные способы моделирования экологических процессов.
3) Сформулировать математические задачи, возникающие в результате моделирования.
4) Разработать алгоритмы задач и решить их.
5) Оформить отчет по данной работе.
Теоретические материалы и методические указания
Известно, что экологические системы являются достаточно сложными, так как прямое экспериментальное исследование их по известным причинам невозможно. Однако имеются простые модели экологических систем, которые стали классическими.
Модель Мальтуса. Пусть рассматривается однородная популяция в условиях неограниченных ресурсов среды обитания. Предполагается, что скорость роста популяции пропорциональна ее численности.
Вводятся обозначения: ![]() -время,
-время,
![]() -численность
популяции,
-численность
популяции, ![]() -
скорость роста популяции. Тогда модель может быть представлена в
виде следующего
дифференциального уравнения:
-
скорость роста популяции. Тогда модель может быть представлена в
виде следующего
дифференциального уравнения:
![]() =
Rx,
(7.1)
=
Rx,
(7.1)
где ![]() –
коэффициент скорости роста популяции. Данное уравнение будет решено при
заданных начальных условиях:
–
коэффициент скорости роста популяции. Данное уравнение будет решено при
заданных начальных условиях:
![]() . (7.2)
. (7.2)
Начальное условие определяет численность популяции в начальный момент времени. Решение дифференциального уравнения, удовлетворяющее начальному условию, имеет следующий вид:
![]() , (7.3)
, (7.3)
что показывает экспоненциальный закон роста численности популяции в условиях неограниченных ресурсов.
Модель Ферхюльста.
Если ресурсы окружающей среды ограничены, т.е. экологическая емкость среды ![]() ограиченное число, то модель может иметь
следующий вид:
ограиченное число, то модель может иметь
следующий вид:
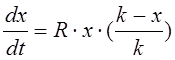 .
(7.4)
.
(7.4)
Полученное уравнение называется логистическим уравнением Ферхюльста, которое показывает, что скорость роста популяции пропорциональна ее численности и остающейся свободной части ресурсов среды обитания.
Модель, учитывающая нижнюю границу численности. В предыдущих моделях считалось, что численност популяции пропорциональна количеству особей. Однако во многих видах популяции скорость роста численности может зависеть от квадрата численности. С другой стороны, плотность популяции некоторых видов не должна быть ниже некоторого уровня, т.е. не должна опускаться ниже некоторого определенного критического количества. Модель, которая учитывает эти требования, может быть записана в следующем виде:
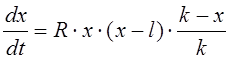 .
(7.5)
.
(7.5)
Здесь ![]() –
нижняя граница численности популяции, ниже которой она может вымирать. Эта
граница зависит от вида популяции.
–
нижняя граница численности популяции, ниже которой она может вымирать. Эта
граница зависит от вида популяции.
Модель системы двух популяций, конкурирующих за общий ресурс. Пусть в экологической системе существуют две популяции, которые используют общий жизненный ресурс. Они находятся в конкурентной борьбе за использование имеющегося ресурса. Рост каждого вида популяции зависит от развития другого вида. Такая модель может иметь следующий вид:
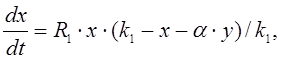
 (7.6)
(7.6)
где ![]() и
и ![]() –
коэффициенты роста численности, а
–
коэффициенты роста численности, а ![]() ,
, ![]() – параметры, характеризующие
экологическую емкость среды для каждого вида популяции. Коэффициенты
– параметры, характеризующие
экологическую емкость среды для каждого вида популяции. Коэффициенты ![]() и
и ![]() отражают
влияние одного вида популяции на другой вид.
отражают
влияние одного вида популяции на другой вид.
Модель системы «хищник-жертва». Пусть в экологической системе для «жертвы» имеется неограниченное количество корма. Рост численности «жертвы» происходит естественным путем и зависит от воздействия со стороны «хищника». Для «хищника» «жертва» является единственным источником питания. Если отсутствует «жертва», то «хищник» также вымирает.
Вводятся обозначения: ![]() - количество
«жертвы»,
- количество
«жертвы», ![]() - количество
«хищника». Тогда модель может иметь следующий вид:
- количество
«хищника». Тогда модель может иметь следующий вид:
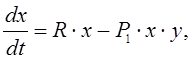
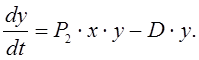 (7.7)
(7.7)
Первое уравнение (7.7)
отражает закономерность изменения популяции «жертв», а второе уравнение -
«хищников». Слагаемое ![]() характеризует
скорость размножения «жертв» в отсутствии «хищника», а слагаемое
характеризует
скорость размножения «жертв» в отсутствии «хищника», а слагаемое ![]() характеризует скорость гибели «жертв» за
счет их уничтожения «хищниками». Слагаемое
характеризует скорость гибели «жертв» за
счет их уничтожения «хищниками». Слагаемое ![]() характеризует
увеличение численности «хищников» за счет поедания «жертв», а слагаемое
характеризует
увеличение численности «хищников» за счет поедания «жертв», а слагаемое ![]() характеризует естественную смертность
«хищников». Коэффициенты
характеризует естественную смертность
«хищников». Коэффициенты ![]() представляют собой
константы, имеющие только положительные значения. Система уравнений (7.7)
называется уравнениями Лотки-Вольтерра.
представляют собой
константы, имеющие только положительные значения. Система уравнений (7.7)
называется уравнениями Лотки-Вольтерра.
Модель Базыкина. Модель «хищник»-«жертва» может быть обобщена моделю Базыкина. Для этого были учтены следующие биологические факторы:
1) По модели Лотки -
Вольтерра интенсивность поедания жертв хищниками линейно растет с ростом
популяции жертв. Однако экспериментальные данные показывает, что эта
зависимость имеет следующий вид: 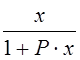 .
.
2) Невозможность
безграничного размножения, которая может быть описана формулой: 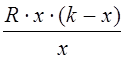 .
.
3) Недостаток
территории приводит к конкуренции, который описывается зависимостью: ![]() .
.
С учетом этих факторов получена модель «хищник»-«жертва», которая имеет следующий вид:
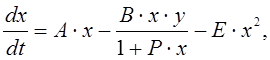
 (7.8)
(7.8)
Рассмотренные модели позволяют сделать определенный анализ путем численного эксперимента. В данном случае все рассмотренные модели привели к решению систем дифференциальных уравнений первого порядка при заданных начальных условиях. Для всех этих моделей можно рассматривать общую задачу для системы дифференциальных уравнений - задачу Коши.
Задача Коши для системы дифференциальных уравнений первого порядка может быть поставлена в следующем виде: требуется решить систему дифференциальных уравнений
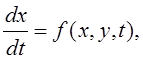
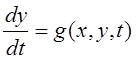 (7.9)
(7.9)
для начального условия:
![]() (7.10)
(7.10)
Решение задачи Коши (9)-(10) ищется в промежутке [0,T]. Для решения данной задачи существуют различные численные методы, в частности, методы Эйлера, Рунге-Кутта и другие.
Метод Эйлера. Для решения
задачи Коши (7.9)-(7.10) производные искомых функций ![]() и
и
![]() заменяются конечно-разностными
соотношениями следующих видов:
заменяются конечно-разностными
соотношениями следующих видов:
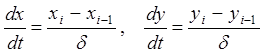 ,
,![]()
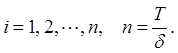 (7.11)
(7.11)
Тогда будут получены рекуррентные формулы:
![]() (7.12)
(7.12)
Здесь ![]() (7.13)
(7.13)
Алгоритм решения задачи состоит из следующих этапов:
- определение начальных значений искомых функций по формулам (7.13);
- начало цикла (![]() );
);
- вычисление значений искомых функций по
формулам для очередного значения счетчика цикла ![]()
- переход к следующему значению счетчика
![]()
- если ![]() то
вычисления повторяются для следующего значения счетчика цикла;
то
вычисления повторяются для следующего значения счетчика цикла;
- вывод результатов.
Требуется составить программу решения задачи, а затем выполнить ее для различных моделей. Результаты могут быть представлены в виде табличных значений искомых функций и их графиков.
Контрольные вопросы:
1) В чем отличие модели Ферхюльста от модели Мальтуса?
2) Почему моделирование экологических систем является сложным?
3) Можно ли показать адекватность модели «хищник-жертва»?
4) Чем отличается модель Базыкина от модели Лотки-Вольтерра?
5) Какие формулы называются конечно-разностными соотношениями?
Лабораторная работа № 8. Модели движений твердого тела
Цель работы: изучение способов математического моделирования движений твердого тела для различных случаев.
Порядок выполнения работы:
1) Изучить теоретические материалы [7,8] и методические указания к выполнению данной работы.
2) Изучить способы математического моделирования движений твердого тела в различной постановке.
3) Сформулировать математические задачи, возникающие в результате моделирования.
4) Разработать алгоритмы и программы решения задач.
5) Решить задачи и оформить отчет по данной работе.
Теоретические материалы и методические указания
Известно, что одной из распространенных задач механики является задача о движениях твердого тела. Эта задача может быть сформулирована в разных постановках и соответственно могут быть разработаны различные математические модели. Целью математического моделирования является определение закона изменения скорости движения тела и закона изменения координаты во времени. Здесь рассматриваются две модели данной задачи о движениях твердого тела.
Модель движения материальной точки по
баллистической траектории. Твердое
тело рассматривается как материальная точка, которая в начальный момент времени
находится в точке с координатами: ![]() Движение тела
начинается с заданной скоростью
Движение тела
начинается с заданной скоростью ![]() под углом к горизонту
под углом к горизонту
![]() Из второго закона Ньютона получены
следующие уравнения:
Из второго закона Ньютона получены
следующие уравнения:
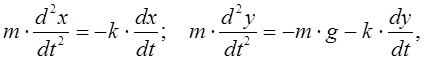
где ![]() масса,
масса, ![]() горизонтальная и вертикальная координаты,
горизонтальная и вертикальная координаты, ![]() время,
время, ![]() коэффициент
сопротивления среды.
коэффициент
сопротивления среды.
Здесь возникает задача Коши для обыкновенных дифференциальных уравнений. Для решения данной задачи вначале необходимо перейти к безразмерным переменным.
Модель движения космического
летательного аппарата (КЛА) по околоземной орбите. Пусть в начальный момент КЛА находится на высоте ![]() от поверхности Земли и в начальный момент
времени
от поверхности Земли и в начальный момент
времени ![]() имеет скорость
имеет скорость ![]() и
координаты
и
координаты ![]() где
где ![]() радиус
Земли. Математическая модель движения КЛА по орбите может иметь следующий вид:
радиус
Земли. Математическая модель движения КЛА по орбите может иметь следующий вид:
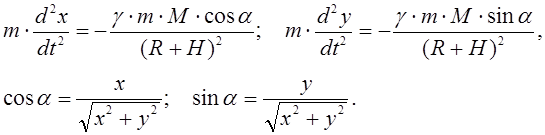
Здесь также возникает задача Коши для обыкновенных дифференциальных уравнений.
Требуется самостоятельно выполнить задание, состоящее из следующих этапов:
- выбрать характерные величины для каждой величины и перейти к безразмерным переменным;
- сформулировать для каждой модели математическую постановку полученных из моделей задач;
- разработать алгоритм решения математических задач, используя один из методов численного решения задачи Коши для обыкновенных дифференциальных уравнений;
- решить задачи численно для конкретных значений параметров;
- провести сравнительный анализ полученных решений этих задач;
- результаты представить в виде графиков, показывающих изменения скоростей и координат.
Контрольные вопросы:
1) Какая траектория движения тела называется баллистической?
2) Как решается система дифференциальных уравнений второго порядка?
3) Для чего осуществляется переход к безразмерным переменным?
4) Как осуществляется переход в уравнениях к безразмерным переменным?
5) Как выбирают характерные величины для перехода к безразмернгым переменным?
6) Что за параметры ![]() ,
, ![]() ?
?
Лабораторная работа № 9. Моделирование процессов, происходящих в электрических цепях»
Цель работы: изучение способов математического моделирования процессов, происходящих в электрических цепях и решение задач, возникающих в результате моделирования.
Порядок выполнения работы:
1) Изучить теоретические материалы [9,10] и методические указания к выполнению данной работы.
2) Изучить способы математического моделирования процессов, происходящих в электрических цепях.
3) Сформулировать математические задачи, возникающие в результате моделирования.
4) Разработать алгоритмы задач и решить их.
5) Оформить отчет по данной работе.
Теоретические материалы и методические указания
Известно, что для описания процессов, происходящих в электрических цепях, могут быть использованы законы электротехники. С помощью этих законов можно разрабатывать математические модели этих процессов. Пусть рассматривается следующая схема (см.рисунок 1).
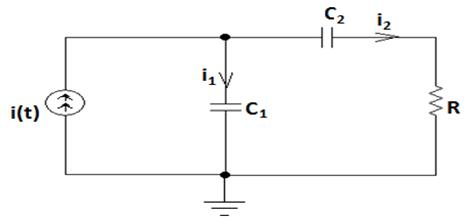
Рисунок 1 – Линейная RC- цепь
Используя законы Кирхгофа для данной цепи, можно получить следующую систему дифференциальных уравнений:
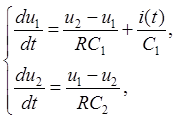 (9.1)
(9.1)
где R – сопротивление резистора; C1 и C2 - емкости конденсаторов; u1(t) и u2(t)– напряжения.
Не ограничивая общность, можно считать, что в
начальный момент (при ![]() ) имелись следующие начальные
условия:
) имелись следующие начальные
условия:
![]() (9.2)
(9.2)
Остальные искомые переменные величины (токи) могут быть определены с помощью следующих формул:
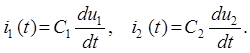 (9.3)
(9.3)
Перед тем как приступить к решению данной задачи,
целесообразно перейти к безразмерным переменным. Для этого выбираются так
называемые характерные величины. Пусть в качестве характерных величин выбраны:
![]() - напряжение,
- напряжение, ![]() ток,
ток, ![]() время. Переход к безразмерным переменным
осуществляется с помощью следующей замены переменных:
время. Переход к безразмерным переменным
осуществляется с помощью следующей замены переменных:
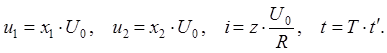 (9.4)
(9.4)
Здесь: ![]() безразмерные
величины. В дальнейших выкладках штрих над
безразмерные
величины. В дальнейших выкладках штрих над ![]() можно
опустить и считать ее безразмерной величиной.
можно
опустить и считать ее безразмерной величиной.
Замена переменных (9.4) позволяет получить из системы уравнений (9.1) следующую систему относительно безразмерных величин:
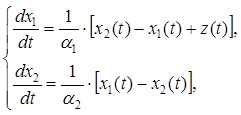
![]() (9.5)
(9.5)
где 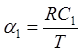 и
и 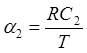 – безразмерные величины.
– безразмерные величины.
Из начальных условий (2) след
![]() (9.6)
(9.6)
Решение задачи (9.5)-(9.6) позволяет определить
искомые функции ![]() и
и ![]() в
аналитические формулы которых входят параметры
в
аналитические формулы которых входят параметры ![]() и
и ![]() Требуется оценить влияние изменения
значений параметров
Требуется оценить влияние изменения
значений параметров ![]() и
и ![]() на
изменение функций
на
изменение функций ![]() и
и ![]()
Решение задачи Коши (9.5)-(9.6) ищется в промежутке [0,1]. Для решения данной задачи существуют различные численные методы, в частности, методы Эйлера, Рунге-Кутта и другие.
Метод Эйлера. Для решения
задачи Коши (9.5)-(9.6) производные искомых функций ![]() и
и ![]() заменяются конечно-разностными
соотношениями следующих видов:
заменяются конечно-разностными
соотношениями следующих видов:
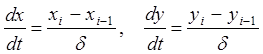 ,
,![]()
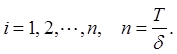 (9.7)
(9.7)
Тогда будут получены рекуррентные формулы:
![]() (9.8)
(9.8)
Здесь ![]() (9.9)
(9.9)
Алгоритм решения задачи состоит из следующих этапов:
- определение начальных значений искомых функций по формулам (9.9);
- начало цикла (![]() );
);
- вычисление значений искомых функций по
формулам для очередного значения счетчика цикла ![]()
- переход к следующему значению счетчика
![]()
- если ![]() то
вычисления повторяются для следующего значения счетчика цикла;
то
вычисления повторяются для следующего значения счетчика цикла;
- вывод результатов.
Требуется составить программу решения задачи, а затем выполнить ее для конкретных значений параметров задачи. Результаты могут быть представлены в виде табличных значений искомых функций и их графиков.
Контрольные вопросы:
1) Какие законы использованы для составления математической модели электрической цепи?
2) Какой процесс в электрической цепи называется переходным?
3) Для чего производится переход к безразмерным переменным?
4) Почему выбран метод Эйлера для решения данной задачи?
5) Какова точность решения данной задачи?
Лабораторная работа № 10. Численное решение краевой задачи для обыкновенных дифференциальных уравнений
Цель работы: изучение одного из популярных методов решения краевой задачи для обыкновенных дифференциальных уравнений.
Порядок выполнения работы:
1) Изучить теоретические материалы [7,8] и методические указания к выполнению данной работы.
2) Сформулировать постановку задачи.
3) Изучить метод решения задачи и разработать алгоритм ее решения.
4) Решить задачу с помощью Excel .
5) Получить решение задачи с помощью компьютерной программы, составленной на одном из языков программирования.
6) Получить результат решения задачи в виде графика искомой функции.
7) Провести анализ полученного решения.
8) Оформить отчет по данной работе.
Теоретические материалы и методические указания
В прикладных задачах физики, механики и инженерных расчетов часто возникает проблема решения краевой задачи для обыкновенных дифференциальных уравнений второго порядка. Решение этой задачи имеет важное значение при изучении динамических процессов, в частности, колебательных процессов.
Постановка задачи. Пусть даны:
дифференциальное уравнение
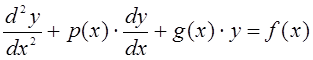 (10.1)
(10.1)
и граничные условия
![]() (10.2)
(10.2)
Здесь ![]() заданные числа,
заданные числа, ![]() известные
функции. Требуется найти значения неизвестной функции
известные
функции. Требуется найти значения неизвестной функции ![]() в
промежутке
в
промежутке![]() , удовлетворяющие уравнению (10.1) и
граничным условиям (10.2).
, удовлетворяющие уравнению (10.1) и
граничным условиям (10.2).
Метод решения задачи. Поставленную задачу (10.1)-(10.2) в практических
случаях невозможно решить аналитическими методами. Поэтому для решения таких
задач используется численный метод, метод конечных разностей. Сущность этого
метода заключается в следующем. Выбирают маленький шаг ![]() и
промежуток
и
промежуток ![]() делится на
делится на ![]() равных
частей. Точки деления определяются следующей формулой:
равных
частей. Точки деления определяются следующей формулой:
![]()
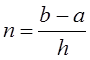 .
.
Значения функции ![]() в этих
точках
в этих
точках ![]() обозначены:
обозначены:
![]() (10.3)
(10.3)
Производится замена производных искомой функции ![]() конечно-разностными соотношениями:
конечно-разностными соотношениями:
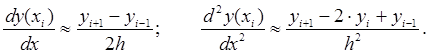 (10.4)
(10.4)
Подставляя формулы (10.4) в формулу (10.1) и учитывая
обозначения (10.3), можно получить следующее уравнение для ![]() :
:
![]() (10.5)
(10.5)
Здесь 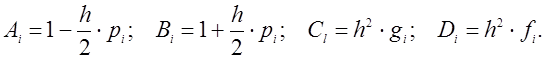
Формула (10.5) определяет систему алгебраических
уравнений относительно неизвестных значений искомой функции ![]() Количество этих уравнений равно
Количество этих уравнений равно ![]() Из гранчных условий (10.2) можно получить
два уравнения:
Из гранчных условий (10.2) можно получить
два уравнения:
![]() (10.6)
(10.6)
Формулы (10.5) и (10.6) представляют собой систему ![]() уравнений с
уравнений с ![]() неизвестными
неизвестными
![]() Если будет решена данная система
алгебраических уравнений, то задача будет решена, т.е. будут найдены значения
искомой функции
Если будет решена данная система
алгебраических уравнений, то задача будет решена, т.е. будут найдены значения
искомой функции ![]() .
.
Метод прогонки. Система уравнений (10.5) является системой с трехдиагональной матрицей. Решение такой системы определяется методом прогонки, сущность которого заключается в следующем. Решение системы определяется следующей формулой:
![]() (10.7)
(10.7)
где ![]() прогоночные
коэффициенты; они пока неизвестные.
прогоночные
коэффициенты; они пока неизвестные.
Процесс определения этих коэффициентов называется прямой прогонкой; для определения их используются формулы:
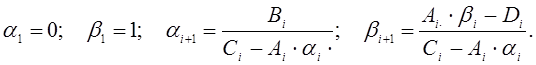 (10.8)
(10.8)
Определение значений искомой функции ![]() называют обратной прогонкой и для этого
используются следующие формулы: сперва вторая формула (10.6), а затем формула
(10.7).
называют обратной прогонкой и для этого
используются следующие формулы: сперва вторая формула (10.6), а затем формула
(10.7).
Алгоритм решения задачи составлен в следующем виде:
- вычисление по известным формулам коэффициентов ![]() системы уравнений (10.5);
системы уравнений (10.5);
- вычисление прогоночных коэффициентов по формулам (10.8);
- определение искомых значений функции по формулам (10.6) и (10.7);
- вывод полученных результатов.
Пример. Пусть рассматривается уравнение:
![]()
Для численного решения использованы следующие значения
параметров: ![]()
Результаты
решения задачи должны быть представлены в виде табличных значений функции ![]() и ее графика.
и ее графика.
Контрольные вопросы:
1) Какая задача называется краевой задачей?
2) В чем сущность конечно-разностного метода решения краевой задачи?
3) Какова погрешность данного метода?
4) В чем заключается сущность метода прогонки?
5) В чем особенность матрицы системы алгебраических уравнений (10.5)?
Лабораторная работа № 11. Явная расчетная схема решения задачи о теплопроводности
Цель работы: изучение одного из методов решения задачи о теплопроводности на основе явной расчетной схемы.
Порядок выполнения работы:
1) Изучить теоретические материалы [7,8] и методические указания к выполнению данной работы.
2) Сформулировать постановку физической задачи о теплопроводности в стержне.
3) Изучить метод решения задачи на основе явной расчетной схемы.
4) Разработать алгоритм решения задачи.
5) Составить программу решения задачи на одном из языков программирования.
6) Отладить программу выполнить ее для конкретных исходных данных.
7) Получить результат решения задачи в виде таблиц и графиков.
8) Провести анализ полученного решения.
9) Оформить отчет по данной работе.
Теоретические материалы и методические указания
Повторить материалы лекции по данной теме и дополнительно изучить вопросы, связанные с математическим моделированием физического процесса о распространении тепла в стержне. Дополнительные материалы можно найти в учебниках физики и теплотехники.
Постановка задачи. Пусть
рассматривается однородный стержень. Параметры этого стержня следующие: длина ![]() , площадь сечения
, площадь сечения ![]() ,
плотность материала
,
плотность материала ![]() , коэффициент теплоемкости
, коэффициент теплоемкости ![]() ,
, ![]() –
коэффициент температурапроводности. На концах этого стержня задана температура
(или может быть она измерена). Требуется определить распределение температуры
во всех сечениях данного стержня в любой момент времени. Предполагается, что
площадь сечения мала в сравнении с его длиной. Это допущение позволяет
считать, что температура во всех точках определенного сечения стержня
одинакова.
–
коэффициент температурапроводности. На концах этого стержня задана температура
(или может быть она измерена). Требуется определить распределение температуры
во всех сечениях данного стержня в любой момент времени. Предполагается, что
площадь сечения мала в сравнении с его длиной. Это допущение позволяет
считать, что температура во всех точках определенного сечения стержня
одинакова.
Математическая модель задачи. Перед математическим моделированием поставленной
задачи необходимо ввести обозначения параметров: ![]() -
время,
-
время, ![]() - координата сечения стержня по оси,
направленной по длине стержня,
- координата сечения стержня по оси,
направленной по длине стержня, ![]() –температура стержня на
сечении стержня с координатой
–температура стержня на
сечении стержня с координатой ![]() и в момент времени
и в момент времени ![]() . Тогда температура может быть
рассмотрена как функция переменных
. Тогда температура может быть
рассмотрена как функция переменных ![]() и
и ![]() :
: ![]() .
.
Для определения температуры, т.е. функцию ![]() используется уравнение параболического
типа:
используется уравнение параболического
типа:
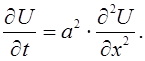 (11.1)
(11.1)
Для решения этого уравнения должны быть заданы:
- начальное условие, которое вытекает из температурного режима стержня в начальный момент времени:
![]() (11.2)
(11.2)
- граничные условия на концах стержня:
![]() (11.3)
(11.3)
![]() (11.4)
(11.4)
Постановка математической задачи. На основе
математической модели задачи (11.1)-(11.4) можно сформулировать следующую
постановку математической задачи: требуется найти такую функцию) ![]() в области
в области ![]() , удовлетворяющую
дифференциальному уравнению (11.1), начальным условиям (11.2) и граничным
условиям (11.3) и (11.4).
, удовлетворяющую
дифференциальному уравнению (11.1), начальным условиям (11.2) и граничным
условиям (11.3) и (11.4).
Переход к безразмерным переменным. Для удобства дальнейших вычислений необходимо перейти к безразмерным параметрам. Пусть в качестве характерных величин выбраны следующие параметры:
![]() – линейный размер,
– линейный размер, ![]() – характерное время,
– характерное время, ![]() – характерная температура: в качестве последнего
можно принять наибольшую температуру на одном из концов стержня. Вводятся новые
переменные:
– характерная температура: в качестве последнего
можно принять наибольшую температуру на одном из концов стержня. Вводятся новые
переменные: ![]() Здесь
Здесь ![]() -
безразмерное время,
-
безразмерное время, ![]() - безразмерная координата,
- безразмерная координата, ![]() – безразмерная температура. В дальнейших
расчетах черточки точки над
– безразмерная температура. В дальнейших
расчетах черточки точки над ![]() и
и ![]() опускаются. После замены переменных
уравнение (11.4) имеет вид:
опускаются. После замены переменных
уравнение (11.4) имеет вид:
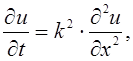 (11.5)
(11.5)
где  .
.
Начальное условие (11.2) имеет вид:
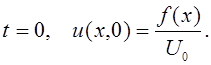 (11.6)
(11.6)
Граничные условия (11.3) и (11.4) будут записаны в виде следующих формул:
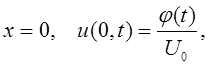 (11.7)
(11.7)
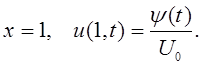 (11.8)
(11.8)
Теперь необходимо решить задачу в безразмерных параметрах (11.5)-(11.8).
Явная расчетная схема. Из уравнения (11.5) следует формула:
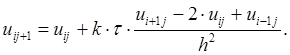 (11.9)
(11.9)
Из начального условия (11.6) следует
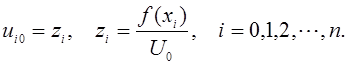 (11.10)
(11.10)
Из граничных условий (11.7) и (11.8) будут получены формулы:
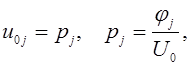 (11.11)
(11.11)
![]()
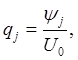
![]() (11.12)
(11.12)
Алгоритм явной расчетной схемы состоит из следующих этапов:
- цикл для вычисления значений искомой функции по формуле (11.10).
-
внешний цикл по счетчику ![]() начало цикла.
начало цикла.
- вычисление граничных значений по формулам (11.11) и (11.12).
-
внутренний цикл по счетчику ![]() вычисления по
формуле (11.9).
вычисления по
формуле (11.9).
-
конец внешнего цикла по ![]() .
.
Индивидуальное задание магистранту выдается преподавателем перед выполнением лабораторной работы.
Контрольные вопросы:
1) Какие законы использованы для получения математической модели задачи о распространении тепла в стержне?
2) В чем отличие темепературопроводности от теплопроводности?
3) Какому типу относится уравнение распространения тепла в стержне?
4) В чем сущность метода, используемого для решения задачи о теплопроводности?
5) В чем преимущества явной расчетной схемы?
6) Какие недостатки являются основными явной расчетной схемы?
Лабораторная работа № 12. Неявная расчетная схема решения задачи о теплопроводности
Цель работы: изучение одного из популярных методов решения задачи о теплопроводности на основе неявной расчетной схемы.
Порядок выполнения работы:
1) Изучить теоретические материалы [7,8 ] и методические указания к выполнению данной работы.
2) Изучить метод решения задачи на основе неявной расчетной схемы.
3) Разработать алгоритм решения задачи.
4) Составить программу решения задачи на одном из языков программирования.
5) Отладить программу и выполнить ее для конкретных исходных данных.
7) Получить результат решения задачи в виде таблицы значений искомой функции.
8) Провести анализ полученного решения.
9) Оформить отчет по данной работе.
Теоретические материалы и методические указания
Перед выполнением данной работы целесообразно повторить теоретические материалы, связанные с постановкой задачи о теплопроводности и математическим моделированием, а также дискретизация математических формул. Здесь решается та же задача (11.5)-(11.8), которая была рассмотрена в предыдущей работе.
Несмотря на трудности, связанные с разработкой компьютерной программы решения задачи, в практических вычислениях в основном предпочтение отдается неявной расчетной схеме.
Неявная расчетная схема. Из уравнения теплопроводности;
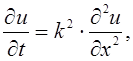
следует формула:
![]() (12.1)
(12.1)
где 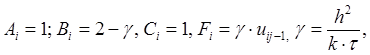 (12.2)
(12.2)
![]()
Из начального условия 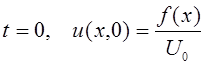 следует
следует
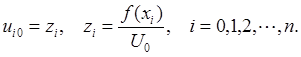 (12.3)
(12.3)
Из граничных условий 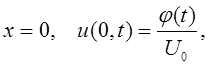
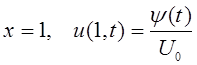 будут получены формулы:
будут получены формулы:
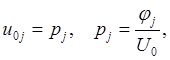 (12.4)
(12.4)
![]()
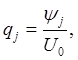
![]() (12.5)
(12.5)
Метод прогонки. Вводятся обозначения:
![]()
Тогда с учетом этой замены будет получена следующая формула:
![]() (12.6)
(12.6)
Здесь: ![]()
Решение системы уравнений (12.6) осуществляется методом прогонки; этот метод был рассмотрен в лабораторной работе №10. Решение системы (12.6) определяется следующей формулой:
![]() (12.7)
(12.7)
где ![]() прогоночные
коэффициенты; они пока неизвестные.
прогоночные
коэффициенты; они пока неизвестные.
Процесс определения этих коэффициентов называется прямой прогонкой; для определения их используются формулы:
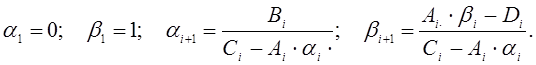 (12.8)
(12.8)
Определение значений искомой функции ![]() называют обратной прогонкой и для этого
используются следующие формулы: сперва вторая формула (12.6), а затем формула
(12.7).
называют обратной прогонкой и для этого
используются следующие формулы: сперва вторая формула (12.6), а затем формула
(12.7).
Алгоритм неявной расчетной схемы состоит из следующих этапов:
- цикл для вычисления начальных значений искомой функции по формуле (12.3);
-
внешний цикл по счетчику ![]() начало цикла;
начало цикла;
- вычисление граничных значений по формулам (12.4) и (12.5);
-
внутренний цикл по счетчику ![]()
- вычисление по известным формулам коэффициентов системы уравнений (12.6);
- прямая прогонка: вычисление прогоночных коэффициентов по формулам (12.8);
- обратная прогонка: определение искомых значений функции по формулам (12.5) и (12.7);
-
конец внутреннего цикла по ![]()
- переход к внешнему циклу и завершение вычислений.
Индивидуальное задание магистранту выдается преподавателем перед выполнением лабораторной работы.
Контрольные вопросы:
1) Какие недостатки у явной расчетной схемы?
2) Что такое устойчивость расчетной схемы?
3) В каких случаях неявная расчетная схема является устойчивой?
4) Какая особенность системы уравнений (12.6)?
5) На каком этапе вычисляются коэффициенты прогонки?
Список литературы
1. Тихонов А.Н., Костомаров Д.. Вводные лекции по прикладной математике. – М.: Наука, 1984.- 192 с.
2. Королев А.Л. Компьютерное моделирование – М.: БИНОМ. Лаборатория знаний, 2010.-230 с.
3. Мышкис А.Д. Элементы теории математических моделей.– М.: Высшая школа.- 2007.-244 с.
4. Голованов Н.Н. Геометрическое моделирование.- М.:Высшая школа.- 2002. – 370 с.
5. Бусленко Н.П. Моделирование сложных систем. – М.:Наука, 1978.- 400 с.
6. Коршунов Ю.М. Математические основы кибернетики: Учеб. пособие для вузов. – М.: Энергия, 1980. – 424 с.
7. Тихонов А.Н., Самарский А.А. Уравнения математической физики.- М.: Наука, 1972. -735 с.
8. Седов Л.И. Методы подобия и размерности в механике. – М.: Наука, 1987.- 432 с.
9. Смирнов В.И. Курс высшей математики. Том 2.- М.: Наука,1974.- 656 с.
10. Бакалов В.П., Дмитриков В.Ф., Крук Б.Е. Основы теории цепкй. Учебник для вузов; Под ред. Бакалова В.П. – М.: Радио и связь, 2000. -592 с.
11. Бухгольц Н.Н. Основной курс теоретической механики (часть вторая).- М.: 1872.-332 с.
12. Құралбаев З.Қ. Алгоритмдеу және программалау тілдері.-Алматы, 2008.-353 бет.
Содержание
Введение
1 Лабораторная работа №1. Линейная аппроксимация статистических данных
2 Лабораторная работа №2. Квадратичная аппроксимация статистических данных
3 Лабораторная работа №3. Уравнения множественной регресии
4 Лабораторная работа №4. Моделирование нормально распределенных случайных величин
5 Лабораторная работа №5. Модель определения цены товара на конкурентном рынке
6 Лабораторная работа №6. Численное решение задачи коши для обыкновенных дифференциальных уравнений
7 Лабораторная работа №7. Модели процессов в экологических системах
8 Лабораторная работа №8. Модели движений твердого тела
9 Лабораторная работа №9. Моделирование переходных процессов, происходящих в электрических цепях
10 Лабораторная работа №10.Численное решение краевой задачи для обыкновенных дифференциальных уравнений
11 Лабораторная работа №11. Явная расчетная схема решения задачи о теплопроводности
12 Лабораторная работа №12. Неявная расчетная схема решения задачи о теплопроводности
13 Список литература
Содержание