Некоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ
И СВЯЗИ
Кафедра компьютерной технологии
МАТЕМАТИЧЕСКОЕ И КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ
Конспекты лекций
для магистрантов, обучающихся по специальности
6М070400 - Вычислительная техника и программное
обеспечение
Алматы 2014
СОСТАВИТЕЛЬ: Куралбаев З.К. Математическое и компьютерное моделирование. Конспекты лекций для магистрантов специальности 6М070400-Вычислительная техника и программное обеспечение. – Алматы: АУЭС, 2013 . – 60 с.
Конспекты лекций содержат теоретические материалы по математическому и компьютерному моделированию, где рассматриваются методы моделирования для решения сложных научных, инженерно-технических, социально-экономических и других важных практических задач.
Рекомендуются магистрантам всех форм обучения по специальности 6М070400 –Вычислительная техника и программное обеспечение.
Ил., табл. 3, библиогр. - 20 назв.
Рецензент: канд.техн.наук, доцент Ни А.Г.
Печатается по плану издания Некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2013 г.
© НАО «Алматинский университет энергетики и связи», 2014 г.
Введение
Преподавание дисциплины «Математическое и компьютерное моделирование» предназначено дать будущим ИТ-спеиалистам знания и основные навыки решения различных научных, инженерно-технических и практических задач с применением математических методов и средств современной компьютерной техники.
Цель курса:
– дать магистрантам основные сведения о современных методах построения, реализации и исследования моделей объектов, процессов и систем различной природы;
- ознакомить с методологией моделирования;
- научить применять компьютер как инструмент познания в различных областях практической деятельности;
- научить и сформировать навыки применения методов моделирования для решения конкретных научных задач.
Задачи курса:
- ознакомить с методами моделирования, применяемых в научных и научно-технических исследованиях;
- ознакомить с современными методами и технологиями построения математических и компьютерных моделей объектов исследования;
- обучить эффективному применению математических и компьютерных моделей для решения практических задач;
- развить творческий потенциал будущих магистров по компьютерным технологиям, необходимый для дальнейшего самостоятельного освоения новых методов и технологий в условиях непрерывного развития и совершенствования информационных технологий.
Компетентность магистранта:
должен знать:
- основные виды моделирования процессов, происходящих в природе и обществе;
- подходы для создания математических моделей задач из различных предметных областей знаний;
- особенности математического и компьютерного моделирования, этапы создания адекватных исследуемому процессу или явлению моделей;
уметь:
- сформулировать постановку задачи из предметной области, используя для этого фундаментальные законы природы;
- разрабатывать математическую модель задачи, осуществляя выбор основных (приоритетных) факторов, влияющих на решение поставленной задачи;
- сформулировать математическую задачу на основе математической модели задачи и выбрать метод ее решения на компьютере;
- проводить вычислительный эксперимент для многих вариантов исходных данных.
Лекция 1. Основные понятия о методах моделирования
Цель лекции: дать обучающимся первоначальные знания о методах моделирования различных объектов исследования, о роли этих методов в научных исследованиях.
Содержание лекции: понятие о моделировании процессов и явлений, происходящих в природе и обществе. Виды моделей и области применения моделей. Роль математического и компьютерного моделирования в развитии науки и техники.
Одной из характерных особенностей современного мира является широкое применение математических методов и компьютерных технологий в самых различных областях человеческой деятельности. Основными методами и инструментами ученых и специалистов в научных исследованиях, в изыскательских и проектных работах стали методы математического и компьютерного моделирования. Этот факт требует от будущих ИТ-специалистов фундаментального знания по применению методов математического и компьютерного моделирования для решения сложных научно-технических и жизненно важных практических задач.
1 Понятия о моделировании. Модели и их разновидности. Познавательные и прагматические модели
Изучение природного явления или происходящие в обществе события, исследование природных и технологических процессов, проектирование объектов или других проблем прежде всего связаны с их предварительным моделированием. Любое серьезное мероприятие человек начинает с изучения рассматриваемого объекта в моделях [1]. Здесь рассматриваются два понятия, связанные между собой: объект моделирования и его модель.
Объектом моделирования называется любая часть реальной действительности, которая может быть рассмотрена как единое целое и подлежащая изучению или исследованию по определенным качественным или количественным признакам [1]. Объектом моделирования могут быть процессы, явления, события, предметы и многие другие [2].
Модель – это любой объект произвольной формы, отражающий основные свойства, характеристики и связи объекта моделирования, которые являются существенными для решения поставленной задачи [1]. Модель отражает только главные свойства объекта моделирования, пренебрегает несущественными или второстепенными. Поэтому конкретная модель не может отражать полностью все свойства и характеристики моделируемого объекта. Известно, что свойства, характеристики и связи любого объекта зависят от множества внутренних и внешних факторов. При создании модели объекта выбираются только существенные факторы для решения поставленной задачи. Поэтому модель будет иметь прямую зависимость от условий постановки задачи. В зависимости от выбора факторов и постановки задачи для одного и того же объекта могут быть составлены различные модели, т.е. речь идет о множестве моделей [2].
В настоящее время моделирование является неотъемлемой частью человеческой деятельности. Особенно оно стало актуальным в научных исследованиях, главным методом изучения сложных явлений и процессов.
Модели могут быть условно разделены на две группы: познавательные и прагматические [3-5]. Познавательные модели являются формой представления знаний, отражением существующих закономерностей в природе и обществе. Прагматические модели являются средством организации практических действий, например, проекты, чертежи, рисунки и т.д.
2 Основные задачи моделирования
Можно считать, что моделирование как форма отражения действительности окружающего мира зародилось с возникновением научного знания. Вначале в качестве модели человечество использовало геометрические изображения, макеты, схему или рисунки объекта изучения. Такие модели могут быть названы геометрическими [1,2].
В процессе развития есетественных наук возникла необходимость использования других способов моделирования, в частности, вместо изучения сложных, труднодоступных для проведения измерений, инструментальных наблюдений или визуального изучения явлений или процессов стали использоваться аналоговые и математические модели.
Аналоговые модели используют подобие, существующее между двумя явлениями или процессами. Одно из явлений является объектом моделирования, а вторая его моделью. Например, изучение сложной сети водоснабжения города может быть заменено изучением электрической сети, созданной на стенде лаборатории. Таких примеров можно привести очень много.
3 Роль моделирования в науке и технике
История развития науки и техники неразрывно связано с развитием математической науки и применением математических методов в различных отраслях как естественных, так и гуманитарных наук. Это связано прежде всего в связи с применением количественных методов исследования вместо традиционных описательных методов, существовавших прежде во многих отраслях науки [4,5]. Примером может служит экономические науки, которые прежде использовали анализ экономических показателей без применения количественных критериев, в частности, для определения оптимальных решений. В последние годы интенсивно используются методы математического моделирования, позволяющие использовать хорошо развитый математический аппарат и быстродействующую вычислительную технику.
Использование компьютерных и телекоммуникационных средств хранения, обработки, передачи и получения информации позволило решать сложные задачи, которые прежде не могли быть решены [6]. Применение компьютерных технологий для решения научных проблем потребовало развитию новых направлений в математике и созданию новых математических моделей процессов и явлений, а также методов решения различных задач. С другой стороны, появление новых математических моделей и методов стимулировало появление новых программных продуктов для ЭВМ, а это, в свою очередь, стимулировало развитие компьютерной техники и технологий. Появился новый термин «компьютерное моделирование» [2].
Моделирование - один из основных методов научного познания. Суть его зключается в том, что из сложного явления выделяются некоторые его главные части и замещаются моделями, более простыми, более удобными для изучения и объяснения.
Любая наука основана на представлениях об объекте исследования, которые сложились в сознании человека. Эти представления определяют концептуальные модели объекта. Для формирования концептуальных моделей исследователь (человек) использует результаты наблюдений, свой исследовательский и теоретический опыт, логические выводы. Здесь должны быть выделены наиболее существенные факторы из множества факторов, влияющих на объект исследования. С помощью концептуальных моделей создаются абстрактные модели, отражающие свойства реальных объектов.
На базе концептуальных моделей и соответствующих научных законов формируются модели явлений и процессов, которые затем образуют научные теории.
Проектирование и эксплуатация сложных технических систем требуют применения научных знаний и методов моделирования. Без предварительного анализа на моделях не выполняется ни один проект. Кроме этого методы моделирования позволяют определять закономерности изменения параметров объекта, устанавливать связи между ними, что очень важно в изучении сложных явлений и процессов.
В научных исследованиях существуют гипотезы, высказанные исследователями на основе наблюдений и своих интиуций. Одним из важных направлений в науке является проверка этих гипотез с помощью лабораторных или натурных испытаний. Гипотеза также может рассматриваться как модель изучаемого объекта. После многократных испытаний и анализа результатов могут быть установлены определенные закономерности, определяющие свойства и характер объекта. Одним словом, гипотеза может превратиться в научную теорию.
Исторически математическая модель стала использоваться как инструмент для изучения природных явлений и процессов, в вопросах проектирования и планирования очень давно, с момента появления обыкновенных арифметических вычислений.
4 Особенности математического и компьютерного моделирования
Особенностью математического моделирования является то, что для его применения не требуются материальные затраты, нет необходимости применять какие-то приборы, инструменты и оборудование для исследования, не нужно создавать макеты или чертежи. Здесь используются только знания, опыт и интуиция исследователя [2].
Можно смело утверждать, что большиство законов природы и общества, выявленные исследователями, получены благодаря использованию математических моделей. В дальнейшем, с развитием науки и техники роль математического моделирования стала еще более важной. Это связано с тем, что изучение многих сложных процессов и явлений затруднено из-за недоступности наблюдения, нельзя определять значения параметров объекта даже с помощью современных инструментов. В некоторых случаях методы математического моделирования являются единственными для исследования сложных явлений.
Появление такого мощного инструмента как вычислительная техника позволило расширить возможности применения методов математического моделирования. Многие проблемы, связанные с решением математических задач, получаемых из математических моделей, обработкой и хранением большого объема информации, были эффективно решены с помощью компьютерной техники. Появились новые методы моделирования, называемые методами компьютерного моделирования [2]. Компьютер стал не только инструментом для решения математических задач, его стали применять для моделирования многих объектов исследования. В настоящее время компьютер стал инструментом для проведения экспериментов. Появился новый вид эксперимента – численный эксперимент, позволяющий выполнить численный анализ с большим объемом информации, причем с огромной скоростью.
Основной особенностью компьютерного моделирования является простота их создания и модификации. Изменению подвергается только математическое и программное обеспечение. Кроме этого компьютерная модель позволяет рассматривать множество вариантов, что очень важно для анализа и выбора наилучшей (эффективной) модели объекта. В настоящее время много внимания уделяется созданию так называемых автоматизированных систем моделирования, которые позволяют выполнить построение моделей, проводить численные эксперименты, обработать информацию и сделать анализ по результатам экспериментов.
5 Этапы разработки математической и компьютерной модели объекта
Создание математической и компьютерной модели объекта начинается с выявления или синтеза структуры объекта, проводится предварительный качественный анализ его свойств, а также факторов, оказывающих влияния на них. Постановкой задач моделирования осуществляет специалист в конкретной предметной области.
Следующий этап требует работу специалиста по математике, который разрабатывает матматическую модель, используя для этого результаты анализа свойств объекта и факторов, влияющих на функционирование объекта. На основе математической модели должна быть сформулирована математическая постановка задачи. В результате, задача из предметной области становится математической задачей.
Для решения математической задачи выбирается метод решения. Обычно для решения математической задачи используется численный метод. Численный метод позволяет создавать расчетную схему решения задачи, по которой разрабатывается алгоритм решения задачи [8,9].
На следующем этапе разрабатывается программа решения задачи на компьютере. Любая программа требует тщательной проверки и тестирования. Этот этап работы называется отладкой программы. Разработка алгоритма, программы и ее отладка являются функциями программиста.
Последними этапами работы являются выполнение программы и анализ результатов ее выполнения. Одной из главных и полезных особенностей компьютерного моделирования является возможность многократного использования программного обеспечения, полученного в результате выполнения всех вышеназванных видов работы.
6 Адекватность моделей
Любая модель определенным образом отличается от оригинала-объекта, т.е. полного совпадения никогда не бывает. Однако модель может с некоторой точностью отражать основные свойства объекта. Модель, с помощью которой успешно решается поставленная задача, называется адекватной. Поэтому адекватность является характеристикой точности отражения моделью свойства моделируемого объекта, необходимой для решения поставленной задачи [11,2].
Различие между объектом и моделью связано с учетом только основных факторов, пренебрегая второстепенными. Здесь возможны два крайних случаев: а) учитываются небольшое количество факторов, что приводит к простой модели и тем самым к простой математической задаче; б) учитываются очень большое количество факторов, при котором приходится решать труднорешаемую математическую задачу. Оба варианта считаются неудачными, поэтому ставится вопрос о выборе оптимального варианта модели.
Лекция 2. Математическое моделирование. Методы исследования моделей
Цель лекции: ознакомить обучающихся с основными подходами применения методов математического моделирования и исследования моделей.
Содержание лекции: введение в математическое моделирование, этапы разработки математической модели. Математическая модель движения твердого тела. Метод подобия. Классификация методов исследования математических моделей. Дискретизация непрерывных переменных. Численные методы и вычислительный эксперимент.
1 Введение в математическое моделирование
В научных исследованиях важное место принадлежит математическому моделированию объектов исследования. В данной лекции будут рассматриваться некоторые сведения о математическом моделировании как метод исследования различных явлений и процессов, приведены примеры построения математических моделей простейших явлений и сформулированы постановки математических задач. Вначале необходимо дать определение математического моделирования и математической модели.
Математическая модель объекта исследования – это математический объект, который по своим свойствам подобен объекту – оригиналу [1,2]. Процесс создания математической модели объекта называется математическим моделированием. Математическая модель представляет собой совокупность математических зависимостей (алгебраические и дифференциальные уранения и их системы, неравенства и их системы, интегралы и другие различные формулы), связывающих основные параметры объекта исследования.
В предыдущей лекции было отмечено, что в зависимости от выбора учитываемых факторов и параметров, модели могут быть разными. Перед составлением математической модели проводится анализ факторов, влияющих на постановку задачи. Из такого анализа будет получена совокупность параметров, являющихся важными (основными) для формулировки решаемой задачи. Выбранным параметрам присваиваются имена (идентификаторы). Этот процесс называется идентификацией параметров. Затем, используя условия задачи, сформулированные в постановке задачи, будут получены математические зависимости относительно выбранных параметров.
В этом процессе для получения формул в основном используются фундаментальные законы природы или развития общества. При этом предполагается, что фундаментальные законы считаются выполненными для кокретной рассматриваемой задачи. Однако для многих задач приходится использовать данные эксперимента или наблюдений, феноменологические законы или эмпирические зависимости.
2 Движение тела под действием силы тяжести в среде с сопротивлением
Пусть рассматривается следующий простой пример. В качестве рассматриваемого объекта принято твердое тело определенной массы, которое падает с некоторой высоты под воздействием силы тяжести и при этом испытывает сопротивление воздуха. Перед составлением математической модели, описывающей движение этого тела, необходимо сделать некоторые допущения.
Пусть:
- тело имеет определенную форму, обеспечивающую прямолинейное его движение;
- масса тела постоянная величина;
- в процессе движения форма тела не изменяется;
- плотность тела намного выше чем плотность воздуха;
- вращение тела отсутствует;
- сопротивление воздуха имеет линейную зависимость от скорости движения тела;
- сила-тяжести постоянная величина.
Тело, которое удовлетворяет всем этим допущениям, в теоретической механике называется материальной точкой [13]. Поэтому для составления математической модели движения такого тела можно пользоваться фундаментальными законами теоретической механики. В данном примере целью составления математической модели является определение закона изменения скорости движения тела и закона изменения координаты, определяющей его местоположения в зависимости от времени.
Идентификация. Пусть вводятся обозначения:
![]() – время,
независимая переменная;
– время,
независимая переменная;
![]() –
координата, определяющая местоположение материальной точки;
–
координата, определяющая местоположение материальной точки;
![]() – масса
тела;
– масса
тела;
![]() –
ускорение силы тяжести;
–
ускорение силы тяжести;
![]() – скорость
движения тела;
– скорость
движения тела;
![]() – коэффициент
сопротивления среды (воздуха);
– коэффициент
сопротивления среды (воздуха);
![]() -
начальная скорость тела (в начальный момент времени);
-
начальная скорость тела (в начальный момент времени);
x0 – начальное положение (в начальный момент времени ![]() ).
).
Используя второй закон Ньютона, с учетом допущений, сделанных выше, можно записать следующие уравнения [13]:
 (1)
(1)
Эти уравнения являются обыкновенными дифференциальными
уравнениями относительно двух неизвестных функций ![]() и
и ![]()
Для определения частного решения этих уравнений должны быть заданы начальные условия, записанные в следующем виде:
![]() (2)
(2)
Полученные формулы (1) и (2) составляют математическую
модель задачи о движении тела под действием силы тяжести и силы сопротивления
среды. Здесь может быть сформулирована математическая задача: требуется
найти такие значения неизвестных функций ![]() и
и ![]() в промежутке
в промежутке ![]() удовлетворяющих
системе уравнений (1) и начальным условиям (2).
удовлетворяющих
системе уравнений (1) и начальным условиям (2).
3 Метод подобия
Практические задачи имеют математические модели в виде математических зависимостей между параметрами, имеющими размерные значения. При выполнении расчетов удобно переходить к безразмерным параметрам. Такой метод, называемый методом подобия [10], является одним из распространенных и широко применяемых в научных исследованиях.
Сущность метода подобия заключается в следующем. Для каждого параметра выбираются характерные величины и рассматриваются отношения размерных параметров к этим характерным величинам. Тогда будут получены безразмерные параметры. Переход к безразмерным параметрам позволяет выполнять расчеты, не думая о проблемах, связанных с размерами параметров.
Для перехода к безразмерным переменным вначале
выбираются так называемые характерные величины для рассматриваемой задачи и
производится замена переменных: каждая безразмерная величина определяется как
отношение размерной величины к характерной величине. В рассмотренном примере о
движении твердого тела в качестве характерных величин могут быть выбраны
следующие параметры: ![]() время,
время, ![]() начальное
положение тела,
начальное
положение тела, ![]() начальная скорость. В данном
случае вводятся обозначения:
начальная скорость. В данном
случае вводятся обозначения:


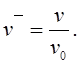 (3)
(3)
Используя эти обозначения (3), из формул (1) и (2) можно получить уравнения в безразмерных переменных.
4 Классификация методов исследования моделей
После того как была составлена математическая модель задачи, сформулирована математическая постановка задачи и преобразование ее к безразмерному виду требуется решить задачу для дальнейшего исследования модели. Здесь приходится решать математическую задачу. Для этого существует достаточно большое количество методов, позволяющих исследовать качественные и количественные свойства объекта. Используемые для решения задач методы могут быть разделены на: точные, асимптотические, приближенные [15].
По видам решений, получаемых при использовании этих методов, они делятся на аналитические и численные. Аналитические методы позволяют получать решения в виде математических формул или зависимостей. В результате использования численных методов решения получаются в виде чисел или числовых таблиц. Каждый вид методов имеют определенные преимущества и недостатки.
Аналитические методы решения дают результаты в виде математических формул, удобных для анализа полученных результатов. Однако аналитические методы могут быть использованы для простых математических задач, получаемых из простых моделей объекта исследования. Очевидно, что создание простых моделей сопровождается пренебрежением большого количества факторов, влияющих на функционирование объекта. Здесь ухудшается адекватность модели объекту исследования. Это является существенным недостатком при решении поставленной задачи.
Поэтому приходится создавать сложные модели, учитывающие достаточное количество факторов. На основе сложных моделей естественно формулируется сложная математическая задача, которая не решается существующими аналитическими методами. В связи с этим появилась необходимость создания быстродействующей вычислительной техники. Появление ЭВМ стимулировало развитие численных методов, с помощью которых можно решать практически задачи любой сложности и любого типа. Такое положение стало основанием для появления компьютерного моделирования, мощного инструмента для модельного исследования различных явлений и процессов.
Преимуществом численных методов является возможность решения практически любой математической задачи. Недостатком их может быть неточность получаемых результатов. Однако этот недостаток может быть разрешен возможностью современных ЭВМ выполнять расчеты с любой точностью и большой скоростью.
5 Дискретизация непрерывных переменных
Определенные трудности для численного решения на ЭВМ возникают при решении задач, описывающих непрерывные процессы или процессы с распределенными параметрами. В этих задачах рассматриваются непрерывные переменные и их производные.
Из курса математики известно [11], что уравнения или их системы называются дифференциальными, если в них присутствуют производные искомых переменных. Если искомые переменные зависят только от одной независимой переменной, то такие уравнения считаются обыкновенными дифференциальными уравнениями. В зависимости от условия постановки исходной задачи могут быть поставлены следующие задачи: задача Коши (задача с начальными условиями) и краевая задача (задача с граничными условиями).
Большую группу прикладных задач составляют задачи т.н. математической физики [8,9], где рассматриваются дифференциальные уравнения в частных производных. В этих уравнениях искомые переменные зависят от многих независимых переменных.
Для применения компьютерной техники для решения этих
задач должна быть произведена дискретизация непрерывных переменных [8,9,15]. Известно, что (по определению производной) производная
функции ![]() является
пределом отношения приращения функции
является
пределом отношения приращения функции ![]() к
приращению аргумента
к
приращению аргумента ![]() при
при ![]()
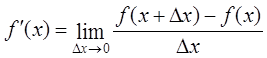 . (4)
. (4)
Следовательно, при достаточно малом значении
приращения аргумента ![]() с достаточной точностью можно
записать следующее выражение:
с достаточной точностью можно
записать следующее выражение:
 (5)
(5)
Формула (5) называется разностным соотношением первого порядка. Если рассматривается производная второго порядка, то она заменяется разностным соотношением второго порядка и т.д.
Для получения формулы (5) область определения функции
разбивается на ![]() равных частей. Длина каждой из
этих частей
равных частей. Длина каждой из
этих частей ![]() называется шагом разбиения. Точки
разбиения области определения функции или узловые точки имеют координаты
называется шагом разбиения. Точки
разбиения области определения функции или узловые точки имеют координаты ![]() . Совокупность дискретных значений
функции
. Совокупность дискретных значений
функции ![]() заменяет в дальнейших расчетах непрерывную
функцию
заменяет в дальнейших расчетах непрерывную
функцию ![]()
6 Численные методы
Когда используются приближенные методы решения
задачи, возникает проблема о точности вычислений [15]. Использование
метода, точность которого не определена, не имеет практическую ценность. При
замене производной функции разностным соотношением погрешность зависит от
выбранного шага ![]() : чем меньше значение шага тем
меньше погрешность вычисления или точность выше и, наоборот. Поэтому стараются
выбирать шаг
: чем меньше значение шага тем
меньше погрешность вычисления или точность выше и, наоборот. Поэтому стараются
выбирать шаг![]() маленьким, но при этом увеличивается
количество шагов
маленьким, но при этом увеличивается
количество шагов ![]() , что приводит к увеличению
объема вычислительной работы.
, что приводит к увеличению
объема вычислительной работы.
При выполнении расчетных работ точность вычисления обычно задается заранее и в качестве значений параметра, определяющего точность вычисления, выбирают следующие маленькие числа: 0,01, 0,001, 0,0001 и т.д.
Численный метод позволяет составить т.н. расчетную схему, по которой производятся арифметические и логические действия [15]. Следует обратить внимание на такой факт, при выполнении расчетов на ЭВМ появляются очень большие числа или многократные повторения без выдачи результатов («зацикливание»). В таких случаях говорят, что расчетная схема неустойчивая. Поэтому перед использованием любой расчетной схемы необходимо убедиться в том, что расчетная схема устойчивая и можно с уверенностью использовать для разработки алгоритма и программы решения задачи. Неустойчивость расчетной схемы может появиться в ходе вычислений из-за накопления ошибок.
7 Компьютерный вычислительный эксперимент
В связи с применением компьютера широко стали применяться численные методы и численное (компьютерное) моделирование. Преимуществом численных методов является возможность решения любых практических задач.
Для решения задачи на компьютере должна быть составлена программа на основе алгоритма. Для практического использования результатов решения задачи должны быть получены численные данные для различных вариантов. Проведение численных расчетов для различных вариантов задачи и анализ их результатов называется вычислительным экспериментом.
Лекция 3. Эконометрические модели
Цель лекции: изучить способы математического моделирования и решения задач эконометрики.
Содержание лекции: о задачах эконометрики. Постановка задачи об определении цены товара на конкурентном рынке и ее эконометрическая модель. Метод и алгоритм решения задачи. Модели корреляционного и регрессионного анализа. Метод наименьших квадаратов.
Одной из областей использования методов математического моделирования и вычислительной техники являются социально-экономические исследования. Здесь используются разнообразные модели: экономико-математические, статистические, имитационные, стохастические, оптимизационные и т.д. Математизация и компьютеризация финансово-экономической отрасли привели к появлению новых направлений и методов научных исследований [1,2].
В данной и следующей лекциях будут рассмотрены вопросы, связанные с моделированием процессов и явлений, протекающих в экономике и социальной сфере.
Математическое моделирование многих экономических задач, в том числе, процесса ценообразования, прогнозирования, циклических процессов в экономике и других, привело к появлению нового направления экономической науки, называемой эконометрикой. Эконометрика стала одним из инструментов исследования таких проблемных вопросов как прогнозирование экономического развития, маркетинговое изучение рынка товаров и услуг, а также для решения других задач.
1 Постановка задачи об определении цены товара на конкурентном рынке
В экономической теории (в микроэкономике) имеется утверждение о том, что цена товара определяется на конкурентном рынке и она зависит от спроса и предложения на этот товар. Требуется определить цену даннного товара на данном рынке и показать процесс установления цены товара с помощью простой модели.
Для решения данной задачи должны быть заданы зависимости от цены товара спроса покупателей на этот товар и объема этого товара, предлагаемого продавцами.
Для создания модели ценообразования должны быть следующие предположения (гипотезы):
- первоначальная цена товара определяется значением цены в предыдущем периоде;
- объем проданного продавцом товара равен объему купленного покупателем товара;
- в каждый период времени на рынке устанавливается равновесная цена.
Пусть рассматривается некоторый рынок определенного товара. Известно, что спрос на товар будет большим, если цена товара будет низкой и, наоборот, спрос будет маленьким, если цена будет большой. Объем товара, предлагаемого продавцами, также зависит от цены товара: если цена товара высокая, то объем предложения также будет большим и, наоборот, при низкой цене товара предложение также будет низким. Тогда функция, определяющая спрос на товар, будет монотонно убывающей функцией цены товара; эта функция называется функцией спроса. Функция предложения будет монотонно возрастающей функцией цены товара. Для простоты здесь рассматриваются линейные зависимости объема продажи и покупки от цены товара.
2 Эконометрическая модель
Пусть вводятся обозначения: ![]() –цена
товара,
–цена
товара, ![]() -функция спроса,
-функция спроса, ![]() –
функция предложения. Для простоты предполагается, что эти функции являются
линейными:
–
функция предложения. Для простоты предполагается, что эти функции являются
линейными:
![]()
![]() , (1)
, (1)
где ![]() –время (период),
–время (период),
![]() – заданные величины, определяющие функции спроса и
предложения. Объемы спроса и предложения должны быть одинаковыми:
– заданные величины, определяющие функции спроса и
предложения. Объемы спроса и предложения должны быть одинаковыми:
![]() . (2)
. (2)
Здесь
параметр ![]() -текущий
момент (период торговли) времени, а
-текущий
момент (период торговли) времени, а ![]() показывает предыдущий
момент (период) торговли времени. Приведенные выше формулы (1)-(2) определяют
эконометрическую модель поставленной задачи.
показывает предыдущий
момент (период) торговли времени. Приведенные выше формулы (1)-(2) определяют
эконометрическую модель поставленной задачи.
3 Метод решения задачи
В данном случае для решения задачи выполняются простые вычисления объема предложения и спроса; в каждом шаге определяется новое значение цены товара. Здесь можно получить окончательную цену товара, не выполняя операций, указанных в алгоритме, приведенном ниже. Для этого было бы достаточно совместное решение простых уравнений (1) и (2). Идея предлагаемой здесь модели для описания процесса определения цены товара заключается в том, чтобы показать, как может происходить торговля между продавцом и покупателем для выяснения окончательной цены товара.
4 Алгоритм решения
Алгоритм решения состоит из следующих этапов:
-
рассматривается координатная система, у которой абсцисса ![]() , а ордината
, а ордината ![]() ;
;
-
необходимо строить графики функций ![]() и
и ![]() ;
;
-
задается начальная цена товара ![]() и для нее
определяется объем товара по формуле для
и для нее
определяется объем товара по формуле для ![]() ;
;
- из
равенства ![]() определяется новая цена товара;
определяется новая цена товара;
- цена
товара определяется с определенной точностью; для этого задается либо
количество повторения ![]() , либо условие точности:
, либо условие точности: ![]()
![]()
![]() если выполняется это условие, то процесс
решения задачи завершается; в противном случае вычисляется следующее значение
цены товара.
если выполняется это условие, то процесс
решения задачи завершается; в противном случае вычисляется следующее значение
цены товара.
5 Модели корреляционного и регрессионного анализа
Как было отмечено неоднократно, одна из важных задач моделирования – это получение зависимости какого-либо показателя (параметра) изучаемого явления или процесса от других параметров (факторов). Для решения данной задачи проводились эксперименты или наблюдения, результаты которых впоследствии анализировались и в итоге были получены искомые зависимости или закономерности. Примером может служить всем известный закон Ома для электрических цепей.
В последние десятилетия этот подход необходимо было использовать для моделирования сложных систем, в которых методология однофакторного эксперимента должна была уступить место многофакторному анализу. Результатом таких исследований является построение уравнений регрессии или регрессионной модели.
6 Метод наименьших квадратов
Пусть проведен эксперимент или наблюдения над объектом
моделирования, в результате которого получена статистическая информация. Эта
информация обычно записывается в виде таблицы. Такая таблица называется статистическим рядом. На основе этой информации требуется получить
зависимость между показателями (параметрами) объекта. Пусть такими параметрами
обозначены ![]() и
и ![]() . Результаты эксперимента
записаны в виде следующей таблицы:
. Результаты эксперимента
записаны в виде следующей таблицы:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В декартевой системе координат ![]() результаты
наблюдений (эксперимента) представляют собой набор точек с координатами
результаты
наблюдений (эксперимента) представляют собой набор точек с координатами ![]() Эти точки называются статистическими или
экспериментальными.
Эти точки называются статистическими или
экспериментальными.
Процесс решения этой задачи осуществляется в два этапа:
- определение общего вида функции, используемой для описания зависимости между показателями;
- определение неизвестных параметров, вошедших в общий вид выбранной функции.
Общий вид функции выбирается исследователем исходя из
собственного опыта, а затем методом наименьших квадратов (МНК) определяется ее
конкретный вид. Пусть общий вид функции, связывающей рассматриваемых
параметров ![]() и y, задан в виде
и y, задан в виде
![]() Она может быть выбрана по-разному. В
данном случае функция
Она может быть выбрана по-разному. В
данном случае функция ![]() называется аппроксимирующей
функцией, ее график называется аппроксимирующей линией, а процесс
определения этой функции – аппроксимацией.
называется аппроксимирующей
функцией, ее график называется аппроксимирующей линией, а процесс
определения этой функции – аппроксимацией.
Если аппроксимирующая функция линейная ![]() , то процесс называется линейной
аппроксимацией. В качестве аппроксимирующей функции может рассматриваться
квадратная функция следующего вида
, то процесс называется линейной
аппроксимацией. В качестве аппроксимирующей функции может рассматриваться
квадратная функция следующего вида ![]() , в которой
, в которой ![]() являются неизвестными величинами. Если
они будут определены, то задача считается решенной. Такую аппроксимацию
статистических данных называют квадратичной аппроксимацией.
являются неизвестными величинами. Если
они будут определены, то задача считается решенной. Такую аппроксимацию
статистических данных называют квадратичной аппроксимацией.
Для достижения наибольшей точности могут быть
использованы полиномы (многочлены) высших порядков. Например, полином ![]() ой степени:
ой степени:
![]()
В этом случае требуется определить значения
неизвестных коэффициентов ![]()
![]()
Пусть рассматривается общий случай, когда в качестве
аппроксимирующей принята следующая функция ![]() .
Сущность метода наименьших квадратов предполагает рассматривать минимум
следующей функции:
.
Сущность метода наименьших квадратов предполагает рассматривать минимум
следующей функции:
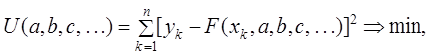
где ![]() статистические значения
показателей
статистические значения
показателей ![]()
![]() неизвестные
параметры, которые должны быть определены из условия минимума функции
неизвестные
параметры, которые должны быть определены из условия минимума функции![]() :
:
 (4)
(4)
Из этих условий (4) будет получена система
алгебраических уравнений, из которой определяются значения неизвестных
параметров ![]() . Количество уравнений будет равно
количеству неизвестных параметров.
. Количество уравнений будет равно
количеству неизвестных параметров.
Если рассматривается линейная аппроксимация, то
решается система из двух алгебраических уравнений. Если в качестве
аппроксимирующей функции используется полином ![]() ой
степени, то решается система
ой
степени, то решается система ![]() линейных алгебраических
уравнений с
линейных алгебраических
уравнений с ![]() неизвестными.
неизвестными.
Лекция 4. Модели регрессионного анализа
Цель лекции: изучить один из популярных методов определения функциональных зависимостей между параметрами (показателями) – уравнений регрессии.
Содержание
лекции:
проблема об определении зависимости между двумя параметрами. Полином ![]() ой степени. Решение системы
ой степени. Решение системы ![]() уравнений. Множественная регрессия. Метод
и алгоритм решения задачи.
уравнений. Множественная регрессия. Метод
и алгоритм решения задачи.
В научных исследованиях, связанных с определением закономерностей в явлениях или процессах, требуется определить функциональные зависимости между основными их параметрами (показателями). Такая проблема существует практически во всех прикладных исследованиях. В данной лекции будет рассматриваться конкретная реализация метода наименьших квадратов (МНК) для двух случаев: когда определяется зависимость между двумя параметрами и между многими параметрами (множественная регрессия).
1 Определение зависимости между двумя параметрами
Пусть требуется определить
функциональную зависимость между двумя параметрами  и
и 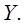 Для этого используются статистические
(экспериментальные) табличные данные, приведенные в предыдущей лекции.
Для этого используются статистические
(экспериментальные) табличные данные, приведенные в предыдущей лекции.
Как было отмечено в предыдущей лекции, для решения данной проблемы используется метод наименьших квадратов. Однако, вначале необходимо выбрать общий вид аппроксимирующей функции. На практике часто используются линейная и квадратичная функции. Как было отмечено выше, в первом случае процесс определения аппроксимирующей функции называется линейной аппроксимацией, а во втором - квадратичной.
Из курса математики, в частности, из математической статистики известно, что для достижения высокой точности при аппроксимации экспериментальных (статистических) данных желательно использовать полином высшей степени. Однако это приводит к сложной проблеме вычислительного характера.
2 Полином ![]() ой степени
ой степени
Если в качестве аппроксимирующей функции использовать
полиномы ![]() ой степени, то решение задачи сводится к
решению системы
ой степени, то решение задачи сводится к
решению системы ![]() линейных алгебраических
уравнений. При достаточно большом значении
линейных алгебраических
уравнений. При достаточно большом значении ![]() приходится
решать систему уравнений с большим количеством неизвестных.
приходится
решать систему уравнений с большим количеством неизвестных.
Пусть в качестве аппроксимирующей функции выбран
полином ![]() ой степени, представленный в следующем
виде:
ой степени, представленный в следующем
виде:
![]() (1)
(1)
где ![]() – неизвестные коэффициенты
полинома. Для определения неизвестных коэффициентов полинома (1) использован
известный метод наименьших квадратов (МНК). По данному методу используется
условие минимума следующей функции:
– неизвестные коэффициенты
полинома. Для определения неизвестных коэффициентов полинома (1) использован
известный метод наименьших квадратов (МНК). По данному методу используется
условие минимума следующей функции:
 .
(2)
.
(2)
Функция ![]() является функцией
является функцией ![]() параметров. Аргументами данной функции
являются коэффициенты полинома (1), выбранного для аппроксимации
экспериментальных данных. Как было отмечено выше, необходимым и достаточным
условием минимума функции (2) является равенство нулю первых ее частных
производных по аргументам
параметров. Аргументами данной функции
являются коэффициенты полинома (1), выбранного для аппроксимации
экспериментальных данных. Как было отмечено выше, необходимым и достаточным
условием минимума функции (2) является равенство нулю первых ее частных
производных по аргументам ![]()
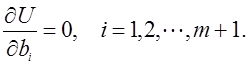 (3)
(3)
Из условия (3) минимума функции вначале определяют первые ее частные производные, которые приравниваются к нулю:
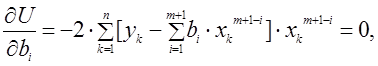 (4)
(4)
В данной формуле ![]() Поэтому
количество уравнений равно
Поэтому
количество уравнений равно ![]() Отсюда можно получить
систему линейных алгебраических уравнений с
Отсюда можно получить
систему линейных алгебраических уравнений с ![]() неизвестными
параметрами
неизвестными
параметрами ![]() :
:
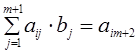 ,
, ![]() (5)
(5)
Коэффициенты и свободные члены данной системы алгебраических уравнений определяются с помощью следующих формул:

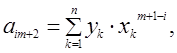
![]() (6)
(6)
где ![]()
![]()
Систему уравнений (5) можно записать в следующем развернутом виде:
 (7)
(7)
Из теории линейных систем алгебраических уравнений (линейной алгебры) известно, что существуют различные методы решения систем линейных алгебраических уравнений. Они широко применяются на практике при решении подобных систем уравнений. Однако решение систем уравнений с большим количеством уравнений и неизвестных связано с определенными трудностями вычислительного характера. Из множества этих методов решения такой системы наиболее удобным для программирования и решения на компьютере является метод Жордана - Гаусса.
В дальнейших расчетах принято использовать в качестве
аппроксимирующей функции полином пятой степени, т.е. ![]() Тогда
система уравнений (7) будет записана в следующем виде:
Тогда
система уравнений (7) будет записана в следующем виде:
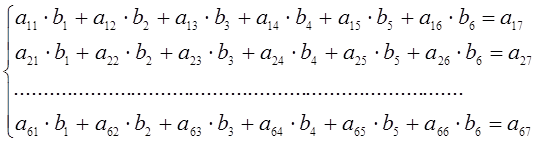 (8)
(8)
Данная система состоит из шести уравнений с шестью неизвестными. Коэффициенты и свободные члены уравнений этой системы определены как суммы значений экспериментальных данных в различных степенях.
3 Решение системы уравнений (8)
Для этого использован метод Жордана-Гаусса. Алгоритм решения системы уравнений (8) данным методом состоит из следующих этапов:
10. Ввод значений аргумента ![]() и функции
и функции ![]() , для
, для ![]()
20. Цикл по параметру ![]() для вычисления коэффициентов системы
алгебраических уравнений по формулам (8).
для вычисления коэффициентов системы
алгебраических уравнений по формулам (8).
30. Начало цикла для решения системы
уравнений методом Жордана-Гаусса: ![]()
![]() . (Здесь p - вспомогательная переменная).
. (Здесь p - вспомогательная переменная).
40. Цикл по параметру ![]() для вычисления коэффициентов
для вычисления коэффициентов ![]() го уравнения по формуле
го уравнения по формуле 
50. Начало цикла по параметру ![]() (номер строки основной матрицы системы
уравнений)
(номер строки основной матрицы системы
уравнений) ![]()
60. Если ![]() то
значение параметра
то
значение параметра ![]() увеличивается на единицу
увеличивается на единицу ![]() , т.е. осуществляется переход к следующему
уравнению (Совпадение номера уравнения с номером разрешающей строки).
, т.е. осуществляется переход к следующему
уравнению (Совпадение номера уравнения с номером разрешающей строки).
70. Если ![]() то
переход к пункту 100 . (Завершение вычислений).
то
переход к пункту 100 . (Завершение вычислений).
80. Цикл по параметру ![]() для вычисления коэффициентов
для вычисления коэффициентов ![]() го уравнения по формуле преобразований
Жордана-Гаусса
го уравнения по формуле преобразований
Жордана-Гаусса ![]() .
.
90. Конец цикла по параметру ![]() . Если
. Если ![]() то
переход к пункту 40.
то
переход к пункту 40.
100. Вывод результатов.
4 Множественная регрессия
В инженерных и экономических исследованиях часто рассматриваются многофакторные модели. В данном случае требуется определить зависимости, связывающие нескольких величин. Такие уравнения называются уравнениями множественной регрессии.
Если переменные ![]() определяют трех экономических (экспериментальных)
показателей, то требуется определить следующие уравнения:
определяют трех экономических (экспериментальных)
показателей, то требуется определить следующие уравнения:
![]() (9)
(9)
где ![]() - неизвестные
пока коэффициенты. Если будут определены значения этих коэффициентов, то задача
считается решенной. Данное уравнение может быть записано и в других формах. Например,
- неизвестные
пока коэффициенты. Если будут определены значения этих коэффициентов, то задача
считается решенной. Данное уравнение может быть записано и в других формах. Например,
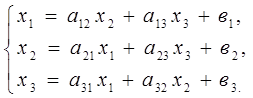 (10)
(10)
Эти уравнения (9) и (10) будут эквивалентными, потому что каждое из них может быть получено из другого с помощью простых преобразований. Если рассматривается первое уравнение (10), то оно из формулы (9) получается с помощью простых преобразований.
5 Метод решения задачи
Для решения задачи используются статистические данные, которые могут быть представлены в следующем виде:
|
X1 : |
x11 |
x12 |
x13 |
… |
x1i |
… |
x1m |
|
X2 : |
x21 |
x22 |
x23 |
… |
x2i |
… |
x2m |
|
X3 : |
x31 |
x32 |
x33 |
… |
x3i |
… |
x3m |
Искомое уравнение может быть записано в следующем виде:
![]() (11)
(11)
где: 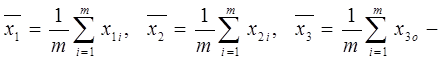 (12)
(12)
средние значения каждого параметра.
Свободный член уравнения определяется с помощью следующей формулы
![]() . (13)
. (13)
Итак, решение задачи может быть ограничено
определением значений только двух неизвестных коэффициентов![]() . Для
определения значений этих коэффициентов можно использовать метод наименьших
квадратов (МНК). Сущность этого метода рассмотрена в предыдущей лекции. Отсюда
следует условие минимума следующей функции:
. Для
определения значений этих коэффициентов можно использовать метод наименьших
квадратов (МНК). Сущность этого метода рассмотрена в предыдущей лекции. Отсюда
следует условие минимума следующей функции:
 .
.
Здесь ![]() рассматривается
как функция двух параметров
рассматривается
как функция двух параметров ![]() и
и ![]() .
.
После простых преобразований можно получить из этой системы уравнений следующую систему:
 (14)
(14)
Здесь коэффициенты системы (14) называются моментами второго порядка:
![]()
![]() (15)
(15)
![]()
Решение системы уравнений (14) может быть представлено в следующем виде:
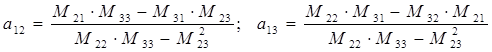 (16)
(16)
6 Алгоритм задачи
Алгоритм задачи является очень простым и может быть записан в следующем виде:
-
по формулам (12) определяются
средние значения ![]() ;
;
- вычисление моментов по формулам (15) ;
-
вычисление параметров ![]() и
и ![]() по формулам (16);
по формулам (16);
-
определение свободного
члена уравнения ![]() по формуле (13).
по формуле (13).
Лекция 5. Моделирование процессов в экологических системах
Цель лекции: изучить методы математического моделирования процессов, происходящих в экологических системах.
Содержание лекции: модели роста и развития отдельной популяции. Модель Мальтуса. Модель Ферхюльста. Модель системы двух популяций, конкурирующих за общий ресурс. Модель, учитывающая нижнюю границу численности. Модель системы «хищник-жертва». Модель Базыкина. Общая постановка задачи для моделей процессов в экологической системе. О методах решения задачи Коши.
Одной из областей применения компьютерного моделирования являются процессы, происходящие в экологических системах. Известно, что экологические системы являются достаточно сложными, так как прямое экспериментальное исследование их по известным причинам невозможно. Однако имеются простые модели экологических систем, которые стали классическими.
1 Модели роста и развития отдельной популяции. Модель Мальтуса
Пусть рассматривается однородная популяция в условиях неограниченных ресурсов среды обитания. Предполагается, что скорость роста популяции пропорциональна ее численности.
Для составления модели вводятся следующие обозначения:
![]() - время,
- время, ![]() - численность популяции;
- численность популяции;
![]() -
скорость роста популяции.
-
скорость роста популяции.
Тогда модель может быть представлена следующим дифференциальным уравнением:
 (1)
(1)
где ![]() – коэффициент скорости роста
популяции. Данное уравнение будет решено при заданных начальных условиях:
– коэффициент скорости роста
популяции. Данное уравнение будет решено при заданных начальных условиях:
![]() .
(2)
.
(2)
Начальное условие определяет численность популяции в начальный момент времени. Решение дифференциального уравнения, удовлетворяющее начальному условию, имеет следующий вид:
![]() (3)
(3)
что показывает экспоненциальный закон роста численности популяции в условиях неограниченных ресурсов. На самом деле в природе неограниченные ресурсы существуют крайне редко. Этот закон может быть использован в тех случаях, когда численность популяции небольшая. Это может быть в начальный период существования популяции.
2 Модель Ферхюльста
Если ресурсы
окружающей среды ограничены, т.е. экологическая емкость среды ![]() ограниченное число, то модель может иметь
следующий вид:
ограниченное число, то модель может иметь
следующий вид:
 . (4)
. (4)
Полученное
уравнение называется логистическим уравнением Ферхюльста, которое показывает,
что скорость роста популяции пропорциональна ее численности и остающейся
свободной части ресурсов среды обитания. Из решения этого уравнения
следует, что при малых значениях численности популяции ![]() , его решение имеет экспоненциальный
характер. Однако с ростом численности популяции она приближается к предельному
значению
, его решение имеет экспоненциальный
характер. Однако с ростом численности популяции она приближается к предельному
значению ![]() . Если же первоначальная численность
популяции больше
. Если же первоначальная численность
популяции больше ![]() , то произойдет монотонное
уменьшение ее численности до равновесного значения.
, то произойдет монотонное
уменьшение ее численности до равновесного значения.
3 Модель, учитывающая нижнюю границу численности
В предыдущих моделях считалось, что численность популяции пропорциональна количеству особей. Однако во многих видах популяции скорость роста численности может зависеть от квадрата численности. С другой стороны, плотность популяции некоторых видов не должна быть ниже некоторого уровня, т.е. не должна опускаться ниже некоторого определенного критического количества. Модель, которая учитывает эти требования, может быть записана в следующем виде:
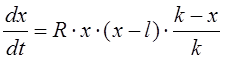 .
(5)
.
(5)
Здесь ![]() – нижняя граница численности
популяции, при которой она может вымирать. Эта граница зависит от вида
популяции.
– нижняя граница численности
популяции, при которой она может вымирать. Эта граница зависит от вида
популяции.
4 Модель системы двух популяций, конкурирующих за общий ресурс
Пусть в экологической системе существуют две популяции, которые используют общий жизненный ресурс. Они находятся в конкурентной борьбе за использование имеющегося ресурса. Рост каждого вида популяции зависит от развития другого вида. Такая модель может иметь следующий вид:

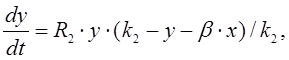 (6)
(6)
где ![]() и
и ![]() –
коэффициенты роста численности, а
–
коэффициенты роста численности, а ![]() и
и ![]() – параметры, характеризующие
экологическую емкость среды для каждого вида популяции. Коэффициенты
– параметры, характеризующие
экологическую емкость среды для каждого вида популяции. Коэффициенты ![]() и
и ![]() отражают влияние одного вида популяции на
другой вид.
отражают влияние одного вида популяции на
другой вид.
5 Модель системы «хищник-жертва»
Пусть в экологической системе для «жертвы» имеется неограниченное количество корма. Рост численности «жертвы» происходит естественным путем и зависит от воздействия со стороны «хищника». Для «хищника» «жертва» является единственным источником питания. Если отсутствует «жертва», то «хищник» также вымирает.
Вводятся
обозначения: ![]() - количество
«жертвы»,
- количество
«жертвы», ![]() - количество
«хищника». Тогда модель может иметь следующий вид:
- количество
«хищника». Тогда модель может иметь следующий вид:

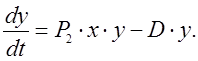 (7)
(7)
Первое уравнение
(7) отражает закономерность изменения популяции «жертв», а второе уравнение -
«хищников». Слагаемое ![]() характеризует
скорость размножения «жертв» в отсутствии «хищника», а слагаемое
характеризует
скорость размножения «жертв» в отсутствии «хищника», а слагаемое ![]() характеризует скорость гибели «жертв»
за счет их уничтожения «хищниками». Слагаемое
характеризует скорость гибели «жертв»
за счет их уничтожения «хищниками». Слагаемое ![]() характеризует
увеличение численности «хищников» за счет поедания «жертв», а слагаемое
характеризует
увеличение численности «хищников» за счет поедания «жертв», а слагаемое ![]() характеризует естественную смертность
«хищников». Коэффициенты
характеризует естественную смертность
«хищников». Коэффициенты ![]() представляют собой
константы, имеющие только положительные значения. Система уравнений (7)
называется уравнениями Лотки-Вольтерра.
представляют собой
константы, имеющие только положительные значения. Система уравнений (7)
называется уравнениями Лотки-Вольтерра.
6 Модель Базыкина
Модель «хищник-жертва» обобщена Базыкиным. Для этого им были учтены следующие биологические факторы:
1) По модели
Лотки - Вольтерра интенсивность поедания жертв хищниками линейно растет с
ростом популяции жертв. Однако экспериментальные данные показывает, что эта
зависимость имеет следующий вид: ![]() .
.
2) Невозможность
безграничного размножения, которая может быть описана формулой: ![]() .
.
3) Недостаток
территории приводит к конкуренции, который описывается зависимостью ![]() .
.
С учетом этих факторов получена модель «хищник-жертва», которая имеет следующий вид:
 (8)
(8)
7 Общая постановка задачи для моделей процессов в экологической системе
В данном случае все рассмотренные модели привели к решению систем дифференциальных уравнений первого порядка при заданных начальных условиях. Для всех этих моделей можно рассматривать общую задачу для системы дифференциальных уравнений - задачу Коши.
Задача Коши для системы дифференциальных уравнений первого порядка может быть поставлена в следующем виде.
Требуется решить систему дифференциальных уравнений первого порядка
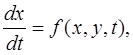
 (9)
(9)
для начального условия:
![]() (10)
(10)
Решение задачи Коши (9)-(10) ищется в некотором
заданном промежутке [0,T]. Здесь ![]() и
и ![]() считаются заданными.
считаются заданными.
8 О методах решения задачи Коши
Практика применения численных методов показала, что
целесообразно использовать метод Рунге – Кутта, который имеет различные
модификации. Достаточно высокую точность (порядка ![]() )
обеспечивает метод Рунге-Кутта четвертого порядка. В данном случае
)
обеспечивает метод Рунге-Кутта четвертого порядка. В данном случае ![]() шаг по
аргументу, т.е. по времени
шаг по
аргументу, т.е. по времени ![]() Для использования этого метода поступают следующим
образом.
Для использования этого метода поступают следующим
образом.
Согласно этому методу, вначале выбирается шаг по
независимой переменной ![]() например,
например, ![]() а затем
отрезок
а затем
отрезок ![]() разбивается на
разбивается на ![]() участков, длина каждого из которых равна
участков, длина каждого из которых равна ![]() . После
этого вводятся следующие обозначения:
. После
этого вводятся следующие обозначения:
![]()
![]() (11)
(11)
 количество
шагов по независимой переменной
количество
шагов по независимой переменной ![]()
Для определения дискретных значений исомых функций (11) методом Рунге - Кутта четвертого порядка точности используются следующие формулы:
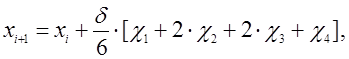
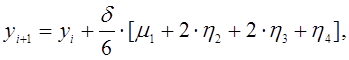 (12)
(12)
где ![]()
![]()
![]()

 (13)
(13)
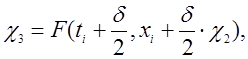

![]()
![]()
Итак, получены формулы (11) - (13) для определения
дискретных значений искомых функций ![]() для
значений
для
значений ![]()
![]()
Лекция 6. Моделирование переходных процессов в электрических цепях
Цель лекции: изучить способы математического моделирования процессов, происходящих в электрических цепях и решение задач, возникающих в результате моделирования.
Содержание лекции: постановка линейной задачи. Математическая модель линейной задачи. Переход к безразмерным переменным. Метод Эйлера. Постановка нелинейной задачи. Математическая модель нелинейной электронной схемы. Переход к безразмерным переменным.
1 Постановка линейной задачи
Известно, что для описания процессов, происходящих в электрических цепях, могут быть использованы законы электротехники. С помощью этих законов можно разрабатывать математические модели этих процессов. Пусть рассматривается простая схема (см.рисунок 1):
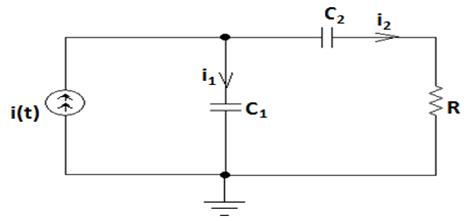
Рисунок 1 – Линейная RC- цепь
Данная схема (см.рисунок 1) является линейной, так как здесь отсутствует нелинейный элемент. Сопротивление резистивного элемента постоянная величина, а конденсаторы имеют постоянные емкости.
2 Математическая модель линейной задачи
Используя законы Кирхгофа [12] для данной цепи, можно получить следующую систему дифференциальных уравнений:
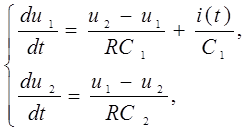 (1)
(1)
Здесь введены следующие обозначения: ![]() время, R – сопротивление резистора, C1 и C2 - емкости
конденсаторов, u1(t) и u2(t)– напряжения.
время, R – сопротивление резистора, C1 и C2 - емкости
конденсаторов, u1(t) и u2(t)– напряжения.
Не ограничивая общность, можно считать, что в
начальный момент (при ![]() ) имелись следующие начальные
условия (по второму закону коммутации):
) имелись следующие начальные
условия (по второму закону коммутации):
![]() (2)
(2)
Остальные искомые переменные величины (токи) могут быть определены с помощью следующих формул:
 (3)
(3)
Полученные формулы (1) – (3) описывают переходный процесс, происходящий в данной электрической цепи и, следовательно, они образуют математическую модель поставленной здесь задачи.
3 Переход к безразмерным переменным
Как было отмечено выше, в тех случаях, когда в задаче
имеются величины с различными размерностями, целесообразно перейти к
безразмерным переменным. Поэтому, перед тем, как приступить к решению данной
задачи, целесообразно перейти к безразмерным переменным. Для этого выбираются
так называемые характерные величины. Пусть в качестве характерных величин
выбраны: ![]() - напряжение,
- напряжение, ![]() ток,
ток, ![]() время. Переход к безразмерным переменным
осуществляется с помощью следующей замены переменных:
время. Переход к безразмерным переменным
осуществляется с помощью следующей замены переменных:
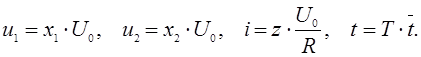 (4)
(4)
Здесь: ![]() безразмерные
величины. В дальнейших выкладках штрих над
безразмерные
величины. В дальнейших выкладках штрих над ![]() можно
опустить и считать ее безразмерной величиной. Замена переменных (4) позволяет
получить из системы уравнений (1) следующую систему относительно безразмерных
величин:
можно
опустить и считать ее безразмерной величиной. Замена переменных (4) позволяет
получить из системы уравнений (1) следующую систему относительно безразмерных
величин:

![]() (5)
(5)
где 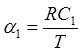 и
и 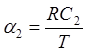 – безразмерные величины.
– безразмерные величины.
Из начальных условий (2) следует
![]() (6)
(6)
Решение задачи (5)-(6) позволяет определить значения искомых функций. В данном случае решение задачи Коши (5)-(6) ищется в промежутке [0,1]. Для решения данной задачи рекомендуется любое из существующих численных методов, в частности, методы Эйлера и Рунге-Кутта.
4 Метод Эйлера
Для решения задачи Коши (5)-(6)
производные искомых функций ![]() и
и ![]() заменяются конечно-разностными
соотношениями следующих видов:
заменяются конечно-разностными
соотношениями следующих видов:
 ,
, ![]()
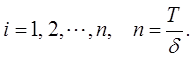 (7)
(7)
Тогда будут получены рекуррентные формулы:
![]() (8)
(8)
Здесь ![]() (9)
(9)
5 Постановка нелинейной задачи
В данном случае вместо линейного элемента рассматривается нелинейный элемент (НЭ). Пусть рассматривается простая схема (см.рисунок 2).
Требуется определить переходный процесс, возникающий в данной схеме. Это означает, что необходимо определить значения напряжений и токов в участках схемы.
6 Математическая модель нелинейной электронной схемы
Методика составления уравнений состояния схемы на основе законов Кирхгофа остается такой же, как и в случае линейных резистивных элементов [12]. Для составления математической модели данной электронной схемы (см.рисунок 2) вводятся следующие обозначения:
![]() токи,
токи,
![]() напряжения,
напряжения,
![]() емкости
конденсаторов,
емкости
конденсаторов, ![]() время.
время.
Здесь ![]() и
и ![]() считаются постоянными величинами, а
величины
считаются постоянными величинами, а
величины ![]() - переменными, функциями времени τ.
- переменными, функциями времени τ.
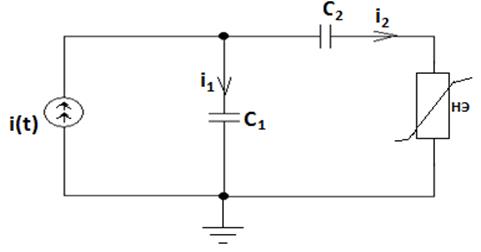
Рисунок 2 – Схема с нелинейным элементом
По законам Кирхгофа для рассматриваемой схемы справедливы следующие формулы:
![]()
![]()
При последовательном соединении конденсатора ![]() и
НЭ ток остается равным, т.е.
и
НЭ ток остается равным, т.е. ![]()
Уравнения, определяющие зависимости тока и напряжения для конденсаторов [12], записываются в виде следующих формул:
а) для первого конденсатора 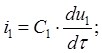
б) для второго конденсатора 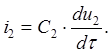
Пусть для аппроксимации ВАХ нелинейного элемента (НЭ) используется следующее выражение
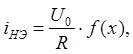
где 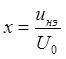 - безразмерное
напряжение,
- безразмерное
напряжение,
![]() -
аппроксимирующая функция зависимости между током и напряжением в нелинейном
элементе. В отличие от задачи, рассмотренной в первой части данной лекции,
вместо линейного элемента с постоянным сопротивлением
-
аппроксимирующая функция зависимости между током и напряжением в нелинейном
элементе. В отличие от задачи, рассмотренной в первой части данной лекции,
вместо линейного элемента с постоянным сопротивлением ![]() в
данной задаче используется нелинейный элемент (НЭ). Причем, напряжение в
нелинейном элементе определяется по формуле
в
данной задаче используется нелинейный элемент (НЭ). Причем, напряжение в
нелинейном элементе определяется по формуле ![]()
8 Переход к безразмерным переменным
Для этого вводятся безразмерные величины. В данном случае необходимо ввести шесть безразмерных переменных:
![]() время;
время;
![]() токи в
ветвях цепи;
токи в
ветвях цепи;
![]() напряжения;
напряжения;
![]() ток в
источнике.
ток в
источнике.
Кроме этого выбираются характерные величины:
![]() время;
время;
![]() -
напряжение;
-
напряжение;
![]() - ток.
- ток.
Производится следующая замена переменных:
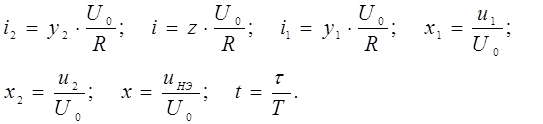
Здесь ![]() безразмерные
величины. В составе этой системы имеется простая формула:
безразмерные
величины. В составе этой системы имеется простая формула:
![]()
которая позволяет сократить количество формул до четырех.
Если будут найдены ![]() и
и ![]() , то
легко определяется
, то
легко определяется ![]() ; поэтому достаточно решить вместо
пяти уравнений систему следующих четырех уравнений относительно четырех
неизвестных функций
; поэтому достаточно решить вместо
пяти уравнений систему следующих четырех уравнений относительно четырех
неизвестных функций ![]()

![]()
Здесь по формуле ![]() определяется
безразмерное значение напряжения в нелинейном элементе
определяется
безразмерное значение напряжения в нелинейном элементе ![]() .
Кроме этого здесь появляются безразмерные коэффициенты в дифференциальных
уравнениях. В данном случае постоянные величины
.
Кроме этого здесь появляются безразмерные коэффициенты в дифференциальных
уравнениях. В данном случае постоянные величины 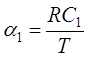 и
и 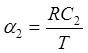 являются безразмерными величинами. Потому
что
являются безразмерными величинами. Потому
что ![]() и
и ![]() -
постоянные времени и они имеют размерности времени.
-
постоянные времени и они имеют размерности времени.
Если будут решены данные уравнения, то будут
определены безразмерные величины ![]() Для определения
размерных величин этих переменных необходимо умножить полученные значения на
характерные величины:
Для определения
размерных величин этих переменных необходимо умножить полученные значения на
характерные величины:
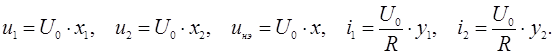
После исключения переменных и ![]() можно получить систему
уравнений относительно трех переменных
можно получить систему
уравнений относительно трех переменных ![]() Итак,
получена следующая система дифференциальных уравнений относительно трех неизвестных
функций
Итак,
получена следующая система дифференциальных уравнений относительно трех неизвестных
функций ![]()
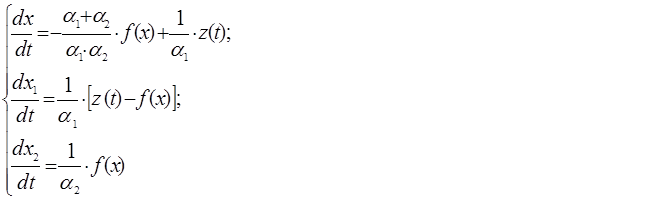 (10)
(10) ![]() Также как
для линейной задачи, для рассматриваемой здесь электронной цепи предполагается,
что в начальный момент времени отсутствовал ток (напряжение):
Также как
для линейной задачи, для рассматриваемой здесь электронной цепи предполагается,
что в начальный момент времени отсутствовал ток (напряжение):
![]() (11)
(11)
Если будут найдены значения безразмерных функций ![]() определяющих напряжения, то безразмерные
величины, определяющие токи
определяющих напряжения, то безразмерные
величины, определяющие токи ![]() и
и ![]() будут найдены из следующих формул:
будут найдены из следующих формул:
![]() (12)
(12)
Совокупность формул (11) – (13) определяет математическую модель поставленной задачи о переходном процессе, происходящем в нелинейной электрической цепи (Рисунок 2). Решение данной задачи может быть осуществлено одним из существующих численных методов.
Лекция 7. Моделирование колебательных явлений
Цель лекции: изучить один из популярных методов решения краевой задачи для обыкновенных дифференциальных уравнений, возникающих в результате моделирования колебательных явлений.
Содержание лекции: математическая модель колебательных движений тела, подвешанного на пружине. Математическая модель математического маятника. Колебательный процесс в электрической цепи. О методе решения задачи Коши для дифференциального уравнения второго порядка.
В прикладных задачах физики и механики, а также в инженерных расчетах часто возникает проблема решения задач для обыкновенных дифференциальных уравнений второго порядка. Решение этих задач имеет важное значение при изучении динамических процессов, в частности, колебательных процессов.
В качестве примеров здесь рассматриваются математические модели ряда задач из разных областей знаний:
- колебания подвешанного на пружине тела;
- колебания математического маятника;
- колебательный процесс в электрической цепи.
1 Математическая модель колебательных движений тела, подвешанного на пружине
Пусть тело массы ![]() подвешено
на упругой пружине и происходит колебания в вертикальном направлении около
положения равновесия. Положение равновесия тела определяется из условия, когда
вес тела уравновешивается упругой силой пружины. Требуется составить уравнения,
описывающие колебания данного тела [13].
подвешено
на упругой пружине и происходит колебания в вертикальном направлении около
положения равновесия. Положение равновесия тела определяется из условия, когда
вес тела уравновешивается упругой силой пружины. Требуется составить уравнения,
описывающие колебания данного тела [13].
Вводятся обозначения: ![]() расстояние
тела по вертикальному направлению от положения равновесия,
расстояние
тела по вертикальному направлению от положения равновесия, ![]() время,
время, ![]() коэффициент
сопротивления среды,
коэффициент
сопротивления среды, ![]() коэффициент, определяющий силу
упругости пружины.
коэффициент, определяющий силу
упругости пружины.
На тело будут действовать следующие силы:
- сила инерции 
- сила упругости ![]() ,
которая стремится вернуть тело в положение равновесия; знак минус означает,
что упругая сила направлена против положительного направления
,
которая стремится вернуть тело в положение равновесия; знак минус означает,
что упругая сила направлена против положительного направления ![]() ;
;
- сила сопротивления среды 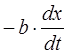 пропорциональна
скорости движения тела и имеет направление, обратное скорости;
пропорциональна
скорости движения тела и имеет направление, обратное скорости;
- сила притяжения Земли ![]() уравновешена
силой упругости пружины.
уравновешена
силой упругости пружины.
Из закона механики (второй закон Ньютона) [13] следует, что движение тела будет описано следующим дифференциальным уравнением:
 (1)
(1)
Для решения данного уравнения (1) должны быть заданы
начальные усорвия при ![]() :
:
 (2)
(2)
Здесь ![]() начальное положение
тела,
начальное положение
тела, ![]() начальная скорость тела. Формулы (1)
и (2) определяют математическую модель колебательного движения тела,
подвешанного на упругой пружине.
начальная скорость тела. Формулы (1)
и (2) определяют математическую модель колебательного движения тела,
подвешанного на упругой пружине.
2 Математическая модель математического маятника
Пусть рассматривается математический маятник длины ![]() . Определение математического маятника
дано в школьном курсе физики. Движение маятника происходит в среде с
сопротивлением, пропорциональным скорости движения маятника.
. Определение математического маятника
дано в школьном курсе физики. Движение маятника происходит в среде с
сопротивлением, пропорциональным скорости движения маятника.
Для составления уравнений, описывающих движение
маятника, вводятся обозначения: ![]() время,
время, ![]() масса маятника,
масса маятника, ![]() коэффициент
сопротивления среды,
коэффициент
сопротивления среды, ![]() ускорение силы тяжести,
ускорение силы тяжести, ![]() угол отклонения маятника от положения
равновесия.
угол отклонения маятника от положения
равновесия.
На маятник действуют силы:
- сила притяжения Земли ![]()
- сила сопротивления среды 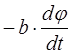 ;
;
- сила инерции ;
;
- внешняя сила, зависящая от времени ![]()
Из закона механики (второй закон Ньютона) [13] следует следующее уравнение:

Здесь рассматриваются малые колебания маятника. Это
означает, что угол наклона маятника ![]() от положения
равновесия считается малым. Для малого значения
от положения
равновесия считается малым. Для малого значения ![]() можно
предположить
можно
предположить ![]() Поэтому полученное уравнение может
быть написано в следующем виде:
Поэтому полученное уравнение может
быть написано в следующем виде:
 (3)
(3)
Начальные условия для решения данного дифференциального уравнения (3) могут быть заданы в виде:
 (4)
(4)
Итак, формулы (3) и (4) являются математической моделью колебания математического маятника.
3 Колебательный процесс в электрической цепи
Пусть рассматривается электрическая цепь, в которой
имеются конденсатор ![]() резистивный элемент
резистивный элемент ![]() и катушка индуктивности
и катушка индуктивности ![]() Требуется определить колебательный
процесс, происходящий в этой цепи.
Требуется определить колебательный
процесс, происходящий в этой цепи.
Вводятся обозначения: ![]() напряжение
на обкладках конденсатора,
напряжение
на обкладках конденсатора, ![]() сила тока в цепи. Из
теории электрических цепей известны следующие зависимости [12]:
сила тока в цепи. Из
теории электрических цепей известны следующие зависимости [12]:
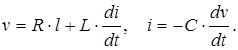 (5)
(5)
Если в цепи существует источник тока с
электродвижущей силой ![]() то первое уравнение (5) будет
иметь следующий вид:
то первое уравнение (5) будет
иметь следующий вид:
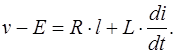 (6)
(6)
Подставляя вторую формулу (5) в формулу (6), можно получить следующее уравнение:
 (7)
(7)
Здесь также могут быть заданы начальные условия для решения данного уравнения (7).
Итак, все рассмотренные задачи были приведены к решению задачи Коши для дифференциальных уравнений второго порядка.
4 О методе решения задачи Коши для дифференциального уравнения второго порядка
Для решения задачи Коши для дифференциального уравнения второго порядка могут быть использованы численные методы Эйлера, Рунге-Кутта и другие.
Перед использованием метода решения задачи необходимо сделать некоторые преобразования. С помощью этих преобразований можно привести дифференциальное уравнение второго порядка к системе двух дифференциальных уравнений первого порядка. Для этого вводится следующее обозначение:
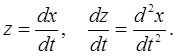
Тогда дифференциальное уравнение второго порядка
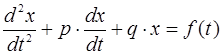
будет записано в виде системы двух дифференциальных уравнений первого порядка:
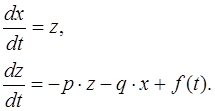 (8)
(8)
Численное решение такой системы уравнений было рассмотрено в предыдущих лекциях. Очевидно, также будут преобразованы начальные условия задачи.
Лекция 8. Численное решение краевой задачи для дифференциального уравнения второго порядка
Цель лекции: изучить метод решения краевой задачи для обыкновенных дифференциальных уравнений второго порядка.
Содержание лекции: постановка краевой задачи. Метод решения задачи. Метод прогонки. Алгоритм решения задачи.
1. Постановка краевой задачи.
Пусть даны:
дифференциальное уравнение
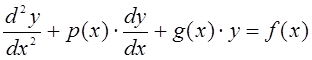 (1)
(1)
и граничные условия
![]() (2)
(2)
Здесь ![]() заданные числа,
заданные числа, ![]() известные
функции. Требуется найти значения неизвестной функции
известные
функции. Требуется найти значения неизвестной функции ![]() в
промежутке
в
промежутке![]() , удовлетворяющие уравнению (1) и
граничным условиям (2).
, удовлетворяющие уравнению (1) и
граничным условиям (2).
2 Метод решения задачи
Поставленную задачу (1)-(2) в
практических случаях невозможно решить аналитическими методами. Поэтому для
решения таких задач используется численный метод, метод конечных разностей.
Сущность этого метода заключается в следующем. Выбирают маленький шаг ![]() и промежуток
и промежуток ![]() делится
на
делится
на ![]() равных частей. Точки деления определяются
следующей формулой:
равных частей. Точки деления определяются
следующей формулой:
![]()
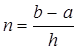 .
.
Значения функции ![]() в этих
точках
в этих
точках ![]() обозначены:
обозначены:
![]() (3)
(3)
Производится замена производных искомой функции ![]() конечно-разностными соотношениями:
конечно-разностными соотношениями:
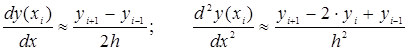 (4)
(4)
Подставляя формулы (4) в формулу (1) и учитывая
обозначения (3), можно получить следующее уравнение для ![]() :
:
![]() (5)
(5)
Здесь 
Формула (5) определяет систему линейных алгебраических
уравнений относительно неизвестных значений искомой функции ![]() Количество этих уравнений равно
Количество этих уравнений равно ![]() Из граничных условий (2) можно получить
две формулы:
Из граничных условий (2) можно получить
две формулы:
![]() (6)
(6)
Таким образом, формулы (5) и (6) представляют собой
систему ![]() уравнений относительно
уравнений относительно ![]() неизвестных величин
неизвестных величин ![]() Если будет решена данная система
алгебраических уравнений, то будут найдены дискретные значения искомой функции
Если будет решена данная система
алгебраических уравнений, то будут найдены дискретные значения искомой функции ![]() . Результаты решения задачи будут
представлены в виде числовых таблиц.
. Результаты решения задачи будут
представлены в виде числовых таблиц.
3 Метод прогонки
Система алгебраических уравнений (5) имеет особую матрицу, составленную из коэффициентов неизвестных величин. Особенностью этой матрицы является ее трехдиагональность, т.е. элементы матрицы, находящиеся на главной ее диагонали и двух параллельных к нему диагоналях, могут быть ненулевыми. А остальные элементы этой матрицы являются нулями. Такая особенность матрицы стала причиной появления метода прогонки для решения таких систем алгебраических уравнений с трехдиагональной матрицей.
Сущность метода прогонки заключается в следующем. Решение системы алгебраических уравнений (5) записывается в виде следующей формулы:
![]() (7)
(7)
где ![]() неизвестные коэффициенты;
они называются прогоночными.
неизвестные коэффициенты;
они называются прогоночными.
Процесс решения системы уравнений (5) методом прогонки состоит из двух этапов:
1) Прямая прогонка; на этом этапе определяются
значения неизвестных прогоночных коэффициентов ![]()
2) Обратная прогонка; на данном этапе определяются
значения искомой функции ![]()
Для определения значений прогоночных коэффициентов используются формулы:
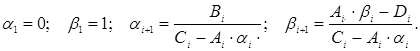 (8)
(8)
Эти формулы являются рекуррентными, при известных
значениях ![]() вычисление значений прогоночных
коэффициентов по формулам (8) не представляет труда.
вычисление значений прогоночных
коэффициентов по формулам (8) не представляет труда.
Определение значений искомой функции ![]() осуществляется по формулам (6) и (7); вначале
по второй формула (6) определяется значение искомой функции на правой границе,
а ее значения в других точках определяются формулой (7) в обратном порядке
изменения индекса
осуществляется по формулам (6) и (7); вначале
по второй формула (6) определяется значение искомой функции на правой границе,
а ее значения в других точках определяются формулой (7) в обратном порядке
изменения индекса ![]() от
от ![]() до 1.
до 1.
4 Алгоритм решения задачи
Алгоритм решения задачи составлен в следующем виде:
- вычисление по известным формулам коэффициентов ![]() системы уравнений (5);
системы уравнений (5);
- вычисление прогоночных коэффициентов по формулам (8);
- определение искомых значений функции по формулам (6) и (7);
- вывод полученных результатов.
Лекция 9. Математическая модель задачи о теплопроводности
Цель лекции: изучить метод математического моделирования одной из важных инженерных задач - задачи о теплопроводности.
Содержание лекции: постановка задачи о теплопроводности в стержне. Математическая модель задачи. Постановка математической задачи. Переход к безразмерным переменным. Математическая модель задачи о диффузии.
Инженерно-физические задачи, имеющие неинерционный характер, могут быть приведены к постановке и решению одного типа математических уравнений. Этот тип уравнений называется уравнениями параболичесокго типа. Эти уравнения относятся к одному из типов задач уравнений математической физики. Несмотря на различия природы этих задач, для решения их используется один и тот же метод. К таким уравнениям приводят задачи о переносе тепла, диффузии, фильтрации жидкостей в пористой среде и другие. В данной лекции рассматривается одна из этих задач – задача о теплопроводности в стержне.
1 Постановка задачи о теплопроводности в стержне
Пусть рассматривается однородный стержень,
теплоизолированный с боков, что изменение температуры в стержне происходит
из-за изменения температуры на концах стержня. Параметры этого стержня следующие:
длина ![]() , площадь сечения
, площадь сечения ![]() ,
плотность материала
,
плотность материала ![]() , коэффициент теплоемкости
, коэффициент теплоемкости ![]() ,
, ![]() –
коэффициент теплопроводности. Плотность и коэффициент теплопроводности
зависят от свойства материала стержня.
–
коэффициент теплопроводности. Плотность и коэффициент теплопроводности
зависят от свойства материала стержня.
Предполагается, что площадь сечения ![]() мала в сравнении с его длиной
мала в сравнении с его длиной ![]() . Это допущение позволяет считать, что
температура во всех точках любого сечения стержня одинакова. На концах этого
стержня задана температура (или может быть она измерена). Изменение температуры
на концах стержня приводит к неравномерности температуры в различных сечениях
стержня. Очевидно, что от более нагретого участка стержня будет перетекать
тепло к менее нагретому участку. Это означает, что в любой момент времени
температура в любом сечении стержня будет переменной величиной, зависящей от
времени и от места расположения сечения стержня.
. Это допущение позволяет считать, что
температура во всех точках любого сечения стержня одинакова. На концах этого
стержня задана температура (или может быть она измерена). Изменение температуры
на концах стержня приводит к неравномерности температуры в различных сечениях
стержня. Очевидно, что от более нагретого участка стержня будет перетекать
тепло к менее нагретому участку. Это означает, что в любой момент времени
температура в любом сечении стержня будет переменной величиной, зависящей от
времени и от места расположения сечения стержня.
Требуется определить распределение температуры во всех сечениях данного стержня в любой момент времени.
2 Математическая модель задачи
Перед математическим моделированием поставленной
задачи необходимо ввести обозначения параметров: ![]() -
время,
-
время, ![]() - координата сечения стержня по оси,
направленной по длине стержня,
- координата сечения стержня по оси,
направленной по длине стержня, ![]() количество тепла,
количество тепла, ![]() –температура стержня на сечении стержня с
координатой
–температура стержня на сечении стержня с
координатой ![]() и в момент времени
и в момент времени ![]() . Тогда температура может быть
рассмотрена как функция независимых переменных
. Тогда температура может быть
рассмотрена как функция независимых переменных ![]() и
и ![]() :
: ![]() .
.
Для составления математической модели данной задачи необходимо использовать фундаментальные законы физики.
По закону Фурье,
«. . . если температура тела неравномерна, то в нем возникают тепловые
потоки, направленные из мест с высокой температурой в места с более низкой
температурой» [9]. Тогда количество тепла, протекающее через сечения с
координатой ![]() за малый промежуток времени
за малый промежуток времени
(![]() ),
),
равно
 , (1)
, (1)
а
через сечения с координатой ![]() равно
равно
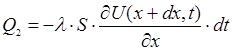 . (2)
. (2)
Знак минус в этих формулах означает, что за положительное
направление роста тепла принято положительное направление координатной оси ![]()
Другой закон физики, известный из школьного курса
физики, определяет количество тепла, которое необходимо сообщить однородному
телу, чтобы повысить его температуру на ![]() , равно
, равно
![]() (3)
(3)
где ![]() объем элементарного
участка стержня длины
объем элементарного
участка стержня длины ![]()
Теперь можно составить уравнение, определяющее баланс тепла:
![]()
или 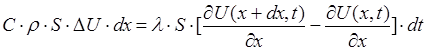 .
.
Если разделить полученное равенство на ![]() то можно получить следующее равенство:
то можно получить следующее равенство:
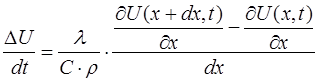 . (4)
. (4)
Вводится обозначение 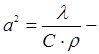 постоянная
величина, зависящая от свойств материала стержня; она называется коэффициентом
температуропроводности.
постоянная
величина, зависящая от свойств материала стержня; она называется коэффициентом
температуропроводности.
Если приращение аргумента ![]() стремится
к нулю
стремится
к нулю ![]() , то левая часть равенства (4) в пределе
равна первой производной по переменной
, то левая часть равенства (4) в пределе
равна первой производной по переменной ![]() функции
функции
![]() , т.е.
, т.е. ![]() , а
дробь в правой части этого равенства равен второй производной по переменной
, а
дробь в правой части этого равенства равен второй производной по переменной ![]() этой же функции, т.е.
этой же функции, т.е.
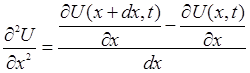 .
.
Учитывая эти формулы и обозначения, из формулы (4) можно получить следующее уравнение:
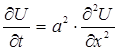 . (5)
. (5)
Полученное уравнение (5) называется уравнением теплопроводности. Оно является дифференциальным уравнением в частных производных и относится к параболическому типу уравнений математической физики.
Для решения этого уравнения должны быть заданы:
- начальное условие, которое вытекает из температурного режима стержня в начальный момент времени:
![]() (6)
(6)
- граничные условия на концах стержня:
![]()
![]() (7)
(7)
![]()
![]() (8)
(8)
Здесь функции ![]() считаются
заданными; функция
считаются
заданными; функция ![]() определяет начальное
распределение температуры в стержне, а функции
определяет начальное
распределение температуры в стержне, а функции ![]() -
изменение температуры на концах стержня.
-
изменение температуры на концах стержня.
Полученная совокупность формул (5) – (8) определяет математическую модель задачи о теплопроводности в однородном стержне.
3 Постановка математической задачи.
На основе математической модели задачи (5)-(8) можно
сформулировать следующую постановку математической задачи: требуется найти
такую функцию) ![]() в области
в области ![]() , удовлетворяющую дифференциальному
уравнению (5), начальным условиям (6) и граничным условиям (7) и (8).
, удовлетворяющую дифференциальному
уравнению (5), начальным условиям (6) и граничным условиям (7) и (8).
Задача будет решена для промежутка времени ![]() где
где ![]() период
времени исследования температурного процесса.
период
времени исследования температурного процесса.
4 Переход к безразмерным переменным
Для удобства дальнейших вычислений, необходимо перейти
к безразмерным параметрам. Пусть в качестве характерных величин выбраны
следующие параметры: ![]() – линейный размер (длина
стержня),
– линейный размер (длина
стержня), ![]() – характерное время,
– характерное время, ![]() – характерная температура; в качестве последнего
можно принять наибольшую температуру на одном из концов стержня. Вводятся новые
переменные:
– характерная температура; в качестве последнего
можно принять наибольшую температуру на одном из концов стержня. Вводятся новые
переменные: ![]() Здесь
Здесь ![]() -
безразмерное время,
-
безразмерное время, ![]() - безразмерная координата,
- безразмерная координата, ![]() – безразмерная температура. В дальнейших
расчетах черточки точки над
– безразмерная температура. В дальнейших
расчетах черточки точки над ![]() и
и ![]() опускаются. После замены переменных
уравнение (4) имеет вид:
опускаются. После замены переменных
уравнение (4) имеет вид:
 (9)
(9)
где ![]() .
.
Начальное условие (6) имеет вид:
 (10)
(10)
Граничные условия (7) и (8) будут записаны в виде следующих формул:
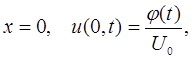 (11)
(11)
 (12)
(12)
Теперь необходимо решить задачу в безразмерных параметрах (9)-(12).
5 Математическая модель задачи о диффузии
Пусть рассматривается некоторая пористая среда в трубке. Если эта среда неравномерно заполнена газом, то происходит диффузия газа. Механизм диффузии простой: из мест с более высокой концентрацией происходит перетекание газа в места с меньшей концентрацией.
Для описания процесса диффузии используется функция ![]() которая определяет концентрацию газа в
сечении
которая определяет концентрацию газа в
сечении ![]() в момент времени
в момент времени ![]()
По закону Нернста масса газа, протекающая через
сечения ![]() за промежуток времени (
за промежуток времени (![]() ), равна
), равна
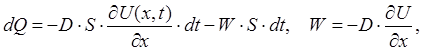
где ![]() коэффициент диффузии,
коэффициент диффузии, ![]() площадь сечения трубки,
площадь сечения трубки, ![]() плотность диффузионного потока, равная
массе газа, протекающего в единицу времени через единицу площади.
плотность диффузионного потока, равная
массе газа, протекающего в единицу времени через единицу площади.
Баланс массы газа на элементарном участке трубки (![]() ) за промежуток времени (
) за промежуток времени (![]() )
)
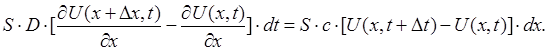
Это равенство делится на ![]() и при
и при ![]() и
и ![]() можно
получить следующее уравнение:
можно
получить следующее уравнение:

где  постоянная величина,
зависящая от свойств газа, параметр
постоянная величина,
зависящая от свойств газа, параметр ![]() называется
коэффициентом диффузии.
называется
коэффициентом диффузии.
Полученное уравнение не отличается от уравнения
теплопроводности в стержне. Подобные уравнения могут быть получены и для других
физических процессов, в которых пренебрегаются инерционными составляющими.
Кроме этого, в обоих случаях рассматривались одномерные задачи, т.е. искомая
функция в них ![]() была функцией только от одной
координатной переменной
была функцией только от одной
координатной переменной ![]() .
.
Эти математические модели могут быть разработаны для
случаев, когда рассматриваются плоские (для двух координатных переменных) и
пространственные (для трех координатных переменных) задачи. Например, для
плоского случая, в системе координат (![]() ):
):
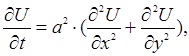
![]()
и для пространственного случая, в системе координат (![]() ):
):

![]()
Лекция 10. Расчетные схемы решения задачи о теплопроводности
Цель работы: изучить популярные методы решения задачи о теплопроводности на основе явной и неявной расчетных схем.
Содержание лекции: о методах решения задачи. Явная расчетная схема. Алгоритм явной расчетной схемы. Неявная расчетная схема. Метод прогонки решения системы алгебраических уравнений. Алгоритм неявной расчетной схемы.
1 О методах решения задачи
Для решения данной задачи используется конечно-разностный метод, рассмотренный при решении краевой задачи для дифференциального уравнения второго порядка (лекция №7). В отличие от краевой задачи для обыкновенного дифференциального уравнения, здесь искомая функция зависит от двух аргументов, поэтому выбираются шаги по двум переменным:
![]() шаг по
времени
шаг по
времени ![]()
![]() шаг по
координате
шаг по
координате ![]()
Область определения искомой функции![]() будет разбита на прямоугольники со
сторонами
будет разбита на прямоугольники со
сторонами ![]() и
и ![]() .
Номера точек разбиения обозначены:
.
Номера точек разбиения обозначены: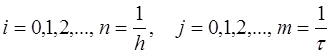 . Пересечения прямых
. Пересечения прямых ![]() и
и ![]() называются
узловыми точками. На область интегрирования наносится сетка, поэтому этот метод
называется методом сеток. Значение искомой функции в узловой точке с
координатами
называются
узловыми точками. На область интегрирования наносится сетка, поэтому этот метод
называется методом сеток. Значение искомой функции в узловой точке с
координатами ![]() обозначено
обозначено ![]()
Производится замена производных искомой функции, имеющихся в уравнении (9). Вторая производная по координате:
 . (13)
. (13)
Для первой производной по времени могут быть использованы различные формулы; популярными из них являются две формулы:
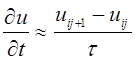 (14)
(14)
и 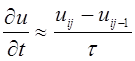 .
(15)
.
(15)
Если для замены производных в уравнении (9) использовать формулы (13) и (14), то будет получена явная расчетная схема, а если использовать вместо формулы (14) формулу (15), то полученная расчетная схема называется неявной.
2 Явная расчетная схема
Используя формулы (13) и (14), из уравнения (9) будет получена формула:
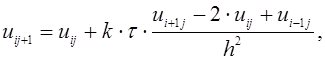 (16)
(16)
Из начального условия (10) следует
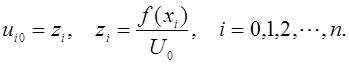 (17)
(17)
Из граничных условий 11) и (12) будут получены формулы:
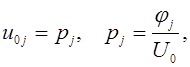 (18)
(18)
![]()
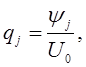
![]() (19)
(19)
3 Алгоритм
Алгоритм явной расчетной схемы состоит из следующих этапов:
- цикл для вычисления значений искомой функции по формуле (17);
-
внешний цикл по счетчику ![]() начало цикла;
начало цикла;
- вычисление граничных значений по формулам (18) и (19);
-
внутренний цикл по счетчику ![]() вычисления по
формуле (16);
вычисления по
формуле (16);
-
конец внешнего цикла по ![]()
4 Неявная расчетная схема
Теперь необходимо рассматривать решение этой же задачи с помощью неявной расчетной схемы.
Следует отметить, что в большинстве случаях предпочтение отдается неявной расчетной схеме. Хотя программировать явную расчетную схему очень легко, однако она имеет существенный недостаток – она не всегда устойчива. Поэтому, несмотря на некоторые трудности программирования, пользователи в большинстве случаях используют неявную схему, так как неявная схема во многих случаях устойчива и более надежна.
Используя замену производных по формулам (13) и (15), из уравнения теплопроводности
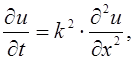
можно получить следующие формулы:
![]() (20)
(20)
где  (21)
(21)
![]()
Формулы (20) представляют собой систему линейных алгебраических уравнений, основная матрица которой имеет особенность; она является трехдиагональной матрицей. Эта особенность позволила использовать метода прогонки для решения этой системы алгебраических уравнений.
Из начального условия  следует
следует
 (22)
(22)
Из граничных условий 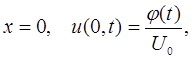
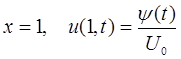 будут получены формулы:
будут получены формулы:
 (23)
(23)
![]()
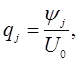
![]() (24)
(24)
5 Метод прогонки решения системы алгебраических уравнений
Вводятся следующие обозначения:
![]()
Тогда с учетом этой замены будет получена следующая формула:
![]() (25)
(25)
Здесь: ![]()
Решение системы уравнений (25) осуществляется методом прогонки; этот метод был рассмотрен ранее, на лекции, когда рассматривалась краевая задача для обыкновенных дифференциальных уравнений.
Особенность основной матрицы системы уравнений позволяет искать решение системы (25) в виде следующей формулы:
![]() (26)
(26)
где ![]() неизвестные пока коэффициенты,
называемые прогоночными.
неизвестные пока коэффициенты,
называемые прогоночными.
Процесс определения этих коэффициентов прогонки называется прямой прогонкой; для определения их используются следующие рекуррентные формулы:
 (27)
(27)
Определение значений искомой функции ![]() называют обратной прогонкой и для этого
используются следующие формулы: сперва формула (24), а затем формула (26).
называют обратной прогонкой и для этого
используются следующие формулы: сперва формула (24), а затем формула (26).
6 Алгоритм
Алгоритм неявной расчетной схемы состоит из следующих этапов:
- цикл для вычисления начальных значений искомой функции по формуле (22);
- внешний цикл по счетчику ![]() начало
цикла;
начало
цикла;
- вычисление граничных значений по формулам (23) и (24);
- внутренний цикл по счетчику ![]()
- вычисление по формулам (25) коэффициентов системы уравнений;
- прямая прогонка: вычисление прогоночных коэффициентов по формуле(27);
- обратная прогонка: определение искомых значений функции поформулам (24) и (26);
- конец внутреннего цикла по ![]()
- переход к внешнему циклу и завершение вычислений.
Лекция 11. Моделирование волновых процессов
Цель лекции: ознакомить с вопросами математического моделирования волновых процессов, часто встречающихся при решении практических задач.
Содержание лекции: уравнения поперечных колебаний струны. Постановка математической задачи. Метод решения задачи. Телеграфное уравнение.
Многие явления природы, имеющие динамический характер, являются причиной волновых процессов, изучение которых является особо важным. Математическое моделирование волновых процессов, приводят к решению задач, связанных с дифференциальными уравнениями в частных производных второго порядка. Причем, математическое моделирование этих, различных по природе, задач природы приводят к одному типу уравнений. Эти уравнения называются уравнениями гиперболического типа и являются составной частью уравнений математической физики. Пусть рассматриваются математические модели некоторых из этих задач.
1 Уравнения поперечных колебаний струны
Пусть рассматривается струна длины ![]() поперечное сечение которой мало. Струна
рассматривается как гибкая упругая нить. Математическое выражение гибкости
заключается в том, что напряжения, возникающие в струне, всегда направлены по
касательной к ее мгновенному профилю. Это означает, что струна не
сопротивляется изгибу. Так как струна рассматривается как упругое тело,
величина натяжения определяется по закону Гука, т.е. пропорциональна удлинению
струны.
поперечное сечение которой мало. Струна
рассматривается как гибкая упругая нить. Математическое выражение гибкости
заключается в том, что напряжения, возникающие в струне, всегда направлены по
касательной к ее мгновенному профилю. Это означает, что струна не
сопротивляется изгибу. Так как струна рассматривается как упругое тело,
величина натяжения определяется по закону Гука, т.е. пропорциональна удлинению
струны.
Вводятся обозначения: ![]() время,
время, ![]() координата,
координата, ![]() поперечное
отклонение точки струны,
поперечное
отклонение точки струны, ![]() плотность материала
струны,
плотность материала
струны, ![]() площадь поперечного сечения струны,
площадь поперечного сечения струны, ![]() сила натяжения, действующая на единицу площади
сечения струны, она постоянная величина для любого сечения струны,
сила натяжения, действующая на единицу площади
сечения струны, она постоянная величина для любого сечения струны,![]() внешняя сила, под действием которой
происходит этот процесс, она действует на единицу длины струны. Процесс
колебания струны описывается функцией
внешняя сила, под действием которой
происходит этот процесс, она действует на единицу длины струны. Процесс
колебания струны описывается функцией ![]() ,
которая определяет положение точки струны, соответствующей координате
,
которая определяет положение точки струны, соответствующей координате ![]() , в момент времени
, в момент времени ![]() Еще
одним допущением является малость колебания струны, т.е. перемещение точек
струны мало и можно пренебречь квадратом производной функции
Еще
одним допущением является малость колебания струны, т.е. перемещение точек
струны мало и можно пренебречь квадратом производной функции  в сравнении с единицей.
в сравнении с единицей.
Пусть рассматривается любой элементарный участок ![]() струны длины
струны длины ![]() . На
струну действуют следующие силы: внешняя сила
. На
струну действуют следующие силы: внешняя сила ![]() сила
инерции, сила натяжения струны
сила
инерции, сила натяжения струны ![]() . По второму закону
Ньютона можно составить следующее уравнение движения:
. По второму закону
Ньютона можно составить следующее уравнение движения:
 (1)
(1)
Это уравнение является проекцией на вертикальную ось. В
данном уравнении ![]() масса элементарного участка
струны,
масса элементарного участка
струны, 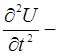 ускорение движения,
ускорение движения, 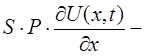 проекция
силы натяжения в сечении с координатой
проекция
силы натяжения в сечении с координатой ![]() а
а  проекция силы натяжения в сечении с
координатой
проекция силы натяжения в сечении с
координатой ![]() внешняя сила
внешняя сила ![]() ,
действующая на этот участок струны определена как произведение площади
сечения и длины участка.
,
действующая на этот участок струны определена как произведение площади
сечения и длины участка.
Если разделить равенство на ![]() затем
рассматривать предел полученных выражений при
затем
рассматривать предел полученных выражений при ![]() то
можно получить следующее уравнение:
то
можно получить следующее уравнение:
 (2)
(2)
где 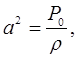
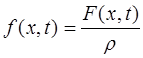 .
.
Здесь ![]() скорость звука, для
различных материалов она имеет различные значения. Уравнение (2) описывает
вынужденные колебания струны. Если внешняя сила отсутствует, т.е
скорость звука, для
различных материалов она имеет различные значения. Уравнение (2) описывает
вынужденные колебания струны. Если внешняя сила отсутствует, т.е ![]() то будет получено уравнение свободных
колебаний струны:
то будет получено уравнение свободных
колебаний струны:
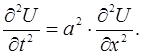 (3)
(3)
Для определения частного решения данной задачи должны
быть заданы начальные и граничные условия. Начальные условия при ![]() определяют начальный профиль струны и
начальную скорость движения ее точек:
определяют начальный профиль струны и
начальную скорость движения ее точек:
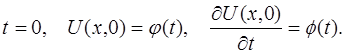 (4)
(4)
Граничные условия для решения данной задачи зависят от условий закрепления концов струны. Если концы струны жестко закреплены, то граничные условия будут записаны в следующем виде:
![]() (5)
(5)
Итак, получена математическая модель задачи о поперечных колебаниях струны: формулы (3) –(5) для свободных колебаний, формулы (2), (4), (5) для вынужденных колебаний.
2 Математическая постановка задачи
Пусть рассматриваются свободные колебания струны. Это означает, что требуется решить уравнение (3) для начальных (4) и граничных (5) условий. Эта задача относится к задачам математической физики гиперболического типа.
3. Метод решения задачи.
Для решения данной задачи используется конечно-разностный метод (метод сеток), использованный ранее для решения другой задачи математической физики – задачи о теплопроводности.
В отличие от задачи о теплопроводности, здесь
используется вторая производная по времени ![]() и две
начальные условия (4).
и две
начальные условия (4).
4. Телеграфное уравнение
Одной из задач, которые приводят к решению уравнения гиперболического типа, является уравнение, названное телеграфным уравнением.
Пусть имеется электрическая цепь, состоящую из прямого
и обратного проводников длины ![]() . Сопротивление
. Сопротивление ![]() , самоиндукция
, самоиндукция ![]() емкость
емкость
![]() утечка изоляции
утечка изоляции ![]() по
всей длине распределены равномерно, рассчитанные на единицу длины проводников.
по
всей длине распределены равномерно, рассчитанные на единицу длины проводников.
Вводятся обозначения: ![]() координата,
координата,
![]() время,
время, ![]() напряжение,
напряжение,
![]() сила тока в сечении цепи на расстоянии
сила тока в сечении цепи на расстоянии ![]() от конца
от конца ![]() Напряжение
Напряжение
![]() и сила тока
и сила тока ![]() являются
функциями переменных
являются
функциями переменных ![]() и
и ![]()
Рассматривается элементарный участок цепи (![]() ). Для этого участка цепи используется
закон индукции, который определяет падение напряжения:
). Для этого участка цепи используется
закон индукции, который определяет падение напряжения:

С другой стороны, это падение напряжения происходит
из-за сопротивления ![]() и индуктивности
и индуктивности  , поэтому можно записать следующее
равенство:
, поэтому можно записать следующее
равенство: 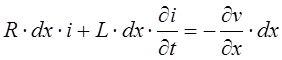 .
.
Разделив полученное равенство на ![]() можно получить следующее уравнение:
можно получить следующее уравнение:
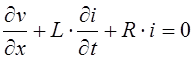 . и (6)
. и (6)
Теперь рассматривается разность между токами,
входящим ![]() в этот элементарный участок цепи и
выходящим
в этот элементарный участок цепи и
выходящим ![]() из него:
из него:
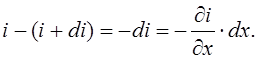
Эта разность между токами состоит из токов заряжения 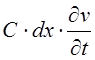 и утечки
и утечки ![]() Тогда
можно записать следующее равенство:
Тогда
можно записать следующее равенство:

Разделив данное равенство на ![]() можно
получить следующее уравнение:
можно
получить следующее уравнение:
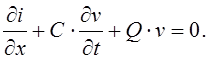 (7)
(7)
Решение полученных двух дифференциальных уравнений
первого порядка (6) и (7) позволяет определить искомые значения напряжения ![]() и силу тока
и силу тока ![]() в
любом сечении проводника
в
любом сечении проводника ![]() и в любой момент
времени
и в любой момент
времени ![]() .
.
Эти уравнения могут быть преобразованы в другую форму.
Для этого вводится дополнительная переменная ![]() ,
которая связана с напряжением
,
которая связана с напряжением ![]() следующей формулой:
следующей формулой:  Подставив эту формулу в формулу (7),
можно получить
Подставив эту формулу в формулу (7),
можно получить
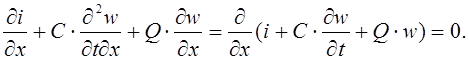
Это означает, что выражение  не
зависит от
не
зависит от ![]() Не ограничивая общность, можно считать,
что это выражение равно нулю, т.е.
Не ограничивая общность, можно считать,
что это выражение равно нулю, т.е. ![]() Отсюда следует, что
Отсюда следует, что
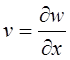 ,
, 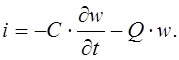 (8)
(8)
Подставив формулу (8) в формулу (6), можно получить следующее уравнение:
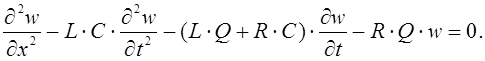 (9)
(9)
Полученное уравнение (9) называется телеграфным уравнением. Это уравнение может быть упрощено, если представить функцию в виде:
![]()
где  .
.
Подставив эту формулу в (9), можно получить следующее уравнение:
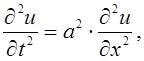 (10)
(10)
где 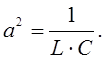
Сравнение формул (3) и (10) показывает, что они одинаковые. Отсюда следует, что одно и то же уравнение может описывать различные процессы.
Лекция 12. Передача информации. Математическая модель сигнала
Цель лекции: изучить методы математического моделирования сигналов, возникающих в процессе передачи информации.
Содержание лекции: система передачи данных. Сигнал. Основные параметры сигнала. Помехи. Математическая модель сигнала и помехи.
В любой информационной системе одним из основных этапов информационного процесса является передача информации. Для передачи информации от источника до потребителя должна существовать система передачи данных.
1 Системой передачи данных
Системой передачи данных называется соскупность технических средств (передатчик, приемник, линия связи), обеспечивающих возможность передачи сообщений от источника к получателю. Обобщенная структура системы передачи информации состоит из: источника сообщений, получателя сообщений, передающего и приемного устройства, линии связи [6]. Известно, что при передаче информации возможны помехи и они также далжны быть в системе передачи информации.
Передающее устройство обеспечивает преобразование сообщения в электрический сигнал, передаваемый по линии связи, в то время как приемное устройство преобразует принятый сигнал обратно в передаваемое сообщение. В современных цифровых системах связи основные функции передатчика и приемника выполняет устройство, называемое модемом.
Линия связи - это среда, используемая для передачи сигналов от передатчика к приемнику. Такой средой может быть кабель, волновод или область пространства, в которых распространяются электромагнитные волны от передатчика к приемнику.
Передающее устройство осуществляет преобразование сообщений в сигналы, удобные для прохождения по конкретной линии связи [6]. В его состав может входить устройство, обеспечивающее помехоустойчивое кодирование. Это устройство называют кодирующим устройством или кодером канала. Потому что первичный электрический сигнал непосредственно не передается по линии связи. В передатчике первичный сигнал преобразуется во вторичный высокочастотный сигнал, пригодный для передачи по линии связи. Такое преобразование осуществляется посредством модулятора, который изменяет один из параметров высокочастотного колебания, генерируемого генератором высокой частоты, в соответствии с изменением первичного сигнала.
2 Сигнал
В процессе передачи сигнала по линии связи он искажается помехой и на входе приемника отличается по форме от переданного. Приемное устройство обрабатывает принимаемый сигнал и восстанавливает по нему переданное сообщение. Принимаемый высокочастотный сигнал фильтруется и усиливается линейными каскадами приемного устройства и поступает на демодулятор, в котором высокочастотный сигнал преобразуется в низкочастотный первичный сигнал. В декодирующем устройстве низкочастотный сигнал преобразуется в кодовую комбинацию символов первичного сигнала. Одновременно в нем осуществляются обнаружение и исправление искаженных символов первичного сигнала. Данная операция осуществляется в случае использования на передающей стороне помехоустойчивого кодирования. Таким образом, на выходе декодирующего устройства имеется кодовая комбинация символов первичного сигнала, соответствующая передаваемому сообщению.
Однако в результате различных искажений и воздействия помех пришедший сигнал может отличаться от переданного. Поэтому возникают гипотезы (предположения) о том, какое сообщение было передано. В связи с этим задачей приемного устройства является решение о том, какое из возможных сообщений в действительности передано источником. Для решения данной задачи проводится анализ всех сведений об источнике, о применяемом помехоустойчивом коде и виде модуляции, о свойствах и природе помех. В результате такого анализа принимается решение о принятом сообщении. Эта часть приемного устройства, которая осуществляет анализ полученног сигнала и принимает решение, называется решающей схемой.
Кодовая комбинация символов первичного сигнала преобразуется в соответствующее сообщение с помощью детектора сигнала, которое поступает на вход получателя информации. Если передача информации между передатчиком и приемником осуществляется одновременно в обе стороны, то такой режим называется дуплексным.
Итак, главной целью системы передачи информации является верность передачи. Верность передачи – это мера соответствия принятого сообщения переданному.
Совокупность средств, предназначенных для передачи сообщений, называют каналом связи. Каналы связи бывают многоканальными, если для передачи информации от группы источников, находящихся в одном пункте, к группе получателей, расположенных в другом пункте.
Из курса физики известно, что излучение электромагнитных волн эффективно, если размеры излучателя соизмеримы с длиной излучаемой волны, поэтому передача электрического сигнала по радиоканалам, кабелям, микроволновым линиям производится на высоких частотах (или на коротких волнах). Одним словом, сигнал передается на несущей частоте. Процесс изменения тех или иных параметров несущей в соответствии с сигналом, передаваемым на этой несущей, называют модуляцией.
Преобразование сообщения в электрический сигнал осуществляется с помощью различных датчиков, называемых преобразователями сообщений. Например, при передаче речи это преобразование выполняет микрофон, при передаче изображения – ЭЛТ (электронно-лучевая трубка). Сигнал на выходе преобразователя сообщения называют первичным. Однако, в большинстве случаях первичный сигнал является низкочастотным колебанием и не может быть передан на большие расстояния. Поэтому для передачи первичного сигнала на большие расстояния его преобразуют в высокочастотный сигнал с помощью модулятора.
3 Основные параметры сигнала
Основными параметрами
сигнала являются длительность сигнала ![]() и
ширина спектра. Любой сигнал имеет начало и конец. Поэтому длительность сигнала
определяет интервал времени
и
ширина спектра. Любой сигнал имеет начало и конец. Поэтому длительность сигнала
определяет интервал времени ![]() , в пределах которого
существует сигнал.
, в пределах которого
существует сигнал.
Спектором сигнала ![]() называется
совокупность его гармонических составляющих (гармоник), образующих ряд Фурье:
называется
совокупность его гармонических составляющих (гармоник), образующих ряд Фурье:

где ![]() – частота повторения сигнала (частота
первой гармоники);
– частота повторения сигнала (частота
первой гармоники);
![]() –
номер гармоники.
–
номер гармоники.
Эта формула может быть записана и в следующем виде:
![]() =
= ![]()
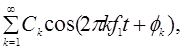
где ![]()
![]() - амплитуда,
- амплитуда, 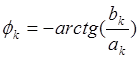 - фаза гармоник.
(Можно использовать ряды по синусам.)
- фаза гармоник.
(Можно использовать ряды по синусам.)
Коэффициенты Фурье определяются с помощью формул:
![]() =
=![]()
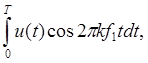
![]() =
=![]()
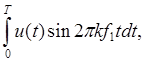
где ![]()
![]() - период повторения сигнала
- период повторения сигнала ![]() .
.
Для определения коэффициентов Фурье используют формулы численного интегрирования (метод прямоугольников):
![]() =
=![]()
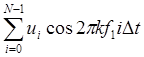 ,
, ![]() =
= ,
,
где ![]() =
=![]() шаг, с которым расположены абсциссы
шаг, с которым расположены абсциссы ![]() .
.
Спектр сигнала
конечной длительности неограничен, однако для любого сигнала можно указать
диапазон частот, в пределах которого сосредоточена его основная энергия. Этим
диапазоном определяется ширина спектра сигнала. Для импульсных
сигналов большая часть энергии сосредоточена в области частот от 0 до 1/![]() , где
, где ![]() -
длительность периодических прямоугольных импульсов. Поэтому ширина спектра
-
длительность периодических прямоугольных импульсов. Поэтому ширина спектра ![]() периодического импульсного сигнала
приблизительно оценивается по формуле
периодического импульсного сигнала
приблизительно оценивается по формуле ![]() = 1/
= 1/![]() (Гц). Например, для речевого сигнала
для телефонной связи ширина спектра ограничивается полосой от 300 до 3400
Гц.
(Гц). Например, для речевого сигнала
для телефонной связи ширина спектра ограничивается полосой от 300 до 3400
Гц.
Объемом сигнала
называют велилчину ![]() , где
, где ![]() -
мощность сигнала (Вт),
-
мощность сигнала (Вт), ![]() - время передачи
сигнала (сек.),
- время передачи
сигнала (сек.), ![]() - ширина спектра (Гц). Базой
сигнала называют
- ширина спектра (Гц). Базой
сигнала называют ![]() . Если база сигнала порядка
единицы, то такие сигналы называются узкополосными, а если
. Если база сигнала порядка
единицы, то такие сигналы называются узкополосными, а если ![]() , то широкополосными.
, то широкополосными.
Сигналы могут дискретными и непрерывными (аналоговыми). Сигнал, дискретный по одному параметру и непрерывный по другому, называют дискретно-непрерывным. Так как источник сообщений выдает каждое сообщение с некоторой вероятностью, поэтому сигнал представляет собой случайное колебание, т.е. сигнал может быть случайным процессом.
4 Помехи
Для получателя информации помеха является случайным воздействием на передаваемый сигнал, приводящее к его изменению. Поэтому помеха считается случайным процессом. Все помехи можно разделить на искусственные и естественные. К искусственным относятся промышленные помехи, помехи от других систем, работающих в данном диапазоне волн, организованные помехи, генерируемые специальными техническими средствами. Естественными помехами являются собственные шумы приемных устройств радиотехнических систем передачи информации, называемые внутренними помехами. Существуют и внешние помехи.
5 Математическая модель сигнала и помех
Для теоретического рассмотрения процессов передачи информации в радиотехнических системах широко используются математическое моделирование сигналов и помех. Математическая модель сигнала (помеха) – это математическая форма представления сигналов и помех. Модель должна быть такой, чтобы она в наибольшей степени соответствовала реальным сигналам. В общем случае математическая модель конкретного сигнала может быть записана в виде обобщенного ряда Фурье [8].
Частный случай,
когда сигнал имеет ступенчатую форму. Пусть теперь предполагается, что ![]() является поступающим сигналом.
является поступающим сигналом.
В литературе приведены различные типы наиболее
распространенных на практике сигналов [8-11]. Здесь рассматривается частный
случай, когда сигнал ![]() задан в виде периодической формы
(см.рисунок 3).
задан в виде периодической формы
(см.рисунок 3).

Рисунок 3 – Сигнал периодической формы
Формула, определяющая сигнала, приведенного на рисунке 1, записывается в следующем виде:
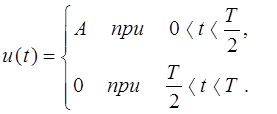
Разложение данной функции ![]() в ряд
Фурье
в ряд
Фурье
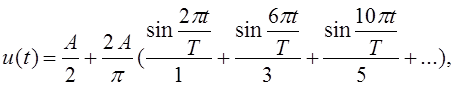
Коэффициенты этого ряда определены в следующем виде:
![]()
![]()
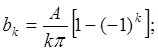 где
где ![]()
Лекция 13. Моделирование сложных систем. Имитационное моделирование
Цель лекции: ознакомить с вопросами, связанными с моделированием сложных систем, в том числе имитационным моделированием.
Содержание лекции: понятие сложной системы. Показатели свойств сложных систем. Имитационное моделирование. Системный подход в моделировании.
1 Понятие сложной системы
Развитие науки и техники, применение их достижений в разных областях человеческой деятельности привели к усложнению применяемых на производстве оборудований и аппаратуры, стали сложными отношения между различными объектами, участвующими в экономической деятельности предприятий и организаций. В связи с этим появилась одна из актуальных проблем современной науки – проблема разработки и внедрения в практику методов исследования сложных систем [3-6]. К сложным системам относятся любые технологические, производственные, коммуникационные, вычислительные системы и другие объекты.
На практике часто встречаются объекты, исследование которых затруднено из-за их сложности. В таких случаях объект расчленяют на определенное число частей. Объект рассматривают как сложная система, а каждую часть объекта - как подсистема. Часть объекта также может быть сложной; тогда она рассматривается как сложная система, состоящая из множества элементов. Таким образом, сложная система может быть представлена как многоуровневая конструкция из взаимодействующих элементов, объединяемых в подсистемы различных уровней. В некоторых случаях подсистема может быть самостоятельно функционирующей частью системы.
В сложных системах главную роль играют вопросы управления [3-6]. Управление представляет собой процесс сбора, передачи и переработки информации, осуществляемый с помощью специальных средств (технических и программных). От элементов системы к управляющим устройствам (УУ) поступает информация, характеризующая состояние элементов системы. Информация на УУ может поступить от вышестоящих органов управления или воздействии внешней среды. УУ перерабатывает поступающую информацию и в результате переработки синтезируются управляющие команды. Эти команды изменяют состояние системы и режимы функционирования элементов системы.
В связи с появлением вычислительной техники и средств коммуникаций в качестве управляющих устройств используются компьютеры. Компьютер работает по программе, реализующую алгоритм переаботки информации. Такой алгоритм называется управляющим алгоритмом.
Если управление сложной системой производится с единого центра, то оно называется централизованным управлением. Однако существуют системы, где осуществляется децентрализация управления.
Для осуществление децентрализации управления сложной системой используется система управления с иерархической структурой. В иерархической системе рассматриваются различные уровни управления. Такая система управления является самым распространенной и эффективной.
Реальные системы функционируют в условиях действия различных факторов, в том числе случайных. Источниками случайных факторов могут быть воздействие внешней среды, ошибки персонала, шумы и помехи в коммуникациях, природные и техногенные события и другие. Одним словом, факторы, влияющие на работу системы могут быть как внешние, так и внутренние.
Сложные системы имеют следующие отличительные черты:
- сложная система состоит из многочисленных взаимосвязанных элементов, каждый из которых может быть также сложной системой;
- для достижения поставленной цели функционирования системы используется достаточно сложная функция;
- сложную систему можно разбить на подсистемы, цели функционирования которых подчинены общей цели функционирования всей системы;
- в системе имеются: система управления, информационная сеть и потоки информации;
- система взаимодействует с внешней средой и функционирует в условиях случайных факторов.
2 Показатели свойств сложной системы
Любая система представляет собой совокупность объектов (подсистем, элементов и т.д.), предназначенная для выполнения определенного вида работ или для решения некоторого класса задач. При этом должна быть четко определена цель функционирования системы и перечень решаемых ею задач. Здесь может быть определен критерий оценки качества функционирования системы. Для этого используется показатель эффективности системы. Показателем эффективности может быть числовая характеристика, которая дает возможность оценивать степень приспособленности системы к выполнению поставленной перед ней задачи.
Расчет показателей эффективности системы является достаточно сложной задачей, поэтому приходится использовать математические методы [3-6]. Для того чтобы показатель эффективности могла полностью характеризовать качество работы системы, он должен учитывать все особенности и свойства системы, с учетом внутренних и внешних факторов, влияющих на функционирование системы. Отсюда следует, что показатель эффективности функционирования системы зависит от структуры самой системы, значений ее параметров, характера воздействий внешней среды, внутренних и внешних случайных факторов.
Отсюда следует, что показателем эффективности является некоторый функционал, заданный на некотором множестве процессов функционирования системы. Для оценки эффективности системы часто используются такие функционалы, характеризующие свойства системы, как надежность, помехозащищенность, качество управления и т.д.
3 Имитационное моделирование
Итак, система является совокупностью объектов, объединенных какой-либо формой регулярного воздействия с целью выполнения определенных функций. Сложность системы требует использование методов имитационного моделирования. Имитационное моделирование предполагает, что поведение элементов сложной системы задается в форме алгоритма их функционирования, т.е. в виде алгоритмической модели. Алгоритмическая модель реализуется компьютерной программой.
4 Системный подход в моделировании
Любой объект исследования представляет собой достаточно сложную систему, состоящую из совокупности взаимодействующих элементов. Причем, каждый элемент объекта также может быть сложной системой. Поэтому объект исследования может рассматриваться как некоторая система и для анализа может быть использована методология, называемая системным подходом.
Сущность системного подхода заключается в следующем. Вначале объект выделяется из состава окружающей среды; это называется определением системы. Система может состоять из подсистем, которые также являются достаточно сложными системами. Подсистемы и элементы системы находятся в определенной взаимозависимости. Информация о свойствах системы в определенный момент времени определяет состояние системы. Движение системы – это процесс перехода системы из одного состояния в другое. Возможность отражения поведения системы зависит от того как она представляет объект моделирования.
Рассмотренные положения системного подхода в определенном смысле составляют методологическую основу моделирования.
Лекция 14. Моделирование стохастических (случайных) процессов
Цель лекции: изучить вопросы, связанные с моделированием стохастических и случайных величин.
Содержание лекции: стохастическое моделирование. Предельные теоремы теории вероятностей. Параметры случайного процесса.
Кроме сложности, характеризующей сложную систему, ее особенностью является влияние случайных факторов. Исследование влияния случайных факторов на поведение системы связано с проведением множества компьютерных экспериментов. Эти эксперименты называются стохастическим моделированием и они позволяют получать статистические данные, на основе которых могут быть сделаны выводы о законах распределения параметров системы как случайные величины.
1 Стохастическое моделирование
Стохастическое моделирование является одно из важнейших направлений имитационного моделирования. Случайные процессы связаны со случайными событиями и функциями, которые являются фундаментальными понятиями в прикладной математике.
В практике моделирования процессов часто приходится иметь дело с системами, которые подвергаются случайным воздействиям окружающей среды или внутренним случайным изменениям параметров системы. Здесь имеются многочисленные факторы, воздействие которых имеет случайный характер.
В задачах, рассмотренных ранее, при моделировании инженерно-технических или физических задач предполагалось, что известны точные значения параметров или параметры являются детерминированными. Однако на практике точные значения параметров изучаемой системы, как правило, неизвестны. Поэтому они рассматриваются как случайные события или процессы, параметры которых могут принимать тое или иное значения с определенной вероятностью.
Когда рассматривается вопрос о случайных явлениях, считается, что они непредсказуемые, хаотичные, недетерминированные. Однако доказано, что случайность – это такой вид неопределенности, которая подчиняется определенной закономерности. Эта закономерность задается в виде распределения вероятностей. При моделировании случайных процессов используется своя методология, которая отличается от методов моделирования детерминированных процессов. Основныеми методами моделирования подобных систем являются стохастическое моделирование и статистическая обработка его результатов.
Стохастическое моделирование – это один из видов имитационного моделирования, представляющий собой метод получения с помощью компьютера статистических данных о процессах, происходящих в моделируемой системе, параметры которой изменяются случайным образом с заданным законом распределения. Иными словами, сущность метода стохастического моделирования сводится к построению некоего моделирующего алгоритма, имитирующего функционирование системы, случайные воздействия на систему, случайные изменения параметров системы и случайные изменения начальных условий. Такой алгоритм реализуется с помощью компьютерных программных средств многократно. В результате этого будет получена информация о свойствах системы.
Если количество такой реализации достаточно много, то полученные результаты с достаточной точностью будут характеризовать процесс функционирования системы. В ходе модельных экспериментов с помощью имитационной модели воспроизводится влияние случайных факторов. При этом необходимо произвести многократное выполнение эксперимента для получения статистичеких данных.
Первоначально изложенный метод назывался методом Монте-Карло, который был использован для решения детерминированных задач, заменяя их эквивалентной схемой некоторой стохастической системы, выходные характеристики которой совпадают с результатом решения этой задачи. Позже этот метод использовался для компьютерной имитации функционирования систем, подверженных случайным воздействиям. Этот метод получил новое название метод стохостического моделирования.
2 Предельные теоремы теории вероятностей
Теоретической основой метода стохастического моделирования являются предельные теоремы теории вероятностей. Как было отмечено выше, случайные явления (события, процессы, величины) подчиняются определенным закономерностям. Эти закономерности позволяют прогнозировать поведение системы, оценивать количественно усредненные характеристики, имеющие определенную устойчивость. Характерные закономерности проявляются в виде распределения вероятности случайных величин, образующихся при сложении множества воздействий. Предельные теоремы или законы больших чисел выражают эти закономерности.
Теорема Бернулли. Если производится ![]() независимых
испытаний, в каждом из которых некоторое событие наступает с вероятностью
независимых
испытаний, в каждом из которых некоторое событие наступает с вероятностью ![]() , то относительная частота появления
этого события
, то относительная частота появления
этого события ![]() при
при ![]() стремится
к
стремится
к ![]() , где
, где ![]() количество
появлений события. На основе этой теоремы можно определить вероятность события
как частота его появления.
количество
появлений события. На основе этой теоремы можно определить вероятность события
как частота его появления.
Теорема Чебышева. Если в ![]() независимых
испытаниях наблюдается ряд значений некоторой случайной величины, то при
независимых
испытаниях наблюдается ряд значений некоторой случайной величины, то при ![]()
![]() среднее
арифметическое значение этой случайной величины стремится к ее
математическому ожиданию.
среднее
арифметическое значение этой случайной величины стремится к ее
математическому ожиданию.
Центральная предельная теорема. Если существует ![]() независимых
случайных величин, имеющих одинаковый закон распределения, математическое
ожидание и дисперсию, то при
независимых
случайных величин, имеющих одинаковый закон распределения, математическое
ожидание и дисперсию, то при ![]()
![]() закон
распределения их суммы неограниченно приближается к нормальному закону.
закон
распределения их суммы неограниченно приближается к нормальному закону.
Эти теоремы гарантируют высокое качество статистичеких оценок при достаточно большом количестве испытаний.
3 Параметры случайного процесса
Параметры случайного процесса являются случайными величинами, которые могут быть как непрерывными, так и дискретными. Случайная величина полностью характеризуется, если известен закон распределения вероятности или плотность распределения вероятности. Обычно ограничиваются некоторыми характеристиками случайной величины.
Математическое ожидание или среднее по вероятности значение случайной
величины: 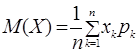 , где
, где ![]() –
дискретная случайная величина,
–
дискретная случайная величина, ![]() - возможные (наблюдаемые)
значения случайной величины
- возможные (наблюдаемые)
значения случайной величины ![]() ;
; ![]() – соответствующие им вероятности принятия
случайной величиной возможных значений. Если рассматривается непрерывная
случайная величина
– соответствующие им вероятности принятия
случайной величиной возможных значений. Если рассматривается непрерывная
случайная величина ![]() , то ее математическое ожидание определяется
формулой:
, то ее математическое ожидание определяется
формулой:  , где
, где ![]() – функция плотности распределения вероятности.
– функция плотности распределения вероятности.
Среднеквадратическое отклонение определяет разброс случайной величины относительно математического ожидания. Для определения значения данной характеристики используется следующая формула:
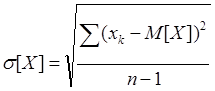 .
(1)
.
(1)
Коэффициента вариабельности случайной величины, характеризующая относительную величину разброса, вычисляется формулой:
![]() =
= 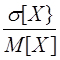 .
(2)
.
(2)
Квадрат среднеквадратического отклонения называется дисперсией случайной величины:
![]() =
= ![]() . (3)
. (3)
В практических вычислениях используются различные законы распределения вероятности для непрерывных случайных величин.
Если рассматривается моделирование случайного изменения системы по времени, то его можно рассматривать как случайное событие перехода от одного состояния в другое. Если вероятность любого возможного состояния системы в будущем зависит только от состояния в текущий момент и не зависит от того, каким путем система пришла в текущее состояние, то такой случайный процесс называется марковским.
Лекция 15. Информационные модели. Заключение
Цель лекции: ознакомить с информационным моделированием, основные понятия и определения информационного моделирования.
Содержание лекции: определения информационной модели. Геоинформационные модели. Электронные карты. Заключение.
1Определения информационной модели
В настоящее время появился термин «информационные модели» и он получил широкое распространение среди исследователей. Однако определение информационной модели различными авторами дается по разному. Это связано с различными точками зрения к проблеме моделирования информационных процессов. В данной лекции будут рассмотрены различные определения информационной модели.
В зависимости от целей моделирования возможно несколько уровней формализованного описания систем: символический, теоретико-множественный, абстрактно-алгебраический, топологический, логико-математический и информационный. На информационном уровне описания систем предполагается, что в любом процессе управления или регулирования происходит переработка входных информационных сигналов в выходные сигналы. В данном случае информация выступает как способность процессов и явлений порождать многообразие состояний, которые передаются от одного объекта к другому посредством отображения состояния источника в состоянии приемника.
Согласно определению академика Ершова А.П., «информационная модель – это модель, в которой изучаемое явление отображается в виде процессов передачи и обработки информации, а параметры модели представлены в числовой, текстовой или иной сигнальной форме». Такое определение подчеркивает информационный аспект изучения объектов и процессов. Из этого определения следует, что при информационном моделировании отображаются в первую очередь процессы передачи и преобразования сигналов. Например, в системах управления и регулирования.
Кроме определения Ершова, существуют и другие определения информационной модели.
По определению Семакина и Хеннера [19,20] «Информационная модель объекта – это его описание». Это означает, что если построено описание объекта, то построена его информационная модель и она содержит определенную информацию об объекте. Однако любая модель содержит подобную информацию, так как основным свойством модели является отражение определенных свойств объекта моделирования. Поэтому данное определение Семакина и Хеннера имеет общий характер, не отражает специфику информационного моделирования.
В толковом словаре по информатике, вышедшем под редакцией Пешинова и Савинкова [16], «Информационную модель характеризует формализованное описание информационных структур и операций над ними или параметрическое представление процесса циркуляции информации, подлежащей автоматизированной обработке в системе управления».
В статье Могилева и Хеннера [7] «О понятии «Информационное моделирование» это поределение звучит так: «Информационная модель это класс знаковых моделей, описывающих информационные процессы (возникновение, передачу, преобразование и использование информации) в системах самой разнообразной природы».
Эти два определения достаточно хорошо согласуются с определением Ершова. В них выделены особенности информационного моделирования Существуют и другие определения информационного моделирования. Во многих случаях по определению понятия информационной модели и математической модели совпадают. Однако главным различием между математическими и информационными моделями определяется соотношением между данными и алгоритмами: если данные больше и важнее алгоритмов, то имеем информационную модель, а иначе – математическую. Например, если рассматривается база данных (каталог книг в библиотеке), то здесь важнее данные чем алгоритмы, поэтому здесь рассматривается информационная модель. Если рассматривается движение космического аппарата, то для описания его движения необходима математическая модель.
Из всего сказанного следует следующий вывод: понятие «информационная модель» находится в стадии становления вследствие быстрого развития и изменения науки по информационным технологиям.
2 Геоинфомационные модели
Одной из разновидностей информационных моделей могут быть геоинформационные модели. Знакомые всем географические карты отражают различные характеристики определенных территорий. Это означает, что географические карты представляют собой систему моделей, которые отображают один и тот же объект, одним и тем же способом, но с разной степенью детализации. Кроме информации, которая отображается на картах, часто возникает необходимость в получении более детального и разнообразного сведения, в поисках объектов определенного рода, определении маршрутов движения и т.п. Решением подобных вопросов средствами современных информационных технологий занимается геоинформационное моделирование.
Геоинформационное моделирование – это один из видов компьютерного моделирования, который базируется на создании многослойных электронных карт. При этом опорный слой описывает географию определенной территории, а остальные слои - различные виды состояния этой территории: экономическое развитие, политическое и административное деление и т.п. На электронную карту могут быть выведены соответствующие слои, которые отражают различные объекты и связи между ними – города, дороги, аэропорты и т.д. геоинформационные карты реализуются с использованием векторной графики и поэтому всегда можно выбрать нужные масштабы при работе с такими моделями.
3 Электронные карты
Электронные карты связаны с базами данных, где хранится необходимая информация об изображенных на карте объектах, что позволяет пользователю таких карт осуществить поиск необходимого ему объекта. Особую ценность такие модели приобретают при их соединении с технологией спутникового геопозиционирования (GPS).
4 Заключение
В предложенных здесь конспектах лекций даны материалы о задачах, часто возникающих в исследовательской работе по различным областям знаний. В современных условиях любая научная или проектная работа связана с математическим и компьютерным моделированием исследуемого процесса или изучаемого явления. В связи с важностью математического и компьютерного моделирования в научно-исследовательской работе каждому будущему научному сотруднику (магистранту) необходимо иметь знания и навыки по применению математических методов и компьютерной техники для решения задач, возникающих в своей области исследования. Рассмотренные в данных лекциях материалы являются первоначальными сведениями для углубленного освоения в дальнейшем методов моделирования различных процессов и явлений.
Список литературы
1 Тихонов А.Н., Костомаров Д.П. Вводные лекции по прикладной математике.- М.: Наука, 1984. – 192 с.
2. Королев А, Л. Компьютерное моделирование. – М.: БИНОМ. Лаборатория знаний, 2010.-230 с.
3. Бусленко Н.П. Моделирование сложных систем.–М.: Наука,1978.-400 с.
4. Кузин Л.Т. Основы кибернетики. Т.1. Математические основы кибернетики. – М.: Энергия, 1973.- 504 с.
5. Коршунов Ю.М. Математические основы кибернетики: Учеб. пособие для вузов. – М.: Энергия, 1980. – 424 с.
6. Информационные технологии в радиотехнических системах. Учебное пособие.– 2-ое изд., перераб. и доп./В.А.Васин, И.Б.Власов, Ю.М.Егоров и др.; под ред. И.Б.Федорова. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. –768 с.
7. Дмитриев В.И. Прикладная теория информации: Учебное пособие для студентов. – М.: Высшая школа, 1989. – 320 с.
8. Тихонов А.Н., Самарский А.А. Уравнения математической физики.- М.: Наука, 1972. -735 с.
9. Джеффрис Г., Свирлс Б. Методы математической физики. Вып.3.- М.: Изд-во «Мир», 1970.- 344 с.
10. Седов Л.И. Методы подобия и размерности в механике. – М.: Наука, 1987.- 432 с.
11. Смирнов В.И. Курс высшей математики. Т.2,3.- М.: Наука, 1974.- 656 с.
12. Бакалов В.П., Дмитриков В.Ф., Крук Б.Е. Основы теории цепкй. Учебник для вузов; Под ред. Бакалова В.П. – М.: Радио и связь, 2000. -592 с.
13. Бухгольц Н.Н. Основной курс теоретической механики (часть вторая).- М.: 1872.-332 с.
14. Құралбаев З.Қ. Алгоритмдеу және программалау тілдері. - Алматы, 2008.-353 бет.
15. Березин И.С., Жидков Н.П. Методы вычислений.- М.: Физматгиз, 1962.- Т.2.-578 с.
16. Першинов В.И., Савинков В.М. Толковый словарь по информатике. – М.: Финансы и статистика, 1995.
17. Могилев А.В., Хеннер Е.К. О понятии «Информационное моделирование»//Информатика и образование. 1997, № 8. С.3-8.
18. Математический энциклопедический словарь. – М.: Сов. Энциклопедия, 1988.
19. Суворова Н.И. Информационное моделирование. Величины, объекты, алгоритмы. –М.: Лаборатория базовых знаний, 2002.
20. Угринович Н.Д. Исследование информационных моделей. Элективный курс. Учебное пособие. 2-ое изд. Испр. – М.: БИНОМ. Лаборатория знаний, 2006.
Содержание
Введение
Лекция 1.Основные понятия о методах моделирования
Лекция 2.Математическое моделирование. Методы исследования моделей
Лекция 3.Эконометрические модели
Лекция 4.Модели регрессионного анализа
Лекция 5.Моделирование процессов в экологических системах
Лекция 6.Моделирование переходных процессов в электрических цепях
Лекция 7.Моделирование колебательных явлений
Лекция 8.Численное решение краевой задачи для дифференциального уравнения второго порядка
Лекция 9.Математическая модель задачи о теплопроводности
Лекция 10.Расчетные схемы решения задачи о теплопроводности
Лекция 11.Моделирование волновых процессов
Лекция 12.Математические модели сигналов и помех
Лекция 13.Моделирование сложных систем. Имитационное моделирование
Лекция 14.Моделирование стохастических (случайных) процессов
Лекция 15.Информационные модели. Заключение
Список литературы
Сводный план 2013 г. поз. 312
Куралбаев Зауытбек Куралбаевич
МАТЕМАТИЧЕСКОЕ И КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ
Конспекты лекций
для магистрантов, обучающихся по
специальности
6М070400-Вычислительная техника и программное
обеспечение
Редактор Н.М.
Голева
Специалист по
стандартизации Н.К.Молдабекова
Подписано в печать
«____» ____2013 г.
Формат 60х84 1/16
Тираж 30 экз.
Бумага типографская
№1
Объем 4,0 уч. изд.л.
Заказ ____ Цена 400 тг.
Копировально-множительное бюро
некоммерческого акционерного общества
«Алматинский университет энергетики и связи»
050013, Алматы, Байтурсынулы, 126