Некоммерческое акционерное общество

Алматинский университет  энергетики и  связи

Кафедра автоматическая электросвязь

 

 

ТЕХНОЛОГИИ ЦИФРОВОЙ СВЯЗИ

Сборник задач 

для студентов очной формы обучения специальности

5В071900 – Радиотехника, электроника и телекоммуникации

 

 

Алматы 2013

 

СОСТАВИТЕЛИ: К.С. Чежимбаева Н.В. Глухова. Технологии цифровой связи. Сборник задач для студентов очной формы обучения специальности 5B071900 – Радиотехника, электроника и телекоммуникации. –  Алматы: АУЭС, 2013. – 43 с.

 

В  данном сборнике изложены основные принципы  и методики расчета по таким основным темам дисциплины «Технологии цифровой связи», как: «Каналы  связи и их характеристики», «Синхронизация в ЦСС», «Методы и устройства помехоустойчивого кодирования». Приведены методы решения типовых задач, а также задачи для самостоятельного выполнения на практических занятиях, список рекомендуемой литературы.

Ил.  1, табл.  15, библиогр. – 3 назв.

 

Рецензент: канд. техн. наук, профессор ТКС Казиева Г.С.

 

Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2013  год.

 

© НАО «Алматинский университет  энергетики и связи», 2013г.

 

Введение

 

Дискретный канал представляет собой совокупность устройств преобразования сигналов, канала связи и предназначен для передачи дискретных сигналов. Дискретный канал характеризуется максимально допустимой скоростью модуляции, вероятностью ошибки p_ош и надежностью.

Синхронизация цифровых сигналов данных (ЦСД) – это процесс установления  и поддержании требуемых фазовых соотношений между значащими моментами двух или нескольких цифровых сигналов данных .

При проектировании УС должны быть заданы исходные параметры: скорость модуляции ; параметры искажений единичных элементов на выходе демодулятора  и ; максимально допустимое время синхронизации  и время поддержания синхронизма ; погрешность синхронизации  либо исправляющая способность приемника. Основными параметрами, характеризующими устройство синхронизации, являются: коррекционный эффект, угол коррекции, минимальный период корректирования, максимальное расхождение по фазе, погрешность (точность) синхронизации, статическая погрешность, динамическая погрешность.

В процессе хранения данных и передачи информации по сетям связи неизбежно возникают ошибки. Контроль целостности данных и исправление ошибок — важные задачи на многих уровнях работы с информацией (в частности, физическом, канальном, транспортном уровнях модели OSI).

Помехоустойчивое, или избыточное, кодирование применяется для обнаружения и (или) исправления ошибок, возникающих при передаче по дискретному каналу. Отличительное свойство помехоустойчивого кодирования состоит в том, что избыточность источника, образованного выходом кодера, больше, чем избыточность источника на входе кодера. Помехоустойчивое кодирование используется в различных системах связи, при хранении и передаче данных в сетях ЭВМ, в бытовой и профессиональной аудио- и видеотехнике, основанной на цифровой записи.

Если экономное кодирование сокращает избыточность источника сообщений, то помехоустойчивое кодирование, напротив, состоит в целенаправленном введении избыточности для того, чтобы появилась возможность обнаруживать и (или) исправлять ошибки, возникающие при передаче по каналу связи.

 

1 Каналы связи и их характеристики. Энтропия источника дискретных сообщений

 

Среднее количество информации Н(А), приходящаяся  на одно сообщение, определяется на основе знания вероятностей P(ai) появления знаков ai на выходе источника:

 

Н(А) = - ∑ P(ai) log₂ P(ai).

 

Аналогично определяется среднее количество информации на один разряд сообщения, состоявшего из n – разрядов.H(x)  = H(A)\ n

 

J _собщ.= 1 \ p₁ log₂ 1 \ p₁ + 1 \ p₂ log₂ 1 \ p₂ =  - p₁ log₂ p₁ – p₂ log₂ p₂ = - p₁ log₂ p₁ – (1 - p₁) log₂(1 - p₁).

 

Скорость модуляции: В = 1\ τ₀,

τ₀ – продолжительность передачи единичного элемента.

Коэффициент ошибок по элементам: n _Ош. = n _Ош \ В ∙ Т:

В – скорость модуляции (Бод);

Т – время измерения (с). Пропускная способность симметричного дискретного канала определяется:

 

С _max = В [ 1 + Р_ош. log₂ Р_ош. + (1 - Р_ош) ].

 

Калькулятор позволяет вычислять десятичные и натуральные логарифмы. При решении задач необходимо произвести вычисления логарифмов по основанию 2. Это делается следующим образом:

 

 

Количество информации в передаваемом символе определяется в битах. Чем меньше вероятность появления символа (сообщения), тем больше количество информации извлекается при его получении. Если источник может выдать один из двух независимых символов (а₁ или а₂), и первый из них выдается с вероятностью р(а₁)=1, то символ а₁ не несет никакой информации, ибо он заранее известен получателю.

Примеры решения

1.     Определить энтропию источника сообщений, если он может выдавать N = 5 знаков с вероятностями: P(a₁) = 0,4; P(a₂) = 0,1; P(a₃) = 0,2; P(a₄) = 0,1; P(a₅) = 0,2.

               Ответ: 2,12 бит\зн.

2. Решить предыдущую задачу при условии одинаковой вероятности появления каждого из 5 –ти знаков. P(ai) = 0,2.

Ответ: 2,32 бит\зн.

Вопросы:

1) Когда энтропия будет равна 0.

(Если вероятность передачи какого-то сообщения (знака) равна 0).

2) Условие максимальной энтропии.

(Если символы источника появляются независимо и с одинаковой вероятностью).

3) Определить H(x)  двоичного кода, в котором каждому предаваемому знаку соответствует кодовая комбинация N = 2⁵ = 32, если известно, что с учетом неравномерности появления знаков текста энтропия источника сообщений Н(А) = 4,36 бит\зн. сообщения.

Определить максимальное значение H _max(x). и избыточность источника:

Н _max (А) = log₂ N ; Н _max (А) = log₂ 32 = 5 бит\ зн.; H _max(x) = 5 \ 5.

Ответ: 1,0 бит \разряд.

Зная H (x) и  H _max(x), можно судить об избыточности источника сообщений:

И = 1 - H (x) \ H _max(x) ; И = 1 – 0,87 = 0,13.

Это означает, что источник выдает разряды сообщения, которые в информационном смысле недогружены на 13 %, по сравнению с потенциальными возможностями.

Количество информации определяется: I = log₂ 1 \ p = log₂ N.

4) По симметричному дискретному каналу связи со скоростью В = 2000 Бод передается последовательность элементов 0 и 1. Вероятность появления элементов одинакова и равна 0,5. Действие помех  появляется в том, что искажается 1% элементов. Определить пропускную способность канала.

Решение.

С _max = В [ 1 + Р_ош. log₂ Р_ош. + (1 - Р_ош) ] ;

Ответ: С _max = 1840 бит\с.

5) Сигналы приходят на два разнесенных приемника. Вероятность правильного приема на первом приемнике 0,8 на втором – 0,9. Прием сигналов обоими приемниками независим. Определить количество информации, содержащейся в сообщении о правильном приеме сигнала.

Решение.

Используется формула:

J _собщ.= 1 \ p₁ log₂ 1 \ p₁ + 1 \ p₂ log₂ 1 \ p₂ =  - p₁ log₂ p₁ – p₂ log₂ p₂ = - p₁ log₂ p₁ – (1 - p₁) log₂(1 - p₁).

Ответ: J _собщ. = 0,03 бит.

6) По каналу связи передаются сообщения х₁,х₂, х₃, х_4, х₅ с вероятностями Р(х₁) = 0,3,

Р(х ₂) = 0,1, Р(х ₃) = 0,25, Р(х ₄ ) = 0,2, Р(х ₅ ) = 0,15 соответственно. Определить среднее количество информации, приходящееся на каждое сообщение.

Ответ: 2,23 бит.

7) На входе двоичного двоичного источника сообщений элементы 0 и 1 появляются с вероятностями р и р-1 соответственно. При каком значении р энтропия источника максимальна?

Ответ: энтропия максимальна при равновероятностных элементах, т.е. р = 0,5.

8) Кодовая комбинация состоит из 14 элементов. Вероятность искажения каждого элемента равна 0,2. применяется корректирующий код, исправляющий все ошибки до трехкратных включительно. Определить количество информации J , содержащейся в сообщении о том, что кодовая комбинация искажена.

Ответ: количество информации J = 1.74 бит.

9) Определить количество информации в слове русского текста из п=8     букв, буквы считать равновероятными и независимыми.

В русском алфавите N=32 буквы. Вероятность появления одной буквы:

p(a_i)=1/N=1/32.

Считаем, что используется двоичный код, т.е. символы «0» и «1».

В одной букве содержится информации:

I(a_i)=log₂ {1/ p(a_i)}= - log₂ p(a_i)= -log₂ (1/32)=5 бит.

Слово содержит 8 букв. Количество информации в этом слове:

I_сл= I(a_i)=8·I(a_i)=40 бит.

Под избыточностью всегда понимают что-то лишнее. Избыточными в источнике считаются сообщения, которые несут малое, а иногда и нулевое, количество информации. Время на их передачу тратится, а полезной информации передается мало. Наличие избыточности означает, что часть сообщений можно и не передавать по каналу связи, а восстановить их на приеме по известным статистическим связям. Так и поступают при передаче телеграмм, исключая из текста союзы, предлоги, знаки препинания, поскольку они легко восстанавливаются по смыслу телеграммы на основании известных правил построения фраз.

Количественно избыточность оценивается коэффициентом избыточности:

К_изб=[H_max(A)- H(A)]/ H_max(A)=1- H(A)/ H_max(A),

где H(A)- энтропия источника, вычисленная на основе учета статистических характеристик сообщений;

H_max(A)= log₂ N – максимальная энтропия источника из N сообщений.

10) Вычислить коэффициент избыточности источника двоичных сообщений при вероятности одного из них: p(a₁)=0,1.

Для двоичного источника: H_max(A)= log₂ 2=1 бит.

Вероятность появления второго сообщения: p(a₂)=1- p(a₁)=0,9.

Энтропия двоичного источника при этих параметрах:

H(A)= -  p(a_i) log₂ p(a_i)= - 0,1 log₂  0,1-0,9 log₂ 0,9=0,47 бит.

Тогда коэффициент избыточности равен:

К_изб=1- H(A)/ H_max(A)= 1-0,47/1=0,53.

Избыточность при передаче сообщений имеет свои положительные и отрицательные стороны. Увеличение избыточности приводит к увеличению времени передачи сообщений, излишней загрузке каналов связи. Одной из задач теории информации и техники кодирования является задача сокращения избыточности.

Однако при увеличении избыточности появляется возможность повышения помехоустойчивости передачи сообщений. У русского, да и у всех европейских языков, К_изб 0,5. На практике обеспечивают компромиссное значение избыточности для заданной скорости и надежности передачи сообщений.

11) Найти максимальное количество информации, которое содержится в квантованном телевизионном сигнале, соответствующем одному телевизионному кадру при 625 строках разложения. Сигнал, соответствующий одной строке изображения, представляет собой последовательность 833 (при отношении сторон кадра 4/3) статистически независимых случайных по амплитуде,  каждый из которых с равной вероятностью принимает одно из 16 значений. Найти избыточность телевизионного сигнала, если фактически кадр изображения с 16 градациями уровней содержит 9,37·10⁵ бит информации.

При равновероятных сообщениях (импульсах) максимальное значение энтропии, т.е. среднее количество информации на один импульс равно:

H_max(A)= log₂ N= log₂ 16=4 бит/сообщ.

Количество элементов изображения (сообщений) в одном кадре:

n=833·625=520625 сообщений.

Количество информации в одном кадре:

I_кадр= n·H_max(A)=520625·4=2,083·10⁶ бит.

Исходя из реальной информации кадра энтропия реального телевизионного изображения при 16 градациях яркости (среднее количество на один элемент изображения), равна:

H(A)= I_{кадр.реал.}/n=9.37·10⁵/520625=1.8 бит/сообщ.

Избыточность реального телевизионного сигнала:

К_изб=1- H(A)/ H_max(A)= 1-1.8/4=0,55.

12) Источник за время Т=10⁶с выдает I=10⁷ бит информации двоичными посылками длительностью τ=10 мс. За какое время и каким количеством двоичных посылок можно передать тот же объем информации, если полностью устранить избыточность источника? Определить избыточность источника.

Заданный объем информации источник передает следующим количеством посылок:

n=Т/ τ=10⁶/10·10 ^-3=10⁸.

Энтропия, т.е. средняя информация на символ:

H(A)= I/ n=10⁷/10⁸=10 ^-1=0,1 бит/симв.

Если избыточность устранена, то при двоичном коде каждый символ несет в себе H_max (A) =1 бит информации и заданный объем информации передается следующим количеством посылок:

n_о= I/ H_max(A)=10⁷/1=10⁷.

Требуемое для этого время:

Т_о= τ· n_о=10·10 ^-3·10⁷=10⁵ с.

Избыточность источника:    К_изб=1- H(A)/ H_max(A)=1-0,1/1=0,9.

Полное устранение избыточности источника позволяет на 90% экономичнее использовать канал связи.

13) Источник сообщений имеет алфавит с объемом N=32 используется двоичный код. Число разрядов в кодовой комбинации п=8. Какое число информационных и проверочных символов содержится в каждой кодовой комбинации. Определить число запрещенных комбинаций. Определить избыточность  и относительную скорость.

Число информационных символов:  k=log₂N= log₂32=5.

Число проверочных символов:  r=n-k=8-5=3.

Количество запрещенных комбинаций равно разности между общим числом возможных и разрешенных кодовых комбинаций:

N_зап.=N_o-N=2⁸-32=256-32=224.

Относительная скорость кода есть относительное число разрешенных кодовых комбинаций и вычисляется по формуле:

R_k= log₂N / log₂N_o= log₂32 / log₂256=5/8.

Коэффициент избыточности кода:

K_k=(1- R_k)=3/8.

 

Самостоятельное выполнение заданий

Задача 1.1

Определить энтропию источника сообщений, если он может выдавать N = 5 знаков с вероятностями: P(a₁) = 0,4; P(a₂) = 0,1; P(a₃) = 0,2; P(a₄) = 0,1; P(a₅) = 0,2.

Задача 1.2

Решить предыдущую задачу при условии одинаковой вероятности появления каждого из 5 –ти знаков. P(ai) = 0,2.

Задача 1.3

Определить H(x) двоичного кода, в котором каждому предаваемому знаку соответствует кодовая комбинация N = 2⁵ = 32, если известно, что с учетом неравномерности появления знаков текста энтропия источника сообщений Н(А) = 4,36 бит\зн.

Определить максимальное значение H _max(x), избыточность источника, пояснить, что означает избыточность.

Задача 1.4

По симметричному дискретному каналу связи со скоростью В = 2000 Бод передается последовательность элементов 0 и 1. Вероятность появления элементов одинакова и равна 0,5. Действие помех  появляется в том, что искажается 1% элементов. Определить пропускную способность канала.

Задача 1.5

Сигналы приходят на два разнесенных приемника. Вероятность правильного приема на первом приемнике 0,8 на втором – 0,9. Прием сигналов обоими приемниками независим. Определить количество информации, содержащейся в сообщении о правильном приеме сигнала.

Задача 1.6

По каналу связи передаются сообщения х₁,х ₂,х ₃,х _4,  х ₅ с вероятностями Р(х₁) = 0,3 , Р(х ₂) = 0,1, Р(х ₃) = 0,25, Р(х ₄ ) = 0,2, Р(х ₅ ) = 0,15, соответственно. Определить среднее количество информации, приходящееся на каждое сообщение.

Задача 1.7

На входе двоичного двоичного источника сообщений элементы 0 и 1 появляются с вероятностями р и р-1 соответственно. При каком значении р энтропия источника максимальна?

Задача 1.8

Кодовая комбинация состоит из 14 элементов. Вероятность искажения каждого элемента равна 0,2. Применяется корректирующий код, исправляющий все ошибки до трехкратных включительно. Определить количество информации J, содержащейся в сообщении о том, что кодовая комбинация искажена.

Примеры решения1.     Определить скорость передачи по двоичному, симметричному каналу связи , если шумы в канале вносят ошибки, таким образом, что в среднем 4 символа из 100 принимаются неверно (т.е. «1» вместо «0» и наоборот).

Решение:

Составим таблицу вероятностей:

p(x₀) = 0,5; p(y₀/ x₀) = 0,96;

p(x₁) = 0,5; p(y₁/ x₀) = 0,04;

p(y₀) = 0,5; p(y₀/ x₁) = 0,04;

p(y₁) = 0,5; p(y₁/ x₁) = 0,96.

Пропускная способность для двоичного, симметричного канала :

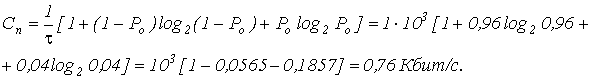
2.     По непрерывному каналу связи, имеющим полосу пропускания F_k = 1 кГц, передается полезный сигнал X(t), представляющий собой нормальный случайный процесс с нулевым математическим ожиданием и дисперсией: = 4 мВ. В канале действует независимый от сигнала гауссов шум F(t) с нулевым математическим ожиданием и дисперсией = 1 мВ.

Определить:

– дифференциальную энтропию входного сигнала;

– дифференциальную энтропию выходного сигнала;

– условную дифференциальную энтропию;

– количество информации в одном непрерывном отсчете процесса Y(t) относительно отсчета X(t);

– скорость передачи информации по непрерывному каналу с дискретным временем;

– пропускную способность непрерывного канала связи;

– емкость канала связи, если время его работы T = 10 м;

– количество информации, которое может быть передано за 10 минут работы канала;

– показать, что информационная емкость непрерывного канала без памяти с аддитивным гауссовым шумом при ограничении на пиковую мощность не больше информационной емкости такого же канала при той же величине ограничения на среднюю мощность.

Решение:

Дифференциальная энтропия входного сигнала:

= 3,05 бит/отсчет.

Дифференциальная энтропия выходного сигнала:

=3,21 бит/отсчет.

Условная дифференциальная энтропия:

= 2,05 бит/отсчет.

Количество информации в одном непрерывном отсчете процесса Y(t) относительно отсчета X(t) определяется по формуле:

I (X, Y) = h(x) – h (x/y) = h(y) – h (y/x) = 3,21–2,05 = 1,16 бит/отсчет.

Скорость передачи информации по непрерывному каналу с дискретным временем определяется по формуле:

= 2×10³× [3,21–2,05] = 2320 бит/с.

Пропускная способность непрерывного канала с помехами определяется по формуле:

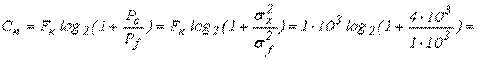2322 бит/с.

  

Самостоятельное выполнение заданий

Задача 1.9

В канал связи передаются сообщения, составленные из алфавита x_1, x₂ и x₃ с, вероятностями p(x₁)=0,25; p(x₂₎=0,025 и p(x₃)=0,5.

Канальная матрица имеет вид:

.

при этом:

.

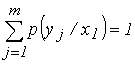Вычислить:

1) Энтропию источника информации H(X) и приемника H(Y).

2) Общую и условную энтропию H (Y/X).

3) Потери информации в канале при передаче к символов (к = 100).

4) Количество принятой информации при передаче к символов.

5) Скорость передачи информации, если время передачи одного символа t = 0,01 мс.

Задача 1.10

По каналу связи передаются символы алфавита x₁, x₂, x₃ и x₄ с вероятностями . Определить количество информации принятой при передаче 500 символов, если влияние помех описывается канальной матрицей:

р (у/х)= .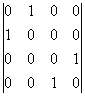

Задача 1.11

Определить потери информации в канале связи при передаче равновероятных символов алфавита, если канальная матрица имеет вид:

.

Определить скорость передачи информации, если время передачи одного символа t = 0,001 сек.

Задача 1.12

Определить потери информации при передаче 1000 символов алфавита источника x₁, x₂ и x₃ с вероятностями p =0,2; p =0,1 и p( )=0,7, если влияние помех в канале описывается канальной матрицей:

.

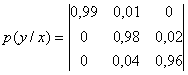Задача 1.13

Определить количество принятой информации при передаче 600 символов, если вероятности появления символов на выходе источника X равны:  а влияние помех при передаче описывается канальной матрицей:

.

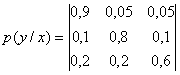Задача 1.14

В канал связи передаются сообщения, состоящие из символов алфавита , при этом вероятности появления символов алфавита равны:

Канал связи описан следующей канальной матрицей:

.

Определить скорость передачи информации, если время передачи одного символа  мс.

Задача 1.15

По каналу связи передаются сигналы x₁, x₂ и x₃ с вероятностями p =0,2;

p=0,1 и p()=0,7. Влияние помех в канале описывается канальной матрицей:

.

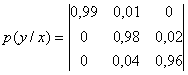Определить общую условную энтропию и долю потерь информации, которая приходится на сигнал x₁ (частную условную энтропию).

Задача 1.16

По каналу связи передаются символы алфавита x₁, x₂, x₃ и x₄ с вероятностями .

Помехи в канале заданы канальной матрицей:

.

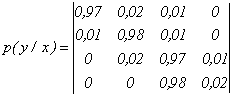Определить пропускную способность канала связи, если время передачи одного символа t = 0,01 сек.

Определить количество принятой информации при передаче 500 символов, если вероятности появления символов на входе приемника Y равны: , а влияние помех при передаче описывается канальной матрицей:

.

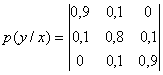Задача 1.17

По непрерывному каналу связи, имеющим полосу пропускания, передается полезный сигнал X(t), представляющий собой нормальный случайный процесс с нулевым математическим ожиданием и дисперсией . В канале действует независимый от сигнала гауссов шум F(t) с нулевым математическим ожиданием и дисперсией . Данные для задания  приведены в таблице 1.1

 

Таблица 1.1 – Исходные данные для расчетов

Вариант	Fk (кГц)	мВ
1	1	3	2
2	3	5	3
3	4	2	1
4	2	5	4
5	5	7	5
6	6	5	3
7	7	3	2
8	1	5	3
9	4	4	2
10	3	5	4
11	2	3	1
12	5	6	5

 

Определить:

– дифференциальную энтропию входного сигнала;

– дифференциальную энтропию выходного сигнала;

– условную дифференциальную энтропию;

– количество информации в одном непрерывном отсчете процесса Y(t) относительно отсчета X(t);

– скорость передачи информации по непрерывному каналу с дискретным временем;

– пропускную способность непрерывного канала связи;

– определить емкость канала связи, если время его работы T = 10 м;

– определить количество информации, которое может быть передано за 10 минут работы канала;

– показать, что информационная емкость непрерывного канала без памяти с аддитивным гауссовым шумом при ограничении на пиковую мощность не больше информационной емкости такого же канала, при той же величине ограничения на среднюю мощность.

 

2 Синхронизация в ЦСС

 

Задача 2.1

В синхронной системе ПДС используется устройство поэлементной синхронизации с дискретным управлением.

Требуется:

объяснить назначение и виды синхронизации в системах передачи сообщений.

Сформулировать основные требования к системам синхронизации и указать, какие факторы влияют на время вхождения и поддержания синхронизации.

Рассчитать параметры схемы синхронизации с дискретным управлением для УПС и привести ее функциональную схему при следующих исходных данных:

а) скорость модуляции В. Бод;

б) смещение левой и правой границы единичных элементов на выходе демодулятора распределено по нормальному закону с параметрами d_кв и d_пр;

в) максимально допустимое время синхронизации Т_с с;

г) время поддержания синхронизма Т_пс с ;

д) исправляющая способность приемника µ_эф%.

 

Таблица 2.1 – Исходные данные

Вариант	Скорость модуляции    В	Параметры искажений единичных элементов на выходе демодулятора σкв левая граница	Параметры искажений единичных элементов на выходе демодулятора σ пр правая граница	Макс. допустимое время синхронизации  tc	Исправляющая  способность приемника µ.эф	Время поддержания синхронизма  t пс
1	1400	2	1,0	0,1	35	0,3
2	1500	7	1,1	0,2	44	0,4

 

Продолжение таблицы 2.1

Вариант	Скорость модуляции    В	Параметры искажений единичных элементов на выходе демодулятора σкв левая граница	Параметры искажений единичных элементов на выходе демодулятора σ пр правая граница	Макс. допустимое время синхронизации  tc	Исправляющая  способность приемника µ.эф	Время поддержания синхронизма  t пс
3	1700	8	1.2	0,5	42	0,7
4	1900	9	1,6	0,4	51	0,6
5	2000	5	1,8	0,2	37	0,3
6	1800	7	1,2	0,3	29	0,5
7	1550	6	1,0	0,1	45	0,4
8	1200	12	1,8	0,2	59	0,3
9	1350	11	1,6	0,4	41	0,5
10	1700	4	1,5	0,1	43	0,3
11	1950	8	1,4	0,3	47	0,4
12	2200	12	1,2	0,4	28	0,5
13	2000	10	1,4	0,5	39	0,6
14	1450	7	1,7	0,2	34	0,3
15	1500	3	1,3	0,5	43	0,6
16	1700	6	1,5	0,3	45	0,4
17	1900	9	1,8	0,5	27	0,6
18	2000	10	1,4	0,6	29	0,7
19	2100	13	1,6	0,8	31	0,9
20	2300	12	1,5	0,7	47	0,8
21	1800	6	1,4	0,6	26	0,7
22	1900	8	1,3	0,4	30	0,5
23	1200	2	1,4	0,2	48	0,5
24	1450	4	1,6	0,4	20	0,7
25	1500	9	1,7	0,5	38	0,6

 

Методические указания к выполнению задачи 2.1

Расчет параметров схемы синхронизации проводится в следующем порядке:

- определяется допустимая погрешность синхронизации по формуле:

e _доп= e_с = 0,5-µ_эф- d_пр,

где e_с – погрешность синхронизации,

µ_эф – эффективная исправляющая способность приемника при краевых искажениях сигнала,

d_пр,- преобладание приемника.

Динамическая составляющая погрешности e_дин рассчитывается исходя из утверждения, что динамическая погрешность не превысит утроенного среднеквадратического значения d_e («правило из трех сигм»), т.е. e_дин = 3d_e ,

d_e ² = 0,628 d_кв/ S_mд,   S_mд = t _nc B,

где S –емкость реверсивного счетчика,

m_д – коэффициент деления частоты задающего генератора.

Допустимая величина коэффициента нестабильности задающего генератора K_f  модулятора и демодулятора находится по формуле:

K_f  < e _доп /(В t _nc).

Допустимая статическая погрешность синхронизации при заданных параметрах краевых искажений  определяется из соотношения:

e_ст= e_с – e_дин,

где e_с – погрешность синхронизации, e_с = e _доп .

При этом, если допустимая величина статической погрешности превышает 1%,то целесообразно задаться   e_ст =0,01.

Коэффициенты m_д  и  S определяется соотношением:

S=Е/[1(m_д S)+4 K_f].

Полученные значения m_д и S следует округлить до ближайших целых чисел и проверить, не превышает ли при этом необходимые значения t_c и e_с.Значения  m_д  находятся из соотношения:

m_д= m_д S/ S.

Частота задающего генератора определяется по формуле:

f₀= m_д f_в ,

где f ₀ – частота модуляции, которая равна скорости модуляции В ,т.е . f₀=В.

Пример.

Рассчитать параметры схемы синхронизации с дискретным управлением для УПС при следующих исходных данных. Скорость модуляции  1800 Бод, смещение левой и правой границ единичных элементов на выходе демодулятора распределено по нормальному закону с параметрами: _{σ кв = 9, σпр =1,2% . Максимально допустимое время синхронизации t c = 0,3 с, время поддержания синхронизма t пс = 0,4 с, исправляющая способность приемника μэф = 44%}

_{Исходные данные:}

 _{= 9% = 0,09}

 _{=  1,2% 0,012σ}

_{В = 1800 Бод}

 _{= 0,3 с}

 _{= 0,4с}

_{44% = 0,44}

Определяется допустимая погрешность синхронизации  по формуле:

.

ε _доп. = 0,5 – 0,44 – 0,012 = 0,048.

Заданное время синхронизации:

Определяем произведение S*m_д:

S*m_д = 0,3 *1800 = 540.

Динамическая составляющая погрешности ε _дин. рассчитывается по формуле:

ε _дин. = 3 √ о,628*0,09 * 540 = 0,03.

Допустимая величина коэффициента нестабильности задающего генератора k_f модулятора и демодулятора рассчитывается по формуле:

Из этой формулы находим коэффициент нестабильности генератора

K _f = ε _{доп .}/ (2 * В* t_пс),

K _f = 0,048/ (2 *1800*0,4) ≈3,3 *10^-5.

Определим допустимую статистическую погрешность синхронизации при заданных  параметрах краевых искажений:

ε _ст. = ε _доп - ε _дин = 0,048 - 0,03 = 0,018.

Для  нахождения m_д и S преобразуем:

К виду  ε _ст. = S[1/ (m_д S) + 4 k _f ] зная, что m_д S = 540 и K _f ≈3,3 *10^-5, найдем требуемое S:

S = ε _ст./ [1/ (m_д S) + 4 k _f ] = 0,018 / (1/540 + 4 * 3,3 *10^-5) = 9,07.

Округлим S до ближайшего целого числа S = 9.  Тогда m_д = 540/9 =60. Частота задающего генератора определяется по формуле f₀ = m_д * f_В,

где f_В – частота модуляции, которая равна скорости модуляции В, т.е. f_В= В.

f₀ = 60*1800 = 108 к Гц.

 

3 Методы и устройства помехоустойчивого кодирования

 

Примеры решения.

1) Пусть требуется закодировать комбинацию вида 1101, что соответствует A(х) =х³ + х² + 1.

Определяем число контрольных символов r = 3. Из таблицы возьмем многочлен P(х) = х³ + х + 1, т. е. 1011.

Умножим A(х) на х^r:

A(x)·x^r = (x³ + x² + 1) · x³ = x⁶ + x⁵ + x³Þ 11010000.

Разделим полученное произведение на образующий полином g(х):

A(x) · x^r ⁄ P(x) = (x⁶ + x⁵ + x³) ⁄ (х³ + х + 1) = х³ + х² + х + 1 + 1 ⁄ (х³ + х + 1) Þ 1111 + 001 ⁄ 1011.

При делении необходимо учитывать, что вычитание производится по модулю 2. Остаток суммируем с h(х)·х^r. В результате получим закодированное сообщение:

F(x) = (x³ + x² + 1) · (x³ + x + 1) = (x³ + x² + 1) · x³ + 1 Þ 1101001.

В полученной кодовой комбинации циклического кода информационные символы A(х)=1101, а контрольные: R(х)=001. Закодированное сообщение делится на образующий полином без остатка.

2) Алгоритм определения ошибки.

Пусть имеем n-элементные комбинации (n = k + r), тогда:

получаем остаток от деления Е(х), соответствующего ошибке в старшем разряде [1000000000], на порождающий полином P_r(x):

E₁(x) ⁄ P_r(x) = R₀(x).

Делим полученный полином Н(х) на P_r(x) и получаем текущий остаток R(x).

Сравниваем R₀(x) и R(x).

- Если они равны, то ошибка произошла в старшем разряде.

- Если нет, то увеличиваем степень принятого полинома на x и снова проводим деления:

H(x) · x ⁄ P_r(x) = R(x).

Опять сравниваем полученный остаток с R₀(x).

- Если они равны, то ошибки во втором разряде.

- Если нет, то умножаем Н(х) · х² и повторяем эти операции до тех пор, пока R(x) не будет равен R₀(x).

Ошибка будет в разряде, соответствующем числу, на которое повышена степень Н(х), плюс один.

Например: H(x) · x³ ⁄ P_r(x) = R₀(x).

Коды Боуза – Чоудхури (БЧХ)

Французский ученый А. Хоквингем (1959 г.) и американцы Р. К. Боуз и Д. К. Рой-Чоудхури (1960 г.) нашли большой класс кодов, обеспечивающий произвольное минимальное кодовое расстояние d_min ≥ 5. Они получили название БЧХ (Боуза-Чоудхури-Хоквингема). Порождающие полиномы для таких кодов в зависимости от предъявляемых к ним требований, можно найти в таблице 3.1.

 

Таблица 3.1 – Таблица порождающих полиномов

k	n	m	s	dmin	Порождающий полином
					Символическая запись	Запись в виде полинома
3	7	4	1	3	13	1011
4	15	11	1	3	23	10011
8	15	7	1	3	721	111010001
10	15	5	3	7	2467	10100110111
5	31	26	1	3	45	100101
10	31	21	2	5	3551	11101101001
15	31	16	3	7	107657	1000111110101111
25	31	11	5	11	5423325	101100010011011010101

где  n — общее число элементов;

m — число информационных элементов;

k — число избыточных элементов (n = m + k).

Процедура построения кода БЧХ по заданным M и d_min:

- по d_min найти значение, при котором обеспечивается необходимое число информационных элементов m при минимальной избыточности k_min;

- найти в таблице соответствующий порождающий полином;

- если d_min четное, умножить найденный полином на (x + 1);

- если m_табл>>m_задан, то можно перейти к укороченному циклическому коду, вычеркивая в порождающей матрице исходного кода с параметрами m_табл; k_min (m_табл − m_задан) столбцов слева и столько же строк сверху.

Образующий полином кода БЧХ определяется по длине кода и заданному кодовому расстоянию. Длина кода определяется из выражения n = 2 ^m – 1,

где m – любое целое число:

m = log ₂(n +1). В отдельных случаях для определения m удобно пользоваться выражением:

2 ^m – 1= nc₀ ,

где c₀ является одним из сомножителей, на которые разлагается число n.

Число проверочных разрядов кода:  r ≤ m (d - 1)\ 2.

Число информационных разрядов:

k ≥ (2m - 1) – m (d -1) \ 2.

Образующий полином кода БЧХ является наименьшим общим кратным (НОК) так называемых минимальных полиномов mi (x), порядок которых равен  d-2, а  i= 1,3,5…

P (x) = НОК _.

 

Таблица 3.2 – Значения минимальных полиномов для степени: m = 2 ÷ 8

	Значения минимального полинома mi (x) при m равном
	1	2	3	4	5	6	7	8
1	-	111	1011	10011	100101	1000011	10001001	100011101
3			1101	11111	111101	1010111*	10001111	101110111*
5				111	110111	110011	10011101	101101001
7				11001	101111	1001001*	11110111	110111101 *
9				1	110111	1101	10111111	111100111
11					111011	1101101	11010101	1000101011
13							10000011	1110110111 *
15								010011
17								101100101
19							11001011	110001011 *

 

Продолжение таблицы 3.2

	Значения минимального полинома mi (x) при m равном
	1	2	3	4	5	6	7	8
21							11100101	101100011
23								100011011 *
25								100111111 *
27
29
31
33
35								101011111
37
39
41
43								111000011
45								100111001 *
47
49
51								011111
53

Примечание: * - Непримитивный многочлен

 

Самостоятельное выполнение заданий

Задача 3. 1

Рассчитать Р_н.о. (n) для кодов (7,4) и (11,7), если дискретный канал характеризуется следующим распределением ошибок различной кратности.

 

Таблица 3.3 – Исходные данные для расчетов

t	1	2	3	4	5	6	7	8	9	10	11
Р(t) n = 7	3∙10-5	1∙10-5	6∙10-6	1∙10-6	5∙10-7	1∙10-7	8∙10-8	-	-	-	-
P (t) n= 11	10-4	7∙10-5	2∙10-5	8∙10-6	3∙10-6	10-6	7∙10-7	5∙10-7	2∙10-7	10-7	7∙10-8

 

Задача 3.2

Рассчитать Р_н.о. (n) для кодов (7,4)  и (11,7), если дискретный канал характеризуется двумя параметрами – вероятность ошибки двоичного элемента _ош = 5∙10^-3 и показателем группирования ошибок α = 0,6.

Из теории линейных кодов известно, что любой линейный двоичный код (n,k) не обнаруживает только 2 ^{k – 1} сочетаний ошибок, совпадающих с ненулевыми кодовыми комбинациями.  Вероятность необнаруженной ошибки для линейных кодов, обнаруживающих ошибки, определяется по формуле:

Р_н.о. (n) ≈ ^,

P(t,n) – частость появления ошибок кратности t.

Для кодов, обнаруживающих пакеты ошибок, вероятность Р_н.о. (n) вычисляется по приближенной формуле:

Р_н.о. (n) ≈ _.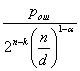

_{где ош}  -  вероятность ошибки двоичного элемента;

α – показатель группирования ошибок.

 

Пример.

Дано n = 7,k = 4, Р(х) = 1101. Построить производящую матрицу с использованием: а) первого и б) второго способов.

Методические указания.

Разрешенные кодовые комбинации циклического кода F (x) могут быть получены двумя способами:

1-й способ: умножение кодовой комбинации Q (х) простого кода на одночлен х^r и добавлением к этому произведению остатка R (x), полученного в результате деления произведения Q (х)∙ х^r на образующий полином Р (х): F (x) = Q (х)∙ х^r + R (x);

2-й способ: умножение кодовой комбинации Q (х) простого кода на образующий полином:

F (x) = Q (х) + Р(x).

Для формирования строк производящей матрицы по первому способу образования циклического кода берут не произвольные комбинации кода Q (х), а только те из них, которые содержат единицу в одном разряде  Q_i (х),

где  i =  1 ÷ k.

Производящая матрица циклического кода имеет вид:

G_n,k= _,

где Е _k ^Т – единичная транспонированная матрица;

С_r,k – подматрица с числом столбцов r  и строк k, образованная остатком R_i(х).

При втором способе образования циклического кода производящая матрица G_n,k формируется умножением образующего полинома Р (х) степени r на одночлен х ^{k -1}  и последующих сдвигов полученной комбинации.

а) так как k = 4, используем следующие единичные векторы Q_i (х): Q₁ (х) = 0001;  Q₂ (х) = 0010; Q₃ (х) = 0100; Q₄(х) = 1000. Производим  следующую операцию над вектором  Q₁ (х):

Q (х)∙ х^r \ Р (х) =  .            Остаток от деления R₁ (x) = 101.

Проделываем аналогичные операции с Q₂ (х); Q₃ (х); Q₄(х), при этом имеем R₂ (x) =111;

R₃ (x) = 011; R₄ (x) = 110.

Производящая матрица имеет вид: G_7,4 = .

Строки полученной матрицы – первые четыре комбинации кода. Пятая комбинация является нулевой, а остальные 11 комбинаций образуются суммированием по модулю 2 всевозможных сочетаний строк производящей матрицы.

б) при втором способе первую строку матрицы получаем из выражения:

Р (х) х ^{k -1}  = 1101 х 1000 = 1101000, а последующие k -1  строк  - с помощью циклического сдвига полученной комбинации. Таким образом, производящая матрица:

G_7,4= .

Задача 3.3

Согласно данным таблицы 3.4 построить производящую матрицу с использованием: а) первого и б) второго способов.

 

Таблица 3.4 – Исходные данные

Вариант	n	k	Р(х)
1	7	4	1001
2			0101
3			1110
4			0111
5			0100
6			0001
7			1111
8			0100
9			1101
10			1100
11	11	7	1000
12			0010
13			1010
14			0110
15			0011
16			1011

 

Задача 3.4

Построить код БЧХ, способный исправлять трехкратные ошибки при n = 15. Определяем кодовое расстояние d = 2∙ t + 1 ; d = 2∙ 3 + 1 = 7 и m = log ₂(n +1) = 4. Число проверочных разрядов r ≤ 4 ∙6 \ 2 = 12 из таблицы 3.2 находим минимальные полиномы:

m₁ (x) = 10011; m₃ (x) =11111; m₅ (x) = 111.

Образующий полином Р (х) определяется, как произведение минимальных полиномов:

Р (х) = 10011 х 11111 х 111 = 10100110111 или

Р (х) = х¹⁰ + х⁸ + х⁵ + х⁴ + х² + х + 1.

Степень Р(х) равна 10, поэтому уточненное значение числа проверочных разрядов r = 10. Следовательно, число информационных разрядов k = n – r = 15 – 10 = 5. На основе образующего полинома  строим образующую матрицу кода (15,5):

G _{15, 5} .

Строки образующей матрицы являются пятью первыми комбинациями кода БЧХ. Остальные комбинации получаются суммированием всевозможных сочетаний строк образующей матрицы.

Задача 3.5

Показать процесс исправления трехкратной ошибки на примере кода, полученного в задаче 3.4

Предположим, передавалась комбинация 101001101110000 и ошибки поражают 13-,3- и 1-й разряды, т.е. ошибочная комбинация имеет вид 100001101110101. Делим принятую комбинацию на образующий полином:

100001101110101  |10100110111

10100110111

  10000000001

    10100110111

        10011011001

        10100110111

            111101110           w= 7.

Так как вес полученного остатка (w= 7) больше числа исправляемых ошибок t _и = 3, производим циклический сдвиг комбинации и деление на образующий полином до получения остатка весом, равным трем. Для данного примера остаток с данным весом (101001) получается при сдвиге комбинации на три разряда. Складываем по модулю два делимых с полученным остатком:

Å      001101110101100

                 101001

         001101110000101.

Затем производим циклический сдвиг полученной комбинации на три разряда вправо (так как в процессе деления комбинация влево была сдвинута на три разряда): 101001101110000.

Таким образом, полученная комбинация не содержит ошибок.

Выполнить самостоятельно:

Задача 3.6 Построить код БЧХ, исправляющий двукратные ошибки, если длина кода n =  21.

Задача 3.7 Построить код БЧХ длиной 15, способный исправлять  двукратные ошибки.

Задача 3.8 Построить код БЧХ длиной 31, способный исправлять пятикратные ошибки.

Задача 3.9 Показать исправление двукратных ошибок в коде, полученном в задаче 3.7.

Задача 3.10 Показать исправление пятикратных ошибок в коде, полученном в задаче 3.8.

Задача 3.11 Для кодовой комбинации  Q (0,1)=1011 сформировать кодовую комбинацию циклического кода (7,4).

Задача 3.12 Принятая кодовая комбинация циклического кода (7,4) имеет вид F¹(0,1)=1010101. Порождающий полином кода G(x)=x³+x+1. Определить и исправить ошибку в принятой кодовой комбинации, если она имеется.

Задача  3.13 В АПД используются циклический код с минимальным кодовым расстоянием d min =3 b и с числом информационных символов К=8.

Требуется:

- определить минимальное число проверочных единичных элементов r и длину кодовой комбинации n;

- объяснить правило выбора образующего полинома Р(х);

- объяснить, какие полиномы называют примитивными, и пояснить, сколько остатков позволяет формировать примитивные полиномы;

- дать определение понятий циклического кода;

- построить порождающую (образующую) и проверочную (контрольную) матрицу;

- произвести декодирование выбранного кода методом вычисления остатка.

Построить функциональную схему соответствующего декодера для выбранного кода.

 

Таблица 3.5 – Исходные данные для расчетов

Параметр	Последняя цифра номера зачетной книжки
	0	1	2	3	4	5	6	7	8	9
1-часть кодового слова	1011	0011	1001	0110	1110	0111	1101	1111	1010	1100

 

Таблица 3.6– Исходные данные для расчетов

Параметр	Предпоследняя цифра номера зачетной книжки
	0	1	2	3	4	5	6	7	8	9
2-часть кодового слова	0011	1001	0111	1011	0101	1111	1101	0110	1110	1100

 

Методические указания к выполнению задания

Прежде чем приступить к выполнению заданию, следует изучить свойства и методы построения циклических кодов.

1.5.1 Выбор числа контрольных символов r. Есть два способа выбора числа r. При первом способе исходят из того, что число контрольных символов r определяется по эмпирической формуле:

r = ЦЧ log2(n+1),

где ЦЧ – означает целое число, округленное в сторону большего значения.

При втором способе число контрольных символов r определяется по эмпирической формуле :

r=ЦЧ log2[(к+1)+ЦЧ log2(к+1)].

Выбор образующего полинома Р(х).

Степень образующего полинома m не может быть меньше числа контрольных символов r. Это значит что может быть выбран любой полином Р(х),начиная с r степени и выше. Для упрощения технической реализации кодирования степень Р(х), следует выбирать равной числу r , т.е m= r. Если в таблице имеется ряд полиномов с данной степенью, то из них следует выбирать самый короткий. Однако число ненулевых членов полинома Р(х) не должно быть меньше минимального кодового расстояния d_min.

Разрешенные кодовые комбинации циклического кода F(x) могут быть получены двумя способами:

а) умножением кодовой комбинации Q(x) простого кода на одночлен x и добавлением к этому произведению остатка R(x),полученного в результате деления произведения Q(x)x r на образующий полином

Р(х):F(x)=Q(x)xr+R(x),

F(x)=Q(x)P(x).

Произвести кодирование с использованием первого и второго способов.

б) умножением кодовой комбинации Q(x) простого кода на образующий полином Р(х):

Указать достоинство и недостатки полученных кодовых комбинации.

Декодирование циклических кодов.

Метод вычисления остатка:

- обнаружение ошибок.

При использовании циклического кода обнаружение ошибок сводится к делению принятой кодовой комбинации на образующий полином.

Получение остатка свидетельствует о наличии ошибок. Остаток от деления в циклических кодах играет роль синдрома (опознавателя) – исправление ошибок.

Исправление ошибок производится путем подсчета веса остатка W. Если вес остатка равен или меньше числа исправляемых ошибок ,т.е W ≤ t, то принятую кодовую комбинацию складывают по модулю 2 с остатком и получают исправленную комбинацию. Если W>t, то производят сдвиг на один символ влево и полученную кодовую снова делят на образующий многочлен Р(х)и снова подсчитывают вес остатка. Если вес полученного остатка по –прежнему W>t,то производят дополнительные циклические сдвиги влево. При этом после каждого циклического сдвига сдвинутую комбинацию делят на образующий многочлен Р(х) и проверяют вес остатка. Если вес остатка равен или меньше числа исправляемых ошибок, т.е.W≤t, то принятую кодовую комбинацию складывают по модулю 2 с остатком и получают исправленную комбинацию.

Следует сказать, что декодирование методом вычисления остатков применимо, если rt>n. Если rt<n, то код будет обнаруживать, но не исправлять ошибки.

Примеры решения.

1. На основе кодовой комбинации номера билета составить кодовую комбинацию помехоустойчивого циклического кода, исправляющего однократные ошибки.

Номер билета- N_б=24.

Решение.

Количество разрядов в кодовой комбинации:

k  log₂ N = log₂ 51=5,7  k=6.

Кодовая комбинация номера билета:

Q(0,1)=011000.

Количество нулей в комбинации – n₀=4.

Количество единиц в комбинации – n₁=2.

Определяем минимальное расстояние d₀  для исправления однократных  ошибок

d₀ 2t_исп+1=2·1+1=3.

Количество дополнительных (проверочных) разрядов r определяется формулой:

2^r k+r+1  r=4.

Тогда количество разрядов кодовой комбинации п равно

п = k+r =6+4=10.

Из таблицы порождающих полиномов для r=4 выбираем

Р(0,1)=10011  Р(х)=х⁴+х+1.

Определяем остаток R(0,1)

^.

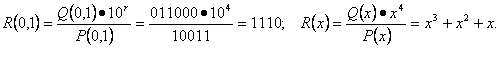
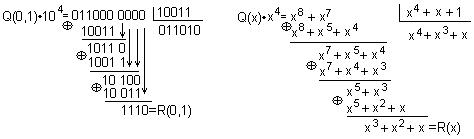Кодовая комбинация помехоустойчивого циклического кода, исправляющего однократные ошибки.

F(0,1) = Q(0,1)·10⁴  R(0,1) = 011000 1110;

F(х) = Q(х)·х⁴  R(х) = х⁸+х⁷+х³+х²+х.

 

2. N=37; N_б=42.

Решение:    

К  log₂ N = log₂ 37=5,21  К=6;

Q(0,1)=101010.

п₀=3 ; п₁=3.

d₀ 2t_исп+1=2·1+1=3.

2^r K+r+1  r=4.

п = K+r =6+4=10.

Р(0,1)=10011  Р(х)=х⁴+х+1.

F(0,1) = Q(0,1)·10⁴  R(0,1) =101010 0111;

F(х) = Q(х)·х⁴  R(х) = х⁹+х⁷+х⁵+х²+х+1.

3. N=53; р(1)=0,5;N_б=33.

Решение:

К  log₂ N = log₂ 53=5,731  К=6;

Q(0,1)=100001.

п₀=4 ; п₁=2.

I=n₀I₀+n₁I₁=4·1+2·1=6 бит.

d₀ 2t_исп+1=2·1+1=3.

2^r K+r+1  r=4.

п = K+r =6+4=10.

Р(0,1)=10011  Р(х)=х⁴+х+1.

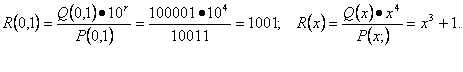
F(0,1) = Q(0,1)·10⁴  R(0,1) =1000011001;

F(х) = Q(х)·х⁴  R(х) = х⁹+х⁴+х³+1.

4. При использовании циклического кода (7,4) с порождающим полиномом

G(x)=x³+x²+1 приняты кодовые комбинации  1)1011010; 2) 0110100;

3) 1101101.

Обнаружить и исправить ошибки в этих кодовых комбинациях, если они имеются.

1) Q₁(0,1)=1011010 → Q₁(x)= x⁶+x⁴+ x³+x;

2) Q₂(0,1)=0110100 → Q₂(x)= x⁵+x⁴+ x²;

3) Q₃(0,1)=1101101 → Q₃(x)= x⁶+x⁵+ x³+x²+1;

Определяем синдромы

^{1) 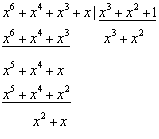 2) 3)}

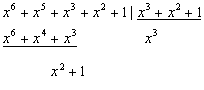
Соответственно получаем:

1)    по таблице синдрому С(х)= x²+x→С(0,1)=110 соответствует символ х⁶. Инвертируя его, получим принятую кодовую комбинацию без ошибки Q_1разр(0,1)=0011010;

2)    остаток нулевой, следовательно, ошибки нет - Q_2разр(0,1)=0110100;

3)    по таблице синдрому С(х)= x²+1→С(0,1)=101 соответствует символ х³. Инвертируя его, получим принятую кодовую комбинацию без ошибки Q_1разр(0,1)=1100101.

Теперь используем другой порождающий полином G(x)=x³+x+1.

Определяем синдромы:

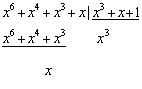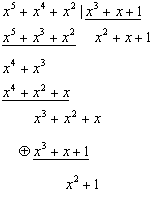^{1)  2) 3)}

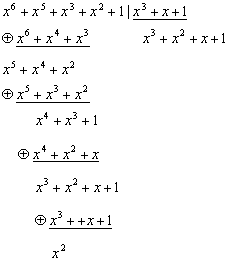
1)     По таблице синдрому С(х)= x→С(0,1)=010 соответствует символ х. Инвертируя его, получим принятую кодовую комбинацию без ошибки Q_1разр(0,1)=1011000.

2)     По таблице синдрому С(х)= x²+1→С(0,1)=101 соответствует символ х⁶. Инвертируя его, получим принятую кодовую комбинацию без ошибки  Q_2разр(0,1)=1110100.

3)     По таблице синдрому С(х)= x²→С(0,1)=100 соответствует символ х². Инвертируя его, получим принятую кодовую комбинацию без ошибки  Q_2разр(0,1)=1101001.

5. Показать, что код с кодовым расстоянием  d_o позволяет обнаружить q_o.ош.≤ d_o-1 ошибок и исправить  q_и.ош.≤ d_o/2-1 при четном  d_o и q_и.ош.≤( d_o-1)/2-1 ошибок при нечетном  d_o.

Если при передаче некоторой разрешенной кодовой комбинации произошло q ошибок, то расстояние по Хэммингу между принятой и переданной комбинациями d_ij=q. Так как между любыми двумя разрешенными комбинациями расстояние по Хэммингу не меньше d_o, то кодовая комбинация отличающаяся от переданной в q=( d_o-1) разрядах, является запрещенной, и ошибки будут обнаружены.

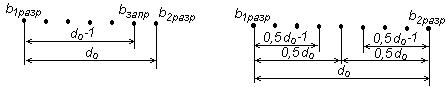
Для доказательства того, что код с кодовым с кодовым расстоянием  d_o может исправить q_и.ош.≤ d_o/2-1 ошибок, достаточно убедиться, что среди разрешенных кодовых комбинаций имеется только одна, которая могла бы превратиться в принятую запрещенную комбинацию.

Допустим, что существуют две разрешенные кодовые комбинации b_1разр и b_2разр, которые при искажении (0,5d_o-1) символов превращаются в одну и ту же запрещенную кодовую комбинацию b. Это означает, что

d(b_1разр, b)= (0,5 d_o-1)< 0,5d_o,   d(b_2разр, b)= (0,5 d_o-1)< 0,5d_o.

Для того чтобы из комбинации b_1разр получить b_2разр, необходимо изменить не более [d(b_1разр, b)+ d(b_2разр, b)] символов, так как выполняется условие

d(b_1разр, b)+ d(b_2разр, b) ≤ d(b_1разр,b_2разр).

Поскольку при сделанном допущении

d(b_1разр, b) < 0,5d_o и  d(b_2разр, b) < 0,5d_o

имеем d(b_1разр,b_2разр) < d_o, что противоречит определению d_o.

Следовательно, при числе ошибок q_и.ош.≤ d_o/2-1 принятой запрещенной комбинации может соответствовать лишь одна разрешенная комбинация. Это означает, что все ошибки будут исправлены. Правило декодирования в этом случае следующее:

- если принята запрещенная комбинация, то считается переданной ближайшая к ней разрешенная комбинация.

 

Самостоятельное выполнение заданий

Вариант 1

1.     Определить количество контрольных символов циклического кода, если обнаруживает t_исп.ош= 4 ошибки при n= 31.

2.     Передано сообщение 11000: построить циклический код, если образующий полином x²+x³+1.

3.     Построить кодирующие устройства для циклического кода, если образующий полином x⁹+x³+1.

4.     Построить код Файра b_r= 4, b_s= 3.

5.     Передано сообщение 10101: проведите кодирование и декодирование методом Хемминга.

Вариант 2

1.     Определить количество контрольных символов циклического кода, если обнаруживает t_исп.ош= 4 ошибки при n= 63.

2.     Передано сообщение 101101: построить циклический код, если образующий полином x⁵+x+1.

3.     Построить кодирующие устройства для циклического кода, если образующий полином x⁵+x+1.

4.     Построить код Файра b_r= 4, b_s= 3.

5.     Передано сообщение 101101: проведите кодирование и декодирование методом Хемминга.

Вариант 3

1.     Определить количество контрольных символов циклического кода, если обнаруживает t_исп.ош= 4 ошибки при n= 63.

2.     Передано сообщение 10000: построить циклический код, если образующий полином x²+x³+1.

3.     Построить кодирующие устройства для циклического кода, если образующий полином x⁶+x³+x+1.

4.     Построить код Файра b_r= 4, b_s= 2.

5.     Передано сообщение 11001: проведите кодирование и декодирование методом Хемминга.

Вариант 4

1.     Определить количество контрольных символов циклического кода, если обнаруживает t_исп.ош= 5 ошибки при n= 31.

2.     Передано сообщение 11101: построить циклический код, если образующий полином x⁴+x³+1.

3.     Построить кодирующие устройства для циклического кода, если образующий полином x⁴+x³+x²+1.

4.     Построить код Файра b_r= 3, b_s= 3.

5.     Передано сообщение 10101: проведите кодирование и декодирование методом Хемминга.

Вариант  5

1.     Определить количество контрольных символов циклического кода, если обнаруживает t_исп.ош= 2 ошибки при n= 63.

2.     Передано сообщение 11111: построить циклический код, если образующий полином x⁴+x³+1.

3.     Построить кодирующие устройства для циклического кода, если образующий полином x⁴+x³+1.

4.     Построить код Файра b_r= 4, b_s= 3.

5.     Передано сообщение 11111: проведите кодирование и декодирование методом Хемминга.

Вариант  6

1.     Определить количество контрольных символов циклического кода, если обнаруживает t_исп.ош= 6 ошибки при n= 31.

2.     Передано сообщение 11100: построить циклический код, если образующий полином x⁴+x³+1.

3.     Построить кодирующие устройства для циклического кода, если образующий полином x⁷+x³+1.

4.     Построить код Файра b_r= 4, b_s= 4.

5.     Передано сообщение 10001: проведите кодирование и декодирование методом Хемминга.

Вариант 7

1.     Определить количество контрольных символов циклического кода, если обнаруживает t_исп.ош= 6 ошибки при n= 31.

2.     Передано сообщение 10001: построить циклический код, если образующий полином x⁴+x+1.

3.     Построить кодирующие устройства для циклического кода, если образующий полином x⁴+x+1.

4.     Построить код Файра b_r= 4, b_s= 4.

5.     Передано сообщение 11110: проведите кодирование и декодирование методом Хемминга.

Вариант 8

1.     Определить количество контрольных символов циклического кода, если обнаруживает t_исп.ош= 5 ошибки при n= 31.

2.     Передано сообщение 101010101: построить циклический код, если образующий полином x⁸+x³+1.

3.     Построить кодирующие устройства для циклического кода, если образующий полином x⁸+x³+1.

4.     Построить код Файра b_r= 3, b_s= 3.

5.     Передано сообщение 10101: проведите кодирование и декодирование методом Хемминга.

Вариант 9

1.     Определить количество контрольных символов циклического кода, если обнаруживает t_исп.ош= 4 ошибки при n= 127.

2.     Передано сообщение 101101: построить циклический код, если образующий полином x⁵+x²+1.

3.     Построить кодирующие устройства для циклического кода, если образующий полином x⁵+x²+1.

4.     Построить код Файра b_r= 4, b_s= 3.

5.     Передано сообщение 101101: проведите кодирование и декодирование методом Хемминга.

Вариант 10

1.     Определить количество контрольных символов циклического кода, если обнаруживает t_исп.ош= 3 ошибки при n= 127.

2.     Передано сообщение 11101101: построить циклический код, если образующий полином x⁷+x³+x+1.

3.     Построить кодирующие устройства для циклического кода, если образующий полином x⁷+x³+x+1.

4.     Построить код Файра b_r= 4, b_s= 3.

5.     Передано сообщение 110101: проведите кодирование и декодирование методом Хемминга.

Вариант 11

1.     Определить количество контрольных символов циклического кода, если обнаруживает t_исп.ош= 6 ошибки при n= 31.

2.     Передано сообщение 11011: построить циклический код, если образующий полином x⁴+x²+x+1.

3.     Построить кодирующие устройства для циклического кода, если образующий полином x⁹+x³+1.

4.     Построить код Файра b_r= 4, b_s= 2.

5.     Передано сообщение 11011: проведите кодирование и декодирование методом Хемминга.

Вариант 12

1.     Определить количество контрольных символов циклического кода, если обнаруживает t_исп.ош= 4 ошибки при n= 31.

2.     Передано сообщение 11111: построить циклический код, если образующий полином x⁴+x³+1.

3.     Построить кодирующие устройства для циклического кода, если образующий полином x⁵+x³+x+1.

4.     Построить код Файра b_r= 4, b_s= 3.

5.     Передано сообщение 11111: проведите кодирование и декодирование методом Хемминга.

Вариант 13

1.     Определить количество контрольных символов циклического кода, если обнаруживает t_исп.ош= 2 ошибки при n= 63.

2.     Передано сообщение 111111: построить циклический код, если образующий полином x⁵+x+1.

3.     Построить кодирующие устройства для циклического кода, если образующий полином x⁵+x+1.

4.     Построить код Файра b_r= 4, b_s= 3.

5.     Передано сообщение 111111: проведите кодирование и декодирование методом Хемминга.

Вариант 14

1.     Определить количество контрольных символов циклического кода, если обнаруживает t_исп.ош= 4 ошибки при n= 127.

2.     Передано сообщение 10000: построить циклический код, если образующий полином x⁴+x³+1.

3.     Построить кодирующие устройства для циклического кода, если образующий полином x⁴+x³+1.

4.     Построить код Файра b_r= 4, b_s= 3.

5.     Передано сообщение 10000: проведите кодирование и декодирование методом Хемминга.

Вариант 15

1.     Определить количество контрольных символов циклического кода, если обнаруживает t_исп.ош= 2 ошибки при n= 127.

2.     Передано сообщение 11000: построить циклический код если образующий полином x⁴+x³+1.

3.     Построить кодирующие устройства для циклического кода если образующий полином x⁴+x³+1.

4.     Построить код Файра b_r= 3, b_s= 3.

5.     Передано сообщение 11000: проведите кодирование и декодирование методом Хемминга.

Вариант 16

1.     Определить количество контрольных символов циклического кода, если обнаруживает t_исп.ош= 4 ошибки при n= 127.

2.     Передано сообщение 1101011: построить циклический код, если образующий полином x⁶+x⁴+x+1.

3.     Построить кодирующие устройства для циклического кода, если образующий полином x⁹+x³+1.

4.     Построить код Файра b_r= 4, b_s= 3.

5.     Передано сообщение 1101011: проведите кодирование и декодирование методом Хемминга.

Вариант 17

1.     Определить количество контрольных символов циклического кода, если обнаруживает t_исп.ош= 2  ошибки при n= 63.

2.     Передано сообщение 100101: построить циклический код, если образующий полином x⁵+x+1.

3.     Построить кодирующие устройства для циклического кода, если образующий полином x⁵+x+1.

4.     Построить код Файра b_r= 4, b_s= 2.

5.     Передано сообщение 100101: проведите кодирование и декодирование методом Хемминга.

Вариант 18

1.     Определить количество контрольных символов циклического кода, если обнаруживает t_исп.ош= 2 ошибки при n= 63.

2.     Передано сообщение 10111: построить циклический код, если образующий полином x⁴+x³+x²+1.

3.     Построить кодирующие устройства для циклического кода, если образующий полином x⁹+x³+1.

4.     Построить код Файра b_r= 4, b_s= 3.

5.     Передано сообщение 101101: проведите кодирование и декодирование методом Хемминга.

Вариант 19

1.     Определить количество контрольных символов циклического кода, если обнаруживает t_исп.ош= 4 ошибки при n= 127.

2.     Передано сообщение 1011101: построить циклический код, если образующий полином x⁶+x⁴+x+1.

3.     Построить кодирующие устройства для циклического кода, если образующий полином x⁶+x⁴+x+1.

4.     Построить код Файра b_r= 4, b_s= 3.

5.     Передано сообщение x⁶+x⁴+x+1: проведите кодирование и декодирование методом Хемминга.

Вариант 20

1.     Определить количество контрольных символов циклического кода, если обнаруживает t_исп.ош= 3 ошибки при n= 127.

2.     Передано сообщение 1011: построить циклический код, если образующий полином x³+x²+1.

3.     Построить кодирующие устройства для циклического кода, если образующий полином x³+x²+1.

4.     Построить код Файра b_r= 4, b_s= 3.

5.     Передано сообщение x³+x²+1: проведите кодирование и декодирование методом Хемминга.

  

Приложение 1

 

Таблица неприводимых порождающих полиномов степени m

 

Приложение 2 

Таблица значений функций Крампа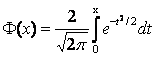

 

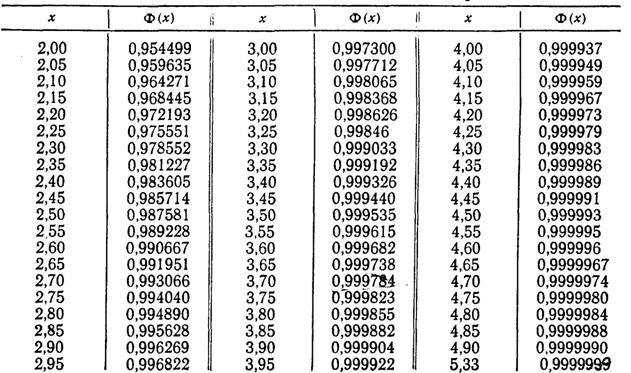
Приложение 3

 

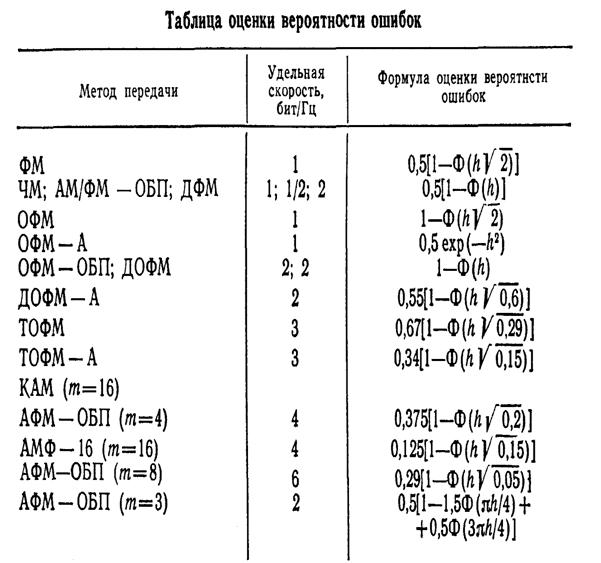
Приложение 4 

Неприводимые многочлены и их эквиваленты

 

Минимальные многочлены циклических кодов

№ М (Х)	Min многочлены различных  l степеней
	2	3	4	5	6	7	8
М1 (Х)	111	1011	10011	100101	1000011	10001001	100011101
М3 (Х)		1101	11111	111101	1010111	10001111	101110111
М5 (Х)			111	110111	1100111	10011101	111110011
М7 (Х)			11001	101111	1001001	11110111	101101001
М9 (Х)				110111	1101	10111111	110111101
М11 (Х)				111011	1101101	11010101	111100111
М13 (Х)						10000011	100101011

 

Образующие многочлены для БЧХ кодов

N	И	S	Образующий полином	N	И	S	Образующий полином
7	4	1	13	127	120	1	211
15	11	1	23		113	2	41567
	7	2	721		106	3	11554743
	5	3	2467		99	4	3447023271
31	26	1	45		92	5	624730022327
	21	2	3551		85	6	130704476322273
	16	3	107657		78	7	26230002166130115
	11	5	5423325		71	9	6255010713253127753
	6	7	313365047		64	10	1206534025570773100045
63	57	1	103
	51	2	12471	255	247		435
	45	3	1701317		239		267543
	39	4	166623567		231		156720665
	36	5	1033500423		223		75626641375
	30	6	1574641656547		215		23157564726421
	24	7	17323260404441		207		1617660567636227
	18	10	1363026512351725		199		7633031270420722341
					191		2663470176115333714567
					187		52755313540001322236351
					179		22624710717340432416300455

Приложение 5

 

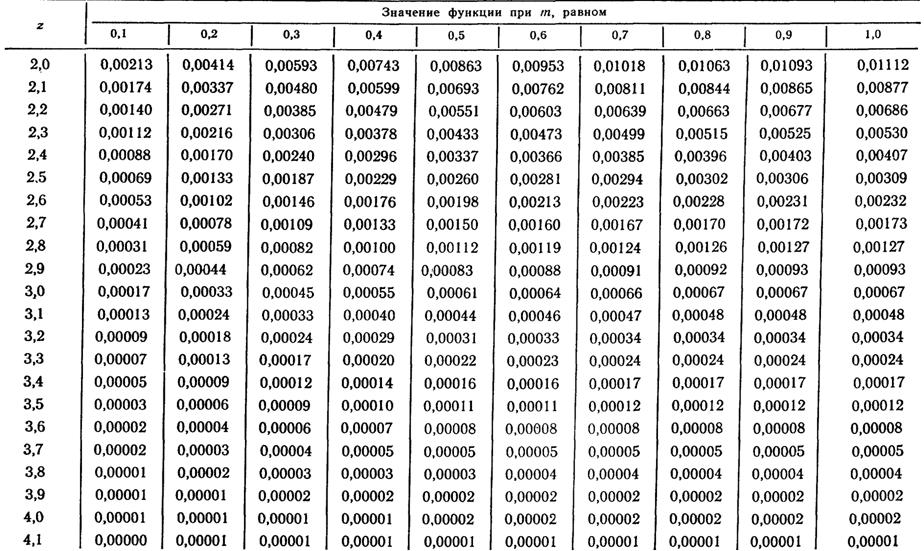
Таблица значений функций Оуэна

Продолжение приложения 5

 

 

Список литературы

 

1.      В. Г. Олифер, Н. А. Олифер . Основы сетей передачи данных. Курс лекций.  Интернет-университет информационных технологий, 2005.

2.      В.А. Кудряшов, В.П. Глушко. Системы передачи дискретной информации. УМК МПС , 2002.

3.      В.В. Ломовицкий, А.И. Михайлов, К.В. Шестак, В.М. Щекотихин.

Основы построения систем и сетей передачи информации. Интернет-университет информационных технологий, 2005.

4.      Хелд Г. Технологии передачи данных. 2003.

5.      Дмитриев В.И. Прикладная теория информации: Учебник.- М.: Высш.шк., 1989.

6.      Скляр Б. Цифровая связь: Теоретические основы и практическое применение. - М.: Вильямс, 2003.

7.      Гаранин М.В., Журавлев В.И., Кунегин С.В. Системы и сети передачи информации. - М.: Радио и связь, 2000.

8.      Телекоммуникационные системы и сети: Учебное пособие. Т.1 /Под ред. В.П. Шувалова: - М.: Горячая линия-Телеком, 2003.

9.      Передача дискретных сообщений: Учебник/Под ред. В.П. Шувалова. - М.: Радио и связь, 1990.

10. Боккер П. Передача данных. Техника связи в системах телеобработки данных./Пер. с нем. Т.1. - М.: Связь, 1980.

 

Содержание

 

Введение	3
1 Каналы связи и их характеристики. Энтропия источника дискретных сообщений	4
2 Синхронизация в ЦСС	14
3 Методы и устройства помехоустойчивого кодирования	17
Приложение 1	35
Приложение 2	36
Приложение 3	37
Приложение 4	38
Приложение 5	39
Список литературы	41

 

Сводный план 2013г., поз. 96