АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ  И СВЯЗИ

 

Кафедра инженерной графики и прикладной  механики

Инженерная и компьютерная  графика

МЕТРИЧЕСКИЕ ЗАДАЧИ

ЧАСТЬ 1

Методические указания к выполнению

семестровой работы

(для студентов всех форм обучения специальностей

050717 – Теплоэнергетика, 050718 – Электроэнергетика,

050719 – Радиотехника, электроника и телекоммуникации)

 

 

 

 

 

 

 

 

Алматы 2006

СОСТАВИТЕЛИ: А.Д. Динасылов, Э.А. Яхъяев, А.Б.Досаева.

Инженерная и компьютерная графика. Метрические задачи. Часть 1. Методические указания к выполнению семестровой работы  (для студентов всех форм обучения специальностей 050717 – Теплоэнергетика, 050718 – Электроэнергетика, 050719 – Радиотехника, электроника и телекоммуникации).- Алматы: АИЭС, 2006. - 27 с.: ил.

В указаниях рассматривается методика и решение задач на тему «Метрические задачи» раздела «Теория построения чертежей», даны графические способы решения метрических задач по определению расстояний.

Приведены индивидуальные задания по вариантам для самостоятельных работ студентов по разделу « Теория построения чертежей».

Указания предназначены для студентов, обучающихся  по всем специальностям бакалавриата и изучающих дисциплину «Инженерная и компьютерная графика», и могут оказаться полезными при подготовке к экзамену.

Ил. 14, библиогр.- 12 назв.

 

Рецензент: канд. техн. наук, доцент Мукашев М. Ш.

Печатается по плану издания Алматинского института энергетики и связи   на 2006 г.

 

                                 ©   Алматинский институт энергетики и связи, 2006 г.

Содержание

 

Введение                                                                                                                     4

1 Определение расстояний                                                                                        5

              1.1  Расстояние между двумя точками                                                          5

1.2  Расстояние от точки до прямой линии                                                      10

1.3  Расстояние между двумя параллельными прямыми                                11

1.4  Расстояние между двумя скрещивающимися прямыми                          13

    1.5  Расстояние от точки до плоскости                                                             16

1.6  Расстояние от точки до поверхности                                                         19

            1.7 Расстояние между двумя параллельными плоскостями                           21

Приложение  А   Комплект задач                                                                            24

Список литературы                                                                                                   26

 

          Введение

Метрическими задачами называются задачи, решение которых связано с определением на чертеже каких-либо метрических свойств образов. К метрическим свойствам относят длины участков линий, величины углов, площадей, объемов и т.п.

Наиболее сложные задачи, при решении которых используют как метрические, так и позиционные свойства геометрических образов, называют комплексными.

При параллельном (ортогональном) проецировании геометрические образы, произвольно расположенные в пространстве, проецируются на плоскости проекций с искажением. В этом случае искажаются проекции величин их линейных и угловых характеристик.

Определение неискаженных величин линейных и угловых характеристик геометрических образов, произвольно расположенных в пространстве, по их проекциям и представляют собой класс метрических задач, который мы рассмотрим в настоящих методических указаниях.

Многие метрические и комплексные задачи, которые встречаются в технике, являются типовыми и решаются с помощью типовых приемов, которые необходимо понять и запомнить. Знание этих приемов и умение применить их на практике позволяют овладеть аппаратом начертательной геометрии, с помощью которого задачи можно решать легко и быстро.

Алгоритмы решения всех метрических задач опираются на два инварианта ортогонального проецирования:

а)  теорему (прямую и обратную) о проецировании прямого угла. Напомним ее. Если одна сторона прямого угла параллельна плоскости проекции, а вторая ей не перпендикулярна, то при ортогональном проецировании прямой угол проецируется на эту плоскость в прямой  угол.

                                    

(ABC = 90 ⁰) Ù ([BC] // p₁, [BA] ^ p ₁) Þ A’B’C’ = 90 ⁰;

б) свойство любой плоской фигуры проецироваться без искажения (в конгруэнтную фигуру) на ту плоскость проекций, которая параллельна  этой фигуре, т.е. (Ф Ì b) Ù (b // p₁) Þ Ф ^’ @ Ф.

   Все многообразие метрических задач может быть подразделено на три группы:

а) включает в себя определение расстояний от точки до другой точки, до прямой, до плоскости, до поверхности;  от прямой до плоскости;

б) включает в себя определение углов между:

                   1) пересекающимися или скрещивающимися прямыми;

                   2) прямой и плоскостью;

                   3) плоскостями (определение величины двугранного угла);

          в) определение величин плоских фигур.

         Для решения этих задач необходимо  изучить типовые приемы решения задач методами  начертательной геометрии.

Первый этап – сосредоточиться и осмыслить постановку задачи. Что дано? Что требуется?  Какие условия ставятся и возможно ли им удовлетворить?

Второй этап – поиск связи между исходными данными и искомыми. Здесь составляется план решения задачи. 

Третий этап – реализация плана; здесь необходим контроль правильности решения и точности графических построений.

Завершающий этап – анализ решения задачи.

Рассмотрим решение некоторых метрических задач, связанных с определением расстояний.

 

1 Определение расстояния

 

К этой группе метрических задач относятся задачи на определение расстояний между двумя точками, точкой и прямой, двумя параллельными линиями, двумя скрещивающимися прямыми линиями, точкой и плоскостью, двумя параллельными плоскостями.

 

1.1     Расстояние между двумя точками

 

Расстояние между двумя точками определяется длиной отрезка прямой линии, соединяющей эти точки.

Если отрезок прямой занимает произвольное (общее) положение, то ни на одной основной плоскости проекций нельзя определить его истинную величину. Отрезок прямой линии проецируется в натуральную величину на параллельную ему плоскость.

Построить изображение отрезка в истинную величину на комплексном чертеже можно следующими способами: 

      а) способ прямоугольного треугольника.

На чертеже выполняют следующие построения.  Одну из проекций отрезка, например горизонтальную А₁В₁ (рисунок 1, а), берем в качестве одного из катетов прямоугольного треугольника, второй катет принимаем равным разности расстояний точек А и В (DZ) от горизонтальной плоскости проекций (p₁). Для определения этой разницы на чертеже через точку В₂ проводим вспомогательную прямую, перпендикулярную к линии связи А₂ А₁. Отрезок А₂1₂- искомый второй катет. В треугольнике А₁В₁В₀  катет В₁В₀ равен разности расстояний точек А и В до горизонтальной плоскости проекций (DZ). Выполнив необходимые построения, найдем истинную величину отрезка АВ (на чертеже А₁В₀).

 

 

 

 

 

 

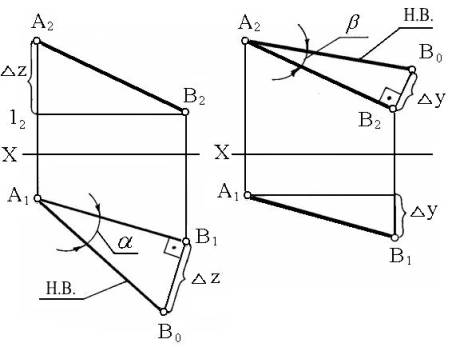
а)                                                                  б)

 

Рисунок 1

На рисунке 1, а видно, что угол наклона прямой к горизонтальной плоскости проекций определяется как угол, составленный прямой с её проекцией на эту плоскость. Угол с вершиной в точке А, т. е. a, будет равен углу наклона прямой АВ к горизонтальной плоскости проекции (p₁).

     Прямоугольный треугольник можно построить, если взять за катет фронтальную проекцию отрезка (рисунок 1, б). В треугольнике А₂В₂В₀ катет В₂В₀ равен разности расстояний точек А и В до фронтальной плоскости проекций      (D U). Угол b будет равен углу, который составляет прямая АВ с фронтальной плоскостью проекций (p₂).

Таким образом, угол между катетом (проекцией) и гипотенузой прямоугольного треугольника равен истинной величине угла наклона отрезка к той плоскости проекций, на которой выполнены построения;

б) способ  перемены плоскостей проекций - суть способа перемены плоскостей проекций - состоит в переходе от данной системы плоскостей проекций к новой системе плоскостей проекций. На рисунке 2 показано решение задачи. Чтобы определить натуральную величину отрезка (сделать прямую общего положения прямой уровня), необходимо дополнительную плоскость проекций расположить параллельно заданному отрезку. Для этой цели необходимо выполнить следующие преобразования. Заменим p₂  плоскостью     p₄ // АВ (Х₁₄ // А₁В₁), т.е. заменим одну систему плоскостей проекций p₂ / p₁ другой p₄ / p₁. Новая плоскость проекций должна быть обязательно перпендикулярна к одной из основных плоскостей проекций, в данном случае p₁, т.е. плоскости старой системы. Из рисунка 2, а видно, что новая ось проекций Х₁₄ располагается параллельно горизонтальной проекции А₁В₁ отрезка (Х₁₄ // А₁В₁).  Проводим через точки А₁ и В₁ линию связи перпендикулярно оси Х₁₄, отметим точку А_X14 и В_X14 и по линии связи отложим координату Z точки А и В – отрезок А₄А_X14  = А_X12А₂ и В₄В_X14= В_X12В₂. Построим точки А₄ и В₄. На плоскость p₄ отрезок АВ проецируется в истинную величину (А₄В₄ = АВ). Расстояние новой плоскости проекций (p₄) от отрезка АВ произвольное. Найдя натуральную величину отрезка на плоскости p₄, получим одновременно и величину угла наклона отрезка к плоскости p₁   (a₄°  =  a°).

Для определения величины угла (b) наклона прямой к плоскости p₂ (рисунок 2, б) проведем ось Х₁₂, например, через точку А₁ и заменим плоскость p₁  на плоскость p₅, проходящую через прямую АВ (А₂В₂ º Х₂₅). В системе p₂ / p₅ прямая АВ станет горизонталью, а угол (b₅ = b).

 

 

 

 

 

 

 

 

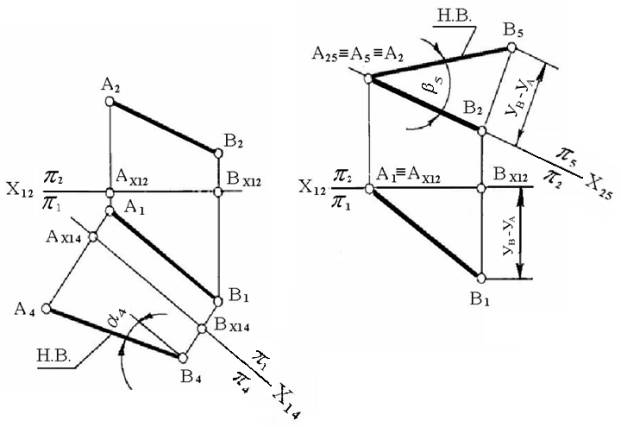
a)                                                                    б)

Рисунок 2

Таким образом, для определения величины отрезка прямой общего положения и угла её наклона к одной из плоскостей проекций необходимо заменить вторую плоскость проекций, расположив новую плоскость параллельно прямой; на этой плоскости отрезок и угол проецируются в натуральную величину;

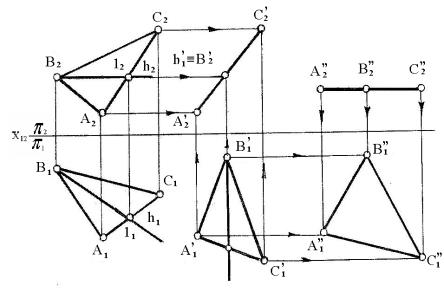
в) способ вращения  состоит в том, что заданная система плоскостей проекций остаётся прежней, а отрезок вращают вокруг неподвижной оси до тех пор, пока она не займёт частное положение. Вращение производят вокруг осей, перпендикулярных или параллельных плоскостей проекций. Для определения натуральной величины отрезка его вращают до положения, параллельного плоскости проекции. Чтобы повернуть на некоторый угол прямую, достаточно повернуть на этот же угол две точки прямой. Однако ось вращения лучше выбирать проходящей через одну из точек отрезка. Тогда при вращении отрезка она остаётся неподвижной как точка, лежащая на оси вращения. Например, примем за ось вращения перпендикуляр к горизонтальной плоскости проекций, проходящей точку А (рисунок 3, а).

 

 

 

 

 

а)                                                                      б)

 

Рисунок  3

Тогда на чертеже горизонтальная проекция этой оси будет совпадать с горизонтальной проекцией А₁ точки А (А₁ º  i₁). Радиусом вращения R точки В в этом случае будет горизонтальная проекция А₁ В₁ отрезка (А₁ В₁ = R). Принимаем точку А₁ за центр вращения, описываем дугу радиусом R до пересечения с прямой, проведённой из точки А₁ параллельно оси X. На чертеже прямая А₁В₁^’– новое положение отрезка АВ, отрезок расположился параллельно плоскости p₂.

 Новое положение фронтальной проекции В₂^’ точки В находим на прямой, проведённой через В₂ параллельно оси проекции X. Эта прямая является фронтальной проекцией плоскости, в которой происходит вращение точки В. Соединив точки А₂ и В₂^’, получим отрезок А₂В₂^’, который является истинной величиной отрезка АВ.

На рисунке 3, б показан пример вращения, выполняемого вокруг оси, перпендикулярной к фронтальной плоскости проекций. Ось вращения проходит через точку В. На рисунке А₁'В₁ – истинная величина отрезка АВ.

1.2  Расстояние от точки до прямой линии

Расстояние от точки до прямой линии равно длине отрезка перпендикуляра, опущенного из точки на прямую. Если заданная в условии прямая линия является прямой общего положения, то для решения задачи необходимо так преобразовать чертёж, чтобы эта прямая стала проецирующей, то есть  проецировалась в точку.

Задачу можно решить, например, двойной заменой плоскостей проекций (рисунок 4), выбрав при первой замене новую плоскость проекций  p₄ параллельно прямой (чтобы прямая стала прямой уровня), а затем осуществить вторую замену, расположив новую плоскость проекций p₅ перпендикулярно к прямой; А₅К₅ – искомое расстояние.

На рисунке 4 показано определение расстояния от точки А до прямой ВС способом двойной замены плоскостей проекций:

а) p₂ ^ p₁ ® p₁ ^ p₄;  p₄  ¤¤  ВС; Х₁₄  ¤¤  В₁С₁;

          б) p₁  ^ p₄ ® p₄ ^ p₅;  p₅ ^ ВС;  Х₄₅ ^ В₄С₄;

          в) А₅К₅ – истинное расстояние от точки А до прямой ВС;

          г) Чтобы построить проекции перпендикуляра АК в исходной системе плоскостей, строим основание перпендикуляра – точку К на прямой ВС из условия, что в системе он занимает положение линии уровня, то есть               А₄К₄  ^ В₄С₄. Горизонтальная и фронтальная проекции точки К определяются по линиям связи из условия принадлежности её прямой ВС.

 

 

 

 

 

 

 

 

 

 

 

 

 

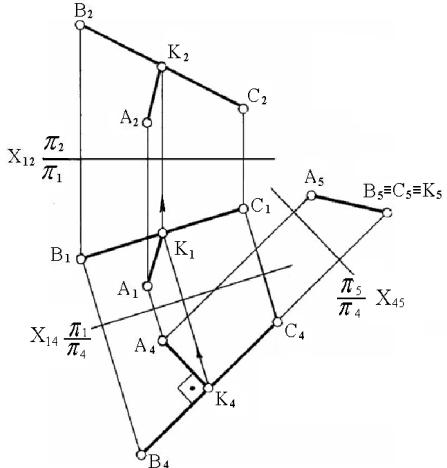
Рисунок 4

1.3     Расстояние между двумя параллельными прямыми

Расстояние между двумя параллельными прямыми измеряется длиной отрезка перпендикуляра, опущенного из произвольной точки одной прямой на другую прямую.

 

 

 

 

 

 

 

 

 

 

Рисунок 5

На рисунке 5 показано определение расстояния между прямыми линиями АВ и СД путем преобразования чертежа прямых линий (двукратная замена плоскостей проекций).

Сначала построено изображение прямых линий АВ и СД на плоскости       p₄ ^ p₁. В этой системе плоскостей проекций прямые линии занимают положение линий уровня: АВ (СД) // π₄,  Х₁₄ // А₁В₁ (С₁Д₁).

В системе плоскостей π₄ ^ π₅ прямые занимают проецирующее положение по отношению к плоскости π₅: π₅ ^ АВ (СД); Х₄₅  ^ А₄В₄ (С₄Д₄). Отрезок М₅N₅ между вырожденными проекциями прямых определяет истинную величину расстояния между прямыми АВ и СД.

1.4          Расстояние между двумя скрещивающимися прямыми линиями

Расстояние между двумя скрещивающимися прямыми линиями измеряется длиной  отрезка  МN  (рисунок 6),  перпендикулярного  данным  прямым  a  и b

(МN ^ a, МN ^ b). Если одна из прямых перпендикулярна плоскости проекций   (b ^ p₁), то перпендикуляр к ней будет параллелен этой плоскости проекций   (МN // p₁) и спроецируется на эту плоскость проекций без искажения М₁N₁ = МN.

 

 

 

 

 

 

 

 

Рисунок 6

Если обе заданные в условии прямые линии являются прямыми общего положения, то решение задачи сводится к такому преобразованию чертежа, в результате которого  проекция одной из данных прямых спроецируется в точку. Это построение можно выполнить плоскопараллельным перемещением или заменой плоскостей проекций.

Рассмотрим пример. Определить кратчайшее расстояние между двумя скрещивающимися прямыми и выразить в проекциях общий к ним перпендикуляр (рисунок 7). В построении, показанном на рисунке 7, одна из скрещивающихся прямых СД спроецирована в точку на новую плоскость проекций (π₅). Выполнен следующий план:

                           а) π₁ ^ π₂ ® π₄ ^ π₁;    π₄ // СД;      Х₁₄  // С₁Д₁;

          б) π₄  ^ π₁ ® π₅ ^ π_4;    π₅ ^ СД;     Х₄₅ ^ С₄Д₄;

          в) Получив на плоскости проекций π₅  проекцию прямой СД в виде точки (С₅ º Д₅)  и проекцию второй прямой А₅В₅ и проведя из С₅ (В₅) перпендикуляр на А₅В₅, нашли искомое расстояние (М₅N₅ = MN) между данными  скрещивающимися прямыми АВ и СД. Далее ход построения указан стрелками. Проекция М₄N₄ проведена через точку N₄ параллельно оси Х₄₅.

 

 

 

 

 

 

 

 

 

 

 

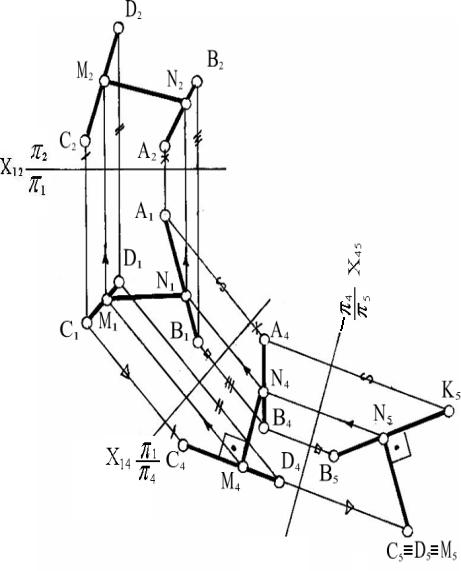
Рисунок 7

1.5  Расстояние от точки до плоскости

Расстояние от точки до плоскости измеряется длиной отрезка перпендикуляра, опущенного из точки на плоскость. Для решения задачи необходимо так преобразовать чертеж, чтобы плоскость в новом положении стала проецирующей. Например, определить расстояние от точки D до плоскости общего положения заданного треугольником АВС. Применим способ замены плоскостей проекций (рисунок 8).

 

Рисунок 8

Построим фронталь f плоскости АВС (f(С,1) = АВС), проведем плоскость  π₄ (π₄ ^ f ® Х₁₄  ^ f₂). Построим проекцию плоскости АВС и точки D на плоскости проекций π₅ (А₄В₄С₄, Д₄). Через точку D₄ проводим D₄К₄ ^ А₄В₄С₄. Отрезок D₄К₄ равен искомому расстоянию. Точки К₂ и К₁ найдем, установив последовательно проекционную связь К₂D₂  // Х₁₄,  К₁ – на расстоянии от оси Х₁₄ до К₄, измеренном на эпюре в системе π₂/ π₄.

На рисунке 9 показано решение задачи без замены плоскостей проекций.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

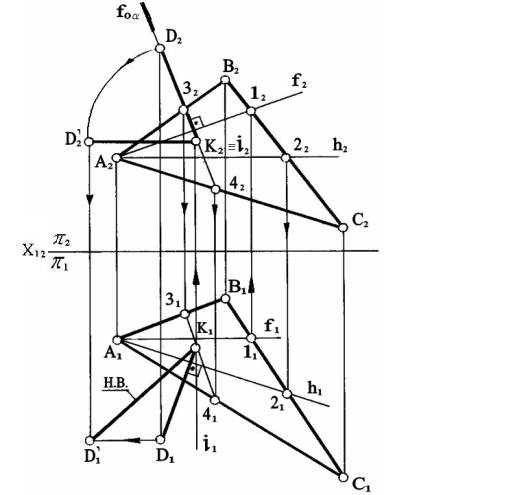
Рисунок 9

Построим перпендикуляр DК. Вначале через точку А проводим горизонталь А – 2 и фронталь А – 1. Фронтальная проекция искомого перпендикуляра проходит через точку D₂  перпендикулярно А₂1₂ (f₂), а горизонтальная – через D₁ перпендикулярно к А₁2₁ (h₁). Основание перпендикуляра (точка К) определяется как точка пересечения этого перпендикуляра с плоскостью. Заключаем его во фронтально – проецирующую плоскость α (задаем ее следом  f_оa) и находим линию пересечения этой плоскости с плоскостью треугольника - прямую 34. Получаем точку К₁ – горизонтальную проекцию основания перпендикуляра – и по К₁ находим К₂.

Действительная величина отрезка DK найдена путем вращения его вокруг оси i (i ^ π₂ и К  ' i ) до положения, параллельного плоскости π₁

[D₁^‘ K ₁] = [K  ABC].

На рисунке 10 в качестве примера показано определение расстояния от точки А до плоскости a, заданной следами, способом замены плоскостей проекций. Этим способом заданная плоскость a преобразуется в проецирующую a ^ π ₄.

 Для этого выбирается новая плоскость проекций (π₁ ^ π₂  ® π₄ ^ π₁;

π₄ ^ a; Х₁₄ ^ h _0a ). На f _0a отмечаем произвольную точку 1₂ и определяем ее новую фронтальную проекцию на плоскости π ₄ (1₄) Через точку Х _a14

 

 

 

 

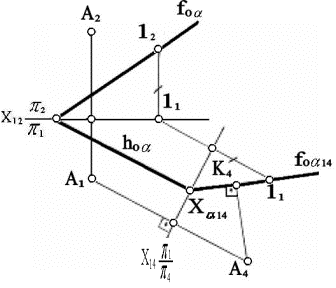
Рисунок 10

(Х_a14 = f_0a14  Ç Х₁₄) и 1₄ проводим f_0a14. Определяем новую фронтальную проекцию точки А ® А₄.

Из точки А₄ опускаем перпендикуляр на f _0a14 и отмечаем точки его пересечения с f _0a14 – К₄. На новую плоскость проекций π₄ расстояние от точки А до плоскости (a) спроецируется без искажения А ₄К ₄ = АК.

1.6     Расстояние от точки до поверхности

На рисунке 11 показано определение расстояние от точки А до ближайшей точки на поверхности конуса.

Искомое расстояние равно расстоянию от заданной точки до ближайшей к ней образующей. Эта образующая лежит в плоскости α, проходящей через точку А и ось конуса. Поворачиваем эту плоскость (α) вокруг оси конуса до положения, параллельного фронтальной плоскости (π₂). Точка А займет новое положение А’(A’₁, A’₂),  и искомое расстояние выразится отрезком А’₂K₂, перпендикулярным к S₂B₂.

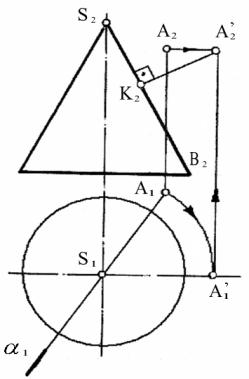
Рисунок 11

На рисунке 12 показано определение расстояния от точки А до ближайшей поверхности сферы. Искомое расстояние измеряется по прямой АО. Повернем прямую АО вокруг оси, проходящей через точку О, перпендикулярную к горизонтальной плоскости проекции (π₁), так, чтобы АО стала параллельна фронтальной плоскости проекции (π₂), получим АК = А’O – R = A’₂O₂ - R.

A’₂K ₂= AK - расстояние от точки до сферы.

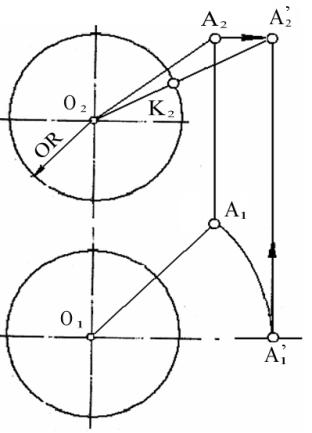
Рисунок 12

1.7     Расстояние между двумя параллельными плоскостями

Расстояние между параллельными плоскостями измеряется длиной отрезка перпендикуляра, опущенного из произвольной точки одной плоскости на другую плоскость.

Истинную величину этого расстояния можно определить несколькими способами.  Наиболее простой из них – способ замены плоскостей проекций.  Суть решения задачи состоит в том, что  новую плоскость проекций  необходимо выбрать так, чтобы заданные в условии плоскости спроецировались на нее в прямые линии. Расстояние между полученными линиями, измеренное по перпендикуляру, и будет искомым.  На рисунке 13 приведен пример определения расстояния между двумя параллельными плоскостями α и β общего положения, заданными следами.  Переходим от системы  π₁ / π₂  к  π₁ / π₄  (p₁  ^ p ₂ ® p₄  ^ p₁) 

X ₁₄ ^ h _{0 a} (h _{0 b}).

Для построения новых проекций плоскостей α и β в одной из заданных плоскостей взята точка 1 (1₂, 1₁), принадлежащая фронтальному следу плоскости, найдена ее новая проекция 1_4, затем построены проекции плоскостей α и β.  На плоскость p ₄  заданные плоскости проецируются в прямые линии α₄ и β₄, так как новая плоскость проекций выбрана перпендикулярно к плоскостям α и β. Искомое расстояние – ι.

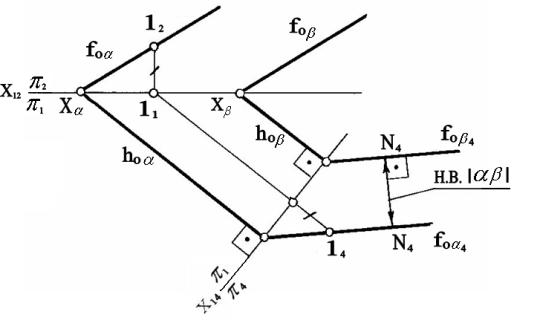
Рисунок 13

Рассмотрим пример. Если плоскости α  и β общего положения, заданными пересекающимися прямыми (рисунок 14 ) α (a Ç b) и β (c Ç d), α // β.

 

 

 

 

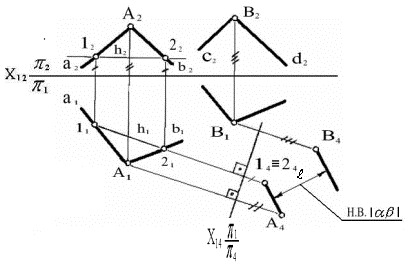
Рисунок 14

Для получения проекций плоскостей в виде линий на новой плоскости проекций π₄  в плоскости α проведена горизонталь h:  h Ì a,  h,  h ∩ a = 1,

 h ∩ b = 2,   h (12) Ì a. Вводим новую плоскость π₄ ^ π₁ (переходим от π₁ ^ π₂ → π₄ ^ π₁,  π₄ ^ α (β),  Х₁₄ ^ h₁). Плоскость  π₄   перпендикулярна к обеим данным плоскостям α  и β. Строим проекцию плоскости α и точки В другой плоскости (β) на плоскости π_4,  плоскости α  и β спроецировались в параллельные прямые линии. Расстояние между полученными линиями, измеренное по перпендикуляру, и будет искомым - i.

Приложение А

Комплект задач

Задача №1

По заданным координатам построить две проекции точек АВСDЕК.     

Задача № 2

Построить горизонтальную проекцию точки F  и провести прямую l,  проходящую через точку F(70; Y; 40) и параллельную плоскости α(AB || DN).

Задача №3

Построить перпендикуляр к плоскости β(АВ ∩ АD) и отложить на нем отрезок АК, равный 40 мм.

Задача №4

Построить точку пересечения прямой DК с плоскостью α(ABС) и определить ее видимость на проекциях.

Задача №5

Построить проекции линии пересечения плоскостей α(ABС) и β(DЕК).

Задача №6

Определить натуральную величину отрезка АВ различными способами.

Задача №7

Определить расстояние от точки D до плоскости α(ABС).

Задача №8

Определить расстояние между скрещивающимися прямыми АВ и DЕ.

Задача №9

Построить точки пересечения прямой АВ со следующими поверхностями:

          а) с конусом, радиус основания которого 30 мм, высота 50мм, а ось вращения проходит через середину отрезка АВ;

          б) с пирамидой СDЕК.

Задача №10

Определить натуральную величину сечения пирамиды АВСЕ с горизонтально-проецирующей плоскостью γ, проходящей через середину ребра АВ и параллельно ребру ВС.

 

Список литературы

1.      Виноградов В. Н., Ройтман И. А. Сборник задач и методические указания по начертательной геометрии. – М.: Просвещение, 1972.

2.       Гордон В. О., Семенцов – Огиевский М. А. Курс начертательной геометрии: Учебное пособие / Под. ред. Иванова Ю. Б. – М.: Наука, 1988. – 288с.

3.      Гордон В. О., Иванов Ю. Б., Солнцева Т. Е. Сборник задач по курсу начертательной геометрии: Учебное пособие для вузов. – 6 – е изд., перераб.

- М.: Наука. Гл. ред. физ. – мат. лит., 1989. – 320 с. - JSBN  5 – 02 – 013926 – 2.

4.      Лаптев О. В., Числив П. А. Задачник по начертательной геометрии. – М., 1999.

5.      Павлова А. А. Начертательная геометрия. Учебник для студентов высших учебных заведений. – М.: ООО “ Издательство Астрель “:  ООО “ Издательство АСТ “, 2001. – 304 с.: ил.

6.      Стрижаков А. В., Мартиросов А. Л., Кубарев А. Е. Начертательная геометрия / Серия “ Высшее образование .“ – Ростов Н/Д: Феникс, 2004. – 320 с.

7.      Тарасов Б. Ф., Дудкина Л. А., Немолотов С. О. Начертательная геометрия. – СПб.: Издательство “ Лань “, 2001. – 256 с.: ил.

8.      Мукашев М. Ш. Инженерная графика. Часть 1. Начертательная геометрия. Лекции и методические указания по выполнению самостоятельных работ. – Алматы, 1999. – 180 с.

9.      Мукашев М. Ш., Дуйсенов С. А., Калиев Б. З. Инженерлік және машиналық графика, 1 – бөлім. Сызба геометрия. Оқу құралы. АЭжБИ. Алматы, 2004. – 8б.

10.  Яхъяев Э.А. Техническое черчение (для учащихся колледжа): Учебное пособие. АИЭС. Алматы, 2005. -  103 с.: ил.

11. Фролов С. А. Начертательная геометрия: Учебное пособие для втузов. – М.: Машиностроение, 1983.

12. Фролов С. А. Сборник задач по начертательной геометрии. – М.: Машиностроение, 1986.

                                                                                   

 

Сводный план 2006 г., поз.

Алмас Даменович Динасылов

Эркин Алимджанович Яхъяев

Айгуль Борибековна Досаева

 

ИНЖЕНЕРНАЯ И КОМПЬЮТЕРНАЯГРАФИКА.

МЕТРИЧЕСКИЕ ЗАДАЧИ

Часть 1

Методические указания к выполнению семестровой работы

 (для студентов всех  форм обучения специальностей

050717 – Теплоэнергетика, 050718 – Электроэнергетика,

050719 – Радиотехника, электроника и телекоммуникации)

 

 

Редактор  Ж.М. Сыздыкова

Подписано в печать ……                                           Формат 60х84 1/16

Тираж …..экз.                                                              Бумага типографская № 1

Объем 2,0 уч.-изд.л.                                                    Заказ …….. Цена ……..

 

Копировально-множительное бюро

Алматинского института энергетики и связи

050013, Алматы, ул. Байтурсынова, 126