АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра Инженерная графика и Прикладная механика
ИНЖЕНЕРНАЯ И КОМПЬЮТЕРНАЯ ГРАФИКА.
ТЕОРИЯ ПОСТРОЕНИЯ ЧЕРТЕЖЕЙ
Конспект
лекций
(для
студентов всех форм обучения и всех специальностей)
Алматы
2006
СОСТАВИТЕЛЬ: М.Ш. Мукашев. Инженерная и компьютерная
графика. Теория построения чертежей.
Конспект лекций. (для студентов
всех форм обучения и всех специальностей). – Алматы: АИЭС, 2006. – 35 с.
Излагаются основные вопросы
теории построения чертежей. Приведены основные методы построения проекций
точки, прямых, плоскостей, гранных поверхностей вращения. В отдельной лекции
даны способы построения стандартных аксонометрических проекций. Конспект лекций
предназначен для студентов 1 курса очной и заочной форм обучения всех
специальностей АИЭС.
Ил.58, библиогр.- 9 назв.
Рецензент: канд. техн. наук,
доцент Яхьяев Э.А.
© Алматинский институт энергетики и связи, 2006 г.
Содержание
1 Лекция 1. Метод проекций 4
1.1 Центральное проецирование 4
1.2 Параллельное проецирование 4
1.3 Ортогональное проецирование 6
1.4 Точка в системе двух плоскостей проекции 6
1.5 Точка в системе трех плоскостей проекции 7
1.6 Система прямоугольных координат 8
1.7 Проекции отрезка прямой линии 8
1.8 Точка на прямой 11
1.9 Определение следов прямой 12
1.10 Взаимное расположение двух прямых 13
2 Лекция 2. Проекции плоскости на чертеже 15
2.1 Способы задания плоскости на чертеже 15
2.2 Проекции плоскостей частного положения 16
2.3 Проекции плоских углов 19
2.4 Взаимное положение двух плоскостей 21
3 Лекция 3. Способы преобразования ортогональных проекций 23
3.1 Способ замены плоскостей проекций 23
3.2 Способ вращения вокруг оси, перпендикулярной к
плоскости
проекции 25
4 Лекция 4. Аксонометрические проекции 27
4.1 Прямоугольная изометрическая проекция 29
4.2 Прямоугольная диметрическая проекция 31
4.3 Некоторые косоугольные аксонометрические проекции 33
Список литературы 35
1 Лекция 1. Метод проекций
Содержание лекции:
- метод ортогонального проецирования элементов геометрических фигур: точки, прямой линии, плоскости.
Цели лекции:
- изучить
метод ортогонального проецирования на две и три взаимно перпендикулярные
плоскости, рассмотреть частные случаи проецирования прямой.
1.1 Центральное
проецирование
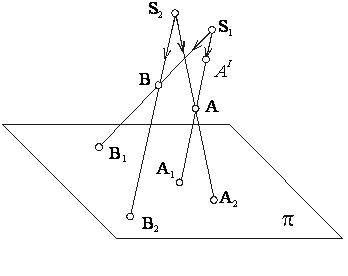
Рисунок 1
В основу построения любого изображения положен метод
проецирования, который заключается в следующем. Пусть дана некоторая плоскость π, которую
называют плоскостью проекций,
и вне ее точка S1, называемая центром
проецирования. Чтобы спроецировать точку А
пространства на плоскость π (рисунок 1),
через центр проецирования S1 проводят
прямую S1A до ее
пересечения с плоскостью π
в точке А1. Точку А1 принято называть
центральной проекцией точки А,
прямую S1A1
– проецирующим лучом. Проекцией фигуры называют множество проекций всех ее
точек. Простейшими фигурами являются точки, прямые и плоскости. Более сложные
фигуры состоят из нескольких или даже бесчисленного множества точек, прямых и
плоскостей.
Не изменяя положения плоскости π и взяв новый центр S2, получаем новую проекцию точки А – точку А2.
Итак, при заданных плоскости проекции и центре проецирования, можно получить проекцию точки. Но, имея одну проекцию (например А1) нельзя по ней определить положение самой точки в пространстве, т.к. любая точка на проецирующей прямой S1A1 проецируется в одну и ту же точку А1 (сравни А и А` на рисунке 1). Для единственного решения, очевидно, необходимо иметь две проекции (например А1 и А2).
1.2
Параллельное
проецирование
Параллельное проецирование является частным случаем
центрального проецирования, когда S=S∞
(бесконечно удалена от плоскости π). В этом случае проецирующие прямые параллельны между
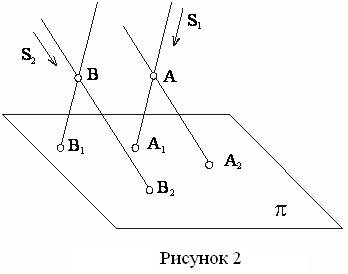
собой (рисунок 2).
Параллельное
Рисунок 2
проецирование полностью определяется положением плоскости (π) и направлением проецирования (S). Для определения положения точки в
пространстве
здесь также необходимо иметь две параллельные проекции, полученные при двух
различных направлениях проецирования. В этом случае положение точки
определяется пересечением прямых, проведенных через А1 А2
параллельно соответствующим направлениям.
В параллельных проекциях также, как и в центральных (рисунок 3):
Рисунок 3
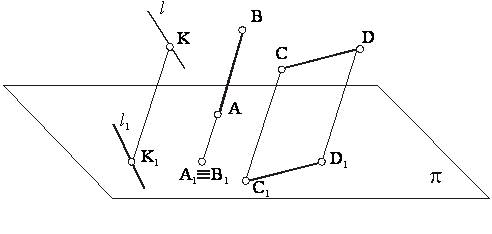
а) прямая линия проецируется на плоскость в виде прямой;
б) каждая точка и линия в пространстве имеют единственную свою проекцию;
в) для построения проекции прямой достаточно спроецировать две ее точки и через полученные проекции этих точек провести прямую линию (С1 и D1);
г) если точка принадлежит прямой, то проекция этой точки принадлежит проекции этой прямой (точка К на прямой ℓ).
Кроме перечисленных свойств, для параллельных проекций можно указать еще следующее:
а) если прямая параллельна направлению проецирования (прямая АВ на рисунке 3), то проекцией этой прямой является точка;
б) отрезок прямой линии, параллельной
плоскости проекции, проецируется на эту плоскость в натуральную величину (на
рисунке 3: CD=C1D1
как отрезки параллельных между параллельными прямыми).
1.3
Ортогональное проецирование
Ортогональное (прямоугольное) проецирование является частным случаем параллельного проецирования, при котором направление проецирования “S” перпендикулярно плоскости проекции (рисунок 4).
Рисунок 5 Рисунок 4
Здесь также для определения положения точки в пространстве необходимо иметь две параллельные проекции, полученные при двух направлениях проецирования. При ортогональном проецировании эти проекции должны быть в двух взаимно перпендикулярных плоскостях π1 и π2 (рисунок 5).
Метод параллельного проецирования на две взаимно перпендикулярные плоскости был изложен французским геометром Гаспаром Монжем (1746-1818) и назван методом Монжа.
В техническом черчении преимущественно применяется параллельное прямоугольное проецирование на две или три взаимно перпендикулярные плоскости, которые мы и будем рассматривать в дальнейшем.
1.4
Точка
в системе двух плоскостей проекции
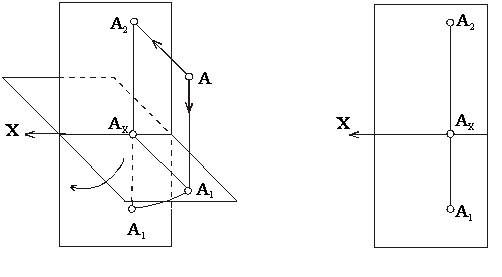
Изложение положения точки в пространстве производится по ее прямоугольным проекциям на две взаимно перпендикулярные плоскости – горизонтальную плоскость (π1) и фронтальную плоскость (π2). Линия пересечения плоскостей называется осью проекции Х (рисунок 6).
Повернув плоскость π1 вокруг оси проекции на 90º, получим одну плоскость – плоскость чертежа. Проекции А1 и А2 расположатся на одном перпендикуляре к оси проекции – линии связи. В результате совмещения плоскостей π1 и π2 получается чертеж, известный под названием “Эпюр Монжа” (рисунок 7).
Рисунок 6 Рисунок 7
1.5
Точка
в системе трех плоскостей проекций
Третья плоскость проекций (π3), перпендикулярная к π1 и π2, называется профильной плоскостью (рисунок 8). Также, как и плоскость π2, она расположена вертикально. Помимо оси Х появляются еще оси проекций У и Z, перпендикулярные к оси Х. Буквой О обозначена точка пресечения всех трех плоскостей проекций.
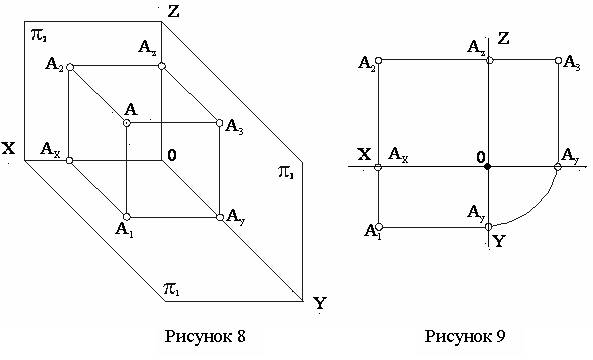
Если “разрезать” плоскости по оси У и повернуть плоскость π1 вокруг оси Х на 90º, а плоскость π3 – вокруг оси Z на 90º, то все три плоскости совместятся в одну
плоскость – плоскость чертежа (рисунок 9). Линии, связывающие проекции точки
между собой, называются линиями связи. Горизонтальная (А1) и фронтальная (А2)
проекции точки А расположены на
одном перпендикуляре к оси Х – на
линии связи А1-А2, фронтальная (А2) и профильная (А3) проекции лежат на одном
перпендикуляре к оси Z – на линии связи А2-А3. Построение профильной проекции точки А (А3)
по фронтальной и горизонтальной проекциям показано на рисунке 9.
1.6
Система
прямоугольных координат
Система прямоугольных координат называется еще “декартовыми координатами” по имени французского математика Декарта (1596-1650). Здесь три взаимно перпендикулярные плоскости (π1, π2 и π3) называются плоскостями координат. Прямые, по которым пересекаются плоскости координат, называются осями координат (X,Y,Z). Точка пересечения осей координат называется началом координат и обозначается буквой О. Плоскости координат в своем пересечении образуют 8 трехгранных углов, деля пространство на 8 частей – октантов (от латинского octo – восемь).
Принимая оси проекций за оси координат, можно найти координаты точки по данным ее проекциям. Координатами точки называются расстояния, отсекаемые линиями связи на осях координат.
Расстояние О-Ах (рисунок 9) называется абсциссой, расстояние О-Ау называется ординатой, расстояние О-Аz – аппликатой. При буквенном обозначении координат абсцисса указывается буквой Х, ордината – буквой У, аппликата – буквой Z.
Если задаются три координаты точки, то этим определяется ее положение в пространстве.
1.7
Проекции
отрезка прямой линии
Рисунок 10
Положим, что даны фронтальные и горизонтальные проекции точек А и В (рисунок 10).
Проведя через одноименные проекции этих точек прямые линии, мы получим проекции
отрезка АВ – фронтальную (А2В2) и горизонтальную (А1В1).
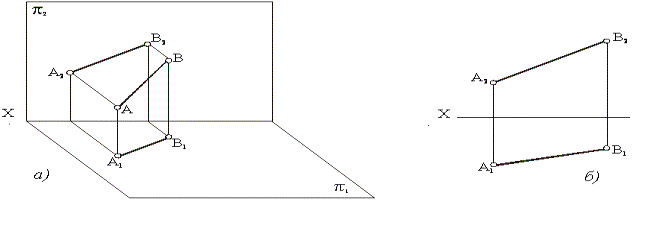
Точки А и В находятся на разных расстояниях от каждой из плоскостей π1, π2, π3, т.е. прямая АВ не параллельна ни одной из них и не перпендикулярна к ним. Такая прямая называется прямой общего положения. Здесь каждая из проекций меньше самого отрезка А1В1<АВ, А2В2<АВ, А3В3<АВ.
Прямая линия может занимать относительно плоскостей особые (частные) положения. Рассмотрим их.
1. Прямая параллельна плоскости π1 (рисунок 11). В этом случае фронтальная проекция прямой параллельна оси проекции, а горизонтальная проекция равна самому отрезку (А2В2║ОХ, А1В1=│АВ│). Такая прямая называется горизонтальной и обозначается буквой “h”.
Рисунок 11
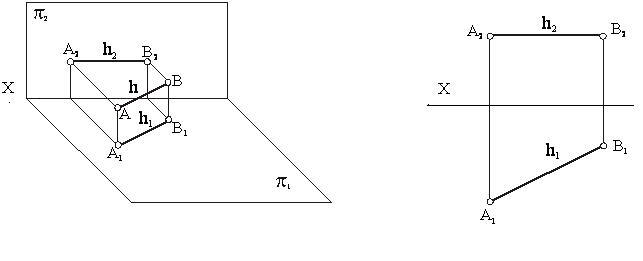
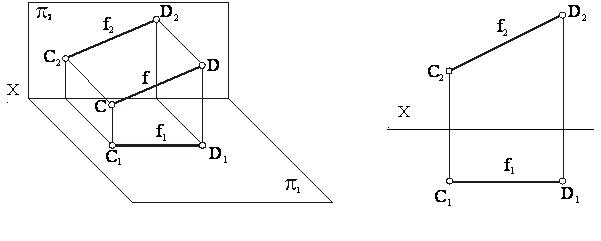
2. Прямая параллельна плоскости π2 (рисунок 12). В этом случае ее горизонтальная проекция параллельна оси проекции (С1D1║ОХ), а фронтальная проекция равна самому отрезку (С2D2=│CD│). Такая прямая называется фронтальной и обозначается буквой “f”.
Рисунок 12
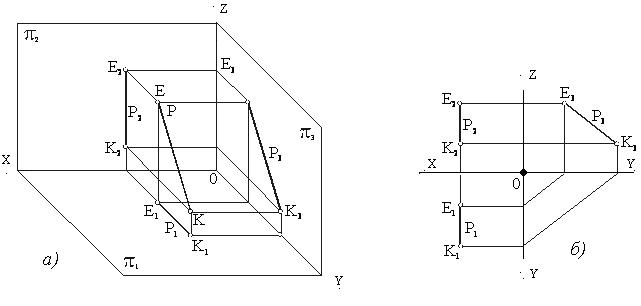
3. Прямая параллельна плоскости π3 (рисунок 13). В этом случае горизонтальная и фронтальная проекции прямой располагаются на одном перпендикуляре к оси проекции ОХ, а ее профильная проекция равна самому отрезку, т.е. Е1К1┴ОХ, Е2К2┴ОХ, Е3К3┴ЕК. Такая прямая называется профильной и обозначается буквой “p”.
Рисунок 13
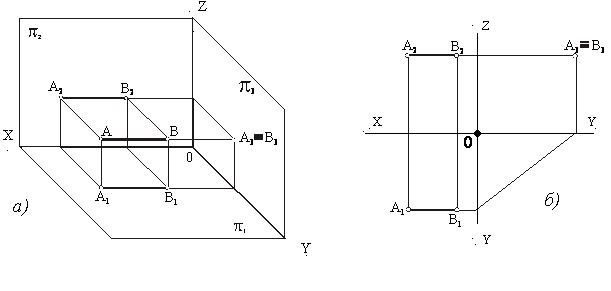
4. Прямая параллельна двум плоскостям – π1 и π2. Тогда она будет перпендикулярна плоскости π3 (рисунок 14). Проекция прямой на плоскости π3 представит собой точку (А3≡В3), а проекции на плоскостях π1 и π2 будут параллельны оси ОХ (А1В1║ОХ, А2В2║ОХ).
Рисунок 14
5. Прямая параллельна плоскостям π1 и π3, т.е. она перпендикулярна плоскости π2 (рисунок 15). Проекция прямой на плоскости π2 представит собой точку (С2≡D2), а проекции на плоскостях π1 и π3 будут параллельны осям У и У, т.е. перпендикулярны осям Х и Z, (C1D1┴OX, C3D3┴Z).
Рисунок 15
6. Прямая параллельна плоскостям π2 и π3, т.е. она перпендикулярна плоскости π1 (рисунок 16). Здесь проекция прямой на плоскости π1 представит собой точку (Е1≡К1), а проекции на плоскостях π2 и π3 будут перпендикулярны оси ОХ и ОУ соответственно (Е2К2┴ОХ, Е3К3┴ОУ).
Рисунок 16
1.8
Точка на прямой
Если точка
принадлежит некоторой прямой, то проекции этой точки лежат на соответствующих
проекциях прямой. Одним из свойств параллельного проецирования является то, что
отношение отрезков прямой линии равно отношению их проекций (рисунок 17). Так как прямые АА1, СС1, ВВ1
параллельны между собой, то 
.
Это
вытекает из теоремы Фаллеса. Напомним ее: если параллельные прямые,
пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они
отсекают равные отрезки и на другой его стороне.
Этим свойством можно воспользоваться для деления отрезка прямой линии в
некотором заданном соотношении.
Рисунок 18
Даны проекции отрезка СD (рисунок 18).
Нужно разделить его в соотношении 2:3. Из произвольной точки концов отрезка
(например, из точки С1)
проведем вспомогательную прямую в
произвольном направлении и отложим на ней пять равных между собой отрезков.
Последнюю точку – 5
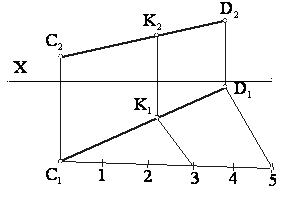соединим
с другим концом отрезка (D1) и
параллельно прямой 5-D1 проведем из точки 3
прямую. Получаем точку К1,
причем К1D1:C1K1=2:3. Затем по линии связи на проекции C2D2 находим К2.
1.9
Определение следов прямой
Точки пересечения прямой с плоскостями проекций называются следами прямой (рисунок 19). Горизонтальная проекция горизонтального следа (точка М1) совпадает с самим следом, а фронтальная проекция этого следа М2 лежит на оси проекции Х. Фронтальная проекция фронтального следа N2 совпадает со следом N, а горизонтальная его проекция N1 лежит на той же оси проекции Х. Следовательно, чтобы найти горизонтальный след, надо продолжить фронтальную проекцию А2В2 до пересечения с осью Х и через точку М2 провести перпендикуляр к оси Х до пересечения с продолжением горизонтальной проекции А1В1. Точка М≡М1 – горизонтальный след прямой АВ. Аналогично находим фронтальный след N≡N2.
Прямая не имеет следа на плоскости проекции в том случае, когда она параллельна этой плоскости.
Рисунок 19
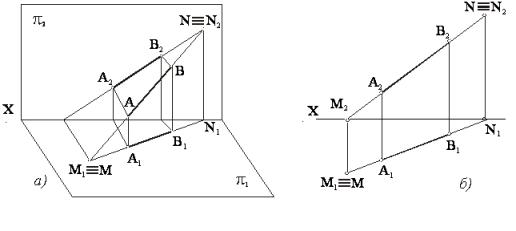
1.10
Взаимное расположение двух прямых
Две прямые в пространстве могут быть параллельными, пересекающимися или скрещивающимися.
Если две прямые в пространстве параллельны между собой, то их проекции на плоскости также параллельны между собой (рисунок 20). Обратное утверждение не всегда верно (сравни прямые С0D0 и CD на этом же рисунке).
Рисунок 20
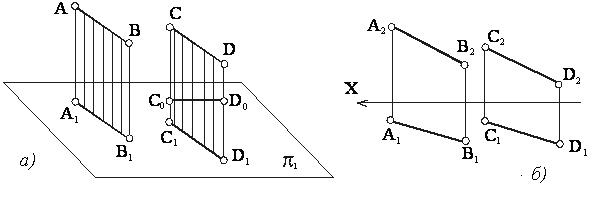
Если прямые линии пересекаются, то их одноименные проекции пересекаются между собой в точке, которая является проекцией точки пересечения этих прямых (рисунок 21).
Рисунок 21
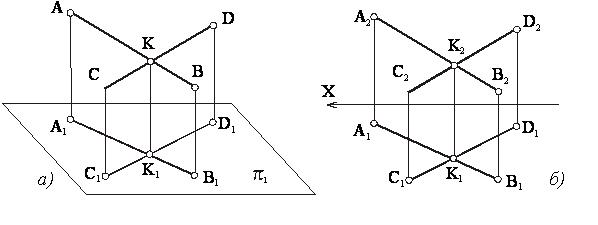
Скрещивающиеся прямые не пересекаются и не параллельны между собой (рисунок 22).
Рисунок 22
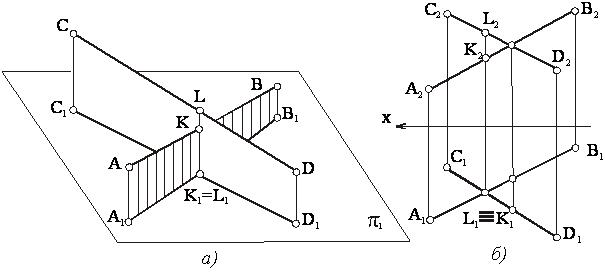
Как видно из данного рисунка, точка с проекциями К2 и К1 принадлежит прямой АВ, а точка с проекциями L2 и L1 принадлежит прямой СD. Эти точки одинаково удалены от плоскости π2, но расстояния их от плоскости π1 различны: точка L расположена выше, чем точка К.
2 Лекция 2. Проекции плоскости на чертеже
Содержание лекции:
- рассмотрение
способа задания проекции плоскости на чертеже;
- рассмотрение плоскости общего и частного положения,
особенности расположения их проекций;
- рассмотрение проекции плоских углов, проецирование
прямого угла в натуральную величину;
- рассмотрение проекции параллельных и пересекающихся
плоскостей.
Цель лекции:
- изучить способы построения проекций различных
плоскостей на чертеже.
2.1 Способы задания
плоскости на чертеже
Плоскость на чертеже может быть задана:
а) проекциями трех точек, не лежащих на одной прямой (рисунок 23 а);
б) проекциями прямой и точки, взятой вне прямой (рисунок 23 б);
в) проекциями двух пресекающихся прямых (рисунок 23 в);
г) проекциями двух параллельных прямых (рисунок 23 г);
д) проекциями любой плоской фигуры – треугольником, многоугольником, кругом и т.д. (рисунок 23 д);
е) более наглядно плоскость может быть изображена при помощи следов – линий пересечения ее с плоскостями проекций (рисунок 23 е).
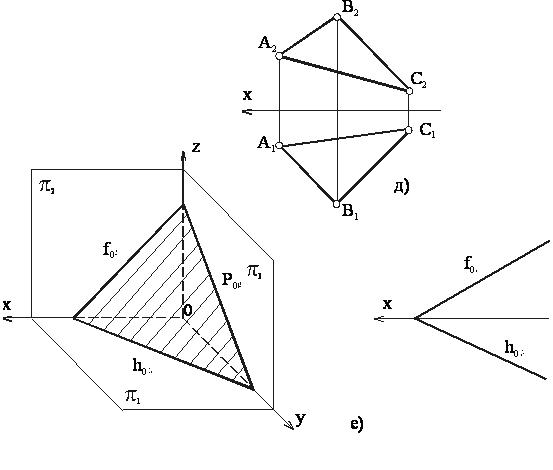
Продолжение рисунка 23
2.2 Проекции плоскостей частного положения
Если плоскость не параллельна и не перпендикулярна ни одной из плоскостей проекций, то она называется плоскостью общего положения.
Рисунок 24
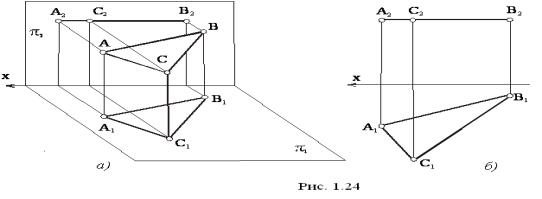
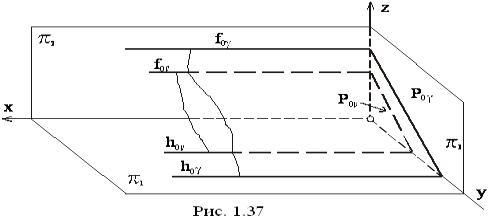
Если плоскость параллельна плоскости π1, то такая плоскость называется горизонтальной. На рисунке 24 плоскость γ (АВС) расположена параллельно плоскости π1. Как видно на рисунке, фронтальная проекция этой фигуры представляет собой прямую линию, параллельную оси Х и совпадающую с фронтальным следом ƒ0γ плоскости, а горизонтальная проекция γ1 (А1В1С1) равна самой фигуре.
Если плоскость параллельна плоскости π2, то такая плоскость называется фронтальной. На рисунке 25 плоская фигура (круг) расположена параллельно плоскости π2. Горизонтальная проекция ее представляет собой прямую линию, параллельную оси Х, а фронтальная проекция равна самой фигуре.
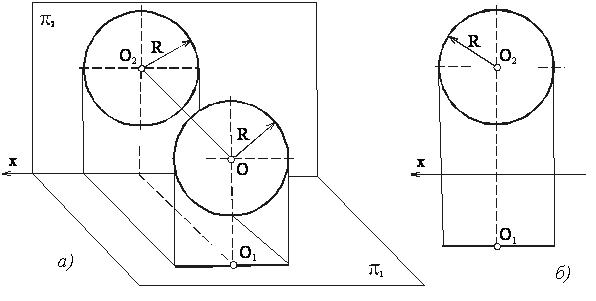
Рисунок 25
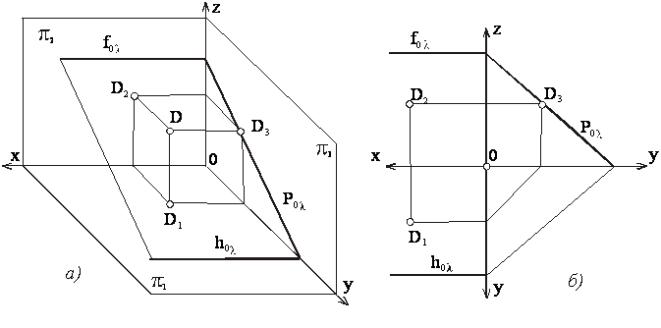
Если плоскость параллельна плоскости π3 , то такая
плоскость называется профильной плоскостью (рисунок 26).
Если плоскость перпендикулярна плоскости π1 (но не параллельна плоскости π2), то такая плоскость называется горизонтально-проецирующей (не путать с горизонтальной). На рисунке 27 горизонтально-проецирующая плоскость β задана следами. Как видно на рисунке, фронтальный след такой плоскости ƒоβ проходит перпендикулярно оси Х, а горизонтальный след hоβ обладает собирательным свойством (горизонтальная проекция любой точки, линии или плоской фигуры, принадлежащей плоскости β, совпадает с горизонтальным следом hоβ).
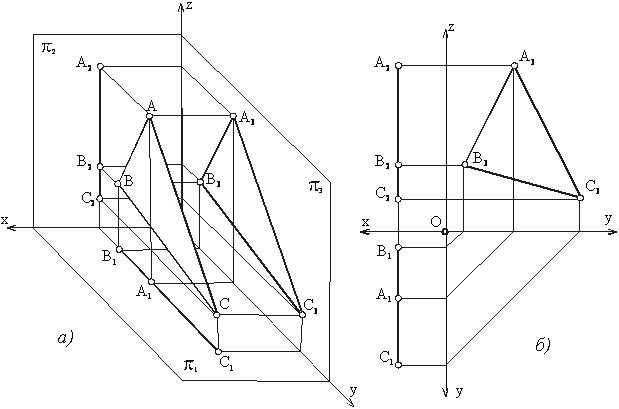
Рисунок 26
Рисунок 27
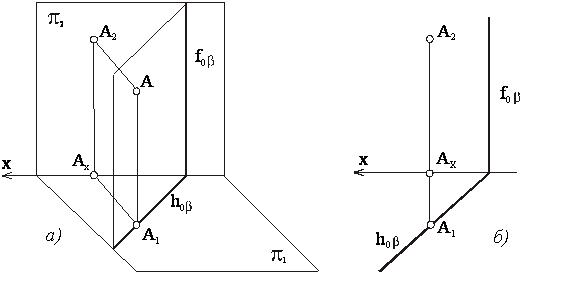
Если плоскость перпендикулярна плоскости π2 (но не параллельна плоскости π1), то такая плоскость называется фронтально-проецирующей (рисунок 28).
Рисунок 28
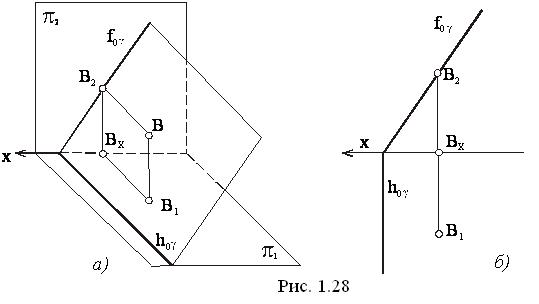
Если плоскость перпендикулярна плоскости π3 (но не перпендикулярна плоскостям π1 и π2), то такая плоскость называется профильно-проецирующей (рисунок 29).
Рисунок 29
2.3 Проекции
плоских углов
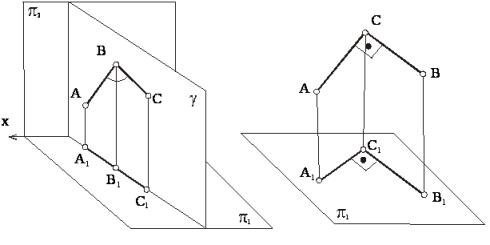
Если плоскость γ, в которой расположен некоторый угол АВС, перпендикулярна к плоскости проекции (π1), то он проецируется на эту плоскость проекции в виде прямой линии (рисунок 30).
Рисунок 31 Рисунок 30
Если плоскость прямого угла не перпендикулярна
к плоскости проекции и хотя бы одна его сторона параллельна этой плоскости, то
прямой угол проецируется на нее в виде прямого угла.
На рисунке 31 сторона ВС
параллельна плоскости π1. Если угол АСВ прямой, то
независимо от положения стороны АС
на проекции угол АСВ будет также
прямым.
Если учесть, что сторона угла параллельна плоскости проекции, она
называется либо горизонтальной (если параллельна плоскости π1), либо фронтальной (если
параллельна плоскости π2), либо профильной прямой (если параллельна плоскости π3), то можно сделать
следующий вывод:
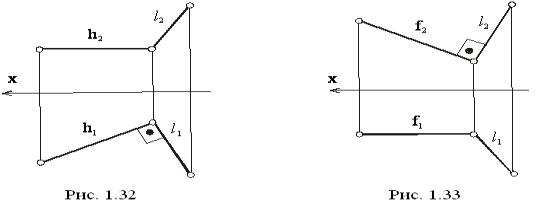
) для того, чтобы построить перпендикуляр к горизонтальной прямой, необходимо, чтобы горизонтальная проекция перпендикуляра (ℓ1) была перпендикулярна к горизонтальной проекции горизонтали (h1). На рисунке 32 ℓ1┴h1. Тогда независимо от расположения проекции ℓ2 эти прямые в пространстве будут взаимно перпендикулярны (ℓ1┴h1);
) для того, чтобы построить перпендикуляр к фронтальной прямой, необходимо, чтобы фронтальная проекция перпендикуляра (ℓ2) была перпендикулярна к фронтальной проекции фронтали (ƒ2). На рисунке 33 ℓ2┴ƒ2. Тогда независимо от расположения ℓ1 эти прямые в пространстве будут взаимно перпендикулярны (ℓ┴ƒ).
Рисунок 33 Рисунок 32
Эти особенности
проецирования прямой угла широко используются при решении геометрических задач.
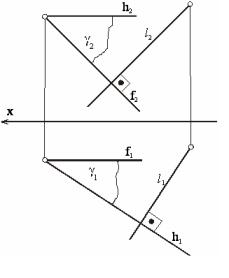
Например, две пересекающиеся
между собой горизонталь h и
фронталь ƒ будут составлять
плоскость γ. Если из некоторой
точки А провести прямую ℓ (рисунок 34), перпендикулярную
горизонтали и фронтали, то эта прямая будет перпендикулярна и плоскости γ.
Рисунок 34
2.4 Взаимное
положение двух плоскостей
Две плоскости могут быть
параллельными либо пересекаться между собой.
Если плоскости β и γ параллельны между собой, то всегда в каждой из них можно
построить две пересекающиеся между собой прямые линии так, чтобы прямые одной
плоскости соответственно были параллельны двум прямым другой плоскости.
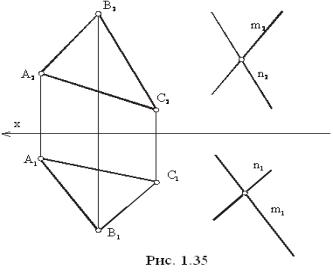
Рисунок 35
На
рисунке 35 плоскость β задана
треугольником АВС, а плоскость γ – двумя пересекающимися прямыми
“m” и “n”. Для того, чтобы плоскости
β и γ были параллельны между собой, необходимо, чтобы прямые “m” и “n” были параллельны сторонам
треугольника АВС, например m║АВ, n║ВС.
Прямые “m” и “n” могут быть
также параллельны любым другим прямым, лежащим в плоскости β(АВС).
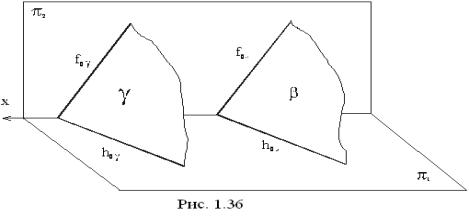
Если плоскости заданы
следами, то для параллельности плоскостей их следы должны быть параллельны
между собой (рисунок 36), т.е. ƒ0γ║ƒ0β, h0γ║h0β.
Рисунок 36
Если следы
плоскостей параллельны оси Х, то эти
плоскости могут быть либо параллельны, либо пересекаться между собой (рисунок 37).
Для определения параллельности нужно построить третий, профильный след.
Рисунок 37
3 Лекция 3. Способы преобразования ортогональных
проекций
Содержание лекции:
- рассмотрение двух наиболее
распространенных способов
преобразования ортогональных проекций: способа замены плоскостей проекций и способа вращения – на основании конкретных примеров.
Цель лекции:
- изучить методы
преобразования ортогональных проекций для использования их при решении
геометрических задач.
Решение геометрических задач значительно
упрощается,
когда мы имеем дело с частным положением геометрических фигур относительно
плоскостей проекций (либо перпендикулярно, либо параллельно ей).
Переход от общего
(произвольного) положения геометрической фигуры к частному может быть достигнут
двумя путями:
) выбором новой плоскости проекций, по отношению к которой проецируемая фигура, не меняющая своего положения в пространстве, окажется в частном положении;
) перемещением в пространстве проецируемой фигуры так, чтобы она заняла частное положение относительно плоскостей проекций, которые при этом не меняют своего положения в пространстве.
Эти два способа преобразования проекций рассматриваются в данной лекции.
3.1 Способ замены плоскостей проекций
Ортогональные
проекции на две взаимно перпендикулярные основные (горизонтальную и
фронтальную) плоскости проекций позволяют изобразить предмет сверху и спереди.
В ряде случаев необходимо построить вид предмета с другой стороны, чтобы более
полно представить его форму и очертание. Дополнительные чертежи предмета могут
быть построены способом замены плоскостей проекций.
Пусть заданы точка А и
система двух взаимно перпендикулярных плоскостей p1 и p2 (рисунок 38). Возьмем новую плоскость
проекций p4 перпендикулярно плоскости p1 и спроецируем на нее точку А (проекция А4). Получаем две системы плоскостей проекций: основную p1 и p2 и дополнительную p1 и p4 . Плоскость p1 будет общей для обеих
систем плоскостей проекций. Как видно из рисунка, высота точки А над плоскостью p1 остается неизменной.
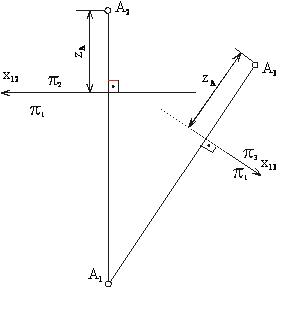Операцию перехода от одной системы плоскостей проекций
к другой легко проследить и на эпюре (рисунок 39).
Здесь дополнительная ось проекций x13 (между плоскостями p1 и p3)
соответствует положению горизонтально - проецирующей плоскости p3.
Линия связи А1А3 проходит перпендикулярно
оси X13, расстояние от точки А3 до оси X13 равно
расстоянию от проекции А2
до оси X12 (координате ZA).
Рисунок 39
Аналогично можно заменить плоскость p1
на новую плоскость проекции p4
(рисунок 40).
Рисунок 40
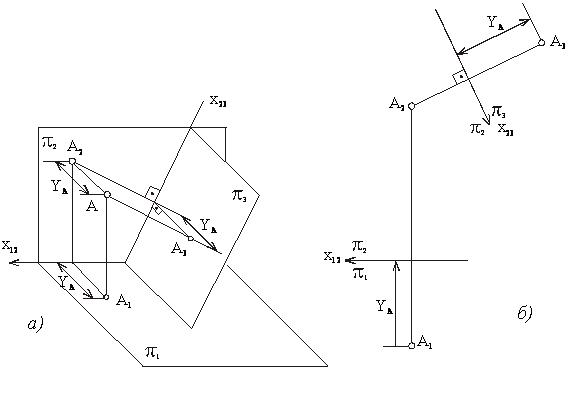
Здесь дополнительная проецирующая плоскость p3 проходит перпендикулярно плоскости p2 . Построение проекции точки А3 проводим следующим образом:
- проводим ось проекций X23, соответствующую положению плоскости p3;
- из проекции А2 проводим линию связи А2А3 перпендикулярно оси X23;
- откладываем на этой линии связи от оси X23 отрезок, равный расстоянию от проекции А1 до оси X12 (Ya) , получаем проекцию A3.
Замена одной из плоскостей проекций не всегда может привести к решению поставленной задачи. Иногда приходится менять две и более плоскости проекций.
Покажем, как
определяются ортогональные проекции точки А
при последовательных заменах
плоскостей проекций (рисунок 41).
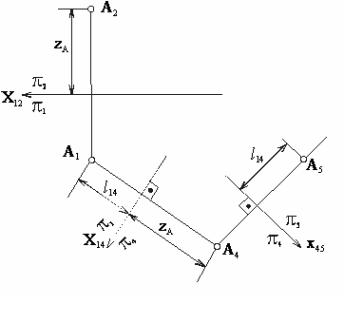Пусть
точка А задана в основной системе
плоскостей проекций p2/p1
. Выбираем новую систему плоскостей проекций p1/p4
и построим проекцию А4 точки А. Методика построения проекции А4 дана выше (рисунки 38, 39).
Рисунок 41
Заменяя в системе плоскостей проекций p1/p4
плоскость p1 на плоскость
проекций p5,
перпендикулярную плоскости p4,
получим третью систему плоскостей проекции p4/p5.
На эпюре ось X45 будет определять
положение плоскости p5
относительно плоскости p4.
Проводя из точки А4 линию
связи A4A5
перпендикулярно оси X45 и отложив на ней от
этой оси расстояние ℓ14 , равное расстоянию от проекции А1 до оси X14, получим новую проекцию точки А5.
Метод замены плоскостей проекций позволяет получить новые, наиболее
удобные для решения задач проекции фигур по заданным неудобным.
3.2
Способ вращения вокруг оси, перпендикулярной к плоскости проекции.
Данный способ противоположен способу замены плоскостей проекций. Способ вращения также дает возможность строить множество чертежей, но в одной системе плоскостей проекций.
Рассматриваемую
фигуру при вращении вокруг оси можно приводить в любое нужное положение и
строить его ортогональные проекции.
Проследим, как будет изменяться положение точки А при ее вращении вокруг оси “i” , перпендикулярной p2 (рисунок 42).
Точка А перемещается по дуге окружности в плоскости b (b^i, и следовательно, b║p2 ), поэтому эта окружность проецируется на плоскость p2 без искажения, а на плоскость p1 - в отрезок прямой, параллельной оси X. Таким образом, если точка А перемещается вокруг оси i по дуге окружности радиуса R на некоторый угол j, то она займет положение А’. При этом фронтальная проекция точки А2 повернется вокруг центра O2 на тот же угол j и займет положение А2'. Горизонтальная проекция точки А1 продвинется по прямой, параллельной оси X, и займет положение А1'. На эпюре это будет выглядеть следующим образом (рисунок 43).
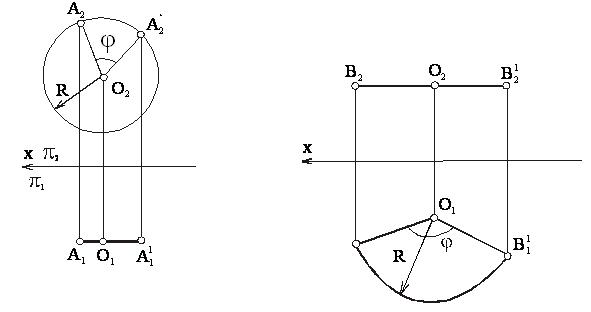
Рисунок 43 Рисунок 44
Аналогично можно показать вращение точки В (рисунок 44) вокруг оси, перпендикулярной горизонтальной плоскости p1. Здесь горизонтальная проекция точки В1 перемещается по дуге окружности радиусом R, а фронтальная проекция - по прямой, параллельной оси X.
Способ вращения геометрических фигур вокруг осей, перпендикулярных плоскостям проекций, широко используется при решении геометрических задач.
4 Лекция 4. Аксонометрические проекции
Содержание лекции:
- рассмотрение способа
построения стандартных аксонометрических проекций: изометрии и диметрии – на
основании конкретных примеров.
Цель лекции:
- изучить способы построения
стандартных аксонометрических проекций: прямоугольных и некоторых косоугольных изометрии
и диметрии, гранных поверхностей и окружностей.
Ортогональные
(прямоугольные) проекции находят широкое применение в технике при составлении
чертежей. Это объясняется тем, что выполнение чертежей с помощью ортогональных
проекций достаточно просто, при этом можно получить проекции, сохраняющие
метрические характеристики оригинала.
Наряду с отмеченными
достоинствами, метод ортогонального проецирования имеет существенный
недостаток. Для того, чтобы получить представление о пространственном
геометрическом образе фигуры, приходится одновременно рассматривать две, три, а
иногда и большее число проекций.
В ряде случаев бывает
необходимо, наряду с чертежом геометрической фигуры, выполненным в
ортогональных проекциях, иметь ее наглядное изображение. Также изображение
может быть получено путем проецирования оригинала на специально выбранную
плоскость. Такие проекции называются аксонометрическими. Название
"аксонометрия" образовано из слов древнегреческого языка:
"аксон" - ось, "метро" - измеряю.
Аксонометрическая проекция
есть прежде всего проекция только на одной плоскости.
Если взять точку А в прямоугольной системе координат с
координатами ОХ=OY=OZ=ℓ (рисунок 45) и
спроецировать ее на некоторую плоскость π0, то координаты точки А, естественно, исказятся и будут равны
ℓх, ℓy, ℓz. Они не равны ℓ и не равны между собой.
Отношения 
называются
коэффициентами искажения по аксонометрическим осям.
Очевидно, принимая различное
взаимное расположение натуральной (декартовой) системы координат и
аксонометрической плоскости π0 и задавая разные
направления проецирования S,
можно получить множество аксонометрических проекций, отличающихся друг от друга
как направлением аксонометрических осей, так и величиной коэффициентов
искажений вдоль этих осей.
Справедливость этого
утверждения была доказана немецким геометром Карлом Польке.
Теорема Польке. Три отрезка
произвольной длины, лежащих в одной плоскости и выходящих из одной точки под
произвольными углами друг к другу, представляют параллельную проекцию трех
равных отрезков, отложенных на прямоугольных осях координат от начала.
На основании этой теоремы
аксонометрические оси и коэффициенты искажений по ним могут выбираться
произвольно.
Однако для унификации
построений в инженерной практике используются стандартные аксонометрические
проекции, часть которых мы и рассмотрим в этом разделе.
Для начала дадим несколько
определений:
)
если
направление проецирования S перпендикулярно плоскости
проецирования π0, то такие проекции
называются прямоугольными аксонометрическими;
)
если
коэффициенты искажений равны по всем аксонометрическим осям (кх=ку=кz),
то такая аксонометрическая проекция называется изометрией;
)
если
коэффициенты искажений одинаковы для каких-либо двух осей (например, кх=кz), то такая аксонометрическая проекция называется
диметрией;
)
если
коэффициенты искажений различны для всех осей (кх≠ку≠кz), то такая
аксонометрическая проекция называется триметрией;
)
независимо
от вида для прямоугольных аксонометрических проекций между коэффициентами
искажений существует следующая зависимость
кх2+ку2+кz2=2.
Данное определение доказуемо, однако, в целях упрощения изложения,
принимаем эту формулу без доказательств.
Как было уже указано, в практике построений используется
ограниченное число аксонометрических проекций, которые стандартизированы и
подлежат обязательному соблюдению.
Рассмотрим некоторые, наиболее распространенные из них.
4.1
Прямоугольная изометрическая проекция
Для изометрической проекции
все коэффициенты искажений по аксонометрическим осям равны между собой, т.е. кх=ку=кz=к. Так как для прямоугольной
аксонометрии
кх2+ку2+кz2=2,
то получаем
3к2=2,
отсюда к=0,82. Такие коэффициенты искажений по осям называются
натуральными.
Для изометрии углы между осями одинаковы и равны 120◦,
обычно ось z принимают вертикальной
(рисунок 46).
На рисунке 47 показана
изометрическая проекция куба с размерами ребер, равными "а".
Как видно из рисунка, размеры куба по осям откладываются
уменьшенными по сравнению с оригиналом. Пользоваться такими коэффициентами
искажений неудобно. Поэтому, для упрощения построений допускается принимать
коэффициенты искажений по осям, равным единице (кх=ку=кz=1), и откладывать по осям неискаженные размеры фигуры. Такие
коэффициенты искажений называются приведенными. В этом случае, увеличение
линейных размеров изображения по сравнению с действительными происходит в
1/0,82=1,22 раза.
Изометрические оси обычно проводят с помощью транспортира, либо
треугольника с углами 60◦ и 30◦. Те же углы
можно построить с помощью циркуля (рисунок 48).
Порядок построений следующий.
1.
Проводим
вертикальную ось Z0 и отмечаем на ней точку
"О".
2.
Из точки "О", как из центра, проводим
окружность любого, по возможности большего радиуса и отмечаем на вертикальной
оси точку "1".
3.
Из
точки "1", не изменяя
раствора циркуля, делаем на дуге окружности засечки (точки "2" и "3").
4.
Соединив
центр "О" с точками "2" и "3", строим оси Х0
и У0.
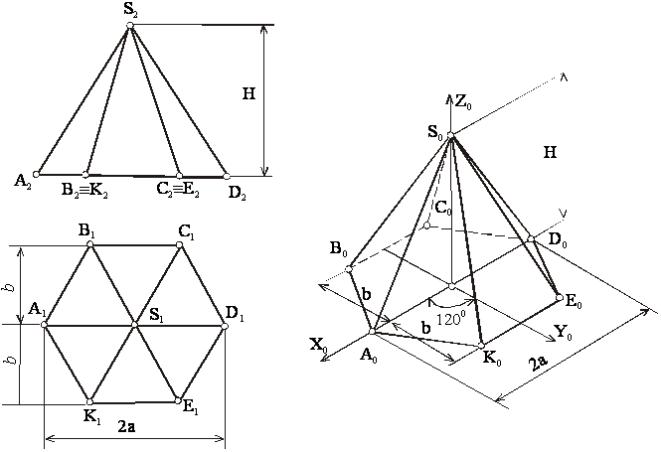
В качестве примера на
рисунке 49 приведена ортогональная проекция пирамиды (а) и ее изометрическая проекция (б). Для упрощения построений начало аксонометрических осей (точку 0) расположили в центре основания
пирамиды.
В практике построений часто
приходится строить изометрические проекции окружностей. Рассмотрим ее
построение. Чтобы иметь наглядное представление о расположении и величине осей
эллипсов, последние вписаны в грани куба с размерами, равными диаметру
окружности d (рисунок 50).
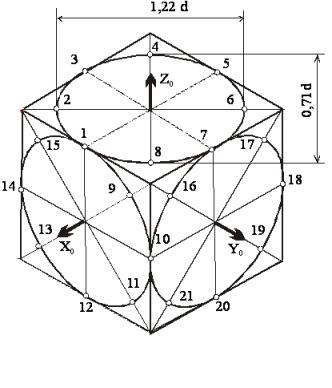Рассмотрим построение
эллипса на верхней грани куба. Как видно из рисунка, для построения эллипса
известны 8 ее точек. Расстояние между точками 1 и 5, 3 и 7 (вдоль
изометрических осей) равно диаметру окружности (отложены без искажения, т.к.
приведенные коэффициенты кх,
ку, кz равны единице). Большая ось эллипса (между точками 2
и 6) равна 0,71d. Соединив плавной линией полученные 8 точек, строим
эллипс, который является изометрической проекцией окружности диаметром d.
Аналогично строим эллипсы на остальных гранях куба.
Расстояния между точками для построений эллипсов следующие.
|
1-5=d 3-7=d 2-6=1,22d 4-8=0,71d |
1-12=d 14-10=d 15-11=1,22d 13-9=0,71d |
7-20=d 10-18=d 21-17=1,22d 16-19=0,71d |
4.2
Прямоугольная диметрическая проекция
Для
диметрических проекций кх=кz=к. Если взять ку=0,5к, то получим
к2+ к2+0,25к2=2,
отсюда к=0,94.
Тогда кх=кz=0,94, ку=0,47.
Следовательно, в прямоугольной диметрической проекции по двум осям
(Х0 и Z0) получается сокращение
линейных размеров до 0,47ℓ от
фактического (ℓ). Такие
коэффициенты искажений называются натуральными.
Для диметрических проекций ось Z0 располагают, как правило, вертикально. Углы между
осями будут следующими (рисунок 51).
Приближенно диметрические оси можно построить, если принять tg7◦10≈1/8,
tg41◦25'=7/8.
Тогда диметрические оси
можно построить, как показано на рисунке 52.
Ось Y0 может быть проведена также
как биссектриса угла x0oz0. Эту биссектрису можно
провести также с помощью циркуля (рисунок 53).
Из точки О проведем дугу окружности произвольным
радиусом. На пересечении ее с осями х0
и z0 отмечаем точки А и В. Далее из точек А и В делаем две засечки этим же радиусом,
через пересечение которых (точку Т)
пройдет биссектриса ОТ, продолжение
которой и будет осью Y0.
Указанными выше
коэффициентами искажений и диметрическими осями пользоваться неудобно. Поэтому
на практике разрешается пользоваться приведенными коэффициентами искажений по
осям (кх=кz=1, ку=0,5).
Для построения диметрической
проекции окружности впишем ее также в грани куба размерами, равными d.
На рисунке 54 показан пример
построения окружности в диметрической проекции.
Как видно из рисунка, здесь
также известны 8 точек, соединив которые, можно построить диметрическую
проекцию окружности.
Расстояния между точками для
построения эллипсов следующие:
|
1-2=d 3-4=d 5-6=1,06d 7-8=0,96d |
11-14=d 3-9=0,5d 10-13=1,06d 15-16=0,35d |
1-18=0,5d 11-20=d 17-21=1,06d 19-22=0,35d |
