Некоммерческое акционерное общество
АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра инженерной графики и прикладной механики
А.Д.Динасылов
ПРИКЛАДНАЯ МЕХАНИКА.
ОСНОВЫ РАСЧЕТОВ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ
Учебное пособие

Алматы 2009
Учебное пособие содержит примеры решения задач по разделу «Сопротивление материалов» дисциплины по выбору «Прикладная механика»/«Механика». Ранее на кафедре Инженерная графика и прикладная механика были выпущены конспекты лекций по этим дисциплинам, в которых ввиду ограниченности объема изложение теоретического материала сопровождалось небольшим числом примеров решения задач. В настоящем учебном пособии количество решенных примеров представляется достаточным для усвоения материала раздела «Сопротивление материалов», изложенного в конспектах лекций, и для подготовки к различного вида контролю знаний, включая экзамен. Решение задач предваряется кратким напоминанием основных теоретических сведений, причем ряд положений не вошел в конспекты лекций, однако на лекциях этот материал излагается.
Учебное пособие предназначено для студентов специальности 050717 - Теплоэнергетика и может использоваться студентами других специальностей, изучающих дисциплину «Механика» или «Прикладная механика».
Содержание
|
Введение |
4 |
|
1 Растяжение и сжатие |
6 |
|
1.1 Эпюры нормальных сил |
6 |
|
1.2 Основные соотношения при растяжении и сжатии |
10 |
|
1.3 Расчеты на прочность и жесткость |
14 |
|
1.4 Расчет статически неопределимых систем |
18 |
|
2 Кручение |
23 |
|
2.1 Эпюры крутящих моментов |
23 |
|
2.2 Касательные напряжения. Угол закручивания и потенциальная энергия деформации |
26 |
|
2.3 Расчеты на прочность и жесткость по методу допускаемых напряжений |
28 |
|
2.4 Статически неопределимые системы |
30 |
|
3 Сдвиг |
31 |
|
4 Геометрические характеристики поперечных сечений стержня |
33 |
|
4.1 Статические моменты сечения |
34 |
|
4.2 Моменты инерции сечений. Радиусы инерции |
35 |
|
5 Прямой изгиб |
40 |
|
5.1 Эпюры поперечных сил и изгибающих моментов |
40 |
|
5.2 Напряжения в поперечных сечениях. Расчеты на прочность по допускаемым напряжениям |
50 |
|
5.3 Перемещения при изгибе и расчеты на сложность |
57 |
|
6 Сложное сопротивление |
61 |
|
6.1 Косой изгиб |
61 |
|
6.2 Внецентренное растяжение (сжатие) |
65 |
|
6.3 Совместное действие изгиба с растяжением (сжатием) |
72 |
|
6.4 Совместное действие изгиба с кручением |
|
|
7 Продольный изгиб (устойчивость сжатых стержней) |
77 |
|
7.1 Расчет сжатых стержней по формулам Эйлера и Ясинского |
78 |
|
7.2 Расчет сжатых стержней по коэффициенту продольного изгиба |
80 |
|
Список литературы |
83 |
Введение
В настоящем пособии рассматриваются простые, наиболее типичные методы расчета элементов конструкций на прочность и жесткость при различных видах нагружения. Под прочностью, как известно, понимают способность твердых тел воспринимать действие внешних сил (а также других факторов) без разрушения. Наряду с этим нарушением прочности считается также возникновение пластических деформаций. В пособии рассматриваются задачи статического расчета, то есть предполагается, что нагрузки, приложенные к конструкции, достаточно медленно (так, что силами инерции можно пренебречь) возрастают от нуля до номинальных значений, и в дальнейшем они либо остаются постоянными, либо так же медленно изменяются.
Основным методом расчета на прочность является расчет по допускаемым напряжениям, согласно которому достижение хотя бы в одной точке рабочим напряжением (в общем случае - эквивалентным напряжением, определяемым по одной из теорий прочности) предельного значения означает нарушение прочности всей конструкции. Примем следующие обозначения: s - расчетное (в общем случае эквивалентное) напряжение для наиболее нагруженной (опасной) точки; [s] - допускаемое напряжение, составляющее [n]-ю долю от предельного напряжения; sпред - предельное напряжение для рассматриваемого материала (предел прочности или предел текучести при статическом нагружении); [n] - требуемый (нормативный) коэффициент запаса прочности; n - фактический (расчетный) запас прочности. Тогда условие прочности записывается в виде
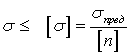
или иногда (что, по существу, одно и то же) в виде
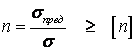 .
.
При таких видах нагружения стержня как растяжение, сжатие, чистый изгиб, а также при кручении прочность определяется единственным напряжением (одним компонентом напряженного состояния), возникающим в поперечных, то есть перпендикулярных оси стержня, сечениях. В первых трех случаях расчет ведется по нормальным напряжениям s, а при кручении - по касательным напряжениям t. В последнем случае в приведенных выше формулах вместо s следует подставлять t. В общем случае нагружения в элементах конструкции возникает сложное напряженное состояние, и тогда в качестве расчетного напряжения следует принимать эквивалентное напряжение, определяемое с использованием так называемых теорий прочности.
Классификацию видов
нагружения стержня производят согласно тому, какие внутренние силовые факторы
возникают в поперечных сечениях бруса. Для определения внутренних силовых
факторов (ВСФ) используют метод сечений (см. рисунок 1). Согласно этому методу
в любом поперечном сечении можно мысленно рассечь стержень, находящийся в
равновесии под действием заданной системы внешних сил (см. рисунок 1,a),
на две части и заменить действие отброшенной части на оставшуюся часть
внутренними силами, распределенными по какому-то неизвестному закону (см.
рисунок 1,б). Из статики известно, что любую систему сил можно привести
к главному вектору и главному моменту. Выбрав в качестве точки приведения центр
тяжести поперечного сечения, приведем внутренние силы к главному вектору ![]() и главному моменту
и главному моменту ![]() (см. рисунок 1,в). Спроецировав
(см. рисунок 1,в). Спроецировав ![]() и
и ![]() на
координатные оси х, у, z, получим шесть ВСФ (см. рисунок 1,г).
Взаимно ортогональные оси х, у, z должны быть направлены следующим
образом: одна из координатных осей (будем направлять ось z) -
перпендикулярно поперечному сечению; две оставшиеся координатные оси должны
совпадать с так называемыми главными осями инерции сечения (в случае сечения,
имеющего хотя бы одну ось симметрии, одна из координатных осей должна совпадать
с ней).
на
координатные оси х, у, z, получим шесть ВСФ (см. рисунок 1,г).
Взаимно ортогональные оси х, у, z должны быть направлены следующим
образом: одна из координатных осей (будем направлять ось z) -
перпендикулярно поперечному сечению; две оставшиеся координатные оси должны
совпадать с так называемыми главными осями инерции сечения (в случае сечения,
имеющего хотя бы одну ось симметрии, одна из координатных осей должна совпадать
с ней).
 |
Так как стержень в целом находится в равновесии, то мысленно отсеченные части его должны находиться в равновесии. Воспользовавшись условиями равновесия для любой из отсеченных частей, при известных внешних силах несложно найти ВСФ.
Для того чтобы определить, какой вид нагружения имеет место в конкретном случае, надо установить, какие ВСФ возникают в поперечных сечениях рассматриваемого стержня. ВСФ в различных сечениях стержня могут иметь различные значения. Принято представлять закон изменения ВСФ вдоль оси стержня в виде графика, называемого эпюрой. Ось эпюры по форме повторяет ось стержня; перпендикулярно оси эпюры откладывают в масштабе (можно приблизительно) отрезки, пропорциональные величине исследуемого ВСФ в соответствующих поперечных сечениях. Эпюру принято штриховать линиями, перпендикулярными к оси стержня, при этом каждый штрих в принятом масштабе представляет собой величину ВСФ в поперечном сечении стержня, соответствующую данной точке на оси эпюры. В случае прямолинейного горизонтального стержня эпюры обычно строят под схемой стержня.
При статическом нагружении конструкций из пластичных материалов, кроме расчета по допускаемым напряжениям, применяется также расчет по предельному состоянию (по разрушающей нагрузке, по несущей способности). В этом случае в качестве предельной нагрузки принимается такая нагрузка, при которой дальнейшее ее возрастание невозможно, так как конструкция превращается в геометрически изменяемую систему вследствие того, что напряжения, равные пределу текучести, возникают не в отдельных ее точках, а охватывают полностью поперечное сечение стержня.
Для проверки или определения размеров конструкций, при которых перемещения, возникающие при действии на конструкцию эксплуатационных нагрузок, не превышают некоторых допустимых по тем или иным соображениям значений, служат расчеты на жесткость. Напомним, что жесткостью называют способность твердых тел воспринимать нагрузку без существенного изменения размеров и формы.
В зависимости от того, как сформулирована задача в конкретном случае, любой метод расчета позволяет решать три вида задач: проверочный расчет, проектный расчет (определение размеров элементов), определение допускаемого значения нагрузки.
1 Растяжение и сжатие
Растяжением называют такой вид нагружения стержня, при котором в его поперечных сечениях возникает только нормальная (продольная) сила N, а все остальные ВСФ равны нулю. Сжатие формально отличается от растяжения только знаком N (при растяжении направление N совпадает с направлением внешней нормали к поперечному сечению стержня, а при сжатии - с направлением внутренней нормали). Вместе с тем есть качественные различия между поведением стержней при растяжении и сжатии. Так, сжатие длинных стрежней сопровождается изгибом и потерей устойчивости. Во всех рассматриваемых в данной главе случаях мы будем считать, что устойчивость обеспечена.
1.1 Эпюры нормальных сил
Согласно методу сечений нормальная сила N в каком-либо поперечном сечении равна алгебраической сумме проекций на продольную ось стержня всех внешних сил, действующих по одну сторону от рассматриваемого сечения (т.е. приложенных к одной из отсеченных частей стрежня),
![]() (1.1)
(1.1)
В случае растяжения N
считается положительной, в случае сжатия - отрицательной, поэтому в выражении
(1.1) проекция какой-либо внешней силы ![]() берется
со знаком “плюс” тогда, когда при разложении этой силы ее составляющая вдоль
продольной оси
берется
со знаком “плюс” тогда, когда при разложении этой силы ее составляющая вдоль
продольной оси ![]() направлена кнаружи от
отсеченной части стержня; когда составляющая
направлена кнаружи от
отсеченной части стержня; когда составляющая ![]() направлена
вовнутрь отсеченной части, ее следует брать со знаком “минус”.
направлена
вовнутрь отсеченной части, ее следует брать со знаком “минус”.
 Обычно растяжение
стержней с прямолинейной осью вызывается внешними силами, действующими вдоль
оси стержня. Если, кроме сосредоточенных сил, имеются продольные распределенные
силы интенсивности
Обычно растяжение
стержней с прямолинейной осью вызывается внешними силами, действующими вдоль
оси стержня. Если, кроме сосредоточенных сил, имеются продольные распределенные
силы интенсивности ![]() , то в правую часть формулы
(1.1) следует добавить выражение
, то в правую часть формулы
(1.1) следует добавить выражение ![]() , где интегрирование
производится по длине каждого участка, на который действует распределенная
нагрузка, а суммирование выполняется по всем участкам, расположенным по одну
сторону от рассматриваемого сечения.
, где интегрирование
производится по длине каждого участка, на который действует распределенная
нагрузка, а суммирование выполняется по всем участкам, расположенным по одну
сторону от рассматриваемого сечения.
Пример 1 - Для изображенного на рисунке 2 а стержня ступенчато-переменного сечения (площади поперечных сечений А1 = 10 см2, A2 = 20 см2), нагруженного силами F1 = 3 кН, F2 = 7 кН и F3 = 14 кН, требуется построить эпюру продольных сил.
Решение. Рассматриваемый стержень имеет 4 участка: ВС, CD, DE, ЕК. В качестве границ участков примем сечения, в которых приложены внешние силы или скачкообразно меняется площадь сечений.
Так как силы F1, F2, F3 действуют вдоль оси стержня (собственный вес не учитываем), то в его поперечных сечениях возникает только нормальная сила N. Конец стержня К жестко защемлен. Поскольку все внешние силы направлены вдоль оси стержня z, то и опорная реакция RK направлена вдоль этой оси (см.рисунок 2,б). Составив уравнение равновесия стержня в виде равенства нулю суммы проекций всех сил на ось z
![]()
найдем реакцию опоры
![]()
Переходим к определению нормальных сил.
Определим нормальную силу в произвольном поперечном сечении I-I участка ВС стержня. Мысленно разрежем стержень по сечению I-I, которое можно провести в любом месте между точками В и С, и отбросим его левую часть, приложив к оставшейся правой части в сечении I-I нормальную силу N1 (см. рисунок 2,в). Согласно выражению (1.1) и правилу знаков найдем силу
![]()
Для всех сечений участка ВС нормальная сила постоянна и равна 3 кН.
Чтобы определить N на участке CD, проведем произвольное сечение II-II и отбросим левую часть от сечения стержня (см. рисунок 2,г). К оставшейся правой части для сохранения ее равновесия должна быть приложена сила N2, значение которой будет равно
![]() кН.
кН.
Проводя сечение III-III и отбрасывая левую часть (см. рисунок 2,д), найдем N на участке DE
![]() кН.
кН.
Замечаем, что N3= N2, то есть изменение площади поперечного сечения не влияет на величину поперечной силы, и два участка CD и DE можно было рассматривать как один участок СЕ.
Найдем N на участке ЕК, для чего проведем сечение IV-IV и отбросим левую часть (см. рисунок 2,е)
![]() кН.
кН.
Напомним, что силу N на каждом участке можно определять, отбрасывая правую от соответствующего сечения часть стержня и рассматривая силы, приложенные к оставшейся левой части. Так, для участка ЕК можно найти (см. рисунок 2,ж)
![]() кН.
кН.
По найденным значениям N построим эпюру. Для этого под схемой стержня проведем ось эпюры параллельно оси стержня (см. рисунок 2,и), спроецируем на ось характерные сечения (границы участков) и отложим с примерным соблюдением масштаба величины нормальной силы. Выше оси будет откладывать положительные значения, ниже - отрицательные. На каждом участке в данном случае N постоянна, поэтому эпюра на каждом участке параллельна оси. Отметим, что изображать отсеченные части стержня, как на рисунках 2,в-ж, необязательно, здесь это сделано для большей наглядности.
Пример 2 - Построить эпюру N для стержня AG, изображенного на рисунке 3,a. На участке CD стержень нагружен распределенной нагрузкой с постоянной интенсивностью q.
Решение. Рассматривая все время правую от сечения отсеченную часть стержня, можно обойтись без определения опорной реакции.
Для построения эпюры N выделим участки, считая границами крайние сечения, в которых приложены сосредоточенные силы, а также сечения, в которых начинается и заканчивается распределенная нагрузка. Проводя произвольное сечение на каждом участке (см. рисунки 3,b-e), найдем N. Положение сечения будет фиксировать с помощью координаты z; начало координат для каждого участка может быть своим.
Участок GE (0 £
z1 £ 0,15 м): ![]() . На участке GE нормальной силы
нет.
. На участке GE нормальной силы
нет.
Участок ЕD (0,15 м £
z2 £ 0,3 м): ![]() кН.
На участке ЕD нормальная сила постоянная, отрицательная. Строим эпюру (см.
рисунок 3,ж).
кН.
На участке ЕD нормальная сила постоянная, отрицательная. Строим эпюру (см.
рисунок 3,ж).
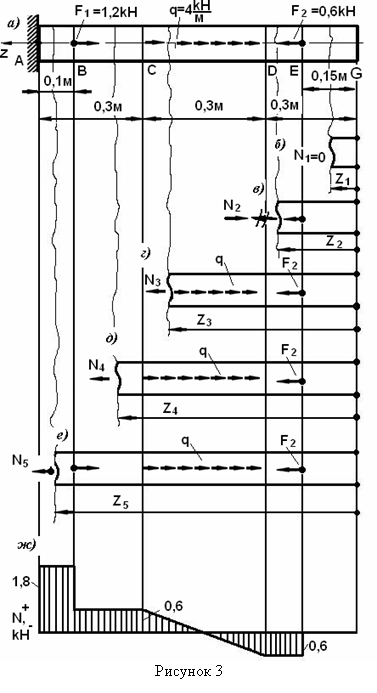 Участок DC (0,3 м £ z3 £
0,6 м):
Участок DC (0,3 м £ z3 £
0,6 м): 
На этом участке величина N зависит от положения сечения, определяемого координатой z3. Зависимость эта линейная, следовательно, эпюра будет представлять собой наклонную к оси прямую, для построения которой достаточно подсчитать значение N3 в граничных сечениях. Имеем: при z3=0,3 м, N3 =-F2=-0,6 кН; при z3=0,6 м, N3=-F2 +g∙0,3=0,6 кН. Откладываем эти значения от оси эпюры в соответствующих сечениях и соединяем две точки прямой (см. рисунок 3,ж).
Участок СВ (0,6м £ z4 £ 0,8 м): N4 =-F2+q×0,3 = 0,6 кН. Эпюра - прямая, параллельная оси, так как N4 от z4 не зависит.
Участок ВА (0,8 м £ z5 £ 0,9 м): N5 = - F2 + g∙0,3 +F1 = 1,8 кН. Здесь эпюра также параллельна своей оси.
Пример 3 - Стальной цилиндрический стержень ступенчатого сечения, изображенный на рисунке 4,a, нагружен силой F = 100 H. Диаметры равны D = =0,2 м, d = 0,15 м. Построить эпюру N с учетом собственного веса стержня.
Решение. Кроме сосредоточенной силы F, стержень нагружен распределенными силами собственного веса с постоянными интенсивностями q1 в нижней части и q2 - в верхней (см. рисунок 4,а). Определим q1 и q2
![]() Н/м,
Н/м,
![]() Н/м.
Н/м.
![]() Здесь r - плотность материала (для стали r = 7,8×10 кг/м3), g - ускорение свободного
падения (g = 9,81 м/с2); А1 и А2
- площадь поперечного сечения нижнего и верхнего
участков соответственно.
Здесь r - плотность материала (для стали r = 7,8×10 кг/м3), g - ускорение свободного
падения (g = 9,81 м/с2); А1 и А2
- площадь поперечного сечения нижнего и верхнего
участков соответственно.
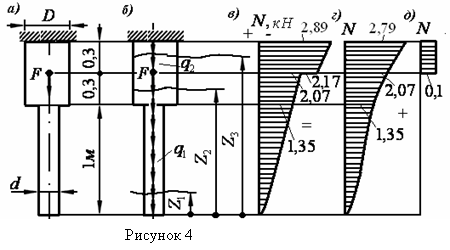 Определим N на каждом участке и построим эпюру (см. рисунок 4,б).
На нижнем участке N определим как сумму всех сил, приложенных к нижней от
выбранного сечения части: тогда, приняв начало z1 на нижнем
конце стержня, запишем
Определим N на каждом участке и построим эпюру (см. рисунок 4,б).
На нижнем участке N определим как сумму всех сил, приложенных к нижней от
выбранного сечения части: тогда, приняв начало z1 на нижнем
конце стержня, запишем ![]() при
при ![]()
![]() при
при
![]()
![]() кН.
кН.
На среднем участке (от сечения, где ступенчато изменяется
сечение стержня, до сечения, где приложена сила F) рассмотрим нижнюю от
произвольного сечения часть стержня. Тогда, выбрав начало z2 там
же, где начало z1, запишем ![]() при
при ![]() м
м ![]() кН; при
кН; при ![]() м
м
![]() кН.
кН.
На верхнем участке – аналогично ![]() при
при
![]() м
м ![]() кН,
при
кН,
при ![]() м
м ![]() кН.
кН.
Отметим, что эпюру N можно было бы получить как сумму двух эпюр, построенных отдельно от собственного веса и от силы F, что изображено на рисунках 4,г и д.
1.2 Основные соотношения при растяжении и сжатии
При растяжении или сжатии в поперечных сечениях стержней возникают нормальные напряжения s, которые распределяются равномерно по сечению и определяются как
![]() (1.2)
(1.2)
где N - нормальная сила в рассматриваемом сечении;
А - площадь поперечного сечения.
Абсолютное удлинение однородного стержня постоянного сечения, нагруженного растягивающими силами F, приложенными по концам стержня, определяется (в случае материала, подчиняющегося закону Гука) по формуле
![]() (1.3)
(1.3)
где Е - модуль упругости 1-го рода (модуль Юнга) материала.
В общем случае ![]() определяется как
определяется как
![]() .
(1.4)
.
(1.4)
Здесь интегрирование производится по длине участка, а суммирование - по числу участков.
Общая формула для определения потенциальной энергии упругой деформации U, накопленной в стержне, имеет вид
![]() (1.5)
(1.5)
где интегрирование и суммирование производится так же, как в (1.4).
Для стержня, растянутого или сжатого силами F по концам, потенциальную энергию можно определить через работу внешних сил как
![]() . (1.6)
. (1.6)
Для определения перемещений в статически определимых шарнирно-стержневых системах поступают следующим образом. Находят из условий статики продольные силы в элементах системы и по закону Гука определяют абсолютное удлинение элементов. Так как элементы системы при деформации не разъединяется, то, пользуясь методом засечек, устанавливают геометрические соотношения между перемещениями, из которых и определяют искомые перемещения. При этом следует иметь в виду, что элементы системы, кроме того, получают удлинения и могут поворачиваться вокруг шарниров. Поэтому каждая точка элемента перемещается вдоль оси и по дуге окружности соответствующего радиуса. Эти дуги (засечки) можно ввиду малости перемещений заменять перпендикулярами к радиусам.
По закону Гука относительная продольная деформация при растяжении или сжатии
![]() (1.7)
(1.7)
а относительная поперечная деформация
![]() (1.8)
(1.8)
где m - коэффициент поперечной деформации материала (коэффициент Пуассона).
Относительное изменение площади поперечного сечения и объема стержня могут быть определены по формулам
![]() , (1.9)
, (1.9)
![]() (1.10)
(1.10)
Для стержня, растянутого или сжатого силами F, приложенными по концам, имеем
![]() . (1.11)
. (1.11)
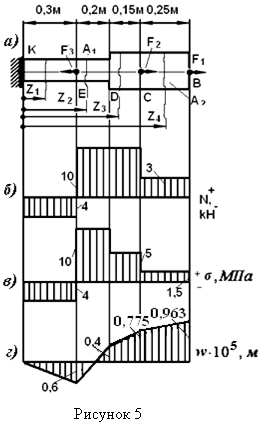
Пример 4 - Для стержня, рассмотренного в примере 1, построить эпюру нормальных напряжений σ и эпюру перемещений w поперечных сечений вдоль оси z, определить потенциальную энергию U, накопленную в стержне. Материал стержня - сталь, модуль упругости E=2∙105 МПа.
Решение. Изобразим стержень и эпюру N, построенную в примере 1 (см. рисунки 5,а,б).
 Напряжения на каждом участке определяются
по формуле (1.2):
Напряжения на каждом участке определяются
по формуле (1.2): ![]()
![]()
![]()
![]()
Эпюра σ изображена на рисунке 5,в.
Переходим к построению эпюры перемещений w (см. рисунок 5,г).
Начинаем строить эпюру от левого конца стержня. Так как левое сечение
закреплено, то его перемещение равно нулю. Проведем произвольное сечение на участке
КЕ, положение которого будем определять с помощью координаты z1.
Очевидно, что перемещение этого сечения w1 вдоль оси равно
абсолютному удлинению ![]() части стержня длиной z1.
Так как N и A на участке постоянны, то
части стержня длиной z1.
Так как N и A на участке постоянны, то ![]() Перемещения w1 линейно зависят от z1,
и эпюра перемещений на участке представляет собой наклонную прямую. Найдем
значения, соответствующие двум граничным сечениям: при z1=0 w1=0; при z1=0,3 м
Перемещения w1 линейно зависят от z1,
и эпюра перемещений на участке представляет собой наклонную прямую. Найдем
значения, соответствующие двум граничным сечениям: при z1=0 w1=0; при z1=0,3 м
![]() .
.
Перемещения на участке ЕК отрицательны, то есть стержень здесь сжат, чему соответствует деформация укорочения, и все сечения перемещаются влево.
На участке ED перемещение w2 равно удлинению
части стержня длиной z2 ![]() Значение w2
линейно зависит от z2, следовательно, эпюра прямая, и ее
значения в граничных сечениях равны: при z2=0,3
м w2=-0,6∙10-5 м; при z2=0,5
м
Значение w2
линейно зависит от z2, следовательно, эпюра прямая, и ее
значения в граничных сечениях равны: при z2=0,3
м w2=-0,6∙10-5 м; при z2=0,5
м ![]()
Аналогично строим эпюру на двух остальных участках.
На участке DC: ![]() при z3=0,5
м w3=0,4∙10-5 м,
при z3=0,65 м w3=0,775∙10-5 м.
при z3=0,5
м w3=0,4∙10-5 м,
при z3=0,65 м w3=0,775∙10-5 м.
На участке CB: ![]() при z4=0,65
м w4=0,775∙10-5 м, при z4=0,9
м w4=0,963∙10-5 м.
Перемещение правого конца стержня, очевидно, равно полному
удлинению стержня.
при z4=0,65
м w4=0,775∙10-5 м, при z4=0,9
м w4=0,963∙10-5 м.
Перемещение правого конца стержня, очевидно, равно полному
удлинению стержня.
Потенциальную энергию деформации найдем по формуле (1.5) как
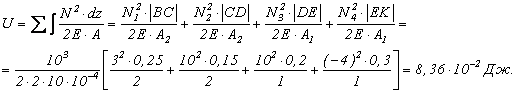
Пример 5 - Определить перемещение точки приложения силы и нормальные напряжения в упругих стержнях системы, изображенной на рисунке 6,а.
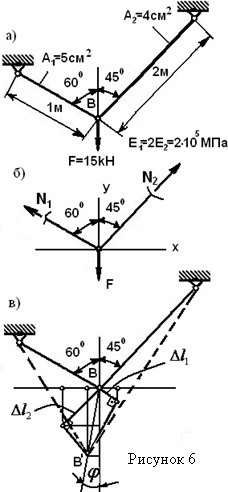 Решение. Воспользовавшись методом вырезания узлов (см. рисунок 6,б),
запишем условие равновесия узла в виде
Решение. Воспользовавшись методом вырезания узлов (см. рисунок 6,б),
запишем условие равновесия узла в виде
![]()
![]()
Решая совместно эти уравнения, найдем нормальные силы в стержнях N1=11,0 кН и N2=13,5 кН.
Нормальные напряжения в стержнях равны
![]()
![]()
Для определения перемещения d точки В найдем сначала абсолютные удлинения стержней
![]()
![]()
Затем воспользуемся методом засечек (см. рисунок 6,в), заменив
дуги окружностей перпендикулярами к положением стержней в недеформированном
состоянии. Положение точки приложения силы в деформированном состоянии
находится на пересечении этих перпендикуляров (точка В'); деформированное
состояние системы показано пунктиром. Вектор ![]() '
представляет собой вектор полного перемещения точки В. Величину этого
перемещения и направление найдем по его проекциям на оси x и y.
Имеем
'
представляет собой вектор полного перемещения точки В. Величину этого
перемещения и направление найдем по его проекциям на оси x и y.
Имеем ![]()
![]()
Тогда ![]()
![]() и
и ![]()
1.3 Расчеты на прочность и жесткость
По методу допускаемых напряжений расчет на прочность при растяжении или сжатии производят по формуле
![]() (1.12)
(1.12)
Здесь σ -
расчетное напряжение в поперечном сечении, N - нормальная сила, A
- площадь поперечного сечения, ![]() - допускаемое
напряжение.
- допускаемое
напряжение.
Допускаемое напряжение ![]() назначается как часть от предельного
для данного материала напряжения
назначается как часть от предельного
для данного материала напряжения ![]()
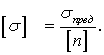 (1.13)
(1.13)
В качестве предельного напряжения σпред для пластических материалов берется предел текучести σт (если материал неодинаково работает на напряжение и сжатие, то, соответственно, σтр - предел текучести при растяжении и σтс - предел текучести при сжатии), а для хрупких - предел прочности (временное сопротивление) σв; в случае материалов, неодинаково сопротивляющихся растяжению и сжатию, соответственно, σвр - предел прочности при растяжении и σвс – предел прочности при сжатии. В формуле (1.13) [n] - нормативный коэффициент запаса (запас прочности), величина которого зависит от ответственности и условий работы рассчитываемой конструкции, точности расчетной схемы и ряда других факторов.
В случае стержня постоянного сечения расчет достаточно выполнить для сечения, где нормальная сила N максимальна по модулю. В случае стержня переменного сечения нужно сначала определить опасное сечение, где максимальны напряжения, и затем выполнить для него расчет.
Если, кроме обеспечения прочности, поставлено условие, чтобы перемещение какой-либо точки системы или сечения δ не превосходило заданной допустимой величины [δ], то производят проверку на жесткость по условию
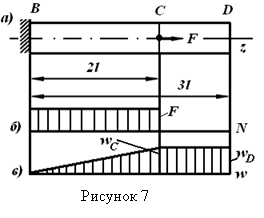
![]() . (1.14)
. (1.14)
Пример 6 - Стальной стержень BD в сечении С нагружен силой F (см. рисунок 7,а). Приняв [σ] = 200 МПа, А = 2 см2, l =0,5 м, Е=2·105 МПа, допускаемую величину перемещения правого торца стержня [δ]D = 0,3 мм, определить величину допускаемой силы [F].
Решение. Участок стержня ВС испытывает растяжение (N = F), а на участке CD продольной силы нет; эпюра N приведена на рисунке 7,б. На рисунке 7,в показана эпюра перемещений сечений стержня w вдоль его оси, причем на участке CD все сечения имеют одинаковое перемещение.
Из условия прочности
![]()
выражаем допускаемое значение силы F
![]()
Из условия жесткости
![]()
также выражаем допускаемое значение силы F
![]()
Сопоставление двух значений [F] показывает, что определяющим является условие жесткости, то есть для того, чтобы удовлетворить обоим условиям, следует принять [F] = [F][d] = 12 кН; при этом wD будет равно [δ]D, а напряжения будут меньше, чем [σ].
 Пример 7 -
Определить объем колонны, представляющей собой каменную кладку для трех случаев:
1) простая призматическая (или цилиндрическая) колонна (см. рисунок 8,а);
2) колонна, состоящая из двух призматических (или цилиндрических) участков (см.
рисунок 8,б); 3) колонна равного сопротивления, в каждом поперечном
сечении которой напряжения одинаковы. Сжимающая сила F равна 2,0 МН,
высота колонны h составляет 30 м, плотность ρ=1,5·103
кг/м3, допускаемое напряжение [σ]=1,2 МПа.
Пример 7 -
Определить объем колонны, представляющей собой каменную кладку для трех случаев:
1) простая призматическая (или цилиндрическая) колонна (см. рисунок 8,а);
2) колонна, состоящая из двух призматических (или цилиндрических) участков (см.
рисунок 8,б); 3) колонна равного сопротивления, в каждом поперечном
сечении которой напряжения одинаковы. Сжимающая сила F равна 2,0 МН,
высота колонны h составляет 30 м, плотность ρ=1,5·103
кг/м3, допускаемое напряжение [σ]=1,2 МПа.
Решение. 1)
В этом случае условие прочности имеет вид ![]() ,
,
откуда
![]()
![]()
2) Условие прочности для верхней части имеет вид  ,
,
откуда
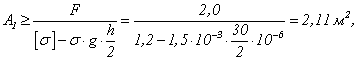
![]()
Из условия прочности для нижней части 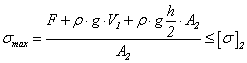
найдем

![]()
Объем колонны составит ![]()
3) Рассматривая элемент бруса, выделенный двумя бесконечно близко
расположенными сечениями (рисунок 1.8 в, г), запишем уравнение
равновесия в виде ![]() откуда
откуда ![]() Интегрируя это
выражение, получим
Интегрируя это
выражение, получим ![]() или
или ![]() . При z=0 уравнение дает площадь
верхнего поперечного сечения стержня Amin, которое должно
быть равно
. При z=0 уравнение дает площадь
верхнего поперечного сечения стержня Amin, которое должно
быть равно ![]() , следовательно
, следовательно ![]() ,
и закон изменения площади поперечного сечения стержня равного сопротивления
получает вид
,
и закон изменения площади поперечного сечения стержня равного сопротивления
получает вид 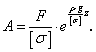 Площадь сечения в основании
колонны равна
Площадь сечения в основании
колонны равна 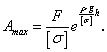 Чтобы определить объем
колонны, найдем сначала ее вес G как разность нормальных сил в нижнем и
верхнем сечениях
Чтобы определить объем
колонны, найдем сначала ее вес G как разность нормальных сил в нижнем и
верхнем сечениях
![]()
Объем колонны определяется как
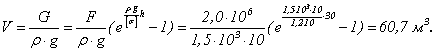
Сравнивая объем колонны для всех трех случаев, видим, что для равнопрочной колонны получается существенный выигрыш.
Пример 8 - Для стержневой системы, изображенной на рисунке 9 а, проверить условие прочности, приняв F=40 кН, [σр]=100 МПа, [σсж]=60 МПа.
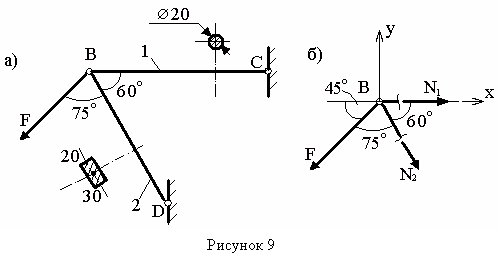
Решение. Прежде всего определим продольные силы в стержнях 1 и 2, для чего мысленно выражаем узел В и рассмотрим от брошенных частей силами N1 и N2. Записывая уравнения равновесия (для плоской системы сходящихся сил) в виде сумм проекций всех сил на оси x и y
![]()
![]()
найдем из этих уравнений силы
![]()
![]()
Знак минус показывает, что сила N2 в действительности направлена противоположно первоначально выбранному направлению, то есть стержень 2 сжат.
Определяем площади поперечных сечений стержней
![]()
![]()
Наконец, определяем нормальные напряжения в поперечных сечениях стержней и сравниваем их с допускаемым напряжением
![]()
![]()
Отсюда заключаем, что условие прочности выполняется для стержня 2 и не выполняется для стержня 1. Значит, для конструкции в целом условие прочности не выполняется, т.е. она может получить значительные пластические деформации или (и) разрушиться.
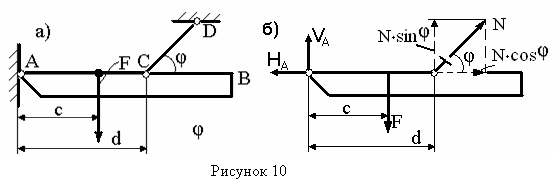 Пример 9 -
Жесткий брус АВ шарнирно закреплен в точке А и поддерживается
стальной тягой круглого поперечного сечения CD (см. рисунок 10,а).
Требуется определить из условия прочности диаметр поперечного сечения тяги CD,
приняв следующие данные:
Пример 9 -
Жесткий брус АВ шарнирно закреплен в точке А и поддерживается
стальной тягой круглого поперечного сечения CD (см. рисунок 10,а).
Требуется определить из условия прочности диаметр поперечного сечения тяги CD,
приняв следующие данные: ![]()
![]()
![]() ,
, ![]()
![]()
![]()
Решение.
Мысленно освободив брус от связей в точке А и разрезав тягу CD,
заменим действие отброшенных связей неизвестными силами НА, VA
и N. Все три силы могут быть определены из трех уравнений
равновесия, которые могут быть составлены для рассматриваемой плоской системы
сил. Однако для решения задачи требуется знать только силу N, поэтому
ограничимся одним уравнением ![]() откуда
откуда
![]()
Из условия прочности
![]() имеем
имеем ![]()
Диаметр тяги должен быть назначен так, чтобы выполнялось условие
![]()
1.4 Расчет статически неопределимых систем
Статически неопределимыми называются такие системы, для которых нельзя определить реакции связей и ВСФ во всех элементах, пользуясь только уравнениями статики. Разность между числом неизвестных и числом независимых уравнений статики называет степенью статической неопределимости системы. Общий план решения статически неопределимых систем состоит в следующем:
а) составляют уравнения статики и определяют степень статической неопределимости;
б) из рассмотрения деформированного состояния системы составляют уравнения, связывающие деформации отдельных элементов (уравнения совместности деформаций);
в) в уравнениях совместности деформаций величины деформаций (удлинений) выражают по закону Гука через усилия;
г) уравнения статики и преобразованные уравнения совместности деформаций, полученные в предыдущем пункте, решаются совместно.
Изменение температуры стержней статически неопределимых систем вызывает температурные деформаций, зависящие от длины стержня l, коэффициента линейного расширения материала α и изменения температуры ∆t. Эти деформации, как правило, не удовлетворяют условием совместности деформаций, вследствие чего в стержнях возникают упругие напряжения и соответствующие им упругие деформации. Суммарные деформации (упругие плюс температурные) должны удовлетворять условиям совместности деформаций. Решение задач о температурных напряжениях производится по общей схеме, рассмотренной выше, при этом суммарное удлинение стержня определяется как
![]() (1.15)
(1.15)
где ![]() – упругое абсолютное удлинение стержня,
определяемое по формуле (1.3) или (1.4);
– упругое абсолютное удлинение стержня,
определяемое по формуле (1.3) или (1.4);
![]() -
температурное абсолютное удлинение, определяемое по формуле
-
температурное абсолютное удлинение, определяемое по формуле
![]() (1.16)
(1.16)
Изготовление статически неопределимых систем требует весьма точного выдерживания размеров стержней с тем, чтобы соединение концов стержней можно было осуществить без приложения усилий. В противном случае возникают напряжения, называемые монтажными или начальными. Определение монтажных напряжений производят также из условий статики и условий совместности деформаций. При этом в последних условиях учитывают наличие заданной неточности в длинах элементов системы. В выражения удлинений по закону Гука подставляют проектные длины, а не фактические, так как они мало отличаются друг от друга.
При расчете на прочность
по допускаемым напряжениям необходимо обеспечить условие ![]() в самом напряженном стержне. Если при
этом допускаемое напряжение
в самом напряженном стержне. Если при
этом допускаемое напряжение ![]() определяется по
отношению к пределу текучести
определяется по
отношению к пределу текучести ![]() то фактический запас
прочности для статически неопределимых систем всегда оказывается больше, чем
для статически определимых. Объясняется это тем, что в статически определимых
системах достижение предела текучести хотя бы в одном элементе означает
выпадение соответствующей связи, что делает систему кинематически изменяемой. В
статически неопределимых системах исчерпание грузоподъемности наступает тогда,
когда напряжения во всех элементах достигнет предела текучести, то есть система
становится кинематически изменяемой тогда, когда текучесть последовательно
охватит все стержни системы.
то фактический запас
прочности для статически неопределимых систем всегда оказывается больше, чем
для статически определимых. Объясняется это тем, что в статически определимых
системах достижение предела текучести хотя бы в одном элементе означает
выпадение соответствующей связи, что делает систему кинематически изменяемой. В
статически неопределимых системах исчерпание грузоподъемности наступает тогда,
когда напряжения во всех элементах достигнет предела текучести, то есть система
становится кинематически изменяемой тогда, когда текучесть последовательно
охватит все стержни системы.
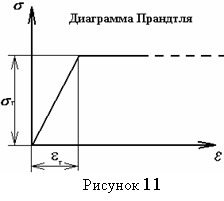 Расчет по несущей
способности (по предельному состоянию) состоит в следующем. Расчетным путем
определяется предельное значение нагрузки, в предположении, что материал стержней
является идеальным упруго-пластическим (принимается диаграмма деформирования
Прандтля, изображенная на рисунке 11). Предельная нагрузка
Расчет по несущей
способности (по предельному состоянию) состоит в следующем. Расчетным путем
определяется предельное значение нагрузки, в предположении, что материал стержней
является идеальным упруго-пластическим (принимается диаграмма деформирования
Прандтля, изображенная на рисунке 11). Предельная нагрузка ![]() определяется тогда только из условий
статики (условия совместности не нужны), так как в предельном состоянии усилия
в стержнях
определяется тогда только из условий
статики (условия совместности не нужны), так как в предельном состоянии усилия
в стержнях ![]() равны
равны ![]() . При
заданном коэффициенте запаса прочности [n] допускаемая сила [F] определяется как
. При
заданном коэффициенте запаса прочности [n] допускаемая сила [F] определяется как ![]() .
.![]()
Пример 10 -
Жесткий брус АВ поддерживается шарнирной опорой А и двумя стальными тягами 1 и
2 (см. рисунок 12,а). Требуется подобрать площади поперечных сечений тяг
из условия прочности по допускаемым напряжениям, если площади связаны соотношением
А1:А2=1:3. В расчетах принять следующие данные: ![]()
![]() [n]=1,5,
a=d=2 м, b=4,5 м, c=e=2,5 м,
[n]=1,5,
a=d=2 м, b=4,5 м, c=e=2,5 м, ![]()
Решение. Приложив к брусу все действующие на него активные и реактивные силы (рисунок 12 б), запишем уравнения равновесия
![]()
![]()
![]()
 Три уравнения равновесия содержат 4 неизвестные силы, следовательно, система
является один раз статически неопределимой.
Три уравнения равновесия содержат 4 неизвестные силы, следовательно, система
является один раз статически неопределимой.
Для составления уравнения совместности перемещений рассмотрим наряду с
исходным состоянием системы ее деформированное состояние (см. рисунок 12,в).
В результате удлинения тяг брус АВ повернется вокруг шарнира А,
оставаясь прямым. В виду малости перемещений будем считать, что все точки бруса
перемещаются вертикально вниз. Тогда перемещение шарнира D равно абсолютному
удлинению тяги 1: ![]() Удлинение тяги 2 получим,
опуская из точки С перпендикуляр на новое положение тяги,
Удлинение тяги 2 получим,
опуская из точки С перпендикуляр на новое положение тяги, ![]() Рассматривая
Рассматривая ![]() и
считая угол β малым, таким что угол α в деформированном состоянии
остается практически прежним, найдем
и
считая угол β малым, таким что угол α в деформированном состоянии
остается практически прежним, найдем ![]()
Из подобия треугольников ADD1 и ACC1 имеем
![]() или
или
![]()
откуда получаем уравнения совместности перемещений в
виде ![]()
На основании закона Гука запишем соотношения ![]()
![]() подставив которые в уравнения
совместности перемещений, найдем
подставив которые в уравнения
совместности перемещений, найдем
![]()
Отсюда, учитывая соотношение А2=3А1,
получим ![]() Подставляя это выражение в последнее
уравнение равновесия, найдем
Подставляя это выражение в последнее
уравнение равновесия, найдем
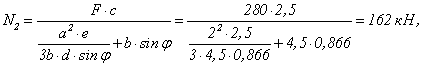 и из
соотношения между продольными силами
и из
соотношения между продольными силами
![]()
Из условия прочности стержней на растяжение по методу допускаемых
напряжений (![]() ) определяем площади поперечных стержней
) определяем площади поперечных стержней
![]()
![]()
Но площади поперечных сечений стержней еще должны удовлетворять
заданному соотношению ![]() Поэтому окончательно назначим
Поэтому окончательно назначим
![]()
![]()
Напряжения в стержнях при этом равны
![]()
![]()
Пример 11 -
Для конструкции, рассмотренной в примере 10, при найденных значениях площадей и
![]() определить напряжения в стержнях,
вызванные изменением их температуры на
определить напряжения в стержнях,
вызванные изменением их температуры на ![]()
Решение. Если бы деформациям стержней ничто не препятствовало в точках D
и C, то при изменении температуры они удлинились бы на величины ![]()
![]() и
и
![]() соответственно (см. рисунок 12,г).
Для стали α равно 1,25·10-5 1/ºС. Поскольку в общем
случае эти удлинения не удовлетворяют условиям совместности деформаций, то в
стержнях возникают усилия
соответственно (см. рисунок 12,г).
Для стали α равно 1,25·10-5 1/ºС. Поскольку в общем
случае эти удлинения не удовлетворяют условиям совместности деформаций, то в
стержнях возникают усилия ![]() и
и ![]() . Для определенности будем считать, что
стержень 1 растянут, а стержень 2 сжат, т.е. брус AB
займет некоторое положение
. Для определенности будем считать, что
стержень 1 растянут, а стержень 2 сжат, т.е. брус AB
займет некоторое положение ![]() такое, что точка
такое, что точка ![]() располагается ниже точки
располагается ниже точки ![]() а точка
а точка ![]() выше
точки
выше
точки ![]() . Если в результате решения знак усилия
окажется отрицательным, то это будет означать, что на самом деле направление
усилия противоположно принятому.
. Если в результате решения знак усилия
окажется отрицательным, то это будет означать, что на самом деле направление
усилия противоположно принятому.
Составим уравнение равновесия в виде ![]() откуда
откуда
![]()
Из подобия треугольников ![]() и
и ![]() принимая ввиду малости угла
принимая ввиду малости угла ![]() ,
, ![]() имеем
имеем
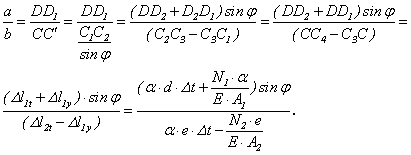
Подставляя сюда полученное выше соотношение между ![]() и
и ![]() и
производя вычисления, получим
и
производя вычисления, получим ![]()
![]()
Итак, в стержне 1 возникают сжимающие напряжение ![]() в стержне 2 - растягивающие
в стержне 2 - растягивающие ![]()
Пример 12 -
Для конструкции, рассмотренной в примере 10, при найденных значениях площадей и
![]() определить напряжения, возникающие
стержнях после сборки, если стержень 2 изготовлен на 0,02% короче
проектной (номинальной) длины.
определить напряжения, возникающие
стержнях после сборки, если стержень 2 изготовлен на 0,02% короче
проектной (номинальной) длины.
Решение.
После сборки конструкции брус ![]() займет наклонное
положение, как показано на рисунке 12,д. Стержень 1 при этом укоротится
на величину
займет наклонное
положение, как показано на рисунке 12,д. Стержень 1 при этом укоротится
на величину ![]() а стержень 2 удлинится на
величину
а стержень 2 удлинится на
величину ![]() направления усилий
направления усилий ![]() и
и ![]() сразу
определяются верно. Величина
сразу
определяются верно. Величина ![]()
Запишем уравнение равновесия в виде
![]() откуда
откуда ![]()
Составляем уравнение совместности перемещений исходя из подобия
треугольников ![]() и
и ![]() .
Имеем
.
Имеем ![]() но, поскольку
но, поскольку ![]()
![]() получим
получим ![]() Выражая удлинения через усилия, запишем
Выражая удлинения через усилия, запишем
![]()
Подставляя сюда выражение ![]() полученное из
уравнения равновесия, получим после преобразований и вычислений
полученное из
уравнения равновесия, получим после преобразований и вычислений ![]()
![]() Тогда
напряжения в стержнях равны
Тогда
напряжения в стержнях равны
![]()
![]()
Пример 13 - Для условий примера 10 подобрать площади поперечных размеров, пользуясь методом предельных состояний; сравнить расход материала в двух случаях.
Решение. Рассматривая предельное состояние системы (см. рисунок 12,е), запишем уравнение равновесия в виде
![]()
где ![]() - предельная нагрузка (несущая способность)
системы.
- предельная нагрузка (несущая способность)
системы.
Разделим это уравнение на ![]() принимая
принимая ![]() и учитывая, что
и учитывая, что ![]() запишем
запишем
![]() откуда
откуда
![]()
![]()
Сравним расход материала для изготовления стержней в случаях расчета по
допускаемым напряжениям ![]() и по предельному
состоянию
и по предельному
состоянию ![]()
![]()
Таким образом, расчет по предельному состоянию дает экономию материала 5%.
2.Кручение
Кручением называется такой вид нагружения стержня, когда в его поперечных сечениях возникает только крутящий момент Т=Мz (см. рисунок 1,г), а все остальные ВСФ равны нулю.
2.1. Эпюры крутящих моментов
Согласно методу сечений крутящий момент Т в каком-либо поперечном сечений стержня численно равен алгебраической сумме моментов относительно продольной оси стержня всех внешних сил, действующих на одну из отсеченных данным сечением частей стержня
![]() (2.1)
(2.1)
Естественно, в правую часть (2.1) входят и моменты пар сил, если таковые имеются.
Крутящий момент Т условно считается положительным, если наблюдатель со стороны внешней нормали ν к поперечному сечению видит его направленным против часовой стрелки (см. рисунок 13) и отрицательным, - если по часовой стрелке (см. рисунок 14).
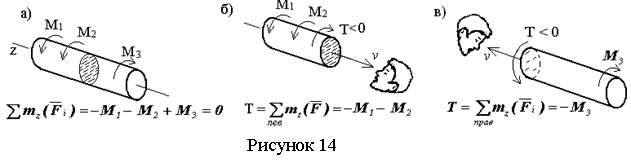
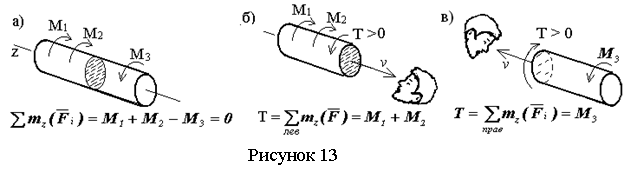 В соответствии с этим в выражении (2.1) момент внешней силы или пары
сил берется со знаком “плюс”, если наблюдатель видит его направленным по часовой
стрелке, и отрицательным – если против часовой стрелки.
В соответствии с этим в выражении (2.1) момент внешней силы или пары
сил берется со знаком “плюс”, если наблюдатель видит его направленным по часовой
стрелке, и отрицательным – если против часовой стрелки.
Кручение стержней с прямолинейной осью обычно вызывается парами сил М, лежащими в плоскостях, перпендикулярных к оси стержня, как на рисунках 13 и 14. Если, кроме того, имеются распределенные по длине моменты с интенсивностью m, тo формулу (2.1) можно переписать в виде
![]() .
(2.2)
.
(2.2)
Для изображения пар сил, лежащих в плоскостях, перпендикулярных плоскости рисунка, применяют условное изображение в виде двух кружков, причем кружок с точкой обозначает силу, направленную на наблюдателя, с крестиком - от наблюдателя.
Рассмотрим примеры построения эпюр Т.
Пример 14 - Построить эпюру Т для стержня на рисунке 15.
Решение. Здесь 2 участка. Будем на обоих участках определять Т, рассматривая равновесие левой от сечения части стержня; при этом реактивный момент в заделке можно не определять.
На 1-м
участке (см. рисунок 15,б): 0£
z1 £ a, T1= ![]() =
M.
=
M.
Ha 2-м
участке (см. рисунок 15,в): а £
z2 £ а+в, Т2=![]() =
М-3М =-2М.
=
М-3М =-2М.
На каждом из участков крутящий момент Т постоянен, эпюра приведена на рисунке 15,г.
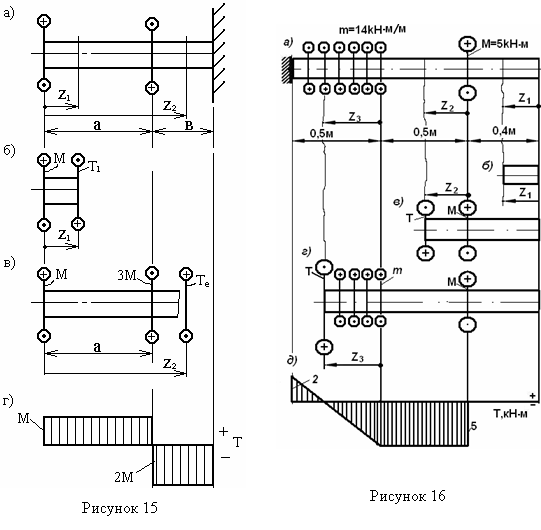
Пример 15 - Построить эпюру Т для стержня на рисунке 16,а.
Решение. Рассмотрим последовательно справа 3 участка, не определяя реактивный момент.
|
На 2-м
участке (см. рисунок 16,в): 0 £
z2 £ 0,5, ![]() кН·м.
кН·м.
На 3-м
участке (см. рисунок 16,г): 0 £
z3 £ 0,5 м, ![]() . Здесь Т линейно
зависит от z3 , значит, эпюра представляет собой наклонную
прямую. Найдем значения Т в граничных сечениях: при z3=0,
T=5 кН·м, при z3=0,5 м, Т=-5+14·0,5=2 кН·м.
. Здесь Т линейно
зависит от z3 , значит, эпюра представляет собой наклонную
прямую. Найдем значения Т в граничных сечениях: при z3=0,
T=5 кН·м, при z3=0,5 м, Т=-5+14·0,5=2 кН·м.
Эпюра Т показана на рисунке 16,д.
2.2 Касательные напряжения. Угол закручивания и потенциальная энергия деформации
При кручении стержня круглого поперечного сечения диаметром d в его поперечных сечениях возникают касательные напряжения τ (см. рисунок 17,а), пропорциональные расстоянию r рассматриваемой точки от центра сечения
 (2.3)
(2.3)
где 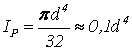 - полярный момент
инерции круглого сечения.
- полярный момент
инерции круглого сечения.
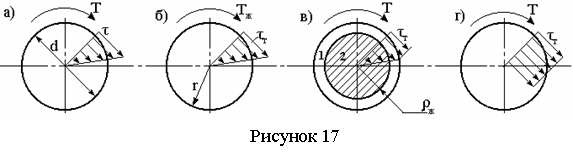 |
Максимальные касательные напряжения возникают в точках, наиболее удаленных от центра, и равны
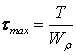 (2.4)
(2.4)
где  - полярный момент
сопротивления круглого сечения.
- полярный момент
сопротивления круглого сечения.
Угол закручивания j стержня круглого сечения на участке длиной l при постоянных Т и d определяют по формуле
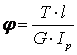 (2.5)
(2.5)
где 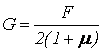 - модуль сдвига
материала.
- модуль сдвига
материала.
Если стержень имеет несколько участков, причем Т и d могут изменяться произвольным образом, тo полный угол закручивания определяется по формуле
 (2.6)
(2.6)
где интегрирование производится по длине каждого участка, а суммирование - по всем участкам стержня.
Для кольцевого сечения пользуются теми же формулами при этом
 , (2.7)
, (2.7)
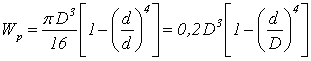 (2.8)
(2.8)
где D и d - наружный и внутренний диаметры сечения соответственно.
В случае стержня некруглого сечения в формулах (2.4) - (2.6) вместо Wр и Ip нужно подставлять соответственно Wк и Iк - момент сопротивления при кручении и момент инерции при кручении, выражения для которых применительно к различным формам сечений приводятся в справочниках и учебниках. Для стержней круглого и кольцевого сечения Wк=Wp, Iк=Ip.
Для определения потенциальной энергии, накопленной в стержне при кручении, служит формула
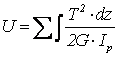 (2.9)
(2.9)
 где интегрирование и суммирование производят так же,
как в (2.6).
где интегрирование и суммирование производят так же,
как в (2.6).
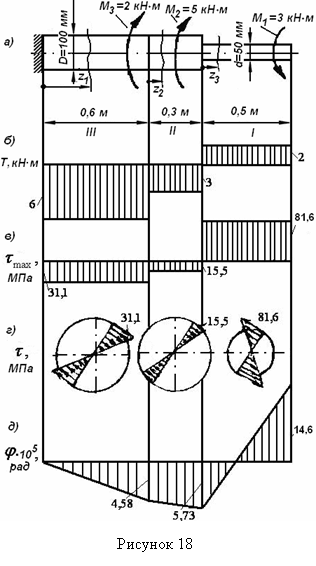
Пример 16 - Построить эпюры крутящих моментов, напряжений и углов закручивания для вала, изображенного на рисунке 18,а. Модуль сдвига G=8·104 МПа. Определить потенциальную энергию, накопленную в стержне.
Решение. Последовательно суммируя моменты, приложенные по правую сторону от текущего сечения вала, построим эпюру крутящих моментов (см. рисунок 18,б).
Максимальные
касательные напряжения на каждом участке определяются по формуле (2.4), причем ![]() см3 на участке I,
см3 на участке I, ![]() см3 на участках II и III.
см3 на участках II и III.![]()
Эпюра изменения τmax вдоль оси вала показана на рисунке 18,в; на рисунке 18,г изображены эпюры изменения τ по радиусу для трех участков.
Эпюру углов закручивания j начинаем строить от заделки, где j=0.
На участке АВ
угол закручивания сечения, расположенного на расстоянии z1 от
заделки, ![]()
![]()
![]() Зависимость
Зависимость ![]() от z1
изображается прямой: при
от z1
изображается прямой: при ![]()
![]() при z1=0,6 м
при z1=0,6 м ![]() рад.
рад.
На участке ВС
к этому углу прибавляется величина ![]() , где z2
отсчитывается от сечения B. Аналогично строится эпюра j на участке СD.
, где z2
отсчитывается от сечения B. Аналогично строится эпюра j на участке СD.
Потенциальная энергия деформации определяется как

2.3. Расчеты на прочность и жесткость по методу допускаемых напряжений
По методу допускаемых напряжений расчет стержня постоянного сечения на прочность при кручении производят по формуле
 (2.10)
(2.10)
где Тmax - наибольший по модулю крутящий момент;
Wк – момент сопротивления поперечного сечения стержня кручению, который в случае стержня круглого сечения совпадает с полярным моментом сопротивления Wр;
![]() -
допускаемое касательное напряжение, которое назначается как часть от предельного
для данного материала напряжения;
-
допускаемое касательное напряжение, которое назначается как часть от предельного
для данного материала напряжения;
 (2.11)
(2.11)
В качестве tпред для пластичных материалов берется предел текучести при сдвиге tт , а для хрупких - предел прочности при сдвиге tв.
Иногда дополнительно ставится условие, чтобы угол закручивания j на длине l не превосходил допускаемый угол закручивания [j]. В этом случае проводят расчет на жесткость по условию, которое при постоянном сечении и постоянном крутящем моменте Т имеет вид
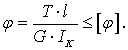 (2.12)
(2.12)
Иногда условие жесткости предъявляют к относительному
углу закручивания ![]() .
.
В случае вращающихся валов бывает необходимым использовать зависимость между передаваемой мощностью Р и моментом на валу, равным крутящему моменту Т,
Р=Т·ω (2.13)
где ![]() - угловая скорость
вращения вала (рад/с),
- угловая скорость
вращения вала (рад/с),
n - число оборотов вала в минуту.
Пример 17 - Полый вал турбины передает мощность 5 МВт при 100 об/мин. Определить диаметр вала d, если внутренний диаметр d1 составляет d/2, допускаемое напряжение равно 30 МПа, допускаемый угол закручивания равен 2 град/м, модуль сдвига G=8·104 МПа.
Решение.
Определяем момент, передаваемый валом![]()
![]() МН·м.
МН·м.
Из условия прочности найдем необходимый полярный момент сопротивления
![]() м3.
м3.
По формуле (2.8)
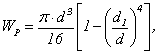
откуда
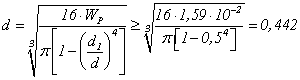 м = 442 мм.
м = 442 мм.
Найдем необходимый момент инерции сечения из условия жесткости
![]() м4.
м4.
Используя формулу (2.7), найдем
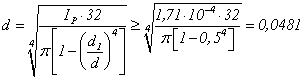 м=48, 1мм.
м=48, 1мм.
Как видно, определяющим является условие прочности, и соответственно назначаем d=442 мм, d1=221 мм.
Пример 18 - Для условий примера 17 определить диаметр dc сплошного вала и сравнить расход материала в двух случаях.
Решение. По найденному в примере 17 требуемому значению WP найдем диаметр
![]() м.
м.
По требуемому IP найдем
![]() м.
м.
Окончательно dc=443 м, а расход материала пропорционален площадям сечений
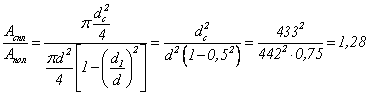 .
.
Таким образом, в случае сплошного вала расход материала увеличивается на 28 %.
2.4. Статически неопределимые системы
Раскрытие статической неопределимости сводится к совместному решению уравнений статики и уравнений, вытекающих из условий совместности перемещений (деформаций).
 Так, для систем, состоящих из нескольких соосных
прямолинейных элементов, жестко заделанных по концам и нагруженных только
внешними парами сил, уравнение равновесия записывается в виде равенства нулю
суммы всех внешних активных и реактивных пар сил. Условие совместности перемещений
записывается в виде равенства нулю алгебраической суммы углов закручивания на
всех участках.
Так, для систем, состоящих из нескольких соосных
прямолинейных элементов, жестко заделанных по концам и нагруженных только
внешними парами сил, уравнение равновесия записывается в виде равенства нулю
суммы всех внешних активных и реактивных пар сил. Условие совместности перемещений
записывается в виде равенства нулю алгебраической суммы углов закручивания на
всех участках.
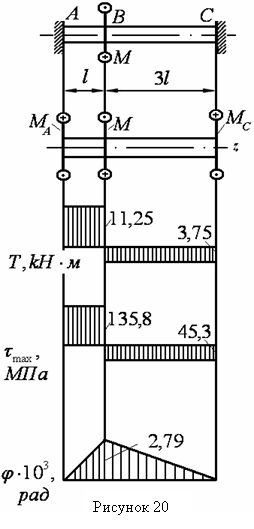
Пример 19 - Для вала, изображенного на рисунке 20,а, определить диаметр из условия прочности, если tт=200 МПа,[n]=1,5 , M=15кН·м , l=1 м. Построить эпюры максимальных касательных напряжений и углов закручивания.
Решение. Обозначив неизвестные реактивные моменты в сечениях А и С через МA и МC (см. рисунок 20,б), запишем уравнение равновесия в виде
SМz=-МА+М-МС=0.
Уравнение совместности перемещений получаем из условия неподвижности сечений А и С
![]() .
.
Решая два
уравнения совместно, получим ![]()
![]() . Строим эпюру крутящих моментов (см. рисунок
20,в).
. Строим эпюру крутящих моментов (см. рисунок
20,в).
Из условия
прочности, учитывая, что ![]() найдем диаметр вала
найдем диаметр вала
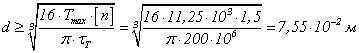 .
.
Можно
округлить значение диаметра до ближайшего значения из стандартного ряда нормальных
линейных размеров, тогда d=75 мм. Так как округление произведено в сторону
уменьшения, вал будет перегружен; напряжения обратно пропорциональны полярным
моментам сопротивления, которые в свою очередь, пропорциональны диаметрам в
третьей степени, так что перегрузка составит ![]()
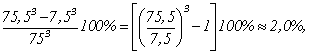 что можно считать допустимым.
что можно считать допустимым.
На рисунках 20,г,д показаны эпюры максимальных касательных напряжений и углов закручивания для выбранного диаметра.
3 Сдвиг
Сдвигом называется такой вид нагружения стержня, когда в его поперечных сечениях возникает поперечная (перерезывающая) сила Q, а все остальные ВСФ отсутствует. Во многих случаях нагружение, близкое к этому, испытывают различные детали, служащие для соединения элементов машин или строительных конструкций - заклепки, штифты, болты (поставленные без зазора) и т.п. (см. рисунок 21).
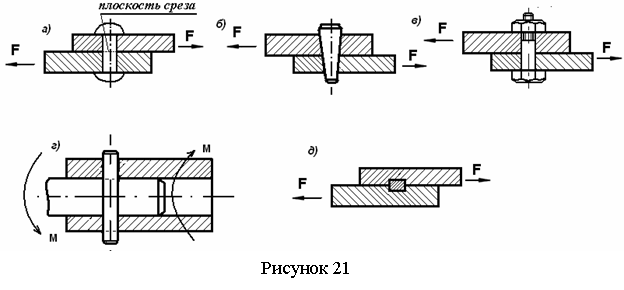
Действительные условия работы перечисленных деталей сложнее. Они существенно зависят от технологии изготовления и сборки конструкции. В поперечных сечениях элементов при этом возникает не только поперечная сила Q, но и изгибающий момент М, а следовательно, и нормальные напряжения s. В инженерной практике же расчет этих деталей носит условный характер, и он основывается на следующих допущениях:
а) в поперечных сечениях возникает только один ВСФ - поперечная сила Q;
б) касательные напряжения в поперечном сечении распределяются равномерно, t = Q/A;
в) если соединение выполнено с помощью нескольких одинаковых соединительных элементов (болтов, заклепок и т.п.), то считается, что между ними нагрузка распределяется равномерно (кроме случаев нагружения парами сил в плоскости стыка соединяемых деталей).
Разрушение соединительных элементов в случае их недостаточной прочности происходит по поверхностям стыка соединяемых деталей. Поэтому говорят, что эти элементы работают на срез, обозначая касательные напряжения в поперечных сечениях tср.
Условие прочности по напряжениям среза имеет вид
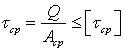 (3.1)
(3.1)
где Q - поперечная сила; при нескольких одинаковых элементах Q=F/i (F - общая нагрузка, i - число элементов);
Aср - площадь среза одного элемента;
[tср] - допускаемое напряжение на срез (обычно [tср] = (0,25...0,3) sт, здесь sт - предел текучести материала элемента).
Расчет на срез, обеспечивая прочность соединительных элементов, не гарантирует надежность конструкции в целом. Если толщины соединяемых деталей малы, тo давления между соединительными элементами и стенками соединяемых деталей вызывают смятие последних, и соединение становится ненадежным. Давления между элементами и стенками принято называть напряжениями смятия и обозначать sсм. Для того, чтобы не допустить смятия стенок деталей производят расчет на смятие по условию прочности
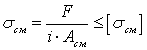 (3.2)
(3.2)
 где
F/i - нагрузка на один соединительный элемент;
где
F/i - нагрузка на один соединительный элемент;
Асм - расчетная площадь смятия;
[sсм] - допускаемое напряжение на смятие (для малоуглеродистых сталей [sсм] = 100....120 МПа).
В качестве расчетной площади смятия при контакте по плоскости (см. рисунок 21,д) принимают действительную площадь контакта, при контакте по цилиндрической поверхности - площадь проекции поверхности контакта на диаметральную плоскость, т.е. Асм = d·d. При различной толщине соединяемых деталей следует подставлять dmin.
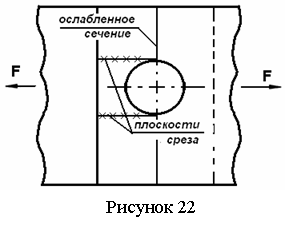
Кроме расчетов на срез и смятие, необходима проверка прочности соединяемых на растяжение по ослабленному сечению и расчет на срез (выкалывание) части элемента вдоль линии действия силы (см. рисунок 22). Все виды расчета рассмотрены в примере 20.
Пример 20 - Тяги 1 и 2 соединены между собой штырем 3, вставленным в проушины (рисунок 23) и нагружены силами F. Определить допускаемое значение силы F, если заданы допускаемые напряжения: на растяжение [sр] = 120 МПа, на срез [tср] = 80 МПа, на смятие [sсм] = 210 МПа.
Решение. Допускаемую силу найдем как наименьшую из значений силы, полученных в расчетах тяг на растяжение, стенок отверстий (проушин) на смятие, краев проушины на срез (выкалывание).
1. Из расчета тяги 1 на растяжение:
а) по сечению I-I
FIдоп.раст
= ![]() кН;
кН;![]()
б) по сечению II-II
FIIдоп.раст = [sр] ·2(b1-dш)·d1=46,1 кН.
2. Из расчета тяги 2 на растяжение:
а) по сечению III-III
FIIIдоп.раст. =[sр] ·b2·d2 =43,2 кН;
б) по сечению II-II
 FIVдоп.раст.
= [sр]·(D-dш)·d2 =28,8 кН.
FIVдоп.раст.
= [sр]·(D-dш)·d2 =28,8 кН.
3. Из расчета штыря на срез
Fдоп.срез
= [tср]![]() кН.
кН.
4. Из расчета стенок отверстий в проушинах на смятие
- для тяги 1: АIсм = 2d1·dш = 320 мм2;
- для тяги 2: АIIсм = d2·dш = 240 мм2.
Наиболее нагружена и тяга 2 с Аmin = 240 мм2. Отсюда
Fдоп.см = [sсм]×AIIсм = 50,4 кН.
5. Из расчета краев проушины на выкалывание:
а) для тяги 1 (выкалывание по ab=см=е1)
FIдоп.вык. = [tср]×2е1×2d1 = 589 кН;
б) для тяги 2 (выкалывание на ак=се»е2)
FIIдоп.вык. = [tср]×2е2×d2=38,4 кН.
Окончательно допускаемая нагрузка Fдоп=28,8 кН. Она лимитируется прочностью тяги 2 на растяжение.
4 Геометрические характеристики поперечных сечений стержня
При решении задач изгиба используются некоторые геометрические характеристики поперечных сечений стержня; в настоящей главе рассматривается их определение, свойства и методы вычисления.
4.1. Статические моменты сечения
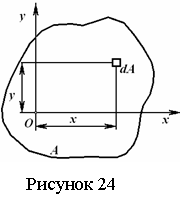
Рассмотрим некоторую плоскую фигуру в системе координат x, y (рисунок 24). Интегралы
![]() ,
, ![]() (4.1)
(4.1)
называются статическими моментами фигуры относительно оси x и оси y соответственно. Здесь А - площадь сечения, dA – бесконечно малый элемент площади, x и y - координаты этого элемента.
Выясним, как изменяются статические моменты сечения при параллельном переносе координатных осей (см. рисунок 25). Очевидно, что x2 = x1 - a; y2 = y1 - b.
Тогда
![]() ,
, ![]() . (4.2)
. (4.2)
Величины
а и b можно подобрать (причем единственным образом) так, чтобы
статические моменты ![]() и
и ![]() были
равны нулю. Ось, относительно которой статический момент равен нулю, называется
центральной. Точка пересечения центральных осей называется центром
тяжести сечения.
были
равны нулю. Ось, относительно которой статический момент равен нулю, называется
центральной. Точка пересечения центральных осей называется центром
тяжести сечения.
 В системе координат (x1, y1) координаты центра тяжести определяются как
В системе координат (x1, y1) координаты центра тяжести определяются как
![]() ,
, ![]() . (4.3)
. (4.3)
По формулам (4.3) можно решать и обратную задачу - определить статические моменты при известных площади и координатах центра тяжести сечения.
При вычислении координат центра тяжести сложных сечений, составленных из простейших фигур или стандартных прокатных профилей, используют формулы
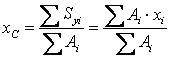 ;
;  ,
(4.4)
,
(4.4)
где Аi , xi , yi - площадь и координаты центра тяжести i-й составляющей фигуры соответственно.
Пример 21 - Определить положение центра тяжести параболического треугольника АОВ (см. рисунок 26) , если ОС=b, a ОВ описывается параболой у=а·хn .
Решение.
Найдем сначала высоту h, h=a·bn. Выразив dА=у·dx=a×xn×dx, найдем площадь ![]()
![]()
Статический момент относительно оси у найдем по формуле (4.1)
![]()
Для определения Sx элемент dA выразим по-другому, dA=(b-x)·dy=(b-x)·n·a·хn-1·dx. Тогда по формуле (4.1) получим
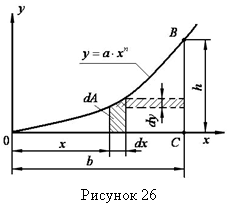
![]()
Координаты центра тяжести найдем по формулам (4.3)


Пример 22 - Определить положение центра тяжести сложного составного сечения, изображенного на рисунке 27.
Решение. Разбиваем сечение на простые фигуры: треугольник, прямоугольник и полукруг. Выбираем систему координат х, у и определяем координаты центров тяжести составляющих фигур.
В треугольнике
центр тяжести находится на расстоянии 1/3 высоты от основания; в прямоугольнике
- на пересечении осей симметрии; в полукруге - на оси симметрии на расстоянии ![]() от вертикального диаметра.
от вертикального диаметра.
Площадь
составной фигуры равна ![]()
По формулам (4.4) находим координаты центра тяжести составной фигуры в системе осей х, у
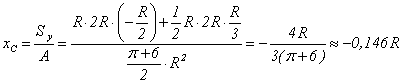 ,
,
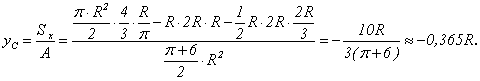
4.2 Моменты инерции сечений. Радиусы инерции
Для любой плоской фигуры (см.рисунок 24) определенные интегралы
![]() ,
, ![]() (4.5)
(4.5)
называют осевыми моментами инерции фигуры относительно осей х и у, а определенный интеграл
![]() (4.6)
(4.6)
- центробежным моментом инерции сечения относительно взаимно перпендикулярных осей х и у.
При переходе от центральных осей х0, у0 к осям x,y, параллельным первым и расположенным на расстояниях a и b от них, моменты инерции вычисляются по формулам
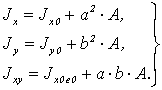 (4.7)
(4.7)
При обратном переходе, от нецентральных осей к центральным, в выражениях (4.7) знаки “плюс” перед вторыми слагаемыми меняются на “минус”.
При повороте координатных осей (см. рисунок 28) осевые и центробежный моменты инерции вычисляются по формулам
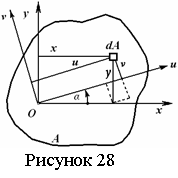
 (4.8)
(4.8)
Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты инерции принимают экстремальные значения, называют главными осями инерции; положение этих осей относительно осей х и у определяются углами a0, которые могут быть вычислены с использованием формулы
 (4.9)
(4.9)
Главными моментами инерции называют осевые моменты инерции относительно главных осей; их значения определяют по формулам
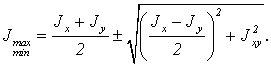 (4.10)
(4.10)
Главные оси, проходящие через центр тяжести сечения, называют главными центральными осями, а моменты инерции относительно этих осей - главными центральными моментами инерции.
В случае, когда сечение имеет хотя бы одну ось симметрии, эта ось и ось, ей перпендикулярная и проходящая через центр тяжести сечения, являются главными центральными осями.
Моменты инерции сложных сечении относительно каких-либо осей определяют, суммируя соответствующие моменты инерции составляющих фигур относительно тех же осей.
Ниже приведены формулы главных центральных моментов инерции для прямоугольника, круга, кольца, показанных на рисунке 29.
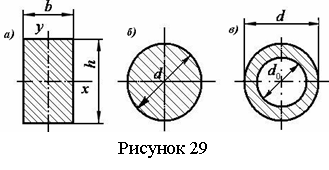 Для
прямоугольника
Для
прямоугольника
 (4.11)
(4.11)
Для круга
![]() (4.12)
(4.12)
Для кольца
![]() .
(4.13)
.
(4.13)
Отметим, что для круга и кольца все центральные оси являются главными и моменты инерции относительно этих осей равны между собой. Таким свойством обладает любое сечение, у которого два главных центральных момента одинаковы (например, квадрат или равносторонний треугольник).
Для прокатных профилей (двутавров, швеллеров, уголков) значения моментов инерции поперечных сечений приводятся в справочниках.
Радиусом инерции плоской фигуры относительно оси х называют величину
 (4.14)
(4.14)
где Jx - осевой момент инерции относительно рассматриваемой оси х;
А - площадь фигуры.
Пример 23 - Определить положение главных центральных осей и вычислить значения главных центральных моментов инерции сечения, имеющего форму полукруга (см. рисунок 30).
Решение.
Определяем положение центра тяжести. Очевидно, он находится на оси симметрии
(на оси у). Выбираем вспомогательную оси х1,у1;
тогда ![]() ,
, ![]() , dA=2R·cosa·dy1, y1=R·sina, dy1=d(R·sina)=R·cosa∙dα и
, dA=2R·cosa·dy1, y1=R·sina, dy1=d(R·sina)=R·cosa∙dα и
![]() ,
,
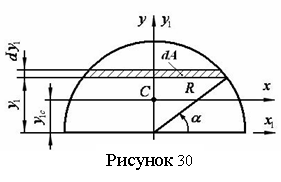

Ось симметрии у и ось х являются главными центральными осями инерции сечения. Вычисляем значения главных центральных моментов инерции
![]() ;
;
 и, так как
и, так как ![]() ,
то
,
то ![]()
Пример 24 - Вычислить главные центральные моменты инерции сечения, изображенного на рисунке 31.
Решение. Так как сечение имеет ось симметрии, то центр тяжести сечения лежит на этой оси. Разбив сечение на 3 прямоугольника, найдем
![]() ,
,
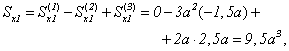
![]() .
.
Момент инерции сечения относительно оси х найдем, используя формулы для прямоугольника (4.11) и формулы перехода (4.7)
![]() Момент инерции относительно оси у
найдем, учитывая, что ось у является центральной как для сечения в
целом, так и для составляющих фигур. Тогда получаем
Момент инерции относительно оси у
найдем, учитывая, что ось у является центральной как для сечения в
целом, так и для составляющих фигур. Тогда получаем
![]() .
.
Пример 25 - Вычислить главные центральные моменты инерции сечения, показанного на рисунке 32,а.
Решение. 1) Определяем координаты центра тяжести, для чего проводим вспомогательные оси х1 и у1. Для швеллера и уголка, составляющих сечение, выписываем необходимые данные из таблиц сортамента и заносим в таблицу 1.
Вычисляем координаты хс и ус
![]()
![]()
Т а б л и ц а 1
|
Фигуры |
Площадь сечения A, см2 |
Положение центра тя-жести z0, см2 |
Моменты инерции относительно собственных осей, см4 |
|||
|
горизонтальной |
вертикальной |
Jx0 (max) |
Jy0 (min) |
|||
|
|
|
|
|
|
|
|
|
Швеллер №20а |
25,2 |
2,28 |
1670 |
139 |
- |
- |
|
Уголок 100*100*10 |
19,2 |
2,83 |
179 |
179 |
284 |
74,1 |
Далее проводим вспомогательные центральные оси х и у. Отметим, что центр тяжести должен лежать на линии, соединяющей центры тяжести уголка и швеллера.
2) Вычисляем моменты инерции относительно осей х и у
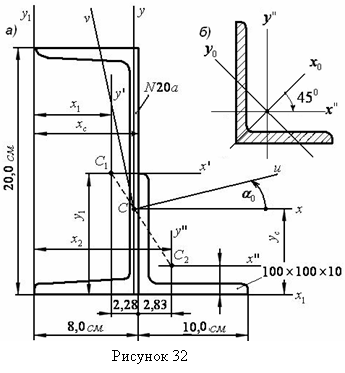
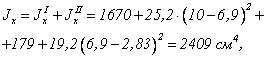

Вычисляем центробежный
момент инерции относительно осей х и у по формуле (4.7). Так как
швеллер имеет горизонтальную ось симметрии ![]() , тo
собственные центральные оси x’, y’ для него являются главными и
, тo
собственные центральные оси x’, y’ для него являются главными и ![]() Для уголка собственные центральные
оси х”, у” не являются главными. Для него главными являются
оси х0, у0, т.к. х0 -
ось симметрии (рисунок 32,б). По третьей формуле (4.8) при
Для уголка собственные центральные
оси х”, у” не являются главными. Для него главными являются
оси х0, у0, т.к. х0 -
ось симметрии (рисунок 32,б). По третьей формуле (4.8) при ![]()
![]() см4.
см4.
Тогда центробежный момент всего сечения относительно осей х и y равен
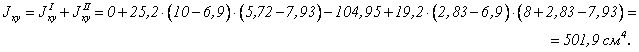 По
формуле (4.9) определяем угол наклона главных осей
По
формуле (4.9) определяем угол наклона главных осей
![]()
Отложим этот угол против часовой стрелки и проведем главные центральные оси u и v.
4) Вычисляем главные центральные моменты инерции по формуле (4.10):
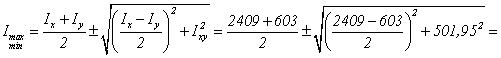
![]() см4.
см4.
Следовательно Jmax=2536 см4, Jmin=476 см4 и, так как Jx>Jy, тo Jmax есть момент инерции оси u, а Jmin - относительно v.
5 Прямой изгиб
Изгибом стержня называют такой вид нагружения, при котором в его поперечных сечениях возникает изгибающий момент M. Если изгибающий момент является единственным ВСФ, то имеем чистый изгиб. Чаще наряду с M в сечениях возникает поперечная сила Q, и в этом случае имеем поперечный изгиб.
 Стержень, работающий на изгиб, обычно называют балкой.
Пролетом называют часть двух опорный балки, находящуюся между опорами. Консольная
балка – это балка с жестким защемлением (заделкой) на одном конце и другим
незакрепленным концом. Консолями называют части балки, выступающие за пределы
пролета (длина балки в этом случае больше длины пролета). Под главной
плоскостью инерции стрежня подразумевается плоскость, проходящая через одну из
главных центральных осей инерции поперечного сечения и его продольную ось. В
случае, когда все внешние силы, включая опорные реакции, лежат в одной плоскости,
совпадающей с одной из главных плоскостей инерции стержня, его изогнутая ось
также лежит в этой плоскости, и такой случай изгиба называется прямым или
плоским. Так, если все внешние силы стержня лежат в плоскости zy
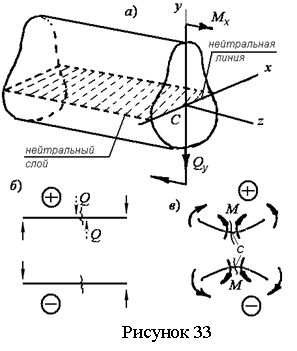
(см. рисунок 33), то в поперечных сечениях стержня возникают поперечная сила Qy и
изгибающий момент Mx. Если ось балки первоначально была прямолинейной, то
она изогнется, и изогнутая ось балки будет лежать в этой же плоскости zy.
Волокна балки со стороны выпуклости будут испытывать удлинение, со сторон вогнутости
– укорочение, и есть так называемый нейтральный слой, на котором волокна не изменяют
длину, а лишь искривляются. Линия пересечения нейтрального слоя с плоскостью
поперечного сечения балки называется нейтральной линией. При прямом изгибе нейтральная
линия совпадает с главной центральной осью инерции поперечного сечения, перпендикулярной
плоскости действия сил.
Стержень, работающий на изгиб, обычно называют балкой.
Пролетом называют часть двух опорный балки, находящуюся между опорами. Консольная
балка – это балка с жестким защемлением (заделкой) на одном конце и другим
незакрепленным концом. Консолями называют части балки, выступающие за пределы
пролета (длина балки в этом случае больше длины пролета). Под главной
плоскостью инерции стрежня подразумевается плоскость, проходящая через одну из
главных центральных осей инерции поперечного сечения и его продольную ось. В
случае, когда все внешние силы, включая опорные реакции, лежат в одной плоскости,
совпадающей с одной из главных плоскостей инерции стержня, его изогнутая ось
также лежит в этой плоскости, и такой случай изгиба называется прямым или
плоским. Так, если все внешние силы стержня лежат в плоскости zy
(см. рисунок 33), то в поперечных сечениях стержня возникают поперечная сила Qy и
изгибающий момент Mx. Если ось балки первоначально была прямолинейной, то
она изогнется, и изогнутая ось балки будет лежать в этой же плоскости zy.
Волокна балки со стороны выпуклости будут испытывать удлинение, со сторон вогнутости
– укорочение, и есть так называемый нейтральный слой, на котором волокна не изменяют
длину, а лишь искривляются. Линия пересечения нейтрального слоя с плоскостью
поперечного сечения балки называется нейтральной линией. При прямом изгибе нейтральная
линия совпадает с главной центральной осью инерции поперечного сечения, перпендикулярной
плоскости действия сил.
5.1. Эпюры поперечных сил и изгибающих моментов.
Поперечной силой Qy
называется проекция равнодействующих внутренних сил в рассматриваемом
поперечном сечении на главную центральную ось поперечного сечения ![]() (см. рисунок 1,в). Она численно
равна алгебраической сумме проекций на ось всех внешних сил, приложенных к
одной из двух мысленно отсеченных рассматриваемым сечением частей стержня.
(см. рисунок 1,в). Она численно
равна алгебраической сумме проекций на ось всех внешних сил, приложенных к
одной из двух мысленно отсеченных рассматриваемым сечением частей стержня.
![]() (5.1)
(5.1)
Поперечная сила считается положительной, если она стремится повернуть отсеченную часть стержня относительное центра тяжести по ходу часовой стрелки. Тогда знаки сил Fk в выражении (5.1) можно брать согласно мнемоническому правилу, изображенному на рисунке 32,б: внешняя сила, стремящаяся повернуть относительную часть стержня по ходу часовой стрелки относительно точки, соответствующей рассматриваемому сечению, вызывает положительную силу.
Изгибающим моментом Mx называют главного вектора внутренних сил в рассматриваемом сечении, получаемого при приведении внутренних сил к центру тяжести поперечного сечения, на главную ось инерции x (см. рисунок 1,в). Иначе, изгибающий момент Mx является результирующим моментом внутренних сил в рассматриваемом поперечном сечении относительно главной центральной оси инерции поперечного сеченияx. Он численно равен алгебраической сумме моментов всех внешних сил, приложенных к стержню по одну сторону от рассматриваемого сечения, относительно оси x
![]() (5.2)
(5.2)
Эпюры изгибающих моментов принято строить на сжатом
волокне. Тогда для балок с горизонтальной в недеформированном состоянии
продольной осью знак момента внешней силы (или пары сил) следует назначать согласно
следующему правилу: со знаком «плюс» момент берется (при условии, что
положительные ординаты эпюры моментов будем откладывать вверх) в том случае,
если эта сила (пара сил) стремится изогнуть рассматриваемую часть балки относительно
рассматриваемого сечения выпуклостью вниз; в противном случае момент следует
взять со знаком «минус». Соответствующее мнемоническое правило показано на
рисунке 32,в. Поскольку обычно на схемах толщину балок не показывают,
вместо ![]() в выражении (5.2) можно писать
в выражении (5.2) можно писать ![]() , где С - точка на оси балки,
через которую проходит рассматриваемое сечение
, где С - точка на оси балки,
через которую проходит рассматриваемое сечение
![]() (5.2)
(5.2)
Аналогично вводятся понятия Qx и My.
Эпюры поперечных сил и изгибающих моментов обычно строят, составляя выражения для Q и M на каждом участке, границами которых являются: крайние сечения; сечения, где приложены внешние силы или пары сил (моменты); сечения, где начинается и заканчивается распределенная нагрузка с интенсивностью q, изменяющейся определенному закону. Быстрее можно построить эпюры по характерным точкам, используя общие закономерности, в том числе вытекающие из дифференциальных зависимостей между изгибающим моментом M, поперечной силой Q и интенсивностью распределенной нагрузки q. Эти зависимости имеют вид.
![]() , (5.3)
, (5.3)
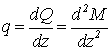 . (5.4)
. (5.4)
Ниже приведены основные закономерности для эпюр Q и M:
а) в сечении, где к балке приложена сосредоточенная сила, на эпюре Q имеет место скачок на величину приложенной силы, а на эпюре M - изменение угла наклона касательной (излом);
б) в сечении, где к балке приложена пара сил (момент), на эпюре M имеет место скачок на величину момента этой пары;
в) для участка балки, на котором отсутствует распределенная нагрузка, поперечная сила постоянна, а эпюра изгибающих моментов – линейна (эпюра Q очерчена прямой, параллельной оси абсцисс, (а эпюра M - наклонной прямой);
г) для участка балки с равномерно распределенной нагрузкой поперечная сила Q изменяется по линейному закону, а изгибающий момент M -по квадратичному (эпюра Q очерчена наклонной прямой, а эпюра M -квадратичной параболой);
д) в сечении, где эпюра Q пересекает ось абсцисс (проходит через ноль), изгибающий момент экстремален;
е) если распределенная нагрузка направлена вниз (q<0), то эпюра M очерчена параболой, обращенной выпуклостью вверх;
ж) изменение значения изгибающего момента, между двумя какими-либо сечениями на участке равно площади эпюры поперечной силы между теми же двумя сечениями.
Пример 25 - Для заданной балки (см. рисунок 34,а) построить эпюры Q и M.
Решение. Для того чтобы построить эпюры Q и M, нужно предварительно определить опорные реакции. Отбрасываем опорные закрепления и заменяем их действие реакциями. В точке B имеем шарнирно-подвижную опору, реакция которой всегда направлена перпендикулярно опорной поверхности – направим ее вверх (см. рисунок 34,б). В точке A имеем шарнирно неподвижную опору, реакция которой в общем случае может быть направлена как угодно в плоскости, то есть реакция имеет 2 составляющие. Поскольку в рассматриваемом случае все остальные силы вертикальны, то и реакция опоры A будет вертикальной – направим ее также вверх. Запишем уравнения равновесия в виде сумм моментов всех сил относительно точек A и B
![]() ,
,
![]() .
.
Отсюда, подставляя числовые значения, найдем
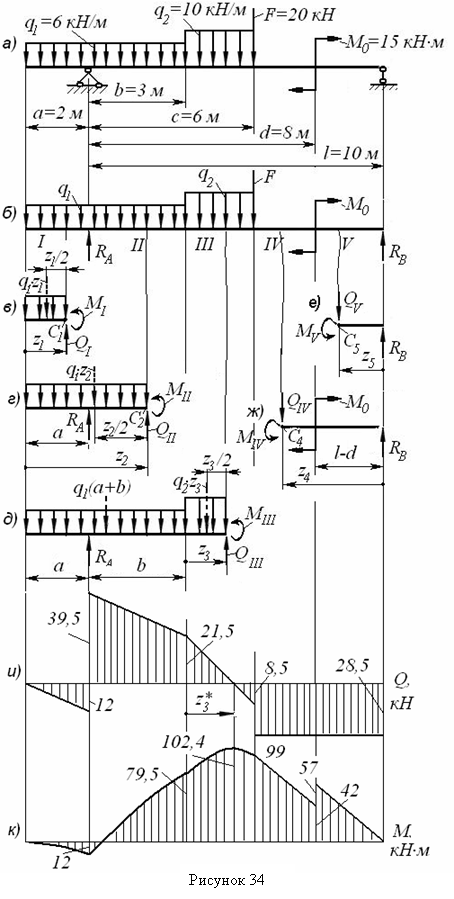
 ,
,
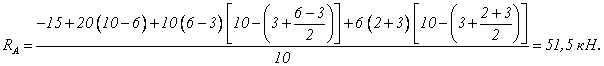
Составив уравнение равновесия в виде суммы проекций всех сил на ось y, убедимся, что реакции определены правильно
![]() .
.
Переходим к построению эпюры. Балка имеет 5 участков.
Проведем
произвольное сечение на участке I и будем
рассматривать левую отсеченную часть балки (см. рисунок
34,в); положение произвольного сечения будем определять с помощью
координаты ![]() . Тогда по формуле (5.1) с учетом
правила знаков
. Тогда по формуле (5.1) с учетом
правила знаков ![]() . Величина Q1 линейно зависит от координаты z1, следовательно, эпюра Q1
будет представлять собой наклонную прямую. Для того чтобы построить эту прямую,
найдем значения Q1 в граничных сечениях:
при
. Величина Q1 линейно зависит от координаты z1, следовательно, эпюра Q1
будет представлять собой наклонную прямую. Для того чтобы построить эту прямую,
найдем значения Q1 в граничных сечениях:
при ![]() , при
, при ![]() . На
эпюре
. На
эпюре ![]() (см. рисунок
34,и) откладываем соответствующие значения и проводим прямую.
(см. рисунок
34,и) откладываем соответствующие значения и проводим прямую.
По формуле
(5.2) с учетом правила знаков определяем изгибающий момент: ![]() . Величина
. Величина ![]() является
квадратичной функцией от
является
квадратичной функцией от ![]() , следовательно,
эпюра М будет представлять собой квадратичную параболу. Парабола может
иметь или не иметь вершину на рассматриваемом участке. Для того, чтобы выяснить
это, обратимся к выражению (5.3), из которого следует, что парабола на рассматриваемом
участке имеет вершину в том сечении, где
, следовательно,
эпюра М будет представлять собой квадратичную параболу. Парабола может
иметь или не иметь вершину на рассматриваемом участке. Для того, чтобы выяснить
это, обратимся к выражению (5.3), из которого следует, что парабола на рассматриваемом
участке имеет вершину в том сечении, где ![]() . В
нашем случае это сечение, которое соответствует
. В
нашем случае это сечение, которое соответствует ![]() . Таким
образом, в рассматриваемом случае достаточно определить значения
. Таким
образом, в рассматриваемом случае достаточно определить значения ![]() в граничных сечениях: при
в граничных сечениях: при ![]() , при
, при ![]() . Соответствующая
эпюра показана на рисунке 34,к; выпуклость эпюры в соответствии с выражением
(5.4) направлена навстречу стрелкам, обозначающим
. Соответствующая
эпюра показана на рисунке 34,к; выпуклость эпюры в соответствии с выражением
(5.4) направлена навстречу стрелкам, обозначающим ![]() .
.
Строим эпюры
для участка ІІ. С этой целью проводим произвольное сечение на участке ІІ.
Будем рассматривать левую от сечения часть балки; положение произвольного сечения
будем определять с помощью координаты ![]() ,
начало которой удобно выбрать на левом конце балки (см. рисунок 34,г). Тогда
,
начало которой удобно выбрать на левом конце балки (см. рисунок 34,г). Тогда ![]() :
: ![]() - линейная зависимость Q2 от
- линейная зависимость Q2 от ![]() ; эпюра
Q2 – прямая; при
; эпюра
Q2 – прямая; при ![]()
![]() при
при ![]()
![]() ; строим эпюру
; строим эпюру ![]() на
участке ІІ (см. рисунок 34,и).
на
участке ІІ (см. рисунок 34,и).
Запишем выражение
для изгибающего момента на втором участке. ![]() -
квадратичная зависимость от
-
квадратичная зависимость от ![]() ; эпюра – парабола;
так как
; эпюра – парабола;
так как ![]() не проходит через ноль, достаточно
определить
не проходит через ноль, достаточно
определить ![]() в граничных сечениях:
в граничных сечениях:
при ![]() ;
;
при ![]() .
.
По найденным
значениям строим эпюру ![]() на участке ІІ (см. рисунок 34,к).
на участке ІІ (см. рисунок 34,к).
Переходим к
участку ІІІ. Произвольным сечением на этом участке рассечем балку на 2
части. Будем по-прежнему рассматривать левую часть балки, определяя положение
произвольного сечения с помощью координаты ![]() ,
начало которой возьмем на левой границе участка ІІІ (см. рисунок 34,д). Координата
,
начало которой возьмем на левой границе участка ІІІ (см. рисунок 34,д). Координата ![]() изменяется в пределах
изменяется в пределах ![]() . Запишем выражение для поперечной силы
. Запишем выражение для поперечной силы ![]() . Это - линейная зависимость от
. Это - линейная зависимость от ![]() ; эпюра
; эпюра ![]() –
прямая; при
–
прямая; при ![]()
![]()
![]() ; при
z3=c-b
; при
z3=c-b ![]()
По найденным значениям строим
эпюру ![]() на участке ІІІ (см. рисунок 34,и).
на участке ІІІ (см. рисунок 34,и).
Запишем
выражение для изгибающего момента на третьем участке ![]() .
Это квадратичная зависимость от
.
Это квадратичная зависимость от ![]() ; эпюра – парабола. Так
как
; эпюра – парабола. Так
как ![]() проходит через ноль на участке,
парабола имеет вершину, соответствующую максимальному значению (поскольку
проходит через ноль на участке,
парабола имеет вершину, соответствующую максимальному значению (поскольку ![]() меняет знак с положительного на
отрицательный); соответствующее значение
меняет знак с положительного на
отрицательный); соответствующее значение ![]() найдем,
приравняв выражение
найдем,
приравняв выражение ![]() нулю:
нулю: ![]() ; отсюда
; отсюда ![]()
![]()
Значения ![]() в трех точках составляют:
в трех точках составляют:
при ![]() ;
;
при ![]()
при ![]() .
.
По найденным значениям строим
эпюру ![]() на участке ІІІ (см. рисунок 34,к).
на участке ІІІ (см. рисунок 34,к).
Для участков IV и V будем рассматривать части балки справа от сечения.
На рисунке 34,е
показана правая от сечения часть балки для построения эпюр ![]() и
и ![]() на
участке V; положение произвольного сечения определяется координатой
на
участке V; положение произвольного сечения определяется координатой ![]() , начало которой совмещено с правым концом
балки
, начало которой совмещено с правым концом
балки ![]() .
.
Тогда ![]() - от
- от ![]() не
зависит; эпюра – прямая, параллельная оси эпюры.
не
зависит; эпюра – прямая, параллельная оси эпюры.
![]() - линейная зависимость от
- линейная зависимость от ![]() ; эпюра – наклонная прямая; при
; эпюра – наклонная прямая; при ![]() ; при
; при ![]() .
Эпюра - на рисунке 33 к.
.
Эпюра - на рисунке 33 к.
На рисунке 33
ж показана правая часть балки для построения эпюр ![]() и
и ![]() на
участке IV; положение произвольного сечения определяется координатой
на
участке IV; положение произвольного сечения определяется координатой ![]() , начало которой совпадает с правым
концом балки
, начало которой совпадает с правым
концом балки ![]() .
.
Тогда ![]() - от
- от ![]() не
зависит; эпюра – та же прямая, параллельная оси эпюры, что и она участке V
(см. рисунок 34,и). Выражение для
изгибающего момента
не
зависит; эпюра – та же прямая, параллельная оси эпюры, что и она участке V
(см. рисунок 34,и). Выражение для
изгибающего момента ![]() - линейная зависимость от
- линейная зависимость от ![]() ; эпюра наклонная прямая: при
; эпюра наклонная прямая: при ![]() ;
;
при ![]() .
.
Эпюра – на рисунке 34,к.
Пример
26 – Построить эпюры ![]() и
и ![]() для балки, изображенный на рисунке 35,а,
если
для балки, изображенный на рисунке 35,а,
если ![]()
![]()
![]() .
.
Решение. Начинаем с определения реакций, для чего составляем уравнения равновесия (реакции показаны пунктиром на рисунке 35,а).
![]()
![]()
откуда 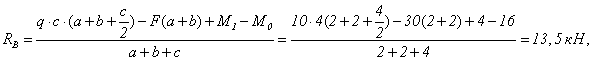
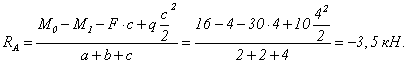
Знак «минус» показывает, что реакция направлена противоположно предварительно принятому направлению; на рисунке 35,б показаны действительные направления.
Проверка показывает, что реакции определены, верно
![]()
Эпюры будем строить по характерным точкам.
На участке І
(см. рисунок 35,б) эпюра
поперечных сил QI постоянна
(распределенная нагрузка отсутствует), равна по модулю RA=3,5
кН, отрицательна (направлена вниз слева от любого сечения на участке І)
– строим эпюру на рисунке 35,в. Эпюра изгибающих моментов здесь
линейная, убывающая (QI отрицательна),
начинается от значения ![]() на
левой границе, а на правой границе участка
на
левой границе, а на правой границе участка ![]() (здесь значение подставляем со знаком
«плюс», так как в выражении для
(здесь значение подставляем со знаком
«плюс», так как в выражении для ![]() мы
учли действительное направление RA
). Эпюра показана на рисунке 35,г.
мы
учли действительное направление RA
). Эпюра показана на рисунке 35,г.
На участке ІІ
эпюра QII имеет такой же вид, как на
участке І: ![]() Изгибающий
момент изменяется по линейному закону и на левой границе имеет
значение
Изгибающий
момент изменяется по линейному закону и на левой границе имеет
значение ![]() (скачок
на
(скачок
на ![]() вверх); правой границе
вверх); правой границе ![]() .
.
На участке ІІІ
поперечная сила меняется по линейному закону (на участке имеется равномерно
распределенная нагрузка). На левой границе участка ІІІ эпюра изменяется
скачком на величину ![]() :
: ![]() . На правой границе, если рассматривать
левую часть балки,
. На правой границе, если рассматривать
левую часть балки, ![]() . Если же смотреть справа, то
в этом сечении
. Если же смотреть справа, то
в этом сечении ![]() и все сходится. Изгибающий момент
на участке ІІІ изменяется по квадратичному закону. Эпюра не левой
границе начинается со значения
и все сходится. Изгибающий момент
на участке ІІІ изменяется по квадратичному закону. Эпюра не левой
границе начинается со значения ![]() , где-то на участке
достигает максимального значения (там, где эпюра
, где-то на участке
достигает максимального значения (там, где эпюра ![]() проходит
через нулевое значение) и на правой границе должна приходить к нулевому
значению. Проверим последнее:
проходит
через нулевое значение) и на правой границе должна приходить к нулевому
значению. Проверим последнее: ![]() . Найдем теперь
значения максимального момента на участке . Из подобия треугольников, составляющих
эпюру
. Найдем теперь
значения максимального момента на участке . Из подобия треугольников, составляющих
эпюру ![]() , запишем
, запишем ![]() ,
откуда
,
откуда ![]() . Поскольку изменение значения изгибающего
момента между левой границей участка и сечением, где момент максимален,
положительно и равно площади под эпюрой поперечной силы между этими двумя
сечениями, то
. Поскольку изменение значения изгибающего
момента между левой границей участка и сечением, где момент максимален,
положительно и равно площади под эпюрой поперечной силы между этими двумя
сечениями, то ![]() .
.
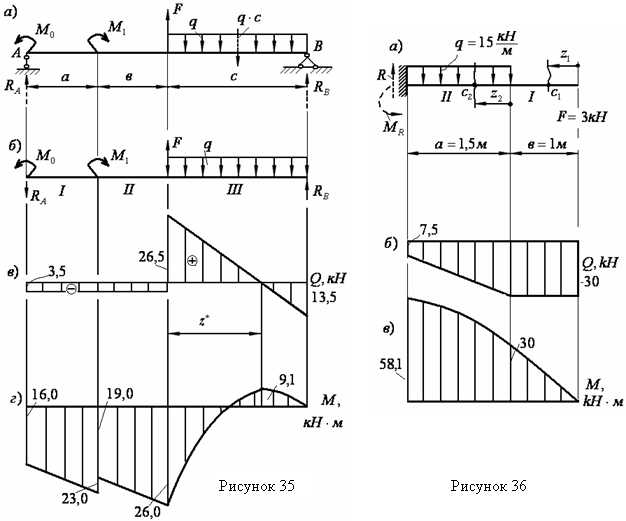
|
Решение. Балка имеет два участка. Для того чтобы не определять реакцию R и реактивный момент MR в заделке, будем рассматривать на обоих участках правую отсеченную часть.
На участке I
![]() :
: ![]() , от z2
не зависит;
, от z2
не зависит; ![]() - уравнение прямой;
при
- уравнение прямой;
при ![]()
![]() , при
, при
![]() ,
, ![]() .
.
На участке II ![]() :
: ![]() - уравнение прямой; при
- уравнение прямой; при ![]()
![]()
![]() , при
, при ![]() ,
, ![]() . Изгибающий момент
. Изгибающий момент
![]() -
уравнение параболы; поскольку Q2
не меняет знак на участке, вершины парабола не имеет; при
-
уравнение параболы; поскольку Q2
не меняет знак на участке, вершины парабола не имеет; при ![]() ,
,
![]() ;
; ![]() .
Эпюры показаны на рисунке 36,б,в.
.
Эпюры показаны на рисунке 36,б,в.
Пример 28 - Определить максимальный по абсолютной величине изгибающий момент для балки ABC (см. рисунок 37,а).
Решение. Нагрузка на балку ABC передается через опоры верхней балки DCE, которую рассмотрим отдельно (см. рисунок 36,). Определим опорные реакции RD и RC, для чего запишем уравнения равновесия для балки DCE
![]() ,
, ![]() , откуда
, откуда
![]() ,
, ![]() .
.
Реакция RD получилась отрицательной, то есть в точке D сила, с которой балка ABC действует на балку DCE, направлена сверху вниз.
 Теперь
рассматриваем нагружение балки ABC (см. рисунок 37,в). В
точке D действует сила
Теперь
рассматриваем нагружение балки ABC (см. рисунок 37,в). В
точке D действует сила ![]() ,
,
![]() и направлена снизу
вверх. В точке C действует сила
и направлена снизу
вверх. В точке C действует сила ![]() ,
,
![]() и направлена cверху вниз. Определяем реакции RA
и RB, которые первоначально направим
вверх. Записываем уравнения равновесия
и направлена cверху вниз. Определяем реакции RA
и RB, которые первоначально направим
вверх. Записываем уравнения равновесия ![]() , откуда
, откуда 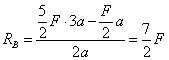 ;
;
![]() , откуда
, откуда 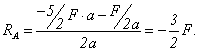
Реакция RA оказалась направленной противоположно тому направлению, которое было принято первоначально. На рисунке 36,г первоначальное направление перечеркнуто и рядом показано действительное направление. Несложно в уме проверить равенство нулю суммы проекций всех сил на вертикальную ось.
Для определения максимального по абсолютной величине, изгибающего момента построим эпюру M. В данном случае нет необходимости в построении эпюры Q, так как распределенной нагрузки нет, так что нет опасности потерять экстремальные значения моментов где-нибудь внутри участков – в пределах каждого участка эпюра M монотонна.
Над опорой A изгибающий момент равен нулю; в
сечении D он
определяется моментом силы RA, то
есть ![]() . В сечении C изгибающий момент равен нулю, а
над опорой B находим
. В сечении C изгибающий момент равен нулю, а
над опорой B находим![]() .
.
Т.о., находим
максимальный по абсолютной величине момент ![]()
Пример 29 - Построить эпюры Q и M для балки на рисунке 38,а.
Решение. Учитывая, что равнодействующая распределенной по закону треугольника равна площади этого треугольника и проходит через его центр тяжести, найдем опорные реакции из уравнений равновесия:
![]() , откуда
, откуда 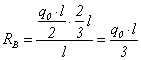 ;
;
![]() , откуда
, откуда  .
.
Проверка
суммы проекций всех сил на вертикальную ось свидетельствует, что реакции
найдены верно ![]() .
.
Имеется всего
один участок. Произвольным сечением на расстоянии z от левой опоры разделим балку на две части и будем рассматривать
левую часть: ![]() ; так как qz=q0∙z/l , то
; так как qz=q0∙z/l , то ![]() - уравнение параболы. Так как Q принимает нулевое значение на участке при z=0, то эпюра будет иметь вершину при z=0, а далее будет монотонно убывающей, так как q<0. Кривизна эпюры - отрицательна, так как
- уравнение параболы. Так как Q принимает нулевое значение на участке при z=0, то эпюра будет иметь вершину при z=0, а далее будет монотонно убывающей, так как q<0. Кривизна эпюры - отрицательна, так как ![]() . Строим эпюру (см. рисунок 38,б): при z=0
. Строим эпюру (см. рисунок 38,б): при z=0
![]() при z=l
при z=l ![]() . Определим
значение z* , при котором Q=0.
Из выражения
. Определим
значение z* , при котором Q=0.
Из выражения ![]() найдем
найдем ![]() . Смысл имеет только положительный
корень
. Смысл имеет только положительный
корень ![]()
Строим эпюру
изгибающих моментов (см. рисунок 38,в).
Очевидно, M=0 на опорах A и B.
Выражение для изгибающих моментов в
сечении z запишем как![]() Находим
при Q=0 максимальный изгибающий момент
Находим
при Q=0 максимальный изгибающий момент ![]()
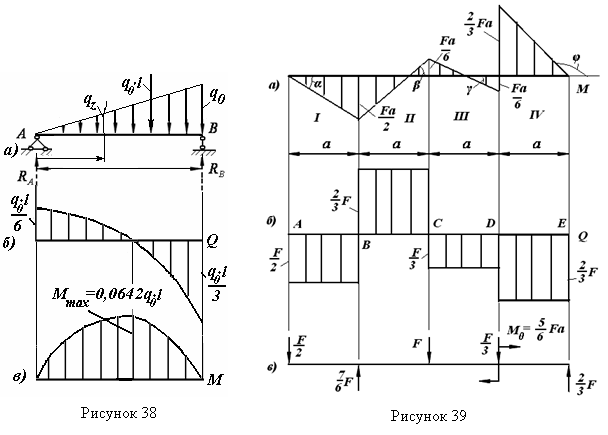
Пример 30 - По заданной эпюре изгибающих моментов (см. рисунок 39,а) построить эпюру поперечных сил и определить нагрузку, под действием которой эпюра имеет такой вид.
Решение. Разбиваем эпюру на 4 участка. Тангенс угла наклона касательной к эпюре дает поперечную силу в соответствующем сечении. На каждом участке углы наклона касательной постоянны.
На участке І: ![]()
На участке
ІІ: ![]()
На участке
ІІІ: ![]()
На участке
IV: ![]()
По найденным значением строим эпюру поперечных сил (см. рисунок 39,б). Так как поперечные силы изменяются при переходе от участка к участку, то балка нагружена сосредоточенными силами в сечениях A, B, C, D, E. Этим силам соответствуют скачки на эпюре Q и изломы на эпюре M. Кроме того, балка нагружена сосредоточенным моментом M0=5/6F∙a (парой сил) в сечении D.
Схема загружения балки показана на рисунке 39,в.
5.2 Напряжения в поперечных сечениях. Расчеты на прочность по допускаемым напряжениям
При поперечном изгибе в поперечных сечениях балки возникают нормальные и касательные напряжения (см. рисунок 40).
Нормальные напряжения в произвольной точке поперечного сечения определяются по формуле
 (5.5)
(5.5)
где M - изгибающий момент в рассматриваемом сечении;
Ix - момент инерции относительно нейтральной линии, совпадающей с главной центральной осью x при изгибе в плоскости yz;
y - расстояние от нейтральной линии до точки, в которой вычисляются напряжения.
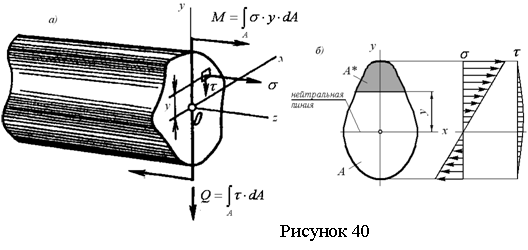
Нормальные напряжения в поперечном сечении балки распределяются по линейному закону и достигают наибольших значений в точках, наиболее удаленных от нейтральной линии (см. рисунок 40,б). В случае балки постоянного сечения они достигают наибольшего значения в том сечении, где максимален изгибающий момент, и определяются как
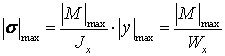 (5.6)
(5.6)
Отношение
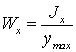 (5.7)
(5.7)
называют моментом сопротивления сечения при изгибе относительно оси x или осевым моментом сопротивления; он имеет размерность длины в третьей степени и является геометрической характеристикой поперечного сечения балки, то есть зависит только от размеров и формы сечения.
Для сечений, изображенных на рисунке 29, осевые моменты сопротивления вычисляют по следующим формулам:
для прямоугольника
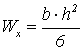 ,
,  ;
(5.8)
;
(5.8)
для круга
 (5.9)
(5.9)
для кольца
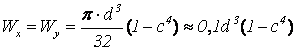 . (5.10)
. (5.10)
Расчет на прочность по методу допускаемых напряжений в случае балок постоянного сечения, изготовленных из материалов, одинаково работающих на растяжение и сжатие, выполняется по условию прочности
 (5.11)
(5.11)
где
![]() -
максимальное по абсолютной величине значение изгибающего момента,
-
максимальное по абсолютной величине значение изгибающего момента,
[σ] - допускаемое напряжение.
Наиболее экономичными являются такие формы поперечных сечений, для которых с наименьшей затратой материала получается наибольшая величина осевого момента сопротивления. К таким рациональным сечениям относятся стандартные двутавровые и швеллерные профили, коробчатые и кольцевые сечения. Для стандартных профилей осевые моменты сопротивления вычислены заранее для каждого типоразмера и проводятся в таблицах.
При использовании материалов, неодинаково сопротивляющихся растяжению и сжатию, возможен следующий случай (речь идет о балках постоянного сечения): сечение балки симметрично относительно нейтральной линии и эпюра изгибающих моментов сохраняет знак по всей длине балки; в этом случае расчет ведется по условию (5.11), где в качестве [σ] берется меньше из допускаемых напряжений на растяжение [σр] и сжатие [σс]. В остальных случаях бывает необходимым выполнять расчет как по максимальным напряжениям растяжения, так и по максимальным напряжениям сжатия, причем, если эпюра изгибающих моментов не сохраняет знак и сечение несимметрично относительно нейтральной оси, нужно производить расчет не только по максимальному по абсолютной величине изгибающему моменту, но и по максимальному изгибающему моменту противоположенного знака.
Касательные напряжения в произвольной точке поперечного сечения балки (см. рисунок 40) определяют по формуле Журавского
 (5.12)
(5.12)
где Qy - поперечная сила в рассматриваемом сечении;
![]() -
статический момент относительно нейтральной линии той части сечения (см. рисунок
4), которая расположена выше прямой, проведенной через данную точку параллельно
нейтральной линии на расстоянии y от нее;
-
статический момент относительно нейтральной линии той части сечения (см. рисунок
4), которая расположена выше прямой, проведенной через данную точку параллельно
нейтральной линии на расстоянии y от нее;
Jx - момент инерции поперечного сечения относительно нейтральной линии;
b - ширина поперечного сечения на уровне, рассматриваемой точки.
В большинстве случаев касательные напряжения невелики и в расчетах на прочность их не учитывают. Исключение составляют тонкостенные балки, нагруженные большими сосредоточенными силами, а также очень короткие балки. В этом случае наряду с расчетом по нормальным напряжениям производят расчет по наибольшим касательным по условию
![]() .
(5.13)
.
(5.13)
Если в точках поперечного сечения одновременно возникают нормальные и касательные напряжения одного порядка, то расчет производят по эквивалентному напряжению с использованием одной из теорий прочности.
Пример
31 - Проверить прочность балки, изображенной на рисунке 34,а,
если поперечное сечение балки представляет собой прямоугольник со сторонами 100х180
мм, а допускаемые напряжения ![]() ,
, ![]() .
.
Решение. Прежде всего, необходимо построить эпюры Q и M. Нами они уже были построены при решении примера 25 (см. рисунок 34,и,к). Рассмотрим два случая I и II расположения балки.
Случай I. Длинная сторона прямоугольника параллельна
плоскости изгиба yz, сечения при изгибе поворачиваются
относительно оси x (рисунок
40 а): b=100 мм, h=180 мм; осевой момент сопротивления по
формуле (5.8) ![]() Расчетный изгибающий момент принимаем равным максимальному по
абсолютной величине изгибающему моменту на эпюре (рисунок 34,к) Mmax=102,4 кН∙м.
Расчетный изгибающий момент принимаем равным максимальному по
абсолютной величине изгибающему моменту на эпюре (рисунок 34,к) Mmax=102,4 кН∙м.
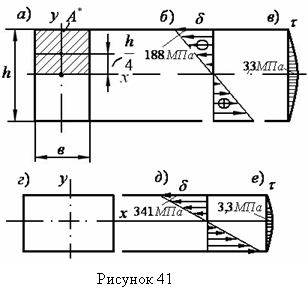 Проверяем выполнение
условия прочности по нормальным напряжениям (5.11)
Проверяем выполнение
условия прочности по нормальным напряжениям (5.11)
![]() - условие
прочности выполняется. Эпюра распределения σ по поперечному
сечению показана на рисунке 41,б.
- условие
прочности выполняется. Эпюра распределения σ по поперечному
сечению показана на рисунке 41,б.
Для проверки
условия прочности по касательным напряжением найдем τmax, воспользовавшись формулой (5.12). Для прямоугольного
сечения b=const,
поэтому максимальные касательные напряжения возникают в точках сечения,
которым соответствует максимальное значения статического момента ![]() . Очевидно, это точки, лежащие на
нейтральной линии, для которых
. Очевидно, это точки, лежащие на
нейтральной линии, для которых ![]() ,
,
![]() и
и ![]() .
.
В наиболее удаленных от нейтральной линии точках поперечного сечения Sx=0, поэтому τ=0. Максимальные касательные напряжения определяем для наиболее нагруженного поперечного сечения (чуть правее сечения А на рисунке 34,и, где Q=39,5 кН)
![]() .
Эпюра распределения τ показана на
рисунке 41,в.
.
Эпюра распределения τ показана на
рисунке 41,в.
Таким образом, в рассматриваемом случае выполнены условия прочности как по нормальным, так и по касательным напряжениям, причем последние весьма малы.
Случай II. Короткая сторона прямоугольника параллельна
плоскости изгиба yz (рисунок 41,г). Тогда
![]() ,
, ![]() ,
, ![]() .
. ![]() -
условие прочности по нормальным напряжениям не выполнено. Величина τmax не изменяется, эпюры – на рисунке 41,д,е.
-
условие прочности по нормальным напряжениям не выполнено. Величина τmax не изменяется, эпюры – на рисунке 41,д,е.
Пример
32 - Балка ABC (рисунок 42,а)
имеет поперечное сечение в виде тавра, ориентированное так, как показано на
рисунке 42,б. Поверить прочность балки, если![]()
Решение. Определяем опорные реакции из уравнений равновесия:
![]() , откуда
, откуда ![]()
![]() , откуда
, откуда![]()
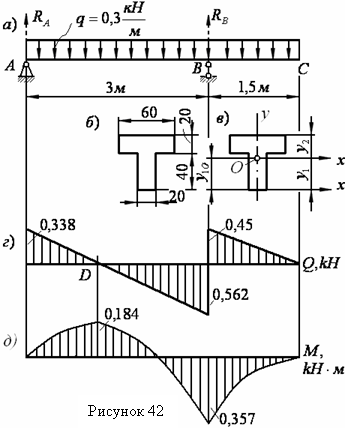
![]() -
проверка сходится.
-
проверка сходится.
Строим эпюры Q и M на рисунке 42,г,д.
Определяем положении центра тяжести сечения О, момент инерции относительно нейтральной линии х, координаты наиболее удаленных от нейтральной линии точек y1 и y2 (см. рисунок 42,в):
![]() ,
,![]() ,
,
![]() ,
, ![]() .
.
Подсчитываем напряжения по формуле (5.5).
В сечении D, где имеет место максимальный
положительный изгибающий момент, имеем ![]() ,
, ![]() . В сечении B, где максимален отрицательный момент,
. В сечении B, где максимален отрицательный момент, ![]()
![]()
![]() . Условие
прочности в рассматриваемом случае выполняется, так как
. Условие
прочности в рассматриваемом случае выполняется, так как ![]() и
и ![]()
![]()
Отметим, что
если сечение балки будет ориентирована полкой вниз, то условие прочности не
будет выполнено, т.к. в этом случае получаем ![]() .
.
Пример
33 - Для балки, изображенный на рисунке 35,а, подобрать сечение
в виде двутавра, приняв ![]() .
.
Решение. Определяем опорные реакции и строим эпюру M, как в примере 26 (эпюра Q в этом случае играет вспомогательную роль – она показывает, имеются ли в пределах участков с распределенной нагрузкой сечения, где момент экстремален).
Из эпюры на
рисунке 35,г определяем максимальное по абсолютной величине значение
изгибающего момента ![]() . Так как выполняется проектный расчет,
выразим из условия прочности (5.11) геометрический фактор – осевой момент
сопротивления
. Так как выполняется проектный расчет,
выразим из условия прочности (5.11) геометрический фактор – осевой момент
сопротивления ![]() . По таблице сортамента, приведенной в приложениях
к [1-4], выбираем двутавр №18а по ГОСТ 8239-72, у которого
. По таблице сортамента, приведенной в приложениях
к [1-4], выбираем двутавр №18а по ГОСТ 8239-72, у которого ![]() . Балка при этом будет испытывать некоторую
перегрузку, т.к.
. Балка при этом будет испытывать некоторую
перегрузку, т.к. ![]() ,однако перегрузка составляет
,однако перегрузка составляет ![]() , что можно считать приемлемым.
, что можно считать приемлемым.
 Пример 34
- Определить максимально допустимое значение интенсивности распределенной
нагрузки q, которую можно безопасно приложить к
балке, изображенной на рисунке 43,а. Cечение
балки показано на рисунке 43,б, допускаемое напряжение
Пример 34
- Определить максимально допустимое значение интенсивности распределенной
нагрузки q, которую можно безопасно приложить к
балке, изображенной на рисунке 43,а. Cечение
балки показано на рисунке 43,б, допускаемое напряжение ![]() .
.
Решение.
Строим эпюру изгибающих моментов, выразив ее характерные ординаты через q и a. Максимальный
изгибающий момент ![]() . Приравняем
его допускаемому изгибающему моменту, выразив последний из условия прочности
(5.11)
. Приравняем
его допускаемому изгибающему моменту, выразив последний из условия прочности
(5.11) ![]() . Отсюда
. Отсюда ![]() Для
круглого сечения
Для
круглого сечения ![]() , и,
таким образом,
, и,
таким образом, ![]()
Пример
35 - Проверить прочность клееной деревянной балки (см. рисунок 44,а,б),
если ![]()
![]() ,
,
![]()
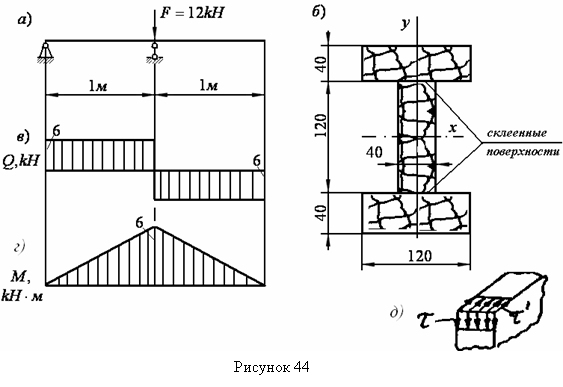
Решение. Эпюры поперечных сил и изгибающих моментов показаны на рисунках 44,в,г.
Вычислим момент инерции и осевой момент сопротивления поперечного сечения
![]()
![]()
Наибольшие
нормальные напряжения в поперечном сечении балки![]()
Максимальные
касательные напряжения возникают в точках на оси x,
где максимален статический момент![]() . Найдем
. Найдем![]() . Тогда
. Тогда ![]() .
.
Проверим
прочность клеевого шва. Касательные напряжения на продольных склеенных
плоскостях подчиняются закону парности (см. рисунок 44,д) и равны ![]() где
где ![]() - статический момент полки
относительно нейтральной оси;
- статический момент полки
относительно нейтральной оси;
Тогда ![]()
Таким образом, прочность балки обеспечена.
5.3 Перемещения при изгибе и расчеты на жесткость
Перемещения поперечных сечений балок характеризуются прогибами и углами поворота (см. рисунок 45). Прогибами v называют линейные перемещения центров тяжести поперечных сечений в направлении, перпендикулярном геометрической оси балки. Углами поворота θ называют угловые перемещения поперечных сечений вокруг нейтральной оси. Перемещения сечений вдоль оси стержня обычно пренебрежимо малы.
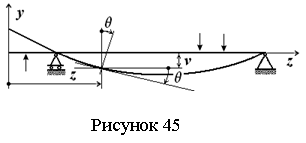 Прогибы и углы поворота сечений могут быть найдены
различными способами. В частности, их можно определить, если известно уравнение
изогнутой оси балки, называемой также упругой линией балки. Так, в случае изгиба
в плоскости yz (см. рисунок 45) достаточно знать уравнение изогнутой оси
Прогибы и углы поворота сечений могут быть найдены
различными способами. В частности, их можно определить, если известно уравнение
изогнутой оси балки, называемой также упругой линией балки. Так, в случае изгиба
в плоскости yz (см. рисунок 45) достаточно знать уравнение изогнутой оси
![]() (ось z направлена вдоль недеформированной оси балки), чтобы
иметь возможность определить прогиб v и угла поворота θ любого
сечения, положение которого характеризуется координатой z,
так как очевидно (считая прогиб малым), что
(ось z направлена вдоль недеформированной оси балки), чтобы
иметь возможность определить прогиб v и угла поворота θ любого
сечения, положение которого характеризуется координатой z,
так как очевидно (считая прогиб малым), что
![]() ;
; ![]() .
(5.14)
.
(5.14)
Уравнение изогнутой оси балки может быть получено различными способами, в том числе путем непосредственного интегрирования дифференциального уравнения изогнутой оси
![]() (5.15)
(5.15)
где M - изгибающий момент;
E - модуль упругости;
Jx - момент инерции поперечного сечения балки относительно нейтральной оси.
Произведение ![]() называют
жесткостью стержня (балки) при изгибе. Если балка имеет несколько участков, то
для каждого участка зависимости M(z) и
называют
жесткостью стержня (балки) при изгибе. Если балка имеет несколько участков, то
для каждого участка зависимости M(z) и ![]() (z)
описываются своими уравнениями; при интегрировании уравнения (5.15) для каждого
участка появляется по две постоянных интегрирования. Последние определяются из
граничных условий, соответствующих условиям закрепления балки (в заделке равны
нулю прогиб и угол поворота сечения, на шарнирных опорах равны нулю прогибы), а
также условиям непрерывности и плавности изогнутой оси на границах смежных участков
(то есть равенства прогибов и углов поворота в смежных сечениях).
(z)
описываются своими уравнениями; при интегрировании уравнения (5.15) для каждого
участка появляется по две постоянных интегрирования. Последние определяются из
граничных условий, соответствующих условиям закрепления балки (в заделке равны
нулю прогиб и угол поворота сечения, на шарнирных опорах равны нулю прогибы), а
также условиям непрерывности и плавности изогнутой оси на границах смежных участков
(то есть равенства прогибов и углов поворота в смежных сечениях).
Отметим, что в рассмотренном методе определения перемещений не учитывается влияние поперечной силы, так как оно оказывается существенным только для очень коротких балок.
Определение перемещений необходимо для выполнения расчетов на жёсткость при изгибе, которое в большинстве случаев сводится к удовлетворению условия
![]() (5.17)
(5.17)
где fmax - максимальный прогиб (стрела прогиба);
[f] - допускаемый прогиб, значение которого зависит от назначения конструкции и обычно устанавливается как некоторая доля от длины пролета l, например, l/200 или l/1000.
Для обеспечения нормальной работы подшипников скольжения и роликовых подшипников качения иногда ставится дополнительное условие жёсткости, ограничивающее углы поворота опорных сечений (0,001 рад)
![]() (5.18)
(5.18)
Ниже во всех примерах жесткость балок считается постоянной.
Пример 36 - Определить прогиб и угол поворота незакрепленного конца консольной балки, нагруженной равномерно распределенной нагрузкой интенсивности (см. рисунок 36).
Решение. Поместив начало координат в заделке, запишем выражение для нагибающего момента в произвольном сечении, расположенном на расстоянии z от начало координат
![]() .
.
Дифференциальное уравнение изогнутой оси имеет, согласно формуле (5.15), вид
![]() .
.
Последовательно интегрируя это уравнение два раза, получаем уравнения для прогибов и углов поворота
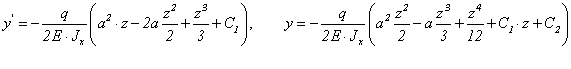 .
.
Постоянные интегрирования C1 и C2 находим из граничных условий в заделке. При z=0 y=0; отсюда с использованием уравнения для прогибов для вытекает, что C2=0. При z=0 y’=0; отсюда из уравнения для углов поворота вытекает, что C1=0
Окончательно получаем уравнения:
- для
прогибов 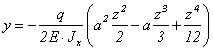 ;
;
- для углов
поворота 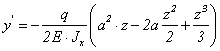 .
.
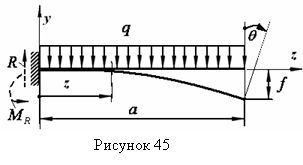 Подставляя
значение z=a,
найдем прогиб f и угол поворота θ незакрепленного
конца балки
Подставляя
значение z=a,
найдем прогиб f и угол поворота θ незакрепленного
конца балки

![]()
 Пример 37
- Найти и проанализировать уравнение упругой линии свободно опертой
балки, нагруженной силой F на расстояниях a и b от концов (см. рисунок
46).
Пример 37
- Найти и проанализировать уравнение упругой линии свободно опертой
балки, нагруженной силой F на расстояниях a и b от концов (см. рисунок
46).
Решение.
Из уравнений равновесия найдем опорные реакции. Они будут равны ![]() .
.
Запишем выражения для изгибающих моментов на двух участках:
![]()
![]() ;
;
![]()
![]() ;
;
Составим дифференциальные уравнения изогнутой оси и дважды их проинтегрируем. Получаем


Четыре постоянных интегрирования C1, C2, C3, C4 найдем из следующих условий:
1) в сечении z=a должны быть равны углы наклона обеих частей изогнутой оси балки;
2) в том же сечении z=a равны прогибы обеих частей балки;
3) в сечении z=0 прогиб равен нулю;
4) в сечении z=l прогиб равен нулю.
Из первого
условия следует, что C1=C3, из второго – что C2=C4.
Третье условие дает C2=0 (и, следовательно,
C4=0) и четвертое – ![]() .
.
Таким
образом, ![]() , C2=C4=0.
, C2=C4=0.
С учетом этих значений уравнение изогнутой оси балки имеет вид
![]()
![]() ;
;
![]()
![]() .
.
Углы поворота сечений определяются выражениями
![]()
![]() ;
;
![]()
![]() .
.
Из последних выражений несложно найти угол поворота любого сечения балки, в частности, на концах балки A и B
![]()
![]()
Максимальный
прогиб fmax балка имеет в сечении,
где касательная к упругой линии горизонтальна, то есть равен нулю угол поворота
поперечного сечения балки. Если a>b,то fmax
находится на участке AC, в противном случае он
лежит на участке CB. Приравнивая значение ![]() нулю, можно найти координату сечения,
где прогиб максимален
нулю, можно найти координату сечения,
где прогиб максимален ![]() (при
условии a>b).
Т.о., при перемещении сечения С, где приложена сила, от середины балки (b=l/2) до правой опоры (точнее, близко к опоре, b≈0),
координата сечения, где имеет место наибольший прогиб, изменяется от 0,5l до
(при
условии a>b).
Т.о., при перемещении сечения С, где приложена сила, от середины балки (b=l/2) до правой опоры (точнее, близко к опоре, b≈0),
координата сечения, где имеет место наибольший прогиб, изменяется от 0,5l до ![]() .
.
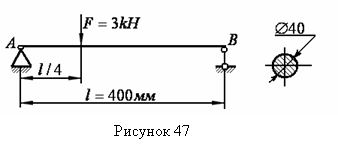 Значение
максимального прогиба, соответствующее координате
Значение
максимального прогиба, соответствующее координате ![]() , составляет
, составляет 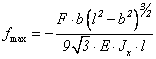 при a>b, а прогиб балки в ее среднем сечении -
при a>b, а прогиб балки в ее среднем сечении -  (также при a>b).
(также при a>b).
В предельном случае, когда b→0, значение fmax отличается от значения f(l/2) всего лишь на 3% ,в остальных случаях отличие и того меньше. Это означает, что приближенно можно считать, что fmax ≈f(l/2).
В случае, когда
сила приложена посредине балки (a=b=l/2), имеем ![]()
![]() .
.
Пример 38 – Проверить выполнение условий жесткости для балки, приведенной на рисунке 47, если максимальный прогиб не должен превышать величину [f]=0,8 мм, а угол поворота сечений над опорами – величины [θ]=10-3 рад. Модуль Юнга Е=2,1∙105 МПа.
Решение.
Прежде всего, определим значение осевого момента сопротивления. Т.к. поперечное
сечение балки круглое, то ![]()
Для того, чтобы найти максимальный прогиб fmax, воспользуемся формулой, полученной в предыдущем примере, принимая во внимание, что a<b. Получаем

Воспользовавшись полученными в предыдущем примере формулами для углов поворота сечений, расположенных над опорами, найдем их
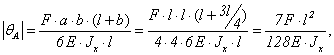
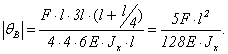
Очевидно, что угол поворота сечения над опорой A больше. Выполним проверку условия жесткости для него. Получаем
![]()
Таким образом, оба условия жесткости выполнены.
6 Сложное сопротивление
Под сложным сопротивлением подразумевают различные комбинации простейших деформаций бруса - растяжения или сжатия, сдвига, кручения и изгиба. На основании принципа независимости действия сил напряжения и деформации в стержне при сложном сопротивлении определяют суммированием напряжений или деформаций, вызванных каждым внутренним силовым фактором в отдельности. Напомним, что этот принцип применим в тех случаях, когда имеют место только упругие деформации, а материал подчиняется закону Гука. Касательные напряжения, вызываемые поперечными силами, не учитываются. Как мы убедились при рассмотрении поперечного изгиба, обычно эти напряжения намного меньше, чем нормальные напряжения. Поэтому здесь считается, что прочность определяется нормальными напряжениями, а также касательными напряжениями, обусловленными кручением (если таковое имеет место). Внутренние силовые факторы при этом могут быть определены без учета деформаций.
6.1 Косой изгиб
Косой изгиб подразделяется на плоский и пространственный. В случае балки постоянного сечения, если все силы, действующие на нее, расположены в плоскости (силовая плоскость), не проходящей через главную ось инерции поперечного сечения, то имеет место плоский косой изгиб. При этом первоначально прямолинейная ось балки искривляется и образует плоскую кривую, плоскость которой не совпадает с силовой плоскостью. Если силы, действующие на балку, не лежат в одной плоскости, то получаем пространственный косой изгиб, при этом изогнутая ось балки представляет собой некоторую пространственную кривую.
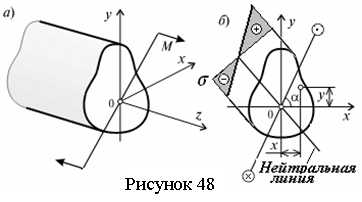 При проведении расчетов на прочность и жесткость при
косом изгибе внешние силы раскладывают на составляющие вдоль главных осей
инерции и затем строят эпюры изгибающих моментов Mx и My в двух
плоскостях. В случае плоского косого изгиба можно построить эпюру полного
изгибающего момента, а затем определить составляющие моменты (см. рисунок 48,а)
как
При проведении расчетов на прочность и жесткость при
косом изгибе внешние силы раскладывают на составляющие вдоль главных осей
инерции и затем строят эпюры изгибающих моментов Mx и My в двух
плоскостях. В случае плоского косого изгиба можно построить эпюру полного
изгибающего момента, а затем определить составляющие моменты (см. рисунок 48,а)
как
![]() (6.1)
(6.1)
где α – угол между осью x и плоскостью изгибающего момента (см. рисунок 48,б).
Нормальное напряжение в точке, имеющей координаты x и y (рисунок 48 б), определяется как
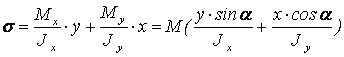 (6.2)
(6.2)
где Jx, Jy – моменты инерции поперечного сечения балки относительно главных осей x и y соответственно.
Напряжения пропорциональны расстоянию точки от нейтральной линии, уравнение которой имеет вид
 .
(6.3)
.
(6.3)
При косом изгибе нейтральная линия не перпендикулярна плоскости действия изгибающего момента, т.к. Jx≠Jy, т.е., стержень «предпочитает» изгибаться не в плоскости изгибающего момента, а в некоторой другой плоскости, где жесткость на изгиб меньше. Если Jx=Jy (например, круглое или квадратное сечение), то любая центральная ось является главной, и имеем прямой изгиб.
Нормальное напряжения в произвольной точке поперечного сечения стержня пропорционального расстоянию от нейтральной линии (см. рисунок 48,б) и достигает максимальных значений в наиболее удаленных от нее точках. Касательные напряжения при косом изгибе длинных стержней сплошного поперечного сечения пренебрежимо малы.
Если максимальное напряжение возникают в точке, наиболее удаленной от обеих главных центральных осей, то условие прочности имеет вид
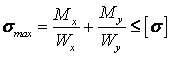 (6.4)
(6.4)
где Wx,Wy - моменты сопротивления изгибу относительно осей x и y соответственно;
[σ] - допускаемое напряжение.
Задача подбора сечения в виде прокатного профиля (двутавра или швеллера) выполняется методом проб и ошибок по выражению
 (6.5)
(6.5)
где ![]() ; для
двутавров с лежит в пределах от 6 до 15.
; для
двутавров с лежит в пределах от 6 до 15.
Прогиб и угол поворота какого-либо сечения при косом изгибе определяют как геометрические суммы прогибов и углов поворота от изгиба в двух главных плоскостях инерции
![]() ,
,
![]() (6.6)
(6.6)
где fx и fy – прогибы в направлении осей x и y;
θxz и θyz – углы поворота сечений в плоскостях xz и yz.
Пример 39 - Подобрать прямоугольное сечение балки (см. рисунок 49) при условии, что h = 2b, [σ]=160 МПа, P=60 кН, α=30°, l=2,8 м.
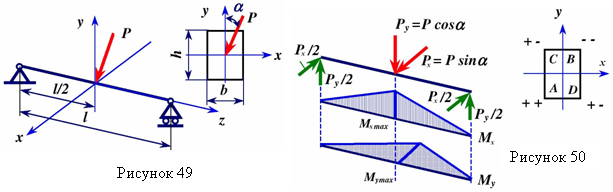
Решение. Разложив силу Р на две составляющие, действующие по направлению главных осей поперечного сечения балки, определяем опорные реакции и строим эпюры изгибающих моментов Mx и Му (рисунок 50).
Наибольшие моменты действуют в среднем сечении, где ![]()
![]() следовательно, это сечение является
опасным.
следовательно, это сечение является
опасным.
Для определения положения опасной точки расставим знаки σ(Mx) и σ(Му) в угловых точках поперечного сечения балки (см. рисунок 50). При действии момента Mx в точках А и D будут иметь место положительные (растягивающие) напряжения, а в точках С и В - отрицательные (сжимающие) напряжения. При действии момента Му в точках А и С будут иметь место положительные σ, а в точках В и D - отрицательные. Точки поперечного сечения А и В, в которых действуют нормальные напряжения одного знака, являются опасными; для них и должны составляться условия прочности.
Судя по условию задачи, балка изготовлена из пластичного материала, ([σ]=160
МПа) и, следовательно, одинаково сопротивляется растяжению и сжатию. Таким
образом, точки А и В являются равноопасными, и для них
используется одно условие прочности (6.4). Выразим моменты сопротивления
поперечного сечения при заданном соотношении высоты и ширины ![]()
![]()
Подставляя эти
выражения в условие прочности (6.4), выразим из него ширину сечения  Окончательно принимаем b=90 мм, h=2b=180 мм.
Окончательно принимаем b=90 мм, h=2b=180 мм.
Пример 40 – При установке на опоры двутавровой балки №60 (Wx=2560 см3, Wy=182 см3), предназначенной для работы на изгиб в вертикальной плоскости, совпадающей с плоскостью стенки, была допущена ошибка, и стенка двутавра отклонилась от вертикали на угол φ= 1°. Определить связанное с этим увеличение наибольших нормальных напряжений.
Решение: Отклонение оси двутавра у от вертикали привело к возникновению косого изгиба (см. рисунок 51) и появлению изгибающих моментов Мx и Мy
Мy =М∙ sinφ = M∙sin1° =0,0175М, Мx =М∙ cosφ = M∙cos1°= =0,9998М.
 Максимальные напряжения при косом изгибе равны
Максимальные напряжения при косом изгибе равны

и, так как Мx ≈М, то ![]() .
.
В случае правильной установки балки, нагрузка F совпадала
бы с вертикальной осью балки у, и имел бы место прямой изгиб. Изгибающий
момент был бы равен М, а напряжения ![]()
Таким образом, незначительное отклонение от вертикали на угол φ= 1° приводит к возрастанию максимальных напряжений на 24,6 %.
Пример 41 – Вычислить максимальные нормальные напряжения в опасном сечении балки (см. рисунок 52,а), испытывающей косой изгиб. Форма сечения - прямоугольник, b = 6 см, h = 12 см. Покажите, как можно вычислить перемещение свободного конца балки.
Решение. На рисунке 52,б,г показаны схемы нагружения балки в вертикальной и горизонтальной плоскостях, а на рисунке 52,в,д - соответствующие эпюры изгибающих моментов Мх, Мy. На эпюрах видно, что опасным сечением является заделка, где Мх = -20 кН∙м, Му = 5 кН∙м. Для прямоугольного сечения Ix = b∙h3/12, Iy = h∙b3/12, и уравнение нейтральной оси (6.3) для опасного сечения принимает вид х-у = 0.
Расположение нейтральной линии (см. рисунок 52,е) показывает, что самыми опасными точками сечения являются точки В и С, как наиболее удаленные от нейтральной линии. Подставляя их координаты в (6.2), вычислим напряжения в этих точках
![]()
На рисунке 52,е изображена эпюра, характеризующая изменение нормальных напряжений в направлении, перпендикулярном нейтральной оси.
Определение перемещения свободного конца балки можно выполнить следующим способом. Сначала определяют перемещения в вертикальной и горизонтальной плоскостях по отдельности, а затем их геометрически складывают.
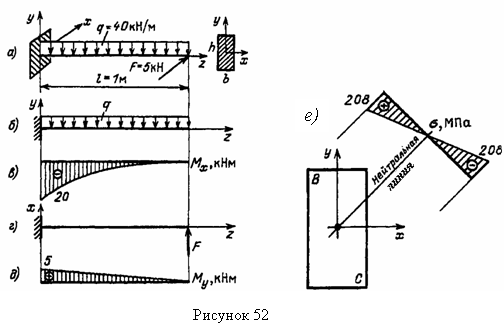 Перемещение
в вертикальной плоскости можно определить по формуле
Перемещение
в вертикальной плоскости можно определить по формуле![]() полученной в примере 36. Перемещение в
горизонтальной плоскости можно получить, используя формулу для прогиба
консольной балки, нагруженной сосредоточенной силой на свободном конце. Эта
формула может быть получена так же, как и в примере 36, непосредственным
интегрированием дифференциального уравнения изогнутой оси балки. Применительно
к рассматриваемому примеру эта формула имеет вид
полученной в примере 36. Перемещение в
горизонтальной плоскости можно получить, используя формулу для прогиба
консольной балки, нагруженной сосредоточенной силой на свободном конце. Эта
формула может быть получена так же, как и в примере 36, непосредственным
интегрированием дифференциального уравнения изогнутой оси балки. Применительно
к рассматриваемому примеру эта формула имеет вид 
Окончательно находим полный прогиб как![]() и вектор полного прогиба составляет с
осью x угол φ,
определяемый через
и вектор полного прогиба составляет с
осью x угол φ,
определяемый через 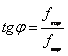 .
.
6.2 Внецентренное растяжение (сжатие)
Внецентренным растяжением (сжатием) называют нагружение стержня двумя растягивающими (сжимающими) силами, линия действия которых смещена относительно оси стержня (см. рисунок 53,а). Точку приложения силы будем называть полюсом и обозначать через P.
ВСФ в поперечных сечениях стержня сводятся к нормальной силе и двум изгибающим моментам
![]() (6.7)
(6.7)
где N - продольная сила;
Mx, My - изгибающие моменты относительно главных центральных осей x и y;
ex, ey - расстояние от полюса, до осей осей x и y (эксцентриситеты).
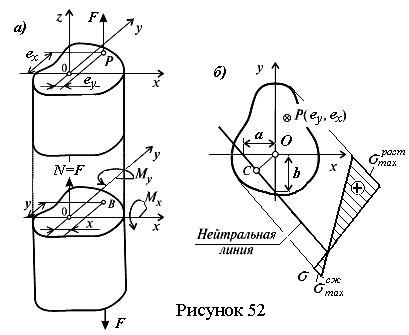
Нормальные напряжения в произвольной точке поперечного сечения определяются, исходя из принципа независимости действия сил, как сумма частных результатов
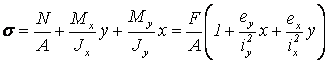 . (6.8)
. (6.8)
Так как знаки перед вторым и третьим слагаемым в правой части выражения (6.8) зависят от того, какого знака напряжения вызывает моменты в первом квадрате, будем назначать оси x и y таким образом, чтобы полюс находился в первом квадранте. В этом случае перед каждым слагаемым будет знак «плюс», и если силу брать в выражениях (6.7) и (6.8) со своим знаками, то и напряжения будут получаться со своими знаками.
Исходя из (6.8), уравнение нейтральной линии записывается в виде уравнения прямой на плоскости поперечного сечения
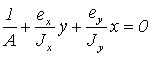 (6.9)
(6.9)
или в виде уравнения прямой в отрезках
![]() (6.10)
(6.10)
где a и b - отрезки, отсекаемые нейтральной линией на осях x и y
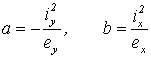 ;
(6.11)
;
(6.11)
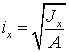 ,
,  - радиусы инерции относительно осей x и y .
- радиусы инерции относительно осей x и y .
Как следует из (6.11), нейтральная линия всегда проходит через квадрант, противоположный тому, в котором находится полюс (см. рисунок 52,б). При этом нейтральная линия может как пересекать поперечное сечение, так и не пересекать его. Во втором случае напряжения во всех точках имеют знак, совпадающий со знаком силы.
Последнее обстоятельство важно, в частности, при расчете кирпичных и каменных колонн, поскольку бетонная кладка практически не сопротивляется растяжению. Для того чтобы напряжения во всех точках сечения были сжимающими, нужно внешнюю сжимающую силу прикладывать достаточно близко к центру тяжести сечения.
В окрестности центра тяжести поперечного сечения стержня можно выделить область называемую ядром сечение. Если полюс (или след силы) находится внутри ядра сечения, напряжение во всех точках сечения имеют знак силы. Для определения ядра сечения нужно представить себе, что нейтральная линия обкатывается вокруг сечения, тогда полюс вычертит границы ядра сечения; при этом используют формулу для определения расстояния от начала координат до нейтральной линии, описываемой управлением (6.10), которая имеет вид
 . (6.12)
. (6.12)
Нормальное напряжение в произвольной точке поперечного сечения пропорционально расстоянию точки от нейтральной линии (см. рисунок 52,в) и достигает максимальных значений в наиболее удаленных от нее точках.
Для симметричных сечений, имеющих точки, наиболее удаленные одновременно от обеих главных центральных осей инерции, максимальные напряжения возникают в этих точках. Условие прочности для них имеет вид
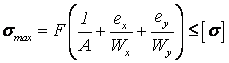 . (6.13)
. (6.13)
Пример 42 - Установить, который из двух стержней, изображенных на рисунках 53,а,б, способен выдержать большую нагрузку без признаков пластичности деформации.
Решение. Сравним максимальные напряжения в двух случаях.
Для случая
(а) 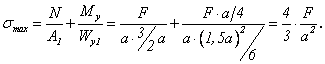
Для случая
(б) ![]() .
.
Таким образом, несмотря на то, что в случае (а) площадь поперечного сечения стрежня больше, прочность стержня оказалась меньше, чем в случае (б).
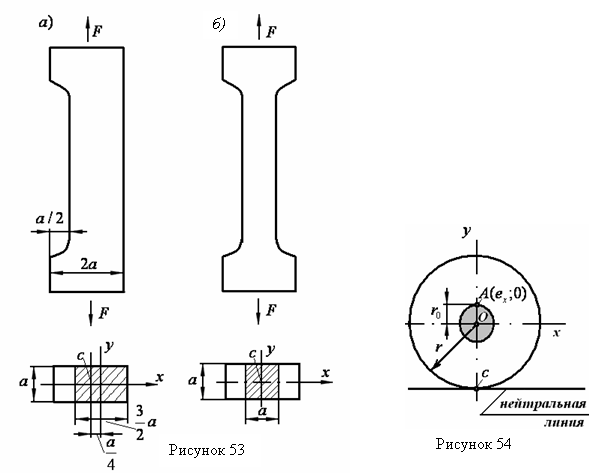 Пример
43 - Определить ядро сечение для стержня круглого поперечного сечения
радиуса r (см. рисунок 54).
Пример
43 - Определить ядро сечение для стержня круглого поперечного сечения
радиуса r (см. рисунок 54).
Решение.
По условиям симметрии понятно, что ядро сечения должно иметь форму круга,
радиус которого обозначим через r0. Пусть полюс находится на
оси y, а нейтральная линия касается контура сечения.
Тогда ![]() Учитывая, что
Учитывая, что 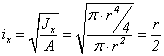 , по формуле (6.12)
запишем
, по формуле (6.12)
запишем 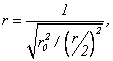 откуда
определяем
откуда
определяем ![]()
Пример 44 - Жесткий брус, имеющий поперечное сечение, изображенное на рисунке 55,а, нагружен продольной сжимающей силой F=100 кН, след которой проходит через точку D. Определить положение нейтральной линии, наибольшие растягивающие и сжимающие напряжения, построить эпюру напряжений и ядро сечения.
Решение. Оси x и y направим так, чтобы полюс был в первом квадранте (см. рисунок 55,б). В данном случае
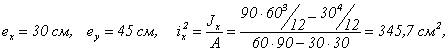
![]()
Уравнение
нейтральной линии имеет вид ![]() или
в отрезках
или
в отрезках ![]() .
.
Наибольшие
сжимающие напряжения возникают в точке D с
координатами ![]() , а наибольшие растягивающие –
в точке E
, а наибольшие растягивающие –
в точке E ![]() ; найдем их
; найдем их
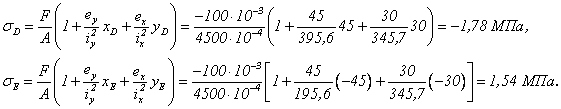
Эпюра напряжений приведена на рисунке 55,б.
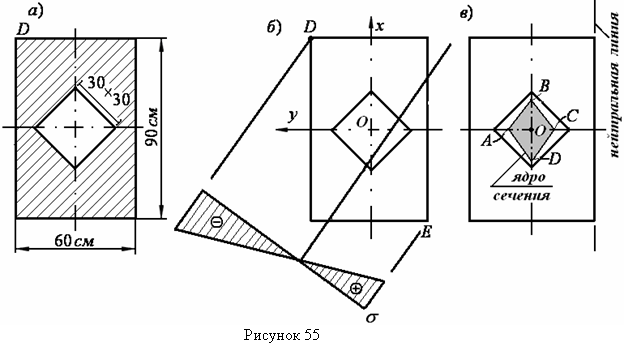 |
Строим ядро сечения. Определим сначала точку пересечения контура ядра сечения с осью (см. рисунок 55,в). Когда нейтральная линия совпадает с правой стороной прямоугольника (OC=30 см), плюс находится в точке A.
Определяем по
формуле (6.12) ![]() откуда
откуда ![]() Аналогично для точки D найдем
Аналогично для точки D найдем ![]()
Можно показать, что для любого сечения, вписывающего в прямоугольник (вершины прямоугольника должны совпадать с вершинами сечения, например, двутавр, швеллер и др.), ядро сечения представляет собой четырехугольную фигуру.
Ядро сечения для рассматриваемого примера показано на рисунке 55,в.
6.3 Совместное действие изгиба с растяжением (сжатием)
При действии сил, вызывающих одновременно прямой изгиб и растяжения (сжатие) стержня, в его поперечных сечениях возникают три ВСФ: продольная сила N, изгибающий момент M, поперечная сила Q. Такой случай нагружения показан на рисунке 56. Здесь не показана эпюра поперечной силы, так как при расчетах на прочность и жесткость ее не учитывают.
Нормальное напряжение в любой точке поперечного сечения вычисляют по формуле
 .
(6.14)
.
(6.14)
При сочетании косого поперечного изгиба и растяжения (сжатия) в поперечных сечениях стержня возникают одновременно пять ВСФ – N, Mx, My, Qx, Qy. Из них при расчетах учитывают три - N, Mx, My. В частности, напряжения определяют по формуле
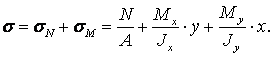 (6.15)
(6.15)
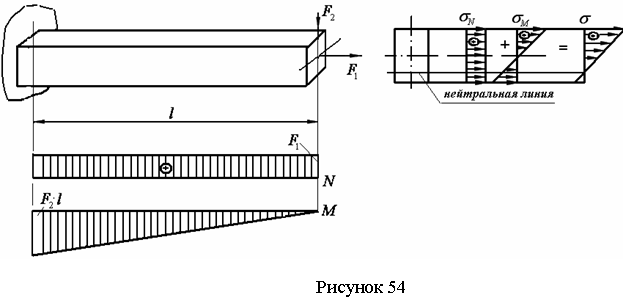 Знак каждого слагаемого в (6.17) и (6.18) целесообразно
устанавливать непосредственно по характеру деформации стержня.
Знак каждого слагаемого в (6.17) и (6.18) целесообразно
устанавливать непосредственно по характеру деформации стержня.
Для того, чтобы выполнить расчет на прочность, надо определить положение опасного сечения и найти опасную точку в этом сечении. Если наибольшие значения различных ВСФ имеют место в разных поперечных сечениях, то приходится выполнять расчет для двух или бóльшего числа сечений.
Для стержней, материал которых работает одинаково на растяжение и сжатие, и в поперечных сечениях которых имеются точки, одновременно наиболее удаленные от обеих главных центральных осей инерции, опасной является та из угловых точек, в которой знаки напряжений по всем ВСФ совпадают. В этом случае условие прочности имеет вид
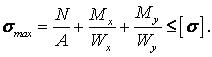 (6.16)
(6.16)
Для стрежней, материал которых неодинаково работает на растяжение и сжатие, бывает необходим расчет как по максимальному напряжению одного знака, так и по максимальному напряжению другого знака.
Пример
45 - Рама изготовлена на кусков стальной трубы, сваренных в колене (см.
рисунок 55,а). Внешний диаметр трубы составляет 60 мм, внутренний – 50 мм. Найти максимальные растягивающие и максимальные сжимающие
напряжения в раме, если ![]()
![]()
Решение. Реакции опор RA=RC и, очевидно, равны F/2.

Обозначая
угол наклона труб к горизонтали через α, разложим реакции на составляющие
![]() Здесь
Здесь
![]()
Под действием
сил R׳ в поперечных сечениях возникает сжимающая
нормальная сила N=-R׳, а под действием R׳׳ – изгибающий момент (эпюры показаны на рисунке 54 б),
максимальное значение которого имеет место в сечении B и равно ![]() . Напряжения в крайних точках этого
поперечного сечения равны
. Напряжения в крайних точках этого
поперечного сечения равны
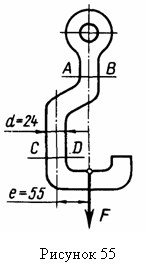
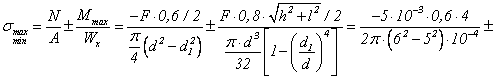
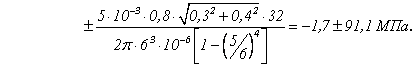
Таким образом, ![]()
Пример 46 – Определить напряжения в сечениях AB и СD стального крюка постоянного круглого сечения (см. рисунок 55), если сила F=3 кН, размеры крюка на рисунке приведены в миллиметрах.
Решение. Применяя метод сечений, видим, что в сечении AB возникает только продольная сила N=F. В этом сечении крюк работает только на растяжение, при этом нормальные напряжения определяются как
σAB=N/A=4F/π∙d2=4∙3∙103/(3,14∙242∙10-6)=6,64∙106 Па=6,64 МПа.
В сечении СD имеет место сочетание растяжения и изгиба. Максимальное напряжение при этом равно σCD=N/A+F∙e/Wx. Так как Wx= π∙d3/16, то получаем
σСD=N/A+ 16F∙e/π∙d3=6,64∙106 +16∙3∙103∙55∙10-3/(3,14∙243∙10-9)=1,26∙108 Па=126 МПа.
6.4 Совместное действие изгиба с кручением
Совместное действие изгиба с кручением необходимо учитывать при расчете валов машин, испытывающих воздействие окружных и радиальных усилий. Сочетание изгиба с кручением имеет место также в пространственных рамах, коленчатых валах и других элементах конструкций.
В предыдущих подразделах рассматривались такие случаи сложного сопротивления (косой изгиб, внецентренное растяжение или сжатие, совместное действие изгиба и растяжения или сжатия), при которых учитывались только нормальные напряжения в поперечных сечениях стержня, и, следовательно, имело место одноосное напряженное состояние. Это позволило при выводе расчетных формул использовать сечения произвольной формы.

В случае изгиба с кручением от действия крутящего момента в поперечных сечениях бруса возникают касательные напряжения, которые необходимо учитывать при расчете на прочность. Наиболее просто расчет выполняется для стержня круглого поперечного сечения, и ниже рассматривается только этот случай.
Пусть в поперечном сечении круглого стержня (см. рисунок 56,а) действуют два изгибающих момента Mx и Мy, которые могут быть приведены к одному суммарному моменту М∑, т.к. все центральные оси круга являются главными
![]() (6.17)
(6.17)
Максимального значения нормальные напряжения от М∑, достигают в точке А (положительные σ) или В (отрицательные σ). Знаки напряжений устанавливают по характеру деформаций.
Кроме того, в поперечном сечении бруса имеет место крутящий момент (Мкр=Мz). Максимального значения касательные напряжения от Мкр достигают в точках на контуре сечения. Следовательно, точка А (или точка В) является опасной, для которой и составляеют условие прочности.
В точке A имеют место напряжения
 (6.18)
(6.18)
причем моменты сопротивления для круглого сечения определяют как
 (6.19)
(6.19)
Анализ показывает (см. рисунок 56,б), что в данном случае имеет место упрощенное плоское напряженное состояние, и расчет на прочность должен вестись по одной из гипотез (теорий) прочности. Для пластичных материалов применяют гипотезу наибольших касательных напряжений (III) или энергетическую гипотезу (IV).
Условие прочности по III и по IV гипотезе в случае упрощенного плоского напряженного состояния записывают в виде
![]()
![]()
В рассматриваемом случае условие прочности можно записать в виде
 (6.20)
(6.20)
где - расчетный момент, который по третьей теории прочности определяют как
![]() (6.21)
(6.21)
а по четвертой теории прочности как
![]() . (6.22)
. (6.22)
Для хрупких материалов может быть использована гипотеза прочности Мора (условно назовем ее V теорией), согласно которой
![]() (6.23)
(6.23)
где k – отношение предела прочности материала
при растяжении к пределу прочности при сжатии, ![]() (если
пределы прочности не даны, а даны допускаемые напряжения, то это отношение
можно выразить через допускаемые напряжения).
(если
пределы прочности не даны, а даны допускаемые напряжения, то это отношение
можно выразить через допускаемые напряжения).
Аналогично выполняют расчет полого вала (с кольцевым сечением).
Пример 47 – Проверить прочность вала зубчатой передачи (см. рисунок 57,а), изготовленного из стали Ст4, предел текучести для которой σт=260 МПа.
Вал передает мощность P=40 кВт и вращается со скоростью n=100 об/мин, нормативный запас прочности [σ]=2,8, диаметр вала d=35 мм. Расчет выполнить по третьей теории прочности, размеры на рисунке 57 даны в миллиметрах. Принять, что зависимость между окружным Ft и радиальным Fr усилиями в зубчатой передаче имеет вид Fr=0,36Ft.

Решение. Определим угловую скорость вала ω=π∙n/30=3,14∙1000/30=104,7 рад /c и передаваемый валом вращающий момент T=P/ ω=40∙103/104,7=382,2 Н∙м.
Вращающий момент связан с окружным усилием зависимостью T=Ft∙D/2, откуда Ft=2T/D=2∙382,2/0,3=2548 Н. Радиальное усилие Fr=0,36Ft=0,36∙2548=917,2 Н.
Изображаем расчетную схему вала как на рисунке 57,б.
Строим эпюры крутящего момента (см.рисунок 57,в), а также изгибающих моментов в двух плоскостях (см.рисунки 57,г,д). По эпюрам видно, что опасное сечение расположено чуть правее середины зубчатого колеса. Используя третью теорию прочности, проверим выполнение условия прочности
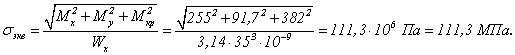
Определяем запас прочности n=σт/ σэкв=260/ 111,3=2,34<[n]=2,8.
Таким образом, прочность вала недостаточна.
Пример 48 – На вал (см. рисунок 58,а) действуют две вертикальные и одна горизонтальная сила, а также три скручивающих момента. Материал вала – сталь 45, σт=360 МПа. Определить диаметр вала из условия статической прочности с использованием 4-й теории прочности, приняв запас прочности равным 2,2.
Решение. Определяем допускаемое напряжение [σ]= =σт/[n]=360/2,2=164 МПа.
Определив реакции опор, строим эпюру изгибающих моментов Mвер (см. рисунок 58,б). Аналогично строим эпюру изгибающих моментов в горизонтальной плоскости Мгор (см. рисунок 58,в). Далее строим эпюру крутящих моментов Мкр (см. рисунок 58,г).
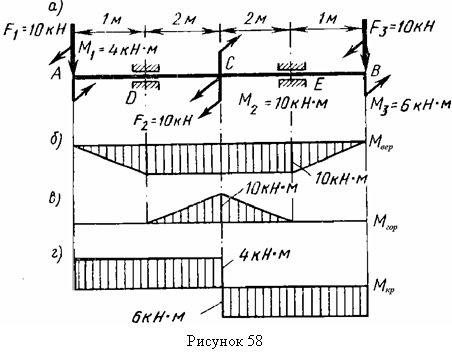
Опасным (наиболее нагруженным) является сечение чуть правее С, так что расчетный эквивалентный момент определяем по (6.22) как
![]()
Из условия
прочности (6.20) выражаем осевой момент сопротивления ![]() Диаметр
вала определяем по формуле (5.8)
Диаметр
вала определяем по формуле (5.8) 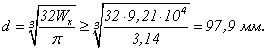 Окончательно
диаметр вала может быть принят равным 100 мм.
Окончательно
диаметр вала может быть принят равным 100 мм.
Пример 50
– На валу (см. рисунок 59,а) установлены два шкива с диаметрами D1=300 мм и D2=600
мм. Усилия на ветвях ременных передач связаны зависимостями S1=2S2,
причем ![]() размер l=800 мм. Приняв допускаемое напряжение [σ]=200 МПа, определить
из расчета на прочность по третьей теории прочности диаметр вала в наиболее
нагруженной части вала.
размер l=800 мм. Приняв допускаемое напряжение [σ]=200 МПа, определить
из расчета на прочность по третьей теории прочности диаметр вала в наиболее
нагруженной части вала.
Решение.
Определяем не заданные в условиях задачи усилия на ветвях ременных передач ![]()
Приводим силы к оси вала, в результате чего появляются скручивающие
моменты![]()
![]()
![]() и силы давления на вал
и силы давления на вал ![]() .
.

Расчетная схема вала приведена на рисунке 59,б.
Строим эпюру крутящих моментов (см. рисунок 59,в).
Далее строим эпюру изгибающих моментов в вертикальной плоскости (см. рисунок 59,г), для чего предварительно определяем опорные реакции из уравнений равновесия YА=9 кН, YB=3 кН.
На рисунке 59,д приведена эпюра изгибающих моментов в горизонтальной плоскости, Для ее построения предварительно нужно было определить реакции опор в этой плоскости XА=1,5 кН, XB=4,5 кН.
Очевидно, что опасным сечением является сечение, расположенное чуть правее середины шкива с диаметром D1; максимальный расчетный момент определяем по (6.21)
![]()
Из условия прочности (6.20) выражаем осевой момент сопротивления
![]()
Диаметр вала определяем по формуле (5.8)

Если принять диаметр вала равным 45 мм, то это приведет к перегрузке, составляющей ≈7%, что недопустимо.
Окончательно принимаем вала равным 48 мм.
7 Продольный изгиб (устойчивость сжатых стержней)
Прямолинейная форма равновесия стержня, нагруженного сжимающей силой F (см. рисунок 60) оказывается устойчивой, пока сжимающая сила меньше некоторого значения. Критической силой Fкр называют наименьшее значение силы F, при котором прямолинейная форма равновесия перестает быть устойчивой (происходит потеря устойчивости). При силе, превышающей критическую силу, устойчивой будет некоторая криволинейная форма равновесия стержня (показана пунктиром на рисунке 60), при этом переход к новой форме равновесия сопровождается большими прогибами стержня, вследствие чего в его поперечных сечениях возникает изгибающий момент (изгиб под действием продольной силы) и резко возрастают напряжения.
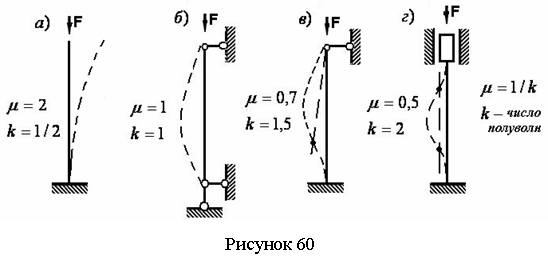
Практически при достижении сжимающей силы критического значения стержень выходит из строя. Поэтому допускаемая нагрузка должна быть меньше критической. Условие устойчивости имеет вид
![]() или
или ![]() (7.1)
(7.1)
где nу и [nу] – фактический и требуемый (нормативный) запас устойчивости.
Значение [nу] зависит от назначения стержня и его материала; для стальных строительных конструкций [nу]=1,75…2,0; для машиностроительных - 3,5…5,0; для чугунных – 5,0 в среднем; деревянных - 3,0.
7.1. Расчет сжатых стержней по формулам Эйлера и Ясинского
Если потеря устойчивости сжатого стержня постоянного сечения происходит в упругой стадии работы, то величину критической силы вычисляют по формуле Эйлера
 (7.2)
(7.2)
где E - модуль упругости материала стрежня;
Jmin - минимальный главный центральный момент инерции поперечного сечения;
l - длина стрежня;
μ – коэффициент приведения длины, зависящий от способов закрепления концов стержня (см. рисунок 60), m=1/k;
k – число полуволн синусоиды, по которой изгибается стержень при потере устойчивости.
Соответствующая величина сжимающих напряжений в поперечном сечении, называемая критическим напряжением, вычисляется по формуле
 (7.3)
(7.3)
где A - площадь поперечного сечения;
λ - гибкость стержня,
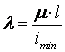 ;
(7.4)
;
(7.4)
imin
- минимальный радиус инерции поперечного сечения, ![]()
Формулы (7.2) и (7.3) справедливы, если критическое напряжение не превышает предела пропорциональности материала σпц, или, что одно и то же, если гибкость стержня превышает значения предельной гибкости
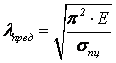 .
(7.5)
.
(7.5)
Значение λпред для стали Ст.3 равно 100, для стали Ст.5 - 85, для серого чугуна - 80, для дерева – 70 и т.д.
Если потеря устойчивости происходит при напряжениях, превышающих предел пропорциональности, то для вычисления критических напряжений используют эмпирическую формулу Ясинского
![]() (7.6)
(7.6)
где a, b и с – коэффициенты, зависящие от материала стержня.
Для стали Ст.3: a=310 МПа, b=11,4 МПа, с=0.
Для стали Ст.5: a=464 МПа, b=3,62 МПа, с=0.
Для чугуна СЧ4: a=776 МПа, b=12 МПа, с=0,053 МПа.
Для дерева (сосна вдоль волокон): a=29,3 МПа, b=0,194 МПа, с=0.
Если гибкость стержня весьма мала (жесткие стержни), расчет на устойчивость не производится, стержень работает просто на сжатие.
Пример 51 - Продольно сжатый стержень, закрепленный как показано на рисунке 60,а, изготовлен из двутаврого профиля №40 и имеет длину 12 м. Вычислить критическую силу для стержня.
Решение.
В таблице сортамента для двутавра №40 находим минимальный радиус инерции
![]() и по формуле (7.4)
подсчитываем гибкость стержня, учитывая, что для рассматриваемой схемы
закрепления стержня m=2. Вычисляем
и по формуле (7.4)
подсчитываем гибкость стержня, учитывая, что для рассматриваемой схемы
закрепления стержня m=2. Вычисляем ![]() . Так как λ>λпред=100 для стали Ст3, то
критическую силу вычисляем по формуле Эйлера, предварительно найдя в таблице
. Так как λ>λпред=100 для стали Ст3, то
критическую силу вычисляем по формуле Эйлера, предварительно найдя в таблице ![]() . Получаем
. Получаем
Пример 52 - Для колонны длиной 5 м, изготовленной из стальной (Ст3) трубы с внешним диаметром и внутренним диаметром и закрепленной как на рисунке 60,в, определить допускаемое значение сжимающей силы, приняв коэффициент запаса устойчивости [nу]=3,0.
Решение.
Определяем минимальный радиус инерции поперечного сечения 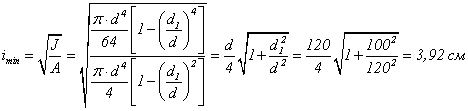 .
.
Отметим, что в рассматриваемом случае любая центральная ось является главной, и все центральные моменты инерции равны между собой.
Далее
определяем гибкость колонны ![]() .
.
Используя формулу Ясинского (7.6) для критического напряжения, найдем критическую силу
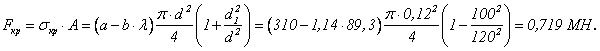 Допускаемое
значение сжимающей силы определяем
как
Допускаемое
значение сжимающей силы определяем
как 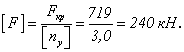
Пример 53 - Оба конца тонкого стержня закреплены неподвижными шарнирами. При каком увеличении температуры стержня произойдет выпучивание (считать, что материал ведет себя упруго, коэффициент температурного расширения и модуль упругости неизменны).
Решение.
При увеличении температуры стержня в шарнирных опорах будут возникать реакции,
сжимающие стержень для компенсации температурной деформации. Выпучивание
(потеря устойчивости) происходит, когда величина сжимающей силы![]() достигает значения критической силы
достигает значения критической силы![]()
Отсюда ![]()
7.2 Расчет сжатых стержней на устойчивость по коэффициенту продольного изгиба
Расчет на устойчивость сжатых стержней некоторых конструкций, металлоконструкций подъемно-транспортных машин и ряда других сооружений выполняют по условию
![]() (7.7)
(7.7)
где [σу], [σсж] - допускаемые напряжения на устойчивость и на сжатие соответственно;
φ - коэффициент продольного изгиба, называемый также коэффициентом снижения основного допускаемого напряжения.
Как видно из (7.7), такой расчет по форме совпадает с расчетом на сжатие. Коэффициент зависит от материала и гибкости стержня и его значения приведены в таблице 2.
Расчет по условию (7.7) не представляет трудностей, если он носит характер проверочного расчета или определения допускаемой нагрузки.
В случае же проектного расчета приходится пользоваться
методом последовательных приближений. При этом нужно стремиться к экономии материала.
Наиболее полно используется свойства материала, если выполняется равенство ![]() .
Тогда из выражения (7.7) следует
.
Тогда из выражения (7.7) следует
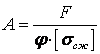 (7.8)
(7.8)
однако заранее, пока площадь сечения неизвестна, невозможно определить гибкость стержня λ и коэффициент φ. Поэтому, задаваясь значением φ, подбирают сечение, и затем нужно добиваются того, чтобы для подобранного сечения фактическое значение φ было близким к предварительно принятому значению.
Приводим среднее значение допускаемого напряжения на
сжатие для некоторых материалов: стали Ст.3, Ст.4 - ![]() , Ст.5 - 175 МПа; чугун - 140 МПа;
дерево - 10 МПа.
, Ст.5 - 175 МПа; чугун - 140 МПа;
дерево - 10 МПа.
Т а б л и ц а 2 - Коэффициент продольного изгиба
|
Гибкость, λ |
Материал |
|||
|
Сталь Ст.2, Ст.3, Ст.4. |
Сталь Ст.5 |
Чугун |
Дерево |
|
|
0 |
1,00 |
1,00 |
1,00 |
1,00 |
|
10 |
0,99 |
0,98 |
0,97 |
0,99 |
|
20 |
0,96 |
0,95 |
0,91 |
0,97 |
|
30 |
0,94 |
0,92 |
0,81 |
0,93 |
|
40 |
0,92 |
0,89 |
0,89 |
0,87 |
|
50 |
0,89 |
0,86 |
0,57 |
0,80 |
|
60 |
0,86 |
0,82 |
0,44 |
0,71 |
|
70 |
0,81 |
0,76 |
0,34 |
0,60 |
|
80 |
0,75 |
0,70 |
0,26 |
0,48 |
|
90 |
0,69 |
0,62 |
0,20 |
0,38 |
|
100 |
0,60 |
0,51 |
0,16 |
0,31 |
|
110 |
0,52 |
0,43 |
- |
0,15 |
|
120 |
0,45 |
0,37 |
- |
0,22 |
|
130 |
0,40 |
0,36 |
- |
0,18 |
|
140 |
0,36 |
0,29 |
- |
0,16 |
|
150 |
0,32 |
0,26 |
- |
0,14 |
|
160 |
0,29 |
0,24 |
- |
0,12 |
|
170 |
0,26 |
0,21 |
- |
0,11 |
|
180 |
0,23 |
0,19 |
- |
0,10 |
|
190 |
0,21 |
0,17 |
- |
0,09 |
|
200 |
0,19 |
0,16 |
- |
0,08 |
Пример
54 - Подобрать диаметр стальной стойки круглого поперечного сечения, нагруженной
как показано на рисунке 60,г, при ![]() (материал – сталь Ст3).
(материал – сталь Ст3).
Решение.
Для данных условий закрепления коэффициент приведения длины ![]() . Подбор сечения производим методом
последовательных приближений.
. Подбор сечения производим методом
последовательных приближений.
Задаемся в
первом приближении значением коэффициента продольного изгиба![]() . Тогда площадь поперечного сечения
стрежня определяется как
. Тогда площадь поперечного сечения
стрежня определяется как ![]()
Определим
диаметр поперечного сечения ![]() .
.
Для круглого сечения ![]()
Гибкость
стержня ![]()
По таблице 2
для стали Ст3 при ![]() коэффициент
коэффициент ![]() , то есть значение коэффициента
продольного изгиба не совпадает с предварительно принятым значением.
, то есть значение коэффициента
продольного изгиба не совпадает с предварительно принятым значением.
Зададимся во
втором приближении значением ![]() .
.
Тогда
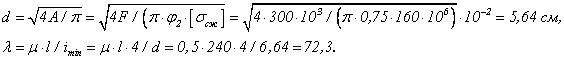
По таблице 2
находим: при ![]()
![]() ; при
; при ![]()
![]() .
.
Путем
интерполяции находим ![]()
Проверим, насколько сошелся полученный результат. Площадь
поперечного сечения равна ![]() Фактическое
напряжение
Фактическое
напряжение ![]() Допускаемое напряжение на устойчивость
Допускаемое напряжение на устойчивость
![]() так что недогрузка составляет
так что недогрузка составляет ![]()
Найдем
критическое напряжение потери устойчивости. Так как λ<λпред=100 для Ст3, то по
формуле Ясинского имеем ![]() Коэффициент
запаса устойчивости равен
Коэффициент
запаса устойчивости равен ![]() Таким
образом, окончательно можно принять d=56,4 мм.
Таким
образом, окончательно можно принять d=56,4 мм.
 Пример 55
- Подобрать номер швеллера для составной колонны из двух швеллеров (см. рисунок
61) при условии равноустойчивости колонны в направлении главных осей инерции.
Определить расстояние между стенками профилей, если
Пример 55
- Подобрать номер швеллера для составной колонны из двух швеллеров (см. рисунок
61) при условии равноустойчивости колонны в направлении главных осей инерции.
Определить расстояние между стенками профилей, если ![]()
![]() Определить коэффициент запаса устойчивости.
Определить коэффициент запаса устойчивости.
Решение.
Для заданных условий закрепления стержня ![]() .
.
Зададимся ![]() . Тогда
. Тогда ![]() Площадь швеллера должна быть равной или
больше половины этой площади
Площадь швеллера должна быть равной или
больше половины этой площади![]() .
По таблице ГОСТ 8240–72 находим швеллер №12 с площадью поперечного
сечения А=13,3 см2.
.
По таблице ГОСТ 8240–72 находим швеллер №12 с площадью поперечного
сечения А=13,3 см2.
Для
определения гибкости требуется значение минимального радиуса инерции. Так как
для отдельно взятого швеллера ![]() ,
то очевидно, что для обеспечения равноустойчивости составного стержня в направлении
главных осей инерции надо несколько разнести два швеллера (на расстояние с),
так чтобы iy был равен ix ; при этом
,
то очевидно, что для обеспечения равноустойчивости составного стержня в направлении
главных осей инерции надо несколько разнести два швеллера (на расстояние с),
так чтобы iy был равен ix ; при этом  Величину
Величину ![]() определяем по таблицам сортамента.
определяем по таблицам сортамента.
Для швеллера №12
![]() , так что гибкость
, так что гибкость ![]() Этому значению соответствует
Этому значению соответствует ![]() (таблица 2), так что расчет
производим снова.
(таблица 2), так что расчет
производим снова.
Задаемся ![]() . Тогда А=23,6
см2, Ашв=11,8 см
- снова выбираем швеллер №12. Так как второе приближение дает тот же
результат, что и первое, то окончательно применяем сечение стойки из двух
швеллеров №12.
. Тогда А=23,6
см2, Ашв=11,8 см
- снова выбираем швеллер №12. Так как второе приближение дает тот же
результат, что и первое, то окончательно применяем сечение стойки из двух
швеллеров №12.
Определим
величину критической силы по формуле Эйлера (поскольку гибкость стержня ![]() )
) 
Коэффициент
запаса устойчивости ![]()
Расстояние между стенками швеллеров вычисляем из условия равенства моментов инерции составленного сечения относительно главных центральных осей xO и yO (см. рисунок 61)
 откуда
откуда 
Список литературы
1. Феодосьев В.И. Сопротивление материалов: Учебник для вузов. – М.: Изд-во МГТУ им. Н.Э.Баумана, 2000. – 592 с.
2. Степин П.А. Сопротивление материалов: Учебник для немашиностроит. спец. вузов. – М.: Высш. шк., 1989. – 367 с.
3. Буланов Э.А. Решение задач по сопротивлению материалов. – М.: Высш. шк., 1994. – 206 с.
4. Винокуров А.И. Сборник задач по сопротивлению материалов. – М.: Высш. шк., 1990. – 383 с.
5. Механика. Конспект лекций /А.Д.Динасылов. Р.К.Койлыбаева. – Алматы: АИЭС, 2008. – 76 с.
6. Прикладная механика. Конспект лекций /А.Д.Динасылов. – Алматы: АИЭС, 2009. – 80 с.
7. Механика. Методические указания и задания к выполнению расчетно-графических работ /А.Д.Динасылов. – Алматы: АИЭС, 2006. – 42 с.
8. Прикладная
механика. Методические указания и задания к выполнению расчетно-графических
работ /А.Д.Динасылов. – Алматы: АИЭС, 2006. – 38 с.