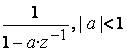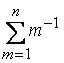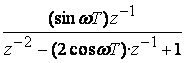Некоммерческое акционерное общество

АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра телекоммуникационных систем

 

 

 

 

ОСНОВЫ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ В ТЕЛЕКОММУНИКАЦИОННЫХ СИСТЕМАХ

Конспект лекций

(для студентов – бакалавров всех видов обучения для специальности 5В071900 – Радиотехника, электроника и телекоммуникации)

  

 

 

Алматы 2011

СОСТАВИТЕЛИ: Г.С. Казиева., Богомолова Л.Г. Основы цифровой обработки сигналов в телекоммуникационных системах.  Конспект лекций для студентов – бакалавров всех форм обучения  специальности 5В071900 – Радиотехника, электроника и телекоммуникации Алматы: АУЭС, 2010 г. – 48 с.

  

Конспект лекций представляет собой базовый курс по основам цифровой обработки сигналов. В нем рассмотрены методы спектрального анализа и цифровой фильтрации, алгоритмы синтеза цифровых фильтров, изложены основы теории дискретных сигналов и систем, а также некоторые аспекты применения цифровой обработки сигналов в системах связи, приведен перечень рекомендуемой литературы.

Конспект лекций предназначен для студентов  дневного и заочного факультетов специальностей специальности 5В071900 – Радиотехника, электроника и телекоммуникации.

Ил. 14, табл.2, библ.7 назв.18

 

Рецензент:

кан.техн. наук зав. кафедрой «АЭС»                                К.С. Чежимбаева

  

Печатается по плану издания некоммерческого акционерного общества «Алматинский институт энергетики и связи» на 2010 год.

 

 

 

 

© НАО «Алматинский университет энергетики и свяэи», 2011 г.

 

 

СОДЕРЖАНИЕ

                                                                                       

Введение         

4 

1. Основные типы сигналов и их спектры

5

2 . Обобщенная схема цифровой обработки сигналов

9

3. Дискретное преобразование Фурье (ДПФ).     Z-преобразование дискретного сигнала.                                        

 14

4. Обратное Z-преобразование     

19

5 Свойства Z-преобразования; алгоритмы и  структурные схемы дискретных систем  

 22  

6. Цифровые фильтры

26

7. Рекурсивные цифровые фильтры (фильтры с бесконечным числом отсчетов импульсной характеристики)-    БИХ- фильтры.

  

30

8. Частотные характеристики цифровых фильтров(ЦФ) ; типовые звенья ЦФ.

36

9 Общие сведения и основные понятия цифровой  интерполяции сигналов с целочисленными   коэффициентами

 39

Список литературы

47


Введение 

Изучение принципов и языка цифровой обработки сигналов не требует глубоких и всесторонних знаний по математике. Все, что необходимо, — это немного опыта в элементарной алгебре, способах декомпозиции (разложения) произвольных сигналов на простейшие составляющие и их обратной реконструкции.

Физические величины макромира, как основного объекта наших измерений и источника информационных сигналов, как правило, имеют непрерывную природу и отображаются непрерывными (аналоговыми) сигналами. Цифровая обработка сигналов (ЦОС или DSP - digital signal processing) оперирует исключительно с дискретными величинами, причем с квантованием как по координатам динамики своих изменений (во времени, в пространстве, и любым другим изменяемым аргументам), так и по амплитудным значениям физических величин. Математика дискретных преобразований зародилась в недрах аналоговой математики еще в 18 веке в рамках теории рядов и их применения для интерполяции и аппроксимации функций, однако ускоренное развитие она получила в 20 веке после появления первых вычислительных машин. В принципе, в своих основных положениях математический аппарат дискретных преобразований подобен преобразованиям аналоговых сигналов и систем. Однако дискретность данных требует учета этого фактора, а его игнорирование может приводить к существенным ошибкам. Кроме того, ряд методов дискретной математики не имеет аналогов в аналитической математике.

Стимулом быстрого развития дискретной математики является и то, что стоимость цифровой обработки данных меньше аналоговой и продолжает снижаться, даже при очень сложных ее видах, а производительность вычислительных операций непрерывно возрастает. Немаловажным является также и то, что системы ЦОС отличаются высокой гибкостью. Их можно дополнять новыми программами и перепрограммировать на выполнение различных функций без изменения оборудования. В последние годы ЦОС оказывает постоянно возрастающее влияние на ключевые отрасли современной промышленности: телекоммуникации, средства информации, цифровое телевидение и пр. Следует ожидать, что в обозримом будущем интерес и к научным, и к прикладным вопросам цифровой обработки сигналов будет нарастать во всех отраслях науки и техники.

В настоящее время методы цифровой обработки сигналов, digital signal processing (DSP) находят все более широкое применение, вытесняя постепенно методы, основанные на аналоговой обработке.

                Благодаря успехам микроэлектроники системы ЦОС не только воплотились в реальность, но и вошли в нашу повседневную жизнь в виде CD- и DVD-проигрывателей, модемов, сотовых телефонов и многого другого. Более того, в некоторых прикладных областях ЦОС стала вытеснять “традиционную” (аналоговую). В значительной степени это произошло в аудиотехнике, телефонии. Интенсивно идет процесс перехода телевизионного вещания на цифровую основу.

Бурное развитие цифровых технологий во многом изменило как стиль самого понятия “радиотехника”, так и требования, предъявляемые к подготовке специалистов в этой области, сделав необходимыми новые знания и умения.

В этом плане в конспекте лекции охвачены некоторые актуальные теоретические вопросы и наиболее употребляемые алгоритмы цифровой обработки сигналов в телекоммуникационных системах.

 

Лекция 1 Основные типы сигналов и их спектры

 

Цель лекции- рассмотреть виды  сигналов и их спектральное представление

         Сигнал – это физический процесс, содержащий в себе некоторую информацию. На практике чаще всего используются электрические сигналы. При этом, носителем информации является изменяющиеся во времени ток или напряжение в электрической цепи. Электрические сигналы легче обрабатывать чем другие, они хорошо передаются на большие расстояния.

Существуют аналоговые, дискретные и цифровые сигналы.

Аналоговые сигналы (АС). Большинство сигналов имеют аналоговую природу, т.е. изменяются непрерывно во времени и могут принимать любые значения на некотором интервале. Аналоговые сигналы описываются некоторой математической функцией времени . Пример АС – гармонический сигнал:

 или экспоненциальный сигнал – .

Аналоговые сигналы используются в телефонии, радиовещании, телевидении. Ввести такие сигналы в компьютер и обработать его невозможно, т.к. на любом интервале времени он имеет бесконечное множество значений, а для точного (без погрешности) представления его значения требуются числа бесконечной разрядности. Поэтому необходимо преобразовать аналоговый сигнал так, чтобы можно было представить его последовательностью чисел заданной разрядности.

Дискретный сигнал. Дискретизация аналогового сигнала состоит в том, что сигнал представляется в виде последовательности значений, взятых в дискретные моменты времени  . Эти значения называются отсчетами. а - называется интервалом дискретизации. Конечную последовательность отсчетов записывают таким образом: .

Например: .

 

 

 Здесь :; ; ; .

Цифровые сигналы. Для того, чтобы представить дискретный сигнал последовательностью чисел конечной разрядности, его следует подвергнуть операции, которая называется квантованием. Вся область значений сигнала разбивается на уровни, количество которых должно быть представлено в числах заданной разрядности.

Расстояния между этими уровнями называется шагом квантования -. Число этих уровней равно N (от 0 до N-1). Каждому уровню присваивается некоторое число: . Отсчеты сигнала сравниваются с уровнями квантования и в качестве сигнала выбирается число, соответствующее некоторому уровню квантования .

Каждый уровень квантования кодируется двоичным числом с п разрядами, например: ; ;  и т.д. Число уровней квантования и наименьшее число разрядов п двоичный чисел, кодирующих эти уровни, связаны соотношением

,

N=4

п=2

 

N=6

п=3

 

N=9

п=4

 

N=32

п=5

и т.д.

Например, при

  

Если кодируемая функция может принимать как отрицательные, так и положительные значения, то знак функции кодируется, как правило, с помощью специального знакового разряда. Пример цифровых сигналов – сигналы импульсно-кодовой модуляции, использующиеся в системах многоканальной связи.

Рассмотрим примеры некоторых дискретных сигналов, полученных из типовых аналоговых.

Единичный ступенчатый сигнал в аналоговой форме:

.

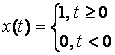В дискретной форме:

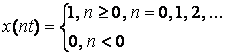
 – сдвинутая последовательность, которая образуется при сдвиге последовательность вправо при  и влево при .

Импульс Дирака или -функция в аналоговой форме:

 

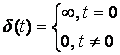
В дискретной форме:

.

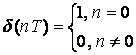
Таким образом, математическая запись любого дискретного сигнала имеет вид:

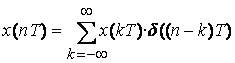,                          (1.1)

 

т.к. все члены при  равны 0.

Например, последовательность  может быть записана в виде:

.

 Итак, согласно выражению (2.1) дискретный сигнал представляет сумму -функций, следующих с интервалом времени Т. Эти функции имеют амплитудные коэффициенты, равные отсчетам сигнала  в точках дискретизации .

Как часто следует брать отсчеты?

Их следует брать так часто, чтобы успевать отследить все, даже самые быстрые изменения сигнала. Иначе, при восстановлении этого сигнала по дискретизированным отсчетам часть информации будет потеряна и форма восстановленного сигнала  будет отличаться от формы исходного  сигнала.

Периодической называют последовательность , удовлетворяю­щей условию:

, где

 

m и N – целые числа,

m = 1, 2, …; NТ – период последовательности.

 

Спектры аналоговых и дискретных сигналов

         Для описания аналоговых и дискретных сигналов в частотной области используется аппарат преобразования Фурье. Спектром  аналогового сигнала  называют прямое преобразование Фурье

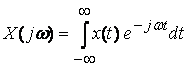,                                         (1.2)

где  – комплексная спектральная плотность.

В свою очередь сигнал  может быть восстановлен по его спектру (обратное преобразование Фурье):

.                                 (1.3)

В соответствии с принципом неопределенности сигнал , имеющий ограниченную протяженность во времени имеет неограниченный по полосе спектр  и наоборот.

Здесь  – модуль комплексной спектральной плотности , или спектр амплитуд. Непериодический сигнал бесконечной протяженности во времени имеет сплошной спектр, ограниченный по частоте.

Если сигнал  является периодическим с периодом , равным его длительности , то его спектр будет дискретным .

Теперь вместо  используют отсчеты . Интервал дискретизации спектра по частоте F определяется, как известно, периодом сигнала, в данном случае  :   

.

Формула для прямого и обратного преобразования Фурье получаются из (1.2) и (1.3) путем замены непрерывной частоты f на дискретные значения пF.

Таким образом, спектр  периодического сигнала вычисляется по формуле

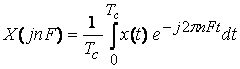,                           (1.4)

 

где  - комплексная амплитуда п-й гармоники.

Сигнал  можно восстановить по его дискретному спектру, воспользовавшись формулой

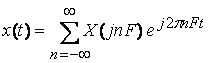 .                                (1.5)

Выражение (1.5) является комплексным представлением ряда Фурье. Из соотношения (1.5) нетрудно увидеть, что спектральное представление периодического сигнала комплексной формой ряда Фурье и содержит как положительные, так и отрицательные частоты. Однако, отрицательных частот в природе не существует, и это не реальное понятие, а математическая абстракция. Они появляются как следствие формального представления гармонических колебаний комплексной формой записи.

Легко доказать, что при переходе к тригонометрической форме записи

,

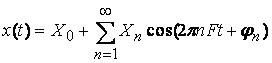где                            ;

понятие “отрицательная частота” теряет смысл.

;  ;  .

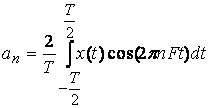В соответствии с принципом дуальности можно сказать: если периодическим является спектр, то дискретным будет сигнал .

Обозначая период повторения спектра дискретного сигнала , получим интервал дискретизации:

.

         Формулы прямого и обратного преобразования Фурье для дискретного сигнала имеют вид:

,                                (1.6)

,                             (1.7)

Величину  называют комплексной спектральной плотностью дискретного сигнала.

 

Лекция 2 . Обобщенная схема цифровой обработки сигналов

 

Цель лекции - ознакомить студентов с задачами ЦОС.

         Первая задача цифровой обработки заключается в оценке искажения исходного сигнала. Дальнейшая обработка состоит в извлечении из полученного сигнала нужной информации и подавлении шумов. Это осуществляется с помощью цифровой фильтрации. Даже оцифрованный сигнал занимает много места, и следующий шаг обработки заключается в сжатии сигнала. Обычно имеется в виду сжатие с потерей информации. Здесь важно установить критерии допустимой потери информации. В зависимости от выбранного критерия выбирается способ сжатия. Хотя последовательность бесконечна, в реальных условиях мы имеем дело лишь с конечными последовательностями. В этой связи нужна оценка потерь, связанных с усечением последовательностей.

         Задачи ЦОС сигнала обычно сводятся к трем действиям:

- ввод цифрового сигнала, или преобразование входного аналогового сигнала в     цифровую форму;

-обработка полученного массива данных с использованием различных алгоритмов;

- вывод полученного результата, или обратное преобразование цифрового сигнала в аналоговую форму.

Перечисленные преобразования должны происходить по определенным правилам, смысл которых отображен на рисунке 2.1, где показаны основные элементы обобщенной схемы ЦОС.

На вход системы поступает ограниченный по длительности аналоговый сигнал . В силу конечной длительности сигнала его спектр бесконечен!

Бесконечность спектра является препятствием для преобразования сигнала  в цифровую форму. Для ограничения спектра используется фильтр нижних частот ФНЧ. Спектр ограничивается верхней частотой . Далее сигнал  поступает на вход аналого-цифрового преобразователя, в котором осуществляется дискретизация сигнала по времени и квантования по уровню. При дискретизации аналоговый сигнал  заменяется отсчетами мгновенных значений , взятыми через интервал времени (интервал дискретизации) Т (рисунок 2.2,а). Чем меньше интервал дискретизации Т,

                           Рисунок 2.1- Обобщенная схема ЦОС

тем точнее последовательность отсчетов  будет отображать исходный сигнал. Интервал дискретизации определяет частоту дискретизации

; .                                         (2.1)

Чем выше , тем труднее вычислителю выполнить большое количество операций над отсчетами в темпе их поступления на переработку, и тем сложнее должно быть его устройство. Таким образом, точность представления сигнала требует увеличить , а стремление сделать вычислитель как можно более простым приводит к желанию понизить .

Однако существует ограничение на минимальное значение : для полного восстановления непрерывного сигнала  по его отсчетам  необходимо и достаточно, чтобы частота дискретизации  была, как минимум, в два раза больше наивысшей частоты  в спектре передаваемого сигнала , т.е.

.                                                  (2.2)

Соотношение (2.2) получило название теоремы Котельникова.

Реальные сигналы ограничены во времени, поэтому их спектр бесконечен (см. рисунок 2.2,б). Отсюда следует, что при  дискретизация невозможна.

         Тем не менее, в спектре любого конечного сигнала есть такие частоты, которые, начиная с некоторой , имеют незначительные амплитуды, и поэтому ими можно пренебречь без заметного искажения самого сигнала. Значения  определяется конкретным типом сигнала и решаемой задачи.

Например, для стандартного телефонного сигнала:

 кГц  - минимальная стандартная частота его дискретизации  кГц. Ограничение спектра до частоты  осуществляется аналоговым ФНЧ, получившем название антиэлайсингового.

Сигнал и его спектр на выходе ФНЧ изображены на рисунке 1.2,в.

Квантование отсчетов по уровням (или квантование) производится с целью формирования последовательности чисел: весь диапазон изменения величины отсчетов разбивается на некоторое количество дискретных уровней N, и каждому отсчету по определенному правилу присваивается значение одного из двух ближайших уровней квантования, между которыми оказался данный отсчет (см. рисунок 2.2,е).

 В результате получается последовательность чисел , представляемых в двоичном коде. Количество уровней определяется разрядностью п АЦП; так если п = 3, то всего можно иметь  уровней квантования, а минимальное и максимальное значения отсчетов соответственно  и . Ясно, что квантованный отсчет отличается от выборки . Это отличие является ошибкой квантования:   

,                                 (2.3)

которое теме больше, чем меньше п. Максимальная ошибка квантования равна половине шага квантования .,т.е

,                                      (2.4)

где

 

Рисунок 2.2- Непериодические сигналы и их спектры


        Отсюда следует, что чем больше разрядность АЦП, тем точнее представляется отсчет и тем сложнее и дороже оказывается АЦП. Современные АЦП имеют разрядность от 8 до 20.

Последовательность  поступает на вычислитель, который по заданному алгоритму каждому отсчету  ставит в однозначное соответствие выходной отсчет

.

Результатом обработки исходного сигнала является новая цифровая последовательность – цифровой сигнал  (см. рисунок 2.2,ж), существенно отличающийся от . Количество операций (умножений, сложений, пересылок и т.д.) для получения одного отсчета  может исчисляться тысячами, поэтому вычислитель должен работать на более высокой тактовой

 

частоте , чем , чтобы успеть произвести все необходимые действия до поступления очередного отсчета , т.е. какой бы сложности не был алгоритм, время переработки  не должно превышать периода дискретизации

.

Именно при этих условиях возможна работа вычислителя в реальном масштабе времени, т.е. в темпе поступления входных отсчетов.

         Например, при обработке стандартного телефонного сигнала с  кГц для обеспечения работы вычислителя в реальном масштабе времени тактовая частота должна быть, по крайней мере, 6 МГц, как в процессорах первого поколения TMS320C10.

Полученные выходные отсчеты подаются на цифро-аналоговый преобразователь (ЦАП), формирующий ступенчатый сигнал  – (см. рисунок 2.2,з), который затем с помощью сглаживающего фильтра НЧ преобразуется в аналоговый выходной сигнал  (см. рисунок 2.2,ж).

Из всего сказанного вытекает ряд ограничений, влияющих на характер и выбор элементной базы для реализации вычислителя:

- разность регистров вычислителя должна быть большой и превышать разность ЦАП во избежание дополнительных ошибок при округлении результатов вычислений;

- тактовая частота, на которой работает вычислитель, должна в сотни раз превосходить частоту дискретизации, если предъявляются требования реального времени. 

 

Лекция 3. Дискретное преобразование Фурье (ДПФ).   Z-преобразование дискретного сигнала.

 

Цель лекции- ознакомить студентов с ДПФ и Z-преобразованием дискретного сигнала. Методы определения преобразования. Таблица

Z-преобразования.

         Мы уже отмечали, что развитие вычислительной техники привело к появлению цифровых систем обработки сигнала. При этом, как сигнал, так и его спектр необходимо перед вводом в вычислительное устройство представить в виде отсчетов, т.е. чисел. В настоящее время обработка сигналов чаще всего производится в частотной области, что диктуется значительным сокращением объема цифровой аппаратуры и времени обработки. Как же представить спектр сигнала в виде отсчетов?

Пусть дискретной обработке подвергается аналоговый сигнал , имеющий спектр  и длительность .

Подвергнем этот сигнал дискретизации, т.е. заменим его отсчетами , взятых в момент времени .

         Полное число отсчетов этого сигнала равно

, где  – интервал дискретизации.

Спектр дискретного сигнала станет периодическим с периодом повторения .

Мысленно продолжим дискретный сигнал с периодом равным длительности сигнала . Поскольку дискретный сигнал стал периодичным, то его спектр станет дискретным с частотой дискретизации спектра;

.

Используя преобразования Фурье для периодического сигнала, найдем комплексные амплитуды соответствующих коэффициентов

этого ряда:

,

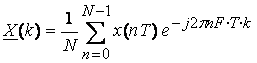так как

, а , то произведение

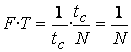 и окончательно получим

, .             (3.1)

Формула (3.1) получила название прямого дискретного преобразования Фурье (ПДПФ).

 – это комплексные отсчеты спектра периодического дискретного сигнала . Поскольку частота дискретизация спектра

,

а , то в интервале  будет укладываться

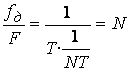
отсчетов спектра дискретного сигнала .

Теперь обработку сигнала можно осуществлять в частотной области, вводя в ЭВМ отсчеты спектра сигнала, что значительно сокращает время обработки дискретного сигнала. Это фундаментальное для дискретных сигналов соотношение представляет собой алгоритм вычисления гармонических составляющих  по заданным дискретным отсчетам  аналогового сигнала .

         Отметим некоторые очевидные свойства ПДПФ.

1)      Дискретное преобразование обладает свойствами линейности: сумме (разности) дискретных сигналов соответствует сумма (разность) их ДПФ.

2)      Число определяемых коэффициентов :  равно числу отсчетов N за период сигнала . При  коэффициент

 

.

3)      Коэффициент  (постоянная составляющая) является средним значением всех отсчетов:

.

4)      Если N – четное число, то

.

5)      Коэффициенты ДПФ, номера которых располагаются симметрично относительно  образуют сопряженные пары

,

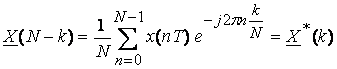т.е. можно считать, что коэффициенты

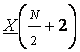, , …,  соответствуют отрицательным частотам . При изучении спектра сигнала они не дают новых сведений.

При изучении теории ДПФ возникает вопрос: можно ли по известным коэффициентам ДПФ   вычислить отсчетные значения  непрерывного сигнала? Да, можно. В этом случае используется обратное дискретное преобразование Фурье (ОДПФ):

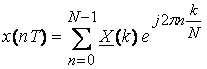,                    (3.2)

Формулы (3.1) и (3.2) являются аналогами прямого и обратного преобразования Фурье для непрерывных сигналов.

 

Прямое Z-преобразование

         Для аналоговых сигналов  известно преобразование Лапласа, позволяющее упростить вычисления. Для дискретных сигналов  используются подобное преобразование, называемое Z-преобразованием. Как известно, дискретный сигнал и его спектр описываются соотношениями

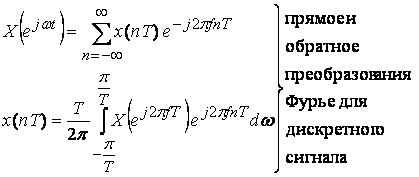
Произведем в первой формуле замену:

.

Тогда формула прямого преобразования Фурье дискретного сигнала примет вид:

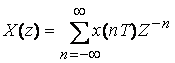.                                  (3.3)

Выражение (3.3) получило название Z-преобразование или Z-изображение дискретного сигнала . Если считать, что  для , то получим одностороннее Z-преобразование:

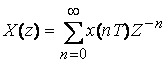.                                  (3.4)

Можно указать на связь Z-преобразования с преобразованием Лапласа

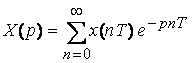
которое получается путем замены . Очевидно, что

 или .

Эти формулы устанавливают связь между точками в плоскостях  и .

Действительно,

для  , т.к. ;

для  .

Если положить , то мы будем перемещаться по оси  в плоскости р. При переходе в Z-плоскость точки мнимой оси  будут располагаться на единичной окружности . Причем точка  на плоскости р переходит в точку +1 на плоскости Z, а точки  в точку . Это означает, что точки отрезка  р-плоскости проецируются в точки на единичной окружности Z-плоскости. Так как функция  – периодична, то последующие отрезки на оси  плоскости р такой же длины вновь будут проецироваться на единичную окружность плоскости Z. Точки левой полуплоскости  соответствуют точкам внутри единичной окружности Z, а точки правой полуплоскости  – точкам вне этой окружности.Из теории комплексных переменных известно, что искусственное изменение независимой переменной посредством ее замены некоторой функцией от новой переменной дает преобразование одной области комплексной переменной в другую. Следовательно, некоторый контур одной области переходит в другой. Так как в Z- преобразовании используется подстановка Z=epT , то происходит отображение мнимой оси в плоскости «р» в единичную окружность в плоскости “Z” (см. рисунок 3.1)

 

 

Рисунок 3.1 –Отображение мнимой оси в плоскости «р» в единичную окружность в плоскости «z»

 

Для значений, соответствующих мнимой оси, вместо «р» необходимо подставить «jω», тогда Z = ejωT       =>   многозначная функция от «ω» с единичной амплитудой и фазовым углом, равным «ωТ».

Если «ω» увеличивается от 0 до ωg/4, то Z изменяется от Z=1 до Z =+j вдоль единичной окружности и в первом квадранте плоскости Z, где Т – период дискретизации и «ωg» = 2π/T.

 вдоль единичной окружности во II квадранте

 вдоль единичной окружности в III квадранте

 в IV квадранте

 

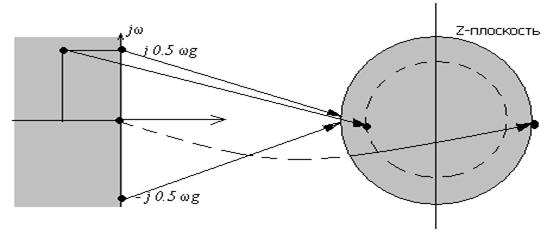
Рисунок 3.2- Отображение точек левой полуплоскости   р   вне  и внутри единичной окружности Z

 

        

         Лекция 4 . Обратное Z-преобразование

 

         Цель лекции - ознакомить студентов с  методами вычисления обратного Z-преобразования, таблица преобразования

Как найти дискретный сигнал по его Z-преобразованию? Для этого можно воспользоваться обратным Z-преобразованием, подобно тому, как мы пользуемся обратным преобразованием Лапласа.

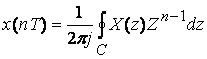.                                  (4.1)

Интегрирование ведется по замкнутому контуру С в Z-плоскости.

Другой способ определения дискретной последовательности заключается в том, чтобы разложить функцию  в степенной ряд по степеням . Тогда коэффициенты при степени  в соответствии с формулой (3.4) будут определять отсчеты дискретного сигнала.

Пример 4.1. Найдем дискретный сигнал , которому соответствует Z-преобразование:

.

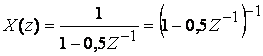Воспользуемся разложением функции  в ряд: … Для заданного Z-преобразования:

запишем Z-преобразвание в виде:

 +…

Сравнивая полученное изображение с общей формулой Z- преобразования  записываем последовательность

Общий член этой последовательности , .

Удобный способ вычисления Z-преобразования заключается в разложении  на простые дроби (если  – дробно-рациональная функция)

      (4.2)

В этом случае, используя свойство линейности Z-преобразования и учитывая условие

,

находим, что 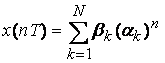             .                                         (4.3)

Пример 4.2.Известно обратное преобразование:

.

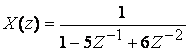         Разложим  на простые дроби:

.

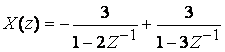Согласно (4.2) и (4.3) значения  будет равны

.

 

Пример 4.3

 

X[n] = Aan,       n ? 0

 

.                      (4.4)

 

Из математики известно, что этот ряд сходится к функции:

 

  .                        ( 4.5)

Как найти дискретный сигнал по его Z-преобразованию (обратное Z-преобразование)

 

Пример 4.4

 

.

Функция X(Z) имеет полюса в точках

 

Z1 =1/2;    Z2=-1/3      =>  корни

 

Или Z1-1 = 2;   Z2-1 = -3

 

Разложим X(Z) на сумму простых дробей:

 

 

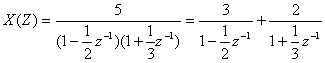.                               (4.6)

 

 

Коэффициенты в числителях каждой дроби вычисляются как при разложении входного сопротивления Z(p) реактивных двухполюсников при синтезе их по схеме Фостера:

 

.

 

 

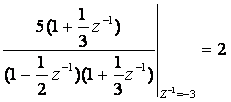Тогда подобно тому, как формула( 4.5 ) представляет сумму

ряда (4.4), простые дроби в (4.6) являются суммами рядов

               и                   .

 

Поскольку Z-преобразование – это линейная операция, последовательность X[n] состоит из суммы двух последовательностей:

     n ? 0

 

После выполнения операции возведения в степень «n» получим:

X[0] = 5;    X[1] = 5/6;   X[2] = 35/36  и т.д.

 

 

Наиболее часто используемые Z-преобразования приведены в таблице 4.1

Таблица 4.1

 

,

1

 

Пример 4.5 Определить обратное  Z- преобразование функции.

 

X(z)=.

 

Решение:

Получим степенной ряд методом деления:

z

Zsin

 

 

zsin

z

z
              sin2

Таким образом

X(z) = z sin

Откуда x (nT) = sin .

 

Лекция 5. Свойства Z-преобразования; алгоритмы и структурные схемы дискретных систем

 

Цель лекции- рассмотреть свойства Z-преобразования.

     Так же, как и для преобразований Лапласа и Фурье, существуют теоремы для Z-преобразования. Приведем наиболее важные.

 

1 Теорема линейности (суперпозиции).

Сумме дискретных сигналов соответствует сумма их изображений:

Если

, , то

, где а и b – const.

2 Теорема задержки

Если дискретный сигнал задержан на N отсчетов, то его Z-преобразование имеет вид

  .                            (5.1)

3 Теорема умножения на

.

4 Теорема умножения на п:

.

5. Теорема свертки

Свертке дискретных сигналов  и  соответствует произведение их Z-преобразований.

 

Алгоритмы и структурные схемы дискретных систем

Теорема дискретной свертки

Известно, что сигнал на выходе аналоговой цепи связан с сигналом на входе цепи интегралом наложения (интегралом свертки):

,                      (5.2)

где  – импульсная характеристика цепи.

При переходе к дискретным сигналам используется выражение для дискретной свертки.

Чтобы не вносить путаницы, время t заменим дискретным значением , а время  дискретным значением . Вместо непрерывного сигнала  мы будем иметь дело с дискретным сигналом , вместо непрерывной импульсной характеристики  – с дискретной импульсной характеристикой . Тогда интеграл (5.2) запишется в виде:

.

Обозначая в этом выражении , , , окончательно получим, что п-ный отсчет дискретной выходной последовательности рассчитывается как

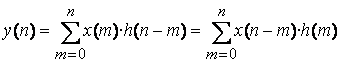.                  (5.3)

 

Поскольку любой отсчет сигнала – это число, то формулу (5.3) можно запрограммировать на ЭВМ. Остается лишь ввести в ЭВМ числа, соответствующие всем дискретным значениям отсчетов входного сигнала  и дискретным значениям отсчетов импульсной характеристики  и она вычислит отсчеты выходного сигнала . Выражение (5.2) на языке вычислительной техники называется алгоритмом вычисления выходного сигнала.

.

 

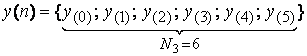Структурные схемы дискретных систем

 

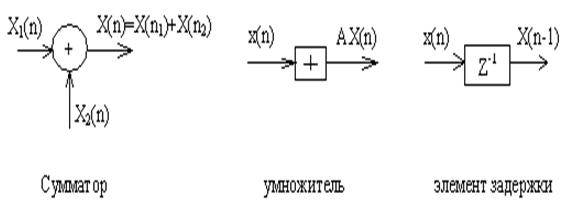
         Анализ формулы (5.3) показывает, что в ней выполняется три действия: умножение, сложение и задержка. Эти действия можно представить в виде элементов структурной схемы (рисунок 5.1).

  

 

             а)                                            б)                                    в)                                        

Рисунок 5.1 –Элементы структурной схемы (а-сумматор;б- умножитель;в- элемент задержки)

 

В отличие от аналоговых цепей, которые представляют собой соединение элементов , дискретная цепь – это структурная схема вычислений выходной последовательности  по выходной последовательности . Она состоит из элементов задержки, сумматоров и усилителей (умножителей).

Приведенные на рисунке 5.1 операции можно осуществить с помощью элементов цифровой или вычислительной техники. Первые представляют собой выпускаемые промышленностью интегральные микросхемы, позволяющие задерживать, складывать, умножать сигналы. Последние – это серийные макро, микро-ЭВМ, либо микропроцессорные устройства. Характерно, что и те и другие работают с цифровыми сигналами, т.е. с отсчетами, представленными в двоичном коде (0; 1). В этом случае любая конкретная цепь может быть реализована с помощью устройства, собранного на ИМС, либо в виде программы для ЭВМ или микропроцессорного устройства.

Заметим, что представление чисел в двоичном коде из-за ограниченности разрядности цифровых устройств выполняется неточно. Операция умножения отсчетов сигнала на число тоже выполняется неточно из-за округления или усечения результата. Это приводит к ошибкам при восстановлении сигнала. Существует только один путь уменьшения этих ошибок – увеличение разрядности устройств обработки.

Вывод: дискретная цепь – это структурная схема алгоритма вычислений, а. цифровая цепь – это воплощение данного алгоритма в виде программных и аппаратных средств.

         Рассмотрим один из элементов дискретной цепи – элемента задержки Элемент задержки (см. рисунок 5.1,в) осуществляет задержку цифрового сигнала на один интервал дискретизации . Сигнал на его входе

, а на выходе       .

Применим Z-преобразование к этим сигналам:

;  – согласно теореме задержки, т.о. .

Передаточная функция дискретной цепи

     Передаточной (системной) функцией дискретной цепи  называют отношение Z-преобразований входного и выходного дискретных сигналов

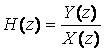.                                              (5.3)

Обратимся к теореме свертки, согласно которой свертке дискретных функций  и  соответствует произведение их Z-преобразований, т.е.

.

 

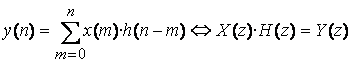Из последнего выражения видно, что Z-преобразование импульсной характеристики цепи  и есть передаточная функция дискретной цепи

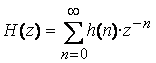 .                                     (5.4)

Пример 5.1. Найти системную функцию дискретной цепи, имеющей импульсную характеристику

.

.

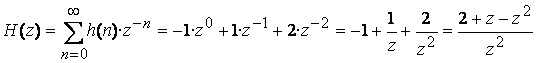Пример 5.2. Найти импульсную характеристику и передаточную функцию дискретной цепи ,описываемой уравнением

.

Выражение для выходного сигнала :

.

Сравним его с выражением, полученным согласно теореме дискретной свертки:

,

отсюда ; .

Согласно (5.4 ), передаточная функция

.

Другой способ нахождения  состоит в том, чтобы найти Z-изображение выходного сигнала , а затем найти

;

;

.

 

 

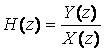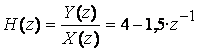Лекция 6. Цифровые фильтры

 

Цель лекции- дать определение цифровых фильтров и показать использование цифровых фильтров; рассмотреть нерекурсивные фильтры

Определение. Система называется физически реализуемой, если сигнал на выходе в момент времени t зависит от входных сигналов в моменты времени .

         Важнейшим примером линейных дискретных систем является линейный цифровой фильтр (ЦФ).

ЦФ-ом называется -некоторый алгоритм, который производит определенные операции во временной или частотной области входного дискретного сигнала и формирует выходной дискретный сигнал.

         Аналогичные действия, но только с непрерывным сигналом, выполняют аналоговые фильтры. При этом ЦФ имеют ряд преимуществ по сравнению с аналоговыми:

-простота реализации и удобство использования (используются одни и те же алгоритмы для проектирования фильтров с различными импульсными характеристиками);

- лучшие качественные характеристики (можно получить практически любую заданную точность обработки сигналов);

- возможность спроектировать фильтр любой сложности;

для перестройки на другую импульсную характеристику следует лишь задать новое ядро для фильтра.

Однако, цифровые фильтры имеют и ряд недостатков:

- невозможность обработки сигналов на сверхвысоких частотах – это определяется частотой дискретизации современных АЦП, которая в настоящее время не превышает нескольких сотен мегагерц. Например, для спектрального анализа света такой частоты дискретизации явно недостаточно, так как частота электромагнитных колебаний света лежит в терагерцовом диапазоне;

- при использовании сложных цифровых фильтров скорость обработки сигнала может существенно замедлиться, вплоть до того, что будет невозможна обработка сигнала в реальном масштабе времени;

- для большой точности и высокой скорости обработки сигналов требуется не только мощный процессор, но и дополнительное, возможно дорогостоящее, аппаратное обеспечение в виде высокоточных и быстрых ЦАП и АЦП.

Тем не менее, эти недостатки не препятствуют все более широкому использованию цифровых фильтров в компьютерных приложениях. В настоящее время цифровые фильтры используются в следующих приложениях:

- обработка звукового сигнала – различные звуковые эффекты (например эхо), эмуляция объемного звука, восстановление и редактирование звукозаписей, синтезирование звучания музыкальных инструментов, синтез и распознавание речи;

- обработка изображений – различные эффекты (например размытие или повышение резкости), сжатие изображений (формат JPEG, фрактальная компрессия);исследование и обработка каких-либо экспериментальных данных, например, ультразвуковое исследование в медицине, обработка сигналов, отраженных от цели и т.д.;

-искусственный интеллект – синтезирование нейронных сетей.

Цифровые фильтры являются прогрессивной технологией обработки сигналов и предназначены, в первую очередь, для вытеснения морально устаревших в некоторых областях аналоговых фильтров, сочетая в себе более высокую точность обработки сигнала, простоту, невысокую стоимость и удобство использования. Ниже представлены наиболее распространенные  формы соединений цифровых фильтров.

а)

 

б)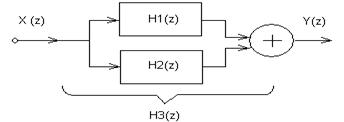

                                  в)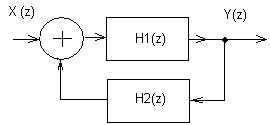

 

Рисунок 6.1-   Формы соединения  дискретных фильтров: последовательное (а), параллельное (б), соединение обратной связи (в).

 

В основном, все цифровые фильтры делятся на две большие группы: фильтры с конечной импульсной характеристикой (КИХ-фильтры)  или нерекурсивные и фильтры с бесконечной импульсной характеристикой (рекурсивные фильтры).

 

Нерекурсивные ЦФ (фильтры с конечной импульсной характеристикой КИХ- фильтры)

 

Цифровая техника позволяет получить высокое качество обработки сигналов несмотря на ошибки квантования: ошибки (шумы) квантования можно привести в норму увеличением разрядности кодовых слов. Рациональные способы конструирования цифровой цепи также способствуют минимизации уровня шумов квантования.

Расчёт цифровой цепи по заданным требованиям к её характеристикам имеет ряд принципиальных особенностей в зависимости от наличия обратной связи. Эти особенности являются следствием конечной длины импульсного отклика  нерекурсивного ЦФ.

Поэтому нерекурсивные фильтры содержат большое число элементов цепи, но вместе с тем имеют целый ряд важных достоинств: нерекурсивные ЦФ всегда устойчивы, позволяют строить фильтры с минимальной линейной фазой, отличаются  простой настройкой.

          Как известно, любая дискретная линейная система обладает некоторой импульсной характеристикой, т.е. реакцией цепи на единичный дискретный импульс (единичную -функцию). При подаче на вход линейной дискретной цепи на выходе будет образовываться некоторая последовательность импульсов различной амплитуды. Для фильтров с конечной импульсной характеристикой (КИХ-фильтров) количество этих импульсов конечно.

КИХ-фильтры реализуются на основе свертки двух функций. Первая функция является входным сигналом ,    а вторая  называется ядром фильтра и определяет его импульсную характеристику:

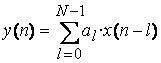    .                                 (6.1)

Как видно из выражения (6.1) значение выходного сигнала  в момент времени  определяется N-взвешенным значением входного сигнала в моменты времени :

.

В зависимости от размера ядра фильтра, т.е. от количества содержащихся в ядре отсчетов, точность обработки сигнала фильтром варьируется. При малом количестве отсчетов в ядре точность обработки невысока. При увеличении числа отсчетов точность повышается. Однако при увеличении числа отсчетов в ядре скорость обработки снижается пропорционально.

Применяя к (6.1) Z-преобразование, получим

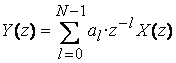   .                                  (6.2)

 

 

Передаточная функция КИХ-фильтра(нерекурсивный фильтр)

     Найдем передаточную функцию  КИХ-фильтра.

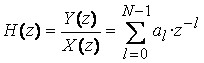                                     (6.3)

Устройство, реализующее ЦФ, выполняет последовательное умножение входной выборки сигнала на коэффициенты фильтра  и сложение полученных произведений. ЦФ более высоких порядков можно реализовать несколькими способами. Наиболее простым способом является так называемая прямая форма реализации ЦФ. В прямой форме ЦФ реализуется в соответствие с формулами (6.1) и (6.2).

Другим способом реализации ЦФ является каскадная (или последовательная) и параллельная формы реализации. При реализации в каскадной форме ЦФ представляется в виде последовательности следующих друг за другом звеньев ЦФ 1-го или 2-го порядка. В этом случае ЦФ реализуется в соответствии с формулой .

.

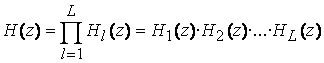При параллельной форме реализации входная последовательность во всех звеньях одна и та же, а выходная последовательность системы равна сумме выходных последовательностей отдельных звеньев.

Передаточная функция ЦФ рассматривается как:

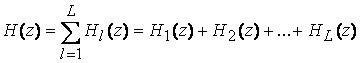
Нерекурсивный ЦФ может быть практически осуществлен, если заданная импульсная характеристика содержит ограниченное число отсчетов (КИХ-фильтр). Для получения же импульсной характеристики с большим числом членов требуется много ячеек памяти. Вместе с тем, нерекурсивные ЦФ имеют целый ряд важнейших достоинств. Они всегда устойчивы, позволяют строить фильтры с точно-линейной фазочастотной характеристикой и минимально-фазовые фильтры, а также отличаются малыми собственными шумами и простотой настройки.

 

Лекция 7. Рекурсивные цифровые фильтры (фильтры с бесконечным числом отсчетов импульсной характеристики)- БИХ- фильтры.

 

         Цель лекции- рассмотреть передаточную характеристику БИХ- фильтра; схемы реализации БИХ- фильтров.

         Возможности ЦФ существенно расширяются при введении в его схему обратных связей. Принцип работы рекурсивных ЦФ заключается в следующем. Каждый последующий отсчет в выходном сигнале, формируемом фильтром, рассчитывается как взвешенная сумма  предыдущих рассчитанных отсчетов выходного сигнала и  предшествующих отсчетов входного сигнала. Алгоритм работы рекурсивного ЦФ записывается в виде разностного уравнения

 .                           (7.1)

Если бы не погрешность представления чисел в ЭВМ, такой фильтр имел бы бесконечное количество затухающих по амплитуде выходных отсчетов при одном единственном входном отсчете, т.е. фильтр имел бы бесконечную импульсную характеристику (БИХ-фильтр). На практике размер импульсной характеристики определяется точностью представления чисел.

Применив Z-преобразование к (7.1) и решив его относительно , найдем передаточную функцию рекурсивного ЦФ

    .                            (7.2)

Рассмотрим некоторые, наиболее часто используемые структурные схемы рекурсивных ЦФ.

 

Прямая форма  рекурсивных фильтров реализуется непосредственно по его разностному уравнению (7.1) или по передаточной функции (7.2). Она содержит один сумматор, умножители и  элемента задержки (для создания цепей, соответствующих числителю и знаменателю передаточной функции  используются отдельные элементы задержки). Порядок фильтра определяется высшим порядком полиномов числителя или знаменателя.

Недостаток такого способа реализации – сравнительно большое число ячеек памяти, применяемой для рекурсивной и нерекурсивной частей. Уменьшить число этих ячеек позволяют каноническая (в смысле оптимального решения) схема, в которой каждый элемент задержки используется для цепей как нерекурсивной, так и рекурсивной частей схемы.

 

Прямая каноническая форма. Канонической называют структурную схему фильтра, содержащую минимальное число элементов задержки. Домножив числитель и знаменатель (7.2) на некоторую функцию , передаточную функцию рекурсивного ЦФ (7.2) можно представить в виде

,

где

     и           .

Передаточным функциям  и  соответствуют разностные уравнения

  .                (7.3)

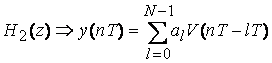         .                               (7.4)

         Алгоритм (7.4) определяет структуру построения нерекурсивного ЦФ, у которого входным сигналом является сигнал , а (7.3) рекурсивного ЦФ, у которого входным сигналом является сигнал . Таким образом, общая схема рекурсивного ЦФ включает в свою структуру 2 части – рекурсивную и нерекурсивную. Так как в фильтрах, реализующих  и  имеет место задержка только сигнала , то дублирующие элементы задержки можно объединить и использовать только один набор элементов задержки .

Прямая каноническая схема содержит минимальное число L элементов задержки:  и два сумматора.

В качестве примера приведем прямую каноническую форму структурной схемы ББ с передаточной функцией вида

,

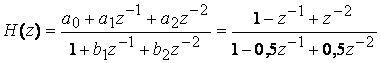здесь .

Структурная схема рекурсивного ЦФ 2-го порядка (так называемого биквадратного блока – ББ) показана на рисунке 7.1 (порядком цифрового фильтра называется количество элементов задержки в схеме фильтра).

 

 

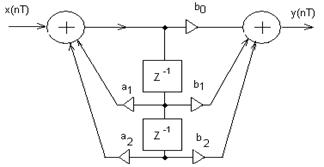
Рисунок 7.1- Прямая каноническая форма структурной схемы  биквадратного блока

 

         Каскадная (последовательная) форма реализации рекурсивных фильтров является одной из наиболее часто применяемых схем реализации ЦФ высоких порядков и соответствует представлению передаточной функции  в виде произведения,                                           (7.5)

 

где  – передаточная функция биквадратного блока:

,                          (7.6)

причем возможно, что в некоторых сомножителях  некоторые коэффициенты равны нулю и, следовательно, реализуются более простой структурной схемой. Параллельная форма реализации соответствует представлению передаточной функции РЦФ в виде суммы

,                                          

    

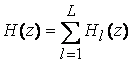где слагаемые  могут быть реализованы в виде упрощенных структур биквадратных блоков.

Основное достоинство рекурсивных фильтров – существенное сокращение числа элементов по сравнению с их числом в нерекурсивных фильтрах, выполняющих те же операции. Это позволяет реализовать цифровые фильтры с импульсными характеристиками, имеющими теоретически бесконечное число отсчетов. Поэтому в радиотехнике рекурсивные ЦФ получили название фильтров с бесконечными импульсными характеристиками (БИХ-фильтров).

 

 

 

Рисунок 7.1-Каскадная последовательная форма рекурсивного фильтра

 

 

 

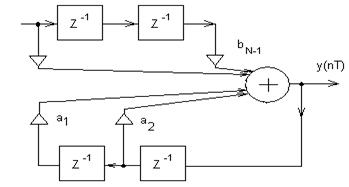
Рисунок 7.2- Прямая форма структуры ББ(биквадратного блока),содержащая сумматор и четыре элемента задержки

 

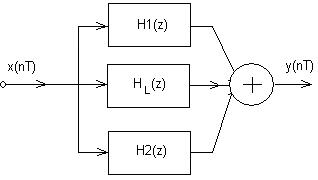
Рисунок7.3. – Параллельная форма  рекурсивного фильтра

 

 

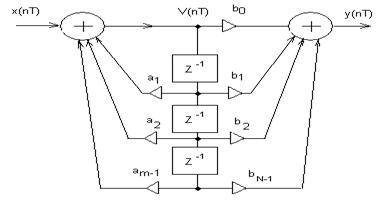
Рисунок 7.4- Прямая каноническая форма структурной схемы рекурсивного фильтра

 

Эффекты квантования в цифровых системах

 

В разделе “Аналоговые, дискретные и цифровые сигналы”  мы обсуждали разницу между дискретными и цифровыми сигналами. До сих пор, строго говоря, речь шла о дискретных сигналах и системах, поскольку отсчеты сигналов и коэффициентов фильтров считались представленными точно (без погрешностей). Сигналы на входе  и выходе  ЦФ являются цифровыми, т.е. последовательностями чисел. Каждое из этих чисел представляется в виде двоичного кода, и в ЦФ в соответствии с алгоритмом

.

выполняются операции пересылки, сложения и умножения кодов. Представить числа точно конечным числом разрядов кода невозможно. При этом алгоритм функционирования реализуется неточно. Ошибки цифровой фильтрации обусловлены следующими факторами:

- ошибки квантования входных и выходных сигналов;

- квантованием коэффициентов фильтра  и ;

- конечной разрядностью операционных устройств;

- округлением промежуточных результатов вычислений.

Поэтому при реализации ЦФ следует учитывать поведение упомянутых ошибок, которые часто называют ошибками квантования. На выходе цифровой системы ошибки квантования воспринимаются в виде шума, который называют шумом квантования. Это значит, что выбранная структура ЦФ, разрядность входных и выходных сигналов, длина регистров арифметических устройств должны быть определены так, чтобы ошибки квантования не превышали допустимой величины.

 

         Эффекты квантования коэффициентов фильтра. Расчет разрядности коэффициентов

 

Коэффициенты передаточной функции фильтра  и  являются сомножителями при вычислении отсчетов выходного сигнала фильтра.

АЧХ фильтра  нормируется так, чтобы при всех значениях  в полосе пропускания , а в полосе задерживания , поэтому для избирательных фильтров справедливо:

, т.е.   .                            ( 7.7)

В силу этого двоичный код коэффициентов КИХ-фильтров содержит лишь знаковый разряд и дробную часть, и не содержит целой части.

Поскольку десятичные числа менее единицы в двоичном коде представит точно невозможно, то найденные “точные”, т.е. представленные семью-четырнадцатью десятичными знаками коэффициенты фильтров  заменяются приближенным представлением в двоичном коде. Процесс округления вносит некоторую погрешность и вместо точного значения  используются их приближенные значения .

Для избирательного фильтра, АЧХ которого должна удовлетворять условию  при , критерием возможности округления коэффициентов до  двоичных разрядов является неравенство:

 для ,                     (7.8)

где  – АЧХ фильтра, рассчитанное при округлении коэффициентов до  двоичных разрядов.

 – АЧХ фильтра с неквантованными коэффициентами.

Существуют разные способы расчета разрядности коэффициентов  по допускам на характеристики фильтров. Самый простой способ – метод проб. Расчет минимального значения  по методу проб начинается с выбора разрядности ориентировочно, субъективно. Затем следует расчет АЧХ с новыми – приближенными значениями коэффициентов, оценка искажений характеристики по (7.8) и соответствующая коррекция разрядности коэффициентов  в ту или иную сторону. Расчет повторяется столько раз, сколько потребуется для удовлетворительного решения задачи по выбору разрядности коэффициентов.

В нерекурсивных ЦФ частотные характеристики линейно связаны с коэффициентами фильтров. Поэтому малые искажения коэффициентов приводят к малым искажениям частотных характеристик и проблемы, связанные с округлением коэффициентов возникают редко. Однако, если фильтр должен иметь очень крутой спад АЧХ между полосами пропускания и задерживания, округление коэффициентов все же может привести к заметным искажениям частотных характеристик.

Значительно серьезнее округления коэффициентов сказывается на характеристиках рекурсивных фильтров, поскольку коэффициенты знаменателя передаточной функции связаны с импульсными характеристиками нелинейно. Как правило, наибольшие искажения происходят в тех случаях, когда АЧХ фильтра имеет крутые скаты в переходных зонах между полосами пропускания и задерживания. Величина этих искажений сильно зависит от формы реализации фильтра. При представлении фильтра в виде каскадного соединения звеньев второго порядка округление коэффициентов влияет на характеристики фильтров значительно слабее, чем при прямой форме реализации.

Таким образом, прослеживается общая закономерность: параметры любого фильтра с резким изменением частотной характеристики в переходной полосе, реализованного в прямой форме, крайне чувствительны к значениям коэффициентов фильтра.

 

Лекция 8. Частотные характеристики цифровых фильтров (ЦФ) ; типовые звенья ЦФ.

 

Цель лекции- построение частотных характеристик  ЦФ; рассмотрение типовых звеньев дискретных цепей.

         Одним из важных показателей ЦФ является комплексный частотный коэффициент передачи

.                                     (8.1)

Если учесть, что

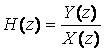 – системная функция ЦФ,

         то для получения  достаточно в выражении для  заменить z на , т.е.

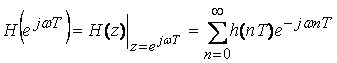 .                     (8.2)

 

Для нерекурсивных ЦФ:

.

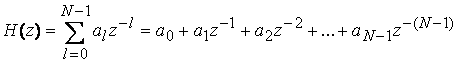Тогда .

Поскольку все частотные характеристики зависят при постоянном Т от произведения , то вместо  можно ввести новую переменную – нормированную частоту. Как правило, используют два способа нормирования частоты. При первом способе полагают

.

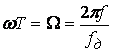В этом случае период всех частотных характеристик равен  и требования к ним следует задавать на интервале . При втором способе полагают , где

.

 В этом случае период дискретизации равен  и требования следует задавать на интервале .

Будем считать, что нормированной частотой является частота:

.

Тогда

.             (8.3)

Из (8.3) легко получить АЧХ и ФЧХ цифрового фильтра

.            (8.4)

 

Для рекурсивного ЦФ

   ,         .                   (8.5)

 

Из выражений (8.3) и (8.5) следует ряд важных свойств:

- все частотные характеристики ЦФ являются непрерывными функциями частоты;

- все частотные характеристики являются периодическими функциями частоты f с периодом повторения частоты дискретизации:

 (или 1 в масштабе нормированных частот ), поскольку в выражении для  входит периодическая функция ;

- АЧХ есть четная функция от частоты, ФЧХ – нечетная функция частоты

 

.

Из этих свойств следует, что требования к частотным характеристикам следует задавать лишь на интервале в половину периода, т.е.

.

Типовые звенья дискретной цепи.

 

        В литературе  (3,4,7,9  ) типовыми звеньями дискретной цепи считаются звенья 1-го и 2-го порядков. Они получаются из общей структуры (канонической схемы), если оставить в ней один или два элемента задержки.

Типовое звено первого порядка с передаточной функцией

имеет АЧХ, равную

.

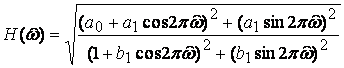Типовое звено 2-го порядка имеет вид имеет передаточную функцию

.

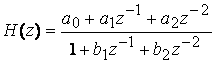Пример 8.1. Построить график АЧХ звена 1-го порядка, у которого

Передаточная функция такого звена

.

         Чтобы цепь была устойчивой необходимо выполнить условие .

При:

.

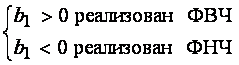Отсюда видно, что достаточно заменить на противоположные знаки нечетных коэффициентов знаменателя передаточной функции фильтра  и фильтр из фильтра нижних частот превращается в фильтр верхних частот.

Вопросы, касающиеся проектирования цифровых фильтров достаточно подробно рассмотрены в [3] и [9].

 

Лекция 9. Общие сведения и основные понятия цифровой интерполяции сигналов с целочисленными коэффициентами

 

Цель лекции- рассмотреть со студентами вопросы интерполяции цифрового сигнала; а также ознакомить их с работой эспандера .

Увеличение частоты дискретизации (интерполяция) цифрового сигнала

         До сих пор рассматривались алгоритмы и устройства обработки цифровых сигналов при определенной (фиксированной) частоте дискретизации  и соответствующем интервале дискретизации

.

         Вместе с тем в современных системах связи и радиотехники часто используются устройства и каналы связи с различными частотами дискретизации. Так, на разных участках канала в современном цифровом оборудовании радиодомов и телецентров приняты следующие стандарты на частоту дискретизации звуковых сигналов:

- 48 кГц – для обработки сигналов;

- 32 кГц – для передачи по каналу связи;

- 44,1 кГц – для лазерного проигрывателя.

Для ТV-сигналов – 13,5 МГц – для формирования и обработки сигналов, а в различных системах компрессии частота дискретизации может понижаться в 40 раз.

Таким образом, для обеспечения совместной работы различных источников сигнала, системы обработки и каналов связи необходимо осуществить сопряжение частот дискретизации, т.е. преобразование сигналов с частотой дискретизации

 в частоту

.

Аналогичная задача возникает в технике многоканальной связи (преобразование стандартной частоты дискретизации 60-канальной группы с частотным разделением каналов, равной 576 кГц, в частоту 512 кГц для передачи по каналу связи).

Процесс преобразования цифрового сигнала от более низкой частоты к более высокой традиционно называют интерполяцией цифрового сигнала.

Процесс преобразования от более высокой частоты к более низкой называется децимацией ЦС.

Процесс преобразования частоты дискретизации стал в дальнейшем использоваться и при построении эффективных в смысле вычислительных затрат многоскоростных систем обработки ЦС, в которых различные этапы обработки выполняются на разных частотах дискретизации.

В настоящей главе мы рассмотрим основные алгоритмы интерполяции ЦС, а также структуры соответствующих устройств ЦОС. Алгоритмы и структуры устройств децимации сигналов будут рассмотрены позднее.

В ЦОС под термином интерполяция подразумевается процесс ЦОС, приводящий к формированию сигнала  с повышенной частотой дискретизации из сигнала  с более низкой частотой дискретизации при определенных ограничениях на временные и спектральные изменения исходного сигнала. Таким образом, новый интервал дискретизации равен

;          – прежний интервал дискретизации.

Можно выделить три разновидности процесса интерполяции при ЦОС:

-увеличение частоты дискретизации осуществляется в соответствии с математическим понятием интерполяции. В этом случае в исходных точках отсчетов  или  отсчеты новой и старой функции совпадают:

.

Т.е. если исходная функция  содержала  отсчет, то полученная функция  содержит  отсчет (между каждой парой отсчетов  добавляется еще несколько отсчетов ).

При увеличении частоты дискретизации исходные отсчеты дискретного сигнала  оказываются утерянными, однако отсчеты выходного сигнала  могут рассматриваться как отсчеты исходного аналогового сигнала  из которого путем дискретизации с интервалом  был образован исходный дискретный сигнал . В этом случае огибающая сигналов  и , а так же их спектр – не изменяются.

-увеличение частоты дискретизации приводит к изменению формы интерполируемого сигнала, однако модуль его спектра не изменяется.

Во всех случаях процесс преобразования описывается структурной схемой (см. рисунок 9.1).

.
 
Входной аналоговый сигнал  поступает на идеальный дискретизатор Д, работающий с интервалом дискретизации  (L – целое число). Выходной дискретный сигнал ,  поступает на идеальный интерполятор ИИ, увеличивающий частоту дискретизации в L раз. Таким образом, сигнал  можно рассматривать как результат дискретизации исходного аналогового сигнала  с интервалом дискретизации .        Выходной сигнал системы ,  получается в результате преобразования выходного сигнала ИИ  линейной дискретной системой с частотной характеристикой

 .                                        (9.1)

Иными словами АЧХ системы :

, т.е. форма модуля спектра не изменяется, а

ФЧХ  для разных случаев может быть разной.

Для случая 1:

Дискретная система  обладает линейной ФЧХ, т.е.

 – целое число, не зависит от частоты,

ФЧХ имеет вид:

 (линейно зависит от частоты).

Для случая 2:

дискретная система  обладает линейной ФЧХ:

дискретная система  обладает линейной ФЧХ:

, т.е. , но

 
 
 – нецелое число.

Случай 3: Дискретная система обладает нелинейной ФЧХ, т.е.

 – зависит от частоты;

 в этом случае огибающая сигнала  не является отсчетами сигнала ,

 

но модуль спектра сигнала  в основной полосе частот по прежнему

 

имеет тот же вид, что и модуль спектра входного сигнала , поэтому по

дискретному сигналу  может быть восстановлен аналоговый сигнал , модуль спектра которого совпадает с модулем спектра исходного сигнала , т.е. информация не будет утеряна.

Рассмотрим теперь частотную интерпретацию процесса интерполяции

цифрового сигнала с целочисленным коэффициентом L = 3.

Пусть спектр исходного сигнала  имеет вид, изображенный на рисунке 9.2,а.

После дискретизации исходного сигнала с частотой дискретизации

  модуль спектра  имеет вид, изображенный на рисунке 9.2,б.

 При дискретизации же с частотой в три раза выше,  или  получим модуль спектра  дискретизированного сигнала  (рисунок 9.2,в).

 Отличие между этими спектрами состоит в том, что (не считая амплитуды) в спектре  имеются “лишние” частотные составляющие с

центральными частотами  и .

     Таким образом, процесс повышения частоты дискретизации сигнала  эквивалентен преобразованию спектра сигнала от вида 9.2,б к виду 9.2,в, т.е. к подавлению “лишних” частотных составляющих исходного спектра с помощью цифрового фильтра.

Эспандер частоты

Процесс интерполяции осуществляется путем цифровой фильтрации с целью подавления “лишних” составляющих спектра. Однако цифровой фильтр работает на определенной частоте дискретизации. Следовательно, перед цифровой фильтрацией сигнала необходимо осуществить предварительное увеличение частоты дискретизации исходного сигнала в

 

 

 

Рисунок 9.2 – Спектры сигналов  при интерполяции   цифрового сигнала

 

нужное число раз L.  

          Эту операцию осуществляет эспандер частоты дискретизации (ЭЧД).

Входным сигналом ЭЧД является дискретный сигнал с интервалом дискретизации  (частотой ) ,

Сигнал  преобразуется в сигнал  по алгоритму:

.

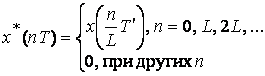Таким образом, формируется выходной дискретный сигнал с интервалом дискретизации

, который в L раз меньше исходного, или частотой дискретизации  – в L раз больше исходной.

Последовательность  получается из последовательности  путем ввода  нулевых отсчетов между каждой парой отсчетов исходной последовательности. Получим связь между спектром  и . Для этого вначале найдем Z-преобразование сигналов  и .

Z-преобразование входной последовательности:

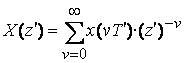,                                     (9.2)

где .

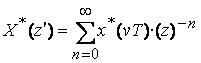,                                     (9.3)

где .

Поскольку , то очевидно, что .

Преобразуем теперь (9.3) учтя, что

 для

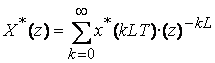.                                  (9.4)

Если учесть, что

, а  и, следовательно,

, то сравнив (9.4) с (9.2), получим:

                                              (9.5)

Это означает, что Z-преобразование входного и выходного сигналов ЭЧД тождественны.

Соотношения для спектров получим из (9.5), подставив вместо

 и

 или

где

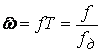 – нормированная частота.

Таким образом, выходной сигнал ЭДЧ:

 , формируемый из входного  по алгоритму (9.1) имеет тот же спектр, что и входной сигнал.

Спектр выходного сигнала ЭЧД периодичен со “старой” частотой дискретизации

, а не с “новой” частотой   ,

как это обычно имеет место для сигналов, интервал дискретизации которых равен Т.

 

Простейшая система интерполяции с целочисленным коэффициентом L

Входным сигналом является сигнал

,  с интервалом дискретизации .

         Предполагается, что сигнал  с ограниченным спектром занимает полосу частот от .

         Частота дискретизации

.

Входной сигнал  поступает на экспандер частоты дискретизации, осуществляющий предварительное увеличение частоты дискретизации в L-раз по алгоритму (9.1):

.

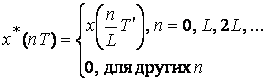Спектры входного и выходного сигналов ЭДЧ равны и периодичны с частотой .

Выходной сигнал ЭДЧ обрабатывается "идеальным" цифровым фильтром НЧ с передаточной функцией  и импульсной характеристикой , задачей которого является подавление “лишних” частотных составляющих спектра

, занимающих область частот

.

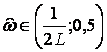         Частотные характеристики фильтра должны удовлетворять условию:

.                            (9.6)

В качестве ФНЧ могут быть использованы как КИХ так и БИХ-фильтры. КИХ-фильтры позволяют достаточно просто строить эффективные системы преобразования частоты дискретизации сигналов. Как известно, КИХ фильтры имеют передаточную функцию

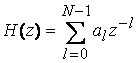                                          (9.7)

и линейную ФЧХ

.

 Они могут иметь нечетное (КИХ-фильтры 1-го вида) и четное (КИХ-фильтры 2-го вида) число отсчетов N импульсной характеристики

 .

Для фильтров 1-го вида (N – нечетное)

 – целое число

         Поскольку величина R определяет задержку числа во временной области, вносимую фильтром при обработке сигнала, то задержка

равна целому числу интервалов дискретизации Т.

При этом процесс интерполяции соответствует варианту 1, т.е. увеличение частоты дискретизации осуществляется в соответствии с математическим понятием интерполяции, когда сохраняются отсчеты входного сигнала, модуль спектра и форма огибающей входного сигнала.

Для КИХ-фильтров 2-го вида (N – четное)

 – нецелое число.

         Процесс интерполяции в этом случае соответствует варианту 2, когда сохраняются и модуль спектра и форма огибающей входного сигнала, но не сохраняются его отсчеты.

Минимально-фазовые КИХ обладают нелинейной ФЧХ

.

Процесс интерполяции соответствует варианту 3: сохраняется модуль спектра, но не сохраняется форма сигнала.

БИХ-фильтры обладают, как правило, нелинейной ФЧХ и в случае их использования тоже сохраняется модуль спектра, но не сохраняется форма исходного сигнала (вариант 3).

  

 Список используемой литературы 

1. Баскаков С. И. Радиотехнические цепи и сигналы. – М.: Высшая школа, 2003. – 462 с.

2. Гоноровский И. С. Радиотехнические цепи и сигналы. – М.: Радио и связь, 1986. – 512 с.

3. Карамов З. С., Колесниченко Г. И. Цифровая обработка сигналов: Учебное пособие/ МИС. – М.: 1990.- 41с.

4. Куприянов М.С. и др. Техническое обеспечение цифровой обработки сигналов: Справочник. – СПб. Форт, 2000.- 752 с .

5. Куприянов М.С., Матюшкин Б. Д.  Цифровая обработка сигналов: процессоры, алгоритмы, средства проектирования. – СПб., 1999. – 592 с.

6. Нефедов В. И. Основы радиоэлектроники и связи. – М.: Высшая школа, 2002. – 510 с.

7. Сергиенко А. Б. Цифровая обработка сигналов. – ЗАО Издательский дом «Питер», 2002. – 608 с.

8. Солонина А. И., Улахович Д. А. и другие. Основы цифровой обработки сигналов. – С-П. «БХВ-Петербург», 2003. – 608 с.

9. Введение в цифровую фильтрацию/ Под ред. Р. Бочнера и А. Константинидиса. – М.: Изд-во” Мир”, 1976. – 215с.

10. Цифровой процессор сигналов TMS 32010 и его применение/ Под ред. А.А. Ланне. – Л.: ВАС,1990. – 296 с.

11. Теоретические основы радиотехники/ Под ред. В. Н. Ушакова. – М.: Высшая школа, 2002. – 306 с.

12. Радиотехнические цепи и сигналы/ Под ред. К. А. Самойло. – М.: Радио и связь, 1982. – 528 с.

13. Гольденберг Л.М.  и др. Цифровые устройства и микропроцессорные системы. Задачи и упражнения: Учебное пособие. – М.: Радио и связь, 1992. – 256с.

14. Казиева Г. С. Основы цифровой обработки сигналов в телекоммуникационных системах: Конспект лекций. – Алматы: АИЭС, 2006.

  Сводный план 2010 г., поз.