АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра высшей математики
Математика 3
Конспект лекций
(для студентов всех форм обучения всех специальностей)
Бакалавриат
Алматы 2008
СОСТАВИТЕЛИ: Жуматаева С.А., Темешева С.М. Математика 3. Конспект лекций (для студентов всех форм обучения всех специальностей). Бакалавриат. – Алматы: АИЭС, 2008. – 67 с.
Настоящий конспект содержит 17 лекций по курсу высшей математики, входящих в раздел “Математика 3” (“Теория поля”, “Дифференциальные уравнения”, “Ряды”, “Теория функций комплексного переменного и операционное исчисление”, “Элементы теории вероятностей”) и соответствует учебному плану второго семестра обучения бакалавров всех специальностей Алматинского института энергетики и связи.
Конспект лекций предназначен для студентов высших технических учебных заведений.
Содержание
|
Предисловие……...…………………………………..……………………....... |
4 |
|
|
1 Лекция 1 |
Теория поля……………………………...…………………... |
5 |
|
2 Лекция 2 |
Дифференциальные уравнения. Обыкновенные дифференциальные уравнения………….... |
9 |
|
3 Лекция 3 |
Однородные дифференциальные уравнения относительно переменных. Уравнения, сводящиеся к однородным. Линейные дифференциальные уравнения первого порядка. Уравнение Бернулли……………...………………………… |
13 |
|
4 Лекция 4 |
Дифференциальные уравнения высших порядков. Дифференциальные уравнения, допускающие понижение порядка. Линейные дифференциальные уравнения высших порядков………………...…....……………………………… |
17 |
|
5 Лекция 5 |
Линейные однородные дифференциальные уравнения. Решение линейного неоднородного дифференциального уравнения. Линейные однородные дифференциальные уравнения с постоянными коэффициентами……………… |
21 |
|
6 Лекция 6 |
Метод подбора частного решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами. Метод неопределенных коэффициентов. Система обыкновенных дифференциальных уравнений…. |
25 |
|
7 Лекция 7 |
Числовые ряды. Основные понятия. Знакоположительные ряды ………………………………………………………….. |
29 |
|
8 Лекция 8 |
Знакопеременные и знакочередующиеся ряды…………… |
33 |
|
9 Лекция 9 |
Функциональные ряды, степенные ряды. Ряды Тейлора. Разложение некоторых функций в ряд Маклорена…..…… |
37 |
|
10 Лекция 10 |
Ряды Фурье…………………………………………………... |
41 |
|
11 Лекция 11 |
Понятие функции комплексного переменного……………. |
43 |
|
12 Лекция 12 |
Определение преобразования Лапласа…………………….. |
47 |
|
13 Лекция 13 |
Нахождение оригинала по изображению. Приложение операционного исчисления…..……………………………... |
51 |
|
14 Лекция 14 |
Элементы теории вероятностей……………………………. |
53 |
|
15 Лекция 15 |
Формула полной вероятности……………………………… |
58 |
|
16 Лекция 16 |
Случайные величины……………………………………….. |
61 |
|
17 Лекция 17 |
Дисперсия дискретной случайной величины……………... |
64 |
|
Список литературы……………………………………..................................... |
67 |
|
Предисловие
Настоящий конспект содержит 17 лекций по курсу высшей математики, входящих в раздел “Математика 3” и соответствует учебному плану второго семестра обучения бакалавров всех форм обучения всех специальностей Алматинского института энергетики и связи.
Конспект лекций будет полезен преподавателям и студентам и предназначен для проведения самостоятельных работ во время аудиторных занятий по следующим разделам курса высшей математики: “Теория поля”, “Дифференциальные уравнения”, “Ряды”, “Теория функций комплексного переменного и операционное исчисление”, “Элементы теории вероятностей”.
Нумерация определений, теорем, формул состоит из двух чисел: первое из них указывает номер лекций, а второе – порядковый номер определения, теоремы, формулы в этой лекции.
Усвоение содержащегося в пособии материала способствует получению хороших знаний студентом по соответствующим разделам курса высшей математики.
1 Лекция 1 Теория поля
Содержание: Определение поля, элементы теории поля. Типы векторных полей. Вычисление потока и циркуляции векторного поля. Теорема Остроградского-Гаусса, теорема Стокса.
Цели лекции: Уметь составлять системы дифференциальных уравнений, определяющих семейство векторных линий, находить дивергенцию и ротор векторного поля. Уметь применять теоремы Остроградского-Гаусса и Стокса при вычислении потока векторного поля.
Определение 1.1 Если в каждой точке ![]() области
области ![]() задан определенный вектор
задан определенный вектор ![]() , то говорят, что в этой
области задано векторное поле, т.е. векторное поле задано, если в каждой точке
, то говорят, что в этой
области задано векторное поле, т.е. векторное поле задано, если в каждой точке ![]() указан соответствующий
вектор
указан соответствующий
вектор ![]() (предполагается,
что функции
(предполагается,
что функции ![]() ,
, ![]() ,
, ![]() непрерывны вместе со своими частными
производными).
непрерывны вместе со своими частными
производными).
Частные случаи векторных полей
1. Векторное поле называется однородным, если вектор ![]() постоянный, т.е. функции
постоянный, т.е. функции
![]() ,
, ![]() ,
, ![]() являются постоянными.
являются постоянными.
2. Векторное поле называется плоским, если в
выбранной системе координат ![]() ,
, ![]() ,
, ![]() являются функциями двух переменных и одна
из проекции вектора равна
являются функциями двух переменных и одна
из проекции вектора равна ![]() , например:
, например: ![]() .
.
3. Если функции ![]() ,
, ![]() ,
, ![]() не зависят от
не зависят от ![]() , то поле называется стационарным.
, то поле называется стационарным.
Определение 1.2 Векторной линией векторного поля называется линия, в каждой точке которой направление касательной в этой точке к линии совпадает с направлением вектора, соответствующего этой точке.
Пусть дано векторное поле ![]() . Пусть векторная линия имеет
параметрическое уравнение:
. Пусть векторная линия имеет
параметрическое уравнение: ![]() ,
, ![]() ,
, ![]() . Касательная к векторной линии в точке
. Касательная к векторной линии в точке ![]() с направляющим
вектором
с направляющим
вектором ![]() имеет
вид:
имеет
вид: 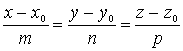 . Из
определения 1.2 следует, что вектора
. Из
определения 1.2 следует, что вектора ![]() и
и ![]() коллинеарны, тогда из условия коллинеарности
векторов получим
коллинеарны, тогда из условия коллинеарности
векторов получим 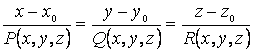 .
Так как,
.
Так как, ![]() есть
приращение аргумента
есть
приращение аргумента ![]() ,
то
,
то ![]() .
Аналогично:
.
Аналогично: ![]() ,
, ![]() .
.
Итак,
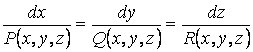 . (1.1)
. (1.1)
Система дифференциальных уравнений (1.1) определяет
семейство векторных линий векторного поля ![]() .
.
Поток вектора
Пусть дано векторное поле ![]() . Возьмем в этом поле некоторую
поверхность
. Возьмем в этом поле некоторую
поверхность ![]() и
выберем на ней определенную сторону.
и
выберем на ней определенную сторону. ![]() – единичный вектор нормали к рассматриваемой
стороне в произвольной точке.
– единичный вектор нормали к рассматриваемой
стороне в произвольной точке.
Определение 1.3
Потоком вектора ![]() через
поверхность
через
поверхность ![]() называется
интеграл по поверхности
называется
интеграл по поверхности ![]() от скалярного произведения вектора поля на
единичный вектор нормали к поверхности:
от скалярного произведения вектора поля на
единичный вектор нормали к поверхности:
![]() (1.2)
(1.2)
или
![]()
![]() . (1.3)
. (1.3)
Дивергенция
Рассмотрим произвольную точку ![]() векторного поля
векторного поля ![]() , окружим ее замкнутой
поверхностью
, окружим ее замкнутой
поверхностью ![]() ,
целиком содержащейся в поле.
,
целиком содержащейся в поле.
Рассмотрим 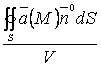 . В поле скоростей жидкости это отношение определяет
количество жидкости, возникающее в единицу времени в области
. В поле скоростей жидкости это отношение определяет
количество жидкости, возникающее в единицу времени в области ![]() , отнесенной к единице
объема, т.е. среднюю объемную мощность источника. Если поток меньше 0, то
говорят о мощности стока.
, отнесенной к единице
объема, т.е. среднюю объемную мощность источника. Если поток меньше 0, то
говорят о мощности стока.
Найдем 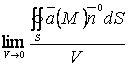 , т.е. предел при условии, что область
, т.е. предел при условии, что область ![]() стягивается в точку
стягивается в точку ![]() . Если предел больше
. Если предел больше ![]() , то точка
, то точка ![]() называется источником,
если предел меньше
называется источником,
если предел меньше ![]() ,
то точка
,
то точка ![]() называется
стоком. Сам предел характеризует мощность источника или мощность стока.
называется
стоком. Сам предел характеризует мощность источника или мощность стока.
Определение 1.4 Дивергенцией или расходимостью векторного поля ![]() называется предел отношения
потока вектора через поверхность, окружающую точку
называется предел отношения
потока вектора через поверхность, окружающую точку ![]() , к объему, ограниченному этой
поверхностью, при условии, что вся поверхность стягивается в точку
, к объему, ограниченному этой
поверхностью, при условии, что вся поверхность стягивается в точку ![]() и обозначают:
и обозначают:
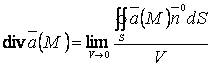 . (1.4)
. (1.4)
Теорема. ![]() дивергенция векторного
поля
дивергенция векторного
поля ![]()
![]() находится по формуле
находится по формуле
 , (1.5)
, (1.5)
где
частные производные берутся в точке ![]() .
.
Теорема Остроградского-Гаусса. Поток вектора изнутри замкнутой поверхности равен тройному интегралу по объему, ограниченному этой поверхностью, от дивергенции поля
![]()
или
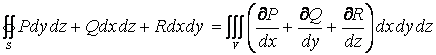 . (1.6)
. (1.6)
Свойства дивергенции
1.
![]() ;
;
2. пусть ![]() – определяет векторное поле, а
– определяет векторное поле, а ![]() – скалярное поле, тогда
– скалярное поле, тогда
![]() .
.
Циркуляция векторного поля
Определение 1.5
Циркуляцией вектора ![]() вдоль
замкнутого контура
вдоль
замкнутого контура ![]() называется
криволинейный интеграл по этому контуру от скалярного произведения вектора
называется
криволинейный интеграл по этому контуру от скалярного произведения вектора ![]() на вектор
на вектор ![]() , касательный к контуру
, касательный к контуру
![]() . (1.7)
. (1.7)
Ротор векторного поля
Определение 1.6 Ротором векторного поля ![]()
![]() называется вектор
называется вектор
 . (1.8)
. (1.8)
Теорема
Стокса. Поток ротора через
поверхность ![]() равен
циркуляции вектора по границе этой поверхности:
равен
циркуляции вектора по границе этой поверхности:![]() или
или
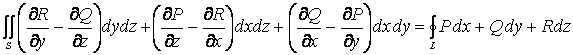 . (1.9)
. (1.9)
Свойства ротора
1.
![]() ;
;
2.
если ![]() –
скалярная функция,
–
скалярная функция, ![]() –
вектор, тогда
–
вектор, тогда
![]() .
.
Оператор Гамильтона
Введем
символический вектор ![]() –
набла-вектор.
–
набла-вектор. 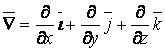 называется
оператором Гамильтона.
называется
оператором Гамильтона.
1. 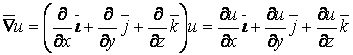 ,
, ![]() .
.
2. 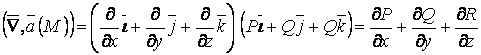 ,
, ![]() .
.
3.  ,
, ![]() .
.
Типы полей
1. Векторное поле называется соленоидальным или
трубчатым, если ![]() .
.
2. Векторное поле называется потенциальным или
безвихревым, если ![]() .
.
3. Если векторное поле соленоидальное и потенциальное, то оно называется гармоническим.
2 Лекция 2 Дифференциальные уравнения. Обыкновенные дифференциальные уравнения
Содержание: Основные определения и понятия. Виды дифференциальных уравнений первого порядка и методы их решения.
Цели лекции: Уметь определять тип дифференциального уравнения и его порядок, применять необходимые подстановки, находить решение или общий интеграл дифференциального уравнения.
Основные определения и понятия
Определение 2.1
Дифференциальным уравнением называется уравнение, связывающее независимую
переменную ![]() ,
неизвестную функцию
,
неизвестную функцию ![]() и
ее производные или дифференциалы различных порядков.
и
ее производные или дифференциалы различных порядков.
Определение 2.2 Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.
Пример 2.1 -
![]() . Данное
уравнение является дифференциальным уравнением, т.к. оно содержит производные
второго и первого порядка. Наивысший порядок производной, входящей в данное
уравнение, равен двум, следовательно, порядок данного дифференциального
уравнения равен двум.
. Данное
уравнение является дифференциальным уравнением, т.к. оно содержит производные
второго и первого порядка. Наивысший порядок производной, входящей в данное
уравнение, равен двум, следовательно, порядок данного дифференциального
уравнения равен двум.
Пример 2.2 -
![]() . Данное
уравнение является дифференциальным уравнением, т.к. оно содержит дифференциалы
первого порядка. Порядок дифференциального уравнения равен одному, так как в
уравнение входят дифференциалы первого порядка.
. Данное
уравнение является дифференциальным уравнением, т.к. оно содержит дифференциалы
первого порядка. Порядок дифференциального уравнения равен одному, так как в
уравнение входят дифференциалы первого порядка.
Определение 2.3
Решением или интегралом дифференциального уравнения называется любая функция ![]() , которая, будучи
подставлена в уравнение, обращает ее в тождество.
, которая, будучи
подставлена в уравнение, обращает ее в тождество.
Дифференциальные уравнения первого порядка
Дифференциальное уравнение первого порядка имеет вид:
![]() .
(2.1)
.
(2.1)
Если уравнение (2.1) удается разрешить относительно производной, т.е.
![]() ,
(2.2)
,
(2.2)
то
такая форма называется нормальной формой дифференциального уравнения первого
порядка или дифференциальным уравнением первого порядка, разрешенным
относительно производной. Известно, что ![]() тогда (2.2) можно представить в виде
тогда (2.2) можно представить в виде
![]() . (2.3)
. (2.3)
Определение 2.4
Решением дифференциального уравнения первого порядка называется функция ![]() ,
, ![]() , которая при подстановке в
уравнение обращает его в тождество.
, которая при подстановке в
уравнение обращает его в тождество.
График решения дифференциального уравнения называется интегральной кривой. Ответ на вопрос, при каких условиях уравнение (2.2) имеет решение, дает теорема Коши, которая называется теоремой о существовании и единственности решения дифференциального уравнения (2.2).
Теорема Коши.
Если ![]() и ее
частная производная
и ее
частная производная ![]() определены
и непрерывны в некоторой области
определены
и непрерывны в некоторой области ![]() плоскости
плоскости ![]() , то какова бы ни была внутренняя точка
, то какова бы ни была внутренняя точка ![]() , в некоторой
окрестности этой точки существует единственное решение уравнения
, в некоторой
окрестности этой точки существует единственное решение уравнения ![]() , удовлетворяющее
условиям
, удовлетворяющее
условиям
![]() при
при ![]() .
(2.4)
.
(2.4)
Условия (2.4), в силу которых ![]() принимает заданное значение
принимает заданное значение ![]() в заданной точке
в заданной точке ![]() , называются начальными
условиями и записываются так:
, называются начальными
условиями и записываются так:
![]() .
(2.4’)
.
(2.4’)
Если поставлена задача отыскания решения уравнения (2.2), удовлетворяющего начальным условиям (2.4), тогда говорят, что поставлена задача Коши.
С геометрической точки зрения решить задачу Коши означает,
что из множества интегральных кривых нужно выделить ту, которая проходит через
заданную точку ![]() плоскости
плоскости
![]() .
.
Точки плоскости, через которые проходит более одной интегральной кривой, либо не проходит ни одной интегральной кривой, называются особыми точками уравнения.
Определение 2.5
Общим решением дифференциального уравнения (2.2) в некоторой области ![]() плоскости
плоскости ![]() называется функция
называется функция
![]() ,
(2.5)
,
(2.5)
зависящая
от ![]() и от
произвольной постоянной
и от
произвольной постоянной ![]() , которая удовлетворяет следующим условиям:
, которая удовлетворяет следующим условиям:
а) если (2.5) удовлетворяет уравнению (2.2) при любом
значении постоянной ![]() ,
,
б) каковы бы ни были начальные условия (2.4), всегда
можно найти значение ![]() такое,
что функция
такое,
что функция ![]() удовлетворяет
данным начальным условиям:
удовлетворяет
данным начальным условиям: ![]() .
.
Определение 2.6 Решение дифференциального уравнения, найденное в виде неявной функции
![]() ,
(2.6)
,
(2.6)
называется общим интегралом уравнения (2.2).
Определение 2.7 Частным решением уравнения (2.2) в области ![]() называется функция
называется функция ![]() , которая получается из
общего решения (2.5) при определенном значении постоянной
, которая получается из
общего решения (2.5) при определенном значении постоянной ![]() .
.
Геометрический смысл дифференциального уравнения первого порядка
Пусть дано дифференциальное уравнение![]() и
и ![]() – его решение. Через любую точку
интегральной кривой можно провести касательную. Из уравнения следует, что
угловой коэффициент
– его решение. Через любую точку
интегральной кривой можно провести касательную. Из уравнения следует, что
угловой коэффициент ![]() касательной
к интегральной кривой в каждой точке
касательной
к интегральной кривой в каждой точке ![]() равен значению в этой точке функции
равен значению в этой точке функции ![]() . Таким образом,
. Таким образом, ![]() устанавливает зависимость
между координатами точки и угловым коэффициентом
устанавливает зависимость
между координатами точки и угловым коэффициентом ![]() касательной к графику интегральной кривой
в той же точке. Сопоставим каждой точке
касательной к графику интегральной кривой
в той же точке. Сопоставим каждой точке ![]() интегральной кривой направленный отрезок,
угловой коэффициент которого равен
интегральной кривой направленный отрезок,
угловой коэффициент которого равен ![]() получим, так называемое, поле направлений
данного уравнения.
получим, так называемое, поле направлений
данного уравнения.
Итак, с геометрической точки зрения уравнение ![]() определяет поле направлений
на плоскости
определяет поле направлений
на плоскости ![]() ,
а решение – интегральная кривая, направление касательной к которой в каждой
точке, совпадает с направлением поля.
,
а решение – интегральная кривая, направление касательной к которой в каждой
точке, совпадает с направлением поля.
Виды уравнений
I. Уравнение вида
![]() (2.7)
(2.7)
называется
простейшим дифференциальным уравнением или ![]() . Функция
. Функция ![]() определяется по формуле:
определяется по формуле: ![]() .
.
II. Уравнение вида
![]() (2.8)
(2.8)
называется уравнением с разделенными переменными.
Решение определяется по формуле: ![]() .
.
III. Уравнение вида
![]() (2.9)
(2.9)
называется уравнением с разделяющимися переменными.
Считая
![]() и
и ![]() разделим обе части
уравнения (2.9) на произведение
разделим обе части
уравнения (2.9) на произведение ![]() , тогда получим:
, тогда получим:  , т.е. свели (2.9) к дифференциальному
уравнению с разделенными переменными.
, т.е. свели (2.9) к дифференциальному
уравнению с разделенными переменными.
Уравнение вида
![]() ,
(2.10)
,
(2.10)
где
![]() и
и ![]() – непрерывные функции,
так же является уравнением с разделяющимися переменными. Для отыскания решения
(2.10) заменим
– непрерывные функции,
так же является уравнением с разделяющимися переменными. Для отыскания решения
(2.10) заменим ![]() ,
получим уравнение
,
получим уравнение
![]() .
(2.11)
.
(2.11)
Предполагая ![]() , разделим (2.11) на
, разделим (2.11) на ![]() , тогда получим уравнение с
разделенными переменными:
, тогда получим уравнение с
разделенными переменными: 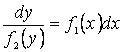 . Интегрируя обе части последнего равенства,
найдем общий интеграл уравнения (2.10):
. Интегрируя обе части последнего равенства,
найдем общий интеграл уравнения (2.10):
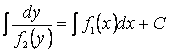 .
.
Пример 2.3 -
![]() – это
простейшее дифференциальное уравнение первого порядка.
– это
простейшее дифференциальное уравнение первого порядка.
Интегрируем:
![]()
![]()
![]() .
.
Пример 2.4 -
![]() – это
уравнение с разделяющимися переменными.
– это
уравнение с разделяющимися переменными.
Разделим обе части уравнения на выражение ![]() , предположив
, предположив ![]() , тогда получим
уравнение с разделенными переменными
, тогда получим
уравнение с разделенными переменными
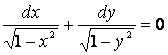 .
.
Интегрируя
это уравнение, получим ![]() , или, используя формулу
, или, используя формулу ![]() , запишем равенство
, запишем равенство
![]() ,
,
которое и является общим интегралом данного дифференциального уравнения.
3 Лекция 3 Однородные дифференциальные уравнения относительно переменных. Уравнения, сводящиеся к однородным. Линейные дифференциальные уравнения первого порядка. Уравнение Бернулли
Содержание:
Определение степени однородности функции, однородные дифференциальные уравнения
относительно переменных ![]() ,
, ![]() . Линейные однородные и неоднородные
дифференциальные уравнения первого порядка. Метод вариации произвольной постоянной.
Уравнение Бернулли.
. Линейные однородные и неоднородные
дифференциальные уравнения первого порядка. Метод вариации произвольной постоянной.
Уравнение Бернулли.
Цели лекции:
Уметь определять степень однородности функции; решать однородные
дифференциальные уравнения относительно переменных ![]() ,
,![]() и уравнения, сводящиеся к ним, линейные
однородные и неоднородные дифференциальные уравнения первого порядка. Уметь
применять метод вариации произвольной постоянной. Решать уравнения Бернулли.
и уравнения, сводящиеся к ним, линейные
однородные и неоднородные дифференциальные уравнения первого порядка. Уметь
применять метод вариации произвольной постоянной. Решать уравнения Бернулли.
IV. Однородные дифференциальные
уравнения первого порядка относительно переменных ![]() и
и ![]() .
.
Определение 3.1 Функция ![]() называется
однородной функцией
называется
однородной функцией ![]() -го
порядка измерения, если выполняется соотношение:
-го
порядка измерения, если выполняется соотношение: ![]() .
.
Например, ![]() . Для этой функции
. Для этой функции
![]() ,
,
т.е.
![]() – однородная
функция 3-го порядка измерения.
– однородная
функция 3-го порядка измерения.
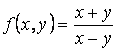 ;
; 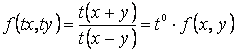 , т.е.
, т.е. 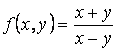 – однородная функция нулевого порядка
измерения.
– однородная функция нулевого порядка
измерения.
Определение 3.2 Уравнение ![]() называется
однородным дифференциальным уравнением первого порядка, если функция
называется
однородным дифференциальным уравнением первого порядка, если функция ![]() однородная функция
относительно переменных
однородная функция
относительно переменных ![]() ,
,![]() нулевого порядка измерения.
нулевого порядка измерения.
Определение 3.3 Дифференциальное уравнение ![]() называется однородным относительно
переменных
называется однородным относительно
переменных ![]() ,
,![]() , если функции
, если функции ![]() и
и ![]() являются однородными функциями
одного и того же порядка измерения.
являются однородными функциями
одного и того же порядка измерения.
Для решения однородного относительно переменных ![]() и
и ![]() дифференциального уравнение первого
порядка применяют подстановку:
дифференциального уравнение первого
порядка применяют подстановку:
![]() (3.1)
(3.1)
после чего оно сводится к уравнению вида III.
V. Уравнение, сводящееся к однородному дифференциальному
уравнению I-порядка относительно переменных ![]() и
и ![]() .
.
Это уравнение вида
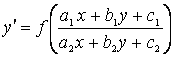 (3.2)
(3.2)
Решение:
1) если 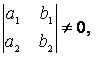 тогда
произведем замену
тогда
произведем замену  ,
где
,
где ![]() и
и ![]() найдем из системы
линейных уравнений
найдем из системы
линейных уравнений  ;
;
2) если  тогда будем делать замену
тогда будем делать замену 
После замены уравнение сводится к уравнению вида IV.
Линейные дифференциальные уравнения
Определение 3.4 Уравнение вида VII
![]() ,
(3.3)
,
(3.3)
где
![]() и
и ![]() – непрерывные функции,
называется линейным дифференциальным уравнением первого порядка, т.е. если
неизвестная функция
– непрерывные функции,
называется линейным дифференциальным уравнением первого порядка, т.е. если
неизвестная функция ![]() и
ее производная
и
ее производная ![]() входят
в это уравнение только в первой степени.
входят
в это уравнение только в первой степени.
Определение 3.5 При ![]() уравнение
(3.3) называется линейным однородным дифференциальным уравнением первого порядка
и имеет вид VI
уравнение
(3.3) называется линейным однородным дифференциальным уравнением первого порядка
и имеет вид VI
![]() .
(3.4)
.
(3.4)
При ![]() уравнение (3.3) называется линейным неоднородным
дифференциальным уравнением первого порядка.
уравнение (3.3) называется линейным неоднородным
дифференциальным уравнением первого порядка.
Определим решение линейного однородного
дифференциального уравнения первого порядка: ![]() ,
, ![]() ,
, ![]() , т.е. получили уравнение с разделяющимися
переменными. Далее разделим переменные и проинтегрируем полученное уравнение:
, т.е. получили уравнение с разделяющимися
переменными. Далее разделим переменные и проинтегрируем полученное уравнение:
 ,
,
![]() .
.
Таким образом,
![]() .
(3.5)
.
(3.5)
(3.5) – общее решение уравнения (3.4).
Приведем алгоритм нахождения решения линейного неоднородного дифференциального уравнения первого порядка (3.3). Для решения (3.3) применим метод вариации произвольной постоянной, который заключается в следующем:
а) сначала найдем общее решение соответствующего уравнения (3.4), т.е. найдем функцию вида (3.5);
б) в (3.5) ![]() будем считать не постоянной, а неизвестной
функцией
будем считать не постоянной, а неизвестной
функцией ![]() . Теперь
общее решение уравнения (3.3) будем искать в виде
. Теперь
общее решение уравнения (3.3) будем искать в виде
![]() .
(3.6)
.
(3.6)
Так как, по нашему предположению, (3.6) является решением (3.3), тогда подставив (3.6) в (3.3) получим тождество, т.е.
![]()
![]()
![]() ,
,
откуда найдем ![]() :
: ![]()
![]()
![]()
![]() . Подставим выражение для
. Подставим выражение для ![]() в (3.6), получим общее
решение дифференциального уравнения (3.3):
в (3.6), получим общее
решение дифференциального уравнения (3.3): ![]() ,
,
которое запишем в виде
![]() . (3.7)
. (3.7)
(3.7) – общее решение линейного неоднородного дифференциального уравнения первого порядка (3.3).
Структура общего решения линейного неоднородного дифференциального уравнения первого порядка
Общее решение линейного неоднородного дифференциального уравнения состоит из общего решения соответствующего линейного однородного дифференциального уравнения и частного решения линейного неоднородного дифференциального уравнения, т.е.
 ,
, ![]() .
.
Пример 3.1 - Найти
общее решение уравнения ![]() .
.
Решение: ![]() – это дифференциальное уравнение вида (3.3).
Запишем соответствующее линейное однородное уравнение:
– это дифференциальное уравнение вида (3.3).
Запишем соответствующее линейное однородное уравнение: ![]() . Решая его, получим:
. Решая его, получим: ![]() ,
,  ,
, ![]() ,
, ![]() – это общее решение линейного однородного
уравнения
– это общее решение линейного однородного
уравнения ![]() .
Общее решение линейного неоднородного уравнения имеет вид
.
Общее решение линейного неоднородного уравнения имеет вид ![]() . Найдем функцию
. Найдем функцию ![]() :
: ![]()
![]()
![]() . Тогда решением
уравнения будет
. Тогда решением
уравнения будет ![]() .
.
Уравнение Бернулли
Уравнение вида VIII
![]() (3.8)
(3.8)
называется уравнением Бернулли.
После замены ![]() ,
, ![]() ,
, ![]() уравнение Бернулли сводится к уравнению
типа VII.
уравнение Бернулли сводится к уравнению
типа VII.
Замечание.
VII. ![]() – линейное неоднородное дифференциальное
уравнение I-порядка относительно неизвестной функции
– линейное неоднородное дифференциальное
уравнение I-порядка относительно неизвестной функции ![]() .
.
VI. ![]() –
линейное однородное дифференциальное уравнение I
порядка относительно
–
линейное однородное дифференциальное уравнение I
порядка относительно ![]() .
.
VIII. ![]() – уравнение Бернулли
относительно
– уравнение Бернулли
относительно ![]() .
.
Уравнение в полных дифференциалах
Определение 3.5 Уравнение вида
![]() (3.9)
(3.9)
называется уравнением в полных дифференциалах, если выполняется равенство
 . (3.10)
. (3.10)
Докажем, что при выполнении условия (3.10) левая часть
(3.9) есть полный дифференциал некоторой функции ![]() , т.е.
, т.е.
![]() .
.
Необходимость. Пусть левая часть (3.9) полный дифференциал ![]() . Тогда
. Тогда ![]()
![]()
![]() и
и ![]()
![]() , тогда
, тогда ![]() и
и ![]() . Так как
. Так как ![]() , то
, то 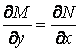 .
.
Достаточность. Пусть выполнено (3.10), т.е. ![]() ,
, ![]() , тогда
, тогда  и
и 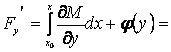
![]() . С другой стороны,
. С другой стороны,  , отсюда
, отсюда ![]() , т.е.
, т.е. ![]() и
и 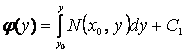 , тогда
, тогда 
 . Таким образом, левая часть (3.9) является
полным дифференциалом функции
. Таким образом, левая часть (3.9) является
полным дифференциалом функции ![]() , а формула
, а формула
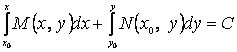 (3.11)
(3.11)
служит для нахождения решения уравнения в полных дифференциалах.
4 Лекция 4 Дифференциальные уравнения высших порядков. Дифференциальные уравнения, допускающие понижение порядка. Линейные дифференциальныеуравнения высших порядков
Содержание: Основные понятия и определения. Линейные дифференциальные уравнения второго порядка. Основное свойство решения линейного однородного дифференциального уравнения. Система линейно зависимых и независимых функций и их вронскиан.
Цели лекции: Дать определение дифференциальных уравнений высших порядков. Показать способы решения дифференциальных уравнений, допускающих понижение порядка. Различать линейные однородные и неоднородные дифференциальные уравнения высших порядков. Для системы функций уметь определять их линейную зависимость или независимость.
Определение 4.1 Уравнение вида ![]() , где
, где ![]() – независимая переменная,
– независимая переменная, ![]() – искомая функция,
– искомая функция, ![]() и
и ![]() – ее производные, называется
дифференциальным уравнением второго порядка.
– ее производные, называется
дифференциальным уравнением второго порядка.
Обычно рассматривают дифференциальное уравнение
второго порядка, разрешенное относительно ![]() , т.е.
, т.е.
![]() . (4.1)
. (4.1)
Решением уравнения (4.1) называется функция ![]() ,
, ![]() , которая при подстановке в
уравнение обращает его в тождество. График решения называется интегральной
кривой.
, которая при подстановке в
уравнение обращает его в тождество. График решения называется интегральной
кривой.
Имеет место теорема существования и единственности решения, которая носит название теоремы Коши.
Теорема Коши.
Если функция ![]() и
ее частные производные
и
ее частные производные ![]() и
и ![]() определены и непрерывны в некоторой области
определены и непрерывны в некоторой области
![]() пространства
переменных
пространства
переменных ![]() ,
то какова бы ни была внутренняя точка
,
то какова бы ни была внутренняя точка ![]() области
области ![]() , в некоторой окрестности точки
, в некоторой окрестности точки ![]() существует единственное
решение уравнения
существует единственное
решение уравнения ![]() удовлетворяющее
условиям
удовлетворяющее
условиям
![]() ,
, ![]() .
(4.2)
.
(4.2)
Условия (4.2) называются начальными условиями.
Задача отыскания решения по заданным начальным условиям называется задачей Коши.
Геометрически это означает, что через заданную точку ![]() плоскости проходит
единственная интегральная кривая с заданным угловым коэффициентом
плоскости проходит
единственная интегральная кривая с заданным угловым коэффициентом ![]() касательной в этой
точке.
касательной в этой
точке.
Определение 4.2 Функция ![]() ,
зависящая от
,
зависящая от ![]() и
от двух произвольных постоянных
и
от двух произвольных постоянных ![]() и
и ![]() , называется общим решением уравнения (4.1)
в некоторой области
, называется общим решением уравнения (4.1)
в некоторой области ![]() ,
если: 1) она является решением уравнения при любых значениях постоянных
,
если: 1) она является решением уравнения при любых значениях постоянных![]() и
и ![]() ; 2) при любых начальных условиях
(4.2) существуют единственные значения постоянных
; 2) при любых начальных условиях
(4.2) существуют единственные значения постоянных ![]() ,
, ![]() такие, что
такие, что ![]() удовлетворяет данным начальным условиям.
удовлетворяет данным начальным условиям.
Определение 4.3 Любая функция ![]() , получающаяся из общего решения
, получающаяся из общего решения ![]() при определенных
значениях постоянных
при определенных
значениях постоянных ![]() ,
,
![]() называется частным
решением уравнения (4.1).
называется частным
решением уравнения (4.1).
Дифференциальные уравнения высших порядков
Дифференциальные уравнения порядка n имеет вид
![]()
или, если оно разрешено относительно старшей производной,
![]() . (4.3)
. (4.3)
Решением уравнения (4.3) называется функция ![]() ,
, ![]() , которая при подстановке в
уравнение (4.3) обращает его в тождество.
, которая при подстановке в
уравнение (4.3) обращает его в тождество.
Общее решение уравнения (4.3) зависит от х и n произвольных
постоянных и имеет вид:![]() .
.
Решения, получающиеся из общего решения при
определенных значениях постоянных ![]() , называется частным решением уравнения
(4.3).
, называется частным решением уравнения
(4.3).
Начальные условия имеют вид:
![]() ,
, ![]() , …,
, …, ![]() . (4.4)
. (4.4)
Отыскания решения уравнения (4.3), удовлетворяющего начальным условиям (4.4), называется решением задачи Коши.
Дифференциальные уравнения, допускающее понижение порядка
Рассмотрим частные случаи, когда решение уравнения ![]() или
или
![]() (4.5)
(4.5)
с помощью замены переменной сводится к решению уравнения более низкого порядка.
1. Уравнение вида ![]() . Данное уравнение не содержит
. Данное уравнение не содержит ![]() , его решение будем
находить путем последовательного интегрирования:
, его решение будем
находить путем последовательного интегрирования:
![]() ,
, ![]() ,
, ![]() , …,
, …,  .
.
2. Уравнение вида ![]() . В этом уравнении отсутствует
. В этом уравнении отсутствует ![]() и ее производные до
и ее производные до ![]() -порядка. Произведя
замену
-порядка. Произведя
замену ![]() ,
, ![]() , …,
, …, ![]() , придем к уравнению
, придем к уравнению ![]() , т.е. получим
дифференциальное уравнение
, т.е. получим
дифференциальное уравнение ![]() -порядка.
-порядка.
3. Уравнение вида ![]() . Это уравнение не содержит явно переменной
. Это уравнение не содержит явно переменной
![]() . Сделаем
замену
. Сделаем
замену ![]() и
будем считать
и
будем считать ![]() независимой
переменной, тогда
независимой
переменной, тогда ![]() ,
,
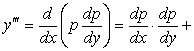
 ,
,
и
т.д. В итоге получим дифференциальное уравнение ![]() -порядка.
-порядка.
Линейные дифференциальные уравнения высших порядков
Линейным дифференциальным уравнением ![]() -го порядка называется
уравнение вида
-го порядка называется
уравнение вида ![]() ,
где
,
где ![]() – искомая
функция,
– искомая
функция, ![]() – ее
производные,
– ее
производные, ![]() –
аргумент,
–
аргумент, ![]() ,
, ![]() – заданные непрерывные
функции.
– заданные непрерывные
функции.
Линейное дифференциальное уравнение называется
неоднородным, если ![]() и
называется однородным, если
и
называется однородным, если ![]() .
.
Мы рассмотрим линейные дифференциальные уравнения
второго порядка. Результаты обобщаются на линейные дифференциальные уравнения ![]() -го порядка.
-го порядка.
Уравнение
![]() , (4.6)
, (4.6)
есть линейное неоднородное дифференциальное уравнение второго порядка.
Уравнение
![]() , (4.7)
, (4.7)
- однородное дифференциальное уравнение второго порядка.
Линейные однородные дифференциальные уравнения ІІ-порядка. Основное свойство решения линейного однородного дифференциального уравнения ІІ-порядка
Теорема 4.1 Если
![]() и
и ![]() решения уравнения (4.7),
то функция
решения уравнения (4.7),
то функция
![]() (4.8)
(4.8)
при
любых значениях постоянных ![]() и
и ![]() также является решением уравнения (4.7).
также является решением уравнения (4.7).
Доказательство. Так как ![]() и
и ![]() является решением (4.7), тогда имеют место
тождества:
является решением (4.7), тогда имеют место
тождества: ![]() ,
,
![]() . Подставим
(4.8) в (4.7), для этого найдем
. Подставим
(4.8) в (4.7), для этого найдем ![]() и
и ![]() :
: ![]() ,
, ![]() , тогда
, тогда ![]() . Теорема доказана.
. Теорема доказана.
Итак, функция (4.8) является решением (4.7). Является ли эта функция общим решением уравнения (4.7)? Чтобы ответить на этот вопрос введем понятия линейной зависимости и линейной независимости системы функций.
Определение 4.4 Функции ![]() ,
,
![]() называются
линейно зависимыми на
называются
линейно зависимыми на ![]() ,
если существуют такие числа
,
если существуют такие числа ![]() не все равные нулю
не все равные нулю ![]() , такие, что
, такие, что ![]() выполнено равенство
выполнено равенство
![]() . (4.9)
. (4.9)
Для ![]() равенство (4.9) примет вид:
равенство (4.9) примет вид: ![]() ,
, ![]() , или
, или ![]()
![]() .
.
Если условие (4.9) нарушено, то система функций называется линейно независимой.
Определение 4.5 Определителем Вронского (вронскианом) называется функция
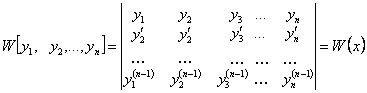 . (4.10)
. (4.10)
Теорема 4.2
Если ![]() и
и ![]() линейно зависимы на
линейно зависимы на ![]() тогда их определитель
Вронского равен нулю.
тогда их определитель
Вронского равен нулю.
Доказательство.
Так как ![]() и
и ![]() линейно зависимы, то
линейно зависимы, то ![]()
![]() , следовательно,
, следовательно, ![]() ,
, ![]() и по свойству определителей
и по свойству определителей ![]() . Теорема доказана.
. Теорема доказана.
Теорема 4.3
Если решения уравнения (4.7) ![]() и
и ![]() линейно независимы на
линейно независимы на ![]() то их вронскиан не равен нулю на
то их вронскиан не равен нулю на
![]() .
.
Доказательство.
Предположим, что существует точка ![]() такая, что
такая, что ![]() , т.е.
, т.е.  . Составим систему:
. Составим систему: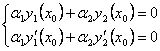 , где
, где ![]() и
и ![]() – неизвестные числа. Так как система
однородная и ее определитель
– неизвестные числа. Так как система
однородная и ее определитель ![]() то система имеет ненулевое решение
относительно
то система имеет ненулевое решение
относительно ![]() и
и
![]() . Рассмотрим
функцию
. Рассмотрим
функцию ![]() , где
, где
![]() и
и ![]() – ненулевое решение составленной
системы, причем, функция
– ненулевое решение составленной
системы, причем, функция ![]() удовлетворяет нулевым начальным условиям
удовлетворяет нулевым начальным условиям ![]() ,
, ![]() . Но этим же условиям
удовлетворяет функция
. Но этим же условиям
удовлетворяет функция ![]() и
она же удовлетворяет уравнению (4.7), тогда, по теореме о
существовании и единственности решения дифференциального уравнения, эти решения
совпадают, т.е.
и
она же удовлетворяет уравнению (4.7), тогда, по теореме о
существовании и единственности решения дифференциального уравнения, эти решения
совпадают, т.е. ![]() на
на
![]() , тогда
, тогда ![]() и
и ![]() линейно зависимы на
линейно зависимы на ![]() , что противоречит условию
теоремы. Следовательно, наше предположение неверно. Итак, если
, что противоречит условию
теоремы. Следовательно, наше предположение неверно. Итак, если ![]() и
и ![]() – решения (4.7) на
– решения (4.7) на ![]() ,тогда
,тогда
1) если ![]() и
и ![]() линейно независимы, то
линейно независимы, то ![]() ,
, ![]() ;
;
2) если ![]() и
и ![]() линейно зависимы, то
линейно зависимы, то ![]() ,
, ![]() .
.
5 Лекция 5 Линейные однородные дифференциальные уравнения. Решение линейного неоднородного дифференциального уравнения. Линейные однородные дифференциальные уравнения с постоянными коэффициентами
Содержание: Общее решение линейного однородного дифференциального уравнения. Метод вариации произвольных постоянных. Решение линейного однородного дифференциального уравнения с постоянными коэффициентами.
Цель лекции: Уметь находить общее решение линейного однородного дифференциального уравнения. Уметь находить частное решение с помощью формулы Остроградского-Лиувилля. Уметь решать линейные неоднородные дифференциальные уравнения, применяя метод вариации произвольных постоянных. Уметь решать линейные однородные дифференциальные уравнения с помощью характеристического уравнения.
Установим, при каких условиях функция ![]() является общим решением
линейного однородного дифференциального уравнения.
является общим решением
линейного однородного дифференциального уравнения.
Теорема 5.1
Если ![]() и
и ![]() – линейно независимые
на
– линейно независимые
на ![]() решения
уравнения
решения
уравнения
![]() , (5.1)
, (5.1)
то функция
![]() ,
(5.2)
,
(5.2)
где
![]() и
и ![]() – произвольные
постоянные, является общим решением (5.1).
– произвольные
постоянные, является общим решением (5.1).
Доказательство.
По теореме 4.1 функция ![]() является решением (5.1). Для того чтобы
доказать, что оно является общим решением, надо из него выделить частное
решение, удовлетворяющее любым начальным условиям. Пусть
является решением (5.1). Для того чтобы
доказать, что оно является общим решением, надо из него выделить частное
решение, удовлетворяющее любым начальным условиям. Пусть ![]() и
и ![]() ,
, ![]() – произвольные начальные условия. Составим
систему:
– произвольные начальные условия. Составим
систему:  где
где
![]() и
и ![]() – неизвестные числа.
– неизвестные числа. ![]() – определитель этой
системы. Так как
– определитель этой
системы. Так как ![]() и
и
![]() линейно независимы,
то
линейно независимы,
то ![]() , тогда эта
система имеет единственное решение:
, тогда эта
система имеет единственное решение: ![]() ,
, ![]() , тогда
, тогда ![]() , т.е., из (5.2) выделили частное решение,
таким образом (5.2) – общее решение (5.1).
, т.е., из (5.2) выделили частное решение,
таким образом (5.2) – общее решение (5.1).
Вывод. Чтобы
найти общее решение линейного однородного дифференциального уравнения II-порядка
достаточно найти два линейно независимых частных решения уравнения (5.1) и
составить выражение (5.2) с произвольными постоянными ![]() и
и ![]() .
.
Формула Остроградского-Лиувилля
Как найти общее решение (5.1), если известно только
одно частное решение этого уравнения? Пусть ![]() – частное решение уравнения (5.1). Введем
новую функцию
– частное решение уравнения (5.1). Введем
новую функцию ![]() ,
полагая
,
полагая ![]() ,
найдем
,
найдем ![]() и
и ![]() :
: ![]() ,
, ![]() . Произведем замену в (5.1):
. Произведем замену в (5.1):
![]()
![]()
![]() .
.
Понизим порядок полученного дифференциального
уравнения с помощью замены ![]() , тогда
, тогда ![]() , и получим линейное однородное дифференциальное
уравнение:
, и получим линейное однородное дифференциальное
уравнение: ![]()
![]()
 , откуда
, откуда ![]()
![]() , таким образом, получили общее
решение (5.1) – функцию
, таким образом, получили общее
решение (5.1) – функцию 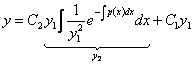 , где
, где
![]() .
(5.3)
.
(5.3)
(5.3) – формула Остроградского-Лиувилля.
Линейные неоднородные дифференциальные уравнения II-порядка
Рассмотрим линейные неоднородные дифференциальные уравнения II-порядка
![]() , (5.4)
, (5.4)
![]() . (5.1)
. (5.1)
Теорема 5.2 Общее решение линейного неоднородного дифференциального уравнения (5.4) есть сумма любого его частного решения и общего решения соответствующего однородного уравнения (5.1), т.е.
![]() (5.5)
(5.5)
Доказательство.
Возьмем функцию ![]() .
Покажем, что эта функция является решением (5.4). Найдем
.
Покажем, что эта функция является решением (5.4). Найдем ![]() ,
, ![]() . Подставим в (5.4):
. Подставим в (5.4):
![]()
![]() , т.е.,
, т.е., ![]() .
.
Покажем, что функция ![]() является общим решением (5.4). Возьмем
является общим решением (5.4). Возьмем ![]() – любое решение
уравнения (5.4), тогда
– любое решение
уравнения (5.4), тогда ![]() есть решение однородного уравнения, так как выполняется равенство
есть решение однородного уравнения, так как выполняется равенство
![]() .
.
Так как ![]() – решение линейного однородного уравнения,
значит, оно имеет вид
– решение линейного однородного уравнения,
значит, оно имеет вид ![]() :
:
![]()
![]() , т.е., из (5.5) мы
выделили некоторое частное решение, тогда (5.5) есть общее решение линейного
неоднородного дифференциального уравнения. Теорема доказана.
, т.е., из (5.5) мы
выделили некоторое частное решение, тогда (5.5) есть общее решение линейного
неоднородного дифференциального уравнения. Теорема доказана.
Покажем, как найти ![]() методом вариации произвольных постоянных.
Пусть
методом вариации произвольных постоянных.
Пусть ![]() –
общее решение линейного однородного уравнения (5.1). Найдем частное решение.
Пусть общее решение имеет вид
–
общее решение линейного однородного уравнения (5.1). Найдем частное решение.
Пусть общее решение имеет вид
![]() .
(5.6)
.
(5.6)
Найдем ![]() , подберем
, подберем ![]() и
и ![]() так, чтобы выполнялось равенство
так, чтобы выполнялось равенство
![]() ,
(5.7)
,
(5.7)
тогда
![]() . Найдем
. Найдем ![]() , подставим в (7.1):
, подставим в (7.1): ![]()
![]() , то есть
, то есть
![]() .
(5.8)
.
(5.8)
Таким образом, (5.6) является решением, если ![]() и
и ![]() удовлетворяют (5.7) и (5.8),
точнее, системе уравнений
удовлетворяют (5.7) и (5.8),
точнее, системе уравнений
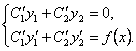 (5.9)
(5.9)
Определителем системы будет  , так как
, так как ![]() и
и ![]() линейно независимы, тогда (5.9) имеет
только одно решение:
линейно независимы, тогда (5.9) имеет
только одно решение: ![]() ,
,
![]() , отсюда
, отсюда ![]() ,
, ![]() . Найденные
. Найденные ![]() и
и ![]() подставим в (5.6) и получим общее решение
линейного неоднородного уравнения (5.4).
подставим в (5.6) и получим общее решение
линейного неоднородного уравнения (5.4).
Линейные однородные дифференциальные уравнения II-порядка с постоянными коэффициентами
Рассмотрим линейное однородное дифференциальное уравнение II-порядка с постоянными коэффициентами
![]() ,
(5.10)
,
(5.10)
где
![]() и
и ![]() – постоянные.
– постоянные.
Уравнение
![]() (5.11)
(5.11)
является характеристическим уравнением, соответствующим (5.10).
Теорема 5.3 1.
Если уравнение (5.11) имеет действительный корень ![]() , тогда функция
, тогда функция ![]() удовлетворяет уравнению (5.10). 2.
Если уравнение имеет комплекс корни
удовлетворяет уравнению (5.10). 2.
Если уравнение имеет комплекс корни ![]() , тогда функции
, тогда функции ![]() и
и ![]() удовлетворяют (5.10).
удовлетворяют (5.10).
Доказательство.
1. Пусть ![]() –
корень уравнения (5.11). Запишем функцию
–
корень уравнения (5.11). Запишем функцию ![]() , вычислим
, вычислим ![]() ,
, ![]() и подставим в уравнение (5.10)
и подставим в уравнение (5.10)
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
т.е.
функция ![]() удовлетворяет
уравнению (5.10).
удовлетворяет
уравнению (5.10).
2. Пусть ![]() ;
; ![]() – корни (5.11). Составим функцию
– корни (5.11). Составим функцию
![]() ,
,
тогда
![]() ,
, ![]() ,
, ![]() . Аналогично
. Аналогично
![]() ,
,
тогда
функции ![]() ,
, ![]() удовлетворяет уравнению
(5.10).
удовлетворяет уравнению
(5.10).
Теорема 5.4 Если корни характеристического уравнения (5.11):
а) действительные ![]() и различные,
и различные, ![]() , тогда общее решение (5.10) имеет вид:
, тогда общее решение (5.10) имеет вид: ![]() ;
;
б) действительные ![]() и равные
и равные ![]() , тогда общим решением (5.10) является
функция
, тогда общим решением (5.10) является
функция ![]() ;
;
в) комплекно-сопряженные ![]() ,
, ![]() , тогда общее решение (5.10) имеет вид:
, тогда общее решение (5.10) имеет вид: ![]() .
.
Доказательство.
а) Пусть ![]() ,
тогда
,
тогда ![]() ,
, ![]() – частные решения
(5.10). Проверим их на линейную зависимость:
– частные решения
(5.10). Проверим их на линейную зависимость: ![]() т.к.
т.к. ![]() , т.е.
, т.е. ![]() ,
, ![]() линейно независимы, тогда
линейно независимы, тогда ![]() .
.
б) Пусть ![]() .
. ![]() – частное решение уравнения (5.10). По
формуле Остроградского-Лиувилля найдём
– частное решение уравнения (5.10). По
формуле Остроградского-Лиувилля найдём ![]() :
: ![]()
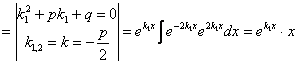 ,
, ![]() .
.
в) Пусть ![]() ,
, ![]() , тогда по теореме 5.3
, тогда по теореме 5.3 ![]() ,
, ![]() – частные решения. Проверим
– частные решения. Проверим ![]() ,
, ![]() на линейную зависимость:
на линейную зависимость: ![]() , т.е. функции
, т.е. функции ![]() ,
, ![]() линейно независимы, тогда
линейно независимы, тогда
![]() .
.
Алгоритм нахождения решения уравнения ![]()
1. Составим соответствующее однородное
дифференциальное уравнение ![]() ;
;
2. решим характеристическое уравнение ![]() ;
;
3. составим ![]() ;
;
4. пользуясь методом вариации произвольных постоянных,
найдем ![]() , для
этого определим функции
, для
этого определим функции ![]() из системы (5.9);
из системы (5.9);
5. запишем ![]() .
.
6 Лекция 6 Метод подбора частного решения линейного Неоднородного дифференциального уравнения с постоянными коэффициентами. Метод неопределенных коэффициентов. Система обыкновенных дифференциальных уравнений
Содержание: Решение линейных неоднородных дифференциальных уравнений с постоянными коэффициентами. Системы обыкновенных дифференциальных уравнений. Нормальные системы линейных однородных дифференциальных уравнений с постоянными коэффициентами.
Цели лекции: Уметь применять метод неопределенных коэффициентов при нахождении частного решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами. Уметь решать системы дифференциальных уравнений методом исключений и с помощью характеристического уравнения.
Рассмотрим линейное неоднородное дифференциальное уравнение II-порядка с постоянными коэффициентами
![]() .
(6.1)
.
(6.1)
Было показано, что ![]() . Если в уравнении (6.1) функция
. Если в уравнении (6.1) функция ![]() может представлена в
виде
может представлена в
виде
![]() , (6.2)
, (6.2)
где
![]() ,
, ![]() – многочлены. Тогда
– многочлены. Тогда ![]() будет иметь вид
будет иметь вид
![]() (6.3)
(6.3)
где
![]() ,
, ![]() и
и ![]() – многочлены степени
– многочлены степени ![]() ;
; ![]() –кратность числа
–кратность числа ![]() среди корней
характеристического уравнения, соответствующего линейному однородному уравнению.
среди корней
характеристического уравнения, соответствующего линейному однородному уравнению.
Пример 6.1 -
![]() .
.
![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() ,
, ![]() ,
,
![]() ;
; ![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
![]() .
.

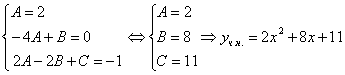
![]() ,
, ![]()
Пример 6.2 -
![]() .
.
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() .
.
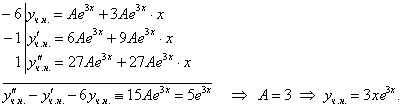
![]() .
.
Система обыкновенных дифференциальных уравнений. Нормальная система дифференциальных уравнений
Определение 6.1
Нормальной системой дифференциальных уравнений порядка ![]() называется совокупность
называется совокупность ![]() дифференциальных
уравнений I-порядка:
дифференциальных
уравнений I-порядка:
 (6.4)
(6.4)
![]() – независимая
переменная,
– независимая
переменная, ![]() –
неизвестные функции,
–
неизвестные функции, ![]() ,
, ![]() ,
, ![]() – их производные.
– их производные.
Комментарии. В нормальной системе:
а)
все уравнения разрешены относительно производных ![]() ,
, ![]() ;
;
б) производные искомых функций имеют только первый порядок.
Определение 6.2 Общим решением системы (6.4) называется совокупность ![]() -функций
-функций
![]() ,
, ![]() , …,
, …, ![]() , (6.5)
, (6.5)
зависящих
от ![]() произвольных
постоянных
произвольных
постоянных ![]() ,
, ![]() ,
, ![]() ,
, ![]() и имеющих непрерывные
частные производные по
и имеющих непрерывные
частные производные по ![]() , если:
, если:
а) (6.5) разрешимы относительно ![]() ,
, ![]() ,
, ![]() ,
, ![]() при всех (
при всех (![]() )
)![]() , где
, где ![]() – область единственности решения
задачи Коши, т.е.
– область единственности решения
задачи Коши, т.е.
![]() ; (6.6)
; (6.6)
б) (6.5) является решением системы (6.4) при всех ![]() ,
, ![]() ,
, ![]() ,
, ![]() , получаемых из соотношения
(6.6).
, получаемых из соотношения
(6.6).
Задача Коши имеет вид – система уравнении (6.4) и начальные условия:
![]() . (6.7)
. (6.7)
Метод исключения позволяет свести решение нормальной
системы ![]() -го
порядка к решению одного дифференциального уравнения
-го
порядка к решению одного дифференциального уравнения ![]() -го порядка. Сущность этого
метода заключается в последовательном исключении искомых функций из уравнений
системы (6.4). Продифференцируем по
-го порядка. Сущность этого
метода заключается в последовательном исключении искомых функций из уравнений
системы (6.4). Продифференцируем по ![]() первое уравнение системы:
первое уравнение системы: ![]() . Учитывая остальные
уравнения системы, перепишем полученное выражение в виде
. Учитывая остальные
уравнения системы, перепишем полученное выражение в виде
![]() или
или ![]() ,
,
![]() или
или ![]() , …,
, …,
![]() , т.е. получим систему:
, т.е. получим систему:
 (6.8)
(6.8)
Из первых ![]() уравнений можно выразить
уравнений можно выразить ![]() через
через ![]() ,
, ![]() ,
, ![]() , …,
, …, ![]() и подставить в последнее уравнение, т.е.
и подставить в последнее уравнение, т.е. ![]() .
.
Нормальная система линейных однородных дифференциальных уравнений с постоянными коэффициентами
Система вида
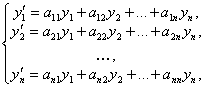 (6.9)
(6.9)
называется нормальной системой линейных однородных дифференциальных уравнений с постоянными коэффициентами.
Введем обозначения:
 ,
, 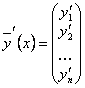 ,
,  .
.
Тогда (6.9) примет вид
![]() .
(6.10)
.
(6.10)
Определение 6.3
Совокупность вектор-функций системы (6.10) ![]() ,
,
![]() ,
…,
,
…, ![]() называется линейно зависимой, если
называется линейно зависимой, если ![]() , где
, где ![]() . В противном случае,
система функций называется линейно независимой.
. В противном случае,
система функций называется линейно независимой.
Определение 6.4
Совокупность ![]() линейно
независимых решений системы (6.10) называется фундаментальной системой решений.
линейно
независимых решений системы (6.10) называется фундаментальной системой решений.
Теорема (о структуре решения нормальной системы
линейных однородных дифференциальных уравнений). Если совокупность вектор-функций ![]() ,
, ![]() , …,
, …, ![]() является
фундаментальной системой решений для системы (6.10), то общим решением системы
является
является
фундаментальной системой решений для системы (6.10), то общим решением системы
является ![]() ;
где
;
где ![]() ,
, ![]() произвольные постоянные.
произвольные постоянные.
Рассмотрим решение системы линейных однородных дифференциальных уравнений второго порядка постоянными коэффициентами:
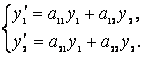 (6.11)
(6.11)
Решение ищем в виде ![]() ,
, ![]() :
:

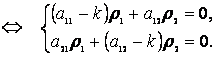 (6.12)
(6.12)
Для того, чтобы система (6.12) имела ненулевые решения необходимо, чтобы
 . (6.13)
. (6.13)
(6.13) – характеристическое уравнение системы (6.11).
Решения уравнения (6.13) – числа ![]() ,
, ![]() называются собственными значениями характеристического
уравнения, вектор
называются собственными значениями характеристического
уравнения, вектор  называется
собственным вектором. Решением системы (6.11) будет функция
называется
собственным вектором. Решением системы (6.11) будет функция
![]() .
.
7 Лекция 7 Числовые ряды. Основные понятия. Знакоположительные ряды
Содержание: числовые ряды, частичные суммы, остаток числового ряда, необходимый признак сходимости числового ряда, достаточные признаки сходимости положительных рядов: признаки сравнения, предельный признак сравнения, признак Д’Аламбера, радикальный признак Коши, интегральный признак Коши.
Цель лекции: Ознакомить студентов с понятием числовых рядов, показать примеры исследования рядов на сходимость.
Выражение вида
![]() , (7.1)
, (7.1)
где
![]() , называется
числовым рядом. Числа
, называется
числовым рядом. Числа ![]() называются членами ряда, число
называются членами ряда, число ![]() – общим членом ряда.
– общим членом ряда.
Суммы
![]()
называются
частичными суммами, а ![]() –
–
![]() -ой частичной
суммой ряда (7.1). Если
-ой частичной
суммой ряда (7.1). Если ![]() существует и равен числу
существует и равен числу ![]() , т.е.
, т.е. ![]() , то ряд (7.1) называется
сходящимся, а
, то ряд (7.1) называется
сходящимся, а ![]() –
его суммой. Если
–
его суммой. Если ![]() не
существует (в частности, бесконечен), то ряд (7.1) называется расходящимся.
не
существует (в частности, бесконечен), то ряд (7.1) называется расходящимся.
Сумма
![]()
называется
![]() -м остатком
ряда (7.1).
-м остатком
ряда (7.1).
Если ряд (7.1) сходится, то
![]() .
.
Пример 7.1 -
Дан ряд ![]() .
Установить сходимость этого ряда и найти его сумму.
.
Установить сходимость этого ряда и найти его сумму.
Решение. Запишем ![]() -ую частичную сумму данного ряда и
преобразуем ее:
-ую частичную сумму данного ряда и
преобразуем ее: ![]()
![]()
![]()
![]()
Поскольку ![]() , то данный ряд сходится и его сумма равна
, то данный ряд сходится и его сумма равна ![]() .
.
Пример 7.2 - Исследовать на сходимость ряд
![]() (7.2)
(7.2)
и в случае сходимости найти его сумму.
Решение. Имеем
![]() .
.
Если ![]() , то
, то ![]() , т.е.
, т.е. ![]() , и, следовательно, ряд (7.2) расходится.
Пусть теперь
, и, следовательно, ряд (7.2) расходится.
Пусть теперь ![]() ,
тогда
,
тогда ![]() .
Положим
.
Положим ![]() , тогда
, тогда
![]() , т.е.
, т.е. ![]() . Если же
. Если же ![]() , то
, то ![]() и, следовательно, конечного
предела
и, следовательно, конечного
предела ![]() , а
значит, и предела последовательности частичных сумм не существует. Наконец, при
, а
значит, и предела последовательности частичных сумм не существует. Наконец, при
![]() предел
предел ![]() также не существует.
также не существует.
Таким образом, ряд ![]() , члены которого составляют бесконечную геометрическую
прогрессию с первым членом
, члены которого составляют бесконечную геометрическую
прогрессию с первым членом ![]() и знаменателем
и знаменателем ![]() , сходится при
, сходится при ![]() и его сумма равна
и его сумма равна ![]() и расходится при
и расходится при ![]() .
.
Теорема 7.1 (необходимый признак сходимости ряда). Если числовой ряд (7.1) сходится, то ![]() .
.
Обратное утверждение неверно.
Пример 7.3 - Доказать, что гармонический ряд
![]()
расходится,
хотя его члены стремятся к нулю при ![]() .
.
Доказательство. Допустим, что ряд ![]() сходится и его сумма равна
сходится и его сумма равна ![]() . Рассмотрим разность
частичных сумм с номерами
. Рассмотрим разность
частичных сумм с номерами ![]() и
и ![]() , тогда
, тогда ![]() . Имеем
. Имеем
![]() .
.
Заменяя каждое слагаемое меньшей величиной ![]() , получаем
, получаем
![]() .
.
Это неравенство означает, что ![]() , т.е. наше допущение неверно и,
следовательно, гармонический ряд расходится.
, т.е. наше допущение неверно и,
следовательно, гармонический ряд расходится.
Теорема 7.2 (достаточный признак расходимости ряда). Если ![]() , то ряд (7.1) расходится.
, то ряд (7.1) расходится.
Пример 7.4 -
Исследовать на сходимость ряд ![]() .
.
Решение. Запишем общий член данного ряда: ![]() . Тогда
. Тогда
![]() ,
,
т.е. ряд расходится.
Сходимость или расходимость числового ряда не нарушается, если в нем отбросить любое конечное число членов. Но его сумма, если она существует, при этом изменяется.
Рассмотрим некоторые достаточные признаки сходимости числовых рядов с положительными членами.
Теорема 7.3 (признаки сравнения). Если даны два ряда
![]() , (7.3)
, (7.3)
![]() (7.4)
(7.4)
и для
всех ![]() выполняются
неравенства
выполняются
неравенства ![]() ,
то:
,
то:
а) из сходимости ряда (7.4) следует сходимость ряда (7.3);
б) из расходимости ряда (7.3) следует расходимость ряда (7.4).
В качестве рядов для сравнения целесообразно выбирать
ряд, представляющий сумму членов геометрической прогрессии ![]() , а также гармонический
(расходящийся) ряд.
, а также гармонический
(расходящийся) ряд.
Теорема 7.4 (предельный признак сравнения). Если существует конечный предел ![]() , причем
, причем ![]() , то ряды (7.3) и (7.4) либо оба
сходятся, либо оба расходятся.
, то ряды (7.3) и (7.4) либо оба
сходятся, либо оба расходятся.
Пример 7.5 -
Зная, что ряд ![]() сходится,
установить сходимость ряда
сходится,
установить сходимость ряда ![]() .
.
Решение. Так как ![]() , то ряд
, то ряд ![]() также сходится.
также сходится.
Теорема 7.5 (признак Д’Аламбера). Пусть для ряда (7.1) ![]() (начиная с некоторого
(начиная с некоторого ![]() ) и существует предел
) и существует предел
![]() .
.
Тогда
при ![]() данный
ряд сходится, при
данный
ряд сходится, при ![]() ряд
расходится. При
ряд
расходится. При ![]() признак
Д’Аламбера не дает ответа на вопрос о сходимости или расходимости ряда.
признак
Д’Аламбера не дает ответа на вопрос о сходимости или расходимости ряда.
Пример 7.6 - Исследовать
на сходимость ряд ![]() .
.
Решение. Поскольку ![]() ,
, ![]() или, что то же самое,
или, что то же самое, ![]() , то
, то
![]()
![]() .
.
Следовательно, ряд расходится.
Теорема 7.6 (радикальный признак Коши). Если, начиная с некоторого ![]() ,
, ![]() и
и ![]() , то при
, то при ![]() ряд (7.1) сходится, а при
ряд (7.1) сходится, а при ![]() расходится. При
расходится. При ![]() признак Коши не
применим.
признак Коши не
применим.
Теорема 7.7 (интегральный признак Коши). Пусть члены ряда (7.1) монотонно убывают, т.е.
![]()
и
функция ![]() ,
непрерывная при
,
непрерывная при ![]() ,
такова, что
,
такова, что ![]() .
Тогда ряд (7.1) и интеграл
.
Тогда ряд (7.1) и интеграл 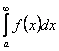 одновременно сходятся или расходятся.
одновременно сходятся или расходятся.
Пример 7.7 - Исследовать
на сходимость ряд ![]()
![]() , называемый рядом Дирихле.
, называемый рядом Дирихле.
Решение. Исследуем на сходимость несобственный
интеграл ![]()
![]() .
.
Так как ![]() . Из последнего равенства видно, что при
. Из последнего равенства видно, что при ![]() несобственный интеграл
несобственный интеграл ![]() расходится, а при
расходится, а при ![]() сходится, причем
сходится, причем ![]() . При
. При ![]() получим интеграл
получим интеграл ![]() , который расходится. Таким
образом, вместе с исследованным несобственным интегралом ряд Дирихле
, который расходится. Таким
образом, вместе с исследованным несобственным интегралом ряд Дирихле ![]() сходится при
сходится при ![]() и расходится при
и расходится при ![]() .
.
Сходимость многих рядов можно исследовать путем сравнения их с соответствующим рядом Дирихле.
8 Лекция 8 Знакопеременные и знакочередующиеся ряды
Содержание: Знакопеременные и знакочередующиеся числовые ряды, признак Лейбница, абсолютная сходимость, условная сходимость.
Цель лекции: Ознакомить студентов с понятием знакопеременных и знакочередующихся числовых рядов, привести их основные свойства, показать примеры исследования рядов на сходимость, нахождения произведения рядов по Коши.
Пусть дан числовой ряд ![]() , где члены ряда имеют различные знаки.
Числовой ряд, знаки членов которого чередуются
, где члены ряда имеют различные знаки.
Числовой ряд, знаки членов которого чередуются
![]() , (8.1)
, (8.1)
называется
знакочередующимся рядом, причем числа ![]() – положительные.
– положительные.
Признак Лейбница
Теорема 8.1 (теорема Лейбница). Знакочередующийся ряд ![]() сходится, если выполняются два условия:
сходится, если выполняются два условия:
а) ![]() – величины членов ряда убывают,
– величины членов ряда убывают,
б) ![]() . (8.2)
. (8.2)
Доказательство.
Рассмотрим ![]() -ую
частичную сумму четного количества членов:
-ую
частичную сумму четного количества членов: ![]() Так как, в силу первого условия, каждая
скобка положительна, то последовательность частичных сумм
Так как, в силу первого условия, каждая
скобка положительна, то последовательность частичных сумм ![]() возрастающая. Распишем
возрастающая. Распишем ![]() в виде
в виде ![]()
![]() . Так как выражения в скобках –
положительные числа, то
. Так как выражения в скобках –
положительные числа, то ![]() . Итак, последовательность
. Итак, последовательность ![]() – возрастающая и ограничена
сверху. Следовательно, эта последовательность имеет конечный предел
– возрастающая и ограничена
сверху. Следовательно, эта последовательность имеет конечный предел ![]() .
.
Рассмотрим частичную сумму для нечетного количества
членов ![]() .
. ![]() (
(![]() в силу второго условия теоремы).
Следовательно,
в силу второго условия теоремы).
Следовательно, ![]() -ая
частичная сумма имеет конечный предел, и знакочередующийся ряд сходится.
Теорема доказана.
-ая
частичная сумма имеет конечный предел, и знакочередующийся ряд сходится.
Теорема доказана.
Пример 8.1 - Исследовать сходимость ряда
![]() .
.
Решение. Применим признак Лейбница. Так как
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
то
![]() . Следовательно,
выполнено первое условие признака Лейбница. Далее, так как
. Следовательно,
выполнено первое условие признака Лейбница. Далее, так как
![]() ,
,
то выполнено и второе условие. Значит, данный ряд сходится.
Пример 8.2 - Исследовать сходимость ряда
![]() .
.
Решение. Первое условие признака Лейбница выполняется:
![]() ;
;
с другой стороны, ![]() ,
, 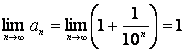 . Так как
. Так как ![]() , то не выполнен необходимый
признак сходимости ряда. Ряд расходится.
, то не выполнен необходимый
признак сходимости ряда. Ряд расходится.
Пример 8.3 - Исследовать сходимость ряда
![]() .
.
Решение. Общий член ряда не стремится к нулю, поэтому ряд расходится.
Возьмем ![]() -ую частичную сумму сходящегося
знакочередующегося ряда, для которого выполняется признак Лейбница:
-ую частичную сумму сходящегося
знакочередующегося ряда, для которого выполняется признак Лейбница:
![]() .
.
Пусть ![]() –
– ![]() -й остаток ряда. Его можно записать как
разность между суммой ряда
-й остаток ряда. Его можно записать как
разность между суммой ряда ![]() и
и ![]() -й частичной суммой
-й частичной суммой ![]() , т.е.
, т.е. ![]() . Нетрудно видеть, что
. Нетрудно видеть, что
![]() .
.
Величина ![]() оценивается с помощью неравенства
оценивается с помощью неравенства ![]() .
.
Остановимся теперь на некоторых свойствах знакопеременных рядов (т.е. знакочередующихся рядов и рядов с произвольным чередованием знаков своих членов).
Абсолютная и условная сходимость рядов
Пусть дан знакопеременный ряд
![]() . (8.3)
. (8.3)
Рассмотрим ряд, составленный из абсолютных величин
![]() . (8.4)
. (8.4)
Ясно, что ряд (8.4) является знакоположительным рядом.
Теорема 8.2 Если сходится ряд (8.4), составленный из абсолютных величин, то сходится и знакопеременный ряд (8.3).
Доказательство.
![]() сходится,
следовательно, по свойству сходящихся рядов ряд
сходится,
следовательно, по свойству сходящихся рядов ряд ![]() сходится. По признаку сравнения рядов
имеет место неравенство
сходится. По признаку сравнения рядов
имеет место неравенство
![]() (8.5)
(8.5)
тогда
ряд ![]() сходится.
Ясно, что члены ряда (8.3) равны разности соответствующих членов двух
сходящихся рядов (8.5) и (8.4) сходятся, следовательно, ряд (8.3) сходится.
Теорема доказана.
сходится.
Ясно, что члены ряда (8.3) равны разности соответствующих членов двух
сходящихся рядов (8.5) и (8.4) сходятся, следовательно, ряд (8.3) сходится.
Теорема доказана.
Пример 8.4 - Исследовать сходимость ряда
![]() .
.
Решение. Составим ряд из абсолютных величин:
![]() .
.
Этот
ряд является геометрическим рядом со знаменателем ![]() и, следовательно, сходится. Вместе с ним и
исследуемый ряд сходится, причем абсолютно.
и, следовательно, сходится. Вместе с ним и
исследуемый ряд сходится, причем абсолютно.
Сходящийся ряд ![]() называется условно сходящимся, если ряд
называется условно сходящимся, если ряд ![]() расходится.
расходится.
Пример 8.5 - Исследовать сходимость ряда
 .
.
Решение. Применим признак Лейбница. Так как
 ,
,
то первое условие признака Лейбница выполнено. Далее, так как
 ,
,
то выполнено и второе условие. Значит, данный ряд сходится. Составим ряд из абсолютных величин данного ряда:
![]() .
.
Члены полученного ряда больше членов ряда
![]() ,
,
который получен из гармонического ряда отбрасыванием первого члена. Значит, по первому признаку сравнения ряд, составленный из абсолютных величин расходится. Таким образом, ряд

сходится условно.
Если ряд ![]() абсолютно сходится, то ряд, полученный
после любой перестановки бесконечного множества его членов, абсолютно сходится
и имеет ту же сумму, что и первоначальный ряд.
абсолютно сходится, то ряд, полученный
после любой перестановки бесконечного множества его членов, абсолютно сходится
и имеет ту же сумму, что и первоначальный ряд.
Если ряд ![]() условно сходится, то при перестановке
бесконечного множества его членов сумма ряда может измениться. В частности, при
соответствующей перестановке членов условно сходящегося ряда можно превратить
его в расходящийся ряд.
условно сходится, то при перестановке
бесконечного множества его членов сумма ряда может измениться. В частности, при
соответствующей перестановке членов условно сходящегося ряда можно превратить
его в расходящийся ряд.
Если ряды ![]() и
и ![]() сходятся абсолютно и имеют соответственно
суммы
сходятся абсолютно и имеют соответственно
суммы ![]() и
и ![]() , то сходится абсолютно
и ряд
, то сходится абсолютно
и ряд
![]() .
.
Этот
ряд называется произведением рядов (по Коши). Его сумма равна ![]() .
.
Пример 8.6 - Возвести в квадрат абсолютно сходящийся ряд
 .
.
Решение.


 .
.
9 Лекция 9 Функциональные ряды, степенные ряды. Ряды Тейлора. Разложение некоторых функций в ряд Маклорена
Содержание: область сходимости функционального ряда, сумма ряда, мажорируемый ряд, область сходимости степенного ряда, интервал и радиус сходимости степенного ряда, теорема Абеля, формулы и ряды Тейлора и Маклорена, разложение функций в степенные ряды.
Цель лекции: Дать понятия часто применяемых в приближенных вычислениях определенного интеграла функциональных, степенных рядов.
Пусть функции ![]() (
(![]() ) определены в области
) определены в области ![]() . Тогда выражение вида
. Тогда выражение вида
![]() (9.1)
(9.1)
называется
функциональным рядом. Он называется сходящимся в точке ![]() , если сходится числовой ряд
, если сходится числовой ряд
![]() . (9.2)
. (9.2)
Множество значений ![]() , при которых ряд (9.1) сходится,
называется областью сходимости функционального ряда.
, при которых ряд (9.1) сходится,
называется областью сходимости функционального ряда.
Так как каждому ![]() из области сходимости соответствует
некоторое число – сумма числового ряда, то указанное соответствие определяет
функцию
из области сходимости соответствует
некоторое число – сумма числового ряда, то указанное соответствие определяет
функцию ![]() ,
которая называется суммой ряда (9.1) в области сходимости функционального ряда.
,
которая называется суммой ряда (9.1) в области сходимости функционального ряда.
Функциональный ряд называется мажорируемым в некоторой
области ![]() , если
существует сходящийся числовой ряд
, если
существует сходящийся числовой ряд
![]() (9.3)
(9.3)
такой,
что для всех ![]() справедливы
неравенства
справедливы
неравенства
![]()
Ряд (9.3) называется мажорантным (мажорирующим) рядом.
Степенным рядом называется функциональный ряд вида
![]() (9.4)
(9.4)
где
![]() – постоянные
числа, называемые коэффициентами ряда,
– постоянные
числа, называемые коэффициентами ряда, ![]() – фиксированное число. При
– фиксированное число. При ![]() получаем степенной ряд
вида
получаем степенной ряд
вида
![]() (9.5)
(9.5)
Все утверждения и теоремы, верные для ряда (9.4), верны и для ряда (9.5).
Интервал и радиус сходимости степенного ряда
Теорема 9.4 (теорема Абеля). 1. Если степенной ряд (9.5) сходится при
некотором значении ![]() ,
то он абсолютно сходится при всяком значении
,
то он абсолютно сходится при всяком значении ![]() , удовлетворяющем условию
, удовлетворяющем условию ![]() . 2. Если
степенной ряд (9.5) расходится при некотором значении
. 2. Если
степенной ряд (9.5) расходится при некотором значении ![]() , то он расходится при любых
, то он расходится при любых ![]() , для которых
, для которых ![]() .
.
Неотрицательное число ![]() , такое, что при всех
, такое, что при всех ![]() степенной ряд (9.5) сходится, а
при всех
степенной ряд (9.5) сходится, а
при всех ![]() расходится,
называется радиусом сходимости ряда. Промежуток
расходится,
называется радиусом сходимости ряда. Промежуток ![]() называется интервалом сходимости ряда
(9.5).
называется интервалом сходимости ряда
(9.5).
Радиус сходимости степенного ряда (9.5) определяется формулой
 или
или 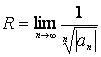 , (9.6)
, (9.6)
если,
начиная с некоторого номера ![]() , все
, все ![]() (предполагается, что указанные пределы
существуют или бесконечны). Формулы (9.6) легко получить, воспользовавшись соответственно
признаком Д’Аламбера или радикальным признаком Коши.
(предполагается, что указанные пределы
существуют или бесконечны). Формулы (9.6) легко получить, воспользовавшись соответственно
признаком Д’Аламбера или радикальным признаком Коши.
Если дан ряд вида (9.4), то его радиус сходимости ![]() определяется также по
формулам (9.6), а интервалом сходимости будет интервал с центром в точке
определяется также по
формулам (9.6), а интервалом сходимости будет интервал с центром в точке ![]() :
: ![]() .
.
Степенные ряды можно почленно интегрировать и дифференцировать в их интервалах сходимости. Радиус сходимости при этом не изменяется.
Формулы и ряды Тейлора и Маклорена. Разложение функций в степенные ряды
Если функция ![]() имеет производные в окрестности точки
имеет производные в окрестности точки ![]() до
до ![]() -го порядка включительно, то
существует точка
-го порядка включительно, то
существует точка ![]()
![]() , такая, что
, такая, что
![]() (9.7)
(9.7)
где
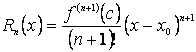 .
.
Формула (9.7) называется формулой Тейлора функции ![]() для точки
для точки ![]() ,
, ![]() – остаточным членом формулы
Тейлора в форме Лагранжа. Многочлен
– остаточным членом формулы
Тейлора в форме Лагранжа. Многочлен
![]()
называется
многочленом Тейлора функции ![]() .
.
При ![]() приходим к частному случаю формулы (9.7):
приходим к частному случаю формулы (9.7):
![]() (9.8)
(9.8)
где
 ,
, ![]()
![]() .
.
Формула (9.8) называется формулой Маклорена функции ![]() .
.
Сформулируем условие разложимости функции в ряд
Тейлора. Если функция ![]() дифференцируема
в окрестности точки
дифференцируема
в окрестности точки ![]() любое
число раз и в некоторой окрестности этой точки
любое
число раз и в некоторой окрестности этой точки ![]() или
или
 , (9.9)
, (9.9)
то
![]() (9.10)
(9.10)
В частности, при ![]()
![]() (9.11)
(9.11)
Ряд (9.10) называется рядом Тейлора, а ряд (9.11) – рядом Маклорена.
Условие (9.9) является необходимым и достаточным для
того, чтобы ряд, построенный по схеме (9.10) или (9.11), сходился к функции ![]() в некоторой окрестности
точки
в некоторой окрестности
точки ![]() . В
каждом конкретном случае необходимо находить область сходимости ряда к данной
функции.
. В
каждом конкретном случае необходимо находить область сходимости ряда к данной
функции.
Приведем разложения в степенные ряды некоторых элементарных функций:
![]() (9.12)
(9.12)
 (9.13)
(9.13)
 (9.14)
(9.14)
![]() (9.15)
(9.15)
![]() (9.16)
(9.16)
Для каждого случая в скобках указана область, в
которой степенной ряд сходится к соответствующей функции. Последний ряд,
называемый биномиальным, на концах интервала сходимости ведет себя по-разному в
зависимости от ![]() :
при
:
при ![]() абсолютно
сходится в точках
абсолютно
сходится в точках ![]() ;
при
;
при ![]() расходится
в точке
расходится
в точке ![]() и
условно сходится в точке
и
условно сходится в точке ![]() ; при
; при ![]() расходится в точках
расходится в точках ![]() .
.
В общем случае разложение в степенные ряды основано на использовании рядов Тейлора или Маклорена. Но на практике степенные ряды многих функций можно найти формально, используя ряды (9.12) – (9.16) или формулу для суммы членов геометрической прогрессии. Иногда при разложении полезно пользоваться почленным дифференцированием или интегрированием рядов. В интервале сходимости ряды сходятся к соответствующим функциям.
Пример 9.1 - Разложить
в ряд по степеням ![]() функцию
функцию
![]() и найти
область сходимости полученного ряда.
и найти
область сходимости полученного ряда.
Решение. Используя формулу понижения степени преобразуем данную функцию
![]() .
.
Теперь воспользуемся разложением (9.13), где вместо ![]() подставим
подставим ![]() , тогда получим
, тогда получим
![]()

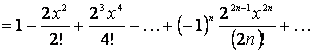 .
.
Найдем радиус сходимости этого ряда. Так как  , то по формуле
, то по формуле  имеем
имеем
 .
.
Таким образом, полученный ряд сходится при всех ![]() .
.
10 Лекция 10 Ряды Фурье
Содержание: Разложение функций в тригонометрические ряды Фурье.
Цель лекции: Дать понятие ряда Фурье, применяемого в колебательном анализе, привести примеры разложения функций в ряды Фурье.
Функциональный ряд вида
![]() , (10.1)
, (10.1)
где
коэффициенты ![]() ,
,
![]()
![]() определяются по
формулам
определяются по
формулам
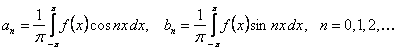 (10.2)
(10.2)
называется
рядом Фурье функции ![]() .
Отметим, что всегда
.
Отметим, что всегда ![]() .
Члены ряда (10.2) можно записать в виде гармоник
.
Члены ряда (10.2) можно записать в виде гармоник
![]()
с
амплитудой ![]() ,
частотой
,
частотой ![]() и
фазой
и
фазой 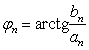 .
.
Функция ![]() называется кусочно-монотонной на отрезке
называется кусочно-монотонной на отрезке ![]() , если этот отрезок
можно разбить на конечное число интервалов
, если этот отрезок
можно разбить на конечное число интервалов ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() таким образом, чтобы в каждом из них
функция была монотонна.
таким образом, чтобы в каждом из них
функция была монотонна.
Теорема 10.1
Если функция ![]() периодическая
(период
периодическая
(период ![]() ),
кусочно-монотонная и ограниченная на отрезок
),
кусочно-монотонная и ограниченная на отрезок ![]() , то ее ряд Фурье сходится в любой точке
, то ее ряд Фурье сходится в любой точке ![]() и его сумма
и его сумма
![]() .
.
Из теоремы следует, что ![]() в точках непрерывности функции
в точках непрерывности функции ![]() и сумма
и сумма ![]() равна среднему
арифметическому пределов слева и справа функции
равна среднему
арифметическому пределов слева и справа функции ![]() в точках разрыва первого рода.
в точках разрыва первого рода.
Если функция ![]() имеет период
имеет период ![]() , то ее ряд Фурье записывается в виде
, то ее ряд Фурье записывается в виде
![]() , (10.3)
, (10.3)
где
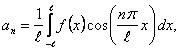
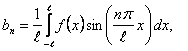
![]() . (10.4)
. (10.4)
Теорема 10.2
Если периодическая функция ![]() с периодом
с периодом ![]() кусочно-монотонная и ограниченная на
отрезке
кусочно-монотонная и ограниченная на
отрезке ![]() , то
ее ряд Фурье (10.3) сходится для любого
, то
ее ряд Фурье (10.3) сходится для любого ![]() к сумме
к сумме
![]() .
.
Если периодическая функция ![]() четная, то она разлагается в ряд
Фурье только по косинусам, при этом
четная, то она разлагается в ряд
Фурье только по косинусам, при этом
 .
.
Если
же периодическая функция ![]() нечетная, то она разлагается в ряд Фурье
только по синусам и
нечетная, то она разлагается в ряд Фурье
только по синусам и
 .
.
Так как для всякой периодической функции ![]() с периодом
с периодом ![]() и любого
и любого ![]() справедливо равенство
справедливо равенство
 ,
,
то коэффициенты Фурье можно вычислять по формулам:
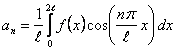 ,
,  ,
,
где ![]() .
.
Пусть функция ![]() кусочно-монотонна и ограничена на отрезке
кусочно-монотонна и ограничена на отрезке ![]()
![]() . Чтобы разложить эту функцию в
ряд Фурье, продолжим ее на интервал
. Чтобы разложить эту функцию в
ряд Фурье, продолжим ее на интервал ![]() так, чтобы она оставалась кусочно-монотонной
и ограниченной в
так, чтобы она оставалась кусочно-монотонной
и ограниченной в ![]() .
Найденную функцию разложим в ряд Фурье, который сходится к заданной функции на
отрезке
.
Найденную функцию разложим в ряд Фурье, который сходится к заданной функции на
отрезке ![]() . Если
заданную функцию продолжить на
. Если
заданную функцию продолжить на ![]() четным образом, то получим ее разложение
только по косинусам, если же продолжить ее нечетным образом, получим разложение
в ряд только по синусам.
четным образом, то получим ее разложение
только по косинусам, если же продолжить ее нечетным образом, получим разложение
в ряд только по синусам.
Например, функция ![]() , определенная на
, определенная на ![]()
![]() и продолженная в
и продолженная в ![]() в соответствии с равенствами
в соответствии с равенствами

разлагается
только по синусам. Сумма ![]() ряда Фурье такой функции равна
ряда Фурье такой функции равна ![]() внутри отрезка
внутри отрезка ![]() , а
, а ![]() ,
, ![]() согласно теореме 10.2.
согласно теореме 10.2.
Поскольку ряд Фурье сходится к значению
соответствующей функции в точках, где функция непрерывна, то ряды Фурье часто
используются для нахождения сумм числовых рядов. Так, например, если в ряде
Фурье функции ![]() ,
,
![]() , по косинусам
положить
, по косинусам
положить ![]() , то
получим:
, то
получим:
![]()
![]() .
.
11 Лекция 11 Понятие функции комплексного переменного
Содержание: Определение функции комплексного переменного. Основные элементарные функции. Дифференцирование, условия Коши-Римана.
Цели лекции: Знать основные элементарные функции, уметь выделять действительную и линейную части. Научить применять правило дифференцирования, проверять условия Коши-Римана.
Определение 11.1 Говорят, что на некотором множестве точек ![]() , изображающих значения
комплексной переменной
, изображающих значения
комплексной переменной ![]() определена функция
определена функция ![]() , если каждой точке
, если каждой точке ![]() из этого множества поставлено
в соответствие одно или несколько значений
из этого множества поставлено
в соответствие одно или несколько значений ![]() .
.
Если ![]() является функцией от
является функцией от ![]() , тогда каждое из переменных
, тогда каждое из переменных ![]() и
и ![]() является функциями от двух действительных
переменных
является функциями от двух действительных
переменных ![]() и
и ![]() , т.е.
, т.е. ![]() и
и ![]() . Если же
. Если же ![]() , где
, где ![]() и
и ![]() – действительные функции действительных
аргументов
– действительные функции действительных
аргументов ![]() и
и ![]() , то
, то ![]() можно рассматривать как функцию
комплексного переменного
можно рассматривать как функцию
комплексного переменного ![]() .
.
Определение 11.2 Число ![]() называется
пределом однозначной функции
называется
пределом однозначной функции ![]() при
при ![]() , если для любого
, если для любого ![]() существует
существует ![]() такое, что как только
такое, что как только ![]() выполняется неравенство
выполняется неравенство
![]() и записывают
и записывают
![]() .
.
Определение 11.3 Функция ![]() называется
непрерывной в точке
называется
непрерывной в точке ![]() ,
если
,
если
![]() .
.
Основные элементарные функции комплексного переменного
1. Рациональная функция ![]() .
.
2. Дробно-рациональная функция  .
.
3. Показательная функция определяется как сумма абсолютно сходящегося степенного ряда во всей комплексной плоскости
![]()
Свойства показательной функции: а) ![]() ; б)
; б) ![]() , т.е. функция
, т.е. функция ![]() есть периодическая
функция с периодом
есть периодическая
функция с периодом ![]() .
.
4. ![]() и
и ![]() можно определить в виде ряда Маклорена
можно определить в виде ряда Маклорена
 ,
,
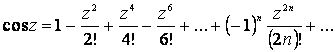 .
.
Эти
ряды абсолютно сходятся при любом ![]() . Функции
. Функции ![]() ,
, ![]() ,
, ![]() связаны между собой формулой Эйлера:
связаны между собой формулой Эйлера: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
5.  ,
,  .
.
6. Гиперболические функции:
 ,
,
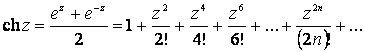 ,
,
![]() ,
,
![]() .
.
Выполняются следующие соотношения: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
7. ![]()
Свойства:
![]() ,
,  ,
, ![]() ,
, ![]() .
.
8. Обратные тригонометрические функции:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
9. ![]() , где
, где ![]() .
.
10.
![]() где
где ![]() .
.
Производная функции комплексного переменного
Пусть функция ![]() определена в некоторой области
определена в некоторой области ![]() комплексного переменного
комплексного переменного
![]() . Дадим
аргументу
. Дадим
аргументу ![]() приращение
приращение
![]() так, чтобы
точка
так, чтобы
точка ![]() принадлежала
области
принадлежала
области ![]() .
Тогда функция
.
Тогда функция ![]() получит
приращение
получит
приращение ![]() .
.
Определение 11.4 Функция ![]() называется
дифференцируемой в точке
называется
дифференцируемой в точке ![]() из области
из области ![]() , если существует предел отношения
, если существует предел отношения ![]() при
при ![]() произвольным образом. Этот
предел называют производной функции
произвольным образом. Этот
предел называют производной функции ![]() и пишут:
и пишут:
 . (11.1)
. (11.1)
Определение 11.5 Функция ![]() ,
имеющая непрерывную производную в каждой точке области, называется
аналитической в этой области.
,
имеющая непрерывную производную в каждой точке области, называется
аналитической в этой области.
Свойства производных:
1. ![]() ;
;
2. ![]() ;
;
3. 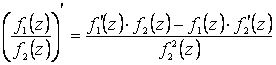 , где
, где ![]() .
.
4. Если сложная функция ![]() , где
, где ![]() – функция комплексного переменного, и
существуют производные
– функция комплексного переменного, и
существуют производные ![]() и
и ![]() , тогда справедлива формула
, тогда справедлива формула
![]() .
.
Таблица производных аналогична таблице производных функции действительного переменного.
Условия Коши-Римана
Пусть ![]() . Пусть
. Пусть ![]() имеет производную, т.е.
имеет производную, т.е.
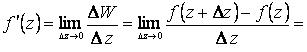
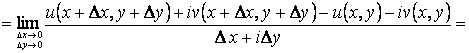 .
.
Так как по определению предел не зависит от выбора пути
стремления ![]() ,
, ![]() к нулю, то рассмотрим
частные случаи:
к нулю, то рассмотрим
частные случаи:
а) пусть ![]() , тогда
, тогда
![]()
![]() ;
;
б) пусть ![]() , тогда
, тогда
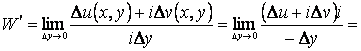
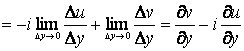 .
.
Так как производные равны, то ![]()
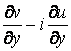 . Следовательно,
. Следовательно,
 (11.2)
(11.2)
(11.2) – условия Коши-Римана.
При выполнении условий Коши-Римана производная ![]() равна:
равна:
![]() .
.
Определение 11.6 Функция ![]() называется
гармонической в области
называется
гармонической в области ![]() , если она имеет непрерывные частные
производные до второго порядка включительно и удовлетворяет уравнению Лапласа в
этой области
, если она имеет непрерывные частные
производные до второго порядка включительно и удовлетворяет уравнению Лапласа в
этой области
 . (11.3)
. (11.3)
(11.3) – уравнение Лапласа.
12 Лекция 12 Определение преобразования Лапласа
Содержание: Определение преобразования Лапласа, его свойства. Свертка двух функций и ее изображение. Таблица изображений.
Цель лекции: Знать определение преобразования Лапласа, уметь применять свойства преобразования при нахождении изображения. Знать таблицу изображений.
Определение 12.1 Преобразованием Лапласа функции действительного переменного ![]() называется функция
комплексного переменного
называется функция
комплексного переменного ![]() , определяемая формулой
, определяемая формулой
![]() .
(12.1)
.
(12.1)
Несобственный интеграл в правой части (12.1),
зависящий от комплексного параметра ![]() , называется интегралом Лапласа.
, называется интегралом Лапласа.
Установим, какие функции ![]() будем рассматривать и какие условия надо
наложить на функцию
будем рассматривать и какие условия надо
наложить на функцию ![]() ,
чтобы несобственный интеграл (12.1) сходился.
,
чтобы несобственный интеграл (12.1) сходился.
Будем предполагать следующее:
1. ![]() при
при ![]() ;
;
2. ![]() – кусочно-непрерывна при
– кусочно-непрерывна при ![]() . Это значит, что она
или непрерывна или на каждом конечном отрезке имеет конечное число точек
разрыва первого рода;
. Это значит, что она
или непрерывна или на каждом конечном отрезке имеет конечное число точек
разрыва первого рода;
3. при ![]() модуль функции
модуль функции ![]() может возрастать, но не быстрее
некоторой показательной функции, т.е. существуют такие постоянные числа
может возрастать, но не быстрее
некоторой показательной функции, т.е. существуют такие постоянные числа ![]() и
и ![]() такие что, для любого
такие что, для любого ![]() выполняется неравенство
выполняется неравенство
![]() .
(12.2)
.
(12.2)
Нижняя грань всех чисел ![]() , для которых выполняется неравенство
(12.2) называется показателем роста функции
, для которых выполняется неравенство
(12.2) называется показателем роста функции ![]() .
.
Функция ![]() , удовлетворяющая условиям 1, 2, 3
называется оригиналом.
, удовлетворяющая условиям 1, 2, 3
называется оригиналом.
Функция ![]() , определяемая формулой (12.1) называется
изображением функции
, определяемая формулой (12.1) называется
изображением функции ![]() и
обозначают:
и
обозначают: ![]() или
или
![]() .
.
Рассмотрим единичную функцию Хевисайда, которая задается следующим образом:
|
|
1
0 t Рисунок 1 |
Покажем,
что функция ![]() является
оригиналом.
является
оригиналом.
Во-первых, ![]() при
при ![]() , во-вторых,
, во-вторых, ![]() непрерывно при
непрерывно при ![]() , как постоянная функция,
в-третьих, 30
, как постоянная функция,
в-третьих, 30 ![]() при
при ![]() , т.е. она ограничена. Таким образом, функция
, т.е. она ограничена. Таким образом, функция
![]() является
оригиналом.
является
оригиналом.
Найдем для нее изображение:
![]() при
при ![]() .
.
Таким образом, изображение ![]() для
для ![]() существует, если
существует, если ![]() и ее изображением
является
и ее изображением
является 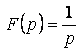 . Для
простоты будем писать, что
. Для
простоты будем писать, что ![]() , тогда
, тогда
![]() . (12.3)
. (12.3)
Вообще, если речь идет о какой-либо функции ![]() , например
, например ![]() ,
, ![]() ,
, ![]() и т.д., то подразумеваем следующее
и т.д., то подразумеваем следующее 
 .
.
С помощью функции ![]() можно записать
можно записать ![]() ,
, ![]() ,
, ![]() , но сокращенно будем писать
, но сокращенно будем писать ![]() ,
, ![]() ,
, ![]() .
.
Теорема 12.1 (теорема существования
изображения). Для всякого оригинала ![]() существует изображение
существует изображение ![]() , определенное в полуплоскости
, определенное в полуплоскости ![]() , где
, где ![]() – показатель роста
оригинала. В каждой точке этой полуплоскости функция
– показатель роста
оригинала. В каждой точке этой полуплоскости функция ![]() аналитична.
аналитична.
Теорема 12.2 (теорема единственности оригинала).
Если ![]() является
изображением двух оригиналов
является
изображением двух оригиналов ![]() и
и ![]() , то эти оригиналы совпадают во всех
точках, в которых они непрерывны.
, то эти оригиналы совпадают во всех
точках, в которых они непрерывны.
Свойства преобразования Лапласа
Теорема линейности. Для любых действительных или комплексных постоянных ![]() и
и ![]()
![]() , где
, где ![]() ,
, ![]() ,
,
т.е. линейной комбинации оригиналов соответствует такая же линейная комбинация изображений.
Теорема подобия. Для любого постоянного ![]() верно соотношение
верно соотношение 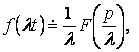 где
где ![]() .
.
Теорема затухания (смещения). Для любого действительного или комплексного числа ![]() :
: ![]() , где
, где ![]() .
.
Теорема запаздывания. Для любого постоянного числа ![]() верно соотношение
верно соотношение ![]() где
где ![]() .
.
Теорема дифференцирования оригинала. Пусть функция ![]() и ее производные
и ее производные ![]() ,
, ![]() , являются оригиналами, причем
, являются оригиналами, причем ![]() , тогда:
, тогда: ![]() ,
,
![]() ,
,
![]() ,
,
…,
![]() .
.
Самым простым является случай, если ![]()
![]() , тогда
, тогда ![]() .
.
Теорема интегрирование оригинала. Если ![]() и
и ![]()
![]() , то
, то  , т.е.
, т.е.  .
.
Теорема дифференцирования изображения. Если ![]() , тогда
, тогда ![]() ,
, ![]() , …,
, …, ![]() .
.
Теорема интегрирования изображения. Если ![]() и функция
и функция ![]() является оригиналом, то
является оригиналом, то 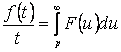 , где
, где  сходится.
сходится.
Свертка функций
Определение 12.2 Сверткой двух функций ![]() и
и ![]() ,
, ![]() , обозначаемой
, обозначаемой ![]() , называется интеграл
, называется интеграл ![]()
![]() .
.
Свойства свертки
1. Свертка коммутативна, т.е. ![]() .
.
2. Если ![]() и
и ![]() оригиналы, то их сверка
оригиналы, то их сверка ![]() также является оригиналом.
также является оригиналом.
Теорема умножения изображений (теорема Бореля). Если ![]() и
и ![]() , то
, то ![]() .
.
Формула Дюамеля
Рассмотрим специальный случай теоремы умножения
изображения ![]() ,
где
,
где ![]() ,
, ![]() ,
, ![]() . Тогда
. Тогда
![]()
 .
.
Итак,
![]() ,
,
или
![]() . (12.5)
. (12.5)
Аналогично можно получить формулы
![]() ,
,
![]() .
.
(12.5) называется интегралом Дюамеля или формулой Дюамеля.
Таблица изображений
|
1. |
|
2. |
|
|
3. |
|
4. |
|
|
5. |
|
6. |
|
|
7. |
|
8. |
|
|
9. |
|
10. |
|
|
11. |
|
12. |
|
|
13. |
|
14. |
|
|
15. |
|
16. |
|
13 Лекция 13 Нахождение оригинала по изображению. Приложение операционного исчисления
Содержание: Нахождение оригинала по изображению. Приложение операционного исчисления.
Цели лекции: Уметь находить оригинал по данному изображению, решать задачу Коши для линейных дифференциальных уравнений с постоянными коэффициентами, решать системы операторным методом.
Если  правильная рациональная дробь, то эту
дробь разлагают на сумму простых дробей и находят оригиналы для каждой простой
дроби, используя свойства преобразования Лапласа и таблицу соответствия.
правильная рациональная дробь, то эту
дробь разлагают на сумму простых дробей и находят оригиналы для каждой простой
дроби, используя свойства преобразования Лапласа и таблицу соответствия.
Пример
13.1 - Найти оригинал по изображению ![]() .
.
Решение.

 .
.
Пример
13.2 - Найти оригинал по изображению 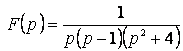 .
.
Решение.
Разложим ![]() на элементарные
дроби:
на элементарные
дроби:
 .
.
Найдем
коэффициенты ![]() ,
тогда получим
,
тогда получим ![]() .
.
Решение задачи Коши для линейного дифференциального уравнения с постоянными коэффициентами
Решение задачи Коши поясним на примере.
Пример 13.3 -
Решить задачу Коши ![]() ,
,
![]() .
.
Пусть
![]() , тогда
, тогда ![]() . Перейдем к изображениям:
. Перейдем к изображениям:
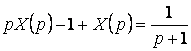 . Полученное
уравнение называется операторным уравнением, соответствующим поставленной
задаче Коши. Решим его относительно
. Полученное
уравнение называется операторным уравнением, соответствующим поставленной
задаче Коши. Решим его относительно ![]() :
:
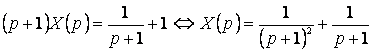 .
.
Перейдем
к оригиналам: ![]() .
Таким образом, функция
.
Таким образом, функция ![]() является решением задачи Коши.
является решением задачи Коши.
Решение системы линейных дифференциальных уравнений операторным методом
Решение системы линейных дифференциальных уравнений операторным методом поясним на примере:
Пример 13.4 -
Решить задачу Коши для системы двух линейных неоднородных дифференциальных
уравнений: 
![]() .
.
Пусть ![]() ,
, ![]() , тогда
, тогда ![]() ,
, ![]() . Перейдем к системе операторных
уравнений:
. Перейдем к системе операторных
уравнений:

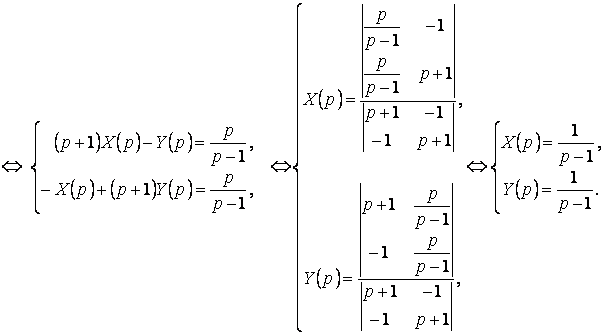
Найдем оригиналы: Следовательно,
решением задачи Коши будет система функций
Следовательно,
решением задачи Коши будет система функций 
14 Лекция 14 Элементы теории вероятностей
Содержание: Основные понятия и определения теории вероятностей. Определение вероятности. Элементы комбинаторики. Алгебра событий.
Цель лекции: Ознакомить с основными понятиями теории вероятностей, методами и способами вычисления вероятности.
Теория вероятностей – математическая наука, изучающая закономерности случайных явлений. При этом изучаемые явления рассматриваются независимо от их конкретной природы, т.е. теория вероятностей рассматривает математические модели случайных явлений. Причем случайным явлением понимают явление, предсказать исход которого невозможно.
Случайные события, их классификация
Пусть проводится некоторый опыт (эксперимент,
испытание), исход которого нельзя предсказать. Случайным событием называется
любой исход опыта, который может произойти или не произойти в результате
осуществления определенной совокупности условий. События обозначаются буквами: ![]() ,
, ![]() ,
, ![]() , … . Непосредственные исходы опыта называются
элементарными событиями и обозначаются через
, … . Непосредственные исходы опыта называются
элементарными событиями и обозначаются через ![]() . Множества всех элементарных событий и
обозначают через
. Множества всех элементарных событий и
обозначают через ![]() .
Наблюдаемые нами события можно разделить на три вида: достоверные, невозможные,
случайные.
.
Наблюдаемые нами события можно разделить на три вида: достоверные, невозможные,
случайные.
Определение 14.1 Событие ![]() называется
достоверным, если оно обязательно произойдет при осуществлении определенной
совокупности условий.
называется
достоверным, если оно обязательно произойдет при осуществлении определенной
совокупности условий.
Определение 14.2 Событие ![]() называется
невозможным, если оно заведомо не произойдет при осуществлении определенной
совокупности условий.
называется
невозможным, если оно заведомо не произойдет при осуществлении определенной
совокупности условий.
Определение 14.3 Событие ![]() называется
случайным, если при осуществлении определенной совокупности условий оно может
произойти или не произойти.
называется
случайным, если при осуществлении определенной совокупности условий оно может
произойти или не произойти.
Каждое случайное событие есть следствие действия очень многих случайных причин. Невозможно учесть влияния на результат всех этих причин, так как неизвестны законы их действия. По иному обстоит дело, если рассматривать случайные события, которые многократно наблюдаются при осуществлении одних и тех же условий. Оказывается, что достаточно большое число однородных случайных событий, независимо от их конкретной природы, подчиняются определенным закономерностям. Установлением этих закономерностей и занимается теория вероятностей.
Итак, предметом теории вероятностей является изучение вероятностных закономерностей массовых однородных случайных событий.
Виды случайных событий
Определение 14.4 События называются несовместными, если появление одного из них исключает появление другого события в одном и том же испытании.
Определение 14.5 События ![]() называются
попарно несовмест-ными, если любые два из них несовместны.
называются
попарно несовмест-ными, если любые два из них несовместны.
Определение 14.6 Несколько событий образуют полную группу, если они попарно несовместны и в результате каждого опыта происходит одно и только одно их них.
Определение 14.7 События называются равновозможными, если есть основание считать, что ни одно из этих событий не является более возможным, чем другое, т.е. все события имеют равные “шансы”.
Действия над событиями
Основные операции над событиями полностью соответствуют основным операциям над множествами.
1. Суммой событий ![]() и
и ![]() называется событие
называется событие ![]() , состоящее в наступлении хотя
бы одного из них, т.е. или наступит событие
, состоящее в наступлении хотя
бы одного из них, т.е. или наступит событие ![]() , или наступит событие
, или наступит событие ![]() , или наступят события
, или наступят события ![]() и
и ![]() вместе.
вместе.
2. Произведением событий ![]() и
и ![]() называется событие
называется событие ![]() , состоящее в совместном
наступлении этих событий.
, состоящее в совместном
наступлении этих событий.
3. Разностью событий ![]() и
и ![]() называется событие
называется событие ![]() , происходящее тогда и только
тогда, когда происходит событие
, происходящее тогда и только
тогда, когда происходит событие ![]() , но не происходит событие
, но не происходит событие ![]() .
.
4. Противоположным событию ![]() называется событие
называется событие ![]() , которое происходит
тогда и только тогда, когда не происходит событие
, которое происходит
тогда и только тогда, когда не происходит событие ![]() (т.е. событие
(т.е. событие ![]() означает, что событие
означает, что событие ![]() не наступило).
не наступило).
5. Событие ![]() влечет событие
влечет событие ![]() (или
(или ![]() является частным случаем
является частным случаем ![]() ), если из того, что
происходит событие
), если из того, что
происходит событие ![]() ,
следует, что происходит событие
,
следует, что происходит событие ![]() ; записывают
; записывают ![]() .
.
6. Если ![]() и
и ![]() , то событие
, то событие ![]() и
и ![]() называются равными и записывают
называются равными и записывают ![]() .
.
Классическое определение вероятности
Существует несколько определений этого понятия.
Простой способ определения вероятности события основывается на равновозможности
любого исхода из конечного числа опытов. Рассмотрим пример. Пусть в урне
содержится шесть одинаковых шаров, причем два из них красных, три шара синие и
один шар белый. Очевидно, что возможность вытянуть красный шар или синий
больше, чем возможность вытянуть белый шар. Число, характеризующее эту
возможность, и есть вероятность события. Случай, который приводит к наступлению
события ![]() ,
называется благоприятствующим.
,
называется благоприятствующим.
Определение 14.4 Вероятностью события ![]() называется отношение числа
называется отношение числа ![]() случаев,
благоприятствующих этому событию, к общему числу
случаев,
благоприятствующих этому событию, к общему числу ![]() элементарных исходов, т.е.
элементарных исходов, т.е.
![]() .
(14.1)
.
(14.1)
Свойства вероятности события
1. Вероятность достоверного события равна 1, т.е. ![]() .
.
2. Вероятность невозможного события равна 0, т.е. ![]() .
.
3. Вероятность случайного события есть положительное
число, заключенное между нулем и единицей, т.е. ![]() .
.
Относительная частота события
Определение 14.5 Относительной частотой события называется отношение число испытаний ![]() , в которых событие
, в которых событие ![]() появилось, к общему
числу
появилось, к общему
числу ![]() фактически
произведенных испытаний. Обозначают относительную частоту
фактически
произведенных испытаний. Обозначают относительную частоту ![]() , т.е.
, т.е. ![]() .
.
Свойства относительной частоты события
1. Относительная частота достоверного события равна 1,
т.е. ![]() .
.
2. Относительная частота невозможного события равна 0,
т.е. ![]() .
.
3. Относительная частота случайного события заключена
между нулем и единицей, т.е. ![]() .
.
4. Свойство статической устойчивости: с увеличением
числа опытов относительная частота принимает значения, близкие к некоторому
постоянному числу. Это постоянное число и есть вероятность появления события ![]() или приблизительно
равно вероятности события
или приблизительно
равно вероятности события ![]() .
.
Элементы комбинаторики
Из определения вероятности события следует, что надо
будет вычислять число благоприятствующих событию ![]() исходов и число общих исходов. Подсчет
числа исходов проводится обычно комбинаторными методами. Многие комбинаторные
задачи могут быть решены с помощью двух правил, называемых правилами сложения и
умножения.
исходов и число общих исходов. Подсчет
числа исходов проводится обычно комбинаторными методами. Многие комбинаторные
задачи могут быть решены с помощью двух правил, называемых правилами сложения и
умножения.
Правило суммы.
Если некоторый объект ![]() можно
выбрать
можно
выбрать ![]() способами,
а объект
способами,
а объект ![]() можно
выбрать
можно
выбрать ![]() способами,
независимых от способов выбора объекта
способами,
независимых от способов выбора объекта ![]() , то любой из указанных объектов (
, то любой из указанных объектов (![]() или
или ![]() ) можно выбрать
) можно выбрать ![]() способами.
способами.
Правило умножения. Если из некоторого конечно множества объект ![]() можно выбрать
можно выбрать ![]() способами и после
каждого такого выбора объект
способами и после
каждого такого выбора объект ![]() можно выбрать
можно выбрать ![]() способами, то оба объекта (
способами, то оба объекта (![]() и
и ![]() ) в указанном порядке можно
выбрать
) в указанном порядке можно
выбрать ![]() способами.
способами.
Для нахождения числа всевозможных исходов используют
комбинаторные формулы. Пусть дано множество, состоящее из ![]() различных элементов.
различных элементов.
Размещением из ![]() элементов по
элементов по ![]() элементов называется любое упорядоченное
подмножество данного множества, содержащее
элементов называется любое упорядоченное
подмножество данного множества, содержащее ![]() элементов. Из определения следует, что
размещения – это выборки (комбинации), состоящие из
элементов. Из определения следует, что
размещения – это выборки (комбинации), состоящие из ![]() элементов, которые отличаются
друг от друга либо составом элементов, либо порядком их расположения. Размещение
обозначается символом
элементов, которые отличаются
друг от друга либо составом элементов, либо порядком их расположения. Размещение
обозначается символом ![]() и вычисляется по формуле
и вычисляется по формуле
 .
(14.2)
.
(14.2)
Перестановкой из ![]() элементов называется размещение из
элементов по
элементов называется размещение из
элементов по ![]() элементов.
Перестановка обозначается символом
элементов.
Перестановка обозначается символом ![]() и вычисляется по формуле
и вычисляется по формуле
![]() .
(14.3)
.
(14.3)
Сочетанием из ![]() элементов по
элементов по ![]() называется любое подмножество, которое
содержит
называется любое подмножество, которое
содержит ![]() элементов
данного множества. Из определения следует, что сочетания – это выборки
(комбинации) из
элементов
данного множества. Из определения следует, что сочетания – это выборки
(комбинации) из ![]() элементов,
которые отличаются друг от друга только составом элементов. Число сочетаний
элементов,
которые отличаются друг от друга только составом элементов. Число сочетаний ![]() элементов из
элементов из ![]() элементов обозначается
символом
элементов обозначается
символом ![]() и
вычисляется по формуле
и
вычисляется по формуле
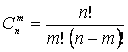 .
(14.4)
.
(14.4)
Алгебра событий. Теорема сложения вероятностей двух несовместных событий
Теорема 14.1 Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий, т.е.
![]() . (14.5)
. (14.5)
Следствие. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий, т.е.
![]() .
.
Теорема 14.2
Сумма вероятностей событий ![]() , образующих полную группу, равна единице,
т.е.
, образующих полную группу, равна единице,
т.е. ![]() .
.
Теорема 14.3 Сумма вероятностей противоположных событий равна 1:
![]() .
(14.6)
.
(14.6)
Зависимые и независимые события
Два события называются независимыми, если вероятность одного из них не зависит от появления или не появления другого события.
Несколько событий называют попарно-независимыми, если каждые два из них события независимые. Два события называются зависимыми, если вероятность появления одного из них зависит от наступления или не наступления другого события.
Умножения вероятностей независимых событий
Теорема 14.4 Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.
![]() .
(14.7)
.
(14.7)
Следствие. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:
![]() .
.
Теорема 14.5
Вероятность появления хотя бы одного из событий ![]() ,
, ![]() , …,
, …, ![]() , независимых в совокупности, равна
разности между единицей и произведением вероятностей противоположных событий
, независимых в совокупности, равна
разности между единицей и произведением вероятностей противоположных событий ![]() , т.е.
, т.е.
![]() ,
(14.8)
,
(14.8)
где
![]() .
.
Условная вероятность
Пусть события ![]() и
и ![]() зависимые. Условной вероятностью
зависимые. Условной вероятностью ![]() называют вероятность
события
называют вероятность
события ![]() ,
вычисленную в предположении, что событие
,
вычисленную в предположении, что событие ![]() уже наступило.
уже наступило.
Теорема умножения вероятностей зависимых событий
Теорема 14.6. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предложении, что первое событие уже наступило.
Замечание:
применим формулу (14.7) к событию ![]() , т.к.
, т.к. ![]() совпадает с
совпадает с ![]() , то
, то ![]() , тогда
, тогда
![]() .
.
Следствие. Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже наступили:
![]() . (14.9)
. (14.9)
Следствие. Из формулы (14.9) можно вычислить условную вероятность
![]() . (14.10)
. (14.10)
Теорема сложения вероятностей совместных событий
Теорема 14.7. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
![]() . (14.11)
. (14.11)
Замечание. При
использовании формулы (14.11) следует иметь в виду, что если ![]() и
и ![]() зависимые, то (14.11) примет
вид
зависимые, то (14.11) примет
вид
![]() .
.
15 Лекция 15 Формула полной вероятности
Содержание: Формула полной вероятности, формула Байеса, формула Бернулли и интегральная теоремы Лапласа, распределение Пуассона. Простейший поток событий и его свойства.
Цель лекции: Ознакомить и показать вычисление вероятностей по соответствующим формулам.
Теорема 15.1
Вероятность события ![]() ,
которое может наступить лишь при условии появления одного из несовместных
событий
,
которое может наступить лишь при условии появления одного из несовместных
событий ![]() , образующих
полную группу, равна сумме произведений вероятностей каждого из этих событий на
соответствующих условную вероятность события
, образующих
полную группу, равна сумме произведений вероятностей каждого из этих событий на
соответствующих условную вероятность события ![]() , т.е.
, т.е.
![]() .
(15.1)
.
(15.1)
Формула (15.1) называется формулой полной вероятности,
события ![]() ,
, ![]() , …,
, …, ![]() называются гипотезами.
называются гипотезами.
Доказательство.
Из условия теоремы следует, что событие ![]() наступит, если наступит одно, безразлично
какое, из несовместных событий
наступит, если наступит одно, безразлично
какое, из несовместных событий ![]() ,
, ![]() , …,
, …, ![]() , то есть
, то есть
![]() . (15.2)
. (15.2)
Вычислим каждое из слагаемых (15.2), имеем
![]() ,
,
![]() ,
,
…,
![]() .
.
Тогда (15.2) примет вид
![]()
![]() .
.
Теорема доказана.
Формула Байеса
Допустим, произведено испытание, в результате которого
появилось событие ![]() .
Определим, как изменились (в связи с тем, что событие
.
Определим, как изменились (в связи с тем, что событие ![]() уже наступило) вероятности гипотез,
т.е. следует найти
уже наступило) вероятности гипотез,
т.е. следует найти ![]() ,
,
![]() , …,
, …, ![]() . Найдем
. Найдем ![]() . По теореме умножения
. По теореме умножения
![]()
 ,
,
или
 .
.
Аналогично
 . (15.3)
. (15.3)
(15.3) – формула Байеса.
Формула Байеса позволяет переоценить вероятность
гипотез после того, как становится известным результат испытания, в котором
наступило событие ![]() .
.
Формула Бернулли
Если производится несколько испытаний, причем
вероятность события ![]() в
каждом испытаний не зависит от исходов других испытаний, то такие испытания
называются независимыми относительно события
в
каждом испытаний не зависит от исходов других испытаний, то такие испытания
называются независимыми относительно события ![]() .
.
Пусть производится ![]() независимых испытаний, в каждом из которых
событие
независимых испытаний, в каждом из которых
событие ![]() может
появиться или нет. Пусть вероятность события
может
появиться или нет. Пусть вероятность события ![]() в каждом испытании
в каждом испытании ![]() , тогда
, тогда ![]() .
.
Задача: вычислить вероятность того, что при ![]() испытаниях событие
испытаниях событие ![]() появится ровно
появится ровно ![]() раз, и не появится
раз, и не появится ![]() раз.
раз.
Важно подчеркнуть, что не требуется, чтобы событие ![]() повторялось ровно
повторялось ровно ![]() раз в определенной
последовательности. Искомую вероятность обозначим
раз в определенной
последовательности. Искомую вероятность обозначим ![]()
![]() .
(15.4)
.
(15.4)
(15.4) – формула Бернулли.
Локальная теорема Лапласа
Если число испытаний ![]() большое, то применение формулы Бернулли затруднительно.
Если вероятность
большое, то применение формулы Бернулли затруднительно.
Если вероятность ![]() появления
события
появления
события ![]() в
каждом испытании постоянна
в
каждом испытании постоянна ![]() , то
, то ![]() приближенно равна значению функции
приближенно равна значению функции 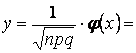
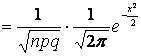 , где
, где 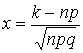 , т.е.
, т.е.
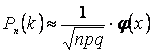 ,
, 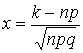 .
(15.5)
.
(15.5)
Функция ![]() табулирована.
табулирована.
Интегральная теорема Лапласа
Если вероятность наступления события ![]() в каждом испытании
равна
в каждом испытании
равна ![]() , причем
, причем
![]() , то
, то ![]() – вероятность того,
что событие
– вероятность того,
что событие ![]() появится
в
появится
в ![]() испытаниях
от
испытаниях
от ![]() до
до ![]() раз равно
раз равно  ;
; ![]() ,
, ![]() или
или

 . (15.6)
. (15.6)
Функция
![]() нечетна.
нечетна.
Распределение Пуассона
Пусть производится ![]() независимых испытаний, в каждом из которых
вероятность события
независимых испытаний, в каждом из которых
вероятность события ![]() равна
равна
![]() . Для
определения вероятности
. Для
определения вероятности ![]() появлений события
появлений события ![]() в
в ![]() испытаниях используют формулу Бернулли.
Если же
испытаниях используют формулу Бернулли.
Если же ![]() велико,
тогда используют асимптотическую формулу Лапласа, но она непригодна, если
велико,
тогда используют асимптотическую формулу Лапласа, но она непригодна, если ![]() . В этих случаях
применяют асимптотическую формулу Пуассона.
. В этих случаях
применяют асимптотическую формулу Пуассона.
Вероятность того, что при очень большом числе
испытаний, в каждом из которых вероятность события мала, событие наступит ![]() раз, равна
раз, равна
![]() , (15.7)
, (15.7)
где
![]() – среднее
число появления события в различных сериях испытаний.
– среднее
число появления события в различных сериях испытаний.
Простейший поток событий
Рассмотрим события, которые наступают в случайные моменты времени. Потоком событий называют последовательность событий, которые наступают в случайные моменты времени.
Свойства потока событий
Свойство стационарности. Свойство стационарности характеризуется тем, что вероятность
появления ![]() событий
на любом промежутке времени зависит только от числа
событий
на любом промежутке времени зависит только от числа ![]() и от длительности
и от длительности ![]() промежутка и не зависит
от начало его отчета. При этом различные промежутки времени предполагаются
непересекающимися.
промежутка и не зависит
от начало его отчета. При этом различные промежутки времени предполагаются
непересекающимися.
Свойство отсутствия последствия. Свойство отсутствия последствия характеризуется тем,
что вероятность появления ![]() событий на любом промежутке времени не
зависит от того, появились или не появились события в моменты времени,
предшествующие началу рассматриваемого промежутка.
событий на любом промежутке времени не
зависит от того, появились или не появились события в моменты времени,
предшествующие началу рассматриваемого промежутка.
Свойство ординарности. Свойство ординарности характеризуется тем, что за бесконечно малый промежуток времени может появиться не более одного события.
Простейшим (пуассоновским) называют поток событий, который обладает свойствами стационарности, отсутствия последствия и ординарности.
Интенсивностью потока ![]() называют среднее число событий, которое
появится в единицу времени. Если постоянная интенсивности потока известна,
тогда вероятность появления
называют среднее число событий, которое
появится в единицу времени. Если постоянная интенсивности потока известна,
тогда вероятность появления ![]() событий простейшего потока за время
событий простейшего потока за время ![]() определяется по формуле
определяется по формуле
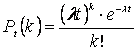 .
(15.8)
.
(15.8)
16 Лекция 16 Случайные величины
Содержание: Понятие дискретной и непрерывной случайной величины, функция распределения и ее свойства, плотность распределения и ее свойства. Числовые характеристики дискретных и непрерывных случайных величин.
Цель лекции: Уметь задать закон распределения случайной величины, строить функцию и многоугольник распределения. Уметь вычислять числовые характеристики дискретных и непрерывных случайных величин.
Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Дискретные и непрерывные случайные величины
Дискретной (непрерывной) называют случайную величину, которая принимает отдельные изолированные возможные значения с определенными вероятностями. Число возможных значений случайной величины может быть конечным или бесконечно.
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, что число возможных значений непрерывной случайной величины бесконечно.
Закон распределение вероятностей дискретной случайной величины
Пусть ![]() – дискретная случайная величина, которая
принимает значения
– дискретная случайная величина, которая
принимает значения ![]() с
некоторыми вероятностями
с
некоторыми вероятностями ![]() .
.
Законом распределения дискретной случайной величины называют соотношение между возможными значениями и их вероятностями.
Закон распределения можно задать таблично, аналитически и графически. При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, вторая – их вероятности:
|
|
|
|
… |
|
|
|
|
|
… |
|
Приняв во внимание, что в одном испытании случайная
величина принимает одно и только одно возможное значение, заключаем, что
события ![]() ,
, ![]() , …,
, …, ![]() образуют полную
группу, т.е.
образуют полную
группу, т.е. ![]() .
.
Биномиальное распределение
Пусть производится ![]() независимых испытаний, в каждом из которых
вероятность события
независимых испытаний, в каждом из которых
вероятность события ![]() может
появиться или не появиться. Вероятность наступления события
может
появиться или не появиться. Вероятность наступления события ![]() во всех испытаниях постоянно и
равно
во всех испытаниях постоянно и
равно ![]() , тогда
, тогда
![]() . Рассмотрим
в качестве дискретной величины
. Рассмотрим
в качестве дискретной величины ![]() – число появлений события
– число появлений события ![]() в этих испытаниях.
Найти закон распределения случайной величины
в этих испытаниях.
Найти закон распределения случайной величины ![]() .
.
Возможные значения дискретной случайной величины ![]() ,
, ![]() ,
, ![]() , …,
, …, ![]() с вероятностями
с вероятностями ![]() ,
, ![]() .
.
Рассмотрим разложение бинома Ньютона: ![]()
![]() .
. ![]() – вероятность появления события
– вероятность появления события ![]() раз в
раз в ![]() независимых испытаниях,
независимых испытаниях,
![]() –
вероятность появления
–
вероятность появления ![]() раз в
раз в ![]() испытаниях, …,
испытаниях, …, ![]() – вероятность того, что событие
не появится ни один раз. Тогда
– вероятность того, что событие
не появится ни один раз. Тогда
|
|
|
|
… |
|
… |
|
|
|
|
|
… |
|
… |
|
т.е.
закон распределения случайной величины ![]() задан таблично.
задан таблично.
Закон распределения дискретной случайной величины
можно задать графически, если на оси абсцисс отложить возможные значения
случайной величины, а на оси ординат – вероятности этих значений. Ломаную, соединяющую
последовательно точки ![]()
![]()
![]() …, называют многоугольником распределения.
…, называют многоугольником распределения.
Функция распределения случайной величины и ее свойства
Одним из способов задания закона распределения
вероятностей является задание функции распределения, обозначаемой ![]() . Функцией распределения
дискретной случайной величины
. Функцией распределения
дискретной случайной величины ![]() называется функция
называется функция ![]() , которая для любого числа
, которая для любого числа ![]() равна вероятности
события
равна вероятности
события ![]() ,
т.е. по определению
,
т.е. по определению
![]() .
(16.1)
.
(16.1)
Функцию распределения ![]() называют интегральной функцией распределения.
Функция распределения обладает следующими свойствами:
называют интегральной функцией распределения.
Функция распределения обладает следующими свойствами:
1. ![]() ограничена, т.е.
ограничена, т.е. ![]() .
.
2. ![]() – неубывающая, т.е. если
– неубывающая, т.е. если ![]() , то
, то ![]() .
.
3. ![]() ,
, ![]() .
.
4. Вероятность попадания случайной величины ![]() в промежуток
в промежуток ![]() равна
равна
![]() .
(16.2)
.
(16.2)
5. ![]() непрерывна слева, т.е.
непрерывна слева, т.е. ![]() .
.
Функция распределения дискретной случайной величины имеет вид
![]() .
(16.3)
.
(16.3)
Функция распределения дискретной случайной величины ![]() есть разрывная функция
со скачками
есть разрывная функция
со скачками ![]() в
точках
в
точках ![]() , при
подходе к точке разрыва слева
, при
подходе к точке разрыва слева ![]() сохраняет значение, ее график имеет
ступенчатый вид.
сохраняет значение, ее график имеет
ступенчатый вид.
Числовые характеристики случайной величины.
Математическое ожидание дискретной случайной величины
Если неизвестен закон распределения случайной величины, то используют число, которое характеризует случайную величину.
Математическим ожиданием дискретной случайной величины
![]() называют
сумму произведений всех ее возможных значений на их вероятности:
называют
сумму произведений всех ее возможных значений на их вероятности:
![]() . (16.4)
. (16.4)
![]() – постоянная величина для
данного события.
– постоянная величина для
данного события.
Вероятностный смысл математического ожидания
Пусть произведено ![]() испытаний, в которых случайная величина
испытаний, в которых случайная величина ![]() приняла
приняла ![]() раз значение
раз значение ![]() ,
, ![]() раз значение
раз значение ![]() , …,
, …, ![]() раз значение
раз значение ![]() , причем
, причем ![]() , тогда сумма всех
значений, принятых случайной величины, равна
, тогда сумма всех
значений, принятых случайной величины, равна ![]() .
. ![]() – среднее арифметическое всех значений,
принятых случайной величиной
– среднее арифметическое всех значений,
принятых случайной величиной ![]() или
или ![]()
![]() , где
, где ![]() – относительная частота
значения
– относительная частота
значения ![]() ,
т.е.
,
т.е. ![]()
![]() . Допустим, что число испытаний велико,
тогда
. Допустим, что число испытаний велико,
тогда ![]() , и
, и ![]() , т.е.
, т.е. ![]() . Таким образом, математическое
ожидание приближенно равно среднему арифметическому наблюдаемых значений
случайной величины (тем точнее, чем больше число испытаний).
. Таким образом, математическое
ожидание приближенно равно среднему арифметическому наблюдаемых значений
случайной величины (тем точнее, чем больше число испытаний).
Замечание.
Ясно, что ![]() больше
наименьшего и меньше наибольшего из возможных значений, т.е. на числовой оси
возможные значения расположены слева и справа от
больше
наименьшего и меньше наибольшего из возможных значений, т.е. на числовой оси
возможные значения расположены слева и справа от ![]() . В этом смысле
. В этом смысле ![]() характеризует расположение
распределения и, поэтому его называют центром распределения.
характеризует расположение
распределения и, поэтому его называют центром распределения.
Свойства математического ожидания
1. ![]() , где
, где ![]() ;
;
2. ![]() , т.е. постоянный множитель можно вынести
на знак математического ожидания.
, т.е. постоянный множитель можно вынести
на знак математического ожидания.
Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая случайная величина.
Произведением двух независимых случайных величин ![]() и
и ![]() называется случайная величина,
равная произведениям каждого возможного значения
называется случайная величина,
равная произведениям каждого возможного значения ![]() на каждое возможное значение
на каждое возможное значение ![]() . Вероятности возможных
значений случайной величины
. Вероятности возможных
значений случайной величины ![]() равны произведениям вероятностей
возможных значений сомножителей.
равны произведениям вероятностей
возможных значений сомножителей.
3. ![]() .
.
4. ![]() .
.
17 Лекция 17 Дисперсия дискретной случайной величины
Содержание: Дисперсия и среднеквадратическое отклонение дискретной случайной величины. Числовые характеристики непрерывных случайных величин.
Цель лекции: Уметь вычислять числовые характеристики дискретных и непрерывных случайных величин.
Зная лишь математическое ожидание, нельзя судить ни о том, какие возможные значения она может принимать, ни о том, как они рассеяны вокруг математического ожидания.
Пусть ![]() – случайная величина,
– случайная величина, ![]() – ее математическое ожидание.
– ее математическое ожидание. ![]() называется отклонением
случайной величины от ее математического ожидания.
называется отклонением
случайной величины от ее математического ожидания.
Пусть дан закон распределения случайной величины ![]() :
:
|
|
|
|
… |
|
|
|
|
|
… |
|
Напишем закон распределения отклонения ![]() . Для того, чтобы
отклонение приняло значение
. Для того, чтобы
отклонение приняло значение ![]() достаточно, чтобы случайная величина
приняла значение
достаточно, чтобы случайная величина
приняла значение ![]() ,
а ее вероятность
,
а ее вероятность ![]() ,
тогда:
,
тогда:
|
|
|
|
… |
|
|
|
|
|
… |
|
Теорема 17.1
Математическое ожидание отклонения равно 0: ![]() .
.
Доказательство.
![]()
![]() .
.
Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания и обозначается
![]() .
(17.1)
.
(17.1)
Теорема 17.2 Дисперсия равна разности между математическим ожиданием квадрата случайной величины и квадратом математического ожидания
![]() .
(17.2)
.
(17.2)
Доказательство.
![]()
![]()
![]() .
.
Свойства дисперсии
1.
![]() , где
, где ![]() .
.
Доказательство.
![]() .
.
2.![]() .
.
Доказательство.
![]()
![]() .
.
3.
![]() ,
,![]() .
.
4.
![]() .
.
Дисперсия числа появлений события в независимых испытаниях
Теорема 17.3
Дисперсия числа появлений события ![]() в
в ![]() независимых испытаниях, в каждом из которых
вероятность появления события постоянна и равна
независимых испытаниях, в каждом из которых
вероятность появления события постоянна и равна ![]() , равна
, равна
![]() .
(17.8)
.
(17.8)
Вероятностный смысл дисперсии: она характеризует степень рассеяния случайной величины вокруг своего среднего значения.
Среднеквадратическим отклонением случайной величины ![]() называют квадратный
корень из дисперсии
называют квадратный
корень из дисперсии
![]() ,
(17.9)
,
(17.9)
т.е.
размерность ![]() совпадает
с размерностью
совпадает
с размерностью ![]() .
.
Модой дискретной случайной величины ![]() называется ее
значение, принимаемое с наибольшей вероятностью по сравнению с двумя соседними
значениями, обозначается через
называется ее
значение, принимаемое с наибольшей вероятностью по сравнению с двумя соседними
значениями, обозначается через ![]() .
.
Плотность распределения и ее свойства
Одной из характеристик непрерывной случайной величины является плотность распределения вероятностей.
Плотностью распределения вероятностей непрерывной
случайной величины ![]() называется
производная ее функции распределения. Обозначают через
называется
производная ее функции распределения. Обозначают через ![]() . Таким образом,
. Таким образом,
![]() .
(17.10)
.
(17.10)
Функцию ![]() также называют дифференциальной функцией
распределения.
также называют дифференциальной функцией
распределения.
Вероятностный смысл дифференциальной функции
По определению производной
![]() .
.
Отсюда
получим ![]() ,
т.е. плотность вероятности определяется как функция непрерывной случайной
величины, удовлетворяющая условию
,
т.е. плотность вероятности определяется как функция непрерывной случайной
величины, удовлетворяющая условию ![]() .
.
Свойства ![]() :
:
1. ![]() , т.е.
, т.е. ![]() неотрицательно.
неотрицательно.
2. ![]() , т.е. вероятность попадания непрерывной
случайной величины
, т.е. вероятность попадания непрерывной
случайной величины ![]() в
промежуток
в
промежуток ![]() равна
определенному интегралу от ее плотности в пределах от
равна
определенному интегралу от ее плотности в пределах от ![]() до
до ![]() .
.
3. Интегральная функция распределения непрерывной случайной величины может быть выражена через плотность вероятности по формуле
![]() . (17.11)
. (17.11)
4. ![]() .
.
Числовые характеристики непрерывной случайной величины
Математическим ожиданием непрерывной случайной
величины ![]() с
плотностью вероятности
с
плотностью вероятности ![]() есть число
есть число
![]() .
(17.12)
.
(17.12)
Если
случайная величина задана на ![]() , то
, то
![]() .
(17.13)
.
(17.13)
Дисперсия непрерывной случайной величины ![]() с плотностью вероятности
с плотностью вероятности
![]() находится по
формулам
находится по
формулам
![]() , (17.14)
, (17.14)
![]() . (17.15)
. (17.15)
Среднее квадратическое отклонение равно
![]() .
(17.16)
.
(17.16)
Для непрерывной случайной величины мода ![]() есть абсцисса точки
максимума функции
есть абсцисса точки
максимума функции ![]() .
.
Медианой ![]() непрерывной случайной величины
непрерывной случайной величины ![]() называют такое ее
возможное значение
называют такое ее
возможное значение ![]() ,
которое определяется равенством
,
которое определяется равенством
![]() . (17.17)
. (17.17)
С помощью функции распределения медиану можно найти из равенства
![]() .
(17.18)
.
(17.18)
Список литературы
1. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа для втузов. – М.: Наука, 1973. – 720 с.
2. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное исчисления. – М.: Наука, 1980. – 432 с.
3. Гмурман В.Е. Теория вероятностей и математическая статистика: Учебное пособие для вузов. – М.: Высш. шк., 2003. – 479 с.
4. Натансон И.П. Краткий курс высшей математики. – СПб.: Издательство Лань, 1997. – 736 с.
5. Письменный Д.Т. Конспект лекций по высшей математике. – 2.– М.: Айрис-пресс, 2003. – 256 с.
6. Хасейнов К.А. Каноны математики: Учебник.– Алматы, 2003. – 686 с.