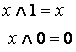ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ

ҒЫЛЫМ МИНИСТРЛІГІ

“Алматы энергетика және байланыс институтының”

Коммерциялық емес акционерлік қоғамы

 

Жоғары математика кафедрасы

 

 

 

Байсалова М.Ж.

 

ДИСКРЕТ  МАТЕМАТИКА

 

Оқу құралы

  

 

 Алматы 2007

 

  

УДК 517

ББК 22.17Я73

Б20  Дискрет математика: оқу құралы  –

Оқу құралы / Байсалова М.Ж.

Алматы, АЭжБИ. 2007. - 76 бет.

ISBN 9965 – 708 – 98 – 3

 

     Жоғары техникалық оқу орындарының оқу бағдарламасына жиындар теориясы, математикалық логика, комбинаторика, графтар теориясы, т.б. математика тарауларын қамтитын курстар еніп жүр. Бұл тараулар информатика есептерінің математикалық жасауына негіз болатыны белгілі. Қазақ тілінде аталған  бөлімдерді қамтитын оқулықтар жеткіліксіз болғандықтан  кейбір терминдердің түпнұсқасын келтірдім. Кемшіліктерді көрсетіп, алып- қосар пікірлеріңіз болса, ризалығымды білдіремін.

      Осы оқулықты шығаруға атсалысқан Алматы энергетика және байланыс институтының жоғары математика кафедрасының доценті Людмила Николаевна Астраханцеваға зор алғысымды білдіремін.

       Алматы энергетика және байланыс институтының Ғылыми кеңесінде жоғары техникалық оқу орындарында оқитын студенттерге арналған оқулық деп ұсынылған (ҒК хаттамасы № 6)

      

                                                                                                             ББК 22.17Я73             

       ПІКІР БЕРУШІ: ҚазҰУ, проф.   Қ.Ж.Наурызбаев.

       АЭжБИ, физ.-мат.ғыл. канд.,проф. С.Е.Базарбаева.

 

 

Б                                                          

ISBN 9965-708-98-3                                               

Көшіріп басуға, көшірмесін жасауға автордың рұхсатынсыз болмайды.

Барлық авторлық, сондай-ақ баспахананың құқығы сақталған.

 

 

ã “Алматы  энергетика және байланыс институтының” КЕАҚ, 2007 ж.

1 Жиындар теориясының негізгі ұғымдары

 1.1 Жиындар

         Жиын математикадағы негізгі ұғымдарының бірі болғандықтан, оған анықтама берілмейді. Жиын деп белгілі математикалық объектілердің жиынтығын түсінеміз. Ол объектілер жиынның элементтері деп аталып, кіші әріптермен, ал жиынның өзі  бас әріппен белгіленеді.

а элементі А жиынына тиістілігін аА, “” - тиістілік кванторымен белгілейді.

b A – b элементі А жиынына тиісті емес.

Бізге белгілі жиындарды атап өтейік:

N – натурал сандар жиыны;

Z – бүтін сандар жиыны;

Q – рационал сандар жиыны;

R – нақты сандар жиыны; 

C – комплекс сандар жиыны;

Ø – бос жиын.

Жиі қолданылатын кванторлар:

 - кез келген,  х  А (кез келген х А жиынында жатады);

 - табылады,  у  В (В жиынынан у элементі табылады);

׃ ( | ) – мынадай, қасиетін сипаттау үшін;

 - бұдан шығатын салдар;

 - тепе-теңдік кванторы, тек сол жағдайда;

 - қатаң енгізу кванторы.

Жиынға енетін элементтер саны шенеулі немесе шексіз көп болуы мүмкін.

          1-мысал: а) қазақ алфавитінің әріптер жиыны (42 элемент бар);

               ә) натурал сандар жиыны ( элементі бар);

               б)  теңдеуінің нақты түбірлерінің жиыны ешқандай да элементтен тұрмайды, бос жиын.

          Ақырлы жиын деп осы жиынның элементтерінің санына тең болатын натурал сан табылатын жиынды айтады. Ақырлы емес жиын ақырсыз жиын деп аталады.

          Ақырлы А және В жиындары тек қана бірдей элементтерден құралса, тең жиындар деп аталып,  А=В деп белгіленеді.

          Егер ақырлы А жиынында ақырлы В жиынына тиісті емес элемент бар болса, және керісінше, онда олар тең емес жиындар  деп аталады.

          2-мысал. {0, 1, 2}={1, 2, 0},  {0, 1}{1, 2, 0, 3}. 

Жиындардың берілу тәсілдері.

1.     Мүшелерін (элементтерін) тізіп жазу арқылы. Ақырлы жиын

, ақырсыз жиын В={1, 3, 5, 7, ..., } – тақ сандар жиыны.

2.     Сипаттау арқылы. Мысалы жиынның кез келген х мүшесі р(х)

қасиетіне ие болсын, онда осы элементтерден тұратын С жиыны былай беріледі: С={х(х)}.

Осы сияқты анықталған жиындар 

Q={}, В={х: х=}.

          А және В жиындары берілсін. Егер А жиынының кез келген х элементі В жиынында да жатса, онда А жиыны В жиынының ішкі жиыны деп аталады.

А  В немесе В А деп белгіленеді. Кванторлар тілінде 

(А  В) (х А  х  В).

Егер В жиынының А ішкі жиыны В жиынынан және Ø-ден өзгеше болса,

онда ол меншікті ішкі жиыны деп аталады. Кванторлар тілінде, А  В  

А  В және А  В.

 Ø кез келген жиынның ішкі жиыны болады: Ø  А.

Қасиеттері:

а) А  А;

          ә) А  В, В  А  А  =  В;

          б) А  В, В  С  А  С.

          В жиынының В және Ø ішкі жиындары оның меншіксіз   ішкі жиындары деп аталады. Егер жиын ең болмағанда екі элементтен тұрса, онда оның меншікті ішкі жиындары болады.

Мысалы: А = {а, в} жиынының ішкі жиындары: {а}, {в}, {Ø}, {а, в}. Бұл ішкі жиындардың ішінде {а}, {в}- меншікті, ал  {а, в}, {Ø}- меншіксіз болып табылады.

 

Ішкі жиындарға қолданылатын амалдар

         U (универсум) деп кең жиынды белгілейік, яғни элементтер осы жиыннан алынып отыратын болсын.

Эйлер – Венн диаграммасы. Тік төртбұрыштың нүктесі U жиынынан алынған деп  есептейік. Мысалға А={1,2,3,4}, В={1,3,5}, С={5,6} жиындарын алайық.

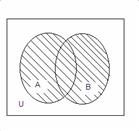
1.     Ең болмағанда А жиынына немесе В жиынына тиісті элементтер

жиынын А және В жиындарының бірігуі (қосындысы) (А  В) деп айтады.

 А  В = {х: х  А немесе х  В}

                                                                                                                                                                                                

          

 

                                      А  В={1,2,3,4,5},  А  С={1,2,3,4,5,6}.

 

 

       1.1 Сурет

  _________________________________________

  Леонард Эйлер (1707-1783)- швейцарлық математик.

Джон Венн (1834-1923) – ағылшын математигі.

          «Бірігу» амалын жалпыласақ,

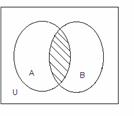
          2. А жиынына да, В      жиынына да тиісті элементтер жиынын А және В жиындарының қиылысуы (көбейтіндісі) (АВ) деп айтады.

           АВ ={х:хА және хВ}.

 

 

 


                                                                                            А  В={1,3},  В  С={5},  АС= Ø.

 

                                     

                         1.2 Сурет                                  

 «Қиылысу» амалын жалпыласақ, .

3. А жиынына тиісті, бірақ В жиынына тиісті емес элементтер жиынын А және В жиынының айырымы (А\В) деп айтады.

А\В = {х:хА және хВ}

 

 

 


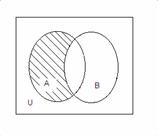                                                    А \ В={2,4}, В \ С={1,3}, А\С=А.

 

 

 

                1.3 Сурет

4.  А және В жиындарының симметриялық айырмасы (АВ) деп келесі

жиынды айтады:     

 АВ=(А\В)  (В\А)= {х:(хА және хВ) немесе (хВ және хА) }.

             

 

 


                                              

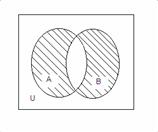              1.4 Сурет

АВ= {2,4}{5}={2,4,5},  АC= {1,2,3,4}{5,6}={1,2,3,4,5,6}.     

            5. U\A жиыны А жиынының толықтауышы деп аталып,  деп белгіленеді.

= U\A

 

 

 

 

 

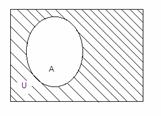
                       1.5 Сурет

Унивесум U={1,2,3,4,5,6,7,8,9} болса, онда ={5,6,7,8,9} болады.

 

1.2 Жиындар алгебрасы

Жиындарға амалдар қолданып, жаңа жиындар алуға болады. Осы амалдардың негізгі қасиеттері мен олардың арасындағы байланыс жиындар алгебрасы деп аталады.

1.1 К е с т е - Қасиеттер

1

(идемпотенттік)  

АА=А

 

АА=А

2

Ауыстырымдылық (коммутативтік)

АВ=ВА

 

АВ=ВА

3

Үлестірімділік

А(ВС) =(АВ) С

 

А (ВС) =(АВ) С

4

Терімділік (дистрибутивтік)

А(ВС) =(АВ) (АС)

 

А (ВС) =(АВ)  (АС)

5

Сіңіру

А(ВА)=А

 

А (ВА)=А

6

Нөлдің қасиеті   А Ø=А

А Ø= Ø

7

Бірдің қасиеті   А U= U

А U= А

8

Қосалқы принципі (де Морган заңы)

 

9

Екі рет теріске шығару    

 

 

10

Толықтауыштың қасиеті

 

 Ø

Жиындар арасындағы қасиеттер (заңдар) жоғарыдағы  келтірілген қасиеттермен шектеліп қоймайды. Қалған қасиеттерді логика алгебрасының ережелері бойынша аталған касиеттерді қолданып алуға болады.

 

Жиындардың декарттық (тура) көбейтіндісі

Математикада жиындардың жай элементтері ғана емес, сонымен бірге олардың реттелген жұп элементтері де кездеседі. (а1,а2,...,аn) элементтері реттелген жиын берілсін, оны жиынтық, вектор, кортеж деп те атайды, аі –

_________________________________________________

Огастес де Морган (1806-1871) – шотландық математик

 

жиынның і-ші мүшесі. (а1,а2,...,аn) – жиынтығының ұзындығы деп n компоненталар санын айтамыз.

А және В жиындарының тура немесе декарттық көбейтіндісі деп (а,в) жұбының жиынын айтамыз.  деп белгілейміз.      

={(a, b): a, b},

=,

,

, {Ø}.

Мысалдар қарастырып өтейік.

1.  A={1,2}, B={1,2,3} жиындары берілсін. Бұл жиындар үшін тура көбейтінділер

{(1,1), (1,2), (1,3), (2,1), (2,2), (2,3)},

{(1,1), (1,2), (2,1), (2,2), (3,1), (3,2)},

{(1,1), (1,2), (2,1), (2,2)}   (2,1)(1,2).

2.  R – нақты сандар жиыны берілсін. Онда

{(x,y}: (x,y) – жазықтықтың нүктелері},

{(x,y,z) : (x,y,z) – кеңістіктің нүктелері}.

3. ,  екі жиынды қарастырайық. Егер жазықтықтағы декарттық координаталар жүйесін қарастырсақ, онда  ұзындығы бірге тең квадрат ретінде қарастыруға болады.

 

 

 

 

  

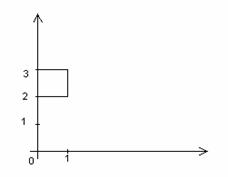1.6 Сурет

1-есеп.  де Морган заңын (қосалқы принципі) дәлелдеу керек.

          Шешуі:  І әдіс Эйлер-Венн диаграммасы арқылы. Ол үшін теңдіктің сол жағындағы жиынды кескіндеп аламыз:

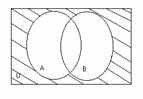          а)                        

 

 

 1.7 Сурет

Ал оң жақтағы жиынды бейнелеу үшін алдымен  жиынын   көлденең жолақпен,  жиынын     тік жолақпен белгілеп аламыз. Сонда бізге керекті жиын осы екі жолақтың қиылысуында, яғни тормен кескінделген жиын болады;

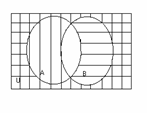          ә)

                                                                  

                                                                                                                                             

 

                                                         1.8 Сурет

Байқасақ, жоғарыдағы диаграммада штрихпен белгіленген жиын мен төмендегі тормен белгіленген жиын бір жиынды береді, бұл екі жиынның теңдігін білдіреді.

ІІ әдіс қасиеттерге сүйеніп, өрнектерді түрлендіру арқылы.

Алдымен U =VUV, VU қасиеті бойынша:

1) ;

2)  енгізулері орындалатынын көрсетейік.

1)  және  және  ;

2) керісінше,  және  және   .

                                 

          Жиынның бүркеуі мен бөлікшесі

         Жиындарға қолданылатын операциялардың тағы бір түрі - жиынды ішкі жиындар жүйесіне бөліктеу операциясы болып табылады. А жиыны мен оның ішкі жиындар жүйесін  A   қарастырайық.

Анықтама. Егер 1)  A  Ø],                   2)

шарттары орындалса, онда A   жиын жүйесін А жиынының бүркеуі деп атайды.

Анықтама.  Егер 1)  A   Ø, ];        2) ;

3)  A     Ø] немесе Ø  

шарттары орындалса, онда A  жиын жүйесі А жиынының бөлікшесі деп аталады.

         Егер бүркеу анықтамасындағы екі шартқа 3) шартты қоссақ, онда бүркеу бөлікше бола алады. Басқаша айтқанда, егер әрбір  элементі тек қана бір  Аі  ішкі жиынына тиісті болса, онда А жиынының бос емес ішкі жиындардың  A  жүйесі оның бөлікшесі бола алады.

1–мысал. жиыны берілсін:

а)  - А жиынының бүркеуі;

ә) - А жиынының бөлікшесі болады;

б)  - қандай-да бір ішкі жиындардың жүйесі, ол бүркеуі де емес, бөлікшесі де емес, себебі .

2–мысал. N – натурал сандар жиынын қарастырайық. N 0 – жұп, N 1 – тақ сандар жиыны болсын. Онда {N 0 , N 1 } –N бөлікшесі бола алады.

1.3 Қатынастар. Унарлы, бинарлы, n-орынды қатынастар

А1, А2, ..., Аn жиындарындағы n – орынды қатынас немесе n – орынды предикат деп А1А2...Аn тура көбейтіндісінің кез келген жиыншасын айтамыз. Басқаша айтқанда, егер (х1,х2,...,xn)Р болса,  х1, х2, ..., xn  элементтері  (мұндағы х1,  х2, xn )   Р қатынасымен байланыстырылған деп аталып, Р(х1,х2,...,xn)  деп белгіленеді.

n=1 болса, онда Р қатынасы А жиынының жиыншасы болады, РА және унарлы қатынас немесе қасиет деп аталады.  

 n=2 болса, онда   жиі кездесетін екі орынды қатынас. Бұл жағдайда олар бинарлы қатынас немесе сәйкестік деп аталады. Сонымен А және В жиындарының арасындағы Р сәйкестігі  АВ жиынының жиыншалары болып табылады,  және (х,у) ,  оны жиі хРу деп жазады.

 – А жиынындағы  n-орынды қатынас. Кейбір оқулықта  бинарлық қатынасы  немесе деп белгіленеді, А1 – қатынасты жіберу облысы, А2 – қатынасты қабылдау  жиыны деп аталады.

1–мысал:

          а)  егер   ал бинарлық қатынас P={(x;y) / x,y, y элементі х-ке бөлінеді, х}, онда  P={(2,2),(2,4),(2,6),(2,8),(3,3),(3,6)};

          ә)  P={(х,у) / x, y} қатынасын R жиынында қарастырайық. Онда  xPy  жазуын   деп түсінуге болады, яғни Р қатынасы “” символымен берілген;

          б) А – нақты сандар жиыны, онда  {(x,y)}  A жиынындағы бинарлы қатынас болады;

          в)  А – адамдар жиыны , онда {(x,y)-тің туысқаны} А-дағы бинарлық қатынас.

         Бинарлы қатынастардың берілу жолдары:

1)  тізіп жазу арқылы,  мысалы  (2,2), (2,4), (2,6), (2,8), (3,3), (3,6);

2)  бинарлық қатынасын график көмегімен кескіндеу қолайлы.

         Өзара перпендикуляр өстер (Ox – көлденең өс,  Oy – тік өс)  сызайық. А және В жиындарының элементтерін сәйкес өстерде белгілейік. XOY жазықтығында координаталары  болатын нүктелерді белгілейік. Алынған нүктелер жиыны Р қатынасына сәйкес келеді;

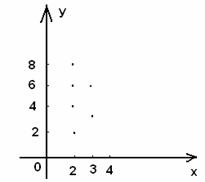
1.9 Сурет

1 мысалдағы Р қатынасы.

3) Р қатынасымен байланысқан  және  элементтері стрелкамен қосылған түрінде.

         2–мысал. мен жиындарының арасындағы  қатына-сын, ал А жиынындағы  қатынасын бейнелеу керек:

а) ;

 ә) ;

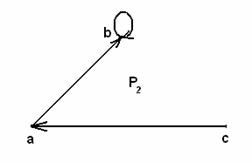
1.10 Сурет

           4) ақырлы жиындардың арасындағы бинарлы қатынас жұптардың тізімімен немесе матрица арқылы беріледі. ,  және  бинарлы қатынасы берілген болсын. Бұл қатынастың матрицасы: ,  өлшемді, мұндағы

.

          Сонымен нөл мен бірден тұратын кез келген матрица - қандай да бір бинарлы қатынастың матрицасы болып табылады.

          3–мысал. а) ,  жиындары мен осы жиындар арасындағы ,  қатынастары берілген. Бұл қатыныстарды матрица арқылы беруге болады

,  ;

ә)  жиынында  қатынасы берілген:             . Бұл қатынасқа сәйкес матрица

.

          Анықтама.  Р қатынасының анықталу облысы (Dp деп белгіленеді) Dpкейбір у үшін . Ал мәндерінің жиыны Еркейбір х үшін  жиындары айтылады.

          Dp – бірінші элементтерден құралған жиын,

          Ер – екінші элементтерден құралған жиын.

          А және В жиындарының арасында Р қатынасы берілсін. .

          Келесі анықтамаларды енгізейік:

          а) кері қатынас:

;

          ә) толықтауыш қатынас:

;

          б)  тепе-тең қатынас:

. Кейде деп белгіленеді, -дағы диагональ деп те атайды;

          в) универсалды қатынас:

 және  кейде толық қатынас деп те атайды.

          4–мысал.  жиынында  x элементі  y –тің бөлгіші}  қатынасы берілген. Олай болса . Бұл қатынас үшін Dp={2,3} – анықталу облысы, Ep={2,3,4,6,8} – мәндерінің жиыны, P-1={(2,2),(4,2),(6,2),(8,2),(3,3),(6,3)} – кері қатынас.

          1. P қатынасына  (предикатына) қатысты Х жиынының бейнесі деп, келесі жиын айтылады: P(x)={y/(x,y), кейбір  үшін}

          2. P предикатына қатысты кері бейнесі деп, Р-1(х) немесе Р-1 предикатына қатысты Х жиынының бейнесін айтады.

         Анықтама.  және  бинарлық қатынастарының  композициясы немесе көбейтіндісі деп  қатынасы немесе жиыны айтылады, ол былай анықталады

 және .

          5-мысал  және  - оң бүтін сандар жиынында берілген бинарлық қатынастар  болсын: -оң бүтін сан},  - оң бүтін сан}. Онда - оң бүтін сан} және - оң бүтін сан}.      

          Теорема.  Кез келген P, Q, R бинарлық қатынастар үшін келесі қасиеттер орындалады:

а) ;

ә) ;

б) .

     Дәлелдеуі [1, 19 бет].

                 Бинарлық қатынас матрицасының негізгі қасиеттері

          Егер  және  , онда

          1.

(матрицалардың элементтерін қосу 0+0=0; 1+1=0+1=1+0=1 ережесі бойынша жүргізіледі);

          2.

матрицалардың элементтерін көбейту кәдімгідей іске асырылады, яғни 00=01=10=0; 11=1).

        1-мысал. 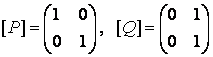 бинарлық қатынастардың матрицалары берілген. Олар үшін

,

.

3. Егер   -кері қатынас болса, онда   .

4. Егер  және  .

5. -тепе-тең қатынас болса, онда    - бірлік матрица.

6.  -ның толықтауышы, онда - бұл  -дағы 0-ді 1-ге, ал 1-ді 0-ге ауыстырған матрица.

7. Егер  , онда композиция   және матрицалар кәдімгі матрицаларды көбейту ережесі бойынша іске асырылады, бірақ матрицаларды көбейту кезінде элементтерді қосып, көбейту бірінші пункттегідей жүргізіледі

.

                    Анықтама.  P  қатынасы  анықталған болсын.

          1. Егер  үшін    болса, онда  P рефлексивті қатынас деп аталады (P-«бір қалада тұру»).

          2. Егер  үшін -дан  шығатын болса, онда P симметриялы қатынас деп аталады  (P-«бір фирмада жұмыс істеу»).

          3. Егер -дан  шығатын болса, онда P антирефлексивті деп аталады  (P-«ұлы болу»).

          4. Егер  және -дан  шығатын болса, онда P антисимметриялы қатынас деп аталады  (P-«бастық болу»).

          5. Егер  және  -да  шығатын болса, онда Р транзитивті қатынас деп аталады  (P-«ағасы болу» немесе ).

          2-мысал. А- нақты оң сандар жиыны болсын. Р қатынасы ретінде”<”, “>”, “=” қарастыруға болады.

          Ескерте кетелік, Р бинарлы қатынасы  жиынында анықталған болсын. Бұл қатынастың қасиеттерін матрицасы арқылы тексеруге болады:

1. P- рефлексивті болсын 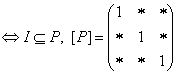,мұнда орнына бір немесе нөлдер белгіленген.

2. P- симметриялы болсын .

3. P- антисимметриялы  немесе . Бұл қасиет  матрицасындағы бас диагональдан басқа жердегі элементтері нөлге тең болады,  бас диагональда да нөлдер болуы мүмкін екендігін көрсетеді.

4. P- транзитивті , яғни егер ,  , онда .

         3-мысал.  матрицасымен берілген Р қатынасының қасиеттерін қарастырайық.  матрицасының бас диагоналінде бірлер тұрғандықтан, Р рефлексивті, яғни .  матрицасы симметриялы емес, олай болса Р қатынасы да симметриялы емес.

.

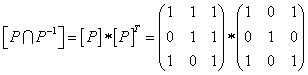         Бұл матрица антисимметриялылықты тексеруге қажет. Бас диагональдан басқа жердегі элементтер нөлге тең емес болғандықтан, Р антисимметриялы емес. Келтірілген мысалдан антисимметриялық қасиет пен симметриялы емес қасиеттері әртүрлі екендігі көрінеді. Енді транзитивті қасиетіне тексерейік.

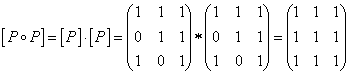
яғни , олай болса транзитивті емес  [4, 93 бет], [6, 13 бет].

          Егер P қатынасы рефлексивті, симметриялы және транзитивті болса, онда ол эквивалентті қатынас деп аталады. Эквиваленттілікті Е немесе ~ (тильда) символымен белгілейді:  , .

          4-мысал. «» теңдік қатынасы кез келген А жиынында эквивалентті қатынас болады, себебі: 

          а) рефлексивті ;

          ә) симметриялы ,  ;

          б) транзитивті ,  .

          5-мысал. Үшбұрыштар жиынын алсақ, ұқсастық қатынасы эквивалентті болады.

          А жиынындағы Е эквиваленттілік қатынасы осы А жиынын элементтері өзара эквивалентті ішкі жиындарға бөледі. Мұндай ішкі жиындар эквиваленттілік класы деп аталады.

           Е – А жиынындағы эквиваленттілік қатынасы және  болсын. А жиынының х-ке эквивалентті элементтердің ішкі жиыны х элементінің эквиваленттілік класы деп аталады. Е(х) немесе  деп белгіленеді


     Эквивалент кластар жиыны А жиынының Е эквивалентке қатысты

фактор жиыны деп аталады,  деп белгіленеді: . Фактор жиын булеанның ішкі жиыны болып табылады.

          6-мысал.  А – АЭжБИ студенттер жиыны, Е – студенттік группаға тиесілік қатынасы. Эквиваленттілік класы – бір группадағы студенттер жиыны. Е–ге қатысты АЭжБИ студенттер жиынындағы фактор жиын АЭжБИ студенттік топтар жиыны болады.

          Анықтама бойынша:

          а) эквиваленттілік класының кез келген элементі эквиваленттілік класын туындайды, яғни егер , онда ;

          ә) әрбір эквиваленттілік класта кем дегенде бір элемент бар, яғни

;

          б) ешқандай элемент екі әртүрлі класқа бірден тиесілі бола алмайды

, онда

          Бөлікше анықтамасын еске түсірсек, онда

          Теорема.  фактор-жиын А жиынының бөлікшесі болып табылады. Керісінше, егер A - А жиынының қандай-да бір бөлікшесі, онда оған сәйкес Е эквиваленттілік қатынасын  орнатуға болады.

          Сонымен, А жиынындағы барлық эквиваленттік қатынасы мен А-дағы барлық бөлікшелер арасында өзара бірмәнді сәйкестік орнатуға болады.

          7-мысал.  жиыны берілсін. 

A– бөлікшесі, ал    –  

осы бөлікшеге сәйкес эквиваленттік қатынас болады.

         8-мысал.   жиыны берілсін.  және

 болсын:

а)  қатынасының эквивалентті қатынас болатындығын көрсетейік, яғни бұл қасиет рефлексивті, симметриялы және транзитивті қасиеттерге ие болатын-дығын тексереміз. Ол үшін

 қатынасының матрицасын құрамыз

.

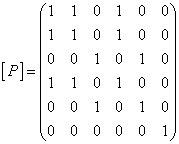1) - рефлексивті, себебі матрицадағы бас диагональда бірлер тұр;

2) - симметриялы, себебі  ;

3)

.

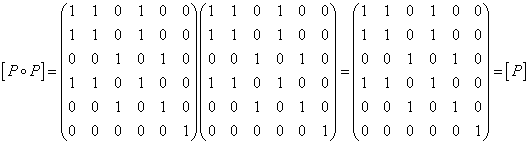Сондықтан - транзитивті. Олай болса, - эквивалентті қатынас;

ә) эквиваленттілік класы мен барлық эквиваленттілік кластарының жиынын (яғни  фактор-жиынын құрайық).

Сонымен үш эквиваленттілік класы бар

Сондықтан фактор-жиын . Сонымен берілген эквивалентті қатынасқа сәйкес А жиынының бөлікшесін алдық.

Бұл мысалдан:

а) эквиваленттілік класының кез келген элементінен  эквиваленттілік класс туындайды (яғни  );

ә) әрбір эквиваленттілік класында ең болмағанда бір элемент болу керек (яғни );

б) әр элемент тек бір ғана класқа тиесілі болу керек ().

 

           1.4 Реттік қатынастар

          Егер А жиынында Р қатынасы антисимметриялы және транзитивті болса, ол реттік қатынас деп аталады. Реттік қатынас рефлексивті болса, онда ол дербес реттілік (қатаң емес,  мысалы ), ал антирефлексивтік қосылса, онда қатаң реттілік (қатаң,  мысалы, ) деп аталады.

          А жиынында реттік қатынас берілген болсын. Егер осы жиынның екі ,  элементтері үшін  немесе  орындалса, онда бұл элементтер салыстырмалы деп аталады, қарсы жағдайда салыстырылмайтын деп аталады.

         Егер А жиынының кез келген екі элементі салыстырылмалы болса, онда осы жиындағы дербес реттілік сызықты (толық, тізбектей) деп аталады.

Дербес (сызықты) реттілік анықталған жиын дербес реттелген жиын (сызықты реттелген жиын) деп аталып, д.р.ж.  (с.р.ж) деп белгіленеді.

          1-мысал. жиыны берілсін:

          а) - дербес реттілік қатынас.

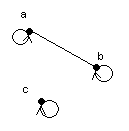Ол сызықты болмайды, себебі  және ,  және  арасында қатынас жоқ, салыстыруға келмейді.                                

 

 

 

 

        1.11 Сурет

 

          Оның матрицасы 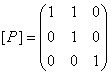- бірлік матрица, рефлексивті (тепе-тең);

          ә) P(A)Ø,.

          Осы P(A) жиынында келесі қатынасты анықтайық:

=

P(A) – дербес реттелген жиын болады, бірақ сызықты реттілік емес, себебі  салыстырмалы, ал   және  салыстырылмайтын элементтер;

б) сызықты реттелген жиын – бұл N, Z, Q, R жиындары (кәдімгі рет бойынша алынған “<”, “>”, “=”…). Бұл сызықты реттелген жиынды <N,>, (Z, ) жұбы ретінде белгілейді.

          Сызықты реттелген жиынды бірінші элементіне қарай бөлуге болады. Мысалы, егер сызықты реттелген жиын ретінде натурал және бүтін сандар жиынын алатын болсақ, онда натурал сандарда кіші элемент бар, ал бүтін сандарда жоқ.

          Егер реттелген А жиынында    орындалатын х элементі болмаса,  элементі  минималды (максималды) деп аталады.

Егер сызықты реттелген жиынның бос емес ішкі жиынында минимальды элемент бар болса, онда ол әбден реттелген деп аталады.

          2-мысал. әбден реттелген жиын.

          3-мысал.  әбден реттелген жиын, себебі , бірақ -де ең кіші элемент жоқ.

 

Лексикографиктік реттілік

          Лексикографиктік реттілікте сөздіктегі сөздердің реттелуі негізге алынған.  Мысалы «арман» сөзі «болат» сөзінен бұрын, себебі алфавитте а әріпі б әріпінен бұрын орналасқан.

бос емес символдар жиыны берілген, ол алфавит деп аталады. Х-тен алынған бірінен соң бірі жазылған символдардың ақырлы жиынтығы сөздер деп аталады, мысалы, .  сөзінің  элементі оның ші координатасы, ал  оның ұзындығы деп аталады. W(x) - Х алфавитіндегі сөздер жиыны.

 X-тегі реттік қатынас болсын, яғни  - реттелген жиыны берілген. W(x) жиынындағы лексикографиктік рет деп  деп белгіленеді) келесі ережеге сүйенетін қатынас айтылады

 және  немесе ) және

 үшін  шарты орындалады.

 .5 Функция. Функционалдық қатынас

         Анықтама.  Егер

а)  ;

ә)  

шарттары орындалса, онда А жиынынан В жиынына  бинарлы қатынасы функционалдық (функция) деп аталады.

(яғни бұл бинарлық қатынаста бірінші элементі бірдей, ал екінші элементі әртүрлі екі жұп болмайды немесе    функция).

         Егер  орнына  орындалса, онда  дербес функция деп аталады. А-дан В-ға бейнеленетін  функциясы былай белгіленеді:  немесе .

         Егер  болса, онда   функциясының мәні, ал аргументі деп аталады) немесе  ( функциясы  элементіне  элементін сәйкес қояды).

         Мысалы:

а) функция;

ә) функция емес, себебі   элементіне  элементтері сәйкес келеді;

б) функция, мұндағы ;

в) функция емес.

         Анықтама.  болсын.

         а) егер   қатынасы дербес функция болса, яғни кез-келген  элементтері үшін -ден  екені шығатын болса (немесе  және , онда  функциясы инъективті (инъекция немесе әртүрлі мәнді) деп аталады;

 

 

 

 


                                                  Инъекция (сюръекция емес)

              1.12 Сурет

ә) егер  болса, онда  функциясы сюръективті (сюръекция) деп аталады.       сюръекция;

 

                                               

 


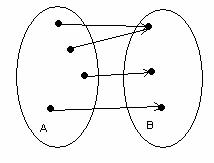
                                                         Сюръекция (инъекция емес)

                  1.13 Сурет

               б) егер  функциясы әрі инъективті, әрі суръективті болса, яғни А жиынының әрбір элементіне В жиынының тек бір элементі және В жиынының әр элементіне А жиынының кейбір элементі сәйкес келетін болса, онда ол биективті (биекция немесе өзара бірмәнді) деп аталады.

Биекция деп белгіленеді.

1-мысал.

                                                       

 

 

 

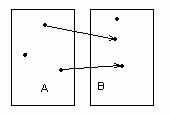
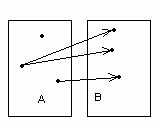
               қатынас емес                       инъекция (сюръекция емес)

 


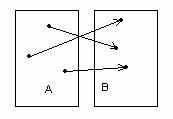                сюръекция (инъекция емес)                 биекция

 

                                                      1.14 Сурет

 

 

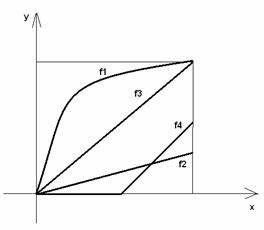
          2-мысал.  

функцияларын қарастырайық.

   1.15 Сурет

  биективті;

инъективті, сюръекция емес;

          сюръекция, инъекция емес;

  инъекция емес, сюръекция емес.                                                                         

          Жиындар қуаты

          Жиындар қуаты түсінігі элементтер санына байланысты жиындарды салыстыру барысында пайда болады.

          Анықтама. Егер  биъекциясы бар болса, онда А және В жиындары эквивалентті деп аталады (А~B – деп белгіленеді).

          Сонымен ақырлы элементтер саны бар екі жиынның элементтер саны тең болса, олар эквивалентті болады. Ал егер элементтер саны шексіз көп болса, онда жиынның қуаты деген түсінік пайда болады.

          Анықтама. А жиынының қуаты деп А жиынына эквивалентті жиындар класы айтылады,  - деп белгіленеді:

          а) егер А жиыны ақырлы  элементтен тұратын жиын болса,  болады. А және В эквивалентті жиындар қуаттары бірдей болып есептеледі;

          ә) егер А элементтер саны ақырсыз жиын және N- натурал сандар жиынына эквивалентті болса, онда А – санамалы (санаулы) жиын деп аталады  (санамалы жиынның элементтерін нөмірлеуге болады). А жиыны мен N натурал сандар жиынымен өзара  бірмәнді байланыс орнатуға болса, онда А санамалы жиын деп аталады;

          б) натурал сандар жиынымен өзара бірмәнді сәйкестік орнатылмайтын ақырсыз жиындар санамалы емес жиындар деп аталады.

          Мысалы, Кантор теоремасы бойынша [0,1] кесіндісінде нақты сандар жиыны санамалы емес. Мұндай жиындар қуатын континуум деп аталады (С деп белгіленеді). Ал жиынның өзін континуалды немесе континуум деп атайды. Сонымен континуалды жиын қуаты , яғни санамалы жиынның барлық ішкі жиындарының жиынының қуатына тең.

          Жалпы кез келген  жиыны үшін, оның қуаты . (U) – жиынның ішкі жиындарынан тұратын жиын немесе булеан.

          1-мысал. Санамалы жиындар:

          а) бүтін сандар жиыны (оң және теріс);

          ә) рационал сандар жиыны (Q);

          б) натурал сандар жиынының (N) кез келген ішкі жиындары;

          в)  санамалы.

          2-мысал. Континуалды жиындар:

          а) нақты сандар жиыны N (сан өсіндегі нүктелер жиыны);

          ә) кеңістіктегі (жазықтықтағы) бүкіл нүктелер жиыны;

          б) санамалы жиынның ішкі жиындарының жиыны  санамалы жиын).

          Жиындар теориясында кез келген қуатты жиын үшін оның ішкі жиындарынан тұратын жиынның қуаты әлдеқайда жоғары. Сондықтан ең жоғары (ең көп, максималды) қуатты жиын болмайды. Жиынның қуатына жаңа көзқараспен қарауға болады, оны қандай да бір жаңа объект ретінде қарастырсақ болады, оны кардинал немесе кардиналды сан деп атайды.

     

          3-мысал.

          а) кез келген натурал сан n (n элементтен тұратын ақырлы жиынның қуаты);

          ә)  және т.б.

  2 Математикалық  логика элементтері

          Математикалық логика екі негізгі бөлімнен тұрады: айтылымдар логикасы және предикаттар логикасы.

          Анықтама. Айтылым деп дәл осы уақытта оның ақиқаттығы немесе жалғандығы белгілі хабарлы сөйлемді айтады.

          Мысалы. Екі қосу екі тең төртке (хабарлы сөйлем, ақиқат). Манат – Қазақстанның валютасы (хабарлы сөйлем, жалған).

          Анықтама. Қарапайым айтылым деп бөліктелмейтін, бүтін бір ұғымды айтады (жиынның элементтері сияқты). Айтылымдарды А, В, С, ... , Р, Q, ...  бас әріптермен белгілейді.

         Анықтама. Күрделі айтылымдар деп логикалық байланыс (операциялар, қисаптар) арқылы байланысқан қарапайым айтылымдардан тұратын сөйлемді айтады.

 2.1 Негізгі логикалық операциялар (қисаптар)

          2.1.1 Конъюкция («және» операциясы, логикалық көбейту), белгіленуі  (“Р  және Q” деп оқылады).

P және Q айтылымдардың конъюкциясы деп тек екеуі де ақиқат болған жағдайда ақиқат болатын, қалған жағдайда  жалған болатын айтылымды айтады.

          2.1.2 Дизъюнкция («немесе» операциясы, логикалық қосынды), белгіленуі  (“Р  немесе Q” деп оқылынады). Екеуі де жалған болған жағдайда жалған болып есептелетін, қалған жағдайда ақиқат айтылым.

          2.1.3 Теріске шығару (инверсия, «бірақ»), белгіленуі (“ емес”, “ теріс” деп оқылынады). Р айтылымның керісі деп Р жалған болғанда ақиқат болатын, ал Р ақиқат болғанда жалған болатын айтылымды айтады.

          2.1.4  Импликация (логикалық салдар), белгіленуі   (“егер Р болса, онда Q” немесе “Р-ның салдары Q”, “Р-дан Q шығады” деп оқылады).

Р ақиқат, ал Q жалған болғанда жалған болатын айтылым. Р айтылымы импликацияның бастамасы, ал Q – қорытындысы деп аталады.

          2.1.5 Эквиваленттілік (эквиваленция, бірдей мәнді), белгіленуі    (“Р  айтылымы Q айтылымына эквивалентті”, “Р , тек егер Q” , “Р мен Q бірмәнді”  деп оқылынады). Р мен Q ақиқат мәндері сәйкес келгенде ақиқат болатын, қарсы жағдайда жалған болатын айтылымдарды эквивалентті айтылымдар деп атайды.

          2.2 Логика алгебрасы

          Логика алгебрасын қолданып, айтылымдар логикасының мазмұнын қарастырайық. Айта кетелік, логика алгебрасында логикалық формулалар алгебралық  өрнектер ретінде қарастырылады, оларды логикалық заңдарға бағынатын ережелер бойынша түрлендіруге болады. Логика алгебрасы математикалық логиканың бір бөлігі ретінде логикалық айтылымдардың (формулалардың) және алгебралық әдістер көмегімен олардың ақиқаттығын анықтайды.

          Р айтылымына х логикалық айнымалысын сәйкес қоямыз. Егер Р ақиқат болса, онда х айнымалысы 1 мәнін, ал  Р жалған болса, онда 0 мәнін  қабылдайды.

          Анықтама-1. Кез келген айнымалы формула болып табылады (ең кішкентай формула – атом, атомарлы формула деп те аталады).

          Анықтама-2. Егер  және  формулалар болса, онда  өрнектері де формула болады.

          Анықтама. Анықтама-1 және анықтама-2 бойынша құрылған формулалардан өзге формула жоқ.

          Егер  формуласы  жиынына тиісті логикалық айнымалылардан құралған болса, онда  деп жазамыз. Логикалық операциялар нәтижесі ақиқат кестесі арқылы беріледі. Мысалы теріске шығару операциясы

            2.1 К е с т е

0

1

1

0

 

 

Қалған логикалық операциялар анықтамасын төменгі кесте арқылы еске түсіруге болады.

          2.2 К е с т е

0

0

0

0

1

1

0

1

0

1

1

0

1

0

0

1

0

0

1

1

1

1

1

1

          Бұл кесте арқылы кез келген формуланың ақиқаттығын анықтай аламыз, яғни олар үшін ақиқат кестесін құруға болады.

                   1-мысал.

 формуласының ақиқаттық кестесі

 2.3 К е с т е

у

0

0

0

1

1

0

1

1

1

0

0

1

1

1

1

1

1

1

0

1

0

1

0

1

1

1

1

0

1

1

1

0

1

1

1

1

1

0

0

0

1

0

0

1

0

1

0

1

0

1

1

0

0

0

1

1

0

1

0

1

0

0

0

1

1

1

1

0

1

0

0

0

 

 

 

 

 

          2-мысал.

 формуласының ақиқаттық кестесі

                            2.4 К е с т е

у

0

0

0

1

1

1

1

0

0

1

1

1

1

1

0

1

0

1

0

1

1

0

1

1

1

0

1

1

1

0

0

0

1

1

1

1

0

1

0

1

1

1

1

1

0

0

0

0

1

1

1

1

0

0

0

0

 Бастапқы бес негізгі  логикалық операциядан басқа тағы үш логикалық операция бар:

         а) Шеффер штрихы (антиконъюнкция),  белгіленуі .

 немесе ;

         ә) Пирс стрелкасы (антидизъюнкция), белгіленуі .

 немесе ;

         б) сақиналы қосынды (логикалық қосынды, екі модуль бойынша қосынды), белгіленуі .

 немесе .

         Анықтамаға сүйеніп, бұл операциялардың ақиқаттық кестесін құруға болады

                                      2.5 К е с т е

0

0

1

1

0

0

1

1

0

1

1

0

1

0

1

1

1

0

0

0

 Математикада өрнекті түрлендіргенде алдымен көбейту, содан соң қосу немесе азайту амалдарын орындаған сияқты, логика алгебрасында да, әр операцияның өз кезегі  бар. Ол үшін төменгі келісімдерді келтірейік:

а) сыртқы жақшаларды жазбауға болады;

Мысалы.  орнына    жазуға болады;

ә)  - логикалық операциялар жиынында  «күштірек» немесе «күштері басым» және ~ «күштері бірдей» транзитивтік қатынастарын келесі сұлба бойынша енгізейік.

 

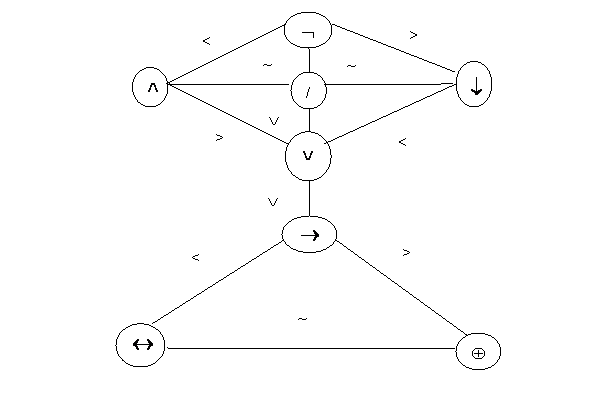
2.1 Сурет

         Бұл келісімдерге сәйкес амалдарды орындау жақша жоқ жерде алдымен «күштірек» байланыстан басталып, «әлсізден» аяқталады, ал «күші бірдей» байланыстар үшін амалдарды солдан оңға қарай орындау керек.

         Келесі  формулаларда амалдар орындау ретіне сай жақша қою керек.

         3-мысал. .

         Жауабы: .

         4-мысал. .

         Жауабы: .

         5-мысал.  өрнегінде жақшаны алып тастауға болмайды, себебі біздің келісім бойынша  өрнегіне  формуласы сәйкес келер еді.

 Логика алгебрасының функциялары

         Әрбір формуланы логикалық айнымалылы логикалық функция деп түсінуге болады, ол функция тек екі мәнді 0 және 1-ді қабылдай алады.

         Анықтама.  n айнымалылы  логика алгебрасының функциясы деп, кез келген  нөлдер мен бірлердің жиынтығына  мәнін сәйкес қоятын кез келген функцияны айтады, яғни .

         Логика алгебрасының функциясы буль функциясы, екілік функция немесе ауыстырып-қосқыш функция деп аталып,  деп белгіленеді. Себебі бұл функциялар белгілі бір қондырғының кіру сигналдарын шығу сигналдарына түрлендіруін сипаттайды. Қондырғының n  кіру (ену) жолы бар, оларға ток берілуі де, берілмеуі де мүмкін және осы қондырғыда бір шығу жолы бар, оған да ток берілуі, берілмеуі кірер жолда токтың берілуіне байланысты.

                                                           

                                                                                                                                                      

                                                           

                                                                           

                                                           

                                                        2.2 Сурет

Бұл жағдайда i-нші кіру    жолына ток берілгенде  мәнін, ал берілмегенде  мәнін қабылдайды.  (мұнда ) мәнін, ток шығу жолынан өткенде, ал    ток өтпеген жағдайда  қабылдайды.

         Мысалға,  функциясы екі кіру жолы және бір шығу жолы бар қондырғыдағы конъюнкция операциясын көрсетеді.

 

                     2.3 Сурет

         Бұл жағдайда егер екі кіру мәні де бірге тең болса, шығу мәні  де бірге тең болады.

 Логикалық функциялардың берілу жолдары

         1. Ақиқаттық кестесі арқылы.

Кестенің сол жағында  аргументтерінің қабылдайтын мәндері, ал оң жағында оған сәйкес  мәні орналасады.

         2. Функцияны 0 мәнін (нөлдік жиынтық) қабылдайтын барлық жиынтықтарды тізу және сол сияқты 1 мәнін (бірлік жиынтық) қабылдайтын жиынтықтарды тізу арқылы беруге болады.

         3. Функцияның берілу тәсілі ретінде формуланы қарастыруға болады.

         Дауыс беру мысалын қарастырайық. Үш мүшеден тұратын комитет қандай да бір резолюцияның қабылдау барысын қадағалайтын құрылғыны қарастырайық. Комитеттің әрбір мүшесі резолюцияны қолдайтын болса, өз кнопкасын басады, егер көпшілігі қолдаса, онда резолюция қабылданады. Бұны қондырғы өзіне белгілейді.

         Сонымен қондырғыны  функциясы іске асырады, ақиқаттық кестесі мына түрде беріледі.

                                         2.4 К е с т е

x

y

z

0

0

0

0

0

0

1

0

0

1

0

0

0

1

1

1

1

0

0

0

1

0

1

1

1

1

0

1

1

1

1

1

Көпшілік дауыс 2 немесе 3 болғанда,   қабылданады. Бұл функцияны нөлдік жиынтықпен қабылдауға болады:  немесе бірлік жиынтық:

         Анықтама.  функциясының мәндерінің векторы деп -тің барлық мәндерінің реттелген жиынтығы айтылады, ал мәндер аргумент жиынынан  () лексикографиктік тәртіппен реттеледі.

         Жоғарыдағы мысалда  мәндерінің векторы (0,0,0,1,0,1,1,1) жиынтығы болады.

         Е с к е р т у - Лексико-графиктік реттілік екі саннан тұратын жиынтықтың өсу ретіне сәйкес келеді. Графтар теориясындағы ағаш ұғымын қолданатын болсақ, 0 және 1 әртүрлі жиынтықтарын келесі жолмен алуға болады: бұл ағаштың әрбір қабатында ұзындығы n болатын () әртүрлі нөлдер мен бірлердің жиынтығы орналасады. І қабатында (жоғарыда) - n; ІІ қабатында - n; ІІІ қабатында - n, ..., т.б.

                                                2.4 Сурет

 

         Сонымен, 0 және 1-ден тұратын барлық мүмкін жиынтықтар n айнымалылы функцияның саны  тең, яғни бір айнымалылы функция үшін 2, екі айнымалылы функция үшін , т.б. Ал барлық мүмкін болатын әртүрлі n функциялардың саны   болғанда, 0 мен 1-дің орналасу жағдайларының санына тең, яғни .

         Егер  деп  функцияның аргументтерінің мәндерінің жиынын белгілесек, ал  барлық  аргументті функциялар болса, онда бұл жиындардың қуаты . Сонымен  тез өседі.

, , ,  т.б.

         Анықтама. Егер , онда  функциясы  және  функцияларының суперпозициясы деп аталады,

         Мысалы:  функциясы  және , ,   функцияларының суперпозициясы.

         Анықтама.   функциясы нөл мен бірлердің барлық жиынтығында 1 мәнін (0 мәнін) қабылдаса,  яғни , онда ол 1 константасы (0 константасы) деп аталады.

 Формулалар эквиваленттігі.

Логика алгебрасының негізгі эквиваленттік қатынастары

         Жоғарыдағы 1-мысалдағы  және  формулаларының ақиқаттық кестелері бірдей болуы мүмкін. Бұл жағдайда эквивалентті формулалар ұғымы пайда болады.

         Анықтама. Егер ,  формулаларының  ақиқаттық кестелері бірдей болса, онда олар эквивалентті (күші бірдей) деп аталып,   деп белгіленеді.

         Мысалы.  формулалары үшін ақиқаттық кестесін құрайық.

 

       2.5  К е с т е

x

y

0

0

1

1

1

1

0

1

0

1

1

1

1

0

1

0

0

0

1

1

0

0

1

1

Ақиқаттық кестесі бірдей, сондықтан

 

 Бұл мысалда формулалар эквиваленттілігін кәдімгі стандарт әдіспен тексердік:

а) әрбір формулаға ақиқаттық кестесін құрдық;

ә) айнымалының мәндерінің жиынтығы бойынша кестедегі нәтижелерді

салыстырдық.

Басқа әдіс - эквивалентті түрлендірулер. Мұнда эквивалент қатынастар (заңдар) мен ауыстыру ережелері қолданылады.

 2.6  К е с т е - Негізгі эквиваленттік қатынастар (заңдар)

1

Орын ауыс-

тырымдылық

(коммутативтік)

2

Терімділік

(ассоциативтік) 

3

Үлестірімділік

(дистрибутивтік) 

4

Идемпотенттік 

5

Сіңіру заңы  

6

Де-Морган заңы 

7

Екі рет теріске шығару                 

8

Константалардың қасиеті

9

- қарама-қайшылық заңы

- шығып қалған үшінші заңы

 2.7  К е с т е - Тағы да басқа керекті эквиваленттік қатынастар

10

Жапсыру заңы

 

10 а

Тарқату

11

Жалпыланған жапсыру

12

13

14

15

16

          Анықтама. Егер формуласы 1 мәнін (0 мәнін) қабылдайтындай айнымалы мәндерінің жиынтығы табылатын болса, онда  формуласы орындалатын (теріске шығарылатын) деп аталады.

         Мысалы.   формуласы бір мезгілде орындалатын (1 және теріске шығарылатын  болады.

         Анықтама. Егер  формуласы айнымалы мәндерінің барлық  жиынтығында 1 мәнін (сәйкес 0 мәнін) қабылдаса (яғни 1 константа немесе 0 константа болса), онда  формуласы тепе-тең ақиқат (жалпы мәнді) немесе «тавтология» (жалпы жалған, қарама-қайшылық) деп аталады.

         Мысалы.   формуласы – тепе-тең ақиқат,         

      формуласы – жалпы жалған болады, себебі

    2.8 К е с т е

х

х

х

0

1

1

0

1

0

1

0

          Егер  тепе-тең ақиқат болса, онда  деп белгілейміз.

          Егер  жалпы жалған болса, онда  деп белгілейміз.

          Е с к е р т у л е р

          1 Егер  формуласы тепе-тең ақиқат болса ғана, онда  ол тепе-тең  жалған болады  .

          2 Егер  формуласы тепе-тең ақиқат болмаса  ғана, оны теріске шығаруға болады .

         3 Егер  формуласы тепе-тең жалған болмаса ғана, ол  орындалатын болады .

         4 Егер  тепе-тең ақиқат,  тепе-тең жалған болса, онда кез-келген  үшін келесі эквиваленттіктер орындалады

                                     

 

 

 

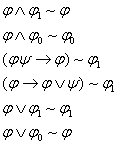
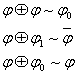
          2.3 Буль алгебрасы

          Алдыңғы тақырыпта көрсетілгендей, бір ғана логикалық функция әртүрлі логикалық операциялардың жиынтығы арқылы беріле алады. Мысалы .

          Анықтама. Егер кез келген логикалық функция сигмадағы () функциялардың суперпозициясы болса, онда сигма () логикалық  функциялардың жүйесі (жиынтығы) функционалды толық жүйе (немесе базис) деп аталады.

          Мысалы логикалық функциялардың толық жүйесі:

т.б.

          Осылардың ішінде жиі қолданылатын  базис болып табылады.

          Айнымалыдан, жақшадан басқа конъюнкция, дизъюнкция және теріске шығару таңбаларынан тұратын формулалар буль формулалары деп аталады.

          Теорема. Кез келген логикалық функция буль формуласы бола алады.

          Бұдан  жүйесінің функционалды толықтығы шығады. Сондықтан қандай-да бір операциялардың жиынтығының толықтығын дәлелдеу үшін операциялар жиынтығы арқылы конъюнкция, дизъюнкция және теріске шығару операцияларын өрнектеуге болады. Бұл тұжырымды жалпыласақ,

          Теорема. Егер  функционалдық толық жүйесінің барлық функцияларын -дағы формулалармен өрнектеуге болса, онда -да функционалдық толық жүйе болады.

          1-мысал.   және  жүйелері,  базисі берілген. ,  функционалды толық болады, себебі олардың әрқайсысындағы   -де жетпей тұрған операцияны қалған екеуі арқылы өрнектеуге болады  (-де «», -де «» жетпей тұр).

 Де  Морган  заңыүшін         

 Де  Морган  заңыүшін        

          2-мысал.   буль формуласын ,  жүйелерінде қарастырайық.

де,

 де.

          Сонымен функционалдық толықтық ретінде  жүйесін кең ауқымды деп есептеуге болады, себебі одан конъюнкцияны немесе дизъюнкцияны  шығарып тастасақ, ол толықтығын жоймайды. Бірақ ,  кең ауқымдыға жеткізу үшін () амалын қолданғанда, теріске шығару амалы шамадан тыс көп енгізіледі.

          2.4 Дизъюнктивті және конъюнктивті қалыпты формалар

             (ДҚФ, КҚФ)

         Анықтама. Айнымалылардың немесе олардың терістерінің конъюнкциясы элементар конъюнкция (конъюнкт) деп аталады (барлық айнымалыларды қамту қажет емес). Осы сияқты элементар дизъюнкция (дизъюнкт) деп айнымалылардың немесе олардың терістерінің дизъюнкциясы айтылады.

          1-мысал.  және дизъюнкт.

          2-мысал.   және конъюнкт.

          3-мысал.  бір мезгілде конъюнкт те, дизъюнкт те болады.

          Анықтама. Элементар конъюнкциялардың (конъюнкттардың) дизъюнкциясы дизъюнктивті қалыпты форма (ДҚФ), ал дизъюнкттардың конъюнкциясы конъюнктивті қалыпты форма деп аталады. (КҚФ).    

          4-мысал: а) конъюнкт;

              ә)ДҚФ.

          5-мысал: а) дизъюнкт;

                            ә) КҚФ.

           Формуланы ДҚФ – ке келтіру ережелері:

          а) формуладағы кездесетін логикалық операцияларды, эквиваленттіктерді қолданып, конъюнкция, дизъюнкция және теріске шығару  арқылы өрнектейміз:

          1) ;

          2) ;

          3) ;

          4) ;

          5) ;

          ә)   де Морган заңына сүйеніп:

         

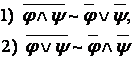
теріске шығаруларды айнымалыларға қолданамыз және  ережесіне сүйеніп, екі еселі теріске шығаруларды жоямыз;

          б) үлестірімділік (дистрибутивтік) заңын қолданып, формуладағы конъюнкциялар дизъюнкциядан бұрын орындалатындай етіп түрлендіреміз.

          6-мысал.   формуласын ДҚФ-ке келтіру керек.

          Ол үшін формуладағы  таңбаларын  таңбаларына ауыстыру керек.

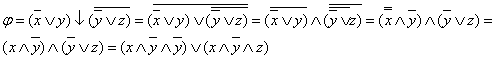
          Соңғы формула [1] бойынша ДҚФ болып есептелінеді. Ал [2] оқулығында әрбір айнымалы конъюнкцияда және дизъюнкцияда бір-ақ рет кездесуі керек.

Сондықтан, артық айнымалыларды жою үшін келесі эквиваленттікті қолданамыз:

а)  (идемпотенттік);

ә) (үшіншіні жою);

    (қарама-қайшылық заңы);

б) ,

     -( константалар қасиеті),

    - [2] бойынша ДҚФ.

          Формуланы КҚФ – ке келтіру ДҚФ-ке келтіру сияқты жүргізіледі, тек 3) пункттегі ереже орнына келесі ереже болу керек: ) үлестірімділік (дистрибутивтік) заңын қолданып, формуладағы дизъюнкциялар конъюнкциялардан бұрын орындалатындай етіп түрлендіру керек. .

          1-есеп.  формуласын КҚФ-ке келтіру керек.

          Шешуі:      алдымен  операциясын ауыстырамыз

 [ Де-Морган заңы,  сосын ] =

 - КҚФ.

Әрі қарай түрлендірейік, ол үшін алдыңғы екі жақша үшін үлестірімділік заңды қолданамыз. 

 - ДҚФ, КҚФ бола алады.

          Сонымен, бір формуланың бірнеше ДҚФ, КҚФ болады, жалғыздық қасиеті орындалмайды.

          Анықтама. Мүлтіксіз дизъюнктивті қалыпты форма (МДҚФ) деп әрбір элементар конъюнкцияға енетін әрбір айнымалы бір-ақ рет кездесетін және енетін не өзі, не оның терісі ғана болатын ДҚФ-ты айтамыз және элементар конъюнкттар  арасында бірдей болмауы керек.

          Анықтама. Мүлтіксіз конъюнктивті қалыпты форма (МКҚФ) дегеніміз келесі шарттарды қанағаттандыратын КҚФ: әрбір элементар дизъюнкцияға енетін әрбір айнымалы бір-ақ рет кездеседі және не айнымалы, не оның терісінің екеуінің біреуі ғана ену керек, элементар дизъюнкттардың бірдей болмау керек.

          7-мысал:

          а)  - МДҚФ;

          ә) - МКҚФ;

          б)  - МДҚФ емес, бірінші және үшінші конъюнкттар бірдей;

          в)  - МДҚФ емес, бірінші конъюнктке екеуі де еніп тұр.

          2-есеп.   формуласын ДҚФ-ке келтіру керек.

          Шешуі

 

.

          3-есеп.  формуласын КҚФ-ке келтіру керек.

          Шешуі

.

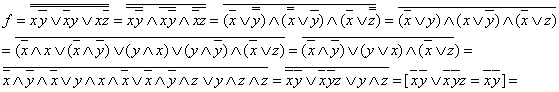
          Теорема  (МДҚФ мен МКҚФ-ның бар болуы мен жалғыздығы) .

Әрбір логикалық формуланы бір ғана жолмен МДҚФ (МКҚФ) түрінде жазуға болады. (Элементар конъюнкттік дизъюнкттің тізілу ретінің дәлдігіне дейін).

МДҚФ-қа келтірудің екі әдісі бар:

          1 әдіс. Алдымен формуланың ДҚФ табамыз, сосын оның конъюнкттарын келесі амалдармен түрлендіреміз:

          а) егер конъюнкт құрамында айнымалымен қоса оның терісі де болса, онда оны ДҚФ-тан алып тастайды;

ә) егер х айнымалысы мен оның терісі  конъюнктқа бірнеше рет енсе, онда біреуін қалдырып, қалғанын алып тастайды (яғни );

б) егер қандай да бір конъюнкт құрамына кейбір у айнымалысы енбесе, онда оны тарқату немесе кері жапсыру заңын қолдану арқылы енгізеді;

в) егер бірдей конъюнкттер кездессе, идемпотенттік заңды қолданып, біреуін қалдырады.

          4-есеп. - ДҚФ, оны МДҚФ-ке келтіру керек.

          Шешуі

.

         2 әдіс. Берілген формуланың ақиқат кестесін құрады. Сосын Шеннон теоремасына негізделген ережені қолданады:

 функцияның МДҚФ-да  мәндер бағанасында қанша 1 болса, сонша конъюнкт болады;  нөл мен бірлердің әрбір бірлік жиынтығына барлық айнымалылардың конъюнктасы сәйкес келеді, егер  болса, онда  терісімен алынады және  болса, онда теріске шығармай өзі алынады.

          5-есеп.  - ДҚФ, оны МДҚФ-ке келтіру керек.

          Шешуі

                    2.9 К е с т е

х

у

0

0

0

1

1

0

1

0

0

0

0

0

1

1

1

0

1

1

0

1

0

1

0

1

0

0

0

0

0

0

0

1

1

1

0

0

0

0

0

1

1

0

0

0

1

0

0

0

1

1

1

0

1

0

1

0

0

0

1

1

1

1

0

0

0

1

0

0

1

1

1

1

1

0

0

1

0

0

1

1

             Бұл кестедегі соңғы бағаннан   бірлік жиынтықтарды теріп жазамыз: . Соңғы әдіс бойынша

.

КҚФ-ны МКҚФ-ға келтіру  ДҚФ-ны МДҚФ-ға келтіру  сияқты жүргізіледі:

          а) эквивалентті түрлендіру;

         ә) ақиқаттық кестесі бойынша МДҚФ-ға келтіру:

функцияның мәндерінің бағанында қанша 0 болса, МКҚФ-да сонша дизъюнкт болады.  нөл мен бірлердің нөлдік жиынтығына барлық айнымалылардың дизъюнктасы сәйкес келеді, егер  болса, онда  терісімен алынады және егер  болса, онда өзгеріссіз қалады (теріске шығармай).

          8-мысал. Алдыңғы есептегі формуланы  МКҚФ-ға келтірейік.

          Бұл бірінші әдіс бойынша. Ал екінші әдіс бойынша 1 кестедегі  нөлдік жиынтықтарды теріп жазамыз: ,  бойынша  .

          2.5 Дизъюнктивті қалыпты формалар класында минимилизациялау.

          Карно картасы

Практикалық есептерді шешкенде, логикалық формулаларды минимилизациялау есебі жиі кездеседі. Релейлі-контакт сұлбасымен мысалды алсақ (немесе коммутациялық сұлба, электр тізбегі), әрбір сұлбаны логикалық формуламен сипаттау керек. Формула неғұрлым қарапайым болса, онда сұлба да соғұрлым қарапайым болады.

Енетін айнымалылар саны минималды болатын дизъюнктивті формаларды табу есептері жақсы зерттелген.

          Айнымалының енуі деп, формуладағы айнымалының алатын орнын тусінуге болады.

         Анықтама.  Айнымалының ену саны ең аз болатын ДҚФ минималды ДҚФ деп аталады.

         Минималды ДҚФ-ны алу жолдарының бірі Карно картасын (диаграммасын) қолдану болып табылады. (Басқа жолы – элементар түрлендірулер арқылы).

         Карно картасы – бұл әрбір клеткасы (ұяшық) конъюнкциядан (конъюнктадан) тұратын кесте.   n айнымалылы функция үшін  элементар конъюнкция бар болады (n айнымалылы функция үшін нөл және бірдің мүмкін болар жиынтықтар саны сияқты). Яғни n=2 үшін :

а) , n=2;

ә) , n=3 және т.б.

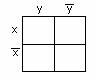          Карно картасы  өлшемді матрица түрінде салынады. Оның бағанына  айнымалыларының мәні сәйкес келеді, жолына  айнымалыларының мәні сәйкес келеді немесе керісінше, ал көрші ұяшық (тігінен не көлденең айырмашылығы жоқ) бір айнымалының мәніне ғана өзгеше болады. Айта кетелік, бір функция үшін бірнеше Карно картасын салуға болады.

          Мысалы:

          а) х, у екі айнымалы функция үшін Карно картасы

                      

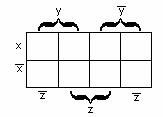ә)  үш айнымалылы функция үшін:

                                                                                                           

 

 

2.5 Сурет                                                                                              2.6 Сурет

 б)  төрт айнымалы функция үшін:         

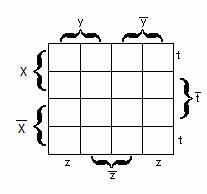  2.7 Сурет                                                                                                                                                                  

z буль функцияның минималды ДҚФ-ын анықтау үшін алдымен оның МДҚФ-ын табу керек (ақиқат кестесі көмегімен), содан соң МДҚФ-ң әрбір элементар конъюнкциясын сәйкес Карно картасындағы ұяшыққа 1 деп белгілеу керек.

         1-мысал. а)  үшін Карно картасы

 

 

 

2.8 Сурет                                                                                                                                                                  

 Егер Карно картасында тігінен не көлденеңінен көршілес 2, 4, 8  (төрт айнымалы функция үшін) ұяшықта 1 болса, онда бұл ұяшықтарды тұтас «блокқа» жинауға болады, яғни сәйкес конъюнкттардың дизъюнкциясын қысқартуға болады.

         Алдыңғы мысалда көлденеңнен екі  ұяшықта 1 тұр, оған сәйкес келетін формула

.

         Сонымен екі  ұяшықтан тұратын блокқа  бір х айнымалысы жауап береді (оны кестеден көруге болады):

 ә)   - МДҚФ

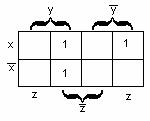
2.9 Сурет

          Белгіленген блокқа жауап беретін конъюнкт . Сондықтан берілген формуланың қысқартылған түрі: ;

б) .

 

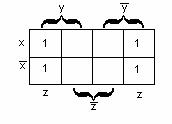
                                                        2.10 Сурет                                                                                                                                                                  

          Карно картасының екі z бағаны да 1-ге толтырылған. Егер осы бағандарды «айналдыра» беттестірсек, төрт ұяшықтан тұратын блок аламыз. Бұл төрт ұяшық z айнымалысын толық  «қамтиды»,  сондықтан берілген формуланы бір айнымалыға дейін қысқартсақ болады ;

        в) .

 

 

 

 

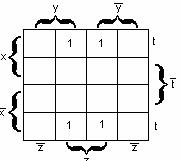 2.11 Сурет                                                                                                                                                                  

          Бұл функцияны сипаттайтын Карно картасын баған бағанға ( -ке), жол жолға ( -ға) беттесетіндей етіп «бұрауға болады». Яғни бұл картада төрт «ұяшықтан» тұратын блок бар. Ол  пен  айнымалыларын қамтиды, сондықтан берілген формулаларды  деп қысқартуға болады.

          г) .

         Құрылған Карно картасы бойынша:

          1) 8 ұяшықты блокқа y айнымалысы сәйкес келеді;

2) 4 ұяшықты блокқа xсәйкес келеді;

          3) 2 ұяшықты блокқа  сәйкес келеді.

          Олай болса, берілген формуланың минимизацияланған түрі

.

  

 

 

 

 

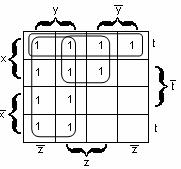
                2.12 Сурет                                                                                                                                                                  

 1-есеп.   формуласы берілген:  

а) ДҚФ-ға келтіру керек;

ә) ақиқаттық таблицасы бойынша МДҚФ құру керек;

б) Карно картасы көмегімен  минималды ДҚФ;

Шешуі:

         а) формуланың ДҚФ-ын   операциясының анықтамасын және  логикалық операциялардың қасиеттерін қолданып таба аламыз: ==[ Де-Морган

заңы]==[екі рет теріске шығару]=

 ==[дистрибутивтік]=

==[идемпотенттік]=

=. Соңғы өрнек формуланың  ДҚФ болып табылады;

         ә) формулалардың ақиқаттық таблицасын құрамыз.

Ақиқаттық таблицасы бойынша формуланың мүлтіксіз дизъюнктивті қалыпты формасын (МДҚФ) құрамыз. Ол үшін формуланың 1 мәнін қабылдайтын (=1) айнымалы мәндерінің жиынтықтарын тізіп жазамыз

{(0011),(0100),(0101),(0110),(0111),(1011),(1111)}. Келесі ережені қолданамыз:   функциясының   мәндерінің бағанында қанша бірлік болса, МДҚФ-ында  сонша конъюнкт болады; әрбір

нөлдік және бірлік жиынтықтарына: егер  болғанда  теріске шығарылып, ал  болғанда  теріске шығарылмай алынған барлық

2.9 К е с т е

A

B

C

D

0

0

0

0

1

0

0

0

1

0

1

0

0

0

0

1

1

0

0

0

1

1

0

0

0

0

1

0

1

0

0

0

1

0

1

0

0

0

1

1

1

0

1

1

0

1

0

1

0

1

0

0

1

1

0

1

0

1

0

1

0

1

0

1

1

1

0

1

0

1

0

1

0

1

1

0

1

1

0

1

0

1

0

1

0

1

1

1

1

1

1

1

0

1

0

1

1

0

0

0

0

0

0

0

1

0

1

0

1

0

0

1

0

0

0

0

1

1

0

0

1

0

1

0

0

0

0

0

1

0

1

0

1

0

1

1

0

0

1

1

0

1

0

1

1

1

0

0

0

0

0

0

1

1

0

0

1

1

0

1

0

0

0

0

1

1

0

0

1

1

1

0

0

0

0

0

1

1

0

0

1

1

1

1

0

0

1

1

0

1

0

1

 айнымалылардың конъюнктасы сәйкес келеді. Сонымен, берілген формуланың МДҚФ   дизъюнкциясы

 түріндегі жеті конъюнкталардан тұрады ( таңбасын жазбадық).

         б) төрт айнымалылы функцияның  Карно картасы  ұяшықтан тұратын  таблицаны білдіреді (төрт айнымалылы функцияның мүмкіндігінше қанша 0 және 1 жиынтықтары болса, сонша ұяшық саны), көрші ұяшықтар бір айнымалының мәніне өзгеше болатын жолдар мен бағандар айнымалы мәндеріне немесе оның терісіне  сәйкес келеді. Минималды ДҚФ алу үшін функцияның МДҚФ-ң әрбір  конъюнктасы Карно картасындағы сәйкес ұяшықта бірмен белгіленеді:

 

 

 

1

 

 

1

 

 

 

 

 

 

1

1

 

 

1

1

 

1

 

 

                   2.13 Сурет                                  

Минималды ДҚФ алу үшін бірліктер қатар тұрған тік және көлденең жолдарды біріктіру керек. Біріктірілген бірліктерді блок деп те атайды.  Блок 2, 4, 8 ұяшықтан тұруы мүмкін, 2 ұяшықтан блок деп қатар тұрған емес, таблицаның бір жақ бұрышында тұрған бірліктерді айтуға болады. Немесе таблицаның төрт бұрышында тұрған 4 бірліктен тұратын да 4 ұяшықты блок болады, бұл жағдайда бағанды бағанға (С-ны С-ға) және жолда жолға (Д-ны Д-ға) “бұрауға” болады. Біздің Карно картасында 4 ұяшықтан тұрған екі блок бар. Төменгі сол бұрыштағы блокты  және айнымалылары жабады, сондықтан оған  конъюнкциясы сәйкес келеді, картаның бұрышындағы 4 ұяшықты блокқа  конъюнкциясы сәйкес келеді. Сонымен,   формуланың минималды ДҚФ.

           Қосалқылық принципі

          Анықтама. Егер  орындалса, онда

функциясы  функциясына қосалқы функция деп аталады. Қосалқылық қатынасы симметриялы, яғни , онда .

 болса, онда  өзіне өзі қосалқы функция.

          Мысалы. Келесі кестені қарастырайық.

                      2.9 К е с т е

1

0

х

0

1

х

 

 

         Бұл кестеден дизъюнкцияға қосалқы қатынас конъюнкция, ал конъюнкцияға – дизъюнкция, 1 константасына – 0 константасы және 0 константасына – 1 константасы болады. Де Морган заңын қолдансақ,

1)  , бұдан теріске шығару өз өзіне қосалқы;

2)  функциясы өз өзіне қосалқы екенін көрсетейік.

1 жолы.

              

2 жолы. Ақиқат кестесі арқылы қосалқы функцияны алуға болады, ол үшін ақиқат кестедегі -тің барлық мәндерін қарама-қарсыға өзгерту керек.

   2.11 К е с т е                                        2.12 К е с т е

х

у

0

0

0

0

0

0

0

0

0

1

0

0

0

0

0

1

0

0

0

0

0

0

1

1

0

0

1

1

1

0

0

0

0

0

0

1

0

1

0

1

0

1

1

1

0

1

0

0

1

1

1

1

1

1

1

1

х

у

1

1

1

0

1

1

0

0

1

0

1

0

1

0

0

1

0

1

1

0

0

1

0

1

0

0

1

1

0

0

0

1

      

 

 

 

 

 Қосалқылық принципі:  функциясын өрнектейтін  формуласында функцияның барлық таңбаларын сәйкес қосалқы функцияның таңбасына өзгертсек, онда алынған  формуласы  функциясына қосалқы  функциясын өрнектейтін болады.

         Буль алгебрасындағы қосалқы принципі: (жоғарыдағы мысалда) егер  функциясын өрнектейтін  формуласында конъюнкцияны дизъюнкцияға, 1-ді 0-ге, 0-ді 1-ге алмастырсақ  -ке қосалқы  функциясын өрнектейтін  формуласын аламыз. Егер функциялар тең, яғни  болса, онда олардың сәйкес қосалқы функциялары да тең болады .

1-есеп.  функциясы берілген:

а) қосалқы функцияның анықтамасына;

ә) Буль алгебрасындағы қосалқы принципіне сүйеніп,

 қосалқы функцияның ДҚФ-ын табу керек.

         Шешуі:

а)

 

 

 ә) .

         Алдымен функциясын қысқартсақ , содан соң буль алгебрасындағы қосалқы принципі бойынша .

         Сонымен, ДҚФ-ға КҚФ сәйкес келеді, КҚФ-ға ДҚФ, МДҚФ-ға МКҚФ сәйкес келеді.

 Буль алгебрасы және жиындар теоремасы

         Жиындарға қолданылатын операциялар (қиылысу, бірігу, 1-10 қасиеттер) мен буль алгебрасындағы логикалық функцияларға қолданылатын эквивалентті қатынастар (1-9, яғни конъюнкция, дизъюнкция, теріске шығару) арасында байланыс байқалады.

         Негізгі эквиваленттілік қатынастарды қанағаттандыратын екі бинарлы және бір унарлы операциядан тұратын кез келген алгебра буль алгебрасы деп аталады.

1.  - конъюнкция, дизъюнкция, теріске шығару операциялары бар буль алгебрасы.

2.  - m  айнымалылы логикалық функцияның буль алгебрасы,  алгебраның ішкі алгебрасы болады, себебі .

3. (P  - қиылысу, бірігу, теріске шығару операциялары бар универсумдағы  жиынның буль алгебрасы.

4.   - ұзындығы n екілік векторлардың буль алгебрасы. Екілік векторларға қолданылатын логикалық операциялар келесі жолмен анықталған.

  векторлары үшін:

а) , мұндағы  егер ; қалған жағдайда ;

ә) .  егер ; қалған жағдайда ;

б) , егер , онда ал  егер  болса, .

         Логикалық функциялардың жиындарының екілік векторларының буль алгебрасы үшін келесі теоремалар орындалады:

         Теорема. Егер  ( қуаты n-ге тең) болса, онда (P  жиынның буль алгебрасы  екілік векторлардың буль алгебрасына изоморфты (яғни өзара бірмәнді) сәйкестік орнатуға болады [20, 156 бет].

         Теорема.  болса, онда жиындардың буль алгебрасы (P  функциялардың буль алгебрасына  изоморфты болады.

         Сонымен, егер  болса, онда берілген буль алгебралар арасында өзара изоморфизм орнатуға болады. Бұл жағдайда  P  және P   және  жиындары арасында өзара бірмәнді сәйкестік орнатуға болады.

         Буль алгебрасының изоморфизмі компъютерлік есептеулерде жиі қолданылады. Мысалы, жиындар немесе логикалық функцияларға қолданылатын операциялар орнына олардың изоморфты аналогтарын -  компъютерде оңай іске асырылатын екілік векторлардың операцияларын қолдануға болады.

 2.6 Коммутациялық сұлбалар

         1938 жылы Клод Шеннон ақиқаттық кестесі мен электр тізбектері арасындағы байланысты байқады. Ток көзі (2.13 сурет) мен электр лампасынан (2.14 сурет)

 

 

 

 

 

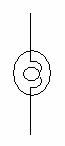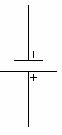            2.14 Сурет                                     2.15 Сурет

тұратын ауыстырып-қосқыш сұлбаны қарастырайық.

 

 

 

 


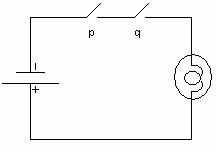
                                                    2.15 Сурет

          Егер p және q ауыстырғыштары тұйық болса, онда оларға 1 мәні беріледі. Қарсы жағдайда 0 мәні беріледі. Лампочка жанғанда схемаға 1 мәні берілді деп есептейміз (яғни электр тогы ол арқылы өтеді). Айта кетелік, тізбектің p және q элементтерін тізбектей қосқанда 3-суреттегідей екі ауыстырып-қосқыштың екеуі де тұйық болғанда, яғни p да, q да 1 мәнін қабылдағанда ғана лампочка жанады және схема мәні 1-ге тең болады. Сонымен схема  тұжырымына сәйкес келеді.

          Ауыстырып-қосқыштың мұндай орналасуы p және q логикалық элементі немесе логикалық көбейту схемасы деп аталады.

Бұл логикалық элемент                                  

                       

 
 немесе


түрінде көрсетіледі.

               2.16 Сурет                                                       2.17 Сурет

 

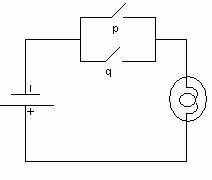          Енді p және q ауыстырып-қосқыштары параллель жалғанған ауыстырып-қосқыш сұлбасын қарастырайық:

         Айта кетелік екі ауыстырғыштың біреуі тұйық болғанда, яғни  немесе  (немесе екеуі де 1-ге тең болғанда) лампочка жанады және сұлба мәні 1-ге тең болады. Бұл сұлба  тұжырымына сәйкес келеді. Ауыстырып-қосқыштың мұндай орналасуы p немесе q немесе логикалық қосу сұлбасы деп аталады. Бұл логикалық элемент келесі символмен белгіленеді:                             

  2.18 Сурет

 

                                             немесе                   

                 2.19 Сурет                                        2.20 Сурет

           Бір p ауыстырып-қосқышты сұлба берілді деп есептейік. Егер p ашық болса ғана лампочка жанады, яғни егер p мәні 0-ге тең болса, схема мәні 1-ге тең. Егер p мәні 1-ге тең болса, сұлба мәні 0-ге тең болады. Бұл сұлба  тұжырымына сәйкес келеді, ал сәйкес логикалық элементі  теріске шығару логикалық элемент немесе инвертор деп аталады.

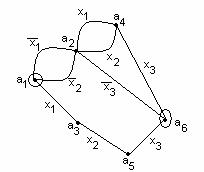1-мысал

                                                                                    2.21 Сурет

                                                                       

                                                                                            

.

              

 

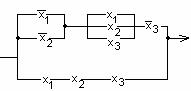
                            2.22 Сурет                                               2.23 Сурет

 

                                                                      

                         

 

 

 

 

                                                                       2.24 Сурет

           2.22 суретте көрсетілген сұлбаға 2.23 суреттегі электр схемасы және 2.24 суреттегі контакттер сұлбасы сәйкес келеді. Бұл сұлбаларға келесі буль формуласы сәйкес келеді

.

         2-мысал.

 

 

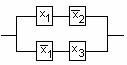2.25 Сурет

  сұлбасына 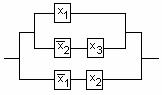 формуласы сәйкес келеді.

 3-мысал.

                                    

 

                           

2.26 Сурет

сұлбасына  формуласы сәйкес

                                       келеді.

       4-мысал.

 

 


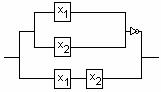2.27 Сурет

 сұлбасына   формуласы сәйкес келеді.

       5-мысал. Үш кіретін және бір шығатын жолы бар сұлба салу керек. Екі кіретін жолда сигнал берілсе, тек сол жағдайда шығатын жолда сигнал болу керек.

          Шешуі:  үш кірер жол болсын. Берілген есептегі

сұлбаны сипаттайтын формула

                      

 

 

                                                                         

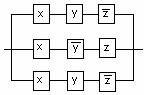
2.28 Сурет

Сонымен, ауыстырғыш функцияны сипаттайтын формула неғұрлым қарапайым болса, соғұрлым сұлба да қарапайым болады. ДҚФ минимизациялау осындай жағдайларда қажет.

6-мысал.  Сұлбаны қысқарту керек

 

 


      

 

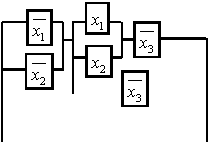
            2.29 Сурет

     Шешуі:      берілген сұлба үшін өткізгіштік функциясын құрайық

. Бұл функцияны белгілі әдістердің (мысалы, элементар түрлендіру, Карно картасы бойынша минимизациялау және т.б. әдістер) бірін қолданып, қысқартамыз  

[дистрибутивтік]==[сіңіру қасиеті]=

=. Алынған формулағы келесі сұлба сәйкес келеді

 

 


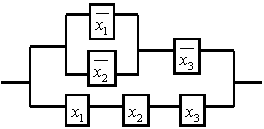
                     2.30 Сурет

 3 Комбинаторика

         - n элементтен тұратын жиын берілген. Оны элементтер санына қарай n-жиын деп те атайды. (n,r) -  жиынынан таңдап алынған r элементтен тұратын ішкі жиын таңдау (выборка), ал r – осы таңдаудың көлемі деп аталады. Егер (n,r) таңдауында элементтердің орналасу реті ескерілсе, ол (n,r)- орын алмастыру (перестановка), ал  элементтердің орналасу реті ескерілмесе (n,r)- теру деп аталады. Теруде элементтердің қайталануы да, қайталанбауы да мүмкін. Элементтері қайталануы мүмкін реттелген (n,r)-таңдау n элементтерден r бойынша қайталанатын орын алмастыру немесе қайталанатын (n,r)- орын алмастыру деп аталады. Егер реттелген (n,r)-таңдаудың элементтері әртүрлі болса, онда мұндай теру қайталанбайтын (n,r)-орын алмастыру деп аталады. (n,r)-таңдаулар саны  немесе , ал  қайталанатын орын алмастырулар саны -  немесе  символдарымен белгіленеді. Кейбір оқулықтарда (n,r) орын алмастыруын орналастыру (размещение) деп атап,  символымен белгіленеді. Орын алмастыру деп (n, n) реттелген таңдауды айтуға болады. Реттелмеген (n,r)-таңдауда элементтері қайталануы мүмкін, оны n элементтен r бойынша қайталанатын теру деп атайды. Қайталанбайтын терудің саны , , , ал қайталанатын ,  деп белгіленеді.

      Мысал.  болсын. Барлық реттелген және реттелмеген қайталанатын және қайталанбайтын үш элементтен екі элемент бойынша таңдауды табу керек.

1.  - тоғыз қайталанатын  орын алмастыру .

2.  - алты қайталанбайтын орын алмастыру .

3.  - үш қайталанбайтын теру .

4.  - алты қайталанатын теру .

 

3.1 Қосу және көбейту ережелері

         1. Қосу ережесі. Егер S n-жиынынан A ішкі жиынын n тәсілімен, A-дан өзге B ішкі жиынын m тәсілмен таңдап алуға болса, онда S жиынынан  жиынын n+m тәсілмен алуға болады, мұндағы A және B жиындарын бірмезгілде алуға болмайды.

         Қосу ережесін жиындар теориясы терминдерінде қолданайық. Егер A

n-жиыны және B m-жиыны берілсе, онда  болғанда,  бірігуі (n+m)- жиын болады. Егер  бөліктеуі берілсе, мұндағы  және жиын болса, онда  S жиыны - -жиын болады.

2. Көбейту ережесі. Егер S n-жиынынан A ішкі жиынын n тәсілмен,  ал осындай әрбір таңдаудан кейін B ішкі жиынын m тәсілмен таңдап алуға болса, онда A және B теруін айтылған рет бойынша nm тәсілмен таңдап алуға болады.

      Жиындар теориясы терминінде бұл ереже жиындардың декарттық көбейтіндісі ұғымына сәйкес келеді: егер A n-жиын, ал B m-жиын болса, онда  - nm-жиын болады. Жалпы жағдайда,  жиын болсын,  . Келесі жиындарды құрайық:     

Онда -жиын болады. Басқаша айтқанда, r амал жасау керек болсын. Бірінші амалды  тәсілмен, екінші амалды  тәсілмен, сол сияқты r амалға дейін  тәсілмен орындауға болатын болсын, онда r амалды  тәсілмен орындауға болады.

         Мысал. Бірінші семестрде студенттерге 9 пән жүргізіледі. Сабақ кестесінде дүйсенбіге 4 әртүрлі сабақты қанша тәсілмен қоюға болады?

         9 элементтен 4 қайталанбайтын орын ауыстыруды есептеу керек. Сабақ кестесінде бірінші сабақты 9 тәсілмен, екінші сабақты 8, үшіншісін 7 және төртіншісін 6 тәсілмен қоюға болады. Көбейту ережесі бойынша кестені құру тәсілдер саны мынаған тең  .

 

3.2 Қайталанбайтын және қайталанатын орын ауыстыру мен теруді есептеу формулалары

         Барлық мүмкін болар (n,r)-орын ауыстыру санын, яғни орналастыруды табайық. Ол үшін көбейту ережесін біртіндеп қолданамыз. Сонымен, - n- жиынында (n,r)-орын ауыстыруының бірінші элементін таңдау үшін n мүмкіндік бар, екінші элементін таңдау үшін n-1 мүмкіндік бар. Себебі бір рет таңдалған элемент қалған таңдауға қатыспайды, қайталанбайтын орын ауыстыру қарастырып жатырмыз. Сол сияқты r-ші элементті таңдау үшін

n-r+1 мүмкіндік қалады. Онда

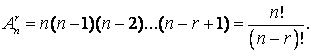
Расында

 

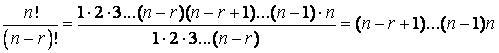
мұндағы  Сонымен келесі теорема дәлелденді.

Теорема. - n-жиынның реттелген r элементті ішкі жиындарының саны  формуласымен анықталады.

Дербес жағдайда

Бұл n- элементті ішкі жиындарды реттеу тәсілдерінің саны.

         Мүмкін болар қайталанатын (n,r)-орын ауыстыру санын есептейік. Бұл жағдайда (n,r)-орын ауыстыруының кез келген элементін таңдап алғаннан кейін де келесі элементті таңдау үшін n мүмкіндік сол күйінде қалып отырады. Олай болса, көбейту ережесі бойынша қайталанатын (n,r)- орын ауыстыру саны мынаған тең болады: .

         Терудің санын есептейік. Элементтері қайталанбайтын реттелмеген (n,r)-таңдаулар берілсін. Барлық мүмкін (n,r)- теруден тұратын жиынның элементтерінің санын  деп белгілейміз.

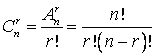 және  сандарын салыстырайық.  - n элементтен r бойынша реттелген  таңдау саны;  - n элементтен r бойынша реттелмеген таңдау саны. r көлемді әрбір реттелмеген теруді  әртүрлі тәсілдермен реттеуге болады, яғни .  Бұдан               .                                                (1)

Алынған нәтижені теорема түрінде тұжырымдауға болады.

        Теорема. - n-жиынының барлық реттелмеген r элементті ішкі жиындарының саны  формуласымен анықталады.

түрінде бөліктеу берілсін, яғни - - n -жиынының -ішкі жиыны және 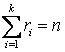. - n-жиынының -бөліктеу санын есептейік. - n -жиынының  -ішкі жиынын таңдап алу үшін  мүмкіндік бар. Содан кейін  -ішкі жиынды қалған  элемент арасынан таңдап алуға болады, себебі . Бұл таңдауды  тәсілмен іске асыруға болады. Осы сияқты қалған ішкі жиындар да таңдап алынады. Көбейту ережесін қолданып, - n-жиынының -бөліктеу саны мынаған тең

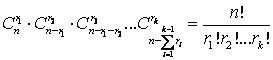.                                 (2)

Расында

.

Сонымен, сәйкес элементтерінің саны -ға тең   k  реттелмеген жиындары берілсе, онда осы жиындардың  қосындысы ретінде - n-жиынын 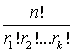 әдіспен көрсетуге болады.

        1-мысал. 4 бірдей математика, 6 бірдей информатика, 2 бірдей  химия оқулықтары бар. Барлығы 12 кітапты  кітап сөресіне қанша тәсілмен қоюға болады?

         2-мысал. “Қазақстан” сөзіндегі әріптердің орнын өзгерткендегі алынатын сөздердің (мағынасыз) санын табу керек.

         “Қазақстан” сөзіндегі әртүрлі әріптер  жиындарын құрайды. Берілген сөзді осы жиындарға бөлсек, олардың бірігулері жаңа мағынасыз сөздер береді. Мұндағы , {а,а,а}, {қ,қ}, {з}, {с}, {т}, {н}. Бұдан .

Берілген жиын ={қ,а,з,а,қ,с,т,а,н}.  (2) формуласы бойынша

         Енді  жиынынан қайталанатын (n,r)-теру санын есептейік.  жиынының элементтері 1,2,…,n сандарымен нөмірленген болсын. - n-жиыны ақырлы және санамалы болғандықтан, бұл қисапты жүргізуге мүмкіндігіміз бар. Онда  жиынынан  (n,r)-терудің орнына өзара бірмәнді сәйкестік арқасында оған эквивалентті  жиындағы (n,r)-теруді қарастырсақ болады.  жиынындағы кез келген (n,r)-таңдау  түрінде жазылады, мұндағы , теңдік таңбасы қайталанатын таңдауды қарастырғандықтан мүмкін болады.  r-таңдауына элементтерді әртүрлі   r-жиынын сәйкес қоямыз.  және   арасындағы сәйкестік бірмәнді  r-жиынынан  n+r-1-жиынынан қайталанбайтын r-теру болып табылады.

(1) формуласы бойынша қайталанбайтын -теру саны мынаған тең .  Онда                 

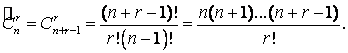
         Мысал. Дүкенде конфеттің 10 әртүрлі түрлері сатылады. 12 конфетті қалай таңдап алуға болады?

         12 конфет 10 әр түрінен қайталанып таңдап алынатын болғандықтан,

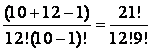  тәсілмен конфетті сатып алуға болады.

 4 Графтар теориясының элементтері

      Кейбір қолданбалы математика есептерінде бірнеше обьектілер арасындағы байланыс жүйелері зерттеледі. Объектілер төбелер деп аталып, олар нүктемен белгіленеді, ал осы төбелер арасындағы байланыс доғалар деп аталып, сәйкес нүктелер арасына стрелкалар қою арқылы белгіленеді.

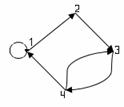Осындай жүйелер графты құрайды. Мысалдар: қаладағы           көшелер жүйесі: граф төбелері - көше қиылыстары болса, ал доғалар -бағыты белгілі көшелер; электр жүйесі; химиялық байланыстағы молекулалар; географиялық карта; адамдар арасындағы байланыс (ата-тегі); программаның блок-схемасы; транспорт, әуе жолдары. Соңғы мысалда бір  пункт-                  

      4.1 Сурет      тен екінші пунктке маршруттар саны бірнешеу болса, онда ең қысқасын, қолайлысын іздестіреміз. Осы сияқты есептерді шешу үшін графтарға есептеулер жүргізу керек  [2, 196 бет].

           4.1 Негізгі ұғымдар мен анықтамалар

          Графта объектілер арасындағы байланысты сипаттайтыны белгілі, ал байланыс бағытталған немесе бағытталмаған болуы мүмкін. Сондықтан графтар теориясында графтың негізгі екі түрін қарастырады: бағытталған граф – орграф, бағытталмаған граф - н-граф.

 4.1 К е с т е

              Н-граф (бағытталмаған)

            Орграф (бағытталған)

1 G бағытталмаған граф дегеніміз екі жиынның жүйесі G=(V,E) не G=G(V,E), мұндағы V–элементтері төбелері деп аталатын ақырлы жиын, E–элементтері қабырға деп аталатын, екі элементтің ішкі жиындарының жиыны, ол V (реттелмеген жұптардан тұратын) жиынының ішкі жиыны, {u,v}єE әрбір қабырғасына u және v– төбелері әртүрлі деп есептелінеді.

2 егер e=(u,v) қабырға болса онда,

а) u және v төбелері қабырғаның шеткі нүктелері (ұштары) деп аталады. uv деп белгіленеді;

ә) {u,v} қабырғасы  u және v төбелеріне инциденттелген, керісінше u және v төбелері {u,v} қабырғасына инциденттелген деп аталады;

б) u және v нүктелері қабырғаның шеткі нүктелері болса (немесе егер төбелері бір қабырғаға инцидентті болса), онда u және v төбелері сыбайлас деп аталады.

3 v төбесінің дәрежесі  деп оған инцидентті қабырғалар санын айталады (ρ(v) деп белгіленеді).

4 шеткі нүктелері беттесетін қабырға тұзақ деп аталады.

5 егер m - G н-графының қабырғалар саны болса, онда =2m, яғни барлық төбелердің дәрежелерінің қосындысы екі еселенген қабырғалар санына тең. Бұл жерде тұзақтың төбе дәрежелеріне  қосатын үлесі 2.

1 G бағытталған граф та екі жиынмен беріледі G=(V,E), мұндағы V– элементтері төбелер деп аталатын ақырлы жиын, E –V-дан алынған реттелген жұптар жиыны, яғни VV жиынының ішкі жиыны, элементтері доға деп аталады.

2 а) егер e=(u,v)  доға болса, онда u- доғаның басы, v-соңы деп аталады. (u,v) доғасын u төбесінен басталатын (шығатын) және v төбесіне бататын (кіретін ) деп атайды.  (немесе ) деп белгіленеді;

ә) u және v төбелері (u,v) доғасына инцидентті деп аталады.

        Егер доға v төбесінен басталса немесе v төбесіне батса, онда ол доға v төбесіне инцидентті деп аталады;

б) доғаның u басы v соңы болатын төбелері сыбайлас деп аталады.

3 v төбесінің шығу дәрежесі v төбесінде басы болатын доғалар санын айтамыз (,      ρ1 (v)  деп белгіленеді);

кіру дәрежесі  деп v төбесі соңы болатын доғалар санын айтамыз (, ρ2(v) деп белгіленеді).

ρ(v)=+ – v төбесінің дәрежесі.

4 доғаның басы мен соңы беттесетін болса, ол тұзақ деп аталады.

5 егер  m – G орграфының доғалар саны болса, онда ==m.  Екі дәрежеге де тұзақтың қосар үлесі 1.

          Ескерте кетелік, кейбір оқулықта доға орнына қабырға деп жазылады.        

          Келесі анықтамаларды енгізейік.

          1. Тек қана екі төбеге инцидентті болатын қабырғалар параллель немесе еселі деп аталады.

          2. Ал еселі қабырғалары бар граф мультиграф деп аталады.

          3. Егер элементтері (төбелері мен қабырғалар жиыны) шектеулі болса, онда граф шектеулі деп аталады.

          4. Егер төбелер жиыны бос (олай болса қабырғалар жиыны да бос) болса, онда граф бос деп аталады.

           Графтардың берілу тәсілдері

          1. Графты V және E  (төбелері мен қабырғалар) жиындарының жұбы түрінде немесе қабырғалар жиыны арқылы беруге болады, онда әрбір қабырға шеткі нүктелерінің жұбын білдіреді.

          Мысалы:   а) V={a,b,c} төбелері мен   E={} қабырғалары арқылы берілген граф;

          ә)  E={{a,b},{b,c}} -  н-граф үшін берілу жолы;

          б)  E={(a,b),(b,c)} -    орграф үшін берілу жолы.

          2. Графты суретте бейнелеу арқылы беруге болады, V={a,b,c}, E={{a,b},{b,c}} қабырғалар жиыны болатын суреттегідей беруге болады.

 

                                         

 

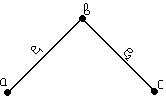
4.2 Сурет                                                4.3 Сурет

          Мұнда  a және b төбелері сыбайлас және олар е1={a,b} қабырғаларына инцидентті, ал е1 қабырғасы a,b төбелеріне инцидентті.

          1-мысал.

 

 

                                         

                                                    

                                                                                                          

 

 

 

 

 

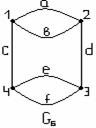
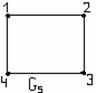
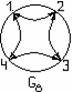
                                                       4.4 Сурет                                               

          Суретте келтірілген графтарды салыстырайық.

          1. G1- G7 - н-графтар,

              G8- G12   - орграфтар.

          2. G1 және G2  -  толық графтар, сонымен қатар G1= G2.

          3. G7  толық емес, себебі төбелерінің жұбы қабырғамен қосылғанымен 1 тұзақ (3 төбеде) бар.

          4. G3  барлық төбелері бөлек-бөлек орналасқан (графтың қабырғалар жиыны бос).

          5. G4 және G5  графтары бір-біріне толықтауыш болады, яғни G4=  және     G5=.

          6. G6 – мультиграф, себебі, a және b,  e және f еселі қабырғалары бар.

          7. G8 – орграф, G5 – н-графына сәйкес келеді.

8. G9  және G10  тең емес, себебі өзгеше доғалар бар: G9  -да  (4,1),  G10 -да (1,4);

         9. G11 – бағытталған мультиграф, себебі а және в доғалары еселі.

         10. G12 – мультиграф болмайды, себебі а және в доғалары әртүрлі бағытталған.

          2-мысал.   G1- G2   графтарының төбелерінің дәрежесін есептеу керек.

                                         

 

 

 

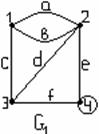
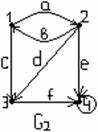
                      4.5 Сурет                                                 4.6 Сурет                                               

           Шешуі.  Екі графтың да төрт төбесі бар.  V={1,2,3,4} төбелерінің дәрежесін табу керек:

          а) алдымен G1 графының төбелерінің дәрежесін табайық.

ρ(1)=3,   ρ(2)=4,   ρ(3)=3,   ρ(4)=4 (н-графта тұзақтың үлесі 2-ге тең). Соныменен,  =14 =2m,   m=7 - графтағы қабырғалар саны;

         ә) G2 графының төбелерінің дәрежесін табамыз:

         1) шығу дәрежесі: ρ1(1)=2,   ρ1(2)=3,   ρ1(3)=1,   ρ1(4)=1  (орграфта тұзақтың  үлесі 1-ге тең);

         2) кіру дәрежесі: ρ2(1)=1,   ρ2(2)=1,   ρ2 (3)=2,   ρ2(4)=3;

         3) .

          3. Графтың берілу жолдарын әрі қарай қарастырайық. Алғашқы екі жол ЭЕМ қолданумен есептерді шығаруға жарамайды. Граф берілуінің тағы бір түрі – графтың инциденттік матрица арқылы берілуі.

          G графының барлық төбелері мен қабырғалары (доғалары) тұзақпен қоса нөмірленген болсын: G=(V,E), мұндағы

V={v1,v2,v3,…vm} - төбелерінің жиыны,

E={e1,e2,e3,…en}   - қабырғаларының жиыны.

          G графының инциденттік матрицасы деп өлшемі mn болатын (аij) матрицасын айтамыз, оның элементтері келесі жолмен анықталады:

          а) G н-графы үшін    

       1, i-ші төбе j-ші қабырғамен инцидентті болса, 

    aij=

      0, қарсы жағдайда;

      ә) G ографы үшін

                                 1,   i-ші төбеден j-ші доға шықса,

       aij=         -1, егер  i төбеге j-ші доға кірсе, j-ші доға түйін емес болу керек,

                          0, қарсы жағдайда.                                                 

 

 

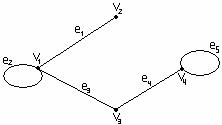3-мысал.

 

 

 

 

                       4.7 Сурет                                               

V={v1,v2,v3, v4}        төбелер жиыны мен                                                         

E={e1,e2,e3, e4, e5}    қабырғалар жиыны берілген.

          Бұл граф үшін инциденттік матрицасы

 A= .

          4-мысал.

 

                                                                        V={а1,а2,а3}       төбелер жиыны мен

                                                                        E={1,2,3,4,5,6}  доғалар жиыны берілген.

                                                                        Бұл графтың инциденттік матрицасы құрамыз 

                                                                       A= .

               4.8 Сурет                                               

          Теориялық зерттеуде инциденттік матрица кең қолданылғанмен, бұл әдіспен есеп шығару өте ұзақ.

4. Графты сыбайлас матрица арқылы беру. Графтың матрица түрде берілуінің қолайлы түрі – сыбайлас  матрица арқылы берілуі.

         G=(V,E) графының В=(bij) сыбайлас матрицасы деп, өлшемі nn болатын шаршы матрица айтылады (n төбелерінің саны). Сыбайлас матрицаның элементтері келесі жолмен анықталады:

 а) G н-графы үшін

              1, i-ші төбе j-ші қабырғамен инцидентті болса, 

   b ij=

      0, қарсы жағдайда;

 

ә) G орграф үшін:

       1, i-ші төбеден j-ші  төбеге доға жүргізілсе, 

   b ij=

      0, қарсы жағдайда;

 

б) G мультиграфы үшін:

                          к, н-граф үшін осы төбелерді қосатын қабырғалар саны,

 

  bij=                  оргаф үшін басы i-ші төбеде соңы j-ші  төбеде болатын доғалар;

                   0, қарсы жағдайда.

 

5-мысал. Суретте көрсетілген н-граф үшін сыбайластық  матрицасы

 

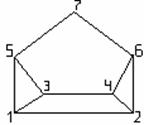                                                               B= .

               4.9 Сурет                                               

           6-мысал. Суретте көрсетілген орграф үшін сыбайластық  матрицасы

 
 

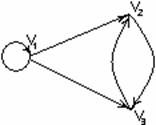                                                                B=.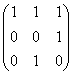

                              4.10 Сурет                                               

 

7-мысал. Суретте көрсетілген мультиграф үшін сыбайластық  матрицасы

 

 

 

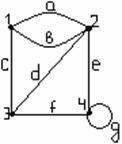                                                                           B=.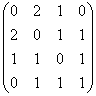

 

                      4.11 Сурет                                               

          Айта кетелік, н-графтың сыбайлас матрицасы А – симметриялы болып табылады, яғни А=Ат   (бұл жағдайда оның барлық қабырғалары жоғарыдағы оң үшбұрышта анықталған). Егер бұл графта тұзақ болмаса, онда бас диагональда нөлдер тұрады.

         Сыбайлас матрица көмегімен төбелер және қабырғалар санын анықтауға болады:      төбелер саны  n -  матрицаның реті,

қабырғалар саны   m=.

         Орграф үшін i-ші жолдағы бірдің саны i-ші төбенің ρ1(vі)  шығу дәрежесіне тең; j-ші бағандағы бірдің саны j-ші төбенің ρ2(vj) кіру дәрежесіне тең.

         Доға саны сыбайлас матрицаның барлық элементтерімен анықталады    

                     

                                          m=.

 5. Графтың қабырғалар (доғалар) тізімі арқылы берілуі.

         Инциденттік қатынасты инциденттік матрицасынан басқа қабырға (доға) тізімі арқылы беруге болады. Доғалар саны төбелер санына қарағанда анағұрлым аз болған кезде қолданған қолайлы. Бұл тізімді екі бағанға тізіп жазу арқылы береді: бірінші бағанға барлық қабырғалар (доғалар), ал екінші бағанға осы қабырғаларға инцидентті төбелерді енгізеді; н-граф үшін төбелер реті (жолда) қалауынша жазылады; ал орграф үшін алдымен доға басының нөмірі жазылады.

8-мысал.                                 4.2 К е с т е

Қабырғалар

Төбелер

a

b

c

d

e

f

g

1   2

1   2

1   3

2   3

2   4

3   4

4   4

                                           

Алдыңғы 3-мысалдағы

графтың қабырғалар тізімімен

берілуі.

 

 

 

 

 9-мысал.

 

 

 

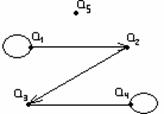                                                          4.9 Сурет                                                

 Сызбада берілген граф аралас типті (кейбір қабырғалар а3, а4                                                                бағытталмаған), а5 алшақ орналасқан, екі тұзақ (а1 және а4 төбелерінде), екі доға бар (а1,а2), (а2,а3).

Доғалар тізімі екі жиынтықпен беріледі

=(1,1,2,3,4,4),

                                                      =(1,2,3,4,3,4).

         Н-графты орграфқа айналдыру үшін бағытталмаған қабырғаға қарама-қарсы бағытталған екі доғаны беру керек. Әрбір тізімде қанша доға болса, сонша элемент болады. Бұл мысалда алты доға бар (1,1) (1,2)  (2,3)  (3,4)  (4,3)  (4,4).

6. Графты сыбайластық тізімі арқылы беру. 

         Кейбір есептерді шығару барысында төбелер мен қабырғалар жиыны өзгеріп отырады (ол жиыннан элементтер алынып та, қосылып та отырады). Бұл жағдайда графтың берілуінің қолайлы түрі сыбайластық тізімі арқылы берілуі. Бұл жағдайды қарастырмаймыз, [5, 292 бет], [3, 244 бет] сипатталған.

4.2 Графтар изоморфизмі

         Графты әртүрлі жолдармен беруге болатынын көрдік. Сызбаға қарап, бір графтың екі кескіні ме, әлде әртүрлі графтар ма екенін білу қиын. Төмендегі екі суретте бір граф берілген.

 


                                                                       

 

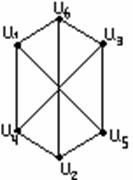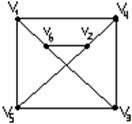
       4.10 Сурет                                                       4.11 Сурет                                            

         Графтың матрицасының және қабырға тізімінің түрі оның төбелері мен қабырғаларының нөмірленуіне байланысты. Егер графтың төбелері нөмірленген болса, онда ол толығымен берілген граф деп есептелінеді.

          Анықтама. Тек қана төбелерінің және қабырғаларының нөмірленуінде ғана айырмашылығы бар графтар изоморфты графтар деп аталады.

          Анықтама. Егер e1=(u,v) e2=(φ(u),φ(v)) сыбайластықты сақтайтын биекция φ: бар болса, онда G1=(V1,E1) және G2=(V2,E2) графтары изоморфты деп аталып,  G1~G2 деп белгіленеді.

         Теорема. Графтың изоморфизмі эквиваленттілік қатынас болып табылады. Расында изоморфизм эквиваленттілік қатынастың барлық қасиетіне сай келеді:

          а) рефлексивті (G~G);

          ә) симметриялы (G1~ G2 G2~G1);

          б) транзитивті (G1~G2, G2~G3 G1~G3).

    Графтарды изоморфизм дәлдігіне дейін қарастыруға болады. Барлық изоморфты графтар үшін бірдей сандық характеристикалар графтың инварианты деп аталады.

          Мысалы, n(G) – төбелерінің саны мен m(G) – қабырғаларының саны G  графының инварианты болып табылады. Бірақ бұл аталған инварианттар изоморфизм дәлдігіне дейін анықтамайды. Мысалы, төмендегі суретте төбелер саны мен қабырғалар саны бірдей, бірақ бұлар изоморфты емес. 

                                     

                     

 

 

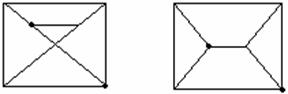
           4.12 Сурет                4.13 Сурет

      Егер екі графтың бір-бірінен айырмашылығы тек төбелерінің нөмірленуінде ғана болса, онда олардың инциденттік және сыбайлас матрицалары әртүрлі болады. Бірақ бір графтың инциденттік (сыбайлас) матрицасын екінші графтың осындай матрицасының жолы мен бағандарын ауыстыру арқылы  алуға болады.

          Мысалы 55 өлшемді матрицада жол мен бағандар ауыстырым саны 5!=n! болады. Сондықтан мұндай жолмен матрицаның изоморфизмін тексеру өте ұзақ.

         Кейде графтың изоморфтілігін графиктік көрініс бойынша көз жеткізуге болады. Суреттегі  және  графтары изоморфты, себебі 3 төбені 2 және 4 төбелер деңгейіне көтерсек және -ні төңкерсек,  және  графтарының формалары бірдей (бірдей графтар шығу үшін төбелерін қайта нөмірлеу керек).

             

 

                                                                                       

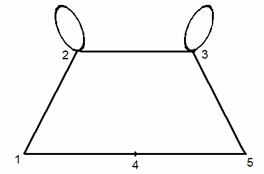
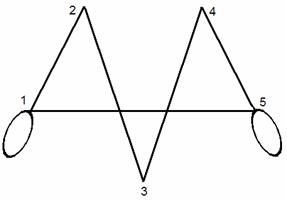
                       4.14 Сурет                                               4.15 Сурет

          Ішкі графтар (подграфы)

         Анықтама. Егер  және E1E орындалса, онда G1=(V1,E1) графы G=(V,E) графының  бөлігі деп аталады.

Анықтама. Ұштары V1 жиынында болатын қабырғалар (доғалар)  G1=(V1,E1) бөлігінде жатса, онда G1=(V1,E1) графы G=(V,E) графының ішкі графы деп айтамыз.

Мысалы

         

 

 

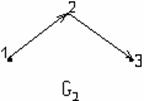
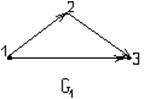
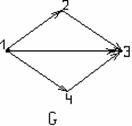
      4.16 Сурет                           4.17 Сурет                            4.18 Сурет

 G1 – G графының ішкі графы {1,2,3} төбелерінен туындаған,

G2 –  G графының бөлігі.

 Графтарға қолданылатын операциялар

        Графтарға қолданылатын операциялардың кейбіреуін келтіріп өтейік:

а) G(V,E) графының толықтауышы деп, мынандай (V,E)  графы  айтылады: кез-келген u,vV,  {u,v}қабырғасы  графында жатып, ал G-да жатпайды;

ә) G1(V1,E1) және G2(V2,E2) графтары берілген:

1) G1 және G2 графтарының бірігуі деп (белгіленуі G1G2).

G1= G1 G2=( V1V2, E1E2)  графын айтамыз;

         2) G1 және G2 графтарының қиылысуы деп (G1G2).

G1= G1 G2=( V1V2, E1E2)  графын айтамыз;

         3) G1 және G2 графтарының жалғауы (соединение) (G1+ G2) деп

G1+ G2 =( V1V2, E1E2 {{u,v}/ u V1, vV2,  u ≠v}) графын айтамыз.

    3-мысал.

                                

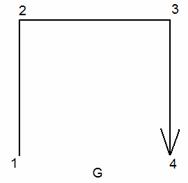
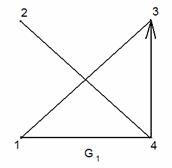
               4.19 Сурет                                                  4.20 Сурет

G1 графы G графының толықтауышы болады.

          4-мысал. G1 және G2 графтары берілген.

                                                                             

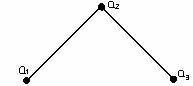
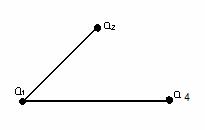
            4.21 Сурет                                                      4.22 Сурет

 

 


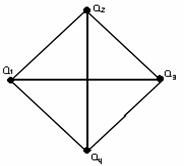G1+ G2

                         4.23 Сурет

 

 


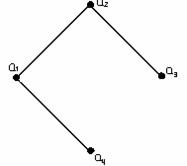G1G2                                                                      G1G2

                               4.24 Сурет                                            4.25 Сурет

          Кез-келген төбелері сыбайлас болатын тұзақсыз н-граф толық деп аталады (яғни қабырғалармен қосылған).  n төбелі толық граф Кn  деп белгіленеді.

          Суретте толық графқа мысал келтірілген.

 

 

 


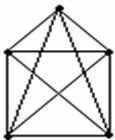                   01000

    К2                         К3                                       К4                                 К5

 4.26 Сурет          4.27 Сурет                    4.28 Сурет                   4.29 Сурет

                    Графтың қабырғалар саны келесі формуламен есептелінеді:

 m(Kn)=

          n -графтың басты класстарының бірі n өлшемді кубтар (немесе n-кубтар) деп аталатын класс болып табылады,  Qn  деп белгіленеді.

          Qn - n өлшемді кубтың төбелері әртүрлі 0 мен 1-ді қабылдайтын «n-ка»-лардан (жиынтықтардан) тұрады, ал қабырғалары келесі ережелерге сүйеніп беріледі: сәйкес «n-ка»-лар бір-бірінен бір координатаға айырмашылығы болғанда ғана, тек сол жағдайда ғана төбелері сыбайлас болады.

          5-мысал.

 

 

 

 

 

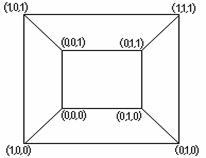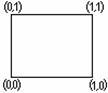    4.30 Сурет                    4.31 Сурет                                      4.32 Сурет

           4.3 Маршруттар, жетерлік (достижимость), байланыстылық

        Н-граф пен орграф үшін тағы да жаңа ұғымдар енгіземіз. G(V,E) графы берілсін.  

Анықтама.  v1,e1, v2,e2, ….., en,vn+1  тізбегі v1  және vn+1 төбелерін қосатын  маршрут  деп аталады, мұндағы v1, v2, ..., vn+1 V,  e1,e2, …, en  E.

    Маршрутты v1 , v2, ...vn+1 төбелерінің тізімімен, e1, e2, ...,en қабырғалар (доғалар) тізімімен беруге болады: v1- маршруттың басы, vn+1 – маршруттың соңы.

Шынжыр (жол) – барлық қабырғалары (доғалары) әртүрлі маршрут.

Цикл (контур) – тұйықталған шынжыр (жол), яғни басы мен соңы тең (v1=vn+1) .

Қарапайым, жай шынжыр (жол), жай цикл (контур) – бірінші және соңғы төбесінен басқа төбелері қайталанбайтын, яғни өз ішінде қиылыспайтын шынжыр (жол), цикл (контур).

Анықтама. Егер графта цикл (контур) болмаса, онда ол  ациклдік (контурсыз) деп аталады.

Анықтама.  Маршруттың қабырғаларының (доғаларының) саны оның ұзындығы деп аталады.

Егер u және v төбелерін қосатын ұзындығы n болатын шынжыр (жол) бар болса, uv деп жазамыз.

Анықтама. Егер басы u және соңы v болатын шынжыр (жол) бар болса, онда v төбесі u төбесінен жетерлік (достижимый) деп аталады.

Анықтама. Егер кез-келген екі беттеспейтін төбелері маршрутпен қосылса, онда G н-графы байланысқан деп аталады.

Анықтама. Егер G орграфына сәйкес н-граф байланысқан болса, онда G орграфы да  байланысқан деп аталады.

Егер кез-келген u және v екі төбесі өзара қолжетерлік болса, яғни, u төбесі v төбесінен, ал v төбесі u төбесінен жетерлік болса, онда орграф мықты байла-нысқан деп аталады.

Анықтама. Келесі шарттар орындалсын:

          а) G1 – бос емес байланысқан (мықты байланысқан) граф;

          ә) егер G2 – G графының байланысқан (мықты байланысқан) ішкі графы және G1 G2 болса, онда G1 = G2, яғни G1 – G графының максималды байланысқан (мықты байланысқан) ішкі графы болады.

         Егер осы екі шарт орындалса, онда G графының G1 ішкі графы G(V,E) графының байланыстық компонентасы (байланыстықтың мықты компонентасы) деп аталады.

1–  мысал. Суретте н–граф берілген:

                                                                        

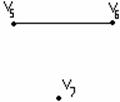
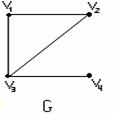а) (v1,v 3,v4) – жай шынжыр;

ә) (v1,v3,v2,v1,v3,v4) – маршрут

(шынжыр, бірақ қарапайым емес);

 

б) (v3,v1,v2, v4) маршрут емес ({v2,v4 } жоқ);

   4.33 Сурет                4.34 Сурет                     в) (v1,v2,v3,v4) – жай цикл;

г) v1,v2,v3,v4 төбелеріне қос-қостан жетуге болады (жетерлік),

v5,v6 – ұзындығы бірге тең шынжыр;

v7 – ұзындығы 0-ге тең шынжыр, алшақ орналасқан төбе;

д) бұл G графы байланысқан емес, себебі ол үш байланыс компонентасынан тұрады {v1,v2,v3,v4},  {v5,v6}, {v7}.

          2 – мысал.  орграфы берілген.

 


а) 1, 2, 4, 5 немесе 1, 2, 3 – жай жол;

ә) 1, 2, 3, 1 – жай контур;

б) 5 төбесі кез-келген төбеден жетерлік,

5 төбесінен ешқандай төбеге жетуге болмайды;

в) 4 төбесі 1, 2, 3 төбесінен жетерлік және 5

                 4.35 Сурет                  төбесінен жетпейді.

         

          Бұл граф байланысқан, бірақ мықты байланысқан емес, оның {1,2,3}, {4}, {5} төбелер жиыны түрінде берілген үш мықты компонентасы бар.

    Теорема. Кез-келген графты қиылыспайтын байланысқан компоненталардың (ал орграф үшін мықты байланысқан)  бірігуі түрінде көрсетуге болады. Граф байланысқан (орграф үшін мықты байланысқан) компоненталарға бір ғана жолмен жіктеледі.

    Сонымен, н-графтың байланысқан (немесе орграфтың мықты байланысқан) компоненталарының төбелерінің жиыны графтың төбелерінің жиынында бөліктеу құрайды.

    G графының байланысқан (орграф үшін мықты байланысқан) компоненталарының саны (K(G) немесе C(G) деп белгіленеді) бірмәнді анықталады.

    Егер  K(G)=1 болса, онда G – байланысқан граф.

    Егер  K(G)>1 болса, онда G  - байланыспаған граф.

2- мысалда G2 орграфы үшін мықты байланысқан компоненталар саны K(G2)=3, ал {1,2,3,4,5} төбелер жиынының  {{1,2,3},{4},{5}} бөліктеуі бар.

         

          Байланыстық компоненталарын және байланыстық   

          компоненталардың мықтысын анықтау

         Графты сипаттайтын тағы бір матрица қарастырайық.

Анықтама. Егер

1, егер j төбесі i-ші төбеден қолжетерлік болса,

0, қарсы жағдайда.

 

             сij элементтерінен тұратын m өлшемді (m=|v| - төбе саны) шаршы С=( сij) матрицасы  жетерлік  матрица деп аталады  (н-граф үшін – сыбайластық матрицасы).

Жетерлік матрицасын келесі жолмен алуға болады: А – сыбайластық матрицасы болсын, B=(bij)=Е+А+А2+...+Аm   құрайық, сонда

сij =

Бұл жетерлік матрицаны табу әдісі тым ұзақ, қолайлы түрінің бірі – Уоршолла алгоритмі [4, 282 бет]. Қарапайым жағдайда С матрицасын графтың графиктік кескінінен табуға болады.

    3-мысал. G графы (алдыңғы 2 – мысалдағы) үшін жетерлік матрица

С=.

          С матрицасында граф элементтерінің маршрут арқылы байланысын бақылауға болады. Н-граф үшін сij=1 болса, онда граф байланысқан. Жалпы, н-графтың байланысқан C матрицасы графтың төбелер жиынын компоненттерге бөліктенуіне сәйкес келетін эквиваленттік қатынасының матрицасы болып табылады.

          1-мысалдағы G графының жетерлік матрицасы.

 

С=

          Бірлерден тұратын блоктар үш байланыстық компоненталарына сәйкес келеді. {1,2,3,4},  {5,6}, {7} төбелер жиыны, яғни төбелер жиынын осы компоненталарға бөліктеуге сәйкес келеді.

    Орграф үшін жетерлік матрица көмегімен графтың мықты компоненталарын табуға болады. С=(cij)  матрицасынан басқа Q=CT=( qij) матрицасын қарастырсақ

        1, егер i төбесі j -ші төбеден қолжетерлік болса,

   qij =

        0, қарсы жағдайда.

          Q-ды кейде жетерлікке қарама-қарсы матрица деп те атайды. S=(sij)=QC матрицасын қарастырамыз, мұндағы  операциясы C және Q матрицаларының  элементін элементке көбейтуді білдіреді, яғни sij=cijqij .

    Егер vi және vj төбелері өзара жетерлік болса, онда олар графтың бір мықты байланысқан компонентасында орналасқандығын білдіреді және S матрицасының сәйкес элементі 1-ге тең, яғни sij=1. Сонымен,  vi  төбесінен тұратын мықты байланысқан компонента  sij=1 болатын vj төбелерін де қамтиды.

    2 – мысалдағы оргафты қарастырайық. Оның С жетерлік және Q жетерлікке қарама-қарсы матрицаларын құрып, олардың S көбейтіндісін қарастырамыз.

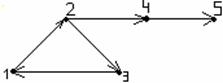                                                                                     С= 

          4.36 Сурет

 

CT=                              S=CQ=

          S матрицасының  бірінші жолы бойынша бір төбесін қамтитын мықты компонента {1,2,3} төбелерінен тұрады. S матрицасынан 1,2,3 төбелеріне сәйкес келетін жолдар мен бағандарды сызып тастаймыз. Мына матрицаны аламыз  S1=.                   

          S1 матрицасының бірінші жолында жалғыз 1 бар, ол 4 төбесіне сәйкес келеді, келесі мықты байланысқан компонента бір төбеден тұрады, ол {4}. S1 –ден 4 төбесінен тұратын жол мен бағанды сызып тастаймыз. Қалған матрица S2= (1). Берілген графтың мықты байланыстықтың үшінші компонентасы екіншісі сияқты бір төбеден тұрады: {5}. Сонымен, графтың мықты байланыстылығының 3 компонентасы бар: {1,2,3}, {4}, {5}.

 

          4.4 Графтардың маршруттарын зерттеу

          Сыбайлас матрицаның негізгі қолданылуы – ол  арқылы  ұзындықты маршрутты анықтау болып табылады.

    Теорема. G=(V,E) графы берілсін, V={v1,v2,…,vn} төбелер жиыны. A – G  графының сыбайлас матрицасы болсын. Ak= AA…A=(aij)  матрицасын қарастырайық.

          Егер aij=m болса, онда vi төбесінен vj төбесіне  ұзындықты m маршрут бар болады.

          1–мысал. Суреттегі аралас типті графты қарастырайық.                                                                                            

                                                                                                                                  

 

 

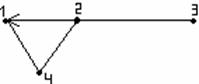
                                                             4.37 Сурет

           Бұл графтың сыбайлас матрицасы –  А=.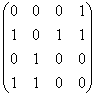

          А2   табайық (матрицаны матрицаға көбейту қарапайым әдіспен іске асырылады):

А2 =    =

а213 =0, ұзындығы 2-ге тең 1-ші төбеден 3-ші төбеге маршрут жоқ (13).

а222 =2, ұзындығы 2-ге тең екі маршрут бар (22): 2-4-2,  2-3-2.

а234 =1, ұзындығы 2-ге тең 1маршрут бар (34): 3-2-4.

 А3 =   =.

          Енді маршруттың өзін анықтайық.

а313 =1, ұзындығы 3-ке тең 1-ден 3-ке дейін 1 маршрут бар (13): 1-4-2-3.

(1,4,2,3) тізбегін матрицаларды көбейткеннен кейін алынған матрица элементінен алуға болады.  А3  матрицада: а313 = а211 а13 + а212 а23+ а213 а33+ а214а43    

                                            1   =     10    +     11   +     00   +     00.

         Басқаша айтқанда, а313 элементінде нөл емес қосылғышты а212 көбейткіші береді, мұндағы а212 үшін нөл емес қосылғышты а14а42  береді (яғни а14а42 а23 ). Сонымен төменгі индекстер бойынша соңынан жоғары қарай жылжысақ, 1-4-2-3 (ал жақшада 1-4-4-2-2-3, қайталанатын 4-4 орнына 4, ал 2-2 орнына 2 санын алу керек).

 Графтағы ара қашықтық

G=(V,E) байланысқан н-граф, ал vi, vj – G графының әртүрлі төбелері болсын.

Анықтама.  vi және vj  төбелерінің арасындағы ара қашықтық  деп ұштары vi және vj болатын қарапайым шынжырдың ең кіші ұзындығын айтамыз. d(vi, vj) деп белгіленеді. Бұл жолмен анықталған ара қашықтық  метриканың барлық аксиомаларын қанағаттандырады:

1)     d(vi, vj)≥0, сонымен қатар d(vi, vj)=0  vi =vj;

2)     d(vi, vj)= d(vj, vi);

3)     d(vi, vj)≤ d(vi, vк)+ d(vк, vj) бұл үшбұрыштар теңсіздігі.

      V={v1,v2,…,vn} графтың төбелер жиыны болсын. D=(dij) матрицасын қарастырайық, мұндағы dij =d(vi, vj). D матрицасы ара қашықтық матрицасы деп аталады. Айта кетелік, D=DT , яғни D – симметриялы матрица.

         Келесі анықтамаларды енгізейік.

1. v төбесінің эксцентриситеті деп  (e(v) деп белгіленеді)  max{d(u,v)/ uv} айтамыз, сонымен эксцентриситет дегеніміз берілген төбеден ең алыс орналасқан төбеге дейінгі арақашықтық. D ара қашықтық матрицасында Vi төбесінің эксцентриситеті деп і-ші жолдағы ең үлкен сан айтылады.

2. G графының диаметрі деп (d(G) деп белгіленеді) төбелерінің эксцентриситетінің ең үлкені айтылады. d(G)=max{e(v)/vV}.

3. Егер e(v)=d(G) болса, онда v  алшақ орналасқан төбе деп аталады.

4. G графның радиусы деп (r(G) деп белгіленеді) эксцентриситеттің ең кішісі айтылады.  r(G)=min{e(v)/vV}.

5. Егер e(v)=r(G) болса, онда  v орталық төбе деп аталады.

6. Орталық төбелердің жиыны графтың центрі деп аталады.

         2-мысал. Суреттегі G графын қарастырайық. Оның ара қашықтық матрицасы  - D.

                                                             D=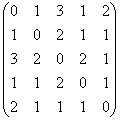

                4.38 Сурет

 Матрицаның әр жолынан ең үлкен санды таңдаймыз, бірінші жолда ең үлкен сан 3, сондықтан e(1) =3. Сол сияқты e(2) =2, e(3) =3, e(4) =2, e(5) =2.  Бұл табылған    эксцентриситеттер арасынан ең үлкенін таңдаймыз, ол  - 3, олай болса диаметр  d(G)=3, ал ең кішісі радиусты береді - r(G)= 2. Бұдан 1, 3 – алшақ орналасқан төбелер, 2,4,5 – орталық төбелер, {2,4,5} – графтың центрі.

 4.5 Графтағы ара қашықтықты зерттеу. Ең қысқа жол туралы есеп

Графтың орталық төбелерін табу есептері практикада жиі кездеседі. Мысалы, графтың төбелеріне  – қалалардың аудандары, ал қабырғасына – олардың арасындағы жолдар сәйкес келеді деп есептейік. Емхана, дүкен және т.б. мекемелерді қолайлы орналастыру талап етіледі, яғни осы мекемеге дейінгі ең алшақ орналасқан аудандардың ара қашықтығын минимализациялау есебі туындап отыр. Олай болса, бұл мекемелерді орналастыру орындары графтың орталық төбелері болу керек. Мұнда қойылған есептердің шарты өмірдегіге сай келе бермейді, себебі аудандардың арақашықтығы, жол уақыты т.б. жағдайларға көңіл бөлуге тура келеді. Әртүрлі жағдайларды ескеру үшін өлшенген графтар қолданылады.

G(V,E) графы берілген. G графының таңбасы (немесе таңбаларды орналастыру) деп 

f:VSv  (f функциясы төбелерінің таңбаларын орналастыру),

g: ESE (қабырғаларының (доғаларының) таңбаларын орналастыру) жұбын айтамыз. Олай болса, (V,E,f,g) төрттігін өлшенген немесе таңбаланған граф деп атаймыз.

Егер vV, онда  f(v) – v төбесінің салмағы, ал eE болса, онда g(e) - e  қабырғасының (доғасының) салмағы.

Графтың тек қана төбелері таңбаланған (онда g=const) немесе доғалары ғана таңбаланған (онда f=const) жағдайлары жиі кездеседі.

1-мысал. Суретте ұзындықтары белгіленген автокөлік жолдарының сұлбасы (V,E,f,g) таңбаланған графымен берілген.

 

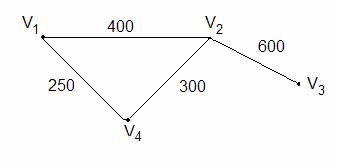
                                                            4.39 Сурет

V1  - Астана

V2  - Екібастұз

V3  - Семей

V4  - Қарағанды

V={V1, V2, V3, V4,V5} ,  Е={{V1, V2 },{V2, V3}, { V1, V4},{ V2, V4}},

f: VSv : S – қалалар жиыны,  f(V1)= Астана,   f(V2)= Екібастұз,   f(V3)= Семей, f(V4)= Қарағанды.

g: ESE :  S – арақашықтық  g({V1, V2})=400,  g({V2, V3})=600,  g({V1, V4})=250,   g({V2, V4})=300.

Өлшенген графтағы доғалардың салмағы туралы ақпаратты W=(wij) салмақ матрицасы түрінде беруге болады. Ол келесі түрде анықталады:

егер (ai,aj) доғасы бар болса, wij – (ai,aj) доғасының салмағы, ал салмақ жоқ жерлердің орнына қосымша мәліметке сай 0 немесе ∞ таңбаларын қояды. (∞ - егер төбелер сыбайлас болмаса). Жоғарыдағы мысалдағы граф үшін салмақ матрицасы:

W=

Өлшенген графтар үшін арақашықтық, эксцентриситет, радиус, т.б. ұғымдар енгізілді.

         G(V,E) өлшенген граф болсын, мұндағы әрбір (v1,v2) доғасының салмағы

(v1,v2) саны болсын. Келесі анықтамаларды енгізейік:

а) v1,v2 ,..., vп+1  (v1vп+1) өзара жалғанған болсын. Өзара жалғанған маршрутының салмағы деп  = саны айтылады;

ә) v1 және vп+1  төбелерінің арасындағы dw(v1,vn+1) (w – арақашықтық) өлшенген арақашықтық деп v1 v п+1 маршрутының ең азы айтылады.

б)  v1   және vп+1 төбелерінің арасындағы ең қысқа маршрут деп, салмағы dw(v1, vn+1)-ге тең болатын маршрут айтылады;

в) v төбесінің өлшенген эксцентриситеті деп  (еw(v) деп белгіленеді)    ew(v)=max{dw(v,u)/ UV} саны айтылады;

г) G графының өлшенген радиусы  (rw(G) деп белгіленеді) деп орталық  төбемен өлшенген эксцентриситетті айтады;

   д) ew(v)=min{еw(u)/uV} орындалатын v төбесі G графының өлшенген орталық төбесі деп айтады.

   2-мысал. Жоғарыдағы мысал үшін ew(V1)=400  V1 төбесінен шығатын ең ұзын жол. Сол сияқты ew(V2)=600, ew(V3)=600, ew(V4)=300.

  Айта кетелік, егер әрбір доғаның ұзындығын 1-ге тең деп алсақ, онда салмақсыз граф аламыз.

 Қысқа маршрутты (жолды) табу

Қысқа маршруттарды анықтаудың бірнеше тәсілдері (алгоритмдері) бар. Ол таңдау есеп шартына (мысалы қабырға өлшемі теріс немесе жоқ болуы мүмкін), шешу жолына (компьютерде, қолмен) байланысты. (Флойд-Уоршолл [4, 611 бет], Форд-Беллман [1, 126 бет])

Барлық қабырғаларының салмағы теріс емес өлшенген графтарға ғана қолданылатын  Дейкстра алгоритмін қарастырайық.

Дейкстра алгоритмінің әртүрлі нұсқаларын кездестіруге болады, мысалы салмақ матрицасын қолданбай ( [4, 613 бет]  ) және осы матрицаның көмегімен ([4, 615 бет], [1, 127 бет]) компьютерде қолдану үшін ([3, 271 бет]).

Біз Судопластовта ұсынылған нұсқаны қарастырамыз.

G(V,E) – n төбелі өлшенген граф берілсін. W=(wij) – оның салмақ матрицасы .

Белгіленген бір vі төбесінен (оны бастамасы деп атаймыз) қандай-да бір басқа төбеге дейінгі өлшенген арақашықтықты табу керек.

Т1 арқылы V \{ v1} төбелер жиынын белгілейік, яғни Т1 – бастамасыз V  барлық төбелер жиыны, D(1)=(d1(1) , d2(1), …, dn(1))  белгілеуін енгізейік, мұндағы di(1)=0,  dj(1)=wij  (i≠j), яғни D(1) – салмақ матрицасындағы і-ші жол.

S қадам жасадық. S- қадамында  TS төбелер жиыны мен D(S)=(d1(S) , d2(S), …, dn(S)) жолдар анықталған болсын. Біздің мақсатымыз TS- тен  TS+1-ке көшу және D(S) -тен D(S+1) -ге көшу.  Енді dj(S)=min{ dk(S)/ vk TS} орындалатындай TS -тен vj төбесін таңдап аламыз.

TS+1= TS\{ }, D(S+1)=( d1(S+1), …, dn(S+1))   болсын, мұндағы

    , егер ,

, егер .

 S=n-1  қадамда D(n-1)=( d1(n-1), d2(n-1)…, dn(n-1))   жолын аламыз, мұндағы d1(n-1) – vі төбесінен vj төбесіне дейінгі өлшенген арақашықтыққа тең d j(n-1)=dw(vі, vj).

3-мысал. Суреттегі графты қарастырайық. A төбесінен F төбесіне дейінгі қысқа ара қашықтықты табу керек.

Шешуі. V={A,B,C,D,E,F} – төбелер жиыны.

 

 

 

 

 

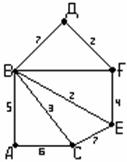                                                                4.40 Сурет

                                   Осы граф үшін салмақ матрицасын құрайық.   

W=

                                                   min=(a,∞)=a

                                                  min=(∞,∞)=∞

                                                 a+∞=∞

∞+∞=∞ деп келісейік

А төбесінен F-ке дейінгі ең қысқа жолды табу керек болғандықтан, А  төбесі бастама болады:

а) Т1=V\{A}={B,C,D,E,F}  бастама нүктесін төбелер жиынынан алып тастаймыз.

D(1)=(0,,6, ∞,∞,∞)  - салмақ матрицасындағы бірінші жол;

ә) Т2  мен D(2) –ге көшу үшін D(1) жолындағы ( -ден басқа) салмақтар ішінен ең кішісін тауып белгілейміз. Ол – 5, келесі қадамдарда ол өзгеріссіз қалып отырады, тағы да өзгеріссіз қалатын параметр – бірінші тұрған 0, бұл А-дан А-ға дейінгі ара қашықтық. Ал 5 саны В төбесіне сәйкес келетін салмақ, оны  Т1- ден алып тастап, Т2 -ні аламыз Т2 ={C,D,E,F}.

D(2) алу үшін В төбесіне сәйкес келетін жолды көшіріп жазайық.

  5  0  3   7    2   10

         5  5   5    5    5

          5  8  12   7   15

Алынған жолды  D(1) -мен салыстырып, D(2) -дегі сәйкес орынға ең кіші санды жазамыз                      D(2)=(0, 5, , 12, 7, 15);

б) Т3  пен D(3)  алу үшін екінші қадамдағы шараларды қайталаймыз.

Т3= Т2\{С}={D,E,F}.   W-дағы С-ға сай үшінші жол:

 6   3   0   ∞   7    ∞

            6   6    6    6

            6  ∞  13   ∞

(алдыңғы екі санды қарастырмаймыз, себебі олардың орнында өзгермейтін 0 және 5 сандары тұр).

Алынған жолды D(2) -мен салыстырып, D(3) -тегі сәйкес орынға ең кішісін жазамыз                    D(3)=(0, 5, 6, 12, 7, 15);

в) D(3)-тегі соңғы үш санның 12,7,15 арасынан  ең кішісін таңдаймыз, ол

7.  Е төбесіне сәйкес келгендіктен, оны да алып тастаймыз  Т4= Т3\{Е}={D,F}.

 

                                            ∞   2   7   ∞   0    4           -Е төбесіне сай бесінші жол.

7   7    7

                                                            ∞   7   11

Алынған жолды D(3) пен салыстырып,  D(4)=(0, 5, 6, 12, 7, 11) аламыз;

г) енді D(4)-тен 15 пен11 сандарының кішісі 11 болғандықтан, оған

сәйкес төбе  F –ті  алып тастаймыз Т5= Т4\{ F}={D}.

 ∞   10   ∞   2    4   0

                     11       11

                     13       11

D(4)-пен салыстырып, D(5)=(0, 5, 6, 12, 7, 11) аламыз. Соңғы жолдан келесі қорытынды жасаймыз dw(A,A)=0,  dw(A,B)=5,   dw(A,C)=6,    dw(A,D)=12,   dw(A,E)=7, dw(A,F)=11.

         Жауабы: dw(A,F)=11.

         Айта кетелік, бұл нұсқада А төбесінен F төбесіне қысқа жол кескінделмеген.

Осы есепті шешудің келесі нұсқасын қарастырайық.

Суреттегі графты келесі түрде өзгертеміз (яғни әр төбеге  координатасын тіркеп жазамыз):

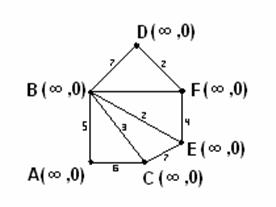
                                                           4.41 Сурет

а) А төбесінен F төбесіне өтетін қысқа жолды салайық. Әр төбеге белгіленген реттелген жұптың  бірінші компонентасы төбеге жеткен кездегі қысқа жолдың ұзындығын, ал екінші компонента қысқа жолдың алдыңғы төбесін білдіреді. Жол табылмайынша, бірінші компонента , ал екіншісі 0 болып тұрады. Компоненталары тұрақтыға айналған төбе ерекше белгіленеді.

         Алгоритмнің бірінші қадамынан кейін  мына суретті   аламыз (А төбесінен жол басталғандықтан, А(0,0));

 

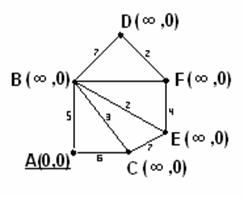
                                                   4.42 Сурет

ә) В және С төбелері А төбесімен сыбайлас болғандықтан, екі қадам жасауға болады. В төбесінің реттелген жұбына (5,А) мәнін береміз, себебі I компонента 5 –бұл А мен В ара қашықтығы, ал II компонента – алдыңғы төбе А.

         Ал С төбесіне  болғандықтан (6,А) мәнін береміз. Реттелген жұптарға өзгерістер жаңа ара қашықтықтар ескісіне қарағанда аз (жол ұзындығы аз) болғанда ғана енгізіледі. В мен С үшін ескі ұзындықтары  болғандықтан өзгеріс енгіздік;

б) үшінші қадамда уақытша енгізілген мәндердің ең азын таңдаймыз. Біздің жағдайда бұл А-дан В-ге дейінгі ара қашықтық, ол 5-ке тең (ал А-дан С-ге дейін 6-ға тең). Сондықтан В(5,А)-ны тұрақты етіп қалдырамыз.

 

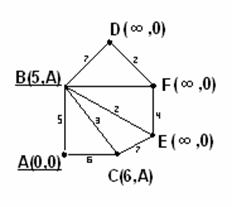
4.43 Сурет

Екінші қадамға қайта оралып, В төбесімен сыбайлас уақытша (себебі оларды әзірге ерекше белгілеген жоқпыз) C,D,E,F төбелерін қарастырамыз.

         Әрбір жағдайда осы төбелерге А-дан В-ге дейінгі ара қашықтықты қосамыз. Сонымен,

С  төбесі үшін 5+3=8;

D төбесі үшін 5+7=2;

E төбесі үшін 5+2=7;

    F төбесі үшін 5+10=15.

         С төбесіне қосқан қашықтығымыз 8, алдыңғысынан (6-дан) көп болғандықтан, ескі компонентасын қалдырамыз. Ал D,E,F үшін алдыңғысынан аз болғандықтан, оларды өзгеріссіз қалдырамыз: D(12,B), E(7,B), F(15,B).

Үшінші қадам жасаймыз: уақытша берілген төбелерге берілген қашықтықтардың ең кішісін табамыз min{6,12,7,15}=6, бұл С-ның компонентасы болғандықтан, оны тұрақты С(6,А) қыламыз.

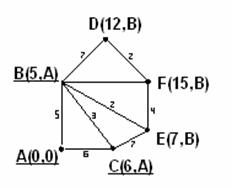
                                                         4.44 Сурет

Енді жаңа С төбесін алайық. Екінші қадамнан ешқандай өзгеріс жоқ (яғни С-ға сыбайлас уақытша төбе қарастыру керек – ол Е төбесі). Үшінші қадамда Е(7,В) төбесін тұрақты етеміз.

 

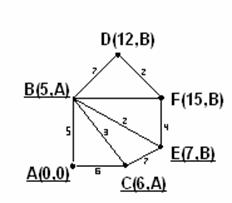
                                                            4.45 Сурет

Жаңа тұрақты Е төбесін қарастырамыз. Екінші қадамда F(15,B)-ны F(11,E) –ге өзгертеміз, себебі F(15,B) ескі компонентаға қарағанда жаңа 7+4=11 аз. Үшінші қадамда F(11,E) тұрақты.

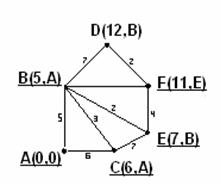
                                                  4.46 Сурет

F төбесі тұрақтыға айналды, 11 – А-дан F-ке дейінгі ең кіші ара қашықтық.

         Егер тұрақты төбелермен сыбайлас төбелер жиынтығы F төбесіне жеткенше дейін бітіп қалса, есептің мағынасы жоқ болар еді, себебі А-дан F-ке дейінгі жол болмас еді.

         Ең қысқа жолдың ұзындығын 11-ді таптық, ал жолдың өзін табу үшін екінші компонентаға қараймыз. F-тың алдында Е, Е-нің алдында В, В-ның алдында А. Сондықтан қысқа жол ABEF.

 4.6 Ағаштар, орман, минималды діңгекті ағаштар

Ағаш деп  циклі жоқ  байланысқан н-граф, яғни тұзағы және еселі қабырға-лары жоқ н-граф айтылады.

Орман деп циклі жоқ байланыспаған н-граф айтылады.

Сонымен, кез-келген орманның байланыстылық компонентасы ағаш болады.

Мысалы.

                                                  

 

 

                                                  Бұл граф ағаш.

 

               4.47 Сурет

 


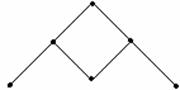   Бұл граф ағаш емес, циклі бар.

               4.48 Сурет

 

 


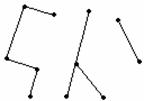        Үш ағаштан құралған орман.

               4.49 Сурет

 1-теорема.  G – тұзақсыз n  қабырғалы н-граф болсын. Келесі шарттар эквивалентті:

а) G – ағаш;

ә) G – n-1 қабырғасы бар байланысқан граф;

б) G – n-1 қабырғалы ациклдік граф;

в) G  графының беттеспейтін екі төбесін жалғыз қарапайым шынжыр қосады;

г) G – ациклді граф.

Егер қандай–да бір сыбайлас емес төбелерін қабырғамен қоссақ, онда алынған графта бір ғана цикл болады.

Анықтама. Егер графтың v төбесінің дәрежесі =1 болса, онда v төбесі соңғы төбе немесе жапырақ (немесе салбырап тұрған төбе) деп аталады. Соңғы төбеге инцидентті қабырға соңғы қабырға деп аталады.

Кез-келген ағашты оның қандай–да бір v төбесіне «іліп» қоюға болады, яғни v төбесін жоғарғы қабатқа, онымен сыбайлас төбелерді бір қабат төмен, т.с.с. орналастыру арқылы.

 

 

 

 

 

 

                                                        4.50 Сурет

Бұл жағдайда v  төбесі ағаштың тамыры деп  аталады.   Ең  төменгі қабатта орналасқан соңғы   төбелер 1 типті деп аталады. Егер ағаштан бірінші типті төбелерді және оған инцидентті соңғы қабырғаларын алып тастасақ, онда ағашта  қалған шеткі төбелер – 2 типті төбелер деп аталады.                                               

Осы сияқты 3,4 ... типті төбелер анықталады. Соңғы ағашта шектеулі типті төбелер қалады және ең көп типті төбелердің саны 1 немесе 2 болады.

         1-мысал. Суреттегі графта v4, v3, v 5, v 6, v 7, v 8 – 1 типті төбелер;

v 1, v 6 – 2 типті төбелер;

v 2 – 3 типті төбелер;

v –  4 типті төбе.

         Әрбір тамырлы бағытталмаған (н-граф) ағаш үшін сәйкес тамырлы бағытталған ағаш анықтауға болады: мұндай ағаштың қабырғалары тамырынан бастап бағытталады, бұл бағыт жалғыз. Басқа төбе–тамырды таңдайтын болсақ, бағытталмаған граф–ағаштан өзге орграф–ағаш аламыз.

2-мысал. Суреттегі G граф–ағашты қарастырайық.

       

 

 

 

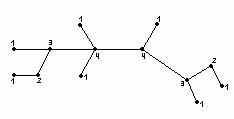
                                               4.51 Сурет

Төбелердің белгілеулері оның типін білдіреді. Максималды 4-ші типті екі төбе бар.  Тамырлары осы максималды типті төбелерде болатын екі әртүрлі бағытталған тамырлы ағаштар тұрғызуға болады:     

    а) тамыр–сол жақтағы  максималды 4-ші типті төбе;

                                                                  

 

                                                                  

 

                                                     4.52 Сурет                                           

     ә) тамыр–оң жақтағы  максималды 4-ші типті төбе.

                                            

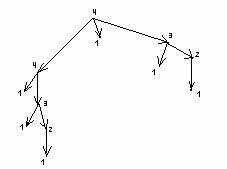
                                                          4.53 Сурет

Егер бағыттарын алып тастасақ, үш суреттегі графтар бір ағашты бейнелейді.

Анықтама. G=(V,E) н-графын қарастырайық, егер  және – G графының кез-келген байланыс компонентасында ағаш құрайтын орман болса, онда G графының  ішкі графы G графы үшін діңгек немесе каркас деп аталады.

Егер G байланысқан граф болса, онда  діңгегі G графының діңгекті ағашы деп аталатын ішкі графы болып табылады. Әрбір графта діңгек болатыны анық: әрбір байланысқан компонентада циклді бұзсақ, яғни артық қабырғаларды алып тастасақ, діңгекті аламыз.

3-мысал. Екі байланысқан компонентасы бар G графын қарастырайық.

 

Қабырғалары цифрлармен берілген.

G графының діңгегі ретінде 2,3,4,6, 7 қабырғалы      

орманды алуға болады (цикл тудыратын       

қабырғалар  санын алып тастадық).

               4.54 Сурет


                                                             

 

 

                   4.55 Сурет

         Бұл мысалдан діңгек бірмәнді анықталмайтыны  көрінеді. Осы графтың тағы бір діңгегі 2,3,4,6,8 қабырғалы орманы.

Діңгек ағаштарды іздеудің әртүрлі жолдары бар және графтың діңгек ағаштарының санын анықтайтын теоремалар да бар. Бірақ біз оған тоқталмаймыз. Әрі қарай қарастырғалы отырған теорема графты сипаттайтын сандарының бірі – цикломатикалық сан туралы.

2-теорема. Кез-келген G н-графының діңгегін алу үшін алып тастау керек қабырғалар саны m-n+c санына тең және ол қабырғаларды алып тастау ретіне тәуелсіз, мұндағы  m – қабырғалар саны, n – төбелер саны,  c – графтың байланыстық компоненталар саны.

Дәлелдеуі. Сi – G графының і-ші байланыстық компоненталар саны болсын (i=).  Сi- дің  ni төбесі болсын. Онда 1-теорема бойынша оның  ki діңгек ағашының (ni -1) қабырғасы болады.

Егер mi –  Сi қабырғалар саны, ni -1–  ki қабырғалар саны болса, онда Сi-ден ki-ді алу үшін (mi-(ni -1)) қабырға алып тастау керек. Барлығы с байланыстық компонентасы болғандықтан, G графының барлық байланыстық компоненталарынан алып тасталынған қабырғаларды қоссақ

= - +=m-n-c.

ν(G)=m-n+c саны G  графының цикломатикалық саны (рангі) деп аталады.

Салдар:

а) ν(G)=0 жағдайда ғана G н-графы ағаш (орман) бола алады;

ә) ν(G)=1 жағдайда ғана G н-графында бір ғана цикл болады.

 4.7  Ең аз салмақты діңгекті ағашты табу

Өлшенген G графының діңгек ағашының салмағы діңгек ағаштың қабырғасына жазылған салмақтардың қосындысына тең.

G графының басқа кез-келген діңгегінің салмағынан кем немесе тең болатын салмақты G графының діңгегін  ең аз салмақты ағаш деп аталады. 

         Ең аз салмақты діңгекті табу есебі жол жүйелерін, электр байланыс жүйелерін және т.б. жоспарлағанда туындайды. Берілген орталықтарды (төбелерді) қандай да бір байланыс жүйесімен (қабырғамен) былай жалғануы керек: екі орталық не тура (бір қабырғамен), не басқа орталықтар арқылы (шынжырмен) және байланыс каналының жалпы ұзындығы арқылы (немесе құны, немесе салмағы).

Ең аз салмақты діңгекті табудың Краскаль алгоритмін қарастырайық.

T=(V,E1) ағашын құрғанда цикл туындамайтындай етіп ең аз қабырғалар таңдап алынады:

а) G=(V,E) графындағы ең аз салмақты е қабырғасын таңдағанда оның (е-ның) тиісті еместігін және E1-ге қосқанда Т ағашында цикл пайда болмайтындығын ескереміз;

ә) осы қабырғаны E1  жиынына қосамыз;

б) осы қасиеттерге ие болатын қабырғалар бар болса, олар біткенше

жалғастыра береміз;

[1]-де бұл алгоритм былай беріледі.

G=(V,E) графы берілген:

а) V төбелер жиынынан және салмағы ең аз е1 жалғыз қабырғасынан тұратын Т1 графын құрамыз;

ә) егер Тi графы құрылған және  (мұндағы n - G графының төбе

саны, с байланыстық компоненталар саны), онда Тi қабырғалар жиынына Тi-дегі қабырғалардың салмағынан аз салмақты және Тi-дегі қабырғалармен цикл құрмайтын  еi+1 қабырғаcын қосу арқылы Тi+1 графын құрамыз.

4-мысал. Суретте G графы берілген. Ең аз салмақты діңгек ағашты табу керек.

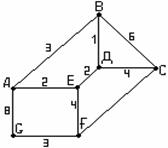                                                         Шешуі:

а) Т1: V ={A,B,C,D,E,F,G} төбелер жиыны,

                                              E1={{B,D}} графтағы ең аз салмақты қабырға  

                                              (салмағы 1);

          ә) T2: V өзгермейді, E2={{B,D},{E,D}}, E1-ге ұшы D төбесінде болатын аз салмақты {E,D} қабырғасын қостық;

           б) T3:  V өзгермейді,

 E3={{B,D},{E,D},{A,E}};

             4.56 Сурет                          в) T4: V өзгермейді,

                                               E4={{B,D},{E,D},{A,E},{E,F}};

           г) T5: V өзгермейді, Е5={{B,D}, {E,D}, {A,E}, {E,F}, {F,G}};

           д) T6: V өзгермейді E6={{B,D}, {E,D}, {A,E}, {E,F}, {F,G}, {C,D}}.

        Басқа қосатын қабырға қалған жоқ, сондықтан ең аз салмақты ізделінді діңгек 2-суретте көрсетілген, оның салмағы 1+2+2+3+4+4=16.

 

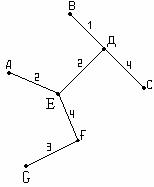
                                                           4.57 Сурет

 Айта кетелік:

а) -лерді анықтағанда оларды бір суретте кескіндейміз, әрбір қадамда бір қабырғадан қосып отырамыз;

ә) келтірілген мысалдағы графта   n=7 төбе, m=10 қабырға болады және ол байланысқан, яғни байланыстық компоненталар саны c=1.

         Сонымен, діңгек алу үшін m-n+c=4 (грфтың цикломатикалық саны) қабырғаны алып тастау керек еді. Расында, {А,В},{А,D},{С,F},{В,C} қабырғалары алып тасталынды.                             

Әдебиеттер  тізімі

1. Судоплатов С.В., Овчинникова Е.В. Элементы дискретной математики. – М.: ИНФРА-М, Новосибирск: изд-во НГТУ, 2002.

2. Москинова Г.И. Дискретная математика. Математика для менеджера в примерах и упражнениях: Учебное пособие. – М.: Логос, 2004. – 240 с.

3. Новиков Ф.А. Дискретная математика для программистов: Учебник для вузов. 2-е изд.  – СПб.: Питер, 2004. – 364 с.: ил. – (Серия «Учебник для вузов»).

4. Андерсон, Д. Дискретная математика и комбинаторика.: Пер. с англ. – М.: Издатель- ский дом «Вильямс», 2004. – 960 с.: ил. – Парал. тит. англ.

5. Белоусов А.И., Ткачев С.Б. Дискретная математика. – М.: изд-во МГТУ им. Н.Э.Баумана, 2001.

6. Шапорев С.Д. Дискретная математика. Курс лекций и практических занятий. – СПб.: БХВ-Петербург, 2006.

7. Яблонский С.В. Введение в дискретную математику. – М. «Высшая школа», 2001.

8. Асеев Г.Г., Абрамов О.М., Ситников Д.Э. Дискретная математика: Учебное пособие.- Ростов н/Д: «Феникс», Харьков: «Торсинг», 2003.

     -144 с.

9. Плотников А.Д. Дискретная математика: учебное пособие/ А.Д.Плотников. – 2-е изд., испр. и доп. – М.: Новое знание, 2006. – 304 с.

10. Оре О. Графы и их применение: пер. с англ./ Под ред. и с предисл. И.М.Яглома. Изд. 3-е, стереотипное. –М.: КомКнига, 2006. – 168 с.

Мазмұны

 1 Жиындар теориясының негізгі ұғымдары

1.1 Жиындар........................................................................................................   3

1.2 Жиындар алгебрасы .....................................................................................   6

1.3 Қатынастар. Унарлы, бинарлы, n-орынды қатынастар  ...........................   9

1.4 Реттік қатынастар  ......................................................................................   16

1.5 Функция. Функционалдық қатынас  .........................................................   18

 2 Математикалық логика элементтері

2.1 Негізгі логикалық операциялар   ................................................................  21

2.2 Логика алгебрасы  ........................................................................................  22

2.3 Буль алгебрасы  ............................................................................................  30

2.4 Дизъюнктивті және конъюнктивті қалыпты формалар  .........................   31

2.5 Дизъюнктивті қалыпты формалар класында минимилизациялау.

      Карно картасы  ............................................................................................   35

2.6 Коммутациялық сұлбалар  .........................................................................   43

 3 Комбинаторика

3.1 Қосу және көбейту ережелері  ..................................................................    47

3.2 Қайталанбайтын және қайталанатын орын ауыстыру мен теруді

есептеу формулалары  ......................................................................................   48

 4 Графтар теориясының элементтері

4.1 Негізгі ұғымдар мен анықтамалар ............................................................   51

4.2 Графтар изоморфизмі  .................................................................................  58

4.3 Маршруттар, жетерлік,  байланыстылық...................................................  62

4.4 Графтардың маршруттарын зерттеу  .........................................................  66

4.5 Графтағы ара қашықтықты зерттеу. Ең қысқа жол туралы  есеп ..............................................................................................................  68

4.6 Ағаштар, орман, минималды діңгекті ағаштар  .......................................  75

4.7 Ең аз салмақты діңгекті ағашты табу  .......................................................  79

Әдебиеттер  тізімі............................................................................................... 81