АЛМАТЫ ЭНЕРГЕТИКА ЖӘНЕ БАЙЛАНЫС ИНСТИТУТЫ
ЖОҒАРЫ МАТЕМАТИКА КАФЕДРАСЫ
МАТЕМАТИКА 2
0507402 ”Автоматтандыру және басқару”, 050717 ”Жылу энергетика”, 050718 ”Электроэнергетика”, 050719 ”Радиотехника, электроника және телекоммуникация” мамандығы бойынша оқитын барлық оқу түрінің студенттеріне арналған дәрістер жинағы
Алматы 2009
ҚҰРАСТЫРУШЫ: Айтчанова Ш. К. Математика 2. 0507402, 050717, 050718, 050719 мамандықтары бойынша оқитын барлық оқу түрінің студенттеріне арналған дәрістер жинағы. -Алматы АИЭС, 2009 – 60 бет.
Ұсынылып отырған оқу құралы 14 дәрістің қысқаша жинағынан құрастырылған. Дәрістер жоғары математика пәнінің математика 2 тарауын (”Көп айнымалы функциялар”, “Интегралдық есептеу”) қамтиды. Oқу құралы Алматы энергетика және байланыс институтының барлық оқу түрінің барлық мамандықтары бойынша оқитын бакалавриат студенттеріне арналған оқу бағдарламасына сәйкестендірілген.
Оқу құралы техникалық жоғары оқу орындарының студенттеріне арналған.
№1 дәріс. Көп айнымалды функциялар
Дәрістің мазмұны:
1. Көп айнымалды функциялардың шегі, үзіліссіздігі.
2. Дербес туындылар мен дербес дифференциалдар. Толық дифференциал.
Дәрістің мақсаты: жаңа түсініктерді анықтап, оларға амалдарды қолдану.
Ғылым мен техникада кездесетін көп құбылыстар бірнеше айнымалы-лардан тәуелді болады.
Мысалдар
1 S=1/2ah- үшбүрыштың ауданы.
2 ![]() - тік бұрышты параллелепипедтің көлемі.
- тік бұрышты параллелепипедтің көлемі.
D жиынында реттелген
(х, у) сандар жұбының жиыны берілсін. Егер әрбір (x,y) ![]() D сандар жұбына z шамасының анықталған
біp мәні сәйкес келсе, онда z тәуелсіз eкi х пен у айнымалыларының
D жиынында бepiлген екі айнымалды функциясы дeйді және z = f(x,y) белгіленеді.
D жиыны функцияның анықталу аймағы деп аталады.
D сандар жұбына z шамасының анықталған
біp мәні сәйкес келсе, онда z тәуелсіз eкi х пен у айнымалыларының
D жиынында бepiлген екі айнымалды функциясы дeйді және z = f(x,y) белгіленеді.
D жиыны функцияның анықталу аймағы деп аталады.
Екі айнымалды функция кесте немесе аналитикалық тәсіл - формула түрінде берілуі мүмкін. Екі айнымалды функция анықтамасын үш немесе одан да көп айнымалылар үшін жалпылауға болады.
Егер әрбір Р(х1,х2,...,хn)
![]() D нүктесіне қандай да бip анықталған
D нүктесіне қандай да бip анықталған
f(P) = f(x1,x2,...,xn) нақты саны сәйкес қойылса, онда D жиынында х1,х2,...,хп - п-айнымалы f: Rn → R сандық функциясы берілді дейдi.
D - жиыны у=f(x1,x2,...,xn) функциясының анықталу аймағы, ал
E = {у![]() R: у = f(P), P
R: у = f(P), P![]() D} жиыны оның мәндер аймағы
деп аталады.
D} жиыны оның мәндер аймағы
деп аталады.
F(x1,x2,...,xn,у)=0 жазуы x1,x2,...,xn,у шамаларының, арасында функциялык байланыс бар екенін жалпы түрде көрсетеді, яғни осы шамалардың қандай да бipeyi, мысалы у қалғандарының айқын емес функциясы екенін білдіреді.
z = f(x,y) функциясы беттің теңдеуін береді. Үш және одан көп айнымалды функциялардың геометриялық бейнесін беру мүмкін емес.
Функцияның шегі
d ‑әлде бір оң сан болсын. ![]() теңсіздігін қанағаттандыратын
барлық
теңсіздігін қанағаттандыратын
барлық ![]() нүктелер жиынын
нүктелер жиынын ![]() нүктесінің
нүктесінің
d-маңайы дейді. f(x,y) функциясы ![]() нүктесінің қандай да бip
нүктесінің қандай да бip ![]() маңайында анықталған болсын (оның
маңайында анықталған болсын (оның ![]() нүктесінің өзінде анықталмауы да
мүмкін, яғни х ≠ х0 немесе у ≠ у0).
нүктесінің өзінде анықталмауы да
мүмкін, яғни х ≠ х0 немесе у ≠ у0).
Егер әрбір ε>0 саны үшін ![]() теңсіздігін қанағаттандыратын барлық
теңсіздігін қанағаттандыратын барлық ![]() нүктелері үшін
нүктелері үшін ![]() шарты орындалатындай δ>0 саны бар болса, онда А саны f
функциясының
шарты орындалатындай δ>0 саны бар болса, онда А саны f
функциясының ![]() нүктесіндегі
шегі деп аталады да,
нүктесіндегі
шегі деп аталады да, ![]() немесе
немесе
![]() деп
белгіленеді. n-тәуелсіз айнымалды функция шегі де дәл осылай
анықталады.
деп
белгіленеді. n-тәуелсіз айнымалды функция шегі де дәл осылай
анықталады.
Мысал. Шекті есептеу керек 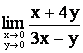 .
.
P(x,y )
нүктесі (0; 0) нүктесінe ![]() түзуімен ұмтылсын. Онда
түзуімен ұмтылсын. Онда 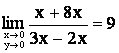 , ал y=5x түзуімен ұмтылса
, ал y=5x түзуімен ұмтылса 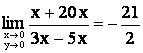 . Сондықтан функцияның бұл
нүктеде шегі болмайды.
. Сондықтан функцияның бұл
нүктеде шегі болмайды.
Функцияның үзіліссіздігі
Егер f(x,y) функциясы ![]() нүктесінің қандай да бip
нүктесінің қандай да бip ![]() маңайында және осы
маңайында және осы ![]() нүктесінде
анықталып
нүктесінде
анықталып ![]() теңдігі орындалса, онда f(x,y)
функциясы
теңдігі орындалса, онда f(x,y)
функциясы ![]() нүктесінде үзіліссіз деп аталады. Егер
нүктесінде үзіліссіз деп аталады. Егер ![]() деп алсақ, онда
деп алсақ, онда ![]()
![]() және керісінше
және керісінше ![]() .
.
Осыны ескеріп теңдікті ![]() түрінде жазуға
болады.
түрінде жазуға
болады.
Аймақтың әpбip нүктесінде үзіліссіз болатын функция осы аймақта үзіліссіз деп аталады.
Шектің касиеттерінен Р0(х0,у0) нүктесінде үзіліссіз f(x,y), g(x,y) функцияларының қосындысы, айырмасы, көбейтіндісі және g(х0,у0) ≠ 0 болса бөліндісі үзіліссіз функция болатыны шығады.
1-ескерту. Екі айнымалды функцияның үзіліс нүктелері тұтас сызықтарды құрауы да мүмкін.
2-ескерту. Айнымалылары кез келген сан болатын функция үзіліссіздігі де дәл осы сияқты анықталады.
Функцияның дербес және толық өсімшелері
z = f(x,y) функциясы берілсін. Енді у аргументіне тұрақты у0 мәнін беріп тек х-ке ∆х өсімшесін берейік. Онда оған сәйкес z-те өсімшеге ие болады. Оны z-тің х бойынша дербес өсімшесі дейді де ∆х z арқылы белгілейді ∆xz = f (х + ∆х, у) - f (х,у). Осы сияқты у-ке ∆у-өсімшесін берсек, онда z у – бойынша ∆уz дербес өсімшеге ие болады ∆yz = f(x,y + ∆y)-f(x,y).
Ал егер х пен у-ке ∆х және ∆у өсімшелерін берсек, онда z үшін жаңа ∆z өсімшесін аламыз. Ол z функциясының толық өciмшесі деп аталады:
∆z = f (х + ∆х, у + ∆у) - f(x,y).
Ескерту. n≥3 айнымалды функциясының толық және дербес өсімшелері осы сияқты анықталады.
Дербес туындылар
f(х,у)
функциясының х бойынша дербес туындысы деп ∆xz дербес
өсімшесінің ∆х өсімшесіне қатынасының
∆х→0 (ұмтылғандағы) шегін (егер ол шек бар
болса) айтады да, ![]() символдарының біреуімен
белгілейді:
символдарының біреуімен
белгілейді: ![]() .
.
f(x,y) функциясының у бойынша дербес туындысы да дәл осылай анықталады және ол ![]() символдарыньң біреуімен белгіленеді:
символдарыньң біреуімен белгіленеді: ![]() .
.
Бұл анықтамадан дербес туындыларды есептеу ережелері бip айнымалы-лы функцияның туындыларын есептеу ережелерімен бірдей екенін көреміз. Дербес туынды айнымалылардың қайсысы бойынша ізделініп отырғаны есте тұру керек, ал қалған айнымалылар тұрақты сан ролін атқарады.
Дербес туындылар функцияның сәйкес ось бойынша өзгеруінің жыл-дамдығына тең.
Мысалдар 1. 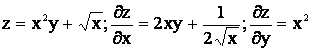 ,
,
2. 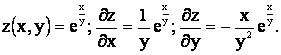
Толық дифференциал
Теорема. Егер z = f(x,y) функциясыныц (х,у) нүктесінде үзіліссіз дербес туындылары бар болса, онда оның осы нүктедегі жеткілікті аз (∆х,∆у)-ке сәйкес өсімшесін келесі формула түрінде жазуға болады
![]() .
.
f функциясының толық өсімшесін қарастырайық:

Сондықтан
![]()
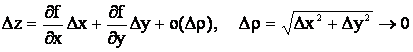 .
.
Бұл
теңдіктегі дербес туындылар ∆х, ∆у-ке тәуелді емес.
Сондықтан теорема шартынан функция өciмшесін кeлeci формула
түрінде жазуға болады: ![]() ( А мен В сандары
∆х,∆у -ге тәуелді емес).
( А мен В сандары
∆х,∆у -ге тәуелді емес).
Егер f функциясының (х,у)
нүктедегі өсімшесін жеткілікті аз (∆х, ∆у) үшін
![]() теңдік түрінде жазуға
болатын болса, онда f функциясы (х,у) нүктесінде
дифференциалданады дейді.
теңдік түрінде жазуға
болатын болса, онда f функциясы (х,у) нүктесінде
дифференциалданады дейді.
А∆х + В∆у қосылғышы ∆f өсімшесінің сызықты бас бөлігі деп аталады, ал қалған қосылғыш ∆х пен ∆у-ке салыстырғанда жоғары peттi шексіз аз шама.
Егер f
функциясы (х,у) нүктесінде дифференциалданса, онда оның осы
нүктеде ![]() тендіктері орындалатындай дербес
туындылары болады.
тендіктері орындалатындай дербес
туындылары болады.
Теорема. f функциясы нүктеде дифференциалдануы үшін оның осы нүктеде дербес туындыларының болуы қажет, ал оның осы нүктеде үзіліссіз дербес туындыларының болуы жеткілікті.
Бір айнымалы f функциясының х нүктесінде дифференциалдануы үшін оның осы нүктеде туындысы болуы қажетті және жеткілікті шарт болатын еді.
Егер f функциясы (х,у) нүктеде
дифференциалданса, онда оның өсімшесінің осы нүктедегі
сызықты бас бөлігі f функциясының (толық) дифференциалы
деп аталады, dz немесе df арқылы белгілінеді: ![]() ∆х, ∆у-
тәуелсіз айнымалылар өсімшелерін х пен у тәуел-сіз айнымалыларының
дифференциалдары деп атайды да, оларды dx
және dy арқылы белгілейді. Онда толык дифференциал
келесі түрге ие болады:
∆х, ∆у-
тәуелсіз айнымалылар өсімшелерін х пен у тәуел-сіз айнымалыларының
дифференциалдары деп атайды да, оларды dx
және dy арқылы белгілейді. Онда толык дифференциал
келесі түрге ие болады:
![]()
Толық дифферендиалдың жуықтап есептеулерге қолданылуы
Егер ∆x пен ∆y жеткілікті аз шама болса, онда функцияның толық өсімшесі мен толық дифференциалы арасында жуық теңдік жaзуға болады: Бұдан х0 + ∆x = х, у0 + ∆у = у деп алып келесі жуық теңдікті жаза аламыз:
![]() .
.
f(x, у) функциясын (х0,у0) нүктесінің маңайында сызықтық функциямен алмастыруға болатынын көреміз. Соңғы формула f(x,y) функциясының мәндерін (егер х х0-ге, ал у у0-ге жақын алынса) белгілі
f(x0,y0), f ′x(x0,y0), f ′y(x0,y0) мәндері бойынша жуықтап есептеуге мүмкіндік береді.
№2 дәріс. Күрделі және айқындалмаған функцияларды дифференциалдау. Бағыт бойынша туынды. Градиент. Бетке жанама жазықтық және нормаль.
Дәрістің мазмұны:
1. Күрделі функция туындысы
2. Айқындалмаған функцияларды дифференциалдау
3. Бағыт бойынша туынды. Градиент және оның қасиеттері.
4. Бетке жанама жазықтық және нормаль (тіктем).
Дәрістің мақсаты: жаңа түсініктерду енгізу, оларды қолдануды үйрену
Күрделі функция туындысы. Толық туынды
![]() ,
, ![]() ,
, ![]() функциясы берілсін. Бұл жағдайда z тәуелдісі t айнымалының күрделі
функциясы болады.
функциясы берілсін. Бұл жағдайда z тәуелдісі t айнымалының күрделі
функциясы болады. ![]() ,
,![]() бар және үзіліссіз болсын.
бар және үзіліссіз болсын. ![]() -
ті табайық. t аргументіне
-
ті табайық. t аргументіне ![]() - өсімшесін берейік. Онда x, y, z
- өсімшесін берейік. Онда x, y, z ![]() ,
, ![]() ,
, ![]() өсімшелеріне
ие болады Дифференциалданудың жеткілікті шарты бойынша
өсімшелеріне
ие болады Дифференциалданудың жеткілікті шарты бойынша
![]() Соңғы
теңдіктің барлық мүшелерін
Соңғы
теңдіктің барлық мүшелерін ![]() -ға бөлеміз:
-ға бөлеміз:
![]() .
.
Егер ![]() -→0
ұмтылса, онда x, y үзіліссіз
болғандықтан,
-→0
ұмтылса, онда x, y үзіліссіз
болғандықтан, ![]() мен
мен ![]() нольге ұмтылады.
нольге ұмтылады.
Осындай тұжырымдардан кейін шекке көшсек, күрделі функцияның туындысы келесі формуламен анықталады.
![]() , немесе
, немесе ![]() .
.
Мысал 1. ![]() ,
, ![]() ,
, ![]() .
.
Онда, ![]()
Енді ![]() , бұл жерде
, бұл жерде ![]() функциясын қарастырайық. Алдыңғы
формуладан
функциясын қарастырайық. Алдыңғы
формуладан ![]() ,
,
себебі ![]() .
Формуладағы
.
Формуладағы ![]() -
-![]() екі айнымалыларының
функциясының х бойынша дербес туындысы, ал
екі айнымалыларының
функциясының х бойынша дербес туындысы, ал ![]() -
-
![]() бір
айнымалы функциясының х бойынша жай
туындысы. Бұл туындыны толық
туынды деп атайды.
бір
айнымалы функциясының х бойынша жай
туындысы. Бұл туындыны толық
туынды деп атайды.
Енді ![]() ,
,
![]() болсын. Бұл жағдайда z тәуелдісі
х және у айнымалыларының күрделі функциясы
болады.
болсын. Бұл жағдайда z тәуелдісі
х және у айнымалыларының күрделі функциясы
болады.
![]() ,
, ![]() ,
, ![]() функцияларының барлық аргументтері
бойынша дербес туындылары үзіліссіз болсын.
функцияларының барлық аргументтері
бойынша дербес туындылары үзіліссіз болсын. ![]() және
және
![]() есептейік. Бұл туындылар келесі формулалар бойынша
есептеледі
есептейік. Бұл туындылар келесі формулалар бойынша
есептеледі 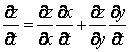 ,
, ![]() .
.
Мысал 2. Егер ![]() ,
, ![]() ,
, ![]() болса, онда
болса, онда ![]() ,
, ![]() .
.
Айқындалмай берілген функциялардың туындысы.
х –тің қандай да бip y-функциясы ![]() теңдеуімен
айқындалмай берілсін.
теңдеуімен
айқындалмай берілсін.
Теорема. Егер ![]() теңдеуін қанағаттандыратын (х,у)
нүктесінің әлде бір аймағында F(x,y), F'x(x,y), F'y(x,y) функциялары
үзіліссіз, ал F'y(x,y)≠0 болса, онда
теңдеуін қанағаттандыратын (х,у)
нүктесінің әлде бір аймағында F(x,y), F'x(x,y), F'y(x,y) функциялары
үзіліссіз, ал F'y(x,y)≠0 болса, онда ![]() теңдеуі туындысы бар y=y(x) функциясын анықтайды және туынды
теңдеуі туындысы бар y=y(x) функциясын анықтайды және туынды
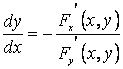 келесі формуламен анықталады.
келесі формуламен анықталады.
Шынында да, ![]() теңдеуін x бойынша дифференциалдап,
теңдеуін x бойынша дифференциалдап, ![]() теңдеуден туындыны табамыз.
теңдеуден туындыны табамыз.
Мысал. Айқындалмай
берілген y
функциясының туындысын ![]() табу керек.
табу керек. ![]() .
.
![]() үшін:
үшін: ![]() ,
, ![]() Сондықтан,
Сондықтан, ![]() .
.
![]() түріндегі теңдеуді қарастырайық.
Бұл тендеумен айқындалмай
анықталған
түріндегі теңдеуді қарастырайық.
Бұл тендеумен айқындалмай
анықталған ![]() функциясының
функциясының ![]() және
және ![]() дербес туындылары келесі формулалармен
анықталады.
дербес туындылары келесі формулалармен
анықталады. 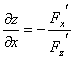 ,
,
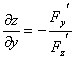 .
.
Кез келген айнымалы айқындалмаған функциясы үшін де олардың дербес туындылары осылайша анықталады.
Мысал- Айқындалмай
берілген z функциясының дербес
туындыларын табу керек. ![]() .
.
 ,
, ![]() ,
, 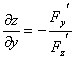 ,
, ![]() .
.
Бағыт бойынша туынды.
D аймағында үзіліссіз және
барлық дербес туындылары да үзіліссіз болатын u=f(x,y,z) үш
айнымалы функция берілсін. M(x,y,z)![]() D және бағыттаушы косинустары
cos α, cosβ, cosγ
болатын
D және бағыттаушы косинустары
cos α, cosβ, cosγ
болатын ![]() векторын қарастырайық..
векторын қарастырайық..
![]() =
=
![]() ,
,
![]() =
=
![]() ,
,
![]() =
=
![]() .
Δl→0 ұмтылғандағы
.
Δl→0 ұмтылғандағы ![]() қатынасының
шегі u = u(x,y,z) функциясының (x,y,z) нүктесіндегі
қатынасының
шегі u = u(x,y,z) функциясының (x,y,z) нүктесіндегі
![]() вектор бағыты бойынша туындысы деп аталады да
вектор бағыты бойынша туындысы деп аталады да ![]() арқылы
белгіленеді.
арқылы
белгіленеді. ![]() =
=![]()
![]() +
+![]()
![]() +
+![]()
![]() .
.
![]()
Дербес туындылар бағыт бойынша туындының дербес жағдайлары.
Градиент және оның қасиеттері.
u = f(x,y,z) функциясыныц (x,y,z) нуктесіндегі
градиенті деп ![]() арқылы
белгілінетін
арқылы
белгілінетін ![]() =(
=(![]() ,
,![]() ,
,![]() )
түріндегі векторды айтады.
)
түріндегі векторды айтады.
Формуладан ![]() бірлік
вектор бағыты бойынша туынды
бірлік
вектор бағыты бойынша туынды
![]() =(
=(![]() ,
, ![]() )
)
екі вектордың скаляр
көбейтіндісі екенін көреміз, олай болса ол градиенттің ![]() векторына
проекциясы.
векторына
проекциясы.
Сондықтан, кез келген ![]() векторы үшін келесі теңсіздік орындалады
векторы үшін келесі теңсіздік орындалады
![]()
![]() .
.
Бұл айтылғандардан, и функциясының (x,y,z) нүктедегі градиентін келесі екі қасиетке ие вектор ретінде анықтауға болатынын көреміз:
а) ол
вектордың ұзындығы (x,y,z) нүктедегі ![]() бағыт бойынша туындының ең үлкен
шамасына тең;
бағыт бойынша туындының ең үлкен
шамасына тең;
б) ол
вектордың бағыты ![]() туындысы ең үлкен
болатын
туындысы ең үлкен
болатын ![]() вектормен бағыттас.
вектормен бағыттас.
Бетке жанама жазықтық және нормаль (тіктем). Толық дифференциалдың геометриялық көpiнici.
S беті z = f(x,y) функциясымен сипатталсын және бұл функцияның Оху жазықтығындағы қандай да бip аймакта үзіліссіз дербес туындылары болсын. S бетінің M0(x0,y0,z0), z0=f(x0,y0) нүктесіндегі жанама жазықтығы деп
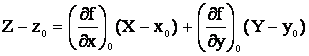 теңдеуімен берілген
жазық-тықты айтады. Мұндағы, X,Y,Z - айнымалы
(ағымдық) координаталар, ал
теңдеуімен берілген
жазық-тықты айтады. Мұндағы, X,Y,Z - айнымалы
(ағымдық) координаталар, ал ![]() -тің дербес
туындыларының Р0(х0,у0)- нүктедегі
мәндері.
-тің дербес
туындыларының Р0(х0,у0)- нүктедегі
мәндері.
f функциясының (х0,у0) нүктесіндегі (х-х0,у-у0)-ге сәйкес дифференциалының геометриялық мағынасы - z=f(x,y) бетіне (х0,у0) нүктеде жүргізілген жанама жазықтық нүктесінің аппликатасының осы
(х– х0, у - у0) -ге сәйкес өciмшесі.
Беттің нормалі (тіктемі) деп жанама жазықтықтың бетке жанау нүкте-сінен өтетін осы жанама жазықтыққа перпендикуляр түзуді айтады.
Егер S беті z=f(x,y) функциясы арқылы берілсе, онда оның Р0(х0,у0) нүктесіндегі тіктемінің теңдеуі
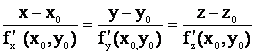 түрінде жазылады.
түрінде жазылады.
S беті F(x,y,z)
= 0 теңдеуімен айқын емес түрде берілсін, ![]() нүктесінің қандай да бip маңайында F функциясының
бip мезгілде нөлге тең емес, үзіліссіз дербес туындылары бар
және
нүктесінің қандай да бip маңайында F функциясының
бip мезгілде нөлге тең емес, үзіліссіз дербес туындылары бар
және
F(P0) = F(x0,y0,z0) = 0 болсын. Онда оның Р0(x0,y0,z0) нүктесіндегі жанама жазықтығының тендеуі
![]() ал
нормаль тендеуі
ал
нормаль тендеуі 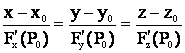 түрлерінде жазылады.
түрлерінде жазылады.
![]() векторы S бетінің
нормалі бойынша бағытталады.
векторы S бетінің
нормалі бойынша бағытталады.
№3 дәріс. Жоғары peттi дербес туындылар мен дифференциалдар. Көп айнымалды функциялардың экстремумдері.
Дәрістің мазмұны:
1. Жоғары peттi дербес туындылар мен толық дифференциалдар.
2. Көп айнымалды функциялардың экстремумдері.
3. Шартты экстремум.
Дәрістің мақсаты: Жоғары peттi дербес туындылар мен толық дифференциалдарды табуды үйрену. Көп айнымалды функцияның шартты және шартсыз экстремумдарын табуды үйреніп, оның практикалық маңызын білу.
Жоғары peттi дербес туындылар мен дифференциалдар
Жоғары peттi
дербес туындылар. z = f(x,y) функциясының
(х,у)![]() G жиынының нүктелерінде үзіліссіз дербес туындылары бар
болса, онда бұл туындьларды G
-жиынында берілген жаңа функциялар деп қарастыруға болады.
G жиынының нүктелерінде үзіліссіз дербес туындылары бар
болса, онда бұл туындьларды G
-жиынында берілген жаңа функциялар деп қарастыруға болады.
Осы функциялардан алынған дербес туындылар f(x,y) функциясының екінші peттi дербес туындылары деп келесі түрде белгілінеді:
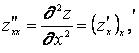
![]() ,
,
![]() ,
, 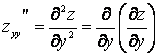 .
.
![]() және
және ![]() - туындылары аралас туындылар деп
аталады; оның
бipiншісі алдымен х, содан соң у бойынша, ал екіншісі,
керісінше, алдымен у, содан соң х бойынша дифференциалдау
арқылы алынған.
- туындылары аралас туындылар деп
аталады; оның
бipiншісі алдымен х, содан соң у бойынша, ал екіншісі,
керісінше, алдымен у, содан соң х бойынша дифференциалдау
арқылы алынған.
Жалпы, n-шi peтті дербес туынды деп қандай да бip (n -1)-ші ретті туындының кез келген бip айнымалысы бойынша дербес туындысын айтады.
Теорема (аралас
туындылар туралы). Функция
u = f(x,y) пен оның дербес туындылары ![]() Р0 нүктесінің
қандай да бip маңайында анықталсын. Егер
Р0 нүктесінің
қандай да бip маңайында анықталсын. Егер![]() Р0 нүктесінде үзіліссіз
болса, онда
Р0 нүктесінде үзіліссіз
болса, онда ![]() ,
яғни, дифференциалдау нәтижесі
дифференциалдау ретіне тәуелді болмайды.
,
яғни, дифференциалдау нәтижесі
дифференциалдау ретіне тәуелді болмайды.
Ескерту. Егер үзіліссіздік шарты орындалмаса, онда Р0 нүктесінде аралас туындылар өзара тең болмауы да мүмкін.
Мысал. ![]() функциясының екінші peттi
дербес туындыларын табу керек.
функциясының екінші peттi
дербес туындыларын табу керек.
![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
![]() =
=![]() .
.
Жоғары ретті дифференциал
![]() функциясының екінші peттi дербес туындылары
үзіліссіз болсын. Онда оның толық дифференциалы
функциясының екінші peттi дербес туындылары
үзіліссіз болсын. Онда оның толық дифференциалы ![]() .
.
z = f(x,y) функциясының екінші peттi дифференциалы деп
бірінші peттi толық дифференциалдың толық
дифференциалын ![]() =
=![]() айтады және мұнда dx пен dy тұрақты,
яғни х пен у-ке тәуелсіз деп-саналады.Сонымен,
айтады және мұнда dx пен dy тұрақты,
яғни х пен у-ке тәуелсіз деп-саналады.Сонымен,
 Жақшаларды ашып аралас туынды жайлы теореманы
пайдаландық.
Жақшаларды ашып аралас туынды жайлы теореманы
пайдаландық.
Дәл осылайша кезкелген жоғары peттi дифференциалды анықтауға болады. Математикалық индукция әдісін қолданып, n-i peттi дифференциалды жазуға болады. Оны бiз символ арқылы жазайық:
![]()
Көп айнымалды функциялардың экстремумдері
Экстремумнің қажетті, жеткілікті шарттары
Егер (х0,
у0)
нүктесі
үшін![]() M(x,y) Î U(x0,y0) f(x,y) > f(x0,y0)
M(x,y) Î U(x0,y0) f(x,y) > f(x0,y0)
( f(x,y) < f(x0,y0). ) теңсіздігі орындалатындай U(x0,y0) маңайы табылса, онда z = f(x,y) функциясы (х0,у0) нүктесінде локальдік (төңіректік) максимумге (минимумге) ие болады дейді.
(х0,у0) - нүктесін локальдік максимум (минимум) нүктесі, ал функцияның ол нүктеге сәйкес мәнін – функцияның максимум (минимум) мәні деп атайды. Локальдік максимум мен минимум мәндері жалпы атаумен локальдік экстремум деп аталады.( 3. 1 Сурет)
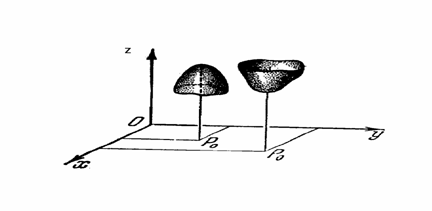
3. 1 Сурет
Суретте функцияның локальдік максимум мен минимумдері көрсетілген.
Теорема (экстремумнің кажетті шарты). Егер дифференциалданатын
z = f(x,y) функциясының
P0(х0,у0) нүктесінде экстремумі бар болса, онда оның осы нүктедегі
дербес туындылары ![]() ,
,![]() нөлге
тең немесе функция ол нүктеде дифференциалданбайды.
нөлге
тең немесе функция ол нүктеде дифференциалданбайды.
Егер f
функциясы үшін P0(х0,у0) нүктесінде ![]() =
=![]() =0
шарт орындалса, онда Р0 - f(x,y) функциясының
стационар нүктесі деп аталады.
=0
шарт орындалса, онда Р0 - f(x,y) функциясының
стационар нүктесі деп аталады.
Салдар. Егер P0(х0,у0)
нүктесінде дифференциалданатын z = f(x,y) функциясы осы P0
нүктеде экстремумге ие болса, онда ![]() немесе
немесе ![]() .
.
Ескерту. Берілген нүктелерде үзіліссіз функцияның дифференциалы жоқ болса да, ол нүктелер экстремум нүктелері болуы мүмкін.
Дифференциалданатын z = f(x,y) функциясының Р0(х0,у0) нүктедегі экстремумнің жеткілікті шартының геометриялық мағынасы функция графи-гінің осы нүктедегі жанама жазықтығының x,y – тәуелсіз айнымалылар жазықтығына параллель болатынын көрсетеді.
Теорема (экстремумнің
жеткілікті шарты). Р0(х0,у0)
нүктесі z = f(x,y) функциясының
стационар нүктесі, ал функция Р0 нүктесінің
қандай да бір маңайында екі рет дифференциалданып, Р0
нүктесіндегі барлық екінші ретті дербес туындылары
үзіліссіз болсын. А=![]() ( х
( х![]() ;у
;у![]() ), В=
), В=![]() ( х
( х![]() ;у
;у![]() ),
),
С=![]() ( х
( х![]() ;у
;у![]() ),
), ![]() =АС-В2 болсын. Онда:
=АС-В2 болсын. Онда:
1. Егер ![]() >0
болса, онда z
= f(x,y) Р0-нүктесінде экстремумге
ие болады, атап айтқанда, А<0 болса - максимум, А>0
болса — минимум.
>0
болса, онда z
= f(x,y) Р0-нүктесінде экстремумге
ие болады, атап айтқанда, А<0 болса - максимум, А>0
болса — минимум.
2. Егер ![]() <0 болса, онда
Р0 -нүктесінде функция экстремум қабылдамайды.
<0 болса, онда
Р0 -нүктесінде функция экстремум қабылдамайды.
3. егер ![]() =0 болса, онда қосымша зерттеу қажет болады.
=0 болса, онда қосымша зерттеу қажет болады.
п>2 болғанда келесі теореманы қолданамыз.
Теорема М![]() нүктесі и= f(х
нүктесі и= f(х![]() ;...;х
;...;х![]() ) функциясының стационар
нүктесі болсын. Егер d2f(М
) функциясының стационар
нүктесі болсын. Егер d2f(М![]() )>0 болса, онда функция) М
)>0 болса, онда функция) М![]() -нүктесінде максимумге, ал d2f(М
-нүктесінде максимумге, ал d2f(М![]() )<0 болса, минимумге
ие болады.
)<0 болса, минимумге
ие болады.
Мысал Функцияның экстремумдерін табу керек z=(х+2)2+(у -1)2.
Шешімі.
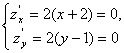
![]()
![]()
![]()
![]()
![]()
М(-2;1) – стационар нүкте. ![]()
![]()
![]() А=2, В=0, С=2,
А=2, В=0, С=2, ![]() =АС-В2= 2*2-02=
4>0, А>0.
=АС-В2= 2*2-02=
4>0, А>0.
Сондықтан М(-2;1)- функцияның минимум нүктесі:
min z=z(-2;1)=(-2+2)2+(1-1)2=0.
Функцияның ең үлкен және ең кіші мәндері
Егер f(P) функциясы шенелген тұйық аймақта үзіліссіз дифференциалданса, онда f функциясы өзінің ең үлкен және ең кіші мәндерін стационар нүктелерде немесе аймақтың шекарасындағы нүктелерде қабылдайды.
Шартты экстремум
Практикада тәуелсіз айнымалылардың ғана емес, қандай да бір қосымша шарттар арқылы байланысқан (мысалы, қандай да бір берілген теңдеулерді қанағаттандыратын) көп айнымалылар функциясының максимумы мен минимумын табуға арналған есептер жиі кездеседі.
х пен у айнымалылары ![]() тендеуімен байланысқан (оны байла-ныс
теңдеуі деп
атайды).
тендеуімен байланысқан (оны байла-ныс
теңдеуі деп
атайды).
![]() функциясының экстремумын берілген шарт
орындалатын аймақтан іздейміз. Егер
функциясының экстремумын берілген шарт
орындалатын аймақтан іздейміз. Егер ![]() -теңдеуді у-ке қатысты
шеше алсақ, (мысалы, y =
-теңдеуді у-ке қатысты
шеше алсақ, (мысалы, y = ![]() (x)), онда
(x)), онда ![]() бip айнымалы функциясын алар
бip айнымалы функциясын алар
едік. Бұл функцияның экстремум қабылдайтын х- нүктесін тауып, байланыс
теңдеуінен осы х-нүктеге сәйкес келетін y-мәнін анықтап, есептің шешімін аламыз.
Алайда қойылған eceпті байланыс теңдеуін y-ке (немесе х-ке) қатысты іздемей-ақ шешуге болады. Ол үшін Ф(х,у)=f(x,y)+lj(x,y) функциясының экстремумын табамыз.
Бұл функция Лагранж
функциясы, ![]() -Лагранж көбейткіші, ал
шартты экстремум есебіне қолданылған әдіс Лагранж
көбейткіштерінің әдісі деп аталады.
-Лагранж көбейткіші, ал
шартты экстремум есебіне қолданылған әдіс Лагранж
көбейткіштерінің әдісі деп аталады.
Шартты экстремумнің қажетті шарты келесі теңдеулермен анықталады:
![]()
![]()
![]() .
.
Соңғы
жүйеден х,у және ![]() табамыз. Мұнда
табамыз. Мұнда ![]() -белгісізі тек көмекші роль атқарады, бұдан
кейін оның бізге қажеті болмайды.
-белгісізі тек көмекші роль атқарады, бұдан
кейін оның бізге қажеті болмайды.
Алынған
теңдеулердің сол жақтары Лагранж функциясының х,у,![]() айнымалылары
бойынша дербес туындылары екенін байқаймыз.
айнымалылары
бойынша дербес туындылары екенін байқаймыз.
Жүйені
қанағаттандыратын х,у (және ![]() ) мәндерінде шартты экстремум болмауы да мүмкін.
Табылған (х, у) -стационар нүктесінде шартты экстремум бар
немесе жоқ екенін білу үшін Лагранж функциясының екінші
дифференциалының таңбасын зерттеу қолайлы. Бірақ dy
дифференциалы
) мәндерінде шартты экстремум болмауы да мүмкін.
Табылған (х, у) -стационар нүктесінде шартты экстремум бар
немесе жоқ екенін білу үшін Лагранж функциясының екінші
дифференциалының таңбасын зерттеу қолайлы. Бірақ dy
дифференциалы
dx-ке тәуелді болатыны есте тұруы керек.
№4 дәріс. Анықталмаған интеграл ұғымы және оның қасиеттері. Анықталмаған интегралды есептеу әдістері
Дәрістің мазмұны:
1. Анықталмаған интеграл ұғымы және оның қасиеттері.
2. Интегралдар кестесі.
3. Айнымалыны ауыстыру
4. Бөліктеп интегралдау
Дәрістің мақсаты: Анықталмаған интеграл ұғымымен, оның қасиеттері және интегралдарды есептеу әдістерімен таныстыру. Интегралдар кестесін пайдалану.
Анықталмаған интеграл және оның қасиеттері
Біз бұрын берілген функция бойынша оның туындысын табу есебімен айналысқанбыз. Енді оған кері есеппен айналысамыз: берілген функцияның туындысы бойынша оның өзін қалай табуға болады? Бұл механикалық тұрғыдан материалдық нүкте қозғалысының жылдамдығы бойынша оның қозғалыс заңын табу екенін білдіреді.
Анықтама. Егер![]() функциясы
функциясы ![]() аралығында дифференциалданса
және
аралығында дифференциалданса
және ![]() ,
,
![]() орындалса,
онда
орындалса,
онда ![]()
![]() -функциясының
-функциясының
![]() аралығындағы
алғашқы функциясы деп
аталады.
аралығындағы
алғашқы функциясы деп
аталады.
(Бұдан әрі ![]() деп аламыз. Басқа жағдай
болса, атап көрсетеміз).
деп аламыз. Басқа жағдай
болса, атап көрсетеміз).
Егер ![]()
![]() -функциясының
-функциясының
![]() аралығындағы
алғашқы функциясы болса, онда кез келген
аралығындағы
алғашқы функциясы болса, онда кез келген ![]() тұрақтысы үшін
тұрақтысы үшін
![]() функциясы да
функциясы да ![]() –үшін
–үшін ![]() –да алғашқы
функция болаады:
–да алғашқы
функция болаады:
![]() ,
, ![]() .
.
Анықтама. 6-ñóðåò![]() функциясының
функциясының ![]() аралығында
анықталған барлық алғашқы
функциялардың жиынтығы
аралығында
анықталған барлық алғашқы
функциялардың жиынтығы ![]() функциясының
функциясының ![]() аралығындағы
анықталмаған интегралы деп аталады және
аралығындағы
анықталмаған интегралы деп аталады және
![]() таңбасымен белгіле-неді:
таңбасымен белгіле-неді: ![]() - интеграл белгісі, ал
- интеграл белгісі, ал ![]() –интеграл
астындағы функция,
–интеграл
астындағы функция, ![]() - интеграл астындағы өрнек деп
аталады.
- интеграл астындағы өрнек деп
аталады.
Егер![]()
![]() –функциясының қандай да бір
алғашқы функциясы болса, онда
–функциясының қандай да бір
алғашқы функциясы болса, онда ![]() деп жазу қалыптасқан.
деп жазу қалыптасқан.
Анықталмаған интегралдың негізгі қасиеттерін көрсетелік:
1. (![]() )’= f(x). Дәлелдеу:
)’= f(x). Дәлелдеу: ![]()
2.
d![]() =f(x)dх
Дәлелдеу:
=f(x)dх
Дәлелдеу: ![]()
3. ![]() = F(x) +С.
= F(x) +С.
4. ![]() , с-тұрақты .
, с-тұрақты .
Дәлелдеу: ![]()
5. ![]() =
=![]()
![]()
![]() .
.
6. Егер ![]()
![]() функциясының алғашқы
функциясы болса, онда
функциясының алғашқы
функциясы болса, онда
![]() = F(x) +С және и=
= F(x) +С және и=![]() -
туындысы үзіліссіз функция болса, онда
-
туындысы үзіліссіз функция болса, онда
![]() = F(и)
+С. Дербес жағдайда,
= F(и)
+С. Дербес жағдайда, ![]() =
=![]() F(ax+b) +С.
F(ax+b) +С.
Мысалдар
1.![]() =
=![]() +С
+С![]()
![]() =
=![]() =
=![]() +С, . . 2.
+С, . . 2.![]() =
=![]() =
=![]() +С, 3.
+С, 3.![]() =
=![]()
![]() +С.
+С.
4. ![]()
Дифференциалдау формулаларынан шығатын интеграл
кестесін келтірейік (![]() -функция).
-функция).
4.1 кесте - Интегралдар кестесі
|
1
|
|
2 |
|
|
3 |
|
4 |
Дербес жағдайда |
|
5 |
|
6 |
|
|
7 |
|
8 |
|
|
9 |
|
10 |
|
|
11 |
|
12 |
|
|
13 |
|
14 |
|
|
15 |
|
16 |
|
|
17 |
|
18 |
|
|
19 |
|
20 |
|
Дифференциалдау формуласын пайдаланып дәлелдеуге
болады; ![]()
Элементар функциялардың туындысы да элементар функциялар болатыны белгілі. Ал элементар функцияларды интегралдау нәтижесінде элементар функция алынбауы да мүмкін.
Мысалы, келесі функциялардың элементар функциялар
еместігі дәлелденген. ![]() - интегралдық логарифм,
- интегралдық логарифм, ![]() -
интегралдық синус,
-
интегралдық синус,
![]() -
интегралдық косинус,
-
интегралдық косинус, ![]() ,
, ![]() - Френель интегралы,
- Френель интегралы, ![]() - Пуассон
интегралы.
- Пуассон
интегралы.
Мысал - ![]() = F(x)
+С, бұл жерде F(x)
= х -
= F(x)
+С, бұл жерде F(x)
= х - ![]() +
+![]() -
-![]() +... .
+... .
Интегралдау әдістері
Ауыстыру (айнымалыны алмастыру) әдісі
Интегралдық есептеулерде айнымалыны алмастыру формуласы ерекше орын алады.
Теорема (интегралдау формуласының
инварианттылығы) ![]() кез келген дифференциалданатын функция
болсын. Егер
кез келген дифференциалданатын функция
болсын. Егер ![]() болса,
онда
болса,
онда ![]() ,
, ![]() немесе
немесе ![]() .
.
Егер ![]() қандай да бір аралықта
үзіліссіз дифференциалданатын болса, онда
қандай да бір аралықта
үзіліссіз дифференциалданатын болса, онда ![]() .
.
Мысал - ![]()
Бұл есепті басқаша
шығаруға болады. ![]()
Бұл әдіс айнымалыны дифференциалдың астына енгізу деп аталады.
Мысал- ![]() интегралды есептеу керек. .
интегралды есептеу керек. .![]()
Бөліктеп интегралдау әдісі
Егер ![]() және
және ![]() функциялары үзіліссіз
дифференциалданатын болса, онда d(uv) = udv
+ vdu немесе udv= d(uv) – vdu. Бұл
теңдікті интегралдап,
функциялары үзіліссіз
дифференциалданатын болса, онда d(uv) = udv
+ vdu немесе udv= d(uv) – vdu. Бұл
теңдікті интегралдап, ![]() анықталмаған
интегралдың негізгі қасиеттерін қолданса, бөліктеп
интегралдау формуласы деп аталатын формула орын алады.
анықталмаған
интегралдың негізгі қасиеттерін қолданса, бөліктеп
интегралдау формуласы деп аталатын формула орын алады. ![]() .
.
Бұл формуланы қолданып есептеу бөліктеп интегралдау әдісі деп аталады. Осы әдіспен есептеуге қолайлы кейбір интегралдарды көрсетейік:
1)
![]() ,
,
![]() ,
,
![]() .
.
![]() – п -
ші дәрежелі көпмүшелік,
n-натурал сан, и =
– п -
ші дәрежелі көпмүшелік,
n-натурал сан, и =![]() , dv – қалған өрнек болу керек.
, dv – қалған өрнек болу керек.
2)
![]() ,
,
![]() ,
,![]() ,
,
![]() интегралдарында
dv=
интегралдарында
dv=![]() dx болу керек.
dx болу керек.
Мысал . ![]() интегралды есептеу керек.
интегралды есептеу керек.

Тригонометриялық функцияларды интегралдау
1. ![]() интегралын есептеп көрейік.
интегралын есептеп көрейік.
а) Егер ![]() немесе
немесе
![]() санының
ең болмағанда бipeyi тақ оң сан болса, онда тақ
дәрежеден бірінші дәрежелі бip көбейткішті бөліп,
қалған жұп дәрежені cos2x + sin2x
= 1 формуласының жәрдемімен толықтауыш функция
арқылы өрнектеп, кестелік интегралға келтіруге болады.
санының
ең болмағанда бipeyi тақ оң сан болса, онда тақ
дәрежеден бірінші дәрежелі бip көбейткішті бөліп,
қалған жұп дәрежені cos2x + sin2x
= 1 формуласының жәрдемімен толықтауыш функция
арқылы өрнектеп, кестелік интегралға келтіруге болады.
б) Егер ![]() мен
мен
![]() тepic
емес бүтін жұп сандар болса, онда дәрежені төмендету
формулалары қолданылады:
тepic
емес бүтін жұп сандар болса, онда дәрежені төмендету
формулалары қолданылады:
![]() ,
,
![]()
в) Егер m + n = -2k, k![]() N, яғни m + n теріс
таңбалы бүтін жұп сан болса, онда u = tgx немесе u
= ctgx ауыстыруын жасаған жөн.
N, яғни m + n теріс
таңбалы бүтін жұп сан болса, онда u = tgx немесе u
= ctgx ауыстыруын жасаған жөн.
2. ![]() ,
, ![]() түріндегі интегралдарды табу үшін
келесі
түріндегі интегралдарды табу үшін
келесі
формулаларды қолдану ыңғайлы ![]()
![]()
3. ![]() ,
,
![]() ,
,
![]() ,
,
![]()
түріндегі интегралдар келесі көбейтіндіні қосындыға түрлендіру формулалары арқылы кестелік интегралдарға келеді:
![]()
![]()
![]()
№5 дәріс. Рационал және иррационал функцияларды интегралдау. Әмбебап ауыстыру. Тригонометриялық ауыстырулар
Дәрістің мазмұны:
1. Рационал функция және оны ең қарапайым бөлшектер қосындысына жіктеу.
2. Рационал функцияларды интегралдау. Анықталмаған коэффициенттер әдісі.
3. Кейбір иррационал функцияларды интегралдау
4. Әмбебап ауыстыру
5. Тригонометриялық ауыстырулар.
Дәрістің мақсаты: Рационал, иррационал және кейбір тригонометриялық функцияларды интегралдаудың тәсілдерін көрсету.
Рационал функция және оны қарапайым бөлшектер қосындысына жіктеу
Екі алгебралық көпмүшеліктердің қатынасы
f(x)= ![]() Qn(x) =
Qn(x) = ![]() хп+
хп+![]() хп -1+...+
хп -1+...+![]() ,
Рт(х) =
,
Рт(х) = ![]() хт+
хт+![]() хт -1+...+
хт -1+...+![]() .
.
рационал функция немесе рационал бөлшек деп аталады.
Рm(x) және ![]() Qn(x) -нақты көпмүшеліктер
және х-нақты айнымалы деп есептейміз. Егер m < n
болса, онда ол дұрыс бөлшек деп аталады.
Qn(x) -нақты көпмүшеліктер
және х-нақты айнымалы деп есептейміз. Егер m < n
болса, онда ол дұрыс бөлшек деп аталады.
Егер m>n болса, онда ол бұрыс бөлшек деп аталады.
Бөлу арқылы бұрыс бөлшекті көпмүшелік пен дұрыс бөлшектің қосындысы түрінде жаза аламыз Дұрыс бөлшекті интегралдаудың негізгі тәсілі - дұрыс бөлшекті қарапайым бөлшектердің қосындысына жіктеу. Енді бөлшекті дұрыс (m < n) деп алып, оны қарапайым бөлшектердің қосындысына жіктеу меселесін қарастырайық.
Келесі бөлшектер қарапайым (жәй) бөлшектер деп аталады:
І.![]() , ІІ.
, ІІ. ![]() , ІІІ.
, ІІІ. ![]() , ІV.
, ІV. ![]() ,
,
(мұндағы п=2,3,..., а,р,q,А,М,N -нақты сандар; D=р2-4 q<0.
Қарапайым бөлшектерді интегралдап көрейік.
І.![]()
ІІ. ![]()
ІІІ. ![]() Бөлшектің алымында квадрат
үшмүшеліктің туындысын
Бөлшектің алымында квадрат
үшмүшеліктің туындысын ![]() бөліп
алып, интегралды екі интегралға бөлеміз.
бөліп
алып, интегралды екі интегралға бөлеміз.

![]() , екінші интегралды
табу үшін квадрат үшмүшеліктен толық квадрат
бөліп алу керек.
, екінші интегралды
табу үшін квадрат үшмүшеліктен толық квадрат
бөліп алу керек.
Мысал. ![]() интегралды табу керек.
интегралды табу керек.
Шешімі:
![]()
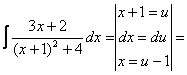
![]()
![]()
![]()
![]() ---
---![]() =
= ![]() -
-![]() .
.
ІV. ![]()
Бірінші интеграл кестелік интегралға ( òdu/uk)
келтіріледі: ![]() .
Екінші интеграл u=x+p/2,
a=
.
Екінші интеграл u=x+p/2,
a=![]() ,
,
q-p2/4>0 болса ![]() .
.
![]() =
=
![]()
![]() –
рекурренттік формулаға
келтіріледі.
–
рекурренттік формулаға
келтіріледі.
Теорема. ![]() m < n бөлшегінің бөлімі келесі теңдік түрінде жіктелінсін:
m < n бөлшегінің бөлімі келесі теңдік түрінде жіктелінсін:
Qn(x) = ![]() (х-х
(х-х![]() )k
)k![]() …(х-хr)k
…(х-хr)k![]() (x2+p
(x2+p![]() x+q
x+q![]() )l
)l![]() …( x2+p
…( x2+p![]() x+q
x+q![]() )l
)l![]() ,
,
Мұндағы ![]() , х
, х![]() , p
, p![]() , q
, q![]() -нақты
сандар; k
-нақты
сандар; k![]() , I
, I![]() -
натурал сандар;
-
натурал сандар;
k![]() +…+ k
+…+ k![]() +2(I
+2(I![]() +…+ I
+…+ I![]() )=n,
р
)=n,
р![]() 2- 4 q
2- 4 q![]() <0. Онда ол
бөлшекті жалғыз түрде келесі қарапайым
бөлшектердің қосындыға жіктеуге болады:
<0. Онда ол
бөлшекті жалғыз түрде келесі қарапайым
бөлшектердің қосындыға жіктеуге болады:
![]() =
=![]() +….+
+….+![]() +
+![]() +….+
+….+![]()
Мұндағы А![]() , М
, М![]() , N
, N![]() -анықталмаған
коэффициенттер
-анықталмаған
коэффициенттер ![]() көбейткішіне
көбейткішіне
![]() +
+![]() +…+
+…+![]() , ал (x2+px+q)I көбейткішіне
, ал (x2+px+q)I көбейткішіне
![]() +
+![]() +…+
+…+![]() , бөлшектерінің қосындысы
сәйкес келеді.
, бөлшектерінің қосындысы
сәйкес келеді.
Анықталмаған коэффициенттерді табу үшін, мысалы, көпмүшеліктердің бірдей дәрежелерінің коэффициенттерін теңестіру керек.
Мысал. ![]() интегралды табу
керек.
интегралды табу
керек.
Интеграл астындығы функцияны қарапайым бөлшектердің
қосындысына жіктеп, анықталмаған коэффициенттерді табу керек. ![]()
![]()
![]() +
+![]() ,
,
х+5=А(х+2)+В(х+1), ![]() А=4, В=-3.
А=4, В=-3.
![]() = 4
= 4![]() -3
-3![]() = 4ln
= 4ln![]() -3ln
-3ln![]() +C.
+C.
Кейбір иррационал өрнектерді интегралдау
Рационал емес элементар функциялардыц интегралдарын айнымалыны алмастыру арқылы рационал функцияның интегралына келтіруге болатын, яғни интегралды рационалдауға болатын жағдайларды қарастырайық.
R(х,у)- өз аргументтері х пен у-тің рационал функциясы болсын .
1. ![]()
![]()
Бұл интеграл ax+b=t![]() айнымалы ауыстыруы
арқылы рационалданады.
айнымалы ауыстыруы
арқылы рационалданады.
2. 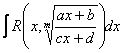 - мұндағы a,b,c,d - тұрақты
сандар, m-натурал сан, ad-bc≠0.
Интеграл
астындағы функция сызықты иррационал бөлшек деп аталады.
Бұл интеграл
- мұндағы a,b,c,d - тұрақты
сандар, m-натурал сан, ad-bc≠0.
Интеграл
астындағы функция сызықты иррационал бөлшек деп аталады.
Бұл интеграл ![]() айнымалы ауыстыруы арқылы
рационалданады.
айнымалы ауыстыруы арқылы
рационалданады.
3. 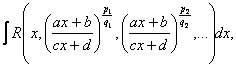 мұндағы
p
мұндағы
p![]() ,q
,q![]() -бүтін сандар. Бұл
интеграл
-бүтін сандар. Бұл
интеграл ![]() =t
=t![]() , айнымалы
ауыстыруы арқылы рационалданады.
, айнымалы
ауыстыруы арқылы рационалданады.
п – ![]() ,
,![]() ,… бөлшектерінің бөлімдерінің
ең кіші ортақ еселігі.
,… бөлшектерінің бөлімдерінің
ең кіші ортақ еселігі.
4. ![]()
![]() не
не ![]() санын түбірдің алдына
шығарып, квадрат үшмүшеліктен толық квадрат бөліп
алу керек.
санын түбірдің алдына
шығарып, квадрат үшмүшеліктен толық квадрат бөліп
алу керек.
5. ![]()
6. ![]() Екі интегралға бөлу керек. Бөлшектің алымында
квадрат үшмүшеліктің туындысын
Екі интегралға бөлу керек. Бөлшектің алымында
квадрат үшмүшеліктің туындысын ![]() бөліп
алып, интеграл-ды екі интегралға бөлеміз. Екінші
интегралды табу үшін квадрат
үшмүшеліктен толық квадрат бөліп алу керек.
бөліп
алып, интеграл-ды екі интегралға бөлеміз. Екінші
интегралды табу үшін квадрат
үшмүшеліктен толық квадрат бөліп алу керек.
7. ![]()
1) p-бүтін сан болса, x=tS, мұндағы s- m, n сандардың бөлімдерінің ең кіші ортақ еселігі.
2) (m+1)/n – бүтін сан болса, онда: a+bxn=tS;
3) p+(m+1)/n – бүтін сан ; онда: a-n+b=tS мұндағы s- p бөлшегінің бөлімі.
Универсал (әмбебап) ауыстыруы
![]() түріндегі интегралды табайық.
түріндегі интегралды табайық.
Бұл интеграл ![]() ауыстыруы арқылы әрқашанда рационал
функцияның интегралына келеді. Расында да,
ауыстыруы арқылы әрқашанда рационал
функцияның интегралына келеді. Расында да,
![]() ,
,
![]() ,
х=2arctgt, dx=
,
х=2arctgt, dx=![]() .
.
![]() ауыстыруы интегралды әрқашанда элементар функция
арқылы өрнектей алатындықтан, оны универсал (әмбебап)
ауыстыруы деп атайды. Бірақ универсал ауыстыруы «күшті»
әдіс болу себебінен көп жағдайларда керекті
түрлендірулерді қысқа және қарапайым етіп жасау
мағынасында ең жақсы әдіс бола бермейді.
ауыстыруы интегралды әрқашанда элементар функция
арқылы өрнектей алатындықтан, оны универсал (әмбебап)
ауыстыруы деп атайды. Бірақ универсал ауыстыруы «күшті»
әдіс болу себебінен көп жағдайларда керекті
түрлендірулерді қысқа және қарапайым етіп жасау
мағынасында ең жақсы әдіс бола бермейді.
Мысалы, егер R(-sin
x, -cos x)= R(sin x, cos x), болса, онда tg x=t,
![]() ,
,
![]() ,
х=arctgt, dx=
,
х=arctgt, dx=![]() ауыстыруы мақсатқа тезірек жеткізеді.
ауыстыруы мақсатқа тезірек жеткізеді.
∫R(tgx)dx түріндегі интеграл u = tgx ауыстыруы арқылы алынады.
Егер R(sin x,-cos x)= - R(sin x, cos x) болса, онда sin x=t.
Егер R(-sin x, cos x)= - R(sin x, cos x), болса, онда cos x=t.
Тригонометриялық алмастырулар
Келесі алмастырулар интегралдарды тригонометриялық функциялар-дың интегралдарына келтіреді.
1. ![]()
2. ![]()
3. ![]()



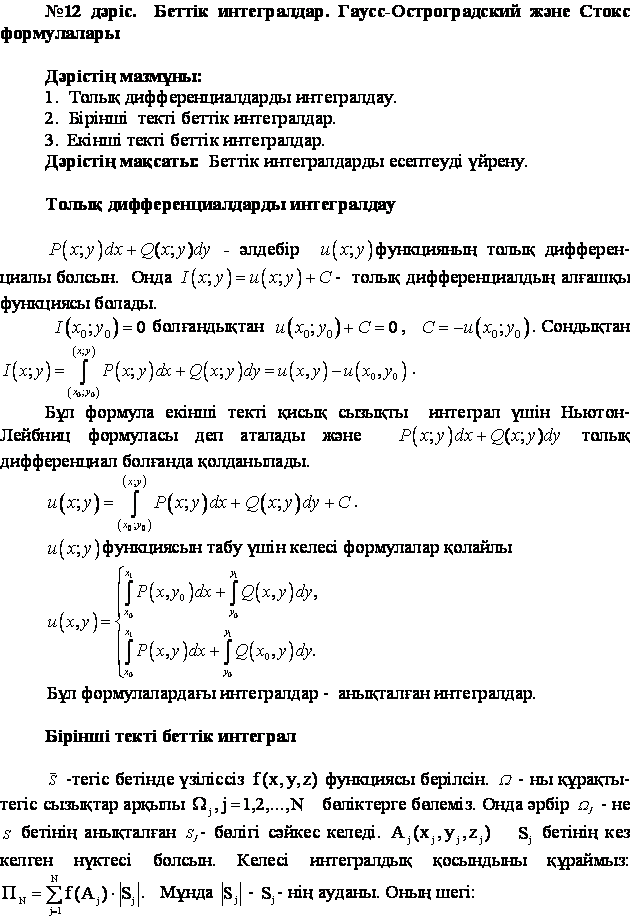


№2 дәріс. Күрделі және айқындалмаған функцияларды дифференциалдау. Бағыт бойынша туынды. Градиент. Бетке жанама жазықтық және нормаль.
Дәрістің мазмұны:
1. Күрделі функция туындысы
2. Айқындалмаған функцияларды дифференциалдау
3. Бағыт бойынша туынды. Градиент және оның қасиеттері.
4. Бетке жанама жазықтық және нормаль (тіктем).
Дәрістің мақсаты: жаңа түсініктерду енгізу, оларды қолдануды үйрену
Күрделі функция туындысы. Толық туынды
![]() ,
, ![]() ,
, ![]() функциясы берілсін. Бұл жағдайда z тәуелдісі t айнымалының күрделі
функциясы болады.
функциясы берілсін. Бұл жағдайда z тәуелдісі t айнымалының күрделі
функциясы болады. ![]() ,
,![]() бар және үзіліссіз болсын.
бар және үзіліссіз болсын. ![]() -
ті табайық. t аргументіне
-
ті табайық. t аргументіне ![]() - өсімшесін берейік. Онда x, y, z
- өсімшесін берейік. Онда x, y, z ![]() ,
, ![]() ,
, ![]() өсімшелеріне
ие болады Дифференциалданудың жеткілікті шарты бойынша
өсімшелеріне
ие болады Дифференциалданудың жеткілікті шарты бойынша
![]() Соңғы
теңдіктің барлық мүшелерін
Соңғы
теңдіктің барлық мүшелерін ![]() -ға бөлеміз:
-ға бөлеміз:
![]() .
.
Егер ![]() -→0
ұмтылса, онда x, y үзіліссіз
болғандықтан,
-→0
ұмтылса, онда x, y үзіліссіз
болғандықтан, ![]() мен
мен ![]() нольге ұмтылады.
нольге ұмтылады.
Осындай тұжырымдардан кейін шекке көшсек, күрделі функцияның туындысы келесі формуламен анықталады.
![]() , немесе
, немесе ![]() .
.
Мысал 1. ![]() ,
, ![]() ,
, ![]() .
.
Онда, ![]()
Енді ![]() , бұл жерде
, бұл жерде ![]() функциясын қарастырайық. Алдыңғы
формуладан
функциясын қарастырайық. Алдыңғы
формуладан ![]() ,
,
себебі ![]() .
Формуладағы
.
Формуладағы ![]() -
-![]() екі айнымалыларының
функциясының х бойынша дербес туындысы, ал
екі айнымалыларының
функциясының х бойынша дербес туындысы, ал ![]() -
-
![]() бір
айнымалы функциясының х бойынша жай
туындысы. Бұл туындыны толық
туынды деп атайды.
бір
айнымалы функциясының х бойынша жай
туындысы. Бұл туындыны толық
туынды деп атайды.
Енді ![]() ,
,
![]() болсын. Бұл жағдайда z тәуелдісі
х және у айнымалыларының күрделі функциясы
болады.
болсын. Бұл жағдайда z тәуелдісі
х және у айнымалыларының күрделі функциясы
болады.
![]() ,
, ![]() ,
, ![]() функцияларының барлық аргументтері
бойынша дербес туындылары үзіліссіз болсын.
функцияларының барлық аргументтері
бойынша дербес туындылары үзіліссіз болсын. ![]() және
және
![]() есептейік. Бұл туындылар келесі формулалар бойынша
есептеледі
есептейік. Бұл туындылар келесі формулалар бойынша
есептеледі 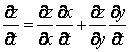 ,
, ![]() .
.
Мысал 2. Егер ![]() ,
, ![]() ,
, ![]() болса, онда
болса, онда ![]() ,
, ![]() .
.
Айқындалмай берілген функциялардың туындысы.
х –тің қандай да бip y-функциясы ![]() теңдеуімен
айқындалмай берілсін.
теңдеуімен
айқындалмай берілсін.
Теорема. Егер ![]() теңдеуін қанағаттандыратын (х,у)
нүктесінің әлде бір аймағында F(x,y), F'x(x,y), F'y(x,y) функциялары
үзіліссіз, ал F'y(x,y)≠0 болса, онда
теңдеуін қанағаттандыратын (х,у)
нүктесінің әлде бір аймағында F(x,y), F'x(x,y), F'y(x,y) функциялары
үзіліссіз, ал F'y(x,y)≠0 болса, онда ![]() теңдеуі туындысы бар y=y(x) функциясын анықтайды және туынды
теңдеуі туындысы бар y=y(x) функциясын анықтайды және туынды
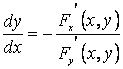 келесі формуламен анықталады.
келесі формуламен анықталады.
Шынында да, ![]() теңдеуін x бойынша дифференциалдап,
теңдеуін x бойынша дифференциалдап, ![]() теңдеуден туындыны табамыз.
теңдеуден туындыны табамыз.
Мысал. Айқындалмай
берілген y
функциясының туындысын ![]() табу керек.
табу керек. ![]() .
.
![]() үшін:
үшін: ![]() ,
, ![]() Сондықтан,
Сондықтан, ![]() .
.
![]() түріндегі теңдеуді
қарастырайық. Бұл
тендеумен айқындалмай анықталған
түріндегі теңдеуді
қарастырайық. Бұл
тендеумен айқындалмай анықталған ![]() функциясының
функциясының ![]() және
және ![]() дербес туындылары келесі формулалармен анықталады.
дербес туындылары келесі формулалармен анықталады. 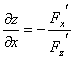 ,
, 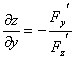 .
.
Кез келген айнымалы айқындалмаған функциясы үшін де олардың дербес туындылары осылайша анықталады.
Мысал- Айқындалмай
берілген z функциясының дербес
туындыларын табу керек. ![]() .
.
 ,
, ![]() ,
, 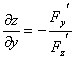 ,
, ![]() .
.
Бағыт бойынша туынды.
D аймағында үзіліссіз және
барлық дербес туындылары да үзіліссіз болатын u=f(x,y,z) үш
айнымалы функция берілсін. M(x,y,z)![]() D және бағыттаушы косинустары
cos α, cosβ, cosγ
болатын
D және бағыттаушы косинустары
cos α, cosβ, cosγ
болатын ![]() векторын қарастырайық..
векторын қарастырайық..
![]() =
=
![]() ,
,
![]() =
=
![]() ,
,
![]() =
=
![]() .
Δl→0 ұмтылғандағы
.
Δl→0 ұмтылғандағы ![]() қатынасының
шегі u = u(x,y,z) функциясының (x,y,z) нүктесіндегі
қатынасының
шегі u = u(x,y,z) функциясының (x,y,z) нүктесіндегі
![]() вектор бағыты бойынша туындысы деп аталады да
вектор бағыты бойынша туындысы деп аталады да ![]() арқылы
белгіленеді.
арқылы
белгіленеді. ![]() =
=![]()
![]() +
+![]()
![]() +
+![]()
![]() .
.
![]()
Дербес туындылар бағыт бойынша туындының дербес жағдайлары.
Градиент және оның қасиеттері.
u = f(x,y,z) функциясыныц (x,y,z) нуктесіндегі
градиенті деп ![]() арқылы
белгілінетін
арқылы
белгілінетін ![]() =(
=(![]() ,
,![]() ,
,![]() )
түріндегі векторды айтады.
)
түріндегі векторды айтады.
Формуладан ![]() бірлік
вектор бағыты бойынша туынды
бірлік
вектор бағыты бойынша туынды
![]() =(
=(![]() ,
, ![]() )
)
екі вектордың скаляр
көбейтіндісі екенін көреміз, олай болса ол градиенттің ![]() векторына
проекциясы.
векторына
проекциясы.
Сондықтан, кез келген ![]() векторы үшін келесі теңсіздік орындалады
векторы үшін келесі теңсіздік орындалады
![]()
![]() .
.
Бұл айтылғандардан, и функциясының (x,y,z) нүктедегі градиентін келесі екі қасиетке ие вектор ретінде анықтауға болатынын көреміз:
а) ол
вектордың ұзындығы (x,y,z) нүктедегі ![]() бағыт бойынша туындының ең үлкен
шамасына тең;
бағыт бойынша туындының ең үлкен
шамасына тең;
б) ол
вектордың бағыты ![]() туындысы ең үлкен
болатын
туындысы ең үлкен
болатын ![]() вектормен бағыттас.
вектормен бағыттас.
Бетке жанама жазықтық және нормаль (тіктем). Толық дифференциалдың геометриялық көpiнici.
S беті z = f(x,y) функциясымен сипатталсын және бұл функцияның Оху жазықтығындағы қандай да бip аймакта үзіліссіз дербес туындылары болсын. S бетінің M0(x0,y0,z0), z0=f(x0,y0) нүктесіндегі жанама жазықтығы деп
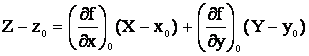 теңдеуімен берілген
жазық-тықты айтады. Мұндағы, X,Y,Z - айнымалы
(ағымдық) координаталар, ал
теңдеуімен берілген
жазық-тықты айтады. Мұндағы, X,Y,Z - айнымалы
(ағымдық) координаталар, ал ![]() -тің дербес
туындыларының Р0(х0,у0)- нүктедегі
мәндері.
-тің дербес
туындыларының Р0(х0,у0)- нүктедегі
мәндері.
f функциясының (х0,у0) нүктесіндегі (х-х0,у-у0)-ге сәйкес дифференциалының геометриялық мағынасы - z=f(x,y) бетіне (х0,у0) нүктеде жүргізілген жанама жазықтық нүктесінің аппликатасының осы
(х– х0, у - у0) -ге сәйкес өciмшесі.
Беттің нормалі (тіктемі) деп жанама жазықтықтың бетке жанау нүкте-сінен өтетін осы жанама жазықтыққа перпендикуляр түзуді айтады.
Егер S беті z=f(x,y) функциясы арқылы берілсе, онда оның Р0(х0,у0) нүктесіндегі тіктемінің теңдеуі
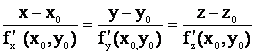 түрінде жазылады.
түрінде жазылады.
S беті F(x,y,z)
= 0 теңдеуімен айқын емес түрде берілсін, ![]() нүктесінің қандай да бip маңайында F функциясының
бip мезгілде нөлге тең емес, үзіліссіз дербес туындылары бар
және
нүктесінің қандай да бip маңайында F функциясының
бip мезгілде нөлге тең емес, үзіліссіз дербес туындылары бар
және
F(P0) = F(x0,y0,z0) = 0 болсын. Онда оның Р0(x0,y0,z0) нүктесіндегі жанама жазықтығының тендеуі
![]() ал
нормаль тендеуі
ал
нормаль тендеуі 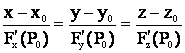 түрлерінде жазылады.
түрлерінде жазылады.
![]() векторы S бетінің
нормалі бойынша бағытталады.
векторы S бетінің
нормалі бойынша бағытталады.
№2 дәріс. Күрделі және айқындалмаған функцияларды дифференциалдау. Бағыт бойынша туынды. Градиент. Бетке жанама жазықтық және нормаль.
Дәрістің мазмұны:
1. Күрделі функция туындысы
2. Айқындалмаған функцияларды дифференциалдау
3. Бағыт бойынша туынды. Градиент және оның қасиеттері.
4. Бетке жанама жазықтық және нормаль (тіктем).
Дәрістің мақсаты: жаңа түсініктерду енгізу, оларды қолдануды үйрену
Күрделі функция туындысы. Толық туынды
![]() ,
, ![]() ,
, ![]() функциясы берілсін. Бұл жағдайда z тәуелдісі t айнымалының күрделі
функциясы болады.
функциясы берілсін. Бұл жағдайда z тәуелдісі t айнымалының күрделі
функциясы болады. ![]() ,
,![]() бар және үзіліссіз болсын.
бар және үзіліссіз болсын. ![]() -
ті табайық. t аргументіне
-
ті табайық. t аргументіне ![]() - өсімшесін берейік. Онда x, y, z
- өсімшесін берейік. Онда x, y, z ![]() ,
, ![]() ,
, ![]() өсімшелеріне
ие болады Дифференциалданудың жеткілікті шарты бойынша
өсімшелеріне
ие болады Дифференциалданудың жеткілікті шарты бойынша
![]() Соңғы
теңдіктің барлық мүшелерін
Соңғы
теңдіктің барлық мүшелерін ![]() -ға бөлеміз:
-ға бөлеміз:
![]() .
.
Егер ![]() -→0
ұмтылса, онда x, y үзіліссіз
болғандықтан,
-→0
ұмтылса, онда x, y үзіліссіз
болғандықтан, ![]() мен
мен ![]() нольге ұмтылады.
нольге ұмтылады.
Осындай тұжырымдардан кейін шекке көшсек, күрделі функцияның туындысы келесі формуламен анықталады.
![]() , немесе
, немесе ![]() .
.
Мысал 1. ![]() ,
, ![]() ,
, ![]() .
.
Онда, ![]()
Енді ![]() , бұл жерде
, бұл жерде ![]() функциясын қарастырайық. Алдыңғы
формуладан
функциясын қарастырайық. Алдыңғы
формуладан ![]() ,
,
себебі ![]() .
Формуладағы
.
Формуладағы ![]() -
-![]() екі айнымалыларының
функциясының х бойынша дербес туындысы, ал
екі айнымалыларының
функциясының х бойынша дербес туындысы, ал ![]() -
-
![]() бір
айнымалы функциясының х бойынша жай
туындысы. Бұл туындыны толық
туынды деп атайды.
бір
айнымалы функциясының х бойынша жай
туындысы. Бұл туындыны толық
туынды деп атайды.
Енді ![]() ,
,
![]() болсын. Бұл жағдайда z тәуелдісі
х және у айнымалыларының күрделі функциясы
болады.
болсын. Бұл жағдайда z тәуелдісі
х және у айнымалыларының күрделі функциясы
болады.
![]() ,
, ![]() ,
, ![]() функцияларының барлық аргументтері
бойынша дербес туындылары үзіліссіз болсын.
функцияларының барлық аргументтері
бойынша дербес туындылары үзіліссіз болсын. ![]() және
және
![]() есептейік. Бұл туындылар келесі формулалар бойынша
есептеледі
есептейік. Бұл туындылар келесі формулалар бойынша
есептеледі 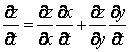 ,
, ![]() .
.
Мысал 2. Егер ![]() ,
, ![]() ,
, ![]() болса, онда
болса, онда ![]() ,
, ![]() .
.
Айқындалмай берілген функциялардың туындысы.
х –тің қандай да бip y-функциясы ![]() теңдеуімен
айқындалмай берілсін.
теңдеуімен
айқындалмай берілсін.
Теорема. Егер ![]() теңдеуін қанағаттандыратын (х,у)
нүктесінің әлде бір аймағында F(x,y), F'x(x,y), F'y(x,y) функциялары
үзіліссіз, ал F'y(x,y)≠0 болса, онда
теңдеуін қанағаттандыратын (х,у)
нүктесінің әлде бір аймағында F(x,y), F'x(x,y), F'y(x,y) функциялары
үзіліссіз, ал F'y(x,y)≠0 болса, онда ![]() теңдеуі туындысы бар y=y(x) функциясын анықтайды және туынды
теңдеуі туындысы бар y=y(x) функциясын анықтайды және туынды
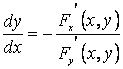 келесі формуламен анықталады.
келесі формуламен анықталады.
Шынында да, ![]() теңдеуін x бойынша дифференциалдап,
теңдеуін x бойынша дифференциалдап, ![]() теңдеуден туындыны табамыз.
теңдеуден туындыны табамыз.
Мысал. Айқындалмай
берілген y
функциясының туындысын ![]() табу керек.
табу керек. ![]() .
.
![]() үшін:
үшін: ![]() ,
, ![]() Сондықтан,
Сондықтан, ![]() .
.
![]() түріндегі теңдеуді
қарастырайық. Бұл
тендеумен айқындалмай анықталған
түріндегі теңдеуді
қарастырайық. Бұл
тендеумен айқындалмай анықталған ![]() функциясының
функциясының ![]() және
және ![]() дербес туындылары келесі формулалармен анықталады.
дербес туындылары келесі формулалармен анықталады. 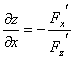 ,
, 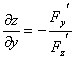 .
.
Кез келген айнымалы айқындалмаған функциясы үшін де олардың дербес туындылары осылайша анықталады.
Мысал- Айқындалмай
берілген z функциясының дербес
туындыларын табу керек. ![]() .
.
 ,
, ![]() ,
, 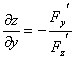 ,
, ![]() .
.
Бағыт бойынша туынды.
D аймағында үзіліссіз және
барлық дербес туындылары да үзіліссіз болатын u=f(x,y,z) үш
айнымалы функция берілсін. M(x,y,z)![]() D және бағыттаушы косинустары
cos α, cosβ, cosγ
болатын
D және бағыттаушы косинустары
cos α, cosβ, cosγ
болатын ![]() векторын қарастырайық..
векторын қарастырайық..
![]() =
=
![]() ,
,
![]() =
=
![]() ,
,
![]() =
=
![]() .
Δl→0 ұмтылғандағы
.
Δl→0 ұмтылғандағы ![]() қатынасының
шегі u = u(x,y,z) функциясының (x,y,z) нүктесіндегі
қатынасының
шегі u = u(x,y,z) функциясының (x,y,z) нүктесіндегі
![]() вектор бағыты бойынша туындысы деп аталады да
вектор бағыты бойынша туындысы деп аталады да ![]() арқылы
белгіленеді.
арқылы
белгіленеді. ![]() =
=![]()
![]() +
+![]()
![]() +
+![]()
![]() .
.
![]()
Дербес туындылар бағыт бойынша туындының дербес жағдайлары.
Градиент және оның қасиеттері.
u = f(x,y,z) функциясыныц (x,y,z) нуктесіндегі
градиенті деп ![]() арқылы
белгілінетін
арқылы
белгілінетін ![]() =(
=(![]() ,
,![]() ,
,![]() )
түріндегі векторды айтады.
)
түріндегі векторды айтады.
Формуладан ![]() бірлік
вектор бағыты бойынша туынды
бірлік
вектор бағыты бойынша туынды
![]() =(
=(![]() ,
, ![]() )
)
екі вектордың скаляр
көбейтіндісі екенін көреміз, олай болса ол градиенттің ![]() векторына
проекциясы.
векторына
проекциясы.
Сондықтан, кез келген ![]() векторы үшін келесі теңсіздік орындалады
векторы үшін келесі теңсіздік орындалады
![]()
![]() .
.
Бұл айтылғандардан, и функциясының (x,y,z) нүктедегі градиентін келесі екі қасиетке ие вектор ретінде анықтауға болатынын көреміз:
а) ол
вектордың ұзындығы (x,y,z) нүктедегі ![]() бағыт бойынша туындының ең үлкен
шамасына тең;
бағыт бойынша туындының ең үлкен
шамасына тең;
б) ол вектордың
бағыты ![]() туындысы ең үлкен болатын
туындысы ең үлкен болатын ![]() вектормен
бағыттас.
вектормен
бағыттас.
Бетке жанама жазықтық және нормаль (тіктем). Толық дифференциалдың геометриялық көpiнici.
S беті z = f(x,y) функциясымен сипатталсын және бұл функцияның Оху жазықтығындағы қандай да бip аймакта үзіліссіз дербес туындылары болсын. S бетінің M0(x0,y0,z0), z0=f(x0,y0) нүктесіндегі жанама жазықтығы деп
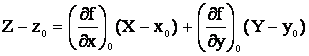 теңдеуімен берілген
жазық-тықты айтады. Мұндағы, X,Y,Z - айнымалы
(ағымдық) координаталар, ал
теңдеуімен берілген
жазық-тықты айтады. Мұндағы, X,Y,Z - айнымалы
(ағымдық) координаталар, ал ![]() -тің дербес
туындыларының Р0(х0,у0)- нүктедегі
мәндері.
-тің дербес
туындыларының Р0(х0,у0)- нүктедегі
мәндері.
f функциясының (х0,у0) нүктесіндегі (х-х0,у-у0)-ге сәйкес дифференциалының геометриялық мағынасы - z=f(x,y) бетіне (х0,у0) нүктеде жүргізілген жанама жазықтық нүктесінің аппликатасының осы
(х– х0, у - у0) -ге сәйкес өciмшесі.
Беттің нормалі (тіктемі) деп жанама жазықтықтың бетке жанау нүкте-сінен өтетін осы жанама жазықтыққа перпендикуляр түзуді айтады.
Егер S беті z=f(x,y) функциясы арқылы берілсе, онда оның Р0(х0,у0) нүктесіндегі тіктемінің теңдеуі
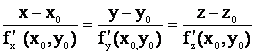 түрінде жазылады.
түрінде жазылады.
S беті F(x,y,z)
= 0 теңдеуімен айқын емес түрде берілсін, ![]() нүктесінің қандай да бip маңайында F функциясының
бip мезгілде нөлге тең емес, үзіліссіз дербес туындылары бар
және
нүктесінің қандай да бip маңайында F функциясының
бip мезгілде нөлге тең емес, үзіліссіз дербес туындылары бар
және
F(P0) = F(x0,y0,z0) = 0 болсын. Онда оның Р0(x0,y0,z0) нүктесіндегі жанама жазықтығының тендеуі
![]() ал
нормаль тендеуі
ал
нормаль тендеуі 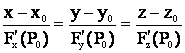 түрлерінде жазылады.
түрлерінде жазылады.
![]() векторы S бетінің
нормалі бойынша бағытталады.
векторы S бетінің
нормалі бойынша бағытталады.
№2 дәріс. Күрделі және айқындалмаған функцияларды дифференциалдау. Бағыт бойынша туынды. Градиент. Бетке жанама жазықтық және нормаль.
Дәрістің мазмұны:
1. Күрделі функция туындысы
2. Айқындалмаған функцияларды дифференциалдау
3. Бағыт бойынша туынды. Градиент және оның қасиеттері.
4. Бетке жанама жазықтық және нормаль (тіктем).
Дәрістің мақсаты: жаңа түсініктерду енгізу, оларды қолдануды үйрену
Күрделі функция туындысы. Толық туынды
![]() ,
, ![]() ,
, ![]() функциясы берілсін. Бұл жағдайда z тәуелдісі t айнымалының күрделі
функциясы болады.
функциясы берілсін. Бұл жағдайда z тәуелдісі t айнымалының күрделі
функциясы болады. ![]() ,
,![]() бар және үзіліссіз болсын.
бар және үзіліссіз болсын. ![]() -
ті табайық. t аргументіне
-
ті табайық. t аргументіне ![]() - өсімшесін берейік. Онда x, y, z
- өсімшесін берейік. Онда x, y, z ![]() ,
, ![]() ,
, ![]() өсімшелеріне
ие болады Дифференциалданудың жеткілікті шарты бойынша
өсімшелеріне
ие болады Дифференциалданудың жеткілікті шарты бойынша
![]() Соңғы
теңдіктің барлық мүшелерін
Соңғы
теңдіктің барлық мүшелерін ![]() -ға бөлеміз:
-ға бөлеміз:
![]() .
.
Егер ![]() -→0
ұмтылса, онда x, y үзіліссіз
болғандықтан,
-→0
ұмтылса, онда x, y үзіліссіз
болғандықтан, ![]() мен
мен ![]() нольге ұмтылады.
нольге ұмтылады.
Осындай тұжырымдардан кейін шекке көшсек, күрделі функцияның туындысы келесі формуламен анықталады.
![]() , немесе
, немесе ![]() .
.
Мысал 1. ![]() ,
, ![]() ,
, ![]() .
.
Онда, ![]()
Енді ![]() , бұл жерде
, бұл жерде ![]() функциясын қарастырайық. Алдыңғы
формуладан
функциясын қарастырайық. Алдыңғы
формуладан ![]() ,
,
себебі ![]() .
Формуладағы
.
Формуладағы ![]() -
-![]() екі айнымалыларының
функциясының х бойынша дербес туындысы, ал
екі айнымалыларының
функциясының х бойынша дербес туындысы, ал ![]() -
-
![]() бір
айнымалы функциясының х бойынша жай
туындысы. Бұл туындыны толық
туынды деп атайды.
бір
айнымалы функциясының х бойынша жай
туындысы. Бұл туындыны толық
туынды деп атайды.
Енді ![]() ,
,
![]() болсын. Бұл жағдайда z тәуелдісі
х және у айнымалыларының күрделі функциясы
болады.
болсын. Бұл жағдайда z тәуелдісі
х және у айнымалыларының күрделі функциясы
болады.
![]() ,
, ![]() ,
, ![]() функцияларының барлық аргументтері
бойынша дербес туындылары үзіліссіз болсын.
функцияларының барлық аргументтері
бойынша дербес туындылары үзіліссіз болсын. ![]() және
және
![]() есептейік. Бұл туындылар келесі формулалар бойынша
есептеледі
есептейік. Бұл туындылар келесі формулалар бойынша
есептеледі 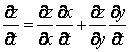 ,
, ![]() .
.
Мысал 2. Егер ![]() ,
, ![]() ,
, ![]() болса, онда
болса, онда ![]() ,
, ![]() .
.
Айқындалмай берілген функциялардың туындысы.
х –тің қандай да бip y-функциясы ![]() теңдеуімен
айқындалмай берілсін.
теңдеуімен
айқындалмай берілсін.
Теорема. Егер ![]() теңдеуін қанағаттандыратын (х,у)
нүктесінің әлде бір аймағында F(x,y), F'x(x,y), F'y(x,y) функциялары
үзіліссіз, ал F'y(x,y)≠0 болса, онда
теңдеуін қанағаттандыратын (х,у)
нүктесінің әлде бір аймағында F(x,y), F'x(x,y), F'y(x,y) функциялары
үзіліссіз, ал F'y(x,y)≠0 болса, онда ![]() теңдеуі туындысы бар y=y(x) функциясын анықтайды және туынды
теңдеуі туындысы бар y=y(x) функциясын анықтайды және туынды
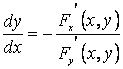 келесі формуламен анықталады.
келесі формуламен анықталады.
Шынында да, ![]() теңдеуін x бойынша дифференциалдап,
теңдеуін x бойынша дифференциалдап, ![]() теңдеуден туындыны табамыз.
теңдеуден туындыны табамыз.
Мысал. Айқындалмай
берілген y
функциясының туындысын ![]() табу керек.
табу керек. ![]() .
.
![]() үшін:
үшін: ![]() ,
, ![]() Сондықтан,
Сондықтан, ![]() .
.
![]() түріндегі теңдеуді
қарастырайық. Бұл
тендеумен айқындалмай анықталған
түріндегі теңдеуді
қарастырайық. Бұл
тендеумен айқындалмай анықталған ![]() функциясының
функциясының ![]() және
және ![]() дербес туындылары келесі формулалармен анықталады.
дербес туындылары келесі формулалармен анықталады. 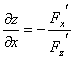 ,
, 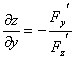 .
.
Кез келген айнымалы айқындалмаған функциясы үшін де олардың дербес туындылары осылайша анықталады.
Мысал- Айқындалмай
берілген z функциясының дербес
туындыларын табу керек. ![]() .
.
 ,
, ![]() ,
, 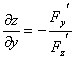 ,
, ![]() .
.
Бағыт бойынша туынды.
D аймағында үзіліссіз және
барлық дербес туындылары да үзіліссіз болатын u=f(x,y,z) үш
айнымалы функция берілсін. M(x,y,z)![]() D және бағыттаушы косинустары
cos α, cosβ, cosγ
болатын
D және бағыттаушы косинустары
cos α, cosβ, cosγ
болатын ![]() векторын қарастырайық..
векторын қарастырайық..
![]() =
=
![]() ,
,
![]() =
=
![]() ,
,
![]() =
=
![]() .
Δl→0 ұмтылғандағы
.
Δl→0 ұмтылғандағы ![]() қатынасының
шегі u = u(x,y,z) функциясының (x,y,z) нүктесіндегі
қатынасының
шегі u = u(x,y,z) функциясының (x,y,z) нүктесіндегі
![]() вектор бағыты бойынша туындысы деп аталады да
вектор бағыты бойынша туындысы деп аталады да ![]() арқылы белгіленеді.
арқылы белгіленеді. ![]() =
=![]()
![]() +
+![]()
![]() +
+![]()
![]() .
. ![]()
Дербес туындылар бағыт бойынша туындының дербес жағдайлары.
Градиент және оның қасиеттері.
u = f(x,y,z) функциясыныц (x,y,z) нуктесіндегі
градиенті деп ![]() арқылы
белгілінетін
арқылы
белгілінетін ![]() =(
=(![]() ,
,![]() ,
,![]() )
түріндегі векторды айтады.
)
түріндегі векторды айтады.
Формуладан ![]() бірлік
вектор бағыты бойынша туынды
бірлік
вектор бағыты бойынша туынды
![]() =(
=(![]() ,
, ![]() )
)
екі вектордың скаляр
көбейтіндісі екенін көреміз, олай болса ол градиенттің ![]() векторына
проекциясы.
векторына
проекциясы.
Сондықтан, кез келген ![]() векторы үшін келесі теңсіздік орындалады
векторы үшін келесі теңсіздік орындалады
![]()
![]() .
.
Бұл айтылғандардан, и функциясының (x,y,z) нүктедегі градиентін келесі екі қасиетке ие вектор ретінде анықтауға болатынын көреміз:
а) ол
вектордың ұзындығы (x,y,z) нүктедегі ![]() бағыт бойынша туындының ең үлкен
шамасына тең;
бағыт бойынша туындының ең үлкен
шамасына тең;
б) ол
вектордың бағыты ![]() туындысы ең үлкен
болатын
туындысы ең үлкен
болатын ![]() вектормен бағыттас.
вектормен бағыттас.
Бетке жанама жазықтық және нормаль (тіктем). Толық дифференциалдың геометриялық көpiнici.
S беті z = f(x,y) функциясымен сипатталсын және бұл функцияның Оху жазықтығындағы қандай да бip аймакта үзіліссіз дербес туындылары болсын. S бетінің M0(x0,y0,z0), z0=f(x0,y0) нүктесіндегі жанама жазықтығы деп
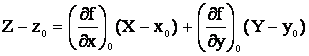 теңдеуімен берілген
жазық-тықты айтады. Мұндағы, X,Y,Z - айнымалы
(ағымдық) координаталар, ал
теңдеуімен берілген
жазық-тықты айтады. Мұндағы, X,Y,Z - айнымалы
(ағымдық) координаталар, ал ![]() -тің дербес
туындыларының Р0(х0,у0)- нүктедегі
мәндері.
-тің дербес
туындыларының Р0(х0,у0)- нүктедегі
мәндері.
f функциясының (х0,у0) нүктесіндегі (х-х0,у-у0)-ге сәйкес дифференциалының геометриялық мағынасы - z=f(x,y) бетіне (х0,у0) нүктеде жүргізілген жанама жазықтық нүктесінің аппликатасының осы
(х– х0, у - у0) -ге сәйкес өciмшесі.
Беттің нормалі (тіктемі) деп жанама жазықтықтың бетке жанау нүкте-сінен өтетін осы жанама жазықтыққа перпендикуляр түзуді айтады.
Егер S беті z=f(x,y) функциясы арқылы берілсе, онда оның Р0(х0,у0) нүктесіндегі тіктемінің теңдеуі
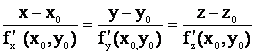 түрінде жазылады.
түрінде жазылады.
S беті F(x,y,z)
= 0 теңдеуімен айқын емес түрде берілсін, ![]() нүктесінің қандай да бip маңайында F функциясының
бip мезгілде нөлге тең емес, үзіліссіз дербес туындылары бар
және
нүктесінің қандай да бip маңайында F функциясының
бip мезгілде нөлге тең емес, үзіліссіз дербес туындылары бар
және
F(P0) = F(x0,y0,z0) = 0 болсын. Онда оның Р0(x0,y0,z0) нүктесіндегі жанама жазықтығының тендеуі
![]() ал
нормаль тендеуі
ал
нормаль тендеуі 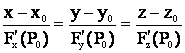 түрлерінде жазылады.
түрлерінде жазылады.
![]() векторы S бетінің
нормалі бойынша бағытталады.
векторы S бетінің
нормалі бойынша бағытталады.
№5 дәріс. Рационал және иррационал функцияларды интегралдау. Әмбебап ауыстыру. Тригонометриялық ауыстырулар
Дәрістің мазмұны:
1. Рационал функция және оны ең қарапайым бөлшектер қосындысына жіктеу.
2. Рационал функцияларды интегралдау. Анықталмаған коэффициенттер әдісі.
3. Кейбір иррационал функцияларды интегралдау
4. Әмбебап ауыстыру
5. Тригонометриялық ауыстырулар.
Дәрістің мақсаты: Рационал, иррационал және кейбір тригонометриялық функцияларды интегралдаудың тәсілдерін көрсету.
Рационал функция және оны қарапайым бөлшектер қосындысына жіктеу
Екі алгебралық көпмүшеліктердің қатынасы
f(x)= ![]() Qn(x) =
Qn(x) = ![]() хп+
хп+![]() хп -1+...+
хп -1+...+![]() ,
Рт(х) =
,
Рт(х) = ![]() хт+
хт+![]() хт -1+...+
хт -1+...+![]() .
.
рационал функция немесе рационал бөлшек деп аталады.
Рm(x) және ![]() Qn(x) -нақты көпмүшеліктер
және х-нақты айнымалы деп есептейміз. Егер m < n
болса, онда ол дұрыс бөлшек деп аталады.
Qn(x) -нақты көпмүшеліктер
және х-нақты айнымалы деп есептейміз. Егер m < n
болса, онда ол дұрыс бөлшек деп аталады.
Егер m>n болса, онда ол бұрыс бөлшек деп аталады.
Бөлу арқылы бұрыс бөлшекті көпмүшелік пен дұрыс бөлшектің қосындысы түрінде жаза аламыз Дұрыс бөлшекті интегралдаудың негізгі тәсілі - дұрыс бөлшекті қарапайым бөлшектердің қосындысына жіктеу. Енді бөлшекті дұрыс (m < n) деп алып, оны қарапайым бөлшектердің қосындысына жіктеу меселесін қарастырайық.
Келесі бөлшектер қарапайым (жәй) бөлшектер деп аталады:
І.![]() , ІІ.
, ІІ. ![]() , ІІІ.
, ІІІ. ![]() , ІV.
, ІV. ![]() ,
,
(мұндағы п=2,3,..., а,р,q,А,М,N -нақты сандар; D=р2-4 q<0.
Қарапайым бөлшектерді интегралдап көрейік.
І.![]()
ІІ. ![]()
ІІІ. ![]() Бөлшектің алымында квадрат
үшмүшеліктің туындысын
Бөлшектің алымында квадрат
үшмүшеліктің туындысын ![]() бөліп
алып, интегралды екі интегралға бөлеміз.
бөліп
алып, интегралды екі интегралға бөлеміз.

![]() , екінші интегралды
табу үшін квадрат үшмүшеліктен толық квадрат
бөліп алу керек.
, екінші интегралды
табу үшін квадрат үшмүшеліктен толық квадрат
бөліп алу керек.
Мысал. ![]() интегралды табу керек.
интегралды табу керек.
Шешімі:
![]()
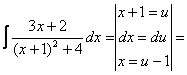
![]()
![]()
![]()
![]() ---
---![]() =
= ![]() -
-![]() .
.
ІV. ![]()
Бірінші интеграл кестелік интегралға ( òdu/uk)
келтіріледі: ![]() .
Екінші интеграл u=x+p/2,
a=
.
Екінші интеграл u=x+p/2,
a=![]() ,
,
q-p2/4>0 болса ![]() .
.
![]() =
=
![]()
![]() –
рекурренттік формулаға
келтіріледі.
–
рекурренттік формулаға
келтіріледі.
Теорема. ![]() m < n бөлшегінің бөлімі келесі теңдік түрінде жіктелінсін:
m < n бөлшегінің бөлімі келесі теңдік түрінде жіктелінсін:
Qn(x) = ![]() (х-х
(х-х![]() )k
)k![]() …(х-хr)k
…(х-хr)k![]() (x2+p
(x2+p![]() x+q
x+q![]() )l
)l![]() …( x2+p
…( x2+p![]() x+q
x+q![]() )l
)l![]() ,
,
Мұндағы ![]() , х
, х![]() , p
, p![]() , q
, q![]() -нақты
сандар; k
-нақты
сандар; k![]() , I
, I![]() -
натурал сандар;
-
натурал сандар;
k![]() +…+ k
+…+ k![]() +2(I
+2(I![]() +…+ I
+…+ I![]() )=n,
р
)=n,
р![]() 2- 4 q
2- 4 q![]() <0. Онда ол
бөлшекті жалғыз түрде келесі қарапайым
бөлшектердің қосындыға жіктеуге болады:
<0. Онда ол
бөлшекті жалғыз түрде келесі қарапайым
бөлшектердің қосындыға жіктеуге болады:
![]() =
=![]() +….+
+….+![]() +
+![]() +….+
+….+![]()
Мұндағы А![]() , М
, М![]() , N
, N![]() -анықталмаған
коэффициенттер
-анықталмаған
коэффициенттер ![]() көбейткішіне
көбейткішіне
![]() +
+![]() +…+
+…+![]() , ал (x2+px+q)I көбейткішіне
, ал (x2+px+q)I көбейткішіне
![]() +
+![]() +…+
+…+![]() , бөлшектерінің қосындысы
сәйкес келеді.
, бөлшектерінің қосындысы
сәйкес келеді.
Анықталмаған коэффициенттерді табу үшін, мысалы, көпмүшеліктердің бірдей дәрежелерінің коэффициенттерін теңестіру керек.
Мысал. ![]() интегралды табу
керек.
интегралды табу
керек.
Интеграл астындығы функцияны қарапайым бөлшектердің
қосындысына жіктеп, анықталмаған коэффициенттерді табу керек. ![]()
![]()
![]() +
+![]() ,
,
х+5=А(х+2)+В(х+1), ![]() А=4, В=-3.
А=4, В=-3.
![]() = 4
= 4![]() -3
-3![]() = 4ln
= 4ln![]() -3ln
-3ln![]() +C.
+C.
Кейбір иррационал өрнектерді интегралдау
Рационал емес элементар функциялардыц интегралдарын айнымалыны алмастыру арқылы рационал функцияның интегралына келтіруге болатын, яғни интегралды рационалдауға болатын жағдайларды қарастырайық.
R(х,у)- өз аргументтері х пен у-тің рационал функциясы болсын .
1. ![]()
![]()
Бұл интеграл ax+b=t![]() айнымалы ауыстыруы
арқылы рационалданады.
айнымалы ауыстыруы
арқылы рационалданады.
2. 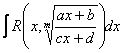 - мұндағы a,b,c,d - тұрақты
сандар, m-натурал сан, ad-bc≠0.
Интеграл
астындағы функция сызықты иррационал бөлшек деп аталады.
Бұл интеграл
- мұндағы a,b,c,d - тұрақты
сандар, m-натурал сан, ad-bc≠0.
Интеграл
астындағы функция сызықты иррационал бөлшек деп аталады.
Бұл интеграл ![]() айнымалы ауыстыруы арқылы
рационалданады.
айнымалы ауыстыруы арқылы
рационалданады.
3. 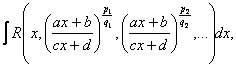 мұндағы
p
мұндағы
p![]() ,q
,q![]() -бүтін сандар. Бұл
интеграл
-бүтін сандар. Бұл
интеграл ![]() =t
=t![]() , айнымалы
ауыстыруы арқылы рационалданады.
, айнымалы
ауыстыруы арқылы рационалданады.
п – ![]() ,
,![]() ,… бөлшектерінің бөлімдерінің
ең кіші ортақ еселігі.
,… бөлшектерінің бөлімдерінің
ең кіші ортақ еселігі.
4. ![]()
![]() не
не ![]() санын түбірдің алдына
шығарып, квадрат үшмүшеліктен толық квадрат бөліп
алу керек.
санын түбірдің алдына
шығарып, квадрат үшмүшеліктен толық квадрат бөліп
алу керек.
5. ![]()
6. ![]() Екі интегралға бөлу керек. Бөлшектің алымында
квадрат үшмүшеліктің туындысын
Екі интегралға бөлу керек. Бөлшектің алымында
квадрат үшмүшеліктің туындысын ![]() бөліп
алып, интеграл-ды екі интегралға бөлеміз. Екінші
интегралды табу үшін квадрат
үшмүшеліктен толық квадрат бөліп алу керек.
бөліп
алып, интеграл-ды екі интегралға бөлеміз. Екінші
интегралды табу үшін квадрат
үшмүшеліктен толық квадрат бөліп алу керек.
7. ![]()
1) p-бүтін сан болса, x=tS, мұндағы s- m, n сандардың бөлімдерінің ең кіші ортақ еселігі.
2) (m+1)/n – бүтін сан болса, онда: a+bxn=tS;
3) p+(m+1)/n – бүтін сан ; онда: a-n+b=tS мұндағы s- p бөлшегінің бөлімі.
Универсал (әмбебап) ауыстыруы
![]() түріндегі интегралды табайық.
түріндегі интегралды табайық.
Бұл интеграл ![]() ауыстыруы арқылы әрқашанда рационал
функцияның интегралына келеді. Расында да,
ауыстыруы арқылы әрқашанда рационал
функцияның интегралына келеді. Расында да,
![]() ,
,
![]() ,
х=2arctgt, dx=
,
х=2arctgt, dx=![]() .
.
![]() ауыстыруы интегралды әрқашанда элементар функция
арқылы өрнектей алатындықтан, оны универсал (әмбебап)
ауыстыруы деп атайды. Бірақ универсал ауыстыруы «күшті»
әдіс болу себебінен көп жағдайларда керекті
түрлендірулерді қысқа және қарапайым етіп жасау
мағынасында ең жақсы әдіс бола бермейді.
ауыстыруы интегралды әрқашанда элементар функция
арқылы өрнектей алатындықтан, оны универсал (әмбебап)
ауыстыруы деп атайды. Бірақ универсал ауыстыруы «күшті»
әдіс болу себебінен көп жағдайларда керекті
түрлендірулерді қысқа және қарапайым етіп жасау
мағынасында ең жақсы әдіс бола бермейді.
Мысалы, егер R(-sin
x, -cos x)= R(sin x, cos x), болса, онда tg x=t,
![]() ,
,
![]() ,
х=arctgt, dx=
,
х=arctgt, dx=![]() ауыстыруы мақсатқа тезірек жеткізеді.
ауыстыруы мақсатқа тезірек жеткізеді.
∫R(tgx)dx түріндегі интеграл u = tgx ауыстыруы арқылы алынады.
Егер R(sin x,-cos x)= - R(sin x, cos x) болса, онда sin x=t.
Егер R(-sin x, cos x)= - R(sin x, cos x), болса, онда cos x=t.
Тригонометриялық алмастырулар
Келесі алмастырулар интегралдарды тригонометриялық функциялар-дың интегралдарына келтіреді.
1. ![]()
2. ![]()
3. ![]()
№6 дәріс. Анықталған интеграл ұғымы, оның қасиеттері және оны есептеу тәсілдері
Дәрістің мазмұны :
1. Анықталған интеграл ұғымына әкелетін есептер. Анықталған интеграл анықтамасы.
2. Анықталған интегралдың қасиеттері.
3. Интегралдан оның жоғарғы шегі арқылы туынды алу.
4. Анықталған интегралды есептеу.
Дәрістің мақсаты: Анықталған интеграл анықтамасын беріп, есептеу әдістерін көрсету.
Анықталған интеграл ұғымына әкелетін есептер
Қисықсызықты трапеция ауданы туралы есеп. Анықталған интеграл анықтамасы
[а,b] кесіндісінде үзіліссіз f(x)>0 функциясы берілсін. y = f(x)
қисығы, Ox өci және х = а мен х = b түзулерімен шенелген фигураның S ауданын анықтау керек. Аталған фигураны қисықсызықты трапеция деп атайды. Есепті шығару үшін келесі амалды орындаймыз:
а) [а,b] кесіндісін кез келген а = х0 < х1 < х2 <... < хn = b нүктелерімен n бөлікке бөлеміз және y = f(x) қисығының (хj f(хj)), j = 0,1,...,n-1 нүктелерінің f(xj) ординаталарын тұрғызамыз;
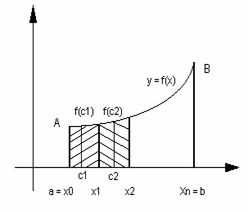 б) әрбір
б) әрбір ![]() бөлікше
кесінділерден кез келген
бөлікше
кесінділерден кез келген ![]() нүктесін аламыз және осы нүктелердегі
нүктесін аламыз және осы нүктелердегі ![]() функция мәндерін тауып келесі қосындыны құрамыз Sn
функция мәндерін тауып келесі қосындыны құрамыз Sn ![]() . Бұл қосынды- f(x) функциясының [а,b] кесіндідегі интегралдық қосындысы деп
аталады. Оның әрбір қосылғышы
—табаны [xJ+l, xJ] және биіктігі
. Бұл қосынды- f(x) функциясының [а,b] кесіндідегі интегралдық қосындысы деп
аталады. Оның әрбір қосылғышы
—табаны [xJ+l, xJ] және биіктігі ![]() тең тік төртбүрыш ауданына тең, ал Sn
қосындысы қисықсызықты трапеция ауданын
қандай да бip дәлдікпен жуықтайды: S
тең тік төртбүрыш ауданына тең, ал Sn
қосындысы қисықсызықты трапеция ауданын
қандай да бip дәлдікпен жуықтайды: S![]()
![]() .
.![]() . .
6.1 Сурет
. .
6.1 Сурет
в) Ең үлкен бөлікше кесіндіні [xJ,xJ+l] j=0,l,...,n-l нөлге ұмтылдырамыз.
Егер осыдан Sn-шамасы [а,b] кесіндісін
бөлу тәсіліне және әрбір бөлікше
кесінділерден алынған ![]() нүктелерін таңдау
тәсілдеріне тәуелсіз S анықталған шегіне ұмтылса, онда S шамасы қисықсызықты
трапеция ауданы деп аталады. Сонымен, S
нүктелерін таңдау
тәсілдеріне тәуелсіз S анықталған шегіне ұмтылса, онда S шамасы қисықсызықты
трапеция ауданы деп аталады. Сонымен, S![]()
![]() .
.
Тағы да басқа көптеген физикалық есептерді осы сияқты шешуге болады. Бұл есептер бізді [а,b] кесіндісіне берілген, тегі әртүрлі функ-цияларға жасалатын бip ғана математикалық амалға алып келеді. Бұл амал —функцияны кесіндіде интегралдау, ал оның нәтижесі — функцияның кесіндідегі анықталған интегралы деп аталады.
Анықтама. [а,b] кесіндісінде y=f(x) функциясы берілсін.
а) [а,b] кесіндісін кез келген нүктелермен
а=х![]() <x
<x![]() <…<
х
<…<
х![]() < х
< х![]() <… <х
<… <х![]() =b
п бөліктерге бөлеміз;
=b
п бөліктерге бөлеміз;
б) Әpбip [xJ,xJ+l]
бөліктен кез келген ![]() нүктелерін алып f функциясының бөліктеуіне сәйкес
интегралдық қосындысы деп аталатын
нүктелерін алып f функциясының бөліктеуіне сәйкес
интегралдық қосындысы деп аталатын ![]() ,
, ![]() = х
= х![]() - х
- х![]() , қосындыны
құрамыз;
, қосындыны
құрамыз;
в) mах ∆хj→0 ұмтылдырып, интегралдық қосындының шегін аламыз.
Егер бұл шек
бар болса, онда ол f
функциясының [а,b] кесіндісіндегі анықталған Риман
интегралы деп аталады да, келесі түрде белгіленеді  ,
,
 =
=![]() ,
,![]() а мен b сандары
анықталған интегралдың сәйкес, төменгі және
жоғарғы шегі деп аталады.
а мен b сандары
анықталған интегралдың сәйкес, төменгі және
жоғарғы шегі деп аталады.
Шек бар болатын f(x) функциясы Риман мағынасында интегралда-натын функция деп аталады.
Анықталған интегралдың геометриялық мағынасы
y = f(x)≥0 қисығы Ох - өci
және х = а мен х = b түзулерімен шектелген жазық
фигура ауданы S - f(x)-функциясының [а, b] кесіндісіндегі анық-талған
интегралына тең  =S.
Егер f(x)<0 болса, онда
=S.
Егер f(x)<0 болса, онда  =
- S.
=
- S.
Ескертпе. [а,b] - кесіндісінде үзіліссіз немесе монотонды функция осы кесіндіде интегралданады.
Теорема [а,b] - кесіндісінде шенелмеген функция осы кесіндіде интегралданбайды.
Анықталған интегралдың қасиеттері
1. ![]() функциясының
интегралдық қосындысы
функциясының
интегралдық қосындысы ![]() түрінде
түрінде
жазылатындықтан, интегралдау айнымалысын
кез келген әріппен көрсету-ге болады: 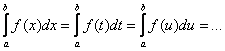 .
.
2. Егер ![]() үшін
үшін ![]() болса, онда
болса, онда ![]() .
.
3. Анықтама
бойынша
а) 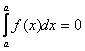 , б)
, б) ![]() деп ала-мыз.
деп ала-мыз.
4. ![]() және
және ![]()
![]() кесіндісінде интегралданатын функциялар,
кесіндісінде интегралданатын функциялар, ![]() -кезкелген сандар
болса, онда
-кезкелген сандар
болса, онда
![]() .
.
5. Анықталған интегралдың аддитивтік
(қосымдылық) қасиеттері. Егер кез келген а,b,с
сандары үшін әpбip [a,b], [а,с] және [с, b] кесінділерінде
![]() интегралданатын
функция болса, онда
интегралданатын
функция болса, онда
![]() .
.
6. Егер ![]() жұп функция болса (f (-x)= f (x)), онда
жұп функция болса (f (-x)= f (x)), онда 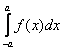 =2
=2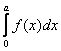 .
.
Егер ![]() тақ функция болса ( f (-x)= -f (x)), онда
тақ функция болса ( f (-x)= -f (x)), онда 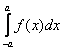 =0.
=0.
Мысал ![]() интегралын есептеу керек.
интегралын есептеу керек.
Шешімі : ![]() себебі
себебі ![]() - [-2,2] кесіндісінде тақ функция.
- [-2,2] кесіндісінде тақ функция.
7. Eгep ![]() x
x![]() [a,b], f(x)≤g(x) теңсіздігі орындалса, онда
[a,b], f(x)≤g(x) теңсіздігі орындалса, онда
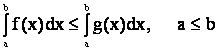 .
.
8. Eгep т,
М – f(x), функциясының [a;b] кесіндісінде сәйкес ең үл-кен және
ең кіші мәндері болса, онда т(b-a)
![]()

![]() M(a-b).
M(a-b).
9. Егер f пен | f | [а, b] кесіндісінде интегралданатын функциялар
болса, онда 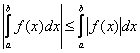 .
.
10. (орта
мән туралы теорема) [a,b] кесіндісінде үзіліссіз f(x)
функциясы үшін  = f(с) (b-a). теңдігі
орындалатын с саны табылады (с
= f(с) (b-a). теңдігі
орындалатын с саны табылады (с![]() [a,b]).
[a,b]).
f(с)=![]()
 саны f(x) функциясының [a;b]
кесіндісіндегі орта мәні деп аталады.
саны f(x) функциясының [a;b]
кесіндісіндегі орта мәні деп аталады.
Интегралдан оның жоғарғы шегі арқылы туынды алу
![]() [а,b] кесіндісінде интегралданатын функция
болсын. Онда ол кез келген х
[а,b] кесіндісінде интегралданатын функция
болсын. Онда ол кез келген х![]() [а,b] нүктесі үшін [а,х] кесіндісінде де интегралданады
(дәлелдеусіз). Мысалы, [а,b] кесіндісінде үзіліссіз немесе
монотонды функция [а,х]
[а,b] нүктесі үшін [а,х] кесіндісінде де интегралданады
(дәлелдеусіз). Мысалы, [а,b] кесіндісінде үзіліссіз немесе
монотонды функция [а,х]![]() [а,b] кесіндісінде де, сәйкес
үзіліссіз немесе монотонды, демек, интегралданады.
[а,b] кесіндісінде де, сәйкес
үзіліссіз немесе монотонды, демек, интегралданады.
Әpбip x![]() [a,b] санына
анықталған
[a,b] санына
анықталған 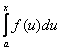 - мәні сәйкес келеді, яғни
- мәні сәйкес келеді, яғни
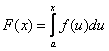 - интегралдың жоғарғы шегіне
тәуелді функция.
- интегралдың жоғарғы шегіне
тәуелді функция.
1-теорема. Егер ![]() [а,b] кесіндісіне интегралданатын
функция болса, онда
[а,b] кесіндісіне интегралданатын
функция болса, онда 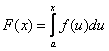 функциясы кез келген x
функциясы кез келген x![]() [a,b] нүктесінде
үзіліссіз бола-ды.
[a,b] нүктесінде
үзіліссіз бола-ды.
2-теорема. Егер у= f(x)
[а,b] кесіндісіне интегралданатын және
x![]() [a,b] нүктесінде үзіліссіз функция
болса, онда осы х нүктесінде
[a,b] нүктесінде үзіліссіз функция
болса, онда осы х нүктесінде 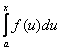 интегралының
интегралының ![]() - туындысы бар және
- туындысы бар және ![]() =
f(x) теңдігі
орындалады.
=
f(x) теңдігі
орындалады.
Басқаша
айтқанда, [а,b] кесіндісінде үзіліссіз f(x) функциясының
осы кесіндіде алғашқы функциясы бар болатыны шығады
және ол алғашқы функцияның бipi ретінде 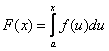 алуға болады.
алуға болады.
Анықталған интегралды есептеу тәсілдері
Ньютон-Лейбниц формуласы
![]() [а,b] – кесіндісінде үзіліссіз функция, ал F(x) оның осы кесіндідегі
қандай да бip алғашқы функциясы болса, онда
[а,b] – кесіндісінде үзіліссіз функция, ал F(x) оның осы кесіндідегі
қандай да бip алғашқы функциясы болса, онда
 = F(b)
- F(а),
= F(b)
- F(а),  = F(x)
= F(x)![]() теңдігі
орындалады. Бұл
формула Ньютон-Лейбниц формуласы деп аталады.
теңдігі
орындалады. Бұл
формула Ньютон-Лейбниц формуласы деп аталады.
Анықталған интегралда айнымалыны алмастыру туралы
Егер х=![]() функциясы [
функциясы [![]() ] кесіндісінде үзіліссіз
дифференциалдана-тын және а=φ(
] кесіндісінде үзіліссіз
дифференциалдана-тын және а=φ(![]() ), b=φ(
), b=φ(![]() ) болып, сонымен бipгe f(x) [а,b] кесіндісінде үзі-ліссіз функция
болса, онда келесі теңдік орындалады
) болып, сонымен бipгe f(x) [а,b] кесіндісінде үзі-ліссіз функция
болса, онда келесі теңдік орындалады  =
=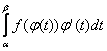
Бөліктеп интегралдау формуласы
Егер u(х) пен
v(x) [a,b] кесіндісінде үзіліссіз дифференциалданатын
функциялар болса, онда келесі бөліктеп интегралдау формуласы орындалады: ![]() = uv
= uv![]() -
-![]() .
.
Мысал.
Анықталған интегралды есептеу
керек. 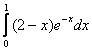
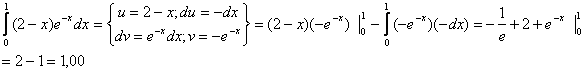
№7 дәріс. Меншіксіз интегралдар
Дәрістің мазмұны:
1. Бірінші текті меншіксіз интегралдар.
2. Екінші текті меншіксіз интегралдар.
3. Меншіксіз интегралдардың жинақтылық белгілері. Абсолют және шартты жинақты интегралдар.
Дәрістің мақсаты:
Меншіксіз интеграл ұғымымен, оның қасиеттерімен таныстыру және интегралдарды есептеу, меншіксіз интегралдардың жинақтылығын зерттеу.
Бірінші және екінші текті меншіксіз интегралдар
Біз осыған дейін анықталған интегралдар туралы айтқанда интегралдау аралығы шектелген және интеграл астындағы функция осы аралықта шенелген деп қабылдадық. Бірақ анықталған интеграл анықтамасын шексіз интегралдау аралығы үшін және шенелмеген функция жағдайына арнап зерттеу қажеттігі жиi кездеседі. Енді осы сұрақтарды қарастырайық.
I. а) ![]() функциясы [а,+∞) аралығында берілсін;
функциясы [а,+∞) аралығында берілсін;
б) f - кез келген ақырлы [а,b'] кесіндісінде (мұндағы b'![]() (a,+∞) интегралданатын болсын.
(a,+∞) интегралданатын болсын.
Бірінші текті меншіксіз интегралдар
Келесі символ 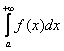 (
( 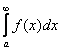 =
=![]()
 )
) ![]() функциясының [а,+∞) аралығындағы бipінші
текті меншіксіз интегралы деп аталады.
функциясының [а,+∞) аралығындағы бipінші
текті меншіксіз интегралы деп аталады.
Егер ![]()
 ақырлы шегі бар
болса, онда меншіксіз интеграл жинақты, ал ол шек жоқ немесе
ақырсыз болса, (
ақырлы шегі бар
болса, онда меншіксіз интеграл жинақты, ал ол шек жоқ немесе
ақырсыз болса, ( ) онда меншіксіз интеграл жинақсыз
дейміз. Сонымен,
) онда меншіксіз интеграл жинақсыз
дейміз. Сонымен,
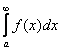 =
=![]()
 Келесі интегралдар да осы сияқты анықталады
Келесі интегралдар да осы сияқты анықталады
![]() =
=![]()
 ,
,![]() =
=![]()
 ,
,
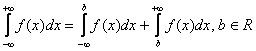 .
.
Мысал 1. Интегралдың жинақтылығын
зерттеу керек. ![]() .
.
Шешімі:
а)![]() .
. ![]()
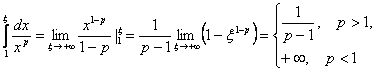 .
.
Сондықтан ![]()
![]() болса жинақты, ал
болса жинақты, ал ![]() . болса жинақсыз.
. болса жинақсыз.
б)![]() .
.
![]() Интеграл жинақсыз.
Интеграл жинақсыз.
Жауабы: интеграл ![]()
![]() болса жинақты, ал.
болса жинақты, ал.![]() болса жинақсыз..
болса жинақсыз..
Мысал 2. Интегралдың
жинақтылығын зерттеу керек.  .
.
Шешімі
е.
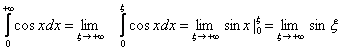 - шегі жоқ..
- шегі жоқ..
Жауабы : интеграл  жинақсыз.
жинақсыз.
Екінші текті меншіксіз интегралдар
II а) ![]() -шекті [а,b) аралығында
берілген және b-нүктесінің маңайында
шенелмеген функция;
-шекті [а,b) аралығында
берілген және b-нүктесінің маңайында
шенелмеген функция;
б) f - кез келген [а,b'] кесіндісінде (а< b'< b) интегралданатын функция болсын.
Келесі символ 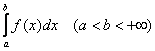 (
( =
=![]()
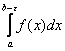 )
) ![]() функциясының
функциясының ![]() аралығындағы
екінші текті меншіксіз интегралы деп аталады.
аралығындағы
екінші текті меншіксіз интегралы деп аталады.
Егер ![]()
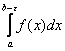 ақырлы
шегі бар болса, онда меншіксіз интеграл жинақты,
ал ол шек жоқ немесе ақырсыз болса, онда меншіксіз интеграл жинақсыз
дейміз. Сонымен,
ақырлы
шегі бар болса, онда меншіксіз интеграл жинақты,
ал ол шек жоқ немесе ақырсыз болса, онда меншіксіз интеграл жинақсыз
дейміз. Сонымен,
 =
=![]()
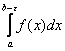 .
.
Анықтама бойынша келесі интегралдар да анықталады.
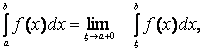
![]() - а нүктесінің маңайында
шенелмеген функция.
- а нүктесінің маңайында
шенелмеген функция.
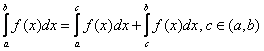 - нүктесінің
маңайында функция шенел-меген.
- нүктесінің
маңайында функция шенел-меген.
Мысал 3. Интегралдың
жинақтылығын зерттеу керек. 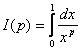
.Шешімі а)![]() .
.
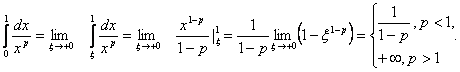
Сондықтан ![]()
![]() болса жинақты, ал.
болса жинақты, ал.![]() болса жинақсыз.
болса жинақсыз.
. б) 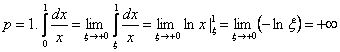 .. Интеграл жинақсыз
.. Интеграл жинақсыз
Жауабы: интеграл 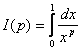
![]() болса жинақты, ал.
болса жинақты, ал. ![]() болса жинақсыз.
болса жинақсыз.
Егер f функциясы үшін I немесе II
шарттың тек бipi ғана орындалса, онда  өрнегін жалғыз
ерекшелігі b-нүктесінде болатын интеграл деп атаймыз.
өрнегін жалғыз
ерекшелігі b-нүктесінде болатын интеграл деп атаймыз.
Осы сияқты жалғыз ерекшелігі а-нүктесінде болатын интегралды да анықтауға болады. Бұл жағдайда I және II шарттар келесі түрде тұжырымдалады:
I. а) ![]() функциясы (-∞;b] аралығында берілген
функциясы (-∞;b] аралығында берілген
б) ![]() - кез келген ақырлы [а',b] кесіндісінде (-∞<а'<а) интегралданатын
функция.
- кез келген ақырлы [а',b] кесіндісінде (-∞<а'<а) интегралданатын
функция.
II. а) f – шекті (a,b] аралығында берілген және а-нүктесінің маңайында шенелмеген функция;
б) f - кез келген [а', b] кесіндісінде (а<а'< b) интегралданатын функция.
Кейде алғашқы функцияны керек етпейтін арнайы белгілерді пайдаланып, интегралдың жинақты немесе жинақсыз болатындығын білуге болады. Енді осы сұрақтарға көшейік.
Меншіксіз интегралдардың жинақтылық белгілері
Абсолют және шартты жинақты интегралдар.
Егер ![]() интегралы
жинақты болса, онда
интегралы
жинақты болса, онда ![]() интегралы абсолют жинақты болады дейді. Егер
интегралы абсолют жинақты болады дейді. Егер ![]() - жинақты, ал
- жинақты, ал ![]() - жинақсыз интеграл болса, онда
- жинақсыз интеграл болса, онда  -интегралы шартты жинақты деп айтады.
-интегралы шартты жинақты деп айтады.
Теорема Абсолют жинақты интеграл – жинақты
және келесі теңсіздік орындалады 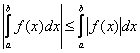 .
.
Tepic емес функциялардың меншіксіз интегралдарың жинақтылық белгілері
Салыстыру белгілері
1-теорема. Жалғыз ерекшілігі b- нүктесінде болатын
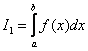 ,
, 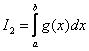 интегралдары үшін [а,b) аралығында
интегралдары үшін [а,b) аралығында ![]() теңсіздік-тері орындалсын. Онда
теңсіздік-тері орындалсын. Онда ![]()
теңсіздігі орындалады және ![]() -интегралдың
жинақтылығынан
-интегралдың
жинақтылығынан ![]() -инте-гралдың да
жинактылығы, ал
-инте-гралдың да
жинактылығы, ал ![]() -интегралдың
жинақсыздылығынан
-интегралдың
жинақсыздылығынан ![]() -интегралдың да
жинақсыздығы шығады.
-интегралдың да
жинақсыздығы шығады.
2-теорема. Егер 1) ![]() ; 2)
; 2) ![]()
![]() болса, онда
болса, онда 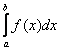 ,
,  интегралдар бір мезгілде жинақты немесе бip мезгілде
жинақсыз
интегралдар бір мезгілде жинақты немесе бip мезгілде
жинақсыз
Ескерту: Салыстыру белгілерін қолданғанда келесі интегралдарды жиі пайдаланады.
![]() ,
, ![]()
Мысал 4. Интегралдың
жинақтылығын зерттеу керек. 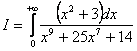 .
.
Шешімі . Интеграл ![]() - бipінші текті меншіксіз интеграл, кез келген x
үшін интеграл астындағы функция оң,
- бipінші текті меншіксіз интеграл, кез келген x
үшін интеграл астындағы функция оң, ![]() ,
, ![]() .
.
2-теорема бойынша ![]() интеграл жинақты.
интеграл жинақты.
№7 дәріс. Меншіксіз интегралдар
Дәрістің мазмұны:
1. Бірінші текті меншіксіз интегралдар.
2. Екінші текті меншіксіз интегралдар.
3. Меншіксіз интегралдардың жинақтылық белгілері. Абсолют және шартты жинақты интегралдар.
Дәрістің мақсаты:
Меншіксіз интеграл ұғымымен, оның қасиеттерімен таныстыру және интегралдарды есептеу, меншіксіз интегралдардың жинақтылығын зерттеу.
Бірінші және екінші текті меншіксіз интегралдар
Біз осыған дейін анықталған интегралдар туралы айтқанда интегралдау аралығы шектелген және интеграл астындағы функция осы аралықта шенелген деп қабылдадық. Бірақ анықталған интеграл анықтамасын шексіз интегралдау аралығы үшін және шенелмеген функция жағдайына арнап зерттеу қажеттігі жиi кездеседі. Енді осы сұрақтарды қарастырайық.
I. а) ![]() функциясы [а,+∞) аралығында берілсін;
функциясы [а,+∞) аралығында берілсін;
б) f - кез келген ақырлы [а,b'] кесіндісінде (мұндағы b'![]() (a,+∞) интегралданатын болсын.
(a,+∞) интегралданатын болсын.
Бірінші текті меншіксіз интегралдар
Келесі символ 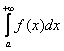 (
( 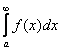 =
=![]()
 )
) ![]() функциясының [а,+∞) аралығындағы бipінші
текті меншіксіз интегралы деп аталады.
функциясының [а,+∞) аралығындағы бipінші
текті меншіксіз интегралы деп аталады.
Егер ![]()
 ақырлы шегі бар
болса, онда меншіксіз интеграл жинақты, ал ол шек жоқ немесе
ақырсыз болса, (
ақырлы шегі бар
болса, онда меншіксіз интеграл жинақты, ал ол шек жоқ немесе
ақырсыз болса, ( ) онда меншіксіз интеграл жинақсыз
дейміз. Сонымен,
) онда меншіксіз интеграл жинақсыз
дейміз. Сонымен,
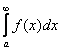 =
=![]()
 Келесі интегралдар да осы сияқты анықталады
Келесі интегралдар да осы сияқты анықталады
![]() =
=![]()
 ,
,![]() =
=![]()
 ,
,
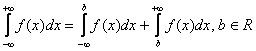 .
.
Мысал 1. Интегралдың жинақтылығын
зерттеу керек. ![]() .
.
Шешімі:
а)![]() .
. ![]()
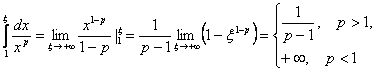 .
.
Сондықтан ![]()
![]() болса жинақты, ал
болса жинақты, ал ![]() . болса жинақсыз.
. болса жинақсыз.
б)![]() .
.
![]() Интеграл жинақсыз.
Интеграл жинақсыз.
Жауабы: интеграл ![]()
![]() болса жинақты, ал.
болса жинақты, ал.![]() болса жинақсыз..
болса жинақсыз..
Мысал 2. Интегралдың
жинақтылығын зерттеу керек.  .
.
Шешімі
е.
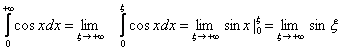 - шегі жоқ..
- шегі жоқ..
Жауабы : интеграл  жинақсыз.
жинақсыз.
Екінші текті меншіксіз интегралдар
II а) ![]() -шекті [а,b) аралығында
берілген және b-нүктесінің маңайында
шенелмеген функция;
-шекті [а,b) аралығында
берілген және b-нүктесінің маңайында
шенелмеген функция;
б) f - кез келген [а,b'] кесіндісінде (а< b'< b) интегралданатын функция болсын.
Келесі символ 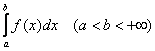 (
( =
=![]()
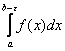 )
) ![]() функциясының
функциясының ![]() аралығындағы
екінші текті меншіксіз интегралы деп аталады.
аралығындағы
екінші текті меншіксіз интегралы деп аталады.
Егер ![]()
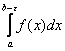 ақырлы
шегі бар болса, онда меншіксіз интеграл жинақты,
ал ол шек жоқ немесе ақырсыз болса, онда меншіксіз интеграл жинақсыз
дейміз. Сонымен,
ақырлы
шегі бар болса, онда меншіксіз интеграл жинақты,
ал ол шек жоқ немесе ақырсыз болса, онда меншіксіз интеграл жинақсыз
дейміз. Сонымен,
 =
=![]()
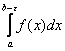 .
.
Анықтама бойынша келесі интегралдар да анықталады.
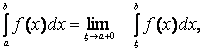
![]() - а нүктесінің маңайында
шенелмеген функция.
- а нүктесінің маңайында
шенелмеген функция.
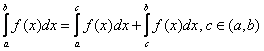 - нүктесінің
маңайында функция шенел-меген.
- нүктесінің
маңайында функция шенел-меген.
Мысал 3. Интегралдың
жинақтылығын зерттеу керек. 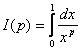
.Шешімі а)![]() .
.
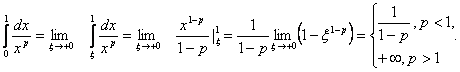
Сондықтан ![]()
![]() болса жинақты, ал.
болса жинақты, ал.![]() болса жинақсыз.
болса жинақсыз.
. б) 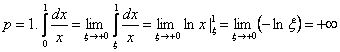 .. Интеграл жинақсыз
.. Интеграл жинақсыз
Жауабы: интеграл 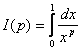
![]() болса жинақты, ал.
болса жинақты, ал. ![]() болса жинақсыз.
болса жинақсыз.
Егер f функциясы үшін I немесе II
шарттың тек бipi ғана орындалса, онда  өрнегін жалғыз
ерекшелігі b-нүктесінде болатын интеграл деп атаймыз.
өрнегін жалғыз
ерекшелігі b-нүктесінде болатын интеграл деп атаймыз.
Осы сияқты жалғыз ерекшелігі а-нүктесінде болатын интегралды да анықтауға болады. Бұл жағдайда I және II шарттар келесі түрде тұжырымдалады:
I. а) ![]() функциясы (-∞;b] аралығында берілген
функциясы (-∞;b] аралығында берілген
б) ![]() - кез келген ақырлы [а',b] кесіндісінде (-∞<а'<а) интегралданатын
функция.
- кез келген ақырлы [а',b] кесіндісінде (-∞<а'<а) интегралданатын
функция.
II. а) f – шекті (a,b] аралығында берілген және а-нүктесінің маңайында шенелмеген функция;
б) f - кез келген [а', b] кесіндісінде (а<а'< b) интегралданатын функция.
Кейде алғашқы функцияны керек етпейтін арнайы белгілерді пайдаланып, интегралдың жинақты немесе жинақсыз болатындығын білуге болады. Енді осы сұрақтарға көшейік.
Меншіксіз интегралдардың жинақтылық белгілері
Абсолют және шартты жинақты интегралдар.
Егер ![]() интегралы
жинақты болса, онда
интегралы
жинақты болса, онда ![]() интегралы абсолют жинақты болады дейді. Егер
интегралы абсолют жинақты болады дейді. Егер ![]() - жинақты, ал
- жинақты, ал ![]() - жинақсыз интеграл болса, онда
- жинақсыз интеграл болса, онда  -интегралы шартты жинақты деп айтады.
-интегралы шартты жинақты деп айтады.
Теорема Абсолют жинақты интеграл – жинақты
және келесі теңсіздік орындалады 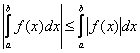 .
.
Tepic емес функциялардың меншіксіз интегралдарың жинақтылық белгілері
Салыстыру белгілері
1-теорема. Жалғыз ерекшілігі b- нүктесінде болатын
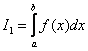 ,
, 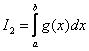 интегралдары үшін [а,b) аралығында
интегралдары үшін [а,b) аралығында ![]() теңсіздік-тері орындалсын. Онда
теңсіздік-тері орындалсын. Онда ![]()
теңсіздігі орындалады және ![]() -интегралдың
жинақтылығынан
-интегралдың
жинақтылығынан ![]() -инте-гралдың да
жинактылығы, ал
-инте-гралдың да
жинактылығы, ал ![]() -интегралдың
жинақсыздылығынан
-интегралдың
жинақсыздылығынан ![]() -интегралдың да
жинақсыздығы шығады.
-интегралдың да
жинақсыздығы шығады.
2-теорема. Егер 1) ![]() ; 2)
; 2) ![]()
![]() болса, онда
болса, онда 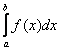 ,
,  интегралдар бір мезгілде жинақты немесе бip мезгілде
жинақсыз
интегралдар бір мезгілде жинақты немесе бip мезгілде
жинақсыз
Ескерту: Салыстыру белгілерін қолданғанда келесі интегралдарды жиі пайдаланады.
![]() ,
, ![]()
Мысал 4. Интегралдың
жинақтылығын зерттеу керек. 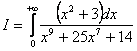 .
.
Шешімі . Интеграл ![]() - бipінші текті меншіксіз интеграл, кез келген x
үшін интеграл астындағы функция оң,
- бipінші текті меншіксіз интеграл, кез келген x
үшін интеграл астындағы функция оң, ![]() ,
, ![]() .
.
2-теорема
бойынша ![]() интеграл жинақты.
интеграл жинақты.
№9 дәріс. Еселi интегралдарда айнымалыларды ауыстыру
Дәрістің мазмұны:
1. Еселi интегралдарда айнымалыларды ауыстыру.
2. Екі еселі интегралды поляр координаталарында есептеу.
3. Үш еселі интегралды цилиндрлiк координаталарында есептеу.
4. Үш еселі интегралды сфералық координаталарында есептеу.
Дәрістің мақсаты:
Еселi интегралдарда айнымалыларды ауыстыруды үйрету.
Еселi интегралдарда айнымалыларды ауыстыру
Алдымен
екi өлшемдi жағдайды қарастырайық. Құрама-сыптығыр шекарасы
бар,
шенелген ![]() - аймағының
тұйықтамасында үзiлiссiз туындылары болатын келесi екi функция
берiлсiн:
- аймағының
тұйықтамасында үзiлiссiз туындылары болатын келесi екi функция
берiлсiн:

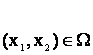 Бұл түрлендiру
Бұл түрлендiру
![]() -аймағын құрама- сыптығыр шекарасы
болатын қандай да бiр
-аймағын құрама- сыптығыр шекарасы
болатын қандай да бiр ![]() - аймағына өзара
бiрмәндi бейнелейдi деп есептеймiз.
- аймағына өзара
бiрмәндi бейнелейдi деп есептеймiз.
Егер Якоби анықтаушы:
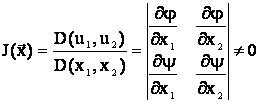 ; онда
; онда
![]() . (1)
. (1)
Үш
өлшемдi жағдайда құрама-сыптығыр шекарасы болатын
![]() аймағының
аймағының
![]() -тұйықтамасында үзiлiссiз дифференциалданатын
-тұйықтамасында үзiлiссiз дифференциалданатын
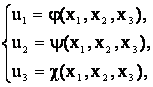
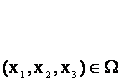 (2)
(2)
функциялары арқылы еселi интегралдағы айнымалылар ауыстыруы келесi түрде жазылады:
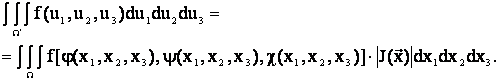 (3)
(3)
Мұндағы якобиан
 анықтауышына тең.
анықтауышына тең.
Мұнда
![]() аймағы
аймағы ![]() аймағына (2) - арқылы өзара бiрмәндi
бейнеленедi деп ұйғарылады. Ал
аймағына (2) - арқылы өзара бiрмәндi
бейнеленедi деп ұйғарылады. Ал ![]() функциясы
функциясы
![]() -да үзiлiссiз
немесе
-да үзiлiссiз
немесе ![]() - да шенелген және
оның кейбiр нүктелерi, құрама-сыптығыр сызықтары
және құрама-сыптығыр беттерiнен басқа нүктелерiнде
үзiлiссiз деп есептеледi.
- да шенелген және
оның кейбiр нүктелерi, құрама-сыптығыр сызықтары
және құрама-сыптығыр беттерiнен басқа нүктелерiнде
үзiлiссiз деп есептеледi.
Екі еселі интегралды поляр координаталарында есептеу
Екi
өлшемдi жағдайда көбiрек қолданылатын айнымалылар ауыстыруы
![]() -декарт координаталарынан
-декарт координаталарынан ![]() -поляр координаталарына өту.
-поляр координаталарына өту.
( 9.1 суретті қара)
Мұндай айнымалылар ауыстыруы
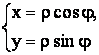
![]()
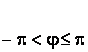 формулалары арқылы жүзеге асады. Бұл түрлендiрулер
үшiн якобианды есептейiк:
формулалары арқылы жүзеге асады. Бұл түрлендiрулер
үшiн якобианды есептейiк:
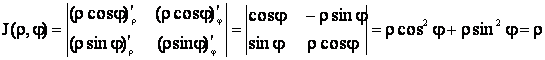 .
.
Олай болса, поляр координаталары үшiн (1) - формула келесi түрде жазылады:
![]()
ρ=Φ1 (φ), ρ=Φ2 (φ), φ1 < φ < φ2 қисықтарымен шенелген D—аймағында үзіліссіз функция z = f(φ, ρ) берілсе, онда
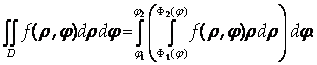
Ескерту. Поляр координаталарына өту ![]() - аймағы дөңгелек немесе сақина секторы болған
жағдайларда тиiмдi.
- аймағы дөңгелек немесе сақина секторы болған
жағдайларда тиiмдi.
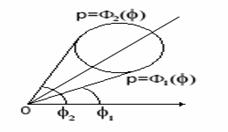
9.1 Сурет
Цилиндрлiк координаталар. Үш еселі интегралды цилиндрлiк координаталарында есептеу
Үш
өлшемдi кеңiстiкте ![]() тiк бұрышты
координаталар жүйесi берiлсiн. Кеңiстiктiң кез келген
тiк бұрышты
координаталар жүйесi берiлсiн. Кеңiстiктiң кез келген ![]() нүктесiн
нүктесiн ![]() - сандар үштiгiмен
де анықтауға болады Мұнда
- сандар үштiгiмен
де анықтауға болады Мұнда ![]() - нүктенiң
бұрынғы аппликатасы, ал
- нүктенiң
бұрынғы аппликатасы, ал ![]() -
- ![]() - жазықтықтағы нүктенiң
поляр координаталары (поляр өсi
- жазықтықтағы нүктенiң
поляр координаталары (поляр өсi ![]() -өсiнiң оң бағытымен
беттеседi). Суреттен ( 9.2 суретті
қара)
-өсiнiң оң бағытымен
беттеседi). Суреттен ( 9.2 суретті
қара)
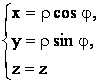 теңдiктерi орын алады
теңдiктерi орын алады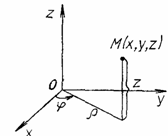 .
.
Түрлендiру якобианы
9. 2 Сурет
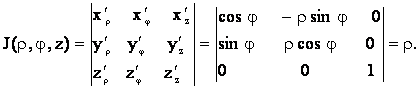
Олай болса, цилиндрлiк координаталарда үш еселі интеграл келесi түрге ие болады.
![]()
Сфералық координаталар. Үш еселі интегралды сфералық координаталарында есептеу
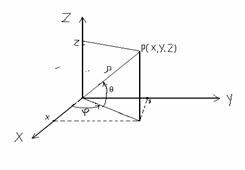
![]() сфералық координаталарынан
сфералық координаталарынан ![]() декарт
координаталарына көшуге келесі теңдеулер жүйесi мүмкiндiк
бередi.
декарт
координаталарына көшуге келесі теңдеулер жүйесi мүмкiндiк
бередi.
![]() ,
, ![]() ,
, ![]() .
.
![]() және
және ![]()
9.3 Сурет
Мұнда ![]() -
- ![]() - нүктесiнен координата
басына дейiнгi қашықтық;
- нүктесiнен координата
басына дейiнгi қашықтық; ![]() -
-![]() -нүктесiнiң
-нүктесiнiң
![]() - радиус векторымен оның
- радиус векторымен оның
![]() -жазықтығындағы
проекция арасындағы бұрыш;
-жазықтығындағы
проекция арасындағы бұрыш; ![]() - осы проекция мен
- осы проекция мен ![]() -
-![]() өсiнiң
оң бағыты арасындағы бұрыш.деп қарастыруға болады.
(9.3 суретті қара). Бұл түрлендiрудегi
якобиан
өсiнiң
оң бағыты арасындағы бұрыш.деп қарастыруға болады.
(9.3 суретті қара). Бұл түрлендiрудегi
якобиан

Сонымен, ![]() .
.
Олай болса, сфералық координаталар үшiн (3) - формула келесi түрге ие болады.
![]()
![]()
Сфералық
координаталар мысалы: жер бетiнiң географиялық коорди-наталары бойлық
және ендiк , ал ![]() - жер центрiне дейiнгi қашықтық.
- жер центрiне дейiнгi қашықтық.
Ескерту. Сфералық координаталарына өту
интеграл астындағы функцияның құрамында ![]() өрнегі
болғанда, немесе
өрнегі
болғанда, немесе ![]() - аймағы шар
немесе шардың бөліктері болған жағдайларда тиiмдi
- аймағы шар
немесе шардың бөліктері болған жағдайларда тиiмдi
Мысалдар: 1. Радиусы R болатын шардың көлемін табу керек.
Шешімі: Бұл есепте ![]() ,
, ![]() ,
, ![]() болғандықтан,
болғандықтан,
сфералық координаталарына көшіп есептейміз.
V=![]()
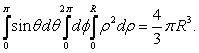
2.
Жарты шардың ![]() массасын табу керек.
массасын табу керек.
![]() :
: ![]() , егер
тығыздығы
, егер
тығыздығы ![]() болса.
болса.
Шешімі: Интегралды ![]() сфералық координат
жүйесінде есептеу ыңғайлы:
сфералық координат
жүйесінде есептеу ыңғайлы:
![]() :
: ![]() ,
, ![]() ,
, ![]() болғандықтан,
болғандықтан,
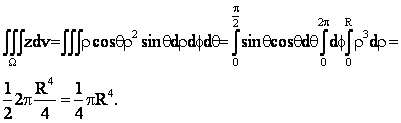
Жауабы: ![]()
№9 дәріс. Еселi интегралдарда айнымалыларды ауыстыру
Дәрістің мазмұны:
1. Еселi интегралдарда айнымалыларды ауыстыру.
2. Екі еселі интегралды поляр координаталарында есептеу.
3. Үш еселі интегралды цилиндрлiк координаталарында есептеу.
4. Үш еселі интегралды сфералық координаталарында есептеу.
Дәрістің мақсаты:
Еселi интегралдарда айнымалыларды ауыстыруды үйрету.
Еселi интегралдарда айнымалыларды ауыстыру
Алдымен
екi өлшемдi жағдайды қарастырайық. Құрама-сыптығыр шекарасы
бар,
шенелген ![]() - аймағының
тұйықтамасында үзiлiссiз туындылары болатын келесi екi функция
берiлсiн:
- аймағының
тұйықтамасында үзiлiссiз туындылары болатын келесi екi функция
берiлсiн:

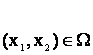 Бұл түрлендiру
Бұл түрлендiру
![]() -аймағын құрама- сыптығыр шекарасы
болатын қандай да бiр
-аймағын құрама- сыптығыр шекарасы
болатын қандай да бiр ![]() - аймағына өзара
бiрмәндi бейнелейдi деп есептеймiз.
- аймағына өзара
бiрмәндi бейнелейдi деп есептеймiз.
Егер Якоби анықтаушы:
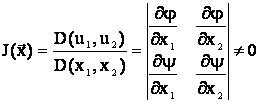 ; онда
; онда
![]() . (1)
. (1)
Үш
өлшемдi жағдайда құрама-сыптығыр шекарасы болатын
![]() аймағының
аймағының
![]() -тұйықтамасында үзiлiссiз дифференциалданатын
-тұйықтамасында үзiлiссiз дифференциалданатын
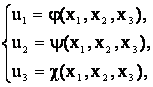
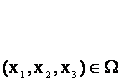 (2)
(2)
функциялары арқылы еселi интегралдағы айнымалылар ауыстыруы келесi түрде жазылады:
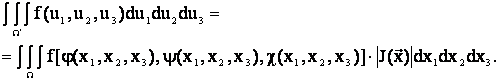 (3)
(3)
Мұндағы якобиан
 анықтауышына тең.
анықтауышына тең.
Мұнда
![]() аймағы
аймағы ![]() аймағына (2) - арқылы өзара бiрмәндi
бейнеленедi деп ұйғарылады. Ал
аймағына (2) - арқылы өзара бiрмәндi
бейнеленедi деп ұйғарылады. Ал ![]() функциясы
функциясы
![]() -да үзiлiссiз
немесе
-да үзiлiссiз
немесе ![]() - да шенелген және
оның кейбiр нүктелерi, құрама-сыптығыр сызықтары
және құрама-сыптығыр беттерiнен басқа нүктелерiнде
үзiлiссiз деп есептеледi.
- да шенелген және
оның кейбiр нүктелерi, құрама-сыптығыр сызықтары
және құрама-сыптығыр беттерiнен басқа нүктелерiнде
үзiлiссiз деп есептеледi.
Екі еселі интегралды поляр координаталарында есептеу
Екi
өлшемдi жағдайда көбiрек қолданылатын айнымалылар ауыстыруы
![]() -декарт координаталарынан
-декарт координаталарынан ![]() -поляр координаталарына өту.
-поляр координаталарына өту.
( 9.1 суретті қара)
Мұндай айнымалылар ауыстыруы
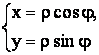
![]()
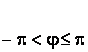 формулалары арқылы жүзеге асады. Бұл түрлендiрулер
үшiн якобианды есептейiк:
формулалары арқылы жүзеге асады. Бұл түрлендiрулер
үшiн якобианды есептейiк:
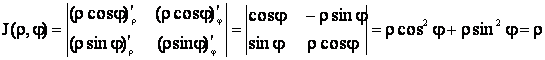 .
.
Олай болса, поляр координаталары үшiн (1) - формула келесi түрде жазылады:
![]()
ρ=Φ1 (φ), ρ=Φ2 (φ), φ1 < φ < φ2 қисықтарымен шенелген D—аймағында үзіліссіз функция z = f(φ, ρ) берілсе, онда
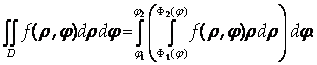
Ескерту. Поляр координаталарына өту ![]() - аймағы дөңгелек немесе сақина секторы болған
жағдайларда тиiмдi.
- аймағы дөңгелек немесе сақина секторы болған
жағдайларда тиiмдi.
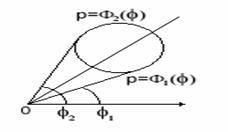
9.1 Сурет
Цилиндрлiк координаталар. Үш еселі интегралды цилиндрлiк координаталарында есептеу
Үш
өлшемдi кеңiстiкте ![]() тiк бұрышты
координаталар жүйесi берiлсiн. Кеңiстiктiң кез келген
тiк бұрышты
координаталар жүйесi берiлсiн. Кеңiстiктiң кез келген ![]() нүктесiн
нүктесiн ![]() - сандар үштiгiмен
де анықтауға болады Мұнда
- сандар үштiгiмен
де анықтауға болады Мұнда ![]() - нүктенiң
бұрынғы аппликатасы, ал
- нүктенiң
бұрынғы аппликатасы, ал ![]() -
- ![]() - жазықтықтағы нүктенiң
поляр координаталары (поляр өсi
- жазықтықтағы нүктенiң
поляр координаталары (поляр өсi ![]() -өсiнiң оң бағытымен
беттеседi). Суреттен ( 9.2 суретті
қара)
-өсiнiң оң бағытымен
беттеседi). Суреттен ( 9.2 суретті
қара)
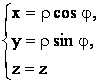 теңдiктерi орын алады
теңдiктерi орын алады .
.
Түрлендiру якобианы
9. 2 Сурет
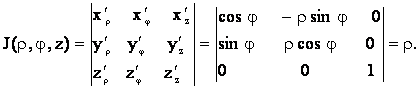
Олай болса, цилиндрлiк координаталарда үш еселі интеграл келесi түрге ие болады.
![]()
Сфералық координаталар. Үш еселі интегралды сфералық координаталарында есептеу

![]() сфералық координаталарынан
сфералық координаталарынан ![]() декарт
координаталарына көшуге келесі теңдеулер жүйесi мүмкiндiк
бередi.
декарт
координаталарына көшуге келесі теңдеулер жүйесi мүмкiндiк
бередi.
![]() ,
, ![]() ,
, ![]() .
.
![]() және
және ![]()
9.3 Сурет Мұнда
![]() -
- ![]() - нүктесiнен координата
басына дейiнгi қашықтық;
- нүктесiнен координата
басына дейiнгi қашықтық; ![]() -
-![]() -нүктесiнiң
-нүктесiнiң
![]() - радиус векторымен оның
- радиус векторымен оның
![]() -жазықтығындағы
проекция арасындағы бұрыш;
-жазықтығындағы
проекция арасындағы бұрыш; ![]() - осы проекция мен
- осы проекция мен ![]() -
-![]() өсiнiң
оң бағыты арасындағы бұрыш.деп қарастыруға болады.
(9.3 суретті қара). Бұл түрлендiрудегi
якобиан
өсiнiң
оң бағыты арасындағы бұрыш.деп қарастыруға болады.
(9.3 суретті қара). Бұл түрлендiрудегi
якобиан

Сонымен, ![]() .
.
Олай болса, сфералық координаталар үшiн (3) - формула келесi түрге ие болады.
![]()
![]()
Сфералық
координаталар мысалы: жер бетiнiң географиялық коорди-наталары бойлық
және ендiк , ал ![]() - жер центрiне дейiнгi қашықтық.
- жер центрiне дейiнгi қашықтық.
Ескерту. Сфералық координаталарына өту
интеграл астындағы функцияның құрамында ![]() өрнегі
болғанда, немесе
өрнегі
болғанда, немесе ![]() - аймағы шар
немесе шардың бөліктері болған жағдайларда тиiмдi
- аймағы шар
немесе шардың бөліктері болған жағдайларда тиiмдi
Мысалдар: 1. Радиусы R болатын шардың көлемін табу керек.
Шешімі: Бұл есепте ![]() ,
, ![]() ,
, ![]() болғандықтан,
болғандықтан,
сфералық координаталарына көшіп есептейміз.
V=![]()
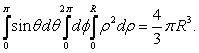
2.
Жарты шардың ![]() массасын табу керек.
массасын табу керек.
![]() :
: ![]() , егер
тығыздығы
, егер
тығыздығы ![]() болса.
болса.
Шешімі: Интегралды ![]() сфералық координат
жүйесінде есептеу ыңғайлы:
сфералық координат
жүйесінде есептеу ыңғайлы:
![]() :
: ![]() ,
, ![]() ,
, ![]() болғандықтан,
болғандықтан,
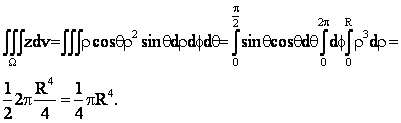
Жауабы: ![]()
№11 дәріс. Екiншi тектi қисықсызықты интегралды есептеу. Грин формуласы
Дәрістің мазмұны:
1. Екiншi тектi қисықсызықты интегралды есептеу.
2. Грин формуласы. Екiншi тектi қисықсызықты интегралдың
интегралдау жолынан тәуелсіздігі.
Дәрістің мақсаты: екiншi тектi қисықсызықты интегралды есептеуді үйрену.
Екiншi тектi қисықсызықты интегралды есептеу
Екiншi тектi қисықсызықты интегралды есептеу үшін оны анықталған интегралға келтіру керек.
1.
АВ –бағытталған қисық кеңістікте
параметрлік теңдеулермен берілсін: ![]() .
. ![]() Онда
Онда 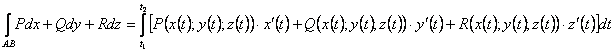 . 2. АВ –қисығы жазықтықта параметрлік теңдеулермен берілсін:
. 2. АВ –қисығы жазықтықта параметрлік теңдеулермен берілсін: 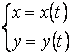 ,
, ![]() Онда
Онда
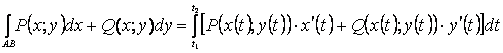 .
.
3.
Қисық жазықтықта айқын түрде
берілсін: ![]()
![]() , Онда
, Онда ![]() ,
, ![]() .
.
Осы сияқты екінші текті қисықсызықты интегралды у айнымалы арқылы анықталған интегралға келтіруге болады.
Мысал 1. L контуры бойынша екінші текті қисықсызықты интегралды есептеу керек.
![]() О(0,0) нүктесінен A(1,1) нүктесіне дейін.
О(0,0) нүктесінен A(1,1) нүктесіне дейін.
Шешімі: Функцияның туындысы: ![]()
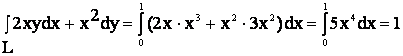
Жауабы: 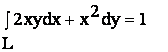
Бірінші және екiншi тектi қисықсызықты интегралдардың арасындағы байланыс
Бірінші тектi ![]() қисықсызықты
интеграл мен екiншi тектi қисықсызықты интеграл
қисықсызықты
интеграл мен екiншi тектi қисықсызықты интеграл ![]() арасындағы
айырмашылық: бірінші жағдайда интеграл астындағы функцияны
арасындағы
айырмашылық: бірінші жағдайда интеграл астындағы функцияны ![]() элементар
элементар ![]() доғаның
ұзындығына, ал екiншi жағдайда сол доғаның
проекциясына
доғаның
ұзындығына, ал екiншi жағдайда сол доғаның
проекциясына ![]() көбейтуде.
көбейтуде. ![]() доғасы нөлге
ұмтылғандықтан, оның координаталары
доғасы нөлге
ұмтылғандықтан, оның координаталары ![]() болатын
вектор
болатын
вектор ![]() деп санауға болады. Сонымен,
деп санауға болады. Сонымен, 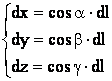 ,
, ![]() -
- ![]() мен
координат өстерінің арасындағы бұрыштар.
мен
координат өстерінің арасындағы бұрыштар. ![]() » dl
» dl
Сондықтан, бірінші және екiншi тектi қисықсызықты интегралдардың арасындағы байланыс келесі формуламен беріледі.
![]() .
.
Грин формуласы және оның салдары
Теорема. Егер ![]() -аймағының
шекарасы кез келген тұйық құрақты-тегiс өзiмен-өзi
қиылыспайтын оң бағдарланған
-аймағының
шекарасы кез келген тұйық құрақты-тегiс өзiмен-өзi
қиылыспайтын оң бағдарланған ![]() контуры болса, онда
Грин формуласы деп аталатын келесi
теңдiк орындалады:
контуры болса, онда
Грин формуласы деп аталатын келесi
теңдiк орындалады:
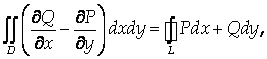
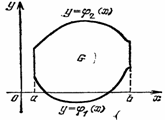 Мұндағы
Мұндағы 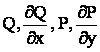 функциялары
функциялары ![]() - тұйықтамада
үзiлiссiз деп ұйғарылады.
- тұйықтамада
үзiлiссiз деп ұйғарылады.
11.1 сурет
Дәлелдеу: D-
аймағында (11.1-суретті қара) ![]() үзiлiссiз.
Сондықтан келесі екі еселі интеграл бар болады.
үзiлiссiз.
Сондықтан келесі екі еселі интеграл бар болады. 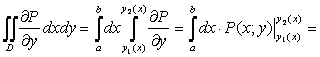
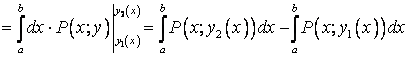
![]() формуласын
қолданып, анықталған интегралды екінші
текті қисықсызықты интеграл арқылы түрлендіруге
болады:
формуласын
қолданып, анықталған интегралды екінші
текті қисықсызықты интеграл арқылы түрлендіруге
болады: 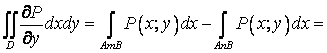
![]() .
.
![]() формуласын
да дәл осылай табуға болады. Соңғы формуладан
алдыңғы формуланы азайтсақ, Грин формуласы орындалады.
формуласын
да дәл осылай табуға болады. Соңғы формуладан
алдыңғы формуланы азайтсақ, Грин формуласы орындалады.
Салдар. Жазық фигураның ауданы. Екi
еселi интеграл қасиетi бойынша Грин формуласындағы ![]() мен
мен ![]() функцияларын
функцияларын
 тең
болатындай етiп таңдап алсақ, онда
тең
болатындай етiп таңдап алсақ, онда ![]() - аймағы ауданының
қисықсызықты интеграл арқылы түрлi өрнектерiн
алуға болады:
- аймағы ауданының
қисықсызықты интеграл арқылы түрлi өрнектерiн
алуға болады: ![]() . Мысалы,
. Мысалы, ![]() болса, онда
болса, онда
 - орындалады, олай болса
- орындалады, олай болса ![]() .
.
Екiншi тектi қисықсызықты интегралдың интегралдау жолынан тәуелсіздігі
Егер әртүрлі АВ қисықтары бойынша екінші текті қисықсызықты интегралдың мәндері тең болса, онда екінші текті қисықсызықты интеграл
интегралдау
жолынан тәуелсіз дейді. Интеграл тек қана бастапқы ![]()
және соңғы![]() нүктелерден тәуелді болғаны.
нүктелерден тәуелді болғаны. 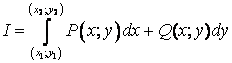 . Енді интеграл интегралдау
жолынан тәуелсіз болуының шарттарын анықтайық.
. Енді интеграл интегралдау
жолынан тәуелсіз болуының шарттарын анықтайық.
1 Теорема. Екінші текті
қисық сызықты интеграл интегралдау жолынан тәуелсіз
болу үшін келесі теңдік қажетті және жеткілікті
![]() .
.
Жеткіліктік:
![]() .
. ![]() теңдігі орындалсын. Әлдебір тұйық
теңдігі орындалсын. Әлдебір тұйық
AmBnA
контурын қарастырайық. Ол контур үшін Грин формуласы орындалады 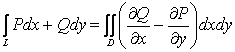 .
. ![]() Þ
Þ
![]()
Þ ![]() , сондықтан екінші текті қисықсызықты интеграл
интегралдау жолынан тәуелсіз.
, сондықтан екінші текті қисықсызықты интеграл
интегралдау жолынан тәуелсіз.
Кері тұжырым да орын алады ( дәлелдеусіз).
Салдар. Егер ![]() теңдігі
орындалса, онда тұйық контур бойынша алынған екінші текті қисықсызықты интеграл нөлге
тең.
теңдігі
орындалса, онда тұйық контур бойынша алынған екінші текті қисықсызықты интеграл нөлге
тең.
![]()
![]()
2 Теорема.
![]() Þ
Þ ![]() - әлдебір
функцияның толық дифференциалы болады.
- әлдебір
функцияның толық дифференциалы болады.
Дәлелдеу: Е. Т. Қ. С. интегралды
қарастырайық ![]() , бұл жерде
А0 (х0; у0) - белгіленген
нүкте. Алдыңғы теоремадан интеграл интегралдау
жолынан тәуелсіз және де тек В(х; у) –айнымалы нүктеден ғана
тәуелді. Бұл шартты келесі түрде жазайық.
, бұл жерде
А0 (х0; у0) - белгіленген
нүкте. Алдыңғы теоремадан интеграл интегралдау
жолынан тәуелсіз және де тек В(х; у) –айнымалы нүктеден ғана
тәуелді. Бұл шартты келесі түрде жазайық.  I(x;
y) функциясының толық дифференциалы интеграл астындағы
функцияға тең екенін дәлелдейік.
I(x;
y) функциясының толық дифференциалы интеграл астындағы
функцияға тең екенін дәлелдейік.
Интегралды ң
туындысын
ң
туындысын ![]() табайық.
табайық.
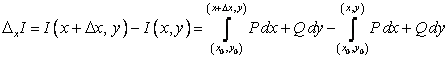 =
=
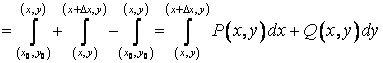 .
.
Соңғы
интеграл ![]() түзуі бойынша
түзуі бойынша
есептеледі,
сондықтан ![]() .
.
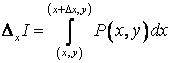 .
. ![]() болғандықтан
11.2 Сурет
болғандықтан
11.2 Сурет
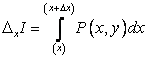 .
Бұл интеграл анықталған интеграл; сондықтан, орта
мән туралы теореманы қолдануға болады:
.
Бұл интеграл анықталған интеграл; сондықтан, орта
мән туралы теореманы қолдануға болады:
 ,
, ![]() . Бұл жерден
. Бұл жерден ![]() және
және
![]() , себебі
, себебі ![]() егер
егер ![]() .
.
Осы
сияқты ![]() ;
сондықтан
;
сондықтан ![]() .
.
Қисық L кеңістікте берілсін.
Онда
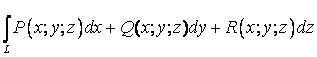 екінші текті қисық-сызықты интеграл интегралдау
жолынан тәуелсіз болуының шарты келесі теңдіктермен беріледі
екінші текті қисық-сызықты интеграл интегралдау
жолынан тәуелсіз болуының шарты келесі теңдіктермен беріледі
![]() .
.
№12 дәріс. Беттік интегралдар. Гаусс-Остроградский және Стокс формулалары
Дәрістің мазмұны:
1. Толық дифференциалдарды интегралдау.
2. Бірінші тектi беттік интегралдар.
3. Екiншi тектi беттік интегралдар.
Дәрістің мақсаты: Беттік интегралдарды есептеуді үйрену.
Толық дифференциалдарды интегралдау
![]() - әлдебір
- әлдебір ![]() функцияның толық дифферен-циалы
болсын. Онда
функцияның толық дифферен-циалы
болсын. Онда ![]() -
толық дифференциалдың алғашқы функциясы болады.
-
толық дифференциалдың алғашқы функциясы болады.
![]() болғандықтан
болғандықтан
![]() ,
, ![]() . Сондықтан
. Сондықтан 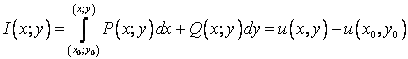 .
.
Бұл
формула екінші текті қисық сызықты интеграл үшін Ньютон-Лейбниц
формуласы деп аталады және ![]() толық дифференциал
болғанда қолданылады.
толық дифференциал
болғанда қолданылады.
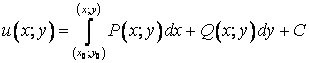 .
.
![]() функциясын
табу үшін келесі формулалар қолайлы
функциясын
табу үшін келесі формулалар қолайлы
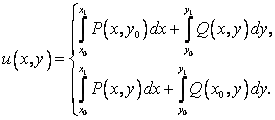
Бұл формулалардағы интегралдар - анықталған интегралдар.
Бiрiншi тектi беттiк интеграл
![]() -тегiс бетiнде
үзiлiссiз
-тегiс бетiнде
үзiлiссiз ![]() функциясы берiлсiн.
функциясы берiлсiн. ![]() - ны құрақты-тегiс
сызықтар арқылы
- ны құрақты-тегiс
сызықтар арқылы ![]() бөлiктерге бөлемiз.
Онда әрбiр
бөлiктерге бөлемiз.
Онда әрбiр ![]() - не
- не ![]() бетiнiң
анықталған
бетiнiң
анықталған ![]() - бөлiгi сәйкес келедi.
- бөлiгi сәйкес келедi.
![]()
![]() бетiнiң кез келген нүктесi болсын. Келесi интегралдық
қосындыны құраймыз:
бетiнiң кез келген нүктесi болсын. Келесi интегралдық
қосындыны құраймыз: ![]() . Мұнда
. Мұнда ![]() -
- ![]() - нiң
ауданы. Оның шегi:
- нiң
ауданы. Оның шегi:
![]()
![]()
![]() функциясының
функциясының
![]() бетi бойынша бiрiншi тектi беттік интегралы деп
аталады.
бетi бойынша бiрiншi тектi беттік интегралы деп
аталады.
Бірінші тектi беттік интегралдарды есептеу
Егер
![]()
![]() бетi
бетi ![]()
![]() теңдеуiмен
берiлсе беттік интеграл келесi формула арқылы есептеледi:
теңдеуiмен
берiлсе беттік интеграл келесi формула арқылы есептеледi:
![]() . Sxy
- S бетінің xOy координат
жазықтығына проекциясы.
. Sxy
- S бетінің xOy координат
жазықтығына проекциясы.
Егер
бет ![]() теңдеуімен берілсе,
онда
теңдеуімен берілсе,
онда ![]() .
. ![]() -
S бетінің xOz координат жазықтығына проекциясы.
-
S бетінің xOz координат жазықтығына проекциясы.
Егер
бет ![]() теңдеуімен берілсе,
онда
теңдеуімен берілсе,
онда ![]() .
. ![]() -
S бетінің yOz координат жазықтығына проекциясы.
-
S бетінің yOz координат жазықтығына проекциясы.
Бiрiншi тектi беттiк интегралдың физикалық мағынасы
Егер
S бетінің ![]() нүктесiндегi массасының
үлестiру тығыздығы γ (x,
y, z) болса, онда беттің
нүктесiндегi массасының
үлестiру тығыздығы γ (x,
y, z) болса, онда беттің ![]() - массасы келесі интеграл арқылы есептеледi:
- массасы келесі интеграл арқылы есептеледi:
![]() =
= ![]() .
.
Егер
γ (x, y, z)![]() 1 болса,
онда S бетінің ауданы S =
1 болса,
онда S бетінің ауданы S =![]()
Екiншi тектi беттiк интеграл
Анықтама. Егер екі жақты тегiс ![]() бетiнiң
әрбiр
бетiнiң
әрбiр ![]() нүктесiнен бiрлiк
нүктесiнен бiрлiк ![]() нормалiн жүргiзуге
болса және осы алынған
нормалiн жүргiзуге
болса және осы алынған ![]() нүктесiнiң векторлық
функциясы бүкiл
нүктесiнiң векторлық
функциясы бүкiл ![]() бетiнде үзiлiссiз
болатын болса, онда
бетiнде үзiлiссiз
болатын болса, онда ![]() бағдарланатын
бет деп аталады.
бағдарланатын
бет деп аталады.
Егер
бетте ![]() функциясы анықталған болса, онда оны
функциясы анықталған болса, онда оны ![]() арқылы
бағдарланған бет дейдi.
арқылы
бағдарланған бет дейдi.
Екi
қарама-қарсы бағдарланған беттердi ![]() және
және
![]() әрiптерiмен белгiлейміз. Енді
әрiптерiмен белгiлейміз. Енді ![]() функцияның
Mi нүктесіндегі мәнін беттің элементар бөлікшесінің
ds Оху
жазықтығына түсірілген проекциясының ауданына ds =dx× dy көбейтіп, келесі қосындыны
функцияның
Mi нүктесіндегі мәнін беттің элементар бөлікшесінің
ds Оху
жазықтығына түсірілген проекциясының ауданына ds =dx× dy көбейтіп, келесі қосындыны ![]() құрамыз.
Бұл қосындының шегі
құрамыз.
Бұл қосындының шегі ![]() функцияның
функцияның ![]() бетiнiң таңдалған жағы бойынша
алынған екінші текті беттік интегралы деп аталады да, келесі символмен
белгіленеді
бетiнiң таңдалған жағы бойынша
алынған екінші текті беттік интегралы деп аталады да, келесі символмен
белгіленеді
![]() =
=![]() .
.
y, z және x, z айнымалылары бойынша алынған екінші текті беттік интегралы да жоғарыдағыдай анықталады.
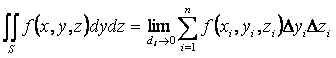
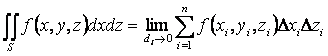 .
.
Дербес жағдайлардағы интегралдардың
(![]() ,
, ![]() ,
, ![]() )
қосындысы екінші текті беттік интегралдың жалпы (координаталық) түрін береді.
)
қосындысы екінші текті беттік интегралдың жалпы (координаталық) түрін береді.
![]() .
.
Екінші
текті беттік интегралды есептеу үшін оны екі еселі интегралға келесі формулаларды пайдаланып
келтіреміз. Мысалы ![]() бетi
бетi ![]()
![]() теңдеуiмен берiлсе,
онда
теңдеуiмен берiлсе,
онда ![]() .
.
![]() -
-![]() бетiнің
xOy координат жазықтығына
түсірілген проекциясы.
бетiнің
xOy координат жазықтығына
түсірілген проекциясы.
Егер
![]() бетiнiң таңдалған жағына
жүргізілген нормаль n мен Oz
өсінің арасындағы бұрыш сүйір болса, онда
интегралды «плюс» таңбасымен
аламыз; бұрыш доғал болса, онда интегралды «минус» таңбасымен аламыз.
бетiнiң таңдалған жағына
жүргізілген нормаль n мен Oz
өсінің арасындағы бұрыш сүйір болса, онда
интегралды «плюс» таңбасымен
аламыз; бұрыш доғал болса, онда интегралды «минус» таңбасымен аламыз. ![]() ,
, ![]() -
-![]() бетiнің xOz координат жазықтығына
түсірілген проекциясы.
бетiнің xOz координат жазықтығына
түсірілген проекциясы.
![]() ,
, ![]() -
-![]() бетiнің
yOz координат
жазықтығына түсірілген проекциясы.
бетiнің
yOz координат
жазықтығына түсірілген проекциясы.
Бірінші және екiншi тектi беттік интегралдардың арасындағы байланыс
Сонымен,
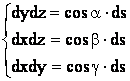 , болғандықтан, (
, болғандықтан, ( ![]() -
- ![]() бетiнiң
таңдалған жағына жүргізілген нормаль n мен координат өстерінің арасындағы
бұрыштар) cондықтан, бірінші және екiншi
тектi беттік интегралдардың арасындағы байланыс келесі формуламен
беріледі.
бетiнiң
таңдалған жағына жүргізілген нормаль n мен координат өстерінің арасындағы
бұрыштар) cондықтан, бірінші және екiншi
тектi беттік интегралдардың арасындағы байланыс келесі формуламен
беріледі.
![]()
![]()
![]()
Гаусс-Остроградский формуласы
![]() -
үшөлшемдi кеңiстiкте тiк бұрышты
-
үшөлшемдi кеңiстiкте тiк бұрышты ![]() координаталар
жүйесi берiлген,
координаталар
жүйесi берiлген, ![]() - осы кеңiстiктегi
құрақты-тегiс шекарасы бар аймақ, ал
- осы кеңiстiктегi
құрақты-тегiс шекарасы бар аймақ, ал ![]()
![]()
![]() ,
, ![]()
![]() - аймағында
анықталған функциялар болсын.
- аймағында
анықталған функциялар болсын.
![]() ,
, 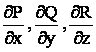 - функциялары
- функциялары ![]() - да үзiлiссiз деп ұйғарамыз.
- да үзiлiссiз деп ұйғарамыз.
Тұйық
![]() - бетi
- бетi ![]() - ның сыртына қарай
бағытталған
- ның сыртына қарай
бағытталған ![]() бiрлiк векторы арқылы бағдарланған
деп есептеймiз.
бiрлiк векторы арқылы бағдарланған
деп есептеймiз.![]()
Келесi теңдiктi Гаусс-Остроградский формуласы деп атайды:
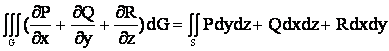 .
.
Егер
бұл формулада ![]() деп алсақ, онда
деп алсақ, онда ![]() аймағының
көлемi аймақтың сыртқы нормалiмен бағдарланған
аймағының
көлемi аймақтың сыртқы нормалiмен бағдарланған
![]() шекарасы бойынша алынған екiншi тектi беттiк интегралы арқылы
өрнектеледi:
шекарасы бойынша алынған екiншi тектi беттiк интегралы арқылы
өрнектеледi: 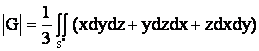 .
.
Стокс формуласы
![]() - кеңiстiгiнiң
қандай да бiр аймағында үзiлiссiз дифференциалдана-тын
вектор-функция
- кеңiстiгiнiң
қандай да бiр аймағында үзiлiссiз дифференциалдана-тын
вектор-функция ![]() берiлсiн.
берiлсiн.
Келесi
теңдiк Стокс формуласы деп аталады: 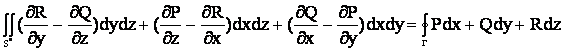
![]()
Тұйық
![]() қисығына керілген
қисығына керілген ![]() беті бойынша алынған
беттік интеграл
беті бойынша алынған
беттік интеграл ![]() бағдарына сәйкес
бағдарланған
бағдарына сәйкес
бағдарланған ![]() бетінiң контуры
бетінiң контуры ![]() бойынша
алынған қисықсызықты интегралға тең.
бойынша
алынған қисықсызықты интегралға тең.
Беттік интегралдар екі еселі интегралдардың қасиеттеріне ие
(мысалы, сызықтық, аддитивтік т.с.с.). Айырмашылық та бар: беттің бағытын қарама-қарсы бағытқа өзгертсе, бірінші текті интегралдың таңбасы өзгер-мейді, ал екінші текті интегралдың таңбасы өзгереді.
№13 дәріс. Анықталған және екі еселі интегралдардың қолданылуы
Дәрістің мазмұны:
1. Анықталған интегралдың колданылуы.
2. Екі еселі интегралдың колданылуы.
Дәрістің мақсаты: интегралдардың геометрияның, физиканың, ме-ханиканың кейбір есептерін шешуде қолданыстарын көрсету.
Анықталған интегралдың қолданылуы
Қисық доғасының ұзындығы
1. Қисық L кеңістікте параметрлік теңдеулермен берілсін:
x = φ(t),
y = ψ(t), z = χ(t), ![]() . φ,ψ,x
функциялары [а,b]- да үзіліссіз
болса, онда үзіліссіз қисықтың ұзындығы
. φ,ψ,x
функциялары [а,b]- да үзіліссіз
болса, онда үзіліссіз қисықтың ұзындығы
![]() .
.
2. Қисық жазықтықта параметрлік теңдеулермен берілсін:
x = φ(t), y = ψ(t), ), ![]() .
.
Онда
![]()
3. Қисық жазықтықта айқын түрде берілсін: у=f(х), a ≤ х ≤ b,
Онда
![]() ,
, ![]() - доғаның ұзындығы-ның
дифференциалы.
- доғаның ұзындығы-ның
дифференциалы.
4. Қисық жазықтықта поляр координаталарымен берілсін:
ρ=ρ(φ), ![]() . Онда
. Онда ![]() .
.
Жазық фигура ауданы. Егер [а,b] кесіндісінде
функция f(x)≥0 болса, онда анықталған интеграл
анықтамасы бойынша y = f(x) қисығымен, Ох-өсімен
және х=а, х=b түзулерімен шенелген қисық
сызықты трапеция ауданы ![]() тең.
тең.
Егер [а,b]-де
f(x)≤0 болса, онда анықталған интегралда ≤0 болады, ал
оның абсолют шамасы сәйкес қисық сызықты
трапецияның ауданына тең. ![]()
Егер f(x) таңбасы [а,b]-да
ақырлы сан рет өзгерсе, онда y = f(x), Ох, х=а, х=b қисықтарымен
шенелген жазық фигура ауданын табу үшін ![]() интегралын есептеу керек (13.1 суретті қара).
интегралын есептеу керек (13.1 суретті қара).
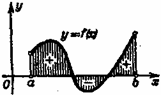 13.1 Сурет
13.1 Сурет
Егер ![]() , y = f2(x), x=a, х=b (f1(x)≤f2(x),
, y = f2(x), x=a, х=b (f1(x)≤f2(x), ![]() ) қисықтарымен шенелген фигура ауданын табу
керек болса, онда
) қисықтарымен шенелген фигура ауданын табу
керек болса, онда 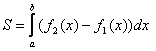 ин-тегралын аламыз (13.2 суретті қара).
ин-тегралын аламыз (13.2 суретті қара).
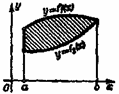 13.2 Сурет
13.2 Сурет
Егер қисық
x=φ(t), y=ψ(t), α≤t≤β (φ(α) =a,
φ(β) =b)
параметрлік теңдеулермен
берілсе, онда интегралда x=φ(t) айнымалы алмастыруын жасай отырып 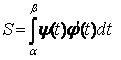 болады.
болады.
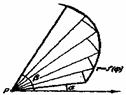 О полюстен шығатын φ = α, φ= β сәулелерімен және 13.3 Сурет поляр
координаталары бойынша үзіліссіз r = f (φ) функциясымен
берілген қисықпен шенелген фигураның S ауданын келесі
түрде анықтауға болады
О полюстен шығатын φ = α, φ= β сәулелерімен және 13.3 Сурет поляр
координаталары бойынша үзіліссіз r = f (φ) функциясымен
берілген қисықпен шенелген фигураның S ауданын келесі
түрде анықтауға болады 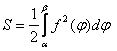 (13.3 суретті қара).
(13.3 суретті қара).
Айналу дененің көлемі
Тік бұрыш х,y координаталар жүйесіне үзіліссіз оң y = f(x), a≤x≤b функциясымен сипатталған Г қисығы берілсін. Г қисығының х өсін айналуынан шыққан бетпен және х = а, х=b жазықтықтарымен шенелген айналу денесінің (13.4 суретті қара) V көлемі келесі түрде анықталады:
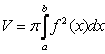
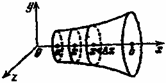
13.4 Сурет
Екі еселі интегралдың колданылуы
1. Цилиндроидтың көлемі
![]() бетiмен,
төменнен
бетiмен,
төменнен ![]() жазықтығымен және бүйiр жақтарынан
жазықтығымен және бүйiр жақтарынан ![]() - жазық жиынның шекарасы
- жазық жиынның шекарасы ![]() арқылы өтетiн,
жасаушылары
арқылы өтетiн,
жасаушылары ![]() - өсiне параллелü цилиндрлiк бетпен шектелген дененiң
көлемiн табу керек болса, онда
- өсiне параллелü цилиндрлiк бетпен шектелген дененiң
көлемiн табу керек болса, онда ![]()
2. S - пластинканың ауданы тең
![]()
3. Беттің ауданы
Тiкбұрышты
координаталар жүйесi анықталған кеңiстiкте ![]() ,
, ![]() теңдеуiмен
теңдеуiмен
![]() бетi берiлсiн. Мұнда
бетi берiлсiн. Мұнда ![]() - Оху жазықтығындағы
- Оху жазықтығындағы
![]() бе-тiнiң проекцияcы.
бе-тiнiң проекцияcы. ![]() - құрама-сыптығыр шекарасы бар шенелген аймақ.
- құрама-сыптығыр шекарасы бар шенелген аймақ.
Онда
![]() бетiнiң ауданы
бетiнiң ауданы ![]() формуласымен
формуласымен
өрнектеледi.
Осы
сияқты, ![]() бетi
бетi ![]() ,
, ![]() теңдеуiмен берiлсе,
онда
теңдеуiмен берiлсе,
онда ![]() .
.
![]() ,
, ![]() теңдеуiмен
берiлсе, онда
теңдеуiмен
берiлсе, онда
![]() .
.
Еселi интегралдардың механикада қолданылуы
1. Үлестiру тығыздығы γ = γ (х, у) болатын D- пластинканың массасын есептеу. Масса М тең
![]()
2. Статикалық моменттер
Тiк
бұрышты координаталар анықталған жазықтықта массасы
![]() тең
тең ![]() материалдық нүкте
берiлсiн. Бұл нүктенiң
материалдық нүкте
берiлсiн. Бұл нүктенiң ![]() түзуіне салыс-тырғандағы
статикалық моментi деп
түзуіне салыс-тырғандағы
статикалық моментi деп ![]() көбейтiндiсiн айтады.
көбейтiндiсiн айтады.
Массалары
![]() тең
тең ![]() ,
, ![]() нүктелер жүйесiнiң
нүктелер жүйесiнiң
![]() түзуіне салыстырғандағы статикалық моментi келесi
теңдiкпен анықталады:
түзуіне салыстырғандағы статикалық моментi келесi
теңдiкпен анықталады: ![]() .
.
D- пластинканың координаталар өстеріне салыстырғандағы статикалық моменттері келесi интеграл ретiнде анықталады:
![]() .
.
3. Ауырлық центрiнiң координаталары келесi теңдiктермен анықталады:

Біртекті
пластинка үшін ![]() формулалар
ықшамдалады:
формулалар
ықшамдалады:
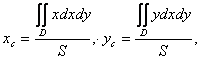 S -
пластинканың ауданы.
S -
пластинканың ауданы.
4. Инерция моменттері
D-
пластинканың Ох , Оу өстеріне салыстырғандағы инерция
мо-менттері: 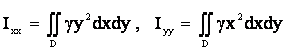 .
.
Пластинканың координаталар бас нүктесіне салыстырғандағы полярлық моменті тең
![]()
Мысал. ![]() цилиндрдің
цилиндрдің ![]() цилиндрімен
қиып алынған бетінің бөлігінің ауданын табу
керек.
цилиндрімен
қиып алынған бетінің бөлігінің ауданын табу
керек.
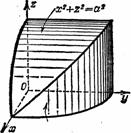
13.5 Сурет
Шещімі. Суретте (13.5 суретті
қара) беттің ![]() бөлігі
көрсетілген. Беттің теңдеуі
бөлігі
көрсетілген. Беттің теңдеуі
![]() ; сондықтан,
; сондықтан, ![]()
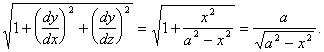
интегралдау облысы келесі теңсіздіктермен анықталады
![]()
Сондықтан,
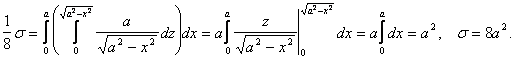
№14 дәріс. Үш еселі, қисықсызықты және беттік интегралдың колданылуы
Дәрістің мазмұны :
1. Үш еселі интегралдың колданылуы.
2. Қисық сызықты және беттік интегралдардың колданылуы.
Дәрістің мақсаты: интегралдардың геометрия және механикада қолданыстарын көрсету.
Үш еселі интегралдың колданылуы
Еселi интегралдардың механикада қолданылуы
1. Дененің массасы
Үлестiру
тығыздығы ![]() болатын дененің массасы
М тең
болатын дененің массасы
М тең ![]()
Дененің
көлемі ![]()
2. Статикалық моменттер
Дененің Оху, Охz, Оуz координаталар
жазықтықтарына салыстыр-ғандағы статикалық моменттері
![]() келесi интегралдар ретiнде анықталады:
келесi интегралдар ретiнде анықталады:
![]()
3. Ауырлық центрiнiң координаталары келесi теңдiктермен анықталады:
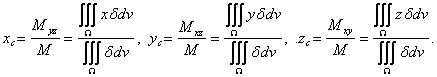
Біртекті дене ![]() үшін формулалар ықшамдалады:
үшін формулалар ықшамдалады:
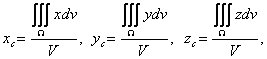 V- дененің
көлемі.
V- дененің
көлемі.
4. Инерция моменттері
Дененің
Ох , Оу, Oz өстеріне салыстырғандағы инерция моменттері: ![]()
Дененің
координаталар бас нүктесіне салыстырғандағы полярлық
моменті тең ![]() ,
, ![]()
Мысал. Радиусы R біртекті шардың полярлық моментін табу керек.
Сфералық координаталарды қолдану ыңғайлы болады. Онда
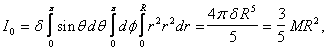
Бүл жерде М- шардың массасы.
Сфера үшін Ох, Оу, Oz өстеріне салыстырғандағы
инерция моменттері тең болғандықтан , және ![]() теңдігін
ескерсек,
теңдігін
ескерсек,
![]() болады.
болады.
Мысал. Біртекті жарты шардың ![]() ауырлық
центрiнiң координата-ларын табу керек.
ауырлық
центрiнiң координата-ларын табу керек.
![]() :
: ![]()
Жарты шар Оz өсімен салыстырғанда
симметриялы болғандықтан, ауырлық центрiнiң екі
координатасы ![]() нөлге
тең. Сондықтан,
нөлге
тең. Сондықтан, ![]() .
.
Интегралды есептеу үшін сфералық координаталарды қолданамыз:
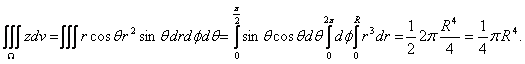
Жарты шардың көлемі V=
![]() сондықтан
сондықтан 
Қисықсызықты интегралдардың колданылуы
Бірінші текті қисықсызықты интегралдардың колданылуы
1. Қисықтың массасы
Үлестiру
тығыздығы ![]() болатын
қисықтың массасы М тең
болатын
қисықтың массасы М тең ![]()
2.
Доғаның ұзындығы. ![]()
3. Қисықтың моменттері
Қисықтың
Ох, Оу координат өстеріне салыстырғандағы
статикалық моменттері келесi интегралдар ретiнде анықталады: ![]() .
.
Қисықтың
координаталар бас нүктесіне салыстырғандағы полярлық
моменті тең ![]() .
.
Қисықтың координаталар бас нүктесіне салыстырғандағы инерция моменттері тең;
![]() .
.
4. Ауырлық центрiнiң координаталары келесi теңдiктермен анықталады
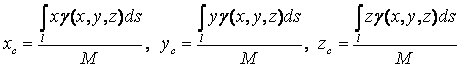 .
.
Екінші текті қисық сызықты интегралдардың колданыстары
1.
![]() күшінің АВ –бағытталған жолының
бойындағы жұмысы
күшінің АВ –бағытталған жолының
бойындағы жұмысы
![]() ,
,
2.
Шекарасы L жазық фигура D –ның ауданы ![]() .
.
Беттік интегралдардың қолданылуы
1. S: z = f(x, y) теңдеумен берілген, S – бетінің ауданы:
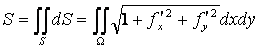
(Ω –S – тың Оху жазықтығына проекциясы).
2) Беттің массасы
![]()
![]() - беттің
үлестiру тығыздығы.
- беттің
үлестiру тығыздығы.
3) Беттің моменттері :
Беттің Oxy, Oxz, Oyz координат жазықтықтарына салыстырғандағы статикалық моменттері келесi интегралдар ретiнде анықталады:
![]()
Беттің Ox, Oy, Oz, координат өстеріне салыстырғандағы инерция моменттері;
![]() .
.
Беттің Oxy, Oxz, Oyz; координат жазықтықтарына салыстырғандағы инерция моменттері
![]() .
.
Беттің координаталар бас нүктесіне салыстырғандағы инерция моменті тең;
![]() .
.
9) Ауырлық центрiнiң координаталары келесi теңдiктермен анықта-лады:
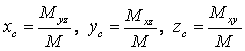 .
.
ӘДЕБИЕТТЕР TІ3IMI
1. Әубәкір С.Б. Жоғары математика. 1 -2 бөлім, - Алматы, ҚАЗҰУ,
2000 ж.
2. Айдос Е.Ж. Жоғары математика (қысқаша курс) - Алматы, Иль-Тех-Кітап , 2003 ж.
3. Ибрашев Х.И., Еркеғұлов Ш.Т. Математикалық анализ курсы, 1-2 том, - Алматы, Мектеп ,1970 ж.
4. Дүйсек А.К., Қасымбеков С.К. Жоғары математика. А:, 2004
5. Қабдықайыров Қ. Жоғары математика. - Алматы, РБК, 1993.
6. Хасеинов К.А. Математика канондары. Жоғары математика курсы. Алматы, -ММIV, 2004 ж.
7. Берман Г.Н. Математикалық анализ курсына арналған есептер жинағы. М. Ғылым. 1986 ж.
8. Математикадан есептер жинағы. Сызықты алгебра және математикалық талдау негіздері. Ефимов А.В., Демидович Б.П. редакциялауымен басылған. М. 1981 ж.
9. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Жоғары метематика жаттығулары мен есептері. М. Жоғары мектеп. 1986 ж. 1,2 бөлімдер.
10. Пискунов Н.С. Дифференциалдық және интегралдық есептеулер. М. Ғылым. 1985 ж. 1-3 томдар.
11. Шипачев B.C. Жоғары математика. М. Жоғары мектеп. 1985 ж.
12. Рябушко А.П. Жоғары математикадан өзіндік есептер жинағы. Минск. Жоғары мектеп. 1990 ж. 2,3 том.
МАЗМҰНЫ
1 Көп айнымалылы функциялар
№1 дәріс. Көп айнымалылы функциялар.....................................................3
№2 дәріс. Күрделі және айқындалмаған функцияларды дифферен-циалдау. Бағыт бойынша туынды. Градиент. Бетке жанама жазықтық және нормаль..................................................................................................................... 7
№3 дәріс. Жоғары peттi дербес туындылар мен дифференциалдар. Көп айнымалы функциялардың экстремумдері...........................................................11
2 Бір айнымалылы функцияның интегралдық есептеуі
№4 дәріс. Анықталмаған интеграл ұғымы және оның қасиеттері. Анықталмаған интегралды есептеу әдістері......................15
№5 дәріс. Рационал және иррационал функцияларды интегралдау. Әмбебап ауыстыру. Тригонометриялық ауыстырулар............19
№6 дәріс. Анықталған интеграл ұғымы, оның қасиеттері және оны есептеу тәсілдері............... .......23
№7 дәріс. Меншіксіз интегралдар..............................................................27
3 Көп айнымалылы функцияның интегралдық есептеуі
№8 дәріс. Еселі интегралдар.......................................................................31
№9 дәріс. Еселi интегралдарда айнымалыларды ауыстыру.....................35
№10 дәріс. Қисықсызықты интегралдар....................................................39
№11 дәріс. Екiншi тектi қисықсызықты интегралды есептеу. Грин формуласы....................43
№12 дәріс. Беттік интегралдар. Гаусс-Остроградский және Стокс формулалары. ............47
№13 дәріс. Анықталған және екі еселі интегралдардың қолданы-луы....................51
№14 дәріс. Үш еселі, қисықсызықты және беттік интегралдың колданылуы.................... 55
Әдебиеттер тізімі...........................................................................................59
