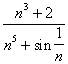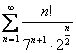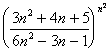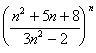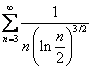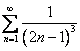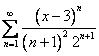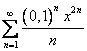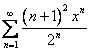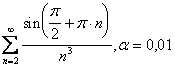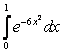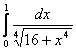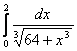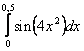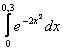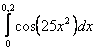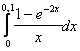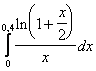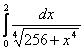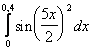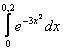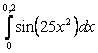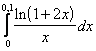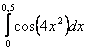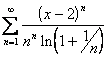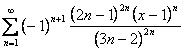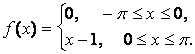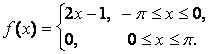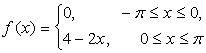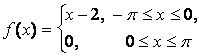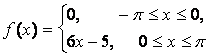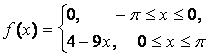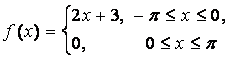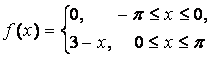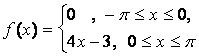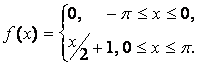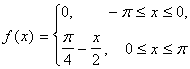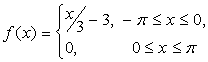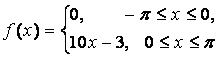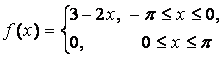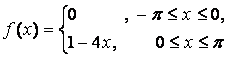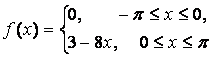Некоммерческое акционерное общество
АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра высшей математики
Математика 3
Методические указания и задания к выполнению расчетно-графической работы для студентов всех специальностей
Часть 3
Алматы 2010
СОСТАВИТЕЛИ: С.А.Жуматаева, Л.Н.Ким. Математика 3. Методические указания и задания к выполнению расчетно-графических работ для студентов всех специальностей. Часть 3.- Алматы: АИЭС, 2010.- 25 с.
Методические указания и задания к расчетно-графической работе содержат дополненное и переработанное издание типового расчета №7 программы второго семестра курса высшей математики для студентов всех специальностей дневного отделения АИЭС 2002 года. Приведены основные теоретические вопросы программы, варианты заданий и решение типового варианта. Расчетные задания разделены на два уровня сложности.
Методические указания предназначены для студентов первого курса всех форм обучения всех специальностей.
Введение
Методические указания представляют собой программу, задания к модулю 3 «Ряды » Математики 3 и решение типового варианта. Задания состоят из тридцати вариантов. Вторая цифра номера задания указывает вариант студента.
Вариант задания контрольной работы для студентов, обучающихся по заочной форме, определяется как остаток от деления номера зачетной книжки на 30. Например: номер зачетной книжки равен 080612. Это число представляется в виде: 080612=2687*30+2. Следовательно, студент должен выполнить задания варианта №2. Если остаток равен нулю, то студент выполняет вариант №30.
Контрольная работа должна быть решена в отдельной тетради, решение задач должно быть кратким и, в то же время, достаточно объяснено ссылками на теорию и сопровождено необходимыми рисунками. Примером для оформления контрольной работы может служить решение типового варианта, которое приведено в данном методическом указании.
1 Типовой расчет 3. Ряды
1.1 Теоретические вопросы
1 Числовые ряды. Сходимость и сумма ряда. Необходимое условие сходимости ряда.
2 Признаки сравнения.
3 Признаки Даламбера и Коши.
4 Интегральный признак сходимости.
5 Знакочередующиеся ряды. Теорема Лейбница. Оценка остатка ряда.
6 Знакопеременные ряды. Абсолютно и условно сходящиеся ряды.
7 Область сходимости функциональных рядов. Понятие равномерной сходимости. Признак Вейерштрасса
8 Почленное интегрирование и дифференцирование равномерно сходящихся рядов.
9 Степенные ряды. Теорема Абеля. Интервал и радиус сходимости степенных рядов.
10 Ряд Тейлора.
Разложение по степеням ![]() функций
функций ![]()
![]()
![]()
11 Тригонометрический ряд Фурье и его коэффициенты. Теорема Дирихле.
12 Ряд Фурье для
функций с периодом ![]() .
.
13 Ряд Фурье для
четных и нечетных функций, для непериодических функций.![]()
1.2 Расчетные задания первого уровня
1. Записать
общий член ряда, найти ![]() (
(![]() ую частичную сумму
ую частичную сумму
ряда), ![]() -остаток ряда и
-остаток ряда и ![]() . Найти
. Найти ![]() сумму ряда.
сумму ряда.
Т а б л и ц а 1
|
1.1 |
1.2 |
1.3 |
|
1.4 |
1.5 |
1.6 |
|
1.7 |
1.8 |
1.9 |
|
1.10 |
1.11 |
1.12 |
|
1.13 |
1.14 |
1.15 |
|
1.16
|
1.17 |
1.18
|
|
1.19
|
1.20 |
1.21 |
|
1.22
|
1.23
|
1.24
|
|
1.25
|
1.26 |
1.27
|
|
1.28
|
1.29 |
1.30
|
2. Выполняется ли необходимое условие сходимости ряда? Если да, то исследовать ряд на сходимость с помощью признаков сравнения.
Т а б л и ц а 2
|
2.1
|
2.2
|
2.3
|
|
2.4
|
2.5
|
2.6
|
|
2.7
|
2.8
|
2.9
|
|
2.10
|
2.11
|
2.12
|
|
2.13
|
2.14
|
2.15
|
|
2.16
|
2.17
|
2.18
|
|
2.19
|
2.20
|
2.21
|
|
2.22
|
2.23
|
2.24
|
|
2.25
|
2.26
|
2.27
|
|
2.28
|
2.29
|
2.30 |
![]()
3. Исследовать ряд на сходимость с помощью признака Даламбера.
Т а б л и ц а 3
|
3.1
|
3.2
|
3.3
|
|
3.4
|
3.5
|
3.6
|
|
3.7
|
3.8
|
3.9
|
|
3.10
|
3.11
|
3.12
|
|
3.13
|
3.14 |
3.15
|
|
3.16
|
3.17
|
3.18 |
|
3.19
|
3.20
|
3.21
|
|
3.22
|
3.23
|
3.24
|
|
3.25
|
3.26
|
3.27
|
|
3.28 |
3.29 |
3.30 |
4. Исследовать ряд на сходимость с помощью радикального признака Коши.
Т а б л и ц а 4
|
4.1 |
4.2 |
4.3 |
|
4.4 |
4.5 |
4.6 |
|
4.7 |
4.8 |
4.9 |
|
4.10 |
4.11 |
4.12 |
|
4.13 |
4.14 |
4.15 |
|
4.16 |
4.17.
|
4.18 |
|
4.19 |
4.20 |
4.21 |
|
4.22 |
4.23 |
4.24 |
|
4.25 |
4.26 |
4.27 |
|
4.28 |
4.29 |
4.30 |
5. Исследовать ряд на сходимость с помощью интегрального признака Коши.
Т а б л и ц а 5
|
5.1 |
5.2 |
5.3 |
|
5.4 |
5.5 |
5.6 |
|
5.7 |
5.8 |
5.9 |
|
5.10 |
5.11 |
5.12 |
|
5.13 |
5.14 |
5.15 |
|
5.16 |
5.17 |
5.18 |
|
5.19 |
5.20 |
5.21 |
|
5.22 |
5.23 |
5.24 |
|
5.25 |
5.26 |
5.27 |
|
5.28 |
5.29 |
5.30 |
6. Сравнением с рядом Дирихле исследовать сходимость ряда.
Т а б л и ц а 6
|
6.1
|
6.2
|
6.3
|
|
6.4
|
6.5
|
6.6
|
|
6.7
|
6.8
|
6.9
|
|
6.10
|
6.11
|
6.12
|
|
6.13
|
6.14
|
6.15
|
|
6.16
|
6.17
|
6.18
|
|
6.19
|
6.20
|
6.21
|
|
6.22
|
6.23
|
6.24
|
|
6.25
|
6.26
|
6.27
|
|
6.28 |
6.29
|
6.30
|
7. Исследовать на абсолютную или условную сходимость знакочередующиеся ряды.
Т а б л и ц а 7
|
7.1 |
7.2 |
7.3 |
|
7.4 |
7.5 |
7.6 |
|
7.7 |
7.8 |
7.9 |
|
7.10 |
7.11 |
7.12 |
|
7.13 |
7.14 |
7.15 |
|
7.16 |
7.17 |
7.18 |
|
7.19 |
7.20 |
7.21 |
|
7.22 |
7.23 |
7.24 |
|
7.25 |
7.26 |
7.27. |
|
7.28 |
7.29 |
7.30 |
8. Задан функциональный
ряд ![]() с общим
членом
с общим
членом ![]() .
Записать
.
Записать ![]() ую
частичную сумму
ую
частичную сумму ![]() и
остаток
и
остаток ![]() для
заданного ряда.
для
заданного ряда.
Т а б л и ц а 8
|
8.1
|
8.2
|
8.3 |
8.4
|
|
8.5
|
8.6
|
8.7
|
8.8
|
|
8.9
|
8.10
|
8.11 |
8.12
|
|
8.13
|
8.14
|
8.15
|
8.16
|
|
8.17
|
8.18
|
8.19
|
8.20
|
|
8.21
|
8.22 |
8.23
|
8.24 |
|
8.25 |
8.26
|
8.27
|
8.28
|
|
8.29
|
8.30
|
8.31
|
8.32
|
9 . Найти область сходимости ряда из задания 8.
10. Вычислить сумму ряда с точностью ![]() .
.
Т а б л и ц а 9
|
10.1
|
10.2
|
|
10.3 |
10.4
|
|
10.5
|
10.6
|
|
10.7
|
10.8
|
|
10.9
|
10.10
|
|
10.11
|
10.12
|
|
10.13
|
10.14
|
|
10.15
|
10.16
|
|
10.17
|
10.178
|
|
10.19
|
10.20
|
|
10.21
|
10.22 |
|
10.23
|
10.24
|
|
10.25
|
10.26
|
|
10.27
|
10.28
|
|
10.29
|
10.30 |
11. Используя разложение подынтегральной функции в степенной ряд, вычислить определенный интеграл с точностью до 0,001.
Т а б л и ц а 10
|
11.1 |
11.2
|
11.3 |
11.4
|
|
11.5 |
11.6 |
11.7
|
11.8
|
|
11.9 |
11.10
|
11.11
|
11.12
|
|
11.13
|
11.14
|
11.15
|
11.16
|
|
11.17
|
11.18
|
11.19
|
11.20
|
|
11.21
|
11.22
|
11.23
|
11.24
|
|
11.25
|
11.26
|
11.27
|
11.28 |
|
11.29
|
11.30
|
|
|
12. Разложить в ряд Фурье периодическую функцию ![]() с периодом
с периодом ![]() , заданную в указанном
интервале.
, заданную в указанном
интервале.
Т а б л и ц а 11
|
12.1 |
12.2 |
12.3 |
|
12.4 |
12.5
|
12.6 |
|
12.7 |
12.8 |
12.9
|
|
12.10
|
12.11
|
12.12
|
|
12.13 |
12.14 |
12.15 |
|
12.16 |
12.17 |
12.18
|
|
12.19 |
12.20 |
12.21 |
|
12.22
|
12.23 |
12.24 |
|
12.25
|
12.26
|
12.27
|
|
12.28 |
12.29
|
12.30
|
1.3 Расчетные задания второго уровня
13. Найти радиус, интервал сходимости и область сходимости ряда.
Т а б л и ц а 12
|
13.1
|
13.2
|
13.3
|
|
13.4
|
13.5
|
13.6
|
|
13.7
|
13.8
|
13.9
|
|
13.10
|
13.11
|
13.12
|
|
13.13
|
13.14
|
13.15
|
|
13.16
|
13.17
|
13.18
|
|
13.19
|
13.20
|
13.21
|
|
13.22
|
13.23
|
13.24
|
|
13.25
|
13.26
|
13.27
|
|
13.28 |
13.29 |
13.30
|
14. Разложить в ряд Фурье периодическую функцию,
заданную на отрезке ![]() .
.
Т а б л и ц а 13
|
14.1 |
14.2
|
|
14.3 |
14.4
|
|
14.5 |
14.6
|
|
14.7 |
14.8
|
|
14.9 |
14.10
|
|
14.11
|
14.12
|
|
14.13
|
14.14
|
|
14.15
|
14.16
|
|
14.17
|
14.18
|
|
14.19
|
14.20
|
|
14.21
|
14.22
|
|
14.23
|
14.24
|
|
14.25
|
14.26
|
|
14.27
|
14.28
|
|
14.29
|
14.30
|
1.4 Решение типового варианта
1. Составить формулу
общего члена ряда 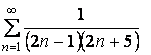 и
написать первые пять членов. Написать
и
написать первые пять членов. Написать ![]() -
- ![]() -ую частичную сумму ряда
-ую частичную сумму ряда 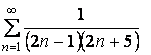 ,
, ![]() - остаток ряда и
- остаток ряда и ![]() . Найти
. Найти ![]() - сумму ряда.
- сумму ряда.
Решение :
Общий член ряда 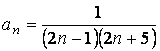 ,
, 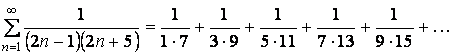
![]() =
=
![]() =
= ,
, ![]() =
=![]() .
.
Представим общий член ряда в виде суммы простейших дробей:
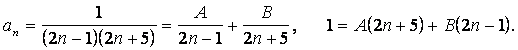
При ![]() имеем:
имеем: ![]() при
при ![]() получим:
получим: ![]()
Таким образом, ![]() Найдем сумму первых
Найдем сумму первых ![]() членов ряда:
членов ряда:

Вычислим сумму ряда: 
2. Выполняется ли необходимое условие сходимости ряда ? Если да, то
исследовать ряд 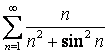 на сходимость с помощью
признаков сравнения.
на сходимость с помощью
признаков сравнения.
Решение:
Выпишем общий член ряда 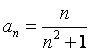 .
. 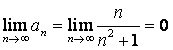 , следовательно, необходимое
условие сходимости ряда выполнено.
, следовательно, необходимое
условие сходимости ряда выполнено.
Так как ![]() , то
, то ![]() и
и 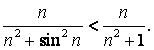
Ряд  расходится по второму признаку сравнения.
Сравнивая ряд
расходится по второму признаку сравнения.
Сравнивая ряд  с
рядом
с
рядом ![]() ,
который расходится и, вычислив
,
который расходится и, вычислив  , убеждаемся, что по первому признаку
сравнения расходится и данный ряд.
, убеждаемся, что по первому признаку
сравнения расходится и данный ряд.
3. Исследовать ряд  на сходимость с помощью признака
Даламбера.
на сходимость с помощью признака
Даламбера.
Решение:
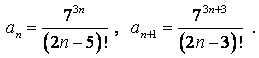 По признаку Даламбера имеем:
По признаку Даламбера имеем:
 следовательно,
ряд сходится.
следовательно,
ряд сходится.
4. Исследовать ряд 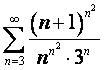 на сходимость с помощью радикального
признака Коши.
на сходимость с помощью радикального
признака Коши.
Решение:
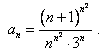
По радикальному признаку Коши имеем: 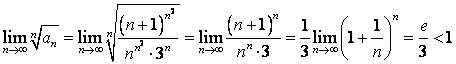 . Следовательно, ряд сходится.
. Следовательно, ряд сходится.
5. Исследовать ряд  на сходимость с помощью интегрального
признака сходимости.
на сходимость с помощью интегрального
признака сходимости.
Решение:
Выпишем общий член ряда 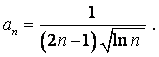 Рассмотрим ряд
Рассмотрим ряд ![]() . По интегральному
признаку Коши он расходится, так как несобственный интеграл
. По интегральному
признаку Коши он расходится, так как несобственный интеграл  расходится. Но
расходится. Но ![]() т.е.
т.е.  и поэтому по
первому признаку сравнения данный ряд также расходится.
и поэтому по
первому признаку сравнения данный ряд также расходится.
6. Сравнением с рядом Дирихле исследовать
сходимость ряда 
Решение:
Выпишем общий член ряда  ,
,
cтепень числителя равна двум,
знаменателя - трем. Разность степеней числителя и знаменателя равна единице.
Следовательно, сравним данный ряд по второму признаку сравнения с рядом Дирихле
:  где
где ![]() т.е. с рядом
т.е. с рядом ![]() (гармонический ряд,
расходится). Так как
(гармонический ряд,
расходится). Так как 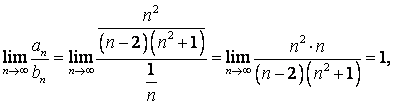 то оба ряда одновременно расходятся.
то оба ряда одновременно расходятся.
7. Исследовать на абсолютную или условную сходимость знакочередующиеся ряды:

Решение:
а) рассмотрим ряд 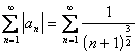 . Этот ряд сходится по второму признаку
сравнения: сравниваем его с рядом
. Этот ряд сходится по второму признаку
сравнения: сравниваем его с рядом  ( это ряд Дирихле
( это ряд Дирихле ![]() сходится); По предельному
признаку сравнения
сходится); По предельному
признаку сравнения  поэтому
оба ряда сходятся одновременно. Так как ряд
поэтому
оба ряда сходятся одновременно. Так как ряд 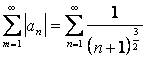 - сходится, то ряд
- сходится, то ряд  сходится
сходится
абсолютно;
б) рассмотрим ряд ![]() Сравним его с рядом
Сравним его с рядом ![]() .
.
По второму признаку сравнения  поэтому приходим к выводу, что
он расходится. Следовательно, исходный ряд не может сходиться абсолютно.
Проверим выполнение условий Лейбница:
поэтому приходим к выводу, что
он расходится. Следовательно, исходный ряд не может сходиться абсолютно.
Проверим выполнение условий Лейбница: 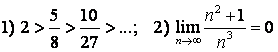 . Они выполняются, следовательно,
исходный ряд сходится условно;
. Они выполняются, следовательно,
исходный ряд сходится условно;
с) для этого ряда не выполняется одно из условий
Лейбница ![]() Действительно,
Действительно,
 Следовательно,
ряд расходится.
Следовательно,
ряд расходится.
8. Задан функциональный ряд 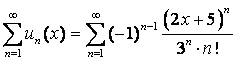 с общим членом
с общим членом 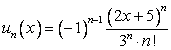 . Записать
. Записать ![]() ую частичную сумму
ую частичную сумму ![]() и остаток
и остаток ![]() для заданного ряда.
для заданного ряда.
Решение:
 =
=![]()
В нашем случае: 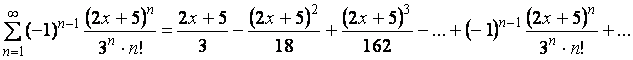
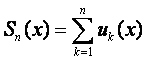 , следовательно,
, следовательно,
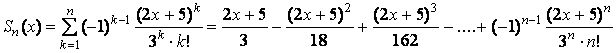 .
.
 ,
,
![]()
9 Найти область сходимости функционального ряда:
а)  ; б)
; б) 
Решение:
а) 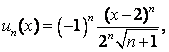
![]()
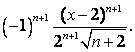
По признаку Даламбера 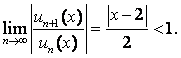 Следовательно,
Следовательно, ![]() или
или ![]() Интервал
Интервал ![]() -интервал сходимости
заданного ряда.
-интервал сходимости
заданного ряда.
Проверим концы интервала: при ![]() получим ряд
получим ряд 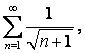 который исследуем на
сходимость по второму признаку сравнения. Сравним с расходящимся рядом
который исследуем на
сходимость по второму признаку сравнения. Сравним с расходящимся рядом 
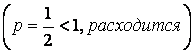 .Поэтому ряд
.Поэтому ряд 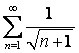 расходится, следовательно,
расходится, следовательно, ![]() не входит в область
сходимости ряда; при
не входит в область
сходимости ряда; при ![]() получим
ряд
получим
ряд 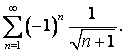 Он
сходится условно, так как выполняются условия признака Лейбница:
Он
сходится условно, так как выполняются условия признака Лейбница:
 Следовательно,
Следовательно, ![]() входит
в область сходимости ряда. Таким образом, область сходимости данного ряда
входит
в область сходимости ряда. Таким образом, область сходимости данного ряда ![]() ;
;
б) ![]() ,
, ![]() Найдем радиус сходимости ряда по формуле:
Найдем радиус сходимости ряда по формуле:

Итак, ряд сходится только в точке ![]() .
.
10. Вычислить сумму ряда  с точностью
с точностью ![]()
Решение:
Так как ряд знакочередующийся и сходящийся, то ![]() ая частичная сумма ряда
ая частичная сумма ряда ![]() является приближением
к его сумме
является приближением
к его сумме ![]() с
абсолютной погрешностью, меньшей, чем абсолютная величина первого члена, не
входящего в
с
абсолютной погрешностью, меньшей, чем абсолютная величина первого члена, не
входящего в ![]() ,
т.е.
,
т.е. ![]()
Вычислим несколько последовательных первых членов
этого ряда: ![]() до
тех пор, пока не получим член по абсолютной величине меньший указанной
точности. В нашем случае это
до
тех пор, пока не получим член по абсолютной величине меньший указанной
точности. В нашем случае это ![]() Тогда по вышеприведенному свойству
знакочередующихся рядов
Тогда по вышеприведенному свойству
знакочередующихся рядов 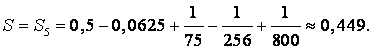
11. Разложить функцию в ряд Тейлора по степеням ![]() .
.
![]()
Решение:
![]() найдем корни квадратного трехчлена
найдем корни квадратного трехчлена ![]()
![]() .
Значит, функцию можно преобразовать так:
.
Значит, функцию можно преобразовать так: ![]()
=
Каждое слагаемое разлагаем в ряд Тейлора по известной формуле:
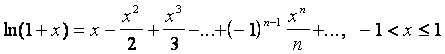
![]() где
второй ряд получен из первого путем замены
где
второй ряд получен из первого путем замены ![]()
Складывая эти ряды, получим ряд Тейлора для исходной функции:

![]() рассмотрим
рассмотрим ![]() как степенной ряд, у которого
коэффициенты всех членов, кроме двух, равны нулю и который сходится на всей
числовой оси. Умножая этот ряд Тейлора для
как степенной ряд, у которого
коэффициенты всех членов, кроме двух, равны нулю и который сходится на всей
числовой оси. Умножая этот ряд Тейлора для ![]() который также сходится на всей числовой
оси, получим искомое разложение:
который также сходится на всей числовой
оси, получим искомое разложение:

12. Вычислить  с точностью до
с точностью до ![]()
Решение:
Разложим подынтегральную функцию в биномиальный ряд
![]()
полагая в нем 
этот ряд сходится при ![]() Почленно проинтегрируем этот ряд в
пределах от 0 до
Почленно проинтегрируем этот ряд в
пределах от 0 до ![]() :
:
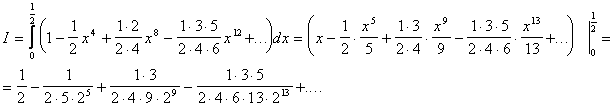
Получили знакочередующийся ряд, сумму которого нужно найти с точностью до 0,0001.
Вычислим несколько последовательных первых членов этого ряда:
![]() Так
как
Так
как ![]() то,
согласно свойству знакочередующихся сходящихся рядов, имеем:
то,
согласно свойству знакочередующихся сходящихся рядов, имеем:
![]()
13. Разложить в ряд Фурье периодическую функцию
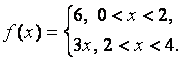
Решение:
Для определения коэффициентов Фурье воспользуемся формулами:
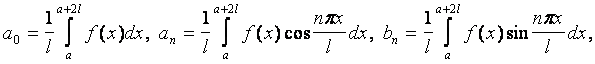
где ![]() тогда
тогда
![]()
Получим:



Подставляя в формулу  где
где ![]() найденные коэффициенты, получим искомое
разложение:
найденные коэффициенты, получим искомое
разложение:

14. Разложить в ряд Фурье периодическую функцию

Решение:
Вычислим коэффициенты Фурье:
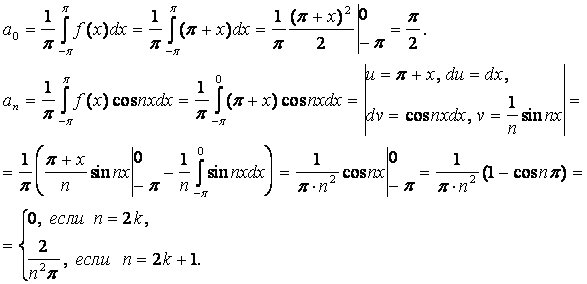

Ряд Фурье для таких функций имеет вид: 
Подставляя в эту формулу найденные коэффициенты, получим искомое разложение:
![]()
15. Разложить функцию ![]() в ряд Фурье на отрезке
в ряд Фурье на отрезке ![]() .
.
Решение:
Ряд Фурье функции ![]() :
:  .
.
Коэффициенты Фурье ![]() находятся
по формулам:
находятся
по формулам:
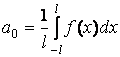 ,
,  ,
,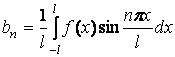 , где
, где ![]() .
.
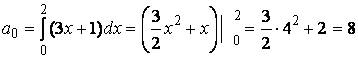 .
.
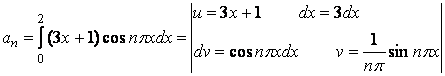
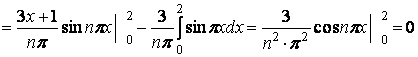
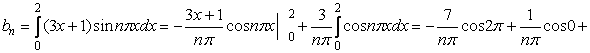
+ .
.
Ряд Фурье заданной функции:
4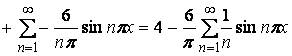 .
.
Список литературы
1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2 ч.- М.: Высш. Шк., 1986. – Ч.2-352 с.
2. Сборник индивидуальных заданий по высшей математике: В 3 ч.
/А.П.Рябушко, В.В.Бархатов и др./ Под редакцией А.П.Рябушко.- Минск: Вышэйшая школа, 1991.-Ч.3-351 с.
3. Кузнецов А.А. Сборник заданий по высшей математике: Типовые расчеты.-М.: Высш.шк., 1983.-176 с.
4. Письменный Д.Т. Конспект лекций по высшей математике. 2 часть.-М.: Айрис-пресс, 2003.-256 с.
5. Хасеинов К.А. Каноны математики. Учебник – Алматы: 2003.-686 с.
6. Математика 3. Конспект лекций для студентов всех форм обучения всех специальностей. Алматинский институт энергетики и связи: 2007.
Содержание
Введение 3
1 Типовой расчет 3. Ряды 3
1.1 Теоретические вопросы 3
1.2 Расчетные задания первого уровня 4
1.3 Расчетные задания второго уровня 12
1.4 Решение типового варианта 15
Список литературы 25