Коммерциялық емес акционерлік қоғам
Алматы энергетика және байланыс Университеті
Жоғары математика кафедрасы
Математика 1
5В071700 – “Жылу энергетика”, 5В071800 – “Электр
энергетика”,
5В071900 – “Радиотехника, электроника және
телекоммуникациялар” мамандықтары бойынша оқитын
студенттер үшін
дәрістер жинағы
Алматы, 2013
Құрастырушылар: Мустахишев К.М., Атабай Б.Ж. Математика 1. 5В071700 – “Жылу энергетика”, 5В071800 – “Электр энергетика”, 5В071900 – “Радиотехника, электроника және телекоммуникациялар” мамандықтары бойынша оқитын студенттер үшін дәрістер жинағы. -Алматы, 2013. - 48 б.
Дәрістер жинағы ҚР БҒМ 2012 жылы бекіткен бағдарламаға сай жазылған. Онда сызықтық алгебра, аналитикалық геометрия және комплекс сандар, бір айнымалы функцияларының дифференциалдық және интегралдық есептеулері, операторлық есептеу бөлімдері қамтылған (барлығы 11 дәріс).
Сурет -17, әдебиет көзі - 10 атау.
Пікір жазған: физ.-мат. ғылым. канд., доцент Дуйсек А.К.
“Алматы энергетика және байланыс университеті” коммерциялық емес акционерлік қоғамының 2013 жылғы жоспары бойынша басылды
© “ Алматы энергетика және байланыс университеті” КЕАҚ, 2013 ж.
2013 ж. жиынтық жоспары, реті 303
1-модуль. Сызықтық алгебра, аналитикалық геометрия және комплекс сандар
1-дәріс. Анықтауыштар, матрицалар және сызықтық теңдеулер жүйелері
Дәріс мақсаты: студенттерді олар үшін жаңа анықтауыш және матрица ұғымдарымен таныстырып, оларға амалдар қолдануды үйрету. Сызықтық теңдеулер жүйесін жаңа әдістермен: Крамер ережесі бойынша және матрицалық тәсілдермен шешуді үйрету.
Сандардың
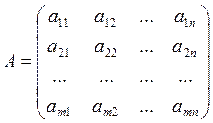 (1.1)
(1.1)
тік бұрышты кестесі ![]() жатық және
жатық және ![]() тік жолдары бар
тік жолдары бар ![]() өлшемді матрица
деп аталады. Егер
өлшемді матрица
деп аталады. Егер ![]() болса,
онда
болса,
онда ![]()
![]() - ретті шаршы матрица
деп аталады. Мұндағы
- ретті шаршы матрица
деп аталады. Мұндағы ![]() сандары оның элементтері деп
аталады.
сандары оның элементтері деп
аталады.
Бір ғана жатық не тік жолдан тұратын матрицаны сәйкес жатық жол-матрица немесе тік жол-матрица деп атаймыз.
Шаршы матрицаның (![]() ) негізгі сипаттамаларының бірі
оның
) негізгі сипаттамаларының бірі
оның ![]() -ретті
анықтауышы немесе детерминанты деп аталып,
-ретті
анықтауышы немесе детерминанты деп аталып,
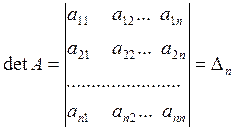 (1.2)
(1.2)
өрнегімен белгіленетін сан. Егер ![]() болса, А-ны ерекше матрица, ал
қарсы жағдайда оны ерекше емес матрица дейміз.
болса, А-ны ерекше матрица, ал
қарсы жағдайда оны ерекше емес матрица дейміз.
Анықтауыштарды есептеу.
Жеке санды бірінші ретті анықтауыш деуге болады. Екінші ретті анықтауыш диагональдарының бойында орналасқан элементтердің көбейтінділерінің айырымына тең:
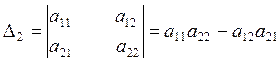 . (1.3)
. (1.3)
Үшінші ретті анықтауыш Саррюс ережесі немесе диагональдар мен үшбұрыштар ережесі деп аталатын әдіспен есептелінеді (1 суретті қара).
Бұл ережені қолдануды жеңілдету үшін анықтауыштың алдыңғы екі жатық не тік жолдарын өздеріне өздерін параллель көшіріп, анықтауыштың соңына тіркеп жазады, ары қарай схема бойынша есептейді (1б суретті қара):
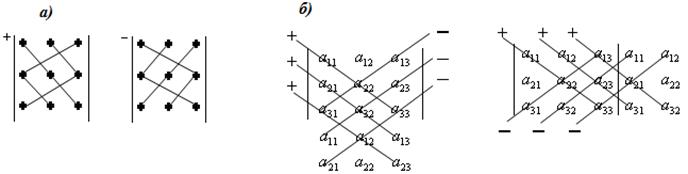
1 сурет - Үшінші ретті анықтауышты есептеу схемасы
Яғни,
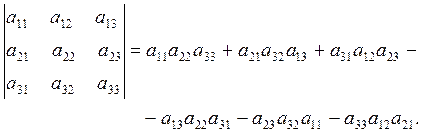 (1.4)
(1.4)
Анықтауыштардың қасиеттері.
Матрицаның не анықтауыштың жатық жолдарын сәйкес номірлі тік жолдарға (немесе керісінше) айналдыру амалы транспондау деп аталады.
1. Бағаналағаннан анықтауыш өзгермейді.
2. Кез келген екі жатық (не тік) жолдарын өзара орын ауыстырғаннан анықтауыштың таңбасы өзгереді.
3. Кез келген жатық (не тік) жолының барлық элементтерін бір санға көбейтсек, анықтауыш та сол санға көбейтіледі. Ортақ көбейткіші анықтауыш белгісінің сыртына шығаруға болады.
4. Кейбір жатық не тік жолының әрбір элементі екі қосылғыштан тұратын анықтауыш екі анықтауыштың қосындысына тең.
5. Анықтауыш нөлге тең, егер:
1) бір жатық (тік) жолының элементтері түгел нөлге тең болса;
2) екі жатық (тік) жолының сәйкес элементтері өзара тең немесе пропорционал болса.
6. Кез келген жатық (тік) жолының элементтерін бір санға көбейтіп, басқа жатық (тік) жолдың сәйкес элементтеріне қосқаннан анықтауыш өзгермейді.
![]() анықтауышының
анықтауышының ![]() жатық және
жатық және ![]() тік жолдарын сызып
тастағаннан пайда болған
тік жолдарын сызып
тастағаннан пайда болған ![]() ретті
ретті ![]() анықтауышы
анықтауышы ![]() элементінің
миноры, ал
элементінің
миноры, ал ![]() анықтауышы
оның алгебралық толықтауышы деп аталады.
анықтауышы
оның алгебралық толықтауышы деп аталады.
7. Лаплас теоремасы. Анықтауыш оның кез келген жатық (тік) жолы элементтері мен олардың алгебралық толықтауыштарының көбейтінділерінің
қосындысына тең:
Бұлар анықтауышты i-жатық және j-тік жолдарының элементтері бойынша ашу формулалары делінеді. Олар жоғарғы ретті анықтауыштарды есептеуде қолданылады.
8. Анықтауыштың бір жатық (тік) жолының элементтері мен басқа жатық (тік) жолының сәйкес элементтерінің алгебралық толықтауыштарының
көбейтінділерінің қосындысы нөлге тең.
Матрицаларға амалдар қолдану.
Матрицаны кез келген санға көбейтсек,
оның барлық элементтері сол санға көбейтіледі: ![]() . Тең
өлшемді матрицаларды өзара қосуға болады. Мұнда
қосылғыш матрицалардың сәйкес элементтері өзара
қосылады.
. Тең
өлшемді матрицаларды өзара қосуға болады. Мұнда
қосылғыш матрицалардың сәйкес элементтері өзара
қосылады.
Матрицалар айырымы ![]() болып табылады.
болып табылады.
Өлшемдері бірдей матрицалардың ішінде сәйкес элементтері тең матрицалар ғана өзара тең.
Өлшемдері ![]() және
және ![]() (біріншісінің тік жолдар саны
- ені екіншісінің
жатық жолдар санына - биіктігіне тең) болып келген матрицаларды
өзара көбейтуге болады:
(біріншісінің тік жолдар саны
- ені екіншісінің
жатық жолдар санына - биіктігіне тең) болып келген матрицаларды
өзара көбейтуге болады:
![]() ,
, 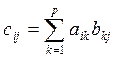
![]() . (1.5)
. (1.5)
Матрицаларды қосу амалы
орын алмастыру заңына (коммутативтік заңға) қанағаттандырады:
яғни ![]() , бірақ, жалпы
жағдайда
, бірақ, жалпы
жағдайда ![]() .
.
1–есеп: Екі А және В.
матрицалары берілген. ![]() -тi табыңыз.
-тi табыңыз.
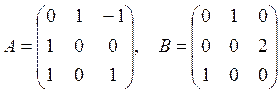 №
№
Шешу.
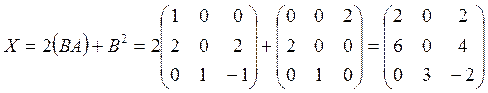 .
.
Нөлдік емес шаршы матрицаның диагоналінің бір бетінде орналасқан элементтері нөлге тең болса, оны үшбұрышты матрица дейміз. Ал бас диагоналінде жатпайтын элементтерінің бәрі нөлге тең болса, онда ол диагональдық матрица деп аталып, ал диагональдық элементтері 1-ге тең болса, онда, n – ретті бірлік матрица
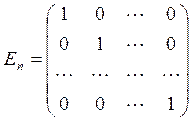
ұғымына келеміз.
Әр уақытта ![]() және тең ретті шаршы матрица А
үшін
және тең ретті шаршы матрица А
үшін ![]() .
.
Кері матрица.
Квадраттық A және А-1
матрицаларының ![]() шартын қанағаттандыруында
олар өзара кері матрицалар делінеді. Тек азбаған шаршы
матрицаның ғана кері матрицасы бар, өйткені
шартын қанағаттандыруында
олар өзара кері матрицалар делінеді. Тек азбаған шаршы
матрицаның ғана кері матрицасы бар, өйткені ![]() .
.
Кері матрица тек біреу ғана және ![]() үшін
үшін
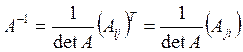 . (1.6)
. (1.6)
Берілген матрица элементтерінің алгебралық
толықтауыштарынан құралып, бағаналанған ![]() матрицасы А-ға
қосақталған (қарымталы) матрица деп аталады.
Сондықтан кері матрицаны (1.6)-нің көмегімен табу
қосақталған матрица әдісі делінеді.
матрицасы А-ға
қосақталған (қарымталы) матрица деп аталады.
Сондықтан кері матрицаны (1.6)-нің көмегімен табу
қосақталған матрица әдісі делінеді.
Сызықтық теңдеулер жүйелері.
Қысқаша ![]() белгісізді
белгісізді ![]() сызықтық теңдеулер жүйесі
сызықтық теңдеулер жүйесі
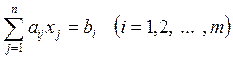 (1.7)
(1.7)
түрінде жазылады. Теңдеулердің коэффициенттері ![]() және бос мүшелері
және бос мүшелері ![]() берілген сандар. Олардан
құралған
берілген сандар. Олардан
құралған ![]() және
және ![]() матрицалары
сәйкес жүйе матрицасы және оның кеңейтілген
матрицасы деп аталады.
матрицалары
сәйкес жүйе матрицасы және оның кеңейтілген
матрицасы деп аталады.
Кем дегенде бір шешуі бар жүйе үйлесімді жүйе
деп, қарсы жағдайда үйлесімсіз жүйе деп аталады. Бір
ғана шешуі бар жүйені анықталған жүйе, ал шексіз
көп шешуі бар жүйені анықталмаған жүйе дейміз.
Шешулер жиындары бірдей жүйелер эквивалент жүйелер делінеді. Егер ![]() , онда (1.7) біртекті, ал
қарсы жағдайда біртексіз деп аталады. Біртекті жүйенің әр
уақытта нөлдік (тривиал) шешуі
, онда (1.7) біртекті, ал
қарсы жағдайда біртексіз деп аталады. Біртекті жүйенің әр
уақытта нөлдік (тривиал) шешуі ![]() бар.
бар.
Крамер ережесі.
Берілген (1.7) сызықтық теңдеулер жүйесінде
![]() болса,
болса, ![]() n-ретті шаршы
матрица болады,
n-ретті шаршы
матрица болады, ![]() жүйе
анықтауышы деп аталады.
жүйе
анықтауышы деп аталады.
Теорема. Егер жүйе анықтауышы ![]() болса, онда жүйе
үйлесімді және оның
болса, онда жүйе
үйлесімді және оның
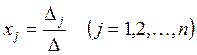 (1.8)
(1.8)
формулаларымен анықталатын бір ғана шешуі бар. Мұнда Dj – жүйе анықтауышының j-тік жолын жүйенің бос мүшелер тік жолымен алмастырудан пайда болған анықтауыш.
(1.8) теңдіктері Крамер формулалары деп аталады.
Бұл теореманың
көмегімен сызықтық теңдеулер жүйесінің
үйлесімділігін дәлелдеп, оның шешуін табу Крамер ережесі
делінеді. Бұл ережеден теңдеулер жүйесінің
анықтауышы ![]() болса, жүйенің бір
ғана нөлдік шешуі болады. Егер
болса, жүйенің бір
ғана нөлдік шешуі болады. Егер ![]() болса, онда жүйенің
нөлден өзгеше шексіз көп шешуі болады.
болса, онда жүйенің
нөлден өзгеше шексіз көп шешуі болады.
2–есеп:
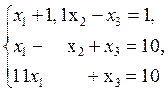
жүйесін шешіңіз.
Шешу. Жүйе үйлесімді, өйткені оның анықтауышы
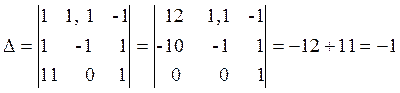 .
.
Қосымша анықтауыштар
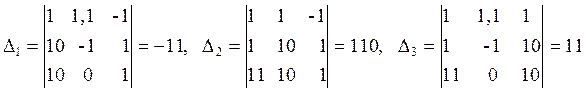 .
.
Крамер формулалары (1.8) бойынша: ![]()
Матрицалық теңдеулер.
Кез келген (1.7) сызықтық теңдеулер жүйесін матрицалық
![]() (1.9)
(1.9)
түрінде жазуға болады. Мұнда ![]() -берілген матрицалар;
-берілген матрицалар; ![]() - белгісіз тік жол матрица. Мұндай
жүйе шешуі:
- белгісіз тік жол матрица. Мұндай
жүйе шешуі:
![]() . (1.10)
. (1.10)
3–есеп. Теңдеуді шешіңіз: ![]() ,
,
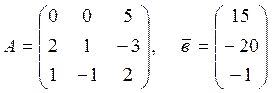 .
.
Шешу. Теңдеу матрицасы азбаған: ![]() . Сонымен,
. Сонымен,
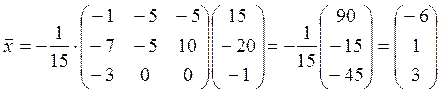 .
.
2-дәріс. Үш өлшемді кеңістіктегі векторлар. Түзу мен жазықтық
Дәріс мақсаты: студенттердің мектептен алған векторлар, түзулер мен жазықтықтар туралы білімдері негізінде оларға векторлық көбейтінді, аралас көбейтінді түсініктерін, сызықтық нысандар теңдеулері мен есептерін, оларды шешу жолдарын түсіндіру.
Тек сан мәнімен ғана сипатталатын шама скалярлық шама деп аталады. Ал, вектор сан мәнімен (ұзындығымен) қатар бағытымен де сипатталады. Вектор бағытталған кесінді, кейде тасымал деп те аталады. Геометриялық түрде екі векторды қосу белгілі параллелограмм (үшбұрыш, 2 суретті қара) ережесі бойынша орындалады.
Бірақ, оны қайталап қолдану
арқылы векторлардың кез келген шекті санын ![]() қосуға
болады(мысалы,
қосуға
болады(мысалы, ![]() ,
2б суретті қара).
,
2б суретті қара).
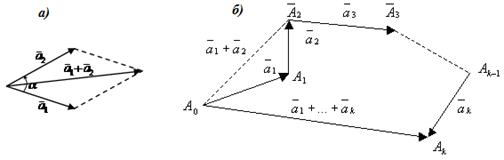
2 сурет - Векторларды қосу
Векторлардың көбейтіндісі.
Тікбұрышты
декарттық координаталар жүйесінде бірлік векторлар (орталар) ![]() координаталар
осьтерінің бағыттарын көрсетеді және декарттық
базис құрайды:
координаталар
осьтерінің бағыттарын көрсетеді және декарттық
базис құрайды: ![]() . Мұнда
. Мұнда ![]() вектордың немесе
вектордың немесе ![]() нүктесінің координаталары.
нүктесінің координаталары.
Үш векторды
![]() (1.11)
(1.11)
қарастыралық.
1. Скалярлық көбейтінді.
Екі вектордың модульдері мен
олардың арасындағы бұрыштың косинусының
көбейтіндісіне тең ![]() санын сол
векторлардың скалярлық көбейтіндісі дейміз:
санын сол
векторлардың скалярлық көбейтіндісі дейміз:
![]() (1.12)
(1.12)
немесе
![]() . (1.13)
. (1.13)
Скалярлық көбейтінді үшін
![]() (1.14)
(1.14)
теңдігі тура болады.
Вектордың ұзындығы
![]() .
.
Екі вектордың арасындағы бұрыш (1.15)-дың көмегімен табылады:
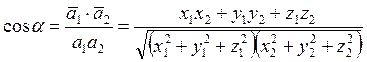 . (1.15)
. (1.15)
Бұдан векторлардың перпендикулярлық белгісі:
![]() . (1.16)
. (1.16)
2. Векторлық көбейтінді.
Егер ![]() -ның ұшынан
қарағанда
-ның ұшынан
қарағанда ![]() -ден
-ден ![]() -ге қарайғы ең
қысқа бұрылу (3 суретті қара) сағат тілінің
жүрісіне қарсы бағытта орындалатын болса, онда декарттық
базис
-ге қарайғы ең
қысқа бұрылу (3 суретті қара) сағат тілінің
жүрісіне қарсы бағытта орындалатын болса, онда декарттық
базис ![]() оң
үштік құрайды, ол анықтайтын координаталар жүйесі
оң
үштік құрайды, ол анықтайтын координаталар жүйесі
![]() оң
дейміз. Қарсы жағдайда бірлік векторлар үштігі де,
сәйкес координаталар жүйесі де сол делінеді.
оң
дейміз. Қарсы жағдайда бірлік векторлар үштігі де,
сәйкес координаталар жүйесі де сол делінеді.
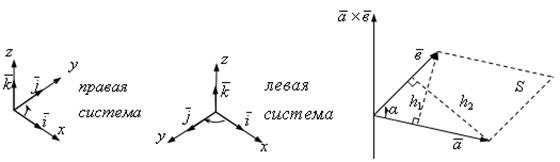
3 сурет - Екі вектордың векторлық көбейтіндісі
Берілген ![]() және
және ![]() векторларының векторлық
көбейтіндісі деп оларға перпендикуляр, оң үштік
құрайтын, модулі олардың абсолют шамалары мен
арасындағы бұрышының синусының көбейтіндісіне
тең
векторларының векторлық
көбейтіндісі деп оларға перпендикуляр, оң үштік
құрайтын, модулі олардың абсолют шамалары мен
арасындағы бұрышының синусының көбейтіндісіне
тең ![]() векторын
айтамыз:
векторын
айтамыз:
![]() . (1.17)
. (1.17)
Геометриялық тұрғыдан (1.17) көбейткіш векторларға тұрғызылған параллелограмның ауданын
![]() . (1.18)
. (1.18)
Базистік векторлардың векторлық көбейтінділері:
![]() ,
, ![]() .
.
Сонымен,
![]() , (1.19)
, (1.19)
немесе
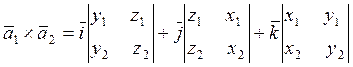 . (1.20)
. (1.20)
Яғни, бірінші жатық жолы арқылы ашылған 3-ретті анықтауыш ретінде:
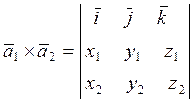 . (1.21)
. (1.21)
Енді анықтауыштар қасиеттерінің көмегімен векторлық көбейтіндінің негізгі қасиеттері оңай алынады:
1) ![]() , 2)
, 2) ![]() , 3)
, 3)![]() ,
,
4)![]() ,
, ![]() .
.
Екі вектордың коллинеарлығының қажет және жеткілікті шарты:
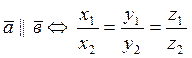 . (1.22)
. (1.22)
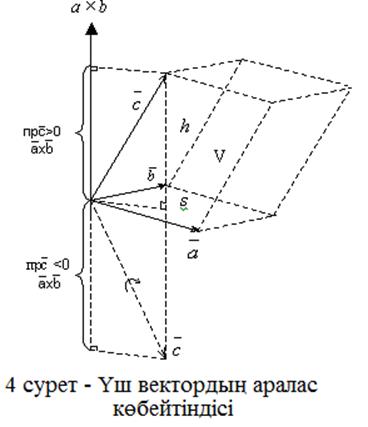
Векторлардың аралас көбейтіндісі.
Берілген үш вектордың
кез келген екеуінің (4 суретті қара) векторлық көбейтіндісінің
үшінші вектормен ![]() скалярлық көбейтіндісіне
тең сан олардың аралас көбейтіндісі деп аталып,
скалярлық көбейтіндісіне
тең сан олардың аралас көбейтіндісі деп аталып, ![]() түрінде
жазылады.
түрінде
жазылады.
Яғни, 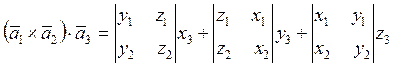
немесе
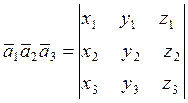 . (1.23)
. (1.23)
 Анықтауыштың жатық жолдарын
орын алмастыру туралы қасиетті пайдаланып, 1)
Анықтауыштың жатық жолдарын
орын алмастыру туралы қасиетті пайдаланып, 1) ![]() , 2)
, 2) ![]() дей аламыз.
Көбейткіш векторлардың кем дегенде екеуі өзара тең не
коллинеар болса, аралас көбейтінді нөлге тең.
дей аламыз.
Көбейткіш векторлардың кем дегенде екеуі өзара тең не
коллинеар болса, аралас көбейтінді нөлге тең.
Үш вектордың
компланарлығының
қажет және жеткілікті шарты қысқаша ![]() түрінде жазылады.
Бұл шарт орындалмаса, берілген векторларға параллелепипед
тұрғызуға болады. Векторлық көбейтіндінің
геометриялық мағынасын және (1.20)–ны пайдаланып, осы
параллелепипедтің көлемін табалық:
түрінде жазылады.
Бұл шарт орындалмаса, берілген векторларға параллелепипед
тұрғызуға болады. Векторлық көбейтіндінің
геометриялық мағынасын және (1.20)–ны пайдаланып, осы
параллелепипедтің көлемін табалық:
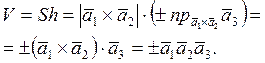
Жалпы ![]() .
.
Кеңістіктегі түзу мен жазықтық.
Кесіндіні берілген қатынаста бөлу.
Кеңістікте не жазықтықта бір ![]() түзуінің
бойында орналасқан
түзуінің
бойында орналасқан ![]() ,
, ![]() нүктелерін қарастыралық
(7 суретті қара). Мұнда
нүктелерін қарастыралық
(7 суретті қара). Мұнда ![]() - бекітілген (координаталары белгілі) нүктелер, ал,
- бекітілген (координаталары белгілі) нүктелер, ал, ![]() – олар арқылы өтетін
– олар арқылы өтетін
түзудің А2 – ден басқа кез келген
нүктесі; ![]() кесіндісін
берілген қатынаста:
кесіндісін
берілген қатынаста:
бөлетін осы ![]() нүктесінің координаталары:
нүктесінің координаталары:
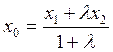 ,
, 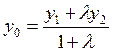 ,
, 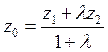 .
.
Ал, кесіндінің ортаңғы нүктесінің координаталарын
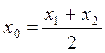 ,
, 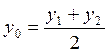 ,
, 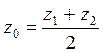 (1.24)
(1.24)
түрінде табамыз.
Кеңістіктегі жазықтық.
Жазықтықтың ![]() кеңістігіндегі жалпы
теңдеуі
кеңістігіндегі жалпы
теңдеуі
![]()
![]()
![]() (1.25)
(1.25)
түрінде жазылады. Алғашқы
үш коэффициент бір мезгілде нөлге тең бола алмайды. Бос
мүше ![]() болса,
жазықтық координаталар осьтерінен
болса,
жазықтық координаталар осьтерінен 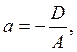
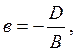
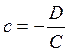 кесінділерін қияды.
Жазықтықтың осы кесінділердегі
кесінділерін қияды.
Жазықтықтың осы кесінділердегі
теңдеуі
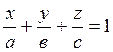 (1.26)
(1.26)
түрінде жазылады. Егер ![]() болса, онда жазықтық координаталардың
бас нүктесі арқылы өтеді
болса, онда жазықтық координаталардың
бас нүктесі арқылы өтеді ![]() .
.
Жазықтықтың нормальдық векторы
деп оған перпендикуляр ![]() векторын айтамыз. Оның жалпы
теңдеуін векторлық түрде жазалық:
векторын айтамыз. Оның жалпы
теңдеуін векторлық түрде жазалық:
![]() .
.
Берілген нүкте арқылы өтетін қалыпты
векторы ![]() жазықтықтың
теңдеуі:
жазықтықтың
теңдеуі:
![]() . (1.27)
. (1.27)
Енді бір түзудің бойында жатпайтын
үш нүкте ![]() берілген
делік. Олар арқылы жалғыз ғана жазықтық Р
өтеді. Оның ағым нүктесін
берілген
делік. Олар арқылы жалғыз ғана жазықтық Р
өтеді. Оның ағым нүктесін ![]() десек,
десек, ![]()
![]() ,
, ![]() векторларының компланарлық шарты
векторларының компланарлық шарты ![]() жазықтығының
теңдеуін береді:
жазықтығының
теңдеуін береді:
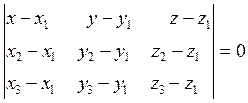 . (1.28)
. (1.28)
Жалпы теңдеулерімен
берілген ![]() ,
, ![]() жазықтықтарының
арасындағы екі жақты:
жазықтықтарының
арасындағы екі жақты:
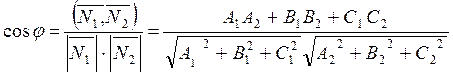 . (1.29)
. (1.29)
Екі жазықтықтың өзара параллельдік және перпендикулярлық белгілері де векторлардың сәйкес белгілерімен бірдей болады:
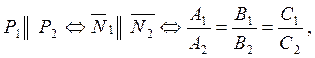
![]() .
.
Векторлар теңдігінің шарты:
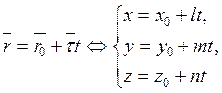 (1.30)
(1.30)
түзудің векторлық және координаталық түрдегі параметрлік теңдеулері деп аталады. Векторлардың коллинеарлық шарты:
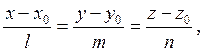
![]() (1.31)
(1.31)
түзудің канондық немесе пропорциялар түріндегі теңдеуі делінеді.
Берілген екі нүкте арқылы өтетін түзудің теңдеуі:
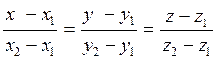 . (1.32)
. (1.32)
Кеңістіктегі түзуді екі
жазықтықтың қиылысу сызығы ![]() деп қарауға болады.
Бұл жазықтықтардың жалпы теңдеулерінің жүйесі
деп қарауға болады.
Бұл жазықтықтардың жалпы теңдеулерінің жүйесі
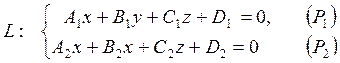 (1.33)
(1.33)
түзудің жалпы теңдеуі деп аталады.
Түзулердің кеңістікте өзара орналасуы олардың бағыттаушы векторларының көмегімен зерттеледі. Екі түзудің арасындағы бұрыш:
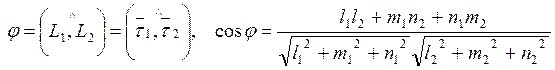 . (1.34)
. (1.34)
Түзулердің өзара параллельдік және перпендикулярлық белгілері:
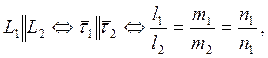 (1.35)
(1.35)
![]() . (1.36)
. (1.36)
Берілген түзу мен жазықтықты:
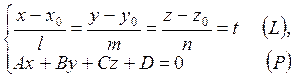 (1.37)
(1.37)
қиылысады деп есептеп, олардың арасындағы бұрышты табалық.
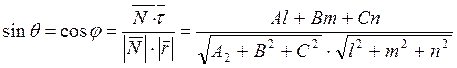 . (1.38)
. (1.38)
Түзу мен жазықтықтың параллельдік және перпендикулярлық белгілері:
![]() ,
,
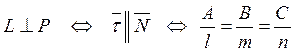 .
.
![]() -дегі түзу.
-дегі түзу.
Егер жалпы теңдеуде ![]()
![]() болса, онда одан табылған
болса, онда одан табылған ![]() теңдігі
түзудің
теңдігі
түзудің 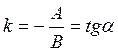 бұрыштық
коэффициентті теңдеуін береді.
бұрыштық
коэффициентті теңдеуін береді.
Берілген ![]() нүктесі арқылы өтетін
түзудің теңдеуі
нүктесі арқылы өтетін
түзудің теңдеуі
![]() (1.39)
(1.39)
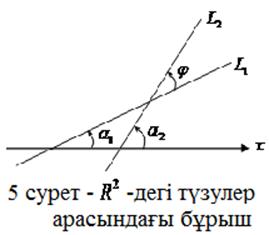 түрінде жазылады.
Бұрыштық коэффициенттері
түрінде жазылады.
Бұрыштық коэффициенттері ![]() берілген екі түзудің
арасындағы бұрыш
берілген екі түзудің
арасындағы бұрыш 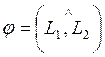 түзулердің
абсцисса осіне көлбеу бұрыштарының айырымы ретінде
анықталады (5 суретті қара):
түзулердің
абсцисса осіне көлбеу бұрыштарының айырымы ретінде
анықталады (5 суретті қара):
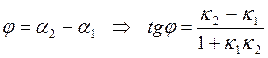 .
.
Бұрыштық коэффициент түзудің жазықтықтағы бағытын анықтайды:
![]() ,
, ![]() .
.
3-дәріс. Екінші ретті қисықтар мен беттер
Дәріс мақсаты: екінші ретті қисықтар мен беттердің жалпы теңдеулерін канондық түрге келтіру, олардың қасиеттерін зерттеу әдістерін баяндау. Комплекс сандардың әртүрлі пішіндерін (түрлерін) келтіріп, оларға амалдар қолдануды үйрету.
Екінші дәрежелі алгебралық теңдеу
![]() (1.40)
(1.40)
![]() координаталар
жүйесінде екінші ретті қисық деп аталатын жазық
сызықты анықтайды. Коэффициенттерінің сан мәндеріне
қарай екінші ретті қисықтардың жалпы теңдеуі (1.40):
эллипсті, шеңберді, гиперболаны немесе параболаны анықтауы
мүмкін.
координаталар
жүйесінде екінші ретті қисық деп аталатын жазық
сызықты анықтайды. Коэффициенттерінің сан мәндеріне
қарай екінші ретті қисықтардың жалпы теңдеуі (1.40):
эллипсті, шеңберді, гиперболаны немесе параболаны анықтауы
мүмкін.
Нәтижесінде (айнымалылардың бұрынғы белгілеулерін сақтай отырып) берілген теңдеуді төмендегі қарапайым түрлердің біріне келтіреміз.
1. 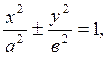 - эллипс (
- эллипс (![]() болғанда шеңбер
болғанда шеңбер ![]() ) және
гипербола.
) және
гипербола.

(1.41)
5. 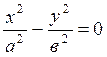 - координаталардың бас
нүктесі арқылы өтетін қос түзу.
- координаталардың бас
нүктесі арқылы өтетін қос түзу.
Эллипс пен гиперболаның канондық
теңдеулерінде (1.41.1), 6а-суретте анықтық үшін ![]() делік. Гиперболаның ордината осімен қиылыспайтынын
делік. Гиперболаның ордината осімен қиылыспайтынын
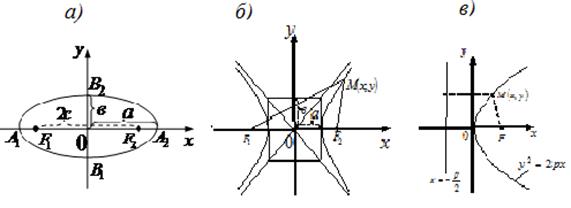
6 сурет - Эллипс және гипербола
көреміз. Сондықтан абсцисса және ордината осьтері, олардың бойында
салынатын ![]() және
және
![]() шамалары
гиперболаның сәйкес заттық және жорамал осьтері деп
аталады. Эллипс үшін бұл сандар үлкен және кіші осьтер
делінеді,
шамалары
гиперболаның сәйкес заттық және жорамал осьтері деп
аталады. Эллипс үшін бұл сандар үлкен және кіші осьтер
делінеді, ![]() мен
мен ![]() сәйкес жарты осьтер деп аталады.
Қисықтардың симметрия осьтерімен қиылысу
нүктелері олардың төбелері делінеді:
сәйкес жарты осьтер деп аталады.
Қисықтардың симметрия осьтерімен қиылысу
нүктелері олардың төбелері делінеді: ![]()
![]() Гипербола жорамал осьтің екі
жағында жатқан симметриялы бөліктерден тұрады. Оларды
гиперболаның оң және сол бұтақтары дейміз.
Гипербола жорамал осьтің екі
жағында жатқан симметриялы бөліктерден тұрады. Оларды
гиперболаның оң және сол бұтақтары дейміз.
Бұл қисықтардың
әрқайсысының екі фокусы ![]() және
және ![]() , оларға сәйкес екі
директрисасы
, оларға сәйкес екі
директрисасы ![]() және
және
![]() бар;
бар; ![]() фокустік қашықтық
деп аталады. Қисықтың эксцентриситеті деп аталатын
фокустік қашықтық
деп аталады. Қисықтың эксцентриситеті деп аталатын
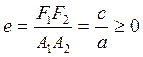
саны қисықтың абсцисса осі бойымен
созылыңқы болу шамасын сипаттайды. Эллипсте ![]() ,
демек,
,
демек, ![]() ,
, ![]() ал, гиперболада
ал, гиперболада ![]() . Жеке жағдайда: шеңбер
үшін
. Жеке жағдайда: шеңбер
үшін ![]() ,
ал теңбүйірлі
,
ал теңбүйірлі ![]() гипербола үшін
гипербола үшін ![]() .
.
Параболаның бір ғана фокусы бар, демек
директрисасы да біреу. Директриса параболамен қиылыспайды, симметрия
осіне перпендикуляр, қисықтың дөңес (сырт)
жағында жатады. ![]() - парболаның төбесі, ал
- парболаның төбесі, ал ![]() оның фокустық қашықтығы (1.41.2, 6в
суретті қара). Олай болса,
оның фокустық қашықтығы (1.41.2, 6в
суретті қара). Олай болса, 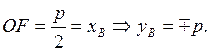 Екінші ретті қисықтар
үшін
Екінші ретті қисықтар
үшін ![]() , фокальдық параметр деп аталады.
Анықтама бойынша
, фокальдық параметр деп аталады.
Анықтама бойынша 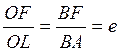
![]() .
.
Қашықтықтар ![]() (6а,б суреттерді қара) қисықтың
ағым нүктесінің
(6а,б суреттерді қара) қисықтың
ағым нүктесінің ![]() фокальдық фокустары деп аталады. Эллипс
үшін
фокальдық фокустары деп аталады. Эллипс
үшін ![]() , ал, гипербола үшін
, ал, гипербола үшін ![]() .
.
Гиперболаның диагональдары 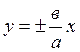 оның асимптоталары
болады.
оның асимптоталары
болады.
Полярлық координаталар жүйесіндегі екінші ретті қисықтар.
Екінші ретті қисық ![]() дегеніміз берілген фокус деп аталатын нүктеден
дегеніміз берілген фокус деп аталатын нүктеден ![]() және директриса деп аталатын түзуден
және директриса деп аталатын түзуден ![]() қашықтықтарының
қатынасы тұрақты
қашықтықтарының
қатынасы тұрақты ![]() болатын
болатын ![]() жазықтығы
нүктелерінің геометриялық орны:
жазықтығы
нүктелерінің геометриялық орны:
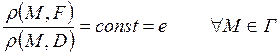 . (1.42)
. (1.42)
Соңғы теңдіктен эллипс пен гиперболаның директрисаларының теңдеулерін табуға болады:
 ;
;
Декарттық және полярляқ координаталары арасындағы байланыс
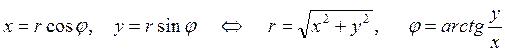 (1.43)
(1.43)
теңдіктерімен анықталады.
Екінші ретті қисықтардың
полярлық координаталардағы жалпы теңдеуін қорыту
үшін фокусты ![]() (6в
суретті қара) полюс ретінде қабылдап, полярлық осьті
(6в
суретті қара) полюс ретінде қабылдап, полярлық осьті ![]() -ға перпендикуляр
оңға қарай бағыттайық. Сонда (1.42) –ден:
-ға перпендикуляр
оңға қарай бағыттайық. Сонда (1.42) –ден:
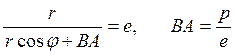 ;
; 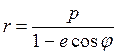 . (1.44)
. (1.44)
Екінші ретті беттер.
Екінші ретті беттердің жалпы теңдеуі координаталық түрде
![]() (1.45)
(1.45)
болып жазылады. Сызықтық түрлендірулердің
көмегімен канондық түрге келтірілгеннен кейін оның
кеңістікте ![]() қандай
геометриялық бейнелерді анықтайтыны айқындалады:
қандай
геометриялық бейнелерді анықтайтыны айқындалады:
1)
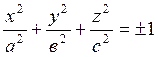 - эллипсоид (центрі бас
нүктеде
- эллипсоид (центрі бас
нүктеде ![]() орналасқан)
немесе жорамал бет;
орналасқан)
немесе жорамал бет;

(1.46)
4) 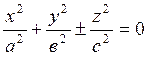 - бір ғана нүкте
- бір ғана нүкте ![]() – жаңа
координаталар жүйесінің бас нүктесі немесе төбесі осы
нүктеде орналасқан конус.
– жаңа
координаталар жүйесінің бас нүктесі немесе төбесі осы
нүктеде орналасқан конус.
Бұлар екінші ретті беттердің координаталар жүйесіндеғі теңдеулері.
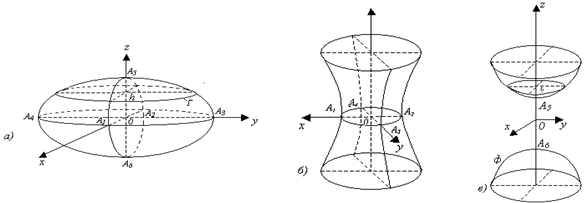 |
Эллипсоидтар мен гиперболоидтардың канондық теңдеулерінде
16 сурет - Эллипсоид және гиперболоидтар
беттердің жарты осьтері деп аталады. Олар әртүрлі
болып, (1.46.1)-де ылғи оң таңбалар алынса, теңдеу
үш осьті эллипсоидты анықтайды дейміз. Оның алты төбесі
бар (7а суретті қара): ![]() . Үш осьті эллипсоидтың барлық
ортогональ қималары
. Үш осьті эллипсоидтың барлық
ортогональ қималары ![]() эллипстер. Егер жарты осьтердің екеуі
өзара тең, мысалы,
эллипстер. Егер жарты осьтердің екеуі
өзара тең, мысалы, ![]() болса, онда эллипсті
болса, онда эллипсті ![]() осінен айналдырудан пайда болған айналу эллипсоидына
осінен айналдырудан пайда болған айналу эллипсоидына
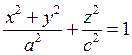
келеміз. Ал, ![]() болса, эллипсоид радиусы
болса, эллипсоид радиусы ![]() сфераға айналады.
Оның канондық теңдеулері:
сфераға айналады.
Оның канондық теңдеулері: ![]() . Егер (1.46.2)-нің оң
жағында
. Егер (1.46.2)-нің оң
жағында ![]() алынса,
онда теңдеу бірқуысты гиперболоидты (7б суретті қара)
анықтайды. Оның төбелері
алынса,
онда теңдеу бірқуысты гиперболоидты (7б суретті қара)
анықтайды. Оның төбелері ![]() .
.
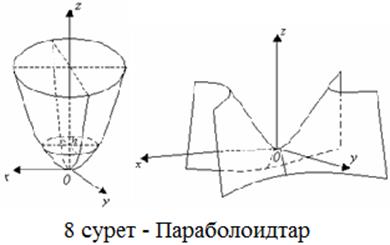 Аталмыш теңдеудің оң
жағында
Аталмыш теңдеудің оң
жағында ![]() алынса,
ол қосқуысты гиперболоидты (7в суретті қара) сипаттайды.
Оның төбелері
алынса,
ол қосқуысты гиперболоидты (7в суретті қара) сипаттайды.
Оның төбелері ![]() аппликата осінің бойында жатады.
Гиперболоидтардың бұл оське перпендикуляр
жазықтықтардағы (
аппликата осінің бойында жатады.
Гиперболоидтардың бұл оське перпендикуляр
жазықтықтардағы (![]() , қосқуысты гиперболоид
үшін
, қосқуысты гиперболоид
үшін ![]() )
қималары эллипстер (
)
қималары эллипстер (![]() болса, шеңберлер), басқа
ортогональ қималары гиперболалар болады.
болса, шеңберлер), басқа
ортогональ қималары гиперболалар болады.
Жеке жағдайда, мысалы, ![]() болса,
гиперболаның бұтақтарын аппликата осінен айналдырудан пайда
болған айналу гиперболоидтары алынады:
болса,
гиперболаның бұтақтарын аппликата осінен айналдырудан пайда
болған айналу гиперболоидтары алынады:
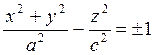 .
.
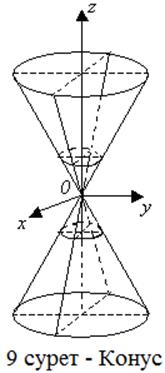 Қос таңбаның қайсысын
алуымызға байланысты (1.46.3) теңдеулерімен анықталатын
беттер сәйкес эллипстік және гиперболалық параболоидтар деп
аталады. Параболоидтардың (8 суретті қара)
төбесі біреу ғана, ол координаталардың бас нүктесінде
орналасқан;
Қос таңбаның қайсысын
алуымызға байланысты (1.46.3) теңдеулерімен анықталатын
беттер сәйкес эллипстік және гиперболалық параболоидтар деп
аталады. Параболоидтардың (8 суретті қара)
төбесі біреу ғана, ол координаталардың бас нүктесінде
орналасқан; ![]() (эллипстік
параболоид үшін
(эллипстік
параболоид үшін ![]() ) жазықтықтарындағы
қималары сәйкес эллипстер (
) жазықтықтарындағы
қималары сәйкес эллипстер (![]() болса, шеңберлер) және
гиперболалар (
болса, шеңберлер) және
гиперболалар (![]() болғанда теңбүйірлі), басқа ортогональ қималары
параболалар. Олардың бұтақтары
болғанда теңбүйірлі), басқа ортогональ қималары
параболалар. Олардың бұтақтары ![]() жазықтықтарында
гиперболалық параболоид үшін төмен қарай
бағытталған. Ал,
жазықтықтарында
гиперболалық параболоид үшін төмен қарай
бағытталған. Ал, ![]() жазықтығындағы
гиперболаның заттық осі
жазықтығындағы
гиперболаның заттық осі ![]() болса, абсцисса осіне,
болса, абсцисса осіне, ![]() болса - ордината
осіне параллель. Бұл гипербола
болса - ордината
осіне параллель. Бұл гипербола ![]() болғанда координаталардың бас
нүктесі арқылы өтетін қос түзуге айналады.
Эллипстік параболоид
болғанда координаталардың бас
нүктесі арқылы өтетін қос түзуге айналады.
Эллипстік параболоид ![]() болғанда
айналу параболоидын
болғанда
айналу параболоидын
![]()
береді. Ол параболаны ![]() осінен айналдыру арқылы алынады.
осінен айналдыру арқылы алынады.
Енді (1.46.4)
теңдеуінде екінші таңбаны алып, онымен анықталатын тік
конусты (9 суретті қара) қарайық. Оның ![]() жазықтықтарындағы
қималары (бағыттаушылары) эллипстер,
жазықтықтарындағы
қималары (бағыттаушылары) эллипстер, ![]() болғанда –
шеңберлер. Соңғы жағдайда әдеттегі тік
дөңгелек конусты аламыз. Басқа ортогональ қималары
гиперболалар. Олар координаталар жазықтықтарында
болғанда –
шеңберлер. Соңғы жағдайда әдеттегі тік
дөңгелек конусты аламыз. Басқа ортогональ қималары
гиперболалар. Олар координаталар жазықтықтарында ![]() бас нүкте
арқылы өтетін қос түзуге айналады. Қаралған
теңдеулерде айнымалыларды орын ауыстыру арқылы координаталар жүйесіне
қарағанда басқаша орналасқан беттерді алуға
болады.
бас нүкте
арқылы өтетін қос түзуге айналады. Қаралған
теңдеулерде айнымалыларды орын ауыстыру арқылы координаталар жүйесіне
қарағанда басқаша орналасқан беттерді алуға
болады.
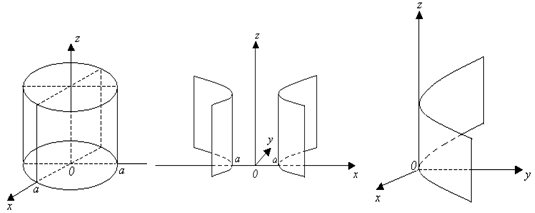 |
10-суретте эллипстік, гиперболалық және параболалық тік цилиндрлер бейнеленген. Эллипстік цилиндр
10 сурет - Цилиндлер
жасаушылары соған сәйкес оське параллель.
Комплекс сандар.
1. Комплекс сандардың алгебралық түрі.
Алгебралық түрдегі комплекс сан (к.с.) деп
аталатын ![]() ,
, ![]() өрнегінде
өрнегінде ![]() жорымал бірлік
делінеді. Қосылғыштар:
жорымал бірлік
делінеді. Қосылғыштар: ![]() және
және ![]() к.с.-ның сәйкес нақты
және жорымал бөліктері,
к.с.-ның сәйкес нақты
және жорымал бөліктері, ![]() -жорымал бөліктің
коэффициенті;
-жорымал бөліктің
коэффициенті; ![]() болса,
онда
болса,
онда ![]() -ны таза
жорымал сан дейміз. К.с. –дар
-ны таза
жорымал сан дейміз. К.с. –дар ![]() және
және ![]() өзара (қарымталы)
түйіндес делінеді. Барлық к.с. жиыны С арқылы белгіленеді,
өзара (қарымталы)
түйіндес делінеді. Барлық к.с. жиыны С арқылы белгіленеді, ![]() ;
; ![]() санын С жиынының
нөлі дейміз.
санын С жиынының
нөлі дейміз.
Теңестіру, қосу және алу амалдарын орындағанда к.с.-ды сандық вектор ретінде қарауға болады:
1) ![]()
![]() ;
; ![]() ;
;
2) ![]()
3) ![]()
![]()
4) 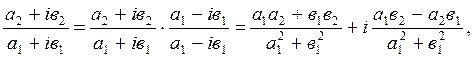
![]()
2. Комплекс сандардың тригонометриялық түрі.
Комплекс айнымалы ![]() оның аффиксі деп аталатын М нүктесінің
полярлық координаталары арқылы да өрнектеледі; (1.43)-ті
қолдансақ, тригонометриялық түрдегі к. с.-ға
оның аффиксі деп аталатын М нүктесінің
полярлық координаталары арқылы да өрнектеледі; (1.43)-ті
қолдансақ, тригонометриялық түрдегі к. с.-ға
![]() (1.47)
(1.47)
келеміз. Мұнда к.с.-ның ![]() -модулі,
-модулі, 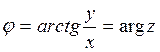 - аргументі (полярлық
бұрыштың:
- аргументі (полярлық
бұрыштың: ![]() бас мәні).
бас мәні).
Көбейту, бөлу, дәрежеге шығару және түбір табу амалдарын орындау үшін к.с.-ды тригонометриялық түрде
![]()
![]()
алған тиімді.
1. Екі бұрыштың қосындысының синусы мен косинусының формулаларын пайдаланып, к.с.-ның көбейтіндісін
![]() (1.48)
(1.48)
түрінде жаза аламыз.
2. К.с.-ды бөлгенде олардың модульдері бір-біріне бөлінеді де, бөлгіштің аргументі бөлінгіштің аргументінен алынады:
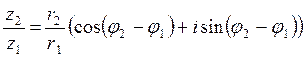 .
.
3. К.с.-ды (1.57) n-дәрежеге шығаруды оны өзіне-өзін біртіндеп n-1 рет көбейту ретінде орындасақ, санның модулі n дәрежеге шығарылып, аргументі n-ге көбейтілетінін көреміз:
![]() (1.49)
(1.49)
Муавр формуласы деп аталатын бұл
теңдік теріс бүтін көрсеткіштер (![]() ) үшін де дұрыс.
) үшін де дұрыс.
4. К.с.-нан n дәрежелі түбір
![]()
табу үшін ол түбірдің n дәрежесі берілген санға тең:
![]() .
.
екенін ескеріп, (1.47)-ды пайдалансақ болғаны.
К.с.-дың теңдігінің шарттарын, модуль (![]() ) мен аргумент туралы
айтылғандарды ескерсек:
) мен аргумент туралы
айтылғандарды ескерсек:
![]() ,
, 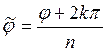 .
.
Сонымен, к.с.-нан n дәрежелі түбір тапқанда оның модулінен сәйкес түбір табылып, аргументі (период қосылған) n –ге бөлінеді:
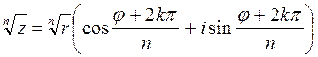 ,
, ![]() .
.
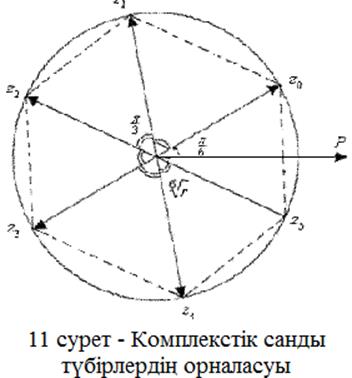 Түбірдің n мәні: z0,
z1, ..., zn-1 бар, олар модульдері бірдей,
аргументтері
Түбірдің n мәні: z0,
z1, ..., zn-1 бар, олар модульдері бірдей,
аргументтері ![]() -нен бастап
-нен бастап ![]() -ге өсіп отыратын к.с. Бұл
мәндердің геометриялық бейнелері (аффикстері) радиусы
-ге өсіп отыратын к.с. Бұл
мәндердің геометриялық бейнелері (аффикстері) радиусы ![]() шеңберге іштей сызылған дұрыс n-бұрыштың
(11-суретте n=6) төбелері.
шеңберге іштей сызылған дұрыс n-бұрыштың
(11-суретте n=6) төбелері.
3. К.с.-ның көрсеткіштік түрі.
Жорымал айнымалының көрсеткіштік функциясын зерттей келе Л.Эйлер
![]() . (1.50)
. (1.50)
формулаларын дәлелдеді. Бұл формулалар (1.47) к.с.-ын
көрсеткіштік түрде ![]() , жазуға мүмкіндік береді.
К.с.-ның бұл түрі алгебралық амалдарды орындауға
қолайлы:
, жазуға мүмкіндік береді.
К.с.-ның бұл түрі алгебралық амалдарды орындауға
қолайлы:
![]() ,
, 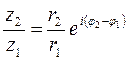 ,
, ![]() ,
, ![]() ,
, ![]() .
.
2-модуль. Бір айнымалы функцияларының дифференциалдық есептеуі
4-дәріс. Функцияның шегі
Дәріс мақсаты: функцияның шегі, шексіз аз және шексіз үлкен функциялар, анықталмағандықтар, тамаша шектер түсініктерімен қатар гиперболалық функцияларды, олардың қасиеттері мен графиктерін беру.
Функция және оның шегі.
Анықтама. Егер х
айнымалысының ![]() жиынынан алынған әрбір мәніне
нақты ереже не заң бойынша
жиынынан алынған әрбір мәніне
нақты ереже не заң бойынша ![]() айнымалысының
айнымалысының ![]() жиынындағы белгілі бір мәні сай
келетін болса, онда
жиынындағы белгілі бір мәні сай
келетін болса, онда ![]() -ті
-ті ![]() -тің функциясы деп атап,
-тің функциясы деп атап,
![]()
деп жазамыз.
Мұнда ![]() – тәуелсіз айнымалы немесе аргумент,
– тәуелсіз айнымалы немесе аргумент, ![]() - тәуелді айнымалы. Тәуелсіз айнымалы
мәндерінің жиыны
- тәуелді айнымалы. Тәуелсіз айнымалы
мәндерінің жиыны ![]() функцияның анықталу аймағы,
функцияның сәйкес мәндерінің жиыны
функцияның анықталу аймағы,
функцияның сәйкес мәндерінің жиыны ![]() оның өзгеру аймағы деп аталады.
оның өзгеру аймағы деп аталады.
Өз кезегінде аргумент басқа айнымалының функциясы болуы мүмкін:
![]() ,
, ![]() . (2.1)
. (2.1)
Егер ![]() болса, онда
болса, онда ![]() жиынында күрделі
жиынында күрделі
![]() (2.1/)
(2.1/)
функциясы анықталған дейіз. (2.1/)-ден ![]() -ды жойып, күрделі функцияны аламыз.
-ды жойып, күрделі функцияны аламыз.
Негізгі элементарар функциялар
математиканың мектептік курсында қаралған. Олардың
қатарына гиперболалық деп аталатын функциялар да жатады.
Экспоненталардың ![]() және
және ![]() жарты айырымы және жарты қосындысы
сәйкес гиперболалық синус және гиперболалық косинус деп
аталып,
жарты айырымы және жарты қосындысы
сәйкес гиперболалық синус және гиперболалық косинус деп
аталып,
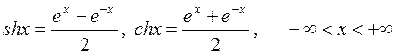 (2.2)
(2.2)
түрінде жазылады. Тригонометриялық функцияларға ұқсас гиперболалық тангенс және гиперболалық котангенс функциялары енгізіледі:
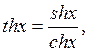
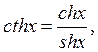
![]() .
.
Нүктенің
![]() өзінде анықталған болуы міндетті болмаса да,
оның
өзінде анықталған болуы міндетті болмаса да,
оның ![]() маңында анықталған
маңында анықталған ![]() функциясын
қарастыралық.
функциясын
қарастыралық.
1-анықтама.
Егер берілген ![]() үшін
үшін
![]()
![]()
![]() (2.3)
(2.3)
болатындай ![]() саны табылса,
онда А санын
саны табылса,
онда А санын ![]() функциясының
функциясының ![]() нүктесіндегі
(
нүктесіндегі
(![]() –дағы) шегі деп атап,
–дағы) шегі деп атап,
![]()
![]()
![]() (2.4)
(2.4)
деп жазамыз.
Егер ![]() және
және ![]() , функцияларының
, функцияларының
![]() да нақты
шектері бар болса, онда:
да нақты
шектері бар болса, онда:
![]() (2.5)
(2.5)
![]() (2.6)
(2.6)
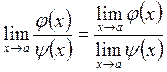 ,
, ![]() . (2.7)
. (2.7)
Функция шегінің теңсіздіктермен өрнектелетін қасиеттері де бар:
1) ![]()
![]()
![]()
![]()
![]() ,
,
2) ![]()
![]()
![]()
![]() , 3)
, 3)![]()
![]()
![]() .
.
Егер
![]()
![]() (2.8)
(2.8)
болатындай ![]() саны бар болса, онда
саны бар болса, онда ![]() функциясы
функциясы ![]() аймағында шектелген дейді.
аймағында шектелген дейді.
Егер ![]() -да
-да ![]() функциясының нақты шегі
функциясының нақты шегі ![]() бар болса, онда
бар болса, онда ![]() нүктесінің функция шектелген және
өзінің сол нүктедегі шегімен
нүктесінің функция шектелген және
өзінің сол нүктедегі шегімен ![]() болғанда) таңбалас болатын қандай да болмасын
болғанда) таңбалас болатын қандай да болмасын
![]() аймағы бар.
аймағы бар.
Теорема (күрделі функцияның шегі туралы). Егер (2.1) күрделі функциясында
![]() болса, онда
болса, онда
![]() . (2.9)
. (2.9)
Егер
(2.4)-де ![]() айнымалысы
айнымалысы
![]() -ға:
кіші (сол жағынан) немесе үлкен (оң жағынан) бола
отырып, ұмтылсын деп талап қойсақ, онда функцияның
нүктедегі сол жақ және оң жақ шектерінің
ұғымына келеміз. Олар сәйкес:
-ға:
кіші (сол жағынан) немесе үлкен (оң жағынан) бола
отырып, ұмтылсын деп талап қойсақ, онда функцияның
нүктедегі сол жақ және оң жақ шектерінің
ұғымына келеміз. Олар сәйкес:
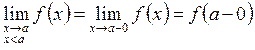
![]()
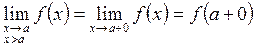
![]()
деп белгіленеді. ![]() функциясының
функциясының ![]() нүктесінде нақты
шегі
нүктесінде нақты
шегі ![]() бар
болу үшін
бар
болу үшін ![]() болуы
қажет және жеткілікті.
болуы
қажет және жеткілікті.
Шексіз аз және шексіз үлкен функциялар.
Егер
![]()
болса, онда ![]() функциясы
функциясы ![]() да шексіз аз деп аталады. Нақты шегі (2.4) бар функция
үшін
да шексіз аз деп аталады. Нақты шегі (2.4) бар функция
үшін
![]()
![]()
![]() ,
, ![]() (2.10)
(2.10)
теоремасы орындалады.
Егер
![]() (2.11)
(2.11)
болса, онда ![]() функциясы
функциясы ![]() да шексіз үлкен деп аталады.
да шексіз үлкен деп аталады.
1–теорема: Егер ![]()
![]() және
және ![]() да: 1)
да: 1) ![]() шексіз аз функция болса, онда
шексіз аз функция болса, онда ![]() шексіз үлкен
функция, 2)
шексіз үлкен
функция, 2) ![]() шексіз
үлкен функция болса, онда
шексіз
үлкен функция болса, онда ![]() шексіз аз функция болады.
шексіз аз функция болады.
2–теорема: ![]() да саны шекті: 1) шексіз аз
функциялардың көбейтіндісі де шексіз аз, 2) шексіз үлкен
функциялардың көбейтіндісі - шексіз үлкен функция болады.
да саны шекті: 1) шексіз аз
функциялардың көбейтіндісі де шексіз аз, 2) шексіз үлкен
функциялардың көбейтіндісі - шексіз үлкен функция болады.
3–теорема: Саны шекті ![]() да шексіз аз функциялардың
қосындысы шексіз аз функция болады.
да шексіз аз функциялардың
қосындысы шексіз аз функция болады.
4–теорема: ![]() маңында шектелген функция мен
маңында шектелген функция мен ![]() да
шексіз аз функцияның көбейтіндісі
да
шексіз аз функцияның көбейтіндісі ![]() да шексіз аз функция. Ал,
да шексіз аз функция. Ал, ![]() :
: ![]()
![]() функциясы мен
функциясы мен ![]() да шексіз үлкен
функцияның көбейтіндісі
да шексіз үлкен
функцияның көбейтіндісі ![]() да шексіз үлкен функция болады.
да шексіз үлкен функция болады.
Функциялар ![]() и
и ![]()
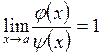
![]()
![]()
![]() ,
, ![]() , (2.12)
, (2.12)
шартына қанағаттандырса, оларды ![]() -да
өзара эквивалент дейміз.
-да
өзара эквивалент дейміз.
Ал, (2.12)-ні басқаша жазсақ:
![]() . (2.12.1)
. (2.12.1)
онда ![]() -да
-да ![]() қосындысының бас
бөлігі де, екінші қосылғыш жуықтап есептеулерде
әдетте еленбей қалдырылатын шексіз аз “қосымша” болады.
қосындысының бас
бөлігі де, екінші қосылғыш жуықтап есептеулерде
әдетте еленбей қалдырылатын шексіз аз “қосымша” болады.
Шексіз аз және шексіз үлкен функцияларға
амалдар қолдану кейде анықталмағандықтар деп аталатын
өрнектерге келтіреді. Шекке тура көшу
анықталмағандықтардың ![]() ,
, ![]() ,
, ![]() және
және ![]() сияқты түрлеріне келтіруі
мүмкін. Дәрежелі анықталмағандықтар деп аталатын
сияқты түрлеріне келтіруі
мүмкін. Дәрежелі анықталмағандықтар деп аталатын ![]() ,
, ![]() және
және ![]() түрлері логарифмдеу
арқылы
түрлері логарифмдеу
арқылы ![]() анықталмағандығына
келтіріледі.
анықталмағандығына
келтіріледі.
Тамаша шектер.
Шек
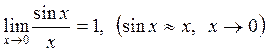 (2.14)
(2.14)
бірінші тамша шек деп аталады.
Екінші тамаша шек деп аталып, ![]() санын анықтайтын
санын анықтайтын
![]()
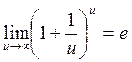 ,
, ![]() (2.15)
(2.15)
формулалары да дәлелденген.
Функциялардың ![]() дағы асимптоталық
теңдіктері:
дағы асимптоталық
теңдіктері:
![]()
![]()
![]() ;
;![]() ,
, ![]()
![]() ,
, ![]() ,
,
![]() . (2.16)
. (2.16)
Көпмүшеліктер
қатынасының ![]() ұмтылысындағы шегін табуда олардың
бас мүшелерін
ұмтылысындағы шегін табуда олардың
бас мүшелерін ![]() және
және
![]() салыстырсақ
болғаны:
салыстырсақ
болғаны:
![]()
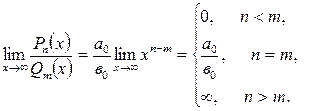
49-есеп. Функцияның шегін табыңыз:
![]()
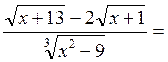
![]()
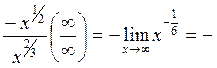
![]()
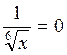 .
.
Ал, ![]() жағдайында
жағдайында ![]() түріндегі
анықталмағандықты ашу үшін алдын ала
иррационалдықтардан құтылып, өрнекті ықшамдау
ұтымды:
түріндегі
анықталмағандықты ашу үшін алдын ала
иррационалдықтардан құтылып, өрнекті ықшамдау
ұтымды:
![]()
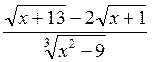
![]() .
.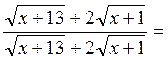
![]()
![]()
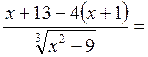
![]()
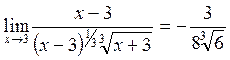
![]()
![]() .
.
5-дәріс. Функцияның үзіліссіздігі
Дәріс мақсаты: функцияның нүктеде үзіліссіздігінің анықтамасын беріп, үзіліс нүктелерін сұрыптау. Кесіндіде үзіліссіз функцияның қасиеттерін (теоремаларды) келтіріп, кесіндіде бірқалыпты үзіліссіз функциялар және бірсарынды функциялар ұғымдарын енгізу.
Егер ![]() функциясы
функциясы ![]() нүктесінің өзінде
және оның
нүктесінің өзінде
және оның ![]() маңында анықталған,
нүктедегі шегі өзінің сол нүктедегі мәніне
тең:
маңында анықталған,
нүктедегі шегі өзінің сол нүктедегі мәніне
тең:
![]()
![]()
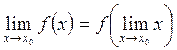 (2.17)
(2.17)
болса, ![]() функциясы
функциясы ![]() нүктесінде үзіліссіз деп
аталады. Егер (2.17) орындалмаса, онда
нүктесінде үзіліссіз деп
аталады. Егер (2.17) орындалмаса, онда ![]() функциясы
функциясы ![]() нүктесінде үзілісті, ал
нүктесінде үзілісті, ал ![]() оның үзіліс нүктесі дейді. Егер функция
оның үзіліс нүктесі дейді. Егер функция ![]() нүктесінде үзіліссіз және
нүктесінде үзіліссіз және ![]()
![]() болса, онда
болса, онда ![]() нүктесінің функция сол нүктедегі
таңбасын сақтайтын қандай да болмасын
нүктесінің функция сол нүктедегі
таңбасын сақтайтын қандай да болмасын ![]() төңірегі бар болады.
төңірегі бар болады.
Кез келген ![]() нүктесін алып,
нүктесін алып, ![]() айырымын аргументтің
айырымын аргументтің ![]() нүктесіндегі өсімшесі (
нүктесіндегі өсімшесі (![]() болуы мүмкін бола тұрса да) деп атайық. Ал,
болуы мүмкін бола тұрса да) деп атайық. Ал,
![]() (2.17.1)
(2.17.1)
айырымы функцияның ![]() нүктесіндегі
нүктесіндегі ![]() - ке сай өсімшесі деп аталады;
- ке сай өсімшесі деп аталады; ![]()
![]() және
және ![]() болғандықтан (2.17) –дегі бірінші
теңдікті
болғандықтан (2.17) –дегі бірінші
теңдікті
![]() . (2.18)
. (2.18)
деп жазуға болады. Сонымен, функция нүктеде үзіліссіз болу үшін сол нүктедегі аргументтің шексіз аз өсімшесіне функцияның шексіз аз өсімшесі сай келуі қажет және жеткілікті.
Егер нүктенің ![]() өзінде және оның сол жақ не оң жақ
жарты маңында анықталған
өзінде және оның сол жақ не оң жақ
жарты маңында анықталған ![]() функциясы үшін
функциясы үшін
![]()
![]()
![]() , (2.19)
, (2.19)
болса, онда функция ![]() нүктесінде сәйкес сол жағынан не
оң жағынан үзіліссіз деп аталады. Функция
нүктесінде сәйкес сол жағынан не
оң жағынан үзіліссіз деп аталады. Функция ![]() нүктесінде үзіліссіз болу үшін нүктеде сол
жағынан да, оң жағынан да үзіліссіз болуы:
нүктесінде үзіліссіз болу үшін нүктеде сол
жағынан да, оң жағынан да үзіліссіз болуы: ![]()
![]() қажет және жеткілікті. Егер
қажет және жеткілікті. Егер
![]()
![]() болса, онда функция
болса, онда функция ![]() нүктесінде тек сол
жағынан ғана үзіліссіз. Демек,
нүктесінде тек сол
жағынан ғана үзіліссіз. Демек, ![]() - функцияның үзіліс нүктесі.
- функцияның үзіліс нүктесі.
1–теорема. Нүктеде үзіліссіз функциялардың кез келген шекті санының алгебралық қосындысы мен көбейтіндісі сол нүктеде үзіліссіз функциялар.
2–теорема. Бөлгіш нөлге тең емес болса, нүктеде үзіліссіз екі функцияның бөліндісі сол нүктеде үзіліссіз функция.
3–теорема (күрделі функцияның үзіліссіздігі
туралы). Егер (2.1)-де ![]() функциясы
функциясы ![]() нүктесінде,
нүктесінде, ![]() функциясы сәйкес
функциясы сәйкес ![]() нүктесінде үзіліссіз болса, онда
нүктесінде үзіліссіз болса, онда ![]() күрделі функциясы
күрделі функциясы ![]() нүктесінде үзіліссіз.
нүктесінде үзіліссіз.
Интервалдың барлық нүктелерінде үзіліссіз
функция сол интервалда үзіліссіз деп аталады. Егер функция (![]() ) интервалында үзіліссіз,
) интервалында үзіліссіз, ![]() және
және ![]() нүктелерінде сәйкес оң және
сол жақтарынан үзіліссіз болса, онда функцияны
нүктелерінде сәйкес оң және
сол жақтарынан үзіліссіз болса, онда функцияны ![]() кесіндісінде
үзіліссіз дейміз.
кесіндісінде
үзіліссіз дейміз.
Үзіліс нүктелерін сұрыптау.
Нүктенің
![]() өзінде
анықталмаған болуы мүмкін болса да, оның маңында
өзінде
анықталмаған болуы мүмкін болса да, оның маңында ![]() анықталған
анықталған ![]() функциясы сол нүктеде
шекті секіру жасаса, яғни нүктеде біржақты шектердің
екеуі де бар, бірақ өзара тең емес:
функциясы сол нүктеде
шекті секіру жасаса, яғни нүктеде біржақты шектердің
екеуі де бар, бірақ өзара тең емес: ![]() болса, онда
болса, онда ![]() функцияның бірінші текті үзіліс
нүктесі деп аталады.
функцияның бірінші текті үзіліс
нүктесі деп аталады.
Егер ![]() бар болғанымен
бар болғанымен ![]() нүктесінде функция анықталмаған болса, онда
нүктесінде функция анықталмаған болса, онда ![]() функцияның құтылуға болатын үзіліс
нүктесі деп аталады.
функцияның құтылуға болатын үзіліс
нүктесі деп аталады.
Біржақты шектердің ![]() кем дегенде біреуі жоқ не
кем дегенде біреуі жоқ не ![]() -ке тең болса, онда
-ке тең болса, онда ![]() функцияның екінші текті үзіліс
нүктесі деп аталады.
функцияның екінші текті үзіліс
нүктесі деп аталады.
Теңбүйірлі гипербола 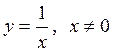 үшін координаталардың бас нүктесі екінші текті
үзіліс нүктесі болады, өйткені
үшін координаталардың бас нүктесі екінші текті
үзіліс нүктесі болады, өйткені ![]() .
.
Кесіндіде үзіліссіз функциялар.
Кесіндіде ![]() үзіліссіз
үзіліссіз ![]() функциясының әрбір
функциясының әрбір ![]() нүктесінде нақты шегі және біржақты
нүктесінде нақты шегі және біржақты ![]() =
=![]()
![]()
![]() шектері бар. Демек, функция шектелген болатын
шектері бар. Демек, функция шектелген болатын
![]() маңдары және Uоң
маңдары және Uоң![]() Uсол
Uсол![]() жарты төңіректері бар. Бұл айтылған төмендегі
теореманы растайды.
жарты төңіректері бар. Бұл айтылған төмендегі
теореманы растайды.
1–теорема: ![]() кесіндісінде үзіліссіз
кесіндісінде үзіліссіз ![]() функциясы осы кесіндіде шектелген, яғни
функциясы осы кесіндіде шектелген, яғни
![]()
![]()
![]()
болатындай ![]() саны табылады.
саны табылады.
2. Вейерштрасс теоремасы: ![]() кесіндісінде үзіліссіз
кесіндісінде үзіліссіз ![]() функциясы осы кесіндіде өзінің
ең кіші және ең үлкен мәндерін қабылдайды,
яғни
функциясы осы кесіндіде өзінің
ең кіші және ең үлкен мәндерін қабылдайды,
яғни
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
болатындай ![]() сандары табылады.
сандары табылады.
3-теорема: ![]() кесіндісінде үзіліссіз
кесіндісінде үзіліссіз ![]() функциясы өзінің осы кесіндідегі кез келген екі
мәнінің:
функциясы өзінің осы кесіндідегі кез келген екі
мәнінің: ![]()
![]()
![]() ,
, ![]() , арасындағы барлық мәндерді
қабылдайды, яғни кез келген сан
, арасындағы барлық мәндерді
қабылдайды, яғни кез келген сан ![]() үшін
үшін ![]()
![]() болатындай
болатындай ![]()
![]() саны табылады.
саны табылады.
1-салдар. Кесіндіде үзіліссіз функция осы
кесіндіде өзінің ең кіші m және ең
үлкен M мәндерінің арасындағы барлық
мәндерді қабылдайды, яғни функцияның мәндер
аймағы ордината осінің ![]() кесіндісі болады.
кесіндісі болады.
2-салдар. Егер ![]() функциясы
функциясы ![]() кесіндісінде үзіліссіз және
кесіндісінде үзіліссіз және ![]() болса, онда
болса, онда ![]() = 0 болатындай кем дегенде бір
= 0 болатындай кем дегенде бір ![]()
![]() нүктесі табылады.
нүктесі табылады.
Монотонды (бірсарынды) функциялар.
Кесіндіде ![]() анықталған және
анықталған және ![]()
![]() ,
, ![]() үшін төмендегі шарттардың біріне қанағаттандыратын
үшін төмендегі шарттардың біріне қанағаттандыратын ![]() функциясы сол кесіндіде
бірсарынды функция деп аталады. Соның ішінде бірсарынды:
функциясы сол кесіндіде
бірсарынды функция деп аталады. Соның ішінде бірсарынды:
1) өспелі: ![]()
![]() ;
;
2) кемімейтін: ![]()
![]() ;
;
3) кемімелі: ![]()
![]() ;
;
4) өспейтін ![]()
![]() функциялар ажыратылады.
функциялар ажыратылады.
Теорема: ![]() кесіндісінде үзіліссіз, бірсарынды
өспелі не кемімелі
кесіндісінде үзіліссіз, бірсарынды
өспелі не кемімелі ![]() функциясына кері,
функциясына кері, ![]() ,
, ![]()
![]()
![]() кесіндісінде үзіліссіз, сәйкес бірсарынды
өспелі не кемімелі
кесіндісінде үзіліссіз, сәйкес бірсарынды
өспелі не кемімелі ![]() функциясы бар.
функциясы бар.
Егер берілген ![]() және
және ![]()
![]() үшін
үшін
![]()
![]() (2.20)
(2.20)
болатындай ![]() саны бар болса, онда
саны бар болса, онда ![]() функциясы
функциясы ![]() кесіндісінде бірқалыпты үзіліссіз деп
аталады.
кесіндісінде бірқалыпты үзіліссіз деп
аталады.
6-дәріс. Функцияның туындылары мен дифференциалдары
Дәріс мақсаты: бастапқы ретті туындылар мен дифференциалдың геометриялық және механикалық мағыналарына, олардың жуықтап есптеулердегі қолданысына көбірек көңіл бөлу. Жоғарғы ретті туындылар мен дифференциалдарды, орташа мән туралы теоремалардың геометриялық талқылауларын және Лопиталь ережесінің қоланылуын баяндау.
Функцияның туындысы.
Функцияның ![]() анықталу аймағынан
анықталу аймағынан ![]() нүктелерін
алайық. Сонда тәуелсіз айнымалының
нүктелерін
алайық. Сонда тәуелсіз айнымалының ![]() өсімшесіне
функцияның
өсімшесіне
функцияның ![]() өсімшесі
сай келеді.
өсімшесі
сай келеді.
Анықтама. Егер функция өсімшесінің ![]() оған сай
тәуелсіз айнымалы өсімшесіне
оған сай
тәуелсіз айнымалы өсімшесіне ![]() қатынасының
қатынасының ![]() -да нақты шегі
бар болса, онда ол сан
-да нақты шегі
бар болса, онда ол сан ![]() функциясының х
нүктесіндегі туындысы деп аталып,
функциясының х
нүктесіндегі туындысы деп аталып, ![]() ,
, 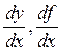 рәміздерімен белгіленеді.
рәміздерімен белгіленеді.
Сонымен,
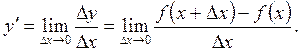 (2.21)
(2.21)
![]() қисығына
қисығына ![]() нүктесінде
жүргізілген жанаманың бұрыштық коэффициенті:
нүктесінде
жүргізілген жанаманың бұрыштық коэффициенті:
![]() . (2.22)
. (2.22)
Жанамаға тұрғызылған
нормаль ![]() (
(![]() ))
)) ![]() қисығына да нормаль
деп аталады. Дәйектендірілген
қисығына да нормаль
деп аталады. Дәйектендірілген ![]() нүктесі үшін
қисыққа
нүктесі үшін
қисыққа ![]() нүктесінде
тұрғызылған жанама және нормальдің теңдеулері:
нүктесінде
тұрғызылған жанама және нормальдің теңдеулері:
![]() , (2.23)
, (2.23)
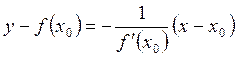 . (2.24)
. (2.24)
түрінде жазылады.
Туынды табу операциясын функцияны дифференциалдау дейді. Нүктеде ![]() диффференциалданатын
диффференциалданатын ![]() функциясының
графигіне
функциясының
графигіне ![]() нүктесінде
бұрыштық коэффициенті функцияның
нүктесінде
бұрыштық коэффициенті функцияның ![]() нүктесіндегі туындысына
тең бір ғана жанама жүргізуге болады. Бұл
тұжырым функция туындысының геометриялық мағынасын
анықтайды.
нүктесіндегі туындысына
тең бір ғана жанама жүргізуге болады. Бұл
тұжырым функция туындысының геометриялық мағынасын
анықтайды.
Функцияның нүктеде үзіліссіздігі оның сол нүктеде дифференциалданатын болуының қажетті шарты. Функцияның нүктеде біржақты үзіліссіздігінің ұғымына байланысты функцияның нүктеде біржақты: сол және оң жақты туындылары қарастырылады:
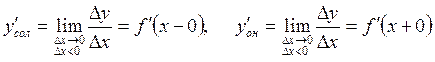 . (2.25)
. (2.25)
Функция нүктеде дифференциалданатын болу
үшін оның сол нүктедегі біржақты туындыларының
екеуі де бар (шекті) және олар өзара тең болуы: ![]() қажет
және жеткілікті. Егер
қажет
және жеткілікті. Егер ![]() функциясының х
нүктесінде біржақты туындыларының екеуі де бар, бірақ,
өзара тең емес:
функциясының х
нүктесінде біржақты туындыларының екеуі де бар, бірақ,
өзара тең емес: ![]() болса, онда
болса, онда ![]() бұл нүктеде
дифференциалданбайтын функция; х функция графигінің қайту
нүктесі деп аталады.
бұл нүктеде
дифференциалданбайтын функция; х функция графигінің қайту
нүктесі деп аталады.
Туынды (2.21) ![]() -ке тең болуы да
мүмкін. Мұндай нүктеде функция
дифференциаланбайды десек те, туындының (
-ке тең болуы да
мүмкін. Мұндай нүктеде функция
дифференциаланбайды десек те, туындының (![]() ) геометриялық мағынасы бар:
) геометриялық мағынасы бар: ![]() қисығына
қисығына ![]() нүктесінде
тұрғызылған жанама абсцисса осіне перпендикуляр.
нүктесінде
тұрғызылған жанама абсцисса осіне перпендикуляр.
Енді функция туындысының
механикалық мағынасын анықтайық. Өз траекториясы
бойымен қозғалыстағы нүктенің жолы s(t) уақыттың
дифференциалданатын функциясы болады. Айталық, ![]() және t1
уақыт кезеңдерінде нүкте сәйкес М және
М1 (12 суретті қара) орындарында болсын, яғни
нүкте
және t1
уақыт кезеңдерінде нүкте сәйкес М және
М1 (12 суретті қара) орындарында болсын, яғни
нүкте ![]() уақыт
аралығында
уақыт
аралығында ![]() жол
жүрді делік. Бұл шамалардың қатынасы
жол
жүрді делік. Бұл шамалардың қатынасы ![]() қозғалушы
нүктенің
қозғалушы
нүктенің ![]() уақыт
аралығындағы орташа жылдамдығы деп аталады. Оның
уақыт
аралығындағы орташа жылдамдығы деп аталады. Оның ![]() -дағы шегін
-дағы шегін
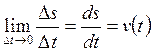 (2.26)
(2.26)
нүктенің кез келген t уақыт кезеңіндегі алгебралық жылдамдығы дейді. Жалпы, қозғалушы нүктенің жылдамдығы траекторияға жанама бойымен бағытталған векторлық шама.
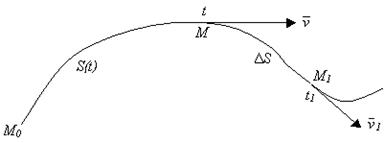
12 сурет – Туындының механикалық мағынасы
Сонымен, жолдан уақыт бойынша туынды қозғалушы нүктенің кез келген уақыт кезеңіндегі жылдамдығына тең. Кез келген дифференциалданатын функция туындысы аргументтің өзгеруіне байланысты функцияның өзгеру жылдамдығын сипаттайды дей аламыз.
Дифференциалдау ережелері.
Функцияны
дифференциалдаудың негізгі ережесі туындының анықтамасынан (2.21)
алынады: аргументке х қалауымызша ![]() өсімше
беріп, функцияның оған сәйкес
өсімше
беріп, функцияның оған сәйкес ![]() өсімшесін
тауып, соңғының алдыңғыға қатынасынан
өсімшесін
тауып, соңғының алдыңғыға қатынасынан
![]() -да шек табамыз.
-да шек табамыз.
Интервалдың әрбір нүктесінде шекті
туындысы бар функция сол интервалда дифференциалданатын функция деп аталады.
Ал, (а,b) интервалында дифференциалданатын, а және в
нүктелерінде біржақты, сәйкес:
оң жақ ![]() және
сол жақ
және
сол жақ ![]() туындылары
бар функция
туындылары
бар функция ![]() кесіндісінде
дифференциалданады дейміз. Мысалы,
кесіндісінде
дифференциалданады дейміз. Мысалы, ![]() ,
, ![]() бүкіл сандық осьте дифференциалданатын
функция. Оның өсімшесі
бүкіл сандық осьте дифференциалданатын
функция. Оның өсімшесі
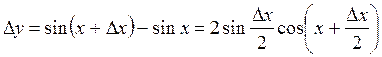 . (2.27)
. (2.27)
Жалпы 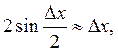
![]() болғандықтан
болғандықтан
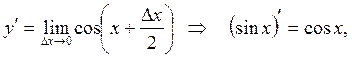
![]() .
.
Ддифференциалдау ережелері.
1. Тұрақты көбейткішті туынды белгісінің сыртына шығаруға болады.
2. Дифференциалданатын функциялардың қосындысының (айырымының) туындысы олардың туындыларының қосындысына (айырымына) тең:
![]() .
(2.28)
.
(2.28)
Бұл қасиет дифференциалданатын функциялардың кез келген шекті санының алгебралық қосындысы үшін дұрыс болғандықтан:
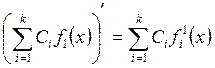 ,
, ![]() ,
, ![]() (2.29)
(2.29)
3. ![]()
![]() . (2.30)
. (2.30)
4. 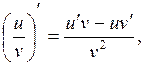
![]() (2.31)
(2.31)
5. Теорема (күрделі функцияның
туындысы туралы). Егер (2.1)-де ![]() функциясы
х нүктесінде,
функциясы
х нүктесінде, ![]() сәйкес
сәйкес ![]() нүктесінде
дифференциалданатын болса, онда
нүктесінде
дифференциалданатын болса, онда ![]() күрделі функциясының х
нүктесінде шекті туындысы бар және
күрделі функциясының х
нүктесінде шекті туындысы бар және
![]() (2.32)
(2.32)
6.
Теорема
(кері функцияның туындысы туралы). Егер ![]() кесіндісінде бірсарынды өспелі не кемімелі
кесіндісінде бірсарынды өспелі не кемімелі ![]() функциясының
функциясының ![]() нүктесінде
нөлден өзгеше шекті туындысы
нүктесінде
нөлден өзгеше шекті туындысы ![]() бар болса, онда оған кері функция
бар болса, онда оған кері функция ![]() сәйкес у
нүктесінде дифференциалданады және
сәйкес у
нүктесінде дифференциалданады және
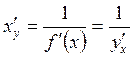 . (2.33)
. (2.33)
Негізгі (күрделі) элементар функциялардың туындылары.
1. ![]() 8.
8. 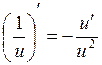 14.
14.
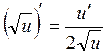
2. ![]() ,
, ![]() 9.
9. ![]() 15.
15.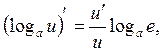
![]() ,
, ![]()
3. 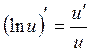 10.
10. ![]() 16.
16. ![]()
4. 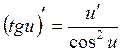 11.
11. 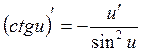 17.
17.
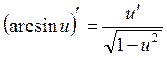
5. ![]()
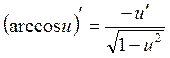 12.
12. 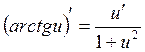 18.
18. 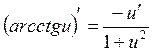
6. ![]() 13.
13. ![]() 19.
19. 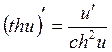
7. 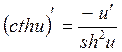 ,
, ![]() .
.
Функция дифференциалы.
Функция ![]()
![]() интервалында дифференциалданатын
және
интервалында дифференциалданатын
және ![]() нүктесіндегі
туындысы
нүктесіндегі
туындысы ![]()
![]() болсын.
Туындының анықтамасынан тәуелсіз айнымалы мен
функцияның сәйкес өсімшелері өзара салыстыруға
келетін шамалар екені байқалады және жазудың (2.12)
үлгісін пайдаланып,
болсын.
Туындының анықтамасынан тәуелсіз айнымалы мен
функцияның сәйкес өсімшелері өзара салыстыруға
келетін шамалар екені байқалады және жазудың (2.12)
үлгісін пайдаланып,
![]() (2.34)
(2.34)
дей аламыз.
Анықтама. Функция ![]() өсімшесінің
өсімшесінің ![]() -ке
қарағанда сызықтық бас бөлігі функцияның х
нүктесіндегі, тәуелсіз айнымалының
-ке
қарағанда сызықтық бас бөлігі функцияның х
нүктесіндегі, тәуелсіз айнымалының ![]() өсімшесіне сай
дифференциалы деп аталып, dy немесе df(х) рәмізімен
белгіленеді:
өсімшесіне сай
дифференциалы деп аталып, dy немесе df(х) рәмізімен
белгіленеді:
![]()
Мысал ретінде ![]() функциясын алсақ, онда
функциясын алсақ, онда ![]() , яғни
, яғни
![]() (2.35)
(2.35)
деп жазуға болады. Сонымен, функцияның дифференциалы
оның туындысы мен аргументтің дифференциалының
көбейтіндісіне тең; функцияның өсімшесі мен дифференциалы
![]() –да балама
шамалар:
–да балама
шамалар: ![]() ,
, ![]() . Бұл
тұжырым жуықтап есептеулерде кеңінен қолданылады. Функцияның
жуық мәнін табу формуласы
. Бұл
тұжырым жуықтап есептеулерде кеңінен қолданылады. Функцияның
жуық мәнін табу формуласы
![]() (2.36)
(2.36)
түрінде жазылады.
Туындының ![]() белгілеуін енді функция мен
аргументтің дифференциалдарының қатынасы деп қарастырамыз.
белгілеуін енді функция мен
аргументтің дифференциалдарының қатынасы деп қарастырамыз.
Дифференциал табу ережелері:
![]()
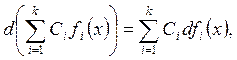
![]() ,
, ![]() ;
;
![]()
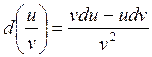 ,
, ![]() ;
; ![]() . (2.37)
. (2.37)
Туындының
геометриялық мағынасы:
![]() функциясының
дифференциалы функция графигіне
функциясының
дифференциалы функция графигіне ![]() нүктесінде
тұрғызылған жанама ординатасының
нүктесінде
тұрғызылған жанама ординатасының ![]() -ке сай өсімшесіне
тең.
-ке сай өсімшесіне
тең.
Берілген аралықта дифференциалданатын ![]() ,
, ![]()
![]() функцияларының
функцияларының ![]() туындысы олардың
диффернциалдарының (
туындысы олардың
диффернциалдарының (![]()
![]() ) қатынасына тең, яғни
) қатынасына тең, яғни
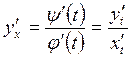 . (2.38)
. (2.38)
5-есеп: ![]() туындысын
табыңыз:
туындысын
табыңыз:
![]()
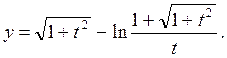
Шешу: 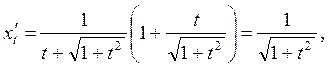
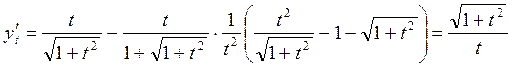 ;
;
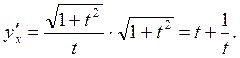
Параметрлік түрде берілген қисыққа
![]() нүктесінде
тұрғызылған жанама мен нормальдің теңдеулерін
((2.23,24):
нүктесінде
тұрғызылған жанама мен нормальдің теңдеулерін
((2.23,24):
![]()
![]()
түрінде жазу ыңғайлы.
Жоғарғы ретті туындылар мен дифференциалдар.
Аймақта ![]() дифференциалданатын
дифференциалданатын ![]() функциясын
қарастыралық. Оның туындысы
функциясын
қарастыралық. Оның туындысы ![]() аймақта немесе оның кейбір
бөлігінде дифференциалданатын функция болсын. Әрі қарай
аймақта немесе оның кейбір
бөлігінде дифференциалданатын функция болсын. Әрі қарай ![]() –ды функцияның бірінші ретті
туындысы немесе бірінші туындысы деп атап, одан табылған туындыны
функцияның екінші ретті туындысы немесе екінші туындысы дейміз.
Соңғыны
–ды функцияның бірінші ретті
туындысы немесе бірінші туындысы деп атап, одан табылған туындыны
функцияның екінші ретті туындысы немесе екінші туындысы дейміз.
Соңғыны
![]() ,
, ![]() ,
, 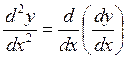 ,
, 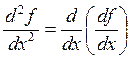
арқылы белгілеп, әрі қарай туындылар табу
мүмкіндігін анықтаймыз. Осылайша функцияның ![]() - ретті туындысы
- ретті туындысы
![]() ,
, ![]() ,
, 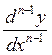 ,
, 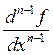
табылды делік. Ол D аймағында не оның қандай да болмасын бөлігінде дифференциалданатын функция болса, одан табылған функцияның n-ретті туындысы
![]() ,
, ![]() ,
,
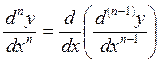 ,
, 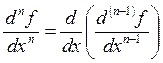 ,
, ![]()
түрінде белгіленеді.
Аймақта u(x) және v(x)
функцияларының n-ретті туындылары бар болсын. Олардың
көбейтіндісінің жоғарғы ретті туындыларын
табайық:![]()
![]()
![]()
![]()
![]()
![]() .
.
Ал, (n -1)- ретті туындылары:
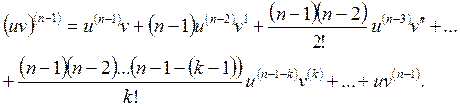
Теңдіктің екі жағынан да туынды алып, ұқсас мүшелерді біріктіргеннен кейін
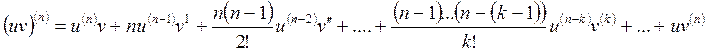 (2.39)
(2.39)
теңдігіне келеміз. (2.39) екі функцияның көбейтіндісінің n-ретті туындысы үшін Лейбниц формуласы деп аталады.
6-есеп: ![]() функциясының
функциясының ![]() туындысын табыңыз.
туындысын табыңыз.
Шешу: ![]() болғанда Лейбниц формуласы
болғанда Лейбниц формуласы
![]()
түрінде жазылады. Шарт бойынша: ![]()
![]()
![]()
![]() ;
;
![]()
![]()
![]()
Дифференциал ![]() немесе
немесе ![]() аргументтің
аргументтің ![]() өсімшесіне сай
функцияның х нүктесіндегі екінші ретті дифференциалы немесе
екінші дифференциалы деп аталады. Функцияның n–ретті дифференциалын
өсімшесіне сай
функцияның х нүктесіндегі екінші ретті дифференциалы немесе
екінші дифференциалы деп аталады. Функцияның n–ретті дифференциалын
![]() оның
оның ![]() -ретті
дифференциалының
-ретті
дифференциалының ![]() дифференциалы ретінде анықтаймыз. Сонымен, функцияның дифференциалы:
дифференциалы ретінде анықтаймыз. Сонымен, функцияның дифференциалы:
![]()
![]() (2.40)
(2.40)
Бұдан n–туындының
![]() белгілеуі функцияның n–дифференциалының
тәуелсіз айнымалы дифференциалының n–дәрежесіне
қатынасы екенін көреміз. Бұл тұжырым жалпы
жағдайда күрделі функция үшін дұрыс емес. Шынында да,
белгілеуі функцияның n–дифференциалының
тәуелсіз айнымалы дифференциалының n–дәрежесіне
қатынасы екенін көреміз. Бұл тұжырым жалпы
жағдайда күрделі функция үшін дұрыс емес. Шынында да, ![]()
(2.38)-ден параметрлік түрде берілген
функцияның ![]() туындысы:
туындысы:
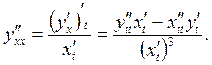 (2.41)
(2.41)
7-есеп. Екінші ретті туындыны ![]() табыңыз:
табыңыз: ![]() .
.
Шешу: 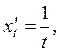
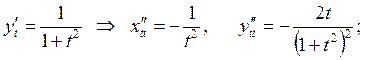
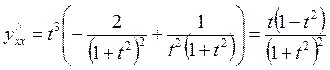 .
.
Орташа мән туралы теоремалар. Лопиталь ережесі.
Интервалда (![]() ) үзіліссіз
) үзіліссіз ![]() функциясы үшін
функциясы үшін
![]() (2.42)
(2.42)
болатындай ![]() нүктесінің
қандай да болмасын
нүктесінің
қандай да болмасын ![]() маңы бар болса, онда
маңы бар болса, онда ![]() функцияның
сәйкес локальдық максимум немесе локальдық минимум
нүктесі деп аталады. Функция өсімшесінің көмегімен (2.42)-ны
функцияның
сәйкес локальдық максимум немесе локальдық минимум
нүктесі деп аталады. Функция өсімшесінің көмегімен (2.42)-ны
![]() (2.43)
(2.43)
түрінде де жазуға болады. Бұл шарттар
орындалған жағдайда ![]() мәні функцияның
мәні функцияның ![]() нүктесіндегі
жергілікті максимумы немесе жергілікті минимумы деп аталады. Ал, максимум
және минимум терминдері экстремум деген атауға біріктіріледі.
Функцияның (
нүктесіндегі
жергілікті максимумы немесе жергілікті минимумы деп аталады. Ал, максимум
және минимум терминдері экстремум деген атауға біріктіріледі.
Функцияның (![]() ) интервалында бірнеше экстремумы бар болуы
мүмкін. Егер (2.42,43) қатынастарында теңдік белгісі
жоқ болса, онда
) интервалында бірнеше экстремумы бар болуы
мүмкін. Егер (2.42,43) қатынастарында теңдік белгісі
жоқ болса, онда ![]() қатаң экстремум деп аталады.
қатаң экстремум деп аталады.
Ролль теоремасы. Егер ![]() функциясы
функциясы ![]() кесіндісінде үзіліссіз, (
кесіндісінде үзіліссіз, (![]() ) интервалында дифференциалданатын және
) интервалында дифференциалданатын және ![]() болса, онда
болса, онда ![]() болатындай кемінде бір
болатындай кемінде бір ![]() нүктесі бар.
нүктесі бар.
Вейерштрасс теоремасы бойынша ![]() -да функция
өзінің ең кіші
-да функция
өзінің ең кіші ![]() және ең үлкен
және ең үлкен ![]() мәндерін
қабылдайды. Егер бұл мәндердің кемінде біреуі кесіндінің
ішкі нүктесінде қабылданса, онда ол нүкте Ролль теоремасына
қанағаттандыратын
мәндерін
қабылдайды. Егер бұл мәндердің кемінде біреуі кесіндінің
ішкі нүктесінде қабылданса, онда ол нүкте Ролль теоремасына
қанағаттандыратын ![]() болады және
болады және ![]() функциясының графигіне
функциясының графигіне ![]() нүктесінде
жүргізілген жанама абсцисса осіне параллель болатынын дәлелдейді. Қарсы
жағдайда
нүктесінде
жүргізілген жанама абсцисса осіне параллель болатынын дәлелдейді. Қарсы
жағдайда ![]() нүктесін
нүктесін
![]() ретінде
қабылдауға болады. Өйткені
ретінде
қабылдауға болады. Өйткені ![]() ,
, ![]() және барлық аралықта
және барлық аралықта
![]() . (2.44)
. (2.44)
(2.48) нүктеде функция экстемумы бар
болуының тек қажетті шарты.
Өйткені, ол орындала тұрса да, ![]() функцияның экстремум нүктесі
болмауы мүмкін.
функцияның экстремум нүктесі
болмауы мүмкін.
Лагранж теоремасы. Егер ![]() функциясы
функциясы ![]() кесіндісінде үзіліссіз, (
кесіндісінде үзіліссіз, (![]() ) интервалында дифференциалданатын болса, онда
) интервалында дифференциалданатын болса, онда
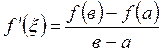 . (2.45)
. (2.45)
болатындай кемінде бір ![]() нүктесі бар.
нүктесі бар.
1-теорема. Егер ![]() нүктесінің
нүктесінің ![]() маңында
маңында ![]() функциялары
функциялары ![]() - да шексіз аз, дифференциалданатын,
- да шексіз аз, дифференциалданатын, ![]() , олардың
туындыларының қатынасының
, олардың
туындыларының қатынасының ![]() -да нақты шегі бар болса, онда
функциялардың өздерінің қатынасының да шегі бар
және
-да нақты шегі бар болса, онда
функциялардың өздерінің қатынасының да шегі бар
және
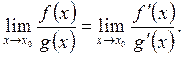 (2.46)
(2.46)
2-теорема. Егер ![]() нүктесінің
нүктесінің ![]() маңында
маңында ![]() функциялары
функциялары ![]() -да шексіз үлкен,
дифференциалданатын,
-да шексіз үлкен,
дифференциалданатын, ![]() ,
олардың туындыларының қатынасының
,
олардың туындыларының қатынасының ![]() -да нақты шегі бар болса,
онда функциялардың өздерінің қатынасының да
-да нақты шегі бар болса,
онда функциялардың өздерінің қатынасының да ![]() -да шегі бар
және ол шектер өзара тең, яғни (2.46) орындалады.
-да шегі бар
және ол шектер өзара тең, яғни (2.46) орындалады.
Бұл теоремалар 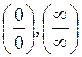 анықталмағандықтарын
ашуға қолданылатын Лопиталь ережесі деп аталатын
әдістің негізін құрайды. Лопиталь ережесінің
көмегімен басқа анықталмағандықтарды ашу үшін
оларды алдын ала түрлендіру не алмастырулар жасау қажет. Лопиталь
ережесін қайталап қолдануға болады:
анықталмағандықтарын
ашуға қолданылатын Лопиталь ережесі деп аталатын
әдістің негізін құрайды. Лопиталь ережесінің
көмегімен басқа анықталмағандықтарды ашу үшін
оларды алдын ала түрлендіру не алмастырулар жасау қажет. Лопиталь
ережесін қайталап қолдануға болады:
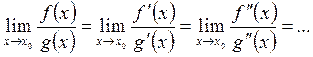 . (2.47)
. (2.47)
8-есеп. Функцияның шегін табыңыз: 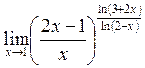
![]()
Шешу. Логарифмдегеннен кейін:
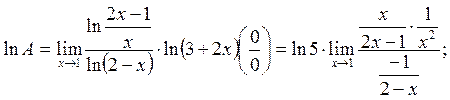
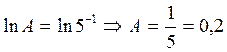 .
.
7-дәріс. Функцияны туындыларының көмегімен зерттеу
Дәріс мақсаты: туындылардың көмегімен дифференциалданатын функцияның қасиеттері мен оның графигінің ерекшеліктерін айқындау әдістерін баяндау. Зерттеу нәтижелері кестесін құрудың және оның көмегімен функция графигінің сұлбасын тұрғызудың үлгісін нақты мысалмен көрсету.
Функция экстремумдары.
1. Функция бірсарындылығының интервалдары.
Функция ![]()
![]() -да үзіліссіз және
-да үзіліссіз және ![]()
![]() -ның кез келген нүктелері (13
суретті қара) болсын. Функцияның кесіндіде
бірсарындылығының
-ның кез келген нүктелері (13
суретті қара) болсын. Функцияның кесіндіде
бірсарындылығының

13 сурет – Функцияның бірсарындылығына
анықтамасынан аргумент пен функцияның
өзара сәйкес өсімшелері ![]() пен
пен ![]() -тің таңбалары: 1) бірдей
болса, функция
-тің таңбалары: 1) бірдей
болса, функция ![]() -
да өспелі, 2) қарама – қарсы болса – кемімелі деп
тұжырымдауға болады. Кері тұжырымда орынды:
-
да өспелі, 2) қарама – қарсы болса – кемімелі деп
тұжырымдауға болады. Кері тұжырымда орынды: ![]() -да өспелі
(кемімелі)
-да өспелі
(кемімелі) ![]() функциясы
үшін
функциясы
үшін
![]() . (2.48)
. (2.48)
1-теорема. ![]() -да үзіліссіз,
-да үзіліссіз, ![]() -да дифференциаланатын
-да дифференциаланатын ![]() функциясы сол кесіндіде өспелі
(кемімелі) болуы үшін
функциясы сол кесіндіде өспелі
(кемімелі) болуы үшін
![]()
![]()
![]()
болуы қажет және жеткілікті.
Туындысының таңбасы тұрақты болатын аралықтар функция бірсарындылығының интервалдары деп аталады.
2-теорема. ![]() -да дифференциаланатын
-да дифференциаланатын ![]() функциясы сол интервалда тұрақты болуы үшін
функциясы сол интервалда тұрақты болуы үшін ![]()
![]() болуы қажет және жеткілікті.
болуы қажет және жеткілікті.
Теңдіктің ((2.48))
![]() (2.49)
(2.49)
түбірлері ![]() функциясының стационарлық нүктелері
деп аталады. Бұларға функцияның шекті туындысы жоқ
нүктелерін қоссақ, олар функцияның сынақ
нүктелері деп аталады. Функция
экстремумдары тек оның сынақ нүктелерінде ғана болуы
мүмкін.
функциясының стационарлық нүктелері
деп аталады. Бұларға функцияның шекті туындысы жоқ
нүктелерін қоссақ, олар функцияның сынақ
нүктелері деп аталады. Функция
экстремумдары тек оның сынақ нүктелерінде ғана болуы
мүмкін.
2. Функцияның жергілікті экстремумдары.
Функцияның сынақ нүктесі
маңындағы тәртібін зерделегенде сол маңда ![]() функцияның тек бір ғана
сынақ нүктесі
функцияның тек бір ғана
сынақ нүктесі ![]() бар деп есептейміз. Егер
бар деп есептейміз. Егер ![]() -нің сол жақ және оң жақ жарты
төңіректерінде функцияның таңбасы қарама -
қарсы болса, онда
-нің сол жақ және оң жақ жарты
төңіректерінде функцияның таңбасы қарама -
қарсы болса, онда ![]() арқылы өткенде функция таңбасын
өзгертеді дейміз.
арқылы өткенде функция таңбасын
өзгертеді дейміз.
3-теорема. Егер функция туындысы ![]()
![]() сынақ нүктесі арқылы
сынақ нүктесі арқылы
өткенде таңбасын өзгертсе, онда ![]() функцияның экстремум нүктесі болады және
функцияның экстремум нүктесі болады және ![]() -ның таңбасы минустан плюске ауса,
онда
-ның таңбасы минустан плюске ауса,
онда ![]() нүктесінде
функцияның минимумы, ал плюстен
минусқа өзгерсе - максимумы бар.
нүктесінде
функцияның минимумы, ал плюстен
минусқа өзгерсе - максимумы бар.
4-теорема. Егер тұрлаулылық нүктесінің ![]() маңында
маңында ![]()
![]() функциясының үзіліссіз
функциясының үзіліссіз ![]() -туындысы бар, нүктенің өзінде
-туындысы бар, нүктенің өзінде ![]() ал,
ал, ![]() болса, онда
болса, онда ![]() жұп болғанда
жұп болғанда ![]() функцияның экстремум нүктесі және
функцияның экстремум нүктесі және ![]() болса, бұл нүктеде функцияның максимумы, ал,
болса, бұл нүктеде функцияның максимумы, ал, ![]() болса – минимумы бар;
болса – минимумы бар; ![]() тақ болса,
тақ болса, ![]() функцияның экстремум нүктесі
емес.
функцияның экстремум нүктесі
емес.
Функцияны экстремумға зерттеудедің екі әдісі: І – дифференциалданатын функцияның бірінші туындысының көмегімен, ІІ – жоғарғы ретті (көбіне екінші ретті) туындыларының көмегімен. Екі әдісте де алдымен (2.49) теңдеуі шешіліп, функцияның тұрлаулылық нүктелері табылады. Оларға функцияның шекті туындылары жоқ нүктелері қосылып сынақ нүктелерінің жиыны анықталады. Сынақ нүктелерінің әрқайсысы жеке зерттеліп, онда функция экстремумының бар – жоғы айқындалады.
3. Функцияның кесіндідегі ең кіші және ең үлкен мәндері.
Вейерштрасс
теоремасы бойынша ![]() кесіндісінде
үзіліссіз
кесіндісінде
үзіліссіз ![]() функциясы сол кесіндіде
өзінің ең кіші және ең үлкен
мәндерін:
функциясы сол кесіндіде
өзінің ең кіші және ең үлкен
мәндерін:
![]() ,
, ![]() (2.50)
(2.50)
қабылдайды. Бұл мәндер
функцияның кесіндідегі глобальдық экстремумдары деп аталады. Олар
не кесіндінің шеткі нүктелерінде, не функцияның ![]() -дағы
сынақ нүктелерінде ғана қабылдануы мүмкін.
Сондықтан (2.50) мәндерін табу үшін функцияның
-дағы
сынақ нүктелерінде ғана қабылдануы мүмкін.
Сондықтан (2.50) мәндерін табу үшін функцияның ![]() нүктелеріндегі
мәндері анықталады. Ақырында осы мәндердің
ең кішісін және ең үлкенін таңдаймыз:
нүктелеріндегі
мәндері анықталады. Ақырында осы мәндердің
ең кішісін және ең үлкенін таңдаймыз:
![]()
![]() . (2.51)
. (2.51)
9-есеп.
Функцияның ![]() кесіндісіндегі ең
кіші және ең үлкен мәндерін табыңыз:
кесіндісіндегі ең
кіші және ең үлкен мәндерін табыңыз: 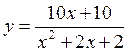 .
.
Шешу: 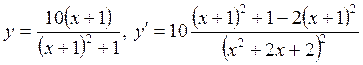 ,
, ![]() ;
;
![]() ;
;
![]()
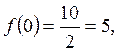
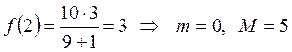 .
.
Функция графигінің қасиеттері.
1. Қисықтың дөңестігі мен ойыстығы.
Интервалда ![]() шекті не шексіз туындысы бар
шекті не шексіз туындысы бар ![]() функциясының графигін ордината осі тік жоғары
қарай бағытталған
функциясының графигін ордината осі тік жоғары
қарай бағытталған ![]() координаталар жүйесінде (14 суретті қара)
қарастыралық.
координаталар жүйесінде (14 суретті қара)
қарастыралық.
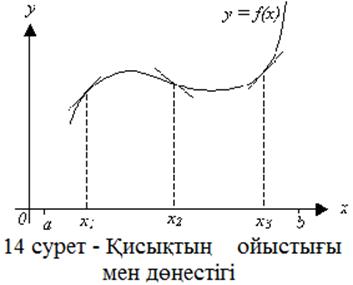 Егер
Егер ![]() нүктесінің
нүктесінің ![]() қисығына
қисығына ![]() нүктесінде
тұрғызылған жанама қисықтан жоғары болса, онда қисық
нүктесінде
тұрғызылған жанама қисықтан жоғары болса, онда қисық ![]() нүктесінде дөңес (ойыс) деп аталады.
Қисықтың дөңестік ойыстыққа немесе
керісінше ауысатын нүктесі оның кері иілу нүктесі делінеді;
34-суретте
нүктесінде дөңес (ойыс) деп аталады.
Қисықтың дөңестік ойыстыққа немесе
керісінше ауысатын нүктесі оның кері иілу нүктесі делінеді;
34-суретте ![]() және
және ![]()
![]() қисығының сәйкес
дөңестік және ойыстық нүктелері, ал
қисығының сәйкес
дөңестік және ойыстық нүктелері, ал ![]() оның кері иілу нүктесі
оның кері иілу нүктесі
5-теорема. Егер ![]() -де
-де ![]() функциясының үзіліссіз екінші ретті
туындысы бар және
функциясының үзіліссіз екінші ретті
туындысы бар және ![]() болса, онда функция графигінің
болса, онда функция графигінің ![]() -де дөңес (ойыс) болуы үшін
-де дөңес (ойыс) болуы үшін
![]()
![]() (2.52)
(2.52)
болуы қажет және жеткілікті.
1-салдар. Егер ![]() функциясының
функциясының ![]() -да екінші туындысы бар болса, онда интервалдың
-да екінші туындысы бар болса, онда интервалдың ![]() -ның таңбасы тұрақты бөліктері функция
графигінің дөңес не ойыс болатын аралықтары болады.
-ның таңбасы тұрақты бөліктері функция
графигінің дөңес не ойыс болатын аралықтары болады.
2-салдар. ![]() нүктесінің өзінде болмауы
мүмкін десек те, оның қандай да болмасын
нүктесінің өзінде болмауы
мүмкін десек те, оның қандай да болмасын ![]() маңында
маңында ![]() функциясының үзіліссіз екінші туындысы
бар болса, онда
функциясының үзіліссіз екінші туындысы
бар болса, онда ![]() функция графигінің кері иілу нүктесі
болуы үшін
функция графигінің кері иілу нүктесі
болуы үшін ![]() арқылы өткенде
арқылы өткенде ![]() -ның таңбасын өзгертуі қажет және жеткілікті.
-ның таңбасын өзгертуі қажет және жеткілікті.
6-теорема. Егер ![]() функциясының
функциясының ![]() нүктесінде үзіліссіз,
нөлден өзгеше үшінші туындысы бар және
нүктесінде үзіліссіз,
нөлден өзгеше үшінші туындысы бар және ![]() болса, онда
болса, онда ![]() функция графигінің кері
иілу нүктесі болады.
функция графигінің кері
иілу нүктесі болады.
Функцияның екінші туындысы нөлге тең
немесе мүлдем жоқ нүктелер функцияның екінші туынды
бойынша сынақ нүктелері деп аталады. Қисықтың ![]() дөңестік не ойыстық аралықтарын, кері иілу
нүктелерін табу үшін
дөңестік не ойыстық аралықтарын, кері иілу
нүктелерін табу үшін
![]() (2.53)
(2.53)
теңдеуінің барлық түбірлерін және шекті
екінші туынды жоқ нүктелерді табу қажет. Олар функция
графигінің дөңестік не ойыстық интервалдарының шекаралары болады. Бұл аралықтарда ![]() -ның таңбасы
тұрақты. Екінші туынды бойынша сынақ нүктесі
арқылы өткенде
-ның таңбасы
тұрақты. Екінші туынды бойынша сынақ нүктесі
арқылы өткенде ![]() -ның таңбасы өзгермесе, ол
-ның таңбасы өзгермесе, ол ![]() қисығының қайту
нүктесі, ал өзгерсе - кері иілу нүктесі болғаны.
қисығының қайту
нүктесі, ал өзгерсе - кері иілу нүктесі болғаны.
2. Функция графигінің асимптоталары.
Қисықтың ![]() тік
асимптоталарынан:
тік
асимптоталарынан: ![]() басқалары
басқалары
![]()
теңдеуімен анықталатынын көрдік.
7-теорема. ![]() түзуі
түзуі ![]() қисығының
асимптотасы болуы үшін
қисығының
асимптотасы болуы үшін
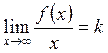 ,
, ![]() (2.54)
(2.54)
нақты шектерінің бар болуы қажет және жеткілікті.
Егер ![]() болса, онда қисықтың көлбеу
асимптотасы бар.
болса, онда қисықтың көлбеу
асимптотасы бар.
Тек ![]() болғанда ғана
болғанда ғана ![]() жатық түзуі
қисықтың асимптотасы болуы мүмкін. Егер (2.54)-де
жатық түзуі
қисықтың асимптотасы болуы мүмкін. Егер (2.54)-де ![]() болса, онда қисықтың асимптотасы жоқ.
болса, онда қисықтың асимптотасы жоқ.
Есеп шығарғанда зерттеулер нәтижесінен функцияның қасиеттерін, сипаттайтын кесте түзіліп, функция графигінің эскизі тұрғызылады.
3-модуль. Бір айнымалы функцияларының интегралдық есептеуі
8-дәріс. Алғашқыбейне функциясы – анықталмаған интеграл
Дәріс мақсаты: функцияны дифференциалдау мен интегралдаудың бір-біріне қарсы амалдар екенін, осы деректі есептеу нәтижелерінің дұрыстығын тексеру үшін қолдануға болатынын көрсету. Интегралдаудың негізгі әдістерін баяндап, оларды нақты есептерге қолдану.
Егер ![]() -да дифференциалданатын
-да дифференциалданатын ![]() функциясының туындысы
функциясының туындысы
![]()
![]() (3.1)
(3.1)
болса, онда ![]()
![]() интервалында
интервалында ![]() -ның алғашқыбейне функциясы деп
аталады.
-ның алғашқыбейне функциясы деп
аталады.
Егер (3.1)–де ![]() болса, онда (
болса, онда (![]()
![]() . Демек, (3.1) орындалса, онда
. Демек, (3.1) орындалса, онда ![]()
![]() , яғни
, яғни ![]()
![]() -да
-да ![]() интервалында
интервалында ![]() -ның алғашқыбейне функциясы болады. Сонымен,
функцияның интервалда бір төркін функциясы бар болса, онда осы
аралықта оның мұндай функцияларының саны шексіз
көп.
-ның алғашқыбейне функциясы болады. Сонымен,
функцияның интервалда бір төркін функциясы бар болса, онда осы
аралықта оның мұндай функцияларының саны шексіз
көп.
Теорема: ![]() -ның
-ның ![]() интервалындағы кез келген екі төркін функциясы бір-бірінен тек тұрақты
қосылғышқа ғана айырылады.
интервалындағы кез келген екі төркін функциясы бір-бірінен тек тұрақты
қосылғышқа ғана айырылады.
Анықтама: ![]() функциясының
функциясының ![]() аралығындағы кез келген
аралығындағы кез келген ![]() төркін функциясы
төркін функциясы ![]() -ның сол интервалдағы анықталмаған
интегралы деп аталып,
-ның сол интервалдағы анықталмаған
интегралы деп аталып, ![]() рәмізімен белгіленеді.
рәмізімен белгіленеді.
Анықтама бойынша
![]() ,
, ![]() . (3.2)
. (3.2)
Мұнда ![]() - интеграл белгісі,
- интеграл белгісі, ![]() - интегралданушы функция,
- интегралданушы функция, ![]() - интеграл астындағы (интегралданушы) өрнек,
- интеграл астындағы (интегралданушы) өрнек, ![]() интегралдау айнымалысы,
интегралдау айнымалысы, ![]() - интегралданушы функцияның
- интегралданушы функцияның ![]() -дағы кез келген төркін функциясы,
-дағы кез келген төркін функциясы, ![]() - кез келген заттық мән қабылдай алатын
(ырықты) тұрақты.
- кез келген заттық мән қабылдай алатын
(ырықты) тұрақты.
Интегралдау операциясын орындау үшін ![]() интегралданушы
функциясының (3.1)-ге қанағаттандыратын бір төркін функциясын
интегралданушы
функциясының (3.1)-ге қанағаттандыратын бір төркін функциясын
![]() тауып, оған
ырықты тұрақтыны
тауып, оған
ырықты тұрақтыны ![]() қоссақ болғаны.
қоссақ болғаны.
Егер (3.1) орындалса, онда
![]() , (3.3)
, (3.3)
яғни, интегралданушы өрнек төркін функцияның дифференциалына тең.
Анықталмаған интегралдың негізгі қасиеттері.
1.
Анықталмаған
интегралдың туындысы интегралданушы функцияға тең: (![]() .
.
2.
Анықталмаған
интегралдың дифференциалы интегралданушы өрнекке тең: ![]() .
.
3.
![]()
4. Тұрақты көбейткішті интеграл белгісінің сыртына шығаруға болады.
5.
Егер ![]() функциялары
функциялары
![]() -да интегралданатын болса, онда
-да интегралданатын болса, онда
![]() (3.4)
(3.4)
![]()
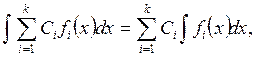
![]() ,
, ![]() (3.5)
(3.5)
түрінде жазуға болады.
Анықталмаған интегралдар кестесі.
1. ![]() , 13.
, 13.
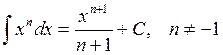 ,
,
2. 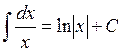 , 14.
, 14. 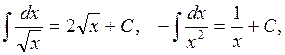
3. 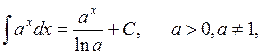 15.
15. ![]() ,
,
4. ![]() , 16.
, 16. ![]() ,
,
5. 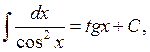 17.
17. 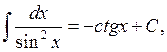
6. 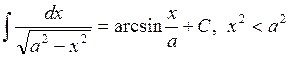 18.
18. 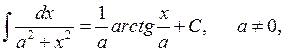
7. 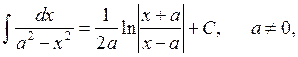
8. 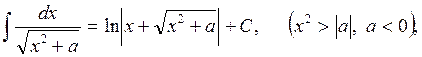
9. 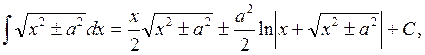
10. 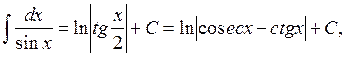
11. 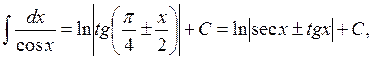
12. ![]() , 19.
, 19. ![]()
20. 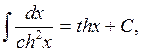 21.
21.
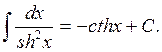
Формулалардың дұрыстығына теңдіктердің оң жақтарын дифференциалдау арқылы көз жеткізуге болады.
Интегралдау әдістері.
Анықталмаған интегралды оның қасиеттерінің және интегралдар кестесінің көмегімен табу тура интегралдау делінеді. Бұлайша интегралдау мүмкін болмаса, онда айнымалыны алмастыру және бөліктеп интегралдау деп аталатын әдістер қолданылады.
1. Интегралдау айнымалысын алмастыру.
Интегралданушы ![]() функциясы
функциясы ![]() - да үзіліссіз
болса, сәйкес
- да үзіліссіз
болса, сәйкес ![]() аралығында
үзіліссіз дифференциалданатын
аралығында
үзіліссіз дифференциалданатын ![]() функциясын таңдап алып және
функциясын таңдап алып және ![]() екенін ескеріп,
екенін ескеріп,
![]()
жүйесі бойынша интегралдау айнымалысын алмастырамыз:
![]() .
(3.6)
.
(3.6)
Егер интегралданушы функция күрделі және құрылымы (3.6)-дің оң жағындағыға ұқсас болса, онда алмастыруды
![]() ,
, ![]()
жүйесі бойынша орындау тиімді. Нәтижесінде анықталмаған интегралда айнымылыны алмастыру формуласы
![]() (3.7)
(3.7)
түріне енеді, өйткені ![]() .
.
Нәтиже интегралдау айнымылысының белгілеуінен тәуелсіз. Квадратурадан кейін табылған төркін функцияда кері алмастырудың көмегімен ескі айнымалыға көшеміз.
Интегралдау айнымалысын
алмастырмай, (3.7)-ның сол жағын ![]() түрінде жазу
түрінде жазу ![]() функциясын дифференциал
белгісінің астына келтіру деп аталады. Қолайлы жағдайларда
бұл амал анықталмаған интегралды күрделі төркін
функция ретінде
функциясын дифференциал
белгісінің астына келтіру деп аталады. Қолайлы жағдайларда
бұл амал анықталмаған интегралды күрделі төркін
функция ретінде
![]()
![]() (3.8)
(3.8)
табуға мүмкіндік береді.
Мысалдар:
а) Интегралданушы
функцияның аргументі сызықтық екімүшелік ![]() болсын делік. Ол
(3.1)-ге қанағаттандырса, онда:
болсын делік. Ол
(3.1)-ге қанағаттандырса, онда:
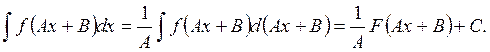
б) Интервалда үзіліссіз дифференциалданатын ![]() функциясы
функциясы
үшін логарифмдік интеграл деп аталатын
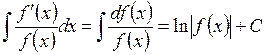 (3.9)
(3.9)
қатынасы орын алады.
2. Бөліктеп интегралдау.
Белгілі бір аймақта
үзіліссіз дифференциалданатын ![]() және
және ![]() функцияларын қарайық.
Олардың көбейтіндісінің дифференциалы
функцияларын қарайық.
Олардың көбейтіндісінің дифференциалы
![]() .
(3.10)
.
(3.10)
Теңдіктің екі жағынан да интеграл алып, анықталмаған интегралдың 3-қасиетін пайдаланып,
![]() (3.11)
(3.11)
түрінде жазылған нәтиже бөліктеп
интегралдау формуласы деп аталады. Теңдіктің сол жағында
табылуға тиіс интеграл орналасқан. Ондағы интегралданушы
өрнектің бір көбейткіші ![]() деп, қалған өрнек (
деп, қалған өрнек (![]() пен қоса)
пен қоса) ![]() деп қабылданады.
Көбіне
деп қабылданады.
Көбіне ![]() арқылы
логарифмдік, кері тригонометриялық функциялар сияқты төркін
функциялары кестелік емес функциялар белгіленеді. Олар жоқ болған
жағдайда
арқылы
логарифмдік, кері тригонометриялық функциялар сияқты төркін
функциялары кестелік емес функциялар белгіленеді. Олар жоқ болған
жағдайда ![]() ретінде
дәрежелі функцияны алу тиімді. Әрі қарай (3.13) -тің
оң жағын құрастырамыз. Бөліктеп интегралдау
формуласын қайталап қолдана беруге болады.
ретінде
дәрежелі функцияны алу тиімді. Әрі қарай (3.13) -тің
оң жағын құрастырамыз. Бөліктеп интегралдау
формуласын қайталап қолдана беруге болады.
10- есеп.
Анықталмаған интегралды ![]() табыңыз.
табыңыз.
Шешу:![]()
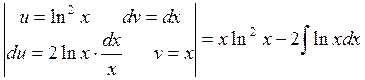 =
=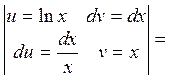
![]() .
.
9-дәріс. Рационал функцияларды интегралдау
Дәріс мақсаты: студенттерді қолайлы алмастыруларды таңдау, интегралданатын функцияны қарапайым бөлшектердің қосындысына жіктеу, интегралды «рационалдау», «мектептік қоржыннан» қажетті тригонометриялық формулаларды тиімді пайдалану тәсілдеріне үйрету.
Дұрыс рационал бөлшектен анықталмаған интеграл табу талап етілсін. Интегралданушы бөлшекті анықталмаған коэффициенттер әдісі деп аталатын тәсілдермен қарапайым бөлшектердің қосындысына жіктейміз. Бөлімі сызықтық екімүшеліктің қандай да болмасын дәрежесі болып келген қарапайым бөлшектің интегралы екімүшелікті дифференциал белгісінің астына енгізу арқылы кестелік түрге келтіріледі. Бұл тәсіл қарапайым бөлшектің бөлімі келтірілмейтін – нақты түбірі жоқ квадрат үшмүшеліктің дәрежелері болып келген жағдайда да қолданылады. Мұндай бөлшектің алымы тұрақты сан болып келсе, онда квадрат үшмүшеліктен екі санның қосындысының не айырымының толық квадратын бөліп шығару:
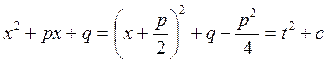 (3.12)
(3.12)
қолайлы. Үшмүшеліктің
дәрежесі ![]() болған
жағдайда бірден кестелік интегралға келеміз.
Ал,
болған
жағдайда бірден кестелік интегралға келеміз.
Ал, ![]() болса,
онда бөліктеп интегралдау формуласын қолдануға болады:
болса,
онда бөліктеп интегралдау формуласын қолдануға болады:
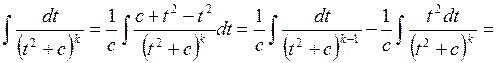
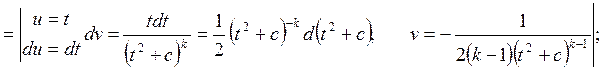
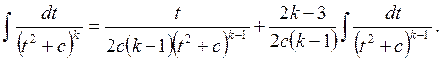 (3.13)
(3.13)
Бастапқы түрдегі нәтижеге қайта оралтатын мұндай теңдік рекурренттік формула деп аталады. Оны керегінше қайталап қолдану кестелік интегралға келтіреді. Заттық n дәрежелі көпмүшелік жәй көбейткіштерге (келтірілмейтін көпмүшеліктерге) бір ғана әдіспен жіктеледі:
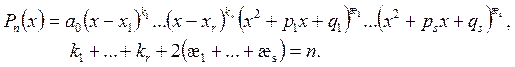 (3.14)
(3.14)
Бөлімі келтірілмейтін көпмүшелік болып келген дұрыс рационал бөлшек қарапайым бөлшек деп аталады.
Теорема. Кез келген дұрыс рационал бөлшек бір ғана әдіспен қарапайым бөлшектердің қосындысына жіктеледі.
Анықталмаған коэффициенттер әдісі.
Дұрыс рационал бөлшекті қарапайым бөлшектердің қосындысына жіктеудің негізгі тәсілі-анықталмаған коэффициенттер әдісі төмендегіше қолданылады.
1. Берілген бөлшектің бөліміндегі көпмүшеліктің барлық түбірлері табылып, ол (3.14) түрінде жәй көбейткіштерге жіктеледі.
2.
Рационал бөлшек
бөлімдері (3.14)-тегі 1,2,...kv , ![]() және 1,2,...,
және 1,2,...,![]() ,
, ![]() дәрежелі сәйкес жәй
көбейткіштер болып келген қарапайым бөлшектердің
қосындысы ретінде өрнектеледі. Мұнда әрбір жәй
көбейткіш өзінің еселігі қанша болса, сонша рет
алынады.
дәрежелі сәйкес жәй
көбейткіштер болып келген қарапайым бөлшектердің
қосындысы ретінде өрнектеледі. Мұнда әрбір жәй
көбейткіш өзінің еселігі қанша болса, сонша рет
алынады.
3.
Бөлімі ![]() -не тең
қарапайым бөлшектің алымы ретінде әзірше белгісіз
-не тең
қарапайым бөлшектің алымы ретінде әзірше белгісіз ![]() саны алынады да,
саны алынады да, ![]() көбейткіштері
үшін
көбейткіштері
үшін
![]()
![]() сызықтық
функциялары алынады.
сызықтық
функциялары алынады.
4.
Қарапайым бөлшектердің
қосындысы ортақ бөлімге ![]() келтіріледі
келтіріледі
де, берілген және соңғы пайда болған бөлімдері бірдей бөлшектердің алымдары теңестіріледі.
5. Теңестіруден кейін бірдей дәрежелері х-тің коэффициенттерін өзара теңестіріліп, n белгісізді n сызықтық теңдеу жүйесі құрылады. Жоғарыдағы теоремалар негізінде бұл жүйесі үйлесімді және бір ғана шешуі бар.
6. Құрылған жүйені шешіп, белгісіз коэффициенттерді тауып, орындарына қоюмен рационал бөлшекті қарапайым бөлшектердің қосындысына жіктеу аяқталады.
Тригонометриялық өрнектерді интегралдау.
Егер ![]() рационал функциясы
аргументтерінің кемінде бірі бойынша тақ болса:
рационал функциясы
аргументтерінің кемінде бірі бойынша тақ болса: ![]()
![]()
![]()
онда сәйкес
![]() (3.15)
(3.15)
алмастыруларының көмегімен ![]() аралық айнымалысының рационал функциясына
аралық айнымалысының рационал функциясына ![]() келеміз. Кейде, (3.15)
функцияларының бірін дифференциал белгісінің астына келтіру
арқылы табуға болады.
келеміз. Кейде, (3.15)
функцияларының бірін дифференциал белгісінің астына келтіру
арқылы табуға болады.
Егер ![]() функциясы өзінің екі аргументі бойынша да
жұп:
функциясы өзінің екі аргументі бойынша да
жұп:
![]()
![]()
болса, онда оны
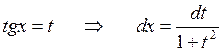 (3.16)
(3.16)
алмастыруының көмегімен интегралдауға болады.
Мысал: 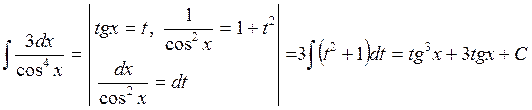 .
.
Егер ![]() функциясы аргументтері бойынша
жұп не тақ болмаса,
оны интегралдау үшін универсал тригонометриялық алмастыру енгізіледі:
функциясы аргументтері бойынша
жұп не тақ болмаса,
оны интегралдау үшін универсал тригонометриялық алмастыру енгізіледі:
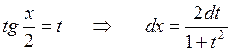 ,
, 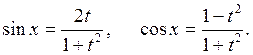 (3.17)
(3.17)
Мысал: 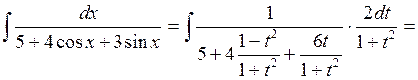
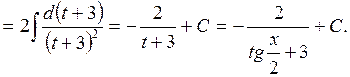
Иррационал функцияларды интегралдау.
Иррационалдықтың негізгі екі түрін: бөлшек – сызықтық және квадрат иррационалдықтарды қарастыралық.
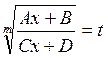
![]()
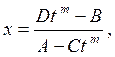
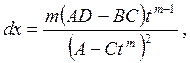
![]() (3.18)
(3.18)
алмастыруы жасалады.
2. Иррцаиональдықтың
![]()
![]()
![]() түрінде рационалдау үшін
төмендегідей алмастырулар жасалады:
түрінде рационалдау үшін
төмендегідей алмастырулар жасалады:
1) ![]()
![]()
![]()
![]()
![]()
![]()
![]() ; (3.19)
; (3.19)
2) ![]()
![]()
![]()
![]()
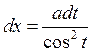
![]()
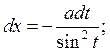 (3.20)
(3.20)
3) ![]()
![]()
![]()
![]()
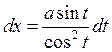
![]()
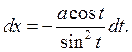 (3.21)
(3.21)
Пример: 1. 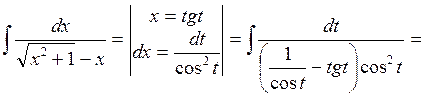
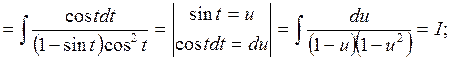
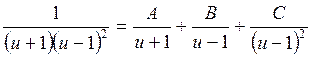
![]()
![]()
![]() .
.
Яғни, 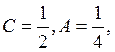
![]()
![]()
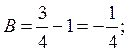
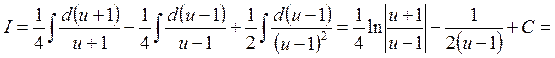
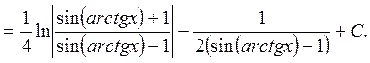
10-дәріс. Анықталған интеграл
Дәріс мақсаты: анықталмаған және анықталған интегралдардың айырмашылығына, соңғының геометриялық және механикалық мағынасына, кейбір айрықша қасиеттеріне (орташа мән туралы теореманы қоса) көңіл аудару. Анықталған интегралдың есептеу әдістерін баяндау, оны меншіксіз интегралдар ретінде жалпылау.
Интегралдың анықтамасы мен қасиеттері.
Кесіндіде ![]() анықталған
анықталған ![]() функциясын қарастыралық. Кесіндіні
функциясын қарастыралық. Кесіндіні ![]() нүктелерімен (15 суретті қара) қалауымызша
нүктелерімен (15 суретті қара) қалауымызша ![]() бөлікке бөлейік. Әр бөліктен еркімізше
бөлікке бөлейік. Әр бөліктен еркімізше ![]() нүктесін таңдап алып, функцияның сол
нүктелердегі мәндерін табайық. Табылған мәндерді
сәйкес құраушы кесінділердің ұзындықтарына
нүктесін таңдап алып, функцияның сол
нүктелердегі мәндерін табайық. Табылған мәндерді
сәйкес құраушы кесінділердің ұзындықтарына ![]() көбейтіп қосайық. Пайда болған өрнек
көбейтіп қосайық. Пайда болған өрнек
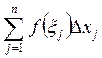 (3.23)
(3.23)
![]() функциясы үшін
функциясы үшін ![]() кесіндісі бойынша құрылған
интегралдық қосынды деп аталады. Құраушы
кесінділердің ең үлкен ұзындығы
кесіндісі бойынша құрылған
интегралдық қосынды деп аталады. Құраушы
кесінділердің ең үлкен ұзындығы ![]()
![]()
кесіндісін бөлшектеудің қадамы
деп аталады: ![]() ,
, ![]() .
.
Анықтама. Егер ![]() -да (3.23) интегралдық қосындысының кесіндіні
бөлшектеу және әр бөліктен
-да (3.23) интегралдық қосындысының кесіндіні
бөлшектеу және әр бөліктен ![]() нүктелерін таңдау әдістерінен тәуелсіз
нақты шегі бар болса, онда сол сан
нүктелерін таңдау әдістерінен тәуелсіз
нақты шегі бар болса, онда сол сан ![]() функциясынан
функциясынан ![]() кесіндісі бойынша
алынған анықталған интеграл деп аталып,
кесіндісі бойынша
алынған анықталған интеграл деп аталып, 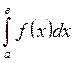 рәмізімен белгіленеді.
рәмізімен белгіленеді.
Анықтама бойынша
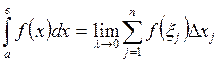 . (3.24)
. (3.24)
Анықталмаған интегралдағы
атаулардың үстіне қосымша: ![]() және
және ![]() интегралдың
сәйкес төменгі және жоғарғы шектері,
интегралдың
сәйкес төменгі және жоғарғы шектері, ![]() интегралдау
аралығы (аймағы) деп аталады.
интегралдау
аралығы (аймағы) деп аталады.
Жоғарыдан ![]() қисығымен, төменнен абсцисса осімен, бүйір
жақтарынан
қисығымен, төменнен абсцисса осімен, бүйір
жақтарынан ![]() және
және ![]() түзулерімен шектелген жазық фигура
түзулерімен шектелген жазық фигура ![]() (15 суретті қара) табаны
(15 суретті қара) табаны ![]() болатын қисықсызықты трапеция деп аталады. Интегралдық қосынды (3.24)
оның ауданын
болатын қисықсызықты трапеция деп аталады. Интегралдық қосынды (3.24)
оның ауданын ![]() жуықтап анықтайды.
жуықтап анықтайды.
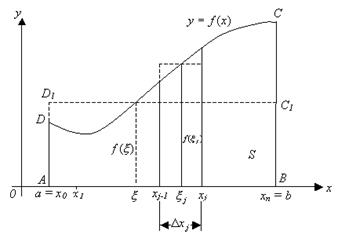
15 сурет - Интегралдық қосынды және орташа мән теорема
Ал, ![]() -да шекке көшкеннен кейін фигура ауданының дәл өрнегі
-да шекке көшкеннен кейін фигура ауданының дәл өрнегі
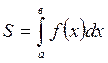 (3.25)
(3.25)
табылады. Бұл теңдік анықталған
интегралдың геометриялық мағынасын айқындайды: ![]() кесіндісінде теріс емес
кесіндісінде теріс емес ![]() функциясынан сол кесінді бойынша алынған
интеграл (3.25) бар болса, оның сан мәні табаны
функциясынан сол кесінді бойынша алынған
интеграл (3.25) бар болса, оның сан мәні табаны ![]() , жоғарыдан интегралданушы
функцияның графигімен шектелген қисықсызықты
, жоғарыдан интегралданушы
функцияның графигімен шектелген қисықсызықты
трапецияның ауданына тең.
Анықталмаған интегралдың 4-5 қасиеттері анықталған интегралға да тән. Анықталған интегралдың кейбір қасиеттері шартты түрде:
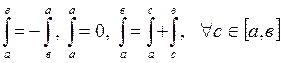 .
(3.26)
.
(3.26)
Анықталған интегралдың кейбір қасиеттері теңсіздіктермен өрнектеледі:
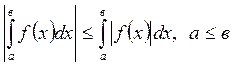 .
.
Функция шегінің қасиеттері
негізінде (![]() ):
):
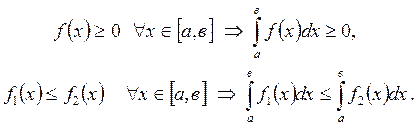
Орташа мән туралы теорема.
Егер ![]() функциясы
функциясы
![]() кесіндісінде
үзіліссіз болса, онда сол кесіндіде
кесіндісінде
үзіліссіз болса, онда сол кесіндіде
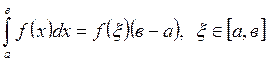 (3.27)
(3.27)
болатындай кемінде бір ![]() нүктесі
табылады.
нүктесі
табылады.
Кесіндіде теріс
емес функция үшін орташа мән туралы теореманың
геометриялық түсініктемесі бар: егер ![]() функциясы
кесіндіде үзіліссіз болса, онда табаны
функциясы
кесіндіде үзіліссіз болса, онда табаны ![]() ,
жоғарыдан
,
жоғарыдан ![]() қисығымен
шектелген қисықсызықты трапециямен ауданы тең табаны
қисығымен
шектелген қисықсызықты трапециямен ауданы тең табаны ![]() ,
биіктігі
,
биіктігі
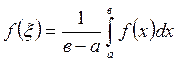 (3.28)
(3.28)
болатын ![]() тіктөртбұрышы
табылады; (3.28) саны интегралданушы функцияның
тіктөртбұрышы
табылады; (3.28) саны интегралданушы функцияның ![]() кесіндісіндегі
орташа мәні деп аталады.
кесіндісіндегі
орташа мәні деп аталады.
Анықталған интегралды есептеу әдістері. Ньютон -Лейбниц формуласы.
 Анықталған интеграл мен орташа
мән туралы теореманың геометриялық түсіндірмелерінен
Анықталған интеграл мен орташа
мән туралы теореманың геометриялық түсіндірмелерінен ![]() -да үзіліссіз функциядан
-да үзіліссіз функциядан ![]() кесіндісі бойынша анықталған интеграл бар деп
қорытынды жасай аламыз. Өйткені (16 суретті қара):
кесіндісі бойынша анықталған интеграл бар деп
қорытынды жасай аламыз. Өйткені (16 суретті қара): ![]() .
.
Соңғы аудан жоғарғы шегі айнымалы анықталған интегралмен өрнектеледі:
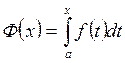 .
.
Бұл функция интегралдау
айнымалысының белгілеуінен тәуелсіз және ![]() интервалында үзіліссіз
дифференциалданады. Туындының анықтамасы мен
интервалында үзіліссіз
дифференциалданады. Туындының анықтамасы мен ![]() кесіндісі үшін орташа мән туралы
теоремадан:
кесіндісі үшін орташа мән туралы
теоремадан:
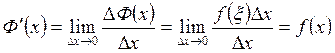
![]() ,
,
яғни ![]() - интегралданушы функцияның
- интегралданушы функцияның ![]() интервалындағы
төркін функциясы. Бұл тұжырым анықталмаған
және анықталған интегралдардың арасындағы
байланысты өрнектейтін
интервалындағы
төркін функциясы. Бұл тұжырым анықталмаған
және анықталған интегралдардың арасындағы
байланысты өрнектейтін
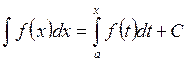 (3.37)
(3.37)
теңдігіне келтіреді.
Төркін функциялар туралы теореманы ескерсек:
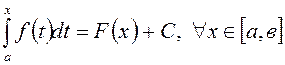 . (3.38)
. (3.38)
Мұнда ![]() интегралданушы функцияның
интегралданушы функцияның ![]() -дағы кез келген төркін функциясы.
Теңдік кесіндінің шекара:
-дағы кез келген төркін функциясы.
Теңдік кесіндінің шекара: ![]() нүктелерінде де орындалады. Бұл мәндерді кезегімен (3.38)-ке қойсақ, алдымен интегралдау тұрақтысын
нүктелерінде де орындалады. Бұл мәндерді кезегімен (3.38)-ке қойсақ, алдымен интегралдау тұрақтысын ![]() табамыз да,
табамыз да,

теңдігіне келеміз. Әрі қарай анықталған интегралды есептеудің негізгі құралы Ньютон – Лейбниц формуласы алынады. Қолдануға ыңғайлы болу үшін ол
 (3.39)
(3.39)
түрінде жазылады.
Есептеу әдістері.
Егер ![]() функциялары және
функциялары және ![]()
![]() кесінділері үшін анықталған
интегралда айнымалыны алмастыру формулалары деп аталатын
кесінділері үшін анықталған
интегралда айнымалыны алмастыру формулалары деп аталатын
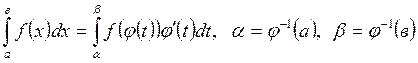 , (3.40)
, (3.40)
 (3.41)
(3.41)
қатынастары орын алады.
Енді ![]() -да үзіліссіз дииференциалданатын
-да үзіліссіз дииференциалданатын ![]() функциялары үшін (3.12) теңдігі құрылды деп, оның
екі жағынан да
функциялары үшін (3.12) теңдігі құрылды деп, оның
екі жағынан да ![]() кесіндісі бойынша анықталған интегралдар алайық.
кесіндісі бойынша анықталған интегралдар алайық.
Анықталған интеграл үшін бөліктеп интегралдау формуласы
 . (3.42)
. (3.42)
11-есеп. Анықталған интегралды  есептеңіз.
есептеңіз.
Шешу: 

Меншіксіз интегралдар.
Анықталған интеграл түсінігі екі алғышартқа негізделген: 1) интегралдау аралығы шекті, 2) интегралданушы функция сол аралықта шектелген. Бұл талаптардың кемінде біреуі орындалмаса, онда анықталған интеграл өзінің тұғырлық мағынасынан айырылып, меншіксіз интеграл деп аталады. Аталмыш шарттардың қайсысы бұзылуына байланысты меншіксіз интегралдардың екі түрі ажыратылады.
І-текті меншіксіз интегралдар.
Шексіз: ![]()
![]() және
және ![]() аралықтарының бірінде
үзіліссіз
аралықтарының бірінде
үзіліссіз ![]() функциясы
қаралады. Алғашқы екі жағдайда сәйкес
жоғарғы және төменгі шектері айнымалы
анықталған интегралдар
функциясы
қаралады. Алғашқы екі жағдайда сәйкес
жоғарғы және төменгі шектері айнымалы
анықталған интегралдар
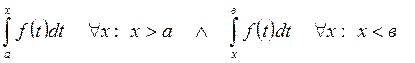 (3.43)
(3.43)
бар болады. Олардың шектері
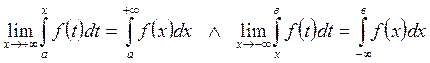 (3.44)
(3.44)
![]() функциясынан
алынған шектері шексіз (І-текті) меншіксіз интеграл деп аталады.
функциясынан
алынған шектері шексіз (І-текті) меншіксіз интеграл деп аталады.
Егер (3.44)-тің сол жақтарындағы
шектер бар және нақты сандар болса, онда оларға тең
меншіксіз интегралдар да бар және жинақты деп аталады. Қарсы
жағдайда (шектер жоқ не ![]() -ке тең) (3.44)-пен анықталатын
меншіксіз интегралдар жинақсыз (тарқамалы) делінеді.
-ке тең) (3.44)-пен анықталатын
меншіксіз интегралдар жинақсыз (тарқамалы) делінеді.
Бүкіл сандық осьте үзіліссіз функция үшін шектерінің екеуі де шексіз
меншіксіз интеграл
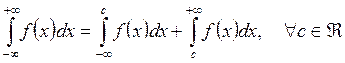 (3.45)
(3.45)
қарастырылады.
Сонымен, І-текті меншіксіз интеграл дегеніміз
интегралдау шектері ![]() -ке ұмтылғандағы
анықталған интегралдың шегі. Сондықтан оны есептеу
үшін Ньютон-Лейбниц формуласы қолданылады. Егер
-ке ұмтылғандағы
анықталған интегралдың шегі. Сондықтан оны есептеу
үшін Ньютон-Лейбниц формуласы қолданылады. Егер ![]() интегралданушы
функцияның
интегралданушы
функцияның ![]() аралықтарындағы төркін функциясы
болса, онда:
аралықтарындағы төркін функциясы
болса, онда:
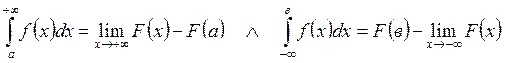 . (3.46)
. (3.46)
Ньютон-Лейбництің жалпыланған формуласын әдеттегіше жаза беруге болады:
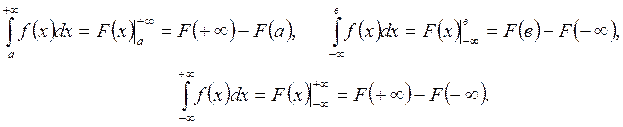 (3.47)
(3.47)
ІІ-текті меншіксіз интегралдар.
Функция екінші текті үзіліс нүктесі
функцияның ерекше нүктесі деп аталады. Интегралдау
кесіндісінің ![]() бастапқы
бастапқы ![]() , соңғы
, соңғы ![]() және кез келген ішкі
және кез келген ішкі ![]() нүктелері интегралданушы функцияның ерекше нүктелері
болып келген жағдайларды қарастыралық. Функция
нүктелері интегралданушы функцияның ерекше нүктелері
болып келген жағдайларды қарастыралық. Функция ![]() тек кесіндінің шеткі нүктелерінің бірінде ғана
шектелмеген болса, онда жеткілікті аз
тек кесіндінің шеткі нүктелерінің бірінде ғана
шектелмеген болса, онда жеткілікті аз ![]() саны үшін
саны үшін
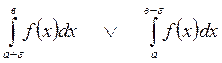 (3.48)
(3.48)
анықталған интегралы бар. Олардың шектері
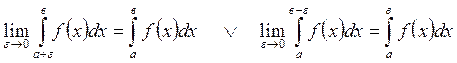 (3.49)
(3.49)
шектелмеген ![]() функциясынан алынған ІІ-текті
меншіксіз интеграл деп аталады.
функциясынан алынған ІІ-текті
меншіксіз интеграл деп аталады.
Егер ![]() функциясының
функциясының ![]() кесіндісіндегі жалғыз
ғана ерекше нүктесі болса, онда
кесіндісіндегі жалғыз
ғана ерекше нүктесі болса, онда
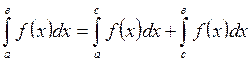 . (3.50)
. (3.50)
Меншіксіз интегралдың геометриялық
мағынасы:. Егер (3.44) және (3.49) интегралдарының
біріншілері жинақты болса, олардың шамалары жоғарыдан ![]() , қисығымен шектелген шексіз, бірақ квадратталатын
қисықсызықты трапециялардың (17а,б-суретті қара)
аудандарына тең. Интегралданушы функцияның интервалда саны шекті
, қисығымен шектелген шексіз, бірақ квадратталатын
қисықсызықты трапециялардың (17а,б-суретті қара)
аудандарына тең. Интегралданушы функцияның интервалда саны шекті ![]() ерекше нүктелері
ерекше нүктелері![]() бар, бірақ оның төркін функциясы
бар, бірақ оның төркін функциясы ![]() бүкіл
бүкіл ![]() кесіндісінде үзіліссіз болса, онда ІІ-текті
меншіксіз интегралды есептеу үшін Ньютон-Лейбниц формуласын (3.39)
түрінде ерекше нүктелерге көңіл аудармай тұтас
кесіндіге
кесіндісінде үзіліссіз болса, онда ІІ-текті
меншіксіз интегралды есептеу үшін Ньютон-Лейбниц формуласын (3.39)
түрінде ерекше нүктелерге көңіл аудармай тұтас
кесіндіге ![]() қолдана беруге болады.
қолдана беруге болады.
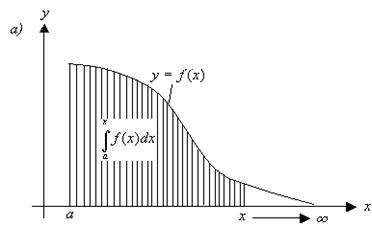
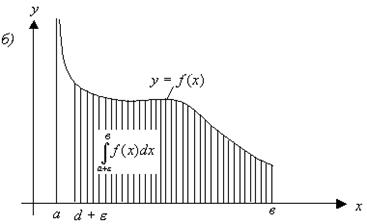
17 сурет - Меншіксіз интегралдардың геометриялық мағынасы
11-дәріс. Операторлық есептеу
Дәріс мақсаты: математиканың «Операторлық (операциялық) есептеу» деп аталатын инженерлік практикада қолданысы мол саласының ғылыми негізін айқындау. Лаплас операторының негізгі қасиеттерін (теоремаларды) баяндап, бұл бөлімнің қолданбалық сипатын зерделеу.
Түпнұсқа деп төмендегі
шарттарға қанағаттандыратын ![]() функциясын айтамыз: 1)
функциясын айтамыз: 1) ![]() болғанда
болғанда ![]() және
және ![]() ; 2) кез келген
; 2) кез келген ![]() кесіндісінде
кесіндісінде ![]() үзіксіз функция
немесе оның саны шекті бірінші текті үзіктік нүктелері бар;
3)
үзіксіз функция
немесе оның саны шекті бірінші текті үзіктік нүктелері бар;
3) ![]() экспонентамен
шектелген, яғни
экспонентамен
шектелген, яғни
![]() (3.51)
(3.51)
болатындай ![]() тұрақтылары
бар.
тұрақтылары
бар.
Соңғы шартты ![]() -да түпнұсқа
модулінің өсуі экспонентаның өсуінен тез емес деп
түсінеміз;
-да түпнұсқа
модулінің өсуі экспонентаның өсуінен тез емес деп
түсінеміз; ![]() саны
саны
![]() функциясының
өсу көрсеткіші деп аталады. Бұл функцияның аргументі
ретінде уақыт
функциясының
өсу көрсеткіші деп аталады. Бұл функцияның аргументі
ретінде уақыт ![]() қабылданады.
Сондықтан түпнұсқаның
қабылданады.
Сондықтан түпнұсқаның ![]() құрамында Хэвисайд
функциясы деп аталатын
құрамында Хэвисайд
функциясы деп аталатын
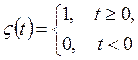 (3.52)
(3.52)
көбейткіші бар деп есептелінеді.
Аталған шарттар орындалса, онда ![]() функциясының
бейнесі деп аталатын меншіксіз интеграл (Лаплас операторы)
функциясының
бейнесі деп аталатын меншіксіз интеграл (Лаплас операторы)
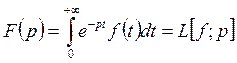 (3.53)
(3.53)
![]() жартыжазықтығында
абсолют және бірқалыпты жинақты. Бұл аймақта
жартыжазықтығында
абсолют және бірқалыпты жинақты. Бұл аймақта ![]() аналитикалық
функция, ол
аналитикалық
функция, ол ![]() түпбейнесінің
Лаплас операторы (35.3) көмегімен түрлендірілген бейнесі. Бұл
дерек шартты түрде
түпбейнесінің
Лаплас операторы (35.3) көмегімен түрлендірілген бейнесі. Бұл
дерек шартты түрде
![]() (3.54)
(3.54)
деп жазылады.
Лаплас интегралы (3.53) жалпы жағдайда комплекс
параметрден ![]() тәуелді.
Ондағы интегралданушы функция
тәуелді.
Ондағы интегралданушы функция ![]() болып,
болып, ![]() -да өшуші экспонентадан тезірек
кемиді:
-да өшуші экспонентадан тезірек
кемиді:
![]()
Ал, (3.53)-те ![]() өшіруші көбейткішінің
енгізілуі тіпті
өшіруші көбейткішінің
енгізілуі тіпті ![]() уақыт
осінде өсетін, бірақ,
уақыт
осінде өсетін, бірақ, ![]() -ден тез емес, функцияларды да
түрлендіруге мүмкіндік береді.
-ден тез емес, функцияларды да
түрлендіруге мүмкіндік береді.
Лаплас түрлендіруінің қасиеттері.
1. Сызықтық қасиет:
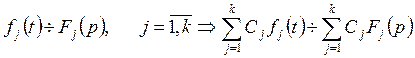 , (3.55)
, (3.55)
![]()
2. Ұқсастық теоремасы:
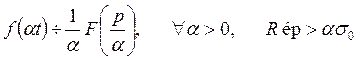 . (3.56)
. (3.56)
3. Ығысу теоремасы:
![]() (3.57)
(3.57)
4. Кешігу теоремасы:
![]() (3.58)
(3.58)
5.
Түпнұсқаны
дифференциалдау. Түпнұсқаның туындылары да ![]() түпнұсқа
болса, онда:
түпнұсқа
болса, онда:
![]()
![]() (3.59)
(3.59)
![]()
6. Бейнені дифференциалдау:
![]() (3.60)
(3.60)
7. Түпнұсқаны интегралдау:
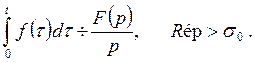 (3.61)
(3.61)
8.
Бейнені интегралдау. Егер ![]() түпнұсқа
болса, онда
түпнұсқа
болса, онда
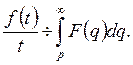 (3.62)
(3.62)
Егер ![]() түпнұсқалар
болса, онда олардың орамасы:
түпнұсқалар
болса, онда олардың орамасы:
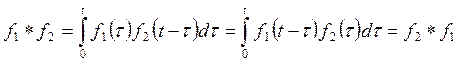 . (3.63)
. (3.63)
9. Бейнелерді көбейту теоремасы:
![]() . (3.64)
. (3.64)
Әдебиеттер тізімі
1. Мустахишев К.М., Ералиев С.Е., Атабай Б.Ж. Математика (толық курс). - Алматы: “TST-Company”, 2009. -429 б.
2. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. –М.: Наука, 2000.
3. Сборник задач по математике для ВТУЗов. Ч.1 Линейная алгебра и основы математического анализа. Под. Ред. А.В. Ефимова, Б.П. Демидовича. - М.: Наука, 2002.
4. Кузнецов Л.А. Сборник заданий по высшей математике (типовые расчеты). - М.: Высшая школа, 2003.
5. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. - М.: Наука, 2001.
6. Курош А.Г. Курс высшей алгебры. - М.: Наука, 1962.
7. Письменный Д.Т. Конспект лекций по высшей математике (полный курс). - М.: Айрис пресс, 2004.
8. Рябушко А.П. и др. Индивидуальные задания по высшей математике. - Минск-Алматы, 2002, чч 1,2,3.
9. Лунгу К.Н. и др. Сборник задач по высшей математике (с контрольными работами). - М: Айрис пресс, 2005, 1,2-курсы.
10. Kazbek Khasseinov Canons of mathematics. - Moscow: Nauka, 2007.
Мазмұны
|
1-модуль. Сызықтық алгебра, аналитикалық геометрия және комплекс сандар |
3 |
|
1-дәріс. Анықтауыштар, матрицалар және сызықтық теңдеулер жүйелері |
3 |
|
2-дәріс. Үш өлшемді кеңістіктегі векторлар. Түзу мен жазықтық |
7 |
|
3-дәріс. Екінші ретті қисықтар мен беттер |
13 |
|
2-модуль. Бір айнымалы функцияларының дифференциалдық есептеуі |
19 |
|
4-дәріс. Функцияның шегі |
19 |
|
5-дәріс. Функцияның үзіліссіздігі |
23 |
|
6-дәріс. Функцияның туындысы мен дифференциалы |
25 |
|
7-дәріс. Функцияны туындыларының көмегімен зерттеу |
33 |
|
3-модуль. Бір айнымалы функцияларының интегралдық есептеуі |
36 |
|
8-дәріс. Алғашқы бейне функциясы – анықталмаған интеграл |
36 |
|
9-дәріс. Рационал функцияларды интегралдау |
39 |
|
10-дәріс. Анықталған интегралдар |
42 |
|
11-дәріс. Операторлық есептеу |
48 |
|
Әдебиеттер тізімі |
50 |