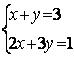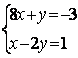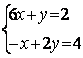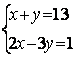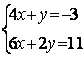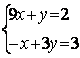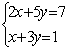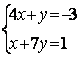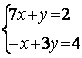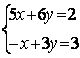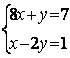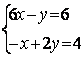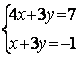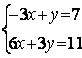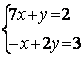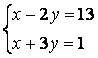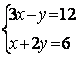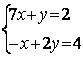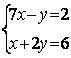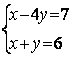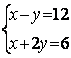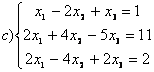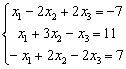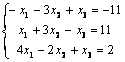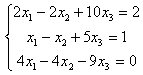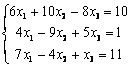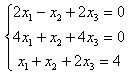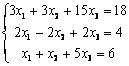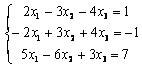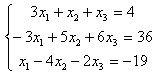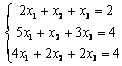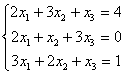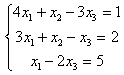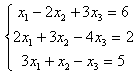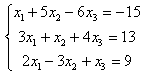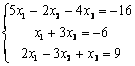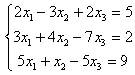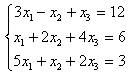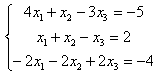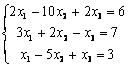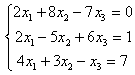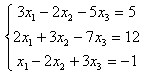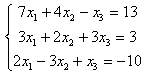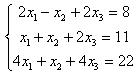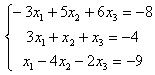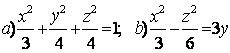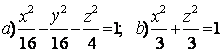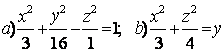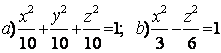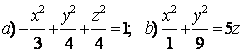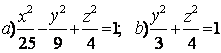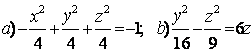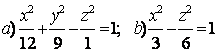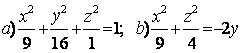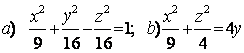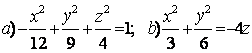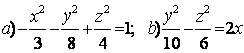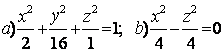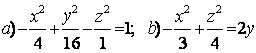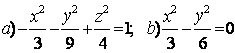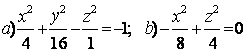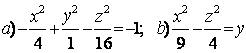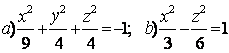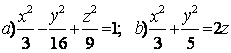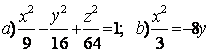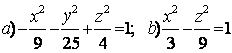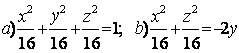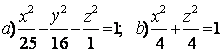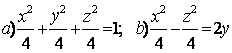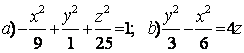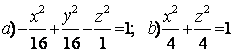Некоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра математики
МАТЕМАТИКА 1
Методические указания и задания к расчетно-графической работе
для студентов всех форм обучения и специальностей 5В071800 – Электроэнергетика, 5В071700- Теплоэнергетика и 5В071900 - Радиотехника, электроника и телекоммуникации и 5В070200 – Автоматизация управления
Часть 1
Алматы 2010
СОСТАВИТЕЛЬ: А.Ж. Масанова, Г.А. Ултаракова. Математика 1. Часть 1. Векторная и линейная алгебры. Аналитическая геометрия. Методические указания и задания к расчетно-графической работе для студентов всех форм обучения всех специальностей, -Алматы: АУЭС, 2010.- 25 с.
Методические указания и задания к расчетно-графической работе содержат раздел программы первого семестра курса математики для студентов всех форм обучения всех специальностей АУЭС: векторная и линейная алгебры, аналитическая геометрия.
Приведены основные теоретические вопросы программы. Дано решение типового варианта.
Эти методические указания могут быть использованы студентами специальностей 5В071800 – Электроэнергетика, 5В071700- Теплоэнергетика и 5В071900 - Радиотехника, электроника и телекоммуникации и 5В070200 – Автоматизация управления в качестве РГР №1 (по курсу «Математика 1») в первом семестре обучения.
1 Типовой расчёт. Векторная и линейная алгебры. Аналитическая геометрия
1.1 Теоретические вопросы
1 Определители, их свойства, вычисление.
2 Матрицы, действия над ними, обратная матрица.
3 Векторы, их длина, линейные операции над векторами. Коллинеарность.
4 Скалярное, векторное, смешанное произведения векторов, их приложения.
5 Различные уравнения прямой на плоскости и в пространстве.
6 Уравнения плоскости.
7 Угол между прямыми, плоскостями, прямой и плоскостью.
8 Расстояние от точки до прямой и до плоскости.
9 Эллипс, гипербола, парабола. Их канонические уравнения.
10 Поверхности второго порядка.
11 Приведение общих уравнений кривых и поверхностей второго порядка к каноническому виду.
12 Ранг матрицы и его вычисление.
13 Различные методы решения систем линейных уравнений:
а) правило Крамера;
б) метод Гаусса;
в) с помощью обратной матрицы.
14 Однородные системы линейных уравнений.
1.2 Расчётные задания
1 Дан определитель третьего порядка. Требуется найти:
а) минор ![]() и алгебраическое дополнение
и алгебраическое дополнение ![]() элемента
элемента ![]() ;
;
б) определитель по правилу треугольника (правилу Саррюса).
Т а б л и ц а 1
|
1.1 |
1.2 |
1.3 |
|
1.4 |
1.5 |
1.6 |
|
1.7 |
1.8 |
1.9 |
|
1.10 |
1.11 |
1.12 |
продолжение таблицы 1
|
1.13 |
1.14 |
1.15 |
|
1.16 |
1.17 |
1.18 |
|
1.19 |
1.20 |
1.21 |
|
1.22 |
1.23 |
1.24 |
|
1.25 |
1.26 |
1.27 |
|
1.28 |
1.29 |
1.30 |
2 Даны матрицы А, В, С. Требуется найти:
а) произведение матриц АВ или ВС, если возможно. Объяснить почему, если невозможно;
б) матрицу ![]() , обратную матрице А.
, обратную матрице А.
Т а б л и ц а 2
|
2.1 |
А= |
|
2.2 |
А= |
продолжение таблицы 2
|
2.3 |
А= |
|
2.4 |
А= |
|
2.5 |
А= |
|
2.6 |
А= |
|
2.7 |
А= |
|
2.8 |
А= |
|
2.9 |
А= |
|
2.10 |
А= |
|
2.11 |
А= |
|
2.12 |
А= |
|
2.13 |
А= |
продолжение таблицы 2
|
2.14 |
А= |
|
2.15 |
А= |
|
2.16 |
А= |
|
2.17 |
А= |
|
2.18 |
А= |
|
2.19 |
А= |
|
2.20 |
А= |
|
2.21 |
А= |
|
2.22 |
А= |
|
2.23 |
А= |
|
2.24 |
А= |
продолжение таблицы 2
|
2.25 |
А= |
|
2.26 |
А= |
|
2.27 |
А= |
|
2.28 |
А= |
|
2.29 |
А= |
|
2.30 |
А= |
3 Даны точки А и В; и вектора ![]() . Требуется найти:
. Требуется найти:
а) модуль (длину) вектора ![]() и середину отрезка АВ;
и середину отрезка АВ;
б) проекцию
вектора![]() ;
;
в) площадь
параллелограмма, полученного из векторов ![]() ;
;
г) объем
пирамиды, построенной из векторов
![]() .
.
Т а б л и ц а 3
|
3.1 |
А(5, -4, 3), В(1, 2, -8), |
3.2 |
А(-3,
1, 0), В(7, 1, -5), |
|
3.3 |
А(0, 4, 5), В(3, -2, 1),
|
3.4 |
А(3, -2, 5), В(4, 5, 7),
|
|
3.5 |
А(2, -3, 7), В(3, 2, 8), |
3.6 |
А(2, -1, 7), В(6, 3, 4) , |
|
3.7 |
А(3, 1, 7), В(2, -3, 9),
|
3.8 |
А(2, 1, -6), В(1, 4, 9) ,
|
|
3.9 |
А(2, -4, 8), В(5, 4, 7),
|
3.10 |
А(3, 2, 5), В(4, 0, -3) ,
|
продолжение таблицы 3
|
3.11 |
А(2, 3, -1),В(-6, 4, 2),
|
3.12 |
А(-4, 2, 3), В(8, 7, -2),
|
|
3.13 |
А(5, 3, 6), В(-2, 3, 5), |
3.14 |
А(0, 6, 0), В(5, 3, -4),
|
|
3.15 |
А(4, 2, 0), В(1, -7, 8), |
3.16 |
А(4, 2, 5), В(-1, 0, 6),
|
|
3.17 |
А(3,-5, 8), В(6, 3, 9),
|
3.18 |
А(7, 2, 2), В(-5, 7, -7) , |
|
3.19 |
А(5, -3, 1), В(2, 3, 7), |
3.20 |
А(8, -6, 4), В(10, 5, 1),
|
|
3.21 |
А(5, 6,-8), В(8, 10,7), |
3.22 |
А(1, -1, 3), В(6, 5, 8),
|
|
3.23 |
А(3, 5,-7), В(8, 4, 1),
|
3.24 |
А(6, -6, 5), В(4, 9, 5),
|
|
3.25 |
А(4,6,11), В(9,3,-4),
|
3.26 |
А(5, 7, 4),В(4,-10, 9), |
|
3.27 |
А(-9, 8, 9), В(7, 1,-2),
|
3.28 |
А(5, 2, 6), В(1, 8, -2),
|
|
3.29 |
А(2, 8, -9), В(7, 5,-5),
|
3.30 |
А(-2, 7, 0), В(6, 3, 5),
|
4 Даны точки ![]() на плоскости и уравнение прямой
на плоскости и уравнение прямой ![]() . Записать
уравнение прямой:
. Записать
уравнение прямой:
а) ![]() -проходящей через эти точки;
-проходящей через эти точки;
б) ![]() - в
виде общего уравнения прямой;
- в
виде общего уравнения прямой;
в) ![]() - в
виде уравнения
прямой с угловым коэффициентом;
- в
виде уравнения
прямой с угловым коэффициентом;
г) ![]() - в виде уравнения прямой в отрезках;
- в виде уравнения прямой в отрезках;
д) ![]() , проходящей через точку
, проходящей через точку ![]() и перпендикулярную
и перпендикулярную ![]() .
.
Т а б л и ц а 4
|
4.1 |
|
4.2 |
|
|
4.3 |
|
4.4 |
|
|
4.5 |
|
4.6 |
6 |
|
4.7 |
|
4.8 |
|
|
4.9 |
|
4.10 |
|
|
4.11 |
|
4.12 |
|
|
4.13 |
|
4.14 |
|
|
4.15 |
|
4.16 |
|
продолжение таблицы 4
|
4.17 |
|
4.18 |
|
|
4.19 |
|
4.20 |
|
|
4.21 |
|
4.22 |
|
|
4.23 |
|
4.24 |
|
|
4.25 |
|
4.26 |
|
|
4.27 |
|
4.28 |
|
|
4.29 |
|
4.30 |
|
5 Даны точки ![]() . Требуется:
. Требуется:
а) составить
уравнение плоскости ![]()
б) записать
![]() в виде общего уравнения плоскости;
в виде общего уравнения плоскости;
в) записать
![]() в виде уравнения плоскости
в отрезках;
в виде уравнения плоскости
в отрезках;
г) записать
![]() в виде общего уравнения плоскости, проходящей через точку
в виде общего уравнения плоскости, проходящей через точку ![]() ;
;
д) составить
каноническое уравнение прямой ![]()
е) записать
параметрическое уравнение прямой ![]() ;
;
д) составить
каноническое уравнение прямой ![]() ;
;
е) записать
параметрическое уравнение прямой ![]() ;
;
ж) составить уравнение прямой ![]() , перпендикулярной плоскости
, перпендикулярной плоскости
![]() .
.
Т а б л и ц а 5
|
5.1 |
|
5.2 |
|
|
5.3 |
|
5.4 |
|
|
5.5 |
|
5.6 |
|
|
5.7 |
|
5.8 |
|
|
5.9 |
|
5.10 |
|
|
5.11 |
|
5.12 |
|
|
5.13 |
|
5.14 |
|
|
5.15 |
|
5.16 |
|
|
5.17 |
|
5.18 |
|
|
5.19 |
|
5.20 |
|
|
5.21 |
|
5.22 |
|
|
5.23 |
|
5.24 |
|
продолжение таблицы 5
|
5.25 |
|
5.26 |
|
|
5.27 |
|
5.28 |
|
|
5.29 |
|
5.30 |
|
6. Решить систему:
а) методом Крамера;
б) матричным методом (с помощью обратной матрицы).
Т а б л и ц а 6
|
6.1 |
|
6.2 |
|
6.3 |
|
|
6.4 |
|
6.5 |
|
6.6 |
|
|
6.7 |
|
6.8 |
|
6.9 |
|
|
6.10 |
|
6.11 |
|
6.12 |
|
|
6.13 |
|
6.14 |
|
6.15 |
|
|
6.16 |
|
6.17 |
|
6.18 |
|
|
6.19 |
|
6.20 |
|
6.21 |
|
|
6.21 |
|
6.23 |
|
6.24 |
|
|
6.23 |
|
6.26 |
|
6.27 |
|
|
6.28 |
|
6.29 |
|
6.30 |
|
7 Дана система уравнений. Требуется:
а) проверить совместность системы методом Гаусса;
б) решить систему, если она совместна:
в) найти ранг матрицы коэффициентов и расширенной матрицы системы.
Т а б л и ц а 7
|
7.1 |
7.2 |
|
7.3 |
7.4
|
|
7.5 |
7.6 |
|
7.7 |
7.8 |
|
7.9
|
7.10 |
|
7.11 |
7.12 |
|
7.13 |
7.14 |
|
7.15 |
7.16 |
|
7.17 |
7.18
|
|
7.19 |
7.20 |
|
7.21 |
7.22 |
|
7.23 |
7.24 |
продолжение таблицы 7
|
7.25 |
7.26 |
|
7.27 |
7.28 |
|
7.29 |
7.30 |
8 Даны точка А; радиус окружности R; полуоси кривых - a,b; уравнение прямой – D. Требуется:
а) записать уравнение окружности с центром в точке А и радиусом R;
б) записать каноническое уравнение эллипса с полуосями а и b. Найти координаты его фокусов, эксцентриситет;
в) записать каноническое уравнение гиперболы с действительной полуосью а и мнимой - b. Найти координаты его фокусов, эксцентриситет, уравнения асимптот;
г) записать каноническое уравнение параболы с вершиной в начале координат и если D ее директриса. Найти координаты его фокуса, эксцентриситет;
д) сделать схематический чертеж эллипса, гиперболы, параболы.
Т а б л и ц а 8
|
8.1 |
A(2,-4), R=4, a=1, b=3, D: x=-5 |
8.2 |
A(-8,2), R=1, a=6, b=5, D: x=-5 |
|
8.3 |
A(1,-4), R=5, a=8, b=3, D: y=-6 |
8.4 |
A(5,-4), R=2, a=6, b=4, D: y=-2 |
|
8.5 |
A(2,-5), R=7, a=3, b=2, D: x=4 |
8.6 |
A(1,8), R=5 , a=3, b=2, D: x=-3 |
|
8.7 |
A(3,-4), R=9, a=7, b=6, D: y=-2 |
8.8 |
A(10,1), R=8, a=1, b=6, D: y=-4 |
|
8.9 |
A(5,-4), R=1, a=6, b=4, D: x=-5 |
8.10 |
A(6,3), R=8 , a=2, b=3, D: x=-5 |
|
8.11 |
A(1,-3), R=5 , a=8, b=2, D: y=6 |
8.12 |
A(5,5), R=2, a=1, b=3, D: y=-7 |
|
8.13 |
A(2,-6), R=7, a=3, b=4, D: x=5 |
8.14 |
A(12,6), R=7, a=6, b=2, D: x=-5 |
|
8.15 |
A(3,4), R=9 , a=2, b=6, D: y=-8 |
8.16 |
A(0,5), R=4, a=6, b=4, D: y=8 |
|
8.17 |
A(2,-9), R=7, a=5, b=2, D: x=6 |
8.18 |
A(-5,0), R=7, a=4, b=5, D: x=1 |
|
8.19 |
A(8,4), R=6 , a=8, b=5, D: y=2 |
8.20 |
A(5,1), R=2, a=9, b=1, D: x=-1 |
|
8.21 |
A(5,-4), R=4, a=6, b=4, D: x=1 |
8.22 |
A(-3,2), R=4, a=8, b=4, D: y=1 |
|
8.23 |
A(1,8), R=5, a=9, b=4, D: y=-6 |
8.24 |
A(9,1), R=6, a=4, b=7, D: x=-3 |
|
8.25 |
A(2,-5), R=7, a=7, b=4, D: x=9 |
8.26 |
A(-9,2), R=7, a=1, b=8, D: y=7 |
|
8.27 |
A(7,4), R=5, a=1, b=7, D: y=8 |
8.28 |
A(11,-4), R=2, a=2, b=4, D: x=8 |
|
8.29 |
A(-2,5), R=5, a=7, b=1, D: x=8 |
8.30 |
A(12,4), R=7, a=3, b=5, D: y=-9 |
9 Определить вид (название) поверхности второго порядка и сделать схематический чертеж.
Т а б л и ц а 9
|
9.1 |
|
9.2 |
|
|
9.3 |
|
9.4 |
|
|
9.5 |
|
9.6 |
|
|
9.7 |
|
9.8 |
|
|
9.9 |
|
9.10 |
|
|
9.11 |
|
9.12 |
|
|
9.13 |
|
9.14 |
|
|
9.15 |
|
9.16 |
|
|
9.17 |
|
9.18 |
|
|
9.19 |
|
9.20 |
|
|
9.21 |
|
9.22 |
|
|
9.23 |
|
9.24 |
|
|
9.25 |
|
9.26 |
|
|
9.27 |
|
9.28 |
|
продолжение таблицы 9
|
9.29 |
|
9.30 |
|
10 Привести к каноническому виду уравнение кривой второго порядка, построить эту кривую
Т а б л и ц а 10
|
10.1 |
|
10.2 |
|
|
|
10.3 |
|
10.4 |
|
|
|
10.5 |
|
10.6 |
|
|
|
10.7 |
|
10.8 |
|
|
|
10.9 |
|
10.10 |
|
|
|
10.11 |
|
10.12 |
|
|
|
10.13 |
|
10.14 |
|
|
|
10.15 |
|
10.16 |
|
|
|
10.17 |
|
10.18 |
|
|
|
10.19 |
|
10.20 |
|
|
|
10.21 |
|
10.22 |
|
|
|
10.23 |
|
10.24 |
|
|
|
10.25 |
|
10.26 |
|
|
|
10.27 |
|
10.28 |
|
|
|
10.29 |
|
10.30 |
|
|
1.3 Решение типового варианта
1 Дан определитель третьего порядка  . Требуется найти:
. Требуется найти:
а) минор ![]() и алгебраическое дополнение
и алгебраическое дополнение ![]() элемента
элемента ![]() ;
;
б) определитель по правилу треугольника (правилу Саррюса).
Решение:
a) минор M![]() элемента a
элемента a![]() равен определителю, полученному
из данного после вычёркивания i-ой строки и j-го столбца. Таким образом,
вычёркиваем в нашем определителе вторую строку и третий столбец, получаем
равен определителю, полученному
из данного после вычёркивания i-ой строки и j-го столбца. Таким образом,
вычёркиваем в нашем определителе вторую строку и третий столбец, получаем ![]() .
Алгебраическое дополнение элемента a
.
Алгебраическое дополнение элемента a![]() вычисляем
по формуле A
вычисляем
по формуле A![]() =(-1)
=(-1)![]() M
M![]() . Значит А
. Значит А![]() =(-1)
=(-1)![]() 11= -11;
11= -11;
б) правило треугольника: определитель третьего порядка равен сумме шести членов; члены со знаком плюс получают при перемножении по три элемента определителя, взятых
по схеме 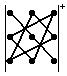 , члены со знаком минус – по схеме
, члены со знаком минус – по схеме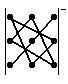 . Поэтому
. Поэтому 
![]()
Формула разложения по третьему столбцу имеет вид 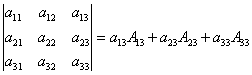 .
Таким образом, вычисляем определитель третьим способом:
.
Таким образом, вычисляем определитель третьим способом:
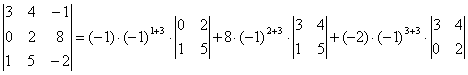 = 2 –
88 – 12= =- 98;
= 2 –
88 – 12= =- 98;
2 Даны матрицы А=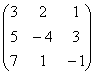 , В=
, В=![]() , С=
, С=![]() . Требуется найти:
. Требуется найти:
а) произведение матриц АВ или ВС, если возможно. Объяснить почему, если невозможно;
б) матрицу ![]() , обратную матрице А;
, обратную матрице А;
Решение:
а)
произведение матриц АВ возможно, если число столбцов матрицы А равно числу
строк матрицы В. Размеры матриц: А![]() , В
, В![]() , С
, С![]() . Таким образом, А
. Таким образом, А![]() В
В![]() =
= ![]() – произведение невозможно. В
– произведение невозможно. В![]() С
С![]() =
= ![]() – произведение возможно. Произведением
матриц ВС является матрица Е, число строк которой равно числу строк матрицы В,
число столбцов равно числу столбцов матрицы :
– произведение возможно. Произведением
матриц ВС является матрица Е, число строк которой равно числу строк матрицы В,
число столбцов равно числу столбцов матрицы : ![]() .
Элемент
.
Элемент ![]() матрицы
Е равен сумме произведений i–ой строки матрицы А на j–ый столбец
матрицы В. Таким образом
матрицы
Е равен сумме произведений i–ой строки матрицы А на j–ый столбец
матрицы В. Таким образом
ВС
= ![]()
![]() =
= ![]() , где
, где ![]() .
.
Итак,
![]()
![]() ;
;
б)
обратная матрица для квадратной матрицы существует, если определитель матрицы
не равен нулю; не существует, если ![]() =0. Обратная матрица А
=0. Обратная матрица А![]() для матрицы А =
для матрицы А =  находится по формуле
находится по формуле 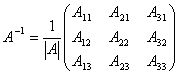 , где
, где ![]() – определитель матрицы
А;
– определитель матрицы
А; ![]() –
алгебраические дополнения элементов
–
алгебраические дополнения элементов ![]() . Найдём определитель матрицы А:
. Найдём определитель матрицы А: ![]() =
= 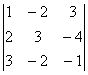 = -30
= -30![]() 0, следовательно А
0, следовательно А![]() существует. Определим
алгебраические дополнения всех элементов матрицы А:
существует. Определим
алгебраические дополнения всех элементов матрицы А: ![]()
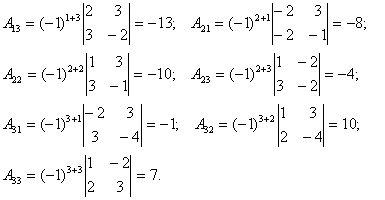
Составим
А![]() по
вышеуказанной формуле
по
вышеуказанной формуле
А![]() = =
= =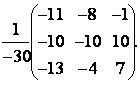
3 Даны точки А(7,
-9, 3) и В(1, 0, -5); и вектора ![]() .
Требуется найти:
.
Требуется найти:
а) модуль (длину) вектора ![]() и середину отрезка АВ;
и середину отрезка АВ;
б) проекцию
вектора![]() ;
;
в) площадь
параллелограмма, полученного из векторов ![]() ;
;
г) объем
пирамиды, построенной из векторов
![]() .
.
Решение:
а) для точек А(![]() ) и В(
) и В(![]() ) координаты вектора
) координаты вектора ![]()
![]() находят по формуле
находят по формуле ![]()
![]() = (
= (![]() ). Таким образом,
). Таким образом, ![]() (1-7, 0-(-9), -5-3) = (-6, 9,
-8); модуль (длина) вектора
(1-7, 0-(-9), -5-3) = (-6, 9,
-8); модуль (длина) вектора ![]() :
: ![]() . Значит,
. Значит, ![]() =
=![]() =
= ![]() ; cередина отрезка АВ имеет
координаты С
; cередина отрезка АВ имеет
координаты С![]() =
=![]() = С( 4, -9/2, -1 );
= С( 4, -9/2, -1 );
б) проекция
вектора![]() есть:
есть: ![]() ; где
; где ![]() - скалярное произведение векторов
- скалярное произведение векторов ![]() . Если векторы
ортогональны, то
. Если векторы
ортогональны, то ![]() ;
;
![]() , так
как
, так
как ![]() , то векторы
, то векторы ![]() и
и
![]() не
ортогональны; вычисляем далее
не
ортогональны; вычисляем далее ![]() ;
;
в) площадь параллелограмма, полученного из векторов ![]() , есть модуль вектора,
полученного от их векторного произведения векторов:
, есть модуль вектора,
полученного от их векторного произведения векторов: ![]() ; сначала находим координаты
; сначала находим координаты
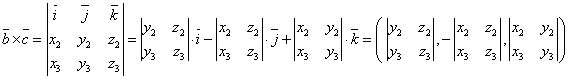 ;
;
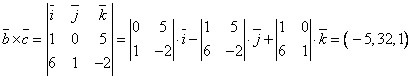 ;
далее определяем модуль вектора:
;
далее определяем модуль вектора: ![]() ;
;
г)
объем пирамиды, построенной из векторов ![]() ,
, ![]() ,
, ![]() , находится из модуля их смешанного
произведения:
, находится из модуля их смешанного
произведения: 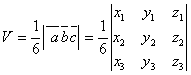
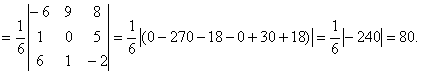
Так как ![]() , то эти векторы не компланарны.
, то эти векторы не компланарны.
4 Даны
точки А![]() (4,
-2), А
(4,
-2), А![]() (8, 1)
на плоскости и уравнение прямой L
(8, 1)
на плоскости и уравнение прямой L![]() : -x + 4y + 5 = 0. Записать
уравнение прямой:
: -x + 4y + 5 = 0. Записать
уравнение прямой:
а) ![]() -проходящей
через эти точки;
-проходящей
через эти точки;
б) ![]() - в виде общего уравнения прямой;
- в виде общего уравнения прямой;
в) ![]() - в виде уравнения прямой
с угловым коэффициентом;
- в виде уравнения прямой
с угловым коэффициентом;
г) ![]() -
в виде уравнения прямой в отрезках;
-
в виде уравнения прямой в отрезках;
д) ![]() ,
проходящей через точку
,
проходящей через точку ![]() и перпендикулярную
и перпендикулярную ![]() .
.
Решение:
a) уравнение прямой, проходящей через две точки (![]() )
и (
)
и (![]() ), находится по формуле
), находится по формуле ![]() .
Значит, уравнение прямой L
.
Значит, уравнение прямой L![]() имеет вид
имеет вид ![]() или
или ![]() ;
;
б) запишем уравнение прямой L![]() в общем виде Ax+By+C=0:
в общем виде Ax+By+C=0: 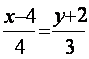
![]() , (A=3, B=-4, C=-20).
, (A=3, B=-4, C=-20).
Геометрический смысл коэффициентов: А,
В, – это координаты нормального (перпендикулярного) вектора прямой L![]() , т. е. вектор
, т. е. вектор ![]() ;
;
в) ![]() через
угловой коэффициент
y=kx+m:
через
угловой коэффициент
y=kx+m: 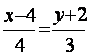
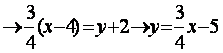 , ( k=
, ( k=![]() , m=-5 );
, m=-5 );
г) ![]() в виде отрезков
x/a+y/b=1:
в виде отрезков
x/a+y/b=1:
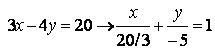 , ( a =
20/3, b = -5 );
, ( a =
20/3, b = -5 );
д) уравнение прямой
, проходящей через точку (![]() ) и
параллельно вектору
) и
параллельно вектору ![]() ,
имеет вид:
,
имеет вид: ![]() . Если вектор перпендикулярный прямой
. Если вектор перпендикулярный прямой ![]() есть
есть
![]() =(A;B)=(-1;4),
а прямая
=(A;B)=(-1;4),
а прямая ![]() также перпендикулярна
также перпендикулярна ![]() , тогда в нашем случае получаем, что направляющим
вектором
, тогда в нашем случае получаем, что направляющим
вектором ![]() будет
будет ![]() и уравнение имеет вид
и уравнение имеет вид
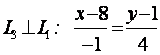 .
.
5 Даны точки А![]() (1,
2, -1), А
(1,
2, -1), А![]() (3, 3, 2), А
(3, 3, 2), А![]() (2, -3, 7). Требуется:
(2, -3, 7). Требуется:
а) составить
уравнение плоскости ![]()
б) записать
![]() в виде общего уравнения плоскости;
в виде общего уравнения плоскости;
в) записать
![]() в виде уравнения плоскости
в отрезках;
в виде уравнения плоскости
в отрезках;
г) записать
![]() в виде общего уравнения плоскости, проходящей через точку
в виде общего уравнения плоскости, проходящей через точку ![]() ;
;
д) составить
каноническое уравнение прямой ![]() ;
;
е) записать
параметрическое уравнение прямой ![]() ;
;
ж) составить
уравнение прямой ![]() ,
перпендикулярной плоскости
,
перпендикулярной плоскости ![]() .
.
Решение:
а) уравнение плоскости, проходящей через точки (![]() ), (
), (![]() ), (
), (![]() ) имеет вид:
) имеет вид: 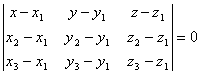 .
.
В нашем случае Р![]() :
: 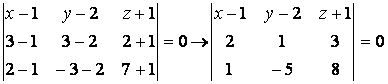 (*);
(*);
б) раскрыв определитель в правой части равенства
(*), получим уравнение плоскости Р![]() в
общем виде Ax+By+Cz+D=0:
в
общем виде Ax+By+Cz+D=0:
23x – 13y – 11z – 8 = 0, (A=23, B=-13, C=-11, D=-8).
Геометрический смысл коэффициентов: А, В, С – это
координаты нормального (перпендикулярного) вектора плоскости, т.
е. вектор ![]() ;
;
в) перенесём в общем уравнении плоскости свободный член –8 в правую часть и разделим обе части на 8. Получим уравнение плоскости в отрезках x/a+y/b+z/c=1:
![]() ,
,
где а=8/23, в=-8/13, с=-8/11 – это величины отрезков, отсекаемых плоскостью на координатных осях, считая от начала координат;
г) раскроем определитель в левой части
равенства (*) по элементам первой
строки: ![]() .
.
Получили уравнение плоскости в виде A(x-x![]() )+B(y-y
)+B(y-y![]() )+C(z-z
)+C(z-z![]() )=0
(
)=0
(![]() );
);
д) каноническое уравнение прямой, проходящей через две
точки (![]() ) и (
) и (![]() ) находится по формуле
) находится по формуле ![]() .
Значит, уравнение прямой L
.
Значит, уравнение прямой L![]() имеет вид
имеет вид ![]() или
или ![]() ;
;
е) уравнения
прямой в виде ![]() называются
каноническими, где a(m,n,p) – ее направляющий
вектор. В предыдущем
пункте уже найдены канонические уравнения прямых. Параметрическими
называются уравнения прямой в виде
называются
каноническими, где a(m,n,p) – ее направляющий
вектор. В предыдущем
пункте уже найдены канонические уравнения прямых. Параметрическими
называются уравнения прямой в виде 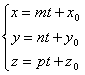 . Чтобы получить параметрические уравнения прямой,
приравняем канонические уравнения к параметру t и из
полученных равенств найдём x, y, z.
. Чтобы получить параметрические уравнения прямой,
приравняем канонические уравнения к параметру t и из
полученных равенств найдём x, y, z.
L![]() :
:![]() =
=
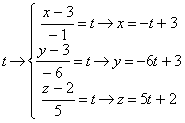 .
.
Итак, параметрическое уравнение L![]() :
: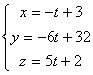 ;
;
ж) так как ![]() , то вектор
, то вектор ![]() оказывается направляющим вектором прямой
оказывается направляющим вектором прямой ![]() . Тогда
каноническое уравнение прямой
. Тогда
каноническое уравнение прямой ![]() имеет вид:
имеет вид:![]() .
.
6. Решить систему 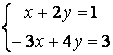
а) методом Крамера;
б) матричным методом (с помощью обратной матрицы).
Решение:
а) решение системы 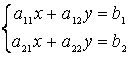 по правилу Крамера имеет вид
по правилу Крамера имеет вид ![]() , где
, где 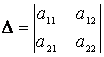 - определитель системы,
- определитель системы,
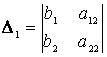 ,
,  - вспомогательные
определители, полученные из определителя системы заменой первого и второго
столбцов столбцом свободных членов.
- вспомогательные
определители, полученные из определителя системы заменой первого и второго
столбцов столбцом свободных членов.
В нашем случае 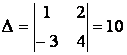 ,
, 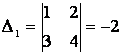 ,
,  . Таким образом, х = -1/5, у =3/5. Ответ
можно записать в виде вектора:
. Таким образом, х = -1/5, у =3/5. Ответ
можно записать в виде вектора: 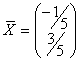 ;
;
б) в матричном виде решение системы 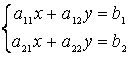 записывается так:
записывается так:![]() , где
, где 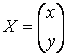 - матрица–столбец
неизвестных,
- матрица–столбец
неизвестных,  -
матрица-столбец свободных членов,
-
матрица-столбец свободных членов, ![]() - матрица, обратная для матрицы системы
- матрица, обратная для матрицы системы  .
.
Найдём обратную матрицу (см. пример
2б) для матрицы системы  . Так как определитель системы
. Так как определитель системы ![]() , то обратная матрица
существует и равна
, то обратная матрица
существует и равна  .
Тогда
.
Тогда 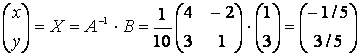 . Или ответ
в обычном виде: х=-1/5, у=3/5.
. Или ответ
в обычном виде: х=-1/5, у=3/5.
7 Дана система уравнений.  .
.
Требуется:
а) проверить совместность системы методом Гаусса;
б) найти ранг матрицы коэффициентов и расширенной матрицы системы;
в) решить систему, если она совместна.
Решение:
а) метод Гаусса заключается в последовательном
исключении неизвестных из уравнений системы с помощью элементарных
преобразований и приведении её к ступенчатому (треугольному) виду расширенной
матрицы системы. Матрица коэффициентов системы есть 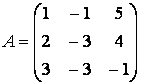 , расширенная
матрица -
, расширенная
матрица - 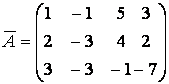 . Так
как матрица
. Так
как матрица ![]() содержится
в матрице
содержится
в матрице ![]() , то
достаточно производить элементарные преобразования только над строками матрицы
, то
достаточно производить элементарные преобразования только над строками матрицы ![]() : умножим первую строку
на -2 и прибавим ко второй, затем умножим первую строку на -3 и прибавим к
третьей. Получим, что матрица
: умножим первую строку
на -2 и прибавим ко второй, затем умножим первую строку на -3 и прибавим к
третьей. Получим, что матрица ![]() , а вместе с ней и матрица
, а вместе с ней и матрица![]() , приводится к
ступенчатой матрице, имеющей три ненулевые строки:
, приводится к
ступенчатой матрице, имеющей три ненулевые строки: 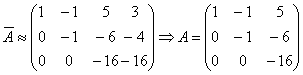 .
.
По теореме Кронекера-Капелли система совместна
(т.е. имеет хотя бы одно решение), если ранг матрицы системы равен рангу
расширенной матрицы ![]() ;
система не совместна (т.е. не имеет решений), если
;
система не совместна (т.е. не имеет решений), если ![]() ;
;
б) далее, по количеству ненулевых строк в ступенчатых
матрицах определяются ранги
матриц ![]() . Значит,
. Значит, ![]() и система совместна. Так как число
неизвестных n равно 3 и равен рангу матрицы системы (n=r), то система имеет одно
решение;
и система совместна. Так как число
неизвестных n равно 3 и равен рангу матрицы системы (n=r), то система имеет одно
решение;
в) таким
образом, данная система сводится к системе, соответствующей последней матрице:  ;
;
поднимаясь по этой системе снизу вверх, найдём
из последнего уравнения ![]() ; из предпоследнего
; из предпоследнего ![]() ; из первого
; из первого ![]() . Ответ: (-4; -2; 1).
. Ответ: (-4; -2; 1).
8 Даны точка А(3, -7); радиус
окружности R=6; ![]() = 2;
= 2; ![]() =
3 – полуоси кривых; D: у = -3 – уравнение прямой. Требуется:
=
3 – полуоси кривых; D: у = -3 – уравнение прямой. Требуется:
а) записать уравнение окружности с центром в точке А и радиусом R;
б) записать каноническое уравнение эллипса с полуосями а=2 и b=3. Найти координаты его фокусов, эксцентриситет;
в) записать каноническое уравнение гиперболы с действительной полуосью а=2 и мнимой – b=3. Найти координаты его фокусов, эксцентриситет, уравнения ассимптот;
г) записать каноническое уравнение параболы с вершиной в начале координат и если D: у = -3 ее директриса. Найти координаты его фокуса, эксцентриситет;
д) сделать чертеж эллипса, гиперболы, параболы.
Решение:
а) уравнение окружности с центром в точке ![]() радиуса R имеет вид
радиуса R имеет вид ![]() ,
значит в нашем варианте:
,
значит в нашем варианте: ![]() ;
;
б) каноническое уравнение эллипса с полуосями ![]() и
и ![]() имеет вид
имеет вид ![]() ; значит в нашем варианте:
; значит в нашем варианте: ![]() .
.
Фокусы эллипса – это точки ![]() , если
, если ![]() и
и ![]() , и эксцентриситет
, и эксцентриситет ![]() эллипса равен
эллипса равен ![]() , или, если
, или, если
![]() , то
, то ![]() и
и ![]() ,
, ![]() .
.
Итак,
в нашем варианте, поскольку ![]() , то,
, то, ![]() эксцентриситет равен
эксцентриситет равен ![]() , (
, (![]() ). Фокусы лежат на оси Оу:
). Фокусы лежат на оси Оу: ![]() . Изобразим эллипс на
координатной плоскости (см.рисунок 1),
где
. Изобразим эллипс на
координатной плоскости (см.рисунок 1),
где ![]() -
вершины эллипса.
-
вершины эллипса.
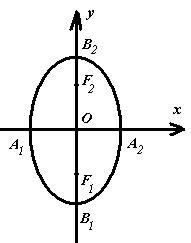
Рисунок 1
в) каноническое уравнение гиперболы с действительной полуосью
![]() , мнимой полуосью
, мнимой полуосью ![]() имеет вид
имеет вид ![]() ; с действительной полуосью
; с действительной полуосью ![]() и мнимой полуосью
и мнимой полуосью ![]() :
: ![]() или
или
![]() . Для гиперболы с действительной полуосью
. Для гиперболы с действительной полуосью ![]() , эксцентриситет равен
, эксцентриситет равен ![]() , где
, где ![]() ; уравнения асимптот гиперболы имеют вид
; уравнения асимптот гиперболы имеют вид ![]() ; фокусы – это точки
; фокусы – это точки ![]() , расположенные на действительной оси.
, расположенные на действительной оси.
По условию ![]() =2,
=2, ![]() =3,
поэтому каноническое уравнение гиперболы с действительной полуосью
=3,
поэтому каноническое уравнение гиперболы с действительной полуосью ![]() будет
будет ![]() . Для
неё полуфокусное расстояние
. Для
неё полуфокусное расстояние ![]() ;
эксцентриситет равен
;
эксцентриситет равен ![]() ;
фокусы:
;
фокусы: ![]() ;
уравнения асимптот:
;
уравнения асимптот: ![]() .
.
Гиперболу легко построить следующим образом: строим
прямоугольник со сторонами ![]() (у
нас
(у
нас ![]() ).
Диагонали прямоугольника являются асимптотами гиперболы, точки пересечения
сторон прямоугольника с действительной осью гиперболы – вершинами гиперболы (см.рисунок
2):
).
Диагонали прямоугольника являются асимптотами гиперболы, точки пересечения
сторон прямоугольника с действительной осью гиперболы – вершинами гиперболы (см.рисунок
2):
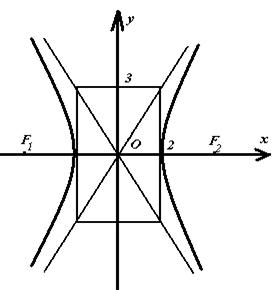
Рисунок 2
г) по условию, если директриса
параболы y=-p/2, то осью
симметрии параболы с вершиной в начале координат является ось Ох. Значит, её
каноническое уравнение имеет вид ![]() ; если директриса параболы x=-p/2, то осью симметрии параболы с вершиной в начале координат
является ось Оy. Значит, её
каноническое уравнение имеет вид
; если директриса параболы x=-p/2, то осью симметрии параболы с вершиной в начале координат
является ось Оy. Значит, её
каноническое уравнение имеет вид ![]() . Так как директриса параболы имеет уравнение у = -3,
то
. Так как директриса параболы имеет уравнение у = -3,
то ![]() и уравнение параболы будет:
и уравнение параболы будет: ![]() . Фокус параболы – это точка
. Фокус параболы – это точка ![]() , лежащая на оси симметрии. В нашем случае
фокус -
, лежащая на оси симметрии. В нашем случае
фокус - ![]() .
Построим параболу(см.рисунок 3).
.
Построим параболу(см.рисунок 3).
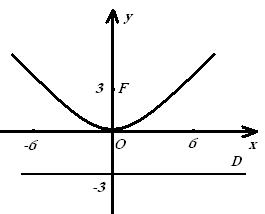
Рисунок 3
9 Определить вид (название) поверхности второго порядка и сделать схематический чертёж:
а) ![]() ; б)
; б) ![]() .
.
Решение:
а) ![]() - это
каноническое уравнение однополостного гиперболоида с осью симметрии Ох. Его
схематический чертёж (см.рисунок 4);
- это
каноническое уравнение однополостного гиперболоида с осью симметрии Ох. Его
схематический чертёж (см.рисунок 4);
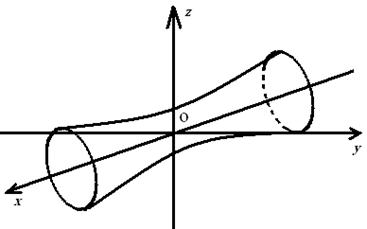
Рисунок 4
б) ![]() - это каноническое уравнение конуса второго порядка с
осью симметрии Оz и вершиной в начале координат. Его
схематический чертёж (см.рисунок 5);
- это каноническое уравнение конуса второго порядка с
осью симметрии Оz и вершиной в начале координат. Его
схематический чертёж (см.рисунок 5);

Рисунок 5
10 Привести к каноническому виду уравнение кривой
второго порядка ![]() и
построить эту кривую.
и
построить эту кривую.
Решение:
Уравнение вида

Определяют соответственно эллипс, гиперболу и
параболу, которые имеют центр симмметрии (эллипса и гиперболы) или вершину
параболы в точке ![]() .
Для этого применим метод выделения полных квадратов:
.
Для этого применим метод выделения полных квадратов:
![]()
Дополним члены, содержащие x, и члены содержащие y, до полных квадратов ![]() ,
,
![]() ,
,
![]() ,
,
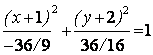 ,
, 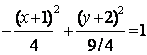 ,
,
т. е. имеем гиперболу, с центром в точке С(-1;-2), действительной полуосью b=3/2 (по оси 0y) и мнимой полуосью a=2. Построим его схематический чертёж (см. рисунок 6).
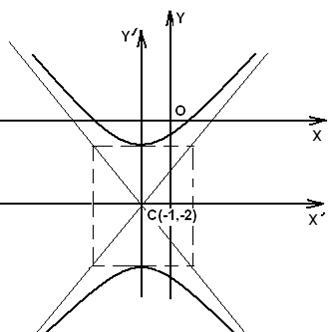
Рисунок 6
Список литературы
1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: в 2 ч. – М.: Высшая школа, 2003. – ч. 1,2.-352 с.
2. Сборник индивидуальных заданий по высшей математике: в 3 ч. (Рябушко А.П., Бархатов В.В. и др.). Под ред. Рябушко А.П. – Минск: Высш. школа, 2000.-ч.1.-396 с.
3. Кузнецов А.А. Сборник заданий по высшей математике: Типовые расчеты. –М.:Высш. Шк., 1983.-176с.
4. Хасеинов К.А. Каноны математики: Учебник. – Алматы, 2003.-686 с.
Содержание
1 Типовой расчёт. Векторная и линейная алгебра. Аналитическая геометрия.
1.1 Теоретические вопросы 3
1.2 Расчётные задания 3
1.3 Решение типового варианта 12
Список литературы 25

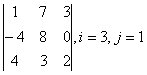
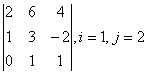
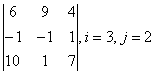
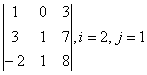
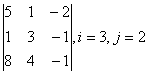
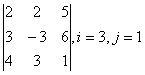
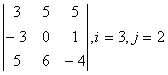
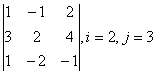

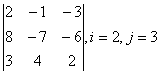
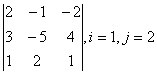
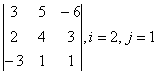
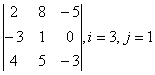
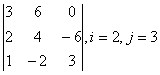

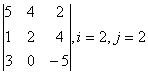
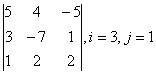
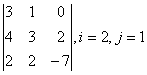
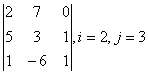
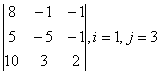
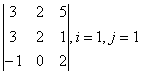
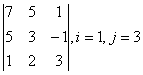

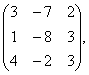 В=
В=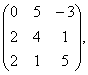 В=
В=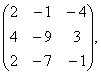 В=
В=
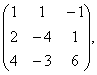 В=
В=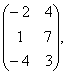 С=
С=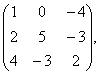 В=
В=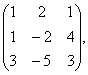 В=
В=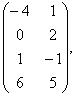 С=
С= В=
В= В=
В= В=
В=
 , В=
, В= С=
С= В=
В=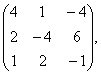 В=
В=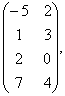 С=
С=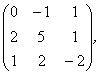 В=
В=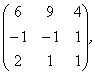 В=
В=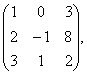 В=
В=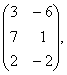
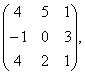 В=
В=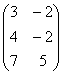 , С=
, С=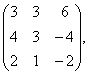 В=
В=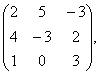 В=
В=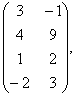 С=
С=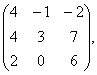 В=
В=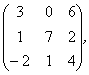 В=
В=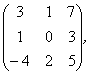 В=
В=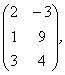
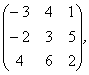 В=
В=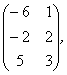 С=
С=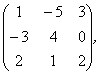 В=
В= В=
В=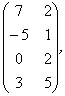 С=
С=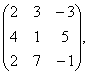 В=
В= В=
В=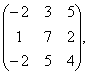 В=
В=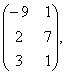
 В=
В=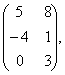 С=
С=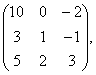 В=
В= В=
В= С=
С=