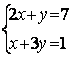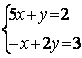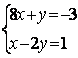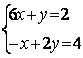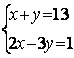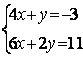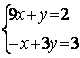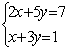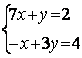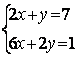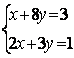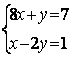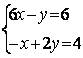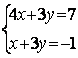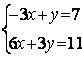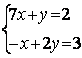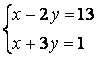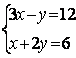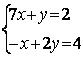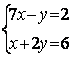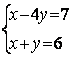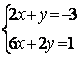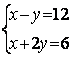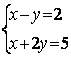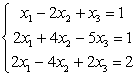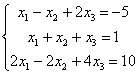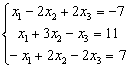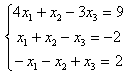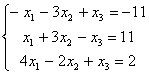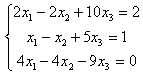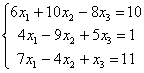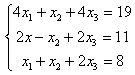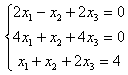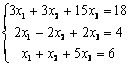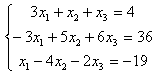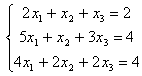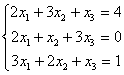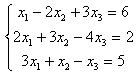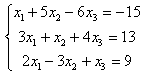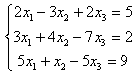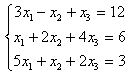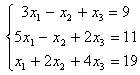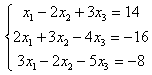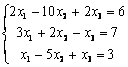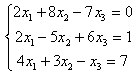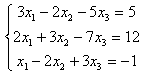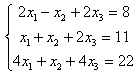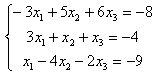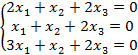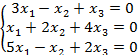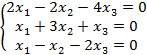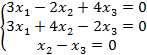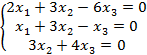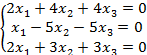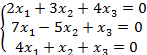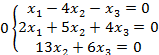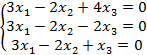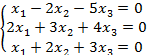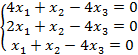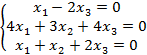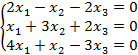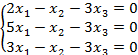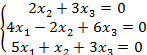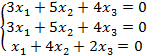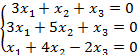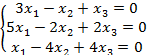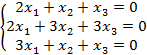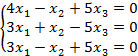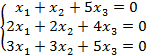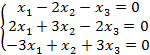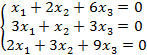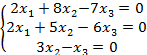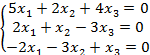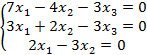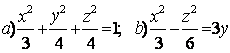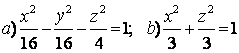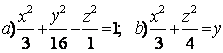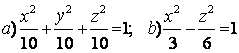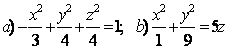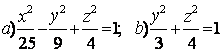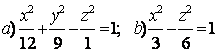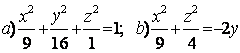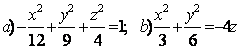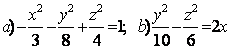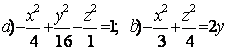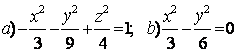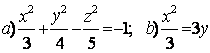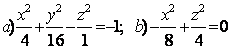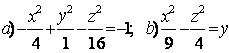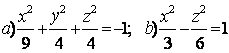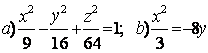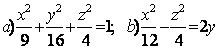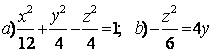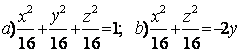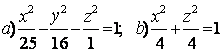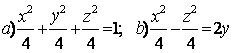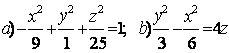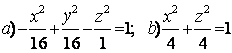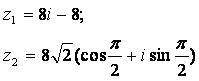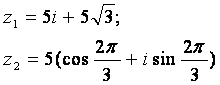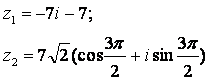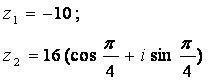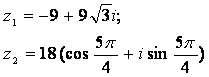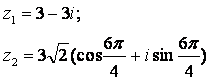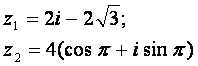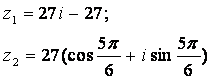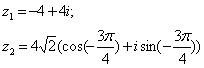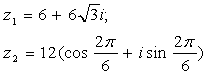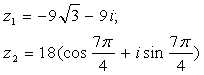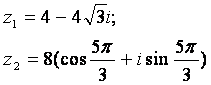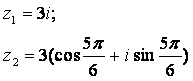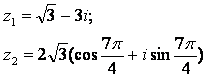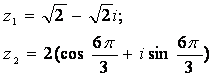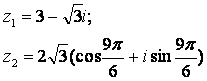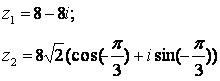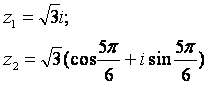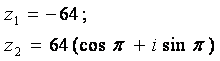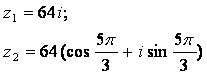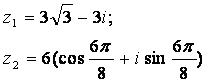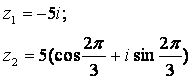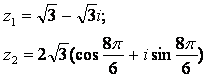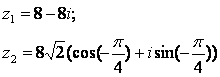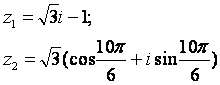Некоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра высшей математики
МАТЕМАТИКА 1
Методические указания и задания к расчетно-графической работе
для студентов специальностей 5В074600 – Космическая техника и технологии
Часть1
Алматы, 2013
Составители: Масанова А.Ж., Ултаракова Г.А. Математика 1. Методические указания и задания к расчетно-графической работе для студентов специальностей 5В074600 – Космическая техника и технологии. Часть1. – Алматы, 2013 –33 с.
Методические указания и задания к расчетно-графической работе содержат разделы программы первого семестра курса математики для студентов АУЭС: векторная и линейная алгебра, аналитическая геометрия, комплексные числа. Приведены основные теоретические вопросы программы. Дано решение задач типового варианта действующих заданий РГР.
Табл. 12, Ил. 6.
Рецензент: преп. Ибраева Л.К.
Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2013 г.
© НАО Алматинского университета энергетики и связи, 2013 г.
Сводный план 2013., поз.183
Введение
Математика играет важную роль в инженерно-технических исследованиях. Она является не только аппаратом количественного расчета, но также методом точного исследования и средством предельно четкой формулировки понятий и проблем. Математические методы стали составной частью любой технической дисциплины. Все это приводит к необходимости усиления прикладной направленности курса математики и повышения уровня фундаментальной математической подготовки.
РГР выполняется на отдельной тонкой тетради, в номере каждого задания вторая цифра указывает на вариант.
Расчётно-графическая работа. Векторная и линейная алгебры. Аналитическая геометрия
Цель: овладение фундаментальными понятиями и методами теории алгебры и геометрии. Получить навыки в вычислении определителей и операциях над матрицами и векторами, которые используются при решении систем уравнений; определять по виду уравнений кривых их геометрические свойства и взаимное расположение на плоскости или в пространстве. Выполнять все арифметические действия над комплексными числами.
Теоретические вопросы
1. Определители, их свойства, вычисление.
2. Матрицы, действия над ними, обратная матрица.
3. Векторы, их длина, линейные операции над векторами. Коллинеарность.
4. Скалярное, векторное, смешанное произведения векторов, их приложения.
5. Различные уравнения прямой на плоскости и в пространстве.
6. Уравнения плоскости.
7. Угол между прямыми, плоскостями, прямой и плоскостью.
8. Расстояние от точки до прямой и до плоскости.
9. Эллипс, гипербола, парабола. Их канонические уравнения.
10. Поверхности второго порядка.
11. Приведение общих уравнений кривых и поверхностей второго порядка к каноническому виду.
12. Ранг матрицы и его вычисление.
13. Различные методы решения систем линейных уравнений:
а) правило Крамера;
б) метод Гаусса;
в) с помощью обратной матрицы.
14. Однородные системы линейных уравнений.
15. Комплексные числа, модуль и главная часть к.ч., операции над к.ч., формула Муавра.
Расчётные задания
Задание 1. Дан определитель третьего порядка. Требуется найти:
а) минор ![]() и алгебраическое дополнение
и алгебраическое дополнение ![]() элемента
элемента ![]() ;
;
б) определитель по правилу треугольника (правилу Саррюса);
в) определитель методом разложения по i-ой строке и j-му столбцу.
|
1.1 |
1.2 |
1.3 |
|
|
1.4 |
1.5 |
1.6 |
|
|
1.7 |
1.8 |
1.9 |
|
|
1.10 |
1.11 |
1.12 |
|
|
1.13 |
1.14 |
1.15 |
|
|
1.16 |
1.17 |
1.18 |
|
|
1.19 |
1.20 |
1.21 |
|
|
1.22 |
1.23 |
1.24 |
|
|
1.25 |
1.26 |
1.27 |
|
1.28 |
1.29 |
1.30 |
|
Задание 2. Даны матрицы А, В, С. Требуется найти:
а) произведение матриц АВ или ВС, или СВ, если возможно. Объяснить, почему, если невозможно;
б) матрицу ![]() , обратную матрице А.
, обратную матрице А.
|
2.1 |
А= |
|
2.2 |
А= |
|
2.3 |
|
|
2.4 |
|
|
2.5 |
|
|
2.6 |
|
|
2.7 |
|
|
2.8 |
|
|
2.9 |
А= |
|
2.10 |
|
|
2.11 |
|
|
2.12 |
|
|
2.13 |
А= |
|
2.14 |
А= |
|
2.15 |
А= |
|
2.16 |
А= |
|
2.17 |
А= |
|
2.18 |
А= |
|
2.19 |
А= |
|
2.20 |
А= |
|
2.21 |
А= |
|
2.22 |
А= |
|
2.23 |
А= |
|
2.24 |
А= |
|
2.25 |
А= |
|
2.26 |
А= |
|
2.27 |
А= |
|
2.28 |
А= |
|
2.29 |
А= |
|
2.30 |
А= |
Задание 3. Даны
точки А и В; и вектора ![]() . Требуется найти:
. Требуется найти:
а) модуль (длину) вектора ![]() и середину отрезка АВ;
и середину отрезка АВ;
б) проекцию
вектора![]() ;
;
в) площадь
параллелограмма, полученного из векторов ![]() ;
;
г) объем
пирамиды, построенной из векторов
![]() .
.
|
3.1 |
А(5, -4, 3), В(1, 2, -8), |
3.2 |
А(-3,
1, 0), В(7, 1, -5), |
|
3.3 |
А(0, 4, 5), В(3, -2, 1),
|
3.4 |
А(3, -2, 5), В(4, 5, 7),
|
|
3.5 |
А(2, -3, 7), В(3, 2, 8), |
3.6 |
А(2, -1, 7), В(6, 3, 4) , |
|
3.7 |
А(3, 1, 7), В(2, -3, 9),
|
3.8 |
А(2, 1, -6), В(1, 4, 9) ,
|
|
3.9 |
А(2, -4, 8), В(5, 4, 7),
|
3.10 |
А(3, 2, 5), В(4, 0, -3) ,
|
|
3.11 |
А(2, 3, -1),В(-6, 4, 2),
|
3.12 |
А(-4, 2, 3), В(8, 7, -2),
|
|
3.13 |
А(5, 3, 6), В(-2, 3, 5), |
3.14 |
А(0, 6, 0), В(5, 3, -4),
|
|
3.15 |
А(4, 2, 0), В(1, -7, 8), |
3.16 |
А(4, 2, 5), В(-1, 0, 6),
|
|
3.17 |
А(3,-5, 8), В(6, 3, 9),
|
3.18 |
А(7, 2, 2), В(-5, 7, -7) , |
|
3.19 |
А(5, -3, 1), В(2, 3, 7), |
3.20 |
А(8, -6, 4), В(10, 5, 1),
|
|
3.21 |
А(5, 6,-8), В(8, 10,7), |
3.22 |
А(1, -1, 3), В(6, 5, 8),
|
|
3.23 |
А(3, 5,-7), В(8, 4, 1),
|
3.24 |
А(6, -6, 5), В(4, 9, 5),
|
|
3.25 |
А(4,6,11), В(9,3,-4),
|
3.26 |
А(5, 7, 4),В(4,-10, 9), |
|
3.27 |
А(-9, 8, 9), В(7, 1,-2),
|
3.28 |
А(5, 2, 6), В(1, 8, -2),
|
|
3.29 |
А(2, 8, -9), В(7, 5,-5),
|
3.30 |
А(-2, 7, 0), В(6, 3, 5),
|
Задание 4. Даны
точки ![]() на
плоскости и уравнение прямой
на
плоскости и уравнение прямой ![]() . Записать
уравнение прямой:
. Записать
уравнение прямой:
а) ![]() , проходящей через эти точки;
, проходящей через эти точки;
б) ![]() - в
виде общего уравнения прямой;
- в
виде общего уравнения прямой;
в) ![]() - в
виде уравнения
прямой с угловым коэффициентом;
- в
виде уравнения
прямой с угловым коэффициентом;
г) ![]() - в виде уравнения прямой в отрезках;
- в виде уравнения прямой в отрезках;
д) ![]() , проходящей через точку
, проходящей через точку ![]() и перпендикулярную
и перпендикулярную ![]() .
.
|
4.1 |
|
4.2 |
|
|
4.3 |
|
4.4 |
|
|
4.5 |
|
4.6 |
|
|
4.7 |
|
4.8 |
|
|
4.9 |
|
4.10 |
|
|
4.11 |
|
4.12 |
|
|
4.13 |
|
4.14 |
|
|
4.15 |
|
4.16 |
|
|
4.17 |
|
4.18 |
|
|
4.19 |
|
4.20 |
|
|
4.21 |
|
4.22 |
|
|
4.23 |
|
4.24 |
|
|
4.25 |
|
4.26 |
|
|
4.27 |
|
4.28 |
|
|
4.29 |
|
4.30 |
|
Задание 5. Даны
точки ![]() . Требуется:
. Требуется:
а) составить
уравнение плоскости ![]()
б) записать
![]() в виде общего уравнения плоскости;
в виде общего уравнения плоскости;
в) записать
![]() в виде уравнения плоскости
в отрезках;
в виде уравнения плоскости
в отрезках;
г) записать
![]() в виде общего уравнения плоскости, проходящей через точку
в виде общего уравнения плоскости, проходящей через точку ![]() ;
;
д) составить
каноническое уравнение прямой ![]() ;
;
е) записать
параметрическое уравнение прямой ![]() ;
;
ж) составить уравнение прямой ![]() , перпендикулярной плоскости
, перпендикулярной плоскости
![]() .
.
|
5.1 |
|
5.2 |
|
|
5.3 |
|
5.4 |
|
|
5.5 |
|
5.6 |
|
|
5.7 |
|
5.8 |
|
|
5.9 |
|
5.10 |
|
|
5.11 |
|
5.12 |
|
|
5.13 |
|
5.14 |
|
|
5.15 |
|
5.16 |
|
|
5.17 |
|
5.18 |
|
|
5.19 |
|
5.20 |
|
|
5.21 |
|
5.22 |
|
|
5.23 |
|
5.24 |
|
|
5.25 |
|
5.26 |
|
|
5.27 |
|
5.28 |
|
|
5.29 |
|
5.30 |
|
Задание 6. Решить систему:
а) методом Крамера;
б) матричным методом (с помощью обратной матрицы).
|
6.1 |
|
6.2 |
|
6.3 |
|
|
6.4 |
|
6.5 |
|
6.6 |
|
|
6.7 |
|
6.8 |
|
6.9 |
|
|
6.10 |
|
6.11 |
|
6.12 |
|
|
6.13 |
|
6.14 |
|
6.15 |
|
|
6.16 |
|
6.17 |
|
6.18 |
|
|
6.19 |
|
6.20 |
|
6.21 |
|
|
6.21 |
|
6.23 |
|
6.24 |
|
|
6.23 |
|
6.26 |
|
6.27 |
|
|
6.28 |
|
6.29 |
|
6.30 |
|
Задание 7. Дана система уравнений. Требуется:
а) проверить совместность системы методом Гаусса;
б) решить систему, если она совместна;
в) найти ранг матрицы коэффициентов и расширенной матрицы системы.
|
7.1 |
7.2 |
|
7.3 |
7.4 |
|
7.5 |
7.6 |
|
7.7 |
7.8 |
|
7.9
|
7.10 |
|
7.11 |
7.12 |
|
7.13 |
7.14 |
|
7.15 |
7.16 |
|
7.17 |
7.18
|
|
7.19 |
7.20 |
|
7.21 |
7.22 |
|
7.23 |
7.24 |
|
7.25 |
7.26 |
|
7.27 |
7.28 |
|
7.29 |
7.30 |
Задание 8. Решить однородную систему линейных уравнений.
|
8.1 |
8.2 |
8.3 |
|
8.4 |
8.5 |
8.6 |
|
8.7 |
8.8 |
8.9 |
|
8.1 |
8.11 |
8.12 |
|
8.13 |
8.14 |
8.15 |
|
8.16 |
8.17 |
8.18 |
|
8.19 |
8.20 |
8.21 |
|
8.22 |
8.23 |
8.24 |
|
8.25 |
8.26 |
8.27 |
|
8.28 |
8.29 |
8.30 |
Задание 9. Даны точка А; радиус окружности R; полуоси кривых - a,b; уравнение прямой – D. Требуется:
а) записать уравнение окружности с центром в точке А и радиусом R;
б) записать каноническое уравнение эллипса с полуосями а и b. Найти координаты его фокусов, эксцентриситет;
в) записать каноническое уравнение гиперболы с действительной полуосью а и мнимой - b. Найти координаты его фокусов, эксцентриситет, уравнения асимптот;
г) записать каноническое уравнение параболы с вершиной в начале координат и если D ее директриса. Найти координаты его фокуса, эксцентриситет;
д) сделать схематический чертеж эллипса, гиперболы, параболы.
|
9.1 |
A(2,-4), R=4, a=1, b=3, D: x=-5 |
9.2 |
A(-8,2), R=1, a=6, b=5, D: x=-5 |
|
9.3 |
A(1,-4), R=5, a=8, b=3, D: y=-6 |
9.4 |
A(5,-4), R=2, a=6, b=4, D: y=-2 |
|
9.5 |
A(2,-5), R=7, a=3, b=2, D: x=4 |
9.6 |
A(1,8), R=5 , a=3, b=2, D: x=-3 |
|
9.7 |
A(3,-4), R=9, a=7, b=6, D: y=-2 |
9.8 |
A(10,1), R=8, a=1, b=6, D: y=-4 |
|
9.9 |
A(5,-4), R=1, a=6, b=4, D: x=-5 |
9.10 |
A(6,3), R=8 , a=2, b=3, D: x=-5 |
|
9.11 |
A(1,-3), R=5 , a=8, b=2, D: y=6 |
9.12 |
A(5,5), R=2, a=1, b=3, D: y=-7 |
|
9.13 |
A(2,-6), R=7, a=3, b=4, D: x=5 |
9.14 |
A(12,6), R=7, a=6, b=2, D: x=-5 |
|
9.15 |
A(3,4), R=9 , a=2, b=6, D: y=-8 |
9.16 |
A(0,5), R=4, a=6, b=4, D: y=8 |
|
9.17 |
A(2,-9), R=7, a=5, b=2, D: x=6 |
9.18 |
A(-5,0), R=7, a=4, b=5, D: x=1 |
|
9.19 |
A(8,4), R=6 , a=8, b=5, D: y=2 |
9.20 |
A(5,1), R=2, a=9, b=1, D: x=-1 |
|
9.21 |
A(5,-4), R=4, a=6, b=4, D: x=1 |
9.22 |
A(-3,2), R=4, a=8, b=4, D: y=1 |
|
9.23 |
A(1,8), R=5, a=9, b=4, D: y=-6 |
9.24 |
A(9,1), R=6, a=4, b=7, D: x=-3 |
|
9.25 |
A(2,-5), R=7, a=7, b=4, D: x=9 |
9.26 |
A(-9,2), R=7, a=1, b=8, D: y=7 |
|
9.27 |
A(7,4), R=5, a=1, b=7, D: y=8 |
9.28 |
A(11,-4), R=2, a=2, b=4, D: x=8 |
|
9.29 |
A(-2,5), R=5, a=7, b=1, D: x=8 |
9.30 |
A(12,4), R=7, a=3, b=5, D: y=-9 |
Задание 10. Определить вид (название) поверхности второго порядка и сделать схематический чертеж.
|
10.1 |
|
10.2 |
|
|
10.3 |
|
10.4 |
|
|
10.5 |
|
10.6 |
|
|
10.7 |
|
10.8 |
|
|
10.9 |
|
10.10 |
|
|
10.11 |
|
10.12 |
|
|
10.13 |
|
10.14 |
|
|
10.15 |
|
10.16 |
|
|
10.17 |
|
10.18 |
|
|
10.19 |
|
10.20 |
|
|
10.21 |
|
10.22 |
|
|
10.23 |
|
10.24 |
|
|
10.25 |
|
10.26 |
|
|
10.27 |
|
10.28 |
|
|
10.29 |
|
10.30 |
|
Задание 11. Привести к каноническому виду уравнение кривой второго порядка, построить эту кривую.
|
11.1 |
|
11.2 |
|
|
|
11.3 |
|
11.4 |
|
|
|
11.5 |
|
11.6 |
|
|
|
11.7 |
|
11.8 |
|
|
|
11.9 |
|
11.10 |
|
|
|
11.11 |
|
11.12 |
|
|
|
11.13 |
|
11.14 |
|
|
|
11.15 |
|
11.16 |
|
|
|
11.17 |
|
11.18 |
|
|
|
11.19 |
|
11.20 |
|
|
|
11.21 |
|
11.22 |
|
|
|
11.23 |
|
11.24 |
|
|
|
11.25 |
|
11.26 |
|
|
|
11.27 |
|
11.28 |
|
|
|
11.29 |
|
11.30 |
|
|
Задание 12. Даны комплексные числа z1 и z2. Требуется найти:
а) модуль комплексного числа z1;
б) аргумент комплексного числа z1;
в) представление комплексного числа z1 в тригонометрической и показательной формах;
г) сумму комплексных чисел z1 и z2 аналитически и графически;
д) (z2)5;
е) произведение z1 z2 в тригонометрической форме;
ж) все комплексные корни ![]() (для вариантов с четными номерами) и
(для вариантов с четными номерами) и ![]() (для вариантов с нечетными номерами). Решение
изобразить на чертеже.
(для вариантов с нечетными номерами). Решение
изобразить на чертеже.
|
12.1 |
|
12.2 |
|
|
12.3 |
|
12.4 |
|
|
12.5 |
|
12.6 |
|
|
12.7 |
|
12.8 |
|
|
12.9 |
|
12.10 |
|
|
12.11 |
|
12.12 |
|
|
12.13 |
|
12.14 |
|
|
12.15 |
|
12.16 |
|
|
12.17 |
|
12.18 |
|
|
12.19 |
|
12.20 |
|
|
12.21 |
|
12.22 |
|
|
12.23 |
|
12.24 |
|
|
12.25 |
|
12.26 |
|
|
12.27 |
|
12.28 |
|
|
12.29 |
|
12.30 |
|
Решение типового варианта
Задание 1. Дан определитель третьего порядка 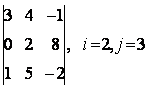 . Требуется найти:
. Требуется найти:
а) минор ![]() и алгебраическое дополнение
и алгебраическое дополнение ![]() элемента
элемента ![]() ;
;
б)определитель по правилу треугольника (правилу Саррюса);
в) определитель методом разложения по 2-ой строке и 3-му столбцу.
Решение:
a) минор M![]() элемента a
элемента a![]() равен определителю, полученному
из данного после вычёркивания i-ой строки и j-го столбца. Таким образом,
вычёркиваем в нашем определителе вторую строку и третий столбец, получаем
равен определителю, полученному
из данного после вычёркивания i-ой строки и j-го столбца. Таким образом,
вычёркиваем в нашем определителе вторую строку и третий столбец, получаем ![]() .
Алгебраическое дополнение элемента a
.
Алгебраическое дополнение элемента a![]() вычисляем
по формуле A
вычисляем
по формуле A![]() =(-1)
=(-1)![]() M
M![]() . Значит, А
. Значит, А![]() =(-1)
=(-1)![]() 11= -11;
11= -11;
б) правило треугольника: определитель третьего порядка равен сумме шести членов; члены со знаком плюс получают при перемножении по три элемента определителя, взятых
по
схеме 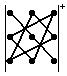 , члены со знаком минус – по схеме
, члены со знаком минус – по схеме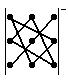 . Поэтому
. Поэтому 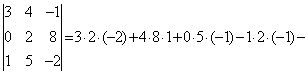
![]()
в)
формула разложения по третьему столбцу имеет вид: 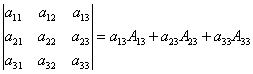 ,
,
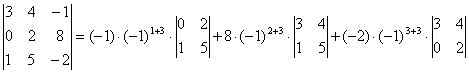 = 2 – 88 – 12=-98;
= 2 – 88 – 12=-98;
аналогично вычисляем определитель, разлагая по второй строке:
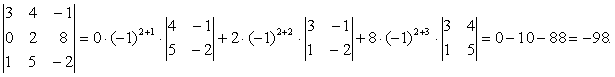
Задание 2. Даны матрицы А= , В=
, В=![]() , С=
, С=![]() . Требуется найти:
. Требуется найти:
а) произведение матриц АВ или ВС, или СВ, если возможно. Объяснить, почему, если невозможно;
б) матрицу ![]() , обратную матрице А.
, обратную матрице А.
Решение:
а) произведение матриц АВ возможно, если число
столбцов матрицы А равно числу строк матрицы В. Размеры матриц: А![]() , В
, В![]() , С
, С![]() . Таким образом, А
. Таким образом, А![]() В
В![]() – произведение невозможно (т.к.
– произведение невозможно (т.к.![]() ); В
); В![]() С
С![]() – произведение возможно (т.к.
– произведение возможно (т.к.![]() ). Произведением матриц
ВС является матрица Е, число строк которой равно числу строк матрицы В, число
столбцов равно числу столбцов матрицы :
). Произведением матриц
ВС является матрица Е, число строк которой равно числу строк матрицы В, число
столбцов равно числу столбцов матрицы : ![]() .
Элемент
.
Элемент ![]() матрицы
Е равен сумме произведений i–ой строки матрицы А на j–ый столбец
матрицы В. Таким образом,
матрицы
Е равен сумме произведений i–ой строки матрицы А на j–ый столбец
матрицы В. Таким образом,
ВС
= ![]()
![]() =
= ![]() , где
, где ![]() .
.
Итак,
![]()
![]() ;
;
б) обратная матрица для квадратной матрицы существует,
если определитель матрицы не равен нулю; и не существует, если ![]() =0. Обратная матрица А
=0. Обратная матрица А![]() для матрицы А =
для матрицы А =  находится по формуле
находится по формуле  , где
, где ![]() – определитель матрицы
А;
– определитель матрицы
А; ![]() –
алгебраические дополнения элементов
–
алгебраические дополнения элементов ![]() . Найдём определитель матрицы А:
. Найдём определитель матрицы А: ![]() =
= 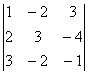 = -30
= -30![]() 0, следовательно А
0, следовательно А![]() существует.
существует.
Определим алгебраические дополнения всех элементов
матрицы А: ![]()
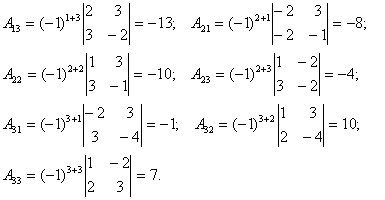
Составим А![]() по вышеуказанной формуле: А
по вышеуказанной формуле: А![]() =
= 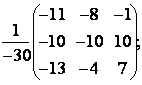 и далее необходимо сделать
проверку:
и далее необходимо сделать
проверку: 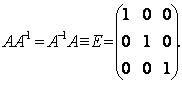
Задание
3. Даны точки А(7, -9, 3) и В(1, 0, -5); и вектора ![]()
![]() . Требуется найти:
. Требуется найти:
а) модуль (длину) вектора ![]() и середину отрезка АВ;
и середину отрезка АВ;
б) проекцию
вектора![]() .;
.;
в) площадь параллелограмма,
полученного из векторов ![]() .;
.;
г) объем
пирамиды, построенной из векторов
![]() .
.
Решение:
а) для точек А(![]() ) и В(
) и В(![]() ) координаты вектора
) координаты вектора ![]()
![]() находят по формуле
находят по формуле ![]()
![]() = (
= (![]() ).
).
Таким образом, ![]() (1-7, 0-(-9), -5-3) = (-6, 9, -8);
(1-7, 0-(-9), -5-3) = (-6, 9, -8);
модуль
(длина) вектора ![]() :
:
![]() . Значит,
. Значит, ![]() =
=![]() =
=![]() ;
;
cередина отрезка
АВ имеет координаты С![]() =
=![]() = С(4, -9/2, -1);
= С(4, -9/2, -1);
б) проекция
вектора![]() есть:
есть: ![]() ; где
; где ![]() - скалярное произведение векторов
- скалярное произведение векторов ![]() .
.
Если
векторы ортогональны, то ![]() ;
; ![]() , так как
, так как ![]() , то векторы
, то векторы ![]() и
и ![]() не ортогональны; вычисляем далее
не ортогональны; вычисляем далее ![]() ;
;
в) площадь параллелограмма, полученного из векторов ![]() , есть модуль вектора,
полученного от их векторного произведения векторов:
, есть модуль вектора,
полученного от их векторного произведения векторов: ![]() ; сначала находим координаты:
; сначала находим координаты:
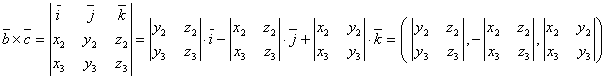 ;
;
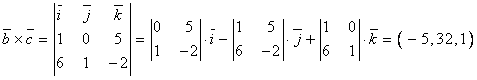 ;
;
далее
определяем модуль вектора: ![]() ;
;
г)
объем пирамиды, построенной из векторов ![]() ,
, ![]() ,
, ![]() , находится из модуля их смешанного
произведения:
, находится из модуля их смешанного
произведения: 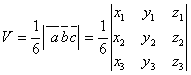
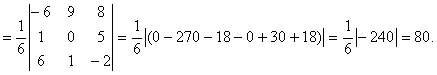
Так как ![]() , то эти векторы не компланарны.
, то эти векторы не компланарны.
Задание 4. Даны точки А![]() (4, -2), А
(4, -2), А![]() (8, 1) на плоскости и уравнение прямой L
(8, 1) на плоскости и уравнение прямой L![]() :
-x + 4y + 5 = 0.
Записать уравнение прямой:
:
-x + 4y + 5 = 0.
Записать уравнение прямой:
а) ![]() -проходящей через эти точки;
-проходящей через эти точки;
б) ![]() - в
виде общего уравнения прямой;
- в
виде общего уравнения прямой;
в) ![]() - в
виде уравнения
прямой с угловым коэффициентом;
- в
виде уравнения
прямой с угловым коэффициентом;
г) ![]() - в виде уравнения прямой в отрезках;
- в виде уравнения прямой в отрезках;
д) ![]() , проходящей через точку
, проходящей через точку ![]() и перпендикулярную
и перпендикулярную ![]() .
.
Решение:
a) уравнение прямой, проходящей через две точки ![]() и
и
![]() , находится по формуле
, находится по формуле ![]() .
.
Значит, уравнение прямой L![]() имеет вид
имеет вид ![]() или
или ![]() ;
;
б) запишем уравнение прямой L![]() в общем виде Ax+By+C=0:
в общем виде Ax+By+C=0: 
![]() , (A=3, B=-4, C=-20).
, (A=3, B=-4, C=-20).
Геометрический смысл коэффициентов: А, В, – это координаты нормального
(перпендикулярного) вектора к прямой L![]() , т. е. вектор
, т. е. вектор ![]() ;
;
в)
![]() через угловой коэффициент y=kx+m:
через угловой коэффициент y=kx+m: 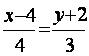
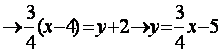 , ( k=
, ( k=![]() , m=-5
);
, m=-5
);
г) ![]() в виде отрезков
x/a+y/b=1:
в виде отрезков
x/a+y/b=1:
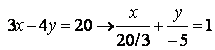 , ( a =
20/3, b = -5 );
, ( a =
20/3, b = -5 );
д) уравнение прямой
, проходящей через точку (![]() ) и
параллельно вектору
) и
параллельно вектору ![]() ,
имеет вид:
,
имеет вид: ![]() .
.
Если
вектор перпендикулярный прямой ![]() есть
есть ![]() =(A;B)=(-1;4), а
прямая
=(A;B)=(-1;4), а
прямая ![]() также перпендикулярна
также перпендикулярна ![]() , тогда в нашем случае получаем, что направляющим
вектором
, тогда в нашем случае получаем, что направляющим
вектором ![]() будет
будет ![]() и уравнение имеет вид
и уравнение имеет вид
 .
.
Задание 5. Даны
точки А![]() (1,
2, -1), А
(1,
2, -1), А![]() (3, 3, 2), А
(3, 3, 2), А![]() (2, -3, 7). Требуется:
(2, -3, 7). Требуется:
а) составить
уравнение плоскости ![]()
б) записать
![]() в виде общего уравнения плоскости;
в виде общего уравнения плоскости;
в) записать
![]() в виде уравнения плоскости
в отрезках;
в виде уравнения плоскости
в отрезках;
г) записать
![]() в виде общего уравнения плоскости, проходящей через точку
в виде общего уравнения плоскости, проходящей через точку ![]() ;
;
д) составить
каноническое уравнение прямой ![]() ;
;
е) записать
параметрическое уравнение прямой ![]() ;
;
ж) составить
уравнение прямой ![]() ,
перпендикулярной плоскости
,
перпендикулярной плоскости ![]() .
.
Решение:
а) уравнение плоскости, проходящей через точки ![]() ,
, ![]() ,
, ![]() имеет вид:
имеет вид: 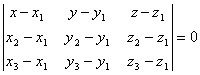 .
.
В нашем случае Р![]() :
: 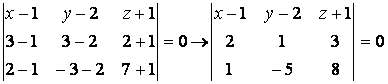 (*);
(*);
б) раскрыв определитель в правой части равенства
(*), получим уравнение плоскости Р![]() в
общем виде Ax+By+Cz+D=0:
в
общем виде Ax+By+Cz+D=0:
23x – 13y – 11z – 8 = 0, (A=23, B=-13, C=-11, D=-8).
Геометрический смысл коэффициентов: А, В, С – это
координаты нормального (перпендикулярного) вектора плоскости, т.
е. вектор ![]() ;
;
в) перенесём в общем уравнении плоскости свободный член –8 в правую часть и разделим обе части на 8. Получим уравнение плоскости в отрезках x/a+y/b+z/c=1:
![]() ,
,
где а=8/23, в=-8/13, с=-8/11 – это величины отрезков, отсекаемых плоскостью на координатных осях, считая от начала координат;
г)
раскроем определитель в левой части равенства (*) по элементам первой строки:
![]() .
.
Получили уравнение плоскости в виде A(x-x![]() )+B(y-y
)+B(y-y![]() )+C(z-z
)+C(z-z![]() )=0
(
)=0
(![]() );
);
д) каноническое уравнение прямой, проходящей через две
точки (![]() ) и (
) и (![]() ), находится по формуле
), находится по формуле ![]() .
Значит, уравнение прямой L
.
Значит, уравнение прямой L![]() имеет вид
имеет вид ![]() или
или ![]() ;
;
е) уравнения
прямой в виде ![]() называются
каноническими, где a={m,n,p} – ее направляющий
вектор. В предыдущем
пункте уже найдены канонические уравнения прямых. Параметрическими
называются уравнения прямой в виде
называются
каноническими, где a={m,n,p} – ее направляющий
вектор. В предыдущем
пункте уже найдены канонические уравнения прямых. Параметрическими
называются уравнения прямой в виде 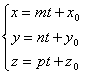 . Чтобы получить параметрические уравнения прямой,
приравняем канонические уравнения к параметру t и из
полученных равенств найдём x, y, z.
. Чтобы получить параметрические уравнения прямой,
приравняем канонические уравнения к параметру t и из
полученных равенств найдём x, y, z.
L![]() :
:![]() =
=
 .
.
Итак, параметрическое уравнение L![]() :
: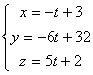 ;
;
ж) так как ![]() , то вектор
, то вектор ![]() оказывается направляющим вектором прямой
оказывается направляющим вектором прямой ![]() . Тогда
каноническое уравнение прямой
. Тогда
каноническое уравнение прямой ![]() имеет вид:
имеет вид:![]() .
.
Задание 6. Решить
систему  :
:
а) методом Крамера;
б) матричным методом (с помощью обратной матрицы).
Решение:
а) решение системы 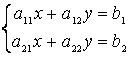 по правилу Крамера имеет вид:
по правилу Крамера имеет вид: ![]() , где
, где 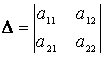 - определитель системы,
- определитель системы,
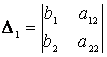 ,
, 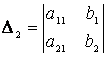 - вспомогательные
определители, полученные из определителя системы заменой первого и второго
столбцов столбцом свободных членов.
- вспомогательные
определители, полученные из определителя системы заменой первого и второго
столбцов столбцом свободных членов.
В нашем случае 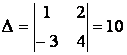 ,
, 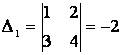 ,
,  . Таким образом, х = -1/5, у =3/5.
. Таким образом, х = -1/5, у =3/5.
Ответ можно записать в виде вектора: 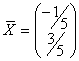 ;
;
б) в матричном виде решение системы 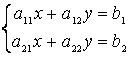 записывается так:
записывается так:![]() , где
, где 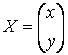 - матрица–столбец
неизвестных,
- матрица–столбец
неизвестных,  -
матрица-столбец свободных членов,
-
матрица-столбец свободных членов, ![]() - матрица, обратная для матрицы системы
- матрица, обратная для матрицы системы  .
.
Найдём обратную матрицу (см. пример
2б) для матрицы системы 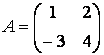 . Так как определитель системы
. Так как определитель системы ![]() , то обратная матрица
существует и равна
, то обратная матрица
существует и равна  .
.
Тогда  . Или ответ в обычном виде: х=-1/5, у=3/5.
. Или ответ в обычном виде: х=-1/5, у=3/5.
Задание 7. Дана
система уравнений.  .
.
Требуется:
а) проверить совместность системы методом Гаусса;
б) найти ранг матрицы коэффициентов и расширенной матрицы системы;
в) решить систему, если она совместна.
Решение:
а) метод Гаусса заключается в последовательном
исключении неизвестных из уравнений системы с помощью элементарных
преобразований и приведении её к ступенчатому (треугольному) виду расширенной
матрицы системы. Матрица коэффициентов системы есть 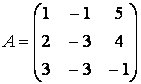 , расширенная
матрица -
, расширенная
матрица -  . Так
как матрица
. Так
как матрица ![]() содержится
в матрице
содержится
в матрице ![]() , то
достаточно производить элементарные преобразования только над строками матрицы
, то
достаточно производить элементарные преобразования только над строками матрицы ![]() : умножим первую строку
на -2 и прибавим ко второй, затем умножим первую строку на -3 и прибавим к
третьей. Получим, что матрица
: умножим первую строку
на -2 и прибавим ко второй, затем умножим первую строку на -3 и прибавим к
третьей. Получим, что матрица ![]() , а вместе с ней и матрица
, а вместе с ней и матрица![]() , приводится к
ступенчатой матрице, имеющих три ненулевые строки:
, приводится к
ступенчатой матрице, имеющих три ненулевые строки:  .
.
По
теореме Кронекера-Капелли система совместна (т.е. имеет хотя бы одно решение),
если ранг матрицы системы равен рангу расширенной матрицы ![]() ; система не совместна (т.е. не
имеет решений), если
; система не совместна (т.е. не
имеет решений), если ![]() .
.
По количеству ненулевых строк в ступенчатых матрицах
определяются ранги
матриц ![]() :
: ![]() и,
следовательно, система совместна;
и,
следовательно, система совместна;
б) так как число неизвестных n равно 3 и равно рангу матрицы системы (n=r), то система имеет одно решение;
в) таким
образом, данная система сводится к системе, соответствующей последней ступенчатой расширенной матрице:  ;
;
поднимаясь по этой системе снизу вверх, найдём
из последнего уравнения ![]() ; из предпоследнего -
; из предпоследнего - ![]() ; из
первого -
; из
первого - ![]() . Ответ: (-4; -2; 1).
. Ответ: (-4; -2; 1).
Задание 8. Решить однородную систему линейных уравнений
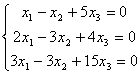 .
.
Решение: однородная
система уравнений всегда совместна (![]() ) и имеет нулевое решение
) и имеет нулевое решение ![]() Для
того чтобы однородная система n уравнений
с n неизвестными имела ненулевые решения, необходимо и
достаточно, чтобы ее определитель был равен нулю (или rankA<n).
Для
того чтобы однородная система n уравнений
с n неизвестными имела ненулевые решения, необходимо и
достаточно, чтобы ее определитель был равен нулю (или rankA<n).
Определитель матрицы коэффициентов
системы 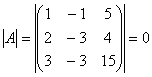 , значит rankA<3. Выберем любой ненулевой минор 2-го порядка в матрице
А:
, значит rankA<3. Выберем любой ненулевой минор 2-го порядка в матрице
А: ![]() .
Значит, система имеет бесчисленное множество решений.
.
Значит, система имеет бесчисленное множество решений.
Так как rankA=2, то в исходной однородной системе одну переменную ![]() определим
в свободные, а третье уравнение отбросим. Далее будем решать неоднородную
систему методом Крамера:
определим
в свободные, а третье уравнение отбросим. Далее будем решать неоднородную
систему методом Крамера:

Таким образом, нахождение ненулевого решения однородной системы сводится к решению неоднородной системы, и ее общее решение имеет вид:
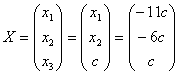 .
.
При с=1, получаем одно частное решение: ![]()
При с=-2, получаем второе частное решение: ![]() и
т.д.
и
т.д.
Задание 9.
Даны точка А(3, -7); радиус окружности R=6; ![]() = 2;
= 2; ![]() =
3 – полуоси кривых; D: у = -3 – уравнение прямой. Требуется:
=
3 – полуоси кривых; D: у = -3 – уравнение прямой. Требуется:
а) записать уравнение окружности с центром в точке А и радиусом R;
б) записать каноническое уравнение эллипса с полуосями а=2 и b=3. Найти координаты его фокусов, эксцентриситет;
в) записать каноническое уравнение гиперболы с действительной полуосью а=2 и мнимой – b=3. Найти координаты его фокусов, эксцентриситет, уравнения ассимптот;
г) записать каноническое уравнение параболы с вершиной в начале координат и если D: у = -3 ее директриса. Найти координаты его фокуса, эксцентриситет;
д) сделать чертеж эллипса, гиперболы, параболы.
Решение:
а) уравнение окружности с центром в точке ![]() радиуса R имеет вид
радиуса R имеет вид ![]() ,
значит, в нашем варианте:
,
значит, в нашем варианте: ![]() ;
;
б) каноническое уравнение эллипса с полуосями ![]() и
и ![]() имеет вид
имеет вид ![]() ; значит в нашем варианте:
; значит в нашем варианте: ![]() .
.
Фокусы эллипса – это точки ![]() , если
, если ![]() и
и ![]() , и эксцентриситет
, и эксцентриситет ![]() эллипса равен
эллипса равен ![]() , или, если
, или, если
![]() , то
, то ![]() и
и ![]() ,
, ![]() .
.
Итак,
в нашем варианте, поскольку ![]() , то,
, то, ![]() эксцентриситет равен
эксцентриситет равен ![]() , (
, (![]() ). Фокусы лежат на оси Оу:
). Фокусы лежат на оси Оу: ![]() . Изобразим эллипс на
координатной плоскости (см.рисунок 1),
где
. Изобразим эллипс на
координатной плоскости (см.рисунок 1),
где ![]() -
вершины эллипса.
-
вершины эллипса.
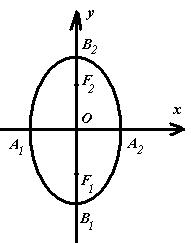
Рисунок 1
в) каноническое уравнение гиперболы с действительной
полуосью ![]() ,
мнимой полуосью
,
мнимой полуосью ![]() имеет
вид
имеет
вид ![]() ;
с действительной полуосью
;
с действительной полуосью ![]() и
мнимой полуосью
и
мнимой полуосью ![]() :
:
![]() или
или ![]() . Для гиперболы с действительной полуосью
. Для гиперболы с действительной полуосью ![]() , эксцентриситет равен
, эксцентриситет равен ![]() , где
, где ![]() ; уравнения асимптот гиперболы имеют вид
; уравнения асимптот гиперболы имеют вид ![]() ; фокусы – это точки
; фокусы – это точки ![]() , расположенные на действительной оси.
, расположенные на действительной оси.
По условию ![]() =2,
=2, ![]() =3,
поэтому каноническое уравнение гиперболы с действительной полуосью
=3,
поэтому каноническое уравнение гиперболы с действительной полуосью ![]() будет
будет ![]() . Для
неё полуфокусное расстояние
. Для
неё полуфокусное расстояние ![]() ;
эксцентриситет равен
;
эксцентриситет равен ![]() ;
фокусы:
;
фокусы: ![]() ;
уравнения асимптот:
;
уравнения асимптот: 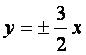 .
.
Гиперболу легко построить следующим образом: строим
прямоугольник со сторонами ![]() (у
нас
(у
нас ![]() ).
Диагонали прямоугольника являются асимптотами гиперболы, точки пересечения
сторон прямоугольника с действительной осью гиперболы – вершинами гиперболы (см.рисунок
2):
).
Диагонали прямоугольника являются асимптотами гиперболы, точки пересечения
сторон прямоугольника с действительной осью гиперболы – вершинами гиперболы (см.рисунок
2):
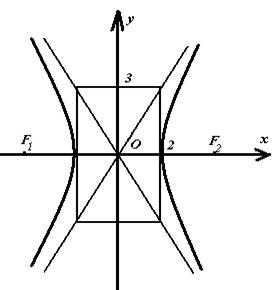
Рисунок 2
г) по условию, если директриса
параболы y = -p/2, то осью
симметрии параболы с вершиной в начале координат является ось Ох. Значит, её
каноническое уравнение имеет вид ![]() ; если директриса параболы x=-p/2, то осью симметрии параболы с вершиной в начале координат
является ось Оy. Значит, её
каноническое уравнение имеет вид
; если директриса параболы x=-p/2, то осью симметрии параболы с вершиной в начале координат
является ось Оy. Значит, её
каноническое уравнение имеет вид ![]() . Так как директриса параболы имеет уравнение у = -3,
то
. Так как директриса параболы имеет уравнение у = -3,
то ![]() и уравнение параболы будет:
и уравнение параболы будет: ![]() . Фокус параболы – это точка
. Фокус параболы – это точка ![]() , лежащая на оси симметрии. В нашем случае
фокус -
, лежащая на оси симметрии. В нашем случае
фокус - ![]() .
Построим параболу (см.рисунок 3).
.
Построим параболу (см.рисунок 3).
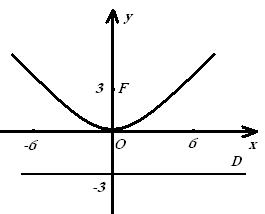
Рисунок 3
Задание 10. Определить вид (название) поверхности второго порядка и сделать схематический чертёж:
а) ![]() ; б)
; б) ![]() .
.
Решение:
а) ![]() - это каноническое уравнение однополостного гиперболоида с
осью симметрии Ох. Его схематический чертёж (см.рисунок 4);
- это каноническое уравнение однополостного гиперболоида с
осью симметрии Ох. Его схематический чертёж (см.рисунок 4);
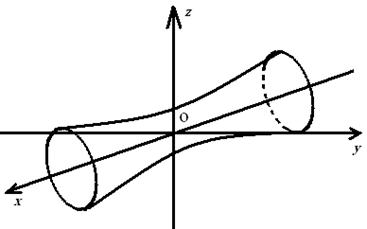
Рисунок 4
б) ![]() - это каноническое уравнение конуса второго порядка с
осью симметрии Оz и вершиной в начале координат. Его
схематический чертёж (см.рисунок 5);
- это каноническое уравнение конуса второго порядка с
осью симметрии Оz и вершиной в начале координат. Его
схематический чертёж (см.рисунок 5);
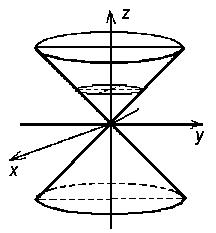
Рисунок 5
Задание 11.
Привести к каноническому виду уравнение кривой второго порядка ![]() и построить эту
кривую.
и построить эту
кривую.
Решение: уравнение вида

определяют соответственно эллипс, гиперболу и
параболу, которые имеют центр симмметрии (эллипса и гиперболы) или вершину
параболы в точке ![]() .
Для этого применим метод выделения полных квадратов:
.
Для этого применим метод выделения полных квадратов:
![]()
Дополним члены, содержащие x, и члены содержащие y, до полных квадратов ![]() ,
,
![]() ,
,
![]() ,
,
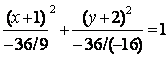 ,
, 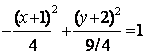 ,
,
т. е. имеем гиперболу, с центром в точке С(-1;-2), действительной полуосью b=3/2 (по оси 0y) и мнимой полуосью a=2 9 (по оси 0х). Построим его схематический чертёж (см. рисунок 6).
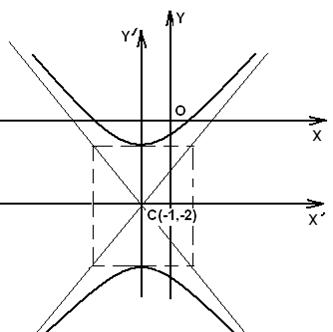
Рисунок 6
Задание 12. Даны комплексные числа:
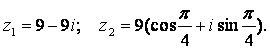
Требуется найти:
а) модуль комплексного числа z1;
б) аргумент комплексного числа z1;
в) представление комплексного числа z1 в тригонометрической и показательной формах;
г) сумму комплексных чисел z1 и z2 аналитически и графически;
д) (z2)5;
е) произведение z1*z2 в тригонометрической форме;
ж)
все комплексные корни ![]()
Решение:
а) если комплексное число в алгебраической форме имеет вид:
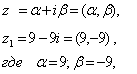
то модуль комплексного числа z1:
![]()
б) аргумент комплексного числа z1:
![]()
в) в тригонометрической и показательной форме комплексное число имеет вид:
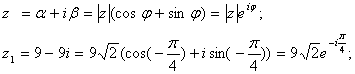
г) сумма комплексных чисел z1 и z2

д) для вычисления(z2)5 воспользуемся формулой Муавра:

е) произведение z1*z2 в алгебраической форме имеет вид:
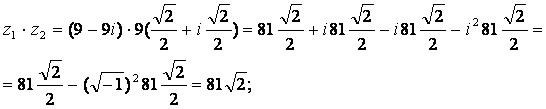
но произведение z1*z2 в тригонометрической форме более просто вычисляется:

ж)
все комплексные корни n-ой степени ![]() вычисляются по формуле Муавра:
вычисляются по формуле Муавра:

Распишем все полученные корни для всех к:
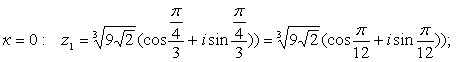
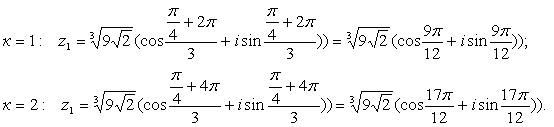
На графике все кубические корни будут расположены на вершинах правильного треугольника.
Список литературы
1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: в 2 ч. – М.: Высшая школа, 2003. – ч. 1,2.-352 с.
2. Сборник индивидуальных заданий по высшей математике: в 3 ч. (Рябушко А.П., Бархатов В.В. и др.). Под ред. Рябушко А.П. – Минск: Высш. школа, 2000.-ч.1.-396 с.
3. Кузнецов А.А. Сборник заданий по высшей математике: Типовые расчеты. –М.:Высш. Шк., 1983.-176 с.
4. Хасеинов К.А. Каноны математики: Учебник. – Алматы, 2003.-686 с.
Содержание
Расчётно-графическая работа. Векторная и линейная алгебра. Аналитическая геометрия
Теоретические вопросы 3
Расчётные задания 3
Решение типового варианта 16
Список литературы 33
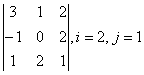
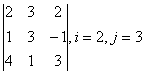

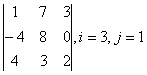
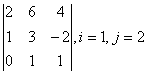
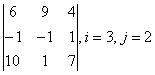

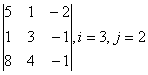
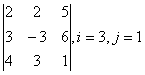
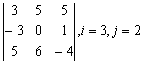
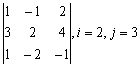
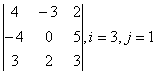

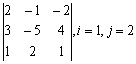


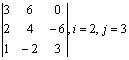

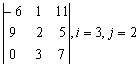
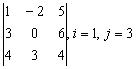
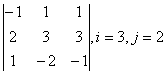
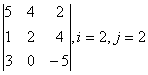
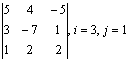
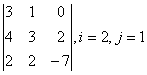
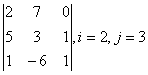

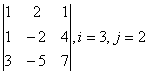
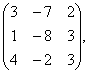 В=
В=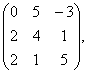 В=
В=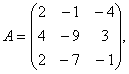
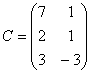
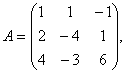
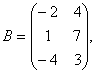
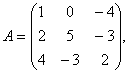
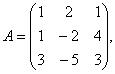
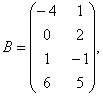


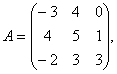
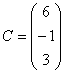

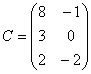
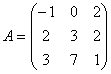 ,
, 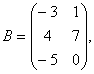
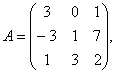
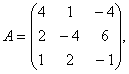
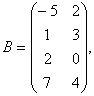
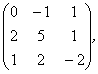 В=
В=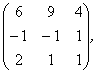 В=
В=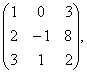 В=
В=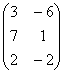
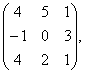 В=
В=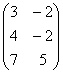 , С=
, С=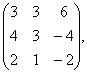 В=
В= В=
В= С=
С=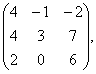 В=
В=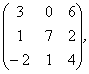 В=
В=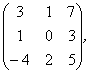 В=
В=
 В=
В=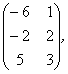 С=
С=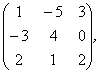 В=
В= В=
В=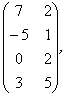 С=
С=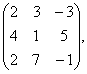 В=
В= В=
В=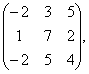 В=
В=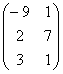
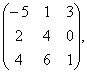 В=
В= С=
С=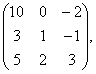 В=
В=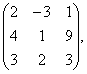 В=
В=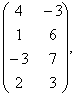 С=
С=