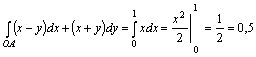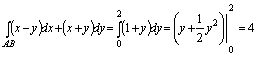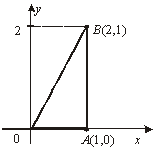ҚАЗАҚСТАН РЕСПУБЛИКСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
«Алматы энергетика және байланыс институтының»
Коммерциялық емес акционерлік қоғамы
С. Е. Ералиев
ӨРІСТЕР ТЕОРИЯСЫ
Оқу құралы
Алматы 2008
4. ҚИСЫҚ СЫЗЫҚТЫ ИНТЕГРАЛДАР
4.1 Бірінші текті қисық сызықты интегралдар
![]() функциясы
функциясы ![]() жазықтығында жататын кез
келген бір
жазықтығында жататын кез
келген бір ![]() аймағында
үзіліссіз функция болсын. Осы аймақта жататын
аймағында
үзіліссіз функция болсын. Осы аймақта жататын ![]() қисығын алып оны
нүктелердің көмегімен қарапайым
қисығын алып оны
нүктелердің көмегімен қарапайым ![]() доғаларына бөлейік.
Әрбір қарапайым
доғаларына бөлейік.
Әрбір қарапайым ![]() доғасының бойынан кез келген
бір
доғасының бойынан кез келген
бір ![]() нүктесін
алып, осы нүктедегі
нүктесін
алып, осы нүктедегі ![]() функциясының мәнін
функциясының мәнін ![]() доғасының
ұзындығы
доғасының
ұзындығы ![]() -ге
көбейтейік. Осындай барлық
-ге
көбейтейік. Осындай барлық ![]() көбейтінділерінің
қосындысы интегралдық қосынды деп аталады.
көбейтінділерінің
қосындысы интегралдық қосынды деп аталады.
Егер ![]() интегралдық қосындысының
шегі бар әрі ол шек
интегралдық қосындысының
шегі бар әрі ол шек ![]() қисығын қарапайым
доғаларға қалай бөлгенімізге де, әрбір
қарапайым
қисығын қарапайым
доғаларға қалай бөлгенімізге де, әрбір
қарапайым ![]() доғаларынан
доғаларынан
![]() нүктелерін
қалай алғанымызға да, байланысты болмаса, онда осы шекті
нүктелерін
қалай алғанымызға да, байланысты болмаса, онда осы шекті ![]() функциясынан
функциясынан ![]() доғасының
ұзындығы бойынша алынған қисық сызықты
интеграл немесе бірінші текті қисық сызықты интеграл деп
аталып былай белгіленеді:
доғасының
ұзындығы бойынша алынған қисық сызықты
интеграл немесе бірінші текті қисық сызықты интеграл деп
аталып былай белгіленеді:
![]() (4.1)
(4.1)
Бірінші текті қисық сызықты интегралдың негізгі қасиеттері:
1. ![]() ;
;
2. ![]() ;
;
3. бірінші текті қисық сызықты интеграл интегралдау жолының бағытынан тәуелсіз болады, яғни
![]() ;
;
4. егер ![]() қисығы
қисығы ![]() және
және ![]() қисықтарына
бөлінсе, онда
қисықтарына
бөлінсе, онда
![]() .
.
Бірінші текті қисық сызықты интегралды есептеу үшін келесі формулалардың біреуі қолданылады:
а) егер ![]() қисық сызығы
қисық сызығы ![]()
![]() теңдеуімен берілсе, онда
бірінші текті қисық сызықты интеграл
теңдеуімен берілсе, онда
бірінші текті қисық сызықты интеграл
![]() (4.2)
(4.2)
формуласымен есептеледі;
б) егер ![]() қисық сызығы параметрлік
қисық сызығы параметрлік
![]()
![]() теңдеуімен
берілсе, онда
теңдеуімен
берілсе, онда
![]() ; (4.3)
; (4.3)
в) егер ![]() қисық сызығы
полярлық координаталар жүйесінде
қисық сызығы
полярлық координаталар жүйесінде ![]()
![]() теңдеуімен
берілсе, онда
теңдеуімен
берілсе, онда
![]() ; (4.4)
; (4.4)
г) егер ![]() қисық сызығы
кеңістікте параметрлік
қисық сызығы
кеңістікте параметрлік ![]()
![]()
![]() теңдеулерімен берілсе, онда үш
айнымалы
теңдеулерімен берілсе, онда үш
айнымалы ![]() функциясының
бірінші текті қисық сызықты интегралы
функциясының
бірінші текті қисық сызықты интегралы
![]() (4.5)
(4.5)
формуласымен есептеледі.
4.2 Бірінші текті қисық сызықты интегралдың қолданылуы
1. ![]() қисығының бойында
анықталған үзіліссіз
қисығының бойында
анықталған үзіліссіз ![]() функциясы бірге тең болса, онда
функциясы бірге тең болса, онда ![]() қисығының
ұзындығы
қисығының
ұзындығы ![]() формуласымен
анықталады.
формуласымен
анықталады.
2. ![]() тұйық қисығымен
шенелген
тұйық қисығымен
шенелген ![]() аймағының
ауданы
аймағының
ауданы
![]() (4.6)
(4.6)
формуласымен анықталады, мұндағы ![]() жиегін айналып өту
бағыты
жиегін айналып өту
бағыты ![]() аймағы
әр уақытта интегралдау жолының сол жағында
қалатындай етіп алынады.
аймағы
әр уақытта интегралдау жолының сол жағында
қалатындай етіп алынады.
3. Егер ![]() қисығының сызықты
тығыздығы
қисығының сызықты
тығыздығы ![]() болса,
онда
болса,
онда
а) ![]() қисығының массасы
қисығының массасы
![]() ; (4.7)
; (4.7)
б) ![]() және
және ![]() осьтеріне қарағандағы
статикалық моменттері
осьтеріне қарағандағы
статикалық моменттері
![]() және
және ![]() ; (4.8)
; (4.8)
в) ауырлық орталығының координаталары
![]() ; (4.9)
; (4.9)
г) ![]() және координаталар
жүйесінің бас нүктесіне қарағандағы
сәйкес
және координаталар
жүйесінің бас нүктесіне қарағандағы
сәйкес ![]() және
және
![]() екпіндік
моменттері
екпіндік
моменттері
![]() (4.10)
(4.10)
формулаларымен есептеледі.
28-мысал. ![]() интегралын
интегралын ![]() параболасының
параболасының ![]() мен
мен ![]() аралығындағы
доғасы бойынша есептеу керек, мұндағы
аралығындағы
доғасы бойынша есептеу керек, мұндағы ![]() .
.
Шешуі. ![]() .
.
Сондықтан
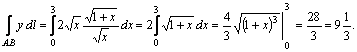
29-мысал. ![]() интегралын
интегралын ![]() шеңберінің
шеңберінің ![]() доғасы бойынша есептеу
керек, мұндағы
доғасы бойынша есептеу
керек, мұндағы ![]() .
.
Шешуі.
![]()
![]() .
.
Сондықтан
![]() .
.
|
21-сурет |
30-мысал. Шешуі. Осында |
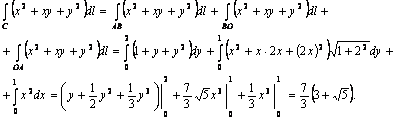
85. ![]() интегралын
интегралын ![]() кесіндісі бойынша есептеу керек,
мұндағы
кесіндісі бойынша есептеу керек,
мұндағы ![]() .
.
86. ![]() интегралын
интегралын ![]() кесіндісі бойынша есептеу керек,
мұндағы
кесіндісі бойынша есептеу керек,
мұндағы ![]() .
.
87. ![]() интегралын
интегралын ![]() ,
, ![]() ,
, ![]() бұранда сызықтың бірінші
айналымы
бұранда сызықтың бірінші
айналымы ![]() бойынша
есептеу керек.
бойынша
есептеу керек.
88. ![]() интегралын
интегралын ![]() шеңбері бойынша есептеу керек
шеңбері бойынша есептеу керек ![]() .
.
89. ![]() интегралын
интегралын ![]() жарты кубтық параболаның
жарты кубтық параболаның ![]() доғасы бойынша
есептеу керек, мұндағы
доғасы бойынша
есептеу керек, мұндағы ![]() .
.
90. ![]() интегралын
интегралын ![]() циклоидасы
циклоидасы ![]() бойынша есептеу керек.
бойынша есептеу керек.
91. ![]() интегралын
интегралын ![]() параболасының
параболасының ![]() доғасы бойын-ша есептеу
керек, мұндағы
доғасы бойын-ша есептеу
керек, мұндағы ![]() .
.
92. ![]() интегралын
интегралын ![]() қисық сызығының
доғасы бойынша есептеу керек
қисық сызығының
доғасы бойынша есептеу керек ![]() .
.
93. ![]() интегралын
интегралын ![]() логарифмдік спи-ралы (шиырмасы) бойынша
есептеу керек.
логарифмдік спи-ралы (шиырмасы) бойынша
есептеу керек.
94. Тығыздығы ![]() болатын
болатын ![]()
![]() қисық сызығының
доғасы массасын табу керек.
қисық сызығының
доғасы массасын табу керек.
95. ![]() циклоидасының доғасы
ауырлық орталығының координаталарын табу керек
циклоидасының доғасы
ауырлық орталығының координаталарын табу керек ![]() .
.
96. ![]() шеңберінің
шеңберінің ![]() ,
, ![]() осьтеріне және координаталық
жүйесінің бас нүктесіне қарағандағы
екпіндік моменттерін табу керек.
осьтеріне және координаталық
жүйесінің бас нүктесіне қарағандағы
екпіндік моменттерін табу керек.
4.3 Екінші текті қисық сызықты интегралдар.
![]() жазықтығындағы
жазықтығындағы ![]() қисық
сызығының бойында жатқан
қисық
сызығының бойында жатқан ![]() доғасының әрбір
нүктесінде анықталған және үзіліссіз
доғасының әрбір
нүктесінде анықталған және үзіліссіз ![]() және
және ![]() функциялары берілсін.
функциялары берілсін. ![]() доғасын кезкелген
ретпен
доғасын кезкелген
ретпен ![]() нүктелерімен
нүктелерімен
![]() қарапайым
доғаларға бөліп, әрбір
қарапайым
доғаларға бөліп, әрбір ![]() доғасынан бір
доғасынан бір ![]() нүктеден таңдап
алайық.
нүктеден таңдап
алайық. ![]() хордасының
хордасының
![]() және
және ![]() осьтеріндегі
сәйкес проекцияларын
осьтеріндегі
сәйкес проекцияларын ![]() және
және ![]() деп белгілейік.
деп белгілейік.
![]() доғасындағы
доғасындағы ![]() және
және ![]() функцияларының
интегралдық қосындысы деп
функцияларының
интегралдық қосындысы деп ![]() қосындысын айтады.
қосындысын айтады.
Егер ![]() ,
, ![]() интегралдық қосындысының
шегі бар және ол шек
интегралдық қосындысының
шегі бар және ол шек ![]() доғасының
доғасының ![]() элементарлық
доғаларға қалай бөлгеніне де, әрбір
элементарлық доғалардан
элементарлық
доғаларға қалай бөлгеніне де, әрбір
элементарлық доғалардан ![]() нүктесінің қалай таңдап
алынғанынан да байланысты болмаса, онда осы шекті
нүктесінің қалай таңдап
алынғанынан да байланысты болмаса, онда осы шекті ![]() және
және ![]() функцияларынан
функцияларынан ![]() доғасы бойынша
алынған екінші текті қисық сызықты интегралы деп атайды
және оны былай белгілейді:
доғасы бойынша
алынған екінші текті қисық сызықты интегралы деп атайды
және оны былай белгілейді:
 (4.11)
(4.11)
Егер ![]() қисығы
қисығы ![]() теңдеуімен берілсе
және
теңдеуімен берілсе
және ![]() ,
, ![]() болса, онда екінші
текті қисық сызықты интеграл
болса, онда екінші
текті қисық сызықты интеграл
![]() (4.12)
(4.12)
формуласымен есептеледі.
Егер ![]() қисығы
қисығы ![]() теңдеулерімен берілсе,
онда
теңдеулерімен берілсе,
онда
![]() . (4.13)
. (4.13)
Егер тегіс ![]() қисық сызығы
кеңістікте
қисық сызығы
кеңістікте ![]() теңдеулерімен
берілсе, онда осы қисықтың бойында анықталған,
үзілссіз
теңдеулерімен
берілсе, онда осы қисықтың бойында анықталған,
үзілссіз ![]() функциялары
үшін екінші текті қисық сызықты интеграл
функциялары
үшін екінші текті қисық сызықты интеграл
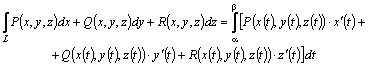 (4.14)
(4.14)
формуласымен есептелінеді.
Екінші текті қисық сызықты интегралдың негізгі қасиеттері:
1. Екінші текті қисық сызықты интегралдың интегралдау жолының бағытын өзгерткенде оның мәнінің таңбасы өзгереді, яғни
![]() ;
;
2. ![]() .
.
Қалған қасиеттері бірінші текті қисық сызықты интегралдың негізгі қасиеттері сияқты болады.
Тұйық ![]() контуры бойынша алынған
қисық сызықты интегралды
контуры бойынша алынған
қисық сызықты интегралды
![]() деп
белгілейді және интегралдау жолының бағыты үшін
сағат тіліне қарама-қарсы бағытты алады.
деп
белгілейді және интегралдау жолының бағыты үшін
сағат тіліне қарама-қарсы бағытты алады.
4.4 Екінші текті қисық сызықты интегралдың қолданылуы:
![]()
айнымалы күшінің ![]() қисық сызығының
бойында істелген жұмысы
қисық сызығының
бойында істелген жұмысы
![]()
формуласымен есептелінеді, мұндағы ![]() өрнегі
өрнегі ![]() және
және ![]() вектор-ларының скаляр
көбейтіндісі, ал
вектор-ларының скаляр
көбейтіндісі, ал
![]() .
.
4.5 Бірінші және екінші текті қисық сызықты интегралдар арасын-дағы байланыс.
Егер ![]() болса, онда
болса, онда ![]()
![]() . Олай болса
. Олай болса
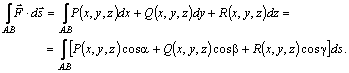 (4.15)
(4.15)
31-мысал. ![]() интегралын
интегралын ![]() параболасының
параболасының ![]() доғасы бойынша есептеу
керек, мұндағы
доғасы бойынша есептеу
керек, мұндағы ![]() ,
, ![]() .
.
Шешуі. ![]() , сондықтан
, сондықтан

32-мысал.
![]() интегралын
интегралын ![]() түзуі бойынша интегралдау керек,
мұндағы
түзуі бойынша интегралдау керек,
мұндағы ![]() .
.
Шешуі. Екі нүкте арқылы өтетін
түзудің теңдеуінің формуласын қолдансақ ![]() немесе
немесе ![]() және
және ![]() болғанда
болғанда ![]() болғанда
болғанда ![]() яғни
яғни ![]() 0-ден 1-ге дейін
өзгереді.
0-ден 1-ге дейін
өзгереді.

33-мысал. ![]() интегралын төбелері
интегралын төбелері ![]()
![]() нүктелері болатын
нүктелері болатын ![]() үшбұрыш контуры (жиегі)
бойынша есептеу керек.
үшбұрыш контуры (жиегі)
бойынша есептеу керек.
|
Шешуі. 1)
2)
|
22-сурет |
.
3)![]() теңдеуі
теңдеуі ![]() 1-ден 0-ге дейін өзгереді.
Сондық-тан
1-ден 0-ге дейін өзгереді.
Сондық-тан
![]()
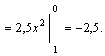
Сонымен
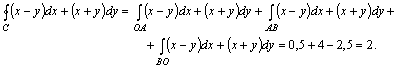
97. ![]() интегралын
интегралын ![]() түзуі бойынша есептеу керек,
мұндағы
түзуі бойынша есептеу керек,
мұндағы ![]() .
.
98. ![]() интегралын
интегралын ![]()
![]() циклоидасы бойынша есептеу керек.
циклоидасы бойынша есептеу керек.
99. ![]() интегралын а)
интегралын а) ![]() түзуі; ә)
түзуі; ә) ![]() параболасы; б)
параболасы; б) ![]() параболасы; в)
параболасы; в) ![]() сынығы; г)
сынығы; г) ![]() сынығы бойынша
есептеу керек, мұндағы
сынығы бойынша
есептеу керек, мұндағы ![]() ,
, ![]() .
.
100. ![]() интегралын 99-есептің шарттары
бойынша есептеу керек.
интегралын 99-есептің шарттары
бойынша есептеу керек.
101. ![]() интегралын төбелері
интегралын төбелері ![]() болатын
болатын ![]() квадрат контуры (жиегі)
бойынша есептеу керек.
квадрат контуры (жиегі)
бойынша есептеу керек.
102. ![]() интегралын
интегралын ![]() эллипс контуры (жиегі) бойынша есептеу
керек.
эллипс контуры (жиегі) бойынша есептеу
керек.
103. ![]() интегралын
интегралын ![]() түзуі бойынша есептеу керек,
мұндағы
түзуі бойынша есептеу керек,
мұндағы ![]() .
.
104. ![]() интегралын
интегралын ![]()
![]() бұранда сызығының бір
айналымы бойынша есептеу керек.
бұранда сызығының бір
айналымы бойынша есептеу керек.
105. ![]() айнымалы күшінің
әсерінен
айнымалы күшінің
әсерінен ![]() пара-боланың
пара-боланың
![]() нүктесімен
нүктесімен
![]() нүктесінің
арасындағы доғасы бойында істелінген жұмысты есеғптеу
керек.
нүктесінің
арасындағы доғасы бойында істелінген жұмысты есеғптеу
керек.
4.5 Екінші текті қисық сызықты интегралдың интегралдау жолынан тәуелсіздігі. Функцияны өзінің толық дифференциалы арқылы анықтау.
![]() және
және ![]() функциялары өздерінің бірінші
ретті дербес туындыларымен бірге бір байланысты
функциялары өздерінің бірінші
ретті дербес туындыларымен бірге бір байланысты ![]() аймағында үзіліссіз болсын.
аймағында үзіліссіз болсын. ![]() аймағында жататын
аймағында жататын
![]() қисығының
бойында
қисығының
бойында ![]() интегралы
интегралдау жолынан тәуелсіз болуы үшін
интегралы
интегралдау жолынан тәуелсіз болуы үшін
![]() (4.16)
(4.16)
теңдігінің орындалуы қажетті және жеткілікті.
(16)-шарты орындалған жағдайда ![]() аймағында
толықтай жататын кезкелген тұйық
аймағында
толықтай жататын кезкелген тұйық ![]() жиегі бойынша алынған
қисық сызықты интеграл нөлге тең болады,
яғни
жиегі бойынша алынған
қисық сызықты интеграл нөлге тең болады,
яғни
![]() .
.
Интегралдау жолынан тәуелсіз болған жағдайда
![]()
интегралын есептеу үшін ![]() нүктесімен
нүктесімен ![]() нүктесін қосатын
нүктесін қосатын ![]() және
және ![]() осьтеріне параллель
осьтеріне параллель ![]() немесе
немесе ![]() сынығын
интегралдау жолы етіп алған тиімді, мұндағы
сынығын
интегралдау жолы етіп алған тиімді, мұндағы ![]() .
.
|
23-сурет |
(16)-шартты қанағаттандыратын
|
![]() функциясын
табу үшін қисық сызықты интегралды
функциясын
табу үшін қисық сызықты интегралды ![]() сынығы бойынша интегралдау
жеткілікті, мұндағы
сынығы бойынша интегралдау
жеткілікті, мұндағы ![]() кезкелген белгілен-ген нүкте,
кезкелген белгілен-ген нүкте, ![]() айнымалы нүкте,
ал
айнымалы нүкте,
ал ![]() . Осыдан
. Осыдан
![]() ,
,
мұндағы ![]() – кезкелген сан.
– кезкелген сан.
Осы сияқты ![]() сынығы бойынша да
интегралдауға болады, мұндағы
сынығы бойынша да
интегралдауға болады, мұндағы ![]() . Яғни
. Яғни
![]() . (4.17)
. (4.17)
4.6 Грин формуласы
Жиегі ![]() болатын жабық
болатын жабық ![]() аймағында
аймағында ![]() функциялары
өздерінің дербес туындыларымен бірге үзіліссіз болса, онда
функциялары
өздерінің дербес туындыларымен бірге үзіліссіз болса, онда
![]() . (4.18)
. (4.18)
35-мысал. ![]() интегралын есептеу керек.
интегралын есептеу керек.
Шешуі. ![]()
![]() . Яғни
. Яғни ![]() болғандықтан берілген интеграл
интегралдау жолынан тәуелсіз. Олай болса интегралдау жолы үшін
болғандықтан берілген интеграл
интегралдау жолынан тәуелсіз. Олай болса интегралдау жолы үшін ![]() сынығын
таңдап аламыз, мұндағы
сынығын
таңдап аламыз, мұндағы ![]() . Оның
. Оның ![]() бөлігі
бөлігі ![]() ,
, ![]() бөлігі
бөлігі ![]() . Осыдан
. Осыдан
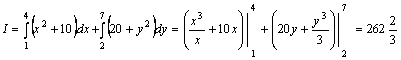 .
.
36-мысал. ![]() өрнегі қандай да бір
өрнегі қандай да бір ![]() функциясының
толық дифференциалы болатындығын не болмай-тындығын тексеру
керек. Болған жағдайда
функциясының
толық дифференциалы болатындығын не болмай-тындығын тексеру
керек. Болған жағдайда ![]() функциясын табу қажет.
функциясын табу қажет.
Шешуі. ![]()
![]() . Яғни
. Яғни ![]() . Осыдан берілген өрнек
. Осыдан берілген өрнек ![]() функциясы-ның
толық дифференциалы болады.
функциясы-ның
толық дифференциалы болады. ![]() деп алсақ, онда
деп алсақ, онда

37-мысал. ![]() эллипсінің ауданын есептеу керек.
эллипсінің ауданын есептеу керек.
Шешуі. ![]() болғандықтан
болғандықтан
![]() .
.
38-мысал.
![]()
![]() интегралын екі әдіспен тікелей
және Грин формуласының көмегімен есептеу керек,
мұндағы
интегралын екі әдіспен тікелей
және Грин формуласының көмегімен есептеу керек,
мұндағы ![]() жиегі
төбелері
жиегі
төбелері ![]() нүктелері
болатын үшбұрыш.
нүктелері
болатын үшбұрыш.
Шешуі. Алдымен интегралды тікелей есептейік
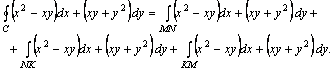
![]() теңдеуі
теңдеуі
![]() 1-ден 2-ге
дейін өзгереді.
1-ден 2-ге
дейін өзгереді.
![]() теңдеуі
теңдеуі
![]() 2-ден 1-ге
дейін өзгереді.
2-ден 1-ге
дейін өзгереді.
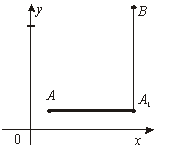
![]() теңдеуі
теңдеуі
![]() 3-тен 1-ге
дейін өзгереді.
3-тен 1-ге
дейін өзгереді.
Осыдан

Енді Грин формуласын пайдаланып, интегралды есептейік.
![]() .
.
Осыдан ![]() ,
мұндағы
,
мұндағы ![]() облысы
облысы
![]() үшбұрышы.
үшбұрышы.
![]() түзуінің
теңдеуі
түзуінің
теңдеуі ![]() ,
,
![]() -нің –
-нің – ![]() . Екі еселі интегралды
есептейік
. Екі еселі интегралды
есептейік
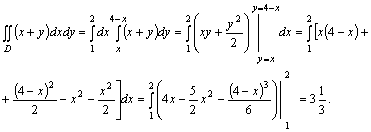
106. ![]() интегралын есептеу керек.
интегралын есептеу керек.
107. ![]() интегралын есептеу керек.
интегралын есептеу керек.
108. ![]() интегралын есептеу керек.
интегралын есептеу керек.
Берілген өрнектердің қандай да бір ![]() функциясының
толық дифференциалы болатындығын не болмайтындығын тексеру
керек. Болған жағдайда
функциясының
толық дифференциалы болатындығын не болмайтындығын тексеру
керек. Болған жағдайда ![]() функциясын анықтау қажет.
функциясын анықтау қажет.
109. ![]() .
.
110. ![]() .
.
111. ![]() .
.
112. ![]() .
.
Грин формуласын пайдаланып қисық сызықты интегралдарды есептеу керек.
113. ![]() , мұндағы
, мұндағы ![]() контуры (жиегі)
контуры (жиегі) ![]() шеңбері.
шеңбері.
114. ![]() , мұндағы
, мұндағы ![]() жиегі төбелері
жиегі төбелері ![]() ,
, ![]() болатын үшбұрыш.
болатын үшбұрыш.
115. ![]() , мұндағы
, мұндағы ![]() жиегі төбелері
жиегі төбелері ![]() ,
, ![]() ,
, ![]() ,
, ![]() болатын төртбұрыш.
болатын төртбұрыш.
116. ![]() , мұндағы
, мұндағы ![]() жиегі төбелері
жиегі төбелері ![]()
![]() , болатын үшбұрыш.
, болатын үшбұрыш.
117. ![]() астроидасымен шектелген пішіннің
ауданын табу керек.
астроидасымен шектелген пішіннің
ауданын табу керек.
118. ![]() кардиоидасымен шек-телген пішіннің
ауданын табу керек.
кардиоидасымен шек-телген пішіннің
ауданын табу керек.
119. ![]() циклоидасымен және
циклоидасымен және ![]() өсімен шектелген
пішіннің ауданын табу керек
өсімен шектелген
пішіннің ауданын табу керек ![]() .
.
120. ![]() параболаларымен шектелген пішіннің
ауданын табу керек.
параболаларымен шектелген пішіннің
ауданын табу керек.
5. БЕТТІК ИНТЕГРАЛДАР
5.1 Бірінші текті беттік интегралдар
![]() кеңістігінде
кеңістігінде ![]() бетінің әрбір
нүктесінде анықталған және үзіліссіз
бетінің әрбір
нүктесінде анықталған және үзіліссіз ![]() функциясы берілсін.
функциясы берілсін. ![]() бетін кезкелген ретпен
бетін кезкелген ретпен ![]() қарапайым
аймақтарға бөлейік. Осы қарапайым
аймақтардың аудандарын
қарапайым
аймақтарға бөлейік. Осы қарапайым
аймақтардың аудандарын ![]() деп, ал диаметрлерін сәйкесінше
деп, ал диаметрлерін сәйкесінше ![]() ,
, ![]() деп белгілейік,
мұндағы аймақтың диаметрі деп осы аймақтың
жиегіндегі екі нүктенің ара қашықтықтарының
ең үлкенін айтады. Әрбір қарапайым аймақтан
кезкелген бір
деп белгілейік,
мұндағы аймақтың диаметрі деп осы аймақтың
жиегіндегі екі нүктенің ара қашықтықтарының
ең үлкенін айтады. Әрбір қарапайым аймақтан
кезкелген бір ![]()
![]() нүктесін
таңдап алып, осы нүктедегі берілген
нүктесін
таңдап алып, осы нүктедегі берілген ![]() функциясының мәнін
функциясының мәнін ![]() ауданына
көбейтейік. Осындай көбейтінділердің қосындысы
ауданына
көбейтейік. Осындай көбейтінділердің қосындысы
![]()
![]() функциясының
функциясының
![]() беті бойынша
алынған интегралдық қосындысы деп аталады. Егер
беті бойынша
алынған интегралдық қосындысы деп аталады. Егер ![]() болғанда осы
интегралдық қосындысының шегі бар және ол шек
болғанда осы
интегралдық қосындысының шегі бар және ол шек ![]() бетін
бетін ![]() қарапайым
аймақтарға қалай бөлгенінен де, әрбір
қарапайым аймақтан
қарапайым
аймақтарға қалай бөлгенінен де, әрбір
қарапайым аймақтан ![]() нүктесін қалай таңдап
алғаннан да тәуелсіз болса, онда осы шек
нүктесін қалай таңдап
алғаннан да тәуелсіз болса, онда осы шек ![]() функциясының
функциясының ![]() бетіндегі бірінші текті
беттік интеграл деп аталып, былай белгіленеді.
бетіндегі бірінші текті
беттік интеграл деп аталып, былай белгіленеді.
![]() . (5.1)
. (5.1)
Бірінші текті беттік интегралдың мәні ![]() бетінің қай
жағын алғанымыздан тәуелсіз болады.
бетінің қай
жағын алғанымыздан тәуелсіз болады.
Бірінші текті беттік интегралдың негізгі қасиеттері екі еселі интегралдың негізгі қасиеттері сияқты болады.
Егер ![]() беті
беті ![]() теңдеуімен берілсе, ал оның
теңдеуімен берілсе, ал оның ![]() жазықтығындағы
проекциясы
жазықтығындағы
проекциясы ![]() болса,
онда бірінші текті беттік интеграл
болса,
онда бірінші текті беттік интеграл
![]() (5.2)
(5.2)
формуласымен есептеледі.
Егер ![]() болса, онда
болса, онда ![]() бетінің ауданы
бетінің ауданы
![]() (5.3)
(5.3)
формуласымен есептеледі.
5.2 Бірінші текті беттік интегралдың механикада және физикада қолданылуы
![]() кеңістігінде аумағы
кеңістігінде аумағы ![]() беті, ал
тығыздығы
беті, ал
тығыздығы ![]() болатын
материалдық беттің массасы
болатын
материалдық беттің массасы
![]() , (5.4)
, (5.4)
ал ![]() жазықтығына
қарағандағы статикалық моменттері сәйкес
жазықтығына
қарағандағы статикалық моменттері сәйкес
![]() ,
, ![]() ,
, ![]() (5.5)
(5.5)
формуласымен есептелінеді. Біртекті материалдың беттер үшін
![]() .
.
Материалдық беттің ауырлық орталығы
![]() . (5.6)
. (5.6)
формулаларымен анықталады.
Координата осьтеріне және бас нүктесіне қарағандағы инерция моменттері
 (5.7)
(5.7)
формулаларымен есептеледі.
38-мысал. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() беті
беті
![]() жазықтығының
бірінші октантадағы бөлігі.
жазықтығының
бірінші октантадағы бөлігі.
Шешуі. ![]()
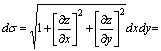
![]() . Осыдан беттік интеграл екі еселі
интегралға айналады:
. Осыдан беттік интеграл екі еселі
интегралға айналады:
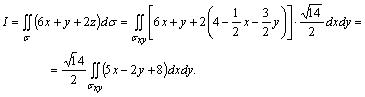
Екі еселі интегралдың интегралдау облысы ![]()
![]() ,
, ![]() түзулерімен
шектелген. Осыдан
түзулерімен
шектелген. Осыдан

39-мысал. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() беті
беті
![]() теңдеуімен
берілген жартысфера
теңдеуімен
берілген жартысфера ![]() .
.
Шешуі. ![]() ,
, ![]() ,
, 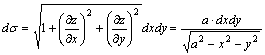 .
.
Осыдан беттік интеграл екі еселі интегралға айналады
![]() .
.
Екі еселі интегралдың интегралдау облысы ![]() шеңберімен шектелген
шеңберімен шектелген
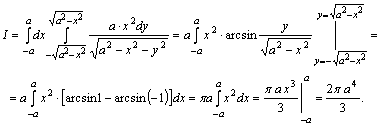
40-мысал. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() беті
беті
![]() параболоиды
және
параболоиды
және ![]() жазықтығымен
шектелген дененің толық беті болады.
жазықтығымен
шектелген дененің толық беті болады.
Шешуі. ![]() беті
беті ![]() және
және ![]() беттерінен тұрады,
мұндағы
беттерінен тұрады,
мұндағы ![]() беті
беті
![]() параболоиды,
ал
параболоиды,
ал ![]() беті
беті ![]() жазықтығының
бөлігі. Яғни
жазықтығының
бөлігі. Яғни
![]() .
.
![]() беті
беті ![]() ,
, ![]() осыдан
осыдан
![]() .
.
![]() беті
беті ![]() ,
, ![]() осыдан
осыдан
![]() .
.
Интегралдау облысы ![]() дөңгелегі болып табылады,
сондықтан полярлық координатаға көшейік:
дөңгелегі болып табылады,
сондықтан полярлық координатаға көшейік: ![]() . Онда
. Онда

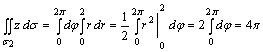 .
.
Сонымен
![]() .
.
121. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() беті
беті
![]() жазықтығының
бірінші октантадағы бөлігі.
жазықтығының
бірінші октантадағы бөлігі.
122. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() беті
беті
![]() жазықтығының
бірінші октантадағы бөлігі.
жазықтығының
бірінші октантадағы бөлігі.
123. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() беті
беті
![]() жазықтығының
бірінші октантадағы бөлігі.
жазықтығының
бірінші октантадағы бөлігі.
124. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() беті
беті
![]() теңдеуімен
берілген жарты сфера
теңдеуімен
берілген жарты сфера ![]() .
.
125. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() беті
беті
![]() конусының
конусының
![]() ,
, ![]() жазықтықтарының
арасындағы бөлігі.
жазықтықтарының
арасындағы бөлігі.
126. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() беті
беті
![]() конусының
конусының
![]() жазықтықтарының
арасындағы бөлігі.
жазықтықтарының
арасындағы бөлігі.
127. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() беті
беті
![]() теңдеуімен
берілген жарты сфера.
теңдеуімен
берілген жарты сфера.
128. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() беті
беті
![]() конусының
бөлігі
конусының
бөлігі ![]() .
.
129. ![]() интегралын есептеу керек,
мұндағы
интегралын есептеу керек,
мұндағы ![]() беті
беті
![]() параболоидының
бөлігі
параболоидының
бөлігі ![]() .
.
130. ![]() жазықтығының
жазықтығының ![]() цилиндрімен
қиғандағы бөлігінің ауданын табу керек.
цилиндрімен
қиғандағы бөлігінің ауданын табу керек.
131. Тығыздығы ![]() болатын
болатын ![]()
![]() параболоидының массасын табу керек.
параболоидының массасын табу керек.
132. Біртекті ![]() жарты сферасының ауырлық
орталығын табу керек.
жарты сферасының ауырлық
орталығын табу керек.
133. Біртекті ![]() параболоидының
параболоидының ![]() жазықтықтар-ының
арасындағы бөлігінің ауырлық орталығын табу
керек.
жазықтықтар-ының
арасындағы бөлігінің ауырлық орталығын табу
керек.
134. ![]() параболоидының
параболоидының ![]() жазықтықтарының
арасындағы бөлігінің
жазықтықтарының
арасындағы бөлігінің ![]() осіне қатысты инерция моментін табу
керек
осіне қатысты инерция моментін табу
керек ![]() .
.
135. ![]() конусының
конусының ![]() жазықтықтарының
арасындағы бөлігінің
жазықтықтарының
арасындағы бөлігінің ![]() осіне қатысты инерция моментін
есептеу керек.
осіне қатысты инерция моментін
есептеу керек.
5.3 Екінші текті беттік интегралдар
![]() кеңістігінде жатық
кеңістігінде жатық ![]() беті берілсін. Осы
беттің,
беті берілсін. Осы
беттің, ![]() жіктемесінің
көмегімен анықталған,
жіктемесінің
көмегімен анықталған, ![]() жағында анықталған
әрі үзіліссіз
жағында анықталған
әрі үзіліссіз ![]() ,
, ![]() функ-циялары берілсін.
функ-циялары берілсін. ![]() бетін кез келген жолмен
бетін кез келген жолмен ![]() қарапайым
аймақтарға бөлейік. Осы қарапайым
аймақтардың аудандарын
қарапайым
аймақтарға бөлейік. Осы қарапайым
аймақтардың аудандарын ![]() , ал сәйкес диаметрлерін
, ал сәйкес диаметрлерін ![]() арқылы
белгілейік, мұндағы аймақтың диаметрі деп осы
аймақтың шекарасында (жиегінде) жататын екі нүктенің
ара қашықтықтарының ең үлкенін айтады.
Әрбір
арқылы
белгілейік, мұндағы аймақтың диаметрі деп осы
аймақтың шекарасында (жиегінде) жататын екі нүктенің
ара қашықтықтарының ең үлкенін айтады.
Әрбір ![]() қара-пайым
аймағынан кез келген жолмен бір
қара-пайым
аймағынан кез келген жолмен бір ![]() нүктесін таңдап алып, осы
нүктедегі
нүктесін таңдап алып, осы
нүктедегі ![]() бетінің
жіктемесін
бетінің
жіктемесін ![]() деп
белгілейік. Төмендегі көбейтінділердің қосындысы:
деп
белгілейік. Төмендегі көбейтінділердің қосындысы:
![]() ;
;
![]() және
және
![]() функцияларының
функцияларының
![]() беті бойынша
алынған интегралдық қосындысы деп аталады.
беті бойынша
алынған интегралдық қосындысы деп аталады. ![]() осы интегралдық
қосындының шегі бар және ол шек
осы интегралдық
қосындының шегі бар және ол шек ![]() бетін
бетін ![]() қарапайым аймақтан
қарапайым аймақтан ![]() нүктесін
қалай таңдап алғаннан да тәуелсіз болса, онда осы шек
нүктесін
қалай таңдап алғаннан да тәуелсіз болса, онда осы шек ![]() және
және ![]() функцияларының
функцияларының ![]() беті бойынша
алынған екінші текті беттік интеграл деп аталып, былай белгіленеді:
беті бойынша
алынған екінші текті беттік интеграл деп аталып, былай белгіленеді:
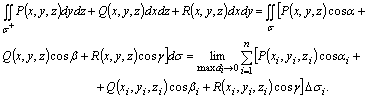 (5.8)
(5.8)
![]() бетінің жағын
ауыстырғанда екінші текті беттік интегралдың таңбасы
өзгереді.
бетінің жағын
ауыстырғанда екінші текті беттік интегралдың таңбасы
өзгереді.
Екінші текті беттік интегралдың негізгі қасиеттері екі еселі интегралдың негізгі қасиеттері сияқты болады.
Екінші текті беттік интегралды есептеу
![]() бетін координата остеріне параллель
(мекендік оқығына қатарлас) жүргізілген түзулер
тек бір нүктеде қисын. Бұл жағдайда
бетін координата остеріне параллель
(мекендік оқығына қатарлас) жүргізілген түзулер
тек бір нүктеде қисын. Бұл жағдайда ![]() бетінің теңдеуін
бетінің теңдеуін ![]() немесе
немесе ![]() немесе
немесе ![]() түрінде
жазуға болады.
түрінде
жазуға болады.
Егер ![]() бетінің
бетінің ![]() жазықтықтарындағы
проекцияларын сәйкес
жазықтықтарындағы
проекцияларын сәйкес ![]() деп белгілесек, онда екінші текті беттік
интегралдар-ды екі еселі интегралға келтіруге болады:
деп белгілесек, онда екінші текті беттік
интегралдар-ды екі еселі интегралға келтіруге болады:
а) ![]() ,
,
мұнда, егер ![]() болса, онда «+» таңбасын, ал
болса, онда «+» таңбасын, ал ![]() болса, онда «–»
таңбасын аламыз;
болса, онда «–»
таңбасын аламыз;
б) ![]() ,
,
мұнда, егер ![]() болса, онда «+» таңбасын, ал
болса, онда «+» таңбасын, ал ![]() болса, онда «–»
таңбасын аламыз;
болса, онда «–»
таңбасын аламыз;
в) ![]() ,
,
мұнда, егер ![]() болса, онда «+» таңбасын, ал
болса, онда «+» таңбасын, ал ![]() болса, онда «–»
таңбасын аламыз.
болса, онда «–»
таңбасын аламыз.
Тұйық жабық ![]() беті бойынша алынатын беттік
интегралды
беті бойынша алынатын беттік
интегралды
![]()
деп белгілейді.
41-мысал. ![]() интегралын
интегралын
|
Шешуі. Берілген интегралды үш интегралдың қосындысы түрінде жазайық
|
24-сурет |
![]() интегралын
есептейік.
интегралын
есептейік. ![]() ,
, ![]() болғандықтан,
болғандықтан,
![]() .
.
![]() бетінің
бетінің
![]() жазықтығында
жазықтығында
![]() проекциясы
проекциясы ![]() ,
, ![]()
![]() түзулерімен шектелген. Осыдан
түзулерімен шектелген. Осыдан
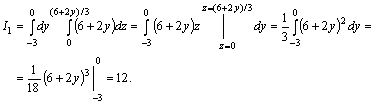
![]() интегралын
есептейік.
интегралын
есептейік. ![]() ,
, ![]() болған-дықтан
болған-дықтан
![]() .
. ![]() бетінің
бетінің ![]() жазықтығындағы
жазықтығындағы
![]() проекциясы
проекциясы ![]() түзулерімен
шектелген. Осыдан
түзулерімен
шектелген. Осыдан
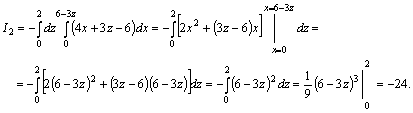
![]() интегралын
есептейік.
интегралын
есептейік. ![]() ,
, ![]() болғандықтан
болғандықтан
![]() .
.
![]() бетінің
бетінің
![]() жазықтығындағы
жазықтығындағы
![]() проекциясы
проекциясы ![]() ,
, ![]() түзулерімен шектелген.
Осыдан
түзулерімен шектелген.
Осыдан
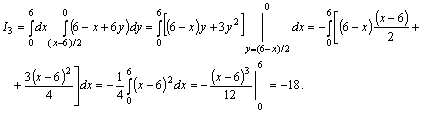
Сонымен
![]() .
.
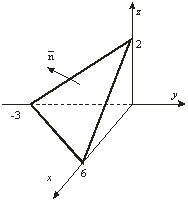
42-мысал. ![]() интегралын
интегралын ![]() бетінің сыртқы жағы
бойынша есептеу керек, мұндағы
бетінің сыртқы жағы
бойынша есептеу керек, мұндағы ![]() беті
беті ![]() конусымен
конусымен ![]() жазықтығының
қиылысынан шығатын дененің толы беті.
жазықтығының
қиылысынан шығатын дененің толы беті.
|
Шешуі. Берілген интегралды үш интегралдың қосындысы түрінде жазайық
Бұл жағдайда |
25-сурет
|
теңдеуімен берілген ![]() беттерінен тұрады.
беттерінен тұрады.
Сондықтан
![]() .
.
![]() бетінде
бетінде
![]() бетінде
бетінде ![]() ,
, ![]() бетінде
бетінде ![]() . Осыдан
. Осыдан
![]() .
.
![]() бетінің
бетінің ![]() жазықтығындағы
жазықтығындағы
![]() проекциясы
проекциясы ![]() түзулермен
шектелген. Осыдан
түзулермен
шектелген. Осыдан

![]()
![]() интегралын есептейік.
интегралын есептейік.
Бұл жағдайда ![]() беті:
беті: ![]() теңдеуімен берілген
теңдеуімен берілген ![]() ,
, ![]() теңдеуімен берілген
теңдеуімен берілген ![]() және
және ![]() теңдеуімен
берілген
теңдеуімен
берілген ![]() беттерінен
тұрады. Сондықтан
беттерінен
тұрады. Сондықтан
![]()
![]() бетінде
бетінде
![]() бетінде
бетінде ![]() ,
, ![]() бетінде
бетінде ![]() . Осыдан
. Осыдан
![]() .
.
![]() бетінің
бетінің
![]() жазықтығындағы
жазықтығындағы
![]() проекциясы
проекциясы ![]() түзулерімен
шектелген. Осыдан
түзулерімен
шектелген. Осыдан
![]() .
.
![]() интегралын есептейік.
интегралын есептейік.
Бұл жағдайда ![]() беті:
беті: ![]() теңдеуімен берілген
теңдеуімен берілген ![]() ,
, ![]() теңдеуімен берілген
теңдеуімен берілген ![]() және
және ![]() теңдеуімен
берілген
теңдеуімен
берілген ![]() беттерінен
тұрады. Сондықтан
беттерінен
тұрады. Сондықтан
![]() .
.
![]() бетінде
бетінде
![]() бетінде
бетінде ![]() . Осыдан
. Осыдан
![]() .
.
![]() бетінің
бетінің
![]() жазықтығындағы
проекциясы
жазықтығындағы
проекциясы ![]() шеңберімен
шектелген. Сондықтан полярлық координаталар жүйесіне
көшеміз:
шеңберімен
шектелген. Сондықтан полярлық координаталар жүйесіне
көшеміз:
![]() ;
яғни
;
яғни
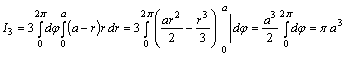 .
.
Сонымен
![]() .
.
136. ![]() интегралын
интегралын ![]() бетінің сыртқы жағы
бойынша есептеу керек, мұндағы
бетінің сыртқы жағы
бойынша есептеу керек, мұндағы ![]() беті
беті ![]() жазықтығы-ның
координаттық жазықтықтармен қиылғандағы
бөлігі.
жазықтығы-ның
координаттық жазықтықтармен қиылғандағы
бөлігі.
137. ![]() интегралын
интегралын ![]() бетінің сыртқы жағы
бойынша есептеу керек, мұндағы
бетінің сыртқы жағы
бойынша есептеу керек, мұндағы ![]() беті
беті ![]() жазықтығының
координаттық жазықтықтармен қиылғандағы
бөлігі.
жазықтығының
координаттық жазықтықтармен қиылғандағы
бөлігі.
138. ![]() интегралын
интегралын ![]() бетінің сыртқы жағы
бойынша есептеу керек, мұндағы
бетінің сыртқы жағы
бойынша есептеу керек, мұндағы ![]() беті
беті ![]() жазықтығының
координаттық жазықтықтармен қиылғандағы
бөлігі.
жазықтығының
координаттық жазықтықтармен қиылғандағы
бөлігі.
139. ![]() интегралын
интегралын ![]() бетінің сыртқы жағы
бойынша есептеу керек, мұндағы
бетінің сыртқы жағы
бойынша есептеу керек, мұндағы ![]() беті
беті ![]() эллипсоидының бірінші
октантындағы (жарты ширегіндегі) бөлігі.
эллипсоидының бірінші
октантындағы (жарты ширегіндегі) бөлігі.
140. ![]() интегралын
интегралын ![]() бетінің сыртқы жағы
бойынша есептеу керек, мұндағы
бетінің сыртқы жағы
бойынша есептеу керек, мұндағы ![]() беті
беті ![]() эллипсоидының бірінші
октантындағы (жарты ширегіндегі) бөлігі.
эллипсоидының бірінші
октантындағы (жарты ширегіндегі) бөлігі.
141. ![]() интегралын
интегралын ![]()
![]() жазықтықтарымен шектелген
тетраэдрдің сыртқы жағы бойынша есептеу керек.
жазықтықтарымен шектелген
тетраэдрдің сыртқы жағы бойынша есептеу керек.
142. ![]() интегралын
интегралын ![]()
![]() жазықтықтарымен шектелген
тетраэдрдің сыртқы жағы бойынша есептеу керек.
жазықтықтарымен шектелген
тетраэдрдің сыртқы жағы бойынша есептеу керек.
143. ![]() интегралын
интегралын ![]() сфера-сының сыртқы жағы
бойынша есептеу керек.
сфера-сының сыртқы жағы
бойынша есептеу керек.
5.4 Стокс формуласы
Егер тұйық жатық ![]() контурымен (жиегінен) шектелген
екі жақты
контурымен (жиегінен) шектелген
екі жақты ![]() бетінде
бетінде
![]() ,
, ![]() функциялары және
олардың бірінші ретті дербес туындылары үзіліссіз болса, онда
функциялары және
олардың бірінші ретті дербес туындылары үзіліссіз болса, онда
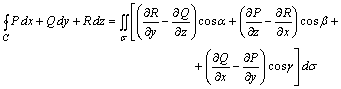 (5.9)
(5.9)
теңдігі Стокс формуласы деп аталады, мұндағы ![]() –
–![]() бетінің жіктемесінің
бағыттаушы косинустары. Тіктеменің бағыты оның
ұшынан қарағанда
бетінің жіктемесінің
бағыттаушы косинустары. Тіктеменің бағыты оның
ұшынан қарағанда ![]() тұйық контурының
(жиегінің) бойымен қозғалыс сағат тілінің
қозғалысына қарсы бағытта болатындай өтіп
таңдап алынады.
тұйық контурының
(жиегінің) бойымен қозғалыс сағат тілінің
қозғалысына қарсы бағытта болатындай өтіп
таңдап алынады.
Грин формуласы Стокс формуласының ![]() және
және ![]() болғандағы
дербес жағдайы.
болғандағы
дербес жағдайы.
43-мысал. ![]() интегралын Стокс формуласының
көмегімен есептеу керек, мұндағы
интегралын Стокс формуласының
көмегімен есептеу керек, мұндағы ![]() контуры төбелері
контуры төбелері ![]() нүктелері
болатын
нүктелері
болатын ![]() үшбұрышы.
үшбұрышы.
Шешуі. ![]() және
және ![]() нүктелері арқылы өтетін
жазықтықтың теңдеуі
нүктелері арқылы өтетін
жазықтықтың теңдеуі ![]() немесе
немесе ![]() болады.
болады.
![]()
![]()
Осыдан Стокс формуласы бойынша
![]() .
.
![]() бетінің
(
бетінің
(![]() үшбұрышының)
үшбұрышының) ![]() жазықтығындағы
жазықтығындағы ![]() проекциясы
проекциясы ![]() түзулерімен
шектелген. Сондықтан
түзулерімен
шектелген. Сондықтан
![]() .
.
144. ![]() интегралын Стокс формуласының
көмегімен есептеу керек, мұндағы
интегралын Стокс формуласының
көмегімен есептеу керек, мұндағы ![]() контуры төбелері
контуры төбелері ![]() нүктелері
болатын
нүктелері
болатын ![]() үшбұрышы.
үшбұрышы.
145. ![]() интегралын Стокс формуласының
көмегімен есептеу керек, мұндағы
интегралын Стокс формуласының
көмегімен есептеу керек, мұндағы ![]() контуры төбелері
контуры төбелері ![]() нүктелері
болатын
нүктелері
болатын ![]() үшбұрышы.
үшбұрышы.
146. ![]() интегралын Стокс формуласының
көмегімен есептеу керек, мұндағы
интегралын Стокс формуласының
көмегімен есептеу керек, мұндағы ![]() контуры төбелері
контуры төбелері ![]() нүктелері
болатын
нүктелері
болатын ![]() үшбұрышы.
үшбұрышы.
5.5 Остроградский-Гаусс формуласы
Тұйық ![]() бетімен шектелген
бетімен шектелген ![]() жабық облысында
жабық облысында ![]() ,
, ![]() функциялары және
олардың бірінші ретті дербес туындылары үзіліссіз болса, онда
функциялары және
олардың бірінші ретті дербес туындылары үзіліссіз болса, онда
![]() , (5.10)
, (5.10)
мұндағы ![]() –
– ![]() бетінің жіктемесінің
бағыттаушы косинустары.
бетінің жіктемесінің
бағыттаушы косинустары.
Бұл теңдеу Остроградский-Гаусс формуласы деп аталады.
44-мысал. 42-мысалдағы берілген есепті Остроградский-Гаусс формуласының көмегімен есептеу керек.
Шешуі. ![]() ,
, ![]() . Осыдан
. Осыдан ![]() . Яғни
. Яғни ![]() болады. Бұл интегралды есептеу
үшін
болады. Бұл интегралды есептеу
үшін ![]() ,
, ![]() цилиндрлік
координаталар (мекендік) жүйесіне көшсек
цилиндрлік
координаталар (мекендік) жүйесіне көшсек
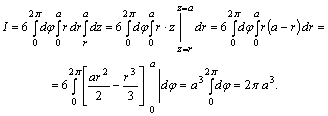
147. 142-есебін Остроградский-Гаусс формуласының көмегімен есептеу керек.
148. 143-есебін Остроградский-Гаусс формуласының көмегімен есептеу керек.
149. ![]() интегралын Остроградский-Гаусс
формуласының көмегімен
интегралын Остроградский-Гаусс
формуласының көмегімен ![]() ,
, ![]() кубының сыртқы беті бойынша
есептеу керек.
кубының сыртқы беті бойынша
есептеу керек.
150. ![]() интегралын Остроградский-Гаусс
формуласының көмегімен
интегралын Остроградский-Гаусс
формуласының көмегімен ![]() жазықтықтары-мен шектелген
тетраэдрдің сыртқы беті бойынша есептеу керек.
жазықтықтары-мен шектелген
тетраэдрдің сыртқы беті бойынша есептеу керек.
6. ӨРІСТЕР ТЕОРИЯСЫНЫҢ ЭЛЕМЕНТТЕРІ
6.1 Скалярлық өріс. Деңгейлік беттер
Кеңістіктің V аймағында жататын
кезкелген бір M нүктесіне белгілі заңдылық бойынша
анықталған ![]() саны сәйкестендірілсе, онда осы
аймақта скалярлық өріс берілді дейді. Егер үш
өлшемді кеңістікте декарттық координаталар
(мекендік)жүйесі енгізілсе, онда скалярлық өрістің
берілуі үш айнымалы функцияның берілуімен бірдей:
саны сәйкестендірілсе, онда осы
аймақта скалярлық өріс берілді дейді. Егер үш
өлшемді кеңістікте декарттық координаталар
(мекендік)жүйесі енгізілсе, онда скалярлық өрістің
берілуі үш айнымалы функцияның берілуімен бірдей:
![]() (6.1)
(6.1)
Екі өлшемді кеңістікте скалярлық өріс
![]() (6.2)
(6.2)
функциясы арқылы беріледі де жазық өріс деп аталады.
![]() теңдігін қанағаттандыратындарын
теңдігін қанағаттандыратындарын
![]() аймағында
жататын
аймағында
жататын ![]() нүктелерінің
жиынтығын
нүктелерінің
жиынтығын ![]() санына
сәйкес деңгейлік беттер деп атайды.
санына
сәйкес деңгейлік беттер деп атайды.
Жазық өріс үшін ![]() теңдеуі
теңдеуі ![]() санына сәйкес
деңгейлік сызықтар үйірін анықтайды.
санына сәйкес
деңгейлік сызықтар үйірін анықтайды.
Егер ![]() функциясы кеңістіктің
функциясы кеңістіктің ![]() аймағында жататын
әрбір нүктедегі температураны анықтаса, онда оны
температураның скалярлық өрісі дейді.
аймағында жататын
әрбір нүктедегі температураны анықтаса, онда оны
температураның скалярлық өрісі дейді.
45-мысал. ![]() скалярлық өрісінің
деңгейлік беттерін табу керек.
скалярлық өрісінің
деңгейлік беттерін табу керек.
Шешуі. ![]() деңгейлік беттер
болғандықтан
деңгейлік беттер
болғандықтан
а) егер ![]() болса, ода деңгейлік беттер екі
қуысты гиперболоидтар жиынтығы болады;
болса, ода деңгейлік беттер екі
қуысты гиперболоидтар жиынтығы болады;
б) егер ![]() болса, ода деңгейлік беттер бір
қуысты гиперболоидтар жиынтығы болады;
болса, ода деңгейлік беттер бір
қуысты гиперболоидтар жиынтығы болады;
в) егер ![]() болса, ода деңгейлік беттер конустар
жиынтығы болады.
болса, ода деңгейлік беттер конустар
жиынтығы болады.
46-мысал. ![]() скалярлық өрісінің
деңгейлік сызықтар үйірін табу керек.
скалярлық өрісінің
деңгейлік сызықтар үйірін табу керек.
Шешуі. ![]() функциясын
функциясын ![]() тұрақтысымен
теңестірейік
тұрақтысымен
теңестірейік ![]() немесе
немесе
![]() .
Яғни деңгейлік сызықтар параболалардың жиынтығы
болады.
.
Яғни деңгейлік сызықтар параболалардың жиынтығы
болады.
6.2 Скалярлық өрістің туындысы
![]() скалярлық өрісінің
скалярлық өрісінің ![]() векторы бойынша
берілген
векторы бойынша
берілген ![]() бағыты
бойынша туындысы
бағыты
бойынша туындысы
![]() ,
,
мұндағы ![]() ;
;
формуласымен анықталады.
![]() скалярлық өрісінің
скалярлық өрісінің ![]() қисығы
бойынша M нүктесіндегі туындысы одан
қисығы
бойынша M нүктесіндегі туындысы одан ![]() қисығының M
нүктесінде жүргізілген
қисығының M
нүктесінде жүргізілген ![]() жанамасы бойынша алынатын туындымен
бірдей.
жанамасы бойынша алынатын туындымен
бірдей.
![]() -ң абсолюттік шамасы
-ң абсолюттік шамасы ![]() скалярлық
өрісінің M нүктесіндегі өзгеру
жылдамдығын, ал оның таңбасы оң болғанда
өсіп, теріс болғанда кемитіндігін анықтайды.
скалярлық
өрісінің M нүктесіндегі өзгеру
жылдамдығын, ал оның таңбасы оң болғанда
өсіп, теріс болғанда кемитіндігін анықтайды.
6.3 Скалярлық өрістің градиенті
![]() скалярлық өрісінің
градиенті деп өрістің деңгейлік бетіне жүргізілген
тіктеме бойымен оның өсу бағытына сай алынған
скалярлық өрісінің
градиенті деп өрістің деңгейлік бетіне жүргізілген
тіктеме бойымен оның өсу бағытына сай алынған
![]() (6.3)
(6.3)
векторын айтады, мұндағы ![]() Гамильтон (набла)
операторы.
Гамильтон (набла)
операторы.
Скалярлық өрістің градиентінің негізгі қасиеттері:
![]() ; (6.4)
; (6.4)
![]() ; (6.5)
; (6.5)
мұндағы
![]() – тұрақтылар;
– тұрақтылар;
![]() ; (6.6)
; (6.6)
![]() ; (6.7)
; (6.7)
![]() ; (6.8)
; (6.8)
![]() ; (6.9)
; (6.9)
6.4 Скалярлық өрістің туындысымен оның градиентінің арасындағы байланыс
![]() скалярлық өрісінен
скалярлық өрісінен ![]() бағытында
алынған туындымен ол өрістің
бағытында
алынған туындымен ол өрістің ![]() нүктесіндегі градиентінің
арасындағы байланыс
нүктесіндегі градиентінің
арасындағы байланыс
![]() (6.10)
(6.10)
формуласымен анықталады, мұндағы ![]() –
– ![]() бағытының бірлік векторы, ал
бағытының бірлік векторы, ал ![]() - градиетпен
- градиетпен ![]() векторының
векторының ![]() нүктесіндегі
бұрышы.
нүктесіндегі
бұрышы.
Градиенттің ұзындығы ![]() өрісінің
өзгеру жылдамдығының
өрісінің
өзгеру жылдамдығының ![]() нүктесіндегі ең үлкен
шамасына тең. Яғни
нүктесіндегі ең үлкен
шамасына тең. Яғни
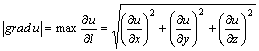 . (6.11)
. (6.11)
47-мысал. ![]() функциясы,
функциясы, ![]() векторы және
векторы және ![]() нүктесі берілген. Табу
керек:
нүктесі берілген. Табу
керек:
а) ![]() функциясының
функциясының ![]() нүктесіндегі градиентін;
нүктесіндегі градиентін;
б) ![]() нүктесіндегі
нүктесіндегі
![]() функциясының
функциясының
![]() векторының
бағыты бойынша туындысын;
векторының
бағыты бойынша туындысын;
в) ![]() нүктесіндегі
нүктесіндегі
![]() функциясының
өсу жылдамдығының ең үлкен шамасын.
функциясының
өсу жылдамдығының ең үлкен шамасын.
Шешуі.
![]()
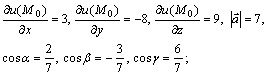
Осыдан
а) ![]() ;
;
б) ![]() ;
;
в) ![]() .
.
6.5 Векторлық өріс
![]() кеңістігінде жататын
кеңістігінде жататын ![]() аймағының
әрбір
аймағының
әрбір ![]() нүктесіне
нүктесіне
![]()
векторының анықталған мәні сәйкес келсе,
онда осы аймақта векторлық өріс берілді дейді.
Мұндағы ![]() және
және
![]() функциялары
функциялары ![]() векторының
сәйкес
векторының
сәйкес ![]() және
және
![]() осьтеріндегі
(оқтықтарындағы) проекциялары.
осьтеріндегі
(оқтықтарындағы) проекциялары.
Егер ![]() векторы күш ретінде
қарастырылса, онда векторлық өрісті күш өрісі
дейді.
векторы күш ретінде
қарастырылса, онда векторлық өрісті күш өрісі
дейді.
Векторлық өрістің векторлық
сызығы деп оның әрбір ![]() нүктесіндегі бағыты осы
нүктедегі
нүктесіндегі бағыты осы
нүктедегі ![]() векторының
бағытымен сәйкес келетін қисық сызықты айтады.
Векторлық сызық (күш сызығы)
векторының
бағытымен сәйкес келетін қисық сызықты айтады.
Векторлық сызық (күш сызығы)
![]() (6.12)
(6.12)
дифференциалдық теңдеулер жүйесі арқылы анықталады.
Векторлық өріс уақыттан тәуелсіз болса, онда оны стационарлық; ал уақыттан тәуелді болса, онда оны стационарлық емес (тұрақты емес) өріс деп атайды.
6.6 Векторлық өрістің ағыны және дивергенциясы. Остроградский-Гаусс формуласы
![]() кеңістігінде жататын
кеңістігінде жататын ![]() аймағында жататын
екі жақты
аймағында жататын
екі жақты ![]() беті
берілсін. Беттің жағы таңдалынып алынған
жаққа тұрғызылған
беті
берілсін. Беттің жағы таңдалынып алынған
жаққа тұрғызылған
![]()
векторы арқылы анықталады.
Егер ![]() беті
беті
![]() (6.13)
(6.13)
теңдеуімен берілсе, онда
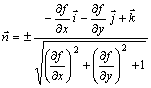 . (6.14)
. (6.14)
Мұндағы плюс таңбасы беттің
жоғары жағына сәйкес алынады, өйткені бұл
жаққа тұрғызылған тіктемемен ![]() оқтығының
арасындағы бұрыш сүйір болғандықтан
оқтығының
арасындағы бұрыш сүйір болғандықтан ![]() оң болады. Минус
таңбасы беттің төменгі жағына сәйкес алынады.
оң болады. Минус
таңбасы беттің төменгі жағына сәйкес алынады.
Егер ![]() беті
беті
![]() (6.15)
(6.15)
теңдеуімен берілсе, онда бірлік тіктеме вектор
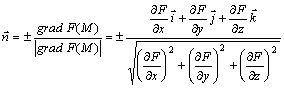 . (6.16)
. (6.16)
Егер бет бірнеше бөліктен тұрса, онда тіктеме бірлік вектор әрбір бөлік үшін бөлек табылады. Бет тұйық болған жағдайда әр уақытта оның сыртқы жағы алынады.
Бірлік тіктеме ![]() бағытындағы
бағытындағы ![]() беті бойынша
өтетін
беті бойынша
өтетін ![]() векторлық
өрісінің ағыны деп
векторлық
өрісінің ағыны деп
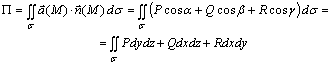 (6.17)
(6.17)
интегралын айтады.
Егер ![]() беті
беті ![]() жазықтығына бірмәнді
проекцияланса, онда
жазықтығына бірмәнді
проекцияланса, онда ![]() векторының
векторының
![]() беті
арқылы өтетін ағыны
беті
арқылы өтетін ағыны ![]() бетінің проекциясы
(көлеңі)
бетінің проекциясы
(көлеңі) ![]() арқылы
алынатын екі еселі интегралмен есептелінеді:
арқылы
алынатын екі еселі интегралмен есептелінеді:
![]() (6.18)
(6.18)
Мұндағы ![]() (6.14), (6.16) – формулаларындағы
(6.14), (6.16) – формулаларындағы ![]() -ң алдындағы
коэффициент. Жоғарыдағыдай
-ң алдындағы
коэффициент. Жоғарыдағыдай ![]() беті
беті ![]() немесе
немесе ![]() жазықтықтарына бірмәнді
проекцияланса, онда ағыны төмендегі формулалармен анықталады.
жазықтықтарына бірмәнді
проекцияланса, онда ағыны төмендегі формулалармен анықталады.
![]() (6.19)
(6.19)
![]() векторлық өрісінің М
нүктесіндегі дивергенциясы деп
векторлық өрісінің М
нүктесіндегі дивергенциясы деп ![]() векторлық өрісінің
ағынының осы нүктедегі көлемдік тығыздығын
айтады:
векторлық өрісінің
ағынының осы нүктедегі көлемдік тығыздығын
айтады:
![]() ,
,
мұндағы ![]() – тұйық
– тұйық ![]() бетімен шенелген
құрамында
бетімен шенелген
құрамында ![]() нүктесі
болатын көлем.
нүктесі
болатын көлем.
Дивергенция декарттық координаталар жүйесінде
![]() (6.20)
(6.20)
формуласымен анықталады.
Егер ![]() болса, онда
болса, онда ![]() бетінен
бетінен ![]() тіктемесінің бағыты бойынша
ағатын сұйықтың мөлшері
тіктемесінің бағыты бойынша
ағатын сұйықтың мөлшері ![]() тіктемесінің
бағытына қарсы ағатын сұйықтың
мөлшерінен көп болады; егер
тіктемесінің
бағытына қарсы ағатын сұйықтың
мөлшерінен көп болады; егер ![]() болса, онда
болса, онда ![]() бетінен
бетінен ![]() тіктемесінің бағыты бойынша
ағатын сұйықтың мөлшері оған қарсы
ағатын сұйықтың мөлшерінен аз болады, яғни
ағын теріс болады. Егер
тіктемесінің бағыты бойынша
ағатын сұйықтың мөлшері оған қарсы
ағатын сұйықтың мөлшерінен аз болады, яғни
ағын теріс болады. Егер ![]() болса, онда
болса, онда ![]() бетінен ағып шығатын
сұйықпен оған құятын сұйықтың
мөлшері бірдей, яғни ағын нөлге тең болады.
бетінен ағып шығатын
сұйықпен оған құятын сұйықтың
мөлшері бірдей, яғни ағын нөлге тең болады.
Дивергенцияның негізгі қасиеттері:
а) ![]() , мұндағы
, мұндағы ![]() тұрақты вектор;
тұрақты вектор;
б) ![]() , мұндағы
, мұндағы ![]() - тұрақты сандар;
- тұрақты сандар;
в) ![]() .
.
Остроградский-Гаусс формуласы
![]() көлемін қоршаған
тұйық
көлемін қоршаған
тұйық ![]() бетінің
сырты арқылы өтетін ағынды анықтау үшін
Огсроградский - Гаусс теоремасын қолданған ыңғайлы:
бетінің
сырты арқылы өтетін ағынды анықтау үшін
Огсроградский - Гаусс теоремасын қолданған ыңғайлы: ![]() векторлық
өрісінің кез келген бағытымен тұйық
векторлық
өрісінің кез келген бағытымен тұйық ![]() беті арқылы
өтетін ағыны
беті арқылы
өтетін ағыны ![]() -дан осы бет қоршаған
-дан осы бет қоршаған ![]() көлемі бойынша
алынатын үш еселі интегралға тең болады. Яғни
көлемі бойынша
алынатын үш еселі интегралға тең болады. Яғни
![]() . (6.21)
. (6.21)
48-мысал. ![]() теңдеуімен берілген
жазықтықтың бір октантадағы (жарты ширектегі) беті
арқылы өтетін
теңдеуімен берілген
жазықтықтың бір октантадағы (жарты ширектегі) беті
арқылы өтетін ![]() векторлық өрісінің
ағынын табу керек. Мұндағы жазықтықтың
тіктемесі
векторлық өрісінің
ағынын табу керек. Мұндағы жазықтықтың
тіктемесі ![]() өсімен
сүйір бұрыш жасайды.
өсімен
сүйір бұрыш жасайды.
Шешуі. Бірлік тіктеме векторы
![]() ,
,
яғни ![]() ;
;
Осыдан

49-мысал. Огсроградский-Гаусс формуласын пайдаланып
координаталар жазықтықтарымен ![]() жазықтығының
қиылысуынан пайда болатын пирамиданың сыртқы беттері
арқылы өтетін
жазықтығының
қиылысуынан пайда болатын пирамиданың сыртқы беттері
арқылы өтетін ![]() векторлық өрісінің
ағынын есептеу керек.
векторлық өрісінің
ағынын есептеу керек.
Шешуі. ![]() . Яғни
. Яғни
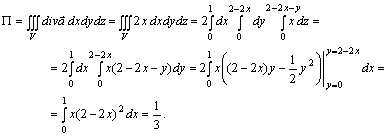
6.7 Сызықтық интеграл және векторлық өрістің циркуляциясы (иірімі). Векторлық өрістің роторы (құйымы). Стокс теоремасы
![]() кеңістігінің бір
аймағында
кеңістігінің бір
аймағында ![]() векторлық
өрісі және осы аймақта жататын бағытталған
векторлық
өрісі және осы аймақта жататын бағытталған ![]() қисығы
берілсін.
қисығы
берілсін. ![]() векторының
өрісінің
векторының
өрісінің ![]() қисығы
бойынша алынған сызықты интеграл деп
қисығы
бойынша алынған сызықты интеграл деп
![]() (6.22)
(6.22)
қисық сызықты интегралды айтады. Мұндағы ![]() – берілген
– берілген ![]() қисығының
бірлік жанама векторы,
қисығының
бірлік жанама векторы, ![]() оның доғасының
диффееренциалы, ал
оның доғасының
диффееренциалы, ал ![]() -
берілген
-
берілген ![]() қисының
бойында жататын нүктелердің радиус-векторы.
қисының
бойында жататын нүктелердің радиус-векторы.
Егер ![]() – күштер өрісі болса, онда
(22) –сызықты интеграл осы күштер өрісінің
– күштер өрісі болса, онда
(22) –сызықты интеграл осы күштер өрісінің ![]() қисығының
бойында істеген жұмысын көрсетеді.
қисығының
бойында істеген жұмысын көрсетеді.
Егер ![]() қисығы
қисығы ![]() параметрлік теңдеулерімен
берілсе әрі бастапқы және соңғы
нүктелеріпараметрдің
параметрлік теңдеулерімен
берілсе әрі бастапқы және соңғы
нүктелеріпараметрдің ![]() және
және ![]() мәндеріне сәйкес болса, онда
мәндеріне сәйкес болса, онда
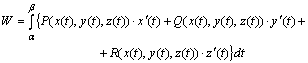 (6.23)
(6.23)
Егер ![]() қисығы
қисығы ![]() (
(![]() ) теңдеулерімен берілсе, онда
сызықты интеграл
) теңдеулерімен берілсе, онда
сызықты интеграл
![]() (6.24)
(6.24)
формуласымен есептелінеді.
![]() қисығының бағыты
өзгергенде сызықты интегралдың таңбасы өзгереді.
қисығының бағыты
өзгергенде сызықты интегралдың таңбасы өзгереді.
![]() векторлық өрісінің
циркуляциясы (иірімі) деп осы өрістен тұйық
векторлық өрісінің
циркуляциясы (иірімі) деп осы өрістен тұйық ![]() қисығы
бойынша алынған сызықты интегралды айтады:
қисығы
бойынша алынған сызықты интегралды айтады:
![]() . (6.25)
. (6.25)
Егер ![]() қисығы
қисығы ![]() бөліктерінен
құралса, онда
бөліктерінен
құралса, онда
![]() . (6.26)
. (6.26)
50-мысал. ![]() векторлық өрісінің,
векторлық өрісінің, ![]() жазықтығының
координаттық жазықтықтармен қиылысуынан пайда
болған,
жазықтығының
координаттық жазықтықтармен қиылысуынан пайда
болған, ![]() қисығының
бойындағы циркуляциясын (иірімі) табу керек.
қисығының
бойындағы циркуляциясын (иірімі) табу керек.
|
26-сурет |
Шешуі.
а)
|
![]() нүктесінен және
нүктесінен және ![]() нүктесіне
қозғалғанда
нүктесіне
қозғалғанда ![]() айнымалысы үштен нөлге дейін
кемиді, сондықтан
айнымалысы үштен нөлге дейін
кемиді, сондықтан
![]()
б) ![]() түзуінің бойында
түзуінің бойында ![]() және
және ![]() , сондықтан
, сондықтан ![]() .
. ![]() теңдеуінен
теңдеуінен ![]() және
және ![]() . Сондықтан
. Сондықтан ![]() және
және
![]()
![]() .
Яғни
.
Яғни
![]()
с) ![]() түзуінің бойында
түзуінің бойында ![]() және
және ![]() , сондықтан
, сондықтан ![]() .
. ![]() теңдеуінен
теңдеуінен ![]() және
және ![]() . Сондықтан
. Сондықтан ![]() және
және
![]() .
.
![]() нүктесінен
және
нүктесінен
және ![]() нүктесіне
қозғалғанда
нүктесіне
қозғалғанда ![]() айнымалысы үштен нөлге дейін
кемиді, сондықтан
айнымалысы үштен нөлге дейін
кемиді, сондықтан
![]() .
.
Сонымен ![]() .
.
![]() векторлық өрісінің
роторы (құйыны) деп
векторлық өрісінің
роторы (құйыны) деп
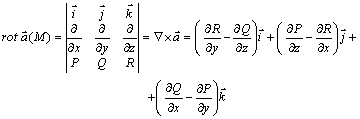 (6.27)
(6.27)
формуласымен есептелінетін векторды айтады.
Құйынның қасиеттері:
1. ![]() , мұндағы
, мұндағы ![]() - тұрақты вектор;
- тұрақты вектор;
2. ![]() , мұндағы
, мұндағы ![]() - тұрақты сандар.
- тұрақты сандар.
3. ![]() , мұндағы
, мұндағы ![]() - скалярлық функция.
- скалярлық функция.
Егер ![]() қисық сызығы екі
жақты жатық
қисық сызығы екі
жақты жатық ![]() бетін қоршаған
тұйық жатық жиек болса, онда Стокс теоремасы оындалады.
Оның векторлық пішіні
бетін қоршаған
тұйық жатық жиек болса, онда Стокс теоремасы оындалады.
Оның векторлық пішіні
![]() , (6.28)
, (6.28)
мұндағы ![]() бірлік векторы
бірлік векторы ![]() бетіне
тұрғызылған тіктеме, оның ұшынан
қарағанда
бетіне
тұрғызылған тіктеме, оның ұшынан
қарағанда ![]() жиегін
айналу сағат бағытына қарсы болуы тиіс.
жиегін
айналу сағат бағытына қарсы болуы тиіс.
![]() болғандықтан
болғандықтан
![]() . (6.29)
. (6.29)
51-мысал. Стокс формуласын пайдаланып
![]() векторлық өрісінің
векторлық өрісінің ![]() ,
, ![]() ,
, ![]() нүктелері арқылы өтетін
нүктелері арқылы өтетін ![]() жиегіндегі иірімін табу
керек.
жиегіндегі иірімін табу
керек.
Шешуі.
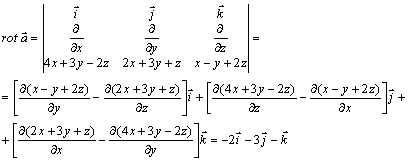
Бағдарлануы оң ![]() үшбұрышынан
тұратын
үшбұрышынан
тұратын ![]() жиегі
жиегі
![]() жазықтығында
жатады. Осыдан
жазықтығында
жатады. Осыдан
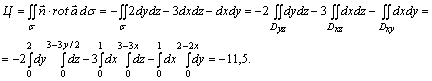
6.8 Потенциалды (дәрменді) және соленоидеалды (түтікшелік) векторлық өрістер
![]() векторлық өрісі потенциалды
өріс деп аталады, егер
векторлық өрісі потенциалды
өріс деп аталады, егер ![]() аймағында анықталған
аймағында анықталған ![]() скаляр өрісі
табылып, ол үшін
скаляр өрісі
табылып, ол үшін
![]() . (6.30)
. (6.30)
![]() функциясы
функциясы ![]() өрісінің потенциалы деп
аталады. Берілген бір байланысты аймақта
өрісінің потенциалы деп
аталады. Берілген бір байланысты аймақта ![]() векторлық өрісі потенциалды
болуы үшін
векторлық өрісі потенциалды
болуы үшін
|
Өріс потенциалды болғанда
сызықты интеграл интегралдау жолының пішініне байланысты
болмайды. Ол тек алғашқы нүктемен соңғы
нүктеге ғана байланысты болады. Сондықтан жолды Бұл жағдайда |
27-сурет |
![]() (6.31)
(6.31)
Егер ![]() потенциалды бірмәнді функция болса,
онда
потенциалды бірмәнді функция болса,
онда
![]() . (6.32)
. (6.32)
![]() жиегі тұйық болғанда
жиегі тұйық болғанда ![]() векторлық
өрісінің иірімі
векторлық
өрісінің иірімі
![]() (6.33)
(6.33)
Егер ![]() векторлық өрісінің
әрбір нүктесінде
векторлық өрісінің
әрбір нүктесінде ![]() болса, онда
болса, онда ![]() векторлық өрісі
түтікшелік векторлық өріс деп аталады. Бұл
жағдайда кез келген тұйық бет арқылы өтетін
вектор өрісінің ағыны нөлге тең болады.
векторлық өрісі
түтікшелік векторлық өріс деп аталады. Бұл
жағдайда кез келген тұйық бет арқылы өтетін
вектор өрісінің ағыны нөлге тең болады.
Егер ![]() векторлық өрісі дәрменді
әрі түтікшелік өріс болса, онда
векторлық өрісі дәрменді
әрі түтікшелік өріс болса, онда
![]() . (6.34)
. (6.34)
Мұндағы
![]() (6.35)
(6.35)
Лаплас операторы, ал ![]() функциясы гармоникалық функция деп аталады.
функциясы гармоникалық функция деп аталады.
52-мысал. ![]() векторлық өрісінің потенциалды
болатындығын тексеру керек және осы өрісінің потенциалы
векторлық өрісінің потенциалды
болатындығын тексеру керек және осы өрісінің потенциалы
![]() -ді табу
керек.
-ді табу
керек.
Шешуі. ![]() болғандықтан
болғандықтан
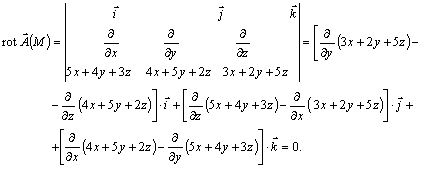
Яғни ![]() өрісі потенциалды өріс.
өрісі потенциалды өріс.
Енді ![]() потенциалын табайық
потенциалын табайық
![]() ,
,
![]() деп алсақ, онда
деп алсақ, онда
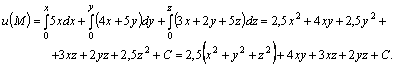
53-мысал. ![]() векторлық өрісі потенциалды,
соленойдалды әрі гормониялық өріс болатындығын
анықтау керек.
векторлық өрісі потенциалды,
соленойдалды әрі гормониялық өріс болатындығын
анықтау керек.
Шешуі.
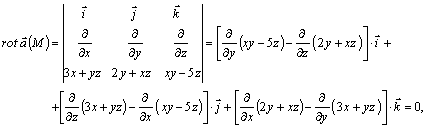
яғни өріс потенциалды.
![]()
яғни өріс соленоидалды.
Берілген өріс потенциалды және соленоидалды болғандықтан, ол гормониялық өріс болып табылады.
151. ![]() скалярлық өрісінің
деңгейлік бетін табу керек.
скалярлық өрісінің
деңгейлік бетін табу керек.
152. ![]() скалярлық өрісінің
деңгейлік бетін табу керек.
скалярлық өрісінің
деңгейлік бетін табу керек.
153. ![]() скалярлық өрісінің
деңгейлік бетін табу керек.
скалярлық өрісінің
деңгейлік бетін табу керек.
154. ![]() скалярлық өрісінің
деңгейлік бетін табу керек.
скалярлық өрісінің
деңгейлік бетін табу керек.
155. ![]() скалярлық өрісінің
деңгейлік сызығын табу керек.
скалярлық өрісінің
деңгейлік сызығын табу керек.
156. ![]() скалярлық өрісінің
деңгейлік сызығын табу керек.
скалярлық өрісінің
деңгейлік сызығын табу керек.
157. ![]() скалярлық өрісінің
деңгейлік сызығын табу керек.
скалярлық өрісінің
деңгейлік сызығын табу керек.
![]() функциясы,
функциясы, ![]() векторы және
векторы және ![]() нүктесі берілген. Табу
керек:
нүктесі берілген. Табу
керек:
а) ![]() функциясының
функциясының ![]() нүктесіндегі градиентін;
нүктесіндегі градиентін;
ә) ![]() нүктесіндегі
нүктесіндегі
![]() функциясының
функциясының
![]() векторының
бағыты бойынша туындысын;
векторының
бағыты бойынша туындысын;
б) ![]() нүктесіндегі
нүктесіндегі
![]() функциясының
өсу жылдамдығының ең үлкен шамасын.
функциясының
өсу жылдамдығының ең үлкен шамасын.
158.
![]()
159.
![]()
160. ![]() .
.
161. ![]() .
.
162. ![]() .
.
![]() векторының
дивергенциясын есептеу керек:
векторының
дивергенциясын есептеу керек:
163. ![]() .
.
164. ![]() .
.
165. ![]() .
.
166. ![]() .
.
167. ![]() теңдеуімен берілген
жазықтықтың бірінші октантадағы беті арқылы
өтетін
теңдеуімен берілген
жазықтықтың бірінші октантадағы беті арқылы
өтетін ![]() векторлық
өрісінің ағынын есептеу керек, мұнда
жазықтық жіктемесі
векторлық
өрісінің ағынын есептеу керек, мұнда
жазықтық жіктемесі ![]() өсімен сүйір бұрыш
жасайды.
өсімен сүйір бұрыш
жасайды.
168. ![]() теңдеуімен берілген жазықтықтың
бірінші октантадағы беті арқылы өтетін
теңдеуімен берілген жазықтықтың
бірінші октантадағы беті арқылы өтетін ![]() век-торлық
өрісінің ағынын есептеу керек, мұнда
жазықтық тіктемесі
век-торлық
өрісінің ағынын есептеу керек, мұнда
жазықтық тіктемесі ![]() өсімен сүйір бұрыш
жасайды.
өсімен сүйір бұрыш
жасайды.
169. ![]() теңдеуімен берілген
жазықтықтың бірінші октантадағы беті арқылы
өтетін
теңдеуімен берілген
жазықтықтың бірінші октантадағы беті арқылы
өтетін ![]() вектор
өрісінің ағынын есептеу керек, мұнда
жазықтық тіткемесі
вектор
өрісінің ағынын есептеу керек, мұнда
жазықтық тіткемесі ![]() өсімен сүйір бұрыш
жасайды.
өсімен сүйір бұрыш
жасайды.
170. ![]() эллипсоидының бірінші
октантадағы беті арқылы өтетін
эллипсоидының бірінші
октантадағы беті арқылы өтетін ![]() векторлық өрісінің
ағынын есептеу керке, мұнда жазықтық тіткемесі
векторлық өрісінің
ағынын есептеу керке, мұнда жазықтық тіткемесі ![]() өсімен
сүйір бұрыш жасайды.
өсімен
сүйір бұрыш жасайды.
171. Остроградский-Гаусс формуласын пайдаланып ![]() жазықтығы
мен координаталар жазықтықтарының қиылысуынан пайда
болған пирамиданың сыртқы беті арқылы өтетін
жазықтығы
мен координаталар жазықтықтарының қиылысуынан пайда
болған пирамиданың сыртқы беті арқылы өтетін ![]() векторлық
өрісінің ағынын есептеу керек.
векторлық
өрісінің ағынын есептеу керек.
172. Остроградский-Гаусс формуласын пайдаланып ![]() жазықтығы
мен координаталар жазықтықтарының қиылысуынан пайда
болған пирамиданың сыртқы беті арқылы өтетін
жазықтығы
мен координаталар жазықтықтарының қиылысуынан пайда
болған пирамиданың сыртқы беті арқылы өтетін ![]() векторлық
өрісінің ағынын есептеу керек.
векторлық
өрісінің ағынын есептеу керек.
173. Остроградский-Гаусс формуласын пайдаланып ![]() жазықтығы
мен координаталар жазықтықтарының қиылысуынан пайда
болған пирамиданың сыртқы беті арқылы өтетін
жазықтығы
мен координаталар жазықтықтарының қиылысуынан пайда
болған пирамиданың сыртқы беті арқылы өтетін ![]() векторлық
өрісінің ағынын есептеу керек.
векторлық
өрісінің ағынын есептеу керек.
174. Остроградский-Гаусс формуласын пайдаланып ![]() сферасы арқылы
өтетін
сферасы арқылы
өтетін ![]() векторлық
өрісінің ағынын есептеу керек.
векторлық
өрісінің ағынын есептеу керек.
175. Остроградский-Гаусс формуласын пайдаланып ![]() цилиндрінің
толық беті арқылы өтетін
цилиндрінің
толық беті арқылы өтетін ![]() векторлық өрісінің
ағынын есептеу керек.
векторлық өрісінің
ағынын есептеу керек.
![]() векторының құйынын
есептеу керек:
векторының құйынын
есептеу керек:
176.
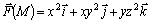 .
.
177. 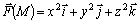 .
.
178. 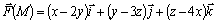 .
.
179. ![]() .
.
180. Стокс формуласын пайдаланып ![]()
![]() векторлық өрісінің
векторлық өрісінің ![]() нүктелері
арқылы өтетін
нүктелері
арқылы өтетін ![]() контуры бойынша иірімін табу керек.
контуры бойынша иірімін табу керек.
181. Стокс формуласын пайдаланып ![]() векторлық
өрісінің
векторлық
өрісінің ![]() нүктелері
арқылы өтетін
нүктелері
арқылы өтетін ![]() контуры бойынша иірімін табу керек.
контуры бойынша иірімін табу керек.
182. Стокс формуласын пайдаланып ![]()
![]() векторлық өрісінің
векторлық өрісінің ![]()
![]() нүктелері арқылы
өтетін
нүктелері арқылы
өтетін ![]() контуры
бойынша иірімін табу керек.
контуры
бойынша иірімін табу керек.
183. Стокс формуласын пайдаланып ![]() векторлық
өрісінің
векторлық
өрісінің ![]() шеңберінің
оң бағыты бойынша иірімін табу керек.
шеңберінің
оң бағыты бойынша иірімін табу керек.
184. Стокс формуласын пайдаланып ![]() векторлық
өрісінің
векторлық
өрісінің ![]() эллипстің
оң бағыты бойынша иірімін табу керек.
эллипстің
оң бағыты бойынша иірімін табу керек.
![]() векторлық өрісінің
потенциалды өріс болатындығын тексеру керек. Потенциалды өріс
болған жағдайда оның потенциалы
векторлық өрісінің
потенциалды өріс болатындығын тексеру керек. Потенциалды өріс
болған жағдайда оның потенциалы ![]() -ді табу керек:
-ді табу керек:
185. ![]() .
.
186. ![]() .
.
187. ![]() .
.
188. ![]() .
.
189. ![]() .
.
![]() векторлық өрісі потенциалды,
соленоидалды, гармониялық болатындығын анықтау керек:
векторлық өрісі потенциалды,
соленоидалды, гармониялық болатындығын анықтау керек:
190. ![]() .
.
191. ![]() .
.
192. ![]() .
.
193. ![]() .
.
194. ![]() .
.
195. ![]() .
.
196. ![]() .
.
ЖАУАПТАРЫ
1 – тарау
1.
![]() - центрі
- центрі ![]() , ал радиусы
, ал радиусы ![]() болатын шеңберімен шектелген
болатын шеңберімен шектелген ![]() жазықтығының бөлігі. 2.
жазықтығының бөлігі. 2. ![]() және
және ![]() параболаларының арасында орналасқан және
параболаларының арасында орналасқан және ![]() нүктесі тиісті емес
нүктесі тиісті емес ![]() жазықтығының бөлігі. 3. Бүкіл
жазықтығының бөлігі. 3. Бүкіл ![]() жазықтығы. 4.
жазықтығы. 4. ![]() түзуінен жоғары орналасқан
түзуінен жоғары орналасқан ![]() жазықтығының бөлігі. 5.
жазықтығының бөлігі. 5. ![]() параболасынан жоғары орналасқан
параболасынан жоғары орналасқан ![]() жазықтығының бөлігі. 6.
жазықтығының бөлігі. 6. ![]() 1 және 3 ширектерінде орналасқан
1 және 3 ширектерінде орналасқан ![]() жазықтығының бөлігі. 7.
жазықтығының бөлігі. 7. ![]() түзуі тиісті емес
түзуі тиісті емес ![]() жазықтығының бөлігі. 8.
жазықтығының бөлігі. 8. ![]() параболасы және
параболасы және ![]() түзуімен шектелген
түзуімен шектелген ![]() жазықтығының бөлігі. 9.
жазықтығының бөлігі. 9. ![]() шеңберімен шектелген және
шеңберімен шектелген және ![]() нүктесі тиісті емес
нүктесі тиісті емес ![]() жазықтығының бөлігі. 11.
жазықтығының бөлігі. 11. ![]()
![]() 12.
12. ![]()
![]()
13.
![]()
![]() 14.
14. ![]()
![]() 15.
15.
![]()
![]()
16.
![]()
![]() 17.
17. ![]()
![]() 18.
18. ![]()
![]()
19.
![]()
![]() 20.
20. ![]()
![]()
21.
![]()
![]() 22.
22. ![]()
![]()
23.
![]()
![]() 24.
24. ![]()
![]()
25.
![]()
![]() 26.
26.![]()
![]() 27.
27. ![]()
![]() 28.
28. ![]()
![]()
29. ![]()
![]() 30.
30. ![]()
![]()
31. ![]()
![]() 32.
32. ![]()
![]()
![]() 33.
33. ![]()
![]()
![]() 34.
34. ![]()
![]()
![]() 35.
35. ![]()
![]()
![]() 36.
36. ![]()
![]()
![]()
37.
![]() 38.
38.
![]()
39.
![]() 40.
40. ![]()
41.
![]() 42.
42. ![]()
43.
![]() 44.
44.![]()
45.
![]()
46.
![]() 47.
47.
![]() 48.
48. ![]() 49.
49. ![]() Ескерту
Ескерту ![]() деп
алу керек. 50. 0,82. 51.
деп
алу керек. 50. 0,82. 51. ![]()
![]()
![]() 52.
52.
![]()
![]()
![]() 53.
53. ![]()
![]()
![]() 54.
54. ![]()
![]()
![]()
55.
![]()
![]()
![]() 56.
56. ![]()
![]()
![]() 57.
57. ![]()
![]()
![]() 58.
58. ![]()
![]()
![]() 59.
59. ![]()
![]()
![]() 60.
60. ![]()
![]()
![]() 61.
61. ![]()
62.
![]()
63.
![]()
64.
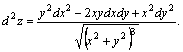 69.
69.
![]()
![]() 70.
70. ![]()
![]()
71.
![]()
![]()
72.
![]()
![]()
73.
![]() 74.
74.
![]()
75.
![]() 76.
76.
![]() 77.
77.
![]()
78.
![]() 79.
79.
![]()
80.
![]() 81.
81.
![]() 82.
82.
![]()
83.
![]() 84.
84.
![]() 85.
85.
![]()
86.
![]() 87.
87.
![]()
![]()
88.
![]()
![]() 89.
89. ![]()
![]() 90.
90.![]()
![]() 91.
91.
![]()
![]()
92.
![]()
![]() 93.
93. ![]()
![]() 94.
94. ![]() 95.
95.
![]()
![]() 96.
96.
![]()
![]()
97.
![]()
![]() 98.
98.
![]()
![]() 99.
99.
![]()
![]()
100.
![]()
![]() 101.
101.
![]()
102.
![]() 103.
103.
![]()
104.
![]() 105.
экстремум
жоқ. 106.
105.
экстремум
жоқ. 106.
![]()
107.
![]() болғанда
болғанда ![]()
108.
![]() болғанда
болғанда ![]()
![]() болғанда
болғанда ![]() 109.
109.
![]()
![]() 110.
110.
![]()
![]() 111.
111.
![]()
![]() 112.
112.
![]()
![]()
113.
![]()
![]() 114.
114.
![]()
![]()
2-6 – тарау
1.
8. 2. 39. 3.
24. 4. 45. 5. 304. 6. ![]() . 7. 168. 8.
3,35. 9.
. 7. 168. 8.
3,35. 9. ![]() . 10. 1,5. 11.
. 10. 1,5. 11. ![]() . 12.
. 12. ![]() . 13. 0,5. 14.
. 13. 0,5. 14.
![]() . 15.
214,65. 16.
. 15.
214,65. 16. ![]() . 17. 16,65.
. 17. 16,65.
18. ![]() .
.
19. ![]() . 20.
. 20. ![]() .
.
21. 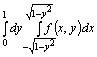 . 22.
. 22. ![]() .
.
23. ![]() .
.
24. ![]() . 25.
. 25. 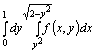 .
.
26. 1,5![]() . 27. 0,5
. 27. 0,5![]() . 28.
. 28. ![]() . 29.
. 29. ![]() .
.
30. ![]() . 31.
. 31. ![]() . 32.
. 32. ![]() . 33.
. 33. ![]() . 34.
. 34. ![]() .
.
35. ![]() . 36. 1,25
. 36. 1,25![]() . 37.
. 37. ![]() . 38.
. 38. ![]() . 39.
. 39. ![]() . 40.
. 40. ![]() .
.
41. 12. 42. ![]() . 43. 24. 44.
. 43. 24. 44. ![]() . 45.
. 45. ![]() . 46.
. 46. ![]() . 47.
. 47. ![]() .
.
48. ![]() . 49.
. 49. ![]() . 50.
. 50. ![]() . 51.
. 51.
![]()
![]() . 52. 0,4. 53.
. 52. 0,4. 53.
![]() .
.
54. ![]() . 55.
. 55. ![]() . 56.
. 56. ![]() .
.
57. ![]() . 58.
. 58. ![]() ;
; ![]() . 59.
. 59. ![]() . 60.
. 60. ![]()
![]() . 61.
. 61. ![]() . 62.
-2,25. 63.
. 62.
-2,25. 63. ![]() .
.
64.
![]() .
65.
.
65. ![]() .
66.
.
66. ![]() .
67.
.
67. ![]() .
68.
.
68. ![]() .
.
69. ![]() . 70.
. 70. ![]() . 71.
. 71. ![]() . 72.
. 72. ![]() . 73.
. 73. ![]() . 74.
4,5.
. 74.
4,5.
75. ![]() . 76.
. 76. ![]() . 77.
. 77. ![]() . 78.
. 78. ![]() .
.
79. ![]() . 80.
. 80. ![]() . 81.
. 81. ![]() .
.
82. ![]() ;
; ![]() . 83.
. 83.
![]()
84. ![]() ;
; ![]() ;
; ![]() .
.
85. 2,5. 86. ![]() . 87.
. 87. ![]() . 88.
. 88. ![]() . 89.
. 89. ![]() .
.
90. ![]() . 91.
. 91. ![]() . 92.
. 92. ![]() . 93.
. 93. ![]() .
.
94. 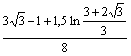 . 95.
. 95. ![]() . 96.
. 96. ![]() .
.
97. ![]() . 98.
. 98. ![]() . 99. а) 2;
ә)
. 99. а) 2;
ә) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
100. а) – г) ![]() . 101. 1. 102.
0. 103.
. 101. 1. 102.
0. 103. ![]() . 104.
. 104.
![]() . 105.
. 105.
![]() . 106.
12. 107. 146. 108. 20,5.
. 106.
12. 107. 146. 108. 20,5.
109.
болады;
![]() .
.
110. болмайды. 111. болады; ![]() .
.
112. болады; ![]() . 113.
. 113. ![]() . 114. -4.
. 114. -4.
115. ![]() . 116. 18. 117.
. 116. 18. 117.
![]() . 118.
. 118.
![]() . 119.
. 119.
![]() . 120.
. 120.
![]() .
.
121. ![]() . 122. 16. 123.
. 122. 16. 123.
![]() . 124.
. 124.
![]() . 125.
. 125.
![]() . 126.
. 126.
![]() .
.
127. 0. 128. ![]() . 129.
. 129. ![]() . 130.
. 130. ![]() . 131.
. 131. ![]() .
.
132. ![]() ;
; ![]() . 133.
. 133. ![]() ;
; ![]() .
.
134. ![]() . 135.
. 135. ![]() . 136. 21. 137.
. 136. 21. 137.
![]() . 138.
3.
. 138.
3.
139. ![]() . 140.
. 140. ![]() . 141. 0. 142.
. 141. 0. 142.
![]() . 143.
. 143.
![]() . 144.
-64. 145. 23,5.
. 144.
-64. 145. 23,5.
146. 1. 147. 148. 149. ![]() . 150.
. 150. ![]() . 151.
центрі
. 151.
центрі ![]() нүктесі
және радиусы
нүктесі
және радиусы ![]() болатын
сфералар жиынтығы. 152. параллель жазықтықтар
жиынтығы. 153. эллипстік параболоидтар жиынтығы. 154.
гиперболалық параболоидтар жиынтығы. 155. центрі
болатын
сфералар жиынтығы. 152. параллель жазықтықтар
жиынтығы. 153. эллипстік параболоидтар жиынтығы. 154.
гиперболалық параболоидтар жиынтығы. 155. центрі ![]() нүктесі
және радиусы
нүктесі
және радиусы ![]() болатын
шеңберлер жиынтығы.
болатын
шеңберлер жиынтығы.
156. параллель түзулер жиынтығы. 157. гиперболар жиынтығы.
158. а) ![]() ;
ә)
;
ә) ![]() ;
б)
;
б) ![]() . 159.
а)
. 159.
а) ![]() ; ә)
2; б)
; ә)
2; б) ![]() .
160. а)
.
160. а) ![]() ; ә)
; ә) ![]() ; б) 1. 161.
а)
; б) 1. 161.
а) ![]() ; ә)
; ә)
![]() ; б)
; б) ![]() . 162. а)
. 162. а)
![]() ; ә)
; ә)
![]() . б)
. б) ![]() . 163. 6.
. 163. 6.
164. ![]() . 165.
3. 166.
. 165.
3. 166. ![]() . 167.
. 167. ![]() . 168. 0,5.
. 168. 0,5.
169. 21. 170. ![]() . 171.
. 171. ![]() . 172. 9. 173.
. 172. 9. 173.
![]() . 174.
. 174.
![]() .
.
175. ![]() . 176.
. 176.
![]() . 177.
0. 178.
. 177.
0. 178. ![]() .
.
179. ![]() . 180.
-5. 181.
. 180.
-5. 181. ![]() . 182. -3. 183.
. 182. -3. 183.
![]() . 184.
. 184.
![]() .
.
185. болады; ![]() .
186. болмайды.
.
186. болмайды.
187. болады; ![]() .
188. болады;
.
188. болады; ![]() .
.
189. болады; ![]() .
190. потенциалды; өріс. 191.
гармониялық өріс. 192. болмайды. 193.
соленоидалды өріс.
.
190. потенциалды; өріс. 191.
гармониялық өріс. 192. болмайды. 193.
соленоидалды өріс.
194. потенциалды өріс. 195. соленоидалды өріс. 196. гармониялық өріс.
ӘДЕБИЕТТЕР ТІЗІМІ
1. Аяпбергенов С.А. Аналитикалық геометрия. Алматы: Мектеп, 1971.
2. Қасымов Қ.Ә., Қасымов Е.Ә. Жоғары математика курсы (Сызықты алгебра). Алматы, «Санат», 1997.
3. Клетеник Д.В. Сборник задач по аналитической геометрии. М.: Наука – 1967.
4. Минорский В.П. Сборник задач по высшей математике. М.: Наука – 1987.
5. Пискунов Н.С. Дифференциальное и интегральное исчисления. – М.: Наука, 1978.
6. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальные уравнения. Кратные интегралы. Функция комплексного переменного. Ряды. – М.: Наука, 1981.
7. Задачи и упражнения по математическому анализу для ВТУЗов (под. ред. Б.П. Демидовича). – М.: Наука, 1977.
8. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. –М.: Высшая школа, 1980.
9. Берман Г.Н. Сборник задач по курсу математического анализа. – М.: Наука, 1977.
10. Минорский Л.П. Сборник задач по высшей математике. – М.: Наука, 1978.
МАЗМҰНЫ
1. Қисық сызықты интегралдар 59
2. Беттік интегралдар 75
3. Өріс теориясының элементтері 91
Жауаптары 110
Әдебиеттер тізімі 118