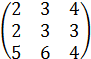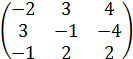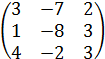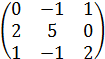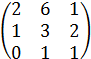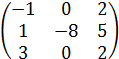Некоммерческое акционерное общество

АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра высшей математики

 

 

АЛГЕБРА

Методические указания к расчетно-графическим работам для студентов

всех форм обучения специальности 5В060200 – Информатика

2-часть  

 

 

Алматы 2011 

СОСТАВИТЕЛИ: Каирбеков Т., Толеуова Б.Ж. Алгебра. Методические указания к выполнению расчетно-графических работ для студентов всех форм обучения  специальности 5В060200 – Информатика. 2-часть -Алматы: АУЭС, 2011.- 19 стр.

 

Методические указания предназначены для выполнения расчетно-графических работ № 2 по дисциплине «Алгебра» и составлены по программе раздела «Линейные пространства. Евклидово пространство» специальности  5В060200 – Информатика. Настоящие методические указания содержат перечень вопросов, необходимых для изучения этого раздела, варианты заданий, теоретические сведения, а также решение типового варианта.

Табл. 12, библиогр. – 9 назв. 

 

Рецензент: канд. физ.-мат.наук., доц. Байсалова М.Ж.

 

 

Печатается по плану издания некоммерческого акционерного общества  «Алматинский университет энергетики и связи» на  2011 г.  

 

ã  НАО «Алматинский университет энергетики и связи», 2012 г.

 

Теоретические вопросы

 

1.     Кольцо многочленов от одной переменной.

2.     Алгоритм Евклида. Взаимно простые многочлены.

3.     Алгоритм деления с остатком. Наибольший общий делитель.

4.     Кратные корни. Схема Горнера. Решение уравнения третьей степени формулой Кардано.

5.     Подпространства, линейная зависимость векторов. Преобразование

координат вектора.

6.     Базис и размерность линейного пространства. Переход от одного базиса к другому.

7.     Скалярное произведение векторов в евклидовом пространстве. Процесс ортогонализации. Неравенство Коши–Буняковского.

8.     Угол между векторами в евклидовом пространстве. Норма вектора.

 

 

1.     Задания

 

1.1 Задания первого уровня

 

1-задание

Найти  и  , используя алгоритм деления с остатком

многочлена  на многочлен  .

№

1.1

1.2

1.3

1.4

1.5

1.6

1.7

1.8

1.9

1.10

1.11

1.12

1.13

1.14

1.15

1.16

1.17

1.18

1.19

1.20

1.21

1.22

1.23

1.24

1.25

1.26

1.27

1.28

1.29

1.30

 

 

 

 

 

 

 

 

 

2- задание

Вычислить , используя схему Горнера.

№

2.1

4

2.2

2.3

3

2.4

-1

2.5

1

2.6

2

2.7

2.8

2

2.9

 

2.10

2

2.11

-2

2.12

1

2.13

2

2.14

-1

2.15

1

2.16

1

2.17

2

2.18

1

2.19

1

2.20

2

2.21

1

2.22

2

2.23

1

2.24

-3

2.25

1

2.26

2

2.27

1

2.28

1

2.29

1

2.30

1

 

 

3- задание

Решить уравнение третьей степени по формуле Кардано.

№

Уравнение

№

Уравнение

3.1

3.2

3.3

3.4

3.5

3.6

3.7

3.8

3.9

3.10

3.11

3.12

3.13

3.14

3.15

3.16

3.17

3.18

3.19

3.20

3.21

3.22

3.23

3.24

3.25

3.26

3.27

3.28

3.29

3.30

 

 

4- задание

Найти наибольший общий делитель данных многочленов.

№

4.1

4.2

4.3

4.4

4.5

4.6

4.7

4.8

4.9

4.10

4.11

4.12

4.13

4.14

4.15

4.16

4.17

4.18

4.19

4.20

4.21

4.22

4.23

4.24

4.25

4.26

4.27

4.28

4.29

4.30



 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5- задание

Исследуйте, являются ли данные векторы в  -линейном пространстве линейно зависимыми.

№

5.1

5.2

5.3

5.4

5.5

5.6

5.7

5.8

5.9

5.10

5.11

5.12

5.13

5.14

5.15

5.16

5.17

5.18

5.19

5.20

5.21

5.22

5.23

5.24

5.25

5.26

5.27

5.28

5.29

5.30

 

 

6- задание

Найти базис векторов из 5-задания и установить размерность пространства.

 

 

7- задание

Доказать, что векторы , ,  образуют базис и найти координаты

вектора    в этом базисе.

№

7.1

7.2

7.3

7.4

7.5

7.6

7.7

7.8

7.9

7.10

7.11

7.12

7.13

7.14

7.15

7.16

7.17

7.18

7.19

7.20

7.21

7.22

7.23

7.24

7.25

7.26

7.27

7.28

7.29

7.30

 

 

8- задание

Даны векторы   и  . Найти координаты вектора .

№

8.1

8.2

8.3

8.4

8.5

8.6

8.7

8.8

8.9

8.10

8.11

8.12

8.13

5.14

8.15

8.16

8.17

8.18

8.19

8.20

8.21

8.22

8.23

8.24

8.25

8.26

8.27

8.28

8.29

8.30

 

 

9- задание

Найти угол между векторами   и     из 8-задания.

 

 

10- задание

Записать матрицу перехода от базиса  , ,    к  базису  ,  ,  .  

№

10.1

10.2

10.3

10.4

10.5

10.6

10.7

10.8

10.9

10.10

10.11

10.12

10.13

10.14

10.15

10.16

10.17

10.18

10.19

10.20

10.21

10.22

10.23

10.24

10.25

10.26

10.27

10.28

10.29

10.30

 

 

11- задание

Проверить, будет ли матрица    матрицей перехода от одного базиса к другому?  

№

№

№

11.1

11.2

11.3

11.4

11.5

11.6

11.7

11.8

11.9

11.10

11.11

11.12

11.13

11.14

11.15

11.16

11.17

11.18

11.19

11.20

11.21

11.22

11.23

11.24

11.25

11.26

11.27

11.28

11.29

11.30

 

 

 

12- задание

Нормировать вектор  .

№

№

№

12.1

12.2

12.3

12.4

12.5

12.6

12.7

12.8

12.9

12.10

12.11

12.12

12.13

12.14

12.15

12.16

12.17

12.18

12.19

12.20

12.21

12.22

12.23

12.24

12.25

12.26

12.27

12.28

12.29

12.30

 

 

1.2 Задания второго уровня

 

13- задание

Вектор   задан в   , , . Разложить этот вектор по базису

,  ,  .

№

13.1

13.2

13.3

13.4

13.5

13.6

13.7

13.8

13.9

13.10

13.11

13.12

13.13

13.14

13.15

13.16

13.17

13.18

13.19

13.20

13.21

13.22

13.23

13.24

13.25

13.26

13.27

13.28

13.29

13.30

 

 

14- задание

В евклидовом пространстве дан базис , , , .  Проверить, можно ли

с помощью векторов этого базиса построить ортонормированный базис того же пространства.

№

14.1

14.2

 

14.3

14.4

 

14.5

 

14.6

14.7

 

14.8

 

14.9

 

14.10

14.11

 

14.12

 

14.13

14.14

14.15

 

14.16

 

14.17

14.18

 

14.19

14.20

 

14.21

14.22

 

14.23

14.24

 

14.25

 

14.26

14.27

 

14.28

 

14.29

 

14.30

 



2  Методические указания к выполнению заданий раздела «Линейные пространства. Евклидово пространство». Решение типового варианта

 

1)      Найти  и  , используя алгоритм деления с остатком

многочлена    на многочлен  .

Решение: По алгоритму деления с остатком многочлена на многочлен, для любых многочленов  и  существуют многочлены   и   такие, что выполняется следующее равенство:

 

,

 

где   – делимое,  – делитель,  – частное,  – остаток.

Степень    менше степени  .

 

                2           

                               

 

 

 

 

                               

 

 

Значит,      и

.   

 

2)       Используя схему Горнера, найти значение многочлена

    в точке  .

Решение: Представим многочлен

   

в следующем виде, разделив его предварительно на  :

,

где   .

Коэффициенты частного и остаток определим по схеме Горнера:

 

 

 

 

 

Для данного многочлена используем эту схему:

 

1

-3

6

-10

16

4

1

 

Значит, .

 

3)       Решить уравнение третьей степени  по формуле Кардано:
                                    .

Решение:  Рассмотрим уравнение третьей степени:

                                    .                                                 (1)

С помощью подстановки  , уравнение приведем к следующему виду:

                                      .                                                         (2)

 

Корни уравнения (2) находим по следующи формулам:

,  где   ,     .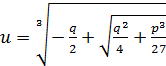

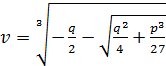Значит,

 .

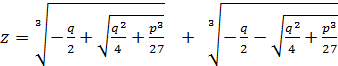Последняя формула называется формулой Кардано.

Корни уравнения (2) имеют вид:

,    ,    ,  где ,    ,  а корни уравнения (1) ищем в виде ,    ,    .

 

          Дано уравнение:

.

 

Применив подстановку  , получим:

                                    , 

,    ,

,      ,     

,

 .

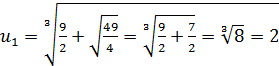Итак,    ,    ,   

.

 

4)       Найти наибольший общий делитель многочленов

      и     .

Решение: Наибольший общий делитель двух многочленов можно найти

по алгоритму Евклида. По этому алгоритму наибольший общий делитель

многочленов  равен тому остатку, на который нацело делится предыдущий остаток:

,

,

 

,

………………………………

,

.

 

Разделим    на  :

 

                                                       

 

 

 

 

 

 

.  Теперь разделим    на  :

___________

                                                   

 

 

 

 

 

                                                   

 

 

 

 

Разделим    на  :

 

 

                     

                                                 

 

 

      

 

 

                                                            0

     Остаток     делится нацело на остаток   , значит    является наибольшим общим делителем многочленов    и  :

.

 

5)       Исследуйте, являются ли векторы ,    и   в  -линейном пространстве линейно зависимыми.

          Решение:  Векторы , ,  называются линейно независимыми, если равенство

                                                                                  (3)

выполняется лишь при  .  Если равенство (3) может выполнится и в том случае, когда не все числа , , равны нулю, то говорят, что векторы , ,   линейно зависимы. Для того, чтобы определить линейную зависимость или линейную независимость векторов, достаточно вычислить определитель матрицы, составленной из координат этих векторов. Если определитель отличен от нуля, то векторы линейно независимы, если равен нулю, то линейно зависимы.

          Составим и вычислим определитель:

 

,  значит векторы линейно независимы.

 

6)       Найти базис векторов ,  , 

         и установить размерность пространства.

Решение: Вычислим определитель:

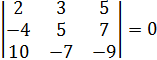,  значит векторы линейно зависимы.

Видно, что векторы   и  линейно независимы, значит они образуют базис. Тогда вектор  можно разложить по   векторам  , :

.

Таким образом, размерность пространства равна 2.

Подставляя компоненты векторов, получим:

                                .

Приравнивая соответствующие компоненты, получим систему уравнений:

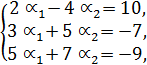
откуда  ,  т.е.   .

 

7)       Доказать, что векторы ,    и   образуют базис и найти координаты вектора    в этом базисе.

 

Решение:            .

 

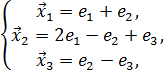
Т.к. 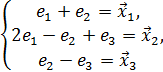     то решим систему относительно   по формулам Крамера:

,    

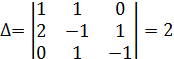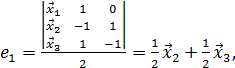
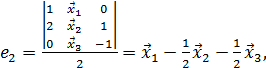
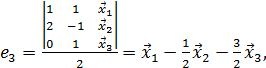     тогда

 

                                        .

 

8)       Даны векторы  ,  . Найти координаты вектора .

Решение:           

.

 

9)       Найти угол между векторами    и   .

Решение:   Угол между двумя векторами вычисляют по формуле:

 ,

где   –скалярное произведение этих векторов.

Т.к.   , ,

,  то    .

 

10)    Записать матрицу перехода от базиса  , ,    к  базису , , , если ,  ,  .

Решение: Матрица перехода имеет вид:

.

 

11)    Проверить, будет ли матрица 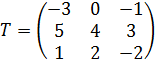   матрицей перехода от одного базиса к другому? 

Решение: Если определитель матрицы  отличен от нуля, то она является матрицей перехода от одного базиса к другому.   

Вычислим определитель этой матрицы:

,

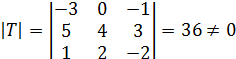значит  будет матрицей перехода от одного базиса к другому.

 

12)    Нормировать вектор  .

Решение: Норму (длину) вектора    обозначают символом  и вычисляют по формуле:

.

Находим нормирующий множитель и умножим на него данный вектор:

 ,   ,

.

 

Список литературы 

1.     Курош А.Г. курс высшей алгебры. – М.: Наука, 1968.

2.     Болгов В.А, Демидович Б.П., Ефимов А.В. и др.  Сборник задач по математике. – М.: Наука, 1986.

3.     Фаддеев Д.К., Соминский И.С. Сборник задач по высшей алгебре. – М.: Наука, 1977.

4.     Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2 ч. Ч.1– М.: Издательский дом «ОНИКС 21 век»: Мир и Образование, 2003.

5.     Апатенок Р.Ф., Маркина А.М., Попова Н.В., Хейнман В.Б. Сборник задач по линейной алгебре. – Мн.: Выш. школа, 1980.

6.     Рябушко А.П., Бархатов В.В., Державец В.В., Юруть И. Е. Индивидуальные задания по высшей математике. – Мн.: Выш. школа, 1980.

7.     Ляпин С.Е., Баранова И.В. Сборник задач по элементарной математике. – М.: Учпедгиз, 1960.

8.      Бурдун А.А., Мурашко Е.А., Феденко А.С. Сборник задач по алгебре и геометрии. – Мн.: Изд-во БГУ, 1979.

9.     Солодовников А.С., Торопова Г.А. Линейная алгебра с элементами аналитической геометрии. – М.: Высш.шк., 1987.

 

Содержание 

 

Теоретические вопросы  

     3

1 Задания 

     3

1.1   Задания первого уровня

1.2   Задания второго уровня

     3

   11

2 Методические указания к выполнению заданий раздела «Линейные преобразования. Евклидово пространство». Решение типового варианта

    13

Список литературы 

   19