Некоммерческое акционерное общество

АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра высшей математики

 

 

 

 

 ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Методические указания и задания

к выполнению расчетно-графических работ

(для студентов всех форм обучения специальности

5В070400 – Вычислительная техника и программное обеспечение,

5В070300 – Информационные системы)

Часть 1

 

 

 

Алматы 2011 

СОСТАВИТЕЛИ: Л.Н. Астраханцева,  М.Ж.Байсалова. Теория вероятностей   и математическая   статистика. Методические  указания  и задания  к выполнению    расчетно-графической   работы    для  студентов всех форм обучения специальности 5В070400–Вычислительная техника и программное  обеспечение,   5В070300 –  Информационные системы. Часть  1. –Алматы: АУЭС, 2011.-  28 с.

  

Методические указания и задания к расчетно-графической работе содержат типовой расчет №1 дисциплины «Теория вероятностей и математическая статистика» для студентов всех форм обучения специальности 5В070400 – Вычислительная техника и программное   обеспечение, 5В070300 – Информационные системы. Приведены основные теоретические вопросы программы. Дано решение типового варианта.

          Табл. 10, библиогр. –  5 назв. 

 

Рецензент: канд.физ.-мат.наук, проф. С.Е.Базарбаева.

 

Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2011 г.

 

ã НАО «Алматинский университет энергетики и связи», 2011 г.

 

         1 Типовой расчёт. Случайные события и случайные величины

 

         1.1 Теоретические вопросы

 

1 Предмет теории вероятностей. Случайные события, частота. Статисти-

ческое и геометрическое определения вероятности.

2 Пространство  элементарных  событий.   Алгебра событий. Классичес-

кое определение вероятности.

3 Теоремы сложения и умножения вероятностей. Условная вероятность.

Зависимые и независимые события.

4 Формула полной вероятности. Формула Байеса.

5 Повторение испытаний. Формула Бернулли.

6 Локальная и интегральная теоремы Лапласа. Функция Лапласа. Фор-

мула Пуассона.

7 Дискретные и непрерывные случайные величины. Закон распределе-

ния дискретной случайной величины. Биномиальное распределение, распределение Пуассона.

8 Интегральная функция распределения (функция распределения), свой-

ства, график.

9 Дифференциальная функция распределения (плотность распределе-

ния), свойства, график.

10 Числовые характеристики случайных величин. Математическое ожи-

дание дискретных и непрерывных случайных величин.

11 Дисперсия и среднее квадратическое отклонение дискретных и

непрерывных  случайных величин.

12   Начальные и центральные моменты распределения, асимметрия,

эксцесс, мода, медиана.

 

         1.2 Расчётные задания

 

         1 В партии N деталей, среди них M бракованных. Найти

а) относительную частоту бракованных деталей;

б) вероятность того, что все m деталей, взятых наугад из партии, будут бракованными;

в) вероятность того, что среди m деталей, взятых наугад из партии, будет m бракованных.

 

Т а б л и ц а 1

№

N

M

m

m

№

N

M

m

m

1.1

100

25

10

8

1.16

70

8

5

3

1.2

90

15

12

7

1.17

75

9

8

4

1.3

85

10

7

4

1.18

85

6

5

2

1.4

80

9

5

3

1.19

90

12

7

4

1.5

95

15

9

3

1.20

87

10

8

3

продолжение таблицы 1

1.6

70

10

9

5

1.21

100

30

15

5

1.7

80

15

7

5

1.22

90

20

9

3

1.8

90

10

6

4

1.23

95

15

10

4

1.9

75

10

8

4

1.24

85

10

7

2

1.10

100

20

10

7

1.25

90

12

6

3

1.11

90

10

8

5

1.26

85

10

5

2

1.12

80

7

5

3

1.27

75

8

5

3

1.13

95

10

8

5

1.28

100

15

9

4

1.14

96

12

7

1

1.29

80

10

7

4

1.15

89

13

5

2

1.30

85

7

5

2

 

2  В ящике изделия четырёх сортов. Первого сорта n изделий, второго - n, третьего - n, четвёртого - n. Наудачу берут m изделий. Найти вероятность того, что среди них m изделий первого сорта, m- второго, m- третьего, m- четвёртого сорта (m+ m+ m+ m= m).

Т а б л и ц а 2

№

n

n

n

n

m

m

m

m

2.1

1

2

3

4

1

1

2

1

2.2

2

2

4

2

1

1

1

2

2.3

2

3

4

1

1

2

3

1

2.4

1

4

2

3

1

2

1

2

2.5

4

2

2

2

3

1

2

1

2.6

3

2

3

2

2

1

3

1

2.7

5

1

2

2

3

1

1

1

2.8

2

5

2

1

1

3

1

1

2.9

4

2

3

2

2

1

2

1

2.10

3

3

4

2

2

1

1

2

2.11

2

3

3

3

1

2

3

1

2.12

1

3

4

3

1

2

2

1

2.13

2

3

4

2

1

2

3

2

2.14

1

2

3

5

1

1

2

3

2.15

2

3

4

2

1

2

2

1

2.16

3

2

2

4

2

1

1

1

2.17

4

3

2

3

2

1

2

1

2.18

3

3

4

2

2

1

2

2

2.19

2

4

5

1

2

2

3

1

2.20

3

4

3

2

2

2

3

2

2.21

2

5

2

3

1

3

1

2

2.22

4

4

2

2

2

2

2

1

2.23

2

7

2

1

1

5

2

1

2.24

3

1

6

2

2

1

3

1

 

продолжение таблицы 2

2.25

1

3

3

2

1

3

1

1

2.26

1

4

2

2

0

2

1

1

2.27

2

3

1

3

1

2

0

1

2.28

3

1

2

3

0

1

1

2

2.29

3

2

3

1

2

2

2

0

2.30

2

2

2

3

1

1

1

2

 

3 В магазин поступили 1000 ламп из трёх заводов: ламп - из первого завода, - из второго,  остальные  из третьего. Среди ламп первого завода % бракованных, второго - % бракованных, третьего - % бракованных.   

Куплена одна лампа:

         а) найти вероятность того, что она бракованная;

         б) купленная лампа оказалась бракованной. Найти вероятность того, что она сделана на i – том заводе ( i =1,2,3).

Т а б л и ц а 3

№

 

i

3.1

100

250

7

8

5

1

3.2

430

180

5

4

7

2

3.3

170

540

6

5

8

3

3.4

650

120

10

9

8

2

3.5

400

180

7

10

5

1

3.6

120

380

10

6

9

2

3.7

270

340

9

5

4

3

3.8

430

120

10

7

6

2

3.9

360

120

5

10

8

1

3.10

420

210

8

7

6

1

3.11

370

130

10

6

5

2

3.12

410

200

5

10

8

3

3.13

280

510

10

6

5

3

3.14

710

120

2

10

4

3

3.15

460

240

5

9

7

1

3.16

520

220

5

8

7

1

3.17

270

410

10

5

9

2

3.18

250

140

8

7

4

2

3.19

190

380

5

9

30

1

3.20

290

610

6

3

3

2

3.21

270

430

10

6

4

2

3.22

280

360

7

10

9

1

3.23

520

110

5

7

10

1

3.24

240

290

9

8

4

3

3.25

310

410

7

2

5

3

 

продолжение таблицы 3

3.26

520

110

3

6

7

2

3.27

280

310

9

8

4

2

3.28

400

320

4

5

8

1

3.29

350

240

9

8

7

1

3.30

190

520

5

2

4

3

 

 

4 Проводится n испытаний, в каждом из которых вероятность появления события А равна p. Найти вероятность того, что событие А появится:

а) ровно  раз;

б) не менее  раз;

в) не более  раз;

г) хотя бы один раз.

Т а б л и ц а 4

№

n

p

№

n

p

4.1

4

2

3

2

0.9

4.16

5

3

4

2

0.8

4.2

4

3

3

2

0.8

4.17

4

3

3

1

0.7

4.3

5

4

4

2

0.7

4.18

4

2

3

2

0.6

4.4

5

3

3

2

0.6

4.19

5

3

4

1

0.5

4.5

6

5

5

1

0.5

4.20

6

4

5

2

0.4

4.6

6

4

4

1

0.4

4.21

7

5

6

2

0.3

4.7

7

5

5

2

0.3

4.22

8

3

7

2

0.2

4.8

7

4

4

1

0.2

4.23

8

4

7

1

0.3

4.9

8

4

7

2

0.3

4.24

7

5

6

2

0.4

4.10

8

3

6

1

0.4

4.25

6

3

5

2

0.5

4.11

7

4

6

2

0.5

4.26

5

2

4

1

0.6

4.12

7

5

6

1

0.6

4.27

4

2

3

2

0.7

4.13

6

3

4

2

0.7

4.28

5

3

3

3

0.8

4.14

6

2

4

2

0.8

4.29

6

4

4

2

0.9

4.15

5

4

4

1

0.9

4.30

7

5

6

1

0.9

 

5 Вероятность «сбоя» в работе телефонной станции при каждом вызове равна р. Поступило n вызовов. Найти вероятность k «сбоев». 

 

Т а б л и ц а 5

№

р

n

k

№

р

n

k

№

р

n

k

5.1

0.002

1000

7

5.11

0.01

200

8

5.21

0.004

500

9

5.2

0.003

1000

7

5.12

0.01

300

8

5.22

0.005

600

9

5.3

0.004

1000

7

5.13

0.02

200

8

5.23

0.01

400

9

5.4

0.005

1000

7

5.14

0.01

500

8

5.24

0.01

500

9

5.5

0.006

1000

7

5.15

0.02

300

8

5.25

0.01

600

9

продолжение таблицы 5

5.6

0.007

1000

7

5.16

0.01

700

8

5.26

0.007

1000

9

5.7

0.008

1000

7

5.17

0.02

400

8

5.27

0.008

1000

9

5.8

0.009

1000

7

5.18

0.01

900

8

5.28

0.009

1000

9

5.9

0.01

1000

7

5.19

0.02

500

8

5.29

0.01

1000

9

5.10

0.011

1000

7

5.20

0.011

1000

8

5.30

0.012

1000

9

  

6 Вероятность наступления события А в каждом испытании равна р. Найти вероятность того, что в n испытаниях событие А наступит

а) ровно  раз;

б) от  до  раз;

в) более  раз;

г) менее  раз.

Т а б л и ц а 6

№

n

p

№

n

p

6.1

100

80

90

0.8

6.16

100

90

95

0.6

6.2

100

85

95

0.8

6.17

100

62

82

0.6

6.3

100

70

95

0.8

6.18

100

50

70

0.8

6.4

100

83

93

0.7

6.19

100

55

75

0.8

6.5

100

50

60

0.7

6.20

100

45

80

0.8

6.6

 100

65

75

0.7

6.21

100

40

60

0.8

6.7

100

70

80

0.7

6.22

100

35

70

0.3

6.8

100

40

50

0.6

6.23

100

50

80

0.3

6.9

100

65

80

0.75

6.24

100

40

65

0.3

6.10

100

70

85

0.75

6.25

200

45

75

0.4

6.11

100

78

92

0.75

6.26

200

100

150

0.4

6.12

100

20

60

0.7

6.27

200

80

170

0.4

6.13

100

30

85

0.7

6.28

300

150

180

0.8

6.14

100

40

79

0.7

6.29

400

100

190

0.6

6.15

100

80

95

0.6

6.30

400

200

295

0.7

7 Дискретная случайная величина Х задана рядом распределения. Найти:

а) её функцию распределения , построить график ;

б) математическое ожидание, дисперсию, среднее квадратическое отклонение, моду;

в) вероятность попадания Х в интервал (a;b).

 

Т а б л и ц а 7

№

Х

х

х

х

х

х

х

а

b

Р

р

р

р

р

р

р

7.1

 

Х

0

1

2

4

6

9

-2

7

Р

0.05

0.15

0.3

0.25

0.15

0.1

продолжение таблицы 7

7.2

Х

-3

-2

-1

0

2

4

-1

3

Р

0.15

0.3

0.02

0.14

0.18

0.31

7.3

 

Х

1

2

3

5

7

8

-3

6

Р

0.3

0.14

0.16

0.1

0.2

0.1

7.4

 

Х

-4

-3

-2

0

1

2

0

1

Р

0.2

0.08

0.23

0.27

0.12

0.1

7.5

 

Х

1

2

4

5

7

9

3

8

Р

0.19

0.21

0.06

0.14

0.12

0.28

7.6

 

Х

-1

0

2

3

5

7

-4

4

Р

0.26

0.14

0.07

0.2

0.03

0.3

7.7

 

Х

-2

-1

0

3

5

7

1

6

Р

0.18

0.09

0.01

0.2

0.22

0.3

7.8

Х

1

2

4

5

6

8

0

6

Р

0.3

0.17

0.13

0.1

0.2

0.1

7.9

Х

1

2

3

4

7

9

5

8

Р

0.11

0.29

0.06

0.14

0.17

0.23

7.10

Х

0

1

2

3

7

9

4

8

Р

0.06

0.14

0.3

0.25

0.15

0.1

7.11

Х

-3

-2

0

1

2

4

-1

3

Р

0.15

0.3

0.01

0.14

0.19

0.31

7.12

Х

-1

0

3

5

7

8

1

6

Р

0.25

0.14

0.16

0.1

0.2

0.15

7.13

Х

-4

-3

-2

0

2

4

-1

3

Р

0.2

0.07

0.24

0.26

0.13

0.1

7.14

Х

-3

-1

0

3

4

7

-2

6

Р

0.12

0.09

0.01

0.2

0.28

0.3

7.15

Х

-1

0

1

3

7

8

2

6

Р

0.26

0.14

0.15

0.2

0.3

0.15

7.16

Х

-2

-1

0

1

2

7

-3

5

Р

0.17

0.09

0.01

0.3

0.23

0.2

7.17

Х

1

2

3

5

6

7

0

4

Р

0.1

0.14

0.16

0.1

0.2

0.3

7.18

Х

-3

-1

0

3

5

6

-2

4

Р

0.16

0.09

0.01

0.3

0.24

0.2

7.19

Х

1

2

5

6

7

8

3

6

Р

0.2

0.15

0.15

0.1

0.3

0.1

7.20

Х

-1

0

2

4

7

8

1

5

Р

0.23

0.18

0.12

0.2

0.1

0.17

7.21

Х

1

2

4

5

6

8

0

7

Р

0.3

0.14

0.16

0.03

0.2

0.17

7.22

Х

-4

-3

-1

0

1

3

-2

2

Р

0.2

0.03

0.24

0.26

0.17

0.1

продолжение таблицы 7

7.23

Х

1

2

3

4

7

9

0

8

Р

0.17

0.23

0.09

0.11

0.12

0.28

7.24

Х

0

1

3

5

7

8

2

6

Р

0.2

0.14

0.16

0.12

0.3

0.08

7.25

Х

-5

-3

-2

0

1

3

-4

2

Р

0.2

0.06

0.21

0.29

0.14

0.1

7.26

Х

1

2

3

5

8

9

4

7

Р

0.18

0.22

0.05

0.15

0.12

0.28

7.27

Х

1

3

4

5

7

8

2

6

Р

0.3

0.16

0.14

0.01

0.2

0.19

7.28

Х

-5

-3

-1

0

1

3

-4

2

Р

0.1

0.03

0.14

0.36

0.17

0.2

7.29

Х

0

2

3

4

6

8

1

7

Р

0.26

0.14

0.05

0.15

0.12

0.28

7.30

Х

-1

0

2

3

7

8

1

6

Р

0.21

0.16

0.14

0.1

0.2

0.19

 

8 Непрерывная случайная величина Х задана функцией распределения . Найти:

а) её плотность распределения ;

б) математическое ожидание, дисперсию, среднее квадратическое отклонение, моду, медиану;

в) вероятность попадания Х в интервал (a;b).

Построить графики  и .

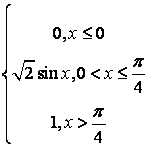
Т а б л и ц а 8

№

а

b

№

а

b

8.1

1

4

8.16

4

5

8.2

1

2

8.17

2

4

8.3

0,5

1

8.18

0,2

0,9

  

продолжение таблицы 8

8.4

 

 

 

 

 

1

8.19

-

8.5

2

4

8.20

0

1,5

8.6

-

8.21

8.7

0,1

0,2

8.22

0,1

0,5

8.8

3

4

8.23

5,5

6

8.9

1

5

8.24

1

2

8.10

3

4

8.25

3

6

 

 продолжение таблицы 8

8.11

5

7

8.26

7,5

8

8.12

-

8.27

5

6

8.13

3,5

6

8.28

0

8.14

2,5

3

8.29

0,1

0,3

8.15

0

2

8.30

-

 

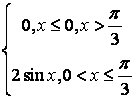
9 Непрерывная случайная величина Х задана плотностью распределения . Найти:

а) её функцию распределения ;

б) математическое ожидание, дисперсию, среднее квадратическое отклонение, моду, медиану;

в) вероятность попадания Х в интервал (a;b).

Построить графики  и .

 

Т а б л и ц а 9

№

а

b

№

а

b

9.1

1

3

9.16

-1

2

9.2

-2,5

0

9.17

0

9.3

0

9.18

0

1,5

9.4

0

9.19

1

2,5

9.5

0

9.20

0,1

1

9.6

0

9.21

0

1

9.7

1

2

9.22

1

9.8

3

4,5

9.23

0

9.9

2

4

9.24

0

1,5

 

продолжение таблицы 9

9.10

1,5

2

9.25

0

9.11

9.26

0

1

9.12

1

3

9.27

1

4

9.13

-1

1

9.28

9.14

0,2

1,2

9.29

0

2

9.15

0

9.30

2

3

  

         10 Найти закон распределения дискретной случайной величины Х, которая принимает два значения   и    (<). Известны математическое ожидание , дисперсия  и вероятность  возможного значения х. 

Т а б л и ц а 10

№

 

№

 

10.1

0.9

3.1

0.09

10.16

0.8

3.2

0.16

10.2

0.8

1.4

0.64

10.17

0.9

1.2

0.36

10.3

0.7

2.6

0.84

10.18

0.8

2.4

0.64

10.4

0.6

3.4

0.24

10.19

0.7

3.3

0.21

10.5

0.5

3

1

10.20

0.6

1.8

0.96

10.6

0.4

3.2

0.96

10.21

0.5

2

1

10.7

0.3

3.7

0.21

10.22

0.4

3.6

0.24

10.8

0.2

2.6

0.64

10.23

0.3

2.4

0.84

10.9

0.1

3.8

0.36

10.24

0.2

3.6

0.64

 

продолжение таблицы 10

10.10

0.2

3.8

0.16

10.25

0.1

3.9

0.09

10.11

0.3

3.4

0.84

10.26

0.2

3.8

0.16

10.12

0.4

2.2

0.96

10.27

0.3

2.4

0.84

10.13

0.5

3.5

0.25

10.28

0.4

3.6

0.24

10.14

0.6

2.8

0.96.

10.29

0.1

2.8

0.36

10.15

0.7

1.6

0.84

10.30

0.9

2.2

0.36

 

11 Решить задачи, используя алгебру событий,  классическое  или геометрическое определения вероятности.

11.1 Для сигнализации об аварии установлены три независимо работающих устройства. Вероятность того, что при аварии первое устройство сработает, равна 0,8; для второго и третьего устройства эти вероятности соответственно равны 0,9 и 0,8. Найти вероятность того, что при аварии сработает только одно устройство.

11.2 В одном ящике 5 белых и 10 чёрных шаров, в другом - 10 белых и 5 чёрных шаров. Из каждого ящика вынуто по одному шару. Найти вероятность того, что хотя бы один из них белый.

11.3 Вероятность попадания в корабль для одной торпеды равна 0,5. Какова вероятность того, что три торпеды потопят корабль, если для этого достаточно одного попадания?

11.4 В шкатулке 10 красных и 6 синих пуговиц. Вынимают наугад две пуговицы. Какова вероятность, что они будут одноцветными?

11.5 Вероятность попадания в цель первым стрелком равна 0,7, вторым – 0,95. Стрелки выстрелили одновременно. Чему равна вероятность того, что один из них попадёт в цель, другой промахнётся?

11.6  Вероятность того, что изготовленная на первом станке деталь будет первого сорта, равна 0,7, для второго станка эта вероятность равна 0,8. На первом станке изготовлены 2 детали, на втором - 3. Найти вероятность того, что хотя бы на одном станке все изготовленные на нём детали будут первого сорта.

11.7  32 буквы русского алфавита написаны на карточках разрезной азбуки. Три карточки вынимаются наугад одна за другой и укладываются в порядке появления. Найти вероятность того, что получится слово «бал».

11.8 В цехе работают 7 мужчин и 3 женщины. По табельным номерам наугад отобраны З человека. Найти вероятность того, что среди отобранных лиц будет хотя бы одна женщина.

11.9 Из партии изделий товаровед отбирает изделия высшего сорта.  Вероятность того, что наудачу взятое изделие будет высшего сорта, равна 0,8. Найти вероятность того, что из 3 проверенных изделий только 2 высшего сорта.

11.10 Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, равна 0,4. Произведены 3 независимые измерения. Найти вероятность того, что только в одном из них допущена ошибка.

11.11  Вероятность одного попадания в цель при одном залпе из двух орудий равна 0,38. Найти вероятность поражения цели при одном выстреле  первым из орудий, если известно, что для второго орудия эта вероятность равна 0,8.

11.12 На полке в библиотеке в случайном порядке расставлено 16 учебников, среди которых 5 по физике. Библиотекарь берёт наудачу 3 учебника. Найти вероятность того, что хотя бы один из них будет по физике.

11.13 Брошены 3 игральные кости. Найти вероятность того, что на каждой из выпавших граней появится 5 очков.

11.14 В круг радиуса 10 вписан правильный треугольник. Внутрь круга наудачу брошены 4 точки. Найти вероятность того, что все 4 точки попадут внутрь треугольника.

11.15 Отрезок длиной 30 разделён на 3 равные части. На этот отрезок наудачу брошены 3 точки. Найти вероятность того, что на каждую из трёх частей отрезка попадёт по одной точке. Предполагается, что вероятность попадания точки на отрезок пропорциональна его длине и не зависит от его расположения.

11.16 Для сигнализации об аварии установлены три независимо работающих устройства. Вероятность того, что при аварии первое устройство сработает, равна 0,7; для второго и третьего устройства эти вероятности соответственно равны 0,9 и 0,6. Найти вероятность того, что при аварии сработает хотя бы одно устройство.

11.17 В одном ящике 6 белых и 12 чёрных шаров, в другом - 11 белых и 5 чёрных шаров. Из каждого ящика вынуто по одному шару. Найти вероятность того, что только один из них белый.

11.18 Вероятность попадания в корабль для одной торпеды равна 0,4. Какова вероятность того, что 2 торпеды потопят корабль, если для этого достаточно одного попадания?

11.19  В шкатулке 14 красных и 8 синих пуговиц. Вынимают наугад две пуговицы. Какова вероятность, что они будут разноцветными?

11.20 Вероятность попадания в цель первым стрелком равна 0,8, вторым — 0,85. Стрелки выстрелили одновременно. Чему равна вероятность того, что хотя бы один из них попадёт в цель?

11.21 Вероятность того, что изготовленная на первом станке деталь будет первого сорта, равна 0,8, для второго станка эта вероятность равна 0,9. На первом станке изготовлены 3 детали, на втором - 2. Найти вероятность того, что все детали, изготовленные на двух станках, будут первого сорта.

11.22 32 буквы русского алфавита написаны на карточках разрезной азбуки. Четыре карточки вынимаются наугад одна за другой и укладываются в порядке появления. Найти вероятность того, что получится слово «вода».

11.23 В цехе работают 8 мужчин и 4 женщины. По табельным номерам наугад отобрано 4 человека. Найти вероятность того, что среди отобранных лиц будут все мужчины.

11.24 Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие будет высшего сорта, равна 0,8. Найти вероятность того, что из 3 проверенных изделий только 1 высшего сорта.

11.25 Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, равна 0,3. Произведены 4 независимые измерения. Найти вероятность того, что хотя бы в одном из них допущена ошибка.

11.26 Вероятность одного попадания в цель при одном залпе из двух орудий равна 0,4. Найти вероятность поражения цели при одном выстреле первым из орудий, если известно, что для второго орудия эта вероятность равна 0,7.

11.27 На полке в библиотеке в случайном порядке расставлено 15 учебников, среди которых 5 по биологии. Библиотекарь берёт наудачу 3 учебника. Найти вероятность того, что только один из них будет по биологии.

11.28 Брошены 4 игральные кости. Найти вероятность того, что на каждой из выпавших граней появится 6 очков.

11.29 В круг радиуса 12 вписан правильный треугольник. Внутрь круга наудачу брошены 3 точки. Найти вероятность того, что все 3 точки попадут внутрь треугольника.

11.30 Отрезок длиной 60 разделён на 4 равные части. На этот отрезок наудачу брошены 4 точки. Найти вероятность того, что на каждую из четырёх частей отрезка попадёт по одной точке. Предполагается, что вероятность попадания точки на отрезок пропорциональна его длине и не зависит от его расположения.

  

1.3 Решение типового варианта

 

1 В партии 120 деталей, среди них 40 бракованных. Найти:

а) относительную частоту бракованных деталей;

б) вероятность того, что все 20 деталей, взятых наугад из партии, будут бракованными;

в) вероятность того, что среди 20 деталей, взятых наугад из партии, будет 9 бракованных.

Решение:

а) относительной частотой события А (обозначается ) называется отношение числа m испытаний, в которых событие А появилось, к общему числу n произведённых испытаний: .

Пусть событие А – появление бракованных деталей в партии, тогда .

В пунктах б) и в) используем классическое определение вероятности события А: , где m – число испытаний, благоприятствующих появлению события А, n – общее число испытаний;

б) пусть событие А - все 20 деталей, взятых наугад из партии, бракованные. Общее число испытаний равно числу различных способов: взять 20 деталей из 120 деталей, т.е. ; число благоприятствующих испытаний равно числу различных способов: взять из 40 бракованных деталей 20, т.е. . Таким образом, ;

в) пусть событие А – среди 20 деталей, взятых наугад из партии, будет 9 бракованных. Как выше сказано, ; число m благоприятствующих испытаний получим, комбинируя каждое из  сочетаний ( равно числу различных способов выбрать 9 бракованных из 40 бракованных деталей) с каждым из  сочетаний ( равно числу различных способов выбрать 11 не бракованных из 80 не бракованных деталей), т.е. . Таким образом, .

При вычислении числа сочетаний была использована функция combin в Mathcad. Ниже приведена копия файла, в котором combin(Q,R) введена как функция пользователя C(Q,R), позволяющая получать значения сочетаний при произвольных Q и R.

,

,

,

,

,

.

 

2 В ящике изделия четырёх сортов. Первого сорта 3 изделия, второго - 4, третьего - 2, четвёртого - 1. Наудачу берут 5 изделий. Найти вероятность того, что среди них 2 изделия первого сорта, 2- второго, 1- третьего, 0- четвёртого сорта.

Решение:

пусть событие А - среди 5, выбранных наудачу изделий, 2 изделия первого сорта, 2 - второго, 1 - третьего, 0 - четвёртого сорта. Для решения задачи также используем классическое определение вероятности события А: Р(А) = m/ n, где n число всех возможных способов выбора 5 изделий из имеющихся 10 (3+4+2+1=10), т.е. . Число m благоприятствующих событию А элементарных событий равно  . Поэтому Р(А) = 36/252=1/7.

Заметим, что при небольших числах число сочетаний проще найти вручную по формуле      ,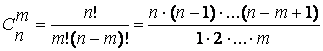

причём дробь лучше начинать заполнять со знаменателя, т.к. в числителе столько же сомножителей, сколько в знаменателе.

 

3 В магазин поступили 1000 ламп из трёх заводов: 100 ламп из первого завода, 300 - из второго, остальные из третьего. Среди ламп первого завода 5% бракованных, второго - 4% бракованных, третьего - 6% бракованных.   

Куплена одна лампа:

         а) найти вероятность того, что она бракованная;

         б) купленная лампа оказалась бракованной. Найти вероятность того, что она сделана на 2–ом заводе.

         Решение:

пусть событие А – куплена бракованная лампа, а события , , –  лампа поступила соответственно из первого, второго, третьего заводов (эти события называются гипотезами).

         а) вероятность события А находится по формуле полной вероятности: , где  Р(А/) – условные вероятности того, что купленная наугад лампа поступила из i– го завода (i=1,2,3). По условию задачи имеем: Р() = 100/1000 = 0,1; Р() = 300/1000 = 0,3; Р() = 600/1000 = 0,6; Р(А/)=0,05; Р(А/)=0,04; Р(А/)=0,06. Поэтому  Р(А) = = 0,053;

         б) в этом пункте требуется найти условную вероятность Р(/А). Используем для этого формулу Байеса:

,

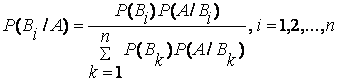которая для нашей задачи перепишется так: =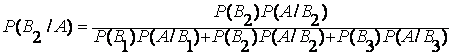

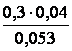= = 0,226.

 

4 Проводится 10 испытаний, в каждом из которых вероятность появления некоторого события  равна 0,8. Найти вероятность того, что событие  появится:

а) ровно 8 раз (событие А);

б) не менее 9 раз (событие В);

в) не более 2 раз (событие С);

г) хотя бы один раз (событие D).

Решение:

для определения вероятности события А используем формулу Бернулли: , где - вероятность появления раз  некоторого события в серии   независимых испытаний, . Вероятности событий В и С определяются как суммы вероятностей: - вероятность того, что событие произойдёт не менее, чем раз в  независимых испытаниях, т.е. или , или +1,…, или раз; - вероятность того, что событие произойдёт не более раз в  независимых испытаниях, т.е. или 0, или 1, или 2,…, или  раз. Эти вероятности называют комулятивными (накопленными). Таким образом,

а)==0,302,

б) 0,376,

в) 0,000078.

Введём противоположное D событие Е - в серии   независимых испытаний некоторое событие не появилось ни разу. Тогда

г) =1.

Ниже приведена копия файла из Mathcad с вычислениями. 

,

,

,

,

.

  

5 Вероятность «сбоя» в работе телефонной станции при каждом вызове равна 0,003. Поступило 1000 вызовов. Найти вероятность 6 «сбоев».

Решение:

поскольку велико,  мало, а произведение  - небольшое число, то вместо формулы Бернулли для определения вероятности появления раз  некоторого события в серии   независимых испытаний удобнее использовать формулу Пуассона .

В нашей задаче =1000, =6, =0,003, , поэтому =0,05.

При вычислении можно использовать таблицу значений функции , приводимую в некоторых учебниках, или функцию dpois в Mathcad. Ниже приведена копия файла, в котором проведены вычисления в Mathcad.

,

.

  

6. Вероятность наступления некоторого события в каждом испытании равна 0,8. Найти вероятность того, что в 100 независимых испытаниях событие  наступит

а) ровно 80 раз (событие А);

б) от 70 до 80 раз (событие В);

в) более 80 раз (событие С);

г) менее 70 раз (событие D).

Решение:

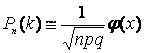поскольку число независимых испытаний велико, то вероятность появления раз  некоторого события в  испытаниях определяется по локальной теореме Муавра-Лапласа и приближённо равна , где 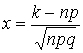, ,  (значения этой функции находят из таблиц или с помощью встроенной функции dnorm в системе Mathcad).

Для определения вероятностей событий В, С и D используют интегральную теорему Муавра-Лапласа: вероятность того, что число появления некоторого события будет находится в промежутке от  до  приближённо равна , где 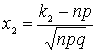, , 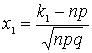 - функция Лапласа, значения которой находятся из специальных таблиц или с помощью встроенной функции pnorm в системе Mathcad.

а) 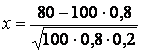=0, ;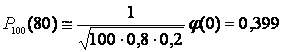

б) , , ;

в) , ;

г) , .

Ниже приведена копия файла, в котором сделаны вычисления в системе Mathcad.

 

,

,

,

,

,

,

,

,

,

,

.

,

,

,

 

или другой вариант

,

. 

,

,

,

,

,

,

,

,

. 

 

7  Дискретная случайная величина Х задана рядом распределения

Х

0

10

20

30

40

50

Р

0,05

0,15

0,3

0,25

0,2

0,05

Найти:

а) её функцию распределения , построить график ;

б) математическое ожидание, дисперсию, среднее квадратическое отклонение, моду;

в) вероятность попадания Х в интервал (15;45).

Решение:

а) функция распределения  (интегральная функция распределения) случайной величины Х определяет вероятность события Х<х. Для дискретной случайной величины она находится по формуле =

, где суммирование ведётся по всем  , для которых .

Итак, 1) если , то ;

2) если , то ;

3) если , то ;

4) если , то ;

5) если , то =

;

6) если , то + +;

7) если , то + +.

         Таким образом, ;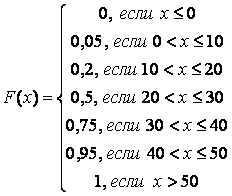

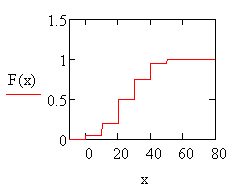
График построен в системе Mathcad (см. ниже).

б) найдём числовые характеристики. Для дискретной случайной величины математическое ожидание равно сумме произведений всех её возможных значений на вероятности этих значений: . Поэтому

25,5.

Дисперсия случайной величины Х находится либо по формуле , либо по формуле . Для дискретной случайной величины эти формулы перепишутся так:  или . Среднее квадратическое отклонение равно ; мода дискретной случайной величины (обозначается ) – это её значение, принимаемое с наибольшей вероятностью; вероятность попадания Х в интервал (а;b) находится по формуле . В нашей задаче эти величины равны:

D(x)=154,75; ;  =20;

=0,75.

Ниже приведена копия файла, в котором сделаны вычисления в системе Mathcad, причём вычисление дисперсии проведено по обеим формулам.

,

,

,

,

 

,

 

,

  

,

  

,

  

,

 

,

 

,

 

,

 

,

 

 

.

 

 

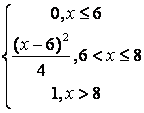
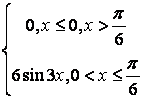
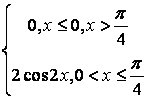
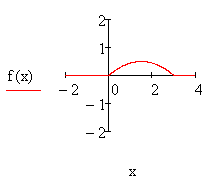
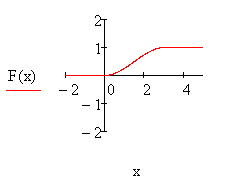
8 Непрерывная случайная величина Х задана функцией распределения.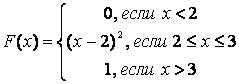   

Найти:

а) её плотность распределения ;

б) математическое ожидание, дисперсию, среднее квадратическое отклонение, моду, медиану;

в) вероятность попадания Х в интервал (1; 2,5).

Построить графики  и .

Решение:

а) плотность распределения вероятностей непрерывной случайной величины равна производной её функции распределения: , поэтому ;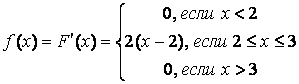

б) числовые характеристики непрерывных случайных величин находятся по формулам: математическое ожидание -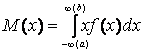;  дисперсия - 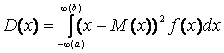или 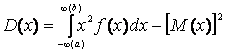 (пределы интегрирования зависят от того, принадлежат ли возможные значения случайной величины всей оси Ох или интервалу (a;b)); среднее квадратическое отклонение - ; модой непрерывной случайной величины  называется то её значение , при котором плотность распределения максимальна; медианой непрерывной случайной величины называется такое её значение , для которого одинаково вероятно, окажется ли случайная величина меньше или больше , т.е. .

Таким образом, в нашей задаче =8/3; ; = 0,236. Для определения моды надо найти максимум функции  на отрезке [2; 3]. Поскольку эта функция монотонна, то её максимум достигается на конце отрезка, т.е. . Итак, =3. Медиану можно найти из условия , где вероятность =  находится по формуле   или по формуле - вероятность попадания случайной величины в промежуток (a; b). Так как 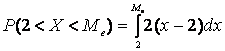=, то, решая уравнение =0,5, получим  два корня 1,29 и 2,71, из которых подходит один: = 2,71;

в) вероятность попадания Х в интервал (1; 2,5) находим по выше приведённым формулам

 или =.

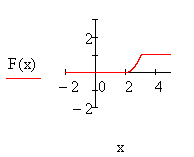
         Графики функций  и  построим в системе Mathcad:

,

,

 

Заметим, что вычисление интегралов и другие вычисления можно проводить в системе Mathcad, например,

,

,

,

 

,

  

.

 

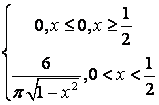
9 Непрерывная случайная величина  Х задана плотностью распределения .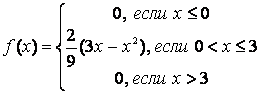

Найти:

а) её функцию распределения ;

б) математическое ожидание, дисперсию, среднее квадратическое отклонение, моду, медиану;

в) вероятность попадания Х в интервал (1;4).

Построить графики  и .

         Решение:

а) функцию распределения находим по формуле. Итак, если , то , поэтому ;

если , то =-;

если , то .

Таким образом, искомая функция распределения имеет вид ;

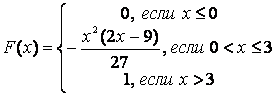б) математическое ожидание, дисперсию, среднее квадратическое отклонение, моду, медиану находим как в предыдущей задаче.

=1,5; 0,45; = 0,671.

Для определения моды надо найти максимум функции  на отрезке [0; 3]. Для этого находим производную и приравниваем её к нулю: ,  при х=3/2, эта точка критическая. Проверяем её на экстремум: , итак, при переходе через точку х=3/2 знак производной сменился с плюса на минус, значит х=3/2 точка максимума, поэтому =3/2.

Медиану находим из условия ,

где = = .  

Так как

 =-,

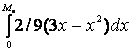то, решая уравнение 

-=0,5,

получим три корня, из которых подходит один:

= 1,5.

Ниже приведёна копия файла с вычислениями в системе Mathcad.

,

,

,

,

 

,

 

 

 

,

 

,

  

.

,

 

,

 

,

 

 

в) вероятность попадания Х в интервал (1;4) равна  0,741

или   =  =

==.

         Ниже приведёна копия файла из Mathcad с вычислениями.

,

  

,

 

,

 

,

  

.

  

Графики функций F(x) и f(x) построим в системе Mathcad:

 

,

 

,

 

,

.

  

10 Найти закон распределения дискретной случайной величины Х, которая принимает два значения   и    (<). Известны математическое ожидание =1,4, дисперсия =0,24  и вероятность =0,6  возможного значения.

Решение:

так как сумма вероятностей всех возможных значений дискретной случайной величины равна единице, то вероятность того, что случайная величина примет значение х равна р= 1- 0,6 = 0,4.

Напишем закон распределения Х:

Х

р

0,6

0,4

Чтобы найти  и  , составим систему двух уравнений, используя формулы вычисления математического ожидания и дисперсии для дискретных случайных величин:  и  . Эта система имеет вид: .

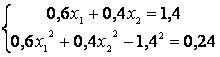Решим её в Mathcad:

.

,

  

,

,

 

.

 

Итак, система имеет два решения =1, =2 и =1,8, =0,8. По условию <, поэтому задаче удовлетворяет первое решение =1, =2. Таким образом, искомый закон распределения: 

Х

1

2

р

0,6

0,4

 

Список литературы 

       1. Ивановский Р.И. Теория вероятностей и математическая статистика. Основы, прикладные аспекты с примерами изадачами в среде Mathcad. - СПб.: БХВ- Петербург, 2008. – 528 с.

       2. Письменный Д. Конспект лекций по теории вероятностей и математической статистики,  случайные процессы. – М.: Айрис -пресс, 2006. – 288 с.

       3. Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие для вузов. – М.: Высш. школа, 2003.- 279 с.

       4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высш. школа, 1999.- 400 с.

         5. Базарбаева С.Е. и др. Теория вероятностей и математическая статистика. Сборник типовых расчетов и методических указании. – Алматы: АИЭС, 2001. – 32 с.

 

Содержание

 

1 Теоретические вопросы                                                                                    3

2 Расчётные задания                                                                                             3

4 Решение типового варианта                                                                            17

Список литературы                                                                                              30

 

                                                                                  Сводный план  2011 г., поз.218
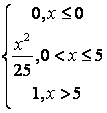
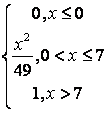
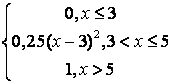
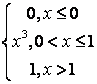
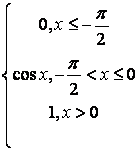
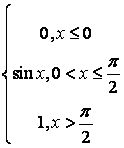
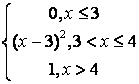
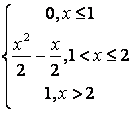
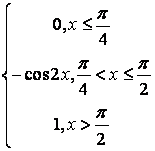
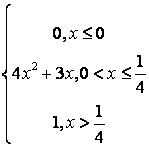
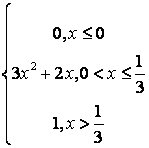
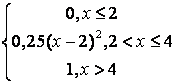
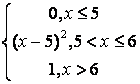
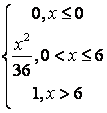
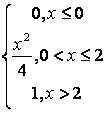
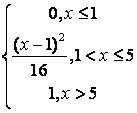
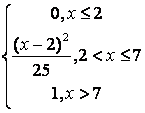
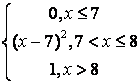
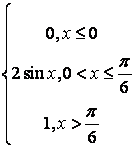
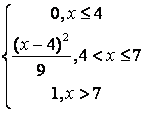
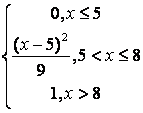
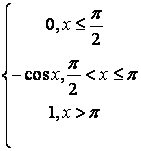
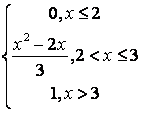
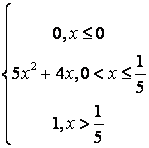
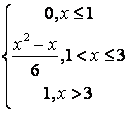
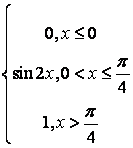
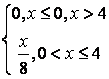
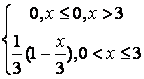
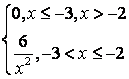
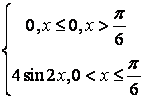
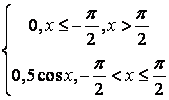
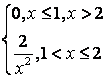
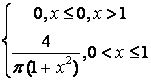
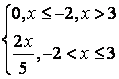
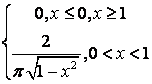
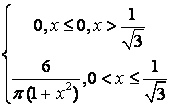
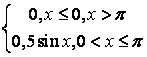
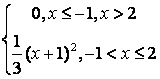
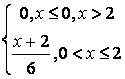
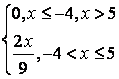
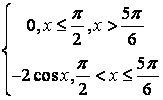
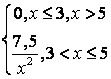
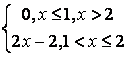
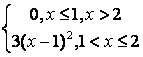
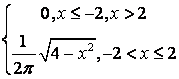
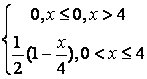
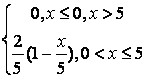
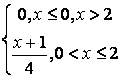
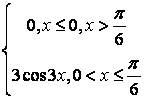
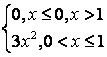
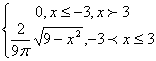
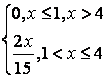
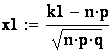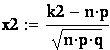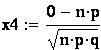
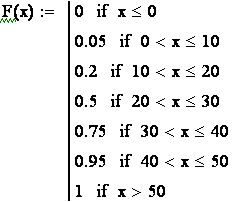
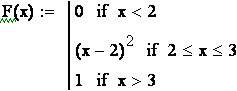
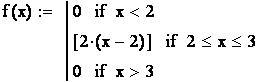
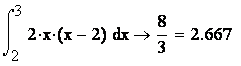
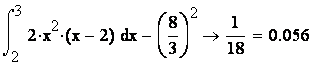
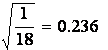
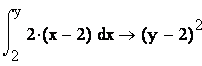
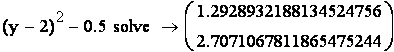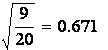
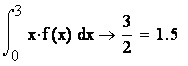
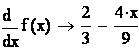
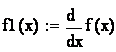
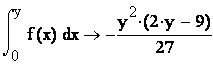
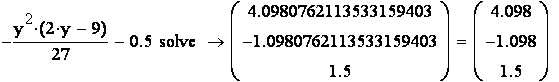
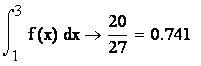
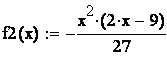
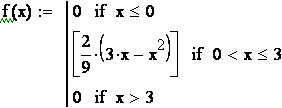
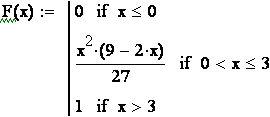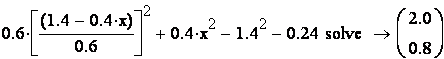