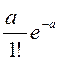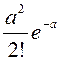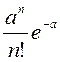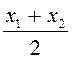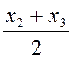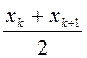Коммерциялық емес акционерлік қоғам
АЛМАТЫ ЭНЕРГЕТИКА ЖӘНЕ БАЙЛАНЫС УНИВЕРСИТЕТІ
Жоғары математика кафедрасы
ЫҚТИМАЛДЫҚТАР ТЕОРИЯСЫ ЖӘНЕ
МАТЕМАТИКАЛЫҚ СТАТИСТИКА
5В070400 – Есептеу техникасы мен
бағдарламалық қамтамасыз ету
және 5В070300 – Ақпараттық
жүйелер мамандықтарының студенттері үшін
дәрістер жинағы
Алматы 2013
ҚҰРАСТЫРУШЫЛАР: Астраханцева Л.Н., Байсалова М.Ж. Ықтималдық теориясы және математикалық статистика. 5В070400 – Есептеу техникасы мен бағдарламалық қамтамасыз ету және 5В070300 – Ақпараттық жүйелер мамандықтарының барлық оқу түрінің студенттері үшін дәрістер жинағы. - Алматы: АЭжБУ, 2013.- 49 б.
Бұл дәрістер жинағы 5В070400 – Есептеу техникасы мен бағдарламалық қамтамасыз ету және 5В070300 – Ақпараттық жүйелер мамандықтарының барлық оқу түрінің студенттеріне «Ықтималдық теориясы және математикалық статистика» пәнін оқып, үйрену үшін арналған.
Бұл материал көрсетілген мамандықтың «Ықтималдық теориясы және математикалық статистика» пәнінің бағдарламасына сәйкес құрылған.
Тапсырмалар берілген және қажет теориялық мәліметтер келтірілген.
Кестелер- 10, без.- 10, әдеб.көрсеткіші – 12 атау.
«Алматы энергетика және байланыс университеті» коммерциялық емес акционерлік қоғамының 2013 ж. жоспары бойынша басылды
ã «Алматы энергетика және байланыс университеті» КЕАҚ, 2013 ж.
1 Ықтималдықтар теориясы элементтері
1.1 Дәріс 1. Кездейсоқ оқиғалар. Элементар оқиғалар кеңістігі. Ықтималдық
Дәріс мазмұны: ықтималдықтар теориясы пәні. Элементар оқиғалар кеңістігі. Оқиғалар алгебрасы. Ықтималдықтың анықтамалары.
Дәріс мақсаты: ықтималдықтар теориясы пәні мен негізгі ұғымдармен танысу.
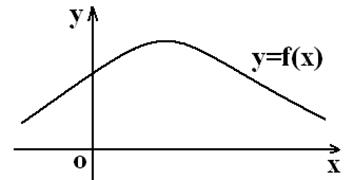
Өмірде болып жатқан оқиғаларды соңы немен аяқталатынын болжап білу мүмкін және мүмкін емес деп бөлуге болады. Ағаштан жасалған кубикті суға лақтырғанда ол міндетті түрде су бетіне қалқып шығады. Бірақ кубиктің жоғарғы жағында қанша ұпаймен шығатынын болжау мүмкін емес. Егер тиынды бір рет лақтырса, онда елтаңба немесе цифр түсуі алдын-ала белгісіз. Бірақ тиынды көп рет лақтырсақ, жобамен жартысында елтаңба, жарты жағдайда сан түсуі мүмкін. Сонымен, қандай да бір заңдылық пайда бола бастайды. Ықтималдықтар теориясы – кездейсоқ құбылыстардың заңдылығын зерттейтін математикалық ғылым. Ол құбылыстарды емес, оның математикалық моделдерін қарастырады. Ықтималдықтар теориясында оқиға - басты ұғым.
Анықтама.
Кездейсоқ оқиға деп берілген шарттар жиынтығында орындалуы да, орындалмауы да мүмкін оқиғаны айтамыз; бұл шарттар жиынтығы сынақ немесе тәжірибе делінеді.
Ықтималдықтар теориясында жиындар теориясының
аппараты қолданылады, кездейсоқ оқиғалар жиындар
сияқты латын алфавитінің бас әріптерімен белгіленеді ![]() ,
т.с.с.
,
т.с.с.
Мысалы 1.1.1 – «Ойын сүйегін лақтыру» сынағын қарастырайық. Келесі кездейсоқ оқиғалар болуы мүмкін: А – 2 ұпайдың түсуі; В – ұпайлар саны тақ болып түсуі; С – 9 ұпайдың түсуі; D – бүтін ұпайлар саны түсуі.
Анықтама.
Тәжірибенің мүмкін болатын нәтижесі элементар оқиғалар
деп аталып, ![]() деп белгіленеді. Элементар
оқиғалардың жиыны элементар оқиғалар
кеңістігі деп аталып,
деп белгіленеді. Элементар
оқиғалардың жиыны элементар оқиғалар
кеңістігі деп аталып, ![]() деп белгіленеді.
деп белгіленеді.
Сонымен, кез келген А жиыны ![]() ішкі
жиыны деп қарастыруға болады:
ішкі
жиыны деп қарастыруға болады: ![]() . Әр есепте
. Әр есепте ![]() әртүрлі.
әртүрлі.
Мысалы 1.1.2 – Жоғарыда келтірілген мысалда ойын сүйегін
лақтырғанда 6 элементар оқиғалар болуы мүмкін: ![]() ,
мұндағы
,
мұндағы ![]() - лақтыру кезінде
- лақтыру кезінде ![]() ұпайының түсуі.
Сонымен, бұл есепте элементар оқиғалар кеңістігі
ұпайының түсуі.
Сонымен, бұл есепте элементар оқиғалар кеңістігі ![]() немесе
немесе ![]() . А кездейсоқ оқиғасын – 2 ұпайдың
түсуін
. А кездейсоқ оқиғасын – 2 ұпайдың
түсуін ![]() ішкі жиыны деп қарастыруға болады:
ішкі жиыны деп қарастыруға болады: ![]() ;
сол сияқты
;
сол сияқты ![]() .
.
Анықтамалар.
1. Егер тәжірибе нәтижесінде оқиғаның алдын ала орындалмайтыны
белгілі болса, онда ол оқиға мүмкін емес деп аталады.
Белгіленуі ![]() - бос жиын.
- бос жиын.
2. Егер тәжірибе нәтижесінде оқиғаның міндетті түрде орындалатыны
белгілі болса, онда ол оқиға ақиқат деп аталады. Ақиқат оқиға
![]() -мен
беттеседі.
-мен
беттеседі.
3. Егер тәжірибе нәтижесінде бір оқиғаның пайда болуы екіншісінің
пайда болуына әсер етпесе, онда бұл оқиғалар үйлесімсіз деп аталады, қарсы жағдайда – үйлесімді. Егер бірнеше оқиғалардың кез келген екеуі үйлесімсіз болса, онда олар жұбымен үйлесімсіз.
Егер оқиғалардың пайда болуға мүмкіндіктері бірдей болса, олар бірдей мүмкіндікті делінеді.
4. Егер бірнеше оқиғалар үшін келесі шарттар орындалса:
а) олар жұбымен үйлесімсіз;
б) әрбір тәжірибе нәтижесінде тек бір оқиға пайда болса,
онда бұл оқиғалар толық топ құрайды.
Сонымен, бірінші мысалда С оқиғасы
- 9 ұпайының түсуі, мүмкін емес: С=![]() ;
D оқиғасы – бүтін ұпайлар саны түсуі, ақиқат:
;
D оқиғасы – бүтін ұпайлар саны түсуі, ақиқат:
![]() ;
А және
;
А және ![]() оқиғалары үйлесімсіз; А және
D үйлесімді.
оқиғалары үйлесімсіз; А және
D үйлесімді. ![]() оқиғалары бірдей
мүмкіндікті және толық топ құрайды.
оқиғалары бірдей
мүмкіндікті және толық топ құрайды.
Оқиғалар алгебрасы
Жиындар теориясының аппаратын
жалғастырып жиындарға қолданылатын амалдар сияқты
кездейсоқ оқиғаларға қолданылатын амалдардарды
анықтауға болады. Бұл жағдайда универсал жиын ретінде элементар
оқиғалар кеңістігін алуға болады ![]() .
Бос жиын
.
Бос жиын ![]() –
мүмкін емес оқиғалар.
–
мүмкін емес оқиғалар.
1. A және B оқиғаларының
қосындысы (бірігуі) деп ең болмағанда екеуінің
біреуінің пайда болуынан құралған C оқиғасы
айтылады (яғни не A, не В, немесе A және B
бірге): ![]()
2. А және B оқиғаларының
көбейтіндісі (қиылысуы) деп екеуінің бірге пайда болуынан
құралған C оқиғасы айтылады: ![]() .
.
3. A және ![]() оқиғаларының айырымы деп A оқиғасы
пайда болып,
оқиғаларының айырымы деп A оқиғасы
пайда болып, ![]() оқиғасы пайда болмауынан тұратын C
оқиғасы айтылады:
оқиғасы пайда болмауынан тұратын C
оқиғасы айтылады: ![]() .
.
4. A оқиғасына
қарама-қарсы оқиға деп A оқиғасы
орындалмағанда орындалатын ![]() оқиғасы айтылады:
оқиғасы айтылады: ![]() .
.
5. Егер A оқиғасының
пайда болуы B оқиғасының пайда болуына ықпал
жасаса, ![]() ,
яғни А жиыны B-ның ішкі жиыны.
,
яғни А жиыны B-ның ішкі жиыны.
Бұл амалдардың анықтамаларын
қасиеттері сияқты Эйлер-Венн диаграммасы көмегімен
кескіндеуге болады. Айта кетелік, кейбір ұғымдар мен
қорытындыларды қысқаша көрсетілген амалдар
көмегімен көрсетуге болады. Мысалы, егер A және B
үйлесімсіз болса, онда ![]() ; Егер
; Егер ![]() толық топ құрса, онда 1)
толық топ құрса, онда 1) ![]() ;
2)
;
2) 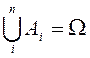 .
.
Салыстырмалы жиілік. Ықтималдық
Анықтама.
n сынақта A оқиғасы m рет
пайда болсын. A оқиғасының салыстырмалы жиілігі деп ( ![]() деп
белгіленеді) A оқиғасының пайда болу санының
жалпы сынақ санына қатынасы айтылады, сонымен
деп
белгіленеді) A оқиғасының пайда болу санының
жалпы сынақ санына қатынасы айтылады, сонымен  .
m санын A оқиғасының
салыстырмалы жиілігі деп атайды.
.
m санын A оқиғасының
салыстырмалы жиілігі деп атайды.
Әрбір сынақта оқиғаның пайда болу мүмкіндігі әртүрлі екендігі белгілі. Осы мүмкіндіктің дәрежесін анықтау есебі туындайды. Осылай оқиғаның ықтималдығы ұғымы пайда болады.
Анықтама.
Оқиғаның ықтималдығы деп осы оқиғаның пайда болу мүмкіндіктерінің сандық өлшемі айтылады.
Ықтималдықты анықтаудың бірнеше түрлері бар. Олардың үшеуін қарастырайық.
Ықтималдықтың статистикалық анықтамасы
Қандай да бір сынақ бірдей
жағдайда сериялап, яғни бірнеше рет жүргізілсін. Әрбір
серияда сынақ саны әртүрлі болсын: біріншісінде - ![]() ,
екіншісінде -
,
екіншісінде - ![]() , және т.б., k – шісінде -
, және т.б., k – шісінде - ![]() .
А оқиғасы i – ші жағдайда
.
А оқиғасы i – ші жағдайда ![]() жиілікпен
пайда болсын, онда салыстырмалы жиілігі
жиілікпен
пайда болсын, онда салыстырмалы жиілігі  (i =1,2,…,k).
(i =1,2,…,k).
Тәжірибе санын тым көп етіп
жүргізгенде ![]() жиілігі тұрақты бір санның
төңірегінде топталады.
жиілігі тұрақты бір санның
төңірегінде топталады.
Анықтама.
A оқиғасының статистикалық
ықтималдығы деп (белгіленуі ![]() ) осы оқиғаның тәжірибе санын
тым көп етіп жүргізгенде қатысты жиілігінің топталатын
санын айтады:
) осы оқиғаның тәжірибе санын
тым көп етіп жүргізгенде қатысты жиілігінің топталатын
санын айтады:![]()
 .
.
Ықтималдық салыстырмалы жиілік сияқты келесі қасиеттерге ие (ықтималдық аксиомалары):
1 ![]() ,
, ![]() ,
, ![]() .
.
2 Егер А және В үйлесімсіз (яғни ![]() ) болса, онда
) болса, онда ![]() .
.
Ықтималдықтың классикалық анықтамасы
![]() (i=1,2,…,n) нәтижелері толық топ
құрайтын n бірдей мүмкіндікті сынақтар
жүргізілсін. Сонымен, элементар оқиғалар кеңістігі деп
келесі жиын айтылады:
(i=1,2,…,n) нәтижелері толық топ
құрайтын n бірдей мүмкіндікті сынақтар
жүргізілсін. Сонымен, элементар оқиғалар кеңістігі деп
келесі жиын айтылады: ![]() , мұндағы
, мұндағы ![]() ,
, 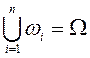 ,
, ![]() . Мұндай элементар оқиғалар
сәтті мүмкіндік немесе шанс деп, ал сынақ – классикалық
деп те аталады. Осы тәжірибемен байланысты A әртүрлі
кездейсоқ оқиғалар
. Мұндай элементар оқиғалар
сәтті мүмкіндік немесе шанс деп, ал сынақ – классикалық
деп те аталады. Осы тәжірибемен байланысты A әртүрлі
кездейсоқ оқиғалар ![]() -ның ішкі жиыны (
-ның ішкі жиыны (![]() ) болады. Мысалы,
) болады. Мысалы, ![]() .
A ішкі жиынына енетін элементар оқиғалар (яғни
олардың пайда болуы A-ның пайда болуына әсер етеді) A
оқиғасына қолайлы оқиғалар деп аталады.
.
A ішкі жиынына енетін элементар оқиғалар (яғни
олардың пайда болуы A-ның пайда болуына әсер етеді) A
оқиғасына қолайлы оқиғалар деп аталады.
Мысалы
1.1.3 – Сынақ
– ойын сүйегінің
лақтырылуы болсын. ![]() =
= ![]() - элементар оқиғалар кеңістігі. A– жұп
ұпайлар түсу саны, яғни
- элементар оқиғалар кеңістігі. A– жұп
ұпайлар түсу саны, яғни ![]() . Сонымен, A оқиғасына
. Сонымен, A оқиғасына ![]() ,
, ![]() ,
, ![]() үш элементар оқиғалары қолайлы болады.
үш элементар оқиғалары қолайлы болады.
Анықтама.
A оқиғасының
ықтималдығы деп A оқиғасына қолайлы m
элементар оқиғалар санының элементар оқиғалар n
жалпы санына қатынасы айтылады, яғни 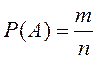 .
.
Қарапайым жағдайларда бұл формуланы қолдану қиындық туғызбайды. Күрделі жағдайда – элементар оқиғалар n жалпы санын және қолайлы m элементар оқиғалар санын анықтағанда комбинаторика формулаларын қолданады ([1], 19-35 бет).
Мысалы 1.1.4 – Электрондық қондырғы 5 элементтен тұрады. Егер барлық элементтері жөнделген болса, ол қалыпты жұмыс істейді. Оның элементтері 1000 элементті партиядан таңдап алынады. Партиядағы элементтердің 950-і жөнделген, ал 50 жөндеуді талап етеді. Кез келген ретпен таңдап алынған 5 элементтен құрылған қондырғының қалыпты жұмыс істеу ықтималдығын табу керек.
A оқиғасы – қондырғы
қалыпты жұмыс істейді. 1000 элементтің арасынан 5 элементті
таңдаудың барлық мүмкін жағдайлар саны (яғни ![]() -ғы
элементар оқиғалар саны) n=
-ғы
элементар оқиғалар саны) n=![]() теру санына тең; қолайлы
жағдайлар саны m=
теру санына тең; қолайлы
жағдайлар саны m=![]() . Сондықтан
. Сондықтан 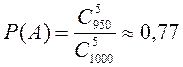 .
.
Ықтималдықтың геометриялық анықтамасы
Егер есепте ![]() элементар оқиғалар кеңістігі шексіз
санамалы емес жиын болса, ал
элементар оқиғалар кеңістігі шексіз
санамалы емес жиын болса, ал ![]() элементар оқиғалар тең
мүмкіндікті болса, онда бұл есепте ықтималдықтың
геометриялық анықтамасын қолдануға болады. Геометриялық
тұрғыдан есеп шартын қарамастан нүктені белгілі бір Q
геометриялық облысқа
лақтыру (кесінді, жазықтықтың немесе
кеңістіктің бөлігі) шартына келтіру. Нүкте
қарамастан лақтырылғандықтан, онда Q облысының q
кез келген щектеулі бөлігіне түсу мүмкіндіктері тең. Сондықтан
нүктенің q
(q
элементар оқиғалар тең
мүмкіндікті болса, онда бұл есепте ықтималдықтың
геометриялық анықтамасын қолдануға болады. Геометриялық
тұрғыдан есеп шартын қарамастан нүктені белгілі бір Q
геометриялық облысқа
лақтыру (кесінді, жазықтықтың немесе
кеңістіктің бөлігі) шартына келтіру. Нүкте
қарамастан лақтырылғандықтан, онда Q облысының q
кез келген щектеулі бөлігіне түсу мүмкіндіктері тең. Сондықтан
нүктенің q
(q![]() Q) облысына түсу ықтималдығы q өлшеміне
(ұзындық, аудан немесе көлем) пропорционал және q-дың пішіні мен орналасуына тәуелді
емес.
Q) облысына түсу ықтималдығы q өлшеміне
(ұзындық, аудан немесе көлем) пропорционал және q-дың пішіні мен орналасуына тәуелді
емес.
Анықтама.
![]() – нүктенің q (q
– нүктенің q (q![]() Q) облысына түсуі.
Онда бұл оқиғаның ықтималдығы осы
нүкте пайда болатын q облысының өлшемінің
барлық Q өлшеміне қатынасына тең:
Q) облысына түсуі.
Онда бұл оқиғаның ықтималдығы осы
нүкте пайда болатын q облысының өлшемінің
барлық Q өлшеміне қатынасына тең: 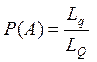 немесе
немесе
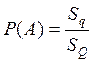 немесе
немесе
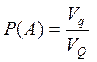 ,
мұндағы L, S, V – сәйкес облыстың
ұзындығы, ауданы немесе көлемі.
,
мұндағы L, S, V – сәйкес облыстың
ұзындығы, ауданы немесе көлемі.
Мысалы 1.1.5 – Радиусы R дөңгелек диск екі секторға бөлінген. Біреуінің доға ұзындығы R. Тез айналып жатқан дискіге оқ атылды. Оның доға ұзындығы R секторға түсу ықтималдығын табу керек .
A оқиғасы
– доға ұзындығы R секторға түсуі. 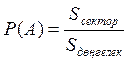 .
.
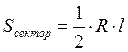 формуласы
бойынша
формуласы
бойынша 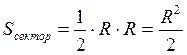 ,
, ![]() . Сондықтан
. Сондықтан 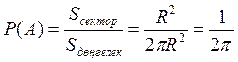 .
.
1.2 Дәріс 2. Ықтималдық теориясының негізгі теоремалары
Дәріс мазмұны: көбейту және қосу теоремалары. Толық ықтималдық, Байес, Бернулли формулалары. Лапластың аймақтық және интегралдық теоремалары. Пуассон теоремасы.
Дәріс мақсаты: ықтималдық теориясының негізгі теоремалары мен формулаларымен танысу.
Анықтама.
1. A және В екі оқиғасы берілген. Егер
біреуінің ықтималдығы екіншісінің пайда болуынан
өзгерсе, онда олар тәуелді деп аталады, қарсы жағдайда
– тәуелсіз; егер ![]() оқиғаларының әрқайсысы
және кез келген қалғандарының комбинациялары
көбейтіндіде тәуелсіз болса, онда
оқиғаларының әрқайсысы
және кез келген қалғандарының комбинациялары
көбейтіндіде тәуелсіз болса, онда ![]() оқиғалары жиынтықта тәуелсіз
деп аталады.
оқиғалары жиынтықта тәуелсіз
деп аталады.
2. A оқиғасының шартты
ықтималдығы (белгіленуі ![]() немесе
немесе ![]() )
деп B оқиғасы орындалған жағдайда A
оқиғасының ықтималдығы айтылады. Егер A және
B тәуелсіз болса, онда
)
деп B оқиғасы орындалған жағдайда A
оқиғасының ықтималдығы айтылады. Егер A және
B тәуелсіз болса, онда ![]() , егер тәуелді болса, онда
, егер тәуелді болса, онда ![]() .
.
Мысалы 1.1.6 – Жәшікте
2 ақ және 1 қара шарлар бар. Екі
адам бір бірден шар алады. A оқиғасы
– бірінші адамда ақ шар пайда болуы, В - екінші
адамда ақ шар пайда болуы. Келесі теңдіктер айқын: 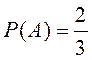 ;
; 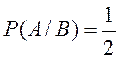 . Сонымен,
. Сонымен, ![]() , сондықтан A және B тәуелді оқиғалар.
, сондықтан A және B тәуелді оқиғалар.
Көбейту теоремасы
A және B екі оқиғаның
көбейтіндісінің ықтималдығы (бірге
пайда болуы) біреуінің ықтималдығының
екіншісінің шартты ықтималдығына көбейткенге тең, бұл
жағдайда бірінші оқиға пайда болу шарты орындалуы керек: ![]() .
.
Салдары:
1)
Егер A және B оқиғалары тәуелсіз болса, онда ![]() .
.
2)
Егер ![]() оқиғалары жиынтықта тәуелсіз, онда олардың
кез
оқиғалары жиынтықта тәуелсіз, онда олардың
кез
келген k үшін ![]() орындалады.
орындалады.
3)
![]() n оқиғалары үшін көбейту теоремасының жалпы
түрі:
n оқиғалары үшін көбейту теоремасының жалпы
түрі:
![]() .
.
Жоғарыда екі тәуелсіз
оқиғаларының қосындысының
ықтималдығын анықтайтын аксиома келтірілген: ![]() ,
, ![]() . Оқиғалардың қосындысының
ықтималдықтарының жалпы ережелері келесі теоремада берілген.
. Оқиғалардың қосындысының
ықтималдықтарының жалпы ережелері келесі теоремада берілген.
Қосу теоремасы
A және B екі оқиғаның
қосындысының ықтималдығы осы оқиғалардың
ықтималдықтарының қосындысынан бірге пайда
болуының ықтималдығын азайтқанға тең болады:
![]() .
.
Егер оқиғалар үйлесімсіз болса, онда ![]() және
және ![]() .
.
Салдар:
4)
1. ![]() n оқиғалары үшін қосу
теоремасының жалпы түрі:
n оқиғалары үшін қосу
теоремасының жалпы түрі:
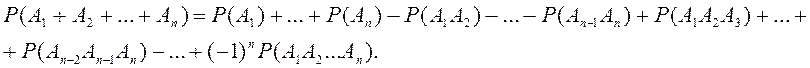 2. Егер
2. Егер ![]() оқиғалары толық топ
құрайтын болса, онда
оқиғалары толық топ
құрайтын болса, онда ![]() ,
, ![]() және
және
![]() болғандықтан
болғандықтан ![]() . Дербес жағдайда
. Дербес жағдайда ![]() және
және
![]() қарама-қарсы оқиғалары толық
топ құрағандықтан
қарама-қарсы оқиғалары толық
топ құрағандықтан ![]() немесе
немесе ![]() .
.
Айта кетелік, бірінші салдарды жиі
қолданбаймыз. Егер A оқиғасы
–![]() оқиғаларының ең болмағанда біреуінің пайда
болуы болса, яғни
оқиғаларының ең болмағанда біреуінің пайда
болуы болса, яғни ![]() , онда
, онда ![]() - осы оқиғалардың бірде
біреуінің пайда болмауы.
Сондықтан
- осы оқиғалардың бірде
біреуінің пайда болмауы.
Сондықтан ![]() =
=
![]() .
.
Толық ықтималдықтар формуласы
Көбейту және қосу теоремаларын бөлек қолдануға болады, ал кейбір есептерде оларды бірге қолдануды талап етеді.
![]() оқиғалары
толық топ құрайды (яғни
оқиғалары
толық топ құрайды (яғни ![]() ;
; 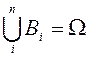 ). А оқиғасы осы оқиғалардың
біреуімен пайда болуы мүмкін.
). А оқиғасы осы оқиғалардың
біреуімен пайда болуы мүмкін. ![]() оқиғаларының
қайсысы пайда болатындығы алдын ала белгісіз, сондықтан оларды
гипотезалар деп атайды.
оқиғаларының
қайсысы пайда болатындығы алдын ала белгісіз, сондықтан оларды
гипотезалар деп атайды. 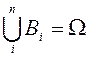 шартына байланысты гипотезалардың
ықтималдықтары
шартына байланысты гипотезалардың
ықтималдықтары ![]() шартын қанағаттандырады
және априорлы немесе тәжірибеге дейінгі деп аталады. Шарт бойынша A
оқиғасы келесі оқиғалардың
шартын қанағаттандырады
және априорлы немесе тәжірибеге дейінгі деп аталады. Шарт бойынша A
оқиғасы келесі оқиғалардың ![]() ең
болмағанда біреуі орындалғанда пайда болады, яғни
ең
болмағанда біреуі орындалғанда пайда болады, яғни ![]() .
Бірақ
.
Бірақ ![]() үйлесімсіз, яғни
үйлесімсіз, яғни ![]() үйлесімсіз,
сондықтан
үйлесімсіз,
сондықтан ![]()
![]() . Көбейту теоремасы бойынша
. Көбейту теоремасы бойынша ![]() . Осы мәндерді
. Осы мәндерді ![]() -ға қойсақ,
-ға қойсақ,
![]()
формуласын аламыз. Бұл – толық ықтималдықтар формуласы.
Байес формуласы
A және ![]() оқиғаларына салыстырмалы шарттар
сақталсын, яғни A оқиғасы толық топ
құрайтын
оқиғаларына салыстырмалы шарттар
сақталсын, яғни A оқиғасы толық топ
құрайтын ![]() оқиғаларының бірімен пайда бола
алады. Сынақ жүргізіліп, A
оқиғасы пайда болсын.
Бұл гипотезалардың ықтималдықтарының
олардың априорлық мәндеріне қарағанда өзгеруіне
әкеп соғады. A оқиғасы орындалды деген шарты
бойынша гипотезалардың ықтималдықтарының мәндері
былай белгіленеді:
оқиғаларының бірімен пайда бола
алады. Сынақ жүргізіліп, A
оқиғасы пайда болсын.
Бұл гипотезалардың ықтималдықтарының
олардың априорлық мәндеріне қарағанда өзгеруіне
әкеп соғады. A оқиғасы орындалды деген шарты
бойынша гипотезалардың ықтималдықтарының мәндері
былай белгіленеді: ![]() және апостериорлы немесе тәжірибеден кейінгі
деп аталады. Олар Байес формуласы бойынша есептелінеді:
және апостериорлы немесе тәжірибеден кейінгі
деп аталады. Олар Байес формуласы бойынша есептелінеді: 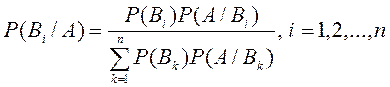 .
.
Бұл формуланы көбейту теоремасынан
оңай алуға болады: ![]() .
.
Соңғы теңдіктен
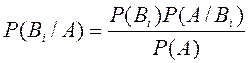 .
.
Теңдіктің оң жағындағы бөлімге толық ықтималдық формуласын қойсақ Байес формуласын аламыз.
Сынақтың қайталануы. Бернулли формуласы
n сынақ жүргізілді, оның екі нәтижесі
ғана бар: A оқиғасы пайда болады және A
оқиғасы пайда болмайды. Бұл сынақтар A
оқиғасына қарағанда тәуелсіз, яғни әрбір
сынақта A оқиғасының пайда болу
ықтималдығы басқа сынақтың нәтижесінен
тәуелсіз. Әрбір сынақта A оқиғасының
пайда болу ықтималдығы бірдей немесе әртүрлі болуы
мүмкін. Сынақтарды жүргізу шарттары бірдей болатын
жағдайларды қарастырайық, сондықтан әрбір
сынақта A оқиғасы пайда болуы бірдей. Ол ![]() санына
тең болсын, онда
санына
тең болсын, онда ![]() –
A оқиғасының пайда болмау
ықтималдығы. Сынақтардың мұндай тізбегі Бернулли
сұлбасы деп аталады.
–
A оқиғасының пайда болмау
ықтималдығы. Сынақтардың мұндай тізбегі Бернулли
сұлбасы деп аталады.
n сынақтан тұратын серияда A оқиғасы k
рет пайда болу ықтималдығын табайық. Бұл
ықтималдықты ![]() деп белгілейік.
деп белгілейік.
Келесі болжам жасайық: n сынақта A
оқиғасының k рет пайда болуы әртүрлі
тізбекте (ретте) жүргізіледі. В күрделі
оқиғасының бір жағдайын қарастырайық: A
оқиғасы k сынақта пайда болды, ал қалған (n-k)
сынақта пайда болмайды, яғни  . A және
. A және ![]() оқиғалары тәуелсіз.
Сондықтан көбейту теоремасы бойынша
оқиғалары тәуелсіз.
Сондықтан көбейту теоремасы бойынша
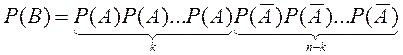 =
=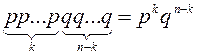 .
.
![]() оқиғасына ұқсас оқиға:
оқиғасына ұқсас оқиға: ![]() оқиғасы k сынақта пайда болатын, ал
қалған (n-k) сынақта пайда болмайтын жағдайлар
саны n-нен k бойынша теруге тең, яғни
оқиғасы k сынақта пайда болатын, ал
қалған (n-k) сынақта пайда болмайтын жағдайлар
саны n-нен k бойынша теруге тең, яғни ![]() .
Бұл оқиғалардың барлығы тәуелсіз, ал
берілген оқиға олардың қосындысына тең.
Сондықтан қосу теоремасы бойынша
.
Бұл оқиғалардың барлығы тәуелсіз, ал
берілген оқиға олардың қосындысына тең.
Сондықтан қосу теоремасы бойынша
![]() =
=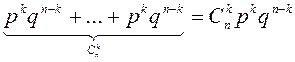 .
.
![]()
![]() формуласы Бернулли формуласы деп аталады.
формуласы Бернулли формуласы деп аталады.
Бернулли формуласымен n сынақта A оқиғасы
k рет пайда болуының ықтималдығын ғана емес,
сонымен бірге n сынақта A оқиғасы k реттен
кем емес, (яғни k немесе k+1, …, немесе n рет, белгіленуі![]() )
және k реттен артық емес (яғни 0 немесе 1,…, немесе k
рет, белгіленуі
)
және k реттен артық емес (яғни 0 немесе 1,…, немесе k
рет, белгіленуі ![]() ) :
) :
![]() =
=![]() ;
;
![]() =
=![]() .
.
Бернулли формуласымен n үлкен (n>10),
ал р өте аз шама болғанда көп есептеулерді талап етеді.
Бұл жағдайда ![]() ықтималдығын есептеу
үшін жуықтап есептеу формулалары қолданылады.
ықтималдығын есептеу
үшін жуықтап есептеу формулалары қолданылады.
Пуассон теоремасы
Егер сынақ саны n шексіз үлкейсе,
ал оқиғаның пайда болу ықтималдығы р әр
сынақта аз болса, бірақ ![]() көбейтіндісі тұрақты
болып қалса, онда
көбейтіндісі тұрақты
болып қалса, онда ![]() ықтималдығы жуық шамамен
ықтималдығы жуық шамамен 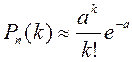 тең.
тең.
Соңғы
формуланы Пуассон формуласы деп атайды, оны
![]() , ал
, ал ![]() болғанда
қолданады. Бұл формуламен есептеулер жүргізгенде кестемен
немесе Mathcad жүйесін қолдануға болады.
болғанда
қолданады. Бұл формуламен есептеулер жүргізгенде кестемен
немесе Mathcad жүйесін қолдануға болады.
Муавр-Лапластың төңіректік теоремасы
Егер
оқиғаның
әрбір ықтималдығы
р тұрақты
және 0 мен 1-ге тең болмаса, ал n сынақ саны шексіз үлкейсе, онда оқиғаның n сынақта k рет
пайда болу ықтималдығы жуық шамамен 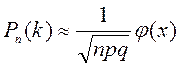 тең;
мұндағы
тең;
мұндағы 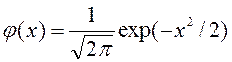 ;
;
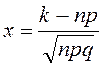 ;
; ![]() .
.
![]() функциясы көмекші функция. Оның
мәнін кестеден аламыз және келесі қасиеттерді ескеру керек:
функциясы көмекші функция. Оның
мәнін кестеден аламыз және келесі қасиеттерді ескеру керек:
1)
![]() жұп, яғни
жұп, яғни ![]() ;
;
2)
![]() болғанда
болғанда
![]() деп
есептеуге болады.
деп
есептеуге болады.
Муавр-Лапластың интегралдық теоремасы
Егер оқиғаның
әрбір ықтималдығы
р тұрақты
және 0 мен 1-ге тең болмаса, ал n сынақ саны шексіз үлкейсе, онда оқиғаның n сынақта ![]() реттен кем емес және
реттен кем емес және ![]() артық емес (белгіленуі
артық емес (белгіленуі ![]() немесе
немесе ![]() ) пайда болу ықтималдығы жуық шамамен
) пайда болу ықтималдығы жуық шамамен ![]() тең,
мұндағы
тең,
мұндағы  ;
;
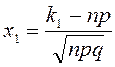 ;
; 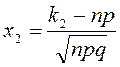 .
.
![]() – Лаплас функциясы немесе ықтималдықтар интегралы
деп аталатын көмекші функция. Оның мәнін кестеден аламыз
және келесі қасиеттерді ескеру керек:
– Лаплас функциясы немесе ықтималдықтар интегралы
деп аталатын көмекші функция. Оның мәнін кестеден аламыз
және келесі қасиеттерді ескеру керек:
1) ![]() тақ, яғни
тақ, яғни ![]() ;
;
2) ![]() болғанда
болғанда![]() =0,5 деп есептеуге болады.
=0,5 деп есептеуге болады.
1.3 Дәріс 3. Кездейсоқ шамалар
Дәріс мазмұны: дискретті жәнеүзіліссіз кездейсоқ шамалары. Олардың үлестірім заңдары. Үлестірім функциясы.
Дәріс мақсаты: кездейсоқ шамалар мен олардың үлестірім заңдарымен танысу.
Анықтама.
Кездейсоқ шама деп мүмкін мәндер жиынынан алдын ала қандай екені белгісіз мәндер қабылдайтын айнымалыны айтамыз.
Кездейсоқ шамаларды латын алфавитінің
бас әріптерімен X,Y,Z,..., ал олардың мүмкін
мәндерін: x,y,z,… немесе ![]() белгілейміз.
белгілейміз.
Кездейсоқ шамалар дискретті және үзіліссіз деп бөлінеді. Егер кездейсоқ шаманың мүмкін мәндер жиыны ақырлы немесе шексіз санамалы болса, онда ол дискретті, егер шексіз санамалы емес болса, онда – үзіліссіз кездейсоқ шама деп аталады
Мысалы 1.3.1 – Дискретті кездейсоқ шамалардың мысалы:
1) Х – үш атыста нысанаға тию. Х мүмкін мәндері: {0,1,2,3} жиыны.
2) X – берілген уақыт ішінде телефон станциясына келіп түскен
қоңыраулар саны. Х мүмкін мәндері: {0,1,2,3,…} жиыны.
Үзіліссіз кездейсоқ шамалардың мысалы:
1) Х – нысана центрі мен оқ тиген нүктенің ара қашықтығы.
2) Х – радиолампаның мүлтіксіз жұмыс істеу уақыты.
Бұл жағдайда мүмкін мәндер қандай да бір аралықты бүтіндей қамтиды.
Кездейсоқ шаманы толық зерттеу үшін оның мүмкін мәндерін ғана емес, оның ықтималдықтарын да білу керек.
Анықтама.
Кездейсоқ шаманың мүмкін мәндері мен оның ықтималдықтарын байланыстыратын ереже (кесте, функция, график) оның үлестірім заңы деп аталады.
Дискретті кездейсоқ шамалардың үлестірім заңдары
Х дискретті кездейсоқ шамасы ![]() мәндерін
мәндерін ![]() ықтималдықтарымен қабылдасын (
ықтималдықтарымен қабылдасын (![]() немесе
немесе ![]() ).
).
Х үлестірім заңы кестемен берілсін:
|
Х |
|
|
… |
|
… |
|
Р |
|
|
… |
|
… |
Бұл кесте үлестірім қатары деп аталады. ![]() ,
,
![]() оқиғалары
үйлесімсіз және толық топ құрайды, яғни
оқиғалары
үйлесімсіз және толық топ құрайды, яғни ![]() .
.
Х үлестірім заңының графиктік
түрде берілуі: тік бұрышты координаталар
жүйесінде абсцисса осі бойына ![]() мәндері,
ал ордината осіне – осы
мәндердің
мәндері,
ал ордината осіне – осы
мәндердің ![]() ықтималдықтары салынады. (
ықтималдықтары салынады. (![]() ,
,![]() ) координаталы
нүктелерді тізбектей кесінділермен қосады. Пайда
болған сынық сызықты үлестірімнің
көпбұрышы деп атайды.
) координаталы
нүктелерді тізбектей кесінділермен қосады. Пайда
болған сынық сызықты үлестірімнің
көпбұрышы деп атайды.
Үлестірім заңының аналитикалық берілуі мүмкін мәндердің өз ықтималдықтарымен байланыстыратын формуланы айқындауды талап етеді. Бұндай формуланы кейбір кездейсоқ шамалар үшін ғана табуға болады.
Бернулли және Пуассон үлестірімдерін «Кездейсоқ шамалардың негізгі үлестірім заңдары» тақырыбында қарастырамыз.
Үзіліссіз кездейсоқ шамалар. Үлестірім функциясы
Үзіліссіз кездейсоқ шаманы үлестірім заңымен немесе үлестірім көпбұрышымен беруге болмайтындығы белгілі. Дискретті және үзіліссіз кездейсоқ шамалар үшін үлестірім заңын берудің универсал жолы бар.
Анықтама.
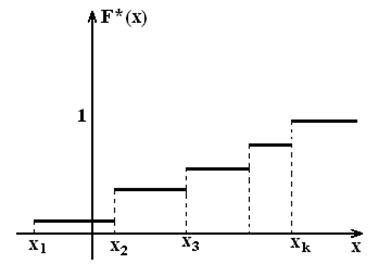
Х кездейсоқ шамасының үлестірім функциясы (немесе интегралдық функциясы, үлестірім заңы) деп әрбір х мәні үшін оқиғалар ықтималдығы X<x, яғни F(x)=P(X<x) (1) анықталатын F(x) функциясы айтылады.
![]() мәндерін қабылдайтын дискретті Х кездейсоқ
шамасы үшін (1) формула келесі түрде жазылады
мәндерін қабылдайтын дискретті Х кездейсоқ
шамасы үшін (1) формула келесі түрде жазылады ![]() ,
мұндағы
,
мұндағы ![]() қосындылау х-тен кіші барлық
қосындылау х-тен кіші барлық ![]() мәндеріне
салыстырмалылығын білдіреді. Сонымен, дискретті кездейсоқ шамасы
үшін бұл функция үзілісті,
мәндеріне
салыстырмалылығын білдіреді. Сонымен, дискретті кездейсоқ шамасы
үшін бұл функция үзілісті, ![]() - оның үзіліс нүктелері. Үзіліссіз
кездейсоқ шама үшін F(x) үзіліссіз.
- оның үзіліс нүктелері. Үзіліссіз
кездейсоқ шама үшін F(x) үзіліссіз.
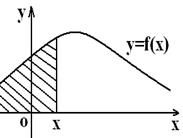
F(x) қасиеттері
1)
барлық х
үшін ![]() .
.
Бұл қасиет ықтималдық сияқты F(x) анықтамасынан шығады
2) F(x) кемімелі емес, яғни егер ![]() ,
онда
,
онда ![]() .
.
Расында, ![]() болсын.
болсын. ![]() оқиғасын екі
оқиғаның қосындысы түрінде жазуға болады:
оқиғасын екі
оқиғаның қосындысы түрінде жазуға болады: ![]() .
Бұл оқиғалар үйлесімсіз болғандықтан, ықтималдықтарды
қосу теоремасы бойынша:
.
Бұл оқиғалар үйлесімсіз болғандықтан, ықтималдықтарды
қосу теоремасы бойынша: ![]() , бұдан
, бұдан
![]()
![]() .
.
Кез келген ықтималдық теріс емес
болғандықтан, онда ![]() , яғни
, яғни ![]() . Қасиет дәлелденді.
. Қасиет дәлелденді.
Салдар 1.
Кездейсоқ шаманың ![]() аралығына түсу ықтималдығы
аралығына түсу ықтималдығы
![]() ,
,
бұл ![]() теңдігінен шығады.
теңдігінен шығады.
Салдар 2.
Кездейсоқ шама белгілі бір мәнді
қабылдау ықтималдығы нолге тең. Егер ![]() формуласында
формуласында ![]() деп алып,
деп алып, ![]() кезде
шекке көшсек, онда
кезде
шекке көшсек, онда ![]() ,
, ![]() үзіліссіздіктерінен және
үзіліссіздіктерінен және ![]() .
.
Салдар 3.
![]() .
.
3) Егер кездейсоқ шаманың
мүмкін мәндері ![]() интервалында жатса, онда
интервалында жатса, онда ![]() және
және ![]() ; үзіліссіз кездейсоқ шама үшін
мүмкін мәндері барлық сан осінде жатса,
; үзіліссіз кездейсоқ шама үшін
мүмкін мәндері барлық сан осінде жатса, ![]() және
және ![]() . Аталып өткен қасиеттер
үзіліссіз кездейсоқ шаманың графигін салуға
мүмкіндік береді:
. Аталып өткен қасиеттер
үзіліссіз кездейсоқ шаманың графигін салуға
мүмкіндік береді:
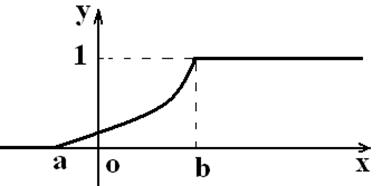
1 сурет
Айта кетелік, үзіліссіз кездейсоқ шаманы көбінесе үзіліссіз үлестірім функциясы бар шама ретінде анықталады.
Үлестірім тығыздығы
Үзіліссіз кездейсоқ шаманы үлестірім функциясынан басқа жолмен де беруге болады. Оның басты сипаттамасы – ықтималдықтардың үлестірім тығыздығы.
Анықтама.
Үзіліссіз кездейсоқ шаманың
ықтималдықтарының үлестірім тығыздығы (жәй үлестірім тығыздығы немесе үлестірімнің дифференциалдық функциясы, белгіленуі ![]() ) деп
оның үлестірім функциясының
туындысы айтылады, яғни
) деп
оның үлестірім функциясының
туындысы айтылады, яғни ![]() .
.
Үлестірім тығыздығының ықтималдық мағынасын анықтайық. Туындының анықтамасы бойынша
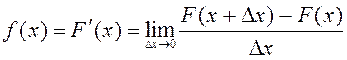 = |
= | ![]() қасиеті| =
қасиеті| =
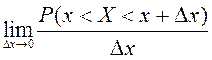 .
.
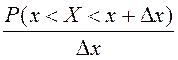 қатынасы
қатынасы ![]() интервалындағы орта ықтималдықты
білдіргендіктен,
интервалындағы орта ықтималдықты
білдіргендіктен, ![]() функциясы
функциясы ![]() нүктесіндегі және
оның аймағындағы ықтималдықты сипаттайды.
нүктесіндегі және
оның аймағындағы ықтималдықты сипаттайды.
Айта кетелік, үлестірімнің дифференциалдық функциясы, интегралдық функция сияқты үлестірім заңының бірі болады, бірақ интегралдық функция сияқты универсалды бола алмайды. Үлестірім тығыздығы тек үзіліссіз кездейсоқ шамалар үшін ғана анықталады.
f(x) қасиеттері
1.
Х-тің ![]() интервалына түсу ықтималдығы келесі
формула бойынша анықталады:
интервалына түсу ықтималдығы келесі
формула бойынша анықталады:
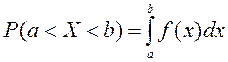 .
.
Расында, 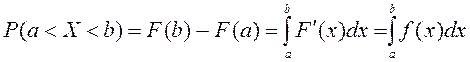 .
.
2.
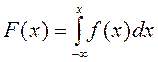 .
.
Расында, 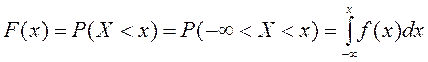 .
.
3. ![]() үшін
үшін ![]() .
.
Расында, ![]() , бірақ
, бірақ ![]() кемімелі емес, сондықтан
кемімелі емес, сондықтан ![]() ,
олай болса
,
олай болса ![]() .
.
4. 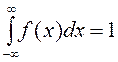 .
.
Бірінші қасиетте ![]() деп есептейік, онда
деп есептейік, онда 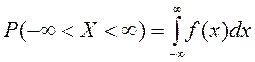 ,
бірақ
,
бірақ ![]() ақиқат оқиға, сондықтан
ақиқат оқиға, сондықтан ![]() .
Яғни
.
Яғни 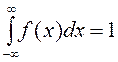 .
.
![]() үлестірім тығыздығының графигі үлестірім
қисығы деп аталады, келесі түрде болады:
үлестірім тығыздығының графигі үлестірім
қисығы деп аталады, келесі түрде болады:
2 сурет
Егер анықталған интегралдың
геометриялық мағынасын еске түсірсек, яғни
қисық сызықты трапецияның ауданы, онда ![]() қасиеттерінің
геометриялық интерпретациясын аламыз.
қасиеттерінің
геометриялық интерпретациясын аламыз.
3 суретте жолақпен белгіленген облыстар сәйкес:
а) Х-тің ![]() интервалына түсу ықтималдығына
тең; б)
интервалына түсу ықтималдығына
тең; б)  ; в)
; в)  .
.
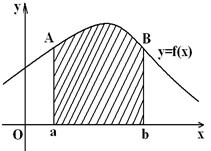
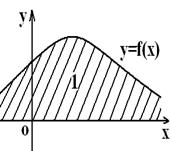
а) б) в)
3 сурет
1.4 Дәріс 4. Кездейсоқ шамалардың сандық сипаттамалары
Дәріс мазмұны: математикалық үміт, дисперсия, орта квадраттық ауытқу.
Дәріс мақсаты: үзіліссіз кездейсоқ шаманың негізгі сандық сипаттама-
ларымен таныстыру.
Кездейсоқ шамалардың сандық сипаттамалары
Кездейсоқ шаманың үлестірім заңы оны ықтималдық көзқараста толық сипаттайды. Бірақ үлестірім заңының тек нақты қасиеттерін ғана білу жеткілікті қолданбалы есептер жиі кездеседі. Мысалы, кездейсоқ шаманың мүмкін мәндері топтасатын орта мән немесе олардың ортаға салыстырмалы шашырауы.
Анықтама.
Кездейсоқ шамалардың сандық сипаттамалары деп олардың үлестірім заңының негізгі ерекшеліктерін өрнектейтін кездейсоқ емес сандық параметрлерді айтады.
Сандық сипаттамаларды шартты түрде орналасу сипаттамасына (математикалық үміт (күтім), мода, медиана, квантиль), үлестірілу сипаттамасына (дисперсия, орта квадраттық ауытқу), сипаттамасының түрі (асимметрия, эксцесс) бөлуге болады. Кейбіреуін қарастырайық.
Математикалық үміт (күтім)
Анықтама.
Х дискретті кездейсоқ шаманың математикалық
үміті деп оның мүмкін мәндерінің ![]() олардың ықтималдықтарына
олардың ықтималдықтарына ![]() көбейтіндісінің
қосындысы айтылады (
көбейтіндісінің
қосындысы айтылады (![]() немесе
немесе ![]() ).
Белгіленуі
).
Белгіленуі ![]() немесе
немесе ![]() :
:
![]() .
.
![]() мәндері шексіз жиын болғанда соңғы
теңдіктің оң жағындағы қатар абсолютті
жинақты болады.
мәндері шексіз жиын болғанда соңғы
теңдіктің оң жағындағы қатар абсолютті
жинақты болады.
Дискретті кездейсоқ шаманың математикалық үмітінің ықтималдық мағынасы: ол жуық шамамен көп тәжірибе нәтижесінде бақыланып отырған мәндердің арифметикалық ортасына тең (немесе сынақ сандары үлкейген сайын бақыланып отырған мәндердің арифметикалық ортасы математикалық үмітке жуықталады).
Расында, n сынақ жүргізілсін, онда ![]() мәні
мәні ![]() рет,
рет, ![]() -
- ![]() рет, т.с.с.
рет, т.с.с. ![]() -
- ![]() рет және де
рет және де 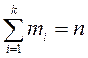 . Онда кездейсоқ шаманың қабылдаған барлық
мәндерінің арифметикалық ортасы:
. Онда кездейсоқ шаманың қабылдаған барлық
мәндерінің арифметикалық ортасы: 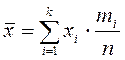 . Бірақ
. Бірақ ![]() - бұл
- бұл ![]() мәнінің қатысты жиілігі, ол
тәжірибе саны көбейген сайын
мәнінің қатысты жиілігі, ол
тәжірибе саны көбейген сайын ![]() ықтималдығына ұмтылады, ал сондықтан арифметикалық орта математикалық үмітке ұмтылады:
ықтималдығына ұмтылады, ал сондықтан арифметикалық орта математикалық үмітке ұмтылады:  .
.
Үзіліссіз кездейсоқ шаманың математикалық үміті де осылай анықталады, тек қосынды интегралдаумен айырбасталынады.
Анықтама.
Мүмкін мәндері [a,b] кесіндісінде (немесе![]() )
жататын, ал үлестірім тығыздығы
)
жататын, ал үлестірім тығыздығы ![]() болатын
үзіліссіз кездейсоқ шаманың математикалық үміті келесі
формула бойынша есептелінеді:
болатын
үзіліссіз кездейсоқ шаманың математикалық үміті келесі
формула бойынша есептелінеді:
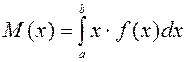 (немесе
(немесе 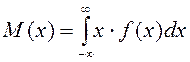 , бұл интеграл абсолютті жинақты деп есептелінеді).
, бұл интеграл абсолютті жинақты деп есептелінеді).
![]() қасиеттері:
қасиеттері:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() , мұндағы
, мұндағы ![]() айырымы кездейсоқ шаманың математикалық
үмітінен ауытқуы деп аталады.
айырымы кездейсоқ шаманың математикалық
үмітінен ауытқуы деп аталады.
4) кез келген ![]() және
және ![]() кездейсоқ
шамалары үшін
кездейсоқ
шамалары үшін ![]() .
.
5) Егер ![]() және
және ![]() тәуелсіз кездейсоқ шамалар
болса, онда
тәуелсіз кездейсоқ шамалар
болса, онда ![]() .
.
2 және 4 қасиеттері кез келген шектеулі кездейсоқ шамалар жағдайына жалпыланады:
![]() ,
мұндағы
,
мұндағы ![]() – тұрақтылар.
– тұрақтылар.
Бұл қасиеттерді дискретті және үзіліссіз кездейсоқ шамаларды анықтайтын формулаларға қойып оңай алуға болады ([1], 138-142 бет).
Тәуелсіз сынақтардағы оқиғаның пайда болу санынының математикалық үмітін анықтайтын формуланы білген пайдалы.
Теорема. Бір сынақта оқиғаның пайда болу санынының математикалық үміті осы оқиғаның ықтималдығына тең; n тәуелсіз сынақтардағы оқиғаның пайда болу санынының математикалық үміті сынақ санының әрбір сынақта пайда болу ықтималдығына көбейтіндісіне тең.
Расында, егер бір сынақ жүргізіліп, онда
оқиғаның пайда болу ықтималдығы ![]() -ға
тең болса, онда пайда болмау ықтималдығы
-ға
тең болса, онда пайда болмау ықтималдығы ![]() .
Бұл кездейсоқ оқиғаның үлестірім заңы:
.
Бұл кездейсоқ оқиғаның үлестірім заңы:
|
|
0 |
1 |
|
|
|
|
Сондықтан
математикалық үміт ![]() ;
;
Егер
![]() – n тәуелсіз
сынақтарда оқиғаның пайда болу саны және
– n тәуелсіз
сынақтарда оқиғаның пайда болу саны және![]() - бірінші сынақта оқиғаның пайда болу саны,
- бірінші сынақта оқиғаның пайда болу саны, ![]() - екіншіде, және т.б.,
- екіншіде, және т.б., ![]() - n-ші оқиғалардың пайда болу
сандары
- n-ші оқиғалардың пайда болу
сандары ![]() . Төртінші қасиет бойынша
. Төртінші қасиет бойынша
![]() .
.
Теңдіктің оң жағындағы
әрбір қосылғыш бір сынақтағы
оқиғаның пайда болу санының математикалық
үміті және ![]() -ға тең.
Сондықтан
-ға тең.
Сондықтан 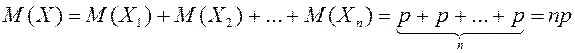 .
.
Дисперсия
Кездейсоқ шаманың таралуының басты сипаттамасы дисперсия болып табылады.
Анықтама.
![]() кездейсоқ шаманың дисперсиясы (белгіленуі
кездейсоқ шаманың дисперсиясы (белгіленуі
![]() )
деп сол кездейсоқ шаманың математикалық үмітінен
ауытқуының квадратының математикалық үміті айтылады:
)
деп сол кездейсоқ шаманың математикалық үмітінен
ауытқуының квадратының математикалық үміті айтылады:
![]() .
.
Дискретті
кездейсоқ шаманың қабылдайтын мүмкін мәндері ![]() (
(![]() немесе
немесе ![]() ), олардың ықтималдықтары
), олардың ықтималдықтары ![]() болсын. Онда дисперсия келесі формула бойынша есептелінеді:
болсын. Онда дисперсия келесі формула бойынша есептелінеді:
![]() .
.
Үзіліссіз кездейсоқ шаманың
қабылдайтын мүмкін мәндері [a,b] (немесе ![]() )
аралығында жатады, ал үлестірім тығыздығы
)
аралығында жатады, ал үлестірім тығыздығы ![]() болса,
дисперсия келесі формула бойынша есептелінеді:
болса,
дисперсия келесі формула бойынша есептелінеді: 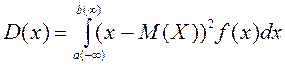 . Бұл формулалар дискретті және
үзіліссіз кездейсоқ шаманың математикалық
үмітінің анықтамасынан шығады.
. Бұл формулалар дискретті және
үзіліссіз кездейсоқ шаманың математикалық
үмітінің анықтамасынан шығады.![]()
Дисперсия есептеудің басқа қолайлы формуласы бар.
Теорема. Дисперсия кездейсоқ шаманың квадратының математикалық үмітінің математикалық үміттің квадратының айырымына тең, яғни
![]() .
.
Расында,
![]() тұрақты болғандықтан,
тұрақты болғандықтан, ![]() және
және ![]() тұрақты болады.
Сондықтан математикалық
үміт қасиеті боынша:
тұрақты болады.
Сондықтан математикалық
үміт қасиеті боынша:
![]()
= ![]()
![]() .
.
Дискретті және үзіліссіз кездейсоқ шаманың математикалық үміт анықтамасынан соңғы формуланы басқаша жазамыз:
дискретті кездейсоқ шама үшін - 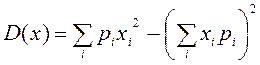 ;
;
үзіліссіз кездейсоқ шама үшін - 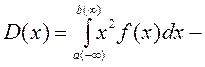
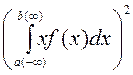 .
.
![]() қасиеттері:
қасиеттері:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() ;
;
4) Егер ![]() –
тәуелсіз кездейсоқ шамалар болса,
–
тәуелсіз кездейсоқ шамалар болса, ![]() .
.
Қасиеттердің жалпылануы мен салдары:
а) ![]() –
тәуелсіз кездейсоқ шамалар болса
–
тәуелсіз кездейсоқ шамалар болса
![]() ,
,
мұндағы ![]() -
тұрақтылар;
-
тұрақтылар;
б) ![]() ;
;
в) ![]() ,
, ![]() .
.
Тәуелсіз сынақтардағы
оқиғалардың пайда болу сандарының дисперсиясын математикалық
үміт сияқты ерекше формула бойынша табуға болады: ![]() – бір сынақта оқиғалардың пайда болу
сандарының дисперсиясы;
– бір сынақта оқиғалардың пайда болу
сандарының дисперсиясы; ![]() – n сынықта
оқиғалардың пайда болу сандарының дисперсиясы (
– n сынықта
оқиғалардың пайда болу сандарының дисперсиясы (![]() –
әрбір сынақтағы оқиғаның пайда болу
ықтималдығы,
–
әрбір сынақтағы оқиғаның пайда болу
ықтималдығы, ![]() – пайда болмау ықтималдығы, n – сынақ
саны).
– пайда болмау ықтималдығы, n – сынақ
саны).
Дисперсия кездейсоқ шаманың квадраты өлшеміне ие, салыстыру үшін сол өлшемді сейілудің сипаттамасын білу керек. Бұндай сипаттама орта квадраттық ауытқуда бар.
Анықтама.
Кездейсоқ шаманың орта квадраттық
ауытқуы немесе стандартты ауытқуы (белгіленуі ![]() )
деп оның дисперсиясының квадрат түбірі айтылады, яғни
)
деп оның дисперсиясының квадрат түбірі айтылады, яғни ![]() .
.
Басқа сандық сипаттамалардың анықтамасы мен қасиеттері ([1] 150-152 бет) берілген.
1.5 Дәріс 5-6. Кездейсоқ шамалардың негізгі үлестірім заңдары
Дәріс мазмұны: биномдық үлестірім заңы, Пуассон, бірқалыпты, көрсеткіштік, қалыпты үлестірімдер.
Дәріс мақсаты: кездейсоқ шамалардың негізгі үлестірім заңдарымен таныстыру.
Биномдық үлестірім заңы
![]() – n тәуелсіз сынақтарда А оқиғасының
пайда болу саны, р – әрбір сынақта А оқиғасының
пайда болу ықтималдығы, q – пайда болмау
ықтималдығы болсын.
– n тәуелсіз сынақтарда А оқиғасының
пайда болу саны, р – әрбір сынақта А оқиғасының
пайда болу ықтималдығы, q – пайда болмау
ықтималдығы болсын. ![]() -тің мүмкін мәндері: 0,1,2,…, n.
Бұл мүмкін мәндердің ықтималдықтары келесі формуламен
есептелінеді
-тің мүмкін мәндері: 0,1,2,…, n.
Бұл мүмкін мәндердің ықтималдықтары келесі формуламен
есептелінеді ![]() =
=![]()
![]() ,
, ![]() (1).
(1).
Анықтама.
![]() дискретті кездейсоқ
шамасының үлестірімі үшін үлестірім заңы (1)
формуласымен берілсе, онда ол биномды үлестірім делінеді.
дискретті кездейсоқ
шамасының үлестірімі үшін үлестірім заңы (1)
формуласымен берілсе, онда ол биномды үлестірім делінеді.
Сонымен, бұл кездейсоқ шаманың үлестірім қатары:
|
Х |
0 |
1 |
2 |
… |
n |
|
Р(Х=k) |
|
|
|
… |
|
Үлестірім функциясы:
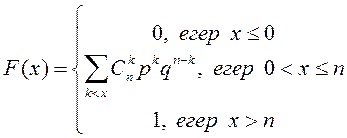 .
.
Сандық сипаттамаларды анықтау
үшін дайын формулаларды қолдануға болады, олар
математикалық үміт пен дисперсияның қасиеттерін
анықтағанда табылған. n тәуелсіз сынақта
оқиғаның пайда болу санының математикалық
үміті мен дисперсиясы: ![]() ,
, ![]() .
.
![]() интервалына түсу ықтималдығы
интервалына түсу ықтималдығы ![]() . формуласы бойынша табылады.
. формуласы бойынша табылады.
Бином заңы бойынша үлестірілген кездейсоқ шамаларды зерттеуді Mathcad жүйесінде арнайы енгізілген функциялар көмегімен жүргізуге болады ([7]).
Пуассон үлестірімі
Пуассон үлестірімі биномдық үлестірім
үшін шектік болып табылады, яғни сынақтар саны n
шексіз өседі, әрбір сынақта оқиғаның пайда
болу ықтималдығы р азаяды, бірақ ![]() көбейтіндісі
тұрақты болып қалады.
көбейтіндісі
тұрақты болып қалады.
Бұл жағдайда оқиғаның k
рет пайда болуы (k=0,1,2,…,n,…) Пуассон формуласы бойынша
есептелінеді 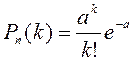 , ал үлестірім заңы осы формуламен
берілетін кездейсоқ шама Пуассон заңымен үлестірілген
делінеді.
, ал үлестірім заңы осы формуламен
берілетін кездейсоқ шама Пуассон заңымен үлестірілген
делінеді.
Бұл кездейсоқ шаманың үлестірім қатары:
|
Х |
0 |
1 |
2 |
… |
n |
… |
|
Р(Х=k) |
|
|
|
… |
|
… |
Сандық сипаттамаларын табамыз.
![]()
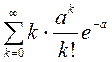 =
=![]()
 =
=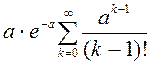 = =
= =![]() . Математикалық үміті
. Математикалық үміті ![]() . Дисперсиясы
. Дисперсиясы
![]() . Сонымен, Пуассон заңымен үлестірілген кездейсоқ
шамалар үшін математикалық үміт пен дисперсия өзара тең. Пуассон заңының бұл қасиетін
практикада зерттеліп отырған кездейсоқ шамалар Пуассон
заңымен үлестірілген гипотезасын тексеруде қолданады. Пуассон
заңы туралы жиі «сирек оқиғалар заңы» деп те
атайды. Пуассон заңымен үлестірілген кездейсоқ
шамалар мысалы: белгілі бір уақыт арасында катодтан ұшып
шығатын электрондар саны;
t уақыт ішінде телефон
станциясына келіп түсетін
қоңыраулар саны және т.с.с.
. Сонымен, Пуассон заңымен үлестірілген кездейсоқ
шамалар үшін математикалық үміт пен дисперсия өзара тең. Пуассон заңының бұл қасиетін
практикада зерттеліп отырған кездейсоқ шамалар Пуассон
заңымен үлестірілген гипотезасын тексеруде қолданады. Пуассон
заңы туралы жиі «сирек оқиғалар заңы» деп те
атайды. Пуассон заңымен үлестірілген кездейсоқ
шамалар мысалы: белгілі бір уақыт арасында катодтан ұшып
шығатын электрондар саны;
t уақыт ішінде телефон
станциясына келіп түсетін
қоңыраулар саны және т.с.с.
Бірқалыпты үлестірім
Мүмкін мәндері белгілі бір интервалда жататын және олардың барлығы бірдей мүмкіндікті болатын үзіліссіз кездейсоқ шамалар практикада кездеседі. Ондай шамалар бірқалыпты үлестірілген дейді.
Анықтама.
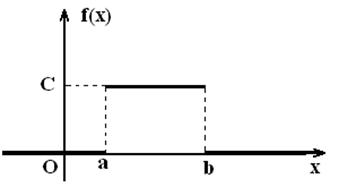
Егер [a,b] кесіндісінде Х
үзіліссіз кездейсоқ шамасының үлестірім
тығыздығы тұрақты, ал оның сыртында нолге
тең болса , онда үзіліссіз кездейсоқ шама
бірқалыпты үлестірілген деп аталады, мұндағы с –
const.
, онда үзіліссіз кездейсоқ шама
бірқалыпты үлестірілген деп аталады, мұндағы с –
const.
Сонымен, тығыздық графигі:
4 сурет
f(x) үлестірім тығыздығының қасиеттері
бойынша f(x) графигі мен ОХ осімен шектелген фигураның
ауданы 1-ге тең, яғни ![]() немесе
немесе 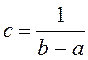 .
.
Олай болса,  .
.
F(x) үлестірім функциясын табайық.
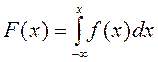 формуласы бойынша
формуласы бойынша ![]() болғанда
болғанда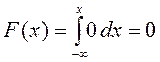 ;
;
егер ![]() ,
онда
,
онда  =
=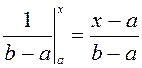 ;
;
егер ![]() ,
онда
,
онда 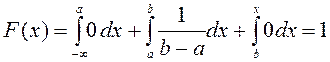 .
.
Сонымен,
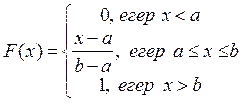 .
.
F(x) графигінің түрі:

5 сурет
Бірқалыпты үлестірімнің
сандық сипаттамалары: математикалық үміт 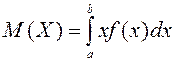 =
=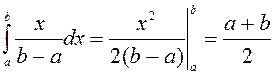 ; дисперсия
; дисперсия 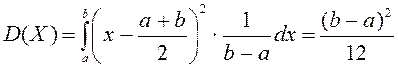 ; орта квадраттық ауытқу
; орта квадраттық ауытқу 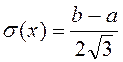 .
. ![]() интервалына түсу ықтималдығы:
интервалына түсу ықтималдығы: 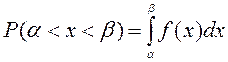 =
= немесе
немесе ![]() . Бұл ықтималдық 6 суреттегі штрихталған
тіктөртбұрыштың ауданына тең
. Бұл ықтималдық 6 суреттегі штрихталған
тіктөртбұрыштың ауданына тең
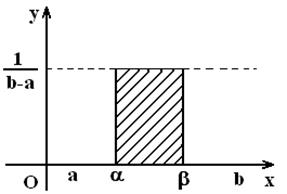
6 сурет
Көрсеткіштік үлестірім
Практикада ықтималдық теориясының қолданылуында, мысалы, сенімділік теориясында, жаппай қызмет ету теориясында және т.б. үлестірімнің көрсеткіштік немесе экспоненциалды заңы қолданылады.
Анықтама.
Егер үлестірім тығыздығы 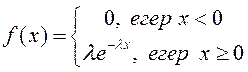 түрінде
берілсе, мұндағы
түрінде
берілсе, мұндағы ![]() >0 – үлестірім параметрі, онда Х үзіліссіз
кездейсоқ шамасы көрсеткіштік заңмен үлестірілген
делінеді.
>0 – үлестірім параметрі, онда Х үзіліссіз
кездейсоқ шамасы көрсеткіштік заңмен үлестірілген
делінеді.
Үлестірім функциясын табайық 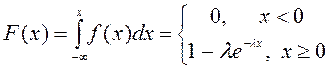 .
.
7 және 8 суреттерінде f(x), F(x) графиктері кескінделген
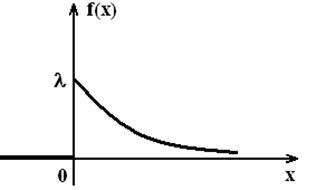

7 сурет 8 сурет
Көрсеткіштік үлестірімнің сандық сипаттамалары:
1) математикалық
үміт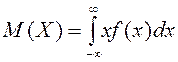 =
= 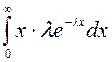 =
= ![]() =
=![]() ;
;
2) дисперсия ![]() =
=  =
= ;
;
3) орта квадраттық
ауытқуы 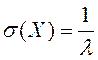 .
.
Сонымен, көрсеткіштік үлестірімнің 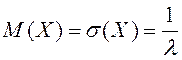 ,
бұл теңдікті практикада кездейсоқ шаманың көрсеткіштік
үлестірілген гипотезасын тексеруде қолданады.
,
бұл теңдікті практикада кездейсоқ шаманың көрсеткіштік
үлестірілген гипотезасын тексеруде қолданады.
![]() интервалына түсу ықтималдығы:
интервалына түсу ықтималдығы:
![]() =
=
![]() .
.
Көрсеткіштік үлестірімнің сенімділік теориясында
қолданылуын қарастырайық. Кейбір қондырғыны,
қарапайым ба, күрделі ме, бұдан былай элемент деп атайтын
боламыз. Элемент ![]() моментінен бастап жұмысын бастасын, ал
моментінен бастап жұмысын бастасын, ал ![]() уақыттан соң жұмысын аяқтасын деп ұйғарайық.
Үзіліссіз кездейсоқ шаманы – элементтің мүлтіксіз
жұмыс істеу уақытын Т арқылы белгілейік.
уақыттан соң жұмысын аяқтасын деп ұйғарайық.
Үзіліссіз кездейсоқ шаманы – элементтің мүлтіксіз
жұмыс істеу уақытын Т арқылы белгілейік. ![]() үлестірім функциясы
үлестірім функциясы ![]() уақыт ішіндегі істен шығу
ықтималдығын анықтайды. Олай болса, сол уақыттағы
мүлтіксіз жұмыс істеу ықтималдығы (яғни
уақыт ішіндегі істен шығу
ықтималдығын анықтайды. Олай болса, сол уақыттағы
мүлтіксіз жұмыс істеу ықтималдығы (яғни ![]() қарама-қарсы
оқиғаның ықтималдығы):
қарама-қарсы
оқиғаның ықтималдығы):
![]()
![]() .
.
функциясын сенімділік функциясы деп атайды, ол ![]() уақыт
ішіндегі мүлтіксіз жұмыс істеу ықтималдығын анықтайды.
Т жиі көрсеткіштік заңмен
уақыт
ішіндегі мүлтіксіз жұмыс істеу ықтималдығын анықтайды.
Т жиі көрсеткіштік заңмен
үлестірілген, сонда ![]() , ал
, ал ![]() =
=![]() . Бұл жағдайда
. Бұл жағдайда ![]() сенімділіктің көрсеткіштік заңы деп атайды, ал
сенімділіктің көрсеткіштік заңы деп атайды, ал ![]() істен шығудың интенсивтілігін анықтайды.
істен шығудың интенсивтілігін анықтайды.
Қалыпты үлестірім
Үлестірімнің қалыпты заңы– ықтималдық теориясында маңызды заң. Мысалы қалыпты заңмен үлестірілген кездейсоқ шамалар: өлшеу және бақылаудың кездейсоқ қателері; оқ атқанда мәреден кездейсоқ жаңылуы кездейсоқ ауытқулары және т.б. Басқа заңдардан қалыпты заңның негізгі ерекшелігі – ол қандай да бір шарттарда басқа үлестірім заңдары ұмтылатын шектік заң болып табылады.
Анықтама.
 тығыздығымен сипатталатын кездейсоқ
шаманың ықтималдығының үлестірім заңы
қалыпты заң деп аталады.
тығыздығымен сипатталатын кездейсоқ
шаманың ықтималдығының үлестірім заңы
қалыпты заң деп аталады.
Сонымен, қалыпты үлестірім екі параметрмен ![]() және
және
![]() анықталады. Осы
параметрлердің ықтималдық мағынасын ашайық.
анықталады. Осы
параметрлердің ықтималдық мағынасын ашайық. ![]() болатындығын
көрсетейік:
болатындығын
көрсетейік:
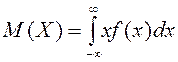 =
=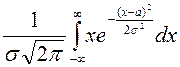 =
= =…=
=…=![]() .
.
Толығырақ мәліметті [1], 145 беттен
қараңыз. Сол сияқты, ![]() :
:
![]()
 =
= =
= =
=
=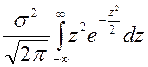 =
= =…=
=…=![]() .
.
Бұдан орта квадраттық ауытқу ![]() .
Егер
.
Егер ![]() =0
және
=0
және ![]() =1,
онда қалыпты үлестірім нормаланған деп аталады.
=1,
онда қалыпты үлестірім нормаланған деп аталады.
Ықтималдықтың қалыпты
үлестірімінің тығыздығының графигі қалыпты
қисық немесе Гаусс қисығы деп аталады.  функциясын математикалық талдау әдістерімен зерттеп,
оның графигін саламыз:
функциясын математикалық талдау әдістерімен зерттеп,
оның графигін саламыз:
а) анықталу облысы ![]() ;
;
б) график ОХ осінен жоғары орналасқан, себебі ![]() үшін
үшін ![]() ;
;
в)
![]() , яғни ОХ – көлденең асимптота;
, яғни ОХ – көлденең асимптота;
г)
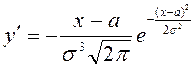 ,
, ![]()
![]()
![]() - кризистік нүкте;
- кризистік нүкте; ![]() егер
егер ![]() және
және ![]() егер
егер ![]() , онда
, онда ![]() ,
, 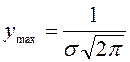 ;
;
д)
екінші туынды арқылы иілу
нүктесін табамыз  және
және
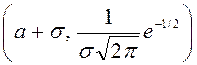 . Сонымен, Гаусс қисығы:
. Сонымен, Гаусс қисығы:
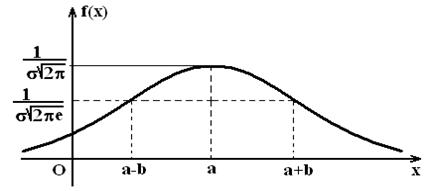
9 сурет
![]() және
және ![]() параметрлерінің өзгерісінің
қалыпты қисықтарға келтіретін әсері:
параметрлерінің өзгерісінің
қалыпты қисықтарға келтіретін әсері:
а) бір ![]() болғанда
болғанда ![]() шамасының өзгеруі қалыпты
қисықтың формасын өзгертпейді, тек ОХ осі бойында
шамасының өзгеруі қалыпты
қисықтың формасын өзгертпейді, тек ОХ осі бойында ![]() болса солға,
болса солға, ![]() болса
оңға жылжиды;
болса
оңға жылжиды;
б)
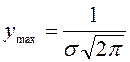 болғандықтан,
болғандықтан, ![]() өскен сайын максималды
ордината кемиді және
керісінше; үлестірім қисығымен шектелген аудан
әрқашан бірге тең болғандықтан,
өскен сайын максималды
ордината кемиді және
керісінше; үлестірім қисығымен шектелген аудан
әрқашан бірге тең болғандықтан, ![]() өзгергенде тек қисықтың формасы
ғана өзгереді:
өзгергенде тек қисықтың формасы
ғана өзгереді: ![]() өскен сайын ол жатық болады және ОХ
осі бойымен созылады.
өскен сайын ол жатық болады және ОХ
осі бойымен созылады.
Қалыпты үлестірілген
кездейсоқ шаманың берілген
интервалға түсу
ықтималдығын табамыз ![]() :
:
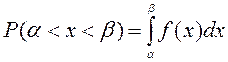 =
= 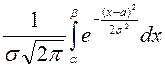 =
= =
=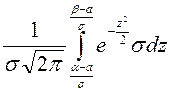 =
=
=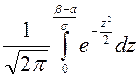 –
– 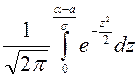 =
=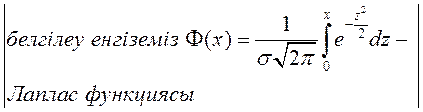 = =
= =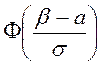 –
–
 .
.
Лаплас функциясының мәндерін арнайы кестеден немесе Mathcad жүйесінде алынады. Бұл функцияның қасиеттері:
1) ![]() кез келген х үшін анықталған;
кез келген х үшін анықталған;
2) ![]() ;
; 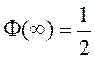 ;
;
3) ![]() , тақ
функция;
, тақ
функция;
4) ![]()
 .
.
Сонымен, Лаплас функциясының графигі:
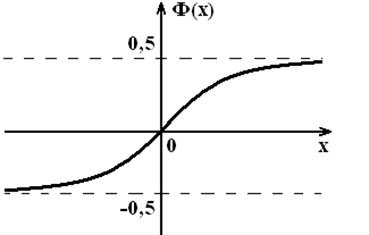
10 сурет
Лаплас функциясы арқылы қалыпты үлестірілген кездейсоқ шаманың F(x) үлестірім функциясы анықталады:
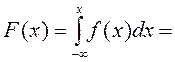
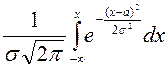 =
=![]()
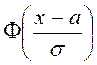 -
-![]() = =
= =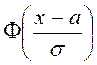 +
+ ![]() = =
= =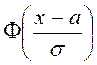 + 0,5.
+ 0,5.
Практикада
![]() қалыпты
үлестірілген кездейсоқ шаманың а – математикалық
үміттен ауытқуының абсолют шамасы бойынша
қалыпты
үлестірілген кездейсоқ шаманың а – математикалық
үміттен ауытқуының абсолют шамасы бойынша ![]() санынан
кіші болу ықтималдығын, яғни
санынан
кіші болу ықтималдығын, яғни ![]() басқаша айтқанда, бұл
кездейсоқ шаманың сейілу центрі
басқаша айтқанда, бұл
кездейсоқ шаманың сейілу центрі ![]() -ға
салыстырмалы симметриялы интервалына түсу ықтималдығын
-ға
салыстырмалы симметриялы интервалына түсу ықтималдығын ![]() есептеуге тура келеді.
есептеуге тура келеді.
Расында,
![]() болғандықтан,
болғандықтан,
![]() =
= ![]()
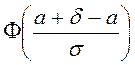 -
- 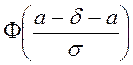 =
=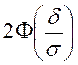 .
.
Сонымен, ![]() аз
болған сайын (яғни сейілу), соғырлым
қалыпты үлестірілген кездейсоқ шаманың
аз
болған сайын (яғни сейілу), соғырлым
қалыпты үлестірілген кездейсоқ шаманың ![]() интервалына
түсу ықтималдығы үлкен.
интервалына
түсу ықтималдығы үлкен. ![]() -тің барлық мәндері
енетіндей центрі а нүктесінде болатын қандай интервал алуға
болатынын анықтайық.
-тің барлық мәндері
енетіндей центрі а нүктесінде болатын қандай интервал алуға
болатынын анықтайық. ![]() мәндерінің кестесін қолданамыз:
мәндерінің кестесін қолданамыз:
![]() =
=![]() =0,6826;
=0,6826;
![]() =
=![]() =0,9594;
=0,9594;
![]() =
=![]() =0,9973;
=0,9973; ![]() =
=![]() =0,999936.
=0,999936.
Сонымен, қалыпты үлестірілген кездейсоқ
шаманың барлық дерлік (~ 99,7%) мәндері ![]() интервалына түседі. Бұл тұжырым «үш сигма
ережесі» деп аталады.
интервалына түседі. Бұл тұжырым «үш сигма
ережесі» деп аталады.
2 Математикалық статистика элементтері
2.1 Дәріс 7. Математикалық статистика пәні және негізгі ұғымдары
Дәріс мазмұны: бас және таңдама жиынтық, таңдау әдістері. Таңдаманың статистикалық үлестірімі. Полигон және гистограмма.
Дәріс мақсаты: математикалық статистика пәнімен және негізгі ұғымдарымен таныстыру.
Математикалық статистика - бұл математиканың бөлімі, ол жалпылама кездейсоқ құбылыстарды бақылау нәтижелерінен алынған тәжірибелік берілімдерді жинау әдістерін, оларды өңдеу және талдауды зерттейді. Ықтималдықтар теориясы математикалық статистика шешетін қолданбалы есептердің теориялық негізі болып табылады.
Жалпы ұғымдар енгізейік. Қандай да бір объектілер жиынтығын сапалы және сандық белгіге бақылау керек болсын. Мысалыға, егер өнімдер партиясы бақыланса, онда сапалы белгі – өнімнің стандартты болуы, сандық белгісі – өнімнің қандай да бір өлшемі.
Анықтамалар.
1. Бас жиынтық деп эксперименттердің (өлшеу, бақылау) барлық мүмкін нәтижелерін жиынын айтамыз.
2. Таңдама жиынтық немесе жәй таңдама деп объектілердің жалпы жиынтығынан кездейсоқ алынған жиынтықты айтамыз.
3. Бас жиынтықтың көлемі деп немесе таңдама көлемі деп осы жиынтықтағы объектілер саны айтылады, белгіленуі N және n.
4. Х белгісін зерттеу үшін бас жиынтықтан
n көлемді ![]() таңдама алынған болсын. Зерттеліп
отырған
таңдама алынған болсын. Зерттеліп
отырған ![]()
![]() мәндері варианталар деп аталады.
мәндері варианталар деп аталады.
5. ![]() мәні
мәні ![]() рет бақылансын
рет бақылансын ![]() және де
және де ![]() .
.
![]() саны
саны ![]() вариантасының
жиілігі, ал
вариантасының
жиілігі, ал  қатынасы – осы вариантаның қатысты жиілігі деп
аталады.
қатынасы – осы вариантаның қатысты жиілігі деп
аталады.
Белгісіз үлестірім заңын анықтау
Қандай да бір ![]() белгісін (
белгісін (![]() кездейсоқ шамасын) зерттеу үшін n тәуелсіз сынақ
жүргізілсін (өлшеу, бақылау). Олардың
әрқайсысында
кездейсоқ шамасын) зерттеу үшін n тәуелсіз сынақ
жүргізілсін (өлшеу, бақылау). Олардың
әрқайсысында ![]() шамасы қандай да бір мәндер
қабылдасын. Кез келген таңдама аламыз (немесе қарапайым
статистикалық қатар):
шамасы қандай да бір мәндер
қабылдасын. Кез келген таңдама аламыз (немесе қарапайым
статистикалық қатар):
1 кесте
|
Зерттеу № |
1 |
2 |
… |
|
варианталар |
|
|
… |
Егер таңдаманы өсу ретімен орналастырсақ, онда вариациалық деп аталатын қатар аламыз:
2 кесте
|
№ |
1 |
2 |
… |
k |
|
|
|
|
|
|
|
|
|
|
… |
|
Мұндағы ![]() ,
, ![]() . Егер
. Егер ![]() вариантасының
вариантасының ![]() және қатысты жиілігі
және қатысты жиілігі 
![]() болса, онда жиіліктердің статистикалық
қатарын (3 кестені қара) және
қатысты жиіліктің статистикалық қатарын алуға болады (4 кестені
қара), мұндағы
болса, онда жиіліктердің статистикалық
қатарын (3 кестені қара) және
қатысты жиіліктің статистикалық қатарын алуға болады (4 кестені
қара), мұндағы ![]() :
:
3 кесте
|
|
|
|
… |
|
|
|
|
|
… |
|
4 кесте
|
|
|
|
… |
|
|
|
|
|
… |
|
Практикада үлкен көлемді таңдама
кездеседі немесе ізделінді белгі үзіліссіз болады (яғни ![]() қандай да бір аралықтың кез келген
мәнін қабылдайды). Бұл жағдайда интервалдық статистикалық
қатар деп аталатын қатар құрады. Ол
үшін бақыланып отырған мәндердің жиынын
қандай да бір аралықтың кез келген
мәнін қабылдайды). Бұл жағдайда интервалдық статистикалық
қатар деп аталатын қатар құрады. Ол
үшін бақыланып отырған мәндердің жиынын ![]() тең ұзындықты
тең ұзындықты ![]() ,
, ![]() , және т.с.с. аралықтарына бөледі.
, және т.с.с. аралықтарына бөледі. ![]() ұзындығы мен аралық санын
анықтау басты сұрақ болып табылады. Келесі
тәсілді қарастырайық:
ұзындығы мен аралық санын
анықтау басты сұрақ болып табылады. Келесі
тәсілді қарастырайық: 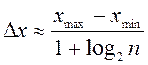 - Стерджес формуласы. Мұндағы
- Стерджес формуласы. Мұндағы ![]() - таңдама құлашы;
- таңдама құлашы; ![]() ;
; ![]() - интервалдар саны, яғни
- интервалдар саны, яғни 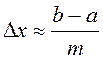 . Бірінші
интервалдың басы ретінде
. Бірінші
интервалдың басы ретінде 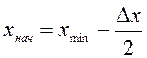 шамасын алуға болады. Интервалдық қатардың
екінші және үшінші жолдарына сәйкес интервалға
түсетін бақылау саны (яғни интервалдың варианталарының жиілігінің
қосындысы) және интервалдың
варианталарының қатысты жиілігінің
қосындысы жазылады. Сонымен, интервалдық қатар:
шамасын алуға болады. Интервалдық қатардың
екінші және үшінші жолдарына сәйкес интервалға
түсетін бақылау саны (яғни интервалдың варианталарының жиілігінің
қосындысы) және интервалдың
варианталарының қатысты жиілігінің
қосындысы жазылады. Сонымен, интервалдық қатар:
5 кесте
|
интервалдар |
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
Егер варианта орнына интервал ортасын алсақ, интервалдық қатардан топталған немесе дискретті статистикалық қатар алуға болады (6 кестені қара):
6 кесте
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
Статистикалық
қатарлар (жиілік, қатысты жиілік, жиілік
және қатысты жиіліктің интервалдық және дискретті қатарлары) үлестірімнің
белгісіз заңының бағасы болады. Бернулли теоремасына
сәйкес оқиғаның пайда болуының
қатысты жиілігі ықтималдығы бойынша осы
оқиғаның ықтималдығына ұмтылады (![]() ). Қатысты жиіліктің статистикалық қатары
қарастырылып отырған кездейсоқ шаманың эмпирикалық
үлестірімі болады деген қорытынды жасауға болады, яғни теориялық
кездейсоқ шаманың үлестірім қатарының аналогы
болады.
). Қатысты жиіліктің статистикалық қатары
қарастырылып отырған кездейсоқ шаманың эмпирикалық
үлестірімі болады деген қорытынды жасауға болады, яғни теориялық
кездейсоқ шаманың үлестірім қатарының аналогы
болады.
Үлестірімнің геометриялық заңының аналогы – үлестірімнің көпмүшелігін алу арқылы вариациалық қатарды басқаша өңдеуге болады.
3 немесе 4 кесте бойынша координаталық жазықтықта ![]() немесе
немесе ![]() нүктелерін
саламыз, сосын оларды кесіндімен жалғаймыз. Алынған фигура
жиілік полигоны немесе қатысты жиілік полигоны
деп аталады (11 суретті қара).
нүктелерін
саламыз, сосын оларды кесіндімен жалғаймыз. Алынған фигура
жиілік полигоны немесе қатысты жиілік полигоны
деп аталады (11 суретті қара).
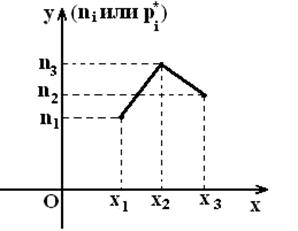
11 сурет
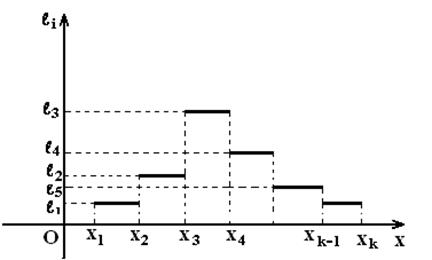
Статистикада басқа геометриялық құрылымы – гистограмма жиі қолданылады. Қатысты жиілік гистограммасы
кездейсоқ шаманың f(x) үлестірімінің
дифференциалдық функциясының (тығыздықтың) статистикалық аналогы
болып табылады. Мысалы, статистикалық гипотезаларды тексеру есептерінде
гистограмманы үлестірімінің теориялық тығыздығының
графигімен салыстырады және қарастырылып отырған
кездейсоқ шаманың үлестірімі туралы болжам жасайды. Гистограмманы
салу үшін интервалдық қатарды қолдануға болады.
Гистограмма – бұл сатылы фигура, ол табаны ![]() интервал ұзындығы, биіктігі
интервал ұзындығы, биіктігі
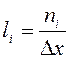 немесе
немесе  болатын тіктөртбұрыштардан тұрады.
Бірінші жағдайда жиілік гистограммасын, екіншісінде – қатысты
жиілік гистограммасы (12 суретті қара).
болатын тіктөртбұрыштардан тұрады.
Бірінші жағдайда жиілік гистограммасын, екіншісінде – қатысты
жиілік гистограммасы (12 суретті қара).
12 сурет
Гистограмма ауданы таңдама көлеміне тең ![]() ,
ал қатысты жиілік гистограммасының ауданы бірге тең
,
ал қатысты жиілік гистограммасының ауданы бірге тең ![]() .
Егер қатысты жиілік гистограммасының әрбір сатысында кез
келген нүкте алсақ, мысалы ортасын, және осы
нүктелерді ирек сызықпен қоссақ, онда f(x)
тығыздығының жуық графигін аламыз.
.
Егер қатысты жиілік гистограммасының әрбір сатысында кез
келген нүкте алсақ, мысалы ортасын, және осы
нүктелерді ирек сызықпен қоссақ, онда f(x)
тығыздығының жуық графигін аламыз.
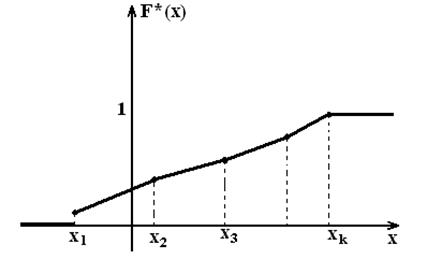
Анықтама.
Үлестірімнің эмпирикалық функциясы деп әрбір
х мәні үшін X<x
оқиғасының қатысты жиілігін анықтайтын ![]() функциясы айтылады, яғни
функциясы айтылады, яғни 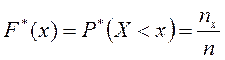 , мұндағы
, мұндағы ![]() -
х-тен кіші
-
х-тен кіші ![]() варианталар саны; n – таңдама
көлемі.
варианталар саны; n – таңдама
көлемі.
![]() функциясының анықтамасынан
функциясының анықтамасынан ![]() қасиеттері
қасиеттері
![]() функциясының
қасиеттерімен бірдей:
функциясының
қасиеттерімен бірдей:
а) оның мәндері [0,1] кесіндісінде жатады;
б) ол кемімелі емес;
в) егер ![]() - ең кіші варианта, ал
- ең кіші варианта, ал
![]() - ең үлкен варианта
болса, онда
- ең үлкен варианта
болса, онда ![]() ;
; ![]() .
.
Бернуллидің
үлкен сандар заңы бойынша оқиғаның
пайда болуының қатысты жиілігі ықтималдығы бойынша осы
оқиғаның ықтималдығына ұмтылады, яғни ![]() , олай болса
, олай болса
![]() . Сонымен,
. Сонымен, ![]() үлестірімнің
эмпирикалық
функциясы
үлестірімнің
эмпирикалық
функциясы ![]() үлестірім функциясының теориялық (интегралалдық)
бағасы болып табылады.
үлестірім функциясының теориялық (интегралалдық)
бағасы болып табылады.
![]() функциясын құру үшін қатысты
жиіліктің статистикалық
қатарын қолданамыз:
функциясын құру үшін қатысты
жиіліктің статистикалық
қатарын қолданамыз:
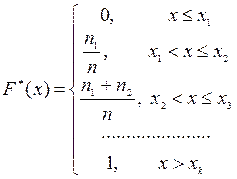 немесе
немесе 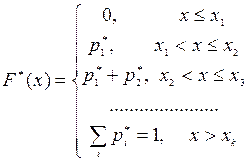 .
.
![]() -тің
графигі сатылы үзілісті сызықтар болады, секірістер бақыланып
отырған мәндерге сәйкес келеді және осы
мәндердің қатысты жиілігіне тең (13 суретті қара).
-тің
графигі сатылы үзілісті сызықтар болады, секірістер бақыланып
отырған мәндерге сәйкес келеді және осы
мәндердің қатысты жиілігіне тең (13 суретті қара).
13 сурет
Егер таңдама көлемі үлкен немесе ізделінді белгі
үзіліссіз болса, онда ![]() варианта орнына интервалдық статистикалық
қатардағы интервалдардың шекарасын алуға болады.
варианта орнына интервалдық статистикалық
қатардағы интервалдардың шекарасын алуға болады. ![]() және
және ![]() екенін ескерсек,
координаталық
жазықтықта
екенін ескерсек,
координаталық
жазықтықта ![]() ,
, ![]() , …,
, …,  , … ,
, … , ![]() нүктелерін
кесінді арқылы немесе ирек сызықпен жалғайды. Бұл
сызық
нүктелерін
кесінді арқылы немесе ирек сызықпен жалғайды. Бұл
сызық ![]() үлестірім
теориялық функциясының жуық
графигі болады (14 суретті қара).
үлестірім
теориялық функциясының жуық
графигі болады (14 суретті қара).
14 сурет
2.2 Дәріс 8. Статистикалық үлестірімнің сандық сипаттамалары. Үлестірімнің параметрлерінің статистикалық бағалары
Дәріс мазмұны: таңдама ортасы және таңдама дисперсиясы. Ығыспаған және тиімді, орнықты бағалар. Бас және таңдама ортасының бағалары. Бас және таңдама дисперсиялар.
Дәріс мақсаты: үлестірімнің параметрлерінің бағаларымен және олардың қасиеттерімен таныстыру.
Математикалық статистикада статистикалық
үлестірімдерге теориялық үлестірімнің сандық сипаттамалары
сияқты сипаттамалар енгізіледі. Математикалық үміттің
ан.алогы таңдама ортасы болады, белгіленуі ![]() (немесе
(немесе ![]() ).
).
Анықтама.
Таңдама ортасы деп барлық таңдама варианталарының арифметикалық ортасы айтылады.
Сонымен, таңдама ортасын жиілік не салыстырмалы жиілік статистикалық қатары бойынша құрады (3 немесе 4 кестені қара):
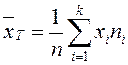 немесе
немесе 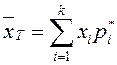 .
.
Егер таңдаманың көлемі
үлкен болса немесе қарастырылып отырған кездейсоқ шама
үзіліссіз болса, онда таңдама ортасын табу үшін сол формулалар
қолданылады, мұндағы ![]() ретінде интервалдық қатардағы интервалдардың
ортасы алынады, яғни 6 кестедегі берілімдер.
ретінде интервалдық қатардағы интервалдардың
ортасы алынады, яғни 6 кестедегі берілімдер.
Анықтама.
![]() таңдама дисперсиясы деп таңдама
мәндерінің таңдама ортасынан ауытқуының квадраттарының
арифметикалық ортасы айтылады:
таңдама дисперсиясы деп таңдама
мәндерінің таңдама ортасынан ауытқуының квадраттарының
арифметикалық ортасы айтылады:
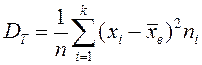 немесе
немесе 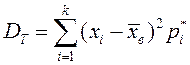 .
.
Теориялық дисперсия сияқты таңдама
дисперсиясын басқа формуламен есептеуге болады: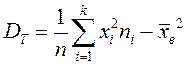 ,
яғни
,
яғни ![]() ,
мұндағы
,
мұндағы ![]() .
.
Таңдама ![]() формуласы бойынша есептелінеді, оның
өлшем бірлігі ізделінді белгінің өлшем бірлігіндей. Практикада
есеп шығарғанда түзетілген таңдама дисперсиясын
және түзетілген орта квадраттық ауытқу қолданылады.
формуласы бойынша есептелінеді, оның
өлшем бірлігі ізделінді белгінің өлшем бірлігіндей. Практикада
есеп шығарғанда түзетілген таңдама дисперсиясын
және түзетілген орта квадраттық ауытқу қолданылады.
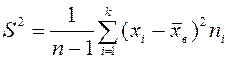 – түзетілген таңдама дисперсиясы. Сонымен,
– түзетілген таңдама дисперсиясы. Сонымен, 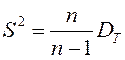 .
. ![]() – түзетілген орта квадраттық
ауытқу. Бұл формулалардың барлығын үзіліссіз белгілер
үшін де қолдануға болады,
тек
– түзетілген орта квадраттық
ауытқу. Бұл формулалардың барлығын үзіліссіз белгілер
үшін де қолдануға болады,
тек ![]() орнына
орнына
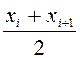 алу
керек.
алу
керек.
Енді математикалық статистиканың
екінші негізгі есебін – үлестірімнің белгісіз параметрлерінің
бағасын қарастырайық. Практикада кездейсоқ шаманың
үлестірім заңының түрі белгілі немесе маңызды
емес болады. Ол бір немесе бірнеше параметрлерге
тәуелді болады. Мысалы, Пуассон заңында – бір ![]() параметріне, қалыпты үлестірім заңы -
параметріне, қалыпты үлестірім заңы - ![]() және
және ![]() параметрлерге, т.с.с. n бақылау нәтижесінде алынған таңдама бойынша осы параметрлерді
бағалау талап етіледі.
параметрлерге, т.с.с. n бақылау нәтижесінде алынған таңдама бойынша осы параметрлерді
бағалау талап етіледі.
Анықтама.
Параметрдің бағасы деп шектелген тәжірибе нәтижесіне негізделген оның жуықталған мәні айтылады.
![]() кездейсоқ шамасының
кездейсоқ шамасының ![]() параметріне тәуелді үлестірім заңын
қарастырайық. n тәжірибе өткізілсін.
Нәтижесінде
параметріне тәуелді үлестірім заңын
қарастырайық. n тәжірибе өткізілсін.
Нәтижесінде ![]() таңдасасы алынсын. Әрбір бақыланып
отырған
таңдасасы алынсын. Әрбір бақыланып
отырған ![]() мәнін
мәнін ![]() кездейсоқ шамасы деп қарастырамыз
(яғни
кездейсоқ шамасы деп қарастырамыз
(яғни ![]() кездейсоқ шамасының n данасын аламыз,
олар
кездейсоқ шамасының n данасын аламыз,
олар ![]() сияқты
үлестірілген) және
сияқты
үлестірілген) және ![]() деп белгілейміз. n бақылау
нәтижесінде алынған баға осы бақылаулардың
қандай да бір функциясы болады, яғни
деп белгілейміз. n бақылау
нәтижесінде алынған баға осы бақылаулардың
қандай да бір функциясы болады, яғни ![]() . Жоғарыда көрсетілгендей,
математикалық үміттің бағасы таңдама ортасы
болады
. Жоғарыда көрсетілгендей,
математикалық үміттің бағасы таңдама ортасы
болады 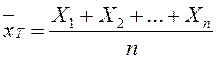 ,
F(x) функциясының бағасы –
,
F(x) функциясының бағасы – ![]() үлестірімнің эмпирикалық
функциясы, тығыздықтың бағасы – гистограмма. Сонымен,
үлестірімнің эмпирикалық
функциясы, тығыздықтың бағасы – гистограмма. Сонымен, ![]() параметрінің
параметрінің ![]() бағасы,
бағасы, ![]() кездейсоқ шамаларының функциясы
болғандықтан, ол да кездейсоқ шама болады. Егер басқа
таңдама алсақ, баға да басқа болады. Егер n бақылау
саны аз болса, онда
кездейсоқ шамаларының функциясы
болғандықтан, ол да кездейсоқ шама болады. Егер басқа
таңдама алсақ, баға да басқа болады. Егер n бақылау
саны аз болса, онда ![]() -ны оның өз бағасымен ауыстыру
қатеге әкеп соғар еді. Сондықтан, параметрдің
бағалары өз мәніне «жақсы» жуықтау үщін келесі
талаптар қойылады.
-ны оның өз бағасымен ауыстыру
қатеге әкеп соғар еді. Сондықтан, параметрдің
бағалары өз мәніне «жақсы» жуықтау үщін келесі
талаптар қойылады.
Статистикалық бағалардың қасиеттері
1. Ығыспағандық.
Анықтама.
Егер ![]() параметрінің
параметрінің ![]() бағасының математикалық үміті бағаланып
отырған параметрге тең болса
бағасының математикалық үміті бағаланып
отырған параметрге тең болса ![]() , онда
, онда ![]() параметрінің
параметрінің ![]() бағасы ығыспаған деп аталады; егер
бағасы ығыспаған деп аталады; егер ![]() ,
онда баға - ығысқан.
,
онда баға - ығысқан.
Ығыспаған баға жүйелік қате болдырмайды, яғни бір таңбалы қате, немесе бір жаққа асыру (баға әруақытта бағаланып отырған параметрден үлкен), немесе бір жаққа кеміту (кем). Бұл таңдаманың көлемі аз болғанда маңызды.
2. Орнықтылық.
Анықтама.
Егер ![]() параметрінің
параметрінің ![]() бағасы ықтималдығы бойынша бағаланып
отырған параметрге жинақты болса, яғни
бағасы ықтималдығы бойынша бағаланып
отырған параметрге жинақты болса, яғни ![]() немесе
немесе ![]() үшін
үшін ![]() орындалса, онда
орындалса, онда ![]() параметрінің
параметрінің ![]() бағасы орнықты деп аталады.
бағасы орнықты деп аталады.
Егер баға орнықты болса, онда таңдаманың көлемі ұлғайғанда параметрдің ақиқат мәні бағасынан айырмашылығы азаяды.
3. Тиімділігі.
Анықтама.
Егер ![]() параметрінің
параметрінің ![]() бағасының осы параметрдің барлық мүмкін
бағасының осы параметрдің барлық мүмкін
ығыспаған бағаларының арасында ең кіші дисперсиясы
болса, онда ![]() параметрінің
параметрінің ![]() бағасы эффективті деп аталады.
бағасы эффективті деп аталады.
Бағаның ығыспағандық және тиімділік қасиеттерінің қатар жүруі практикалық тұрғыдан маңызды. Осы екі қасиеттерге ие бағаны оптималды деп атайды.
Берілген бағаның қасиеттерін анықтау үшін әртүрлі әдістер қолданылады (мысалы, [2] 227 бет). Үш қасиетке ие бағаны табу қиын.
Үлестірім параметрлерінің нүктелік бағалары
Анықтама.
Нүктелік баға деп бір санмен анықталатын баға айтылады.
Жоғарыда қарастырылған
статистикалық үлестірімдердің сандық
сипаттамаларының барлық бағалары ![]() ,
,
![]() ,
,
![]() ,
,
![]() нүктелік
болып табылады. Олардың жоғарыда көрсетілген
қасиеттердің қайсысына ие болатынын анықтайық.
нүктелік
болып табылады. Олардың жоғарыда көрсетілген
қасиеттердің қайсысына ие болатынын анықтайық.
![]() -
- ![]() кездейсоқ
шамасының n тәуелсіз бақылауының нәтижесінде
алынған таңдама болсын.
кездейсоқ
шамасының n тәуелсіз бақылауының нәтижесінде
алынған таңдама болсын. ![]() кездейсоқ мәндер
болғандықтан, оны кездейсоқ шамалар ретінде
қарастырамыз
кездейсоқ мәндер
болғандықтан, оны кездейсоқ шамалар ретінде
қарастырамыз ![]()
![]() (яғни n дана Х:
(яғни n дана Х: ![]() кездейсоқ шамалар аламыз. Сондықтан
кездейсоқ шамалар аламыз. Сондықтан ![]() ,
,
![]() ,
,
![]() .
Таңдама ортасы
.
Таңдама ортасы 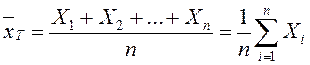 математикалық үміттің
ығыспаған және орнықты бағасы екенін
көрсетейік.
математикалық үміттің
ығыспаған және орнықты бағасы екенін
көрсетейік.
Расында, 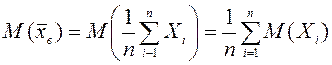 =
=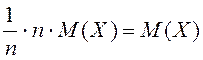 . Сонымен,
. Сонымен, ![]() , яғни
, яғни ![]() - математикалық үміттің
ығыспаған бағасы. Бағаның орнықтылығын
көрсету үшін Чебышев теоремасын қолданамыз:
шектеулі дисперсиясы
бар
- математикалық үміттің
ығыспаған бағасы. Бағаның орнықтылығын
көрсету үшін Чебышев теоремасын қолданамыз:
шектеулі дисперсиясы
бар ![]() тәуелсіз
кездейсоқ шамалардың арифметикалық ортасы ықтималдығы
бойынша олардың математикалық орталарының арифметикалық
ортасына ұмтылады, кездейсоқ шамалар
тәуелсіз
кездейсоқ шамалардың арифметикалық ортасы ықтималдығы
бойынша олардың математикалық орталарының арифметикалық
ортасына ұмтылады, кездейсоқ шамалар ![]() үшін
үшін 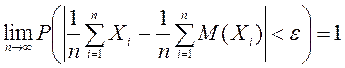 орын алады. Біздің жағдайда соңғы
теңдікті былай жазуға болады:
орын алады. Біздің жағдайда соңғы
теңдікті былай жазуға болады:
![]() , яғни
, яғни ![]() және математикалық үміттің орнықты
бағасы болады.
және математикалық үміттің орнықты
бағасы болады. ![]() математикалық үміттің анағұрлым тиімді
бағасы болады, ал
қалыпты үлестірім
үшін де тиімді бағасы болады. Практикада математикалық
үмітті бағалау үшін
математикалық үміттің анағұрлым тиімді
бағасы болады, ал
қалыпты үлестірім
үшін де тиімді бағасы болады. Практикада математикалық
үмітті бағалау үшін ![]() таңдама ортасын алады.
таңдама ортасын алады.
Енді D(X) дисперсияның
бағасы –![]() қарастырамыз, ол былай жазылады
қарастырамыз, ол былай жазылады 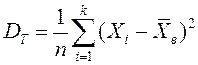 немесе
немесе 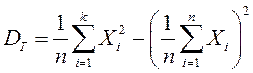 . Келесі теңдік дәлелденген
. Келесі теңдік дәлелденген  , яғни бұл баға
ығысқан. Сондықтан таңдама дисперсиясын
, яғни бұл баға
ығысқан. Сондықтан таңдама дисперсиясын  шамасына
көбейтіп түзейді. Алынған баға – түзетілген
таңдама дисперсиясы деп аталады:
шамасына
көбейтіп түзейді. Алынған баға – түзетілген
таңдама дисперсиясы деп аталады: 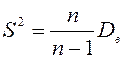 . Бұл баға ығыспаған болады. n үлкен болғанда
. Бұл баға ығыспаған болады. n үлкен болғанда
![]() және
және ![]() арасындағы айырмашылық көп емес, сондықтан
арасындағы айырмашылық көп емес, сондықтан ![]() -ні
-ні ![]() болғанда
дисперсияны бағалау үшін қолданады.
болғанда
дисперсияны бағалау үшін қолданады.
Интервалдық бағалар
Нүктелік бағалар бағаланып отырған параметрге жақсы жуықтамайды, әсіресе таңдама көлемі аз болғанда. Сонымен қатар, олар бағаның дәлдігін және сенімділігін анықтауға мүмкіндік бермейді.
Анықтама.
Екі санмен – интервалдың шеткі нүктелерімен анықталатын баға интервалдық баға деп аталады.
Бағаның дәлдігі және сенімділігі
ұғымдарының мағынасын анықтайық. Таңдаманың
берілімдері бойынша ![]() параметрінің
параметрінің ![]() нүктелік бағасы алынған болсын.
нүктелік бағасы алынған болсын. ![]() шамасы
аз болған сайын
шамасы
аз болған сайын ![]() параметрінің
параметрінің ![]() нүктелік бағасы дәлірек
болатындығы белгілі. Басқаша айтқанда, егер
нүктелік бағасы дәлірек
болатындығы белгілі. Басқаша айтқанда, егер ![]() және
және ![]() ,
, ![]() аз болған сайын
аз болған сайын ![]() бағасы дәлірек болады.
бағасы дәлірек болады.
Анықтама.
![]() орындалатындай
орындалатындай ![]() оң саны бағаның дәлдігін
анықтайды;
оң саны бағаның дәлдігін
анықтайды; ![]() аз болған сайын баға дәлірек болады.
аз болған сайын баға дәлірек болады.
Статистикалық әдістерде ![]() теңсіздігінің орындалу ықтималдығын
бағалау қажет. Сондықтан сенімділік ұғымы пайда болады.
теңсіздігінің орындалу ықтималдығын
бағалау қажет. Сондықтан сенімділік ұғымы пайда болады.
Анықтама.
![]() параметрінің
параметрінің ![]() бағасының сенімділігі (сенімділік)
деп
бағасының сенімділігі (сенімділік)
деп ![]() теңсіздігі орындалатындай
теңсіздігі орындалатындай ![]() ықтималдығы айтылады, яғни
ықтималдығы айтылады, яғни ![]()
![]() .
.
![]() теңдігін түрлендіреміз:
теңдігін түрлендіреміз:
![]() немесе
немесе ![]() .
.
Сонымен, ![]() сенімділігі
(сенімділілік ықтималдығы) дегеніміз
сенімділігі
(сенімділілік ықтималдығы) дегеніміз ![]() параметрінің
ақиқат мәні
параметрінің
ақиқат мәні ![]() интервалында жату ықтималдығы.
интервалында жату ықтималдығы.
Анықтама.
![]() параметрінің ақиқат мәндерін берілген
параметрінің ақиқат мәндерін берілген
![]() сенімділікпен
бүркейтін
сенімділікпен
бүркейтін ![]() интервалы сенімділік интервалы айтылады.
интервалы сенімділік интервалы айтылады.
![]() шамасын алдын ала таңдайды,
шамасын алдын ала таңдайды, ![]() = 0,9 (0,95; 0,99…) деп алады. Сонда
= 0,9 (0,95; 0,99…) деп алады. Сонда ![]() -ның дәл мәні
-ның дәл мәні ![]() сенімділік
интервалында жатады.
сенімділік
интервалында жатады.
Қалыпты үлестірімнің математикалық
үмітін бағалау үшін сенімділік интервалы. Қалыпты
үлестірімнің ![]() белгілі болғандағы математикалық
үмітін бағалау үшін сенімділік интервалы
белгілі болғандағы математикалық
үмітін бағалау үшін сенімділік интервалы
Ізделінді ![]() кездейсоқ шамасы
кездейсоқ шамасы ![]() және
және ![]() параметрлерімен қалыпты үлестірілген болсын. Орта квадраттық
ауытқу
параметрлерімен қалыпты үлестірілген болсын. Орта квадраттық
ауытқу ![]() белгілі болсын. Белгісіз
белгілі болсын. Белгісіз ![]() математикалық үмітті бағалау керек болсын. Берілген
математикалық үмітті бағалау керек болсын. Берілген ![]() сенімділікпен
сенімділікпен
![]() параметрін бүркейтін сенімділік интервалын табу есебін
талдайық.
параметрін бүркейтін сенімділік интервалын табу есебін
талдайық. ![]() кездейсоқ шамасына n сынақ
жүргізіп,
кездейсоқ шамасына n сынақ
жүргізіп, ![]() таңдамасын аламыз. Әрбір вариантаны
таңдамасын аламыз. Әрбір вариантаны ![]() кездейсоқ
шамасының данасы ретінде қарастырамыз, яғни
кездейсоқ
шамасының данасы ретінде қарастырамыз, яғни ![]() n кездейсоқ шамалар аламыз, олар
n кездейсоқ шамалар аламыз, олар ![]() сияқты
үлестірілген, яғни
сияқты
үлестірілген, яғни ![]() ,
, ![]() . Осы бақылаулар негізінде таңдама
бағаларын табамыз:
. Осы бақылаулар негізінде таңдама
бағаларын табамыз: 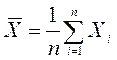 - таңдама ортасы;
- таңдама ортасы;
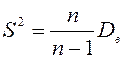 =
=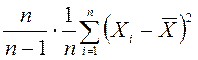 =
= – түзетілген таңдама
дисперсиясы (мұнда жиілік
– түзетілген таңдама
дисперсиясы (мұнда жиілік ![]() ). Орталық шектік теорема негізінде
қорытынды жасаймыз:
). Орталық шектік теорема негізінде
қорытынды жасаймыз: ![]() – кедейсоқ шама, ол
– кедейсоқ шама, ол ![]() сияқты
қалыпты үлестірілген. Математикалық үміт пен дисперсия
қасиеттері бойынша
сияқты
қалыпты үлестірілген. Математикалық үміт пен дисперсия
қасиеттері бойынша ![]() параметрлерін
табамыз:
параметрлерін
табамыз:
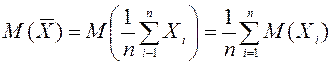 =
=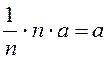 ;
;
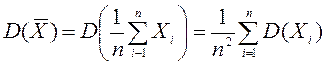 =
=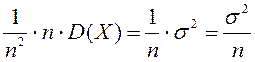 ;
;
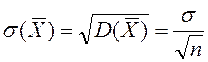 .
.
Енді сенімділік интервалын
құруға кірісейік, ![]() кездейсоқ шамасының
кездейсоқ шамасының ![]() математикалық үмітінің ақиқат мәнін
математикалық үмітінің ақиқат мәнін
![]() сенімділікпен
қамтитын (бүркейтін), яғни
сенімділікпен
қамтитын (бүркейтін), яғни ![]() шартының орындалуы талап етіледі. Қалыпты
үлестірім үшін
шартының орындалуы талап етіледі. Қалыпты
үлестірім үшін 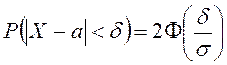 формуласы белгілі. Сондықтан,
формуласы белгілі. Сондықтан, ![]() –
–
![]() және
және ![]() параметрлері болғандықтан
параметрлері болғандықтан
 .
.
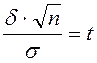 белгілеуін
енгізейік, онда
белгілеуін
енгізейік, онда  . Осы белгілеуден кейін соңғы теңдік
былай жазылады:
. Осы белгілеуден кейін соңғы теңдік
былай жазылады: 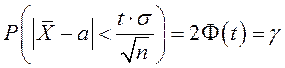
немесе 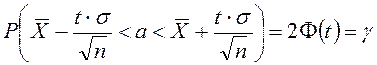 . Сонымен,
. Сонымен, ![]() белгілі болғанда
белгілі болғанда ![]() математикалық үмітті бағалау үшін сенімділік
интервалы:
математикалық үмітті бағалау үшін сенімділік
интервалы: 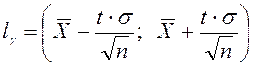 .
. ![]() сенімділік өлшемі алдын ала
таңдап алынады. Таңдау есепке байланысты, мысалы, авиа жолаушылары
үшін ұшақтың сенімділік дәрежесі, сатып алушы
үшін телевизордың сенімділік дәрежесіне
қарағанда жоғарырақ болу керек. Әдетте
сенімділік өлшемі алдын ала
таңдап алынады. Таңдау есепке байланысты, мысалы, авиа жолаушылары
үшін ұшақтың сенімділік дәрежесі, сатып алушы
үшін телевизордың сенімділік дәрежесіне
қарағанда жоғарырақ болу керек. Әдетте ![]() сенімділігін
0,9; 0,95; 0,99 деп алады. Сонда
сенімділігін
0,9; 0,95; 0,99 деп алады. Сонда ![]() параметрі сенімділік интервалына
түсетіндігі белгілі. t мәнін
параметрі сенімділік интервалына
түсетіндігі белгілі. t мәнін ![]() шартынын
табады
шартынын
табады  ;
берілген
;
берілген ![]() бойынша
бойынша ![]() Лаплас функциясының кестесінен t
аргументі табылады.
Лаплас функциясының кестесінен t
аргументі табылады.  теңдігінен, n (таңдама
көлемі) үлкен болған сайын,
теңдігінен, n (таңдама
көлемі) үлкен болған сайын, ![]() аз
болады (соғырлым баға дәлірек);
аз
болады (соғырлым баға дәлірек);
![]() теңдігінен
теңдігінен ![]() сенімділігінің үлкейгендігінен t үлкейеді, себебі
сенімділігінің үлкейгендігінен t үлкейеді, себебі
![]() функциясы өспелі, сондықтан
функциясы өспелі, сондықтан  теңдігінен
теңдігінен
![]() үлкейеді,
яғни дәлдік азаяды.
үлкейеді,
яғни дәлдік азаяды.
Мысалы 2.8.1 - Егер орта вадраттық ауытқу ![]() =5,
таңдама ортасы
=5,
таңдама ортасы ![]() =14, таңдама көлемі n =25 болғанда,
0,95 сенімділікпен берілген қалыпты үлестірілген кездейсоқ
шаманың сенімділік интервалын табу керек.
=14, таңдама көлемі n =25 болғанда,
0,95 сенімділікпен берілген қалыпты үлестірілген кездейсоқ
шаманың сенімділік интервалын табу керек.
Шешуі:
 формуласын
қолданамыз.
формуласын
қолданамыз.
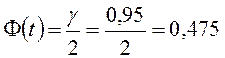 теңдігінен t
белгісізін табамыз, кестеден
t=1,96. Олай
болса,
теңдігінен t
белгісізін табамыз, кестеден
t=1,96. Олай
болса,
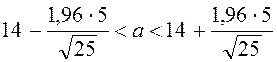 немесе
немесе ![]() . Сонымен, сенімділік
интервалы
. Сонымен, сенімділік
интервалы ![]() .
.
А қосымшасы
Үлестірім моменттері туралы ұғым. Мода, медиана, квантилдер.
Кейбір негізгі сандық сипаттамалар үлестірім моменттері ұғымның дербес жағдай болып табылады. «Момент» термины механикадан алынған, ол массаның үлестірілуін сипаттайды. Ықтималдық теориясында екі түрлі моменттер қарастырылады: бастапқы және орталық.
Анықтама.
![]() кездейсоқ шамасының k – ші ретті бастапқы
моменті деп
кездейсоқ шамасының k – ші ретті бастапқы
моменті деп ![]() кездейсоқ шамасының математикалық
үміті айтылады, яғни
кездейсоқ шамасының математикалық
үміті айтылады, яғни ![]() .
.
Олай болса, дискретті кездейсоқ шамалар үшін
бастапқы момент 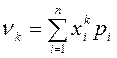 формуласымен, ал үзіліссіз үшін –
формуласымен, ал үзіліссіз үшін –  формуласымен
өрнектеледі. Бірінші ретті бастапқы момент – бұл математикалық
үміт:
формуласымен
өрнектеледі. Бірінші ретті бастапқы момент – бұл математикалық
үміт: ![]() . Жоғарғы ретті бастапқы моменттер
негізінде орталық моменттерді есептеу үшін қолданылады.
. Жоғарғы ретті бастапқы моменттер
негізінде орталық моменттерді есептеу үшін қолданылады.
Анықтама.
![]() кездейсоқ шамасының k – ші ретті орталық моменті
деп
кездейсоқ шамасының k – ші ретті орталық моменті
деп ![]() кездейсоқ шаманың математикалық үміті айтылады,
яғни
кездейсоқ шаманың математикалық үміті айтылады,
яғни ![]() .
.
Дискретті кездейсоқ шама үшін
орталық момент 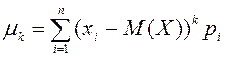 формуласымен; ал үзіліссіз –
формуласымен; ал үзіліссіз –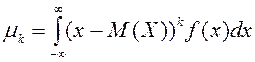 формуласымен өрнектеледі. Жоғарыда көрсетілгендей,
формуласымен өрнектеледі. Жоғарыда көрсетілгендей, ![]() ,
,
![]() .
Кездейсоқ шаманың қасиеттерін сипаттау үшін үшінші
және төртінші ретті орталық моменттер қолданылады: олар
пішінін сипаттайды – симметриялы немесе симметриялы емес, сүйір
төбелі немесе жазық төбелі.
.
Кездейсоқ шаманың қасиеттерін сипаттау үшін үшінші
және төртінші ретті орталық моменттер қолданылады: олар
пішінін сипаттайды – симметриялы немесе симметриялы емес, сүйір
төбелі немесе жазық төбелі.
Үшінші ретті орталық момент ![]() симметриялылықты
анықтайды. Егер кездейсоқ шама өзінің математикалық
үмітіне қатысты симметриялы үлестірілсе, онда
симметриялылықты
анықтайды. Егер кездейсоқ шама өзінің математикалық
үмітіне қатысты симметриялы үлестірілсе, онда ![]() =
0 (барлық тақ ретті орталық моменттер
=
0 (барлық тақ ретті орталық моменттер ![]() ).
).
![]() кездейсоқ шаманың өлшемі куб бірлікте
болғандықтан, әдетте өлшемсіз сипаттаманы
қарастырады:
кездейсоқ шаманың өлшемі куб бірлікте
болғандықтан, әдетте өлшемсіз сипаттаманы
қарастырады: 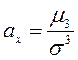 - асимметрия коэффициенті немесе жәй асимметрия.
Үлестірім қисығының пішіні
- асимметрия коэффициенті немесе жәй асимметрия.
Үлестірім қисығының пішіні ![]() -ке
байланысты, егер
-ке
байланысты, егер ![]() , онда қисық математикалық
үміттің оң жағында, егер
, онда қисық математикалық
үміттің оң жағында, егер ![]() , онда сол жағында жатық (А.1 суретін
қара).
, онда сол жағында жатық (А.1 суретін
қара).
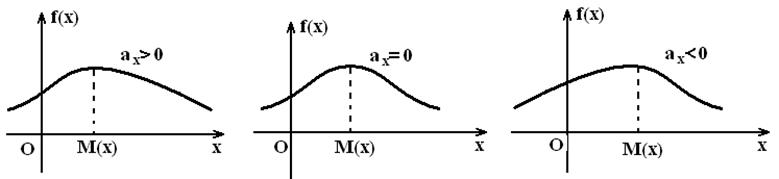
А.1 сурет
Төртінші ретті орталық момент ![]() үлестірімнің
сүйір төбелі немесе жазық төбелігін анықтайды.
үлестірімнің
сүйір төбелі немесе жазық төбелігін анықтайды.
Анықтама.
Х кездейсоқ шаманың эксцессі
деп  шамасы
айтылады.
шамасы
айтылады.
Қалыпты үлестірім үшін 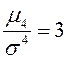 және
және
![]() . Барлық үлестірім заңдары арасында қалыпты
үлестірім «пішіннің эталоны» болғандықтан (
. Барлық үлестірім заңдары арасында қалыпты
үлестірім «пішіннің эталоны» болғандықтан (![]() және
және ![]() ), эксцесс асимметрия сияқты, үлестірім пішінінің
өзгешелігін бағалауға мүмкіндік береді. Үлестірім
қисықтары қалыпты қисыққа
қарағанда сүйір төбелі болып үлестірілген (А.2 суретін қара).
), эксцесс асимметрия сияқты, үлестірім пішінінің
өзгешелігін бағалауға мүмкіндік береді. Үлестірім
қисықтары қалыпты қисыққа
қарағанда сүйір төбелі болып үлестірілген (А.2 суретін қара).
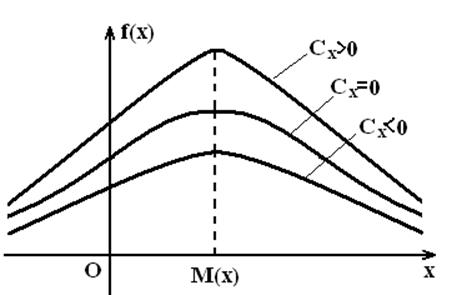
А.2 сурет
Орталық моменттерді есептегенде бастапқы
моменттер арқылы есептелінетін формулаларды қолданған
қолайлы: ![]() ;
; ![]() ;
; ![]() . Жоғарғы ретті моменттер практикада
сирек қолданылады.
. Жоғарғы ретті моменттер практикада
сирек қолданылады.
Математикалық үміттен өзге практикада басқа сипаттамалар – мода, медиана, квантиль кездеседі.
Дискретті кездейсоқ шаманың модасы
деп оның ең үлкен ықтимал мәні айтылады; үзіліссіз
кездейсоқ шаманың модасы деп үлестірім тығыздығы
максимум болатын мәнін айтамыз. Максимумдары жоқ немесе бір не бірнеше максимумдары
бар үлестірімдер бар. Модалар
![]() немесе
немесе ![]() деп
белгіленеді.
деп
белгіленеді.
Егер кездейсоқ шаманың белгілі бір ![]() мәнінде
мәнінде
![]() орындалса, онда
орындалса, онда ![]() кездейсоқ
шаманың медианасы деп аталады, яғни
кездейсоқ
шаманың медианасы деп аталады, яғни
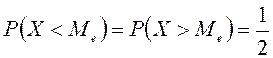 . Үлестірім
функциясы
. Үлестірім
функциясы ![]() , онда соңғы теңдікті былай
жазуға болады
, онда соңғы теңдікті былай
жазуға болады 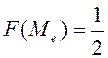 . Медиананы
. Медиананы 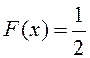 теңдеуінің түбірі деп табуға
болады.
теңдеуінің түбірі деп табуға
болады.
![]() ретті квантиль деп кездейсоқ шаманың
ретті квантиль деп кездейсоқ шаманың ![]() орындалатындай
орындалатындай
![]() мәні
айтылады. Сонымен, медиана
дегеніміз
мәні
айтылады. Сонымен, медиана
дегеніміз ![]() =1/2 болғандағы квантиль.
=1/2 болғандағы квантиль. ![]() квантильдерін кейде сәйкес төменгі квантиль, медиана және жоғарғы квантиль деп
атайды, олар кездейсоқ шаманың анықталу обласын
төрт бөлікке бөледі, әр бөлікке түсу
ықтималдығы бірдей және ¼-ге тең.
квантильдерін кейде сәйкес төменгі квантиль, медиана және жоғарғы квантиль деп
атайды, олар кездейсоқ шаманың анықталу обласын
төрт бөлікке бөледі, әр бөлікке түсу
ықтималдығы бірдей және ¼-ге тең.
Б қосымшасы
Ықтималдық теориясының шектік теоремалары.
Ықтималдық теориясының математикалық заңдары жаппай кездейсоқ құбылыстарға тән статистикалық заңдылықтардың абстракциясы болып табылады. Егер кездейсоқ шама жалпы сипатталған болса, онда оның сипаттамалары орнықты болады және кездейсоқ болмайды. Мысалы, кездейсоқ оқиғаның n сынақта пайда болу жиілігі n ұлғайғанда орнықты болады және тұрақты шамаға – ықтималдыққа ұмтылады; кездейсоқ шамалардың арифметикалық ортасы математикалық үмітке жуықталады және т.с.с. Шектік теоремалардың екі түрі қарастырылады: 1) үлкен сандар заңы; 2) орталық шектік теорема.
Үлкен сандар заңы
Үлкен сандар заңы теоремалары кездейсоқ шамалардың жеткілікті үлкен саны қоса алғанда кездейсоқ қасиетін жоғалтып, заңдылыққа айналу шарттарын қарастырады. Осындай теоремаларға Чебышев және Бернулли теоремалары жатады (басқалары да бар, біз оларды қарастырмаймыз). Алдымен теориялық маңызы зор Чебышев теңсіздігін қарастырамыз.
Теорема.
Кездейсоқ шаманың
оның математикалық үмітінен ауытқуының абсолют
шамасы бойынша оң ![]() санынан кем болмау ықтималдығы
жоғарыдан
санынан кем болмау ықтималдығы
жоғарыдан 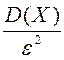 шамасымен
шектелген, яғни
шамасымен
шектелген, яғни
![]()
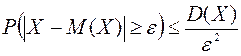
немесе, егер қарама қарсы оқиғаға көшсек,
 .
.
Чебышев теңсіздігінің бұл екі формасы оқиғаның ықтималдығының сәйкес жоғарғы және төменгі шекараларын көрсетеді.
Айта кетелік, бұл жерде және де
ықтималдық теориясының басқа теоремаларында «ықтималдық
бойынша жинақты» ұғымы қолданылады: егер кез келген ![]() үшін
үшін ![]() оқиғасының
ықтималдығы
оқиғасының
ықтималдығы ![]() кезде бірге ұмтылса, яғни
кезде бірге ұмтылса, яғни ![]() ,
онда
,
онда ![]() кездейсоқ
шамалары ықтималдық бойынша А шамасына жинақты. Оны
былай жазуға болады
кездейсоқ
шамалары ықтималдық бойынша А шамасына жинақты. Оны
былай жазуға болады ![]() . Математикалық талдаудағы
жинақтылық пен айырмашылығы, ықтималдық бойынша
жинақтылық
. Математикалық талдаудағы
жинақтылық пен айырмашылығы, ықтималдық бойынша
жинақтылық ![]() теңсіздігі
теңсіздігі ![]() тізбегінің
көпшілік мүшелері үшін орындалуын талап етеді, математикалық
талдауда бұл теңсіздік тізбектің N номерден бастап (яғни
тізбегінің
көпшілік мүшелері үшін орындалуын талап етеді, математикалық
талдауда бұл теңсіздік тізбектің N номерден бастап (яғни
![]() )
барлық мүшелері үшін орындалуы керек.
)
барлық мүшелері үшін орындалуы керек.
Чебышев теоремасы. Егер ![]() қос қостан тәуелсіз кездейсоқ шамалар болса
және олардың дисперсиялары шектеулі болса (яғни С саны
табылып,
қос қостан тәуелсіз кездейсоқ шамалар болса
және олардың дисперсиялары шектеулі болса (яғни С саны
табылып, ![]() орындалса), онда n өскенде осы кездейсоқ
шамалардың арифметикалық ортасы ықтималдық бойынша
олардың математикалық үміттерінің арифметикалық
ортасына жинақты, яғни кез келген
орындалса), онда n өскенде осы кездейсоқ
шамалардың арифметикалық ортасы ықтималдық бойынша
олардың математикалық үміттерінің арифметикалық
ортасына жинақты, яғни кез келген ![]() үшін
үшін 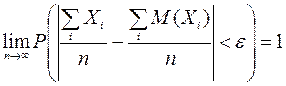 .
Егер
.
Егер ![]() ,
онда Чебышев теоремасының дербес жағдайын аламыз
,
онда Чебышев теоремасының дербес жағдайын аламыз 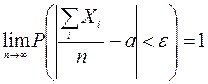 .
.
Чебышев теоремасының мағынасы: егер жеке
тәуелсіз кездейсоқ шамалар өздерінің математикалық
үміттерінен алыс мәндер қабылдай алса, онда
ықтималдықтары үлкен жеткілікті үлкен санды кездейсоқ
шамалардың арифметикалық ортасы белгілі санға жуық
мәнді қабылдайды (атап айтқанда 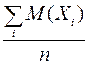 ).
Чебышев теоремасының практикада маңызы зор. Оған статистикада
жиі қолданылатын таңдама әдісі негізделген. Ол әдіс
бойынша азғана кездейсоқ таңдама негізінде барлық
объектілер жиынтығы туралы қорытынды жасалады (азғана
үлгі негізінде бидай сапасы туралы). Әрине, бұл әдісті теорема
шарттары орындалғанда ғана қолдана аламыз.
).
Чебышев теоремасының практикада маңызы зор. Оған статистикада
жиі қолданылатын таңдама әдісі негізделген. Ол әдіс
бойынша азғана кездейсоқ таңдама негізінде барлық
объектілер жиынтығы туралы қорытынды жасалады (азғана
үлгі негізінде бидай сапасы туралы). Әрине, бұл әдісті теорема
шарттары орындалғанда ғана қолдана аламыз.
Бернулли теоремасы
Бернулли теоремасы маңызды және тарихта үлкен сандар заңының бірінші формасы болып табылады. n тәуелсіз сынақта оқиғаның пайда болу жиілігі мен ықтималдығы арасындағы байланысты көрсетеді.
Теорема. Бір бірінен тәуелсіз n рет
тәжірибе жүргізгенде, А оқиғасының пайда
болу саны m болсын. Егер әрбір тәжірибе А оқиғасы ![]() ықтималдығымен пайда болса, онда кез келген
ықтималдығымен пайда болса, онда кез келген ![]() :
:
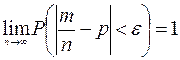 .
.
Салыстырмалы жиіліктің оның
ықтималдығынан ауытқуының абсолют шамасының ![]() кіші
болу ықтималдығы өскенде бірге жақындайды,
кіші
болу ықтималдығы өскенде бірге жақындайды, 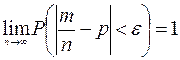 ,
демек А оқиғасының салыстырмалы жиілігі
ықтималдығы бойынша А оқиғасының
ықтималдығына жинақты.
,
демек А оқиғасының салыстырмалы жиілігі
ықтималдығы бойынша А оқиғасының
ықтималдығына жинақты.
Орталық шектік теорема
Орталық шектік теоремалар жеткілікті үлкен санды кездейсоқ шамалардың қосындылары үшін үлестірім заңын орнатады. Бұл шектік теоремалар қалыпты үлестірілген кездейсоқ шамалары пайда болатын шарттарын қарастырады. Орталық шектік теорема шарттарға байланысты әртүрлі формада болады. Ляпунов теоремасын қарастырайық.
Егер
![]() кездейсоқ шамалары өзара тәуелсіз және бір
заңмен үлестірілген, математикалық үміті
кездейсоқ шамалары өзара тәуелсіз және бір
заңмен үлестірілген, математикалық үміті ![]() және
дисперсиясы
және
дисперсиясы ![]() , және де,
3-ші ретті абсолютті
орталық момент
, және де,
3-ші ретті абсолютті
орталық момент ![]() бар
болса, онда n шексіз ұлғайғанда
бар
болса, онда n шексіз ұлғайғанда 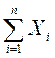 қосындының үлестірім заңы
қалыпты заңға шексіз жақындайды.
қосындының үлестірім заңы
қалыпты заңға шексіз жақындайды.
Табиғатта және қоғамда кездесетін кездейсоқ құбылыстардың көбі Ляпунов теоремасымен түсіндіріледі. Мысалы:
1) Қандай да бір а шамасын өлшеу жүргізілсін. Көп факторлардың әсер
ету нәтижесінде ![]() бақылау мәндері а–дан әртүрлі ауытқулар
алынды, оның әрбіреуі
бақылау мәндері а–дан әртүрлі ауытқулар
алынды, оның әрбіреуі ![]() аз қатені туындатады және
аз қатені туындатады және ![]() . Онда қателер қосындысы (қорытындысы) Ляпунов теоремасы
бойынша қалыпты үлестірілген кездейсоқ шама болып табылады.
. Онда қателер қосындысы (қорытындысы) Ляпунов теоремасы
бойынша қалыпты үлестірілген кездейсоқ шама болып табылады.
2) Оқ атқанда көп кездейсоқ себептер әсерінен үлкен ауданда снарядтар шашырайды. Снарядтың траекториясына кездейсоқ әсерді тәуелсіз деп есептеуге болады. Әрбір себеп траектория өзгеруіне барлық себептердің біріге жасаған әсеріне қарағанда байқаусыз өзгеріс енгізеді, Сондықтан снарядтың көздеген мәресінен ауытқуын қалыпты үлестірілген кездейсоқ шама деп күтуге болады.
3) Ляпунов теоремасы бойынша ер адамның бойы қалыпты заң бойынша үлестірілген кездейсоқ шама деуге болады.
Айта кетелік, қарастырылған Муавр-Лаплас интегралдық теоремасы
![]() кездейсоқ шамалары бірдей
үлестірілген, дискретті және тек екі мән 0 және 1 қабылдағандағы
шектік теореманың қарапайым дербес жағдайы болып табылады.
кездейсоқ шамалары бірдей
үлестірілген, дискретті және тек екі мән 0 және 1 қабылдағандағы
шектік теореманың қарапайым дербес жағдайы болып табылады.
Әдебиеттер тізімі
1. Жаңбырбаев Б.С., Жаңбырбаева Ү.Б. Ықтималдықтар теориясы мен
математикалық статистика. Оқу құралы. – Алматы: «Сa Fa» баспасы, 2006. -280 бет.
2. Письменный Д. Конспект лекций по теории вероятностей и мате-
матической статистике, случайные процессы.- М.: Айрис- пресс, 2006.- 288 с.
3. Гмурман В.Е. Теория вероятностей и математическая статистика.
Учебное пособие для вузов.- М.: Высш. школа, 2003.- 279 с.
4. Гмурман В.Е. Руководство к решению задач по теории вероятностей и
математической статистике. –М.: Высш. школа, 1999.- 400 с.
5. Астраханцева Л.Н. Дискретная математика. Учебное пособие.- Алматы: АУЭС, 2011.- 78 с.
6. Астраханцева Л.Н., Байсалова М.Ж. Ықтималдықтар теориясы және
математикалық статистика. 5В070400 – «Есептеу техникасы және бағдарламалық қамтамасыз ету», 5В070300 - «Ақпараттық жүйелер» мамандықтары бойынша оқитын барлық бөлім студенттері үшін есептеу- графикалық жұмыстарды орындауға арналған әдісістемелік нұсқаулар мен тапсырмалар. - Алматы: АЭжБУ, 2011. -1 бөлім.-30 б.
7. Астраханцева Л.Н., Байсалова М.Ж. Ықтималдықтар теориясы және математикалық статистика. 5В070400 – «Есептеу техникасы және бағдарламалық қамтамасыз ету», 5В070300 - «Ақпараттық жүйелер» мамандықтары бойынша оқитын барлық бөлім студенттері үшін есептеу- графикалық жұмыстарды орындауға арналған әдісістемелік нұсқаулар мен тапсырмалар. - Алматы: АЭжБУ, 2011. -2 бөлім.- 27 б.
Мазмұны
|
1 Ықтималдықтар теориясы элементтері |
|
|
1.1 Дәріс 1. Кездейсоқ оқиғалар. Элементар оқиғалар кеңістігі. Ықтималдық |
3 |
|
1.2 Дәріс 2. Ықтималдық теориясының негізгі теоремалары |
7 |
|
1.3 Дәріс 3. Кездейсоқ шамалар |
11 |
|
1.4 Дәріс 4. Кездейсоқ шамалардың сандық сипаттамалары |
16 |
|
1.5 Дәріс 5-6. Кездейсоқ шамалардың негізгі үлестірім заңдары |
19 |
|
2 Математикалық статистика элементтері |
|
|
2.1 Дәріс 7. Математикалық статистика пәні және негізгі ұғымдары |
27 |
|
2.2 Дәріс 8. Статистикалық үлестірімнің сандық сипаттамалары. Үлестірімнің параметрлерінің статистикалық бағалары. |
32 |
|
А қосымшасы. Үлестірім моменттері туралы ұғым. Мода, медиана, квантилдер |
39 |
|
Б қосымшасы. Ықтималдық теориясының шектік теоремалары |
42 |
|
Әдебиеттер тізімі |
45 |
2013 ж. жиынтық жоспары, реті 307
Астраханцева Людмила Николаевна
Байсалова Мәншүк Жұмамұратқызы
ЫҚТИМАЛДЫҚТАР ТЕОРИЯСЫ ЖӘНЕ МАТЕМАТИКАЛЫҚ СТАТИСТИКА
5В070400 – Есептеу техникасы мен
бағдарламалық қамтамасыз ету
және 5В070300 – Ақпараттық
жүйелер мамандықтарының студенттері үшін
дәрістер жинағы
Редактор Кегенбаева
А.
Стандарттау бойынша
маман Молдабекова Н.К.
Басуға
қол қойылды_______
Пішіні 60х84 1/16
Таралымы 100 дана
№1 типографиялық
қағаз
Көлемі 2,9 баспа
табақ
Тапсырыс______Бағасы
290 тг.
«Алматы энергетика және байланыс университеті»
Коммерциялық емес акционерлік
қоғамының
көшірме-көбейткіш бюросы
050013, Алматы, Байтурсынұлы
көшесі, 126