Коммерциялық емес акционерлік қоғам

Алматы энергетика және байланыс Университеті

Жоғары математика кафедрасы

Дифференциалдық теңдеулер

5В060200 – Информатика мамандығы бойынша

оқитын студенттер үшін дәрістер жинағы

Алматы, 2013

2012 ж. жиынтық жоспары, реті 348

Құрастырушылар: К.М. Мустахишев, Б.Ж. Атабай. Дифференциалдық теңдеулер. 5В060200 – Информатика мамандығы бойынша оқитын студенттер үшін дәрістер жинағы. - Алматы: АЭжБУ, 2013. -46 б.

Дәрістер жинағында «Дифференциалдық теңдеулер» курсы бойынша 12 дәріс, қолданыстағы тапсырмалардың үлгі нұсқасындағы есептер мен теориялық материалды жете түсінуге арналған мысалдардың (барлығы 26 есеп) шығарылулары келтірілген.

Ил. 5, библиограф. – 7 атау.

Пікір жазған: физ.-мат.ғылым. канд., доцент Ұ.К. Қойлышов

“Алматы энергетика және байланыс университеті” коммерциялық емес акционерлік қоғамының 2012 жылға арналған басылымдар жоспарына сай баспаға шығарылған.

1-модуль. Бірінші ретті дифференциалдық теңдеулер

1-дәріс. Негізгі түсініктер. Геометриялық талқылау

Дәрістің мақсаты: дифференциалдық теңдеу (ДТ) түсінігіне келтіретін есептерді қарап, студенттерді ДТ-ның негізгі түсініктерімен таныстыру.

Белгісіздер туынды не дифференциал белгісінің астында болып келген теңдеу дифференциалдық теңдеу (ДТ) деп аталады. Теңдеудегі белгісіз функция туындыларының ең жоғарғы реті ДТ-ның реті делінеді. Ғылым мен техниканың көптеген есептері ДТ ұғымына келтіреді. Солардың кейбіреулерін қарастыралық.

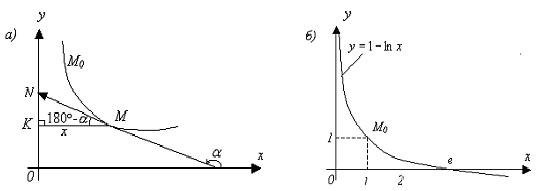
1. Кез келген нүктесінде жүргізілген, ұшы осінде жататын жанама векторының (1a)-суретті қара) сол оське проекциясы 1-ге тең болатын, нүктесі арқылы өтетін сызықты табыңыз.

Шешу. Тікбұрышты -нен:

1 сурет - Болжалды және дәлденген интегралдық қисық

Туындының геометриялық мағынасын ескерсек:

. (1.1)

Бұл бірінші ретті дифференциалдық теңдеу.

2. Қатаңдығы с серіппеге (2 суретті қара) ілініп, еркіне жіберілген массасы m жүктің қозғалыс заңын табыңыз.

Шешу. Жүкке оның ауырлық күші және серіппенің созылу не сығылу шамасына пропорционал серпінділік күші әсер етеді. Бұл күштердің ортақ әсер сызығын тік төмен қарай бағытталған осі ретінде қабылдайық. Координаталардың бас нүктесі 0 ретінде жүктің ауырлық центрінің статикалық тепе-теңдік орны деп аталатын нүктені алайық (суретте l арқылы жүксіз серіппенің ұзындығы белгіленген). Ньютонның екінші заңы бойынша

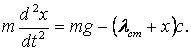
2 сурет - Серіппеге ілінген жүк тербелісі

Мұнда - серіппенің статикалық созылуы; белгілеуін енгізсек, екінші ретті ДТ-ға келеміз:

(1.2)

Жалпы түрде n-ретті DТ

(1.3)

деп жазылады. Мұнда -тәуелсіз айнымалы, - белгісіз функция, - оның туындылары. Теңдеуге оның ретін анықтайтын ең жоғарғы ретті туындының қатынасуы міндетті. Қалған аргументтердің қай-қайсысы да (1.3)-ке айқын түрде енбеуі мүмкін. Айқын емес функцияның бар болу шарттарына [1] ұқсас талаптар орындалған жағдайда (16.3)-ті арқылы шешіп,

(1.4)

деп жаза аламыз.

Қаралып отырған аймақта -ретті туындысы бар, (1.3)-ке қанағаттандыратын функциясы сол теңдеудің шешуі деп, оның графигі теңдеудің интегралдық қисығы деп аталады. Сонымен, функциясы мен оның туындыларын (1.3)-ке қойғанда теңдеу тепе-теңдікке (ақиқат теңдікке) айналады.

1-есеп: функциясы ДТ-сының шешуі болама?

Шешу. Көрсетілген функция мен оның екінші туындысын берілген теңдеуге қоялық:

Жауап: иә, болады.

ДТ-ны шешу деп белгісіз функциясын туынды не дифференциал белгілерінен босатып, табуды айтамыз. Бұл ДТ-ның ретіне сай рет анықталмаған интеграл табуға әкеледі. Әрбір квадратура сайын шешуде жаңа интегралдау тұрақтысы С пайда болады. Құрамында тәуелсіз тұрақты бар, -ретті ДТ-ның барлық мүмкін шешуін қамтитын функциясы теңдеудің жалпы шешуі деп аталады. Ондай шешу айқын емес түрде табылса, оны ДТ-ның жалпы интегралы дейді.

Белгісіз функцияның және оның ()-ретке дейінгі (қоса алғанда) туындыларының аймақтың бір нүктесіндегі мәндерінің жиыны:

. (1.5)

ДТ-ның (есептің) бастапқы шарттары делінеді. Бұл мәндерді жалпы шешуге және оның (n-1)-ретке дейінгі туындыларына қойып, белгісізі бар алгебралық теңдеулер жүйесіне келеміз. Тұрақтылардың одан табылған нақты мәндерін жалпы шешудегі орындарына қойғаннан пайда болған функция ДТ-ның берілген бастапқы шарттарға қанағаттандыратын дербес шешуі деп аталады. ДТ-ның (1.5) түріндегі бастапқы шарттарға қанағаттандыратын дербес шешуін табу туралы есепті алғаш рет Коши қойып, ондай шешудің бар және біреу ғана екені туралы теореманы дәлелдеді.

DТ-мен қоса, белгісіз функцияның аймақтың дәйектендірілген нүктесіндегі мәндері

(1.6)

берілетін есептер класстары да кездеседі. Олар шекаралық есептер, (1.6) –шекаралық шарттар деп аталады.

2-дәріс. Коши есебі (бастапқы есеп). Айнымалылары ажыратылатын теңдеулер

Дәрістің мақсаты: коши есебінің (бастапқы есептің) қойылуын, сол есеп шешуінің бар және біреу ғана болуы туралы теореманы түсіндіру. Студенттерге айнымалылары ажыратылатын ДТ-ларды интегралдау әдістерін көрсету.

Бірінші ретті () DТ жалпы түрде және туынды арқылы шешілген түрде сәйкес:

(1.7)

деп жазылады. Бастапқы шарттары

(1.8)

түрінде беріледі. Белгісіз функция мен тәуелсіз айнымалы дифференциалдарының қатынасы болғандықтан бірінші ретті ДТ дифференциалдық түрде де

(1.9)

берілуі мүмкін.

Шешудің бар және жалғыз болуы туралы теорема.

Егер функциясы тұйық аймақта (тіктөртбұрышта, 3 суретті қара)

үзіліссіз, у бойынша шектелген дербес туындысы: бар болса, онда

кесіндісінде ДТ-сының (1.8): бастапқы шартына қанағаттандыратын дербес шешуі бар және ол біреу ғана; функциясы -де үзіліссіз дифференциалданады және .

3 сурет - Берілген нүктесі арқылы өтетін интегралдық қисық

Коши теоремасының шарттары орындалса, онда нүктесі арқылы теңдеуінің

тіктөртбұрышында жататын бір ғана интегралдық қисығы өтеді.

Айнымалылары ажыратылатын теңдеулер.

Егер (1.7) және (1.9) теңдеулеріндегі екі айнымалының функциялары жеке айнымалылар бойынша функциялардың көбейтіндісіне жіктелсе, олар айнымалылары ажыратылатын ДТ-лар қатарына жатады. Мысалы:

айнымалылары ажыратылатын теңдеулер. Қарапайым түрлендірулерден кейін айнымалылары ажыратылған:

теңдеулеріне келеміз. Бұл теңдіктерден мүшелеп анықталмаған интегралдар алсақ, берілген теңдеулердің жалпы шешулері не жалпы интегралдары табылады.

Айнымалылары ажыратылатын (1.1) теңдеуі:

үшін Коши есебінің шешуін табайық. Квадратура (1.1)-дің жалпы шешуін береді:

Бастапқы шартты пайдаланып: , оған қанағаттандыратын дербес шешуді табамыз. Енді есепте талап етілген нүктесі арқылы өтетін интегралдық қисықты дәлірек (1б)-сурет) тұрғызуға болады.

2-есеп. ДТ-ның жалпы шешуін (жалпы интегралын) табыңыз:

Шешу. Теңдеудің екі жағын да 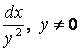өрнегіне көбейтсек, айнымалылары ажыратылған теңдеуге келеміз:

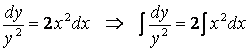Квадратураны орындап, берілген теңдеудің сәйкес жалпы интегралын немесе жалпы шешуін табамыз:

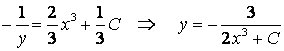3-есеп. Коши есебінің шешуін табыңыз және оған сай интегралдық қисықты тұрғызыңыз:

Шешу. Алдымен айнымалылары ажыратылған ДТ-ның жалпы шешуін табалық:

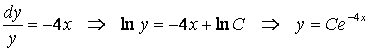Бастапқы шартты пайдаланып, интегралдау тұрақтысының мәнін табамыз:

Абсцисса осі Коши есебінің шешуі болатын функциясы графигінің – интегралдық қисықтың жатық асимптотасы болады (4-суретті қара).

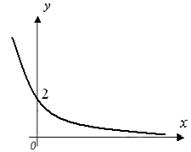
4 сурет - функциясының графигі

4-есеп. Коши есебінің шешуін табыңыз:

Шешу. Айнымалыларды ажыратып, теңдуді

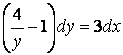түрінде жазалық. Оның жалпы интегралы

Бұған бастапқы шартты енгізсек: . Берілген бастапқы шартқа қанағаттандыратын дербес интеграл

түрінде жазылады.

3-дәріс. Біртекті, сызықтық және толық дифференциалды теңдеулер

Дәрістің мақсаты: тыңдаушыларды бірінші ретті ДТ-лардың интегралданатын түрлерімен: біртекті, сызықтық, толық дифференциалды және соларға келтірілетін теңдеулермен таныстыру.

1. Біртекті теңдеулер.

Кез келген t параметрі үшін шартына қанағаттандыратын функциясы m-дәрежелі біртекті функция деп аталады. Туынды арқылы шешілген (1.7) теңдеуінің оң жағы нөл дәрежелі біртекті функция: болса, ол біртекті ДТ деп аталады.

Егер және дәрежелері бірдей біртекті функциялар болса, онда (1.9) да біртекті ДТ-лар қатарына жатады. Ол (1.7)–ге оңай келтірілетін болғандықтан, соңғыда

(1.10)

жүйесі бойынша белгісіз функцияны алмастыралық.

Біртекті функцияның анықтамасындағы параметрді деп алып, (1.7)-нің оң жағын

түрінде жаза аламыз. Белгісіз функцияны алмастырғаннан кейін квадратура арқылы шешілетін теңдеуге келеміз:

;

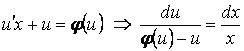болған ерекше жағдайда:

яғни DТ-ның интегралдық сызықтары координаталардың бас нүктесі арқылы өтетін түзулер үйірін құрайды.

5-есеп. ДТ-ның жалпы шешуін (жалпы интегралын) табыңыз:

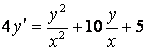Шешу. Берілгені айнымалылары бойынша біртекті теңдеу. Ондағы белгісіз функцияны алмастырып: , , айнымалылары ажыратылатын теңдеуге келеміз:

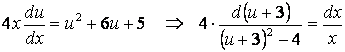Интегралдап, логарифмдерден құтылғанннан кейін берілген ДТ-ның жалпы интегралын:

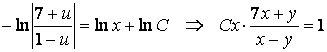
түрінде жазуға болады. Бұдан жалпы шешу

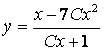2. Сызықтық теңдеулер.

Құрамында белгісіз функция мен оның туындылары тек бірінші дәрежеде ғана кездесетін теңдеу сызықтық DТ деп аталады. Бірінші ретті сызықтық DТ келтірілген түрде

(1.11)

деп жазылады. Мұнда , -да берілген үзіліссіз функциялар; болса, (1.11) біртекті, қарсы жағдайда: біртекті емес делінеді; (1.11)-ге сәйкес біртекті сызықтық теңдеу

айнымалылары ажыратылатын теңдеулер қатарына жатады. Оның жалпы шешуі:

, . (1.12)

Интегралдау тұрақтысын әзірше белгісіз u(х) функциясымен алмастырып,

(1.13)

біртексіз теңдеудің (1.11) шешуі болсын деп талап етейік; (1.13) функциясын және оның туындысын (1.11)–ге қойып, пайда болған тепе-теңдіктен белгісіз функцияны u(х) табамыз. Оны (1.13)–ге қойсақ, біртексіз теңдеудің жалпы шешуі табылады:

(1.14)

Қолданылған тәсіл ырықты тұрақтыны вариациялау (variatio-өзгеру, лат.): әдісі деп аталады. Есеп шығарғанда қорыту жолын қайталамай-ақ, (1.14) –ті дайын формула ретінде қолдануға болады.

6-есеп. Коши есебінің шешуін табыңыз:

Шешу. Берілген теңдеуді (1.11)-мен салыстырсақ:

Бұл функцияларды (1.14)-ке енгізелік:

Жалпы шешуге

бастапқы мәндерді қойсақ:

Коши есебінің шешуі:

3. Интегралданатын түрлерге келтірілетін теңдеулер. Біртекті теңдеулерге келтірілетін ДТ-лар

Дифференциалдық теңдеу

(1.15)

сызықтық түрлендірудің :

(1.16)

көмегімен біртекті ДТ-ға келтіріледі. Белгісіз тұрақтылар (1.15)-те функция аргументіндегі бөлшек-сызықтық өрнекте алмастырудан кейін бос мүшелер болмайтындай етіп таңдап алынады:

(1.17)

Алмастыруда (1.16):

болғандықтан берілген теңдеу (1.15) жаңа айнымалылар арқылы

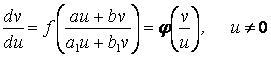1.18)

түрінде жазылады. Бұл бірінші ретті біртекті DТ, (1.10) тәріздес:

(1.19)

алмастыруының көмегімен айнымалылары ажыратылатын теңдеуге келтіріледі.

7-есеп. ДТ-ның жалпы инт егралын табыңыз:

Шешу. (1.17) жүйесін құрып, шешелік:

;

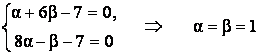1) , , 2) , алмастыруларын біртіндеп орындайық:

Соңғы теңдеуде айнымалыларды ажыратып, квадратураларды орындалық:

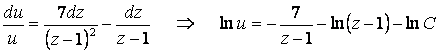Логарифмдерден құтылып, ескі айнымалыларға көшелік:

Бастапқы теңдеудің жалпы интегралы:

Бернулли теңдеуі.

Сызықтық емес бірінші ретті DТ

(1.20)

Бернулли теңдеуі деп аталады. Мұнда - берілген үзіксіз функциялар; және болғанда Бернулли теңдеуі сызықтық сәйкес біртекті және біртексіз DТ-ға айналады. Теңдеуді -ге көбейтіп, белгісіз функцияны алмастырайық:

. (1.21)

Түрлендірілген

теңдеуіне

белгілеулерін енгізсек, (1.11) типтес

1.22)

теңдеуіне келеміз.

Бернулли (1.22)-нің шешуін

(1.23)

түрінде іздеп, белгісіз , функцияларын олардың көбейтіндісі (1.23) біртексіз (1.22) теңдеуінің шешуі болсын:

(1.24)

деген талаптан табуды ұсынды. Әрі қарай шығару жолы тұрақтыны вариациялау әдісімен бірдей: функциясы (1.24) –те жақшаның ішіндегі өрнек нөлге тең болатындай етіп таңдап алынады. Табылған функцияны қайтадан (1.24) –ке қойып, айнымалылары ажыратылатын теңдеуге келеміз. Одан -ды тауып, -ға көбейтсек, нәтиже (1.14)-пен бірдей болады. Ақырында ескі айнымалыға көшу: жеткілікті. Бернулли теңдеуін біртексіз сызықтық теңдеуге келтірмей-ақ, ырықты тұрақтыны вариациялау немесе Бернулли әдісімен тура интегралдай беруге де болады.

8-есеп. ДТ-ның жалпы шешуін табыңыз:

Шешу. болғандықтан (1.16) алмастыруы:

түрінде орындалып, (1.11) теңдеуіне келтіреді:

Мұнда ; (1.14)-ті қолданып, жалпы шешуді табамыз:

;

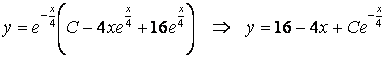4. Толық дифференциалды теңдеулер

Толық дифференциалды интегралдау.

Дифференциалдық түрдегі (1.9) теңдеуінің сол жағы қаралып отырған аймақта 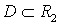дифференциалданатын бір 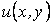функциясының дифференциалына тең болса:

(1.25)

онда ол толық дифференциалды теңдеу деп аталады. Бұл шарттың орындалуы үшін

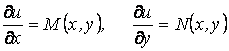(1.26)

болуы қажет және жеткілікті. Аралас дербес туындылар туралы теорема [1] бойынша

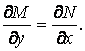(1.27)

Бұл шарт көбіне (1.9) –дың толық дифференциалды екенін тексеру үшін қолданылады. Жалпы, (1.25-27) шарттары қос-қостан тең қуатты (балама).

Егер (1.26) орындалса, онда:

(1.28)

Соңғы теңдік толық дифференциалды теңдеудің жалпы интегралы болады. Оны табу үшін (1.26) теңдеулерінің бірін сәйкес айнымалы бойынша интегралдаймыз. Екінші айнымалы әзірше дәйектендірілген деп саналады. Мысалы, бірінші теңдеуді бойынша интегралдасақ:

. (1.29)

Интегралдау тұрақтысы ретінде енгізілген белгісіз функциясын табу үшін (1.26) -дағы екінші шартты пайдаланымыз:

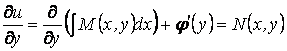Бұдан:

болсын делік. Табылған функциясын (1.29) – ға қойып, толық дифференциалы берілген (16.9) теңдеуінің сол жағына тең болатын функциясын табамыз. Бұл функцияны басқаша:

(1.30)

деп алып та табуға болды. Мұнда ал, ретінде -тен құрамында бар, бірақ, -де кездеспейтін қосылғыштар алынады.

9-есеп. ДТ-ның жалпы шешуін табыңыз:

Шешу. (19)-бен салыстырып:

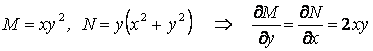яғни берілген теңдеудің толық дифференциалды ДТ екенін көреміз.

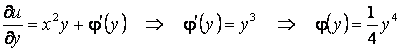Бастапқы теңдеудің жалпы интегралы

Интегралдаушы көбейткіш.

Егер (1.27) орындалмаса, онда (1.9) толық дифференциалды теңдеу емес. Бірақ, кейбір жағдайларда оны интегралдаушы көбейткіш деп аталатын функциясына көбейту арқылы толық дифференциалды теңдеуге келтіруге болады. Жалпы жағдайда интегралдаушы көбейткішті табу үшін дербес туындылы ДТ–ны шешуге тура келеді. Шынында да, интегралдаушы көбейткіш бар болса, онда:

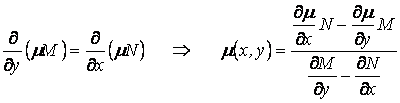(1.31)

Интегралдаушы көбейткіш бір айнымалының ғана: -тің немесе -тің функциясы болған жағдайда (1.31) –де сәйкес:

деп, интеграл алсақ:

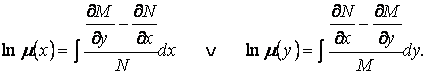(1.32)

1-мысал: Интегралдаушы көбейткішті тауып, теңдеуді шешіңіз:

(1)

Шешу: (1.27) шарты орындалмайды, өйткені

;

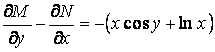(1.32)-нің біріншісінен:

Табылған функцияға көбейткеннен кейін (1)-ді

деп жазайық. Енді (1.27) орындалады және (1.30)-да:

Берілген теңдеудің жалпы интегралы:

4-дәріс. Шешудің бар және біреу ғана болуы туралы теореманың графиктік интерпретациясы

Дәрістің мақсаты: студенттерге Коши теоремасының геометриялық мағынасын - графиктік талқылауларын түсіндіру. Лагранж және Клеро теңдеулерін қарап, ДТ-ға параметр енгізу әдісін түсіндіру.

Туынды арқылы шешілген бірінші ретті ДТ (1.7) шешудің бар және біреу ғана болуы туралы теоремаға қанағаттандырады және (3 суретті қара) делік. Туындының геометриялық мағынасы бойынша

интегралдық қисығына нүктесінде жүргізілген жанаманың абсцисса осіне көлбеу бұрышы. Нүктелердің , демек, болатын геометриялық орны теңдеуінің изоклинасы (isos –тең, klino – көлбетемін, гр.) - теңкөлбеулігі деп аталады. Мұндай сызықтың нүктелерінде интегралдық қисықтың абсцисса осіне көлбеу бұрышы тұрақты, яғни қисығына жанамалар өзара параллель болып, бірдей бағытталады. Бұл бағыттар теңкөлбеулікті қуалай қойылған жебелермен ( векторларымен) көрсетіледі. Аймақтағы барлық , векторларының жиыны теңдеуінің бағыттар өрісі деп аталады. Бұрыштық коэффициенттің әртүрлі мәндері үшін теңкөлбеуліктер жүргізіліп, ДТ-ның бағыттар өрісі тұрғызылған делік; нүктесі арқылы өтетін, әрбір нүктесінде өріс бағыты - векторы оған жанама болатын (“өрісті бойлап” жүретін) сызық ізделініп отырған интегралдық қисық болады. Ол Коши есебінің: жуық шешуін береді.

Теңкөлбеуліктер жеткілікті жиі тұрғызылған болса, интегралдық қисықтың “көрші” теңкөлбеуліктер арасындағы доғасын жуықтап оған жүргізілген жанаманың кесіндісімен алмастыруға болады. Сондықтан нүктесі арқылы өтетін интегралдық қисығы ретінде жуықтап -ден екі бағытта да тұрғызылған, буындары “алдыңғы” теңкөлбеуліктің векторына параллель сынық сызық қабылданады.

Мысал ретінде (1.1) теңдеуінің нүктесі арқылы өтетін интегралдық қисығын тұрғызайық, немесе графиктік әдіспен Коши есебінің:

шешуін табайық.

Ізделініп отырған , интегралдық қисығы ордината осін қиып өте алмайды, өйткені нүктесінде функциясы анықталмаған. Демек, Коши теоремасына қанағаттандыратын аймағы оң жақ жарты жызықтықта орналасқан. Тең көлбеуліктер: , ордината осіне параллель түзулер. Ордината осі қисығының тік асимптотасы болады, өйткені да 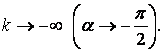Дәлелдеуіміз бойынша: және яғни

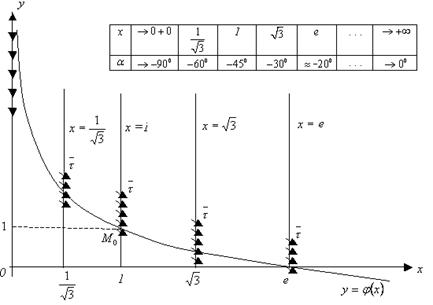
5 сурет - Теңкөлбеуліктер әдісіне

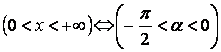Бұл шарттар үшін сәйкестік кестесін құрып, көрнектілік мақсатында осьтер бойынша әртүрлі масштабтар қабылдап, теңдеудің бағыттар өрісін және нүктесі арқылы өтетін интегралдық қисығын тұрғызалық (5 суретті қара).

ДТ-ға параметрлер енгізу әдісі.

Туынды арқылы шешілген (1.7) ДТ-сындағы үш айнымалының функциясы параметрлік түрде:

жазылуы мүмкін екені белгілі [1]. Алғашқы екеуін қаралып отырған аймақта өз аргументтері аргументтері бойынша дифференциалданатын функциялар деп санап, олардың дифференциалдарын теңдігіне қоялық:

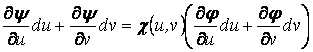Бұл теңдікті, мысалы, -ды тәуелсіз айнымалы, -ны белгісіз функция ретінде қарап, туынды арқылы шешілген бірінші ретті ДТ

түрінде жаза аламыз.

Бұлайша құрылған ДТ-ның шешуі квадратура арқылы табыла бермеуі мүмкін. Бірақ, оның жалпы шешуін таба алсақ, (1.33)-тің алғашқы екі теңдеуі бастапқы теңдеуінің параметрлік түрдегі жалпы шешуін береді:

Параметрлер енгізу немесе дифференциалдау әдісі деп аталатын бұл тәсілді теңдеуі немесе арқылы оңай шешілетін жағдайларда қолдану тиімді. Бұл жағдайларда пааметрлер ретінде сәйкес пен немесе пен алынады.

Лагранж теңдеуі.

Айнымалыларға пен қарағанда сызықтық бірінші ретті ДТ

(1.34)

Лагранж теңдеуі деп аталады. Мұндағы барлық коэффициенттер параметрінің қаралып отырған аймақта дифференциалданатын белгілі функциялары; десек, (1.34)-ті

(1.35)

түрінде жаза аламыз. Параметр -ны -тің функциясы деп есептеп, (1.35)-ті бойынша дифференциалдайық:

Енді -ны тәуелсіз айнымалы, -ті белгісіз функция ретінде қарасақ ДТ-ға келеміз:

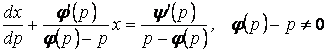. (1.36)

Бұл теңдеудің жалпы шешуін (1.14)-тің көмегімен тауып, оны (1.35)-ке қойсақ, Лагранжа теңдеуінің жалпы интегралын түрінде табуға да болады.

. (1.37)

Қажетті шарттар орындалған жағдайда (1.37)-ден параметрін қойып, Лагранж теңдеуінің жалпы интегралын түрінде табуға да болады.

2-мысал. ДТ-ны шешіңіз:

Шешу. Берілгені (1.35) түріндегі Лагранж теңдеуі:

Одан -ны -тің функциясы деп туынды табалық:

Бұл теңдікті (1.36) сызықиық ДТ түрінде жазып, оған (1.14)-ті қолданайық:

, ;

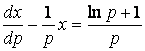Бұл өрнекті бастапқы теңдеуге қойып, оның жалпы шешуін параметрлік түрде табамыз:

Клеро теңдеуі.

Лагранж теңдеуінің (1.35) болғандағы жеке жағдайы

(1.38)

Клеро теңдеуі деп аталады. Оның сипаттық ерекшелігі ретінде бойынша дифференциалдағаннан кейін теңдеудің екі теңдікке ажырауын:

1) , 2)

айтуға болады. Бұл теңдіктерді (1.38)-бен қоса қарасақ: 1) Клеро теңдеуінің жалпы шешуін

2) оның параметрлік түрдегі ерекше шешуі деп аталатын

өрнектерін табамыз.

Бұдан Клеро теңдеуін шешудің практикалық ережесі [4] қорытылады: (1.38)-де -ны -ға алмастырып, теңдеудің жалпы шешуін аламыз. Оны бойынша дифференциалдап және пайда болған екі теңдеу (жалпы шешу және дифференциалдау нәтижесі) жүйесінен -ны жойып, Клеро теңдеуінің ерекше шешуін табамыз.

3-мысал. ДТ-ны шешіңіз:

Шешу. Практикалық ереже бойынша теңдеудің жалпы шешуі

бойынша дифференциалдағаннан кейін:

Ырықты тұрақтыны жойып, ерекше шешуді табамыз:

Жоғарғы ретті дифференциалдық теңдеулер

Реті төмендетілетін теңдеулер.

1. Құрамында белгісіз функция және оның бастапқы туындылары жоқ ДТ-лар.

I. Ең жоғарғы ретті туынды арқылы шешілген ДТ-ның (1.4) қарапайым түрі

(1.39)

берілсін; - қаралып отырған аймақта үзіліссіз функция. Теңдеудің ретін біртіндеп интегралдау арқылы төмендетуге болады. Әрбір квадратура сайын (1.39)-дің реті 1-ге кеміп, интегралдау тұрақтысы қосылып отырады. Теңдеудің жалпы шешуін

. (1.40)

II. Айталық, -ретті ДТ-ның (1.3) құрамына белгісіз функция мен оның -ретке дейінгі туындылары айқын түрде енбеген, яғни теңдеу

(1.41)

түрінде берілген болсын. Жаңа белгісіз функцияны:

, (1.42)

енгізу арқылы (1.41)-тің ретін бірлікке төмендете аламыз. Алмастырудан пайда болған -ретті

теңдеуінің жалпы шешуі табылса, онда кері алмастыру жасап, алдыңғы тармақта қаралған

теңдеуіне келеміз. Сонымен, реті ДТ-ның құрамына айқын түрде енбеген болса, теңдеудің ретін төмендету үшін ондағы ең төменгі ретті туындыны жаңа белгісіз функция деп қабылдаймыз.

10-есеп. ДТ-ның жалпы шешуін табыңыз:

Шешу. Дифференциал белгісінің астына енгізу тәсілін қолданып, теңдеуді тізбектей екі рет интегралдасақ, жалпы шешу табылады:

;

2. Құрамында тәуелсіз айнымалы жоқ ДT.

Тәуелсіз айнымалы х айқын түрде қатынаспаған 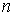-ретті ДТ

(1.43)

берілсін. Ескі белгісіз функцияны тәуелсіз айнымалының орнына қабылдап, жаңа белгісіз функцияны енгізелік. Сонда:

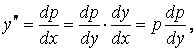
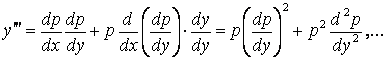(1.44)

Бұл теңдіктердің әрқайсысының оң жағындағы туындылардың ең жоғарғы реті сол жағындағылардан 1-ге кем. Оларды (1.42)-ке енгізсек, () -ретті ДТ

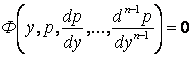(1.45)

пайда болады. Бұл теңдеудің жалпы шешуі табылса, ескі айнымалыға көшіп, оны

(1.46)

деп жазуға болар еді. Бұл айнымалылары ажыратылатын бірінші ретті ДТ.

4-мысал. Коши есебінің шешуін табыңыз:

Шешу. Берілген теңдеу үшін (1.45)-ні жазып, айнымалыларды ажыратайық:

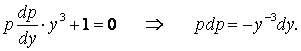
Теңдікті интегралдап, екенін ескерейік:

;

(1.46)-дің орнында:

теңдіктері болады. Интегралдағаннан кейін:

Бұдан (1;-1) нүктесі арқылы өтетін интегралдық қисық параболасы екенін көреміз.

2-модуль. Жоғарғы ретті сызықтық дифференциалдық теңдеулердің жалпы теориясы

5-дәріс. Коэффициенттері үзіліссіз сызықтық ДT-лар

Дәрістің мақсаты: коэффициенттері үзіліссіз және тұрақты жоғарғы ретті ДТ-лар жалпы теориясының негіздерін баяндау. Негізгі түсініктермен: шешулердің іргелік жүйесі (ШІЖ), Вронский анықтауышы (вронскиан), n-ретті біртекті және біртексіз теңдеулер жалпы шешулерінің құрылымы, т.б. таныстыру. Лиувилль формуласын келтіру.

Келтірілген түрде ((1.11), 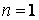) n-ретті біртексіз сызықтық DT

(2.1)

деп жазылады. Мұнда -да берілген үзіліссіз функциялар. Теңдеудің сол жағы – белгісіз функция мен оның туындыларының коэффициенттері 1, болып келген сызықтық комбинациясы қысқаша деп белгіленеді. Шартты түрде -ға қайталап дифференциалдау және сызықтық амалдар жиынтығын қолдануды белгілейтін рәміз: L (linea-сызық, лат.) сызықтық дифференциалдық оператор деп аталады. Егер болса, (2.1) біртекті делініп, қарсы жағдайда: біртексіз деп аталады. Біртексіз (2.1) және оған сәйкес біртекті сызықтық ДT қысқаша

(2.2)

деп жазылады.

Функция туындылары сияқты операторы да біртектілік және аддитивтік қасиеттерге ие:

Бұл оператор

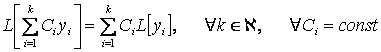(2.3)

болғандықтан да сызықтық деп аталады.

Сызықтық ДТ-лар (2.2) үшін интервалында (1.5) бастапқы шарттарына қанағаттандыратын шешудің бар және жалғыз болуы туралы теорема орындалады. Егер функциялары біртекті сызықтық теңдеудің (2.2) шешулері болса, онда (2.3)-1ен олардың кез келген сызықтық комбинациясы да сол теңдеудің шешуі болатынын байқаймыз. Векторлардың сызықтық тәуелділік және тәуелсіздік ұғымдары ортақ аймақта анықталған функцияларға да тән екені белгілі [1]; -ретті біртекті сызықтық ДТ-ның -да сызықтық тәуелсіз шешулерінің саны -нен артпайды. теңдеуінің -да сызықтық тәуелсіз кез келген дербес шешуінің жиынтығы

(2.4)

шешулердің фундаменттік(іргелік) жүйесі деп аталады. Сызықтық біртекті теңдеудің кез келген шешуі (2.4) функцияларының сызықтық комбинациясы түрінде өрнектеледі. Сондықтан

(2.5)

функциясы теңдеуінің жалпы шешуі болады. Мұнда -тәуелсіз ырықты тұрақтылар. Олардың әрқайсысы кез келген заттық мән қабылдай алады. Сонымен, шешулерінің іргелік жүйесі табылса, онда (2.2) –дағы біртекті теңдеуді шешілді деп есептеуге болады.

Теорема: -да -ретті туындылары бар және теңдеуіне қанағаттандыратын: функцияларының жиынтығы сол теңдеу шешулерінің іргелік жүйесі болуы үшін олардан құралған Воронский анықтауышы [1] интервалда нөлге тең болмауы:

қажет және жеткілікті.

Шешулерінің іргелік жүйесі вронскиан біртекті теңдеулерінің коэффициенттерімен байланыстыратын

, (2.6)

қатынасы Лиувилль формуласы деп аталады. Ол, мысалы, екінші ретті біртекті сызықтық ДТ-ның кез келген нөлдік емес дербес шешуі белгілі болса, оның жалпы шешуін квадратура арқылы табуға мүмкіндік береді.

Біртексіз (2.1) теңдеуінің кез келген дербес шешуі және оған сәйкес біртекті теңдеудің жалпы шешуі (2.5) белгілі болса, яғни

болса, онда функциясы бастапқы біртексіз сызықтық ДТ-ның жалпы шешуі болады. Мұндай құрылым, мысалы, (1.40)-та орын алып тұр.

6-дәріс. Коэффициенттері тұрақты сызықтық ДT

Дәрістің мақсаты: коэффициенттері тұрақты -ретті сызықтық ДТ-ларды: біртектісін сипаттама теңдеулерінің түбірлеріне қарай ШІЖ құрып, ал, біртексізін оң жағы квазимүшелік болса, анықталмаған коэффициенттер, жалпы, Лагранждың тұрақтыларды вариациялау әдістерімен шешуді баяндау.

Сызықтық біртекті ДТ.

Біртекті сызықтық

(2.7)

теңдеуінде болсын. Дифференциалданатын функция мен оның туындыларының сызықтық комбинациясы -да тек олар бір класқа қарасты функциялар болған жағдайда ғана нөлге тепе-тең бола алады. Мұндай қасиет тек экспонентаға ғана тән. Сондықтан (2.7)-тің дербес шешуі

(2.8)

түрінде ізделінеді. Бұл өрнектерді (2.7)-ке қойып, екенін ескерсек,

(2.9)

дәрежелі алгебралық теңдеуге келеміз. Ол (2.7) ДТ-сының мінездеме теңдеуі деп аталады. Оның түбірі бар; (2.7)-тің жалпы шешуінің құрылымы оның мінездеме теңдеуі түбірлерінің түріне байланысты. Жеке жағдайларды қарастыралық.

1. Мінездеме теңдеудің (2.9) барлық түбірлері де жәй (әртүрлі) және заттық түбірлер: болсын. Оларға сәйкес дербес шешулер

іргелік жүйе құрайды. Өйткені олардың вронскианы:

Мұндағы сандарының дәрежелерінен тұратын анықтауыш дәрежелі анықтауыш немесе Вандермонд анықтауышы деп аталады; (2.7) –нің жалпы шешуі

(2.10)

түрінде жазылады.

11-есеп. ДТ-ның жалпы шешуін табыңыз:

Шешу. Мінездеме теңдеудің

жай заттық түбірлері бар:

ДТ-ның жалпы шешуі

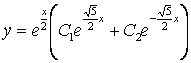2. Мінездеме теңдеудің (2.9) түбірлері заттық сандар, бірақ, кейбіреулері өзара тең (еселі) болсын. Мысалы, түбірі еселі болса, онда (2.7)-нің жалпы шешуінде оған

(2.11)

қосылғышы сай келеді. Мысалы, (1.39)-ғе сәйкес біртекті теңдеу үшін

3. Түйіндес комплекс сандар (2.9)-дың жәй түбірлері болсын. Бұл түбірлерге (2.7)-нің жалпы шешуінде

(2.12)

қосылғышы сай келеді.

Мысалы, (1.2) үшін мінездеме теңдеу және оның түбірлері: .

Жүктің (2 суретті қара) тербеліс заңы – (1.2)-нің жалпы шешуі

(2.13)

Интегралдау тұрақтыларын алмастырып:

жүктің өзіндік гармониялық тербелісінің заңын аламыз:

(2.14)

Тербелістің: амплитудасы ( нүктесінің тербеліс центрінен 0 ең үлкен ауытқуы), -фазасы, -бастапқы базасы, -оралу жиілігі. Тербеліс периоды

Теориялық тұрғыдан тербеліс шексіз ұзақ жалғасуы тиіс. Іс жүзінде тербеліс кедергілі ортада орын алады. Мысалы, ортаның кедергісі жылдамдыққа пропорционал-кедергі күші болса, онда қозғалыстың дифференциалдық теңдеуі

түрінде жазылады. Оның жалпы шешуі

немесе

өшер (-ортаның кедергі коэффициенті) гармониялық тербелістің заңы болады.

Бос мүшесі периодты функция (ұйытқытушы күш) болып келген коэффициенттері тұрақты екінші ретті біртексіз сызықтық ДТ материялық нүктенің кедергісіз не кедергілі ортадағы еріксіз тербелістерін сипаттайды.

12-есеп. Коши есебінің шешуін табыңыз

Шешу. Мінездеме теңдеудің

түбірлері жай комплекс сандар

Жалпы шешу мен оның туындысы:

Бұларға бастапқы мәндерді қойсақ:

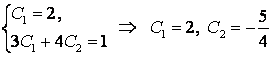Коши есебінің шешуі

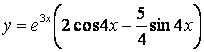Коэффициенттері тұрақты сызықтық біртексіз квазимүшелікті ДT

Анықталмаған коэффициенттер әдісі.

Коэффициенттері тұрақты n-ретті сызықтық біртексіз ДТ-ның

(2.15)

жалпы шешуін табу үшін енді оның кез келген бір дербес шешуін тапсақ болғаны. Ол үшін анықталмаған коэффициенттер және тұрақтыларды вариациялау (1.13) әдістері қолданылады.

Егер (2.15)-тің оң жағы квазикөпмүшелік деп аталатын

(2.16)

түрде берілсе, онда ізделініп отырған дербес шешудің де түрін соған ұқсастырып,

(2.17)

деп аламыз. Мұнда - сәйкес дәрежелі берілген көпмүшеліктер, ал, -дәрежелері бірдей, коэффициенттері әзір белгісіз көпмүшеліктер. Белгісіз коэффициенттер функциясы (2.15)-нің шешуі болсын деген талаптан анықталады. Егер (2.9)-дың еселі түбірі болса, онда (2.15) теңдеуімен сипатталатын процесте резонанс құбылысы бар деп, ізделінуші дербес шешуге көбейткіші енгізіледі. Резонанс жоқ болса, онда болғаны.

13-есеп. ДТ-ның жалпы шешуін табыңыз:

Шешу. Сәйкес біртекті теңдеудің мінездеме теңдеуінің

екі еселі заттық түбірі бар. Демек,

Резонанс жоқ болғандықтан берілген біртексіз теңдеудің дербес шешуін

функциясы түрінде іздейміз. Оның өзін жеке туындыларын: , бастапқы ДТ-ға қойып, пайда болған жүйені шешейік:

Талап етілген жалпы шешу

14-есеп. ДТ-ның жалпы шешуін табыңыз.

Шешу. Алдыңғы есептегі сияқты сәйкес біртекті теңдеудің мінездеме теңдеуінің түбірлерін табайық:

Біртекті теңдеудің жалпы шешуі

«Үш еселі» резонанс бар болғандықтан:

Бұл функцияларды берілген ДТ-ға қойсақ:

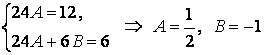Ізделініп отырған жалпы шешу

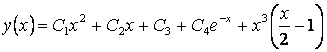Теорема. Егер функциялары сәйкес теңдеулерінің шешулері болса, олардың қосындысы теңдеуінің шешуі болады.

Теореманың тұжырымы операторының аддитивтік қасиетінен туындайды.

5-мысал. ДТ-ның жалпы шешуін табыңыз:

Шешу. Алдыңғы есептердің шығару жолдарын ұстанайық:

Дербес шешу туралы теореманы қолданып, теңдеуінде резонанс орын алатынын ескерсек:

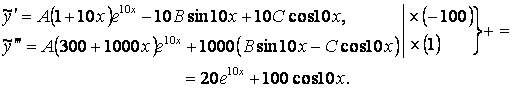
Сызықтық тәуелсіз функцияларының коэффициенттерін теңестірейік:

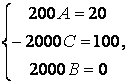
Ақырында, жалпы шешу

.

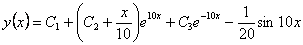Лагранждың ырықты тұрақтыларды вариациялау әдісі.

Сызықтық біртексіз ДТ-ның оң жағы “арнаулы” түрде (2.16) берілмеген болса, онда теңдеудің жалпы шешуін табу үшін ырықты тұрақтыларды вариациялау әдісі қолданылады. Ол үшін алдымен сәйкес біртекті ДТ-ның іргелік шешулер системасын (2.4) тауып, оның жалпы шешуін (2.5) құрамыз. Одан кейін интегралдау тұрақтылары С_і вариацияланады, яғни оларды әзірше белгісіз функциялар деп есептеп,

(2.18)

функциясының (2.1) немесе (2.15) біртексіз теңдеуіне қанағаттандыруы талап етіледі. Аталған белгісіз функцияларды табу үшін төмендегідей тәсілмен сызықтық теңдеулер системасы құрылады: (2.15)-дің туындысын тауып, оның түрі С_і коэффициенттері тұрақты болғандағыдай болсын деп шарт қойылады. Бұл талап

қатынастарына пара-пар. Осы процесті ()-қадамға дейін жалғастырайық:

Соңында:

Функцияны (2.18) және оның табылған туындыларын біртексіз теңдеуге қойып,

екенін ескерсек, сызықтық теңдеу системасына:

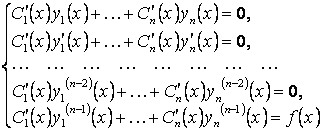(2.19)

келеміз. Система анықтауышы

өйткені (2.4) функциялары -да сызықтық тәуелсіз [1]. Олай болса, (2.19) үйлесімді және бір ғана шешуі бар:

Бұлар -да үзіліссіз, демек, интегралданатын функциялар:

Табылған функцияларды (2.18)-ке қойып, берілген біртексіз ДT-ның жалпы шешуін аламыз:

. (2.20)

Мұнда да мен функцияларының қосындысы ретінде жалпы шешудің құрылымы сақталатыны байқалады.

15-есеп. Коши есебінің шешуін табыңыз:

Шешу: .

(2.19) жүйесін құрып, шешелік:

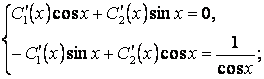
Берілген теңдеудің жалпы шешуі мен оның туындысы:

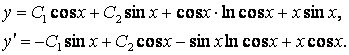
Бастапқы шарттарға қанағаттандырсақ: . Талап етілген дербес шешу

7-дәріс. Сызықтық ДТ-лар жүйелерінің жалпы теориясы

Дәрістің мақсаты: студенттерді сызықтық ДТ-лар жүйесі жалпы теориясының векторлық-матрицалық түрде баяндалған негіздерімен (анықтамалар, шешудің қасиеттері, ШІЖ, іргелік матрица, вронскиан, Лиувилль формуласы, т.б. түсініктер) таныстыру.

Сызықтық біртекті жүйелер.

Сызықтық біртекті ДТ-лардың жүйесі

(2.21)

түрінде, ал, векторлық-матрицалық белгілеулерде

, (2.22)

деп жазылады. Мұнда - белгісіз функциялардың коэффициенттерінен тұратын жүйе матрицасы, - аралығында берілген үзіліссіз функциялар (немесе сандар), - белгісіз функциялар векторы (ұстыншасы); интервалында (2.21) немесе (2.22) жүйесі Коши теоремасының шарттарына қанағаттандырады.

Айталық

(2.23)

векторы (2.22) жүйесінің шешуі болсын. Векторлар жүйесінің Вронский анықтауышын (вронскианын) бұрынғыша

(2.24)

деп белгілесек, онда болғанда (2.23) векторлары интервалында сызықтық тәуелсіз және керісінше. Интервалдың кем дегенде бір нүктесінде болса, онда бұл шарт аралықтың барлық нүктелерінде де орындалады.

Қалыпты жүйенің -да сызықтық тәуелсіз кез келген шешуінің жиынтығын оның шешулерінің іргелік жұйесі (ШІЖ) дейміз. Тік жолдары ШІЖ құрамындағы векторлар болып келген матрицасы (2.22) жүйесінің іргелік матрицасы деп аталады. Координталары тәуелсіз ырықты тұрақты вектор үшін (2.22) жүйесінің жалпы шешуі

(2.25)

түрінде жазылады.

Бастапқы шарттары түрінде берілген Коши есебін шешу үшін (3.13)-ке мәнін қойып, тұрақты вектордың сәйкес мәнін табамыз:

Табылған мәнді (2.25)-ке қойып, Коши есебінің шешуін аламыз:

Коши матрицасы деп аталатын матрицасының көмегімен Коши есебінің шешуін

(2.26)

түрінде беруге болады.

Лиувилль формуласы (2.22) жүйесі үшін

(2.27)

түрінде жазылады.

Сызықтық біртексіз жүйелер.

Бос мүшелерінің кем дегенде біреуі интервалында нөлге тепе-тең болмаса, сызықтық ДТ-лардың қалыпты жүйесі

(2.28)

біртексіз делінеді. Қаралып отырған аралықта нөл-векторға тепе-тең емес вектор-функциясын енгізіп, (2.28)-ді матрицалық түрде

(2.29)

жазайық. Коэффициенттерінің үзіліссіздік аймағында (2.28) немесе (2.29) жүйесі Коши есебінің шешуі бар және біреу ғана болуы туралы теореманың шарттарына қанағаттандырады. Қаралған (2.21)-ді біртексіз (2.28) жүйесіне сәйкес біртекті жүйе дейміз.

Айнымалы матрицаның туындысы оның элементтерінің туындыларынан тұратынын ескеріп, тура қою арқылы

(2.30)

векторы (2.29) жүйесінің шешуі екеніне көз жеткізуге болады. Мұнда бірінші қосылғыш (2.29)-ға сәйкес (2.22) біртекті жүйесінің жалпы шешуі де, біртексіз (2.29) жүйесінің кез келген дербес шешуі. Сондықтан сәйкес біртекті жүйе шешілген болса, біртексіз жүйенің шешуін табу үшін оның қандай да болмасын бір дербес шешуін тапсақ болғаны. Ол үшін Лагранж ұсынған төмендегі әдісті қолдануға болады.

Лагранждың ырықты тұрақтыны вариациялау әдісі.

Біртекті (2.22) жүйесінің жалпы шешуі (2.25) түрінде табылған делік. Мұндағы тұрақты векторды енді әзірше белгісіз вектор-функция деп алып, оны

(2.31)

векторы (2.29) біртексіз жүйесінің шешуі болатындай етіп таңдап алалық. Болжамды шешуді (2.29) жүйесіне қояйық:

Біртекті (2.22) жүйесі үшін іргелік матрица болғандықтан

. (2.32)

Соңғы -ға қарағанда сызықтық біртексіз алгебралық теңдеулердің жүйесі үйлесімді, бір ғана шешуі

бар. Өйткені оның анықтауышы іргелік матрицаның анықтауышы. Интегралдағаннан кейін

немесе (шартты түрде)

. (2.33)

Кез келген тұрақты вектор үшін (2.31) біртексіз (2.29) жүйесінің жалпы шешуін, ал болғанда оның дербес шешуін береді және сызықтық біртексіз ДТ-лар жүйесі жалпы шешуінің құрылымы туралы бұрын айтылған тұжырымды растай түседі.

Көп жағдайларда біртексіз (2.28) жүйесін -ретті бір сызықтық ДТ-ға келтіру арқылы интегралдау тиімді.

8-дәріс. Коэффициенттері тұрақты сызықтық жүйелер

Дәрістің мақсаты: алдыңғы дәрісте баяндалған негізгі заңдылықтар мен әдістерді (сипаттама теңдеулер, белгісіз функцияларды жою, сызықтық ДТ-лар жүйесіне қолдану, тиімді әдісті таңдау.

Мінездеме теңдеулер жүйесі.

Енді (2.28)-те барлық коэффициенттер берілген сандар деп, сызықтық біртексіз ДТ-лар жүйесін

(2.34)

қарайық. Сызықтық ДТ-лардың қалыпты жүйелері туралы бұрын айтылғандардың бәрі (2.34) үшін де орындалады.

Сәйкес бәртекті

, (2.35)

жүйесінің іргелік матрицасын табу үшін сызықтық алгебраның әдістері қолданылады. Сандық матрицаның (оператордың [1]) мінездеме теңдеуі

(2.36)

(2.35) жүйесінің мінездеме теңдеуі болады. Ол (2.35)-ке балама коэффициенттері тұрақты -ретті біртекті сызықтық ДТ-ның мінездеме теңдеуімен ((2.16)) бірдей.

Алгебралық теңдеудің (2.36) жәй (еселіктері 1-ге тең) заттық түбірлері болған жағдайды қараумен шектелейік. Мұндай әрбір түбіріне ( матрицасының меншікті мәніне) оператордың бір меншікті векторы , ал, оларға (2.35) жүйесінің бір шешуі сай келеді. Меншікті векторлар, демек, жүйе шешулері сызықтық тәуелсіз. Соңғылар, (2.35) жүйесінің іргелік матрицасын

(2.37)

құрайды. Нәтижесінде біртекті жүйенің жалпы шешуі табылады:

. (2.38)

Біртексіз жүйенің дербес не жалпы шешуін Лагранж әдісімен немесе жүйені (2.15) түріндегі коэффициенттері тұрақты -ретті сызықтық біртексіз ДТ-ға келтіру арқылы табуға болады.

16-есеп. ДТ-лар жүйесін шешіңіз:

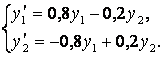
Шешу. Берілген сызықтық біртекті жүйенің мінездеме теңдеуінің

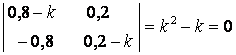
түбірлері: . Оларға сәйкес меншікті векторларды: , табайық;

1) , .

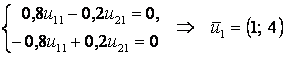Мұнда ыңғайлырақ болуы үшін еркін айнымалының мәні деп алынған.

2) , .

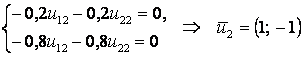Шешудің іргелік жүйесі:

Жүйенің жалпы шешуі:

. (1)

Тексеру. Берілген теңдеулерді мүшелеп қоссақ:

Табылған шешудегі функцияларды да қоссақта, осы қорытындыға келеміз.

Коэффициенттері тұрақты екінші ретті сызықтық ДТ немесе екі сызықтық ДТ жүйесі мінездеме теңдеуінің түбірлері таза жорамал сандар болған жағдайда тербелмелі қозғалысты сипаттайды. Мысалы, (1.2)-ні ДТ-лардың қалыпты жүйесі ретінде

деп жазуға болады. Оның мінездеме теңдеуінің түбірлері таза жорамал сандар:

Жүктің (2 суретті қара) тербеліс заңы (2.13) немесе (2.14) түрінде жазылады.

6-мысал. ДТ-лар жүйесінің жалпы шешуін табыңыз:

Шешу. Жүйенің мінездеме теңдеуінің

түбірлері . Оларға сәйкес меншікті векторларды табайық:

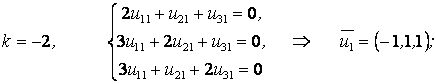
2) ;

3) .

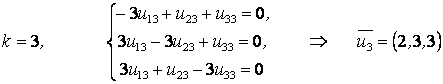Қаралған сызықтық біртекті алгебралық теңдеулер жүйелері матрицаларының ранглері 2-ге тең. Сондықтан олардың бәрінде де үшінші теңдеу артық, ал, еркін белгісіз деп саналған.

Шешулердің іргелік жүйесі:

Жүйенің жалпы шешуі:

Белгісіз функцияларды жою әдісі.

Бұл тарауда айтылғандардан ДТ-ның қалыпты жүйесі бір -ретті ДТ-ға балама және керісінше екенін байқаймыз. Олай болса, (2.34) жүйесін бір -ретті коэффициенттері тұрақты сызықтық біртексіз ДТ-ға келтіруге болады. Ол үшін теңдеулердің бірін, мысалы, біріншісін бойынша мүшелеп рет, қалғандарын рет дифференциалдап, берілген және дифференциалдау арқылы табылған теңдеулерден белгісіз функциялары мен олардың туындыларын жоямыз. Нәтижесінде (2.2) түріндегі ДТ-ға келеміз.

17-есеп. Белгісіз функцияларды жою әдісімен 16-есептегі жүйені шешіңіз.

Шешу. Бірінші теңдеуді мүшелеп дифференциалдап нәтижені «Тексерудегі» теңдікпен қоса қарасақ:

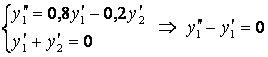Бұл коэффициенттері тұрақты екінші ретті сызықтық біртекті ДТ. Оның және берілген жүйенің мінездеме теңдеулері бірдей. Демек, алынған теңдеудің жалпы шешуі.

Енді теңдігін интегралдайық:

Табылған функцияларды жүйе теңдеулерінің біріне қойып, интегралдау тұрақтысын табамыз. Сонда жүйенің шешуі бұрынғы (1) түрінде жазылады.

7-мысал. Ырықты тұрақтыларды вариациялау әдісімен Коши есебінің шешуін табыңыз:

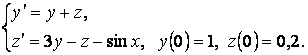(1)

Шешу. Сәйкес сызықтық біртекті жүйенің

(2)

мінездеме теңдеуін құрып, шешелік:

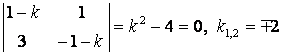Табылған меншікті мәндерге сай меншікті векторларды табайық:

1) , .

2) , .

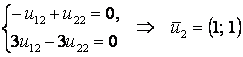Сонысен, шешулердің іргелік жүйесі:

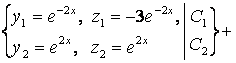Оның жалпы шешуі

Әрі қарай Лагранж әдісіндегі (2.31,32) теңдеулерін құрып, шешейік:

; (3)

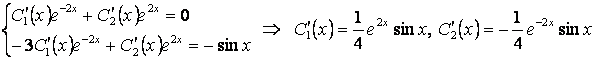Интегралдағаннан кейін:

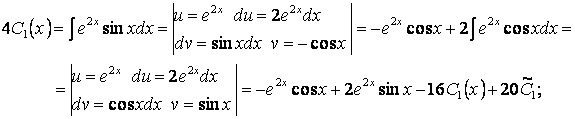
Бұл нәтижені пайдалану үшін алмастыруын жасасақ:

Табылған функцияларды (3)-ке қойып, (1)-дің жалпы шешуін табамыз:

. (4)

Бастапқы шарттарды қолдансақ:

Коши есебінің шешуі:

Бұл мысалда белгісіз функцияларды жою және анықталмаған коэффициенттер әдістерін тізбектей пайдалану табылған нәтижеге тезірек әкеледі. Шынында да, теңдеулерді мүшелеп қосайық және біріншісін бойынша дифференциалдайық:

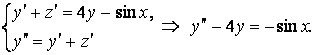
Пайда болған коэффициенттері тұрақты екінші ретті сызықтық біртексіз ДТ-ны анықталмаған коэффициенттер әдісімен шешейік:

;

Шарт бойынша болғандықтан жүйенің жалпы шешуі (4) түріне келеді.

3-модуль. Екінші ретті сызықтық ДТ-лар үшін шекаралық есептер

9-дәріс. Шекаралық есептердің қойылуы

Дәрістің мақсаты: студенттерге екінші ретті сызықтық ДТ-үшін шекаралық есептің әртүрлі шекаралық шарттар жағдайында қойылуын түсіндіру. Шекаралық шарттарды Коши шарттарымен салыстыру. Шекаралық есеп шешуінің бар және біреу ғана болуы туралы теореманы баяндау.

Сызықтық біртексіз ДТ (2.1) болғанда

(3.1)

түрінде, ал, оған сәйкес біртекті ДТ

(3.2)

болып жазылады. Мұндағы қаралып отырған аймақта үзіліссіз функциялар. Бұл теңдеулер (3.1-2) үшін кез келген -ретті (2.2) теңдеулері туралы айтылған тұжырымдар орындалады. Коши есебі үшін бастапқы шарттар

(3.3)

түрінде беріледі. Бастапқы есептің шешуі сандарының кез келген мәндері үшін де бар және біреу ғана.

Бір қатар физикалық есептерде ДТ-ның шешуін берілген бастапқы шарттар бойынша емес, оның интервалдың шеткі нүктелеріндегі мәндері арқылы іздеуге тура келеді. Оларды шекаралық есептер деп, ал, берілген мәндерді шекаралық шарттар дейді. Шекаралық шарттарды аралығы үшін жалпы түрде

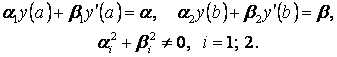(3.4)

деп жазуға болады. Егер болса, (3.4) шарттарын біртекті деп, ал қарсы жағдайда біртексіз деп атаймыз. Мұны қандай да болмасын , функциялары (3.4)-ке болғанда қанағаттандырса, олардың сызықтық комбинациясы да: , сол шартқа қанағаттандырады деп түсінеміз. Егер теңдеуде де (3.2), қойылған шарттар да біртекті болса, онда шекаралық есеп біртекті делінді. Ал, олардың кемінде біреуі (теңдеу немесе шарт) біртексіз болса, шекаралық есепті біртексіз дейміз. Периодтық түрдегі деп аталатын:

, (3.5)

шекаралық шарттар да кездеседі. Олар біртекті шекаралық шарттарға жатады.

Шекаралық есептерді шешу Коши есебін шешу тәртібі бойынша орындалады. Алдымен (3.1) немесе (3.2) түрінде берілген теңдеудің жалпы шешуін тауып, оны берілген шекаралық шарттарға қоямыз. Пайда болған алгебралық теңдеулер жүйесінен интегралдау тұрақтылары табылады.

8-мысал. Интервалда берілген шекаралық есепті: 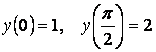шешіңіз.

Шешу. Берілген біртексіз теңдеудің дербес шешуі , ал, оған сәйкес біртекті теңдеудің жалпы шешуі бар. Олардың қосындысын шекаралық шарттарға қойсақ: . Ізделініп отырған шешу .

Коэффициенттері және бос мүшесі кесіндісінде үзіліссіз функциялар болатын екінші ретті сызықтық ДТ жалпы түрде

. (3.6)

деп жазылады. Ол болғанда теңдеуді -ға бөлу арқылы (3.1) түріне келтіріледі. Бірақ, шекаралық есептерді зерттеуде кесіндінің жеке нүктелерінде болатын жағдайлар да қамтылады. Оларды (3.6) теңдеуінің ерекше нүктелері дейміз. Кесіндіні бөлшектеу мүмкіндігін ескеріп, ерекше нүктелер кесіндінің шеткі нүктелерімен дәл келеді, яғни немесе деуге болады. Бұл жағдайларда сәйкес шекаралық шартты шешудің немесе мәндерінің шектелген болуы туралы талаппен алмастыруға болады. Кейде бұл талаптардың орнына шешу модулінің өсуі туралы шарттарды:

(3.7)

қабылдауға болады.

Коши теоремасынан (3 суретті қара) бастапқы есептің қойылуында шешудің бүкіл кесіндісінде бар болуы талап етілмейді. Шешу бастапқы нүктесінің белгілі бір аймағында анықталған болса болғаны. Ал, шекаралық есепте шешудің бүкіл кесінді бойында бар болуы талап етіледі және оның біреу ғана болуы міндетті емес. Осындай маңызды ерекшеліктердің салдарынан шекаралық есептің шешуі ылғи табыла бермейді.

Біртекті шекаралық есеп кем дегенде бір нөлдік емес шешуі бар болғанда ғана шешілетін есептер қатарына жатады және функциясы да оның шешуі болады. Сондықтан біртекті шекаралық есептің нөлдік емес шешуі тек тұрақты көбейткішке дәлдікпен ғана анықтала алады.

Теорема (шекаралық есептің шешуі бар және біреу ғана болуы туралы): (3.1) ДТ-ның кез келген (3.4) шекаралық шарттарына қанағаттандыратын бір ғана шешуі бар болу үшін оған сәйкес біртекті есептің ((3.2) ) тек қана нөлдік шешуі болуы қажет және жеткілікті.

10-дәріс. Штурм-Лиувилль есебі

Дәрістің мақсаты: Штурм-Лиувилль есебі коэффициенттері үзіліссіз сызықтық екінші ретті ДТ үшін жалпы шекаралық есептің жеке жағдайы екенін көрсету. Сызықтық алгебрадан белгілі оператордың меншікті мәндері мен меншікті функциялары және кесіндіде ортогональ функциялар туралы түсініктерді қолдану. Шеттік есептің шекаралық функциялары, мысалы, Грин функциясы туралы ұғымды беріп, оның қатысуымен шекаралық есеп шешуінің интегралдық функциясын келтіру.

Ыңғайлы болуы үшін (3.6)-ға сызықтық дифференциалдық операторды

(3.8)

енгізіп, екінші ретті біртекті ДТ-ны

. (3.9)

қарайық. Бұл теңдеудің (3.4) шарттарына болғанда қанағаттандыратын нөлдік емес шешуін табу туралы есеп Штурм-Лиувилль есебі деп аталады. Параметрдің Штурм-Лиувилль шекаралық есебінің шешуі бар болатын мәндерін операторының меншікті мәндері деп, ал, оларға сәйкес шешулерін оператордың немесе есептің меншікті функциялары деп атаймыз.

Тәжірибелік зерттеулерде (3.8) операторын

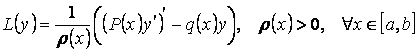түрінде қолдану ыңғайлырақ деп саналады. Мұнда

;

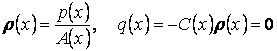Кесіндіде -үзіліссіз, ал, - үзіліссіз дифференциалданатын функциялар; оператордың салмақ функциясы делінеді.

Штурм-Лиувилль есебінде меншікті мәндер теріс емес сандардың өспелі тізбегін

құрайды және сандық қатары ылғи да жинақты. Меншікті мәндер тізбегіне меншікті функциялар тізбегі

. (3.10)

сай келеді. Тұрақты көбейткішке дейінгі дәлдікпен әрбір пеншікті мәнге сәйкес жалғыз ғана меншікті функция табылады. Периодтық түрдегі шекаралық шарттар (3.5) жағдайында бір меншікті мәнге сызықтық тәуелсіз екі меншікті функция сай келуі де мүмкін.

Әртүрлі және меншікті мәндеріне сай және меншікті функциялары

теңдігіне қанағаттандырады. Олар кесіндісінде салмағымен ортогональ [1] функциялар деп аталады. Бұл мағынада өрнегін (3.10) меншікті функциялар жүйесі үшін ортогональдаушы көбейткіш деуге болады.

Теорема: кесіндісінде үзіліссіз дифференциалданатын, үзбе-үзіліссіз екінші туындысы бар, (3.4) біртекті () шекаралық шарттарына қанағаттандыратын функциясы (3.10) меншікті функциялар жүйесі бойынша абсолют және бірқалыпты жинақты

қатарына жіктеледі. Қатар коэффициенттері

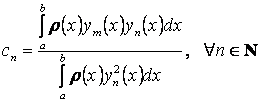Шектік есептің шекаралық функциялары. Грин функциясы.

Кесіндіде біртекті шекаралық есепті:

(3.11)

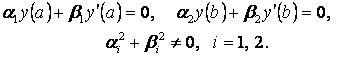(3.12)

қарайық. Теңдеудің (3.11) іргелік шешулер жүйесін десек, шекаралық есептің кез келген екі (әртүрлі) дербес шешулері

түрінде жазылады.

Кез келген және шекараларын алып, кесіндісінде нөлге тепе-тең емес, бірақ, нүктесінде

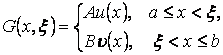
функциясын құрайық. Бұл функция қаралып отырған аймақтың -ден басқа нүктелерінің бәрінде (3.11-12) шекаралық есебінің шешуі болады. Ырықты тұрақтыларды

теңдеулерінен анықтап, функциясының нүктесінде де үзіліссіз болуын, ал, оның туындысының сол нүктеде берілген секіріске ие болуын қамтамасыз етуге болады.

Келтірілген шарттардың бәріне қанағаттандыратын функциясын болғандағы Штурм-Лиувилль жүйесі (есебі) үшін Грин функциясы деп аталады. Интегралдық теңдеудің

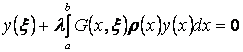
әрбір шешуі (3.12) шкаралық шарттары үшін

теңдеудің де шешуі болады және керісінше екені, яғни бұл теңдеулердің эквивалентті (теңмағыналы) екені дәлелденген.

11-дәріс. ДТ-лардың қалыпты жүйесі

Дәрістің мақсаты: студенттерді ДТ-лар жүйесінің жалпы, канондық және қалыпты түрлерімен таныстыру. Қалыпты жүйенің интегралы және алғашқы интегралы ұғымдарын беріп, симметриялы түрдегі қалыпты жүйеден интегралданатын комбинацияларды бөліп шығару әдістерін үйрету. Қалыпты жүйе үшін Коши есебінің қойылуын, оның шешуінің бар және біреу ғана болуы туралы теореманы баяндау.

ДТ-лар жүйесі жалпы түрде былай жазылады:

. (3.13)

Мұнда - тәуелсіз айнымалы, - белгісіз функциялар, қалған аргументтер олардың -ретке дейінгі туындылары. Жүйені (3.13) шешуі деп ондағы барлық белгісіз функцияларды табуды айтамыз.

Керекті шарттар орындалған жағдайда (3.13) жүйесін белгісіз функциялардың ең жоғарғы ретті туындылары арқылы шешуге болады:

. (3.14)

Мұны ДТ-лар жүйесінің канондық түрі дейді. Жаңа белгісіз функциялар енгізіп, (3.14) жүйесін туындылар арқылы шешілген бірінші ретті теңдеудің жүйесі

(3.15)

түрінде жазуға болады.

ДТ-лар жүйесінің қалыпты түрі деп аталатын (3.15) жүйесінің аралығындағы шешуі деп сол аралықта үзіліссіз дифференциалданатын және жүйе теңдеулерін бойынша тепе-теңдікке айналдыратын функциялардың жиынтығын айтамыз. Айнымалылардың белгілі бір өзгеру аймағында дербес туындыларымен 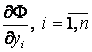бірге анықталған, үзіліссіз және оған жүйенің кез келген шешуін қойғанда үшін тұрақты мән қабылдайтын функциясын (3.15) қалыпты жүйесінің интегралы дейді. Ал, ырықты тұрақтыға теңестірілген интеграл

, (3.16)

жүйенің алғашқы интегралы делінеді.

Интегралданатын комбинацияларды бөліп шығару үшін (3.15) жүйесін кейде симметриялы (тәуелсіз айнымалы мен белгісіз функциялар «теңсалмақты») деп аталатын

(3.17)

түрінде жазып, тең бөлшектердің-пропорциялардың белгілі қасиетін:

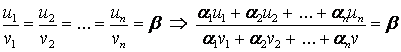(3.18)

қолдану ыңғайлырақ. Қолданыста сандары (3.18)-дегі соңғы бөлшектің бөлімі нөлге тең немесе оның алымы бөлімінің толық дифференциалы болатындай етіп таңдалады.

9-мысал. ДТ-лар жүйесінің жалпы шешуін табыңыз:

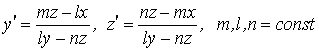Шешу. Жүйені симметриялы түрде жазайық:

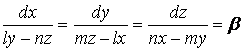Енді (3.18)-де алдымен , одан кейін , деп алсақ:

Бұл бөлшектердің алымдарын да нөлге теңеп, интегралдағаннан кейін берілген жүйенің жалпы шешуін айқын емес түрде анықтайтын оның алғашқы интегралдары табылады:

Қалыпты (3.15) жүйесі үшін Коши есебі: жүйенің

(3.19)

бастапқы шарттарына қанағаттандыратын шешуін табыңыз деп қойылады.

Коши теоремасы. Қалыпты (3.15) жүйесінің оң жақтары айнымалылары өзгеруінің өлшемді аймағында анықталған делік. Егер нүктесінің қандай да болмасын аймағында функциялары үзіліссіз және олардың шектелген дербес туындылары 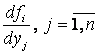бар болса, онда жүйенің (3.19) бастапқы шарттарына қанағаттандыратын шешуі бар және ол біреу ғана болатын айнымалысының өзгеруінің интервалы табылады.

Құрамында ырықты (тәуелсіз) тұрақтылары бар, олардың жарамды мәндерінің бәрінде де жүйе теңдеулерін тепе-теңдіктерге айналдыратын

(3.20)

функцияларының жиынтығынан шешудің бар және біреу ғана болуы туралы теореманың шарттары орындалатын аймақта Кошидің кез келген есебінің шешуін алуға болатын болса, онда (3.20) функциялары (3.15) жиынының жалпы шешуін құрайды.

12-дәріс. Дербес туындылы бірінші ретті дифференциалдық теңдеулер

Дәрістің мақсаты: бірінші ретті дербес туындылы ДТ үшін Коши есебін қойып, екі тәуелсіз айнымалы жағдайында оның геометриялық мағынасын ашу. Сызықтық біртекті дербес туындылы теңдеудің жалпы және дербес шешулерін табу есептерін қарастыру.

Коши есебінің қойылуы.

Бірінші ретті дербес туындылы ДТ жалпы түрде былай жазылады:

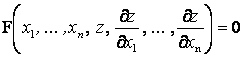, (3.21)

мұнда - тәуелсіз айнымалылар, - белгісіз функция, - оның дербес туындылары.

Керекті шарттар орындалған жағдайда (3.21)-дің жалпы шешуі бар және оның құрамында ырықты тұрақтылармен қатар кейбір ырықты функциялар да болуы мүмкін. Сондықтан (3.21) түріндегі ДТ-лардың жалпы шешулерін табу талап етіле бермейді. Әдетте Кошидің бастапқы шарттарына немесе шешуді бірмәнді анықтайтын басқа шарттарға қанағаттандыратын дербес шешулер ізделінеді. Мұндай есептерді шешуде (3.21) тәрізді теңдеулер ДТ-лар жүйелеріне келтіріліп, интегралданады.

Дербес туындылардың бірі, мысалы, бойынша, арқылы шешілген (3.21) теңдеуі

(3.22)

үшін Коши есебі төмендегіше қойылады: теңдеудің -дің берілген мәнінде қалған тәуелсіз айнымалылардың

(3.23)

функциясына айналатын

(3.24)

шешуін табыңыз.

Екі тәуелсіз айнымалы жағдайында

(3.25)

теңдеулерін интегралдау есебін және Коши шарттарын

(3.26)

геометриялық тұрғыдан мағыналауға болады. Кеңістікте (3.25) теңдеуінің шешуі

(3.27)

сол теңдеудің интегралдық беті деп аталатын бетті анықтайды. Интегралдық бетке нүктесінде жүргізілген жанама жазықтықтың теңдеуі

(3.28)

түрінде жазылады. Демек, дербес туындылы ДТ (3.25) оның интегралдық бетіндегі нүктесінің координатары мен бетке сол нүктеде тұрғызылған нормальдің бұрыштық коэффиценттерінің арасындағы қатынасты өрнектейді. Ал, (3.26) теңдеулері кеңістіктегі қисықты анықтайды.

Сонымен, (3.25) теңдеуі үшін қойылған Коши есебін жазықтығында жатқан (3.26) жазық қисығы арқылы өтетін интегралдық бетті табу талабы деп санауға болады.

Дербес туындыларының бірі арқылы шешілмеген (3.25) теңдеуі үшін Коши есебі жалпы түрде: берілген қисық

(3.29)

арқылы өтетін интегралдық бетті табыңыз деп қойылады. Берілген (3.25) теңдеуінің мінездемелері деп аталатын (3.29) қисықтарының кейбіреулері арқылы кеңістікте шексіз көп интегралдық беттердің жиыны өтеді.

Келтірілген геометриялық мағыналауды (3.21) теңдеуіне де таратуға болады. Мұнда теңдеудің шешуі (3.24) өлшемді кеңістікте интегралдық гипербетті, ал, (3.23) бастапқы шартты өлшемді кеңістіктегі бетті анықтайды.

Сызықтық біртекті теңдеулер.

Бірінші ретті дербес туындылы сызықтық біртекті ДТ

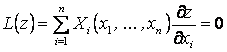, (3.30)

түрінде жазылады. Мұнда - қаралып отырған аймақта үзіліссіз дифференциалданатын берілген функциялар. Қатынастар

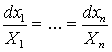(3.31)

(3.30) -ға сәйкес байырғы ДТ-лар жүйесін береді. Бұл жүйенің (3.16) түріндегі кез келген алғашқы интегралының сол жағы (3.30)-ның шешуі болады. Керісінше, (3.30)-ның ырықты тұрақтығы теңерілген кез келген шешуі (3.31)-дің алғашқы интегралы болады.

Жалпы түрдегі (3.21) теңдеуінен (3.30)-ның айырмашылығы сызықтық біртекті ДТ үшін жалпы шешуді табу туралы есепті қоюға болады. Егер (3.31) жүйесінің қаралып отырған аймақта анықталған қандай да болмасын тәуелсіз алғашқы интегралының жиынтығы

(3.32)

белгілі болса, онда берілген аймақта дифференциалданатын кез келген

(3.33)

күрделі функциясы (3.30)-дың жалпы шешуі бола алады. Бұл қорытынды (3.21)-дің жалпы шешуінің құрамына ырықты функциялар кіре алады деген қағидаға қайшы келмейді.

Сызықтық оператордың қасиеттерінен-ақ (3.33) функциясының (3.30) теңдеуіне қанағаттандыратынын көруге болады. Шынында да, және

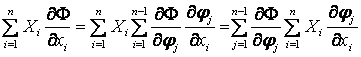
болғандықтан

Мысал ретінде

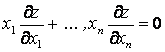
теңдеуінің жалпы шешуін табайық. Оған сәйкес (3.31) жүйесі

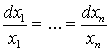
деп жазылады. Оның тәуелсіз алғашқы интегралдарының жүйесін, мысалы, болғанда

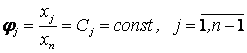
түріне келтіруге болады. Сондықтан берілген дербес туындылы ДТ-ның жалпы шешуі өлшемі нөлге тең ырықты біртекті функция

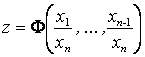
болып табылады.

Коши есебі: (3.30) теңдеуінің

, (3.34)

болатындай шешуін табыңыз; (3.34)-те - берілген сан, - берілген дифференциалданатын функция.

Коши есебінің шешуін табу үшін (3.31)-дің тәуелсіз алғашқы интегралының жүйесін (3.32) құрып, оны тәуелсіз айнымалылар арқылы шешеміз:

Сонда Коши есебінің (3.34) бастапқы шартына қанағаттандыратын шешуі:

түрінде жазылады [3].

10-мысал. Коши есебін шешіңіз:

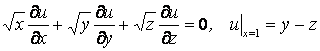Шешу. (3.31) жүйесі және оның тәуелсіз алғашқы интегралдары:

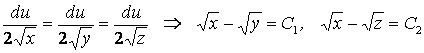болып жазылады; болғанда

Коши есебінің шешуі

Әдебиеттер тізімі

1. Мустахишев К.М., Ералиев С.Е., Атабай Б.Ж. Математика (толық курс). –Алматы: «TST-Company», 2009. -410 б.

2. Базарбаева С.Е., Дулэпо В.М. Жоғарғы математика. Есептеу-сызба жұмысы үшін әдістемелік нұсқаулар мен тапсырмалар. 6-б. –Алматы: АЭжБУ, 2002. -34 б.

3. Степанов В.В. Дифференциалдық тепңдеулер курсы. –М.: ГИФМЛ, 1959. -468 б.

4. Ефимов А.В., Демидович Б.П. (ред.). ЖТОО үшін математикадан есептер жинағы. Математикалық талдаудың арнаулы бөлімдері. –М.: Ғылым, 1986. -366 б.

5. Бугров Я.С., Никольский С.М. Дифференциалдық теңдеулер. Еселі интегралдар. Қатарлар. Комплекс айнымалының функциялары. –М.: Ғылым, 1985. -464 б.

6. Камке Э. Бірінші ретті дербес туындылы дифференциалдық теңдеулер бойынша анықтама. –М.: Ғылым, 1966. -260 б.

7. Трикоми Ф. Дифференциальные уравнения. –М.: ИЛ, 1962.

Мазмұны

1-модуль. Бірінші ретті дифференциалдық теңдеулер	3
1-дәріс. Негізгі түсініктер. Геометриялық талқылау	3
2-дәріс. Коши есебі (бастапқы есеп). Айнымалылары ажыратылатын теңдеулер	5
3-дәріс. Біртекті, сызықтық және толық дифференциалды теңдеулер	8
4-дәріс. Шешудің бар және біреу ғана болуы туралы теореманың графиктік интерпретациясы	15
2-модуль. Жоғары ретті сызықтық дифференциалдық теңдеулердің жалпы теориясы	21
5-дәріс. Коэффициенттері үзіліссіз сызықтық ДТ-лар	21
6-дәріс. Коэффициенттері тұрақты сызықтық ДТ	23
7-дәріс. Сызықтық ДТ-лар жүйелерінің жалпы теориясы	29
8-дәріс. Коэффициенттері тұрақты сызықтық жүйелер	32
3-модуль. Екінші ретті сызықтық ДТ-лар үшін шекаралық есептер 9-дәріс. Шекаралық есептердің қойылуы	37 37
10-дәріс. Штурм-Лиувилль есебі.	39
11-дәріс. ДТ-лардың қалыпты жүйесі	41
12-дәріс. Дербес туындылы бірінші ретті дифференциалдық теңдеулер	43
Әдебиеттер тізімі	47