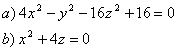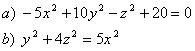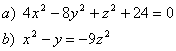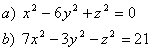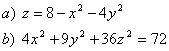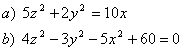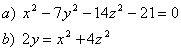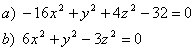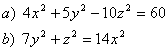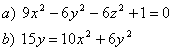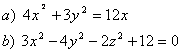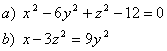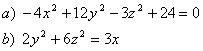АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ
Алгебра и геометрия.
Методические указания и задания
к выполнению расчетно-графических работ
(для студентов очной формы обучения специальности
050704 – Вычислительная техника и программное обеспечение)
Алматы 2007
СОСТАВИТЕЛИ: Л.Н. Астраханцева, Л.Н.Ким, М.Ж.Байсалова. Алгебра и геометрия. Методические указания и задания к выполнению расчетно-графической работы для студентов очной формы обучения специальности 050704 – Вычислительная техника и программное обеспечение. -Алматы: АИЭС, 2007.- 26 с.
Методические указания и задания к расчетно-графической работе содержат типовой расчет №3 дисциплины «Алгебра и геометрия» для студентов очной формы обучения специальности 050704 – Вычислительная техника и программное обеспечение. Приведены основные теоретические вопросы программы. Дано решение типового варианта.
Ил. 7, табл. 7, библиогр. – 4 назв.
Рецензент: канд.физ.-мат.наук, проф. С.Е.Базарбаева.
Печатается по плану издания некоммерческого акционерного общества «Алматинский институт энергетики и связи» на 2007 г.
ã НАО «Алматинский институт энергетики и связи», 2007 г.
1 Типовой расчёт 3. Аналитическая геометрия, квадратичные формы
1.1 Теоретические вопросы
1 Прямая на плоскости. Различные уравнения прямой на плоскости.
2 Угол между прямыми. Условия параллельности и перпендикулярности прямых. Расстояние от точки до прямой.
3 Различные уравнения плоскости. Угол между плоскостями.
4 Различные уравнения прямой в пространстве. Угол между прямыми в пространстве, между прямой и плоскостью.
5 Кривые второго порядка. Окружность, эллипс, гипербола, парабола.
6 Поверхности второго порядка.
7 Квадратичные формы. Приведение квадратичных форм к каноническому виду.
8 Приведение уравнений кривых второго порядка к каноническому виду. Применение квадратичных форм к упрощению уравнений кривых второго порядка.
1.2 Расчётные задания
1
Даны точки А
и А
на плоскости и уравнение
прямой L:
а) составить уравнение прямой L, проходящей через эти точки;
б) записать уравнение прямой L в виде: 1) y=kx+m; 2) Ax+By+C=0;
3) x/a+y/b=1; 4) y-y
=k(x-x). Сделать чертёж и на нём указать геометрический
смысл k, m, A, B, a, b, x, y;
в) найти угол между прямыми Lи L.
Будут ли эти прямые параллельны, перпендикулярны?
Т а б л и ц а 1
|
№ варианта и задание для 1 |
№ варианта и задание для 1 |
|
1.1 А |
1.2 А |
|
1.3 А |
1.4 А |
|
1.5 А |
1.6 А |
|
1.7 А |
1.8 А |
|
1.9 А |
1.10 А |
|
1.11 А |
1.12 А |
|
1.13 А |
1.14 А |
продолжение таблицы 1
|
1.15 А |
1.16 А |
|
1.17 А |
1.18 А |
|
1.19 А |
1.20 А |
|
1.21 А |
1.22 А |
|
1.23 А |
1.24 А |
|
1.25 А |
1.26 А |
|
1.27 А |
1.28 А |
|
1.29 А |
1.30 А |
2
Даны точки А,А,А
и плоскость Р:
а) составить уравнение плоскости Р, проходящей
через точки А,
А,А;
б) записать уравнение плоскости Р в виде: 1) Ax+By+Cz+D=0;
2) x/a+y/b+z/c=1; 3) A(x-x)+B(y-y)+C(z-z)=0;
Как называются уравнения
1), 2)? Указать
геометрический смысл А, В, С, а, в, с, x, y, z;
в) найти угол между плоскостями Р1 и Р.
Будут ли эти плоскости параллельны, перпендикулярны?
Т а б л и ц а 2
|
№ варианта и задание для 2 |
|
2.1 А |
|
2.2 А |
|
2.3 А |
|
2.4 А |
|
2.5 А |
|
2.6 А |
|
2.7 А |
|
2.8 А |
|
2.9 А |
|
2.10 А |
|
2.11 А |
|
2.12 А |
|
2.13 А |
|
2.14 А |
|
2.15 А |
|
2.16 А |
|
2.17 А |
продолжение таблицы 2
|
2.18 А |
|
2.19 А |
|
2.20 А |
|
2.21 А |
|
2.22 А |
|
2.23 А |
|
2.24 А |
|
2.25 А |
|
2.26 А |
|
2.27 А |
|
2.28 А |
|
2.29 А |
|
2.30 А |
3
Даны точки А,А,А и плоскость Р ( в
задании 2):
а) составить уравнение прямой L, проходящей через точки А и А, и
прямой L, проходящей через точки Аи А;
б) записать канонические и параметрические уравнения
прямой L;
в) найти угол между прямыми Lи L;
г) найти угол между прямой L и плоскостью Р.
4 Даны: A – точка, лежащая на кривой; R – радиус окружности;
a, b - полуоси кривых; ось симметрии (Оx или Оy); D – директриса кривой:
а) составить уравнение окружности с центром в точке А и радиусом R;
б) составить уравнение и сделать чертёж эллипса с
полуосями а и в. Найти эксцентриситет 
, фокусы F, F;
в) составить уравнения и сделать чертёж гипербол с
действительной и мнимой полуосями а и в (два варианта: а – действительная; в – мнимая; а – мнимая; в – действительная). Найти эксцентриситет , фокусы Fи F,
уравнения асимптот;
г) составить уравнение и сделать чертёж параболы с осью симметрии Оx или Оy, вершина параболы в начале координат, D – директриса параболы. Найти фокус F.
Таблица 3
|
№ варианта и задание для 4 |
№ варианта и задание для 4 |
|
4.1A(2, -4), R=4,a=1, b=3, OX,D: x=-3 |
4.2 A(-5, 1),R=3,a=2, b=4, OY,D: y=2 |
|
4.3A(1, -4), R=5,a=8, b=3, OY,D: y=-6 |
4.4 A(7, 1),R=6,a=4, b=1, OX,D: x=2 |
продолжение таблицы 3
|
4.5A(2, -5), R=7,a=3, b=2, OX,D: x=4 |
4.6 A(-6, 2),R=8,a=7, b=4, OY,D: y=5 |
|
4.9A(5, -4), R=1,a=6, b=4, OX,D: x=-5 |
4.10A(-5, 2),R=4,a=9,b=4, OY,D: y=7 |
|
4.11A(1, -3),R=5,a=8, b=2, OY,D: y=6 |
4.12 A(8, 1),R=6,a=4,b=2, OX,D: x=3 |
|
4.13A(2, -6),R=7,a=3, b=4, OX,D: x=5 |
4.14A(-7, 2),R=8,a=1,b=4, OY,D: y=3 |
|
4.15A(3, 4),R=9,a=2, b=6, OY,D: y=-8 |
4.16 A(6, 3),R=2,a=3,b=1,OX,D: x=-8 |
|
4.17A(2, -9),R=7,a=5, b=2,OX, D: x=6 |
4.18A(-1, 2),R=8,a=5, b=4,OY,D: y=4 |
|
4.19A(8, -4),R=9,a=7, b=5,OY, D: y=2 |
4.20A(5, 1), R=2,a=9, b=1,OX,D: x=-1 |
|
4.21A(5, -4),R=1,a=6, b=4,OX, D: x=2 |
4.22A(-3, 2),R=4,a=8,b=4,OY, D: y=1 |
|
4.23A(1, 8),R=5,a=9, b=2,OY, D: y=-6 |
4.24A(9, 1), R=6,a=4,b=7,OX,D: x=-3 |
|
4.25A(2, -5),R=7,a=7, b=4,OX, D: x=9 |
4.26A(-9, 2),R=8,a=1,b=8,OY, D: y=7 |
|
4.27A(7, 4),R=9,a=2, b=7, OY, D: y=8 |
4.28A(11, 3),R=2,a=3,b=4,OX,D: x=8 |
|
4.29A(-7, 4),R=6,a=3, b=7,OY, D: y=4 |
4.30A(10, 4),R=4,a=3,b=5,OX,D: x=8 |
5 Определить вид (название) поверхности второго порядка и сделать схематический чертёТ а б л и ц а 4
|
№ варианта и задание для 5 |
№ варианта и задание для 5 |
|
5.1 |
5.2 |
|
5.3 |
5.4 |
|
5.5 |
5.6 |
|
5.7 |
5.8 |
|
5.9 |
5.10 |
|
5.11 |
5.12 |
|
5.13 |
5.14 |
|
5.15 |
5.16 |
|
5.17 |
5.18 |
|
5.19 |
5.20 |
|
5.21 |
5.22 |
продолжение таблицы 4
|
5.23 |
5.24 |
|
5.25 |
5.26 |
|
5.27 |
5.28 |
|
5.29 |
5.30 |
6 Задача по аналитической геометрии
6.1 Даны две точки А(3, 5, 6) и В(5, -7, 4). Составить уравнение плоскости,
проходящей через точку А перпендикулярно к отрезку АВ.
6.2 Составить уравнение плоскости, проходящей через точки (3, 2, -1) и
(4, -3, 2) и параллельной оси ОУ.
6.3 Плоскость проходит через точку М(2, -6, 5) и отсекает на оси абсцисс
отрезок а = 4, а на оси ординат отрезок в = 3. Составить уравнение этой
плоскости.
6.4 Составить канонические уравнения прямой, проходящей через точку
М(1, 5, 7) и точку пересечения прямой 
с
плоскостью
2х – 3у + z – 14 = 0.
6.5 Привести к каноническому виду уравнения прямой 
.
6.6 Даны вершины треугольника А(5, 7, 4), В(3, 2, -1), С(1, 4, -3). Написать канонические уравнения медианы, проведённой из вершины А.
6.7 Доказать, что следующие две прямые параллельны: 
и
.
6.8 Доказать, что следующие прямые взаимно перпендикулярны: 
и 
.
6.9 Составить уравнение прямой, проходящей через точку М(1, -1, 3)
параллельно линии пересечения плоскостей х – 2у + 3z – 5 = 0 и
3x + y – 2z + 1 = 0.
6.10 Вычислить угол между прямой 
и
плоскостью
4х + 2y – 2z + 5 = 0.
6.11 Вычислить угол между прямой, проходящей через точки А(3, 6, 2),
В(4, 5, -2), и плоскостью 2x + y - 2z – 5 = 0.
6.12 Составить уравнение прямой, проходящей через точку М(-2, 3, 4)
перпендикулярно к плоскости 3x – 2y + 5z – 6 =0.
6.13 Найти расстояние между плоскостями 2x – 11y +10z – 15 = 0 и
2x - 11y +10z + 45 = 0.
6.14 Найти точку В, симметричную точке А(1, 2, -4) относительно плоскости 3x – 2y +z – 23 = 0.
6.15 Составить уравнение плоскости, проходящей через точку М(5, 3, 2)
параллельно двум векторам 
(4, 1, 2), 
(5, 3, 1).
6.16 Составить уравнение плоскости, проходящей через начало координат и
точки (-2, 1, 4), (3, 2, 5).
6.17 Составить уравнение плоскости, проходящей через точку М(3, -2, 6) и
отсекающей на осях координат равные отрезки.
6.18 Составить уравнение плоскости, проходящей через ось Оу и точку
М(2, 4, 1).
6.19 Составить параметрические уравнения прямой 
.
6.20 Составить уравнение плоскости, проходящей через начало координат и
точку М(3, 5, 2) перпендикулярно к плоскости 2х – 3у = 0.
6.21 Написать уравнение плоскости, проходящей через точку А(2,5,-3)
перпендикулярно вектору 
, где 
6.22 Найти угол между плоскостями 
6.23 Найти точку пересечения прямой 
и
плоскости 
6.24 Найти точку 
, симметричную точке 
относительно
прямой 
6.25 Найти точку , симметричную точке 
относительно
плоскости 
6.26 Написать уравнение плоскости, проходящей через точку А(0,-3,5)
перпендикулярно вектору , где 
6.27 Найти угол между плоскостями 
6.28 Найти точку пересечения прямой 
и
плоскости 
6.29 Найти точку , симметричную точке 
относительно
прямой 
6.30 Найти точку , симметричную точке 
относительно
плоскости 
7 Привести уравнение кривой второго порядка к каноническому виду, построить эту кривую
Т а б л и ц а 5
|
№ варианта и задание для 7 |
|
|
7.1 |
7.2
|
|
7.3 |
7.4 |
|
7.5 |
7.6 |
|
7.7 |
7.8 |
|
7.9 |
7.10 |
|
7.11 |
7.12 |
|
7.13 |
7.14 |
|
7.15 |
7.16 |
продолжение таблицы 5
|
7.17 |
7.18 |
|
7.19 |
7.20 |
|
7.21 |
7.22 |
|
7.23 |
7.24 |
|
7.25 |
7.26 |
|
7.27 |
7.28 |
|
7.29 |
7.30 |
8 Привести уравнение поверхности второго порядка к каноническому виду. Сделать схематический чертёж
Т а б л и ц а 6
|
№ варианта и задание для 8 |
|
|
8.1
|
8.2 |
|
8.3
|
8.4
|
|
8.5
|
8.6
|
|
8.7
|
8.8
|
|
8.9
|
8.10 |
|
8.11 |
8.12
|
|
.813
|
8.14
|
|
8.15
|
8.16
|
|
8.17
|
8.18
|
|
8.19 |
8.20
|
|
8.21 |
8.22
|
продолжение таблицы 6
|
8.23 |
8.24
|
|
8.25
|
8.26
|
|
8.27 |
8.28
|
|
8.29
|
8.30
|
9 Привести квадратичную форму F(x,y) к каноническому виду; найти ортогональное преобразование, приводящее квадратичную форму к каноническому виду
Т а б л и ц а 7
|
F(x,y) |
F(x,y) |
F(x,y) |
|
9.1 |
9.11 |
9.21 |
|
9.2 |
9.12 |
9.22 |
|
9.3 |
9.13 |
9.23 |
|
9.4 |
9.14 |
9.24 |
|
9.5 |
9.15 |
9.25 |
|
9.6 |
9.16 |
9.26 |
|
9.7 |
9.17 |
9.27 |
|
9.8 |
9.18 |
9.28 |
|
9.9 |
9.19 |
9.29 |
|
9.10 |
9.20 |
9.30 |
10 Привести уравнение кривой второго порядка f(x, y)=0 к каноническому виду; построить эту кривую
Т а б л и ц а 8
|
f(x, y)=0 |
f(x, y)=0 |
|
10.1 |
10.2 |
|
10.3 |
10.4 |
|
10.5 |
10.6 |
|
10.7 |
10.8 |
|
10.9 |
10.10 |
|
10.11 |
10.12 |
|
10.13 |
10.14 |
|
10.15 |
10.16 |
|
10.17 |
10.18 |
|
10.19 |
10.20 |
|
10.21 |
10.22 |
|
10.23 |
10.24 |
|
10.25 |
10.26 |
|
10.27 |
10.28 |
|
10.29 |
10.30 |
1.3 Решение типового варианта
1
Даны точки А(4, -2), А(8, 1) на
плоскости и уравнение прямой
L: -x + 4y + 5 = 0:
а) составить уравнение прямой L, проходящей через эти точки;
б) записать уравнение прямой Lв виде: 1) y=kx+m; 2) Ax+By+C=0;
3)
x/a+y/b=1; 4)
y-y=k(x-x). Сделать чертёж и указать геометрический
смысл k, m, A, B, a, b, x, y;
в) найти угол между прямыми L и L. Будут ли эти прямые параллельны, перпендикулярны?
Решение:
a) уравнение прямой, проходящей через две точки (
) и (
)
находится по формуле 
.
Значит уравнение прямой L
имеет вид 
или 
;
б) запишем уравнение прямой Lв нужном виде.
1) y=kx+m: 
, ( k=
, m=-5 );
2) Ax+By+C=0: 
,
( A=3, B=-4, C=-20 );
3) x/a+y/b=1: 3x - 4y – 20 = 0 
, ( a = 20/3, b = -5 );
4) y-y=k(x-x): 
,
(k=, 
).
Построим прямую L по двум точкам А(4, -2), А(8, 1)
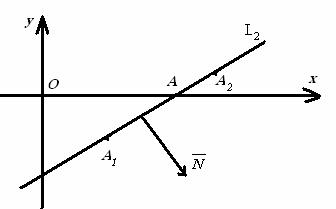
Рисунок 1
Укажем
геометрический смысл коэффициентов: k== tg
– это угловой коэффициент прямой L; m =-5= OB – величина отрезка, отсекаемого прямой Lна оси Оу, считая от начала координат; А=3, В=-4 –
координаты нормального вектора прямой L, т.
е. 
.
Уравнение y = kx+m называют уравнением прямой с угловым коэффициентом; Ax+By+C=0 – общим уравнением прямой; x/a+y/b=1 – уравнением прямой в отрезках;
в) угол между
прямыми L и Lможно найти по одной из двух формул. Если уравнения
прямых заданы в общем виде L: 
; L:
, то находим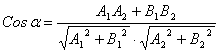 
; если заданы уравнения с угловым коэффициентом L:
, L:
, то
находим 
, если 
или
; 
,
если 
или 
.
Так как
по условию уравнение L
задано в общем виде L:
-х + 4у+5=0, то возьмём уравнение Lтоже в общем виде L: 3х – 4у –20 = 0 и воспользуемся первой формулой
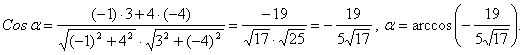
Ввиду
того, что 
и 
, то прямые L и L не
параллельны и не перпендикулярны.
2–3
Даны точки А(1, 2, -1), А(3, 3, 2), А(2, -3, 7) и плоскость Р:
2x +3y + z – 1 = 0.
2
а) составить уравнение плоскости Р,
проходящей через точки А, А, А;
б) записать уравнение плоскости Р в виде:
1) Ax+By+Cz+D=0;
2) x/a+y/b+z/c=1; 3) A(x-x)+B(y-y)+C(z-z)=0;
Как называются уравнения 1),
2)? Указать геометрический смысл А, В, С, а, в, с, x, y, z;
в) найти угол между плоскостями Р и Р.
Будут ли эти плоскости параллельны, перпендикулярны?
Решение:
а) уравнение плоскости, проходящей через точки (
), (
), (
)
имеет вид: 
.
В нашем случае Р:
(*);
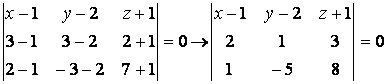б) 1) раскрыв определитель в правой части равенства (*),
получим уравнение плоскости Р в виде Ax+By+Cz+D=0: 23x – 13y – 11z – 8 = 0, (A=23, B=-13, C=-11, D=-8). Этот вид уравнения плоскости называется общим;
2) перенесём в общем уравнении плоскости свободный член –8
в правую часть и разделим обе части на 8. Получим уравнение плоскости в виде x/a+y/b+z/c=1: 
,
(а=8/23, в=-8/13, с=-8/11). Этот вид называется уравнением плоскости в отрезках;
3) раскроем определитель в левой части равенства (*) по
элементам первой строки: 
.
Получим уравнение плоскости
в виде A(x-x)+B(y-y)+C(z-z)=0 (
).
Геометрический смысл коэффициентов: А, В, С – это координаты
нормального
(перпендикулярного) вектора плоскости, т. е. вектор 
; а, в, с – это величины отрезков, отсекаемых
плоскостью на координатных осях, считая от начала координат. Значит
а=8/23 – отрезок, отсекаемый на Ох, в=-8/13 –на Оу, с=-8/11– на Oz; 
-
координаты точки, лежащей на плоскости, т. е. точка (1, 2, -1) принадлежит
плоскости Р;
в) косинус угла между плоскостями Р
и Р
находится
по формуле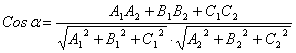 
. Если 
, то 
; если 
или 
, то 
. В
нашем случае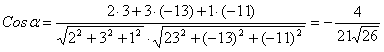 
.Так как 
и 
, то Ри Рне
параллельны и не перпендикулярны.
4 а) составить уравнение прямой L, проходящей через точки А и
А, и прямой L, проходящей через точки А и А;
б) записать канонические и параметрические уравнения
прямой L;
в) найти угол между прямыми L и L;
г) найти угол между прямой L и плоскостью Р.
Решение:
а) уравнение прямой, проходящей через две точки () и
() находится по
формуле 
.Таким образом, уравнение прямой L, проходящей через точки А(1, 2, -1), А(3, 3, 2), имеет вид: 
, а уравнение прямой L, проходящей через точки А(1, 2, -1) и А(2, -3, 7): 
;
б) уравнения прямой в виде 
называются
каноническими. В предыдущем пункте уже найдены канонические уравнения прямых: L:
и L:
. Параметрическими называются уравнения
прямой в виде 
. Чтобы получить параметрические уравнения
прямых, приравняем канонические уравнения к параметру t и из полученных равенств найдём x, y, z.
L:= 
.
Итак, параметрические уравнения L:
;
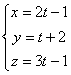в) косинус угла между прямыми L: 
и L:
находится по формуле 
. Итак, 
;
г) синус угла 
между прямой и
плоскостью 
находится по формуле 
.
Следовательно, синус угла между прямой L: и плоскостью Р
равен 
.
5
Даны: точка А(3, -7), лежащая на кривой; R = 6 – радиус окружности; 
= 2, 
= 3 – полуоси кривых; Оу – ось симметрии параболы, вершина
которой лежит в начале координат; D: у = -3
– уравнение директрисы параболы:
а) составить уравнение окружности с центром в точке А и радиусом R;
б) составить уравнение и сделать чертёж эллипса с
полуосями и . Найти эксцентриситет , фокусы F, F;
в) составить уравнения и сделать чертёж гипербол с
действительной и мнимой полуосями и . (два
варианта: –
действительная, – мнимая;
–
мнимая, –
действительная). Найти эксцентриситет , фокусы F и F, уравнения асимптот;
г) составить уравнение и сделать чертёж параболы с осью симметрии Ох или Оу, вершина параболы в начале координат, D – директриса параболы. Найти фокус F.
Решение:
а) уравнение окружности с центром в точке 
радиуса R имеет вид 
, значит в нашем варианте: 
;
б) каноническое уравнение эллипса с полуосями и имеет вид 
;
эксцентриситет эллипса
равен 
, где 
, если 
, (т. е. -
большая полуось). Если 
, (т. е. - большая полуось), то и следует поменять местами. Фокусы эллипса – это точки 
, если ; или 
, если 
. Итак, каноническое уравнение эллипса в нашем
варианте 
. Поскольку , то
, а эксцентриситет равен 
, (
). Фокусы
лежат на оси Оу: 
. Изобразим
эллипс на координатной плоскости:
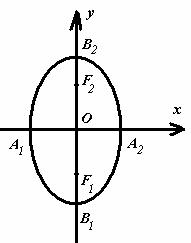
Рисунок 2
-
вершины эллипса.
в) каноническое уравнение гиперболы с действительной
полуосью , мнимой
полуосью имеет
вид 
; с
действительной полуосью и
мнимой полуосью : 
или 
. Для гиперболы с уравнением эксцентриситет равен , где 
; уравнения
асимптот гиперболы имеют вид 
; фокусы – это точки , расположенные на действительной оси.
По условию =2, =3, поэтому каноническое уравнение гиперболы с действительной
полуосью будет 
, а с действительной полуосью
:
или 
.
Рассмотрим
гиперболу . Для неё
полуфокусное расстояние 
;
эксцентриситет равен 
; фокусы: 
; уравнения асимптот: 
.
Гиперболу легко построить следующим образом: строим прямоугольник со сторонами 
(у нас 
). Диагонали прямоугольника являются асимптотами гиперболы, точки
пересечения сторон прямоугольника с действительной осью гиперболы – вершинами
гиперболы:
Рисунок 3
г) по условию осью симметрии параболы с вершиной в начале
координат является ось Оу, значит её каноническое уравнение имеет вид 
. Так как директриса параболы имеет уравнение у = - 3,
то в уравнении параболы будет знак +, т. е.: 
. Для определения параметра 
учитываем, что уравнение директрисы этой
параболы будет 
; таким образом, 
.
Итак, уравнение нашей параболы: 
. Фокус параболы – это точка 
, лежащая на оси симметрии. В нашем случае фокус - 
. Построим параболу.
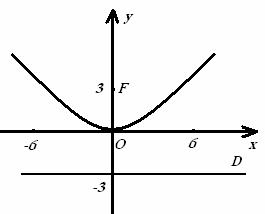
Рисунок 4
6 Определить вид (название) поверхности второго порядка и сделать схематический чертёж:
а) 
; б) 
.
Решение:
а) дано каноническое уравнение однополостного гиперболоида с осью симметрии Ох, его схематический чертёж:
Рисунок 5
б) Дано каноническое уравнение конуса второго порядка с осью симметрии Оz и вершиной в начале координат, его схематический чертёж;
Рисунок 6
Указания к выполнению заданий 9-10
9 Привести квадратичную
форму F(x,y)=
к каноническому виду; найти ортогональное
преобразование, приводящее квадратичную форму к каноническому виду.
Решение
Квадратичную форму
F(x,y)=
всегда можно привести к
каноническому виду F(
)=
. Матрица квадратичной
формы в старом базисе (старой систему координат Оху) будет 
, в новом
базисе (новой системе координат О
) – 
, где 
–
собственные значения матрицы А. Матрицы A и D подобные, т.е. связаны равенством 
или
,
где 
– матрица ортогонального
оператора, приводящего квадратичную форму к диагональному виду; её столбцами
являются координаты нормированных собственных векторов матрицы А, составляющих
базис, в котором матрица квадратичной формы имеет диагональный вид. Если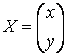 
–
столбец координат вектора в старом базисе,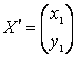 
– в новом, то
,
или в координатной форме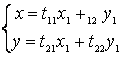 
– формулы преобразования
координат при переходе к новому базису.
В нашей задаче матрица
квадратичной формы в старом базисе будет 
. Найдём её собственные
значения и собственные векторы.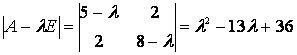 
. 
– собственные
значения. Таким образом, в новом базисе квадратичная форма примет канонический
вид 
F()=
. Матрица этой
квадратичной формы имеет диагональный вид 
.
Найдём собственные
векторы, отвечающие собственным значениям .
1) 
: 
. Пусть 
,
тогда 
, 
– собственный
вектор. Нормируем его: 
.
2) 
: 
. Пусть 
,
тогда 
. 
, 
.
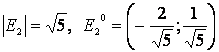Итак,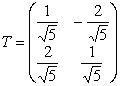 
– матрица ортогонального
оператора, приводящего квадратичную форму к каноническому виду. 
–
формулы преобразования координат при переходе к новому базису.
10 Привести уравнение
кривой второго порядка 
к каноническому виду; построить эту кривую.
Решение
Рассмотрим квадратичную
форму F(x,y)=, составленную из старших членов уравнения
кривой, и приведём её к каноническому виду (см. задачу 9). Матрица 
–
матрица ортогонального оператора, приводящего квадратичную форму к
каноническому виду (этот оператор является оператором поворота системы
координат Оху вокруг начала координат на некоторый угол и перехода к системе
координат О), а также это матрица перехода от базиса 
в
системе координат Оху к базису 
в новой системе координат О.
Формулы 
являются формулами преобразования
системы координат при повороте. Старшие члены уравнения кривой преобразуются
так:
F(x,y)=F()=, младшие –
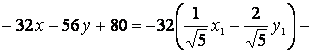
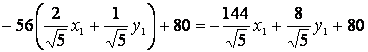. Таким образом, в системе координат О уравнение
линии примет вид 
.
Дальнейшее упрощение
уравнения кривой можно осуществить с помощью преобразования параллельного
переноса системы координат. Для этого дополним члены с 
и 
в
последнем уравнении до полного квадрата:
. Обозначим 
– формулы
преобразования координат при параллельном переносе системы координат. Точка 
–
новое начало координат. В системе координат 
уравнение кривой
примет канонический вид 
или 
– это уравнение
эллипса. Чтобы построить этот эллипс, повернём сначала систему Оху до
системы О. Для этого, имея матрицу 
оператора
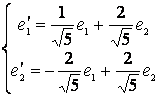
поворота, запишем разложение нового базиса через старый : 
.
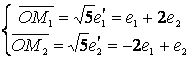Векторы 
и 
направлены по новым
осям координат О и О, что позволяет построить
эти оси. Затем параллельно перенесём систему О, совмещая начало
координат О с точкой 
, получим систему , в которой
построим эллипс по его каноническому уравнению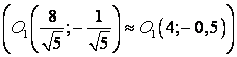 
.
Рисунок 7
Список
литературы
1. Апатенок Р.Ф., Маркина А.М. Сборник задач по линейной алгебре. - Мн.: Выш. Школа, 1980. – 192 с.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: в 2 ч. – М.: Высшая школа, 2003. – ч. 1,2.-352 с.
3. Сборник индивидуальных заданий по высшей математике: в 3 ч. (Рябушко А.П., Бархатов В.В. и др.). Под ред. Рябушко А.П. – Минск: Высш. школа, 2000.-ч.1.-396 с.
4. Хасеинов К.А. Каноны математики: Учебник. – Алматы, 2003.-686 с.
Содержание
1 Типовой расчёт 3. Аналитическая геометрия, квадратичные формы............3
1.1 Теоретические вопросы.………………………………….....…………….….3
1.2 Расчётные задания……………………………………..………………….….3
1.3 Решение типового варианта……….……………………..………………….12
Список литературы ………………………………………..……………………25
Сводный план 2007 г., поз.
Астраханцева Людмила Николаевна
Ким Людмила Николаевна
Байсалова Маншук Жумамуратовна
АЛГЕБРА И ГЕОМЕТРИЯ
Методические указания и задания
к выполнению расчетно-графической работы для студентов очной формы обучения специальности 050704 – Вычислительная техника и программное обеспечение
Редактор Т.С.Курманбаева
Подписано в печать Формат 6084 1/16
Тираж 500 экз Бумага типографская №1
Объем 2,6 уч.-изд.л. Заказ______ Цена_____ тг.
Копировально-множительное бюро
некоммерческого акционерного общества
«Алматинский институт энергетики и связи»
050013, Алматы, Байтурсынова, 126