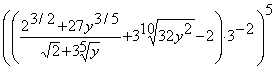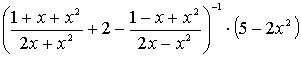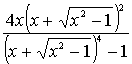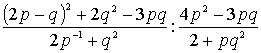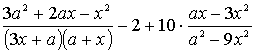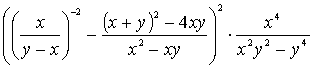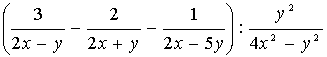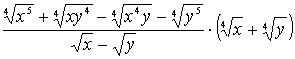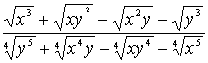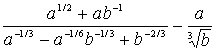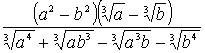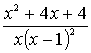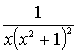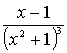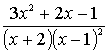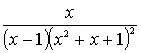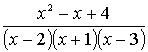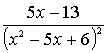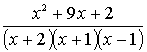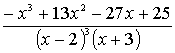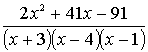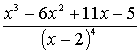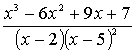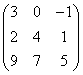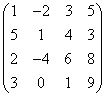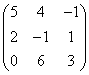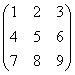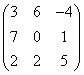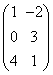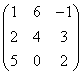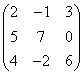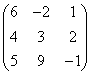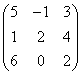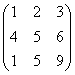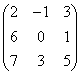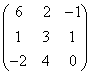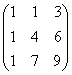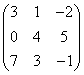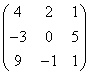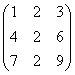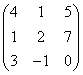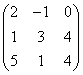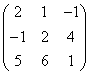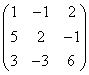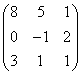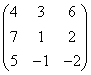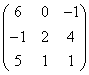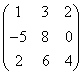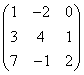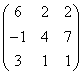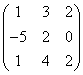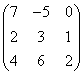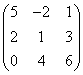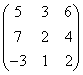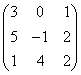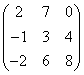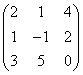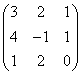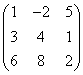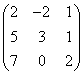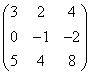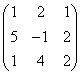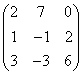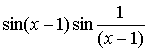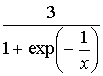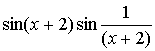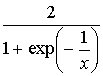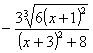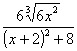АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ
Алгебра и геометрия
Методические указания к
выполнению лабораторных работ
( для студентов очной формы
обучения специальности
050704- Вычислительная техника
и программное обеспечение)
Алматы 2006
СОСТАВИТЕЛИ: Л.Н. Астраханцева, Л.Н.Ким,
М.Ж.Байсалова.
Алгебра и геометрия.
Методические указания к выполнению лабораторных работ (для студентов очной
формы обучения специальности 050704-Вычислительная техника и программное
обеспечение). –Алматы: АИЭСЮ, 2006.-51с.
Методические указания и
задания к лабораторным работам для
студентов очной формы обучения специальности 050704-Вычислительная техника и
программное обеспечение содержат четыре
лабораторные работы с заданиями по 30 вариантов и указаниями к выполнению.
![]()
Рецензент: канд.физ.-мат.наук, профессор С.Е.Базарбаева
Печатается по плану издания Алматинского института
энергетики и связи на 2006 г.
Ó Алматинский институт энергетики и связи, 2006 г.
1 Лабораторная работа №1. Работа с компьютерной
системой Mathcad. Задачи элементарной
математики
1.1 Цель работы
Целью настоящей лабораторной работы является
знакомство с компьютерной системой Mathcad,
приобретение навыков в технике арифметических вычислений, в преобразовании алгебраических выражений, в
решении уравнений, в построении графиков элементарных функций в декартовой и
полярной системах координат.
1.2 Описание центральных вопросов при решении задач
элементарной математики
Для того чтобы преобразовать алгебраическое выражение,
вычислить значение функции, построить график функции или решить уравнение,
необходимо прежде всего ввести соответствующее выражение в рабочий документ Mathcad. Большинство вычислений в Mathcad можно выполнить тремя способами: выбором операции в
меню, с помощью кнопочных панелей инструментов или обращением к соответствующим
функциям.
1.3 Рабочее
задание
1.3.1
Вычислить.
Варианты индивидуальных заданий для 1.3.1.
|
№ |
Задание |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
21 |
|
|
22 |
|
|
23 |
|
|
24 |
|
|
25 |
|
|
26 |
|
|
27 |
|
|
28 |
|
|
29 |
|
|
30 |
|
1.3.2 Упростить выражение
Варианты индивидуальных заданий для 1.3.2.
|
№ |
Задание |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
21 |
|
|
22 |
|
|
23 |
|
|
24 |
|
|
25 |
|
|
26 |
|
|
27 |
|
|
28 |
|
|
29 |
|
|
30 |
|
1.3.3 Раскрыть
скобки и привести подобные члены
Варианты индивидуальных заданий для 1.3.3.
|
№ |
Задания |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
21 |
|
|
22 |
|
|
23 |
|
|
24 |
|
|
25 |
|
|
26 |
|
|
27 |
|
|
28 |
|
|
29 |
|
|
30 |
|
1.3.4 Разложить на множители многочлен f(x)
Варианты индивидуальных заданий для 1.3.4.
|
№ |
f(x) |
№ |
f(x) |
|
1 |
|
2 |
|
|
3 |
|
4 |
|
|
5 |
|
6 |
|
|
7 |
|
8 |
|
|
9 |
|
10 |
|
|
11 |
|
12 |
|
|
13 |
|
14 |
|
|
15 |
|
16 |
|
|
17 |
|
18 |
|
|
19 |
|
20 |
|
|
21 |
|
22 |
|
|
23 |
|
24 |
|
|
25 |
|
26 |
|
|
27 |
|
28 |
|
|
29 |
|
30 |
|
1.3.5 Разложить на сумму простейших дробей
рациональные дроби
Варианты индивидуальных заданий для 1.3.5.
|
№ |
Задание |
№ |
Задание |
|
1 |
|
2 |
|
|
3 |
|
4 |
|
|
5 |
|
6 |
|
|
7 |
|
8 |
|
|
9 |
|
10 |
|
|
11 |
|
12 |
|
|
13 |
|
14 |
|
|
15 |
|
16 |
|
|
17 |
|
18 |
|
|
19 |
|
20 |
|
|
21 |
|
22 |
|
|
23 |
|
24 |
|
|
25 |
|
26 |
|
|
27 |
|
28 |
|
|
29 |
|
30 |
|
1.3.6
Выполнить задания:
а) решить
уравнение f(x)=0, где f(x)- многочлен из задания 1.3.4 Сравнить полученный
результат с ответом в задании 1.3.4;
б) решить уравнение.
Варианты индивидуальных заданий для 1.3.6 (б)
|
№ |
Задание |
№ |
Задание |
|
1 |
|
2 |
|
|
3 |
|
4 |
|
|
5 |
|
6 |
|
|
7 |
|
8 |
|
|
9 |
|
10 |
|
|
11 |
|
12 |
|
|
13 |
|
14 |
|
|
15 |
|
16 |
|
|
17 |
|
18 |
|
|
19 |
|
20 |
|
|
21 |
|
22 |
|
|
23 |
|
24 |
|
|
25 |
|
26 |
|
|
27 |
|
28 |
|
|
29 |
|
30 |
|
2 Примеры выполнения заданий и указания к выполнению лабораторной работы №1
Пример
1. Вычислить![]()
 .
.
Указание. Набрать выражение с клавиатуры, причём, смешанная дробь набирается как сумма целой и дробной частей, в десятичной дроби вместо запятой набирается точка, знак умножения не опускается. Выделить всё синим угловым курсором и нажать клавишу =.
Выполнение примера
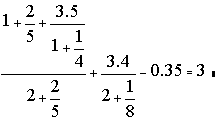
Пример 2. Упростить выражение .
.
Указание. Набрать выражение с клавиатуры с учётом указания
для первого примера, выделить всё синим угловым курсором, щёлкнуть по позиции Символы, Упростить или вызвать панель Символические операторы, Simplify.
Выполнение примера в рабочем окне программы Mathcad
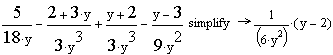 .
.
Пример 3. Раскрыть скобки и привести подобные члены в
выражении ![]() .
.
Указание. Набрать выражение с клавиатуры с учётом
указания для пер-
вого
примера, выделить всё синим угловым курсором, щёлкнуть по позиции Символы,
Расширить или вызвать панель Символические операторы, Expand.
Выполнение
примера в
рабочем окне программы Mathcad
![]() .
.
Пример 4.
Разложить на множители выражение ![]() .
.
Выполнение примера 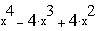 .
.
Указание.
Набрать выражение с клавиатуры с учётом указания для первого примера, выделить
всё синим угловым курсором, щёлкнуть по позиции
Символы, Фактор.
Ответ:![]() .
.
Пример 5. Разложить рациональную дробь 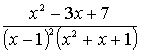 на сумму
на сумму
простейших дробей.
Указание. Набрать выражение с
клавиатуры с учётом указания для первого примера, выделить синим угловым
курсором переменную х, щёлкнуть по позиции Символы,
Переменные, Преобразовать в частичные доли или вызвать панель Символические операторы, Parfrac.
Выполнение примера в рабочем окне программы Mathcad
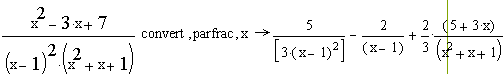 .
.
Пример 6. а) Решить уравнение f(x)=0, где f(x)=![]() . Сравнить результаты с ответом в задании 4. б) Решить
уравнение
. Сравнить результаты с ответом в задании 4. б) Решить
уравнение ![]() .
.
Указание. Привести уравнение к виду f(x)=0, набрать с
клавиатуры левую часть уравнения, вызвать панель Символические операторы, Solve, заполнить просвет переменной, относительно которой
решается уравнение и щелкнуть по свободному месту страницы.
Выполнение примера в рабочем окне программы Mathcad:
а)

Т.к. уравнение
![]() =0 имеет два
двукратных корня x=0 и x=2, то левая часть уравнения
разлагается на множители -
=0 имеет два
двукратных корня x=0 и x=2, то левая часть уравнения
разлагается на множители - ![]() , что совпадает с результатом в примере 4;
, что совпадает с результатом в примере 4;
б)
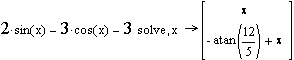 .
.
Итак, множество решений уравнения ![]() :
: 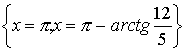 .
.
3 Лабораторная работа №2. Задачи векторной и линейной алгебры
3.1
Цель работы
Целью настоящей лабораторной работы
является изучение правил и приемов использования MathCad для выполнения операций с
векторами и с
матрицами, решения систем линейных уравнений.
3.2 Описание центральных
вопросов выполнения операций с векторами и с матрицами, решение систем линейных уравнений. Рассмотрим
векторы ![]() ,
, ![]() и
и ![]() :
:
- умножение вектора ![]() на число
на число ![]()
![]() ;
;
- скалярным произведением векторов ![]() и
и ![]() называется число
называется число
![]() ;
;
- длина вектора ![]() равна
равна ![]() ;
;
- смешанное произведение
векторов ![]() ,
, ![]() и
и
![]() равно
равно 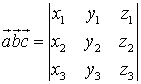 ;
;
- если векторы ![]() ,
, ![]() и
и ![]() параллельны одной и
той же плоскости, то
параллельны одной и
той же плоскости, то
они называются компланарными. Необходимым и
достаточным условием компланарности трех векторов является равенство нулю их
смешанного произведения ![]() ;
;
- любые три некомпланарные
векторы образуют базис трехмерного
пространства, т.е. четвертый вектор может быть
разложен единственным образом по данным трем векторам.
Рассмотрим матрицы 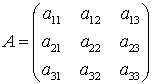 ,
,  ,
,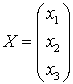 :
:
- если ![]() ,то матрица
,то матрица ![]() имеет обратную
матрицу
имеет обратную
матрицу ![]() , т.е. такую
, т.е. такую
матрицу, для которой
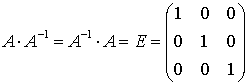 ;
;
- система ![]() может быть решена следующим способом:
может быть решена следующим способом:
- если
определитель матрицы![]() не равен нулю, то система имеет
не равен нулю, то система имеет
единственное решение,
которое можно найти по формулам Крамера
![]() , где
, где ![]()
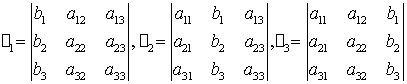 ;
;
- если ![]() , то единственное решение системы
, то единственное решение системы ![]() можно
можно
найти также с помощью
обратной матрицы ![]() .
.
3.3 Рабочее
задание
3.3.1 Даны векторы ![]() и числа
и числа ![]() . Найти:
. Найти:
а)![]() ;
;
б) ![]() ;
;
в) скалярное произведение векторов ![]() и
и ![]() ;
;
г)
векторное произведение векторов ![]() и
и ![]() ;
;
д) длину вектора ![]() и вектора, полученного в предыдущем пункте;
и вектора, полученного в предыдущем пункте;
е) смешанное произведение векторов ![]() ;
;
ж) являются ли заданные три вектора
линейно зависимыми или нет? Могут ли они образовывать базис пространства?
Варианты индивидуальных
заданий для 3.3.1
|
№ |
|
|
|
|
|
|
|
1 |
(2, -3, 1) |
(1, 2, 5) |
(6, 2, -3) |
2 |
1 |
3 |
|
2 |
(4, -2, 0) |
(4, -2, 0) |
(1, 2, -5) |
1 |
2 |
2 |
|
3 |
(5, -1, 0) |
(3, 2, 4) |
(3, 2, -3) |
-1 |
-2 |
1 |
|
4 |
(1, 2,-3) |
(1, -2,5) |
(4, 1, -3) |
7 |
3 |
-1 |
|
5 |
(5, 1, 2) |
(2, 1, -4) |
(6, 2, -3) |
2 |
4 |
-3 |
|
6 |
(7, -1, 0) |
(3, -6, 5) |
(1, 5,- 4) |
5 |
1 |
2 |
|
7 |
(2, -3, 4) |
(7, 2, 4) |
(6, 2,-3) |
6 |
2 |
-1 |
|
8 |
(5, -1, 3) |
(3, -1, 6) |
(7, 2,-3) |
3 |
-3 |
2 |
|
9 |
(6, 2, -5) |
(2, 2, -3) |
(1,-7, 5) |
4 |
-5 |
1 |
|
10 |
(4, -1, 0) |
(3, -3, 4) |
(5, 2, -1) |
-2 |
4 |
2 |
|
11 |
(7, 0, 6) |
(1, 2, -5) |
(3, -2,-1) |
1 |
3 |
4 |
|
12 |
(1, -1, 5) |
(-1, -5, 1) |
(1, 3,-3) |
2 |
4 |
3 |
|
13 |
(5, -1, 2) |
(-3, 2, 4) |
(4, 2,-5) |
4 |
2 |
5 |
|
14 |
(6, -1, 4) |
(1, 0, 7) |
(2, -1, 0) |
3 |
-1 |
1 |
|
15 |
(5, -1, 3) |
(6, 2, -3) |
(-5, 1 ,-3) |
5 |
-2 |
2 |
|
16 |
(5, -1, 0) |
(1, 2, 1) |
(5,2,-2) |
3 |
-1 |
1 |
|
17 |
(5, -1, 0) |
(4, 3, 1) |
(4,6,-1) |
2 |
3 |
1 |
|
18 |
(5, -1, 0) |
(3, 1, 4) |
(2,1,0) |
1 |
4 |
2 |
|
19 |
(5, -5, 4) |
(7, 2,6) |
(1,6,-5) |
-7 |
3 |
1 |
|
20 |
(7, 5, 0) |
(3, 1,4) |
(2,2,-3) |
2 |
4 |
3 |
|
21 |
(1, -3, 2) |
(1, 2,4) |
(5,4,-1) |
5 |
1 |
-1 |
|
22 |
(3, -4, 1) |
(7, 2,4) |
(3,2,-4) |
3 |
-1 |
1 |
|
23 |
(4, 2, 0) |
(3, 1,3) |
(5,1,-1) |
-2 |
3 |
4 |
|
24 |
(5, 6, -3) |
(1, 2,0) |
(6,1,-3) |
1 |
-2 |
2 |
|
25 |
(6, -1, 2) |
(7, 2,5) |
(1,2,-2) |
5 |
3 |
1 |
|
26 |
(1, -3, 1) |
(3, 2,6) |
(3,2,-4) |
2 |
-1 |
7 |
|
27 |
(4, 2, -2) |
(1, 2,4) |
(2,1,-5) |
1 |
-2 |
4 |
|
28 |
(7, -1, 5) |
(3, 0,5) |
(1,2,-2) |
-3 |
2 |
1 |
|
29 |
(6, 2, 0) |
(6, 4,1) |
(4,2,-4) |
1 |
4 |
-2 |
|
30 |
(3, -4, -1) |
(1, 2,3) |
(7,1,-1) |
2 |
3 |
1 |
3.3.2 Даны матрицы А, В, С.
а) найти определители матриц А и
С;
б) определить матрицу ![]() ;
;
в)
найти матрицы обратные к матрицам А и С, если они существуют;
г)
найти ранги матриц А и С;
д) найти произведение матриц А и В;
е)
найти матрицу ![]() .
.
Варианты индивидуальных
заданий для 3.3.2
|
№ |
A |
B |
C |
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
7 |
|
|
|
|
8 |
|
|
|
|
9 |
|
|
|
|
10 |
|
|
|
|
11 |
|
|
|
|
12 |
|
|
|
|
13 |
|
|
|
|
14 |
|
|
|
|
15 |
|
|
|
|
16 |
|
|
|
|
17 |
|
|
|
|
18 |
|
|
|
|
19 |
|
|
|
|
20 |
|
|
|
|
21 |
|
|
|
|
22 |
|
|
|
|
23 |
|
|
|
|
24 |
|
|
|
|
25 |
|
|
|
|
26 |
|
|
|
|
27 |
|
|
|
|
28 |
|
|
|
|
29 |
|
|
|
|
30 |
|
|
|
3.3.3 Дана система уравнений ![]() :
:
а) решить эту систему по
формулам Крамера;
б) решить систему матричным
способом, т.е. с помощью обратной
матрицы по формуле ![]() ;
;
в)
решить систему с помощью операции (встроенной функции)
![]() .
.
Варианты индивидуальных
заданий для 3.3.3
1 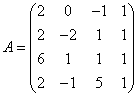 ,
, 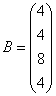 2
2 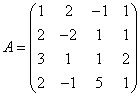 ,
, 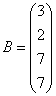
3 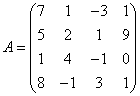 ,
, 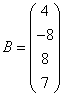 4
4 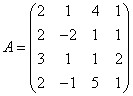 ,
, 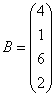
5 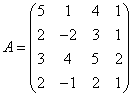 ,
, 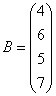 6
6 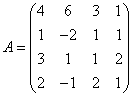 ,
,  7
7 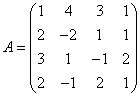 ,
, 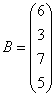 8
8  ,
, 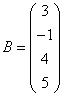
9 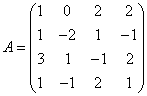 ,
, 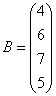 10
10 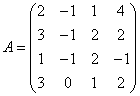 ,
, 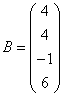
11  ,
,  12
12  ,
, 
13 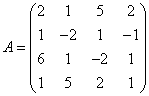 ,
, 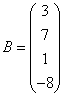 14
14 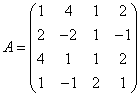 ,
, 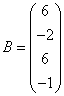
15  ,
, 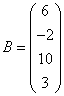 16
16 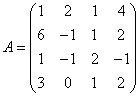 ,
, 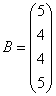
17 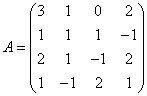 ,
, 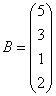 18
18 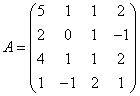 ,
, 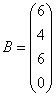
19 ,
, 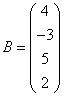 20
20 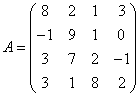 ,
,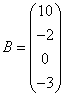
21 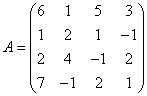 ,
,  22
22 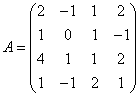 ,
, 
23 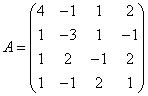 ,
, 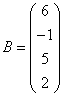 24
24 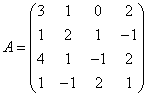 ,
, 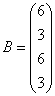
25 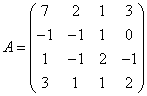 ,
,  26
26 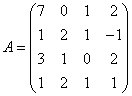 ,
, 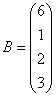
27 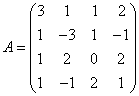 ,
, 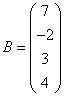 28
28 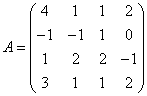 ,
, 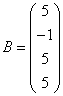
29 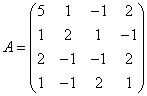 ,
, 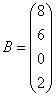 30
30 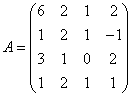 ,
, 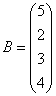
4 Примеры выполнения заданий и указания к выполнению лабораторной работы №2
Пример
1. Даны векторы ![]() и числа
и числа ![]() . Найти:
. Найти:
а) ![]() ;
;
б) ![]() ;
;
в)
скалярное произведение векторов ![]() и
и ![]() ;
;
г)
векторное произведение векторов ![]() и
и ![]() ;
;
д)
длину вектора ![]() и вектора, полученного в предыдущем пункте;
и вектора, полученного в предыдущем пункте;
е)
смешанное произведение векторов ![]() ;
;
ж)
являются ли заданные три вектора линейно зависимыми или нет?
Могут ли они образовывать базис пространства?
Указание.
Набрать с использованием панели Матрицы
три вектора как матрицы- столбцы (три строки и один столбец) и три числа, затем
последовательно выполнить все 7 заданий.
Выполнение задания
Замечание: Текст и большинство формул набираются в системе WORD; вычисления, решение уравнений производятся в системе
MATHCAD параллельно, затем копируются в документе WORD.
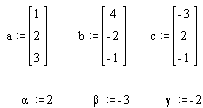
а)-б) набрать с
клавиатуры выражения ![]() и
и ![]() , причём знак умножения не опускать, выделить всё синим
уголком (для этого использовать клавишу Пробел)
и нажать знак =:
, причём знак умножения не опускать, выделить всё синим
уголком (для этого использовать клавишу Пробел)
и нажать знак =: 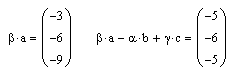
в)-г) вызвать панель Матрицы, Скалярное (затем Векторное)
произведение в пробелы ввести сомножители, выделить всё синим уголком и нажать
знак =:
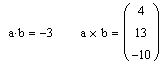
д)
вызвать панель Матрицы, Вычисление
определителя, заполнить пробел вектором ![]() или
или ![]() , выделить всё синим уголком и нажать знак =:
, выделить всё синим уголком и нажать знак =:![]()
е)
набрать с помощью панели Матрицы,
Скалярное и Векторное произведения выражение ![]() , выделить всё синим уголком и нажать знак =:
, выделить всё синим уголком и нажать знак =: ![]() или
или ![]() .
.
ж) три вектора будут
линейно независимыми, если определитель, составленный из координат этих
векторов не равен нулю (или их смешанное произведение не равно нулю); они будут
зависимыми, если этот определитель равен нулю. Поэтому составим матрицу из
координат векторов ![]() и вычислим определитель этой матрицы, как
указано выше:
и вычислим определитель этой матрицы, как
указано выше:
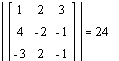 . Таким образом, векторы
. Таким образом, векторы ![]() являются линейно независимыми и могут образовывать базис
пространства.
являются линейно независимыми и могут образовывать базис
пространства.
Пример
2. Даны матрицы
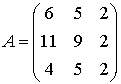 ,
, 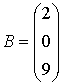 ,
, 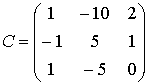 .
.
а) найти определители матриц А и
С;
б) определить матрицу ![]() ;
;
в)
найти матрицы обратные к матрицам А и С, если они существуют;
г)
найти ранги матриц А и С;
д)
найти произведение матриц А и В;
е)
найти матрицу ![]() .
.
Указание. Набрать с
использованием панели Матрицы
три матрицы, затем последовательно
выполнить все 6 заданий:
Выполнение задания

а) определители матриц А и С найти, как
указано в задании 1.7: ![]() ,
, ![]() ;
;
б) задание выполняется с помощью панели Матрицы, Транспонирование матриц: ![]() ;
;
в) задание выполняется с помощью панели Матрицы, Инверсия, причём если
определитель матрицы равен нулю, то матрица не имеет обратной:
![]() - не существует, т.к. её
определитель равен нулю,
- не существует, т.к. её
определитель равен нулю, 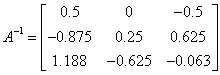 ;
;
г) ранги матриц
определяются с помощью функции rank, которую
набирают с клавиатуры: ![]()
д)-е) задания выполняются с помощью
операций умножение и
возведение в степень либо с
клавиатуры, либо используя панель Арифметика:
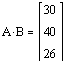
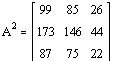 .
.
Пример 3. Дана система
уравнений ![]() , где
, где
 ,
, 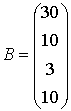 ,
, 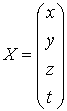 .
.
а) решить эту систему по
формулам Крамера;
б) решить систему матричным
способом;
в) решить систему с помощью функции lsolve(A,B).
Указание. Набрать матрицы A и B с использованием панели Матрицы, затем последовательно выполнить все 3 задания.
Выполнение задания

а) для решения системы
по правилу Крамера следует набрать ещё четыре матрицы, затем по формулам Крамера
найти решение: 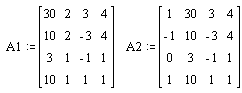
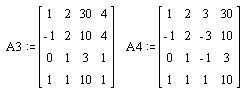
 . Таким образом, система имеет
одно решение
. Таким образом, система имеет
одно решение ![]() ;
;
б) для решения системы
матричным способом нужно набрать ещё матрицу ![]() , затем умножить
, затем умножить ![]() на B и нажать знак
=:
на B и нажать знак
=:
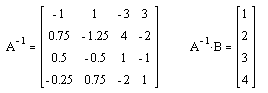 . Ответ:
. Ответ: ![]() ;
;
в) для решения системы с помощью функции lsolve следует набрать эту функцию с клавиатуры, в качестве аргументов записать матрицы А и В, вызвать знак стрелки с панели Символические операторы, щёлкнуть по свободному месту и после появившихся записей нажать знак =:
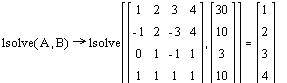 . Ответ:
. Ответ: ![]() .
.
5 Лабораторная работа №3. Задачи математического анализа
5.1
Цель работы
Целью настоящей лабораторной работы является обучение
студентов правилам и приемам использования MathCad для построения графиков функций, вычисления пределов, сравнения
бесконечно малых, определения непрерывности
и точек разрыва функции.
5.2 Описание центральных вопросов построения графиков и
вычисления пределов.
Рассмотрим функцию ![]() , определенную на промежутке
, определенную на промежутке ![]() :
:
- функция ![]() называется
непрерывной в точке
называется
непрерывной в точке ![]() , если выполняются равенства
, если выполняются равенства ![]() (1);
(1);
- если хотя бы одно из равенств (1) нарушается, и при
этом ![]() являются конечными
числами, то
являются конечными
числами, то ![]() называют точкой
разрыва I рода, если же хотя бы одно
из чисел
называют точкой
разрыва I рода, если же хотя бы одно
из чисел ![]() бесконечно большое,
то
бесконечно большое,
то ![]() называют точкой
разрыва II рода.
называют точкой
разрыва II рода.
Пусть функции ![]() и
и ![]() определены на
промежутке
определены на
промежутке ![]() и
и ![]() :
:
- если ![]() , то
, то ![]() называется бесконечно
малой функцией при
называется бесконечно
малой функцией при ![]() ;
;
- для сравнения двух бесконечно малых функций при ![]() находят предел их отношения:
находят предел их отношения: 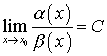 ;
;
- если![]() , то
, то ![]() и
и ![]() называются бесконечно
малыми величинами одного и того же порядка;
называются бесконечно
малыми величинами одного и того же порядка;
- если ![]() , то
, то ![]() называется бесконечно малой более высокого порядка по
сравнению с
называется бесконечно малой более высокого порядка по
сравнению с ![]() , а
, а ![]() - бесконечно малой более низкого порядка по сравнению с
- бесконечно малой более низкого порядка по сравнению с ![]() ;
;
- если ![]() , то
, то ![]() и
и ![]() называются
эквивалентными величинами:
называются
эквивалентными величинами: ![]() .
.
5.3 Рабочее задание
5.3.1 Построить график функции y=f(x) в декартовой системе координат
Варианты индивидуальных заданий для 5.3.1
|
№ |
f(x) |
№ |
f(x) |
|
1 |
|
16 |
|
|
2 |
|
17 |
|
|
3 |
|
18 |
|
|
4 |
|
19 |
|
|
5 |
|
20 |
|
|
6 |
|
21 |
|
|
7 |
|
22 |
|
|
8 |
|
23 |
|
|
9 |
|
24 |
|
|
10 |
|
25 |
|
|
11 |
|
26 |
|
|
12 |
|
27 |
|
|
13 |
|
28 |
|
|
14 |
|
29 |
|
|
15 |
|
30 |
|
5.3.2
Построить график функции y=f(x) в декартовой
системе координат Построить в том же графике касательную и нормаль в указанной
точке.
Варианты индивидуальных
заданий для 5.3.2
|
№ |
f(x) |
|
№ |
f(x) |
|
№ |
f(x) |
|
|
1 |
|
-10 |
11 |
|
10 |
21 |
|
-5 |
|
2 |
|
-3 |
12 |
|
3 |
22 |
|
-5 |
|
3 |
|
-8 |
13 |
|
8 |
23 |
|
-3 |
|
4 |
|
-3 |
14 |
|
3 |
24 |
|
-5 |
|
5 |
|
-1 |
15 |
|
1 |
25 |
|
-1 |
|
6 |
|
-2 |
16 |
|
2 |
26 |
|
5 |
|
7 |
|
-1 |
17 |
|
1 |
27 |
|
5 |
|
8 |
|
-2 |
18 |
|
2 |
28 |
|
3 |
|
9 |
|
0,5 |
19 |
|
-0,5 |
29 |
|
5 |
|
10 |
|
0,5 |
20 |
|
-0,5 |
30 |
|
1 |
5.3.3 Построить график функции, заданной
параметрически
Варианты индивидуальных
заданий для 5.3.3
|
№ |
x(t) |
y(t) |
№ |
x(t) |
y(t) |
|
1 |
|
|
16 |
|
|
|
2 |
|
|
17 |
|
|
|
3 |
|
|
18 |
|
|
|
4 |
|
|
19 |
|
|
|
5 |
|
|
20 |
|
|
|
6 |
|
|
21 |
|
|
|
7 |
|
|
22 |
|
|
|
8 |
|
|
23 |
|
|
|
9 |
|
|
24 |
|
|
|
10 |
|
|
25 |
|
|
|
11 |
|
|
26 |
|
|
|
12 |
|
|
27 |
|
|
|
13 |
|
|
28 |
|
|
|
14 |
|
|
29 |
|
|
|
15 |
|
|
30 |
|
|
5.3.4
Построить график функции в полярной системе координат
Варианты индивидуальных
заданий для 5.3.4
|
№ |
|
№ |
|
№ |
|
|
1 |
|
11 |
- |
21 |
|
|
2 |
|
12 |
|
22 |
|
|
3 |
|
13 |
|
23 |
|
|
4 |
|
14 |
|
24 |
|
|
5 |
|
15 |
|
25 |
|
|
6 |
|
16 |
|
26 |
|
|
7 |
|
17 |
|
27 |
|
|
8 |
|
18 |
|
28 |
|
|
9 |
|
19 |
|
29 |
|
|
10 |
|
20 |
|
30 |
|
5.3.5 Найти предел функции f(x) в точке а
Варианты индивидуальных заданий для 5.3.5
|
№ |
f(x) |
а |
№ |
f(x) |
а |
№ |
f(x) |
а |
|
1 |
|
2 |
11 |
|
1 |
21 |
|
-1 |
|
2 |
|
3 |
12 |
|
1 |
22 |
|
4 |
|
3 |
|
|
13 |
|
|
23 |
|
0 |
|
4 |
|
0 |
14 |
|
1 |
24 |
|
-2 |
|
5 |
|
1 |
15 |
|
0 |
25 |
|
2 |
|
6 |
|
4 |
16 |
|
4 |
26 |
|
|
|
7 |
|
1 |
17 |
|
|
27 |
|
0 |
|
8 |
|
2 |
18 |
|
1 |
28 |
|
-1 |
|
9 |
|
b |
19 |
|
-1 |
29 |
|
-1 |
|
10 |
|
2 |
20 |
|
|
30 |
|
|
5.3.6 Определить, что указанные функции являются
бесконечно малыми при ![]() . Сравнить эти бесконечно малые
. Сравнить эти бесконечно малые
Варианты индивидуальных заданий для 5.3.6
|
№ |
|
|
№ |
|
|
|
1 |
|
|
16 |
|
|
|
2 |
|
|
17 |
|
|
|
3 |
|
|
18 |
|
|
|
4 |
|
|
19 |
|
|
|
5 |
|
|
20 |
|
|
|
6 |
|
|
21 |
|
|
|
7 |
|
|
22 |
|
|
|
8 |
|
|
23 |
|
|
|
9 |
|
|
24 |
|
|
|
10 |
|
|
25 |
|
|
|
11 |
|
|
26 |
|
|
|
12 |
|
|
27 |
|
|
|
13 |
|
|
28 |
|
|
|
14 |
|
|
29 |
|
|
|
15 |
|
|
30 |
|
|
5.3.7 Найти
точки разрыва заданных функций и определить их тип
Варианты индивидуальных
заданий для 5.3.7
|
№ |
f(x) |
g(x) |
№ |
f(x) |
g(x) |
|
1 |
|
|
2 |
|
|
|
3 |
|
|
4 |
|
|
|
5 |
|
|
6 |
|
|
|
7 |
|
|
8 |
|
|
|
9 |
|
|
10 |
|
|
|
11 |
|
|
12 |
|
|
|
13 |
|
|
14 |
|
|
|
15 |
|
|
16 |
|
|
|
17 |
|
|
18 |
|
|
|
19 |
|
|
20 |
|
|
|
21 |
|
|
22 |
|
|
|
23 |
|
|
24 |
|
|
|
25 |
|
|
26 |
|
|
|
27 |
|
|
28 |
|
|
|
29 |
|
|
30 |
|
|
6 Примеры выполнения заданий и указания к выполнению лабораторной работы №3
Пример
1. Построить график функции в декартовой системе координат.
Указание. Набрать с клавиатуры заданную
функцию. Вызвать с панели
Графики Декартов
график. Заполнить чёрную метку возле оси Ох именем переменной х, метку
возле оси Оу именем функции f(x),заполнить метки для масштаба и щёлкнуть по
свободному месту вне поля графика.
Выполнение задания
f(x)=![]()
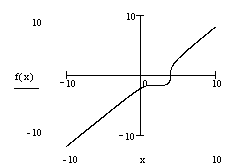
Пример
2. Построить график функции в декартовой
системе координат. Построить в том же графике касательную и нормаль в
указанной точке.
Указание. Набрать с клавиатуры заданную
функцию, угловой коэффициент касательной, вычисленный в указанной точке,
уравнения касательной и нормали. Вызвать с панели Графики Декартов график,
заполнить метки (причём набор трёх
функций по оси Оу производить через запятую) и щёлкнуть по свободному месту вне
поля графика.
Выполнение задания
![]() ,
, ![]() ;
;
![]() - угловой
коэффициент касательной;
- угловой
коэффициент касательной;
![]() - угловой коэффициент
касательной, вычисленный в точке
- угловой коэффициент
касательной, вычисленный в точке ![]() ;
;
![]() - уравнение
касательной;
- уравнение
касательной;
![]() - уравнение
нормали.
- уравнение
нормали.
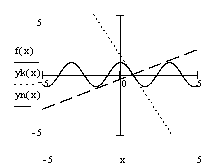
Пример 3. Построить график функции,
заданной параметрически.
Указание. Набрать с клавиатуры заданную
функцию, вызвать с панели Графики Декартов график, заполнить метки,
причём по оси Ох набрать x(t), а по оси Оу
- y(t) и щёлкнуть по свободному месту вне поля
графика.
Выполнение задания
![]()
![]()
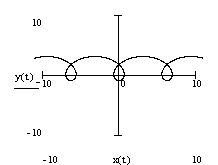
Пример 4. Построить график функции в полярной системе
координат.
Указание. Набрать с клавиатуры заданную функцию,
вызвать с панели Графики Полярный график, заполнить метки и щёлкнуть по
свободному месту вне поля графика.
Выполнение задания
![]()
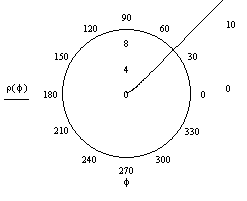
Пример 5. Найти предел функции f(x) в точке a.
Указание. Вызвать с панели Математический
анализ знак Пределы, заполнить его,
вызвать с панели Символические операторы знак стрелки и щёлкнуть
по свободному месту.
Выполнение задания
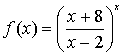 , a=
, a=![]()
![]()
Пример 6. Определить, что указанные
функции являются бесконечно малыми при ![]() . Сравнить эти бесконечно малые.
. Сравнить эти бесконечно малые.
Указание. Найти пределы для каждой из
заданных функции при ![]() , как указано выше,
затем найти предел отношения этих
функций при
, как указано выше,
затем найти предел отношения этих
функций при ![]() и сделать выводы.
и сделать выводы.
Выполнение задания
![]()
![]()
![]()
![]() -вычисление пределов заданных функций, т.к. пределы равны
0, то обе функции являются бесконечно
малыми при
-вычисление пределов заданных функций, т.к. пределы равны
0, то обе функции являются бесконечно
малыми при ![]() .
.
![]() -т.к. предел отношения этих
функций при
-т.к. предел отношения этих
функций при ![]() равен 1, то
бесконечно малые эквивалентны.
равен 1, то
бесконечно малые эквивалентны.
Пример 7. Найти точки разрыва заданной
функции и определить их тип.
Указание. Найти односторонние пределы для
каждой из заданных функций в точках,
где функции не определены (для этого надо вызвать с панели Математический
анализ знаки Левого и Правого Пределов), в зависимости от
найденных пределов определить тип точки разрыва.
Выполнение задания
![]() .
.
Для данной функции точка х=-6 не входит в её область
определения, но функция определена в окрестности этой точки, значит х=-6
является точкой разрыва.
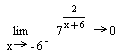
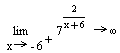 -вычисление односторонних пределов в точке разрыва.
-вычисление односторонних пределов в точке разрыва.
Левый предел функции равен 0, правый-![]() . Т.к. один из односторонних пределов равен
. Т.к. один из односторонних пределов равен![]() , то точка х=-6 является точкой разрыва второго рода.
, то точка х=-6 является точкой разрыва второго рода.
7 Лабораторная работа №4
Исследование функций и
построение графиков
7.1
Цель работы
Целью настоящей лабораторной работы является вычисление производных функции одной переменной, исследование функции с помощью производных и построение графиков.
4.2
Описание центральных вопросов полного исследования функции и построения
графиков.
Рассмотрим
функцию ![]() , определенную на промежутке
, определенную на промежутке ![]() . Характер поведения функции в области определения можно
исследовать, опираясь на следующие утверждения:
. Характер поведения функции в области определения можно
исследовать, опираясь на следующие утверждения:
- если ![]() то график функции в
точке
то график функции в
точке ![]() пересекает ось
абсцисс;
пересекает ось
абсцисс;
- если в точке ![]() функция имеет
бесконечный разрыв, то график
функция имеет
бесконечный разрыв, то график
функции имеет вертикальную
асимптоту ![]()
- если существуют и конечны пределы ![]()
то прямая ![]() - наклонная
асимптота графика функции при
- наклонная
асимптота графика функции при ![]()
- если ![]() и существует такое
число
и существует такое
число ![]() что
что ![]() для любого
для любого ![]() то исследуемая
функция периодична с периодом
то исследуемая
функция периодична с периодом ![]() в этом случае
достаточно построить график функции на промежутке
в этом случае
достаточно построить график функции на промежутке ![]() и доопределить его по
периодичности на всю числовую ось;
и доопределить его по
периодичности на всю числовую ось;
- если ![]() для любого
для любого ![]() то исследуемая
функция четная. В этом случае график симметричен относительно оси ординат; достаточно построить график функции на
промежутке
то исследуемая
функция четная. В этом случае график симметричен относительно оси ординат; достаточно построить график функции на
промежутке ![]() и отобразить его
симметрично относительно оси ординат на промежуток (-
и отобразить его
симметрично относительно оси ординат на промежуток (-![]() ,0);
,0);
- если ![]() для любого
для любого ![]() то исследуемая
функция нечетная; в этом случае график симметричен относительно начала
координат; достаточно построить график функции на промежутке
то исследуемая
функция нечетная; в этом случае график симметричен относительно начала
координат; достаточно построить график функции на промежутке ![]() а затем отобразить
его на промежуток
а затем отобразить
его на промежуток ![]() симметрично относительно
начала координат;
симметрично относительно
начала координат;
- если существует окрестность точки ![]() такая, что в этой
окрестности
такая, что в этой
окрестности ![]() при
при ![]() и
и ![]() при
при ![]() то функция имеет в
точке
то функция имеет в
точке ![]() максимум. Если же
максимум. Если же ![]() при
при ![]() и
и ![]() при
при ![]() то функция имеет в
точке
то функция имеет в
точке ![]() минимум;
минимум;
- если дважды дифференцируемая на промежутке ![]() функция
функция ![]() имеет на нем
положительную вторую производную, то функция выпукла на
имеет на нем
положительную вторую производную, то функция выпукла на ![]() . Если же вторая производная отрицательна на промежутке
. Если же вторая производная отрицательна на промежутке ![]() , то функция на нем вогнута.
, то функция на нем вогнута.
Если же вторая производная равна нулю в точке ![]() а слева и справа от
нее имеет значения разных знаков, то точка
а слева и справа от
нее имеет значения разных знаков, то точка ![]() - точка перегиба.
- точка перегиба.
7.3 Рабочее
задание
7.3.1 Дана
функция f(x) и точка![]() . Найти производную функции f(x) по
определению.
. Найти производную функции f(x) по
определению.
7.3.2 Найти
производные:![]() .
.
Варианты индивидуальных
заданий для 7.3.1 и 7.3.2.
|
№ |
|
|
№ |
|
|
№ |
|
|
|
1 |
|
|
2 |
|
1 |
3 |
|
0 |
|
4 |
|
0 |
5 |
|
0 |
6 |
|
0 |
|
7 |
|
|
8 |
|
1 |
9 |
|
2 |
|
10 |
|
0 |
11 |
|
0 |
12 |
|
2 |
|
13 |
|
|
14 |
|
|
15 |
|
|
|
16 |
|
|
17 |
|
1 |
18 |
|
0 |
|
19 |
|
0 |
20 |
|
1 |
21 |
|
0 |
|
22 |
|
2 |
23 |
|
|
24 |
|
|
|
25 |
|
|
26 |
|
0 |
27 |
|
|
|
28 |
|
2 |
29 |
|
0 |
30 |
|
|
7.3.3 Дана
функция f(x). Найти точки пересечения графика функции f(x) с осями
координат.
7.3.4 Найти
асимптоты графика функции f(x).
7.3.5
Построить график функции f(x) и сравнить
полученные результаты с данными на графике.
Варианты индивидуальных
заданий для 7.3.3, 7.3.4 и
7.3.5.
|
№ |
|
№ |
|
№ |
|
|
1 |
|
2 |
|
3 |
|
|
4 |
|
5 |
|
6 |
|
|
7 |
|
8 |
|
9 |
|
|
10 |
|
11 |
|
12 |
|
|
13 |
|
14 |
|
15 |
|
|
16 |
|
17 |
|
18 |
|
|
19 |
|
20 |
|
21 |
|
|
22 |
|
23 |
|
24 |
|
|
25 |
|
26 |
|
27 |
|
|
28 |
|
29 |
|
30 |
|
7.3.6 Дана
функция f(x). Найти точки экстремума и экстремальные значения f(x).
7.3.7 Построить график функции f(x) и сравнить полученные результаты с данными на графике.
Варианты индивидуальных заданий для 7.3.6 и 7.3.7.
|
№ |
|
№ |
|
|
1 |
|
2 |
|
|
3 |
|
4 |
|
|
5 |
|
6 |
|
|
7 |
|
8 |
|
|
9 |
|
10 |
|
|
11 |
|
12 |
|
|
13 |
|
14 |
|
|
15 |
|
16 |
|
|
17 |
|
18 |
|
|
19 |
|
20 |
|
|
21 |
|
22 |
|
|
23 |
|
24 |
|
|
25 |
|
26 |
|
|
27 |
|
28 |
|
|
29 |
|
30 |
|
7.3.8 Дана
функция f(x). Найти интервалы выпуклости, вогнутости и
точки перегиба графика функции.
7.3.9
Построить график функции f(x) и сравнить
полученные результаты с данными на графике.
Варианты индивидуальных заданий для 7.3.8 и 7.3.9.
|
№ |
|
№ |
|
№ |
|
|
1 |
|
2 |
|
3 |
|
|
4 |
|
5 |
|
6 |
|
|
7 |
|
8 |
|
9 |
|
|
10 |
|
11 |
|
12 |
|
|
13 |
- |
14 |
|
15 |
|
|
16 |
|
17 |
|
18 |
|
|
19 |
|
20 |
|
21 |
|
|
22 |
|
23 |
|
24 |
|
|
25 |
|
26 |
|
27 |
- |
|
28 |
|
29 |
|
30 |
|
7.3.10 Провести полное исследование функции f(x) и построить график.
Варианты индивидуальных заданий для задания 7.3.10.
№ |
|
№ |
|
№ |
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
11 |
|
12 |
|
13 |
|
14 |
|
15 |
-
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
|
21 |
|
22 |
|
23 |
|
24 |
|
25 |
|
26 |
|
27 |
|
28 |
|
29 |
|
30 |
|
8 Примеры выполнения заданий и указания к выполнению лабораторной работы №4.
Пример 1. Дана функция ![]() и точка
и точка ![]() =
=![]() .
.
а) найти производную функции f(x) по
определению;
в) найти производные![]() .
.
Указание. В математической программе MATHCAD набрать с клавиатуры заданную функцию. Вызвать с
панели Математический анализ знак Пределы, заполнить его и вычислить предел отношения приращения функции
к приращению аргумента при ![]() . Полученное
выражение будет производной заданной
функции, найденной по определению. Затем вызвать с панели Математический анализ знак Производной,
заполнить его и вычислить производную
средствами системы MATHCAD. Набрать с клавиатуры
точку
. Полученное
выражение будет производной заданной
функции, найденной по определению. Затем вызвать с панели Математический анализ знак Производной,
заполнить его и вычислить производную
средствами системы MATHCAD. Набрать с клавиатуры
точку ![]() и вычислить
производные, как указано ниже.
и вычислить
производные, как указано ниже.
Выполнение задания в рабочем окне программы Mathcad.
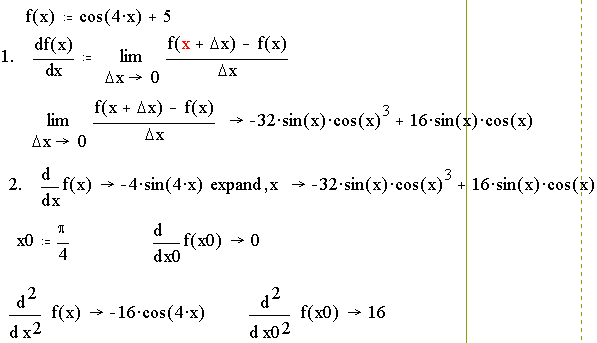
Пример 2. Дана функция ![]() .
.
а)найти координаты точек
пересечения f(x) с осями координат;
б) найти асимптоты графика
функции;
в) построить график функции
и сравнить полученные результаты с
данными на
графике.
Указание. а) набрать с
клавиатуры заданную функцию. Вычислить значение f(0) – это точка пересечения
с осью ОУ. Решить уравнение f(x)=0 – его корни являются
точками пересечения с осью ОХ;
б) найти точку разрыва f(x),
вычислить односторонние пределы в этой точке. Записать уравнение вертикальной
асимптоты. Вычислить пределы ![]() ,
, ![]() . Составить уравнение наклонной (или горизонтальной, если k=0)
асимптоты y=kx+b;
. Составить уравнение наклонной (или горизонтальной, если k=0)
асимптоты y=kx+b;
в) построить график f(x). Сделать выводы о
совпадении или нет проведённых выше исследований с данными на графике.
Замечание: все указанные
действия выполнялись в предыдущих лабораторных работах № 1, 2, 3.
Выполнение задания в рабочем окне программы Mathcad.
а)
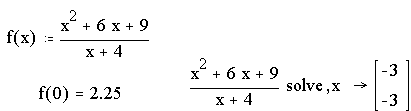
Таким образом,
точка пересечения с осью ОХ– (-3;0), с осью ОУ- (0;2,25).
б) х=-4 является точкой разрыва функции, т.к. функция не определена в этой точке. Вычислим односторонние пределы в этой точке:
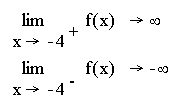 .
.
Итак, х=-4 – вертикальная асимптота.
Найдём наклонную асимптоту y=kx+b:
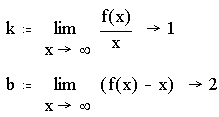
Итак, y=x+2 – наклонная асимптота;
в) построим график функции и его асимптоты:
f1(x)=x+2, f2(x)=x+4.
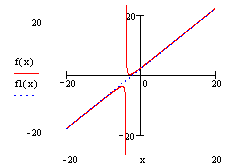
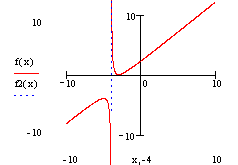
Пример 3. Дана функция ![]() .
.
а) найти точки экстремума и экстремальные значения;
б) построить график функции и сравнить полученные
результаты с
данными
на графике.
Указание. а) найти производную функции![]() . Найти критические точки, т.е. точки, в которых
. Найти критические точки, т.е. точки, в которых ![]() =0 или не существует. Разбить критическими точками область
определения на части, найти знак производной в каждой части. Сделать выводы.
Все данные занести в таблицу;
=0 или не существует. Разбить критическими точками область
определения на части, найти знак производной в каждой части. Сделать выводы.
Все данные занести в таблицу;
б) построить график функции и сравнить полученные
результаты с данными на графике.
Выполнение задания в рабочем окне программы Mathcad.
а)
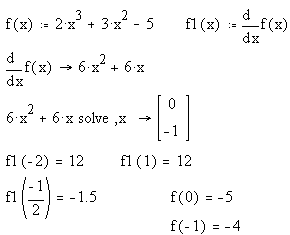
|
x |
|
-1 |
|
0 |
|
|
|
+ |
0 |
- |
0 |
+ |
|
y |
|
-4 |
|
-5 |
|
Итак, точка максимума - (-1;-4); точка минимума -
(0;-5). Интервалы возрастания - ![]() и
и ![]() , интервал убывания -
, интервал убывания - ![]() ;
;
б) построим график функции:
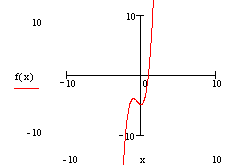
Данные
на графике совпадают с данными исследования.
Пример 4. Дана функция  .
.
а) найти интервалы выпуклости и вогнутости графика
функции, точки перегиба;
б) построить график функции f(x) и сравнить
полученные результаты с данными на графике.
Указание: а) найти производную второго порядка функции![]() . Найти точки, где
. Найти точки, где ![]() =0 или не существует. Разбить область определения функции
полученными точками на части. Сделать выводы о выпуклости и вогнутости и
наличии точек перегиба. Все данные занести в таблицу;
=0 или не существует. Разбить область определения функции
полученными точками на части. Сделать выводы о выпуклости и вогнутости и
наличии точек перегиба. Все данные занести в таблицу;
б) построить график функции f(x) и сравнить
полученные результаты с данными на графике.
Выполнение задания в рабочем окне программы Mathcad.
а) 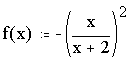
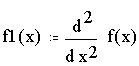
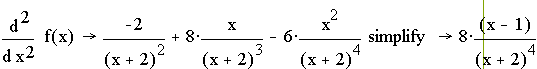
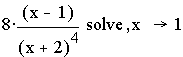
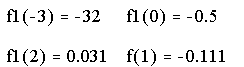
|
x |
|
|
1 |
|
|
|
- |
- |
0 |
+ |
|
y |
|
|
-0,111 |
|
Итак, (1,-0.111)- точка перегиба.
![]() и
и ![]() - интервалы выпуклости,
- интервалы выпуклости, ![]() - интервал вогнутости;
- интервал вогнутости;
б)
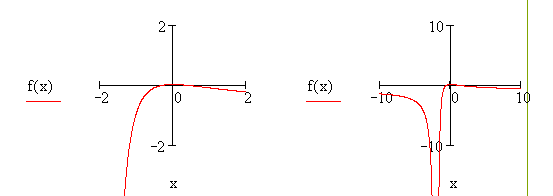
Для
большей наглядности график построен в двух масштабах. Данные на графике
совпадают с данными исследования.
Пример 5. Дана функция f(x)=![]() . Провести полное исследование функции и построить график.
. Провести полное исследование функции и построить график.
Указание. Найти: а) область определения и точки
разрыва;
б)
асимптоты графика функции; в) точки пересечения графика с осями координат; г)
чётность и нечётность; д) интервалы монотонности, точки экстремума; е)
интервалы выпуклости, вогнутости, точки перегиба; ж) построить график функции.
Выполнение задания в рабочем окне программы Mathcad.
а) f(x)= ![]() ,
, ![]() ,
, ![]() -точки разрыва. Д(f):
-точки разрыва. Д(f):![]() ;
;
б) f(x)= ![]() , т.к.
, т.к.
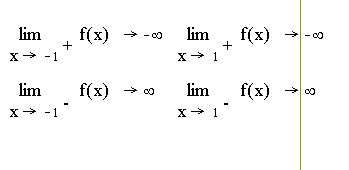
![]() - вертикальные асимптоты.
- вертикальные асимптоты.
Найдём наклонную асимптоту y=kx+b:
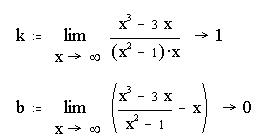 .
.
Таким образом,
y=x - наклонная
асимптота;
в) точки пересечения графика функции с
осями координат:
с OX: y=0![]()
![]() ,
,
c
OY: x=0![]() y=0
y=0![]() ;
;
г) так как 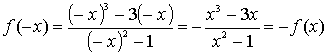 , то функция нечётная;
, то функция нечётная;
д) найдём интервалы монотонности, точки
экстремума: 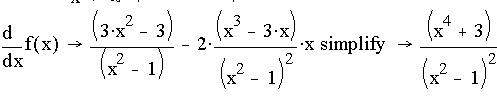
Так
как ![]() , то функция f(x) везде в области определения возрастает. Точек
экстремума нет;
, то функция f(x) везде в области определения возрастает. Точек
экстремума нет;
е) найдём интервалы выпуклости,
вогнутости, точки перегиба:
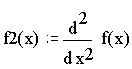
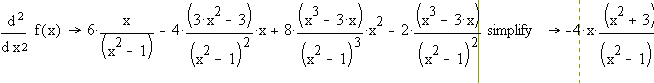 f2(x)=0:
f2(x)=0:
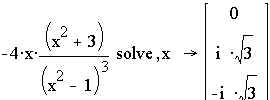 .
.
Итак, х=0 может быть абсциссой точки перегиба.
Заполним таблицу.
|
x |
|
|
0 |
|
|
|
|
+ |
- |
0 |
+ |
- |
|
y |
|
|
0 |
|
|
Определение знаков второй производной в указанных
интервалах:  .
.
Таким образом,
(0,0) -точка перегиба;
ж) построим графики функции и асимптоты: ![]()
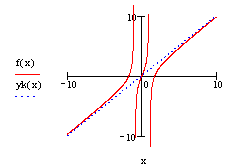
Замечание. Текст и большинство формул набираются в
системе WORD;
вычисления, решение уравнений, построение графиков производятся в системе MATHCAD параллельно, затем копируются и переносятся в документ WORD.
Литература
1. Дъяконов В.П.,
Абраменкова И.В. ![]() 7.0 в математике,
физике и в
7.0 в математике,
физике и в ![]() . – М.: Нолидж, 1998.-352 с.
. – М.: Нолидж, 1998.-352 с.
2. Плис
А.И., Сливина Н.А. ![]() :
математический практикум для
:
математический практикум для
экономистов и инженеров:
Учеб. пособие. – М.: Финансы и статистика, 1999.-656 с.
3. Хасеинов К.А. Каноны
математики. - Алматы, 2003.-686 с.
4. Киръянов Д.В. ![]() 12. – С.Пб.: БХВ –
Петербург, 2005. – 576 с.
12. – С.Пб.: БХВ –
Петербург, 2005. – 576 с.
Содержание
1 Лабораторная работа № 1 1
2 Примеры выполнения заданий и указания к выполнению
лабораторной работы № 1 10
3 Лабораторная работа № 2 13
4 Примеры выполнения заданий и указания к выполнению
лабораторной работы № 2 20
5 Лабораторная работа № 3 25
6 Примеры выполнения заданий и указания к выполнению
лабораторной работы № 3 33
7 Лабораторная работа № 4 37
8 Примеры выполнения заданий и указания к выполнению
лабораторной работы № 4 41
Литература 50
Сводный
план 2006г.,поз.112
Людмила Николаевна Астраханцева
Людмила
Николаевна Ким
Маншук Жумамуратовна Байсалова
Алгебра
и геометрия
Методические
указания к выполнению лабораторных работ
(для
студентов очной формы обучения специальности
050704
– Вычислительная техника и программное обеспечение)
Редактор Ж.М.Сыздыкова
Подписано в печать
Формат 6084 1/16
Тираж 100 экз. Бумага типографская №1
Объем 2,6 уч.-изд.л. Заказ Цена
Копировально-множительное бюро
Алматинского института энергетики и связи
050013, Алматы,
Байтурсынова,126