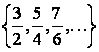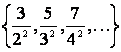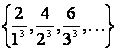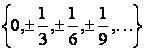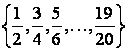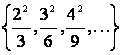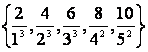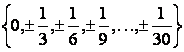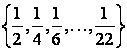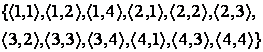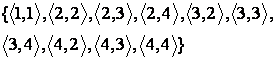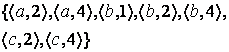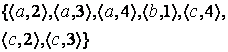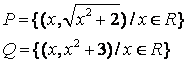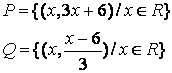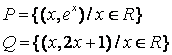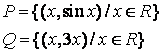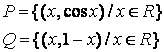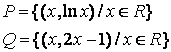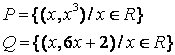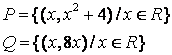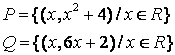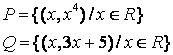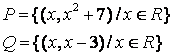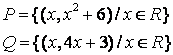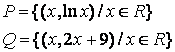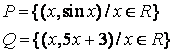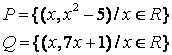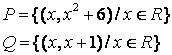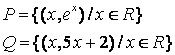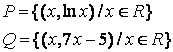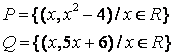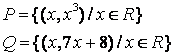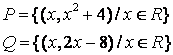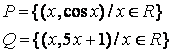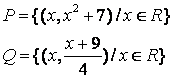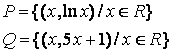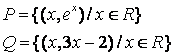Типовой расчёт №1 (Дискретная математика)

АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ

КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ

Дискретная математика

Методические указания и задания

к выполнению расчетно-графических работ

(для студентов очной формы обучения специальности

050704 – Вычислительная техника и программное обеспечение)

Часть 1

СОСТАВИТЕЛИ: Л.Н. Астраханцева, Л.Н.Ким, М.Ж.Байсалова.

Алгебра и геометрия. Методические указания и задания к выполнению расчетно-графической работы для студентов очной формы обучения специальности 050704 – Вычислительная техника и программное обеспечение.

Методические указания и задания к расчетно-графической работе содержат типовой расчет №3 дисциплины «Алгебра и геометрия» для студентов очной формы обучения специальности 050704 – Вычислительная техника и программное обеспечение. Приведены основные теоретические вопросы программы. Дано решение типового варианта.

1 Типовой расчёт 1. Множества, отношения

1.1 Теоретические вопросы

1 Множества, их способы задания. Подмножества, булеан. Операции над множествами.

2 Свойства операции над множествами. Разбиения и покрытия множеств.

3 Прямое произведение множеств. Отношения (унарные, бинарные, n-арные). Способы задания бинарных отношений. Обратное отношение, дополнение отношения, тождественное отношение. Композиция бинарных отношений.

4 Основные свойства матриц бинарных отношений. Свойства бинарных отношений (рефлексивность, симметричность, антисимметричность, транзитивность).

5 Отношение эквивалентности. Классы эквивалентности, фактор-множество.

6 Отношение порядка. Лексигографический порядок.

7 Функциональные отношения. Инъекция, сюръекция, биекция. Понятие о мощности множеств.

1.2 Расчётные задания

1 Данное множество задать перечислением элементов

Т а б л и ц а 1

1.1	1.2
1.3	1.4
1.5	1.6
1.7	1.8
1.9	1.10
1.11	1.12
1.13	1.14
1.15	1.16
1.17	1.18
1.19	1.20
1.21	1.22

продолжение таблицы 1

1.23	1.24
1.25	1.26
1.27	1.28
1.29	1.30

2 Данное множество задать общим свойством

Т а б л и ц а 2

2.1	2.2
2.3	2.4
2.5	2.6
2.7	2.8
2.9	2.10
2.11	2.12
2.13	2.14
2.15	2.16
2.17	2.18
2.19	2.20
2.21	2.22
2.23	2.24
2.25	2.26
2.27	2.28
2.29	2.30

3 Для данного множества:

a) составить булеан (т.е. множество всех подмножеств);

б) какое-нибудь покрытие;

в) какое-нибудь разбиение;

г) произвольное множество его подмножеств (ни булеан, ни покрытие, ни разбиение).

Т а б л и ц а 3

3.1 {x,y,z}	3.2 {2,3,4}
3.3 {a,b,c}	3.4 {e,f,g}
3.5 {m,n,p}	3.6 {x,y,z,t}
3.7 {2,3,4,5}	3.8 {a,b,c,d}
3.9 {e,f,g,k}	3.10 {m,n,p,q}
3.11 {6,7,8}	3.12 {v,w,z}
3.13 {5,6,7}	3.14 {b,c,d}
3.15 {4,5,6}	3.16 {y,z}
3.17 {3,4}	3.18 {b,c}
3.19 {f,g}	3.20 {n,p}
3.21 {y,z,t}	3.22 {3,4,5}
3.23 {b,c,d}	3.24 {f,g,k}
3.25 {n,p,q}	3.26 {7,8}
3.27 {w,z}	3.28 {6,7}
3.29 {c,d}	3.30 {5,6}

4 Для данных множеств А и В найти:

а);

б);

в);

г).

Т а б л и ц а 4

	A	B		A	B
4.1	{a,b,d}	{b,d,e,h}	4.2	{3,4,5,6}	{2,3,6,7,8}
4.3	{d,f,g,h}	{f,g,j,k}	4.4	{7,8,9}	{3,4,5,6,7}
4.5	{r,t,y}	{t,y,u,v}	4.6	{3,4,7,8}	{7,8,9,10}
4.7	{q,w,e}	{w,e,r,t}	4.8	{2,4,6,8}	{1,2,3,4,5}
4.9	{m,n,p,q}	{p,q,u,v}	4.10	{a,b,c,d}	{b,c,d,e,h}
4.11	{1,3,5,6}	{2,3,6,7,8}	4.12	{f,g,h}	{f,g,j,k}
4.13	{6,7,8,9}	{4,5,6,7}	4.14	{w,r,t,y}	{t,y,u,v,w}
4.15	{3,4,8}	{4,8,9,10}	4.16	{q,w,e,h}	{w,e,r,t}
4.17	{1,4,6,8}	{1,2,3,4}	4.18	{n,p,q}	{p,q,u,v}
4.19	{b,c,d}	{c,d,e,h}	4.20	{1,3,5}	{2,3,5,7,8}
4.21	{f,g,h,e}	{e,g,j,k}	4.22	{6,7,8}	{5,6,7}
4.23	{w,r,t}	{t,y,v,w}	4.24	{3,4,7}	{4,7,9,10}
4.25	{w,e,h}	{w,r,t}	4.26	{4,6,8}	{1,2,3,4,5,6}
4.27	{n,p,q,w}	{q,u,v,w}	4.28	{1,3,5,7}	{4,5,6,7}
4.29	{e,a,I,o}	{a,j,o}	4.30	{1,3,4,6}	{1,4,9,10}

5 Пусть универсальное множество U={0,1,2,3,4,5,6,7,8,9}. Для данных множеств А и В найти:

а);

б) ;

в) ;

г) .

Т а б л и ц а 5

	A		B				A		B
5.1	{1,2,3}		{4,5}		5.2		{3,4,5}		{7,8}
5.3	{7,8,9}		{1,2,3}		5.4		{7,8,9}		{3,4,5}
5.5	{4,5}		{2,3}		5.6		{4,7,8}		{9,0}
5.7	{3,4}		{6,7,8}		5.8		{2,6,8}		{1,2,3}
5.9	{3,5,7}		{1,4,6}		5.10		{8,9,0}		{1,2,4}
5.11	{1,3,5}		{6,7,8}		5.12		{0,1,2}		{8,9}
5.13	{6,7,8}		{4,5}		5.14		{4,5,6}		{1,2}
5.15	{3,4,8}		{1,9}		5.16		{2,9,5}		{3,4}
5.17	{4,6,8}		{1,2,3}		5.18		{2,3}		{4,7,9}
5.19	{1,5,6}		{2,3}		5.20		{1,3,5}		{2,7,8}
5.21	{6,7,9}		{5,8}		5.22		{6,7,8}		{5,9}
5.23		{2,4,6}		{3,5}		5.24		{3,4,7}		{8,9}
5.25		{5,6,0}		{1,2}		5.26		{6,8}		{2,3}
5.27		{1,3,4}		{7,8}		5.28		{1,3,5}		{6,7}
5.29		{7,8}		{4,6,9}		5.30		{3,4,6}		{1,9}

6 Доказать тождество:

а) с помощью диаграмм Эйлера-Венна;

б) используя определения операций над множествами или свойства операций.

Т а б л и ц а 6

6.1 A\(BC)=(A\B)∩(A\C)	6.2 ABC= A∩C
6.3 A\(B∩C)=(A\B) (A\C)	6.4
6.5 A\(A\B)=A∩B	6.6
6.7 A\B=A\(A∩B)	6.8
6.9 A∩(B\C)=(A∩B)\(A∩C)=(A∩B)\C	6.10
6.11 (A\B)\C=(A\C)\(B\C)	6.12
6.13 AB=A(B\A)	6.14
6.15 (A∩B) (A∩B )=A	6.16
6.17 (AB)∩(AB )=A	6.18
6.19 ( AB)∩A=A∩B	6.20
6.21 (AB)\C=(A\C) (B\C)	6.22
6.23 A\(B\C)=(A\B) (A∩C)	6.24
6.25 A\(BC)=(A\B)\C	6.26 A(B∩C)=(AB)∩(AC)
6.27 (A\B)C=(AC)\B	6.28 (AB)∩A=(A∩B) A=A
6.29 (A\B)C=(AC)	6.30

7 Даны множества А={a,b,c,d}, В={1,2,3,4} и отношения :

a) построить матрицы отношений и ;

б) изобразить отношения графически;

в) найти ;

г) проверить, является ли отношение рефлексивным, симметричным, антисимметричным, транзитивным.

Т а б л и ц а 7


7.1
7.2
7.3
7.4
7.5
7.6
7.7
7.8
7.9
7.10
7.11
7.12
7.13
7.14
7.15
7.16
7.17
7.18
7.19
7.20
7.21
7.22
7.23

продолжение таблицы 7

7.24
7.25
7.26
7.27
7.28
7.29
7.30

8 Доказать, что отношение является отношением эквивалентности на множестве . Построить классы эквивалентности и фактор-множество.

Т а б л и ц а 8


8.1
8.2
8.3
8.4
8.5
8.6
8.7
8.8
8.9
8.10
8.11
8.12
8.13
8.14
8.15
8.16
8.17
8.18
8.19
8.20
8.21
8.22
8.23

продолжение таблицы 8

8.24
8.25
8.26
8.27
8.28
8.29
8.30

9 Даны два отношения и :

а) доказать, что эти отношения являются функциями;

б) найти композиции ;

в) какими свойствами обладают отношения (инъективность, сюръек-тивность, биективность).

Т а б л и ц а 9

9.1	9.2
9.3	9.4
9.5	9.6
9.7	9.8
9.9	9.10
9.11	9.12
9.13	9.14
9.15	9.16
9.17	9.18
9.19	9.20

продолжение таблицы 9

9.21	9.22
9.23	9.24
9.25	9.26
9.27	9.28
9.29	9.30

1.3 Решение типового варианта

1 Множество задать перечислением элементов

Решение:

2 Множество задать общим свойством

Решение:

3 Для множества :

a) составить булеан (т.е. множество всех подмножеств);

б) какое-нибудь покрытие;

в) какое-нибудь разбиение;

г) произвольное множество его подмножеств (ни булеан, ни разбиение, ни покрытие).

Решение:

а) так как состоит из трёх элементов, то булеан P имеет элементов: P ;

б) например, - покрытие ;

в) например, или - разбиение ;

г) например, - ни булеан, ни разбиение, ни покрытие.

4 Для данных множеств и найти множества:

а);

б);

в);

г).

Решение:

а) ;

б) ;

в) ;

г) .

5 Пусть универсальное множество U={0,1,2,3,4,5,6,7,8,9}. Для данных множеств и найти:

а);

б) ;

в) ;

г) .

Решение:

а) ;

б) ;

в)

;

г)

6 Доказать тождество :

а) с помощью диаграмм Эйлера-Венна;

б) используя определения операций над множествами или свойства операций.

Решение:

а)

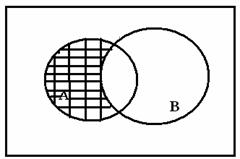
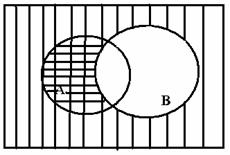
Рисунок 1 Рисунок 2

Таким образом, на обоих рисунках фигуры, изображающие множества и , одни и те же (заштрихованы решеткой );

б) если , то ( и ) ( и ) .

Если , то ( и ) ( и ), что и требовалось доказать.

7 Даны множества и и отношения и

а) построить матрицы отношений и ;

б) изобразить отношения графически;

в) найти ;

г) проверить, является ли отношение рефлексивным, симметричным, антисимметричным, транзитивным.

Решение:

а) -матрица отношения , где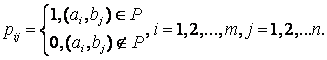

Таким образом, , ;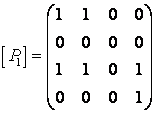

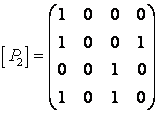б)

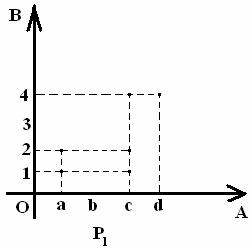
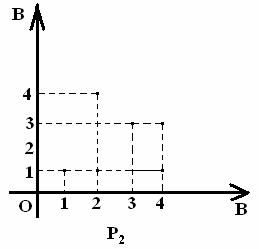
Рисунок 3 Рисунок 4

Заметим, что существуют другие способы графического изображения отношений. Например, отношение можно изобразить как на рисунке 5, а отношение – как на рисунке 6;

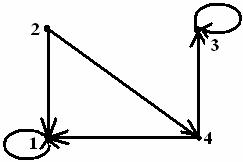
Рисунок 5 Рисунок 6

в) так как , то , . Поскольку , и

, то дополнением к будет отношение

Поскольку и , что, где , то ;

г) свойства отношения проще определить по его матрице . Так как на главной диагонали этой матрицы не все единицы, то отношение не рефлексивно, так как , то оно не симметричное. Поскольку все элементы вне главной диагонали не являются нулями, то не антисимметричное, так как, например, , но , то не транзитивное.

Решение:

отношение является отношением эквивалентности, если оно рефлексивно, симметрично, транзитивно. Построим матрицу отношения и по ней определим его свойства.

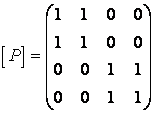. Так как эта матрица содержит единицы на главной диагонали, то - рефлексивно; так как , то оно симметрично. Построим , его матрица

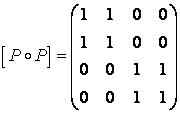. Для рефлексивности отношения надо, чтобы или , если , то . Сравнивая отношения и , а также их матрицы, видим, что и , что доказывает, что - рефлексивно.

Классом эквивалентности элемента называется множество . Множество всех классов эквивалентности называется фактор-множеством множества по отношению . Множество является разбиением множества .

Построим классы эквивалентности для каждого элемента множества :

;

Таким образом, . Фактор-множество множества по отношению будет: .

9 Даны два отношения и :

а) доказать, что эти отношения являются функциями;

б) найти композиции ;

в) какими свойствами обладают отношения (инъективность, сюръек-тивность, биективность).

Решение:

а) отношение является функцией, если или для любого существует единственный , что .

В нашем случае и являются функциями, так как для любого действительного числа , числа и существуют и будут единственными.

б) ,

;

в) проверим данные функции на инъективность. Функция называется инъективной, если или . Для функции условие инъективности не выполняется, т.е. не существуют пары значений , которым соответствует одно : , но и , т.е. .

Функция инъективна, так как для любых действительных выполняется . Проверим функции на сюръективность. Функция называется сюръективной, если для любого существует , что или область значений отношения совпадает с .