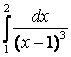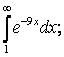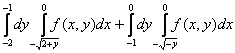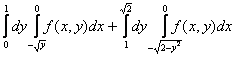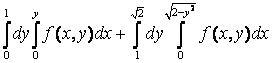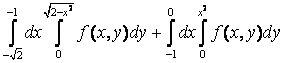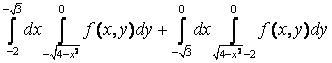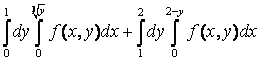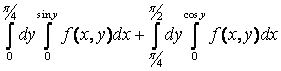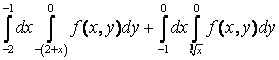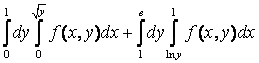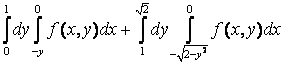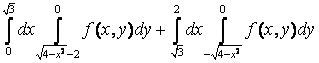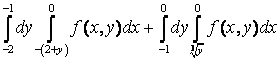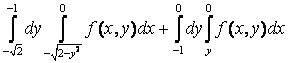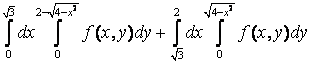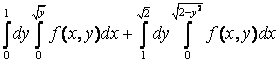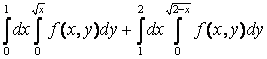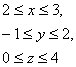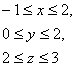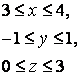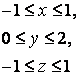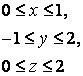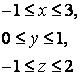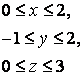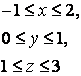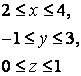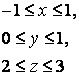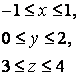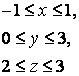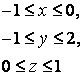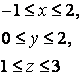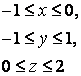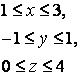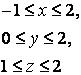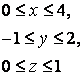АЛМАТЫ ЭНЕРГЕТИКА ЖӘНЕ БАЙЛАНЫС ИНСТИТУТЫ
ЖОҒАРЫ МАТЕМАТИКА КАФЕДРАСЫ
Математикалық талдау
050704 – Есептеу техникасы және бағдарламалық қамтамасыз ету,
050703- Ақпараттық жүйелер мамандықтары бойынша
оқитын барлық бөлім студенттері үшін
есептеу-графикалық жұмыстарды орындауға
арналған әдістемелік нұсқаулар мен тапсырмалар
2- бөлім
Алматы 2009
ҚҰРАСТЫРУШЫЛАР: Л.Н. Астраханцева, М.Ж.Байсалова. Математикалық талдау. 050704 – Есептеу техникасы және бағдарламалық қамтамасыз ету, 050703- Ақпараттық жүйелер мамандықтары бойынша оқитын барлық бөлім студенттері үшін есептеу-графикалық жұмыстарды орындауға арналған әдістемелік нұсқаулар мен тапсырмалар. 2- бөлім - Алматы: АЭжБИ, 2009. - 33 б.
1 есептеу-графикалық жұмыс. Көп айнымалылы функциялар. Бір және көп айнымалы функцияларды интегралдау
1.1 Теориялық сұрақтар
1 Алғашқы функция, анықталмаған интеграл, оның қасиеттері, интегралдар кестесі.
2 Интегралдау әдістері: жіктеу әдісі, айнымалыны ауыстыру әдісі (бір ауыстыру көмегімен алынатын интегралдар тобы).
3 Квадраттық үшмүшеліктің интегралы, тригонометриялық ауыстырулар. Бөліктеп интегралдау.
4 Рационал бөлшектерді, кейбір иррациональных функцияларды интегралдау.
5 Кейбір тригонометриялық функцияларды интегралдау, тригонометриялық ауыстырулар.
6 Анықталған интеграл және оның қасиеттері.
7 Жоғарғы шектік функция ретінде қарастырылып анықталған интеграл. Ньютона-Лейбница формуласы. Анықталған интегралдар үшін айнымалыны ауыстыру, бөліктеп интегралдау.
8 Шекаралары шексіздікке тең меншіксіз интегралдар (1-і текті) және шектелмеген функциялардың меншіксіз интегралдары (2-і текті).
9 Көп айнымалы функциялар. Шек және үзіліссіздік.
10 Дербес өсімшелер және дербес туындылар. Жоғарғы ретті дербес туындылар.
11 Дербес дифференциалдар. Толық өсімшелер және толық дифференциал.
12 Жоғарғы ретті дифференциалдар. Толық дифференциалдың инварианттық түрі.
13 Күрделі және айқын емес түрде берілген көп айнымалылы функцияны дифференциалдау.
14 Екі айнымалы функцияның экстремумы. Экстремумның қажетті және жеткілікті шарттары.
15 Шартты экстремум. Екі айнымалылы функцияның тұйық жиындағы ең үлкен және ең кіші мәндері.
16 Еселі интеграл ұғымына келтірілетін есептер. Екі және үш еселі интегралдар, олардың қасиеттері.
17 Тік бұрышты координаталарда екі және үш еселі интегралдарды есептеу.
18 Еселі интегралда айнымалы ауыстыру, полярлық, цилиндрлік және сфералық координаталарға көшу.
1.2 Есептік тапсырмалар
1 Интегралды есептеу керек
1 К е с т е
|
1.1
а) |
|
1.2 а) |
|
1.3
а) |
|
1.4 а) |
|
1.5 а) |
|
1.6 а) |
|
1.7 а) |
|
1.8 а) |
|
1.9 а) |
|
1.10
а) |
|
1.11
а) |
|
1.12
а) |
|
1.13
а) |
|
1.14
а) |
|
1.15
а) |
|
1.16
а) |
1 кестенің жалғасы
|
1.17 а) |
|
1.18 а) |
|
1.19 а) |
|
1.20 а) |
|
1.21 а) |
|
1.22 а) |
|
1.23 а) |
|
1.24 а) |
|
1.25 а) |
|
1.26 а) |
|
1.27 а) |
|
1.28
а)
|
|
1.29
а) |
|
1.30
а) |
2 Бөліктеп интегралдау формуласын қолданып, итегралды есептеу керек.
2 К е с т е
|
2.1 |
2.2 |
|
2.3 |
2.4 |
|
2.5 |
2.6 |
|
2.7 |
2.8 |
|
2.9 |
2.10 |
|
2.11 |
2.12 |
|
2.13 |
2.14 |
|
2.15 |
2.16 |
|
2.17 |
2.18 |
|
2.19 |
2.20 |
|
2.21 |
2.22 |
|
2.23 |
2.24 |
|
2.25 |
2.26 |
|
2.27 |
2.28 |
|
2.29 |
2.30 |
3 Интегралды есептеу керек
3 К е с т е
|
3.1 |
3.2 |
3.3 |
|
3.4 |
3.5 |
3.6 |
|
3.7 |
3.8 |
3.9 |
|
3.10 |
3.11 |
3.12 |
|
3.13 |
3.14 |
3.15 |
|
3.16 |
3.17 |
3.18 |
|
3.19 |
3.20 |
3.21 |
|
3.22 |
3.23 |
3.24 |
3 кестенің жалғасы
|
3.25 |
3.26 |
3.27 |
|
3.28 |
3.29 |
3.30 |
4 Интегралды есептеу керек
4 К е с т е
|
4.1 а) б) |
4.2 а) б) |
4.3 а) б) |
|
4.4 а) б) |
4.5 а) б) |
4.6 а) б) |
|
4.7 а) б) |
4.8 а) б) |
4.9 а) б) |
|
4.10 а) б) |
4.11 а) б) |
4.12 а) б) |
|
4.13 а) б) |
4.14 а) б) |
4.15 а) б) |
|
4.16 а) б) |
4.17 а) б) |
4.18 а) б) |
|
4.19 а) б) |
4.20 а) б) |
4.21 а) б) |
|
4.22 а) б) |
4.23 а) б) |
4.24 а) б) |
4 кестенің жалғасы
|
4.25 а) б) |
4.26 а) б) |
4.27 а) б) |
|
4.28 а) б) |
4.29 а) б) |
4.30 а) б) |
5 Интегралды есептеу керек
а) универсал айырбастауды қолданып;
б) дәрежесін төмендетіп
5 К е с т е
|
5.1 а) б) |
5.2 а) б) |
5.3 а) б) |
|
5.4 а) б) |
5.5 а) б) |
5.6 а) б) |
|
5.7 а) б) |
5.8 а) б) |
5.9 а) б) |
|
5.10 а) б) |
5.11 а) б) |
5.12 а) б) |
|
5.13 а) б) |
5.14 а) б) |
5.15 а) б) |
|
5.16 а) б) |
5.17 а) б) |
5.18 а) б) |
|
5.19 а) б) |
5.20 а) б) |
5.21 а) б) |
5 кестенің жалғасы
|
5.22 а) б) |
5.23 а) б) |
5.24 а) б) |
|
5.25 а) б) |
5.26 а) б) |
5.27 а) б) |
|
5.28 а) б) |
5.29 а) б) |
5.30 а) б) |
6 Анықталған интегралды есептеу керек
6 К е с т е
|
6.1 а) б) |
6.2 а) б) |
6.3 а) б) |
|
6.4 а) б) |
6.5 а) б) |
6.6 а)
б) |
|
6.7 а) б) |
6.8 а) |
6.9 а) б) |
|
6.10 а) б) |
6.11 а) б) |
6.12 а) б) |
|
6.13 а) б) |
6.14 а) б) |
6.15 а) б) |
6 кестенің жалғасы
|
6.16 а) б) |
6.17 а) б) |
6.18 а) б) |
|
6.19 а) б) |
6.20 а) б) |
6.21 а) б) |
|
6.22 а) б) |
6.23 а) б) |
6.24 а) б) |
|
6.25 а) б) |
6.26 а) б) |
6.27 а) б) |
|
6.28 а) б) |
6.29 а) б) |
6.30 а) б) |
7 Меншіксіз интегралды есептеу керек немесе оның жинақсыздығын дәлелдеу керек
7 К е с т е
|
7.1 а) |
7.2 а) |
7.3а) |
|
7.4а) |
7.5 а) |
7.6а) |
|
7.7а) |
7.8а) |
7.9а) |
7 кестенің жалғасы
|
7.10а) |
7.11а) |
7.12а) |
|
7.13 а) б) |
7.14 а) б) |
7.15 а) б) |
|
7.16 а) б) |
7.17 а) б) |
7.18 а) б) |
|
7.19 а) б) |
7.20 а) б) |
7.21а) б) |
|
7.22 а)
б) |
7.23 а) б) |
7.24 а) б) |
|
7.25 а) б) |
7.26 а) б) |
7.27 а) б) |
|
7.28 а) б) |
7.29 а) б) |
7.30 а) б) |
8 z=f(x,y) функциясы үшін табу керек
а)![]() ; б)
; б) ![]() ;
;
б)
![]()
8 К е с т е
|
8.1 |
8.2 |
8.3 |
|
8.4 |
8.5 |
8.6 |
|
8.7 |
8.8 |
8.9 |
|
8.10 |
8.11 |
8.12 |
|
8.13 |
8.14 |
8.15 |
|
8.16 |
8.17 |
8.18 |
|
8.19 |
8.20 |
8.21 |
|
8.22 |
8.23 |
8.24 |
|
8.25 |
8.26 |
8.27 |
|
8.28 |
8.29 |
8.30 |
9 Табу керек:
а)
F(x,y,z)=0 бетіне
![]() нүктесінде
жүргізілген жанама мен нормальдың теңдеуін жазу керек;
нүктесінде
жүргізілген жанама мен нормальдың теңдеуін жазу керек;
б)
F(x,y,z)=0
теңдігімен айқын емес түрде берілген z функцясының ![]() туындыларын.
туындыларын.
9 К е с т е
|
F(x,y,z) |
|
F(x,y,z) |
|
|
9.1 |
(2,1,-1) |
9.2 |
(-2,1,2) |
|
9.3 |
(1,2,1) |
9.4 |
(-1,1,2) |
|
9.5 |
(2,1,-1) |
9.6 |
(-2,1,2) |
|
9.7 |
(1,2,1) |
9.8 |
(-1,1,2) |
|
9.9 |
(2,1,-1) |
9.10 |
(-2,1,2) |
|
9.11 |
(1,2,1) |
9.12 |
(-1,1,2) |
|
9.13 |
(2,1,-1) |
9.14 |
(-2,1,2) |
|
9.15 |
(1,2,1) |
9.16 |
(-1,1,2) |
|
9.17 |
(2,1,-1) |
9.18 |
(-2,1,2) |
|
9.19 |
(1,2,1) |
9.20 |
(-1,1,2) |
|
9.21 |
(2,1,-1) |
9.22 |
(-2,1,2) |
|
9.23 |
(1,2,1) |
9.24 |
(-1,1,2) |
|
9.25 |
(2,1,-1) |
9.26 |
(-2,1,2) |
|
9.27 |
(-1,2,1) |
9.28 |
(-1,1,2) |
|
9.29 |
(1,2,1) |
9.30 |
(-1,1,2) |
10 z=f(x,y) функцияны экстремумға зерттеу керек
10 К е с т е
|
f(x,y) |
f(x,y) |
f(x,y) |
|
10.1 |
10.2
|
10.3
|
|
10.4 |
10.5
|
10.6 |
|
10.7
|
10.8 |
10.9
|
|
10.10 |
10.11 |
10.12
|
|
10.13
|
10.14
|
10.15 |
|
10.16 |
10.17 |
10.18 |
|
10.19 |
10.20 |
10.21 |
|
10.22 |
10.23 |
10.24
|
|
10.25
|
10.26 |
10.27
|
|
10.28
|
10.29 |
10.30 |
11 Берілген сызықтармен шектелген D облысы бойынша екі еселі интегралды есептеу керек
11 К е с т е
|
|
D |
|
D |
|
11.1 |
x=-1, x=2, y=1, y=3 |
11.2 |
x=2, x=5, y=-1,y=2 |
|
11.3 |
x=0, x=2, y=1, y=2 |
11.4 |
x=1, x=5, y=-1, y=1 |
|
11.5 |
x=-1, x=1, y=1, y=2 |
11.6 |
x=2, x=3, y=-1, y=2 |
|
11.7 |
x=0, x=1, y=1, y=4 |
11.8 |
x=-1, x=3, y=-1, y=2 |
|
11.9 |
x=-1, x=1, y=1, y=3 |
11.10 |
x=4, x=5, y=-1, y=1 |
|
11.11 |
x=-1, x=2, y=1, y=3 |
11.12 |
x=2, x=4,y=-1, y=1 |
11 кестенің жалғасы
|
11.13 |
x=-1, x=1,y=1, y=3 |
11.14 |
x=2, x=3,y=-1, y=2 |
|
11.15 |
x=-1, x=1 y=1, y=2 |
11.16 |
x=3 x=6,y=-1, y=2 |
|
11.17 |
x=-1, x=2, y=2 y=4 |
11.18 |
x=2, x=3,y=-1, y=1 |
|
11.19 |
x=-1, x=3,y=1, y=4 |
11.20 |
x=2, x=4,y=-1, y=5 |
|
11.21 |
x=-1, x=2, y=1, y=4 |
11.22 |
x=2, x=5, y=2,y=4 |
|
11.23 |
x=0 x=1 y=1, y=2 |
11.24 |
x=2, x=5, y=-1, y=3 |
|
11.25 |
x=-1, x=1y=1, y=4 |
11.26 |
x=-1,=3,y=-1, y=2 |
|
11.27 |
x=-1, x=2, y=1, y=3 |
11.288 |
x=2, x=3,y=0,y=2 |
|
11.29 |
x=1,x=3,y=-1, y=2 |
11.30 |
x=0,x=3 ,=-1, y=2 |
12 Интегралдау ретін өзгерту керек
12 К е с т е
|
12.1 |
12.2 |
|
12.3 |
12.4 |
|
12.5 |
12.6 |
|
12.7 |
12.8 |
|
12.9 |
12.10 |
12 кестенің жалғасы
|
12.11 |
12.12
|
|
12.13 |
12.14
|
|
12.15
|
12.16
|
|
12.17
|
12.18
|
|
12.19
|
12.20
|
|
12.21
|
12.22
|
|
12.23
|
12.24
|
|
12.25
|
12.26
|
|
12.27
|
12.28
|
|
12.29
|
12.30
|
13 Полярлық координаталарды қолданып екі еселі интегралды есептеу керек
13 К е с т е
|
|
D |
|
D |
|
13.1 |
|
13.2 |
|
|
13.3 |
|
13.4
|
|
|
13.5 |
|
13.6 |
|
|
13.7 |
|
13.8
|
|
|
13.9
|
|
13.10 |
|
|
13.11
|
|
13.12
|
|
|
13.13
|
|
13.14
|
|
|
13.15
|
|
13.16 |
|
|
13.17 |
|
13.18
|
|
|
13.19 |
|
13.20 |
|
|
13.21 |
|
13.22 |
|
|
13.23 |
|
13.24 |
|
|
13.25 |
|
13.26 |
|
|
13.27 |
|
13.28 |
|
|
13.29 |
|
13.30 |
|
14 Үш еселі интегралды есептеу керек
14 К е с т е
|
|
T |
|
Т |
|
14.1 |
|
14.2 |
|
|
14.3 |
|
14.4 |
|
|
14.5 |
|
14.6 |
|
|
14.7 |
|
14.8 |
|
|
14.9 |
|
14.10 |
|
|
14.11 |
|
14.12 |
|
|
14.13 |
|
14.14
|
|
|
14.15
|
|
14.16
|
|
|
14.17 |
|
14.18 |
|
14 кестенің жалғасы
|
14.19
|
|
14.20 |
|
|
14.21 |
|
14.22 |
|
|
14.23 |
|
14.24 |
|
|
14.25 |
|
14.26 |
|
|
14.27 |
|
14.28 |
|
|
14.29 |
|
14.30 |
|
15 Берілген бетпен шектелген беттің көлемін табу керенк
15 Кесте
|
15.1 |
15.2 |
|
15.3 |
15.4
|
|
15.5 |
15.6
|
|
15.7 |
15.8
|
15 кестенің жалғасы
|
15.9
|
15.10
|
|
|
15.11
|
15.12 |
|
|
15.13
|
15.14
|
|
|
15.15
|
15.16
|
|
|
15.17
|
15.18
|
|
|
15.19
|
15.20
|
|
|
15.21
|
15.22
|
|
|
15.23
|
15.24
|
|
|
15.25
|
15.26
|
|
|
15.27
|
15.28
|
|
|
15.29
|
15.30 |
|
1.3 Типтік нұсқаның шешуі
![]() функциясының анықталмаған интегралы
функциясының анықталмаған интегралы
![]() деп
белгіленеді, мұндағы
деп
белгіленеді, мұндағы ![]() - алғашқы функциялардың
жиынтығы (яғни
- алғашқы функциялардың
жиынтығы (яғни
![]()
![]() немесе
немесе ![]() ).
).
Анықталмаған интегралдың қасиеттері
1)
![]() ;
2)
;
2) ![]() ;
;
3)![]() ; 4)
; 4)![]() .
.
Интегралдау ережелері
1)
![]() ;
;
2)
![]() ,
, ![]() - тұрақты;
- тұрақты;
3)
Егер ![]() и
и ![]() , то
, то ![]() .
.
16 К е с т е –Негізгі интегралдар
|
1 |
1а 1б |
2 |
|
3 |
3а |
4 |
|
5 |
6 |
7 |
|
8 |
8а |
9
|
|
9а |
10 |
11 |
|
12 |
13 |
|
1 Интегралды табу керек
а)![]() ;
;
б)
![]() ;
;
в)![]()
Шешуі:
а) интеграл астындағы функция таблицалық интегралдардың алгебралық қосындысы, сондықтан 1) және 2) ережелері мен 16 кестесінің 1, 5, 9 а формулаларынан:
![]() =
=![]() =
=
=![]()
![]() =
=![]() .
.
б) және в) мысалдарда үш әдістің бірін қолдануға болады:
1)
![]() немесе
немесе
![]() формуласы бойынша айнымалы ауыстыру қолдануға
болады;
формуласы бойынша айнымалы ауыстыру қолдануға
болады;
2)
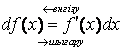 формуласы бойынша дифференциал
таңбасы астына интеграл астындағы функцияның бір
бөлігін енгізіп, 3) ережесі бойынша интегралдауға болады;
формуласы бойынша дифференциал
таңбасы астына интеграл астындағы функцияның бір
бөлігін енгізіп, 3) ережесі бойынша интегралдауға болады;
3)
егер ![]() , онда
, онда ![]() формуласын қолдануға болады.
формуласын қолдануға болады.
б)
![]() =( 16 кестедегі 4 формула және
=( 16 кестедегі 4 формула және ![]() =2 болғандағы үшінші әдіс) =
=2 болғандағы үшінші әдіс) = ![]() ;
;
в)
бұл интегралды
бірінші және екінші әдістермен шешеміз: 1) ![]() = =
= = =
=![]() ; 2)
; 2) ![]() = (дифференциал таңбасы астына
= (дифференциал таңбасы астына ![]() -ті енгіземіз) =
-ті енгіземіз) =![]() = (дифференциал таңбасы астынан вынесем 1/5-ді шығарамыз,
= (дифференциал таңбасы астынан вынесем 1/5-ді шығарамыз, ![]() деп
3) ережені қолданамыз) =
деп
3) ережені қолданамыз) = ![]() .
.
2
Интегралды табу
керек ![]() .
.
Шешуі:
Бөліктеп интегралдау формуласынан ![]() :
:
![]() =
= 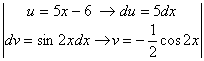 =
= ![]()
-![]() =
=![]()
![]() .
.
3
Интегралды табу
керек ![]() .
.
Шешуі:
квадратты үшмүшеліктің толық квадратын бөліп алып, жаңа айнымалы енгіземіз:
![]() =
=  =
=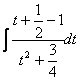 =
=
=![]() =
= ![]() =
= ![]()
![]() =
= ![]() .
.
4 Интегралды табу керек
а)
![]() ;
;
б)
![]()
Шешуі:
бұл
рационал функцияның интегралы. ![]() түріндегі функция рационал
функция деп аталады (немесе рационал
бөлшек), мұндағы
түріндегі функция рационал
функция деп аталады (немесе рационал
бөлшек), мұндағы ![]() және
және
![]() -
- ![]() және
және ![]() дәрежелі
көпмүшеліктер. Егер
дәрежелі
көпмүшеліктер. Егер ![]() , онда рационал бөлшек дұрыс, егер
, онда рационал бөлшек дұрыс, егер ![]() , онда – дұрыс
емес. Дұрыс бөлшектердің
ішінде төрт қарапайым түрін қарастырайық: 1)
, онда – дұрыс
емес. Дұрыс бөлшектердің
ішінде төрт қарапайым түрін қарастырайық: 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() мұндағы
мұндағы ![]() - нақты сандар,
- нақты сандар,
![]() - натурал сандар,
- натурал сандар,
![]() квадрат үшмүшеліктің нақты түбірлері
жоқ. Алдыңғы үш типті интегралдар
оңай алынады (жоғарыдағы мысалдар), төртінші
типті интеграл рекуррентті
формуламен есептелінеді (мысалы [1], 238 бет). Рационал функцияларды
интегралдау ережелері:
квадрат үшмүшеліктің нақты түбірлері
жоқ. Алдыңғы үш типті интегралдар
оңай алынады (жоғарыдағы мысалдар), төртінші
типті интеграл рекуррентті
формуламен есептелінеді (мысалы [1], 238 бет). Рационал функцияларды
интегралдау ережелері:
1)
егер интеграл астындағы
бөлшек дұрыс емес болса, онда алымын бөліміне бөлгенде
бүтін бөлігі бөлініп шығады, яғни
бөлшекті ![]() =
= ![]() түрінде
жазамыз, мұндағы
түрінде
жазамыз, мұндағы ![]() - көпмүшелік,
- көпмүшелік, ![]() - дұрыс бөлшек;
- дұрыс бөлшек;
2)
бөлшектің
бөліміндегі көпмүшелікті көбейткіштерге ![]() ;
;
3)
дұрыс бөлшекті
![]() қарапайым бөлшектерге жіктейміз:
қарапайым бөлшектерге жіктейміз:
![]() =
=![]()
![]() +…+
+…+![]() +…+
+…+![]() +
+![]() +…+
+…+![]() …;
…;
4)
![]() анықталмаған коэффициенттерді
табайық, ол үшін оң жақтағы бөлшектерді
ортақ бөлімге келтіріп, алымдарын теңестіреміз. Егер соңғы
теңдіктің оң және сол жақтарындағы
анықталмаған коэффициенттерді
табайық, ол үшін оң жақтағы бөлшектерді
ортақ бөлімге келтіріп, алымдарын теңестіреміз. Егер соңғы
теңдіктің оң және сол жақтарындағы ![]() -тің
бірдей дәрежесі алдындағы
коэффициенттерді, онда
берілген коэффициенттерге қатысты сызықты теңдеулер
жүйесін аламыз. Коэффициенттерді басқа жолмен алуға болады,
ол үшін
-тің
бірдей дәрежесі алдындағы
коэффициенттерді, онда
берілген коэффициенттерге қатысты сызықты теңдеулер
жүйесін аламыз. Коэффициенттерді басқа жолмен алуға болады,
ол үшін ![]() айнымалысына кез келген мән бер керек.
айнымалысына кез келген мән бер керек.
Сонымен, рационал функцияның интегралы әрқашанда алынады, себебі оны көпмүшеліктің немесе қарапайым бөлшектердің интегралына келтіруге болады.
а)
Интеграл астындағы
бөлшек дұрыс емес, себебі алымындағы және
бөліміндегі дәрежелері тең
(![]() ). Алдын ала бөліміндегі жақшаларды
ашып, алымын бөліміне бөлеміз:
). Алдын ала бөліміндегі жақшаларды
ашып, алымын бөліміне бөлеміз:
|
|
|
|
|
2 |
|
|
Сонымен,![]() =
=![]() =
= 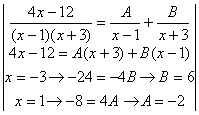 =
= ![]()
![]()
![]() =
= ![]() =
= ![]() ;
;
б)
![]() =
= =
=
=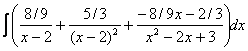 =
=![]() =…=
=…=![]()
![]()
![]() .
.
5 Интегралды табу керек
а)
![]() ;
;
б)
![]() ;
;
в)![]() .
.
Шешуі:
![]() түріндегі интеграл, мұндағы
түріндегі интеграл, мұндағы ![]() -
рационал функция,
-
рационал функция, ![]() универсал ауыстыруы арқылы рационал функцияның
интегралына келтіріледі
универсал ауыстыруы арқылы рационал функцияның
интегралына келтіріледі
![]() ;
;
![]()
![]() ;
;
![]() ;
; ![]() .
.
а)
![]() =
= ![]() =
= 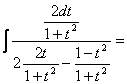
![]()
![]() =
=
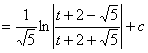 =
= 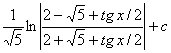 .
.
Универсал ауыстыруы әруақытта қолайлы емес. Егер
(1)![]() ;
; ![]() ;
;
(2)![]() ;
;
(3)![]() ,
, ![]() ;
;
(4)![]() ,
, ![]() ,
, ![]() ,
,
кездессе, келесі ережелердің бірі қолданылады:
1)
(1) түріндегі интеграл ![]() тақ болғанда келесі формулалар бойынша дәрежені
төмендетуге болады:
тақ болғанда келесі формулалар бойынша дәрежені
төмендетуге болады:
![]() ;
; ![]() ;
; ![]() ;
;
2)
![]() тақ болғанда (1) түріндегі
интегралды есептеу үшін осы дәрежеден көбейткішті бөліп
алып, кофункциясын жаңа айнымалымен ауыстыру керек;
тақ болғанда (1) түріндегі
интегралды есептеу үшін осы дәрежеден көбейткішті бөліп
алып, кофункциясын жаңа айнымалымен ауыстыру керек;
3)
(2) түріндегі интегралды
қарастырайық. Егер ![]() және
және ![]() екеуі де жұп болғанда 1) ережесімен табуға болады Егер
екеуі де жұп болғанда 1) ережесімен табуға болады Егер
![]() немесе
немесе ![]() (немесе
(немесе ![]() де,
де, ![]() де)
тақ болса 2) ережесімен табуға болады;
де)
тақ болса 2) ережесімен табуға болады;
4) (3) түріндегі интегралды ![]() немесе
немесе ![]() жаңа айнымалымен ауыстыру арқылы
табуға болады;
жаңа айнымалымен ауыстыру арқылы
табуға болады;
5) (4) түріндегі интегралды
![]() ;
;
![]()
![]() ;
;
![]() .
.
формулалары бойынша қосылғыштарға жіктеу арқылы табуға болады.
б)![]() =( 1) ережесі бойынша дәрежені
төмендетеміз) = =
=( 1) ережесі бойынша дәрежені
төмендетеміз) = =![]() =
= 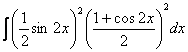 =
=![]()
![]() =
=
![]() =
=![]()
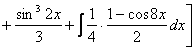 =
=![]() ;
;
в)![]() = (2) ережесі бойынша көбейткішті бөліп
алып
= (2) ережесі бойынша көбейткішті бөліп
алып ![]() және оның кофункциясы
және оның кофункциясы ![]() -ты
-ты
![]() арқылы
белгілейміз) =
арқылы
белгілейміз) =![]() =
= =
=
= ![]() =
= ![]() =
=![]() .
.
6 Анықталған интегралды табу керек
а)
 ;
;
б)![]() .
.
Анықталған интегралды табу үшін Ньютон-Лейбниц формуласы:
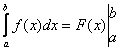 =
=![]() , мұндағы
, мұндағы ![]() -
- ![]() -тің
алғашқы функциясы.
-тің
алғашқы функциясы.
Анықталған интегралдың негізгі қасиеттері
1)
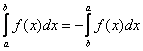 ;
2)
;
2) 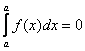 ;
;
3) 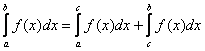 ; 4)
; 4)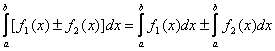 ;
;
5)
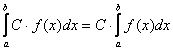 , С – тұрақты;
, С – тұрақты;
6)
егер ![]() -да
-да ![]() , онда
, онда  ;
;
7)
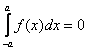 , егер
, егер ![]() - тақ
функция;
- тақ
функция;
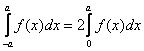 , егер
, егер ![]() - жұп функция.
- жұп функция.
Интегралдау әдістері:
1)
бөліктеп интегралдау: 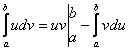 ;
;
2)
айнымалы ауыстыру: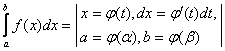 =
= 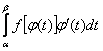 .
.
а) Берілген интегралдың алғашқы функциясын табу үшін тригоно-
метриялық ауыстырулардың бірін қолданады. Бұл
ауыстырулар ![]() және
және ![]() қатысты рационал функциялардың интегралына
келтіріледі:
қатысты рационал функциялардың интегралына
келтіріледі:
![]() -
- ![]() ауыстыруы;
ауыстыруы;
![]() -
- ![]() ауыстыруы;
ауыстыруы;
![]() -
- ![]() ауыстыруы.
ауыстыруы.
 =
=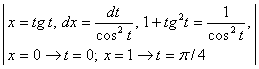 =
=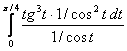 =
= =
=
= =
=![]() =
=![]() ;
;
б) бөліктеп интегралдау әдісі бойынша: ![]() =
=
=
= =
=![]()
![]() =
=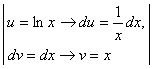 =
=
=![]() =
=![]() .
.
7 Меншіксіз интегралдарды есептеу керек немесе оның жинақсыздығын дәлелдеу керек
а) 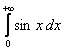 ;
;
б)  .
.
Шешуі:
меншіксіз интегралдардың түрлері:
1) шексіз шекаралары бар интегралдар;
2) шектелмеген функциялардың интегралдары айтылады.
Шексіз шекаралары бар меншіксіз интегралдар анықтама бойынша
табылады: 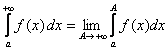 ;
;
![]() ;
;
![]() =
=![]()
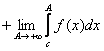 , немесе
, немесе
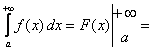
![]() (қалған интегралдар сол
сияқты) формуласымен есептелінеді.
(қалған интегралдар сол
сияқты) формуласымен есептелінеді.
Шексіз үзіліс нүктелері бар функциялардың
меншіксіз интегралдары анықтама бойынша табылады: 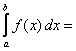 =
=
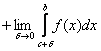 ,
мұндағы
,
мұндағы ![]() - шексіз үзіліс нүктесі, дербес
жағдайда үзіліс нүктесі аралықтың шекара
нүктесінде
- шексіз үзіліс нүктесі, дербес
жағдайда үзіліс нүктесі аралықтың шекара
нүктесінде ![]() немесе
немесе ![]() нүктелерінде болуы мүмкін. Егер жоғарыда
көрсетілген шектер бар болса, онда меншіксіз интеграл жинақты, егер
жоқ болса жинақсыз деп аталады.
нүктелерінде болуы мүмкін. Егер жоғарыда
көрсетілген шектер бар болса, онда меншіксіз интеграл жинақты, егер
жоқ болса жинақсыз деп аталады.
а) 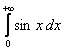 =
=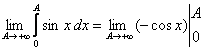 =
=![]() +
+![]() = 1-
= 1-![]() - шектері жоқ, бұдан меншіксіз интеграл жинақсыз.
- шектері жоқ, бұдан меншіксіз интеграл жинақсыз.
б)
 =[
=[![]() - екінші текті үзіліс нүктесі]=
- екінші текті үзіліс нүктесі]=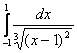 + +
+ +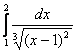 =
=![]()
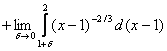 =
=![]() +
+ ![]() =
=![]() +
+![]() =
=![]() .
.
8
![]() функциясы үшін табу керек
функциясы үшін табу керек
а)![]() ;
;
б) ![]() ;
;
в) ![]()
Шешуі:
Көп айнымалылы функцияны ![]() әрбір айнымалы (аргумент) бойынша дифференциалдауға
болады, бұл жағдайда қалған аргументтер
тұрақты боп есептелінеді. Дербес туындылар
әрбір айнымалы (аргумент) бойынша дифференциалдауға
болады, бұл жағдайда қалған аргументтер
тұрақты боп есептелінеді. Дербес туындылар ![]() белгілі бір айнымалы функцияны дифференциалдау
ережелері бойынша табылады. Жоғарғы ретті дербес туындыларды
белгілі бір айнымалы функцияны дифференциалдау
ережелері бойынша табылады. Жоғарғы ретті дербес туындыларды ![]() сол ережелер бойынша табады: екінші ретті дербес туынды –бұл бірінші
ретті дербес туындының туындысы, үшінші – бұл екіншіден
алынған, т.с.с.
сол ережелер бойынша табады: екінші ретті дербес туынды –бұл бірінші
ретті дербес туындының туындысы, үшінші – бұл екіншіден
алынған, т.с.с.
![]() функцияның толық дифференциалы
функцияның толық дифференциалы
![]()
формуласымен есептелінеді.
а) ![]() функциясы үшін дербес туындылардың
түрі
функциясы үшін дербес туындылардың
түрі ![]() ,
, ![]() ;
;
б) 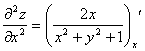 =
=![]() ,
,
![]() =
=![]() ,
, ![]()
![]() ;
;
в)
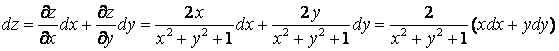 .
.
9 Табу керек
а) ![]() нүктесінде
нүктесінде
![]() бетке
жүргізілген жанама
бетке
жүргізілген жанама
жазықтық пен нормальдің теңдеуін;
б) ![]() теңдеуімен
берілген айқын емес z функциясының
теңдеуімен
берілген айқын емес z функциясының
![]() дербес
туындыларын
дербес
туындыларын
Шешуі:
а) егер бет ![]() теңдеуімен берілген берілсе және
теңдеуімен берілген берілсе және ![]()
нүктесі осы бетте жатса, онда бетке жүргізілген жанама жазықтық
![]()
теңдеуімен өрнектеледі; осы нүктедегі беттің нормаль теңдеуі
![]()
![]() .
.
Сонымен, ![]() болғандықтан
болғандықтан
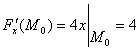 ;
;
 ;
;
 .
.
Жанама жазықтық теңдеуі ![]() немесе
немесе ![]() ; нормаль теңдеуі -
; нормаль теңдеуі - ![]()
![]() ;
;
б) ![]() теңдеуімен
берілген айқын емес
теңдеуімен
берілген айқын емес ![]() функциясының
функциясының
![]() келесі формулалармен табамыз
келесі формулалармен табамыз
![]() ;
;
![]() ,….
,….
Дербес жағдайда, егер ![]() бір
бір ![]() айнымалыға
тәуелді
айнымалыға
тәуелді ![]() теңдеуімен берілген айқын емес функция болса,
теңдеуімен берілген айқын емес функция болса,
![]() .
.
Біздің мысалда ![]() теңдеуі айқын емес z
функциясын өрнектейді,
теңдеуі айқын емес z
функциясын өрнектейді, ![]() , сондықтан
, сондықтан ![]() ;
; ![]() .
.
10 ![]() функциясын экстремумға зерттеу керек
функциясын экстремумға зерттеу керек
Шешуі:
егер ![]() функциясының
функциясының
![]() нүктесіндегі мәні оның
жақын нүктелеріндегі мәндерінен үлкен (кіші) болса,
онда осы нүктеде функцияның максимумы
(минимумы) бар
дейміз. Максимумдер немесе
минимумдер (экстремумдер) функцияның
анықталу облысында жататын дербес туындылары нөлге тең немесе
жоқ болатын нүктелерде ғана болады. Мұндай
нүктелер кризистік нүктелер деп аталады. Кез келген кризистік
нүкте экстремум нүктесі болмайды. Кризистік нүктені экстремумға
тексеру үшін жеткілікті шартты қолданады:
нүктесіндегі мәні оның
жақын нүктелеріндегі мәндерінен үлкен (кіші) болса,
онда осы нүктеде функцияның максимумы
(минимумы) бар
дейміз. Максимумдер немесе
минимумдер (экстремумдер) функцияның
анықталу облысында жататын дербес туындылары нөлге тең немесе
жоқ болатын нүктелерде ғана болады. Мұндай
нүктелер кризистік нүктелер деп аталады. Кез келген кризистік
нүкте экстремум нүктесі болмайды. Кризистік нүктені экстремумға
тексеру үшін жеткілікті шартты қолданады: ![]() функциясы берілген.
функциясы берілген. ![]() - кризистік нүктесі болсын.
Белгілеу енгізейік
- кризистік нүктесі болсын.
Белгілеу енгізейік 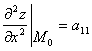 ,
,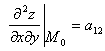 ,
,  ;
; 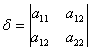 =
= ![]() . Егер
. Егер ![]() , онда
, онда ![]() - минимум нүктесі;
егер
- минимум нүктесі;
егер ![]() , онда
, онда
![]() -
максимум нүктесі; егер
-
максимум нүктесі; егер ![]() , онда
, онда ![]() нүктесінде
экстремум жоқ; егер
нүктесінде
экстремум жоқ; егер
![]() , онда қосымша зерттеулер керек.
, онда қосымша зерттеулер керек.
![]() функциясының
дербес туындыларын және кризистік
нүктелерін табамыз:
функциясының
дербес туындыларын және кризистік
нүктелерін табамыз: ![]() ;
; ![]() .
. 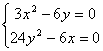 жүйесін
шешіп,
жүйесін
шешіп, ![]() және
және ![]() нүктелерін табамыз. Екеуі де кризистік
нүктесі болады, себебі функция хОу жазықтығының
барлық нүктелерінде анықталған. Жеткіліктілік шарты
бойынша экстремумға тексереміз:
нүктелерін табамыз. Екеуі де кризистік
нүктесі болады, себебі функция хОу жазықтығының
барлық нүктелерінде анықталған. Жеткіліктілік шарты
бойынша экстремумға тексереміз: ![]() ,
, ![]() ,
, ![]() .
. ![]() нүктесі үшін
нүктесі үшін  ,
,
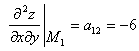 ,
,
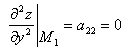 ,
,
![]() ,
сондықтан
,
сондықтан ![]() нүктесінде экстремум жоқ.
нүктесінде экстремум жоқ. ![]() нүктесі үшін
нүктесі үшін ![]() ,
, ![]() ,
, ![]() ,
, ![]() , сондықтан
, сондықтан ![]() - минимум нүктесі
- минимум нүктесі ![]() .
.
11 D облысы келесі сызықтармен шектелген: x=0, x=3, y=-1, y=2.
D облысы бойынша ![]() екі еселі интегралды есептеу керек.
екі еселі интегралды есептеу керек.
Шешуі:
D интегралдау облысы координата осьтеріне параллель түзу сызықтармен шектелген, яғни тіктөртбұрыш. Интегралдау шекаралары сандар болғандықтан интегралдау ретін ескермеуге болады (алдымен х айнымалысы бойынша, содан соң у бойынша немесе керісінше). Сондықтан
![]() =
=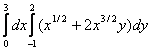 =
=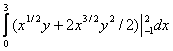
=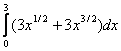 =
=![]() .
.
12 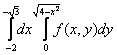 +
+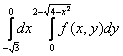 интегралдау ретін өзгерту керек
интегралдау ретін өзгерту керек
Шешуі:
![]() және
және ![]() екі облыстан тұратын интегралдау облысын
салайық.
екі облыстан тұратын интегралдау облысын
салайық. ![]() келесі сызықтармен шектелген:
келесі сызықтармен шектелген: ![]() .
Ал
.
Ал ![]() :
:
![]() .
.
![]() және
және ![]() қисықтарын салу үшін оны
канондық түрге келтіреміз.
қисықтарын салу үшін оны
канондық түрге келтіреміз. ![]()
![]()
![]()
![]() .
Сонымен,
.
Сонымен, ![]() - центрі координаталар басында болатын шеңбердің
жоғарғы бөлігінің теңдеуі, радиусы 2-ге тең.
- центрі координаталар басында болатын шеңбердің
жоғарғы бөлігінің теңдеуі, радиусы 2-ге тең.
![]()
![]()
![]() . Сонымен,
. Сонымен, ![]() - центрі (0,2) нүктесінде, радиусы
2-ге тең болатын шеңбердің төменгі
бөлігінің теңдеуі.
- центрі (0,2) нүктесінде, радиусы
2-ге тең болатын шеңбердің төменгі
бөлігінің теңдеуі.
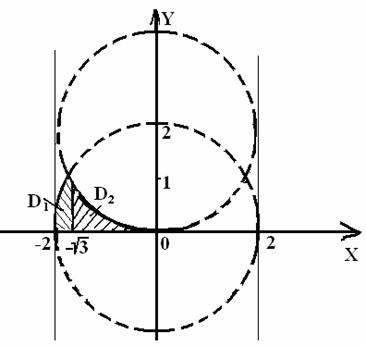
1 Сурет
Суретте ![]() және
және ![]() қосылып
қосылып ![]() облысын береді.
облысын береді. ![]() облысы сол жағынан
облысы сол жағынан ![]() жарты
шеңберімен, оңынан –
жарты
шеңберімен, оңынан –![]() жарты шеңберімен шектелген.
жарты шеңберімен шектелген. ![]() облысы
бойынша интегралдау ретін өзгертсек:
облысы
бойынша интегралдау ретін өзгертсек: 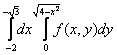 +
+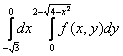 =
= .
.
13 Полярлық координатаға көшіп, екі еселі интегралды есептеу керек
![]() ,
, ![]() .
.
Шешуі:
полярлық координатаға көшу формуласы:
![]() =
=![]() .
.
Интегралдау облысы - центрі координаталар басында болатын
дөңгелек, яғни полюс облыстың ішінде
болғандықтан ![]() =
=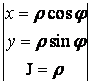 =
=
=![]() =
=![]() =
=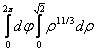 =
=![]() .
.
14 Үш еселі интегралды есептеу керек
![]() ,
, ![]() .
.
Шешуі:
Интегралдау облысы ![]() -
жақтары координата
жазықтықтарына параллель тік бұрышты параллелепипед, сондықтан берілген үш еселі интеграл қайталама
интегралға келтіріледі, оның шекаралары тұрақты
және интегралдау ретін ескермеуге болады:
-
жақтары координата
жазықтықтарына параллель тік бұрышты параллелепипед, сондықтан берілген үш еселі интеграл қайталама
интегралға келтіріледі, оның шекаралары тұрақты
және интегралдау ретін ескермеуге болады:
![]() =
=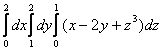 =
=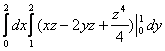 =
=
=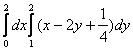 =
=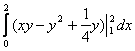 =
= =
=![]() .
.
15
![]() ,
, ![]() ,
, ![]() беттерімен шектелген дененің көлемін табу
керек.
беттерімен шектелген дененің көлемін табу
керек.
Шешуі:
V үш өлшемді
облысының v көлемі ![]() формуласымен есептелінеді. Берілген
беттердің теңдеуі бойынша V облысын саламыз.
формуласымен есептелінеді. Берілген
беттердің теңдеуі бойынша V облысын саламыз. ![]()
![]() ,
, ![]()
![]() - құраушы Oz осіне
параллель параболалық
цилиндрлердің теңдеуі;
- құраушы Oz осіне
параллель параболалық
цилиндрлердің теңдеуі; ![]() - xOy координата
жазықтығының теңдеуі;
- xOy координата
жазықтығының теңдеуі;
![]() - Oy осіне параллель және Ox-ті (2,0,0) нүктесінде, Oz – (0,0,4) нүктесінде
қиятын жазықтың теңдеуі. Облыстың
түріне қарап үш еселі
интегралды қайталама
интегралға келтіргенде келесі интегралдау ретін таңдап аламыз:
- Oy осіне параллель және Ox-ті (2,0,0) нүктесінде, Oz – (0,0,4) нүктесінде
қиятын жазықтың теңдеуі. Облыстың
түріне қарап үш еселі
интегралды қайталама
интегралға келтіргенде келесі интегралдау ретін таңдап аламыз: ![]() =
= =
=
=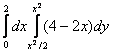 =
=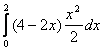 =
=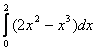 =
=![]() .
.
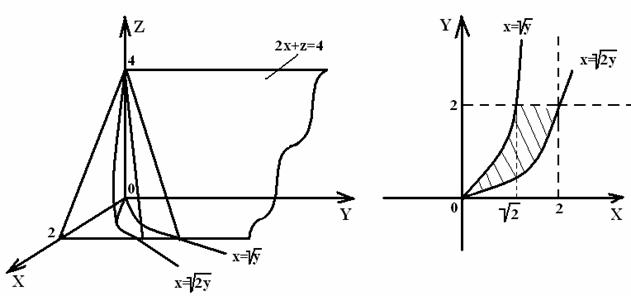
2 Сурет
Әдебиеттер тізімі
1. Хасеинов К.А. Каноны математики. Учебник -Алматы, 2003 -686 с.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: в 2 ч. – М.: Высшая школа, 2003. – ч. 1,2.-352 с.
3. Сборник индивидуальных заданий по высшей математике: в 3 ч. (Рябушко А.П., Бархатов В.В. и др.). Под ред. Рябушко А.П. – Минск: Высш. школа, 2000.-ч.2,3 .-396 с.
4. Дүйсек А.К., Қасымбеков С.К. Жоғары математика (оқу құралы) - Алматы: ҚБТУ, 2004. - 440 б.
Мазмұны
1 Теориялық сұрақтар………………………………….....………......…….….3
2 Есептік тапсырмалар………………………………….....….....………….….3
3 Типтік нұсқаның шешуі…………………………………….....…………….20
Әдебиеттер тізімі ...............................................................................................33
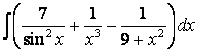


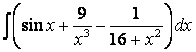

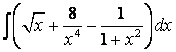
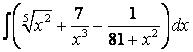 , б)
, б)


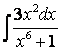
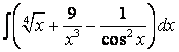 ,
б)
,
б)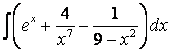 ,
б)
,
б)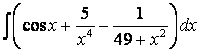 , б)
, б)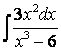
 ,
б)
,
б) ,
б)
,
б)
 , б)
, б) , б)
, б) , б)
, б) , б)
, б)  , б)
, б) 
 ,
,  ,
,  , б)
, б)
 , б)
, б)  , б)
, б)  ,
,  ,
,














 б)
б)













 ; б)
; б)  ; б)
; б)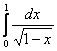
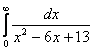 ; б)
; б) 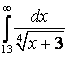

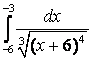




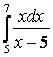

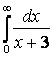
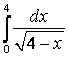
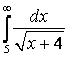 ;
;
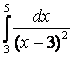
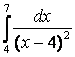
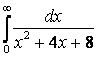
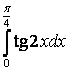
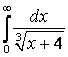
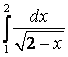
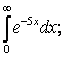


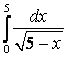
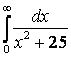

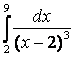
 ;
;