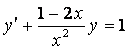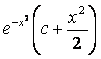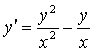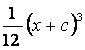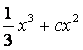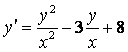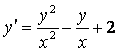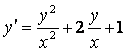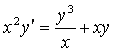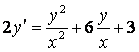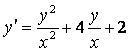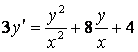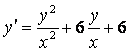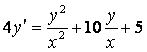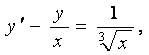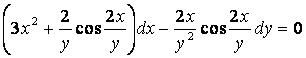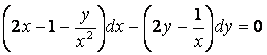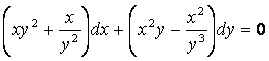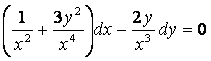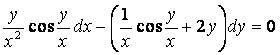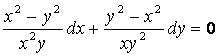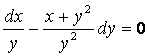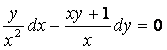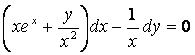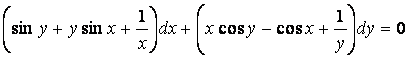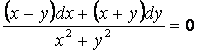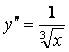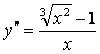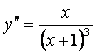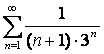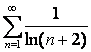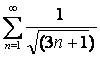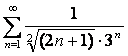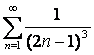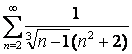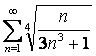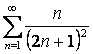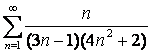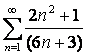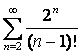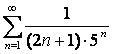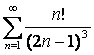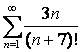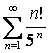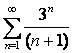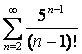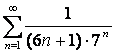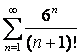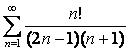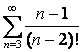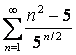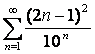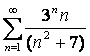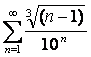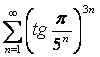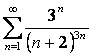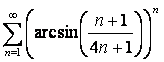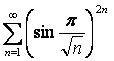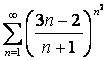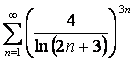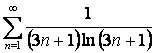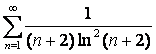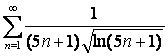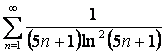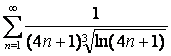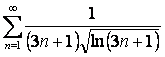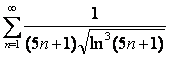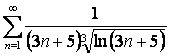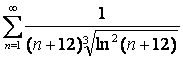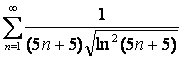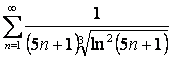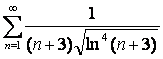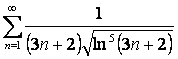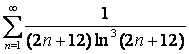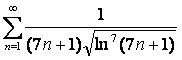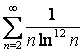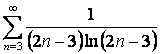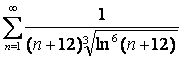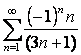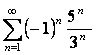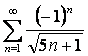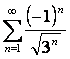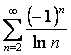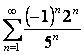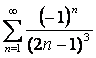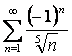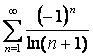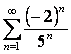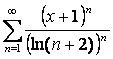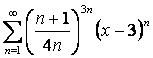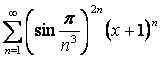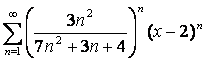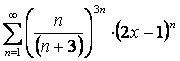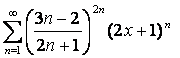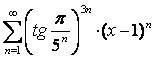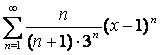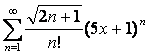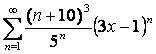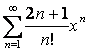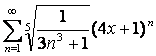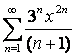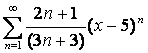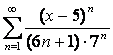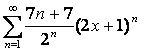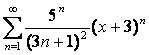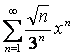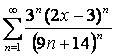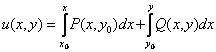АЛМАТЫ ЭНЕРГЕТИКА ЖӘНЕ БАЙЛАНЫС ИНСТИТУТЫ
ЖОҒАРЫ МАТЕМАТИКА КАФЕДРАСЫ
Математикалық талдау
Есептеу-графикалық жұмыстарды орындауға
арналған әдістемелік нұсқаулар мен тапсырмалар
(050704 – Есептеу техникасы және бағдарламалық қамтамасыз ету, 050703–Ақпараттық жүйелер мамандықтары бойынша оқитын барлық бөлім студенттері үшін)
3 бөлім
Алматы 2009
ҚҰРАСТЫРУШЫЛАР: Ким Р.Е., Масанова А.Ж.
Математикалық талдау. 050704– Есептеу техникасы және бағдарламалық қамтамасыз ету, 050703–Ақпараттық жүйелер мамандықтары бойынша оқитын барлық бөлім студенттері үшін есептеу-графикалық жұмыстарды орындауға арналған әдістемелік нұсқаулар мен тапсырмалар. 3 бөлім. - Алматы: АЭжБИ, 2009. - 37 б.
«Есептеу техникасы және бағдарламалық қамтамасыз ету», «Ақпараттық жүйелер» мамандықтары бойынша оқитын барлық бөлім студенттеріне арналған есептеу графикалық жұмыстарды орындауға арналған әдістемелік нұсқаулар мен тапсырмалар
«Математикалық талдау» пәнінің №3 типтік есептеулерден тұрады. Бағдарламаның теориялық сұрақтары енгізілген. Типтік варианттың шешімі келтірілген.
1 3-типтік есептеулер. Дифференциалдық теңдеулер. Қатарлар
1.1 Теориялық сұрақтар
1. Дифференциалдық теңдеулердің (ДТ) негізгі ұғымдары (анықтама, реті, жалпы және дербес шешімі, жалпы интеграл, Коші есебі, болу және жалғыздық теоремасы).
2. Бірінші ретті дифференциалдық тендеулер. Айнымалылары ажыратылатын дифференциалдық теңдеулер. Айнымалылар арқылы біртекті бірінші ретті дифференциалдық теңдеулер. Біртекті теңдеулерге келтіретін дифференциалдық теңдеулер.
3. Бірінші ретті біртекті сызықты дифференциалдық тендеулер, Бернулли теңдеуі, толық дифференциалды дифференциалдық тендеулер.
4. Жоғарғы ретті дифференциалдық теңдеулер (негізгі түсініктер). Ретін төмендетуге болатын дифференциалдық теңдеулер.
5. Жоғарғы ретті сызықты дифференциалдық теңдеулер. Сызықты дифференциалдық оператор, оның қасиеттері. Сызықты біртекті дифференциалдық теңдеулер (СБТ), жалпы шешімінің құрылымы.
6. Коэффициенттері тұрақты жоғарғы ретті біртекті сызықты дифференциалдық теңдеулер.
7. Біртекті емес сызықты (СБЕТ) дифференциалдық теңдеулер, жалпы шешімінің құрылымы. Тұрақтыларды вариациялау әдісі.
8. Коэффициенттері тұрақты СБЕТ. Дербес шешімін таңдау әдісі.
9. Сандық қатарлар. Қатардың жинақтылығы және қосындысы. Қатардың жинақтылығының қажетті шарты.
10. Қатарларды салыстыру белгілері.
11. Даламбер және Коши белгілері.
12. Кошидің интегралдық белгісі.
13. Мүшелерінің таңбалары ауыспалы қатарлар. Лейбниц теоремасы.
14. Айнымалы таңбалы қатарлар. Абсолютті және шартты жинақталатын қатарлар.
15. Дәрежелік қатарлар. Абель теоремасы. Дәрежелік қатардың жинақталу интервалы және жинақталу радиусы.
16. Тейлор қатары. ![]() функцияларды х арқылы дәрежелік
қатарларға жіктеу.
функцияларды х арқылы дәрежелік
қатарларға жіктеу.
1.2 Есептеу тапсырмалары
1 Көрсетілген ![]() функциясы берілген
дифференциалдық тендеудің (ДТ) шешімі бола ма? (С – ерікті
тұрақты)
функциясы берілген
дифференциалдық тендеудің (ДТ) шешімі бола ма? (С – ерікті
тұрақты)
1 К е с т е
|
№ |
|
ДТ |
|
1.1 |
|
|
|
1.2 |
|
|
|
1.3 |
|
|
|
1.4 |
|
|
|
1.5 |
|
|
|
1.6 |
|
|
|
1.7 |
|
|
|
1.8 |
|
|
|
1.9 |
|
|
|
1.10 |
|
|
|
1.11 |
|
|
|
1.12 |
|
|
|
1.13 |
|
|
|
1.14 |
|
|
|
1.15 |
|
|
|
1.16 |
|
|
|
1.17 |
|
|
1 кестенің жалғасы
|
1.18 |
|
|
|
1.19 |
|
|
|
1.20 |
|
|
|
1.21 |
|
|
|
1.22 |
|
|
|
1.23 |
|
|
|
1.24 |
|
|
|
1.25 |
|
|
|
1.26 |
|
|
|
1.27 |
|
|
|
1.28 |
|
|
|
1.29 |
|
|
|
1.30 |
|
|
2 Дифференциалдық тендеудің жалпы шешімін (жалпы интегралын) табу керек
2 К е с т е
|
2.1 |
|
2.2 |
|
2.3 |
|
|
2.4 |
|
2.5 |
|
2.6 |
|
|
2.7 |
|
2.8 |
|
2.9 |
|
|
2.10 |
|
2.11 |
|
2.12 |
|
|
2.13 |
|
2.14 |
|
2.15 |
|
|
2.16 |
|
2.17 |
|
2.18 |
|
|
2.19 |
|
2.20 |
|
2.21 |
|
2 кестенің жалғасы
|
2.22 |
|
2.23 |
|
2.24 |
|
|
2.25 |
|
2.26 |
|
2.27 |
|
|
2.28 |
|
2.29 |
|
2.30 |
|
3 Коши есебін шешу керек
3 К е с т е
|
3.1 |
|
3.2 |
|
|
3.3 |
|
3.4 |
|
|
3.5 |
|
3.6 |
|
|
3.7 |
|
3.8 |
|
|
3.9 |
|
3.10 |
|
|
3.11 |
|
3.12 |
|
|
3.13 |
|
3.14 |
|
|
3.15 |
|
3.16 |
|
|
3.17 |
|
3.18 |
|
|
3.19 |
|
3.20 |
|
|
3.21 |
|
3.22 |
|
|
3.23 |
|
3.24 |
|
|
3.25 |
|
3.26 |
|
|
3.27 |
|
3.28 |
|
|
3.29 |
|
3.30 |
|
4 Айнымалылар арқылы біртекті дифференциалдық теңдеудің жалпы шешімін (жалпы интегралын) табу керек
4 К е с т е
|
4.1 |
|
4.2 |
|
|
4.3 |
|
4.4 |
|
|
4.5 |
|
4.6 |
|
4 кестенің жалғасы
|
4.7 |
|
4.8 |
|
|
4.9 |
|
4.10 |
|
|
4.11 |
|
4.12 |
|
|
4.13 |
|
4.14 |
|
|
4.15 |
|
4.16 |
|
|
4.17 |
|
4.18 |
|
|
4.19 |
|
4.20 |
|
|
4.21 |
|
4.22 |
|
|
4.23 |
|
4.24 |
|
|
4.25 |
|
4.26 |
|
|
4.27 |
|
4.28 |
|
|
4.29 |
|
4.30 |
|
5 Коши есебін шешу керек
5 К е с т е
|
5.1 |
|
5.2 |
|
|
5.3 |
|
5.4 |
|
|
5.5 |
|
5.6 |
|
|
5.7 |
|
5.8 |
|
|
5.9 |
|
5.10 |
|
|
5.11 |
|
5.12 |
|
5 кестенің жалғасы
|
5.13 |
|
5.14 |
|
|
5.15 |
|
5.16 |
|
|
5.17 |
|
5.18 |
|
|
5.19 |
|
5.20 |
|
|
5.21 |
|
5.22 |
|
|
5.23 |
|
5.24 |
|
|
5.25 |
|
5.26 |
|
|
5.27 |
|
5.28 |
|
|
5.29 |
|
5.30 |
|
6 Дифференциалдық теңдеудің жалпы интегралын табу керек
6 К е с т е
|
6.1 |
|
|
6.2 |
|
|
6.3 |
|
|
6.4 |
|
|
6.5 |
|
|
6.6 |
|
|
6.7 |
|
|
6.8 |
|
|
6.9 |
|
|
6.10 |
|
6 кестенің жалғасы
|
6.11 |
|
|
6.12 |
|
|
6.13 |
|
|
6.14 |
|
|
6.15 |
|
|
6.16 |
|
|
6.17 |
|
|
6.18 |
|
|
6.19 |
|
|
6.20 |
|
|
6.21 |
|
|
6.22 |
|
|
6.23 |
|
|
6.24 |
|
|
6.25 |
|
|
6.26 |
|
|
6.27 |
|
|
6.28 |
|
|
6.29 |
|
|
6.30 |
|
7 Бернуллидің дифференциалдық теңдеуінің жалпы шешімін табу керек
7 К е с т е
|
7.1 |
|
7.2 |
|
|
7.3 |
|
7.4 |
|
|
7.5 |
|
7.6 |
|
|
7.7 |
|
7.8 |
|
|
7.9 |
|
7.10 |
|
|
7.11 |
|
7.12 |
|
|
7.13 |
|
7.14 |
|
|
7.15 |
|
7.16 |
|
|
7.17 |
|
7.18 |
|
|
7.19 |
|
7.20 |
|
|
7.21 |
|
7.22 |
|
|
7.23 |
|
7.24 |
|
|
7.25 |
|
7.26 |
|
|
7.27 |
|
7.28 |
|
|
7.29 |
|
7.30 |
|
8 Жоғарғы ретті дифференциалдық теңдеулердің жалпы шешімін табу керек
8 К е с т е
|
8.1 |
|
8.2 |
|
|
8.3 |
|
8.4 |
|
|
8.5 |
|
8.6 |
|
|
8.7 |
|
8.8 |
|
|
8.9 |
|
8.10 |
|
|
8.11 |
|
8.12 |
|
8 кестенің жалғасы
|
8.13 |
|
8.14 |
|
|
8.15 |
|
8.16 |
|
|
8.17 |
|
8.18 |
|
|
8.19 |
|
8.20 |
|
|
8.21 |
|
8.22 |
|
|
8.23 |
|
8.24 |
|
|
8.25 |
|
8.26 |
|
|
8.27 |
|
8.28 |
|
|
8.29 |
|
8.30 |
|
9 Коэффициенттері тұрақты біртекті сызықты дифференциалдық теңдеулердің жалпы шешімін табу керек
9 К е с т е
|
9.1 |
|
9.2 |
|
|
9.3 |
|
9.4 |
|
|
9.5 |
|
9.6 |
|
|
9.7 |
|
9.8 |
|
|
9.9 |
|
9.10 |
|
|
9.11 |
|
9.12 |
|
|
9.13 |
|
9.14 |
|
|
9.15 |
|
9.16 |
|
|
9.17 |
|
9.18 |
|
|
9.19 |
|
9.20 |
|
|
9.21 |
|
9.22 |
|
|
9.23 |
|
9.24 |
|
|
9.25 |
|
9.26 |
|
|
9.27 |
|
9.28 |
|
|
9.29 |
|
9.30 |
|
10 Коэффициенттері тұрақты біртекті емес сызықты дифференциалдық теңдеулердін жалпы шешімін табу керек
10 К е с т е
|
10.1 |
|
10.2 |
|
|
10.3 |
|
10.4 |
|
|
10.5 |
|
10.6 |
|
|
10.7 |
|
10.8 |
|
|
10.9 |
|
10.10 |
|
|
10.11 |
|
10.12 |
|
|
10.13 |
|
10.14 |
|
|
10.15 |
|
10.16 |
|
|
10.17 |
|
10.18 |
|
|
10.19 |
|
10.20 |
|
|
10.21 |
|
10.22 |
|
|
10.23 |
|
10.24 |
|
|
10.25 |
|
10.26 |
|
|
10.27 |
|
10.28 |
|
|
10.29 |
|
10.30 |
|
11 ![]() қатары берілген:
қатары берілген:
а) қатардың ![]() жалпы мүшесінің формуласын және бірінші бес
мүшесін жазу керек;
жалпы мүшесінің формуласын және бірінші бес
мүшесін жазу керек;
б)
қатардың n-дербес қосындысын ![]() жазу;
жазу;
в)
қатардың калдығы![]() жазу;
жазу;
г) қатардың жинақтығының қажетті шартын тексеру.
11 К е с т е
|
11.1 |
|
11.2 |
|
11.3 |
|
|
11.4 |
|
11.5 |
|
11.6 |
|
|
11.7 |
|
11.8 |
|
11.9 |
|
|
11.10 |
|
11.11 |
|
11.12 |
|
11 кестенің жалғасы
|
11.13 |
|
11.14 |
|
11.15 |
|
|
11.16 |
|
11.17 |
|
11.18 |
|
|
11.19 |
|
11.20 |
|
11.21 |
|
|
11.22 |
|
11.23 |
|
11.24 |
|
|
11.25 |
|
11.26 |
|
11.27 |
|
|
11.28 |
|
11.29 |
|
11.30 |
|
12 Дирихле ![]() қатарымен салыстыра отырып,
қатардың жинақтылығын зерттеу және p параметрін
табу
қатарымен салыстыра отырып,
қатардың жинақтылығын зерттеу және p параметрін
табу
12 К е с т е
|
12.1 |
|
12.2 |
|
12.3 |
|
|
12.4 |
|
12.5 |
|
12.6 |
|
|
12.7 |
|
12.8 |
|
12.9 |
|
|
12.10 |
|
12.11 |
|
12.12 |
|
|
12.13 |
|
12.14 |
|
12.15 |
|
|
12.16 |
|
12.17 |
|
12.18 |
|
|
12.19 |
|
12.20 |
|
12.21 |
|
|
12.22 |
|
12.23 |
|
12.24 |
|
12 кестенің жалғасы
|
12.25 |
|
12.26 |
|
12.27 |
|
|
12.28 |
|
12.29 |
|
12.30 |
|
13 Даламбер белгісімен қатардың жинақтылығын зерттеу
13 К е с т е
|
13.1 |
|
13.2 |
|
13.3 |
|
|
13.4 |
|
13.5 |
|
13.6 |
|
|
13.7 |
|
13.8 |
|
13.9 |
|
|
13.10 |
|
13.11 |
|
13.12 |
|
|
13.13 |
|
13.14 |
|
13.15 |
|
|
13.16 |
|
13.17 |
|
13.18 |
|
|
13.19 |
|
13.20 |
|
13.21 |
|
|
13.22 |
|
13.23 |
|
13.24 |
|
|
13.25 |
|
13.26 |
|
13.27 |
|
|
13.28 |
|
13.29 |
|
13.30 |
|
14 Коши белгісімен қатардың жинақтылығын зерттеу
14 К е с т е
|
14.1 |
|
14.2 |
|
14.3 |
|
|
14.4 |
|
14.5 |
|
14.6 |
|
14 кестенің жалғасы
|
14.7 |
|
14.8 |
|
14.9 |
|
|
14.10 |
|
14.11 |
|
14.12 |
|
|
14.13 |
|
14.14 |
|
14.15 |
|
|
14.16 |
|
14.17 |
|
14.18 |
|
|
14.19 |
|
14.20 |
|
14.21 |
|
|
14.22 |
|
14.23 |
|
14.24 |
|
|
14.25 |
|
14.26 |
|
14.27 |
|
|
14.28 |
|
14.29 |
|
14.30 |
|
15 Кошидің интегралдық белгісімен қатардың жинақтылығын зерттеу
15 К е с т е
|
15.1 |
|
15.2 |
|
|
15.3 |
|
15.4 |
|
|
15.5 |
|
15.6 |
|
|
15.7 |
|
15.8 |
|
|
15.9 |
|
15.10 |
|
|
15.11 |
|
15.12 |
|
15 кестенің жалғасы
|
15.13 |
|
15.14 |
|
|
15.15 |
|
15.16 |
|
|
15.17 |
|
15.18 |
|
|
15.19 |
|
15.20 |
|
|
15.21 |
|
15.22 |
|
|
15.23 |
|
15.24 |
|
|
15.25 |
|
15.26 |
|
|
15.27 |
|
15.28 |
|
|
15.29 |
|
15.30 |
|
16 Мүшелерінің таңбалары ауыспалы қатарлардың абсолютті немесе шартты жинақтылығын зерттеу
16 К е с т е
|
16.1 |
|
16.2 |
|
16.3 |
|
|
16.4 |
|
16.5 |
|
16.6 |
|
|
16.7 |
|
16.8 |
|
16.9 |
|
|
16.10 |
|
16.11 |
|
16.12 |
|
|
16.13 |
|
16.14 |
|
16.15 |
|
16 кестенің жалғасы
|
16.16 |
|
16.17 |
|
16.18 |
|
|
16.19 |
|
16.20 |
|
16.21 |
|
|
16.22 |
|
16.23 |
|
16.24 |
|
|
16.25 |
|
16.26 |
|
16.27 |
|
|
16.28 |
|
16.29 |
|
16.30 |
|
17 Дәрежелік қатар ![]() берілген.
Қатардың жинақтылық радиусы мен жинақтылық
интервалын табу
берілген.
Қатардың жинақтылық радиусы мен жинақтылық
интервалын табу
17 К е с т е
|
17.1 |
|
17.2 |
|
|
17.3 |
|
17.4 |
|
|
17.5 |
|
17.6 |
|
|
17.7 |
|
17.8 |
|
|
17.9 |
|
17.10 |
|
|
17.11 |
|
17.12 |
|
|
17.13 |
|
17.14 |
|
|
17.15 |
|
17.16 |
|
|
17.17 |
|
17.18 |
|
17 кестенің жалғасы
|
17.19 |
|
17.20 |
|
|
17.21 |
|
17.22 |
|
|
17.23 |
|
17.24 |
|
|
17.25 |
|
17.26 |
|
|
17.27 |
|
17.28 |
|
|
17.29 |
|
17.30 |
|
1.3 Типтік нұсқасын шешу
1. ![]() функциясы
функциясы ![]() тендеуінің шешімі бола ма?
тендеуінің шешімі бола ма?
Шешуі:
Тапсырманы орындау үшің мыналар қажетті:
а) берілген функцияның туындысын табу керек:
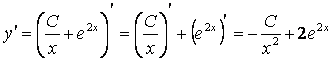 ;
;
б)![]() және
және ![]() өрнектерін берілген теңдеуге қойып, оның тепе-теңдікке
түрленетінін тексеру керек:
өрнектерін берілген теңдеуге қойып, оның тепе-теңдікке
түрленетінін тексеру керек:
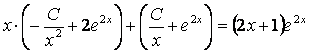 ;
;
![]() ;
;
![]() – тепе-теңдік, яғни берілген функция
дифференциалдық тендеудің жалпы шешімі болады.
– тепе-теңдік, яғни берілген функция
дифференциалдық тендеудің жалпы шешімі болады.
Ескерту. Егер
![]() и
и ![]() теңдеуге қойғанда тепе-теңдік болмаса, онда берілген
функция теңдеудің шешімі болмайды.
теңдеуге қойғанда тепе-теңдік болмаса, онда берілген
функция теңдеудің шешімі болмайды.
2. ![]() дифференциалдық теңдеуінің жалпы
шешімін (жалпы интегралын) табу керек
дифференциалдық теңдеуінің жалпы
шешімін (жалпы интегралын) табу керек
Шешуі:
![]()
![]()
![]() – айнымалылары ажыратылатын теңдеу (1.4.1 -анықтамалық
материалға қараңыз).
– айнымалылары ажыратылатын теңдеу (1.4.1 -анықтамалық
материалға қараңыз).
![]()
![]()
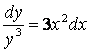 – айнымалылары ажыратылған теңдеу. Оны
былай шешеміз:
– айнымалылары ажыратылған теңдеу. Оны
былай шешеміз:
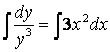
![]()
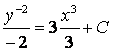
![]()
 .
.
Жауабы:  –
теңдеудің жалпы интегралы.
–
теңдеудің жалпы интегралы.
3. ![]() ,
, ![]() теңдеу үшін Коши есебінің шешімін табу керек
теңдеу үшін Коши есебінің шешімін табу керек
Шешуі:
![]()
![]()
![]()
![]()
![]() – айнымалылары ажыратылатын теңдеу, оны
– айнымалылары ажыратылатын теңдеу, оны ![]()
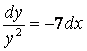 – айнымалылары ажыратылған теңдеуге келтіріп, интегралдап,
жалпы шешімін табамыз:
– айнымалылары ажыратылған теңдеуге келтіріп, интегралдап,
жалпы шешімін табамыз:
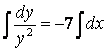
![]()
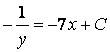
![]()
![]() .
.
Бастапқы шартты қанағаттандыратын дербес шешімді табайық:
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
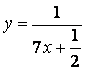
![]()
![]() - дербес
шешімі.
- дербес
шешімі.
Ескерту. Тендеуді ![]() -қа бөлгенде
-қа бөлгенде ![]() немесе
немесе ![]() болса, онда дербес шешімді жоғалтып алуымыз мүмкін. Сондықтан
бұл дербес шешімді бастапқы тендеуге қойып,
болса, онда дербес шешімді жоғалтып алуымыз мүмкін. Сондықтан
бұл дербес шешімді бастапқы тендеуге қойып, ![]() функциясы теңдеуді қанағаттандыратынына
көзімізді жеткіземіз. Бірақ та
функциясы теңдеуді қанағаттандыратынына
көзімізді жеткіземіз. Бірақ та ![]() теңдеудің ерекше шешімі болмайды, себебі
ол - ерекше шешім, бастапқы шартты қанағаттандырмайды.
теңдеудің ерекше шешімі болмайды, себебі
ол - ерекше шешім, бастапқы шартты қанағаттандырмайды.
Жауабы: ![]() .
.
4. ![]() дифференциалдық теңдеудің жалпы
шешімін (жалпы интегралын) табу керек
дифференциалдық теңдеудің жалпы
шешімін (жалпы интегралын) табу керек
Шешуі:
![]() – қос аргументі бойынша біртекті теңдеу (1.4.1
қөріңіз).
– қос аргументі бойынша біртекті теңдеу (1.4.1
қөріңіз).
Берілген теңдеуді жаңа айнымалы ![]()
![]()
![]()
![]()
![]() .
.
енгізу арқылы мына тендеуге келтіреміз: ![]() ;
;
![]() ;
бұл айнымалылары
ажыратылатын теңдеу. Оны шешеміз:
;
бұл айнымалылары
ажыратылатын теңдеу. Оны шешеміз:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
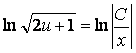
![]()
![]()
![]()
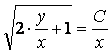 – жалпы интеграл.
– жалпы интеграл.
Жауабы: 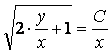 .
.
5. ![]() ,
, ![]() . Коши есебін шешу керек
. Коши есебін шешу керек
Шешуі:
Берілген теңдеу біртектісіз сызықты теңдеу болады (1.4.1көріңіз).
Бұл тапсырманы екі тәсілмен шығарайық:
1) ![]() (Бернулли әдісі);
(Бернулли әдісі);
2) ерікті тұрақтыларды вариациялау әдісі.
(Шығару тәсілін студент өзі таңдайды).
1) Бернулли әдісі.
Ауыстыру жасайық ![]() (мұнда u = u(x), v
= v(x) – жаңа
белгісіз функциялар)
(мұнда u = u(x), v
= v(x) – жаңа
белгісіз функциялар) ![]()
![]() ; - оны теңдеуге
қоямыз:
; - оны теңдеуге
қоямыз:
![]()
![]()
![]() ;
;
v функциясын
![]() теңдеуінің шешімі болатындай таңдайық. Бұл
теңдеу-айнымалары
ажыратылатын тендеу:
теңдеуінің шешімі болатындай таңдайық. Бұл
теңдеу-айнымалары
ажыратылатын тендеу: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Табылған v функциясын ескере отырып, бастапқы теңдеуден
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
u = u(x) функциясы табылды .
Сондықтан  – жалпы шешімі.
– жалпы шешімі.
Бастапқы шарт ![]() болғандықтан
болғандықтан
![]()
![]()
![]() .
.
Жауабы: ![]() ;
;
2) ерікті тұрақтыларды вариациялау әдісі.
![]() – 1-ретті біртекті емес сызықты дифференциалдық
теңдеуі.
– 1-ретті біртекті емес сызықты дифференциалдық
теңдеуі.
Оған сайкес біртекті тендеу ![]() . Бұл айнымалылары ажыратылатын теңдеу
. Бұл айнымалылары ажыратылатын теңдеу
![]()
![]()
![]()
![]()
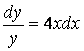
![]()
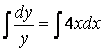
![]()
![]()
![]()
![]() – біртекті
сызықтық теңдеудің жалпы шешімі.
– біртекті
сызықтық теңдеудің жалпы шешімі.
Біртекті емес тендеудің шешімін мына түрде іздейміз: ![]() ; бұл жерде
; бұл жерде ![]() – белгісіз функция.
– белгісіз функция.
![]() ,
, ![]() бастапқы
тендеуге қоямыз
бастапқы
тендеуге қоямыз
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Сонымен,  – бастапкы теңдеудің жалпы шешімі.
Бастапқы шартты
– бастапкы теңдеудің жалпы шешімі.
Бастапқы шартты ![]() қолданып, тұрақты С-ны
табамыз:
қолданып, тұрақты С-ны
табамыз: ![]()
![]()
![]() .
.
Жауабы: ![]() .
.
6. ![]() дифференциалдық
теңдеудің жалпы интегралын табу керек
дифференциалдық
теңдеудің жалпы интегралын табу керек
Шешуі:
теңдеудың құрылымы ![]() .
.
![]() және
және ![]() табамыз:
табамыз:
 .
.
Сондықтан берілген теңдеу - и функциясы арқылы толық
дифференциалды теңдеу: ![]() ; бұл
- u функциясының толық дифференциалы (1.4.1көріңіз).
; бұл
- u функциясының толық дифференциалы (1.4.1көріңіз).
Белгісіз функция ![]() келесі формула бойынша
табылады:
келесі формула бойынша
табылады: 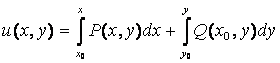 .
.
х0 = 0, у0 = 0 болсын; сонда
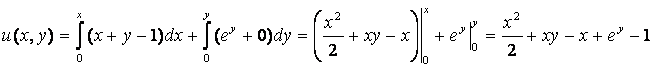
![]() болғандықтан, и = С – дифференциалдық
теңдеудің жалпы интегралы.
болғандықтан, и = С – дифференциалдық
теңдеудің жалпы интегралы.
Жауабы: 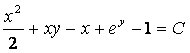 .
.
7. ![]() дифференциалдық тендеудің жалпы
шешімін табу керек
дифференциалдық тендеудің жалпы
шешімін табу керек
Шешуі:
![]() – Бернулли теңдеуі (1.4.1
көріңіз).
– Бернулли теңдеуі (1.4.1
көріңіз).
Ауыстыру жасайық: ![]()
![]()
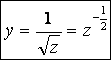
![]()
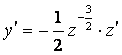 .
Табылған
.
Табылған ![]() ,
, ![]() функцияларды берілген теңдеуге қоямыз:
функцияларды берілген теңдеуге қоямыз:
 .
Теңдеуді
.
Теңдеуді ![]() -қа көбейтеміз:
-қа көбейтеміз:
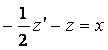
![]()
![]() – біртекті емес сызықты бірінші ретті дифференциалдық
теңдеу. Бұл теңдеуді Бернулли әдісімен шығарамыз
(5-тапсырмасының 1-әдісімен шешіні көру керек).
– біртекті емес сызықты бірінші ретті дифференциалдық
теңдеу. Бұл теңдеуді Бернулли әдісімен шығарамыз
(5-тапсырмасының 1-әдісімен шешіні көру керек).
Ауыстыру жасайық ![]()
![]()
![]() .
.
![]()
![]()
![]() (*)
(*)
v функциясын
![]() теңдеуінің
шешімі болатындай таңдайық. Бұл тендеу - айнымалары ажыратылатын тендеу :
теңдеуінің
шешімі болатындай таңдайық. Бұл тендеу - айнымалары ажыратылатын тендеу :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Таңдалған v функциясын ескере отырып, (*)-теңдеуден и функциясын табамыз:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
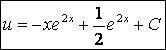 , функциясы табылды.
, функциясы табылды.
Сонымен, 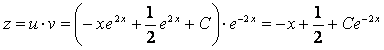
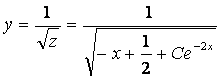 –берілген теңдеудін жалпы
шешімі.
–берілген теңдеудін жалпы
шешімі.
Жауабы: 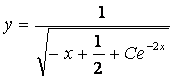 .
.
8. ![]() дифференциалдық теңдеудің жалпы шешімін табу керек
дифференциалдық теңдеудің жалпы шешімін табу керек
Шешуі:
![]() –
– ![]() түріңдегі екінші
ретті дифференциалдық теңдеу.Теңдеудің ретін екі рет интегралдау арқылы теңдеудің жалпы шешімін табамыз:
түріңдегі екінші
ретті дифференциалдық теңдеу.Теңдеудің ретін екі рет интегралдау арқылы теңдеудің жалпы шешімін табамыз:

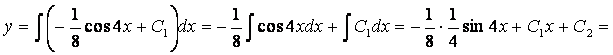
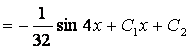 .
.
Жауабы: 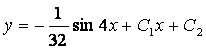 .
.
9. Коэффициенттері тұрақты жоғарғы ретті әртүрлі:
а) ![]() ,
,
б) ![]() ,
,
в) ![]() ;
;
біртекті сызықты дифференциалдық теңдеулердің жалпы шешімдерін табу керек
а) ![]() .
.
Шешуі:
![]() -
берілген теңдеудің сипаттаушы
квадраттық теңдеуі.
-
берілген теңдеудің сипаттаушы
квадраттық теңдеуі.
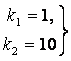 – оның әртүрлі
нақты түбірлері.
– оның әртүрлі
нақты түбірлері.
Жалпы шешімі: ![]() .
.
Жауабы: ![]() .
.
б) ![]() .
.
Шешуі:
![]() - сипаттаушы теңдеу.
- сипаттаушы теңдеу.
![]() – сипаттаушы теңдеудің өзара тең түбірлері.
– сипаттаушы теңдеудің өзара тең түбірлері.
Жалпы шешімі: ![]() .
.
Жауабы: ![]() .
.
в) ![]() .
.
Шешуі:
![]() -
сипаттаушы теңдеу
-
сипаттаушы теңдеу
![]() – сиптатаушы теңдеудің комплекс жорамал түбірлері. (
– сиптатаушы теңдеудің комплекс жорамал түбірлері. (![]() ,
, ![]() (1.4.2
көріңіз)).
(1.4.2
көріңіз)).
Жалпы шешімі: ![]() .
.
Жауабы: ![]() .
.
10. Коэффициенттері
тұрақты жоғарғы ретті біртексіз сызықты дифференциалдық
теңдеудің ![]() жалпы шешімін табу керек
жалпы шешімін табу керек
Шешуі:
Теңдеудің жалпы шешімінің
құрылымы ![]() (1.4.3 көріңіз).
(1.4.3 көріңіз).
![]() – біртексіз теңдеудің сәйкес
біртекті
– біртексіз теңдеудің сәйкес
біртекті
![]() теңдеудің
жалпы шешімі;
теңдеудің
жалпы шешімі;
![]() – берілген біртексіз теңдеудің дербес
шешімі.
– берілген біртексіз теңдеудің дербес
шешімі.
1) белгісіз ![]() функциясын
табайық:
функциясын
табайық:
![]() – сипаттаушы теңдеу.
– сипаттаушы теңдеу.
 – сиптатаушы теңдеудің
комплекс түберлері (
– сиптатаушы теңдеудің
комплекс түберлері (![]() ,
, ![]() (1.4.2 көріңіз)). Сонымен,
(1.4.2 көріңіз)). Сонымен, ![]() .
.
2) біртекті теңдеудің оң жағына
f(x) жазып,
анықтылмаған коэффициенттер
әдісін пайдаланып ![]() табайық.
табайық.![]() ,
P0(x)– нөлінші дәрежелі көпмүше
(С = 6,
,
P0(x)– нөлінші дәрежелі көпмүше
(С = 6,![]() ).
).
Егер де ![]() сипаттаушы теңдеудің түбірі
болмаса, онда дербес шешім мына түрде ізделеді:
сипаттаушы теңдеудің түбірі
болмаса, онда дербес шешім мына түрде ізделеді: ![]() . Белгісіз түрақты А санын
. Белгісіз түрақты А санын
табу үшін берілген
теңдеуге ![]() ,
,
![]() ,
, ![]() қоямыз:
қоямыз:
![]() ,
, ![]() ,
, ![]() ;
;
![]() .
.
Осыдан мынаны аламыз: ![]()
![]()
![]()
![]()
![]() ;
;![]()
Сондықтан да, берілген теңдеудің жалпы шешімі мына түрде болады: ![]() .
.
Жауабы: ![]() .
.
11. 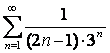 қатар берілген:
қатар берілген:
а) осы қатардың жалпы мүшесінің формуласын және оның бірінші бес мүшесін жазу керек;
б)
қатардың n-дербес қосындысы ![]() жазу керек;
жазу керек;
в)
қатардың калдығы ![]() жазу керек;
жазу керек;
г) қатар үшін жинақтылықтың қажетті шартын тексеру керек.
Шешуі:
а)
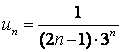 ;
;
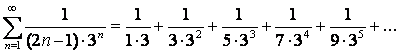 ;
;
б)
Қатардың бірінші n
мүшесінің
қосындысын ![]() табайық -
табайық -
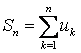 :
:
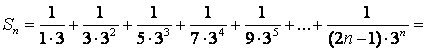
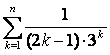 ;
;
в) егер 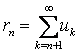 , онда
, онда
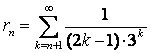 - қатардың
калдығы;
- қатардың
калдығы;
г) 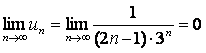 ; сондықтан қатардың
жинақтылығының қажетті шарты орындалған (1.4.4
көріңіз).
; сондықтан қатардың
жинақтылығының қажетті шарты орындалған (1.4.4
көріңіз).
12. 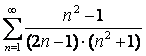 қатарын
Дирихле қатарымен салыстыра отырып, оның жинақтылығын
зерттеу керек және параметр p табу керек
қатарын
Дирихле қатарымен салыстыра отырып, оның жинақтылығын
зерттеу керек және параметр p табу керек
Шешуі:
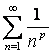 - Дирихле қатары
- Дирихле қатары ![]() -де
жинақты,
-де
жинақты, ![]() -де
жинақсыз болады.
-де
жинақсыз болады.
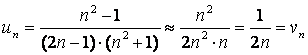 , - Дирихле қатарының
, - Дирихле қатарының 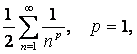 n-мүшесі. Сондықтан
2-і салыстыру белгісі бойынша қатар жинақсыз (
n-мүшесі. Сондықтан
2-і салыстыру белгісі бойынша қатар жинақсыз (![]() -гармониялық
қатары жинақсыз).
-гармониялық
қатары жинақсыз).

екі қатар да жинақсыз болады.
13. Даламбер белгісін колданып,  қатардың жинақтылығын
зерттеу керек
қатардың жинақтылығын
зерттеу керек
Шешуі:
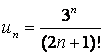 ,
, 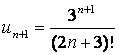 - берілген қатардың n-,
n+1-мүшелері.
- берілген қатардың n-,
n+1-мүшелері.
Даламбер белгісі бойынша (1.4.4 көріңіз):
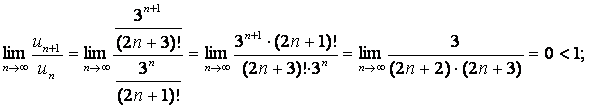 сондықтан қатар жинақты.
сондықтан қатар жинақты.
14. Коши белгісін колданып, 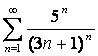 қатардың жинақтылығын
зерттеу керек
қатардың жинақтылығын
зерттеу керек
Шешуі:
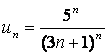 - берілген қатардың n-мүшесі.
- берілген қатардың n-мүшесі.
Коши белгісі бойынша (1.4.4 көріңіз):
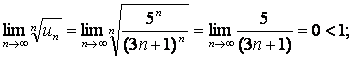
сондықтан қатар жинақты.
15. Кошидің
интегралдық белгісін қолданып, 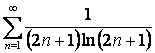 қатардың жинақтылығын зерттеу керек
қатардың жинақтылығын зерттеу керек
Шешуі:
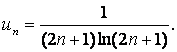 - берілген қатардың n-мүшесі.
- берілген қатардың n-мүшесі.
Қатардың барлық ![]() мүшелері оң және өспейді,
яғни u1 ³ u2 ³ u3 ³ …
мүшелері оң және өспейді,
яғни u1 ³ u2 ³ u3 ³ …
сонымен қатар, 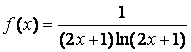 – функциясы үзіліссіз, өспейтін;
– функциясы үзіліссіз, өспейтін;
f (1) = u1, f (2) = u2 , …, f (п) = uп .
Берілген қатар Кошидің интегралдық белгісі бойынша жинақсыз болады, себебі (1.4.4 көріңіз)
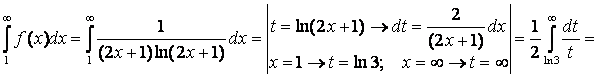
 - интегралы жинақсыз.
- интегралы жинақсыз.
16. Мүшелерінің таңбалары ауыспалы мына қатарлардың абсолютті және шартты жинақтылығын зерттеу керек:
а) 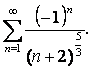 ,
,
б) 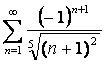 ,
,
в) 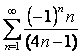 .
.
Шешуі:
а) 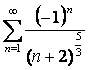 ;
;
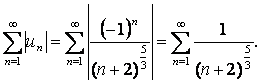 қатарын қарыстырайық. Ол
2- қатар салыстыру белгісі бойынша жинақты:
қатарын қарыстырайық. Ол
2- қатар салыстыру белгісі бойынша жинақты:
қатарды ![]() қатарымен салыстырамыз (бұл
қатарымен салыстырамыз (бұл
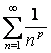 Дирихле қатары,
Дирихле қатары,  , -
жинақты);
, -
жинақты); 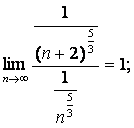 сондықтан
екі қатар да жинақты.
сондықтан
екі қатар да жинақты.
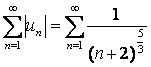 қатары
жинақты
болғандықтан,
қатары
жинақты
болғандықтан,  қатары абсолютті жинақты.
қатары абсолютті жинақты.
б) 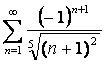 ;
;
Шешуі:
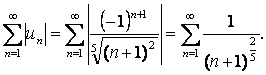 қатарын қарыстырайық. Оны жинақсыз
қатарын қарыстырайық. Оны жинақсыз 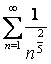 қатарымен салыстырайық (бұл
- Дирихле қатары
қатарымен салыстырайық (бұл
- Дирихле қатары 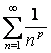 ,
, 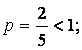 жинақсыз);
жинақсыз);
 , 2-і салыстыру белгісі бойынша берілген қатар да жинақсыз.
Сондықтан берілген қатар абсолютті жинақты бола алмайды. Лейбниц теоремасының шарттарының
орындалуын тексерейік (1.4.4 көріңіз):
, 2-і салыстыру белгісі бойынша берілген қатар да жинақсыз.
Сондықтан берілген қатар абсолютті жинақты бола алмайды. Лейбниц теоремасының шарттарының
орындалуын тексерейік (1.4.4 көріңіз):
1) 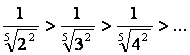 ; 2)
; 2) 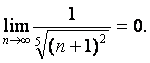
Шарттар орындалғандықтан, берілген қатар шартты жинақты.
в)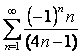 ;
;
Шешуі:
Бұл қатар үшін Лейбниц теоремасының
шарттарының біреуі орындалмайды (![]() ) (1.4.4 көріңіз):
) (1.4.4 көріңіз):
Шынында, 1) 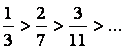 ;
2)
;
2) 
Сондықтан қатар жинақсыз.
17. Дәрежелік қатарлар берілген
а) 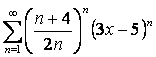 ;
;
б) 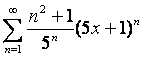 .
.
Олардың жинақтылық радиусы мен жинақтылық аралығын табу керек.
Радиусты төменгі формулалардың бірін қолданып табамыз (1.4.5 көріңіз) :
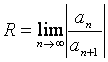 немесе
немесе 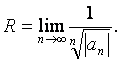
а)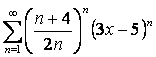 ;
;
Шешуі:
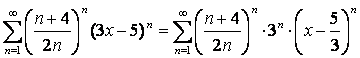 . Берілген қатарды мына стандартты түрге
келтірелік:
. Берілген қатарды мына стандартты түрге
келтірелік:
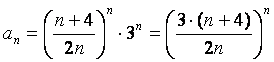 ,
, 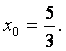
Сонда

Қатардың жинақтылық аралығын ![]() келесі теңсіздіктен табамыз:
келесі теңсіздіктен табамыз:
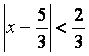
![]()
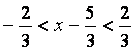
![]()
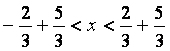
![]()
 .
.
Жауабы: 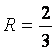 -
қатардың жинақтылық радиусы,
-
қатардың жинақтылық радиусы,  - жинақтылық
аралығы.
- жинақтылық
аралығы.
б) 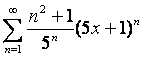 ;
;
Шешуі:
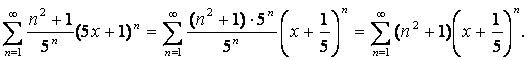
Қатарды стандартты түрге келтірелік:
![]() ,
,
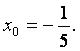
Сонда 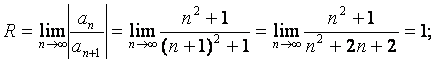
![]() - қатардың
жинақтылық радиусы.
- қатардың
жинақтылық радиусы.
Қатардың жинақтылық аралығын ![]() келесі теңсіздіктен табамыз:
келесі теңсіздіктен табамыз:
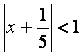
![]()
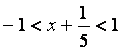
![]()
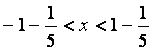
![]()
 .
.
Жауабы : ![]() жинақтылық радиусы,
жинақтылық радиусы,  - жинақтылық
аралығы.
- жинақтылық
аралығы.
1.4 Анықтама материалдар.
1. Дифференциалдық теңдеудің негізгі түрлерінің кестесі
|
№ |
Теңдеу- дің типі |
Теңдеудің түрлері |
Шешу әдісі |
Ескерту |
|
1 |
Айны-малылары ажыраты-латын |
а) б) |
а) б) |
|
|
2 |
Біртекті |
а)
б) бірдей біртекті функциялар: |
|
1-типтік теңдеуге келтіріледі. бірақ оның бір жақтарында
|
|
3 |
Сызықты |
|
а) Бернулли әдісі. б) Вариациялық әдісі. С-кез келген тұрақтыны функция С(х) рет тінде қарастырып, оны (*)-теңдеуін қанағаттандыратындай етіп табу керек. |
а) С = 0 |
|
4 |
Бернулли теңдеуі |
|
а) Бернулли әдісі. б) |
|
|
5 |
Толық дифференциалды диф. теңдеулер |
|
Шешімі |
Тексеру
|
2. Коэффициенттері тұрақты екінші ретті біртекті сызықты дифференциалдық теңдеу мына түрде болады:
у¢¢ + pу¢ + qу = 0, p, q ÎR.
Оның жалпы шешімі k 2 + pk + q = 0 сиптатаушы теңдеудің түбірлерінің түріне байланысты.
Сипаттаушы тендеудің түбірлері:
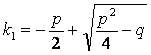 ;
; 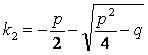 .
.
Мүмкін жағдайлар:
а) егер сиппатаушы теңдеудің түбірлері k1 , k2 Î R ( k1 ≠ k2 ) әртүрлі нақты сандар болса, онда жалпы шешім
![]() түрінде болады;
түрінде болады;
б) егер сиптатаушы тендеудің түбірлері , k1 , k2 Î R өзара тең болса ( k1 = k2 ), онда жалпы шешім
![]() түрінде
жазылады;
түрінде
жазылады;
в) егер сиптатаушы тендеудің түбірлері k1
, k2 Î C екі ![]() ,
,
![]() ,
,
![]()
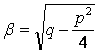 комплекс сандар болса, онда жалпы шешім
комплекс сандар болса, онда жалпы шешім
![]() түрінде жазылады.
түрінде жазылады.
3. Коэффициенттері тұрақты екенші ретті біртекті емес сызықты дифференциалдық теңдеу түрі мынадай болады:
у¢¢ + ру¢ + qу = f (x), p, q Î R;
оның жалпы шешімі ![]() түрінде жазылады;
түрінде жазылады;
бұл жерде ![]() – сәйкес у¢¢ + ру¢ + qу = 0 біртекті
тендеудің жалпы шешімі;
– сәйкес у¢¢ + ру¢ + qу = 0 біртекті
тендеудің жалпы шешімі;
![]() – берілген біртекті емес теңдеудің
дербес шешімі.
– берілген біртекті емес теңдеудің
дербес шешімі.
Дербес шешім![]() -і
анықтау біртекті емес теңдеудің
оң жағы f(x) функцияға байланысты.
-і
анықтау біртекті емес теңдеудің
оң жағы f(x) функцияға байланысты.
3.1 Егер де теңдеудің оң жағындағы
функция ![]() ,
мүнда Pn(x) – п-дәрежелі көпмүше
түрінде болса, дербес шешім
,
мүнда Pn(x) – п-дәрежелі көпмүше
түрінде болса, дербес шешім ![]() сипаттама теңдеудің k 2
+ pk + q = 0 түбірі a болуболмауына
байланысты. Сондықтан мынадай нұсқалар болуы мүмкін:
сипаттама теңдеудің k 2
+ pk + q = 0 түбірі a болуболмауына
байланысты. Сондықтан мынадай нұсқалар болуы мүмкін:
а) егер де a саны сипаттаушы теңдеудің түбірі болмаса, онда дербес шешім мына түрде ізделеді:
![]() ,
,
яғни Qn(x) –коэффициенттері ![]() белгісіз
п-дәрежелі көпмүше
(Pn(x) сияқты);
белгісіз
п-дәрежелі көпмүше
(Pn(x) сияқты);
б) егер де a саны сипаттаушы теңдеудің бір еселі нақты түбірі болса, онда ![]() .
.
в) егер де a саны сипаттаушы теңдеудің еселігі екіге тең түбірі болса, онда ![]() .
.
3.2 Егер де теңдеудің оң
жағындағы ![]() функция мына түрде болса
функция мына түрде болса ![]() ,
мұнда Pп(x), Qт(x)
– п- және т-
дәрежелі көпмүшелер,
онда мынадай нұсқалар болуы мүмкін:
,
мұнда Pп(x), Qт(x)
– п- және т-
дәрежелі көпмүшелер,
онда мынадай нұсқалар болуы мүмкін:
егер де a ± ib саны сипаттаушы теңдеудің комплекс түбірлері болмаса, онда
![]() ,
,
мұнда Up(x), Vp(x)
– коэффициенттері белгісіз р-дәрежелі
көпмүшелер, ![]() .
.
а) егер де a ± ib саны сиппатаушы теңдеудің комплекс түбірлері болса, онда
![]() .
.
Дербес жағдайлар:
б) егер f (x) = М cos bx + N sin bx, мұндағы М, N – тұрақты сандар, онда:
1) егер де ± ib саны сиптатаушы теңдеудің жорамал түбірлері болмаса, онда
![]() ,
,
(А , В – анықталатын белгісіздер);
2) егер де ± ib сандары сиптатаушы теңдеудің жорамал түбірлері болса, онда
![]() ,
,
(А , В – анықталатын белгісіздер).
4. Сандық қатарлар
 (1)
(1)
мұнда ип Î R (n = 1, 2, …), өрнегін саңдық қатар дейді.
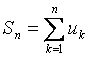 – қатардың n-дербес қосындасы,
– қатардың n-дербес қосындасы, 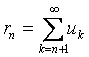 – қатардың қалдығы.
– қатардың қалдығы.
Егер де 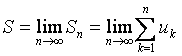 шегі болса, қатар жинақты; S санын қатардың
қосындысы деп атайды.
шегі болса, қатар жинақты; S санын қатардың
қосындысы деп атайды.
Егер де қатар жинақты болса, онда ![]() .
.
Осы шартты сандық қатардың жинақтылығының қажетті белгісі деп атайды.
4.1 Оң қатардың жинақтылығының белгілері
1) Даламбердің белгісі.
Егер де 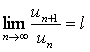 шегі бар болса, онда қатар
шегі бар болса, онда қатар
l < 1 де жинақты;
l > 1 де жинақсыз;
l = 1 де белгіні қолданбайды.
Егер де ип де көрсеткішті немесе факториалды функциялар болса, онда Даламбер белгісін қолдануға болады.
2) Коши белгісі.
Егер де ![]() шегі бар болса
шегі бар болса
онда қатар l < 1 де жинақты;
l > 1 де жинақсыз;
l = 1 де белгіні қолданбайды.
3) Салыстыру белгілері.
(1) – қатармен қосымша
 (2)
(2)
қатарын қарастырамыз.
Салыстырудың 1-белгісі:
а) егер де un £ vn (п = 1, 2, …) және де (2)-қатар жинақты болса, онда (1) -қатар да жинақты;
б) егер де un ³ vn (п = 1, 2, …) және (1)-қатар да жинақсыз болса, онда (2)-қатар да жинақсыз.
Салыстырудың 2-белгісі:
Егер де 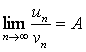 (
А ≠ 0, А ≠ ∞ ), шегі бар болса, онда (1), (2) –қатарлар не
жинақты, не жинақсыз.
(
А ≠ 0, А ≠ ∞ ), шегі бар болса, онда (1), (2) –қатарлар не
жинақты, не жинақсыз.
4) Интегралдық белгісі (Кошидің интегралдық белгісі)
(1)- қатардың мүшелері оң жәңе өспейтін: u1 ³ u2 ³ u3 ³ …болсын, сонымен қатар, f (x) функциясы үзіліссіз және мынадай теңдіктер болсын:
f (1) = u1, f (2) = u2 , …, f (п) = uп .
Сонда (1) – қатар мен өзіндік емес интеграл 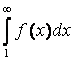 бірдей не жинақты, не жинақсыз.
бірдей не жинақты, не жинақсыз.
4.2 Таңбалары ауыспалы қатарлар
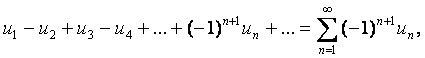 (3)
(3)
мұнда uп ³ 0 (п = 1, 2, …), қатарын мүшелері монотонды кемитін,
яғни: 1) u1 > u2 > u3 > және де 2) ![]() болса, онда (3) – қатар жинақты,
оның қосындысы оң , u1 мүшесінен кіші:
0 < S < u1.
болса, онда (3) – қатар жинақты,
оның қосындысы оң , u1 мүшесінен кіші:
0 < S < u1.
Лейбниц теоремасы.
Егер де (3) және 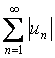 қатарлары жинақты болса, онда (3) –
қатар абсолютті жинақты дейді; егер де (3) – қатар жинақты,
қатарлары жинақты болса, онда (3) –
қатар абсолютті жинақты дейді; егер де (3) – қатар жинақты, 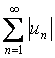 –
қатар жинақсыз болса, онда (3) – қатарды шартты жинақты
дейді.
–
қатар жинақсыз болса, онда (3) – қатарды шартты жинақты
дейді.
5. Функционалдық қатарлар
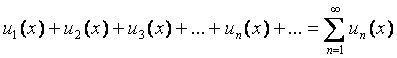 қатарын функционалдық қатар деп атайды;
қатарын функционалдық қатар деп атайды;
функционалдық қатардың дербес жағдайы дәрежелік (х-дәрежесімен):
 ,
,
қатары болады; мұнда ап (п = 1, 2, …) – тұрақты дәрежелік қатардың мүшелері.
Дәрежелік қатар (–R; R) аралығында жинақты, оның сыртында жинақсыз. R санын қатардың жинақтылық радиусы дейді де
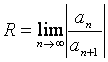 немесе
немесе

формуларымен есептейді.
Жалпы жағдайда (х – х0) – арқылы дәрежелі қатардың түрі мынадай:
 ,
,
мұнда ап (п = 1, 2, …), қатардың коэффициенттері.
Соңғы қатардың жинақтылық радиусы R - ортасы х0 нүктесі болатын аралық (х0 – R; х0 + R). Жинақтылық радиусы жоғарыдағы формулалармен есептеледі.
Егер де R = ∞ болса, онда қатардың жинақтылық радиусы бүкіл сандық түзу болады; егер де R = 0 болса, онда жинақтылық интервал х = х0 нүктесіне айналады.
Әдебиеттер тізімі
1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: В 2 ч.–М.: Высшая школа, 1986.–Ч.1–352 с.
2. Сборник индивидуальных заданий по высшей математике: В 3 ч./А.П. Рябушко, В.В. Бархатов и др./Под редакцией А.П. Рябушко.–Минск: Вышейшая школа, 1991.–Ч.3.–351с.
3. Кузнецов А.А. Сборник заданий по высшей математике: Типовые расчеты.–М.: Высшая школа, 1983.– 176 с.
4. Хасеинов Математикасының каноныА.-2003
Мазмұны
1 3-типтік есептеу. Дифференциалдық теңдеулер. Қатарлар....…….....…..3
1.1 Теориялық сұрақтар.…………....……………………….....……………….3
1.2 Есептелетін тапсырмалар....……………………..……………………........4
1.3 Типтік нұсқаларды шығару....……….……………………..………………18
1.4 Анықтамалық материалдар………………………………………………...31
Әдебиеттер тізімі...………………………………..…………………….............37