Некоммерческое акционерное общество

АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра физики 

 

 

ФИЗИКА 1 

Методические указания  к выполнению расчетно – графических работ

для студентов всех форм обучения всех специальностей

  

Алматы 2009

         СОСТАВИТЕЛИ: М.Ш. Карсыбаев, А.М. Саламатина, Т.С. Байпакбаев / Под редакцией д.п.н. проф. Мажитовой Л.Х. ФИЗИКА 1. Методические указания к          выполнению расчетно – графических работ для студентов всех форм          обучения всех специальностей.– Алматы: АИЭС, 2009 - 24 с. 

         Методические указания содержат темы курса, по которым составлены задания РГР, формулировки типовых задач, описание общих методов их решения и примеры применения этих методов к решению конкретных задач. Методическая разработка предназначена для помощи при самостоятельном выполнении студентами заданий РГР.

 

Введение

Решение задач при изучении курса физики во втузе имеет исключи­тельно большое значение для будущих специалистов. Оно учит анализиро­вать изучаемые явления, выделять главные факторы, отвлекаясь от случай­ных и несущественных деталей, учит моделировать реальные физические и физико-технические процессы. Задачи развивают навык в использовании общих законов материального мира для решения конкретных вопросов, имеющих практическое или познавательное значение.

В основной части данного руководства приведены темы курса физики, по которым составлены задания для РГР; по каждой теме перечисле­ны основные понятия, законы, соотношения, сформулированы основные (ти­повые) задачи, описаны общие методы их решения, рассмотрены примеры.

Невозможно научиться решать задачи по физике, не зная и не понимая теории. Поэтому необходима самостоятельная работа при подготовке к ауди­торному занятию, которая заключается в проработке теоретического мате­риала по заданной теме и усвоении основных понятий, определений физиче­ских величин, законов, и т.п. Приведенные в данном руководстве описания методов решения основных типов задач, должны помочь студентам как на аудиторном занятии, так и при выполнении самостоятельной расчетно-графической работы.

Процесс решения поставленной физической задачи состоит, как прави­ло, из трех основных этапов. На первом, физическом, этапе проводится ана­лиз условия задачи, выполняется рисунок, схема или векторная диаграмма для ее наглядной интерпретации; затем, на основании тех или иных законов составляется система уравнений, в число неизвестных которой входят и ис­комые величины.

На втором, математическом, этапе находят решение системы уравне­ний, т.е. получают решение задачи сначала в общем виде, а затем, произведя вычисления, числовой ответ задачи.

После того как получено общее решение, необходимо провести его анализ. На этом, третьем, этапе выясняют, как и от каких физических вели­чин зависит найденная величина, в каких условиях эта зависимость проявля­ется. При анализе числового ответа проверяют размерность полученной ве­личины и соответствие числового ответа физически возможным значениям искомой величины. 

 

Требования к оформлению РГР

 

Каждую расчетно-графическую работу следует выполнять в отдельной тетради, на обложке которой указывают номер работы, вариант, кем работа выполнена, кто ее проверил, дату сдачи на проверку; например, согласно следующему образцу:

                  Физика 1 РГР №__ Вариант №__

                  Выполнил студент ___(Ф.И.О, группа)

                  Проверил ___(Ф.И.О. преподавателя)

                  Сдана на проверку ___(дата)

Работу выполняют шариковой (или иной) ручкой, рисунки - при по­мощи карандаша и линейки.

Условие задачи следует переписывать полностью, без сокращений. За­тем его записывают с помощью общепринятых символических обозначений в краткой форме, под заглавием «Дано». Если в задаче заданы числовые вели­чины, то необходимо выразить их в системе единиц СИ.

Решение каждой задачи необходимо сопроводить пояснениями, рас­крывающими смысл и значение используемых обозначений, указать физиче­ские законы и принципы, положенные в основу решения. Необходимо обос­новывать применение в каждом конкретном случае того или иного закона, принципа или соотношения. После того, как задача решена в общем виде, т.е. получен ответ в виде расчетной формулы, производят вычисления, руково­дствуясь при этом правилами приближенных вычислений. 

 

1 Кинематика материальной точки и твердого тела

 

Основные понятия, законы, соотношения

Радиус-вектор r точки, его компоненты. Закон движения частицы. Траектория движения. Векторы скорости v и ускорения а, их компоненты. Тангенциальное , нормальное  и полное а ускорения. Радиус кривиз­ны траектории .

Угол поворота  при вращении твердого тела. Угловая скорость ω. Угловое ускорение ε. Связь между угловой ω и линейной скоростями v, между угловым   и тангенциальным   ускорениями.

[1] §§2-5; [2] §§1-4.

Прямая основная задача кинематики заключается в нахождении любо­го параметра движения (v, а, ω, ε) по известному закону движения  r = r(t)  или .

Метод решения основной задачи кинематики состоит в последователь­ном применении определений кинематических величин и соотношений, свя­зывающих эти величины. Зная закон движения, можно определить любой параметр движения.

Пример 1.

Радиус-вектор частицы изменяется со временем по закону r(t) = 3t²i+2tj +4k (м). Найти скорость v, ускорение а и модуль скорости v для произвольного момента времени  .

Решение. Запишем компоненты радиус-вектора и получим кинематические уравнения движения:

x(t)=3 (м),   y(t)=2t  (м),    z(t)=4 (м)

Согласно определению, скорость – это первая производная по времени от радиус-вектора, а ее компоненты – первые производные от соответствующих координат:

v_x =  (м/с);      v_y===2  (м/с);    v_z==0.

Ускорение, согласно определению, - это первая производная по времени от скорости:

 (м/с²)      ,  .

Таким образом:  v=6ti+2j,      a=6i.

Модуль любого вектора, как известно, равен корню квадратному из суммы его компонентов. Соответственно, модули векторов скорости и ускорения будут равны:

=  (все – в м/с),    a=6 (м/с²).

Пример 2.

Обратная задача кинематики заключается в определении закона движения по какому-либо известному параметру движения и заданным на­чальным условиям.

Метод решения обратной задачи также основан на применении зако­нов кинематики, но вместо дифференцирования по времени t, теперь выпол­няется интегрирование дифференциальных уравнений. Появляющиеся при этом константы интегрирования находят из начальных условий.

Пример 3.

Поезд движется прямолинейно со скоростью . Внезапно на пути возникает препятствие, и машинист включает тормозной механизм. С этого момента скорость поезда изменяется по закону , где . Каков тормозной путь поезда? Через какое время после начала торможения он остановится?

Решение:

Т.к. движение одномерное, то для нахождения закона его движения достаточно найти закон изменения одной координаты, например, .Согласно определению скорости: ,

или .

Интегрируя последнее уравнение, получим:

                                               .

         Чтобы определить константу интегрирования , воспользуемся начальными условиями: при , , которые подставим в закон движения. В результате получим , откуда следует, что .

         Время  торможения поезда до его остановки найдем из уравнения

         , откуда    .

         Тормозной путь равен:  .

2 Основная задача динамики и методы ее решения для частицы, системы частиц и твердого тела

 

Основные понятия, законы, соотношения

Масса. Импульс. Сила. Первый закон Ньютона. Инерциальные системы отсчета. Второй закон Ньютона (две формулировки). Третий закон Ньютона.

Центр масс системы частиц. Движение центра масс твердого тела.

Момент силы, плечо силы. Момент импульса. Уравнение моментов. Момент инерции тела относительно оси. Уравнение динамики вращательно­го движения твердого тела относительно неподвижной оси.

[1] §§ 6, 8, 10, 30, 31; [2] §§ 5-7, 9, 16, 18, 19.

Основная задача динамики заключается в определении механического состояния системы в произвольный момент времени по заданным силам и состоянию системы в начальный момент времени.

Метод решения основной задачи динамики базируется на применении соответствующих рассматриваемой системе законов динамики. Интегриро­ванием полученных при этом уравнений движения находят зависимости Р(t) и  L(t), которые показывают, как в процессе движения изменяются, соответственно, импульс и момент импульса частицы или твердого тела.

Пример 4.

Частице массой  сообщена начальная скорость  под уг­лом а к горизонту. Траектория полета частицы лежит в плоскости . Пре­небрегая сопротивлением воздуха, найти зависимость от времени:

а) импуль­са частицы ;

б) момента импульса  частицы относительно точки бросания 0.

Решение:

Движение материальной точки подчиняется законам динамики

                                     ,                                                      (2.1)                    

                                     .                                                   (2.2)

Тело, брошенное под углом к горизонту, описывает параболическую траекторию (рисунок 1).

Рисунок 1

Единственная сила, действующая на тело, - это сила тяжести, поэтому,

                   dp=mg·dt                                                 (2.3) 

интегрируя дифференциальное уравнение (2.3), получим:

                                               p(t)- p₀ = - mgt,  или:

                                        p(t) = mV₀- mgt                                        (2.4)

         Момент силы, по определению, равен векторному произведению радиус-вектора точки приложения силы на вектор силы:

                                               =.

         Векторное произведение двух векторов всегда перпендикулярно плоскости, в которой лежат сомножители, в данном случае - момент силы тяжести перпендикулярен плоскости , вдоль отрицательного направления оси . Модуль момента силы равен произведению силы на плечо (кратчайшее расстояние от точки 0 до линии действия силы, которое в нашем случае равно координате  тела):     M=mgx(t).

Таким образом,  

                                               M(t)= - j mgx(t).                                       (2.5) 

         Подставив полученное выражение в (2.2):

                                               dL= - jmgx(t)·dt.                                        (2.6)

Интегрированием получим искомый результат:

                                      L(t)= - jmgV₀ t²cosα                                   (2.7)

Второй общий метод решения задач динамики состоит в опреде­лении ускорения частицы или центра масс твердого тела. В этом случае необходимо выполнить следующие действия:

▪ выяснить, с какими телами взаимодействует рассматриваемое тело, найти величину, направление и точку приложения каждой из сил;

▪ сделать схематический рисунок и указать на нем направление каждой из приложенных сил и ускорения;

▪ выбрать  инерциальную  систему  отсчета  и  записать  для  рассматриваемого тела уравнение динамики в векторной форме:

                                      ma = F_{+F₂+...+F_N .                                (2.8)

Если силы действуют не по одной прямой, то выбирают две взаимно перпендикулярные оси  и . Спроектировав все векторы, входящие в векторное уравнение на эти оси, записывают второй закон Ньютона в виде двух скалярных уравнений:

                                     ma_x=ΣF_ix,                     

                                      ma_y=ΣF_iy,                                                  (2.9)

Если задано криволинейное движение, то одну из осей направляют вдоль касательной к траектории, а другую – по нормали к ней.

          Если в задаче рассматривается движение системы связанных между
собой тел, то следует уравнение движения записать для каждого тела в от­дельности. Затем записывают в виде уравнений кинематические условия,
связывающие ускорения отдельных тел системы.

          Проверив, совпадает ли число неизвестных с числом уравнений, решают полученную систему уравнений.

          После того, как найдено ускорение частицы (или центра масс твердого
тела), определение скорости (импульса) и закона движения сводится к решению обратной задачи кинематики.     

         

3 Законы сохранения импульса, момента импульса и энергии

 

Основные понятия, законы, соотношения

          Импульс системы частиц. Внешние и внутренние силы. Замкнутая (изолированная) система частиц. Закон сохранения импульса.

Закон сохранения момента импульса.

Работа силы. Кинетическая энергия частицы, вращающегося твердого тела. Консервативные силы. Потенциальная энергия. Полная механическая энергия. Закон сохранения механической энергии.

[1]т.1§§ 15-17,21-27; [2] §§9,11-13,19.

         Законы сохранения в механике позволяют рассматривать общие свой­ства движения без решения дифференциальных уравнений и детальной ин­формации о развитии процессов во времени.

Общим для всех законов сохранения является утверждение о сохране­нии какой-то физической величины, обозначим ее , при определенных ус­ловиях. Набор этих условий обозначим через .

Метод применения законов сохранения в самом общем виде предполагает следующие действия:

          ▪ выяснить, какие тела следует включить в рассматриваемую физиче­скую систему;

          ▪ рассмотреть процесс взаимодействия тел в данной системе, выделив:
а) состояние системы до взаимодействия;

б) состояние тел после их взаимодействия;

в) сам процесс взаимодействия;

▪ проверить, выполняются ли условия  в данной системе;

          ▪ выбрать инерциальную систему отсчета, относительно которой определяют значение величины  А] (до взаимодействия);

          ▪ определить значение величины А₂ в конце взаимодействия;

          ▪ записать закон сохранения в виде уравнения:

                                               А_х = А₂

и решить его относительно искомой величины;

▪ если сохраняющаяся величина векторная, то полученное векторное уравнение спроецировать на соответствующие оси координат.

Пример 5.

Платформа в виде диска радиусом  может вращаться во­круг вертикальной оси, проходящей через ее центр. На краю платформы сто­ит человек массой . С какой угловой скоростью  будет вращаться плат­форма, если человек пойдет вдоль края со скоростью  относительно плат­формы? Масса платформы - . Трением пренебречь.

    Решение.

1) Физическая система включает человека и платформу.

2)    Первоначально оба тела неподвижны относительно земли. Затем человек начинает идти по краю платформы. При этом человек взаимодействует с ней, в результате чего платформа начинает вращаться в обратную сторону. Однако характер взаимодействия (величина этой, внутренней для рассматриваемой системы, силы) нам неизвестен, поэтому применить уравнение дина­мики вращательного движения к платформе невозможно. Закон сохранения механической энергии здесь также неприменим, поскольку первоначально , но, перемещаясь по платформе, человек совершает работу, увеличивая механическую энергию системы, а значит .

3) В рассматриваемой системе тел действуют внешние силы - это силы
тяжести и реакции опоры (на которой установлена платформа). Момент этих
сил относительно оси вращения  равен нулю , так как линия действия силы тяжести параллельна оси , а линия силы реакции опоры
пересекает ось . Следовательно, суммарный момент импульса тел относи­тельно оси вращения  остается постоянным:  

                                               L_]Z = L_2Z,,                                                 (3.1)

где индексы 1 и 2 относятся соответственно к начальному и конечному со­стояниям системы.

4) В инерциальной системе отсчета, связанной с Землей, оба тела первоначально находились в состоянии покоя, поэтому L_]Z=0.

5) При движении скорость v человека относительно выбранной системы отсчета (согласно закону сложения скоростей) складывается из скорости его движения относительно платформы   и линейной скорости  точек края вращающейся платформы:

                                      ,                                                 (3.2)

где учтено, что эти скорости направлены в противоположные стороны. Момент импульса системы при этом равен:

                                     ,                        (3.3)

здесь  - момент инерции платформы.

         6) Применим закон сохранения момента импульса:

                                     .                           (3.4)

Решив полученное уравнение относительно искомой величины, получим ответ:

                                               .                                       (3.5) 

         4 Основы молекулярно-кинетической теории строения вещества. Статистические распределения. Законы термодинамики.

 

Основные понятия, законы, соотношения

Уравнение состояния идеального газа. Изопроцессы.

Внутренняя энергия и теплоемкость идеального газа. Работа газа. Первое начало термодинамики. Второе начало термодинамики.

Молекулярно-кинетическая теория. Давление газа на стенку сосуда.

Средняя энергия поступательного движения молекул. Среднеквадра­тичная скорость молекул. Число степеней свободы молекул и теплоемкость газа.

Функция распределения Максвелла молекул газа по скоростям. Сред­няя арифметическая и наиболее вероятная скорости молекул.

Барометрическая формула. Распределение Больцмана.

[1] §§61-68, 71-76; [2] §§ 41-45, 50-53, 58, 59.

Основная задача термодинамики равновесных процессов заключается в нахождении всех макросостояний физической системы. Если известны на­чальное и все промежуточные состояния системы, то можно определить из­менение внутренней энергии, найти работу, совершенную системой, рассчи­тать количество теплоты, полученное (или отданное) системой и т.д.

Метод решения типовых задач термодинамики основан на применении уравнения состояния (например, идеального газа), первого и второго законов термодинамики, соотношений для теплоемкостей, которые дает классическая теория. Но, прежде всего, приступая к решению задачи, необходимо выяснить характер процесса, протекающего в газе (если об этом не оговорено в усло­вии).

Пример 6.

Баллон емкостью  с известным газом, находящимся при давлении  и температуре , нагревают до . Какое количество теплоты при этом поглощает газ?

Решение. Объем  баллона постоянный, поэтому процесс нагревания газа является изохорным. Применим первое начало термодинамики к изо-хорному процессу:

                                     .                                                     (4.1)

Внутренняя энергия идеального газа равна:

                                      ,                        (4.2)

здесь  мы использовали уравнение Менделеева-Клапейрона и выражение для молярной теплоемкости  идеального газа (согласно классической теории теплоемкости) при постоянном объеме.

Таким образом, искомое  количество теплоты равно:

                                      ,   (4.3)

так как по закону Шарля для изохорного процесса

                                      .

Окончательно:              .                                            (4.4) Основные задачи, решаемые статистическим методом - это задачи:

а) нахождения средних и наиболее вероятных значений различных физических величин;

б) определение среднего числа частиц  или доли  от общего их числа, обладающих некоторым свойством.

Статистический метод решения указанных задач основан на приме­нении математических понятий и законов теории вероятности и известных функций распределения.

Пример 7.

Какая часть от общего числа молекул азота, находящегося при температуре  и атмосферном давлении, обладает скоростями, отличающимися от наиболее вероятной не более, чем на 2,0 м/с?

Решение. При атмосферном давлении и температуре 300 К азот можно считать идеальным газом. В отсутствие внешних сил молекулы идеального газа подчиняются закону распределения Максвелла. Согласно закону Мак­свелла число молекул , относительные скорости которых лежат в интервале от  до  при условии, что , равно:

                                      .                             (4.5)

Относительная скорость   в нашем случае равна и=1, поэтому

                                      .                                           (4.6)

Вычислим наиболее вероятную скорость v_в

                                      ;

                                      .

Таким образом, условие  выполняется. Следовательно:

                                      .

Итак, молекулы азота, обладающие при  скоростями, которые лежат в интервале от (v_в – 2,0) м/с  до  (v_в + 2,0) м/с, составляют от общего числа долю, равную

∆N/N =0,84%.

Пример 8.

Найти среднюю потенциальную энергию молекул воздуха в поле тяготения Земли. Температуру воздуха считать постоянной и равной 300 К.

Решение.

Газ (воздух) находится в поле тяготения Земли. Следова­тельно, его молекулы распределены по энергиям согласно функции распре­деления Больцмана:

                                     ,

где  – потенциальная энергия молекулы в поле силы тяжести;

 – концентрация молекул (или других взвешенных в  среде частиц) в той области пространства, где их потенциальная энергия имеет значение ;

 – концентрация молекул на нулевом уровне потенциальной энергии, в нашем примере – у поверхности Земли.

Среднее значение потенциальной энергии молекулы определяется по формуле:

         .                            (4.7)

Поскольку  известные табличные интегралы равны соответственно:

         ,       ,

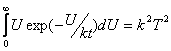то получим следующий результат:  .

Численный ответ: .

 

5 Взаимодействие электрических зарядов. Электрическое поле. Основные характеристики электрического поля

 

Основные понятия, законы и соотношения

Электрический заряд. Закон Кулона. Электрическое поле. Напря­женность Е электрического поля (определение). Формула напряженности поля точечного заряда. Принцип суперпозиции полей. Однородное поле.

Работа по перемещению заряда в электрическом поле. Потенциал .

Потенциал поля точечного заряда.

Теорема о циркуляции вектора Е. Связь между Е и  .

[1] т.2 §§ 1-4, 8, 9; [2] §§ 77-80, 83-86.

Основная задача электростатики заключается в расчете электриче­ского поля, созданного произвольным распределением зарядов. Рассчитать электростатическое поле - это значит в каждой его точке определить вектор напряженности  Е  или потенциал .

Основной универсальный метод расчета электростатического поля в вакууме базируется на применении принципа суперпозиции.

В том случае, если поле создано системой  точечных зарядов , сна­чала определяют напряженность E_i (или потенциал ), которую создает в рассматриваемой точке каждый из зарядов в отдельности. На рисунке следу­ет показать расположение зарядов и направление векторов E_i в указанной точке. Затем по принципу суперпозиции находят результирующее поле, т.е. вектор E  как геометрическую сумму векторов:  

                                     E = E₁ + E₂ + E₃ + …,                              (5.1)

а потенциал результирующего поля  как алгебраическую сумму:

                                                                           (5.2)

В общем случае, когда поле создано произвольным распределением зарядов, необходимо в первую очередь, разделить весь заряд на столь малые элементы, чтобы их можно было бы считать точечными. Если заряд распре­делен на нити, то эту нить следует разделить на бесконечно малые отрезки длиной . Заряд такого элемента равен  ( - линейная плотность заряда). Напряженность dE поля этого точечного заряда определяется по известной формуле. Поскольку направление векторов dE от элементов нити различны, постольку необходимо выбрать координатные оси (две или три), найти проекции вектора dE на эти оси и затем по принципу суперпозиции интегрированием найти проекции, например, Е_х, Е_у, E_z вектора напряженно­сти результирующего поля в интересующей нас точке.

Подобным образом поверхность, по которой непрерывно распределен заряд, следует разделить на малые элементы площадью , заряд которых  можно рассматривать как точечный. Определив по известной фор­муле напряженность поля dE, создаваемого выделенным элементом, затем по принципу суперпозиции находят результирующее поле.

Пример 9.

Положительный заряд  равномерно распределен по тон­кому проволочному кольцу радиуса  (рисунок 2). Определить напряжен­ность E  поля в точке , лежащей на оси кольца на расстоянии  от его центра 0.        

Решение:

Разделим кольцо на элементарные (т.е. очень малые) участки dℓ так, чтобы заряд dq каждого такого участка можно было считать точечным. Тогда модуль напряженности dE  поля, создаваемого выделенным (рисунок 2) точечным зарядом в точке ,  равен:

.      (5.3)

 

 

Рисунок 2 

Найдем проекцию вектора   dE  на ось 0Z:

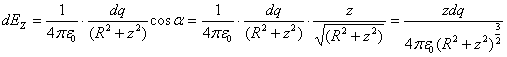.    (5.4)

В соответствии с принципом суперпозиции сложим проекции dE_z полей, создаваемых в искомой точке всеми участками заряженного кольца. Предел этой суммы - это криволинейный (контурный) интеграл:

,                                (5.5)

где интегрирование производится вдоль контура кольца.

Из соображений симметрии (при равномерном распределении заряда по кольцу) следует, что в точке , лежащей на оси кольца, напряженность поля направлена вдоль этой оси. Следовательно, ее остальные проекции равны нулю   E_y = E_x = 0, а модуль равен:

                                     .                                  (5.6)

 

6 Проводники и диэлектрики в электростатическом поле. Энергия электрического поля

 

Основные понятия, законы, соотношения

Электростатическая индукция. Распределение заряда на проводнике.

Электростатическая индукция. Распределение заряда на проводнике.

Вектор электрического смещения D . Поляризованность Р. Теорема Гаусса. Условия на границе раздела двух сред.

Энергия заряженного конденсатора. Объемная плотность энергии
электрического поля.                   

[1] т. 2 §§ 12-15,18-23; [ 2 ] §§ 88-90, 92-95.

Основная задача электростатики - расчет поля при наличии провод­ника решается с помощью метода суперпозиции и метода зеркальных изо­бражений.

Идея метода зеркальных изображений заключается в том, что ищется другая задача - такая, которая решается просто и решение которой может быть использовано. Например, необходимо рассчитать поле, созданное то­чечным зарядом q, находящимся около безграничной проводящей плоско­сти (рисунок За). В этом случае можно использовать решение задачи с двумя точечными зарядами q и -q. Поле этой системы известно, его эквипотенциали и линии вектора Е показаны на рисунке 3б. Если совместить со средней эк­випотенциальной поверхностью (её потенциал φ= 0) проводящую плос­кость и убрать заряд - q, то поле в верхнем полупространстве останется прежним (рисунок Зв).

Рисунок  3

Итак, в рассматриваемом случае поле отлично от нуля только в верхнем полупространстве и для вычисления этого поля достаточно ввести фиктивный заряд - «изображение» данного заряда (-q), противоположный по знаку заряду q, поместив его по другую сторону проводящей плоскости на таком же расстоянии от нее, что и заряд q. Фиктивный заряд q создает в верхнем полупространстве точно такое же поле, как и индуцированные заряды на плоскости. Именно это подразумевают, когда говорят, что фиктивный заряд (-q) заменяет собой "действие" всех индуцированных зарядов.

При расчете поля в диэлектриках используют следующие два метода. Первый метод основан на принципе суперпозиции. Здесь сначала рас­считывают поле свободных, или (как иногда их называют) «сторонних», зарядов Е₀. Затем определяют поле связанных зарядов E'. И, наконец, напря­женность поля Е в диэлектрике в соответствии с принципом суперпозиции, находят как сумму Е = Е₀ + Е'.

Второй метод основан на применении теоремы Гаусса, с помощью которой находят вектор электрического смещения D, затем определяют на­пряженность электрического поля Е. Использование теоремы Гаусса в инте­гральной форме для расчета полей эффективно в тех случаях, когда поле об­ладает специальной симметрией. Симметрия, а следовательно, и конфигура­ция поля должны быть такими, чтобы можно было подобрать сферическую или цилиндрическую замкнутую поверхность, вычисление потока электриче­ского смещения сквозь которую свелось бы к умножению D (или Е) на площадь S этой гауссовой  поверхности (или ее части).

Метод Гаусса предполагает поэтапное выполнение следующих дейст­вий:

1) определить, исходя из симметрии заданного распределения сторон­
них зарядов, конфигурацию линий вектора  D (или Е); 

2)  подобрать форму и размеры замкнутой поверхности с учетом симметрии поля;

3)    изобразить на рисунке линии вектора D и вспомогательную поверхность;

4)    выразить поток электрического смещения Ф_D сквозь эту поверхность через значение модуля D (или Е) в точках на выбранной поверхности и ее (поверхности) параметры (т.е. радиус, длину и т.п.);

5)    найти суммарный сторонний заряд Q, охватываемый этой поверхностью, т.е. находящейся внутри нее;

6)    на основании теоремы Гаусса составить уравнение, приравняв по­ток Ф_D найденному заряду Q, и найти электрическое смещение D(r)  или
D(x) (в зависимости от симметрии поля).

         Пример 10.

         Два бесконечно длинных тонкостенных коаксиальных цилиндра радиусов R₁ и R₂ равномерно заряжены с поверхностными плотностями заря­дов σ₁ и σ₂  Пространство между цилиндрами заполнено однородным и изо­тропным диэлектриком с диэлектрической проницаемостью ε. Определить напряженность Е во всех точках поля.

         Решение.

1) Сторонние заряды в рассматриваемой физической систе­ме распределены равномерно на двух цилиндрических поверхностях, имею­щих общую ось. Эта ось и является осью симметрии. Исходя из симметрии системы можно заключить, что как напряженность Е, так и смещение D направ­лены радиально, а их модули зависят от одной координаты - расстояния  r точки поля до оси.

2) Вспомогательную (гауссову) поверхность выберем в форме цилинд­ра произвольного радиуса r и длины ℓ, коаксиального с заданным цилиндром (рисунок 4)

 

 

                   Рисунок 4                                                  Рисунок 5

3) На рисунке 5 изображена картина линий вектора электрического смещения D для случая, когда внутренний цилиндр заряжен положительно, а внешний - отрицательно (σ₂ < 0).

4) Поток электрического смещения сквозь выбранную поверхность в нашем случае равен:

                                     Ф_D = D(r)·2πrℓ,                                         (6.1)

здесь учтено, что линии вектора D пронизывают только цилиндрическую часть поверхности (по радиальным линиям), а через торец вспомогательного цилиндра поток равен нулю, т.к. линии поля лишь скользят вдоль, но не про­низывают его.

5) Величина стороннего заряда Q, охватываемого гауссовой поверхно­стью, равна:

а)    Q  = 0, если  r < R₁ (точка А на рисунке  4);

б)    Q  =  σ₁·2πRℓ , если R₁ ≤ r ≤ R₂  (точка B);

в)     Q  = (σ₁·R₁ + σ₂·R₂)·2πℓ,   если  r ≥ R₂  (точка С).

6) в соответствии с теоремой Гаусса:

                                   0,                                            r < R₁

     σ₁·2πRℓ,                                 R₁ ≤ r ≤ R₂                              (6.2)

                                   σ₁·R₁ + σ₂·R₂)·2πℓ,                 r ≥ R₂ .

           

 

Таким образом, из (6.2) получим:

                                   0,                                            r < R₁

D(r)     =            ,                                  R₁ ≤ r ≤ R₂                              (6.3)

                                                              r ≥ R₂ .

В однородном диэлектрике справедливо:

                                               D = εε₀E,                                                                     (6.4)

откуда                      

0 ,                                           r < R₁,

E(r)  =             ,                                   R₁ ≤ r ≤ R₂ ,,                             (6.5)

                                    ,                         r ≥ R₂.

 

7 Постоянный ток. Законы постоянного тока

 

Основные понятия, законы, соотношения

Сила тока. Плотность тока. Классическая электронная теория электро­проводности металлов.

Электродвижущая сила. Падение напряжения. Закон Ома для неодно­родного участка цепи в интегральной и дифференциальной форме. Работа и мощность тока. Полезная и полная мощность.

[1] т.2 §§ 24,25,26,28, 30; [2] §§ 96-100,102.

Основная задача теории постоянного тока — это расчет электрической цепи, когда задана некоторая произвольная электрическая цепь и отдельные ее параметры, например, ЭДС и сопротивление, и требуется найти силы то­ков, напряжение на некотором участке цепи, работу, мощность, коэффициент полезного действия и т.п.

Самой важной фундаментальной величиной в явлении постоянного тока служит сила тока , поэтому основная задача в теории постоянного тока заключается в нахождении токов, протекающих в цепи. Существуют различные методы решения этой задачи. В курсе  «физика 1»  мы рассматриваем лишь один из них.

Этот метод основан на последовательном применении закона Ома для замкнутой цепи и закона Ома для неоднородного (или однородного) участка цепи. Применение законов Ома позволяет полностью рассчитать токи в цепи с одним источником ЭДС, либо несколькими источниками ЭДС, соединенными последовательно, а также в тех случаях, когда имеются батареи, состоящие из совершенно одинаковых источников тока. В послед­нем случае такую батарею в расчетах заменяют одним эквивалентным источником тока (E _экв , r_экв).

При последовательном соединении  одинаковых источников, ЭДС каждого из которых равна E, а внутреннее сопротивление равно r, пара­метры эквивалентной батареи вычисляют согласно формулам:

                                      E_экв = NE,                                                   (7.1)

                                      r_экв = Nr.                                                     (7.2)

При параллельном соединении одинаковых источников:

                                      E_экв = E,                                                      (7.3)

                                      r_экв = r/N.                                                   (7.4)

  

Пример 11.

Три группы из двух  последовательно соединенных одина­ковых элементов соединены параллельно. ЭДС каждого элемента , внутреннее сопротивление . Полученная батарея замкнута на внешнее сопротивление . Найти силу тока во внешней цепи.

 

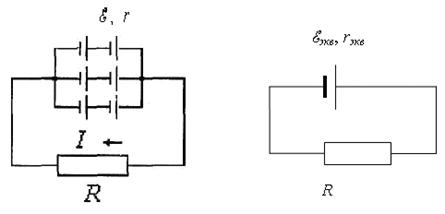
         Рисунок 6                                                 Рисунок 7

Решение.

Электрическая схема заданной цепи изображена на рисунке 6. Преобразуем эту схему в более простую. Для этого сначала заменим группу из двух последова­тельно соединенных элементов одним эквива­лентным источником с , . Три таких источника, соединенных параллельно, в свою очередь, можно заменить одним эквива­лентным источником с параметрами: , .

Получается, таким образом, очень простая эквивалентная схема (рисунок 7). Согласно закону Ома для замкнутой цепи:

                                     .

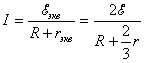Произведя  вычисления, получим искомый ответ: .

 

8  Магнитное поле в вакууме

 

Основные понятия, законы, соотношения

Магнитное поле. Вектор магнитной индукции В. Линии магнитной индукции. Закон Био-Савара-Лапласа. Принцип суперпозиции.

Теорема о циркуляции вектора В.

[1]т.2 §§35, 36, 38; [2] §§109,110,118,119.

Основная задача теории магнитного поля заключается в расчете магнитной индукции поля, созданного системой токов и движущихся электрических зарядов.

Общий метод расчета магнитных полей основан на применении закона Био-Савара-Лапласа в дифференциальной форме и принципа супер­позиции. Здесь в общем случае необходимо:

1)    сделать рисунок, указать на нем токи и указать точку поля, в которой требуется вычислить индукцию В;

2)    выделить произвольный элемент тока Idℓ и найти с помощью за­кона Био-Савара-Лапласа модуль и направление вектора dB магнитной индукции, создаваемого выделенным элементом тока в искомой точке;

3) в соответствии с принципом суперпозиции магнитная индукция в произвольной точке поля равна векторной сумме магнитных индукций dB,
созданного в этой точке всеми элементами тока, т.е.:

                                      B = ∫dB ,                                                   (8.1)

где интегрирование производится по контуру проводника с током;

4) если проводник с током и точка, в которой находят вектор В, ле­жат в одной плоскости, то все элементарные вектора dB направлены вдоль одной прямой. Тогда геометрическое сложение заменяется алгебраическим и вместо (8.1) определяют модуль магнитной индукции:

                                                                                           (8.2)

В остальных случаях нужно ввести координатные оси и находить соответствующие проекции, например:

                                                                                         (8.3)

Второй метод расчета полей основан на применении теоремы о цир­куляции вектора магнитной индукции. Однако его применение ограничено симметричными полями, когда через точку, в которой требуется определить вектор В, можно провести такой замкнутый контур , совпадающий с лини­ей индукции поля, во всех точках которого индукция была бы одинакова по модулю. В этом случае циркуляция вектора В по контуру  находится как произведение:

                                     ∫B·dℓ=  B·ℓ,                                               (8.4)

где  - длина данного контура.

Расчет магнитного поля по второму методу выполняется в следующей последовательности:

1)   подбирают контур , удовлетворяющий указанным выше условиям,
выбирают направление его обхода;

2)   определяют циркуляцию вектора магнитной индукции через произве­дение (8.4) и алгебраическую сумму токов, охватываемых контуром ;

3)   на основании теоремы о циркуляции вектора В составляют уравнение;

4)   решают полученное уравнение и находят модуль вектора магнитной
индукции в искомой точке.

Пример 11.

По сплошному бесконечному цилиндрическому проводу ра­диуса  течет постоянный ток плотности  . Найти индукцию В поля внутри провода.

Решение. Из симметрии задачи следует, что линии вектора В представ­ляют собой окружности, центры которых лежат на оси провода, а модуль вектора  одинаков во всех равноотстоящих от оси провода точках. Иначе говоря, он зависит только от одной координаты  -  расстояния до оси.

1)     Проведем вспомогательный контур в виде окружности радиуса r < R

(рисунок 8). Направление его обхода свяжем с направлением тока правилом правого винта. На рисунке крестиками обозначено направление «от нас» вектора плотности тока j .

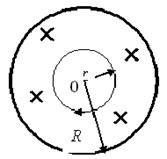
Рисунок 8

 

         2) Циркуляция вектора B по выбранному нами контуру равна:

                                               ,                                      (8.5)

т.к. во всех точках данного контура индукция по величине одинакова, а по направлению совпадает с касательной к окружности.

         3) Ток, охватываемый нашим контуром, равен:

                                               .                                        (8.6)

4) Согласно теореме о циркуляции:

                                      .                                       (8.7)

5)   откуда следует, что внутри провода индукция поля прямо пропорциональна расстоянию r до оси провода:

                                     .                                       (8.8)

 

9 Силовое действие магнитного поля. Работа перемещения проводника с током в магнитном поле

 

Основные понятия, законы, соотношения.

Сила Лоренца. Сила Ампера.

Магнитный момент витка с током. Момент сил, действующих на виток с током в магнитном поле.

Магнитный поток. Теорема Гаусса.

Работа перемещения проводника с током в магнитном поле.

[1] т. 2 §§ 37-41; [ 2 ] §§ 11 V_t114,120,121.

Основные типы задач по данной теме - это задачи на:

•  расчет силового действия магнитного поля и работы по перемещению в нем проводника с током;

•     расчет магнитного потока сквозь заданную поверхность.

Задачи первого типа решаются с применением соответствующих фор­мул, выражающих

- силу Лоренца; силу Ампера в интегральной форме (если поле однородное, а проводник - прямолинейный), либо в дифференциальной форме с по­следующим интегрированием;

- момент силы, действующей на виток с током в магнитном поле; работу силы.

Расчет магнитного потока в общем случае неоднородного поля вы­полняется в следующей последовательности:

1)  на рисунке изобразить линии магнитной индукции заданного по ус­ловию задачи поля и контур поверхности, через которую нужно вычислить
поток ;

2)   выделить бесконечно малый элемент поверхности площадью ,
таким образом, чтобы во всех его точках величина модуля  (или нормаль­
ной к поверхности проекции ), была бы одинакова. В зависимости от кон­
фигурации и симметрии поля это может быть, например, узкая прямая по­
лоска или тонкое кольцо и т.п.;

3)  определить, элементарный магнитный поток, пронизывающий вы­
деленный элемент поверхности, по формуле:

                                               .

Пример 12.

В одной плоскости с бесконечно длинным прямым прово­дом, по которому идет ток силы , расположена прямоугольная рамка со сто­ронами а и b (рисунок 9). Ближайшая из двух, параллельных току, сторон рамки находится на расстоянии . Определить магнитный поток  через рамку.

Решение.

1) Индукция магнитного поля В прямого бесконечного про­вода с током равна по модулю:

                                     ;

его линии представляют собой концентрические окружности, центры кото­рых лежат на оси прямого провода.

                   2) Разделим площадь рамки на узкие полоски так, чтобы в пределах каждой по­лоски магнитное поле можно было бы
считать однородным. Выделим одну из
таких полосок шириной , находящую­ся на расстоянии    от оси прямого тока.

         3) Выберем положительную нормаль к плоскости рамки в направлении магнит­ной индукции, обозначенном на рисунке 9 крестиками («от нас»).

Тогда элементарный магнитный поток

         Рисунок 9                          через выделенную полоску равен:

                                               .                                (9.4)

         4) Полный магнитный поток через рамку равен сумме элементарных потоков, пронизывающих каждую полоску. Предел этой суммы есть интеграл:

                                      .   (9.5)

 

 

Список литературы

 

         1. Савельев И.В. Курс физики: в 3-х т. -М., 1989.

2.     Трофимова Т.И. Курс физики. -М., 1998.

 

 

Содержание

         Введение……

         Требования к содержанию и оформлению самостоятельной работы (РГР)…

         1 Кинематика материальной точки и твердого тела…

         2 Основная задача динамики и методы ее решения для частицы, системы частиц и твердого тела…

         3 Законы сохранения импульса, момента импульса и энергии…

         4 Основы молекулярно - кинетической теории строения вещества. Статистические распределения. Законы термодинамики…

         5 Взаимодействие электрических зарядов. Электрическое поле. Основные характеристики электрического поля……

         6 Проводники и диэлектрики в электростатическом поле. Энергия электрического поля …

         7 Постоянный ток. Законы постоянного тока…

         8 Магнитное поле в вакууме

         9 Силовое действие магнитного поля. Работа перемещения проводника с током в магнитном поле…

         Список литературы.

         Содержание…