Некоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра физики
ФИЗИКА 2
Конспект лекций
для студентов всех форм обучения специальностей
5В071900 - Радиотехника, электроника и телекоммуникации,
5В070400 – Вычислительная техника и программное обеспечение,
5В070300 – Информационные системы
Алматы 2011
СОСТАВИТЕЛИ: Т.Д. Дауменов, М.Ш. Карсыбаев, А.М. Саламатина. ФИЗИКА 2. Конспект лекций для студентов всех форм обучения специальностей 5В071900 – Радиотехника, электроника и телекоммуникации, 5В070400 – Вычислительная техника и программное обеспечение, 5В070300 – Информационные системы. – Алматы: АУЭС, 2011 – 102 с.
Излагается краткое содержание лекций по дисциплине «Физика 2» для радиотехнических, информационно-технологических специальностей бакалавриата.
Конспект лекций «Физика 2» представляет собой еще один элемент системы методического обеспечения учебного процесса по дисциплине и может быть использован в качестве раздаточного материала на лекционных занятиях, а также в самостоятельной работе над теоретическим материалом при подготовке к практическим, лабораторным занятиям и экзаменам.
Ил. 49 , табл. 2, библиогр. – 9 назв.
Рецензент: канд. физ.-мат. наук, доц. Тонконогая Л.А.
Печатается по дополнительному плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2011г.
Ó НАО «Алматинский университет энергетики и связи», 2011 г.
Содержание
|
Содержание |
3 |
|
Введение |
5 |
|
1 Лекция. Явление электромагнитной индукции |
7 |
|
1.1 Электромагнитная индукция |
7 |
|
1.2 Закон электромагнитной индукции как следствие закона сохранения энергии |
8 |
|
1.3 Индукционные токи |
8 |
|
1.4 Зависимость э.д.с. индукции от индуктивности |
9 |
|
1.5 Коэффициент взаимной индукции |
10 |
|
1.6 Магнитная энергия тока. Энергия магнитного поля |
10 |
|
2 Лекция. Уравнения Максвелла |
11 |
|
2.1 Максвеллова трактовка закона индукции |
11 |
|
2.2 Дифференциальная форма записи закона электромагнитной индукции |
12 |
|
2.3 Токи смещения |
13 |
|
2.4 Система уравнений Максвелла |
14 |
|
2.5 Относительность электрического и магнитного полей |
15 |
|
3 Лекция. Колебательные процессы |
15 |
|
3.1 Колебания – общее понятие и классификация |
15 |
|
3.2 Общая характеристика гармонических колебаний. Дифференциальное уравнение гармонических колебаний |
16 |
|
3.3 Гармонические осцилляторы |
17 |
|
3.4 Энергия гармонических колебаний |
19 |
|
3.5 Векторная диаграмма. Сложение колебаний. Биения |
20 |
|
4 Лекция. Затухающие и вынужденные колебания |
23 |
|
4.1 Дифференциальное уравнение затухающих колебаний. Амплитуда и частота затухающих колебаний |
23 |
|
4.2 Вынужденные колебания, их амплитуда и фаза. Резонанс. Резонансные кривые |
25 |
|
4.3 Переменный ток как вынужденные колебания. Закон Ома для переменного тока. Мощность, выделяемая в цепи переменного тока |
27 |
|
4.4 Ангармонические колебания |
31 |
|
5 Лекция. Волновые процессы |
32 |
|
5.1 Упругие волны |
32 |
|
5.2 Уравнения плоской и сферической волн |
32 |
|
5.3 Длина волны. Фазовая скорость |
34 |
|
5.4 Волновое уравнение |
35 |
|
5.5 Энергия упругих волн. Вектор Умова-вектор плотности потока энергии упругой волны |
37 |
|
6 Лекция. Электромагнитные волны |
39 |
|
6.1 Волновое уравнение для электромагнитного поля |
39 |
|
6.2 Свойства электромагнитных волн |
42 |
|
6.3 Энергия и импульс электромагнитной волны. Вектор Пойнтинга |
44 |
|
6.4 Излучение диполя |
46 |
|
7 Лекция. Свет как электромагнитная волна |
47 |
|
7.1 Суперпозиция волн. Волновой пакет. Групповая скорость |
47 |
|
7.2 Дисперсия волн |
49 |
|
7.3 Свет как электромагнитная волна |
49 |
|
7.4 Интерференция света |
50 |
|
7.5 Временная и пространственная когерентность |
52 |
|
7.6 Методы наблюдения интерференции света |
54 |
|
8 Лекция. Дифракция волн |
55 |
|
8.1 Принцип Гюйгенса-Френеля |
55 |
|
8.2 Метод зон Френеля |
56 |
|
8.3 Дифракция на одной и многих щелях |
59 |
|
8.4 Спектральное разложение |
60 |
|
9 Лекция. Тепловое излучение |
61 |
|
9.1 Характеристики и законы теплового излучения |
61 |
|
9.2 Проблемы излучения абсолютно черного тела |
63 |
|
9.3 Квантовая гипотеза и формула Планка |
64 |
|
10 Лекция. Корпускулярные свойства электромагнитного излучения |
64 |
|
10.1 Фотоэффект |
64 |
|
10.2 Энергия и импульс световых квантов |
64 |
|
10.3 Гипотеза и уравнение Эйнштейна |
65 |
|
10.4 Эффект Комптона |
65 |
|
11 Лекция. Корпускулярно-волновой дуализм вещества как универсальное свойство материи. Уравнение Шредингера |
67 |
|
11.1 Гипотеза де Бройля и ее экспериментальное подтверждение |
67 |
|
11.2 Волновые свойства микрочастиц и соотношение неопределенностей Гейзенберга |
68 |
|
11.3 Уравнение Шредингера. Состояние частицы в квантовой механике. Пси-функция. Временное и стационарное уравнения Шредингера |
68 |
|
11.4 Решение уравнения Шредингера для простейших квантовых систем. Задача о частице в одномерной прямоугольной яме |
70 |
|
11.5 Атом водорода. Энергетический спектр атома водорода. Пространственное квантование |
71 |
|
11.6 Спин электрона |
74 |
|
12 Лекция. Элементы квантовых статистик и физики твердого тела |
75 |
|
12.1 Понятие о квантовой статистике |
75 |
|
12.2 Распределение Бозе-Эйнштейна и Ферми-Дирака |
76 |
|
12.3 Вырожденный электронный газ в металлах |
77 |
|
13 Лекция. Конденсированные состояния |
79 |
|
13.1 Теплоемкость кристаллической решетки |
79 |
|
13.2 Фононный газ |
81 |
|
13.3 Электропроводность металлов |
82 |
|
13.4 Энергетические зоны в кристаллах |
83 |
|
13.5 Полупроводники |
84 |
|
14 Лекция. Контактные явления |
86 |
|
14.1 Контактная разность потенциалов в металлах |
86 |
|
14.2 Полупроводниковые p-n переходы. Транзисторы |
88 |
|
14.3 Вентильный фотоэффект |
90 |
|
15 Лекция. Атомное ядро и классификация элементарных частиц |
91 |
|
15.1 Основные свойства и строение ядра |
91 |
|
15.2 Энергия связи ядер |
92 |
|
15.3 Ядерные силы. Модели ядра |
93 |
|
15.4 Радиоактивное излучение и его виды. Закон радиоактивного распада |
94 |
|
15.5 Ядерные реакции |
96 |
|
15.6 Виды взаимодействий и классы элементарных частиц |
97 |
|
15.7 Кварки |
99 |
|
15.8 Понятие об основных проблемах современной физики и астрофизики |
100 |
|
Список литературы |
102 |
Введение
«Физика 2. Конспект лекций» представляет собой изложение содержания материала лекций по этой дисциплине и предназначен для студентов, которые обучаются по программам бакалавриата на факультетах ФРТиС и ФИТ.
Курс «Физика 2» включает в себя некоторые разделы классической и современной физики. Ясная физическая и мировоззренческая интерпретация представлений классической и современной физики формирует у студентов способность перестраивать свое мышление к восприятию неизбежных трансформаций старых научных и технических представлений в принципиально новые.
В каждой лекции отражены основные вопросы темы в их логической связи и структурной целостности, но без детальной проработки математических выкладок или примеров. Поэтому данная учебно-методическая разработка может и должна служить лишь ориентировочной основой для учебной деятельности студента при подготовке к практическим занятиям, рубежному и итоговому контролю.
1 Лекция. Явление электромагнитной индукции
1.1 Электромагнитная индукция
Электромагнитная индукция была открыта Фарадеем в 1831 г. Электромагнитной индукцией называется возникновение электродвижущих сил под действием магнитных полей. Для демонстрации этого явления берут неподвижный магнит и проволочную катушку, концы которой соединены с гальванометром. При движении катушки в постоянном магнитном поле в ней возбуждается электрический ток, прекращающийся, когда катушка останавливается. Этот ток называется индукционным током, а само явление – электромагнитной индукцией. В частности, когда катушка равномерно вращается в постоянном магнитном поле, индукционный ток периодически меняет свою силу и направление. Возбуждение электрического тока при движении проводника в магнитном поле объясняется действием силы Лоренца, возникающей при движении проводника. Рассмотрим случай, когда два параллельных провода АВ и СD помещены в постоянное однородное магнитное поле, перпендикулярное к плоскости рисунка и направленное к читателю (см.рисунок 1). Слева провода АВ и СD замкнуты, справа разомкнуты. Вдоль проводов может свободно скользить проводящий мостик ВС. Когда мостик движется вправо со скоростью v, вместе с ним движутся и электроны. На каждый движущийся заряд е в магнитном поле действует сила Лоренца
![]() .
(1.1)
.
(1.1)
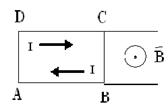
В результате электроны начнут перемещаться по мостику вверх, т.е. по нему потечет ток, направленный вниз. Это и есть индукционный ток. Сила Лоренца в описанном опыте играет роль сторонней силы, возбуждающей электрический ток.
Соответствующая напряженность стороннего поля равна Рисунок 1
![]() . (1.2)
. (1.2)
Электродвижущая сила, создаваемая этим полем,
называется электродвижущей силой индукции и обозначается ![]() . В рассматриваемом случае
. В рассматриваемом случае
![]() .
(1.3)
.
(1.3)
Знак
минус поставлен потому, что стороннее поле направлено против положительного обхода
контура, определяемого вектором ![]() по правилу правого винта. Величина
по правилу правого винта. Величина ![]() есть приращение
площади контура ABCD в единицу времени, или скорость приращения этой площади.
Поэтому величина
есть приращение
площади контура ABCD в единицу времени, или скорость приращения этой площади.
Поэтому величина ![]() равна
равна
![]() т.е.
скорости приращения магнитного потока, пронизывающего площадь контура
ABCD.
Таким образом,
т.е.
скорости приращения магнитного потока, пронизывающего площадь контура
ABCD.
Таким образом,
![]() .
(1.4)
.
(1.4)
Единица измерения э.д.с. индукции – вольт (В), действительно:
![]() .
.
Результат
(1.4) справедлив и в том случае, когда однородное магнитное поле ![]() направлено под любым
углом к плоскости контура ABCD. Тогда не составляет труда распространить формулу (1.4)
на случай любого замкнутого провода, движущегося произвольным образом в
постоянном неоднородном магнитном поле.
направлено под любым
углом к плоскости контура ABCD. Тогда не составляет труда распространить формулу (1.4)
на случай любого замкнутого провода, движущегося произвольным образом в
постоянном неоднородном магнитном поле.
1.2 Закон электромагнитной индукции как следствие закона сохранения энергии
К формуле (4) можно прийти также с помощью закона
сохранения энергии, как это впервые сделал Гельмгольц (1821-1894).
Рассматривается замкнутый виток провода, в которой включен гальванический
элемент с электродвижущей силой ![]() . Виток движется в постоянном магнитном
поле. За время dt амперовы силы совершают над витком работу
. Виток движется в постоянном магнитном
поле. За время dt амперовы силы совершают над витком работу ![]() . Кроме того, в витке
выделяется джоулево тепло
. Кроме того, в витке
выделяется джоулево тепло ![]() . Сумма этих работ должна равняться
работе гальванического элемента
. Сумма этих работ должна равняться
работе гальванического элемента ![]() т.е.
т.е.
![]() ,
(1.5)
,
(1.5)
отсюда
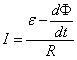 .
(1.6)
.
(1.6)
Таким
образом, движущемся витке ток определяется не только электродвижущей силой
гальванического элемента, к ней добавляется слагаемое -![]() которое и есть электродвижущая
сила индукции.
которое и есть электродвижущая
сила индукции.
1.3 Индукционные токи
Индукционные токи могут возникать и в неподвижных проводниках. Возьмем замкнутый провод и постоянный магнит. При движении провода возникает индукционный ток. Что произойдет, если, оставляя провод неподвижным, двигать магнит? Покой и движение – понятия относительные. Явление индукции должно зависеть только от относительного движения провода и магнита. Отсюда следует, что при движении магнита будет возбуждаться такой же индукционный ток, что и при соответствующем движении провода. Опыт подтверждает это заключение. Таким образом, для возбуждения индукционного тока существенно изменение магнитного потока через контур проводника, а не способ, каким это изменение достигается. Всякий раз, когда меняется магнитный поток, пронизывающий контур неподвижного или движущегося замкнутого провода, в проводе возникает индукционный ток, причем во всех случаях электродвижущая сила индукции определяется формулой (1.4). Эта формула определяет не только величину, но и направление индукционного тока, которое определяется правилом Ленца: индукционный ток всегда имеет такое направление, что он ослабляет действие причины, возбуждающей этот ток.
1.4 Зависимость э.д.с. индукции от индуктивности
Электрический ток, текущий в замкнутом контуре, создает вокруг себя магнитное поле, индукция которого, по закону Био-Савара-Лапласа, пропорционально току. Сцепленный с контуром магнитный поток Ф, поэтому пропорционален току I в контуре:
![]() ,
(1.7)
,
(1.7)
где коэффициент пропорциональности L называется индуктивностью контура.
При изменении силы тока в контуре будет изменяться также и сцепленный с ним магнитный поток; следовательно, в контуре будет индуцироваться э.д.с. Возникновение э.д.с. индукции в проводящем контуре при изменении в нем силы тока называется самоиндукцией.
Единица измерения индуктивности - генри (Гн):
1 Гн=1 Вб/А=1 В с/А.
Используя
формулу (7), можно получить выражение для индуктивности соленоида, которая
зависит от числа витков соленоида N, его длины ![]() , площади S и
магнитной проницаемости
, площади S и
магнитной проницаемости![]() вещества, из которого изготовлен сердечник
соленоида:
вещества, из которого изготовлен сердечник
соленоида:
![]() .
(1.8)
.
(1.8)
Применяя к явлению самоиндукции закон Фарадея, при условии, что контур не деформируется и магнитная проницаемость не изменяется, получим
![]() .
(1.9)
.
(1.9)
1.5 Коэффициент взаимной индукции
Рассмотрим два неподвижных контура (1 и 2),
расположенных достаточно близко друг от друга. Пусть в контуре 1 течет ток ![]() , а в контуре 2 -
, а в контуре 2 - ![]() . Пусть
. Пусть ![]() - часть магнитного
потока, создаваемого первым током, который пронизывает контур второго тока.
Тогда
- часть магнитного
потока, создаваемого первым током, который пронизывает контур второго тока.
Тогда
![]() .
(1.10)
.
(1.10)
Если
ток в первом контуре изменяется, то в контуре индуцируется э.д.с ![]() :
:
![]() . (1.11)
. (1.11)
Если изменяется ток во втором контуре, то э.д.с., индуцируемая в первом контуре, аналогично может быть записана в виде
![]() .
(1.12)
.
(1.12)
Явление
возникновения э.д.с. в одном из контуров при изменении силы тока в другом
называется взаимной индукцией. Коэффициенты пропорциональности ![]() называются взаимной
индуктивностью контуров. Расчеты, подтверждаемые опытом, показывают, что
называются взаимной
индуктивностью контуров. Расчеты, подтверждаемые опытом, показывают, что
![]() .
(1.13)
.
(1.13)
Можно
показать, что взаимная индуктивность двух катушек с количествами витков ![]() , намотанных на общий
тороидальный сердечник имеет вид:
, намотанных на общий
тороидальный сердечник имеет вид:
![]() .
(1.14)
.
(1.14)
1.6 Магнитная энергия тока. Энергия магнитного поля
Магнитное поле является носителем энергии. Выражение
для магнитной энергии тока можно получить через работу, которая затрачивается
током на создание магнитного поля. Для изменения магнитного потока на величину ![]() необходимо совершить
работу
необходимо совершить
работу ![]() .
Тогда работа по созданию магнитного потока будет равна
.
Тогда работа по созданию магнитного потока будет равна
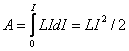 .
.
Следовательно, магнитная энергия тока может быть определена этой работой
![]() .
(1.15)
.
(1.15)
Энергию магнитного поля можно представить как функцию величин, характеризующих это поле в окружающем пространстве. Можно показать, что формула (1.15) может быть преобразована к виду
![]() ,
(1.16)
,
(1.16)
где V - объем пространства, занятого магнитным полем.
Исследование свойств переменных полей, в частности, распространения электромагнитных волн, явилось доказательством того, что энергия магнитного поля (16) локализована в пространстве, причем в единице объема пространства заключена энергия с объемной плотностью, равной
![]() .
(1.17)
.
(1.17)
Формула (1.17) справедлива как для однородного, так и для неоднородного полей. Она справедлива также и для переменных полей. Отметим, что это выражение справедливо только для сред, для которых зависимость В от Н линейная, т.е. оно относится только к пара- и диамагнетикам.
2 Лекция. Уравнения Максвелла
2.1 Максвеллова трактовка закона индукции
Когда проводник движется в постоянном магнитном поле,
индукционный ток вызывается магнитной составляющей силы Лоренца (1). Какая же сила
возбуждает индукционный ток в неподвижном проводнике, находящемся в переменном
магнитном поле? Ответ был дан Максвеллом. Согласно Максвеллу, всякое изменение
магнитного поля во времени возбуждает в окружающем пространстве электрическое
поле. Циркуляция вектора напряженности ![]() этого поля по любому неподвижному
замкнутому контуру
этого поля по любому неподвижному
замкнутому контуру ![]() определяется
выражением
определяется
выражением
![]() .
(2.1)
.
(2.1)
Между максвелловым и фарадеевым пониманием явления
электромагнитной индукции имеется существенное различие. Согласно Фарадею, электромагнитная
индукция состоит в возбуждении электрического тока. Для ее наблюдения
необходимо наличие замкнутого проводника. Максвелл, напротив, видит сущность
электромагнитной индукции, прежде всего в возбуждении электрического поля, а не
тока. Электромагнитная индукция может наблюдаться и тогда, когда в пространстве
вообще нет никаких проводников. Появление индукционного тока в замкнутом
проводнике при внесении последнего в переменное магнитное поле есть лишь одно
из проявлений электрического поля![]() , возникшего в результате изменения поля
магнитного. Но поле
, возникшего в результате изменения поля
магнитного. Но поле ![]() может
производить и другие действия, например, поляризовать диэлектрик, вызвать
пробой конденсатора, ускорять и тормозить заряженные частицы и т. п. Оно может
вызвать электрический ток и в незамкнутом проводнике.
может
производить и другие действия, например, поляризовать диэлектрик, вызвать
пробой конденсатора, ускорять и тормозить заряженные частицы и т. п. Оно может
вызвать электрический ток и в незамкнутом проводнике.
Максвеллова формулировка закона индукции более общая, чем формулировка Фарадея. Она принадлежит к числу наиболее важных обобщений электродинамики.
2.2 Дифференциальная форма записи закона электромагнитной индукции
Математически закон индукции в понимании Максвелла
выражается формулой (2.1), где интеграл берется по замкнутому контуру, который
может быть проведен и в диэлектрике, а не обязательно в проводнике, как было у
Фарадея. Магнитный поток ![]() определяется интегралом
определяется интегралом
![]() ,
(2.2)
,
(2.2)
взятым
по произвольной поверхности S, натянутой на контур ![]() . Поэтому формулу (2.1) можно представить
в виде
. Поэтому формулу (2.1) можно представить
в виде
![]() . (2.3)
. (2.3)
Применив к последнему выражению теорему Стокса, получим
![]() .
(2.4)
.
(2.4)
Это - дифференциальная форма закона электромагнитной индукции. Уравнение (2.3) или эквивалентное ему уравнение (2.4) – одно из основных соотношений теории электромагнитного поля. Оно входит в систему уравнений Максвелла.
2.3 Токи смещения
Основные уравнения электромагнитного поля в неподвижных средах, применимые не только к постоянным, но и к переменным электромагнитным полям, были установлены Максвеллом. К уравнениям Максвелла можно прийти путем последовательного обобщения опытных фактов. Надо решить, какие из полученных ранее уравнений могут быть сохранены, какие должны быть отброшены и какие надо обобщить. Можно сохранить только такие уравнения, которые не противоречат представлениям теории поля.
К основным уравнениям электродинамики присоединим закон сохранения электрического заряда:
![]() .
(2.5)
.
(2.5)
Если электромагнитное поле стационарно, то это уравнение переходит в
![]() .
(2.6)
.
(2.6)
Известная теорема о циркуляции напряженности магнитного поля
![]() (2.7)
(2.7)
также может быть преобразована в дифференциальную форму
![]() ,
(2.8)
,
(2.8)
а
потому удовлетворяет требованиям теории поля. Однако она не может входить в
число основных уравнений электродинамики, потому что уравнение (2.8)
противоречит закону сохранения электрического заряда (2.5). Чтобы устранить это
противоречие, продифференцируем по времени соотношение
![]()
![]()
или ввиду уравнения (1)
![]() .
(2.9)
.
(2.9)
Величину
![]() (2.10)
(2.10)
Максвелл
назвал током смещения, а сумму ![]() - полным током
(точнее - плотностью
полного тока). А условие замкнутости тока должно быть записано для полного тока
- полным током
(точнее - плотностью
полного тока). А условие замкнутости тока должно быть записано для полного тока
![]() ,
(2.11)
,
(2.11)
т.е.
полный ток всегда соленоидален. Поэтому противоречие с уравнением (2.5) устранится,
если в уравнении (2.8) ток проводимости ![]() заменить полным током, т.е. написать
заменить полным током, т.е. написать
![]() . (2.12)
. (2.12)
2.4 Система уравнений Максвелла
Дополнив основные факты из области электромагнетизма установлением магнитных действий токов смещения, Максвелл мог написать систему фундаментальных уравнений электродинамики. Таких уравнений четыре.
В интегральной форме они имеют вид
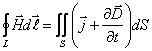 ,
(I)
,
(I)
![]() ,
(II)
,
(II)
![]() , (III)
, (III)
![]()
![]() . (IV)
. (IV)
В дифференциальной форме
![]() ,
(Iа)
,
(Iа)
![]() ,
(IIа)
,
(IIа)
![]() ,
(IIIа)
,
(IIIа)
![]() .
(IVа)
.
(IVа)
Уравнения Максвелла показывают, что источниками электрического поля могут быть либо электрические заряды, либо магнитные поля, меняющиеся во времени. Магнитные же поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями. Уравнения Максвелла в интегральной форме справедливы и в тех случаях, когда существуют поверхности разрыва, на которых свойства среды или напряженности электрического и магнитного полей меняются скачкообразно. Поэтому в этой форме уравнения Максвелла обладают большей общностью, чем в дифференциальной форме, которая предполагает, что все величины в пространстве и во времени меняются непрерывно. Поэтому дифференциальные уравнения Максвелла должны быть дополнены граничными условиями
![]() (2.13)
(2.13)
Здесь
![]() -
поверхностная плотность электрических зарядов, а
-
поверхностная плотность электрических зарядов, а ![]() - поверхностная плотность тока
проводимости на рассматриваемой границе раздела.
- поверхностная плотность тока
проводимости на рассматриваемой границе раздела.
В случаях, когда поверхностные заряды и токи отсутствуют, граничные условия (2.13) преобразуются к виду
![]() (2.14)
(2.14)
Отметим, что уравнения Максвелла не могут быть выведены. На них следует смотреть как на основные аксиомы классической электродинамики, полученные путем обобщения опытных фактов.
2.5 Относительность электрического и магнитного полей
К электромагнитному полю применим только принцип относительности Эйнштейна, так как факт распространения электромагнитных волн в вакууме во всех системах отсчета с одинаковой скоростью не совместим с принципом относительности Галилея.
Из принципа относительности вытекает, что отдельное рассмотрение электрического и магнитного полей имеет относительный смысл. Так, если электрическое поле создается системой неподвижных зарядов, то эти заряды, являясь неподвижными относительно одной инерциальной системы отсчета, движутся относительно другой и, следовательно, будут порождать не только электрическое, но и магнитное поле. Аналогично, неподвижный относительно одной инерциальной системы отсчета проводник с постоянным током, возбуждая в каждой точке пространства постоянное магнитное поле, движется относительно других инерциальных систем, и создаваемое им переменное магнитное поле возбуждает вихревое электрическое поле.
3 Лекция. Колебательные процессы
3.1 Колебания – общее понятие и классификация
Колебания – широко распространенный вид движения; они наблюдаются в системах самой разнообразной природы. Колебания относятся к процессам, которые точно или приблизительно повторяются через одинаковые промежутки времени. В случае механических колебаний повторяются изменения положений (координат) и скоростей тел; в электрических колебаниях повторяются изменения напряжений и сил токов в электрических цепях, кроме того, изменения характеристик электрического и магнитного полей (векторов E и B) вокруг этих цепей. Существуют также «смешанные» колебания, например, электромеханические колебания, которые происходят в электроакустических преобразователях, таких как мембрана телефона, микрофон, электродинамический преобразователь.
Независимо от своей природы колебания подчиняются одним и тем же закономерностям, поэтому для их описания используют один и тот же формальный математический аппарат.
Различают свободные и вынужденные колебания, автоколебания и параметрические колебания.
Свободными (или собственными) называются колебания, которые: а) происходят в отсутствие переменных внешних воздействий на колебательную систему, б) возникают вследствие какого-либо начального отклонения данной системы от состояния её устойчивого равновесия.
Автоколебания – это незатухающие колебания, энергия которых периодически за счет обратной связи пополняется из какого-либо источника.
Важной кинематической характеристикой является форма колебаний. Она определяется видом той функции времени, которая описывает изменение данной физической величины при колебаниях. По форме колебания различают гармонические, пилообразные, П-образные и другие.
3.2 Общая характеристика гармонических колебаний. Дифференциальное уравнение гармонических колебаний
Периодические колебания величины ξ(t) называются гармоническими, если они происходят по закону синуса или косинуса:
ξ(t) =Acos(ωt+φ0), (3.1)
здесь ξ(t) характеризует изменение какой-либо физической величины при колебаниях;
A – амплитуда колебаний, т. е. максимальное положительное значение колеблющейся величины. Значение колеблющейся величины ξ(t) в произвольный момент времени t определяется значением фазы колебаний:
φ(t)=ωt+φ0, (3.2)
где ω - циклическая (круговая) частота;
а φ0 – начальная фаза, то есть фаза в момент времени t=0.
ω=2πν=2π ⁄ Т, (3.3)
где ν=1⁄Т – частота колебаний, которая определяет число колебаний в единицу времени и измеряется в Гц.
При частоте колебаний 1 Гц одно полное колебание происходит за одну секунду: 1 Гц=1 с-1.
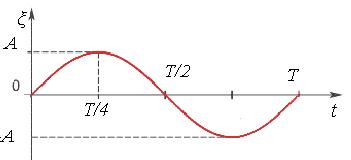
Рисунок 3.1
Период колебания Т – это время, за которое происходит одно полное колебание. За промежуток времени, равный периоду Т, фаза гармонических колебаний изменяется на 2π.
Амплитуда и начальная фаза определяются начальными условиями, а частота (или период) – параметрами колебательной системы.
Найдем первую и вторую производные колеблющейся по гармоническому закону физической величины ξ(t):
dξ/dt= –Aωsin(ωt+φ0)=Acos ωt+φ0 +π/2), (3.4)
d2ξ/dt2= -Aω2cos(ωt+φ0)=Aω2cos(ωt+φ0+ π). (3.5)
В случае механических колебаний величина ξ имеет смысл координаты колеблющейся материальной точки, а dξ/dt и d2ξ/dt2 – соответственно ее скорости и ускорения.
Сравнивая (1) и (5), можно увидеть, что в случае гармонических колебаний справедливо следующее соотношение:
d2ξ/dt2 = - ω2ξ(t),
или
d2ξ/dt2 + ω2ξ(t)=0. (3.6)
Дифференциальное уравнение гармонических колебаний (3.6) – это дифференциальное уравнение второго порядка, линейное относительно функции ξ(t) с положительным коэффициентом, равным ω2, однородное.
3.3 Гармонические осцилляторы
Система, закон движения которой имеет вид (3.1), называется линейным гармоническим осциллятором. Примером такой системы служит пружинный маятник – груз массы m, закрепленный на упругой пружине.
Если груз сместить из положения равновесия, то пружина деформируется и в ней возникает сила упругости, которая сообщает грузу ускорение. По второму закону Ньютона с учетом закона Гука Fупр= - kx , пренебрегая трением и сопротивлением среды, получим:
m∙d2x∕dt2 = - kx,
поделив обе части равенства на m и произведя перенос, получим:
d2x∕dt2+(k/m) x=0.
Сравнив полученное дифференциальное уравнение с (3.6), можно найти собственную частоту ω0 свободных незатухающих колебаний пружинного маятника:
![]() .
(3.7)
.
(3.7)
Рассмотрим свободные гармонические колебания в электрическом колебательном контуре – электрической цепи, состоящей из конденсатора электроемкости C, катушки индуктивности L и сопротивления R (см.рисунок 3.3). При замыкании на катушку предварительно заряженного конденсатора в колебательном контуре возникают свободные колебания заряда q конденсатора и силы тока в катушке i.
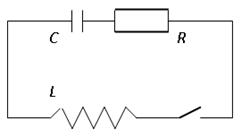
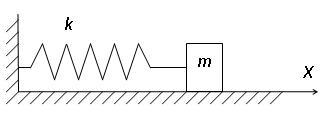
Рисунок 3.2 Рисунок 3.3
Согласно обобщенному закону Ома
![]() , (3.8)
, (3.8)
так как по определению силы тока
![]() ,
,
то уравнение (3.8) примет вид
![]() (3.9)
(3.9)
в случае идеального контура сопротивление R=0, поэтому:
![]() . (3.10)
. (3.10)
Решение дифференциального уравнения (3.10) имеет вид:
![]() (3.11)
(3.11)
и описывает гармонические колебания заряда на обкладках конденсатора с частотой
![]() . (3.12)
. (3.12)
3.4 Энергия гармонических колебаний
Энергия гармонического осциллятора в случае колебательного контура складывается из электрической энергии заряженного конденсатора и магнитной энергии катушки индуктивности:
![]() , (3.13)
, (3.13)
где
учтено, что ![]() ,
а также, что
,
а также, что ![]() .
.
Соотношение (3.13) означает, что в идеализированном колебательном контуре, сопротивление R которого бесконечно мало, полная энергия сохраняется. Если в начальный момент времени заряженный конденсатор с запасенной в нем энергией W0 замкнуть на катушку индуктивности, то вся энергия из электрической через четверть периода перейдет в магнитную энергию катушки, а через следующие четверть периода опять превратится в электрическую. При этом максимальные значения
![]() . (3.14)
. (3.14)
В случае механических колебаний полная энергия гармонического осциллятора (в котором отсутствуют силы трения и сопротивления среды), складывающаяся из кинетической и потенциальной энергий, также остается постоянной, испытывая периодические превращения из кинетической в потенциальную и наоборот:
![]() .(3.15)
.(3.15)
3.5 Векторная диаграмма. Сложение колебаний. Биения
Гармонические колебания можно изобразить графически с помощью вращающегося вектора на плоскости. Для этого из начала координат О на плоскости проводят вектор А (см.рисунок 3.4), модуль которого равен амплитуде А колебаний и составляет с осью координат OX угол φ=ωt+φ0, равный фазе колебаний в данный момент времени t. С течением времени угол φ увеличивается так, что вектор А равномерно вращается вокруг точки 0 с угловой скоростью, равной циклической частоте колебаний ω. Соответственно, проекция вектора А на ось ОX совершает гармонические колебания по закону
![]() .
.
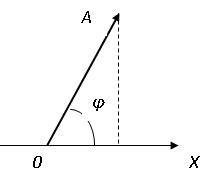

Рисунок 3.4 Рисунок 3.5
3.5.1 Рассмотрим сложение гармонических колебаний одинакового направления и одинаковой частоты
![]() ,
, ![]() .
.
Результирующее колебание – гармоническое, с той же
частотой ![]() :
:
![]() .
.
На векторной диаграмме (см.рисунок 3.5) результирующее колебание изображается вектором A.
![]() , (3.16)
, (3.16)
![]() .
(3.17)
.
(3.17)
Как следует из (3.11), амплитуда результирующего колебания зависит не только от амплитуд, но и от разности фаз складываемых колебаний (φ2 – φ1).
Колебания одинаковой частоты, разность фаз которых со временем не изменяется, называются когерентными. При сложении когерентных колебаний наибольший интерес представляют следующие случаи:
а) разность фаз равна нулю или четному числу π : (φ2 – φ1)=2πn, где n = 0, 1, 2, (любое целое число). В этом случае cos(φ2 – φ1)=1 и A=A1+A2 , т.е. амплитуды складываются;
б) разность фаз равна нечетному числу π: (φ2 – φ1) = (2n+1) π , где n = 0, 1, 2,… Тогда cos(φ2 – φ1)= -1 и A=|A1-A2|, т.е. амплитуды вычитаются;
в) разность фаз равна (φ2 –
φ1) =![]() , где n = 0, 1, 2,… В этом
случае cos(φ2 –
φ1)=0
и
, где n = 0, 1, 2,… В этом
случае cos(φ2 –
φ1)=0
и ![]() .
.
3.5.2 Особый интерес представляет случай, когда частоты складываемых колебаний немного отличаются друг от друга:
х1=Acosωt, х2=A2cos(ω+∆ω) t.
Складывая эти выражения и учитывая, что ∆ω/2 <<ω , получим:
![]() . (3.18)
. (3.18)
В результате получаются колебания с периодически
изменяющейся амплитудой Aб=|2Acos![]() |. Такие колебания называются биениями.
Частота биений - ωб=∆ω, период биений - Tб=
|. Такие колебания называются биениями.
Частота биений - ωб=∆ω, период биений - Tб=![]() .
.
Метод биений заключается в определении частоты биений между эталонными и измеряемыми колебаниями. Он широко применяется для настройки музыкальных инструментов, анализа слуха и т. д.
3.5.3 Сложение взаимно перпендикулярных колебаний с одинаковыми частотами. Пусть точка М одновременно колеблется вдоль осей координат ОХ и ОУ по законам х=A1cosωt и y=А2cos(ωt+φ).
Уравнение траектории результирующего колебания точки М в плоскости ХОУ найдем, исключив из уравнений параметр t:
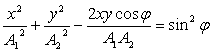 . (3.19)
. (3.19)
Уравнение (3.14) – это уравнение неприведенного эллипса, ориентированного относительно осей произвольным образом. Точка М описывает этот эллипс (см.рисунок 3.6а) за время, равное периоду складываемых колебаний T . Результирующее движение точки М называют эллиптически поляризованными колебаниями. Ориентация в плоскости ХОУ осей эллипса, а также его размеры, зависят от амплитуд А1 и А2 складываемых колебаний и разности их начальных фаз.
3.5.3.1 Если φ2-φ1 =(2m+1)π/2, где m=0, ±1, ±2, …, то
![]() ,
,
в этом случае оси эллипса совпадают с осями ОХ и ОY, а размеры полуосей соответственно равны амплитудам А1 и А2 (см.рисунок 3.6b).
В случае равенства амплитуд А1 = А2, траектория точки М представляет собой окружность. Такие колебания носят название циркулярно-поляризованных или колебаний, поляризованных по кругу.
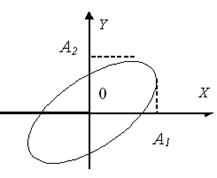
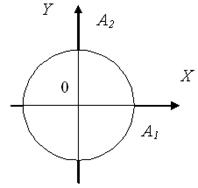
Рисунок 3.6 a Рисунок 3.6 b
3.5.3.2
Если φ = πm , где m = 0,±1,±2, … , то эллипс
вырождается в прямую y= ± , при этом знак "плюс"
соответствует четным m, т.е. сложению синфазных колебаний (см.рисунок
3.7а), «минус» - нечетным m, т.е. сложению колебаний, происходящих
в противофазе (см.рисунок 3.7b). В этих случаях точка М совершает
линейно поляризованные колебания. Она гармонически колеблется с частотой
складываемых колебаний и амплитудой A =
, при этом знак "плюс"
соответствует четным m, т.е. сложению синфазных колебаний (см.рисунок
3.7а), «минус» - нечетным m, т.е. сложению колебаний, происходящих
в противофазе (см.рисунок 3.7b). В этих случаях точка М совершает
линейно поляризованные колебания. Она гармонически колеблется с частотой
складываемых колебаний и амплитудой A =![]() , вдоль прямой линии, составляющей с ОХ
угол α: tg α =
(A2/A1)cos πm.
, вдоль прямой линии, составляющей с ОХ
угол α: tg α =
(A2/A1)cos πm.
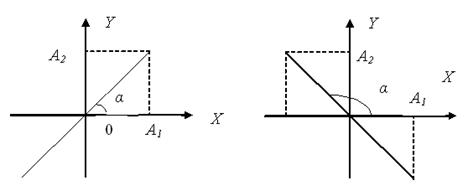
Рисунок 3.7 а Рисунок 3.7 b
3.5.4 Сложение взаимно перпендикулярных колебаний с разными циклическими частотами приводит к возникновению сложных кривых, называемых фигурами Лиссажу. Их форма зависит от соотношения амплитуд, частот и начальных фаз складываемых колебаний. При отношении частот ω1/ω2 = n2/n1 , где n1 и n2 - числа пересечений с осями соответственно OX и OY, траектория представляет собой устойчивую замкнутую кривую. Это свойство можно использовать для определения неизвестной частоты при сравнении с колебаниями известной частоты.
4 Лекция. Затухающие и вынужденные колебания
4.1 Дифференциальное уравнение затухающих колебаний. Амплитуда и частота затухающих колебаний
Рассмотрим затухающие колебания на примере электрических колебаний в колебательном контуре, состоящем из катушки индуктивности L, конденсатора емкости С и активного сопротивления R (см.рисунок 4.1). Как показано в предыдущей лекции, применение обобщенного закона Ома приводит к уравнению (3.9).
Введем обозначения: коэффициент затухания:
![]() ,
(4.1)
,
(4.1)
собственная частота ω0 незатухающих колебаний системы:
![]() . (4.2)
. (4.2)
Тогда дифференциальное уравнение затухающих колебаний примет вид:
![]() . (4.3)
. (4.3)
Решение данного уравнения зависит от соотношения его коэффициентов ω0 и β. В случае слабого затухания (β2<<ω02 ) решение имеет вид:
q(t) = q0 e-βt cos(ωt+α), (4.4)
где q0 - амплитуда в начальный момент времени;
α - начальная фаза затухающих колебаний (определяются из начальных условий);
ω - частота свободных затухающих колебаний, равная:
![]() .
(4.5)
.
(4.5)
Период затухающих колебаний равен:
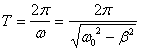 .
(4.6)
.
(4.6)
Для колебательного контура:
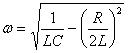 (4.7)
(4.7)
|
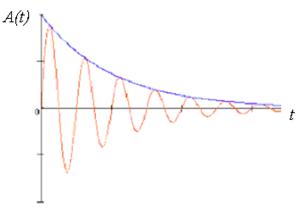
A(t) =q0e – βt, (4.8)
Рисунок 4.1
то (4.4) примет вид гармонического колебания ![]() , но в данном
случае амплитуда затухающих колебаний A(t) убывает со временем по
экспоненциальному закону (см.рисунок 4.1).
, но в данном
случае амплитуда затухающих колебаний A(t) убывает со временем по
экспоненциальному закону (см.рисунок 4.1).
Напряжение Uc на конденсаторе изменяется по тому же закону, что и заряд на его обкладках:
![]() =
=![]() q0 e-βt
cos(ωt+α). (4.9)
q0 e-βt
cos(ωt+α). (4.9)
Ток в контуре при наличии активного сопротивления R опережает по фазе Uc более чем на π∕2:
![]() , (4.10)
, (4.10)
где
![]() .
(4.11)
.
(4.11)
Натуральный логарифм отношения амплитуд двух колебаний, взятых через период Т, называют логарифмическим декрементом затухания θ:
θ
= ln![]() , (4.12)
, (4.12)
θ
= ln
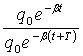 =βT.
(4.13)
=βT.
(4.13)
Логарифмический декремент затухания – это величина, обратная числу полных колебаний,
совершенных за время релаксации τ (![]() ,
, ![]() ),
),
![]() . (4.14)
. (4.14)
Добротностью колебательной системы Q называют величину
![]() .
(4.15)
.
(4.15)
Добротность тем выше, чем слабее затухание. При слабом затухании
![]() .
(4.16)
.
(4.16)
При β2≥ω02 колебаний в контуре не возникает, происходит апериодический разряд конденсатора. Активное сопротивление контура, при котором наступает апериодический процесс, называют критическим:
![]() .
. ![]() (4.17)
(4.17)
4.2 Вынужденные колебания, их амплитуда и фаза. Резонанс. Резонансные кривые
Вынужденными называются колебания системы, происходящие под действием внешнего периодически изменяющегося воздействия.
Пусть на пружинный маятник действует внешняя
сила, изменяющаяся по гармоническому закону ![]() ; помимо этого, действуют силы
упругости (по закону Гука) и сопротивления среды Fсопр. Если
тело движется с малой (по сравнению со скоростью звука в данной среде)
скоростью
v, то сила сопротивления пропорциональна скорости
v:
; помимо этого, действуют силы
упругости (по закону Гука) и сопротивления среды Fсопр. Если
тело движется с малой (по сравнению со скоростью звука в данной среде)
скоростью
v, то сила сопротивления пропорциональна скорости
v: ![]() .
.
Дифференциальное уравнение движения в среде с трением тела, прикрепленного к пружине, по второму закону Ньютона:
![]() ,
,
или, в каноническом виде:
![]() .
(4.18)
.
(4.18)
Учитывая (3.7) ![]() и введя обозначение
и введя обозначение ![]() (сравни с
4.1), перепишем дифференциальное уравнение вынужденных колебаний: в виде
(сравни с
4.1), перепишем дифференциальное уравнение вынужденных колебаний: в виде
![]() .
(4.19)
.
(4.19)
Решение неоднородного дифференциального уравнения II-ого порядка (4.19) представляет собой сумму общего решения однородного уравнения (без правой части) и частного решения неоднородного уравнения. Нас интересуют только установившиеся колебания, т.е. частное решение этого уравнения, так как общее решение однородного уравнения, как мы уже установили в предыдущем параграфе (4.1), описывает затухающие колебания и по прошествии некоторого времени обращается в нуль. Частное решение имеет вид:
![]() ,
(4.20)
,
(4.20)
где А – амплитуда установившихся вынужденных колебаний; она зависит от частоты ω вынуждающей силы.
Амплитуда смещения определяется выражением:
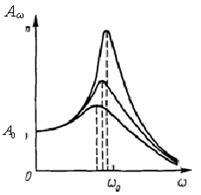
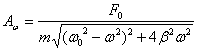 .
(4.21)
.
(4.21)
Сдвиг фаз φ между внешней гармонической силой и вызываемыми ею колебаниями находится по формуле:
![]() . (4.22)
. (4.22)
Рисунок 4.2
На рисунке 4.2 приведен график зависимости амплитуды
вынужденных колебаний Aω от частоты ω
вынуждающей силы. При ω→0 колебания отсутствуют; под
действием приложенной постоянной силы F0 тело смещается от
положения равновесия и растягивает пружину на величину A0,
называемую статическим отклонением и равную (по закону Гука) ![]() . При
возрастании ω амплитуда также растет, достигая максимума при
частоте, близкой к собственной частоте ω0, а затем
убывает, стремясь в пределе к нулю при
. При
возрастании ω амплитуда также растет, достигая максимума при
частоте, близкой к собственной частоте ω0, а затем
убывает, стремясь в пределе к нулю при ![]() .
.
Резкое возрастание амплитуды вынужденных колебаний при приближении частоты ω вынуждающей
силы к собственной частоте ω0 колебательной системы
называется резонансом. Точное
значение частоты ωр, при которой амплитуда смещения
достигает максимального значения, можно найти, приравняв производную от Aω
(4.21) по ω нулю (исследование функции на экстремум): ![]() .
.
|
![]() . (4.23)
. (4.23)
Амплитуда смещения при резонансе равна:
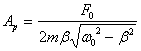 , (4.24)
, (4.24)
|
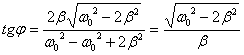 . (4.25)
. (4.25)
4.3 Переменный ток как вынужденные колебания. Закон Ома для переменного тока. Мощность, выделяемая в цепи переменного тока
Переменным током называют установившиеся вынужденные колебания тока в цепи.
|
Пусть подаваемое напряжение изменяется со временем по гармоническому закону
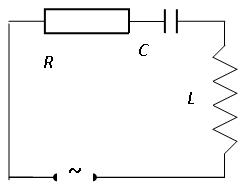 u=Um cos ωt. (4.26)
u=Um cos ωt. (4.26)
В этом случае применение обобщенного закона Ома приводит к дифференциальному уравнению вынужденных колебаний в контуре:
![]() ,
(4.27)
,
(4.27)
или:
Рисунок 4.3
![]() . (4.28)
. (4.28)
Частное решение (4.20) имеет вид:
![]()
![]() , (4.29)
, (4.29)
где qm – амплитуда, а y- разность фаз между колебаниями заряда q на обкладках конденсатора и приложенного напряжения u.
Продифференцируем (4.29) по времени и получим закон изменения силы тока в контуре
![]() .
(4.30)
.
(4.30)
Запишем это выражение в виде:
![]() ,
(4.31)
,
(4.31)
где Im - амплитуда силы тока, причем
![]() ;
;
φ - сдвиг по фазе между колебаниями тока i и приложенного напряжения u.
Наша задача - найти значения Im и φ. Представим уравнение (4.27) в виде
![]() , (4.32)
, (4.32)
т.е. сумма падений напряжения на индуктивности L, активном сопротивлении R и емкости С в каждый момент времени равна мгновенному значению приложенного извне напряжения u:
а) по закону Ома падение напряжения на резисторе
![]() ,
,
откуда следует, что колебания напряжения ![]() совпадают по
фазе с колебаниями тока, а его амплитудное значение равно
совпадают по
фазе с колебаниями тока, а его амплитудное значение равно ![]() ;
;
б) разность потенциалов между обкладками конденсатора
![]() ,
,
следовательно, колебания напряжения ![]() по фазе на
по фазе на ![]() отстают от
колебаний тока, а их амплитудное значение равно
отстают от
колебаний тока, а их амплитудное значение равно ![]() ;
;
в) падение напряжения uL на катушке индуктивности
![]() ,
,
по фазе эти колебания на ![]() опережают колебания тока;
опережают колебания тока; ![]() .
.
Величину R называют активным сопротивлением
цепи, а величины ![]() и
и ![]() называются соответственно реактивным
емкостным и реактивным индуктивным сопротивлением.
называются соответственно реактивным
емкостным и реактивным индуктивным сопротивлением.
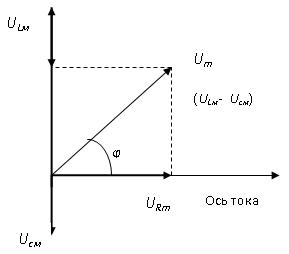 Используем полученные соотношения при построении векторной
диаграммы напряжений. При последовательном соединении
элементов ток в цепи везде один и тот же, если его можно считать квазистационарным.
В этом случае все векторы амплитуд напряжений на резисторе
URm, на катушке ULm и на конденсаторе UCm
откладывают относительно оси тока с учетом их фазовых соотношений с
током (см.рисунок 4.4).
Используем полученные соотношения при построении векторной
диаграммы напряжений. При последовательном соединении
элементов ток в цепи везде один и тот же, если его можно считать квазистационарным.
В этом случае все векторы амплитуд напряжений на резисторе
URm, на катушке ULm и на конденсаторе UCm
откладывают относительно оси тока с учетом их фазовых соотношений с
током (см.рисунок 4.4).
Рисунок 4.4
Напряжение на резисторе
UR
совпадает
по фазе с током, поэтому вектор амплитуды ![]() откладывают вдоль оси тока;
поскольку напряжение на конденсаторе отстает по фазе на
откладывают вдоль оси тока;
поскольку напряжение на конденсаторе отстает по фазе на ![]() от тока, то вектор
амплитуды напряжения
от тока, то вектор
амплитуды напряжения ![]() повернут на диаграмме на угол (-
повернут на диаграмме на угол (- ![]() ) и так далее.
) и так далее.
По правилу сложения векторов находим их сумму, которая согласно (4.24) равна амплитуде приложенного внешнего напряжения Um. Сдвиг по фазе φ между напряжением и током на диаграмме равен углу, который образует вектор Um с осью тока; тангенс этого угла равен:
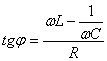 .
(4.33)
.
(4.33)
По теореме Пифагора ![]() и далее, подставляя полученные
выше соотношения
и далее, подставляя полученные
выше соотношения ![]() ,
,
получим соотношение, связывающее амплитудные значения тока Iм и Uм:
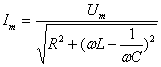 . (4.34)
. (4.34)
Согласно (4.34) амплитудное значение тока прямо пропорционально амплитудному значению приложенного напряжения. Это соотношение рассматривают как закон Ома для переменного тока (при последовательном соединении). В общем случае произвольного соединения этот закон записывают в виде:
![]() , (4.35)
, (4.35)
где Z – полное сопротивление цепи переменному току, или импеданс, которое зависит от параметров цепи (R, L, C), соединения всех ее элементов и частоты ω приложенного напряжения.
При ![]() падения напряжений на конденсаторе и
катушке индуктивности одинаковы по амплитуде
падения напряжений на конденсаторе и
катушке индуктивности одинаковы по амплитуде ![]() и противоположны по фазе, значение
амплитуды тока в последовательном колебательном контуре достигает максимально
возможного значения
и противоположны по фазе, значение
амплитуды тока в последовательном колебательном контуре достигает максимально
возможного значения ![]() , а сдвиг фаз обращается в ноль
, а сдвиг фаз обращается в ноль ![]() . Это явление
называют резонансом тока. Резонансная частота для силы
тока совпадает с собственной частотой контура
. Это явление
называют резонансом тока. Резонансная частота для силы
тока совпадает с собственной частотой контура
![]() . (4.36)
. (4.36)
Мгновенная мощность тока в цепи равна:
![]() . (4.37)
. (4.37)
Практический интерес имеет среднее за период Τ значение мощности
![]() .
(4.38)
.
(4.38)
Такую же мощность развивает постоянный ток
![]() . (4.39)
. (4.39)
Величины ![]() и
и ![]() называют действующими
(или эффективными) значениями тока и напряжения. Все амперметры и
вольтметры для цепей переменного тока проградуированы именно по действующим
значениям I и U .
называют действующими
(или эффективными) значениями тока и напряжения. Все амперметры и
вольтметры для цепей переменного тока проградуированы именно по действующим
значениям I и U .
Средняя мощность, потребляемая цепью переменного тока:
![]() , (4.40)
, (4.40)
где cosφ - коэффициент мощности, равный
![]() . (4.41)
. (4.41)
4.4 Ангармонические колебания
Примером ангармонических колебаний служат колебания математического или физического маятника при больших отклонениях α его от положения равновесия. Дифференциальное уравнение в этом случае нелинейное:
![]() , (4.42)
, (4.42)
где m – масса тела;
J - момент инерции тела относительно точки О подвеса;
g – ускорение свободного падения;
l – расстояние между точкой О подвеса и центром С тяжести тела.
Решение этого уравнения не является гармоническим. Отличительные особенности ангармонических колебаний состоят в том, что:
а) они не изохронны, то есть их период (и частота) зависит от амплитуды;
б) для них не выполняется принцип суперпозиции.
Однако, любое колебание, каким сложным по форме оно бы не было, всегда можно представить в виде совокупности гармонических составляющих. Согласно теореме Фурье «любое повторяющееся движение можно рассматривать как результат наложения простых гармонических движений; любую волну, независимо от ее формы можно рассматривать как сумму простых гармонических волн».
В теории рядов Фурье, всякая периодическая функция, ограниченная на отрезке, может быть представлена в виде тригонометрического ряда:
![]() , (4.43)
, (4.43)
где ![]()
![]() - период функции
- период функции ![]() , коэффициенты
разложения:
, коэффициенты
разложения:
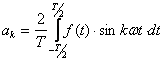 ,
, 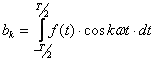 .
.
Таким образом, любое периодическое колебание может быть представлена в виде суммы гармонических колебаний кратных частот ω, 2ω, 3ω, …; частота ω называется основной частотой, остальные – гармониками.
Совокупность гармонических составляющих сложного колебания называется его спектром. Нахождение амплитуд и частот гармоник произвольного периодического процесса с помощью рядов Фурье носит название гармонического анализа. Эта возможность реализуется на практике с помощью приборов – анализаторов спектра.
5 Лекция. Волновые процессы
5.1 Упругие волны
Волновые процессы окружают нас всюду: волны и зыбь океанов, волны сейсмические, волны звука, волны в натянутой струне или кристалле кварца, который используется для излучения или приема ультразвука, электромагнитные волны – свет, радиоволны, рентгеновское излучение.
При всех различиях в происхождении и проявлении волн они обладают целым рядом общих свойств. Главная замечательная особенность волнового движения – оно может переносить энергию на громадные расстояния с очень малыми потерями.
Рассмотрим волны механической природы. Каким образом можно возбудить механические волны? Для этого надо в упругую среду поместить некоторую колебательную систему. В первом приближении все среды, кроме разреженных газов, можно считать абсолютно упругими (линейными), так как внутренние силы, возникающие в них при малых деформациях, пропорциональны величине деформации. Источник – колебательная система (мембрана телефона или ножки камертона), колеблясь, взаимодействует с частицами, находящимися в прилегающем слое среды. При этом создается непрерывный ряд импульсов деформаций, следующих один за другим и распространяющихся в среде.
5.2 Уравнения плоской и сферической волн
Положим, система колеблется по гармоническому закону ![]() тогда вынуждающая
сила, с которой она действует на прилегающие частицы среды, заставляя их колебаться,
также меняется по гармоническому закону с частотой ω вынуждающей
силы, то есть с частотой колебания системы. Эти частицы приходят в
колебательное движение одновременно с возникновением колебаний в системе. Но
частица, отстоящая от источника на расстоянии x, начнет совершать
колебания тогда, когда до нее дойдет начало распространяющегося в среде возмущения.
Если скорость распространения возмущения в среде
v, то возмущение дойдет до данной точки за промежуток
времени, равный v/t. Тогда колебания
частиц среды с координатой равновесного положения x будут происходить по
закону:
тогда вынуждающая
сила, с которой она действует на прилегающие частицы среды, заставляя их колебаться,
также меняется по гармоническому закону с частотой ω вынуждающей
силы, то есть с частотой колебания системы. Эти частицы приходят в
колебательное движение одновременно с возникновением колебаний в системе. Но
частица, отстоящая от источника на расстоянии x, начнет совершать
колебания тогда, когда до нее дойдет начало распространяющегося в среде возмущения.
Если скорость распространения возмущения в среде
v, то возмущение дойдет до данной точки за промежуток
времени, равный v/t. Тогда колебания
частиц среды с координатой равновесного положения x будут происходить по
закону:
![]() (5.1)
(5.1)
Уравнение (5.1) описывает бегущую плоскую гармоническую волну.
Распространяясь от источника колебаний, волновой процесс охватывает все новые и новые области среды. Таким образом, упругая волна – это распространение возмущения в упругой среде. При этом происходит распространение именно возмущения частиц среды, но сами частицы не перемещаются на большие расстояния, а лишь колеблются около своих положений равновесия.
Различают продольные и поперечные волны в зависимости от того, вдоль или поперек направления распространения волны колеблются частицы. Оказывается, что в газах и жидких средах могут распространяться лишь продольные волны, а в твердых телах распространяются и продольные, и поперечные волны. Например, если где-нибудь происходит землетрясение, то в земной коре от его эпицентра распространяются (с разными скоростями) одна продольная и две поперечные сейсмические волны.
|
Геометрическое место точек, до которых доходят колебания к данному моменту времени, называется фронтом волны. Фронт волны представляет собой ту поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли.
Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. В отличие от фронта волны, который все время перемещается, волновые поверхности не перемещаются.
В зависимости от формы волновых поверхностей различают плоские и сферические волны. Волна называется плоской, если волновые поверхности имеют форму плоскости (множество параллельных друг другу плоских поверхностей). В том случае, когда плоская волна распространяется вдоль оси OX, ее волновые поверхности – это плоскости, перпендикулярные данной оси (при условии однородной по своим свойствам среды). Соответственно, волновые поверхности сферической волны, распространяющейся в изотропной и однородной среде, – это множество концентрических сфер.
Уравнение сферической гармонической волны имеет вид:
![]() (5.2)
(5.2)
где a0 - коэффициент, численно равный амплитуде колебаний на расстоянии 1 м от точечного источника.
5.3 Длина волны. Фазовая скорость
Если зафиксировать определенное значение времени t, то уравнения 1 и 2 дадут распределение смещений частиц в зависимости от их расстояния до источника. Смещения точек, отстоящих друг от друга на расстоянии, равном vT, в один и тот же момент времени будут одинаковы, поскольку их фазы отличаются на 2π. Распространение колебаний – процесс периодический не только во времени (с периодом T=1/ν=2π/ω), но и в пространстве.
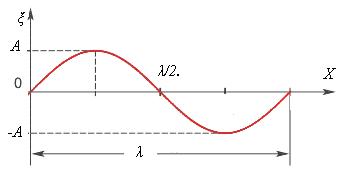 Расстояние λ между ближайшими точками
среды (вдоль направления распространения волны), в которых частицы колеблются с
разностью фаз 2π, называется длиной волны (см.рисунок 5.1).
Длина волны – это расстояние, на которое распространяется фиксированная
фаза за время, равное периоду T колебаний,
Расстояние λ между ближайшими точками
среды (вдоль направления распространения волны), в которых частицы колеблются с
разностью фаз 2π, называется длиной волны (см.рисунок 5.1).
Длина волны – это расстояние, на которое распространяется фиксированная
фаза за время, равное периоду T колебаний,
Рисунок 5.1 ![]() .
(5.3)
.
(5.3)
Другой важной характеристикой волны является волновое число k
![]() ω/v , (5.4)
ω/v , (5.4)
|
С введением волнового числа уравнение волны можно записать:
![]() . (5.5)
. (5.5)
Уравнения 2,3 и 6 описывают плоскую гармоническую волну, которая не затухает. На самом деле в любой среде упругая волна затухает. Если среда однородная, то затухание происходит по экспоненциальному закону:
ξ(x,t)=A0exp(-γx)cos(ωt-kx). (5.6)
Здесь γ – коэффициент поглощения среды, численно равный величине, обратной тому расстоянию, на котором в данной среде амплитуда колебаний убывает в e раз.
Уравнение бегущей сферической гармонической волны, распространяющейся в однородной изотропной поглощающей среде имеет вид:
![]() (5.7)
(5.7)
5.4 Волновое уравнение
Аналогично тому, как существуют основные уравнения динамики, которым подчиняются разнообразные механические движения (материальной точки, твердого тела), так и для волновых движений открыты основные уравнения, описывающие волновые процессы независимо от их природы и конкретного вида.
Найдем эту связь для волн типа (плоских волн произвольной формы)
ξ(x,t) =f( t x/v).
Обозначим фазу волны φ=tx/v. Тогда
![]() ,
,
так как
![]() ,
,
![]() ,
,
так как
![]() .
.
Из сопоставления полученных выражений следует, что справедливо:
![]() .
.
Это уравнение, однако, описывает лишь волны, которые распространяются в положительном направлении оси ОХ. При изменении направления знак «минус» в уравнении меняется на знак «плюс». Таким образом, можно написать:
![]() .
(5.8)
.
(5.8)
Это уравнение является одним из простейших волновых
уравнений. Производная по времени ![]() представляет собой скорость (проекцию
вектора скорости на ось ОХ) частиц среды, с которой они колеблются вблизи
своего положения равновесия.
представляет собой скорость (проекцию
вектора скорости на ось ОХ) частиц среды, с которой они колеблются вблизи
своего положения равновесия.
Чтобы уяснить физический смысл производной ![]() , мысленно
выделим в среде цилиндрический объем, ось которого совпадает с направлением распространения
плоской продольной волны - осью ОХ. Выделим теперь в этом объеме малый
элемент длины ∆x, ограниченный в отсутствие волны поперечными
сечениями с координатами x и x+∆x. Если сечение с
координатой x имеет в некоторый момент времени смещение ξ, то
смещение частиц среды, положение которых в отсутствие волны определяется
координатой x+∆x, будет равно ξ+∆ξ.
Поскольку при прохождении волны смещения частиц, расположенных в разных
сечениях, неодинаковы, то рассматриваемый элемент среды оказывается деформированным
– он получает удлинение ∆ξ, которое может принимать как
положительные, так и отрицательные, а также равные нулю значения.
, мысленно
выделим в среде цилиндрический объем, ось которого совпадает с направлением распространения
плоской продольной волны - осью ОХ. Выделим теперь в этом объеме малый
элемент длины ∆x, ограниченный в отсутствие волны поперечными
сечениями с координатами x и x+∆x. Если сечение с
координатой x имеет в некоторый момент времени смещение ξ, то
смещение частиц среды, положение которых в отсутствие волны определяется
координатой x+∆x, будет равно ξ+∆ξ.
Поскольку при прохождении волны смещения частиц, расположенных в разных
сечениях, неодинаковы, то рассматриваемый элемент среды оказывается деформированным
– он получает удлинение ∆ξ, которое может принимать как
положительные, так и отрицательные, а также равные нулю значения.
Отношение ∆ξ/∆x дает среднее
значение![]() <ε>
относительного удлинения элемента стержня. Чтобы получить относительную
деформацию ε нужно устремить ∆x к нулю. Таким образом,
производная ε=
<ε>
относительного удлинения элемента стержня. Чтобы получить относительную
деформацию ε нужно устремить ∆x к нулю. Таким образом,
производная ε=![]() имеет смысл относительной деформации
среды в сечении с координатой х.
имеет смысл относительной деформации
среды в сечении с координатой х.
В общем виде волновое уравнение, описывающее распространение волн в произвольном направлении, представляет собой линейное однородное дифференциальное уравнение в частных производных второго порядка:
![]() ,
(5.9)
,
(5.9)
здесь v – фазовая скорость;
![]() - оператор Лапласа. В декартовых
координатах он имеет вид:
- оператор Лапласа. В декартовых
координатах он имеет вид:
Δξ=![]() .
(5.10)
.
(5.10)
Волновое уравнение (5.9) справедливо лишь в случае однородных и изотропных сред, затухание в которых пренебрежимо мало.
Всякая функция, удовлетворяющая уравнению вида (5.9), описывает некоторую волну. Нетрудно непосредственно подстановками убедиться, что гармонические волны также удовлетворяют данному уравнению. Так, в случае плоской гармонической волны, распространяющейся вдоль оси ОХ:
Δξ=![]() =-Ak2cos(ωt-kx),
=-Ak2cos(ωt-kx), ![]() =- Aω2cos(ωt-kx).
=- Aω2cos(ωt-kx).
Таким образом, в случае плоской волны волновое уравнение имеет вид:
![]() . (5.11)
. (5.11)
5.5 Энергия упругих волн. Вектор Умова – вектор плотности потока энергии упругой волны
Источник волнового движения – колебательная система. За счет ее энергии возникают колебания частиц. Передача энергии от колеблющегося тела к частицам среды называется излучением. Упругая среда, в которой распространяется механическая волна, обладает дополнительной энергией, которая складывается из кинетической энергии колебательного движения частиц среды и потенциальной энергии упругой деформации этой среды. Эту энергию и называют энергией упругой волны.
Объемная плотность кинетической энергии среды плотностью ρ, в которой распространяется волна, равна:
wk=![]() .
(5.12)
.
(5.12)
Наличие
деформации растяжения (сжатия) означает, что в рассматриваемом сечении (с координатой
х) имеется нормальное напряжение σ=![]() , которое согласно закону Гука равно
σ=Eε=E
, которое согласно закону Гука равно
σ=Eε=E![]() , где E – модуль Юнга упругой среды.
, где E – модуль Юнга упругой среды.
Фазовая скорость продольных упругих волн, как следует из расчетов, которые основываются на применении второго закона Ньютона и закона Гука, равна корню квадратному из модуля Юнга, деленного на плотность вещества:
v=![]() .
(5.13)
.
(5.13)
Потенциальная энергия упругой деформации, которой обладает единичный объем среды, равна
wp=![]() =
=![]() . (5.14)
. (5.14)![]()
Таким образом, объемная плотность энергии упругой волны равна
w=![]() =wk+wp=
=wk+wp=![]() .
(5.15)
.
(5.15)
Поскольку согласно (5.9) оба слагаемых в (5.15) равны друг другу, то плотности кинетической и потенциальной энергии упругой деформации в упругой волне одинаковы и меняются синфазно, поэтому справедливо:
w = ρ![]() 2 ;
(5.16)
2 ;
(5.16)
например, для плоской гармонической волны:
w = ρА2ω2sin2(ωtkx)
= ![]() ρА2ω2
ρА2ω2![]() . (5.17)
. (5.17)
Из (5.17) следует, что мгновенное значение плотности энергии изменяется с частотой 2ω в пределах от wmin=0 до wmax=ρA2ω2.
Усредненное за период значение объемной плотности энергии упругой плоской гармонической волны равно:
<w>
= ![]() ρА2ω2.
(5.18)
ρА2ω2.
(5.18)
Возбужденная за счет излучаемой энергии источника волна осуществляет передачу энергии в среде. Скорость переноса энергии волной равна скорости перемещения в пространстве поверхности, соответствующей максимальному значению w. В случае гармонической волны она равна фазовой скорости v.
Энергия течет в направлении распространения волны. Количество энергии, переносимое волной через некоторую поверхность площадью S в единицу времени, называется потоком энергии через эту поверхность:
Φw=![]() .
(5.19)
.
(5.19)
Плотностью потока энергии волны называется физическая величина, численно равная потоку энергии через единичную площадку, перпендикулярную направлению переноса энергии
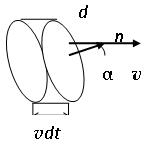
Рисунок 5.2
jw=![]() .
(5.20)
.
(5.20)
Выделим мысленно в среде элемент объема в виде очень малого наклонного цилиндра с площадью основания dS и образующей длиной dl=vdt. Размеры этого цилиндра должны быть малы настолько, чтобы во всех его точках плотность энергии w была бы одинакова. Тогда количество энергии, заключенной в этом объеме, равно:
dW=wdV=w·v·dt·dS·cosα,
где α – угол между нормалью n к площадке dS и вектором v скорости распространения волны. За промежуток времени dt это количество энергии протечет через площадку dS, следовательно, плотность потока энергии будет равна
jw=![]() =
= ![]() wv . (5.21)
wv . (5.21)
Для того чтобы охарактеризовать направление распространения энергии волной вводят вектор Умова:
jw=wv. (5.22)
Интенсивностью I волны называют усредненное по времени значение плотности потока энергии:
![]() .
(5.23)
.
(5.23)
В случае плоской гармонической волны:
I=![]() ρA2ω2v .
(5.24)
ρA2ω2v .
(5.24)
Зная вектор Умова во всех точках интересующей нас поверхности S, можно найти поток энергии через данную поверхность:
![]() .
(5.25)
.
(5.25)
6 Лекция. Электромагнитные волны
6.1 Волновое уравнение для электромагнитного поля
Согласно теории Максвелла, подтвержденной огромной совокупностью опытных фактов, электрические и магнитные явления взаимосвязаны: переменное электрическое поле порождает магнитное поле и, в свою очередь, изменяющееся магнитное поле создает в окружающем пространстве вихревое электрическое поле. Таким образом, если в некоторой области пространства возбудить с помощью колеблющихся зарядов переменное электромагнитное поле, то оно не остается локализованным в этой области. В окружающем пространстве возникает последовательность взаимных превращений электрического и магнитного полей, распространяющихся с определенной скоростью от точки к точке. Этот процесс, периодический во времени и в пространстве, представляет собой волну.
Можно показать, что существование электромагнитных волн вытекает из уравнений Максвелла.
Рассмотрим особенно простой случай плоской электромагнитной волны, распространяющейся вдоль оси ОХ в однородной и изотропной диэлектрической среде, в которой отсутствуют свободные электрические заряды и макроскопические токи, то есть выполняются условия j=0 и ρq=0. В этом случае уравнения Максвелла имеют следующий вид
rotE= -![]() (I)
(I)
divD =0 (II)
rotH
= ![]() (III)
divB
=0
(IV)
(III)
divB
=0
(IV)
D= εε0E (V)
B= μμ0H. (VI)
Распишем (I) ротор вектора E по компонентам с учетом (VI):
![]() rotE=
rotE=
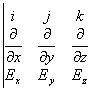 = i
= i
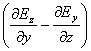 +j
+j
![]() +
k
+
k  =
=
- i
![]() -
j
-
j
![]() -
k
-
k
![]() = - μμ0 (i
= - μμ0 (i![]() +
j
+
j![]() +
k
+
k![]() ). (6.1)
). (6.1)
Поскольку волна плоская и распространяется вдоль оси ОХ, постольку производные компонентов E, D, B и H по координатам y и z равны нулю:
![]() 0 ,
0 , ![]() =0. (6.2)
=0. (6.2)
Из уравнений (6.1) и (6.2) вытекают следующие равенства:
![]() 0,
0, ![]() ,
, ![]() .
(6.3)
.
(6.3)
Аналогично, из уравнений (III) и (6.2) можно получить следующую группу равенств:
![]() =0,
=0, ![]() ,
, ![]() .
(6.4)
.
(6.4)
Чтобы получить волновое уравнение для электромагнитного поля и тем самым показать, что электромагнитные волны могут существовать, продифференцируем по x второе и третье из уравнений (6.3)
![]() .
.
Таким образом доказана справедливость соотношений
![]() , (6.5)
, (6.5)
![]() . (6.6)
. (6.6)
Каждое из уравнений (6.5) и (6.6) представляет собой волновое уравнение для компонентов Ez и Ey электрического вектора волны, а коэффициент пропорциональности перед второй производной по времени – это величина, обратная квадрату фазовой скорости электромагнитной волны:
v=![]()
![]() ,
(6.7)
,
(6.7)
где ![]() - скорость света в вакууме.
- скорость света в вакууме.
Аналогично, можно получить волновые уравнения для Hz и Hy:
![]() ,
, ![]() .
(6.8)
.
(6.8)
Таким образом показано, как из уравнений Максвелла вытекает существование электромагнитных волн.
6.2 Свойства электромагнитных волн
6.2.1 Из равенства нулю производных Ex и Hx как по координатам y и z, так и по времени t, следует, что Ex и Hx не зависят ни от координат, ни от времени. Следовательно, для переменных электрического и магнитного полей плоской волны, распространяющейся по оси ОX, выполняется условие:
Ex=Hx=0,
то есть векторы E и H перпендикулярны к направлению распространения волны - оси ОХ. Это означает, что электромагнитная волна поперечная.
6.2.2 Векторы E и H не только перпендикулярны к направлению распространения волны, но и взаимно перпендикулярны. Для доказательства рассмотрим следующую пару уравнений: второе из (6.3) и третье из (6.4)
![]() ,
, ![]() .
.
Из
последних уравнений следует, что изменяющееся во времени электрическое поле Ez,
направленное вдоль оси OZ, порождает магнитное поле Hy,
направленное вдоль оси OY, а изменение во времени магнитного поля Hy,
в свою очередь, порождает электрическое поле Ez, направленное
вдоль оси OZ. При этом ни поля Ey, ни поля Hz
не возникает. Аналогично, если взять другую пару уравнений (6.3) и (6.4),
то из них следует, что если изменяющееся во времени электрическое поле E
направлено вдоль оси OY, то оно порождает магнитное поле H,
направленное вдоль оси OZ. Все это свидетельствует о том, что E
![]() H.
H.
6.2.3 Мгновенные значения электрического и магнитного полей волны взаимосвязаны. Покажем это на примере плоской электромагнитной волны произвольной формы (то есть не обязательно гармонической по форме), распространяющейся вдоль положительного направления оси ОХ:
Ey=Ey(t-x/v), Hz=Hz(t-x/v).
Введя обозначение φ=t-x/v, найдем производные Ey по x и Hz по y
![]() ,
,
![]()
и подставим их в третье уравнение (6.4)
![]() ,
,
поскольку
v=![]() , то
, то
![]() .
.
Получается, что между мгновенными значениями электрического и магнитного полей существует связь:
![]() . (6.9)
. (6.9)
6.2.4 Это выражение также означает, что векторы E и H не только взаимно перпендикулярны, но и составляют вместе с вектором v скорости распространения волны правовинтовую тройку векторов: если вращать рукоять правого винта по кратчайшему направлению от вектора E к вектору H, то направление поступательного движения винта совпадает с направлением распространения волны (см.рисунок 6.1).
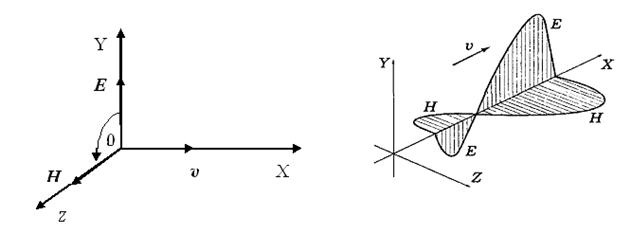
Рисунок 6.1 Рисунок 6.2
6.2.5 Соотношение (14) также означает, что поля E и H изменяются по одному и тому же закону (с одинаковой частотой и в одинаковой фазе), то есть синфазны: проекции Ey и Hz одинаковы по знаку, они одновременно обращаются в ноль и одновременно достигают максимума (см.рисунок 6.2).
Уравнения плоской гармонической электромагнитной волны, распространяющейся вдоль оси OX:
E=jEmcos(ωt-kx+φ0), (6.10)
H=kHmcos(ωt-kx+φ0), (6.11)
где j и k - единичные вектора, направленные вдоль осей OY и OZ;
k=2π/λ – волновое число;
λ=vT – длина волны.
6.2.6 В однородной диэлектрической среде фазовая скорость электромагнитных волн зависит от электрических и магнитных свойств этой среды - диэлектрической ε и магнитной μ проницаемостей (6.7).
Тот факт, что скорость распространения
электромагнитных волн в вакууме совпадает со скоростью света ![]() = 3,0·108
м/с, послужил Максвеллу основанием для физического вывода об электромагнитной
природе света и разработки электромагнитной теории света (1865 г.).
= 3,0·108
м/с, послужил Максвеллу основанием для физического вывода об электромагнитной
природе света и разработки электромагнитной теории света (1865 г.).
Первые эксперименты с электромагнитными волнами выполнил в 1888 году Г. Герц. Результаты этих экспериментов полностью соответствовали теории Максвелла.
6.3 Энергия и импульс электромагнитной волны. Вектор Пойнтинга
Энергия электромагнитной волны складывается из энергии электрического и магнитного полей волны. Поэтому плотность энергии, распределенной в области пространства, в которой распространяется электромагнитная волна, равна:
w=we+wm= ![]() . (6.12)
. (6.12)
С учетом (14) связи между значениями напряженностей электрического и магнитных полей получается, что плотности энергии обоих полей волны (в вакууме и диэлектрической среде) равны между собой:
![]() . (6.13)
. (6.13)
Таким образом, плотность энергии электромагнитной волны равна
![]() . (6.14)
. (6.14)
Умножив выражение для w на скорость v волны, получим соотношение, определяющее плотность потока энергии электромагнитной волны:
jw= wv=EH. (6.15)
Векторы E и H взаимно перпендикулярны и образуют с вектором v скорости волны правовинтовую тройку векторов. Следовательно, векторное произведение [E,H] по направлению совпадает с направлением переноса энергии, а модуль этого вектора равен плотности потока энергии jw . Вектор плотности потока энергии электромагнитной волны называют вектором Пойнтинга:
jw= wv= [E,H]. (6.16)
Напомним, что аналогичный по своему физическому смыслу вектор плотности потока энергии упругой волны называется вектором Умова. По модулю векторы Умова и Пойнтинга равны количеству энергии, переносимой волной в единицу времени через единичную площадку, перпендикулярную направлению распространения волны, поэтому единица их измерения 1Вт/м2.
Интенсивность волны, по определению, равна усредненной за период (или за очень большой по сравнению с периодом промежуток времени) плотности потока энергии волны:
I=<jm>= <w>v. (6.17)
В случае плоской гармонической волны вида (15) плотность энергии равна
w=![]() = εε0E2=
εε0Еm2cos2(ωt-kx) .
(6.18)
= εε0E2=
εε0Еm2cos2(ωt-kx) .
(6.18)
Интенсивность такой волны, согласно (6.17), (6.18) и с учетом равенства <cos2(ωt-kx)>=0,5
I=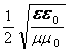 Em2,
(6.19)
Em2,
(6.19)
то есть, интенсивность электромагнитной I волны пропорциональна квадрату амплитуды ее электрической напряженности Em.
Максвелл показал, что электромагнитные волны, отражаясь или поглощаясь в телах, на которые падают, оказывают на них давление. Это давление объясняется силовым действием магнитного поля волны на электрические токи, которые возбуждаются электрическим полем той же волны.
Поскольку электромагнитная волна оказывает давление на тело, следовательно, она обладает импульсом. Иначе говоря, распространение электромагнитной (так же как и упругой) волны сопровождается переносом импульса. Если энергия, переносимая волной, равна W, то величина переносимого ею импульса
p=W/c. (6.20)
Импульс
волны, отнесенный к единице объема, можно выразить через вектор плотности
потока энергии (вектор Пойнтинга)![]()
![]() .
(6.21)
.
(6.21)
6.4 Излучение диполя
Согласно представлениям классической электродинамики электромагнитные волны возбуждаются электрическими зарядами, движущимися с ускорением. Простейшей излучающей системой является электрический диполь, момент которого изменяется периодически.
Рассмотрим излучение гармонического осциллятора – элементарного диполя, размер ℓ которого много меньше длины волны ℓ<<λ, а электрический момент изменяется со временем по гармоническому закону
p=pmcosωt . (6.22)
Примером такой системы служит неподвижный точечный заряд +q и колеблющийся около него точечный заряд – q. Вблизи диполя картина электромагнитного поля очень сложная. Она упрощается в так называемой волновой зоне диполя, то есть на расстояниях r, значительно превышающих длину волны r>>λ. Если волна распространяется в однородной и изотропной среде, то волновые поверхности в волновой зоне имеют сферическую форму. Направление векторов E и H в каждой точке перпендикулярно к лучу; при этом E направлен по касательной к «меридиану», а H – по касательной к «параллели» (см.рисунок 6.3).
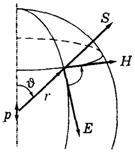
![]() В каждой точке векторы E и H
колеблются по закону cos(ωt-kr), иначе говоря, заряд, совершающий
гармонические колебания с частотой ω, излучает монохроматическую
волну той же частоты. Амплитуды Em и Hm
зависят от расстояния r до излучателя и от угла
В каждой точке векторы E и H
колеблются по закону cos(ωt-kr), иначе говоря, заряд, совершающий
гармонические колебания с частотой ω, излучает монохроматическую
волну той же частоты. Амплитуды Em и Hm
зависят от расстояния r до излучателя и от угла ![]() между направлением радиус-вектора и осью диполя, для
вакуума эта зависимость имеет вид:
между направлением радиус-вектора и осью диполя, для
вакуума эта зависимость имеет вид: ![]()
Em
~Hm~![]() .
.
Рисунок 6.3
Интенсивность волны согласно (6.19) равна:
I~![]() . (6.23)
. (6.23)
Из (6.23) следует, что интенсивность волны изменяется
вдоль луча обратно пропорционально квадрату расстояния r. Кроме того,
она сильно зависит от угла
![]() .
На рисунке 6.4 приведена полярная диаграмма направленности излучения. Вдоль
оси диполя излучение отсутствует (I=0), а в направлениях,
перпендикулярных к оси, интенсивность излучения максимальна.
.
На рисунке 6.4 приведена полярная диаграмма направленности излучения. Вдоль
оси диполя излучение отсутствует (I=0), а в направлениях,
перпендикулярных к оси, интенсивность излучения максимальна.
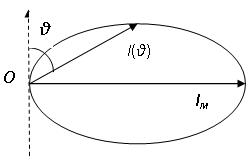 Теоретические расчеты показывают, что мощность излучения диполя (энергия,
излучаемая в единицу времени) пропорциональна квадрату второй производной дипольного
момента по времени:
Теоретические расчеты показывают, что мощность излучения диполя (энергия,
излучаемая в единицу времени) пропорциональна квадрату второй производной дипольного
момента по времени:
P~![]() ,
(6.24)
,
(6.24)
Рисунок 6.4
для гармонически осциллирующего диполя:
P~ pm2ω4cos2ωt. (6.25)
Усреднение за период колебания T=2π/ω дает:
<P>~ pm2ω4. (6.26)
Таким образом, средняя мощность излучения диполя пропорциональна квадрату амплитуды его дипольного момента и четвертой степени частоты.
При решении некоторых проблем в оптике (дисперсия, поглощение в средах, поляризация) атом рассматривают как излучающий диполь, в котором оптический электрон совершает колебания около ядра. Также, всякая реальная передающая антенна может быть представлена как совокупность точечных диполей.
7 Лекция. Свет как электромагнитная волна
7.1 Суперпозиция волн. Волновой пакет. Групповая скорость
Уравнение гармонической волны описывает волну бесконечную во времени и безграничную в пространстве. Но в реальности волновое движение ограничено во времени, поскольку излучение любой волны длится конечный промежуток времени. Значит, реальные волны, которые представляют практический интерес, не являются гармоническими и монохроматическими. В этом случае так же, как и в случае ангармонических колебаний, можно применить разложение в ряд Фурье по гармоническим функциям. Но сначала рассмотрим обратную задачу: что происходит, если в некоторой области пространства одновременно распространяется несколько волн?
Опыт показывает, что в линейных средах волны распространяются независимо друг от друга и справедлив принцип суперпозиции:
ξ
= ![]() ξi
, (7.1)
ξi
, (7.1)
при распространении в линейной среде нескольких волн каждая из них распространяется независимо от других так, что результирующее смещение частицы среды равно геометрической сумме смещений в каждой из волн в отдельности.
Линейными называют среды, свойства которых не зависят от внешних полей. Например, диэлектрическая проницаемость ε такой среды не зависит от величины E напряженности электрического поля. Упругая среда является линейной, если ее модуль Юнга не зависит от величины деформаций.
Особую роль играют одиночные возмущения (короткий волновой импульс от выстрела, взрыва или вспышки); их можно представить как волновые пакеты.
Волновой пакет – это группа близких по волновым числам и по частотам монохроматических волн, амплитуды и фазы которых таковы, что в любой момент времени их сложение дает локализованный в некотором объеме пространства одиночный волновой импульс.
Волновой пакет характеризуется средними значениями волнового числа k0 и частоты ω0, и интервалами ∆k и ∆ω в спектральных разложениях волнового пакета по волновым числам и частотам:
(k0 - ∆k) ≤ k ≥ (k0 + ∆k), ∆k<< k0 ,
(ω0 - ∆ω) ≤ ω ≥ (ω0+∆ω), ∆ω<< ω0 .
Установлено, что чем меньше временная длительность ∆t пакета, тем больше интервал частот ∆ω в его спектральном разложении; и - чем короче его пространственная протяженность Δx, тем больше интервал волновых чисел ∆k.
Пусть в одном направлении с одной и той же скоростью v распространяются две плоские гармонические волны с одинаковыми амплитудами A0 и близкими по значению частотами (ω и ω+dω) и волновыми числами (k и k+dk).
Согласно принципу суперпозиции:
![]()
![]() .
.
Формально полученное выражение можно рассматривать как уравнение квазигармонической волны с медленно периодически изменяющейся амплитудой:
![]() .
(7.2)
.
(7.2)
За скорость u распространения этой несинусоидальной волны принимают скорость перемещения точки M, в которой амплитуда имеет максимальное значение. Следовательно, точка M движется по закону (tdω-xdk)=const. Величина
![]() (7.3)
(7.3)
называется групповой скоростью (скоростью группы волн). Поскольку в этой точке максимальна и плотность энергии, то групповая скорость и есть скорость перемещения энергии волны.
Связь между групповой и фазовой скоростями волны имеет вид:
![]() .
(7.4)
.
(7.4)
7.2 Дисперсия волн
Дисперсией
называется зависимость фазовой скорости распространения монохроматической
волны от ее частоты ω или длины волны λ, то есть
зависимость
v=f(ω), либо ![]() .
.
Для
всех прозрачных бесцветных сред с увеличением длины λ волны в
видимой части спектра показатель преломления n=![]() уменьшается, а
скорость v увеличивается. В этом случае дисперсия называется нормальной.
уменьшается, а
скорость v увеличивается. В этом случае дисперсия называется нормальной.
Рассмотрим распространение произвольной волны как совокупности монохроматических составляющих. Если дисперсия отсутствует, то все эти составляющие распространяются с одинаковыми фазовыми скоростями и потому не смещаются друг относительно друга. Значит, при отсутствии дисперсии (например, в случае электромагнитных волн в вакууме и звуковых волн в воздухе) любая волна сохраняет в процессе распространения свою форму.
При наличии дисперсии сложные (негармонические) волны изменяют свою форму, в частности происходит расплывание волновых пакетов. При этом групповая скорость (7.4) может быть как больше, так и меньше фазовой.
7.3 Свет как электромагнитная волна
Согласно теории Максвелла свет – электромагнитное
излучение, длины волн которого лежат в пределах от 0,001 мкм до 100 мкм, то
есть свет, в широком смысле слова, включает ультрафиолетовую, видимую и
инфракрасную области спектра. Длины волн видимого света лежат в
интервале от 380 нм до 770 нм (в вакууме), а частоты занимают диапазон
ν=(0,39 ![]() . Белый свет – составной, он
представляет собой наложение волн, длины
λ
которых охватывают весь диапазон воспринимаемых глазом электромагнитных волн.
. Белый свет – составной, он
представляет собой наложение волн, длины
λ
которых охватывают весь диапазон воспринимаемых глазом электромагнитных волн.
При переходе из вакуума в прозрачную (диэлектрическую) среду частота ν световых колебаний не изменяется, а фазовая скорость и длина волны уменьшаются в n раз:
![]() ,
, ![]() ; (7.5)
; (7.5)
здесь
![]() -
длина волны в вакууме, n – показатель преломления этой среды.
-
длина волны в вакууме, n – показатель преломления этой среды.
Для подавляющего большинства прозрачных веществ ![]() и зависит от
и зависит от
![]() .
.
В
электромагнитной волне колеблются векторы E и H.
Физиологическое, фотохимическое, фотоэлектрическое и другие действия света
вызываются колебаниями электрического вектора E, поэтому его
называют световым вектором. Интенсивность монохроматической световой
волны пропорциональна квадрату амплитуды светового вектора ![]() .
.
7.4 Интерференция света
Пусть в некоторой области перекрываются две световые, то есть электромагнитные волны. В линейных средах и в вакууме взаимодействие между полями отсутствует. Поэтому волны распространяются независимо друг от друга и в области перекрытия имеет место суперпозиция полей
E=E1+E2 .
Все без исключения приемники света инерционны. Для глаза время разрешения составляет по порядку величины τ ≈ 0,1 с, у фотоматериалов τ ≈ 10-2÷10-4 с, в ячейках Керра (оптические затворы) τ ≈ 10-9 с. Наиболее быстродействующие современные фотоэлементы имеют τ ≈ 10-10 с, но и в этом случае τ>>T, то есть время разрешения τ много больше периода T световых колебаний, так как в области видимого света T≈10-15 с. Поэтому все приемники света могут измерить величину, пропорциональную среднему за время разрешения τ квадрату напряженности <E2>, то есть интенсивность света I.
В области, в которой перекрываются две световые волны, приемник может зафиксировать величину, равную
I=<(E1+E2 )2>= I1 + I2 +2<E1E2>. (7.6)
Последнее слагаемое в выражении (6.9) называется интерференционным членом. Его величина может быть выражена в виде
![]() <cosδ>, (7.7)
<cosδ>, (7.7)
где δ – разность фаз складываемых колебаний.
Результаты сложения волн определяются тем, являются ли волны когерентными или нет:
а) если две волны излучаются двумя независимыми источниками, то разность фаз таких волн в каждой точке (например, экрана) непрерывно изменяется случайным образом, принимая с равной вероятностью любые значения от 0 до 2π, тогда <cos δ> = 0, І12 = 0 и
I = I1 + I2 . (7.8)
Таким образом, при наложении некогерентных волн наблюдаемая интенсивность равна сумме интенсивностей каждой из волн в отдельности;
б) если разность фаз δ, возбуждаемых волнами колебаний, остается постоянной во времени, то волны называются когерентными и в этом случае
I=I1 + I2 +2![]() . (7.9)
. (7.9)
Рассмотрим случай, когда обе волны строго монохроматичны и имеют одну и ту же частоту ω. Монохроматическая волна – это строго синусоидальная волна с постоянными во времени частотой ω, амплитудой A и начальной фазой φ; при этом амплитуда и начальная фаза могут меняться от одной точки пространства к другой, а частота одна и та же везде.
В точках пространства, где выполняется условие cos δ = 1, или
δ=0, 2π, 4π, 6π,…, (7.10)
при
разности фаз, равной четному числу
π, возникают максимумы интенсивности Imax
=I1 + I2 +2![]() .
.
Минимумы возникают в таких точках, в которых cos δ = -1, значит, условие образования интерференционного минимума имеет вид:
δ=π, 3π, 5π,…, (7.11)
то есть, разность фаз должна быть равна нечетному числу π. При этом
Imin
=I1 +
I2
- 2![]() .
.
Таким образом, при наложении когерентных волн происходит перераспределение потока в пространстве, в результате чего в одних местах возникают максимумы, а в других – минимумы интенсивности. Это явление называется интерференцией волн.
Частным случаем интерференции является образование стоячей волны. Стоячая волна образуется при наложении двух когерентных волн, распространяющихся в противоположных направлениях.
Пусть вдоль оси OX распространяются во встречных направлениях две монохроматические с частотой ω и одинаковой амплитудой A0 волны
E1=A0cos(ωtkx) и E2=A0cos(ωt+kx).
В результате их наложения образуется волна
E =E1 + E2 = 2 A0coskx·cosωt. (7.12)
Амплитуда полученной волны определяется выражением
![]() .
(7.13)
.
(7.13)
В отличие от бегущей волны амплитуда стоячей волны зависит от координаты x. В точках, в которых │coskx│= 1, амплитуда удваивается (максимальна) и равна 2A0, а в точках, где │coskx│= 0, амплитуда равна нулю (минимальна). Эти точки называют соответственно пучностями и узлами стоячей волны.
7.5 Временная и пространственная когерентность
Излучение обычных источников (не лазеров) некогерентно; это обусловлено тем, что оно складывается из волн, излучаемых громадными совокупностями его атомов. Процесс излучения атома продолжается в течение времени, длительностью порядка 10-8 с. За это время успевает образоваться цуг волн длиной примерно 3 м. Свет от обычного источника представляет хаотичную последовательность отдельных цугов. Поэтому при наложении световых волн от разных источников фазовые соотношения между колебаниями многократно изменяются случайным образом, и устойчивой интерференционной картины не возникает.
Тем не менее, когерентные световые волны можно получить даже от обычных источников. Общий метод таков: волну, излучаемую одним источником света, разделяют каким–либо способом на две части, которые затем в некоторой области пространства перекрываются. В области перекрытия происходит наложение интерференция расщепленных «половинок» элементарных волновых цугов, излученных отдельными атомами.
Оптическая длина пути
L – это произведение расстояния ℓ, которое
проходит волна в некоторой среде, на показатель
n
преломления в данной среде ![]() . Разность оптических длин проходимых
волнами путей от точки расщепления до точки их наложения называют оптической
разностью хода:
. Разность оптических длин проходимых
волнами путей от точки расщепления до точки их наложения называют оптической
разностью хода:
![]() . (7.14)
. (7.14)
Связь между разностью фаз двух волн и оптической разностью хода
![]() . (7.15)
. (7.15)
Тогда условие образования интерференционных максимумов:
![]() , m=0, 1, 2, 3,…
(7.16)
, m=0, 1, 2, 3,…
(7.16)
Интерференционные минимумы наблюдаются, если волны приходят в противофазе, при этом оптическая разность хода равна нечетному числу полуволн:
![]() , m=0,
1, 2, 3,… (7.17)
, m=0,
1, 2, 3,… (7.17)
Когерентностью называется согласованное протекание нескольких колебательных или волновых процессов.
Согласованное протекание волновых
процессов, происходящих в одной и той же точке, но в разные моменты
времени, называют временной когерентностью.
Промежуток времени τког, в
течение которого случайные изменения начальной фазы волны в данной точке
достигают значения порядка π, называется временем когерентности. За
это время колебание становится некогерентным по отношению к самому себе.
Расстояние, на которое перемещается волна за время τког,
называют длиной когерентности ![]() . Следовательно, расщепленные волны,
приходящие в точку наблюдения с разностью хода, равной или превышающей ℓког,
не образуют интерференционной картины, т.к. некогерентны.
. Следовательно, расщепленные волны,
приходящие в точку наблюдения с разностью хода, равной или превышающей ℓког,
не образуют интерференционной картины, т.к. некогерентны.
Соответствующий расчет дает, что время ![]() когерентности
обратно пропорционально интервалу частот
когерентности
обратно пропорционально интервалу частот ![]() , представленных в данной световой
волне:
, представленных в данной световой
волне: ![]() .
Это означает, что чем уже интервал частот, представленных в данной световой
волне, тем больше время когерентности этой волны. Для монохроматической волны
.
Это означает, что чем уже интервал частот, представленных в данной световой
волне, тем больше время когерентности этой волны. Для монохроматической волны ![]() и время
когерентности
и время
когерентности ![]() .
.
Длину когерентности можно оценить с помощью
соотношения ![]() . Для солнечного света λ=0,50 мкм
(зеленая часть спектра) и Δλ=0,40 мкм, тогда
. Для солнечного света λ=0,50 мкм
(зеленая часть спектра) и Δλ=0,40 мкм, тогда
ℓког≈(0,50)2/0,40 мкм ≈0,6 мкм=0,6·10-3 мм.
Пространственная когерентность – это согласованное протекание колебательных процессов, которые совершаются в один и тот же момент времени в разных точках поверхности, перпендикулярной направлению распространения волны (так называемой квазиволновой поверхности). Пространственная когерентность зависит от условий излучения и формирования световых волн. В реальной световой волне, излучаемой множеством независимых атомов протяженного источника света, разность фаз колебаний в двух точках квазиволновой поверхности Q, - случайная функция времени.
Радиусом
когерентности ρког называют расстояние между двумя
точками поверхности Q, случайные изменения разности фаз δ, в
которых достигают порядка π. Если источник имеет форму диска, диаметр
которого виден из данной точки под углом φ, то![]() . Для Солнца φ≈0,01
рад, λ≈0,50 мкм, ρког ≈0,05 мм.
. Для Солнца φ≈0,01
рад, λ≈0,50 мкм, ρког ≈0,05 мм.
7.6 Методы наблюдения интерференции света
7.6.1 Опыт Юнга. В опыте Юнга пучок яркого солнечного света пропускался через узкую щель S. Прошедшим светом освещались две узкие параллельные и близко расположенные щели S1 и S2 во втором непрозрачном экране. На экране в области перекрытия пучков наблюдались параллельные чередующиеся темные и светлые интерференционные полосы.
 Расстояние между двумя соседними максимумами интенсивности называют
расстоянием между интерференционными полосами, а расстояние между соседними
минимумами интенсивности – шириной интерференционной полосы. Расстояние между
полосами и ширина полосы имеют одинаковое значение, равное
Расстояние между двумя соседними максимумами интенсивности называют
расстоянием между интерференционными полосами, а расстояние между соседними
минимумами интенсивности – шириной интерференционной полосы. Расстояние между
полосами и ширина полосы имеют одинаковое значение, равное
![]() .
(7.18)
.
(7.18)
Рисунок 7.1
7.6.2 Интерференция в тонких пленках. Пусть на
плоскопараллельную пленку толщины d с показателем преломления n
падает параллельный пучок монохроматического света с длиной волны λ0.![]() При отражении
от обеих поверхностей пленки разность хода между волнами 1 и 2 (см.рисунок
7.1) равна
При отражении
от обеих поверхностей пленки разность хода между волнами 1 и 2 (см.рисунок
7.1) равна
![]() .
.
«Потеря» полуволны обусловлена тем, что при
отражении от оптически более плотной среды (с бóльшим показателем
преломления n)
фаза отраженной волны скачком изменяется на ![]() , а при
отражении от оптически менее плотной среды – не изменяется.
, а при
отражении от оптически менее плотной среды – не изменяется.
После геометрических преобразований и с учетом закона преломления света:
![]() . (7.19)
. (7.19)
7.6.3 Кольца Ньютона. При отражении света от поверхностей зазора между стеклянной пластиной и прижатой к ней плоско-выпуклой линзой наблюдаются кольца Ньютона. При нормальном падении света интерференционная картина имеет вид чередующихся темных и светлых концентрических колец. В отраженном свете в центре картины - темное пятно; радиусы темных колец:
![]() , (7.20)
, (7.20)
где m - номер кольца, m=1, 2, 3, …;
R – радиус кривизны линзы.
8 Лекция. Дифракция волн
8.1 Принцип Гюйгенса-Френеля
В однородных и изотропных средах распространение волн происходит прямолинейно и подчиняется законам геометрической оптики.
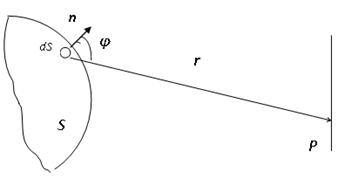 В средах с резкими неоднородностями, например, вблизи
краев непрозрачного экрана или отверстия, наблюдается дифракция - огибание волнами препятствий (соизмеримыми с
длиной волны падающего света) и проникновение в область
геометрической тени (отклонение от законов геометрической оптики).
В средах с резкими неоднородностями, например, вблизи
краев непрозрачного экрана или отверстия, наблюдается дифракция - огибание волнами препятствий (соизмеримыми с
длиной волны падающего света) и проникновение в область
геометрической тени (отклонение от законов геометрической оптики).
Рисунок 8.1
Для объяснения и расчета дифракционных явлений в теории волн применяется принцип Гюйгенса-Френеля.
Согласно принципу Гюйгенса-Френеля каждый элемент волновой поверхности (в общем случае - любой вспомогательной поверхности, до которой доходит излучение) dS можно рассматривать как источник вторичной сферической волны. Поскольку эти вторичные волны являются составными частями единой исходной волны, они когерентны между собой, поэтому в произвольной точке наблюдения P, в которую приходят вторичные волны, будет происходить их наложение (интерференция), в результате чего волны либо усиливают друг друга, либо гасят.
Амплитуда вторичной волны пропорциональна площади элемента волновой поверхности dS, на расстоянии r от него она убывает по закону 1/r. Следовательно, от каждого элемента волновой поверхности в точку наблюдения P (см.рисунок 8.1) приходит колебание светового вектора
dE=K(φ)![]() cos(ωt-kr+α), (8.1)
cos(ωt-kr+α), (8.1)
где (ωt+α) – фаза колебания в месте расположения поверхности S;
r – расстояние от элемента dS поверхности до точки P;
A – множитель, определяемый амплитудой световой волны в том месте, где находится площадка dS;
K(φ) – коэффициент, зависящий от угла φ между нормалью n к площадке dS и направлением от нее к точке P. При φ =0 этот коэффициент максимален, при φ = π/2 он обращается в нуль.
Результирующее колебание в точке P представляет собой суперпозицию колебаний (8.1), взятых по той части волновой поверхности S, которая открыта для точки наблюдения P:
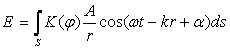 . (8.2)
. (8.2)
Формула (8.2) - аналитическое выражение принципа Гюйгенса – Френеля.
8.2 Метод зон Френеля
В тех случаях, когда источники света имеют симметричную форму и соответственной симметрией обладают волновые поверхности излучаемых ими волн, амплитуду результирующего колебания можно найти простым алгебраическим или геометрическим суммированием.
Этот простой и эффективный метод носит название метода зон Френеля и заключается в следующем. В качестве вспомогательной поверхности выбирается одна из волновых поверхностей (во всех точках которой фазы волны одинаковы). Эта поверхность разбивается на участки, называемые зонами Френеля, таким образом, чтобы разность хода волн от внутреннего и внешнего краев каждого участка до точки наблюдения была равна половине длины волны λ/2. В некоторых случаях вместо точки наблюдения задается некоторое направление в пространстве, тогда половине длины волны должна равняться разность хода волн от краев участка в данном направлении.
Рассмотрим метод зон Френеля на примере точечного источника света S, волновые поверхности которого представляю собой (в однородной и изотропной среде) концентрические сферы. Рассмотрим одну из этих сфер, удаленную от точки наблюдения на расстоянии b. Разобьем эту волновую поверхность на кольцевые зоны таким образом, что расстояния от краев (внутреннего и внешнего) каждой зоны отличались на λ/2. Ясно, что расстояние от края первой (центральной) зоны до точки P, равно (b+λ/2), а от внешнего края m–ой зоны – (b+mλ/2).
Колебания, приходящие в точку P от аналогичных участков (например, лежащих в середине зон, или у внешних краев) двух соседних зон, приходят в противофазе. Поэтому и результирующие колебания, создаваемые каждой из зон в целом, будут для соседних зон отличаться по фазе на π. Следовательно, вторичные волны двух соседних зон будут приходить в точку наблюдения в противофазе и при наложении друг друга гасить.
Точный расчет дает, что площади кольцевых зон при не слишком больших m примерно одинаковы. Расстояние bm от зоны до точки P медленно растет с ростом номера m. Все это приводит к тому, что амплитуда Am колебания, возбуждаемого m–ой зоной в рассматриваемой точке P, монотонно убывает с ростом m, так что
A1> A2>A3>A4> … > Am-1>Am>Am+1> …
Вследствие монотонного убывания амплитуд оказывается, что амплитуда Am колебания от некоторой m–й зоны Френеля равна среднему арифметическому от амплитуд примыкающих к ней зон
Am =![]() .
(8.3)
.
(8.3)
Фазы колебаний, возбуждаемых соседними зонами, отличаются на π, поэтому амплитуда A результирующего колебания в точке P может быть представлена в виде знакопеременного ряда
A= A1 – A2 + A3 – A4+ A5- … (8.4)
Перепишем выражение (6.4) следующим образом
![]() (8.5)
(8.5)
С учетом соотношения (8.3) при m→ ∞ (на пути от источника S до экрана P нет никаких препятствий) выражение (8.5) упрощается
A = A1/2. (8.6)
Полученное соотношение означает, что амплитуда, создаваемая в некоторой точке P всей сферической волновой поверхностью, равна половине амплитуды, создаваемой одной лишь центральной зоной.

Рисунок 8.2
Если на пути волны поставить непрозрачную преграду с вырезанным в ней круглым отверстием, оставляющим открытой лишь одну центральную зону, то амплитуда в точке P будет равна A1, то есть в два раза будет больше, чем A. Соответственно интенсивность света в этом случае будет в четыре раза больше, чем в отсутствие преград между источником и экраном (между точками S и P).
Внешний радиус m–ой кольцевой зоны можно определить по формуле
![]() .
(8.7)
.
(8.7)
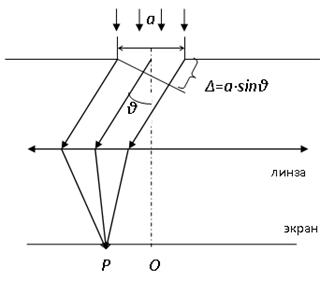 Из соотношения (8.4) следует, что если между
источником S
и экраном P находится круглая
диафрагма (отверстие в непрозрачной преграде), то интенсивность света в точке
наблюдения P – центре дифракционной картины - будет зависеть от того,
сколько зон укладываться в этом отверстии.
Из соотношения (8.4) следует, что если между
источником S
и экраном P находится круглая
диафрагма (отверстие в непрозрачной преграде), то интенсивность света в точке
наблюдения P – центре дифракционной картины - будет зависеть от того,
сколько зон укладываться в этом отверстии.
Минимумы интенсивности будут наблюдаться при четном числе зон m =2,4,6,… (поскольку колебания от каждой пары соседних зон взаимно гасят друг друга), а максимумы – при нечетном числе зон m =1,3,5,… В целом, дифракционная картина от круглого отверстия имеет вид чередующихся светлых и темных колец.
Рисунок 8.3
8.3 Дифракция на одной и многих щелях
Пусть на узкую длинную щель шириной a падает по нормали к ней плоская световая волна. Поместим за щелью собирающую линзу, а в фокальной плоскости линзы - экран (см.рисунок 8.3).
Дифракционная картина на экране при освещении узкой щели монохроматическим светом от лазера представляет собой систему симметрически расположенных вдоль прямой линии светлых (того же цвета, что и лазерное излучение) пятен, при этом в центре картины располагается максимум, по интенсивности значительно превосходящий остальные максимумы. Максимумы разделены минимумами.
Дифракционные минимумы наблюдаются при таких углах дифракции θ, для которых в щели укладывается четное число зон Френеля:
![]() , (8.8)
, (8.8)
где m – порядок минимума, принимает значения 1, 2, 3, …
Дифракционная решетка представляет собой совокупность большого числа расположенных в одной плоскости, отстоящих друг от друга на одно и то же расстояние, одинаковых параллельных щелей.
Расстояние d между серединами соседних щелей называется периодом (или постоянной) решетки. Период решетки равен сумме ширины щели a и непрозрачного промежутка между щелями: d=a+b.
Для получения более четкой дифракционной картины между дифракционной решеткой и экраном располагают собирающую линзу так, что экран находится в ее фокальной плоскости (см.рисунок 8.4).
При прохождении через дифракционную решетку имеет место, во-первых, интерференции световых волн, дифрагировавших на каждой щели в отдельности; во-вторых, интерференция волн, дифрагировавших от разных щелей. При этом положение минимумов (8.8), соответствующих дифракции на одной щели, остается неизменным и при дифракции на N щелях.
Положение главных дифракционных максимумов при нормальном падении параллельного пучка монохроматического света длиной волны λ на дифракционную решетку определяется из формулы:
dsinθ = mλ , m=0, 1, 2, 3, …, mпред , (8.9)
где
mпред – наибольший порядок наблюдаемого максимума,
равный целому числу ![]() , ближайшему к отношению d/λ
с меньшей стороны.
, ближайшему к отношению d/λ
с меньшей стороны.
8.4 Спектральное разложение
Положение дифракционных максимумов (кроме центрального) зависит от длины волны λ. Поэтому при падении на решетку немонохроматического (например, белого) света разным длинам волн будут соответствовать сдвинутые относительно друг друга максимумы, то есть все максимумы ненулевого порядка (m=1, 2,…) разложатся в спектр.
Таким образом, дифракционная решетка позволяет установить спектральный состав направленного на нее излучения и потому представляет собой спектральный прибор. Если излучение состоит из нескольких монохроматических волн, например, λ1 и λ2, то и каждый из максимумов (кроме центрального) будет состоять из отдельных (двух - в нашем примере) спектральных линий; причем очень важно, что максимумы для каждой длины волны (при большом числе N щелей в дифракционной решетке) получаются очень узкими. Поэтому решетка – это спектральный прибор высокого разрешения.
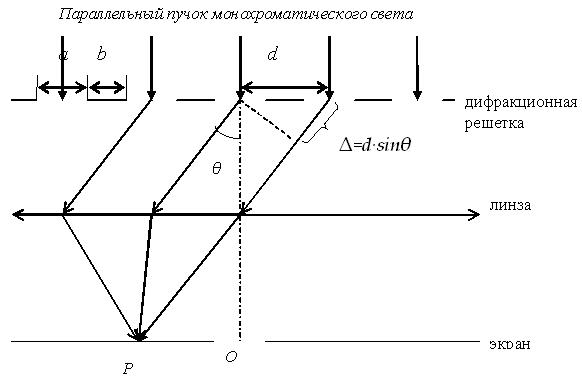
Рисунок 8.4
В отличие от стеклянной призмы дифракционная решетка:
а) сильнее отклоняет не фиолетовые, а наоборот, красные лучи – с большей длиной волны λ;
б) равномерно растягивает спектр, в то время как призма – неравномерно, т. к. длинноволновая (красная) часть ее спектра сжата, а коротковолновая (фиолетовая) более растянута.
9 Лекция. Тепловое излучение
9.1 Характеристики и законы теплового излучения
Свечение тел, т.е. излучение телами электромагнитных волн, может осуществляться за счет различных видов энергии. Испускание электромагнитных волн за счет внутренней энергии тел - тепловое излучение. Все остальные виды свечения, возбуждаемые за счет любого вида энергии, кроме внутренней – люминесценция: хемилюминесценция, электролюминесценция, катодолюминесценция, фотолюминесценция. Тепловое излучение – равновесное, все остальные виды излучения неравновесные. К равновесным состояниям и процессам применимы законы термодинамики.
Энергетическая
светимость тела R, испускательная способность тела
![]() связаны
между собой соотношением
связаны
между собой соотношением
 .
(9.1)
.
(9.1)
Пусть поток лучистой энергии, падающий
на элемент площади - dФw, а
dФ![]() часть потока,
поглощенная телом. Безразмерная величина
часть потока,
поглощенная телом. Безразмерная величина
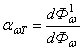 ,
(9.2)
,
(9.2)
называется поглощательной способностью
тела. Для абсолютно черного тела ![]() , если
, если ![]() , то тело – серое.
, то тело – серое.
Закон Кирхгофа гласит: отношение испускательной и поглощающей способностей не зависит от природы тела, оно является для всех тел одной и той же (универсальной) функцией частоты (длины волны) и температуры:
![]() (9.3)
(9.3)
или
![]()
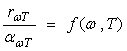 .
. ![]() (9.4)
(9.4)
Функция f (w, Т) может быть названа испускательной способностью абсолютно черного тела.
При теоретических исследованиях для характеристики спектрального состава равновесного теплового излучения удобнее пользоваться функцией частоты f (w, Т). В экспериментальных работах - функцией длины волны. Обе функции связаны друг с другом формулой
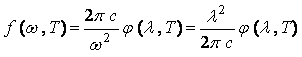 . (9.5)
. (9.5)
Абсолютно черных тел в природе
не существует. Однако можно создать устройство, сколь угодно близкое по своим
свойствам к абсолютно черному телу. Такое устройство представляет собой почти
замкнутую полость, снабженную малым отверстием и излучение, проникшее внутрь
через отверстие, прежде чем выйти обратно из отверстия, претерпевает
многократные отражения. При каждом отражении часть энергии поглощается, в
результате чего практически все излучение любой частоты поглощается такой полостью.
Согласно закону Кирхгофа испускательная способность такого устройства очень
близка к f (w, Т) Т – температура стенок
полости. Если стенки полости поддерживать при некоторой температуре Т, то из
отверстия выходит излучение, близкое по спектральному составу к излучению абсолютно
черного тела. Результаты опытов по исследованию поведения функции ![]() приведены на
рисунке 9.1.
приведены на
рисунке 9.1.![]()
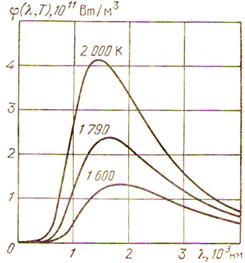 В равновесном состоянии энергия
излучения будет распределена в объеме полости с определенной плотностью энергии
u =
u (T). Спектральное распределение этой энергии можно
охарактеризовать функцией u
(w, Т), определяемой условием
В равновесном состоянии энергия
излучения будет распределена в объеме полости с определенной плотностью энергии
u =
u (T). Спектральное распределение этой энергии можно
охарактеризовать функцией u
(w, Т), определяемой условием ![]() где
где ![]()
![]() доля плотности энергии,
приходящаяся на интервал частот
доля плотности энергии,
приходящаяся на интервал частот ![]() Полная плотность энергии
u (T)
связана с функцией u (w, Т) формулой
Полная плотность энергии
u (T)
связана с функцией u (w, Т) формулой
 (9.6)
(9.6)
Рисунок 9.1
Универсальная
функция ![]() связана
со спектральным распределением плотности энергии
связана
со спектральным распределением плотности энергии ![]() выражением:
выражением:
![]() .
(9.7)
.
(9.7)
Закон Стефана-Больцмана связывает энергетическую светимость абсолютно черного тела с его абсолютной температурой
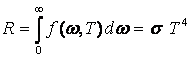 ,
(9.8)
,
(9.8)
где s - постоянная Стефана-Больцмана.
Закон смещения Вина связывает абсолютную температуру и
длину волны ![]() на которую приходится максимум функции
на которую приходится максимум функции
![]()
![]() ,
(9.9)
,
(9.9)
где b - константа, численно равная (экспериментальное значение):
b = 2,90 10![]() м.К.
м.К.
9.2 Проблемы излучения абсолютно черного тела
Полученная по классической теория формула Релея-Джинса выглядит следующим образом:
![]() (9.10)
(9.10)
или
![]() . (9.11)
. (9.11)
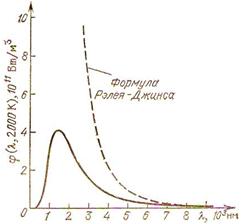 Эта формула удовлетворительно согласуется с экспериментальными
данными лишь при больших длинах волн и резко расходится с опытом для малых
длин волн (рисунок 9.2). Подстановка формулы (9.10) в (9.6) дает для равновесной
плотности энергии u (T) бесконечно большое значение. Этот результат, получивший
название ультрафиолетовой катастрофы, также находится в противоречии с
опытом.
Эта формула удовлетворительно согласуется с экспериментальными
данными лишь при больших длинах волн и резко расходится с опытом для малых
длин волн (рисунок 9.2). Подстановка формулы (9.10) в (9.6) дает для равновесной
плотности энергии u (T) бесконечно большое значение. Этот результат, получивший
название ультрафиолетовой катастрофы, также находится в противоречии с
опытом.
Равновесие между излучением и излучающим телом устанавливается при конечных значениях u (T). Рисунок 9.2
9.3 Квантовая гипотеза и формула Планка
Формула Планка (1900 г.): h или
![]() -
постоянная Планка. Величина энергии квантов пропорциональна частоте излучения
-
постоянная Планка. Величина энергии квантов пропорциональна частоте излучения
![]() .
(9.12)
.
(9.12)
Можно показать, что средняя энергия излучения частоты w равна
![]() ,
(9.13)
,
(9.13)
тогда
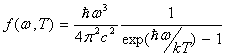 (9.14)
(9.14)
(9.14) – формула Планка, дает исчерпывающее описание равновесного теплового излучения.
10 Лекция. Корпускулярные свойства электромагнитного излучения
10.1 Фотоэффект
Явление фотоэффекта (1887 г.) – Г. Герц. Опыты А.Г. Столетова по исследованию явления фотоэффекта (1888 – 1889 гг.) Опыты Ленарда и других исследователей по усовершенствованию прибора А.Г. Столетова (1898 г.)
10.2 Энергия и импульс световых квантов
Опыт Боте. Фотоны. Энергия и импульс фотона. Масса покоя фотона. Согласно гипотезе световых квантов Эйнштейна, свет испускается, поглощаются и распространяется дискретными порциями (квантами), названными фотонами. Масса фотона может быть определена из закона взаимосвязи массы и энергии
![]() (10.1)
(10.1)
Фотон - элементарная частица, которая всегда движется со скоростью света с и имеет массу покоя, равную нулю.
Импульс фотона определяется по формуле
![]() (10.2)
(10.2)
Фотон,
как и любая другая частица, характеризуется энергией, массой и импульсом. Выражения
(1), (2) связывают корпускулярные характеристики фотона – массу, импульс и энергию
с волновой характеристикой света – его частотой ![]() .
.
Поскольку фотоны обладают импульсом, то свет, падающий на тело, должен оказывать на него давление:
![]() (10.3)
(10.3)
![]() есть энергия
всех фотонов, падающих на единицу поверхности в единицу времени, т.е.
энергетическая освещенность поверхности,
есть энергия
всех фотонов, падающих на единицу поверхности в единицу времени, т.е.
энергетическая освещенность поверхности, ![]() - коэффициент отражения света.
- коэффициент отражения света.
Формула (3) выведенная на основе квантовых представлений, совпадает с выражением, получаемым из электромагнитной теории Максвелла.
10.3 Гипотеза и уравнение Эйнштейна
Идея А. Эйнштейна по объяснению закономерностей фотоэффекта. Формула Эйнштейна
![]() . (10.4)
. (10.4)
Условие возникновения фотоэффекта
 , (10.5)
, (10.5)
где А – работа выхода.
![]()
или
![]() . (10.6)
. (10.6)
Частота w0 или длина волны l0 - красная граница фотоэффекта.
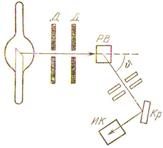 10.4 Эффект Комптона
10.4 Эффект Комптона
Эффект Комптона (1923 г.). А. Комптон, исследуя рассеяние рентгеновских лучей различными веществами, обнаружил, что в рассеянных лучах наряду с излу
чением первоначальной длины волны ![]() содержатся также лучи
большей длины волны
содержатся также лучи
большей длины волны ![]() .
.
Рисунок 10.1
Оказалось, что
![]() (10.7)
(10.7)

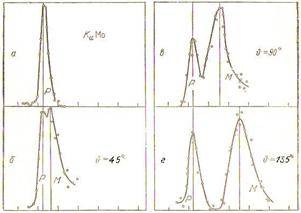
![]() угол,
образуемый направлением рассеянного излучения с направлением первичного пучка.
Т.е. разность Dl от длины волны
l и от природы вещества не зависит. Схема опыта
показана на рисунке 10.1. На рисунке 10.2 приведены результаты исследования
рассеяния монохроматических (характеристических) рентгеновских лучей (линия
угол,
образуемый направлением рассеянного излучения с направлением первичного пучка.
Т.е. разность Dl от длины волны
l и от природы вещества не зависит. Схема опыта
показана на рисунке 10.1. На рисунке 10.2 приведены результаты исследования
рассеяния монохроматических (характеристических) рентгеновских лучей (линия ![]() ) молибдена
на графите. Кривая а характеризует первичное излучение. Остальные кривые
относятся к разным углам рассеяния
) молибдена
на графите. Кривая а характеризует первичное излучение. Остальные кривые
относятся к разным углам рассеяния ![]() , значения которых указаны на рисунке. По
оси ординат отложена интенсивность излучения, по оси абсцисс – длина волны. Рисунок
10.2 Все особенности эффекта Комптона можно объяснить, рассматривая
рассеяние как процесс упругого столкновения рентгеновских фотонов с практически
свободными электронами. Если на первоначально покоящийся свободный электрон
падает фотон с энергией
, значения которых указаны на рисунке. По
оси ординат отложена интенсивность излучения, по оси абсцисс – длина волны. Рисунок
10.2 Все особенности эффекта Комптона можно объяснить, рассматривая
рассеяние как процесс упругого столкновения рентгеновских фотонов с практически
свободными электронами. Если на первоначально покоящийся свободный электрон
падает фотон с энергией ![]() и импульсом
и импульсом ![]() (см.рисунок
10.3), то используя законы сохранения энергии и импульса, можно показать, что:
(см.рисунок
10.3), то используя законы сохранения энергии и импульса, можно показать, что:
Рисунок 10.3
![]() ,
(10.8)
,
(10.8)
где
![]() (10.9)
(10.9)
носит название комптоновской длины волны. Определяемая выражением (10.6) дает для комптоновской длины волны электрона значение
![]() .
.
Результаты измерений
Комптона и последующих измерений находятся в полном согласии с формулой (10.9),
если подставить в неё значение для ![]() .
.
11 Лекция. Корпускулярно-волновой дуализм вещества как универсальное свойство материи. Уравнение Шредингера
11.1 Гипотеза де Бройля и ее экспериментальное подтверждение
Гипотеза де Бройля (1924 г.) – дуализм не является особенностью одних только оптических явлений, но имеет универсальное значение. Фотон обладает энергией
![]()
и импульсом
![]() .
.
По идее де Бройля движение электрона или какой-либо другой частицы связано с волновым процессом, длина волны которого равна
![]() , (11.1)
, (11.1)
а частота
![]() .
(11.2)
.
(11.2)
 Опыт Дэвиссон – Джермер (1927 г.) – отражение электронов от монокристалла
никеля (кубическая система) (см.рисунок 11.1). Рассеяние оказалось особенно интенсивным
при определенном значений угла рассеяния
j, который
соответствовал отражению от атомных плоскостей, расстояние между которыми
d
было известно из рентгенографических исследований (см.рисунок 11.2). Рисунок
11.1
Опыт Дэвиссон – Джермер (1927 г.) – отражение электронов от монокристалла
никеля (кубическая система) (см.рисунок 11.1). Рассеяние оказалось особенно интенсивным
при определенном значений угла рассеяния
j, который
соответствовал отражению от атомных плоскостей, расстояние между которыми
d
было известно из рентгенографических исследований (см.рисунок 11.2). Рисунок
11.1

Рисунок 11.2
Вычисленная по
формуле (11.1) длина волны для максимального тока (U![]() )
равна 1,67 А
)
равна 1,67 А![]() .
Брэгговская длина волны, отвечающая условию
.
Брэгговская длина волны, отвечающая условию
2dSin![]() ,
,
равнялась 1,65 А![]() . Опыты Дэвиссона –
Джермера подтвердили идеи де Бройля.
. Опыты Дэвиссона –
Джермера подтвердили идеи де Бройля.
В 1927 г. Г.П. Томсон и независимо от него П.С. Тартаковский получили дифракционную картину при прохождении электронного пучка через металлическую фольгу.
Было обнаружено, что дифракционные явления обнаруживаются также у атомных и молекулярных пучков.
Л.М. Биберман, Н.Г. Сушков, В.А. Фабрикант (1949 г.) – опыт со слабым электронным пучком.
11.2 Волновые свойства микрочастиц и соотношение неопределенностей Гейзенберга
В классической механике состояние материальной точки определяется заданием динамических переменных (координата, импульс, энергия и т.д.).
Своеобразие микрочастиц - при измерениях не для всех переменных получаются определенные значения:
![]() .
(11.3)
.
(11.3)
Любая микрочастица
не может иметь одновременно точных значений координаты
x и компоненты
импульса р![]() .
Если одна из переменных имеет точное значение, другая переменная при этом
оказывается совершенно неопределенной.
.
Если одна из переменных имеет точное значение, другая переменная при этом
оказывается совершенно неопределенной.
В.Гейзенберг (1927 г.): Произведение неопределенностей значений двух сопряженных переменных не может быть по
порядку величины меньше постоянной Планка ![]() . (Принцип неопределенности
Гейзенберга). Энергия Е и время
t - также канонически сопряженные величины, поэтому
. (Принцип неопределенности
Гейзенберга). Энергия Е и время
t - также канонически сопряженные величины, поэтому
![]() .
(11.4)
.
(11.4)
11.3 Уравнение Шредингера. Состояние частицы в квантовой механике. Пси-функция. Временное и стационарное уравнения Шредингера
Э. Шредингер (1926 г.) – в развитие идеи де Бройля о волновых свойствах вещества получил свое временное уравнение
![]() . (11.5)
. (11.5)
![]() - комплексная функция (пси- функция) координат и
времени, характеризует состояние микрочастицы. Это основное уравнение нерелятивистской
квантовой механики. Для стационарных состояний оно имеет вид:
- комплексная функция (пси- функция) координат и
времени, характеризует состояние микрочастицы. Это основное уравнение нерелятивистской
квантовой механики. Для стационарных состояний оно имеет вид:
![]() . (11.6)
. (11.6)
В квантовой механике большую роль играет понятие оператора. Под оператором подразумевают правило, посредством которого одной функции сопоставляется другая функция:
![]() .
.
Здесь ![]() -
символическое обозначение оператора. Под символом оператора скрывается
совокупность действий, с помощью которых исходная функция (j) превращается в другую функцию (f). Оператор
может, в частности, представлять собой умножение исходной функции
-
символическое обозначение оператора. Под символом оператора скрывается
совокупность действий, с помощью которых исходная функция (j) превращается в другую функцию (f). Оператор
может, в частности, представлять собой умножение исходной функции ![]() на некоторую
функцию U. Тогда
на некоторую
функцию U. Тогда ![]() = U
= U![]() и,
следовательно,
и,
следовательно, ![]() . Если рассматривать функцию
U в
уравнении (11.6) как оператор, действие которого на пси-функцию сводится к
умножению
. Если рассматривать функцию
U в
уравнении (11.6) как оператор, действие которого на пси-функцию сводится к
умножению ![]() на
U, то уравнению (11.6) можно придать вид
на
U, то уравнению (11.6) можно придать вид
![]() . (11.7)
. (11.7)
В этом уравнении символом ![]() обозначен
оператор энергии Е, его называют оператором Гамильтона или гамильтонианом:
обозначен
оператор энергии Е, его называют оператором Гамильтона или гамильтонианом:
![]() . (11.8)
. (11.8)
По Борну (1926 г.) квадрат модуля ![]() функции
определяет вероятность dP того, что частица будет обнаружена в пределах объема
dV
функции
определяет вероятность dP того, что частица будет обнаружена в пределах объема
dV
![]() . (11.9)
. (11.9)
А - коэффициент пропорциональности, для пси-функции выполняется следующее условие нормировки:
![]() . (11.10)
. (11.10)
Из смысла ![]() функции
вытекает, что квантовая механика имеет статистический характер. Уравнение
Шредингера позволяет найти пси – функцию данного состояния и, следовательно,
определить вероятность нахождения частицы в различных точках пространства. Из
уравнения (11.6) и условий, налагаемых на пси – функцию, непосредственно вытекают
правила квантования энергии.
функции
вытекает, что квантовая механика имеет статистический характер. Уравнение
Шредингера позволяет найти пси – функцию данного состояния и, следовательно,
определить вероятность нахождения частицы в различных точках пространства. Из
уравнения (11.6) и условий, налагаемых на пси – функцию, непосредственно вытекают
правила квантования энергии.
Пси – функция должна быть однозначной, непрерывной и конечной, кроме того она должна иметь непрерывную и конечную производную – стандартные условия.
В уравнение Шредингера входит в качестве параметра полная энергия частицы Е. В теории дифференциальных уравнений доказывается, что уравнения вида (11.6) имеют решения, удовлетворяющие стандартным условиям, не при любых значениях энергии Е, а лишь при некоторых избранных значениях. Эти избранные значения называются собственными значениями соответствующей величины, т.е. энергии. Решения, соответствующие собственным значениям Е, называются собственными функциями задачи. Совокупность собственных значений называется спектром величины. Если эта совокупность образует дискретную последовательность, спектр называется дискретным. Если собственные значения образуют непрерывную последовательность, спектр называют непрерывным или сплошным.
11.4 Решение уравнения Шредингера для простейших квантовых систем. Задача о частице в одномерной прямоугольной яме
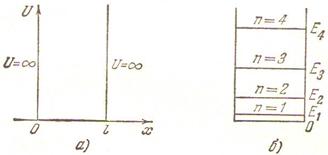 Найдем собственные значения энергии и соответствующие
им собственные функции для частицы, находящейся в бесконечно глубокой одномерной
потенциальной яме. Предположим, что частица может двигаться только вдоль оси
x.
Пусть движение ограничено непроницаемыми для частицы стенками:
x = 0
и x =l. Потенциальная энергия в этом случае равна нулю при
Найдем собственные значения энергии и соответствующие
им собственные функции для частицы, находящейся в бесконечно глубокой одномерной
потенциальной яме. Предположим, что частица может двигаться только вдоль оси
x.
Пусть движение ограничено непроницаемыми для частицы стенками:
x = 0
и x =l. Потенциальная энергия в этом случае равна нулю при ![]() и обращается
в бесконечность при x
<
0 и x
>
l (см.рисунок 11.3а). Уравнение Шредингера для такой
задачи упрощается:
и обращается
в бесконечность при x
<
0 и x
>
l (см.рисунок 11.3а). Уравнение Шредингера для такой
задачи упрощается:
Рисунок 11.3
![]() , (11.11)
, (11.11)
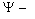 функция
удовлетворяет условию
функция
удовлетворяет условию
![]() , (11.12)
, (11.12)
l - ширина ямы.
Можно показать, что собственные значения энергии частицы являются дискретными:
![]() (n =
1, 2, 3, . . .). (11.13)
(n =
1, 2, 3, . . .). (11.13)
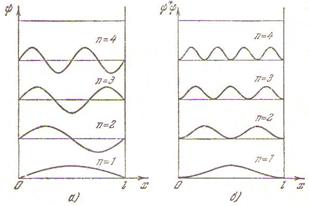 Таким образом, энергия частицы в «потенциальной яме» с бесконечно высокими
«стенками» принимает лишь определенные дискретные значения, т. е. квантуется (см.рисунок
11.4 б). Квантованные значения энергии
Таким образом, энергия частицы в «потенциальной яме» с бесконечно высокими
«стенками» принимает лишь определенные дискретные значения, т. е. квантуется (см.рисунок
11.4 б). Квантованные значения энергии ![]() называются уровнями энергии, а число
n,
определяющее энергетические уровни частицы, называется главным квантовым
числом. Собственные функции имеют вид:
называются уровнями энергии, а число
n,
определяющее энергетические уровни частицы, называется главным квантовым
числом. Собственные функции имеют вид:
Рисунок 11.4
![]() (n =1, 2, 3, . .
.). (11.14)
(n =1, 2, 3, . .
.). (11.14)
Рассмотрение плотности вероятности обнаружения частицы на различных расстояниях от «стенок» ямы показывает, что поведение микрочастицы указывает на то, что представления о траекториях в квантовой механике несостоятельны (см.рисунок 11.3 а,б). Из выражения (11.13) вытекает, что энергетический интервал между соседними уровнями равен
![]() .
(11.15)
.
(11.15)
Если рассмотреть относительное расстояние между уровнями DЕn/En ~1/n, то будет иметь место сближение уровней с ростом n. Этот результат является частным случаем принципа соответствия Бора (1923 г.), согласно которому законы квантовой механики должны при больших значениях квантовых чисел переходить в законы классической физики. Более общая трактовка принципа соответствия: всякая новая, более общая теория, являющаяся развитием классической, не отвергает её полностью, а включает в себя классическую теорию, указывая границы её применения, причем в определенных случаях новая теория переходит в старую.
11.5 Атом водорода. Энергетический спектр атома водорода. Пространственное квантование
Эта задача сводится к задаче о движении электрона в кулоновском поле ядра.
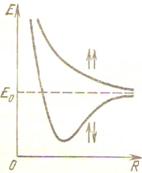 Потенциальная энергия взаимодействия электрона с
ядром, обладающим зарядом Ze (для атома водорода
Z = 1),
Потенциальная энергия взаимодействия электрона с
ядром, обладающим зарядом Ze (для атома водорода
Z = 1),
![]() , (11.16)
, (11.16)
где r - расстояние между электроном и ядром (рисунок 11.3). U(r) с уменьшением r (при приближении электрона к ядру) неограниченно убывает.
Рисунок 11.3
С учетом (11.6) стационарное уравнение Шредингера примет следующий вид:
![]() (11.17)
(11.17)
где m – масса электрона;
Е – полная энергия электрона в атоме.
Поле, в котором
движется электрон, является центрально -симметричным. Поэтому нужно
воспользоваться сферической системе координат:
r, ![]()
Можно показать, что уравнение (11.17), в сферической системе координат, имеет требуемые (т.е. однозначные, конечные и непрерывные) решения в следующих случаях:
1) при любых положительных значениях Е;
2) при дискретных отрицательных значениях энергии, равных:
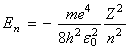 (n = 1, 2, 3, …).
(11.18)
(n = 1, 2, 3, …).
(11.18)
Самый нижний уровень
![]() отвечающий
минимальной возможной энергии, - основной, все остальные (
отвечающий
минимальной возможной энергии, - основной, все остальные (![]() n = 2,3, …) –
возбужденные. При отрицательных энергиях движение электрона является
связанным – он находится внутри гиперболической «потенциальной ямы». По мере
роста главного квантового числа n энергетические уровни располагаются теснее и при
n =
n = 2,3, …) –
возбужденные. При отрицательных энергиях движение электрона является
связанным – он находится внутри гиперболической «потенциальной ямы». По мере
роста главного квантового числа n энергетические уровни располагаются теснее и при
n = ![]() При Е
При Е ![]() движение
электрона является свободным, эта область непрерывного спектра соответствует ионизованному
атому. Энергия ионизации атома водорода равна
движение
электрона является свободным, эта область непрерывного спектра соответствует ионизованному
атому. Энергия ионизации атома водорода равна
![]() .
.
Выражение (12.8) совпадает с аналогичной формулой, полученной Бором для энергии атома водорода. Однако если Бору пришлось вводить свои постулаты, то в квантовой механике дискретные значения энергии, являясь следствием самой теории, вытекают из решения уравнения Шредингера.
В квантовой механике
доказывается, что уравнению Шредингера (12.7) удовлетворяют собственные функции
![]() , определяемые
тремя квантовыми числами: главным
n,
орбитальным l ,
и магнитным
, определяемые
тремя квантовыми числами: главным
n,
орбитальным l ,
и магнитным ![]() .
.
Главное квантовое число n определяет энергетические уровни электрона в атоме и может принимать любые целочисленные значения, начиная с единицы:
n = 1,2,3, …
Из решения уравнения Шредингера вытекает, что момент импульса (механический орбитальный момент) электрона квантуется, т.е. не может быть произвольным, а принимает дискретные значения, определяемые формулой:
![]() (11.19)
(11.19)
где l – орбитальное квантовое число, которое при заданном n принимает значения
l = 0,1, …, (n – 1),
т.е. всего n значений, и определяет момент импульса электрона в атоме.
Из решения уравнения Шредингера следует
также, что вектор ![]() момента импульса электрона может иметь
лишь такие ориентации в пространстве, при которых его проекция
момента импульса электрона может иметь
лишь такие ориентации в пространстве, при которых его проекция ![]() на
направление z внешнего магнитного поля принимает квантованные
значения, кратные
на
направление z внешнего магнитного поля принимает квантованные
значения, кратные ![]() :
:
![]() (11.20)
(11.20)
где ![]() - магнитное
квантовое число, которое при заданном
l может принимать значения
- магнитное
квантовое число, которое при заданном
l может принимать значения
![]() (11.21)
(11.21)
т.е. всего 2l + 1
значений. Таким образом, магнитное квантовое число ![]() определяет проекцию
момента импульса электрона на заданное направление, причем вектор момента
импульса электрона в атоме может иметь в пространстве 2l
+ 1 ориентаций. Число различных состояний, соответствующих данному
n,
равно
определяет проекцию
момента импульса электрона на заданное направление, причем вектор момента
импульса электрона в атоме может иметь в пространстве 2l
+ 1 ориентаций. Число различных состояний, соответствующих данному
n,
равно
![]() (11.22)
(11.22)
Вероятность обнаружения электрона в различных частях атома различна. Электрон при своем движении как бы «размазан» по всему объему, образуя электронное облако, плотность которого характеризует вероятность нахождения электрона в различных точках объема атома. Квантовые числа n и l характеризуют размер и форму электронного облака в пространстве.
В атомной физике, по аналогии со спектроскопией, состояние электрона, характеризующееся квантовыми числами l = 0, называют s- состоянием, l = 1 – p- состоянием, l = 2 – d- состоянием, l = 3 – f- состоянием и т.д. Значение главного квантового числа указывается перед условным обозначением орбитального квантового числа. Например, электроны в состояниях с n = 2 и l = 0 и 1 обозначаются соответственно символами 2s и 2p.
Квантовые
числа n,
l, и ![]() позволяют более полно описать спектр испускания
(поглощения) атома водорода, полученный в теории Бора.
позволяют более полно описать спектр испускания
(поглощения) атома водорода, полученный в теории Бора.
В квантовой механике вводятся правила отбора, ограничивающие число возможных переходов электронов в атоме, связанных с испусканием и поглощением света:
1) изменение орбитального квантового
числа ![]() удовлетворяет
условию
удовлетворяет
условию
![]() (11.23)
(11.23)
2)
изменение магнитного квантового числа ![]() удовлетворяет условию
удовлетворяет условию
![]() (11.24)
(11.24)
11.6 Спин электрона
Опыты О. Штерна и В. Герлаха по прямым измерениям магнитных моментов в неоднородном магнитном поле (1922 г.).
Для объяснения тонкой структуры спектральных линий, а также ряда других трудностей в атомной физике американские физики Д. Уленбек и С. Гаудсмит предположили, что электрон обладает собственным неуничтожимым механическим моментом импульса, не связанным с движением электрона в пространстве, - спином.
Спин электрона (и всех других микрочастиц) – квантовая величина, у неё нет классического аналога; это внутреннее неотъемлемое свойство электрона, подобное его заряду и массе.
Если электрону
приписывается собственный механический момент импульса (спин) ![]() , то ему
соответствует собственный магнитный момент
, то ему
соответствует собственный магнитный момент ![]() . Спин квантуется по закону
. Спин квантуется по закону
![]() (11.25)
(11.25)
где s – спиновое квантовое число.
По аналогии с
орбитальным моментом импульса, проекция ![]() спина квантуется так, что вектор
спина квантуется так, что вектор ![]() может
принимать 2s + 1 ориентаций. Так как в опытах Штерна и Герлаха наблюдались
только две ориентаций, то 2s + 1 = 2, откуда S=1/2. Проекция
спина на направление внешнего магнитного поля, являясь квантованной величиной, определяется
выражением, аналогичным (11.20):
может
принимать 2s + 1 ориентаций. Так как в опытах Штерна и Герлаха наблюдались
только две ориентаций, то 2s + 1 = 2, откуда S=1/2. Проекция
спина на направление внешнего магнитного поля, являясь квантованной величиной, определяется
выражением, аналогичным (11.20):
![]() ,
(11.26)
,
(11.26)
где ![]() - магнитное
квантовое число; оно может иметь только два значения:
- магнитное
квантовое число; оно может иметь только два значения:
![]()
![]() .
.
Таким образом, опытные данные привели к необходимости характеризовать электроны (и микрочастицы вообще) добавочной внутренней степенью свободы. Поэтому для полного описания состояния электрона в атоме необходимо наряду с главным, орбитальным и магнитным квантовыми числами задавать ещё магнитное спиновое квантовое число.
12 Лекция. Элементы квантовых статистик и физики твердого тела
12.1 Понятие о квантовой статистике
В квантовой статистике системы, состоящие из огромного числа частиц, исследуются с помощью законов квантовой механики, в основе которых лежат корпускулярно – волновой дуализм частиц вещества и принцип неразличимости тождественных частиц. Последний означает, что все одинаковые частицы (например, электроны в металле) являются неразличимыми друг от друга.
В квантовой статистике ставится задача о распределении частиц по
ячейкам фазового пространства (шестимерного пространства координат и скоростей),
элемент которого равен ![]() , а также задача определения
средних значений физических величин, характеризующих макроскопическое состояние
системы. Состоянию частицы в фазовом пространстве, с учетом соотношения
неопределенностей Гейзенберга, соответствует не точка, а ячейка фазового
объема h3, где
h –
постоянная Планка.
, а также задача определения
средних значений физических величин, характеризующих макроскопическое состояние
системы. Состоянию частицы в фазовом пространстве, с учетом соотношения
неопределенностей Гейзенберга, соответствует не точка, а ячейка фазового
объема h3, где
h –
постоянная Планка.
Частицы, число которых равно ΔNi в объеме ΔГi , могут различными способами распределиться между Δgi состояниями с энергией Ei. Тогда число квантовых состояний в объеме ΔГi с энергиями от Ei до Ei + ΔEi равно
![]() . (12.1)
. (12.1)
Среднее значение любой функции определяется с помощью функции распределения, которая позволяет также найти вероятность данного состояния системы.
12.2 Распределения Бозе-Эйнштейна и Ферми-Дирака
В квантовой механике различают два вида частиц: бозоны – частицы с
целым или нулевым спином (в единицах ![]() ), на которые не распространяется
принцип Паули и подчиняющиеся распределению Бозе-Эйнштейна (например,
некоторые ядра, фотоны, фононы) и фермионы – частицы с полуцелым спином
(электроны, протоны, нейтроны и т.д.). Последние описываются квантовой статистикой
Ферми-Дирака и подчиняются принципу Паули, согласно которому в каждом
квантовом состоянии может находиться только одна частица. Функция
распределения Бозе-Эйнштейна fБ
выражает
среднюю “населенность” бозонами состояний с данной энергией или среднее их
число в одном состоянии:
), на которые не распространяется
принцип Паули и подчиняющиеся распределению Бозе-Эйнштейна (например,
некоторые ядра, фотоны, фононы) и фермионы – частицы с полуцелым спином
(электроны, протоны, нейтроны и т.д.). Последние описываются квантовой статистикой
Ферми-Дирака и подчиняются принципу Паули, согласно которому в каждом
квантовом состоянии может находиться только одна частица. Функция
распределения Бозе-Эйнштейна fБ
выражает
среднюю “населенность” бозонами состояний с данной энергией или среднее их
число в одном состоянии:
![]() ,
,
где ![]() - число частиц с энергией в интервале от
Ei до
Ei +
ΔEi;
- число частиц с энергией в интервале от
Ei до
Ei +
ΔEi;
![]() - число
квантовых состояний в этом интервале энергий.
- число
квантовых состояний в этом интервале энергий.
Распределение бозонов по энергиям получается из канонического распределения Гиббса при условии сохранении энергии E в системе и числа частиц N:
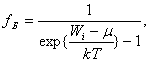 (12.2)
(12.2)
где k – постоянная Больцмана;
Т – термодинамическая температура;
μ – химический потенциал, равный работе, совершаемой в изобарно-изотермических условиях при увеличении числа частиц в системе на единицу. μ≤0, иначе среднее число бозонов в данном состоянии становится отрицательным, что лишено смысла.
Функция распределения Ферми-Дирака определяется аналогично:
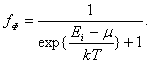 (12.3)
(12.3)
Здесь μ, в отличие от (12.2), может быть положительным.
Функции распределения в классической (Максвелла-Больцмана) и квантовой статистиках, интерпретируемые как среднее число частиц в одном состоянии, можно выразить единой формулой:
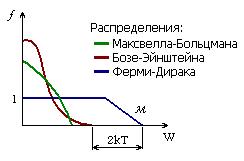
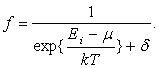 (12.4)
(12.4)
Для распределения Максвелла-Больцмана δ = 0 и μ = 0, для распределения Бозе-Эйнштейна δ = -1 и для распределения Ферми-Дирака δ = +1. Все три распределения показаны на рисунке 12.1.
Рисунок 12.1
Система частиц называется вырожденной, если ее свойства описываются квантовыми закономерностями. Вырождение становится существенным для бозе- или ферми-газов при низких температурах и больших плотностях.
Параметром
вырождения А называется величина ![]() При
A<<1
(малое вырождение) в (12.4) можно пренебречь величиной δ и квантовые
функции распределения переходят в классическую. Параметр А определяется из условия
сохранения общего числа частиц:
При
A<<1
(малое вырождение) в (12.4) можно пренебречь величиной δ и квантовые
функции распределения переходят в классическую. Параметр А определяется из условия
сохранения общего числа частиц:
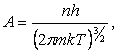 (12.5)
(12.5)
где n – концентрация частиц;
m – масса частицы;
Т – температура;
k –постоянная Больцмана;
h – постоянная Планка.
Примером вырожденного газа являются электроны в металле, которые не подчиняются классической статистике Максвелла-Больцмана.
12.3 Вырожденный электронный газ в металлах
Распределение электронов в металле по энергиям описывается функцией распределения Ферми-Дирака:
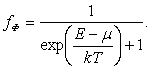 (12.6)
(12.6)
Число квантовых состояний электронов в единице объема металла в интервале энергий от E до E+dE равно:
 (12.7)
(12.7)
Здесь была использована связь между импульсом р и энергией E электрона:
p2 = 2mE,

Число электронов в единице объема металла для энергий от E до E+dE равно:
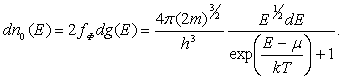 (12.8)
(12.8)
Коэффициент 2 учитывает, что электроны подчиняются принципу Паули. Итак, получен закон распределения электронов по энергиям.
При абсолютном нуле (Т = 0 К) при E<μ0, где μ0 – химический потенциал, имеем fФ → 1 и при E >μ0 fФ → 0. График функции распределения Ферми-Дирака fФ при Т = 0 К показан на рис.12.1. Понятно, что μ0 представляет собой максимальную энергию электронов. Она называется энергией Ферми: μ0 = EF. Наивысший уровень, занятый электронами в металле, называется уровнем Ферми.
Закон распределения электронов проводимости в металле при Т = 0 К имеет вид:
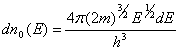 .
(12.9)
.
(12.9)
Общее число электронов в единице объема металла равно:
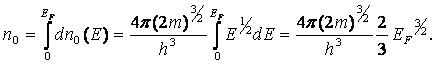 (12.10)
(12.10)
Отсюда можно определить энергию Ферми
 (12.11)
(12.11)
и среднюю энергию электрона при Т = 0 К:
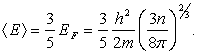 (12.12)
(12.12)
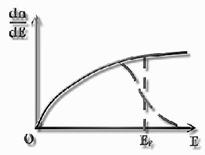
Взяв концентрацию n0 = 6.1028 м-3 и соответствующие значения констант, получим <E> = 9.10-19 Дж = 5,4 эВ.
При Т ≥ 0 К функции распределения Ферми-Дирака имеет вид, изображенный на рисунке 12.2.
Рисунок 12.2
13 Лекция. Конденсированное состояние
Теплоемкость кристаллической решетки. Фононный газ. Электропроводность металлов. Носители тока как квазичастицы.
13.1 Теплоемкость кристаллической решетки
По классическим представлениям твердое тело с N атомами имеет 3N колебательных степеней свободы. На каждую степень свободы приходится энергия kT, тогда молярная теплоемкость кристаллической решетки
![]() (13.1)
(13.1)
где NA – число Авогадро;
R – мольная газовая постоянная.
Опыт дает, что закон Дюлонга-Пти (13.1) справедлив для химически простых веществ при достаточно высоких температурах. При низких температурах С убывает с Т, стремясь к нулю при Т→ 0.
Квантовая теория теплоемкости твердых тел, разработанная Эйнштейном в предположении, что квантовые гармонические осцилляторы, каковыми являются атомы кристалла, колеблются независимо друг от друга с одинаковой частотой, дает, что при Т→ 0 теплоемкость С → 0, что качественно согласуется с опытом. Однако количественного совпадения с опытом не наблюдается. В квантовой теории Дебая полагается, что кристалл является системой N упруго связанных атомов, колебания которых не являются независимыми. Каждому нормальному колебанию решетки соответствует стоячая волна с частотой, определяемой определенными условиями. Число нормальных колебаний (число фононов с частотами от ν до ν+ dν) равно:
 (13.2)
(13.2)
где dg – число квантовых состояний (ячеек) в объеме V, равное
![]() (13.3)
(13.3)
где p = hν/vз – квазиимпульс фонона;
vз- скорость звука в кристалле.
Тогда
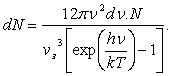 (13.4)
(13.4)
Внутренняя энергия кристалла U с точностью до нулевой энергии равна
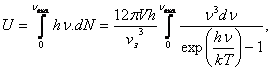 (13.5)
(13.5)
где
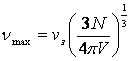 -
максимальная частота фононов, дающих вклад в энергию тепловых колебаний
кристалла.
-
максимальная частота фононов, дающих вклад в энергию тепловых колебаний
кристалла.
При вычислении U вводится характеристическая температура Дебая
![]() ,
под которой для каждого вещества понимается температура, ниже которой
становится существенным квантование энергии колебаний, и рассматриваются два предельных
случая:
,
под которой для каждого вещества понимается температура, ниже которой
становится существенным квантование энергии колебаний, и рассматриваются два предельных
случая:
а) высокие температуры T>>ΘD. Тогда
![]()
и
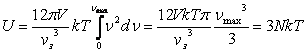 .
.
Для 1 моля N=NA и молярная теплоемкость соответствует закону Дюлонга-Пти:
![]() ; (13.6)
; (13.6)
б) низкие температуры Т<<ΘD:
При
вычислении интеграла вводится новая переменная ![]() и верхний предел заменяется на
∞:
и верхний предел заменяется на
∞:

Тогда молярная теплоемкость С, пропорциональная кубу температуры, подчиняется закону Дебая:
C = const.T3. (13.7)
Формула Дебая хорошо описывает зависимость теплоемкости от температуры только для химически простых веществ, а для тел со сложной структурой она неприменима в виду того, что у таких тел спектр колебания является чрезвычайно сложным.
13.2 Фононный газ
Положение системы с s степенями свободы можно задать с помощью s величин qi, называемых обобщенными координатами системы. Их можно выбрать так, что изменение каждой из них будет представлять собой независимое гармоническое колебание со своей частотой. Тогда энергию кристалла можно выразить как сумму энергий нормальных колебаний решетки:
![]() (13.8)
(13.8)
где N – число элементарных ячеек в кристалле;
r – число атомов в ячейке;
ni – колебательное квантовое число.
За вычетом энергии нулевых колебаний энергия нормального колебания
частоты ![]() слагается
из порций величины
слагается
из порций величины
![]() , (13.9)
, (13.9)
называемой фононом. Фонон имеет квазиимпульс
![]() , (13.10)
, (13.10)
где
![]() - волновой вектор нормального колебания.
- волновой вектор нормального колебания.
Фонон, в отличие от обычных частиц (электронов, фотонов и т.д.), не может возникнуть в вакууме. Он существует только в среде, поэтому является квазичастицей.
При тепловом равновесии среднее число фононов частоты ![]() равно
равно
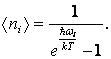 (13.11)
(13.11)
Из (13.11) следует, что в кристалле одновременно может возбуждаться неограниченное количество фононов.
Таким образом, колебания кристаллической решетки можно представить как фононный газ в пределах образца, подобно тому как электромагнитное излучение можно представить как фотонный газ, заполняющий полость. Однако между ними есть существенное различие: фотоны являются истинными частицами, а фононы – квазичастицами.
13.3 Электропроводность металлов
Согласно квантовой теории удельная электрическая проводимость металла равна выражению
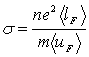 , (13.12)
, (13.12)
напоминающему
классическую формулу, но имеющую отличное физическое содержание. Здесь ![]() - средняя
длина свободного пробега электрона с энергией, равной энергии Ферми, и
- средняя
длина свободного пробега электрона с энергией, равной энергии Ферми, и ![]() - средняя
скорость теплового движения такого электрона. Формула (13.12) дает результаты,
соответствующие опытным данным. В рамках квантовой теории можно объяснить
аномально большие значения средней длины свободного пробега электронов в металле,
превышающие период решетки в сотни раз, а также зависимость σ ~ 1/T:
величина
- средняя
скорость теплового движения такого электрона. Формула (13.12) дает результаты,
соответствующие опытным данным. В рамках квантовой теории можно объяснить
аномально большие значения средней длины свободного пробега электронов в металле,
превышающие период решетки в сотни раз, а также зависимость σ ~ 1/T:
величина ![]() определяется
выражением
определяется
выражением
![]() ,
,
где Е – модуль Юнга;
d – период решетки,
тогда
 , (13.13)
, (13.13)
т.е. σ ~ 1/T, тогда как по классической теории
σ
~![]() .
.
13.4 Энергетические зоны в кристаллах
Согласно зонной теории, существующее в твердых телах периодическое электрическое поле существенно изменяет энергетические состояния электронов. Вместо характерного для изолированного атома энергетического уровня в кристалле, содержащей N взаимодействующих атомов, образуются энергетические зоны, содержащие N уровней, разделенных интервалом порядка 10-23 эВ. Такие разрешенные энергетические зоны разделены запрещенными зонами (см.рисунок 13.1).
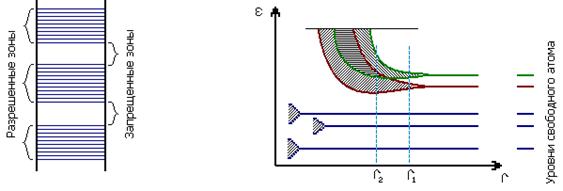
Рисунок 13.1 Рисунок 13.2
На рисунке 13.2 показано расщепление уровней как функция расстояния r между атомами. Заметно расщепляются лишь уровни валентных электронов и вышележащие, не занятые электронами, уровни. При расстоянии типа r1 между зонами имеется запрещенная зона, при расстоянии типа r2 происходит перекрытие соседних зон.
Существование энергетических зон позволяет объяснить существование металлов, полупроводников и диэлектриков. Разрешенную зону, возникшую из уровня валентных электронов в основном состоянии атома, называют валентной зоной. В зависимости от степени заполнения этой зоны возможны три случая: в случае (а) эта зона заполнена электронами не полностью. Данный кристалл является металлом.
То же самое будет при перекрытии соседних разрешенных зон. Во втором случае на рисунке 13.3 (б) валентная зона полностью заполнена электронами и отделена от ближайшей разрешенной зоны (зоны проводимости) небольшой шириной запрещенной зоны ΔЕ (порядка десятых долей эВ). Такой кристалл является полупроводником. Если же ширина ΔЕ велика (порядка нескольких эВ), как в случае (в) кристалл является диэлектриком.
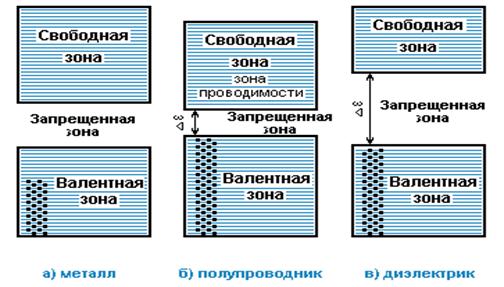
Рисунок 13.3
13.5 Полупроводники
Полупроводниками (см.рисунок 13.4) являются вещества, удельное сопротивление которых изменяется в широком интервале от 10-5 до 108 Ом.м и очень быстро уменьшается с ростом температуры. Наиболее широко применяются такие полупроводники как Si и Ge. Различают собственные и примесные полупроводники.
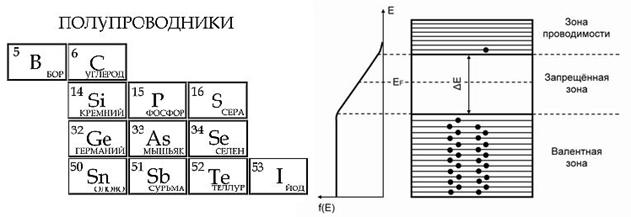
Рисунок 13.4 Рисунок 13.5
Собственными являются химически чистые полупроводники. В них при Т = 0 К все уровни валентной зоны (ВЗ) заполнены электронами и в зоне проводимости электроны отсутствуют.
Электрическое поле не может перебросить их из валентной в зону проводимости (ЗП), поэтому собственные полупроводники при Т = 0К ведет себя как диэлектрики. При Т > 0 К в результате тепловой генерации часть электронов переходит с верхних уровней ВЗ на нижние уровни ЗП. Вследствие образования вакантных уровней в ВЗ поведение электронов ВЗ может быть представлено как движение положительно заряженных квазичастиц, называемых дырками.
Распределение электронов по уровням ВЗ и ЗП подчиняется распределению Ферми-Дирака (см.рисунок 15.5). У собственных полупроводников значение уровня Ферми равно
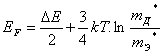 , (13.14)
, (13.14)
где ΔЕ – ширина запрещенной зоны;
mД* и mЭ* - эффективные массы дырки и электрона в ЗП. Обычно второе слагаемое мало и EF = ΔE/2.
Электропроводность собственных полупроводников зависит от температуры по следующему закону
![]() (13.15)
(13.15)
где ΔЕ – ширина ЗЗ;
σ0 – константа.
Имея температурную зависимость lnσ от 1/T можно по графику определить ширину запрещенной зоны полупроводника ΔЕ.
Примесная проводимость делится на электронную (или n-типа) и дырочную (р-типа) проводимость. Для получения полупроводника n-типа (например, кремния (Si) – элемента IY группы) вводят донорную примесь, т.е. элемент Y группы (фосфор, мышьяк и т.д.). Атом Si имеет по своему строению 4 соседних атома, с которыми, отдавая по одному электрону, образует ковалентные связи. Пятый электрон атома примеси остается «лишним». Энергетические уровни таких электронов располагаются ниже дна ЗП, для перевода электронов в которую требуется небольшая энергия (для As в Si ΔEД = 0,054 эВ), получаемая, например, при тепловом возбуждении. При замещении атома Si трехвалентным атомом акцепторной примеси (бор, алюминий и т.д.) возникает недостаток одного электрона для образования насыщенных ковалентных (атомных) связей. Недостающий электрон может быть позаимствован у соседнего атома Si, у которого появляется при этом положительная дырка. Последовательное заполнение дырок соседними электронами эквивалентно движению дырок и приводит к проводимости полупроводника. Акцепторные уровни возникают в ЗЗ полупроводника выше потолка ВЗ (для В в Si ΔEА = 0,08 эВ), переход электронов из ВЗ на акцепторные уровни приводит к появлению в ВЗ дырок. Обратный переход соответствует разрыву одной из четырех ковалентных связей атома примеси с соседями и рекомбинации образовавшегося при этом электрона и дырки.
При повышении температуры концентрация примесных носителей быстро достигает насыщения, т.е. примесная проводимость доминирует при низких Т, с ростом температуры увеличивается вклад собственной проводимости. Таким образом, проводимость полупроводника при высоких Т становится смешанной.
14 Лекция. Контактные явления
14.1 Контактная разность потенциалов в металлах
Валентные электроны в металле (М) находятся в потенциальной яме, т.е. Еp= Евне – U0, где U0 = - еφ. Обычно принимают Евне = 0, Еp = - U0 < 0, потенциал внутри металла φ > 0 (см.рисунок 14.1).
Сообщение металлу избыточного q > 0 увеличивает φ на поверхности и внутри М, Wp электрона уменьшается.
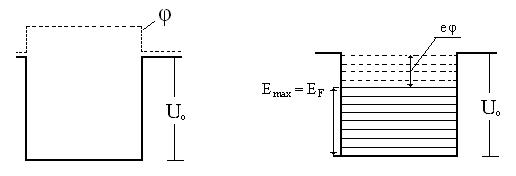
Рисунок 14.1 Рисунок 14.2
Ее = Ек + Ер. При Т = 0 Ек имеет значения от 0 до ЕF. Для удаления е– с нижнего уровня требуется энергия U0, с уровня Ферми – энергия (U0 – EF) (см.рисунок 14.2).
Работа выхода:
![]() . (14.1)
. (14.1)
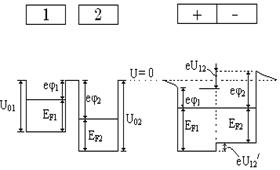 Между двумя разными металлами при соприкосновении
возникает контактная разность потенциалов (см.рисунок 14.3). Она
обусловлена тем, что часть электронов из одного М переходит в другой. В
результате М1 заряжается положительно, а М2-отрицательно. Вокруг возникает
электрическое поле. φ1 возрастает, φ2 убывает; напротив, Ер1
уменьшается, Ер2 увеличивается. Равновесие устанавливается при
совпадении уровней Ферми. Также видно, что Ер электрона вблизи поверхности
М1 меньше, чем у М2, на величину (еφ2 – еφ1). Рисунок
14.3
Между двумя разными металлами при соприкосновении
возникает контактная разность потенциалов (см.рисунок 14.3). Она
обусловлена тем, что часть электронов из одного М переходит в другой. В
результате М1 заряжается положительно, а М2-отрицательно. Вокруг возникает
электрическое поле. φ1 возрастает, φ2 убывает; напротив, Ер1
уменьшается, Ер2 увеличивается. Равновесие устанавливается при
совпадении уровней Ферми. Также видно, что Ер электрона вблизи поверхности
М1 меньше, чем у М2, на величину (еφ2 – еφ1). Рисунок
14.3
Внешняя контактная разность равна
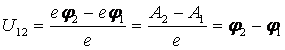 . (14.2)
. (14.2)
Между внутренними точками металлов имеет место внутренняя контактная разность потенциалов:
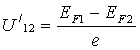 . (14.3)
. (14.3)
На такую величину уменьшается потенциал φ при переходе из М1 в М2.
Для различных пар металлов внешняя ![]() изменяется
от десятых вольта до нескольких вольт. Контактная разность потенциалов
возникает также между М и П/П, р- и n- полупроводниками.
изменяется
от десятых вольта до нескольких вольт. Контактная разность потенциалов
возникает также между М и П/П, р- и n- полупроводниками.
Эффект Зеебека (1821) – появление тока в замкнутой цепи спаев двух разнородных металлов, находящихся при разных температурах. Термо-ЭДС обусловлено:
1) зависимостью EF от Т;
2) диффузией электронов или дырок;
3) увлечение электронов фононами.
![]() . (14.4)
. (14.4)
Термо-ЭДС в цепи из разнородных металлов или полупроводников АВ равна:
![]() , (14.5)
, (14.5)
где ![]() - удельная или дифференциальная
термо-ЭДС (для М
- удельная или дифференциальная
термо-ЭДС (для М ![]() ~ 10-4-10-5 В/К;
для полупроводников
~ 10-4-10-5 В/К;
для полупроводников ![]() ~ 10-3 В/К.
~ 10-3 В/К.
Эффект используется для измерения температуры с помощью термопар или термостолбиков.
Эффект Пельтье (1834) – выделение или поглощение теплоты в спаях при протекании тока в цепи из разнородных М или П/П:
![]() , (14.6)
, (14.6)
где С - коэффициент Пельтье.
Объяснение 1: если носители тока одинаковы (например, 2 П/П n-типа), по разные стороны от спая они имеют разные средние полные энергии и при переходе через спай или отдают избыток энергии решетке (нагрев), или забирают часть энергии (охлаждение спая).
Объяснение 2: на одном спае электроны и дырки движутся навстречу друг другу и рекомбинируют (нагрев), на другом – убыль носителей восполняется появлением электронов и дырок (электроны переходят из ВЗ р-типа в ЗП n-типа) за счет энергии решетки и спай охлаждается.
Эффект Томсона. В 1856 г. Томсон предсказал, исходя из термодинамических соображений, что при прохождении тока по однородному проводнику, вдоль которого имеется градиент температуры, должно выделяться (или поглощаться) тепло, что было подтверждено позже экспериментально. В элементе длиной dl за 1 с выделяется количество тепла:
![]() , (14.7)
, (14.7)
где τ – коэффициент Томсона;
I – сила тока;
![]() – градиент температуры.
– градиент температуры.
Объяснение: в предположении, что ток течет в направлении возрастания температуры и носителями тока являются электроны, последние будут переходить из мест с более высокой температуры (и с большей средней энергией) в места с меньшей температурой, отдавая избыток энергии решетке, что приведет к выделению тепла. Если носителями будут дырки, будет иметь место поглощение тепла.
14.2 Полупроводниковые p-n переходы. Транзисторы
P-N переходом называют тонкий слой между двумя областями одного и того же полупроводникового кристалла (например, кремния), отличающимися типом примесной проводимости.
В контактном слое полупроводника n - типа образуется объемный заряд, образованный неподвижными положительными ионами донорной примеси (элемента V - группы) после диффузии электронов из n-области в р-область, а в р-типе – объемный заряд отрицательных ионов акцепторной примеси (элемента III группы) (см.рисунок 14.4а) после диффузии дырок в обратном направлении. Диффузия прекращается после того, как уровень Ферми, находящийся в запрещенной зоне полупроводника, становится одинаковым в обеих областях.
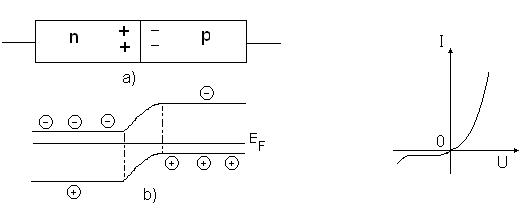
Рисунок 14.4 Рисунок 14.5
Эти объемные заряды образуют собственное поле p-n перехода, которое связано с контактной разностью потенциалов и препятствует дальнейшему переходу основных носителей заряда – электронов из n – области в р – область и дырок из р – области в n – область (см.рисунок 14.4b, зонная диаграмма). Изгибание энергетических зон в области перехода связано с тем, что потенциал р – области при равновесии ниже, чем в n – области (соответственно потенциальная энергия электрона в р – области больше, чем в n – области). На рисунке 4b выше запрещенной зоны лежит зона проводимости, в которой находятся свободные электроны, ниже – валентная зона, в которой при отрыве электронов от атомов (ионизации) образуются дырки, которые могут перемещаться и давать вклад в общий ток.
При приложении к p – n переходу внешнего напряжения в прямом (пропускном) направлении (плюс подается на р – область) высота потенциального барьера снижается, ширина самого p – n перехода также уменьшается, сопротивление перехода мало. Это приводит к резкому росту тока основных носителей по экспоненциальному закону (прямая ветвь вольтамперной характеристики, см.рисунок 14.5).
При приложении обратного напряжения (минус подключен к р – области) высота потенциального барьера возрастает, основные носители не могут перейти в соседнюю область, ток определяется только неосновными носителями, которые могут переходить в соседнюю область (электроны из р –области в n – область, а дырки – в противоположном направлении) и число которых невелико и определяется тепловой генерацией при данной температуре. Таким образом, обратный ток постоянен и лишь при значительном обратном напряжении начинает резко возрастать, что обусловлено электрическим пробоем перехода (левая ветвь, см.рисунок 14.5).
Из данной характеристики следует, что p – n переход в обратном направлении имеет гораздо большее сопротивление, чем в прямом. Это позволяет использовать p – n переходы для выпрямления переменного тока.
Полупроводниковые триоды (транзисторы) представляют собой кристаллы с двумя p – n переходами. Средняя часть транзистора называется базой (Б), которая может иметь любую проводимость, поэтому различают p-n-p или n-p-n транзисторы. Рядом с базой области имеют иной тип проводимости и называются эмиттером (Э) и коллектором (К).
Рассмотрим принцип действия n-p-n транзистора, подключенного в цепь усилителя (см.рисунок 14.6).
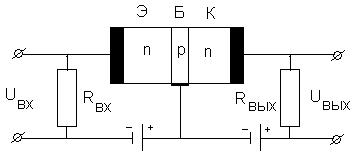
Рисунок 14.6
На переход транзистора Э – Б подается постоянное смещающее напряжение UЭ в прямом направлении, а на переход Б – К - постоянное напряжение UК в обратном направлении. Усиливаемое переменное напряжение Uвх подается на небольшое входное сопротивление Rвх, а усиленное выходное напряжение Uвых снимается с большого выходного сопротивления Rвых. Последнее необходимо для согласования схемы, поскольку второй переход имеет большое сопротивление. Подключение UЭ обеспечивает проникновение электронов в область базы, которые диффундируют к коллектору. Обычно ширина базы незначительна и почти все электроны, не успев рекомбинировать (с дырками), достигают коллектора, т.е. IК ≈ IЭ. Выразив токи через соответсвующие напряжения и сопротивления, получим: Uвх / Rвх ≈ Uвых/ Rвых, откуда следует Uвых/ Uвх ≈ Rвых / Rвх. Так как Rвых >> Rвх , то Uвых >> Uвх. Таким образом, транзистор усиливает напряжения и мощности.
14.3 Вентильный фотоэффект
В диэлектриках и полупроводниках наблюдается внутренний фотоэффект, заключающийся в увеличении электропроводности вещества под действием света. Если энергия светового кванта ћω должна превышать ширину запрещенной зоны ΔЕg, тогда поглотивший квант электрон переходит из валентной зоны в зону проводимости, т.е. становится свободным, соответственно в валентной зоне возникает дырка. Эти дополнительные носители заряда увеличивают электрическую проводимость вещества. Это явление носит название собственной фотопроводимости. Если в веществе имеются примеси, под действием света электроны могут переходить из валентной зоны на уровни примеси или с примесных уровней в зону проводимости. Первым переходам соответствует дырочная, а вторым – электронная примесная фотопроводимость.
На внутреннем фотоэффекте базируется действие фотосопротивлений, в основном из полупроводников – PbS, PbSe, PbTe и InSb, в которых фотопроводимость пропорционально световому потоку, т.е. они используются в фотометрии.
В p-n переходе, а также на границе металла с полупроводником, может наблюдаться вентильный фотоэффект, заключающийся в возникновении фото-ЭДС. Возникшие при освещении p-n перехода неосновные для каждой области носители заряда (дырки в n – области и электроны в р – области) беспрепятственно проходят через переход и там накапливаются, т.е. в n – области возникает избыточный отрицательный заряд, а в р – области - избыточный положительный заряд. Это приводит к возникновению приложенного к переходу напряжения, являющегося фото-электродвижущей силой. Возникающие неравновесные основные носителя составляют ничтожно малую долю от равновесных носителей и не дают ощутимого вклада. Соединенные последовательно кремниевые p-n переходы образуют солнечные батареи, используемые для питания радиоаппаратуры на спутниках и космических станциях.
15 Лекция. Атомное ядро и классификация элементарных частиц
15.1 Основные свойства и строение ядра
Ядром является центральная часть атома, в котором сосредоточена практически вся масса атома и его положительный электрический заряд. Все ядра, кроме ядра атома водорода, включающего один протон, состоят из нуклонов - протонов и нейтронов (модель Иваненко-Гейзенберга).
Заряд ядра равен Ze, где е – величина заряда протона, Z – зарядовое число, равное порядковому номеру химического элемента (атомному номеру) в периодической системе Менделеева. В настоящее время известны ядра с Z от 1 (водород) до 118 (юнуноктий).
Число нуклонов в ядре A = N + Z называется массовым числом, где N – число нейтронов. Для определения числа нуклонов в ядре им приписывается массовое число, равное 1, электрону – нулевое значение числа А.
Ядра с одинаковыми Z, но разными А, называются изотопами; ядра с одинаковыми А, но разными Z, - изобарами; ядра с одинаковыми N называют изотонами; существуют также изомеры – радиоактивные ядра с равными A и Z, отличающиеся периодом полураспада.
В настоящее время известно около 300 устойчивых и более 2000 радиоактивных изотопов химических элементов.
Для обозначения ядер применяют символ ZXA или A ZX, например, 1Н1.
Радиус ядра задается эмпирической формулой: r = r0A1/3, где r0 = (1,3-1,7)10-15 м. Таким образом, объем ядра пропорционален числу нуклонов, т.е. плотность ядерного вещества является константой, составляющей по порядку величины 1017 кг/м3.
Нуклоны в ядрах являются фермионами. Спин ядра – собственный момент
импульса ядра равен ![]() , где
I – внутреннее
(полное) спиновое квантовое число. Спин ядра определяется числом нуклонов.
Нуклоны также обладают собственными магнитными моментами, которыми определяется
магнитный момент ядра, единицей измерения которого является ядерный
магнетон
, где
I – внутреннее
(полное) спиновое квантовое число. Спин ядра определяется числом нуклонов.
Нуклоны также обладают собственными магнитными моментами, которыми определяется
магнитный момент ядра, единицей измерения которого является ядерный
магнетон ![]() , где
mp
– масса
протона.
, где
mp
– масса
протона.
15.2 Энергия связи ядер
Энергией связи ядра называется физическая величина, равная работе по расщепления ядра на нуклоны без сообщения им кинетической энергии. Она является разностью между энергией всех свободных нуклонов, составляющих ядро, и их энергией в ядре.
![]() (15.1)
(15.1)
где Δm – дефект масс, характеризующий уменьшение суммарной массы при образовании ядра из нуклонов;
с – электродинамическая постоянная.
![]() (15.2)
(15.2)
где mp, mn – массы соответственно протона и нейтрона;
МЯ – масса ядра. Обычно массы выражают в атомных единицах массы (а.е.м.).
Обычно массы ядра и протона заменяют массами соответственно атома Ма и водородного атома mH, тогда
![]() (15.3)
(15.3)

Рисунок 15.1
На рисунке 15.1 представлена зависимость удельной энергии связи от массового числа А. Сильнее всего связаны нуклоны в ядрах с 50≤А≥ 60 (Cr-Zn). У них Есв = 8,7 МэВ/нуклон. У самого тяжелого природного ядра Есв = 7,5 МэВ/нуклон.
Такая зависимость делает энергетически возможным деление тяжелых ядер и слияние (синтез) легких ядер.
15.3 Ядерные силы. Модели ядра
В атомных ядрах действуют особые ядерные силы притяжения, отличные от гравитационных и электромагнитных сил и намного превышающие их. Эти силы относятся к классу сильных взаимодействий.
Основные свойства ядерных сил:
1) Ядерные силы являются короткодействующими. Радиус их действия порядка 1ферми (10-15 м );
2) Они обнаруживают зарядовую независимость, т.е. силы взаимодействия двух протонов, двух нейтронов или протона с нейтроном являются одинаковыми;
3) Им свойственно насыщение, т.е. каждый нуклон взаимодействует с ограниченным числом других нуклонов;
4) Ядерные силы зависят от ориентации спинов взаимодействующих нуклонов.
Например, дейтрон – ядро изотопа 1Н2 образуется из протона и нейтрона только при параллельной ориентации их спинов;
5) Ядерные силы не являются центральными, т.е. действующими по линии, соединяющей центры нуклонов.
Ядерные силы носят обменный характер. По современным представлениям нуклоны виртуально обмениваются π-мезонами- квантами ядерного поля. Такая гипотеза впервые была высказана в 1935 году японским физиком Х.Юкавой и подтверждена их экспериментальным обнаружением в 1947 г. Оккиалини и Поуэллом.
В результате виртуальных процессов нуклон оказывается окруженным облаком образующих ядерное поле виртуальных π-мезонов:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Обменное взаимодействие между нуклонами можно описать виртуальными процессами:
![]() ;
;
![]() ;
;
![]() .
.
Из-за сложного характера сильного взаимодействия до сих пор нет единой последовательной теории атомного ядра. Из множества существующих моделей ядра рассмотрим: капельную и оболочечную.
Капельная модель Бора и Френкеля (1936 г.) основана на аналогии между поведением нуклонов в ядре и поведением молекул в капле жидкости – короткодействующие силы, свойство насыщения, постоянная плотность, пропорциональность объема числу частиц. Модель позволила получить формулу для энергии связи ядра и объяснить реакцию деления ядер. Однако она не смогла объяснить повышенную устойчивость ядер с магическими (2, 8, 20, 28, 50, 82, 126) числами нуклонов.
В оболочечной модели Марии Гепперт-Майер и др. (1949 г.) нуклоны заполняют дискретные энергетические уровни в соответствии с принципом Паули. Уровни образуют оболочки, в которых находится определенное число нуклонов. Ядра с полностью заполненными оболочками являются наиболее устойчивыми. Кроме того, модель позволила объяснить спины и магнитные моменты ядер, периодичность изменения их свойств.
15.4 Радиоактивное излучение и его виды. Закон радиоактивного распада
Радиоактивностью называется превращение одних ядер в другие, сопровождаемое испусканием некоторых частиц. Различают естественную радиоактивность существующих в природе неустойчивых изотопов и искусственную радиоактивность изотопов, полученную в результате ядерных реакций.
Основными видами радиоактивного излучения являются α-, β- и γ-излучение. Различают и другие виды, связанные с испусканием протонов или позитронов, а также спонтанное деление ядер, К-захват.
Альфа-излучение представляет собой поток ядер гелия, заряд α-частицы равен +2е, масса совпадает с массой ядра 2Не4. Это излучение обладает высокой ионизирующей и малой проникающей (задерживается листом бумаги) способностью.
Бета-излучение является потоком быстрых электронов с меньшей ионизирующей (~ на 2 порядка), но большей проникающей способностью, чем у α-частиц.
Гамма-излучение – коротковолновое электромагнитное излучение с λ< 10-10 м, по существу, поток частиц (γ-квантов или фотонов), не отклоняющийся электрическим и магнитным полями и обладающий относительно слабой ионизирующей и очень большой проникающей (проходит через свинец толщиной 5 см) способностью.
Теория радиоактивного распада основана на предположении, что ядра претерпевают радиоактивные превращения независимо друг от друга. Тогда число ядер dN, распадающихся за малый промежуток времени dt, пропорционально числу имеющихся ядер N и времени dt:
![]() , (15.4)
, (15.4)
где λ – характерная для данного радиоактивного вещества постоянная, называемая постоянной радиоактивного распада.
После интегрирования получим закон радиоактивного распада
![]() , (15.5)
, (15.5)
где N0 – начальное число нераспавшихся ядер;
N – число нераспавшихся ядер в момент времени t.
Закон (15.5) можно трактовать так: число нераспавшихся ядер убывает со временем по экспоненте.
Число ядер, распавшихся за время t, находится из выражения
![]() (15.6)
(15.6)
Время, за которое распадается половина первоначального числа ядер, называется периодом полураспада Т, которое можно определить из условия
![]() ,
,
откуда
![]() . (15.7)
. (15.7)
Среднее время жизни τ радиоактивного ядра связано с λ и Т соотношениями:
![]() . (15.8)
. (15.8)
Таким образом, среднее время жизни τ есть величина, обратная постоянной радиоактивного распада.
Активностью нуклида, т.е. ядра, отличающегося от других ядер значениями А и Z, называется число распадов ядер за 1 секунду:
![]() . (15.9)
. (15.9)
Единицей активности в СИ служит беккерель (Бк), когда за 1 с происходит один распад. В ядерной физике используется внесистемная единица, называемая кюри (Ки): 1 Ки = 3,7.1010 Бк.
Распад ядер происходит в соответствии с правилами смещения, позволяющими определить, какое ядро возникнет в итоге:
Для α-распада:
ZXA → Z-2YA-4 + 2He4. (15.10)
Для β-распада:
ZXA → Z+1YA + -1e 0. (15.11)
Правила смещения являются следствием законов сохранения электрического заряда и массового числа.
15.5 Ядерные реакции
Ядерной реакцией называется процесс сильного взаимодействия атомного ядра с элементарной частицей или другим ядром, приводящий к преобразованию ядра (или ядер). Символически ядерная реакция записывается в виде
X+ a→ Y+b или X(a,b)Y,
где Х и Y – исходное и конечное ядра;
a и b – налетающая и испускаемая(ые) частица(ы).
Количество выделяющейся энергии называется энергией реакции.
![]() , (15.12)
, (15.12)
где 1-я сумма масс берется для исходных ядра и частицы;
а 2-я – для конечных. Если (m1+m2)>(m3+m4), энергия выделяется и реакция называется экзотермической, в противном случае – энергия поглощается и реакция называется эндотермической.
Ядерная реакция характеризуется эффективным сечением σ:
![]() (15.13)
(15.13)
где N – число частиц, падающих за 1 с на единичную площадь поперечного сечения вещества, имеющего в единице объема n ядер;
dN – число этих частиц, участвующих в реакции в слое толщиной dx. Сечение σ характеризует вероятность того, что при падении частиц на вещество произойдет реакция, и измеряется в барнах. 1барн=10-28м2.
В 1936 г. Н. Бор установил, что реакции, вызываемые не очень быстрыми частицами, протекают в два этапа. При захвате Х-ядром а- частицы образуется составное (или компаунд-) ядро, которое на втором этапе испускает частицу b:
![]() . (15.14)
. (15.14)
Некоторые реакции протекают без образования промежуточного ядра, их называют прямыми ядерными взаимодействиями.
Особое место в ядерных реакциях занимают реакции деления тяжелых ядер под действием нейтронов, сопровождающиеся испусканием двух-трех вторичных нейтронов. При этом образуются осколки деления, близких по массе. Большинство нейтронов испускаются почти мгновенно (t < 10-14 c, их называют мгновенными), а небольшая часть (около 0,7%), называемых запаздывающими нейтронами, испускается через период от 0,05 с до 60 с. В этих реакциях высвобождается энергия, равная примерно 1,1 МэВ/нуклон. Испускаемые при делении вторичные нейтроны могут вызвать новые акты деления, что делает возможным осуществление цепной реакции деления. Последняя характеризуется коэффициентом размножения k нейтронов, который должен быть больше единицы для развития цепной реакции. Цепные реакции делятся на управляемые и неуправляемые. Первые осуществляются в атомных реакторах, вторые – при взрыве при достижении критической массы.
Реакции синтеза атомных ядер характерны тем, что в них энергия, выделяемая на один нуклон, значительно больше, чем в реакциях деления тяжелых ядер. Например, при делении ядра 92U238 выделяется примерно 200 МэВ или 0,84 МэВ/нуклон, тогда как при синтезе дейтерия и трития эта величина равна примерно 3,5 МэВ/нуклон.
Реакции синтеза легких ядер в более тяжелые, происходящие при сверхвысоких температурах (Т > 107 К) называются термоядерными реакциями. Управляемый термоядерный синтез открывает человечеству возможность доступа к практически неисчерпаемому источнику энергии.
15.6 Виды взаимодействий и классы элементарных частиц
Под элементарными частицами можно понимать такие микрочастицы, внутреннюю структуру которых на современном уровне развития физики нельзя представить как объединение других частиц. Они ведут себя как единое целое и могут превращаться друг в друга.
Известны 4 вида взаимодействия между элементарными частицами: сильное, электромагнитное, слабое, гравитационное. В таблице 1 приведены порядки величины констант разных видов взаимодействия и среднее время жизни частиц, распадающихся за счет данного взаимодействия.
По данным таблицы 1 можно судить, когда и при каких условиях преобладает тот или иной вид взаимодействия. Так, например, гравитационное взаимодействие не ограничено по радиусу действия, является универсальным, но в процессах микромира заметной роли не играет, являясь самым слабым по интенсивности взаимодействия.
Элементарные частицы принято делить на 3 основных класса:
- к первому классу относится лишь одна частица – фотон. Это – квант электромагнитного излучения;
- второй класс образуют лептоны. Они участвуют в электромагнитном и слабом взаимодействиях. К ним относятся нейтрино, электрон, мюон, таон (τ-лептон) и их античастицы;
- третьему классу принадлежат адроны. Они обладают, помимо электромагнитного и слабого, сильным взаимодействием. К ним относятся протон, нейтрон, пионы и каоны.
Т а б л и ц а 1
|
Взаимодейcтвие |
αi |
R,м |
τ, с |
Законы сохранения |
Участники* |
Переносчики |
Изменяются Цвет / Аромат |
|
S E
W
G |
~1 ~10-2
~10-10
~10-38 |
10-15 ∞
~10-18
∞ |
~10-23 ~10-20
~10-13
? |
Все Все,кроме Т p,E,J q,B,L
? |
q(H) q(H),ℓ± W± q(H), ℓ все |
gi(i=1...8) γ
W±
G |
+ - - -
- +
? ? |
Обозначения: S – сильное, Е – электромагнитное, W – слабое, G –гравитационное, q – кварки, H – адроны, ℓ - лептоны.
Для всех видов взаимодействия выполняются законы сохранения энергии, импульса, момента импульса и электрического заряда. Кроме того, в сильных взаимодействиях выполняется закон сохранения изотопического спина. Это- одна из внутренних характеристик, показывающая только число членов в изотопическом мультиплете, например, в мультиплете нуклонов изоспин I = ½ (число членов в мультиплете нуклона равно двум – протон, нейтрон).
Гипотеза об античастицах была выдвинута П. Дираком в 1928 г. Через 4 года К. Андерсон обнаружил в космических лучах позитрон – античастицу электрона. Из квантовой теории следует, что частица и античастица должны иметь одинаковые массы, времена жизни в вакууме, одинаковые по модулю, но противоположные по знаку электрические заряды и магнитные моменты, одинаковые спины и изоспины, а также остальные квантовые числа элементарных частиц, служащие для описания закономерностей их взаимодействия (лептонное и барионное числа, странность, очарование и т.д.). В 1956 году было доказано, что такая симметрия имеет место для сильного и электромагнитного взаимодействий, но нарушается для слабого. Античастицы были обнаружены экспериментально для протона (1955) и нейтрона (1956), π+-мезона, каонов и гиперонов. Однако существуют истинно нейтральные частицы, не имеющие античастиц. Это- фотон, π0-мезон, η-мезон. Они не способны к аннигиляции, но обладают фундаментальным свойством элементарных частиц к взаимным превращениям.
15.7 Кварки
В 1964 г. Гелл-Манн и Цвейг выдвинули гипотезу о существовании
фундаментальных частиц, названных кварками, на основании которых можно построить
все адроны. В настоящее время для объяснения существования всех известных
адронов введены шесть видов кварков u, d, s, c, b,
t и соответствующих антикварков ![]() .
.
Характеристики кварков указаны в таблице 2. Кварки имеют дробное значение элементарного электрического заряда, их спин равен 1/2, поскольку только из фермионов можно сконструировать как фермионы, так и бозоны.
Адроны строятся из кварков следующим образом: мезоны состоят из пары кварк-антикварк, барионы – из трех кварков (антибарионы - из трех антикварков. Для некоторых барионов была введена специфическая квантовая характеристика кварка – цвет: «желтый» , «синий», «красный». Теперь кварки с разной «окраской» не противоречили принципу Паули. Открытие в 1974 году истинно нейтрального (J/Ψ)-мезона массой около 6000 me привело к введению нового кварка – с-кварка и новой сохраняющейся величины – «очарования».
Т а б л и ц а 2
|
Кварк (анти- кварк) |
Электрический заряд в единицах е |
Барионное число В |
Спин, в единицах ħ |
Странность S |
|
u (
d (
s (
c ( b ( t ( |
+2/3 (-2/3) -1/3 (+1/3) -1/3 (+1/3) +2/3 (-2/3) -1/3 (+1/3) +2/3 (-2/3) |
+1/3 (-1/3) +1/3 (-1/3) +1/3 (-1/3) +1/3 (-1/3) +1/3 (-1/3) +1/3 (-1/3) |
1/2 1/2 1/2 1/2 1/2 1/2 |
0 0 -1(+1) 0 0 0 |
Кварковая модель оказалась очень плодотворной, она позволила определить все основные квантовые числа адронов. Из этой модели получаются, как и в эксперименте, целочисленный спин для мезонов и полуцелый – для барионов. По ней была предсказана новая частица – Ω—гиперон. Но возникли и трудности: по ней невозможно определить массу адронов. Для построения открытого в 1977 г. сверхтяжелого мезона массой около 20 000me был введен новый тип кварка – b-кварк, являющийся носителем новой сохраняющейся величины – «прелести». Предполагается существование и шестого кварка, который уже решено назвать “истинным”.
По аналогии с квантами полей различных взаимодействий были введены частицы – переносчики взаимодействий между кварками, названные глюонами. Они переносят цвет от одного кварка к другому, в результате чего кварки удерживаются вместе.
Еще одна характеристика – “аромат”, объединяющая все указанные признаки, кроме цвета, сохраняется в сильных и электромагнитных взаимодействиях.
В настоящее время общепринятой считается такое мнение относительно кварков, согласно которой кварки, будучи цветными объектами, в принципе не могут существовать в свободном состоянии, а могут находиться только внутри адронов. Решение проблемы связано с необычным свойством сил, действующих между кварками – энергия взаимодействия возрастает с ростом расстояния между ними.
С помощью кварков удалось объяснить все многообразие свойств и превращений адронов. Результаты экспериментов по рассеянию высокоэнергетических лептонов на нейтронах и протонах позволили установить наличие кварков внутри адронов, равенство их спинов ½, дробный электрический заряд и существование в трех цветовых разновидностях.
Итак, составными элементами материи являются кварки шести ароматов (и трех цветов) и лептоны также шести ароматов. Взаимодействия между этими фундаментальными частицами обеспечиваются за счет обмена переносчиками – глюонами, фотонами, промежуточными бозонами и гравитонами.
15.8 Понятие об основных проблемах современной физики и астрофизики
В современной физике первоочередной является задача построения единой теории всех фундаментальных взаимодействий. Уже создана теория, объединяющая электромагнитное и слабое взаимодействия. Эти фундаментальные взаимодействия при низких энергиях выступают как разные проявления единого электрослабого взаимодействия и различие между которыми исчезает по мере роста энергии частиц.
Во многом успешны и попытки «великого объединения» электрослабого и сильного взаимодействий в одно электроядерное взаимодействие и на очереди – решение грандиозной проблемы объединенного описания всех четырех фундаментальных взаимодействий («расширенная супергравитация»). Однако до сих пор не разрешены некоторые проблемы этого «суперобъединения».
Особенно выдающиеся открытия были совершены на стыке физики частиц, астрофизики и космологии. Наиболее неожиданным было открытие так называемой «темной энергии», плотность которой составляет ¾ полной плотности энергии во Вселенной. Пока единственным необычным проявлением этой субстанции является то, что, в отличие от гравитационного притяжения обычной материи, она не замедляет космологический разлет далеких галактик, а ускоряет его. Это проявляется в спектрах далеких сверхновых.
В отличие от «темной энергии», «темная материя» известна с 30-х годов прошлого века, но из каких частиц состоит эта темная материя, пока неясно. Она группируется внутри и вокруг галактик, что приводит к слишком быстрому вращению вокруг центра галактик. Видимая масса звезд и межгалактического газа примерно в пять раз меньше, чем масса темного вещества, вызывающего аномально быстрое вращение звезд в галактиках и галактик в скоплениях. Так что обычное вещество составляет в среднем не более 5% средней плотности энергии Вселенной. Попытки обнаружить частицы невидимого вещества в подземных низкофоновых лабораториях и в околоземном пространстве пока успеха не принесли.
Список литературы:
Основная литература:
1. Савельев И.В. Курс физики: Кн. 2: Электричество и магнетизм. –М.: «Издательство АСТ», 2004.
2. Савельев И.В. Курс физики: Кн. 4: Волны. Оптика. –М.: «Издательство АСТ», 2004.
3. Савельев И.В. Курс физики: Кн. 5: Квантовая оптика. Атомная физика. Физика твердого тела. Физика атомного ядра и элементарных частиц. –М.: «Издательство АСТ», 2004.
4. Детлаф А.А., Яворский Б.М. Курс физики. -М.: Высш. шк., 2004.
5. Трофимова Т.И. Курс физики. - М.: Высш. шк., 2004.
6. Курс физики. Под ред. Лозовского В.Н. – СПб.: Лань, 2001. – т. 1.
7. Курс физики. Под ред. Лозовского В.Н. – СПб.: Лань, 2001. – т. 2.
Дополнительная литература:
8. Джанколи Дж. Физика. М.: Мир, 1989, т.1-2.
9. Иродов И.Е. Электромагнетизм. Основные законы. – М.: Лаборатория Базовых знаний, 2000.
Св.план 2011 г., поз. 315