МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН
«Алматинский институт энергетики и связи»
М.Ш. Карсыбаев
ФИЗИКА. РЕШЕНИЕ ЗАДАЧ
В КОМПЬЮТЕРНОЙ СРЕДЕ MATHCAD
Учебное пособие
Алматы 2008
Учебное пособие содержит классификацию и методы решения задач по всем разделам физики в компьютерной системе MathCAD. Даны общие рекомендации по работе в среде MathCAD. Практически ко всем задачам даны указания по их решению и ответы. Пособие может оказаться полезным не только для студентов, но и для всех, кто осваивает работу в системе MathCAD.
Учебное пособие предназначено для студентов всех форм обучения всех специальностей.
СОДЕРЖАНИЕ с.
ВВЕДЕНИЕ …4
1 Некоторые сведения о системе MathCAD 2001 …5
1.1 Общая характеристика системы MathCAD 2001 …5
1.2 Работа в среде MathCAD 2001 …5
1.3 О применении единиц измерений в системе MathCAD …8
2 Классификация задач, решаемых на компьютере …9
3 Общие методические указания к решению физических задач …9
4 Физические основы механики …10
4.1 Методы решения задач в кинематике …10
4.2 Методы решения задач по динамике …12
4.3 Задачи по механике …14
5 Молекулярная физика и термодинамика …18
5.1 Указания к решению задач по молекулярной физике и термодинамике …18
5.2 Задачи по молекулярной физике и термодинамике …18
6 Электричество и магнетизм …19
7 Колебания и волны …20
8 Оптика. Квантовая природа излучения …21
9 Элементы квантовой физики …22
10 Список литературы …22
11 Приложение А …23
12 Приложение В …26
13 Приложение С …30
14 Ответы к задачам …31
Введение
В данном учебном пособии рассматриваются решения задач по различным разделам физики с помощью компьютерной системы MathCAD /1- 2/, признанной во всем мире одной из лучших для научно-технических расчетов.
Аналитический метод решения задач из стандартных задачников по физике является в значительной степени ограниченным, поскольку в них даются идеализированные задачи, которые, по существу, служат только для иллюстрации того или иного закона физики. Так, в задачах по механике не учитываются силы сопротивления, учет которых изменяет реальную картину не только количественно, но и качественно. Многие "реальные" задачи попросту не решаются аналитическим способом.
С помощью компьютера можно решать задачи любого типа. Помимо численных ответов к задачам, которые практически выдаются мгновенно, можно также получать любые сложные траектории, отдельные графики и семейства графиков. Применение среды MathCAD в компьютере при решении задач или моделировании физических процессов позволяет получать так называемые "живые графики", т.е. графики, которые можно получать мгновенно, изменяя задаваемые параметры. Это особенно полезно для студентов при анализе полученных результатов и для понимания изучаемых физических явлений. Возможно также решение задач, исходные данные которых заданы в виде таблиц или графиков.
Особое место занимают задачи, в которых рассматриваются явления, описываемые с помощью дифференциальных уравнений. В частности, в классической механике это задачи на второй закон Ньютона, когда действующие силы являются переменными.
Используемые здесь методы решения дифференциальных уравнений первого и второго порядка достаточно просты для понимания студентами и вполне применимы (в отношении точности вычислений) для решения рассматриваемых физических задач.
Использование компьютера для решения задач на практических занятиях требует разработки своей методики проведения таких занятий. Целесообразно, на наш взгляд, проведение практического занятия с использованием компьютера как итогового после изучения соответствующего раздела или модуля физики. Подобные задачи можно предложить студентам при выполнении расчетно-графических (семестровых) работ на компьютере, в качестве олимпиадных задач и для представления научных разработок на студенческие конференции по физике.
Пособие включает некоторые сведения по системе MathCAD, классификацию физических задач и методические указания к их решению, примеры решения задач, предлагаемые для решения задачи по различным разделам физики, приложения и ответы к большинству предложенных задач.
Цель данного пособия заключается в том, чтобы помочь учащимся освоить систему MathCAD для решения физических задач.
1 Некоторые сведения о системе Mathcad 2001
1.1 Общая характеристика системы MathCAD 2001
Системы MathCAD /1-3/ являются одними из лучших математических систем при выполнении научно-технических вычислений. Начиная с MathCAD 2000 Pro, появилась возможность программирования в среде MathCAD. В данном пособии выбран MathCAD 2001, поскольку для него в Интернете есть русская версия книги Кирьянова Д.В./3/, подробно описывающая работу пользователя в этой среде. Последняя из версий на данное время–MathCAD 14.
MathCAD является математическим редактором для расчетов, начиная от арифметики и заканчивая сложными реализациями численных методов.
Главной отличительной особенностью системы MathCAD является общепринятая форма записи математических выражений физических формул и графиков, что очень удобно при решении физических задач. Благодаря простоте применения, наглядности математических действий, обширной библиотеке встроенных функций и численных методов, возможности символьных вычислений, а также превосходному аппарату представления результатов (графики самых разных типов, мощных средств подготовки печатных документов и Web-страниц), MathCAD стал наиболее популярным математическим приложением.
Система MathCAD позволяет выполнять как численные, так и аналитические (символьные) вычисления, имеют чрезвычайно удобный математико-ориентированный интерфейс и прекрасные средства графики /1/. Она работает под управлением графических операционных систем Windows и располагает удобными и наглядными средствами описания алгоритмов решения математических задач. Кроме того, MathCAD позволяет готовить электронные книги с использованием новейших средств мультимедиа, включая гипертекстовые и гипермедиа-ссылки, изысканные графики (в том числе анимационные), фрагменты видеофильмов и звуковое сопровождение.
1.2 Работа в среде MathCAD 2001
Рабочий документ или окно MathCAD вместе с набором панелей инструментов появляются сразу после нажатия курсора мыши на ярлык программы на рабочем столе компьютера (рисунок 1).
Рисунок 1 - Окно системы MathCAD 2001
(фрагмент верхней части)
В верхней строке окна указаны имена системы и файла. В следующей строке – главное меню в следующем порядке: Файл, Правка, Вид, Вставка, Формат, Математика (Вычисления), Графика, Символьное вычисление, Окна, Помощь. Каждая позиция меню становится активной при нажатии на нее левой клавишей мыши (или клавишей F10 на клавиатуре, стрелками “вправо, влево и Enter).
На третьей строке в левой части – панель инструментов наиболее распространенных команд и операций (аналогично Word), в правой – “горячие“ клавиши: Математические функции MathCAD, Единицы измерения, Вычисления, Приложения.
На четвертой строке – перемещаемые наборные панели MathCAD для вывода шаблонов математических знаков (цифр, знаков арифметических операций, матриц, векторов, интегралов, производных и т.д.).
В простейшем случае работа с системой MathCAD сводится к подготовке в окне редактирования задания на вычисления и к установке форматов для их результатов. Входной язык MathCAD максимально приближен к обычному математическому языку описания вычислительных задач и практически не требует их программирования, необходимо лишь точное описание алгоритма решения задачи.
Фактически система MathCAD объединяет три редактора: формульный, текстовой и графический.
Для запуска формульного редактора необходимо установить курсор мыши в свободном месте окна редактирования и щелкнуть левой клавишей. Появится визир в виде маленького красного крестика, который можно перемещать клавишами перемещения курсора. С местонахождения визира начинается набор формул – вычислительного блока.
Текстовой редактор позволяет задавать текстовые комментарии. Установив в нужное место визир, нажмите на Вставку (Insert), появится прямоугольник, в который можно начать вводить текст после перевода языка комментария на русский и установки Шрифта на Ариэль Кириллицу. Текст редактируется обычными средствами (аналогично Word). Вместо Вставки можно нажать на “горячие” клавиши клавиатуры – (Shift+2) или @.
В системе MathCAD имеется программный графический процессор, позволяющий строить графики в декартовой и полярной системе координат, трехмерные поверхности, графики уровней и т.д. Для построения графиков используются 7 шаблонов, перечень которых содержится в подменю Graph позиции Insert главного меню. Для создания шаблона двумерного декартового графика нужно выбрать X-Y Plot. После появления шаблона необходимо ввести х по оси абсцисс с соответствующими пределами и конкретную функцию у(х) на оси ординат. Шаблон можно вывести с помощью пиктограммы графиков (вторая слева на нижней строке рисунка 1). Для удаления графика из рабочего документа нужно обвести его рамкой с помощью курсора и нажать на Ctrl+X.
Есть еще один способ создания графика – задать переменную х, указав диапазон ее изменения и шаг. Шаг h указывается заданием начального значения х0, а затем (через запятую) значения х0 + h. Нужно через знак “;” (точка с запятой) задать также конечное значение х. Затем записать функцию у(х) и вывести шаблон двумерного графика – большой пустой прямоугольник с местами ввода х и у(х) в виде темных маленьких прямоугольников (рисунок 2а). Если строятся графики нескольких функций (рисунок 2б) в одном шаблоне, то они разделяются запятыми. Крайние шаблоны данных служат для указания граничных значений х и у. Если шаблоны не заполняются, то масштабы графика по осям устанавливаются автоматически (рисунок 2б).

Рисунок 2
Графики, как и другие объекты документа, можно выделять, заносить в буфер обмена, вызывать их оттуда и переносить в любое новое место. Их можно просто перетаскивать с места на место курсором мыши, а также изменять их размеры по горизонтали, вертикали или диагонали, цепляясь за специальные маркеры выделенных графиков курсором мыши.
Для построения трехмерного графика z(x,y) необходимо
сначала вычислить матрицу Z с
элементами Zm,n для каждой пары xm, yn. Пусть
мы располагаем функцией ![]() , для которой укажем число точек по осям х
и у: N:=50 m:=0..N n:=0..N и значения элементов xm и yn,
далее запишем Zm,n := f(xm, yn). Вызвав
трехмерный шаблон командой Alt+2 или щелкнув по нему,
укажите в светлом квадратике имя матрицы (Z) и нажмите Ent.
, для которой укажем число точек по осям х
и у: N:=50 m:=0..N n:=0..N и значения элементов xm и yn,
далее запишем Zm,n := f(xm, yn). Вызвав
трехмерный шаблон командой Alt+2 или щелкнув по нему,
укажите в светлом квадратике имя матрицы (Z) и нажмите Ent.
В системе MathCAD автоматизированы процессы вычисления, построения графиков и программирования. Достаточно освоить правила пользования, перечисленные в таблице 1. Рабочий язык в среде MathCAD – английский. Комментарии можно записывать на русском языке. Для этого необходимо нажать Insert (Вставка) и далее Текстовая область. Во второй графе четвертой строки установить Ариэль Кириллицу и использовать русский шрифт.
Т а б л и ц а 1
|
Чтобы получить |
Необходимо набрать |
|
Знак присвоения := |
: (двоеточие) |
|
Цикл по j от 1 до 10 с шагом 1 |
j:1;10 |
|
Цикл по x от 1 до 10 с шагом 0,1* |
x:1,1.1;10 |
|
Умножение 3 х 5 |
3*5 |
|
Корень квадратный |
\ (черта с левым наклоном) |
|
Деление |
/ (черта с правым наклоном) |
|
Элемент вектора с индексом хi |
x[i |
|
Элемент матрицы Мi,j |
M[(I,j) |
|
|
x?f(x) |
*- примечание: после запятой указывается следующее значение, а не шаг.
В таблице указан минимальный список средств MathCAD, с полным списком можно ознакомиться в /1, 3/.
1.3 О применении единиц измерений в системе MathCAD
В системе MathCAD возможно использование размерных величин, например, длина измеряется в метрах (символ – m ), масса – в кг (kg), время – в секундах (sec или s) и т.д. Обозначения основных физических величин (на английском языке) в системе СИ (SI) даны в таблице 2.
Т а б л и ц а 2
|
Фундаментальные единицы SI |
Дополнительные единицы |
||
|
m |
м - метр |
N |
Н - ньютон |
|
kg |
кг - килограмм |
J или joul |
Дж - джоуль |
|
sec |
С - секунда |
rad |
рад - радиан |
|
К |
К - кельвин |
km/hr |
км/ч |
|
A |
А - ампер |
deg |
градус |
|
cd |
кд - кандела |
min |
мин |
|
mole |
моль |
cm, mm |
см, мм |
Приведем пример расчета в MathCad с использованием единиц измерения физических величин в одной из задач по механике.

2 Классификация задач, решаемых на компьютере
Классификация физических задач проводится на различных основаниях в зависимости от поставленной задачи. Например, задачи классифицируются по содержанию (относятся к тому или иному разделу или теме физики), по дидактическим целям (тренировочные, обучающие, творческие), по способам задания (текстовые, графические, экспериментальные); их можно делить на качественные и расчетные и т.д.
Внедрение компьютеров в учебный процесс меняет методику и методологию решения задач. Это позволяет выделить компьютерно-ориентированные задачи (КОЗ), т.е. физические задачи, решаемые математическими методами на компьютере, которые также можно классифицировать по различным признакам.
Среди КОЗ можно выделить следующие типы задач, в которых:
1) производятся многократные вычисления по одной формуле, например, при построении графиков;
2) необходимо найти определенный интеграл, вычисляемый только численными методами;
3) возникают уравнения высоких степеней или трансцендентные уравнения, решаемые только численными методами;
4) необходимо решение систем уравнений;
5) данные заданы графически или в виде массива;
6) необходимо решение дифференциальных уравнений;
т.е. такие задачи, которые без компьютера не решаются или их решение очень громоздко.
Большинство задач данного пособия взяты из задачников /4-7/.
3 Общие методические указания к решению физических задач
Необходимым условием для решения физических задач является предварительное знакомство с теоретическим материалом курса общей физики /8-9/. Именно самостоятельное решение задач по каждому разделу является показателем усвоения физических законов и умения применить их к тем или иным практическим условиям. В некоторых случаях, помимо знания физических законов, необходимо и знание специальных методических приемов, общих для определенного типа задач. С этим чаще всего можно иметь дело при решения задач по механике.
При решении задач целесообразно руководствоваться следующими методическими указаниями:
а) необходимо досконально понять условие задачи, записать его в кратком виде, выражая заданные величины в системе СИ, и, при возможности, сделать схематический рисунок, поясняющий ее сущность;
б) применив соответствующие физические законы к данной задаче, получить решение задачи, если оно не является слишком громоздким, в общем виде. В противном случае можно провести поэтапное решение задачи. При этом полученная величина должна быть выражена через исходные данные. Неиспользование какой-либо физической величины может свидетельствовать о том, что задача решена неверно. Не лишним будет и проверка размерности полученного результата;
в) подставить числовые значения заданных величин в конечную формулу и получить необходимый ответ, проанализировав, по возможности, его достоверность. Особенно это необходимо при решении задач на компьютере.
4. Физические основы механики
4.1 Методы решения задач в кинематике
Для решения задач по кинематике нужно знать закон движения тела, т.е. уравнение (или систему уравнений), определяющее в любой момент времени его положение в выбранной системе координат /8-9/. Далее можно определить кинематические параметры – скорость и ускорение, а также рассчитать траекторию движения тела.
При движении тела вдоль прямой линии (одномерное
движение) по определению скорость ![]() и ускорение
и ускорение ![]() , поэтому скорость
, поэтому скорость ![]() и координату
и координату ![]() можно выразить в виде
можно выразить в виде
![]() ,
откуда следует, что
,
откуда следует, что ![]() при
равномерном движении (
при
равномерном движении (![]() ) и
) и
![]() при равноускоренном
движении.
при равноускоренном
движении.
![]() при
равноускоренном движении (
при
равноускоренном движении (![]() ) и
) и
![]() при равномерном движении.
при равномерном движении.
При двумерном движении для вычисления y, vy и ay используются аналогичные выражения.
При решении в среде MathCAD в соответствии с условием задачи необходимо задать: 1. исходные данные вместе с физическими константами; 2. начальные условия. Их удобно задавать в виде матрицы (значения t0, x0, y0 в примере 1), выводя предварительно ее шаблон с помощью мыши, щелкнув по третьей пиктограмме в четвертой строке (рисунок 1). Кроме того, в примере 1 заданы формулы для начальной скорости. 3. Следующий шаг – организация вычислительных циклов (в примере 1 временной цикл для 50 значений и угловой цикл для 4 значений). Для этого записываются итерационные расчетные формулы (в примере 1 в виде матрицы). Последний этап - построение графика. Такой алгоритм вычисления справедлив для всех задач по кинематике.
Пример 1. Тело брошено под углом ![]() к горизонту с
начальной скоростью
к горизонту с
начальной скоростью ![]() .
Пренебрегая сопротивлением воздуха, построить траектории движения тела при
.
Пренебрегая сопротивлением воздуха, построить траектории движения тела при ![]() .
.
Ниже приводится решение задачи, импортированное
из MathCAD. Здесь не используется язык
программирования, а организованы циклы для переменных ![]() и
и ![]() .
.
В правой части рабочего документа даются комментарии. Решение:


![]() Углы
a
= 30, 45, 60 и 75 град.
Углы
a
= 30, 45, 60 и 75 град.
![]()
(Первое значение угла при k = 0 равно
![]() + s = 15+15 = 30 градусов)
+ s = 15+15 = 30 градусов)

Для получения графика необходимо вывести шаблон двумерного графика, как было указано ранее. По осям координат занести по 4 аргумента и функции (через запятую), указать их пределы и щелкнуть левой кнопкой мыши в свободном месте. График получается автоматически. Можно также получить значения у и х в любой точке траектории, поставив после них знак равенства.
Полученный график представлен ниже на рисунке 3.
В среде MathCAD все кривые можно получить различного
цвета (малиновый, зеленый, синий, красный) и различного вида (штрих-пунктирный,
пунктирный, штриховой, сплошной), здесь же они изображены одним цветом. По
полученным графикам проводится анализ. Так, например, наибольшая дальность при
прочих равных условиях полета соответствует углу ![]() , а высота подъема - максимальному углу
бросания
, а высота подъема - максимальному углу
бросания ![]() ,
дальность полета получается одинаковой при углах
,
дальность полета получается одинаковой при углах ![]() и
и ![]() .
.
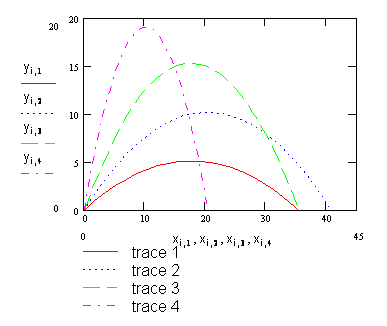
Рисунок 3 - Баллистические кривые
4.2 Методы решения задач по динамике
В динамике основная задача остается прежней, но нужно учитывать все силы, действующие на исследуемое тело (или систему тел). Уравнением движения является второй закон Ньютона, который обязательно нужно записывать в векторном виде, а затем переходить к скалярной форме уравнений, связывающих проекции ускорений и сил на координатные оси, выбранные в зависимости от условия задачи.
В уравнении движения ![]() в правой части сила
в правой части сила ![]() может быть постоянной,
тогда задача решается просто, а может зависеть от координаты, скорости или
времени, тогда получается дифференциальное уравнение, решаемое только в
простейших случаях. В общем случае решение таких уравнений без компьютера практически
невозможно. Численный метод решения дифференциальных уравнений на компьютере
дан в Приложении 1.
может быть постоянной,
тогда задача решается просто, а может зависеть от координаты, скорости или
времени, тогда получается дифференциальное уравнение, решаемое только в
простейших случаях. В общем случае решение таких уравнений без компьютера практически
невозможно. Численный метод решения дифференциальных уравнений на компьютере
дан в Приложении 1.
Пример 2. Условия задачи такие же, как и в задаче
примера 1. Добавлена масса ![]() тела и указан один угол
тела и указан один угол ![]() . Учитывается сила
сопротивления, выражаемая формулой
. Учитывается сила
сопротивления, выражаемая формулой ![]() , где
, где ![]() ,
, ![]() . Вначале записаны данные задачи (первая
строка): масса тела, угол, под которым брошено тело относительно горизонта,
ускорение силы тяжести, константы А и В, входящие в выражение для силы
сопротивления, значение начальной скорости и шаг по времени. В приведенном
примере после задания исходных данных задачи используются средства
программирования системы MathCAD /3/. В программе
определяется траектория движения тела на плоскости XOY
(баллистическая кривая), выражаемая в виде функции
. Вначале записаны данные задачи (первая
строка): масса тела, угол, под которым брошено тело относительно горизонта,
ускорение силы тяжести, константы А и В, входящие в выражение для силы
сопротивления, значение начальной скорости и шаг по времени. В приведенном
примере после задания исходных данных задачи используются средства
программирования системы MathCAD /3/. В программе
определяется траектория движения тела на плоскости XOY
(баллистическая кривая), выражаемая в виде функции ![]() , в которой имеется возможность учитывать
, в которой имеется возможность учитывать
![]() или не
учитывать
или не
учитывать ![]() силу
сопротивления воздуха. Полученные для каждого из указанных случаев графики
представлены на рисунке 4.
силу
сопротивления воздуха. Полученные для каждого из указанных случаев графики
представлены на рисунке 4.

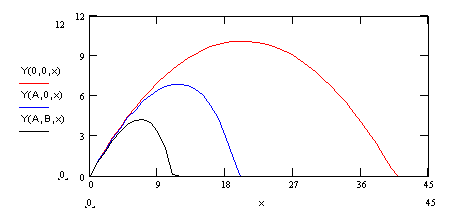
Рисунок 4
Для аргумента х заданы 45 точек (45 м). При отсутствии силы сопротивления получается траектория в виде параболы (верхняя кривая). При
наличии силы сопротивления воздуха кривые ![]() и
и ![]() качественно отличаются по форме (это – не
параболы), а также – количественно по значениям высоты подъема тела и дальности
полета. Все кривые приведены для угла бросания
качественно отличаются по форме (это – не
параболы), а также – количественно по значениям высоты подъема тела и дальности
полета. Все кривые приведены для угла бросания ![]() , однако программа может быть использована
для любого другого значения. В правой части решения для демонстрации возможностей
системы MathCAD в виде столбцов выведены численные
значения функции
, однако программа может быть использована
для любого другого значения. В правой части решения для демонстрации возможностей
системы MathCAD в виде столбцов выведены численные
значения функции ![]() .
.
4.3 Задачи по механике
4.3.1 Задачи первого уровня
Здесь представлены задачи первого уровня сложности (простейшие) по кинематике и динамике, решение которых будет полезным на начальном этапе знакомства с системой MathCAD.
4-1 Два автомобиля движутся прямолинейно и равномерно в одном направлении со скоростями v1 = 90 км/ч и 108 км/ч. В начальный момент времени расстояние между ними равнялось 15 км. 1) Через какое время 2-й автомобиль догонит идущий впереди первый автомобиль? 2) Получить графики зависимости координат автомобилей от времени.
4-2 Найдите положения свободно падающего в глубокий колодец камня через 0,05; 0,10;…1,00 c после начала падения. Сопротивлением воздуха пренебречь. Результаты представить в виде таблицы и получить график зависимости пути от времени.
4-3 Тело брошено вертикально вверх со скоростью v0. Через какое время от начала движения оно пройдет высоту Н? Задайте сами значения скорости v0 и высоты H. Проведите анализ решений получаемого квадратного уравнения.
4-4 Из аэростата, находящегося на высоте H = 540 м, выпал груз. 1) Через какой промежуток времени t груз достигнет поверхности Земли, если аэростат поднимался со скоростью v0 = 6 м/c? 2) Построить графики зависимости времени t от высоты полета аэростата, изменяя ее от 0 до 540 м; 3) Построить аналогичные графики, изменяя значения v0 .
4-5 Из аэростата, находящегося на высоте H = 300 м, выпал груз. 1) Через какой промежуток времени t груз достигнет поверхности Земли, если а) аэростат поднимался со скоростью v0 = 5 м/c? б) аэростат опускался со скоростью v0 = 5 м/c? в) был неподвижен? 2) Построить графики зависимости времени t от высоты полета аэростат для случаев а, б и в.
4-6 Тело брошено под углом к горизонту с начальной скоростью v0 = 20 м/c. Начальные координаты x0 = 0 (по оси абсцисс) и у0 = 100 м. 1) Определите полное время полета; максимальную высоту подъема; координаты х, у и проекции скоростей vx , vy в моменты времени t = 0, 1, 2…10 c. 2) Построить траектории движения тела для углов 20, 40, 60, 800.
4-7 Автомобиль движется по горизонтальному участку пути со скоростью v0 = 72 км/ч. Водитель, заметив препятствие, начинает тормозить. 1) Определить тормозной путь автомобиля S, если коэффициент трения μ = 0,25; 2) Построить график зависимости тормозного пути от скорости автомобиля; 3) То же для различных значений μ .
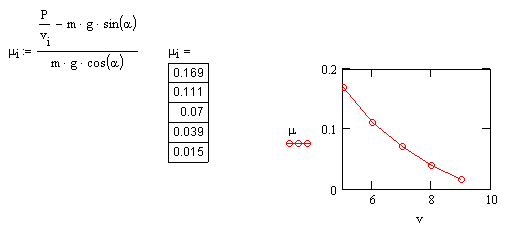
4-8 Грузовой автомобиль массой m = 6 т движется на подъеме со скоростью v = 5 м/с, Угол наклона к горизонту α = 100. 1) Определить коэффициент трения μ, если мощность двигателя N = 100 кВт. 2) Построить график зависимости μ от v.
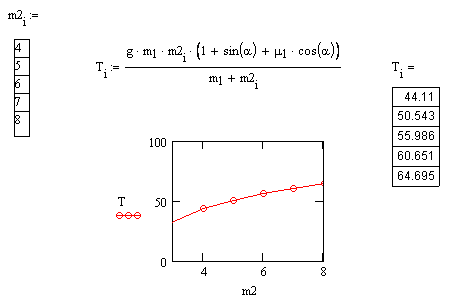
4-9 По наклонной плоскости с углом наклона к горизонту α = 340, перемещается вверх тело массой m1 = 7 кг. Его тянет второе тело массой m2 = 6 кг. Тела связаны нитью, перекинутой через неподвижный блок. 1) Определите силу натяжения нити Fн, если коэффициент трения первого тела μ = 0,25. (Трением в блоке можно пренебречь); 2) Варьируя массу второго тела, определите силу натяжения нити и постройте график этой зависимости; 3) Постройте график зависимости силы натяжения от угла наклона при постоянных значениях m1, m2 и μ. Сформулируйте соответствующие выводы по полученным результатам.
4-10 Два тела, скрепленные нитью, перекинутой через неподвижный блок, движутся равноускоренно по наклонным плоскостям. Углы наклона плоскостей равны 440 и 350. 1) Найти ускорения тел, если масса m1 = 1 кг, а масса m2 = 4 кг. Коэффициенты трения тел о плоскости равны μ1 = 0,2 и μ2 = 0,3; 2) Изменяя массу второго тела, найти ускорения тел
4-11 Шар массой m = 0,4 кг привязан нитью к подвесу и описывает окружность в горизонтальной плоскости со скоростью v = 6 м/c. 1) Какова длина L нити, если угол α, который нить составляет с вертикалью, равен 350 ? 2) То же для разных углов α и построить график зависимости L от α .
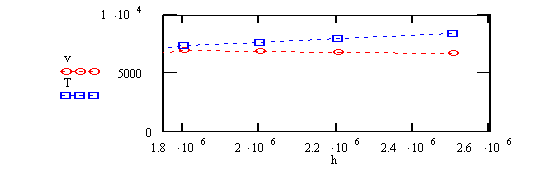
4-12 Средняя высота спутника h над поверхностью Земли равна 2000 км. 1) Определить скорость v спутника и период обращения T, если радиус Земли R = 6400 км, масса Земли M = 6.1024 кг. Гравитационная постоянная G = 6,67.10-11 Н.м2 / кг2; 2) Изменяя высоту спутника над поверхностью Земли, постройте графики зависимостей скорости и периода от высоты.
4-13 На плиту массой M = 1,5 кг, укрепленную на пружине с коэффициентом жесткости k = 900 Н/м, с некоторой высоты падает шар массой m = 0,6 кг. В момент удара скорость шара равна v = 7 м/c. 1) Найдите удлинение пружины х при различных значениях m, если время удара ничтожно мало и удар неупругий; 2) Построить график зависимости х от скорости шара в момент удара при постоянных m, M, k.
4-14 Три четверти своего пути автомобиль прошел со скоростью V1 = 60 км/ч, остальную часть пути – со скоростью V2 = 80 км/ч. 1) Какова средняя путевая скорость <V> автомобиля? 2) Построить график зависимости средней скорости автомобиля от скорости его движения на первой половине пути при постоянном значении V2.
4-15 Первую половину пути тело двигалось со скоростью V1 = 2 м/с, вторую – со скоростью V2 = 8 м/с. 1) Какова средняя скорость <V> тела? 2) Построить график зависимости средней скорости автомобиля от скорости его движения на первой половине пути при постоянном значении V2.
4.3.2 Задачи второго уровня
4-16 Тело массой m = 70 кг падает в воздухе с большой высоты. Сила сопротивления воздуха Fтр = Аv + Bv3, где А = 5 Н.с/м; B = 103 Н.с3/м3. Найти скорость и путь в зависимости от времени, прошедшего после начала падения. Сравните с падением в пустоте. Постройте графики полученных зависимостей.
4-17 Указанные в задаче № 4-16 константы А и Б используйте для задачи, в которой парашютист совершает затяжной прыжок с высоты Н = 7 км. Оцените приблизительно, как долго парашютист может не раскрывать парашют, если до земли должно остаться не менее 1 км и не менее 0,5-1 мин. запаса времени.
4-18 Постройте график зависимости скорости равномерного движения моторной лодки от мощности установленного мотора. Сила сопротивления Fc = Av + Bv3, где А = 40 кг/c; В = 32 кг.с/м2. (Указание: записать мощность через силу и скорость, откуда найти силу и подставить в уравнение движения. Полученное биквадратное уравнение решить для каждого значения мощности от 0 до 5000 Вт через 500).
4-19 С какой максимальной скоростью тепловоз, развивающий силу тяги 25 т, может вести состав массой 2000 т ? Учесть силу трения Fтр = Av + Bv3, где А = 104 кг/c; В = 30 кг.с/м2. Какую мощность развивает тепловоз ?
4-20 Трамвай развивает силу тяги 1,5 т при массе 10 т. Сила сопротивления равна Av, где v – скорость, А = 10 кг/c. Через какое время от начала движения можно считать движение трамвая равномерным ?
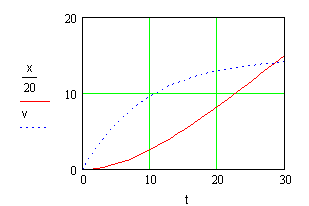
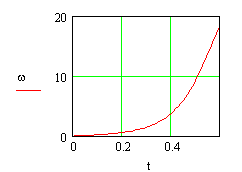
4-21 Если бы на поезд метро при начале движения сразу начала бы действовать постоянная сила, то пассажиры ощутили бы резкий толчок. Для избежания этого силу тяги, и, следовательно, ускорение увеличивают постепенно, например, так, как показано на рисунке 5. Найдите скорость и путь, пройденный поездом за первые 30 секунд через каждые 2 с, взяв данные об ускорении из графика.
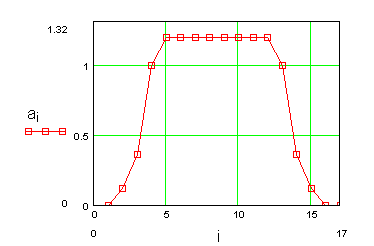
Рисунок 5
Пояснение к рисунку 5: ускорение плавно растет от 0 до 1,2 м/c2 за 10 с (i = 2 c). Далее ускорение постоянно в течение 10 с и в следующие 10 с падает от 1,2 м/c2 до 0.
4-22 На какое расстояние за 3 минуты отойдет от остановки состав массой 2000 т, если сила тяги тепловоза составляет 25 т ? Дайте два ответа: а) без учета трения; б) с учетом вязкого трения о воздух и в осях Fтр = Av + Bv3,где А = 104 Н.с/м; B = 30 Н.с3/м3.
4-23 Колесо массой 1 кг, распределенной по ободу радиусом 0,35 м, вращается с угловой скоростью 10,5 рад/c на оси с жидкой смазкой и тормозится только трением в оси. Момент тормозящих сил равен Mтр = - aω – bω3 , где a = 2,8.10-2 Н.м.с; b = 9,1.10-1 Н.м.с3. Колесо останавливается, когда угловая скорость колеса становится равной 0,1 рад/c. Найдите время и число оборотов до остановки. (Указание: При наращивании угловой скорости используйте условие: ω ≤ 0,1).
4-24 Определите время падения карандаша длиной 15 см, поставленного на острие. В исходном состоянии карандаш неизбежно отклонен от вертикали на 10 и не соскальзывает.
4.3.3 Задачи третьего уровня
4-25 Ракета массой 300 т стартует с Земли. Через какое время она достигнет высоты 40 км, если каждую секунд выбрасывает 1000 кг продуктов сгорания со скоростью u = 4 км/c ? Учесть трение о воздух и уменьшение силы тяжести с высотой.
4-26 Космический объект массой 1т подлетает к Луне. Когда расстояние a становится равным 2.104 км, а прицельное расстояние р = 7.103 км, то скорость объекта vx0 = 1500 м/с. Рассчитайте траекторию полета вблизи Луны. Масса Луны равна 7,3.1022 кг, радиус Луны – 1,7.103 км.
4-27 Космический объект массой 1000 кг подлетает к Луне. Когда расстояние а становится равным 1.104 км, а прицельное расстояние р = 6,5.103 км, то скорость объекта vx0 = 670 м/с. Рассчитайте траекторию полета вблизи Луны. Масса Луны равна 7,3.1022 кг, радиус Луны – 1,7.103 км.
4-28 Колесо массой 1 кг, распределенной по ободу радиусом 35 см, вращается с угловой скоростью 10,5 рад/с на оси с
жидкой смазкой и тормозится только трением в оси. Момент тормозящих сил равен ![]() , где
, где ![]() Н.м.с,
Н.м.с, ![]() Н.м.с3.
Колесо останавливается, когда угловая скорость становится равной 0,1 рад/с.
Найти время и число оборотов до остановки.
Н.м.с3.
Колесо останавливается, когда угловая скорость становится равной 0,1 рад/с.
Найти время и число оборотов до остановки.
5 Молекулярная физика и термодинамика
5.1 Указания к решению задач по молекулярной физике и термодинамике
В данном разделе рассматриваются задачи, в основном, относящиеся к типу 1 КОЗ, в которых имеют место многократные вычисления.
Уравнение состояния идеального газа (уравнение
Клапейрона-Менделеева ![]() , где
, где ![]() – давление газа,
– давление газа, ![]() – его объем,
– его объем, ![]() – абсолютная температура,
– абсолютная температура, ![]() - масса,
- масса, ![]() - молярная масса,
- молярная масса, ![]() = 8,31 Дж/(моль.К) –
газовая постоянная, применяется к газу, находящемуся в условиях, близких к
нормальным (t = 0o C,
p
=1,01.105 Па).
= 8,31 Дж/(моль.К) –
газовая постоянная, применяется к газу, находящемуся в условиях, близких к
нормальным (t = 0o C,
p
=1,01.105 Па).
Для решения задач распределение Максвелла
удобно выразить через относительную скорость 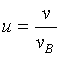 , где
, где  - наиболее вероятная скорость:
- наиболее вероятная скорость:
 .
.
Здесь ![]() .
.
5.1.1 Задачи по молекулярной физике
5-1
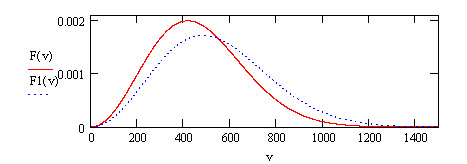
Зависимость распределения молекул по скоростям от температуры. Начертите
график зависимости ![]() от
скорости
от
скорости ![]() для
кислорода при температуре T=300K. Измените температуру. Как изменится при этом распределение?
для
кислорода при температуре T=300K. Измените температуру. Как изменится при этом распределение?
5-2
Доля молекул, имеющих определенные скорости. Найдите долю молекул азота,
имеющих скорости от 700 до 2000м/с при температуре ![]() . Измените температуру. Как
изменится эта доля молекул?
. Измените температуру. Как
изменится эта доля молекул?
5-3 Политропа. Начертите кривую зависимости V(p) для политропического процесса, если показатель политропы равен 1,28. Давление изменяется от 0,2 до 3 атм. Изменяйте показатель политропы от 1 (изотерма) до 1,5. как изменяется вид кривых?
5-4
Кривая Ван-дер-Ваальса. Начертите кривые для функции ![]() для количества вещества
реального газа (азота), равного 1кмоль и имеющего поправки
для количества вещества
реального газа (азота), равного 1кмоль и имеющего поправки
![]() Н
Н![]() и
и ![]() при разных температурах. Газовая постоянная
при разных температурах. Газовая постоянная
![]()
5-5 Объем азота. Найдите объем азота массой 20 г при давлении p=100атм. Значения поправок a и b возьмите из предыдущей задачи 53.
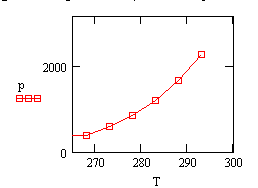
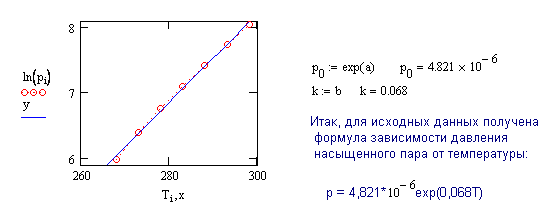
5-6. Давление насыщенного пара. Пользуясь приведенной ниже таблицей, подберите аналитическую формулу, по которой изменяется давление насыщенного водяного пара от температуры.
|
|
-5 |
0 |
5 |
10 |
15 |
20 |
25 |
|
|
3,96 |
6,02 |
8,61 |
12,1 |
16,8 |
23,0 |
31,3 |
Методом наименьших квадратов (Приложение 2) подберите наилучшие значения параметров.
6 Электричество и магнетизм
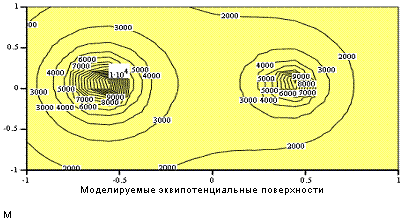
6-1 Построить эквипотенциальные поверхности и трехмерный график изменения потенциала
![]() , если
электростатическое поле создано зарядами
, если
электростатическое поле создано зарядами ![]() и
и ![]() , находящимися друг от друга на расстоянии
, находящимися друг от друга на расстоянии
![]() .
.
6-2 Аккумулятор с внутренним сопротивлением r = 0,08 Ом при силе тока I1 = 4 A выделяет на внешнюю цепь мощность N1 = 8 Вт. Какую мощность N2 выделит аккумулятор на внешнюю цепь при силе тока I2 = 6 A?
6-3 Три источника с ЭДС Е1 = 11 В, Е2 = 4 В, Е3 = 6 В и три реостата с сопротивлениями R1 = 5 Ом, R2 = 10 Ом и R3 = 2 Ом соединены так, как показано на рисунке.

Рисунок 6
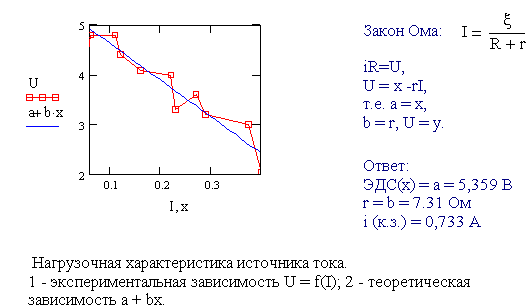
6-4 Нагрузочная характеристика источника тока. Источник тока исследовали
путем подключения к нему различных резисторов (нагрузок) и измерение силы тока ![]() и напряжения
U на
клеммах источника. Получили следующие данные:
и напряжения
U на
клеммах источника. Получили следующие данные:
|
|
0,06 |
0,11, |
0,12 |
0,16 |
0,22 |
0,23 |
0,27 |
0,29 |
0,375 |
0,40 |
|
U, В |
4,8 |
4,8 |
4,4 |
4,1 |
4,0 |
3,3 |
3,6 |
3,2 |
3,0 |
2,05 |
Обработайте
данные методом наименьших квадратов определите ЭДС (![]() ), ток короткого замыкания
), ток короткого замыкания ![]() и внутреннее
сопротивление источника.
и внутреннее
сопротивление источника.
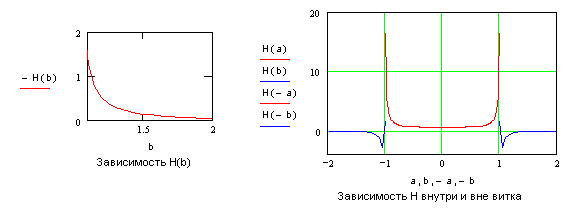
6-5
Магнитное поле витка. Найдите напряженность магнитного поля плоского витка
радиусом R с силой тока ![]() =1А в центре и на расстоянии
=1А в центре и на расстоянии ![]() от центра в плоскости витка
(см. рисунок 7)
от центра в плоскости витка
(см. рисунок 7)
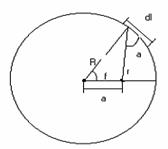
Рисунок 7
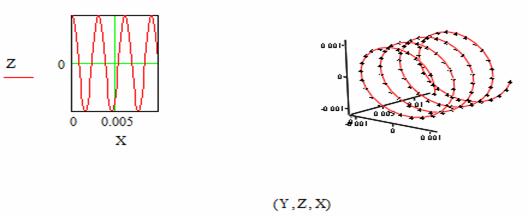
6-6 Позитрон влетает в магнитное поле со скоростью ![]() под углом
под углом ![]() к вектору магнитной индукции
к вектору магнитной индукции ![]() , модуль которого равен
0,01 Тл. Найти радиус и шаг винтовой линии, вдоль которой движется позитрон, а
также построить пространственную траекторию движения заряженной частицы.
, модуль которого равен
0,01 Тл. Найти радиус и шаг винтовой линии, вдоль которой движется позитрон, а
также построить пространственную траекторию движения заряженной частицы.
7 Колебания и волны
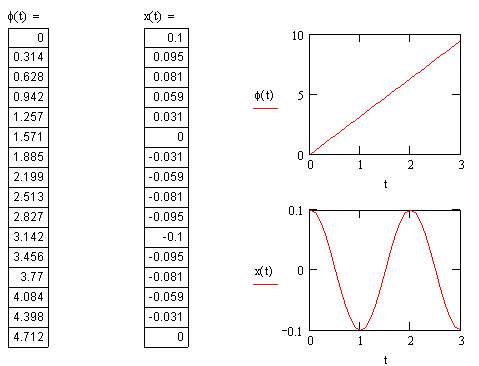
7-1 Амплитуда гармонических колебаний ![]() см, а частота
см, а частота ![]() Гц. Определите период Т
колебания и циклическую частоту ω0. Постройте таблицу зависимости
фазы
Гц. Определите период Т
колебания и циклическую частоту ω0. Постройте таблицу зависимости
фазы ![]() и
смещения
и
смещения ![]() от
времени t, которое изменяется от 0 до 3 с.
от
времени t, которое изменяется от 0 до 3 с.
7-2 Груз на невесомом жестком подвесе длиной ![]() колеблется с большой амплитудой. Как
зависит период колебаний от величины максимального угла отклонения?
колеблется с большой амплитудой. Как
зависит период колебаний от величины максимального угла отклонения?
7-3 Получите зависимость от времени положения акробата, прыгающего на
батуте. Указание: Следует учесть силу тяжести акробата (![]() ), силу упругости (-
), силу упругости (-![]() ) батута и силу трения
в пружинах батута (
) батута и силу трения
в пружинах батута (![]() ).
).
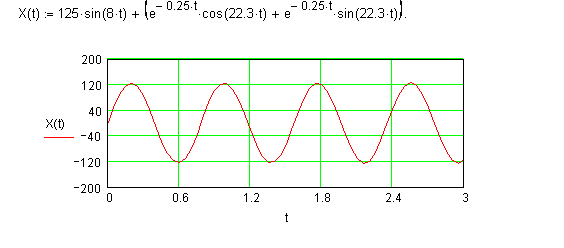
7-4 На тело массой m = 0.1,кроме возмущающей силы F = - kx (k = 50) и силы
трения ![]() (
(![]() ), действует переменная
возбуждающая сила
), действует переменная
возбуждающая сила ![]() ,
где
,
где ![]() ,
, ![]() . Какими будут
колебания при начальных условиях
. Какими будут
колебания при начальных условиях ![]() ,
, ![]() ? Рассмотрите первые 50-100 периодов.
Получите затухающие колебания.
? Рассмотрите первые 50-100 периодов.
Получите затухающие колебания.
7-5 Если длину маятника изменять с частотой, вдвое превышающей собственную
ω0, то энергия от источника с 2 ω0 будет
перекачиваться в систему. Рассмотрите такое параметрическое возбуждение
колебаний на примере качели в предположении, что если дважды за период
приседать в крайних точках, то амплитуда будет возрастать. Указание: Принять
![]() , где
, где ![]() .
.
7-6 Складываются два взаимно перпендикулярных колебания с различными амплитудами, частотами и разностями фаз. Получите фигуры Лиссажу.
7-7 Подберите функции синусоидального сигнала и сигналов однополупериодного и двухполупериодного сигналов и постройте их графики.
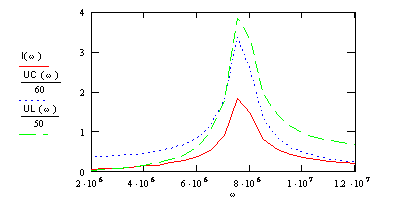
7-8 Резонанс напряжений. Как будут изменяться напряжения на конденсаторе,
на катушке индуктивности, сила тока в цепи, мощность и ![]() при подаче на вход цепи синусоидального
напряжения 20В и при изменении частоты этого напряжения от 0 до 2 МГц. (R=10
Ом, L=14,2мкГ; С=1,2нФ)?
при подаче на вход цепи синусоидального
напряжения 20В и при изменении частоты этого напряжения от 0 до 2 МГц. (R=10
Ом, L=14,2мкГ; С=1,2нФ)?
8 Оптика. Квантовая природа излучения
8-1 Каково расстояние от наблюдателя до оазиса в пустыне, если путник утром
видит в небе мираж под углом ![]() к горизонту, а показатель преломления
из-за сильного охлаждения поверхности пустыни за ночь убывает с высотой
z по
закону :
к горизонту, а показатель преломления
из-за сильного охлаждения поверхности пустыни за ночь убывает с высотой
z по
закону : ![]() где
где
![]() м?
м?
8-2 Световод с линейным изменением показателя преломления. В световоде типа «Градан» луч света искривляется и все время возвращается обратно к оси благодаря тому, что показатель преломления убывает от оси к краям.
8-3 Электростатическая линза. Пусть электроны разлетаются из некоторой точки. Полые цилиндры А и В с боковыми стенками, но без донышек на торцах заряжены так, как показано на рисунке. Влетая в пространство между цилиндрами, электрон ускоряется. Покажите, что, кроме того, расходящийся поток электронов фокусируется после такого устройства приблизительно в одну точку. Изобразите траектории электронов.
8-4
Кольца Ньютона. Рассчитайте и изобразите на графическом дисплее
интерференционные картинки, получающиеся при освещении красным светом ![]() плоской пластины с
прижатыми к ней плосковыпуклыми линзами радиусами
R от 0 до 20 см.
плоской пластины с
прижатыми к ней плосковыпуклыми линзами радиусами
R от 0 до 20 см.
8-5 Дифракция на щели. Постройте график распределения интенсивности по
экрану, находящемуся на расстоянии L=4м от щели, приняв ![]()
![]()
![]() .
.
8-6
Дифракционная решетка. Постройте график распределения интенсивности по экрану,
находящемуся на расстоянии L=4м от решетки, приняв ![]() мм.
мм.
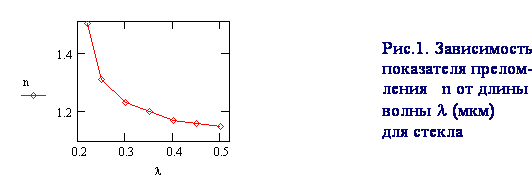
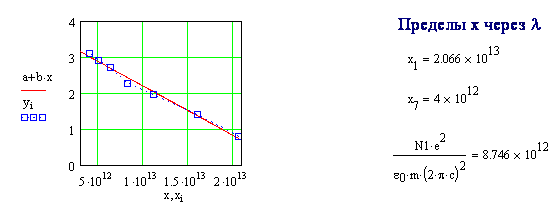
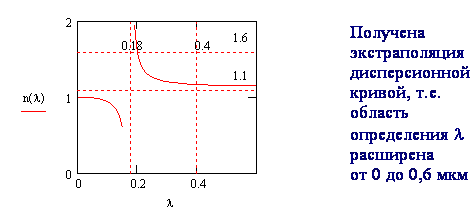
8-7 Экстраполяция
дисперсионной кривой. На опыте для конкретного сорта стекла получена
следующая зависимость показателя преломления от длины волны:![]()
|
|
0,22 |
0,25 |
0,3 |
0,35 |
0,40 |
0,45 |
0,5 |
|
n |
1,5 |
1,31 |
1,23 |
1,20 |
1,17 |
1,16 |
1,15 |
Предполагая,
что показатель преломления n зависит от ![]() по закону (28), восстановите примерно
ход
по закону (28), восстановите примерно
ход ![]() в более
широких пределах и найдите длину волны резонанса
в более
широких пределах и найдите длину волны резонанса ![]() .
.
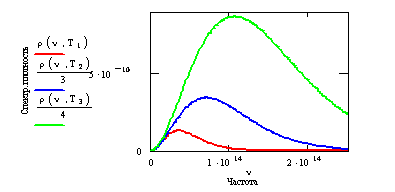
8-8 Построение кривой Планка. Начертите ![]() , если значение
, если значение ![]() изменяется от 0 до
10мкм при температуре 600 К; 1200 К; 1800 К.
изменяется от 0 до
10мкм при температуре 600 К; 1200 К; 1800 К.
8-9 На платиновую пластинку падают ультрафиолетовые лучи. Для прекращения фотоэффекта нужно приложить задерживающее напряжение Uз1 = 3,7 В. Если пластинку заменить другой металлической пластинкой, то задерживающее напряжение Uз2 нужно увеличить до 6 В. Определите работу выхода А2, если для платиновой пластинки она равнялась 10-18 Дж. Заряд электрона е = 1,6.10-19 Кл. Варьируя Uз для металла, найдите работу выхода, постройте график А = f(Uз).
9 Элементы квантовой физики
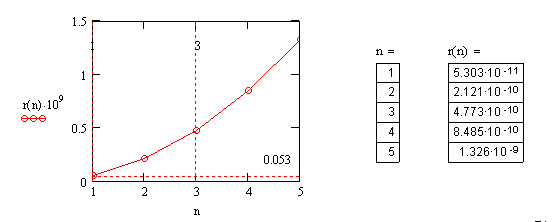
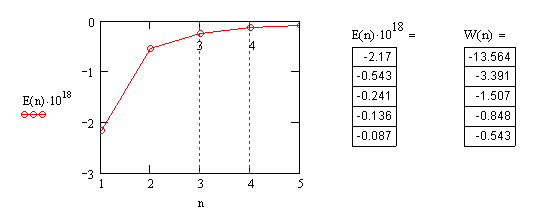
9-1 Определите радиусы орбит электрона и
значения энергии атома водорода для значений главного квантового числа
n = 1,2,3,4,5.
(![]() ,
,
![]() ).
).
9-2 Рассеяние ![]() частиц.
частиц.
![]() частицы с
энергией 4 МэВ рассеиваются тонкой золотой фольгой. Начертите траекторию
частицы, приближающейся к ядру Au. Прицельное расстояние
частицы с
энергией 4 МэВ рассеиваются тонкой золотой фольгой. Начертите траекторию
частицы, приближающейся к ядру Au. Прицельное расстояние ![]() равно
равно
![]() .
На
какой угол
.
На
какой угол ![]() рассеивается
частица? Проведите небольшое исследование: как зависит угол
рассеивается
частица? Проведите небольшое исследование: как зависит угол ![]() от прицельного расстояния
от прицельного расстояния
![]() при рассеивании
при рассеивании ![]() частиц ядрами золота?
частиц ядрами золота?
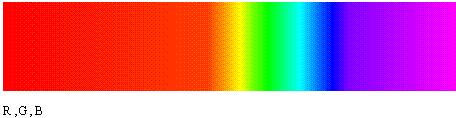
9-3 В спектре водорода с точностью до 0,1 нм найдите значения длин
волн ![]() восьми
линий в каждой из первых пяти серий в спектре излучения водорода. Сделайте таблицу
длин волн. Изобразите на экране вид спектра.
восьми
линий в каждой из первых пяти серий в спектре излучения водорода. Сделайте таблицу
длин волн. Изобразите на экране вид спектра.
9-4 Электрон в потенциальном ящике. Дан потенциальный ящик шириной ![]() и со стенками высотой
U=20
эВ. Найдите, какие значения энергии может
иметь электрон. Изобразите на экране монитора соответствующие волновые функции
и распределение электронной плотности (вероятность нахождения электрона в
разных точках). Сопоставьте со случаем потенциального ящика с бесконечно
высокими стенками, где допустимые зачения энергии
и со стенками высотой
U=20
эВ. Найдите, какие значения энергии может
иметь электрон. Изобразите на экране монитора соответствующие волновые функции
и распределение электронной плотности (вероятность нахождения электрона в
разных точках). Сопоставьте со случаем потенциального ящика с бесконечно
высокими стенками, где допустимые зачения энергии ![]() (n=1,2,3,… энергия
отсчитывается от дна ящика).
(n=1,2,3,… энергия
отсчитывается от дна ящика).
Решите ту же задачу для ящика произвольной формы, где в
пределах от ![]() до
до
![]() потенциальная энергия изменяется по закону
потенциальная энергия изменяется по закону ![]() (
(![]() ,
, ![]() ). В этом случае трудно даже качественно
предугадать решение, но компьютер решает эту задачу так же легко, как и
предыдущую.
). В этом случае трудно даже качественно
предугадать решение, но компьютер решает эту задачу так же легко, как и
предыдущую.
СПИСОК ЛИТЕРАТУРЫ
1. Дьяконов В.П., Абраменкова И.В. Mathcad 7 в математике, физике и в Internet. – M.: Нолидж, 1998. – 352 с.
2. В.М. Дулэпо, С.Е. Базарбаева, С.К. Касымбеков. Высшая математика. Компьютерное решение задач. Методические указания к лабораторным занятиям. – Алматы.: АИЭС, 1999. – 46 с.
3. Д.В. Кирьянов. Электронный учебник. [http://prodav.narod.ru/mathbook.htm].
4. Э.В. Бурсиан. Физика. 100 задач для решения на компьютере. – Санкт-Петербург.: M и М, 1997. – 356 с.
5. В.А. Извозчиков, А.М. Слуцкий. Решение задач по физике на компьютере. – М.: Просвещение, 1999. – 256 с.
6. Физика. Задания к практическим занятиям. Под общей редакцией Ж.П. Лагутиной. – Мн.: Выш. шк., 1989. – 236 с.
7. А.Г.Чертов, А.А. Воробьев. Задачник по физике. – М.: Высшая школа, 1983. – 496 с.
8. И.В. Савельев. Курс общей физики, т.1-3. – M.: Наука, 1987-9.
9. А.А. Детлаф, Б.М. Яворский. Курс физики. – М.: Высшая школа, 1989. – 608 с.
ПРИЛОЖЕНИЕ А
1 Решение физических задач с дифференциальными уравнениями I порядка
Дифференциальное уравнение первого порядка имеет вид
![]() (1)
(1)
Если вид функции f(x,y) известен, то в некоторых случаях уравнение (1) можно решить аналитически, в других случаях это невозможно. С помощью компьютера можно решить любое уравнение типа (1) численным методом. В методе Эйлера дифференциалы dy и dx приближенно заменяются приращениями ∆у и ∆х, т.е.
![]() ;
; ![]() . (2)
. (2)
Тогда, зная х n и уn ( например, из начальных условий известно значение у0 при заданном х0 ), можно найти уn+1 по формуле (2) и хn+1 по формуле
![]() . (3)
. (3)
Затем определяется следующая пара значений yn+2 и хn+2 и, таким образом, получается вся зависимость у(х) в виде двух последовательностей чисел. Алгоритм решения можно представить в виде схемы на рисунке 10.
|
![]()
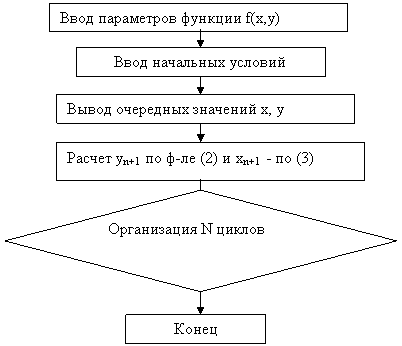 |
Рисунок 8
2 Решение физических задач с дифференциальными уравнениями II порядка
Дифференциальное уравнение II порядка вида
![]() (4)
(4)
можно свести к к двум дифференциальным уравнениям I порядка.
![]() (5)
(5)
и
![]() , (6)
, (6)
или приближенно получим
![]() ;
(7)
;
(7)
и
![]() . (8)
. (8)
Если при каком-то x n известны y n и z n = ( dy /dx ) n , то формулы (7) и (8) позволяют переходить от x 0 , y 0 , z 0 к x 1 , y 1 , z 1 и т.д. и получить решение, т.е. значения x, y, z.
В системе MathCAD возможно решение дифференциальных уравнений с помощью стандартных методов. Рассмотрим пример такого решения дифференциального уравнения второго порядка методом Рунге-Кутта.
Шарик массой 2.2 г и радиусом 4.1 мм падает в масле с плотностью 1000 кг/ м, встречая силу сопротивления 6p r h v, где h = 0.96 кг.м/c. Найти зависимость скорости v, ускорения a и пути s от времени падения t. Решение:



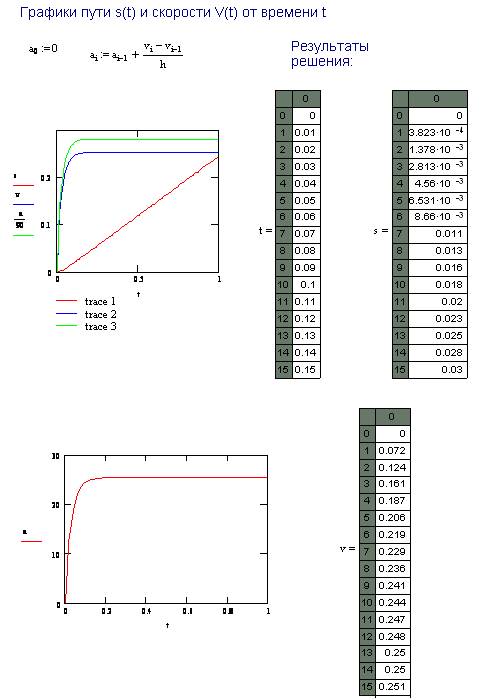
Рисунок 9
ПРИЛОЖЕНИЕ В
Метод наименьших квадратов
В лабораторном практикуме одним из основных методов обработки полученных экспериментальных данных является метод наименьших квадратов (МНК), который используется не только для линейной функциональной зависимости физических величин, но также и для степенной и экспоненциальной зависимостей, наиболее часто встречающихся в курсе физики.
В случае линейной зависимости ![]() между
экспериментальными данными yi и
xi задача решается таким образом, чтобы
между
экспериментальными данными yi и
xi задача решается таким образом, чтобы ![]() была минимальной, т.е.
нужно найти такие значения констант а и b для уравнения
прямой
была минимальной, т.е.
нужно найти такие значения констант а и b для уравнения
прямой ![]() , чтобы
, чтобы
![]() имело
минимум. Тогда должно быть
имело
минимум. Тогда должно быть ![]() и
и
![]() . Подставляя сюда
. Подставляя сюда ![]() и
и ![]() и выполнив дифференцирование, можно
получить окончательные выражения для определения постоянных
и выполнив дифференцирование, можно
получить окончательные выражения для определения постоянных ![]() и
и ![]() :
:
![]() ;
b =
;
b =
![]() ,
где
,
где ![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
,
 |
Пусть имеется совокупность пар значений xi и yi , представленная в среде MathCad в следующем виде:
Рисунок 10
где
N - число измерений, т.е. число пар (![]() ,
, ![]() ).
).
Экспериментальные данные, обозначенные кружочками, как видно из рис.10, имеют значительный разброс и не укладываются на прямой.
Используем МНК для правильной обработки и интерпретации полученных данных. Выполним вышеуказанные процедуры:

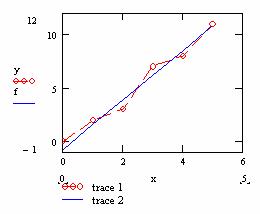
Рисунок 11
На рисунке 11 видно, как должна быть проведена прямая, но основная цель, достигаемая при применении МНК, - это получение правильных значений постоянных а и b, что может иметь в физических задачах принципиальное значение.
По геометрическому смыслу значение а дает пересечение прямой с осью ординат, b равняется тангенсу угла наклона прямой, и даже небольшая погрешность наклона прямой может привести к существенным ошибкам при определении конечного результата (тангенс меняется от 0 до ∞).
В случае нелинейной зависимости повторяются все процедуры МНК, но предварительно исходная зависимость сводится к линейной путем логарифмирования и замены переменных. Рассмотрим решение такой задачи в системе MathСad:
а) рассмотрим степенную зависимость на примере экспериментальной проверки закона Стефана-Больцмана R = σ T n для теплового излучения. Исходные данные для температуры t 0C ( или T, K) и мощности излучения вольфрамовой нити накаливания Р=I·U=R·S:
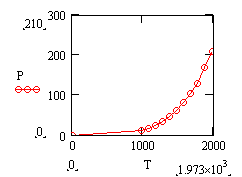 |
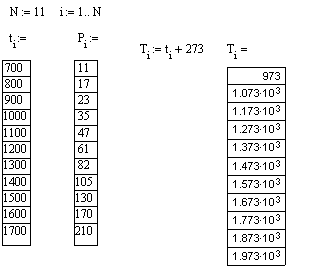
Рисунок 12
Логарифмируя исходное выражение, получим линейную зависимость:
![]() , где σ =
5,67·10-8 Вт/(м2К4) - постоянная Стефана Больцмана.
, где σ =
5,67·10-8 Вт/(м2К4) - постоянная Стефана Больцмана.
Введем обозначения: Y= ℓn R, a1 = ℓn σ, n = b1, X = ℓn T. R = P/S, где S = 10-4 м2- излучающая площадь нити накаливания. На рис. 12 представлен график зависимости мощности излучения нити накаливания от температуры. Приведем вычисления в среде MathCad:
Вычислим излучательность R через мощность Р, затем – значения ℓnR и ℓnT.

Мы ввели новые обозначения, чтобы воспользоваться МНК.
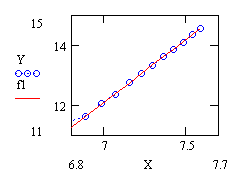 Получено значение
b1=n, близкое к 4, что соответствует значению показателя
степени в законе Стефана-Больцмана:
Получено значение
b1=n, близкое к 4, что соответствует значению показателя
степени в законе Стефана-Больцмана:
![]() .
.
Рисунок 13
Итак, получено подтверждение проверяемого закона, погрешность в определении n составляет всего 3,7%. Совпадение достаточно хорошее, чего трудно было бы ожидать без применения МНК;
б)
в экспоненциальной зависимости ![]() путем логарифмирования и замены
переменных вновь получаем линейную зависимость, к которой можно применить МНК.
Пример вычислений в MathCAD:
путем логарифмирования и замены
переменных вновь получаем линейную зависимость, к которой можно применить МНК.
Пример вычислений в MathCAD:
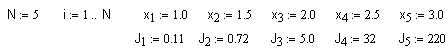
 |
На рисунке 14 представлена исходная зависимость и на рисунке 15 - график полученной с помощью МНК линейной зависимости. Получено также аналитическое выражение для исходных экспериментальных данных.
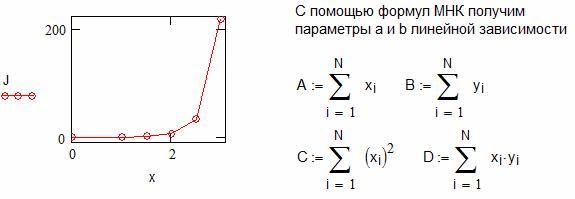
Рисунок 14
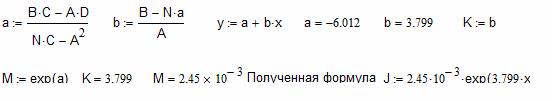
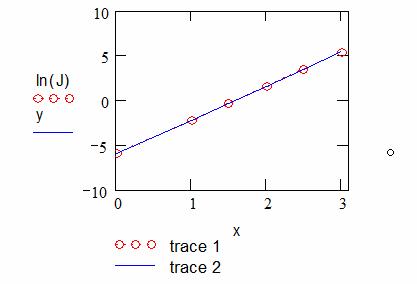
Рисунок 15
Полученный
график зависимости ![]() показывает
прекрасное совпадение с экспериментальными данными, но это справедливо лишь в
случае, когда погрешность измерений примерно одинакова во всем диапазоне. В противном
случае на тех участках, где погрешность больше, следует проводить большее число
измерений.
показывает
прекрасное совпадение с экспериментальными данными, но это справедливо лишь в
случае, когда погрешность измерений примерно одинакова во всем диапазоне. В противном
случае на тех участках, где погрешность больше, следует проводить большее число
измерений.
Приведенные примеры наглядно демонстрируют полезность и большие возможности MathCAD при решении физических задач.
ПРИЛОЖЕНИЕ С
Справочные данные по физическим константам
Т а б л и ц а - Основные физические константы
|
g = 9,81 м/с2 – ускорение свободного падения |
|
с = 3 x 108 м/с – скорость света в вакууме |
|
G = 6,672 x 10-11 м3/(кг.с2) – гравитационная постоянная |
|
NA = 6,022.1023 моль-1 – число Авогадро |
|
k = 1,38 х 10-23 Дж/К – постоянная Больцмана |
|
R = 8,31 Дж/ (моль.К) – универсальная газовая постоянная |
|
ε0 = 8,85 х 10-12 Ф/м – электрическая постоянная |
|
μ0 = 4π х 10-7 Гн/м – магнитная постоянная |
|
e = 1,6 х 10-19 Кл – элементарный заряд (заряд электрона) |
|
me = 9,11 х 10-31 кг – масса покоя электрона |
|
mр = 1,67 х 10-27 кг – масса покоя протона |
|
F = 9,65 x 104 Кл/моль – число Фарадея |
|
h = 6,625 x 10-34 Дж.с – постоянная Планка |
|
1 а.е.м. = 1,66 х 10-27 кг – атомная единица массы |
Ответы к задачам
№ 4-1 t = 50 мин. Указания. Уравнения движения автомобилей: x1 = s +v1t и x2 = v2t, откуда t = s/(v2 –v1).
№ 4-2 Представлено решение, импортированное из среды MathCad.
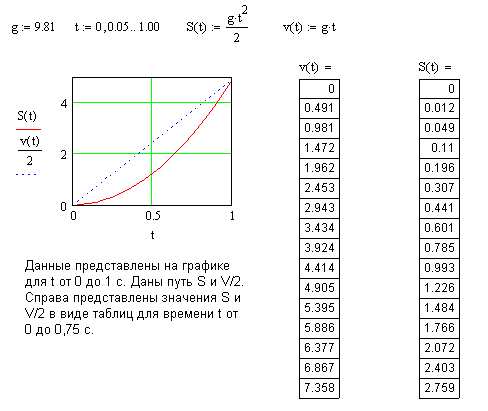
№
4-3 Из зависимости текущей высоты у от времени
t следует получить
t как решение
квадратного уравнения ![]() . Наличие только мнимых корней означает,
что при данной v0 высота Н
недостижима. В случае двух вещественных корней тело проходит данную высоту
дважды.
. Наличие только мнимых корней означает,
что при данной v0 высота Н
недостижима. В случае двух вещественных корней тело проходит данную высоту
дважды.
№ 4-4

№ 4-5 t1 = 8,4 с; t2 = 7,3 с; t3 = 7,8 с. (см. предыдущую задачу).
№ 4-6 Составьте программу, аналогичную приведенной в примере из кинематики.
№ 4-7 Запишем аналитически полученное выражение для тормозного пути

№ 4-8 μ = 0,169; График получен для v в пределах от 5 до 9 м/с.
№ 4-9 Т = 56 Н. Масса второго тела изменяется от 4 до 8 кг.
№ 4-10 Рассмотрим движение тел только влево.

№ 4-11 ![]() L=9,14 м. График зависимости
L от
L=9,14 м. График зависимости
L от ![]() строится по аналогии с предыдущей
задачей.
строится по аналогии с предыдущей
задачей.
№ 4-12 Ответ:
![]()
![]()

№ 4-13 На основе законов сохранения энергии и импульса получите выражение для удлинения пружины:
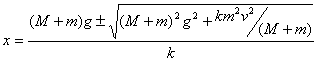 , x = 0,12 м.
, x = 0,12 м.
№ 4-14 ![]() .
.

№ 4-15 ![]()
№ 4-16 Решение задачи выполнено с помощью стандартного метода Рунге-Кутта, находящегося в Центре Ресурсов MathCad 2001.

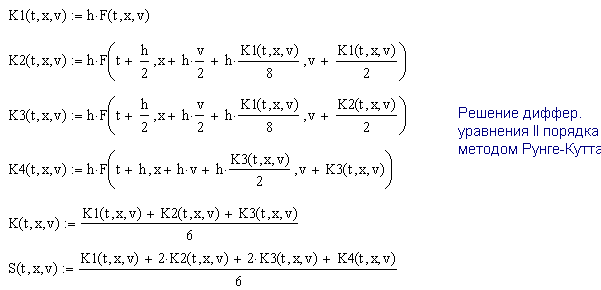


№ 4-17 Учитывая результат предыдущей задачи, получим, что в течение 125 секунд парашют можно не раскрывать.
№ 4-18
![]()
![]()

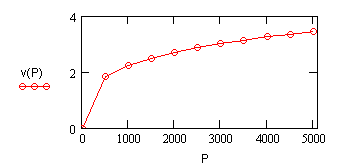
№
4-19 Уравнение движения ![]() , где
Ft-сила тяги,
при равномерном движении (
, где
Ft-сила тяги,
при равномерном движении (![]() ) переходит в кубическое уравнение для
F(t,v),
которое решается методом Кардано (см. Центр ресурсов
MathCad). В
нижеприведенной программе выбран шаг h
и N=100 точек.
) переходит в кубическое уравнение для
F(t,v),
которое решается методом Кардано (см. Центр ресурсов
MathCad). В
нижеприведенной программе выбран шаг h
и N=100 точек.

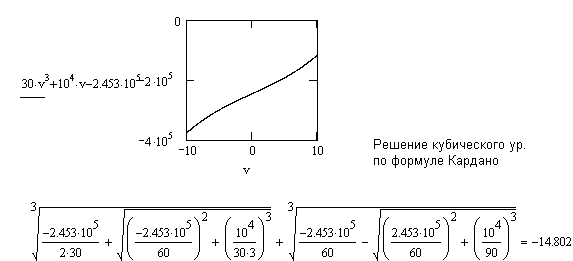
Итак, vmax =14,8 м/с =53,5 км/ч; Р = Ft.vmax=3.68 МВт.
№ 4-20 Задача аналогична № 4-19. Задав начальные условия t0 = 0 и х0=0, составим циклы увеличения t, x и v:
 ,
,
где h = 1, N = 30. Получим: t = 22,5 c; v = 13,5 м/с, S = 209 м.
№ 4-21 Решение задачи, приведенное ниже, выполнено с помощью стандартного метода Рунге-Кутта, находящегося в Центре Ресурсов MathCad.




№ 4-22 a) S1 = 4 км; b) S1 = 2068 м.
№ 4-23
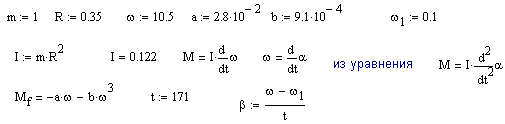
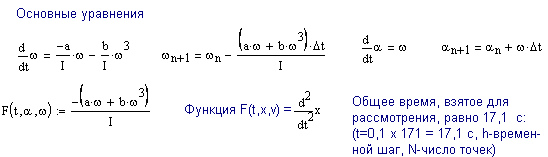




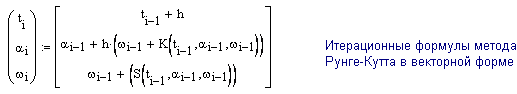

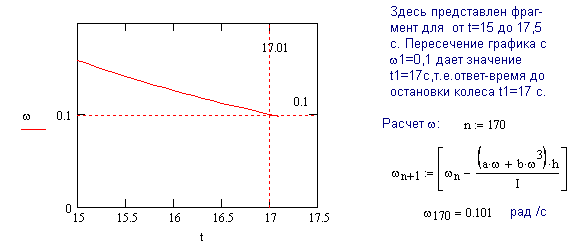

№ 4-24 Графический метод решения задачи.



№ 4-25 Используйте уравнение Мещерского /9/: t = 120 c.
№ 4-26 Ниже приводится программа полета корабля около Луны по гиперболе при определенных значениях скорости корабля и прицельного параметра.


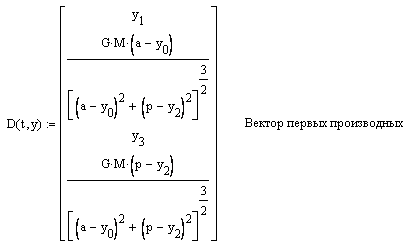

![]()


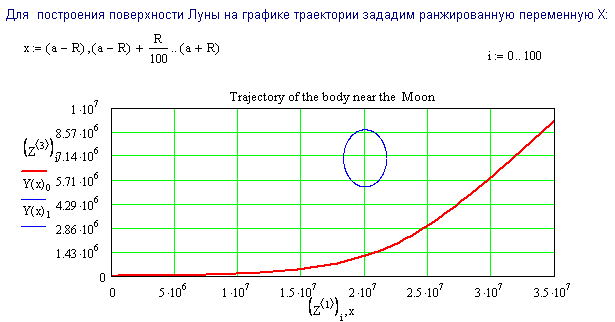
№ 4-27 Приводится аналогичная программа облета Луны по параболе.




Примечание: В данной и предыдущей задаче, как и практически в любой другой задаче, можно получить анимацию траектории полета корабля вблизи Луны. Для этого нужно нажать Вид→Анимация→В в появившемся окне в левой части установить число кадров от 0 до 90→обвести с помощью курсора рабочую область, в которой производится анимация, и нажать в правой части Анимация. Тогда в основном рабочем поле в верхнем левом углу появится окно анимации, нажав в нем на треугольную стрелку, получите движение корабля.
№ 4-28




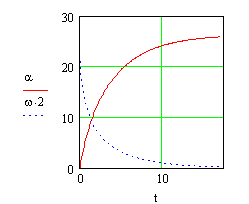 Графики зависимости угла
Графики зависимости угла ![]() и угловой скорости
и угловой скорости ![]() от времени
t
от времени
t
позволяют определить время торможения колеса до полной остановки. Оно определяется по
точке пересечения этих кривых
и равно 17 секунд.
Определив угол ![]() =25,9 рад в этот
=25,9 рад в этот
момент времени, найдем число обо-
ротов колеса: ![]() (об.).
(об.).
№ 5-1 Приведем программу построения кривых распределения Максвелла при температурах 300 К и 400 К.


№ 5-2 Интегралы вычисляются в среде MathCad мгновенно после их набора и нажатия на знак равенства.
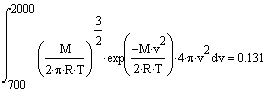
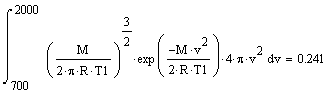
Графики строятся так же, как и в предыдущей задаче.
№ 5-3



![]()

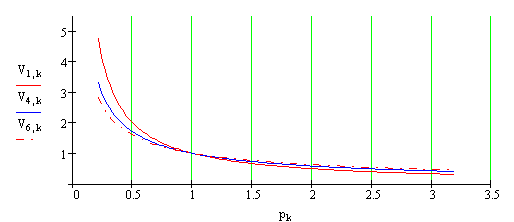
Видно, что с ростом n кривые становятся положе и все кривые пересекаются в одной точке.
№ 5-4 Вычисления в программе представлены для 6 кривых Ван дер-Ваальса, графики – для четырех для более четкого их разделения.
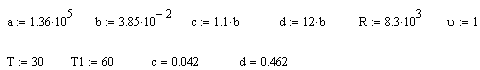
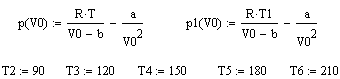

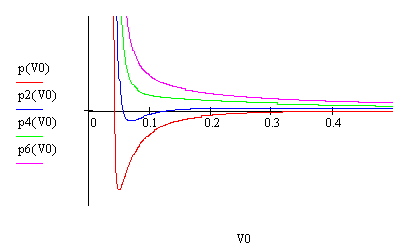
№ 5-5


![]()
№ 5-6



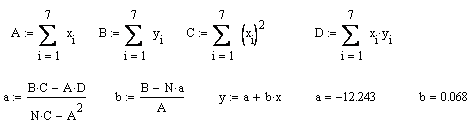
№ 6-1



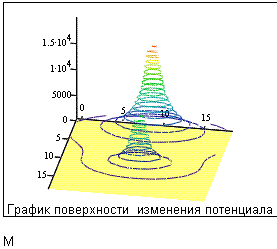
№ 6-2
![]()
![]()

![]()
Дополнительные задания: 1) изменение r ; 2) рис. к задаче
![]()

№ 6-3
Составим уравнения по правилам Кирхгофа (слева), определитель системы уравнений А и вектор свободных членов В. Искомые токи выражаются с помощью вектора В и равны соответственно: I1 = 0,8 A; I1 = - 0,3 A; I1 = 0,5 A. Знак «минус» указывает, что истинное направление тока противоположно указанному на рисунке.
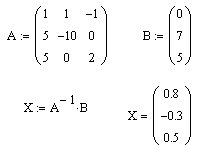
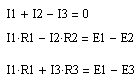
№ 6-4
Исходные данные (сила тока I в А, напряжение U в В):

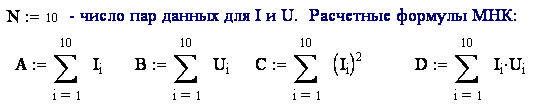

№ 6-5



№ 6-6


7-1
![]()
![]()

7-2
![]()
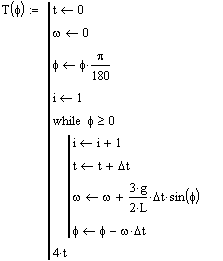

7-3 Примем следующие условия задачи:
![]()
m – масса
гимнаста; k – коэффициент упругости батута;
r – коэффициент пропорциональности
между силой трения ![]() в пружинах батута скоростью
v, т.е.
в пружинах батута скоростью
v, т.е. ![]() . Запишем начальные
условия, итерационные формулы и полученный график.
. Запишем начальные
условия, итерационные формулы и полученный график.

7-4
![]()

- дифференциальное уравнение
![]()

Характеристическое уравнение:
![]()





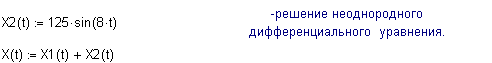

Вынужденные колебания - решение
неоднородного дифференциального уравнения
![]() .
.
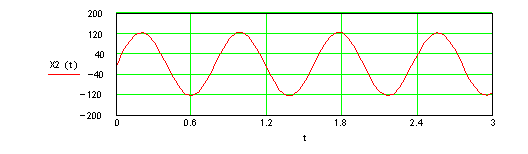
2. Затухающие колебания - решение однородного дифферeнциального уравнения:
(![]() ).
).
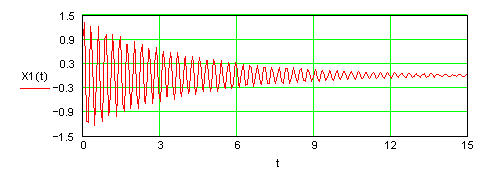
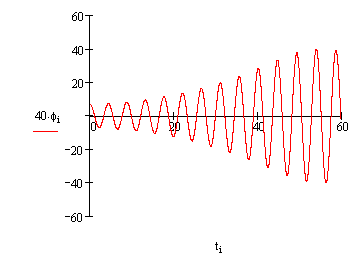
7-5 Параметрические колебания
![]()
![]()

7-6 Фигуры Лиссажу
![]()
![]()
![]()
![]()
![]()

7-7
![]()
![]()
Графики функций:
a) синусоидальный сигнал b) сигнал однополупериодного выпрямления


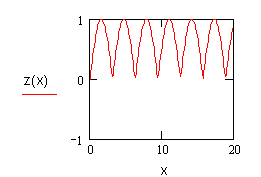
c) сигнал двухполупериодного выпрямления
7-8
![]()
![]()
![]()

Графики резонансных кривых
8-1
По условию задачи: ![]() –
показатель преломления воздуха на нулевой высоте,
g – коэффициент
изменения показателя преломления с высотой
z. Примем шаг
изменения по высоте
–
показатель преломления воздуха на нулевой высоте,
g – коэффициент
изменения показателя преломления с высотой
z. Примем шаг
изменения по высоте ![]() .
k – число итераций до максимальной высоты;
.
k – число итераций до максимальной высоты; ![]() – текущая высота;
– текущая высота; ![]() –текущий показатель
преломления;
–текущий показатель
преломления; ![]() –
текущая длина;
–
текущая длина; ![]() –
угол видимости миража на каждом слое;
–
угол видимости миража на каждом слое;![]() – максимальная высота хода
луча;
– максимальная высота хода
луча;![]() –
расстояние, соответствующее максимальной высоте хода луча.
–
расстояние, соответствующее максимальной высоте хода луча.

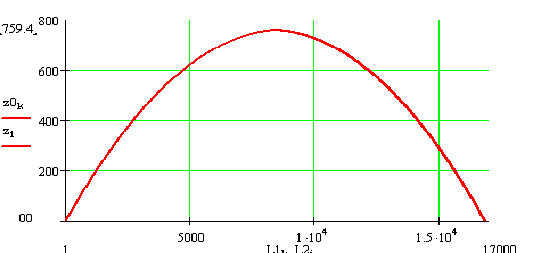
Расчеты показывают, что расстояние от объекта до наблюдателя составляет L =16830 м и максимальная высота хода луча z1 = 759.4 м.
График
зависимости высоты хода луча от пройденного пути при ![]() дает траекторию оптических
лучей при наблюдении миража и представлен на рисунке. Кроме того, по
представленной программе были рассчитаны траектории оптических лучей при меньших
углах наблюдения миража
дает траекторию оптических
лучей при наблюдении миража и представлен на рисунке. Кроме того, по
представленной программе были рассчитаны траектории оптических лучей при меньших
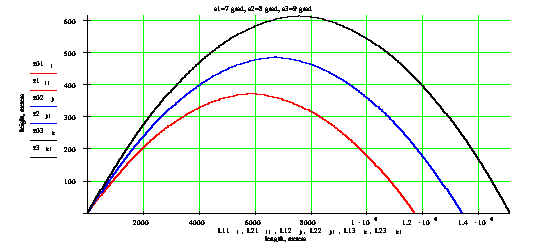
углах наблюдения миража ![]()
![]() ,
, ![]() . Эти данные приведены на следующем рисунке.
. Эти данные приведены на следующем рисунке.
8-2
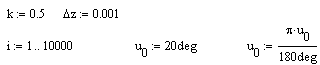


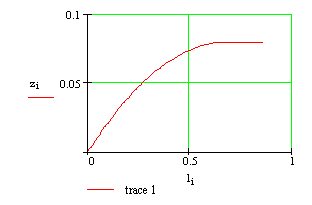
8-3
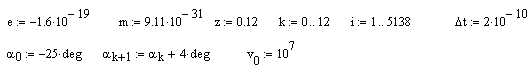



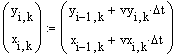
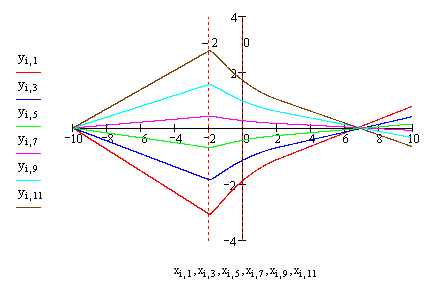
8-4
![]()

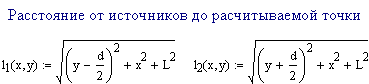
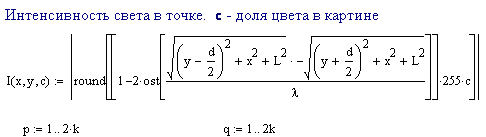
Построение интерференционной картины в виде матрицы с значениями интенсивности в каждой точке. Изменяя с от 0 до 1, можно получить разные цвета.
![]()

8-5
![]()
Если ф-угол дифракции, то х = L*ф и Q= (pb/l)*sinф, тогда:
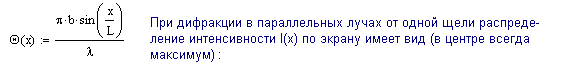
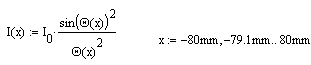
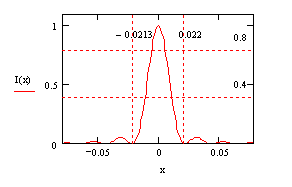
8-6
![]()
![]()
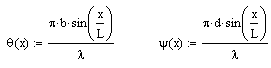


Изменяя значения N, можно получить дифракционные картины для решетки с различным
числом щелей.
8-7



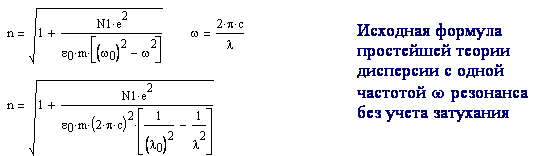





8-8
![]()

8-9
![]()

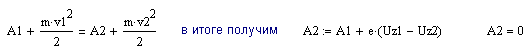
![]()
![]()

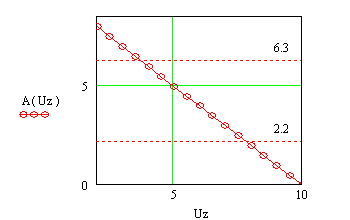
9-1
![]()
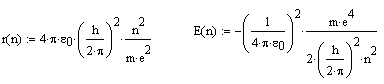

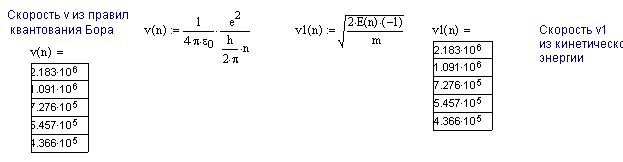
9-2
На рисунке представлена траектория движения α-частицы при ее рассеянии в виде гиперболы. Символ "р" обозначает прицельное расстояние, т.е. длину перпендикуляра, опущенного из ядра, находящегося в точке О, на невозмущенную прямолинейную траекторию альфа-частицы.
 Fi - угол рассеяния α-частицы при взаимодействии с
ядром. Произведем расчет углов рассеяния и траектории α-частиц с кинетической
энергией (EK =
4 MeV) при взаимодействии с тонкой золотой фольгой, приняв
прицельное расстояние р, равное 2∙10-15 м. Построить
траектории при разных прицельных расстояниях
p.
Составим программу на языке программирования
MathCad, задав
начальные параметры, указанные в условии поставленной задачи. Ниже дана
программа и вычисления в компьютерной среде
MathCad, в которой
используются символьная процедура математических вычислений.
Fi - угол рассеяния α-частицы при взаимодействии с
ядром. Произведем расчет углов рассеяния и траектории α-частиц с кинетической
энергией (EK =
4 MeV) при взаимодействии с тонкой золотой фольгой, приняв
прицельное расстояние р, равное 2∙10-15 м. Построить
траектории при разных прицельных расстояниях
p.
Составим программу на языке программирования
MathCad, задав
начальные параметры, указанные в условии поставленной задачи. Ниже дана
программа и вычисления в компьютерной среде
MathCad, в которой
используются символьная процедура математических вычислений.
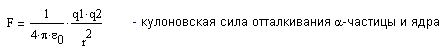
![]()
C помощью символьного процессора MathCad выполним необходимые подстановки:

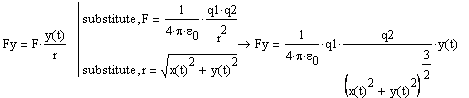
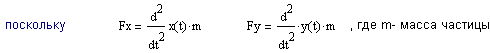
то окончательно уравнения движения по осям x и y имеют вид:
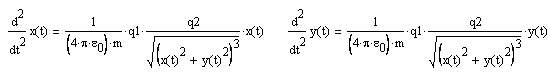
Для определения вектора начальных условий выразим проекцию скорости на ось х, воспользовавшись соотношением:
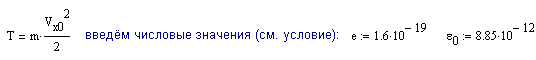
![]()
![]()
![]()
![]()
тогда вектор начальных условий можно записать в следующем виде:


Задача решена, построим траектории движения α-частицы при четырех значениях прицельного расстояния "р".
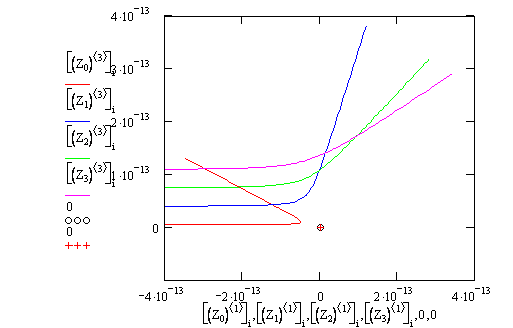 |
значком "плюс", обведенным кругом, указано положение ядра.
9-3


![]()
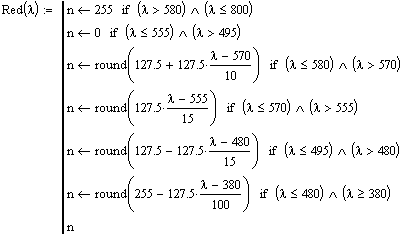


![]()
![]()

![]()
