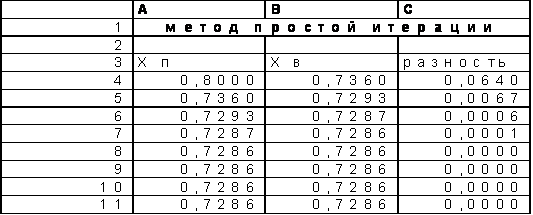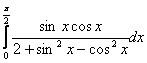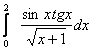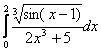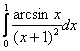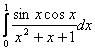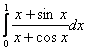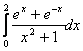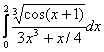АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
КАФЕДРА ИНЖЕНЕРНОЙ КИБЕРНЕТИКИ
Учебно-ознакомительная практика
Методические указания к выполнению заданий для студентов специальности
050702-Автоматизация и управление
Алматы 2009г.
СОСТАВИТЕЛИ: М.Д. Ешпанова. Учебно-ознакомительная практика. Методические указания к выполнению заданий для студентов специальности 050702-Автоматизация и управление. Алматы: АИЭС, 2009. 38-с.
Представлены методические указания к выполнению заданий по учебно-ознакомительной практике. Методическое указание содержит семь заданий. Описание каждого задания содержит необходимую для выполнения информацию, пример решения аналогичной задачи.
Содержание
Введение 3
Задание 1. Приближенное решение конечных уравнений 4
Задание 2. Методы численного интегрирования 11
Задание 3. Метод наименьших квадратов 17
Задание 4. Методы численного решения дифференциальных уравнений с помощьюMS Excel 21
Задание 5. Построение поверхности 25
Задание 6. Решение задач оптимизации с помощью надстройки Поиск решения 29
Задание 7. Функции просмотра и ссылок 34
Список литературы
Введение
Учебно-ознакомительная практика студентов предполагает применение знаний, полученных студентами за время обучения, для решения практических задач. Во время прохождения практики студенты должны изучить численные методы решения инженерных задач и приобрести навыки их применения: методы решения трансцендентных уравнение, методы численного интегрирования, методы решения дифференциальных уравнений.
Студенты на различных примерах изучают широкие возможности MS Excel для решения математических, экономических и других задач. Представленные в методическом пособии задания предназначены для углубленного освоения возможностей табличного процессора и интегрированных сред разработки программных средств.
При прохождении практики студент должен представить письменный отчет по каждому заданию. Отчет должен содержать:
формулировку задачи;
описание метода;
программу на одном из языков программирования или (и) таблицу решения;
результаты работы программы.
Описание каждого задания содержит необходимую для его выполнения информацию из сопутствующего курса, пример решения аналогичной задачи. Некоторые задания предполагают наряду с MS Excel использование алгоритмического языка для выполнения. Также приводятся практические примеры применения методов и функций.
Задание 1. Приближенное решение конечных уравнений
Цель работы: научиться выполнять типовые задачи вычислительной математики, решение алгебраических и трансцендентных уравнений, часто встречающихся в инженерной практике.
Рассматривается численное решение уравнений вида
f(x)=0, (1.1)
где f – заданная функция.
Если уравнение (1.1) имеет следующий вид:
A 0 + A 1 x + A 2 x 2 + . . . + A n x n = 0,
(где A i -известные коэффициенты), то оно называется алгебраическим уравнением n-ой степени. Во всех других случаях уравнение (1.1) называется трансцендентным
Наиболее универсальные методы решения уравнений вида (1.1): метод Ньютона, метод дихотомии, метод хорд, метод простой итерации.
Метод Ньютона. Очередное приближение корня уравнения находится по формуле
хn+1=xn-f(xn)/f 1(xn).
Метод дихотомии (метод деления отрезка пополам). На каждой итерации отрезок [a,b] делится пополам и выбирается та из половин, на концах которой функция f(x) имеет значения разных знаков.
Метод хорд. Очередное приближение находится по формуле
хn+1=xn- (xn – xn-1)* f (xn)./ (f(xn)- f(xn-1)).
Метод простой итерации. Очередное приближение корня находится по формуле
xn= w(xn-1);
начальное приближение можно найти графически. Метод сходится, если |w1(х)| <1 в окрестности корня.
Численное решение уравнения (1) обычно начинают с нахождения грубого решения – начального приближения.
Пример.
Дано уравнение
х3-17х+12=0 (1.2)
Перед решением уравнения численным методом его нужно привести к стандартной форме. Будем рассматривать две стандартные формы.
Таблица 1.1
|
Форма |
Пример |
Где используется |
|
1 уравнение с нулевой правой частью |
х3-17х+12=0 |
Графический метод, метод хорд, дихотомии, Пакет Поиск решения |
|
2 уравнение, в левой части которого стоит неизвестная величина |
х3+12 х=w(х)=---------- 17 |
Метод итерации в ячейке |
Для решения заданного примера рассмотрим следующие способы:
1. Поиск корней уравнения с помощью графика (можно рассматривать как начальное приближение);
2. Метод итерации.
3. Решение уравнения с помощью надстройки Поиск решения.
4. Программа на языке С++ (метод половинного деления – дихотомия).
1.1 Графический метод для поиска корней
При использовании графического метода для поиска корней удобна первая форма уравнения, в которой все его члены перенесены в одну часть.
Уравнение переписывается в виде
f(x)= х3-17х+12. (1.3)
Вводится в электронную таблицу столбец значений х в интервале -5 <=x <=5, затем для каждого х вычисляется значение f(x). Строится точечная диаграмма - график функции f(x).

Рисунок 1.1
Из графика видно, что корни находятся возле точек х=0,8, х=3,7 и х=-4,5.
Графический метод нахождения корней прост, но не совсем точен. Для нахождения корней с более высокой точностью применяются численные итерационные методы. Применяя эти методы, следует указывать начальные приближения, замечательным средством получения которых является графический метод.
1.2 Методы итерации
Суть метода простой итерации (метод прямой подстановки) – использование вычисленного на предыдущем шаге значения в качестве предполагаемого значения для последующей итерации. Для этого следует применить стандартную форму 2 -
![]() (1.4)
(1.4)
Изолированная переменная в левой части уравнения называется вычисляемым значением. Обозначим ее хв. Переменная х в правой части уравнения называется предполагаемым значением. Обозначается как хп .
![]() (1.5)
(1.5)
В ячейке А4 вводится начальное предполагаемое значение – (0,8). Для вычисления в ячейке В4 вычисляемого значения по формуле (1.5) используется предполагаемое значение в ячейке А4.
Каждое новое предполагаемое значение, содержащееся в столбце А, равно вычисляемому значению предыдущего шага из столбца В. Например, в ячейке А5 – вводится формула (=В4).
Чтобы получить новое вычисляемое значение, скопировать формулу из ячейки В4 в ячейку В5.
Для последующих итераций ячейки копируются по мере необходимости из строки 5 в нижние строки. Разность хп-хв в столбце С позволяет оценить скорость сходимости метода.
|
|
Рисунок 1.2
Из рисунка 1.2 видно, что с помощью метода простой итерации (прямой подстановки) удалось найти корень х=0,7286 всего за несколько шагов.
Так как w1(x)= 3*х2 /17 <1 в окрестности х=0,8, то необходимое условия для сходимости метода выполнено.
Преимущество метода простой итерации – легко осуществим в электронной таблице.
Недостатки: иногда метод расходится – с его помощью нельзя получить все корни.
1.3 Надстройка Поиск решения
Программа MS Excel предоставляет другой метод – Надстройка Поиск решения. Этот метод устраняет недостатки метода простой итерации.
Примечание: эта надстройка не устанавливается по умолчанию и не активизируется по умолчанию. Чтобы активизировать надстройку Поиск решения, надо выполнить: Сервис – Надстройки- в окне со списком Надстройки установить флажок Поиск решения.
Уравнение записывается в форме 1. В ячейку В3 вводится начальное приближение - (0,8), а в ячейку В4 – формула =В3^3-17*В3+12 (рисунок 1.3).

Рисунок 1.3
Далее Сервис – Поиск решения.
В поле Установить целевую ячейку в качестве целевой ячейки выбирается ячейка В4, содержащая формулу.
Надстройка Поиск решения будет продолжать поиск решения, пока значение в целевой ячейке не будет равным нулю (так как в правой части уравнения стоит ноль).
Для этого переключатель устанавливается в положение по значению:, а в соответствующем поле введено значение 0.
В поле Изменяя ячейки: вводится адрес ячейки, в которой находится предполагаемое значение, - В3.
После ввода всех параметров щелкнуть на кнопке Выполнить.
С помощью надстройки Поиск решения найден корень, равный 0,73.
Чтобы найти другие корни, следует изменить предполагаемое значение и повторно запустить надстройку Поиск решения.
Преимущества надстройки Поиск решения: проста в применении и позволяет найти все корни уравнения.
1.4 Алгоритм деления отрезка пополам (метод дихотомии)
Требуется определить значение корня с погрешностью, не превосходящей данного положительного числа e. Можно применить метод деления отрезка пополам.
Взяв середину отрезка [a,b], на котором находится корень, то есть точку с координатой с=(а+b)/2, можно сузить диапазон поиска корня: перейти от отрезка [a,b] к отрезку [a,c] или [c,b] в зависимости от знака f (с): если f(a)f(c)<0, то перейти к отрезку [а,с], если f(a)f(c)>0, то перейти к отрезку [c,b]. Если затем найти середину меньшего отрезка и вычислить для нее значение функции f(x), то можно будет вновь сузить диапазон поиска и так далее. После нескольких шагов получится отрезок, длина которого будет меньше данного числа e.
Использование этого метода демонстрируется на программе, написанной на алгоритмическом языке (С++).
Схема программы, реализующий этот алгоритм. Для переменных a и b остаются в силе неравенства a<b и f(a)f(b)[0. Значением fa является f (a), с – обозначает середину отрезка [a,b], fc принимает значение, равное f(c).
Эта программа позволяет получать один из корней. Поэтому предварительно надо определить границы а и b настолько точно (можно использовать графический метод), что в отрезке содержался ровно один корень. Это позволит, задавая различные а и b, получать различные корни.
Для конкретной функции f(x)=x3-17*x+12; один из корней принадлежит отрезку [0,2]; а=0,b=2. тогда программа примет следующий вид.
#include<iostream.h>
#include<conio.h>
#include<math.h>
float f(float x) //функция, вычисляющая значение конкретной функции
{float ff;
ff=x*x*x-17*x+12;
return ff;}
void main() // Главная функция
{float a,b,c,fa,fc,eps; int n=0;
clrscr();
cin>>a>>b>>eps;
fa=f(a);
do
{ c=(b+a)/2;
fc=f(c);
if (fa*fc<0) b=c;
else
{
a=c;fa=fc;
} cout<<c<<endl;n=n+1;
} while (b-a>eps) ;
cout<<a<<endl;
cout<<n<<endl;
}
Преимущества метода: легко осуществим и в электронной таблице, и на языке С++. На языке С++ позволяет найти все корни.
Недостатки метода: по приближенному значению f(x) не всегда можно установить, справедливо ли неравенство f(x)<= 0, когда f(x) мало и погрешность вычисления значения f(x) превосходит само это значение.
1.5 Практический пример. Расчет площади детали
Конструируется некоторый механизм, для которого нужна деталь данной площади, имеющая форму кругового сегмента. Решением должна быть не формула (выражение, зависящее от r и s), а явно указываемое число, которое должно отличаться от истинного значения корня на некоторую малую величину.
Площадь кругового сегмента с радиусом r и с заданным в радианах центральным углом А равна s=r2(А-sinА)/2.
Рассмотрим задачу определения величины центрального угла по данному радиусу r и площади s. Получим уравнение
x-sin x – 2s/r2=0 (1.6)
По смыслу задачи 0<x<2p и 0<s<pr2.. Уравнение (1.6) - это трансцендентное уравнение.
Точную аналитическую формулу для решения этого уравнения найти трудно. Но можно воспользоваться численными методами для решения такого рода уравнений, учитывая, что надо получить некоторое значение.
Решить самостоятельно эту задачу.
1.6 Контрольные вопросы
1.6.1.Перечислить методы численного решения уравнений.
1.6.2 С чего начинается обычно численное решение уравнения?
1.6.3 В чем суть метода простой итерации?
1.6.4 Какое условие должно выполняться для сходимости метода простой итерации?
1.6.5 В чем преимущество и недостаток метода простой итерации?
1.6.6 В чем суть метода половинного деления?
1.6.7 Какие условия должны выполняться при использовании метода половинного деления?
1.6.8 В чем суть метода Поиск решения?
1.7 Варианты заданий
Дано действительное положительное число е. Методом деления отрезка пополам, методом итерации и с помощью Поиска решения найти приближенное решение уравнения f(x)=0. Абсолютная погрешность найденного значения не должна превосходить е. Рядом с уравнением дополнительно указан отрезок (в квадратных скобках), содержащий корень, или начальное приближение к корню (в круглых скобках). Если не указано, то для получения отрезков, содержащих по одному корню уравнения, или для получения начальных приближений к корням исследовать график функции. Задания выполнить, используя MS Excel, также написать программу на одном из языков программирования (C++ или Pascal).
1. x+ln(x+0.5)-0.5=0, [0, 2];
2. x5 – x - 0.2=0, [1, 1.1];
3. x4 + 2x3 – x-1=0, [0, 1];
4. x3 –0.2x2 –0.2x-1.2=0, [1, 1.5];
5. x*2x – 1=0, [0, 1];
6. x2 – sin5x = 0, [0.5, 0.6];
7. 5x – 8* ln x = 8; (4.32);
8. 3 x2 – cos 2x – 1 = 0;
9. 2 ln x – 1/x +0.5=0;
10. x2 cos 2x + 1=0, [0, pi/2];
11. 2 x – cos x = 0, [0, pi/2];
12. 0.9 x – sin √ x – 0.1=0, [0, 1.5];
13.
tg x ![]()
![]()
![]() = 0, [0, pi/4];
= 0, [0, pi/4];
14. (4+x2) (ex –e - x)-18, [1.2, 1.3];
15.
![]() + 1
= cos(0.5x) ;
+ 1
= cos(0.5x) ;
16. x*2x-1=0, [0,1];
17. x2-1.3*ln(x+0.5)-2.8*x+1.15=0, [2.1, 2.5];
18. x4+cos x -2=0, [0, 2];
19. tg x – x =0, (4.67);
20. 1.8*x4 – sin 10*x = 0, (0.22);
21. x – sin x = 0.25, (1.17);
22. 3*x – sin x-7=0;
23. x – cos x -1 =0;
24. x2 – sin5x = 0, [0.5, 0.6];
25. 2 x – cos x = 0, [0, pi/2];
Задание 2. Методы численного интегрирования
Цель работы: изучение методов численного интегрирования, применение этих методов для инженерных расчетов при решения практических задач.
Многие интегралы даже от элементарных функций не выражаются через элементарные функции. Кроме того, функция, которую надо проинтегрировать, может быть задана не формулой, а как-либо иначе. Интегралы могут выражаться через хорошо изученные и затабулированные неэлементарные «специальные» функции, например, функция ошибок, интегральный синус и интегральный косинус. Наиболее универсальными методами, пригодными к интегралам от произвольных функций, заданных любым способом, в особенности таблично, являются методы численного интегрирования. Формулы численного интегрирования дают приближенные значения определенного интеграла, если известны значения подынтегральной функции в некоторых точках (узлах) интервала интегрирования.
Рассматриваются следующие методы численного интегрирования
1. Приближенное вычисление площади с помощью разбиения на прямоугольники.
![]()
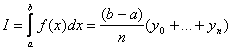
где n – количество отрезков разбиения; y0 бy1,… yn -- значения функции на концах отрезков.
2. Приближенное вычисление площади с помощью разбиения на трапеции.
I=![]() f(x)dx=
f(x)dx=![]() (y0+2y1+…+2yn-1+yn),
(y0+2y1+…+2yn-1+yn),
где n- количество отрезков разбиения; y0 , y1, yn – значения функции на концах отрезков.
3. Метод Симпсона
I=![]() f(x)dx=
f(x)dx=![]() (y0+4y1+2y2+…+4y
2n-1+y 2n),
(y0+4y1+2y2+…+4y
2n-1+y 2n),
где 2n – количество разбиения; у0, у1, у2n – значения функции на концах отрезков.
Метод Симпсона можно использовать при условии, что количество точек нечетное, и по оси абсцисс точки расположены на одинаковых расстояниях, то есть, интервал постоянный. Шаг интегрирования состоит из двух соседних интервалов между данными.
При применении формулы трапеции, ошибка имеет порядок h2, формулы Симпсона – h4, где h – интервал – расстояние между двумя точками интегрирования. При уменьшении h точность увеличивается.
Методы будут проиллюстрированы на примере данных, описывающих функцию у=соs(х) на интервале от 0 до pi/2.
![]() соs(х)dx=sin(pi/2)
-sin(0)=1 (2.1)
соs(х)dx=sin(pi/2)
-sin(0)=1 (2.1)
Процесс вычисления можно разделить на этапы:
1. ввод данных;
2. ввод формулы для вычисления площади одного прямоугольника или трапеции;
3. копирование формулы во все интервалы (обратить внимание, что их количество может не совпадать с количеством точек данных);
4. вычисление суммы площадей отдельных фигур разбиения.
2.1 Вычисление интеграла с помощью разбиения на прямоугольники
В электронную таблицу (рисунок 2.1), в столбец А ввести значения х – от 0 до 1,57 (pi/2) с шагом 0,057, вычислить у - значения подынтегральной функции в этих точках.
В столбце с названием Sпр ввести формулу расчета площади каждого прямоугольника; высота прямоугольника равна значению функции на левом краю интервала разбиения. Вычислить суммарную площадь.
Аналогично вычислить интеграл, где высота прямоугольника равна значению функции на правом краю интервала. Сравнить полученные значения интеграла.

Рисунок 2.1
2.2 Вычисление интеграла с помощью разбиения на трапеции
Ввод формулы для вычисления площади одной трапеции.
Площадь трапеции выражается формулой Sтрап=(уп+ул)*(хп-хл)/2.
Вычислить площадь каждой трапеции, используя уже посчитанные значения у.
Посчитать суммарную площадь трапеции. Сравнить три полученных результата.
Пример: численное интегрирование, выполненное на языке С++.
Float f(float x) //вычисление подинтегрального выражения
{float c;
c=cos(x);
return c;}
float integ(float a,float b, int n) //вычисление интеграла
{float s,h;
int i;
h=(b-a)/n;
s=(f(a)+f(b))/2;
for(i=1;i<n;i++)
s=s+f(a+h*i);
return s*h;}
void main() //главная функция
{float a,b,i;
int n=10;
i=integ(0, 1.57,n);
cout<<”integral value=”<<i<<endl;}
2.3 Практический пример. Подпорная стенка из бетона
Разработан проект подпорной бетонной стенки сложной формы, толщина которой равна 20 см. Чтобы заказать бетон, нужно определить объем, исходя из размеров. Стена имеет вид, приведенный на графике, рисунок 2.2.
Разбить эту задачу на следующие этапы:
1. Ввод в электронную таблицу размеров стенки;
2. Вычисление площади боковой поверхности верхней части стенки;
3. Вычисление площади нижней части стенки.
4. Вычисление суммарной площади боковой поверхности.
5. Умножить полученный результат на толщину стенки, чтобы вычислить объем.
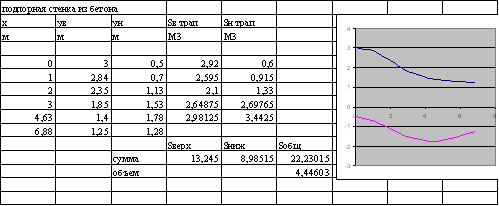
Рисунок 2.2
Выполнить самостоятельно следующие практические примеры.
1. Работа, которую нужно затратить, чтобы растянуть пружину. С помощью устройства, изображенного на рисунке 2.3, можно определить, какая работа необходима для растяжения пружины. Устройство состоит из пружины, динамометра и линейки. Длина нерастянутой пружины равна 1,3 см. затем пружина постепенно растягивается. При каждом удлинении пружины на 0,4 см записывалось показание динамометра, в результате чего получился набор данных, приведенных в таблице. 2.1. Работа, необходимая для растяжения пружины, вычисляется по формуле:
А=![]() (2.2)
(2.2)
где х – удлинение пружины.
Вычислить работу, которую нужно затратить, чтобы растянуть пружину от 0 до 3.6 см..

Рисунок 2.3
Таблица 2.1 Результаты опытов с пружиной
|
Длина (см) |
Исходная длина (см) |
Удлинение (см) |
Сила (Н) |
|
1.3 |
1.3 |
0.0 |
0.0 |
|
1.7 |
1.3 |
0.4 |
0.88 |
|
2.1 |
1.3 |
0.8 |
1.76 |
|
2.5 |
1.3 |
1.2 |
2.64 |
|
2.9 |
1.3 |
1.6 |
3.52 |
|
3.3 |
1.3 |
2.0 |
4.4 |
|
3.7 |
1.3 |
2.4 |
5.28 |
|
4.1 |
1.3 |
2.8 |
6.16 |
|
4.5 |
1.3 |
3.2 |
7.04 |
|
4.9 |
1.3 |
3.6 |
7.92 |
2. Энтальпия, необходимая для нагревания газа. Чтобы нагреть n молей газа от температуры Т1 до температуры Т2, необходимо затратить энтальпию, которая вычисляется с помощью теплоемкости газа по формуле:
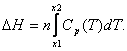 (2.3)
(2.3)
Однако теплоемкость зависит от температуры. Для описания этой зависимости часто применяется уравнение, в правой части которого фигурирует полином третьего порядка относительно Т:
![]() (2.4)
(2.4)
Зная значения коэффициентов a,b,c,d для определенного газа, можно вычислить теплоемкость этого газа при любом значении Т ( в тех пределах, в которых работает уравнение (2.4). В таблице 2.2. приведены коэффициенты для нескольких распространенных газов (температура выражена в градусах Цельсия).
Таблица 2.2 - Коэффициенты для вычисления теплоемкости
|
Название газа |
a |
b |
c |
d |
Интервал применимости |
|
Воздух |
28.94х10-3 |
0.4147х10-5 |
0.3191х10-8 |
-1.965х10-12 |
0 – 1500 0 С |
|
СО2 |
36.11х10-3 |
4.233х10-5 |
-2.877х10-8 |
7.464х10-12 |
0 – 1500 0 С |
|
СН4 |
34.31х10-3 |
5.469х10-5 |
0.3661х10-8 |
-11.00х10-12 |
0 – 1500 0 С |
|
Н2О |
33.46х10-3 |
0.6880х10-5 |
0.7604х10-8 |
-3.593х10-12 |
0 – 1500 0 С |
(варианты: воздух, СО2, СН4, Н2О)
А) Вычислить теплоемкость газа в диапазоне температур от 200 до 800 0 С с шагом 20 0 С.
Б) Вычислить с помощью метода численного интегрирования энергию (изменение энтальпии), необходимую для нагревания 100 моль газа от 200 до 800 0 С.
С) Сравнить результат, полученный в пункте Б), с вычисленным аналитически. Для этого в интеграл из уравнения (2.3) подставить выражения для теплоемкости в виде полинома (2.4).
2.4 Контрольные вопросы
2.4.1 Перечислить формулы численного интегрирования.
2.4.2 Используя формулу прямоугольников для вычисления интеграла, сколько можно получить значений? С чем это связано?
2.4.3 В чем суть метода трапеций?
2.4.4 Какой из методов численного интегрирования дает более высокую точность?
2.4.5 Какой порядок имеет ошибка при применении метода трапеций?
2.4.6 В чем особенность метода Симпсона? Какие условия должны выполняться при использовании метода Симпсона?
2.4.7 Каков порядок ошибки при применении метода Симпсона?
2.4.8 Что означают «интервал между соседними точками » и «шаг интегрирования»?
2.4.9 Чему равен шаг интегрирования при применении метода Симпсона?
2.5 Варианты заданий
Задания выполнить, используя предложенные методы, на MS Excel, написать программу на одном из языков программирования (C++ или Pascal). Результаты сравнить.
|
1 |
|
14 |
|
|
2 |
|
15 |
|
|
3 |
|
16 |
|
|
4 |
|
17 |
|
|
5 |
|
18 |
|
|
6 |
|
19 |
|
|
7 |
|
20 |
|
|
8 |
|
21 |
|
|
9 |
|
22 |
|
|
10 |
|
23 |
|
|
11 |
|
24 |
|
|
12 |
|
25 |
|
|
13 |
|
|
|
Задание 3. Метод наименьших квадратов
Цель работы: изучение методов математико-статистической и компьютерной обработки результатов экспериментов, испытаний и статистических наблюдений.
Для установления закономерностей при изучении многих природных явлений проводятся эксперименты или осуществляют сбор статистических данных об объекте исследования. После этого требуется определить функциональную зависимость между выбранными параметрами, описывающими изучаемое явление. Такую операцию называют аппроксимацией, полученную при этом функцию называют аппроксимирующей функцией, а ее график аппроксимирующей линией.
Пусть изучается связь между двумя переменными x и y; для этого рассматривается таблица значений этих переменных, полученных из эксперимента или в результате сбора данных:
A=(
![]() (3.1)
(3.1)
B=( ) (3.2)
) (3.2)
3.1 Задание: изучается зависимость температуры от времени. Необходимо найти коэффициенты прямой линии, которая лучше всего описывает набор данных, введенных в столбцы х и у (рисунок 3.1).
Коэффициенты прямой А и В вычисляются по формулам (3.1), (3.2).
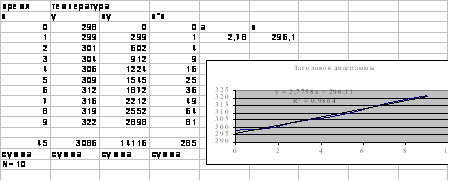
Рисунок 3.1
1.В ячейки А3:A12 (рисунок 3.1) вводятся значения времени, в В3:В12- температуры. В ячейке Е4 вычисляется коэффициент А по формуле (3.1), в F4 - коэффициент В по формуле (3.2).
2.Для определения углового коэффициента А, используя приемы регрессионного анализа в Excel, линии предназначена функция НАКЛОН(). Значение В можно найти с помощью функции ОТРЕЗОК.
Для этого установить курсор в ячейку Е5(F5) и выполнить действия:
Вставка – функции- статистические – НАКЛОН (ОТРЕЗОК) – выделяется столбец у(В3:В12), затем столбец х(А3:A12).
3.2 Выполнение линейной регрессии с помощью линии тренда
Представить данные в графическом виде.
Выделить данные: А3:В12. Вставка – диаграмма – точечный график. Левая кнопка – на графике появляются маркер. Правая кнопка – добавить линию тренда. Выбрать вид линии– (линейная), вкладка параметры – установить – «показать уравнение на диаграмме» и «поместить на диаграмму величину достоверности аппроксимации», «прогноз».
На графике (рисунок 3.1) показаны линия тренда, уравнение регрессии и величина достоверности.
Величина достоверности аппроксимации является одним из показателей, которые следует разместить на диаграмме. По этой величине можно судить о правомерности использовании я того или иного уравнения регрессии.
Если коэффициент лежит в диапазоне 0,9-1, то данную зависимость можно использовать для предсказания результата. Чем ближе к 1 коэффициент корреляции, тем более достоверна используемая модель.
Часто для аппроксимации произвольной выборки и разброса данных подходит полиномиальное уравнение той или иной степени. Однако при прогнозировании уравнениями таких линий следует иметь в виду, что возможны большие ошибки в прогнозах и истории данных. В таких случаях, если находится другая функция с близким коэффициентом корреляции, следует иметь в виду ее уравнение регрессии.
Сравнить все три полученных результата.
Алгоритм данного метода имеет следующий вид:
· ввод исходных данных – одномерных массивов X, Y;
· простой цикл для вычисления сумм по формулам
· вычисление искомых коэффициентов по формулам
Если аппроксимирующая функция имеет следующий вид y = a x 2 + b x + c, то этот случай называется квадратичной аппроксимацией. В этом случае для определения трех неизвестных параметров a , b , c будет получена из условия минимума функции U система трех алгебраических уравнений.
3.3 Практический пример: повторная калибровка измерителя расхода
Измеритель расхода с завода-изготовителя попадает на производство, будучи укомплектованным градуированными таблицами, построенными для стандартных веществ (обычно это воздух или вода). Однако при критическом подходе калибровку необходимо проверять, чтобы убедиться, что после определенного периода эксплуатации инструмент продолжает давать надежные показания.
Во время покупки вертушечного расходомера его градуированная таблица описывалась уравнением (), связывающим показания расходомера (частота в Герцах) со скоростью потока воды vь/с).
V=0.0023+0.0674f (3.3)
По истечении года прибор снят с эксплуатации для повторной калибровки. Предварительное тестирование дало результаты, приведенные в таблице 3.1.
Надо выяснить:
1. Нужно ли прибору повторная калибровка?
2. Если нужна, то каким будет новое калибровочное уравнение?
Во-первых, можно вычислить значения скоростей потока, предсказываемые уравнением (3.3), и с помощью графика проверить, насколько хорошо это уравнение описывает полученные данные.
Таблица 3.1
|
Частота (Гц) |
Скорость(м/с) Экспериментальная |
Скорость(м/с) Предсказываемая |
|
0,8 |
0,05 |
0,1 |
|
4,2 |
0,27 |
0,3 |
|
8,2 |
0,53 |
0,6 |
|
10,9 |
0,71 |
0,7 |
|
13,1 |
0,86 |
0,9 |
|
16,8 |
1,1 |
1,1 |
|
20,5 |
1,34 |
1,4 |
|
23 |
1,5 |
1,6 |
|
26,6 |
1,74 |
1,8 |
|
28,4 |
1,85 |
1,9 |
|
32,9 |
2,15 |
2,2 |
|
35,6 |
2,33 |
2,4 |
|
38,5 |
2,52 |
2,4 |
|
42,1 |
2,75 |
2,8 |
В таблице 3.1приведены сравнительные данные экспериментальной и предсказываемой (вычисленной по формуле (3.3) скоростей. Отдельно построить графики для предсказываемой и экспериментальной скоростей.
Экспериментальные значения несколько отличаются от тех, которые вычислены с помощью уравнения. Это говорит о том, что пришло время выполнить повторную калибровку. Построим на диаграмме линию тренда в виде прямой и отобразим ее уравнение.
3.4 Контрольные вопросы
3.4.1.Какая функция предназначена для определения углового коэффициента прямой линии, лучше всего описывающей данные?
3.4.2 Как построить на диаграмме линию тренда?
3.4.3 Можно ли на диаграмме показать уравнение регрессии?
3.4.4 Какие есть модели линии регрессии?
3.4.5 Как поместить на диаграмму величину достоверности аппроксимации?
3.5 Варианты заданий
Имеются две наблюдаемые величины х и у, например, объемы потребления какого-либо вида продукции за несколько месяцев (х – месяц, у – объем потребления). Необходимо найти математическую модель, наилучшим образом описывающую наблюдаемые значения. Сделать вывод о подходящей математической модели. Выполнить задание в MSExcel.
Варианты 1-5
|
Х |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
У |
87 |
80 |
75 |
80 |
70 |
65 |
68 |
62 |
57 |
54 |
Варианты 6-10
|
Х |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
У |
76 |
134 |
155 |
167 |
153 |
152 |
148 |
130 |
148 |
178 |
Варианты 11-15
|
Х |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
У |
98 |
54 |
108 |
65 |
54 |
63 |
87 |
90 |
92 |
78 |
Варианты 16-20
|
Х |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
У |
9 |
16 |
20 |
27 |
34 |
39 |
44 |
52 |
58 |
64 |
Варианты 21-25
|
Х |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
У |
12 |
35 |
23 |
65 |
34 |
67 |
24 |
34 |
87 |
90 |
Задание 4. Методы численного решения дифференциальных уравнений с помощьюMS Excel
Цель работы – ознакомиться с методами численного решения дифференциальных уравнения и приобрести навыки использования этих методов в инженерных расчетах.
Математические модели физических процессов часто формулируются на языке дифференциальных уравнений.
Y1=f(x,y) на [a,b]; y(a)=y0; (4.1)
Рассматриваются
1. Метод Эйлера: значения в узловых точках вычисляются по формуле
yi+1 =f(xi,yi)h+yi на [a,b]; y(a)=y0; (4.2)
2. Метод Рунге-Кутта: значения в узловых точках вычисляются по формуле:
yi+1 = yi +h/6(k1+2k2+2k3+k4) I=0, 1, 2,… (4.3)
где
k1=f(xi, yi); k2=f(xi+h/2, yi+h 1k1/2);
k3=f(xi+h/2, yi+hk2/2); k4=f(xi+h, yi+hk3)
4.1 Задание: решить дифференциальное уравнение первого порядка с начальными условиями
у1 =x+y, [0, 1.4], h=0.02 y(0)=0;
Для решения применяется формула Эйлера:
f(x,y)=x+y
yi+1 =(xi +yi)h+yi (4.4)
на [0, 1.4]; y(a)=y0;
В ячейки A3:A73 с шагом 0,02 заносятся значения x. В ячейку B3 заносится начальное условие y(0)=0; в ячейку B4 вводится формула (4.4) - B4(=(A3+B3)*0.02+B3); протянуть маркер автозаполнения – рассчитываются значения во всех узловых точках.
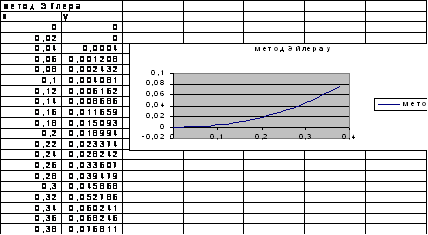
Рисунок 4.1
4.2 Практический пример. Задача изменения температуры тела в зависимости от температуры воздуха
Согласно закону излучения тепла, скорость изменения температуры тела в воздухе пропорциональна разности между температурой воздуха и тела:
![]() (4.5)
(4.5)
где x(t) – температура тела в момент времени
t,
u(t) –
температура воздуха в этот же момент, ![]() - положительный коэффициент, определяемый
свойствами тела. Если, например,
- положительный коэффициент, определяемый
свойствами тела. Если, например, ![]() и температура воздуха зависит от времени
t
как 20 – 1/(1+t2), то
уравнение запишется в виде
и температура воздуха зависит от времени
t
как 20 – 1/(1+t2), то
уравнение запишется в виде
![]() (4.6)
(4.6)
Используя вышесказанное, решить следующие задачи.
1. Пусть в момент времени температура воздуха была
равна 300, а впоследствии опускалась на 0.010 за каждую
секунду, то есть при ![]() выполнено
u(t)=30-0.01t. пусть для рассматриваемого тела
выполнено
u(t)=30-0.01t. пусть для рассматриваемого тела
![]() .
.
Требуется выяснить, сколько потребуется времени для того, чтобы тело, имевшее в момент времени t =0 температуру 1000, остыло до температуры 900.
2. Рассматривается уравнение изменения температуры
тела. Полагается, что для рассматриваемого тела ![]() . Пусть при
. Пусть при ![]() выполнено
u(t)=30-0.1+5 sin t. Написать вариант программы для решения этой задачи,
предприняв некоторые меры по контролю точности. Первоначально вычисления
проводить с шагом h=1, затем они повторяются с шагом
h=1/2
и так далее до тех пор, пока модуль разности двух последних приближений в точке
х(5) не окажется меньшим, чем заданное число
eps.
выполнено
u(t)=30-0.1+5 sin t. Написать вариант программы для решения этой задачи,
предприняв некоторые меры по контролю точности. Первоначально вычисления
проводить с шагом h=1, затем они повторяются с шагом
h=1/2
и так далее до тех пор, пока модуль разности двух последних приближений в точке
х(5) не окажется меньшим, чем заданное число
eps.
3. Рассматривается дифференциальное уравнение, описывающее вымывание инертного материала из резервуара, который взбалтывается:
![]() (4.7)
(4.7)
где
С![]() -
концентрация инертного материала (компонента А) в контейнере и вытекающем из
этого контейнера потоке (мг/мл);
-
концентрация инертного материала (компонента А) в контейнере и вытекающем из
этого контейнера потоке (мг/мл);
Свход – концентрация компонента А во входящем в контейнер потоке (мг/мл);
![]() - продолжительность
обработки сточных вод в системе (
- продолжительность
обработки сточных вод в системе (![]() );
);
V – объем контейнера (константа) (мл);
V1 – скорость входящего и выходящего потока (мл/с);
Начальная концентрация компонента в резервуаре, а также параметры системы: концентрация компонента А во входном потоке, объем резервуара и скорость потока приведены в таблице 4.1.
Таблица 4.1- Параметры системы
|
Название параметра |
Значение параметра |
|
Первоначальная концентрация компонента А в резервуаре |
100 мг/мл |
|
Концентрация компонента А во входном потоке |
0 мг/мл |
|
Объем резервуара |
10 л |
|
Скорость потока |
100 мл/с |
Найти концентрацию компонента в каждый момент времени,
решая дифференциальное уравнение численным методом. Построить график.
Полученные результаты сравнить с аналитическим решением
![]()
4.3 Контрольные вопросы
4.3.1 В каких случаях применяют численные методы решения дифференциального уравнения?
4.3.2 Перечислить наиболее известные методы решения дифференциальных уравнений.
4.3.3 В чем суть метода Эйлера? В чем преимущество этого метода и в чем его недостаток?
4.3.4 В чем суть метода Рунге-Кутта? В чем преимущество этого метода и в чем его недостаток?
4.4.5 Привести пример физического закона, который описывается дифференциальным уравнением.
4.4.6 Сформулировать математически следующее явление: скорость изменения температуры тела в воздухе пропорциональна разности между температурой воздуха и тела.
4.4.7 Сформулировать математически второй закон Ньютона: сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорения, для силы, изменяющейся со временем по известному закону и направленной вдоль фиксированной прямой.
4.4.8 Что понимается по термином «начальное условие»?
4.5 Варианты заданий
С помощью пакета MS Excel, а также языка программирования реализовать алгоритмы численного решения дифференциального уравнения и построить графики для приближенного решения по методу Эйлера и Рунге-Кутта, результаты сравнить.
После уравнения в скобках записаны исходные данные для решения: x0 - начальное значение аргумента, y0 – начальное значение функции от x0, далее – отрезок, на котором решается уравнение, h – шаг.
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
|
|
19 |
|
|
20 |
|
|
21 |
|
|
22 |
|
|
23 |
|
|
24 |
|
|
25 |
|
Задание 5. Построение поверхности
Цель работы – ознакомиться с методикой построения поверхности в MSExcel и приобрести навыки построения поверхности.
В курсе информатики рассматривалось построение графиков – линий, использование двух координат. Но часто возникает необходимость построения поверхности – использование трех координат.
5.1 Построение поверхностей
Построение поверхностей предполагает использование следующей методики:
1. Подготовить диапазон изменения функции по двум координатам, расположив изменения одной координаты вдоль некоторого столбца вниз, а другой – вдоль, прилегающий строки вправо.
2. Ввести на пересечении координат необходимую формулу для построения поверхности и с помощью маркера автозаполнения выполнить ее копирование на всю область построения поверхности.
3. Выделить подготовленные данные и воспользоваться мастером построения диаграмм ( тип диаграммы – Поверхность).
5.2 Задание 1: построить поверхность
![]()
![]() (5.1)
(5.1)
Решение:
1. Подготовить диапазон изменения функции: от -1 до 1.
2. Формула для расчета значения z введена в ячейку С3: =($B3^3/2-(C$2+2)^2.
Подготовленный диапазон и построенная поверхность представлены на рисунке 5.1.
5.3 Построение поверхностей второго порядка (третья координата входит в уравнение поверхности в квадрате)
При построении поверхности второго порядка используется следующая методика:
1. Подготовить диапазон изменения функции по двум координатам, расположив изменения одной координаты вдоль некоторого столбца вниз, а другой – вдоль прилегающий строки вправо.
2. Ввести на пересечении координат необходимую формулу для построения поверхности и с помощью маркера автозаполнения выполнить ее копирование на всю область построения поверхности. В формуле учесть поправку на положительные и отрицательные значения квадратного корня на данной области определения.
3. Выделить подготовленные данные и воспользоваться мастером построения диаграмм ( тип диаграммы – Поверхность).

Рисунок 5.1
5.4 Задание 2: построить сферу
![]() (5.2)
(5.2)
Решение:
1. Подготовить диапазон области определения функции. В диапазон B5:B46 вводятся значения от -1 до 1 (интервал изменения по х и у) с шагом 0,1. Причем, каждое значение дублируется последовательно дважды. Аналогично вводятся значения и для диапазона C4:AR4. На рисунке 5.2 показан диапазон.
2. В диапазон А6:А47 добавить повторяющиеся числа 2 и 3 (для использования в формуле
3. Формула ввода для ячейки С5: =(1-$B5*$B5-D$4*D$4)^(1/2)*ЕСЛИ(ОСТАТ($A6;2)=0;1;-1)
4. Выделить диапазон В4:AR46 и использовать мастер построения диаграмм (тип диаграммы – поверхность). Получится сфера (рисунок 5.3).

Рисунок 5.2

Рисунок 5.3
5.5 Контрольные вопросы
5.5.1 Какова методика построения поверхности?
5.5.2 Какой тип диаграммы следует выбрать при построении поверхности?
5.5.3 Как учесть поправку на положительные и отрицательные значения квадратного корня при построении поверхностей второго порядка?
5.6 Варианты заданий
|
1 |
|
14 |
|
|
2 |
|
15 |
|
|
3 |
|
16 |
|
|
4 |
|
17 |
|
|
5 |
|
18 |
|
|
6 |
|
19 |
|
|
7 |
|
20 |
эллиптический цилиндр |
|
8 |
|
21 |
гиперболический цилиндр |
|
9 |
|
22 |
параболический цилиндр |
|
10 |
|
23 |
|
|
11 |
|
24 |
|
|
12 |
|
25 |
|
|
13 |
|
|
|
Задание 6. Решение задач оптимизации с помощью надстройки Поиск решения
Цель работы – ознакомиться с постановкой задач оптимизации, приобрести навыки решения этих задач, используя MSExcel.
Многие проблемы производства, проектирования,
прогнозирования сводятся к широкому классу задач оптимизации, для решения
которых применяется математические методы. Например: ассортимент продукции –
максимизация выпуска товаров при ограничениях на сырье для производства этих
товаров; планирование перевозок – минимизация затрат на транспортировку
товаров; штатное расписание – составление штатного расписания для достижения
наилучших результатов при наименьших расходах;
Для решения такого типа задач используется линейное программирование.
Это раздел математики, ориентированный на нахождение экстремума (минимума или
максимума) в задачах, которые описываются линейными уравнениями при
дополнительных ограничениях на входные переменные. Задачи линейного
программирования могут быть решены графически и аналитически.
В MS Excel существует возможность с помощью надстройки Поиск решения найти решение, оптимальное при нескольких входных значениях и наборе ограничений на решение.
В общем случае задачу линейного программирования можно сформулировать следующим образом:
Найти экстремум целевой функции
F =с1х1+с2х2….+сnxn ->max (min) (6.1)
При ограничениях в виде равенств
a11x1 +a12x2+…........+a1n xn=b1;
....................................................... (6.2)
an1xn +an2x2+...........+ann xn=bn;
при ограничения в виде неравенств
a11x1 +a12x2+…........+a1n xn <b1;
....................................................... (6.3)
an1xn +an2x2+...........+ann xn <bn;
и условиях неотрицательности входных параметров:
Таблично задачу оптимизации можно сформулировать следующим образом (таблица 6.1).
Таблица 6.1- Постановка задачи оптимизации в общем случае
|
№ |
Название |
Математическая запись |
Описание |
|
1 |
Целевая функция (критерий оптимизации |
F=f(xj)- max(min,const) J=1,n |
Показывает, в каком смысле решение должно быть оптимальным, то есть наилучшим. Возможны три вида целевой функции: максимизация, минимизация, назначение заданного значения. |
|
2 |
Ограничения |
Gi(xj)<=(=;>=)bi, i=1,m, j=1,n. Xj=1,m<=k<=n – целые (для задач целочисленного программирования); |
Устанавливают зависимости между переменными. Зависимости могут быть односторонними и двусторонними. При решении задач двустороннее ограничение записывается в виде двух односторонних. |
|
3 |
Граничные условия |
dj<=xj<=Dj,j=1,n |
Показывает, в каких пределах могут быть значения искомых переменных в оптимальном решении. |
Решение задачи, приведенной в таблице 6.1, удовлетворяющее всем ограничениям и граничным условиям, называется допустимым.
Важная характеристика задачи оптимизации – ее размерность, которая определяется числом переменных n и числом ограничений m. При n<m задачи решения ни имеют.
Необходимым требованием задач оптимизации является условие n>m. Систему уравнений, для которых n=m рассматривают как задачу оптимизации, имеющую одно допустимое решение.
Следовательно, задача имеет оптимальное решение, если она удовлетворяет двум требованиям:
- имеет более одного решения, то есть существуют допустимые решения:
- имеется критерий, показывающий в каком смысле принимаемое решение должно быть оптимальным, то есть наилучшим из допустимых.
Настройка Поиск решения запускается командой Сервис – поиск решения.
Опции настройки приведены в таблице 6.2.
Таблица 6.2 - Опции окна Поиск решения
|
Опции |
Описание |
|
Установить целевую ячейку |
Указывается ячейка, содержащая целевую функцию (критерий оптимизации) рассматриваемой задачи |
|
Равной |
Следует выбрать из трех переключателей (максимальному значению, минимальному значению, значение) тот, который определяет тип взаимосвязи между решением и целевой ячейкой. |
|
Ограничения |
Отображаются ограничения, налагаемые на переменные задачи. Допускаются ограничения в виде равенств, неравенств, а также – требование целочисленности переменных. Ограничения добавляются по одному с помощью кнопки Добавить |
|
Кнопка Параметры |
Позволяет изменять условия и варианты поиска решений исследуемой задачи, а также загружать и сохранять оптимизируемые модели. Значения и состояния элементов управления, используемые по умолчанию, подходят для решения большинства задач.
|
6.1 Задание: планирование производства материалов
Фирма выпускает два типа строительных материалов: А и В. Продукция обоих видов поступает в продажу. Для производства материалов используются два исходных продукта: I и II. Максимально возможные суточные запасы этих продуктов на 7 и 9 тонн соответственно. Расходы продуктов I и II на 1 тонну соответствующих материалов приведены в таблице 6.3.
Изучение рынка сбыта показало, что суточный спрос на материал В никогда не превышает спроса на материал А более чем на 1 т. Кроме того, спрос на материал А никогда не превышает 3 т в сутки. Оптовые цены одной тонны материалов равны: для В – 4000 у.е. для А – 3000 у.е. Какое количество материала каждого вида должна производить фабрика, чтобы доход от реализации был максимальным.
Таблица 6.3 - Расход ресурсов
|
Исходный продукт |
Расход исходных продуктов, т (на одну тонну материалов) |
Максимально возможный запас,т |
|
|
Материал А |
Материал В |
||
|
I |
3 |
2 |
7 |
|
II |
2 |
3 |
9 |
Решение
1.Формулировка математической модели задачи:
- переменные для решения задачи: х1 – суточный объем производства материала А, х2 – суточный объем производства материала В.
- определение функции цели (критерия оптимизации). Суммарная суточная прибыль от производства х1 материала А и х2 материала В:
F=4000*х2+3000*х1.
Цель фабрики – среди всех допустимых х1 и х2 найти такие, которыемаксимизируют суммарную прибыль от производства материалов F:
F=4000*х2+3000*х1. – max.
- Ограничения на переменные:
объем производства не может быть отрицательным, то есть
х2>=0, х1>=0;
расход исходного продукта для производства не может превосходить максимального возможного запаса данного исходного продукта, то есть:
2*х2+3*х1<=7,
3*х2+2*х1<=9.
Ограничения на величину спроса на материалы:
х1-х2<=1,
х1=<3.
Получается следующая математическая модель:
- найти максимум функции
F=4000*х2+3000*х1. – max. (6.4)
- при ограничениях
2*х2+3*х1<=7,
3*х2+2*х1<=9, (6.5)
х1-х2<=1,
х1=<3.
Х2>=0, х1>=0;
2. Подготовить лист рабочей книги MSExcel для вычислений: переменные х1 и х2 находятся соответственно в ячейках С3 и С4.
Целевая функция (6.4) находится в ячейке С6 и содержит формулу = 4000*С4+3000*С3.
Ограничения на задачу (6.5) учтены в ячейках С8:D11 (условие неотрицательности не входит).
3. Работа с надстройкой Поиск решения: Сервис – Поиск решения, вводятся необходимые данные для рассматриваемой задачи.
6.2 Контрольные вопросы
6.2.1 Какие задачи относятся к задачам линейного программирования?
6.2.2 Что означает термин «допустимое решение»?
6.2.3 Сформулировать необходимое требование к задачам оптимизации.
6.2.4 Как задаются границы области допустимых решений?
6.2.5 Для решения какого типа задач ориентирован раздел Линейное программирование?
6.2.6 Сформулировать задачу оптимизации математически.
6.2.7 Какая надстройка используется для решения задач оптимизации?
6.2.8 Назвать опции окна Поиск решения.
6.3 Варианты заданий
1-5 Предприятие выпускает продукцию четырех видов П1-П4, для изготовления которой используются ресурсы трех видов: трудовые, сырье и оборудование. Нормы расхода каждого вида ресурса на изготовление единицы каждого вида продукции приведены в таблице 6.4.
Таблица 6.4
|
Ресурс |
Вид продукции |
Объем ресурса |
|||
|
П1 |
П2 |
П3 |
П4 |
||
|
Трудовой |
1 |
1 |
1 |
1 |
16 |
|
Сырье |
6 |
5 |
4 |
3 |
110 |
|
Оборудование |
4 |
6 |
10 |
13 |
100 |
Прибыль, получаемая от реализации единицы продукции, равна: для продукции П1 – 60 у.е., для П2 – 70 у.е., для П3 – 120 у.е., для П4 – 130 у.е. определить оптимальный план производства каждого вида продукции, максимизирующий прибыль данного предприятия.
6-10 Магазин реализует три вида продукции П1, П2, П3. Для этого используются два ограниченных ресурса – полезная площадь помещений, которая с учетом коэффициента оборачиваемости составляет 450 м2, и рабочее время работников магазина – 600 человекочасов. Товарооборот должен быть не менее 240000у.е. Необходимо разработать план товарооборота, доставляющего максимум прибыли. Затраты ресурсов на реализацию и полученная при этом прибыль представлены в таблице 6.5.
Таблица 6.5
|
Ресурсы |
Затраты ресурсов на реализацию, тыс. у.е. |
Объем ресурсов |
||
|
П1 |
П2 |
П3 |
||
|
Полезная площадь, м3 |
1,5 |
2 |
3 |
450 |
|
Рабочее время, человекочас |
3 |
2 |
1,5 |
600 |
|
Прибыль, тыс. у.е. |
50 |
65 |
70 |
|
11-15 Предприятию предложен на выбор выпуск трех новых изделий, за счет которых можно было бы расширить номенклатуру продукции предприятия при тех же запасах ресурсов. Нормы затрат ресурсов и прибыль от реализации единицы продукции для этих изделий представлены в таблице 6.6.
Таблица 6.6
|
Ресурсы |
Объективно обусловленные ресурсы |
Затраты ресурсов на одно изделие |
||
|
А |
Б |
В |
||
|
Труд |
40/3 |
6 |
4 |
2 |
|
Сырье |
0 |
2 |
1 |
3 |
|
Оборудование |
20/3 |
3 |
1 |
2 |
|
Прибыль на одно изделие |
|
80 |
70 |
45 |
16-20 Для изготовления изделий типа А1 и А2 склад может выделить не более 80 кг металла. Деталей типа А1 завод может изготовить за сутки не более 30 штук, типа А2 – не более 40 штук. Стоимость одного изделия типа А1 составляет 3 у.е., а типа А2 – 5 у.е. На изготовление одного изделия типа А1 идет 2 кг металла, типа А2 – 1 кг. Требуется найти такой план выпуска изделий, который позволит заводу получить максимальную прибыль.
21-25 На основании информации, приведенной в таблице 6.7, составить план производства, максимизирующий объем прибыли.
Таблица 6.7
|
Ресурсы |
Затраты ресурсов на единицу продукции |
Наличие ресурсов |
|
|
А |
В |
||
|
Труд |
2 |
4 |
2000 |
|
Сырье |
4 |
1 |
1400 |
|
Оборудование |
2 |
1 |
800 |
|
Прибыль на единицу продукции |
40 |
60 |
|
Задание 7. Функции просмотра и ссылок
Цель работы – ознакомиться с функцией обработки информации – Функции просмотра и ссылок (Вставка – Функции – Ссылки и массивы) и приобрести навыки использования этой функции на практике.
Функции ВПР() И ГРП () используются для поиска информации в прямоугольных таблицах. Данные функции имеют следующий синтаксис:
=ВПР (искомое_знач;таблица;номер_столбца;тип_просмотра);
=ГПР (искомое_знач;таблица;номер_строки;тип_просмотра);
где:
- искомое_знач – это значение, которое необходимо найти в первом столбце (строке) таблицы;
- таблица – массив или имя диапазона, который определяет таблицу с данными. Первый столбец (строка) должны быть упорядочены в алфавитном порядке текстовых значений или в порядке возрастания числовых данных, а также значений даты/времени;
- Номер_столбца (номер_строки) – указывает, из какого столбца (строки) таблицы следует выбирать возвращаемое значение;
- Тип_просмотра – определяет логическое значения для указания типа соответствия: точное или приближенное.
7.1 Задание: сформировать ведомость заработной платы, в которой надбавка за стаж определяется исходя из соответствующих надбавок за количество отработанных лет
Решение:
Сформировать ведомость (основная таблица) и дополнительную таблицу, как показано на рисунке 7.1.
В ячейку D2 ввести формулу: = C2*ВПР (B2; $F$16:$B$20;2),
где:
В2 – искомое значение (стаж сотрудника), которое необходимо найти в крайнем левом столбце таблицы, определяемой диапазоном $F$16:$B$20;
Индекс 2 определяет номер столбца таблицы, из которого будет возвращено значение (в данном случае, процент надбавки);
С2 – оклад сотрудника.
В ячейку Е2 ввести формулу =С2+D2.
Скопировать формулы в соответствующие диапазоны.
Отформатировать таблицы.
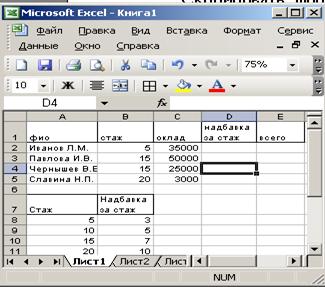
Рисунок 7.1
7.2 Контрольные вопросы
7.2.1 Для чего предназначена функция ВПР?
7.2.2 Какое условие накладывается на первый столбец вспомогательной таблицы?
7.2.3 Что означает «искомое значение»?
7.2.4 Что необходимо учесть при заполнении поля Таблица?
7.2.5 Номер столбца какой таблицы указывается в поле Номер столбца?
7.3 Варианты заданий
Сформировать основную и вспомогательную таблицы в MS Excel. Использовать для вычислений данные вспомогательной таблицы.
Выполнить это задание также на языке С++ (использовать структуры).
Варианты 1-5
|
№ |
Тип площади |
Стоимость 1 кв.м |
Требуемая площадь |
Итого за месяц
|
|
1 |
Офис |
|
15 |
|
|
2 |
Производство |
|
250 |
|
|
3 |
Стоянка |
|
210 |
|
|
4 |
Склад |
|
60 |
|
|
Тип площади |
Офис |
Производство |
склад
|
стоянка |
|
Стоимость 1 кв.м |
3000 |
500 |
400 |
450 |
Варианты 6-10
|
№ |
Название предприятия |
Вид металла |
Количество э/энергии на 1 т |
Объем выплавки |
Потребление э/энергии |
|
1 |
Казахмыс |
Медь |
|
15000 |
|
|
2 |
ПАЗ |
Алюминий |
|
2500 |
|
|
3 |
Казцинк |
Цинк |
|
2100 |
|
|
4 |
УКСЦК |
Свинец |
|
3500 |
|
|
5 |
УКСЦК |
Цинк |
|
4500 |
|
|
6 |
Балхашмедь |
Медь |
|
7000 |
|
|
Вид металла |
Количество э/энергии на 1 т |
|
Алюминий |
300 |
|
Медь |
200 |
|
Свинец |
250 |
|
Цинк |
190 |
Варианты 11-15
|
Дата |
Направление |
Код |
Длительность |
Цена |
Сумма |
|
15.02.06 |
Ксеll |
|
3 |
46,9 |
|
|
13.03.06 |
Kmobile |
|
4 |
46,9 |
|
|
21.03.06 |
Астана |
|
5 |
10 |
|
|
09.04.06 |
Kcell |
|
3 |
46,9 |
|
|
30.04.06 |
Калининград |
|
3 |
53 |
|
|
11.05.06 |
Зона Интернет |
|
35 |
4 |
|
|
20.05.06 |
Астана |
|
2 |
10 |
|
|
31.05.06 |
Зона Интернет |
|
22 |
4 |
|
|
Направление |
Код |
|
Kcell |
300 |
|
Kmobile |
333 |
|
Астана |
317 |
|
Калининград |
401 |
|
Зона Интернет |
750 |
Варианты 16-20
|
Материалы и продукты плавки |
Количество, кг |
Температура, С |
Теплоемкость, ккал/кг*С |
Количество тепла |
|
Штейн горячий |
100 |
1100 |
|
|
|
Воздух |
99 |
60 |
|
|
|
Шлак |
111 |
1200 |
|
|
|
Черновая медь |
29,6 |
1200 |
|
|
|
Черновая медь |
50 |
1200 |
|
|
|
Штейн горячий |
200 |
1100 |
|
|
|
Шлак |
210 |
1000 |
|
|
|
Материал и продукты плавки |
Теплоемкость, ккал/кг*С |
|
Штейн горячий |
0,2 |
|
Шлак |
0,295 |
|
Воздух |
0,31 |
|
Черновая медь |
0,108 |
Количество тепла вычисляется по формуле: Q=c*m*t, где Q – количество тепла,
с = теплоемкость, m – количество материала, t – температура.
Варианты 21-25
|
Наименование металла |
Количество э/энергии на переработку 1 т металла |
Количество металла (т) |
Расход э/энергии |
Стоимость |
|
Медь черновая |
|
3000 |
|
|
|
Титан |
|
500 |
|
|
|
Цинк |
|
2000 |
|
|
|
Магний |
|
1500 |
|
|
|
Цинк |
|
1700 |
|
|
|
Титан |
|
200 |
|
|
|
Медь черновая |
|
4000 |
|
|
|
Магний |
|
1200 |
|
|
|
Цинк |
|
1900 |
|
|
|
Итого |
|
|
|
|
|
Наименование металла |
Количество э/энергии на 1 т |
|
Цинк |
100 |
|
Титан |
250 |
|
Магний |
140 |
|
Медь |
95 |
Список литературы
1. Павловская Т.А., Щупак Ю.А. С/С++ Структурное программирование. –Санкт-Петербург: Питер, 2005.
2. Рональд У. Ларсен. Инженерные расчеты в Excel. – М.: Вильямс, 2002.
3. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1964.
4. Агальцов В.П., Волдайская И.В. Математические методы в программировании. – М: Форум, 2008
5. Бараненков Г.С., Демидович Б.П и др. Задачи и упражнения по математическому анализу М.: Наука, 1970