Некоммреческое акционерное общество
АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра тепловых энергетических установок
Компьютерные технологии
в теплоэнергетических расчетах
Конспект лекций
(для студентов всех форм обучения специальности
050717-Теплоэнергетика)
Алматы 2010
СОСТАВИТЕЛЬ: Н.Г. Борисова Компьютерные технологии в теплоэнергетических расчетах. Конспект лекций для студентов всех форм обучения специальности 050717-Теплоэнергетика.- Алматы: АИЭС, 2010. – 56 с.
В конспектах лекций по дисциплине «Компьютерные технологии в теплоэнергетических расчетах» представлены элементы численных методов и приемы их алгоритмизации для проведения вычислительного эксперимента. Рассмотрены примеры использования численных методов для интерполирования и интегрирования функций, поиска корней алгебраических уравнений и систем уравнений, решения обыкновенных дифференциальных уравнений и краевых задач, а также задач оптимизации при исследованиях и расчетах процессов, установок и систем теплоэнергетики и теплотехнологии.
Конспекты лекций, при отсутствии цельного учебника по курсу, обширной и разрозненной информации по вопросам применения численных методов и компьютерных технологий для исследования объектов теплоэнергетики, позволят студентам усвоить теоретический материал, подготовиться к текущему и итоговому контролю, выполнению и защите расчетно-графических, контрольных и лабораторных работ.
1 Лекция. Тема: введение. Компьютерные технологии в моделировании теплоэнергетических систем, процессов и установок. Модели и виды моделирования
План: введение. Цели и задачи курса. Политика курса. Состояние и перспективы использования компьютерных технологий в моделировании теплоэнергетических систем, процессов и установок. Классификация моделей и видов моделирования.
Курс «Компьютерные технологии в теплоэнергетических расчетах» является дисциплиной по выбору для студентов бакалавриата и включен в учебные планы в качестве базовой дисциплины.
Цель курса – формирование знаний, умений и навыков применения компьютерных технологий для расчета объектов теплоэнергетики и теплотехнологии.
Задачи курса: овладение элементами численных методов; приемами алгоритмизации; закрепление навыков, приобретенных в курсе «Информатика», использования языков программирования; проведение вычислительного эксперимента; использование компьютерных технологий и пакетов прикладных программ для исследования процессов, установок и систем теплоэнергетики и теплотехнологии.
Политика курса дана в силлабусе.
Дисциплина «Компьютерные технологии в теплоэнергетических расчетах» базируется на знаниях и умениях, приобретенных студентами при изучении курсов «Математика», «Информатика», «Физика», «Химия», «Материаловедение», «Техническая термодинамика», «Механика жидкости и газа», «Тепломассообмен». Знания, умения и навыки, полученные студентами, используются при изучении специальных дисциплин, в частности, курса «Методы моделирования и оптимизации теплоэнергетических и теплотехнологических процессов и установок», выполнении курсовых, дипломной и научно-исследовательских работ.
В результате изучения дисциплины бакалавры должны:
- иметь представление о возможностях компьютерных технологий при решении прикладных задач теплоэнергетики и теплотехники;
- владеть:
- способами алгоритмизации и программирования, хранения, обработки и представления информации;
- методами:
- интерполирования функций;
- численного интегрирования;
- решения трансцендентных уравнений, систем алгебраических уравнений, обыкновенных дифференциальных уравнений;
- решения задач оптимизации;
- решения задач стационарной и нестационарной теплопроводности, конвективного теплообмена и т.д.;
- уметь:
- выбирать эффективный численный метод для решения конкретной задачи, оценивать его точность и надежность;
- использовать:
- языки высокого уровня для составления программ расчета;
- текстовые и графические редакторы, мультимедийные средства и компьютерную сеть;
- готовые пакеты прикладных программ для выполнения теплоэнергетических расчетов;
- автоматизированные экзаменационно – обучающие компьютерные системы для самообучения и самоконтроля;
- разрабатывать и использовать информационно-справочные системы и базы данных для обеспечения моделирования теплоэнергетических объектов.
- быть компетентным в выборе:
- численных методов и их программного обеспечения для решения профессиональных задач;
- средств их компьютерной реализации.
Для современного этапа развития теплоэнергетики характерны две тенденции. Первая - увеличение разнообразия условий функционирования теплоэнергетических установок, вызванное расширением диапазона видов, качества и стоимости сжигаемого топлива, типов применяемых систем охлаждения и режимов использования. Вторая – увеличение числа типов и модификаций, используемых и разрабатываемых теплоэнергетических установок, что связано с развитием атомных энергоустановок различных типов, созданием высокоманевренных модификаций паротурбинных, газотурбинных и парогазовых установок.
Эти тенденции приводят к возрастанию значимости технико-экономических исследований по определению оптимальных значений параметров, рационального вида технологической схемы и профилей оборудования энергоустановок различных типов. В настоящее время решение таких задач немыслимо без широкого использования компьютерных технологий и методов моделирования.
Специалист в области теплоэнергетики должен иметь достаточную подготовку в области информационных технологий - использовать программные средства общего пользования: Microsoft Office, Corel Draw, Adobe Photoshop и т.д., специализированные программные средства: AutoCAD, MathCAD, Mathlab, уметь работать в сети, с электронной почтой, в Интернете, знать языки высокого уровня, составлять алгоритмы и программы для решения профессиональных задач.
Трудно назвать отрасль знаний, указать сферы человеческой деятельности, где бы ни применялись и куда бы ни внедрялись в настоящее время методы моделирования.
Использование методов моделирования обусловлено:
- общей тенденцией расширения и углубления исследования процессов в реальном физическом мире;
- длительностью ряда процессов (например, экологических);
- практической невозможностью получать необходимую информацию путем исследования объекта-оригинала (микро- и макрообъекты);
- неполнотой данных о реальных процессах и высокой стоимостью исследований объекта-оригинала, когда с экономических позиций наиболее приемлемо перенести их на объект-модель;
- наличием критических режимов функционирования объекта, когда исследования в некоторых областях изменения экзогенных параметров являются попросту опасными, а результаты исследования не поддаются прогнозу;
- отсутствием условий, а иногда и недостаточной квалификацией персонала для исследования объекта-оригинала;
- необходимостью большого числа экспериментов;
- уникальностью объекта исследования;
- отсутствием объекта-оригинала и т.д.
Моделирование – метод исследования объектов познания на их моделях; построение и изучение моделей реально существующих предметов и явлений (инженерных устройств, физико-химических процессов) и конструируемых объектов для определения либо улучшения их характеристик, рационализации способов их построения, управления ими и т.п.
Модель – аналог (схема, структура, знаковая система) определенного фрагмента природной или социальной реальности – оригинала модели. Такой аналог служит для: хранения и расширения знаний об оригинале, конструирования оригинала, преобразования или управления им.
Формы моделирования разнообразны и зависят от используемых моделей и сферы применения моделирования.
Предметным называется моделирование, в ходе которого исследование ведется на модели, воспроизводящей определенные геометрические, физические, динамические либо функциональные характеристики объекта моделирования – оригинала. К предметному относится аналоговое моделирование, когда оригинал и модель описываются едиными математическими соотношениями.
При знаковом моделировании моделями служат чертежи, схемы, формулы.
Важнейшим видом знакового моделирования является математическое моделирование.
Моделирование применяется вместе с другими общенаучными методами исследования: экспериментом, абстрагированием, идеализацией и т.д.
Модели и виды моделирования можно разделить на три группы:
- первая – определяется характером функционирования объекта;
- вторая – средствами моделирования;
- третья (относится к математическим моделям) – типом математического описания.
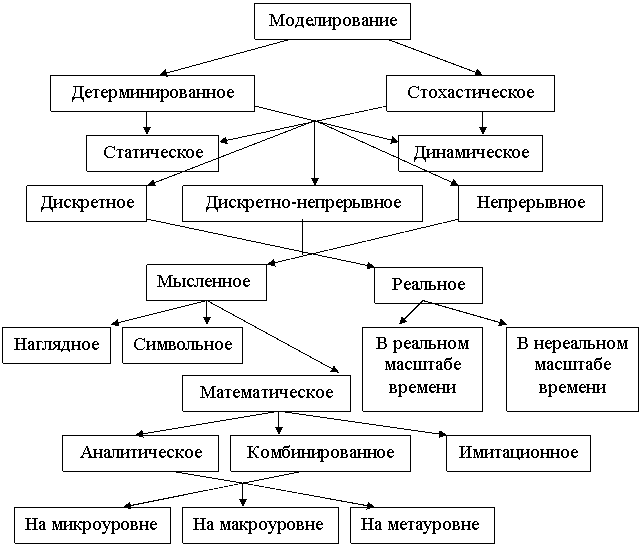
Рисунок 1.1 - Классификация видов моделирования
Поскольку все процессы могут протекать при наличии или отсутствии случайных воздействий, их моделирование носит детерминированный или стохастический характер. Статическое или динамическое моделирование определяется стационарностью и нестационарностью процессов в исследуемом объекте. Периодичность функционирования объекта-оригинала отражается дискретным, дискретно-непрерывным и непрерывным моделированием.
Наглядное моделирование связано с описанием модели на основе представлений, гипотез, выдвигаемых человеком, и применения аналогий различных уровней.
Символьное моделирование отображает свойства объекта-оригинала определенной заранее отработанной системой символов.
Модели на микроуровне обычно формализуют объекты с распределенными параметрами и описываются системами дифференциальных уравнений в частных производных.
Модели на макроуровне обычно представляются обыкновенными дифференциальными уравнениями (задача Коши и краевая задача) и алгебраическими уравнениями. Они используются для моделирования процессов с сосредоточенными параметрами в стационарной и нестационарной постановках.
Модели на метауровне создаются для сложных технических объектов и используются в основном при моделировании систем массового обслуживания и систем автоматического управления.
Имитационное моделирование заключается в создании модели-имитатора работы сложных (чаще при наличии стохастических факторов) систем и процессов при неполных знаниях о ряде процессов в моделируемых объектах. Они не позволяют в отличие от аналитических моделей формировать решение в обычном виде, но за счет перебора вариантов позволяют выбрать приемлемое решение.
Комбинированное моделирование состоит из аналитического моделирования, включая элементы имитационного моделирования, и наоборот.
Реальное моделирование представляет разработку физических полноразмерных или масштабных моделей агрегатов (процессов).
В 2007г. кафедрами ТЭУ и ПТЭ приобретен программный продукт МЭИ «ТВТ Shell» и материалы Электронной Энциклопедии Энергетики.
Электронная Энциклопедия Энергетики включает следующие разделы: общие вопросы теплоэнергетики; теоретические основы теплотехники; тепломеханическое оборудование ТЭС; теплообменное оборудование ТЭС; водоподготовка; водно-химический режим; КИП и автоматика; энергосбережение, экология и охрана труда; топливоиспользование и технология масел; эксплуатация оборудования; тепловые сети. Кроме того, энциклопедия содержит виртуальные лабораторные работы, программы тестирования и тренажеры.
Достаточно большое количество материалов по применению компьютерных технологий в теплоэнергетике и теплотехнике представлено в настоящее время в Интернете. Это – интерактивные справочники по теплоэнергетике и теплотехнике, каталоги энергетического оборудования, нормативно-правовая документация (ГОСТ, СНиП, СН, СО, РД и т.п.), типовые энергетические характеристики и их расчеты, тренажеры и программно-технические средства для производственного персонала энергетических предприятий, таблицы теплофизических свойств энергоносителей и т.д.
Литература: [1],[5],[8],[11],[13],[18].
2 Лекция. Тема: математическое и физическое моделирование в теплоэнергетике. Процесс разработки и использования математических моделей
План: основные понятия математического и физического моделирования. Аналоговое моделирование. Процесс разработки и использования математических моделей. Методы и средства ускорения моделирования. Использование системного анализа при моделировании.
В дальнейшем будем рассматривать физическое моделирование и аналоговое - из предметного; математическое моделирование - из знакового.
Введем ряд определений.
Математическая модель – приближенное описание какого-либо класса явлений внешнего мира, выраженное с помощью математической символики.
Математическое моделирование - процесс изучения явления с помощью математической модели.
Процесс математического моделирования можно подразделить на четыре этапа:
первый - формулирование законов, связывающих основные объекты модели, результат - запись в математических терминах сформулированных качественных представлений о связях между объектами модели;
второй – исследование математических задач, к которым приводят математические модели, основной вопрос – решение прямой задачи – получение в результате анализа модели выходных данных (теоретических следствий) для сопоставления их с результатами наблюдений изучаемых явлений;
третий - выяснение того соответствует ли принятая модель (гипотетичная) критерию практики, т.е. выяснение вопроса о том, согласуется ли результат наблюдений с теоретическими следствиями модели в пределах точности наблюдений. Задачи, в которых определяются характеристики модели таким образом, чтобы выходная информация была сопоставима в пределах точности наблюдений с результатами наблюдений – обратная задача;
четвертый – последующий анализ модели в связи с накоплением данных об изучаемых явлениях и модернизация модели.
Метод математического моделирования занимает ведущее место среди других методов исследования.
Физическое моделирование – экспериментальный метод научного исследования, состоящий в замене изучаемого физического процесса, явления или объекта другим, ему подобным – моделью. Геометрически подобная оригиналу модель имеет увеличенный или уменьшенный по сравнению с оригиналом размер. Модель может отличаться от реального процесса или явления количественными физическими характеристиками.
В основе физического моделирования лежит теория подобия и анализ размерностей.
Кроме прямого физического моделирования, при исследовании различных физических процессов используются различные аналогии, позволяющие на основе однотипности математических уравнений, описывающих различные физические процессы, заменять изучение исследуемого процесса изучением другого процесса.
Например, при моделировании процессов теплообмена используется электротепловая аналогия, в которой исследуемое поле температур заменяется полем электрического потенциала в контуре CR (С- электрическая емкость, R-омическое сопротивление) .
При физическом моделировании сохраняется физическая природа исследуемого объекта. В случае моделирования аналогиями модель воспроизводит иное физическое явление, отличное по своей природе от натурного, но описываемого теми же уравнениями. Метод аналогий основан на формальной идентичности дифференциальных уравнений, описывающих различные по своей физической природе процессы (проявление единства природы).
На существование электрогидродинамической аналогии (ЭГДА) указывал еще Г.Кирхгоф в 1845 г. Метод ЭГДА основан на аналогии уравнений движения электрического тока и уравнений потенциального течения жидкости. Метод магнитогазодинамической аналогии (МАГА) использует аналогию между уравнениями магнитного поля и уравнениями потенциального течения газа. Газогидравлическая аналогия (ГГА) основана на аналогии между уравнениями движения невязкой несжимаемой жидкости в открытом канале и уравнениями плоского потенциального движения газа. Ни один из указанных методов аналогий не позволяет моделировать силы вязкости. Электротепловая аналогия основана на замене поля температур полем электрического потенциала в CR контуре, аналогом коэффициента температуропроводности является величина 1/CR. Гидротепловая аналогия дает возможность моделирования процессов стационарной теплопроводности по аналогии с безвихревым потоком идеальной жидкости.
Начало
практическому применению метода ЭГДА к решению задач, связанных с движением
жидкости, было положено Д.Тома, который применил метод ЭГДА при изучении
движения воды в направляющем аппарате колеса гидротурбины. В качестве
электропроводного материала он использовал листы константана, в которых
вырезались исследуемые решетки профилей направляющих аппаратов гидротурбин.
Листы зажимались в медных шинах, к которым подводился электрический ток
(постоянный). Широкое применение метод ЭГДА получил для решения задач обтекания
турбинных и компрессорных решеток. На установке ЭГДА может быть непосредственно
исследовано обтекания тел поступательно-циркуляционным потоком. Для
решения практически важных задач необходимо уметь определять значение скоростей
и давлений не только в контуре профиля, но и в любой точке исследуемой области
поступательно-циркуляционного потока. Аналитическое решение такой задачи для
одиночного профиля требует чрезвычайно сложных и громоздких вычислений.
Для решетки профилей аналитическое решение подобной задачи неизвестно. Поэтому
можно воспользоваться методом ЭГДА. Этим методом решались задачи обтекания тел
плоским потоком сжимаемого газа с дозвуковой скоростью (используется
электролитическая ванна с переменной глубиной электролита), нелинейные задачи
газодинамики, обтекания крылового профиля, движения трехмерных потоков
несжимаемой ![]()
жидкости в проточной части турбомашин. Широкое применение нашел метод
электрогидродинамической аналогии в вихревых полях (ВЭГА).
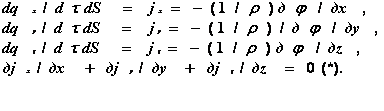 |
Для установления аналогов рассмотрим уравнения движения электрических зарядов в проводниках:
![]()
Подставив первые три уравнения в уравнение (*), получим:
В уравнениях j – плотность электрического тока, φ – электрический потенциал, ρ – удельное сопротивление проводника. Первые три уравнения представляют собой математическую запись закона Ома, уравнение, помеченное (*), – запись закона сохранения заряда.
Для потенциального течения несжимаемой жидкости:
![]()
Уравнение неразрывности для несжимаемой жидкости имеет вид
![]()
Подставив первые три уравнения в уравнение (**), получим
![]()
где φ(x,y,z,τ) – потенциал скоростей.
Потенциал скоростей аналогичен электрическому потенциалу, удельная плотность электрического тока - скорости. Если область течения электрического тока подобна области течения жидкости, а граничные условия аналогичны, то интегралы уравнений Лапласа для этих функций будут отличаться лишь произвольными постоянными. Эквипотенциальные поверхности в электрическом поле тождественны эквипотенциальным поверхностям в потоке жидкости. Силовые линии электрического поля тождественны линиям тока в потоке жидкости.
Это трехмерный случай. В двумерном случае, при геометрическом подобии областей, когда граничные условия для электрического потенциала тождественны граничным условиям для потенциала скоростей, эквипотенциальные линии в электрическом поле тождественны эквипотенциальным линиям в потоке жидкости, силовые линии электрического поля тождественны линиям тока в жидкости.
Установка ЭГДА состоит из двух основных частей: модели и электрической схемы. Модель представляет собой область движения электрического тока, предназначенную воспроизводить исследуемую область движения жидкости. Для ее создания используют различные электропроводные материалы в сочетании с диэлектриками, образующими границы области. Электрическая схема ЭГДА состоит из питательной и измерительной цепей и контрольно-измерительных приборов. Все существующие установки ЭГДА работают по принципу мостовой или компенсационной схемы (или комбинированной).
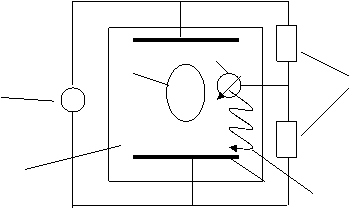
1 7
6
2 =
3
4 5
1-модель из диэлектрика, 2 - источник постоянного или переменного тока; 3 – водный раствор соли, 4 – шина; 5 – щуп, 6- резисторы, 7 – гальванометр
Рисунок 2.1 - Установка ЭГДА
Для идеальной жидкости функция тока удовлетворяет уравнению Лапласа. Гармонически сопряженная с ней функция – потенциал скоростей потока. Линии равных потенциалов и равных функций тока ортогональны. Распределение температуры в двумерном поле также подчиняется уравнению Лапласа, т.е. линии теплового потока и температурного потенциала аналогичны линиям тока и потенциалу скоростей идеального потока жидкости (гидротепловая аналогия).
Электротепловая аналогия заключается в том, что перенос тепла аналогичен переносу электрических зарядов (электропроводность аналогична теплопроводности).
Поток электрического заряда (сила тока):
I=Δq/Δτ = Δφ γ S/Δl= Δφ/RЭ.
Тепловой поток:
qТ=ΔQ/Δτ = ΔТ λ S/Δl= ΔТ/RТ.
Таким образом, тепловое сопротивление аналогично электрическому.
|

|

![]() Δl
Δl
Т2
RЭ= Δl/γS
Δl
Рисунок 2.2 - Одномерная модель стационарной теплопроводности через однослойную стенку и ее электрический аналог
|


 Т1
Т1
|
|

|
|
|
![]()
![]()
![]()
![]()
![]()
![]() Т2 Δl1
Δl2 Δl3
Т2 Δl1
Δl2 Δl3
![]() Т3 RЭ1
RЭ2 RЭ3
Т3 RЭ1
RЭ2 RЭ3
Т4
Δl1 Δl2 Δl3
RT1 RT2 RT3
Рисунок 2.3 - Одномерная модель стационарной теплопроводности через многослойную стенку и ее электрический аналог (последовательное соединение слоев)
При последовательном соединении слоев по аналогии с теорией электричества
qт=ΔT14/(Rт1+ Rт2+ Rт3).
Электротепловую аналогию можно использовать и для решения более сложных задач. Например, если теплопроводность протекает в материалах, расположенных параллельно.
|
|
![]()
![]()
![]()
![]()
![]() RT1
RT1
γ2 λ2 ![]()
![]()
 φ1
φ2
φ1
φ2
![]()
![]() RT2
RT2
![]() Т2
RЭ2
Т2
RЭ2
Рисунок 2.4 - Одномерная модель стационарной теплопроводности через многослойную стенку и ее электрический аналог (параллельное соединение слоев)
При этом по аналогии с теорией электричества
qт=ΔT12/(1/Rт1+ 1/Rт2).
К достоинству метода можно отнести: простоту электрической схемы, простоту измерения напряжения, большую точность результатов.
При разработке электрических моделей, имитирующих процессы теплопроводности, применяются два способа. В первом электрическая модель повторяет геометрию оригинальной тепловой системы и изготавливается из материала с непрерывной проводимостью. Такие модели – с непрерывными параметрами процесса. Во втором – тепловые системы заменяются электрическими цепями. Модели при этом будут с сосредоточенными параметрами процесса.
Метод исследования, основанный на идее физической аналогии, является наиболее сильным средством обобщенного анализа. Из курса физики вам известно, что существует тройная аналогия в явлениях переноса. Аналогия объединяет в единое целое разнородные явления, воспринимаемые как теплообмен, массообмен и гидродинамическое сопротивление. Аналогия является следствием единого молекулярного физического механизма процессов.
Уравнение Фурье (теплопроводность)
q = - λgrad T,
уравнение Фика (диффузия)
j = - D grad с,
уравнение Ньютона (вязкость)
σ = - η grad u.
Большинство промышленных технических объектов являются сложными системами. Характерные признаки сложной системы: невозможность рассмотрения отдельно каждого ее элемента (без установления связей с другими элементами и внешней средой); неопределенность в большом числе состояний системы; неопределенность достоверности информации; разнообразие вариантов достижения конечной цели функционирования системы; адаптивность (приспособляемость системы к возмущающим факторам воздействия среды).
Характерные особенности сложных систем вызывают необходимость использования в ходе создания их моделей методологии системного подхода.
Система - совокупность элементов, находящихся в отношениях и связях друг с другом, которая образует определенную целостность, единство.
Системные принципы:
- целостности (принципиальная не сводимость свойств системы к сумме свойств составляющих ее элементов и не выводимость из последних свойств целого);
- структурности (возможность описания системы через установление ее структуры, т.е. сети связей и отношений системы; обусловленность поведения системы не столько поведением ее отдельных элементов, сколько свойствами ее структуры);
- взаимозависимости системы и среды (система формирует и проявляет свои свойства в процессе взаимодействия со средой, являясь при этом активным, ведущим компонентом взаимодействия);
- иерархичности (каждый компонент системы в свою очередь может рассматриваться как система, а используемая в данном случае система представляет один из компонентов более широкой системы);
- множественности описания каждой системы.
Важной особенностью систем является передача в них информации и наличие процессов управления.
Системы бывают: замкнутые, открытые, статичные, динамичные, детерминированные и вероятностные.
Математическое описание модели в общем случае можно представить так
Y(τ)= F(X(τ), V(τ), S(τ), τ)
![]()
где F – закон функционирования системы;
X(τ) - входные параметры;
V(τ) - воздействия внешней среды;
S(τ) - собственные параметры системы;
Y(τ) - выходные параметры;
τ - время.
Параметры X,V,S часто называют экзогенными (независимыми), а Y - эндогенными (зависимыми).
Существует определенная последовательность реализации моделирования, показанная на схеме рис.2.5.
Основным количественным критерием адекватности модели является степень соответствия вычислительного эксперимента данным экспериментальных работ. При отсутствии последних или для предварительного анализа критерием можно считать непротиворечивость полученных результатов принятым при моделировании гипотезам и допущениям, а так же здравому смыслу.
Любая созданная модель должна удовлетворять ряду требований:
- адекватность ее объекту;
- доступность, простота и понятность для пользователя;
- универсальность (ее модули должны легко адаптироваться к другим модулям;
- точность (высокое совпадение результатов вычислительного эксперимента и параметров реального объекта);
- устойчивость и достоверность функционирования в широком диапазоне изменения рабочих параметров;
- открытость и модульность, способность к развитию без существенного изменения базового варианта;
- экономичность, реализуемая с помощью сравнительно простых алгоритмов и программ, не требующих больших ресурсов ВТ.
Многие из перечисленных требований противоречат друг другу, что требует от разработчиков добиться их оптимального сочетания в зависимости от поставленной цели моделирования.

Рисунок 2.5 – Схема последовательности реализации моделирования
Использование системного подхода в некоторой степени ускоряет процесс моделирования, поскольку предлагает разработчику методологию моделирования. Конкретизация этапов моделирования позволяет систематизировать виды его обеспечения: математическое, программное, информационное и техническое.
Можно предложить ряд средств ускорения моделирования в области этих видов обеспечения.
При решении задач моделирования сложных систем приходится периодически использовать разнообразную информацию. Для тепловых процессов необходимы три группы данных: об индивидуальных свойствах газообразных и конденсированных веществ; о свойствах газообразных, жидких и твердых топлив; о химических реакциях и механизме их протекания. Выполнение требования адекватности математической модели невозможно без соблюдения требования максимальной достоверности этой информации. Для ее хранения используются банки данных (БнД). Преимущество использования БнД для информационного обеспечения при моделировании заключается в том, что с помощью системы управления базой данных (СУБД) программы прикладной области получают необходимую информацию из базы данных. Это позволяет представлять данные независимо от структуры прикладных программ в наиболее удобной логической форме и соответственно обеспечивает независимость прикладных программ от данных.
Принципиально новые возможности появляются при использовании в математическом моделировании и вычислительном эксперименте инструментальных систем (ИС). ИС принято называть программную систему, средства которой могут быть использованы для создания и развития пакетов прикладных программ (ППП) и прикладных программных комплексов (ППК) и для накопления базы знаний (БЗ), т.е. формализованной совокупности сведений о некоторой предметной области, содержащей данные о свойствах объектов, закономерностях процессов и явлений и правила использования этих знаний для принятия решения.
Оперативность моделирования обеспечивается следующими качествами ИС: возможностью оперирования языковыми конструкциями конкретной предметной области; автоматическим синтезом программ; возможностью оперативного рассмотрения различных вариантов математических моделей и их модификаций; организацией « дружественного интерфейса», состоящего в интерактивном диалоговом взаимодействии пользователя и системы с выполнением требований простоты и удобства общения для пользователя. Степень целесообразности использования ИС для решения задач математического моделирования зависит от их структуры, оценки уровня сложности модели, требований к ней, квалификации пользователя моделью.
Литература: [5],[13-18].
3 Лекция. Тема: численные методы в математическом моделировании теплотехнических задач и их программная реализация. Методы интерполирования
План: элементы численных методов и их компьютерная реализация. Приближение функций. Интерполирование, полиномиальное интерполирование, интерполирование сплайнами, аппроксимация кривыми при решении задач приближения функций и расчета теплотехнических таблиц.
В настоящее время численные методы являются мощным математическим средством решения научно-технических задач и проблем. Это связано с тем, что в большинстве случаев невозможно получить точное аналитическое решение, а также со стремительным развитием компьютерной техники. Существует множество стандартных программ и объектно- ориентированных пакетов прикладных программ (ППП). Однако научным и инженерным работникам необходимо понимать сущность основных численных методов и алгоритмов, поскольку интерпретация результатов вычислительного эксперимента нетривиальна и требует специальных знаний особенностей применяемых методов.
Численный анализ является завершающей составляющей математической подготовки теплоэнергетика. Знание основ теории и способов реализации численных методов необходимо при проектной проработке и расчетном обосновании процессов, установок, агрегатов, систем теплоэнергетики и теплотехнологии.
Вы познакомитесь с методами аппроксимации функций, численного решения алгебраических и трансцендентных уравнений, а также систем линейных и нелинейных уравнений, задачами численного интегрирования и дифференцирования, методами решения обыкновенных дифференциальных уравнений, кратким введением в методы решения дифференциальных уравнений в частных производных и задач оптимизации. Практически все методы иллюстрируются алгоритмами и примерами их применения при решении теплотехнических задач. Рассматриваются вопросы реализации изучаемых численных методов на персональном компьютере (РС) с применением программных математических пакетов, которые широко используются в практических вычислениях. Закрепление теоретических знаний достигается при выполнении лабораторного практикума по дисциплине.
3.1 Интерполирование функций
Интерполяция применяется во многих задачах, связанных с вычислениями. Укажем некоторые из этих задач.
Обработка физического эксперимента – построение приближенных формул для характерных величин по табличным данным, полученным экспериментально.
Построение приближенных формул по данным вычислительного эксперимента. Здесь возникают нестандартные задачи интерполяции, так как обычно записываются формулы, с возможно более простой структурой.
Субтабулирование - сгущение таблиц применяется в тех случаях, когда непосредственное вычисление функций трудно или когда имеется мало экспериментальных данных. В РС вводится небольшая таблица, а нужные при расчетах значения функции находятся по мере необходимости по интерполяционной формуле.
Интерполяция применяется также в задаче обратного интерполирования: задана таблица уi = y(xi); найти хi как функцию от уi. Примером обратного интерполирования может служить задача о нахождении корней уравнения.
Интерполяционные формулы используются также при вычислении интегралов, при написании разностных аппроксимаций для дифференциальных уравнений на основе интегральных тождеств.
В общем случае при постановке задачи приближения нужно следовать по алгоритму:
- определить, какой класс приближенных функций нужно выбрать;
- выбрать критерий близости («согласия») исходной и приближающей функции (совпадение в узловых точках – метод Лагранжа, или метод наименьших квадратов);
- указать правило, позволяющее с заданной степенью точности, получить значение функции в промежуточных точках между узлами (какие узлы использовать и как их расположить).
Часто требуется восстановить функцию f(x) для всех значений х на отрезке а ≤ х ≤ b, если известны ее значения в некотором конечном числе точек этого отрезка. Эти значения могут быть найдены в результате наблюдений (измерений) в каком-то натурном эксперименте, либо в результате вычислений. Кроме того, может оказаться, что функция f(x) задается формулой и вычисления ее значений по этой формуле очень трудоемки, поэтому желательно иметь для функции более простую (менее трудоемкую для вычислений) формулу, которая позволяла бы находить приближенное значение рассматриваемой функции с требуемой точностью в любой точке отрезка. В результате возникает следующая математическая задача.
Пусть на отрезке а £ x £ b задана сетка ω ={х0 = а < х1 <¼< хn = b } и в ее узлах заданы значения функции у (х), равные у (х0) = у0, …, у(хi) = уi, …, у(хn) = уn. Требуется построить интерполянту – функцию f(х), совпадающую с функцией у(х) в узлах сетки:
f (xi) = yi, i = 0, 1, …, n. (3.1)
Основная цель интерполяции – получить быстрый (экономичный) алгоритм вычисления значений f(x) для значений х, не содержащихся в таблице данных.Основной вопрос: как выбрать функцию - интерполянту f(х) и оценить погрешность у(х) - f(х)?
Интерполирующие функции f(х), как правило, строятся в виде линейных комбинаций некоторых элементарных функций:
f(x) =![]()
![]()
![]()
где {Ф![]() (х)} - фиксированные линейно независимые
функции;
(х)} - фиксированные линейно независимые
функции;
с0, с1,
…, сn - не определенные пока коэффициенты. ![]()
![]()
Из условий
(3.1) получим систему n+1 уравнений относительно
коэффициентов {с![]() }:
}:
![]()
Предположим,
что система функций Ф![]() (х)
такова, что при любом выборе узлов а = х0< х1 <
…< хn
= b отличен от нуля определитель системы:
(х)
такова, что при любом выборе узлов а = х0< х1 <
…< хn
= b отличен от нуля определитель системы:
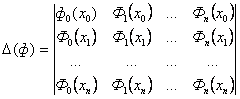 .
.
Тогда по
заданным уi (i =
0,1,…, n ) однозначно определяются коэффициенты с![]() (
(![]() = 0, 1, …, n).
= 0, 1, …, n).
В качестве
системы линейно независимых функций {Ф![]() (х)} чаще всего выбирают: степенные функции Ф
(х)} чаще всего выбирают: степенные функции Ф![]() (х) = х
(х) = х![]() (в этом случае f = Pn
(x) – полином степени n ); тригонометрические функции { Ф
(в этом случае f = Pn
(x) – полином степени n ); тригонометрические функции { Ф![]() (х) = соs kх, sin kx} (в этом случае f
- полином тригонометрический). Используются также рациональные функции
(х) = соs kх, sin kx} (в этом случае f
- полином тригонометрический). Используются также рациональные функции
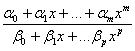
и другие виды интерполирующих функций.
Рассмотрим полиномиальную интерполяцию.
Известно, что любая непрерывная на отрезке [а, b] функция f(x) может быть хорошо приближена некоторым полиномом Рn(х).
Будем искать интерполяционный полином в виде
Рn(x) = ![]() (
3.2 )
(
3.2 )
где с![]() - неопределенные пока
коэффициенты.
- неопределенные пока
коэффициенты.
Полагая f (xi) = yi, получим систему линейных уравнений вида
![]() с0+с1 х0+…+сnх0n= y0,
с0+с1 х0+…+сnх0n= y0,
с0+с1 х1+…+сnх1n= y1,
…………………..…,
с0+с1 хn+…+сnхnn= yn.
Определитель этой системы отличен от нуля, т.е. полином вида (3.2) существует и единственен. Форм записей такого полинома существует множество.
В качестве
базиса {Ф![]() (х)}
мы взяли базис из одночленов 1, х, х2, …, хn.
Для вычислений более удобным является базис полиномов Лагранжа {l
(х)}
мы взяли базис из одночленов 1, х, х2, …, хn.
Для вычислений более удобным является базис полиномов Лагранжа {l![]() (x)} степени n или коэффициентов
Лагранжа:
(x)} степени n или коэффициентов
Лагранжа:
l![]() (xi) = 1,
если i = k,
(xi) = 1,
если i = k,
0, если i ≠ k , i, k = 0, 1, …, n.
Нетрудно видеть, что полином степени n
l![]() (x)
= l
(x)
= l![]() (x) =
(x) = ![]()
удовлетворяет этим условиям.
Полином l![]() (x),
очевидно, определяется единственным образом.
(x),
очевидно, определяется единственным образом.
Полином l![]() (x) y
(x) y![]() принимает значение у
принимает значение у![]() в точке х
в точке х![]() и равен нулю во всех остальных
узлах х
и равен нулю во всех остальных
узлах х![]() при j ¹ k. Отсюда следует, что
интерполяционный полином
при j ¹ k. Отсюда следует, что
интерполяционный полином
Рn(x) = ![]() (3.3)
(3.3)
имеет степень не выше n и Рn (xi) = yi. Формулу (3.3) называют формулой Лагранжа. К достоинствам формулы можно отнести то, что число арифметических действий для вычисления пропорционально n2.
Для оценки близости полинома Рn(х) к функции f(х) предполагают, что существует (n+1)-я непрерывная производная f(n+1) (х).
Тогда формула для погрешности
f(x) - Pn(x) = ![]()
![]()
![]() (x-xj),
(x-xj), ![]() [a,b].
[a,b].
Формула (3) содержит значения функций в узлах интерполяции, она применима как для равноотстоящих, так и для неравноотстоящих узлов. К недостаткам формулы можно отнести то, что при изменении числа узлов все расчеты необходимо проводить заново.
При вычислениях на РС в том случае, когда шаг сетки постоянен, удобна интерполяционная формула Ньютона. Для ее записи надо ввести так называемые разделенные разности.
Разделенная разность нулевого порядка совпадает со значением функции в узлах.
Разделенная разность первого порядка определяется так
у(xi, xj) = [y (xi) - y(xj)]/(xi - xj).
Разделенная разность второго порядка –
y(xi,xj,x![]() )
= [y(xi,xj) - y(xj,x
)
= [y(xi,xj) - y(xj,x![]() )]/(xi - x
)]/(xi - x![]() ) и т.д.
) и т.д.
Тогда функция-интерполянта приобретает вид
f(x) = yo +![]() (3.4)
(3.4)
Уравнение (3.4) определяет полином Ньютона.
После того как вычислены разделенные разности, вычислять полином Ньютона удобно по схеме Горнера:
f(x) = y(xo) + (x-xo) [y (xo,x1) + (х-х1) [y (xo,x1,x2) + …]] . (3.5)
Вычисление f(x) по (3.5) для каждого х требует n умножений и 2n сложений и вычитаний.
Следует иметь в виду, что применение полинома высокой степени может приводить к трудным проблемам, связанным с погрешностями округления.
Важным вопросом является сходимость интерполяции, т.е. выяснение условий, при которых погрешность метода стремится к нулю. Для уменьшения погрешности можно, сохраняя степень интерполяционного полинома, уменьшать шаг сетки, либо, сохраняя шаг сетки, увеличивать число используемых узлов, т.е. степень многочлена.
На практике, если 3-5 узлов не обеспечивают требуемой точности, то нужно не увеличивать число узлов, а уменьшить шаг таблицы.
Для данного порядка интерполяции n ошибка имеет порядок n.
Ошибка ограничения или «усечения» (разложение в ряд «усечено» до некоторого порядка) определяется так
εr = sup|f(x)-P(x)| = hnM/n!, h = |xn-x1|, M = sup|fn(x)|.
К ошибке ограничения добавляют ошибку округления.
3.2 Сплайн - интерполяция
Приближение сплайнами - кусочно-полиномиальное приближение функции f(x) по ее значениям в узлах. Степень полинома на каждом участке одинакова, и называется порядком сплайна. Часто между любыми соседними узлами сетки функция интерполируется кубическим полиномом - кубическая сплайн-интерполяция. Коэффициенты кубического полинома на каждом участке определяются из условий сопряжения (согласования) в узлах.
f(xi)=yi, f'(xi-0) = f'(xi+0), f"(xi-0) = f"(xi+0), для i = 0,1,…, n-1.
На границе участка ставятся условия f"(x0)=0, f"(xn)=0.
Условия согласования звеньев сплайна с исходной функцией используются для вывода формулы одного звена на заданном отрезке. Количество согласований соответствует степени сплайна.
Компьютерная реализация методов интерполирования в Excel описана в [23-24,26].
Литература: [1 - 4],[6],[22-24].
4Лекция. Тема: численное интегрирование в теплотехнических расчетах. Методы численного интегрирования
План: численное интегрирование при расчете площади поверхности нагрева теплообменного аппарата. Методы численного интегрирования: прямоугольника, трапеций, парабол, Гаусса. Компьютерная реализация теплового расчета теплообменного аппарата.
4.1 Численное интегрирование в теплотехнических расчетах
Необходимость численного интегрирования часто возникает при анализе инженерных и научных данных. Например, численные методы вычисления применяют в тех случаях, когда интеграл не удается найти в аналитическом виде или когда этот вид сложен. Численное интегрирование применяют и тогда, когда нужно найти интеграл от табулированной функции, измеряемой в эксперименте.
Например, для определения количества теплоты, передаваемого от одного теплоносителя к другому через поверхность теплообмена, необходимо воспользоваться уравнением теплопередачи вида
dQ = k<Dt>dF. (4.1)
Из уравнения (4.1) tx2
F=òdQ ¤ k<Dt> = òGхcрхdtх ¤ k<Dt>(tx,tг ),
tx1
т.е задача сводится к взятию интеграла, что не всегда можно сделать аналитически.
Задача численного интегрирования состоит в нахождении приближенного значения интеграла вида:
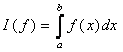
где f(x) – заданная функция.
На отрезке [а,b] вводится сетка
ω ={xi;; x0 = а<x1<x2…<xn = b}.
В качестве приближенного значения интеграла рассматривают число
 (4.2)
(4.2)
где f(xi) – значения функции в узлах сетки;
сi – весовые или квадратурные множители (веса), которые зависят только от узлов и не зависят от вида функции.
Формула (4.2) - квадратурная формула. Задача численного интегрирования будет состоять в отыскании таких узлов {xi;} и таких весов {сi;}, чтобы погрешность квадратурной формулы была минимальна для функций из заданного класса
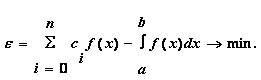
В зависимости от разбиения отрезка [а,b] различают два подхода к построению квадратурных формул. В первом - местоположение и длина интервалов разбиения выбираются заранее. В этом случае используется квадратурная формула Ньютона - Котеса (к этим методам относятся метод трапеции и метод Симпсона). Во втором - местоположение и длина интервалов заранее не задается, а подбирается так, чтобы достичь наивысшей точности при заданном числе интервалов (метод Гаусса).
Определенный интеграл
b
I=ò f(x)dx (4.2)
a
представляет собой площадь, ограниченную кривой f(x),осью х и прямыми х0 = a, х n= b. Мы будем пытаться вычислить интеграл, разбивая интервал от a до b на множество меньших интервалов, находя приблизительную площадь каждой полоски.
y f (xi) f (xi+1)
![]()
![]()

y = f (x)
![]()
![]()
![]()
![]()
![]() a
xi xi+1 b x
a
xi xi+1 b x
Рисунок 4.1 – Геометрическая интерпретация численного интегрирования
4.2 Методы численного интегрирования
4.2.1.Формула прямоугольников
Впишем в каждую полоску прямоугольник. Для нахождения площади такого прямоугольника найдем координату средней точки хср = (xi+xi+1)/2 и значение функции в ней f (xср). Площадь под кривой определяется так
I=ΣIi= Σf((xi+xi+1 )/2)*( xi+1- xi). (4.3)
Формула (4.3) - формула прямоугольников.
Оценим погрешность метода прямоугольников, для чего разложим функцию в ряд Тейлора и отбросим соответствующие члены ряда, содержащие h в степени больше 3.
Эта погрешность может быть определена так:
ei = - (h3/24)* f ′′ (xi), h=(b-a)/n,
ε = ∑ ei = - (h2/24)* (b-a ) * f ′′ ( ξ ) (4.4)
где ξ є [ a , b ].
4.2.2 Метод трапеций
Впишем в каждую полоску трапецию. Площадь под кривой определяется так
I=ΣIi= Σ1/2 (f (xi+1)- f((xi)) *( xi+1- xi) + f(xi) *( xi+1- xi).
Формула трапеций на равномерной сетке шагом h =(xi+1- xi):
I = ∑ сi * f (xi) = h/2*( y0 + 2y1 + 2y2 +... + yn ), (4.5)
i
h = (b -а)/ n; у0 = f (x0); у1 = f (x1) и т.д.
Оценим погрешность метода трапеций, для чего разложим функцию в ряд Тейлора и отбросим соответствующие члены ряда, содержащие h в степени больше 3. Эта погрешность может быть определена так:
ei = - (h3/12)* f ′′ (xi),
ε = ∑ ei = - (h2/12)* (b-a ) * f ′′ ( ξ ), где ξ є [ a , b ] . (4.6)
4.2.3 Метод Симпсона
Этот метод аналогичен правилу трапеций в той части, где интегрирование производится путём разбиения общего интервала на множество более мелких отрезков. Однако теперь для вычисления площади каждой полоски через каждые три последовательные ординаты разбиения проводят квадратичную параболу.
Предположим, что число отрезков чётное:
n = (b-a) / h.
Воспользуемся методом трапеции:
I h= h/2*( y0 + 2y1 + 2y2 +... + yn ). (4.7)
Площадь под кривой I = I h+с h2. (4.8)
Увеличим шаг в два раза k = 2h:
I k= k/2*( y0 + 2y2 + 2y4 +... + yn ). (4.9)
Площадь под кривой I = Ik+с k2. (4.10)
Исключив из системы уравнений (4.8) и (4.10) с, получим формулу Ричардсона для лучшего приближения интеграла
I = I h+ (I h - Ik)/ (k2/ h2-1). (4.11)
Подставим (4.7) и (4.9) в (4.11), получаем формулу Симпсона
I = h/3*( y0 + 4y1 + 2y2 + 4y3 + 2y4 +... + yn ). (4.12)
Ошибка ограничения, допускаемая в методе Симпсона,
ei = - (h4/180)* f (IV) (xi),
ε = ∑ ei = - (h4/180)* (b-a ) * f (IV) ( ξ ) (4.13)
где ξ є [a, b].
Метод трапеций и Симпсона наиболее часто используется при численном интегрировании.
Оценка погрешности ограничения рассмотренных методов численного интегрирования по выражениям (4.4), (4.6) и (4.13) оказываются малоэффективными из-за трудностей оценки производных высокого порядка подынтегральных функций. На практике для достижения требуемой точности прибегают к методу последовательного удвоения числа шагов. Задают значение допустимой погрешности ε и число интервалов разбиения n (шаг интегрирования h) находят In. Удваивают число интервалов (шаг интегрирования h/2) и находят I 2n. Оценивают погрешность Δ=( In- I 2n)/3 – для метода трапеций и Δ=( In- I 2n)/15 – для метода Симпсона. Если Δ≥ ε, количество интервалов еще раз удваивают. Вычисления заканчивают при выполнении условия Δ< ε.
4.2.4 Метод Гаусса
Гауссом предложен метод, позволяющий уменьшить ошибку ограничения при заданном числе интервалов за счет расположения концов интервалов там, где это требуется из условий достижения наивысшей точности интегрирования.
В заданном интеграле b
I=ò f(x)dx,
a
изменим пределы интегрирования так, чтобы они стали равны +1и –1, для чего введем новую переменную μ = (2х- (b+a))/(b-a)
1
I=ò φ (μ)dμ, где φ (μ)=(1/2)(b-a) f((b-a) μ /2+(b+a)/2).
-1
Можно показать, что
1
I=ò φ (μ)dμ = φ (-1/√3) + φ (1/√3) + ε (4.14)
-1
где ε= φ (IV)/135.
Уравнение (4.14)– формула Гаусса для двух ординат.
Можно вывести Гауссовы формулы численного интегрирования более высокого порядка с использованием полиномов Лежандра [1]. На практике предпочтение отдается методу Симпсона.
Интегрирование по квадратурным формулам сопровождается ошибками округления. Они носят случайный характер и с увеличением числа интервалов разбиения n возрастают пропорционально √n. Для функций высокой гладкости формула Гаусса дает значительно более точные результаты, чем формула Симпсона при одинаковом числе узлов, а последняя более точные, чем формула трапеций. Формула Гаусса обеспечивает высокую точность при небольшом числе узлов. Формула Симпсона в достаточной степени точна при умеренном числе узлов и поэтому получила широкое применение. Компьютерная реализация методов интегрирования описана в [9], [23-26].
Литература: [1-4],[6],[22-24].
5 Лекция Тема: численные методы нахождение корней алгебраических и трансцендентных уравнений
План: нахождение корней алгебраических и трансцендентных уравнений при решении уравнений тепло - и массообмена. Методы нахождения корней уравнений: дихотомии, хорд, Ньютона, секущих, последовательных приближений.
5.1 Нахождение корней алгебраических и трансцендентных уравнений при решении задач тепло - и массообмена.
В научной и инженерской практике часто приходится решать алгебраические уравнения. Так при решении задачи нестационарной теплопроводности по определению температурного поля в бесконечной пластине толщиной 2δ было получено уравнение вида
Θ=Σ(2Θ0sinμn/(μn+ sinμnсosμn)) сos(μnх/δ)exp(-μn2Fo),
в котором μn являлось корнем характеристического трансцендентного уравнения
μn/Bi=ctg μn.
Критериальные уравнения тепломассообмена, многие уравнения гидродинамики относятся к трансцендентным уравнениям [14-17].
Скорость и эффективность решений таких уравнений существенно влияют на применимость вычислительного процесса и определяются классом задачи. Алгебраические задачи могут быть классифицированы по числу уравнений, типу и количеству решений.
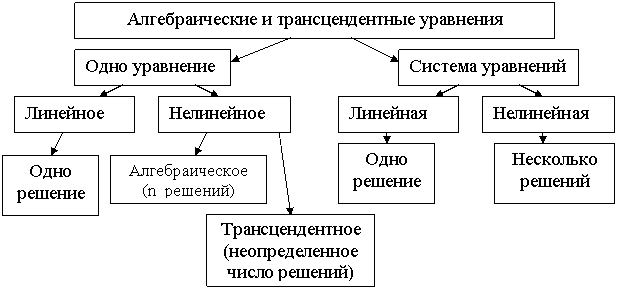
Рисунок 5.1 –Схема классификации алгебраических уравнений
Методы решения алгебраических уравнений делятся на прямые и итерационные.
Прямые это, например, нахождение корня квадратного уравнения.
В итерационных методах процедура решения задаётся в виде многократного применения некоторого алгоритма.
При решении таких задач предполагается, что корни являются действительными.
Отыскание корней уравнения состоит обычно из двух этапов. На первом этапе необходимо выяснить существуют ли решения, какого их количество, оценить примерное значение, оценить количество и величину интервалов, на котором функция меняет знак. Второй этап – нахождение корня в заданном интервале.
При решении задачи нахождения корней функции одной переменной вида f(x)=0, где f(x) – алгебраическая или трансцендентная функция, можно говорить только о приближенном вычислении корней уравнения, т. е. таких значений аргумента x=х*, при которых выполняется равенство f(х*)=0 с заданной точностью. Рассмотрим некоторые методы решения задач такого типа.
5.2 Метод половинного деления (дихотомия)
Дихотомия применяется, когда требуется надежность счета, а скорость сходимости не имеет значения.
 f(хn+1)
f(хn+1)
Y
f(хср)
хn хcр2 х* хcр1 хn+1 Х
f(хn)
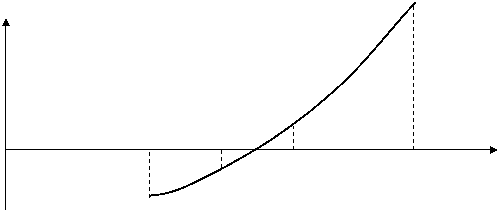
Рисунок 5.2 – Геометрическая интерпретация метода дихотомии
Пусть дано уравнение f(x)=0 и отделен простой корень х*, то есть найден такой отрезок [хn, хn+1], х* принадлежит [хn, хn+1] и на концах интервала функция имеет значения, противоположные по знаку. Отрезок
[хn, хn+1] называется начальным интервалом неопределенности, потому что известно, что корень ему принадлежит, но его местоположение с требуемой точностью не определено.
Алгоритм метода дихотомии.
1. Вычисляют значения функции через равные интервалы значений х до смены знака, при переходе от f(xn) к f(xn+1)
2. Вычисляют среднее значение аргумента xср и находят f(xср).
3. Если знак f(xср) совпадает со знаком f(xn), то в дальнейших расчетах вместо xn используют xcp. Если f(xcp) совпадает с f(xn+1), то вместо xn+1 берут xcp.
4. Интервал, в котором заключено значение корня, сужается. Если f(xcpk) ≤ 0 + ε, где ε положительное наперед заданное достаточное малое число – точность расчета, то процесс заканчивается за k итераций, при этом ширина интервала уменьшается в 2k раз. Если f(xcpk) > 0 + ε, повторяют пп.2-3 алгоритма.
Метод имеет линейную, но безусловную сходимость, и его погрешность за каждую итерацию уменьшается в два раза.
Метод не применим к корням четной кратности, т.е. тогда когда, f(x)=g(x)(x-x1)m, где x1 корень кратности m.
5.3 Метод хорд
В основе этого метода, как и в методе дихотомии, лежит линейная интерполяция по двум значениям функции, имеющим противоположные знаки, но он обеспечивает более быстрое нахождение корня.
Y f(хn+1)
x1* x2* x3* x4* x*
хn хn+1 X
f(хn)
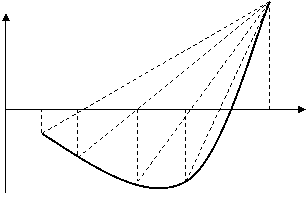
Рисунок 5.3 – Геометрическая интерпретация метода хорд
Алгоритм метода хорд.
1. Вычисляют значения функции через равные интервалы значений х до смены знака при переходе от f (xn) к f (xn+1).
2. Прямая, проходящая через эти две точки, пересекает ось х в точке
х* = xn – f (xn)( xn+1 - xn)/ (f (xn+1) – f (xn)). (5.1)
3. Находят значение f (xk*), которое сравнивают с известными f (xn),
f (xn+1). Если знак f(xк*) совпадает со знаком f(xn), то в дальнейших расчетах вместо xn используют xk*. Если f(xk*) совпадает с f(xn+1), то вместо xn+1 берут xk*.
4. Проверяют близость f(xk*) к нулю c заданной точностью ε. Если f(xk*) ≤ 0 + ε, то процесс заканчивается за k итераций. Если f(xk*) > 0 + ε, повторяют пп.2-3 алгоритма.
В знаменателе формулы (5.1) стоит разность значений функций. Вдали от корня она несущественна, но вблизи корня эти значения близки и малы. Возникает потеря значащих цифр, приводящая к «разболтке» счета. Это ограничивает точность, с которой можно найти корень. Для простых корней это ограничение невелико, а для кратных – существенно. Можно использовать метод Гарвика. Выбирают не очень малое ε, ведут итерации до выполнения условия |xn+1 - xn| < ε и затем продолжают расчет до тех пор, пока |xn+1 - xn| убавает.
5.4 Метод Ньютона
Метод последовательных приближений, разработанный Ньютоном, используется наиболее часто среди всех итерационных алгоритмов.
Функция f(x), дважды дифференцируемая на отрезке [a, b], который содержит корень х*. При этом f(x*)=0. Для определения интервала, в котором заключен корень, в методе Ньютона, не требуется находить значения функции с противоположными знаками. Вместо интерполяции по двум значениям функции будем проводить экстраполяцию с помощью касательной в данной точке.
![]() Y
Y

 М0
М0
х*

![]()
![]() X
X
х1 х2 х0
М1
Рисунок 5.4 – Геометрическая интерпретация метода Ньютона
Алгоритм метода:
1. Находят значение xn+1, которое соответствует точке, в которой касательная к кривой в точке xn пересекает ось х
xn+1 = xn - f(xn)/f ′(xn). (5.2)
2. Процедуру повторяют до выполнения условия близости функции к нулю с заданной точностью f(xn) ≈ ε.
Быстрота сходимости метода Ньютона в большой мере зависит от выбора исходной точки. Если в процессе итераций тангенс угла наклона касательной f ′(xn) обращается в ноль, то применение метода усложняется. В случае бесконечно больших f ′′(x) метод также недостаточно эффективен. При кратности корней (условие f (x)=f ′(x)=0) метод Ньютона не обеспечивает сходимости.
5.5 Метод секущих
Одним из недостатков метода Ньютона является необходимость дифференцирования заданной функции f(x). Если нахождение производной затруднено, можно воспользоваться некоторым приближением, которое положено в основу метода секущих. Заменим производную f ′(xn) для расчета
xn+1 = xn - f(xn)/f ′(xn) разностью последовательных значений функции, отнесенных к разности последовательных значений аргумента, т.е. разделенной разностью первого порядка
F*(xn)= (f(xn)- f(xn-1))/( xn- xn-1),
тогда
xn+1 = xn - f(xn)/ F*(xn). (5.3)
Схема алгоритма остается, как и в методе Ньютона, изменяется только вид итерационной формулы (5.3).
5.6 Метод простой итерации (последовательных приближений)
Для применения этого метода уравнение f(x)=0 приводится к виду
х = g(х). Задаются начальным значением х0, а последующие приближения вычисляются с помощью итерационной процедуры
xn+1= g(хn). (5.4)
Для сходимости метода необходимо выполнение условия
0< g′ (хn)<1
![]() Y
Y

 x
x
![]()
![]()
![]() g(x)
g(x)

![]() X
X
х0 х1 х2
Рисунок 5.5 – Геометрическая интерпретация метода простых итераций
Компьютерная реализация методов в Excel описана в [9], [23-24, 26].
Литература: [1-4],[6], [9], [14-17], [23-24].
6 Лекция. Тема: численные методы решения систем алгебраических уравнений
План: постановка задачи нахождения решения систем линейных и нелинейных алгебраических уравнений. Примеры решения систем уравнений в теплоэнергетических расчетах. Методы решения систем алгебраических уравнений (Гаусса, Зейделя, Ньютона).
6.1 Решение систем линейных и нелинейных алгебраических уравнений
С подобной задачей инженер сталкивается, пожалуй, чаще всего в своей практике. Уравнения, содержащие суммы целых степеней х, называются алгебраическими. К решению систем алгебраических уравнений приводят многие задачи анализа и синтеза физических явлений различной природы (механические, гидравлические, и т.д.). В теплоэнергетике к решению систем алгебраических уравнений приводят задачи: теплового и массового баланса процессов, гидравлического расчета тепловых сетей, систем теплоснабжения, анализа размерности при физическом моделировании и т.д.
В общем случае система линейных уравнений имеет вид:
![]() a11 x1 + a22 x2 +
. . . + a1n xn = b1
a11 x1 + a22 x2 +
. . . + a1n xn = b1
a21 x1 + a22 x2 + . . . + a2n xn = b2
. . . . . . . . . . . . . . . . . . . . . . . . . . . ( 6.1 )
an1 x1 + an2 x2 + . . . + ann xn = bn
Систему (6.1) можно представить в векторно-матричной форме:
![]()
![]() -
матрица коэффициентов будет иметь вид
-
матрица коэффициентов будет иметь вид
a11 a12 . . . a1n
a21 a22 . . . a2n
A = . . . . . . . . . . ;
an1 an2 . . . ann
![]()
![]() -
вектор -столбец свободных
членов ( 6.2 )
-
вектор -столбец свободных
членов ( 6.2 )
b1
b2
b = …… ;
bn
- вектор-столбец неизвестных
![]()
![]() x1
x1
x2
x = ….. .
xn
Свернем (6.2):
Ax = b. (6.3)
Если матрица А невырожденная, то есть ее определитель отличен от нуля, можно найти единственное решение системы (6.1) или (6.3) в виде:
xi=![]() (6.4)
(6.4)
где в числителе определитель матрицы Ai.
Матрица Ai может быть получена из матрицы А, заменой ее i-го столбца, столбцом свободных членов. Такой метод решения мало эффективен, чаще всего используются численные методы решения, которые делятся на: прямые (точные) и итерационные (приближенные). К прямым относится метод Гаусса, к приближенным - метод Зейделя.
![]() Распространенной
вычислительной задачей является нахождение решений систем нелинейных
алгебраических трансцендентных уравнений с n
неизвестными, которые в общем виде можно записать так:
Распространенной
вычислительной задачей является нахождение решений систем нелинейных
алгебраических трансцендентных уравнений с n
неизвестными, которые в общем виде можно записать так:
f1(x1,x2, . . . xn)=0
f2(x1,x2, . . . xn)=0
. . . . . . . . . . . . . . . (6.5)
fn(x1,x2, . . . xn)=0
Решением такой системы называется множество значений x1,x2, . . . xn, одновременно удовлетворяющих каждому из уравнений системы.
Введем векторы столбцы:
![]()
![]()
![]()
![]() x1 f1
x1 f1
x2 f2
x = . . . , f = . . . , тогда (6.5) преобразуется к виду
xn fn
f(x)=0. ( 6.6 )
Такие системы решаются только итерационными методами Ньютона и Зейделя.
6.2 Метод Гаусса с выбором главного элемента (метод последовательного исключения неизвестных)
Процесс решения системы уравнений методом Гаусса делится на два этапа. На первом этапе (прямой ход) последовательным исключением неизвестных составляется преобразованная, эквивалентная система уравнений с треугольной матрицей, в которой все элементы под главной диагональю равны нулю. При этом одно из уравнений в системе содержит только одну неизвестную, а в каждом следующем - добавляется еще по одной неизвестной. На втором этапе (обратный ход) решается преобразованная система уравнений.
6.2.1 Алгоритм метода Гаусса
Прямой ход:
а) среди элементов матрицы А аij, i,j=1…n выбирается наибольший по модулю аpq, называемый главным элементом. Соответственно строка с этим элементом будет главной строкой. Предположим, что аpq=a11, если это не так, то меняют местами первую строку со строкой p и первый столбец со столбцом q, при этом совершают перенумерацию коэффициентов и неизвестных. Информацию о перенумерации необходимо запомнить. Теперь первая строка становится главной;
б) полученное первое уравнение системы делится на a11 = apq и получают уравнение вида:
x1+c12x2+… +c1nxn=d1 (6.7)
где cij=a1j/a11, d1=b1/a11, j=2…n;
в) исключают неизвестную величину х1 из каждого уравнения исходной системы, начиная со второго, путем вычитания уравнения шага б), умноженного на коэффициент аi1, при х1 в соответствующем уравнении. Отбрасывают главную строку и первый столбец матрицы А и получают преобразованную систему уравнений:
![]() c22x2+c23x3+…
+c2nxn=d2
c22x2+c23x3+…
+c2nxn=d2
. . . . . . . . . . . . . . . . . . . . (6.8)
cn2x2+cn3x3+… +cnnxn=dn
где cij=aij-cijai1, di=bi-diai1; (6.9)
г) над системой шага в) (6.8) повторяют операции шагов а) - в), в результате чего получают систему уравнений, содержащих неизвестные х3… хn. Такие преобразования продолжают до тех пор, пока не получат одно уравнение с одним неизвестным:
cnnxn=dn . (6.10)
Это уравнение также считают главным;
д) объединяют все главные уравнения и получают систему с треугольной матрицей, эквивалентную исходной:
![]() x1+c12x2+c13x3+…
+c1nxn=d1
x1+c12x2+c13x3+…
+c1nxn=d1
c22x2+c23x3+… +c2nxn=d2
c33x3+… +c3nxn=d3 . (6.11 )
. . . . . . . . . . . . .
cnnxn=dn
Обратный ход.
Из системы шага д) (6.11) неизвестные определяются в обратном порядке:
xn=dn/cnn
![]() xn-1=dn-1-cn-1xn
xn-1=dn-1-cn-1xn
. . . . . . . . . . . . . . . ( 6.12 )
x1=d1-c12x2-c13x3-… -c1nxn
В случае вырожденной матрицы сnn= 0, получить хn невозможно -метод Гаусса неприменим.
Выбор в качестве главного наибольшего по модулю элемента матрицы А обеспечивает наименьшую величину коэффициента, на который умножается главная строка в процессе последовательного исключения неизвестных, что обеспечивает меньшую погрешность вычисления. Метод Гаусса надежен, прост и широко применяется при решении на ЭВМ.
6.3 Метод Зейделя
![]()
![]()
![]() Суть итерационного метода Зейделя состоит в том, что
задается некоторый произвольный вектор х [0], являющийся началом приближения к
искомому решению х*. Затем строят последовательность приближенных значений
{x[k]}, где k=0,1,2,…, сходящихся к х*
Суть итерационного метода Зейделя состоит в том, что
задается некоторый произвольный вектор х [0], являющийся началом приближения к
искомому решению х*. Затем строят последовательность приближенных значений
{x[k]}, где k=0,1,2,…, сходящихся к х*
lim x[k]=x*, при k→∞.
Последовательность векторов х[0], x[1], … , x[k] сходится к х* в том случае, если для любого ε > 0 существует натуральное число N, начиная с которого (k ≥ N) , выполняется условие
||x*-x[k]|| < ε
где ||·|| - норма вектора.
6.3.1 Алгоритм метода Зейделя:
а) исходную систему линейных алгебраических уравнений
![]() x1+c12x2+c13x3+…
+c1nxn=d1
x1+c12x2+c13x3+…
+c1nxn=d1
x2+c21x1+c23x3+… +c2nxn=d2
. . . . . . . . . . . . . . . . . . . . . . (6.13)
cn1x1+cn2x2+cn3x3+… +xn=dn
разрешают относительно неизвестных х1, х2, … , хn и приводят к виду:
![]() x1=c12x2+… +c1nxn+d1
x1=c12x2+… +c1nxn+d1
x2=c21x1+… +c2nxn+d2 . (6.14)
. . . . . . . . . . . . . . . . . .
xn=cn1x1+… +cnnxn+dn
Такое преобразование всегда можно выполнить, если определитель системы отличен от нуля;
б) задают начальные значения вектора x[0]={x1[0], x2[0], … , xn[0]}. Начальный вектор может быть выбран произвольно, однако необходимо использовать всю информацию, чтобы вектор x[0] был близок к х*;
в) в первое уравнение системы (6.14) подставляют координаты точки x[0] и вычисляют значение первой координаты:
x1[1]=c12x2[0]+c13x3[0]+… +c1nxn[0]+d1.
В следующее уравнение подставляем х1[1] и значения xn[0]:
х2[1]=c21x1[1]+c23x3[0]+… +c2nxn[0]+d2.
Аналогично для xn[1]:
xn[1]=cn1x1[1]+cn2x2[1]+… +dn
В результате будет найдено
x[1]={x1[1],…,xn[1]};
г) начальный вектор x[0] заменяют x[1] и вычисляют следующее приближение. В общем случае k+1 приближение определяется по формуле:
![]() x1[k+1]=c12x2[k]+…+c1nxn[k]+d1
x1[k+1]=c12x2[k]+…+c1nxn[k]+d1
x2[k+1]=c21x1[k+1]+…+c2nxn[k]+d2
. . . . . . . . . . . . . . . . . . . . . . . . . . .
xn[k+1]=cn1x1[k+1]+…+dn
.
Итерационный процесс будет продолжаться до тех пор, пока все xi[k+1] не будут близки с xi[k], то есть выполнится условие:
![]() ||xi[k+1]-xi[k]|| <
ε
(6.15)
||xi[k+1]-xi[k]|| <
ε
(6.15)
где ε - точность вычисления.
Можно показать, что с помощью метода Зейделя строится сходящаяся к точному решению последовательность векторов {x[k]}, если матрица А системы уравнений удовлетворяет условию:
|aij| > |ai1| + |ai2| +…+ |ain| . (6.16)
Для всех i или хотя бы для одного i должно удовлетворятся условие:
|aii| > |ai1| + |ai2| +…+ |ain| . (6.17)
6.4 Сравнение метода Гаусса и Зейделя для решения систем линейных алгебраических уравнений
Выбор в каждом отдельном случае конкретного метода решения систем линейных алгебраических уравнений определяется следующими факторами:
- особенностями матрицы коэффициентов системы А;
- порядком системы;
- быстродействием и объемом памяти компьютера.
Метод Гаусса наиболее универсален и эффективен, применение его особенно целесообразно для систем общего вида с плотно заполненной матрицей коэффициентов А.
При решении систем (n=103-108) с разреженной матрицей коэффициентов наиболее эффективно применять итерационный метод Зейделя или метод прогонки [1].
Ошибки округления в итерационных методах оказываются существенно меньше, чем в прямых методах. Метод Зейделя является самоисправляющимся, так как отдельная ошибка, допущенная в вычислениях, не отражается на конечном результате, так как ошибочное приближение рассматривается как новый начальный вектор. Важным преимуществом итерационных методов является удобство их программирования.
Для решения систем нелинейных уравнений используются методы Ньютона и Зейделя [1].
Компьютерная реализация методов в Mathcad описана в [9-10,26].
Литература: [1-4],[6], [9-10], [14-17], [23-24].
7 Лекция. Тема: численные методы решения обыкновенных дифференциальных уравнений
План: задача Коши для обыкновенных дифференциальных уравнений. Примеры использования обыкновенных дифференциальных уравнений, в теплотехнических расчетах. Методы решения обыкновенных дифференциальных уравнений (одношаговые и многошаговые).
7.1 Задача Коши для обыкновенного дифференциального уравнения первого порядка
Уравнение, содержащее одну или несколько производных, называют дифференциальным. Поскольку большинство физических законов науки и техники записаны в форме дифференциальных уравнений, их решение является повседневной необходимостью. Задачи моделирования, связанные с движением массы или энергии, теплотехнологическими процессами и теплоэнергетическими системами, изменяющимися во времени, также неизбежно ведут к дифференциальным уравнениям. К сожалению, число уравнений, которые можно успешно решить аналитическими методами, очень ограничено. Поэтому при рассмотрении научных и инженерных задач особенно важен вопрос о решении дифференциальных уравнений с помощью персонального компьютера.
В зависимости от числа независимых переменных и, следовательно, типа входящих в них производных, дифференциальные уравнения делятся на две категории: обыкновенные, содержащие одну независимую переменную и производные по ней, и уравнения в частных производных, содержащие несколько независимых переменных и производные по ним, которые называют частными.
Дифференциальным уравнением называется уравнение, содержащее неизвестные функции у, независимые переменные x, производные неизвестных функций:
![]() .
(7.1)
.
(7.1)
Решить дифференциальное уравнение - найти его общий интеграл, функцию Ф, связывающую независимую переменную х, искомую функцию у и n постоянных интегрирования с помощью уравнения Ф(х,у,с1,. с2,….,сn) = 0.
Чтобы решить обыкновенное дифференциальное уравнение (ОДУ), необходимо знать значения зависимой переменной и (или) её производных при некоторых значениях независимой переменной. Если эти дополнительные условия заданы при одном значении независимой переменной, то такую задачу называют задачей с начальными условиями или задачей Коши. Если же условия заданы при двух значениях независимой переменной, задачу называют краевой. В задаче Коши дополнительные условия называют начальными, а в краевой задаче ¾ граничными.
Численное решение – это построение таблицы приближенных значении у1,y2, y3,…, yn. решения уравнения y = f (x) в точках x1,x2,x3,…xn.
Чаще всего полагают xi = x0+ih, где i = 0,1,2…n. Точки xi носят название узлов сетки, а величина h – шага сетки.
Численные методы разделяются на одношаговые, дающие формулу для вычисления значения yk+1 по одному предыдущему значению yk, и многошаговые, при которых для вычисления значения yk+1 требуется k предыдущих значений функции уl,yl-1, yl-2,…, yl-(k+1).
К одношаговым относятся методы Эйлера и Рунге-Кутты, к многошаговым – методы прогноза и коррекции.
Для оценки погрешности метода на одном шаге сетки разложим точное решение уравнения в ряд Тейлора в окрестности узла xk:
y(хk+1)= y(хk)+ (h/1!) y'(хk)+ (h2/2!) y''(хk) +….+(hр/р!) y(р)(хk)+.. . (7.2)
Численный метод решения дифференциального уравнения имеет порядок р, если его расчетные формулы согласуются с разложением в ряд Тейлора до членов порядка hр. Погрешность, связанная с тем, что вместо бесконечного ряда рассматривается аппроксимация функции несколькими первыми членами ряда, называется погрешностью усечения (ограничения). Источником погрешностей будет представление чисел с ограниченным числом значащих цифр – погрешности округления и погрешность распространения – результат накопления погрешностей, появившихся на предыдущих этапах счета.
7.2 Одношаговые методы решения задачи Коши
Различные методы данной группы отличаются объемом проводимых вычислений и получаемой при этом точностью.
7.2.1 Метод Эйлера
Дано уравнение у' = f(x,y) с начальным условием у(х0)= у0.
В методе Эйлера производная у' заменяется приближенной формулой
у'= Δу/Δх = f(x,y).
В результате на первом отрезке [х0,х1] искомое решение приближенно представляется линейной функцией
Δу/Δх = f(x0,y0),
или у-у0 = f(x0,y0)(х-х0), у = у0 + f(x0,y0)(х-х0).
При х=х1 получим
у1 = у0 + f(x0,y0)(х1-х0).
Таким образом, на отрезке [х0,х1] искомая интегральная кривая (точное решение) заменяется отрезком прямой ММ0, касательной к кривой в точке М0.
Тангенс угла наклона этой прямой равен f(x0,y0). Аналогично находят остальные приближенные значения
yi+1 = уi + K1h (7.3)
где K1= f(xi,yi), h=(хi-хi-1).
Из (7.3) следует, что интегральная кривая в методе Эйлера заменяется ломаной линией с вершинами в точках М0(x0,y0), М1(x1,y1),…, Мn(xn,yn) (см. рисунок 7.1).
Метод Эйлера является наиболее простым и наименее точным методом решения ОДУ. Он применяется для поиска оценочных решений на [х0,хn].
 У
У
у(х)
М2
М1
М0
Х
х0 х1 х2
Рисунок 7.1-Геометрическая интерпретация метода Эйлера
В рассмотренном методе переход от точки (xi,yi) в точку (xi+1,yi+1) осуществляется путем смещения на вектор (h, К1). Ошибка метода имеет порядок h2, так как члены, содержащие h во второй и более высоких степенях, отбрасываются, кроме того, метод часто оказывается неустойчивым – малая ошибка увеличивается с ростом х. Этот метод можно усовершенствовать различными способами [1].
Рассмотрим модифицированный метод Эйлера. Хотя тангенс угла наклона касательной к истинной кривой в исходной точке известен и равен y¢(x0), он изменяется в соответствии с изменением независимой переменной. Поэтому в точке (x0+h) наклон касательной уже не таков, каким он был в точке x0. Следовательно, при сохранении начального наклона касательной на всем интервале h в результаты вычислений вносится погрешность. Точность метода Эйлера можно существенно повысить, улучшив аппроксимацию производной. Это можно сделать, например, используя среднее значение производной в начале и в конце интервала. В модифицированном методе Эйлера сначала вычисляют значение функции в следующей точке по методу Эйлера
y*n+1=yn + hf (x n, y n ). (7.4)
Его используют для вычисления приближенного значения производной в конце интервала f(xn+1,y*n+1). Вычислив среднее между этим значением производной и ее значением в начале интервала, найдем более точное значение yn+1:
yn+1=yn+ (f (xn, yn)+f (xn+1,y*n+1))/2h. (7.5)
Модифицированный метод Эйлера имеет второй порядок точности, т.е погрешность метода имеет порядок h3.
7.2.2 Методы Рунге-Кутты
Наибольше распространение при решении обыкновенных дифференциальных уравнений получил методы Рунге-Кутты.
В методах Рунге-Кутты более высокого порядка точности смещение из
точки (xi,yi), в точку (xi+1,yi+1) происходит не сразу, а через промежуточные точки (внутренние для интервала [хi,хi+1]), в каждой из которых определяется направление касательной. В результате смещение выполняется вдоль некоторого усредненного направления. Методы Рунге-Кутты дает набор формул для расчета координат внутренних точек, требуемых для реализации этой идеи. Так как существует несколько способов расположения внутренних точек и выбора относительных весов для найденных производных, то метод Рунге-Кутты, в сущности, объединяет целое семейство методов решения дифференциальных уравнений первого порядка, которым можно отнести метод Эйлера и его модификации.
Наиболее распространенным является метод Рунге-Кутты четвертого порядка точности, для которого ошибка на шаге имеет порядок h5.
В этом методе значения величины yi+1 рассчитывается по формуле
yi+1=yi+h (K1+2K2+2K3+K4)/6 (7.6)
где K1=f (x i, yi);
K2=f (xi+ h /2,yi+ h k1/2);
K3=f (xi+ h /2, yi+ h k2/2);
K4=f (xi+h, yi+ h k3).
Метод Рунге-Кутты применим к системам уравнений первого порядка, а также к уравнениям любого порядка, которые можно свести к системам уравнений первого порядка путем замены переменных.
Так для уравнения второго порядка метод Рунге-Кутты имеет следующий алгоритм.
Исходное уравнение задачи Коши
y´´= f (x, y, y´) (7.7)
с начальными условиями y0 = у(х0) и y´0 = y´ (х0) преобразуется к системе двух уравнений
y´= z = g (x, y, y´), при y´0 = y´ (х0) = z (х0) = z0;
z´= f (x, y, y´) при y0 = у(х0). (7.8)
Далее
уi+1 = уi + К (7.9)
где К = h (К1 + 2К2 +2К3 + К4)/6 ;
К1 = g (x i, y i, z i), К2 = g (x i + h/2, yi + К1h/2, z i + L1h/2):
К3 = g (x i + h/2, yi + К2h/2, z i + L2h/2), К4 = g (x i + h, y i + К3h, z i + L3h);
z i+1 = z i + L (7/10)
где L = h (L 1 + 2 L 2 + 2L 3 + L 4)/6 ;
L 1 = f (x i, y i, z i), L 2 = f (x i + h/2, yi + К1h/2, zi + L1h/2);
L 3 = f (x i + h/2, yi + К2h/2, zi + L2h/2), L 4 = f (x i + h, yi + К3h, z i + L3h).
Метод Рунге-Кутты обладает достаточно высокой точностью, легко программируется. С помощью этого метода можно начинать решение – он самостартующий, так как нужно знать одно значение yi. Величину шага можно изменять на любом этапе вычислений. К недостаткам метода можно отнести большие затраты времени, так как в каждой точке функция рассчитывается четыре раза, и сложность определения ошибки метода.
Погрешность метода Рунге-Кутты на одном шаге сетки равна Mh5, но поскольку на практике М оценить сложно, пользуются правилами Рунге удвоения шага. Выполняют расчет функции уi+1(1) в точке хi+1 методом Рунге-Кутты четвертого порядка точности с шагом h, а затем рассчитывают этим же методом уi+1(2) в точке хi+1 с шагом h/2. По полученным значениям функции определяют погрешность
δ=Σаi(уi+1(1)- уi+1(2) )/15. (7.11)
Если δ > ε, где ε – заданная точность, то шаг уменьшают вдвое. Если
δ < ε, результаты счета с шагом h достаточно точные. Если δ < ε/50, шаг удваивают.
7.3 Многошаговые методы решения задачи Коши
Можно построить более эффективный вычислительный процесс нахождения решения задачи Коши, если использовать информацию о предыдущих точках (хi-2,уi-2), (хi-1,уi-1). Методы, основанные на этой идее, многошаговые. С помощью этих методов нельзя начать решение – они не самостартующие, поэтому используются в сочетании с методами Рунге-Кутты. К многошаговым методам относятся методы прогноза и коррекции [], в которых по формуле прогноза и исходным значениям переменных определяют уi+1(j). Затем находят производную функции и по формулам коррекции уточняют прогнозируемое значение, рассчитывая уi+1(j+1). Среди многошаговых методов наиболее известны метод Хемминга и метод Адамса-Башфорта [].
Методы решения жестких ОДУ, которые не могут быть решены рассмотренными выше методами, приведены в литературе.
Компьютерная реализация методов в Excel описана в [23-24, 26].
Литература: [1-4],[6], [14-17], [23-24].
8 Лекция. Тема: численные методы решения краевых задач
План: численные методы решения краевых задач тепломассообмена и гидродинамики. Основные понятия метода конечных разностей.
8.1 Численные методы решения задач тепломассообмена и гидродинамики
При поиске количественного описания процессов тепломассообмена обычно рассматривают некоторую систему ОДУ или уравнений с частными производными, справедливую в определенной области, с соответствующими начальными и граничными условиями, являющуюся математической моделью процесса.
Существующими аналитическими методами можно решить только самые простые уравнения с тривиальными краевыми условиями. Для решения более сложных задач необходимо свести задачу к алгебраической форме, что возможно при использовании методов дискретизации непрерывных функций, входящих в математическую модель процесса.
Наиболее распространенные численные методы решения таких задач – метод конечных разностей (МКР) и метод конечных элементов (МКЭ). Последний метод применим для процессов, протекающих в системах со сложной геометрией.
8.2 Метод конечных разностей: основные понятия
Для приближенного решения краевых задач теплопроводности широко используется метод конечных разностей.
Идея метода конечных разностей состоит в следующем. Область непрерывного изменения аргументов заменяется расчетной сеткой – дискретным множеством узлов (точек). Вводятся функции дискретных переменных – сеточные функции. Частные производные, входящие в дифференциальные уравнения и граничные условия, заменяются (аппроксимируются) разностными соотношениями.
В результате такой замены краевая задача в частных производных сводится к системе разностных (алгебраических) уравнений, называемых разностной схемой.
Если решение системы разностных уравнений существует и при измельчении сетки стремится к решению поставленной задачи (т.е. сходится), то это решение и является искомым приближенным решением краевой задачи. Число неизвестных в такой системе может быть велико, но решение ее математически более простое.
При решении конкретной задачи методом конечных разностей необходимо рассмотреть следующие вопросы:
- каким образом выбрать сетку;
- как построить разностную схему;
- определить точность, с которой разностная схема аппроксимирует исходную задачу;
- проверить устойчивость разностной схемы;
- выяснить скорость сходимости решения разностной задачи к решению исходной.
8.2.1 Построение сеток. Сеточные функции и сеточные аналоги норм
Заменим область непрерывного изменения аргументов Ω искомой функции Т некоторым конечным множеством точек, лежащих в этой области. Это множество назовем разностной сеткой, сами точки - узлами сетки, а функции, определяемые тем или иным способом на этой сетке, u - сеточными функциями.
Разложение узлов сетки в области может быть произвольным и определяется спецификой решаемой задачи.
Примеры сеток:
а) в простейшем случае одномерной задачи отрезок [0, l] разобьем на N равных частей точками хk=kh, k=0,1,…, N.
Расстояние между узлами h=(хk+1 - хk) называется шагом сетки. В рассматриваемом случае h = l/N = const, поэтому множество узлов хk, k=0,1,…, N представляет собой равномерную сетку на отрезке 0 ≤ х ≤ l и
обозначается Ωk = { хk=kh, k=0,1,…, N }.
0 h хk = kh хk+1/2 = хk +h /2 l
![]()
0 1 2 … k-1 k k+1…. N-1 N x
Рисунок 8.1 – Одномерная равномерная сетка на отрезке
В качестве области определения сеточных функций, кроме узлов, называемых еще целыми точками, часто используют полуцелые точки хk+1/2 = хk +h /2 (на рисунке отмечены крестиком).
Если отрезок [0, l] разобьем на N частей произвольно взятыми точками 0 <х1 <х2<х3…< хk< хk+1< …< хN-1< l, причем х0=0, хN=l, то получим неравномерную сетку с шагом hk= хk- хk-1, зависящим от номера узла k;
б) сетка на плоскости.
Пусть Ω = {0 ≤ х ≤ d, 0 ≤ y ≤ b } – прямоугольник. Отрезки [0, d] и [0, b] разобьем соответственно на N и M частей и через точки хk=kh, k=0,1,…, N, h=d/N, yj=jρ, j=0,1,…, M, ρ=b/M, проведем прямые, параллельные координатным осям. Множество точек (xk,yj) образует сетку в прямоугольнике Ω. Полученная сетка равномерна по каждой переменной х и у. Если h #ρ – сетка прямоугольная, при h = ρ – квадратная.
Если построить сетку неравномерной хотя бы по одной координате, то сетка будет неравномерной.
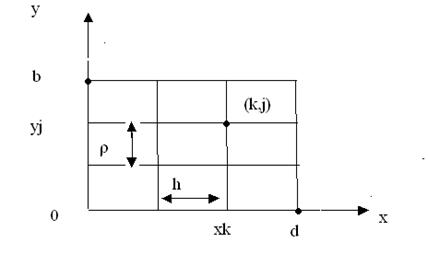
Рисунок 8.2 - Равномерная сетка на плоскости
Для решения одномерной по пространственным координатам нестационарной задачи используют произведение сеток
Ωhη=Ωh х Ωη={(хk, τi ), хk+1= хk + hk, τi+1 = τi + ηi , k=0,1,…, N, i=0,1, …, M, х0=0, хN=l, τ0=0, τM=t}, представляющих собой пространственно-временную разностную сетку.
Совокупность узлов сетки, лежащих на τ = τi, называют i-м слоем.
Для простых областей всегда можно ввести такую сетку, чтобы «крайние» естественнее узлы сетки попадали на границу области. Эти узлы называются граничными, а остальные – внутренними. Граничные условия задачи следует задавать именно в этих граничных узлах.
Для областей более сложной формы естественные узлы сетки невсегда попадают на границу области. Тогда следует рассматривать два подхода к заданию граничных условий:
- ввести дополнительные узлы в точках пересечения линий сетки с границей и в них задавать граничные условия;
- границу области аппроксимировать ломаной, проходящей через ближайшие к границе естественные узлы, и перенести заданные граничные условия на эту ломанную.
Вопрос оптимального выбора шага сетки и, следовательно, количества узлов является непростым. С одной стороны, чем больше требуется точность, тем более мелкий шаг желателен. Но слишком мелкий шаг значительно увеличивает число неизвестных, что повышает требования к быстродействию и объему памяти РС. Очевидно, что должны существовать некоторые «оптимальные» сетки со сравнительно небольшим числом узлов. Такие сетки принято называть грубыми или реальными.
Построение разностной схемы проводится таким образом, чтобы получаемая в результате решения сеточная функция u была как можно ближе к решению Т соответствующей краевой задачи теплопроводности. Так как u – функция дискретного аргумента, а Т – непрерывного, они принадлежат разным функциональным пространствам.
Для определения степени близости этих функций обычно поступают так. Осуществляют переход от непрерывных функций к сеточным по правилу: значение сеточной функции в узле равно значению непрерывной функции в этой же точке. Например, в узле (хk,τi) сетки одномерной нестационарной задачи Tki=T(хk,τi), пространственные узлы сетки обозначают подстрочными индексами, временные – надстрочными. В этом случае говорят так, что сеточная функция Tki является проекций функции Т на пространство сеточных функций, либо Тh. Для оценки близости функций u и Т рассматривается величина ||u -Тh||, где ||·|| некоторая норма в пространстве сеточных функций. Чаще всего ||u||С = mах ||u|| для хk є Ωk – сеточный аналог чебышевской нормы в пространстве непрерывных функций [15].
8.2.2 Построение разностных схем. Порядок аппроксимации
Решение исходной краевой задачи сводится к нахождению таблицы числовых значений функции Тh в точках сетки на соответствующей области. Для приближенного вычисления этой таблицы необходимо дифференциальный оператор А краевой задачи, заданный в классе непрерывного аргумента, приближенно заменить (аппроксимировать) разностным оператором Аh , заданном на множестве сеточных функций.
Разностный аналог можно построить различными способами. В связи с этим возникает задача построения такой разностной схемы, которая была бы оптимальна в определенном смысле. Обычно требуют, чтобы построенная разностная схема на сравнительно грубых сетках обеспечивала необходимый уровень точности для получения приближенного решения. Важнейшие свойства исходных операторных уравнений должны сохраняться у их разностных аналогов.
Среди множества возможных конструктивных подходов к построению разностных аналогов для дифференциальных операторов выделяют:
- метод формальной замены производных конечно-разностными выражениями;
- метод интегральных тождеств (интегро - интерполяционный метод);
- вариационные методы построения разностных схем;
- метод неопределенных коэффициентов.
8.2.3 Метод формальной замены производных конечно-разностными выражениями
Этот метод основан на использовании разложения в ряд Тейлора достаточно гладкой функции, что позволяет сохранить локальные свойства дифференциальных уравнений. Каждая из производных заменяется разностным отношением, содержащим значения сеточной функции в нескольких узлах сетки, образующих некоторую конфигурацию. Такая совокупность узлов называется шаблоном. Узлы, в которых разностная схема записана на шаблоне, называются регулярными, остальные – нерегулярными.
Рассмотрим возможные способы аппроксимации дифференциального оператора вида
А[T] =dT/dx, (8.1)
определенного на множестве непрерывных в области Ω={d<x<b} функций, имеющих ограниченные производные до третьего порядка включительно. Пусть Ωh = {хk=kh, 0<k<N, h=(b-d)/N} – равномерная сетка на отрезке Ω. Наиболее естественным способом замены производной будет
dT/dx = lim [ T(x+h) - T(x)]/h
![]() h 0.
h 0.
Если зафиксировать h в этом равенстве, то получим приближенную формулу для первой производной через конечные разности
dT/dx ≈ [ T(x+h) - T(x)]/h
или в k-м узле имеем правое разностное отношение
Tx,k = (Tk+1 -Tk)/h . (8.2)
Аналогично вводится левое разностное отношение
T*x,k = (Tk -Tk-1)/h . (8.3)
Можно рассмотреть линейную комбинацию (8.2) и (8.3):
σ Tx,k+ (1 - σ) T*x,k (8.4)
где σ – любое вещественное число.
При σ=1/2 получим центральное разностное отношение:
Tx,k 0 = (Tk+1 -Tk-1)/2h. (8.5)
При замене оператора А [T] разностными выражениями (8.2) –(8.5) допускается погрешность аппроксимации 0(hn), где n=1 для (8.2) – (8.4) и
n =2 для (8.5).
Таким образом, выбор шаблона существенно влияет на свойства разностного оператора.
Для аппроксимации второй производной
А[T] =d2T/dx2
выбираем трехточечный шаблон (хk-1, xk, xk+1).
Тогда в k-м узле получим разностный оператор
![]() Txx,k= (Tk+1 -2Tk + Tk-1)/h2 . (8.6)
Txx,k= (Tk+1 -2Tk + Tk-1)/h2 . (8.6)
Порядок аппроксимации в этом случае равен 2, погрешность аппроксимации 0(h2).
Рассмотрим оператор одномерного уравнения теплопроводности
А[T] = dT/dτ - аd2T/dx2 (8.7)
в области Ω = {(0<х<d, 0<τ<t)}, предполагая, что функция температуры непрерывна со своими производными до четвертого порядка по переменной х и до второго по - τ.
Область непрерывного изменения аргументов заменим сеточной областью Ωhη={(хk, τi ), хk =k·h, τi =i·η , 0 <k< N, 1< i < M, η=t/M }.
Аппроксимируем производную по времени правым разностным соотношением Tiτ = (Tk i+1 - Tk I)/ η, а для второй производной по переменной х можно записать отношение (8.6) на временном слое i:
Txx,k i = (Tk+1i -2Tk i + Tk-1 i)/h2 ,
или на временном слое i+1:
Txx,k i+1 = (Tk+1i+1 -2Tk i+1 + Tk-1 i+1)/h2 .
![]() В соответствии с этим можно рассмотреть
две различные аппроксимации оператора (8.7):
В соответствии с этим можно рассмотреть
две различные аппроксимации оператора (8.7):
А[T]hη = Tiτ - а Txx,k i , (8.8)
![]() А[T]hη
= Tiτ - а Txx,k i+1 (8.9)
А[T]hη
= Tiτ - а Txx,k i+1 (8.9)
на шаблонах явной и неявной схем (см. рисунок 8.3).
|
|
|
а) б)
Рисунок 8.3 - Шаблоны явной (а ) и неявной (б) схем
Погрешность локальной аппроксимации оператора (8..7) разностными операторами (8.8) и (8.9) равна 0(η + h2).
Оператор (8.7) можно аппроксимировать и на шеститочечном шаблоне Кранка-Николсона
Рисунок 8.4 – Шаблон неявной схемы Кранка-Николсона
Погрешность локальной аппроксимации оператора (8.7) разностным оператором при этом равна 0(η2 + h2).
Таким образом, метод формальной замены производных конечно-разностными отношениями прост и шаблонен. Полученный в результате разностный аналог дифференциального уравнения аппроксимирует это уравнение в узле сетки, т.е. не совсем справедливо в межузловом пространстве. Недостатком данного метода является отсутствие наглядности и физического содержания.
Компьютерная реализация методов описана в [9-10], [23-26].
Литература: [1-4],[6], [9-10], [14-17], [23-24].
9 Лекция. Тема: численные методы решения задач оптимизации
План: задачи оптимизации в теплоэнергетике и теплотехнике. Методы решения задач оптимизации. Классификация методов. Применение метода прямого спуска, методов безусловной оптимизации первого порядка (метод наискорейшего спуска).
9.1 Задачи оптимизации в теплоэнергетике и теплотехнике
Решение многих теоретических и практических задач теплоэнергетики сводится к отысканию экстремума (максимума или минимума) скалярной функции f(x) n-мерного векторного аргумента х.
|
х = |
х1 х2 х3 … хn |
х – вектор-столбец (точка в n-мерном пространстве).
Например: достижение максимального КПД котельного агрегата; обеспечение минимальной себестоимости тепловой энергии, отпускаемой ТЭЦ; обеспечение минимального значения теплопотерь через теплоизоляцию теплопровода, обмуровку котла, оболочку здания; достижение минимального значений выбросов загрязняющих веществ ТЭС и т.п.
Оптимизируемую функцию f(x) называют целевой функцией или критерием оптимальности.
В дальнейшем мы будем говорить о поиске минимального значения f(x)
|
f(x) |
|
Min. |
Вектор х*, доставляющий min целевой функции f(x), называют оптимальным.
Задачу нахождения минимума функции f(x) можно заменить эквивалентной задачей поиска максимума функции - f(x).
Если х* - точка минимума для функции у=f(x), то для функции у = -f(x) она является точкой максимума
min f(x) = -max (- f(x)),
аналогично и для случая многих переменных.

Рисунок 9.1 – Графическая интерпретация поиска экстремума функции
В реальных условиях на переменные хi , i=1,2, .. n и некоторые функции gi(x) и hj(x), характеризующие качественные свойства объекта, системы, процесса, могут быть наложены ограничения (условия) вида:
gi(x) = 0, i = 1,2, .. n
hj(x) £ 0, j = 1,2, .. m
a £x £b
где
|
а = |
а1 а2 а3 … аn |
|
b = |
b1 b2 b3 … bn |
, .
Такую задачу называют задачей условной оптимизации. При отсутствии ограничений имеет место задача безусловной оптимизации.
Точка х* доставляет глобальный минимум функции одной переменной f(x), заданной на числовой прямой Х, если х ÎХ и f(x*) £ f(x) для всех х ÎХ.
Точка х* называется точкой строгого глобального минимума, если это неравенство выполняется строго.
Если же в выражении f(x*) £ f(x) равенство возможно при х ¹ х*, то реализуется нестрогий минимум, а под решением в этом случае понимают х* ={ х ÎХ : f(x) = f(x*)}.
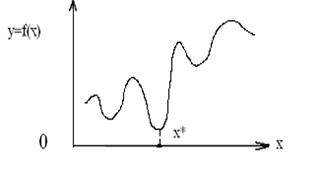
Рисунок 9.2 –Глобальный минимум функции одной переменной

Рисунок 9.3 –Нестрогий минимум функции одной переменной
Точка х*ÎХ доставляет локальный минимум функции f(x) на множестве Х, если при некотором достаточно малом ε > 0 для всех х ¹х*, хÎХ, удовлетворяющих условию | х-х*| < ε , выполняется неравенство f(x*) ≤ f(x), если неравенство строгое, то х* является точкой строгого локального минимума.
Рисунок 9.4 –Экстремумы функции одной переменной на участке [a,b]
На рисунке 9.4: х1, х3, х5, х6, х7, х11 – точки локального максимума (х1 – нестрогого); х2, х6, х8, х10 (х6-нестрогого) – локального минимума; х4 - глобального минимума; х9 – глобального максимума.
9.2 Классификация методов решения задач оптимизации
Возможны два подхода к решению задачи отыскания минимума функции многих переменных f(x)=f(x1,х2,х3,…хn) при отсутствии ограничений на диапазон изменения неизвестных.
Первый подход лежит в основе косвенных методов оптимизации и сводит решение задачи оптимизации к решению системы нелинейных уравнений, являющихся следствием условий экстремума функции многих переменных
(∂f/∂xi)x=x*= 0, i=1,...,n.
Вектор f′(x), составленный из первых производных функций по каждой переменной, т.е. f′(x) = (∂f/∂x1, ∂f/∂x2,…, ∂f/∂xn)т, называют градиентом скалярной функции f(x). В точке минимума градиент равен нулю. Решение системы нелинейных уравнений – задача весьма сложная и трудоемкая, поэтому на практике используют второй подход к минимизации функций, составляющих основу прямых методов.
Суть их состоит в построении последовательности векторов х[0], х[1],…, х[n], таких, что f(х[0])>f(х[1])>…>f(х[n]), > …. В качестве начальной точки х[0] может быть выбрана произвольная точка, однако стремятся использовать всю имеющуюся информацию о поведении функции f(x), чтобы точка х[0] располагалась как можно ближе к точке минимума.
Переход (итерация) от точки х[k], к точке х[k+1], k=0,1,…n состоит из двух этапов:
1) выбор направления движения из точки х[k];
2) определение шага вдоль этого направления.
Методы построения таких последовательностей часто называют методами спуска (т.к. происходит переход от больших значений функции к меньшим). Впервые такая задача была рассмотрена О.Коши в 1845г.
Математически методы спуска описываются соотношением
х [k+1] = х [k] + акр[k], k=0,1, … (9.1)
где р[k] – вектор, определяющий направление спуска;
ак – длина шага.
В координатной форме:
х1[k+1] = х1 [k] + ак р1 [k],
х2[k+1] = х2 [k] + ак р2 [k],
……………………………. .
хn[k+1] = хn [k] + ак рn [k].
Различные методы спуска отличаются друг от друга способами выбора двух параметров – направления спуска и длины шага вдоль этого направления. На практике применяются только методы, обладающие сходимостью, число итераций k →∞.
На практике вычисления прекращаются при выполнении некоторых критериев (условий), например: ||х[k] – х[k-1]|| ≤ ε – условие малости приращения аргумента или - функции ||f(х[k]) – f(х[k-1])|| ≤ γ.
Методы поиска минимума называются детерминированными, если оба элемента перехода от х [k] к х [k+1] (направление движения и величина шага) выбираются однозначно, по доступной в х[k] информации. Если же при переходе используется случайный механизм, то алгоритм называется случайным поиском минимума.
Детерминированные алгоритмы безусловной минимизации делятся на классы в зависимости от вида используемой информации. Если на каждой итерации используется лишь значение минимизируемой функции f′(x), то метод называется методом нулевого порядка. Если требуется вычисления первых производных минимизируемой функции, то - методы первого порядка, вторых – второго порядка.
В настоящее время разработано множество методов для задач условной и безусловной оптимизации. Качество численного метода характеризуется:
- скоростью сходимости;
- временем выполнения одной итерации;
- объемом памяти РС;
- классом решаемой задачи.
9.2.1 Общая характеристика методов нулевого порядка
В этих методах для определения направления спуска не требуется вычисления производных целевой функции. Направление минимизации в данном случае полностью определяется последовательностью вычисленных значений функции. К ним относятся методы:
- прямого спуска (Хука-Дживса);
- деформируемого многогранника (Нелдера-Мида);
- вращающихся координат (Розенброка);
- параллельных касательных (Пауэлла) [].
9.3 Метод прямого спуска (Хука-Дживса)
Суть этого метода состоит в следующем. Задаются некоторой начальной точкой х[0]. Изменяя компоненты вектора х[0], обследуют окрестности данной точки, в результате чего находят направление, в котором происходит уменьшение минимизируемой функции f(x). В выбранном направлении осуществляют спуск до тех пор, пока значение функции уменьшается. После того, как в данном направлении не удается найти точку с меньшим значением функции, уменьшают величину шага спуска. Если последовательные дробления шага не приводят к уменьшению функции, от выбранного направления спуска отказываются и осуществляют новое обследование окрестности и т.д.
Алгоритм метода прямого спуска.
1.Задаются: значениями координат хi[0], i = 1,2,3,…,n начальной точки х[0]; вектором изменения координат Δx в процессе обследования окрестности; наименьшим допустимым значением ε компонентов Δx.
2.Полагают, что х[0] является базисной точкой хБ, вычисляют f(xБ).
3.Циклически изменяют каждую координату хБi, i=1,2,…,n. базисной точки хБ на величину Δxi, т.е. хi[k] = хБi + Δxi, хi[k] = хБi - Δxi. Вычисляют значение f(x[k]) и сравнивают с f(xБ). Если f(x[k]) < f(xБ), то соответствующая координата хi, i = 1,2,3,…,n, приобретает новое значение, вычисленное по одному из выше приведенных выражений. В противном случае значение этой координаты остается неизменным. Если после изменения последней n-ой координаты f(x[k]) < f(xБ), то переходят к пункту 4., в противном случае - к пункту 7.
4.Полагают, что x[k] является новой базисной точкой xБ и вычисляют значение f(xБ).
5.Осуществляют спуск из точки x[k]: x[k+1] =2xi[k]- хБi, i=1,2,…,n, хБi- координаты предыдущей базисной точки. Вычисляют f(x[k+1]).
6. Как в п.3. циклически изменяют каждую координату точки x[k+1], осуществляя сравнение соответствующих значений функции f(x) со значениями f(x[k+1]), полученными в п.5. После изменения последней координаты сравнивают соответствующие значения функции f(x[k+1]) со значением f(xБ), полученным в п.4. Если f(x[k+1]) < f(xБ), то переходят к п.4, в противном случае - к п.3. при этом в качестве базисной точки используют последнюю из полученных базисных точек.
7. Сравнивают значения Δx и ε. Если Δx<ε, то вычисления прекращают. В противном случае уменьшают Δx и переходят к п.3.
Достоинством метода является простота его программирования. Он не требует знания целевой функции в явном виде, легко учитывает ограничения на отдельные переменные, а также сложные ограничения на область поиска.
Недостаток – в случае сильно вытянутых, изогнутых или обладающих острыми углами линий уровня целевой функции он может оказаться неспособным обеспечить продвижение к точке минимума.
 х2
х2
с1
• с2
с3
х΄
0 х1
Рисунок 9.5 –Линии уровня и выбор направления движения к минимуму целевой функции
Как видно из рисунка, каким бы малым ни брать шаг в направлении х1 или х2 из х΄ нельзя получить уменьшения значения целевой функции (с1> >с2>с3).
Поверхностью уровня (на плоскости – линией уровня) является поверхность, получаемая приравниванием выражения функции f(x) некоторой постоянной величине с, т.е. f(x)=с. Во всех точках этой поверхности функция имеет значение с. Изменяя значения постоянной с1, с2, с3, …, сn, получаем ряд поверхностей, геометрически иллюстрирующих характер функции. Как в топографии изобразим рельеф поверхности линиями уровня Ф(х,у) = const.
Равноотстоящие плоскости Ф(х,у) = const имеют линии пересечения с поверхностью Ф(х,у,z). Проекции этих линий на плоскости – линии уровня. Направление убывания функции можно показать штрихами.
![]()
 Ф(х,у,z)
Ф(х,у,z)
![]() Ф(х,у)
Ф(х,у)
![]() Линии уровня
Линии уровня
![]()
min Ф(х,у,z)
Рисунок 9.6 –Линии уровня для функции Ф(х,у,z)
По виду линий уровня можно условно выделить три типа рельефа: котловинный, овражный и неупорядоченный.

• min
. х
Рисунок 9.7 - Линии уровня для котловинного рельефа
(например, Ф(х,у) = х2/а2+у2/b2)
 у
у
• min
х
Рисунок 9.8 - Линии уровня для овражного рельефа
(например, Ф(х,у) = 10(у - sinx)2+0,1x2)
Линии уровня для неупорядоченного рельефа, имеют много максимумов, минимумов и седловин.
y
• min
x
Рисунок 9.9 - Линии уровня для неупорядоченного рельефа
(например, Ф(х,у) = (1+ sin2x)(1+sin2y))
К численным методам решения задач оптимизации первого порядка относятся градиентные методы [].
Градиентные методы, а также численные методы решения задач условной оптимизации будут рассмотрены в курсе «Методы моделирования и оптимизации теплоэнергетических процессов и установок».
Компьютерная реализация методов в Excel описана в [9], [23-26].
Литература: [7], [20].
Список литературы
1. Амосов А.А. Вычислительные методы для инженеров.- М.: МЭИ, 2003. – 596с.
2. Пирумов У.Г. Численные методы. - М.: ДРОФА, 2007.- 221с.
3. Численные методы: Сборник задач /Под ред. У.Г. Пирумова. - М.: ДРОФА, 2007.- 144 с.
4. Киреев В.И.,Пантелеев А.В. Численные методы в примерах и задачах.- М.: МАИ, 2000.- 376с.
5. Очков В.Ф. Современные информационные технологии в теплоэнергетике.- М.: МЭИ, 2007.- 67с.
6. Васильков Ю.В. Компьютерные технологии вычислений в математическом моделировании.- М.: ВШ, 2001.- 256 с.
7. Соболь Б.В. Методы оптимизации: Практикум.- Ростов н/Д.: Феникс, 2009.- 380с.
8. Основы современных компьютерных технологий. / Под ред.
А.Д. Хоменко.- СПб.: КОРОНА, 2005.- 672с.
9. Кирьянов Д.В. Mathcad - 14.- СПб.: БХВ - Петербург, 2007.-704с.
10. Охорзин В.А. Компьютерное моделирование в системе Mathcad.-М.: Финансы и статистика, 2006.-144с.
11. Голицина О.В. Информационные технологии. – М.: ФОРУМ: ИНФРА - М, 2008.- 608 с.
12. Максимов Н.В. Технические средства информатизации.- М.: ФОРУМ: ИНФРА - М, 2008.- 6592 с.
13. Теплоэнергетика и теплотехника. Общие вопросы: Справочник / Под ред. А.В. Клименко, В.М. Зорина. - М.: МЭИ, 1999. - 528 с.
14. Пасконов В.М., Полежаев В.И., Чудов Л.А. Численное моделирование процессов тепло - и массообмена. – М.: Наука, 1984.- 288с.
15. Патанкар С. Численные методы решения задач теплообмена и динамики жидкости. – М.: Энергоатомиздат, 1984.- 152 с.
16. Андерсон Д, Таннехилл Дж. Вычислительная гидромеханика и теплообмен. – М.: Мир, 1990.ч.1, 2 -728 с.
17. Основные процессы и аппараты химической технологии: Пособие по проектированию / Под. ред. Ю.И. Дытнерского. – М.: Химия, 1991.- 496 с.
18. Кафаров В.В., Глебов М.Б. Математическое моделирование основных процессов химических производств. – М.: ВШ.,1991.- 400 с.
19. Зайцев А.И. и др Математическое моделирование источников энергоснабжения промышленных предприятий. - М.: Энергия, 1991.-163 с.
20. Клима И. Оптимизация энергетических систем. - М.: ВШ, 1991.- 247 с.
21. Рыжиков Ю.И. Решение научно-технических задач на персональном компьютере. – СПб.: КОРОНА, 2000.- 272 с.
22. Шуп Т. Е. Прикладные численные методы в физике и технике. - М.: ВШ, 1990.- 255 с.
23. Ларсен Р. Инженерные расчеты в в Excel.- М.:. ИД Вильямс, 2002.-545с.
24. Васильев А.Н. Excel-2007 на примерах.- СПб.: БХВ Петербург, 2007.- 656с.
25. Кульгин Н Б Программирование в Turbo Pascal 7.0 и Delphi.- СПб.: БХВ Петербург, 2007.-400с.
26. Борисова Н.Г. Компьютерные технологии в теплоэнергетических расчетах. Методические указания к выполнению лабораторных работ. – А.: АИЭС, 2005.-36с.
Содержание
|
1 Лекция Введение. Компьютерные технологии в моделировании теплоэнергетических систем, процессов и установок. Модели и виды моделирования……………………………………………………………… |
3 |
|
2 Лекция Математическое и физическое моделирование в теплоэнергетике. Процесс разработки и использования математических моделей………………………………………………….. |
8 |
|
3 Лекция Численные методы в математическом моделировании теплотехнических задач и их программная реализация. Методы интерполирования………………………………………………………….. |
17 |
|
4 Лекция Численное интегрирование в теплотехнических расчетах. Методы численного интегрирования……………………………………... |
22 |
|
5 Лекция Численные методы нахождение корней алгебраических и трансцендентных уравнений………………………………………………. |
26 |
6 Лекция Численные методы решения систем алгебраическихуравнений…………………………………………………………………… |
31 |
|
7 Лекция Численные методы решения обыкновенных дифференциальных уравнений…………………………………………… |
36 |
|
8 Лекция Численные методы решения краевых задач…………………… |
41 |
|
9 Лекция Численные методы решения задач оптимизации……………… |
47 |
|
Список литературы………………………………………………………… |
55 |