МИНИСТЕРСТВО ОБРАЗОВАНИЯ
И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН
Некоммерческое акционерное общество
«Алматинский институт энергетики и связи»
Д.Ж.Темирбаев
ТЕПЛОМАССООБМЕН
Конспект лекций
Алматы 2009
СОСТАВИТЕЛЬ: Д.Ж.Темирбаев. Тепломассообмен: Конспект лекций для студентов всех форм обучения специальности 050717 - Теплоэнергетика. - Алматы: АИЭС, 2009. – 79 с.
Конспект лекций по дисциплине «Тепломассообмен» представляет собой краткое изложение основ учения о тепломассообмене в объеме 32 часов (с учетом графика самостоятельных расчетно-графических работ студентов) и соответствует типовой программе высшего образования для студентов специальности: 050717 - Теплоэнергетика.
Он написан (автором указанной программы) на основе одноименного учебного пособия автора (содержащего задания и методические указания по всем видам занятий с примерами и решениями задач) [13].
Они полезны также для студентов родственных специальностей.
Предисловие. Методика построения дисциплины
Для сокращения объема лекций по дисциплине предприняты ряд мер.
Стационарная теплопроводность без источника тепла излагается путем решения простого уравнения закона Фурье, а не дифференциального уравнения Фурье в форме уравнения Лапласа. Это расширяет и прикладные аспекты самого закона Фурье. А уравнение стационарной теплопроводности Фурье изучается с внутренним источником тепла (в форме уравнения Пуассона) для плоской стенки и стержня неограниченной и конечной длины.
По аналогии с электрическим током определяются тепловой поток и термическое сопротивление. Это позволяет последнее структурно разделить на физическое и геометрическое факторы и получить все обычные расчетные формулы стационарной теплопроводности.
Дифференциальное уравнение нестационарной теплопроводности Фурье подробно изучается для плоской стенки. Его результаты обобщаются для тел различной канонической формы, а также для тел конечных размеров с помощью известной [15] теоремы «о перемножении решений».
Рассмотренные кратко приближенные методы расчета теплопроводности во многом носят методический характер, иллюстрирующий возможности численного решения нелинейных дифференциальных уравнений с частными производными второго порядка, прикладное значение рассмотренных ряда понятий (теоремы о направляющей точке и др.), а также авторские находки.
Система дифференциальных уравнений конвективного теплообмена упрощается на основе модели слабой неизотермичности и слабой сжимаемости потоков. Сами уравнения во многом решаются в безразмерном виде. Это позволяет автору уменьшить и делать более обозримым объем излагаемого материала, проводить аналогию и анализы процессов в критериях подобия и др.
Такая система дифференциальных уравнений конвективного теплообмена для примера точно решается для случаев теплообмена крыловидного профиля, обтекаемого с большой скоростью, и для теплообмена при ламинарном течении Куэтта. В первом случае, по-существу, тестируется сама система уравнений конвективного теплообмена, а во-втором случае, наглядно вводятся понятия собственной температуры и температуры торможения, коэффициента восстановления, а также показывается необходимость их учета даже при далеко дозвуковых течениях, что обычно игнорируется.
Далее изучаются приближенные теории подобия и пограничного слоя, гидродинамическая теория теплообмена, метод интегральных соотношений и расчетные методы теплоотдачи пластины, цилиндра и пучка труб.
Значительное сокращение объема материалов достигается и при изложении тепломассообмена при фазовых и химических превращениях путем обобщения в критериальных уравнениях и массообмена в тройных аналогиях, а также - теплообмена излучением путем его рассмотрения в общем виде для тела в оболочке и использования его результатов для частных случаев.
Особое внимание при изложении дисциплины уделяется межпредметной взаимосвязи, сравнительному анализу и методам повышения интенсивности тепломассообмена, как фундаментальной основы спецкурсов теплоэнергетиков и теплотехников, а также учебно-методическому обеспечению лабораторных и практических занятий и расчетно-графических работ студентов [5,6,7, 13].
1 лекция
Предмет и метод тепломассообмена
Предметом дисциплины тепломассообмен является изучение процессов и закономерностей распространения тепла и массы под действием разности соответственно температуры и плотности.
Различают три механизма теплообмена: теплопроводность (q = (λ/δ)(t1 – t2) = Qτ/(Fτ) = Q/F), конвекцию (q = α(t1 – t2), теплопередача (q = k(t1 – t2))) и излучение (E ~ T4), где Qτ – тепловая энергия (тепло), Дж, Q – тепловой поток (теплота), Вт, q (Е) – плотность теплового потока (теплоты), Вт/м2.
Методом дисциплины является разделение сложного тепломассообмена
на его сравнительно простые виды и изучение их методами математической физики и
научного эксперимента. Феноменологическая
теория
продуктивна, когда размеры объектов исследования ℓ достаточно велики по сравнению со средней длиной свободного
пробега молекул![]() (число
Кнудсена Kn =
(число
Кнудсена Kn =![]() /ℓ < 10-3)
и вещество представляется сплошной средой. При Kn = 10-3÷0 имеем газодинамику, при Kn >
1 среда представляет собой
молекулярный поток.
/ℓ < 10-3)
и вещество представляется сплошной средой. При Kn = 10-3÷0 имеем газодинамику, при Kn >
1 среда представляет собой
молекулярный поток.
Раздел первый. Теплопроводность
1. Закон Фурье и его применение к решению задач стационарной
теплопроводности
1.1
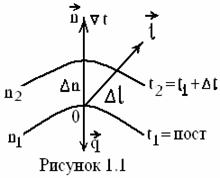 Температурное поле и
градиент температуры
Температурное поле и
градиент температуры
Совокупность значений температуры во всех точках тела в данный момент времени называется температурным полем. Нестационарное температурное поле представляется в виде
![]() . (1.1)
. (1.1)
Температурное поле, независящее от времени (t), - стационарное. Градиент температуры (см. рисунок 1.1)
 (1.2)
(1.2) ![]() (1.3)
(1.3)
![]()
![]()
![]() (1.4)
(1.4)
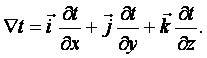 (1.5)
(1.5)
1.2 Закон Фурье. Коэффициент теплопроводности
Количество тепла (тепло) (Qτ, Дж), проходящее через единицу изотермической поверхности (F, м2) в единицу времени (τ, с), называется плотностью теплового потока (ниже и далее черта – знак осреднения)
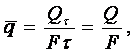
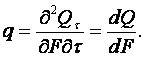 (1.6)
(1.6)
Плотность теплового потока прямо пропорциональна градиенту температуры, что записывается в виде закона Фурье (вывод см. в [15, 16])
![]() (1.7)
(1.7)
Множитель в законе Фурье - коэффициент теплопроводности
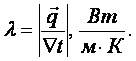 (1.8)
(1.8)
Он слабо зависит от температуры и структуры тела и часто
![]() (1.9)
(1.9)
Различные тела и вещества по теплопроводности делятся на три группы.
1. Теплопроводность газов определяется взаимодействием молекул при их хаотичном движении: 0,006 ÷ 0,06 Вт/(мК).
2. Теплопроводность строительных и
теплоизоляционных материалов, диэлектриков, капельных жидкостей обуславливается упругими колебаниями элементов вещества,
находящихся в различных тепловых и механических состояниях: ![]() 0,07 ÷ 0,7 для капельных жидкостей
и 0,02 ÷ 3,0 для диэлектриков и строительных материалов.
Теплоизоляционными условно называются материалы при
0,07 ÷ 0,7 для капельных жидкостей
и 0,02 ÷ 3,0 для диэлектриков и строительных материалов.
Теплоизоляционными условно называются материалы при ![]() 0,25 Вт/(мК).
0,25 Вт/(мК).
3. Теплопроводность металлов определяется движением электронов. Это подтверждается законом Видемана-Франца, показывающим, что отношение коэффициентов тепло- и электропроводности постоянное,.
Коэффициенты теплопроводности металлов (при 0°С, (Вт/(мК)): серебро 458, чистая медь 396, алюминий 202, латунь 102, сталь 25 ÷ 57, ртуть 4,9.
1.3 Вывод общей формулы теплоты теплопроводности
Тепловой поток через изотермическую поверхность ![]()
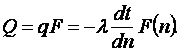 (1.10)
(1.10)
При стационарном процессе тепловые потоки
![]() . (1.11)
. (1.11)
Интеграл (1.10) с учетом (1.11) можно записать в виде
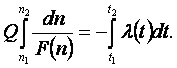 (1.12)
(1.12)
Интегралы в (1.12) можем записать
через ![]() и
и ![]() в виде
в виде
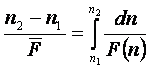 и
и 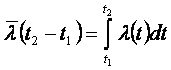 (1.13)
(1.13)
где ![]() - толщина слоя (стенки) (см.
рисунок 1.1).
- толщина слоя (стенки) (см.
рисунок 1.1).
Формулу теплоты теплопроводности получаем, подставляя (1.13) в (1.12)
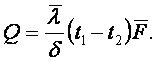 (1.14)
(1.14)
1.4 Аналогия между тепловым потоком и электрическим током
Представим тепловой поток (1.14) в виде, аналогичном закону Ома
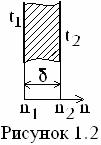

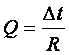 (1.15) ÷ (1.16)
(1.15) ÷ (1.16)
где ![]() - разность
термических потенциалов;
- разность
термических потенциалов;
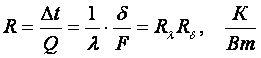 (1.17)
(1.17)
- термическое сопротивление теплопроводности.
Оно структурно определяется физическим механизмом и геометрическим фактором теплопроводности
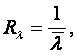
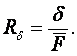 (1.18)
÷ (1.19)
(1.18)
÷ (1.19)
1.5 К расчету геометрического фактора, средних значений
поверхности теплообмена и коэффициента теплопроводности
Согласно (1.19) и (1.13) получаем, что
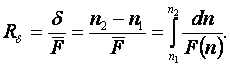 (1.20)
(1.20)
1. Для плоской стенки (см. рисунок 1.2) очевидно, что
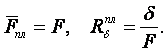 (1.21)
(1.21)
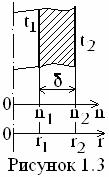
2. Для цилиндрической стенки (см. рисунок 1.3)
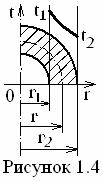
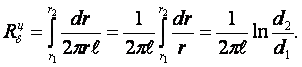 (1.22)
(1.22)
Средняя боковая поверхность цилиндра (по (1.19))
![]()
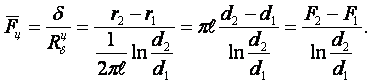 (1.23)
(1.23)
3. Для сферического слоя (F(r) = 4pr2, см. рисунок 1.4)
 (1.24)
(1.24)
![]() (1.25)
(1.25)
Cредний интегральный
коэффициент теплопроводности по (1.13) и (1.9) 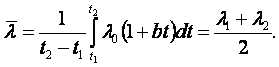 (1.26)
(1.26)
1.6 Составление расчетных формул теплоты теплопроводности
Расчетные формулы теплоты теплопроводности для тел различной формы
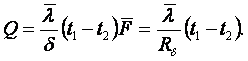 (1.27)
(1.27)
1. Для плоской стенки (см. рисунок 1.2)
 , Вт,
, Вт, 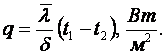 (1.28)
(1.28)
2. Для цилиндрической стенки (см. рисунок 1.3)
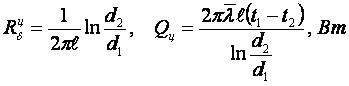 (1.29)
(1.29)
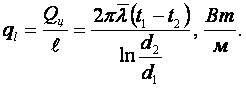 (1.30)
(1.30)
Поверхностные плотности теплоты через цилиндрическую стенку
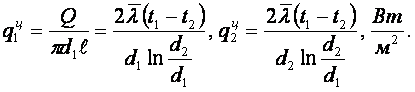 (1.31)
(1.31)
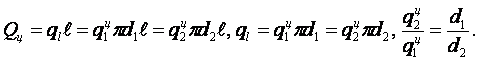 (1.32)
(1.32)
 3. Для сферического слоя (см. рисунок 1.4)
3. Для сферического слоя (см. рисунок 1.4)
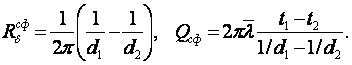 (1.33)
(1.33)
Поверхностные плотности теплоты тел различной формы
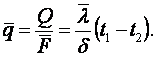 (1.34)
(1.34)
2 лекция
1.7 Температурный профиль стенки постоянной теплопроводности
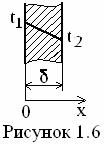 Распределение температуры в стенке найдем по (1.12) и (1.27)
Распределение температуры в стенке найдем по (1.12) и (1.27)
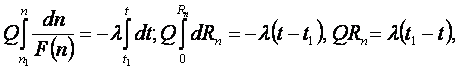
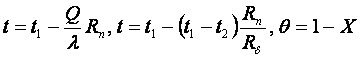 (1.35)
(1.35)
 где
где 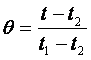 и
и ![]() .
.
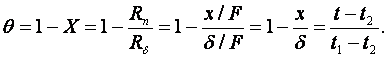 (1.36)
(1.36)
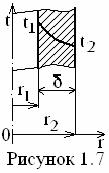
Аналогично получаются формулы распределения t(r) в цилиндрической стенке (см. рисунок 1.7) и в сферическом слое (см. рисунок1.4) постоянной теплопроводности (и для l(t))
 (1.37)
(1.37)
1.8 Стационарная теплопроводность многослойной стенки
Стенка, состоящая из различных однородных слоёв (см. рисунок 1.8), называется многослойной.
При стационарном режиме тепловой поток через каждый слой равняется
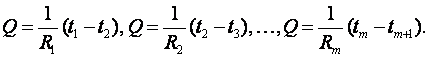 (1.38)
(1.38)
Сложение температурных напоров всех слоёв по (1.38) даёт
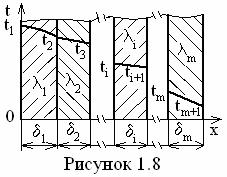
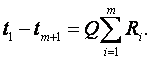 (1.39)
(1.39)
Отсюда (если j = m+1, то m = j-1)
 (1.40)
(1.40)
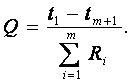 (1.41)
(1.41)
Легко получить расчётные формулы теплоты теплопроводности и ее плотности для многослойной стенки различной формы.
1. Для плоской многослойной стенки
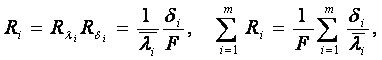
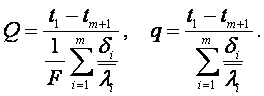 (1.42)
(1.42)
2. Для цилиндрической многослойной стенки
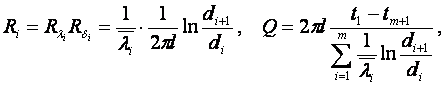 (1.43)
(1.43)
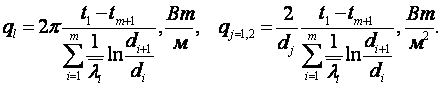 (1.44)
(1.44)
3. Для сферической многослойной стенки
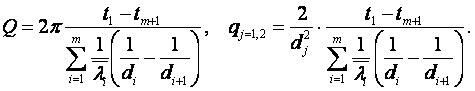 (1.45)
(1.45)
2. Математическая формулировка задач теплопроводности
2.1 Дифференциальное уравнение теплопроводности. Коэффициент
температуропроводности
Выделим некоторую часть тела объёмам V, поверхностью F и объёмной мощностью внутреннего источника теплоты qV, Вт/м3.
Внутренняя энергия U его за время dτ изменится на величину
![]() (2.1)
(2.1)
где изменение тепла внутреннего источника
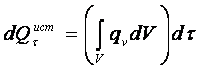 (2.2)
(2.2)
и изменение вытекающего по нормали к наружной поверхности тепла запишем с учётом теоремы Гаусса-Остроградского (как для непрерывной среды)
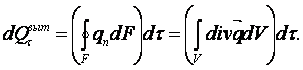 (2.3)
(2.3)
Изобарное изменение внутренней энергии контрольного объёма тела плотности ρ, кг/м3 и теплоёмкости ср, Дж/(кгּК) за время dτ записывается в виде
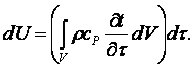 (2.4)
(2.4)
Подставляя (2.2.) ÷ (2.4) в (2.1), найдём
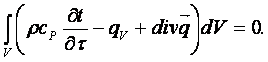 (2.5)
(2.5)
Для сплошной среды (2.5) справедливо и для dV
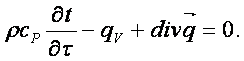 (2.6)
(2.6)
С учётом закона Фурье (1.7) в (2.6) получаем дифференциальное нелинейное уравнение Фурье для нестационарной теплопроводности в виде
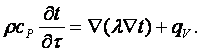 (2.7)
(2.7)
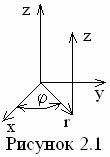 Для случаев с λ = пост и qV = 0 (2.7) записывается в виде линейного дифференциального
уравнения второго порядка
Для случаев с λ = пост и qV = 0 (2.7) записывается в виде линейного дифференциального
уравнения второго порядка
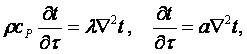 (2.8)
(2.8)
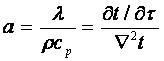 (2.9)
(2.9)
- коэффициент температуропроводности - относительная скорость изменения температурного поля со временем, м2/с;
 (2.10)
(2.10)
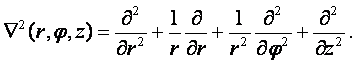 (2.11)
(2.11)
- оператор Лапласа в декартовой (х, у, z) и цилиндрической (r – радиус вектор, φ – полярный угол, z – аппликата) системах координатах (см. рисунок 2.1).
2.2 Условия однозначности решения дифференциального уравнения
теплопроводности
Условия однозначности (краевые условия) состоят из геометрических, физических, временных и граничных условий.
Временные условия
![]() . (2.12)
. (2.12)
Граничные условия 1-го и 2-го на поверхностях стеки (с)
![]() (2.13)
(2.13)
![]() . (2.14)
. (2.14)
Граничные условия четвёртого рода
 (2.15)
(2.15)
2.3 Коэффициент теплоотдачи. Граничные условия третьего рода.
Критерий Био
Теплоотдача характеризуется формулой Ньютона-Рихмана
![]() (2.16)
(2.16)
являющейся, определением среднего и местного коэффициента теплоотдачи
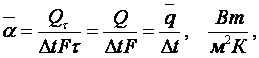 (2.17)
(2.17)
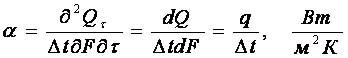 (2.18)
(2.18)
где ![]() – температурный напор между стенкой и
жидкостью, К(0С).
– температурный напор между стенкой и
жидкостью, К(0С).
![]() (2.19)
(2.19)
Уравнение граничного условия 3-го рода находим из теплового баланса
ql = qa, ![]() (2.20)
(2.20)
записанном в проекции на нормаль к изотермической поверхности теплообмена
 (2.21)
(2.21)
Запишем коодинаты и уравнение граничного условия третьего рода в безразмерном виде (см. рисунок 2.2)

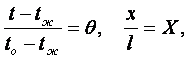 (2.22)
(2.22)
 (2.23)
(2.23)
где 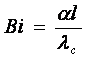 – число (критерий)
Био;
– число (критерий)
Био;
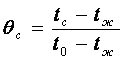 – безразмерная температура на
поверхности стенки;
– безразмерная температура на
поверхности стенки;
Критерий Био характеризуется следующим образом
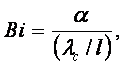

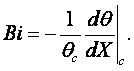 (2.24)
(2.24)
Для удобства выполнения РГР рассмотрим здесь главы 6 и 7 [13].
3 лекция
Раздел второй. Тепловой расчёт теплообменников
6 Теплопередача при постоянных температурах теплоносителей
6.1 Теплопередача и температуры многослойной стенки
Тепловой поток теплоотдачей можно представить в виде
![]() (6.1)
(6.1)
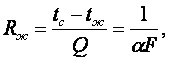
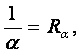
 (6.2) ÷ (6.4)
(6.2) ÷ (6.4)
Если сложить температурные напоры слоёв стационарной теплопередачи многослойной стенки (см. рисунок 6.1), то получим выражения (6.6) ÷ (6.8)
![]() , (6.5)
, (6.5)
для температурного напора между жидкостями, термического сопротивления и мощности теплопередачи многослойной стенки
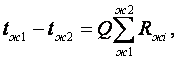
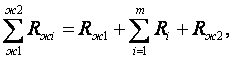
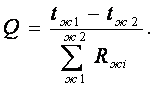
Из (6.5) найдем формулы для расчёта температур между слоями стенок
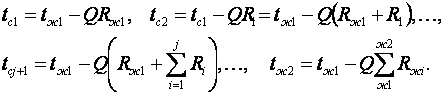 (6.9)
(6.9)
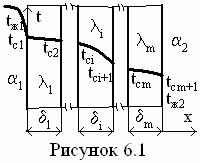 Множитель
пропорциональности между плотностью теплового потока теплопередачи
и температурным напором между жидкостями называется коэффициентом
теплопередачи
Множитель
пропорциональности между плотностью теплового потока теплопередачи
и температурным напором между жидкостями называется коэффициентом
теплопередачи
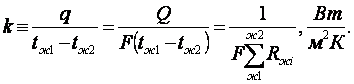 (6.10)
(6.10)
6.2 Коэффициент теплопередачи тел различной формы
1. Коэффициент теплопередачи для плоской многослойной стенки
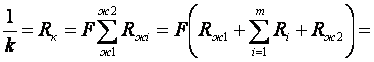
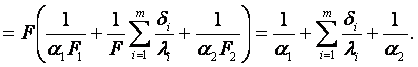 (6.11)
(6.11)
Коэффициент теплопередачи однородной плоской стенки (m = 1)
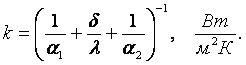 (6.12)
(6.12)
2. Коэффициент теплопередачи цилиндрической стенки по (6.10) и (1.42)
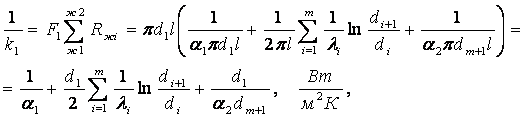 (6.13)
(6.13)
 (6.14)
(6.14)
Если m = 1, то, например, по (6.14)
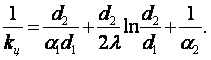 (6.15)
(6.15)
Если d2/d1→1, то (для d2/d1 < 2 с точностью 4 % [1])
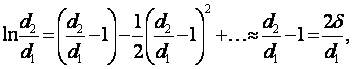 (6.16)
(6.16)
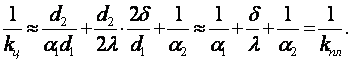 (6.17)
(6.17)
При этом величина теплоты получается более точным, если из d1 и d2 в (6.17) принимать тот диаметр поверхности цилиндра, где a меньше (aм)
![]() , Вт.
, Вт.
Линейный коэффициент теплопередачи цилиндра согласно (6.10)
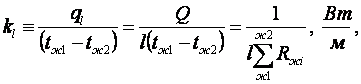 (6.18)
(6.18)
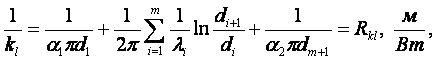 (6.19)
(6.19)
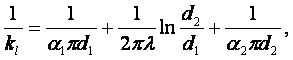 (m=1). (6.20)
(m=1). (6.20)
3. Коэффициент теплопередачи для сферической стенки по (6.10) и с учетом (6.2) и (1.45) рекомендуется получить аналогично (6.13) ÷ (6.15).
6.3 Критический диаметр цилиндрической стенки
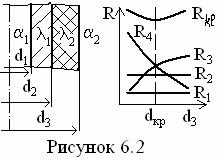 Термическое
сопротивление и критический диаметр цилиндрической стенки
с наружным теплоизоляционным слоем определяются согласно
(6.19) по формулам (см. рисунок 6.2)
Термическое
сопротивление и критический диаметр цилиндрической стенки
с наружным теплоизоляционным слоем определяются согласно
(6.19) по формулам (см. рисунок 6.2)
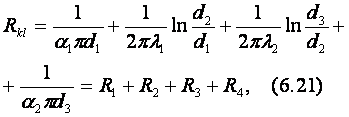
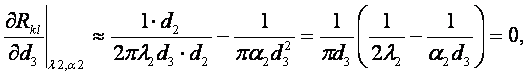
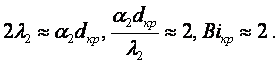 (6.22)
(6.22)
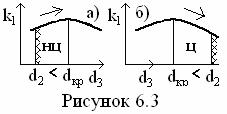
При d2 < dкр (см.
рисунок 6.3а) тепловые потери вначале растут (тепловая изоляция данным
материалом нецелесообразна (нц)) за счёт большего
влияния роста поверхности, чем рост толщины слоя, а при dкр
< d2 (см. рисунок 6.3б) тепловые потери уменьшаются (тепловая
изоляция целесообразна (ц)) за счёт
большего  влияния роста толщины слоя, чем влияние роста поверхности
с увеличением d3. Согласно
(6.22) теплоизоляционный материал пригоден для уменьшения тепловых потерь при
λиз ≤ λкр и α2 ≥
α2кр (см. рисунок 6.4). В противном случае такой материал будет не теплоизоляционным, а интенсификатором
теплообмена.
влияния роста толщины слоя, чем влияние роста поверхности
с увеличением d3. Согласно
(6.22) теплоизоляционный материал пригоден для уменьшения тепловых потерь при
λиз ≤ λкр и α2 ≥
α2кр (см. рисунок 6.4). В противном случае такой материал будет не теплоизоляционным, а интенсификатором
теплообмена.
6.4 Пути интенсификации теплопередачи
Согласно формуле теплового потока теплопередачи
![]() (6.23)
(6.23)
Q
можно увеличивать за счет увеличения k, ∆tж и F. Однако увеличение tж1
связано с опасностью термомеханических разрушений
оборудования. Влияние F рассмотрим в
следующем параграфе. Так как расчёт
kц может сводиться к расчёту kпл, влияние его рассмотрим на примере коэффициента теплопередачи плоской (и
для наглядности) металлической (![]() )
стенки
)
стенки
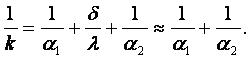
Пусть ![]() (где м-меньший,
б-больший). Тогда
(где м-меньший,
б-больший). Тогда
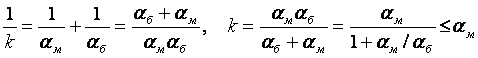 , т.е. k ~ αм.
, т.е. k ~ αм.
Таким образом, k меньше меньшего из αм и αб и поэтому необходимость увеличения k сводится к необходимости увеличения αм.
6.5 Теплопередача ребристой плоской стенки
У
теплопередающей стенки средняя температура ребра будет меньше
температуры у его основания (![]() < t0
= tс2) (см. рисунок 6.5). Это
учитывается коэффициентом эффективности ребра (Е = 0 ¸ 1), определяемым отношением теплоты реального ребра к
теплоте идеального ребра
с t = t0
= const
< t0
= tс2) (см. рисунок 6.5). Это
учитывается коэффициентом эффективности ребра (Е = 0 ¸ 1), определяемым отношением теплоты реального ребра к
теплоте идеального ребра
с t = t0
= const
![]() . (6.24)
. (6.24)
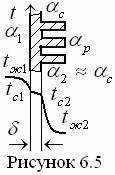 Коэффициент
теплоотдачи ребристой стенки найдем из выражения теплоты ребристой стенки,
складывающейся из тепловых потоков через ребра (р) и гладкую часть стенки (с) (
Коэффициент
теплоотдачи ребристой стенки найдем из выражения теплоты ребристой стенки,
складывающейся из тепловых потоков через ребра (р) и гладкую часть стенки (с) (![]() )
)
![]() ,
(6.25)
,
(6.25)
![]() (6.26)
(6.26)
Коэффициент теплопередачи ребристой стенки kр.с найдем, складывая температурные напоры для каждого слоя
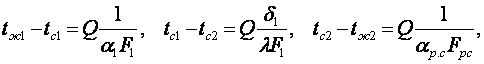
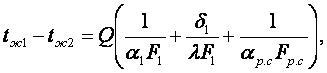 (6.27)
(6.27)
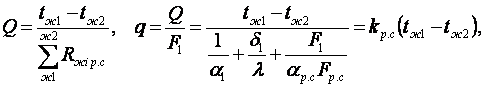
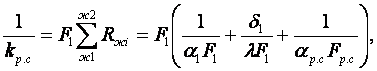
 (6.28)
(6.28)
Прямая пропорциональность коэффициента теплопередачи ребристой стенки kр.с коэффициенту ее оребрения (Fр.с/F1) называется эффектом оребрения стенки.
4 лекция
7 Теплопередача при переменных температурах теплоносителей
7.1 Общие понятия теплового расчёта теплообменников
В формуле теплоты теплопередачи
![]() (7.1)
(7.1)
берётся среднее интегральное значение температурного напора
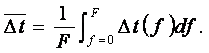 (7.2)
(7.2)
Теплообменные аппараты делятся на поверхностные (рекуперативные), смесительные и регенеративные. Поверхностные теплообменники делятся по методам расчётов на конструкторские и поверочные и по направлениям течения теплоносителей на прямоточные, противоточные и перекрёстные. Горячие и холодные жидкости обозначаются подстрочными индексами 1 и 2, а на входе и выходе – надстрочными (') и (''). У противоточных - входные и выходные значения Δt - по горячей жидкости (см. рисунок 7.1).
7.2 Средний температурный напор прямо и
противоточных теплообменников
Выражение среднего температурного напора прямоточных (а)прм) и противоточных (б)прт) теплообменников определим на примере схемы их типа «труба в трубе» (см. рисунок 7.1). В результате теплового потока
![]() (7.3)
(7.3)
изменяются энтальпии горячей и холодной жидкостей на величину
![]() (7.4)
(7.4)
где знаки по dt/df : ²+² для прямотока, ²-² для противотока;
![]() (7.5)
(7.5)
- параметр одновременного рассмотрения прямо и противотока
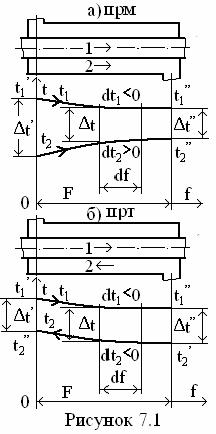
 (7.6)
(7.6)
Если (7.3) подставить в (7.5), то
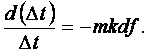 (7.7)
(7.7)
При постоянных значениях m и k (7.7) имеем
 (7.8)
(7.8)
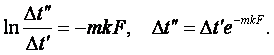 (7.9)
(7.9)
По (7.8), (7.2), (7.9)

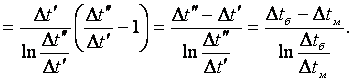 (7.10)
(7.10)
Индексы «б» - больший и «м» - меньший удобны для практических расчётов. При Δtб < 2Δtм приближенные значения
![]() (7.11)
(7.11) ![]() (7.12)
(7.12)
7.3 Расчёт выходных температур теплоносителей прямоточных и
противоточных теплообменников
Для определения ![]() и
и ![]() при поверках в прямотоках
рассматрим
при поверках в прямотоках
рассматрим
![]() (7.13)
(7.13)
![]() (7.14)
(7.14)
Из (7.14) находим (заметим, что в (7.14) – (7.16) m = mпрм для прямотока)
![]() (7.15)
(7.15)
и подставив в (7.13), исключаем её
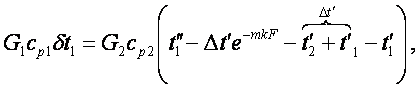
![]()
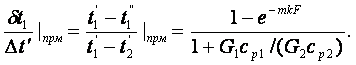 (7.16)
(7.16)
Подставляя t1” из (7.16) в
(7.15), находим ![]() .
.
Аналогично получаем
расчётные формулы для ![]() и
и ![]() противотока
противотока
 (7.17)
(7.17)
![]() (7.18)
(7.18)
7.4 Сравнение эффективностей прямоточных и
противоточных теплообменников
Для одних и тех же жидкостей с
одинаковыми расходами, ![]() и
и ![]()
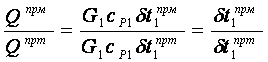 ,
(7.19)
,
(7.19)
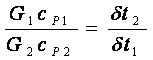 и
и 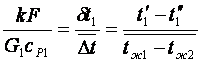 .
(7.20)
.
(7.20)
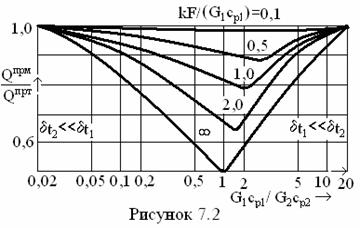
Из рисунка 7.2 видно, что эффективность прямотока мень-ше, чем у противотока, когда изменения температур жидкостей и температурные напоры между ними одного порядка, а когда эти темпера-турные разности сильно отличаются друг от друга, эффек-тивности их одного порядка.
7.5 Средний температурный напор сложных теплообменников
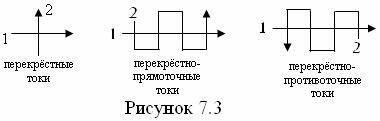
Средний температурный напор между жидкостями перекрестных токов (см. рисунок 7.3) имеет промежуточное значение между температурными напорами прямо-противотоков
![]() (7.21)
(7.21)
и определяется следующим образом:
а)если ![]() то
то ![]() (7.22)
(7.22)
б)если ![]() , то
, то ![]() (7.23)
(7.23)
где ψ – множитель пропорциональности, определяемый из номограмм с
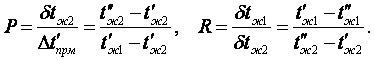 (7.24)
(7.24)
5 лекция
3 Решения задач стационарной теплопроводности с внутренним
источником теплоты
3.1 Стационарная теплопроводность пластины с внутренним
источником теплоты постоянной мощности
Задана однородная пластина источник теплоты с qv = пост (см. рисунок 3.1). Целью решения задачи является определение, как обычно, t(х) и Q.
Уравнение Фурье (2.7) в рассматриваемых условиях принимает вид

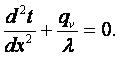 (3.1)
(3.1)
В условиях симметрии задачи
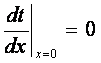 (3.2)
(3.2)
рассматриваем половину пластины с δ и (2.21) в виде
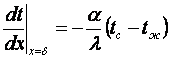 . (3.3)
. (3.3)
Интегрирование (3.1) выполним следующим образом
 (3.4)
(3.4)
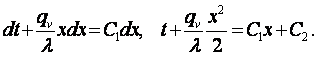 (3.5)
(3.5)
Из (3.4) в условиях (3.2) находим, что С1 = 0. При граничных условиях первого рода (tх=δ = tс) из (3.5) получим, что
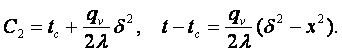 (3.6)
(3.6)
В условиях (3.3) из (3.4) находим, что
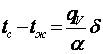 .
(3.7)
.
(3.7)
Распределение
температуры в пластине при (3.3), ![]() и
и ![]() , складывая (3.6) и (3.7), получаем в виде
, складывая (3.6) и (3.7), получаем в виде
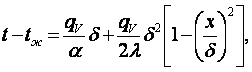 (3.8)
(3.8)
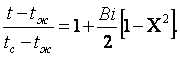 (3.9)
(3.9)
 При a = ¥ согласно (3.7) tc = tж и (3.8) переходит в
(3.6). При х = 0 (3.9) преобразуется к виду
При a = ¥ согласно (3.7) tc = tж и (3.8) переходит в
(3.6). При х = 0 (3.9) преобразуется к виду
 (3.10)
(3.10)
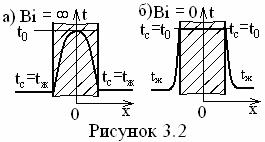
При Bi = ¥, 0 согласно (3.10) ![]() и задача становится
соответственно внутренней (см. рисунок 3.2а) и внешней (см. рисунок 3.2б). Во
всех других значениях числа Био распределение температуры имеет вид, показанный
на рисунке 3.1.
и задача становится
соответственно внутренней (см. рисунок 3.2а) и внешней (см. рисунок 3.2б). Во
всех других значениях числа Био распределение температуры имеет вид, показанный
на рисунке 3.1.
Плотность теплоты в пластине получаем по закону Фурье с (3.4) в виде
 (3.11)
(3.11)
что очевидно из теплового
баланса источника. При ![]() (3.11) имеет вид (3.7)
(3.11) имеет вид (3.7)
![]() . (3.12)
. (3.12)
Тепловой поток через полную поверхность пластины равняется
![]() (3.13)
(3.13)
Аналогично решаются задачи теплопроводности когда ![]()
3.2 Стационарная теплопроводность стержня неограниченной длины
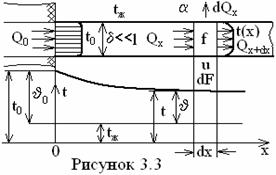 Находим распределение темпратуры и мощ-ность источника тепла Q0 (см.
рисунок 3.3).
Находим распределение темпратуры и мощ-ность источника тепла Q0 (см.
рисунок 3.3).
Распределение
температуры в стержне можно считать одномерным
вдоль оси х ![]() тем строже, чем число
тем строже, чем число ![]() будет ближе
к нулю.
будет ближе
к нулю.
На элементарном участке стержня dx с
периметром «u» и температурным
напором ![]() в окружающую среду отдается
теплота
в окружающую среду отдается
теплота ![]() (3.14)
(3.14)
и мощность источника теплоты стержня в рассматриваемом элементе с объёмом dV уменьшается на величину
![]() (3.15)
(3.15)
Из (3.15) и (3.14) находим объёмную мощность внутреннего источника теплоты
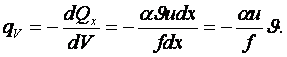 (3.16)
(3.16)
Подставляя (3.16) в (3.1), получаем ДУТ стержня
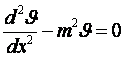 (3.17)
(3.17)
где 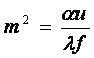 - размерный параметр уравнения, м-2.
- размерный параметр уравнения, м-2.
Решение уравнения (3.17) известно и записивается в виде
![]() ,
, ![]()
![]() . (3.18) ÷ (3.20)
. (3.18) ÷ (3.20)
Для выполнения
условия (ℓ » d) ![]() х=∞
= 0 в (3.20) должно быть С1
= 0, а в начальном сечении
х=∞
= 0 в (3.20) должно быть С1
= 0, а в начальном сечении ![]() х=0
=
х=0
= ![]() 0, следовательно, согласно (3.20)
С2 =
0, следовательно, согласно (3.20)
С2 =![]() 0. Итак
0. Итак
![]() (3.21)
(3.21)
 (3.22)
(3.22)
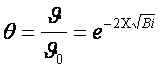 (3.23)
(3.23)
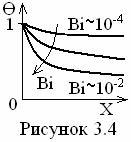
где ![]() и
и  (см. рисунок 3.4).
(см. рисунок 3.4).
Тепловой поток через основание стержня с учётом (3.21) определяем как
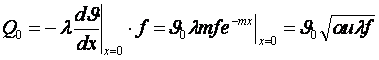 , Вт. (3.24)
, Вт. (3.24)
3.3 Стационарная теплопроводность стержня конечной длины
Решение задачи (3.20) при х = 0 имеет вид
![]() . (3.25)
. (3.25)
Для стержня конечной длины x = l третье граничное условие имеет вид
 (3.26)
(3.26)
Подстановка (3.20) в (3.26) даёт
 (3.27)
(3.27)
где (по условию одномерности решения задачи)
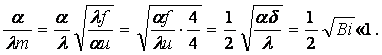 (3.28)
(3.28)
Поэтому (3.27) можем упростить и записать в виде
![]() (3.29)
(3.29)
Из (3.25) и (3.29) находим постоянные интегрирования общего решения
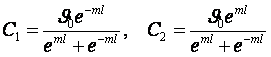 (3.30)
(3.30)
и, подставляя их в (3.20), получаем уравнение для стержня конечной длины
 (3.31)
(3.31)
где ![]() - гипорболический косинус.
- гипорболический косинус.
Температурный напор в конце стержня (x = ℓ) согласно (3.31) равняется
 (3.32)
(3.32)
Уравнение теплового потока через основание стержня конечной длины
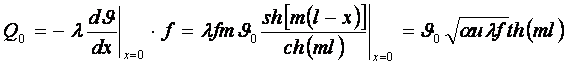 .(3.33)
.(3.33)
Для стержня большой длины (ℓ » d)
![]() и
и ![]() (3.34)
(3.34)
Поэтому (3.32) и (3.33)
переходит к результатам для стержня бесконечной длины (3.23) (![]() )
и (3.24).
)
и (3.24).
4 Нестационарная теплопроводность
4.1 Безразмерное дифференциальное уравнение теплопроводности
(ДУТ). Критерий Фурье
Заменяя размерные величины J, х, у и z безразмерными в ДУТ
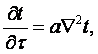 (2.8)
(2.8) 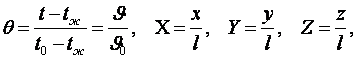 (4.1)
(4.1)
получаем безразмерное ДУТ в виде
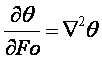 (4.2)
(4.2)
где число Фурье – безразмерое время
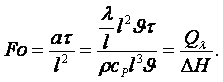 (4.3)
(4.3)
4.2 Решение нестационарного ДУТ плоской стенки методом Фурье
Задача решается при следующей математической формулировке
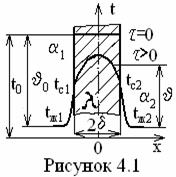
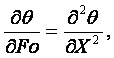
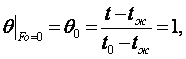

 (4.4) ÷ (4.7)
(4.4) ÷ (4.7)
При заданном числе Био ![]() представляется как (см. рисунк 4.1) [1]
представляется как (см. рисунк 4.1) [1]
![]() (4.8)
(4.8)
Решение для нестационарной теплопроводности пластины находим в виде
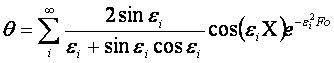 (4.9)
(4.9)
где εi – корни трансцендентного уравнения
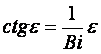 (4.10)
(4.10)
возникающиеся при решении (4.10) графическим методом (в точках пересечения котангенсоид y1 = ctge c прямой линией y2 = e/Bi, см. рисунок 4.2)
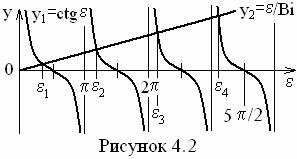
![]() , (4.11)
, (4.11)
причём при Bi→∞
![]()
и при Bi→0
![]() .
.
Уменьшение энтальпии тела

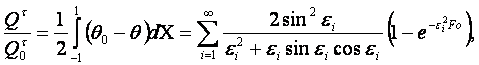 (4.12)
(4.12)
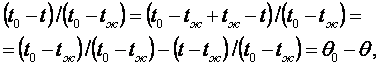

6 лекция
4.3 Анализ решения нестационарного ДУТ плоской стенки
 1. Рост
значений корней характеристического уравнения с ростом
номера (4.11) и (–ε2i×Fo), находящегося в степени числа е,
обеспечивают такое быстрое схождение ряда (4.9), что, начиная,
например, с момента времени F0 >
Fo* = 0,3, 0,5, сумму ряда можно
заменить с точностью 1; 0,1% [2]
первым членом ряда
1. Рост
значений корней характеристического уравнения с ростом
номера (4.11) и (–ε2i×Fo), находящегося в степени числа е,
обеспечивают такое быстрое схождение ряда (4.9), что, начиная,
например, с момента времени F0 >
Fo* = 0,3, 0,5, сумму ряда можно
заменить с точностью 1; 0,1% [2]
первым членом ряда
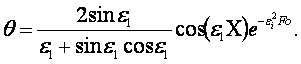 (4.13)
(4.13)
2. Значения
температуры на оси и поверхностях пластины (4.13) с учётом
(4.10) (аналогично для цилиндра) представлены
в виде номограмм (![]() , см. рисунок 4.3) и таблиц
(eI,
eI2,
N, P= f(Bi))
, см. рисунок 4.3) и таблиц
(eI,
eI2,
N, P= f(Bi))
![]()
![]()
 3.
Теорема о направляющей точке.
3.
Теорема о направляющей точке. 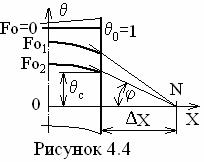 Касательные
к профилям температуры в точках на поверхности тела в любой момент времени
проходят через одну и ту же точку, называ-емую направляющей.
Касательные
к профилям температуры в точках на поверхности тела в любой момент времени
проходят через одну и ту же точку, называ-емую направляющей.
Сравнивая выраже-ние убыли температуры на стенке (см. рисунок 4.4)
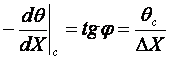 с уравнением третьего граничного условия (2.23)
с уравнением третьего граничного условия (2.23)
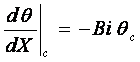 (2.23)
(2.23)
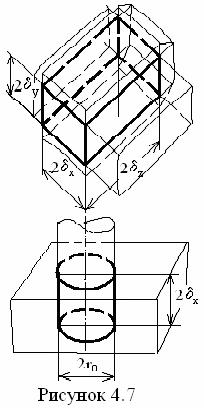 находим, что
расстояние от стенки до направляющей точки определяется заданным числом Био
находим, что
расстояние от стенки до направляющей точки определяется заданным числом Био
DХ = 1/Ві = idem (одно и то же). (4.14)
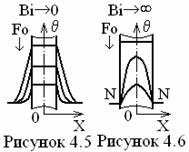
Для предельных значений числа Био Ві = 0 (DХ = µ) и µ (DХ = 0) распределение температуры соответственно будет как на рисунках 4.5 (внешняя задача) и 4.6 (внутренняя задача), а для Ві » 0,1 ¸ 10 - как на рисунке 4.4.
4.4 Нестационарная теплопроводность тел
конечных размеров
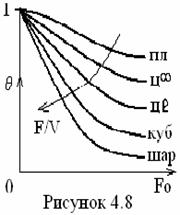
Прямоугольные стержни (пст), паралелепипе-ды (пп) и цилиндры конечных размеров (цℓ) можно рассматривать как тела, образованные пересечением взаимно перпендикулярных соответственно двух, трех пластин (пл), бесконечного цилиндра (цµ) и пластины (см. рисунок 4.7). Поэтому распределение температуры в телах конечных размеров (с постоянными теплофизическими свойствами, то есть для линейного ДУТ) можно представить в виде произведения температуры составляющих тел
![]() (4.15)
(4.15)
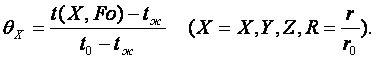
Это положение известно как теорема о перемножении решений [15].
Скорость распространения тепла в телах зависит от отношения поверхности к его объему F/V. Например, для пластины (n = 1), цилиндра бесконечной длины (n = 2) и куба (то же для шара, n = 3) в соответствии с (4.13) при Ві = 0(0) (см. рисунок 4.8)
![]() (4.16)
(4.16)
4.5 Метод регулярного теплового режима
Для тел различной формы при F0 > Fo*
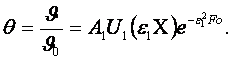 (4.17)
(4.17)
Его для любой точки тела представим как
![]() (4.18)
(4.18)
где 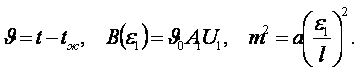
Логарифм и логарифмическая производная (4.18) имеет вид
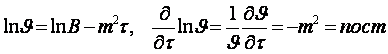 .
(4.19)
.
(4.19)
Относительная скорость изменения температурного тела m2 называем темпом выравнивания температурного поля (темп охлаждения (нагрева) [1]).
 Процесс нестационарной
теплопроводности с постоянной относительной скоростью изменения температурного
поля (4.19) называется регулярным тепловым режимом (РТР). На основе опытных данных и для произвольных
состояний 1 и 2 линейной зависимости (4.19) определяют значение m2
следующим образом (см. рисунок 4.9)
Процесс нестационарной
теплопроводности с постоянной относительной скоростью изменения температурного
поля (4.19) называется регулярным тепловым режимом (РТР). На основе опытных данных и для произвольных
состояний 1 и 2 линейной зависимости (4.19) определяют значение m2
следующим образом (см. рисунок 4.9)
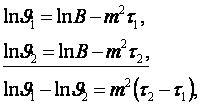
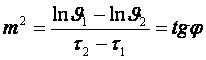 (4.20)
(4.20)
и по (4.18) вычисляют коэффициент температуропроводности
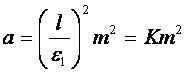 (4.21)
(4.21)
где ![]() - коэффициент формы тела [1]. Например, для шара
- коэффициент формы тела [1]. Например, для шара
![]() (4.22)
(4.22)
Аналогично
находятся коэффициенты теплопроводности, теплового
излучения серого тела, теплоотдачи, теплоёмкости. Режим при Bi→∞
и tж = пост называется тепловым режимом первого рода.
Применяются и режимы с ![]() (РТР 2-
рода) и
(РТР 2-
рода) и ![]() (РТР 3- рода), где tт
и ν – амплитуда и частота колебаний температуры, b – постоянная [26, 1, 2, 15].
(РТР 3- рода), где tт
и ν – амплитуда и частота колебаний температуры, b – постоянная [26, 1, 2, 15].
5 Приближенные методы расчета теплопроводности
5.1 Графический метод расчета теплопроводности
Найдем распределение температуры в полуограниченном теле графическим методом. Для этого уравнение процесса (2.8) записываем
приближенно в конечных разностях (см. рисунок 5.1)

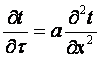 ,
, 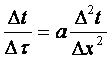 . (5.1) ÷ (5.2)
. (5.1) ÷ (5.2)
В k- момент
времени в центре n- элемента тела с температурой ![]() будут пересекаться два отрезка
температурной кривой
будут пересекаться два отрезка
температурной кривой
 и
и  . (5.3)
. (5.3)
Соответствующие им изменения второго порядка составляет
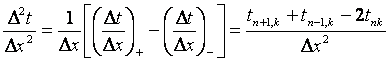 .
(5.4)
.
(5.4)
Скорость изменения температуры n- элемента равняется
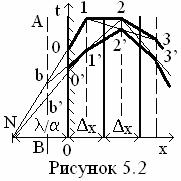
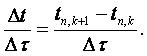 (5.5)
(5.5)
Подстановка (5.5) и (5.4) в (5.2) даёт
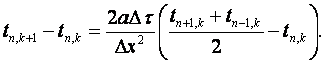 (5.6)
(5.6)
Благодаря свободе выбора интервалов
![]() и
и ![]() Э.Шмидт,
приняв значение числа Фурье в (5.6) равным
Э.Шмидт,
приняв значение числа Фурье в (5.6) равным
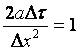 (5.7)
(5.7)
обосновал приём построения ломанной линии профиля температуры для каждого последующего момента времени и назвал "Методом срезания углов".
Местоположение
направляющей точки в каждый
момент времени изменяется с
учетом переменности ![]() и
и
![]() (см. рисунок 5.2) и решаются
аналитически нерешаемые нелинейные дифференциальные уравнения.
(см. рисунок 5.2) и решаются
аналитически нерешаемые нелинейные дифференциальные уравнения.
5.2 Численный метод (метод сеток) расчета теплопроводности
Рассмотрим численное решение двухмерной стационарной теплопровод-ности, описываемой дифференциальным уравнением (2.8) и уравнением в
конечных разностях в виде (см. рисунок 5.3)
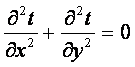 ,
, 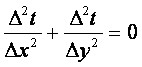 , (5.8) ÷ (5.9)
, (5.8) ÷ (5.9)
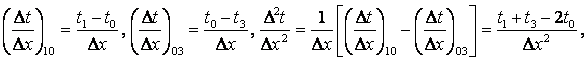 (5.10)
(5.10)
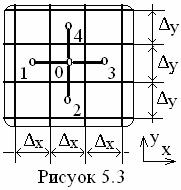
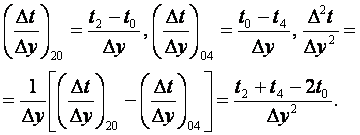 (5.11)
(5.11)
Подстановка (5.10) и (5.11) в (5.9) дает
![]() . (5.12)
. (5.12)
Расчет температурного поля сводится к решению системы уравнений вида (5.12).
При численном решении методом релаксации первоначально задаются значения температур в узловых точках сообразно граничным значениям рассматриваемой задачи [19]. При этом возникает дебаланс
![]() . (5.13)
. (5.13)
Дебаланс быстро сводится к значению близкому нулю путем деления предыдущего дебаланса на 4
![]() . (5.14)
. (5.14)
5.3 Исследование теплопроводности методом аналогии
Аналогичные явления различной физической природы описываются формально одинаковыми уравнениями и условиями однозначности.
В электротепловой аналогии идентичны уравнения
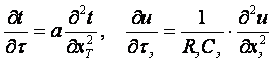 (5.15)
(5.15)
где ![]() и
и ![]() - электрическое сопротивление и емкость
на единицу длины;
- электрическое сопротивление и емкость
на единицу длины;
t и u - тепловые и электрические потенциалы.
Аналогия выполняется, если принять числовое равенство
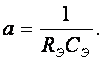 (5.16)
(5.16)
Аналогичны тепловой поток, электрический ток и расход жидкости
 (5.17)
(5.17)
7 лекция
Раздел третий. Конвективный теплообмен в однородной среде
8 Основы теории конвективного теплообмена в однородной среде
8.1 Общие понятия и задачи конвективного теплообмена.
Характеристика коэффициента теплоотдачи
Для расчета теплоты теплоотдачи по формуле Ньютона-Рихмана (2.17)
![]() (8.1)
(8.1)
требуется знание значений местного и средного коэффициентов теплоотдачи
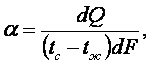
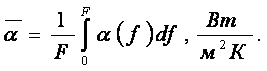 (8.2) ÷ (8.3)
(8.2) ÷ (8.3)
При постоянном поперечном размере поверхности теплообмена средние по длине значения коэффициента теплоотдачи (8.3) рассчитываются для граничных условий первого (tс = const) и второго (qс = const) рода по формулам
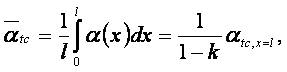
![]() (8.4) ÷ (8.5)
(8.4) ÷ (8.5)
где k
– степень зависимости коэффициента теплоотдачи (с, k = const) от координаты в виде (![]() , см. рисунок 8.1)
, см. рисунок 8.1)
![]() (8.6)
(8.6)
Очевидно, что (см. задачу 6.1)
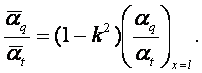 (8.7)
(8.7)
Характерные температуры теплоотдачи
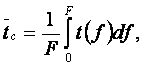
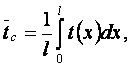 (8.8)
÷ (8.9)
(8.8)
÷ (8.9)
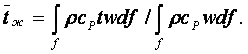 (8.10)
(8.10)
Среднеэтальпийние значения (8.10) при ρ, сР, w = пост
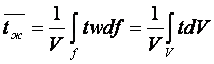 ,
, 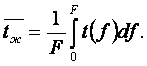 (8.11) ÷ (8.12)
(8.11) ÷ (8.12)
8.2 Уравнение теплоотдачи. Пути определения коэффициента
теплоотдачи
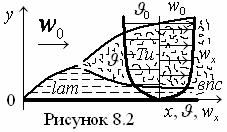 Для составления
уравнения теплоотдачи используется физический факт о
наличии вязкого подслоя (впс) ньютоновской жидкости у
поверхности стенки при любых режимах (lam, Tu) её обтекания (см. рисунок 8.2). Поэтому тепловой баланс жидкости у стенки можем выразить формулами
Ньютона-Рихмана и Фурье
Для составления
уравнения теплоотдачи используется физический факт о
наличии вязкого подслоя (впс) ньютоновской жидкости у
поверхности стенки при любых режимах (lam, Tu) её обтекания (см. рисунок 8.2). Поэтому тепловой баланс жидкости у стенки можем выразить формулами
Ньютона-Рихмана и Фурье
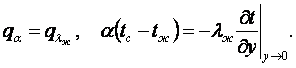 (8.13)
(8.13)
Отсюда получаем уравнение теплоотдачи в виде
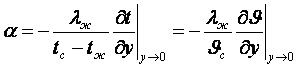 (8.14)
(8.14)
где
![]() и
и ![]() - текущий и
полный температурные напоры.
- текущий и
полный температурные напоры.
8.3 Система дифференциальных уравнений конвективного
теплообмена и условия однозначности их решения
Составим дифференциальные уравнения конвективного теплообмена для стационарного слабонеизотермического и слабосжимаемого течения жидкости.
Уравнение теплоотдачи (8.14)
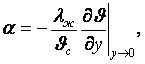 (8.15)
(8.15)
уравнение энергии
![]() , (8.16)
, (8.16)
 |
векторная форма трех уравнений движения в проекциях на оси
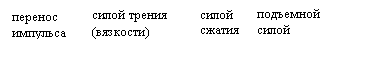
![]() (8.17)
(8.17)
уравнение неразрывности
![]() (8.18)
(8.18)
где силы
тяжести ![]() преобразованы
в подъёмные силы
преобразованы
в подъёмные силы ![]() с точностью выполнения закона
Гей-Люссака (
с точностью выполнения закона
Гей-Люссака (![]() )
)
![]() . (8.19)
. (8.19)
Термический коэффициент объемного расширения при постоянном давлении (для идеального газа β = 1/Т)
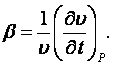 (8.20)
(8.20)
При ![]() (8.19)
можно представить (с точностью до 2-го слагаемого геометрической прогрессии) в виде
(8.19)
можно представить (с точностью до 2-го слагаемого геометрической прогрессии) в виде ![]() и показать, что
и показать, что
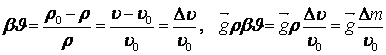 (8.21)
(8.21)
- относительные подъёмные силы (с массой Δm, где v = 1/ρ – удельный объем).
8.4 Повышение температуры вследствие адиабатического сжатия
При больших значениях w∞ можно можно уравнения энергии (8.16) и движения (8.17) и их решения записать как (см. рисунок 8.3)

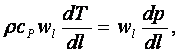 (8.22)
(8.22)
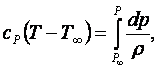 (8.23)
(8.23)
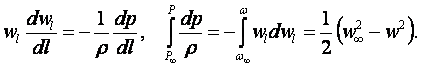 (8.24)
(8.24)
Учитывая (8.24) в (8.23) и значение w = w0 = 0 в лобовой точке, получаем
![]() , (8.25)
, (8.25)
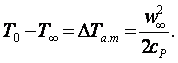 (8.26)
(8.26)
При малых температурных напорах значение температуры вследствие адиабатического сжатия DТа.т = Т0 - Т∞ следует учитывать и при невысоких скоростях потока, например, для w∞=100 м/с»0,3 М воздуха (сР = 1005 Дж/(кгК)
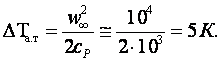 (8.27)
(8.27)
9 Теория подобия конвективного теплообмена в однородной среде
9.1 Безразмерные дифференциальные уравнения и
критерии подобия конвективного теплообмена
Подставим безразмерные величины
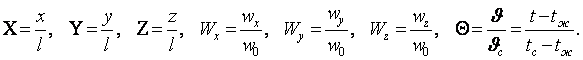 (9.1)
(9.1)
в (8.15) ÷ (8.18), получим их в безразмерных видах
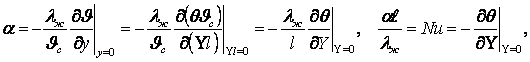 (9.2)
(9.2)
![]() , (9.3)
, (9.3)
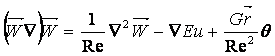 , (9.4)
, (9.4)
![]() .
(9.5)
.
(9.5)
Условия однозначности записываются аналогично размерным видам.
Здесь ![]() и
и ![]() - числа Рейнольдса и Эйлера.
- числа Рейнольдса и Эйлера.
Комплексы величин ![]() и
и ![]() - критерии Нуссельта и
Пекле - соотношение
изменения энтальпии и теплоты теплопроводности
- критерии Нуссельта и
Пекле - соотношение
изменения энтальпии и теплоты теплопроводности
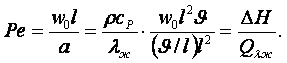 (9.6)
(9.6)
Комплекс величин ![]() - критерий Грасгофа. Он для сред дискретных
называется критерием Архимеда
(
- критерий Грасгофа. Он для сред дискретных
называется критерием Архимеда
(![]() - число Галлилея)
- число Галлилея)
 (9.7)
(9.7)
Комплекс величин ![]() – число Эккерта. Он характеризует
соотношение теплоты сжатия и изменения энтальпии
потока (его порядок 1)
– число Эккерта. Он характеризует
соотношение теплоты сжатия и изменения энтальпии
потока (его порядок 1)
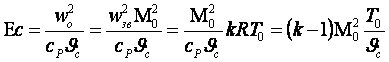 (9.8)
(9.8)
не
только при больших скоростях (число Маха Μ ~ 1),
когда температурный напор, возникающий за счет теплоты сжатия, порядка
абсолютной температуры среды (Jс ~ Т0), как это обычно имеют в виду, но и при умеренных
скоростях течения (М < 1), когда ![]() (см. (8.26) и (8.27), (Ес≈1))
(см. (8.26) и (8.27), (Ес≈1))
 (9.9)
(9.9)
9.2 Критериальные уравнения конвективного теплообмена
Функциональные зависимости критериев - критериальные уравнения
![]() (9.10)
(9.10)
Критериальное уравнение для среднего коэффициента теплоотдачи
 (9.11)
(9.11)
Значение критериального уравнения не изменяется от видоизменения
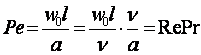 ,
(9.12)
,
(9.12)
![]() , (
, (![]() ).
(9.13)
).
(9.13)
В результате (9.11) равносильно уравнению
![]() (9.14)
(9.14)
Число независимых переменных в (9.14) может уменьшаться
![]() , (9.15)
, (9.15)
![]() (9.16)
(9.16)
Результаты решения и данные экспериментов представляются в виде
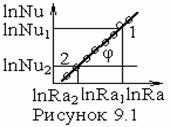
![]() (9.17)
(9.17)
Постоянные значения С и n (9.17) определяются следующим образом (см. рисунок 9.1)
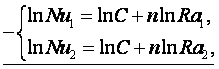
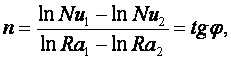 (9.18)
(9.18)
![]() (9.19)
(9.19)
9.3 Моделирование процессов конвективного теплообмена
Способ, приём познания, позволяющий посредством одной системы воспроизвести другую, более сложную систему, являющуюся объектом исследования, называется научным моделированием; система же, воспроизводящая объект исследования (натуру), – её моделью.
Идея моделирования заключается в том, что любое явление, описанное в безразмерных переменных, отражает признаки подобных явлений.
Принципы моделирования.
1. Подобные процессы должны быть одной физической природы и описываться одними и теми же дифференциальными уравнениями.
2. Условия однозначности подобных процессов должны быть одинаковы во всём, кроме численных значений размерных величин.
3. Одноимённые определяющие безразмерные переменные подобных процессов должны быть численно равны.
Разработаны методы приближённого моделирования, основанные на понятиях стабильности (профили скорости одинаковы, коэффициент теплоотдачи постоянный и т.п.), локальности (местный результат обобщается на весь объект) и автомодельности (определяемый параметр перестает зависить от определяющих параметров, например, 3-тий закон термодинамики).
8 лекция
10 Основные положения теории теплового пограничного слоя
10.1 Особенности и система дифференциальных
уравнений ламинарного пограничного слоя
При взаимодействии потока со стенкой на поверхности теплообмена возникают тонкие гидрадинамический и тепловой пограничные слои, в пределах которых происходит изменение скорости и температуры от значений на стенке (у = 0 wх = 0, t = tс) до значений их вдали от стенки.
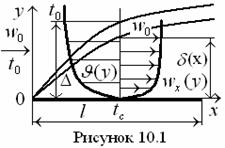 Характерные
особенности пограничного слоя (см. рисунок 10.1) позволяют
значительно
Характерные
особенности пограничного слоя (см. рисунок 10.1) позволяют
значительно
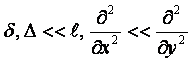 ~1 (10.1)
~1 (10.1)
упростить систему дифференциальных уравнений конвективного теплообмена
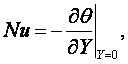 (10.2)
(10.2)
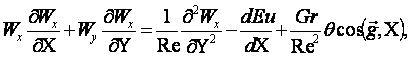 (10.3)
(10.3)
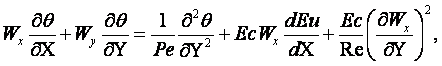 (10.4)
(10.4)
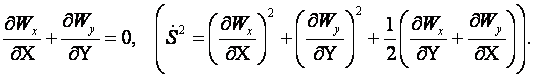 (10.5)
(10.5)
Эта значительно упрощённая система из 4-х уравнений позволяет определить θ, Wх, Wу и Nu. Искомая величина Wz отпала в виду двухмерности задачи, величина Eu перешла из статуса искомой величины в статус заданной величины и определяется по уравнению Бернулли для потенциального потока, так как по оценке слагаемых уравнения движения в проекции на ось Y приводит к
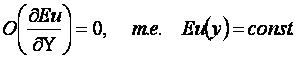 (10.6)
(10.6)
Из (10.3) и (10.4) получаются порядок значений и соотношения
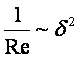 ,
, 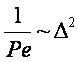 ,
, 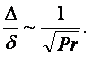 (10.7) ÷ (10.8)
(10.7) ÷ (10.8)
Из (10.3) также следует, что подъёмные силы должны учитываться, если
![]() ,
(10.9)
,
(10.9)
а из (10.4) следует, что теплоты трения и сжатия учитываются, если Ес ~ 1.
10.2 Турбулентный перенос импульса и тепла. Система
дифференциальных уравнений турбулентного пограничного слоя
Турбулентный перенос теплоты и импульса описываетя в виде
 (10.10)
(10.10)
![]() .
(10.11)
.
(10.11)
Турбулентные переносы импульса и теплоты представим по гипотезе Ж. Буссинеска и законами Ньютона и Фурье (знаки осреднения опускаем)
 (10.12)
(10.12) 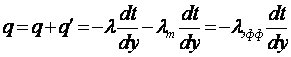 (10.13)
(10.13)
где ![]() и
и ![]() .
.
В результате такого подхода система дифференциальных уравнений турбулентного пограничного слоя записывается внешне как для ламинарного
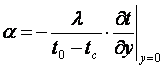 , (10.14)
, (10.14)
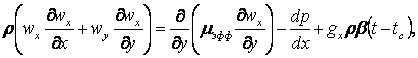 (10.15)
(10.15)
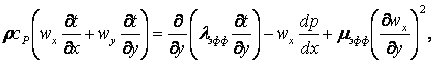 (10.16)
(10.16)
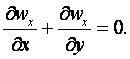 (10.17)
(10.17)
11 Гидродинамическая теория теплообмена
11.1 Физическое и турбулентное числа Прандтля
Из сравнения уравнения энергии (8.16) без учёта теплоты трения и сжатия и уравнения (8.17) для безнапорного движения без учёта подъёмных сил
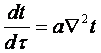 ,
, 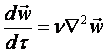 (11.1) ÷ (11.2)
(11.1) ÷ (11.2)
видно, что при ν = a (физическое число Pr = ν/а = 1 поля t и w полностью совпадают. Однако физическое число Прандтля различных сред различное. Больший интерес представляют турбулентные свободные течения, для которых аналогичное турбулентное число Прандтля Prт = νт/ат = 0,72 ¸ 0,75, а вблизи стенок Prт»1. Изучение процессов теплообмена на основе аналогии с переносом импульса носит название гидродинамической теории теплообмена.
11.2 Аналогия Рейнольдса
При условиях подобия полей температуры θ и скорости Wх соотношение (11.4)
 (11.3)
(11.3)
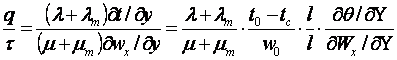 (11.4)
(11.4)
(где ![]() ) преобразуется к виду
) преобразуется к виду
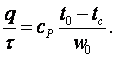 (11.5)
(11.5)
Подставив в (11.5) известные выражения
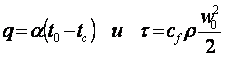 (11.6)
(11.6)
(где α и сf – коэффициенты теплоотдачи и трения) найдем, что
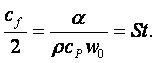 (11.7)
(11.7)
Это выражение (критерий Стэнтона) получено О. Рейнольдсом для определения коэффициента теплоотдачи через известный из гидродинамики коэффициент трения (в 1874 г.) и называется аналогией Рейнольдса. Ее можно представить в виде критериального уравнения теплоотдачи
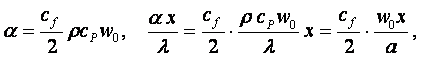
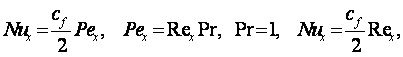 (11.8)
(11.8)
![]() . (11.9)
. (11.9)
Она развита для Pr = разное и Prт = 1 Прандтлем (1910г) и Тейлором (1919г) и для Pr и Prт = разные Т.Карманом (1939г), Г.Райхардта (1950г) [12].
12 Теплообмен при ламинарном течении Куэтта
Течение Куэтта (см. рисунок 12.1) безнапорное
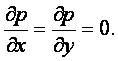 (12.1)
(12.1)
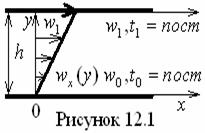 Для
непроницаемой стенки и при пренебрежимо малой естественной
конвекции
Для
непроницаемой стенки и при пренебрежимо малой естественной
конвекции
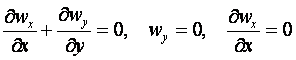 (12.2)
(12.2)
уравнение движения вязкой жидкости и его решение
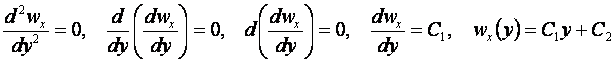
при![]() имеет
вид
имеет
вид
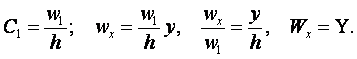
![]() (12.3)
(12.3)
Уравнение энергии
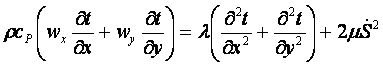 , (12.4)
, (12.4)
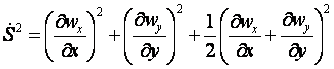
 сравнительной
оценкой слагаемых сводится к виду
сравнительной
оценкой слагаемых сводится к виду
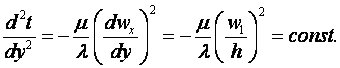 (12.5)
(12.5)
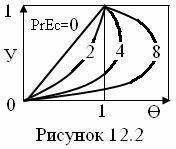
Решение (12.5) при постоянных значениях t1 и t0 (при у = h и 0) аналогично предыдущему и решению уравнения теплопроводности плоской стенки с источником теплоты постоянной мощности. Поэтому его решение приведём в следующем конечном виде (см. рисунок 12.2)
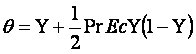 (12.6)
(12.6)
где 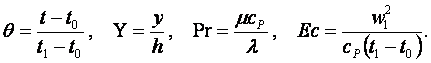
Отсюда видно, что при
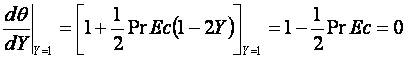 (12.7)
(12.7)
стенка не обменивается теплом с жидкостью и ее температура называется равновесной или собственной температурой
![]() (12.8)
(12.8)
Эта адиабатная температура трения на стенке связана с адиабатной
температурой сжатия потока на стенке следующим образом
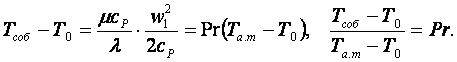 (12.9)
(12.9)
Заметим, что известный коэффициент
восстановления r - соотношение адиабатных температур
теплоты трения и сжатия. Он для ламинарного течения Куэтта (12.9)
и ламинарного и турбулентного обтекания пластины безграничным потоком соответственно равняется ![]() [12, 9,
1].
[12, 9,
1].
Очевидно, что при (по сравнению с (12.7))
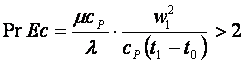 (12.10)
(12.10)
горячая стенка вместо ожидаемого охлаждения жидкостью может нагреваться за счёт теплоты ее трения (см. рисунок 12.2) с плотностью теплового потока
![]() (12.11)
(12.11)
9 лекция
13 Теплоотдача при вынужденном обтекании плоской стенки
13.1 Результаты теоретических решений уравнений
ламинарного пограничного слоя
 Точное решение динамической
задачи для ламинарного обтекания пластины Г. Блязиусом (1908 г) даёт для Pr = 0,6 ÷ 10 следующие результаты
(см. рисунок 13.1)
Точное решение динамической
задачи для ламинарного обтекания пластины Г. Блязиусом (1908 г) даёт для Pr = 0,6 ÷ 10 следующие результаты
(см. рисунок 13.1)

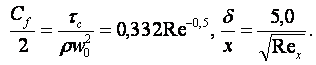 (13.1)
(13.1)
Решение тепловой задачи Э. Польгаузеном (1921 г) в той же в области числа Pr = 0,6 ÷ 10 показывает, что в условиях tc = const [12, 1, 9, 13]
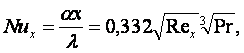 (13.2)
(13.2)
![]() (13.3)
(13.3)
 (13.4)
(13.4)
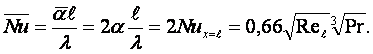 (13.5)
(13.5)
Приближённые решения этих задач с помощью интегральных соотношений с профилями скорости и температуры дают точность 3%:
![]() (13.6)
(13.6)
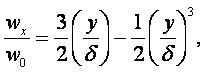 (13.7)
(13.7)
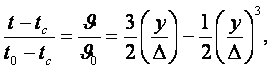 (13.8)
(13.8)
 (13.9)
(13.9)
13.2 Теплоотдача при ламинарном обтекании плоской стенки
Для теплоотдачи плоской стенки в ламинарном потоке
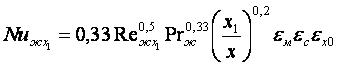 (13.10)
(13.10)
где поправки
М.А.Михеева и на изменение температуры стенки
по х ![]()

![]() (13.11)÷(13.12)
(13.11)÷(13.12)
и на наличие необогреваемого начального участка стенки длиной х0 = x1 - x
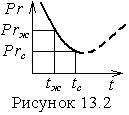
![]() (13.13)
(13.13)
где х1 и х отсчитываются от начала необогреваемого и обогреваемого участков соответственно.
В (13.12) для граничных условий tc
и qc = const ![]() соответственно.
соответственно.
Поправка на неизотермичность (13.11) получена
для части ![]() (см.
сплошную линию на рисунке 13.2) зависимости
(см.
сплошную линию на рисунке 13.2) зависимости ![]() и не применима для части
и не применима для части ![]() (см. пунктирную линию
на рисунке 13.2) той же зависимости
(см. пунктирную линию
на рисунке 13.2) той же зависимости ![]() .
.
13.3 Теплоотдача при турбулентном обтекании плоской стенки
Если известное ![]() подставить в аналогию
Рейнальдса
подставить в аналогию
Рейнальдса
![]() , (13.14)
, (13.14)
то получится критериальное уравнение теплоотдачи для числа Pr = 1 в виде
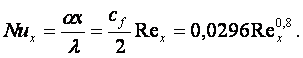 (13.15)
(13.15)
Экспериментальные описываются при Reжх = 105-7 уравнением
![]() (13.16)
(13.16)
Отсюда видно, что α(х)~х-0,2 и при tc = пост
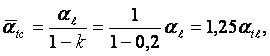 (13.17)
(13.17)
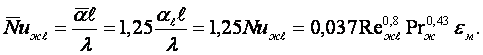 (13.18)
(13.18)
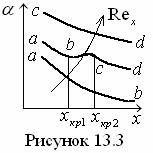 Ламинарный режим течения у плоской
стенки ав (cм. рисунок 13.3) с ростом значения числа Рейнольдса Reх переходит в смешанный
режим авсd с участками ламинарного ав,
переходного вс и турбулентного сd режимов течения, а затем с дальнейшим ростом значения числа Рейнольдса
переходный режим вс перемещается к началу течения и
устанавливается режим развитого турбулентного течения сd.
Ламинарный режим течения у плоской
стенки ав (cм. рисунок 13.3) с ростом значения числа Рейнольдса Reх переходит в смешанный
режим авсd с участками ламинарного ав,
переходного вс и турбулентного сd режимов течения, а затем с дальнейшим ростом значения числа Рейнольдса
переходный режим вс перемещается к началу течения и
устанавливается режим развитого турбулентного течения сd.
14 Теплоотдача при вынужденном течении жидкости в трубе
14.1 Уравнение Лайона
Для
гидродинамически стабилизированного ламинарного течения жид-кости в трубе ![]() длина участка термической
стабилизации
длина участка термической
стабилизации
при условиях
![]() равняется (см. рисунок 14.1)
равняется (см. рисунок 14.1)
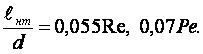 (14.1)
(14.1)
Для решения уравнения энергии без учета теплоты трения и сжатия

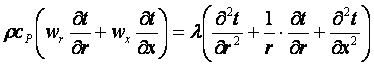 . (14.2)
. (14.2)
Lyon R.N. (1951г) представил (14.2) для ![]() (х) = пост с
учетом
(х) = пост с
учетом ![]() и
и ![]() для турбулентного
течения
для турбулентного
течения
 (14.3)
(14.3)
 В условиях qc =
пост qc/α = tc – tж = cont (что справедливо и при tc = const) из уравнения теплового баланса находим (см. рисунок
14.2)
В условиях qc =
пост qc/α = tc – tж = cont (что справедливо и при tc = const) из уравнения теплового баланса находим (см. рисунок
14.2)
 (14.4)
(14.4)
С учетом (14.4) уравнение энергии (14.3) записывается в виде обыкновенного дифференциального уравнения
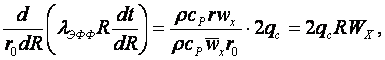 (14.5)
(14.5)
где ![]() и
и ![]() .
.
Первое интегрирование (14.5) дает
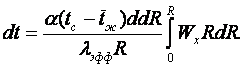 (а)
(а)
Температуру жидкости в (а) определим как среднюю расходную величину
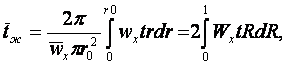
интеграл которой вычислим по частям
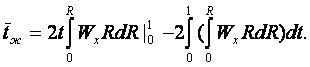 (б)
(б)
Вычислим первое слагаемое (б)
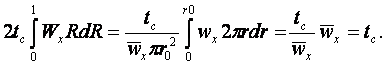 (в)
(в)
Подставив (в) в (б) и заменяя в полученном dt с помощью (а)
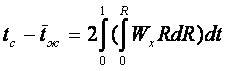
найдем уравнения Лайона для турбулентного и ламинарного (λт = 0) течений
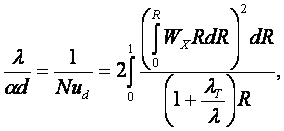 (14.6)
(14.6)
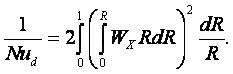 (14.7)
(14.7)
14.2 Теплоотдача при ламинарном течении жидкости в трубе
При гидродинамический стабилизированном ламинарном течении жидкости в трубе профиль скорости описывается уравнением Пуазейля
![]() (14.8)
(14.8)
Подставляя (14.8) в (14.7), получим ![]() . Аналогичное решение
для
. Аналогичное решение
для ![]() пост дает
значение
пост дает
значение ![]()
Для ламинарного вязкостного режима
течения при ![]() =
пост и
=
пост и ![]() Ма-Тун-цзе предложил формулу (1962г) [1]
Ма-Тун-цзе предложил формулу (1962г) [1]
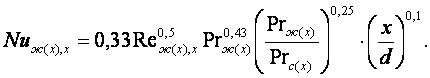 (14.9)
(14.9)
Для ламинарного вязкостно - гравитационного режима течения жидкости в трубе академик Михеев М.А. предложил эмпирическую формулу (1951г)
![]() (14.10)
(14.10)
где ![]() - поправка на изменение среднего
коэффициента теплоотдачи по длине участка стабилизации [1, 3].
- поправка на изменение среднего
коэффициента теплоотдачи по длине участка стабилизации [1, 3].
10 лекция
14.3 Теплоотдача при турбулентном течении жидкости в трубе
Для турбулентного течения в трубе с учетом коэффициента трения
![]() (14.11)
(14.11)
аналогия Рейнольдса (11.8) запишется в виде
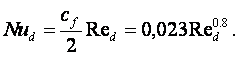 (14.12)
(14.12)
М.А.Михеев обобщил литературные данные в виде (1952г)
![]() (14.13)
(14.13)
Местные значения коэффициента теплоотдачи определяются по [1]
![]() (14.14)
(14.14)
где ![]() при
при ![]() и при t < 2000C, М <
1 для газов
и при t < 2000C, М <
1 для газов ![]() ;
;
![]() (14.15)
(14.15)
Неизотермичность нагрева газа в (14.13)
и (14.14) при ![]() учитывается
температурным фактором (
учитывается
температурным фактором (![]() )
)
![]() . (14.16)
. (14.16)
Для охлаждения турбулентного сверхзвукового
горячего потока в трубе ![]() εt в (14.4)
имеет вид (у пластины 0,38 вместо
0,42)
εt в (14.4)
имеет вид (у пластины 0,38 вместо
0,42)
![]() ,
, 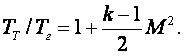 (14.17), (14.18)
(14.17), (14.18)
Уравнение Лайона для турбулентного течения жидких металлов: Prт = 1,
при tc = пост (Себан и Шимазаки) и ![]() = пост (Субботин
В.И. и др. 1963г)
= пост (Субботин
В.И. и др. 1963г)
![]() ,
, ![]() (14.19), (14.20)
(14.19), (14.20)
Для турбулентного стабилизированного течения жидкости в трубе (14.13)
α ~ λ, α ~ w0,8, αw ~ d-0,2, αG ~ d-1,8. (14.21)
Однако с уменьшением диаметра d по (14.21) увеличивается
не только ![]() ,
но и увеличивается коэффициент трения по (14.11) сf
,
но и увеличивается коэффициент трения по (14.11) сf![]() ~ dw-0,2, dG-0,4.
~ dw-0,2, dG-0,4.
14.4 Теплоотдача при переходном режиме течения жидкости в трубе
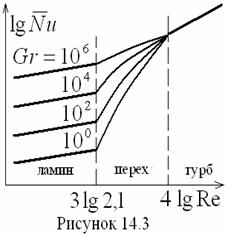
Теплоотдача при переходном режиме тече-ния жидкости в трубе рассчитывается по релакса-ционной схеме Л.А. Вулиса в следующем виде
![]() (14.22)
(14.22)
![]() (14.23)
(14.23)
![]()
![]() (14.13)
(14.13)
14.5 Влияние формы, изогнутости и шероховатости трубы на теплоотдачу
 1. Теплоотдача при турбулентном течении жидкости в некруглых каналах
рассчитывается по формулам теплоотдачи круглой трубы с помощью значения эквивалентного
диаметра dэ = 4f/u = 4πd2/(4πd) = d. Теплоотдача
при турбулентном течении
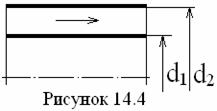
жидкости в кольцевом канале (с Pr = 0,7 ÷ 100, d2/d1 = 1,2 ÷ 14, ℓ = 50 ÷ 460dэ, см. рисунок 14.4) - по формуле
1. Теплоотдача при турбулентном течении жидкости в некруглых каналах
рассчитывается по формулам теплоотдачи круглой трубы с помощью значения эквивалентного
диаметра dэ = 4f/u = 4πd2/(4πd) = d. Теплоотдача
при турбулентном течении
жидкости в кольцевом канале (с Pr = 0,7 ÷ 100, d2/d1 = 1,2 ÷ 14, ℓ = 50 ÷ 460dэ, см. рисунок 14.4) - по формуле
![]() (14.24)
(14.24)
где d1 и d2 - внутренний и внешний диаметры кольцевого канала и dэ = d2 - d1.
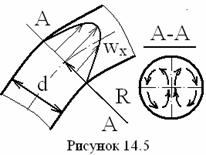
2. Теплоотдача в изогнутых трубах рассчитывается по формулам теплоотдачи при ламинарном (14.7) - (14.10) и турбулентном (14.13) течениях жидкости в прямых трубах следующим образом (ниже R- радиус изгиба, см. рисунок 14.5):
а) при ![]() (14.25)
(14.25)
![]() ;
(14.10)
;
(14.10)
б) при (для ![]() )
) ![]() (14.26)
(14.26)
![]() ; (14.13)
; (14.13)
в) при ![]() по (14.13) с поправкой
по (14.13) с поправкой
![]()
![]() .
(14.27)
.
(14.27)
3. Для расчета теплоотдачи труб с регулярной шероховатостью поверхности с относительным шагом s/h = 8 ÷ 15 (h - высота выступов, см. рисунок 14.6) академик Гомелаури В.И. рекомендовал формулу (Pr = 1 ÷ 80)
![]() (14.28)
(14.28)
где при ![]()
![]() (14.29)
(14.29)
и при ![]()
![]() (14.30)
(14.30)
14.6 Теплоотдача при поперечном обтекании цилиндра
 Поперечное обтекание цилиндра при
Поперечное обтекание цилиндра при ![]() - непрерывное (стоксовое). При Re > 5 с нарастанием толщины пограничного слоя по
периметру цилиндра (φ) происходит его торможение (0<dp/dx, dwx/dx<0) и в условиях
- непрерывное (стоксовое). При Re > 5 с нарастанием толщины пограничного слоя по
периметру цилиндра (φ) происходит его торможение (0<dp/dx, dwx/dx<0) и в условиях ![]() - отрыв от стенки с дальнейшим образованием вихревого следа
Кармана в кормовой части цилиндра.
- отрыв от стенки с дальнейшим образованием вихревого следа
Кармана в кормовой части цилиндра.
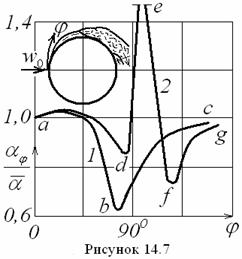
Для иллюстрации влияния гидродинами-ки на теплоотдачу на рисунке 14.7 приводятся две характерные линии с отрывами ламинар-ного 1 и турбулентного 2 пограничных слоев.
Критериальное уравнение теплоотдачи при поперечном обтекании цилиндра записывается в виде
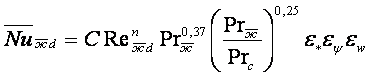 (14.31)
(14.31)
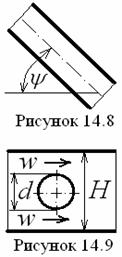 где
где ![]() (14.32)
(14.32)
- поправка на интенсивность турбулентности Tu (Е.П.Дыбан
и др. RеTu = ![]() , 1972г);
, 1972г);
![]() (14.33)
(14.33)
- угол атаки (![]() = 30÷900, Re =
5÷2·105, см. рисунок 14.8);
= 30÷900, Re =
5÷2·105, см. рисунок 14.8);  ; (14.34)
; (14.34)
- поправка на стесненность потока (H – поперечный
размер канала, см. рисунок 14.9);
w – определяющая скорость потока в стесненном месте (С и n см. в [1, 3]).
14.7 Теплоотдача при поперечном обтекании пучка труб
Средний коэффициент теплоотдачи i- ряда труб определяется критериальным уравнением (Re =103 ÷ 105, см. рисунки 14.10, 14.11)
![]() (14.35)
(14.35)
где значения поправок ![]() - на номера ряда и шага труб и угла атаки и постоянных C и n
приводятся в справочниках, задачниках [1,
3 и др.].
- на номера ряда и шага труб и угла атаки и постоянных C и n
приводятся в справочниках, задачниках [1,
3 и др.].
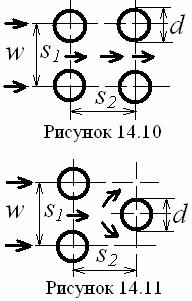 Средний коэффициент теплоотдачи пучка труб
Средний коэффициент теплоотдачи пучка труб
 (14.36)
(14.36)
Для расчета теплоотдачи глубинных рядов коридорных и
шахматных пучков труб при ![]() применяется формула
применяется формула
![]() (14.37)
(14.37)
Для тесно расположенных десяти рядных пучков труб (![]() ) используется формула (Сшах = 1,8 (Re = 10 ÷ 200), Cкор
= 1,2 (Re = 10 ÷ 150))
) используется формула (Сшах = 1,8 (Re = 10 ÷ 200), Cкор
= 1,2 (Re = 10 ÷ 150))
![]() (14.38)
(14.38)
15 Теплоотдача при свободной конвекции
15.1 Теоретические результаты исследования
теплоотдачи при свободной конвекции
Конечные результаты решения уравнений ламинарного пограничного
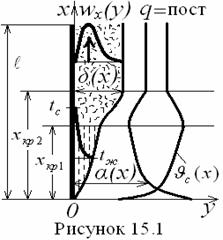 слоя при tc = const
представлены в виде критериальных
уравнений местного и среднего коэффициентов теплоотдачи (см. рисунок 15.1)
слоя при tc = const
представлены в виде критериальных
уравнений местного и среднего коэффициентов теплоотдачи (см. рисунок 15.1)
 (15.1)
(15.1)
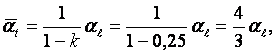
![]() (15.2)
(15.2)
![]() (15.3)
(15.3)
15.2 Результаты экспериментального исследования
теплообмена при свободной конвекции
1. Данные для теплоотдачи вертикальных стен и труб при свободной
конвекции при ![]() пост представим уравнением и
таблицей 15.1
(αq/αt = 1,07)
пост представим уравнением и
таблицей 15.1
(αq/αt = 1,07)
![]() (15.4)
(15.4)
2. Для расчета теплоотдачи горизонтальных труб и плит при![]() и
и ![]() И.М.Михеевой (1959г) предложена
формула
И.М.Михеевой (1959г) предложена
формула
![]() (15.5)
(15.5)
Т а б л и ц а 15.1
|
Режимы |
Плёночный |
Ползучий |
Ламинарный |
Переход- ный |
Турбулент- ный |
|
Rai |
< 10-3 |
|
|
|
|
|
С
|
0,5 (Л.С.Эй- генсон) |
(М.А.Ми- хеев) |
(И.М.Пчел-кин) |
|
(М.А.Ми- хеев) |
|
n |
0 |
1/8 |
1/4 |
|
1/3 |
|
i |
cгd |
cгd |
|
|
|
|
εм |
|
|
εм |
|
εм |
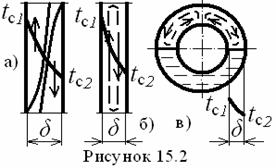 3. Теплоотдача при свободной конвекции в ограниченном пространстве определяется
аналогично плотности теплового потока для теплопроводности в виде (см. рисунок
15.2)
3. Теплоотдача при свободной конвекции в ограниченном пространстве определяется
аналогично плотности теплового потока для теплопроводности в виде (см. рисунок
15.2)
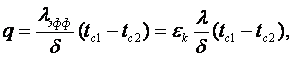 (15.6)
(15.6)
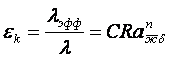 , (15.7)
, (15.7)
С = 1, 0,105; 0,40; n =
0; 0,3; 0,2 для ![]() .
.
11 лекция
Раздел четвертый. Тепломассообмен при фазовых
и химических превращениях
16 Теплообмен при конденсации чистого пара
16.1 Термодинамические понятия и особенности фазовых переходов

В зависимости от того жидкость смачивает или не смачивает
поверхность стенки, конденсация пара на стенке бывает пленочной или
капельной (см. рисунок 16.1).
Характер конденсации опеделяется
поверхностным натяжением пар - жидкость σпж, стенка - жидкость σсж, стенка - пар
σсп (H/м) и краевым углом ![]() в виде
в виде
![]() (16.1)
(16.1)
 Капля
жидкости в паровом пространстве подвержена дополнительному давлению силы
поверхностного натяжения, определяемому формулой Лапласа (здесь и далее σпж = σ)
Капля
жидкости в паровом пространстве подвержена дополнительному давлению силы
поверхностного натяжения, определяемому формулой Лапласа (здесь и далее σпж = σ)
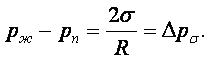 (16.2)
(16.2)
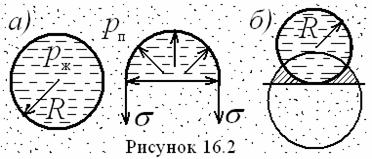
Ее можно найти из равенства сил (см. рисунок 16.2а), как (16.3)
![]() Равновесное давление насыщенного пара над выпуклой поверхностью
Равновесное давление насыщенного пара над выпуклой поверхностью ![]() жидкой капли
больше, чем над плоской поверхностью
жидкой капли
больше, чем над плоской поверхностью ![]() жидкости на величину, определяемой формулой
Кельвина (см. рисунок 16.2б)
жидкости на величину, определяемой формулой
Кельвина (см. рисунок 16.2б)

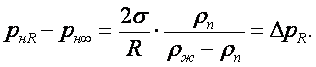 (16.4)
(16.4)
Под действием разности давлений насыщенного пара над выпуклыми и плоскими частями поверхности капли пар в пристенном слое перемещается к корням растущих капель (см. рисунок 16.3).
16.2 Теплоотдача при пленочной конденсации неподвижного пара
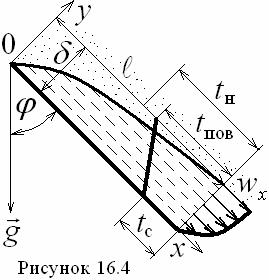 Система
дифференциальных уравнений теплообмена (8.15) – (8.18) для пленочной конденсации пара на наклонной плоской стенке (см. рисунок 16.4) будет иметь
вид
Система
дифференциальных уравнений теплообмена (8.15) – (8.18) для пленочной конденсации пара на наклонной плоской стенке (см. рисунок 16.4) будет иметь
вид
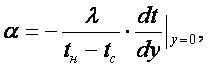 (16.5)
(16.5)
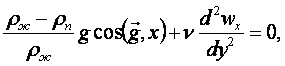 (16.6)
(16.6)
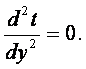 (16.7)
(16.7)
Граничные условия
при у = 0 wx = 0, t = tc = пост, (16.8)
при у = ![]() dwx/dy =
0, t = tн =
пост.(16.9)
dwx/dy =
0, t = tн =
пост.(16.9)
Решение
Нуссельта (16.5) с учетом (16.8) и (16.9) сводит определение
коэффициента теплоотдачи к нахождению толщины слоя конденсата ![]()
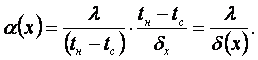 (16.10)
(16.10)
Решение (16.7) с учетом (16.8) и (16.9)
![]()
![]()
![]()
![]()
![]()
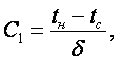

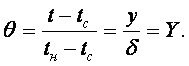 (16.11)
(16.11)
Решение (16.6) с учетом (16.8) и (16.9) имеет вид
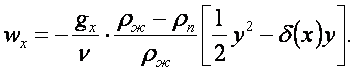 (16.12)
(16.12)
С помощью уравнения теплового баланса на отрезке dx слоя конденсата
dQx = rdGx (16.13)
где r – удельная теплота конденсации пара, Дж/кг;
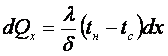 ,
, ![]() (16.14)
(16.14)
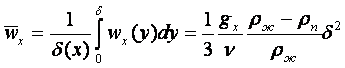 (16.15)
(16.15)
- средняя скорость потока конденсата, находим
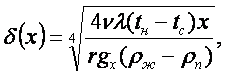 (16.16)
(16.16)
 (16.17)
(16.17)
Среднее значение коэффициента теплоотдачи
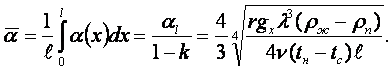 (16.18)
(16.18)
Решение Нуссельта (16.18) представим в виде критериального уравнения
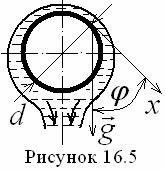
![]() , (16.19)
, (16.19)

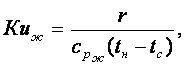
![]() числа Грасгофа, Кутателадзе и Прандтля;
числа Грасгофа, Кутателадзе и Прандтля;
![]() - поправка на φ
стенки.
- поправка на φ
стенки.
Аналогичное решение получено для теплоотдачи конденсирующегося пара на горизонтальной трубе (см. рисунок 16.5) Нуссельтом (при tc = пост, С = 0,728) и Лабунцовым Д.А. (в 1965г при qс = пост, С = 0,693)
![]() (16.20)
(16.20)
16.3 Анализ решения Нуссельта для теплоотдачи
при пленочной конденсации пара
Кружилин Г.Н. и Лабунцов Д.А. (1937г) решили задачу с учетом конвективного переноса теплоты и импульса и показали:
а) Nuуточн = NuN ("N" - решение Нуссельта) для Pr = 1 ÷ 100 и Ku > 5, а для
Ku < 5 (т.е. для больших температурных напоров (tн - tc) и малых r/cр, что имеет
место в околокритической зоне фазового перехода) Nuуточн > NuN;
б) Nuуточн < NuN для Pr << 1 в широком диапазоне изменения tн - tc.
В 1957 году Д.А. Лабунцов предложил поправку на неизотермичность
pадачи (для
диапазона изменения ![]() и
и ![]() ) в виде
) в виде
![]() (16.21)
(16.21)
В 1948 году академик Капица П.Л. учитывает влияние
волнообразования на поверхности пленки конденсата и показывает, что ![]() .
.
В результате критериальные уравнения теплоотдачи при ламинарном течении пленки конденсата вдоль плоской стенки (16.19) и для ламинарного стекания пленки конденсата с горизонтальной трубы (16.20) имеют вид
![]() (16.22)
(16.22)
![]() (16.23)
(16.23)
В (16.23) вводят поправку на волнообразование при ![]() .
.
Критериальное уравнение теплоотдачи при турбулентном
режиме течения пленки конденсата на вертикальной охлаждаемой стенке,
наступающем при ![]() (300 -
500) или
(300 -
500) или ![]() , имеет вид
, имеет вид
![]() (16.24)
(16.24)
16.4 Теплоотдача при пленочной конденсации движущегося пара
1. Для случая конденсации движущегося пара вдоль вертикальной стенки и трубы критериальное уравнение теплоотдачи имеет вид
![]() , (16.25)
, (16.25)
 (16.26)
(16.26)
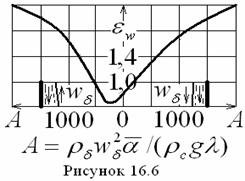 - поправка на
перегрев пара;
- поправка на
перегрев пара;
![]() термодинамический
параметр пара (см. рисунок 16.6);
термодинамический
параметр пара (см. рисунок 16.6);
С = 1,15 и 0,068, n = 1/4 и 1/3 для ламинарного и турбулентного стекания пленки конденсата вдоль вертикальной стенки;
С = 0,728 и n = 1/4 для ламинарного стекания пленки конденсата вдоль вертикаль-
ной трубы (ℓ = d).
2. Теплоотдача при пленочной конденсации движущегося
сверху вниз пара на горизонтальных одиночных и пучках труб определяется той же
формулой (16.25) при ℓ = d, С = 0,728, n = 1/4, εпп и εw (![]() = 400 ÷ 6000)
= 400 ÷ 6000)
 (16.27)
(16.27)
Теплоотдача нижележащих труб уменьшается из-за стекания конденсата с верхних труб, что учитывается введением в (16.25) множителя (Берман Л.Д.)
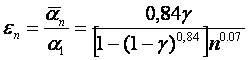 (16.28)
(16.28)
где ![]() - степень
конденсации пара с расходом D;
- степень
конденсации пара с расходом D;
n – номер рядов труб по высоте коридорного пучка или половины номера рядов труб по высоте шахматного пучка.
16.5 Теплоотдача при пленочной конденсации
движущегося пара внутри трубы
Для ламинарного течения пленки конденсата движущегося
сверху вниз насыщенного пара коэффициент теплоотдачи определяется в сравнении с местным коэффициентом теплоотдачи Нуссельта (16.17)
в виде (Исаченко В.И. и др. 1974г, Reпdн = wпd/νп ≤ 1,7·103, ![]() = 3,6 ÷ 33,5 м/с, Reжх = qcx/rμж)
= 3,6 ÷ 33,5 м/с, Reжх = qcx/rμж)
![]() , (16,29)
, (16,29)
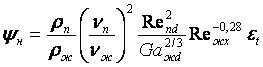 (для
(для ![]() ). (16.30)
). (16.30)
Для турбулентного течения конденсата сверху вниз местный коэффициент теплоотдачи определяется по формуле (Reцdн = wпd/νп > 103, Prж = 1, χ1, χ2 = 0 ÷ 1, рn = 1,22 ÷ 8,82 MПа)
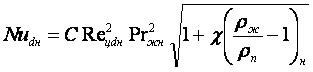 (16.31)
(16.31)
где ![]() - массовое
расходное паросодержание в сечении;
- массовое
расходное паросодержание в сечении;
![]() - скорость циркуляции;
- скорость циркуляции;
С = 0,024, 0,026 и 0,032 - для стальных, латунных и медных труб.
Среднее значение коэффициента теплоотдачи определяется как среднее арифметическое его значений на входе с χ1 и на выходе с χ2 трубы по (16.31)
![]() (16.32)
(16.32)
Для пленочной конденсации движущегося пара в трубе Reжкр = qcxкр/rμж ≈ 200.
12 лекция
16.6 Механизм и расчетные формулы теплообмена
при капельной конденсации пара
С учетом соотношения пропорциональности достаточно малых ∆Тн и ∆рн (16.33), (16.4) и уравнения Клапейрона-Клаузиуса
![]() (16.33)
(16.33)

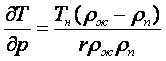 (16.34)
(16.34)
(16.33) можно записать в виде
 (16.35)
(16.35)
Это указывает на наличие минимального радиуса зарождения капли (например, при р = 1 бар и ∆Тохл = 10, 0,1 0C отсюда получаем, что Rмин = 0,2·10-8 м = 0,002 мк и 0,2 мк соответственно)
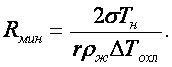 (16.36)
(16.36)
В действительности из-за того, что, согласно Кельвину (16.4), равновесное давление насыщенного пара над выпуклой поверхностью рнR жидкой капли больше, чем над плоской поверхностью pн∞ жидкости, конденсат образуется у стенки в виде пленки и под действием термокапиллярных сил по Клапейрону-Клаузиусу (16.34) быстро приобретает форму капли (см. рисунок 16.7), что подтверждено визуально картинами скоростных киносъемок Зубера.
Теплоотдача при капельной конденсации неподвижного насыщенного водяного пара на вертикальных стенках и трубах и горизонтальном пучке труб (в диапазоне изменения Prж = 1,75 ÷ 3,65, Рп = 0,12 ÷ 1 бар и критерия термокапиллярных сил Пк = (0,98 ÷ 4,5)·10-2) описывается уравнением [1]
![]() (16.37)
(16.37)
где 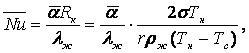
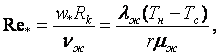

 - скорость отвода теплоты капли
теплопроводностью;
- скорость отвода теплоты капли
теплопроводностью;
 -
отношение сил натяжения к силам вязкости;
-
отношение сил натяжения к силам вязкости;
 - тампературный коэффициент натяжения;
- тампературный коэффициент натяжения;
![]() - число Лапласа;
- число Лапласа;
![]() - относительное изменение коэффициента поверхностного
- относительное изменение коэффициента поверхностного
натяжения в диапазоне изменения температуры капли от Тc до Тн;
![]() - сила поверхностного натяжения на длине,
равной радиусу капли;
- сила поверхностного натяжения на длине,
равной радиусу капли;
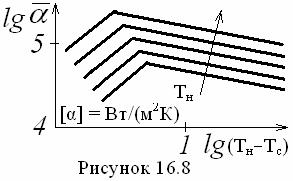 С = 3,2·10-4, 5·10-6,
n = - 0,84, -1,57 при Re* = 8·10-4 ÷3,3·10-3 и
3,3·10-3÷3,5·10-2 соответственно.
С = 3,2·10-4, 5·10-6,
n = - 0,84, -1,57 при Re* = 8·10-4 ÷3,3·10-3 и
3,3·10-3÷3,5·10-2 соответственно.
Из (16.37) следует, что в диапазоне tн
= 50 ÷ 100 0С и Тн
÷ Тс = 0,8 ÷ 14 0С ![]() (
(![]() ) при Re* < или > 3,3·10-3 (см. рисунок
16.8).
) при Re* < или > 3,3·10-3 (см. рисунок
16.8).
Это
обусловлено тем, что в области меньших значений Re* рост числа капель способствует интенсификации
теплоот-дачи при капельной конденсации. При Re* > 3,3·10-3 происходит такое пресыщение (кризис) капельной
конденсации, что термическое сопротивление конденсата подавляет влияние роста
числа капель и ![]() уменьшается
с ростом
уменьшается
с ростом ![]() .
.
Влияние скорости пара на теплоотдачу при капельной конденсации для движения насыщенного пара сверху вниз вдоль вертикальной пластины в диапазоне Re* = 8·10-4 ÷ 3,3·10-3 учитывается поправкой к (16.37) в виде [1]
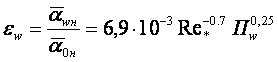 (16.38)
(16.38)
где ![]() - средняя скорость пара.
- средняя скорость пара.
Из (16.38) следует, что ![]() и при
и при ![]() и
и
![]() коэффициент
теплоотдачи максимально увеличивается в 3,5 раза и достигает значения
коэффициент
теплоотдачи максимально увеличивается в 3,5 раза и достигает значения ![]() = 425 кВт/(м2К).
В области кризиса капельной конденсации (Re* > 3,3·10-3) влияние
скорости пара на телообмен сводится на нет.
= 425 кВт/(м2К).
В области кризиса капельной конденсации (Re* > 3,3·10-3) влияние
скорости пара на телообмен сводится на нет.
Содержание 1% воздуха в водяном паре уменьшает α на 60%. Это влияние резко снижается с увеличением скорости пара.
17 Теплоотдача при кипении жидкости
17.1 Факторы, влияющие на теплоотдачу при кипении жидкости
1. Минимальный радиус образования пузырька. Пузырек пара радиуса R с давлением рn в жидкости с давлением рж подвержен дополнительному давлению поверхностного натяжения (по формуле Лапласа (16.2) (рn > рж))
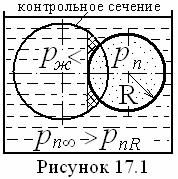
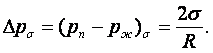 (17.1)
(17.1)
Выход молекул с вогнутой поверхности жидкости в
паровое пространство пузырька сопряжен преодолением дополнительного давления
(по сравнению со случаем с плоской поверхностью), обусловленного притяжением
молекул, находящихся в заштрихованной области, показаной на рисунке 17.1 (рпr < рn![]() ), и определяемого формулой Кельвина (16.3)
), и определяемого формулой Кельвина (16.3)
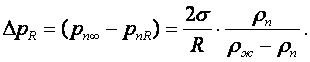 (17.2)
(17.2)
Существование образовавшегося пузырька возможно, если давление насыщенного пара будет достаточным для преодоления сил поверхностного натяжения (17.1) и кривизны фазовых границ (17.2)
 (17.3)
(17.3)
Этому превышению давления соответствует перегрев жидкости
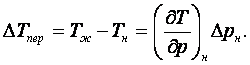 (17.4)
(17.4)
Это (Тж > Тн) известно как необходимое условие парообразования.
Подставляя (17.3) в (17.4) и учитывая уравнение Клапейрона – Клаузиуса
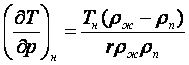 (17.5)
(17.5)
получим
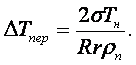 (17.6)
(17.6)
Данному термодинамическому равновесию параметров отвечает начальный (минимальный) радиус пузырька
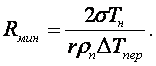 (17.7)
(17.7)
Расчеты показывают, что при ∆tпер = 250C и рн = 1, 100 бар пузырька воды Rмин = 1,3·10-3 и 0,12·10-3мм. Малость R мин позволяет принять ∆Тпер = Тc – Тн.
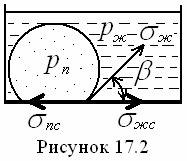 2. Работа образования пузырька. Пузырек пара с объемом V и поверхностью
F, образующийся на участке поверхности стенки нагрева Fc, удерживается силами натяжения жидкости σж(F - Fc) и адгезии поверхности стенки (σпс - σжс)Fс (см. рисунок 17.2).
2. Работа образования пузырька. Пузырек пара с объемом V и поверхностью
F, образующийся на участке поверхности стенки нагрева Fc, удерживается силами натяжения жидкости σж(F - Fc) и адгезии поверхности стенки (σпс - σжс)Fс (см. рисунок 17.2).
Работа образования пузырька L и возникшая разность конечной и начальной потенциальной энергии давления пара и жидкости затрачиваются против действия сил поверхностного натяжения жидкости и адгезии стенки
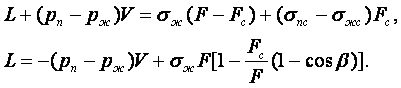 (17.8)
(17.8)
Из (17.8) следует, что при Fc = 0 (образование пузырька в объеме жидкости) эта работа максимальна
![]() (17.9)
(17.9)
 и минимальна, когда поверхность стенки нагрева пузырька Fc стремится к полной поверхности пузырька F (см. рисунок
17.3).
и минимальна, когда поверхность стенки нагрева пузырька Fc стремится к полной поверхности пузырька F (см. рисунок
17.3).
Вероятность образования пузырька тем больше, чем меньше L, т.е. чем больше Fc/F. Поэтому различные неровности поверхности стенки нагрева пузырька (щели, выступы) служат центрами парообразования (второе условие кипения жидкости). Согласно (17.7) с ростом ∆Тпер уменьшается Rмин образования пузырька и резко увеличивается число центров парообразования.
3. Рост и отрыв пузырьков при кипении жидкости. Для пузырьков принимаем ![]() и записываем приток тепла к
сферической оболочке пузырька за время
и записываем приток тепла к
сферической оболочке пузырька за время ![]()
 (17.10)
(17.10)
В результате произойдет увеличение объема и массы пузырька
![]()
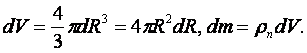 (17.11)
(17.11)
Закон роста пузырька пара можно найти из теплового баланса
![]()
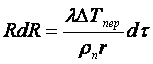 и при ТФС и
и при ТФС и ![]()
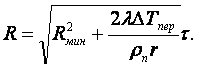 (17.12)
(17.12)
Из условия равновесия подъемный силы пузырька и силы адгезии стенки находится максимальный радиус роста пузырька [1]
![]() (17.13)
(17.13)
Расчеты для воды β = 500C при ∆Тпер = 250C и рn = 1 и 100 бар показывают, что Rмакс = 1,25 и 0,625 мм, Rмакс/Rмин = 103 и 5,2·103, Vмакс/Vмин ≈ 109 и 1011, τ = 0,062 и 1,08с соответственно.
В перегретой жидкости после отрыва от поверхности нагрева продолжается рост и подъем пузырьков вне граничного слоя и далее они разрушаются в объеме и на поверхности жидкости, перенося горячую массу пара и отдавая тепло.
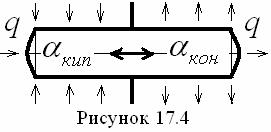 Все
указанные факторы, а также высокие значения
λ и ср воды настолько интенсифицируют теплообмен, что
значение коэффициента теплоотдачи при кипении может
достигать миллиона Вт/(м2К).
Все
указанные факторы, а также высокие значения
λ и ср воды настолько интенсифицируют теплообмен, что
значение коэффициента теплоотдачи при кипении может
достигать миллиона Вт/(м2К).
Особенности теплообмена при фазовых переходах широко используются на практике. Особую роль, например, тепловые трубки играют в электронике, в космической технике и энергетике для передачи тепла с очень высокой интенсивностью (см. рисунок 17.4).
13 лекция
17.2 Переход пузырькового режима кипения к пленочному режиму
Рассмотрим типичные зависимости коэффициента теплоотдачи α и плотности теплового потока q = α(Tc - Tн) от ∆Tпер = Tc - Tн на примере кипения воды в большом объеме при атмосферном давлении (см. рисунок 17.5).
При![]() Тпер < 5 0C (до точки А) кипение слабое и его закономерности теплоотдачи
примерно такие же как для некипящей жидкости. При
Тпер < 5 0C (до точки А) кипение слабое и его закономерности теплоотдачи
примерно такие же как для некипящей жидкости. При ![]() Тпер = 5 ÷ 30 0С
(между точками А и В) происходит интенсивное пузырьковое кипение. Здесь α
и q резко возрастают с увеличением
Тпер = 5 ÷ 30 0С
(между точками А и В) происходит интенсивное пузырьковое кипение. Здесь α
и q резко возрастают с увеличением ![]() Тпер. Затем после
достижения максимальных значений
Тпер. Затем после
достижения максимальных значений ![]() и
и ![]() (называемой первой
критической нагрузкой) величины α и q
стремительно падают, несмотря на рост ∆Tпер. Начиная с
точки В число образующихся пузырьков превышает число
пузырьков, покидающих пристенный слой. Правее точки С на поверхности стенки
возникает устойчивая паровая пленка, оттесняющая кипящую жидкость от стенки, и
устанавливается пленочный режим кипения. При этом все
факторы интенсификации теплообмена при кипении жидкости подавляются
и теплоотдача определяется слабым механизмам теплопроводности с λп
пара, что в десятки раз меньше λж жидкости
(называемой первой
критической нагрузкой) величины α и q
стремительно падают, несмотря на рост ∆Tпер. Начиная с
точки В число образующихся пузырьков превышает число
пузырьков, покидающих пристенный слой. Правее точки С на поверхности стенки
возникает устойчивая паровая пленка, оттесняющая кипящую жидкость от стенки, и
устанавливается пленочный режим кипения. При этом все
факторы интенсификации теплообмена при кипении жидкости подавляются
и теплоотдача определяется слабым механизмам теплопроводности с λп
пара, что в десятки раз меньше λж жидкости ![]() . Значение
α падает почти в 30 раз до уровня 1,2 кВт/(м2К) и имеет слабую тенденцию к росту за
счет теплового излучения, так как.
. Значение
α падает почти в 30 раз до уровня 1,2 кВт/(м2К) и имеет слабую тенденцию к росту за
счет теплового излучения, так как. ![]() достигает 700 ÷ 1000 0С.
достигает 700 ÷ 1000 0С.
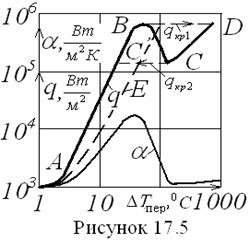 При паровом
обогреве стенки (Тс = const) кривая АВСD реализуется как при увеличении, так и при уменьшении
При паровом
обогреве стенки (Тс = const) кривая АВСD реализуется как при увеличении, так и при уменьшении ![]() .
.
При ![]() в точке В происходит
резкий скачок
в точке В происходит
резкий скачок ![]() по
пунктирной прямой в точку D. В результате температура
поверхности нагрева возрастает настолько, что может произойти термомеханическое
разрушение стенки. Если после достижения устойчивого пленочного кипения снижать
тепловую нагрузку от точки D при qс
= пост = различная, то кривая повторится только до точки С. При qпост
по
пунктирной прямой в точку D. В результате температура
поверхности нагрева возрастает настолько, что может произойти термомеханическое
разрушение стенки. Если после достижения устойчивого пленочного кипения снижать
тепловую нагрузку от точки D при qс
= пост = различная, то кривая повторится только до точки С. При qпост ![]() qкр2
qкр2 ![]() 230 кВт/м2
(кр2 - вторая критическая тепловая нагрузка) в точке С происходит скачок от
пленочного режима в режим пузырькового кипения по прямой пунктирной линии СС’ в
точку С’. Это явление известно под названием теплового гистерезиса (С’ВDСС’, (греческое)
запаздывание).
230 кВт/м2
(кр2 - вторая критическая тепловая нагрузка) в точке С происходит скачок от
пленочного режима в режим пузырькового кипения по прямой пунктирной линии СС’ в
точку С’. Это явление известно под названием теплового гистерезиса (С’ВDСС’, (греческое)
запаздывание).
Известен и третий кризис кипения, когда происходит непосредственный переход однофазной конвекции к пленочному режиму, минуя стадию пузырькового кипения (линия АЕ).
17.3 Теплоотдача при саободном кипении жидкости
Обширные опытные данные для теплоотдачи при свободном кипении различных жидкостей обобщены Д.А.Лабунцовым (р = 0,045 ÷ 175 бар, 1960г)
![]()
![]() (17.14)
(17.14)
где 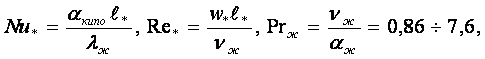 С =
С =
0,0625 и 0,125, n = 0,5 и 0,65 при Re* = 10-5 ÷ 10-2 и 10-2 ÷ 104.
В качестве определяющего размера в (17.14) принята величина, пропорциональная минимальному радиусу пузырька (17.7)
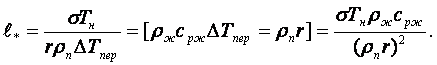 (17.15)
(17.15)
Характерная скорость в (17.14) определяется по тепловому балансу
![]() (17.16)
(17.16)
При кипении
воды в диапазоне ![]() используется формула
используется формула
![]() (17.17)
(17.17)
где [q] = Вт/м2 и [р] = бар [1].
17.4 Теплоотдача при течении кипящейся жидкости в трубе
Для
расчета теплоотдачи при течении кипящейся жидкости
в трубе дополнительно к (17.14) учитывается влияние скорости циркуляции
двухфазной среды ![]() с
помощью формулы Д.А.Лабунцова
с
помощью формулы Д.А.Лабунцова
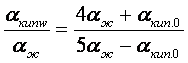 (17.18)
(17.18)
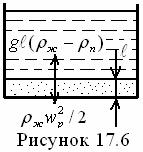 где
где ![]() - коэффициент теплоотдачи,
определяемый по формулам при конвекции
однофазной жидкости при wц;
- коэффициент теплоотдачи,
определяемый по формулам при конвекции
однофазной жидкости при wц;
![]() - коэффициент теплоотдачи, вычисляемый по
(17.14).
- коэффициент теплоотдачи, вычисляемый по
(17.14).
Для (17.18) выделяются три области:
а) при ![]() принимается
принимается ![]()
б) при ![]() принимается
принимается ![]() ;
;
в) при ![]() расчет производится
по (17.18).
расчет производится
по (17.18).
17.5 К расчету критической тепловой нагрузки при кипении жидкости
Плотность подъемной силы пленки пара толщины ℓ на стенке равняется встречному динамическому напору жидкости (см. рисунок 17.6)
![]() (17.19)
(17.19)
где wp – равновесная скорость притока жидкости и отвода пара, равная
![]() ; (17.20)
; (17.20)
qкрит – критическая тепловая нагрузка стенки.
Равенствам (17.19) и (17.20) соответствует критическое число
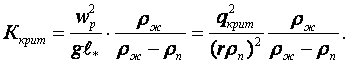 (17.21)
(17.21)
За характерный размер в (17.21) принят ℓ* = Rмин/2 (17.15). Критическая
интенсивность теплообмена определяется следующими соотношениями
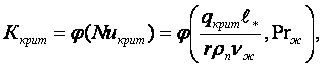

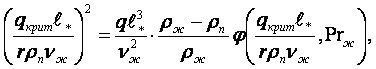
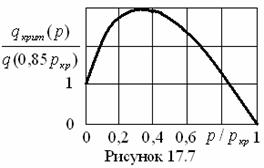
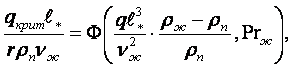 (17.22)
(17.22)
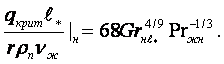 (17.23)
(17.23)
Экстремальная зависимость ТФС жидкости обусловливает
оптимальную критическую нагрузку для кипения воды ![]() при р = 0,26 ркр = 60 бар (см.
рисунок 17.7). Этому соответствует понятие предельной температуры перегрева
поверхности нагрева
при р = 0,26 ркр = 60 бар (см.
рисунок 17.7). Этому соответствует понятие предельной температуры перегрева
поверхности нагрева ![]() определяемой
с помощью (17.23) и (17.14).
определяемой
с помощью (17.23) и (17.14).
14 лекция
18 Массообмен
18.1 Понятия, механизмы и законы диффузии
Диффузией (молярным массообменном) называют самопроизвольный процесс выравнивания поля концентрации. Перенос вещества по нормали к поверхности одной концентрации в единицу времени называют потоком массы J, кг/с. Плотность потока массы
![]()
молекулярной диффузией одного из компонентов в неподвижной двухкомпонентной смеси с ρ при Т и р = пост определяется законом Фика
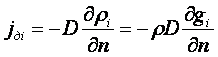 (18.1)
(18.1)
где D – коэффициент молекулярнoй диффузии одного компонента относительно другого, м2/с.
Закон Фика аналогичен закону Фурье. В газовых смесях концентрацию ρ можно записывать через парциальное давление по уравнению состояния
 (18.2)
(18.2)
где Dpi = D/RiT - коэффициент молекулярной диффузии, отнесенный к градиенту парциального давления рассматриваемого компонента, с.
Если Т и р смеси переменны, то возникает термо– и бародиффузия. В результате возникает дополнительный тепловой поток (термоэффект).
Далее рассмотрим общие положения только концентрационной диффузии, определяемые градиентом плотностей при р и Т = постоянные.
В движущейся среде вещество и тепло переносятся
молекулярной диффузией и конвекцией ![]()
![]() (18.3)
(18.3)
![]() (18.4)
(18.4)
где ![]() - удельные энтальпии смеси из i
компонентов, Дж/кг.
- удельные энтальпии смеси из i
компонентов, Дж/кг.
18.2 Массоотдача. Уравнения Стефана и массоотдачи
1. Массоотдача. Аналогично теплоотдаче конвективный массообмен между поверхностью жидкости и окружающей средой называют массоотдачей и аналогично формуле Ньютона – Рихмана для теплоотдачи
![]() (18.5)
(18.5)
введена формула для массоотдачи
![]() (18.6)
(18.6)
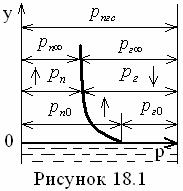 где β - коэффициент массоотдачи, м/с;
где β - коэффициент массоотдачи, м/с;
Если i–й компонент смеси близок состоянию идеального газа, то (18.6) можно записать в виде
![]() (18.7)
(18.7)
где
![]() -
коэффициент массоотдачи, с/м.
-
коэффициент массоотдачи, с/м.
2. Уравнение Стефана. При испарении жидкости в парогазовую среду (ПГС) gn + gг = 1 и pn + pг = p (закон Дальтона). Поэтому газ диффундирует в направлении, обратном направлению диффузии пара (см. рисунок 18.1)
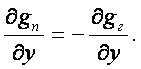 (18.8)
(18.8)
Однако при температуре насыщения пара поверхность испарения данной жидкости для газа (воздуха), имеющего другую температуру насыщения, будет непроницаемой преградой. Это приводит к накоплению газа, увеличению рr0 и возникновению обратного от поверхности оттока газа к периферии. Такой отток газа называется Стефановым потоком. Его скорость обозначим через wcn. В результате пар переносится от поверхности испарения молекулярной диффузией и Стефановым потоком
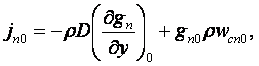 (18.9)
(18.9)
а суммарный поток газа у поверхности испарения жидкости равняется нулю
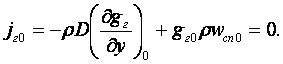 (18.10)
(18.10)
Отсюда скорость Стефанового потока с учетом (18.8)
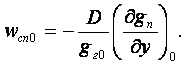 (18.11)
(18.11)
Если подставить (18.11) в (18.10), то
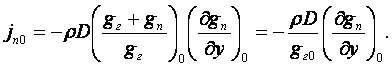 (18.12)
(18.12)
Это уравнение, полученное Стефаном, отличается от закона Фика (18.1), относящегося к условиям беспрепятственного распространения обоих компонентов смеси, множителем полупроницаемости поверхности 1/gr0 > 1.
3. Уравнение массоотдачи. Формула массоотдачи (18.6) и уравнение Стефана (18.12) выражают одну и ту же плотность потока массы у стенки. Приравнивая их, получаем уравнение массоотдачи
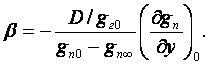 (18.13)
(18.13)
То же имеем при сублимации, десорбции, вдува газа через пористую стенку.
18.3 Тройная аналогия. Дифференциальные и
критериальные уравнения массообмена
Уравнения переноса импульса, теплоты и массы в общем виде и условия однозначности на примере ламинарного течения у плоской стенки
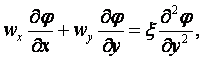 (
(![]() )
(18.14)
)
(18.14)
при ![]()
при ![]()
![]() (18.15)
(18.15)
Отсюда
видно, что математические формулировки задач теплообмена,
массообмена и переноса импульса идентичны во всем, кроме
значений скорости wy = 0 и wcn![]() при y = 0. Если wcn мала
при y = 0. Если wcn мала ![]() , то можно говорить о
тройной аналогии процессов переноса импульса, тепла и массы. При этом числа
Льиюса Le = D/а = 1, Прандтля Pr = v/a = 1
и диффуционное число Прандтля (число Шмидта) PrD =
, то можно говорить о
тройной аналогии процессов переноса импульса, тепла и массы. При этом числа
Льиюса Le = D/а = 1, Прандтля Pr = v/a = 1
и диффуционное число Прандтля (число Шмидта) PrD =
![]()
Критериальное уравнение массоотдачи записывается аналогично уравнению конвективного теплообмена в виде
![]() (18.16)
(18.16)
где ![]() - диффузионное число Нуссельта.
- диффузионное число Нуссельта.
18.4 Тепломассообмен при конденсации пара из парогазовой смеси
Коэффициент
теплоотдачи парогазовой смеси (пара и воздуха) ПГС ![]() определяется по формуле Ньютону-Рихмана
определяется по формуле Ньютону-Рихмана
![]() (18.17)
(18.17)
Сумма термических сопротивлений диффузионного переноса, фазового перехода и конденсата в ПГС (см. рисунок 18.2)
![]() ,
(18.18)
,
(18.18)
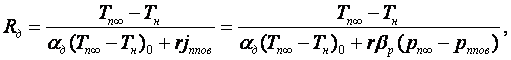 (18.19)
(18.19)
![]() . (18.20)
. (18.20)
Во многих задачах Rф << Rд, Rк. Это позволяет принимать Тппов = Тн.
Коэффициент массоотдачи βр в (18.19) при пленочной конденсации пара из движущейся сверху вниз ПГС на горизонтальных одиночных и шахматных пучках труб в диапазоне рпгс = 0,0627 - 0,089 МПа, определяется по уравнению
![]() (18.21)
(18.21)
где ![]() ,
, ![]() ;
;
при Re = 350 ÷ 4800 n = - 0,6 и С = 0,47 для одиночной трубы, а для первого ряда труб пучка С = 0,53, для третьего и последующих рядов С = 0,82;
при Re =40 ÷ 350 для пятого ряда труб пучка n = - 0,7 и С = 0,52.
Число Рейнольдса в (18.21) рассчитывается по внешнему диаметру труб, скорости и коэффициенту вязкости ПГС перед трубой или рядом труб [1]
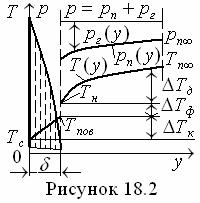
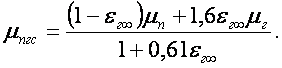 (18.22)
(18.22)
Значение Тн, по которому вводят в расчет рн, определяется методом последовательного приближения с использованием уравнения
![]() (18.23)
(18.23)
где αк - коэффициент теплоотдачи пленки конденсата чистого пара.
18.5 ТМО при испарении жидкости в ПГС
При адиабатном испарении вся теплота, передаваемая от ПГС к жидкости, затрачивается на испарение и возвращается в ПГС с паром. Из этого теплового баланса определяется температура мокрого термометра
![]() (18.24)
(18.24)
ТМО при испарении воды из металлической пористой пластины в продольный турбулентный поток ПГС определяется по уравнениям
![]() (18.25)
(18.25)
![]() (18.26)
(18.26)
![]() (18.27)
(18.27)
18.6 ТМО при химических превращениях
В задачах с химическими реакциями используется энтальпия, в которую включается теплота образования данного компонента h0i. Полные энтальпии і-го компонента и смеси газов определяются соответственно как
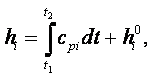
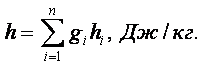 (18.28), (18.29)
(18.28), (18.29)
Когда наряду с химическими реакциями происходят фазовые превращения, энтальпия должна учитывать и теплоту фазовых переходов. В общем случае химические реакции, фазовые переходы и тепломассообмен взаимосвязаны и многие ранее полученные соотношения учитываются в энтальпиях (18.28) и (18.29). Например, плотность теплового потока в диффундирующей смеси описывается уранением (18.4).
При химических реакциях формула Ньютона-Рихмана
записывается с учетом (18.28) и (18.29), ![]() в виде
в виде
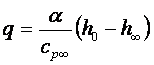 (18.30)
(18.30)
Если химические реакции происходят в газовом потоке с большой скоростью, то диссипация механической энергии учитывается путем замены h∞ в (18.30) на полную энтальпию восстановления с коэффициентом восстановления r
 (18.31)
(18.31)
Значения α в (18.30) определяются в первом приближении как для течений без химических реакций. Наличие химических реакций приводят к изменению полей температуры, скорости и концентрации. Однако их влияние на α мало по сравнению с тепловыми эффектами реакций.
15 лекция
Раздел пятый. Теплообмен излучением
19 Основы теории теплового излучения
19.1 Основные понятия и законы теплового излучения
Тепловое излучение определяется температурой, длиной волны тепловых (инфракрасных) лучей (λ = 0,8..800 мк), состоянием поверхности и взаиморасположением тел, а для газов – еще толщиной слоя и давлением.
Суммарное тепловое излучение с поверхности тела по всем направлениям полусферического пространства и длинам волн называется интегральным или полным лучистым потоком, или лучистой теплотой (Q, Вт, см. рисунок 19.1).
 Теплота,
излучаемая с единицы поверхности тела в полусферическое пространство,
называется излучательной способностью или плотностью интегрального излучения
тела
Теплота,
излучаемая с единицы поверхности тела в полусферическое пространство,
называется излучательной способностью или плотностью интегрального излучения
тела
![]() (19.1)
(19.1)
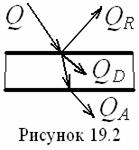 где dQ - элементарный лучистый поток, испускаемый
поверхностью dF.
где dQ - элементарный лучистый поток, испускаемый
поверхностью dF.
Лучистый поток, падающий на тело, может частью поглощаться, отражаться или проходить через него. При этом (см. рисунок 19.2)
![]() (19.2)
(19.2)
где A = QA/Q, R = QR/Q, D = QD/Q – коэффициенты поглощения, отражения и проницаемости.
При A, R, D = 1 тела называются соответственно абсолютно черными, белыми, прозрачными.
Плотность лучистого потока монохроматического излучения, отнесенная к единице волны называется интенсивностью (спектрального) излучения
![]() (19.3)
(19.3)
Относительное изменение интенсивности монохроматического излучения
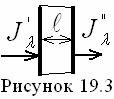
![]() (19.4)
(19.4)
называется спектральным коэффициентом поглощения.
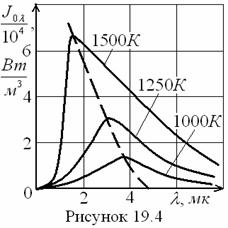 Связь между
интенсивностями излучения на выходе Jλ” и входе Jλ’ cлоя толщиной ℓ
и постоянным коэффициентом абсорбции
χλ выражается законом Бугера (см. рисунок 19.3)
Связь между
интенсивностями излучения на выходе Jλ” и входе Jλ’ cлоя толщиной ℓ
и постоянным коэффициентом абсорбции
χλ выражается законом Бугера (см. рисунок 19.3)
![]() (19.5)
(19.5)
![]() (19.6)
(19.6)
Подстановка (19.6) в (19.4) дает
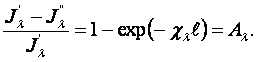 (19.7)
(19.7)
Отсюда видно, что излучение и поглощение газов и
жидкостей (χλ мал) носит объемный характер, а - твердых
тел (![]() ) - поверхностный
характер. В 1900г Марк Планк установил зависимость интенсивности излучения
абсолютно черного тела (A=1) от температуры и длины волны в виде, известном под
названием закона Планка (см. рисунок 19.4)
) - поверхностный
характер. В 1900г Марк Планк установил зависимость интенсивности излучения
абсолютно черного тела (A=1) от температуры и длины волны в виде, известном под
названием закона Планка (см. рисунок 19.4)
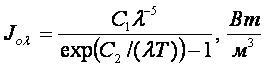 (19.8)
(19.8)
где C1 = 0,374·10-15 Вт·м2, С2 = 1,4387·10-2 м·К.
Исследуя (19.8) на экстремум, получено соотношение, известное как закон смещения Вина (см. пунктирную линию на рисунке 19.4)
![]() (19.9)
(19.9)
Спектрография поверхности Солнца показала, что ![]() . По (19.9)
температура поверхности Солнца получена равной 6000 К.
. По (19.9)
температура поверхности Солнца получена равной 6000 К.
Из (19.3) и (19.8) получается известный закон Стефана – Больцмана
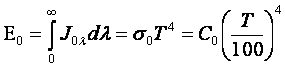 (19.10)
(19.10)
где ![]() , Вт/(м2К4) -
постоянная излучения Стефана-Больц-мана и C0 = 5,672,
Вт/(м2К4) - коэффициент излучения абсолютно черного тела.
, Вт/(м2К4) -
постоянная излучения Стефана-Больц-мана и C0 = 5,672,
Вт/(м2К4) - коэффициент излучения абсолютно черного тела.
 Согласно (19.10) при температуре 40·106 К устойчивой плазмы,
полученной впервые советскими физиками в 1963 году, черный шарик диаметром 1 мм имеет в 1,65·1015 раз большую интенсивность излучения, чем Солнце, и может заменить
его (1325 Вт/м2 вне атмосферы) при размещении на расстоянии 5225 км от Земли [1].
Согласно (19.10) при температуре 40·106 К устойчивой плазмы,
полученной впервые советскими физиками в 1963 году, черный шарик диаметром 1 мм имеет в 1,65·1015 раз большую интенсивность излучения, чем Солнце, и может заменить
его (1325 Вт/м2 вне атмосферы) при размещении на расстоянии 5225 км от Земли [1].
В условиях выполнения для каждой длины волны (см. рисунок 19.5)
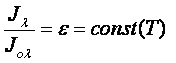 (19.11)
(19.11)
тело называется серым, а
![]() - степенью черноты серого
тела. Для серых тел (19.10) записывается в виде
- степенью черноты серого
тела. Для серых тел (19.10) записывается в виде
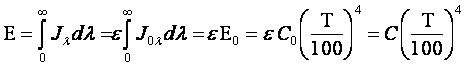 (19.12)
(19.12)
где ![]() - коэффициент излучения серого тела.
- коэффициент излучения серого тела.
Согласно закону Кирхгофа отношение излучательной и поглощательной равновесных способностей серых тел одно и то же и равняется излучательной равновесной способности черного тела (что следует также из (19.12))
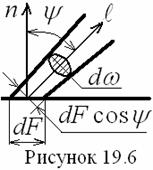
![]() (19.13)
(19.13)
Отсюда, а также из определения (19.11) следует, что для равновесного излучения серого и абсолютно черного тел
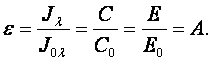 (19.14)
(19.14)
Отношение излучательной способности тела к телесному углу называется угловой плотностью излучения (см. рисунок 19.6)
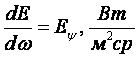 . (19.15)
. (19.15)
Отношение
плотности теплового излучения d2Q к площади dFℓ, нормальной к данному направлению ℓ, и к
телесному углу ![]() называется яркостью излучения
называется яркостью излучения
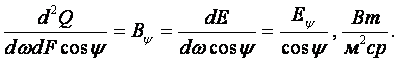 (19.16)
(19.16)
Связь между угловой плотностью и яркостью излучения носит название закона Ламберта (1760 г)
![]() . (19.17)
. (19.17)
Яркость диффузного излучения серого тела
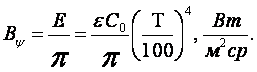 (19.18)
(19.18)
19.2 Методы исследования процессов лучистого теплообмена
Их два – метод многократных отражений (ММО) и метод cальдо (МС).
 Если тело поглощает лучистую энергию с плотностью
интегрального излучения Епогл и излучает собственную энергию
Есоб, то остаток лучистой энергии в теле соответствует
плотности лучистого сальдо (см. рисунок 19.7)
Если тело поглощает лучистую энергию с плотностью
интегрального излучения Епогл и излучает собственную энергию
Есоб, то остаток лучистой энергии в теле соответствует
плотности лучистого сальдо (см. рисунок 19.7)
Есальдо = Епогл - Есоб. (19.19)
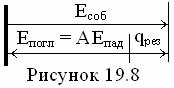 То же можно представить
как результирующий поток (см. рисунок 19.8)
То же можно представить
как результирующий поток (см. рисунок 19.8)
qрез = - Есальдо = Есоб - Епогл = Есоб - АЕпад. (19.20)
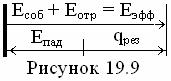 Сумма собственного Есоб и отраженного (Еотр
= REпогл)
излучений называется эффективным (фактическим) излучением тела (Есоб
+ Еотр = Еэфф).
Сумма собственного Есоб и отраженного (Еотр
= REпогл)
излучений называется эффективным (фактическим) излучением тела (Есоб
+ Еотр = Еэфф).
Результирующий поток через эффективное излучение (см. рисунок 19.9)
qрез = Еэфф - Епад. (19.21)
Подставляя сюда Епад из (19.20), находим
Еэфф= qрез+
Епад = qрез +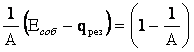 qрез +
qрез +![]() . (19.22)
. (19.22)
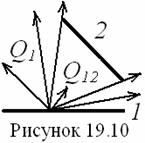 19.3 Геометрические характеристики системы
19.3 Геометрические характеристики системы
излучающихся тел и свойства лучистых потоков
Отношение лучистого потока Q12 , падающего с первого тела на второе, к лучистому потоку первого тела Q1 называется угловым коэффициентом излучения (см. рисунок 19.10)
![]() (19.23)
(19.23)
Отношение лучистого потока Q12 к плотности интегрального излучения первого тела E1 называется взаимной поверхностью рассматриваемых тел
Q12/E1=H12. (19/24)
С учетом (19.23) можем (19.24) представить в виде
![]() (19.25)
(19.25)
При расчете лучистого теплообмена используются основные свойства лучистых потоков, сформулированные в виде аксиом и теорем.
1. Аксиома существования (свойство затеняемости). Для плоского и выпуклого тела самооблучение отсутствует Qii, Hii, φii = 0, а для вогнутого тела Qii, Hii, φii ≠ 0 (см. рисунок 19.11).
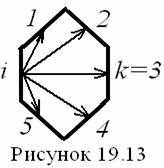

 2. Аксиома аддитивности (свойство
распределительности). Лучистый поток от одного тела к другому арифметически
складывается из лучистых потоков между отдельными частями этих тел (см.
рисунок 19.12)
2. Аксиома аддитивности (свойство
распределительности). Лучистый поток от одного тела к другому арифметически
складывается из лучистых потоков между отдельными частями этих тел (см.
рисунок 19.12)
Qik = Q11 + Q12 + Q21 + Q22 + … . (19.26)
3.Аксиома замкнутости (свойство замыкаемости). Для замкнутой системы тел суммарный лучистый поток, посылаемый одним из них на все остальные, равен лучистому потоку этого тела (см. рисунок 19.13)

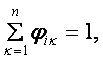 (19.27)
(19.27)
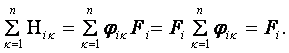 (19.28)
(19.28)
4. Теорема взаимности (свойство взаимности). Взаимные поверхности взаимно инвариантны
![]()
![]() (19.29)
(19.29)
19.4 Теплообмен излучением между телами в прозрачной среде
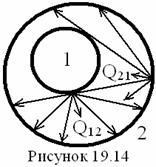 Рассмотрим теплообмен излучением между телами, одно из
которых заключено внутри другого (см. рисунок 19.14). Пусть наружная
поверхность внутреннего тела 1 не имеет вогнутостей (
Рассмотрим теплообмен излучением между телами, одно из
которых заключено внутри другого (см. рисунок 19.14). Пусть наружная
поверхность внутреннего тела 1 не имеет вогнутостей (![]() ). В силу замкнутости системы и
стационарности процессов теплообмена во времени сумма результирующих потоков
равна нулю
). В силу замкнутости системы и
стационарности процессов теплообмена во времени сумма результирующих потоков
равна нулю
Q12 + Q21 = 0. (19.30)
Эффективное
излучение тела 1 полностью падает на внешнее тело 2. Поэтому ![]() Эффективное излучение
тела 2 не полностью падает на тело 1. Поэтому по свойству замкнутости
Эффективное излучение
тела 2 не полностью падает на тело 1. Поэтому по свойству замкнутости ![]()
![]()
![]() и по свойству взаимности
и по свойству взаимности
Н12 = Н21,
![]()
![]() (19.31)
(19.31)
Результирующий тепловой поток
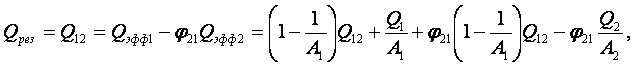
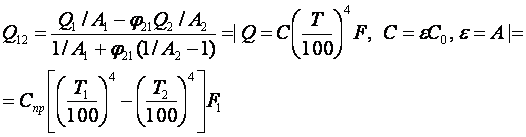 (19.32)
(19.32)
где приведенный коэффициент излучения системы тел
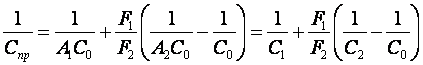 (19.33)
(19.33)
или то же в виде приведенного коэффициента степени черноты

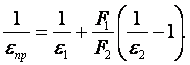 (19.34)
(19.34)
Рассмотрим частные случаи.
1. При F1 = F2 получается решение задачи для лучистого теплообмена между близко расположенными концентрическими цилиндри-ческими и сферическими или плоскопараллельными поверхностями (см. рисунок 19.15). При этом (19.33) и (19.34) будут иметь вид (F1/F2 = 1)

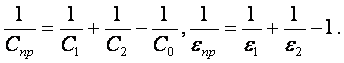 (19.35)
(19.35)
2. Если F1 << F2 (например, для излучения проволки в комнате, см. рисунок 19.16), то согласно (19.33 и (19.34) Спр = С1 и εпр = ε1. Такой же результат получается из (19.33) и (19.34), если второе тело абсолютно черное, но при различных соотношениях F1/F2 и геометрии их взаиморасположения. В последнем случае
 (19.36)
(19.36)
Отсюда также следует справедливость закона Кирхгофа (Е1/А1 = Е0) для равновесного излучения (q12 = 0) тел с различным отношением F1/F2 .
16 лекция
19.5 Действие теплозащитных экранов
Согласно стационарности тепловых потоков (см. рисунок 19.17)
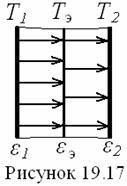 q
1э = qэ2 = q1э2. (19.37)
q
1э = qэ2 = q1э2. (19.37)
Это условие в соответствии с (19.32) запишется в виде
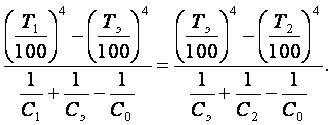 (19.38)
(19.38)
Исключая Тэ из (19.38), находим, что
 (19.39)
(19.39)
В случае отсутствия экрана при тех же температурах поверхностей имеем
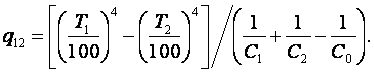 (19.40)
(19.40)
Найдем отношение этих тепловых потоков
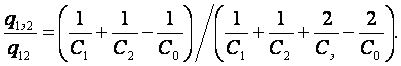 (19.41)
(19.41)
 Расчеты показывают, что для экрана с никелированной
поверхностью с
Расчеты показывают, что для экрана с никелированной
поверхностью с ![]() =
0,05 при
=
0,05 при ![]() =
=![]() = 0,8 тепловой поток
согласно (19.41) уменьшается почти в 30 раз (
= 0,8 тепловой поток
согласно (19.41) уменьшается почти в 30 раз (![]() = 0,0495,
= 0,0495, ![]() = 0,67). При
= 0,67). При ![]() =
=![]() =
=![]() установка одного экрана уменьшает
лучистый поток в 2 раза, а n экранов – в n +1 раз (q12/q1э2 = n +
1).
установка одного экрана уменьшает
лучистый поток в 2 раза, а n экранов – в n +1 раз (q12/q1э2 = n +
1).
19.6 Лучистый теплообмен между телами с высокими
коэффициентами поглощения.
Доказательство теоремы взаимности
Пусть
выпуклые тела 1 и 2 с температурами Т1 и Т2, коэффициентами
поглощения A1, A2 > 0,8 и поверхностями F1 и F2
произвольно расположены в пространстве (см. рисунок 19.18). Согласно определению
яркости (19.16) для диффузного излучения (когда она не зависит от направления и
![]() ) лучистые
потоки, падающие с dF1 на dF2 и с dF2 на dF1
) лучистые
потоки, падающие с dF1 на dF2 и с dF2 на dF1
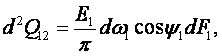 (19.42)
(19.42)
 (19.43)
(19.43)
Здесь удобно попутно рассмотреть доказательство теоремы взаимности
 (19.44)
(19.44)
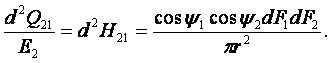 (19.45)
(19.45)
Правые части (19.44) и (19.45) равны между собой. Поэтому
![]()
![]() (19.46)
(19.46)
Для тел с высокими значениями коэффициентов поглощения можем ограничиться рассмотрением одного акта поглощения и принять, что элементы dF1 и dF2 поглощают тепло соответственно A1d2Q21 и A2d2Q12. Результирующий тепловой поток от тела 1 к телу 2 будет тогда равняться их разности
![]() (19.47)
(19.47)
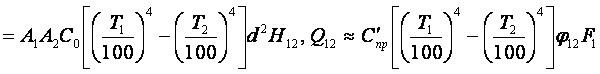
где Спр = А1А2С0 = Е1Е2С0 – приведенный коэффициент излучения.
Угловые коэффициенты излучения определяются методом поточной алгебры, аналитически, графоаналитически с помощью (19.44) – (19.46) или экспериментально. Например, согласно (19.44)
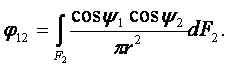 (19.48)
(19.48)
19.7 Определение угловых коэффициентов
излучения методом поточной алгебры
Метод поточной
алгебры строится с применением свойств лучистых потоков и простейших
алгебраических действий. Многие сложные системы излучающих тел можно
представить как совокупность систем из трех  невогнутых тел (см.
рисунок 19.19). Пусть продольные размеры излучающей системы велики по сравнению
с поперечными размерами. Требуется найти средние взаимные поверхности излучения
Fik и
средние угловые коэффициенты излучения
φik (i, k = 1, 2, 3).
невогнутых тел (см.
рисунок 19.19). Пусть продольные размеры излучающей системы велики по сравнению
с поперечными размерами. Требуется найти средние взаимные поверхности излучения
Fik и
средние угловые коэффициенты излучения
φik (i, k = 1, 2, 3).
По свойству замыкаемости 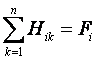 (19.28)
(19.28)
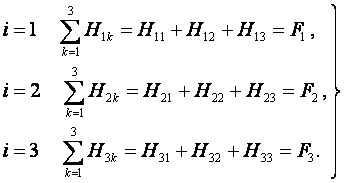 (19.49)
(19.49)
По свойству затеняемости Hii = 0, φii = 0
H11 = H22 = H33 = 0 и φ11 = φ22 = φ33 = 0. (19.50)
По свойству взаимности Hik = Hki (19.29)
H12 = H21, H13 = H31, H23 = H32, (19.51)
Суммируя (19.49) с учетом (19.50) и (19.51), получим
 (19.52)
(19.52)
Вычитая из (19.52) почленно (19.49), найдем, что
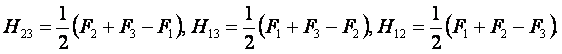 (19.53)
(19.53)
Отсюда угловые коэффициенты излучения равняются
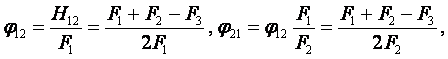 (19.54)
(19.54)
аналогично находятся φ13, φ31, φ23, φ32.
20 Теплообмен излучением в полупрозрачных средах
20.1 Особенности излучения и поглощения газов
Одной
из особенностей излучения газов является объемный его характер, что отмечали
при анализе коэффициента поглощения с помощью закона Бугера. Если одно– и
двухатомарные газы практически прозрачны, то наличие трех и более атомарных
газов среду делает полупрозрачной. Например, в дымовых газах при атмосферном
давлении ![]() =
0,13 и
=
0,13 и ![]() =
0,11.
=
0,11.
Другой особенностью взаимоизлучения и поглощения газов является их селективность (выборочность) по диапазонам длин волн. В результате закон Стефана – Больцмана выполняется нестрого. Например,
![]() (20.1)
(20.1)
где ![]() - длина хода луча, толщина слоя газов.
- длина хода луча, толщина слоя газов.
20.2 Расчет излучения продуктов сгорания
1. Степень черноты продуктов сгорания определяется в виде
![]() (20.2)
(20.2)
слагаемые
которого находятся с помощью номограмм Хоттеля (англ. 1935г) в зависимости от
температуры и произведения ![]() , а коэффициент β учитывает
дополнительное влияние парциального давления пара
, а коэффициент β учитывает
дополнительное влияние парциального давления пара ![]() к гипотезе Бера о
к гипотезе Бера о ![]() , то-есть к εН2О(
, то-есть к εН2О(![]() ). Поправка
). Поправка ![]() учитывает эффект
частичного наложения диапазонов излучения и поглощения СО2 и Н2О
(
учитывает эффект
частичного наложения диапазонов излучения и поглощения СО2 и Н2О
(![]() не
превышает 5%).
не
превышает 5%).
2. А. М. Гурвич и В. В. Митор показали, что расчет суммарной поглощательной способности потухших трехатомных газов СО2 и Н2О может производиться по (19.7) в виде
![]() (20.3)
(20.3)
где ![]()
![]() (20.4)
(20.4)
– коэффициент ослабления лучей.
То же с учетом частичного взаимоналожения спектров излучения и поглощения СО2 и Н2О
![]() (20.5)
(20.5)
что
применимо в диапазоне: tг = 450¸1650°С; ![]() = 0,008¸1,64 м×бар,
= 0,008¸1,64 м×бар, ![]() = 0,04¸1,30 м×бар,
= 0,04¸1,30 м×бар, ![]() = 0,05¸5,0.
= 0,05¸5,0.
3. Результирующий лучистый поток
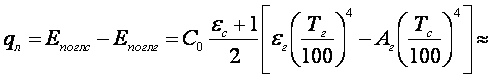
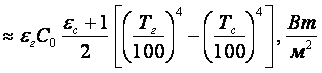 (20.6)
(20.6)
где 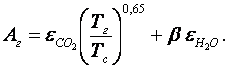 (20.7)
(20.7)
При ![]() неточность приближения в (20.6)
незначительна.
неточность приближения в (20.6)
незначительна.
4. В расчетах сложного теплообмена
![]() (20.8)
(20.8)
где ![]() (20.9)
(20.9)
5. Эффективную толщину теплового излучения можно определить следующим образом. Для излучения газов в объеме V с поверхностью F
![]() (20.10)
(20.10)
Для гладкотрубных пучков эффективная толщина излучающего слоя рассчитывается по формулам
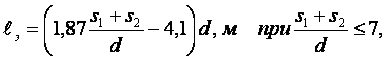 (20.11)
(20.11)
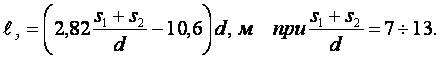 (20.12)
(20.12)
20.3 Тепловое излучение пламени
Приближенный расчет лучистого теплообмена светящегося пламени (факела) со стенками может производиться по формуле
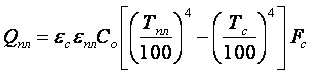 (20.13)
(20.13)
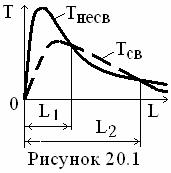 где
где ![]() - средняя геометрическая (эффективная)
температура пламени, К;
- средняя геометрическая (эффективная)
температура пламени, К;
Т1 – теоретическая температура горения, К;
Т2 – температура продуктов сгорания на выходе из топочной камеры, К;
Fс – радиационная поверхность, м2;
![]() и
и ![]() - степень черноты стенок и пламени.
- степень черноты стенок и пламени.
Эффективность излучения светящегося (св) и несветящегося (несв) пламени различна в различных зонах камеры (к) (см. рисунок 20.1) [1].
Заключение
Рассмотренные выше все программные вопросы могут позволить лектору сообразно конкретной аудитории сконцентрировать и углубить приведенные мысли и дифференцированно изложить учение о «Тепломассообмене» с учетом конкретного графика других видов занятий по дисциплине.
Список литературы
1. Исаченко В.П., Осипова В.А., Сукомел А.С. Теплопередача. - М.: Энергоиздат, 1981. - 416с.
2. Кутателадзе С.С. Основы теории теплообмена.- М.: Атомиздат, 1979. – 415 с.
3. Краснощеков Е.А., Сукомел А.С. Задачник по теплопередаче. Изд. 3-е, перераб. и доп. - М.: Энергия, 1980. – 288 с.
4. Дульнев Г.Н. и др. Применение ЭВМ для решения задач теплообмена: Учебное пособие для теплофизич. и теплоэнергетич. спец. ВУЗов / Г.Н. Дульнев, В.Г. Парфенов, А.В. Сигалов. - М.: Высш. шк., 1990. – 207 с.
5. Темирбаев Д.Ж. Тепломассообмен: Методические указания к практическим занятиям с использованием ЭВМ. - Алматы: АИЭС, 2004. – 62 с.
6. Темирбаев Д.Ж. Тепломассообмен: Методические указания к лабораторным занятиям, 4-е перер. изд. - Алматы: АИЭС, 2003. – 44 с.
7. Темирбаев Д.Ж. Тепломассообмен: Методические указания к рассчетно-графическим работам. - Алматы: АИЭС, 2007. - 38 с.
8. Темирбаев Д.Ж., Ермекбаев К.Б. Основы теории теплопроводности и теплового излучения: Учебное пособие. - Алма-Ата: КазПТИ, 1980. – 80 с.
9. Темирбаев Д.Ж., Ермекбаев К.Б. Основы теории конвективного теплообмена в однородной среде: Учеб. пособие. - Алма-Ата: КазПТИ, 1978. – 100 с.
10. Темирбаев Д.Ж. Теплообмен при фазовых и химических превращениях. Тепловой расчет теплообменных аппаратов: Учебное пособие. - Алма-Ата: КазПТИ - АЭИ, 1988. – 46 с.
11. Авчухов В.В., Паюсте Б.Я. Задачник по процессам тепломассообмена: Учебное пособие для вузов. - М.: Энергоатомиздат, 1986. - 144 с.
12. Шлихтинг Г. Теория пограничного слоя.- М.: Наука, 1969. - 743 с.
13. Темирбаев Д.Ж. Тепломассообмен: Учебное пособие. - Алматы: TST-company, 2009. – 251 c.
14. Юдаев Б.Н. Техническая термодинамика. Теплопередача. - М.: Высш. шк., 1988. - 479 с.
15. Лыков А.В. Теория теплопроводности: Учебное пособие для вузов. - М.: Высш. шк., 1967. - 600 c.
16. Шорин С.Н. Теплопередача: Учебное пособие для вузов. - М.: Высш. шк., 1964. – 490 с.
17. Темирбаев Д.Ж. Некоторые особенности изложения курса тепломассообмена // Теплотехника. Вып. 7: Проблемы преподавания теплотехники в ВУЗах. - М.: МПИ, 1991, с. 48 - 52.
18. Ермекбаев К.Б., Темирбаев Д.Ж. Термодинамические основы теплотехники: Учеб. пособие. - Алма-Ата: КазПТИ, 1979. – 58 с.
19. Гребер Г., Эрк С., Григулль. Основы учения о теплообмене. - М.: Иностранная литература, 1969.
20. Лабораторный практикум по теплопередаче/Под ред.Д.Ж.Темирбаева. – 2-е изд., перераб. и доп. – Алма-Ата: КазНИИНТИ, 1976. – 143 с.
21. Промышленная теплоэнергетика и теплотехника: Справочник / Под общей ред. В.Н.Юренева и П.Д.Лебедева. В 2-х т., Т2. – 2-е изд., перераб. - М.: Энергия, 1975. - 896 с.
22. Теплотехнический справочник / Под общей ред. В.А.Григорьева и В.М.Зорина. Книга 4. – 2-е изд., перераб. - М.: Энергоатомиздат, 1991. - 588 с.
23. Сакипов З.Б., Темирбаев Д.Ж. Перенос импульса и тепла в свободной турбулентной струе // Тезисы докладов на 2-м Всесоюзном совещании по тепломассообмену. - Минск: Наука и техника, 1964 (0,05 п.л.), // Сб. Проблемы теплоэнергетики и прикладной теплофизики, вып.1, АН Каз. ССР, Алма-Ата, 1964, с. 47-72.
24. Шец Дж. Турбулентное течение. Процессы вдува и перемешивания. Пер. с англ.- М.: Мир, 1984.- 247 с.
25. Ибраев А., Руденко И.М., Темірбаев Д.Ж. Ерікті ағынның үлдірлі тәртібіндегі жылуалмасу // «Қазақстанның индустриальды-инновациялық даму Стратегиясы аясында энергетика және телекоммуникациялық даму проблемалары» атты ғылыми практикалық конференцияның тезистер жинағы. - Алматы: АЭжБИ, 2005, с. 5.
26. Кондратьев Г.М. Регулярный тепловой режим. - М.: ГИТТЛ, Гостехиздат,1954. – 408 с.
27. Осипова В.А. Экспериментальное исследование процессов теплообмена. – М.: Энергия, 1969. – 392 с.
28. Практикум по теплопередаче / Под ред. А.П.Солодова. – М.: Энергоатомиздат, 1986. – 296 с.
29. Спэрроу Э.М., Сесс Р.Д. Теплообмен излучением. – Л.: Энергия, 1971. – 295 с.
30. Теория теплообмена: Учебник для ВУЗов / С.И.Исаев, И.А.Кожанов, В.И.Кофанов и др. Под ред. А.И.Леонтьева. – М.: Высш. шк., 1979. – 495 с.
31. Патанкар С., Сполдинг Д. Тепло- и массообмен в пограничных слоях: Пер. с англ. – М.: Энергия, 1971. – 128 с.
32. Шуп Т. Прикладные численные методы в физике и технике / Пер. с англ. – М.: Высш. шк., 1990. – 255 с.
33. Новожилов Б.В. Метод Монте-Карло. – М.: Знание, 1966. – 48 с.
34. Математическое обеспечение ЕС ЭВМ. – Минск: Высш. шк., 1980.
35. Мак Кракен Д., Дорн У. Численные методы и программирование на Фортране. – М.: Мир, 1977.
36. Флетчер К. Вычислительные методы в динамике жидкостей: В 2-х томах: Т.1 / Основные положения и обшие методы, Пер. с англ. – М.: Мир, 1991. – 504 с.
37. Флетчер К. Вычислительные методы в динамике жидкостей: В 2-х томах: Т.2 / Методы расчета различных течений: Пер. с англ. – М.: Мир, 1991. – 552 с.
Содержание
с. Предисловие. Методика построения дисциплины. . . . . . . . . . . . . . . . . . . . . 3
1 лекция. Предмет и метод тепломассообмена . . . . . . . . . . . . . . . . . . . . . . . . . 4
Раздел первый. Теплопроводность . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .4
1 Закон Фурье и его применение к решению задач стационарной
теплопроводности . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.1 Температурное поле и градиент температуры . . . . . . . . . . . . . . . . . . . . . . 4
1.2 Закон Фурье. Коэффициент теплопроводности . . . . . . . . . . . . . . . . . . . . . 5
1.3 Вывод общей формулы теплоты теплопроводности . . . . . . . . . . . . . . . . . 5
1.4 Аналогия между тепловым потоком и электрическим током . . . . . . . . . 6
1.5 К расчету геометрического фактора, средних значений
поверхности теплообмена и коэффициента теплопроводности . . . . . . . .6
1.6 Составление расчетных формул теплоты теплопроводности . . . . . . . . . .7
2 лекция.
1.7 Температурный профиль стенки постоянной теплопроводности. . . . . . . . .8
1.8 Стационарная теплопроводность многослойной стенки . . . . . . . . . . . . . 8
2 Математическая формулировка задач теплопроводности . . . . . . . . . . . . . . . 9
2.1. Дифференциальное уравнение теплопроводности. Коэффициент
температуропроводности . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
2.2 Условия однозначности решения дифференциального уравнения
теплопроводности . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
2.3 Коэффициент теплоотдачи. Граничные условия третьего рода.
Критерий Био . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
3 лекция. Раздел второй. Тепловой расчёт теплообменников. . . . . . . . . . 12
6 Теплопередача при постоянных температурах теплоносителей. . . . . . . . . . 12
6.1 Теплопередача и температуры многослойной стенки. . . . . . . . . . . . . . . 12
6.2 Коэффициент теплопередачи тел различной формы. . . . . . . . . . . . . . . . 13
6.3 Критический диаметр цилиндрической стенки . . . . . . . . . . . . . . . . . . . . 14
6.4 Пути интенсификации теплопередачи . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
6.5 Теплопередача ребристой плоской стенки . . . . . . . . . . . . . . . . . . . . . . . .15
4 лекция. 7 Теплопередача при переменных температурах теплоносителей16
7.1 Общие понятия теплового расчёта теплообменников . . . . . . . . . . . . . . .16
7.2 Средний температурный напор прямо и противоточных
теплообменников. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
7.3 Расчёт выходных температур теплоносителей прямоточных и
противоточных теплообменников. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .17
7.4 Сравнение эффективностей прямоточных и противоточных
теплообменников. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
7.5 Средний температурный напор сложных теплообменников . . . . . . . . . 18
5 лекция. 3 Решения задач стационарной теплопроводности
с внутренним источником теплоты . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
3.1 Стационарная теплопроводность пластины
с внутренним источником теплоты постоянной мощности . . . . . . . . . .19
3.2 Стационарная теплопроводность стержня неограниченной длины . . . .20
3.3 Стационарная теплопроводность стержня конечной длины . . . . . . . . . .21
4 Нестационарная теплопроводность . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .22
4.1 Безразмерное дифференциальное уравнение теплопроводности.
Критерий Фурье . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .22
4.2 Решение нестационарного ДУТ плоской стенки методом Фурье. . . . . .23
6 лекция. 4.3 Анализ решения нестационарного ДУТ плоской стенки. . . . 24
4.4 Нестационарная теплопроводность тел конечных размеров . . . . . . . . . .25
4.5 Метод регулярного теплового режима . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
5 Приближенные методы расчета теплопроводности . . . . . . . . . . . . . . . . . . . .26
5.1 Графический метод расчета теплопроводности. . . . . . . . . . . . . . . . . . . . . . 26
5.2 Численный метод (метод сеток) расчета теплопроводности . . . . . . . . . .27
5.3 Исследование теплопроводности методом аналогии . . . . . . . . . . . . . . . .28
7 лекция. Раздел третий. Конвективный теплообмен в однородной среде28
8 Основы теории конвективного теплообмена в однородной среде . . . . . . . .28
8.1 Общие понятия и задачи конвективного теплообмена.
Характеристика коэффициента теплоотдачи . . . . . . . . . . . . . . . . . . . . . .28
8.2 Уравнение теплоотдачи.
Пути определения коэффициента теплоотдачи. . . . . . . . . . . . . . . . . . . . 29
8.3 Система дифференциальных уравнений конвективного
теплообмена и условия однозначности их решения . . . . . . . . . . . . . . . . 30
8.4 Повышение температуры вследствие адиабатического сжатия. . . . . . . 31
9 Теория подобия конвективного теплообмена в однородной среде. . . . . . . .31
9.1 Безразмерные дифференциальные уравнения и критерии подобия
конвективного теплообмена. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
9.2 Критериальные уравнения конвективного теплообмена . . . . . . . . . . . . .32
9.3 Моделирование процессов конвективного теплообмена . . . . . . . . . . . . 33
8 лекция. 10 Основные положения теории теплового пограничного слоя . .34
10.1 Особенности и система дифференциальных уравнений
ламинарного пограничного слоя . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .34
10.2 Турбулентный перенос импульса и тепла. Система
дифференциальных уравнений турбулентного пограничного слоя . . 35
11 Гидродинамическая теория теплообмена. . . . . . . . . . . . . . . . . . . . . . . . . . . 35
11.1 Физическое и турбулентное числа Прандтля . . . . . . . . . . . . . . . . . . . . 35
11.2 Аналогия Рейнольдса. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
12 Теплообмен при ламинарном течении Куэтта. . . . . . . . . . . . . . . . . . . . . . . .36
9 лекция. 13 Теплоотдача при вынужденном обтекании плоской стенки. . . 38
13.1 Результаты теоретических решений уравнений ламинарного
пограничного слоя. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .38
13.2 Теплоотдача при ламинарном обтекании плоской стенки. . . . . . . . . . 39
13.3 Теплоотдача при турбулентном обтекании плоской стенки. . . . . . . . .39
14 Теплоотдача при вынужденном течении жидкости в трубе. . . . . . . . . . . . .40
14.1 Уравнение Лайона. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .40
14.2 Теплоотдача при ламинарном течении жидкости в трубе . . . . . . . . . . 42
10 лекция. 14.3 Теплоотдача при турбулентном течении жидкости в трубе. . . . 42
14.4 Теплоотдача при переходном режиме течения жидкости в трубе. . . .43
14.5 Влияние формы, изогнутости и шероховатости трубы
на её теплоотдачу. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .43
14.6 Теплоотдача при поперечном обтекании цилиндра. . . . . . . . . . . . . . . .44
14.7 Теплоотдача при поперечном обтекании пучка труб. . . . . . . . . . . . . . .45
15 Теплоотдача при свободной конвекции. . . . . . . . . . . . . . . . . . . . . . . . . . . . .45
15.1 Теоретические результаты исследования теплоотдачи
при свободной конвекции. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .45
15.2 Результаты экспериментального исследования теплообмена
при свободной конвекции. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .46
11 лекция. Раздел четвертый. Тепломассообмен при фазовых
и химических превращения. . . . . . . . . . . . . . . . . . . . . . . . .47
16 Теплообмен при конденсации чистого пара. . . . . . . . . . . . . . . . . . . . . . . . . 47
16.1 Термодинамические понятия и особенности фазовых переходов. . . . 47
16.2 Теплоотдача при пленочной конденсации неподвижного пара . . . . . .48
16.3 Анализ решения Нуссельта для теплоотдачи при пленочной
конденсации пара . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
16.4 Теплоотдача при пленочной конденсации движущегося пара. . . . .50
16.5 Теплоотдача при пленочной конденсации движущегося пара
внутри трубы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .51
12 лекция. 16.6 Механизм и расчетные формулы
теплообмена при капельной конденсации пара . . . . . . . . . . . . . . . . . . 51
17 Теплоотдача при кипении жидкости. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
17.1 Факторы, влияющие на теплоотдачу при кипении жидкости. . . . . . . .53
13 лекция. 17.2 Переход
пузырькового режима кипения к пленочному режиму. . . . . . . . . . . . . .56
17.3 Теплоотдача при свободном кипении жидкости. . . . . . . . . . . . . . . . . . 57
17.4 Теплоотдача при течении кипящейся жидкости в трубе. . . . . . . . . . . .57
17.5 К расчету критической тепловой нагрузки при кипении жидкости. . .58
14 лекция. 18 Массообмен. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
18.1 Понятия, механизмы и законы диффузии. . . . . . . . . . . . . . . . . . . . . . . .59
18.2 Массоотдача. Уравнение Стефана и массоотдачи. . . . . . . . . . . . . . . . .60
18.3 Тройная аналогия. Дифференциальные и критериальные
уравнения массообмена. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
18.4 Тепломассообмен при конденсации пара из парогазовой смеси. . . . . 61
18.5 ТМО при испарении жидкости в ПГС. . . . . . . . . . . . . . . . . . . . . . . . . . 62
18.6 ТМО при химических превращениях . . . . . . . . . . . . . . . . . . . . . . . . . . .63
15 лекция. Раздел пятый. Теплообмен излучением. . . . . . . . . . . . . . . . . . 63
19 Основы теории теплового излучения. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .63
19.1 Основные понятия и законы теплового излучения. . . . . . . . . . . . . . . . 63
19.2 Методы исследования процессов лучистого теплообмена. . . . . . . . . .66
19.3 Геометрические характеристики системы излучающихся тел и
свойства лучистых потоков. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
19.4 Теплообмен излучением между телами в прозрачной среде. . . . . . . .67
16 лекция. 19.5 Действие теплозащитных экранов. . . . . . . . . . . . . . . . . . . 69
19.6 Лучистый теплообмен между телами с высокими коэффициентами
поглощения. Доказательство теоремы взаимности. . . . . . . . . . . . . . . .69
19.7 Определение угловых коэффициентов излучения методом
поточной алгебры. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
20 Теплообмен излучением в полупрозрачных средах. . . . . . . . . . . . . . . . . . . 71
20.1 Особенности излучения и поглощения газов. . . . . . . . . . . . . . . . . . . . . 71
20.2 Расчет излучения продуктов сгорания. . . . . . . . . . . . . . . . . . . . . . . . . . 72
20.3 Тепловое излучение пламени. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
Заключение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73