АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра «Электропривод и автоматизация промышленных установок"
Электрические машины
Конспект лекции
(для студентов всех форм обучения специальности 050718 - Электроэнергетика)
Алматы 2007
СОСТАВИТЕЛЬ: К.К.Жумагулов. Р.М. Шидерова. Электрические машины.
Конспект лекций для студентов всех форм обучения специальности 050718 – Электроэнергетика. – Алматы: АИЭС, 2007. - 74 с.
Конспект лекций по курсу “Электрические машины” разработан в соответствии с учебной программой и рассчитан на 34 часа для бакалавров специальности 050718 – Электроэнергетика.
Рассмотрены история развития электромашиностроения, устройства, принцип действия, основные характеристики, векторные диаграммы, схемы замещения электрических машин общепромышленного назначения.
Конспект лекций предназначен для бакалавров дневной и заочной форм обучения специальностей электроэнергетического направления.
Содержание
1 Лекция 1.Введение. История развития электромашиностроения.......4
2 Лекция 2. Трансформаторы. Элементы конструкций. Режим холостого хода......6
3 Лекция 3. Векторная диаграмма трансформатора при холостом ходе..10
4 Лекция 4. Режим короткого замыкания.......................................................13
5 Лекция 5. Работа трансформаторов под нагрузкой...............................16
6 Лекция 6. Электродвижущие силы в обмотках машин переменного тока.................20
7 Лекция 7. Устройство и принцип действия асинхронных двигателей. Трехфазная асинхронная машина при вращающемся роторе.....25
8 Лекция 8. Пуск в ход асинхронных двигателей.....................................29
9 Лекция 9. Регулирование скорости вращения асинхронных двигателей................34
10 Лекция 10.Синхронные машины..........................................................40
11 Лекция 11. Синхронные двигатели......................................................44
12 Лекция 12. Машины постоянного тока, элементы конструкции, обмотки якоря и их э.д.с. ......47
13 Лекция 13. Машины постоянного тока, элементы конструкции, обмотки якоря и их э.д.с. ....51
14 Лекция 14.Реакция якоря машины постоянного тока........................56
15 Лекция 15. Генераторы постоянного тока...........................................59
16 Лекция 16.Двигатели постоянного тока. Способы пуска, характеристики двигателей..........63
17 Лекция 17. Регулирование частоты вращения двигателей постоянного тока...................68
Список литературы ………………………………………………………72
1 Лекция №1. Введение. История развития электромашиностроения
Содержание лекции:
- общие вопросы курса;
- история развития электромашиностроения.
Цель лекции
Ознакомить студентов с историей развития электромашиностроения.
Электромашиностроение начало развиваться с середины XIX в. Исследования электромагнитных полей, проведенные в то время учеными, позволили приступить к созданию моделей для практического применения.
Выдающиеся значения имели работы французского физика А.Ампера, английского физика М.Фарадея и русских ученых Э.Ленца, Б.Якоби и
М.О. Доливо-Добровольского, работы которых дали мощный толчок к использованию переменного тока. К началу XX в. стали вполне очевидными достоинствами и широкие возможности использования в народном хозяйстве электрической энергии. Были доказаны и практически реализованы такие замечательные свойства электрической энергии, как простота выработки, преобразование, трансформация, распределение и передача на большие расстояния. Продолжительный период времени электрический генератор и электрический двигатель развивались независимо друг от друга, и, только в 70-х годах XIX в. пути их развития объединились.
Электрические машины постоянного тока прошли четрые этапа развития:
а) магнитоэлектрические машины с постоянными магнитами;
б) машины с электромагнитами с независимым возбуждением;
в) электрические машины с самовозбуждением с элементарными якорями;
г)электрические машины с усовершенстованными якорями и многополюстными системами.
Начальный период развития электрических машин связан, главным образом с постоянным током. Объясняется это тем, что потребителями электрической энергии являлись установки, работающие исключительно на постоянном токе (дуговые лампы, установки гальванопластики и др.).
Развитие электрических железных дорог значительно увеличило спрос на электродвигатели и генераторы. В 80-х годах XVIII века возникла необходимость передавать электроэнергию на расстояние. В 1882г. Были проведены первые опыты по передаче электроэнергии на постоянном токе. Однако высокое напряжение в генераторах постоянного тока ухудшало работу коллектора и часто приводило к авариям.
Большая заслуга в развитии переменного тока принадлежит русскому ученому П.Н. Яблочкову, который в 1876г. применил трансформатор для питания изобретенных им электрических свечей. Трансформатор П.Н. Яблочкова имел незамкнутый сердечник. Трансформаторы с замкнутым магнитопроводом, применяемые в настоящее время, появились значительно позднее, в 1884г. С изобретением трансформатора возник технический интерес к переменному току, который до этого времени не имел применения.
Выдающийся русский электротехник М.О. Доливо-Добровольский в 1889г. предложил трехфазную систему переменного тока, построил первый трехфазный асинхронный двигатель и первый трехфазный трансформатор. На электрической выставке во Франкфруте-на Майне в 1891г. Доливо-Добровольский демонстрировал опытную высоковольтную электропередачу переменного тока протяженностью 175 км (местечка Лауфен во Франкфруте-на Майне). Трехфазный генератор имел мощность 230 кВА при напряжении 95В. С помощью трехфазных трансформаторов напряжение генератора в Лауфене повышалось до 15 кВ и понижалось во Франкфруте-на Майне до 65 В (фазного значения), при котором осуществлялось питание трехфазного асинхронного двигателя для насосной установки мощностью 75 кВт. При дальнейших опытах напряжения в линии электропередачи повышалось до 28 кВ посредством последовательного включения обмоток высшего напряжения двух трансформаторов. Коэффициент полезного действия (к.п.д.) электропередачи 77,4% и считался тогда высоким.
Последнее столетие характеризует быстрый рост промышленности и транспорта на базе электрификации. К трансформаторам и электрическим машинам предъявлялись более высокие требования: повышение экономичности, уменьшение массы и габаритов. Проводилась большая работа по изучению электромагнитных и тепловых процессов, происходящих при работе трансформаторов и электрических машин, поиску новых изоляционных материалов и улучшению свойств электротехнической стали. Синхронные машины — это бесколлекторные машины переменного тока. По своему устройству они отличаются от асинхронных машин лишь конструкцией ротора, который может быть явнополюсным или неявнополюсным. Что же касается свойств, то синхронные машины отличаются синхронной частотой вращения ротора (n2 = n1= const) при любой нагрузке, а также возможностью регулирования коэффициента мощности, устанавливая такое его значение, при котором работа синхронной машины становится наиболее экономичной. Синхронные машины обратимы и могут работать как в режиме генератора, так и в режиме двигателя. Синхронные генераторы составляют основу электротехнического оборудования электростанций, т.е. практически вся электроэнергия вырабатывается синхронными генераторами. Единичная мощность современных синхронных генераторов достигает миллиона киловатт и более. Синхронные двигатели применяются главным образом для привода устройств большой мощности. Такие двигатели по своим технико-экономическим показателям превосходят двигатели других типов. В крупных электроэнергетических установках синхронные машины иногда используются в качестве компенсаторов — генераторов реактивной мощности, позволяющих повысить коэффициент мощности всей установки.
2 Лекция №2.Трансформаторы, элементы конструкций, режим холостого хода
Содержание лекции:
-общие сведения о трансформаторах;
-назначение трансформаторов;
-элементы конструкции трансформаторов;
-режим холостого хода.
Цель лекции
Ознакомить студентов с элементами конструкции трансформаторов;
-с режимом холостого хода.
2.1 Назначение и принцип действия трансформаторов
Трансформатор представляет собой статический электромагнитный преобразователь с двумя или больше обмотками, предназначенный (наиболее часто) для преобразования переменного тока одного напряжения в переменный ток другого напряжения. Преобразование энергии в трансформаторе осуществляется переменным магнитным полем. Трансформаторы широко применяют при передаче электрической энергии на большие расстояния, при распределении ее между приемниками, а также в различных выпрямительных, усилительных, сигнализационных и других устройствах. При передаче электрической энергии от электростанции к потребителям сила тока в линии обусловливает потери энергии в этой линии и расход цветных металлов на ее устройство. Если при одной и той же передаваемой мощности увеличить напряжение, то сила тока в такой же мере уменьшится, а, следовательно, можно будет применить провода с меньшим поперечным сечением. Это сократит расход цветных металлов при устройстве линии электропередачи и снизит потери энергии в ней. Электрическая энергия вырабатывается на электростанциях синхронными генераторами при напряжении 11—20 кВ; в отдельных случаях применяется напряжение 30—35 кВ. Хотя такие напряжения являются слишком высокими для их непосредственного использования в производстве и для бытовых нужд, они недостаточны для экономичной передачи электроэнергии на большие расстояния. Дальнейшее повышение напряжения в линиях электропередачи (до 750 кВ и более) осуществляют повышающими трансформаторами.
Приемники электрической энергии (лампы накаливания, электродвигатели и др.) из соображений безопасности рассчитывают на более низкое напряжение (110—380 В). Кроме того, изготовление электрических аппаратов, приборов и машин на высокие напряжения связано со значительными конструктивными сложностями, так как токоведущие части этих устройств при высоком напряжений требуют усиленной изоляции. Поэтому высокое напряжение, при котором происходит передача энергии, не может быть непосредственно использовано для питания приемников и подводится к ним через понижающие трансформаторы.
Электрическую энергию переменного тока по пути от электростанции, где она вырабатывается, до потребителя приходится трансформировать 3—4 раза. В распределительных сетях понижающие трансформаторы нагружаются неодновременной нагрузкой и не на полную мощность. Поэтому полная мощность трансформаторов, устанавливаемых для передачи и распределения электроэнергии, в 7—8 раз больше мощности генераторов, устанавливаемых на электростанциях.
Каждая
обмотка
размещается
на обоих стержнях так, что половины двух
обмоток находятся на левом, а вторые половины
— на
правом стержне магнитопровода. При таком расположении обмоток достигается лучшая магнитная
связь
между
ними, благодаря чему снижаются потоки рассеяния, которые не участвуют в процессе трансформирования
энергии.
Действие трансформатора основано на явлении взаимной индукции. Если
первичную обмотку трансформатора включить в сеть
источника переменного тока, то по ней
будет протекать переменный ток ![]() , который создает в сердечнике
трансформатора переменный магнитный поток. Этот магнитный поток, пронизывая
витки
вторичной обмотки, будет индуктировать в ней э.д.с.
, который создает в сердечнике
трансформатора переменный магнитный поток. Этот магнитный поток, пронизывая
витки
вторичной обмотки, будет индуктировать в ней э.д.с.
![]() . Если
вторичную обмотку
замкнуть на какой-либо приемник энергии
,
то под действием индуктируемой э.д.с.
. Если
вторичную обмотку
замкнуть на какой-либо приемник энергии
,
то под действием индуктируемой э.д.с.
![]() по этой обмотке и
через приемник энергии начнет протекать
ток 12. Одновременно в первичной обмотке также
появится нагрузочный ток
по этой обмотке и
через приемник энергии начнет протекать
ток 12. Одновременно в первичной обмотке также
появится нагрузочный ток![]() , который в сумме с током
, который в сумме с током ![]() составит
ток первичной обмотки
составит
ток первичной обмотки![]() . Таким образом,
электрическая энергия, трансформируясь, будет передаваться из первичной сети во вторичную при напряжении, на которое рассчитан приемник энергии, включенный
во вторичную сеть.
. Таким образом,
электрическая энергия, трансформируясь, будет передаваться из первичной сети во вторичную при напряжении, на которое рассчитан приемник энергии, включенный
во вторичную сеть.
В целях улучшения магнитной связи между первичной и вторичной обмотками их помещают на стальном магнитопроводе. Обмотки изолируют как друг от друга, так и от магнитопровода. Обмотку более высокого напряжения называют обмоткой высшего напряжения (ВН), а обмотку более низкого напряжения — обмоткой низшего напряжения (НН). Обмотку, включенную в сеть источника электрической энергии, называют первичной; обмотку, от которой энергия подается к приемнику,— вторичной. Обычно напряжения первичной и вторичной обмоток неодинаковы. Если первичное напряжение меньше вторичного, трансформатор называют повышающим, если же первичное напряжение больше вторичного — понижающим. Любой трансформатор может быть использован и как повышающий и как понижающий. Повышающие трансформаторы применяют для передачи электроэнергии на большие расстояния, а понижающие - для распределения электроэнергии между потребителями.
В трехобмоточных трансформаторах на сердечнике помещают три изолированные друг от друга обмотки. Такой трансформатор дает возможность получить два различных напряжения и снабжать электрической энергией две различные группы приемников. Помимо обмоток ВН и НН трехобмоточный трансформатор имеет обмотку среднего напряжения (СН). Обмоткам трансформатора придают преимущественно цилиндрическую форму, выполняя их при малых токах из круглого медного изолированного провода, а при больших токах из медных шин прямоугольного поперечного сечения. Ближе к сердечнику располагают обмотку НН, так как ее легче изолировать от него, чем обмотку ВН. Обмотку НН изолируют от сердечника прослойкой из какого-либо изоляционного материала. Такая же изолирующая прокладка имеется между обмотками ВН и НН. При цилиндрических обмотках поперечному сечению стержня магнитопровода желательно придать круглую форму, чтобы в площади, охватываемой обмотками, не оставалось немагнитных промежутков. Чем меньше немагнитные промежутки, тем меньше длина витков обмоток, а следовательно, и масса меди при заданной площади сечения стального стержня. Однако стержни круглого сечения изготовить сложно. Магнитопровод набирают из тонких стальных листов и для получения стержня круглого сечения понадобилось бы большое число стальных листов различной ширины, а это потребовало бы изготовления множества штампов. Поэтому в трансформаторах большой мощности сердечник имеет ступенчатое поперечное сечение с числом ступеней не более 9 - 10. Число ступеней сечения сердечника определяется числом углов в одной четверти круга. Ярмо магнитопровода, т. е. та его часть, которая соединяет стержни, имеет также ступенчатое сечение.
Холостым
ходом трансформатора является такой предельный
режим его работы, когда вторичная
обмотка трансформатора разомкнута и ток вторичной обмотки ![]() . Опыт хх позволяет
определить
коэффициент трансформации, токи, потери и сопротивления
хх
трансформатора. При опыте хх первичную обмотку трансформатора включают в сеть переменного тока с
напряжением
. Опыт хх позволяет
определить
коэффициент трансформации, токи, потери и сопротивления
хх
трансформатора. При опыте хх первичную обмотку трансформатора включают в сеть переменного тока с
напряжением ![]() (рисунок 2.1). Под действием приложенного напряжения по
первичной
обмотке протекает ток
(рисунок 2.1). Под действием приложенного напряжения по
первичной
обмотке протекает ток ![]() , равный току хх, который составляет 5—10% номинального, а в
трансформаторах малой мощности
(десятки
вольт-ампер) — >30%.
, равный току хх, который составляет 5—10% номинального, а в
трансформаторах малой мощности
(десятки
вольт-ампер) — >30%.
Для измерения тока хх.,
приложенного к первичной обмотке напряжения и
потребляемой мощности в цепь первичной обмотки трансформатора, включены измерительные приборы (амперметр А,
вольтметр
V
и ваттметр
W).
Вторичная обмотка
трансформатора замкнута на вольтметр, сопротивление которого очень велико
так что, ток вторичной
обмотки
![]()
Ток хх
возбуждает в магнитопроводе трансформатора магнитный поток, который
индуктирует э.д.с. как в первичной, так
и во вторичной обмотках. Действующие значения э. д. с. обмоток ![]() и
и ![]() ,
где
,
где ![]() и
и ![]() - числа витков
первичной и вторичной обмоток трансформатора;
- числа витков
первичной и вторичной обмоток трансформатора; ![]() — амплитуда
магнитного потока;
f—
частота тока.
— амплитуда
магнитного потока;
f—
частота тока.
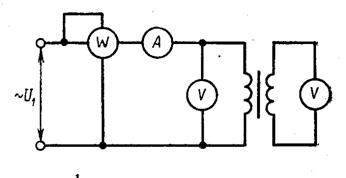
Рисунок 2.1 - Схема опыта хх однофазного трансформатора
Так как
во вторичной обмотке трансформатора тока нет и, следовательно, нет
падения напряжения в сопротивлении этой обмотки, то э.д.с. ![]() , которая определяется
показанием вольтметра, включенного в эту обмотку.
, которая определяется
показанием вольтметра, включенного в эту обмотку.
В первичной обмотке протекает ток хх очень малый по сравнению с номинальным, так что падение напряжения в сопротивлении первичной обмотки будет очень мало по сравнению с приложенным напряжением.
Поэтому
приложенное напряжение практически уравновешивается э.д.с. первичной обмотки: ![]() .
Следовательно, э.д.с.
первичной обмотки определяется показанием
вольтметра, включенного в цепь первичной
обмотки при опыте х.х.
.
Следовательно, э.д.с.
первичной обмотки определяется показанием
вольтметра, включенного в цепь первичной
обмотки при опыте х.х.
Коэффициентом трансформации называют отношение напряжения обмотки ВН к напряжению обмотки НН при хх
![]() .
(2.1)
.
(2.1)
При
опыте хх помимо напряжений первичной и вторичной обмоток измеряются ток хх
![]() и мощность
и мощность
![]() , потребляемая
трансформатором.
Ток хх в фазе обмотки трехфазного трансформатора
, потребляемая
трансформатором.
Ток хх в фазе обмотки трехфазного трансформатора
![]() при соединении
первичной обмотки в звезду равен измеренному току
при соединении
первичной обмотки в звезду равен измеренному току ![]() , а при соединении первичной обмотки в
треугольник
- в
, а при соединении первичной обмотки в
треугольник
- в
![]() раза меньше
измеренного
раза меньше
измеренного ![]() .
Мощность, потребляемая трансформатором при х.х.
.
Мощность, потребляемая трансформатором при х.х.
![]() практически расходуется на покрытие
потерь в стали за счет гистерезиса и вихревых
токов
практически расходуется на покрытие
потерь в стали за счет гистерезиса и вихревых
токов ![]() , так как потери в проводах
первичной обмотки
ничтожно малы. При испытании трехфазного трансформатора
в этих выражениях
следует иметь в виду фазные значения напряжения и тока, а также мощность, отнесенную к
одной фазе,
, так как потери в проводах
первичной обмотки
ничтожно малы. При испытании трехфазного трансформатора
в этих выражениях
следует иметь в виду фазные значения напряжения и тока, а также мощность, отнесенную к
одной фазе, ![]() (
(![]() -
показания ваттметра).
Так как токи в фазах при хх трехфазного трансформатора различны, то за
значение тока хх условно принимают его среднее значение для трех фаз
-
показания ваттметра).
Так как токи в фазах при хх трехфазного трансформатора различны, то за
значение тока хх условно принимают его среднее значение для трех фаз ![]() .
.
3 Лекция №3. Векторная диаграмма трансформатора при холостом ходе
Содержание лекции:
-режим холостого хода;
-векторная диаграмма трансформатора при холостом ходе.
Цель лекции
Ознакомить студентов с принципом построения векторной диаграммы трансформаторов.
Основной магнитный поток в
магнитопроводе трансформатора
индуктирует в первичной и во вторичной обмотках э.д.с. ![]() и
и ![]() .
Помимо основного
магнитного потока существует поток рассеяния
первичной обмотки
.
Помимо основного
магнитного потока существует поток рассеяния
первичной обмотки ![]() . Так как при хх
во вторичной обмотке
тока нет, то эта обмотка не возбуждает поток рассеяния.
Магнитные линии, образующие
поток рассеяния, пронизывают витки только первичной обмотки, в которой
. Так как при хх
во вторичной обмотке
тока нет, то эта обмотка не возбуждает поток рассеяния.
Магнитные линии, образующие
поток рассеяния, пронизывают витки только первичной обмотки, в которой
индуктирует э.д.с.
рассеяния ![]() .
Поток
рассеяния, замыкающийся через магнитную среду и
встречающий на своем пути большое немагнитное
сопротивление, очень мал по сравнению с основным магнитным потоком в магнитопроводе трансформатора
.
Поток
рассеяния, замыкающийся через магнитную среду и
встречающий на своем пути большое немагнитное
сопротивление, очень мал по сравнению с основным магнитным потоком в магнитопроводе трансформатора ![]() . Поэтому э.д.с. рассеяния также очень
мала по сравнению с э.д.с, индуктированной
основным магнитным потоком
. Поэтому э.д.с. рассеяния также очень
мала по сравнению с э.д.с, индуктированной
основным магнитным потоком ![]() .
.
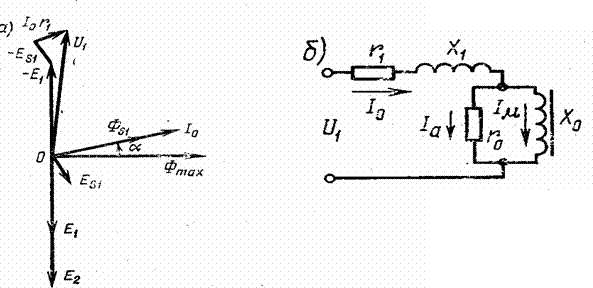
Рисунок 3.1 - Векторная диаграмма (а) и эквивалентная схема (б) трансформатора при хх.
Таким
образом, в первичной обмотке трансформатора
помимо приложенного напряжения
![]() возникают э.д.с. от основного магнитного потока
Е1 и от
потока
рассеяния Еs1.
Первичная обмотка обладает активным сопротивлением
возникают э.д.с. от основного магнитного потока
Е1 и от
потока
рассеяния Еs1.
Первичная обмотка обладает активным сопротивлением ![]() падение напряжения на
котором при хх равно
падение напряжения на
котором при хх равно ![]() . Согласно второму закону Кирхгофа, геометрическая сумма э.д.с. равна сумме падений
напряжений в сопротивлении цепи
. Согласно второму закону Кирхгофа, геометрическая сумма э.д.с. равна сумме падений
напряжений в сопротивлении цепи
![]() . (2.2)
. (2.2)
Записав ![]() (
(
![]() - индуктивное
сопротивление первичной обмотки), уравнению напряжений первичной обмотки
трансформатора
можно придать следующий вид
- индуктивное
сопротивление первичной обмотки), уравнению напряжений первичной обмотки
трансформатора
можно придать следующий вид ![]() или
или ![]() .
.
На рисунке 3.1, а изображена
векторная диаграмма трансформатора при хх. По горизонтальной оси направлен вектор
амплитуды основного
магнитного потока Фm, который
индуктирует в первичной и вторичной обмотках э.д.с. ![]() и
и
![]() , отстающие от магнитного потока по фазе на четверть периода. Поэтому
действующие значения э.д.с. обмоток трансформатора изображены векторами, повернутыми в сторону отставания (по часовой
стрелке) относительно вектора
магнитного потока на четверть периода. При построении векторной диаграммы предполагалось, что трансформатор, повышающий и э.д.с. вторичной обмотки больше, чем
э.д.с. первичной (
, отстающие от магнитного потока по фазе на четверть периода. Поэтому
действующие значения э.д.с. обмоток трансформатора изображены векторами, повернутыми в сторону отставания (по часовой
стрелке) относительно вектора
магнитного потока на четверть периода. При построении векторной диаграммы предполагалось, что трансформатор, повышающий и э.д.с. вторичной обмотки больше, чем
э.д.с. первичной (![]() ). Для понижающего
трансформатора наоборот:
). Для понижающего
трансформатора наоборот: ![]() .
Ток хх возбуждающий магнитный поток, изображен вектором
.
Ток хх возбуждающий магнитный поток, изображен вектором ![]() , повернутым в
сторону опережения относительно вектора магнитного потока
на угол а, называемый углом гистерезисного опережения или углом
магнитного запаздывания. Обычно этот угол мал и составляет несколько градусов. Основной
магнитный поток, магнитные линии
которого замыкаются через сталь магнитопровода,
отстает на угол
d
от тока за счет потерь
в стали на гистерезис и на вихревые токи. Поток рассеяния
Фs1, магнитные линии которого
замыкаются через немагнитную среду, совпадает по
фазе с вектором тока, его создающим. Э.д.с.
рассеяния отстает
от потока рассеяния на четверть периода и показана вектором
, повернутым в
сторону опережения относительно вектора магнитного потока
на угол а, называемый углом гистерезисного опережения или углом
магнитного запаздывания. Обычно этот угол мал и составляет несколько градусов. Основной
магнитный поток, магнитные линии
которого замыкаются через сталь магнитопровода,
отстает на угол
d
от тока за счет потерь
в стали на гистерезис и на вихревые токи. Поток рассеяния
Фs1, магнитные линии которого
замыкаются через немагнитную среду, совпадает по
фазе с вектором тока, его создающим. Э.д.с.
рассеяния отстает
от потока рассеяния на четверть периода и показана вектором
![]() ,
повернутым
относительно вектора
Фs1, на
,
повернутым
относительно вектора
Фs1, на ![]() сторону отставания. Вектор
приложенного напряжения
U1
определяется
как геометрическая
сумма трех векторов, стоящих в правой части
уравнения равновесия э.д.с. Для этого, из
начальной точки диаграммы 0 строим вектор -
сторону отставания. Вектор
приложенного напряжения
U1
определяется
как геометрическая
сумма трех векторов, стоящих в правой части
уравнения равновесия э.д.с. Для этого, из
начальной точки диаграммы 0 строим вектор -![]() ,
равный и противоположно направленный вектору э.д.с.
первичной обмотки
,
равный и противоположно направленный вектору э.д.с.
первичной обмотки
![]() .
Из конца вектора -
.
Из конца вектора -
![]() строим вектор
строим вектор ![]() , равный
и противоположный вектору
, равный
и противоположный вектору ![]() . Из конца вектора -
. Из конца вектора - ![]() строим вектор
строим вектор![]() , параллельный
вектору тока хх.
Начало вектора -
, параллельный
вектору тока хх.
Начало вектора -![]() и конец вектора
и конец вектора
![]()
![]() соединим вектором
соединим вектором ![]() , представляющим собой геометрическую
сумму векторов -
, представляющим собой геометрическую
сумму векторов -![]() ,-
,-![]() и
и ![]() . Следует иметь в виду,
что векторная диаграмма изображена в
искаженном масштабе. В действительности
векторы
. Следует иметь в виду,
что векторная диаграмма изображена в
искаженном масштабе. В действительности
векторы ![]() и
и
![]() очень малы по сравнению с векторами
очень малы по сравнению с векторами ![]() и -
и -![]() .
Поэтому при изображении диаграммы в масштабе
векторы
.
Поэтому при изображении диаграммы в масштабе
векторы
![]() и -
и -
![]() будут близки к
совпадению.
будут близки к
совпадению.
Первичная
обмотка трансформатора помимо активного сопротивления
r1
имеет индуктивное
Xt.
Полное сопротивление
этой обмотки ![]() .
.
Вектор -
![]() можно представить произведением тока
можно представить произведением тока ![]() на некоторое сопротивление. Это сопротивление
непостоянно и содержит как индуктивное
на некоторое сопротивление. Это сопротивление
непостоянно и содержит как индуктивное ![]() , так и активное сопротивление,
так как угол между векторами -
, так и активное сопротивление,
так как угол между векторами -
![]() и
и
![]() больше
нуля, но меньше 90°. Таким
образом, -
больше
нуля, но меньше 90°. Таким
образом, - ![]() .
.
Так как
ток ![]() равен геометрической сумме активной
равен геометрической сумме активной ![]() и реактивной
и реактивной ![]() составляющей, то сопротивление
составляющей, то сопротивление ![]() может быть
представлено в виде двух параллельных
ветвей, одна из которых содержит
активное сопротивление
может быть
представлено в виде двух параллельных
ветвей, одна из которых содержит
активное сопротивление ![]() , через которое протекает ток
, через которое протекает ток ![]() а другая - реактивное
а другая - реактивное ![]() , через которое протекает
ток
, через которое протекает
ток ![]() .
.
Уравнение
напряжений первичной обмотки с учетом приведенных выше обозначений примет
следующий вид: ![]() ,
т. е.
трансформатор
при х. х. может быть представлен эквивалентной
схемой, состоящей из двух последовательно включенных
сопротивлений
,
т. е.
трансформатор
при х. х. может быть представлен эквивалентной
схемой, состоящей из двух последовательно включенных
сопротивлений ![]() и
и ![]() , как изображено на рисунке 2.4. На эквивалентной схеме индуктивное сопротивление
, как изображено на рисунке 2.4. На эквивалентной схеме индуктивное сопротивление ![]() , учитывает действие основного магнитного потока, а активное сопротивление
, учитывает действие основного магнитного потока, а активное сопротивление ![]() эквивалентно
потерям в стали магнитопровода, т.е. мощность,
выделяющаяся
эквивалентно
потерям в стали магнитопровода, т.е. мощность,
выделяющаяся![]() в этом сопротивлении
в этом сопротивлении ![]() . Так как основной
магнитный поток в магнитопроводе много больше потока рассеяния, то
. Так как основной
магнитный поток в магнитопроводе много больше потока рассеяния, то
![]() ,
,![]() , поэтому полное сопротивление
, поэтому полное сопротивление
![]() .
.
Полное
сопротивление хх. ![]() . По
данным опыта хх. полное, активное и
реактивное сопротивления
будут:
. По
данным опыта хх. полное, активное и
реактивное сопротивления
будут:
![]() , где
, где ![]() . В этих выражениях
. В этих выражениях ![]() - соответственно мощность, напряжение и ток, измеренные при опыте хх.
- соответственно мощность, напряжение и ток, измеренные при опыте хх.
Для трехфазного трансформатора векторная диаграмма и эквивалентная схема изображаются для одной фазы и имеют такой же вид, как векторная диаграмма и эквивалентная схема однофазного трансформатора.
4 Лекция № 4 . Режим короткого замыкания
Содержание лекции:
- режим короткого замыкания;
- векторные диаграммы;
-схемы замещения.
Цель лекции
Ознакомить студентов с режимом короткого замыкания;
-с построением векторной диаграммы.
Короткие
замыкания в электрических установках возникают
обычно вследствие каких-либо неисправностей в сетях (при
механическом повреждении изоляции, при ее
электрическом пробое в результате
перенапряжений и др.) или при ошибочных действиях эксплуатационного персонала. Для трансформатора к.з. представляет собой серьезную опасность, так
как при этом возникают очень большие
токи. При к.з. зажимов вторичной обмотки
сопротивление нагрузки ![]() , и, следовательно, напряжение на зажимах вторичной обмотки
, и, следовательно, напряжение на зажимах вторичной обмотки ![]() .
.
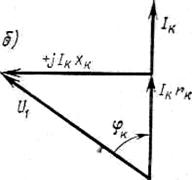
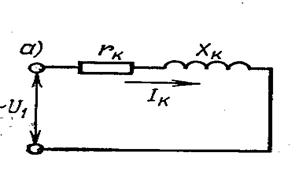
Рисунок 4.1 - Эквивалентная схема (а) и векторная диаграмма (б) трансформатора при к.з.
Таким
образом, напряжение ![]() , приложенное к первичной обмотке, будет
уравновешено падением напряжения в полных сопротивлениях первичной и вторичной
обмоток:
, приложенное к первичной обмотке, будет
уравновешено падением напряжения в полных сопротивлениях первичной и вторичной
обмоток:![]() . Эквивалентная схема
для одной фазы трансформатора при к.з. изображена на рисунке. 4.1,
а.
. Эквивалентная схема
для одной фазы трансформатора при к.з. изображена на рисунке. 4.1,
а.
Уравнение
равновесия э.д.с. первичной обмотки трансформатора при к.з. вторичной обмотки
запишется в следующем виде: ![]() где
где ![]() - ток к.з.
На рисунке
4.1 б, построена
векторная диаграмма для одной фазы
трансформатора при
к.з. Вертикально вверх
направлен вектор тока к.з.
- ток к.з.
На рисунке
4.1 б, построена
векторная диаграмма для одной фазы
трансформатора при
к.з. Вертикально вверх
направлен вектор тока к.з. ![]() ,
параллельно ему - вектор напряжения в активном сопротивлении к.з.
,
параллельно ему - вектор напряжения в активном сопротивлении к.з. ![]() . На
. На ![]() повернут относительно вектора тока в сторону
опережения вектор падения напряжения на
индуктивном сопротивлении к.з. трансформатора
повернут относительно вектора тока в сторону
опережения вектор падения напряжения на
индуктивном сопротивлении к.з. трансформатора
![]() . Геометрическая сумма векторов
. Геометрическая сумма векторов
![]() и
и
![]() дает вектор приложенного
к первичной обмотке
напряжения
дает вектор приложенного
к первичной обмотке
напряжения ![]() который
оказался повернутым относительно вектора тока
который
оказался повернутым относительно вектора тока
![]() в сторону опережения на угол
к.з.
в сторону опережения на угол
к.з. ![]() . Этот угол зависит
от соотношения сопротивлений
. Этот угол зависит
от соотношения сопротивлений ![]() и
и ![]() . Чем больше индуктивное
сопротивление
. Чем больше индуктивное
сопротивление ![]() и меньше активное
и меньше активное ![]() , тем большим будет
угол
, тем большим будет
угол
![]() . Таким образом, сила
тока к.з.
трансформатора
. Таким образом, сила
тока к.з.
трансформатора
![]() .
.
Так как
падение напряжения в полном сопротивлении обмоток трансформатора при номинальном токе ![]() составляет несколько процентов от номинального напряжения, т.е.
составляет несколько процентов от номинального напряжения, т.е. ![]() , то ток
, то ток ![]() окажется больше номинального
тока во столько раз, во сколько номинальное
напряжение больше падения напряжения
в полном сопротивлении обмоток при номинальном токе
окажется больше номинального
тока во столько раз, во сколько номинальное
напряжение больше падения напряжения
в полном сопротивлении обмоток при номинальном токе
![]() . (4.1)
. (4.1)
Отношение ![]() называют кратностью
тока короткого замыкания. Потери в проводах обмоток трансформатора пропорциональны току во второй степени
называют кратностью
тока короткого замыкания. Потери в проводах обмоток трансформатора пропорциональны току во второй степени ![]() , так что в случае, когда ток к.з. окажется, например, в 20 раз больше
номинального тока, потери в проводах
обмоток будут в 400 раз больше (если не учитывать увеличения сопротивления обмоток от нагрева). Выделение большой мощности в проводах обмоток вызывает
резкое повышение их температуры,
вследствие которого возможно нарушение
целости изоляции и выход трансформатора из строя. В трансформаторе имеется очень много параллельных
друг другу витков, каждый из которых
можно рассматривать как отдельный
провод. В витках какой-либо обмотки (первичной или вторичной) протекают токи одинакового направления, так
что все витки одной обмотки взаимно
притягиваются. Намагничивающие силы первичной и вторичной обмоток имеют
встречное направление, поэтому обмотки
стремятся оттолкнуться одна от другой. Механические силы, действующие на обмотки, зависят от конструкции обмоток, размещения витков и токов, протекающих в
обмотках. В концентрических
симметричных обмотках силы, действующие на обмотки, направлены перпендикулярно
оси катушек, в дисковых чередующихся обмотках силы направлены
параллельно оси катушек. Так как
силы, действующие на провода с током,
зависят от произведения токов в проводах, то и силы
, так что в случае, когда ток к.з. окажется, например, в 20 раз больше
номинального тока, потери в проводах
обмоток будут в 400 раз больше (если не учитывать увеличения сопротивления обмоток от нагрева). Выделение большой мощности в проводах обмоток вызывает
резкое повышение их температуры,
вследствие которого возможно нарушение
целости изоляции и выход трансформатора из строя. В трансформаторе имеется очень много параллельных
друг другу витков, каждый из которых
можно рассматривать как отдельный
провод. В витках какой-либо обмотки (первичной или вторичной) протекают токи одинакового направления, так
что все витки одной обмотки взаимно
притягиваются. Намагничивающие силы первичной и вторичной обмоток имеют
встречное направление, поэтому обмотки
стремятся оттолкнуться одна от другой. Механические силы, действующие на обмотки, зависят от конструкции обмоток, размещения витков и токов, протекающих в
обмотках. В концентрических
симметричных обмотках силы, действующие на обмотки, направлены перпендикулярно
оси катушек, в дисковых чередующихся обмотках силы направлены
параллельно оси катушек. Так как
силы, действующие на провода с током,
зависят от произведения токов в проводах, то и силы ![]() действующие на обмотки трансформаторов при к.з.
будут во много раз больше сил,
которые возникают при номинальной нагрузке. Под действием очень больших механических сил обмотки трансформатора деформируются настолько, что может быть
нарушена изоляция и резко уменьшена
их электрическая прочность. Поэтому конструкция
обмоток должна быть рассчитана на такую механическую прочность, которая
противостояла бы силам, возникающим в
первый момент от мгновенных токов
действующие на обмотки трансформаторов при к.з.
будут во много раз больше сил,
которые возникают при номинальной нагрузке. Под действием очень больших механических сил обмотки трансформатора деформируются настолько, что может быть
нарушена изоляция и резко уменьшена
их электрическая прочность. Поэтому конструкция
обмоток должна быть рассчитана на такую механическую прочность, которая
противостояла бы силам, возникающим в
первый момент от мгновенных токов ![]() , превышающих установившиеся токи
, превышающих установившиеся токи
![]() примерно
в два раза
примерно
в два раза ![]() .
.
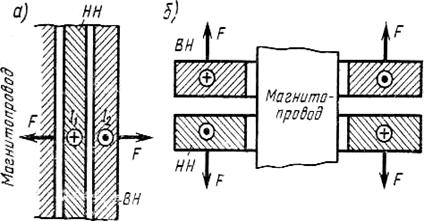
Рисунок 4.2 - Направление сил, действующих на концентрические симметричные (а) и дисковые (б) обмотки трансформатора
Опыт к.з.
производится при значительно пониженном напряжении и является вторым предельным
режимом работы трансформатора,
который наряду с опытом х. х. позволяет определить параметры трансформатора при любой нагрузке. При опыте к.з. вторичную обмотку трансформатора замыкают накоротко,
а к первичной подводят такое
пониженное ![]() ,
при котором в обмотках трансформатора
протекают номинальные токи. Это напряжение называют напряжением короткого
замыкания, измеряется оно в процентах от номинального:
,
при котором в обмотках трансформатора
протекают номинальные токи. Это напряжение называют напряжением короткого
замыкания, измеряется оно в процентах от номинального: ![]() .
.
При опыте к.з. по обмоткам трансформатора протекают номинальные токи и приложенное к первичной обмотке напряжение
![]() (4.2)
(4.2)
где ![]() - номинальный ток
первичной обмотки;
- номинальный ток
первичной обмотки;
![]() - соответственно полное,
активное и реактивное сопротивления к.з.;
- соответственно полное,
активное и реактивное сопротивления к.з.;
![]() - соответственно
активная и реактивная составляющие напряжения
к.з.
- соответственно
активная и реактивная составляющие напряжения
к.з.
![]() .
.
На основании (3.6) может быть построена векторная диаграмма, которая примет вид треугольника напряжений (см. рисунок 4.2).
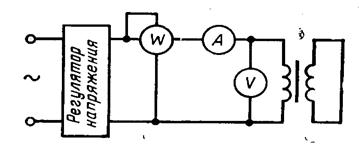
Рисунок 4.3- Схема опыта к.з. трансформатора
Такую
векторную диаграмму называют треугольником короткого
замыкания,
а угол ![]() — углом короткого
замыкания. Этот угол
— углом короткого
замыкания. Этот угол ![]() зависит от соотношения активного и реактивного
сопротивлений к.з.
зависит от соотношения активного и реактивного
сопротивлений к.з.
Опыт
к.з. позволяет определить напряжение ![]() , потери в обмотках трансформатора
, потери в обмотках трансформатора
![]() и
сопротивления к.з. трансформатора
и
сопротивления к.з. трансформатора
![]() .
.
Напряжение
![]() определится
показанием вольтметра при номинальном токе трансформатора, потери в обмотках
определится
показанием вольтметра при номинальном токе трансформатора, потери в обмотках
![]() (потери в меди) -
показанием ваттметра. При опыте к.з. полезная мощность
трансформатора равна
нулю, а потери в стали ничтожно малы,
так как мал магнитный поток в сердечнике.
Поэтому мощность,
потребляемая трансформатором при опыте к.з. расходуется на
нагревание проводов
обмоток
(потери в меди) -
показанием ваттметра. При опыте к.з. полезная мощность
трансформатора равна
нулю, а потери в стали ничтожно малы,
так как мал магнитный поток в сердечнике.
Поэтому мощность,
потребляемая трансформатором при опыте к.з. расходуется на
нагревание проводов
обмоток
![]()
где
![]() - номинальный ток первичной обмотки.
Сопротивления к.з.: активное
- номинальный ток первичной обмотки.
Сопротивления к.з.: активное ![]() полное
полное ![]() ,
индуктивное
,
индуктивное ![]() .
.
Если опыт
к.з. производят при «холодном» (неработающем) трансфрматоре, то параметры к.з.
надо привести к рабочей температуре
750 С, при изменении которой меняются активное сопротивление и потери в обмотках. Таким образом,
приведенные к ![]() температуре 750С активное
сопротивление
температуре 750С активное
сопротивление ![]() в
обмотках
в
обмотках ![]() полное
сопротивление
полное
сопротивление ![]() .
.
При
температуре 750С напряжение которого замыкания ![]() , а его активная и реактивная
составляющие
, а его активная и реактивная
составляющие
![]() .
(4.3)
.
(4.3)
5 Лекция №5. Работа трансформаторов под нагрузкой
Содержание лекции:
- векторная диаграмма;
- эквивалентная схема трансформатора при нагрузке ;
- уравнения равновесия э.д.с. для первичной и вторичной обмоток трансформатора.
Цель лекции
Ознакомить студентов:
- с работой трансформаторов под нагрузкой;
-с уравнением равновесия э.д.с. для первичной и вторичной обмоток трансформатора.
При построении векторных
диаграмм и эквивалентных схем необходимо
сравнивать величины, относящиеся к первичной и вторичной обмоткам, которые при коэффициенте
трансформации, не равном единице,
могут быть существенно различными. Для удобства построения вторичную обмотку трансформатора приводят к
виткам первичной, т.е. условно полагают, что вместо вторичной обмотки с числом витков ![]() имеется обмотка с числом
витков
имеется обмотка с числом
витков ![]() , равным
числу витков первичной обмотки, но так, чтобы мощность, потери энергии и фазовые углы между электрическими величинами оставались после приведения трансформатора
неизменными. Э.д.с. вторичной обмотки трансформатора пропорционально числу
витков обмотки изменится и ее э.д.с:
, равным
числу витков первичной обмотки, но так, чтобы мощность, потери энергии и фазовые углы между электрическими величинами оставались после приведения трансформатора
неизменными. Э.д.с. вторичной обмотки трансформатора пропорционально числу
витков обмотки изменится и ее э.д.с: ![]() . Напряжение
приведенной обмотки
. Напряжение
приведенной обмотки ![]() . Приведенное значение вторичного тока
найдем из условия постоянства полной мощности, т.е.
полная мощность приведенной вторичной обмотки должна оставаться равной полной
мощности действительной вторичной обмотки:
. Приведенное значение вторичного тока
найдем из условия постоянства полной мощности, т.е.
полная мощность приведенной вторичной обмотки должна оставаться равной полной
мощности действительной вторичной обмотки:
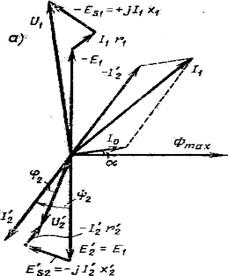
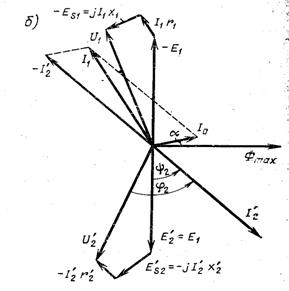
Рисунок 5.1 -Векторная диаграмма трансформатора при активно-индуктивной (а) и активно-емкостной (б) нагрузках
![]() ,
откуда
,
откуда ![]() Активное
сопротивление приведенной
вторичной обмотки трансформатора найдем из условия
постоянства
потерь в меди при приведении вторичной обмотки:
Активное
сопротивление приведенной
вторичной обмотки трансформатора найдем из условия
постоянства
потерь в меди при приведении вторичной обмотки:![]() ,
откуда
,
откуда ![]() . Индуктивное сопротивление,
так же как и
индуктивность, пропорциональна квадрату числа витков, следовательно, индуктивное
сопротивление приведенной вторичной обмотки
. Индуктивное сопротивление,
так же как и
индуктивность, пропорциональна квадрату числа витков, следовательно, индуктивное
сопротивление приведенной вторичной обмотки ![]() После приведения вторичной обмотки трансформатора
к виткам первичной мы можем
перейти к построению векторной диаграммы. На
рисунке. 5.1 показана векторная диаграмма для активно-индуктивной
После приведения вторичной обмотки трансформатора
к виткам первичной мы можем
перейти к построению векторной диаграммы. На
рисунке. 5.1 показана векторная диаграмма для активно-индуктивной ![]() и для активно-емкостной
и для активно-емкостной ![]() нагрузок. В стороне опережения относительно вектора основного потока
трансформатора на угол
нагрузок. В стороне опережения относительно вектора основного потока
трансформатора на угол ![]() построен вектор тока
построен вектор тока
![]() ,
а в сторону отставания
,
а в сторону отставания ![]() на угол
на угол ![]() - векторы э.д.с. первичной и приведенной
вторичной обмоток
- векторы э.д.с. первичной и приведенной
вторичной обмоток ![]() . В сторону отставания
при индуктивном характере нагрузки
. В сторону отставания
при индуктивном характере нагрузки ![]() и в сторону опережения при емкостном характере нагрузки
и в сторону опережения при емкостном характере нагрузки ![]() на угол строим вектор приведенного
вторичного тока
на угол строим вектор приведенного
вторичного тока ![]() . Напряжение на зажимах вторичной обмотки
трансформатора при нагрузке равно сумме э.д.с. вторичной обмотки минус падение напряжения в активном сопротивлении этой
обмотки, т. е. уравнение напряжений
для вторичной обмотки трансформатора
имеет
следующий вид
. Напряжение на зажимах вторичной обмотки
трансформатора при нагрузке равно сумме э.д.с. вторичной обмотки минус падение напряжения в активном сопротивлении этой
обмотки, т. е. уравнение напряжений
для вторичной обмотки трансформатора
имеет
следующий вид
![]() (5.1)
(5.1)
где ![]() - э.д.с,
индуктированная во вторичной обмотке основным
магнитным потоком трансформатора;
- э.д.с,
индуктированная во вторичной обмотке основным
магнитным потоком трансформатора;
![]() - э.д.с. от потока
рассеяния
вторичной обмотки;
- э.д.с. от потока
рассеяния
вторичной обмотки;
![]() - индуктивное
сопротивление этой обмотки.
- индуктивное
сопротивление этой обмотки.
При нагрузке трансформатора током вторичной обмотки будет создан поток рассеяния, магнитные линии которого замыкаются через воздух и пронизывают витки только вторичной обмотки. После приведения вторичной обмотки к виткам первичной мы запишем это уравнение в следующем виде
![]() .
(5.2)
.
(5.2)
Следовательно,
для определения вектора напряжения на зажимах вторичной обмотки трансформатора при
нагрузке из конца
вектора э.д.с. ![]() строим вектор
строим вектор ![]() , отстающий от вектора тока
, отстающий от вектора тока
![]() на
на ![]() , и затем вектор
, и затем вектор ![]() , параллельный
и противоположно
направленный вектору тока
, параллельный
и противоположно
направленный вектору тока
![]() . Геометрическая сумма этих трех
построенных векторов дает приведенное вторичное
напряжение трансформатора
. Геометрическая сумма этих трех
построенных векторов дает приведенное вторичное
напряжение трансформатора
![]() .
.
Для
определения тока первичной обмотки нам нужно, согласно
уравнению равновесия намагничивающей
силы построить геометрическую сумму векторов тока
![]() для приведенного тока вторичной обмотки с
обратным
знаком
-
для приведенного тока вторичной обмотки с
обратным
знаком
-![]() .
Для определения
первичного напряжения воспользуемся уравнением равновесия напряжений обмотки
.
Для определения
первичного напряжения воспользуемся уравнением равновесия напряжений обмотки
![]() .
.
Строим
вектор ![]() ,
равный и противоположно направленный
вектору
,
равный и противоположно направленный
вектору ![]() . Из конца вектора
. Из конца вектора
![]() :
строим вектор
:
строим вектор ![]() ,
повернутый
относительно вектора тока
,
повернутый
относительно вектора тока ![]() на
на
![]() в сторону опережения, и затем вектор
в сторону опережения, и затем вектор ![]() , параллельный
вектору тока
, параллельный
вектору тока ![]() . Геометрическая сумма трех построенных нами
векторов - вектор приложенного напряжения
. Геометрическая сумма трех построенных нами
векторов - вектор приложенного напряжения ![]() . Из векторных
диаграмм видно, что вторичное напряжение зависит от величины тока нагрузки трансформатора
. Из векторных
диаграмм видно, что вторичное напряжение зависит от величины тока нагрузки трансформатора ![]() и от характера нагрузки, т.е. от угла
и от характера нагрузки, т.е. от угла ![]() . При индуктивном характере
нагрузки вторичное напряжение по
абсолютной величине меньше, чем э.д.с,
. При индуктивном характере
нагрузки вторичное напряжение по
абсолютной величине меньше, чем э.д.с, ![]() ,—-понижение
напряжения; при емкостном характере нагрузки вторичное напряжение по абсолютной
величине больше, чем э.д.с.
,—-понижение
напряжения; при емкостном характере нагрузки вторичное напряжение по абсолютной
величине больше, чем э.д.с. ![]() -
повышение напряжения.
-
повышение напряжения.
Так же, как и в случае х.х. трансформатора, для рабочего режима строится эквивалентная схема (рисунок. 5.2).
Э.д.с.
рассеяния первичной обмотки с обратным знаком ![]() ,
выше представлено в виде падения напряжения в
индуктивном сопротивлении
,
выше представлено в виде падения напряжения в
индуктивном сопротивлении ![]() , обусловленном потоком рассеяния
, обусловленном потоком рассеяния
![]() , т.е.
, т.е.
![]() . Э.д.с. рассеяния
вторичной обмотки
. Э.д.с. рассеяния
вторичной обмотки ![]() представим в виде
падения напряжения на индуктивном сопротивлении
представим в виде
падения напряжения на индуктивном сопротивлении ![]() , обусловленном потоком рассеяния
, обусловленном потоком рассеяния
![]() . После приведения
вторичной обмотки к
первичной, получим
. После приведения
вторичной обмотки к
первичной, получим ![]() .
Тогда уравнениям
равновесия э.д.с. для первичной и
вторичной обмоток трансформатора можем придать
следующий вид
.
Тогда уравнениям
равновесия э.д.с. для первичной и
вторичной обмоток трансформатора можем придать
следующий вид ![]() и
и
![]() , где
, где ![]() и
и ![]()
полные сопротивления первичной и приведенной вторичной обмоток трансформатора.
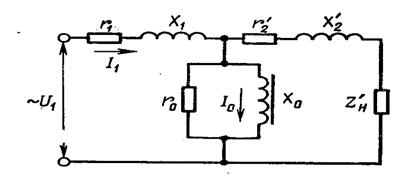
Рисунок 5.2 - Эквивалентная схема трансформатора при нагрузке
Введем
обозначение: ![]()
![]() , где
, где ![]() - вектор тока хх
- вектор тока хх
![]() — полное
сопротивление трансформатора при х.х.
Напряжение вторичной обмотки трансформатора при нагрузке
— полное
сопротивление трансформатора при х.х.
Напряжение вторичной обмотки трансформатора при нагрузке
![]() ,
где
,
где ![]() - полное приведенное
сопротивление внешней нагрузки.
Из
уравнения равновесия н.с. имеем:
- полное приведенное
сопротивление внешней нагрузки.
Из
уравнения равновесия н.с. имеем: ![]() . Уравнение равновесия э.д.с. для
вторичной обмотки трансформатора записывается в измененном виде
. Уравнение равновесия э.д.с. для
вторичной обмотки трансформатора записывается в измененном виде ![]() . Отсюда ток хх
. Отсюда ток хх
![]() .
.
Подставив
![]() в
уравнение равновесия э.д.с. для первичной обмотки, получим
в
уравнение равновесия э.д.с. для первичной обмотки, получим ![]() .
Откуда эквивалентное сопротивление
трансформатора
.
Откуда эквивалентное сопротивление
трансформатора
![]() (5.3)
(5.3)
представляет собой
два последовательно включенных сопротивления, из которых первое - полное сопротивление
первичной обмотки трансформатора, второе - параллельное соединение двух сопротивлений:
сопротивления хх трансформатора и последовательное
соединение приведенных
полных сопротивлений вторичной обмотки трансформатора и нагрузки.
Ток
![]() , - малая величина по сравнению с
номинальным током
первичной обмотки трансформатора. Кроме того, ток
, - малая величина по сравнению с
номинальным током
первичной обмотки трансформатора. Кроме того, ток ![]() и ток нагрузки
и ток нагрузки ![]() не совпадают по
фазе. Так, например, при активной нагрузке ток
не совпадают по
фазе. Так, например, при активной нагрузке ток
![]() будет активным и окажется близким к
совпадению с э.д.с, тогда как ток хх почти чисто реактивный и близок к
совпадению с основным магнитным потоком по фазе. Поэтому ток
первичной обмотки
численно незначительно отличается от приведенного тока вторичной обмотки:
будет активным и окажется близким к
совпадению с э.д.с, тогда как ток хх почти чисто реактивный и близок к
совпадению с основным магнитным потоком по фазе. Поэтому ток
первичной обмотки
численно незначительно отличается от приведенного тока вторичной обмотки: ![]() .
.
Если пренебречь током хх, то упрощенная эквивалентная схема трансформатора при нагрузке будет более простой. Для этой схемы можно ввести следующие обозначения
![]()
![]()
![]() (5.4)
(5.4)
где ![]() ,
, ![]() и
и ![]() - соответственно
полное, активное и реактивное сопротивление
к.з. трансформатора. На рисунке 5.3(а, б)
показана
видоизмененная эквивалентная схема трансформатора при
нагрузке.
- соответственно
полное, активное и реактивное сопротивление
к.з. трансформатора. На рисунке 5.3(а, б)
показана
видоизмененная эквивалентная схема трансформатора при
нагрузке.
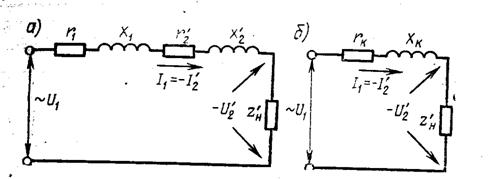
Рисунок 5.3 - Упрощенная (а) и видоизмененная (6) эквивалентные схемы трансформатора
6 Лекция №6. Электродвижущие силы в обмотках машин переменного тока
Содержание лекции:
-электродвижущая сила проводника;
-электродвижущая сила витка и катушки;
- электродвижущая сила фазы обмотки.
Цель лекции
Ознакомить студентов с ээлектродвижущими силами в обмотках
- машин переменного тока.
Необходимо, чтобы
индуктируемые в обмотках ЭДС были синусоидальными, т.е. не содержали высшие
гармоники, вызывающие дополнительный нагрев и тормозные моменты. Так как ЭДС
индуктируются вращающимися магнитными потоками, то для этого необходимо, чтобы
распределение магнитной индукции вдоль воздушного зазора было синусоидальным. Для
этого применяются различные конструктивные меры. Например, для улучшения кривой
поля возбуждения явнополюсных синхронных генераторов их полюсные наконечники
выполняют с радиусом, несколько меньшим, чем радиус воздушного зазора т.е.
делают зазор (![]() )
у краев полюсного наконечника больше зазора посередине (δ). Хорошие
результаты дает полюсный наконечник с соотношением
)
у краев полюсного наконечника больше зазора посередине (δ). Хорошие
результаты дает полюсный наконечник с соотношением ![]()
В неявнополюсных машинах синусоидальный характер распределения магнитной индукции создается подбором соответствующего отношения между частью окружности ротора без пазов и частью его окружности с пазами, в которые укладывается обмотка возбуждения. Обычно это отношение равно 2/3. Однако и в этих случаях кривая магнитной индукции лишь приближается к синусоиде, поэтому ЭДС обмотки статора остается несинусоидальной и наряду с основной гармоникой содержит высшие гармоники. В силу симметрии кривой ЭДС обмотки статора относительно оси абсцисс, в кривой ЭДС не будет четных гармоник.
Определим ЭДС, индуктируемую в обмотке статора основной пространственной гармоникой вращающегося поля (к=1).
Вращающееся со скоростью υ=2τf
![]() синусоидальное
магнитное поле индуктирует в каждом проводнике витка ЭДС действующее значение
синусоидальное
магнитное поле индуктирует в каждом проводнике витка ЭДС действующее значение
![]() ,
,
![]()
![]()
где Bδ=Bml - амплитуда индукции основной гармоники поля в зазоре;
lδ - расчетная активная длина машины;
τ- полюсное деление.
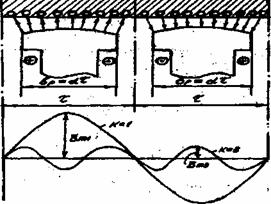
Рисунок 6.1- Распределение магнитной индукции поля возбуждения явнополюсной синхронной машины вдоль поверхности статора
В ряде случаев для улучшения формы ЭДС обмотки статора осуществляется скос пазов относительно бегущего магнитного поля. При этом фаза ЭДС, индуктируемая в отдельных участках проводника синусоидально распределенным магнитным полем, беспрерывно изменяется вдоль проводника и элементарные ЭДС ∆E, индуктируемые на обоих концах проводника, сдвинуты по фазе на угол
![]()
где вс - величина скоса.
В этом случае, для определения ЭДС проводника необходимо сложить векторы ЭДС отдельных участков проводника ∆Е. В пределе, если рассматривать бесконечно малые участки, ∆Е→0 и геометрическая сумма векторов ∆−Е изобразится дугой и будет равна хорде окружности, опирающейся на центральный угол γс.
Отношение длины хорды к ее дуге
![]()
определяет степень уменьшения ЭДС Eпр при наличии скоса и называется коэффициентом пазов обмотки.
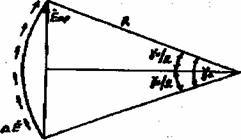
Рисунок 6.2 - Определение ЭДС проводника при скосе пазов
Подставив значение γс, получим
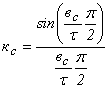 ,
,
так как скос невелик, то
kс ![]() 1. Например, при
1. Например, при
![]()
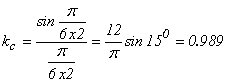 ,
,
т.е. ЭДС Епр уменьшается на 1,1 %. Окончательно
![]() ;
;
а) ЭДС проводника
б) электродвижущая сила витка и катушки.
Шаг витка и катушки обмоток
переменного тока у, чаще всего несколько укорачивают по сравнению с
полюсным делением τ, так что относительный шаг β=у /![]() обычно меньше
единицы.
обычно меньше
единицы.
ЭДС проводников витка имеют одинаковую величину, но сдвинуты по фазе на угол βπ, так как активные проводники витка сдвинуты в магнитном поле на такой же угол.
ЭДС витка равна Ев, = Епр – Eпр и согласно рисунку 3
![]()
где ky = sinπβ/2- коэффициент укорочения шага обмотки. eв максимальна при полном шаге (y=π;β=1), когда ky= 1.
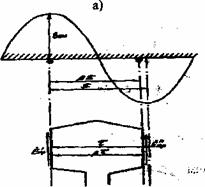
Рисунок 6. 3 - ЭДС витка
Группа последовательно соединенных витков, вместе с общей пазовой изоляцией стенок паза, называется катушкой.
Если катушка содержит ω к витков, то ЭДС катушки
![]() .
.
Поток одного полюса при синусоидальном распределении индукции
![]()
и после подстановки значения Bбlбτ в (11) получим окончательно
Eк=π![]() fωк ку кс ф;
fωк ку кс ф;
в) электродвижущая сила катушечной группы.
Для получения достаточного количества проводников и витков в фазе и сохранения в то же время приемлемых размеров пазов, количество пазов машине делают больше единицы. При этом ряд (q) катушек, имеющих по одинаковому количеству витков ωк и лежащих в соседних пазах, соединяют последовательно. Такую группу катушек, принадлежащих одной фазе, называют катушечной группой.

Рисунок 6.4 - Катушечная группа в магнитном поле (q =4)
ЭДС соседних катушек группы сдвинуты на угол
![]() .
.
Вся группа из q катушек занимает по окружности якоря угол (электрический)
а=
qγ=![]()
![]()
называемый углом фазной зоны. ЭДС катушечной группы Eq равна геометрической сумме ЭДС отдельных катушек группы и меньше арифметической суммы ЭДС этих катушек qEk . Отношение Eq / qEk=kр называется коэффициентом распределения обмотки.
Таким образом, Eq= kрqEк.
Из рисунка 5 следует, что
Eq =2Rsinα/2 и Ek =2Rsinγ /2=2Rsinα/2q.
Подставив эти значения, получаем
Кр=![]()
![]() .
.
Рисунок 6.5 - Определение ЭДС катушечной группы
При q=1,имеем кр = 1, а при q >1, kp< 1.
На основании выражений (13) и (16) получим
Еq=π![]() fωккобксф=4,44fωкqкобксф
fωккобксф=4,44fωкqкобксф
где коб=кукр - коэффициент обмотки;
г) электродвижущая сила фазы обмотки.
В многополюсной машине каждая фаза обмотки содержит ряд катушечных групп, лежащих под разными полюсами. Если группы содержат одинаковое число катушек q, то они занимают одинаковые углы α и сдвинуты относительно друг друга на целое число полюсных делений. В этом случае ЭДС катушечных групп равны по величине и сдвинуты по фазе на 360° (при сдвиге группы на четное число τ) или на 180° (при сдвиге на нечетное число τ). Такие катушечные группы можно соединить последовательно таким образом, что ЭДС групп будут складываться арифметически. Возможно также их параллельное соединение так, что ЭДС всех параллельных ветвей будут одинаковы по величине и совпадут по фазе.
Если в каждой ветви соединено
последовательно п катушечных групп, то действующее значение ЭДС каждой
ветви и фазы обмотки в целом будет: Е =π![]() ωкобксф=4,44fωҝобксф,
ωкобксф=4,44fωҝобксф,
где ω=nq ω - число последовательно соединенных витков каждой параллельной ветви и называется числом витков фазы.
Если
m - фазная обмотка имеет
Z naзов и α
параллельных ветвей, то: ω=![]()
где Sn - число эффективных проводников в пазу.
7 Лекция №7. Устройство и принцип действия асинхронных
двигателей. Трехфазная асинхронная машина при вращающемся роторе
Содержание лекции:
- устройство и принцип действия асинхронных двигателей;
- вращающий момент асинхронных двигателей;
-энергетическая диаграмма асинхронного двигателя;
-механическая характеристика асинхронного двигателя.
Цель лекции
Ознакомить студентов:
-с принципом образования вращающего магнитного поля асинхронных двигателей;
- с эксплутационными характеристиками асинхронных двигателей;
-с механической характеристикой асинхронного двигателя.
Асинхронная машина состоит из двух основных частей - неподвижной части - статора и подвижной части - ротора. Между статором и ротором имеется воздушный зазор. Увеличение воздушного зазора резко уменьшает коэффициент мощности (cosφ) и вращающий момент двигателя.
Сердечник статора собирают из листов электротехнической стали в виде колец, на внутренней окружности которых штампуют пазы для укладки обмотки статора. Обмотка выполняется из изолированных медных проводов. Стальные листы изолируют друг от друга лаком для уменьшения потерь от вихревых токов.
В зависимости от типа ротора асинхронные двигатели делятся на: а) двигатели с короткозамкнутым ротором; б) двигатели с контактными кольцами. Работа асинхронного двигателя основана на принципе электромагнитной индукции.
При подаче в обмотку статора
трехфазного переменного тока возникает вращающееся магнитное поле, которое
перемещается в воздушном зазоре между статором и ротором с частотой вращения
п1 и при своем вращении пересекает проводники обмотки ротора,
индуктируя в этой обмотке ЭДС
e2. В результате взаимодействия тока в
проводнике обмотки ротора с вращающимся магнитным полем статора возникает сила ![]() , которая перемещает
проводник в направлении, определяемом правилом «левой руки». Если умножим силу
F
на расстояние от оси ротора до проводника,
то получим вращающий момент М=FR,
развиваемый
током этого проводника. Так как на роторе помещено большое количество
проводников, то произведения сил, действующих на каждый проводник, на
расстояние этих проводников до оси ротора определяет вращающий момент
двигателя. Под действием вращающего момента ротор двигателя вращается в
направлении вращения магнитного поля.
, которая перемещает
проводник в направлении, определяемом правилом «левой руки». Если умножим силу
F
на расстояние от оси ротора до проводника,
то получим вращающий момент М=FR,
развиваемый
током этого проводника. Так как на роторе помещено большое количество
проводников, то произведения сил, действующих на каждый проводник, на
расстояние этих проводников до оси ротора определяет вращающий момент
двигателя. Под действием вращающего момента ротор двигателя вращается в
направлении вращения магнитного поля.
Активная мощность, потребляемая двигателем из сети, равна
Р1=т1U1I1cosφ1=m1E1I1cosψ1+m1I12γ1.
Окончательное выражение для подводимой к статору активной мощности
P1=m 1I 1 2γ1 + m1 E1 I0 sinδ +m1 E 1I2 cosψ2= pм1 + pc1 + рэм
где Рм1 - электрические потери в обмотке статора;
Pс1 — магнитные потери в сердечнике статора;
Рэм - электромагнитная мощность, передаваемая вращающимся магнитным полем в цепь ротора.
Для реактивной мощности, потребляемой двигателем, имеем
Q1=m1 U1 I1 sin φ1= m1 E1 I1sin ψ1 +m1 I1 2x1 .
После аналитических преобразований получим
Q1 = m1 U1 I1 sin ψ2+ m1 I12x1 + m1E 1I0 cos.
Преобразование
энергии и потери в асинхронном двигателе
иллюстрируются энергетической диаграммой.
Рисунок 7.1- Энергетическая диаграмма асинхронного двигателя
Рмех - механические потери в роторе;
Рм2 - электрические потери в обмотке ротора;
Рдоб - прочие добавочные потери
Электромагнитная мощность вращающегося магнитного поля
Рэм= Р1 – (Рм1+ Рс1).
Мощность, передаваемая со статора на вал ротора
Р2= Рэм – Рм2 .
Полезная механическая мощность на валу двигателя
Р2 = Р2 – Рмех- Рдоб .
Обозначив угловую скорость поля статора через Ω1, а ротора через Ω2 имеем Рэм = М Ω1; Р2 = М Ω2.
Следовательно Рм2 = Рэм – Р2 = М (Ω1 –Ω2).
Таким образом, потери в обмотках роторной цепи равны мощности вращающегося поля, умноженной на скольжение, т.е. чем больше скольжение (меньше частота вращения), тем больше потери в цепи ротора.
Вращающий момент асинхронного двигателя
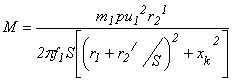
где xk=x1+x2 - индуктивное сопротивление короткого замыкания.
Отсюда вытекает, что момент М пропорционален квадрату напряжения сети U12, т.е. асинхронный двигатель уменьшает перегрузочную способность при понижении напряжения. Напряжение сети будем считать постоянным, поэтому момент является функцией скольжения S.
Имея параметры двигателя r1, x1, r2 и x2 / и задаваясь различными значениями скольжения от S = 1 до S=0, можем построить механическую характеристику двигателя M=f(S), показанную на рисунке 7.2
Рисунок 7.2- Механическая характеристика асинхронного двигателя
При пуске двигателя развивается пусковой момент (точка а) при S=1, проходит через максимальный момент (точка в) при S = SM. Равновесие между вращающим моментом двигателя и моментом сопротивления на валу со стороны приводного механизма наступает тогда, когда момент двигателя становится равным моменту сопротивления М=Мс (точка с).
Пусковой момент Мпуск. составляет одну из его важнейших эксплутационных характеристик. Значение пускового момента получается из общего выражения момента при S=1
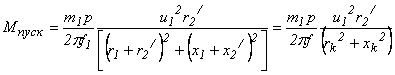 .
.
Из формулы видно, что пусковой момент:
- при заданной частоте f1 и параметрах двигателя прямо пропорционален квадрату напряжения статора U1 2;
- достигает максимума при условии, что активное сопротивление ротора равно индуктивному сопротивлению рассеяния
![]() r2+rдоб=х1+х2.
r2+rдоб=х1+х2.
Пусковой момент обычно
выражается отношением: кп=![]() ,
,
называемым кратностью пускового момента.
Максимальный или опрокидывающий момент Ммакс находим, взяв производную dM/dS и приравняв её к нулю. Из полученного равенства
r12 +xk
2=![]() определим
скольжение
Sm,,
при котором момент будет максимальным. Скольжение,
соответствующее максимальному моменту
определим
скольжение
Sm,,
при котором момент будет максимальным. Скольжение,
соответствующее максимальному моменту
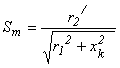 .
.
Таким образом получаем выражение максимального момента
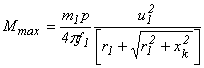 .
.
В нормальном асинхронном двигателе r1 значительно меньше хk, и поэтому можно считать r1=0. Тогда выражение для максимального момента приобретает вид
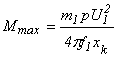 .
.![]()
Отсюда следует, что максимальный момент:
- при заданной частоте и заданных параметрах двигателя пропорционален квадрату напряжения статора U21;
- не зависит от активного сопротивления цепи ротора.
8 Лекция №8. Пуск в ход асинхронных двигателей
Содержание лекции:
- пуск в ход асинхронных двигателей.
Цель лекции
Ознакомить студентов:
-со способами включения асинхронного двигателя в сеть;
-со схемами включения асинхронного двигателя в сеть.
Пусковые характеристики асинхронных двигателей тесно связаны с их конструкцией. Двигатели с фазной обмоткой ротора имеют, по сравнению с двигателями с короткозамкнутой обмоткой ротора, лучшие пусковые характеристики, так как включением в цепь ротора пускового реостата можно уменьшить пусковой ток Iп и одновременно увеличить пусковой момент Мп. Но двигатели с короткозамкнутой обмоткой ротора дешевле, надежнее в работе и имеют лучшие рабочие характеристики. Многочисленные попытки сочетать в одной конструктивной форме преимущества обоих типов двигателей, избежав их недостатков или сведя их до минимума, показали, что эту задачу пока нельзя считать решенной. Наилучших результатов добились, применяя двигатели с короткозамкнутой обмоткой ротора специального исполнения. В связи с ростом пропускной способности распределительных сетей такие двигатели в настоящее время выполняются на мощности порядка тысяч киловатт.
Главными способами пуска асинхронных двигателей являются: а) пуск в ход с помощью реостата, вводимого в цепь ротора двигателя с фазной обмоткой ротора; б) включение в сеть двигателей с короткозамкнутой обмоткой ротора при Un = UH (прямое включение); в) то же при Un < UH.
а) пуск двигателей с фазной обмоткой ротора.
Сопротивление rд пускового реостата (рисунок 22) выбирается из соображений ограничения пускового тока. Обычно величина пускового тока получается допустимой при таком сопротивлении rд, когда начальное значение пускового момента Мп равно максимальному моменту Мт. Тогда Sм = 1 и по формуле
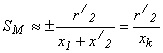 ,
,
![]() .
.
Плавность пуска двигателя достигается устройством в реостате нескольких ступеней сопротивления. На рисунке 8.2, а) приведены механические характеристики двигателя для пяти значений сопротивления, а rД на рисунке 8.3, б) - соответствующие зависимости тока от скорости вращения ротора.
Включение в сеть двигателя с разомкнутой обмоткой ротора может вызвать значительные всплески тока, как это имеет место при включении ненагруженного трансформатора. Поэтому начала первых ступеней сопротивления трех фаз реостата соединяются в общую точку. Наличие замкнутой вторичной цепи предохраняет также от перенапряжений в обмотках статора и ротора при выключении двигателя.
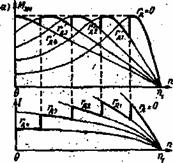
Рисунок 8.1- Включение Рисунок 8.2- Пуск двигателя Рисунок 8.3 – Включение симметричного пускового с реостатом в цепи ротора: несимметричного
реостата а- изменение момента; реостата
б- изменение тока
Для уменьшения числа контактов и удешевления пускового реостата иногда добавочные сопротивления вводят только в две фазы обмотки poтоpа (рисунок 8.4), что вызывает асимметрию тока ротора. Асимметричную систему токов в общем случае можно разложить на три симметричные системы с различным порядком следования фаз. Но система нулевой последовательности токов в данном случае отсутствует, так как средние точки реостата и обмотки ротора не соединяются. Система прямого следования фаз и система обратного следования фаз вращаются относительно ротора с одинаковой скоростью
![]()
но в противоположные стороны. Ротор вращается со скоростью n = n1(1-s). Следовательно, скорость вращения прямого поля относительно статора
n+n2=n1(1-s)+n1s=n1;
скорость вращения обратного поля
n-n2=n1(1-s)- n1s=n1(1-2s).
Таким образом, прямое поле вращается синхронно с полем статора, их взаимодействие создает на валу машины вращающий момент (линия 1 на рисунке 8.5).
Обратное поле ротора вращается в пространстве с переменной скоростью, причем при изменении скольжения от s = 1 до s = 0,5 обратное поле вращается против вращения ротора; при S = 0,5 скорость обратного поля n1 (l -2s) = 0, а при изменении скольжения от s = 0,5 до нуля направление вращения обратного поля совпадает с направлением вращения ротора.
а)
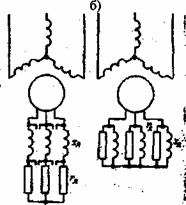
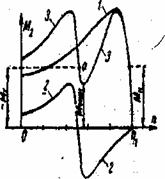
Рисунок 8.4- Включение Рисунок 8.5 - Механическая
в цепь ротора характеристика при
индуктивного сопротивления несимметрии токов ротора
а—последовательно с rд
б — параллельно с rд
Для обратно вращающегося поля
ротора можно считать обмотку статора замкнутой накоротко, так как сопротивление
сети очень мало. Поэтому взаимодействие обратного поля ротора с короткозамкнутой
обмоткой статора при скорости вращения ротора
n<n1/2 приводит к увеличению вращающего момента двигателя, а при
n<n1/2 момент, создаваемый обратным полем, является тормозящим, как
показано на рисунке 8.5 (линия 2). Результирующий момент представлен линией
3. Резкое снижение вращающего момента наблюдается при
n![]() 05n1
и, если нагрузочный момент
Mмин, то
двигатель не достигнет нормальной для него скорости вращения, а будет устойчиво
работать в точке а механической характеристики.
05n1
и, если нагрузочный момент
Mмин, то
двигатель не достигнет нормальной для него скорости вращения, а будет устойчиво
работать в точке а механической характеристики.
Такое же явление наблюдается вследствие асимметрии токов обмотки ротора при нарушении контактов в цепи ротора.
Для автоматизации процесса пуска, в некоторых случаях в цепь ротора включают активное сопротивление rд и последовательно или параллельно с ним индуктивное сопротивление хд.
По схеме (рисунок 8.5, a) в первый момент пуска, когда s = 1 и f2 = f, индуктивное сопротивление велико и в основном ограничивает пусковой ток. По мере увеличения скорости вращения ротора частота f2 = fs уменьшается, соответственно чему уменьшаются э. д. с. ротора Е2s и индуктивное сопротивление Xds= Xd . В результате ток в цепи ротора спадает медленнее, чем при наличии только сопротивления rд, т. е. пусковая операция идет более плавно;
б) прямое включение асинхронного двигателя в сеть.
При этом способе включения
двигателя с короткозамкнутой обмоткой ротора явления, имеющие место в первый
момент включения, те же, что и в короткозамкнутом трансформаторе. На рисунке 8.6,
а показана схема включения двигателя 1 и индуктивного сопротивления
2. При пуске сначала замыкают рубильник 3, а затем при вращении
ротора рубильник 4. Величина индуктивного сопротивления подбирается
таким образом, чтобы кратность пускового тока
In
/
Iн =2 ![]() 2,5; для этого нужно понизить напряжение на двигателе в 2-3
раза. Включение регулируемого индуктивного сопротивления позволяет осуществить
плавный пуск двигателя. Начальное значение пускового момента уменьшается
пропорционально (Un /
UH )2,
т. е. в 4-9 раз.
2,5; для этого нужно понизить напряжение на двигателе в 2-3
раза. Включение регулируемого индуктивного сопротивления позволяет осуществить
плавный пуск двигателя. Начальное значение пускового момента уменьшается
пропорционально (Un /
UH )2,
т. е. в 4-9 раз.
Понижение напряжения автотрансформатором
Вместо индуктивного
сопротивления можно применить автотрансформатор 5 (рисунок 8.6,б). Применение
автотрансформатора позволяет получить большую величину пускового момента, чем в
случае индуктивного сопротивления при одинаковых токах в линии. Если сохранить
прежнее значение
In
/
Iн =2 ![]() 2,5, то требуется понижение напряжения автотрансформатором
только в 1,5-2 раза, а это приводит к уменьшению пускового момента в 2-4 раза.
2,5, то требуется понижение напряжения автотрансформатором
только в 1,5-2 раза, а это приводит к уменьшению пускового момента в 2-4 раза.
Рисунок 8.6-Понижение напряжения при пуске: Рисунок 8.7 - Пуск двигателя а - индуктивным сопротивлением; с переключением со звезды на
б - автотрансформатором треугольник
Недостатком обоих способов пуска является значительная стоимость пусковой аппаратуры.

Рисунок 8.8 - Рабочие характеристики асинхронного двигателя при соединении обмотки статора треугольником и звездой
Пусковой ток в линии при соединении статора
звездой в три раза меньше; чем при соединении треугольником. Это весьма ценное
преимущество рассматриваемого способа пуска. Но, так как при соединении
обмоток
статора звездой фазное напряжение в -![]() раз меньше, чем при соединении
треугольником, то пусковой момент Мп тоже уменьшается в три
раза
раз меньше, чем при соединении
треугольником, то пусковой момент Мп тоже уменьшается в три
раза
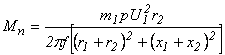 .
.
Способ переключения
треугольник - звезда применяется не только для пуска двигателей в ход, но также
для улучшения
cosφ и кпд двигателей при малых нагрузках (не
превышающих 0,4 номинальной). Переключив обмотки статора с треугольника на
звезду, уменьшают фазное напряжение в ![]() раза при том же линейном напряжении.
Следовательно, э. д. с. Ег и поток Фбм
уменьшаются, так как
e1 ≈
U1 и П1 и
Фбм =
e1
.Это приводит к уменьшению
намагничивающего тока
I0 несколько больше, чем в
раза при том же линейном напряжении.
Следовательно, э. д. с. Ег и поток Фбм
уменьшаются, так как
e1 ≈
U1 и П1 и
Фбм =
e1
.Это приводит к уменьшению
намагничивающего тока
I0 несколько больше, чем в ![]() раз, так как
магнитная цепь двигателя обычно насыщена, а также к уменьшению потерь в стали
приблизительно в 3 раза, так как они зависят от магнитного потока во
второй степени.
раз, так как
магнитная цепь двигателя обычно насыщена, а также к уменьшению потерь в стали
приблизительно в 3 раза, так как они зависят от магнитного потока во
второй степени.
9 Лекция №9. Регулирование скорости вращения асинхронных двигателей
Содержание лекции:
-регулирование скорости асинхронного двигателя
изменением напряжения;
- регулирование скорости вращения изменением скольжения;
- регулирование скорости вращения изменением числа пар полюсов двигателя.
Цель лекции
Ознакомить студентов:
- с регулированием скорости асинхронного двигателя изменением напряжения;
- с регулированием скорости вращения изменением скольжения;
- с регулированием скорости вращения изменением числа пар полюсов двигателя.
Асинхронный двигатель, как правило, используется в электроприводе с постоянной скоростью вращения, однако, в ряде случаев требуется эту скорость регулировать.
Из формулы
s=![]() следует, что скорость вращения ротора асинхронного
двигателя
следует, что скорость вращения ротора асинхронного
двигателя
![]() .
.
Таким образом, чтобы изменить скорость вращения ротора, необходимо изменить либо скольжение s, либо скорость вращения поля статора n1. Последнее достигается изменением числа пар полюсов обмотки статора или же частоты тока в обмотке статора.
Перечисленные способы имеют существенные недостатки, и поэтому было предложено большое число соединений (каскадов) асинхронного двигателя с другими электрическими машинами для получения необходимых характеристик скорости:
а) изменение скольжения.
Проще всего регулирование скольжения осуществляется в двигателе с фазной обмоткой ротора введением добавочного активного сопротивления (рисунок 9.1). Процесс регулирования скорости вращения ротора этим способом рассматривается при постоянстве подведенного, к двигателю напряжения U1 и частоты f. Момент М2 считается также постоянным.
При отсутствии добавочного сопротивления в цепи ротора скольжение двигателя в установившемся режиме определяется точкой А пересечения линии нагрузочного момента (Мт) и характеристики скорости 1 (рисунок 9.1), соответствующей скорости вращения n'. Если ввести сопротивление в цепь ротора, то U1 останется постоянным согласно условию, следовательно, останутся постоянными э.д.с. Е1 и поток Фбт. Так как ротор обладает инерцией, то в ближайший момент времени после введения реостата скорость вращения ротора останется прежней и, соответственно этому, сохраняется величина э. д. с. ротора E2s=E2s. Ток ротора
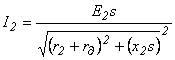
уменьшается вследствие увеличения сопротивления цепи ротора до значения r2+rd, а это приводит к уменьшению вращающего момента
![]() .
.
Рисунок 9.1 - Скорость вращения при различных сопротивлениях цепи ротора
Так как нагрузочный момент Мт остается постоянным, то он будет превышать вращающий момент, на валу двигателя появится отрицательный динамический момент Mj = М2 + Мт и скорость вращения ротора начнет уменьшаться. Соответственно возрастающему скольжению s будет также увеличиваться э. д. с. Е2s и ток I2. Процесс уменьшения скорости вращения и увеличения тока I2 будет происходить до тех пор, пока активная составляющая этого тока I2 cosφ2 не достигнет прежнего значения. Вращающий момент М2 станет равным нагрузочному моменту (- Мт) и ротор будет вращаться с установившейся скоростью п", меньшей, чем до введения реостата (точка В характеристики).
Так как ток ротора и
магнитный поток при уменьшении скорости вращения не претерпевают изменений, то
ток статора
I1 и
cosφ также остаются без
изменений,
поэтому потребляемая двигателем мощность ![]() не изменяется. Полезная мощность
уменьшается вследствие уменьшения скорости вращения и при постоянном моменте М2.
Следовательно, кпд двигателя
не изменяется. Полезная мощность
уменьшается вследствие уменьшения скорости вращения и при постоянном моменте М2.
Следовательно, кпд двигателя
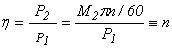
уменьшается пропорционально уменьшению скорости вращения.
С уменьшением скорости вращения происходит ухудшение вентиляции двигателя, поэтому одновременно необходимо также понижать нагрузочный момент Мm.
Наклон характеристик скорости с увеличением сопротивления цепи ротора увеличивается, это понижает устойчивость работы двигателя, т. е. малые изменения нагрузочного момента вызывают большие колебания скорости вращения.
В случае резко нарастающих
нагрузок «смягчение», т. е. увеличение наклона характеристики скорости
желательно для использования кинетической энергии
Jω 2 /2, запасенной во вращающихся частяx привода с общим моментом инерции
J.
При
повышении нагрузки скорость вращения двигателя понижается, и динамический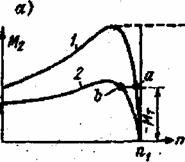

Рисунок 9.1 - Регулирование скорости асинхронного двигателя
изменением напряжения
а - при малом активном сопротивлении ротора; б – при большом сопротивлении
момент
J![]() способствует
преодолению нагрузочного момента Мт, уменьшая таким образом
вращающий момент М2 двигателя. Это позволяет выбрать
двигатель меньшей мощности и понизить наибольший ток статора.
способствует
преодолению нагрузочного момента Мт, уменьшая таким образом
вращающий момент М2 двигателя. Это позволяет выбрать
двигатель меньшей мощности и понизить наибольший ток статора.
Изменение скольжения может быть получено также за счет изменения подведенного к двигателю напряжения U1; однако при малом сопротивлении цепи ротора скольжение изменяется в узких пределах вследствие большого угла наклона механической характеристики. Механическая характеристика 1 построена для номинального напряжения U1H, критическое скольжение SM = 0,2 (в двигателях средней и большой мощности SM значительно меньше). При уменьшении напряжения ординаты механической характеристики уменьшаются пропорционально (U1/UIH)2. Характеристика 2 соответствует уменьшению напряжения на 0,3U1H. При заданном нагрузочном моменте скольжение будет изменяться в пределах между точками а и в, т. е. скорость вращения изменится не более чем на 15%. Но при этом пусковой момент Mn, становится меньше момента (Мт), вследствие чего резко снижается перегрузочная способность двигателя.
Пределы регулирования скольжения зависят также от характера изменения нагрузочного момента от скорости вращения, эти пределы уменьшаются, если момент Мт возрастает с увеличением скорости вращения;
б) изменение числа пар полюсов.
При изменении числа пар полюсов обмотки статора изменяется скорость вращения поля статора, а следовательно, и скорость вращения ротора. Число полюсов может быть только целым, поэтому изменение скорости вращения будет ступенчатым. Особенно большие ступени получаются при малом числе полюсов.
Изменение числа полюсов может быть достигнуто двумя способами: на статоре можно уложить две обмотки, каждая из которых имеет требуемое число полюсов, или же использовать одну обмотку, допускающую переключение на разное число полюсов.
В двигателе с переключением числа полюсов ротор обычно выполняется с короткозамкнутой обмоткой, так как применение фазной обмотки с переключением числа полюсов значительно усложняет изготовление ротора.
Наиболее простая схема переключения числа полюсов обмотки получается при отношении скоростей вращения 1:2.
Двухслойные обмотки предпочтительнее, так как они обеспечивают лучшую форму магнитного поля в зазоре. Шаг обмотки выбирается таким образом, чтобы он был близким к полюсному делению при большем числе полюсов. На рисунке 9.2 представлена схема обмотки, фаза которой состоит из двух катушек АВ и CD. Показанное на рисунке 9.2,а направление тока при соединении конца катушки В с началом катушки С создает четыре полюса. При изменении направления тока в катушке CD получается два полюса (рисунок 9.2 б). Изменение направления тока в катушке CD может быть получено и при параллельном соединении катушек (рисунок 9.2, в). При этом требуется только три выведенных конца вместо четырех а при внутреннем соединении трехфазной обмотки звездой или треугольником только шесть концов. При изменении числа полюсов может изменяться также индукция в зазоре и приблизительно пропорционально ей — вращающий момент двигателя.
Индукция в зазоре зависит от величины вращающегося магнитного потока и полюсного деления. Магнитный поток определяется приложенным к обмотке напряжением, числом последовательно соединенных витков и обмоточным коэффициентом.
При одинаковом фазном напряжении магнитный поток при параллельном соединении будет в 2,5 раза больше, чем при последовательном (в два раза за счет половинного числа последовательно соединенных витков и в 1,25 раза за счет меньшего обмоточного коэффициента). При переходе от удвоенного числа полюсов к меньшему полюсное деление увеличивается в два раза. Таким образом, индукция в зазоре Bб и, следовательно, вращающий момент при переходе к большей скорости вращения возрастает в 1,25 раза. Соединение фазных обмоток при высшей скорости вращения выполняется звездой с двумя параллельными ветвями (YY ), а при низшей - звездой (Y).
Рисунок 9.2 - Регулирование скорости вращения изменением числа пар полюсов двигателя
Эта схема переключения обмоток пригодна для двигателей привода вентиляторов.
Для получения приблизительно
одинакового вращающего момента при обеих скоростях вращения, например, у
двигателя для привода компрессора; применяется схема соединения обмоток
YY/A. В этом
случае фазное напряжение при переходе к высшей скорости вращения уменьшается в-![]() , следовательно,
магнитный поток увеличивается только в 1,45 раза. Вследствие увеличения
полюсного деления в два раза индукция в зазоре и вращающий момент при высшей
скорости вращения составляют 0,7 индукции и момента при низшей скорости.
Увеличение вращающего момента может быть достигнуто за счет соответствующего
выбора шага обмотки и повышения плотности тока при высшей скорости вращения.
, следовательно,
магнитный поток увеличивается только в 1,45 раза. Вследствие увеличения
полюсного деления в два раза индукция в зазоре и вращающий момент при высшей
скорости вращения составляют 0,7 индукции и момента при низшей скорости.
Увеличение вращающего момента может быть достигнуто за счет соответствующего
выбора шага обмотки и повышения плотности тока при высшей скорости вращения.
При необходимости сохранения одинаковой мощности на обеих ступенях скорости вращения (для привода металлорежущих станков) применяется схема переключения обмотки ∆/YY;
в) изменение частоты питающей сети.
Этот способ применяется в тех случаях, когда требуется регулировать скорость вращения одного или нескольких двигателей одновременно или получить скорость вращения более 3000 об/мин.
В качестве примера можно привести привод гребных винтов на судах, привод двигателей в деревообделочной промышленности со скоростью вращения 12000 об/мин, привод электрошпинделей для шлифовки со скоростью вращения до 150 000 [об/мин].
При питании двигателей от синхронного генератора изменение частоты достигается изменением скорости приводного двигателя. Это возможно только в сравнительно узких пределах. Существуют специальные схемы, которые позволяют регулировать частоту тока без изменения скорости приводного двигателя.
С изменением частоты тока будут изменяться в общем случае все величины, характеризующие работу двигателя: напряжение на зажимах, поток, ток холостого хода, вращающий момент, мощность, перегрузочная способность, скорость вращения. Анализ этого способа регулирования скорости отличается значительной сложностью. Поэтому приводятся только конечные результаты без вывода их.
Пусть поставлено условие, чтобы двигатель работал при переменной частоте, но с практически постоянными значениями кпд, cos<p, перегрузочной способности Мт. и постоянным абсолютным скольжением s. Если двигатель не насыщен, то поставленные условия соблюдаются при следующем соотношении между напряжением, частотой и вращающим моментом
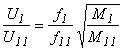
где U 1 и М 1, — напряжение и вращающий момент при частоте f1 ;
U 11 и М11 - те же величины при частоте f11 .
Если М1=М11
= const,
то
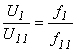 , т. е. напряжение, подводимое к
двигателю, должно изменяться пропорционально частоте.
, т. е. напряжение, подводимое к
двигателю, должно изменяться пропорционально частоте.
При использовании в качестве источника электроэнергии синхронного генератора изменение частоты и напряжения получается при постоянном возбуждении и изменяющейся скорости вращения.
Если двигатель работает на
центробежный вентилятор или нагребной винт, то
M2=f2. В этом случае
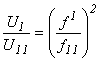 , т. е. напряжение на зажимах должно изменяться пропорционально
частоте во второй степени. Этот режим соответствует работе синхронного
генератора с током возбуждения, изменяющимся пропорционально скорости вращения.
, т. е. напряжение на зажимах должно изменяться пропорционально
частоте во второй степени. Этот режим соответствует работе синхронного
генератора с током возбуждения, изменяющимся пропорционально скорости вращения.
Иногда подобное регулирование частоты применяется для пуска крупных асинхронных двигателей.
![]() .
.
10 Лекция №10. Синхронные машины
Содержание лекции:
-типы синхронных машин и их устройство;
- магнитное поле обмотки возбуждения явнополюсной машины;
-магнитное поле и параметры обмотки якоря;
-продольная и поперечная реакции якоря.
Цель лекции
Ознакомить студентов:
-с типами синхронных машин и их устройством;
- с магнитным полем обмотки возбуждения явнополюсной машины;
-с продольной и поперечной реакцией якоря.
Синхронные машины — это бесколлекторные машины переменного тока. По своему устройству они отличаются от асинхронных машин лишь конструкцией ротора, который может быть явнополюсным или неявнополюсным. Что же касается свойств, то синхронные машины отличаются синхронной частотой вращения ротора (n2 = n1= const) при любой нагрузке, а также возможностью регулирования коэффициента мощности, устанавливая такое его значение, при котором работа синхронной машины становится наиболее экономичной. Синхронные машины обратимы и могут работать как в режиме генератора, так и в режиме двигателя. Синхронные генераторы составляют основу электротехнического оборудования электростанций, т.е. практически вся электроэнергия вырабатывается синхронными генераторами. Единичная мощность современных синхронных генераторов достигает миллиона киловатт и более. Синхронные двигатели применяются главным образом для привода устройств большой мощности. Такие двигатели по своим технико-экономическим показателям превосходят двигатели других типов. В крупных электроэнергетических установках синхронные машины иногда используются в качестве компенсаторов — генераторов реактивной мощности, позволяющих повысить коэффициент мощности всей установки. В данном разделе рассмотрены, главным образом, трехфазные синхронные машины.
10.1 Типы синхронных машин и их устройство
Синхронная машина состоит из неподвижной части — статора — и вращающейся части — ротора. Статоры синхронных машин в принципе не отличаются от статоров асинхронных двигателей, т.е. состоят из корпуса, сердечника и обмотки.
Конструктивное исполнение статора синхронной машины может быть различным в зависимости от назначения и габаритов машины. Так, в многополюсных машинах большой мощности при наружном диаметре сердечника статора более 900 мм пластины сердечника делают из отдельных сегментов, которые при сборке образуют цилиндр сердечника статора. Корпуса статоров крупногабаритных машин делают разъемными, что необходимо для удобства транспортировки и монтажа этих машин.
Роторы синхронных машин могут иметь две принципиально различающиеся конструкции: явнополюсную и неявнополюсную.
Обмотка возбуждения создает магнитный поток возбуждения синхронной машины, который сцепляется с обмоткой якоря (статора) и индуктирует в ней ЭДС.
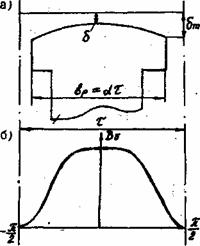
Рисунок 10.1 - Магнитное поле обмотки возбуждения
явнополюсной машины
На рисунке 10.1 кривая I представляет собой распределение магнитной индукции поля возбуждения bs на поверхности якоря. Кривую - Bg разлагают на основную и высшие гармоники, которые индуктируют в обмотке якоря основную и высшие гармоники ЭДС. Высшие гармоники ЭДС малы, так как малы высшие гармоники поля и, кроме того, выбором шага и распределением обмотки якоря достигается уменьшение высших гармоник ЭДС. Поэтому учитывается только основная гармоника ЭДС якоря и соответственно потоком взаимной индукции между индуктором (ротором) и якорем считается основная гармоника поля возбуждения. Коэффициент формы кривой поля
 .
.
Магнитодвижущая сила (МДС) обмотки возбуждения на один полюс
![]()
где ωв - число витков обмотки возбуждения;
IB - ток возбуждения.
Амплитуда основной гармоники поля возбуждения
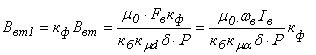
где kб- коэффициент зазора;
kµd - коэффициент насыщения по продольной оси (оси полюсов).
Так как зазор δ переменен, то величину kδ принято рассчитывать для среднего расчетного зазора
![]() .
.
Поток основной гармоники поля возбуждения
![]() .
.
![]() Потокосцепление
с фазной обмоткой якоря, когда ось этой фазы совпадает с осью полюсов синхронной
машины
Потокосцепление
с фазной обмоткой якоря, когда ось этой фазы совпадает с осью полюсов синхронной
машины
Ψвад=WФв1коб1.
При повороте ротора потокосцепление основной гармоники поля возбуждения изменяется по закону
Ψваdt= Ψваdcosω1t=MadIвcosω1
где взаимоиндуктивность равна
![]() .
.
При этом в якоре индуктируется ЭДС
![]() .
.
Амплитуда и действующее значение этой ЭДС
![]() ;
;
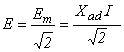
где хad = ω1Mad - сопротивление взаимной индукции обмотки возбуждения с обмоткой якоря.
10.2 Магнитное поле и параметры обмотки якоря. Продольная и поперечная реакции якоря
При нагрузке генератора, когда по обмотке якоря протекает ток, обмотка создает собственное магнитное поле, называемое полем реакции якоря. Реакция якоря синхронной машины оказывает существенное влияние на характеристики и поведение машины как при установившихся, так и при переходных режимах работы.
Ввиду несимметричного устройства ротора явнополюсной синхронной машины возникает необходимость рассматривать действие реакции якоря по продольной и поперечной осям в отдельности. Метод такого рассмотрения называется методом наложения или теорией двух реакций. Метод двух реакций основан на принципе наложения, при котором предполагается, что магнитные потоки, действующие по поперечной оси, не влияют на величину потоков, действующих по продольной оси, и наоборот.
Индуктивная нагрузка (ψ=900). При индуктивной нагрузке ток статора I1 отстает по фазе от ЭДС E1 на 90°. Поэтому он достигает максимума после поворота ротора вперед на 90° относительно его положения, соответствующего максимуму ЭДС. При этом МДС реакции якоря Fa действует по оси полюсов ротора встречно МДС обмотки возбуждения Fв (рисунок 10.2,б). Такое действие МДС реакции якоря ослабляет магнитное поле машины. Следовательно, реакция якоря в синхронном генераторе при чисто индуктивной нагрузке оказывает продольно-размагничивающее действие.
Емкостная нагрузка (iy=-90°). Так как ток при емкостной нагрузке опережает по фазе ЭДС на 90°, то он достигает максимума раньше, чем ЭДС. МДС реакции якоря fo, действует как и в предыдущих случаях по оси полюсов, но теперь уже согласно с МДС обмотки возбуждения Fв, следовательно, реакция якоря в синхронном генераторе при чисто емкостной нагрузке оказывает продольно-намагничивающее действие.
Смешанная нагрузка. При смешанной нагрузке синхронного генератора ток статора I1 сдвинут по фазе относительно ЭДС на угол ψ, значения которого лежат в пределах 0<ψ<90°.
При активно-индуктивной нагрузке вектор Fa отстает от вектора ЭДС на угол 0 < ψ< 90°. Раскладываем вектор Fa на составляющие: продольную составляющую МДС, реакции якоря Fad=Fasinψ и поперечную составляющую Fad= Fa cosψ. Поперечная составляющая МДС Fag пропорциональна активной составляющей тока I^lacosi/f, продольная составляющая МДС пропорциональна реактивной составляющей IafIaSiny/. Если реактивная составляющая тока отстает от ЭДС (ψ=0), то МДС
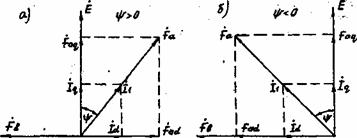
Рисунок 10.2 - Векторные диаграммы при смешанной нагрузке
а) активно-индуктивная нагрузка
б) активно-емкостная нагрузка
размагничивает генератор, если же реактивная составляющая тока I1 опережает ЭДС (ψ< 0), то МДС Fad подмагничивает генератор.
При определении поперечной составляющей МДС реакции якоря для явнополюсной машины это уменьшение потока учитывается коэффициентом kg
Faq=kqFacosψ
где kq - коэффициент формы поперечной реакции якоря, представляющий отношение магнитного потока реакции якоря по поперечной реи в явнополюсной машине к составляющей магнитного потока реакции якоря по той же оси в неявнополюсной машине (обычно kq=0.3-0.5).
Продольная составляющая МДС реакции якоря в явнополюсной машине
Fad=kdFasinψ
где kd - коэффициент формы продольной реакции якоря.
11 Лекция №11. Синхронные двигатели
Содержание лекции:
-назначение синхронных двигателей;
-U-образные и рабочие характеристики синхронного двигателя;
- работа синхронной машины в двигательном режиме.
Цель лекции
Ознакомить студентов:
-с назначением синхронных двигателей;
-с U-образными и рабочими характеристиками синхронного двигателя;
-с работой синхронной машины в двигательном режиме.
Синхронная машина может работать как в режиме генератора, так и в режиме двигателя, т.е. потреблять из сети электрическую энергию и преобразовывать ее в механическую. Если после подключения синхронной машины к электрической сети приложить к его валу тормозной момент, т.е. момент нагрузки, направленный против вращения ротора, то вектор ЭДС сместится на угол Ґ относительно его положения в режиме холостого хода в сторону а отставания. При этом в цепи статора появится результирующая ЭДС ∆ Е = Е+ Uс, создающая в обмотке статора ток I1, опережающий по фазе ЭДС Е £~ на угол ψ. Ток 11 создает вращающееся синхронно с ротором магнитное поле, ось которого d' - d' смещена относительно продольной оси полюсов ротоpa d-d на угол Ґ.
Возникшие при этом тангенциальные составляющие сил магнитного взаимодействия F1 = Fm SinҐ создадут на роторе двигателя вращающий электромагнитный момент М, направленный согласно с вращающим магнитным полем статора и приводящий во вращение ротор с синхронной частотой ω1. При этом синхронная машина потребляет из сети электрическую энергию и преобразует ее в механическую энергию вращения. Вращающий электромагнитный момент преодолевает момент холостого хода и создает полезный момент Mс, под действием которого приводится во вращение производственный механизм
Мэм =Мс+М0 .
Отношение максимального момента к номинальному определяет перегрузочную способность синхронного двигателя
![]() .
.
Рисунок 11.1 - Работа синхронной машины в двигательном режиме
11.1 U-образные и рабочие характеристики синхронного двигателя
При неизменном напряжении сети Uc результирующее магнитное поле синхронного двигателя постоянно. Поэтому при изменении МДС возбуждения Fв, МДС статора Fa изменяется таким образом, чтобы их совместное действие оставалось неизменным, т.е. оставалось неизменным результирующее магнитное поле. Это изменение МДС Fa может происходить за счет изменения значения и фазы тока, т.е. за счет изменения реактивной составляющей тока статора. При увеличении тока возбуждения от Iв=0, возрастает МДС ротора и уменьшается МДС статора, за счет уменьшения индуктивной (по отношению к напряжению сети) составляющей тока статора Id, которая оказывает на магнитную систему подмагничивающее воздействие (рисунок 11.2). При этом полный ток статора I1=Ia+Id уменьшается, коэффициент мощности двигателя costφ1 увеличивается. При некотором значении тока возбуждения Iв, индуктивная составляющая тока статора уменьшается до нуля. Ток статора станет чисто активным, а коэффициент мощности cosφ1 =1.
При увеличении тока возбуждения сверх значения 1ен, т.е. перевозбуждение вызывает увеличение тока Id, но теперь увеличивается емкостная (по отношению к напряжению сети) составляющая тока I1. Таким образом, при недовозбуждении синхронный двигатель работает с отстающим, а при перевозбуждении - с опережающим током.
Зависимость тока статора от тока возбуждения для синхронного двигателя представлена U-образными характеристиками (рисунок 55). Синхронный двигатель является генератором реактивного тока: индуктивного по отношению к сети - при недовозбуждении и емкостного - при перевозбуждении. Указанная способность синхронных двигателей является их ценным качеством, которое используется для повышения коэффициента мощности электрических установок.
Рабочие характеристики синхронного двигателя представляют собой зависимости частоты вращения п2, потребляемой мощности Р1, полезного момента M2, коэффициента мощности cosφ и тока статора I1 от полезной мощности двигателя Р2 (рисунок 11.3).
Рисунок 11.2 - U-образные Рисунок 11.3 - Рабочие
характеристики характеристики синхронного
синхронного двигателя двигателя
Частота вращения ротора п2 = const и поэтому характеристика п2 =f(P2) прямая параллельная оси абсцисс. Полезный момент на валу M2=f(P2 /ω1) характеристика M2=f(P2) имеет вид прямой, выходящей из начала координат.
Мощность, потребляемая из сети, Р1= Р2+∆Р, а так как с ростом нагрузки на валу растут и потери мощности ∆Р, то характеристика P1=f(P2) имеет несколько криволинейный характер.
Характеристика cosφ1=f(P2) зависит от характера возбуждения двигателя при холостом ходе. Если Соsφ10 = 1, то при увеличении нагрузки он уменьшается.
Ток в обмотке статора ![]() с увеличением
нагрузки на валу двигателя растет быстрее, чем потребляемая мощность
p1
,
вследствие уменьшения
cosφ1.
с увеличением
нагрузки на валу двигателя растет быстрее, чем потребляемая мощность
p1
,
вследствие уменьшения
cosφ1.
12 Лекция №12. Машины постоянного тока, элементы конструкции, обмотки якоря и их э.д.с.
Содержание лекции
- принцип действия машин постоянного тока;
– диаграмма распределения магнитной индукции под полюсом;
- устройство и основные элементы конструкции машины постоянного тока.
Цель лекции
Ознакомить студентов:
-с принципом действия машин постоянного тока;
-с-диаграммой распределения магнитной индукции под полюсом;
-с устройством и основными элементами конструкции машины постоянного тока.
12.1 Принцип действия машин постоянного тока
Простейшим генератором постоянного тока может служить виток из проводника в виде рамки, вращающийся в магнитном поле между двумя постоянными магнитами N и S (рисунок 12.1).
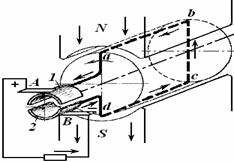
Рисунок 12.1 – Схема работы машины постоянного тока
Концы витка abсd присоединяются к двум медным пластинам коллектора, изолированным друг от друга и от вала, на котором они помещены. На пластинах помещены неподвижные щетки А и В, к которым присоединена внешняя цепь, состоящая из каких-либо приемников электроэнергии. При вращении витка с постоянной частотой проводники ab и cd пересекают магнитные линии, при этом в проводниках индуктируется э.д.с. При равномерном распределении магнитного поля в пространстве э.д.с. проводника
е = Е sin ωt (12.1)
где ω= 2πf – угловая частота;
f – частота э.д.с.
Таким образом, при условии равномерного распределения магнитного поля в витке индуктируется переменная синусоидальная э.д.с. (рисунок 1.2, а). Направление индуктируемой в проводнике э.д.с. определяется правилом правой руки, т.е. при перемещении проводника ab под северным полюсом в нем наводится э.д.с., направленная из-за плоскости чертежа, а когда он проходит под южным полюсом, – за плоскость чертежа. Таким образом, в проводнике ab наводится переменная во времени э.д.с., изменяющая свое направление 2 раза за один оборот витка.
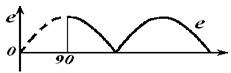

а) б)
Рисунок 12.2 – Э.д.с., индуктируемая в витке (а) и на внешнем участке цепи (б)
Для нормальной работы генератора нужно установить щетки так, чтобы наводимая в витке э.д.с. была равна нулю в момент перехода щетки с одной пластины на другую. Каждая из щеток будет соприкасаться только с той коллекторной пластиной и соответственно только с тем из проводников, которые находятся под полюсом данной полярности. Например, в момент времени, показанный на рисунке 12.1, щетка А соприкасается с пластиной 1 и имеет положительный потенциал, так как к ней подводится э.д.с. от проводника ab, находящегося под северным полюсом. При повороте якоря на 90° виток будет расположен так, что его проводники перемещаются вдоль магнитных линий поля, не пересекая их. Поэтому э.д.с., наведенная в витке, равна нулю. Щетки соединяют коллекторные пластины между собой и тем самым замыкают виток накоротко. При повороте витка на 180° щетка А соприкасается с пластиной 2, но по-прежнему она имеет положительный потенциал, так как к ней подводится э.д.с. от проводника cd, заменившего проводник ab под северным полюсом. Аналогично можно видеть, что щетка В имеет всегда только отрицательный потенциал. Таким образом, по витку abсd по-прежнему протекает переменный ток; при этом по внешнему участку цепи ток проходит только в одном направлении, а именно от положительной щетки А к отрицательной щетке В, т. е. происходит выпрямление переменной э.д.с., наведенной в витке, в пульсирующую на внешнем участке цепи (рисунок 12.2, б). Как видно из рисунка 12.2, кривая э.д.с. помимо постоянной содержит большую переменную составляющую, называемую пульсацией э.д.с. Для ее уменьшения следует увеличить число коллекторных пластин. Если, например, в магнитном поле полюсов поместить два витка, оси которых сдвинуты на 90° в пространстве, и концы этих витков соединить с четырьмя коллекторными пластинами, то при вращении витков индуктируемые в них э.д.с. окажутся сдвинутыми по фазе на угол π/2. Щетки в такой машине надо поместить так, чтобы они соприкасались с пластинами того витка, в котором в данный момент э.д.с. имеет наибольшее значение и на щетках будет э.д.с., пульсация которой много меньше, чем при двух коллекторных пластинах. При дальнейшем увеличении числа коллекторных пластин пульсация уменьшается и при 16 пластинах на пару полюсов становится менее 1%.
В действительности распределение магнитного поля в пространстве неравномерно (рисунок 12.3).
Рисунок 12.3 – Диаграмма распределения магнитной индукции под полюсом
12.2 Устройство и основные элементы конструкции машины постоянного тока
Машина постоянного тока состоит из неподвижной части – статора и вращающейся части – якоря, в котором происходит процесс преобразования механической энергии в электрическую (генератор) или обратно – электрической энергии в механическую (электродвигатель). Между неподвижной и вращающейся частями имеется зазор. Неподвижная часть (рисунок 1.4) состоит из станины 3, главных полюсов, предназначенных для создания основного магнитного потока, добавочных полюсов 2, служащих для достижения безискровой работы щеток на коллекторе (улучшения коммутации). К станине крепят болтами подшипниковые щиты, главные и дополнительные полюсы.
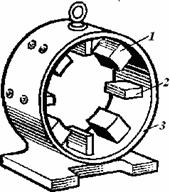
Рисунок 12.4 – Неподвижная часть машины постоянного тока
Основной (главный) полюс (рисунок 12.5, а) имеет сердечник 4, набранный из листов электротехнической стали толщиной 0,5 – 1 мм, стянутых шпильками. На сердечник насажены две катушки обмоток возбуждения 2. Нижнюю часть сердечника – полюсный наконечник выполняют так, чтобы воздушный зазор увеличивался от центра полюса к его концам. Это делается для того, чтобы уменьшить искажение поля под действием реакции якоря и рассеяние главного поля в зоне коммутации. У компенсированных машин постоянного тока в полюсных наконечниках выштамповывают пазы для размещения компенсационной обмотки. Число главных полюсов всегда четное, причем северные и южные полюсы чередуются, что достигается соответствующим соединением катушек обмотки возбуждения полюсов. Катушки всех полюсов соединяют последовательно. Полюсы крепятся к станине 1 болтами или шпильками.
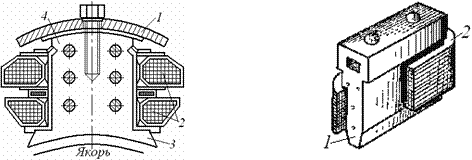 |
а) б)
Рисунок 12.5 – Основной (а) и добавочный (б) полюсы
Добавочный полюс (рисунок 12.5, б) состоит из сердечника 1, изготовляемого из стали, и обмотки 2, изготовляемой из медных шин прямоугольного сечения. Обмотки добавочных полюсов соединяют последовательно с обмоткой якоря, а полюсы устанавливают между главными полюсами и крепят к станине болтами. Воздушный зазор под добавочными полюсами значительно больше, чем под главными. Поперечное сечение добавочных полюсов расширяется в сторону корпуса. Это увеличивает поверхность прилегания добавочного полюса к корпусу, что дает большую устойчивость и предупреждает насыщение от большого потока рассеяния добавочных полюсов.Для создания электрического контакта с поверхностью коллектора в машине устанавливают щетки, которые прикрепляют к щеткодержателю. Щеткодержатель (рисунок 12.6) состоит из нажимных пластин 1; пружины 2, передающей давление на щетку 3; из обоймы 4.
Рисунок 12.6 – Щеткодержатель
13 Лекция №13. Магнитная цепь машины постоянного тока
Содержание лекции:
-порядок расчета магнитной цепи электрической машины;
-характеристика намагничивания машины;
Цель лекции
Ознакомить студентов:
-с порядком расчета магнитной цепи электрической машины;
-с характеристикой намагничивания машины.
13.1 Порядок расчета магнитной цепи электрической машины
Намагничивающая сила н.с. обмотки возбуждения машины постоянного тока создает магнитное поле, магнитные линии которого замыкаются через участки машины, образующие ее магнитную систему. На поперечном разрезе машины (рисунок 13.1) показан путь магнитного потока. Весь магнитный поток Фп полюса делится на две неравные части. Большая часть – основной магнитный поток Фδ проникает через воздушный зазор в якорь и разветвляется в его сердечнике, подходит к соседним полюсам и замыкается через ярмо.
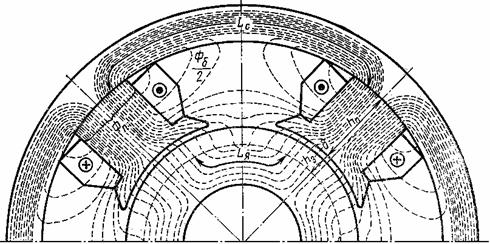
Рисунок 13.1 – Магнитная цепь машины постоянного тока
Под основным магнитным потоком машины постоянного тока понимают поток в зазоре Фδ на площади, соответствующей одному полюсному делению τ, при холостом ходе машины. Меньшая часть потока рассеяния Фσ замыкается между полюсами, минуя якорь. Тогда магнитный поток полюса

где 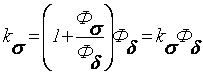 – коэф. рассеяния основных полюсов.
– коэф. рассеяния основных полюсов.
Для машин постоянного тока kσ=1,12÷1,25. Путь основного магнитного потока в машине состоит из замкнутых магнитных цепей, каждая из которых охватывает пару полюсов. Вследствие магнитной симметрии отдельные магнитные цепи многополюсной машины одинаковы и магнитные потоки (а также их составляющие Фδ и Фσ) равны между собой, поэтому рассматривается магнитная цепь одной пары полюсов. Участки магнитной цепи отличаются друг от друга как своими геометрическими размерами, так и физическими свойствами. По закону полного тока для замкнутого контура н.с. одной пары полюсов
F=IВωB=ΣНl=ΣI (13.1)
где IВ – ток возбуждения;
ωB – число витков обмотки возбуждения;
H – напряженность магнитного поля, зависящая от магнитной индукции; l – средняя длина данного участка магнитной цепи.
В магнитной цепи электрической машины напряженность магнитного поля изменяется на границе участков из различных материалов. По этому признаку магнитную цепь машины постоянного тока можно разделить на пять участков: зазор, зубцовый слой (зубцы), сердечник якоря, сердечник полюса с
наконечником, ярмо (станина).
Рассчитанная на пару полюсов основная н. с. машины равна
F0=Fδ+FЗ+FЯ+FП+FС . (13.2)
Это уравнение показывает, что для определения н.с. нужно для каждого из пяти участков найти соответствующую ему напряженность магнитного поля Н и умножить ее на длину пути потока на этом участке. Размеры участков магнитной цепи или известны (в выполненной машине), или устанавливаются по рекомендуемым магнитным индукциям (при проектировании машины), поэтому для необходимого магнитного потока на всех участках магнитной цепи может быть определена индукция В=Ф/S, где Ф – магнитный поток на участке; S – площадь сечения участка. В соответствии с рисунком 13.1 основная н.с. машины
F0=Нδ2δ+НЗ2hЗ+НЯLЯ+НП2hП+НСLC (13.3)
где δ – длина воздушного зазора, м;
hЗ – высота зубцов якоря, м;
hП – высота главных полюсов, м;
LЯ – длина участка по сердечнику якоря, м;
LС – длина участка по станине (ярмо), м;
Н – соответственно напряженность магнитного поля участка цепи, А/м.
Будем считать, что номинальному значению напряжения и номинальной частоте вращения машины соответствует номинальное значение основного потока Ф0=1. Задавшись рядом значений основного потока: 0,5Ф0; 0,8Ф0; 1Ф0; 1,2Ф0, можем для каждого из них рассчитать F0
Намагничивающая сила воздушного зазора. Наибольшее сопротивление магнитному потоку оказывает воздушный зазор. В зубчатом якоре магнитное поле в зазоре распределяется неравномерно: у поверхности зубцов плотность магнитных линий больше, а в пазах меньше (рисунок 13.3), так как магнитное сопротивление на участке с зубцом меньше, чем с пазом. На рисунке 13.4 показано распределение магнитной индукции в воздушном зазоре в поперечном и продольном разрезах машины. Так как магнитная индукция в зазоре изменяется как по окружности якоря, так и по его длине, то вводят понятие о расчетной индукции в зазоре, используя для этого метод приведения. Сущность этого метода заключается в следующем. Заменяют сложную кривую распределения магнитной индукции в зазоре равновеликим прямоугольником с высотой Вδ. Основание такого прямоугольника в первом случае дает расчетную полюсную дугу b', а во втором случае – расчетную длину якоря l'. Отношение b/τ=α' называют расчетным коэффициентом полюсного перекрытия, от величины которого зависит максимальное значение напряжения между коллекторными пластинами. В машинах постоянного тока с добавочными полюсами α'=0,62–0,72 с достаточной точностью определяют расчетную длину якоря l"=(lП+l')/2, где lП – длина полюса по оси машины; l' – длина якоря без вентиляционных каналов. Если bB – ширина вентиляционного канала, а пВ – число каналов, то l=lЯ–пВbB, где lЯ – длина якоря в осевом направлении. Пользуясь расчетными величинами Вδ, b', l', определяем основной магнитный поток машины Ф0=Вδb'l'=Вδ α'τl' откуда Вδ=Ф0/(α'τl'). Необходимая для проведения магнитного потока через зазор намагничивающая сила
Fδ=2Вδδ'/μ0=2Вδδkδ/μ0. (13.4)
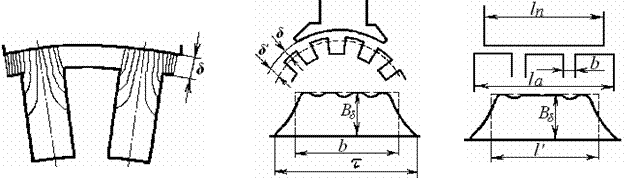 а) б)
а) б)
Рисунок 13.3 – Магнитная индукция Рисунок 13.4 – Распределение
в зазоре зубчатого якоря магнитной индукции под полюсом:
а – на полюсном делении;
б – по длине полюса
Намагничивающая сила зубцового слоя. При определении магнитной индукции в зубцах якоря могут быть рассмотрены два случая: первый, когда ВЗ<1,8 Тл и когда B3>1,8 Тл. Принимаем, что в первом случае весь поток проходит через зубцы, во втором – часть потока проходит через пазы.
Второй случай является более общим. Расчет н.с. при этом будем вести на один зубцовый шаг. Приходящийся на один зубцовый шаг магнитный поток Фt=Bδt1l'=ФЗ+Фпаз, где ФЗ, Фпаз – потоки в зубце и пазе соответственно. Расчетная магнитная индукция
ВЗ'=ВЗ+ВПkЗ (13.5)
где ВЗ=ФЗ/SЗ – действительная индукция в зубце;
ВП=ФП/SП – индукция паза;
kЗ – зубцовый коэффициент, определяемый геометрическими размерами зубца и паза.
Пользуясь (13.5) и эскизом зубца и паза якоря, находим величину магнитной индукции в верхнем, среднем и нижнем сечениях зубца (рисунок 13.5). В зависимости от этих значений индукция по кривым намагничивания зубцов BЗ=f(HЗ) (рисунок 3.2), определяем напряженность магнитного поля зубцов верхнего, среднего и нижнего сечений. Для зубцов расчетное значение напряженности магнитного поля НЗ=(НЗ1+4НЗ.ф+НЗ2)/6, значение н.с. FЗ=HЗ2hЗ.
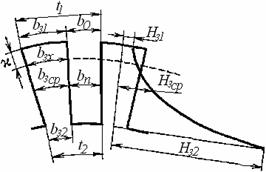
Рисунок 13.5 – Намагничивающая сила зубцов
Намагничивающая сила сердечника якоря, полюсов и станины. Магнитный поток в сердечнике якоря ФЯ=0,5Ф0=ВЯSЯя. Площадь поперечного сечения якоря SЯ=hЯlkС, где hЯ – высота сердечника якоря, kС=0,88÷0,93 – коэффициент заполнения сталью. Для сердечника якоря магнитная индукция ВЯ=Ф0/(2hЯlkС). По кривой намагничивания для стали рассматриваемой марки находим напряженность поля якоря Hя, и тогда н.с. сердечника якоря FЯ=НЯLЯ, где LЯ – длина средней магнитной линии в сердечнике якоря. В сердечнике полюса магнитная индукция ВП=ФП/SП=Ф0kσ/SП, где ФП – магнитный поток полюса; SП – поперечное сечение полюса. По кривой намагничивания стали полюса находим напряженность поля НП и тогда н.с. полюса FП=HПLП=HП2hП, где hП – высота сердечника полюса. В станине магнитный поток ФС=0,5ФП=0,5Ф0kσ, индукция ВС=ФС/SС=Ф0kσ/(2SС). Сечение SС определяют по геометрическим размерам ярма. По характеристике намагничивания для материала ярма находим напряженность поля НC, тогда намагничивающая сила FC=HCLC
где  – длина средней магнитной
линии в ярме.
– длина средней магнитной
линии в ярме.
13.2 Характеристика намагничивания машины
Зависимость Ф0=f(F0) построенная в прямоугольных координатах, называется кривой намагничивания машины или магнитной характеристикой (рисунок 3.6). В начальной части магнитная характеристика имеет прямолинейный характер, так как при малых значениях потока Фδ сталь машины слабо насыщена и н.с. затрачивается на проведение потока через зазор. Продолжение прямолинейной части кривой позволяет выделить н.с. для зазора при различных значениях потока Фδ (линия 0b) т.е. получить зависимость Fδ=f(Фδ). По мере увеличения магнитного потока большая часть н.с. затрачивается на проведение потока по стальным участкам. Эта часть н.с. соответствует отрезку bс. По отношению kН=ac/ab, называемым коэффициентом насыщения, можно судить о степени насыщения магнитной цепи машины при заданном значении потока Фδ. Строить машину с насыщенной магнитной цепью невыгодно, так как при этом материалы будут недоиспользованы и машина получится тяжелой.
Рисунок 13.6 – Характеристика намагничивания
Нецелесообразна также чрезвычайно насыщенная магнитная цепь, так как в этом случае необходимо выполнить мощную обмотку возбуждения с большим расходом меди или алюминия и с большими потерями мощности на возбуждение. По этим причинам электрические машины изготовляют с умеренным насыщением при номинальном режиме. При этом рабочая точка лежит несколько выше колена магнитной характеристики. Обычно kН=1,1÷1,35, а в некоторых случаях kН≈1,7÷2.
14 Лекция №14. Реакция якоря машины постоянного тока
Содержание лекции:
-определение реакции якоря машины постоянного тока;
-распределение магнитной индукции в зазоре под полюсом;
-распределение магнитного поля якоря;
-поперечная и продольная намагничивающие силы якоря.
Цель лекции
Ознакомить студентов:
-с распределением магнитной индукции в зазоре под полюсом;
-с распределением магнитного поля якоря;
-с поперечной и продольной намагничивающими силами якоря
При нагрузке электрической машины, когда возникает ток в цепи якоря, состоящей из нескольких обмоток (якоря, добавочных полюсов, последовательного возбуждения и компенсационной), кроме основного магнитного потока, существуют магнитные поля обмоток цепи якоря. Поэтому магнитный поток в воздушном зазоре и пространственное распределение магнитного поля при нагрузке машины будут определяться совместным действием н.с. полюсов и цепи якоря. Таким образом, магнитный поток, который существует в машине при работе ее под нагрузкой, следует рассматривать как результирующий поток, созданный результирующей н.с. Воздействие н.с. якоря на н.с. основных полюсов называют реакцией якоря. При анализе этого явления мы воспользуемся методом наложения, для этого отдельно строим распределение основного поля полюсов и поля якоря, а затем совмещаем их в результирующее магнитное поле машины. Для выведения выражения н.с. якоря вводится понятие о линейной нагрузке. Для этого зубчатый якорь приводится к гладкому с расчетным воздушным зазором и с равномерно распределенным по окружности якоря слоем проводников.
Распределение основного потока в двухполюсной машине при х.х., показанное на рисунке 14.1, а, имеет симметричный характер как относительно осевой линии dd основных полюсов, так и относительно геометрической нейтрали, занимающих неизменное положение в пространстве. Распределение магнитной индукции в зазоре под полюсом представляет собой трапецеидальную кривую (рисунок 14.1, б).
На рисунке 14.2, а показано распределение магнитного поля якоря. Машина не возбуждена а якорь неподвижен: IB=0 и n=0. Щетки поставим по линии геометрической нейтрали и подведем к ним ток от какого-нибудь постороннего источника постоянного тока в таком направлении, чтобы направления токов в ветвях обмотки совпадали с направлением э.д.с., изображенными на рисунке 14.1, а..
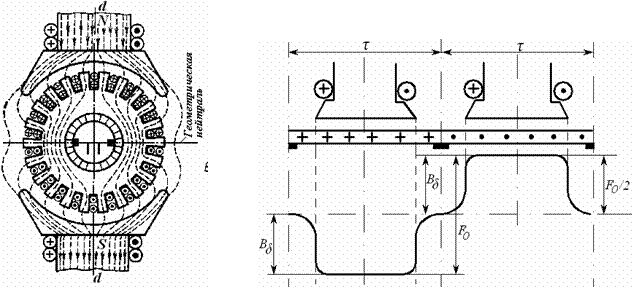
а) б)
Рисунок 14.1 – Основной магнитный поток машины при х.х. (а)
и кривая распределения н.с. и индукции под главными полюсами (б)

а) б)
Рисунок 14.2 – Магнитное поле якоря (а) и кривая н.с. индукции поля якоря (б)
Так как магнитные линии выходят из северного полюса и входят в южный, то левая сторона якоря обладает северной полярностью, а правая – южной. Такое поле якоря называется поперечным полем и определяется поперечной н.с. якоря FЯq. Как видно из рисунка 14.2, б, якорь представляет собой электромагнит, ось которого совпадает с линией щеток. Н.с. якоря по линии геометрической нейтрали имеет максимальное значение, так как соответствующая магнитная линия охватывает наибольший ток (кривая 1), однако магнитная индукция от потока якоря в этих точках имеет небольшое значение (кривая 2), что объясняется увеличением магнитного сопротивления потоку якоря в межполюсном пространстве.
14.1 Поперечная и продольная намагничивающие силы якоря
а) б) в)
Рисунок 14.3 – Направление н.с. якоря
Если щетки стоят на линии геометрической нейтрали qq (рисунок 14.3, а), то поле якоря направлено под углом 90°, т.е. поперек осевой линии основных полюсов dd. Такое поле якоря называют поперечным, и определяется оно поперечной намагничивающей силой якоря FЯq. При сдвиге щеток с нейтрали на угол ±90° ось поля якоря устанавливается по оси полюсов dd вверх или вниз от оси абсцисс (рисунок 14.3, б). Такое поле якоря называют продольным, и определяется оно продольной н.с. якоря FЯd. В общем случае щетки могут быть сдвинуты с нейтрали на угол β или соответственно по окружности якоря на дугу bC (рисунок 14.3, в). В этих условиях можно рассматривать якорь как два совмещенных электромагнита, из которых один, образованный частью обмотки и находящийся в двойном углу 2β, создает продольную намагничивающая сила якоря FЯd=2AbС, а другой, образованный остальной частью обмотки по дуге τ–2bС, создает поперечную н.с. якоря FЯq=А(τ–2bС).
Рисунок 14.4 – Результирующее магнитное поле машины
При нагрузке машины будет иметь место результирующее магнитное поле (рисунок 14.4), которое уже не является симметричным относительно оси полюсов. Причина деформации магнитного поля заключается в том, что направления магнитных линий поперечного поля якоря и поля полюсов под сбегающим краем полюса совпадают, отчего результирующее поле под сбегающим краем полюса усиливается, а под набегающим краем полюса эти поля направлены встречно, поэтому результирующее поле уменьшается. Следствием искажения распределения магнитного поля является смещение по направлению вращения физической нейтрали на некоторый угол β, величина которого зависит от нагрузки машины. Физической нейтралью называют прямую, проходящую через центр, и точки на окружности якоря с нулевой магнитной индукцией, т.е. прямую, перпендикулярную оси результирующего магнитного поля. Для получения удовлетворительной работы щеток (без искрения) в машинах без дополнительных полюсов щетки приходится сдвигать с геометрической нейтрали в том же направлении на угол α, являющийся несколько большим угла β.
15 Лекция №15. Генераторы постоянного тока
Содержание лекции:
-область применения генераторов постоянного тока;
- генератор независимого возбуждения;
-генератор параллельного возбуждения;
-генератор последовательного возбуждения;
-генератор смешанного возбуждения.
Цель лекции
Ознакомить студентов:
-с областью применения генераторов постоянного тока;
-с генераторами различного возбуждения.
В тех случаях, когда по условиям производства необходим или предпочтителен большой ток (предприятия химической и металлургической промышленности, транспорт и др.), его получают, преобразуя переменный ток в постоянный с помощью преобразователей, в качестве которых широко применяют установки двигатель-генератор. В качестве источника энергии генераторы постоянного тока работают, главным образом, в изолированных установках (как возбудители синхронных машин), на автомашинах, самолетах, при сварке дугой, для освещения поездов, на кораблях и др.
Характеристики генератора постоянного тока. Свойства генераторов анализируют с помощью характеристик, устанавливающих зависимость между основными величинами, определяющими работу генератора: э.д.с. Е, напряжение на зажимах генератора U, ток возбуждения IВ, ток в якоре IЯ и частота вращения п. Так как генераторы чаще всего работают с постоянной частотой вращения, то основную группу характеристик снимают при неизменной частоте вращения (n=const). Напряжение U имеет наибольшее значение, поскольку оно определяет свойства генератора в отношении той сети, на которую он работает. Поэтому основными характеристиками являются:
а) нагрузочная U=f(IВ) при IЯ–const. В частном случае, когда IЯ=0, нагрузочная характеристика переходит в характеристику хх., имеющую важное значение для оценки генератора и построения других характеристик;
б) внешняя U=f(IЯ) при RВ=соnst;
в) регулировочная IВ=f(I) при U=const. В частном случае, когда U=0, регулировочная характеристика переходит в характеристику к.з. IК=f(IВ). Режим работы электрической машины при условиях, для которых она предназначена, называют номинальным режимом работы. Номинальный режим работы характеризуется величинами, обозначенными на заводском щитке машины как номинальные: напряжение, мощность, ток, частота вращения.
Рисунок 15.2 – Схема работы генератора
При работе нагруженного генератора в проводах обмотки якоря появляется ток iЯ=IЯ/(2a), в результате взаимодействия которого с основным магнитным полем машины на каждый проводник обмотки якоря действует сила
FЭМ=BСРliЯ (15.4)
где BСР – среднее значение магнитной индукции в зазоре;
l – длина якоря.
Величина электромагнитного момента (Н·м)
M=FЭМ0,5DN=BСРliЯ0,5DN
где N – число активных проводников обмотки якоря.
Имея в виду, что iЯ=IЯ/(2a); πD=2рτ; и магнитный поток возбуждения Ф=ВСРlτ, получим M=BСРl(IЯ/2a)·(2рτ/2π); N=рNIЯФ/(2πа), или
М=СМIЯ Ф (15.5)
где СМ=рN/(2πа) – величина, постоянная для данной машины.
Нагрузочная характеристика.
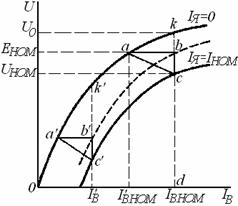
Рисунок 15.5 – Нагрузочная характеристика генератора
независимого возбуждения
Внешняя характеристика.
а) б)
Рисунок 15.6 – Внешняя характеристика генератора независимого возбуждения (а) и ее построение (б).
Регулировочная характеристика.
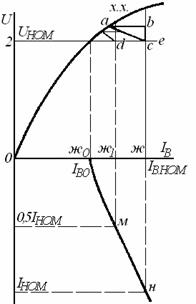
а) б)
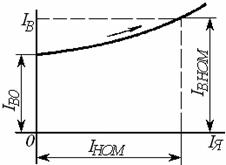
Рисунок 15.7 – Регулировочная характеристика генератора независимого возбуждения (а) и ее построение (б)
Генератор параллельного возбуждения
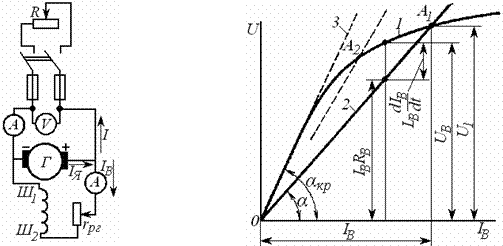 |
Рисунок 15.8 – Схема генератора Рисунок 15.9 – Самовозбуждение генератора
параллельного возбуждения параллельного возбуждения
Характеристика холостого хода.
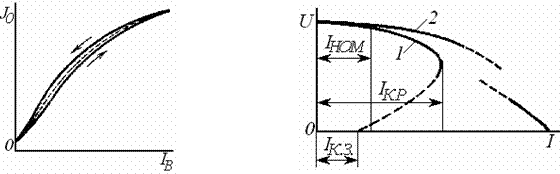
Рисунок 15.10 – Характеристика Рисунок 15.11 – Внешние характеристики
х.х. генератора параллельного генераторов параллельного 1 и
возбуждения независимого 2 возбуждения
Генератор последовательного возбуждения
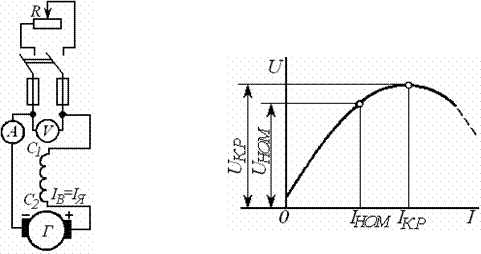
а) б)
Рисунок 15.12 – Схема (а) и внешняя характеристика (б) генератора последовательного возбуждения
16 Лекция №16. Двигатели постоянного тока. Способы пуска, характеристики двигателей
Содержание лекции:
-общие сведения о двигателях постоянного тока;
- способы пуска;
-характеристики двигателей.
Цель лекции
Ознакомить студентов:
-с классификацией двигателей постоянного тока;
- характеристиками двигателей постоянного тока.
Общие сведения о двигателях постоянного тока
Двигатели постоянного тока находят широкое применение в промышленных, транспортных, крановых и других установках, где требуется широкое плавное регулирование частоты вращения. Одна и та же электрическая машина может работать как в режиме генератора, так и в режиме двигателя. Это свойство электрических машин называют обратимостью.
Предположим, что к двигателю подведено напряжение UСЕТИ = const. При заданной на рисунке 16.1 полярности полюсов и направлении тока IЯ в якоре (обмотка якоря показана только одним проводником) на валу двигателя создается вращающий электромагнитный момент М, направленный против вращения часовой стрелки. Под действием этого момента двигатель вращается в направлении момента с постоянной частотой п.
Рисунок 16.1 – Направление момента и противо-э.д.с. обмотки якоря двигателя
Для двигателя, работающего с постоянной частотой вращения, можно составить уравнение э.д.с.
UСЕТИ=ЕЯ+IЯRЯ
где ЕЯ и IЯ – э.д.с и ток, соответствующие установившемуся режиму работы;
IЯRЯ – падение напряжения в сопротивлениях цепи якоря двигателя.
Уравнение моментов двигателя. Электромагнитный момент двигателя
М=(1/π)NIЯpФ/(2а)=CМIЯФ (16.1)
создается в результате взаимодействия основного магнитного поля Ф и тока в обмотке якоря IЯ и расходуется на преодоление тормозящих моментов:
а) момента хх. М0;
б) полезного момента М2;
в) динамического момента Mj.
Момент х.х. М0 существует при любом режиме работы двигателя и определяется трением в подшипниках, трением щеток о коллектор, вентиляционными потерями и потерями в стали. Полезный момент М2 определяется свойствами рабочей машины и характером производственного процесса. Динамический момент возникает при всяком изменении частоты вращения двигателя
Mj=±J(dω/d) (16.2)
где J – момент инерции всех вращающихся частей;
ω – угловая скорость вращения якоря.
Если частота вращения двигателя увеличивается, то момент Еj положителен и, складываясь с моментами М0 и М2, увеличивает тормозной момент на валу двигателя. При уменьшении п момент Mj отрицателен и уменьшает общий тормозной момент. Зависимость между вращающим и тормозным моментами двигателя на его валу определяется законом равновесия моментов: в любых условиях работы двигателя эти моменты находятся во взаимном равновесии, т.е. равны друг другу по величине, но направлены в противоположные стороны. При n=const момент Mj=0 и тогда
М=М0+М2=МСТ (16.3)
где МСТ – статический момент сопротивления на валу двигателя.
Энергетическая диаграмма двигателя. На рисунке 16.2 изображена энергетическая диаграмма двигателя параллельного возбуждения, работающего в установившемся режиме, т.е. при n=const. К двигателю из сети подводится мощность P1=UCI, которая покрывает потери в цепи возбужденияRВ и электрические потери в цепи якоря I2ЯRЯ, а оставшаяся ее часть составляет электромагнитную мощность якоря РЭМ=ЕЯIЯ преобразующуюся в полную механическую мощность РМ двигателя. Полезная механическая мощность на валу двигателя Р2 меньше полной механической мощности РМ на величину мощности P0 необходимой для покрытия потерь в стали РС и механических потерь РМЕХ, т.е.
Р2=РМ – (РС+РМЕХ).
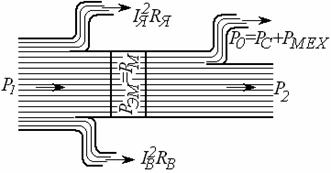
Рисунок 16.2 – Энергетическая диаграмма двигателя
параллельного возбуждения
В зависимости от способа включения обмотки возбуждения и обмотки якоря различают следующие типы двигателей постоянного тока:
а) параллельного возбуждения;
б) последовательного возбуждения;
в) смешанного возбуждения, в которых имеются две обмотки возбуждения: параллельная и последовательная. Двигатели постоянного тока оцениваются по совокупности следующих видов характеристик: пусковых, рабочих, регулировочных и механических.
Пусковые характеристики.
Пусковые характеристики определяются следующими величинами:
а) пусковым током IПУСК характеризуемым отношением IПУСК/IНОМ;
б) пусковом моментом МПУСК, характеризуемым отношением МПУСК/МНОМ;
в) плавностью пусковой операции;
г) временем пуска в ход tПУСК;
д) экономичностью операции, определяемой стоимостью пусковой аппаратуры.
В начальный момент пуска двигателя его якорь неподвижен, противо-э.д.с. в обмотке якоря равна нулю и ток в якоре двигателя IЯ=UС/RЯ. Сопротивление цепи якоря невелико, поэтому пусковой ток превышает номинальный в 20 и более раз. Резкий скачок тока при пуске создает на валу двигателя большой пусковой момент, который может вызвать механические разрушения, как самого двигателя, так и исполнительного механизма, привести к резкому падению напряжения в сети и вызвать интенсивное искрение под щетками. Поэтому при пуске двигателя в ход для ограничения пускового тока применяют пусковые реостаты, включаемые последовательно в цепь якоря (рисунок 16.3). По мере увеличения частоты вращения якоря противо-э.д.с. увеличивается, а ток якоря уменьшается, поэтому сопротивление реостата следует уменьшить так, чтобы в конце пуска оно было полностью выведено, и чтобы пусковой ток превышал номинальный не более чем в два-три раза.
Рисунок 16.3 – Схема включения пускового реостата в цепь двигателя
параллельного возбуждения
Двигатель параллельного возбуждения
Для пуска в ход двигателей постоянного тока применяют двух-, трех- и четырехзажимные пусковые реостаты. На рисунке 16.4 представлена схема включения трехзажимного пускового реостата для двигателя параллельного возбуждения.
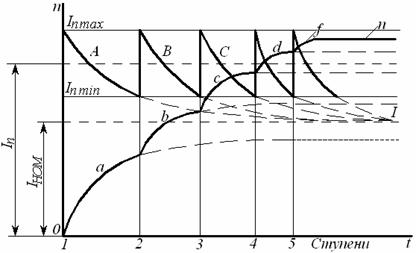
Рисунок 16.4 – Диаграмма процесса пуска двигателя в ход
Реостат имеет шесть контактов: пять рабочих (1, 2, 3, 4, 5) и один холостой (нулевой 0); три зажима Л, Ш, Я, которые соответственно подключаются к линии, обмотке возбуждения и к якорю. Скользящий контакт реостата перемещается по неподвижным контактам и контактной дуге Д, благодаря которой обмотка возбуждения оказывается включенной на полное напряжение сети. Регулировочный реостат в цепи возбуждения rРГ следует вывести, так как в этом случае ток возбуждения IВ, магнитный поток Ф и вращающий момент двигателя достигают наибольшей величины, что облегчает пуск двигателя в ход. Рабочие характеристики двигателя имеют вид М,I, η=f(IЯ) при U=UНOM=const и ТB=cons( рисунок 16.5, б). Схема двигателя показана на рисунке 16.5, а.
а) б)
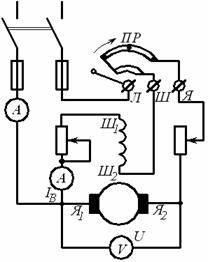
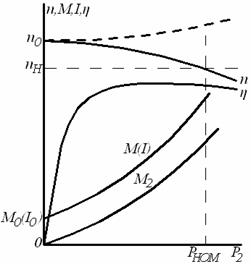
Рисунок 16.5 – Схема двигателя параллельного возбуждения (а)
и его рабочие характеристики (б)
17 Лекция № 17. Регулирование частоты вращения двигателей постоянного тока
Содержание лекции:
- регулирование частоты вращения двигателей постоянного тока.
- изменением напряжения сети;
- изменением падения напряжения в сопротивлениях цепи якоря;
- изменением потока возбуждения.
Цель лекции
Ознакомить студентов:
-с регулированием частоты вращения двигателей постоянного тока.
Одним из основных достоинств двигателей постоянного тока является возможность плавного регулирования частоты вращения в широких пределах. В общем случае в цепь якоря двигателя может быть включен регулировочный реостат Rрг. Тогда из формулы п=[U–IЯ(RЯ+Rрг)]/(сеФ) следует, что частоту вращения двигателей постоянного тока можно регулировать:
а) изменением напряжения сети U;
б) изменением падения напряжения в сопротивлениях цепи якоря IЯ(RЯ+Rрг);
в) изменением потока возбуждения, а следовательно, изменением тока возбуждения IЯ.
Первый способ возможен только в специальных установках, допускающих регулирование напряжения сети U. Реостат Rpг в цепи якоря должен быть подобран так, чтобы можно было регулировать частоту вращения в желаемых пределах. Предположим, что напряжение сети и ток возбуждения остаются постоянными, т.е. U=const и IЯ=const, кроме того, статический момент МСТ=М0+М2 не зависит от частоты вращения двигателя. При выведенном реостате Rpг установившийся режим работы двигателя характеризуется вращающим моментом М2, частотой вращения п1, и током в цепи якоря I21. Сразу же после введения регулировочного реостата Rpг частота вращения и противо-э.д.с. остаются без изменения вследствие значительного момента инерции якоря, а ток в цепи якоря уменьшается до значения I21'. Соответственно уменьшается и вращающий момент двигателя.
Превышение нагрузочного момента над вращающим моментом приводит к снижению частоты вращения якоря, уменьшению противо-э.д.с. и увеличению тока в цепи якоря (рисунок17.1). На рисунке 17.2 представлены две регулировочные характеристики двигателя, снятые при различных значениях тока якоря: при IЯ<IНОМ и при IЯ=IНОМ. Из этих характеристик видно, что при малом значении тока возбуждения, а тем более при обрыве цепи возбуждения IВ=0 частота вращения неограниченно возрастает, что приводит к «разносу» двигателя.
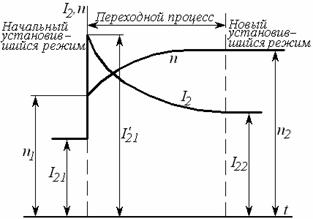
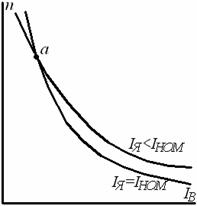
Рисунок 17.1-Процесс регулирования Рисунок 17.2 – Регулировочная
частоты вращения реостатом в характеристика двигателя
цепи якоря (а) и в цепи возбуждения (б)
На рисунке 17.3 приведена схема включения двигателя последовательного возбуждения.
Рабочие характеристики двигателя имеют вид М и η=f(IЯ) при U=UНОМ=const. В двигателях последовательного возбуждения ток якоря одновременно является током возбуждения (IЯ=IВ=I), поэтому магнитный поток Ф при различной нагрузке машины испытывает значительные изменения, и это составляет его характерную особенность. При работе двигателя последовательного возбуждения главное значение имеет изменение основного магнитного потока полюсов, если не учитывать падения напряжения IЯRЯ и реакцию якоря.
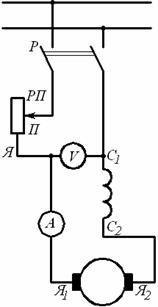
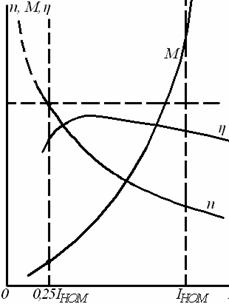
Рисунок 17.3-Схема двигателя Рисунок 17.4 – Рабочие характеристики
последовательного возбуждения двигателя последовательного
возбуждения
Регулирование частоты вращения изменением магнитного потока возбуждения. При обычной схеме включения обмоток двигателя ток в обмотке возбуждения равен току якоря. Если замкнуть рубильник Р1 (рисунок 17.5, б), то ток возбуждения уменьшится, увеличивая частоту. При повышении частоты вращения условия коммутации ухудшаются и ограничивают верхний предел частоты вращения якоря, который не превышает 1,4 номинальной. Для оценки этого способа регулирования частоты вращения введено понятие о коэффициенте ослабления поля kО.П.=RШ.В/(RВ+RШ.В), где RШ.В – шунтирующее сопротивление параллельной обмотки возбуждения. Аналогичное увеличение частоты вращения якоря можно получить, если выполнить обмотку возбуждения секционированной, т.е. сделать отводы от некоторых витков обмотки возбуждения и производить изменения намагничивающая сила этой обмотки (рисунок 17.5, в). Изменение сопротивления регулировочного реостата в цепи якоря также позволяет регулировать частоту вращения двигателя (UД – напряжение на двигателе).
а) б) в)
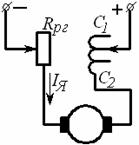
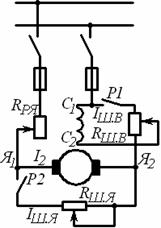
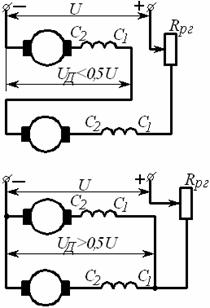
Рисунок 17.5 – Схемы регулирования частоты вращения двигателя последовательного возбуждения:
а – изменением схемы включения; б – изменением тока возбуждения;
в – секционированием обмотки возбуждения
Двигатель смешанного возбуждения имеет две обмотки возбуждения, одна Ш из которых включается параллельно обмотке якоря, а вторая С – последовательно (рисунок 17.5 б).
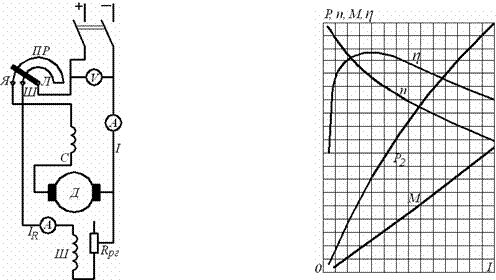
Рисунок17.6–Схема включения Рисунок 17.7–Рабочие характеристики
двигателя смешанного возбуждения двигателя смешанного возбуждения
Соотношение намагничивающих сил обмоток может быть различным, но обычно одна из обмоток создает большую намагничивающую силу, ее называют основной. Частота вращения двигателя п=(U–IЯRЯ)[се(Ф1±Ф2)], где Ф1, Ф2– магнитные потоки параллельной и последовательной обмоток возбуждения соответственно. Поэтому магнитный поток с увеличением нагрузки возрастает, что ведет к уменьшению частоты вращения двигателя. При встречном включении обмоток магнитный поток Ф2 при увеличении нагрузки размагничивает машину (знак минус), увеличивая частоту вращения. При пуске двигателя смешанного возбуждения со встречным включением обмоток возбуждения магнитный поток последовательной обмотки Ф2 может заметно ослабить результирующий поток двигателя и этим осложнить процесс пуска. Чтобы избежать этого, последовательную обмотку таких двигателей иногда замыкают накоротко на все время пуска.
Список литературы
1.Копылов И.П. Электрические машины.-М.: Высшая школа, Логос, 2000.
2.Проектирование электрических машин. /Под общей редакцией И.П. Копылова.- М.: Энергия, 2002.
3.Брускин Д.Э., Зорохович А.Е., Хвостов В.С. Электрические машины.- М., 1987.
4.Вольдек А.И. «Электрические машины»: Учебник для студентов выс. техн. учебн. заведений. Изд. 2-е.-М.: «Энергия», 1974.