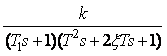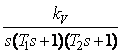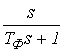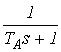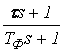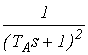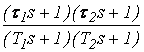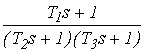Некоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра электропривода и автоматизации промышленных установок
НЕЛИНЕЙНЫЕ И ЦИФРОВЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
методические указания к выполнению
лабораторных работ
для магистрантов специальности 6М071800 – Электроэнергетика
Алматы 2011
СОСТАВИТЕЛИ: П.И. Сагитов, Ю.А. Цыба, Ю.И. Шадхин, Н.К. Алмуратова. Нелинейные и цифровые системы автоматического управления. Методические указания к выполнению лабораторных работ для магистрантов специальности 6М071800 – Электроэнергетика. – Алматы: АИЭС, 2011. – 33с.
Методические указания содержат необходимые теоретические сведения, программу выполнения работ, методику подготовки, проведения экспериментов и анализа полученных результатов.
Методические указания предназначены для магистрантов, обучающихся по специальности 6М071800– Электроэнергетика.
Ил. 9, табл. 2, библиогр. – 4 назв.
Рецензент: д-р. техн. наук, проф. К.К. Жумагулов.
Печатается по плану издания некоммерческого акционерного общества ,,Алматинский университет энергетики и связи” на 2011 г.
Ó НАО ,,Алматинский университет энергетики и связи”, 2011 г.
1 Лабораторная работа № 1. Исследование устойчивости нелинейных разомкнутых и замкнутых систем автоматического управления
Цель работы: исследование устойчивости автоматических систем различной структуры.
1.1 Общие сведения
Математическая устойчивость невозмущенного движения оценивают по характеру возмущенного движения как способность приходить в результате возмущенного движения к невозмущенному движению, если действие возмущения прекратилось. По этой причине возмущенное движение чаще рассматривают как свободное движение системы, поскольку проще решать однородное дифференциальное уравнение с ненулевыми начальными условиями, чем неоднородное уравнение.
Если невозмущенное движение характеризуется функциями,
![]() а
возмущенное – функциями
а
возмущенное – функциями ![]() , то возмущенное движение можно описать
отклонением величин от тех значений, которые они имеют при невозмущенном
движении:
, то возмущенное движение можно описать
отклонением величин от тех значений, которые они имеют при невозмущенном
движении:
![]() (1.1)
(1.1)
Начальными
условиями для свободного движения, записанного в отклонениях, будут значения
величин, ![]() Они
возникли в результате действия возмущения, которое затем прекратилось. Поэтому
функции
Они
возникли в результате действия возмущения, которое затем прекратилось. Поэтому
функции ![]() описывают процесс свободных движений в системе.
Как трактуется определение устойчивости в этом
случае? Невозмущенное движение будет устойчивым, если для всякого
положительного числа
описывают процесс свободных движений в системе.
Как трактуется определение устойчивости в этом
случае? Невозмущенное движение будет устойчивым, если для всякого
положительного числа ![]() , как бы мало оно ни было, можно
подобрать другое число
, как бы мало оно ни было, можно
подобрать другое число ![]() , зависящее от
, зависящее от ![]() такое, что для всех
возмущенных движений, для которых в начальный момент
такое, что для всех
возмущенных движений, для которых в начальный момент
![]() (1.2)
(1.2)
при всех ![]() выполняется неравенство
выполняется неравенство
![]() (1.3)
(1.3)
Из уравнения (1.3) следует, что при оценке устойчивости отклонения не должны
превосходить некоторой достаточно малой величины ![]() , а из уравнения (1.2) – что начальные
условия при этом отличны от нуля, но не превосходят некоторого значения
, а из уравнения (1.2) – что начальные
условия при этом отличны от нуля, но не превосходят некоторого значения ![]() , зависящего от
выбранного значения
, зависящего от
выбранного значения ![]() . Если выполняется условие,
. Если выполняется условие, ![]() то система
называется неограниченно устойчивой, т.е. она будет устойчивой при любых
начальных отклонениях. Если система устойчива при
то система
называется неограниченно устойчивой, т.е. она будет устойчивой при любых
начальных отклонениях. Если система устойчива при ![]() и неустойчива при
и неустойчива при ![]() то она является устойчивой в
малом и неустойчивой в большом ( при
то она является устойчивой в
малом и неустойчивой в большом ( при ![]() . Если выполняется условие
. Если выполняется условие ![]() то система называется
асимптотически устойчивой.
то система называется
асимптотически устойчивой.
Прежде чем рассматривать математическую устойчивость нелинейной системы, рассмотрим, как можно оценить, устойчивость линейной автоматической системы.
Предполагаем, что свободное движение линейной системы описывается линейным однородным дифференциальным уравнением
![]() .
(1.4)
.
(1.4)
С начальными условиями
![]() где
где ![]() - порядок производной.
- порядок производной.
Решение этого уравнения (1.4) представляет собой сумму членов вида
![]() (1.5)
(1.5)
где ![]() - корни характеристического уравнения
- корни характеристического уравнения
![]() (1.6)
(1.6)
![]() - постоянные интегрирования, зависящие
от начальных условий
- постоянные интегрирования, зависящие
от начальных условий
![]()
Корни характеристического уравнения (1.6) в общем случае могут быть вещественными и комплексно сопряженными.
Если в характеристическом уравнении все вещественные части комплексных корней и простые корни отрицательны, то система будет устойчива. Если хотя бы один из вещественных корней или вещественная часть пары комплексных корней окажется положительной, то система будет неустойчива. Если вещественная часть хотя бы одного корня равна нулю, а вещественные части остальных корней – отрицательные, то система находится на границе устойчивости.
При наличии кратных корней с нулевыми вещественными частями система будет неустойчивой.
Итак, установлено, что необходимое и достаточное условие устойчивости линейных систем автоматического управления является отрицательность вещественных частей всех корней характеристического уравнения. Но почти все реальные системы являются нелинейными, и только приближенно некоторые из них можно описать линейными уравнениями. Можно ли по устойчивости линеаризованной системы судить об устойчивости исходной нелинейной системы?
Этот вопрос был решен А.М. Ляпуновым, который сформулировал теоремы об устойчивости линеаризованных систем.
Первая теорема.
Если линеаризованная система устойчива, то устойчива и исходная нелинейная система.
Вторая теорема.
Если линеаризованная система неустойчива, то неустойчива и исходная нелинейная система.
Третья теорема.
Если линеаризованная система находится на границе устойчивости, то для определения устойчивости исходной нелинейной системы необходимо произвести дополнительные исследования по исходным нелинейным уравнениям системы.
Таким образом, теоремы Ляпунова позволяют судить об устойчивости нелинейной системы по линейному уравнению.
Следует отметить, что нелинейная система автоматического управления может быть представлена в виде структурной схемы, состоящей из передаточных функций линеаризованных звеньев системы.
1.2 Программа работы
1.2.1 Построить схему и образовать передаточную функцию разомкнутой системы из звеньев, представленных в вариантах заданий (вариант задания задается преподавателем).
1.2.2 Оценить устойчивость разомкнутой системы нахождением корней характеристического уравнения.
1.2.3 Замкнуть разомкнутую систему отрицательной единичной обратной связью, получить передаточную функцию замкнутой системы и график переходного процесса этой системы. Если замкнутая система неустойчива или находится на границе устойчивости, необходимо улучшить динамику системы так, чтобы система была устойчива с допустимыми качественными характеристиками переходного процесса.
1.2.4 Исследовать влияние коэффициента системы ![]() и постоянных
и постоянных
времени
![]() на
устойчивость разомкнутой и замкнутой систем.
на
устойчивость разомкнутой и замкнутой систем.
Варианты заданий:
Вариант 1
![]()
![]()
Вариант 2
![]()
![]()
Вариант 3
![]()
![]()
Вариант 4
![]()
![]()
Вариант 5
![]()
![]()
Вариант 6
![]()
![]()
Вариант 7
![]()
![]()
Вариант 8
![]()
![]()
Вариант 9
![]()
![]()
Вариант 10
![]()
![]()
Вариант 11
![]()
![]()
Вариант 12
![]()
![]()
1.3 Порядок и методика выполнения работы
Предполагаем, что разомкнутая система состоит из последовательно соединенных звеньев
![]()
где
![]()
Образуем передаточную функцию разомкнутой системы.
В этом случае программа образования передаточной функции разомкнутой системы, с помощью математической системы MATLAB, будет иметь вид:
>> k1=5;k2=70;k3=12;
>> T1=0.5;T2=2;T3=1.5;
>> n1=[T1 1]; m1=[T2 1];
>> W1=tf(n1,m1)
Transfer function:
0.5 s + 1
---------
2 s + 1
>> W1=k1*W1;
>> n2=[k2]; m2=[1.5 1 0];
>> W2=tf(n2,m2)
Transfer function:
70
-----------
1.5 s^2 + s
>> n3=[k3]; m3=[1];
>> W3=tf(n3,m3)
Transfer function:
12
>> G1=W1*W2*W3
Transfer function:
2100 s + 4200
-------------------
3 s^3 + 3.5 s^2 + s
Передаточная функция G1 является передаточной функцией разомкнутой системы.
Определение устойчивости системы осуществляем на
основании численных значений корней характеристического уравнения. Для этого
создаем одномерный массив ![]() из коэффициентов характеристического
уравнения передаточной функции G1 и с помощью функции
из коэффициентов характеристического
уравнения передаточной функции G1 и с помощью функции ![]() получаем корни характеристического
уравнения.
получаем корни характеристического
уравнения.
>> P=[3 3.5 1 0];
>> r = roots(P)
r =
0
-0.6667
-0.5000
где
![]() корни
характеристического уравнения.
корни
характеристического уравнения.
Исходя из выше описанного условия устойчивости движения разомкнутой системы – «если вещественная часть хотя бы одного корня равна нулю (в нашем случае результаты определения корней характеристического уравнения показывают, что один из корней характеристического уравнения равен нулю), а вещественные части остальных корней – отрицательные, то система находится на границе устойчивости». Таким образом, можно сделать вывод, что разомкнутая система находится на границе устойчивости.
Получение передаточной функции замкнутой системы на
основании передаточной функции разомкнутой системы ![]() с единичной отрицательной
обратной связью реализуется с помощью функции
с единичной отрицательной
обратной связью реализуется с помощью функции ![]()
>> GOS=feedback(G1, [1])
Transfer function:
2100 s + 4200
-------------------------------
3 s^3 + 3.5 s^2 + 2101 s + 4200,
здесь передаточная функция замкнутой системы обозначена как GOS.
Переходной
процесс замкнутой системы с единичной отрицательной обратной связью можно
получить после реализации функции ![]()
>> step(GOS)
График переходного процесса замкнутой системы представлен на рисунке 1.1.
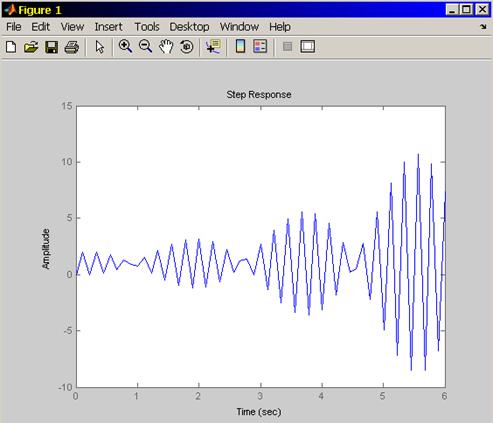
Рисунок 1.1- График переходного процесса замкнутой системы
Как видно из рисунка 1.1, переходной процесс замкнутой системы
неустойчив.
Однако для обеспечения устойчивости разомкнутой системы (как один из вариантов), можно замкнуть систему гибкой обратной связью по производной. В качестве обратной связи (ОС) выбираем блок с передаточной функцией
![]()
где
![]() .
.
Рассмотрим
передаточную функцию ![]() при
при
![]()
В основную программу вводим
>> n4=[0.5 1];
>> m4=[1];
>> W4=tf(n4,m4);
>> GOS=feedback(G1, [W4])
Transfer function:
2100 s + 4200
--------------------------------
3 s^3 + 1054 s^2 + 4201 s + 4200
Переходной
процесс замкнутой системы с гибкой обратной связью можно получить после
реализации функции ![]()
>> step(GOS).
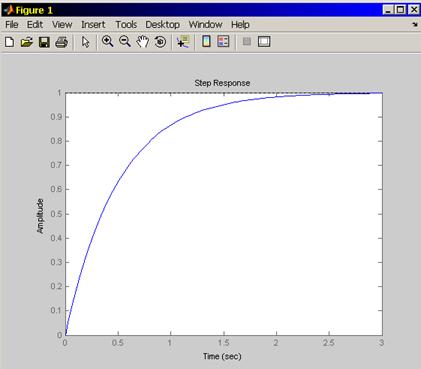
Рисунок 1.2 - График переходного процесса замкнутой
системы с гибкой ОС при ![]()
Вывод: переходной процесс сходится к значению, ![]() следовательно,
система устойчива.
следовательно,
система устойчива.
1.4 Содержание отчета
1.4.1 Краткое описание основных теоретических положений.
1.4.2 Структурная схема разомкнутой и замкнутой САУ.
1.4.3 Графики переходных процессов замкнутой САУ.
1.4.4 Оценка качества переходных процессов замкнутой САУ.
1.5 Контрольные вопросы
1.5.1 Условия устойчивости (теоремы Ляпунова).
1.5.2 Основные функции MATLAB для создания передаточных функций, опеределения устойчивости систем и получения переходных процессов систем.
1.5.3 Способы улучшения динамики систем.
2 Лабораторная работа № 2. Исследование нелинейного двухканального корректирующего устройства
Цель работы: Изучить принципы построения и функционирования двухканального нелинейного корректирующего устройства
2.1 Общие сведения
Линейные минимально – фазовые корректирующие
устройства (ЛКУ) часто не могут обеспечить синтезируемой САУ желаемые
качественные показатели, особенно в условиях неполной информации о состоянии
объекта управления. Ограниченные возможности ЛКУ объясняются в первую очередь
тем, что для них характерна жесткая однозначная связь между амплитудными (АХЧ)
и фазовыми (ФЧХ) частотными характеристиками. Такая связь не позволяет,
например, создать апериодическое звено с опережающей ФЧХ в некотором диапазоне
частот. В псевдолинейных корректирующих устройствах в отличие от ЛКУ
используются разрывные (релейные) режимы работы, которые формируют управления в
виде комбинаций определенных частей сигналов с положительными и отрицательными
знаками. Псевдолинейные двухканальные нелинейные корректирующие устройства (ДНКУ)
позволяют синтезировать ФЧХ независимо от АЧХ, что открывает возможность
получения устойчивых систем, имеющих заданную точность и хорошие фильтрующие
свойства на высоких частотах. На рисунке 2.1 приведена структура системы,
состоящая из объекта управления (ОУ) с передаточной функцией ![]() и ДНКУ, в котором
верхний канал является амплитудным и содержит линейный фильтр
и ДНКУ, в котором
верхний канал является амплитудным и содержит линейный фильтр ![]() и блок определения
модуля.
и блок определения
модуля.
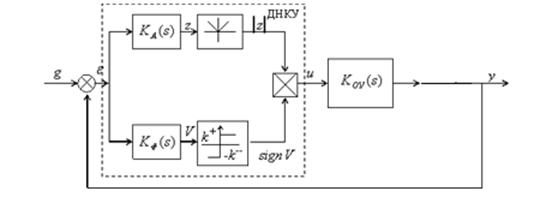
Рисунок 2.1 - Структура системы с ДНКУ
Фазовый фильтр ![]() и реле с коэффициентами усиления
и реле с коэффициентами усиления ![]() и
и
![]() образуют канал фазы (реверса). Выходные сигналы двух
каналов перемножаются в блоке умножения, в результате чего создается
управляющее воздействие
образуют канал фазы (реверса). Выходные сигналы двух
каналов перемножаются в блоке умножения, в результате чего создается
управляющее воздействие
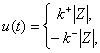
![]() (2.1)
(2.1)
где ![]() - модуль сигнала
- модуль сигнала ![]() с выходом фильтра
с выходом фильтра
![]() ;
;
![]() сигнал с выхода фильтра
сигнал с выхода фильтра
![]() .
.
Если ошибка ![]() является гармоникой
является гармоникой ![]() , то выход ДНКУ
будет изменяться по закону
, то выход ДНКУ
будет изменяться по закону
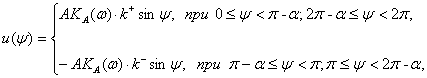 (2.2)
(2.2)
где ![]()
![]() АЧХ
амплитудного фильтра;
АЧХ
амплитудного фильтра;
![]() значение ФЧХ фазового фильтра на частоте
значение ФЧХ фазового фильтра на частоте
![]() рассматриваемой
гармоники.
рассматриваемой
гармоники.
Согласно закону (2.2) , моменты изменения знака
сигнала ![]() а
следовательно, моменты перехода от разгонных режимов к тормозным (или наоборот)
зависят от величины фазового сдвига
а
следовательно, моменты перехода от разгонных режимов к тормозным (или наоборот)
зависят от величины фазового сдвига ![]()
На рисунке 2.2 приведена геометрическая интерпретация
алгоритма работы ДНКУ в виде ![]() построенная для двух значений
построенная для двух значений
![]()
где
![]() Углы
Углы ![]() регулируются выбором
соответствующих коэффициентов
регулируются выбором
соответствующих коэффициентов ![]()
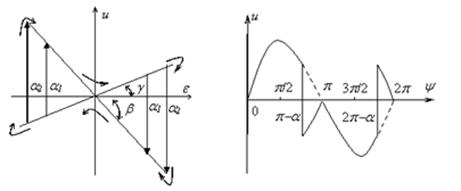
а б
Рисунок 2.2 - Геометрическая интерпретация алгоритма работы ДНКУ
Из рисунка 2.2 а, следует, что ДНКУ создаёт такой же
эффект, как и регулируемая петля положительного гистерезиса с направлением
обхода по часовой стрелке. Известно, что такая петлевая характеристика вносит
во входные гармоники переменные фазовые опережения, зависящие от значения ![]() , что позволяет
получить в САУ существенный запас по фазе в определенном частотном диапазоне.
Форма сигнала
, что позволяет
получить в САУ существенный запас по фазе в определенном частотном диапазоне.
Форма сигнала ![]() (2.2)
изображенная на рисунке 2.2 б, свидетельствует о том, что ДНКУ создает фазовое
опережение за счёт инвертирования наиболее запаздывающих в каждом полупериоде
частей гармоники.
(2.2)
изображенная на рисунке 2.2 б, свидетельствует о том, что ДНКУ создает фазовое
опережение за счёт инвертирования наиболее запаздывающих в каждом полупериоде
частей гармоники.
Выбирая соответствующим образом передаточные функции
![]() ,
, ![]() и
коэффициенты
и
коэффициенты ![]() , можно
целенаправленно и независимо друг от друга изменять АЧХ и ФЧХ корректируемой
системы, приближая её качественные показатели к желаемым значениям.
, можно
целенаправленно и независимо друг от друга изменять АЧХ и ФЧХ корректируемой
системы, приближая её качественные показатели к желаемым значениям.
Полагая, что
![]() (2.3)
(2.3)
и
учитывая, что на частоте среза ![]() канал фазы при
канал фазы при ![]() дает фазовое опережение
дает фазовое опережение
![]() (2.4)
(2.4)
а канал амплитуды вызывает ослабление спектра сигналов
с ростом частоты, можно синтезировать высококачественную систему, не используя
дополнительную информацию о состоянии ОУ, кроме величины ошибки ![]() Пусть, например, ОУ
системы (см. рисунок 2.1) имеет передаточную функцию вида
Пусть, например, ОУ
системы (см. рисунок 2.1) имеет передаточную функцию вида
![]() (2.5)
(2.5)
а коэффициенты ![]()
На рисунке 2.3 приведены ЛАЧХ ![]() и ФЧХ
и ФЧХ ![]() соответствующие выражению (2.5).
Из этих частотных характеристик следует, что замкнутая нескорректированная
система находится на границе устойчивости. Найдем такое ДНКУ с фильтрами
соответствующие выражению (2.5).
Из этих частотных характеристик следует, что замкнутая нескорректированная
система находится на границе устойчивости. Найдем такое ДНКУ с фильтрами ![]() и
и ![]() (2.3), которое
обеспечит запас по фазе на частоте среза
(2.3), которое
обеспечит запас по фазе на частоте среза ![]() и хорошую фильтрацию помех на высоких
частотах, т.е. создаст ЛФЧХ с крутизной
и хорошую фильтрацию помех на высоких
частотах, т.е. создаст ЛФЧХ с крутизной ![]() , начиная с частоты
, начиная с частоты ![]() Для решения этой задачи
выбираем фильтры (2.3) с параметрами
Для решения этой задачи
выбираем фильтры (2.3) с параметрами ![]()
![]() Тогда канал фазы, согласно уравнению
(2.4), будет вносить на частоте среза
Тогда канал фазы, согласно уравнению
(2.4), будет вносить на частоте среза ![]() фазовое опережение
фазовое опережение ![]() , что гарантирует требуемый
запас по фазе.
, что гарантирует требуемый
запас по фазе.
Из приведенных на рисунке 2.3 желаемых частотных
характеристик ![]() и
и
![]() следует,
что скорректированная система, с выбранным ДНКУ, отвечает всем требованиям.
Дополнительное улучшение качества САУ можно получить, варьируя коэффициентами
следует,
что скорректированная система, с выбранным ДНКУ, отвечает всем требованиям.
Дополнительное улучшение качества САУ можно получить, варьируя коэффициентами ![]() .
.
2.2 Программа работы
2.2.1 Создание структурной схемы модели САУ с ДНКУ в системе MATLAB
2.2.2 Набор параметров звеньев модели САУ.
2.2.3 Анализ переходных процессов на составленной модели.
2.3 Порядок и методика выполнения работы
Структурная схема системы приведена на рисунке 2.3,
где включение коэффициента ![]() происходит при
происходит при ![]() а
а ![]() при
при ![]() Объект управления, кроме
линейной части с передаточной функцией ,
Объект управления, кроме
линейной части с передаточной функцией , ![]() может содержать и нелинейную часть в
виде люфта редуктора, находившего на выходе ОУ.
может содержать и нелинейную часть в
виде люфта редуктора, находившего на выходе ОУ.
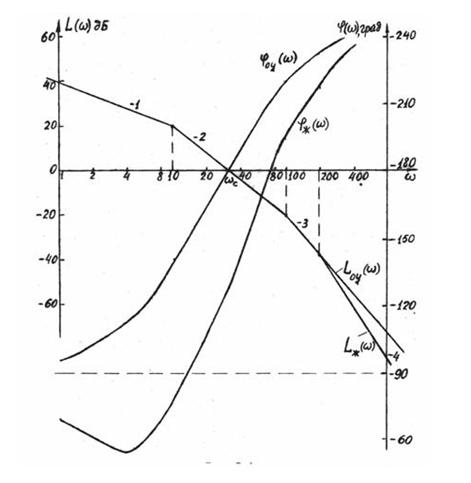
Рисунок 2.3 - Частотные характеристики замкнутой системы
Схема набора системы с использованием прикладных
программ Matlab
представлена
на рисунке 2.4. Вначале анализируется нескорректированная система (без ДНКУ),
для чего на вход ОУ подается сигнал ошибки ![]() После регистрации переходного процесса
на единичную ступенчатую функцию
После регистрации переходного процесса
на единичную ступенчатую функцию ![]() моделируется замкнутая система с ДНКУ
при различных фильтрах в каналах амплитуды и фазы.
моделируется замкнутая система с ДНКУ
при различных фильтрах в каналах амплитуды и фазы.
Необходимо найти такие фильтры
![]() ,
,
![]() и подобрать такие коэффициенты
и подобрать такие коэффициенты
![]() и
и ![]() , чтобы
ДНКУ создавало запас по фазе не менее
, чтобы
ДНКУ создавало запас по фазе не менее ![]() и крутизну желаемой ЛАЧХ на высоких
частотах не хуже
и крутизну желаемой ЛАЧХ на высоких
частотах не хуже ![]() , начиная
с частоты
, начиная
с частоты ![]() При
этом нужно погасить колебания в системе, если они возникают.
При
этом нужно погасить колебания в системе, если они возникают.
Сведения о линейной части и нелинейности типа люфта
приведены в таблице 2.1. Виды передаточных функций фазовых и амплитудных
фильтров, одинаковые при все вариантов, приведены в таблице 2.2. В таблице 2.2
также указан диапазон изменения коэффициентов ![]() . Параметры ОУ и фильтров задаются
преподавателем.
. Параметры ОУ и фильтров задаются
преподавателем.
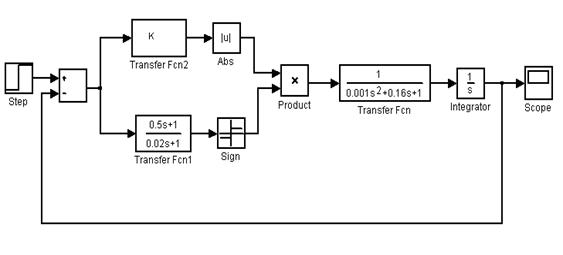
Рисунок 2.4 - Структурная схема модели объекта управления с ДНКУ в Matlab
Таблица 2.1 – Передаточные функции ОУ и характеристики нелинейности
|
Номер задания |
Передаточная функция линейной части объекта КОУ(s) |
Нелинейная часть ОУ |
||||||||
|
|
|
|
Люфт с шириной
петли гистерезиса |
|||||||
|
|
|
Т |
|
|
|
|
|
Т |
||
|
1 |
1.5 |
0,25 |
0,05 |
0,7 |
1.2 |
0.2 |
0.05 |
2 |
0.4 |
+ |
|
2 |
1.7 |
0,2 |
0,03 |
0,5 |
1.1 |
0.4 |
0.05 |
4 |
0.2 |
+ |
|
3 |
1.8 |
0,15 |
0,025 |
0,4 |
1.5 |
0.3 |
0.02 |
3 |
0.1 |
+ |
|
4 |
1.0 |
0,1 |
0,02 |
0,45 |
1.6 |
0.15 |
0.04 |
1.5 |
0.35 |
+ |
|
Продолжение таблицы 2.1 |
||||||||||
|
5 |
1.1 |
0,08 |
0,015 |
0,6 |
1.3 |
0.25 |
0.04 |
5 |
0.25 |
+ |
|
6 |
1.3 |
0.04 |
0.02 |
0.3 |
1.6 |
0,05 |
0,05 |
2.5 |
0.15 |
+ |
|
7 |
1.2 |
0.02 |
0.01 |
0.2 |
1.22 |
0,04 |
0,015 |
3.5 |
0.24 |
+ |
|
8 |
1.4 |
0.01 |
0.04 |
0.35 |
1.07 |
0,02 |
0,04 |
4.5 |
0.33 |
+ |
|
9 |
1.35 |
0.03 |
0.022 |
0.55 |
1.4 |
0,03 |
0,02 |
3.1 |
0.11 |
+ |
|
10 |
1.45 |
0.02 |
0.05 |
0.6 |
1.2 |
0,01 |
0,1 |
4.1 |
0.17 |
+ |
|
11 |
1.33 |
0.01 |
0.02 |
0.5 |
1.44 |
0.02 |
0.4 |
5 |
0,25 |
- |
|
12 |
1.41 |
0.02 |
0.04 |
0.4 |
1.34 |
0.01 |
0.5 |
6 |
0,2 |
- |
|
13 |
1.52 |
0.03 |
0.05 |
0.3 |
1.25 |
0.03 |
0.44 |
7 |
0,15 |
- |
|
14 |
1.66 |
0.04 |
0.02 |
0.25 |
1.11 |
0.04 |
0.52 |
8 |
0,1 |
- |
|
15 |
1.30 |
0.05 |
0.04 |
0.15 |
1.37 |
0.015 |
0.33 |
9 |
0,08 |
- |
Таблица 2.2 - Виды передаточных функций фазовых и амплитудных фильтров
|
Вид фильтров в канале фазы |
Вид фильтров в канале амплитуды |
Пределы изменения k+ и k - |
|
|
|
|
|
|
|
|
|
|
|
2.4 Содержание отчета
2.4.1 Краткое описание ДНКУ.
2.4.2 Структурная схема модели ОУ с ДНКУ в MATLAB.
2.4.3 Графики переходных процессов, полученные в результате моделирования нескорректированной и скорректированной САУ.
2.4.4 Выводы о работе ДНКУ с разными фильтрами и
коэффициентами ![]()
2.5 Контрольные вопросы
2.5.1 В чем заключается отличия ДНКУ от ЛКУ?
2.5.2 Как влияют на динамику САУ коэффициенты ![]() ?
?
2.5.3 Для чего предназначены амплитудный и фазовый фильтры ДНКУ?
2.54 Выводы о работе ДНКУ с различными фильтрами и
коэффициентами ![]() ?
?
3 Лабораторная работа № 3. Синтез регуляторов с переменной структурой для управления нелинейной системой управления
Цель работы: синтез регуляторов с переменной структурой для управления нелинейной системой управления
3.1 Общие сведения
В последнее время существенно возрос интерес к исследованию систем с переменной структурой (СПС). Это связано с тем, что подобные системы обладают свойством нечувствительности к изменению параметров системы и инвариантности к внешним возмущениям. Задача синтеза в СПС обычно сводится к выбору гиперповерхностей в фазовом пространстве, на которых функции управления будут претерпевать разрывы. При выполнении определенных соотношений, о которых будет сказано ниже, в таких системах с необходимостью возникает специфический вид движения – так называемый скользящий режим (СР). СР – это особое движение САУ , при котором изображающая точка колеблется с бесконечно большой частотой в некоторой малой окрестности гиперповерхности разрыва ( или на пересечении гиперповерхностей). Следует отметить, что движение системы в скользящем режиме описывается дифференциальными уравнениями (ДУ) меньшего порядка, чем собственные движения системы. При этом качественные показатели синтезированной САУ обуславливаются только положением гиперповерхности переключения и не зависят от собственных параметров системы. Рассмотрим условия, при которых в СПС будет существовать скользящий режим.
Пусть
![]() (3.1)
(3.1)
есть уравнение гиперповерхности переключения.
В этом случае можно рассматривать
![]() как отклонение изображающей точки от этой
гиперповерхности. Для того чтобы в системе существовал СР, необходимо
сформировать управление таким образом, чтобы изображающая точка, один раз попав
на гиперповерхность переключения, уже не могла сойти с неё и дальше двигалась
только вдоль этой поверхности. Пусть в некоторый момент времени
как отклонение изображающей точки от этой
гиперповерхности. Для того чтобы в системе существовал СР, необходимо
сформировать управление таким образом, чтобы изображающая точка, один раз попав
на гиперповерхность переключения, уже не могла сойти с неё и дальше двигалась
только вдоль этой поверхности. Пусть в некоторый момент времени ![]() Тогда производная по
времени
Тогда производная по
времени ![]() (
скорость изменения
(
скорость изменения ![]() )
должна быть отрицательна. В этом случае
)
должна быть отрицательна. В этом случае ![]() отклонение от гиперповерхности разрыва
будет убывать до нуля, т.е. изображающая точка будет двигаться по направлению к
отклонение от гиперповерхности разрыва
будет убывать до нуля, т.е. изображающая точка будет двигаться по направлению к
![]() . Пусть
изображающая точка перескочила поверхность
. Пусть
изображающая точка перескочила поверхность ![]() и теперь
и теперь ![]() . Соответственно
должно измениться и значение производной, т.е. должно выполняться условие
. Соответственно
должно измениться и значение производной, т.е. должно выполняться условие
![]() . В этом случае изображающая
точка будет двигаться по направлению к поверхности скольжения. Исходя из всего
выше сказанного, можно записать уравнение существования СР
. В этом случае изображающая
точка будет двигаться по направлению к поверхности скольжения. Исходя из всего
выше сказанного, можно записать уравнение существования СР
![]() (3.2)
(3.2)
Таким образом, можно выделить 2 стадии в процессе синтеза СПС, работающих в скользящем режиме:
- определение закона управления и выбор поверхности (поверхностей) переключения, на которых функция будет претерпевать разрывы;
- анализ существования в системе СР.
Описанный подход обладает существенным недостатком – до сих пор не существует общих методов, позволяющих выбрать поверхность переключения для нелинейного объекта таким образом, чтобы синтезированная САУ работала в СР. Для преодоления этого недостатка предложено определять выражение для закона управления, исходя из выполнения условия существования СР. Это условие можно представить следующим образом
![]() (3.3)
(3.3)
где
![]() -
положительно – определенная функция фазовых переменных, такая, что
-
положительно – определенная функция фазовых переменных, такая, что
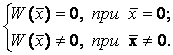
Уравнение гиперповерхности скольжения ![]() выбираем в виде
линейной комбинации фазовых координат системы:
выбираем в виде
линейной комбинации фазовых координат системы:
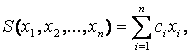 (3.4)
(3.4)
где
![]() некоторые
коэффициенты, определяющие положение гиперповерхности переключения в
пространстве.
некоторые
коэффициенты, определяющие положение гиперповерхности переключения в
пространстве.
При движении вдоль гиперповерхности переключения система будет описываться линейным дифференциальным уравнением, соответствующим выражению (3.4)
![]() (3.5)
(3.5)
где ![]() производная
производная ![]() -го порядка.
-го порядка.
Можно заметить, что при движении в скользящем режиме вдоль гиперповерхности (3.4) будет происходить линеаризация нелинейной системы.
Для того чтобы система устойчиво двигалась в
скользящем режиме, необходимо выбирать коэффициенты ![]() таким образом, чтобы линейное
дифференциальное уравнение (3.5) имело устойчивое решение. Для проверки
устойчивости можно использовать любой алгебраический критерий (Гурвица, Рауса и
другие).
таким образом, чтобы линейное
дифференциальное уравнение (3.5) имело устойчивое решение. Для проверки
устойчивости можно использовать любой алгебраический критерий (Гурвица, Рауса и
другие).
В качестве функции W можно принять норму вектора фазовых координат
![]() . (3.6)
. (3.6)
Тогда выражение (3.3) с учетом (3.6) примет вид
![]() .
(3.7)
.
(3.7)
Если помножить обе части (3.7) на
![]() , то можно заметить, что производная
, то можно заметить, что производная
![]() (3.8)
(3.8)
постоянно
будет менять знак, противоположный знаку ![]() . Таким образом, будет постоянно
выполняться условие существования скользящего режима, т.е. система будет
входить в СР при любых значениях начальных условий. Теперь рассмотрим синтез
закона управления, обеспечивающего существование скользящего режима для
существенно нелинейного объекта, описываемого системой дифференциальных
уравнений вида
. Таким образом, будет постоянно
выполняться условие существования скользящего режима, т.е. система будет
входить в СР при любых значениях начальных условий. Теперь рассмотрим синтез
закона управления, обеспечивающего существование скользящего режима для
существенно нелинейного объекта, описываемого системой дифференциальных
уравнений вида
 (3.9)
(3.9)
Гиперповерхность
![]() выбираем
следующего вида
выбираем
следующего вида
![]() (3.10)
(3.10)
где коэффициент ![]() для простоты примем
для простоты примем ![]() , а коэффициенты
, а коэффициенты ![]() и
и ![]() выбираем из условия
симметрирования в пространстве гиперплоскости скольжения:
выбираем из условия
симметрирования в пространстве гиперплоскости скольжения:
![]()
В этом случае будет удовлетворяться условие устойчивости решения соответствующего дифференциального уравнения.
Уравнение гиперповерхности скольжения в этом случае запишется следующим образом:
![]() (3.11)
(3.11)
Полная производная, по времени ![]() взятая в силу системы (3.9) и
с учетом (3.11), будет иметь вид
взятая в силу системы (3.9) и
с учетом (3.11), будет иметь вид
![]() (3.12)
(3.12)
Подставим полученное выражение для производной в (3.8), откуда найдем выражение для закона управления
![]() (3.13)
(3.13)
Полученный алгоритм управления содержит в себе операции взятия модуля и присвоения знака, которые легко реализуются с помощью цифровой системы управления. Кроме этого, следует отметить, что нелинейности объекта управления входят в функцию управления непосредственно, т.е. от нас не требуется обращать или дифференцировать нелинейности, входящие в структуру объекта. Это является существенным преимуществом предложенного метода перед другими методами синтеза нелинейных САУ.
3.2 Программа работы
3.2.1 Создание структурной схемы модели системы с переменной
структурой в системе MATLAB
3.2.2 Расчет и набор параметров звеньев СПС.
3.2.3 Анализ переходных процессов на модели СПС.
3.3 Порядок и методика выполнения работы
Модель системы ((3.9) и (3.13)), в качестве примера, набранная в пакете прикладных программ Matlab, представлена на рисунке 3.1.
В соответствии с вариантом задания необходимо получить выражение для оптимального закона управления.
Исходя из полученного закона управления, составить структуру скорректированной замкнутой системы (объект управления и регулятор) и набрать её в пакете Matlab.
Цель моделирования заключается в сравнении динамики
работы синтезированной САУ при различных значениях (![]() )
)
параметров
синтезированного регулятора. Значения коэффициенто рекомендуется принимать
следующие: ![]()
Для получения более полного представления о динамике
процессов, происходящих в синтезированной системе, необходимо снять следующие
зависимости: переходной процесс по координате ![]() фазовый портрет в плоскости координат
фазовый портрет в плоскости координат ![]() и
и ![]() , функцию управления
, функцию управления ![]()
Варианты задания
Объект управления описывается системой дифференциальных уравнений следующего вида:
1) 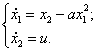 2)
2)
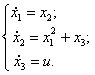
3) 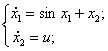 4)
4)
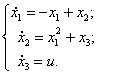
![]()
5) 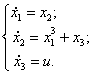 6)
6)

7) 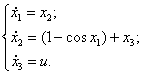 8)
8)
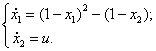
9) 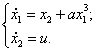 10)
10)
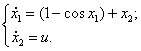
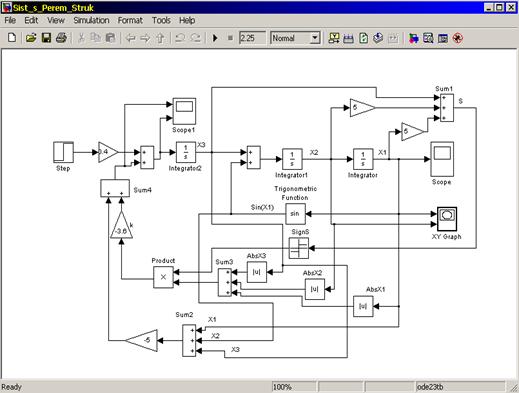
Рисунок 3.1 - Структура системы с переменной структурой в Matlab
3.4 Содержание отчета
3.4.1 Общие сведения об СПС.
3.4.2 Структурную схему модели СПС в системе Matlab.
3.4.3 Графики переходных процессов, фазовые портреты
системы и графики изменения функции управления при различных параметрах
синтезированного регулятора ![]() .
.
3.4.4 Анализ сравнения поведения системы в различных
режимах работы при различных значениях параметров ![]() и
и ![]() .
.
3.5 Контрольные вопросы
3.5.1 Каковы особенности системы с переменной структурой?
3.5.2 Почему функция ![]() должна быть положительно –
определенной?
должна быть положительно –
определенной?
3.5.3 Для чего предназначен регулятор СПС?
4 Лабораторная работа № 4. Аналитическое конструирование оптимального регулятора для нелинейного объекта управления
Цель работы: ознакомиться с методом аналитического конструирования оптимальных регуляторов, исследовать качественные показатели нелинейной системы с оптимальным регулятором.
4.1 Общие положения
Поведение многих промышленных электромеханических объектов управления можно представить в виде системы нелинейных дифференциальных уравнений с линейным вхождением сигнала управления. Например, возмущенное движение объекта управления (ОУ) часто записывают в следующем виде
 (4.1)
(4.1)
где
![]() координаты
состояния объекта;
координаты
состояния объекта;
![]() управляющее
воздействие;
управляющее
воздействие;
![]() -
коэффициенты;
-
коэффициенты;
![]() - нелинейные функции, дифференцируемые по своим аргументам, причём
- нелинейные функции, дифференцируемые по своим аргументам, причём
![]()
Задача синтеза оптимального управления для ОУ (4.1) с использованием
желаемого притягивающего многообразия заключается в определении закона управления с обратными связями
![]() (4.2)
(4.2)
который сначала обеспечивает сближение изображающей точки, находящейся в произвольном начальном состоянии, с выбранным притягивающим многообразием, а затем желаемое устойчивое движение вдоль него к началу координат фазового пространства. При этом на траекториях движения должен минимизироваться обобщенный функционал
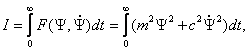 (4.3)
(4.3)
где
![]() некоторая
произвольная непрерывная и дифференцируемая по своим аргументам функция фазовых
координат и, возможно, управления;
некоторая
произвольная непрерывная и дифференцируемая по своим аргументам функция фазовых
координат и, возможно, управления;
![]() положительные
коэффициенты.
положительные
коэффициенты.
Необходимое уравнение оптимальности для функционала (4.3)
![]()
приводит к уравнению экстремалей
![]()
которое можно представить в следующем виде
![]() (4.4)
(4.4)
где ![]()
Выражение (4.4) явно свидетельствует о наличии неустойчивого и устойчивого подсемейств экстремалей. Для устойчивых экстремалей функционала (4.3) справедливо уравнение
![]() (4.5)
(4.5)
которое имеет решение
![]() .
(4.6)
.
(4.6)
Если
начальные условия (НУ), ![]() таковы, что удовлетворяется тождество
таковы, что удовлетворяется тождество ![]() , то согласно решению
(4.6), для любого текущего времени
, то согласно решению
(4.6), для любого текущего времени ![]() будет выполняться условие
будет выполняться условие ![]() . Таким образом,
множество
. Таким образом,
множество ![]() является
инвариантным притягивающим многообразием в том смысле, что если изображающая
точка попадет на него в начальный момент времени, то множество
является
инвариантным притягивающим многообразием в том смысле, что если изображающая
точка попадет на него в начальный момент времени, то множество ![]() будет представлять
собой траектории движения системы для любого текущего времени.
будет представлять
собой траектории движения системы для любого текущего времени.
Поэтому многообразие
![]() (4.7)
(4.7)
можно
рассматривать как заданную программу движения САУ, у которой координаты ![]() удовлетворяют
уравнению (4.7). Это означает, что областью притяжения программного
(невозмущенного) движения
удовлетворяют
уравнению (4.7). Это означает, что областью притяжения программного
(невозмущенного) движения ![]() является вся область фазового
пространства. Для решения сформулированной задачи синтеза оптимального
регулятора определим полную производную функции
является вся область фазового
пространства. Для решения сформулированной задачи синтеза оптимального
регулятора определим полную производную функции ![]()
![]()
которая, с учетом уравнений ОУ (4.1), примет вид
![]() (4.8)
(4.8)
Подставляя
значение производной ![]() (4.8) в уравнение для устойчивых
(4.8) в уравнение для устойчивых
экстремалей (4.5) , получим основное функциональное уравнение
![]()
![]() (4.9)
(4.9)
из которого можно определить искомый оптимальный закон управления (4.2) , доставляющий минимум функционалу (4.3) на траекториях замкнутой САУ. Функциональное уравнение (4.9) является необходимым и достаточным условием для того, чтобы соотношение (4.7) было инвариантным притягивающим многообразием синтезированной системы. Процедура синтеза оптимальных законов управления (4.2) на основе притягивающих многообразий обычно выполняют в три этапа:
1) для известного ОУ (4.1) и выбранного функционала качества (4.3)
задаются
функцией, ![]() например,
в виде
например,
в виде
![]() (4.10)
(4.10)
где
![]() -
настроечные параметры;
-
настроечные параметры; ![]() - произвольная, непрерывно дифференцируемая функция по своим
аргументам нелинейная функция;
- произвольная, непрерывно дифференцируемая функция по своим
аргументам нелинейная функция;
2)
определяют частные производные ![]() и подставляют их
и подставляют их
вместе
с функцией (4.10) в основное функциональное уравнение (4.9), откуда находят
искомый оптимальный закон управления ![]()
3)
из условия ![]() выражают координату
выражают координату ![]() и, подставив её в
и, подставив её в
первые ![]() уравнений объекта (4.1), получают
систему
уравнений объекта (4.1), получают
систему
![]() ,
,
которая
описывает движение изображающей точки вдоль притягивающего многообразия ![]() к началу координат
фазового пространства. Выбором значений настроечных параметров
к началу координат
фазового пространства. Выбором значений настроечных параметров ![]() и вида произвольной
функции
и вида произвольной
функции ![]() этому движению
придают желаемый характер.
этому движению
придают желаемый характер.
Пусть, например, ОУ, типа (4.1), описывается нелинейной системой дифференциальных уравнений второго порядка
 (4.11)
(4.11)
Для объекта (4.11) необходимо синтезировать
оптимальный по критерию (4.3) закон управления ![]() который обеспечивает сближение
изображающей точки, находящейся в произвольном начальном состоянии, с
притягивающим инвариантным многообразием
который обеспечивает сближение
изображающей точки, находящейся в произвольном начальном состоянии, с
притягивающим инвариантным многообразием
![]() (4.12)
(4.12)
где для настроечного
параметра ![]() примем
для простоты условие
примем
для простоты условие ![]()
Подставив частные производные
![]()
в функциональное уравнение (4.9), с учетом (4.11) и (4.12) получим
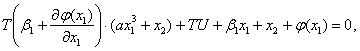
откуда найдем оптимальное
управление ![]() в
виде
в
виде
![]()
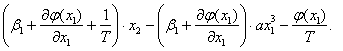 (4.13)
(4.13)
Подставив координату
![]() из
равенства (4.12) в первое уравнение ОУ (4.11), получим выражение
из
равенства (4.12) в первое уравнение ОУ (4.11), получим выражение
![]() (4.14)
(4.14)
которое
описывает невозмущенное (программное) движение замкнутой системы вдоль
многообразия (4.12) к началу координат фазового пространства. Выбором значения
настроечного параметра ![]() и вида произвольной функции
и вида произвольной функции
![]() можно придать системе желаемые свойства, например, гарантировать её асимптотическую
устойчивость в целом. Для этого, согласно (4.14), необходимо выполнить
следующие условия:
можно придать системе желаемые свойства, например, гарантировать её асимптотическую
устойчивость в целом. Для этого, согласно (4.14), необходимо выполнить
следующие условия:
![]()
которые
обеспечивают отрицательность производной ![]() . Тогда закон управления (4.13) и
уравнение движения (4.14) примут соответственно вид
. Тогда закон управления (4.13) и
уравнение движения (4.14) примут соответственно вид
![]() (4.15)
(4.15)
![]() (4.16)
(4.16)
где ![]()
В зависимости от значений параметра ![]() можно получать
различные качественные показатели замкнутой системы. Если
можно получать
различные качественные показатели замкнутой системы. Если ![]() , то, согласно уравнению (4.16),
изображающая точка будет двигаться в начало координат вдоль многообразия
, то, согласно уравнению (4.16),
изображающая точка будет двигаться в начало координат вдоль многообразия ![]() по прямой с угловым
коэффициентом наклона, равным
по прямой с угловым
коэффициентом наклона, равным ![]() . Тогда поведение САУ с нелинейным ОУ (4.11)
описывается линейным дифференциальным уравнением. Найдем характеристическое
уравнение замкнутой системы при
. Тогда поведение САУ с нелинейным ОУ (4.11)
описывается линейным дифференциальным уравнением. Найдем характеристическое
уравнение замкнутой системы при ![]() . Используя выражения (4.11) и (4.15),
получим
. Используя выражения (4.11) и (4.15),
получим
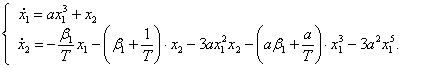 (4.17)
(4.17)
Из первого уравнения системы (4.17) следует , что
![]()
Подставляя
эти значения ![]() и
и
![]() во второе
уравнение (4.17), получим
во второе
уравнение (4.17), получим
![]()
![]() ,
,
откуда после приведения подобных членов будем иметь линейное дифференциальное уравнение замкнутой системы
![]()
и соответствующее ему характеристическое уравнение
![]()
с корнями ![]()
Если для ОУ (4.11) известен лишь диапазон изменения коэффициент
![]() , то соответствующим выбором
коэффициента
, то соответствующим выбором
коэффициента ![]() можно
всегда обеспечить нужное качество и асимптотическую устойчивость замкнутой
системы.
можно
всегда обеспечить нужное качество и асимптотическую устойчивость замкнутой
системы.
Структура системы представлена на рисунке 4.1.
Функциональная схема исследуемой нелинейной САУ содержит последовательно
соединенные блоки: ОУ, описываемый уравнениями (4.11), оптимальный регулятор,
оптимальный регулятор, формирующий закон управления ![]() (4.15). Для исследования
нескорректированной САУ, возбужденной начальными условиями на интеграторе,
необходимо на вход системы подать сигнал
(4.15). Для исследования
нескорректированной САУ, возбужденной начальными условиями на интеграторе,
необходимо на вход системы подать сигнал ![]() В случае анализа замкнутой
скорректированной системы на вход объекта поступает сигнал
В случае анализа замкнутой
скорректированной системы на вход объекта поступает сигнал
![]() с регулятора.
с регулятора.
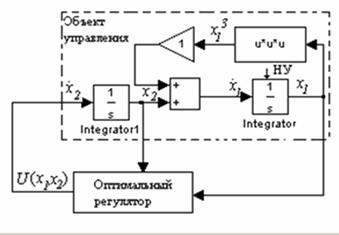
Рисунок 4.1 - Структура системы с оптимальным регулятором
Модель системы, набранная в пакете прикладных программ
Matlab, представлена на рисунке 4.2. При этом основные
параметры были выбраны следующими: ![]()

Рисунок 4.2 - Модель системы, набранная в пакете Matlab
4.2 Программа работы
4.2.1 Создание структурной схемы модели системы с
оптимальным регулятором в системе MATLAB
4.2.2 Расчет и набор параметров регулятора
4.2.3 Анализ переходных процессов на модели с оптимальным
регулятором.
4.3 Порядок и методика выполнения работы
В соответствии с вариантом задания получить выражение для оптимального закона управления. Исходя из полученного закона управления, составить структуру скорректированной замкнутой системы (объект управления и регулятор) и набрать её в пакете Matlab.
Сначала моделируется система без регулятора (с начальными условиями на интеграторе). После исследования и регистрации переходного процесса и фазового портрета ОУ моделируется система с оптимальным регулятором.
Цель моделирования заключается в сравнении выходных характеристик САУ( переходного процесса и фазового портрета) при различных значениях настроечных параметров регулятора и начальных условий на интеграторе (для каждого из параметров в варианте задания представлен диапазон их изменения).
Варианты заданий
Объект
управления описывается системой дифференциальных уравнений следующего вида:
![]()
1) 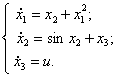 2)
2)

![]()
3) 4)
4)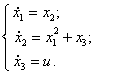
5) 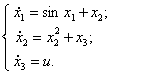 6)
6)
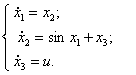
7) 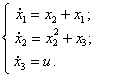 8)
8) 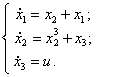
9) 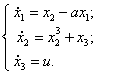 10)
10)
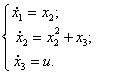
11)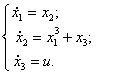 12)
12)
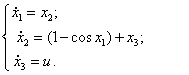
13) 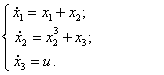
4.4 Содержание отчета
4.4.1Краткое описание метода притягивающих многообразий для аналитического конструирования оптимальных регуляторов.
4.4.2 Структура замкнутой скорректированной системы в Matlab.
4.4.3 Графики переходных процессов.
4.4.4 Анализ сравнения поведения системы при различных настройках регулятора и при начальных условиях.
4.5 Контрольные вопросы
4.5.1 Для чего предназначен функционал качества (4.3)?
4.5.2 Какими параметрами и функцией можно обеспечить желаемый характер движению нелинейного объекта управления?
4.5.3
Основное условие, предъявляемое к функции ![]() ?
?
Список литературы
1. Бесекерский В.А., Попов Е.П. «Теория систем автоматического регулирования». – СПб.: Профессия, 2004. – 752с.
2.Лурье Б.Я., Энрайт П.Ж. Классические методы автоматического управления. – СПб.: БХВ – Петербург, 2004. – 640с.
3. Попов Е.П. « Теория нелинейных систем автоматического регулирования и управления»: Учебное пособие. – М.: Наука, 1988. – 256с.
4. Лазарев Ю. Моделирование процессов и систем в MATLAB. Учебный курс. – СПб.: БХВ – Петербург, 2005. – 512с.
5. Половко А.М., Бутусов П.Н. MATLAB для студента. – СПб.: БХВ – Петербург,2005. – 320 с.
Содержание
|
1 Лабораторная работа № 1 Исследование устойчивости нелинейных разомкнутых и замкнутых систем автоматического управления |
3 |
|
2 Лабораторная работа № 2 Исследование нелинейного двухканального корректирующего устройства |
12 |
|
3 Лабораторная работа № 3 Синтез регуляторов с переменной структурой для управления нелинейной системой управления |
18 |
|
4 Лабораторная работа № 4 Аналитическое конструирование оптимального регулятора для нелинейного объекта управления |
24 |
|
Список литературы |
32 |
Св. пл. 2011 поз. 85