МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАН
Некоммерческое акционерное общество
Алматинский университет энергетики и связи
Цыба Ю.А.
Шадхин Ю.И.
Алмуратова Н.К.
НЕЛИНЕЙНЫЕ И ЦИФРОВЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Учебное пособие
Алматы 2013
УДК 62-83: 681.3
ББК 31.965Я73
Ц 93 Нелинейные и цифровые системы автоматического управления:
Учебное пособие / Цыба Ю.А, Шадхин Ю.И., Алмуратова Н.К.;
АУЭС. Алматы, 2013 – 96 с.
ISBN 978-601-7327-12-5
Учебное пособие «Нелинейные и цифровые системы автоматического управления» разработано в соответствии с типовой учебной программой для специальности 6М071800 – Электроэнергетика, специализация «Электропривод и автоматизация технологических комплексов» и является частью курса «Системы управления электроприводами».
С целью улучшения качества автоматического управления технологическими процессами рассмотрены современные методы исследования нелинейных и принципы построения цифровых систем автоматического управления электроприводами, выполняющих функции стабилизации скорости и момента, точного позиционирования, слежения и работы с программным и адаптивным управлениями.
Учебное пособие предназначено для магистрантов, обучающихся по специальности 6М071800 – Электроэнергетика, а также может быть использовано инженерно-техническими работниками, занимающимися вопросами автоматизации.
Ил. 48, библиогр. – 18 назв.
ББК 31.965Я73
РЕЦЕНЗЕНТЫ: Каз.НТУ, канд. тех. наук, Д.Б. Акпанбетов. АУЭС, канд. тех. наук, проф. А.С. Байкенов.
Печатается по плану издания Министерства образования и науки Республики Казахстан на 2012г.
ISBN 978-601-7327-12-5
© НАО «Алматинский университет энергетики и связи», 2013г.
|
Содержание |
|
|
|
|
|
Введение |
4 |
|
1 Нелинейные системы автоматического управления и их особенности. Линеаризация нелинейных характеристик |
5 |
|
1.1 Классификация и характеристики нелинейных элементов |
5 |
|
1.2 Особенности нелинейных систем автоматического управления |
10 |
|
1.3 Метод гармонической линеаризации нелинейных характеристик |
15 |
|
2 Методы исследования нелинейных систем |
22 |
|
2.1 Метод гармонического баланса |
22 |
|
2.2 Исследование нелинейных систем с помощью статистической линеаризации |
27 |
|
2.3 Фазовый метод |
33 |
|
3 Устойчивость нелинейных систем автоматического управления |
48 |
3.1 Абсолютная устойчивость вынужденного процесса в нелинейной системе |
48 |
3.2 Теоремы прямого метода Ляпунова и их применение |
51 |
|
3.3 Частотный критерий устойчивости Попова |
56 |
|
4 Качество нелинейных систем автоматического управления |
61 |
|
4.1 Оценка качества нелинейных систем автоматического управления |
61 |
|
4.2 Синтез корректирующих устройств нелинейных систем по логарифмическим частотным характеристикам |
67 |
|
5 Цифровые системы автоматического управления электроприводом |
70 |
|
5.1 Принципы построения цифровых систем автоматического управления |
70 |
5.2 Цифровые системы стабилизации скорости |
74 |
|
5.3 Цифровые системы управления положением позиционного электропривода |
76 |
|
5.4 Цифровые системы управления следящего электропривода и основные принципы их построения |
79 |
|
5.5 Системы программного управления электроприводами, принципы их построения и классификация |
81 |
|
5.6 Адаптивные системы управления и принципы их построения |
90 |
|
Список литературы |
96 |
Введение
Развитие техники, интенсификация производства, необходимость увеличения производительности труда выдвинули перед учеными, работающими в области автоматического управления, задачи создания высококачественных систем автоматического управления (САУ), которые способны решать всё более сложные задачи управления.
Как правило, многие системы автоматического управления являются нелинейными, так как объект управления и управляющее устройство могут иметь нелинейные характеристики и нелинейные элементы. Существует большое количество САУ, процессы, в которых принципиально не могут быть описаны линейными дифференциальными уравнениями. Сложность решения нелинейных дифференциальных уравнений вызывает необходимость создания ряда приближенных методов, позволяющих судить о характере процессов, наблюдаемых в системе. При этом нелинейные характеристики реальных элементов САУ заменяют некоторыми идеализированными приближенными характеристиками, которые обусловлены как характером нелинейного элемента, так и методом анализа систем. В связи с чем в настоящем учебном пособии рассматриваются современные методы исследования нелинейных САУ с целью улучшения качества управления технологическими процессами.
Наряду с этим в последнее время при автоматизации самых разнообразных технологических процессов всё большее применение находят цифровые системы управления электроприводами. Это связано с повышением точности работы систем в статических и динамических режимах, их быстродействия и производительности промышленного оборудования.
Развитие цифровой техники привело к тому, что системы управления электроприводами в настоящее время строятся не аппаратными средствами, а с использованием ЭВМ, в которых требуемые алгоритмы управления закладываются программно. Это упрощает задачи проектирования и изготовления таких систем, а также создаёт возможность управлять электроприводами больших промышленных установок, связанных единым технологическим процессом от единого информационно управляющего комплекса, что особенно важно при создании гибких управляющих производств. Использование цифровых управляющих систем электропривода открывает новые возможности их работы, обусловленные созданием систем диагностики и контроля работы электропривода на дисплее.
Глубокое понимание методов автоматического управления и физических процессов в них, знание современных технологических решений, умение оценивать и сопоставлять их возможности, применять на практике – все это необходимо специалистам, чей труд связан с созданием или эксплуатацией технических объектов, в которых широко используются САУ. Именно поэтому в учебном пособии рассмотрены не только нелинейные, но цифровые системы управления, а автоматическое управление как техническая дисциплина входит в программу такой специальности, как электроэнергетика.
1 Нелинейные системы автоматического управления и их особенности. Линеаризация нелинейных характеристик
1.1 Классификация и характеристики нелинейных элементов
Имеется обширных класс нелинейных систем, которые с помощью линейной теории исследовать невозможно [1,2.3,4,5,6,7,8].
Нелинейными называются системы автоматического управления, содержащие хотя бы один нелинейный элемент или элемент с ограниченным по величине воздействием (ограниченной мощностью, перемещением и т. п.).
К нелинейным относятся элементы, имеющие переменный коэффициент усиления. Если с увеличением отклонения коэффициент усиления уменьшается, то это аналогично насыщению или ограниченной мощности. Однако в некоторых случаях специально конструируется нелинейные элементы, у которых с увеличением отклонения коэффициент усиления увеличивается. К нелинейным элементам относятся также логические устройства, с помощью которых могут быть сформированы нелинейности весьма разнообразных форм.
Принцип суперпозиции (наложения), широко применяемый для исследования линейных систем, в случае исследования нелинейных систем неприменим, так как эффект входного сигнала на выходе зависит от других сигналов и от уровня сигнала.
В нелинейных системах возможны автоколебания, которые являются периодическим движением, вызываемые внутренними свойствами системы, а не под влиянием внешних периодических воздействий.
По характеру переходных процессов и условиям устойчивости нелинейных системы в ряде случаев существенно отличаются от линейных. Устойчивая линейная система остается устойчивой при любых начальных отклонениях от установившегося состояния. Нелинейные системы могут быть устойчивыми при малых отклонениях и потерять устойчивость при больших отклонениях. Все это затрудняет исследование нелинейных систем, и к тому же современная теория нелинейных систем не дает общих аналитических методов исследования, с помощью которых можно было бы получить ответы, интересующие инженерную практику с такой же полнотой, с какой их дает линейная теория.
Далее будут рассмотрены методы исследования нелинейных систем, получившие наибольшие распространение. К ним относятся: 1) метод фазовой плоскости; 2) метод гармонической линеаризации.
А.В. Башариным [2] разработан приближенный графический метод исследования систем автоматического управления, который дает возможность произвести также синтез корректирующих устройств в нелинейных системах. Он не дает решения задачи в общем виде и не позволяет установить зависимость между параметрами системы и качеством переходного процесса, однако в некоторых случаях он может быть очень полезен.
Характеристики нелинейных элементов могут быть различимыми. Так, на рисунке 1.1 приведены нелинейные характеристики, наиболее часто встречающиеся на практике.

а - элемент с насыщением; б - элемент с нечувствительностью и ограниченной мощностью или ограниченным перемещением; в – элемент с сухим трением или мертвым ходом; г – гистерезис в стали; д – идеальная релейная характеристика; е – релейная характеристика с зоной нечувствительности; ж – релейная характеристика с коэффициентом возврата kв<1; з - релейная характеристика с зоной нечувствительности с коэффициентом возврата kв<1.
Рисунок 1.1 - Характеристики нелинейных элементов
Нелинейные системы могут содержать один или несколько нелинейных элементов, образующих различные сочетания с линейными элементами. В настоящей главе рассмотрен наиболее распространенный и простой случай, когда система имеет только один нелинейный элемент. Перечислим виды нелинейных звеньев:
1) звено релейного типа;
2) звено с кусочно-линейной характеристикой, а также звенья, описываемые кусочно-линейными дифференциальными уравнениями;
3) звено с криволинейной характеристикой любого очертания;
4) звено, уравнение которого содержит произведение переменных или их производных и другие их комбинации;
5)нелинейное звено с запаздыванием, причем
запаздывание
понимается в смысле, а нелинейность может иметь любой вид;
6) нелинейное импульсное звено;
7) логическое звено.
Различают статические и динамические нелинейности. Первые представляются в виде нелинейных статических характеристик, а вторые – в виде нелинейных дифференциальных уравнений.
Общий метод составления уравнений для нелинейных систем состоит в следующем. Сначала производится линеаризация уравнений всех звеньев системы, для которых это допустимо, кроме существенно линейных звеньев (чаще всего одного-двух). Затем составляются уравнения этих последних звеньев со всеми допустимыми упрощениями их характеристик.
В результате получается система обыкновенных линейных уравнений, к которым добавляется одно-два (иногда более) нелинейных. В соответствии с этим обобщенную структурную схему любой нелинейной системы автоматического регулирования в случае одного нелинейного звена можно представить в виде (см. рисунок 1.2, а), где линейная часть может иметь структуру любой сложности (с обратными связями и т. п., как, например, рисунок 1.2, б или в). В случае двух нелинейных звеньев могут быть разные комбинации, в зависимости от того, в какие цепи системы они входят (см. рисунок 1.3).

Рисунок 1.2 – Структурная схема нелинейной системы автоматического управления в случае одного нелинейного звена

Рисунок 1.3 – Структурная схема нелинейной системы автоматического управления в случае двух нелинейных звеньев
Часто при исследовании нелинейных систем автоматического регулирования удается выделить нелинейность так, чтобы она описывалась непосредственно зависимостью между выходной и входной величинами
![]() ,
(1.1)
,
(1.1)
которая может иметь любую форму (релейного типа, кусочно-линейного или криволинейного). Но иногда, как будет показано далее, не удается этого сделать, и приходится исследовать нелинейные дифференциальные зависимости вида
![]() ,
(1.2)
,
(1.2)
![]() и т.п. (1.3)
и т.п. (1.3)
Встречаются и более сложные случаи, когда обе величины (входная и выходная) оказываются под знаком нелинейной функции раздельно
![]() (1.4) или же вместе
(1.4) или же вместе
![]() .
(1.5)
.
(1.5)
Разделим все нелинейные системы регулирования на три больших класса.
К первому классу нелинейных систем отнесем такие, в которых уравнение нелинейного звена приводится к любому из видов (1.1) – (1.3), т. е. когда под знаком нелинейной функции стоит только входная величина (и ее производные) либо только выходная величина (и ее производные). При этом имеется в виду, что схема системы в целом может быть приведена к виду (см. рисунок 1.2) с одним нелинейным звеном. К этому классу сводится, например, также случай с двумя нелинейными звеньями, (см. рисунок 1.3, в), так как там они могут быть объединены в одно нелинейное звено. Сюда же относится и случай, показанный на рисунке 1.3, г, где имеются два нелинейных звена (если их уравнения содержат под знаком нелинейности только входную величину х, например, вида (1.1) или (1.2)).
Второй класс нелинейных систем включает системы с любым числом нелинейных звеньев, когда под знаки нелинейных функций входят различные переменные, связанные между собой линейной передаточной функцией. Так будет в случае системы с одним нелинейным звеном вида (1.4) или (1.5), а также в системе с двумя нелинейными звеньями (см. рисунок 1.3, а или г), если в первом из них под знак нелинейности входит входная величина, а во втором – выходная. Система же (см. рисунок 1.3, б) относится ко второму классу, если под знаки нелинейностей входят в обоих звеньях либо только входные, либо только выходные величины нелинейных звеньев.
К третьему классу нелинейных систем относятся такие системы с двумя и более нелинейностями, в уравнениях которых под знаки нелинейных функций входят разные переменные, связанные между собой нелинейными дифференциальными уравнениями (т. е. связанные через линейные части и нелинейные звенья). К таким системам относится, например, система (см. рисунок 1.3, а), если в ее уравнениях под знаками нелинейных функций находятся входные (или выходные) величины обоих нелинейных звеньев, и многие другие системы.
Системы с логическими устройствами относятся обычно к нелинейным системам второго и третьего классов.
Заметим, что во всех случаях, когда под знак нелинейной функции входит какая-либо линейная комбинация разных переменных, их следует обозначать одной буквой, а данную линейную комбинацию учесть при составлении общего уравнения линейной части системы. Это бывает, например, в тех случаях, когда на вход нелинейного звена подаются производные или включается обратная связь. Так, если для рисунка 1.2, б
![]() ,
,
то,
обозначая ![]() , (1.6)
, (1.6)
можно привести уравнение нелинейного звена к виду (1.1).
Из всех уравнений линейных звеньев, а также добавочных линейных выражений типа (1.6), получаемых при выделении нелинейности, составляется общее уравнение линейной части системы
![]() ,
(1.7)
,
(1.7)
где Q(р) и R(р) — операторные многочлены или передаточная функция линейной части системы
![]() .
(1.8)
.
(1.8)
Составление уравнений будет проиллюстрировано ниже на примерах.
1.2 Особенности нелинейных систем автоматического управления
Процессы в нелинейных системах автоматического регулирования имеют целый ряд весьма существенных особенностей, которые не встречаются в линейных системах [5,6,7.8].
Благодаря этим существенным особенностям даже вопрос об устойчивости системы становится здесь более сложным. Кроме структуры системы и значений ее параметров для устойчивости того или иного установившегося процесса, имеют значение здесь, в отличие от линейных систем, также и начальные условия. Возможен новый вид установившегося процесса – автоколебания, т. е. устойчивые собственные колебания с постоянной амплитудой при отсутствии внешних колебательных воздействий. Когда в системе возникают автоколебания, то установившееся состояние, соответствующее постоянному значению регулируемой величины, часто становится невозможным.
Следовательно, в общем случае на плоскости параметров системы могут быть не два вида областей (устойчивости и неустойчивости), как в линейных системах, а больше: 1) область устойчивости равновесного состояния с постоянным значением регулируемой величины; 2) область устойчивых автоколебаний; 3) область неустойчивости системы; 4) области, соответствующие другим, более сложным случаям.
Если процессы в системе имеют вид, указанный на рисунке 1.4, а, то равновесное состояние (х = 0) неустойчиво. В том случае, когда оба указанных на рисунке 1.4, а колебания в переходных процессах стремятся к одной и той же амплитуде и к одной и той же частоте, система будет обладать устойчивыми автоколебаниями с амплитудой а.
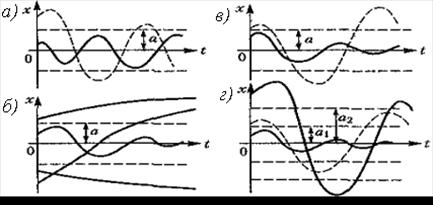
Рисунок 1.4 – Виды переходных процессов
На рисунках 1.4, б и 1.4, в показаны случаи, когда равновесное состояние (х=0) системы устойчиво «в малом», т. е. при начальных условиях, не выводящих отклонения в переходном процессе за определенную величину а, и неустойчиво «в большом», т. е. при начальных условиях, выводящих отклонение в переходном процессе за пределы величины а. Здесь граничным процессом является неустойчивый периодический процесс собственного движения системы с амплитудой а (переходные процессы расходятся от него в обе стороны).
На рисунке 1.4, г показан случай трех возможных установившихся состояний:
- равновесное состояние (х=0);
- колебания с постоянной амплитудой а1;
- колебания с постоянной амплитудой а2.
При этом колебания с амплитудой а1 неустойчивы. В результате система будет устойчива «в малом» по отношению к равновесному состоянию х=0, а «в большом» система будет обладать устойчивыми автоколебаниями с амплитудой а2.
Для иллюстрации особенностей нелинейной системы исследуем переходной процесс и автоколебания в релейной системе стабилизации температуры.
Пусть объект представляет собой некоторую камеру. Учитывая инерционность процесса нагрева и охлаждения, запишем его уравнение в виде
![]() (1.9)
(1.9)
где θ - отклонение температуры;
φ - отклонение управляющего органа;
f(t) - внешние возмущения.
При отклонении температуры θ появляется ток в диагонали моста того или иного направления и замыкается соответствующий контакт реле, включающего постоянное напряжение в ту или иную обмотку возбуждения электродвигателя. Приняв во внимание некоторое отставание в этом процессе включения, получим релейную характеристику. Далее, считая, что ток I пропорционален отклонению температуры объекта θ, а скорость dφ/dt отклонения управляющего органа пропорциональна напряжению на обмотках возбуждения электродвигателя, можно в данном случае выходной величиной релейной характеристики считать dφ/dt, а входной - θ (см. рисунок 1.5, а).
Следовательно, уравнения управляющего устройства запишутся следующим образом
![]() при
при ![]() когда
когда ![]() (1.10)
(1.10)
![]()
![]() при
при ![]()
![]() при
при ![]() когда
когда ![]() (1.11)
(1.11)
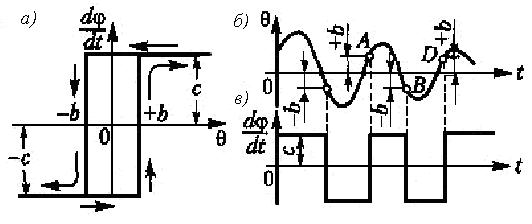
Рисунок 1.5 - Переходной процесс и автоколебания в релейной системе стабилизации температуры
Рассмотрим два произвольных участка переходного процесса (при f(t)=0) в данной системе (участки AB и CD на рисунке 1.5, б).
На участке AB уравнение управляющего устройства согласно рисунку 1.5, в будет dφ/dt = +с.
Дифференцируя (1.9) по t и подставляя туда +с, получаем при (t=0) следующее уравнение системы на участке AB
![]() (1.12)
(1.12)
а на участке BD
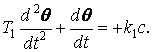 (1.13)
(1.13)
Решение уравнения (1.12) будет
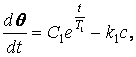 (1.14)
(1.14)
откуда получаем
![]() (1.15)
(1.15)
Условимся для простоты
время t
от начала участка
AB (см. рисунок
1.6, а). Тогда начальные
условия будут ![]() dθ
/dt=
dθ
/dt=![]() при
t
= 0, где
при
t
= 0, где ![]() пока
неизвестно. Используя начальные условия, находим произвольные постоянные
уравнения (1.15)
пока
неизвестно. Используя начальные условия, находим произвольные постоянные
уравнения (1.15)
![]()
![]() (1.16)
(1.16)
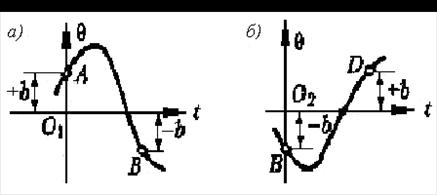
Рисунок 1.6 - Переходной процесс на участках AB и BD
Аналогично для участка BD согласно (1.13), отсчитываем время t тоже от начала этого участка (см. рисунок 1.6, б), получим решение:
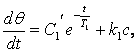 (1.17)
(1.17)
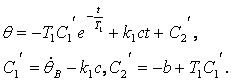
Все остальные участки кривой переходного процесса
будут определяться, очевидно, такими же решениями, но только с другими
значениями величин ![]() . Заметим, что величины
. Заметим, что величины ![]() и
и ![]() , необходимые для
определения произвольных постоянных, находятся как значения
, необходимые для
определения произвольных постоянных, находятся как значения ![]() в конце предшествующих им
участков. Поэтому, если будет задана величина
в конце предшествующих им
участков. Поэтому, если будет задана величина ![]() в начальной точке первого участка
процесса, то выше написанное решение для переходного процесса в системе станет
определенным, такой метод решения задачи называется методом припасовывания.
в начальной точке первого участка
процесса, то выше написанное решение для переходного процесса в системе станет
определенным, такой метод решения задачи называется методом припасовывания.
Выясним теперь, возможны ли в данной системе автоколебания,
т.е. устойчивое периодическое решение. Для этого нужно, очевидно, чтобы в конце
D одного периода колебаний (см. рисунок 1.5, б) получилось точно такие же
значения ![]() и
и
![]() , какие
были в начале его A. Легко заметить, что при этом оба полупериода (AB
и BD) должны быть одинаковыми вследствие симметрии
характеристики (см. рисунок 1.5, а). Поэтому для определения
автоколебаний достаточно рассмотреть только один участок АВ и потребовать,
чтобы
, какие
были в начале его A. Легко заметить, что при этом оба полупериода (AB
и BD) должны быть одинаковыми вследствие симметрии
характеристики (см. рисунок 1.5, а). Поэтому для определения
автоколебаний достаточно рассмотреть только один участок АВ и потребовать,
чтобы
![]() (1.18)
(1.18)
Обозначив период искомых автоколебаний через 2Т, а длительность участка АВ через Т, из (1.14) найдем
![]()
Подставляя сюда (1.18) и замечая, что из (1.16) ![]() получаем выражение
получаем выражение
![]() (1.19)
(1.19)
в
котором содержатся две неизвестные: С1 и Т. Величину Т
(длительность участка АВ) можно выразить из (1.15), так как известно, что в
конце участка ![]() из
(1.15) и (1.16) при этом находим
из
(1.15) и (1.16) при этом находим
![]()
Подставив сюда значение С1 из (1.19), получим уравнение для определения полупериода автоколебаний
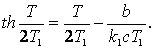 (1.20)
(1.20)
Это трансцендентное уравнение для Т легко решается
графически пересечением двух кривых:![]() и
и ![]() [5].
[5].
Если найдено вещественное положительное значение для Т, то это свидетельствует о наличии периодического решения в данной системе. Чтобы доказать, что это соответствует автоколебаниям, нужно исследовать их устойчивость, т.е. показать, что в переходном процессе система ведет себя, как изображено на рисунке 1.4, а, но не так, как на рисунке 1.4, б, это будет показано ниже.
Амплитуда найденных автоколебаний определяется как ![]() на участке АВ (см. рисунок
1.6, а) путем исследования функции (1.15) на максимум обычным путем.
на участке АВ (см. рисунок
1.6, а) путем исследования функции (1.15) на максимум обычным путем.
1.3 Метод гармонической линеаризации нелинейных характеристик
Метод гармонической линеаризации является приближенным, полученным в результате распространения частотных методов на исследование нелинейных систем [1,3,5,6,7].
Предложено несколько разновидностей применения гармонической линеаризации (метод гармонического баланса Н. И. Крылова и Н. Н Боголюбова, метод Б. В. Булгакова), но все они близки между собой. В основу этих разновидностей положены частотная или гармоническая линеаризация нелинейностей и понятие об эквивалентном коэффициенте усиления нелинейного элемента.
Метод гармонической линеаризации позволяет:
- определить условия устойчивости нелинейной системы (найти значения изменяемых параметров, при которых система будет устойчива);
- определить возможные автоколебания в системе;
- найти частоту и амплитуду автоколебаний.
Применение метода возможно при условии, что характеристики элементов не меняются с течением времени и что выходная величина нелинейного элемента зависит от значений входной величины и не зависит от ее производных и интегралов.
Сущность гармонической линеаризации состоит в следующем. Предположим, что имеется нелинейный элемент, в котором зависимость между выходной и входной величинами представляет нелинейную функцию вида
![]() (1.21)
(1.21)
т.е. выходная величина в общем случае является нелинейной функцией входной величины и ее производной. Подадим на вход нелинейного элемента гармонического воздействие
![]() (1.22)
(1.22)
тогда
![]() .
(1.23)
.
(1.23)
Подставим значения x1 и px1 из выражений (1.22) и (1.23) в выражение (1.21) и заменив ωt = ψ, получим
![]() (1.24)
(1.24)
Это сложная периодическая функция, содержащая гармонические составляющие с частотами, увеличивающимися до бесконечности. Разложив правую часть выражения (1.24) в ряд Фурье, получим
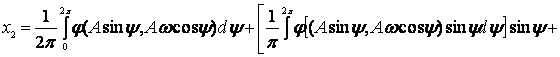
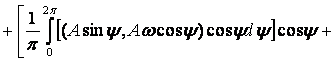 высшие гармоники. (1.25)
высшие гармоники. (1.25)
Первое слагаемое в приведенном разложении представляет собой постоянную составляющую. В наиболее распространенных нелинейностях постоянная составляющая отсутствует, и поэтому в дальнейшем будем считать первое слагаемое равным нулю. Можно провести линеаризацию и в том случае, если постоянная составляющая не равна нулю. Этот вопрос рассмотрен в [1,3,5]. Высшие гармоники разложения отбрасываются, и во внимание принимается только первая (основная) гармоника разложения. Это вносит погрешность в окончательный результат, однако в практических расчетах она, как правило, допустима, поскольку в реальных системах автоматического регулирования линейная часть является фильтром низких частот, т. е. такой динамической системой, которая пропускает только низкие частоты. Высокие частоты гасятся элементами, содержащими индуктивности, механические массы и т. п., и ими можно пренебречь.
Из выражений (1.22) и (1.23) получим
![]()
![]() (1.26)
(1.26)
Обозначим через ![]() и
и ![]() коэффициенты первой гармоники
разложения (1.25), деленные на А будут:
коэффициенты первой гармоники
разложения (1.25), деленные на А будут:
 |
(1.27)
Учитывая сказанное выше и применяя обозначения (1.26) и (1.27), выражение (1.25) может быть переписано в виде
![]() (1.28)
(1.28)
Выражение (1.28) является линейным. Таким образом, гармоническая линеаризация заключается в том, что нелинейная функция вида (1.21) с точностью до высших гармоник заменяется линейной функцией вида (1.28).
Выражение
![]() (1.29)
(1.29)
по аналогии с коэффициентом при x1 в частотном анализе линейных систем называется приближенной передаточной функцией нелинейного элемента.
Если в выражении (1.29) заменить ![]() на
на ![]() при
при ![]() то получим приближенное
значение эквивалентного комплексного коэффициента усиления нелинейного элемента
то получим приближенное
значение эквивалентного комплексного коэффициента усиления нелинейного элемента
![]() (1.30)
(1.30)
или в показательной форме
![]() (1.31)
(1.31)
Здесь
![]() (1.32)
(1.32)
модуль эквивалентного комплексного коэффициента усиления, а его аргумент
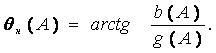 (1.33)
(1.33)
Таким образом, эквивалентным комплексным коэффициентом
усиления нелинейного элемента называется комплексное число, модуль которого
представляет отношение амплитуды первой гармоники на выходе нелинейного
элемента к амплитуде синусоидального воздействия на его входа, а аргумент –
разность фаз первой гармоники на выходе и синусоидального воздействия на входе.
При изменении амплитуда и частота синусоидального воздействия на входе значение
эквивалентного комплексного коэффициента усиления ![]() меняется.
меняется.
В настоящее время коэффициенты разложения в ряд Фурье g(A) и b(A) для значительного количества нелинейностей вычислены, что облегчает применение метода гармонической линеаризации. На рисунке 1.7 приведены нелинейные характеристики, для которых коэффициенты разложения имеют следующий вид:
– для характеристики на рисунке 1.7, а
![]()
![]()
– для характеристики на рисунке 1.7, б
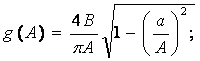
![]()
– для характеристики на рисунке 1.7, в

![]() ;
; ![]() ;
;
– для характеристики на рисунке 1.7, г
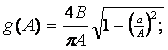
![]()
![]()
Буквенные обозначения, приведенные в формулах, ясны из рисунка 1.7.
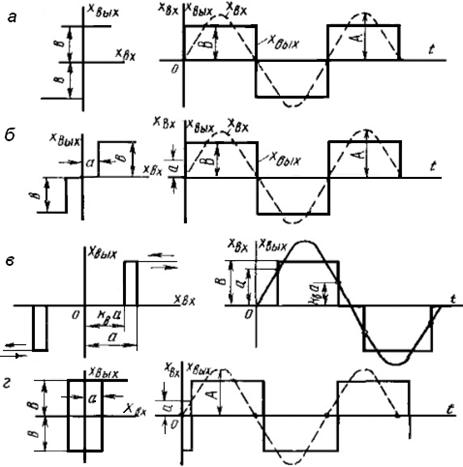
Рисунок 1.7 - К определению коэффициентов гармонической линеаризации нелинейных элементов
Ограничение справедливости формул условием ![]() имеет тот смысл, что
если амплитуда А входной синусоиды будет меньше половины зоны
нечувствительности а, то нелинейный элемент не сработает и движение в
системе будет отсутствовать. Поэтому все расчеты начинаются с предельного
значения
имеет тот смысл, что
если амплитуда А входной синусоиды будет меньше половины зоны
нечувствительности а, то нелинейный элемент не сработает и движение в
системе будет отсутствовать. Поэтому все расчеты начинаются с предельного
значения ![]() .
Обращаем внимание на то, что если нелинейная характеристика однозначна, не
имеет гистерезиса, то коэффициент
.
Обращаем внимание на то, что если нелинейная характеристика однозначна, не
имеет гистерезиса, то коэффициент ![]()
![]() и эквивалентный комплексный коэффициент
усиления, вычисленный по формуле (1.30), будет числом вещественным.
и эквивалентный комплексный коэффициент
усиления, вычисленный по формуле (1.30), будет числом вещественным.
Рассмотрим систему автоматического регулирования, состоящую из нескольких линейных звеньев и одного нелинейного. Все линейные звенья могут быть объединены в один эквивалентный линейный элемент, и тогда структурная схема примет вид, изображенный на рисунке 1.8.

Рисунок 1.8 - Структурная схема системы с нелинейным элементом
Рассмотрим нелинейный элемент. Предположим, что на его вход подано синусоидальное воздействие
![]()
Тогда, пользуясь гармонической линеаризацией, находим эквивалентный коэффициент усиления и с точностью до высших гармоник можем определить выходную величину:
![]() (1.34)
(1.34)
Рассмотрим линейную часть. Обозначив ее передаточную функцию через W(p), получим уравнение в оперативной форме:
![]() (1.35)
(1.35)
В частном случае, когда величина x2 является гармонической функцией с неизменными амплитудой А1 и частотой ω, она может быть представлена в показательной форме
![]() (1.36)
(1.36)
Установившееся значение на выходе линейного элемента при этом будет равно
![]() (1.37)
(1.37)
Здесь
![]() называется
комплексным коэффициентом усиления части, получающимся из
W(p), если вместо
называется
комплексным коэффициентом усиления части, получающимся из
W(p), если вместо ![]() подставить
подставить ![]() .
.
В соответствии с уравнением (1.37) на выходе линейной
части получаются также гармонические колебания, отличающиеся от ![]() по амплитуде и фазе,
причем это отличие полностью определяется комплексным коэффициентом усиления
по амплитуде и фазе,
причем это отличие полностью определяется комплексным коэффициентом усиления
![]() .
.
Модуль ![]() представляет собой отношение выходной
амплитуды к входной, аргумент
представляет собой отношение выходной
амплитуды к входной, аргумент ![]() - разность фаз выходной и входной
синусоид. Для линейной части комплексный коэффициент изменяется при изменении
частоты, но не зависит от амплитуды входного сигнала.
- разность фаз выходной и входной
синусоид. Для линейной части комплексный коэффициент изменяется при изменении
частоты, но не зависит от амплитуды входного сигнала.
Рассмотрим теперь систему в целом. Предположим, что
система находится на грани устойчивости, и в ней возникли незатухающие
колебания с частотой ![]() и амплитудой на входе нелинейного
элемента
и амплитудой на входе нелинейного
элемента ![]() .
Тогда уравнения системы в соответствии с выражениями (1.34), (1.35) и рисунком
1.8 будут иметь вид:
.
Тогда уравнения системы в соответствии с выражениями (1.34), (1.35) и рисунком
1.8 будут иметь вид:
![]()
![]()
![]() (1.38)
(1.38)
Исключая из этих уравнений ![]() и
и ![]() , получим
, получим
![]() . (1.39)
. (1.39)
Так как в системе происходят незатухающие колебания,
то ![]() и, следовательно
и, следовательно
![]() (1.40)
(1.40)
Это – уравнение свободных колебаний системы. Левая
часть уравнения является комплексной величиной. Приравнивая отдельно ее вещественную
и мнимую части нулю, получим два уравнения с двумя неизвестными: частотой ![]() и амплитудой
и амплитудой ![]() . Если в результате
решения этих уравнении получаются вещественные числа, то в системе возможны
колебания с найденными частотой и амплитудой. Если при решении получаются
мнимые числа, то колебания в системе невозможны, система устойчива. Проще и
нагляднее это решение произвести графически.
. Если в результате
решения этих уравнении получаются вещественные числа, то в системе возможны
колебания с найденными частотой и амплитудой. Если при решении получаются
мнимые числа, то колебания в системе невозможны, система устойчива. Проще и
нагляднее это решение произвести графически.
Перепишем уравнение (1.40) следующим образом
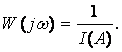 (1.41)
(1.41)
Левая часть уравнения при изменении частоты ![]() от 0 до
от 0 до ![]() представляет
амплитудно-фазовою частотную характеристику линейной части системы в
разомкнутом состоянии.
представляет
амплитудно-фазовою частотную характеристику линейной части системы в
разомкнутом состоянии.
Правая часть уравнения при изменении амплитуды от 0
или от ![]() до
до ![]() представляет
обратную амплитудную характеристику нелинейного элемента системы регулирования.
Обе характеристики могут быть вычерчены в одной системе координат. Точка
пересечения характеристик дает решение уравнения (1.41). При этом частота
колебаний определяется частотой на амплитудно-фазовой характеристике в точке
пересечения кривых, а амплитуда колебаний определяется значением амплитуды на
амплитудной характеристике нелинейного элемента в той же точке (см. рисунок 1.9,
а).
представляет
обратную амплитудную характеристику нелинейного элемента системы регулирования.
Обе характеристики могут быть вычерчены в одной системе координат. Точка
пересечения характеристик дает решение уравнения (1.41). При этом частота
колебаний определяется частотой на амплитудно-фазовой характеристике в точке
пересечения кривых, а амплитуда колебаний определяется значением амплитуды на
амплитудной характеристике нелинейного элемента в той же точке (см. рисунок 1.9,
а).
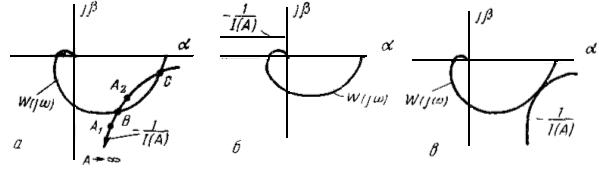
Рисунок 1.9 - Графическое решение линейного и линеаризованного уравнений
Если амплитудно-фазовая характеристика линейного элемента и амплитудная характеристика нелинейного элемента не пересекаются (см. рисунок 1.9, б), то в системе автоколебания невозможны. Если указанные кривые касаются друг друга (см. рисунок 1.9, в), то система (приближенно) находится на границе устойчивости.
Имея амплитудную характеристику линейного элемента, можно так выбрать параметры линейной части системы, чтобы указанные кривые не пересекались и следовательно, система была устойчивой.
Устойчивость колебаний в системе можно оценить
следующим способом, который не является достаточно строгим, но в большинстве
случаев дает правильные результаты. Дадим небольшое приращение амплитуде
колебаний в точке В (см. рисунок 1.9, а). При положительном приращении
+∆А на обратной амплитудной характеристике получим, например,
точку ![]() , а
при отрицательном приращении - ∆А – точку
, а
при отрицательном приращении - ∆А – точку ![]() .
.
Если амплитудно-фазовая характеристика устойчивой
разомкнутой линейной части не охватывает точку ![]() , соответствующую положительному
приращению амплитуды ∆А, и охватывает точку
, соответствующую положительному
приращению амплитуды ∆А, и охватывает точку ![]() , соответствующую
отрицательному приращению амплитуды ∆А, то автоколебания будут
устойчивы. В соответствии с этим определением автоколебания в точке В, где
на рисунке 1.9, а – устойчивы, а в точке С – неустойчивы.
, соответствующую
отрицательному приращению амплитуды ∆А, то автоколебания будут
устойчивы. В соответствии с этим определением автоколебания в точке В, где
на рисунке 1.9, а – устойчивы, а в точке С – неустойчивы.
Метод гармонической линеаризации позволяет правильно выбрать параметры изменяемой части нелинейной системы. Метод гармонической линеаризации применим и при наличии в системе нескольких нелинейности при различном их сочетании с линейными звеньями.
2 Методы исследования нелинейных систем
2.1 Метод гармонического баланса
Периодические режимы во многих нелинейных системах характерны тем, что в некоторых точках системы изменения координат происходят по законам, близким к синусоидальным [5,6,7,8].
Рассмотрим, например, процессы, происходящие в цепи возбуждения генератора Г с вибрационным регулятором напряжения (см. рисунок 2.1, а).
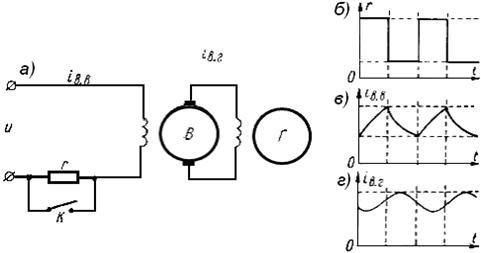
Рисунок 2.1 – Переходные процессы в цепи возбуждения генератора с вибрационным регулятором напряжения
Регулятор периодически замыкает и размыкает свои
контакты К, шунтирующие активное сопротивление r. Сопротивление
цепи при этом изменяется по закону
прямоугольника (см. рисунок 2.1, б), ток возбуждения ![]() возбудителя В -
по пилообразной кривой (см. рисунок 2.1, в), ток возбуждения генератора
возбудителя В -
по пилообразной кривой (см. рисунок 2.1, в), ток возбуждения генератора
![]() - по
сглаженной кривой, более или менее близкой к синусоиде (см. рисунок 2.1, г).
Несмотря на то что на вход системы подается прямоугольная волна, обладающая
резко выраженными высшими гармониками, на выходе ее выделяется достаточно
ощутимо лишь основная гармоника колебаний, остальные гармонические сильно
ослабляются благодаря тому, что система в силу своей инерционности обладает
свойством фильтра, не пропускающего высших гармонических.
- по
сглаженной кривой, более или менее близкой к синусоиде (см. рисунок 2.1, г).
Несмотря на то что на вход системы подается прямоугольная волна, обладающая
резко выраженными высшими гармониками, на выходе ее выделяется достаточно
ощутимо лишь основная гармоника колебаний, остальные гармонические сильно
ослабляются благодаря тому, что система в силу своей инерционности обладает
свойством фильтра, не пропускающего высших гармонических.
В других случаях выделение основной гармонической составляющей обусловлено наличием в системе резонансных цепей, настроенных на эту основную гармоническую частоту. Все остальные гармоники находятся в удалении от резонансного пика и резко ослабляются.
Метод гармонического баланса применим к системам,
состоящим, вообще говоря, из нескольких нелинейных и линейных частей. Если в
системе установилось гармоническое периодическое движение с частотой ω,
то, как известно, в какой-либо ![]() -й линейной части системы, описываемой
уравнением
-й линейной части системы, описываемой
уравнением ![]() , связь между
выходным и входным периодическими значениями дается следующими зависимостями
, связь между
выходным и входным периодическими значениями дается следующими зависимостями
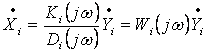 , (2.1)
, (2.1)
или
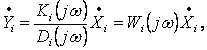 (2.2)
(2.2)
где точки над обозначениями переменных указывают на то, что это периодические величины, выраженные в комплексной форме:
![]()
![]() (2.3)
(2.3)
иными словами, значения Xi и Уi можно связать с помощью комплексных передаточных функций (амплитудно-фазовых частотных характеристик) – прямой Wi или обратной Gi.
Аналогично связь между основными гармониками выходной и входной периодических величин нелинейного элемента устанавливается с помощью комплексной функции, носящей название гармонического коэффициента передачи или, по американской терминологии, описывающей (describing) функции (в литературе можно встретить и другие ее названия: комплексный коэффициент усиления или проводимость нелинейного элемента).
Пусть на вход нелинейного элемента действует гармоническая величина, которую можно записать в виде
![]() . (2.4)
. (2.4)
Рассмотрим сначала безынерционный нелинейный элемент, для которого входная величина х и выходная у связаны между собой нелинейной зависимостью
![]() (2.5)
(2.5)
где функция f (х) удовлетворяет условиям Дирихле.
Тогда первая гармоника периодической величины выхода нелинейного элемента:
![]() , (2.6)
, (2.6)
где В и С определяются как коэффициенты Фурье:
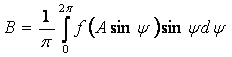 ,
,
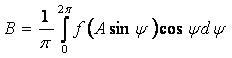 .
.
В методе гармонического баланса вводят в рассмотрение, вместо коэффициентов В и С, их отношения к амплитуде входного колебания А:
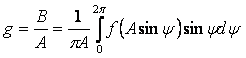 , (2.7)
, (2.7)
 , (2.8)
, (2.8)
тогда
![]() .
(2.9)
.
(2.9)
Представим х и y в комплексной форме
![]() ,
(2.10)
,
(2.10)
![]() . (2.11)
. (2.11)
Как обычно, для упрощения математического описания х
и у выражают в укороченной комплексной форме; например, полагают,
что ![]() , т.
е. рассматривают только те слагаемые, которые соответствуют положительным
частотам. Тогда из выражения (2.11)
, т.
е. рассматривают только те слагаемые, которые соответствуют положительным
частотам. Тогда из выражения (2.11)
![]() , (2.12)
, (2.12)
а
отношение 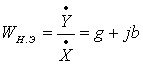 (2.13)
(2.13)
называют гармоническим коэффициентом передачи, или описывающей функцией нелинейного элемента.
Если принять ![]() , т. е. рассматривать область
отрицательных частот, то в этом случае
, т. е. рассматривать область
отрицательных частот, то в этом случае ![]() . Это означает, что
. Это означает, что ![]() имеет две симметричные
относительно вещественной оси ветви, соответствующие положительным и
отрицательным частотам так же, как это имеет место и для характеристик
имеет две симметричные
относительно вещественной оси ветви, соответствующие положительным и
отрицательным частотам так же, как это имеет место и для характеристик ![]() и
и ![]() . Поэтому общее
выражение для,
. Поэтому общее
выражение для, ![]() следовало
бы записать так:
следовало
бы записать так:
![]() .
(2.14)
.
(2.14)
Рассмотрим гармонические коэффициенты передачи некоторых нелинейных элементов.
Характеристики f(x) нелинейных элементов делятся на две основные группы – однозначные и неоднозначные.
При гармоническом воздействии основная гармоника
выходных колебаний безынерционных нелинейных элементов с однозначными
характеристиками совпадает по фазе с входной величиной, поэтому косинусная
составляющая в выражении (2.11) отсутствует. Для этих элементов ![]() и гармонический
коэффициент передачи является величиной вещественной:
и гармонический
коэффициент передачи является величиной вещественной:
![]() .
(2.15)
.
(2.15)
Многие нелинейные элементы имеют характеристики, симметричные относительно начала координат (см. рисунок 2.2). Для этих характеристик функция f(x) есть функция нечетная:
![]() . (2.16)
. (2.16)
В качестве примера рассмотрим кусочно-линейную
характеристику, показанную на рисунке 2.2, а. На этой характеристике
можно указать три зоны: зона нечувствительности ![]() , зона линейности
, зона линейности ![]() , зона насыщения
, зона насыщения ![]() . В зоне нечувствительности
на выходе нелинейного элемента ничего нет; в зоне линейности изменения выходной
величины пропорциональны изменениям входной; в зоне насыщения выходная величина
остается постоянной:
. В зоне нечувствительности
на выходе нелинейного элемента ничего нет; в зоне линейности изменения выходной
величины пропорциональны изменениям входной; в зоне насыщения выходная величина
остается постоянной:
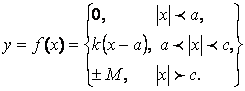 (2.17)
(2.17)
очевидно, что
![]() ,
(2.18)
,
(2.18)
так
как характеристика однозначна, ![]() .
.
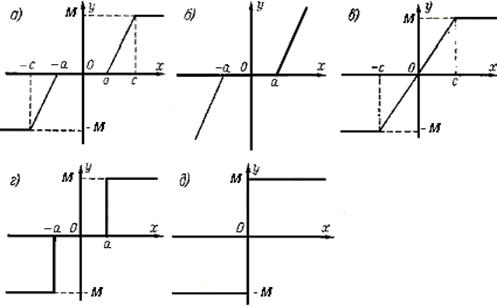
Рисунок 2.2 - Характеристики нелинейных элементов
На рисунке 2.2 также представлены кусочно-линейные характеристики нелинейных элементов с зоной нечувствительности и зоной линейности (см. рисунок 2.2, б) и без зоны нечувствительности (см. рисунок 2.2, в). На рисунке 2.2, г и рисунке 2.2, д приведены характеристики релейного элемента с зоной нечувствительности и без зоны нечувствительности соответственно.
На рисунке 2.3 приведены кривые изменения входной
величины нелинейного элемента х(t)
и выходной величины у(t). Кривая 1 на этом рисунке изображает изменение
входной величины нелинейного элемента ![]() .
.
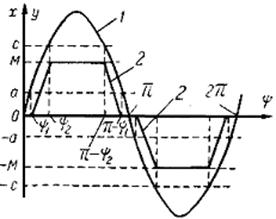
Рисунок 2.3 - Кривые изменения входной величины нелинейного элемента х и выходной величины у
Кривая 2 изображает изменение выходной
величины у(t).
От
момента ![]() до
того момента, когда х(t)
станет равным а, выходная величина
до
того момента, когда х(t)
станет равным а, выходная величина ![]() . В этот момент
фазовый угол Ψ определяется из равенства
. В этот момент
фазовый угол Ψ определяется из равенства ![]() и будет соответственно равен
и будет соответственно равен
![]() . (2.19)
. (2.19)
2.2 Исследование нелинейных систем с помощью статистической линеаризации
Наибольшее распространение в практике расчета нелинейных систем при случайных воздействиях получил приближенный метод, называемый методом статистической линеаризации, разработанный в 1954 г. одновременно И. Е. Казаковым в СССР и Р. Бутоном в США [1,5].
Идея метода основана на приближенной замене нелинейных преобразований процессов, происходящих в системе, статистически эквивалентными им линейными преобразованиями, при этом нелинейный элемент заменяется статистически эквивалентным линейным элементом. В результате такой замены система в целом линеаризуется и для ее исследования можно применять аппарат линейной теории.
Возможны различные критерии статистической эквивалентности, которые могут быть положены в основу метода статистической линеаризации. В тех случаях, когда линеаризуют безынерционный нелинейный элемент, у которого нелинейная зависимость между входным y(t) и выходным x(t) сигналами имеет вид
![]() ,
,
где φ – статическая характеристика нелинейного элемента, применяют следующие два критерия:
1) Критерий равенства математического ожидания и дисперсии случайного процесса на выходе нелинейного элемента и эквивалентного ему линейного элемента.
2) Критерий минимума математического ожидания квадрата разности случайных процессов на выходе нелинейного элемента и эквивалентного ему линейного элемента.
Познакомимся с этими критериями, ограничиваясь рассмотрением только однозначных нелинейных характеристик, которые могут быть либо нечетными, либо четными.
Напомним, что для нечетных и четных характеристик соответственно справедливы соотношения
![]() ,
(2.20)
,
(2.20)
![]() . (2.21)
. (2.21)
Случайные процессы на входе и выходе нелинейного элемента могут быть представлены следующим образом
![]() , (2.22)
, (2.22)
![]() , (2.23)
, (2.23)
где my(t), mx(t) – математические ожидания входного и выходного сигналов соответственно, включающие медленно меняющиеся регулярные составляющие;
![]() – центрированные случайные
составляющие процессов на входе и выходе нелинейного элемента соответственно.
– центрированные случайные
составляющие процессов на входе и выходе нелинейного элемента соответственно.
Заметим, что для четных нелинейных характеристик, обладающих выпрямляющими свойствами, математическое ожидание отлично от нуля даже при my(t) = 0.
В общем случае для однозначной нелинейной
функции ![]() произвольного
вида сигнал на выходе эквивалентного линеаризованного элемента
произвольного
вида сигнал на выходе эквивалентного линеаризованного элемента
![]() , (2.24)
, (2.24)
где ![]() –
математическое ожидание нелинейной функции
–
математическое ожидание нелинейной функции ![]() ;
;
![]() – эквивалентный статистический
коэффициент усиления по случайной центрированной составляющей.
– эквивалентный статистический
коэффициент усиления по случайной центрированной составляющей.
Таким образом, в общем случае нелинейный безынерционный элемент (см. рисунок 2.4, а) заменяют двумя безынерционными элементами: нелинейным по математическому ожиданию и линейным по случайной центрированной составляющей (см. рисунок 2.4, б).
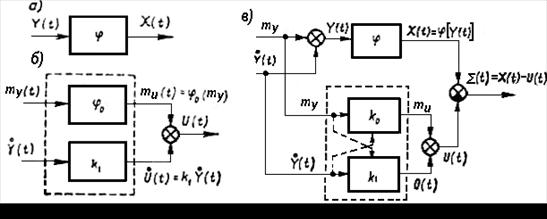
Рисунок 2.4 - Преобразование нелинейных элементов
В частном случае, когда нелинейный
безынерционный элемент имеет нечетную характеристику, функция ![]()
![]() может быть представлена в
виде:
может быть представлена в
виде:
![]() , (2.25)
, (2.25)
где ![]() –
эквивалентный статистический коэффициент усиления нелинейного элемента по математическому
ожиданию (по средней составляющей).
–
эквивалентный статистический коэффициент усиления нелинейного элемента по математическому
ожиданию (по средней составляющей).
В этом случае нелинейный элемент можно
эквивалентно заменить двумя линейными элементами с коэффициентами усиления ![]() и
и ![]() (см.
рисунок 2.4 в). Числовые значения этих коэффициентов при заданной
нелинейной зависимости
(см.
рисунок 2.4 в). Числовые значения этих коэффициентов при заданной
нелинейной зависимости ![]() определяются значениями математического
ожидания и дисперсии случайного сигнала на входе нелинейного элемента.
определяются значениями математического
ожидания и дисперсии случайного сигнала на входе нелинейного элемента.
Покажем сначала, как находят коэффициенты ![]() ,
, ![]() ,
, ![]() в случае
статистической линеаризации, которая основана на первом критерии статистической эквивалентности, состоящем в выполнении равенства математического
ожидания и дисперсии случайного процесса на выходе нелинейного элемента и
эквивалентного ему линейного элемента, т. е. когда
в случае
статистической линеаризации, которая основана на первом критерии статистической эквивалентности, состоящем в выполнении равенства математического
ожидания и дисперсии случайного процесса на выходе нелинейного элемента и
эквивалентного ему линейного элемента, т. е. когда
![]() ,
(2.26)
,
(2.26)
![]() .
(2.27)
.
(2.27)
Принимая во внимание (2.24), получаем
![]() . (2.28)
. (2.28)
Для нечетных нелинейностей, учитывая (2.25), получим
![]() . (2.29)
. (2.29)
Чтобы найти статистический эквивалентный коэффициент k1, перепишем (2.27) следующим образом
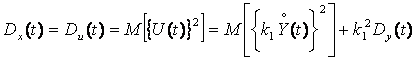 ,
,
откуда
![]() . (2.30)
. (2.30)
Обозначение
![]() показывает,
что коэффициент
показывает,
что коэффициент ![]() найден
по первому критерию эквивалентности.
найден
по первому критерию эквивалентности.
Статистические коэффициенты можно также выразить через
нелинейную зависимость φ и плотность вероятности ![]() случайного
сигнала Y(t)
на входе
нелинейного элемента:
случайного
сигнала Y(t)
на входе
нелинейного элемента:
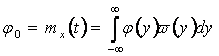 , (2.31)
, (2.31)
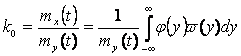 ,
(2.32)
,
(2.32)
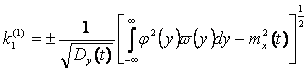 . (2.33)
. (2.33)
Знаки в (2.30) и (2.33) следует выбирать такими, чтобы знаки ![]() и
и ![]() совпадали.
совпадали.
Второй критерий статистической эквивалентности требует выполнения условия минимума математического ожидания квадрата разности процессов на выходе нелинейного элемента и эквивалентного линейного элемента, т. е.
![]() . (2.34)
. (2.34)
Подставляя в (2.34) значения X (t) и U(t), определяемые по (2.23) и (2.24), получим
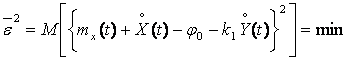 .
.
После выполнения операции возведения в квадрат и вычисления математического ожидания имеем
![]() , (2.35)
, (2.35)
где mx(t) – математическое ожидание случайного процесса на выходе нелинейного элемента;
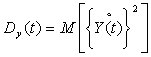 ,
, 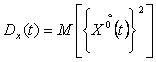 – дисперсия центрированного случайного
процесса на входе и выходе нелинейного элемента соответственно;
– дисперсия центрированного случайного
процесса на входе и выходе нелинейного элемента соответственно;
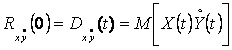 – математическое ожидание (среднее
значение) произведения двух случайных функций
– математическое ожидание (среднее
значение) произведения двух случайных функций ![]() и
и ![]() , равное начальному значению взаимной
корреляционной функции
, равное начальному значению взаимной
корреляционной функции ![]() .
.
При заданных значениях
mx(t),
Dy(t),
Dx(t),
Rx°y(0)
величина ![]() является функцией
параметров
является функцией
параметров ![]() и
k1.
и
k1.
Значения φ0 и k1,
при которых выполняется (2.34), найдем, если приравняем нулю частные
производные функции ![]() по параметрам
по параметрам ![]() и
и ![]() . Имеем
. Имеем ![]() , откуда
, откуда
![]() . (2.36)
. (2.36)
В случае нечетной нелинейной характеристики φ, учитывая (2.25), получаем следующее выражение для коэффициента k0
![]() . (2.37)
. (2.37)
Значение коэффициента k1 находим из выражения:
![]() ,
,
откуда
![]() . (2.38)
. (2.38)
Обозначение ![]() показывает, что коэффициент k1
найден по второму критерию эквивалентности.
показывает, что коэффициент k1
найден по второму критерию эквивалентности.
Статистический коэффициент ![]() можно выразить также
через плотность вероятности
можно выразить также
через плотность вероятности
![]() входного случайного сигнала
Y(t)
и
нелинейную зависимость φ < р, т. е.
входного случайного сигнала
Y(t)
и
нелинейную зависимость φ < р, т. е.
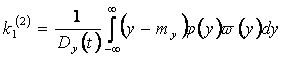 ,
,
где 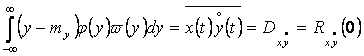 .
.
Обычно значение коэффициента ![]() , определенное из
первого критерия по (2.30), является несколько завышенным,
a
, определенное из
первого критерия по (2.30), является несколько завышенным,
a
![]() ,
определенное из второго критерия по (2.38), – несколько заниженным, поэтому
при расчетах рекомендуется брать их среднее арифметическое значение, т. е.
,
определенное из второго критерия по (2.38), – несколько заниженным, поэтому
при расчетах рекомендуется брать их среднее арифметическое значение, т. е.
![]() .
(2.39)
.
(2.39)
Сравнивая (2.28) и (2.29) с (2.36) и (2.37),
видим, что коэффициенты ![]() и
и ![]() получаются одинаковыми при
статистической линеаризации как по первому, так и по второму критерию.
получаются одинаковыми при
статистической линеаризации как по первому, так и по второму критерию.
Из (2.31) и (2.32) видно, что статистически
эквивалентные коэффициенты усиления зависят не только от вида характеристики
нелинейного элемента ![]() , но и от закона распределения
(плотности вероятности) случайного процесса на входе нелинейного элемента
, но и от закона распределения
(плотности вероятности) случайного процесса на входе нелинейного элемента ![]() .
.
При использовании метода статистической линеаризации приближенно полагают, что закон распределения случайного процесса является нормальным. Такое предположение можно сделать потому, что при прохождении случайного сигнала с любым законом распределения через линейные инерционные звенья на выходе последних закон распределения случайного сигнала оказывается близкими нормальному.
Таким образом, чем инерционнее система, тем закон распределения случайного сигнала на ее выходе ближе к нормальному. Наличие нелинейного элемента в системе нарушает это, однако при достаточно узкой полосе пропускания линейной части системы имеется тенденция к восстановлению нормального закона распределения.
При нормальном законе распределения плотность вероятности однозначно определяется математическим ожиданием и дисперсией случайного процесса, поэтому в этом случае коэффициенты k0 и k1 будут лишь функциями математического ожидания ту и дисперсии Dy входного сигнала, т. е.
![]() . (2.40)
. (2.40)
Формулы (2.31), (2.32), (2.37) и (2.38) при нормальном законе распределения будут иметь следующий вид:
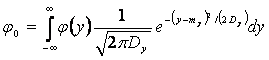 . (2.41)
. (2.41)
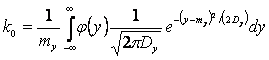 . (2.42)
. (2.42)
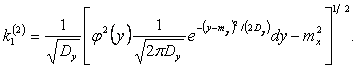 (2.43)
(2.43)
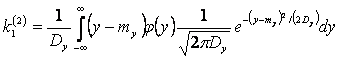 . (2.44)
. (2.44)
Если умножить выражение (2.42) на ![]() , затем продифференцировать
произведение
, затем продифференцировать
произведение ![]() по
по
![]() и
сопоставить полученное выражение с (2.44), то можно убедиться в выполнении
следующего равенства:
и
сопоставить полученное выражение с (2.44), то можно убедиться в выполнении
следующего равенства:
![]() . (2.45)
. (2.45)
Соотношение (2.45) может быть использовано
как для нахождения коэффициента ![]() вместо (2.44), так и для проверки
правильности определения коэффициентов
вместо (2.44), так и для проверки
правильности определения коэффициентов ![]() и
и ![]() .
.
2.3 Фазовый метод
2.3.1 Метод изображения переходных процессов в фазовом пространстве в фазовой плоскости был введен в теорию регулирования академиком Андроновым [1,5,6,7,8]. Им был решен ряд классических задач теории регулирования, в том числе задача Вышнеградского с учетом сухого трения в регуляторе.
Метод дает возможность получить наглядную и точную картину всей совокупности переходных процессов при любых начальных условиях для свободных колебаний в системах второго порядка, содержащих нелинейные элементы. Андронов решил одну из задач для уравнений третьего порядка [5]. Большое количество задач построения «фазовых портретов» различных нелинейных систем было решено Казакевичем, Петровым и Улановым и рядом других авторов [1].
Хотя исследование систем второго порядка для теории регулирования имеет ограниченный интерес, знакомство с основами метода фазовой плоскости весьма полезно благодаря его исключительной наглядности и изяществу.
Фазовой плоскостью называется плоскость, в которой по осям координат откладываются какие-либо две переменные, характеризующие переходный процесс в системе. Наиболее часто в качестве таких переменных принимают отклонение регулируемой величины х и скорость ее изменения по времени:
![]() .
(2.46)
.
(2.46)
При изображении процессов на фазовой плоскости уравнение второго порядка удобно свести к двум уравнениям первого порядка:
 (2.47)
(2.47)
где ![]() и
и
![]() - в общем
случае нелинейные функции координат.
- в общем
случае нелинейные функции координат.
Чтобы изобразить переходный процесс на фазовой плоскости, из уравнений (2.47) исключим время, для чего поделим второе уравнение на первое:
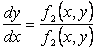 . (2.48)
. (2.48)
Мы получили нелинейное дифференциальное уравнение, общих методов точного решения которого не существует, и в каждой задаче приходится изыскивать частный метод его решения. Решением уравнения (2.48) будет некоторая функция
![]() , (2.49)
, (2.49)
графическое изображение которой, на фазовой плоскости называется фазовой траекторией.
Как известно, каждой совокупности
начальных условий ![]() ,
,
![]() будет
соответствовать свое решение и своя фазовая траектория. Фазовая плоскость для
каждого уравнения покрывается множеством фазовых траекторий, однако это
множество обладает весьма ценным свойством: если функции
будет
соответствовать свое решение и своя фазовая траектория. Фазовая плоскость для
каждого уравнения покрывается множеством фазовых траекторий, однако это
множество обладает весьма ценным свойством: если функции ![]() и
и ![]() однозначны, то каждой точке (х,у)
на плоскости (за исключением, может быть, ограниченного числа изолированных особых точек) соответствует только одно значение
производной dy/dx.
Это означает что через каждую точку фазовой плоскости
(за исключением особых точек) проходит только одна фазовая траектория и что
фазовые траектории не пересекаются друг с другом. Данное обстоятельство и
позволяет получать наглядные нечеткие «фазовые портреты» исследуемой системы,
на которых ясно виден характер возможных движений, подобно тому, как с помощью
магнитных силовых линий получаем наглядное представление о магнитном поле.
однозначны, то каждой точке (х,у)
на плоскости (за исключением, может быть, ограниченного числа изолированных особых точек) соответствует только одно значение
производной dy/dx.
Это означает что через каждую точку фазовой плоскости
(за исключением особых точек) проходит только одна фазовая траектория и что
фазовые траектории не пересекаются друг с другом. Данное обстоятельство и
позволяет получать наглядные нечеткие «фазовые портреты» исследуемой системы,
на которых ясно виден характер возможных движений, подобно тому, как с помощью
магнитных силовых линий получаем наглядное представление о магнитном поле.
Однако многие нелинейности характерны тем, что при возрастании
координаты, т. е. при ![]() , движение происходит по одной
ветви кривой, а при ее убывании, т. е. при
, движение происходит по одной
ветви кривой, а при ее убывании, т. е. при ![]() , по другой. Тогда, хотя характеристика
элемента неоднозначна, па фазовой плоскости будем иметь опять-таки непересекающиеся
фазовые траектории, так как области
, по другой. Тогда, хотя характеристика
элемента неоднозначна, па фазовой плоскости будем иметь опять-таки непересекающиеся
фазовые траектории, так как области ![]() и
и ![]() разграничены осью абсцисс
разграничены осью абсцисс ![]() , которую можно при
этом назвать линией переключения, поскольку на этой оси происходит переходу
фазовой траектории, определяемой одним уравнением, на траекторию, описываемую
другим уравнением.
, которую можно при
этом назвать линией переключения, поскольку на этой оси происходит переходу
фазовой траектории, определяемой одним уравнением, на траекторию, описываемую
другим уравнением.
И лишь в том случае, если неоднозначность является более сложной, может оказаться, что в точках некоторых областей фазовой плоскости будут пересекаться несколько фазовых траекторий. В этом случае прибегают к понятию многополюсных фазовых плоскостей.
Мы упомянули о том, что однозначность фазовых
траекторий, проходящих через данную точку, может не иметь места в так
называемых «особых точках». Эти особые точки представляют собой те точки, в
которых происходит одновременное обращение в нуль функций ![]() и
и ![]() :
:
 (2.50)
(2.50)
Особые точки, определяемые решением системы уравнений (2.50),
отмечены нами нулевым индексом вверху, чтобы отличить их от начальных условий ![]() ,
, ![]() , отмечаемых нулевым индексом
внизу.
, отмечаемых нулевым индексом
внизу.
Заметим, что на основании (2.47) в особых точках dx/dt и dy/dt обращаются в нуль, т. е. движение системы прекращается. Это означает, что особые точки представляют собой точки равновесия системы. Заметим сразу же, что эти точки могут быть как реализуемыми физически, т.е. устойчивыми, так и нереализуемыми, т.е. неустойчивыми, и в неустойчивых точках возможность прекращения движения существует только формально.
Мы говорили о том, что чаще всего за координату y принимают скорость изменения координаты х. Тогда уравнения (2.47) принимают вид:
 (2.51)
(2.51)
Фазовые траектории при этом приобретают некоторые
дополнительные свойства. Прежде всего, из уравнений (2.51) следует, что х всегда
возрастает в верхней полуплоскости (где ![]() ), т. е. движение вдоль фазовой
траектории при возрастании t
происходит
слева направо. В нижней же полуплоскости (где
), т. е. движение вдоль фазовой
траектории при возрастании t
происходит
слева направо. В нижней же полуплоскости (где ![]() ) координата х убывает, и
движение по фазовой траектории происходит справа налево.
) координата х убывает, и
движение по фазовой траектории происходит справа налево.
Следующее интересное свойство вытекает из уравнения (2.48), которое в данном случае принимает вид:
![]() . (2.52)
. (2.52)
При у=0, величина dy/dx становится бесконечно большой во всей фазовой плоскости, за исключением точек равновесия, где f(х, у) = 0. Это означает, что в точках пересечения фазовых траекторий с осью х касательные к фазовым траекториям перпендикулярны к оси х.
Хотя метод фазовых траекторий разработан применительно к нелинейным системам, однако представляет интерес сначала рассмотреть фазовые траектории колебательного линейного звена второго порядка, так как можно легко проследить получение фазовых траекторий и особых точек наиболее важных типов, которые встречаются и нелинейных системах.
2.3.2 Для наглядного представления о сложных нелинейных процессах регулирования часто прибегают к понятию фазового пространства, которое заключается в следующем. Дифференциальное уравнение замкнутой системы регулирования n-го порядка можно преобразовать к системе п дифференциальных уравнений первого порядка в виде:
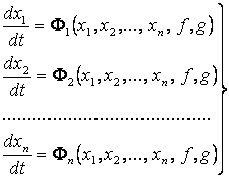 (2.53)
(2.53)
с
начальными условиями: ![]() ,
, ![]() при
при ![]() ,
,
где
![]() – переменные, являющиеся искомыми функциями
времени, причем х1 может обозначать регулируемую
величину, а
– переменные, являющиеся искомыми функциями
времени, причем х1 может обозначать регулируемую
величину, а ![]() – вспомогательные переменные;
– вспомогательные переменные;
![]() и
и ![]() – возмущающее
и задающее воздействия.
– возмущающее
и задающее воздействия.
Пусть, например, в уравнениях (2.53) будет п = 3 (система третьего порядка). Переменные x1, х2, хз здесь могут иметь любой физический смысл. Но условно их можно представить мысленно как прямоугольные координаты некоторой точки М, которую называют изображающей точкой (см. рисунок 2.5, а).
В реальном процессе регулирования в каждый момент
времени величины ![]() имеют
вполне определенные значения. Это соответствует вполне определенному
положению точки М в пространстве (см.
рисунок 2.5, а). С течением
времени в реальном процессе величины
имеют
вполне определенные значения. Это соответствует вполне определенному
положению точки М в пространстве (см.
рисунок 2.5, а). С течением
времени в реальном процессе величины ![]() определенным образом изменяются. Это
соответствует определенному перемещению точки М в пространстве по
определенной траектории. Следовательно, траектория движения точки М может
служить наглядной геометрической иллюстрацией динамического поведения системы в
процессе регулирования.
определенным образом изменяются. Это
соответствует определенному перемещению точки М в пространстве по
определенной траектории. Следовательно, траектория движения точки М может
служить наглядной геометрической иллюстрацией динамического поведения системы в
процессе регулирования.
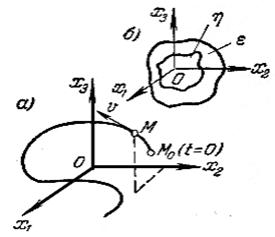
Рисунок 2.5 - Прямоугольные координаты некоторой точки М
Точка М называется изображающей точкой, ее
траектория называется фазовой траекторией, а пространство (![]() ) называется фазовым
пространством.
) называется фазовым
пространством.
Так как производные по времени от координат точки представляют
проекции ее скорости ![]() на оси координат, то
дифференциальные уравнения системы в форме (2.53) представляют собой выражения
для проекций скорости
на оси координат, то
дифференциальные уравнения системы в форме (2.53) представляют собой выражения
для проекций скорости ![]() ; изображающей точки М (см. рисунок
2.5, а) на оси координат. Следовательно, по значениям правых частей
уравнений (2.53) в каждый момент времени можно судить о направлении движения
изображающей точки М, а вместе с тем и о поведении соответствующей
реальной системы в процессе регулирования.
; изображающей точки М (см. рисунок
2.5, а) на оси координат. Следовательно, по значениям правых частей
уравнений (2.53) в каждый момент времени можно судить о направлении движения
изображающей точки М, а вместе с тем и о поведении соответствующей
реальной системы в процессе регулирования.
Начальные условия процесса регулирования (![]() ) определяют
координаты начальной точки фазовой траектории
) определяют
координаты начальной точки фазовой траектории ![]() (см. рисунок 2.5, а).
(см. рисунок 2.5, а).
Если переменных в уравнениях (2.53) будет всего две: ![]() и
и ![]() (система
второго порядка), то изображающая точка будет двигаться не в пространстве, а
на плоскости (фазовая плоскость).
(система
второго порядка), то изображающая точка будет двигаться не в пространстве, а
на плоскости (фазовая плоскость).
Если переменных будет любое число ![]() (система п-го порядка),
то фазовое пространство будет не трехмерным, а
(система п-го порядка),
то фазовое пространство будет не трехмерным, а ![]() -мерным.
-мерным.
Итак, фазовое пространство и фазовые траектории представляют собой лишь геометрический образ динамических процессов, протекающих в системе. В этом геометрическом представлении участвуют координаты и исключено время. Фазовая траектория сама по себе дает лишь качественное представление о характере поведения системы. Чтобы определить количественно положение изображающей точки (а значит, и состояние системы) в любой момент времени, нужно найти решение заданных дифференциальных уравнений (2.53) во времени.
Если уравнения (2.53) составлены в отклонениях от
установившегося состояния, то последнее характеризуется значениями ![]() . Следовательно,
изображением установившегося состояния системы является начало координат
фазового пространства.
. Следовательно,
изображением установившегося состояния системы является начало координат
фазового пространства.
Отсюда вытекает, что фазовые траектории устойчивой линейной системы будут асимптотически приближаться к началу координат при неограниченном увеличении времени. Фазовые траектории неустойчивой линейной системы будут неограниченно удаляться от начала координат.
Для нелинейной системы вследствие ряда особенностей процессов, отмечавшихся выше, фазовые траектории могут принимать самые разнообразные очертания. Если имеется асимптотическая устойчивость для определенного круга начальных условий, то все фазовые траектории, которые начинаются внутри определенной области η, окружающей начало координат фазового пространства (см. рисунок 2.5, б), будут асимптотически приближаться к началу координат. Если устойчивость неасимптотическая, то фазовые траектории, начинающиеся внутри определенной области η вокруг начала координат фазового пространства, могут иметь любые очертания, но не будут выходить за пределы некоторой определенной области ε, окружающей начало координат (см. рисунок 2.5, б).
2.3.3 Рассмотрим формулировку понятия устойчивости по Ляпунову. Невозмущенное движение (установившийся процесс) называется устойчивым, если при заданной сколь угодно малой области ε (см. рисунок 2.5, б) можно найти такую область η, что при начальных условиях, расположенных внутри этой области, возмущенное движение (переходный процесс) будет таким, что изображающая точка не выйдет из области ε при любом сколь угодно большом значении времени t.
В аналитической записи формулировка понятия устойчивости по Ляпунову будет следующей. Невозмущенное движение (установившийся процесс) будет устойчивым, если при заданном положительном сколь угодно малом числе ε можно найти такое положительное число η (зависящее от заданного значения ε), что при начальных условиях
![]() ;
; ![]() (2.54)
(2.54)
решение дифференциальных уравнений возмущенного движения (переходного процесса) удовлетворяет неравенствам
![]() ;
; ![]()
при любом сколь угодно большом t.
Представим себе для этой аналитической записи
геометрический образ в фазовом пространстве. Очевидно, что при ограничении
начальных условий по каждой координате неравенствами (2.54) получается п
- мерный куб со стороной 2η, внутри которого должна лежать
начальная точка фазовой траектории М0 (![]() ). На фазовой плоскости
(п = 2) он обращается в квадрат. Аналогично и второе из написанных неравенств
геометрически означает, что фазовые траектории не должны выходить из куба со
стороной 2 ε.
). На фазовой плоскости
(п = 2) он обращается в квадрат. Аналогично и второе из написанных неравенств
геометрически означает, что фазовые траектории не должны выходить из куба со
стороной 2 ε.
В формулировке Ляпунова содержится требование сколь угодной малости указанных областей. Однако практически это определение так же, как и теоремы Ляпунова, которые будут приведены ниже, применяется и тогда, когда эти области имеют определенные конечные размеры.
2.3.4 Для изучения метода фазовых траекторий предварительно рассмотрим фазовые траектории для обыкновенных линейных систем. Пусть переходный процесс в некоторой системе описывается уравнением второго порядка:
![]() .
(2.55)
.
(2.55)
Введем
обозначение для скорости изменения отклонения регулируемой величины ![]() . Тогда уравнение
системы (2.55) преобразуется к виду
. Тогда уравнение
системы (2.55) преобразуется к виду
 (2.56)
(2.56)
Исключим из уравнений (2.56) время
t,
разделив первое из них на второе (при
х и ![]() ),
получим
),
получим
![]() (2.57)
(2.57)
Решение ![]() этого дифференциального
уравнения с одной произвольной постоянной определяет собой некоторое семейство
интегральных кривых на фазовой плоскости (х,у), каждая из которых
соответствует одному определенному значению произвольной постоянной.
этого дифференциального
уравнения с одной произвольной постоянной определяет собой некоторое семейство
интегральных кривых на фазовой плоскости (х,у), каждая из которых
соответствует одному определенному значению произвольной постоянной.
Вся совокупность интегральных кривых представит собой все возможные фазовые траектории, а значит, и все возможные виды переходного процесса в данной системе автоматического регулирования при любых начальных условиях. Рассмотрим отдельно различные случаи.
Уравнению (2.55) соответствуют корни характеристического уравнения
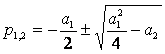 ,
,
причем возможны шесть случаев:
1) корни, чисто мнимые, при ![]() ,
, ![]() (граница устойчивости
линейной системы);
(граница устойчивости
линейной системы);
2) корни комплексные и имеют отрицательные
вещественные части при ![]() ,
, ![]() ,
, ![]() (устойчивая линейная система);
(устойчивая линейная система);
3) корни комплексные и имеют положительные
вещественные части при ![]() ,
, ![]() ,
, ![]() (неустойчивая линейная система);
(неустойчивая линейная система);
4) корни, вещественные отрицательные, при ![]() ,
, ![]() ,
, ![]() (устойчивая линейная
система);
(устойчивая линейная
система);
5) корни, вещественные положительные, при ![]() ,
, ![]() ,
, ![]() (неустойчивая линейная
система);
(неустойчивая линейная
система);
6) корни вещественные и имеют разные знаки при ![]() (неустойчивая
линейная система), в частности, один из корней будет равен нулю при
(неустойчивая
линейная система), в частности, один из корней будет равен нулю при ![]() (граница
устойчивости линейной системы).
(граница
устойчивости линейной системы).
Теперь рассмотрим систему автоматического управления с объектом без самовыравнивания и с приводом управляющего органа, имеющим постоянную скорость.
Уравнение объекта будет
![]() .
(2.58)
.
(2.58)
Для управляющего устройства без массы и демпфера
жесткой обратной связью, т.е. при ![]() получим
получим
![]() (2.59)
(2.59)
где
![]() и
и ![]() – относительные изменения управляемой величины,
смещения чувствительного элемента, управляющего органа, элемента обратной связи
и управляющего золотника;
– относительные изменения управляемой величины,
смещения чувствительного элемента, управляющего органа, элемента обратной связи
и управляющего золотника;
![]() – коэффициент.
– коэффициент.
Пусть привод управляющего органа имеет постоянную
скорость в двух вариантах: с мгновенным переключением при переходе управляющего
элемента (золотника, струйной трубки) через нейтральное положение(![]() =0;2); с зоной
нечувствительности вследствие наличия «перекрытия» золотника или струйной
трубки. В первом случае уравнении привода управляющего органа будет
=0;2); с зоной
нечувствительности вследствие наличия «перекрытия» золотника или струйной
трубки. В первом случае уравнении привода управляющего органа будет
![]() (2.60)
(2.60)
![]() а во втором:
а во втором:
![]() при
при ![]()
![]() при
при ![]() (2.61)
(2.61)
Возьмем фазовую плоскость (х,у), приняв
![]() ,
, ![]() (2.62)
(2.62)
Из уравнений (2.58), (2.59) и (2.62) имеем
![]() ,
, ![]() (2.63)
(2.63)
Следовательно, переключения привода в первом варианте
(![]() ) будет
иметь место
) будет
иметь место
![]() (2.64)
(2.64)
что
соответствует прямой АВ (см. рисунок 2.6, а) на фазовой плоскости,
причем согласно (2.63) значением ![]() соответствует часть плоскости слева от
прямой АВ, а
соответствует часть плоскости слева от
прямой АВ, а ![]() -
справа.
-
справа.
На основании первого из соотношений (2.63) с учетом
(2.60) при ![]() получаем
получаем
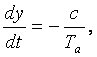 (2.65)
(2.65)
а из (2.62) определится
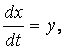 (2.66)
(2.66)
откуда находим уравнения фазовых траекторий
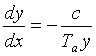 (2.67)
(2.67)
или после интегрирования будет
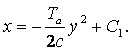
Это есть семейство парабол, показанное на рисунке 2.6,
а справа от линии АВ (они симметричны относительно оси х). Так
как (2.65) и (2.66) являются проекциями скорости ![]() , изображающей точки М на оси х и
у, то имеем
, изображающей точки М на оси х и
у, то имеем ![]() ,
а знак
,
а знак ![]() совпадает
со знаком у.
совпадает
со знаком у.
В соответствии с этим на рисунке 2.6, а укажем стрелочками направление движения изображающей точки М по фазовым траекториям. Аналогичным путем легко строятся параболы слева от прямой АВ.
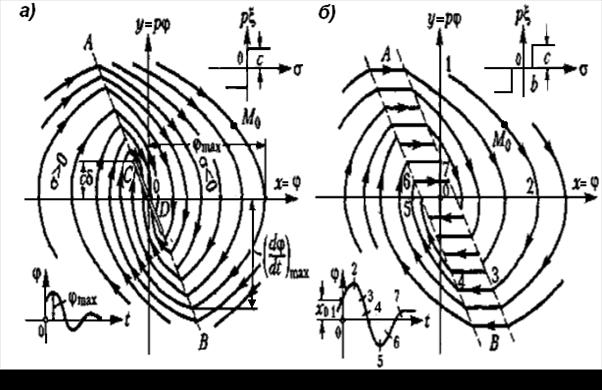
Рисунок 2.6 – Картина общего расположения фазовых траекторий на фазовой плоскости включающая нелинейность релейного типа с зоной нечувствительности
В результате, как видно из общего расположения фазовых
траекторий на фазовой плоскости (см. рисунок 2.6, а), получается
устойчивая система с затухающим колебательным переходным процессом. Но число
колебаний будет конечным. В самом деле, здесь имеется особый отрезок
CD, в
который вливаются все фазовые траектории, чтобы выявить поведение системы на
этом отрезке, вспомним, что для него согласно (2.62) и (2.64) ![]() или
или
![]()
Следовательно, попав на отрезок CD, изображающая точка не может с него уйти, и система будет апериодически приближаться к установившемуся состоянию, т.е. изображающая точка будет «сползать» по отрезку CD к началу координат 0. Таким образом, имевший место вначале колебательный переходный процесс после конечного числа колебаний вырождается в этот, так называемый, скользящий процесс.
Крайние точки особого отрезка
CD
определяются, очевидно, как точки, в которых прямая АВ касается одной из
парабол соответственно правого и левого семейств. Поэтому, подставив значения ![]() из (2.64) в выражение
(2.67), найдем точку С:
из (2.64) в выражение
(2.67), найдем точку С: ![]()
По найденной картине расположения фазовых траекторий
можно качественно представить себе кривую переходного процесса ![]() при любых начальных
условиях. Начальными условиями определяется начальное положение изображающей
точки М и тем самым – определенная фазовая траектория, иллюстрирующая
протекание процесса. Она показывает (см. рисунок 2.6, а)
максимальное отклонение управляемой величины
при любых начальных
условиях. Начальными условиями определяется начальное положение изображающей
точки М и тем самым – определенная фазовая траектория, иллюстрирующая
протекание процесса. Она показывает (см. рисунок 2.6, а)
максимальное отклонение управляемой величины ![]() , максимальную скорость
, максимальную скорость ![]() , а также все
последующие отклонения, число колебаний и т.п.
, а также все
последующие отклонения, число колебаний и т.п.
Рассмотрим теперь ту же систему, но с учетом зоны
нечувствительности. В этом случае переключениям привода (при ![]() и
и ![]() ) на фазовой плоскости
соответствуют согласно (2.63) две наклонные прямые (см. рисунок 2.6, б):
) на фазовой плоскости
соответствуют согласно (2.63) две наклонные прямые (см. рисунок 2.6, б):
![]() и
и
![]()
Между этими прямыми ![]() , правее их
, правее их ![]() , левее их
, левее их ![]() (причем
(причем ![]()
![]() ).
).
При ![]() из (2.61), (2.63) и (2.61) получаем
из (2.61), (2.63) и (2.61) получаем
![]() ,
,
![]()
откуда
(при ![]() )
)
![]() или
или ![]()
(прямые, параллельные оси х в полосе АВ на рисунке 2.6, б).
При ![]() получим прежние параболы. В результате
снова система оказывается устойчивой и имеет колебательный переходный процесс,
но вместо особой точки 0 получаем особый отрезок (у=0,
получим прежние параболы. В результате
снова система оказывается устойчивой и имеет колебательный переходный процесс,
но вместо особой точки 0 получаем особый отрезок (у=0, ![]() ), т.е. установившееся
состояние определяется неоднозначно. Это соответствует тому, что система может
находиться в равновесии в любом месте внутри зоны нечувствительности. Здесь
точно так же возможен скользящий процесс, как и в случае изображенном на
рисунке 2.6, а.
), т.е. установившееся
состояние определяется неоднозначно. Это соответствует тому, что система может
находиться в равновесии в любом месте внутри зоны нечувствительности. Здесь
точно так же возможен скользящий процесс, как и в случае изображенном на
рисунке 2.6, а.
Пример 1. Осциллятор с сухим трением [5]. Сила сухого трения f направлена навстречу движению и постоянна по величине. Обозначая через т – массу осциллятора, через с – жесткость пружины, имеем:
![]() , х' < 0,
, х' < 0,
![]() ,
х' >0.
,
х' >0.
Если в некоторый момент х' = 0 и сила пружины по модулю не превышает силы трения, то осциллятор будет находиться в покое, удерживаясь силой трения: х = const, х' = 0, |сх|<fтр.
Обозначив ![]() ,
, ![]() , получим уравнения
осциллятора в следующем
виде:
, получим уравнения
осциллятора в следующем
виде:
![]() , х' <
0; (2.68)
, х' <
0; (2.68)
х=const, х' =0, | х|<ε; (2.69)
![]() , х' > 0. (2.70)
, х' > 0. (2.70)
Уравнение (2.68) говорит о том, что в нижней фазовой полуплоскости (х' < 0) фазовые траектории представляют собой половинки концентрических эллипсов, центр которых находится в точке +ε на вещественной оси. Из уравнения (2.70) следует, что в верхней полуплоскости центры полуэллипсов находятся в точке – ε (см. рисунок 2.7). Уравнение (2.69) свидетельствует о том, что на оси абсцисс (х' = 0) движение продолжается, если х находится вне отрезка (-ε, +ε), и прекращается, если х находится внутри этого отрезка, который называется отрезком покоя.
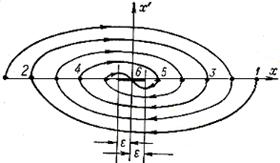
Рисунок 2.7 - Фазовые траектории осциллятора с сухим трением
Таким образом, в целом фазовые траектории, состоящие из отрезков эллипсов, скручиваются к отрезку покоя, и отрезок покоя представляет собой геометрическое место устойчивых состояний равновесия.
Построим кривую переходного процесса при начальных
условиях ![]() .
Решая уравнение (2.68), получаем
.
Решая уравнение (2.68), получаем ![]() ; движение, начавшись в точке 1 (см.
рисунок 2.7 и рисунок 2.8), будет продолжаться до тех пор, пока х' будет
оставаться отрицательным, т. е. до момента
; движение, начавшись в точке 1 (см.
рисунок 2.7 и рисунок 2.8), будет продолжаться до тех пор, пока х' будет
оставаться отрицательным, т. е. до момента ![]() , где х станет равным
, где х станет равным ![]() (точка 2). Далее
движение в соответствии с уравнением (2.70) происходит по
закону
(точка 2). Далее
движение в соответствии с уравнением (2.70) происходит по
закону ![]() (отсчет времени
перенесен в точку
(отсчет времени
перенесен в точку ![]() ).
При
).
При ![]() получим
получим
![]() (точка
3).
(точка
3).
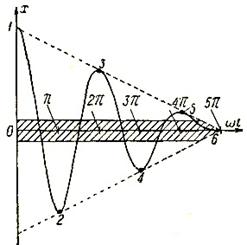
Рисунок 2.8 - Кривая
переходного процесса при начальных условиях ![]()
Продолжив построение, убедимся, что амплитуды верхних
полуволн равны: ![]() а
нижних:
а
нижних: ![]() (см.
рисунок 2.8). Линии, проведенные через вершины полуволн, представляют собой
прямолинейные лучи, в отличие от экспонент в линейном осцилляторе с вязким
демпфированием. Движение прекращается внутри заштрихованной на рисунке зоны
нечувствительности в тот момент, когда х' становится равным нулю.
(см.
рисунок 2.8). Линии, проведенные через вершины полуволн, представляют собой
прямолинейные лучи, в отличие от экспонент в линейном осцилляторе с вязким
демпфированием. Движение прекращается внутри заштрихованной на рисунке зоны
нечувствительности в тот момент, когда х' становится равным нулю.
Пример 2. Осциллятор с переменным сухим трением [5]. Рассмотренный выше осциллятор представляет собой нелинейное устройство, которое нельзя исследовать методами линейной теории регулирования. Но из опыта известно, что многие чувствительные механические органы регуляторов, не имеющих демпфирующих элементов с вязким трением, ведут себя примерно так же, как линейные осцилляторы с вязким трением.
Как известно, колебания коротких пружин затухают весьма быстро. При этом опыты не обнаруживают колебаний, которые изображены на рисунке 2.7, с прямолинейными огибающими амплитуд. Огибающие оказываются криволинейными, причем довольно близкими к экспонентам. Зона застоя при этом оказывается также гораздо меньшей (практически отсутствует), чем это вытекает из предыдущего примера. При некоторых допущениях осцилляторы подобного рода можно представить как линейные.
Сила сухого трения, как известно, пропорциональна нормальному давлению, сжимающему трущиеся поверхности. По аналогии с этим допустим, что сила сухого внутреннего трения в пружинах пропорциональна напряжениям, возникающим в сечениях пружины при ее упругих деформациях, т. е. в конечном итоге, если мы не выходим за пределы действия закона Гука, пропорциональна деформации. Вместе с тем эта сила направлена, как и обычная сила кулоновского трения, навстречу движению. Тогда уравнения линейного осциллятора с переменным сухим внутренним трением можно будет записать в следующем виде:
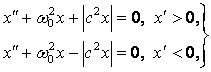 (2.71)
(2.71)
где ![]() - величина переменного внутреннего
трения.
- величина переменного внутреннего
трения.
Уравнения (2.71) можно переписать иначе

Таким образом, в первом и третьем квадрантах фазовой
плоскости, где знаки ![]() и
и ![]() совпадают, фазовые траектории
представляют собой отрезки концентричных по отношению к началу координат
эллипсов с отношением вертикальной полуоси к горизонтальной, равным
совпадают, фазовые траектории
представляют собой отрезки концентричных по отношению к началу координат
эллипсов с отношением вертикальной полуоси к горизонтальной, равным ![]() ; во втором и
четвертом квадрантах это соотношение равно
; во втором и
четвертом квадрантах это соотношение равно ![]() .
.
Фазовые траектории, как это видно из рисунка 2.9, скручиваются к началу координат. Таким образом, качественно фазовый портрет данного осциллятора напоминает фазовый портрет линейного осциллятора с вязким трением.
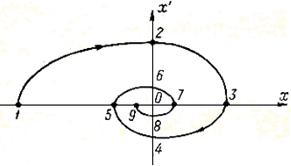
Рисунок 2.9 - Фазовый портрет осциллятора с переменным сухим трением
Аппроксимируем данный нелинейный осциллятор линейным, поставив условием для аппроксимации совпадение периодов и амплитуд их колебаний. Амплитуды совпадут, если фазовые траектории обоих осцилляторов будут пересекать ось абсцисс в одних и тех же точках. Нетрудно определить, что отношение амплитуд в начале и конце периода в рассматриваемом случае равно
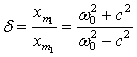 .
(2.72)
.
(2.72)
Свободные колебания изображаются кривой, составленной из четвертей
синусоид с периодами ![]() и
и ![]() (см. рисунок 2.10). Период затухающих колебаний равен
(см. рисунок 2.10). Период затухающих колебаний равен
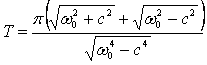 ; (2.73)
; (2.73)
для обычных
случаев для малых значений – ![]()
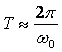 . (2.74)
. (2.74)
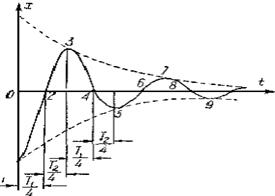
Рисунок 2.10 - Свободные колебания нелинейного осциллятора
Для того чтобы амплитуды и периоды колебаний эквивалентной линейной системы, описываемой уравнением
![]() ,
(2.75)
,
(2.75)
совпали с амплитудами и периодами колебаний данной системы, необходимо выполнить следующие условия:
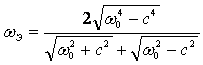 , (2.76)
, (2.76)
для
малых значений – ![]() :
:
![]() ,
(2.77)
,
(2.77)
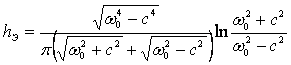 ,
(2.78)
,
(2.78)
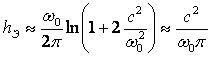 .
.
3 Устойчивость нелинейных систем автоматического управления
3.1 Абсолютная устойчивость вынужденного процесса в нелинейной системе
В нелинейных системах в ряде случаев необходимо определить не только положение равновесия системы, но также и устойчивость определенных процессов, поскольку в общем случае устойчивость равновесия в нелинейной системе может и не совпадать с устойчивостью процесса [1,5,7].
Условие абсолютной устойчивости вынужденного процесса в нелинейной системе определяется выражением:
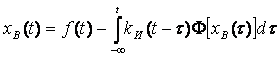 . (3.1)
. (3.1)
Путем соответствующей замены переменных в интеграле выражение (3.1) можно представить в виде:
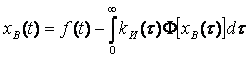 . (3.2)
. (3.2)
Допустим, что существует вынужденный процесс и что в момент t=0 к системе приложено исчезающее воздействие f1(t). Тогда f1(t) налагается на действовавшее ранее f(t), а процесс хв (t) также получает вариацию ξ(t):
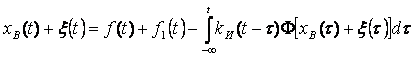 . (3.3)
. (3.3)
Из уравнения (3.3), выражающего возмущенный процесс, вычтем уравнение (3.1) вынужденного процесса и получим уравнение для отклонения:
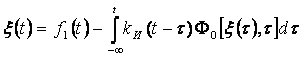 , (3.4)
, (3.4)
где 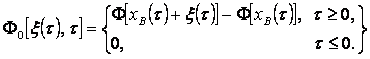 (3.5)
(3.5)
Учитывая (3.5) и (3.2), уравнение (3.4) представим в таком виде:
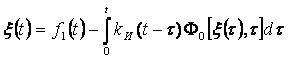 . (3.6)
. (3.6)
Это уравнение отличается от уравнения, для которого
был выведен критерий устойчивости Попова [1,5,8], тем, что функция ![]() теперь зависит явно
от времени, поскольку нелинейный элемент обладает нестационарной
характеристикой.
теперь зависит явно
от времени, поскольку нелинейный элемент обладает нестационарной
характеристикой.
В [5,6] доказано следующее условие: для того чтобы процесс
в нелинейной системе, вызванный ограниченным внешним воздействием, был
абсолютно устойчив, достаточно, чтобы при заданном значении
r
преобразованная
линейная часть была устойчива и чтобы частотная характеристика линейной части ![]() удовлетворяла
условию:
удовлетворяла
условию:
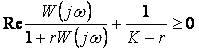 ;
; ![]() , (3.7)
, (3.7)
а производная
нелинейной характеристики ![]() принадлежала
бы полосе
принадлежала
бы полосе ![]() ,
т. е.
,
т. е.
![]() (3.8)
(3.8)
где
![]() - сколь
угодно малая положительная величина.
- сколь
угодно малая положительная величина.
В случае, если линейная часть (непреобразованная)
устойчива, полагаем ![]() и получаем Ф(х)
и получаем Ф(х)
![]()
или
![]()
Геометрически это означает, что характеристика
разомкнутой линеаризованной системы ![]() , которая получается из исходной
нелинейной системы в результате замены нелинейного элемента линейным с
коэффициентом передачи К, должна лежать правее прямой
, которая получается из исходной
нелинейной системы в результате замены нелинейного элемента линейным с
коэффициентом передачи К, должна лежать правее прямой ![]() , или же
характеристика
, или же
характеристика ![]() должна
лежать правее прямой,
должна
лежать правее прямой, ![]() (см. рисунок 3.1, а).
При этом характеристики нелинейного элемента должны удовлетворять условиям:
(см. рисунок 3.1, а).
При этом характеристики нелинейного элемента должны удовлетворять условиям:
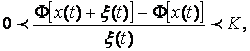 (3.9)
(3.9)
т.
е. характеристика должна лежать в секторе (01,К1)
новой системы координат (см. рисунок 3.1, б). Очевидно, наклон 01К1
равен наклону ОК, если выполняется условие ![]() .
.
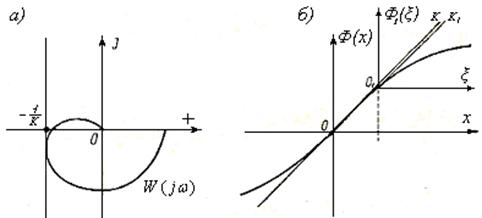
Рисунок 3.1 - Характеристика разомкнутой линеаризованной системы
В общем случае, когда разомкнутая линейная система неустойчива или нейтральна и r отлично от нуля, имеем:
![]() (3.10)
(3.10)
где
![]() .
.
Пусть ![]() . Тогда, заменяя неравенство (3.10)
равенством, получаем уравнение границы области, внутрь которой не должна
входить характеристика
. Тогда, заменяя неравенство (3.10)
равенством, получаем уравнение границы области, внутрь которой не должна
входить характеристика ![]() :
:
![]()
что можно привести к виду:
 (3.11)
(3.11)
Уравнение (3.11) определяет семейство окружностей,
центр которых лежит на отрицательной вещественной полуоси и которые имеют общую
точку касания ![]() .
.
Теперь можно дать следующую геометрическую интерпретацию
критерию абсолютной устойчивости процессов в общем случае: для того чтобы
процессы в нелинейной системе при ограниченных воздействиях были абсолютно
устойчивы достаточно, чтобы производная от характеристики нелинейного элемента ![]() принадлежала полосе
принадлежала полосе ![]() , где
, где ![]() сколь угодно малая
положительная величина и чтобы частотная характеристика линеаризованной
разомкнутой системы
сколь угодно малая
положительная величина и чтобы частотная характеристика линеаризованной
разомкнутой системы ![]() , удовлетворяя частотному критерию
Найквиста, находилась вне соответствующей точке А окружности (см. рисунок
3.2, а), или же чтобы характеристика
, удовлетворяя частотному критерию
Найквиста, находилась вне соответствующей точке А окружности (см. рисунок
3.2, а), или же чтобы характеристика ![]() лежала вне окружности, пересекающей ось
абсцисс в точках
лежала вне окружности, пересекающей ось
абсцисс в точках ![]() и
и
![]() (см.
рисунок 3.2, б).
(см.
рисунок 3.2, б).
Рисунок 3.2 - Геометрическая интерпретация критерия абсолютной устойчивости процессов в нелинейной системе
3.2 Теоремы прямого метода Ляпунова и их применение
3.2.1 При изложении прямого метода Ляпунова будем пользоваться дифференциальными уравнениями автоматической системы в форме уравнений первого порядка, или уравнениями состояния, полагая, что они записаны для переходного процесса в отклонениях всех переменных от их значений в установившемся процессе при новых постоянных значениях возмущающего f = f0 и задающего g = g0 воздействий. Следовательно, эти уравнения для нелинейной системы n- го порядка будут:
![]()
![]() (3.12)
(3.12)
……………………
![]()
где
функции ![]() произвольны
и содержат любого вида нелинейности, но всегда удовлетворяют условию
произвольны
и содержат любого вида нелинейности, но всегда удовлетворяют условию
![]() при
при ![]() (3.13)
(3.13)
так как в установившимся состоянии все отклонения переменных величин и их производные равны нулю по самому определению понятия этих отклонений, то понадобятся в дальнейшем понятие о знакоопределенных, знакопостоянных и знакопеременных функциях.
Пусть имеется функция нескольких переменных ![]() Представим себе
n-мерное
фазовое пространство, в котором
Представим себе
n-мерное
фазовое пространство, в котором ![]() являются прямоугольными координатами
(это будут, в частности, фазовая плоскость при
n=2 и обычное
трехмерное пространство при n=3). Тогда в каждой точке указанного пространства
функция
являются прямоугольными координатами
(это будут, в частности, фазовая плоскость при
n=2 и обычное
трехмерное пространство при n=3). Тогда в каждой точке указанного пространства
функция ![]() будет
иметь некоторые определенные значения. Нам понадобятся в дальнейшем функции
будет
иметь некоторые определенные значения. Нам понадобятся в дальнейшем функции ![]() (
(![]() ), которые обращаются в нуль в
начале координат (т.е. при
), которые обращаются в нуль в
начале координат (т.е. при ![]() ) и непрерывны в некоторой области
вокруг него.
) и непрерывны в некоторой области
вокруг него.
Функция ![]() называется знакоопределенной некоторой
области, если она во всех точках этой области вокруг начала координат сохраняет
один и тот же знак и нигде не обращается в нуль, кроме только самого начала
координат.
называется знакоопределенной некоторой
области, если она во всех точках этой области вокруг начала координат сохраняет
один и тот же знак и нигде не обращается в нуль, кроме только самого начала
координат.
Функция ![]() называется знакопостоянной, если она
сохраняет один и тот же знак, но может обращаться в нуль не только в начале
координат, но и в других точках данной области.
называется знакопостоянной, если она
сохраняет один и тот же знак, но может обращаться в нуль не только в начале
координат, но и в других точках данной области.
Функция ![]() называется знакопеременной, если она в
данной области вокруг начала координат может иметь разные знаки.
называется знакопеременной, если она в
данной области вокруг начала координат может иметь разные знаки.
Приведем примеры всех трех типов функций ![]() . Пусть
n=2
и
. Пусть
n=2
и ![]() , это
будет знакоопределенная (положительная) функция, так как
, это
будет знакоопределенная (положительная) функция, так как ![]() только тогда, когда
одновременно
только тогда, когда
одновременно ![]() и
и
![]() , и
, и ![]() при всех
вещественных значениях
при всех
вещественных значениях ![]() и
и ![]() . Аналогично при любом
n
функция
. Аналогично при любом
n
функция ![]() будет
знакоопределенной положительной, а
будет
знакоопределенной положительной, а ![]() знакоопределенной
отрицательной (см. рисунок 3.3, а).
знакоопределенной
отрицательной (см. рисунок 3.3, а).
Если взять функцию ![]() при
n=3, то она
уже не будет знакоопределенной, так как, оставаясь положительной при любых
при
n=3, то она
уже не будет знакоопределенной, так как, оставаясь положительной при любых ![]() и
и ![]() , она может
обращаться в нуль не только при
, она может
обращаться в нуль не только при ![]() но также и при любом значении
но также и при любом значении ![]() , если
, если ![]() (т.е. на всей оси
(т.е. на всей оси ![]() , см. рисунок.3.3, б)
следовательно, это будет знакопостоянная (положительная) функция.
, см. рисунок.3.3, б)
следовательно, это будет знакопостоянная (положительная) функция.
Наконец, что в некоторых частных задачах нам
понадобится также же функция ![]() , которая обращается в нуль не в начале
координат, а на заданном конечном отрезке АВ (см. рисунок 3.3, в). Тогда
знакоопределенность функции
, которая обращается в нуль не в начале
координат, а на заданном конечном отрезке АВ (см. рисунок 3.3, в). Тогда
знакоопределенность функции ![]() будет обозначать ее неизменный знак и
не обращение в нуль в некоторой области вокруг этого отрезка.
будет обозначать ее неизменный знак и
не обращение в нуль в некоторой области вокруг этого отрезка.
Рисунок 3.3 - Графические примеры изображения знакоопределенной, знакопостоянной и знакопеременной функций
3.2.2 Функция Ляпунова и ее производная по времени. Любую функцию
![]() (3.14)
(3.14)
тождественно
обращающуюся в нуль при ![]() будем называть функцией Ляпунова, если
в ней в качестве величин
будем называть функцией Ляпунова, если
в ней в качестве величин ![]() взяты те отклонения переменных в
переходном процессе:
взяты те отклонения переменных в
переходном процессе:
![]() ,
, ![]()
в которых записываются уравнения (3.12) для этой системы.
Производная от функции Ляпунова (3.14) по времени будет
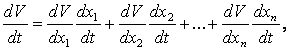 (3.15)
(3.15)
подставив
сюда значения ![]() из
заданных уравнений системы (3.12), получим производную от функции Ляпунова по
времени в виде:
из
заданных уравнений системы (3.12), получим производную от функции Ляпунова по
времени в виде:
![]() (3.16)
(3.16)
где ![]() - правые части уравнений (3.12),
представляющие собой заданные функции от отклонений
- правые части уравнений (3.12),
представляющие собой заданные функции от отклонений ![]() .
.
Следовательно, производная от функции Ляпунова по
времени так же, как и сама ![]() , является некоторой функцией
отклонений, т.е.
, является некоторой функцией
отклонений, т.е.
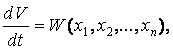 (3.17)
(3.17)
причем
согласно (3.14) эта функция W
так
же, как и сама ![]() , тождественно обращаются в нуль при
значениях
, тождественно обращаются в нуль при
значениях ![]() .
Поэтому к ней в одинаковой степени можно применять все те же понятия
знакоопределенности, знакопостоянства и знакопеременности в некоторой области
вокруг начала координат, о которых говорилось выше по отношению к функции
.
Поэтому к ней в одинаковой степени можно применять все те же понятия
знакоопределенности, знакопостоянства и знакопеременности в некоторой области
вокруг начала координат, о которых говорилось выше по отношению к функции ![]() .
.
Если же функция
W будет не знакоопределенной, а
знакопостоянной, то, очевидно, что траектория изображающей точки М
невезде будет пересекать поверхности ![]() , а может их касаться в тех точках, где
W
обращается в нуль (помимо начала координат). Но так как во всех других местах
фазового пространства функция W имеет один и тот же знак, вследствие чего
изображающая точка может идти только из вне внутрь поверхности
, а может их касаться в тех точках, где
W
обращается в нуль (помимо начала координат). Но так как во всех других местах
фазового пространства функция W имеет один и тот же знак, вследствие чего
изображающая точка может идти только из вне внутрь поверхности ![]() , то при решении
задачи остается только проверить, не «застрянет» ли изображающая точка там, где
W =0.
, то при решении
задачи остается только проверить, не «застрянет» ли изображающая точка там, где
W =0.
Вообще же метод Ляпунова может применяться и при наличии времени t в явном виде, в частности, для уравнений (линейных и нелинейных) с переменными коэффициентами.
Базируясь на этих предварительных сведениях, дадим общую формулировку теорем Ляпунова об устойчивости и неустойчивости нелинейных систем и покажем их справедливость. Теоремы эти годятся для исследования устойчивости систем регулирования не только при малых, но и при больших отклонениях, если для них справедливы исходные уравнения данной системы регулирования. Устойчивость системы при любых больших начальных отклонениях называется коротко устойчивостью в целом.
3.3.3 Теорема Ляпунова об устойчивости нелинейных
систем. Теорема формулируется следующим образом: если при заданных в форме (3.13)
уравнениях системы п-го порядка можно подобрать такую знакоопределенную
функцию Ляпунова ![]() ,
чтобы ее производная по времени
,
чтобы ее производная по времени ![]() тоже была знакоопределенной (или
знакопостоянной), но имела знак, противоположный знаку
V,
то данная система устойчива.
При
знакоопределенной функции W
будет
иметь место асимптотическая устойчивость.
тоже была знакоопределенной (или
знакопостоянной), но имела знак, противоположный знаку
V,
то данная система устойчива.
При
знакоопределенной функции W
будет
иметь место асимптотическая устойчивость.
Проиллюстрируем справедливость этой теоремы на наглядных геометрических образах. Для простоты возьмем систему третьего порядка (п = 3). Уравнения для нее в общем, можно записать следующим образом:
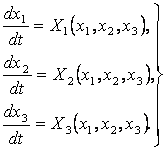 (3.18)
(3.18)
Возьмем знакоопределенную положительную функцию Ляпунова в виде:
![]() , (3.19)
, (3.19)
где а, b, с - произвольно заданные вещественные числа.
Будем придавать величине ![]() возрастающие постоянные значения:
V =
0,
возрастающие постоянные значения:
V =
0, ![]() что
означает:
что
означает:

первое
из этих выражений соответствует одной точке ![]() (началу координат фазового
пространства), а остальные - поверхностям эллипсоидов в фазовом пространстве,
причем каждый последующий эллипсоид содержит внутри себя целиком предыдущий (см.
рисунок 3.4).
(началу координат фазового
пространства), а остальные - поверхностям эллипсоидов в фазовом пространстве,
причем каждый последующий эллипсоид содержит внутри себя целиком предыдущий (см.
рисунок 3.4).
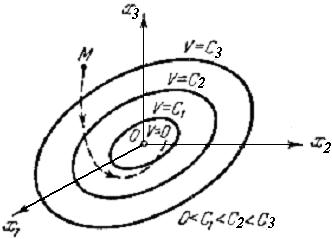
Рисунок 3.4 – Иллюстрация теоремы Ляпунова на наглядных геометрических образах
Возьмем теперь производную от функции Ляпунова по времени. Согласно (3.16) и (3.19)
![]()
где функции ![]() берутся из заданных уравнений системы
регулирования (3.18).
берутся из заданных уравнений системы
регулирования (3.18).
Если полученная таким путем функция W(x1, x2, xs) окажется знакоопределенной отрицательной, т.е. если
![]() (3.20)
(3.20)
во
всех точках исследуемого фазового пространства, кроме одного только начала
координат, где ![]()
![]() при
при ![]() ), то при любых
начальных условиях изображающая точка М (см. рисунок 3.4)
вследствие (3.20) будет двигаться в сторону уменьшения значения
F,
т. е. будет пересекать эллипсоиды, изображенные на рисунке 3.4, извне внутрь. В
результате с течением времени изображающая точка М будет стремиться к
началу координат 0 фазового пространства и уже никак не сможет выйти
за пределы тех эллипсоидов, в которые она проникла.
), то при любых
начальных условиях изображающая точка М (см. рисунок 3.4)
вследствие (3.20) будет двигаться в сторону уменьшения значения
F,
т. е. будет пересекать эллипсоиды, изображенные на рисунке 3.4, извне внутрь. В
результате с течением времени изображающая точка М будет стремиться к
началу координат 0 фазового пространства и уже никак не сможет выйти
за пределы тех эллипсоидов, в которые она проникла.
Это и означает затухание всех отклонений ![]() в переходном
процессе с течением времени. Таким образом, установлена устойчивость данной
системы регулирования, что иллюстрирует справедливость теоремы для системы
третьего порядка в случае знакоопределенной функции
W.
в переходном
процессе с течением времени. Таким образом, установлена устойчивость данной
системы регулирования, что иллюстрирует справедливость теоремы для системы
третьего порядка в случае знакоопределенной функции
W.
Отсюда вытекает справедливость теоремы и в общем
случае, рассуждения остаются аналогичными, только вместо трех уравнений (3.18)
будет п уравнений (3.12). Как и раньше, для любой знакоопределенной
положительной функции Ляпунова ![]() получим некоторые замкнутые
поверхности, окружающие начало координат (см. рисунок 3.4), но уже не в
обычном трехмерном, а в n
-
мерном фазовом пространстве. Поэтому, если производная
получим некоторые замкнутые
поверхности, окружающие начало координат (см. рисунок 3.4), но уже не в
обычном трехмерном, а в n
-
мерном фазовом пространстве. Поэтому, если производная ![]() окажется знакоопределенной
отрицательной, то траектория изображающей точки М в
n
- мерном
пространстве при любых начальных условиях с течением времени будет пересекать
указанные поверхности только извне внутрь, что и свидетельствует об устойчивости
данной системы.
окажется знакоопределенной
отрицательной, то траектория изображающей точки М в
n
- мерном
пространстве при любых начальных условиях с течением времени будет пересекать
указанные поверхности только извне внутрь, что и свидетельствует об устойчивости
данной системы.
3.3 Частотный критерий устойчивости Попова
Рассмотрим нелинейные системы, структурные схемы которых можно привести к виду, показанному на рисунке 3.5. В этой структурной схеме имеется безынерционный нелинейный элемент с характеристикой
![]() (3.21)
(3.21)
и
линейная часть с передаточной функцией
W (s),
имеющей статический коэффициент
передачи, равный единице, и импульсной переходной функцией ![]() . Все воздействия
приведены к одному входу и обозначены
. Все воздействия
приведены к одному входу и обозначены ![]() .
.
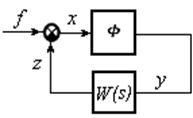
Рисунок 3.5 - Структурная схема системы с безынерционным нелинейным элементом
Изображение решения дифференциального уравнения
системы выразим через изображения воздействия
F (s)
и координаты ![]() :
:
![]() .
(3.22)
.
(3.22)
Переходя к оригиналам, получаем интегральное уравнение Вольтерра второго рода:
 . (3.23)
. (3.23)
Будем рассматривать систему при таких воздействиях,
которые ограничены по модулю и являются исчезающими функциями времени.
Обозначим максимальное воздействие ![]() (supremum).
(supremum).
Исчезающей функцией времени ![]() назовем функцию, стремящуюся
с течением времени к нулю:
назовем функцию, стремящуюся
с течением времени к нулю:
![]() .
.
Если воздействие отсутствует, то из (3.23) следует
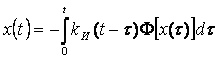 . (3.24)
. (3.24)
Если нелинейная характеристика проходит через начало координат, т. е. Ф(0)=0, то уравнение (3.24) имеет тривиальное решение:
![]() (3.25)
(3.25)
которое соответствует положению равновесия.
Положение равновесия устойчиво в смысле Ляпунова, если
существует такое положительное число ![]() , что при
, что при ![]()
имеет
место неравенство ![]() (3.26)
(3.26)
где А — сколь угодно малое положительное число.
В зависимости от того, при каких значениях ![]() выполняется
неравенство (3.26) будем различать три вида устойчивости: устойчивость в малом,
если
выполняется
неравенство (3.26) будем различать три вида устойчивости: устойчивость в малом,
если ![]() бесконечно
малая величина; устойчивость в большом, если
бесконечно
малая величина; устойчивость в большом, если ![]() - конечная величина, и устойчивость в
целом, если
- конечная величина, и устойчивость в
целом, если ![]() не
ограничено.
не
ограничено.
Изложим частотный метод определения устойчивости, предложенный В. М. Поповым [5], при использовании которого задача решается более просто приемами, аналогичными частотным способам исследования устойчивости линейных систем.
Если в системе автоматического регулирования имеется лишь одна однозначная нелинейность
![]() ,
(3.27)
,
(3.27)
то, объединив вместе все остальные (линейные) уравнения системы, можно всегда получить общее уравнение линейной части системы (см. рисунок 3.6, а) в виде:
![]() , (3.28)
, (3.28)
где ![]() ,
,
![]() ,
,
причем будем считать т < п.

Рисунок 3.6 - Система автоматического регулирования с однозначной нелинейностью
Пусть нелинейность y=F(x) имеет любое очертание, не выходящее за пределы заданного угла arctg k (см. рисунок 3.6, б), т. е. при любом х,
0< F(x)< kx. (3.29)
Пусть многочлен
Q(p),
или что
одно и то же, характеристическое уравнение линейной части
Q(p)=0, имеет все корни с отрицательными вещественными
частями или же, кроме них, имеется еще не более двух нулевых корней. Другими
словами, допускается, чтобы ![]() или
или ![]() и
и ![]() в выражении
Q(p),
т. е.
не более двух нулевых полюсов в передаточной функции линейной части
системы:
в выражении
Q(p),
т. е.
не более двух нулевых полюсов в передаточной функции линейной части
системы:
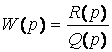 .
.
Приведем без доказательства формулировку теоремы
В.М.Попова: для установления устойчивости нелинейной системы достаточно
подобрать такое конечное действительное число
h, при
котором при всех ![]()
![]() , (3.30)
, (3.30)
где
![]() - амплитудно-фазовая частотная характеристика линейной
части системы.
- амплитудно-фазовая частотная характеристика линейной
части системы.
При наличии одного нулевого полюса требуется еще, чтобы
![]() при
при ![]() ,
,
а
при двух нулевых полюсах ![]() при
при ![]() , a
, a ![]() при малых
при малых ![]() .
.
Теорема справедлива также и при наличии в знаменателе Q(p) передаточной функции линейной части не более двух чисто мнимых корней, но при этом требуются некоторые другие простые добавочные условия [5], называемые условиями предельной устойчивости.
Другая формулировка той же теоремы, дающая удобную графическую
интерпретацию, связана с введением видоизмененной частотной характеристики ![]() , которая определяется
следующим образом:
, которая определяется
следующим образом:
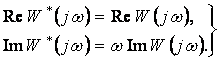
График ![]() имеет вид (см. рисунок 3.7, а),
аналогичный
имеет вид (см. рисунок 3.7, а),
аналогичный ![]() ,
когда в выражениях Q(p)
и R(p)
разность степеней п- т>1.
Если же разность степеней
,
когда в выражениях Q(p)
и R(p)
разность степеней п- т>1.
Если же разность степеней ![]() , то конец графика
, то конец графика ![]() будет на мнимой оси
ниже начала координат (см. рисунок 3.7, б).
будет на мнимой оси
ниже начала координат (см. рисунок 3.7, б).
Далее, выполнив соответствующие математические преобразования, рассмотрим следующую графическую интерпретацию теоремы В. М. Попова.
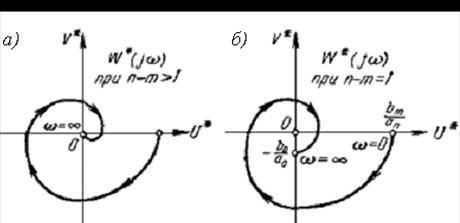
Рисунок 3.7 - Видоизмененные частотные характеристики ![]() к формулировке
теоремы В. М. Попова
к формулировке
теоремы В. М. Попова
Преобразуем левую часть неравенства (3.30):
![]() . (3.31)
. (3.31)
Тогда, положив
![]()
и использовав соотношение (3.31), получим вместо (3.30) для теоремы В. М. Попова условие:
![]() (3.32)
(3.32)
при
всех ![]() .
.
Очевидно, что равенство
![]() (3.33)
(3.33)
представляет
уравнение прямой на плоскости ![]() .
.
Отсюда вытекает следующая графическая интерпретация
теоремы В. М. Попова: для установления
устойчивости нелинейной системы достаточно подобрать такую прямую на плоскости ![]() , проходящую через
точку
, проходящую через
точку ![]() ,
чтобы вся кривая
,
чтобы вся кривая ![]() лежала
справа от этой прямой.
лежала
справа от этой прямой.
На рисунке 3.8 приведена графическая интерпретация теоремы В. М. Попова для установления устойчивости нелинейной системы. Как видно, рисунки 3.8, а и 3.8, б соответствуют устойчивым системам, а рисунки 3.8, в и 3.8, г – неустойчивым.
Рисунок 3.8 - Графическая интерпретация теоремы В. М. Попова для определения устойчивости нелинейной системы
4 Качество нелинейных систем автоматического управления
4.1 Оценка качества нелинейных систем автоматического управления
То обстоятельство, что вблизи границы устойчивости качество процесса регулирования ухудшается, дает основание полагать, что любой критерий устойчивости может послужить основой для выработки тех или иных оценок качества процесса.
Так, в линейных системах все критерии
устойчивости устанавливали неравенства, дающие условия нахождения всех корней
характеристического уравнения слева от мнимой оси. Когда мы конкретизировали
эти неравенства и потребовали, чтобы, кроме того, все корни были удалены от
мнимой оси не менее чем на величину ![]() , мы уже ввели простейшую оценку
качества – степень устойчивости. Однако в практике качество
оценивается по иным прямым показателям, поэтому потребовалось дополнительно
установить связь степени устойчивости с прямыми показателями качества.
, мы уже ввели простейшую оценку
качества – степень устойчивости. Однако в практике качество
оценивается по иным прямым показателям, поэтому потребовалось дополнительно
установить связь степени устойчивости с прямыми показателями качества.
С помощью критерия Попова понятие степени устойчивости может быть использовано и для оценки качества нелинейных систем, как это было указано Я.З. Цыпкиным [7,8].
Будем говорить, что нелинейная система
автоматического управления обладает затуханием или степенью устойчивости ![]() не меньше заданной,
если для отклонения координаты от положения равновесия при любых
t
остается справедливым неравенство:
не меньше заданной,
если для отклонения координаты от положения равновесия при любых
t
остается справедливым неравенство:
![]() , (4.1)
, (4.1)
где М = const.
Чтобы неравенство (4.1) могло иметь место при любых t, необходимо, чтобы
![]() .
.
Если данный предел будет равным нулю, т.
е. ![]() , это
будет означать, что
, это
будет означать, что ![]() стремится к нулю быстрее, чем
стремится к нулю быстрее, чем ![]() .
.
Составим интегральное уравнение
относительно функции ![]()
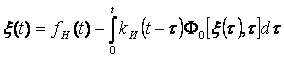 ,
(4.2)
,
(4.2)
где ![]() –
исчезающая функция времени, приложенная к системе в момент
t
= 0. В частности, это может быть реакция
линейной системы на возмущение начальных условий.
–
исчезающая функция времени, приложенная к системе в момент
t
= 0. В частности, это может быть реакция
линейной системы на возмущение начальных условий.
Умножим обе части (4.2) на ![]() , получим
, получим
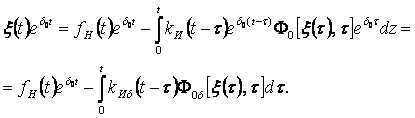 (4.3)
(4.3)
К уравнению (4.3) можно будет применить
критерий Попова, но только при условии, если мы накладываем дополнительное
ограничение на функцию ![]()
![]() . (4.4)
. (4.4)
Тем самым мы требуем, чтобы затухание
линеаризованной системы было большим, чем заданная нижняя граница затухания ![]() . Это обстоятельство
понятно. Оно аналогично условию, что для абсолютной устойчивости системы
необходимо, чтобы линеаризованная система была устойчивой.
. Это обстоятельство
понятно. Оно аналогично условию, что для абсолютной устойчивости системы
необходимо, чтобы линеаризованная система была устойчивой.
Если условие (4.4) выполняется, то в соответствии с критерием Попова система, описываемая уравнением (4.3), обладает абсолютно устойчивым положением равновесия, если
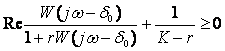 , (4.5)
, (4.5)
где 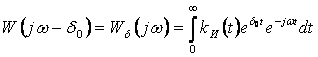
можно назвать смещенной частотной характеристикой системы.
Если критерий абсолютной
устойчивости преобразованной таким образом системы выполняется, то
![]() , и, следовательно, исходная система обладает затуханием не
меньше заданного
, и, следовательно, исходная система обладает затуханием не
меньше заданного ![]() .
.
В частном случае, когда разомкнутая линейная система
устойчива, мы можем, как это было показано ранее, положить ![]() и выражение (4.5) свести к
более простому виду
и выражение (4.5) свести к
более простому виду
![]() . (4.6)
. (4.6)
Наконец, если мы исследуем не затухание отклонения
процесса ![]() от
вынужденного, а затухание отклонения координаты от положения равновесия, то в
соответствии с критерием абсолютной устойчивости положения равновесия для того,
чтобы затухание отклонения было не меньше заданного
от
вынужденного, а затухание отклонения координаты от положения равновесия, то в
соответствии с критерием абсолютной устойчивости положения равновесия для того,
чтобы затухание отклонения было не меньше заданного ![]() , достаточно,
чтобы выполнялось следующее неравенство
, достаточно,
чтобы выполнялось следующее неравенство
![]() . (4.7)
. (4.7)
Перейдем к интегральным оценкам.
По аналогии с линейными системами для оценки качества нелинейной системы можно применить интегральную квадратичную оценку
 ,
(4.8)
,
(4.8)
где
![]() – выходная координата нелинейного элемента.
– выходная координата нелинейного элемента.
В общем виде определить или оценить величину интеграла J, по крайней мере при современном состоянии математики, не представляется возможным. Но если наложить некоторые ограничения на класс нелинейных функций Ф(х), то, как это было показано В. М. Поповым [5], оценка величины интеграла (4.8) становится возможной.
Дополнительное ограничение, налагаемое на функцию Ф(х), сводится к следующему.
Будем полагать, что рассматриваемый класс функций удовлетворяет условиям
![]() . (4.9)
. (4.9)
Кроме того, считаем, что касательная к кривой Ф (х),
проведенная из начала координат, имеет угловой коэффициент ![]() , меньший, чем
, меньший, чем ![]() (см. рисунок
4.1):
(см. рисунок
4.1):
![]()
и
что кривая Ф(х) лежит ниже касательной во всех точках, кроме точки
касания. Это означает, что характеристика Ф(х) не подходит
вплотную к границе запретного сектора ![]() и не стремится к ней асимптотически:
и не стремится к ней асимптотически:
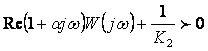 .
(4.10)
.
(4.10)
Имеется известный запас, поэтому должно удовлетворяться также неравенство
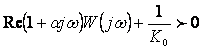 .
(4.11)
.
(4.11)
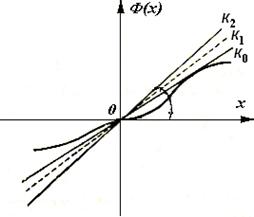
Рисунок 4.1 - Положение нелинейной функции Ф(х) при некоторых ограничениях
Используем для оценки
J величину ![]() , которая была введена
при выводе критерия Попова:
, которая была введена
при выводе критерия Попова:
 . (4.12)
. (4.12)
Исходим из того, что равновесие рассматриваемой
системы устойчиво, поэтому ![]() ; устремив
; устремив ![]() в (4.12) к
бесконечности, а
в (4.12) к
бесконечности, а ![]() –
к нулю, получаем
–
к нулю, получаем
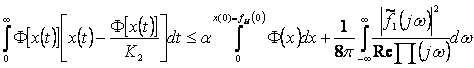 . (4.13)
. (4.13)
Рассмотрим левую часть неравенства (4.13):
 , (4.14)
, (4.14)
очевидно,
что, так как по нашему условию ![]() лежит ниже касательной (за
исключением точки касания), то
лежит ниже касательной (за
исключением точки касания), то
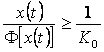 .
.
Заменяя ![]() в выражении (4.14) на меньшую
величину
в выражении (4.14) на меньшую
величину ![]() ,
усиливаем неравенство. Сделав эту подстановку, после некоторых преобразований
находим:
,
усиливаем неравенство. Сделав эту подстановку, после некоторых преобразований
находим:
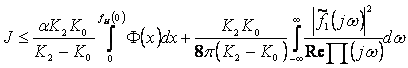 . (4.15)
. (4.15)
Выберем теперь промежуточный параметр ![]() , величина
которого заключена между
, величина
которого заключена между ![]() и
и ![]() (см. рисунок 4.1)
(см. рисунок 4.1)
![]() .
(4.16)
.
(4.16)
Заметим, что если мы во втором интеграле неравенства
(4.15) заменим величину ![]() на меньшую величину
на меньшую величину ![]() , то
неравенство усилится, (числитель уменьшится в меньшей степени, чем знаменатель).
, то
неравенство усилится, (числитель уменьшится в меньшей степени, чем знаменатель).
Поэтому
 (4.17)
(4.17)
конечно,
неравенство усилилось бы еще больше, если бы аналогичную замену ![]() на
на ![]() мы выполнили
бы и в первом слагаемом правой части, но такая замена для нас бесполезна,
поэтому мы ее делать не будем.
мы выполнили
бы и в первом слагаемом правой части, но такая замена для нас бесполезна,
поэтому мы ее делать не будем.
Теперь остается заменить сложное для вычисления оценки выражение функции Попова в знаменателе подынтегрального выражения второго слагаемого.
Функция Ф(х) принадлежит, на основе всего
сказанного выше, не только к классу А (0, К2), но и к
подклассам А (0, К1) и А (0, К0),
поэтому при выводе выражения ![]() мы могли бы везде ставить 1/К1
вместо 1/К2 и считать:
мы могли бы везде ставить 1/К1
вместо 1/К2 и считать:
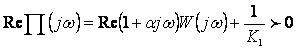 .
(4.18)
.
(4.18)
Вычтем и прибавим 1/К1 в правой части неравенства (4.18):
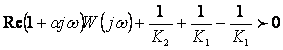 ,
,
или
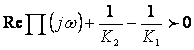 ,
,
 . (4.19)
. (4.19)
Заменив ![]() в (4.19) меньшей величиной (К2
- К1)/К1К2, усиливаем
неравенство:
в (4.19) меньшей величиной (К2
- К1)/К1К2, усиливаем
неравенство:
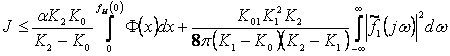 . (4.20)
. (4.20)
Величина оценки существенным образом зависит от параметра
![]() . При
. При ![]() или
или ![]() правая часть
неравенства обращается в бесконечность, и оценка теряет всякий смысл. Чтобы она
имела какое-то практическое значение, параметр
правая часть
неравенства обращается в бесконечность, и оценка теряет всякий смысл. Чтобы она
имела какое-то практическое значение, параметр ![]() надлежит выбрать так, чтобы
правая часть имела наименьшее значение. Определим значение
надлежит выбрать так, чтобы
правая часть имела наименьшее значение. Определим значение ![]() внутри полосы
внутри полосы ![]() ,
, ![]() так, чтобы правая
часть (4.20) стала минимальной.
так, чтобы правая
часть (4.20) стала минимальной.
Решая уравнение (4.20), находим:
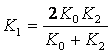 . (4.21)
. (4.21)
Подставив (4.21) в (4.19), окончательно получим:
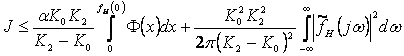 . (4.22)
. (4.22)
Таким образом, мы свели оценку интеграла
![]() к
выражению, которое может быть всегда определено путем интегрирования графика
функции Ф(х) в заданных пределах и вычисления интеграла:
к
выражению, которое может быть всегда определено путем интегрирования графика
функции Ф(х) в заданных пределах и вычисления интеграла:
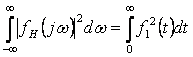 .
(4.23)
.
(4.23)
Так как ![]() – реакция
линейной части на возмущение начальных условий, этот интеграл вычисляется
методами, рассмотренными в линейной теории регулирования.
– реакция
линейной части на возмущение начальных условий, этот интеграл вычисляется
методами, рассмотренными в линейной теории регулирования.
Величину ![]() следует выбирать как можно
меньшей. В пределе это может быть угловой коэффициент касательной, проведенной
из точки
следует выбирать как можно
меньшей. В пределе это может быть угловой коэффициент касательной, проведенной
из точки 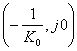 к
видоизмененной частотной характеристике системы.
к
видоизмененной частотной характеристике системы.
Оценка дает удовлетворительные результаты, если ![]() достаточно
отличается от
достаточно
отличается от ![]() .
Если эти величины оказываются близкими друг к другу, пользоваться оценкой
уже не имеет смысла.
.
Если эти величины оказываются близкими друг к другу, пользоваться оценкой
уже не имеет смысла.
4.2 Синтез корректирующих устройств нелинейных систем по логарифмическим частотным характеристикам
В предыдущих параграфах были рассмотрены условия, которым
должны удовлетворять частотные характеристики линейной части, чтобы выполнялись
условия абсолютной устойчивости или заданного показателя качества для замкнутой
нелинейной системы. Условия эти геометрически сводятся к установлению
запретной области, внутрь которой не должна входить амплитудно-фазовая
характеристика линейной системы. Если же в некотором интервале частот ![]() характеристика
характеристика ![]() вошла в
запретную зону и пересекла ее границу при частотах
вошла в
запретную зону и пересекла ее границу при частотах ![]() и
и ![]() , то в линейную часть системы
нужно ввести корректирующее звено с тем, чтобы в указанном интервале частот деформировать
характеристику и вывести ее из запретной
зоны.
, то в линейную часть системы
нужно ввести корректирующее звено с тем, чтобы в указанном интервале частот деформировать
характеристику и вывести ее из запретной
зоны.
Рассмотрим методы последовательной коррекции системы с целью обеспечить ее абсолютную устойчивость.
В [5] было показано, что если производная нелинейной характеристики заключена в пределах
![]()
то,
для того чтобы процессы в нелинейной системе были устойчивы, достаточно, чтобы частотная
амплитудно-фазовая характеристика ![]() линейной части системы не входила
внутрь А - окружности, где
линейной части системы не входила
внутрь А - окружности, где ![]() .
.
А - окружность, как это следует из выражения
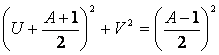 ,
,
пересекает
действительную ось в двух точках: правая точка ![]() , левая -
, левая - ![]() . Сопоставим это с Р -
окружностью, которая используется для построения ординат вещественной частотной
характеристики замкнутой системы по амплитудно-фазовой характеристике
разомкнутой системы [5]. Р - окружность пересекает
действительную ось в точках
. Сопоставим это с Р -
окружностью, которая используется для построения ординат вещественной частотной
характеристики замкнутой системы по амплитудно-фазовой характеристике
разомкнутой системы [5]. Р - окружность пересекает
действительную ось в точках ![]() и
и ![]() .
.
Таким образом, мы можем воспользоваться диаграммами Р - окружностей, если пересчитаем индекс окружности, поставив условием совпадение точек пересечения окружностей с осью. Одна пара из этих точек совпадает, остается выполнить условие совпадения другой пары точек:
![]() или
или ![]() , (4.24)
, (4.24)
откуда
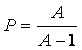 . (4.25)
. (4.25)
Для синтеза корректирующих устройств удобнее
пользоваться логарифмическими частотными характеристиками, поэтому вместо А
- окружностей в плоскости ![]() , необходимо отобразить А -
окружности на плоскость координат
, необходимо отобразить А -
окружности на плоскость координат ![]() и
и ![]() . Аналогичные отображения, построенные
В. В. Солодовниковым, приводятся во всех курсах автоматического регулирования,
и мы можем воспользоваться этими кривыми, пересчитав их индексы по формуле (4.25).
. Аналогичные отображения, построенные
В. В. Солодовниковым, приводятся во всех курсах автоматического регулирования,
и мы можем воспользоваться этими кривыми, пересчитав их индексы по формуле (4.25).
Ранее было показано, что значение индекса Р связано
со значениями ![]() и
и
![]() следующей
зависимостью:
следующей
зависимостью:
![]() . (4.26)
. (4.26)
Воспользовавшись формулой (14.26), можем без труда пересчитать эту зависимость для индекса А – окружности:
![]() ,
,
откуда 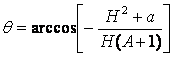 , (4.27)
, (4.27)
а,
в частности, для ![]()
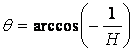 .
(4.28)
.
(4.28)
Пусть нам задано граничное значение 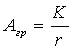 и построена А -
кривая в плоскости
и построена А -
кривая в плоскости ![]() ,
,
![]() (см. рисунок
4.2, а). Амплитудно-фазовая характеристика, пересчитанная к этим
осям, т. е. кривая
(см. рисунок
4.2, а). Амплитудно-фазовая характеристика, пересчитанная к этим
осям, т. е. кривая ![]() , пересекает А - кривую
в точках, соответствующих
, пересекает А - кривую
в точках, соответствующих ![]() и
и ![]() , и в интервале
, и в интервале ![]() входит в запретную область.
Соответствующие ей логарифмические амплитудная и фазовая характеристики показаны
на рисунке 4.2, б сплошной линией.
входит в запретную область.
Соответствующие ей логарифмические амплитудная и фазовая характеристики показаны
на рисунке 4.2, б сплошной линией.
Рисунок 4.2 - Синтез корректирующих устройств нелинейных систем по логарифмическим частотным характеристикам
Чтобы достаточные условия устойчивости не нарушились,
можем потребовать, чтобы вне интервала ![]() логарифмические частотные
характеристики линейной части или совпадали с характеристикой
логарифмические частотные
характеристики линейной части или совпадали с характеристикой ![]() , или шли ниже их, а
внутри интервала совпадали бы с граничной А - кривой или шли ниже ее.
, или шли ниже их, а
внутри интервала совпадали бы с граничной А - кривой или шли ниже ее.
Задавшись произвольно несколькими точками на А -
кривой, соответствующими значениям ![]() переносим эти точки на логарифмические характеристики и, соединяя их плавной
кривой, получаем деформацию ЛАХ и ЛФХ, обеспечивающую соблюдение достаточных
условий абсолютной устойчивости.
переносим эти точки на логарифмические характеристики и, соединяя их плавной
кривой, получаем деформацию ЛАХ и ЛФХ, обеспечивающую соблюдение достаточных
условий абсолютной устойчивости.
Граничная допустимая амплитудно-фазовая характеристика на рисунке 4.2, а отмечена штриховкой, а на рисунке 4.2, б заштрихованы области, внутри которых должны лежать скорректированные логарифмические характеристики. При последовательной коррекции, поскольку ЛАХ скорректированной системы лежит ниже криволинейного сектора, равного разности между новым и старым значениями ЛАХ (прерывистая линия на рисунке 4.2, б), ЛАХ корректирующего звена может, например, представлять собой трапецию.
После того, как определена передаточная функция скорректированной системы, необходимо проверить, обеспечивается ли нахождение фазовой характеристики скорректированной системы в заштрихованной области.
Аналогичный метод коррекции можно применить
и в том случае, если требуется обеспечить выполнение условия, чтобы степень
устойчивости нелинейной системы была не меньше заданной ![]() . А - кривую в
плоскости
. А - кривую в
плоскости ![]() ,
,
![]() при этом
наносим таким же способом, но вместо логарифмических характеристик исходной
системы
при этом
наносим таким же способом, но вместо логарифмических характеристик исходной
системы ![]() строим
логарифмические характеристики для смещенной амплитудно-фазовой характеристики
строим
логарифмические характеристики для смещенной амплитудно-фазовой характеристики ![]() .
.
Более детально метод синтеза корректирующих устройств нелинейных систем по логарифмическим частотным характеристикам, базирующийся на критерии В. М. Попова, рассмотрен в [5].
5 Цифровые системы автоматического управления электроприводом
5.1 Принципы построения цифровых систем автоматического управления
Цифровые системы регулирования – это такие системы, в которых информация о переменных преобразуется в цифровой код [9,10,11].
В настоящее время цифровые системы создают на базе микропроцессоров, реализующих в цифровой форме функции регулятора и информационно-преобразовательного устройства.
Обычно в системах управления электроприводами обеспечивается контроль координат электропривода (ЭП), например, скорости, и контроль состояния объекта управления - ОУ (исполнительного органа рабочей машины ИОРМ), например, его положения, осуществляемое с помощью датчиков ДСЭП и ДСОУ (рисунок 5.1). Применение в таких системах цифровых задающих устройств (ЗУ) с цифроаналоговыми преобразователями цифрового сигнала в аналоговый (ЦАП) повышает точность задающих воздействий и позволяет осуществить их точную индикацию (см. рисунок 5.1, а). Использование цифровых устройств задания ЗУ, обратной связи ДСОУ и сравнения УС с ЦАП (см. рисунок 5.1, б) повышает точность регулирования в целом. При этом в цифровых системах появилась возможность использования точных цифровых регуляторов ЦР с аналоговой системой управления электропривода (см. рисунок 5.1, в) с аналоговым регулятором АР или с полностью цифровой (см. рисунок 5.1, г).
Как было отмечено ранее, разделение устройств на цифровые и аналоговые связано с формой представления информации, обрабатываемой этими устройствами, и соответствующей аппаратурой для реализации этих устройств. Аналоговая форма представления переменных характеризуется пропорциональностью их различным физическим величинам – напряжению, току, скорости, частоте, углу поворота вала и т. п. Цифровая (числовая) форма представления – обозначение величины цифровым кодом числа с использованием только двух чисел 1 и 0 (двоичный код).
а – с цифровым заданием; б – с цифровым заданием и контролем положения; в – с цифровым управлением положения; г – с цифровым управлением положения и скорости.
Рисунок 5.1 - Цифроаналоговые системы управления электроприводом
При цифровом представлении сигнала фиксируется уровень аналогового сигнала на определенном дискретном промежутке времени или уровне сигнала. Тогда непрерывная функция аналогового сигнала аппроксимируется ступенчатой функцией, представляющей собой последовательность значений непрерывной функции в дискретном ряде точек. Эта операция называется квантованием сигнала [10,11]. Если дискретность осуществляется по времени через равные промежутки времени Т0, то такое квантование называется квантованием по времени (см. рисунок 5.2, а), а если по уровню выходного сигнала, через равные значения q (см. рисунок 5.3, а), то – квантованием по уровню. Интервалы Т0 и q называют шагом квантования.
При квантовании по времени непрерывный сигнал (см. рисунок 5.2, а) заменяется решетчатой функцией (см. рисунок 5.2, б):
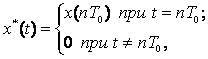 (5.1)
(5.1)
где Т0 – период дискретности.
Эта операция осуществляется импульсным элементом дискретизатором, условное обозначение которого показано на рисунке 5.2, в. Обычно дискретизатором является модулятор, который модулирует последовательность импульсов с периодом дискретности Т0 непрерывным входным сигналом по амплитуде импульсов (см. рисунок 5.2, г, амплитудно-импульсная модуляция – АИМ), по длительности, т. е. по ширине импульсов (см. рисунок 5.2, д, широтно-импульсная модуляция – ШИМ). Применяются также модуляции по частоте следования импульсов – частотно-импульсная модуляция (ЧИМ) и по фазе импульсов фазоимпульсная модуляция (ФИМ).
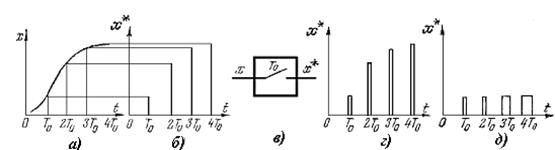
а – непрерывная функция; б – решетчатая функция; в – условное обозначение импульсного элемента; г – амплитудно-импульсная модуляция; д – широтно-импульсная модуляция.
Рисунок 5.2 - Дискретизация величин по времени
В результате дискретизации с частотой квантования ![]() о=2
о=2![]() /То=2
/То=2![]() fо
дискретная
функция
fо
дискретная
функция
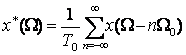 , (5.2)
, (5.2)
записанная при х(0)=0, содержит полезный сигнал
при частоте ![]() о,
полученный из (5.2) при п=0, и боковые высоко-частотные гармоники,
сдвинутые влево и вправо от пТ0 на частоту, кратную основной
частоте, появление которых вызвано потерей информации в интервале между
моментами дискретизации.
о,
полученный из (5.2) при п=0, и боковые высоко-частотные гармоники,
сдвинутые влево и вправо от пТ0 на частоту, кратную основной
частоте, появление которых вызвано потерей информации в интервале между
моментами дискретизации.
В цифровых устройствах большее использование находит квантование по уровню, при котором непрерывная функция заменяется дискретной, определяемой по времени на интервалах кванта (см. рисунок 5.3, а). В этом случае непрерывный сигнал представляется в виде его цифрового значения:
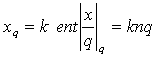 ,
(5.3)
,
(5.3)
где k – крутизна характеристики квантователя (см. рисунок 5.3) которая равна k = 1;
ent – целая часть;
n = 0, ±1, ±2,… – номер интервала шкалы квантователя.
Квантование по уровню осуществляется с погрешностью, равной разности между выходным хq и входным х сигналами
![]() ,
(5.4)
,
(5.4)
показанной на рисунке 5.3, а.
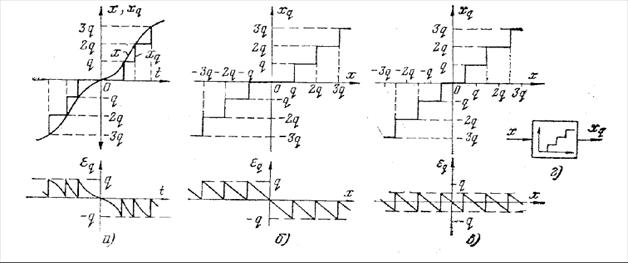
а – замена непрерывной функции дискретной при квантовании по уровню; б, в – статические характеристики квантователей и соответствующие им погрешности квантования; г – условное обозначение квантователя.
Рисунок 5.3 - Квантование величин по уровню
Модуль погрешности зависит от вида характеристики
квантователя и равен ![]() q и
q и
![]() q/2 соответственно для характеристик, приведенных на
рисунках 5.3, б и 5.3, в. Условное изображение
квантователя как аналого-цифрового преобразователя (АЦП) показано на
рисунке 5.3, г.
q/2 соответственно для характеристик, приведенных на
рисунках 5.3, б и 5.3, в. Условное изображение
квантователя как аналого-цифрового преобразователя (АЦП) показано на
рисунке 5.3, г.
Преобразование дискретизированных сигналов в
аналоговые при квантовании по времени называется демодуляцией, а восстановление
огибающей решетчатой функции – интерполяцией. Такие преобразования осуществляют
устройства, называемые демодуляторами или интерполяторами. Они являются
фильтрами нижних частот. Их условное изображение приведено на рисунке 5.4, а.
Дискретизация осуществляется с частотой дискретизации ![]() 0 согласно
теореме Котельникова [10,11], непрерывная функция х(t) полностью определяется своими ординатами, заданными
во временной области для последовательных моментов времени, следующих через Тс
, если функция х(t) не содержит частот выше 0,5 Тс.
Отсюда следует, что частота дискретизации должна быть
0 согласно
теореме Котельникова [10,11], непрерывная функция х(t) полностью определяется своими ординатами, заданными
во временной области для последовательных моментов времени, следующих через Тс
, если функция х(t) не содержит частот выше 0,5 Тс.
Отсюда следует, что частота дискретизации должна быть
![]() ,
(5.5)
,
(5.5)
где –![]() =2
=2![]() / Тс =2
/ Тс =2![]() f0
наибольшая частота спектра функции
х(t).
f0
наибольшая частота спектра функции
х(t).
В системах управления электроприводами наибольшее
распространение получили простейшие интерполяторы нулевого порядка, которые
фиксируют значение дискретного сигнала в момент дискретизации на весь период
дискретности и преобразуют решетчатую функцию в кусочно-постоянную (см. рисунок
5.4, в). Это преобразование происходит с погрешностью интерполяции ![]() = = х=
– х, которая может быть уменьшена
= = х=
– х, которая может быть уменьшена
при использовании сложных интерполяторов более высоких порядков.
Преобразование цифровой информации в аналоговую при квантовании сигналов по уровню выполняется цифроаналоговым преобразователем (ЦАП), условное обозначение которого показано на рисунке 5.4, б. ЦАП осуществляет линейное цифроаналоговое преобразование цифрового сигнала хq в цифроаналоговую величину xц,а. Фактически величина xц,а не является аналоговой, а в статическом режиме имеет вид исходной кусочно-постоянной квантованной функции хq, показанной ранее на рисунке 5.3, а.
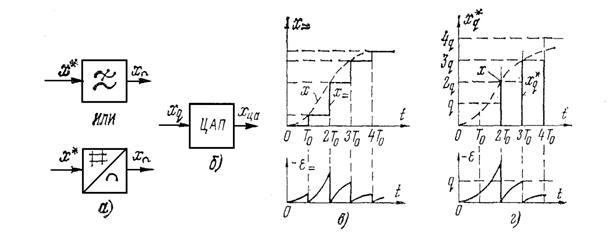
а – условное обозначение фильтра нижних частот – интерполятора; б – условное обозначение цифроаналогового преобразователя; в – восстановление огибающей решетчатой функции и ее погрешность; г – квантованная по уровню решетчатая функция и погрешность восстановления ее интерполятором.
Рисунок 5.4 - Интерполяция величин
В цифроаналоговых устройствах и системах управления электроприводами дискретные величины могут представляться как в аналоговой форме х*(t) (см. рисунок 5.2, б), так и в цифровой х*q(t), в виде решетчатой функции, квантованной по уровню с погрешностью e =хq - х, (см. рисунок 5.4, г). В первом случае устройства называют импульсными, а во втором – импульсно-кодовыми.
5.2 Цифровые системы стабилизации скорости
Более точная система регулирования скорости электропривода получается при наличии цифрового регулятора. Функциональная схема системы приведена на рисунке 5.5. В такой системе электропривода задание скорости вводится в форме числа NЗС с помощью устройства ввода задания SZ. с использованием цифрового задатчика интенсивности SJZ, обеспечивающего требуемый темп нарастания сигнала задания скорости N’ЗС(nT0) и соответственно скорости двигателя. Сигнал обратной связи по скорости обеспечивается импульсным датчиком скорости ВRZ. Импульсы датчика скорости подсчитываются счетчиком РС за фиксированный дискретный интервал времени Т0, определяемый частотой дискретизации f0 цифровой системы (Т0=1/f0). Частота дискретизации задается от выcокостабильного кварцевого генератора эталонной частоты GZ через делитель частоты АZ (f0=fЭ/kд). Текущая скорость электродвигателя в момент времени t=пТ0 пропорциональна числу подсчитанных импульсов:
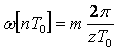 , (5.6)
, (5.6)
где m – число импульсов датчика скорости за интервал времени [(п-1)Т0 – пТ0];
z – число импульсов датчика за один оборот его вала.
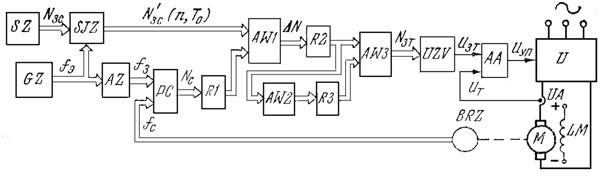
Рисунок 5.5 - Функциональная схема цифровой системы стабилизации скорости электропривода
На выходе счетчика РС по истечении интервала времени получается число Nc[пТ0] как цифровой сигнал обратной связи по скорости. Это число запоминается в регистре R1 до начала следующего периода [пТ0 - (n +1)Т0] и затем сравнивается в сумматоре АW1 с числом задания скорости NЗС . На выходе АW1 получается разница в виде числового сигнала управления:
![]() , (5.7)
, (5.7)
которое запоминается в регистре R2
и далее через сумматор
AW3 подается в ЦАП
UZV, если
в системе используется пропорциональный регулятор скорости, работающий по
алгоритму:
![]() ,
(5.8)
,
(5.8)
где k1 – масштабный коэффициент.
Если в системе используется ПИ-регулятор скорости, работающий по алгоритму
![]() , (5.9)
, (5.9)
то в цифровой части применяются дополнительно сумматор
AW2
и регистр R3.
Интегральная составляющая получается
посредством последовательного алгебраического суммирования текущих значений
отклонения скорости ![]() [пТ0] в накапливающем
сумматоре AW2
и
последующего запоминания результата в регистре
R3.
[пТ0] в накапливающем
сумматоре AW2
и
последующего запоминания результата в регистре
R3.
Аналоговая часть схемы включает силовой преобразователь U и двигатель М, а также контур тока с аналоговым сумматором АА и датчиком тока UА.
Цифровой регулятор скорости и другие цифровые устройства реализуются на базе стандартных блоков, выпускаемых промышленностью [9]. Реализация этих устройств упрощается, если управление электроприводом производится от ЭВМ, в которую заложена соответствующая программа [12].
В последнее время разрабатываются системы регулирования скорости с управлением тиристорным преобразователем в электроприводах постоянного тока или преобразователем частоты в электроприводах переменного тока непосредственно от ЭВМ без системы импульсно-фазового управления (СИФУ), которое назвали прямым управлением. В таких системах аналоговой частью системы является только силовая часть – „выпрямитель – двигатель” или преобразователем частоты – асинхронный двигатель, а контуры тока и скорости – цифровые. «Прямое» управление обеспечивает ЭВМ, которая также выполняет функции СИФУ, т. е. формирует и в требуемые моменты времени подает импульсы управления на тиристоры выпрямителя. Работа цифровых регуляторов скорости и тока обеспечивается в ЭВМ программными способами.
5.3 Цифровые системы управления положением
позиционного электропривода
При автоматизации механизмов, основным рабочим движением которых является угловое или линейное перемещение исполнительного органа и его остановка в требуемых положениях, широкое распространение получил позиционный электропривод с системами управления положением. Автоматическое управление положением бывает двух видов [10,11]:
а) дискретное позиционирование электропривода в заданных точках пути по дискретным сигналам путевых датчиков;
б) непрерывное автоматическое управление положением по отклонению для осуществления дозированных перемещений или по заданной программе.
Независимо от способа управления электропривод обеспечивает дискретное или непрерывное задание позиции или значения перемещения; контроль перемещения в позиции, определяемый требуемой точностью останова исполнительного органа и производительностью рабочей машины, зависящей от скорости перемещения в заданную позицию; точный останов в заданной позиции.
При дискретном позиционировании задается определенное конечное положение движения исполнительного органа. Контроль этого положения осуществляют дискретные датчики положения – контактные и бесконтактные конечные или путевые выключатели с погрешностью срабатывания 1– 0,01 мм. В этом случае обычно используются разомкнутые системы управления электроприводом, обеспечивающие остановку электродвигателя в заданной позиции с наложением механического тормоза. Такой вид управления применяется при невысокой точности позиционирования с редко переналаживаемым циклом перемещений.
При непрерывном управлении положением контроль положения исполнительного органа производится непрерывно в течение всего перемещения до остановки в заданном положении. С этой целью используют непрерывные аналоговые или цифровые датчики перемещения, характеризуемые высокой точностью (до 0,001 мм). В этом случае применяют замкнутые системы электропривода. Такой вид управления целесообразен в системах позиционирования высокой точности с часто переналаживаемым циклом перемещений. Точные системы позиционирования строятся по принципам подчиненного регулирования с двигателями постоянного тока, причем к внутренним контурам тока и скорости добавляется аналоговый или цифровой контур положения.
В настоящее время разрабатываются системы позиционного электропривода с ЭВМ [12], осуществляющие цифровое управление положением. Функциональная схема такой системы приведена на рисунке 5.6.
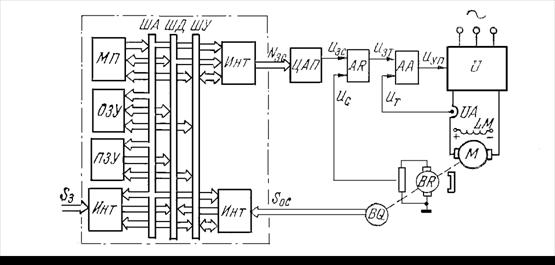
Рисунок 5.6 - Функциональная схема цифровой системы управления положением с микро-ЭВМ
Формирование графиков скорости и тока электропривода обеспечивается аналоговыми контурами скорости и тока. Контур положения, отрабатывающий заданное линейное перемещение S, выполняется программным способом, осуществляемым с микро-ЭВМ. Микро-ЭВМ содержит микропроцессор МП, оперативное ОЗУ и постоянное П3У, запоминающие устройства, интерфейсы входов и выходов ИнТ и шины данных ШД, адреса ША и управления ШУ. Связь микро-ЭВМ с аналоговой частью электропривода, которая содержит аналоговый регулятор AR и сумматор АА, осуществляется через ЦАП.
Программным способом с помощью микро-ЭВМ можно реализовать
регулятор положения РП любого типа П, ПИ параболический. Наиболее сложным
является РП с линейно параболической характеристикой (см. рисунок
5.7). Эта характеристика кодируется в числовом коде и записывается в ОЗУ
в виде таблицы соответствия цифрового задания скорости
NЗС и приращения
перемещения ![]() S=Sз-Sос. В примере,
поясняющем принцип действия системы, кодирование
NЗС и
S=Sз-Sос. В примере,
поясняющем принцип действия системы, кодирование
NЗС и
![]() S
выполнено с помощью четырех разрядов
двоичного кода. При этом получается большая погрешность записи
NЗС* по сравнению с
требуемой NЗС.
Реально в микро-ЭВМ используются
восемь разрядов двоичного кода и кодируется 28 = 256 точек,
обеспечивающих достаточную точность воспроизведения зависимости
NЗС=f(
S
выполнено с помощью четырех разрядов
двоичного кода. При этом получается большая погрешность записи
NЗС* по сравнению с
требуемой NЗС.
Реально в микро-ЭВМ используются
восемь разрядов двоичного кода и кодируется 28 = 256 точек,
обеспечивающих достаточную точность воспроизведения зависимости
NЗС=f(![]() S). Работа контура положения строится по алгоритму,
показанному на рисунке 5.8.
S). Работа контура положения строится по алгоритму,
показанному на рисунке 5.8.
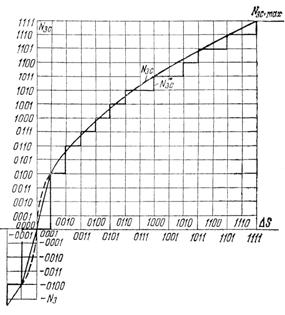
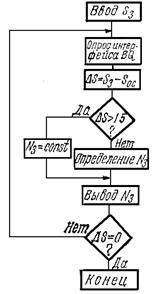
Рисунок 5.7 - Характеристика регулятора Рисунок 5.8 - Алгоритм работы положения контура положения
Задание на движение
Sз
записывается в ПЗУ, и микро-ЭВМ сравнивает
значения SЗ и
SОС и вырабатывает рассогласование![]() S,
согласно которому определяет
NЗС по характеристике
РП, записанной в ОЗУ. В начале движения, когда
Sос мало,
S,
согласно которому определяет
NЗС по характеристике
РП, записанной в ОЗУ. В начале движения, когда
Sос мало,
![]() S
имеет большое значение и микро-ЭВМ выдает
NЗС
мах, чему соответствует
UЗC мах, и электропривод обеспечивает максимальную скорость.
Когда
S
имеет большое значение и микро-ЭВМ выдает
NЗС
мах, чему соответствует
UЗC мах, и электропривод обеспечивает максимальную скорость.
Когда ![]() S
станет меньше значения 1111, микро-ЭВМ начнет уменьшать
NЗС и
UЗC и скорость перемещения будет снижаться. В конце
перемещения, когда Sос =
Sз
и
S
станет меньше значения 1111, микро-ЭВМ начнет уменьшать
NЗС и
UЗC и скорость перемещения будет снижаться. В конце
перемещения, когда Sос =
Sз
и ![]() S=0, то
NЗС = 0 и
UЗC =0
и двигатель остановится, отработав
заданное перемещение. Если возникает перерегулирование, то
S=0, то
NЗС = 0 и
UЗC =0
и двигатель остановится, отработав
заданное перемещение. Если возникает перерегулирование, то
![]() S
получит отрицательное значение, что обеспечит NЗС
и -UЗC, двигатель реверсируется и приближает ИОРМ к
заданному положению.
S
получит отрицательное значение, что обеспечит NЗС
и -UЗC, двигатель реверсируется и приближает ИОРМ к
заданному положению.
5.4 Цифровые системы управления следящего электропривода и основные принципы их построения
Система управления следящего электропривода (СУ СЭП) – это замкнутая динамическая система, которая получает на вход переменную, произвольно меняющуюся во времени, и обеспечивает ее отработку на выходе таким образом, чтобы погрешность слежения не превышала допустимых (заданных) значений. Следящие электроприводы производственных механизмов подразделяются по назначению на электроприводы со слежением по угловому или линейному перемещениям ИОРМ, по исполнению – на электрические с двигателями постоянного и переменного тока, по системе управления – на системы с суммирующим усилителем и с подчиненным регулированием координат, по принципу действия – на аналоговые, дискретные (релейные и импульсные) и цифровые системы [11,13].
По своему действию СУ СЭП является астатической, обеспечивающей полную отработку управляющего воздействия с небольшой погрешностью, определяемой возмущающими воздействиями и параметрами системы. Точность работы СУ СЭП при управлении оценивают по точности воспроизведения задающего сигнала, который при исследованиях изменяют с постоянной скоростью, с постоянным ускорением или по гармоническому закону.
В качестве измерительных устройств в СУ СЭП используются потенциометры, сельсины и синусно-косинусные вращающиеся трансформаторы (СКВТ), имеющие погрешность отработки рассогласования у потенциометров 0,2 – 0,6%, у сельсинов 0,25 – 1o и поворотных трансформаторов – единицы угловых минут, а также цифровые датчики линейных и угловых перемещений.
Исполнительным устройством в СУ СЭП являются тиристорные и транзисторные электроприводы постоянного и переменного тока. В электроприводах постоянного тока широкое применение находят высокомоментные двигатели серий ДПМ и ПБВ [13], обеспечивающие высокое быстродействие за счет малых индуктивностей обмоток и моментов инерции якоря, а также за счет обеспечения высоких пусковых моментов, превышающих номинальные значения до восьмикратных.
Питание следящих электроприводов осуществляется от индивидуальных источников постоянного тока и от промышленных сетей переменного тока с частотой 50 Гц. Маломощные электроприводы питаются от источников с частотой 400 Гц. Измерительные и преобразующие устройства, а также промежуточные усилители, питаются преимущественно от источников переменного тока с частотой 400 Гц. Это уменьшает габариты и снижает инерционности этих устройств.
В общем виде цифровая СУ СЭП может быть представлена структурной схемой, приведенной на рисунке 5.9.
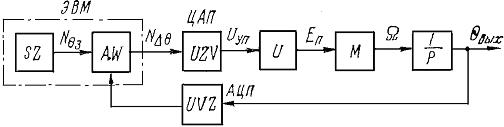
Рисунок 5.9 - Структурная схема цифровой СУ СЭП
Управление положением осуществляется от ЭВМ. Она
задает алгоритм управления и контролирует его отработку. Задание осуществляется
в цифровом коде NӨЗ
с помощью устройства ввода задания SZ. Сигнал обратной связи по
положению обеспечивается также в цифровом коде
NӨвых, получаемый
с помощью
АЦП
UVZ. АЦП осуществляет квантование непрерывной величины по
уровню и времени и обеспечивает кодирование, т.е. преобразование аналоговых
сигналов в цифровые. Сравнивающее устройство АW
от ЭВМ производит сравнивание цифровых сигналов задания и обратной связи и
вырабатывает цифровой сигнал управления ![]() . Далее этот цифровой сигнал
декодируется в ЦАП и превращается в аналоговый сигнал задания скорости
UУП,
управляющий электроприводом; если ЭВМ обеспечивает
регулирование скорости и тока в цифровом виде, то осуществляется прямое
управление электроприводом.
. Далее этот цифровой сигнал
декодируется в ЦАП и превращается в аналоговый сигнал задания скорости
UУП,
управляющий электроприводом; если ЭВМ обеспечивает
регулирование скорости и тока в цифровом виде, то осуществляется прямое
управление электроприводом.
Возможности используемой цифровой техники определяют основные достоинства цифровых СУ СЭП: высокие точность и помехозащищенность, реализацию сложных алгоритмов управления с помощью ЭВМ и организацию цифровой индикации работы электропривода.
Цифроаналоговые СУ СЭП позволяют получить высокую статическую точность регулирования (погрешность 0,01 — 0,001%), присущую цифровым устройствам, и хорошие динамические показатели, т.е. высокое быстродействие с хорошим качеством переходного процесса, обеспечиваемые аналоговой частью системы. Статическая точность цифровых систем определяется шагом квантования по времени, минимальное значение которого ограничено точностью измерения параметра регулирования и точностью преобразования его значений в цифровую форму.
Применение цифровых систем быстро увеличивается в связи с развитием ЭВМ и созданием микро-ЭВМ и микропроцессоров [11,12,14].
5.5 Системы программного управления электроприводами, принципы их построения и классификация
5.5.1 Системами программного управления (СПУ) являются системы автоматического управления рабочей машиной или ее отдельным исполнительным органом — объектом управления (ОУ), осуществляющие управления в соответствии с заданной управляющей программой [9,10,11,15].
Обобщенная структурная схема СПУ приведена на рисунке 5.10. Она включает в себя программное (ПУ), управляющее (УУ) и исполнительное (ИУ) устройства, объект управления (ОУ) и обратную связь (ОС). ПУ содержит программоноситель (ПН), вводное (ВУ) и считывающее (СУ) устройства. ПН, в качестве которого используются перфоленты, магнитные ленты, дискеты и диски, штекерные и другие матрицы или ЭВМ, хранит информацию задания или чертежа, введенную в него программистом или ЭВМ в виде управляющей программы. ВУ вводит информацию управляющей программы в управляющее устройство с помощью СУ, если она записана на ПН или непосредственно от ЭВМ. УУ корректирует потоки информации управляющей программы в соответствии с информацией обратной связи или других источников информации, например, интерполяторов, производит требуемые математические операции и вырабатывает управляющие воздействия на исполнительные элементы – электроприводы.
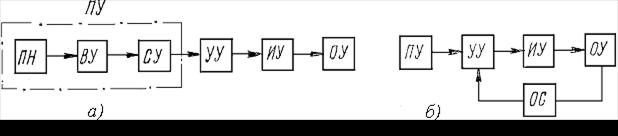
а – разомкнутая; б – замкнутая.
Рисунок 5.10 - Структурная схема системы программного управления
В СПУ применяются быстродействующие регулируемые и следящие электроприводы постоянного и переменного тока, которые приводят в движение объект управления в соответствии с информацией управляющей программы. Обратную связь осуществляют датчики обратной связи, вырабатывающие поток информации о фактическом положении ИОРМ, которая может определяться непосредственно при установке на исполнительном органе или косвенно при установке датчика на валу электрического двигателя электропривода.
Программное управление используется во всех отраслях промышленности, но особенно широкое распространение получило в металлообрабатывающей промышленности, где оно позволяет изготовлять изделия сложной формы с высокой точностью и производительностью без непосредственного участия человека.
СПУ классифицируется следующим образом: по принципу задания программы; по принципу управления; по принципу действия; по назначению.
По принципу задания управляющей программы СПУ разделяются на аналоговые и числовые. В аналоговых СПУ задание управляющей программы производится аналоговым сигналом в виде задания уровня напряжения постоянного тока или фазы напряжения переменного тока.
Числовые СПУ получили распространение в станкостроении. Поэтому термины и определения для них приводятся согласно ГОСТу 20523-81 «Устройства числового программного управления металлообрабатывающего оборудования». В соответствии с этим ГОСТом программное управление с записью программы числовым кодом называется числовым программным управлением (ЧПУ) и определяется как управление обработкой заготовки на станке по управляющей программе, в которой данные записаны в цифровой (числовой) форме. Существует множество различных числовых кодов, с помощью которых кодируется числовая информация управляющей программы. Наибольшее распространение в СПУ получили единичный, двоичный и двоично-десятичные коды.
Управляющее устройство в ЧПУ называется устройством ЧПУ (УЧПУ), а система, определяемая как совокупность функционально взаимосвязанных и взаимодействующих технологических и программных средств, обеспечивающих ЧПУ, называется системой ЧПУ (СЧПУ).
В соответствии с международной классификацией СЧПУ по уровню технических возможностей делятся на следующие классы:
NC (Numerical Control) – СЧПУ с покадровым считыванием программы при обработке каждой заготовки;
SNC (Stored Numerical Control) – СЧПУ с однократным считыванием программы перед обработкой партии одинаковых заготовок;
СNC (Computer Numerical Control) – СЧПУ с мини-ЭВМ (микропроцессором);
DNC (Direct Numerical Control) – СЧПУ группами станков от одной ЭВМ;
HNC (Handled Numerical Control) – оперативные СЧПУ с ручным набором программ на пульте управления.
По принципу управления СПУ выполняются разомкнутыми и замкнутыми. Разомкнутые СПУ (см. рисунок 5.10, а) имеют один поток априорной информации от управляющей программы (УП). Они обеспечивают невысокую, но достаточную по технологии работы машины, точность отработки программы. Замкнутые СПУ (см. рисунок 5.10, б) имеют два потока информации от программы УП и обратной связи ОС. Они обеспечивают высокую точность отработки за счет непрерывного контроля и наличия информации о состоянии ИОРМ.
По принципу действия СПУ подразделяются на аналоговые, импульсные, комбинированные (аналого-импульсные и импульсно-аналоговые) и кодовые [10,11]. Необходимо отметить, что в связи с развитием ЧПУ с ЭВМ такие СПУ, выполненные на аппаратных средствах уже, устарели. В настоящее время выпускаются только цифровые СЧПУ с импульсным шаговым электроприводом и с электроприводом постоянного и переменного тока непрерывного действия [10,11,15,16].
По назначению согласно технологическому признаку СПУ делятся на цикловые, позиционные и контурные.
Цикловые СПУ, или системы с цикловым программным управлением (ЦПУ), осуществляют управление одним или несколькими исполнительными органами рабочих машин ИОРМ, обеспечивающими требуемый технологический цикл, т. е. определенную обычно повторяющуюся последовательность отдельных ИОРМ или группы машин [17,18]. Последовательность действия определяется управляющей программой, задаваемой обычно в виде простых дискретных команд на включение и отключение электроприводов, приводящих в движение ИОРМ. Системы ЦПУ выполняются в основном разомкнутыми, а наличие датчиков положения, фиксирующих положения ИОРМ и дающих команды на включение и отключение электроприводов, рассматриваются как квазиобратные связи.
Наиболее характерно деление СПУ на позиционные и контурные в ЧПУ металлорежущими станками, где согласно ГОСТ 20523-81 позиционное ЧПУ определяется как числовое программное управление станком, при котором перемещение его рабочих органов происходит в заданные точки, причем траектории перемещения не задаются. Позиционное ЧПУ используется не только для управления движением в металлорежущих станках, но и в любых рабочих машинах, исполнительный орган которых требует перемещения с позиционированием. В таких системах важна точность установки заданного конечного положения исполнительного органа, а не траектории его перемещения.
Позиционные системы обычно осуществляют управление положением ИО в нескольких координатах на плоскости, где обеспечивается его точное позиционирование. В этом случае движение ИОРМ от одной координаты к другой происходит по любой траектории, но с минимальным временем перемещения для повышения производительности. Позиционные СПУ строятся на базе позиционных систем управления, в которых сигналы задания изменяются по заданной программе.
В позиционных ЧПУ применяются быстродействующие электроприводы в основном постоянного тока, удовлетворяющие требованиям позиционных электроприводов.
Под контурным ЧПУ понимается числовое программное управление станком (любой рабочей машины), при котором перемещение его исполнительных органов происходит по заданной траектории и с заданной скоростью для получения необходимого контура обработки (движения по контуру).
Контурные СЧПУ предназначены для управления перемещением ИОРМ (объекта управления) с непрерывно изменяющейся информацией управления, сигналы которой являются функциями времени, скорости, пути или любого другого параметра. Такие СПУ реализуют криволинейное движение объекта по заданному контуру как на плоскости, так и в пространстве. Характерная особенность таких СПУ состоит в непрерывной координации движений ИО в каждый момент времени как по пути, так и по скорости.
Контурные системы более сложны, чем позиционные как по алгоритмам управления, так и по требованиям к электроприводу. Обязательными блоками управляющих устройств контурных СПУ являются линейные и круговые интерполяторы, которые осуществляют программирование траекторий движения ИОРМ по опорным точкам в управляющей программе и преобразуют информацию цифрового кода программы в информацию в унитарном коде, обеспечивающую сигналы управления электроприводом.
Разработка самоприспосабливающихся адаптивных систем расширило классификацию ЧПУ по числу потоков информации. Создано адаптивное ЧПУ (АЧПУ), определяемое как числовое программное управление, при котором происходит автоматическое приспособление процесса обработки заготовки к изменяющимся условиям обработки по определенным критериям. Поэтому в современных ЧПУ появились дополнительные потоки информации, кроме основных потоков, определяемых только управляющей программой и главной обратной связью.
5.5.2 Цикловые СПУ обеспечивают работу одного или нескольких объектов управления, в которых ИОРМ осуществляют различные движения с повторяющимися одинаковыми циклами. Последовательность этих движений задается управляющей программой [18].
Управляющие программы в системах ЦПУ выполняются в виде жесткой неизменяемой и изменяемой программ. Жесткая неизменяемая управляющая программа задается в виде определенной схемы электроавтоматики, включение и отключение управляющих элементов которой производится по времени или по технической готовности ИОРМ.
Изменяемые жесткие управляющие программы в цикловых СПУ обычно строятся по схеме матрицы с заданием программы в виде наборов переключателей, штепсельных коммутаторов, командоаппаратов с переставными кулачками и с помощью программируемых контроллеров, представляющих собой электронные вычислительные устройства, реализующие логические функции релейных схем.
Управляющие программы в сложных цикловых СПУ задаются также в цифровом виде (ЧПУ) и памяти ЭВМ. Однако такие программы содержат только информацию о цикле и технологических режимах, а перемещение задается установкой упоров, воздействующих на путевые переключатели.
В цикловых СПУ используются электроприводы постоянного, а чаще переменного тока.
Более надежны цикловые СПУ, схемы которых собраны на бесконтактных логических элементах с применением микросхем. Однако создание схем цикловых СПУ на контактных аппаратах и бесконтактных логических элементах с жесткой неизменяемой программой требует большой затраты труда по их установке, монтажу и наладке.
Для осуществления больших схем цикловых СПУ используются программируемые контроллеры (программируемые командоаппараты) – ПК, представляющие собой специализированную управляющую мини-ЭВМ с устройствами входа и выхода, которые осуществляют логические функции любой схемы управления, записанные в виде введенной в память ЭВМ программы. ПК подключается к объекту управления каналами связи и работает с ним в непосредственном взаимодействии в реальном масштабе времени. Такая СПУ (см. рисунок 5.11) включает в себя программируемый контроллер ПК, входные и выходные устройства ВУ, устройства силовой автоматики УСА и источники питания ИП. ПК содержит центральное процессорное устройство ЦПУ (УВМ), обеспечивающее хранение и реализацию управляющей программы, и устройства сопряжения с входами УСвх и выходами УСвых, осуществляющие согласование параметров электрических внешних и внутренних цепей СПУ, и автономный источник питания АИП. Входными устройствами являются командные органы КО и датчики индикации состояния объекта управления Д, выходными – исполнительные элементы управления ИЭУ и сигнализации ИЭС и электрические двигатели ЭД.
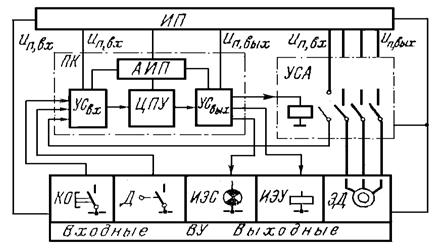
Рисунок 5.11 - Функциональная схема цикловой системы программного управления с программируемым контроллером
Такие ПК надежны, имеют малую трудоемкость введения и отладки программы и позволяют осуществлять индикацию работы схемы с помощью световой сигнализации и дисплея и проводить диагностику их работы. Два источника питания в ПК (ИП и АИП) обеспечивают энергозависимую и энергонезависимую памяти. При этом первая не сохраняет (обнуляет) свои данные при отключении внешних источников энергии, являясь как бы нулевой защитой ПК, а вторая сохраняет свои данные при отключении энергии, сохраняя тем самым алгоритм работы процессора, содержание команд, необходимых для реализации рабочей программы.
Структура ПК организуется по блочно-модульному принципу, что позволяет подобрать конкретный комплект модулей в соответствии с характеристиками автоматизированного объекта. При этом можно реализовать как простые схемы управления циклами, так и сложные системы комплексного управления оборудованием с решением задач технической диагностики, неисправностей и т. д.
Принцип действия ПК объясняется его функциональной схемой (см. рисунок 5.12). Вначале ПК работает в режиме записи программы, которая набирается на программной панели (загрузчике программы) и записывается (загружается) в постоянное запоминающее устройство (ПЗУ). Далее ПК переключается в режим работы, в котором сканнер (генератор тактовых импульсов) последовательно опрашивает ПЗУ, входные и выходные регистры устройств сопряжения с входами и выходами, согласно адресу программы (операнда) выбираются соответствующие ячейки регистров ввода и вывода и подключаются к процессору. Процессор в соответствии с командами (шагами) программы, поступающих из ПЗУ, совершает логические операции над сигналами входов и выходов и преобразует состояние входов в состояние выходов. Если состояние входов не изменилось по сравнению с предыдущим циклом опроса, то процессор подтверждает текущее состояние выходов; если изменилось, то процессор изменяет состояние выходов, согласно программе, записанной в ПЗУ. Опрос участков программы производится циклично, один за другим, в порядке размещения их в программе с возвращением к началу программы после окончания полного цикла опроса.
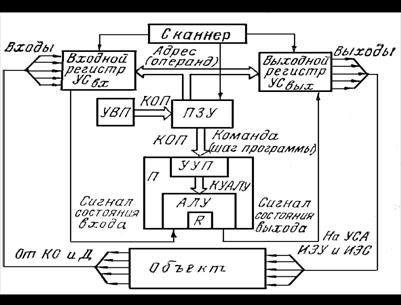
Рисунок 5.12 - Функциональная схема программируемого контроллера
Центральной частью ПК является процессор П, структура которого определяет параметры ПК: быстродействие, систему команд, число входов и выходов, количество таймеров и счетчиков, объем памяти для хранения программы. Процессором выполняются операции считывания и обработки команд, запроса операндов из памяти, передачи управляющих команд на выходные устройства. Процессор состоит из арифметическо-логического устройства АЛУ, которое осуществляет логические операции программы; устройства управления процессора УУП, обеспечивающего преобразование кода программы в код управления АЛУ; регистра памяти результата вычисления R; счетчиков адресов шагов программы (САШП) и адресов запоминающего устройства САЗУ, считывающих соответственно шаги программы и операнды (адреса входа); шин адреса для передачи адреса шагов программы и шин данных для передачи операндов.
Связь процессора с модулями „вход – выход” реализуется через модули процессора, называемые адаптерами, с их помощью осуществляются передача текущего значения входного сигнала в ПЗУ и выдача управляющих воздействий на выходные модули, адрес которых задан операндом. Если управление в модулях выхода выполняется не дискретными исполнительными сигналами, а аналоговыми, то используются устройства ЦАП и АЦП.
Рабочий цикл ПК разделяется на три этапа. На первом этапе, называемом сканированием входных сигналов, происходит загрузка в П3У опрашиваемых входных модулей. На втором этапе обеспечивается обработка программы, а на третьем, заключительном — передача управляющих сигналов выходные модули. Возможно совмещение во времени этих этапов. Время цикла определяется длиной программы. Окончание программы и переход к другому циклу в ПК осуществляются двумя способами: командой конца программы и обработкой всего объема ПЗУ.
5.5.3 Система числового программного управления (СЧПУ) состоит из устройства ЧПУ (УЧПУ) и исполнительного устройства в виде следящего электропривода [18]. Структура канала управления СЧПУ приведена на рисунке 5.13. Она включает в себя устройство ввода информации программы УВП, пульт ручного управления ПРУ, блок запоминания информации программы БЗП, интерполятор И, блок преобразования сигналов управления электроприводом БПСУ, электропривод ЭП, объект управления ИОРМ и датчик обратной связи по положению ДОСП.
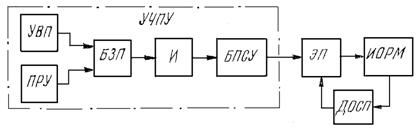
Рисунок 5.13 - Структура канала управления СЧПУ
УВП содержит программоноситель ПН, вводное ВУ и считывающее СУ устройства (см. рисунок 5.10). В качестве ПН в УЧПУ, на которые записывается программа в двоичном коде, используются дискеты, диски и т.д. Числовая информация о перемещении ИОРМ записывается количеством импульсов унитарного кода, определяющим нужное перемещение в миллиметрах, при известном шаге перемещения ИОРМ от одного импульса.
Информация из программоносителя ПН поступает в БЗП (см. рисунок 5.13), который запоминает информацию, считанную с ПН, осуществляет ее контроль и формирует сигнал при ошибке в записи программы. БЗП необходим, так как информация считывается с ПН последовательно (построчно), а используется в УЧПУ параллельно, т. е. вся сразу в пределах одного кадра. В контурных СПУ перерыв информации недопустим, поэтому в БЗП используются два блока памяти, из которых в один записывается информация, а из другого считывается и наоборот после переключения этих блоков. Блок, в который записывается информация, называют буферным (БП), а из которого считывается – рабочим (РП).
После записи информации каждого кадра информация переписывается из буферной памяти в рабочую или блоки памяти переключаются, т. е. меняются местами.
Информация из рабочей памяти поступает в интерполятор, который преобразует информацию, записанную в РП в двоичном коде в число импульсов, следующих в единичном унитарном коде, и обеспечивает линейную или круговую интерполяцию траектории движения ИОРМ между двумя или более заданными точками в двухкоординатной СЧПУ.
При использовании шагового электропривода используются простые разомкнутые импульсно-шаговые ЧПУ с шаговыми двигателями ШД [11,16], функциональная схема одной координаты, которой приведена на рисунке 5.14.
Импульсы программы из интерполятора УЧПУ в унитарном коде поступают по двум информационным каналам, определяющим направление движения ИОРМ «вперед» (+) и «назад» (–), в усилитель-формирователь УФ, где усиливаются и формируются в импульсы требуемой длительности и формы с крутыми фронтами. Далее импульсы управления поступают в распределитель импульсов РИ, усиливаются усилителями мощности УМ и распределяются по обмоткам ШД. В ЧПУ на металлорежущих станках применяется двигатель типа ШД5Д-1М с шагом 6º и моментом на валу 0,06 Н·м, использующийся с гидроусилителем [16]. В принципе можно взять любой силовой ШД, например, четырехфазный индукторный ШД типа ШДА-Ф с шагом 22,5° и моментом до 1 Н·м.
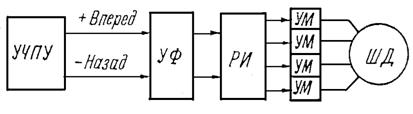
Рисунок 5.14 - Функциональная схема одной координаты импульсно-шаговой СЧПУ
Распределитель импульсов служит для преобразования импульсов управления в многоканальную систему напряжений питания ШД. Схем РИ существует много. Они построены на основе реверсивных счетных кольцевых схем. В последнее время в связи с развитием микроэлектроники РИ выполняются на интегральных микросхемах, построенных на основе сдвиговых регистров и счетчиков с дешифраторами.
Широкое распространение в СПУ получили ЭВМ, начиная с использования их для расчета и составления управляющих программ и до управления электроприводами, осуществляющими движения ИОРМ [12]. В связи с развитием микроэлектроники и появлением микро-ЭВМ и микропроцессоров в СПУ произошел переход от использования малогабаритных ЭВМ с микросхемами малой и средней степени интеграции к микро-ЭВМ с микропроцессорными наборами и большими интегральными схемами памяти (БИС) [14]. Это обусловило коренные изменения структуры ЧПУ и появление оперативных СЧПУ с преимущественной подготовкой управляющих программ непосредственно у рабочей машины (станка), так называемой ОСУ – оперативной системы управления класса CNC (Computer Numerical Control). Используются также универсальные СЧПУ (универсальная система управления – УСУ) с подготовкой управляющих программ в вычислительном центре и непосредственно у станка.
Центральным узлом современных УЧПУ является микрокомпьютер, состоящий из микропроцессора и БИС-памяти. В качестве примера рассмотрим двухкоординатную контурную оперативную СЧПУ с ЭВМ, предназначенную для токарных станков. Функциональная схема СЧПУ приведена на рисунке 5.15.
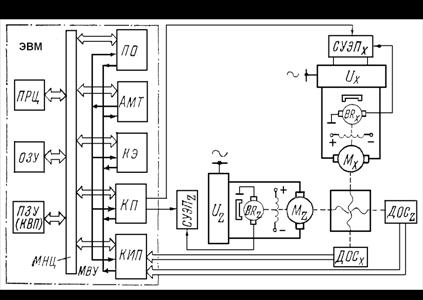
Рисунок 5.15 - Функциональная схема СЧПУ с ЭВМ
Эта СЧПУ обеспечивает управление двумя исполнительными органами станка по координатам X и Z поперечного и продольного перемещения по 999999 импульсов каждое. Движение осуществляется двумя следящими электроприводами с фотоимпульсными датчиками обратной связи, контуры которых осуществлены в ЭВМ программно. УЧПУ выполнено на ЭВМ, которая включает в себя пульт оператора ПО; процессор ПРЦ; оперативное ОЗУ и постоянное ПЗУ запоминающие устройства, где ПЗУ выполнено в виде кассеты внешней памяти КВП; адаптер магистрали и таймеров АМТ. В ЭВМ имеются интерфейсы выводов в виде контроллеров привода КП и импульсных преобразователей датчиков обратных связей КИП, и электроавтоматики КЭ.
Программа с ПО задается в цифровом двоичном коде. Ввод информации программы осуществляется по кадрам. При наборе программы используется буквенная и цифровая информации. При этом применяются буквы: N — номер кадра; X и Z – поперечное и продольное перемещения; S – частота вращения шпинделя; F – скорость подачи; G – подготовительная и M – вспомогательная функции и др. Перемещения задаются числом импульсов в соответствии с ценой импульсов в миллиметрах. При введении программы каждая команда в ЭВМ кодируется в восьмеричном коде и поступает в регистр кодов клавиатуры. Процессор по программе обслуживания пульта оператора опрашивает регистр кода клавиатуры и преобразует записанную в нем информацию во внутреннее представление ЭВМ и переводит ее в ОЗУ.
При подаче команды «ОТРАБОТКА ПРОГРАММЫ» процессор считывает из ОЗУ последовательно все кадры управляющей программы и с помощью программы «интерполятор» разбивает заданное перемещение X или Z с учетом скорости перемещения F на дискреты задания N за время Δt = 10мс равные NЗ = (X / F) Δt .
Процессор опрашивает АЦП обратной связи, преобразуя сигналы датчика обратной связи ДОС также в числовые дискреты обратной связи NОС . Далее процессор определяет числовой сигнал управления в виде дискрет, равных Nу = NЗ – NОС , который в ЦАП преобразуется в напряжение uЗС, подаваемое в систему управления электропривода, обеспечивающую работу электропривода, отрабатывающего заданное перемещение ИОРМ.
Адаптер магистрали и таймеров АМТ выполняет преобразование интерфейса общей шины управления, называемой магистралью МНЦ, в интерфейс контроллеров связи. Управление осуществляется по магистрали внешних устройств МВУ.
Системы числового программного управления с ЭВМ используются не только для управления движением в металлорежущих станках, но и в любых рабочих машинах, исполнительный орган которых требует перемещения с позиционированием. В таких системах важна точность установки заданного конечного положения исполнительного органа, а не траектории его перемещения.
5.6 Адаптивные системы управления и принципы их построения
5.6.1 Адаптивные системы электропривода – это системы, которые требуют учета изменения характеристик и пополнения информации об объекте в процессе работы. Здесь имеется некоторая «дуальность» управления: система сама определяет текущую информацию об объекте и использует ее для оптимального управления объектом [10,11].
В адаптивных системах управления электропривода управляющие воздействия или алгоритмы управления автоматически изменяются с целью осуществления лучшего в каком-либо смысле управления объектом.
На рисунке 5.16 представлена простейшая функциональная схема адаптивной системы управления с изменчивостью характеристик и неполной информацией, позволяющая описать принцип работы адаптивной системы управления. В схеме обозначено: УУ – управляющее устройство; ОУ – объект управления; УА – устройство адаптации; f – помехи; u, n – сигналы управления; x, y – входной и выходной сигналы.
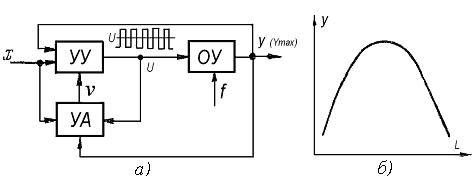
а – схема; б – характеристика объекта.
Рисунок 5.16 - Функциональная схема системы адаптивного управления
Принцип действия простейшей адаптивной системы состоит в том, что она имеет заданный критерий качества и должна заставить объект управления работать так, чтобы выполнялся экстремум критерия качества.
В адаптивной системе основная роль принадлежит устройству адаптации УА, которое получает сигналы входа x и выхода y, а также сигнал управления объектом u.
Эти сигналы могут иметь высокую размерность и служат
для подсчета значений критерия качества. УА вырабатывает сигнал ![]() , который также может
иметь высокую размерность, и управляет УУ таким образом, чтобы при
определенных значениях сигнала
x, при
наличии обратной связи по y и любой сложности возмущений
f
получать в каждый момент времени в объекте отработку с экстремальным значением
показателя качества (производительности, себестоимости и др.).
, который также может
иметь высокую размерность, и управляет УУ таким образом, чтобы при
определенных значениях сигнала
x, при
наличии обратной связи по y и любой сложности возмущений
f
получать в каждый момент времени в объекте отработку с экстремальным значением
показателя качества (производительности, себестоимости и др.).
К классу адаптивных систем управления относятся самонастраивающиеся и самоорганизующиеся системы. В самонастраивающихся системах устройство адаптации на основе собранной информации о входных x, выходных y и управляющих u сигналах подает команды в УУ на изменение уставок или параметров регуляторов таким образом, чтобы добиться заданной цели управления. В самоорганизующихся системах наряду с этим производится изменение структуры системы так, чтобы лучше осуществить цель управления.
В самонастраивающихся системах целью управления может быть, например, достижение экстремума некоторого статического показателя качества, причем положение экстремума, обусловленное контролируемыми координатами системы управления и неконтролируемыми возмущающими воздействиями, может в процессе эксплуатации изменяться неопределенным образом. В таких системах для достижения цели управления и работы в области экстремума управляющее устройство изменяет соответствующим образом задания регуляторов системы.
Целью управления может быть и достижение требуемого динамического показателя качества, характеризующего динамические свойства системы управления электропривода. Обычно это функционал, зависящий от координат и параметров системы, например, один из интегральных критериев погрешности. В этом случае достижение экстремума показателя качества обеспечивается автоматическим изменением параметров системы управления (коэффициентов усиления, постоянных времени регуляторов и обратных связей). Такие системы называют системами с самонастраивающимися корректирующими устройствами.
В зависимости от информации об электроприводе и объекте управления различают два вида самонастраивающихся систем с динамическим показателем качества. В беспоисковых адаптивных системах на основе имеющейся информации создается эталонная модель объекта, обеспечивающая работу системы с требуемым показателем качества. В поисковых адаптивных системах информация об объекте не полная и заранее получена быть не может, а должна быть измерена в процессе работы.
5.6.2 В беспоисковых адаптивных системах управления требуемый показатель качества достигается с помощью эталонной модели объекта управления. Такая модель создается на основании заранее известной информации об объекте и включается в адаптивную систему управления, как показано на рисунке 5.17, а. Эталонная модель (ЭМ) входит в устройство управления УУ, но для наглядности на рисунке 5.17 вынесена из него [11].
Модель управляется сигналом nм из устройства адаптации. Она также получает сигнал управляющих воздействий uм, идущий от сигнала u, но через УУ. Выходным сигналом модели является сигнал yм, поступающий на вход УУ. Модель выполняет функции корректирующего устройства, по сигналам которого УУ изменяет характеристики системы. Модель создается по известному показателю качества объекта, причем желательно, чтобы показатели модели и объекта были близки. Одна из схем включения модели приведена на рисунке 5.17, б. На модель ЭМ и на объект ОУ подается один задающий сигнал x, характеризующий требуемый показатель качества объекта. В процессе работы системы выходные сигналы модели yм и объекта y, характеризующие соответственно показатели качества модели и объекта, сравниваются вычислителем критерия соответствия (ВКС) модели объекту. При отклонении сигнала объекта y от сигнала модели yм ВКС вырабатывает воздействие n, пропорциональное отклонению y от yм, и подает его на управляющее устройство УУ, которое в свою очередь подает соответствующий сигнал uу на регулятор Р, системы управления объектом. Регулятор изменяет (корректирует) управляющий сигнал объекта u, в результате чего объект изменяет свой выходной сигнал y, приближая его к эталонному сигналу модели yм. Такая самонастройка системы с изменением параметров регулятора называется параметрической.
Корректирующие сигналы УУ в таких системах могут подаваться не на регулятор, а на вход системы управления объектом, как показано на рисунке 5.17, а; в этом случае параметры регулятора не меняются. Такая самонастройка называется сигнальной.
В беспоисковых адаптивных системах осуществляется стабилизация динамических свойств электропривода. Поэтому эталонная модель может быть представлена в виде динамического звена с определенной передаточной функцией. ВКС при этом должен получать информацию или непосредственно о динамических характеристиках объекта управления или определять ее косвенно по возможным измеряемым координатам. При непосредственном измерении y и yм ВКС может выполнять роль сумматора, определяющего отклонение D y = yм – y.
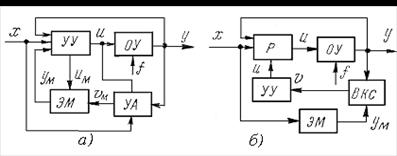
а – общая; б – с моделью, включенной параллельно объекту.
Рисунок 5.17 - Функциональная схема системы адаптивного управления с моделью
Адаптивную систему с параметрической настройкой можно представить упрощенной структурной схемой на рисунке 5.18, а, а с сигнальной настройкой – структурной схемой на рисунке 5.18, б.
а – при параметрической самонастройке; б – при сигнальной самонастройке.
Рисунок 5.18 - Структурная схема системы адаптивного управления с моделью
Рассмотрим схему с сигнальной настройкой (см. рисунок 5.18, б). Сигнал задания x поступает параллельно на систему управления объектом и модель. Их выходные сигналы y и yм сравниваются сумматором AW2, выполняющим роль ВКС, а их разница, D y = yм – y, подается в виде сигнала обратной связи uу на вход системы управления объектом с помощью сумматора AW3.
Передаточная функция такой системы имеет вид:
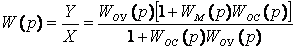 , (5.10)
, (5.10)
где Wоу, Wм(р), Wос(р) – передаточные функции соответственно объекта управления, модели и цепи обратной связи.
Если обеспечить большой коэффициент обратной связи, то единицей в слагаемых числителя и знаменателя по сравнению с Wм(р), Wос(р) можно пренебречь. Тогда
![]() или
или
![]() . (5.11)
. (5.11)
Из (5.11) видно, что выходная координата объекта управления определяется лишь динамическими свойствами модели.
5.6.3 Поисковыми называются системы, решающие задачу оптимального управления с автоматическим поиском при неполной информации об объекте и изменяющихся его характеристиках.
Сущность автоматического поиска можно объяснить, обратившись к рисунку 5.16, а и приняв для упрощения, что поисковая адаптивная система является однокоординатной. Пусть устройство УУ дает на управляемый объект УО пробные воздействия в виде импульсных или гармонических сигналов. Устройство адаптации УА анализирует их результаты и через УУ управляет объектом, приводя его в «оптимальное состояние».
Часто требуется осуществлять автоматический поиск в поисковой адаптивной системе управления электропривода, имеющей статические характеристики y(u) и требующей автоматического управления с выходом на экстремум этой характеристики (см. рисунок 5.16, б). Если состояние поисковой адаптивной системы в данный момент времени характеризует точка A, то при увеличении сигнала управления на Du имеем приращение сигнала y на Dy. Здесь
![]() .
(5.12) Для точки Б, наоборот,
.
(5.12) Для точки Б, наоборот,
![]() .
(5.13)
.
(5.13)
Очевидно, что для выхода на максимум Ymax в первом случае u должно возрастать, а во втором – уменьшаться. При этом объект управления имеет экстремальную статическую характеристику, которая в процессе работы может изменяться в зависимости от f и t.
Задачей поисковой адаптивной системы электропривода является максимальное приближение значений выходной координаты y в точке экстремума к Ymax, которая со временем сама может изменяться.
Следует отметить, что переходные процессы здесь могут происходить в виде отработки подаваемых на объект сигналов uА + DuА или uБ + DuБ. Приближение к максимуму координаты y осуществляется при этом за несколько «шагов». Принцип поиска экстремума показан на рисунке 5.19.

Рисунок 5.19 - Принцип поиска экстремума в адаптивной поисковой системе
Для поиска сигнал управления u объекта УО сначала увеличивается, а затем уменьшается. Увеличение сигнала u происходит до момента, когда выходной сигнал достигает экстремума Ymax и начнет снижаться согласно характеристике объекта управления. При фиксации устройством адаптации УА зоны поиска ЗП, равной Dy, оно подает команду на уменьшение сигнала управления, при этом выходная координата y сначала возрастает, а потом согласно характеристике ОУ снижается. При уменьшении y на Dy, определяемой зоной поиска, УА вновь реверсирует сигнал управления.
При смещении характеристики объекта и повышении значения Ymax сигнал u не реверсируется, пока y не достигнет нового экстремального значения. Теперь поиск будет осуществляться так же, но с другим значением Ymax.
Список литературы
1. Егоров К.В. «Основы теории автоматического регулирования»: Учебное пособие для ВУЗов. – М.: Энергия, 1978. – 648 с.
2. Башарин А.В., Новиков В.А., Соколовский Г.Г. Управление электроприводами. – Л.: Энергоиздат, 1982. – 392 с.
3. Лукас В. А. Теория автоматического управления. – М.: Недра, 1990. – 416 с.
4. Зимин Е.Н., Яковлев В.И. Автоматическое управление электроприводами. – М.: Высш. Школа, 1991. – 318 с.
5. Попов В.М. Теория нелинейных систем автоматического регулирования и управления: Учеб. пособие. – 2-е изд., стер. – М.: Наука. Гл. ред. Физ.-мат. лит, 1998. – 256 с.
6. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – СПб, Изд.-во «Профессия», 2004. – 752 с.
7. Лурье Б.Я., Энрайт П.Дж. Классические методы автоматического управления/под ред. А.А. Ланне. – СПб.: БХВ – Петербург, 2004. – 640 с.
8. Цыба Ю.А., Сагитов П.И. «Элементы теории автоматического управления»: Учебное пособие для ВУЗов. – Алматы: КАУ, 2006. – 144 с.
9. Каган В.Г. и др. Цифровые электромеханические системы. – М.: Энергоатомиздат, 1996.
10. Елисеев В.А. Цифровые системы управления электроприводами. – М.: МЭИ, 2005. – 104 с.
11. Цыба Ю.А. «Автоматическое управление электромеханическими системами»: Учебное пособие для ВУЗов. – Алматы: АИЭС, 2008.– 77с.
12. Управление автоматическими линиями с помощью ЭВМ / Крыленко В.В. и др. – М.: Машиностроение, 2002. – 152 с.
13. Ахиетжанов А.А., Кочемасов А.В. Следящие системы и регуляторы. – М.: Энергоатомиздат. 2001. – 288 с.
14. Бутырин Н.Г. Микропроцессоры в системах автоматического управления: Учебное пособие. – Ленинград: Гос. техн. ун-т., 1991. – 132с.
15. Станки с числовым программным управлением / Под ред. В.А. Лещенко. – М.: Машиностроение, 2003. – 592 с.
16. Ивоботенко Б.А. Козаченко В.Ф. Шаговый электропривод в робототехнике. – М.: МЭИ, 2005. – 104 с.
17. Срибнер Л.А. Цикловое программное управление оборудованием – М.: Машиносроение, 1999. – 152 с.
18. Станки с числовым программным управлением / Под ред. В.А. Лещенко. – М.: Машиностроение, 2000. – 592 с.