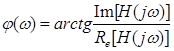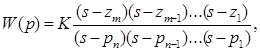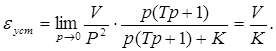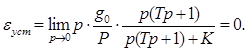Некоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра электропривода и автоматизации промышленных установок
 ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Методические указания по выполнению лабораторных работ для студентов специальности 5В071800 

Алматы 2014

СОСТАВИТЕЛИ: Ю.А. Цыба, Ж.Ж. Тойгожинова, М.Б. Жаркымбекова. Теория автоматического управления. Методические указания по выполнению лабораторных работ для студентов специальности 5В071800. - Алматы: АУЭС, 2014. – 24 с.

 Методические указания содержат необходимые теоретические положения, принципы работы в среде MATLAB Simulink программу выполнения работ, методику подготовки и проведения экспериментов,  анализа полученных результатов.

Методические указания предназначены  для студентов специальности 5В071800 – Электроэнергетика.

Ил. 10, табл. 5, библ. – 5 назв.

Рецензент: кан.тех.наук, профессор А.С. Бакенов

Печатается по плану издания некоммерческого акционерного общества «Алматинский  университет энергетики и связи» на 2014 г.

© НАО «Алматинский университет энергетики и связи», 2014г.

Содержание

Введение

4

1

Лабораторная работа №1. Переходные характеристики типовых динамических звеньев систем автоматического управления

4

2

Лабораторная работа №2. Исследование точности систем автоматического управления

9

3

Лабораторная работа №3. Синтез и исследование систем автоматического регулирования с последовательной коррекцией

16

4

Лабораторная работа №4. Исследование автоколебаний в нелинейных системах автоматического управления                                                            

18

Список литературы

23

Введение

Настоящие указания составляют учебно методическую базу для выполнения лабораторных работ по курсу «Теория автоматического управления» (ТАУ).

Цель работы: развить и закрепить у студентов навыки практического анализа и проектирования систем управления.

В процессе выполнения лабораторных работ студенты должны исследовать такие вопросы, как:

- изучение динамических свойств и построение динамических характеристик различных звеньев автоматических систем во временной и частотной областях;

- исследование точности систем автоматического управления;

- изучение частотных, корневых и других методов синтеза корректирующих устройств для улучшения динамических свойств и повышения показателей качества;

- исследование автоколебаний в нелинейных системах автоматического управления.

Выполнение лабораторных работ предполагает использование популярного мощного пакета моделирования MATLAB с расширениями Control System Toolbox и Simulink. Каждая работа содержит описание команд MATLAB, которые могут быть использованы при выполнении заданий.

1 Лабораторная работа №1. Переходные характеристики типовых динамических звеньев систем автоматического управления

Цель работы: изучить пакет моделирования MATLAB-Simulink. Освоить основные приемы моделирования линейных систем автоматического управления.

1.1   Краткие теоретические сведения

Модель как средство осмысления помогает выявить взаимозависимости переменных, характер их изменения во времени, найти существующие закономерности. При составлении модели становится более понятной структура исследуемого объекта, вскрываются важные причинно-следстенные связи. В процессе моделирования постепенно происходит разделение свойств исходного объекта на существенные и второстепенные с точки зрения сформулированных требований к системе. Также, модель как средство прогнозирования позволяет предсказывать поведение объекта и управлять им, испытывая различные варианты управления.

Модели можно условно разделить на три группы: физические, аналоговые и математические. Физическими принято называть такие модели (макеты), в которых реальный объект заменен его увеличенной или уменьшенной копией. Аналоговое моделирование основано на замене исходного объекта объектом другой физической природы, обладающим аналогичным поведением. Математическая модель является математическим описанием реального физического объекта.

Свойства объекта, представленного математической моделью, могут изучаться с использованием аналитических и вычислительных методов. Аналитические методы исследования математических моделей имеют существенные ограничения. Они позволяют в полной мере исследовать системы, которые описываются дифференциальными уравнениями первого и второго порядка. Системы, описываемые уравнениями третьего и четвертого порядка, поддаются аналитическому решению, но влияние параметров системы приходится исследовать уже численными методами. Системы более высоких порядков исследуются только численными методами.

Численные методы базируются на использовании компьютерного моделирования. Компьютерная модель — это программная реализация математической модели, дополненная различными служебными программами (например, рисующими и изменяющими графические образы во времени). Для исследования динамических систем широко используются пакеты MATLAB - Simulink фирмы Math Work. При моделировании с использованием Simulink реализуется принцип визуального программирования, в соответствии с которым пользователь на экране из библиотек стандартных блоков создает модель устройства и осуществляет расчеты. При этом, в отличие от классических способов моделирования, пользователю не нужно досконально изучать язык программирования и численные методы математики, а достаточно общих знаний, требующихся при работе на компьютере, и, естественно, знаний той предметной области, в которой он работает.

Наиболее распространенными способами математического описания систем автоматического управления является:

- дифференциальные уравнения, записываемые в той или иной форме;

- уравнения состояний – система дифференциальных уравнений, записанных в нормальной форме Коши;

- передаточные функции;

- системные функции (амплитулно-частотные, фазо-частотные, амплитудно- фазовые характеристики);

- нули и полюсы передаточной функции.

Дифференциальное уравнение, описывающее линейную динамическую систему (или ее часть), в общем случае имеет вид:

         (1.1)

где u - входной сигнал;

x - переменная состояния.

Это же уравнение в операторной форме можно записать в виде:

 

(1.2)

 

где - оператор дифференцирования.

          Из последнего уравнения находится отношение выходного сигнала к

 входному

                                                                          (1.3)

Выражение 1.3, совпадающее по форме с передаточной функцией, назовем операторной передаточной функцией. Заметим, что модели пакетов MATLAB - Simulink оперируют именно с операторным представлением дифференциальных уравнений.

Уравнения состояний (система дифференциальных уравнений, записанных в нормальной форме Коши) имеют вид:

(1.4)

где X - вектор состояния;

U,Y - векторы входа и выхода системы;

A - матрица коэффициентов;

B - матрица управления;

C - матрица выхода;

D - матрица, характеризующая связь входного сигнала с выходным.

В частном случае, в простых системах, выход является скалярной величиной. В этом случае матрица С - это вектор строка, а матрица X – вектор столбец, и их произведение дает скалярную величину.

Передаточная функция (отношение преобразованного по Лапласу выходного сигнала к преобразованному по Лапласу входному сигналу), составленная по уравнению 1.1, записывается в виде:

                                             (1.5)

где s = a + jω – комплексная величина.

Если принять s = jω, то получим системную функцию (амплитудно-фазовую характеристику):

 

                          (1.6)

Системная функция может быть записана в алгебраической или показательной форме как:

(1.7)

где

(1.8)

амплитудно-частотная характеристика,

(1.9)

фазо-частотная характеристика.

Числитель и знаменатель передаточной функции (1.5) представляют собой полиномы переменной s. Корни полинома числителя обращают выражение в ноль, и потому называются нулями (Zero), а корни полинома знаменателя обращают выражение в бесконечность и называются полюсами (Pole) передаточной функции. Передаточная функция, записанная при использовании нулей (z) и полюсов (p), представляется в виде:

(1.10)

где К – коэффициент усиления.

1.2           Программа и методика выполнения работы

1.2.1 По варианту, предложенному преподавателем, выбрать из таблицы 1.1. задание и на рабочей области пакета MATLAB-Simulink с помощью библиотек стандартных блоков и представленных уравнений построить схему моделирования линейной системы автоматического управления.

1.2.2 Моделирование произвести для нулевых начальных условий и при подаче на вход системы ступенчатого сигнала – возмущение по нагрузке – (блок Step библиотеки Sources) u = 1(t) и синусоидального сигнала (блок Sine Wave библиотеки Sources) u = 2cos(t).

1.2.3 Выход модели подключить к рабочему окну (блок To Workspace библиотеки Sinks) и графическому дисплею (блок Scope библиотеки Sinks). На графический дисплей выводить графики сигналов y(t) и u(t). Временные интервалы фиксирования выбрать самостоятельно.

1.2.4              Осуществить моделирование свободного движения системы с нулевыми и ненулевыми начальными условиями (см. таблицу 1.2). Снять выходные характеристики y(t) системы. Получить фазовый портрет.

1.2.5         Скопируйте полученные графики в отчет в формате Word. Для этого в меню File выберите пункт Print to Figure. В  появившемся  новом  окне графика переходного процесса выберите в меню Edit пункт Copy Figure, а затем в документе Word вставьте график клавишами Ctrl + V.

Таблица 1.1 – Варианты параметров моделей

Вариант

порядок модели, n

a0

a1

a2

b0

b1

b2

1

3

9

6

3

12

2

0,1

2

3

5

4

3

2,5

2

3

3

3

5

4

2

7,5

0

5

4

3

8

6

2

12

1

10

5

3

7

5

10

10

3

1,5

6

3

15

5

0

15

0,5

1

7

2

7

3

0

10

6

0

8

2

2

0,5

0

4

2

0

9

2

1

0,5

0

25

2

0

10

2

25

1

0

30

2

0

11

2

30

0,8

0

7,5

3

0

12

2

8

6

0

12

2

0

13

2

7

5

0

10

2

0

14

2

15

5

0

15

0

0

15

2

0,1

1

0

0,1

1

0

Таблица 1.2 – Варианты начальных условий моделий

Вариант

1

2

3

4

5

6

7

8

9

10

11

12

13

Порядок модели n

3

3

3

3

3

3

2

2

2

2

2

2

2

y(0)

1

1

1

1

1

1

1

1

1

1

1

1

1

y(1)

(0)

0,5

-0,2

-0,4

0,1

-0,5

0,5

0,4

1

-0,5

0

0,5

0,1

-0,5

y(z)

(0)

0

0,1

0,2

-0,1

0

0,1

-

-

-

-

-

-

-

1.3 Содержание отчета

        

Отчет должен содержать следующие разделы:

1) Титульный лист.

2) Цель и порядок выполнения работы.

3) Краткое изложение теоретической части.

4) Математические модели типовых динамических звеньев.

5) Графики переходных характеристик указанных типовых звеньев.

6) Выводы.

1.4 Контрольные вопросы

1.4.1        Суть и виды моделирования.

1.4.2        Назовите виды математических моделей.

1.4.3        Какие существуют способы математического описания систем автоматического управления?

1.4.4        Для решения каких задач используется пакет MATLAB-Simulink?

1.4.5        Для чего используются блоки интегрирования?

1.4.6        Поясните принцип составления модели вход – выход.

2 Лабораторная работа №2. Исследование точности систем автоматического управления

Цель работы: исследование точности систем автоматического регулирования в различных типовых режимах.

2.1 Краткие теоретические сведения

Одним из основных требований, предъявляемых к САУ, является точность воспроизведения задающего воздействия, которая определяется формой установившегося процесса управления (y(t)). При этом установившаяся ошибка системы будет

e (t ) = y(t)- g(t).

(2.1)

Установившееся значение ошибки в САУ можно определить, воспользовавшись теоремой о предельном значении оригинала из операционного исчисления.

Если функции ε(t) и έ(t) – оригинал и Е(Р) – изображение функции ε(t), то

(2.2)

Обычно точность САУ определяют для типовых режимов работы. Простейшими из них являются режимы:

-   при постоянной величине внешнего воздействия;

-   при изменении внешнего воздействия с постоянной скоростью;

-   при квадратично нарастающем изменении внешнего воздействия;

-   при гармоническом воздействии.

Найдем значение установившейся ошибки в замкнутой САУ при постоянной величине внешнего задающего воздействия g(t) = const = g0.

Пусть передаточная функция разомкнутой цепи – W(p). Тогда передаточная функция замкнутой системы для ошибки будет равна:

 

(2.3)

Согласно теореме о предельном значении оригинала (2.2), выражение установившейся ошибки принимает вид:

(2.4)

При  и  где М(Р) и Q(P) не содержат множителя Р, с учетом (2.2) получим:

(2.5)

Это значение ошибки называется статической ошибкой.

Пусть задающее воздействие изменяется с постоянной скоростью

(2.6)

По формулам (2.2) и (23), с учетом того, что в этом случае найдем:

(2.7)

Чтобы ликвидировать нарастание ошибки в этом случае, передаточная функция разомкнутой цепи САУ – W(p) должна иметь нулевой полюс. Тогда, как следует из формулы (2.7), получим εуст = V/K. Это постоянное значение называется скоростной ошибкой.

Например. Пусть  (один нулевой полюс).

Тогда из (2.7) получим

Если в этом примере задающее воздействие постоянное, то установившаяся ошибка в САУ будет равна нулю

Итак, система, имеющая нулевой полюс в передаточной функции разомкнутой цепи W(p), не будет иметь статической ошибки и даст постоянное значение скоростной ошибки.

Такая система называется астатической системой. В передаточной функции разомкнутой цепи W(p) необходимо присутствие интегрирующего звена.

Следящие системы и системы программного управления должны проектироваться как астатические. Системы, настраиваемые на поддержание постоянного значения регулируемой величины, могут иметь и статические ошибки.

В следящей системе интегрирующим звеном, создающим астатизм, является исполнительный двигатель. Угол поворота вала (или линейное перемещение) будет пропорционален интегралу от входного управляющего сигнала (напряжения).

Как видно из формул ошибок (2.5) и (2.7), для уменьшения величины ошибки надо увеличивать общий коэффициент усиления К разомкнутой цепи системы. Поэтому величина К именуется добротностью системы.

Можно строить САУ также с астатизмом второго и более высокого порядка и не только по отношению к задающему воздействию, но и по отношению к возмущающему воздействию. Условие астатизма при этом будет другим и будет определяться из условия.

(2.8)

Точность при гармоническом воздействии. Установившаяся ошибка в этом случае определяется частотными характеристиками замкнутой системы, рассмотренными ранее.

Пусть входное воздействие изменяется по закону

(2.9)

В линеаризованной системе в установившемся режиме ошибка будет меняться также по гармоническому закону

(2.10)

Точность САУ в этом режиме можно определить по амплитуде ошибки, воспользовавшись определением АЧХ замкнутой САУ по ошибке

(2.11)

Обычно система управления проектируется таким образом, чтобы εm была много меньше амплитуды входного сигнала gm. Следовательно, должно выполняться условие на рабочей частоте ωр. Тогда выражение (2.11) можно заменить приближенным

(2.12)

Эта формула позволяет вычислить амплитуду ошибки в установившемся режиме, а также решить задачу синтеза САУ, обеспечивающую заданную точность в установившемся режиме. Например, при построении желаемой ЛАЧХ на частоте управляющего воздействия (рабочей частоте – ωр) при заданной амплитуде входного воздействия – gm и допустимой амплитуде ошибки – εm определяется, так называемая, контрольная точка с координатами ωр и 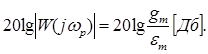 Желаемая ЛАЧХ должна пройти через эту точку (или чуть выше). Часто при проектировании и испытании систем управления пользуются синусоидальным задающим сигналом и в том случае, когда требования к системе поставлены по максимальной скорости и максимальному ускорению входного воздействия. В этом случае можно определить эквивалентный синусоидальный сигнал.

Если  то скорость и ускорение будут

   

Следовательно,

  

Отсюда вычисляются частота ωр и амплитуда gm синусоидального задающего воздействия, соответствующие требуемым максимальной скорости и ускорению, а именно:

 

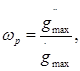
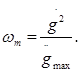
Эти значения используются для нанесения координат контрольной точки на поле построения желаемой ЛАЧХ разомкнутого контура системы управления.

В этой лабораторной работе будут рассмотрены установившиеся ошибки системы при постоянном, линейно-нарастающем и квадратично-нарастающем внешнем воздействиях.

2.2 Программа и методика выполнения работы

2.2.1 В соответствии со своим вариантом построить схему системы, показанной на рисунке 2.1. При исследовании системы с астатизмом нулевого порядка принять R(p)=K и использовать в качестве внешнего задающего воздействия только g=A, g=vt (параметры выбрать из таблиц 2.1), а при исследовании астатических систем принять R(p)=K/p и использовать в качестве внешнего задающего воздействия g=A, g=vt (параметры выбрать из таблиц 2.1) и 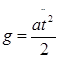 (параметры выбрать из таблицы 2.2).

Рисунок 2.1 - Структурная схема системы

где 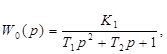  - для астатической системы.

2.2.2  Провести исследование системы с нулевым порядком астатизма при воздействии постоянного сигнала. Для этого необходимо с помощью пакета MATLAB-Simulink собрать схему модели, как показано на рисунке 2.2. Генератором постоянного сигнала является блок Constant из библиотеки Sources, параметром которого является постоянный сигнал g=A. Роль R(p)= K играет усилитель Gain из библиотеки Math.  Передаточная функция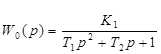 реализуется с помощью блока Transfer Fcn библиотеки Continuous, с помощью параметров которого в модель записываются K1, Т1, Т2. На выходе устанавливается осциллограф Scope из библиотеки Sinks. Для просмотра одновременно двух сигналов и их сравнения на его вход одновременно подаем два сигнала: g =A (с выхода генератора сигнала Constant); y(t) (c выхода системы). Такое позволяет сделать блок Mux (черный четырехугольник на рисунке) из библиотеки Signals & Systems.

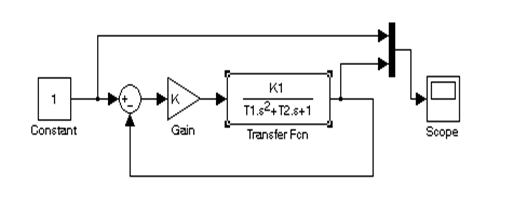
Рисунок 2.2 - Схема модели на MATLAB-Simulink для системы с нулевым порядком астатизма при подаче на вход сигнала g=A

2.2.3 Изменяя К = 1, 5, 10, получить переходные процессы и определить предельные значения установившейся ошибки для каждого К.

2.2.4  Собрать аналогично п.п. 2.2. схему модели для системы с нулевым порядком астатизма при подаче на вход линейно-нарастающего сигнала g = v·t как показано на рисунке 2.3. Для получения входного воздействия g = v·t, последовательно генератору постоянного сигнала соединяется блок Integrator из библиотеки Continuous.

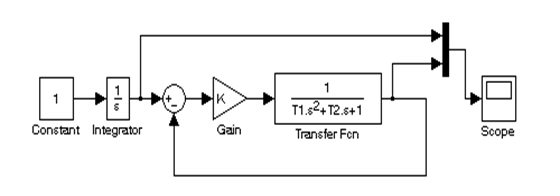
Рисунок 2.3 - Схема модели на MATLAB-Simulink

для системы с нулевым порядком астатизма при подаче на вход сигнала g = v·t

2.2.5 Также для трех значений К = 1, 5, 10 получить переходные процессы и определить предельные значения установившейся ошибки для каждого К.

2.2.6 Исследование систем с астатизмом первого порядка. Для таких систем R(p) = K/p и поэтому последовательно к усилителю Gain присоединяется блок Integrator из библиотеки Continuous. Схема модели показана на рисунке 2.4. Квадратично нарастающее входное воздействие  можно получить, если включить последовательно с генератором воздействующих сигналов два интегратора. Параметры передаточной функции для соответствующих вариантов показаны в таблице 2.2, а параметры воздействующих сигналов - в таблицах 2.1. и 2.2.

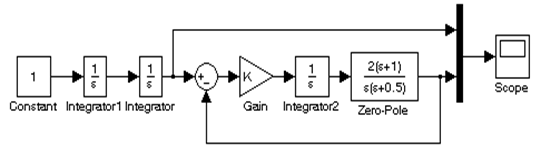
Рисунок 2.4 - Схема модели на MATLAB-Simulink

для системы с астатизмом при подаче на вход сигнала

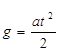  (в качестве примера на схеме показана передаточная функция

2.2.7   По полученным данным проанализировать влияние параметров на точность системы.

Таблица 2.1 - Варианты параметров систем с нулевым порядком астатизма

Вариант

К1

Т1

Т2

К

Типовые входные воздействия

g=A

g=vt

g = at2/2

1

1

0

3

1, 5, 10

1

t

0.2 t 2

2

1.5

0

2.5

1, 5, 10

4

  2t

0.25 t 2

3

1.5

0

0.5

1, 5, 10

2

t

0.3 t 2

4

2

0

1

1, 5, 10

2

  2t    

0.45 t 2

5

3

0

1

1, 5, 10

1

2t

0.4 t 2

6

2.5

0.5

5

1, 5, 10

1

0.5t

0.35 t 2

7

2.5

2.5

3

1, 5, 10

2

4t

0.3 t 2

8

8

0.5

3

1, 5, 10

2

t

0.2 t 2

9

5

0.1

2

1, 5, 10

1

2t

0.2 t 2

10

3

1

2

1, 5, 10

1

t

0.25 t 2

11

1.5

1

0.7

1, 5, 10

2

3t

0.25 t 2

12

2

1

0.6

1, 5, 10

2

2t

0.5 t 2

13

3

2

2

1, 5, 10

2

2t

0.45 t 2

14

4

2

3

1, 5, 10

1

0.5t

0.2 t 2

15

5

1

0.5

1, 5, 10

2

2t

0.3 t 2

Таблица 2.2 - Варианты для исследования астатических систем

Вариант

W0(p)

g = at2/2

Вариант

W0(p)

g = at2/2

1

0,2t2

8

0,25t2

2

0,5t2

9

0,2t2

3

0,2t2

10

0,5t2

4

0,4t2

11

0,3t2

5

0,3t2

12

0,45t2

6

0,45t2

13

0,4t2

7

0,25t2

14

0,5t2

2.3 Содержание отчета

 

Отчет должен содержать следующие разделы:

1) Титульный лист.

2) Цель и порядок выполнения работы.

3) Краткое изложение теоретической части.

4) Математические модели исследуемых систем и кривые переходных процессов.

5) Графики экспериментально полученных зависимостей ε в зависимости от коэффициента К.

6) Выводы.

2.4            Контрольные вопросы

2.4.1    Какие существуют типовые воздействия для исследования точности?

2.4.2        С помощью какого блока Simulink реализуется увеличение порядка астатизма в модели системы?

2.4.3    Как определить порядок астатизма системы автоматического управления?

2.4.4    Суть и виды моделирования.

2.4.5    Назовите виды математических моделей.

2.5.6    Поясните принцип составления модели вход – выход.

3 Лабораторная работа №3. Синтез и исследование САР с последовательной коррекцией

Цель работы: экспериментальная проверка на модели (на ЭВМ) теоретических результатов и эффективности коррекции.

        

3.1           Краткие теоретические сведения

На рисунке 3.1 представлена структурная схема  следящей системы, в которой отсутствует корректирующее звено. Передаточная функция нескорректированной следящей системы в разомкнутом состоянии

(3.5)

где Т1=1с; Т2=0,1с; КР=10

Рисунок 3.1 - Структурная схема  нескорректированной следящей системы


Для данной САР (Приложение А) с помощью метода  логарифмических амплитудно-частотных характеристик произведен синтез корректирующего звена. Передаточная функция полученного звена введена в структуру следящей системы и представлена элементами Matlab Simulink (см. рисунок 3.2).

Рисунок 3.2 – Схема модели скорректированной следящей системы

3.2 Программа и методика выполнения работы

3.2.1 Для структурной схемы следящей системы (см. рисунок 3.1) набрать схему модели из элементов и блоков Matlab Simulink. Получить переходный процесс при UЗ=10В, результаты сохранить.

3.2.2 Набрать схему модели скорректированной системы. Снять переходный процесс при UЗ = 10В, результаты сохранить.

3.2.3 Сопоставить качественные показатели. Сделать выводы.

3.3 Содержание отчета

 

Отчет должен содержать следующие разделы:

1) Титульный лист.

2) Цель и порядок выполнения работы.

3) Краткое изложение теоретической части.

4) Структурные  схемы САР. Схемы моделей.

5) Результаты экспериментов в виде осциллограмм.

6) Выводы.

3.4 Контрольные вопросы

3.4.1 Назначение коррекции.

3.4.2 Методы синтеза КУ.

3.4.3 Расскажите порядок синтеза с помощью ЛАЧХ.

3.4.4 Порядок построения желаемой ЛАЧХ.

3.4.5 Определение передаточной функции КУ по ЛАЧХ.

3.4.6 Виды КУ. Порядок расчета параметров.

4 Лабораторная работа №4. Исследование автоколебаний в нелинейных системах автоматического управления

Цель работы: теоретическое и экспериментальное определение параметров автоколебаний нелинейных САУ

4.1 Краткие теоретические сведения

В состав автоматических систем часто входят существенно нелинейные элементы, которые существенно изменяют характер системы и придают ей такие свойства, которые никогда не могут быть исследованы в рамках линейной теории. Среди нелинейных элементов автоматических систем особую роль играют так называемые безынерционные нелинейности, не обладающих заметным запаздыванием. Элементарным безынерционным звеном будем называть любую систему, выходная переменная которой в каждый данный момент времени зависит только от значения входной переменной в тот же момент времени и не зависит от того, как изменяется входная переменная до данного момента. Таким образом, оператором элементарного безынерционного звена является обычная функциональная зависимость между входной и выходной переменными. Эта функциональная зависимость называется характеристикой элементарного безынерционного звена. Характеристики элементарных нелинейных звеньев можно разделить на слабые и существенные нелинейности. К первой группе относятся такие нелинейные характеристики, которые при малом диапазоне изменения входного сигнала или при малом его отклонении от изменяющегося среднего значения могут быть заменены линейными. Ко второй группе относятся нелинейные характеристики, которые являются существенно нелинейными функциями, например, разрывными или близкими к разрывным. Зависимость между входной и выходной переменными для таких элементов чаще всего может быть приближенно представлена в виде кусочно-линейных функций.

На рисунке 4.1 представлены характеристики нелинейных элементов,  применяемых в работе.


Рисунок 4.1 - Характеристики НЭ

Для исследования режима автоколебаний составляют и набирают схему модели, соответствующую структурной схеме системы (см. рисунок 4.2). Амплитуда и частота автоколебаний на входе нелинейного элемента, т.е. на выходе САУ определяются по осциллографу. Параметры блоков приведены в таблице 4.1.


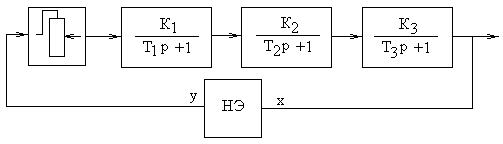Рисунок 4.2 - Структурная схема

4.2           Программа и методика выполнения работы

4.2.1 Набрать схемы подготовленные  при домашней подготовке.

4.2.2 Снять зависимость амплитуды и частоты автоколебаний на выходе САУ от коэффициента усиления линейной части системы. Убедиться в том, что линейная часть является фильтром низких частот.

4.2.3 Сравнить экспериментальные зависимости с расчетными, оценить их совпадение и проанализировать причины их расхождения.

4.2.4 Методические указания к выполнению работы

        

Таблица 4.1 – Параметры исследуемых блоков

№ варианта

Т1, с

Т2, с

Т3, с

Вид нелинейности

U1

U2

t1

t2

1

1

0.1

0.1

Блок 2,а

50

-

2

1

1

0.1

Блок 2,а

70

-

3

0.2

0.1

0.1

Блок 2,а

60

-

4

1

0.1

0.1

Блок 2,б

50

10

5

1

1

0.1

Блок 2,б

60

5

6

1

0.5

0.1

Блок 2,в

80

-

4.3 Содержание отчета

        

Отчет должен содержать следующие разделы:

1) Титульный лист.

2) Цель и порядок выполнения работы.

3) Краткое изложение теоретической части.

4) Структурные  схемы САР. Схемы моделей.

5) Результаты экспериментов в виде осциллограмм.

6) Выводы.

4.4 Контрольные вопросы

4.4.1 На каком допущении основан метод гармонической линеаризации?

4.4.2    Какой вид имеет эквивалентная передаточная функция для рассматриваемой в работе системы?

4.4.3    Как определить условия возникновения и параметры автоколебаний в нелинейной САУ по критерию Гурвица, Михайлова, Найквиста?

4.4.4        Сформулируйте общую постановку задачи  анализа  нелинейной системы методом гармонического баланса.

4.4.5        Что такое автоколебания?

4.4.6        Сформируйте понятие устойчивости системы управления в режиме автокалебаний.

Приложение А

В настоящее время разработано большое число в основном приближенных методов синтеза корректирующих устройств. Наибольшее распространение в инженерной практике получили графо-аналитические методы синтеза, основанные на построении инверсных и логарифмических частотных характеристик разомкнутой системы. При этом широко используются косвенные оценки качества переходного процесса, не требующие решения системы дифференциальных уравнений, такие как запас по фазе, запас по модулю, колебательность, частота среза, которые можно непосредственно определить по частотным характеристикам.

К другой группе относятся аналитические методы синтеза. Для них находятся выражения, аналитически связывающие показатели качества системы с параметрами корректирующего устройства, и определяются значения параметров, соответствующих экстремальному значению функции.

К этим методам относится синтез системы по интегральным критериям качества переходного процесса и критерию среднеквадратичной ошибки.

Применение современных средств вычислительной техники снимает трудности, связанные с непосредственным решением дифференциальных уравнений и построением переходных процессов. В связи с этим наблюдается тенденция решать задачу не приближенными методами, а путем направленного перебора решений исходной системы дифференциальных уравнений при вариации интересующих исследователя параметров корректирующего устройства.

Рассмотрим подробнее удобный из графо-аналитических методов синтеза - метод логарифмических амплитудных характеристик. Он применяется для синтеза минимально-фазовых САР, у которых имеется однозначная связь между амплитудной и фазовой частотной характеристиками.

Процесс синтеза включает в себя следующие этапы:

- строится ЛАЧХ исходной нескорректированной системы LНС(ω) с учетом требуемого коэффициента усиления системы КР в разомкнутом состоянии, который выбирается, исходя из условия обеспечения заданной точности системы в установившемся режиме;

- по заданным показателям качества: -перерегулированию σmax, времени регулирования - строится желаемая ЛАЧХ системы LЖ(ω);

- вычитанием ординат желаемой ЛАЧХ ординат ЛАЧХ исходной нескорректированной системы определяют ЛАЧХ корректирующего устойства LК(ω);

 - по полученной LК(ω) находится WK(p) и подбирается наиболее простой способ технической реализации.

Пусть передаточная функция нескорректированной следящей системы в разомкнутом состоянии.

Пусть передаточная функция нескорректированной следящей системы в разомкнутом состоянии

где Т1=1с; Т2=0,1с; КР=10.

         Соответствующая ей структурная схема.

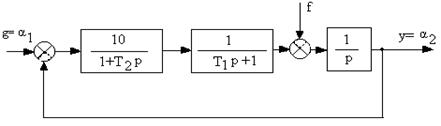
Рисунок А.1 – Структурная схема

Требуется обеспечить следующие показатели качества: перерегулирование ;

         Проведем синтез последовательного корректирующего устройства.

Построим ЛАЧХ разомкнутой нескорректированной системы. Для этого находим  и сопрягающие частоты (см. рисунок А.2):

Для построения желаемой ЛАЧХ, LЖ находим частоту среза ω = 6 с-1, Рmax  = 1.2,

Находим ЛАЧХ корректирующего устройства, как .

Определим передаточную функцию и блок схему реализации КУ:


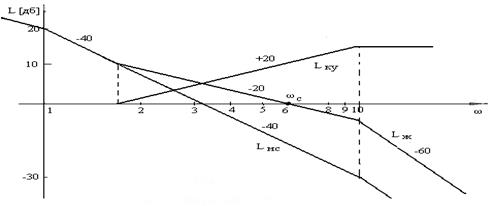Рисунок А.2 - Логарифмические частотные характеристики

Cписок литературы

1.Москаленко В.В. Системы автоматизированного управления электропривода. - М.: «Академия», 2009.

2.Яковлева  В.Б. Теория автоматического управления. - М.: «Академия», 2009.

3.Советов Б.Я. Теоретические основы автоматизированного управления. - М.: «Академия», 2006.

4. Сагитов П.И., Цыба Ю.А. Системы автоматического управления. Конспект лекций. - Алматы: АИЭС, 2006.

5.Сагитов П.И., Цыба Ю.А. Элементы теории автоматического управления. Учебное пособие. - Алматы: АИЭС, 2006.

Сводный план 2014г., поз. 27

Юрий Александрович Цыба
Жанар Жумакановна Тойгожинова
Макпал Бексултановна Жаркымбекова
ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Методические указания по выполнению лабораторных работ для студентов специальности 5В071800 

Редактор Л.Т. Сластихина
Специалист по стандартизации Н.К. Молдабекова

Подписано в печать ________
Формат 60x84 1/16
Тираж 150 экз.
Бумага типографская № 1
Объем 1,5 уч.–изд. л.
Заказ____. Цена 750 тг.

Копировально – множительное бюро
Некоммерческого акционерного общества
«Алматинский университет энергетики и связи»
050013, Алматы, ул. Байтурсынова, 126