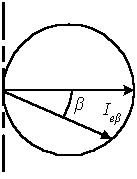АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ

 И СВЯЗИ

 

Кафедра электроснабжения промышленных предприятий

 

 

 

 

 

 

 

 

 

 

 

 

ОСНОВЫ СВЕТОТЕХНИКИ И ФОТОМЕТРИЯ

 

Методические указания и задания к расчетно-

графической работе по курсу Основы светотехники и фотометрия

для специальности 330540- Светотехника и источники света

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Алматы 2004

АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ

 

Кафедра электроснабжения промышленных предприятий

 

 

                                                                                УТВЕРЖДАЮ

                                                            Проректор по учебно-методической работе

                                                                                ______________________

                                                                                “___”_________________2004 г.

 

 

 

 

 

ОСНОВЫ СВЕТОТЕХНИКИ И ФОТОМЕТРИЯ

Методические указания и задания к расчетно-

графической работе по курсу Основы светотехники и фотометрия

для специальности 330540- Светотехника и источники света

 

 

 

 

 

 

 

 

СОГЛАСОВАНО                                                    Рассмотрено и одобрено на

Начальник УМО                                                     заседании кафедры ЭПП

________________                                                Протокол № _______

“___”___________2004г.                                      от “___”___________2004г.

 

                                                                                 Зав.кафедрой ЭПП,

                                                                                 д.т.н., профессор

                                                                                 _____________А.В.Болотов

 

Редактор                                                                Составитель:

________________                                               Старший преподаватель                       кафедры ЭПП

“___”___________2004г.                                      ___________А.С.Алданова

                                                           

 

 

 

Алматы 2004

СОСТАВИТЕЛЬ: А.С.Алданова.  Методические указания и задания  к расчетно-графической работе по курсу Основы светотехники и фотометрия для специальности 330540 – Светотехника и источники света.  - Алматы, АИЭС, 2004. - 38 с.

 

 

 

 

 

 

 

Данная разработка включает задания на расчетно-графическую работу и методические указания по их выполнению, а также список необходимой литературы.

          Ил. 34  , табл. 44, библиогр. - 19 назв.

 

 

 

 

 

Рецензент: д-р. техн. наук, проф. В.Н.Мукажанов

 

 

 

 

 

 

 

 

          Печатается по плану издания Алматинского института энергетики и связи на 2004 год.

 

 

 

 

 

 

 

 

 

 

                                   ©  Алматинский институт энергетики и связи, 2004г.

 

 

 

 

 

 

 

Содержание

 

 

 

1 Введение

 

4

2 Задание № 1. Энергетические характеристики оптического излучения

 

 

4

3 Задание № 2. Световые характеристики излучения

 

12

4 Задание № 3. Световое поле

 

23

5 Задание № 4. Фотометрические характеристики тел

 

31

Список литературы

39

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

          Введение

 

Согласно учебному плану студенты специальности 330540 – Светотехника и источники света изучают курс «Основы светотехники и фотометрия», в котором предусмотрена расчетно-графическая работа, предполагающая самостоятельное закрепление студентами пройденных разделов дисциплины.

Расчетно-графическая работа состоит из четырех заданий. Студент выбирает к каждому заданию только одну задачу из десяти согласно либо первой букве фамилии (задание № 1), либо последней цифре номера зачетной книжки (задание № 2, задание № 4), либо предпоследней цифре номера зачетной книжки (задание № 3).

          К сдаче экзамена по курсу Основы светотехники и фотометрия студенты допускаются после успешного выполнения и защиты РГР.

 

 

ЗАДАНИЕ № 1. ЭНЕРГЕТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ОПТИЧЕСКОГО ИЗЛУЧЕНИЯ

 

Краткие теоретические сведения

 

Излучение является одним из видов энергии. Излучение испускается телами естественного и искусственного происхождения. Такие тела называют источниками излучения. Тела, поглощающие энергию излучения и преобразующие ее в другие виды энергии, называются приемниками излучения.

Энергию, переносимую излучением оптической области спектра, называют энергией излучения Qe. Мощность (количество энергии в единицу времени) излучения оптического диапазона спектра называется потоком излучения Фе.

Поток излучения за конечный интервал времени t определяется по формуле

,
где Qe - энергия излучения источника за интервал t.

Поток излучения характеризуется распределением во времени, по спектру, в пространстве и по приемной и излучающей поверхностям. Источники испускают поток излучения неодинаково в различных направлениях. Для того чтобы охарактеризовать его распределение в пространстве, вводят величину, характеризующую пространственную (угловую) плотность потока излучения - силу излучения. Понятие силы излучения используется для точечных источников. Точечность источника зависит не от его линейных размеров, а от их отношения к расстоянию до точки, в которой оценивается действие источника. Совокупность направлений в пространстве определяется телесным углом. Телесным углом ω называют часть пространства, ограниченную конической поверхностью, образуемой множеством прямых линий, проходящих через общую точку - вершину телесного угла, и замкнутым криволинейным контуром.

При равномерном распределении потока излучения Фе в пределах ω сила излучения Ie в направлении оси телесного угла

.

При неравномерном распределении потока излучения в различных направлениях говорят о бесконечно малом телесном угле dω, внутри которого элементарный поток dФe можно считать равномерно распределенным

.

Сила излучения или энергетическая сила света источника в некотором направлении - это отношение потока излучения dФe, исходящего от источника и распространяющегося внутри телесного угла dω, имеющего заданное направление, к этому элементарному телесному углу. Единицей силы излучения является Вт/ср - сила излучения источника в направлениях, в которых он испускает поток излучения, равный 1 Вт, и равномерно распределенный внутри телесного угла 1 ср.

Фотометрическое тело - это часть пространства, ограниченная поверхностью, проведенной через концы радиусов-векторов силы излучения. Сечение фотометрического тела плоскостью, проходящей через точечный источник, определяет кривую силы излучения источника для данной плоскости сечения.

Для оценки равномерности распределения потока излучения по поверхности источника вводится понятие энергетической светимости (излучательности) Ме. Энергетическая светимость равна отношению элементарного потока излучения ΔФе к площади элементарного, т.е. бесконечно малого, излучающего элемента dАи

.

Для излучателя, имеющего поверхность конечных размеров с равномерно распределенным потоком излучения по всей ее площади А,

.

Единица измерения светимости - Вт/м2. Она численно равна поверхностной плотности потока излучения, при которой поверхность площадью 1 м2  испускает поток излучения, равный 1 Вт.

Плотность потока излучения на поверхности, на которую он падает, называется энергетической освещенностью (облученностью) Ее. Энергетическая освещенность равна отношению элементарного потока излучения, падающего на элементарный элемент приемной поверхности и равномерно распределенного на ней, к площади этого элемента

.

Для облучаемой поверхности конечных размеров и равномерно распределенного по ней потока излучения

.

Единица энергетической освещенности (облученности) - Вт/м2. Она численно равна значению энергетической освещенности поверхности площадью 1 м2, на которую падает поток излучения, равный 1 Вт.

Для характеристики пространственного распределения плотности потока излучения вводится понятие энергетической яркости Le. Энергетическая яркость Le поверхности, по которой равномерно распределен поток излучения Фе, в направлении α равна

.

Единица энергетической яркости - Вт/(ср·м2). Она численно равна яркости равномерно излучающей поверхности площадью 1 м2 в перпендикулярном к ней направлении при силе излучения, равной 1 Вт/ср.

При неравномерном распределении потока излучения по поверхности излучателя энергетическая яркость рассчитывается для элементарных участков площади dA и телесных углов dω, в пределах которых поток излучения можно считать равномерно распределенным

.

Энергетическую яркость часто (особенно для первичных источников) определяют исходя из силы излучения элемента поверхности излучателя, так как именно эта величина характеризует распределение потока излучения в пространстве. Для поверхности конечных размеров, если все ее элементы имеют одинаковую силу излучения в направлении α,

.

Для неравномерно излучающей поверхности

.

Таким образом, энергетическая яркость - это отношение силы излучения элемента поверхности в выбранном направлении к площади его проекции на плоскость, перпендикулярную этому направлению.

У большинства используемых излучателей - как тепловых, так и люминесцентных - яркость в различных направлениях пространства приблизительно одинакова. Это означает, что излучение подчиняется закону Ламберта, т.е. яркость источника постоянна во всех направлениях пространства, иначе говоря, не является функцией направления, определяемого углом α. В этом случае сила излучения описывается зависимостью

,
где Ie0 - сила излучения в направлении α = 0.

Для равнояркой поверхности площадью А

,   
откуда .

Следовательно, для оценки равномерности распределения излучения по поверхности, излучающей по закону Ламберта, можно использовать понятия как поверхностной плотности излучения Ме, так и энергетической яркости Le.

 

Задачи к заданию № 1

 

Номер задачи к заданию №1 выбирается по таблице 1 согласно первой букве фамилии студента. Исходные данные для каждой задачи выбираются по последней цифре номера зачетной книжки.

 

Таблица 1 – Номер задачи

№ задачи

Первая буква фамилии

А,М

Б,Н,Я

В,Г,Ф

Д,Х,У

Е,Ш,Ю

Ж,О

З,П,Ц

И,Р

К,С,Щ

Л,Т,Э

1.2

1.4

1.6

1.8

1.10

1.3

1.5

1.7

1.9

1.1

 

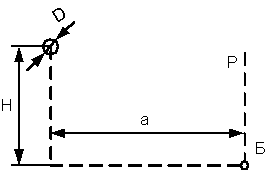
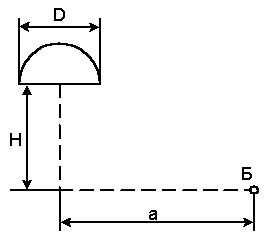
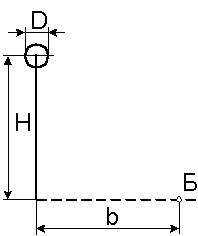
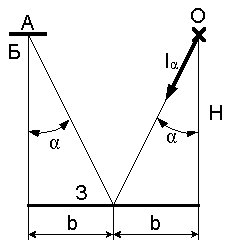
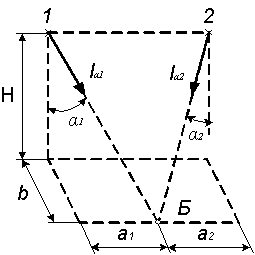
1.1 Ртутная лампа сверхвысокого давления имеет излучающее тело в виде шара диаметром D с энергетической светимостью Ме. Считая лампу равнояркой, определить облученности в точке Б (рисунок 1.1): а) минимальную, б) максимальную, на горизонтальной плоскости, г) на вертикальной плоскости Р. Исходные данные в таблице 1.1.

 

Таблица 1.1

Исходные данные

Последняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

D, мм

4

8

7

6

5

13

10

12

9

13

Ме, Вт/см2

300

350

400

450

500

550

600

650

700

750

H, м

4

5

6

7

8

4

5

6

7

8

а, м

6

7

8

9

10

6

7

8

9

10

 

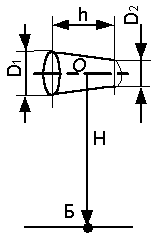
1.2  Равнояркий усеченный конус (рисунок 1.2) создает в точке Б горизонтальной плоскости облученность ЕеБ. Определить энергетическую яркость поверхности усеченного конуса. Как изменится горизонтальная облученность в точке Б, если усеченный конус повернуть около О так, чтобы его основания стали параллельными горизонтальной плоскости? Исходные данные в таблице 1.2.

Таблица 1.2

Исходные данные

Последняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

D1, см

2,5

1,5

3

1

2

1

1,5

2

2,5

3

D2, см

0,2

0,4

0,6

0,8

1

0,2

0,4

0,6

0,8

1

h, cм

1

2

3

4

5

1

2

3

4

5

H, м

3

4

5

6

7

3

4

5

6

7

ЕеБ, Вт/м2

4

3,5

3

2,5

2

4

3,5

3

2,5

2

 

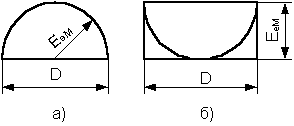
1.3  По круглой пластике, имеющей диаметр D, облученность распределяется, как указано на рисунке 1.3, а и б. Определить лучистые потоки, падающие на пластинку в одном и другом случаях. Исходные данные в таблице 1.3.

Таблица 1.3

Исходные данные

Последняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

D, см

11

12

10

8

9

8

9

10

11

12

ЕеМ, Вт/см2

2

2,5

3

3,5

4

2

2,5

3

3,5

4

 

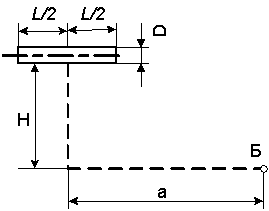
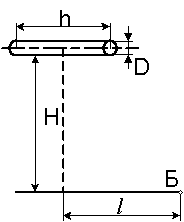
1.4  Определить энергетическую яркость равнояркого цилиндра при известных его размерах, если излучает только боковая поверхность цилиндра. Цилиндр создает в точке Б горизонтальную облученность ЕеБ  (рисунок 1.4). Определить облученность горизонтальной плоскости в точке Б при энергетической яркости цилиндра Le, если излучает вся поверхность. Исходные данные в таблице 1.4.

Таблица 1.4

Исходные данные

Последняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

D, мм

20

25

10

15

10

30

15

20

25

30

L, мм

55

60

50

40

45

40

45

50

55

60

а, м

4

5

6

7

8

4

5

6

7

8

H, м

3

4

5

6

7

3

4

5

6

7

ЕеБ ·10-4, мкВт/м2

45

55

40

60

50

60

55

50

45

40

Le·10-4, Вт/(м2·ср)

5

5,5

4

4,5

6

5

5,5

4

4,5

6

 

1.5  Внутренняя поверхность полой равнояркой полусферы с внутренним диаметром D имеет энергетическую светимость Ме. Определить горизонтальную облученность, создаваемую излучением внутренней поверхности полусферы в точке Б (рисунок 1.5). Исходные данные в таблице 1.5.

 

Таблица 1.5

Исходные данные

Последняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

D, мм

25

15

30

10

20

10

15

20

25

30

Ме, Вт/см2

300

200

350

150

250

150

200

250

300

350

H, м

4

5

6

7

8

4

5

6

7

8

a, м

3

4

5

6

7

3

4

5

6

7

 

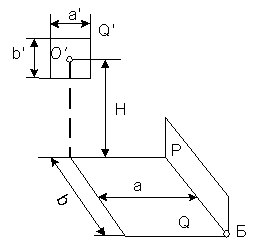
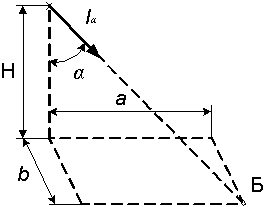
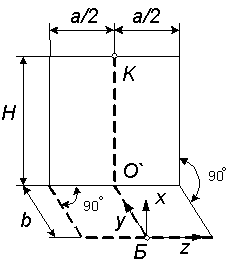
1.6  Равнояркий светящийся прямоугольник с размерами а' и b' (рисунок 1.6) имеет энергетическую яркость Le. Определить максимальную и горизонтальную облученности, создаваемые в точке Б этим прямоугольником. Плоскости Q' и Q параллельны. При каком положении прямоугольника он будет создавать в точке Б максимальное значение горизонтальной облученности. Положение прямоугольника а'b' изменяется путем вращения около точки О'. Исходные данные в таблице 1.6.

Таблица 1.6

Исходные данные

Последняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

a', cм

1,0

1,5

2,0

2,5

3,0

1,0

1,5

2,0

2,5

3,0

b', cм

4,0

5,5

6,0

4,5

5,0

4,0

4,5

5,0

5,5

6,0

Le, Вт/(см2·ср)

140

170

180

150

160

140

150

160

170

180

a, м

6

5

4

3

2

2

3

4

5

6

b, м

3

4

5

6

7

3

4

5

6

7

H, м

7

8

6

4

5

4

5

6

7

8

 

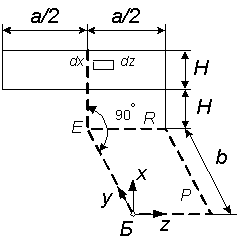
1.7  Плоскость равнояркого светящего прямоугольника Q' расположена перпендикулярно горизонтальной плоскости Q (рисунок 1.7). Определить облученности, создаваемые этим прямоугольником в точке Б горизонтальной плоскости Q и вертикальной Р, если известна энергетическая яркость прямоугольника Le. Исходные данные в таблице 1.7.

Таблица 1.7

Исходные данные

Последняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

a', cм

3,0

2,5

2,0

1,5

1,0

1,0

1,5

2,0

2,5

3,0

b', cм

5,0

5,5

6,0

4,5

4,0

4,0

4,5

5,0

5,5

6,0

Le, Вт/(см2·ср)

150

170

180

140

160

140

150

160

170

180

a, м

6

5

2

3

4

2

3

4

5

6

b, м

3

4

5

6

7

3

4

5

6

7

H, м

4

5

6

7

8

4

5

6

7

8

 

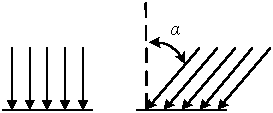
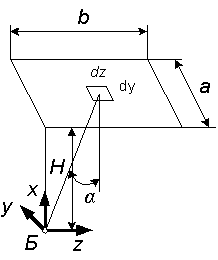
1.8  На две плоские одинаковые по площади поверхности падают одинаковые лучистые потоки (рисунок 1.8). На первую поверхность лучистый поток падает нормально, а на вторую – под углом α. Определите соотношение облученностей этих поверхностей. Исходные данные в таблице 1.8.

Таблица 1.8

Исходные данные

Последняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

α, %

30

35

40

45

50

55

60

65

70

75

 

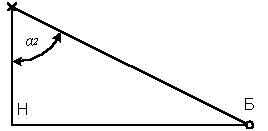
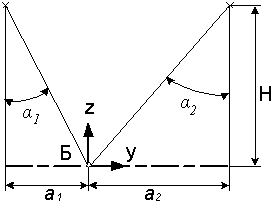
1.9  Точечный источник излучения, расположенный на расстоянии H от облучаемой горизонтальной поверхности, создает на ней равномерную облученность Ее в зоне от α1 до α2 (рисунок 1.9). Определить выражение, описывающее продольную кривую силы излучения в этой зоне углов α. Исходные данные в таблице 1.9.

Таблица 1.9

Исходные данные

Последняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

Ее, Вт/м2

1,5

2

2,5

3

3,5

1,5

2

2,5

3

3,5

H, см

1

2

3

4

5

1

2

3

4

5

α1 °

0

20

15

30

25

40

5

10

35

0

α2°

30

45

35

60

55

65

25

40

60

20

 

1.10       Продольная кривая силы излучения источника – окружность (рисунок 1.10) равна Ieβ = ncosβ. Определить лучистый поток этого источника излучения. Исходные данные в таблице 1.10.

Таблица 1.10

Исходные данные

Последняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

n

100

50

250

150

300

200

150

100

250

200

β °

70

35

60

75

50

55

40

65

30

45

 

 

 

 

Рисунок 1.1

 

 

Рисунок 1.2

 

 

 

 

 

 

 

 

Рисунок 1.3

 

 

 

Рисунок 1.4

 

 

 

 

 

Рисунок 1.5

 

 

Рисунок 1.6

 

 

Рисунок 1.7

 

 

 

 

 

 

 

 

Рисунок 1.8

 

 

 

 

 

 

 

 

Рисунок 1.9

 

 

 

 

 

Рисунок 1.10

 

 

 

 

 

 

 

 

 

ЗАДАНИЕ № 2. СВЕТОВЫЕ ХАРАКТЕРИСТИКИ ИЗЛУЧЕНИЯ

 

 

Краткие теоретические сведения

 

Эффективный поток в системе световых величин и единиц принято называть световым потоком. По определению Международной комиссии по освещению (МКО) световой поток оценивается действием потока излучения на селективный приемник, которым является стандартный фотометрический наблюдатель. В системе световых величин и единиц используются буквенные обозначения, принятые для потока излучения, но без индекса е. Наряду со стандартным фотометрическим наблюдателем в качестве приемника может использоваться фотоэлемент, спектральная чувствительность которого приведена с помощью светофильтра к кривой V(λ). В этом случае световой поток - это мощность излучения, ослабленного для различных λ пропорционально значениям относительной спектральной световой эффективности глаза.

За единицу светового потока принят люмен (лм). Люмен - это излучаемый черным телом световой поток с площади выходного отверстия, равной 0,5305 м2, при нормальном атмосферном давлении и при температуре затвердевания платины 2046 К. Приведение потока излучения к световому, как отмечалось выше, осуществляется с помощью функции V(λ). Зная V(λ), можно определить для всех λ значения спектральной световой эффективности глаза S(λ). Для практики важно знать максимальное значение S(λ)max при λ= 555 нм. Многочисленными измерениями установлено соотношение между единицами потока излучения и световыми единицами - ваттом и люменом: 1 Вт однородного потока излучения с λ=555 нм равен 683 лм светового потока. Следовательно, S(λ)max =683 лм/Вт. Это означает, что 1 Вт однородного потока излучения с λ=555 нм оказывает такое же действие, как световой поток, равный 683 лм.

Таким образом, Ф(λ) - однородный световой поток с длиной волны λ - можно выразить так:

.

Световой поток источника с линейчатым спектром

,
где Фе(λi) - поток излучения i-й линии; n - число линий; V(λi)- значение относительной спектральной световой эффективности для длины волны λi.

Для источника со сплошным спектром

,     
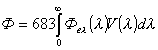где Феλ(λ) - спектральная плотность потока излучения.

Поскольку функция V(λ) стремится к нулю при λ<380 нм и λ>780 нм, световой поток

;             ,
где Δλ - ширина спектрального интервала; n - число участков, на которые разбивается видимая область спектра; Феλ - значение спектральной плотности потока излучения для середины i-го спектрального интервала; V(λ) - значение относительной спектральной световой эффективности глаза для середины i-го спектрального интервала. Значения Феλ(λ)  и V(λ) даны в таблицах.

Световой поток Ф, падающий на тело, в общем случае можно разделить на три части: поток, отраженный от тела, Фρ, поток, поглощенный телом, Фα, и поток, проходящий через тело, Фτ т. е.

    

Учитывая спектральные характеристики тела - спектральные коэффициенты отражения ρ(λ), поглощения α(λ) и пропускания τ(λ), а также распределение энергии в спектре падающего на тело потока излучения Феλ(λ), можно записать выражение для интегральных коэффициентов отражения, поглощения и пропускания в системе световых величин и единиц:

   
где λ1=380 нм; λ2=780 нм.

Очевидным является равенство .

Пространственную плотность светового потока в заданном направлении в системе световых величин и единиц называют силой света I. Она равна отношению элементарного светового потока dФ к элементарному телесному углу dω, в пределах которого заключен и равномерно распределен этот световой поток

.

Для равномерно распределенного светового потока в пределах телесного угла ω

.

За единицу силы света принята условная величина, получаемая при помощи основного светового эталона. Единица силы света - кандела. Это сила света, излучаемого в перпендикулярном направлении поверхностью черного тела площадью 0,5305 см2 при температуре затвердевания платины, при нормальном атмосферном давлении и температуре 2045 К. Связь люмена с канделой выражается следующим образом: один люмен равен световому потоку, испускаемому точечным источником света с силой света в одну канделу внутрь телесного угла, равного одному стерадиану, т. е. 1 лм =1 кд/1 ср.

Аналогично энергетической освещенности в системе световых величин и единиц введена плотность светового потока по освещаемой поверхности - освещенность. Освещенность - отношение светового потока Ф к площади поверхности, на которую он падает. Для равномерного распределения светового потока по освещаемой им поверхности конечного размера площадью А

,

для неравномерно распределенного светового потока

,
где dA - элементарный участок освещаемой поверхности, в пределах которого элементарный световой поток dФ можно считать равномерно распределенным.

Единица освещенности - люкс (лк). Один люкс - освещенность, создаваемая равномерно распределенным световым потоком 1 лм на освещаемой поверхности площадью 1 м2, т. е. 1 лк=1 лм/м2.

Освещенность пропорциональна силе света источника в данном направлении и обратно пропорциональна квадрату расстояния от источника до освещаемого элемента поверхности. Это - так называемый закон квадратов расстояний. Освещенность пропорциональна косинусу угла падения света на освещаемую поверхность. Это - закон Ламберта.

Указанные законы действительны и для энергетической освещенности, однако наиболее широкое применение они находят в практической фотометрии. Если источник имеет конечные размеры, то его обычно разбивают на части, которые по своим относительным размерам можно считать точечными, определяют их силу света, затем освещенности, создаваемые каждым из этих участков, освещенность поверхности, равную сумме создаваемых освещенностей.

Плотность распределения светового потока по поверхности излучателя в системе световых величин и единиц называется светимостью, т. е. плотностью светового потока по поверхности первичного или вторичного источника.

Светимость М поверхности излучателя конечных размеров площадью А, по которой равномерно распределен световой поток Ф,

.

Для неравномерно распределенного по поверхности излучателя светового потока


где М - светимость элементарного участка поверхности излучателя dA, на которой элементарный световой поток dФ можно считать равномерно распределенным. Единица светимости - лм/м2.

Светимость можно также выразить через спектральную плотность энергетической светимости излучающего тела Меλ(λ):

.

Пространственную плотность в системе световых величин и единиц характеризуют яркостью L. Яркость L - это сила света dI(α) с площади проекции dA' элемента поверхности излучающего тела dA на плоскость Р, перпендикулярную направлению излучения.

Определения и выражения для яркости аналогичны соответствующим определениям и выражениям для энергетической яркости (лучистости), только вместо потока излучения и силы излучения в них рассматривают световой поток Ф и силу света I. Единица яркости - кд/м2

Излучатели, яркость которых практически одинакова как по поверхности излучателя, так и по направлению, называются равнояркими излучателями. Простейшими излучателями обычно считают излучатели, у которых излучающее тело имеет форму диска, шара, полусферы и цилиндра.

Для равнояркого диска, имеющего яркость L и площадь А, сила света под углом α

,     
так как проекция излучателя на плоскость, перпендикулярную заданному направлению, .

Если известна зависимость силы света излучателя от направления, то его полный поток находится путем интегрирования силы света по всем направлениям пространства. В большинстве случаев распределение силы света измеряется, а затем задается графиком или таблицей. Поэтому интегрирование выполняется численным методом. Функция силы света задана аналитически и интегрирование выполняется аналитически. Для диска необходимо изменить пределы интегрирования, так как будем считать, что диск излучает с одной стороны

,
откуда

.

Связь между светимостью и яркостью диска, излучающего по закону Ламберта

.

Для равнояркого шара диаметром D площадь проекции  одинакова для любого направления, следовательно, сила света равнояркого шара одинакова по всем направлениям

.

Световой поток шара

.  

Для излучающей полусферы площадь проекции складывается из площади половины круга и эллипса

.

Следовательно,

,   
где .

Световой поток полусферического излучателя

.

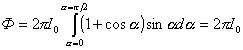Для цилиндрического излучателя (причем излучает только боковая поверхность цилиндра) осью симметрии является ось цилиндра, составляющая угол π/2 относительно направления максимальной силы света. Равнояркий цилиндр с темными торцами имеет светораспределение

,
где ; D и h — диаметр и высота цилиндра.

Световой поток, излучаемый равноярким цилиндром,

.

 

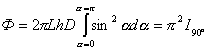Задачи к заданию № 2

 

Номер задачи к заданию №2 выбирается по таблице 2 по последней цифре номера зачетной книжки. Исходные данные для каждой задачи выбираются по предпоследней цифре номера зачетной книжки.

 

Таблица 2 – Номер задачи

№ задачи

Последняя цифра зачетной книжки

1

2

3

4

5

6

7

8

9

0

2.2

2.4

2.6

2.8

2.10

2.3

2.5

2.7

2.9

2.1

 

2.1   Равнояркие шар и цилиндр создают в точке Б (рисунок 2.1) горизонтальную облученность ЕеБгор. Шар излучает монохроматический поток с длиной волны λ1, а цилиндр – с длиной волны λ2. Определить яркости шара и цилиндра, если лучистые яркости Lец=nLеш. У цилиндра излучает только боковая поверхность. Исходные данные в таблице 2.1.

 

 

Таблица 2.1

Исходные данные

Предпоследняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

ЕеБгор, Вт/м2

0,95

0,80

0,85

0,90

0,75

0,90

0,80

0,75

0,95

0,85

λ1, мкм

0,5

0,45

0,4

0,55

0,45

0,4

0,5

0,55

0,4

0,45

λ2, мкм

0,6

0,5

0,55

0,65

0,55

0,6

0,65

0,6

0,5

0,6

D= h, см

6

5

7

4

7

5

6

4

7

6

d, см

3

2,5

4

2

3,5

2

3,5

2,5

4,5

2

H, м

2

4

5

2,5

3

2

5

3,5

5

4,5

b, м

3

6

7

4

5

3

6

5

6

7

n

2

3

4

2

3

4

2

3

4

2

 

2.2  а) Равнояркие шар и диск создают в точке Б (рисунок 2.2) горизонтальную освещенность ЕБгор. Если яркость шара равна яркости диска и диаметр шара равен диаметру диска, определите световые потоки, излучаемые шаром и диском. Относительно точки Б оба источника точечные. Как изменится освещенность в точке Б, если диск повернуть относительно центра до вертикального положения? Толщиной диска пренебречь. б) Определить горизонтальную освещенность, создаваемую источниками в точке Б, если равнояркие шар и диск излучают одинаковые световые потоки Фш=Фд. Исходные данные в таблице 2.2.

Таблица 2.2

Исходные данные

Предпоследняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

ЕБгор, лк

100

200

150

250

50

200

150

100

250

300

H, м

2

1

0,5

1,5

2,5

1

1,5

2

0,5

2,5

b, м

1,5

2,5

3

2

1

2,5

2

1,5

2

1

Фш=Фд, лм

5000

6000

4000

5500

4500

6500

4500

5000

6000

4000

 

2.3  Точечные источники света (шар и диск) освещают (рисунок 2.3) две грани равноугольной трехгранной призмы. Источники излучают одинаковые по значению световые потоки  Фш=Фд. Шар расположен на расстоянии b1 от середины освещаемой грани. На каком расстоянии bх от второй грани нужно расположить диск, чтобы грани имели одинаковые яркости при освещении их шаром и диском? Определите яркость грани, если коэффициент отражения ее поверхности ρ. Толщиной диска пренебречь. Исходные данные в таблице 2.3.

 

 

 

Таблица 2.3

Исходные данные

Предпоследняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

Фш=Фд, лм

2000

1000

1500

2500

1500

1000

2000

2500

1000

2000

b1, м

2

1

0,5

1,5

2,5

1

1,5

2

0,5

2,5

ρ

0,6

0,8

0,7

0,9

0,6

0,8

0,7

0,9

0,6

0,8

 

2.4  Равнояркий цилиндр, у которого светится вся поверхность, имеет яркость L и расположен, как показано на рисунке 2.4. а) Определить коэффициент яркости в направлении θ участка горизонтальной плоскости, лежащего в окрестностях точки Б, если яркость его Lθ. б) Чему будет равен коэффициент яркости этого участка в том же направлении, если ось цилиндра расположить горизонтально в плоскости рисунка, не изменяя положения центра цилиндра. Исходные данные в таблице 2.4.

Таблица 2.4

Исходные данные

Предпоследняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

L·105, кд/м2

1,0

0,8

0,5

1,2

0,9

1,1

0,7·

1,3·

1

0,6

Lθ, кд/м2

0,5

0,9

0,6

0,8

0,7

1

1,2

0,4

1,1

0,3

H, м

2

4

1,5

2,5

3

0,5

1

3,5

5

4,5

b, м

1

2,5

0,5

2

1,5

3

1

2,5

2

1,5

D, см

2

1

3

1,5

2,5

3,5

1

2

3

2,5

h, см

6

5

8

7

6

8

4

5

6

4

 

2.5  Равнояркий шар диаметром D излучает световой поток Ф. Определить яркость шара и расстояние H, на котором следует расположить шар над горизонтальной плоскостью, чтобы получить в точке Б максимальную горизонтальную освещенность (рисунок 2.5). Исходные данные в таблице 2.5.

Таблица 2.5

Исходные данные

Предпоследняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

Ф, лм

2000

3000

3500

2500

1500

1000

2000

4500

4000

3000

D, см

4

5

3

6

5

4

2

3

4

5

b, м

1,5

0,5

1

2

0,8

1,2

1,4

0,9

0,7

0,8

 

2.6  Равнояркий шар создает в точке Б горизонтальной плоскости (рисунок 2.6) освещенность Е. Определить яркость шара, если его диаметр D, коэффициент отражения зеркала ρз. Как изменится освещенность в точке Б горизонтальной плоскости, если шар заменить равноярким диском, имеющим те же яркость и диаметр, что и шар, и плоскость диска расположить параллельно горизонтальной плоскости? Исходные данные в таблице 2.6.

Таблица 2.6

Исходные данные

Предпоследняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

Е, лк

100

80

60

90

70

50

110

120

40

130

D,см

8

10

5

9

6

4

7

11

3

12

ρз

0,6

0,9

0,8

0,65

0,7

0,75

0,85

0,6

0,75

0,8

H, м

2

4

5

2,5

3

1,5

2,5

3,5

3

4,5

b, м

1

2,5

0,5

2

1,5

3

1

2,5

2

1,5

 

2.7  Луч света попадает на белую бариевую пластинку А после отражения от трех зеркал (рисунок 2.7). Определить силу света в направлении центра первого зеркала, если яркость бариевой пластинки в точке Б равна L, коэффициент отражения каждого зеркала ρз и бариевой пластинки ρ. Исходные данные в таблице 2.7.

Таблица 2.7

Исходные данные

Предпоследняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

L, кд/м2

100

80

60

90

70

50

110

120

40

130

ρз

0,85

0,75

0,65

0,8

0,85

0,9

0,6

0,75

0,6

0,75

ρ

0,6

0,9

0,8

0,65

0,7

0,75

0,85

0,6

0,75

0,8

H, м

7

7,5

5

2,5

6,5

6

2,5

3,5

5,5

4,5

b, м

1

2,5

0,5

2

1,5

3

1

2,5

2

1,5

 

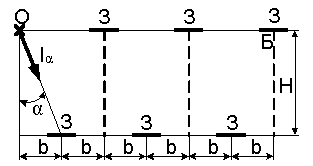
2.8  Определить яркость в точке Б белой гипсовой пластинки с коэффициентом отражения ρ (рисунок 2.8). Световой поток попадает на эту пластинку от источника света О после пяти отражений от зеркал З, коэффициент отражения каждого из которых ρз, если известна сила света Iα. Исходные данные в таблице 2.8.

Таблица 2.8

Исходные данные

Предпоследняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

Iα·107, кд

0,8

0,6

0,9

1,2

1,0

1,5

0,7

1,1

1,4

0,5

ρз

0,85

0,75

0,65

0,8

0,85

0,9

0,6

0,75

0,6

0,75

ρ

0,6

0,9

0,8

0,65

0,7

0,75

0,85

0,6

0,75

0,8

H, м

3

2

5

2,5

6,5

6

2,5

3,5

5,5

4,5

b, м

4

2,5

5

4,5

1,5

3,5

6

2,5

5,5

6,5

 

2.9  Точечный источник О освещает площадку А отраженным от зеркала З светом (рисунок 2.9). Сила света по направлению к центру зеркала Iα. Изображение источника полностью укладывается в пределах зеркала. Размеры, определяющие взаимное положение источника света, зеркала и площадки А: H и b. Принимая коэффициент отражения зеркала ρ, определить горизонтальную освещенность площадки А в точке Б. Исходные данные в таблице 2.9.

Таблица 2.9

Исходные данные

Предпоследняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

Iα, кд

2000

3000

4000

2500

3500

4500

1500

1000

5000

5500

ρ

0,6

0,9

0,8

0,65

0,7

0,75

0,85

0,6

0,75

0,8

H, м

3

2

5

2,5

6,5

6

2,5

3,5

5,5

4,5

b, м

1

0,5

2

1,5

3

3,5

1

2,5

3

2

 

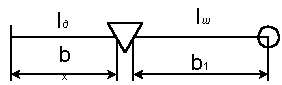
2.10     У равнояркого цилиндра боковая поверхность излучает лучистый монохроматический поток с длиной волны λ1, а основание – с длиной волны λ2. Определить горизонтальную освещенность в точке Б (рисунок 2.10), если известны H, l, D, h. Лучистые потоки, излучаемые боковой поверхностью и основаниями, соответственно равны Фе(λ1,dλ) и Фе(λ2,dλ). Исходные данные в таблице 2.10.

Таблица 2.10

Исходные данные

Предпоследняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

λ1, мкм

0,5

0,45

0,4

0,55

0,45

0,4

0,5

0,55

0,4

0,45

λ2, мкм

0,6

0,5

0,55

0,65

0,55

0,6

0,65

0,6

0,5

0,6

H, м

3

2,5

4

2

3,5

2

3,5

2,5

4,5

2

l, м

6

5

7

4

7

5

6

4

7

6

D, см

2

4

1,5

2,5

3

2

1,5

3,5

3

4

h, см

3

6

4,5

4

5,5

3

3,5

5

4,5

6,5

 

 

 

 

 

Рисунок 2.1

 

 

 

 

 

Рисунок 2.2

 

 

 

 

 

 

 

 

 

 

 

Рисунок 2.3

 

 

 

Рисунок 2.4

 

 

 

Рисунок 2.5

 

 

Рисунок 2.6

 

 

Рисунок 2.7

 

 

 

 

Рисунок 2.8

 

 

Рисунок 2.9

 

 

 

Рисунок 2.10

 

 

 

 

 

ЗАДАНИЕ № 3. СВЕТОВОЕ ПОЛЕ

 

 

Краткие теоретические сведения

 

Распространение световой энергии и светового потока происходит в некотором пространстве, которое называют световым полем. В световом поле рассматриваются распределение в пространстве световых потоков и соотношения, характеризующие это распределение. Количественной характеристикой светового поля является расход световой энергии в единицу времени сквозь единицу площади поверхности, на которой лежит исследуемая точка поля. Таким образом, можно говорить о поверхностной плотности светового потока (освещенности) в данной точке поля.

Если источник имеет конечные размеры, то освещенность, создаваемую на освещаемой поверхности, определяют, разбивая источник на элементарные площадки dA, которые рассматривают как точечные источники.

Освещенность dE от элементарной площадки dA равна

,
где dI - сила света излучающей площадки dA в направлении рассматриваемой точки освещаемой поверхности; α' - угол падения света на эту поверхность; l - расстояние до освещаемой точки.

Так как , где L — яркость площадки dA; α - угол между нормалью к dA и направлением на освещаемую точку, то

,
где — телесный угол, под которым элемент поверхности dA виден из освещаемой точки.

Освещенность, создаваемая в точке источником,

,       
где ω - телесный угол, под которым источник виден из освещаемой точки.

В общем случае яркость меняется от точки к точке вдоль поверхности источника в зависимости от углов, определяющих направления излучения и положения точки на поверхности. Если излучение подчиняется закону Ламберта, то яркость зависит от углов, а если яркость постоянна по направлению и по поверхности источника, то

.       

Освещенность, создаваемая протяженным источником постоянной яркости, подчиняющимся закону Ламберта, определяется его яркостью, размерами и контуром источника относительно освещаемой площадки. От формы поверхности источника освещенность не зависит. Это свойство называется светотехническим подобием.

Интегральная характеристика светового поля С определяет среднюю освещенность выбранной поверхности, расположенной в данной точке поля. Эта характеристика светового поля - функция точки и направления. Она зависит от распределения яркости в пространстве

, 
где L(β, φ) - яркость излучения в направлении, определяемом значениями углов β и φ в исследуемой точке поля; f(β) - функция, определяющая ценность излучения, поступающего с данного направления на выбранную поверхность, расположенную в данной точке поля (рассматривается ниже); dω - элементарный телесный угол, в пределах которого из данной точки пространства виден участок поверхности с яркостью L(β, φ).

Если излучающие поверхности равнояркие, то

.

Функция ценности излучения зависит от положения точечного источника, освещающего выбранную поверхность, и формы этой поверхности. Она определяется отношением площадей σ/А, где σ - площадь проекции выбранной поверхности приемника излучения на плоскость, перпендикулярную направлению от точечного источника к данной точке поля; А — площадь выбранной поверхности приемника излучения, содержащая данную точку поля, средняя освещенность которой является интегральной характеристикой светового поля в этой точке.

Наиболее простая интегральная характеристика - освещенность плоскости Е

  , 
где ω - телесный угол, в пределах которого расположена излучающая свет поверхность, в поле которой определяется освещенность; Ен — нормальная освещенность.

Другой интегральной характеристикой светового поля является пространственная освещенность E0 в данной точке светового поля. Она равна сумме нормальных освещенностей, причем f(β) = l:

.

Если приемник излучения – сфера малого радиуса r, то отношение площади проекции сферического приемника равно

.
Тогда сферическая освещенность Е4π равна

   

Если световые излучения поступают в исследуемую точку преимущественно из одного полупространства, то в качестве интегральной характеристики светового поля используют среднюю полусферическую освещенность.

,
где — освещенность плоскости основания полусферы; dEн — нормальная освещенность площадки, перпендикулярной оси телесного угла ω.

Средняя полусферическая освещенность выражает среднюю плотность светового потока (освещенность) на полусфере исчезающе малого радиуса, расположенной в исследуемой точке поля.

Для оценки насыщенности светом используют среднюю цилиндрическую освещенность, под которой понимают среднюю освещенность боковой поверхности цилиндра с вертикальной ориентацией и малыми размерами (основание и высота цилиндра стремятся к нулю)

.

Для характеристики светового поля введен усредненный по времени, вектор плотности переноса световой энергии - световой вектор е. Световой вектор определяет в любой точке поля значение (модуль) и направление вектора переноса световой энергии, в единицу времени через единицу площади, перпендикулярной направлению переноса. Поток светового вектора Ф' через некоторую поверхность равен разности световых потоков, падающих на одну и другую сторону этой поверхности:

.

Проекция светового вектора εN  на любое направление определяется разностью освещенностей двух сторон некоторой площадки, на нормаль к которой спроектирован вектор

,
где Eβ, Eπ-β - освещенности сторон поверхности; β - угол между направлением и нормалью к поверхности.

 

 

Задачи к заданию № 3

 

Номер задачи к заданию №3 выбирается по таблице 3 по предпоследней цифре номера зачетной книжки. Исходные данные для каждой задачи выбираются по последней цифре номера зачетной книжки.

 

Таблица 3 – Номер задачи

№ задачи

Предпоследняя цифра зачетной книжки

1

2

3

4

5

6

7

8

9

0

3.5

3.2

3.1

3.10

3.3

3.9

3.7

3.6

3.4

3.8

 

3.1  Определить значение и направление светового вектора в точке Б поля двух точечных излучателей (рисунок 3.1). Продольная кривая силы света каждого излучателя описывается уравнением Iα=Ncosα, кд. Исходные данные в таблице 3.1.

Таблица 3.1

Исходные данные

Последняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

N

1200

1000

800

1500

900

1800

2000

1600

600

1300

a1, м

4

2

5

3

6

2

3

4

5

6

a2, м

6

3

4

5

3

4

5

6

3

4

H, м

5

6

3

6

4

5

6

3

4

3

 

3.2  Построить продольное сечение тела освещенности, создаваемое в точке Б точечным источником с силой света  Iα=Nsinα, кд, и определить значение светового вектора в точке Б (рисунок 3.2). Исходные данные в таблице 3.2.

Таблица 3.2

Исходные данные

Последняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

N

1200

1000

800

1500

900

1800

2000

1600

600

1300

a1, м

4

2

5

3

6

2

3

4

5

6

a2, м

6

3

4

5

3

4

5

6

3

4

H, м

5

6

3

6

4

5

6

3

4

3

 

3.3  Два точечных источника света 1 и 2 (Iα1=Ncosα1, кд; Iα2=Msinα2, кд) расположены как, указано на рисунке 3.3. Определить тело распределения освещенности в точке Б и световой вектор, создаваемый источниками в точке Б. Исходные данные в таблице 3.3.

Таблица 3.3

Исходные данные

Последняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

N

1200

1000

800

1500

900

1800

2000

1600

600

1300

M

500

700

1200

1000

1600

1300

1500

900

1800

2000

2a1= a2, м

4

2

5

3

6

2

3

4

5

6

b, м

6

3

4

5

3

4

5

6

3

4

H, м

5

6

3

6

4

5

6

3

4

3

 

3.4  Определить световой вектор и среднюю сферическую освещенность, создаваемые в точке Б равноярким прямоугольником (рисунок 3.4). Плоскость прямоугольника параллельна плоскости yБz. Исходные данные в таблице 3.4.

Таблица 3.4

Исходные данные

Последняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

L·103, кд/м2

7

11

18

20

5

10

15

12

9

17

H = a, м

1

2

0,5

1,5

1

2

0,5

1,5

1

2

b, м

5

3

4

5

3

4

5

2

3

4

 

3.5  Равнояркий светящийся прямоугольник (рисунок 3.5) имеет яркость L. Определить световой вектор и среднюю сферическую освещенность в точке Б. Исходные данные в таблице 3.5.

Таблица 3.5

Исходные данные

Последняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

L·103, кд/м2

7

11

18

20

5

10

15

12

9

17

a, м

1

2

0,5

1,5

1

2

0,5

1,5

1

2

b, м

5

3

4

5

3

4

5

2

3

4

H, м

2

5

3

4

5

3

2

4

5

3

 

3.6  Равнояркий прямоугольник (рисунок 3.6) создает в точке Б среднюю сферическую освещенность Е4π. Определить значение и направление светового вектора в точке Б. Исходные данные в таблице 3.6.

 

 

 

 

Таблица 3.6

Исходные данные

Последняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

Е4π, лк

500

200

800

400

600

1000

700

300

900

1100

a, м

1

2

0,5

1,5

1

2

0,5

1,5

1

2

b, м

5

3

4

5

3

4

5

2

3

4

H, м

2

5

3

4

5

3

2

4

5

3

 

3.7  Определить значение и направление светового вектора в точке Б (рисунок 3.7). Известна горизонтальная освещенность в этой точке, создаваемая равноярким светящим прямоугольником ЕБ. Размеры прямоугольника и положение точки Б даны на рисунке. Исходные данные в таблице 3.7.

Таблица 3.7

Исходные данные

Последняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

ЕБ, лк

500

200

800

400

600

1000

700

300

900

1100

a, м

1

2

0,5

1,5

1

2

0,5

1,5

1

2

b, м

5

3

4

5

3

4

5

2

3

4

H, м

2

5

3

4

5

3

2

4

5

3

 

3.8  Светящая полоса имеет светораспределение Iγα=Ncos2α, кд, в продольной плоскости, проходящей через точку Б и ось полосы (рисунок 3.8). Определить световой вектор и косинусы направляющих углов его в точке Б светового поля полосы. Исходные данные в таблице 3.8.

Таблица 3.8

Исходные данные

Последняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

N

3000

2000

2500

1500

1000

4000

3500

3000

2500

1500

H = a, м

1

2

3

4

1

2

3

4

1

2

b, м

5

3

4

5

3

4

5

2

3

4

 

3.9  Равнояркий шар с диаметром D имеет яркость L. Определить интегральные характеристики в точке Б светового поля этого шара: средние цилиндрическую, сферическую и полусферическую освещенности. Положение шара относительно точки Б показано на рисунке 3.9. Исходные данные в таблице 3.9.

 

 

 

 

 

Таблица 3.9

Исходные данные

Последняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

D, мм

50

30

20

40

60

45

35

25

55

15

L·106, кд/м2

10

15

12

8

18

20

13

9

16

11

H, м

5

6

3

4

5

6

3

4

5

6

a, м

4

5

2

3

4

2

4

5

4

3

b, м

5

3

4

5

3

4

5

2

3

4

 

3.10     Точечный источник света О создает в точке Б плоскости Р среднюю полусферическую освещенность с плоскостью ориентации, совпадающей с плоскостью Р, Е2πР (рисунок 3.10). Определить в точке Б средние освещенности: цилиндрическую, сферическую и полусферическую с плоскостью ориентации, совпадающей с плоскостью Q. Исходные данные в таблице 3.10.

Таблица 3.10

Исходные данные

Последняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

Е2πР, лк

150

200

120

240

160

145

235

125

155

215

H, м

5

6

3

4

5

6

3

4

5

6

a, м

4

5

2

3

4

2

4

5

4

3

b, м

5

3

4

5

3

4

5

2

3

4

 

 

 

 

Рисунок 3.1

 

 

 

 

Рисунок 3.2

 

Рисунок 3.3

 

 

 

Рисунок 3.4

 

Рисунок 3.5

 

 

 

Рисунок 3.6

 

 

Рисунок 3.7

 

Рисунок 3.8

 

Рисунок 3.9

 

 

 

 

Рисунок 3.10

 

 

ЗАДАНИЕ № 4. ФОТОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ТЕЛ

 

Краткие теоретические сведения

 

При распространении излучения в какой-либо материальной среде в результате их взаимодействия энергия излучения претерпевает количественные и качественные изменения. Для всех превращений и видоизменений энергии излучения должен выполняться закон сохранения энергии.

Оптические свойства среды определяются коэффициентами отражения ρ, пропускания τ и поглощения α, причем спектральные характеристики обычно выражаются спектральными коэффициентами отражения, пропускания и поглощения ρ(λ), τ(λ) и α(λ). Геометрическая оптика является частным случаем волновой оптики, которая рассматривает излучение как совокупность световых лучей. Под световым лучом понимается геометрическая линия, не имеющая размеров в поперечном сечении. Поэтому геометрическую оптику называют также лучевой. Основу геометрической оптики составляют: закон прямолинейного распространения света (явление дифракции не учитывается), законы отражения и преломления света и закон независимости распространения световых пучков.

Если лучи встречают на своем пути другую среду и преломляются, то луч падающий и луч преломленный лежат в одной плоскости (плоскости падения) с перпендикуляром к поверхности в точке падения; отношение синуса угла падения к синусу угла преломления постоянно для двух оптических сред

,
где n2,1 - показатель преломления, второй среды относительно первой. Возможна и такая запись:

,
где n1 и n2 - показатели преломления сред; произведение показателя преломления среды на синус угла между нормалью и лучом при каждом преломлении постоянно и называется оптическим инвариантом.

Для количественной оценки модификации излучения в различных средах используется модель пучка лучей. Пучок лучей - это ряд прилегающих друг к другу световых лучей, образующих световую трубку, т.е. часть пространства, по которому происходит перенос световой энергии.

Прохождение излучения в материальной среде сопровождается его ослаблением, поскольку часть его энергии переходит в другие виды. Вещества по-разному поглощают излучение: у металлов оно очень сильное, у диэлектриков гораздо меньше. В большинстве случаев поглощение зависит от длины волны излучения, поэтому изучение этого явления проводится, как правило, для однородного излучения с последующим суммированием полученных результатов для всех длин волн.

Закон Бугера гласит: доля поглощенного излучения не зависит от потока излучения Фе и поток dФе, поглощенный в элементарном слое dx, пропорционален толщине этого слоя:

,
где а - показатель поглощения, м-1.

В светотехнической практике для упрощения расчетов показатель поглощения определяют при десятичном основании логарифма

   
где а10=0,434а - десятичный показатель поглощения.

Показатель поглощения зависит также от длины волны.

Закон Бугера можно записать и для прозрачности вещества


где  - прозрачность вещества - величина, численно равная коэффициенту пропускания излучения веществом единичной толщины (d'=1 м). Для удобства расчета в этом случае вместо показательной функции толщины вводят понятие оптической плотности среды D. Очевидно, при =0,l D =l, а при =0,01 D =2.

Применяют также понятие удельной оптической плотности

.

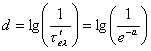В зависимости от показателя поглощения все вещества условно делят на прозрачные и непрозрачные. Это деление проводится на основании средней глубины проникновения излучения в вещество

.

Это понятие имеет физический смысл глубины, на которой вошедший в вещество поток излучения уменьшается в е раз. Потери на пропускание излучения определяются не только отражением на преломляющих поверхностях, но и поглощением. Поэтому на практике под коэффициентом пропускания и оптической плотностью подразумевается величина, учитывающая эти два фактора, ослабляющие проходящее излучение. Например, коэффициент пропускания пластины из стекла с учетом отражения от граничных поверхностей

,
где ρ - коэффициент френелевского отражения; а - коэффициент поглощения проходящего излучения; d - толщина.

Коэффициент поглощения

.

Оптическая плотность

,
где -оптическая плотность, зависящая от поглощаю­щей способности среды;  - оптическая плотность, обусловленная потерями на отражение ( постоянно при любой толщине пластины).

Когда вещество оптически избирательно, то интегральный коэффициент пропускания определяется выражением

.

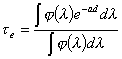Для эффективного потока

,
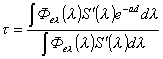где  - относительная спектральная чувствительность приемника излучения (глаз, фотоэлемент);  - спектральная плотность падающего потока.

Широкое применение в светотехнике находят светофильтры - пластины с оптически однородной (не рассеивающей) средой, с избирательным поглощением энергии излучения в той или иной части спектра. Такие светофильтры называются поглощающими (абсорбционными). Светофильтры, пропускание которых в пределах видимой области спектра незначительно меняется с длиной волны, и которые почти не меняют цвета проходящего через них излучения, называют нейтральными.

Основными характеристиками светофильтров являются их зависимости коэффициента пропускания или оптической плотности от длины волны – τ(λ) и D(λ). Светофильтры могут также характеризоваться длиной волны , соответствующей максимуму области пропускания светофильтра, или предельной длиной волны , соответствующей границе полосы пропускания, при этом под границей пропускания понимают то значение λ, при котором коэффициент пропускания в 2 раза меньше максимального.

Эффективный интегральный коэффициент пропускания светофильтра рассчитывается для заданных спектральных составов падающего излучения и приемника

.

Пределы интегрирования определяются длинами волн, в диапазоне которых изменяются подынтегральные функции.

Эффективная оптическая плотность светофильтра

.

Для характеристики пропускания светофильтра используют также понятие кратности светофильтра

 , 
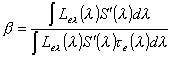где  - спектральная плотность энергетической яркости;  - относительная спектральная чувствительность приемника излучения, причем .

 

Задачи к заданию № 4

 

Номер задачи к заданию №4 выбирается по таблице 4 по последней цифре номера зачетной книжки. Исходные данные для каждой задачи выбираются по последней цифре номера зачетной книжки.

 

Таблица 4 – Номер задачи

№ задачи

Последняя цифра зачетной книжки

1

2

3

4

5

6

7

8

9

0

4.4

4.9

4.10

4.1

4.8

4.2

4.7

4.6

4.5

4.3

 

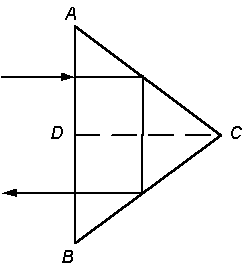
4.1 Определить коэффициент пропускания стеклянной призмы при перпендикулярном падении пучка лучей естественного света середину грани призмы AB (рисунок 4.1). Показатель преломления стекла призмы n, прозрачность стекла призмы τ'. Исходные данные в таблице 4.1.

Таблица 4.1

Исходные данные

Предпоследняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

AB=BC, см

3

4

5

6

7

3

4

5

6

7

n

1,5

1,6

1,7

1,55

1,65

1,75

1,5

1,6

1,7

1,55

τ', см-1

0,991

0,995

0,999

0,992

0,996

0,994

0,993

0,997

0,99

0,998

 

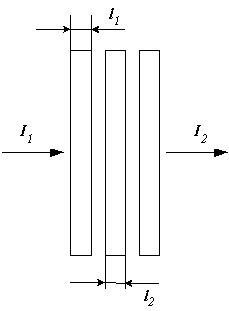
4.2 Имеются три нейтральных светофильтра (рисунок 4.2). Удельные оптические плотности первого и второго светофильтров соответственно d1 и d2. Определить коэффициент пропускания третьего светофильтра, если известно, что три светофильтра ослабляют силу света с I1 до I2. Толщины первого и второго светофильтров соответственно l1 и l2. Исходные данные в таблице 4.2.

Таблица 4.2

Исходные данные

Предпоследняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

d1, см-1

0,31

0,35

0,38

0,32

0,36

0,39

0,33

0,37

0,34

0,3

d2, см-1

0,45

0,48

0,42

0,44

0,4

0,49

0,47

0,41

0,49

0,46

I1, кд

100

140

120

110

90

150

130

80

160

70

I2, кд

5

7

6

5

4

8

7

4

8

4

l1, мм

2

3

2,5

3,5

1,5

2

3

2,5

3,5

1,5

l2, мм

1

1,5

1,5

2

0,5

1

2

1,5

2,5

1

 

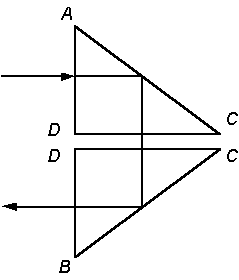
4.3 Пучок лучей естественного света падает перпендикулярно на грань призмы AB и выходит из призмы через ту же грань (рисунок 4.3,а). Как изменятся потери, если призму ABC заменить двумя призмами: ACD и DCB (рисунок 4.3,б). Все три призмы выполнены из стекла с показателем преломления n. Прозрачность стекла призмы τ'. Исходные данные в таблице 4.3.

Таблица 4.3

Исходные данные

Предпоследняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

AC=CB, см

3

4

5

6

7

3

4

5

6

7

n

1,5

1,6

1,7

1,55

1,65

1,75

1,5

1,6

1,7

1,55

τ', см-1

0,991

0,995

0,999

0,992

0,996

0,994

0,993

0,997

0,99

0,998

 

4.4 Естественный свет падает на стеклянную плоскопараллельную пластинку под углом i. Определить потери на отражение от двух граней пластинки и степень поляризации пучка лучей, прошедшего через пластинку. Показатель преломления стекла n. Поглощением света в пластинке пренебречь. Исходные данные в таблице 4.4.

Таблица 4.4

Исходные данные

Предпоследняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

i,°

30

10

20

40

15

25

35

40

5

25

n

1,5

1,6

1,7

1,55

1,65

1,75

1,5

1,6

1,7

1,55

 

4.5 Два нейтральных стеклянных светофильтра толщиной l1 и l2 имеют соответственно прозрачности τ1' и τ2', и показатели преломления n1 и n2. эти светофильтры склеены канадским бальзамом. Определить кратность полученного светофильтра для естественного света при углах падения i1=0° и i2=45°. Исходные данные в таблице 4.5.

 

Таблица 4.5

Исходные данные

Предпоследняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

l1, мм

1,5

2,0

2,5

3,0

1,5

2,0

2,5

3,0

2,0

2,5

l2, мм

0,5

1,0

1,5

2,0

1,0

0,5

1,0

1,5

0,5

1,0

τ1', мм-1

0,3

0,35

0,4

0,45

0,5

0,3

0,35

0,4

0,45

0,5

τ2', мм-1

0,6

0,65

0,7

0,75

0,8

0,6

0,65

0,7

0,75

0,8

n1

1,5

1,51

1,52

1,53

1,54

1,54

1,53

1,52

1,51

1,5

n2

1,53

1,54

1,55

1,52

1,51

1,5

1,52

1,54

1,53

1,55

 

4.6  а) Стеклянная пластинка толщиной l имеет показатель преломления n. Стекло, из которого изготовлена пластинка, обладает прозрачностью τ'. Определить коэффициент пропускания этой пластинки для пучка лучей естественного света, если угол падения i. б) Определить толщину стеклянной плоскопараллельной пластинки, если при угле падения i неполяризованного света на эту пластинку ее коэффициент пропускания τ. Прозрачность стекла пластинки τ'. Показатель преломления n. Исходные данные в таблице 4.6.

Таблица 4.6

Исходные данные

Предпоследняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

l, см

1

1,5

2

2,5

3

1

1,5

2

2,5

3

i,°

20

35

30

0

15

25

35

10

0

25

τ', см-1

0,991

0,993

0,995

0,997

0,99

0,992

0,994

0,996

0,998

0,993

n

1,5

1,6

1,7

1,55

1,65

1,75

1,5

1,6

1,7

1,55

 

4.7 Три стеклянные пластинки с показателями преломления n1, n2 и n3 сложены в стопу так, что пластинка с коэффициентом преломления n2 находится в середине стопы, и склеены канадским бальзамом. Поглощение в стекле и многократные отражения не учитывать. Стопа пластинок находится в воздухе. Угол падения пучка лучей неполяризованного излучения на стопу пластинок i. В каком порядке следует расположить их в стопе, чтобы иметь минимальные потери на отражение? Как изменится коэффициент пропускания этой стопы, если оставить воздушные промежутки между каждыми двумя соседними пластинками? Исходные данные в таблице 4.7.

Таблица 4.7

Исходные данные

Предпоследняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

i,°

0

10

20

30

0

10

20

30

0

10

n1

1,6

1,7

1,5

1,7

1,5

1,6

1,7

1,5

1,6

1,7

n2

1,5

1,6

1,7

1,5

1,6

1,7

1,5

1,6

1,7

1,5

n3

1,6

1,5

1,6

1,6

1,7

1,6

1,6

1,5

1,5

1,7

 

 

4.8  Прожектор освещает цель. Определить яркость цели, видимой наблюдателем, расположенным у прожектора, если расстояние между целью и прожектором l. Диаметр прожектора Dп. Коэффициент отражения его отражателя ρ. Яркость источника света прожектора L. Поверхность цели отражает свет диффузно и имеет коэффициент отражения ρц. Угол падения света на цель α. Средняя прозрачность атмосферы τ' = 0,9 км-1. Рассеянием пренебречь. Исходные данные в таблице 4.8.

Таблица 4.8

Исходные данные

Предпоследняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

l, км

5

6

7

8

9

10

9

8

7

6

Dп, м

2

1,5

1

2,5

2

1,5

1

2,5

2

1

ρ

0,7

0,75

0,8

0,85

0,9

0,7

0,75

0,8

0,85

0,9

L·109, кд/м2

1,2

1,1

1,0

0,9

0,8

1,2

1,1

1,0

0,9

0,8

ρц

0,5

0,55

0,6

0,65

0,7

0,5

0,55

0,6

0,65

0,7

α, °

0

30

45

0

30

45

0

30

45

0

 

4.9  а) Нейтральный светофильтр толщиной l1 имеет оптическую плотность D. Определить оптическую плотность и коэффициент пропускания светофильтра из того же материала, имеющего толщину l2. б) Нейтральный светофильтр имеет показатель преломления n и коэффициент поглощения α. Определить коэффициент пропускания светофильтра, если угол падения пучка лучей неполяризованного излучения на этот светофильтр i. Исходные данные в таблице 4.9.

Таблица 4.9

Исходные данные

Предпоследняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

l1, мм

1,5

2

2,5

3

1,5

2

2,5

3

2

2,5

l2, мм

0,7

0,8

0,9

2,2

1,0

1,5

1,1

2,0

1,2

1,5

D

0,4

0,45

0,5

0,55

0,6

0,4

0,45

0,5

0,55

0,6

n

1,5

1,52

1,54

1,56

1,51

1,53

1,54

1,55

1,53

1,51

α

0,45

0,5

0,55

0,6

0,45

0,5

0,55

0,6

0,5

0,55

i, °

0

30

45

0

30

45

0

30

45

0

 

4.10      Заданный светофильтр имеет спектральный коэффициент пропускания τλ в интервале длин волн от λ1 до λ2. Приняв для остальных участков спектра τλ=0, определить коэффициенты пропускания этого светофильтра для излучения черного тела τs и вольфрама τw, температура которых Т. Исходные данные в таблице 4.10.

 

 

 

Таблица 4.10

Исходные данные

Предпоследняя цифра номера зачетной книжки

0

1

2

3

4

5

6

7

8

9

Тип свето-фильтра

КС18

ОС17

КС15

ЖС18

КС19

ЖС10

КС10

ОС13

ЖС11

ОС14

τλ

0,98

0,96

0,96

0,92

0,92

0,94

0,92

0,92

0,94

0,96

λ1, нм

680

540

660

520

700

380

600

570

440

580

λ2, нм

2700

3000

2600

2600

2500

2800

2700

2800

2700

2700

Т, К

2900

3400

2500

3100

2700

3000

3300

2800

3200

2600

 

 

 

 

Рисунок 4.1

 

Рисунок 4.2

 

 

 

Рисунок 4.3,а

 

 

Рисунок 4.3,б

 

 

 

Список литературы

 

 

1.     Гуторов М.М. Основы светотехники и источники света. – М., 1983.

2.     Мешков В.В. Основы светотехники: Учебное пособие для вузов. Ч.1 – М., 1979.

3.     Мешков В.В., Матвеев А.Б. Основы светотехники: Учебное пособие для вузов. Ч.2 – М., 1989.

4.     Щепина Н.С. Основы светотехники. – М.,1985.

5.     Гуторов М.М. Сборник задач по основам светотехники. – М., 1988.

6.     Ламехов О.А., Фрид Ю.В., Журкин Г.В. Светотехника и светоизмерения. – М., 1980.

7.     Рыков В.И., Четвергов Д.И. Методы и средства измерения световых параметров источников света.- Саранск, 1988.

8.     Тиходеев П.М. Световые измерения в светотехнике. – М., 1962.

9.     Епанешников М.М. Электрическое освещение. – М., 1973.

10. Бухштаб М.А., Дойников А.С., Коромысличенко В.А. Фотометрия для инженеров. – Л., 1991.

11. Кривошеев М.А., Кустарев А. К. Цветовые измерения. – М., 1990.

12. Гуревич М.М. Фотометрия (теория, методы, приборы). – Л., 1983.

13. Дойников А.С. Прикладная  фотометрия. – М., 1983.

14. Справочная книга  по светотехнике//Под ред. М.Б.Айзенберга. – М., 1983.

15. Тищенко Г.А. Осветительные установки. – М., 1984.

16. Скоков И.В. Оптические спектральные приборы. – М., 1984.

17. Справочная книга для проектирования электрического освещения //Под ред. Г.М. Кнорринга. – Л., 1976.

18. Трофимова Т.И. Курс физики. – М., 2001.

19.  Борн М., Вольф Э. Основы оптики. – М., 1973.

Доп. план 2004 г., поз. 14

 

 

 

Айгуль Сапаровна Алданова

 

 

 

ОСНОВЫ СВЕТОТЕХНИКИ И ФОТОМЕТРИЯ

Методические указания и задания к расчетно-

графической работе по курсу Основы светотехники и фотометрия

для специальности 330540- Светотехника и источники света

 

 

 

 

 

Редактор                         В.В.Шилина

 

 

 

 

Подписано в печать _____                Формат 60х84 1/16

Тираж 70 экз.                                      Бумага типографская №1

Объем 2,5 уч.-изд.л.                           Заказ ____.Цена   80 тг.

 

 

 

 

 

 

 

 

 

Копировально-множительное бюро

 Алматинского института энергетики и связи

480013 Алматы, Байтурсынова, 126