Некоммерческое акционерное общество

Алматинский институт энергетики и связи

Кафедра электроснабжения промышленных предприятий

 

 

 

ТЕОРИЯ И ПРАКТИКА

ТЕХНИЧЕСКОГО ЭКСПЕРИМЕНТА

В ЭЛЕКТРОЭНЕРГЕТИКЕ

 

 

Конспект лекций 

для студентов всех форм обучения специальности 6М0718 – Электроэнергетика

 

 

 

Алматы 2010

 

СОСТАВИТЕЛЬ: Фадеев В.Б. Теория и практика технического эксперимента в электроэнергетике.

 

Конспект лекций для студентов всех форм  обучения специальности 6М0718 – Электроэнергетика. - Алматы: АИЭС, 2010. – 52 с.

Конспект  лекций содержит сведения по теории случайных ошибок и обработке результатов измерений, рассматриваются  вопросы анализа экспериментальных данных, определения необходимого объема измерений, нахождения грубых ошибок эксперимента, проверки данных на достоверность и воспроизводимость. Для экспериментальных данных, имеющих стохастический характер, рассмотрено применение статистических критериев, корреляционного и регрессионного анализа.

Особое внимание уделено применению встроенных инструментов Excel для обработки  и анализа результатов эксперимента и  нахождения эмпирических формул к опытным  данным.

 

Содержание

1Классификация, характеристики, задачи и организация  эксперимента	4
2  Базовые понятия теории относительности	8
3. Статистическая обработка экспериментальных данных	12
4  Основные статистические характеристики  выборочной совокупности	16
5  Теория ошибок. Обработка результатов измерений	20
6 Методы определения грубых ошибок экспериментального ряда	24
7 Исследование экспериментального ряда на достоверность и воспроизводимость.	28
8 Применение статистических гипотез при обработке экспериментальных данных.	32
9 Применение  статистических критериев для анализа экспериментальных данных.	36
10 Корреляционно – регрессионный  анализ экспериментальных данных	40
11Методы графической обработки  экспериментальных данных. Интерполяция и аппроксимация данных	44
12 Нахождение   эмпирических формул к экспериментальным данным	48
Литература	51

 

 

 

 

 

 

 

 

 

 

 

 

1 Лекция.   Классификация, характеристики, задачи и организация  эксперимента

Содержание лекции:

 классификация, типы и задачи эксперимента, организация эксперимента, составление программы эксперимента.

Цель лекции:

знакомство с основными   понятиями и терминологией дисциплины.

1.1. Классификация, характеристики  и задачи эксперимента

В научном языке и исследовательской работе термин «эксперимент» обычно используется в значении опыта и целенаправленного наблюдения. Основной целью эксперимента является изучение свойств исследуемых объектов, проверка  гипотез и на этой основе более  глубокое изучение объекта исследования. Постановка и организация эксперимента определяются его назначением.

Эксперименты могут быть классифицированы по различным признакам, в частности:

     - по способу формирования условий, (естественные и искусственные эксперименты);

     - по организации проведения эксперимента (лабораторные, натурные, производственные и т.п.);

     - по контролируемым величинам (пассивный и активный эксперимент);

     - по числу варьируемых факторов (однофакторный и многофакторный эксперимент).

1.2. Краткие характеристики  экспериментов

Естественный эксперимент  проводится в естественных условиях существования объекта исследования. Используется в биологических, социаль­ных, педагогических и психологических науках.

Искусственный эксперимент проводится в искусственных условиях, создаваемых с целью проверки выдвинутых гипотез. Широко приме­няется в естественных и технических науках.

Лабораторный эксперимент проводится в лабораторных условиях. Чаще всего в лабораторном экспе­рименте изучается не сам объект, а его модель или образец. Этот эксперимент позволяет изучить влияние одних характеристик при варьировании других, получить ин­формацию с минимальными затратами времени и ре­сурсов. Однако такой эксперимент не всегда пол­ностью моделирует реальный ход изучаемого процесса, поэтому возникает потребность в проведении натурного эксперимента.

 Натурный эксперимент прово­дится в естественных условиях и на реальных объектах. Основная пробле­ма натурного эксперимента -  обеспечить соответствие условий эксперимента ре­альной ситуации, в которой будет работать впоследст­вии создаваемый объект.

Пассивный  эксперимент предусматривает из­мерение и наблюдение за объектом  без искусственного вмешательства в его функционирова­ние.

Активный эксперимент связан с выбором специальных входных сигналов (факторов) и контроли­рует входные  и выходные сигналы исследуемой системы.

Однофакторный эксперимент предполагает варьирование  исследуемого фактора и  стабилизацию мешающих факторов.

Стратегия многофакторного эксперимента состоит в том, что варьируются все переменные сразу и каждый эффект оценивается по результатам всех опытов, проведенных в данной серии экспериментов.

1.3. Организация эксперимента

Для  организации и проведения эксперимента  необхо­димо:

    - выдвинуть  гипотезу, подлежащую проверке;

    - написать  методику и программу  проведения  экспериментальных работ;

    - обеспечить условия для выполнения экспериментальных работ;

    - подготовить журнал для   фиксирования хода и результатов эксперимента.

  Выбор методики проведения эксперимента  должен проводиться особенно тщательно. Необходимо убедиться в том, что она соответствует современному уровню науки и условиям, в которых выполняется исследование.

1.4. Составление программы эксперимента

До начала проведения  эксперимента составляется  план (программа) выполнения экспериментальных исследований, который включает в себя:

    - цель и задачи эксперимента;

    - выбор   исследуемых    факторов;

    - обоснование объема эксперимента (числа  измерений и опытов);

    - порядок проведения  опытов;

    - обоснование средств измерений;

    - описание проведения эксперимента;

    -обоснование способов обра­ботки и анализа результатов эксперимента.                

Важным этапом подготовки к эксперименту являет­ся определение его целей и задач. Количество задач для конкретного эксперимента не должно быть слишком большим (3...4).

При экспериментальном исследовании одного и того же процесса (наблюдения и измерения) повторные отсчеты на приборах, как правило, неодинаковы. Отклонения объясняются различными причинами: неодно­родностью свойств изучаемого тела, особенностями изучаемого  явления, качеством приборов, классом их точности, субъективными особенностями экспериментатора и проч.

Чем больше случайных факторов, влияющих на опыт, тем больше расхождения в значениях, получаемых при измерениях, т. е. тем больше отклонения отдельных измерений от среднего значения. Это требует повторных измерений, а, следовательно, необходимо знать их минимальное количество. Под необходимым минимальным количеством измерений понимают такое количество измерений, которое в данном опыте обеспечивает устойчивое среднее значение измеряемой величины, удовлетворяющее заданной степени точности. Установление необходимого минимального количества измерений имеет большое значение, поскольку обеспечивает получение наиболее объективных результатов при минимальных затратах времени и средств.

При обработке экспериментальных данных особое внимание должно быть уделено математическим методам обработки и анализу опыт­ных данных, например, нахождению  эмпирических формул, применению корреляционного и регрессионного анализа.

1.5. Порядок обработки  результатов эксперимента

Все анализы, определения и наблюдения необходимо записывать в специальный журнал, форма которого должна наилучшим образом соответствовать исследуемо­му процессу с максимальной фиксацией всех фактов и условий их появления. При получении в одном стати­стическом ряду результатов, резко отличающихся от со­седних измерений, исполнитель должен, тем не менее, записать все данные без искажений и указать обстоя­тельства, сопутствующие указанному измерению. Это по­том позволит установить причины отклонений (искаже­ний) и соответствующим образом квалифицировать та­кие измерения. Если в процессе измерения необходимы простейшие расчеты, то они должны быть внесены в жур­нал или в отдельную тетрадь с указанием дня или меся­ца проведения опыта, номера и серии опытов.

Лабораторные журналы и тетради - важные документы. Поэтому они должны содержаться в порядке и обеспечивать возможность легкой проверки. Нужно не допускать исправлений, а в случае необ­ходимости они должны делаться так, чтобы не происхо­дило путаницы при расчетах. Каждое исправление долж­но сопровождаться подписью экспериментатора и крат­кой справкой о причинах исправлений. Никаких записей или пометок, не относящихся к делу, в лабораторных журналах и тетрадях делать нельзя!

Важное место в экспериментальных исследованиях за­нимают измерения. Теорией и практикой измерения занимается метроло­гия, являющаяся  наукой  об измерениях, методах и средствах обеспе­чения их единства. Напомним  некоторые  основные  понятия из курса метрологии, которые понадобятся нам в дальнейшем.

1.6. Некоторые понятия из курса метрологии 

Различают прямые и косвенные измерения. Наиболее простым является прямое измерение, при котором искомое значение величины находят непосредственно с помощью измерительного прибора. Например, длина измеряется линейкой, напряжение – вольтметром,  и т.п.

 Если прямые измерения невозможны, используют косвенные измерения. В них искомое значение величины находят на основании известной зависимости этой величины от других, допускающих прямое измерение. Например, среднюю плотность тела можно измерить по его массе и геометрическим размерам, электрическое сопротивление резистора – по падению напряжения на нем и току через него и т.п.

Измерительные приборы  ха­рактеризуются величиной погрешности, ста­бильностью измерений и чувствительностью.

Погрешно­сти приборов бывают абсолютными и относительными.

Под абсолютной погрешностью измерительного прибора понимается величина

,

где  - показа­ния прибора;

 -  действительное значение измеренной вели­чины, полученное более точным методом.

 Однако абсолютная погрешность не отражает качества измерений: например, абсолютная погрешность 1 мм при измерении размеров помещения свидетельствует о высоком качестве измерения, та же погрешность совершенно неприемлема при измерении диаметра тонкой проволоки.

Критерием качества измерения является отношение абсолютной погрешности к окончательному результату измерения:

.

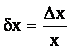Это отношение безразмерно. Величину  называют относительной погрешностью. Высокой точности измерения соответствует малое значение относительной погрешности.

Погрешности  измерения   делятся на систематические погрешности и случайные.

Систематическая погрешность – это погрешность измерения, остающаяся постоянной при повторных измерениях одной и той же величины. В дальнейшем под систематической погрешностью мы будем понимать погрешность прибора.

 Случайные погрешности обусловлены сочетаниями случайных факторов – ошибками отсчета, свойствами исследуемого объекта, вариацией, параллаксом и проч. Случайная погрешность  при повторных измерениях изменяется случайным образом, и результат измерения заранее предсказать невозможно.

Хотя исключить случайные погрешности отдельных измерений невозможно, математическая теория, в основу которой положена теория вероятности и математическая статистика, позволяет не только учесть, но и  уменьшить влияние случайных  погрешностей на окончательный результат.

Поэтому изучение вопросов обработки результатов эксперимента мы начнем с базовых понятий теории вероятности.

 

 

2 Лекция.  Базовые понятия теории относительности

 

Содержание лекции:

случайные  события, вероятность события, дискретные и непрерывные  случайные величины, математическое ожидание,  дисперсия и моменты, законы распределения вероятностей, нормальный  закон распределения, стандартное нормальное распределение, правило трех сигм.

Цель лекции:

знакомство с основными понятиями и терминологией теории вероятности, являющейся теоретической базой  методов обработки экспериментальных данных и измерений.

2.1 Введение

Обработка  данных, полученных  при выполнении измерений  или результатов научных опытов и  исследований, выполняется на основе методов математической статистики, теоретической основой которой является теория вероятности.

2.2 Основы теории вероятностей

В теории вероятностей изучаются общие закономерности для случайных событий. Для понимания предмета и методов теории вероятностей ознакомимся с некоторыми ее базовыми понятиями.

2.3 Базовые понятия теории вероятностей

Основополагающим является понятие случайного события (или просто событие). Это такое событие, которое может произойти, а может и не произойти в результате эксперимента или измерения. Другими словами, наперед, до проведения  опыта, нельзя однозначно сказать, случится это событие или нет. В теории вероятностей каждое такое событие принято характеризовать численной мерой степени объективной возможности события. Эта численная мера называется вероятностью события, или просто вероятностью. Вероятность — это число в диапазоне от 0 до 1.

 Достоверным является событие с вероятностью 1 (т.е. это такое событие, которое обязательно произойдет). Если вероятность события равна нулю, то такое событие называется невозможным, и оно никогда не произойдет. Кроме того, важным является понятие полной группы событий.  В результате проведения опыта  в такой группе обязательно  произойдет хотя бы одно событие из этого набора. Если в качестве опыта рассматривать процесс подбрасывания шестигранного кубика с цифрами от одного до шести, то в качестве примеров полных групп событий могут быть приведены группа из шести  событий (выпадение числа 1, 2 и т.д. до 6) или группа из двух событий (выпадение четного числа или выпадение нечетного числа).

С практической точки зрения больший интерес представляет понятие случайной  величины. Аналогично случайному событию, это такая величина, значение которой  до проведения опыта нельзя предсказать абсолютно достоверно. Случайные величины бывают дискретными и непрерывными. Возможными реализациями дискретной случайной величины в процессе проведения опыта (измерения) являются отдельные числа, в то время как непрерывная случайная величина может в процессе измерения принимать непрерывный набор значений из какого-то интервала, который, в принципе, может быть и неограниченным.

 Важное место в наборе числовых характеристик случайных величин занимает математическое ожидание, которое для непрерывной случайной величины определяется  как

,

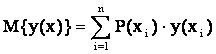 а для дискретной величины, как

   .

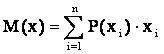Кроме математического ожидания, важной характеристикой  является также и дисперсия.

 Дисперсией случайной величины называют ее числовую характеристику, которая определяется для непрерывной случайной величины по формуле:

,

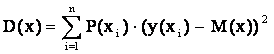а для дискретной случайной величины по формуле:      .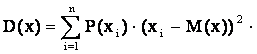

 2.4 Законы распределения вероятностей

 Зная распределение вероятностей интересующих нас случайных величин можно делать выводы о событиях, в которых участвуют эти величины. Конечно,   эти выводы также будут носить случайный характер.

Среди всех вероятностных распределений есть такие, которые на практике исполь­зуются  особенно часто. Эти распределения детально изучены, и свойства их хорошо известны. Многие из этих распределений лежат в основе целых областей знания — таких как теория массового обслуживания, теория надежности, теория измерений, теория игр и т. п.

Большинство применяемых на практике распределений являются дискретными или непрерывными. Среди дискретных распределений наиболее важными являются бино­миальное и пуассоновское распределения, а  среди непрерывных – нормальное распределение  и распределения, связанные с нормальным: Стьюдента, Фишера,  хи-квадрат. Для  нас наибольший интерес представляет нормальное распределение, которое и рассмотрим.

 

Нормальный закон  распределения

Большинство экспериментальных исследований в технике, в различных областях естественных наук, биологии, медицине, и проч. связаны с измерениями, результаты которых могут принимать практически любые значения в заданном интервале, и описываются моделью не­прерывных случайных величин. Одним из важнейших непрерывных распределе­ний является нормальное, или гауссово распределение.

Нормальное распределение получило широкое распространение для приближен­ного описания многих случайных явлений, в которых на результат воздействует большое количество независимых случайных факторов, среди которых нет сильно выделяющихся. Например, рассеяние снарядов при стрельбе. Кроме того, многие распределения, связанные со случайной выборкой, при увеличении  объема выборки  пе­реходят в нормальное распределение. Однако следует иметь в виду, что в природе встречаются экспериментальные распре­деления, для описания которых модель нормального распределения  может оказаться  и  не пригодной.

Плотность вероятностей нормально распределенной случайной величины задает­ся формулой Гаусса:

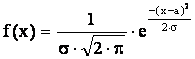,                                             (2.1)    

Здесь  а и    - параметры распределения.

График плотности (нормальная кривая) представлен на рисунке 2.1

 

 

 

 

 

 

 

 

 

 

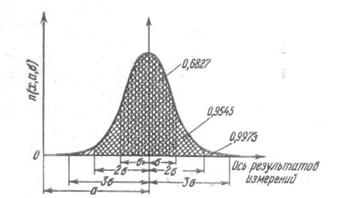
Рисунок 2.1 -  Нормальная кривая распределения

 

Площади под кривой на рисунке представляют собой вероятности получения результатов измерений.

Площадь, отвечающая какому- либо интервалу оси абсцисс, изображает вероятность попадания случайной величины  в данный интервал. В среднем доля (или процент) или, как еще говорят частость тех измерений, которые попадают в рассматриваемый интервал, приближенно соответствует величине вероятности, при том тем точнее, чем больше общее число измерений. Из рисунка 2.1 видно, что основная масса получаемых результатов будет  группироваться около центрального или среднего значения а, которому при отсутствии систематических, т.е. постоянно имеющих место погрешностей отвечает неизвестная истинная величина измеряемого параметра. Параметр , называемый средним квадратическим отклонением характеризует степень сжатия или растяжения (плотности) диаграм­мы. Чем больше , тем «шире» кривая, а ее максимальная высота ниже. Кривая как бы растягивается в стороны. В выделенный на рисунке 2.1  диапазон        нормально распределенная слу­чайная величина попадает с вероятностью 0,682. Следовательно,  из 1000  измерений  в 682 случаях  полученное значение будет попадать в данный интервал. В диапазон   случай­ная величина попадает с вероятностью 0,954, а в диапазон  -  с веро­ятностью 0,997. В последнем случае из тысячи испытаний только в трех из них полученное значение будет находиться вне указанного  интервала. Можно утверждать, что лишь ничтожная часть результатов измерений будет находиться вне указанного предела. Последняя закономерность трактуется  как правило трех сигм или правило трех стандартов.

При уменьшении параметра, т.е. при повышении точности измерений (рисунок 2.2), результаты измерений теснее группируются около центра, кривая (нанесена пунктиром) поднимается в центре и круче спадает к оси абсцисс при удалении от него. С увеличением  параметра, т.е. при снижении точности метода измерения рассеивание результатов измерений увеличивается, и кривая приобретает более пологий вид.

 

 

 

 

 

 

 

 

 

 

 

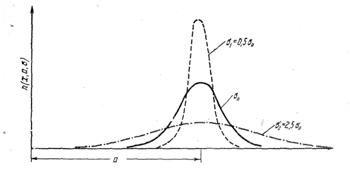
Рисунок 2.2  - Изменение формы нормальной кривой  при  измерениях методами различной точности

 

3 Лекция. Статистическая обработка экспериментальных данных

Содержание лекции:

  математическая статистика, задачи и основные разделы математической статистики, генеральная  и выборочная совокупности, выборка, репрезентативность выборки, параметризация выборки, применение встроенных инструментов Excel для  статистической обработки данных выборки.

Цель лекции:

 знакомство с предметом математической статистики и задачами, решаемыми с ее  помощью.

При выполнении  эксперимента  часто приходится сталкиваться с необходимостью обработки и анализа экспериментальных данных, которые формируются под действием множества факторов, многие из которых носят случайный характер. В качестве примера можно привести  электрическую  нагрузку   промышленных предприятий. Можно сказать, что стохастическому характеру подвержены падение и колебания напряжения сети, частота сети и другие электрические параметры в электрических сетях промышленных предприятий и энергосистем.

Стохастическая природа экспериментальных  данных обусловливает необходимость применения специальных статисти­ческих методов для их анализа и обработки, т.е. применения математической статистики, основная задача которой заключается в получении по данным выборки основных статистических характеристик изучаемого явления.

Приступая к рассмотрению темы, необходимо вначале дать  основные определения понятия математической статистики и  методов статистического исследования.

3.1. Основные понятия и определения

Математической статистикой называется  раздел математики, посвященный методам сбора, анализа и обработки статисти­ческих данных для научных и практических целей.

Статистические данные представляют собой данные, полученные в результате об­следования большого числа объектов или явлений.

Математическая статистика подразделяется на две основные области:

 1. Описатель­ная статистика;

 2. Аналитическая  статистика.

 Описательная статистика охватывает методы описания статистических данных, представления их в форме таблиц и распределений.

Аналитическая статистика или теория статистических выводов ориентирована на обработку данных, полученных в ходе эксперимента, с целью формулировки вы­водов, имеющих практическое значение.

Пакет Excel оснащен средствами статистической обработки данных. И хотя Excel существенно уступает специализированным статистическим пакетам обработки данных, тем не менее, этот раздел математики представлен в Excel наиболее полно.

 В него включены основные, наиболее часто используемые статистические проце­дуры: средства описательной статистики, критерии различия, корреляционные и другие методы, позволяющие проводить необходимый статистический анализ экспериментальных данных.

При рассмотрении применения методов обработки статистических данных мы на практических занятиях  огра­ничимся только простейшими и наиболее часто используемыми методами, реали­зованными в  пакете анализа Excel.

3.2. Выборочный метод

По охвату статистической совокупности исследование может быть сплошное или не сплошное. При сплошном статистическом исследовании группа наблюдения формируется путем полного охвата всех единиц изучаемого явления.

 Множество всех единиц наблюдения, охватываемых таким сплошным наблюдением, называ­ется генеральной совокупностью.

Если интересующая нас совокупность слишком многочисленна, либо ее элементы ма­лодоступны, а также, если имеются другие причины, не позволяющие изучать сразу все ее элементы, прибега­ют к изучению какой-то части этой совокупности. Эта выбранная для  исследования группа элементов называется выборкой или выборочной совокуп­ностью.

Основным методом не сплошного наблюдения является выборочный метод.

Выборка - это группа элементов, выбранная для исследования из всей совокуп­ности элементов.  Задача выборочного метода состоит в том, чтобы сделать правиль­ные выводы относительно  свойств генеральной  совокупности. Так, например, пробуя пищу, повар по одной ложке делает заключения о качестве приготавливае­мой пищи  во всей кастрюле.

Конечной целью изучения выборочной совокупности всегда является получе­ние информации о генеральной совокупности. Поэтому естественно стремиться сделать выборку так, чтобы она наилучшим образом представляла всю генераль­ную совокупность, то есть была бы репрезентативной или представительной.

 Для получения репрезентативной выборки необходимо четко определять, что понимается под генеральной совокупностью. Ее состав и численность зависят от объектов и целей проводимого исследования.

В тех случаях, когда генеральная совокупность недостаточно известна, обычно не удается предложить лучшего способа получения представительной выборки, чем случайный выбор. При этом случайная выборка формируется случайным отбо­ром - из генеральной совокупности с помощью генератора случайных чисел  извлекается по одному объекту.

3.3. Выборочная функция распределения

В теории вероятности характеристики случайной величины опираются на знание закона ее распределения.  Для практических задач такое знание -  редкость. Здесь закон распределения обычно неизвестен.

Первая и основная задача математической стати­стики заключается в получении по данным выборки наиболее рацио­нально построенных статистических характеристик распределения. Выяснение или оценка закона распределения по данным выборки (так называемая параметризация) и составляет существенную про­блему математической статистики: только зная закон распре­деления изучаемой величины, мы можем решать возникающие на практике задачи по анализу, сравнению и предсказанию резуль­татов исследуемого явления. На практике во многих задачах вид или, иначе говоря, форма теоретического распределения, с точностью до некоторых неизвестных параметров может считаться известной.

 Так, например, при обработке деталей на металлорежу­щих станках по методу автоматического получения размера (при устойчивом технологическом процессе) можно считать, что распре­деление погрешностей деталей подчиняется нормальному закону распределения. Точно так же на практике очень часто исходят из того, что нормальному закону следуют и погрешности измере­ний. Суммарную погрешность измерения можно рассматривать как результат действия большого числа независимых или слабо зависи­мых причин, и поэтому наблюденную ошибку можно представлять как сумму «элементарных ошибок»; последние же в свою очередь позволяют с высокой степенью приближения считать наблюдаемую  ошибку нормально распределенной.

Такое положение наблюдается всегда, когда рассматриваемый процесс может быть с некоторым приближением подведен под тео­ретическую схему, анализируемую средствами теории вероятностей.

Во всех этих случаях мы можем считать, что теоретический закон распределения принадлежит к некоторому семейству, завися­щему от одного или нескольких параметров. Если бы точные зна­чения параметров таких, как, например, математическое  ожидание  и дисперсия  при нормальном законе распределения   были известны, закон распределения для данного случая был бы пол­ностью определен. Иными словами, здесь задача нахождения закона распределения изучаемой величины (или величин) сводится к нахож­дению неизвестных значений параметров, т. е. к параметризации. Именно ради определения этих параметров весьма часто и производится само статистическое исследование. Так знание математического ожидания  и дисперсии, параметров, связанных с нормальным распределением дает возможность решать инженерные задачи  из области точности обработки и точности измерения. Как мы рассмотрим далее, для их нахождения используются значения среднего арифметического и дисперсии выборки, благодаря чему с некоторым приближением считается, что найдена и теоретическая функция нормального распределения вероятностей данной задачи.

На практике сведения о законе распределения случайной величины получают независимыми многократными повторениями опыта, в котором изме­ряются значения интересующей исследователей случайной величины.

 На основе информации из полученной выборки  можно построить  приблизитель­ные значения для функции распределения и другие характеристики  случайной ве­личины.

По аналогии с  теорией вероятностей  на практике вводится понятие  о статистической   вероятности.

По этому определению вероятность равна отношению числа испытаний (m), в ко­торых событие появилось, к общему количеству произведенных испытаний (n). Такая вероятность называется еще  статистической частотой.

Для построения выборочной функции распределения весь диапазон изменения случайной величины X разбивают на ряд интервалов одинаковой ширины. Число интервалов обычно выбирают не менее 5 и не более 15. Затем определяют число значений случайной величины X, попавших в каждый интервал. Поделив это число на общее количество наблюдений (n)., находят относительную частоту попадания случайной величины X в заданные интервалы. По найденным относительным частотам строят гистограммы выборочных функций распределения. Если соответствующие точки относительных частот соединить ломаной линией, то полученная диаграмма будет называться полигоном частот.

 При увеличении размера выборки до бесконечности, как мы уже отмечали ранее, эмпирическая частота приближается к вероятности, а выборочные функции распределения превращаются в теоретические: гистограмма превращается в график  плотности распределения.

Как мы увидим далее совсем  необязательно для получения данных о характеристиках генеральной совокупности доводить размер выборки до очень больших значений.

В Excel для построения выборочных функций распределения используются спе­циальная функция Частота и процедура пакета анализа Гистограмма. Работа с ними изучается  на практическом занятии.

 

4 Лекция. Основные статистические характеристики выборочной совокупности

Содержание лекции:

 мода, медиана, среднее значение, интервал, дисперсия выборки,  среднее квадратичное отклонение, стандартная ошибка, эксцесс, асимметрия, инструменты Excel для вычисления выборочных характеристик.

Цель лекции:

 знакомство с основными характеристиками выборочной совокупности и их определением с помощью формул и  встроенных инструментов Excel.

4.1. Определение основных статистических характеристик

На предыдущей лекции мы познакомились с понятием выборки или, иначе, выборочной совокупности. Выборка характеризуется вариационным рядом, под которым в статистике понимают ряд, построенный по количественному признаку. Любой вариационный ряд состоит из двух элементов - вариантов и частот. Вариантами считаются отдельные значения признака, т.е. конкретное значение  варьирующего признака. Частоты – это числа, показывающие, как часто встречаются варианты в ряду распределения. Сумма всех частот определяет объем выборки. Частостями называются частоты, выраженные в долях  единицы или в процентах  относительно объема выборки.

Замена теоретической функции распределения  на ее выборочный аналог  в определении математического ожидания, дисперсии, стандартного отклонения и других характеристик приводит нас к понятиям выборочного среднего, выборочной дисперсии, выборочному стандартному отклонению и т.д. Выборочные характеристики являются оценками соответствующих характеристик генеральной совокупности, поэтому эти оценки должны удовлетворять определенным требованиям, т.е.  они  должны быть:

- несмещенными, т.е. должны стремиться к истинному значению характеристики генеральной совокупности при неограниченном увеличении количества испытаний;

- состоятельными, т.е.  с ростом размера выборки оценка должна стремиться к соответствующему параметру генеральной совокупности с вероятностью, приближающейся к 1;

- эффективными, т.е. для выборок равного объема используемая оценка должна  иметь минимальную дисперсию.

 Среди выборочных характеристик выделяют:

 -  показатели, относящиеся к центру распределения;

 -  показатели рассеяния;

 - показатели, характеризующие   форму  распределения.

 К показателям, характеризующим центр рас­пределения, относятся: среднее значение,  мода  и медиана.

Простейшим показателем, характеризующим центр выборки, является мода.

Мода — это элемент выборки с наиболее часто встречающимся значением (наибо­лее вероятная величина).

Средним значением выборки  называется  величина

 

 

 

Иначе говоря, среднее значение — это центр выборки, вокруг которого группиру­ются элементы выборки.  При увеличении числа наблюдений среднее  выборки приближается к среднему генеральной совокупности, т.е. к  математическому ожиданию, поэтому среднее значение  генеральной совокупности  часто обозначается, как и математическое ожидание,   буквой М.

 Медиана –  это число, которое является серединой выборки.

Основными показателями рассеяния вариант являются:  интервал, дисперсия выбор­ки, стандартное отклонение и стандартная ошибка.

Интервал -  это разница между максималь­ным и минимальным значениями элементов выборки. Интервал является про­стейшей и наименее надежной мерой вариации или рассеяния элементов в вы­борке.

Более точно отражают рассеяние показатели, учитывающие не только крайние, но и все значения элементов выборки. К таким показателям относится дисперсия. Дисперсией выборки  называется величина

 

 

 

 

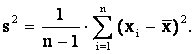
Дисперсия выборки  - это параметр, характеризующий степень разброса элемен­тов выборки относительно среднего значения.

 Чем больше дисперсия, тем дальше отклоняются значения элементов выборки от среднего значения.

 Выборочным стандартным отклонением  или средним  квадратичным отклонением называется  величина:

 

 

Это параметр, также характеризующий степень разброса элементов выборки от­носительно среднего значения. Чем больше среднее квадратичное отклонение, тем дальше отклоняются значения элементов выборки от среднего значения.  Параметр аналогичен дисперсии и используется в тех случаях, когда необходимо, чтобы по­казатель разброса случайной величины выражался в тех же единицах, что и сред­нее значение этой случайной величины.

 Стандартная ошибка или ошибка среднего находится из выражения:

 

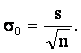
Стандартная ошибка — это параметр, характеризующий степень возможного от­клонения среднего значения  исследуемой  выбор­ки от истинного среднего значения генеральной совокупности элементов. С помощью стандартной ошибки задается так называемый доверительный интер­вал.  

Например,  95%-ный доверительный интервал, равный  , обозначает диапазон, в ко­торый с вероятностью р  = 0,95 при  условии достаточно большого  числа  наблюдений (n > 30) попадает  среднее значение генеральной совокупности.

В этом случае можно сказать, что с   вероятностью р =  0,95  из 100 случаев в 95 результат испытания будет находиться в интервале    и только в 5 случаях результат испытания будет за пределами интервала.

Показателями, характеризующими форму распределения, являются  эксцесс и асимметрия.

Эксцесс  - это степень выраженности «хвостов» распределения, то есть частоты появления  величин  удаленных от среднего значения.

Асимметрия - величина, характеризующая несимметричность распределения эле­ментов выборки относительно среднего значения. Принимает значения от -1 до 1. В случае симметричного распределения асимметрия равна 0.

Часто значения асимметрии и эксцесса используют для проверки гипотезы о том, что данная выборка  принадлежат к определенному теоретическому распределе­нию, в частности, к  нормальному распределению. Для нормального распределения асимметрия равна нулю, а эксцесс — трем.

Как отмечалось выше, в результате наблюдений или эксперимента  мы получаем  наборы данных, называ­емые выборками.

 Для проведения их анализа  эти данные подвергаются статистиче­ской обработке.
 Первое, что всегда делается при обработке данных, это вычисле­ние элементарных статистических характеристик выборок, как минимум: среднего, среднеквадратичного отклонения, ошибки среднего по каждому исследуемому параметру и по каждой группе. В Excel для  вычисления статистических характеристик выборки служит процедура Описательная статистика из   пакета  анализа, работа с которой выполняется на практическом занятии.

4.2. Анализ однородности выборки

 Одним из важных вопросов, возникающих при анализе выборки, является вопрос: относится та или иная варианта к данной ста­тистической совокупности? Решение вопроса не представляет сложности, если распределение в этой совокупности является нормальным. Для этого достаточно использовать правило трех стандартов. Согласно этому правилу, в пределах  интервала  на­ходится 99,7% всех вариант. Поэтому, если варианта попадает в этот интервал, то она считается принадлежащей к данной совокупности. Если не попадает, то она может быть отброшена. Хотя этот метод и предполагает нормальность исходного распределения, на практике он успешно работает и может быть использован в боль­шинстве  случаев.

При числе элементов в выборке n < 30 границы  доверительного интервала  определяют  по формуле:

 

    

где

 - среднее значение выборки;

 - табличное значение распределения Стьюдента с числом степеней свободы  n и  доверительной вероятностью р.

В MS Excel для вычисления границ доверительного интервала можно воспользоваться программой  «Описательная статистика»  из пакета анализа Excel.

 

5 Лекция. Теория ошибок. Обработка результатов измерений

Содержание лекции:

 основы теории случайных ошибок; методы оценки случайных погрешностей в измерениях; доверительные  интервалы и доверительная вероятность; уровень значимости; определение минимального объема выборки.

Цель лекции:

 изучение методов и приемов   статистической обработки результатов измерений.

5.1.Основы теории случайных ошибок и методов оценки случайных погрешностей в измерениях

Анализ случайных погрешностей основывается на тео­рии случайных ошибок.

Тео­рия случайных ошибок дает возможность с опреде­ленной гарантией вычислить действительное значение измеренной величины и оценить возможные ошибки при ее вычислении.

Основу теории случайных ошибок составляют пред­положения о том, что при большом числе измерений:

 1. слу­чайные погрешности одинаковой величины, но разного знака встречаются одинаково часто;

2. большие погрешно­сти встречаются реже, чем малые (вероятность появле­ния погрешности уменьшается с ростом ее величины);

3. при бесконечно большом числе измерений истинное зна­чение измеряемой величины равно среднеарифметичес­кому значению всех результатов измерений,

4. появление того или иного результата измерения как случайного со­бытия описывается нормальным законом распределения.

В теории ошибок различают генеральную и выборочную совокупность измерений.

 Под генеральной совокупностью подразуме­вают все множество возможных значений измерений  или возможных значений погрешностей . Для выбо­рочной совокупности число измерений n  ограничено, и в каждом конкретном случае строго определяется. Обычно считают, если n >30, то среднее значение дан­ной совокупности измерений x достаточно приближается к его истинному значению.

Теория случайных ошибок позволяет решать следующие задачи:

 1. оценить точ­ность и надежность измерения при данном количестве замеров;

2. определить минимальное количество заме­ров, гарантирующее требуемую (заданную) точность и надежность измерений;

3. выявить   и исключить грубые ошибки, допущенные при проведении эксперимента;

 4. определить достоверность полученных данных.

 

5.2. Интервальная оценка с помощью доверительной веро­ятности

Для большой выборки и нормального закона распределения оценочными характеристиками выполненных изме­рений являются  среднее арифметическое выборки, стандартное отклонение  и средняя ошибка выборки:

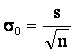
где

 s – Среднеквадратичное отклонение (стандартное отклонение) выборки;

 n – Количество выполненных замеров.

Ошибка выборки для выборочной относительной величины (доли) определяется по выражению:

.

В теории ошибок достаточно важными являются понятия доверительной вероятности и  доверительного интервала.

Доверительной ве­роятностью (достоверностью) измерения называется вероятность того, что истинное значение измеряемой ве­личины попадает в  интервал, называемый доверительным интервалом.

Доверительный интервал определяет  точность измерения и называется предельной  ошибкой  выборки.

Предельная ошибка выборки определяется по формуле:

 

                    (5.1)

где

- гарантийный коэффициент или нормированное отклонение.

Значения  t и соответствующие им доверительные вероятности  приведены в справочной литературе.

При числе опытов n > 30 их значения определяются по таблице Лапласа, а при n < 30 по таблице Стьюдента.

  Для наиболее часто встречающихся случаев, для  n > 30 они имеют следующие значения: для t =1 =0.683; t =2 =0.95; t =3 =0.997.

На практике наиболее часто статистические расчеты производятся с доверительной вероятностью 0,95. Доверительный интервал характеризует погрешность измерения, а доверительная вероятность — достоверность (надежность) из­мерения.

Рассмотрим пример.

Пусть, например, выполнено 30 измерений напряжения сети. Среднее  напряжение сети  220В   среднеквадратическое откло­нение  =3,1 В.

Требуется определить  значение напряжения сети (среднее генеральной совокупности) с доверительной вероятностью 0,95.

Решение:

Средняя ошибка выборки

 

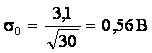
Предельная ошибка выборки

Зная предельную ошибку, рассчитываем  интервал, в котором с доверительной вероятностью 0,95 находится измеряемая величина – напряжение сети     = 220±1,12, т.е.  напряжение сети составляет не менее 219В и не более 221В.

Если  нам  заранее задана предельная ошибка  измерения, то по ней можно определить  доверительную вероятность попадания измеряемой величины в данный интервал.

 Пусть, напри­мер, задана  предельная  ошибка    то для нахождения доверительного интервала по формуле (5.1) находим вначале нормированное отклонение . Для  найденного значения t по таблице Лапласа находим . Это означает, что в заданный доверительный интервал  из 100  результатов измерений попадет  97, и только 3 результата  из 100 будут вне найденного интервала.

Значение  называют уровнем значимости.

 Из него следует, что при нормальном законе распреде­ления погрешность, превышающая доверительный интер­вал, будет встречаться один раз  из  измерений, где

.       (5.2)

Или иначе приходится браковать одно из   измерений.

По данным приведенного выше примера можно вы­числить количество измерений, из которых одно изме­рение превышает доверительный интервал.

 По формуле (5.2) при р_д=0,95 определяем   = 0,95 /(1—0,95) = 19 из­мерений. При доверительной вероятности  , равной  0,997,  это будет уже   332 измерения.

   5.3. Определение минимального количества измерений

Для проведения опытов с заданной точностью и достоверностью необходимо знать то количество измерений,  при котором экспериментатор будет уверен в положительном  исходе. В связи с этим одной из первоочередных задач при статических методах оценки является установление минимального, но достаточного числа измерений для данных условий.

 Задача сводится к установлению минимального объема выборки (числа измерений) ,  при заданных значениях предельной ошибки выборки и заданной  доверительной вероятности.

Предельная ошибка выборки равна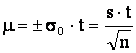  

Из данного выражения можно найти минимальный объем выборки, который при заданной доверительной вероятности, определяемой гарантийным коэффициентом t, обеспечит  требуемую точность результатов выборки .

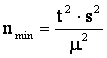         (5.3)

 

В исследованиях часто используется и такая форма записи

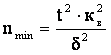
где

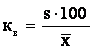 -  коэффициент вариации,  в  %;

- погрешность измерительного прибора,   в  %.

В зависимости от исходных условий  по формуле  (5.3) могут решаться различные задачи, например:

1. Определение объема выборки, необходимого для получения  требуемой точности результатов с заданной вероятностью (рассмотрено выше);

2. Определение возможного предела ошибки репрезентативности, гарантированного с заданной вероятностью и сравнение его  с величиной допустимой погрешности;

3.Определение вероятности того, что ошибка выборки не превысит допустимой погрешности.

 

 

6 Лекция. Методы определения грубых ошибок экспериментального ряда

 Содержание лекции:

кривые распределения Стьюдента, определение доверительного интервала малой выборки, способы определения грубых ошибок экспериментального ряда, округление результатов измерения.

Цель лекции:

  продолжение изучения  методов и приемов   статистической обработки результатов экспериментальных исследований.

6.1 Определение доверительного интервала малой выборки. Кривая распределения Стьюдента

 Как мы уже отмечали ранее,  при числе измерений  n >30  нормированное отклонение t находится по таблице Лапласа. Для нахождения границы доверительного интервала при малых значениях  применяют метод, предложенный в 1808 г. английским математиком В.С. Госсетом (псевдоним Стьюдент).

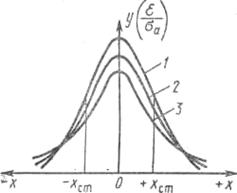
Кривые распределения Стьюдента в случае

(практически при   n >20) переходят в кривые нормального распределения (см. рисунок 6.1).

Для малой выборки доверительный интервал определяется по формуле

,

 где - коэффициент Стьюдента, принимаемый по таблице Стьюдента в зависимости  от  числа измерений и принятого значения доверительной вероятности   .

Зная , можно вычислить действительное значение изучаемой величины для малой выборки  .

.

 

 

 

 

 

 

 

 

 

 

Рисунок 6.1 -  Кривые распреде­ления   Стьюдента  для  раз­личных значений n: 1 -   2 -   n = 10;   3 -  n = 2

 

Возможна и иная постановка задачи. По n известным значениям измерений малой выборки необходимо определить доверительную вероятность  при условии, чтобы погрешность  среднего значения не выходила  за пределы  предельной ошибки выборки .

Задачу решают в такой последовательности:

1)  вначале вычисляется среднее  значение, средняя ошибка и

коэффициент Стьюдента ;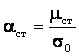

2) далее  на базе  известных значений  n и  по таблице Стьюдента определяют доверительную вероятность.

В процессе обработки экспериментальных данных следует исключать грубые ошибки ряда. Появление этих ошибок вполне вероятно, а наличие их ощутимо влияет на результат измерений. Однако прежде чем исключить то или иное измерение, необходимо убедиться, что это действительно грубая ошибка, а не отклонение вследствие статистического разброса.

6.2  Определение грубых ошибок экспериментального ряда

 Известно несколько методов определения грубых ошибок статистического ряда.

 Наиболее простым способом исключения из ряда резко выделяющегося измерения является правило трех стандартов, согласно которому разброс случайных величин от среднего значения не должен превышать

.

Более достоверными являются методы, базируемые на использовании критериев появления грубых ошибок.

 Пусть имеется статистический ряд малой выборки, подчиняющийся закону нормального распределения. При наличии грубых ошибок критерии их появления вычисляются по  формулам:

;

.

 

где  - наибольшее и наименьшее значения  из n  измерений.

По  таблице «Критерии появления грубых ошибок»[1]   в зависимости от заданной доверительной вероятности  находят максимальное значение , возникающее вследствие статистического разброса.  Если , то значение  необходимо исключить из статистического ряда как грубую погрешность. Если  , исключается величина. После исключения грубых ошибок определяют новые значения  и  из  (n - 1) или (n - 2) измерений.

Второй метод установления грубых ошибок основан на использовании критерия В. И. Романовского и приме­ним также для малой выборки. Методика выявления грубых ошибок сводится к следующему. Задаются дове­рительной вероятностью,  и по таблице «Коэффициенты предельно допустимых ошибок измерения» в зависимости от числа измерений n  находят коэффициент q. Вычисляют предельно до­пустимую абсолютную   ошибку   отдельного   измерения   .

Если , то   данное измерение  исключают из ряда наблюдений.  Этот метод более требователен к очи­стке ряда.

В настоящее время в связи с внедрением в практику обработки данных статистических программ из пакета анализа Excel, нахождение грубых ошибок экспериментального ряда (выпадающих вариант) может быть выполнено  следующим образом.

С помощью программы « Описательная статистика» определяются статистические характеристики для исследуемого ряда данных, и вычисляется диапазон, в котором с задаваемой доверительной вероятностью находится измеряемая величина по формуле:

.

Все данные, которые находятся вне найденного диапазона, считаются, с точностью  до заданной вероятности, ошибками.

6.3 Обработка результатов прямых измерений

При обработке результатов прямых измерений рекомендуется следующий порядок операций:

    1. Выполнить необходимые   измерения  и результаты занести в таблицу.

    2. Найти грубые ошибки, удалить их,  вычислить среднее арифметическое.

    3. Найти погрешность отдельных измерений.

    4. Вычислить квадраты погрешностей  отдельных измерений.

    5. Вычислить стандартную ошибку среднего арифметического.

    6.Задаваясь уровнем надежности, для проделанного числа измерений по таблице Стьюдента найти  коэффициент Стьюдента.

          7.Вычислить  доверительный интервал нахождения случайной ошибки, т.е. погрешность измерения, обусловленную случайными факторами.

Если  погрешность измерения, обусловленная случайными факторами, окажется сравнимой с величиной погрешности прибора, то границы доверительного интервала находятся по формуле:

 

,

 

где

 - половина доверительного интервала для заданного уровня надежности;

- погрешность измерения, обусловленная случайными ошибками;

- абсолютная погрешность прибора.

Если одна из ошибок меньше другой в три и более раз, меньшую ошибку  отбрасывают.

8. Окончательный результат записывается в виде[2]:

.

 

9. Оценивается относительная погрешность измерения:

.

6.4 Округление результатов измерения

Обработку  результатов измерений необходимо выполнять с учетом определенных установленных  правил. Рассмотрим эти правила.

Погрешность измерения  следует округлять  до первой значащей цифры, всегда увеличивая ее на единицу.

Значащими называют  цифры, кроме нулей, стоящих впереди числа. Например, 0,00807 – в этом числе имеется три значащих цифры: 8, ноль между 8 и 7 и 7; первые три нуля незначащие.
Примеры:

8.27 ≈ 9;

0.237 ≈ 0.3;

0.00035 ≈ 0.0004;

0.0862 ≈ 0.09;

857.3 ≈ 900;

43.5 ≈ 50.

Результаты измерения округляют с точностью «до погрешности», т.е. последняя значащая цифра в результате должна находиться в том же разряде, что и  погрешность.

Примеры:

243.871 ± 0.026 ≈ 243.87 ± 0.03;
243.871 ± 2.6 ≈ 244 ± 3;
1053 ± 47 ≈ 1050 ± 50.

 

7 Лекция. Исследование экспериментального ряда на достоверность и воспроизводимость

Содержание лекции:

исследование экспериментальных данных на достоверность и воспроизводимость результатов измерений. Обработка данных косвенных измерений. Определение  оптимальных условий измерения. Обработка результатов экспериментальных данных при однократном измерении.

Цель лекции:

  продолжение изучения  методов и приемов   статистической обработки результатов экспериментальных исследований.

7.1 Исследование экспериментальных данных на достоверность

В исследованиях часто возникает вопрос о достовер­ности данных, полученных в опытах. Решение такой за­дачи можно проиллюстрировать следующим примером.

Пусть установлена прочность контрольных образцов бетона    до     виброперемешивания    и прочность бетонных образцов после перемешивания . Прирост прочности составляет 15%. Это упрочнение относительно небольшое и его можно отнести за счет разброса опытных данных. В этом случае следует провести проверку на достоверность экспериментальных данных по условию:

.

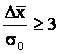Разница средних значений равна 23 – 20 = 3,0, а разница ошибок измерения равна 0,78, поэтому 3 /0,78 = 3,84 > 3.

Следовательно, полученный прирост прочности бетона является достоверным, а не случайным.

7.2 Исследование  экспериментальных данных на воспроизводимость

Выше был рассмотрен  метод проверки экспериментальных измерений на  достовер­ность. Ответственные эксперименты должны быть проверены также и на воспроизводимость результатов, т.е. на их повторяемость в определенных пределах измерений с заданной доверительной достоверностью. Суть такой проверки сводится к следующему. Имеется несколько па­раллельных опытов (серий). Для каждой серии вычис­ляют среднеарифметическое значение . Далее вычисляют дисперсию. Чтобы оценить воспроизводимость, рассчитывают критерий Кохрена:

 

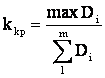
где max  - наибольшее значение дисперсии из числа рассматриваемых параллельных серий опытов;

m  –  число серий опытов;

-  сумма дисперсий m серий.

 Рекомендуется принимать .

Опыты считают воспроизводимыми при выполнении условия

где  табличное значение критерия Кохрена принимаемое в зависимости от доверительной ве­роятности  и числа степеней свободы

q = n— 1.

 В таблице  m -  число серий опытов; n - число измерений в серии.

Пример:

Проведено  3 серии опытов по 5 измерений в каждой серии.

По результатам обработки полученных данных имеем наибольшее значение из дисперсий равное 3,7, а суммарное значение всех дисперсий   3 серий опытов равно 6,7.Следовательно, расчетный коэффициент Кохрена равен 3,7/6,7 = 0,55, а найденный по таблице для m =3 и q=4 равен 0,74.

Так как    0,55 < 0.74 , то измерения в эксперименте следует считать воспроизводимыми. Если бы было наоборот, то необходимо было бы увеличить число серий m  или  число измерений n.

7.3 Обработка экспериментальных данных  косвенных измерений

Во многих случаях в процессе экспериментальных ис­следований приходится иметь дело с косвенными изме­рениями, когда искомая величина Z и ее  погрешность определяется по резуль­татам прямых измерений других величин, связанных с Z  определенной зависимостью.

 В общем случае решение этой задачи оказывается весь­ма сложным. Однако есть несколько случаев, когда оценить пределы погрешно­сти результата косвенного измерения просто.

 

Случай № 1. Величины X и Y измерены с абсолютными погрешностями ∆Х и ∆Y, соот­ветственно и  определяется  величина Z, связанная зависимостью:

.

В этом случае определяется абсолютная погрешность Z как сумма  абсолютных   погрешностей  величин X и Y  без учета знака, а именно: .

 

Случай № 2. Величины X и Y измерены с абсолютными погрешностями ∆Х и ∆Y, соот­ветственно и  определяется  величина Z, связанная зависимостями:  или .

В этом случае  определяется относительная погрешность Z, которая находится через  составляющие относительных погрешностей величин X и Y, которые  суммируются без учета знака, а именно:

.

 

Случай № 3.Величины  X и Y измерены с абсолютными погрешностями ∆Х и ∆Y  и  определяется  величина Z, связанная с X и Y функциональной зависимостью Z = F(X, Y). В этом случае для оценки предела абсолютной погрешности следует  использовать выражение:

Легко видеть, что предыдущие формулы  для погрешностей следуют из послед­него, более общего, соотношения.

Приведенные выше  способы оценки предельной погрешности косвенных измерений могут дать  завышенную оценку значения результирующей погрешности. Однако с точки зрения достоверности результата измерения и с учетом простоты описанного решения такой подход считается вполне приемлемым.

 

7.4. Определение оптимальных условий измерений

Одной из задач теории измерений является установ­ление оптимальных, т. е. наиболее выгодных, условий из­мерений. Оптимальные условия измерений в данном экс­перименте имеют место при условии обеспечения минимальной относительной погрешности  .

 Методика ре­шения этой задачи сводится к следующему. Если исследуется функция с одним неизвестным переменным, то вначале следует взять первую производную по аргументу  х, при­равнять ее нулю и определить . Если вторая производ­ная по аргументу  положительная, то функция y(x) в случае  имеет минимум. При наличии нескольких пере­менных поступают аналогичным образом, но берут про­изводные по всем переменным.

В результате минимизации функций устанавливают оптимальную об­ласть измерений (интервал температур, напряжений, силы тока, угла поворота стрелки на приборе и т.д.) каждой функции , при которой относительная ошибка измерений минимальна, т. е.   .

 

 

7.5 Обработка результатов экспериментальных данных при однократном измерении

Выше были рассмотрены примеры обработки экспериментальных данных, которые носят  стохастический характер, вследствие чего для повышения точности измерений  приходится выполнять измерения с многократным повторением опыта в одинаковых условиях с использованием одного и того же средства измерения.

Однако на практике часто имеют дело с результатами, полученными  при однократном измерении.

Однократные измерения  выполняются в тех случаях, когда требуется лишь грубая оценка  измеряемого параметра или когда погрешность, обусловленная случайными факторами,  мала, и ее можно не учитывать.

 При проведении однократных измерений эксперимент стремятся  организовать так, чтобы результирующая погрешность измерения определялась главным образом погрешностью прибора[3]. В этом  случае погрешность измерения оценивают исходя из точности прибора измерения.

Пример 1.

Вольтметр имеет класс точности . Верхний предел измерения . Прибор показывает значение 127В.

 Определить чему равно измеряемое напряжение?

Решение:

Абсолютная погрешность вольтметра равна

.

Значение измеряемого напряжения лежит в пределе от 126В до 128В.

Пример 2

Омметр класса точности 4,0 имеет неравномерную шкалу. Прибор показывает 50Ом.

Чему равно  измеряемое сопротивление?

Решение:

Абсолютная  погрешность Омметра равна

.

Истинное значение измеряемого сопротивления лежит в пределах от 48Ом до 52 Ом.

 

   

8 Лекция. Проверка статистических  гипотез

 

Содержание лекции:

 статистическая гипотеза, нулевая и альтернативная гипотезы, вероятность ошибки и уровень значимости, проверка статистических гипотез, проверка гипотезы о соответствии нормальному распределению, критерий согласия хи – квадрат.

 Цель лекции:

 изучение вопросов, связанных с анализом экспериментальных данных и проверкой на основе полученных выборок статистических гипотез о параметрах и свойствах генеральной совокупности.

8.1 Применение аналитической статистики для анализа экспериментальных данных

Помимо описательной статистики, основные положения которой были рассмотрены на предыдущих занятиях, важное место при обработке экспериментальных данных занимает  также и аналитиче­ская статистика.

Аналитическая статистика или теория статистических выводов ориенти­рована на обработку данных, полученных в ходе эксперимента, с целью формули­ровки выводов, имеющих прикладное значение.

С помощью аналитической статистики решается вопрос, отражают ли полученные  данные объективно существующую реальность.

 Указанный вопрос решается проверкой соответствующих статистических гипотез. При этом мо­гут выявляться достоверность различия между выборками, формы  взаимосвязи между выборками, влияющие факторы и т. п.

8.2 Принятие статистических решений

Статистическая гипотеза — это предположение о виде или отдельных параметрах распределения вероятностей, которое подлежит проверке на  базе имеющихся данных. Проверка статистических гипотез — это процесс формирования решения о возмож­ности принять или отвергнуть утверждение (гипотезу), основанный на информации, полученной из анализа выборки. Методы проверки гипотез называются критериями. В большинстве случаев рассматривают так называемую нулевую гипотезу (нуль-гипотезу - Н_о), о том, что рассматриваемые   события произошли случайным образом и полученные данные носят стохастический характер.

 Альтернативная гипотеза (H₁) состоит в том, что события случай­ным образом произойти не могли, и имело место воздействие некого фактора.

Обычно нулевая гипотеза формулируется таким образом, чтобы на основании эк­сперимента или наблюдений ее можно было отвергнуть с заранее заданной веро­ятностью ошибки . Эта, заранее заданная вероятность ошибки, называется уров­нем значимости.

Уровень значимости  - максимальное значение вероятности появления события,  которое  считается практически невозможным. В статистике наиболь­шее распространение получил уровень значимости, равный . Поэтому, если вероятность, с которой интересующее нас событие может произойти случайным обра­зом  равно р < 0,05, то принято считать это событие маловероятным, но если оно все же произошло, то это не было случайным.

 В наиболее ответственных случаях, когда требуется особая уверенность в достоверности полученных результатов, надежно­сти выводов  уровень значимости принимают равным    или даже .

Величину  называют доверительной вероятностью (уровнем на­дежности), то есть вероятностью, признанной достаточной для того, чтобы уве­ренно судить о принятом статистическом решении. Соответственно, в качестве до­верительных вероятностей выбирают значения 0,95, 0,99 и 0,999. Интервал, в котором с заданной доверительной вероятностью  находится оцениваемый параметр, называется доверительным интервалом.

 

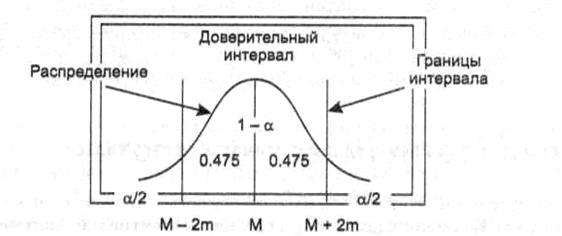
Рисунок 8.1 – 95%- доверительный интервал для среднего значения

 

В соответствии с доверительными вероятностями на практике используются 95%-, 99%-, 99,9%-ные доверительные интервалы. Граничные точки доверительного интервала называют доверительными пределами (см. рисунок 8.1).

Выбор того или иного уровня значимости, выше которого результаты отвергаются как статистически не подтвержденные, или, соответственно, выбор доверительной веро­ятности, в общем случае является произвольным.

 Окончательное решение зави­сит от исследователя, традиций и накопленного практического опыта в данной области исследований.

8.3 Проверка соответствия теоретическому распределению

 Важной  задачей, воз­никающей при анализе экспериментальных данных, является оценка меры соответствия  полученных данных  какому-либо теоретическому рас­пределению. Это связано с тем, что в большинстве случаев при решении реальных задач закон распределения и его параметры неизвестны.

 В то же время применяе­мые статистические методы в качестве предпосылок часто требуют определенного закона распределения.

Наиболее часто проверяется предположение о нормальном распределении генераль­ной совокупности, поскольку большинство статистических процедур ориентировано на выборки, полученные из нормально распределенной генеральной совокупности.

Для оценки соответствия имеющихся экспериментальных данных нормальному закону распределения обычно используют:

- графический метод;

- выборочные пара­метры формы распределения;

- критерии согласия.

Графический метод позволяет дать ориентировочную оценку расхождения или совпадений распределений (см. рисунок 8.2).

При большом числе наблюдений (n > 100) неплохие результаты дает использование выборочных параметров формы распределения: эксцесса и асимметрии, которые определяются с помощью программы описательной статистики. Принято говорить, что предположение о  случайном характере  опытных данных справедливо, если асимметрия близка к нулю, то есть лежит в диапазоне от -0,2 до 0,2, а эксцесс — от 2 до 4.

Наиболее убедительные результаты дает использование критериев согласия. Кри­териями согласия называют статистические критерии, предназначенные для про­верки соответствия  опытных данных теоретической модели.

 Здесь нулевая гипотеза Н_о представляет собой утверждение о том, что распределение генеральной сово­купности, из которой получена выборка, не отличается от нормального, т.е. данные выборки  носят случайный характер.

 Среди кри­териев согласия большое распространение получил непараметрический критерий  (хи-квадрат). Он основан на сравнении эмпирических частот с теоретическими частотами, рассчитанными по форму­лам нормального распределения.

Принято считать, что  уверенно о нормальном характере  распределения можно судить, если имеется не менее 50 результатов наблюдений. В случаях мень­шего числа данных можно говорить только о том, что данные не противоречат нор­мальному закону, и в этом случае обычно используют графические методы оценки соответствия. При большем числе наблюдений целесообразно совместное исполь­зование графических и статистических методов оценки, естественно дополняющих друг друга.

8.4 Использование критерия согласия хи-квадрат

Для применения критерия жела­тельно, чтобы объем выборки n > 50, выборочные данные были сгруппированы в интервальный ряд с числом интервалов не менее 7, а в каждом интервале находи­лось не менее 5 наблюдений (частот).

При этом, как и любой другой статистический критерий, крите­рий хи-квадрат не доказывает справедливость нулевой гипотезы, т.е. соответствия эмпирического распределения нормальному закону, а только позволяет ее отверг­нуть с определенной вероятностью (уровнем значимости).

В MS Excel критерий хи-квадрат реализован в функции ХИ2ТЕСТ. Функция ХИ2-ТЕСТ вычисляет вероятность совпадения экспериментальных (фактических) значений и теоретических (гипотетических) значений.

 Если полученная вероятность будет  ниже уровня значимости (0,05), то нулевая гипотеза отвергается и утверждается, что полученные  данные не соответствуют нормальному закону распределения.

 Если  же вычисленная вероятность будет больше 0,05, а тем более близка к 1, то можно говорить о высокой степени соот­ветствия экспериментальных данных нормальному закону распределения.

 

 

                                                       

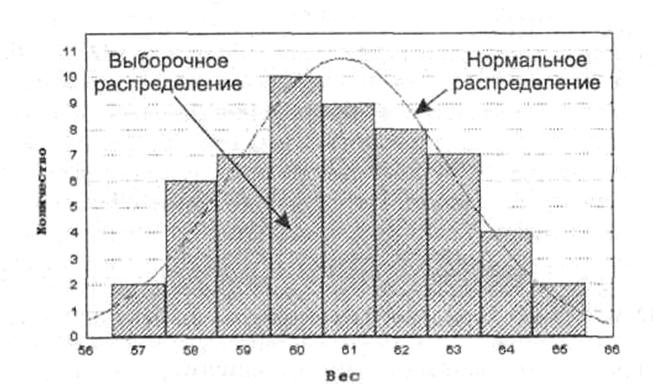
Рис. 8.2.-  Сопоставление выборочного распределения веса студентов и кривой нормального распределения

 

Проверка соответствия экспериментальных данных нормальному закону распределения рассматривается на практических занятиях.

9 Лекция 9. Применение  статистических критериев для анализа экспериментальных данных

 

Содержание лекции:

анализ двух выборок. Выявление достоверности различий, параметрические критерии, критерий Фишера, непараметрические критерии, критерий согласия Пирсона (хи – квадрат).

Цель лекции:

изучение вопросов, связанных с обработкой экспериментальных данных с помощью критериев  t - Стьюдента F - Фишера и хи-квадрат Пирсона().

9.1 Анализ двух выборок. Выявление достоверности различий

 Следующей задачей статистического ана­лиза, решаемой после определения основных выборочных характеристик и ана­лиза одной выборки, является совместный анализ нескольких выборок. Важ­нейшим вопросом, возникающим при анализе двух выборок, является вопрос о наличии различий между этими выборками. Обычно для этого проводят провер­ку статистических гипотез о принадлежности обеих выборок одной генеральной совокупности или о равенстве генеральных средних. Для решения задач такого типа используются так называемые критерии различия.

 Для проверки одной и той же гипотезы могут быть использованы разные статис­тические критерии. Правильный выбор критерия определяется как спецификой данных и проверяемых гипотез, так и уровнем статистической подготовки иссле­дователя.

 Статистические критерии различия подразделяются на параметрические и непа­раметрические критерии. Параметрические критерии служат для проверки гипо­тез о параметрах определенных распределений генеральной совокупности (чаще всего нормального распределения). Непараметрические критерии для проверки гипотез не используют предположений о законе распределения генеральной сово­купности и не требуют знания параметров распределения.

9.2 Параметрические критерии. Критерий Стьюдента

 Параметрические критерии служат для проверки гипотез о положении и рассеивании. Из параметрических критериев наибольшей популярностью при проверке гипотез о равенстве генеральных средних (матема­тических ожиданий) пользуется t-критерий Стьюдента (t-критерий различия).

Критерий Стьюдента (t) по­зволяет найти вероятность того, что средние двух выборок  относятся к одной и той же сово­купности. Если эта вероятность р ниже уровня значимости (р < 0,05), то принято считать, что выборки относятся к двум разным совокупностям.

При использовании t - критерия можно выделить два случая.

 В первом случае его применяют для проверки гипотезы о равенстве генеральных средних двух неза­висимых, несвязанных выборок (так называемый двухвыборочный  t-критерий). В этом случае есть контрольная и опытная группы, состоящие, например, из разных пациентов, количество которых в группах может быть различно.

Во втором случае, когда одна и та же группа объектов порождает числовой матери­ал для проверки гипотез о средних, используется так называемый парный t -критерий. Выборки при этом называют зависимыми, связанными. Например, измеряет­ся содержание лейкоцитов у здоровых животных, а затем у тех же самых животных после облучения.

 В обоих случаях в принципе должно выполняться требование нормальности рас­пределения исследуемого признака в каждой из сравниваемых групп и равенстве дисперсий в сравниваемых совокупностях. Однако на практике по большому сче­ту корректное применение t -критерия Стьюдента для двух групп часто бывает за­труднительно, поскольку достоверно проверить эти условия удается далеко не всегда.

Для оценки достоверности отличий по критерию Стьюдента принимается нулевая гипотеза, что средние выборок равны между собой. Затем вычисляется значение вероятности того, что изучаемые события произошли случайным образом.

В MS Excel для оценки достоверности отличий по критерию Стьюдента используется специальная функция ТТЕСТ и процедуры пакета анализа.

 Все перечисленные инструменты вычисляют вероятность, соответствующую критерию Стьюдента, и используются, чтобы определить, насколько вероятно, что две выборки взяты из генеральных совокупностей, имеющих одно и то же среднее. Применение различных типов критерия Стьюдента мо­жет приводить к различным результатам на основании одних и тех же исходных данных. Предлагается  следующий приблизительный способ выбора типа критерия: если не ясно, какой тип критерия выбирать, выбирается тип 3; если оче­видно, что выборки зависимы, связаны (например, это одни и те же студенты), то следует выбирать тип 1.

9.3 Критерий Фишера

 Критерий Фишера используют для проверки гипотезы о при­надлежности двух дисперсий одной генеральной совокупности и, следовательно, их равенстве. При этом предполагается, что данные независимы и распределены по нормальному закону. Гипотеза о равенстве дисперсий принимается, если отно­шение большей дисперсии к меньшей меньше критического значения распределе­ния Фишера.

          ,

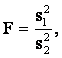
где  зависит от уровня значимости и числа степеней свободы для дисперсий в числителе и знаменателе.

В MS Excel для расчета уровня вероятности выполнения гипотезы о равенстве дисперсий могут быть использованы функция ФТЕСТ  и процеду­ра пакета анализа Двухвыборочный F-тест для дисперсий.

Пример применения критерий  различия

Имеются данные о продажах электрооборудования ТОО « Электросервис» до и после проведения  этой фирмой рекламной компании.

В результате применения критерия Стьюдента к этим данным  была получена вероятность р = 0,006.

Вывод: Поскольку  полученная  вероятность значительно меньше 0.05, делается вывод, что сравниваемые данные существенно  отличаются друг от друга и это различие далеко не случайное, а имеется влияние некоего фактора. В нашем случае это, по всей видимости,  влияние проведенной рекламной компании.

 Аналогичный результат  можно получить и   применяя  критерий  Фишера.

Если бы  вероятность р была бы больше 0,05, то  вывод об эффективности рекламной компании  делать нельзя: различие в данных для принятого уровня значимости  носит, по всей видимости, случайный характер.

9.4 Непараметрические критерии

 Непараметрические критерии используются в тех случаях, когда закон распределения данных отличается от нормального закона  или неиз­вестен. Из большого числа непараметрических критериев рассмотрим критерий Пирсона  (хи- квадрат).

9.5 Критерий Пирсона

 Бывают ситуации, когда необходимо сравнить две относи­тельные или выраженные в процентах величины (доли). Примером может слу­жить случай проверки успешности трудоустройства молодых специалистов, когда известен процент трудоустроившихся выпускников двух институтов. Для провер­ки достоверности различий здесь критерий Стьюдента применить не удастся. В та­ких задачах обычно используют критерий  (хи-квадрат). Критерий хи-квадрат относится к непараметрическим критериям.

Здесь, как и в случае с критерием Стьюдента, принимается нулевая гипотеза о том, что выборки принадлежат к одной генеральной совокупности. Кроме того, опреде­ляется ожидаемое значение результата. Обычно это среднее значение между вы­борками рассматриваемого показателя. Затем оценивается вероятность того, что ожидаемые значения и наблюдаемые принадлежат к одной генеральной совокуп­ности.

В MS Excel критерий хи-квадрат реализован в функции ХИ2ТЕСТ. Функция ХИ2-ТЕСТ вычисляет вероятность совпадения наблюдаемых (фактических) значений и теоретических (гипотетических) значений. Если вычисленная вероятность ниже уровня значимости (0,05), то нулевая гипотеза отвергается и утверждается, что наблюдаемые значения не соответствуют теоретическим значениям.

Если  полученная величина вероятности будет меньше уровня значимости 0,05, то нулевая гипотеза отвергается  и делается вывод о не случайности различий между двумя выборками. И, наоборот, если полученная вероятность будет больше 0,05,  делается вывод, что различие между выборками может носить  случайный характер.

Рассмотрим пример.

Дано:

 После окончания двух институтов энергетического профиля трудоустроились по специальности из первого института 90 человек, а из второго института 60 человек (обе группы  молодых специалистов включали по сто человек).

Вопрос - Случайны ли различия в трудоустройстве выпускников этих вузов?

Решение:

Определяется ожидаемое значение результата -  среднее значение между двумя выборками – 75 человек. В данном случае выдвигается гипотеза о том, что разницы между группами нет, и  в обоих случаях должно было трудоустроиться по 75 человек. С помощью функции ХИ2ТЕСТ определяется значение вероятности. В нашем случае оно равно  0,01436.

Выводы:

Поскольку величина вероятности  меньше уровня значимости 0.05, то нулевая гипотеза отвергается. Следовательно, различия между выборками не могут быть случайными и выборки считаются достоверно отличающимися от друга.

Поэтому на основании применения критерия хи- квадрат можно сделать вывод о том, что в двух группах выпускников выявлены достоверные отличия по успешности трудоустройства, что явилось, по всей видимости, результатом более высокой репутации выпускников первого института.

 

10 Лекция. Корреляционно-регрессионный анализ экспериментальных данных

 

Содержание лекции:

корреляционный анализ, коэффициент корреляции, корреляционная матрица, регрессионный анализ, уравнения регрессии, коэффициенты регрессии, коэффициент детерминации.

Цель лекции:

изучение  возможностей применения корреляционного и регрессионного анализа   для обработки  экспериментальных данных.

10.1 Корреляционный анализ

Важным разделом статистического анализа экспериментальных данных является корреляционный анализ, слу­жащий для выявления взаимосвязей между данными выборок. Одна из наиболее распространенных задач статисти­ческого исследования состоит в изучении связи между исследуемыми переменными. Знание взаимозависимостей отдельных признаков дает возмож­ность решать одну из кардинальных задач любого научного исследования: возмож­ность предвидеть, прогнозировать развитие ситуации при изменении конкретных характеристик объекта исследования. Например, основное содержание любой эко­номической политики, в конечном счете, может быть сведено к регулированию эко­номических переменных, осуществляемому на базе выявленной тем или иным обра­зом информации об их взаимовлиянии. Поэтому проблема изучения взаимосвязей показателей различного рода является одной из важнейших в  научном и статистическом ана­лизе. В общем случае взаимосвязь между переменными носит не функциональный, а вероятност­ный, т.е. стохастический характер. В этом случае нет строгой, однозначной зави­симости между величинами.  Для изучения стохастических связей между переменными  применяется регрессионный и корреляционный анализ. С помощью регрессионного анализа определяется фор­ма  (характер)  зависимости между случайной величиной Y и значениями одной или несколь­ких переменных величин X. С помощью корреляционного  анализа   определяют степень связи между двумя слу­чайными величинами X и Y. В качестве меры такой связи используется коэффи­циент корреляции. Коэффициент корреляции оценивается по выборке объема n связанных пар наблюдений  из совместной генеральной совокупности X и Y.

Для оценки степени взаимосвязи большое распространение получил коэффи­циент линейной корреляции (Пирсона), предполагающий нормальный закон рас­пределения экспериментальных данных.

Коэффициент корреляции (R, r) - параметр, характеризующий степень линей­ной взаимосвязи между двумя выборками. Коэффициент корреляции изменяется от -1 (строгая обратная линейная зависимость) до 1 (строгая прямая пропорцио­нальная зависимость). При значении 0 линейной зависимости между двумя вы­борками нет. Под прямой зависимостью понимают зависимость, при кото­рой увеличение или уменьшение значения одного признака ведет, соответственно, к увеличению или уменьшению второго. При обратной зависимости увеличение одного признака приводит к умень­шению второго и наоборот. Выборочный коэффициент линейной корреляции между двумя случайными ве­личинами X и  Y  рассчитывается по формуле:

 

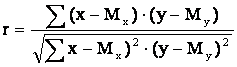
Коэффициент корреляции является безразмерной величиной и его значение не зависит от единиц измерения случайных величин X и Y.

На практике коэффициент корреляции принимает некоторые промежуточные зна­чения между 1 и -1 (рисунок 10.1). Для оценки степени взаимосвязи можно руковод­ствоваться следующими эмпирическими правилами. Если коэффициент корреля­ции (r) по абсолютной величине (без учета знака) больше, чем 0,95, то принято считать, что между параметрами существует практически линейная зависимость (прямая -  при положительном r и обратная -при отрицательном r).

 Если коэф­фициент корреляции r лежит в диапазоне от 0,8 до 0,95, говорят о сильной степе­ни линейной связи между параметрами.

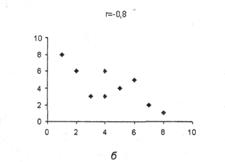 Если 0,6 < r < 0,8, говорят о наличии ли­нейной связи между параметрами. При r < 0,4 обычно считают, что линейную взаимосвязь между параметрами выявить не удалось.

 

 

 

 

 

 

 

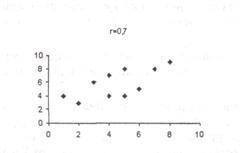
Рисунок 10.1- Примеры прямой (r = 0.7, а) и обратной (r = - 0.8, б) корреляционной зависимости

 

В MS Excel для вычисления парных коэффициентов линейной корреляции исполь­зуется специальная функция КОРРЕЛ. Параметрами функции являются КОРРЕЛ (массив1; массив2), где: массив1 — это диапазон ячеек первой случайной величины; массив2 — это второй интервал ячеек со значениями второй случайной величины.

10.2 Корреляционная матрица

При большом числе наблюдений, когда коэффициенты корреляции необходимо по­следовательно вычислять из нескольких рядов числовых данных, для удобства полу­чаемые коэффициенты сводят в таблицы, называемые корреляционными матрицами.

Корреляционная матрица — это квадратная (или прямоугольная) таблица, в кото­рой на пересечении соответствующей строки и столбца находится коэффициент корреляции между соответствующими параметрами. В MS Excel для вычисления корреляционных матриц используется процедура Кор­реляция. Процедура позволяет получить корреляционную матрицу, содержащую коэффициенты корреляции между различными параметрами.

10.3 Регрессионный анализ

При исследовании взаимосвязей между выборками помимо корреляции различа­ют также и регрессию. Регрессия используется для анализа воздействия на отдель­ную зависимую переменную значений одной или более независимых переменных. Соответственно, наряду с корреляционным анализом еще одним инструментом изучения стохастических зависимостей является регрессионный анализ. С помощью регрессионного  анализа устанавливается форма зависимости между случайной ве­личиной Y (зависимой) и значениями одной или нескольких переменных величин (независимых), причем значения последних считаются точно заданными. Такая зависимость обычно определяется некоторой математической моделью (уравне­нием регрессии), содержащей несколько неизвестных параметров. В ходе регрес­сионного анализа на основании экспериментальных данных находят оценки этих пара­метров, определяются статистические ошибки оценок или границы доверительных интервалов и проверяется соответствие (адекватность) принятой математической модели экспериментальным данным. В линейном регрессионном анализе связь между случайными величинами пред­полагается линейной. В самом простом случае в линейной регрессионной модели имеются две переменные X и Y.

 Требуется по n  парам наблюдений   построить (подобрать) прямую линию, называемую линией рег­рессии, которая «наилучшим образом» приближает наблюдаемые значения. Урав­нение этой линии  является регрессионным уравнением. С помощью регрессионного уравнения можно предсказать ожидаемое значение зависимой ве­личины , соответствующее заданному значению независимой переменной  .

Таким образом, можно сказать, что линейный регрессионный анализ заключается в подборе графика и его уравнения для имеющихся экспериментальных данных. Мерой эффективности регрессионной модели является коэффициент детермина­ции R² (R-квадрат). Коэффициент детерминации (R-квадрат) определяет, с какой степенью точности полученное регрессионное уравнение описывает (аппроксими­рует) исходные данные. Например,  R²=0,98 означает, что на 98%  значение Y определяется исследуемым фактором Х, а на 2 % - другими причинами.

В случае, когда рассматривается зависимость между одной зависимой переменной  и несколькими независимыми    говорят о множественной линейной регрессии.

 В этом случае регрессионное уравнение имеет вид

где

- требующие определения коэффициенты при независимых пере­менных ;

            -  константа.

В регрессионном ана­лизе все признаки (переменные), входящие в уравнение, должны иметь непрерыв­ную, а не дискретную природу.

Для выполнения регрессионного анализа и  получения коэффициентов регрессии используется процедура Регрессия из пакета анализа Excel.

Значимость  регрессионной модели  оценивается с помощью F -критерия Фи­шера. Если величина F-критерия значима (р < 0,05), то и  регрессионная модель яв­ляется значимой.

Достоверность отличия коэффициентов    от нуля проверяется с по­мощью критерия Стьюдента. В случаях, когда p  > 0,05, коэффициент может счи­таться нулевым, а это означает, что влияние соответствующей независимой пере­менной на зависимую переменную статистически недостоверно, и эта независимая переменная может быть исключена из уравнения.

В MS Excel экспериментальные данные можно аппроксимировать   линейным уравнени­ем до 16 порядка. Корреляционно- регрессионный анализ экспериментальных данных с использованием инструментов Excel  выполняется на практических занятиях.

11 Лекция. Методы графической обработки  экспериментальных данных. Интерполяция и аппроксимация данных

 

Содержание лекции:

методы графической обработки экспериментальных данных, типы  координатных систем и координатных сеток; интерполяция и аппроксимация экспериментальных данных

  Цель лекции:

рассмотрение основных вопросов, связанных с графической обработкой экспериментальных данных, применением современных возможностей ЭВМ для нахождения эмпирических формул к полученным данным.

11.1 Методы графической обработки экспериментальных данных

При обработке экспериментальных данных, т.е. результатов измерений или наблюдений широко используются методы графического изображе­ния, так как результаты измерений, представленные в табличной форме,  не позволяют достаточно на­глядно характеризовать закономерности изучаемых про­цессов. Графическое изображение дает наиболее нагляд­ное представление о результатах эксперимента, позволя­ет лучше понять физическую сущность исследуемого процесса, выявить общий характер функциональной за­висимости изучаемых переменных величин, установить наличие максимума или минимума функции.

Для графического изображения результатов измере­ний (наблюдений), как правило, применяют систему прямоугольных координат.

Обычно графики (смотри рисунок11.1)  имеют плавный характер, поэтому резкое искривление графика чаще всего объясняется погрешностями измерения. Если  эксперимент повторить с применением средств измерений более высокой точности и более тщательно, ло­маная кривая больше соответствует плавной кри­вой.      Иногда при построении графика некоторые  точки могут рез­ко удаляться от кривой. В таких случаях вначале сле­дует проанализировать физическую сущность явления, и, если нет основания полагать наличие скачка функции, то такое резкое отклонение можно объяснить грубой ошибкой или промахом. Это может возникнуть тогда, когда данные измерений предварительно не исследова­лись на наличие грубых ошибок измерений. В таких слу­чаях необходимо повторить измерение в диапазоне рез­кого отклонения данных замера. Если прежнее измере­ние оказалось ошибочным, то на график наносят новую точку. Если же повторные измерения дадут прежнее значение, необходимо к этому интервалу кривой отнестись особенно внимательно и тщательно проанализировать  физическую сущность явления.

 

 

 

 

 

 

 

           

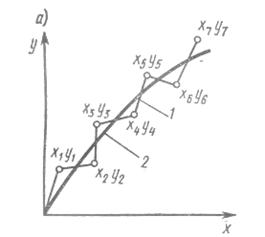
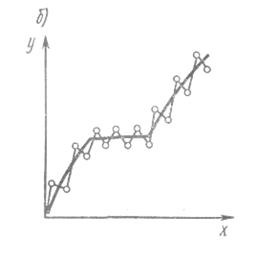
Рисунок 11.1 -  Графическое изображение функции

а) - плавная зависимость: б) - при наличии скачка

1 - кривая по результатам непосредственных измерений; 2- плавная кривая

 

 11.2 Типы  координатных систем и координатных сеток

При графическом изображении результатов экспериментов большую роль играет выбор системы координат или координатой сетки. Координатные сетки бывают равномерными и неравномерными. У равномерных координатных сеток ординаты и абсциссы имеют равномерную шкалу. Например, в системе прямоугольных координат длина откладываемых единичных отрезков на обеих осях одинаковая.

Из неравномерных координатных сеток наиболее  распространены полулогарифмические, логарифмические и вероятностные. Полулогарифмическая сетка имеют  равномерную ординату и логарифмическую абсциссу (рисунок11.2,а). Логарифмическая координатная сеть имеет обе оси логарифмические (рисунок 11.2,6), вероятностная - ординату обычно равномерную и по абсциссе — вероятностную шкалу (рисунок 11.2, в).

Неравномерные сетки применяют для более наглядного изображения функций. Функция  имеет различную форму при различных сетках. Так,  многие криволинейные функции спрямляются на логарифмических сетках.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

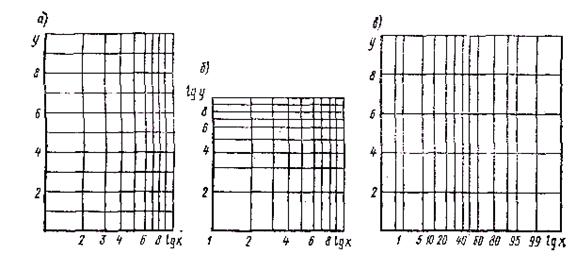
Рисунок 11.2. Координатная сетка: а)-  полулогарифмическая;

б) - логарифмическая;   в) - вероятностная   сетка

 

Масштаб по координатным осям обычно применяют различный.

 От выбора его зависит форма графика — он может быть  узким или широким вдоль оси (рисунок 11.3). Узкие графики дают большую по­грешность по оси у;  широкие -  по оси х.  Из рисунка видно, что пра­вильно подобранный масштаб (нормальный график) позволяет существенно повысить точность отсчетов.  Расчетные графики, имеющие экстремум функции или какой-либо сложный вид, особо тщательно необходимо проверять в зонах изгиба. На та­ких участках количество экспериментальных точек для построения графика долж­но быть значительно больше, чем на плавных участках.

 

        

 

 

 

 

 

 

 

 

 

 

 

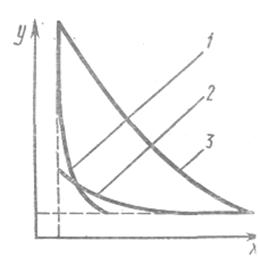
Рисунок 11.3.-Форма графика в зависимости от масштаба

1- узкий; 2- широкий; 3-нормальная.

 

11.3 Интерполяция и аппроксимация экспериментальных данных

 К одной из  важных задач, встречающихся при обработке экспериментальных данных, относится задача нахождения по набору экспериментальных значений функции  в узловых точках аргумента  аналитической зависимости или, как еще ее часто  называют, эмпирической формулы. Обычно функция  ищется в таком виде, чтобы график, построенной на основании найденной функции,  проходил бы  через все узловые точки (т.е. ).

 Такая задача называется задачей интерполяции, а сама функция  - интерполяционной.

 Достаточно популярным для решения этой задачи является применение степенной функции, т.е. полинома имеющего порядок  степени равный количеству узловых точек минус единица. При выполнении этого условия функция будет проходить через все узловые точки. Если возможности (или необходимости) в том, чтобы функция проходила через все узловые точки, нет, функцию выбирают из условия минимальности отклонений от экспериментальных значений, исходя при этом из принимаемой погрешности и практических потребностей.

Но в этом случае говорят не о решении задачи интерполяции, а о решении задачи аппроксимации. А найденную функцию называют аппроксимирующей функцией. Для нахождения эмпирических формул достаточно популярным является применение  встроенных процедур  и инструментов Excel. Применение Excel для нахождения интерполирующих и аппроксимирующих функций рассматриваются на практических занятиях.

 

12 Лекция. Определение эмпирических формул

 

Содержание лекции:

 эмпирические формулы, подбор формулы по виду графика экспериментальных данных, методы оптимизации, метод наименьших квадратов, надстройка Excel « Поиск решения» и ее применение для решения задач оптимизации и  определения эмпирических формул.

Цель лекции:

 в дополнении к лекции 11 дать дополнительные  теоретические сведения по обработке экспериментальных данных, подбору к полученным графикам эмпирических формул, применение для этой цели задач оптимизации и встроенных инструментов Excel.

12.1 Методы подбора эмпирических формул

В процессе экспериментальных исследований получается статистический ряд измерений двух величин, когда каж­дому значению функции  соответствует опре­деленное значение аргумента.

На основе экспериментальных данных можно подоб­рать алгебраические выражения функции , которые называют эмпирическими формулами.

 Такие формулы подбираются лишь в пределах измеренных значений аргумента и имеют тем большую цен­ность, чем больше соответствуют результатам экспери­мента. Необходимость в подборе эмпирических формул воз­никает во многих случаях. Так, если аналитическое вы­ражение  сложное, требует громоздких вычисле­ний, составления программ для ЭВМ или вообще не имеет аналитического выражения, то эффективнее пользо­ваться упрощенной приближенной эмпирической форму­лой. Эмпирические формулы должны быть по возможно­сти наиболее простыми и точно соответствовать экспери­ментальным данным в пределах изменения аргумента. Таким образом, эмпирические формулы являются при­ближенными выражениями аналитических формул. За­мену точных   аналитических  выражений   приближенными называют аппроксимацией, а функции – аппроксимирующими. При подборе  эмпирических формул можно воспользоваться практическими рекомендациями, связывающими форму графика, построенного по   экспериментальным данным, с рекомендуемой формулой для ее аппроксимации.

 Так, например, если экспериментальный гра­фик имеет вид, показанный на рисунке 12.1а, то рекомендуется  применить формулу   .

Если эксперименталь­ный график имеет вид, показанный на рисунке 12.1б, то це­лесообразно использовать выражение  .

Если экспериментальный график имеет вид, представленный на рисунке 12.1в,  то эмпирическая формула принимает вид 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

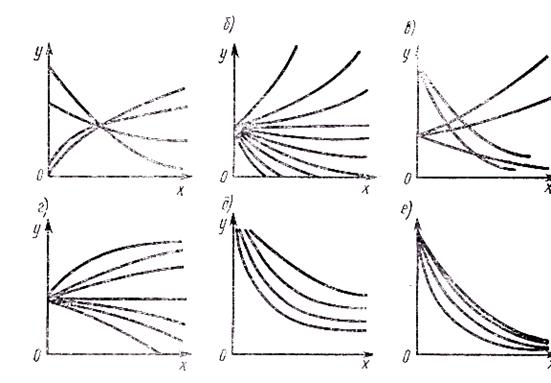
Рисунок 12.1 -  Основные виды графиков эмпирических формул

Если экспериментальный график имеет вид, показанный на рисунке 12.1г, то нужно пользоваться формулой     .

Если график имеет вид, соответствующий кривым на рисунке 12.1д, то применяется выражение    .

Если график имеет вид, соответствующий кривым на рисунке 12.1е, то используют формулу     .

Кроме приведенных выше выражений в качестве эмпирических формул широкое применение нашли полиномы:

Ценность полинома определяется тем, что с его помощью можно аппроксимировать любые результаты измерений, если они графически выражаются непрерывными функциями.

На практических  занятиях  мы рассмотрели некоторые возможности Excel для нахождения эмпирических формул, в частности  применение для этой цели утилит:  линия тренда и регрессия.

На сегодняшнем занятии мы рассмотрим новые возможности Excel для решения оптимизационных задач и  для  нахождения параметров эмпирических формул к полученным экспериментальным данным.

 

 

12.2 Задачи оптимизации.  Метод наименьших квадратов

Очень широкий класс задач составляют задачи оптимизации или, как их еще на­зывают, экстремальные задачи. В этой теме  будут рассмотре­ны некоторые типы задач оптимизации: задачи линейного программирования и метод наименьших квадратов.

В задачах оптимизации требуется найти значения параметров  , реа­лизующих максимум или минимум некоторой зависящей от них, так называемой,  целевой функции

,

На область нахождения параметров    могут быть наложены, при необходимости,   дополнительные условия -  ограничения   в виде   равенств или  неравенств:                               

                                                                 ( i =1,2…n). 

В случае, когда оптимизируемая целевая функция и ограничения ли­нейны, задача оптимизации решается методами линейного программирования и называется задачей линейного программирования.     

Во многих инженерных и экономических задачах, например, желательно найти максимум меры выполнения или минимум стоимости. В задачах электроэнергетике таким задачам можно отнести задачи нахождения минимума потерь электроэнергии, минимума приведенных затрат, максимума выработки электрической и тепловой энергии и проч.

Другим приложением задач оптимизации является нахождение параметров эмпирических формул. Хорошие результаты при их определении дает использование метода наименьших квадратов. Суть этого метода заключается в том, что минимизируется  сумма квадратов отклонений теоретических значений функции, найденной по эмпирической формуле и  значений, полученных из эксперимента.

 Максимум и минимум функции объединяются общим названием экстремума фун­кции. Для поиска экстремумов существуют различные методы. Часто случается, что при отыскании максимумов и минимумов функций многих переменных получают сложную систему уравнений, в этих случаях экстремумы находятся численными методами, то есть при помощи последовательного применения метода проб. При этом применение компьютера является практически единственным способом ре­шения задачи.

Инструментом решений задач оптимизации в Excel служит надстройка  «Поиск решения», внешний вид диалогового окна которой приведен на рисунке 12.2

 

 

Рисунок12.2 – Диалоговое окно Поиск решения

 

Применение данной надстройки для решения оптимизационных задач и для нахождения параметров эмпирических формул  рассматривается на соответствующем практическом  занятии.

 

Список литературы

Основная литература

1.     Дж. Тейлор Введение в теорию ошибок. - М.,- Мир, 1985, 271с.

2.     Маркин Н.С. Основы теории обработки результатов измерений,- М., Издательство стандартов, 1991, 176с.

3.     Агапьев Б.Д., Белов В.Н., Козловский В.В., Марков С.И. Обработка экспериментальных данных: Учеб. пособие / СПбГТУ. СПб., 2001.

4.     Горелова Г.В. Теория вероятностей и математическая статистика в примерах и задачах с применением Excel. – М.: Феникс, 2005. – 476 с.

     5.  Кассандрова О.Н., Лебедев В.В. Обработка результатов наблюдений.- М.: Наука, 1970. 104 с.

Дополнительная литература

1.     Щеголев Б.М. Математическая обработка наблюдений. - М.:Физматгиз, 1962.

2.     Козлов М.В. Прохоров Л.В. введение в математическую статистику.- М., 1987, 264с.

3.     Кузнецов В.А. Якунина Е.В. Основы метрологии.- М., Издательство стандартов, 1995, 279 с.

4.     Селиванов М.Н. Фридман А.Э. Кудряшова Ж. Ф. Качество измерений. Метрологическая справочная книга.- Л., 1987, 295с.

5.     Зайдель А.Н. Ошибки измерений физических величин. -Л.: Наука, 1974. 101 с.

6.     Макарова Н.В., Трофимец В.Я. Статистика в Excel. –М.: Финансы и статистика, 2002.

7.     Светозаров В.В. Основы статистической обработки результатов измерений.-  М.: Изд-во МИФИ, 1983.40 с.

8.     Линник Ю.В. Метод наименьших квадратов и основы теории обработки наблюдений.-  М.: Физматгиз, 1968. 390 с.

9.     Теория вероятностей и математическая статистика. Базовый курс с примерами и задачами. – М.: Физматлит, 2002. – 223 с.

10.Решение математических задач средствами Excel: Практикум /В.Я. Гельман.- СПб.: Питер, 2003.

 

[1] Все указанные в конспекте лекций таблицы приведены в методических указаниях к соответствующим  практическим занятиям.

[2] В научных статьях, как правило, приводят доверительный интервал "плюс-минус одна среднеквадратичная ошибка":

Этот интервал соответствует  доверительной вероятности р = 0,68. Такой интервал называют стандартным и при указании ошибки часто не приводят значение доверительной вероятности.

[3] Погрешность, обусловленная случайными  факторами,  может быть сведена до •7необходимого минимума увеличением числа измерений.