Некоммерческое акционерное общество

“Алматинский университет  энергетики и связи”

Кафедра электроснабжения промышленных предприятий

 

 

 

 

 

ТЕОРИЯ И ПРАКТИКА ТЕХНИЧЕСКОГО ЭКСПЕРИМЕНТА В ЭЛЕКТРОЭНЕРГЕТИКЕ

 Методические указания и  задания  к  расчетно-графическим работам  

для студентов всех форм обучения специальности 6М071800 – Электроэнергетика

 

 

 

Алматы 2010 

 

СОСТАВИТЕЛЬ: Фадеев В.Б. Теория и практика технического эксперимента.

 Методические указания и  задания  к  расчетно- графическим работам для студентов всех форм  обучения специальности 6М071800 – Электроэнергетика. - Алматы: АУЭС, 2010. – 34 с.

 

Данная работа включает в себя задания к   расчетно-графическим работам и  методические указания по их выполнению.

Выполнение данных работ предназначено для выработки у  студента практических навыков  по обработке экспериментальных данных: определению необходимого объема измерений, нахождению грубых ошибок эксперимента, проверке данных на достоверность и воспроизводимость и прочее, а также умение применять встроенные инструменты Excel для обработки результатов эксперимента и  нахождению эмпирических формул к опытным  данным.

 

 

Содержание

 

 

Введение

1

Расчетно- графическая работа  №1. Основные положения и понятия теории вероятности и математической статистики

1.1

Задания к работе 1

1.2

Методические указания к работе 1 

2

Расчетно- графическая работа  №2. Теория случайных ошибок. Обработка экспериментальных данных результатов измерений

2.1

Задания к работе 2

2.2

Методические указания к работе 2

3

Расчетно- графическая работа  №3. Статистическая обработка результатов экспериментальных исследований

3.1

Задания к работе 3

3.2

Методические указания к работе  3

4

Расчетно- графическая работа  №4. Методы графической обработки результатов экспериментальных исследований

4.1

Задания к работе 4

4.2

Методические указания к работе 4

5

Таблицы  вариантов  исходных данных к заданиям

 

 Список  литературы

  

Введение 

В  соответствии с учебным  планом по курсу « Теория и практика технического эксперимента» учащиеся должны выполнить 4 самостоятельные расчетно-графические работы (РГР).

Исходные данные – варианты заданий  по каждой РГР определяются по последней цифре зачетной книжки.

Подробное описание работы с  приведенными  ниже функциями и процедурами  Excel  можно найти в [2, 3 , 5, 6, 13, 14].

 

1. Расчетно графическая работа  №1. Основные положения и понятия теории вероятности и математической статистики

 Теоретический материал  по данной теме содержится в лекциях 2 – 4. Примеры выполнения заданий по данной теме рассматриваются на практических занятиях 1-3.

В результате изучения темы учащиеся должны знать и уметь объяснять основные понятия и определения теории вероятности и математической статистики в пределах лекционного материала по теме.

А также должны  уметь:

- вычислять основные параметры исследуемых данных: математическое ожидание, дисперсию, среднее арифметическое выборочной и генеральной совокупности, стандартную ошибку и прочие параметры  в пределах материала темы;

- использовать инструменты Excel для определения основных статистических характеристик выборки   и    построения кривых нормального распределения и гистограмм.

 

1.1 Задания  к работе

 1.1.1 Задание. Расчет основных характеристик для непрерывных и дискретных  случайных  величин

Исходными данными являются возможные значения экспериментального ряда    и вероятности их появления , а также функция  для непрерывных случайных величин.

Исходные данные к заданию 1 приведены  в таблицах 1.1 и 1.2.

 Требуется:

- рассчитать  математическое ожидание, дисперсию и среднее квадратичное отклонение для заданных значений экспериментального ряда;

- по найденным  значениям математического ожидания и среднего квадратичного отклонения построить кривую нормального распределения.

1.1.2 Задание. Построение выборочных характеристик распределения экспериментального ряда с использованием Excel

Исходными данными являются результаты замеров электрической нагрузки  фидера промышленного предприятия, приведенные в таблице 1.3.

Требуется   по данным выборки  рассчитать и          построить   эмпирические функции распределения относительных частот электрической нагрузки фидера.

1.1.3 Задание. Определение  основных статистических характеристик выборок с использованием пакета анализа Excel

Исходными данными являются результаты замеров электрической нагрузки  фидера промышленного предприятия, приведенные в таблице 1.3.

Требуется:

  определить все характеристики заданной выборки и  интервал, в котором будет находиться исследуемая величина  для следующих доверительных вероятностей: 0,683; 0,95 и 0,997.

 

1.2 Методические указания  по выполнению заданий  

 Методические указания  к  заданию  1.1.1

 Краткие теоретические сведения

В теории вероятностей изучаются закономерности для случайных событий. Случайные события – это такие события,  результат которых заранее предсказать невозможно. В теории вероятностей каждое такое событие принято характеризовать численной мерой возможности события. Эта численная мера называется вероятностью. Вероятность — это число в диапазоне от 0 до 1.

Случайные величины бывают дискретными и непрерывными. Возможными реализациями дискретной случайной величины являются отдельные числа, в то время как непрерывная случайная величина может принимать непрерывный набор значений.

 Важное место в наборе числовых характеристик случайных величин занимает математическое ожидание, которое для непрерывной случайной величины, определяется  по формуле:

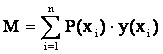                            ,                                                     (1.1)

 а для дискретной величины по формуле:

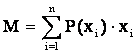                            .                                                          (1.2)

Математическое ожидание характеризует центр, вокруг которого группируются  случайные величины.

Кроме математического ожидания важной характеристикой  является дисперсия.

 Дисперсией случайной величины называют ее числовую характеристику, которая определяется для непрерывной случайной величины по формуле:

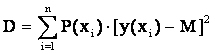                      ,                                                (1.3)

а для дискретной случайной величины по формуле:  

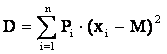                      .                                                          (1.4)

Дисперсия характеризует степень разброса или отклонений случайных величин от своего центра – математического ожидания.

Большинство экспериментальных исследований в технике и  в различных областях естественных наук  связаны с измерениями, результаты которых могут быть описаны с помощью кривой  нормального  распределения, которое задает­ся формулой Гаусса:

.

Здесь  а - математическое ожидание;

            - среднее квадратичное отклонение.                            (1.5)

 

График  нормальной  кривой  представлен на рисунке 1

 

 

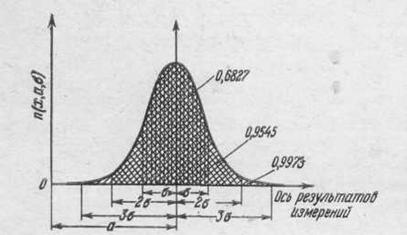
Рисунок 1.1 -  Нормальная кривая распределения

 

Порядок выполнения задания

Для нахождения математического ожидания дискретных случайных величин следует применить формулу (1.2). После чего по формуле (1.4) найти дисперсию, а затем  по формуле  (1.5)  среднее квадратичное отклонение.

Для нахождения математического ожидания для непрерывных случайных величин следует применить формулу (1.1). После чего по формуле (1.3) найти дисперсию  и  далее по формуле (1.5)  среднее квадратичное отклонение.

Зная математическое ожидание и среднее квадратичное отклонение, можно построить и кривую нормального распределения по формуле Гаусса.

Для этой цели можно воспользоваться функцией НОРМРАСП, находящейся в группе статистических функций  Excel.

 Методические указания к  заданию 1.1.2

 Краткие теоретические сведения

Математической статистикой называется  раздел математики, посвященный методам сбора, анализа и обработки статисти­ческих данных.

Статистические данные представляют собой данные, полученные в результате об­следования большого числа объектов или явлений.

По охвату статистической совокупности исследование может быть сплошное или несплошное. При сплошном статистическом исследовании группа наблюдения формируется путем полного охвата всех единиц изучаемого явления.

 Множество всех единиц наблюдения, охватываемых таким сплошным наблюдением, называ­ется генеральной совокупностью.

Если интересующая совокупность слишком многочисленна, либо ее элементы ма­лодоступны, прибега­ют к изучению какой-то части этой совокупности. Эта выбранная для  исследования группа элементов называется выборкой или выборочной совокуп­ностью.

Основным методом не сплошного наблюдения является выборочный метод. Задача выборочного метода состоит в том, чтобы сделать правиль­ные выводы относительно  свойств генеральной  совокупности.

В Excel для построения выборочных функций распределения используются процедура пакета анализа Гистограмма.

Результат работы процедуры приведен на рисунке 1.2

Порядок выполнения задания

По  имеющимся экспериментальным данным, приведенным в таблице 1.3, с помощью процедуры пакета анализа Гистограмма  построить эмпирическую функцию распределения. При анализе полученной  диаграммы, следует помнить, что эмпирическое распределение случайных величин с увеличением числа данных приближается к теоретической – кривой нормального распределения.

 

 

 

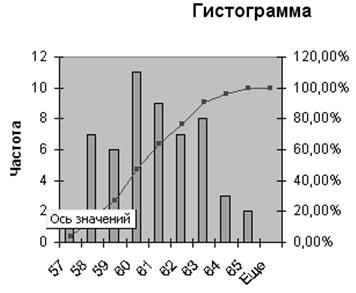
Рисунок 1.2- Диаграмма, построенная с помощью процедуры Гистограмма

.

Методические указания к  заданию  1.1.3

 Краткие теоретические сведения

К основным характеристикам выборки можно отнести: среднее арифметическое, дисперсию, стандартное отклонение и стандартную ошибку.

Средним значением выборки  называется  величина

 

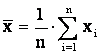                                                                                                               (1.6)

 

Дисперсией выборки  называется величина

 

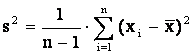                                                                                                   (1.7)

 

Стандартным отклонением  или средним  квадратичным отклонением называется  величина:

 

                                     .                                                                          (1.8)

 

При достаточно большой выборке, при числе элементов   n > 30, с помощью стандартного отклонения задается   доверительный интер­вал.

  Доверительный  интервал обозначает диапазон, в который с определенной вероятностью попадает исследуемая величина (среднее генеральной совокупности) и  определяется  по формуле:

 

 

                                                                                                                 (1.9)

где

      t   - нормированный коэффициент, определяемой из таблицы Лапласа, исходя из задаваемой доверительной вероятности.

Например,  95%-ный доверительный интервал, равный  , обозначает диапазон, в ко­торый с вероятностью р  = 0,95 при  условии достаточно большого  числа  наблюдений (n > 30) попадает  среднее значение генеральной совокупности.

В этом случае можно сказать, что с   вероятностью р =  0,95  из 100 случаев в 95 результат испытания будет попадать в интервал  , и только в 5 случаях результат испытания будет за пределами интервала.

При небольшом  числе элементов в выборке n < 30  границы доверительного интервала  определяют  по формуле:

 

                                                                                                (1.10)

    где     - стан­дартная ошибка (или ошибка среднего), определяется по формуле:

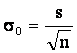                                                               .                                                   (1.11)

Стандартная ошибка — это параметр, характеризующий степень возможного от­клонения среднего значения  исследуемой  выбор­ки от истинного среднего значения генеральной совокупности элементов.

   - табличное значение распределения Стьюдента.

Порядок выполнения задания

Используя формулы 1.6 -1.11, рассчитать все основные статистические характеристики выборочной совокупности и сравнить их  с аналогичными характеристиками, полученными с помощью процедуры Описательная статистика Excel. Сравнение оформить в виде таблицы.

 

2 Расчетно - графическая работа  №2.  Теория случайных ошибок. Обработка экспериментальных данных результатов измерений

Теоретический материал по данной теме содержится в лекциях 5-7. Примеры выполнения заданий по теме рассматриваются на практических занятиях 4-6.

В результате изучения темы, учащиеся должны:

  - иметь представления  о доверительном интервале и доверительной вероятности;

- уметь определять  предельную  ошибку выборки с помощью таблиц Лапласа и  Стьюдента, а также, используя функции и процедуры Excel;

  - уметь определять   необходимый объем выборки  для требуемой точности измерений и заданной доверительной вероятности;

- находить грубые ошибки  экспериментального ряда, используя существующие методы для их определения;

-  уметь проверять  экспериментальные данные  на достоверность и воспроизводимость;

- уметь находить погрешности результатов серии измерений при заданной доверительной вероятности;

- уметь обрабатывать результаты экспериментальных данных при однократном измерении.

2.1 Задания к работе

2.1.1Задание. Методы оценки случайных погрешностей в измерениях

Исходные условия: При выполнении эксперимента  по снятию параметров электрической сети были получены следующие результаты:

 - произведено n замеров силы тока;

 - вычисленное значение стандартного отклонения составило s ампер;

 -допускаемая  погрешность измерительного прибора  равна   ампер.

Требуется:

 1) Определить, с какой доверительной вероятностью (достоверностью) оцениваются результаты  измерения.

2) Определить минимальное количество измерений, которое необходимо выполнить  в данном эксперименте с доверительной надежностью = 0,95 при использовании прибора с относительной погрешностью .

Варианты задания, приведены таблице 2.1.

2.1.2 Задание. Интервальная оценка с помощью доверительной вероятности

Исходные данные:

На ТОО с электролампового завода поступило  партия из  n    электроламп.

Для проверки качества изделий  было проведено испытание 100 ламп.

Средняя продолжительность их горения составило  часов со средним квадратичным отклонением  S часов.

Количество электроламп горевших менее установленного лимита составило n1 штук.

Требуется:

1) Определить количество  электроламп во всей партии, продолжительность горения которых будет меньше низшего предела интервала, найденного с  доверительной вероятностью = 0,95.

2) Определить с той же доверительной вероятностью   долю ламп,  срок службы  которых  будет меньше установленного лимита.

Варианты задания, приведены таблице 2.2.

2.1.3 Задание. Методы определения грубых ошибок экспериментального ряда

Исходные условия:

Выполнено 18   измерений тока в линии ЛЭП 35 кВ.

Варианты заданий приведены в таблице 2.3.

Требуется выполнить анализ экспериментальных данных.

При проведении анализа необходимо:

- выполнить статистическую обработку данных для исходного статистического ряда;

- выявить грубые ошибки в данных эксперимента. Удалить при необходимости  из статистического  ряда найденные ошибки, т.е. выполнить очистку  ряда;

- вычислить относительные погрешности результатов измерения для исходного и очищенного ряда;

   - задаваясь относительной  точностью  прибора равной соответственно 3 и 5 %, найти минимальное количество опытов, необходимое для обеспечения такой точности при  доверительной вероятности р = 0,95.

2.1.4 Задание. Исследование экспериментальных данных на достоверность

Исходные данные:

Известны средние арифметические прочности изделия до и после испытания, а также значения предельных ошибок измерения прочности до и после испытания изделия.

Требуется выполнить анализ экспериментальных данных и ответить на вопрос:  является ли  изменение прочности изделия достоверным, а не следствием разброса опытных данных?

Варианты заданий приведены в таблице 2.4.

2.1.5 Задание. Исследование экспериментальных данных на воспроизводимость результатов эксперимента

Исходные данные:

имеется 4 серии опытов. В  каждой серии проведено по 5 замеров электрического тока в цепи. Варианты заданий приведены в таблице 2.5.

Требуется: используя критерий Кохрена, сделать вывод о воспроизводимости   опытов.

2.2 Методические указания к работе

Методические указания к заданию  2.1.1

 Краткие теоретические сведения

Анализ случайных погрешностей при измерениях основывается на тео­рии случайных ошибок. Тео­рия случайных ошибок дает возможность с опреде­ленной гарантией вычислить действительное значение измеренной величины и оценить возможные ошибки при ее вычислении.

Для большой выборки и нормального закона распределения оценочными характеристиками выполненных изме­рений являются  среднее арифметическое выборки, стандартное отклонение  и средняя ошибка выборки:

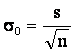                                                                                                                 (2.1)

где

       s - среднеквадратичное отклонение (стандартное отклонение) выборки;

       n  -  количество выполненных замеров.

Ошибка выборки для выборочной относительной величины (доли) определяется по выражению:

                                                     .                                               (2.2)

В теории ошибок достаточно важными являются понятия доверительной вероятности и  доверительного интервала.

Доверительной ве­роятностью (достоверностью) измерения называется вероятность того, что истинное значение измеряемой ве­личины попадает в  интервал, называемый доверительным интервалом.

Доверительный интервал определяет  точность измерения и называется предельной  ошибкой  выборки.

Предельная ошибка выборки определяется по формуле:

 

                                                                                              (2.3)

где

     - гарантийный коэффициент или нормированное отклонение.

Значения  t и соответствующие им доверительные вероятности  приведены в справочной литературе.  При числе опытов n > 30 их значения определяются по таблице Лапласа, а при n < 30 -  по таблице Стьюдента.

  Зная предельную ошибку выборки , можно рассчитать  интервал, в котором с доверительной вероятностью  находится измеряемая величина А:

 

                                        .                                                          (2.4)

 

Порядок выполнения задания

 Для нахождения доверительной вероятности,  с которой оцениваются результаты  измерения необходимо выполнить следующее.

По формуле (2.1) вычисляем среднюю ошибку выборки.

По формуле (2.3) для  предельной ошибки выборки   находим  нормированный коэффициент  .

По таблице Лапласа для  полученного нормированного коэффициента  t находим  доверительную вероятность, с которой оцениваются результаты измерения.

Для того чтобы определить минимальное количество измерений, которое необходимо выполнить  в данном эксперименте с доверительной надежностью = 0,95 при использовании прибора с относительной погрешностью  воспользуемся формулой

 

.

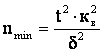Неизвестное значение коэффициента вариации вычисляется  по формуле

   .

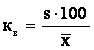Методические указания к  заданию  2.1. 2

Для оценки качества продукции по формуле 2.1 определяем среднюю  ошибку    выборки

С вероятностью 0,95 предел возможной ошибки можно найти по формуле 2.3:

Далее по формуле 2.4 можно рассчитать доверительный интервал, который с доверительной вероятностью 0,95  определяет продолжительность горения электроламп. После чего, используя правило 3 стандартов,  можно найти количество электроламп,  срок горения которых будет меньше  низшего предела  доверительного интервала.

Для нахождения   доли  ламп из всей партии,  срок службы  которых  будет меньше установленного лимита,  выполним следующее.

В соответствии с условием   вычисляем   долю  некачественных   ламп  по формуле

где

   n  –  количество  испытанных электроламп (в нашем случае  ).

  Средняя воз­можная ошибка для  выборочной относительной величины (доли) определяется по формуле  (2.2)

С вероятностью 0,95 предел ошибки доли некачественных электроламп составит

 .

Следовательно,  во всей партии с доверительной вероятностью 0,95 можно ожидать долю электроламп, срок горения которых меньше установленного лимита,  равную .

Методические указания к  заданию  2.1. 3

 Краткие теоретические сведения

Известно несколько методов определения грубых ошибок статистического ряда.

 Наиболее простым способом исключения из ряда резко выделяющегося измерения является правило трех стандартов, согласно которому разброс случайных величин от среднего значения не должен превышать

                                              .                                        (2.5)

Более достоверными, как считают некоторые авторы, являются методы, базируемые на использовании критериев появления грубых ошибок.

 Пусть имеется статистический ряд малой выборки, подчиняющийся закону нормального распределения. При наличии грубых ошибок критерии их появления вычисляются с помощью  формул:

                                          ,                         (2.6)

                                         .                       (2.7)

 

где  - наибольшее и наименьшее значения  из n  измерений.

По  таблице «Критерии появления грубых ошибок», в зависимости от заданной доверительной вероятности  находят значение , возникающее вследствие статистического разброса.  Если , то значение  необходимо исключить из статистического ряда как грубую погрешность. Если  -  исключается величина. После исключения грубых ошибок определяют новые значения  и  из  (n - 1) или (n - 2) измерений.

Следующий  метод установления грубых ошибок основан на использовании критерия В. И. Романовского и приме­ним также для малой выборки. Методика выявления грубых ошибок сводится к следующему: задаются дове­рительной вероятностью  и по таблице «Коэффициент    для вычисления предельно   допустимой ошибки измерения» в зависимости от числа измерений  n  находят коэффициент q.

Вычисляют предельно до­пустимую абсолютную   ошибку   отдельного   измерения

 Если ,  то   данное измерение  исключают из ряда наблюдений.  Этот метод более требователен к очи­стке ряда.

В настоящее время, в связи с внедрением в практику обработки данных статистических программ, нахождение грубых ошибок экспериментального ряда (выпадающих вариант) может быть выполнено  следующим образом.

С помощью программы Описательная статистика  из пакета анализа Excel определяются статистические характеристики для исследуемого ряда данных и вычисляется диапазон, в котором с задаваемой доверительной вероятностью находится измеряемая величина по формуле:

                                                                                (2.8)

где

       - уровень надежности для заданной доверительной вероятности;

      n – число измерений.

Все данные, которые находятся вне найденного диапазона, считаются, с точностью  до заданной вероятности,  грубыми ошибками.

Порядок выполнения  задания

Грубые ошибки следует определять по формулам (2.5-2.8). Необходимые для этой цели таблицы приведены  в  [2].

Статистические характеристики экспериментального ряда рекомендуется находить  с помощью процедуры «Описательная статистика».

Округление результатов  следует выполнять с обязательным применением установленных  правил [1,2].

Методические указания к  заданию 2.1.4

 Краткие теоретические сведения

В исследованиях часто возникает вопрос о достовер­ности данных, полученных в опытах. Решение такой за­дачи можно проиллюстрировать следующим примером.

Пусть установлена прочность контрольных образцов бетона    до     виброперемешивания    и прочность бетонных образцов после перемешивания . Прирост прочности составляет 15%. Это упрочнение относительно небольшое и его можно отнести за счет разброса опытных данных. В этом случае следует провести проверку на достоверность экспериментальных данных по условию:

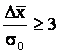                                                       .                                             (2.9)

Разница средних значений равна 23 – 20 = 3,0, а разница ошибок измерения равна 0,78, поэтому 3 /0,78 = 3,84 > 3.

Следовательно, полученный прирост прочности бетона является достоверным, а не случайным.

Порядок выполнения задания

Для выполнения задания следует применить формулу 2.9.

Методические указания к  заданию 2.1.5

 Краткие теоретические сведения

Ответственные эксперименты должны быть проверены также и на воспроизводимость результатов, т.е. на их повторяемость в определенных пределах измерений с заданной доверительной достоверностью. Суть такой проверки сводится к следующему. Имеется несколько па­раллельных опытов (серий). Для каждой серии вычис­ляют среднеарифметическое значение . Далее вычисляют дисперсию. Чтобы оценить воспроизводимость, рассчитывают критерий Кохрена:

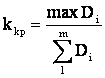                                                                                       (2.10)

где - наибольшее значение дисперсии из всех опытов;

            m   – число серий опытов;

           -  сумма дисперсий m серий.

 Рекомендуется принимать .

Опыты считают воспроизводимыми при выполнении условия

    

где  - табличное значение критерия Кохрена принимаемое в зависимости от доверительной ве­роятности  и числа степеней свободы

 

где n  – число измерений в серии.

Порядок выполнения задания

При выполнении задания по формуле 2.10 следует рассчитать критерий Кохрена и затем сравнить его с табличным значением. Таблица Кохрена, необходимая для выполнения  задания приведена в [2].

 

 

 

3 Расчетно- графическая работа  №3. Статистическая обработка результатов экспериментальных исследований

 Теоретический материал по данной теме содержится в лекциях 8-10. Примеры выполнения заданий по теме рассматриваются на практических занятиях 7-9.

В результате изучения темы  учащиеся должны:

-   уметь применять статистические критерии Стьюдента, Фишера и Пирсона для анализа экспериментальных данных;

- уметь применять корреляционный анализ для оценки  степени стохастической  взаимосвязи между параметрами   данных выборок;

- уметь применять регрессионный анализ  для оценки формы стохастической взаимосвязи между параметрами данных выборок.

3.1 Задания к работе

3.1.1 Задание. Применение   статистических гипотез для проверки соответствия экспериментальных данных нормальному закону распределения

Исходные данные:  известны результаты замера электрических нагрузок, которые приведены в таблице 3.1.

Требуется проверить соответствие данных эксперимента  нормальному закону распределения.

3.1.2 Задание. Применение  критерия Стьюдента для анализа двух выборок

Исходные условия: известны данные о продажах электрооборудования до проведения рекламной компании и после. Данные приведены в таблице 3.2.

 Требуется: дать оценку эффективности рекламной компании,  используя для этой цели  критерий Стьюдента.

3.1.3 Задание. Применение   критерия Фишера для анализа двух выборок

Исходные условия:

 известны данные о зарплате персонала в  электротехнической компании.  Данные приведены в таблице 3.3

 Требуется: используя критерий Фишера, оценить  фактор влияния образования на уровень зарплаты сотрудников в компании.

З.1.4 Задание. Корреляционный анализ экспериментальных данных

Исходные условия: имеются результаты семимесячных наблюдений о количестве грозовых дней и аварий на  ЛЭП 6 кВ. Данные приведены в таблице 3.4.

Требуется, используя корреляционный анализ, найти коэффициент корреляции и оценить наличие взаимосвязи между количеством грозовых дней и количеством аварий на ЛЭП.

3.1.5 Задание. Дисперсионный  анализ экспериментальных данных

Исходные условия: имеются результаты семимесячных наблюдений о количестве грозовых дней и аварий на  ЛЭП 6 кВ. Данные приведены в таблице 3.4.

Требуется, используя дисперсионный анализ, оценить взаимосвязь между количеством грозовых дней и количеством аварий на ЛЭП и  найти регрессионное уравнение к этой связи.

3.2 Методические указания к работе

Методические указания к заданию 3.1.1

 Краткие теоретические сведения

Статистическая гипотеза — это предположение о виде или отдельных параметрах распределения экспериментального ряда, которое подлежит проверке на  базе полученных данных. Методы проверки гипотез называются критериями. В большинстве случаев рассматривают так называемую нулевую гипотезу (нуль-гипотезу - Но), о том, что рассматриваемые   события произошли случайным образом и полученные данные носят стохастический характер и изменяются по нормальному закону.

 Альтернативная гипотеза (H1) состоит в том, что события случай­ным образом произойти не могли, и имело место воздействие некого фактора, а поэтому экспериментальные данные имеют не случайный характер и не могут изменяться по нормальному закону.

 Обычно нулевая гипотеза формулируется таким образом, чтобы на основании эк­сперимента или наблюдений ее можно было отвергнуть с заранее заданной веро­ятностью ошибки . Эта, заранее заданная вероятность ошибки, называется уров­нем значимости.

Уровень значимости  - максимальное значение вероятности появления события,  которое  считается практически невозможным. В статистике наиболь­шее распространение получил уровень значимости, равный . Поэтому, если вероятность, с которой интересующее нас событие может произойти случайным обра­зом  равно р < 0,05, то принято считать это событие маловероятным, но если оно все же произошло, то это не было случайным.

Важной  задачей, воз­никающей при анализе экспериментальных данных, является оценка меры соответствия  полученных экспериментальных  данных  нормальному закону  рас­пределения. Для оценки соответствия имеющихся экспериментальных данных нормальному закону распределения обычно используют  критерии согласия. Среди кри­териев согласия большое распространение получил критерий  (хи-квадрат). Он основан на сравнении эмпирических частот с теоретическими частотами, рассчитанными по форму­лам нормального распределения.

В MS Excel критерий хи-квадрат реализован в функции ХИ2ТЕСТ. Функция ХИ2-ТЕСТ вычисляет вероятность совпадения экспериментальных (фактических) значений и теоретических (гипотетических) значений.

 Если полученная вероятность будет  ниже уровня значимости (0,05), то нулевая гипотеза отвергается и утверждается, что полученные  данные не соответствуют нормальному закону распределения.

 Если  же вычисленная вероятность будет больше 0,05, а тем более близка к 1, то можно говорить о высокой степени соот­ветствия экспериментальных данных нормальному закону распределения.

 

Порядок выполнения задания 3.1.1

 Используя теоретические сведения и опыт выполнения заданий 1 РГР, следует вначале определить  относительные частоты экспериментальных данных, затем найти среднее арифметическое и стандартное отклонение.

 После этого, используя функцию НОРМРАСП,  найти теоретические частоты, соответствующие нормальному распределению. Затем  с помощью функции ХИ2ТЕСТ сравнить теоретические и эмпирические частоты исследуемого параметра и сделать  вывод  о характере изучаемого явления (имеет он  стохастический характер или нет?)

Методические указания к заданию 3.1.2

Краткие теоретические сведения

Важной задачей статистического ана­лиза, решаемой после определения основных выборочных характеристик и ана­лиза одной выборки, является совместный анализ нескольких выборок. Важ­нейшим вопросом, возникающим при анализе двух выборок, является вопрос о наличии различий между этими выборками. Обычно для этого проводят провер­ку статистических гипотез о принадлежности обеих выборок одной генеральной совокупности. Для решения задач такого типа используются так называемые критерии различия. При проверке гипотезы о равенстве генеральных средних (матема­тических ожиданий) часто  используется t-критерий Стьюдента.

Критерий Стьюдента  по­зволяет найти вероятность того, что средние двух выборок  относятся к одной и той же сово­купности. Если эта вероятность р ниже уровня значимости (р < 0,05), то принято считать, что сравниваемые данные носят случайный характер и не связаны между собой.

При использовании t - критерия выделяют  два случая.

 В первом случае  применяется двухвыборочный  t-критерий. Он используется  для  анализа двух неза­висимых и несвязанных выборок. В этом случае при выполнении  эксперимента имеются  контрольная и опытная группы.

Во втором случае используется так называемый парный t – критерий.

Он применяется,  когда одна и та же группа объектов порождает числовой матери­ал. Выборки при этом называют зависимыми. Например,  в эксперименте измеряет­ся содержание лейкоцитов у здоровых животных, а затем у тех же самых животных после облучения.

В MS Excel для оценки достоверности отличий по критерию Стьюдента используется специальная функция ТТЕСТ и процедуры  из пакета анализа Excel

Порядок выполнения задания 3.1.2

Для выполнения задания следует воспользоваться функцией ТТЕСТ, находящейся в категории статистических функций Excel.

В качестве параметров функции ввести данные о продажах электрооборудования до и после проведения рекламной компании.

 По полученному значению критерия Стьюдента следует сделать вывод об эффективности рекламной компании. Если Критерий Стьюдента будет меньше уровня значимости (α = 0,05), то нулевая гипотеза отвергается. Следовательно, различия между выборками   считаются не случайными, и средние выборок считаются  статистически достоверно отличающимися друг от друга.

Методические указания к заданию 3.1.3

Краткие теоретические сведения

Критерий Фишера используют для проверки гипотезы о при­надлежности двух дисперсий одной генеральной совокупности и, следовательно, их равенстве. При этом предполагается, что данные независимы и распределены по нормальному закону. Гипотеза о равенстве дисперсий принимается, если отно­шение большей дисперсии к меньшей меньше критического значения распределе­ния Фишера.

                                     

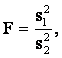
   где   зависит от уровня значимости и числа степеней свободы для дисперсий в числителе и знаменателе.

Критерий Фишера используют для проверки гипотезы о при­надлежности двух дисперсий одной генеральной совокупности и, следовательно, их равенстве. В  Excel для проведения однофакторного дисперсионного анализа использует­ся процедура «Однофакторный дисперсионный анализ».

Порядок выполнения задания 3.1.3

Для выполнения задания следует воспользоваться процедурой  Однофакторный дисперсионный анализ. В качестве вводных параметров следует ввести данные  к заданию, т.е. данные таблицы 3.3 .

Если выходной параметр P-Значение   будет меньше уровня значимости , то  влияние исследуемого фактора считается статистически доказанным.

 

Методические указания к заданию 3.1.4

Краткие теоретические сведения

Важным разделом статистического анализа экспериментальных данных является корреляционный анализ, слу­жащий для выявления взаимосвязей между данными выборок. Одна из наиболее распространенных задач статисти­ческого исследования состоит в изучении связи между исследуемыми переменными. Знание взаимозависимостей отдельных признаков дает возмож­ность решать одну из кардинальных задач любого научного исследования: возмож­ность предвидеть, прогнозировать развитие ситуации при изменении конкретных характеристик объекта исследования.

Проблема изучения взаимосвязей показателей различного рода является одной из важнейших в  научном и статистическом ана­лизе. В общем случае взаимосвязь между переменными  может носить не функциональный, а вероятност­ный, стохастический характер. В этом случае нет строгой, однозначной зави­симости между величинами.  Для изучения стохастических связей между переменными  применяется корреляционный   и регрессионный анализ.

С помощью регрессионного анализа определяется фор­ма  (характер)  зависимости между случайной величиной Y и значениями одной или несколь­ких переменных величин X. С помощью корреляционного  анализа   определяют степень связи между двумя слу­чайными величинами X и Y. В качестве меры такой связи используется коэффи­циент корреляции.

Для оценки степени взаимосвязи большое распространение получил коэффи­циент линейной корреляции Пирсона, предполагающий нормальный закон рас­пределения экспериментальных данных

Коэффициент корреляции (R)   это    параметр, характеризующий степень линей­ной взаимосвязи между двумя выборками. Коэффициент корреляции изменяется от -1 (строгая обратная линейная зависимость) до 1 (строгая прямая пропорцио­нальная зависимость). При значении 0 линейной зависимости между двумя вы­борками нет.

На практике коэффициент корреляции принимает некоторые промежуточные зна­чения между 1 и -1.

 Для оценки степени взаимосвязи рекомендуется руковод­ствоваться следующими эмпирическими правилами. Если коэффициент корреля­ции по абсолютной величине (без учета знака) больше, чем 0,95, то можно считать, что между параметрами существует практически линейная зависимость (прямая -  при положительном R и обратная - при отрицательном R).

Если коэф­фициент корреляции R лежит в диапазоне от 0,8 до 0,95, говорят о сильной степе­ни линейной связи между параметрами.

 Если 0,6 < R < 0,8, говорят о наличии ли­нейной связи между параметрами. При R < 0,4 обычно считают, что линейную взаимосвязь между параметрами выявить не удалось.

В MS Excel для вычисления парных коэффициентов линейной корреляции исполь­зуется специальная функция КОРРЕЛ.

Порядок выполнения задания 3.1.4

Для выявления статистической связи между количеством  грозовых дней и  количеством аварий на  ЛЭП следует воспользоваться функцией КОРРЕЛ.

В качестве параметров функции ввести исходные данные. По полученному коэффициенту корреляции сделать вывод о наличии или отсутствии связи.

Методические указания к заданию 3.1.5

Краткие теоретические сведения

При исследовании взаимосвязей между выборками помимо корреляции различа­ют также и регрессию. Регрессия используется для анализа воздействия на отдель­ную зависимую переменную значений одной или нескольких независимых переменных. Соответственно, наряду с корреляционным анализом еще одним инструментом изучения стохастических зависимостей является регрессионный анализ. С помощью регрессионного  анализа устанавливается форма зависимости между случайной ве­личиной Y (зависимой) и значениями одной или нескольких переменных величин (независимых), причем значения последних считаются точно заданными. Такая зависимость обычно определяется некоторой математической моделью (уравне­нием регрессии), содержащей несколько неизвестных параметров. В ходе регрес­сионного анализа на основании экспериментальных данных находят оценки этих пара­метров, определяются статистические ошибки оценок или границы доверительных интервалов и проверяется соответствие (адекватность) принятой математической модели экспериментальным данным. В линейном регрессионном анализе связь между случайными величинами пред­полагается линейной. В самом простом случае в линейной регрессионной модели имеются две переменные X и Y.

Можно сказать, что линейный регрессионный анализ заключается в подборе графика и его уравнения для имеющихся экспериментальных данных. Мерой эффективности регрессионной модели является коэффициент детермина­ции R2 ,  где R   коэффициент  линейной корреляции.

Коэффициент детерминации  определяет, с какой степенью точности полученное регрессионное уравнение описывает (аппроксими­рует) экспериментальные  данные. Например,  R2=0,98 означает, что на 98%  значение Y определяется исследуемым фактором Х, а на 2 % - другими причинами (случайными факторами).

Если R2 > 0,95,  то говорят о высокой точности аппроксимации (модель хорошо описывает явление). Если R2 лежит в диапазоне от 0,8 до 0,95, говорят об удовлетворительной аппроксимации (модель в целом адекват­на описываемому явлению). Если R2 < 0,6, принято считать, что точность аппроксимации недостаточна и модель требует улучшения (введения новых неза­висимых переменных, учета нелинейностей и т. д.).

В случае, когда рассматривается зависимость между одной зависимой переменной  и несколькими независимыми   , говорят о множественной линейной регрессии.

 В этом случае регрессионное уравнение имеет вид

где

- требующие определения коэффициенты при независимых пере­менных ;

            -  константа.

В регрессионном ана­лизе все  переменные, входящие в уравнение, должны иметь непрерыв­ную, а не дискретную природу.

Для выполнения регрессионного анализа и  получения коэффициентов регрессии используется процедура Регрессия из пакета анализа Excel.

Значимость  регрессионной модели  оценивается с помощью F - критерия Фи­шера. Если величина F-критерия значима (р < 0,05), то и  регрессионная модель яв­ляется значимой.

Достоверность отличия коэффициентов    от нуля проверяется с по­мощью критерия Стьюдента. В случаях, когда p  > 0,05, коэффициент может счи­таться нулевым, а это означает, что влияние соответствующей независимой пере­менной на зависимую переменную статистически недостоверно, и эта независимая переменная может быть исключена из уравнения.

 

Порядок выполнения задания 3.1.5

Для выполнения следует воспользоваться процедурой  Регрессия.

Ввести в качестве входных параметров исходные данные  и по выданным коэффициентам  составить регрессионное уравнение.

 

4 Расчетно - графическая работа  №4. Методы графической обработки результатов экспериментальных исследований

 Теоретический материал по данной теме содержится в лекциях 11-12. Примеры выполнения заданий по теме рассматриваются на практических занятиях 10-11.

В результате изучения темы, учащиеся должны  уметь, используя процедуры Excel:  Линия тренда, Регрессия и Поиск решения – находить эмпирические формулы к исследуемым  экспериментальным данным.

4.1 Задания к работе

4.1.1 Задание. Аппроксимация и интерполяция экспериментальных данных с помощью процедуры Линия тренда

Исходные условия: в результате проведения эксперимента получена таблица  двух параметров X  и Y

Требуется: используя  процедуру Линия тренда, подобрать эмпирическую  формулу к экспериментальным  данным.

Варианты заданий приведены в таблице 4.1.

4.1.2 Задание. Аппроксимация и интерполяция экспериментальных данных с помощью процедуры Регрессия

Исходные условия: в результате проведения эксперимента получена таблица  двух параметров X  и Y

Требуется: используя  утилиту Регрессия из пакета анализа Excel, подобрать  интерполирующий полином к экспериментальным  данным.

Варианты заданий приведены в таблице 4.2.

 

4.1.3 Задание. Применение метода наименьших квадратов для нахождения эмпирических формул

Исходные условия: в результате проведения эксперимента получена таблица  двух параметров X  и Y.

Требуется: используя метод наименьших квадратов, подобрать эмпирическую формулу к экспериментальным данным.

Варианты заданий приведены в таблице 4.2.

4.2 Методические указания к работе

Методические указания к заданиям 4.1.1  и 4.1.2

Краткие теоретические сведения

К одной из  важных задач, встречающихся при обработке экспериментальных данных, относится задача нахождения по набору экспериментальных значений функции  в узловых точках аргумента  аналитической зависимости или, как еще ее часто  называют, эмпирической формулы. Обычно функция  ищется в таком виде, чтобы график, построенной на основании найденной функции,  проходил бы  через все узловые точки (т.е. ).

 Такая задача называется задачей интерполяции, а сама функция  - интерполяционной.

 Достаточно популярным для решения этой задачи является применение степенной функции, т.е. полинома имеющего порядок  степени равный количеству узловых точек минус единица. При выполнении этого условия функция будет проходить через все узловые точки. Если возможности (или необходимости) в том, чтобы функция проходила через все узловые точки, нет, функцию выбирают из условия минимальности отклонений от экспериментальных значений, исходя при этом из принимаемой погрешности и практических потребностей.

Но в этом случае говорят не о решении задачи интерполяции, а о решении задачи аппроксимации. А найденную функцию называют аппроксимирующей функцией.

Порядок выполнения заданий  4.1.1   и 4.1.2

Для выполнения задания 4.1.1 следует применить   процедуру  Линия тренда, для выполнения задания 4.1.2 утилиту  Регрессия из пакета анализа.

 Более подробно материал изложен в  [3].

Методические указания к заданию 4.1.3

Краткие теоретические сведения

На практике часто приходится сталкиваться с задачей  аппроксимации экспериментальных данных. Аппроксимацией называется процесс подбора эмпирической формулы   для установленной из опыта функ­циональной зависимости .

 Эмпирические формулы служат для аналити­ческого представления опытных данных.

Обычно задача аппроксимации распадается на две части.

1. Сначала устанавливают вид зависимости   и, соответственно, вид будущей  эмпирической формулы. Решают, является ли она линейной, квадратичной, логарифмической или какой-либо другой.

2. После  выбора вида формулы определяют ее параметры.

 Для наилучшего выбора параметров задают меру близости аппроксимации экспериментальных данных.

Обычно определение параметров при известном виде зависимости осуществляют по методу наименьших квадратов, предложенному  Гауссом.

 При этом функция  считается наилучшим приближением к f(х), если для нее сумма квадратов невязок δ, или отклонений «теоретических» значений , найденных по эмпирической формуле, от соответствующих  опытных зна­чений  имеет наименьшее значение:

      

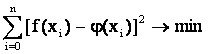
Как мы видим, данное выражение представляет собою  целевую функцию, а сама задача  является разновидностью задачи оптимизации,  поэтому  для ее решения можно  использовать надстройку Excel « Поиск решения».

Порядок выполнения заданий 4.1.3

 Для нахождения параметров эмпирической формулы   методом наименьших квадратов  необходимо применить процедуру « Поиск решения».

 

 

 

5 Таблицы исходных данных

Таблица 1.1 – Значения экспериментального ряда

Номер варианта

Значения 

1

5

8

11

13

16

19

21

24

27

29

2

6

7

9

10

11

12

13

14

15

16

3

7

8

9

10

11

12

13

14

15

17

4

7

9

11

12

14

15

17

19

20

22

5

8

11

14

18

21

24

27

30

34

37

6

9

11

13

15

17

19

21

24

26

28

7

4

6

9

11

13

15

17

19

21

24

8

3

4

6

7

9

11

12

14

15

17

9

4

8

12

15

19

23

27

30

34

38

0

5

7

10

13

15

18

21

24

26

29

 

Таблица 1.2 – Значения  вероятности появления   

Номер варианта

Значения 

1

0,32

0,37

0,43

0,48

0,53

0,05

0,08

0,11

0,13

0,16

2

0,32

0,37

0,43

0,48

0,53

0,05

0,08

0,11

0,13

0,16

3

0,21

0,24

0,27

0,29

0,32

0,05

0,11

0,16

0,21

0,27

4

0,05

0,27

0,48

0,69

0,91

0,11

0,19

0,27

0,35

0,43

5

0,21

0,27

0,32

0,37

0,43

0,11

0,21

0,32

0,43

0,53

6

0,27

0,32

0,37

0,43

0,48

0,11

0,20

0,30

0,40

0,49

7

0,21

0,32

0,43

0,53

0,64

0,21

0,32

0,43

0,53

0,64

8

0,16

0,27

0,37

0,48

0,59

0,05

0,09

0,12

0,15

0,18

9

0,13

0,19

0,25

0,31

0,37

0,13

0,19

0,25

0,30

0,36

0

0,19

0,25

0,32

0,38

0,44

0,06

0,14

0,21

0,29

0,36

 

Таблица 1.3 – Результаты замеров  электрических нагрузок 

 

Номер варианта

Номер опыта

1

2

3

4

5

6

7

8

9

0

1

64

65

176

176

170

176

57

156

160

153

2

62

64

174

176

193

176

58

158

159

158

3

65

72

178

175

175

175

58

156

161

169

4

68

63

174

185

169

175

57

156

159

160

5

67

68

179

168

181

174

60

159

159

158

6

68

65

179

170

179

176

59

158

159

156

7

61

65

177

172

190

176

60

158

157

161

8

65

61

176

175

172

175

57

161

160

158

9

67

64

175

179

184

176

58

156

151

159

10

63

64

175

174

174

174

58

155

161

156

11

64

66

176

171

171

174

58

159

160

156

12

62

63

176

177

176

176

59

157

157

157

13

61

65

177

174

168

177

59

161

159

154

14

63

63

173

169

166

175

59

157

155

157

15

63

63

174

181

176

175

58

159

157

152

16

61

64

178

175

166

174

59

162

157

162

17

64

66

173

173

167

177

59

158

159

167

18

64

71

177

175

178

176

59

154

164

154

19

65

68

176

173

185

175

60

160

166

156

20

64

70

181

176

185

174

60

158

161

160

21

64

59

176

174

162

174

60

161

158

154

22

64

62

175

180

174

176

60

160

160

160

23

68

65

176

164

193

174

59

159

160

153

24

65

62

175

177

180

175

59

158

161

158

25

65

66

173

175

168

174

61

156

158

171

26

64

62

176

173

166

173

58

159

155

154

27

69

67

170

166

185

178

60

159

155

154

28

67

74

178

175

184

175

57

157

154

150

29

70

61

171

181

167

175

59

159

159

158

30

64

60

175

182

164

174

59

162

161

163

 

Таблица 2.1 – Исходные данные к заданию 2.1

Номер варианта

 Число изделий в выборке,  шт.

Стандартное отклонение s, часов

Средняя продолжительность работы  изделия t, часов

Всего изделий в партии, тыс. шт.

1

100

40

1500

5

2

200

50

1400

7

3

150

30

1300

10

4

300

50

1450

6

5

200

40

1300

5,4

6

100

60

1400

4,8

7

200

50

1500

2,5

8

100

40

1300

3,8

9

250

55

1200

4,2

0

400

65

1100

5,1

 

 

 

 

 

 

 

 

 

 

Таблица 2.2 – Исходные данные к заданию 2.2

Номер варианта

Число опытов n

Стандартное отклонение s, А

Погрешность прибора  ∆ , А

1

35

0,4

0,1

2

24

0,5

0,2

3

48

0,3

0,1

4

52

0,5

0,2

5

60

0,15

0,1

6

75

0,25

0,2

7

84

0,3

0,1

8

75

0,4

0,2

9

80

0,28

0,15

0

25

0,31

0,25

 

 

 

 

 

 

 

 

Таблица 2.3 – Исходные данные к заданию 2.3

 

Номер варианта

Номер опыта

1

2

3

4

5

6

7

8

9

0

1

67

67

67

67

67

67

67

67

67

67

2

67

67

67

67

67

67

67

67

67

67

3

68

65

68

68

68

68

68

68

68

68

4

68

68

68

68

68

68

68

68

68

68

5

69

69

69

69

69

69

69

69

69

69

6

70

70

70

70

70

70

70

70

70

70

7

71

72

77

76

74

79

56

72

63

71

8

73

73

73

73

73

73

73

73

73

73

9

74

74

74

74

74

74

74

74

74

74

10

75

75

75

75

75

75

75

75

75

75

11

76

76

76

76

76

76

76

76

76

76

12

77

77

77

77

77

77

77

77

77

77

13

78

78

78

78

78

78

78

78

78

78

14

79

79

79

79

79

79

79

79

79

79

15

80

80

80

80

80

80

80

80

80

80

16

81

81

81

81

81

81

81

81

81

81

17

82

82

82

82

82

82

82

82

82

82

18

92

92

92

92

92

92

92

92

92

92

 

Таблица 2.4 – Исходные данные к заданию 2.4

Номер варианта

Среднее арифметическое до испытания изделия

Среднее арифметическое после испытания изделия

Предельная ошибка измерения до испытания изделия

Предельная ошибка измерения после испытания изделия

1

21

20,8

5

6

2

10,6

12

2,1

0,6

3

38,1

45,7

3,0

2,3

4

24,8

99,1

5,0

1,5

5

48,5

58,2

2,0

2,9

6

5,7

22,9

1,1

0,3

7

23,5

94

4,7

1,4

8

32,3

38,8

2,0

1,9

9

45,1

54,1

1,5

2,7

0

17,5

69,8

3,5

1,0

 

 

 

 

 

 

 

 

 

 

Таблица 2.5-  Исходные данные к заданию 2.5

Для вариантов 0-3

№ серии опытов

Результаты измерения тока в цепи,   А

1

2

3

4

5

1

2,5

1,2

2,0

1,0

2,2

2

4,9

2,5

3,9

2,0

4,4

3

7,4

3,7

5,9

3,0

6,7

4

9,9

4,9

7,9

3,9

123,3

 

 

 

 

Для вариантов 4 -7

№ серии опытов

Результаты измерения тока в цепи,   А

1

2

3

4

5

1

2,1

1,0

1,6

0,8

1,9

2

4,1

2,1

3,3

1,6

3,7

3

6,2

3,1

4,9

2,5

5,6

4

8,2

4,1

6,6

3,3

102,8

 

 

 

 

Для вариантов 8 – 9

№ серии опытов

Результаты измерения тока в цепи,   А

1

2

3

4

5

1

3,5

1,8

2,8

1,4

3,2

2

7,1

3,5

5,7

2,8

6,4

3

10,6

5,3

8,5

4,3

9,6

4

14,2

7,1

11,3

5,7

12,8

        

 

 

 

Таблица 3.1 – Исходные данные к заданию 3.1

 

Номер варианта

Номер опыта

1

2

3

4

5

6

7

8

9

0

1

64

65

176

176

170

176

57

156

160

153

2

62

64

174

176

193

176

58

158

159

158

3

65

72

178

175

175

175

58

156

161

169

4

68

63

174

185

169

175

57

156

159

160

5

67

68

179

168

181

174

60

159

159

158

6

68

65

179

170

179

176

59

158

159

156

7

61

65

177

172

190

176

60

158

157

161

8

65

61

176

175

172

175

57

161

160

158

9

67

64

175

179

184

176

58

156

151

159

10

63

64

175

174

174

174

58

155

161

156

11

64

66

176

171

171

174

58

159

160

156

12

62

63

176

177

176

176

59

157

157

157

13

61

65

177

174

168

177

59

161

159

154

14

63

63

173

169

166

175

59

157

155

157

15

63

63

174

181

176

175

58

159

157

152

16

61

64

178

175

166

174

59

162

157

162

17

64

66

173

173

167

177

59

158

159

167

18

64

71

177

175

178

176

59

154

164

154

19

65

68

176

173

185

175

60

160

166

156

20

64

70

181

176

185

174

60

158

161

160

21

64

59

176

174

162

174

60

161

158

154

22

64

62

175

180

174

176

60

160

160

160

23

68

65

176

164

193

174

59

159

160

153

24

65

62

175

177

180

175

59

158

161

158

25

65

66

173

175

168

174

61

156

158

171

26

64

62

176

173

166

173

58

159

155

154

27

69

67

170

166

185

178

60

159

155

154

28

67

74

178

175

184

175

57

157

154

150

29

70

61

171

181

167

175

59

159

159

158

30

64

60

175

182

164

174

59

162

161

163

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Таблица 3.2 – Исходные данные к заданию 3.2

Номер варианта 0-3

Данные о продажах электрооборудования до  проведения рекламной компании

Данные о продажах электрооборудования после   проведения рекламной компании

83

85

81

87

79

86

81

85

86

89

82

87

 

Номер варианта 4-7

Данные о продажах электрооборудования до  проведения рекламной компании

Данные о продажах электрооборудования после   проведения рекламной компании

60

61

58

63

56

62

58

61

62

64

59

62

Номер варианта 8-9

Данные о продажах электрооборудования до  проведения рекламной компании

Данные о продажах электрооборудования после   проведения рекламной компании

90

92

88

95

85

93

87

92

93

97

89

94

 

Таблица 3.3 – Исходные данные к заданию 3.3

Номер варианта 0-3

Образование

Зарплата

Магистратура

229196

214872

186222

143248

136085

136085

Бакалавриат

186222

143248

143248

136085

128923

121761

Колледж

143248

136085

136085

128923

121761

121761

 

Номер варианта 4-7

Образование

Зарплата

Магистратура

239021

224083

194205

149388

141919

141919

Бакалавриат

194205

149388

149388

141919

134450

126980

Колледж

149388

141919

141919

134450

126980

126980

 

Номер варианта 8-9

Образование

Зарплата

Магистратура

136968

128408

111287

85605

81325

81325

Бакалавриат

111287

85605

85605

81325

77045

72764

Колледж

85605

81325

81325

77045

72764

72764

 

Таблица 3.4 – Исходные данные к заданию 3.4

Номер варианта 0-3

№

Количество грозовых дней

Количество аварий

1

120

20

2

121

15

3

105

18

4

92

16

5

113

19

6

90

16

7

80

15

 

 

Номер варианта 4-7

№

Количество грозовых дней

Количество аварий

1

200

20

2

121

15

3

30

5

4

92

16

5

150

19

6

90

16

7

80

15

 

Номер варианта 8-9

№

Количество грозовых дней

Количество аварий

1

5

2

2

121

15

3

105

18

4

40

16

5

113

19

6

30

16

7

80

15

 

 

 

 

 

 

Таблица 4.1  – Исходные данные к заданию 4.1

Xi

Значения Yi  по  вариантам

1

2

3

4

5

6

7

8

9

0

0,5

1,2

10,2

10,1

1,7

6,4

0,4

0,2

9,9

9,6

0,4

1,0

2,4

10,4

10,2

3,2

6,7

1,0

0,4

9,8

9,7

0,9

2,0

4,0

10,5

10,5

5,8

7,4

2,2

0,9

9,5

9,4

1,7

3,0

6,0

11,0

10,7

7,7

8,1

3,3

1,5

9,4

9,0

2,4

4,0

8,0

11,5

11,1

9,3

8,8

4,5

2,1

9,1

8,5

3,0

5,0

10,0

12,1

11,5

10,5

9,5

5,8

2,7

7,9

8,2

3,4

6,0

12,0

12,9

11,7

11,7

10,2

6,7

3,3

6,1

8,2

3,8

7,0

15,0

13,9

12,5

12,0

10,9

5,4

4,0

7,4

8,3

4,0

8,0

12,0

15,2

14,0

16,0

11,6

4,3

4,7

8,4

8,5

3,5

9,0

7,0

17,0

11,7

15,4

13,0

2,3

6,1

7,6

8,7

3,3

 

 

 

 

 

 

 

 

Таблица 4.2 – Исходные данные к заданию 4.2-4.3

Xi

Значения Yi  по  вариантам

1

2

3

4

5

6

7

8

9

0

0

0

0

0

0

0

0

0

0

0

0

0,15

0,16

0,16

0,16

0,16

0,2

0,16

0,18

0,15

0,12

0,165

0,31

0,33

0,4

0,38

0,5

0,6

0,4

0,33

0,33

0,33

0,33

0,46

0,42

0,42

0,42

0,42

0,4

0,38

0,39

0,41

0,42

0,42

 

 

 

 

 

0,61

0,59

0,59

0,59

0,59

0,59

0,59

0,59

0,59

0,59

0,59

0,77

0,72

0,72

0,72

0,72

0,72

0,72

0,72

0,72

0,72

0,72

0,92

0,75

0,75

0,68

0,7

0,74

0,71

0,73

0,65

0,75

0,75

1,01

0,88

0,88

0,88

0,88

0,88

0,88

0,88

0,88

0,88

0,88

1,16

0,95

0,95

0,94

0,95

0,96

0,95

0,95

0,98

0,97

0,92

1,32

0,96

0,94

0,96

0,92

0,93

0,99

0,93

0,96

0,93

0,96

1,47

0,99

1,2

0,99

0,99

0,99

0,99

0,99

0,99

0,99

0,99

 

 

 

 

 

 

  

 

Список литературы

Основная

1. Фадеев В.Б. Теория и практика технического эксперимента в электроэнергетике. Конспект лекций.- Алматы: АУЭС, 2010.  -52 с.

2. Фадеев В.Б. Теория и практика технического эксперимента в электроэнергетике. Методические указания  и задания к практическим работам 1-6.-  Алматы. АУЭС, 2010.-46с. Электронная версия.

3. Фадеев В.Б. Теория и практика технического эксперимента в электроэнергетике. Методические указания  и задания к практическим работам 7-12.-  Алматы. АУЭС, 2010.-52с. Электронная версия.

Дополнительная  

4. Тюрин Ю.Н., Макаров А.А. Анализ данных на компьютере.- М.: Финансы и статистика.- Инфра – М, 1995.

5. Макарова Н.В., Трофимец В.Я. Статистика в Excel. –М.: Финансы и статистика, 2002.

6. Решение математических задач средствами Excel: Практикум /В.Я. Гельман.- СПб.: Питер, 2003.

7. Айвазян С.А., Мхитарян В.С. Теория вероятности и прикладная статистика. Т.1: Учебник для вузов. - М.: ЮНИТИ, 2001.

8. Елисеева И.И., Юзбашев М.М. Общая теория статистики.- М.: Финансы и статистика, 2004.

9. Романовский В.И. Основные задачи теории ошибок.  Гостехиздат, М. – Л., 1947.

10.Яковлев К.П. Математическая обработка результатов измерений.- М - Л., Гостехиздат, 1950.

11.Гутер Р.С. Овчинский Б.В. Элементы численного анализа и математической обработки результатов опыта. - М.: Физматгиз, 1962.

12.Щеголев Б.М. Математическая обработка наблюдений.- М.: Физматгиз, 1962.

13.Гончаров А. Excel 97  в примерах – СПб.:Питер, 1997.

14.Васильев А.Н. Научные вычисления в Microsoft Excel. –М.:Издательский дом «Вильямс», 2004.