Некоммерческое акционерное общество
АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра электроснабжения промышленных предприятий
ТЕОРИЯ И ПРАКТИКА ТЕХНИЧЕСКОГО ЭКСПЕРИМЕНТА
В ЭЛЕКТРОЭНЕРГЕТИКЕ
Методические указания к выполнению лабораторных работ
(для специальности 6М071800-Электроэнергетика)
Алматы 2012
СОСТАВИТЕЛЬ: Н.Н. Арыстанов, К.М. Асанова. Теория и практика технического эксперимента в электроэнергетике. Методические указания к выполнению лабораторных работ (для специальности 6М071800 - Электроэнергетика). – Алматы: АУЭС, 2012. - 15 с.
Методические указания соответствуют курсу «Теория и практика технического эксперимента в электроэнергетике», включают задание на выполнение лабораторных работ, исходные данные, указания и перечень рекомендуемой литературы.
Ил. 1 , табл. 10, библиогр. - 3 назв.
Рецензент: канд.техн.наук, доц. С.А.Бугубаев
Печатается по плану издания некоммерческого акционерного общества «Алматинский университет энергетики и связи» на 2012 год.
© НАО «Алматинский университет энергетики и связи», 2012 г.
Содержание
|
1 |
Лабораторная работа №1. «Определение условного центра электрических нагрузок» |
4 |
|
2 |
Лабораторная работа №2. «Определение потери мощности и энергии в двухобмоточных трансформаторах» |
6 |
|
3 |
Лабораторная работа №3. «Статический анализ результатов экспериментальных исследований» |
8 |
|
4 |
Лабораторная работа №4. «Применение Excel для аппроксимации данных однофакторного эксперимента» |
12 |
|
5 |
Лабораторная работа №5. «Расчет мощности батарей конденсаторов для компенсации реактивной мощности в узле нагрузки» |
14 |
|
Список литературы |
15 |
|
1 Лабораторная работа № 1. Определение условного центра электрических нагрузок
Цель работы: освоить методику выбора размещения подстанции ГПП с помощью расчета центра электрических нагрузок.
1.1 Краткие теоретические сведения
Проектирование систем электроснабжения (СЭС) промышленных предприятий осуществляется на основе генерального плана, на который наносятся все цеха и участки, которые получают питание от ГПП предприятия.
ГПП является основным звеном СЭС любого предприятия. Поэтому правильное расположение ее на территории предприятия является основой рационального построения схемы распределения электроэнергии на предприятии.
При выборе местоположения подстанции руководствуются положениями курса теоретической механики о нахождении центра тяжести фигуры.
Проводя аналогию между массами и электрическими нагрузками цехов, координаты центра электрических нагрузок предприятия определяют по следующим формулам:
 ,
, 
где Xi, Yi – координаты цехов, совпадающих с их геометрическим центром;
Pi, Qi – электрические нагрузки цехов;
n – количество цехов на предприятии.
Данный метод позволяет определить ЦЭН как некоторую постоянную точку на генеральном плане. Однако в виду того, что нагрузки цехов в реальности меняются, не будет постоянным и ЦЭН. Поэтому найденный центр рассматривают как условный.
1.2 Задание
Используя данные, приведенные в таблице 1.1, и программу Excel найти ЦЭН предприятия в соответствии со своим вариантом.
Т а б л и ц а 1.1 – Исходные данные
|
№ варианта |
№ цеха |
Координата X, м |
Координата Y, м |
Нагрузка цеха P, кВт |
|
1 |
2 |
3 |
4 |
5 |
|
1 |
1 |
23 |
140 |
3050 |
|
2 |
69 |
18 |
960 |
|
|
3 |
135 |
20 |
2100 |
|
|
4 |
30 |
71 |
450 |
|
|
5 |
88 |
165 |
760 |
|
|
2 |
1 |
730 |
25 |
880 |
|
2 |
611 |
117 |
420 |
|
|
3 |
298 |
380 |
655 |
|
|
4 |
0 |
325 |
1290 |
|
|
3 |
1 |
23 |
140 |
3050 |
|
2 |
69 |
18 |
960 |
|
|
3 |
135 |
20 |
2100 |
|
|
4 |
30 |
71 |
450 |
|
|
5 |
88 |
165 |
760 |
|
|
4 |
1 |
190 |
20 |
1480 |
|
2 |
515 |
0 |
5470 |
|
|
3 |
30 |
401 |
4480 |
|
|
4 |
70 |
631 |
58 |
|
|
5 |
12 |
82 |
1627 |
|
|
5 |
1 |
730 |
235 |
850 |
|
2 |
411 |
17 |
1120 |
|
|
3 |
258 |
381 |
6655 |
|
|
4 |
10 |
355 |
120 |
|
|
5 |
404 |
105 |
700 |
|
|
6 |
1 |
412 |
380 |
1749 |
|
2 |
561 |
345 |
95 |
|
|
3 |
28 |
8 |
123 |
|
|
4 |
143 |
96 |
2380 |
|
|
5 |
160 |
190 |
2421 |
|
|
7 |
1 |
240 |
145 |
1540 |
|
2 |
0 |
40 |
4120 |
|
|
3 |
615 |
550 |
2380 |
|
|
4 |
235 |
279 |
250 |
|
|
5 |
84 |
160 |
610 |
|
|
8 |
1 |
60 |
35 |
2300 |
|
2 |
310 |
4 |
3220 |
|
|
3 |
235 |
10 |
2110 |
|
|
4 |
211 |
71 |
3250 |
|
|
5 |
32 |
610 |
4210 |
|
|
9 |
1 |
430 |
345 |
3050 |
|
2 |
65 |
260 |
4820 |
|
|
3 |
43 |
65 |
480 |
|
|
4 |
23 |
46 |
1450 |
|
|
5 |
543 |
260 |
2310 |
|
|
0 |
1 |
630 |
45 |
2050 |
|
2 |
25 |
26 |
820 |
|
|
3 |
413 |
115 |
380 |
|
|
4 |
243 |
326 |
170 |
|
|
5 |
53 |
160 |
210 |
2 Лабораторная работа № 2. Определение потери мощности и энергии в двухобмоточных трансформаторах
Цель работы: изучить метод расчета потери мощности и энергии в двухобмоточных трансформаторах
2.1 Краткие теоретические сведения
Потери в трансформаторе разделяются на электрические и магнитные.
Электрические потери обусловлены нагревом обмоток трансформатора при прохождении по ним электрического тока.
Магнитные потери происходят в магнитопроводе трансформатора. Вследствие чего он и нагревается. Магнитные потери обусловлены потерями на гистерезис и вихревые токи.
Поскольку магнитные потери зависят от напряжения, а электрические от тока, то электрические потери называют переменными, а магнитные постоянными.
Для определения потерь мощности в трансформаторе используют его паспортные данные.
Необходимые данные определяются из двух опытов: опыта холостого хода и короткого замыкания.
Потери активной мощности в трансформаторе определяются по формуле:
![]() ,
,
где ![]() , кВт – потери
холостого хода (паспортные данные);
, кВт – потери
холостого хода (паспортные данные);
![]() , кВт – потери
короткого замыкания при номинальной нагрузке (паспортные данные);
, кВт – потери
короткого замыкания при номинальной нагрузке (паспортные данные);
n – количество трансформаторов равной мощности;
β - коэффициент нагрузки.
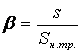 ,
,
где s - текущая электрическая нагрузка, изменяющаяся согласно заданному шагу;
Sн.тр - номинальная мощность трансформатора (паспортные данные).
Потери реактивной мощности в трансформаторе определяются по формуле:
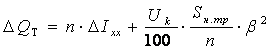 ,
,
где ![]() - ток холостого хода в %
(паспортные данные);
- ток холостого хода в %
(паспортные данные);
Uk - напряжение короткого замыкания в % (паспортные данные).
Годовые потери активной и реактивной энергии:
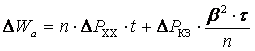 ,
, 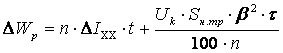
где t- число часов работы трансформатора;
τ - время наибольших потерь.τ зависит от T max – времени использования максимума нагрузки:
![]()
Принять условно T max=5000 ч.
2.2 Задание
В соответствии с вариантом задания, используя программу Excel, рассчитать потери трансформаторов.
Расчет провести для двух вариантов работы трансформаторной подстанции: одиночная работа трансформатора и параллельная работа. Построить графики зависимости потерь от коэффициента нагрузки.
Варианты задания выбираются из таблицы 2.1. Паспортные данные некоторых типов трансформаторов приведены в таблице 2.2.
Таблица 2.1 - Варианты задания исходных данных
|
№ варианта |
Тип трансформатора |
t, ч. |
Коэффициент нагрузки
|
|
1 |
ТМ- 630/10 |
8760 |
0 – 1,3 |
|
2 |
ТМ -1000/10 |
8000 |
0 – 1,3 |
|
3 |
ТМ-1600/10 |
8700 |
0 – 1,3 |
|
4 |
ТМ-2500/10 |
7200 |
0 – 1,3 |
|
5 |
ТМ-1000/10 |
8700 |
0 – 1,3 |
|
6 |
ТМ-630/10 |
8000 |
0 – 1,3 |
|
7 |
ТМ-6300/10 |
6300 |
0 – 1,3 |
|
8 |
ТМ-4000/10 |
7000 |
0 – 1,3 |
|
9 |
ТМ-6300/10 |
5000 |
0 – 1,3 |
|
0 |
ТМ-1600/10 |
8000 |
0 – 1,3 |
Таблица 2.2 - Паспортные данные некоторых типов трансформаторов
|
Тип трансформатора |
Sнт, кВА |
Px, кВт |
Pk, кВт |
Uk, % |
Ix, % |
|
ТМ- 630/10 |
630 |
2,27 |
7,6 |
5,5 |
2 |
|
ТМ -1000/10 |
1000 |
3,3 |
11,6 |
5,5 |
1,4 |
|
ТМ-1600/10 |
1600 |
4,5 |
16,5 |
5,5 |
1,3 |
|
ТМ-2500/10 |
2500 |
6,2 |
23,5 |
5,5 |
1,0 |
|
ТМ-4000/10 |
4000 |
6,45 |
33,5 |
5,5 |
0,9 |
|
ТМ-6300/10 |
6300 |
7,65 |
46,5 |
5,5 |
0,8 |
3 Лабораторная работа № 3. Статический анализ результатов экспериментальных исследований
Цель работы: изучить статический анализ и методику расчета вероятности отклонения напряжения.
3.1 Краткие теоретические сведения
Из теории вероятности известно, что для математического описания случайных процессов необходимо иметь большое количество статистической информации по изучаемому явлению. Однако при большом числе наблюдений простая статистическая совокупность перестает быть удобной формой записи статистического материала, так как становится громоздкой и не наглядной. Для придания большому объему статистической информации компактности и наглядности строится так называемый статистический ряд. Статистический ряд – это таблица, в которой приведены разряды в порядке их расположения вдоль оси абсцисс и соответствующие частоты попадания случайной величины в данный ряд (см.таблицу 3.1).
Таблица 3.1
|
Разряды |
X1, X2 |
X2, X3 |
… |
Xk, X k+1 |
|
Частоты |
P1 |
P2 |
… |
Pk |
Частоты определяются по формуле:
P= Mi/n,
где Mi - количество значений случайной величины, попадающих в i-ый разряд;
n - общее число наблюдений случайной величины.
Число разрядов, на которые следует группировать статистическую информацию, не должно быть слишком большим, так как в этом случае ряд становится невыразительным и в нем трудно проследить закономерность. С другой стороны число разрядов не должно быть маленьким, так как при этом свойства распределения случайной величины описываются слишком грубо. Практика показывает, что рационально выбирать число разрядов от 8 до 20.
Длины разрядов могут быть как одинаковыми, так и различными, однако чаще их берут одинаковыми.
Статистический ряд часто оформляется графически в виде гистограммы, что придает ему большую наглядность и удобство применения.
Гистограмма - это графическое приближенное представление плотности распределения вероятностей случайной величины, построенное по выборке конечного объема.
Она строится следующим образом. По оси абсцисс откладываются разряды, и на каждом из разрядов на их основании строится прямоугольник, площадь которого равна частоте данного разряда. Для построения диаграммы нужно частоту каждого разряда разделить на его длину и полученное число взять в качестве высоты прямоугольника. Если все разряды по длине равны, то высоты прямоугольников пропорциональны соответствующим частотам. Полная площадь гистограммы равна единице, что вытекает из способа ее построения.
Рассмотрим методику построения гистограммы на примере обработки данных отклонений напряжения.
Отклонение напряжения – это величина, равная разности между действительным и заданным значениями напряжения, выраженная в абсолютных единицах или в процентах номинального значения. Отклонение напряжения является одним из показателей качества электроэнергии и регламентируется «Нормами качества электрической энергии в системах электроснабжения общего назначения». Согласно этим нормам нормально-допустимое отклонение напряжения в сетях до 1 КВ не должно превышать ±5%, а максимально допустимое (послеаварийном режиме работы электрической сети) не более ±10%.
Для контроля соответствия действительного напряжения в сети существующим нормам применяются гистограммы отклонений напряжения.
Гистограмма отклонений напряжения – это зависимость вероятности попадания значений напряжения в определенный интервал. Их получают с помощью специальных приборов таких, как статистический анализатор качества напряжения (САКН), измеритель отклонений напряжения 43203, измерительно-вычислительный комплекс «Качество». Гистограммы отклонений напряжения позволяют обслуживающему персоналу принимать решения организационно-технического характера с целью приведения режима напряжения в сети в соответствие с принятыми нормами (например, регулирование напряжения в конкретных узлах схемы, установка стабилизаторов, конденсаторов, изменения в схеме и т.д.).
Методику построения гистограмм отклонений напряжения рассмотрим на примере замеров, полученных прибором САКН. Он имеет восемь разрядов, каждому из которых соответствует счетчик импульсов, который фиксирует и на длительное время запоминает число попаданий отклонений напряжения в тот или иной диапазон за весь период измерений. В результате измерений получаем статистический ряд (см.таблица 3.2).
Таблица 3.2
|
Разряды |
V1 |
V2 |
… |
V8 |
|
Замер 1 |
n1 |
n2 |
… |
n8 |
|
Замер 2 |
m1 |
m2 |
… |
m8 |
Число попаданий отклонений напряжения в i–ый интервал определяется как:
Mi = |(mi – ni)| .
Вероятность попадания отклонения напряжения в интервал определяем следующим образом:
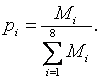
В результате для построения гистограммы получаем таблицу 3.3.
Таблица 3.3
|
Разряды |
V1 |
V2 |
… |
V8 |
|
Вероятность |
p1 |
p2 |
… |
p8 |
Определим диапазон нахождения напряжения сети для данного участка сети с доверительной вероятностью 0,683.
Для этого:
1) Вычислим значения напряжения для каждого разряда по формуле:
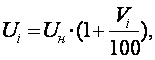
где Uн – номинальное напряжение сети, примем равной 220 В.
2) Вычислим среднее арифметическое напряжения сети по формуле:
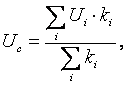
где ki=ni+mi - суммарное количество случайной величины (напряжения сети), попадающих в i–ый разряд, получаемых из замеров 1 и 2.
3) Вычислим отклонение напряжение от среднего для каждого разряда:
![]()
4) Вычислим дисперсию напряжения сети:
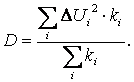
5) Вычислим среднее квадратичное отклонение напряжения:
![]()
6) Вычислим нижнее значение диапазона появления напряжения сети для доверительной вероятности 0,683
![]()
7) Вычислим верхнее значение диапазона появления напряжения сети для доверительной вероятности 0,683
![]()
8) Делаем вывод: с доверительной вероятностью 0,683, т.е. из 1000 выполненных замеров в 683 случаях напряжение сети будет находиться в диапазоне Umin ¸ Umax.
3.2 Задание
Используя данные, приведенные в таблицах 3.4, 3.5 и программу Excel в соответствии со своим вариантом, выполнить необходимые вычисления, определить диапазон напряжения сети для доверительной вероятности 0,683 и построить гистограмму.
Таблица 3.4 - Число попаданий отклонений напряжения по разрядам прибора
|
№ Вар. |
Показания счетчиков |
||||||||
|
№ замера |
1 разряд |
2 разряд |
3 разряд |
4 разряд |
5 разряд |
6 разряд |
7 разряд |
8 разряд |
|
|
1 |
Замер 1 |
9986 |
1765 |
0898 |
0957 |
3868 |
0369 |
5998 |
7820 |
|
Замер 2 |
9986 |
3063 |
2643 |
2047 |
5395 |
1224 |
8686 |
7930 |
|
|
2 |
Замер 1 |
5078 |
1690 |
0628 |
5051 |
5294 |
2042 |
8919 |
5313 |
|
Замер 2 |
5083 |
1974 |
0874 |
5778 |
5638 |
2237 |
8919 |
5313 |
|
|
3 |
Замер 1 |
5083 |
1974 |
0874 |
5778 |
5638 |
2237 |
8919 |
5313 |
|
Замер 2 |
5084 |
2076 |
1233 |
6654 |
6957 |
2632 |
8919 |
7669 |
|
|
4 |
Замер 1 |
9986 |
1101 |
2373 |
5435 |
7346 |
6771 |
3344 |
7669 |
|
Замер 2 |
9986 |
1651 |
2543 |
5866 |
8272 |
7441 |
3510 |
3790 |
|
|
5 |
Замер 1 |
0635 |
0147 |
0152 |
1314 |
2371 |
2101 |
3294 |
3790 |
|
Замер 2 |
0637 |
0246 |
1907 |
9391 |
3742 |
4077 |
3391 |
7569 |
|
|
6 |
Замер 1 |
9980 |
0967 |
2194 |
5000 |
7067 |
6714 |
3344 |
7569 |
|
Замер 2 |
9980 |
1101 |
2373 |
5435 |
7346 |
6771 |
3344 |
9790 |
|
|
7 |
Замер 1 |
0635 |
0147 |
0152 |
9361 |
2371 |
2101 |
3294 |
9976 |
|
Замер 2 |
0635 |
0153 |
0776 |
9552 |
3450 |
2950 |
3754 |
5313 |
|
|
8 |
Замер 1 |
5083 |
1974 |
1874 |
5778 |
5638 |
2237 |
8919 |
5313 |
|
Замер 2 |
5086 |
2331 |
2744 |
7784 |
8499 |
4082 |
8929 |
5313 |
|
|
9 |
Замер 1 |
5078 |
1690 |
0628 |
5051 |
5294 |
2042 |
8919 |
5313 |
|
Замер 2 |
5083 |
1974 |
0874 |
5778 |
5638 |
2237 |
8919 |
7569 |
|
|
0 |
Замер 1 |
9980 |
0967 |
2194 |
5000 |
7067 |
6714 |
3344 |
7569 |
|
Замер 2 |
9980 |
1101 |
2373 |
5435 |
7346 |
6771 |
3344 |
7569 |
|
Таблица 3.5 - Отклонения напряжений по разрядам прибора
|
№ Вар. |
Разряды |
|||||||
|
1 разряд |
2 разряд |
3 разряд |
4 разряд |
5 разряд |
6 разряд |
7 разряд |
8 разряд |
|
|
1 |
-4,5 |
-3,75 |
-2,5 |
-1,25 |
1,25 |
2,5 |
3,75 |
4,5 |
|
2 |
-10 |
-7,5 |
-5,0 |
-2,5 |
2,5 |
5,0 |
7,5 |
10 |
|
3 |
-4,0 |
-3,0 |
-2,0 |
-1,0 |
1,0 |
2,0 |
3,0 |
4,0 |
|
4 |
-2,0 |
-1,5 |
-11,0 |
-0,5 |
0,5 |
1,0 |
1,5 |
2,0 |
|
5 |
-1,5 |
-11,25 |
-7,5 |
-3,75 |
3,75 |
7,5 |
11,25 |
15,0 |
|
6 |
-1,0 |
-0,75 |
-0,5 |
-0,25 |
0,25 |
0,5 |
0,75 |
1,0 |
|
7 |
-8,0 |
-6,0 |
-4,0 |
-2,0 |
2,0 |
4,0 |
6,0 |
8,0 |
|
8 |
-4,8 |
-3,6 |
-2,4 |
-1,2 |
1,2 |
2,4 |
3,6 |
4,8 |
|
9 |
-15 |
-11,25 |
-7,5 |
3,75 |
3,75 |
7,5 |
11,25 |
15 |
|
0 |
-4,5 |
-3,75 |
-2,5 |
-1,25 |
2,5 |
2,5 |
3,75 |
4,5 |
4 Лабораторная работа № 4. Применение Excel для аппроксимации данных однофакторного эксперимента
Цель работы: освоить методы аппроксимации данных однофакторного эксперимента.
4.1 Краткие теоретические сведения
При решении многих инженерных задач часто возникает необходимость в представлении экспериментальных данных, выраженных в табличной форме в форме аналитических выражений, например, в виде полинома:

Замена табличного представления функции формулой позволяет автоматизировать процесс расчета и находить точки экстремума.
Нахождение аргумента, при котором функция имеет минимальное значение, важно при проектировании, например, при проведении технико-экономических расчетов различных вариантов решения инженерной задачи.
4.2 Задание
В соответствии с вариантом задания, приведенным в таблице 4.1, используя программу Excel, для различных степеней полинома исследовать процесс приближения функции F(x), определяемой с помощью полинома к экспериментальной функции Y(x), заданной в задании.
4.3 Порядок выполнения работы
С помощью мастера диаграмм построить график Y(x) по данным варианта.
Используя контекстное меню и добавить линию тренда.
Выбрать тип полиномиальный, степень 1., т.е. задать полином вида:
![]() .
.
В параметрах установить флажок, в меню показать уравнение на диаграмме.
По найденным коэффициентам b вычислить значение величины среднего квадратичного отклонения по формуле:
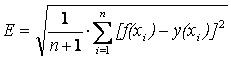 ,
,
где f (x)- расчетное значение аппроксимирующего полинома;
Y(x) - экспериментальное значение функции.
Полученное значение E сравнивается со средней погрешностью табличных значений Y(x), которая определяется по формуле:
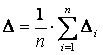 ,
,
где Δi - абсолютная погрешность результата измерения Y(xi),
![]() ,
,
где di = (2,5-5) % - относительная погрешность результата измерения Y (xi).
В технико-экономических задачах электроснабжения считают аппроксимацию достаточно хорошей, если среднеквадратичная погрешность не превышает 10% среднего арифметического табличных значений эмпирической функции.
Если окажется, что E >Δ, то увеличиваем степень полинома и проводим новый расчет, и так далее до нахождения оптимального варианта.
Оптимальный вариант: наибольшая точность при наименьшей степени полинома.
Таблица 4.1 - Исходные данные
|
Xi |
Значения Yi по вариантам |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
|
|
0,5 |
1,2 |
10,2 |
10,1 |
1,7 |
6,4 |
0,4 |
0,2 |
9,9 |
9,6 |
0,4 |
|
1,0 |
2,4 |
10,4 |
10,2 |
3,2 |
6,7 |
1,0 |
0,4 |
9,8 |
9,7 |
0,9 |
|
2,0 |
4,0 |
10,5 |
10,5 |
5,8 |
7,4 |
2,2 |
0,9 |
9,5 |
9,4 |
1,7 |
|
3,0 |
6,0 |
11,0 |
10,7 |
7,7 |
8,1 |
3,3 |
1,5 |
9,4 |
9,0 |
2,4 |
|
4,0 |
8,0 |
11,5 |
11,1 |
9,3 |
8,8 |
4,5 |
2,1 |
9,1 |
8,5 |
3,0 |
|
5,0 |
10,0 |
12,1 |
11,5 |
10,5 |
9,5 |
5,8 |
2,7 |
7,9 |
8,2 |
3,4 |
|
6,0 |
12,0 |
12,9 |
11,7 |
11,7 |
10,2 |
6,7 |
3,3 |
6,1 |
8,2 |
3,8 |
|
7,0 |
15,0 |
13,9 |
12,5 |
12,0 |
10,9 |
5,4 |
4,0 |
7,4 |
8,3 |
4,0 |
|
8,0 |
12,0 |
15,2 |
14,0 |
16,0 |
11,6 |
4,3 |
4,7 |
8,4 |
8,5 |
3,5 |
|
9,0 |
7,0 |
17,0 |
11,7 |
15,4 |
13,0 |
2,3 |
6,1 |
7,6 |
8,7 |
3,3 |
5 Лабораторная работа № 5. Расчет мощности батарей конденсаторов для компенсации реактивной мощности в узле нагрузки
Цель работы: изучить метод расчета и выбор компенсации реактивной мощности в узле нагрузки БК.
5.1 Исходные данные
Узел нагрузки изображен на рисунке 5.1.
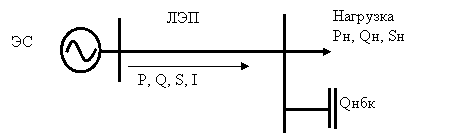
Рисунок 5.1
До компенсации реактивной мощности тангенс угла коэффициента мощности был tgj1.
Требуется определить мощность конденсаторных батарей, установленных в узле нагрузки ТП.
Мощность батареи должна обеспечить снижение тангенса угла коэффициента мощности до уровня tgj2.
Мощность батареи определяется из выражения:
![]() ,
,
где Pн - активная мощность в узле нагрузки.
Полная мощность и ток в ЛЭП до компенсации:
![]() ,
, 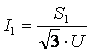 .
.
Полная мощность и ток после установки конденсаторных батарей:
![]() ,
, 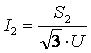 .
.
5.3 Задание
В соответствии с исходными данными варианта задания, приведенными в таблице 5.1, используя программу Excel, выполнить расчет мощности батареи конденсаторов.
Таблица 5.1 – Исходные данные
|
№ Варианта |
Pн, кВт |
Qн, кВАр |
tgj1 |
tgj2 |
U, кВ |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
1800 |
900 |
0,48 |
0,36 |
6,3 |
|
2 |
2500 |
1600 |
0,45 |
0,14 |
10,5 |
|
3 |
1500 |
1000 |
0,33 |
0,3 |
0,4 |
|
4 |
750 |
300 |
0,48 |
0,2 |
37 |
|
5 |
3700 |
1800 |
0,38 |
0,1 |
6,3 |
|
6 |
200 |
30 |
0,3 |
0,2 |
0,4 |
|
7 |
1000 |
620 |
0,4 |
0,35 |
37 |
|
8 |
670 |
220 |
0,37 |
0,15 |
6,3 |
|
9 |
1200 |
100 |
0,29 |
0,22 |
10,5 |
|
0 |
800 |
630 |
0,46 |
0,32 |
10,5 |
Список литературы
1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. - М.: «Лаборатория базовых знаний», 2002.
2. Поршнев С.В. Вычислительная математика: Курс лекций: - С.Пб.: БХВ-Петербург, 2004.
3. Волков Е.А. Численные методы. – М.: Наука, 1987.
Св. план 2012 г. поз 18